Prerpints.org logo
Preprint
Article

Model-Based Adaptive Collaboration of Multi-Terminal Internal Force Tracking

Altmetrics

Downloads

105

Views

45

Comments

0

A peer-reviewed article of this preprint also exists.

This version is not peer-reviewed

Submitted:

18 May 2023

Posted:

19 May 2023

You are already at the latest version

Alerts
Abstract
This paper proposes a multi-terminal adaptive collaborative operation method to solve the problem of unstable internal force tracking in clamping and handling unknown objects by multi-terminal robots. In the proposed method, the internal command force changes the complex internal force control problem into an internal force tracking problem from multi-slave to master. Moreover, we develop an algorithm for multi-slave setups to estimate object stiffness and motion uncertainty in the direction of the internal command force according to Lyapunov theory. Finally, the impedance control generates a reference trajectory for the multi-slave to maintain the desired internal force and track the master’s motion. Several experiments are conducted on a self-made robot equipped. The experimental results show that the oscillation amplitude of each slave end is less than 1 mm, the directional oscillation amplitude is less than 1 degree during the tracking of the desired commanded internal force. For objects with low stiffness, the error of the commanded internal force is less than 1 N (6%) per slave. The error in tracking the commanded internal force for objects with high stiffness is less than 2 N (8%). The results prove the feasibility and effectiveness of the proposed method.
Keywords: 
Subject: Engineering  -   Control and Systems Engineering

1. Introduction

Compared with single-arm gripping end effector robots, multi-arm multi-terminal robots can perform more complex and uncertain tasks in a wider range of application scenarios, such as rapid and stable handling or rescue of larger objects in non-structural hazardous environments that require the cooperation of two arms or multi-arm and multi-terminal setups. In these collaborative systems, a closed operation chain is developed where the contact forces form a set of motion constraints. Thus, the freedom of the closed operation chain is significantly reduced to develop a task chain. In this process, effectively controlling the time-varying complex internal force working space generated on the dynamic system formed by terminals and objects is crucial to ensure task stability. Controller designs for multi-terminal robotic systems are more complex and unstable due to motion and force uncertainty. Specifically, when the multi-terminal system manipulates the unknown object, the double uncertainty of the object and the master terminal motion will lack control of the interconnected system’s closed operation chain. Due to the complexity and diversity of multi-terminal system control sources, there is no perfect solution for collaborative control under kinematics and mechanical uncertainty in multi-terminal collaborative operations. To solve the kinematic uncertainty when manipulating unknown objects with dual-end terminals, researchers have proposed several solutions by applying advanced control theory. For example, [1,2] proposed a sliding mode control that improves trajectory tracking accuracy, and [3,4] developed an adaptive control scheme appropriate for objects with unknown information to control multi-arm robots collaboratively. In [5,6], the authors introduced the absolute relative motion scheme for grasping (Closure of forces in the fixture) large moving objects.
Complex internal force tracking (Synergistic force closure) is critical for a successful task when a multi-terminal without a fixed connection manipulates unknown objects, solely relying on contact time-varying forces. The internal force control scheme within the cooperation range of two arms and two terminals includes impedance control and mixed position/force control. Current solutions involve the adaptive control [7,8] to improve the time-varying force tracking performance of unknown stiffness objects or the hybrid position/force control of the decoupling task space [9,10,11,12], as position and force subspace. To a certain extent, both schemes rely on known environmental information and the kinematic model. To our knowledge, current research has not been expanded to manipulate tasks through multi-terminal contact. Furthermore, there is no related report about a multi-terminal system solving the time-varying complex internal force tracking and controlling problems formed in the contact clamping and handling tasks of unknown objects.
The research on reference algorithms related to time-varying internal force tracking in the multi-terminal collaborative force closure control studied in this article mainly focuses on the cooperation of dual-terminal actuators. Specifically, [13] solved the time-optimal path-tracking problem of two robots executing collaborative grasping tasks. In this method, dynamic programming determines the time-optimal path and a task space admittance control scheme is used to generate a contact model. This method is suitable for grasping general objects in surface contact with robots. However, the time-varying internal force tracking problem for uncertain targets has not been resolved yet. In [14], after analyzing the robot end-effector and the environment, the contact force is used as a position-based impedance controller feedback force to track the desired dynamic uncertainty of the environmental force actively. Alternative approaches reduced the force tracking error caused by environmental position uncertainty via a variable impedance control based on an online impedance parameter adjustment scheme that compensated for the unknown environment and dynamic desired forces. Among them, the adaptive hybrid impedance control method for two-armed robots proposed in [15] introduced variable stiffness impedance control to regulate internal forces. Although this method is the most informative, the variable stiffness adaptive impedance control for robot terminals requires high settings of control parameters, which can easily produce system instability. For multi-terminal time-varying internal force tracking control, it is more difficult to achieve control objectives.
This paper aims to solve the time-varying complex internal force tracking and control problem for strong, stable clamping and handling of unknown objects through a multi-terminal system. Specifically, in the proposed solution, the latter system is based on multi-terminal internal force workspace transformation, an adaptive control algorithm for time-varying force tracking from multi-slave to a single master. Moreover, we study estimating uncertain and unknown motion and the adaptive reference trajectory generation method using absolute relative motion strategies.
The proposed clamping and handling model-based multi-terminal internal force transformation and the adaptive collaboration scheme are simple and robust for operating unknown arbitrary objects. The overall control process simulates the gripping and handling of humans on unknown objects. Compared to the existing literature, the main contributions of this paper can be summarized as follows:
  • Based on the absolute relative motion strategy, this paper proposes the time-varying force tracking control mode and command internal force concept of contact single-master multi-slave terminal. Furthermore, the time-varying complex internal force working space is simplified and transformed according to the concept of command internal force;
  • A method for estimating the unknown stiffness and motion of the direction of multi-internal force commands is proposed. The suggested method is simple and robust for object stiffness, shape changes, and uncertain motion of contact points;
  • Based on the estimation of stiffness and motion in the command internal force direction, we use the uncertain motion and force of impedance model in the command internal force direction to track the formation method of the adaptive reference trajectory. This means that the force of the contact point measured by the force sensor and kinematics can stabilize the collaborative task without building a dynamic object model;
The remainder of this paper is organized as follows: Part 2 describes a complex time-varying internal force workspace comprising multi-terminals and absolute and relative motion control. Part 3 introduces the methods of estimating the unknown dynamic parameters in the command internal force direction and the adaptive reference trajectory formation. Part 4 evaluates the proposed algorithms on a self-made multi-terminal collaborative robot platform. Finally, Part 5 concludes this paper and discusses future research directions.

2. Model Establishment of Multi-Terminal Clamping System

2.1. Formalizing the Workspace

The following symbols represent the position, velocity, and force of each system part used throughout the paper. Note that in the symbols below, the superscripts and subscripts are omitted.
h  Vector composed of F  and N
F  Force vectors of various parts of the system
N  Torque vector of each part of the system
q  A vector composed of h  from multiple terminals
O  Origin of coordinate systems for various parts of the system
v  Translation velocity vector of various parts of the system
p  Position vectors of various parts of the system
Q  Direction vectors of various parts of the system
l  Virtual rod vector from the coordinate origin O h i of each terminal to object coordinate origin O o
ω  Angular velocity vectors of various parts of the system
The following subscripts are defined to distinguish the position, velocity, and force vectors of each part of the system.
o  Position, velocity, and force related to objects
l i  Position, velocity, and force of the i th virtual rod tip
h i  Position, velocity, and force at the root of the virtual rod (at the i th contact terminal)
h j  The position and speed of the root of the virtual rod (at the i th slave terminal) after system simplification
i  Contact point or terminal serial number
j  Represents the simplified serial numbers of each slave terminal,  j = a , b , c
r  Relative (internal) position, velocity, and force
m  Generalized relative (internal) position, velocity, and force vectors
e  Measure position, velocity, and force
The following superscript is defined in the upper left corner of the vector to distinguish the coordinate system represented by the vector.
w  Robot coordinate system Σ w
h i  Simplified coordinate systems for each terminal Σ h i , i = a , b , c , d
h j  Simplified coordinate systems for each slave terminal Σ h j , j = b , c , d  Please refer to the text for other symbols not defined here.
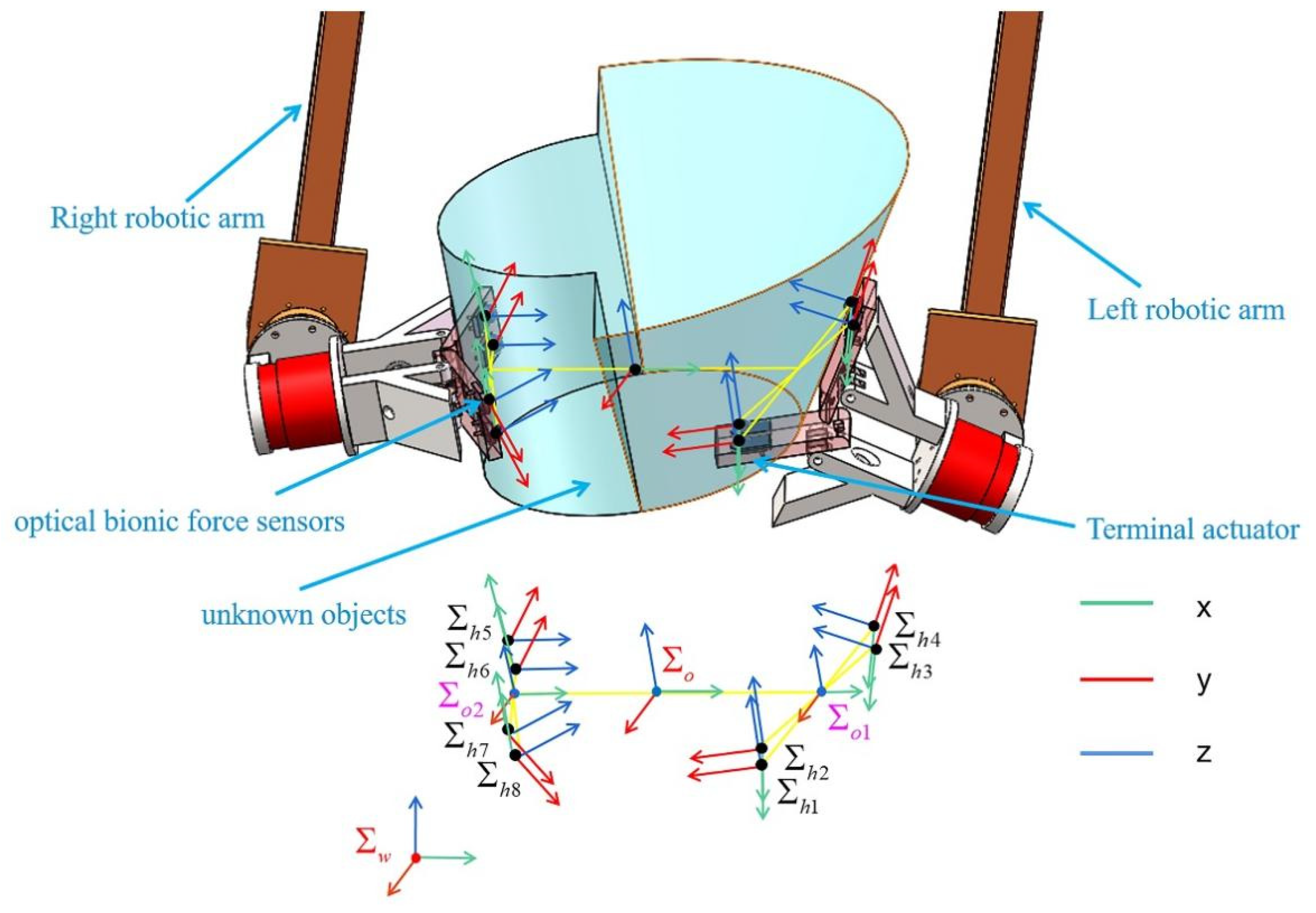
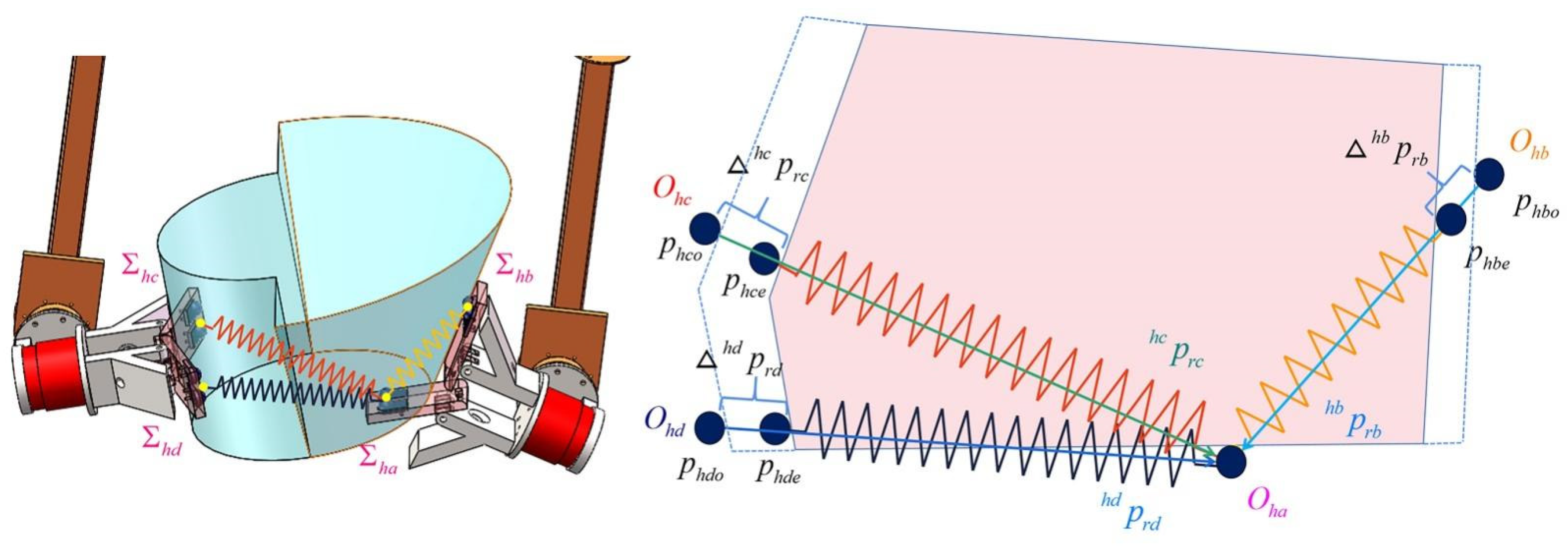
This paper considers the process of a humanoid remote operation robot equipped with 4 end effectors to manipulate objects with unknown information other than visual. Figure 1 illustrates each terminal having two customized optical bionic force sensors. These 4 terminals cooperate to stably clamp unknown objects and maintain adaptive stable handling without relative sliding during any collaboration of the remote operation or on the planning path. This paper makes the following assumptions:
  • Remote operation enables each force-sensing contact point installed at the terminal to reach a reasonable, cooperative position on the object's surface, and all contact points contact the object's surface.
  • The remote operation causes the four terminals to form an origin  O o  in the coordinate system  Σ o , as illustrated in Figure 1, which is close to the object's center of gravity.
A virtual rod defines the force space control vector in a multi-terminal multi-contact point collaborative system [16]. The contact point of this paper is a three-dimensional optical bionic force sensor (Figure 1). The coordinate system  Σ h i i = 1 , … , n represents the contact point coordinate system ( n = 8 ). Nevertheless, the proposed method applies to more contact points and terminals.
Coordinate system, respectively. Σ o 1  and Σ o 2  represent the planar center coordinate system formed by the four coordinate system origins at the contact points of the two terminals installed on a single robotic arm.
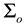
In this paper, O o  is set at the midpoint of the connected line of O 1 and O 2 . The virtual rod l h i w from O hi  to  O o is equivalent to a rigid rod structure fixed at the contact point. The virtual rod top coordinate system Σ h i i = 1 , … , 8  initially coincides with the object coordinate system Preprints 74087 i001.
The force vector generated at the top of l h i w is defined as
h l i w ≡ F l i T w   N l i T w T  
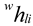
Where F l i o  and N l i o  are the force and moment applied at the tip of the virtual rod  i . The prefix w indicates that the vector is defined in the robot's coordinate system  Σ w . The vector h l i w is calculated from the force and moment applied to the object by the contact terminal  i . The sum of the combined forces on an object F w o  and moment N o w  is calculated from the sum of Preprints 74087 i002.
h o w ≡ F o T w N o T w T =   G w q l
Where  G   ≡   I 6   I 6   I 6   … , q l w ≡ h l 1 T w h l 2 T w h l 3 T w … h l n T w T , and I 6  is a 6 ∗ 6 identity matrix with a rank of 6 because the matrix G  maps n ∗ 6  dimensional vectors to 6-dimensional vectors. Therefore, its null space range is 6 ∗ n − 6 -dimensional, n = 8 in this paper. We define  V  as the null space basis of  G . The general interpretation of Equation (2) is
q l w = G −   h o w + V h w m
Where h m w is an arbitrary  6 ∗ n − 6 -dimensional vector corresponding to  V  and G −  is a generalized inverse matrix of  G .
Note that   V w h m belongs to the null space of  G . So  h w m corresponds to the internal force/moment that can be controlled separately without affecting the net force. Besides, V  and h w m are not fixed, which is important for the follow-up force tracking control.
Equation (3) can be rewritten as
q l w = G − V h o w h m w = U w h  
U ≡   G − V   ∈   ℝ 6 n ∗ 6 n , w h ≡   h o w h m w   ∈   ℝ 6 n   .  
Where  h w is a generalized force vector. The internal forces  h w m can be expressed as  n − 1 6  dimensional force vector set
h m w ≡ h r 1 w h r 2 w ⋮ h r ( n − 1 ) w
For the given  q l w , the force/moment vector h w is obtained by solving Equation (4).
h w = U − 1   q l w  
Next, we introduce stable clamping and handling with multi-contact points in inner and outer working spaces, utilizing simultaneously and independently controlling vectors and the required coordinate systems. The physical meaning of this setup is summarized as follows. Matrix  G  maps the forces exerted by multi-terminals and multi-contact points to the external forces of the object. Matrix  V  is the null space basis of  G , and matrix  U  maps a set of external and internal forces to the forces of multi-terminal contact points.

2.2. Simplification and Transformation of Internal Force Space

Next, we discuss the stable clamping internal force of the multi-point contact collaborative handling system proposed in this paper. When more than two contact points conduct a collaborative clamp, it is difficult to determine the null space basis  V  proposed in Section 2.1 because  V  does not represent the intuitive meaning of the internal force/moment. Hence, we write Equation (6) as follows
h o w = h l 1 w + h l 2 w + .   .   . + h l 8 w   , h r 1 w = c 1 , 1 h l 1 w + c 1 , 2 h l 2 w + .   .   . + c 1 , n h l 8 w   , h r 2 w = c 2 , 1 h l 1 w + c 2 , 2 h l 2 w + .   .   . + c 2 , n h l 8 w   , . . . h r 7 w = c 7 , 1 h l 1 w + c 7 , 2 h l 2 w + .   .   . + c 7 , 8 h l 8 w   .
Thus, Equation (6) becomes
h w = h o w h m w = G C   q l w = U − 1   q l w  
Once the 7 internal force vectors h r 1 w   .   .   .   h r , 7 w  are given, matrix C is determined automatically. However, under the same net force requirement, the internal force vector  h r 1 w   .   .   .   h r , 7 w  has an infinite number of values. This paper determines the internal force direction of stable clamping according to the terminal model. Thus, the desired internal force for stable clamping is adaptively tracked under this set of internal force directions. Therefore, we extract the internal force vector Equation (9) from Equation (8)
  h m w = C w q l
We simplify the internal force workspace according to the terminal model characteristics to reduce computation and for system simplicity. Specifically, considering that the model involves internal and external forces for stable clamping without losing generality, we make the following reasonable assumptions:
  • No torque vector is formed at a single contact point.
  • No internal force is generated between two parallel contact points on a terminal.
  • No internal torque is generated between all contact points, so only internal forces are involved in control based on reference trajectories.
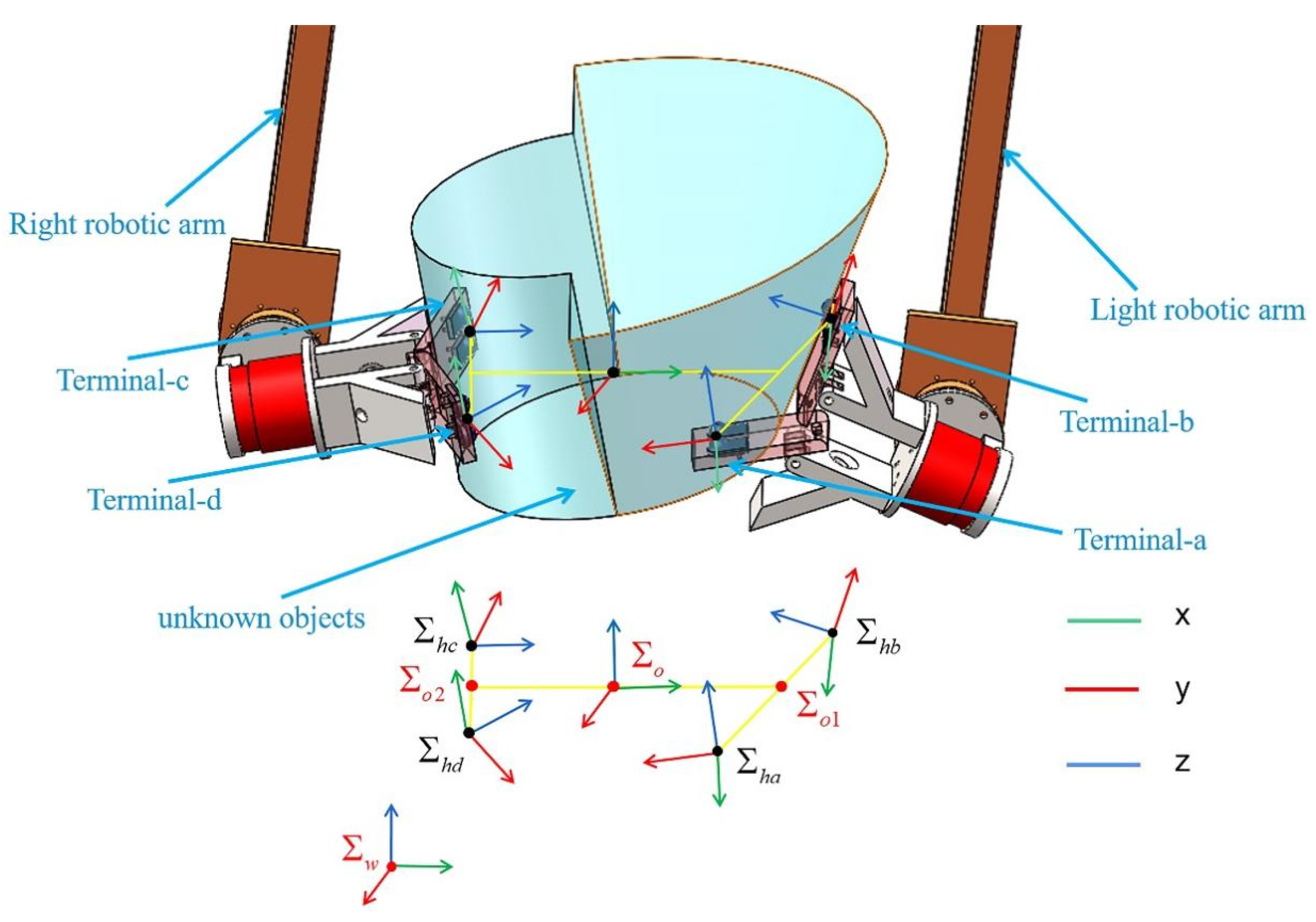
Based on the above assumptions, the initial internal force workspace becomes a four-contact terminal force vector workspace. According to the system model depicted in Figure 2, the coordinate system at the contact points  Σ h 1  and  Σ h 2  are merged into  Σ h a . The new coordinate direction remains unchanged, while the origin changes to  O h a  at the midpoint of the connected line  O h 1  and  O h 2 . Furthermore, Σ h a  as a new cooperation terminal, its force vector is determined by the force vector combination at the contact point Σ h 1  and Σ h 2 . We merge Σ h 3  and Σ h 4  to form  Σ h b , and merge Σ h 5  and Σ h 6 to form  Σ h c , and merge Σ h 7  and  Σ h 8 to form  Σ h d in the same way. As presented in Figure 2, the force vector is simplified similarly. Therefore, the force vector applied to the object by the 8 terminal contact points q h w ≡ h w h 1 T h w h 2 T h w h 3 T … h w h 8 T T  described in Section 2.1 becomes q h w ≡ h w h a T h w h b T h w h c T h w h d T T , and accordingly, the force/moment vector at the tip of the virtual rod  q l w ≡ h w l 1 T h w l 2 T h w l 3 T … h w l 8 T T becomes q l w ≡ h w l a T h w l b T h w l c T h w l d T T . So Equation (7) becomes
h o w = h l a w + h l b w + h l c w + h l d w   h r 1 w = c 1 , 1 h l a w + c 1 , 2 h l b w + c 1 , 3 h l c w + c 1 , 4 h l d w   h r 2 w = c 2 , 1 h l a w + c 2 , 2 h l b w + c 2 , 3 h l c w + c 2 , 4 h l d w h r 3 w = c 3 , 1 h l a w + c 3 , 2 h l b w + c 3 , 3 h l c w + c 3 , 4 h l d w
Defining the direction of the intuitive force while handling the object with the human hand is trivial. Therefore, the following internal force group is used as an intuitive force given to the expected internal force group
h r 1 w = 1 2 ( h l a w   -   h l b w   )   h r 2 w = 1 2 ( h l c w   -   h l d w   )   h r 3 w = 1 2 ( h l a w + h l b w   )   -   1 2 ( h l c w + h l d w   )  
So, matrix C from Equation (11) is determined as the intuitive expectation value matrix C d  as follows
C d = 0.5 I 6 − 0.5 I 6 0 6 0 6 0 6 0 6 0.5 I 6 − 0.5 I 6 0.5 I 6 0.5 I 6 − 0.5 I 6 − 0.5 I 6
The simplified generalized internal force vector  q m d w ≡ h w r 1 T h w r 2 T h w r 3 T T is the expected generalized internal force vector. Thus, Equation (11) becomes
q m d w ≡ C d ∗ q l w
Although the expected internal force vector  q m d w  determined in Equation (13) is intuitive and in line with conventional thinking from the perspective of understanding, it significantly increases the difficulty of setting the parameters. It even makes it impossible to achieve favorable control from the perspective of control. Therefore, we perform a favorable transformation of the internal force workspace appropriate for the control method proposed in this paper. Considering the robustness of the multi-terminal adaptive scheme introduced in this paper, it is necessary to determine one of the terminals and control its absolute motion to afford to realize the other terminals to control the force tracking the relative motion of this terminal.
Note that the internal force vector does not contribute to the object's motion but represents the mechanical stress exerted on the object. There are infinite representations of internal force vectors as null space vectors. One of this paper’s contributions is that the time-varying complex internal force space is difficult to determine and accurately control the collaborative task of manipulating unknown objects using multi-terminals, which is modeled as an accurate controllable space.
Based on the model Equation (10), the selected internal force group is used as the control variables and converted to meet the control needs. In this paper, the desired internal force group in Equation (13) and the internal force group from the slave terminal position to the master terminal are converted as follows to achieve the control goal. The internal force group from the slave terminal to the master terminal is defined as follows
h r b w = 1 2 ( h l a w   -   h l b w   ) , h r c w = 1 2 ( h l a w   -   h l c w   ) ,   h r d w = 1 2 ( h l a w + h l d w   )   .  
Matrix C determined by Equation (14) will be named C e as the internal command force parameter
C e = 0.5 I 6 − 0.5 I 6 0 6 0 6 0.5 I 6 0 6 − 0.5 I 6 0 6 0.5 I 6 0 6 0 6 − 0.5 I 6
When q m e w ≡ h w r b T h w r c T h w r d T T is determined as a generalized command internal force vector, then Equation (14) becomes
q m e w ≡ C e ∗ q l w  
If we determine the expected internal force set, the command internal force group is uniquely determined since we can make the following conversion between Equations (13) and (16).
C d −   q w m d = q w l   q w m e = C e C d −   q w m d  
Where C d −  is the generalized inverse of C d . The transformation in Equation (17) is critical for introducing force-tracking adaptive control.
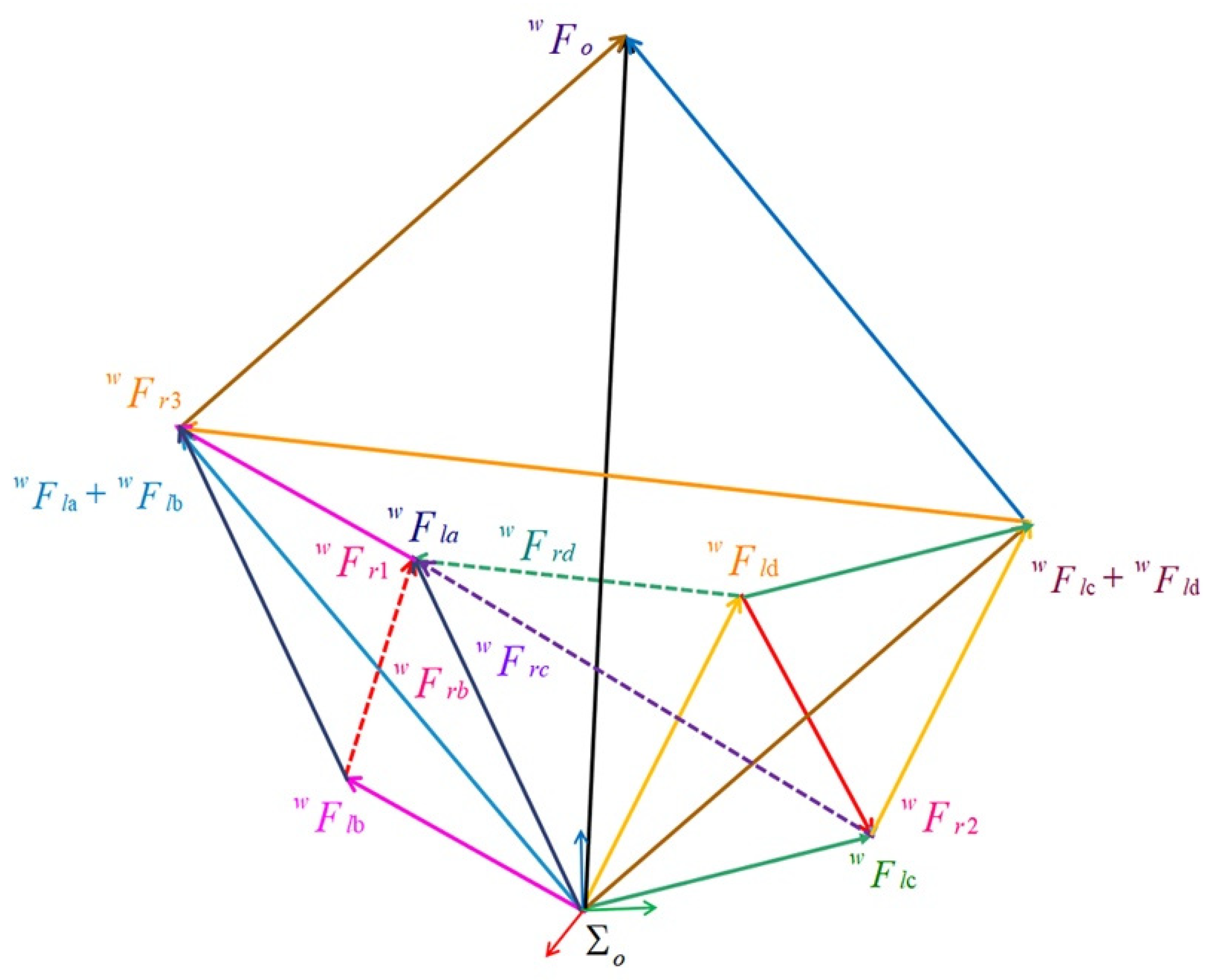
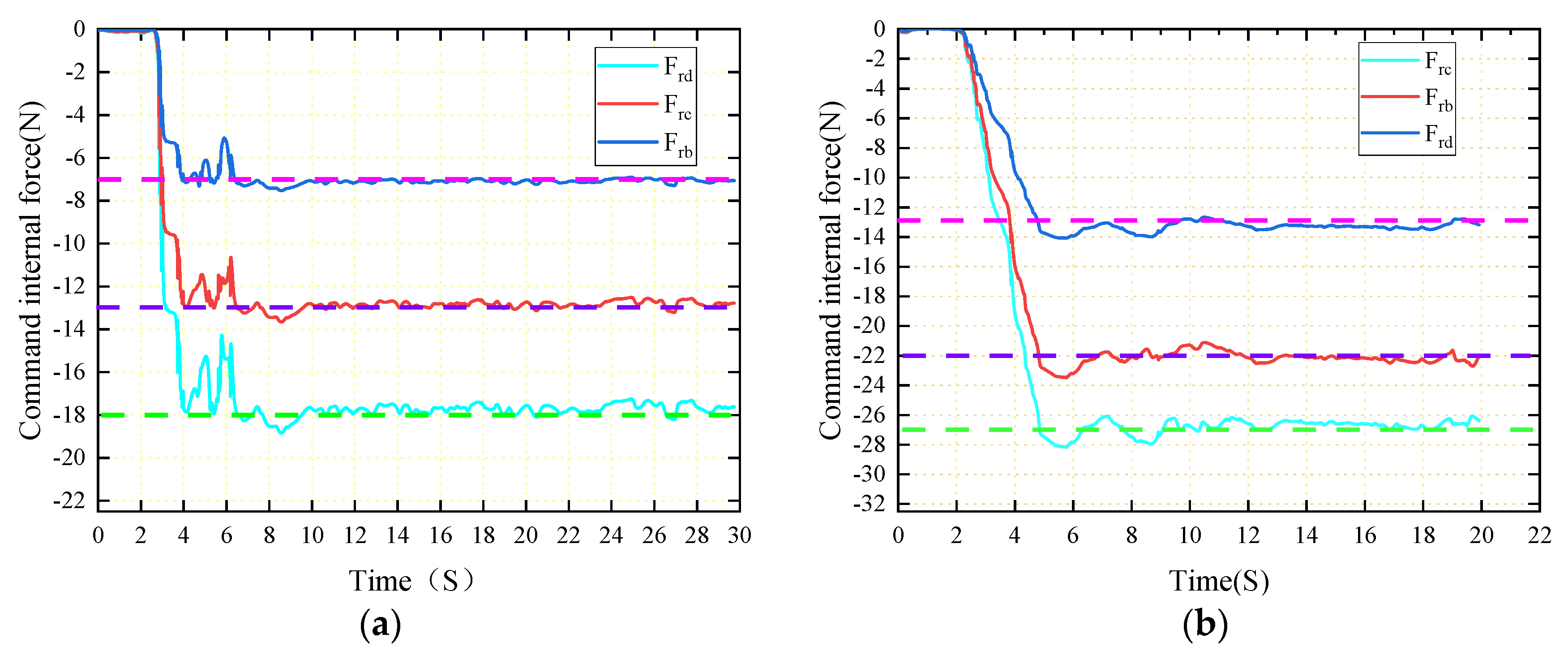
The relationship between the expected and the command internal force in Equation (17) is represented in Figure 3, where the force applied by each terminal on the object is transferred to the origin of the object coordinate system through a virtual rod. F w r 1 , F w r 2 , F w r 3 represents the intuitive expected internal force extracted from Equation (11) in h w r 1 , h w r 2 , h w r 3 , and F w r b , F w r c , F w r d is the internal instruction force as the key control quantity in this article. Due to the four terminals in zero space, the combined external force F w o applied to the object is controlled near a fixed value according to the internal force in changing the demand of the object's movement. It is easy for operators to regularly observe the internal force F w r 1 , F w r 2 , F w r 3 Through observation, we conclude that it meets the demand for stable clamping of objects. However, as a control variable, achieving internal force tracking tasks is difficult because a tracked end is a tracking end itself, which poses significant difficulties to the controller design. Due to the four terminals in zero space, the combined external force F applied to the object is controlled near a fixed value according to the internal force in changing the demand of the object's movement. In order to solve such difficulties, this article proposes the instruction of the internal force F w r b , F w r c , F w r d (extracted from h w r 1 , h w r 2 , h w r 3 in Equation (14)) through (11) - (17). As shown in Figure 3, F w r b , F w r c , F w r d  is the internal force between one terminal and the other terminals, which is crucial for force tracking control. If this end is determined as the absolute motion control object, it will solve the problem that the tracked end itself is the tracking end. This greatly reduces the uncertainty of control. As shown in Equation (17), F w r b , F w r c , F w r d is uniquely determined when F w r 1 , F w r 2 , F w r 3 is determined. In Section 3, we will track a fixed  F w r b , F w r c , F w r d  on a one-dimensional holding line while determining  F w r 1 , F w r 2 , F w r 3 .

2.3. Absolute Relative Motion Control

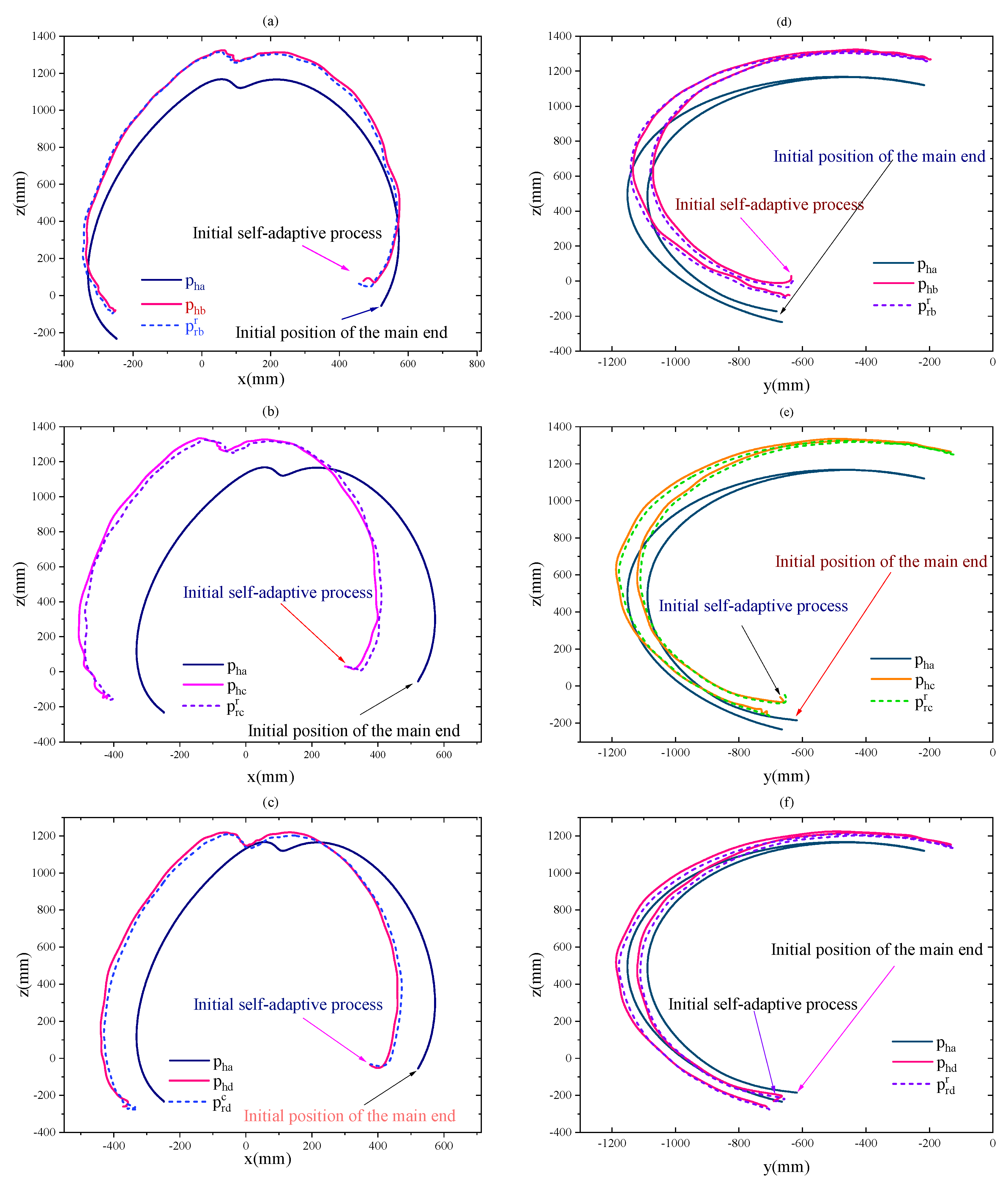
Human hands can hold and handle unknown large objects of any shape in any way stably and flexibly. It is worth highlighting how complex time-varying internal forces and motion are regulated through perceptual intelligence. This paper simulates the ability of humans to develop a multi-terminal robot control algorithm. In the above human process, the person can perceive that any part of his palm is in contact with the object and can be consciously determined as the master terminal, while other parts of the palm in contact with the object can be determined as the slave terminal. Moreover, the slave terminal clamp (increase the internal force) to the master terminal is determined by consciousness to stabilize the clamping. Furthermore, it is important to keep the relative movement between the master and the slave terminal within a small stable range (time-varying force and motion tracking). Similarly, the task space of the robot can be broadly divided into the combined motion of the absolute motion of the master terminal and the relative motion from the slave terminal.
The absolute motion is performed by the master terminal and is designed to achieve accurate and robust tracking of the target reference trajectory. On the other hand, relative motion is conducted by the slave terminal, designed to accept the movement of the master terminal. Thus, the so-called closed kinematic chain constraints can be satisfied. In this paper, the  Σ h a  presented in Figure 2 is identified as the master terminal, Terminal-a, responsible for absolute motion control. The rest Σ h j , ( j = b , c , d )  are slave terminals, named Terminal-j  ( j = b , c , d ) , responsible for relative motion control.
Figure 2 illustrates the relationship between each terminal and object motion in the robot coordinate system. which can be explained with the following equation
P w h i = P w o − R w h i l h i i p w h i · = p w o · − R w h i l h i i × ω w o ω w h i = ω w o
Where p w h i ( i   =   a , b , c , d ) is the position vector of the simplified four terminals in the robot coordinate system, · ×  is the cross product executed by the oblique symmetry matrix operator, R w h i ( i = a , b , c , d ) represents the transformation matrix of each terminal coordinate system relative to the robot coordinate system, p w o ·  and  ω w o  are the translation velocity and angular velocity of the object in the robot coordinate system, respectively, and  l h i i  is the virtual rod represented by the terminal coordinate system.
The relative position p h j r j and orientation Q h j r j  of the three slave terminals Terminal-j j = b , c , d  and the one master Terminal-a in Equation (18) are expressed in the slave terminal coordinate system as follows
p h j r j = R w h j T p w h a − p w h j
  Q h j r j = R w h j T Q w h a
In an ideal state, there is no relative motion between each terminal, so the relative position  p h j r j and orientation  Q h j r j should remain constant.
The robot coordinate system is the default and will be omitted in subsequent equations. For time t, the expected translation velocity and angular velocity corresponding to the object are expressed by  p · o d t  and  ω o d t   . According to Equation (18), we will get the expected translation velocity  p · h a d t  and angular velocity ω h a d t  of the master terminal as follows
p · h a d t = p · o d t + (   R h a   t   l a h i   ) ×   ω o d t  
ω h a d t = ω o d t  
e p h a t = p h a d t   -   T   -   p h a   t  
e Q h a t = Q h a d t   -   T − Q h a t    
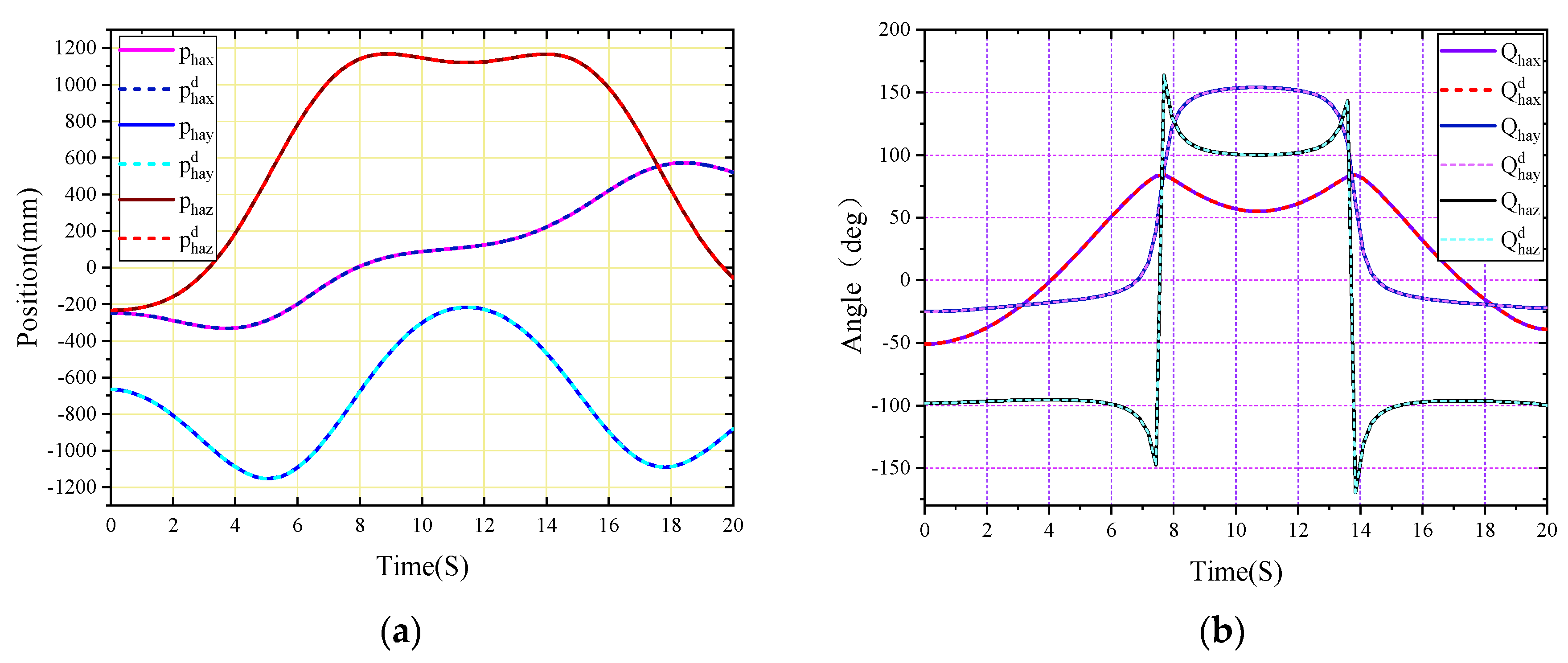
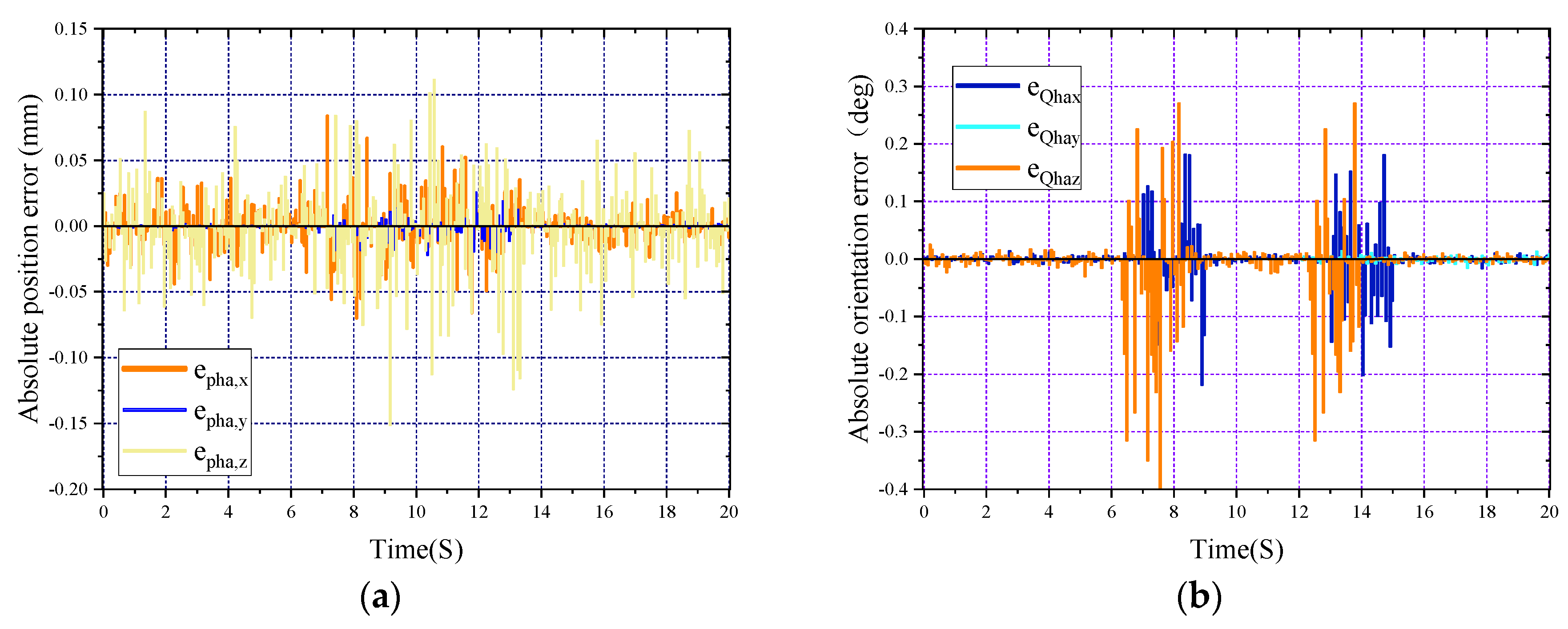
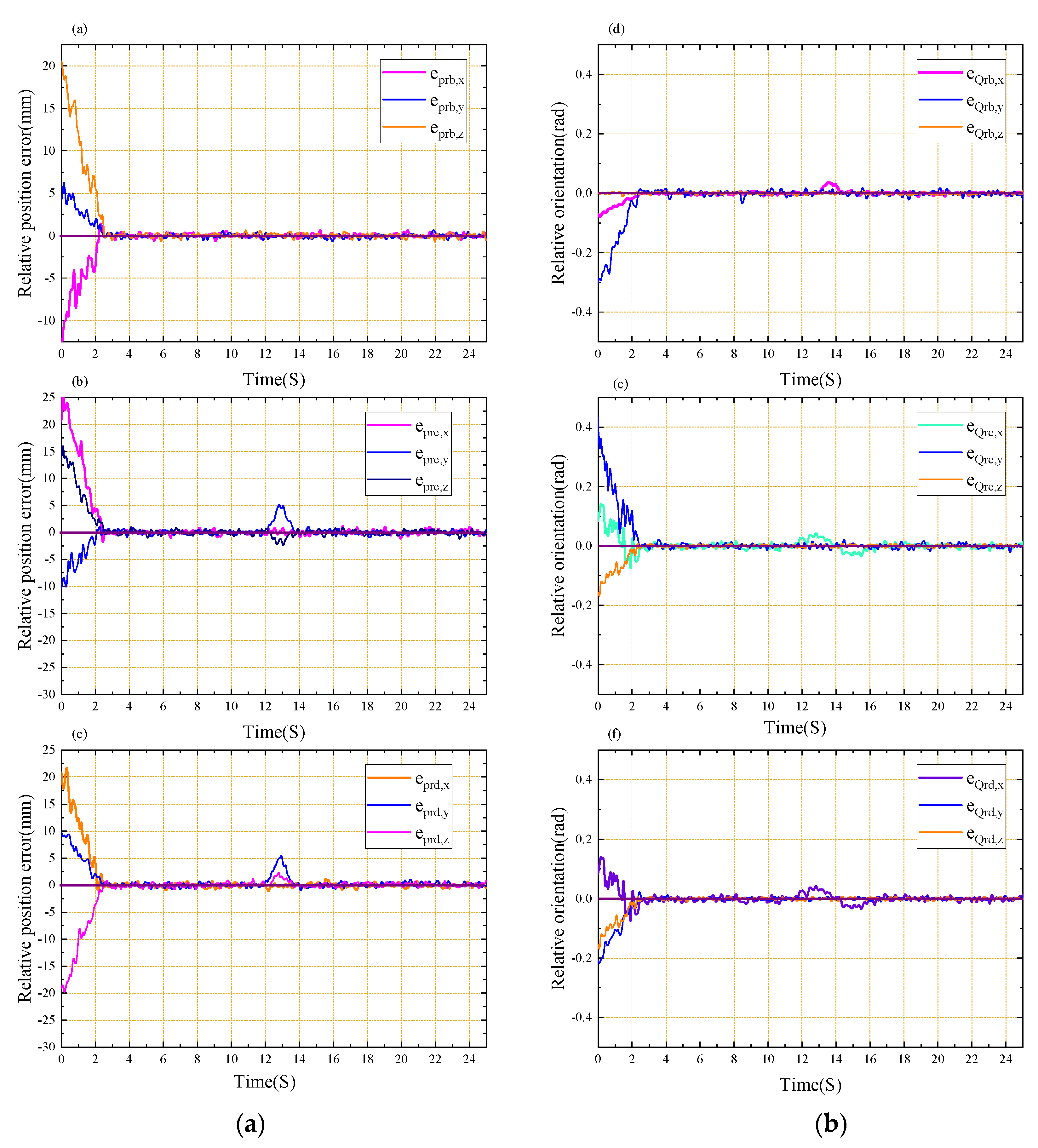
Where e p h a t represents the absolute position error of the master terminal, e Q h a t indicates the absolute direction error of the master terminal, and T  is the sampling time step; p h a d t   -   T is the command position of the last sampling time. p h a   t    is the measurement position of the current time, Q h a d t   -   T  is the desired direction at the last sampling time, with Q h a ( t )  representing the direction measured at the current moment. Note that only Q h a d t   -   T  and Q h a ( t ) are consistent, while e Q h a will be zero.
Once the Cartesian velocity of the master terminal is established, the desired velocity of the slave actuator can be determined by
p · h j d t = v h a t   -   p h a d h j ×   ω h a t
ω h j d t = ω h a t
Where  j = b , c , d , v h a t  is the master terminal translation velocity, h j p h a d   =   h j p h a t 0  is the relative position initialized from the terminal coordinate system extracted from the terminal gesture by (19).
Consider relative errors
e p r j t = R w h j t   h j p h a d   -   h j p h a t  
e Q r j t = R w h j t Q h a d h j − Q h a h j ( t )
Where e p r j t indicates the relative position error of each slave actuator under the robot coordinate system and e Q r j t  indicates the relative direction error of each slave terminal under the robot coordinate system. Similarly, h j p h a d   =   h j p h a t 0  and  Q h i h a d   =   Q h i h i t 0 represent the expected relative position and direction expressed in the slave actuator coordinate system, respectively.
With the above closed-chain constraint method, we can quantitatively calculate the absolute and relative motion of the four terminals accordingly for the desired position and orientation of the object. The advantage of using a master-slave closed chain constraint control is that multi-terminal systems can perform collaborative tasks without knowing the information about the shape, size, and stiffness of the object.

3. Multi-Terminal Adaptive Motion

Each terminal in this paper’s system interacts with the object in point contact, so only the translational force is considered without considering rotational torque in the force of a single terminal on the object. Multi-terminal collaborative forces provide the rotational torque of an object.
The intrinsic transformation relationship between multiple terminals for the desired internal force direction and the command internal force system is established in Section 2.2 (Equation (17)). Furthermore, controlling the absolute relative motion with closed chain constraints is described in Section 2.3 (Equations (18)–(20)). Thus, we create the adaptive reference trajectory control model for time-varying force-tracking multi-slave terminals in the specified internal force direction.

3.1. Problem Description

Since the exact position and motion of the object during the time-varying motion are uncertain, and the stiffness k e  of the object is unknown, completing the time-varying internal force tracking directly from the terminal relative motion control is impossible. Therefore, this paper proposes an adaptive scheme for tracking the expected internal forces for multiple terminals.
The internal command force is defined in Section 2.2. In the next derivation, the slave Terminal -j j = b , c , d will track the relative position P h j r j between its coordinate system and the master terminal Arm-a, i.e., the reference position trajectory of the direction  O h j O h a → , to achieve the desired command internal force. The time-varying force tracking for this specified direction can be transformed into a virtual spring two-stage motion, as depicted in Figure 4. p r j e , ( j = b , c , d ) is defined as the measurement position of the slave terminal in the O h j O h a → direction and p r j o is defined as the position on the initial contact point between the slave terminal and the object and the initial  O h j O h a → , p r j o = p , h j e ( j = b , c , d ) . Extracting the expected command internal force F r j d , ( j = b , c , d )  from the generalized command internal force vector  q w m e of Equation (17) and the internal force error can be expressed as  Δ F r j = F r j − F r j d . In position control mode, assume  p r j e d = p r j e , and the stiffness of an unknown object is  k e . Then the internal command force can be expressed by
F r j = k e p r j o − p r j e  
Equation (29) shows that if it is known to depend on the exact position of the object p r j o , ( j = b , c , d )  and the exact stiffness of the object  k e , the reference position  p r j r , ( j = b , c , d ) of the direction  O h j O h a → can be calculated from the required and desired internal force  p r j r , ( j = b , c , d ) .
p r j r = p r j o   -   F r j d k e
However, the object's exact position during the handling process is uncertain in the actual control. In Figure 4  p r j o , ( j = b , c , d )  is the initial contact point position, and in the subsequent control process, it completely depends on the dynamic environment composed of the master terminal and objects to calculate. The time-varying internal force is kept near the fixed value in this dynamic environment and thus fully considers the impact of the master terminal and objects' motion on the internal force. Because of the stiffness of unknown objects  k e , the error of the model parameters, the control accuracy, and the existence of uncertain factors (such as noise), the trajectory  p r j o , ( j = b , c , d ) is uncertain, so it is impossible to directly calculate the relative motion reference position trajectory of the slave terminal.
Note: The internal force workspace transformation in Section 2.2 proposed the direction of the internal command force, which meets the control requirements. In the same sense, each slave terminal coordinate system origin O h j j = b , c , d tracks the desired position at the holding line O h j O h a →  pointing to the origin of the master terminal coordinate system  O h a . Therefore, next, we will focus on one-dimensional variables at the holding line  O h j O h a →  of p h j o , ( j = b , c , d )  and p h j e , ( j = b , c , d ) in dynamic and uncertain environments.

3.2. Unknown Motion Estimation of the Internal Command Force Direction

Next, we will use the internal command force F r j , ( j = b , c , d ) to estimate the relative position vector  P h j r j shown in Figure 4, i.e., the unknown time-varying position  p r j o of the direction  O h j O h a → , which is critical for p r j r presented in Section 3.3. In general, we model p r j o as the following time-varying trajectories
p r b 0 t = b 0 + b 1 t + b 2 t 2 + .   .   . + b n − 1 t n − 1   p r c 0 t = c 0 + c 1 t + c 2 t 2 + .   .   . + c n − 1 t n − 1   p r d 0 t = d 0 + d 1 t + d 2 t 2 + .   .   . + d n − 1 t n − 1  
Where t is time  b n − 1   ,   c n − 1   ,   d n − 1 , where n = 1 , 2 , 3 ⋯  which is considered a constant for a certain period. For the conciseness of the subsequent formula, we will set  g n − 1   =   b n − 1   ,   c n − 1   ,   d n − 1 . Thus in Equation (31), the corresponding velocity and acceleration will be
p r j o t = g 0 + 2 g 1 t + .   .   . + g n − 1 t n − 1   , p · r j o t = g 1 + 2 g 2 t + .   .   . + ( n − 1 ) g n − 1 t n − 2   ,   ( g = b , c , d ) , ( j = b , c , d )   p ·   · r j o t = 2 g 2 + .   .   . + ( n − 1 ) ( n − 2 ) g n − 1 t n − 3   .  
Based on the model in Equation (32), the estimate of p r j o is described as follows
p r j o ∧ = g 0 ∧ + g 1 ∧ t + g 2 ∧ t 2 p ^ · r j o = g 1 ∧ + 2 g 2 ∧ t p ^ ·   · r j o = 2 g 2 ∧
Where * ^ is an estimated value of ∗ , defined according to Equation (33).
F r j ∧ = k e ∧ ( p r j o ∧ − p r j e )  
Where F r j ∧  and  k e ∧  are the estimated command internal forces and the Hooke coefficient of the object, respectively. By subtracting Equations (34) and (29), we get:
F ∧ r j   -   F r j   = k ^ e   g 0 ∧   +   g 1 ∧ t   +   g 2 ∧ t 2   −   p r j e   - k e g 0   + g 1 t +   g 2 t 2   −   p r j e = p r j e 1 t t 2   H j .         ( g = b , c , d ) ,   (   j = b , c , d   )
In this equation
H j = - k e ∧ + k e k e ∧ g 0 ∧   -   k e g 0 k e ∧ g 1 ∧   -   k e g 1 k e ∧ g 2 ∧   -   k e g 2
Equation (36) represents the estimated error for the unknown total kinetic parameters set. Then we design the adaptive renewal law of H j based on Lyapunov theory
H j · = - k ^ · e   k ^ · e g ^ o + k ^ e g ^ · o k ^ · e g ^ 1 + k ^ e g ^ · 1 k ^ · e g ^ 2 + k ^ e g ^ · 2 = -   Γ j − 1 p r j e 1 t t 2 ( F ^ r j -   F r j ) , (   j = b , c , d   ) , (   g = b , c , d   )
So the adaptive renewal law of k ∧ e  and g i ∧ in Equation (37) can be analyzed as
k ^ · o = γ j 1 − 1 p r j e ( F ^ r j   -   F r j )   ,   j = b , c , d .
g ^ · i − 1 = - 1 k ^ e ( γ j , i + 1 − 1 t i − 1 ( F ^ r j - F r j ) + k ^ · e g ^ i − 1 )   ,   g = b , c , d .   i = 1 , 2 , 3 . j = b , c , d .
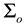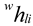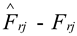Where the renewal rate in the equation is γ j , i . In Equation (37) Γ j   =   diag γ j , 1 ,   γ j , 2 ,   γ j , 3 ,   γ j , 4   ,   j   =   b , c , d  is a positive-definite matrix. In the following equation, we prove the adaptive renewal law in this equation. From Equations (36) to (39), we conclude that the force estimation error of Preprints 74087 i003 converges to 0.
Next, we construct a Lyapunov function
V j = 1 2 H j T Γ j H j   ,   j = b , c , d
Taking the derivative of Equation (40) concerning time will yield
V j · = H j T Γ j H j ·
Taking the transposition on both sides of the Equation (35) will provide
( F ∧ r j   -   F r j ) T = H j T p r j e 1 t t 2   .   j = b , c , d .
Substituting the adaptive renewal law (37) into Equation (41) and considering Equation (42) provides
V j · = − H j T p h j 1 t t 2   ( F ^ r j   -   F r j ) = -   ( F ^ r j   -   F r j ) T ( F ^ r j   - F r j ) .  
Equation (43) shows that when there is a force estimation error of  F ~ r j   =   F ^ r j − F r j , then V j ·   ≤   0 , and V j will decrease. Thus, when the renewal law in Equation (37) eventually leads to  t   →   ∞ , then  F ~ r j → 0 .

3.3. Tracking the Generation of Reference Trajectory of Expected Command Internal Force

Next, we develop an algorithm to generate  p r j r , ( j = b , c , d ) , the reference trajectories p r j e , j = b , c , d  by estimating the uncertain motion of P r j o , j = b , c , d  and the object’s deformation △ p r j , j = b , c , d , as depicted in Figure 4, so that the internal forces required to stabilize clamping are around a fixed value when the object is moved.
As shown in Figure 4, according to Equation (29), we set a required command internal force group
F r j d = k e p r j o − p r j e d , j = b , c , d  
It corresponds to the desired trajectory
  p r j e d = p r j o − 1 k e F r j d , j = b , c , d  
Where F r j d  represents the desired command internal force,  p r j e d represents the desired trajectory at the holding line  O h j O h a → from the terminal actuator Terminal-j, j = b , c , d . According to Section 3.2, if we estimate  p r j o  and  k e , we get the expected trajectory of p r j e d using Equation (45), which will be used to compare with the upcoming impedance model-based method.
In Equation (46), we define the target impedance model at the holding line O h j O h a →  from the terminal actuator Terminal-j  j = b , c , d ,
M p r j e · · + B p r j e · + K ( p r j e   -   p r j e d ) = e r j   ,   j = b , c , d
Where e r j   =   F r j − F r j d  is the internal command force tracking error, and  F r j d is the expected command internal force, while  M , B  and K  are the impedance parameter diagonal matrix.
According to Equation (29), there will be
p r j e = − 1 k e F r j + p r j o = − 1 k e ( F r j d + e r j ) + p r j o , j = b , c , d
Substituting Equation (47) into the impedance model (46) provides
M e · · r j + B e · r j + ( K + k e I 3 ) e r j = − ( M F r j d · · + B F r j d · + K F r j d ) + k e ( M p · · r j o + B p · r j o + K p r j o ) − k e K p r j e d  
Where I 3  represents the 3*3 identity matrix. Since  F r j d is constant, Equation (48) becomes
M e · · r j + B e · r j + ( K + k e I 3 ) e r j = − K F r j d + k e ( M p · · r j o + B p · r j o + K p r j o ) − k e K p r j e d   .
For the force tracking error dynamics in Equation (49), the steady-state error is
e r j , s s = k e K + I 3 k e − 1 ( − 1 k e K F r j d + ( M p · · r j o + B p · r j o + K p r j o ) − K p r j e d )
Therefore, to eliminate the steady-state error  p r j e d , the desired trajectory of p r j e , j = b , c , d , must meet
p r j e d = K − 1 ( M p · · r j o + B p · r j o + K p r j o − 1 k e K F r j d )
Replace the p r j o  and  k e in Equation (51) with the renewal law p r j o ∧  and k e ∧  established in Section 3.2, and the reference trajectory of p r j e , j = b , c , d will provide
p r j e r = 1 K ( M p ∧ · · r j o + B p ∧ · r j o + K p ∧ r j o − K k ∧ e F r j d ) , j = b , c , d
As demonstrated in [21], we finally obtain the command internal force system F r j   →   F r j d , ( j = b , c , d ) using  p r j e r , a reference trajectory of p r j e , j = b , c , d , to eliminate the steady-state error  e r j , s s .
Summary: We obtain  F r j ∧ → F r j → F r j d , ( j = b , c , d ) , F r j ∧ → F r j    as described in Section 3.2 and F r j → F r j d  as described in Section 3.3. Hence, adaptively adjusting the internal forces based on multi-holding lines by referencing trajectories  p r j e r , ( j = b , c , d ) based on motion estimation and impedance models cause the object’s clamping command internal force to converge to its desired value. As transformed and defined in Section 2.2, the user provides the intuitive meaning and expected clamping internal force group, and then the system transforms it into a command internal force group. That is how the force tracking control from the slave to the master is realized.

4. Experiments

4.1. Experimental Description

The experiment was carried out using two self-made 6 degrees of freedom manipulators, with two actuator terminals at the ends and robotic arms with two parallel contact points at the actuator terminals. A three-dimensional bionic optical force sensor is installed at each contact point to measure the contact force. All sensors and motors are connected to a PC via a hub. The absolute and relative motion is controlled with classic proportional gain, and an adaptive time-varying force tracking control algorithm is used to integrate the overall controller based on the force/bit hybrid control model. Due to its length, mature algorithms are not mentioned. For further details, the reader is referred to [15].
To prove the performance of the proposed algorithm, a multi-terminal system is designed to manipulate two objects with different shapes and stiffnesses:
  • The first manipulative object is soft-wrapped, and its surface is soft and uneven.
  • The second manipulative object is a container with a hard and flat surface.
The geometry of the manipulated object and the related dimensions, position, and stiffness are arbitrary and unknown. In addition, experiments are performed under unknown non-ideal conditions (e.g., deformable objects of any shape, arbitrary clamping, arbitrary position, direction trajectories, sliding, and friction), which are suitable for non-structural applications such as rescue. Under the above experimental setup, the reliability and robustness of the proposed multi-terminal adaptive collaboration method are verified.
The software architecture is based on the Robot Operating System (ROS), and the implementation of the control module benefits from a set of software packages that implement the control algorithms. When autonomous control is realized, it can communicate with the robot through the read-write port. Figure 6a,b present the expected experimental trajectories. The soft body package has a position movement and direction change, while the container has only position translation, where the translational trajectory is the same as for the soft body package.
Due to the reference trajectory Terminal-j, j = b , c , d requires some time to stabilize and smooth the reference trajectory by  p r j e r 1 = p r j e r ( 1 − e − μ t η ) , j = b , c , d . Therefore, starting from 0  p r j e r 1  is gradually dominated by  p r j e r . In all cases, we set  μ = 0.02 , η = 2 .
Regarding the remaining parameters, the initial values are  k ∧ e = 10 , k ∧ · e = 0 , b ∧ 0 , c ∧ 0 , d ∧ 0 = 0.55 , 0.55 , 0.55 , b ∧ · 0 , c ∧ · 0 , d ∧ · 0 = 0 , 0 , 0 , b ∧ 1 , c ∧ 1 , d ∧ 1 = 0 , 0 , 0 , b ∧ · 1 , c ∧ · 1 , d ∧ · 1 = 0 , 0 , 0 , b ∧ 2 , c ∧ 2 , d ∧ 2 = 0 , 0 , 0 , and b ∧ · 2 , c ∧ · 2 , d ∧ · 2 = 0 , 0 , 0 . MBK is given as  M   =   diag 0.01 ,   0 . 01 ,   0.01 , B   =   diag 0.1 ,   0 . 1 ,   0.1 , and K   =   diag 5 ,   5 ,   5 .

4.2. Soft-Package Manipulation Experiment

4.2.1. Motion Control Analysis

A soft package is an elastomer with an uneven and irregular surface close to any shape. The mechanical response to the applied force is nonlinear. Soft body wrapping can quickly absorb and regenerate the force during the translation and rotation of multi-terminal gripping objects.
The key poses for the entire experimental process are presented in Figure 5. In the first stage, the operator visually judges the shape of the object through remote operation commands and gives the initial clamping posture to the four terminals, ensuring that each contact point (3D biomimetic optical force sensor) has a contact force of about 1N with the object. Based on the first stage, the second stage will trigger the proposed command internal force adaptive tracking algorithm. Each slave terminal actuator from the end effector is close to the master terminal along the direction of its hold line O h j O h a → , ( j = b , c , d ) until it adaptively obtains the desired command internal force. In the third stage, the object's specified position trajectory and direction trajectory are manipulated under the joint operation of absolute, relative, and reference trajectory control of unknown adaptive motion. The absolute motion position trajectory is depicted in Figure 6a, and the direction trajectory is illustrated in Figure 6b, revealing that the main end actuator trajectory is smoother, suggesting that the master terminal actuator tracks the desired trajectory well.
Preprints 74087 g005
Figure 5. Time-varying force tracking converted into a virtual spring two-stage motion.
Figure 5. Time-varying force tracking converted into a virtual spring two-stage motion.
Preprints 74087 g005
Preprints 74087 g006
Figure 6. The absolute motion control: (a) Absolute position trajectory; (b) Absolute direction trajectory.
Figure 6. The absolute motion control: (a) Absolute position trajectory; (b) Absolute direction trajectory.
Preprints 74087 g006
The projection of each slave relative position trajectory on the xz and yz planes of the robot's coordinate system is illustrated in Figure 8. The slave trajectory highlights that after triggering the adaptive tracking algorithm of the internal command force in the second stage, each reference trajectory is generated by adaptively estimating unknown parameters from the terminal, each slave terminal is close to the master terminal along the holding line, tracking the trajectory of the internal command force. At first, the holding line  O h j O h a → , ( j = b , c , d ) , which is the vector p h b r b , p h c r c , p h d r d in Figure 4, varies and oscillates in a certain range of directions within its coordinate system. Thus, special attention should be paid to the fact that the internal forces traced on the holding line do not necessarily satisfy the desired internal forces, assuming an artificially given initial relative position between each terminal, including frictional requirements. Therefore, the expected value of the commanded internal force F w r b , F w r c , F w r d directly given without considering the expected internal force F w r 1 , F w r 2 , F w r 3 in Figure 3 is insufficient to meet the system stability requirements. If a reasonable expected internal force F w r 1 , F w r 2 , F w r 3 is given according to Equation (17), it is converted to a reasonable expected value of  F w r b , F w r c , F w r d , avoiding the above instability. The k ∧ e and the unknown parameters introduced in Section 3 are estimated in a stable range around the holding line under reasonable desired commanded internal force conditions, with each slave end being under the control constraint of constant relative position and the feedback force controller. Thus, the relative trajectory is well maintained with the help of the reference trajectory. The relative position and direction trajectory errors are depicted in Figure 9a,b. Under reasonable initial position and expected command internal force conditions, each slave adaptively estimates unknown parameters to the absolute position and direction errors are presented in Figure 7a,b. Due to unknown uncertainties, such as coordinate calibration error, numerical error, and kinematic uncertainty, the absolute error has a small and acceptable oscillation around zero.
Generate a reference trajectory and gradually stabilizes to the final relative position under the influence of the reference trajectory. The subsequent process of unknown motion estimation and tracking reveals that the relative position and direction error remain near zero, the position oscillation amplitude is less than 1mm, and the directional oscillation amplitude is below 1 degree. These errors may combine many factors, such as self-made model error, unknown uncertain dynamic environment estimation, and renewal rate. When the two slave terminals far from the main terminal change rapidly toward the absolute motion direction due to the object's inertia, there is a large return deviation and Other position and direction errors. The maximum deviation can reach 5 mm, which is believed to be related to parameter adjustment. Therefore, future work will focus on solving such problems by optimizing the parameters, model, and algorithm. Overall, the effectiveness of the multi-terminal collaboration algorithm proposed in this paper is proven.

4.2.2. Internal Force Tracking Analysis

The following experiments aim to prove the effectiveness and superiority of the proposed method for arbitrary trajectory handling of large objects with unknown information in an arbitrary way using multi-terminal actuators. These experiments focus on simplification, transformation, and adaptive tracking methods for complex internal force spaces.
Here the operator observes the desired internal force  F w r 1 , F w r 2 , F w r 3 = − 7 N , − 5 N , − 24 N , which satisfies the clamping motion requirement in a given intuitive sense, and converts it into the desired commanded internal force  F w r b , F w r c , F w r d = − 7 N , − 13 N , − 18 N employing Equation (17), as presented in Section 4.2.1. The above operation is essential for multi-terminal arbitrary clamping and handling of unknown objects of arbitrary shape due to the reasonableness of the desired
Internal force  F w r 1 , F w r 2 , F w r 3 = − 7 N , − 5 N , − 24 N enhancing the possibility of tracing the desired command internal force on the holding line  O h j O h a → , ( j = b , c , d )  and failing the task because of slippage or insufficient internal force between the slave ends is avoided. Figure 3 fully illustrates this point. Besides, the internal forces exerted on the object from the three slave terminals are shown in Figure 10a When the reference position begins to be adaptively updated in the direction of the hold line, the initial overshoot of each slave terminal is about 25%. The internal command force stabilizes at the desired command internal force group − 7 N , − 13 N , − 18 N  in about 7 seconds. During the subsequent operation, the internal force is always controlled near the expected command internal force with the help of the reference trajectory. Note that the initial trajectory time is calculated from the beginning of the second stage of the entire experiment, and the internal force history is recorded from the first stage. The direction of  F w r b , F w r c , F w r d  is along the holding line  O h j O h a → , ( j = b , c , d ) , and Figure 3 highlights that the force  F w l a  at the Master end is time-varying. In this case, adaptively tracking the direction of F w r b , F w r c , F w r d to the holding line O h j O h a → , ( j = b , c , d ) and the desired value under the constraint that the relative motion direction of the multiple slave to the master end remains constant is a unique contribution of this paper.
Figure 10a illustrates the error response, which despite the uncertainty of object stiffness and position, the tracking command internal force error of each slave is less than 1 N (6%). When the adaptive control is disabled, the system's overshoot increases. One of the main goals of such controllers is to avoid force overshoot during the contact phase while maintaining internal force tracking errors. In the next experiments, this phenomenon will become even more critical. The advantages and disadvantages of other control algorithms for force-tracking uncertain, unknown moving targets have been fully demonstrated in [14,15]. However, no similar research has been found on internal force tracking methods between multiple terminals, making it impossible to conduct a comparative analysis.

4.3. Manipulating Containers

In practice, the stiffness of objects varies significantly depending on the materials. To prove that the proposed method is suitable for anthropomorphic clamping and handling objects of any stiffness and shape, a container weighing up to 3 kilograms containing debris was manipulated. Unlike a soft package, the container's surface is hard, flat, and conical in shape. The high stiffness of the container means that adaptive force tracking becomes more difficult.
To demonstrate the environmental adaptability and user-friendliness of the proposed method, all control parameters are the same as in the previous experiments. Since the container is loaded with debris and the container's surface is smooth, the model contact point is not enough to fill the friction required by rotation. Note that this experiment only did the translational operation of the previous experiment’s position trajectory. If there are enough contact points, the arbitrary rotation task can be completed. The key poses of this experiment are depicted in Figure 11.
The corresponding expected internal force is F w r 1 , F w r 2 , F w r 3 = − 13 N , − 5 N , − 36 N , and the expected internal command force group is F w r b , F w r c , F w r d = − 13 N , − 22 N , − 27 N , with historical records illustrated in Figure 10b, inferring that the adaptive process is longer than the specified internal force tracking error and the time amplitude is larger. The tracking command internal force error of each slave is less than 2 N (8%).
The absolute position trajectory is depicted in Figure 6a. Similarly, the relative position trajectory and position tracking error are presented in Figure 12 and Figure 13. Note that due to the translational manipulation, there is no significant deviation from the relative position after the internal force stabilizes in Figure 9b. However, due to high stiffness and smooth surface, the position fluctuates greatly, and the tracking the expected command internal force in the initial stage requires more time.
So far, the effectiveness and accuracy of the proposed adaptive reference trajectory method have been proven. This method allows for manipulating unknown objects with arbitrary shapes through multi-terminal collaboration, which tracks the expected command internal force and relative motion control algorithm in the specified internal force direction. Compared with pure motion control and constant impedance control, ineffectiveness in manipulating unknown objects has been demonstrated in [13], and thus no comparative experiments will be conducted in this paper. Thus, we conclude that:
  • The proposed method effectively extracts holding lines for complex internal force spaces during multi-terminal force closure collaborations and regulates holding lines and maintains contact forces.
  • The motion estimation in the proposed multi-terminal collaboration method is important for dealing with multi-terminal time-varying motions.

5. Conclusions

This paper proposes a multi-terminal actuator adaptive cooperation method to manipulate unknown objects for a system with closed chain motion and dynamic uncertainty of the multi-arm, multi-terminal actuator, and multi-contact sensing model. Drawing on the intelligent behavior of human clamping and handling unknown objects, simplification and conversion to effective control is established for the complex time-varying internal force working space when multi-terminal collaborative clamping and handling of unknown objects. Based on the Lyapunov theory, an algorithm for multi-slave to estimate objects' stiffness and motion uncertainty in the direction of the internal command force is proposed. Moreover, the impedance control is used to generate a reference trajectory for multi-slave ends, maintaining the desired command internal force on a reasonable holding line to maintain the desired internal force to track the motion of the master terminal. That is how the stability and accuracy of the entire control system are realized. The proposed method is simple, stable, and robust to object shape, position, and stiffness changes.
Experiments in the robot system of two-arm, multi-terminal, and multi-contact sensing points verify that the proposed control method shows good position and force tracking performance when the multi-terminal actuator clamps and manipulates unknown objects of any shape or stiffness in any way. The specific results, such as experimental data, show that the relative position oscillation amplitude of each slave position p h b , p h c , p h d under the reference trajectory of motion estimation after tracking the expected command internal force to a stable position is less than 1mm (except for the violent change of direction motion of the main end), and the directional oscillation amplitude is less than 1 degree. For objects with low stiffness, the internal force error of each command from the terminal is less than 1 N (6%). Additionally, the internal force error of the tracking command for objects with high stiffness is less than 2 N (8%). Besides, the method proposed in this article focuses on the collaborative force closure collaboration of multiple terminals (rather than the internal force closure collaboration of fixtures) and is limited to the model being formulated with 8 sensing contact points and 4 terminals. However, the proposed algorithm can extend to the collaborative force closure collaboration of n  multiple sensing contact points (tactile research) and  n  multiple terminal actuators. Future work will focus on developing anthropomorphic robots with multiple terminals, utilizing self-adjusting expected internal forces based on sliding perception, more functional and nuanced models, and manipulated objects accepting complex and variable external forces. Accordingly, the new algorithms are expected to have more requirements and difficulties.

Author Contributions

Conceptualization, Z.W.; methodology, Z.W and J.D.; software, Z.W.; validation, F.S.; writing—original draft preparation, Z.W and F.S.; writing—review and editing, J.D.; supervision, J.D.; funding acquisition, J.D.; All authors have read and agreed to the published version of the manuscript.

Funding

This research was funded by the National Natural Science Foundation of China, grant number 62275066.

Institutional Review Board Statement

Not applicable.

Informed Consent Statement

Not applicable.

Data Availability Statement

Not applicable.

Acknowledgments

The authors would like to gratefully acknowledge the National Natural Science Foundation of China, the authors would like to thank the editors and reviewers for their valuable comments and constructive suggestions. The authors would like to express their gratitude to Edit Springs (https://www.editsprings.cn) for the expert linguistic services provided.

Conflicts of Interest

The authors declare no conflict of interest.

References

  1. Galicki, M. Finite-time trajectory tracking control in a task space of robotic manipulators. Automatica 2016, 67(5), 165–170. [CrossRef]
  2. Corradini, M.; Fossi, V.; Giantomassi, A. Minimal resource allocating networks for discrete time sliding mode control of robotic manipulators. IEEE Transactions on Industrial Informatics 2012,8(4), 733–745. [CrossRef]
  3. Wang, H. Adaptive control of robot manipulators with uncertain kinematics and dynamics. IEEE Transactions on Automatic Control 2017,62(2), 948–954. [CrossRef]
  4. Duan, J.; Gan, Y.; Chen, M.; Dai, X. Adaptive variable impedance control for dynamic contact force tracking in uncertain environment. Robotics and Autonomous Systems 2018, 102(4), 54–65. [CrossRef]
  5. Liu, T.; Yan, L.; Han, L.; Xu, W. Coordinated resolved motion control of dual-arm manipulators with closed chain. International Journal of Advanced Robotic Systems 2016, 13(3), 80–94. [CrossRef]
  6. Yan, L.; Yang, Y.; Xu, W.; Vijayakumar, S. Dual-arm coordinated motion planning and compliance control for capturing moving objects with large momentum. In Proceedings of the 2019 IEEE/RSJ international conference on intelligent robots and systems, vol 2019, 713 ,7137–7144. [CrossRef]
  7. Heck, D.; Saccon, A.; Wouw, N.; Nijmeijer, H. Guaranteeing stable track-ing of hybrid position–force trajectories for a robot manipulator interacting with a stiff environment. Automatica 2016, 63(1), 235–247. [CrossRef]
  8. Sun, D.; Liao, Q.; Stoyanov, Q.; Kiselev, A.; Loutfi, A. Bilateral telerobotic system using Type-2 fuzzy neural network based moving horizon estimation force observer for enhancement of environmental force compliance and human perception. Automatica 2019, 106(3), 358–373. [CrossRef]
  9. Yang, G.; Wang, S.; Yang, J. Hybrid knowledge base for care robots. International Journal of Innovative Computing, Information and Control 2021,17(1), 335–343. [CrossRef]
  10. Baigzadehnoe, B.; Rahmani, Z.; Khosravi, A.; Rezaie, B. On position/force tracking control problem of cooperative robot manipulators using adaptive fuzzy backstepping approach. ISA Ransactions 2017, 70(9), 432–446. [CrossRef]
  11. Li, C., Zhang, Z.; Xia, G.; Xie, X.; Zhu, Q. Efficient force control learning system for industrial robots based on variable impedance control. Sensors 2018, 18(8), 25–39. [CrossRef]
  12. Yang, Z.; Peng, J.; Liu, Y. Adaptive neural network force tracking impedance control for uncertain robotic manipulator based on nonlinear velocity observer. Neurocomputing 2019, 331(2), 263–280. [CrossRef]
  13. Kaserer, D.; Gattringer, H.; Müller, A. Time Optimal Motion Planning and Admittance Control for Cooperative Grasping. Robottics and Automation Letter 2020, 5, 2216-2223. [CrossRef]
  14. Duan, J.; Gan Y.; Chen, M.; Dai, X. Adaptive variable impedance control for dynamic contact force tracking in uncertain environment. Robotics and Autonomous Systems2018,102 ,54–65. [CrossRef]
  15. Jiao, C.; Yu, L.; Su X.; Wen, Y.; Dai, X. Adaptive hybrid impedance control for dual-arm cooperative manipulation with object uncertainties. Automatica 2022,140 ,1-13. [CrossRef]
  16. Uchiyama M.; Dauchez P. Symmetric kinematic formulation and non-master/slave coordinated control of two-arm robots. Adv. Robot 1993,7,361–383. [CrossRef]
  17. Hirata, Y.; Fukaya, Z. K.; Kosuge, K. Transporting an object by a passive mobile robot with servo brakes in cooperation with a human. Advanced Robotics 2009, 23, 387–404. [CrossRef]
  18. Iqbal, K.; Zheng, Y. F. Arm-manipulator coordination for load sharing using predictive control. in Proceedings 1999 IEEE International Conference on Robotics and Automation (Cat. No. 99CH36288C) 1999, 4, 2539–2544. [CrossRef]
  19. Ikeura, R.; Inooka, H. Variable impedance control of a robot for cooperation with a human. in Proceedings of 1995 IEEE International Conference on Robotics and Automation 1995, 3, 3097–3102. [CrossRef]
  20. Ficuciello, F.; Villani, L.; Siciliano, B. Variable impedance control of redundant manipulators for intuitive human–robot physical interaction. IEEE Transactions on Robotics 2015,31, 850–863. [CrossRef]
  21. Seraji, H.; Colbaugh, R. Force tracking in impedance control. The International Journal of Robotics Research 1997, 16, 97–117. [CrossRef]
  22. Jung, S.; Hsia, T. C.; Bonitz, R. G. Force tracking impedance control of robot manipulators under unknown environment. IEEE Transactions on Control Systems Technology 2004, 12, 474–483. [CrossRef]
  23. Zhang, X.; Khamesee, M. B. Adaptive force tracking control of a magnetically navigated microrobot in uncertain environment. IEEE/ASME Transactions on Mechatronics 2017, 22, 1644– 1651. [CrossRef]
  24. Stephens, T. K.; Awasthi, C.; Kowalewski, T. M. Adaptive impedance control with setpoint force tracking for unknown soft environment interactions. in 2019 IEEE 58th Conference on Decision and Control (CDC) 2019, 1951–1958.
  25. Wojtara, T.; Uchihara, M.; Murayama, H.; Shimoda, S.; Sakai, S.; Fu-jimoto, H.; Kimura, H. Human–robot collaboration in precise positioning of a three-dimensional object. Automatica 2009, 45, 333–342. [CrossRef]
  26. Lee, S. Y.; Lee, K. Y.; Lee, S. H.; J. Kim, W.; Han, C. S. Humanrobot cooperation control for installing heavy construction materials. Autonomous Robots2007, 22, 305–319. [CrossRef]
  27. Agravante, D. J.; Cherubini, A.; Bussy, A.; Gergondet, P.; Kheddar, A. Collaborative human-humanoid carrying using vision and haptic sensing.in 2014 IEEE international conference on robotics and automation (ICRA) 2014, 607–612. [CrossRef]
Preprints 74087 g001
Figure 1. Four terminals equipped with two optical bionic force sensor contact points cooperate to clamp and stably handle heavy objects of any shape.
Figure 1. Four terminals equipped with two optical bionic force sensor contact points cooperate to clamp and stably handle heavy objects of any shape.
Preprints 74087 g001
Preprints 74087 g002
Figure 2. Simplified system workspace.
Figure 2. Simplified system workspace.
Preprints 74087 g002
Preprints 74087 g003
Figure 3. Relationship between expected internal force and commanded internal force.
Figure 3. Relationship between expected internal force and commanded internal force.
Preprints 74087 g003
Preprints 74087 g004
Figure 4. Time-varying force tracking converted into a virtual spring two-stage motion.
Figure 4. Time-varying force tracking converted into a virtual spring two-stage motion.
Preprints 74087 g004
Preprints 74087 g007
Figure 7. The absolute motion error: (a) Absolute position trajectory error; (b) Absolute direction trajectory error.
Figure 7. The absolute motion error: (a) Absolute position trajectory error; (b) Absolute direction trajectory error.
Preprints 74087 g007
Preprints 74087 g008
Figure 8. Relative position trajectory xz plane and yz  plane projection of each slave.
Figure 8. Relative position trajectory xz plane and yz  plane projection of each slave.
Preprints 74087 g008
Preprints 74087 g009
Figure 9. The relative motion error: (a) Relative position trajectory error of each slave; (b) Absolute direction trajectory error of each slave.
Figure 9. The relative motion error: (a) Relative position trajectory error of each slave; (b) Absolute direction trajectory error of each slave.
Preprints 74087 g009
Preprints 74087 g010
Figure 10. The internal force tracking error: (a) History of the internal force group of the soft manipulation package; (b) History of the internal force group of the manipulation container.
Figure 10. The internal force tracking error: (a) History of the internal force group of the soft manipulation package; (b) History of the internal force group of the manipulation container.
Preprints 74087 g010
Preprints 74087 g011
Figure 11. Key pose of translational high-stiffness container.
Figure 11. Key pose of translational high-stiffness container.
Preprints 74087 g011
Preprints 74087 g012
Figure 12. Container translational relative motion trajectory  xz  and  yz  plane projection.
Figure 12. Container translational relative motion trajectory  xz  and  yz  plane projection.
Preprints 74087 g012
Preprints 74087 g013
Figure 13. Relative position trajectory error of each slave terminal of container translation.
Figure 13. Relative position trajectory error of each slave terminal of container translation.
Preprints 74087 g013
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.
Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.
Prerpints.org logo

Preprints.org is a free preprint server supported by MDPI in Basel, Switzerland.

facebook logotwitter logolinkedin logo
MDPI Initiatives
Important Links
Subscribe

Disclaimer

Terms of Use

Privacy Policy

© 2024 MDPI (Basel, Switzerland) unless otherwise stated