1. Introduction
With the continuous development of the chemical industry, more chemical products are used in social life and production, which accelerates the rapid development of the national economy. However, most chemical products are flammable, explosive, toxic, radioactive and other dangerous characteristics, if not handled properly in the process of production, storage, transportation and use, major safety accidents will easily occur, which will cause serious personal casualties, property losses and environmental pollution. Although chemical enterprises and relevant departments have done a lot of work to reduce safety production accidents, there are still loopholes in safety supervision and production process, which leads to frequent safety production accidents in China’s chemical industry. The typical example is ‘1.15′ Liaoning Panjin major explosion and fire accident. On January 15, 2023, a leakage, explosion, and fire accident occurred in the alkylation unit of Liaoning Panjin Haoye Chemical Corporation, resulting in 13 deaths and 35 injuries. Chemical enterprises generally store a large amount of flammable and explosive hazardous materials, which pose high risks during the production process. Once a fire occurs, it will cause extremely serious consequences. These major safety accidents have exposed some problems in safety supervision of chemical industry, such as weak awareness, unclear main responsibility, inadequate investigation of hidden dangers, etc. It is of great practical significance to study the safety supervision and governance of chemical enterprises.
One important reason for the frequent occurrence of chemical safety accidents in enterprises is that the safety supervision system is not perfect, there are serious supervision gaps in the production, transportation, storage and use of chemical products, resulting in loopholes in supervision [
1,
2].Lefebvre and Leveneur [
3] summarized the causes of chemical accidents as leakage, fire, explosion, and thermal runaway. Therefore, it is necessary to conduct safety analysis and management of chemical enterprises to prevent major chemical accidents from occurring. Zhu L [
4] took the local government’s supervision behavior in the chemical industry safety as the research object, and analyzed the current situation of chemical safety supervision in Shandong Province, as well as some problems, such as imperfect supervision system, inadequate safety planning, weak law enforcement ability, lagging construction of basic supervision information, etc. Dai X [
5] analyzed the current situation of supply and demand of China’s chemical safety supervision, and the outstanding problems such as the lack of specialized laws and standards, the single supervision means, and the arbitrariness of supervision from the perspective of government safety supervision. Makin and Winder [
6] pointed out that improving the government’s supervision can have an important impact on the safety production of enterprises, and analyzed the role of external environment in improving the safety production management level. Wachter and Yorio [
7] analyzed the influence of the establishment of safety production supervision system on employees’ behavior from the perspective of internal safety management. Chen H [
8] analyzed the problems and causes of the safety supervision and management of dangerous chemicals in Huian County from the aspects of the supervision object, the supervision subject and the supervision links. Shi Lichen et al. [
9] pointed out that the boundary between government supervision and enterprise management of hazardous chemicals was unclear, and the public participation in major hazard source construction projects was insufficient. Yang and Sun [
10] also pointed out that the probability of related accidents and risks can be reduced by setting quantitative standards, constructing safety indicators, and government support and policy guidance.
Strengthening the internal safety management and control of chemical enterprises by reasonable and scientific methods to ensure the safety of personnel and production equipment is an inevitable means for the stable and rapid development of enterprises [
11]. In view of the problems existing in the safety supervision of chemical enterprises, Wang H [
12] discussed the safety supervision of hazardous chemicals in China from the perspectives of enterprise management, government management, scientific and technological means, laws and regulations, linkage mechanism, etc., and defined the main responsibility of enterprises, the safety supervision responsibility of government departments and the effective mechanism of multi-department linkage supervision in the supervision system. Ale et al. [
13] described a number of recent incidents in the Netherlands and the subsequent investigations, the study found that only a minority of companies make safety of their workers and their environment really a priority. Hence the authorities need to continue to insist that multiple layers of defense be designed and installed and not leave inspection and oversight to the companies or the industry itself. Smith et al. [
14] further proposed to strengthen safety training and guidance for employees engaged in dangerous work in enterprises, and timely monitor and identify the information of employees who are prone to harm. Lee et al. [
15] discussed the systematic changes in laws, regulations, business cultures, and accident responses of organizations on a national level for chemical safety management after a large chemical release accident, and hold that it is possible to cope with disasters more efficiently through cooperation among relevant agencies. Campos et al. [
16] researched how different stakeholders (industry, government and the public) view the current application of omics data in chemical safety assessment, and what key progress needs to be made so that valuable solutions can be provided to improve our confidence in chemical safety assessment, and finally incorporated into the global regulatory framework.
The safety production of chemical enterprises involves many stakeholders. In view of the interest game of the participants, the existing research analyzes the safety production supervision of enterprises with the help of game theory. Taking the supervision failure of Xiangshui ‘3.21′ explosion accident in Jiangsu Province as an example, Jiang Y [
17] made a multi-dimensional dynamic analysis of the value choice and behavior game between the government and enterprises from the project introduction stage, the business development stage to the post-accident stage by using the evolutionary game model and the benefit analysis method based on the hypothesis of bounded rational behavior. The study concluded that the government safety supervision game strategy needs the benefit value lever reconstruction based on the cost-benefit balance. Zhang Z [
18] took the evolutionary game model as the main theoretical tool, constructed a perceived income matrix which is different from the traditional income matrix, and applied it to the research on the safety management behavior of chemical products production in enterprises, analyzed the evolution process of the supervision of unsafe behaviors among employees in enterprises, obtained the objective conditions for the system to reach the ideal state of safety, and provided a theoretical basis for formulating reasonable and effective management regulations and built a tripartite dynamic evolution game system between government and enterprises based on public participation, and analyzed the interaction mechanism of main stakeholders’ behaviors and the factors that influence the system evolution. Shen B [
19] analyzed the supervision effect of the government safety supervision department based on the game model, and the research pointed out that the penalty amount collected by the government safety supervision department after the production safety accident in the enterprise had a significant influence on the evolution effect. Liu S et al. [
20] based on the consideration of industrial cluster enterprises’ safe production behavior and its supervision characteristics, through the analysis of the evolution model of the interaction process between enterprise groups, revealed the evolution law of enterprises’ safe production behavior choice.
The multi-party game subjects involved in the supervision of chemical enterprises have the characteristics of information uncertainty and bounded rationality, and the traditional game theory can no longer be applied to analysis. Evolutionary game theory is different from the traditional game theory, which assumes that all game participants are completely rational. It takes game participants with limited rationality as an analysis, and opens up a new research angle of game theory. Evolutionary game theory was put forward by Smith and Price [
21] when analyzing the phenomenon of biological evolutionary process. It is an asymptotic evolutionary process with some adaptive learning ability, and individuals with high adaptability will be retained. The Evolutionarily Stable Strategy (ESS) in evolutionary game theory is given. Guo and Chen [
22], based on methods such as situation awareness, situation construction, and situation deduction, constructed an emergency management CIA-DISM model to further analyze the evolution process of a chemical park disaster after the Wenchuan earthquake and provide technical support for enterprise accident prevention.Bin et al. [
23] considered the problem of random mutation in the process of evolution, and comprehensively discussed the mechanism of individuals’ dynamic entry into and exit from the population and imitation, thus obtaining the concept of dynamic imitator in evolutionary game theory. Sethi [
24] considered that the possibility of learning strategies by imitation is different, and some strategies are almost difficult to observe, so it will be more difficult to learn by imitation, and put forward a generalized replication dynamic equation. Evolutionary game theory overcomes the limitations of traditional game theory and brings bounded rational participants into the research. Therefore, the study of evolutionary game theory provides a theoretical basis for analyzing the regulatory governance of chemical enterprises.
To sum up, although some articles have done relevant research on chemical safety and its supervision, there is still a lack of analysis of the game mechanism between government regulatory authorities and chemical enterprises from the perspective of game theory, and there are few researches on the strategic choice and reward and punishment mechanism between the two parties. Different from previous studies, the research innovations of this paper are mainly reflected in:
- (1)
Based on the perspective of ‘special rectification’ and ‘normal regulation’, the evolutionary game analysis of chemical safety supervision in different modes is carried out;
- (2)
The probability of chemical safety accident risk is introduced, and the influence of the probability of chemical safety accident on the strategy choice of two game players is analyzed.
- (3)
Considering the evolution process of each game subject’s strategy choice under the government punishment mechanism, and comparing and analyzing the evolution, stability and balance of the behavior strategies of chemical enterprises and government supervision departments, and simulating the evolution process of the game under Matlab software environment, simulating the evolution trend of the two players under different conditions, and analyzing the influence of each factor on the strategy choice.
4. Conclusions and Recommendations
4.1. Conclusions
The aim of this paper is to investigate the game behavior of the government supervision departments and chemical enterprises in the process of chemical safety supervision, based on the perspective of ‘special rectification’ and ‘normal regulation’, the evolutionary game models of chemical enterprises and government supervision departments under different supervision modes are established. Based on the evolutionary game theory, this paper studies the evolutionary process of the two game players’ strategy choices, and compares and analyzes the evolutionary stability and equilibrium of the behavior strategies of chemical enterprises and government supervision departments. Finally, based on the numerical simulation, the numerical experiment and simulation analysis of the model are carried out. Combined with the simulation results, the results show that: (1) Under the ‘special rectification’ mode, the strategic choice of chemical enterprises engaging in safety investment depends on the difference between the benefits and costs of safety non-investment. (2) In the ‘normal regulation’ mode, the choice of its safety non-investment strategy depends on the difference between the cost of engaging in safety investment and the cost of safety non-investment. (3) Increasing the government’s punishment will encourage chemical enterprises to take safety investment behavior under the two supervision modes. (4) Increasing the punishment has a significant impact on the safety investment behavior of enterprises under the ‘normal regulation’ mode, but it has no significant impact on the behavior of chemical enterprises under the ‘special rectification’ mode. At the same time, increasing the punishment will inhibit the government’s strict supervision behavior.
4.2. Insights and Recommendations
(1) Under the ‘special rectification’ mode, the strategic choice of safety investment in chemical enterprises depends on the difference between the benefits and costs of safety investment. In order to obtain high profits, chemical enterprises will adopt a strategy of safety investment to reduce their safety investment. At this point, the government can use administrative means to increase penalties for chemical enterprises engaged in safety non-investment, increase the cost of safety non-investment, and reduce the benefits of safety non-investment, which can encourage chemical enterprises to choose safety investment strategies.
(2) In the ‘normal regulation’ mode, the choice of safety investment strategy depends on the difference between the cost of engaging in safety investment and the cost of safety investment. In addition to increasing the cost of safety investment in chemical enterprises, it is also necessary to consider reducing the cost of safety investment in chemical enterprises. Increasing rewards for safety investment behavior in chemical enterprises and reducing the cost of safety investment are important measures to achieve effective supervision. By constructing a reasonable reward and punishment mechanism, chemical enterprises can promote the transformation towards safety investment behavior.
(3) To improve the efficiency of government regulation of chemical enterprises, information technology can be used to reduce the regulatory costs of government departments and improve the efficiency of strict government regulation. For example, a data analysis platform for big data regulation can fully utilize the advantages of internet information, reduce regulatory costs, and strengthen government regulatory behavior supervision under the ‘normal regulation’ model.
4.3. Limitations
However, there are still some shortcomings in this model. Chemical enterprises are a complex dynamic game evolution process, and many influencing factors and conditions have not been considered in the game process. In the next step, more game conditions will be considered for simulation analysis. At the same time, with the rapid development of new media, it also has a new impact on the behavior strategy of game players. The model has not considered the impact of new media environment on the safety production of chemical enterprises, which will be further analyzed in the follow-up research.
Figure 1.
Evolution process of safety investment strategy adopted by chemical enterprises under ‘special rectification’ mode.
Figure 1.
Evolution process of safety investment strategy adopted by chemical enterprises under ‘special rectification’ mode.
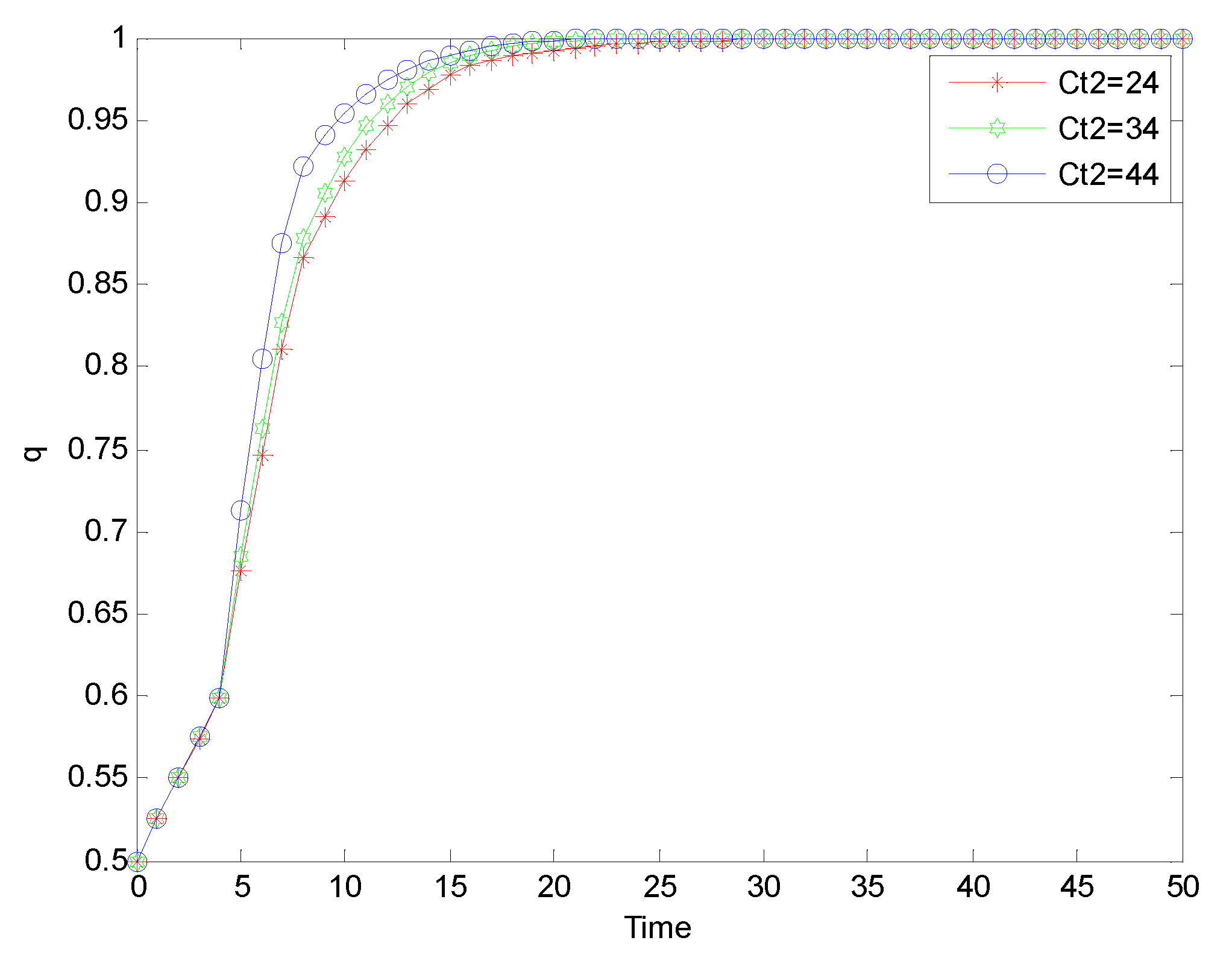
Figure 2.
Evolution process of safety investment strategy adopted by chemical enterprises under ‘normal regulation’ mode.
Figure 2.
Evolution process of safety investment strategy adopted by chemical enterprises under ‘normal regulation’ mode.
Figure 3.
Evolution process of strict supervision strategy adopted by government supervision departments under ‘special rectification’ mode.
Figure 3.
Evolution process of strict supervision strategy adopted by government supervision departments under ‘special rectification’ mode.
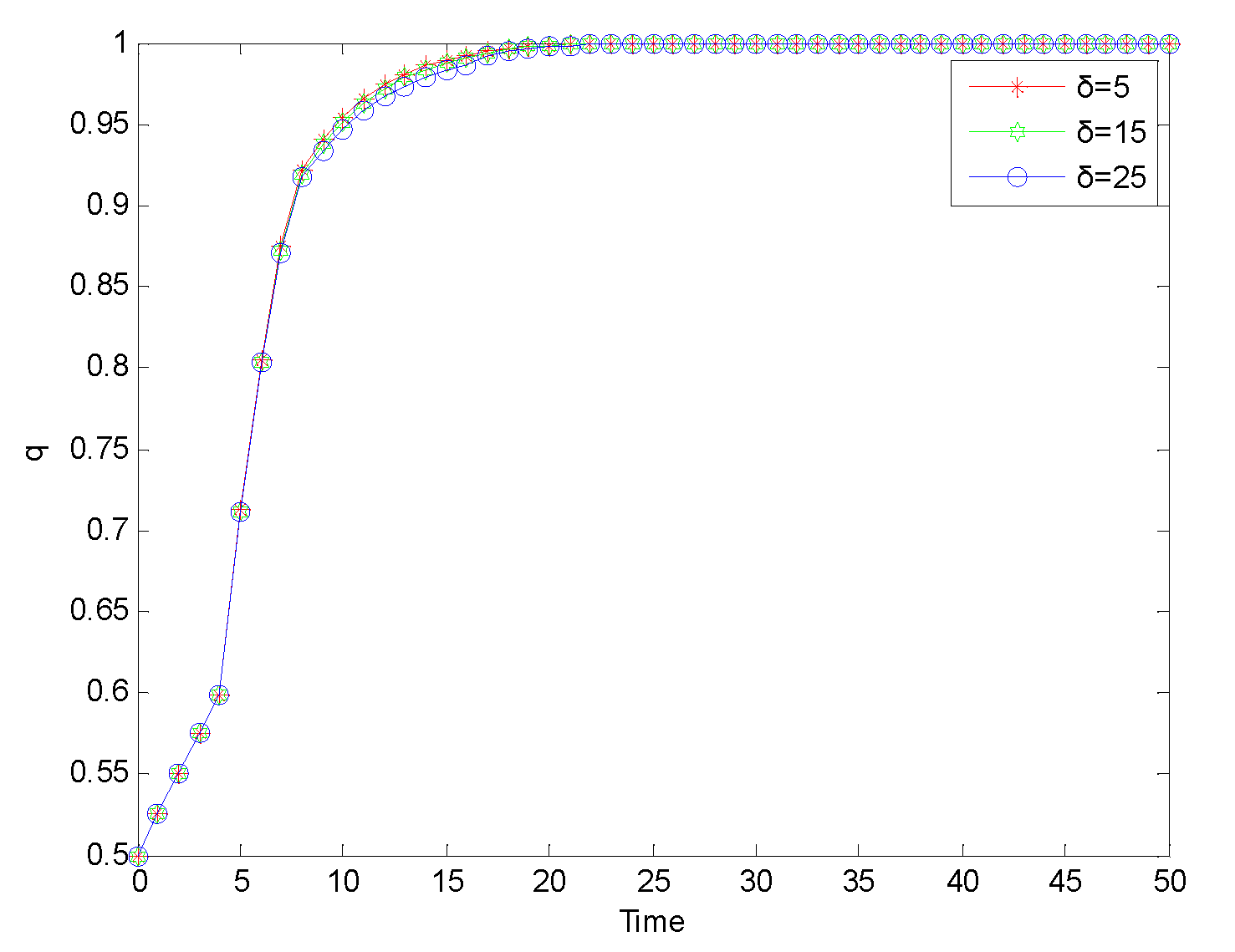
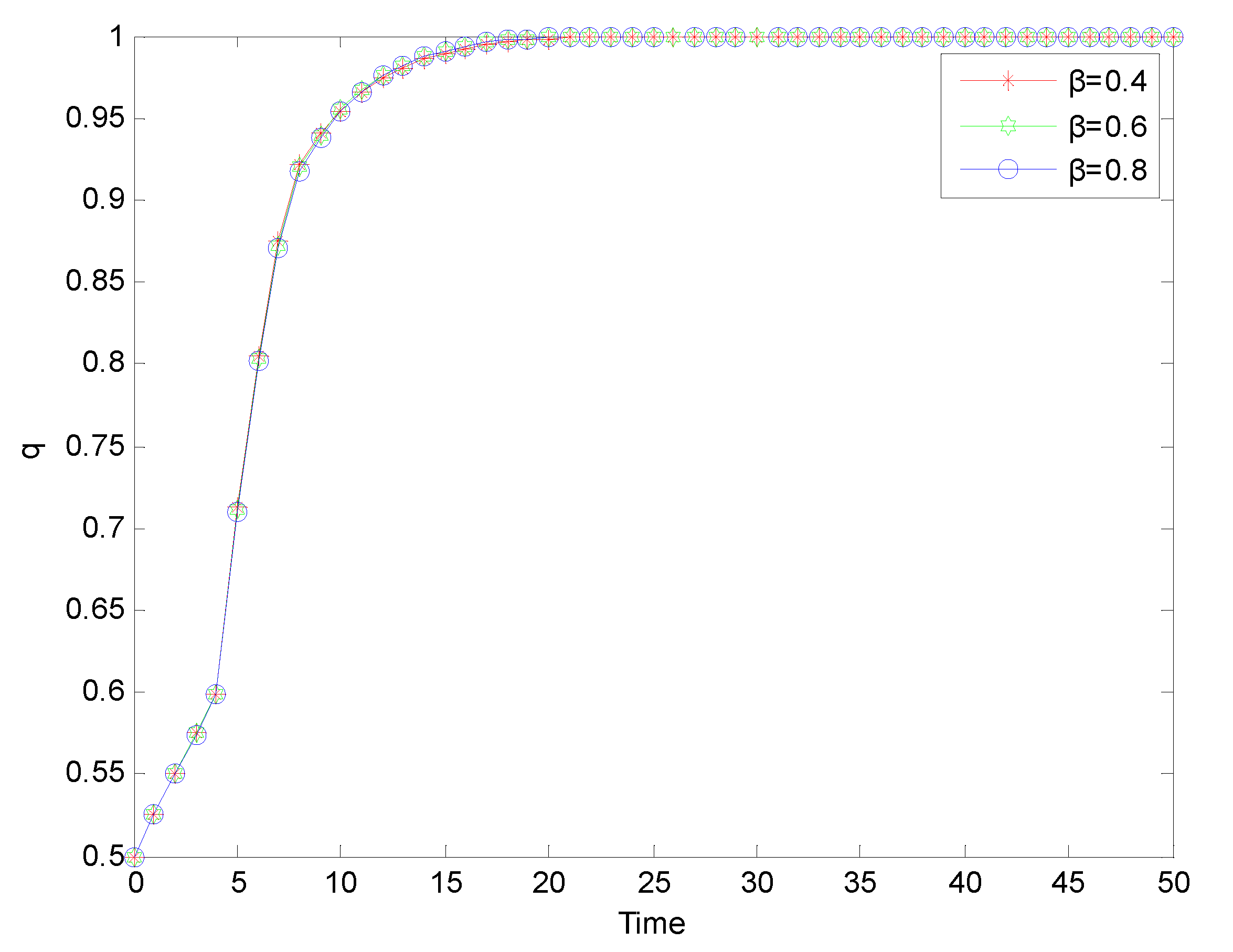
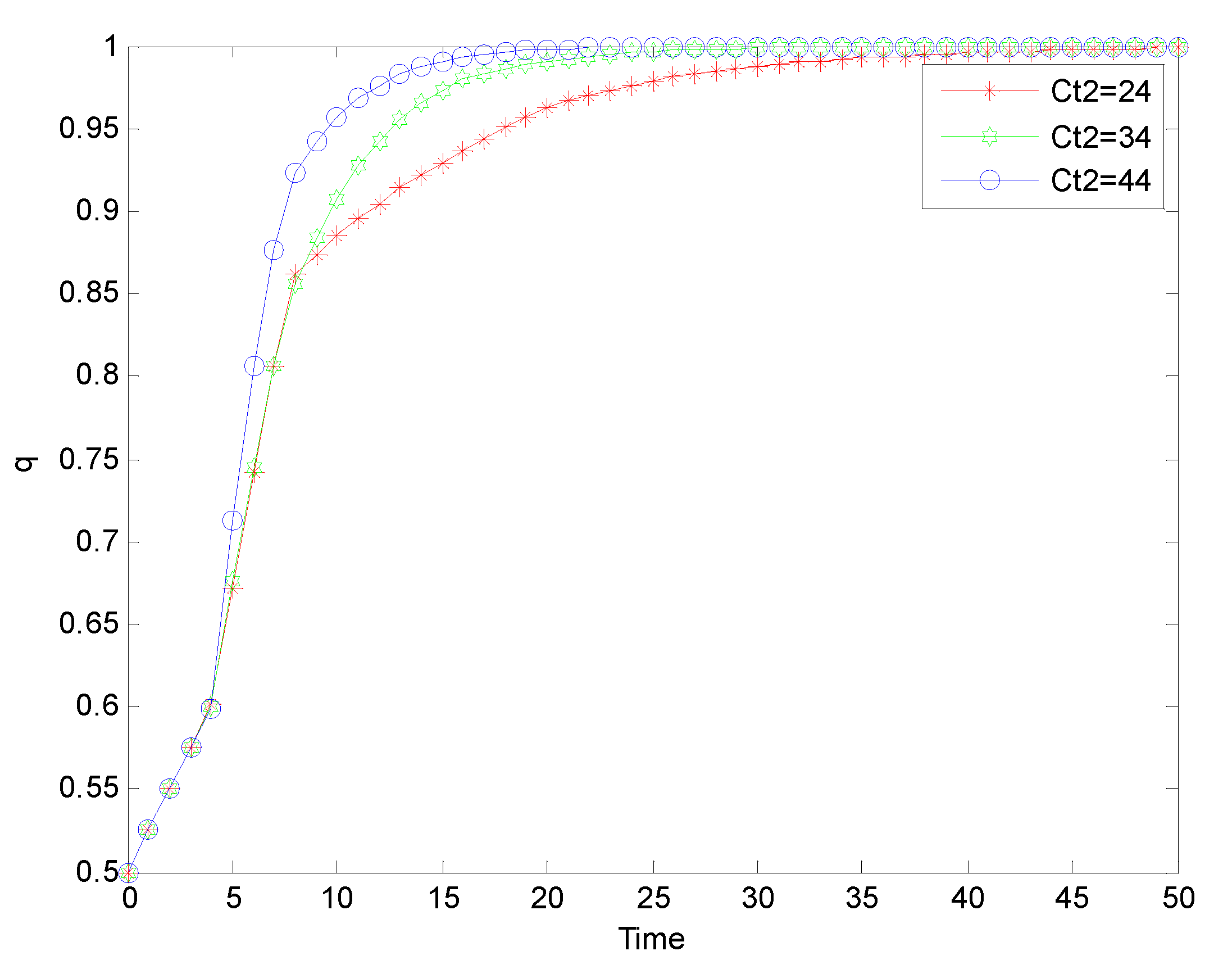
Figure 4.
Evolution process of strict supervision strategy adopted by government supervision departments under ‘normal regulation’ mode.
Figure 4.
Evolution process of strict supervision strategy adopted by government supervision departments under ‘normal regulation’ mode.
Figure 5.
Evolution process of safety investment strategy adopted by chemical enterprises under ‘special rectification’ mode.
Figure 5.
Evolution process of safety investment strategy adopted by chemical enterprises under ‘special rectification’ mode.
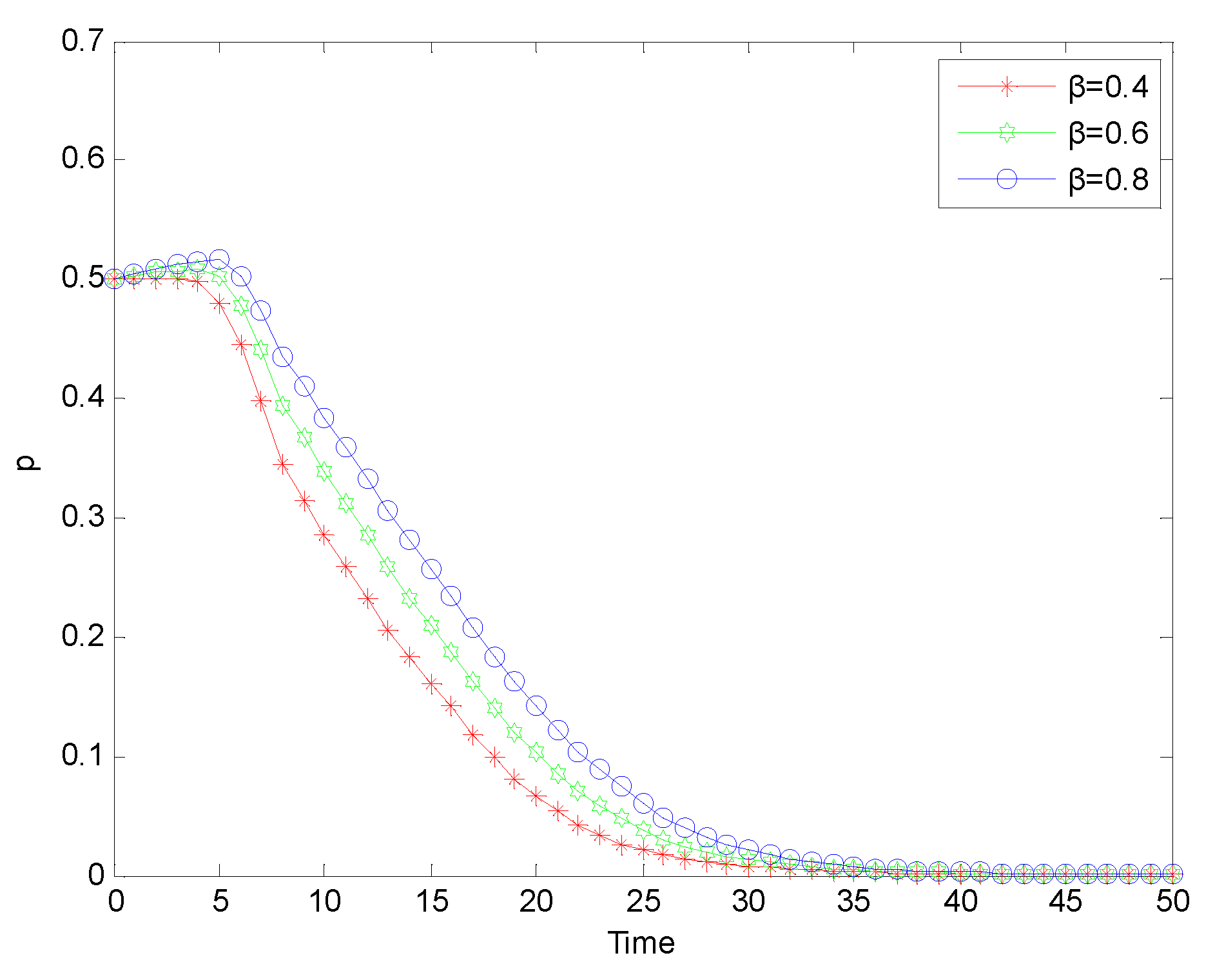
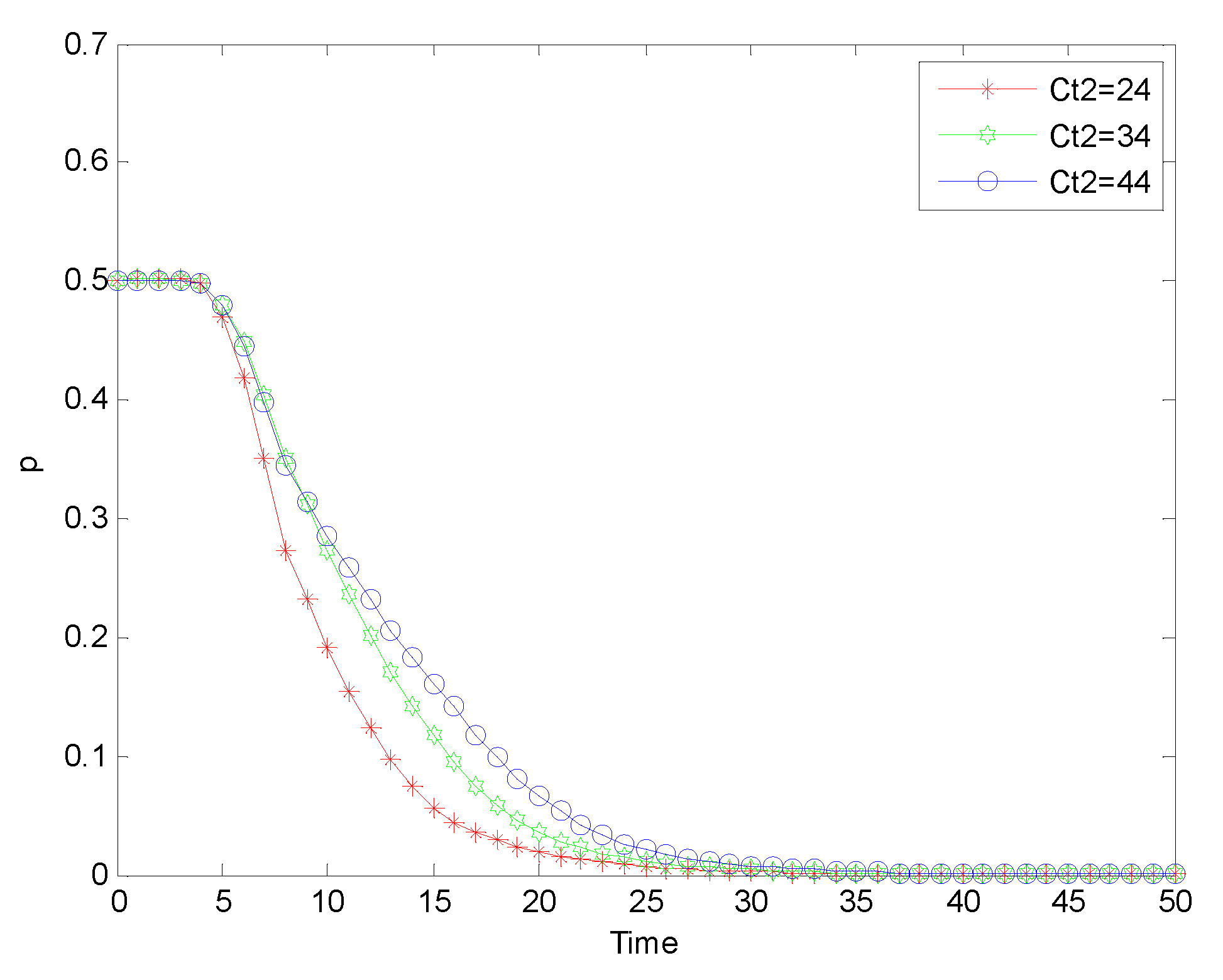
Figure 6.
Evolution process of safety investment strategy adopted by chemical enterprises under ‘normal regulation’ mode.
Figure 6.
Evolution process of safety investment strategy adopted by chemical enterprises under ‘normal regulation’ mode.
Figure 7.
Evolution process of strict supervision strategy adopted by government supervision departments under ‘special rectification’ mode.
Figure 7.
Evolution process of strict supervision strategy adopted by government supervision departments under ‘special rectification’ mode.
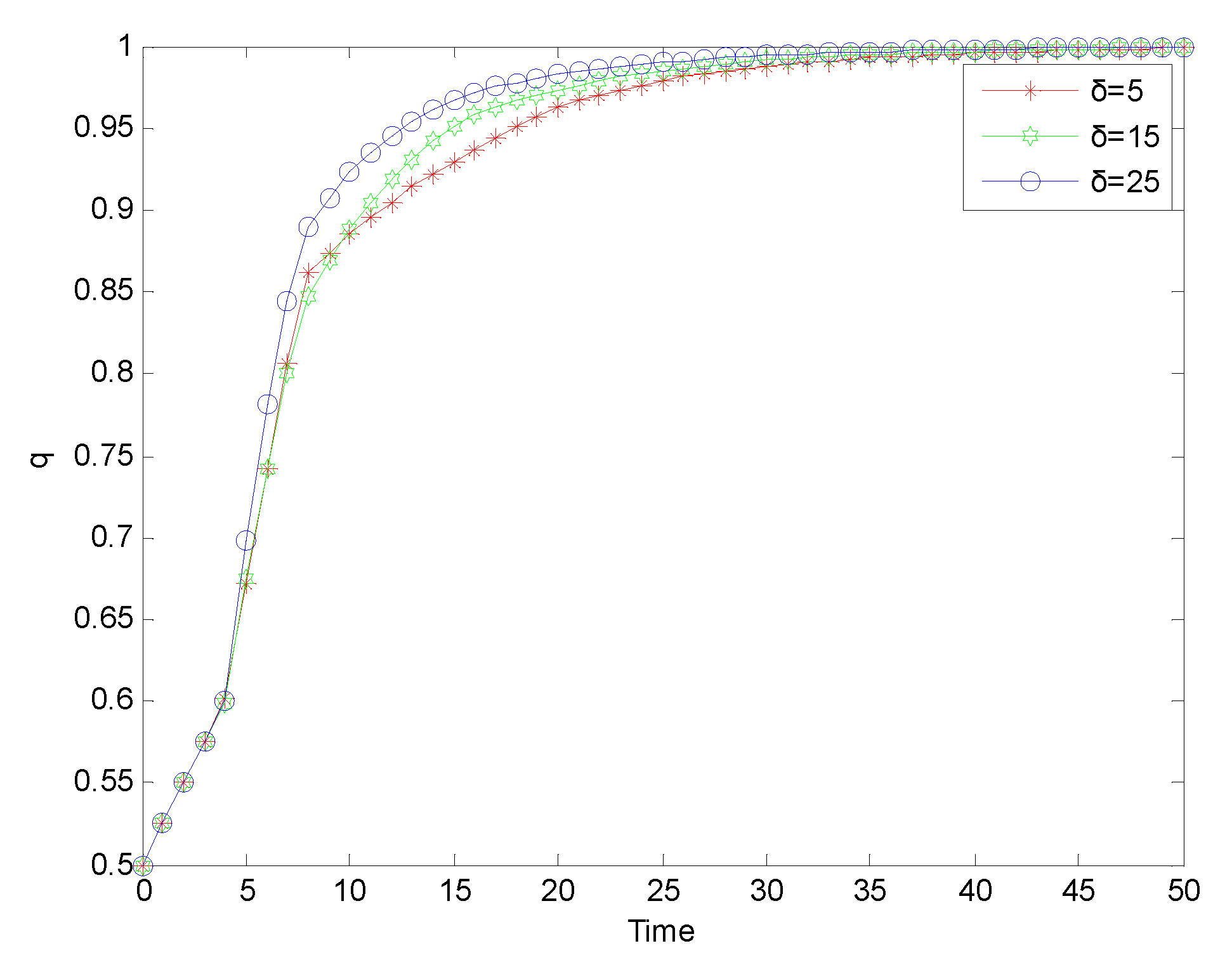
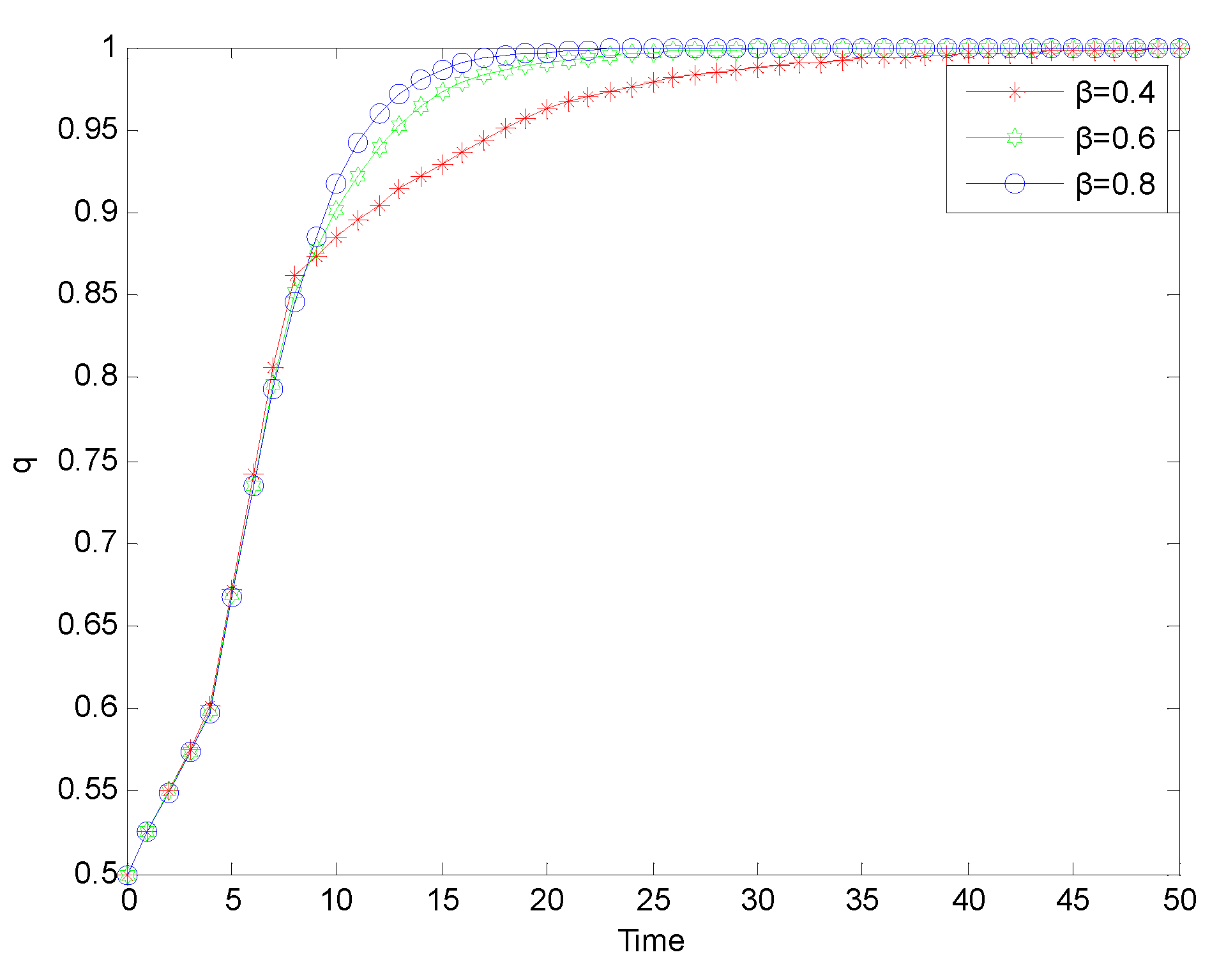
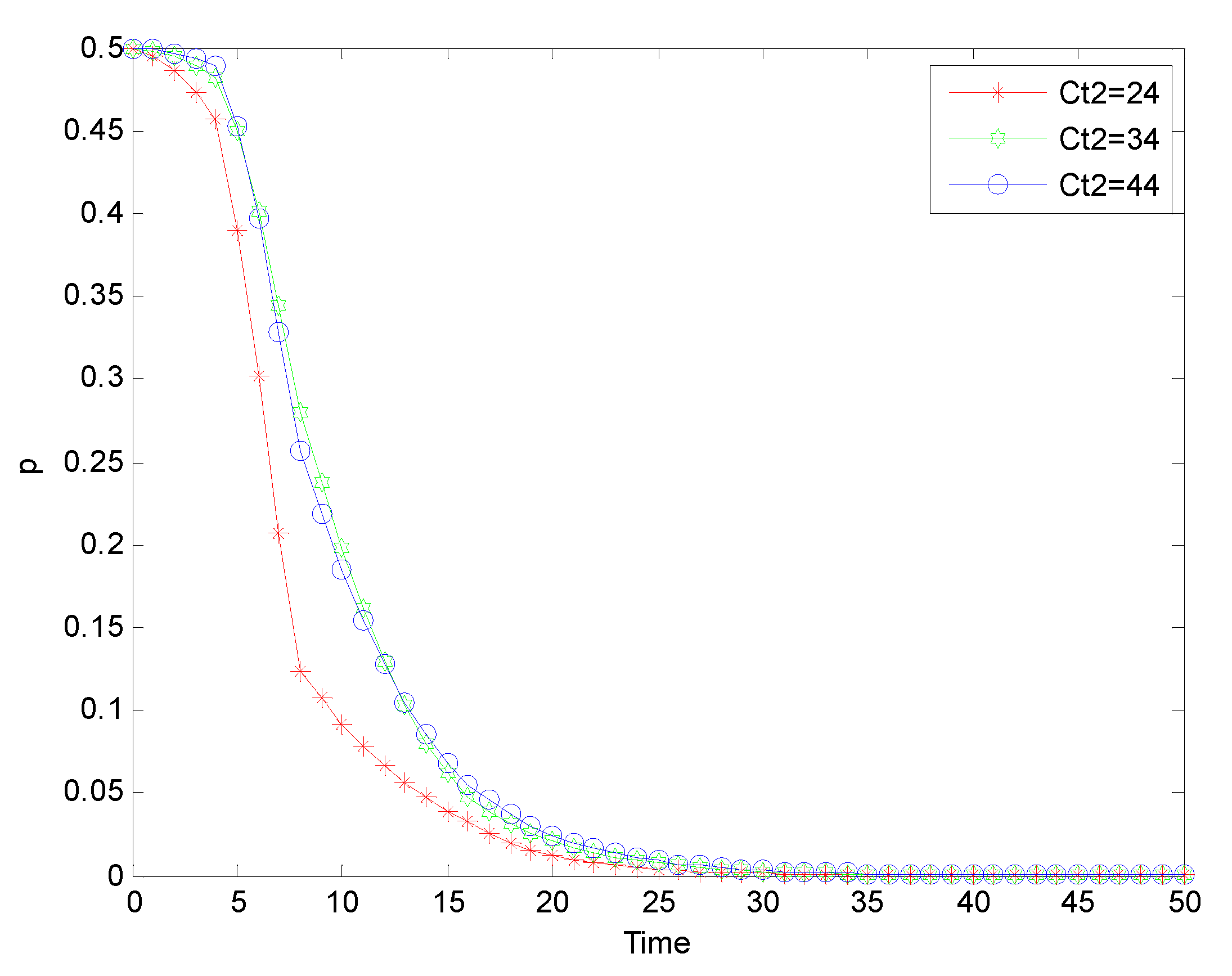
Figure 8.
Evolution process of strict supervision strategy adopted by government supervision departments under ‘normal regulation’ mode.
Figure 8.
Evolution process of strict supervision strategy adopted by government supervision departments under ‘normal regulation’ mode.
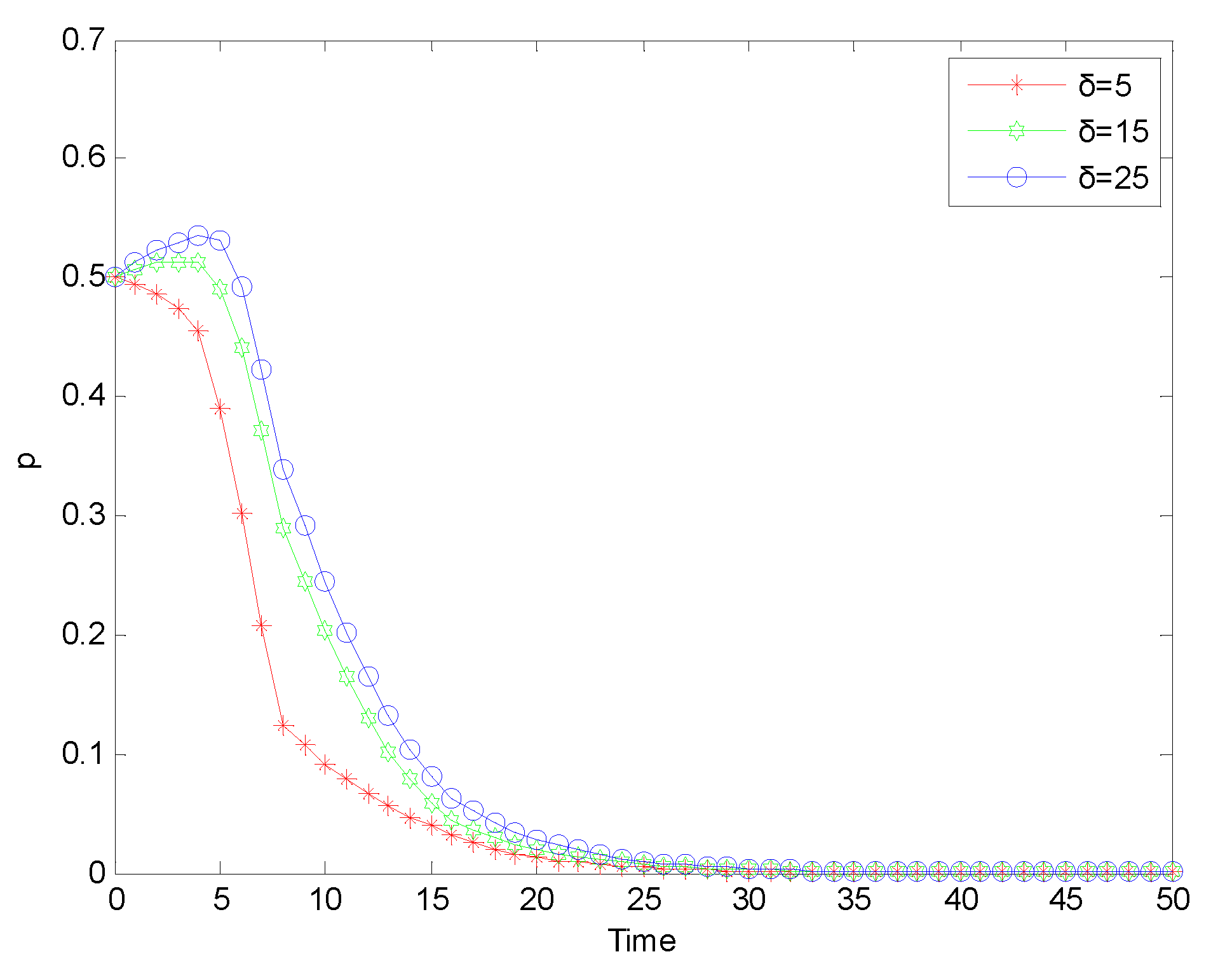
Figure 9.
Evolution process of safety investment strategy adopted by chemical enterprises under ‘special rectification’ mode.
Figure 9.
Evolution process of safety investment strategy adopted by chemical enterprises under ‘special rectification’ mode.
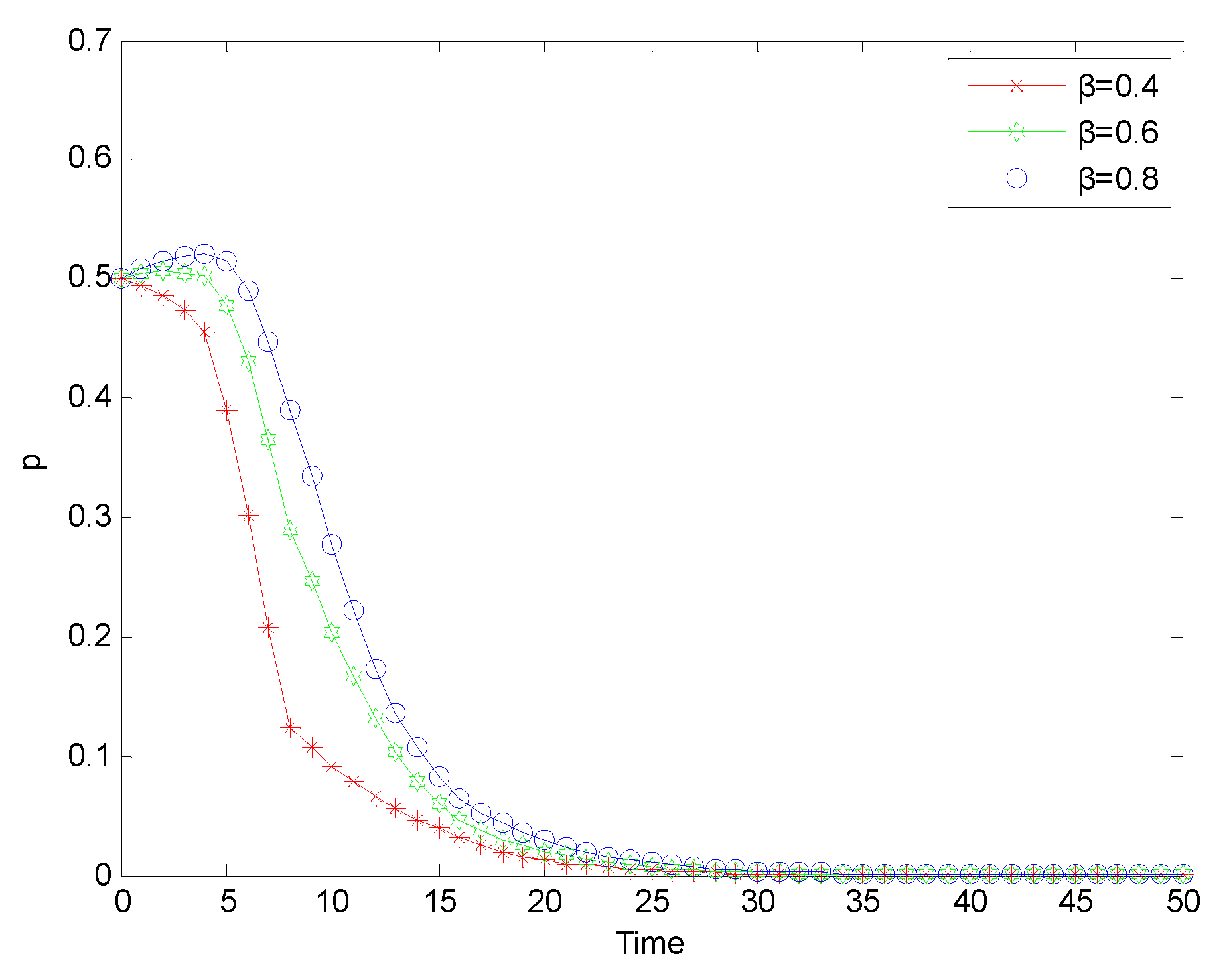
Figure 10.
Evolution process of safety investment strategy adopted by chemical enterprises under ‘normal regulation’ mode.
Figure 10.
Evolution process of safety investment strategy adopted by chemical enterprises under ‘normal regulation’ mode.
Figure 11.
Evolution process of strict supervision strategy adopted by government regulatory authorities under ‘special rectification’ mode.
Figure 11.
Evolution process of strict supervision strategy adopted by government regulatory authorities under ‘special rectification’ mode.
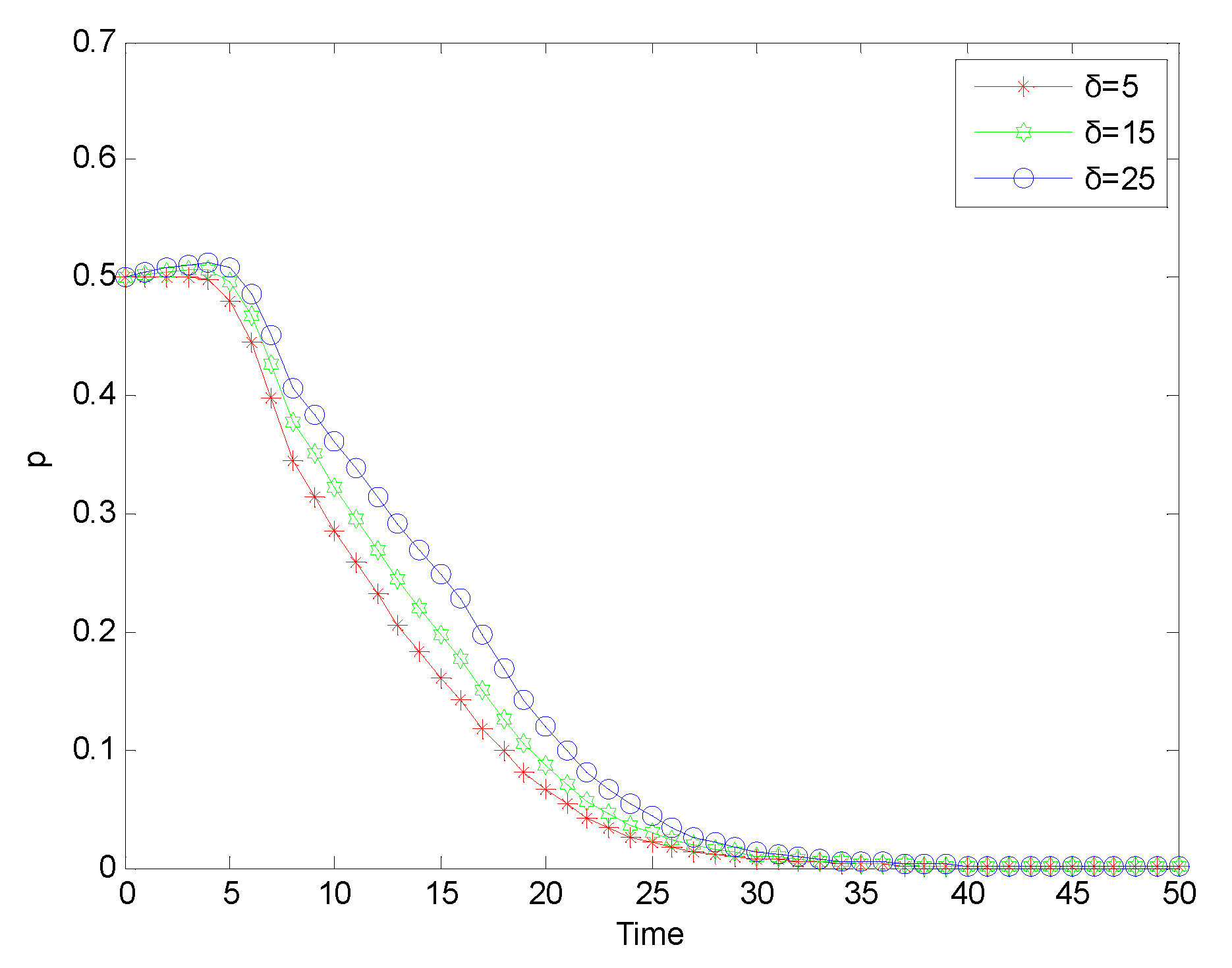
Figure 12.
Evolution process of strict supervision strategy adopted by government regulatory authorities under ‘normal regulation’ mode.
Figure 12.
Evolution process of strict supervision strategy adopted by government regulatory authorities under ‘normal regulation’ mode.
Table 1.
Game income matrix between government regulatory authorities and chemical enterprises.
Table 1.
Game income matrix between government regulatory authorities and chemical enterprises.
| |
|
Government Supervision Department |
Strict Supervision
|
Loose Supervision
|
| Chemical Enterprise |
Safety Investment
|
|
|
Safety Non-investment
|
|
|
Table 2.
‘Special rectification’ mode game return matrix.
Table 2.
‘Special rectification’ mode game return matrix.
| |
|
Government Supervision Department |
Strict Supervision
|
Loose Supervision
|
| Chemical Enterprise |
Safety Investment
|
|
|
Safety Non-investment
|
|
|
Table 3.
System (I) equilibrium point and local stability analysis.
Table 3.
System (I) equilibrium point and local stability analysis.
|
|
|
result |
| (0, 0) |
+ |
|
ESS |
| (0, 1) |
+ |
|
ESS |
| (1, 0) |
+ |
|
ESS |
| (1, 1) |
+ |
|
saddle point |
|
not the equilibrium point |
Table 4.
Game return matrix under ‘normal regulation’ mode.
Table 4.
Game return matrix under ‘normal regulation’ mode.
| |
|
Government Supervision Department |
Strict Supervision
|
Loose Supervision
|
| Chemical Enterprise |
Safety Investment
|
|
|
Safety Non-investment
|
|
|
Table 5.
System (II) equilibrium point and local stability analysis.
Table 5.
System (II) equilibrium point and local stability analysis.
|
|
|
result |
| (0, 0) |
+ |
|
ESS |
| (0, 1) |
+ |
|
ESS |
| (1, 0) |
+ |
|
ESS |
| (1, 1) |
+ |
|
saddle point |
|
not the equilibrium point |