Prerpints.org logo
Preprint
Article

Exploring the Performance Boundaries of a Reconfigurable Multi-Mission Military UAV through Multidisciplinary Analysis

Altmetrics

Downloads

182

Views

77

Comments

0

A peer-reviewed article of this preprint also exists.

  ‡ These authors contributed equally to this work.

This version is not peer-reviewed

Submitted:

18 May 2023

Posted:

22 May 2023

You are already at the latest version

Alerts
Abstract
The performance of a small reconfigurable unmanned aerial vehicle (UAV) is evaluated, 1 combining a multidisciplinary approach in computational analysis of additive manufactured struc- 2 tures, fluid dynamics, and experiments. Reconfigurable UAVs promise cost savings and efficiency 3 without sacrificing performance, while demonstrating versatility to fulfill different military mission 4 profiles. The use of computational fluid dynamics (CFD) in UAV design produces higher accuracy 5 aerodynamic data, which is particularly important for complex aircraft concepts such as blended 6 wing bodies. To address challenges relating to anisotropic materials, the Tsai-Wu failure criterion is 7 applied to structural analysis, using CFD solutions as load inputs. Aerodynamic performance results 8 show the low-speed variant attains an endurance of 1 hour, 48 minutes, whereas for its high-speed 9 counterpart, it is 29 minutes at 66.7% higher cruise speed. Each variant serves different aspects of 10 small UAS deployment in combat, with low-speed envisioned for close surveillance, and high-speed 11 for incursions. Experimental and simulation results suggest room for design iteration, in wing area 12 and geometry adjustments. Structural simulations demonstrated the need for airframe improvements 13 in the low-speed configuration. This paper highlights the potential of reconfigurable UAVs to disrupt 14 the industry, advocating for further research and design improvements.
Keywords: 
Subject: Engineering  -   Aerospace Engineering

1. Introduction

Reconfigurable unmanned aerial vehicles offer certain advantages over systems that are designed for a specific mission, wherein if these systems are operated for off-design conditions they are likely to experience reduced performance. Reconfigurable unmanned aerial systems present an alternative to off-the-shelf products and are designed for various mission profiles, providing cost savings up to 26% with virtually no sacrifice in performance due to the optimal use of common and unique airframe modules between variants [1,2]. This idea is the basis for the Switchblade UAV design, a concept envisioned in previous work [3,4].
At present, Unmanned Aerial Vehicles (UAVs) are primarily utilized in the military for ISTAR (Information, Surveillance, Target Acquisition, and Reconnaissance) operations. These missions typically involve the integration of numerous sensors, each serving unique functions, with the goal of forming a comprehensive picture of the battlefield that field commanders can utilize in real-time [5]. UAVs are invaluable in boosting the effectiveness of these operations, as they are versatile platforms capable of housing an array of advanced sensors. Consequently, UAVs have become the mainstay in such operations across all recent war scenarios, particularly those targeting guerilla groups or non-traditional armies. Recent simulation studies indicate that small UAS considerably enhance the probability of military personnel survival, and that using a hybrid strategy for planning UAV patrol 36 patterns might be successful, incorporating a blend of short and long-range patrols for 37 optimal effectiveness [6]. In a reconfigurability context, a single system can be devised for distinct missions at high performance. The Switchblade small UAS concept assumes a hybrid role in the form of two main aircraft variants for long endurance, slow flight, or long range, fast operation.
The application of additive manufacturing methods in the aircraft industry is widespread and offers many advantages in the production of parts, such as shortened production cycle times, reduction in costs, lighter component weights, and even the globalization of the aircraft industry [7]. Additionally, 3-D printing can be used for efficient production of wind tunnel models, a task that is usually time consuming and costly [8,9]. In this work, one of the goals is to take full advantage of additive manufacturing for prototyping and testing purposes. However, there are still challenges related to the use of this technology for aircraft structures, such as the low strength of Fused Deposition Modeling (FDM) materials, anisotropy, porosities, manufacturing process variability, and imperfections that can be critical to thin-walled features [10,11]. It is necessary to address these issues when designing aircraft structures for safe operation and full life cycles.
The outstanding development of Computational Fluid Dynamics (CFD) software and computational resources in the last couple of decades has benefited the aircraft industry, and by association, UAV designers. CFD methods are increasingly used in early stages of UAV design, with varying fidelity depending on the level of development [12,13]. Extensive analyses with RANS, URANS and DES simulations have been performed on an Unmanned Combat Aerial Vehicle (UCAV) [14], resulting in accurate prediction of vortical flow over a delta wing configuration. Determination of the dynamic stability characteristics of an aircraft - a task that is normally difficult to predict with numerical simulations and usually accomplished empirically or experimentally - was successfully done in [15], where CFD results had great correlation with flight test data. Dynamic stability derivatives for an airfoil were obtained in [16], also with good correlation of experimental data. Even the use of active and passive flow control methods applied to UAV performance enhancement has been studied in computational frameworks [17,18]. The use of higher fidelity CFD models and simulations for the Switchblade UAV is critical to obtain higher accuracy aerodynamic data, and evaluate the performance of both variants: Low-Speed, High-Endurance (LSHE) and High-Speed, Long-Range (HSLR). Moreover, in this study, CFD work serves to inform the structural analysis and wind tunnel experiments, by giving essential input to FEA studies and is a basis for comparison to experimental results.

1.1. Background

Previous design efforts have been made to develop a family of unmanned aerial vehicles that inherit a unique reconfigurability feature to allow multiple missions of different regimes using the same unmanned aerial system (UAS). This UAS is to be referred to as ‘Switchblade’ and offers a vehicle with a modular framework assuming one of four variants based on the mission requirements. The scope of the Switchblade project is to obtain a balance between flight performance and wide-mission adaptability, providing an economic advantage in that only a single UAS is needed by an operator. The conceptual design framework for Switchblade was previously conducted in [3]. Considering a variety of missions in commercial sectors in which UAVs are utilized, three different mission profiles were studied to examine the required flight performance, resulting in four distinguishable UAV variants. The Switchblade UAS consists of a blended wing body (BWB) acting as the common module among all UAV variants, connecting to wing modules. Tailless aircraft have many advantages over traditional aircraft such as; lower weight and drag, smaller cross sections, and higher aerodynamic efficiency [19]. Figure 1 shows the Switchblade family concept. The ‘parent’ UAV variant is the High-Speed Long-Range (HSLR) variant which is prioritized in the design process due to its higher cruise speed and thus propulsion demand. The Low-Speed High-Endurance (LSHE) variant is the ‘child’ variant, where its propulsion demand is automatically satisfied. Both variants can be enabled for vertical takeoff and landing (VTOL) by exchanging its vertical stabilizer with two removable fins that contain electric motor propulsion units.

1.2. Research Objectives

The overarching goal of this work is to push the boundaries of reconfigurable design with consideration to the aerodynamics and structural integrity of two UAV variants designed with functional 3-D printed materials and with significantly different cruise speed. Both the HSLR and LSHE variants utilize the same BWB, and the notion of reaching a reconfigurable design ‘boundary’ is defined in this study as when one of the two variants begins to perform considerably sub-optimal in simulated flight. This notion is discussed throughout the computational and experimental results. The performance criteria considered are: (i) the aerodynamic efficiency, (ii) structural minimum factor of safety (FoS) and deformation.
The first objective is to carry out a refined CFD analysis of the UAV variants, giving continuity to the work performed during the conceptual design phase in [3]. This is accomplished by more detailed geometries, larger fluid domains and finer meshes. The second objective is to identify maximum stress locations and magnitudes through FEA. Considering that the Switchblade prototypes are manufactured by advanced 3-D printing processes almost in their entirety, it is crucial to acknowledge that manufacturing imperfections or defects may occur, and that high stresses are identified and mitigated. However, the use of newly introduced commercial materials, such as carbon fiber-reinforced nylon, may present a challenge to aircraft prototyping because UAV structures can be very thin at certain locations, and therefore particularly susceptible to manufacturing imperfections that reduce the strength and/or stiffness [11].
Finally, the third objective is to test the Switchblade prototypes in a wind tunnel. In this investigation, the main experimental results sought are aerodynamic coefficients at static angles of attack. Secondary aims are to assess control surface and propulsion performance. A modular half-body model is used to test the LSHE and HSLR wing designs. One particular challenge is the complex geometry of the wings, where each configuration contains three different airfoils throughout the wing. Also, most of the empirical formulations for aerodynamic parameters are developed for large scale aircraft, and the lower Reynolds number of UAVs in the laminar and transitional flow regime may cause the empirical and computational results to be less accurate than expected, making wind tunnel testing even more important.

2. Materials and Methods

2.1. Computational Fluid Dynamics Studies

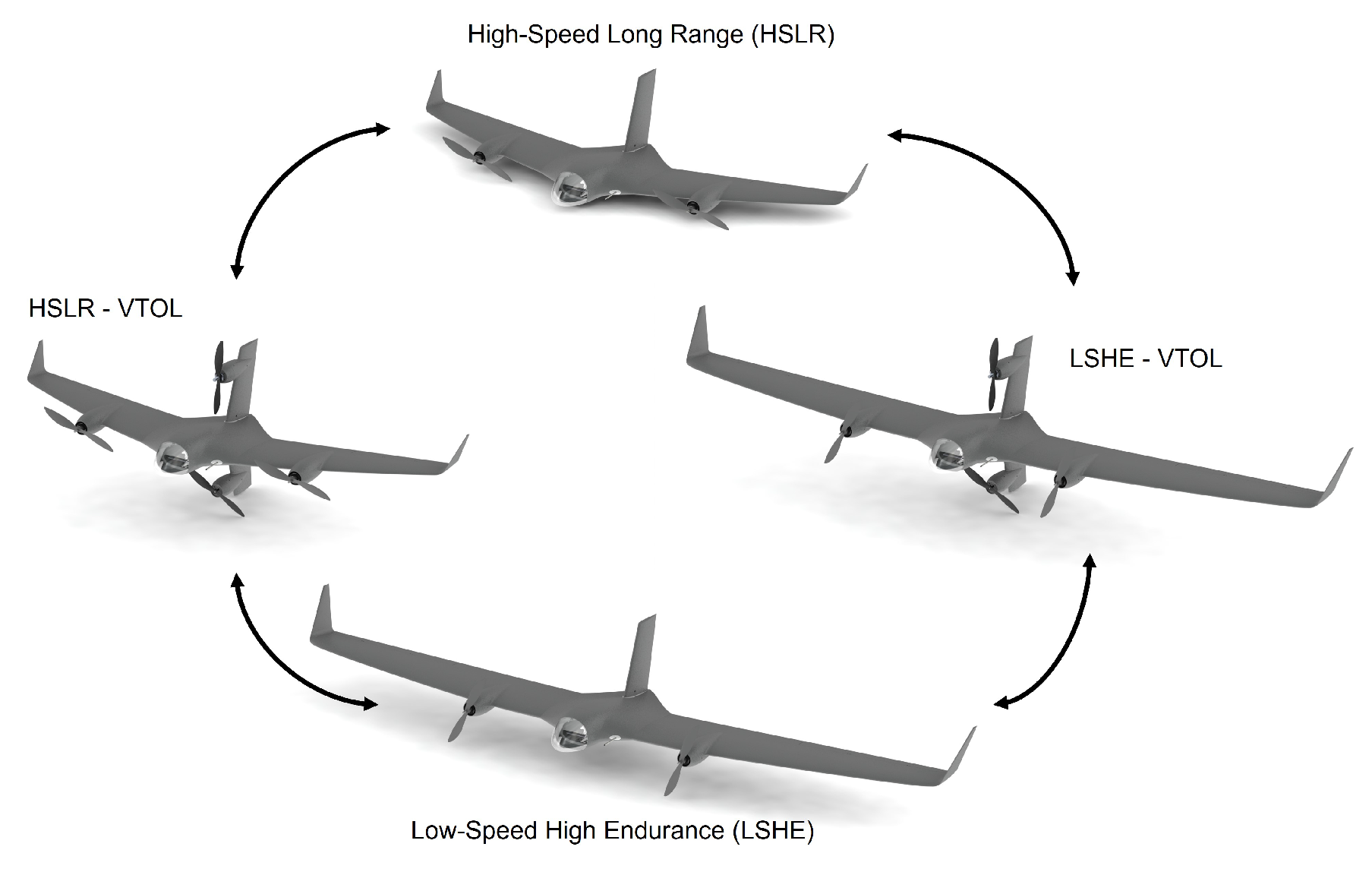
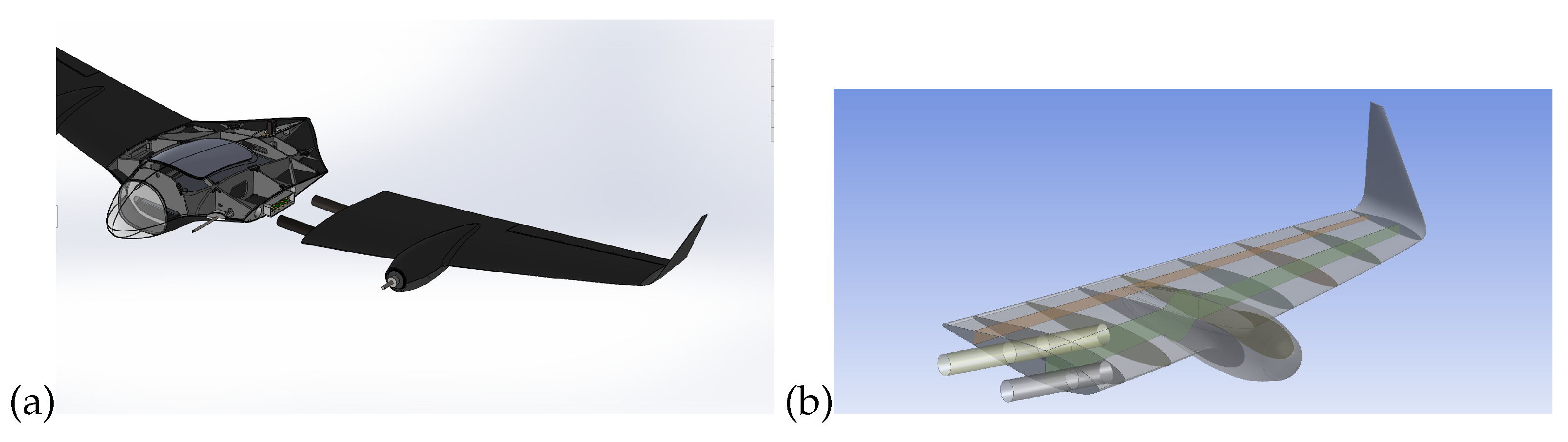
2.1.1. CFD Geometries

The wing geometries used for the CFD studies were based on two main variants: low-speed, high-endurance (LSHE) and high-speed, long-range (HSLR), according to the multi-mission ideas explored in the conceptual design phase (Fig. 1). Although Switchblade can be enabled for vertical take-off and landing (VTOL), this analysis focuses on the standard forward flight configurations. Within these two variants, different CAD versions were created to analyze the effect of geometry complexity on aerodynamic results. The “clean wing” versions consist of the center blended wing body (BWB) geometry connected to its respective wing panels depending on mission type — LSHE or HSLR. The “actual wing” versions consists of the same center body geometry, but connected to wing panels that contain motor nacelles and winglets, more closely resembling the aircraft in its final configuration. For nomenclature reasons, the “clean wing" models and associated geometries are named LSHE and HSLR while the “actual wing” versions are named LSHEWN and HSLRWN. The “W” and “N” refers to “winglet" and “nacelle”, respectively. Figure 2 shows the geometries used for the CFD simulations.
The reconfigurability of Switchblade signifies that some airfoils are shared between 140 different variants. The center body is designed from an MH 81 reflex airfoil, modified to attain a maximum thickness ratio of 20% for increased internal volume required for electronics. The interface between the center body and the wing panel - the wing root - was designed with a symmetric airfoil, and each wing panel has a different wing tip 1airfoil. Both variants have reflex airfoils at the wing tip, with LSHE having more significant reflex to compensate for its lower wing sweep. The airfoils used in each variant and wing characteristics are shown in Table 1 and Table 2, respectively.
In preparing the wing geometries for meshing, some practices were followed to ensure that mesh generation would run smoothly, therefore facilitating convergence and good results. Rounding the wing trailing edges into fillets revealed to be critical in improving mesh quality, and a radius value between 0.2% and 0.4% of the local wing chord was used, depending on the geometry. Sectioning surfaces into areas separated by leading and trailing edges, and chord regions improved meshing by providing the software with edges to seed element nodes.
In each case, half of the aircraft wing-body was analyzed, taking advantage of the symmetric flow field to reduce the time to achieve a converged solution. The size of the fluid domain needs to be sufficiently large so that the far field of the fluid surrounding the wing does not interfere with the physical flow phenomena close to the wing. To achieve this, the fluid domain dimensions were defined using the recommendations from [20] to have at least 25 body lengths around a three-dimensional aircraft. The fluid domain consisted of a half elliptical volume with a semi-major axis of 26 m and minor axis of 13 m. These dimensions have increased dramatically since early CFD simulations were conducted. The nose of the airplane is located at the center of the semi-major axis and faces the upstream direction, towards the elliptical surface.

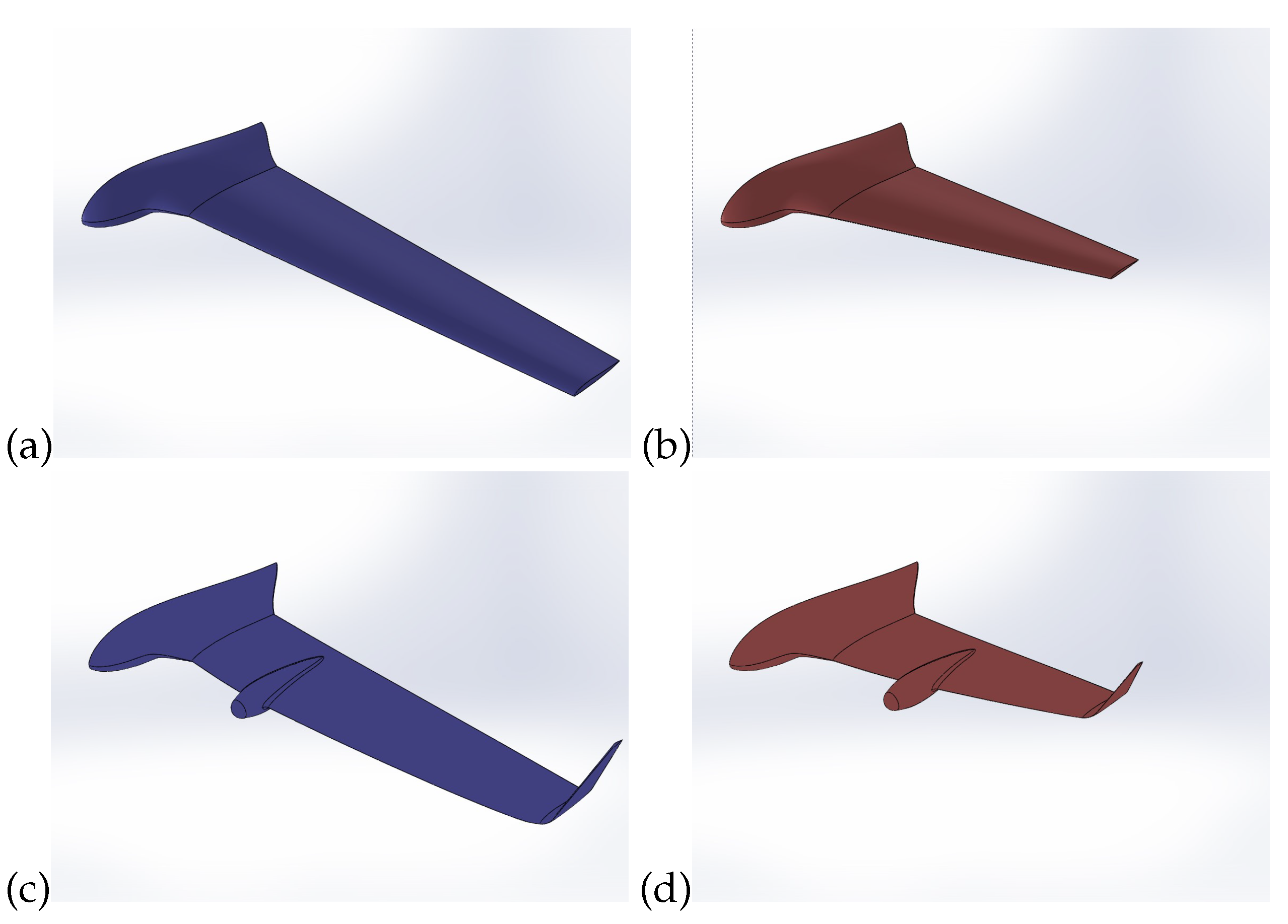
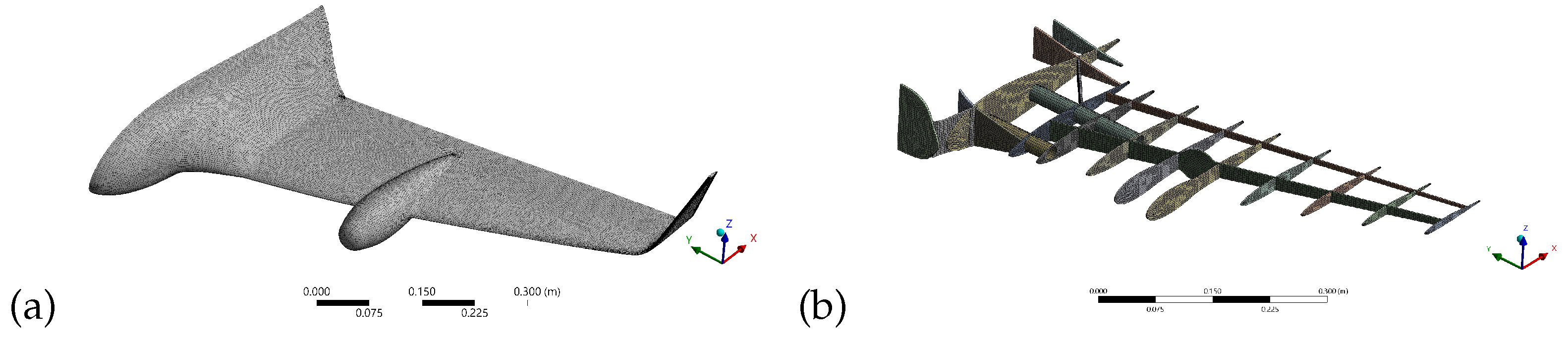
2.1.2. CFD Meshes

The CFD studies performed after the conceptual and preliminary analyses in [3] were characterized by finer meshes with a drastic increase in the number of cells in the fluid domain. This was done primarily to generate a better discretization of the regions close to the wall boundaries. Whereas in the conceptual study the mesh size was below 3.4 million cells, in this study some meshes surpassed the 15 million cell mark. This was accomplished, in part, by utilizing mosaic-meshing in ANSYS Fluent Meshing. This meshing method incorporates poly-hexcore cells and is characterized by filling the bulk volume geometry with hexahedral elements while filling areas with more complex geometries, especially near the wing surface, with polyhedral elements. Mosaic mesh is able to connect the hexahedral and polyhedral elements to one another, thereby incorporating the best parts of each element into every section of the geometry [21]. The result is a more efficient mesh that carefully resolves the boundary layers, capturing flow variables more accurately. Emphasis was given to first-cell height at the wall boundaries, with the goal of obtaining y+ values in the order of one to accurately resolve the viscous sub-layer, a practice well discussed by [20], and [22]. To estimate the first cell height, equations 2.1.2 were used:
Preprints 74084 i006
where Rex is the Reynolds number, ρ is the air density, V∞ is the free-stream velocity, L is the reference length (the mean aerodynamic chord), µ is the air dynamic viscosity; Cf is the skin friction coefficient, τw is the wall shear stress and ∆S is the first cell height, to be determined. From these calculations, the estimate of first cell height was approximately 0.01mm. To reduce the mesh cell count, a value of 0.05mm was implemented. From the first cell at the wall, 25 to 30 inflation layers were created, depending on the final number of cells in the model.
To the extent possible, meshes were generated with at least a hundred cells across the minimum chord length (excluding the winglet), a guideline based on common CFD practices. This meant computing the average face size for the wall boundaries from the mean aerodynamic chord of both variants, and making adaptations to reduce the computational cost of calculations. Details about the meshes used in the CFD work are presented in Table 3. Wall faces refer to the number or polygonal faces generated on the aircraft surface. The mesh quality measure used was orthogonal quality. Figure 3 shows a 195 mesh example for the HSLRWN geometry.

2.1.3. CFD Turbulence Method and Flow Conditions

The turbulence model used for the simulations was the k-ω shear stress transport (SST) model. It was chosen for its capability to accurately model boundary layer flow and non-sensitivity to free stream conditions [23]. The k-ω SST model provides a hybrid, robust approach to turbulence formulation as it uses the k-ω model in the near-wall region and incorporates the k-ϵ model in the free-stream far field. However, the k-ω model can be sensitive to inlet velocity boundary conditions leading to inaccurate turbulence formulation [24]. To avoid this issue, the k-ω SST model switches to the k-ϵ model in the far-field regions of the fluid domain. This model solves two transport equations that are dependent on the turbulent kinetic energy, k, and the specific turbulence dissipation rate, ω, shown in equations 1 and 2, respectively [25].
Preprints 74084 i007
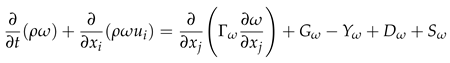
Preprints 74084 i008
Here, Γk is the effective diffusivity of k, G˜k is a generation term for turbulence kinetic energy due to mean velocity gradients, Yk is the dissipation of k, and Sk is a source term. Γωis the effective diffusivity of ω, Yω is the dissipation of ω, and Dω is a cross-diffusion term.
For the steady state, the inlet conditions were adjusted with flow velocity set at 33.62 m/s for the high-speed design cruise speed and 20.16 m/s for the low-speed model. The inlet turbulence intensity was set at 1%, a reasonable amount for undisturbed atmospheric conditions. The outlet condition is set at a gauge pressure of zero. Convergence criteria were applied to the residuals to improve simulation time and results. The convergence requirement for the velocity components, k, and omega residuals was set to 10−5 and the continuity residual to 10−3. For the monitored quantities — lift, drag and pitching moment — the convergence criterion was set to 10−3.

2.2. Finite Element Analysis Studies

The challenges with 3-D printed materials arise from the lack of consistency. 3-D printed materials can differ from model to model due to variables such as printing direction and fill density. For instance in Gu et al’s publication on composite structures, there is an increased risk due to complexity from high anisotropy and a variety of failure modes [26]. For simplicity, Von Mises failure criterion is commonly used on 3-D printed materials, however, it assumes the material to be isotropic [26]. In this study, the Tsai-Wu failure criterion was more suitable since 3-D printed and composite materials are inherently anisotropic and Tsai-Wu is a generally acceptable failure criteria for anisotropic materials. FEA analysis was performed using ANSYS to identify stresses and locations where the wing is more likely to fail.

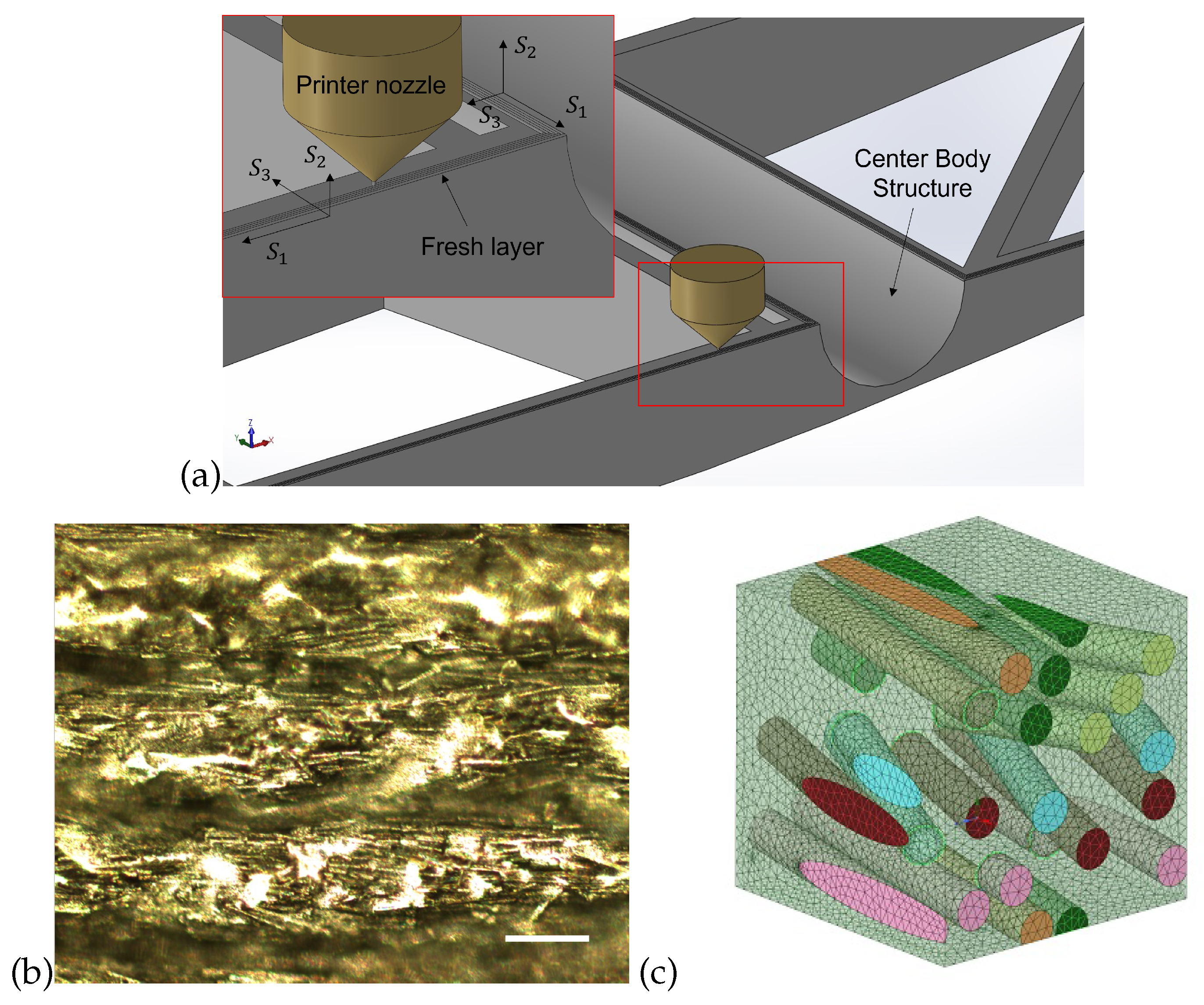
2.2.1. FEA Geometry

In the FEA investigation on the reconfigurable UAV design, it is important to highlight the key techniques used in modeling the geometry for the static structural analysis in ANSYS workbench. The solid model of each variant (LSHE and HSLR) was provided by Stratasys and from these models, the internal structure, wing skin, and winglets could be modeled for the static structural simulation. The models were shelled out and an internal structure was designed, with ribs and shear webs. The CAD drawing of the prototype manufactured is shown in Figure 4 (a). The wing module connects to the center body via two tubular carbon fiber spars and is locked in place with a spring mechanism (not shown). The wing structure analyzed is shown in Figure 4 (b).

2.2.2. Material Properties

Nylon 12 CF was used for 3D printing and testing of the Switchblade aircraft. This material consists of a polymer matrix (nylon) containing short carbon fibers predominantly oriented in the print bead direction. For the finite element analysis of the aircraft, the material was modeled as a representative volume element (RVE) in ANSYS with Material Designer, which calculated the elastic constants necessary for the orthotropic material. Figure 5 (a) shows the macrostructure of the printed material surface, which was used as a basis for modeling the RVE shown in Figure 5 (b).
The material strength limits were obtained from Stratasys [27]. Nylon 12 CF properties differ depending on its printing direction, therefore when modeling the material in ANSYS, its property directions were defined similarly to composite laminates, where 1 is the fiber direction (or the print bead direction), 2 is across fibers (same as the print layering direction) and 3 is the out of plane direction (or across the beads). This was done to allow orienting the material according to the way it is printed throughout the structure components.
Considering the orthotropic properties of the nylon 12 CF material, it was critical that a failure criterion better suited to this material was used in the setup model in ANSYS. The chosen failure criterion was the Tsai-Wu criterion of composite materials. Chen et al. [28] have used the Tsai-Wu failure criterion in their analysis of a 3-D printed bracket made of polylactic acid. The Tsai-Wu failure criterion is introduced below,
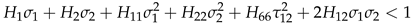
Preprints 74084 i009
Where the components H1, H11, H2, H22, H66 and H12 are dependent on the strength terms of the material in many directions:
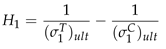
Preprints 74084 i010
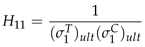
Preprints 74084 i011
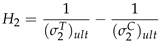
Preprints 74084 i012
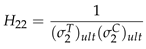
Preprints 74084 i013
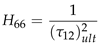
Preprints 74084 i014
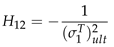
Preprints 74084 i015

2.2.3. FEA Meshes

A quadrilateral-dominant mesh was used to discretize the wing geometry, with a target mesh size of 3 mm in the wing surface. This size was particularly chosen to bring the FEA mesh close to the CFD surface grid on the wing, facilitating the interpolation of the pressure data into the FEA model. The mesh for the high-speed, long-range aircraft is shown in Figure 6. Mesh information for both variants is summarized on Table 4.

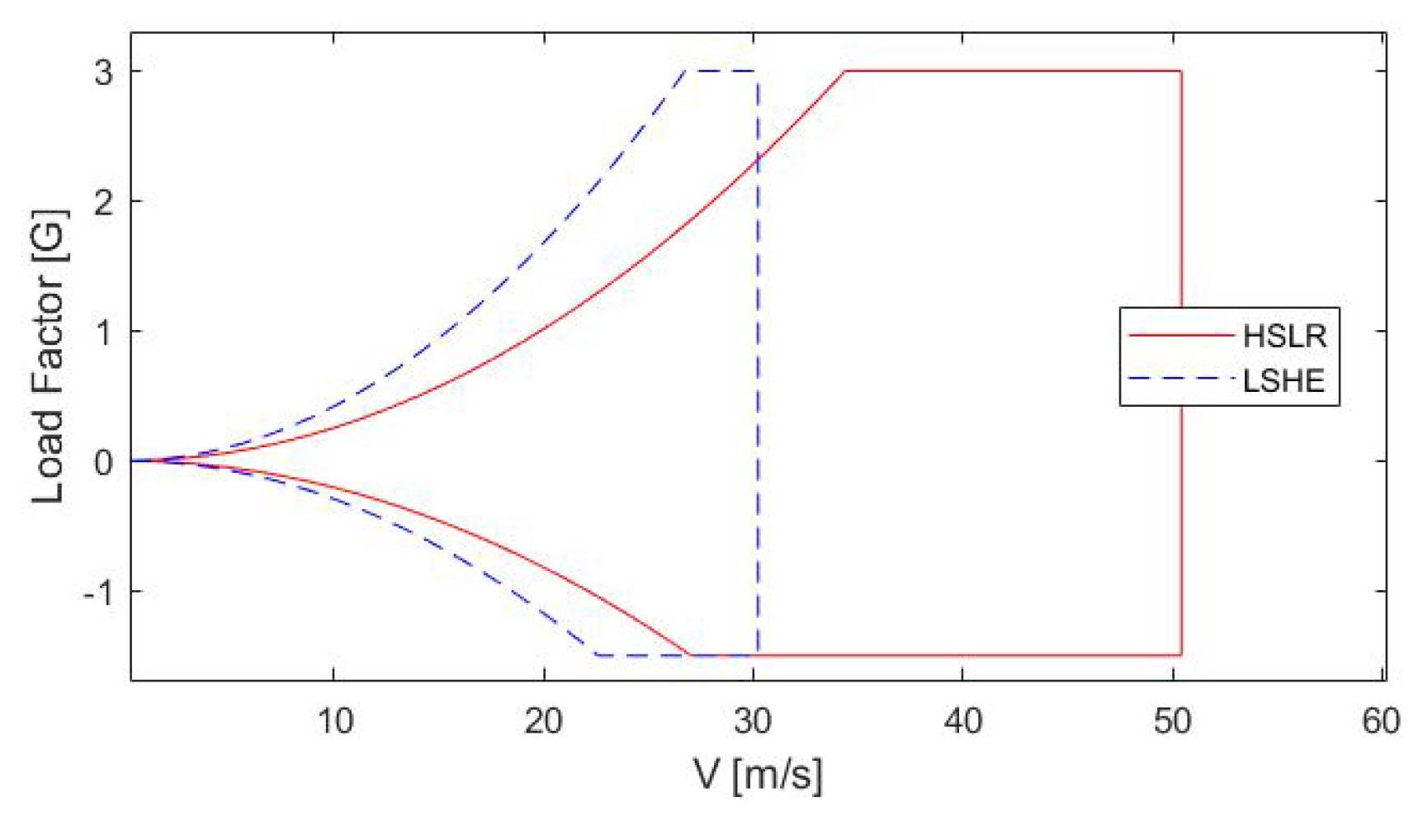
2.2.4. Load and Boundary Conditions

To determine loading in the FEA simulation, V-n diagrams of the HSLR and LSHE models were constructed. The geometry of the aircraft and design performance parameters were used to calculate graphs from which points of interest for the analysis were taken. The V-n diagrams for each variant are shown in Figure 7. From V-n diagram data, speed and angle of attack at each flight condition can be calculated. Results are elaborated in Table 5.
These parameters are then used as inputs in a dedicated CFD simulation to generate the pressure field over the wing surface. The resulting pressure data is directly imported to the FEA simulation with interpolation to be used as a pressure load over the wing surface.

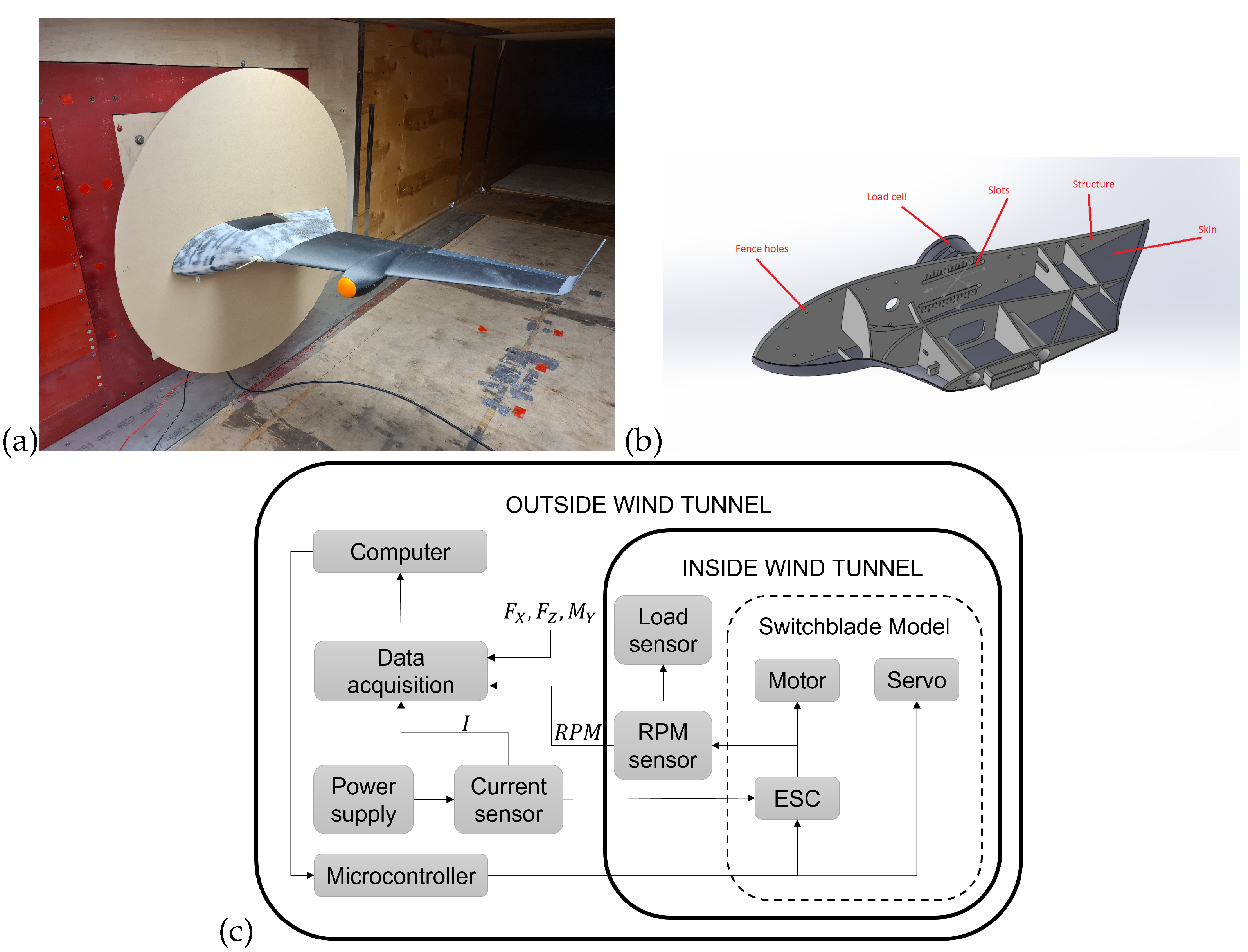
2.3. Wind Tunnel Experiments

The CFD analysis allows for a good prediction of aerodynamic coefficients, but demands confirmation; this is accomplished through wind tunnel testing. The flying wing concept adopted may also pose a challenge from a stability viewpoint, and control surface tests can show whether each variant is stable. Additionally, in the Switchblade project, where advanced prototyping techniques are widely used, it is invaluable to test the airframe strength and stiffness, observing how it reacts to consistent forces provided in wind tunnel setting.
The experiments were conducted in the National Wind Institute (NWI) closed-loop, subsonic wind tunnel at the Reese Technology Center. The test section is 1.2m tall and 1.8m wide, large enough to accommodate the aircraft half-model in its true scale, as shown in Figure 8 (a). The half-model is attached to a circular splitter plate and connected to an ATI 9150 Net Gamma 6-DoF load sensor with a resolution of 0.025 N for the lift and drag forces and 0.00125 N-m for the pitching moment. Figure 8 (b) shows the center body, attached to the load cell through slotted holes, which allows the UAV model to be installed in different longitudinal positions so the aerodynamic center can be identified. Figure 8 (c) shows a schematic of the components in the system. The setup is also equipped with an Arduino microcontroller and servo for setting the elevon at different deflection angles.

2.3.1. Aerodynamic Center Finding Procedure.

The aerodynamic center position was estimated analytically prior to wind tunnel testing, however, as seen in Figure 9, there is great variation of the moment about that position with angle of attack. Illustrated in Figure 8 (b) are the slots used to move the model forward and back to determine the location of the aerodynamic center. By finding the point where the pitching moment remains constant as the angle of attack changes, the center is known. Although this was possible with the HSLR variant model, the limitations on the center body slots did not allow exact placement of the aerodynamic center in the LSHE variant. In that case, the most forward position was used for all force and moment measurements.

2.3.2. Lift, Drag, and Moment Measurements

The objective for this experiment was to gather data on the lift and drag forces, as well as the pitching moment, which ideally should remain constant for the linear regime. The airspeed was set to each variant’s cruise condition, with load cell data acquired using a National Instruments DAQ model 6353 with a sampling rate of 1,000 Hz for a 30 second sample. The static angles of attack were set manually using a pitch link and a digital protractor with an error of ±0.1°. The ranges of angle of attack were -2° to 17° for HSLR and -2° to 14° for LSHE, with increments of 1°.

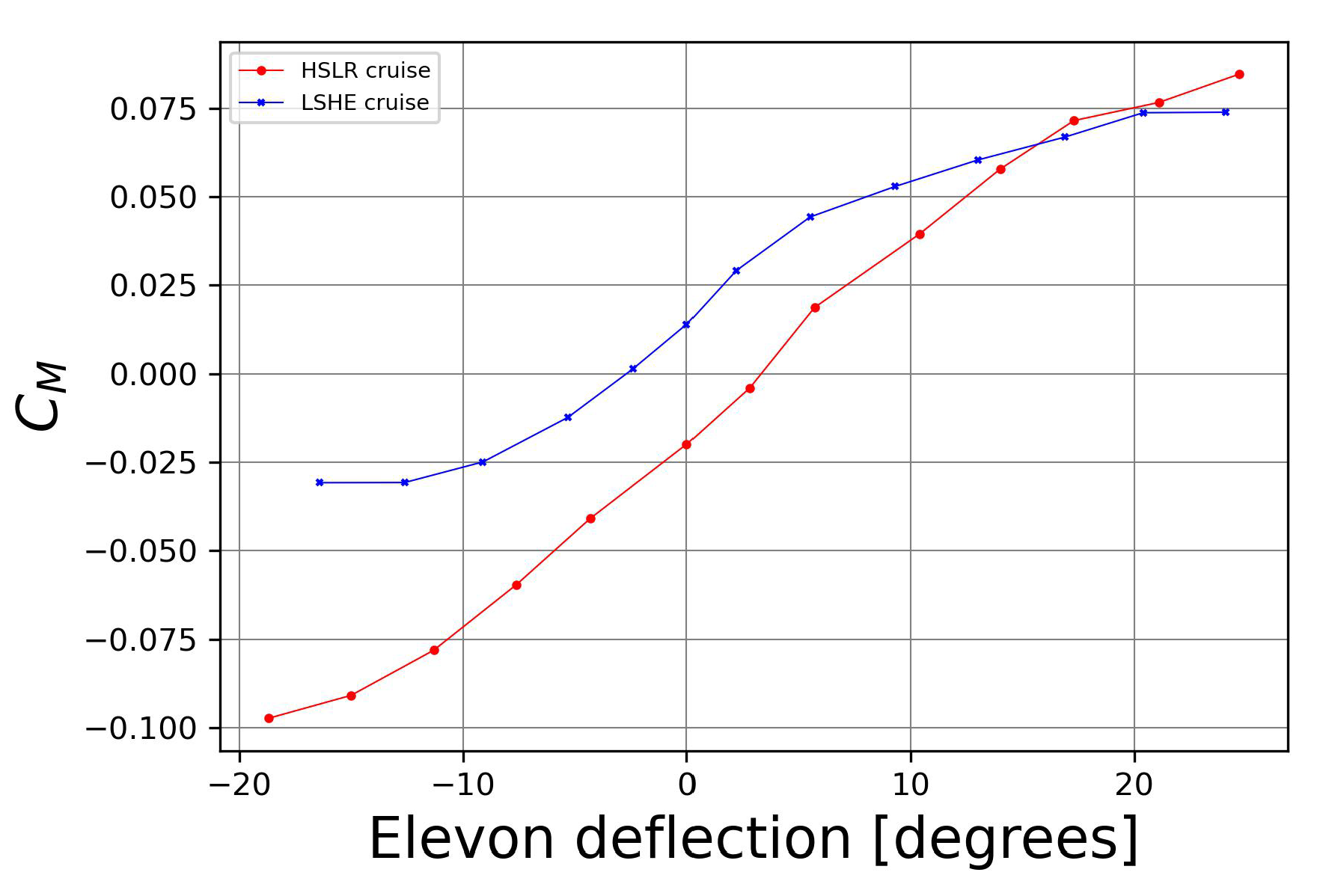
2.3.3. Elevon effectiveness and Trimming Procedure

Since Switchblade is a tailless aircraft, its neutral point location is the same as the aerodynamic center. This may have implications to stability and control better understood when running trimming experiments around the cruise condition for each variant. Ideally, there must not be a need for great control surface deflection to trim the tailless aircraft due to the reflex airfoils used. The experiments to find the cruise trim condition and necessary deflections on the wing control surface were required to evaluate its effectiveness. For these, the aircraft was fixed to the load cell at the longitudinal position that best approximated its aerodynamic center (hence, its neutral point) and commands were given to the wingmounted servo to deflect the elevon at various angles to record the pitching moment coefficient.

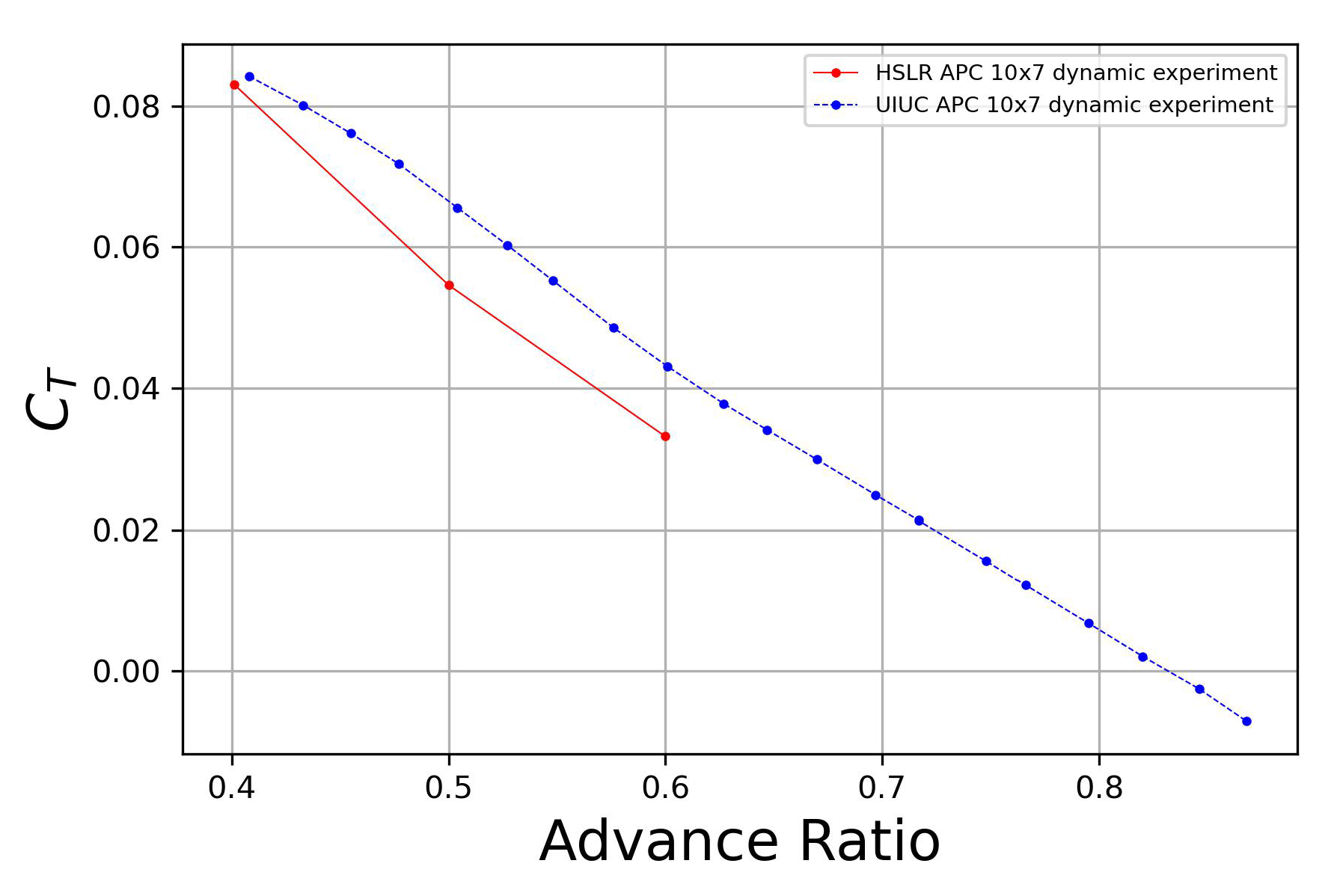
2.3.4. Thrust Experiment

A thrust experiment was performed to compare the installed thrust with the available propeller performance data and to estimate endurance and range for each variant. The propeller used was the APC 10x7 electric. For this experiment, measurements of the generated thrust, motor rotational speed, and free stream velocity were recorded. As shown in Figure 8, the power supply is connected in series with a current sensor, which is then connected to the electronic speed controller (ESC) housed in the motor nacelle. The ESC receives signal input from an Arduino micro-controller outside the wind tunnel. The RPM sensor, connected to two phases of the motor, provides instant measurement of rotational speed, an important parameter for establishing the advance ratio J = V ∞ n ϕ , where V∞ is the free stream velocity, n is rotational speed and ϕ, the propeller diameter.

3. Results and Discussion

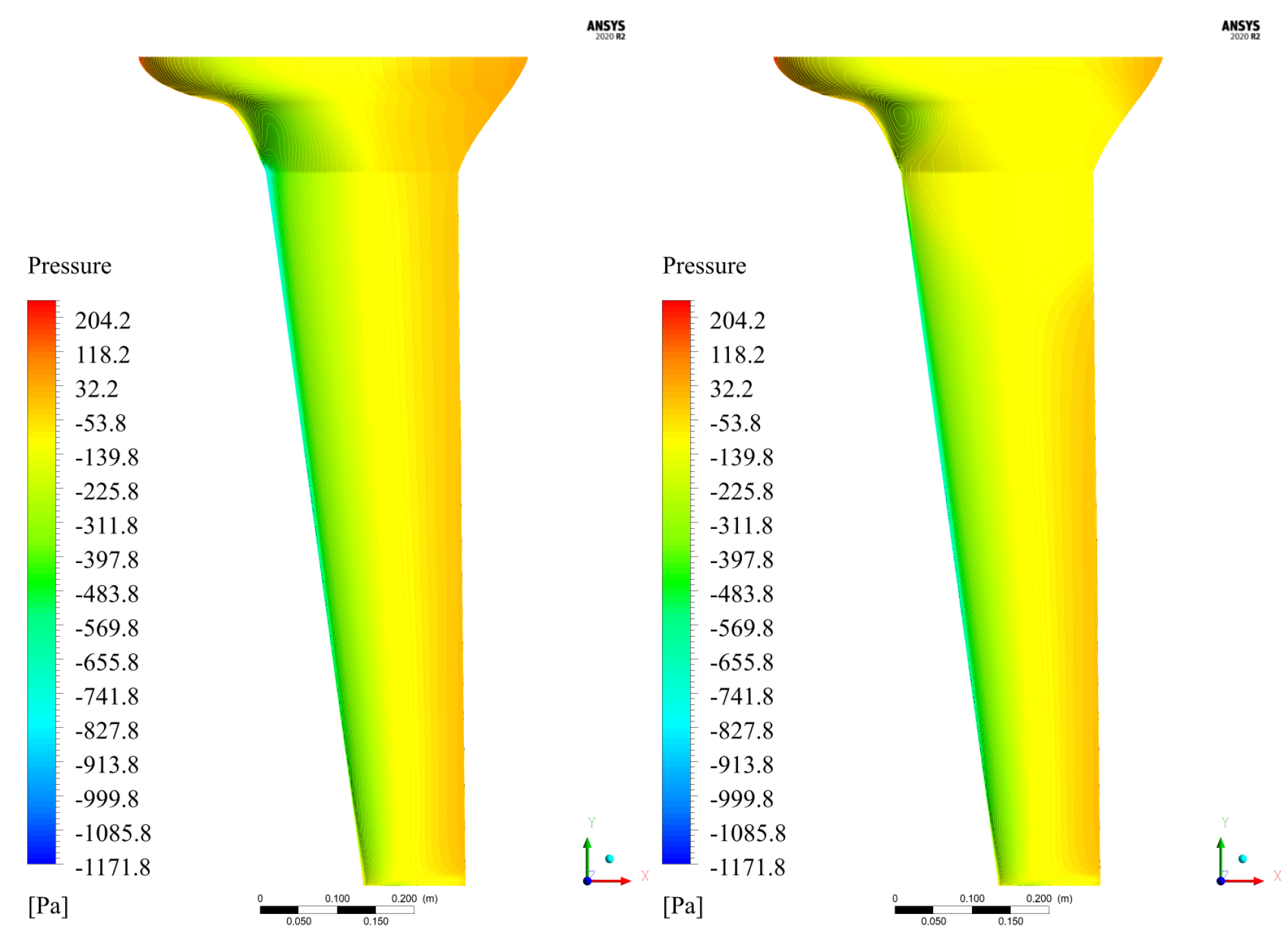
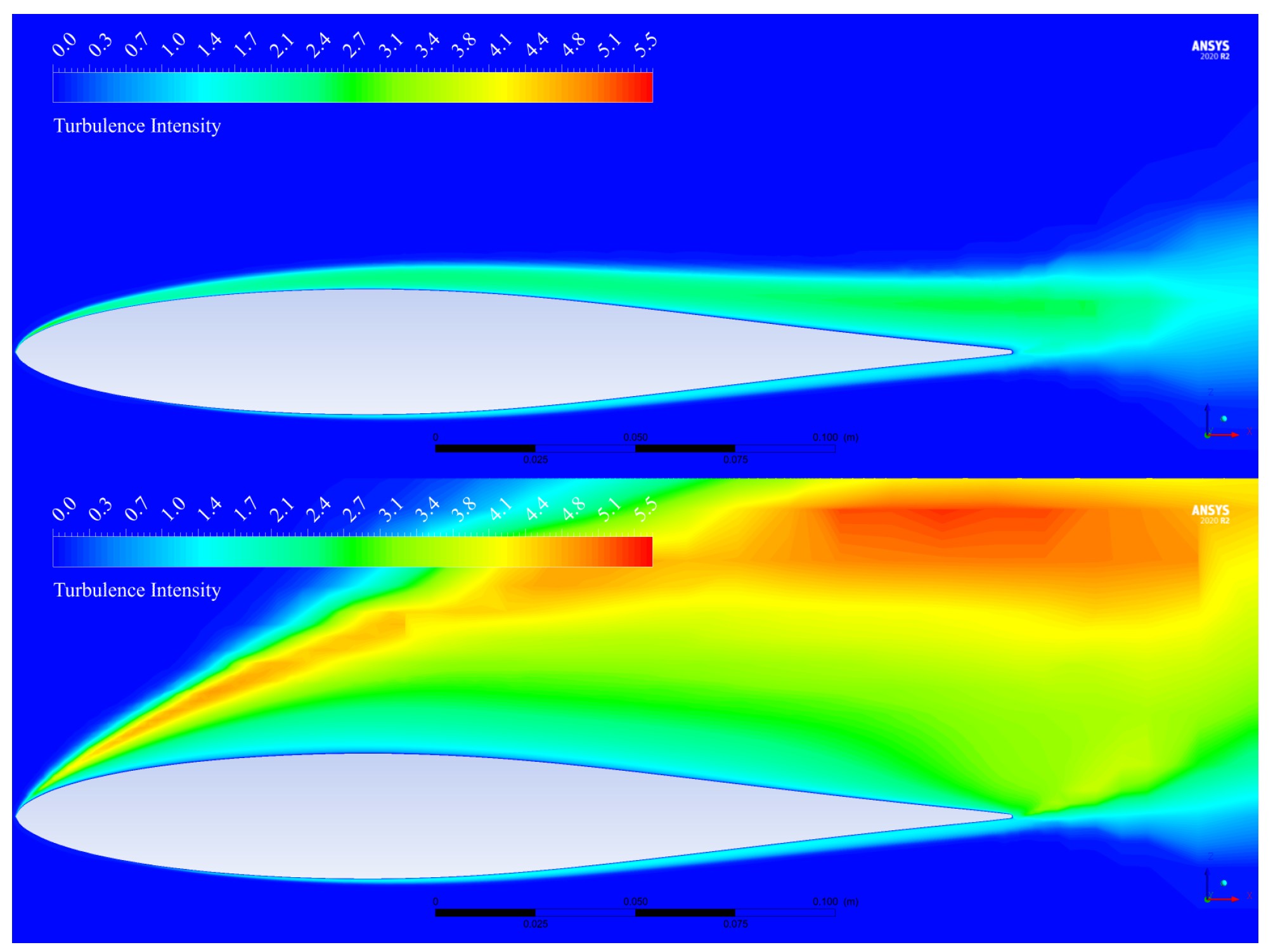
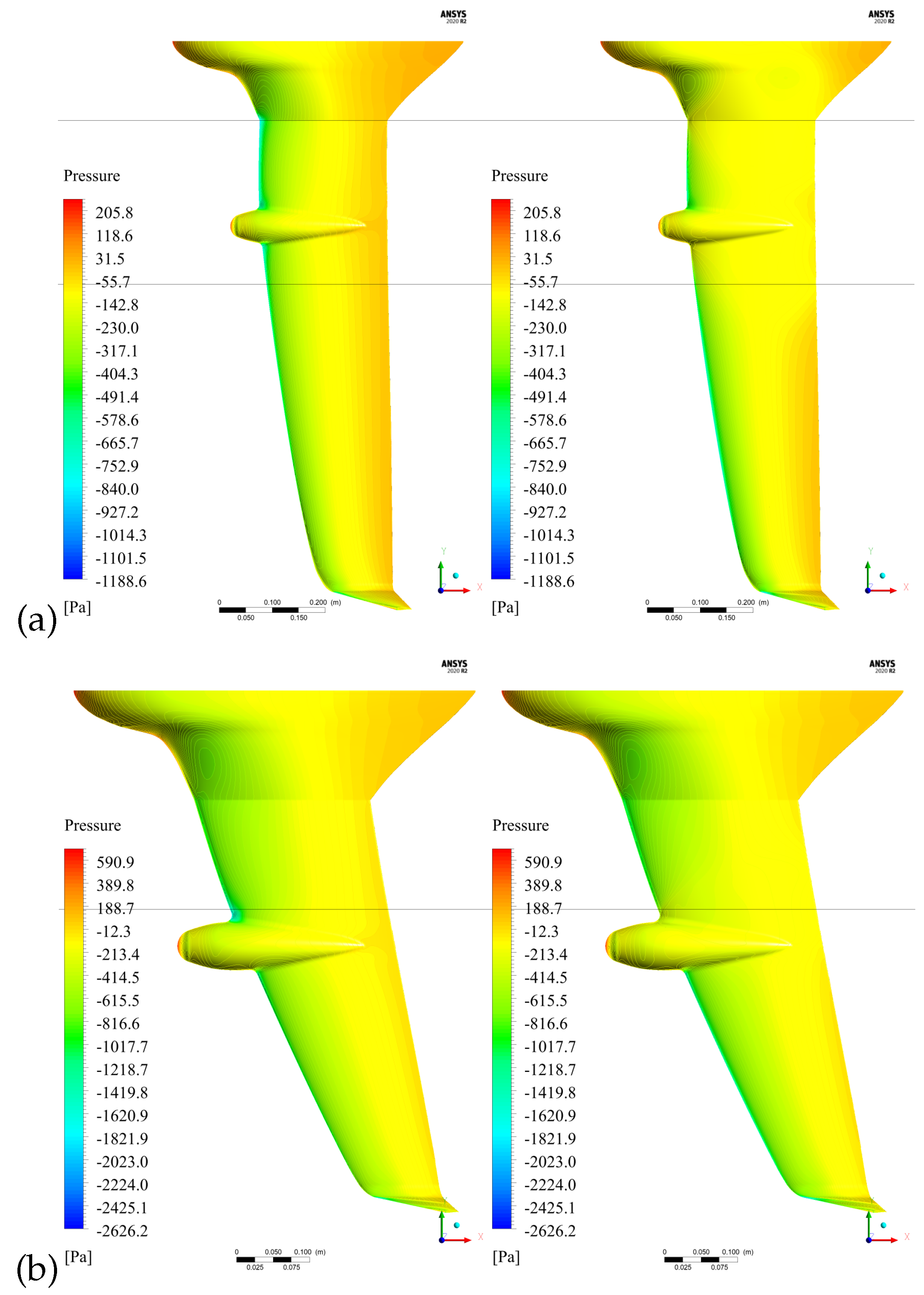
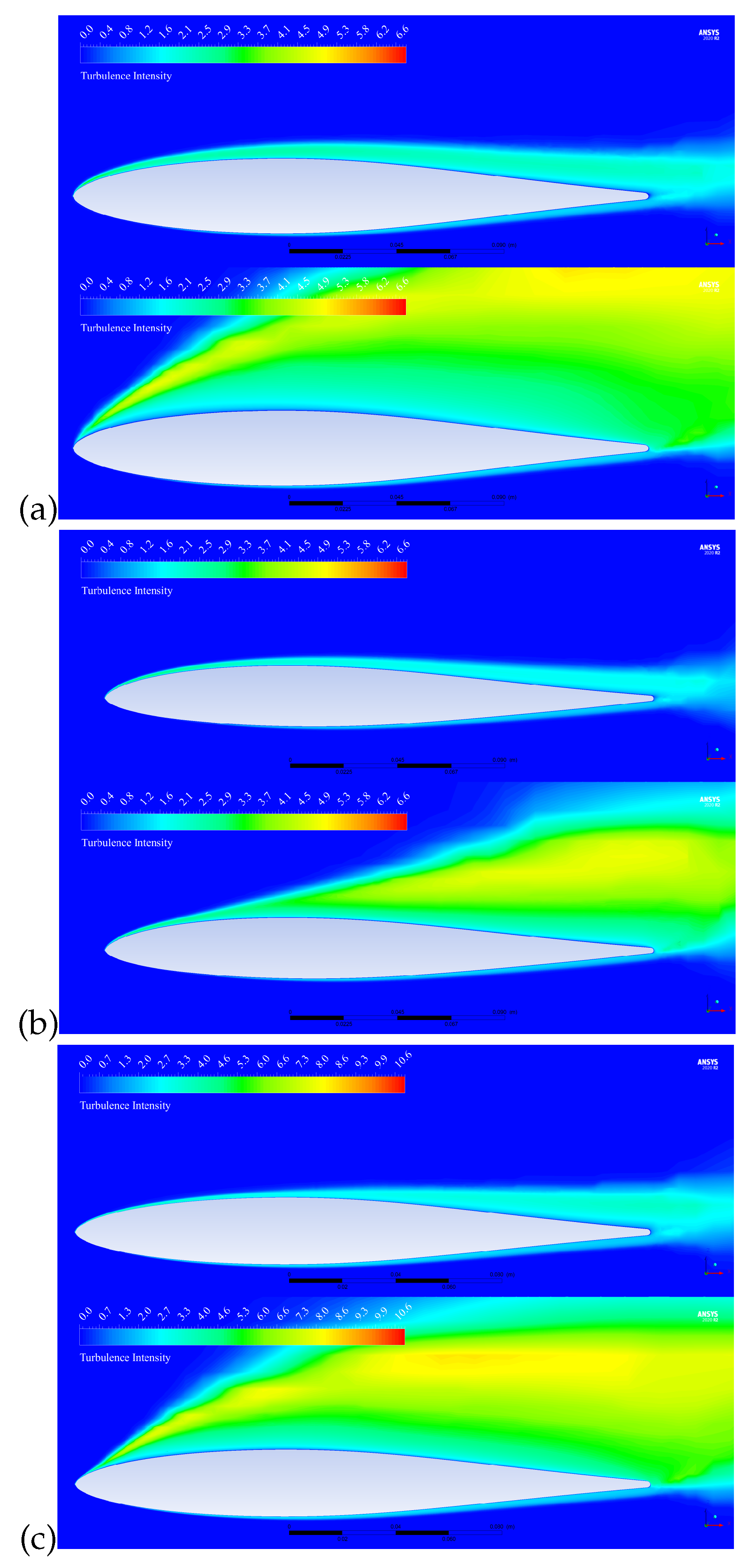
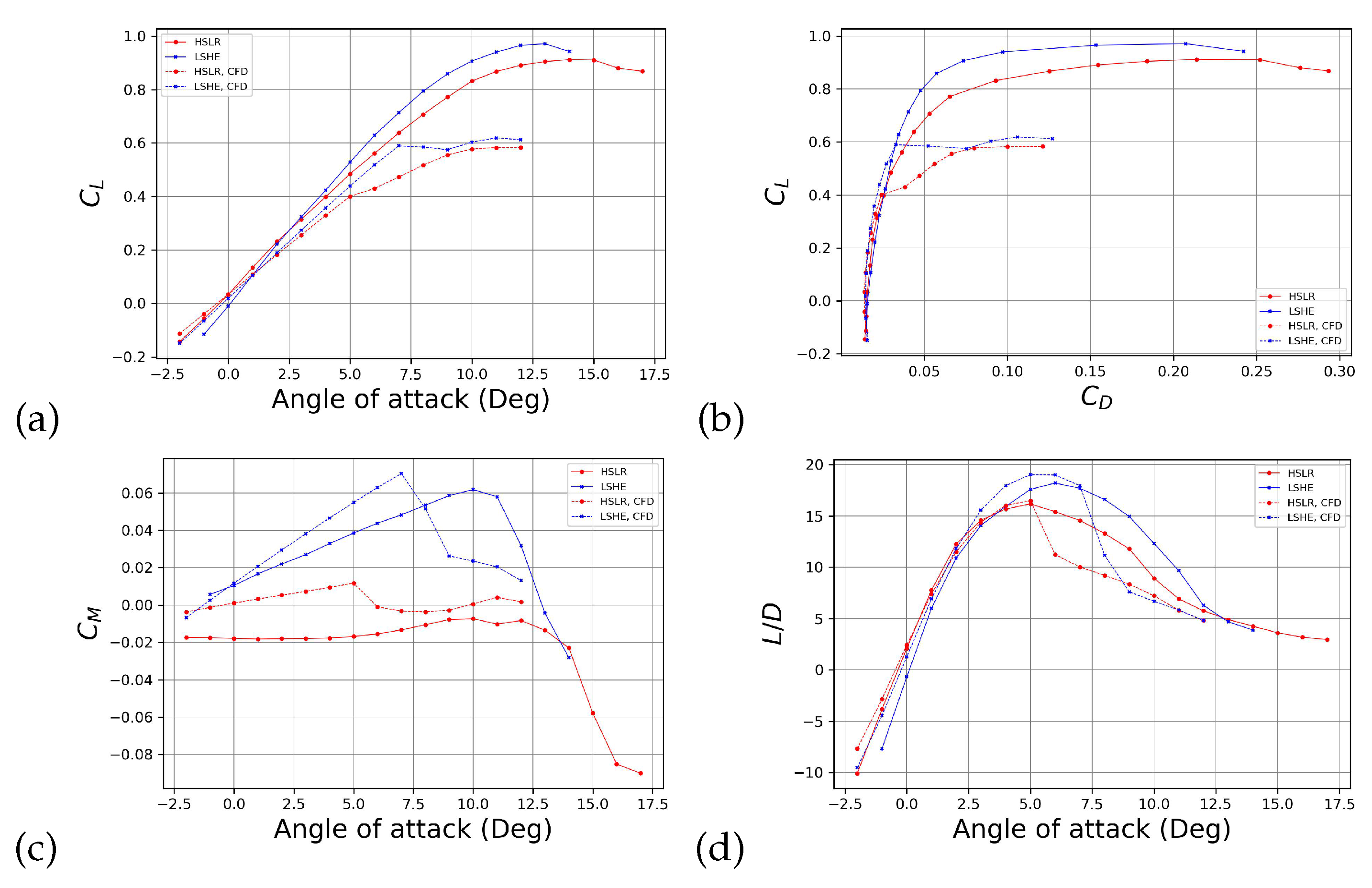
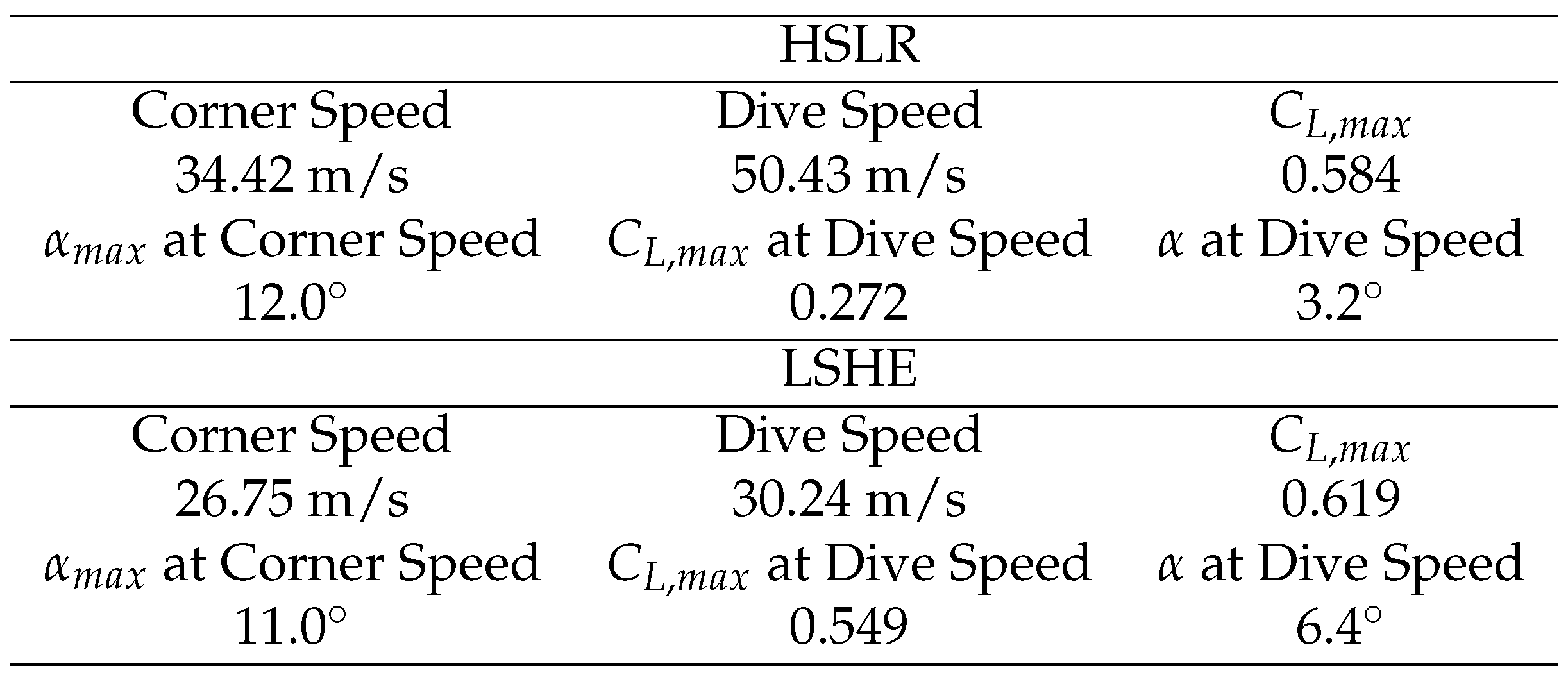
3.1. CFD Aerodynamic Results

In the first CFD simulations, the clean wing versions — LSHE and HSLR — were analyzed to obtain all aerodynamic coefficients and lift-to-drag, L/D ratios, a direct measure of aerodynamic efficiency. Figure 9 shows the results for the clean wing versions of the aircraft. The lift coefficients show expected trends, where the LSHE has a lift-curve slope of 0.078, which is greater than the HSLR slope of 0.070. That is associated with their difference in aspect ratio, LSHE having a slender wing with smaller sweep. The stall angle of attack for the HSLR variant is approximately 11 degrees, with a very smooth stall behavior, as expected in low aspect ratio wings. Meanwhile, the LSHE variant shows an interesting behavior at α = 8°. Lift grows linearly up to that point, after which there is a sudden loss in lift and recovery at α = 9°. Past this angle, lift grows non-linearly, a trend shown in other aerodynamic coefficients; there is great increase in drag generated for the LSHE variant and drastic change in pitching moment. The maximum L/D ratio is 19.68 for LSHE, at α = 6° and 17.86 for HSLR, at α = 6° as well. The base drag coefficient for both variants isvery similar, approximately 0.014 for LSHE and 0.013 for HSLR.
To investigate the reason for the loss in lift seen in the low-speed variant, pressure fields were plotted for the clean wing at α = 8°, where the lift coefficient is still within the linear portion of the graph, and α = 9° for comparison. The results are shown in Figure 10. The pressure plot shows that at the higher angle of attack, the pressure distribution at the interface between the wing panel and the center body becomes more homogeneous, increasing the pressure closer to the leading edge of the wing. Such a phenomenon is an indication that flow separation occurs in this condition, which is revealed in the turbulence plot shown in Figure 11.
While at α = 8°, the turbulence intensity does not reach above approximately 3%. However, at α = 9° it surpasses the 5% mark, indicating a highly turbulent state. This may be caused by the change in curvature between the center body and the wing at that location 3on the UAV.
The second set of simulations involved analyzing the more detailed versions of the wings, with winglets and motor nacelles. The nacelles are expected to add drag penalties to the aircraft, and it was uncertain whether the first winglet designs created during the conceptual design phase would provide a perceivable benefit in aerodynamic efficiency. The first simulations were run with the LSHEWN model, with the lowest cell count. The results show good agreement with the data previously obtained for the clean wing, achieving the same lift curve slope at the linear section of the graph and similar lift decrease past that section. However, for the LSHEWN version this drop in lift is smoother than what is observed for the LSHE.
The CFD analysis for the high-speed variant with winglet and nacelle revealed similar trends in the aerodynamic coefficients associated with flow separation facilitated by the nacelle. However, in this case the change in lift generation was not as abrupt as seen in the low-speed variant. There is no decrease in lift coefficient value with angle of attack, but rather a change in lift curve slope. These results are also shown in Figure 9. The drag coefficients and drag buckets of all wings are very similar up to CL = 0.4, then there is a significant change in drag as seen in the drag polar. For the same lift coefficient, the drag on the HSLRWN wing is much higher than for the LSHEWN wing, due to the flow separating earlier on the former. These differences are reflected on the lift-to-drag ratios seen on both variants. While the maximum L/D for HSLRWN is approximately 16.5, at α = 5°, LSHEWN attains an L/D of 19.0, at α = 6°, or 15.1% higher aerodynamic efficiency. The lift coefficients for the cruise condition for LSHE and HSLR are 0.412 and 0.204, respectively, which indicates that the LSHE variant operates very near its optimal point. The HSLR variant, however, is operating approximately at a L/D ratio of 12.5, which is 24.3% less than desired. Considering this, it is necessary to further reduce the wing dimensions and planform area accordingly. The pitch moment coefficients in Figure 9 show even greater difference between variants, because the aerodynamic center location of the wing with the center body was uncertain, having been estimated with the simple graphic method [29]. The complex geometry of the center body, as well as the use of 3 different airfoils across total span of the aircraft makes it difficult to estimate the correct aerodynamic center location accurately. Wind tunnel experiments were used later to find this location.
Similar to the analysis done on the clean wing low-speed geometry, pressure plots for the detailed wings were created to show what causes the changes in lift production on the top suction surface of the aircraft. Figure 12 presents those results. The low-speed variant shows a big region of homogeneous pressure around the motor nacelle at α = 9°. When comparing this pressure plot with Figure 10, it is suspected that the addition of the nacelle results in two separation regions: one associated with the wing - center body interface and the other associated with the nacelle alone. On the high-speed variant, however, the pressure change region is much smaller at α = 6°. This difference may be due to the smaller aspect ratio of this wing, which produces flow re-circulation from the wing tips to reduce separation.
Figure 13 shows turbulence intensity plots at certain wing span locations where the pressure change is significant. They indicate that high turbulence occurs in the low-speed, high- endurance aircraft, with values of 6% and 5% at y/b = 14% and y/b = 43%, respectively. For the high-speed, long-range aircraft, turbulence levels can reach 9%.
Observing the CFD results, it is necessary to make further changes to the high-speed variant in order to operate near its maximum efficiency point. Flow separation occurring past the linear portion of the lift coefficient graphs was investigated further, using wind tunnel experiments to confirm aerodynamic results and to determine if flow behavior is similar. The simulations did not include propeller downwash effects, which can have a very important role in energizing the flow, keeping it attached to the wing.

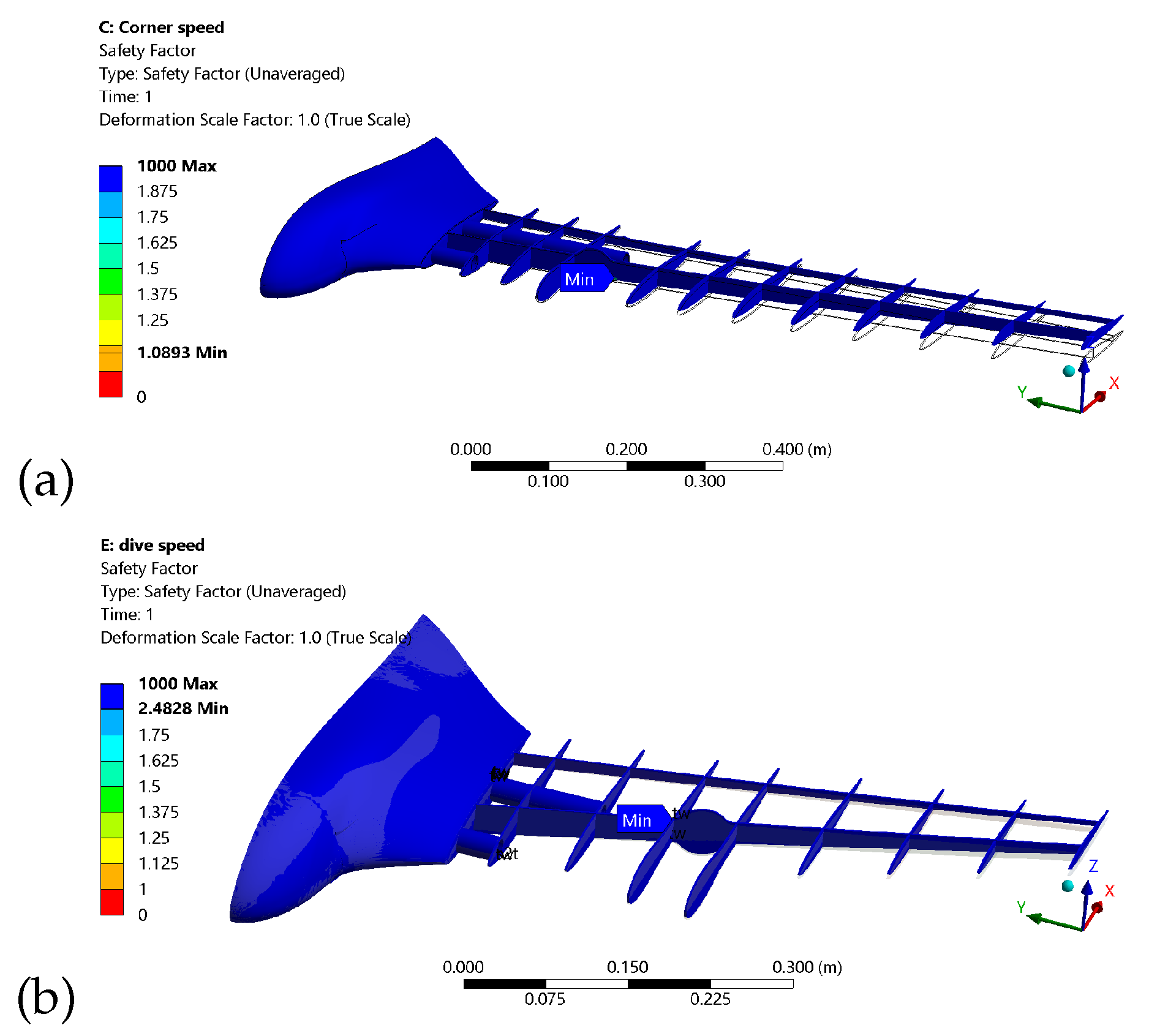
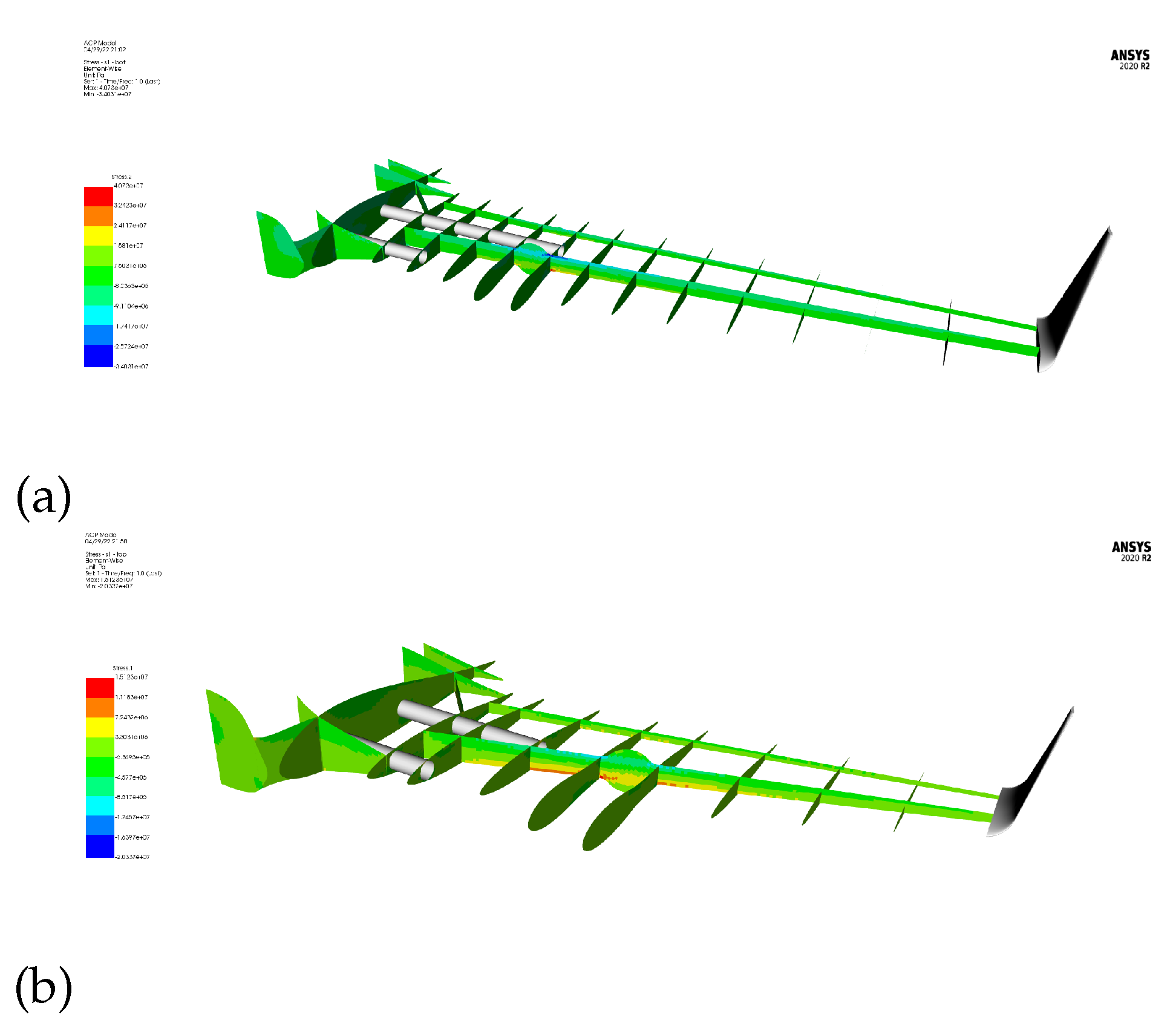
3.2. FEA Results

Results were obtained for maximum load factor conditions: at corner speed with maximum CL angle of attack, and for dive speed, or the highest speed that the aircraft should experience. Figure 14 (a) and (b) show the Factor of Safety (FoS) plots for LSHE at corner speed and HSLR at dive speed, respectively. Computing factors of safety based on the Tsai-Wu failure criterion for each of the cases revealed that LSHE is very close to its strength limit in both conditions, with FoS being 1.09 and 1.16 for corner and dive speeds, respectively. The HSLR variant presents much higher FoS due to its lower aspect ratiowing, despite the higher operating flight speeds. The FoS for that variant is 2.61 for cornerspeed and 2.48 for dive speed.
It was found that in all load cases studied, the minimum factor of safety occurs in the same region of the aircraft, the front spar where it meets the nacelle. Due to its printing orientation, the internal structure is stiffer than the wing skin in the Y direction, which explains the higher stresses in the spar. In addition, the rounded nacelle contour in the spar acts as a stress concentration, contributing to peak stress at one of either sides of the nacelle. Figure 15 shows the plot of the stress component S1 in the internal structure for LSHE corner speed and HSLR dive speed cases. Corresponding maximum stresses are summarized in Table 6. The maximum wing tip displacements, δtip are 25.4 mm for the low-speed and 8.8 mm for the high-speed variant. The higher displacement on the lowspeed aircraft was expected, given its greater wingspan, although higher speed operation would subject the aircraft to excessive deformation and stresses leading to a prohibitive factor of safety.
The reaction forces were computed to check the accuracy of the imported load in each case, since it consists of the pressure data interpolated from the CFD mesh into the FEA mesh. These reaction forces can be converted into the lift being produced in the condition under analysis, as shown in Table 6. LR is the lift calculated from the reaction forces RX and RZ, and Ltrue refers to the actual lift in the flight condition, calculated from aerodynamic coefficients in Figure 9. The reaction lift is 8.3% higher than actual lift in the LSHE dive case, and 6.2% higher in the HSLR corner speed case.

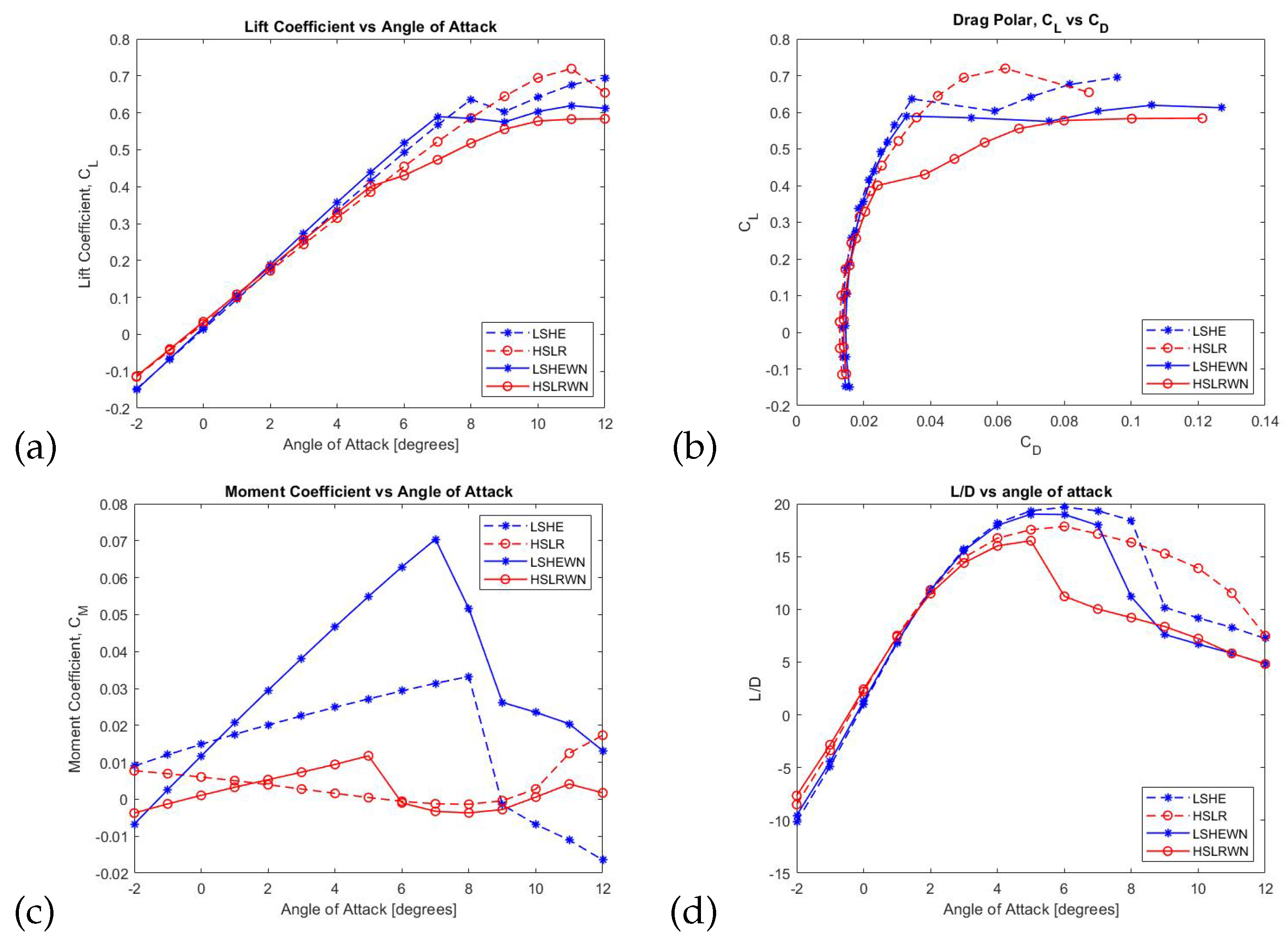
3.3. Experimental Results

The aerodynamic results are shown in Figure 16. The lift coefficient curves in (a) indicate the LSHE variant produces more lift than its counterpart. The maximum lift coefficient, CLmax for this variant is 0.97, at α = 13°, whereas for the HSLR variant it is 0.91, at α = 14°, a 6.1% smaller CLmax. The design lift coefficients for cruise speed on HSLR is 0.21, at an angle of attack of α = 2.0°, while on LSHE it is 0.42, at α = 4.0°. The difference in shape of the lift coefficient curves is in accordance with wings that have different aspect ratios, with the lower aspect ratio HSLR variant having a smoother stall region, as well as higher stall angle of attack.
The drag polars in Figure 16 (b) show both variants produce similar drag up to CL = 0.48. For higher CL, where induced drag effects predominate, the LSHE variant produces less drag due to its higher aspect ratio. The base drag coefficients for LSHE and HSLR are 0.016 and 0.015, respectively. The lift-to-drag ratio curves in Figure 16 (c) indicate the LSHE variant has a maximum L/D of 18.2, or 12.6% higher than HSLR, with L/D = 16.2. At its cruise speed, LSHE operates with L/D = 15.9, which is 29.9% more aerodynamically efficient than HSLR at its cruise speed, with L/D = 12.3. Due to its higher cruise speed, the high-speed variant operates further from its maximum L/D, around % less than optimal, which indicates the aircraft should have its wing area reduced accordingly. The low-speed variant operates closer to maximum L/D, although 12.5% less than optimal.
The pitching moment coefficients are shown in Figure 16 (d). For the HSLR variant, it does not change considerably with angle of attack for the linear range in the lift curve. Past α = 13°, CM decreases abruptly due to stall propagation effects throughout the wing. This behavior shows the aircraft pitches down during stall, which is a desirable tendency. The LSHE variant presents considerable change in CM with angle of attack due to the point of measurement lying behind the aerodynamic center of the aircraft. This is demonstrated by the positive slope of the CM vs α curve.
When comparing experimental and computational results at cruise angles of attack, HSLR and LSHE produce 26.9% and 18.8% higher CL than predicted with CFD. This difference increases at higher angles, with CL for HSLR and LSHE being 52.6% and 57.7% higher at α = 12°. The drag coefficient remains very similar at the lower CL region of Figure 16 (b), with HSLR showing 19.0% higher CD than CFD results at cruise condition, whereas LSHE experimental results show 33.6% higher drag. Above CL = 0.4 for HSLR and approximately 0.6 for LSHE, the drag from experiments is much smaller, since the early separation shown in the CFD model does not occur. This causes the lift-to-drag ratio of the variants to diverge past α = 5° (HSLR) and 7° (LSHE).
The experimental aerodynamic coefficients show a considerable difference from the CFD results, which can be attributed to the challenges in modeling turbulence accurately–particularly in transitional flow. The reduction in lift slope predicted from CFD is not present in the experimental data, which points to the k-ω SST model’s tendency to over- predict flow separation regions [30]. The inlet boundary condition assumptions and flow domain size in the CFD analysis also contribute to the difference in results. The decay of turbulence from the inlet to the aircraft results in very low turbulence intensity at the free-stream close to the aircraft, as opposed to real conditions experienced in the wind tunnel [31]. The CFD incoming flow, as shown in Figure 11 and Figure 13, is perfectly laminar upon reaching the aircraft geometry, while recent measurements from a different workhave shown stream wise turbulence intensity at the center of the test section is 1.2% at an average flow velocity of 10.85m/s [32]. Higher-than-expected turbulence intensity delays flow separation in the wind tunnel model, leading to higher lift coefficients for both variants and separation phenomena of different behavior from the CFD results. Wind tunnel experiments on a 2-D wind turbine blade have shown higher inlet turbulence intensity can result in lift increase of up to 46.2% [33], suggesting that this effect is at play in the wind tunnel tests, in combination with increased 3-D effects from the finite wings, leading to higher CL and CD.
Control surface effectiveness in trimming is shown in Figure 17. The elevon deflection angle is defined as positive for a pitch-up attitude. For the HSLR variant, the elevon is capable of trimming the aircraft with a deflection of δe = 3°, and it can provide a wide range of CM, from approximately 0.10 at δe = 19° to 0.08 at δe = 25°. For the LSHE variant, since its neutral point could not be found, a positive pitching moment exists at δe = 0. Trimming the aircraft in this condition would require a deflection of δe =2.4°. The elevon is capable of providing a minimum CM of -0.03, which is not as low as with the HSLR variant. However, it is believed that the pitch-down moment would be higher if measured at the adequate location. In future experiments, the center body must be altered to allow more travel for load cell adjustment.
The thrust experiment shows that the installed thrust is lower than available data measured for the same propeller in [34], with the difference being up to 23% at J = 0.6. Assuming the difference in thrust is due to installation effects and the wind tunnel environment, the experimental data was used as a starting point for propeller efficiency estimates. Due to limitations in the setup, higher advance ratios were not tested. To evaluate the installed thrust at higher advance ratios, CT was considered to be 23% lower than the available data. An extensive experimental database on small propellers is found in [35].
Preprints 74084 g018
Figure 18. Thrust coefficient vs advance ratio, comparison with available data [35].
Figure 18. Thrust coefficient vs advance ratio, comparison with available data [35].
Preprints 74084 g018
At cruise, the thrust coefficient required from the aircraft and the advance ratio are given by,
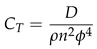
Preprints 74084 i016
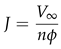
Preprints 74084 i017
substituting the advance ratio into CT and writing drag as a coefficient lead to,
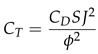
Preprints 74084 i018
Using this equation is an iterative process, since choosing a value for advance ratio J allows for calculation of the thrust coefficient at cruise, but not necessarily will CT match the real performance of the propeller at such advance ratio. Moreover, each Switchblade variant has a different cruise drag, wing area, and advance ratio due to different cruise speeds, which will result in different propeller efficiencies ηp. Using this equation for HSLR, J = 0.74 and CT = 0.013; for LSHE, J = 0.68 and CT = 0.023. Propeller efficiencies at those conditions are 58% and 68%, respectively.
The aircraft performance was evaluated in terms of the endurance and range for both variants by using the equation for electric propulsion derived in [36]:
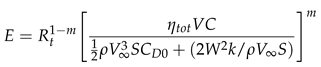
Preprints 74084 i019
Where E is the endurance in hours, Rt is the battery hour rating, m is a discharge parameter, V is the voltage and C is the battery capacity in Ampere-hour, where a capacity of 10 Ampere-hours is used on the Switchblade and calculations. The results from equation 8 are 528 shown in Table 7.
The low-speed, high-endurance variant has an endurance of 1.8h, enabling it to attain a range of 131km. The high-speed, long-range aircraft has reduced endurance due to its lower propeller efficiency and suboptimal L/D ratio at cruise. At a higher speed, the power drawn from the battery is higher, thus reducing operating time. In this case, the endurance and range are 0.49h and 59km. Despite the lower endurance, the HSLR variant is capable of operating outside of the flight envelope of the LSHE, as shown previously in Figure 7. This signifies it can sustain a 66.7% higher cruise speed for time-critical tasks without exceeding load limits established in the maneuver diagram. Additionally, to obtain better performance from higher-speed flight, the HSLR variant must be further modified to bring its operating point closer to the maximum L/D ratio. This could be attained by resizing its wing, causing it to fly at higher angles of attack, therefore at higher efficiency.

4. Conclusions

This paper presents a multidisciplinary analysis approach for a reconfigurable UAV intended for multi military missions, consisting of computational design, numerical simulations in CFD and FEA, as well as wind tunnel experiments for validation. Previous studies by the authors have indicated, at a conceptual level, reconfigurable unmanned aircraft have the potential to disrupt the UAV industry by offering significant cost reduction and supply chain benefits due to fewer 3-D printed airframe parts. These benefits increase with the number of UAV variants in the system, however design challenges and performance tradeoffs become more numerous. While the flight performance of each variant may be on par with individual dedicated unmanned aircraft for each specific mission by simultaneously designing each variant to operate in cruise at its peak aerodynamic efficiency, it was shown that this is difficult to achieve, in part due to the complex aerodynamics of the blended wing body, which is difficult to model analytically prior to CFD analysis. Both the CFD and the experimental results revealed that the low-speed, high-endurance Switchblade variant operate off-optimally aerodynamically, and the high-speed, long-range variant especially would benefit from a design iteration to adjust its wing geometry and reduce planform area. The CFD underestimated lift for most of the angles of attack examined and overestimated drag for higher angles due to flow separation effects that are not indicated in the wind tunnel experimental results. Control surface effectiveness was also evaluated via experimental testing, showing that both variants can be trimmed for cruise flight. Propulsion experiments provided an estimate of how much the installed thrust differs from propeller data, serving as a basis to calculate endurance and range for both Switchblade variants. The Low-Speed, High-Endurance (LSHE) aircraft has an estimated flight endurance of 1 hour and 48 minutes, with a maximum range of 131 km. The High-Speed, Long Range (HSLR) variant shows endurance and range of approximately half-hour and 59km, respectively. Although this variant operates off-optimally, it is able to sustain speeds beyond the flight envelope of its counterpart safely. Further design improvements can cause both variants to operate at maximum efficiency. In the finite element studies, the 3-D printing material Nylon 12 CF was modeled with orthotropic properties, and the Tsai-Wu failure criterion for composites was used. The simulation showed that the HSLR variant operates safely in both critical loading conditions, namely corner speed and dive speed, with factors of safety (FoS) of 2.61 and 2.48, respectively; in the same flight conditions, the LSHE variant operates with lower FoS, 1.09 and 1.16. This indicates that improvements in the airframe are necessary to account for the higher aspect ratio of that variant.

Author Contributions

Conceptualization, D.S. and V.M.; methodology, D.S. and J.R.; software, J.R.; validation, D.S., J.R. and A.R.; formal analysis, J.R. and A.R.; investigation, D.S.; resources, A.R.; data curation, A.R.; writing—original draft preparation, D.S., A.R. and J.R.; writing—review and editing, V.M.; visualization, D.S.; supervision, V.M.; project administration, V.M. and D.S.; funding acquisition, V.M. The authors have contributed equally to all sections and tasks. All authors have read and agreed to the published version of the manuscript.

Funding

This work was supported by the Department of Mechanical Engineering, Texas Tech University, as part of the startup package of Victor Maldonado.

Data Availability Statement

Data will be provided upon request.

Acknowledgments

The authors would like to acknowledge Mr. David Myers for his indispensableexperience and help in manufacturing the experimental setup used in this work. Without him, most of the experiments would not have been possible.

Conflicts of Interest

The authors declare no conflict of interest.

Abbreviations

The following abbreviations are used in this manuscript: Preprints 74084 i022

References

  1. Chowdhury, S.; Maldonado, V.; Tong, W.; Messac, A. New Modular Product-Platform-Planning Approach to Design Macroscale Reconfigurable Unmanned Aerial Vehicles. Journal of Aircraft 2016, 53, 309–322. [Google Scholar] [CrossRef]
  2. Pate, D.J.; Patterson, M.D.; German, B.J. Optimizing Families of Reconfigurable Aircraft for Multiple Missions. Journal of Aircraft 2012, 49, 1988–2000. [Google Scholar] [CrossRef]
  3. Maldonado, V.; Santos, D.; Wilt, M.; Ramirez, D.; Shoemaker, J.; Ayele, W.; Beeson, B.; Lisby, B.; Zamora, J.; Antu, C. ‘Switchblade’: Wide-Mission Performance Design of a Multi-Variant Unmanned Aerial System. In Proceedings of the AIAA Scitech 2021 Forum. [CrossRef]
  4. Santos, D.; Ramirez, D.; Rogers, J.; Zamora, J.; Rezende, A.; Maldonado, V. Full-Cycle Design and Analysis of the Switchblade Reconfigurable Unmanned Aerial System. In Proceedings of the AIAA Aviation 2022 Forum. [CrossRef]
  5. Gargalakos, M. The role of unmanned aerial vehicles in military communications: application scenarios, current trends, and beyond. The Journal of Defense Modeling and Simulation 15485129211031668. [CrossRef]
  6. Christensen, C.; Salmon, J. An agent-based modeling approach for simulating the impact of small unmanned aircraft systems on future battlefields. The Journal of Defense Modeling and Simulation 2022, 19, 481–500. [Google Scholar] [CrossRef]
  7. Wang, Y.C.; Chen, T.; Yeh, Y.L. Advanced 3D printing technologies for the aircraft industry: a fuzzy systematic approach for assessing the critical factors. International Journal of Advanced Manufacturing Technology 2019, 105, 4059–4069. [Google Scholar] [CrossRef]
  8. Zhu, W. Models for wind tunnel tests based on additive manufacturing technology. Progress in Aerospace Sciences 2019, 110, 100541. [Google Scholar] [CrossRef]
  9. Raza, A.; Farhan, S.; Nasir, S.; Salamat, S. Applicability of 3D Printed Fighter Aircraft Model for Subsonic Wind Tunnel. In Proceedings of the 2021 International Bhurban Conference on Applied Sciences and Technologies (IBCAST); pp. 730–735. [CrossRef]
  10. Taylor, R.M.; Niakin, B.; Lira, N.; Sabine, G.; Lee, J.; Conklin, C.; Advirkar, S. Design Optimization, Fabrication, and Testing of a 3D Printed Aircraft Structure Using Fused Deposition Modeling. In Proceedings of the AIAA Scitech 2020 Forum; 2020. [Google Scholar] [CrossRef]
  11. Skawinski, I.; Goetzendorf-Grabowski, T. FDM 3D printing method utility assessment in small RC aircraft design. Aircraft Engineering and Aerospace Technology 2019, 91, 865–872. [Google Scholar] [CrossRef]
  12. Ayele, W.; Maldonado, V. Conceptual Design of a Robotic Ground-Aerial Vehicle with an Aeroelastic Wing Model for Mars Planetary Exploration. Aerospace 2023, 10. [Google Scholar] [CrossRef]
  13. Panagiotou, P.; Yakinthos, K. Aerodynamic efficiency and performance enhancement of fixed-wing UAVs. Aerospace Science and Technology 2020, 99, 105575. [Google Scholar] [CrossRef]
  14. Tormalm, M.; Schmidt, S. Computational Study of Static And Dynamic Vortical Flow over the Delta Wing SACCON Configuration Using the FOI Flow Solver Edge. In Proceedings of the 28th AIAA Applied Aerodynamics Conference. [CrossRef]
  15. Sandoval, P.; Cornejo, P.; Tinapp, F. Evaluating the longitudinal stability of an UAV using a CFD-6DOF model. Aerospace Science and Technology 2015, 43, 463–470. [Google Scholar] [CrossRef]
  16. Mumtaz, M.S.; Maqsood, A.; Sherbaz, S. Computational Modeling of Dynamic Stability Derivatives for Generic Airfoils. MATEC Web Conf. 2017, 95, 12006. [Google Scholar] [CrossRef]
  17. Kim, M.; Kim, S.; Kim, W.; Kim, C.; Kim, Y. Flow Control of Tiltrotor Unamnned-Aerial-Vehicle Airfoils Using Synthetic Jets. Journal of Aircraft 2011, 48, 1045–1057. [Google Scholar] [CrossRef]
  18. Bliamis, C.; Vlahostergios, Z.; Misirlis, D.; Yakinthos, K. Numerical Evaluation of Riblet Drag Reduction on a MALE UAV. Aerospace 2022, 9. [Google Scholar] [CrossRef]
  19. Guiler, R.; Huebsch, W. Wind Tunnel Analysis of a Morphing Swept Wing Tailless Aircraft. In Proceedings of the 23rd AIAA Applied Aerodynamics Conference. [CrossRef]
  20. Goetten, F.; Finger, D.; Marino, M.; Bil, C.; Havermann, M.; Braun, C. A Review of Guidelines and Best Practices for Subsonic Aerodynamic Simulations Using RANS CFD. In Proceedings of the Asia Pacific International Symposium on Aerospace Technology.
  21. Zore, K.; Shah, S.; Stokes, J.; Sasanapuri, B.; Sharkey, P. ANSYS CFD Study for High Lift Aircraft Configurations. In Proceedings of the 2018 Applied Aerodynamics Conference; 2514. [Google Scholar] [CrossRef]
  22. Menter, F.R.; Smirnov, P.E.; Liu, T.; Avancha, R. A One-Equation Local Correlation-Based Transition Model. Flow Turbulence Combust 2015, 95, 583–619. [Google Scholar] [CrossRef]
  23. Menter, F. Two-Equation Eddy-Viscosity Turbulence Models for Engineering Applications. AIAA Journal 1994, 32. [Google Scholar] [CrossRef]
  24. Vostruha, K.; Pelant, J. Perturbation Analysis of "kω" and "kϵ" Turbulent Models. Wall Functions. EPJ Web of Conferences 2013, 45, 01097. [Google Scholar] [CrossRef]
  25. Rodriguez, S. Applied Computational Fluid Dynamics and Turbulence Modeling: Practical Tools, Tips and Techniques; Springer International Publishing, 2019. [Google Scholar]
  26. Gu, J.; Chen, P.; Su, L.; Li, K. A theoretical and experiemental assessment of 3D macroscopic failure criteria for predicting 652 pure inter-fiber fracture of transversely isotropic UD composites. Composite Structures 2020. [Google Scholar]
  27. Stratasys. Nylon 12 Carbon Fiber, 2015.
  28. Chen, R.; Ramachandran, A.; Liu, C.; Chang, F.K.; Senesky, D. Tsai-Wu Analysis of a Thin-Walled 3D-Printed Polylactic Acid (PLA) Structural Bracket. In Proceedings of the 58th AIAA/ASCE/AHS/ASC Structures, Structural Dynamics, and Materials Conference. [CrossRef]
  29. Raymer, D. Aircraft Design: A Conceptual Approach; American Institute of Aeronautics and Astronautics: Reston, VA, 2012. [Google Scholar] [CrossRef]
  30. Evans, S.; Lardeau, S. Validation of a turbulence methodology using the SST k ω model for adjoint calculation. In Proceedings of the 54th AIAA Aerospace Sciences Meeting. [CrossRef]
  31. Spalart, P.R.; Rumsey, C.L. Effective Inflow Conditions for Turbulence Models in Aerodynamic Calculations. AIAA Journal 2007, 45, 2544–2553. [Google Scholar] [CrossRef]
  32. Castillo, R.; Pol, S. Wind tunnel studies of wind turbine yaw and speed control effects on the wake trajectory and thrust stabilization. Renewable Energy 2022, 189, 726–733. [Google Scholar] [CrossRef]
  33. Maldonado, V.; Castillo, L.; Thormann, A.; Meneveau, C. The role of free stream turbulence with large integral scale on the aerodynamic performance of an experimental low Reynolds number S809 wind turbine blade. Journal of Wind Engineering and Industrial Aerodynamics 2015, 142, 246–257. [Google Scholar] [CrossRef]
  34. Brandt, J.; Selig, M. Propeller Performance Data at Low Reynolds Numbers. In Proceedings of the 49th AIAA Aerospace Sciences Meeting including the New Horizons Forum and Aerospace Exposition. [CrossRef]
  35. Ananda, G. UIUC Propeller Database, Volume 1, 2015.
  36. Traub, L.W. Range and Endurance Estimates for Battery-Powered Aircraft. Journal of Aircraft 2011, 48, 703–707. [Google Scholar] [CrossRef]
Preprints 74084 g001
Figure 1. Switchblade multi-mission variants.
Figure 1. Switchblade multi-mission variants.
Preprints 74084 g001
Preprints 74084 g002
Figure 2. (a) LSHE; (b) HSLR; (c) LSHEWN; (d) HSLRWN.
Figure 2. (a) LSHE; (b) HSLR; (c) LSHEWN; (d) HSLRWN.
Preprints 74084 g002
Preprints 74084 g003
Figure 3. (a) Mesh at symmetry boundary; (b) Mesh at wall boundary close to the nacelle.
Figure 3. (a) Mesh at symmetry boundary; (b) Mesh at wall boundary close to the nacelle.
Preprints 74084 g003
Preprints 74084 g004
Figure 4. (a) HSLR assembly detail; (b) HSLR wing structure.
Figure 4. (a) HSLR assembly detail; (b) HSLR wing structure.
Preprints 74084 g004
Preprints 74084 g005
Figure 5. (a) Printing direction relationship with stress components (b) Surface profile taken at 10x magnification, scale bar is 140 µm; (c) Representative volume element.
Figure 5. (a) Printing direction relationship with stress components (b) Surface profile taken at 10x magnification, scale bar is 140 µm; (c) Representative volume element.
Preprints 74084 g005
Preprints 74084 g006
Figure 6. (a) HSLR Surface FEA Mesh; (b) HSLR internal structure.
Figure 6. (a) HSLR Surface FEA Mesh; (b) HSLR internal structure.
Preprints 74084 g006
Preprints 74084 g007
Figure 7. Maneuver diagram for Switchblade variants.
Figure 7. Maneuver diagram for Switchblade variants.
Preprints 74084 g007
Preprints 74084 g008
Figure 8. (a) Wind Tunnel Setup with HSLR variant; (b) Wind Tunnel Center Body; (c) Experimental Setup Schematics.
Figure 8. (a) Wind Tunnel Setup with HSLR variant; (b) Wind Tunnel Center Body; (c) Experimental Setup Schematics.
Preprints 74084 g008
Preprints 74084 g009
Figure 9. (a) CL vs α; (b) Drag polars; (c) CM vs α; (d) L/D vs α.
Figure 9. (a) CL vs α; (b) Drag polars; (c) CM vs α; (d) L/D vs α.
Preprints 74084 g009
Preprints 74084 g010
Figure 10. LSHE Suction Side Pressure Field Comparison: Left: α = 8°, Right: α = 9◦.
Figure 10. LSHE Suction Side Pressure Field Comparison: Left: α = 8°, Right: α = 9◦.
Preprints 74084 g010
Preprints 74084 g011
Figure 11. LSHE Turbulence Intensity at Span Location y/b = 14%: Top: α = 8°, Bottom: α = 9◦.
Figure 11. LSHE Turbulence Intensity at Span Location y/b = 14%: Top: α = 8°, Bottom: α = 9◦.
Preprints 74084 g011
Preprints 74084 g012
Figure 12. (a) LSHEWN Suction Side Pressure Field: Left: α = 7, Right: α = 9°; (b) HSLRWN Suction Side Pressure Field: Left: α = 5°, Right: α = 6◦.
Figure 12. (a) LSHEWN Suction Side Pressure Field: Left: α = 7, Right: α = 9°; (b) HSLRWN Suction Side Pressure Field: Left: α = 5°, Right: α = 6◦.
Preprints 74084 g012
Preprints 74084 g013
Figure 13. (a) LSHEWN Turbulence Intensity at y/b = 14%: Top: α = 7, Bottom: α = 9°; (b) LSHEWN Turbulence Intensity at y/b = 43%: Top: α = 7°, Bottom: α = 9°; (c) HSLRWN Turbulence Intensity at y/b = 42%: Top: α = 5°, Bottom: α = 6◦.
Figure 13. (a) LSHEWN Turbulence Intensity at y/b = 14%: Top: α = 7, Bottom: α = 9°; (b) LSHEWN Turbulence Intensity at y/b = 43%: Top: α = 7°, Bottom: α = 9°; (c) HSLRWN Turbulence Intensity at y/b = 42%: Top: α = 5°, Bottom: α = 6◦.
Preprints 74084 g013
Preprints 74084 g014
Figure 14. Factors of safety: (a) LSHE corner speed; (b) HSLR dive speed.
Figure 14. Factors of safety: (a) LSHE corner speed; (b) HSLR dive speed.
Preprints 74084 g014
Preprints 74084 g015
Figure 15. Internal structure S1 stress component: (a) LSHE, corner speed; (b) HSLR, dive speed.
Figure 15. Internal structure S1 stress component: (a) LSHE, corner speed; (b) HSLR, dive speed.
Preprints 74084 g015
Preprints 74084 g016
Figure 16. Experimental Results. (a) CL vs α; (b) Drag polars; (c) CM vs α; (d) L/D vs α.
Figure 16. Experimental Results. (a) CL vs α; (b) Drag polars; (c) CM vs α; (d) L/D vs α.
Preprints 74084 g016
Preprints 74084 g017
Figure 17. Pitching moment coefficient vs elevon deflection.
Figure 17. Pitching moment coefficient vs elevon deflection.
Preprints 74084 g017
Table 1. Wing airfoil characteristics.
Table 1. Wing airfoil characteristics.
Preprints 74084 i001
Table 2. Wing characteristics.
Table 2. Wing characteristics.
Preprints 74084 i002
Table 3. Mesh Summary.
Table 3. Mesh Summary.
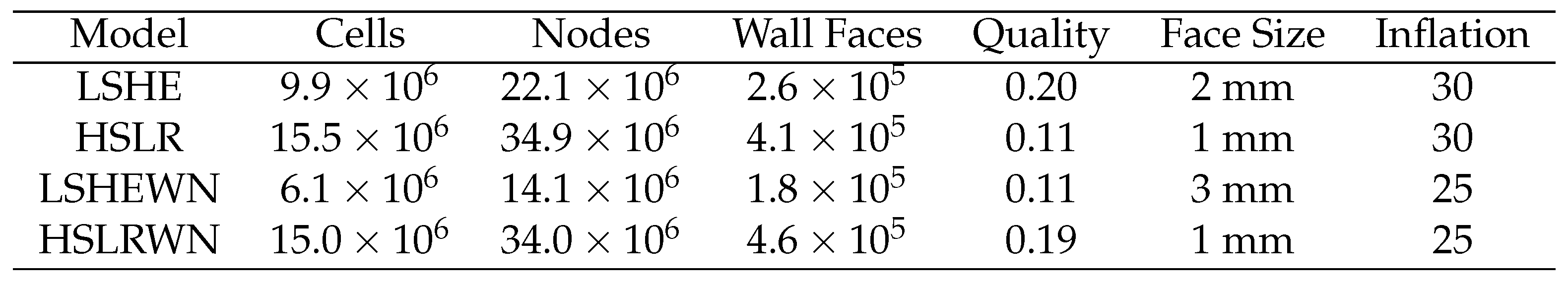
Preprints 74084 i003
Table 4. FEA Mesh Summary.
Table 4. FEA Mesh Summary.
Preprints 74084 i004
Table 5. V-n diagram results for HSLR and LSHE variant.
Table 5. V-n diagram results for HSLR and LSHE variant.
Preprints 74084 i005
Table 6. FEA Results Summary.
Table 6. FEA Results Summary.
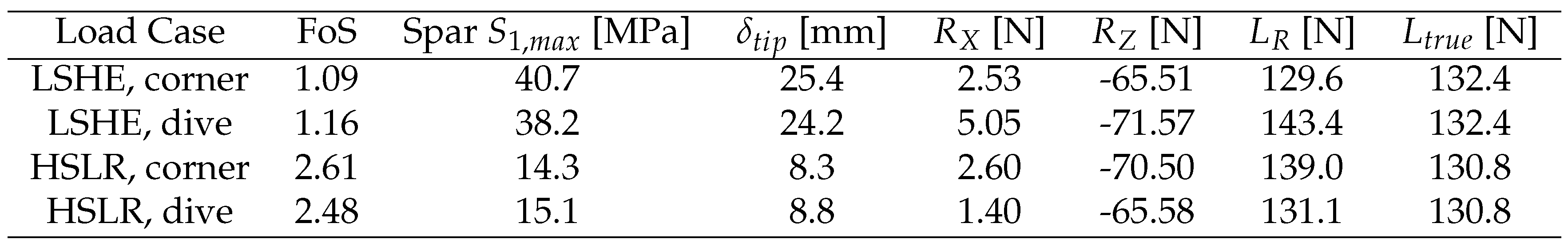
Preprints 74084 i020
Table 7. Endurance and Range by Variant.
Table 7. Endurance and Range by Variant.
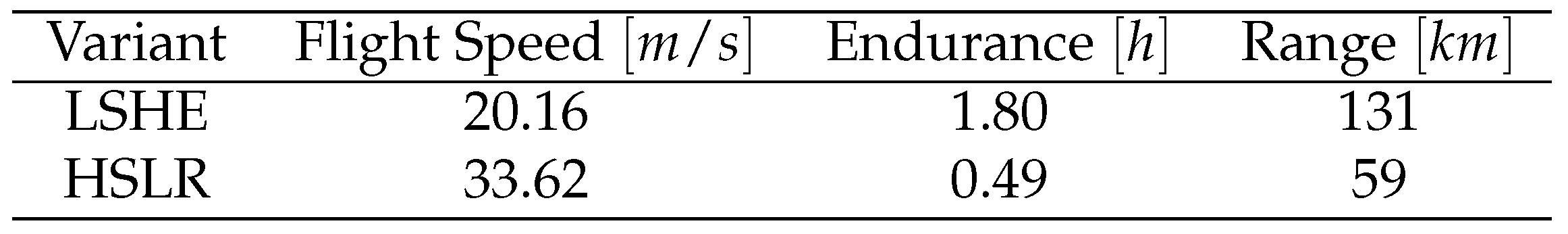
Preprints 74084 i021
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.
Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.
Prerpints.org logo

Preprints.org is a free preprint server supported by MDPI in Basel, Switzerland.

facebook logotwitter logolinkedin logo
MDPI Initiatives
Important Links
Subscribe

Disclaimer

Terms of Use

Privacy Policy

© 2024 MDPI (Basel, Switzerland) unless otherwise stated