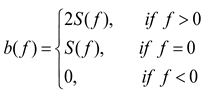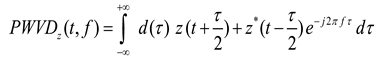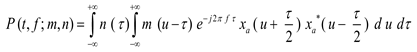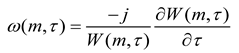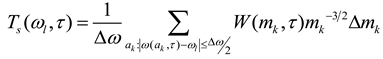Preprint

Article

Post-Earthquake Damage Identification of the Buildings with LMSST

Altmetrics

Downloads

115

Views

Comments

A peer-reviewed article of this preprint also exists.

This version is not peer-reviewed

Submitted:

22 May 2023

Posted:

23 May 2023

You are already at the latest version

Alerts

Abstract

The natural frequency of buildings decreases during a strong-motion earthquake, and the structure loses its stiffness. As a result, understanding the damaging process in the structure owing to changes in structural properties is critical during a seismic excitation. The time-frequency technique can detect the damaged building’s time-varying frequency contents. Wigner distributions (WD), Wigner-Ville distributions (WVD), pseudo-Wigner-Ville distributions (PWVD), smoothed pseudo-Wigner-Ville distributions (SPWVD), and synchrosqueezing transforms (SST) have all become popular in recent years for a variety of earthquake engineering applications, including building damage detection. This study proposes the local maximum synchrosqueezing transform (LMSST) for detecting frequency shifts in buildings during strong earthquakes. The data presented in the research show that the suggested method outperforms as compared to the conventional time-frequency methods for detecting frequency shifting in earthquake-damaged structures.

Keywords:

Subject: Engineering - Safety, Risk, Reliability and Quality

1. Introduction

In recent decades the number of multi-story buildings has exponentially increased due to the urbanization and availability of modern technology and construction material. Post-earthquake damage assessment of buildings is necessary for seismic risk mitigation and resilience planning [1]. With recent progress in signal processing and sensor technology, damage detection using data collected from the sensors attached to buildings is becoming very popular in structural health monitoring (SHM)[2,3]. Modal parameters such as damping ratio, mode shape, and natural frequency are the key concepts to assess the dynamic characteristics of a building. When a structural system changes in mass, stiffness, or structural damping, the values of the parameters tend to vary. This approach can identify the damaged state of the structure [4]. Recently, many researchers have employed time history analysis and Fourier transform (FT) for damage detection. The shifting of a structure’s frequency components during an earthquake may be caused by nonlinearities such as the surrounding environment, degree of excitement, and earthquake ground motion. If the frequency fluctuation ceases after the earthquake and returns to the pre-event frequency of the building (i.e., the natural frequency of the building), there is no structural damage. However, if there is permanent structural damage then the natural frequency of the building changes permanently[5]. Damage identification and real-time health monitoring can be done by comparing the pre-event and post-event frequencies of the building [6]. For this purpose, a joint time-frequency (TF) method is required as this method provides the time and frequency information of a signal simultaneously. Black (1996) [7] applied a short-time Fourier transform (STFT) on the data collected from the Sheraton Universal hotel located in Los Angeles, USA to identify the damage. The study demonstrated that the natural frequency of the building remained stationary even after the earthquake, hence it was concluded that there was no damage in the building. The damage to the buildings has also been identified using Wigner-Ville distribution (WVD). The presence of cross-terms in WVD hinders the interpretations and creates a significant barrier to understanding the response of the building. To overcome this drawback extended versions of the WVD, such as pseudo-Wigner-Ville distribution (PWVD), smoothed pseudo-Wigner-Ville distribution (SPWVD), and reassigned smoothed pseudo-Wigner-Ville distribution (RSPWVD), were employed for damage detection and other signal processing applications [8,9,10,11]. Similarly, various TF methods, like STFT, S-transform (ST), and local time-frequency transform (LTFT) were also employed for damage detection [12]. It was reported that the TF method with less cross-term interference and the least Renyi entropy is suitable for damage detection. Similarly, the performance of the Gabor-Wigner transform (GWT), S-transform, Synchrosqueezing transform (SST), and other time-frequency methods were compared in [13]. It was concluded that the SST is the best among all. However, SST suffers from a smearing problem and is not capable of capturing the pre-event and post-event frequency of the structure.

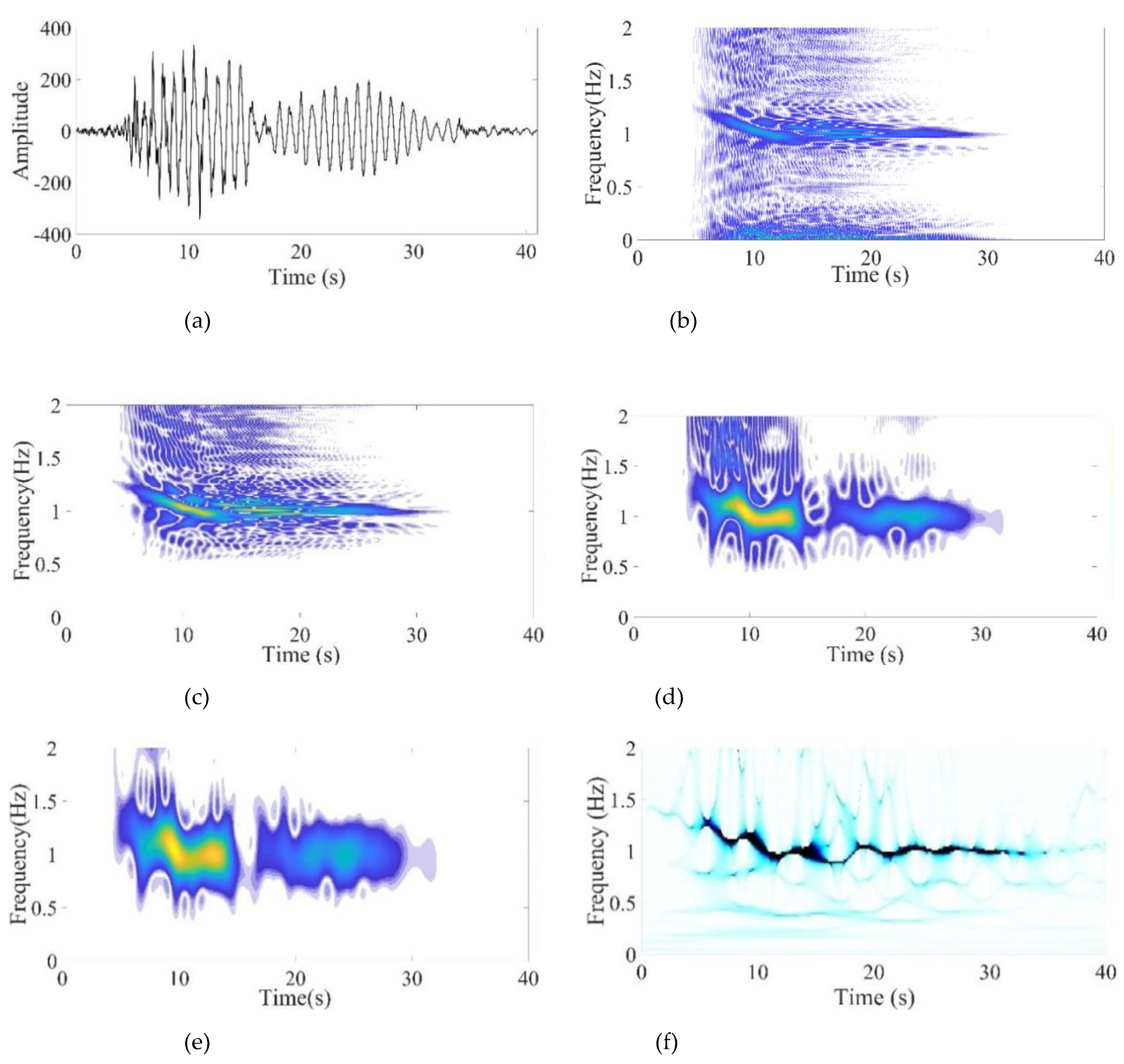
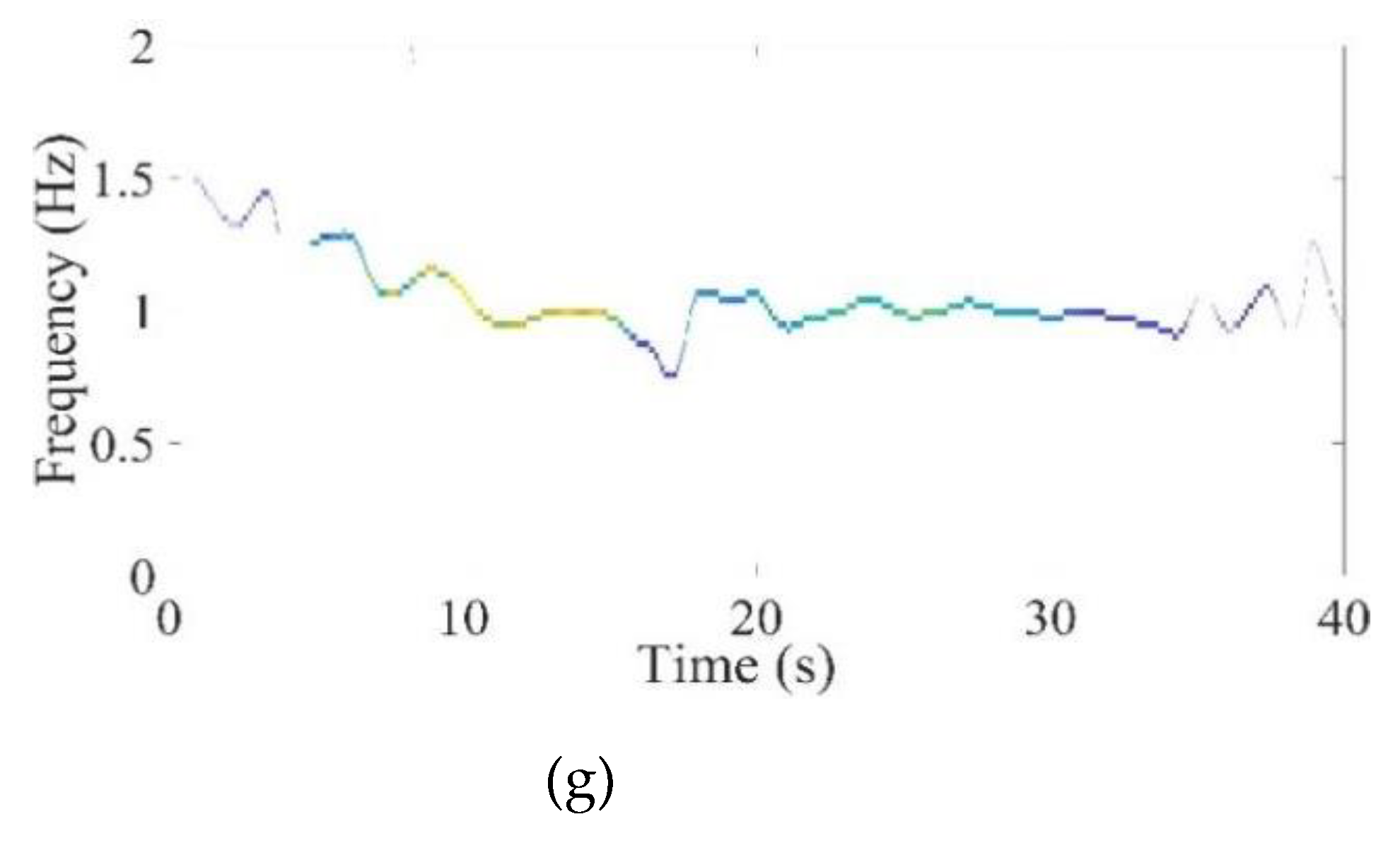
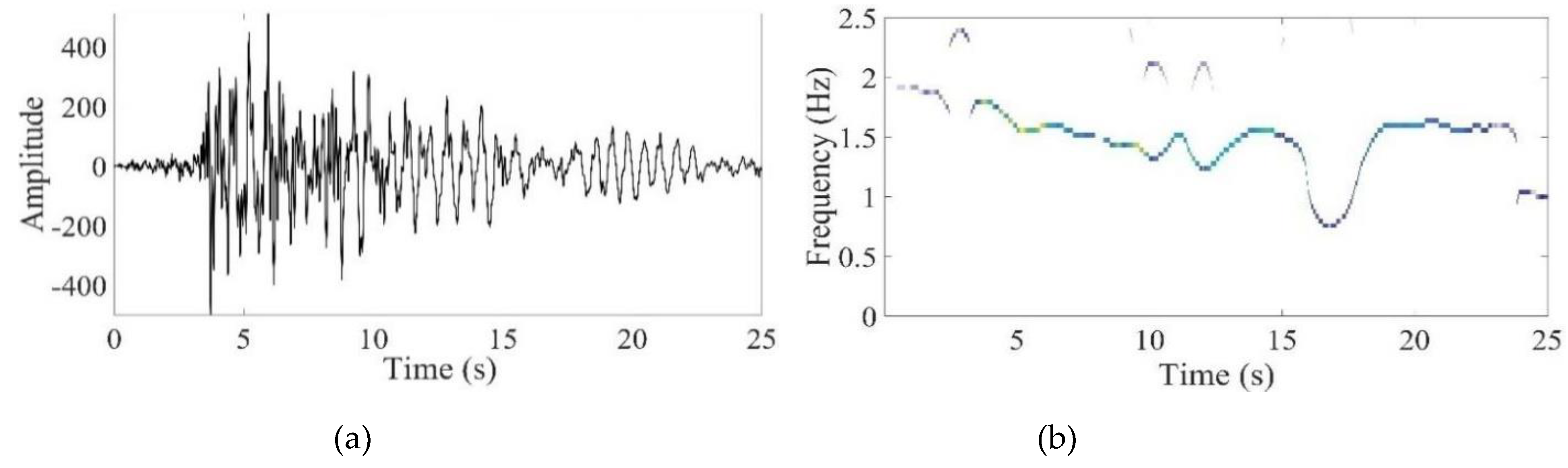
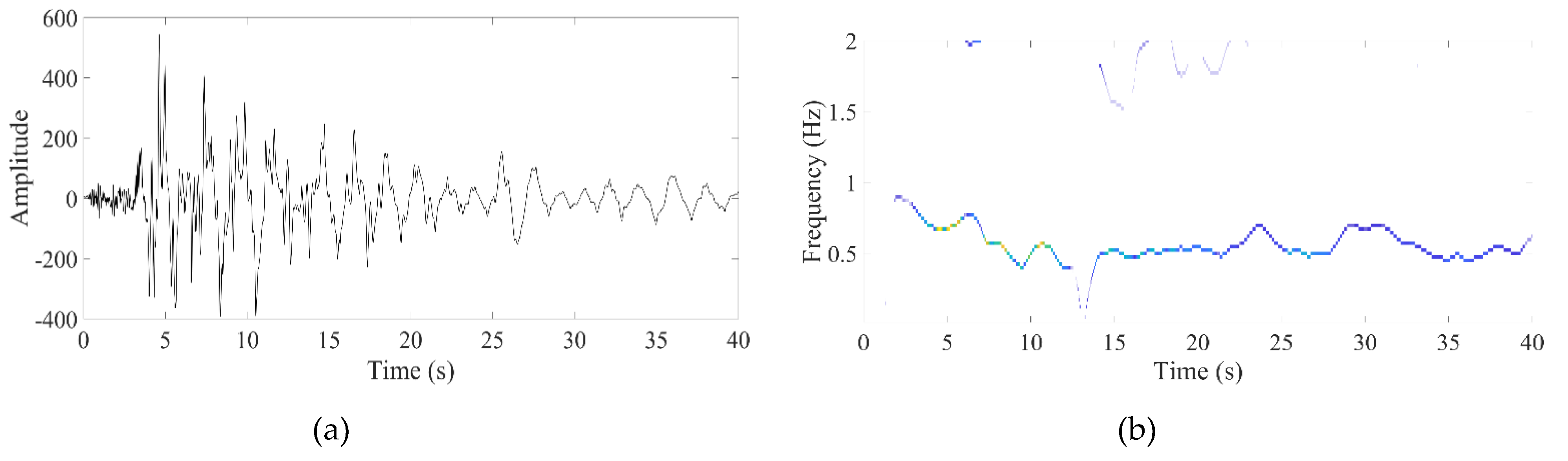
During the seismic event, the amplitude of the signal captured by the sensors is relatively high due to external excitation (i.e., an earthquake). The inertia of the building may prevent a sudden decline in the magnitude of the post-event signal following an earthquake. A certain amount of time must pass before the structure settles and reaches a stable state. In post-earthquake damage detection, the primary goal is to analyze the building’s fundamental frequency during this stable state, both before and after seismic events. In both cases, the amplitude of the signal captured by the sensors is relatively low; with traditional TF methods, it is challenging to deal with low-amplitude signals [14]. In this regard, the local maximum synchrosqueezing transform (LMSST) stands out as a highly sensitive method for detecting amplitude-weak modes [14], making it a suitable choice for post-earthquake damage detection.

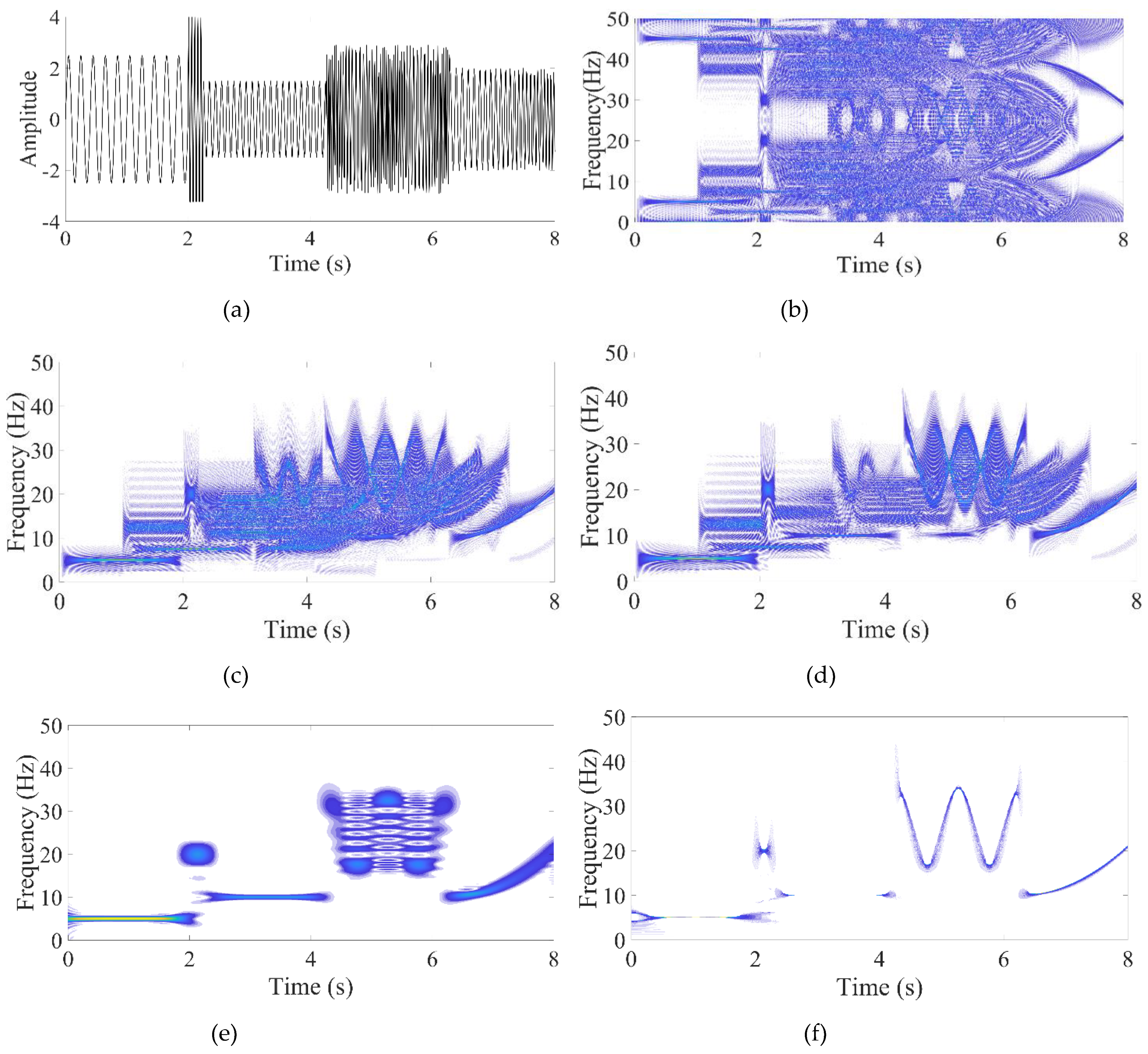
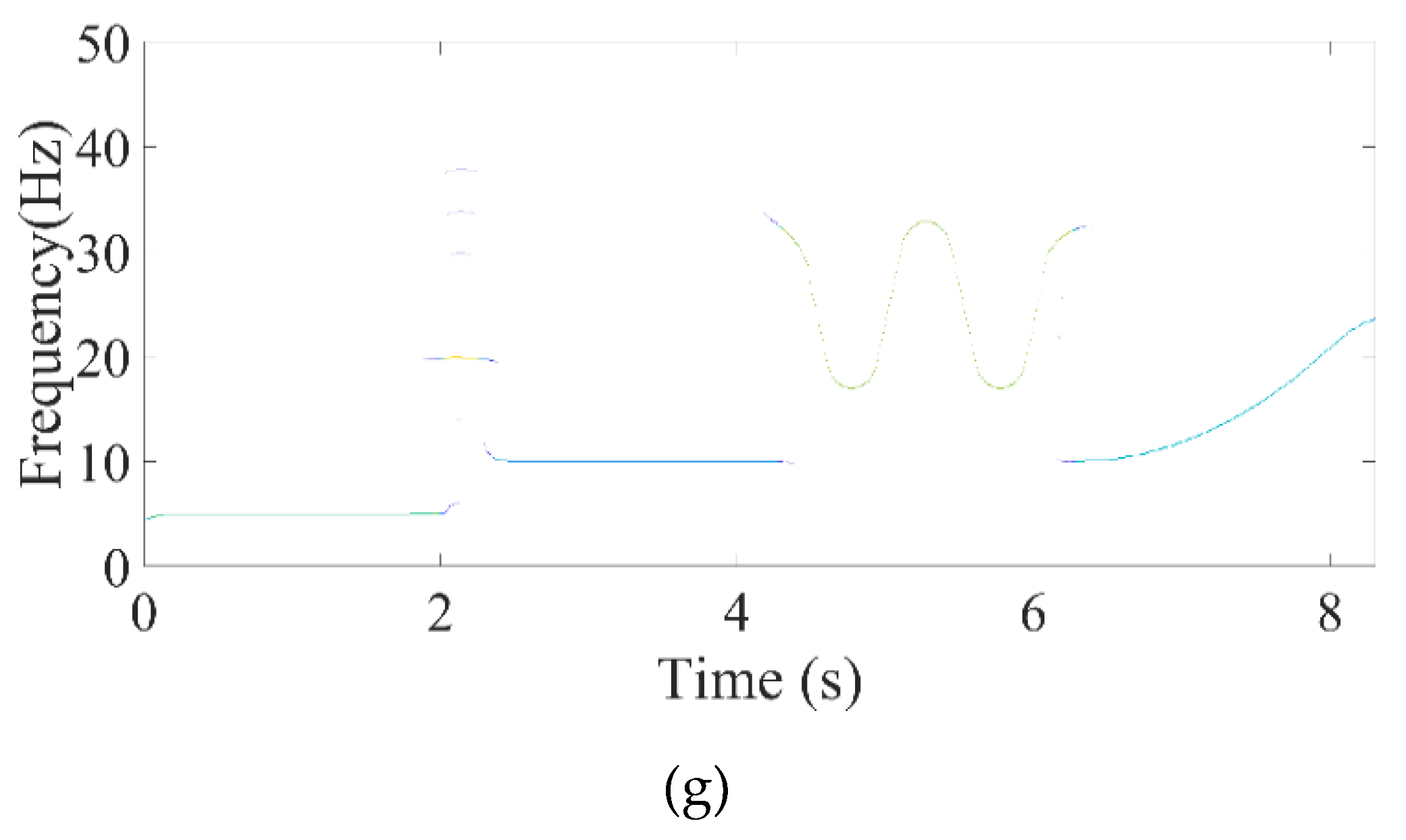
In this research work LMSST is employed for damage detection. The usefulness of LMSST is demonstrated using multi-component synthetic signals and various real earthquake data. Through visual representation and qualitative measures, it is observed that LMSST has better TF resolution and can detect post and pre-event frequency of the structure, which plays a very critical role in structural health monitoring. The amount of permanent shift in the natural frequency of the building after any seismic event determines the health of the building[3,6,11]. This research work is organized in the following manner, in section 2 various TF methods are discussed, followed by a discussion on Rényi entropy and result and analysis in sections 3 and 4 respectively. The paper is concluded in section 5.

2. Time-frequency methods

2.1. Wigner Distribution

The Fourier transform of the autocorrelation of the input signal is defined as the Wigner distribution. WD is mathematically expressed by the equation,

(1)

where * is the complex conjugate of a real signal. WD enhances time and frequency resolutions. However, low frequencies artifact due to the interaction of positive and negative frequencies in the time-frequency plane were studied [8,15,16]. By modifying the WD with the analytic signal, these artifacts can be reduced and it is now called Wigner-Ville Distribution (WVD). Mathematically, WVD could be expressed by,

(2)

where

b (t)

is the Hilbert transform of the input signal. The analytic signal’s Fourier transform is given by

(3)

where

b (t)

is an analytic signal of

s (t)

. Thus, it can be assumed the WVD is an extension of WD. Analytic signal removes the low-frequency artifacts; however, the cross-term interference caused by the actual frequency components cannot be eliminated which exhibits the disturbing tendency in the time-frequency plane and provides misleading information [15,17]. Despite these drawbacks, it has been shown that the WVD concentrates signal energy along with the instantaneous frequency. As a result, the WVD serves as the foundation for separating seismic events in the time-frequency plane.

2.2. Smoothed Wigner-Ville Distribution

Pseudo Wigner-Ville Distribution (PWVD) is expressed by the following equation.

(4)

WVD provides time-frequency resolution to a large extent. However, one of the major challenges in WVD is the cross-term interference which can be suppressed in the time-frequency plane with a sliding window,

d (τ)

. PWVD improves the resolution, although it has interference terms that can make elucidation difficult [18]. Because of this problem, PWVD has now been modified is known as SPWVD that can be expressed mathematically as follows,

(5)

SPWVD is a windowed version of WVD that achieves a better time-frequency resolution by using independent time and frequency window functions. Window functions m and n suppress cross-term interference along the time axis and the frequency axis respectively. SPWVD is also used in pulse oximetry to reduce motion artifacts, which enhances the accuracy of wearable devices [19]. In addition to this, decompositions of seismic spectral of a sandstone dam were performed using the SPWVD in the West Sichuan depression to detect the hydrocarbon. The degree of smoothing depends on the width of the window function. However, the time and frequency resolution of SPWVD losses due to the smoothing effect.

2.3. Synchrosqueezing Transform

Synchrosqueezing transform is a widely used joint time-frequency method that reassigns the signal’s energy along the frequency axis while preserving the signal’s time resolution. Secondly, this method controls the leakage/spreading effect caused by the mother wavelet and in turn, enhances the time-frequency resolution to some extent [20]. The SST is a consistent and powerful mathematical tool that is used to detect frequency components which have been further used in various applications [21,22]. Wavelet transform mathematical equation is defined as,

W (m, τ) = \int_{- \infty}^{\infty} s (t) \frac{1}{m} ψ^{*} (\frac{t - τ}{m}) d t

(6)

where s(t) is the time domain signal,

ψ (t)

is the mother wavelet,

τ

indicates translation of the window function, and

m

is the scale of the mother wavelet which is responsible for dilating and compressing the window. After computing the wavelet coefficient

W (m, τ)

from the input signal, the instantaneous frequency is to be extracted at any point

(m, τ)

(7)

The wavelet coefficient is calculated only on a discrete scale

m_{k}

. The SST

T_{s} (ω, τ)

can be computed at the centers of the frequency

ω_{l}

with

ω_{l} - ω_{l - 1} = Δ ω

(8)

SST improves the time-frequency resolution to some extent. However, the variation of frequency components are difficult to distinguish due to the blurring effect.

2.4. Local Maximum Synchrosqueezing Transform

The analysis initiates with the fundamental concept of STFT which has become the most powerful mathematical tool for analysis of the seismic signals. The STFT is expressed by the equation.

S T F T (t, w) = \int_{- \infty}^{\infty} s (t) w^{*} (t - τ) e^{- j ω τ} d

(9)

where

w (t)

is a window function and

τ

indicates the position of the window. STFT divides the signal into a small segment called windowed signal, i.e.,

s (t) w^{*} (t - τ)

, and the width of the window function determines its resolution [15,23,24]. Taking the square of the magnitude of the STFT yields the spectrogram shown below,

S P_{S T F T} (t, f) = {| S T F T (t, f) |}^{2} = {| \int s (t) w^{*} (t - τ) e^{- j ω τ} d τ |}^{2}

(10)

It is possible to model a multi-component signal with the frequency-modulated (FM) and amplitude-modulated (AM) laws as

s (t) = \sum_{k = 1}^{n} a_{k} (t) e^{i ϕ_{k} (t)}

(11)

where

a_{k} (t)

is the instantaneous amplitude (IA) and

ϕ_{k}^{'} (t)

is an instantaneous frequency (IF). The IA and IF are two significant features that are used to gain insight into the signals’ time-varying characteristics. However, STFT has poor time and frequency resolutions and provides smeared energy distribution. To obtain sharper results, SST was recently introduced, which reassigns the existing time-frequency coefficients into the newly measured time-frequency position. However, the SST method also provides a poor energy concentration in the time-frequency plane. Recently, a local maximum synchrosqueezing transform (LMSST) is proposed which increases the time-frequency resolution of a signal to a large extent [14]. The mathematical expression for LMSST is as follows,

L M S S T (t, η) = \int_{- \infty}^{+ \infty} S T F T (t, ω) \partial (η - ω_{m} (t, ω)) d ω

(12)

Further,

ω_{m} (t, ω)

is a frequency-reassignment operator and can be defined as

ω_{m} (t, ω) = {\begin{matrix} a r g m a x | S T F T (t, ω) |, ω \in [ω - Δ, ω + Δ], i f | S T F T (t, ω) | \neq 0 \\ 0, i f | S T F T (t, ω) | = 0 \end{matrix}

(13)

to separate the two arbitrary modes, with the frequency distance

{ϕ^{'}}_{k + 1} (t) - {ϕ^{'}}_{k} (t) > 4 Δ k \in {1, 2..... n - 1}

. The picking of a smoothing filter is an important task. Furthermore, it is supposed that a window function’s Fourier transform reaches its maximum at zero. The operator for frequency reassignment can be written as

ω_{m} (t, ω) = {\begin{array}{l} {ϕ^{'}}_{k} (t), i f ω \in [{ϕ^{'}}_{k} (t) - Δ, {ϕ^{'}}_{k} (t) + Δ] \\ 0, o t h e r w i s e \end{array}

(14)

where

{ϕ^{'}}_{k} (t)

is the instantaneous frequency. LMSST diminishes the blurring effect and offers a promising approach that can further be utilized in the area of earthquake engineering to detect damage of buildings.

3. Assessment Criteria of Time-Frequency Method

In most cases, it has been observed that visual inspection does not provide a consistent result. Therefore, an objective evaluation method has been developed to identify the best time-frequency method. In this work, Renyi entropy is designated to identify the appropriate time-frequency method.

3.1. Renyi Entropy

Shannon first proposed the concept of entropy measurement in 1949. Later, in signal processing, entropy measures were used to quantify information. Renyi entropy is defined mathematically as

R_{α} = \frac{1}{1 - α} \log_{2} \int_{- \infty}^{+ \infty} \int_{- \infty}^{+ \infty} ρ^{α}_{n o r m} (t, f) d t d f

(15)

Here

α = 3

is selected for analysis [25,26].

ρ^{α}_{n o r m}

is the normalized time-frequency distribution can be expressed as

ρ_{n o r m} (t, f) = \frac{ρ (t, f)}{\int_{- \infty}^{+ \infty} \int_{- \infty}^{+ \infty} ρ (t, f) d t d f}

(16)

The time-frequency methods are quantified using Renyi entropy. Since the selection of time-frequency methods through visual inspection becomes hard when there are slight changes in two different time-frequency plots. As a result, researchers used Renyi entropy to classify the best time-frequency method and concluded that the lowest Renyi entropy provides the most concentrated time-frequency method [26,27]. Hence, Renyi entropy is employed to inspect the suitable time-frequency method which can further be applied in damage detection of buildings.

4. Results and Discussion

To demonstrate the superiority of the LMSST method over WD, WVD, PWVD, SPWVD, and SST, a multi-component synthetic signal and the real earthquake data recorded during the San Fernando Earthquake 1971, and the Northridge Earthquake 1994 are used.

4.1. Synthetic signal

A synthetic signal comprises of a constant frequency signal, exponentially decaying signal, nonlinear frequency varying signal, and chirp signal is generated using the following equation.

x_{1} = 2.5 \sin (2 π 5 t); 0 \leq t \leq 2

x_{2} = e^{- (t^{2} / 10)} \cos (2 π 20 t); � 2 < t \leq 2.23

x_{3} = 1.5 s i n (2 π 10 t); 2.24 < t \leq 4

x_{4} = 3 s i n (3 (150 π t + 3 s i n (2 π t))); 4 < t \leq 6

y_{t} = \sum_{i = 1}^{5} x_{i}

(17)

The multi-component signal

y_{t}

contains five components with epochs of 2 sec, 0.23 sec, 1.76, and 2 sec for the rest of the components, respectively. The time domain representation of a signal is plotted in Figure 1(a) with a sampling frequency of 100 Hz. The synthetic signal is processed with the help of WD, WVD, PWVD, SPWVD, SST, and LMSST and the results are plotted in Figure 1(b)-(g), respectively.

From Figure 1(b) it can be observed that there are many cross-terms present in the TF plot, therefore it is almost impossible to extract any meaningful information from it. WD uses the real signal, hence the positive and negative frequencies generate those cross-terms products. In WVD the cross-terms are minimized by using an analytical signal instead of a real one [23,28]. The analytic signal does not contain negative frequencies and reduces the cross-terms. From Figure 1(c) it can be observed that there are still significant cross-terms present between each pair of harmonics and obstructing proper interpretation of the given synthetic signal.

In PWVD, frequency domain filtering is applied to the signal obtained from WVD, which enhances the frequency domain resolution of the signal but resolution in the time domain is still very poor which can be observed in Figure 1(d). In SPWVD, signals obtained from WVD have been filtered in the time domain as well as the frequency domain with the help of the window function. The consequence of using the windowing function is that SPWVD fails to precisely localize the time and frequency component of the signal [9,10]. From Figure 1(e), it can be observed that the energy band of each frequency component is very thick and hinders the detection of neighboring frequency components. The result of the SST method is shown in Figure 1(g), from the result it can be observed that it suffers from the blurring effects in the frequency plane. The result of LMSST is presented in Figure 1(g). From the TF plot, it can be observed that LMSST has the sharpest TF plane among all mentioned methods. It achieves such superior TF resolution by detecting the local maxima of the spectrogram in the frequency direction [14].

The Renyi entropy measures of test signal-1 for various TF methods are calculated and presented in Table 1. From the table, it can be observed that among all the employed methods LMSST has the lowest Renyi entropy. Thus, it can be concluded that it has the most concentrated TF plane among all TF methods discussed so far. Due to the concentrated TF plane provided by LMSST, all the frequency components present in the synthetic signal with their respective occurrence in time epoch can be easily identified in Figure 1(g).

4.2. Earthquake Data

The presence of damage in the structures permanently alters their natural frequencies. By examining the pre-earthquake and post-earthquake frequencies of the structures their respective health can be determined. With appropriate TF tools, this assessment can be quickly and reliably conducted.

Seismic Data-1: San- Fernando Earthquake, 1971:

Millikan Library is a popular and historical nine-story instrumented building constructed in 1966. The San Fernando earthquake occurred in 1971 with a magnitude of 6.6, as mentioned in Table 2. Before the event, two 3-axis Teledyne Geotech RFT-250 accelerometers were placed in the basement and on the roof of the buildings. Figure 2(a) depicts the time domain response of the data recorded from the sensor placed on the top floor of the building. The data recorded by the sensor can be classified into three parts, pre-seismic, co-seismic, and post-seismic data [11].

The signal from 0-5 sec is pre-seismic, 5 sec to 32 sec is co-seismic, and the rest is the post-seismic signal. TF representations of earthquake signals for various TF methods such as WD, WVD, PWVD, SPWVD, and SST are illustrated in Figs. 2(b)-2(f), respectively. From the figures, it can be observed that the WD, WVD, PWVD, SPWVD, and SST are not capable of capturing the pre-seismic frequency as well as the tail end of the post-seismic frequency. A similar conclusion can be found in [3,11]. Whereas LMSST has a very well-defined TF plane irrespective of the time epoch. This attribute makes it a very effective and reliable technique for structural health monitoring. It can provide the frequency components of the pre-seismic, co-seismic, and post-seismic events. By comparing these frequencies, the health of the building can easily be determined.

From Figure 2(g), it can be observed that the pre-seismic frequency of the building is around 1.5 Hz, during the co-seismic phase the frequency of the building gradually decreases and at the post-seismic phase it tries to regain the natural frequency but fails to regain it. A substantial shift of around 33% is recorded. As reported in [29], the building is said to be damaged if its natural frequency is changed by 5%. Thus, it can be concluded that the building is damaged by the earthquake. Building assessment reports after the earthquake and result obtained by [3,11] is in line with our findings. The Renyi entropies obtained for all TF methods are tabulated in Table 3, where LMSST yields minimum entropy.

Seismic Data-2: Northridge Earthquake, 1994

A 10-storey residential building was designed in 1974 at Northridge. Before the earthquake, four accelerometer sensors were installed on the first, fourth, and eighth floors of the building. Earthquake data was collected from the top floor of the building for approximately 60 seconds. Only the first 25 seconds of seismic signals are analyzed because the remaining signals do not provide useful information. The time-domain representation of the signal and its LMSST response could be seen in Figure 3(a) and Figure 3(b) respectively.

The pre-event frequency of the building is about 2 Hz, during the seismic event the frequency of the building keeps fluctuating. The fluctuation in the building can be attributed to seismic events, ground motion, and other parameters related to the building. After the seismic event, the building tried to regain its pre-event frequency, but the building could not regain its natural frequency and a significant drop of around 25% can be observed. As a result, we can conclude that the building has sustained permanent structural damage due to the earthquake, as also reported in (http://www.strongmotioncenter.org/vdc/scripts/download_tar.plx).

Seismic Data-3: Northridge Earthquake, 1994

The seven-story Van Nuys Hotel was built in 1966. The hotel was lavishly outfitted with sensors on every floor. The time history of the earthquake data collected from the building’s roof, as well as the time-frequency response obtained with the LMSST technique, are plotted in Figure 4(a) and 4(b), respectively. From the figure, it can be observed that the pre-event frequency of the building is around 1 Hz, and during the earthquake, it gradually decreases up to 0.5 Hz. After the earthquake, the building tried to regain its pre-event frequency but could not achieve it. The post-event frequency has dropped by almost 50%. Thus, it can be concluded that the building is permanently damaged by the earthquake, as also reported in (http://www.strongmotioncenter.org/vdc/scripts/download_tar.plx).

5. Conclusions

The health of the structure after any seismic event can be accessed by comparing its pre-event and post-event natural frequencies when there is no influence of external excitation (i.e., an earthquake). The amplitude of the post-event and pre-event signals captured by sensors is relatively low compared to the signal captured during seismic events. Consequently, traditional TF methods like WD, WVD, PWVD, SPWVD, and SST, which don’t have concentrated TF planes, cannot detect the post-event and pre-event frequencies of the building. To overcome this problem, in this research, for the first time, a new TF method called LMSST is employed for post-earthquake damage detection. Through a multi-component synthetic signal, we have shown that it has the most concentrated TF plane and the best temporal and frequency localization capability. Besides that, we have also analyzed the performance of LMSST for three different real-time recorded earthquake data sets and found that, unlike traditional methods, it can precisely and comprehensively detect the post and pre-event frequencies of the building. Thus, it was concluded that it is the most suitable TF method for the post-earthquake damage identification of the buildings.

References

Omoya, M.; Ero, I.; Esteghamati, M.Z.; Burton, H.V.; Brandenberg, S.; Sun, H.; Yi, Z.; Kang, H.; Nweke, C.C. A relational database to support post-earthquake building damage and recovery assessment. Earthq. Spectra 2022, 38, 1549–1569. [Google Scholar] [CrossRef]
Doebling, S.W.; Farrar, C.R.; Prime, M.B.; Shevitz, D.W. Damage Identification and Health Monitoring of Structural and Mechanical Systems from Changes in Their Vibration Characteristics: A Literature Review; Los Alamos National Lab: Washington, DA, USA, 1996. [Google Scholar] [CrossRef]
Clinton, J.F. The Observed Wander of the Natural Frequencies in a Structure. Bull. Seism. Soc. Am. 2006, 96, 237–257. [Google Scholar] [CrossRef]
Bradford, Samuel Case, V, “Time-frequency analysis of systems with changing dynamic properties,” California Institute of Technology, 2006. [CrossRef]
Ozer, E.; Özcebe, A.G.; Negulescu, C.; Kharazian, A.; Borzi, B.; Bozzoni, F.; Molina, S.; Peloso, S.; Tubaldi, E. Vibration-Based and Near Real-Time Seismic Damage Assessment Adaptive to Building Knowledge Level. Buildings 2022, 12, 416. [Google Scholar] [CrossRef]
Leonardo Cano and José, A. Martínez-Cruzado, “Damage identification of structures using instantaneous frequency changes,” in Proceedings of International Conference on Computational Methods in Structural Dynamics and Earthquake Engineering, 2007.
Black and Ventura, “Joint time-frequency analysis of a 20 story instrumented building during two earthquakes,” in Proceedings of the XVIlth International Modal Analysis Conference, Kissimee, Florida, 1999.
Case Bradford, Jing Yang, and Thomas Heaton, “Variations in the dynamic properties of structures: the Wigner-Ville distribution,” 8th U.S. National Conference on Earthquake Engineering, 2006.
Li, Y.; Zheng, X. Wigner-Ville distribution and its application in seismic attenuation estimation. Appl. Geophys. 2007, 4, 245–254. [Google Scholar] [CrossRef]
Wu, X.; Liu, T. Spectral decomposition of seismic data with reassigned smoothed pseudo Wigner–Ville distribution. J. Appl. Geophys. 2009, 68, 386–393. [Google Scholar] [CrossRef]
Michel, C.; Gueguen, P. Time-Frequency Analysis of Small Frequency Variations in Civil Engineering Structures Under Weak and Strong Motions Using a Reassignment Method. Struct. Heal. Monit. 2009, 9, 159–171. [Google Scholar] [CrossRef]
Liu, N.; Schumacher, T.; Li, Y.; Xu, L.; Wang, B. Damage Detection in Reinforced Concrete Member Using Local Time-Frequency Transform Applied to Vibration Measurements. Buildings 2023, 13, 148. [Google Scholar] [CrossRef]
Kumar, R.; P. , S.; Kumar, A. Synchrosqueezing Transform-Based Frequency Shifting Detection for Earthquake-Damaged Structures. IEEE Geosci. Remote. Sens. Lett. 2017, 14, 1393–1397. [Google Scholar] [CrossRef]
Yu, G.; Wang, Z.; Zhao, P.; Li, Z. Local maximum synchrosqueezing transform: An energy-concentrated time-frequency analysis tool. Mech. Syst. Signal Process. 2018, 117, 537–552. [Google Scholar] [CrossRef]
Qian, S.; Chen, D. Joint time-frequency analysis. IEEE Signal Process. Mag. 1999, 16, 52–67. [Google Scholar] [CrossRef]
Kumar R, Wei Zhao, Vikash Singh, “Joint time-frequency analysis of seismic signals: A critical review,” Structural Durability & Health Monitoring, vol. 12, no. 2, pp. 65–83, 2018.
Cohen, L. Time frequency distributions—A review. Proc. IEEE 1989, 77, 941–981. [Google Scholar] [CrossRef]
Staszewski, W.J.; Robertson, A.N. Time–frequency and time–scale analyses for structural health monitoring. Philos. Trans. R. Soc. A: Math. Phys. Eng. Sci. 2006, 365, 449–477. [Google Scholar] [CrossRef] [PubMed]
Yan, Y.-S.; Poon, C.C.; Zhang, Y.-T. Reduction of motion artifact in pulse oximetry by smoothed pseudo Wigner-Ville distribution. J. Neuroeng. Rehabilitation 2005, 2, 3–3. [Google Scholar] [CrossRef] [PubMed]
Daubechies, I.; Lu, J.; Wu, H.-T. Synchrosqueezed wavelet transforms: An empirical mode decomposition-like tool. Appl. Comput. Harmon. Anal. 2011, 30, 243–261. [Google Scholar] [CrossRef]
Herrera, R.H.; Tary, J.B.; van der Baan, M.; Eaton, D.W. Body Wave Separation in the Time-Frequency Domain. IEEE Geosci. Remote. Sens. Lett. 2014, 12, 364–368. [Google Scholar] [CrossRef]
Tary, J.; Herrera, R.; van der Baan, M. The Synchrosqueezing Transform for High-resolution Time-frequency Representation of Microseismic Recordings. 75th EAGE Conference and Exhibition incorporating SPE EUROPEC 2013. LOCATION OF CONFERENCE, United KingdomDATE OF CONFERENCE;
Kumar, R.; Zhao, W. Predominant frequency detection of seismic signal based on Gabor–Wigner transform for earthquake early warning systems. Asian J. Civ. Eng. 2018, 19, 927–936. [Google Scholar] [CrossRef]
Kumar, R.; Zhao, W. Theory and Applications of Time-Frequency Methods for Analysis of Non-Stationary Vibration and Seismic Signal. ICVISP 2018: The 2nd International Conference on Vision, Image and Signal Processing. LOCATION OF CONFERENCE, United StatesDATE OF CONFERENCE; p. 39.
C. L. Saldana, “On time-frequency analysis for structural damage detection,” PhD thesis, University of Puerto Rico, Mayaguez Campus, June, 2014.
Aviyente, S.; Williams, W. Minimum entropy time-frequency distributions. IEEE Signal Process. Lett. 2004, 12, 37–40. [Google Scholar] [CrossRef]
Yu, G.; Yu, M.; Xu, C. Synchroextracting Transform. IEEE Trans. Ind. Electron. 2017, 64, 8042–8054. [Google Scholar] [CrossRef]
Boashash, B.; Black, P. An efficient real-time implementation of the Wigner-Ville distribution. IEEE Trans. Acoust. Speech, Signal Process. 1987, 35, 1611–1618. [Google Scholar] [CrossRef]
Creed, S. G, “Assessment of large engineering structures using data collected during in-service loading in structural assessment,” Butterworths and Company Publishers, Limited, 1987.

Figure 1. (a) Synthetic signal with five components (b) WD (c) WVD (d) PWVD (e) SPWVD (f) SST (g) LMSST.

Figure 2. (a) Time domain representation Seismic Data-1 (b) WD (c) WVD (d) PWVD (e) SPWVD (f) SST (g) LMSST.

Figure 4. (a) Time domain representation: Seismic data-2 (b) Corresponding LMSST.

Figure 5. (a) Time domain representation: Seismic data-3 (b) Corresponding LMSST.

Table 1. Renyi entropy measure.

Time-frequency methods	Renyi Entropy
Time-frequency methods	Test Signal-1
WD	18.278
WVD	17.190
PWVD	16.132
SPWVD	15.613
SST	11.020
LMSST	10.910

Table 2. Details of damaged buildings.

Parameters	Data-1	Data-2	Data-3
Earthquake, Year	San Fernando Earthquake, 1971	Northridge earthquake, 1994	Northridge earthquake, 1994
Magnitude	6.6	6.7	6.7
Epicentre	31 Km	21 Km	18 Km
Name of buildings	Millikan library, Pasadena, US	Ten-storey inhabited building, Burbank, US	Seven-storey Van Nuys Hotel
Sensor’s Position	EW roof	Roof-Center	Roof
Sampling frequency	50 Hz	50 Hz	50Hz
Peak acceleration	340.8 cm/s²	511.99 cm/s²	550.22 cm/s²

Table 3. Renyi entropy measures.

Time-frequency methods	Renyi Entropy
Time-frequency methods	Data-1 San- Fernando Earthquake, 1971
WD	17.256
WVD	15.980
PWVD	15.816
SPWVD	15.444
SST	12.797
LMSST	10.797

Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.

© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).

Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.