Prerpints.org logo
Preprint
Article

Biodiversity as a Firewall to Engineered Microbiomes for Restoration and Conservation

Altmetrics

Downloads

338

Views

294

Comments

1

A peer-reviewed article of this preprint also exists.

This version is not peer-reviewed

Submitted:

19 October 2023

Posted:

24 October 2023

You are already at the latest version

Alerts
Abstract
The possibility of abrupt transitions threatens to poise ecosystems into irreversibly degraded states. Recently, it has been proposed the use of engineered microbiomes in endangered ecosystems to prevent them to cross tipping points and avoid collapse. Potential targets for such interventions include some of the most prominent life-support systems in the biosphere: drylands and coral reefs. Since engineering can require the introduction of microorganisms not present in resident communities, how can we weight the potential outcomes? One way is to use general models of species interactions where the "synthetic" strain is incorporated into a standard multispecies model. Here we follow this approach by modelling a resource-consumer community where one of the species is a modified one that acts by preserving some key resource. We show how the indirect effect of damping the decay of shared resources results in biodiversity increase, and last but not less, the successful incorporation of the synthetic within the ecological network. Further extensions and implications for future restoration and terraformation strategies are discussed.
Keywords: 
Subject: Biology and Life Sciences  -   Ecology, Evolution, Behavior and Systematics

1. Introduction

Ecosystems are resilient entities capable of dealing with multiple sources of change, from environmental fluctuations to the undesirable outcomes of invader species. However, as with any other complex system involving positive feedbacks, they also involve breakpoints associated to changes in key parameters beyond given thresholds (Scheffer et al. 2001, Scheffer 2009, Lenton 2011, Barnovsky et al. 2012) . The increasing stressors associated with Anthropogenic drivers, from global warming to the increasing use of land associated with a growing human population. These factors already affect extant populations globally, regarding biodiversity declines and defaunation. Because of the accelerated pace of change, rapid transitions are expected to occur in the following decades (Sole and Levin 2022). Such changes will profoundly affect ecosystem services on an unprecedented scale.
Different strategies have been proposed to protect ecological communities across scales, from conservation to restoration. A commonality in all these cases is biodiversity conservation: biodiversity is a firewall to invasion and an indicator of ecosystem health. However, the time window for response is shrinking rapidly, and other paths might need to be taken. These include the engineering of ecosystems that target their fragilities (Solé, 2015; Solé et al., 2015; de Lorenzo, 2016; Piaggio et al., 2017). Such strategies include different microbial engineering strategies, from probiotics to the design of simple genetic circuits to perform specific functionalities. Can ecosystem bioengineering provide the right restoration effect while maintaining (or enhancing) biodiversity? What is the difference between using probiotic strains versus genetically modified cells? To answer these questions, dedicated efforts will be necessary to test them under controlled conditions to evaluate their effectiveness and safety. At this stage, models (both mathematical and computational) can provide great insight into potential implementations that fulfill our previous requirements. The aim of this paper is to provide such insight using a population dynamics approach.
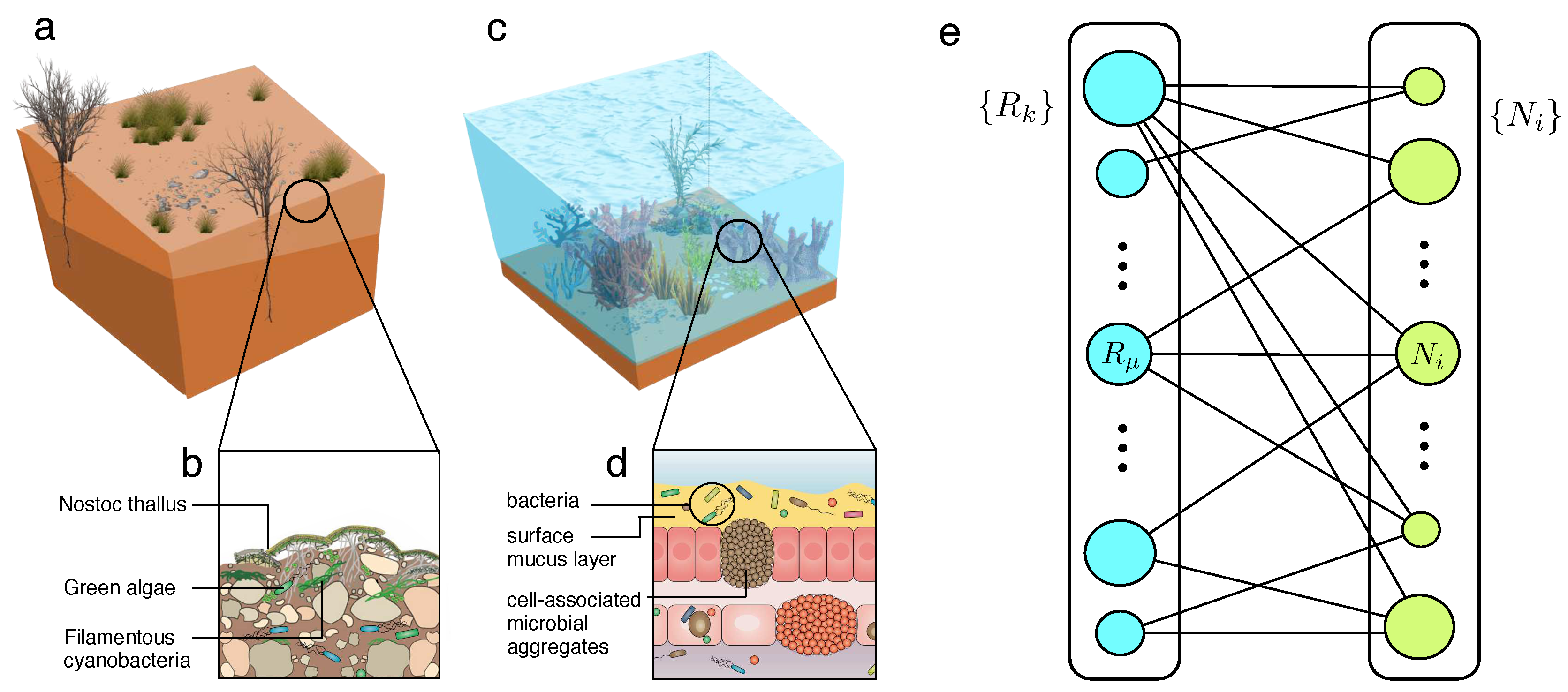
Two potential examples for such an engineering approach are shown in Figure 1a–d. These involve drylands (a,b) and corals (c,d). Both have been extensively analysed and in both cases major declines (or even collapse) are likely to occur over the next decades (Solé and Levin 2022). In both cases too, increasing temperatures trigger community-level effects that jeopardize the stability of these communities. In both cases, the microbial compartment plays a crucial role. Coral reef shrinking is one of the most obvious manifestations of the effects of increasing temperatures, along with overfishing and eutrophication, but also due to pathogens. As a result, rapid declines have taken place in the last decades. What kind of interventions can be used? Within the context of coral reefs, they are known to be holobionts, including a microbial community (Figure 1c) involving a small number of taxa. The health of the corals is correlated with microbiome composition and treatments against undesirable pathogens or microbial diversity imbalances have been approached with probiotics following dysbiosis (Peixoto et al., 2021) but engineered bacteria have also been pointed out as a promising alternative (van Oppen et al., 2015; Van Oppen and Blackall, 2019).
Drylands on the other hand, despite the obvious differences in habitat and physical context, share some commonalities with the coral reef scenario. Here too, global warming can trigger community-level shifts as aridity thresholds are reached (Berdugo et al., 2017; 2020). The soil microbiome, along with soil organic carbon is known to be crucial to preserve diversity, which is a major driver of multifuncionality (Delgado-Baquerizo et al., 2016; 2017). Interventions have also been used in the past to restore degraded drylands (Maestre et al., 2006; Bowker 2007). Several studies involving inoculation of cyanobacteria have shown the potential for recovery, at least over some time scale (Abed et al., 2009, Sabarinathan et al., 2021). But a more directed approach using microbial bioengineering could provide a more efficient and durable effect (Maestre et al., 2017; de Lorenzo 2022). How reliable is this alternative and what can we expect from this kind of intervention? Are there unintended effects (such as extinction cascades) associated to such intervention? What kind of guidance can we get from a population-level study? Mathematical and computational models suggest that some well-defined “motifs” can be implemented to modify the location and nature of tipping points (Solé 2015a, 2015b; Solé et al., 2018; Vidiella et al., 2018, 2020). But these are low-dimensional models and cannot be used to test the potential effects of synthetic strains on a multi species system.
In a previous work (Maull and Solé, 2022) we explored the problem of engineering a given species from a resident microbiome in such a way that the modified strain would be reintroduced afterwards. This was a first-order approach to the more general problems outlined above. By design, we considered a modification of the resident community where the synthetic strain is obtained from a small change of one of its members. As a result, the synthetic organism would inherit most (if not all) the links of the wild type used as a target. Such a requirement is relevant because we start from a stable community with an associated ecological network. In this context, the introduced strain would be expected to be almost redundant and remain in place or replace the wild type. Such scenarios were shown to occur under very general conditions within a multispecies competition model (Maull and Solé, 2022). However, the engineered strain was not performing a specific functionality. In this paper we explore this situation using a resource-consumer multi species model, where we target one species that will be modified to reduce the loss of one of the resources. As will be shown below, this approach does not produce diversity losses while an improvement in the abundance of the key resource is obtained.

2. Methods

2.1. Consumer-Resource Model

This study builds upon the established framework of consumer-resource models, specifically drawing from the foundational work of MacArthur in the 1970s (Macarthur, 1970, Chesson, 1990). However, we have made slight modifications to the model to accommodate our synthetic intervention requirements. We propose a set of differential equations that govern the model, consisting of one equation for resource abundance and another for population density over time. The consumer-resource equations can be expressed as follows:
d R k d t = ρ k − ∑ i n ξ k i N i R k − F ( R k , N s y n )
d N i d t = η i N i ∑ k m ξ i k R k − σ i N i + ϵ
In the proposed model, the resource abundance is denoted by R k , where k = 1 , 2 , . . . m , and the population abundance of each species is denoted by N i , where i = 1 , 2 , . . . n . The growth rates for each resource and species are represented by ρ ∈ ( 0 , 1 ) and η ∈ ( 0 , 1 ) , respectively. Notably, ρ is not resource-dependent and is treated as a general growth rate for each inorganic resource. In contrast, η represents classic replication. The growth of species is also dependent on resource uptake, which is mediated by a matrix ξ k i that weighs the strength of the interaction between each resource and its consumer. The terms of the resource-consumer matrix ξ come up from a uniform rectangular distribution U [0, 1], with a connectivity C = 0.3 .
Species decay rate is represented by σ ∈ ( 0 , 1 ) , and to prevent unrealistically low biomass, a small immigration factor of ϵ = 0.01 is introduced. Resource decay is driven by resource uptake by the species, mediated by the ξ matrix, and a decay rate function F ( R k , N s ) .
F ( R k , N s ) = β k R k 1 + δ k α N s λ
The function F ( R k , N s y n ) introduces a non-linear modulation of the resource degradation process. Specifically, the presence of a synthetic species in the community triggers a damping effect on the degradation of a specific resource α . The maximum decay rate for a given resource k is represented by β ∈ ( 0 , 1 ) , while the constant λ ∈ ( 0 , 1 ) represents the rate of inhibition of the degradation process ( β ) due to the presence of the synthetic strain, N s . Lastly, δ k α is the Dirac’s delta function, i. e. δ k α = 1 when k = α and zero otherwise. Therefore, the damping process will only affect the targeted resource.

2.2. Synthetic Invasion

The core idea is to numerically test the effect of a synthetic invader, under a fundamental control framework, if such organism can have an influence in the extant environment. We take as a fundamental control framework the ideas particularly outlined in (Maull and Solé, 2022). The underlying idea, in contrast with standard microbial invasions (Mallon et al., 2015; Vila et al., 2019) we propose a designed invasion scenario that considers both cell-level features as well as higher-order phenomena connected with community diversity. In order to modify ecosystems by means of introducing new functions using synthetic biology, there are key aspects worth implementing in the design process. The use of an extant species (wild type) as a chasis for the synthetic strain (that will be introduced) can provide of control and effective colonisation outcome. The synthetic, under this specific layout, will have the same or almost the same community interactions than the wild type, therefore the spread potential will be constrained by its niche. At the same time the chances of successful establishment can increase substantially.
Here we use a resource-consumer model to make explicit the relationship between the biotic community and the abiotic resource environment. The species compete for the resource pool through a bipartite network ξ , as specified in Equations (1) and (2). The synthetic species is thus deployed within a resident community C R , therefore creating a new, synthetic community C S . Because of our designed intervention, the synthetic species will essentially share the same interactions and similar growth rate than the wild type strain. The simplest formulation is to assume that ξ s k = ξ w k , but it seems reasonable to consider that a genetic modification process on a given strain can potentially change the metabolic balances and therefore alter their R-C interactions. To incorporate these deviations, we randomly shift the matrix elements by adding a noise term, i. e. ξ s k = ξ w k ± Δ ξ , with Δ ξ ∈ ( 0 , 0.1 ) a random number with a uniform distribution. The functional impact of the synthetic species will take place on a randomly chosen resource R α . This effect, as discussed above, involves a dampening in the resource degradation rate, as specified in Equation (3). Additionally, the engineered strain is likely to have a fitness that might be different from the wild type. It can have a direct positive feedback effect on the metabolic performance or conversely, it can imply a metabolic burden. To incorporate these two options we modify the efficiencies using η s = η w ± 0.1 η w . The neutral scenario ( η s = η w ) will also be considered.
The intervention approach thus starts with an m-resources, n-species ecosystem. Each population will start the simulation with a small initial value of N i ( 0 ) = 0.01 and an initial resource amount of R k ( 0 ) = 0.01 . The community state C R is followed over a transient of τ 1 = 800 time steps. At that moment the community is considered stable and is therefore invaded with an extra species, N s , which will be based on a randomly chosen wild type N w . The chosen mold species must have a population N w ( τ 1 ) > 0.2 . We invade with a small inoculation of synthetic strain as N s ( τ 1 ) = 0.01 . It is important to notice that the set of species that compose the C R does not change in terms of diversity because there is an immigration factor of ϵ that prevents for total extinctions. Once the C R is stable, the invasion takes place, leading the community to the synthetic state C S , after time τ 2 = 2000 time steps, until the system reaches stability again. The R-C interaction matrix goes from:
X R = ξ 1 , 1 ξ 1 , 2 ⋯ ξ 1 , n ξ 2 , 1 ξ 2 , 2 ⋯ ξ 2 , n ⋮ ⋮ ⋱ ⋮ ξ m , 1 ξ m , 2 ⋯ ξ m , n
That is replaced by the “synthetic” R-C interaction matrix, namely
X R = ξ 1 , 1 ξ 1 , 2 ⋯ ξ 1 , n + 1 ξ 2 , 1 ξ 2 , 2 ⋯ ξ 2 , n + 1 ⋮ ⋮ ⋱ ⋮ ξ m , 1 ξ m , 2 ⋯ ξ m , n + 1
Alternatively, it has been also considered the control scenario where the invader is a random species. Meaning by random that it does not come from a wild type species present in the community. Therefore, such introduced strain will have unknown random connections in the ξ matrix and a random η growth rate. We considered two interesting scenarios under this approach. First, the random invader do positively affect a randomly chosen resource, just at it is depicted in Equation (3). This scenario mimics the introduction of a enginered microorganism (not based on an extant species) in order to perform the restoration task. Second, the random invader do not have a specific positive interaction with any resource.
A statistical analysis of the synthetic invasion impact is performed by determining the population change of the community from τ 1 to τ 2 . Population change in terms statistical biotic increase of the present species. Both the wild type and the synthetic species are excluded from the change counting. We generate 500 random stable resident communities C R of m = 10 resources and n = 20 species. Each C R community is randomly generated. Once each community is stable, they are subsequently invaded. To simulate the dynamics of the resource-consumer model, we used a fourth-order Runge-Kutta algorithm.

3. Results

In this section we will study the general properties of the model described by Equations (1) and (2). The first step is to consider the simplest model that captures the main assumptions, but with some extra assumptions that allow to obtain a one-dimensional version. The general model is then considered using numerical experiments where the synthetic strain is introduced within a stable RC community and the statistical patterns of population change are analysed and compared with those associated to a random invader performing the same functionality.

3.1. Two Resources and Two Consumers

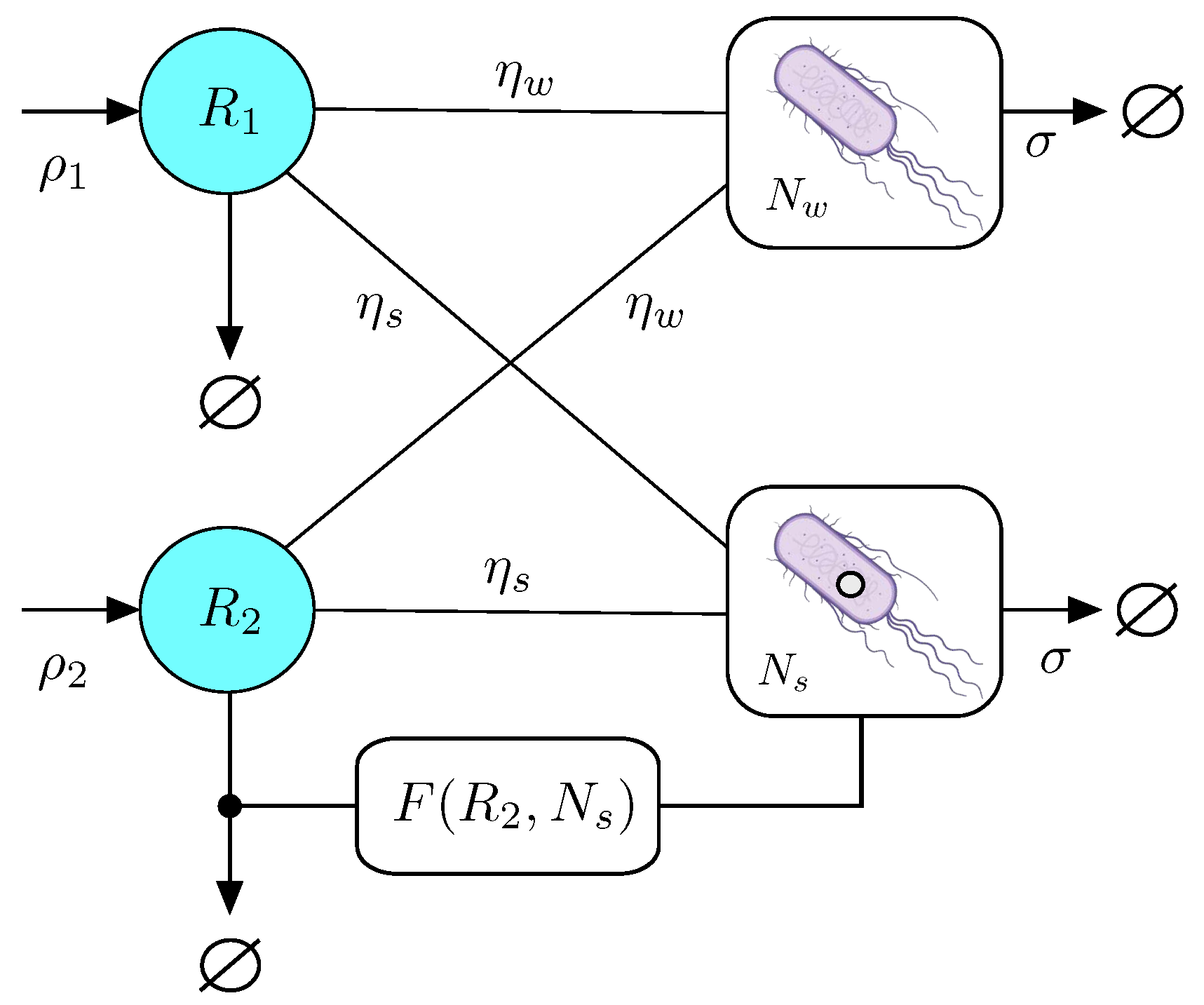
Before we proceed to the general analysis of the multidimensional model, let us consider a simpler scenario that allows to perform some analytics and define the bounds required for a synthetic strain to persist. As defined above, this engineered microorganism is designed to enhance the stability of one of the resources by reducing its loss. The basic diagram of this model is summarised in Figure 2. In this section we exploit the simplicity of this low-dimensional scenario along with an extra constraint that allows to define basic inequalities required for the synthetic strain to be successful.
For simplicity, we fix ξ k = 1 and assume a constant population constraint for the consumer populations, i.e., N s + N w is a fixed quantity. This choice allows for reducing the initial system to a single-equation model. The equations now read:
d R 1 d t = ρ 1 − ( N w + N s ) R 1 − β R 1
d R 2 d t = ρ 2 − ( N w + N s ) R 2 − β R 2 1 + N s λ
for the resource dynamics and we also consider a modified set for the microbiome dynamics, namely:
d N w d t = η w N w ( R 1 + R 2 ) − σ N w − N w Φ
d N s d t = η s N s ( R 1 + R 2 ) − σ N s − N s Φ
where we indicate Φ = Φ ( N w , N s ) .
A general analysis is given in the SM without the previous assumptions, but leading to the same basic result. Using this simplified model, we can further reduce its dimensionality by assuming that the dynamics of the resources is fast and thus we can consider that
d R 1 d t = d R 2 d t ≈ 0
and thus write the resource terms as a function of microbiome populations, i.e., after some algebra we obtain
R 1 = ρ 1 1 + β
for the first resource and
R 2 ( N s ) = ρ 2 ( λ + N s ) ( 1 + β ) λ + N s
Now, because of the assumption that the total population N remains the same, we consider for convenience that N = 1 and, from the condition d N / d t = d ( N w + N s ) / d t = 0 , it is possible to show that:
Φ ( N s , N w ) = ( η s N s + η w N w ) ( R 1 + R 2 ) − σ
Our main goal in this context is to guarantee that the synthetic strain can persist and define the conditions for such persistence. Using N w = 1 − N s and the previous result, we have now, after rearranging some terms we obtain:
d N s d t = ( R 1 + R 2 ) ( η s − η w ) ( 1 − N s ) N s
Since R 1 + R 2 > 0 , this single equation provides a threshold condition for growth of the synthetic strain ( d N s / d t > 0 ), which in this case is simply namely
η s > η w .
This result, under all the simplifications involved, suggests that a synthetic microorganism able to reduce the loss of a common good will likely establish itself provided that its efficiency of resource use is large enough. Our derivation seems far from the multispecies problem, but -as shown below- this result turns out to be robust.
A more general case can be considered if deviations in the interaction matrix between the wild and synthetic components occur (as expected) when a genetic modification is introduced. Therefore upgrading the coarse-grained model with ξ w k ≠ ξ s k states an scenario worth exploring. Therefore, the quartet of equations is the following:
d R 1 d t = ρ 1 − ( ξ w k N w + ξ s k N s ) R 1 − β R 1
d R 2 d t = ρ 2 − ( ξ w k N w + ξ s k N s ) R 2 − β R 2 1 + N s λ
Rearranging ψ = η ξ :
d N w d t = ψ w k N w ( R 1 + R 2 ) − σ N w − N w Φ ( N w , N s )
d N s d t = ψ s k N s ( R 1 + R 2 ) − σ N s − N s Φ ( N w , N s )
We can reduce again the dimensionality by using the fast dynamics condition for resources(8) along with the constant population constraint. It can be shown that:
Φ ( N s , N w ) = ( ψ s k N s + ψ w k N w ) ( R 1 + R 2 ) − σ
And finally rearranging the synthetic strain differential equation to the following expression. For the sake of clarity we recover η ξ = ψ :
d N s d t = ( R 1 + R 2 ) ( η s ξ s k − η w ξ w k ) ( 1 − N s ) N s
Notice that now ( R 1 + R 2 ) , assuming again fast dynamics, reads:
ρ 1 β − N s ( ξ w k − ξ s k ) + ξ w k + ρ 2 β λ N s + λ − N s ( ξ w k − ξ s k ) + ξ w k
Even though it changes in relation to (9,10), since populations are normalized to one, the sum still positive for all scenarios. Which, overall, provides a new threshold condition, namely:
η s > ξ w k ξ s k η w
Here, the ξ term plays a multiplicative role with the intrinsic growth rate. In the multispecies extrapolation, in general terms, it can be stated that the pairwise dynamics between the wild type and the synthetic will fall on the same space of the possible: competitive exclusion, failure and coexistence (when they are dynamically the same species), depending on the η ξ relation.

3.2. Multiple Species and Resources

Consider now the full model, as described by the set of Equations (1) and (2), along with the functional modulation of one resource given by (3). This section aims to study, under general conditions, the effect of different strains (engineered or not) that invade an extant community. Two types of interventions are considered, namely synthetic and random. We define as synthetic a genetically modified strain obtained from a wild-type species present in the resident community. The synthetic invaders can display different growth rate performances in relation to the wild-type organism. They can present a metabolic boost, a metabolic burden or remain unchanged. On the contrary, we define those strains as random, genetically modified or not, and thus not based on any previous existing wild-type species of the extant community. Therefore all the attributes are entirely random.
Two different families of results are presented. We numerically generate the time series of the deployment scenarios. Those time series highlight the pairwise dynamics between the wild type and the synthetic, and the possible impacts of a random invasion on the community. By analysing multiple runs of these time series, a statistical analysis is performed by measuring the frequency distributions of population shifts. Specifically, the population change of the j-th species after inoculation is computed as:
Δ ( N j ) = N j ( τ 1 ) − N j ( τ 2 )
associated to the reconfiguration event post invasion, accumulated through all the statistical trials. Here τ 1 is the last time step before the introduction of the synthetic, once the resident population has reached its stable state, and the final population is computed after τ 2 steps (see methods).
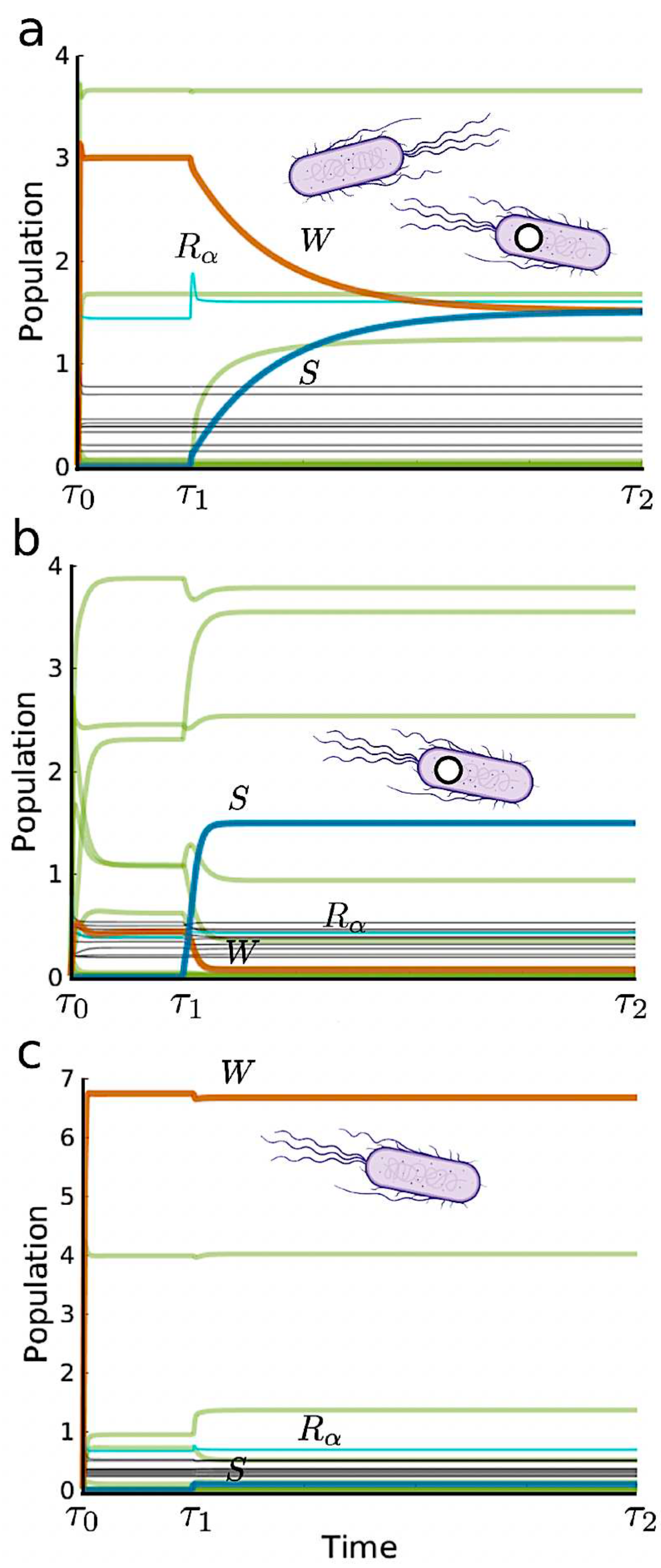
In Figure 3a–c we display the three outcomes emerging from our intervention scenario as described above. As predicted by the two-species, two-resource scenario, the efficiency of the introduced strain largely determines the result of the bioengineering. However, now we can also evaluate its impact on community diversity: is the synthetic strain triggering community shifts? The answer seems to be negative, as illustrated by the time series. Here we use thick orange and blue to represent wild type and synthetic populations, respectively, while all other species abundances are shown in green. The resources are draw in black and the enhanced resource ( R α ) in light blue. In (a) we show a typical time series for the symmetric scenario ( η w t = η s y n ). As we appreciate, the two populations converge to the same population level. In contrast, if η s y n = η w t + 0.1 η w t (b), a switch occurs. Finally, in (c) the growth rate of the synthetic is a 10 % smaller than the wild type due the extra metabolic load (I.e. η s y n = η w t − 0.1 η w t ). In this case, the synthetic fails to establish itself. In each run, a random wild type species has been chosen from the pool with a population greater than 0.2 and the initial N s ( τ 1 ) = 0.1 . Here the connectivity is C = 0.3 . Notice that in both scenarios b and c, the species that end up failing, are not complete washed out due to the (small) immigration term ϵ in Equation (2).
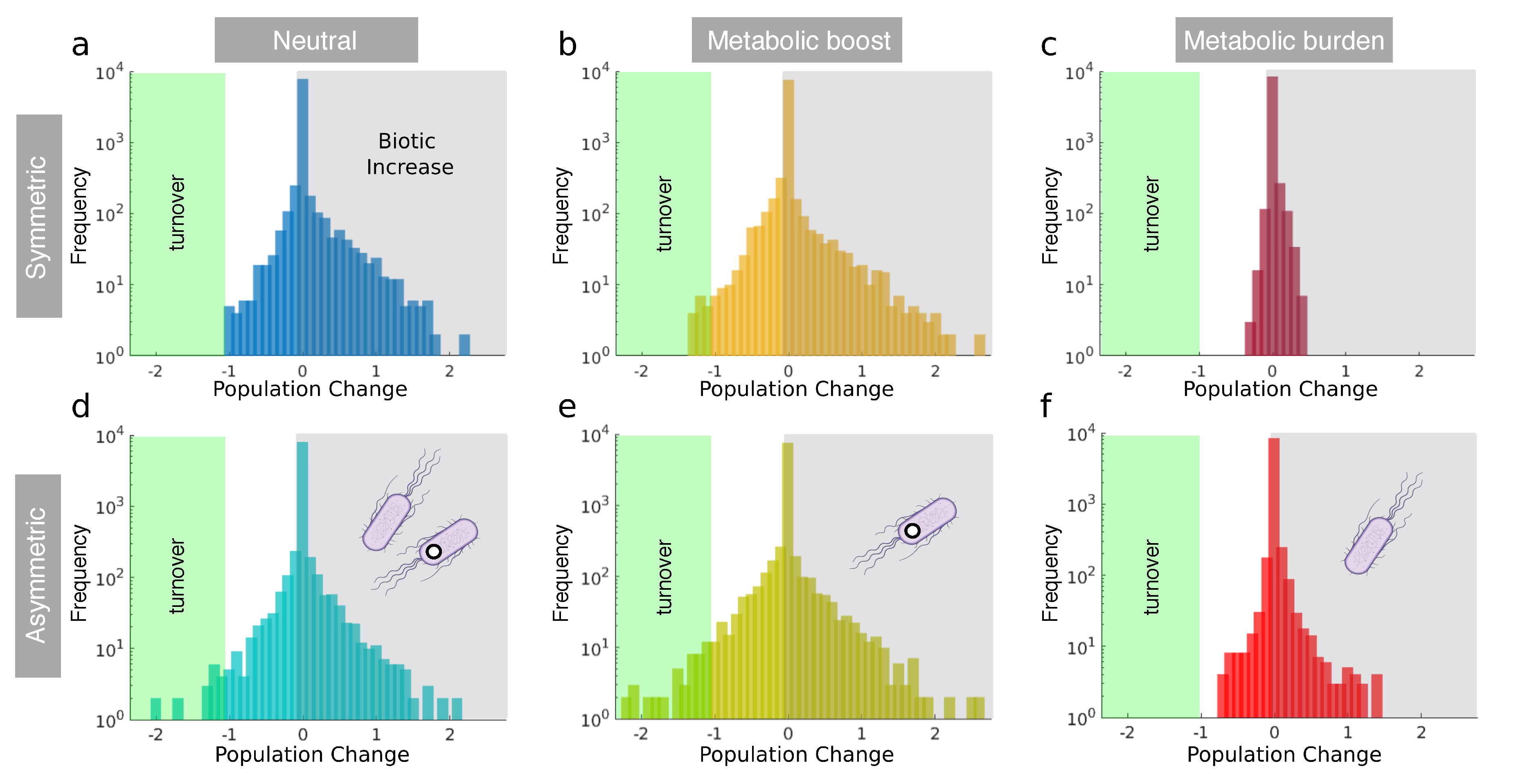
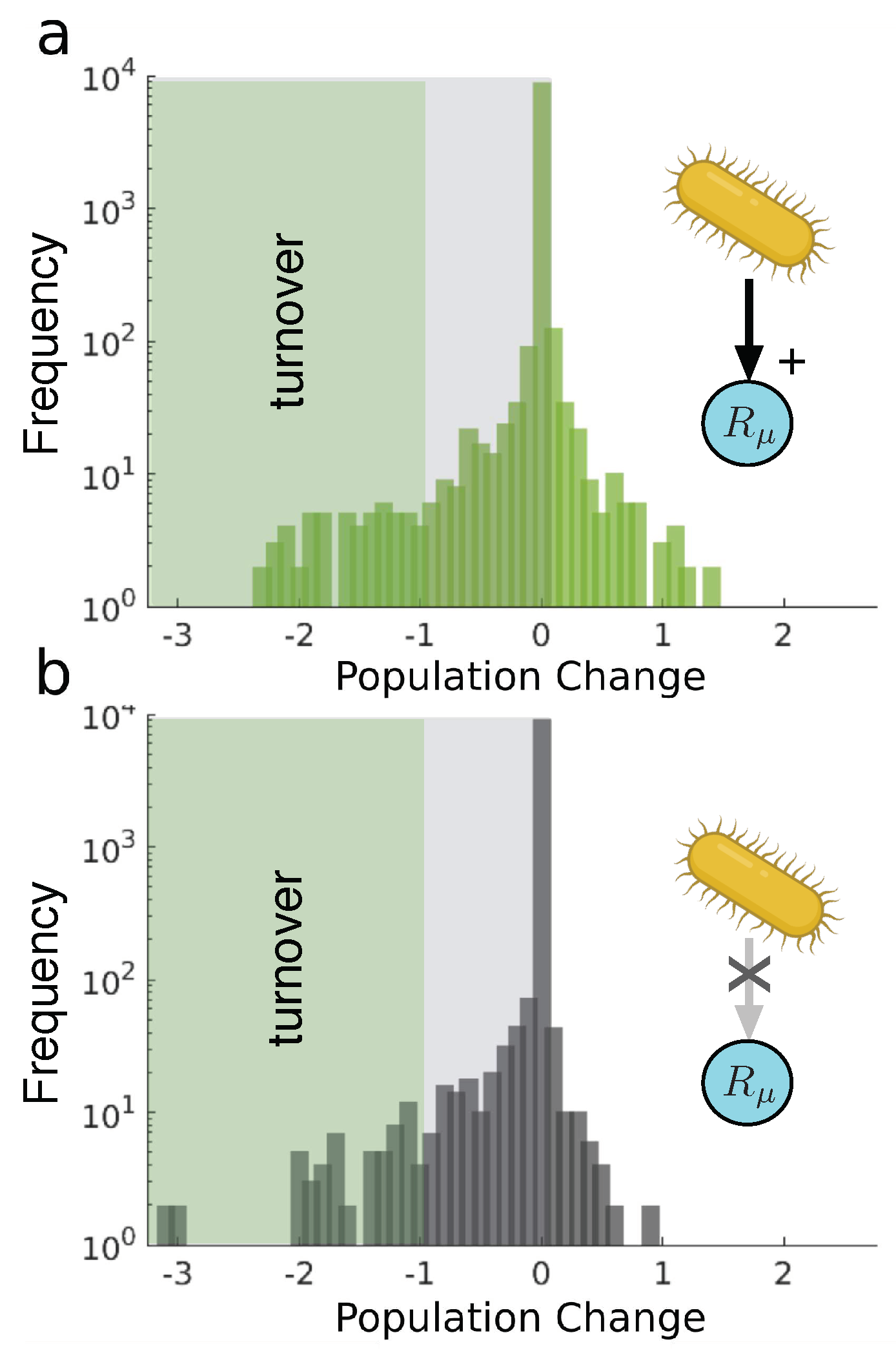
What is the statistical nature of the previous patterns? Specifically, we want to analyse the expected impact of the synthetic “invader” on community structure. Exploring this question is strongly tied to the problem of whether such intervention can trigger “unintended consequences”. In Figure 4, we display the distribution of changes in population density under the three different growth performances under the two previous matrix choices. The plots are represented in linear-log scale, thus helping to detect asymmetries. But they also point into a first important result: the vast majority of population shifts are very small, thus indicating that the introduced strains have little impact at this level. In all plots we have indicated the domain of Δ ( N j ) ≤ − 1 . These are associated to those (rare) cases where population shifts push the given species to extinction. However, since we use a constant immigration rate ϵ , this corresponds to a turnover event. In any case, the fraction of events under this threshold gives us a measure of the frequency of community changes that involve a marked reduction of a component at time τ 1 .
In the first row, a, b and c correspond to the (neutral) unchanged growth rate, metabolic boost and metabolic burden respectively. All of them entail symmetric interactions between the wild type and the synthetic ( ξ s k = ξ w k ). In the same figure, d, e and f correspond to the same scenarios regarding the intrinsic growth rate, but the R-C interactions between the species is slightly randomized. Interestingly, there is a robust statistical skewness towards the positives in all scenarios, which indicates a statistical biotic increase as a result of the synthetic intervention. In other words, the introduced strain triggers population improvements over population decreases. This skewness is more dramatic in the symmetric case (a, b, c).
The positive statistical biotic increase gets highlighted when compared against a random invader, see Figure 5. Here we find two scenarios which correspond to two interesting cases. The first one (a) corresponds to a random invader in all regards. However, the newcomer still possesses the ability to reduce a randomly chosen resource decay rate (here indicated by an arrow with a positive impact). Therefore representing a potentially engineered species, i.e., synthetic, yet not a copy of someone in the community. Secondly (b), we display the results for a random invader with no effect on resources. In both cases, the results show a dramatic difference. The skewness in the distribution of changes drives to the negatives, depicting a statistically biotic decrease resulting from the invasion.
The comparison between the synthetic and random scenarios reveals important insights. In the first set of cases, it is observed that the synthetic invader consistently thrives. Whether the growth rate remains unchanged or experiences a boost, the synthetic invader successfully establishes itself by either coexisting with the wild type or by outcompeting it. On the contrary, the random invader fails more frequently. The frequency distributions reveal a high kurtosis value can be expected, since the distributions peak around zero (notice that the frequency is in logarithmic scale). The synthetic intervention scenarios exhibit right-skewed distributions, indicated by positive skewness values, while the random scenarios are left-skewed.
Notably, the symmetric scenarios (4a-b) exhibit higher skewness values than the asymmetric scenarios (4d-e). However, among the asymmetric scenarios, when the synthetic experiences a metabolic burden (Figure 4f), it demonstrates the highest positive skewness compared to all cases. This finding raises intriguing questions regarding the potential impact of positive and transient interventions. Can temporary synthetic invasions enhance the ecosystem at a broader scale and subsequently disappear, leaving behind a reorganised and healthier ecosystem? Furthermore, does this approach align with concerns regarding the control of organism release in natural environments? These problems are addressed again in the discussion below.

4. Discussion

Microbial bioengineering might be a necessary step to improve the resilience of some ecosystems that face major challenges associated to climate change. Can this strategy improve ecosystem reliability? Will instead engineered strains trigger undesirable, community-level effects that prevent their use within natural communities? The truth is that, despite the sometimes heated debate concerning the use of engineered strains in conservation biology, no real test nor serious theoretical attempts have been promoted to truly address the previous questions. As a consequence, the potential outcomes are poorly understood. Moreover, there is a chasm between most of the research approaches used within synthetic biology (dominated by the molecular and cellular scales) and those ecosystem-level studies that consider the community dynamics on meso- or global scales.
In this paper we have introduced a model of resource-consumer interactions aimed at testing the potential population-level changes when an engineered microbial strain has been introduced. In contrast with a previous paper (Maull and Solé, 2022), where the new strain simply competed with the resident community, here a specific functional improvement of the resource pool has been included. Specifically, for a given resource, a synthetic strain designed from a member of the resident community acts by reducing its decay or spillover. Our results indicate that the impact is typically positive, dominated by small population changes, consistently with our previous findings. This suggests that, against the idea of unintended consequences, a properly designed bioengineering can fulfil to important goals: modify what is needed while preserving diversity. In this context, this is an engineering strategy that exploits emergent properties: by maintaining (and even increasing) biodiversity, multifunctionality will also be protected. By contrast with standard ecological engineering (Odum and Odum, 2003), here a global property (diversity) is also the target. In other words, our strategy includes a specific top-down controlled feature along with a bottom-up, emergent property. This is, we believe, an important conceptual novelty of the proposed intervention that is grounded in a systems-level view of engineering where emergent dynamics is at the center (Holling 1996; Solé 2015; Krakauer, 2019; Gorochowski et al., 2020).
We consider these results a starting point to a more ambitious roadmap to further ways to terraform ecosystems. Many open problems remain. On the theoretical side, evolutionary, spatial and network dynamics and the architecture of the environment have been neglected. Space, for example, can play a key role as a biodiversity enhancer. One key result from the early days of spatial ecology is that complex spatial dynamics (not considered here) can be crucial to maintain ecological diversity (Solé et al., 1992; Bascompte and Solé 1995; see also Pierce et al., 2020). In this context, the trade offs between resource and species dynamics in both space and time will need to be integrated in a more rich context where stochastic dynamics might also play a relevant role. Network architecture, on the other hand, is known to influence the propagation of changes across trophic or mutualistic webs (Montoya et al., 2011). Further exploration needs to be done in relation with realistic web architectures. Similarly, we have reduced our bioengineering design to a single species change, but potential multi species consortia might be of relevance to achieve the desired effects, perhaps targeting different resources. Above all, experimental tests using micro- and mesocosm frameworks are much needed to put to test the theoretical ideas outlined here.

Acknowledgments

The authors want to thank Dani Amor, Fernando Maestre, Victor de Lorenzo, Nuria Conde, Jordi Piñero and Jordi Pla for useful discussions, with special mention to T. Builds-the-Fire for his inspiring ideas. RS is thankful for useful discussions at the EMBL symposium “The organism and the environment”. This research has been supported by the PR01018-EC-H2020-FET- Open MADONNA project and an AGAUR FI-SDUR 2020 grant. Special thanks to the Santa Fe Institute, where much of this work was done.

References

  1. Abed, R.M.; Dobretsov, S.; Sudesh, K. Applications of cyanobacteria in biotechnology. J Appl Microbiol. 2009, 106, 1–12. [Google Scholar] [CrossRef]
  2. Bascompte, J.; Solé, R. Rethinking complexity: Modelling spatiotemporal dynamics in ecology. Trends in Ecology and Evolution 1995, 10, 361–366. [Google Scholar] [CrossRef] [PubMed]
  3. Berdugo, M.; Kefi, S.; Soliveres, S.; Maestre, F.T. Plant spatial patterns identify alternative ecosystem multifunctionality states in global drylands. Nature ecology and evolution 2017, 1, 0003. [Google Scholar] [CrossRef]
  4. Berdugo, M.; Delgado-Baquerizo, M.; Soliveres, S.; Hern ez-Clemente, R.; Zhao, Y.; Gaiten, J.J.; Gross, N.; Saiz, H.; Maire, V.; Lehmann, A.; Rillig, M.C. Global ecosystem thresholds driven by aridity. Science 2020, 367, 787–790. [Google Scholar] [CrossRef] [PubMed]
  5. Berdugo, M.; Vidiella, B.; Solé, R.; Maestre, F.T. Ecological mechanisms underlying aridity thresholds in global drylands. Functional Ecology 2022, 36, 4–23. [Google Scholar] [CrossRef]
  6. Bowker, M.A. Biological soil crust rehabilitation in theory and practice: An underexploited opportunity. Restoration Ecology 2007, 15, 13–23. [Google Scholar] [CrossRef]
  7. Chesson, P. MacArthur’s consumer-resource model. Theoretical Population Biology 1990, 37, 26–38. [Google Scholar] [CrossRef]
  8. de Lorenzo, V.; Marliere, P.; Solé, R. Bioremediation at a global scale: From the test tube to planet Earth. Microbial biotechnology 2016, 9, 618–625. [Google Scholar] [CrossRef] [PubMed]
  9. de Lorenzo, V. Environmental Galenics: Large-scale fortification of extant microbiomes with engineered bioremediation agents. Philosophical Transactions of the Royal Society B 2022, 377, 20210395. [Google Scholar] [CrossRef]
  10. Delgado-Baquerizo, M.; Maestre, F.T.; Reich, P.B.; Jeffries, T.C.; Gaitan, J.J.; Encinar, D.; Berdugo, M.; Campbell, C.D.; Singh, B.K. Microbial diversity drives multifunctionality in terrestrial ecosystems. Nature communications 2016, 7, 10541. [Google Scholar] [CrossRef]
  11. Delgado?Baquerizo, M.; Eldridge, D.J.; Ochoa, V.; Gozalo, B.; Singh, B.K.; Maestre, F.T. Soil microbial communities drive the resistance of ecosystem multifunctionality to global change in drylands across the globe. Ecology letters 2017, 20, 1295–1305. [Google Scholar] [CrossRef] [PubMed]
  12. Gorochowski, T.E.; Hauert, S.; Kreft, J.U.; et al. Toward engineering biosystems with emergent collective functions. Frontiers in bioengineering and biotechnology 2020, 8, 705. [Google Scholar] [CrossRef]
  13. Green, J.L.; Hastings, A.; Arzberger, P.; et al. Complexity in ecology and conservation: Mathematical, statistical, and computational challenges. BioScience 2005, 55, 501–510. [Google Scholar] [CrossRef]
  14. Holling, C.S. Resilience and stability of ecological systems. Annual review of ecology and systematics 1973, 4, 1–23. [Google Scholar] [CrossRef]
  15. Holling, C.S. Engineering resilience versus ecological resilience. In Engineering within ecological constraints; Schulze, P.C., Ed.; National Academy Press, Washington, 1996; Volume 31, p. 32.
  16. Kefi, S.; Rietkerk, M.; Alados, C.L.; et al. Spatial vegetation patterns and imminent desertification in Mediterranean arid ecosystems. Nature 2007, 449, 213–217. [Google Scholar] [CrossRef] [PubMed]
  17. Knowlton, N. Thresholds and multiple stable states in coral reef community dynamics. American Zoologist 1992, 32, 674–682. [Google Scholar] [CrossRef]
  18. Knowlton, N. The future of coral reefs. Proceedings of the National Academy of Sciences 2001, 98, 5419–5425. [Google Scholar] [CrossRef] [PubMed]
  19. Krakauer, D.C. Emergent engineering: Reframing the grand challenge for the 21st century. In Worlds Hidden in Plain Sight; SFI Press: Santa Fe, New Mexico, 2019; pp. 349–355. [Google Scholar]
  20. Lagerstrom, K.; et al. From coral reefs to Joshua trees: What ecological interactions teach us about the adaptive capacity of biodiversity in the Anthropocene. 2022. Phil. rans. R. Soc. B. 2022, 377, 20210389. [Google Scholar] [CrossRef]
  21. MacArthur, R. Species packing and competitive equilibrium for many species. Theoretical population biology 1970, 1, 1–11. [Google Scholar] [CrossRef]
  22. Maestre, F.T.; Martin, N.; Daez, B.; Lopez-Poma, R.; Santos, F.; Luque, I.; Cortina, J. Watering, fertilization, and slurry inoculation promote recovery of biological crust function in degraded soils. Microbial Ecology 2022, 52, 365–377. [Google Scholar] [CrossRef]
  23. Maestre, F.T.; Solé, R.; Singh, B.K. Microbial biotechnology as a tool to restore degraded drylands. Microbial biotechnology 2017, 10, 1250–1253. [Google Scholar] [CrossRef] [PubMed]
  24. Mallon, C.A.; Van Elsas, J.D.; Salles, J.F. Microbial invasions: The process, patterns, and mechanisms. Trends in microbiology 2015, 23, 719–729. [Google Scholar] [CrossRef] [PubMed]
  25. Martin, P.V.; Bonachela, J.A.; Levin, S.A.; Muñoz, M.A. Eluding catastrophic shifts. Proceedings of the National Academy of Sciences 2015, 112, E1828–E1836. [Google Scholar]
  26. Maull, V.; Solé, R. Network-level containment of single-species bioengineering. Phil. rans. R. Soc. B. 2022, 377, 20210396. [Google Scholar] [CrossRef] [PubMed]
  27. Montoya, J.M.; Pimm, S.L.; Sole, R.V. Ecological networks and their fragility. Nature 2006, 442, 259–264. [Google Scholar] [CrossRef] [PubMed]
  28. Odum, H.T. Scales of ecological engineering. Ecological Engineering 1996, 6, 7–19. [Google Scholar] [CrossRef]
  29. Peixoto, R.S.; Sweet, M.; Villela, H.D.; Cardoso, P.; Thomas, T.; Voolstra, C.R.; Hej, L.; Bourne, D.G. Coral probiotics: Premise, promise, prospects. Annual review of animal biosciences 2021, 9, 265–288. [Google Scholar] [CrossRef]
  30. Peñuelas, J.; Sardans, J.; Estiarte, M.; et al. Evidence of current impact of climate change on life: A walk from genes to the biosphere. Global change biology 2013, 19, 2303-2338.Piaggio, A.J.; Segelbacher, G.; Seddon, P.J.; et al. Is it time for synthetic biodiversity conservation? Trends in ecology and evolution 2017, 32, 97-107.
  31. Rocha, J.C.; Peterson, G.; Bodin, O.; Levin, S. Cascading regime shifts within and across scales. Science 2018, 362, 1379–1383. [Google Scholar] [CrossRef]
  32. Sabarinatham, K.G.; Gomathy, M.; Kumar, D.A.; Kannan, R.; Aiyanathan, E.A. Cyanobacteria-Mediated Bioremediation of Problem Soils. Microbial Rejuvenation of Polluted Environment. Microorganisms for Sustainability, vol 25. Springer, Singapore, 2021.
  33. Scanlon, T.M.; Caylor, K.K.; Levin, S.A.; Rodriguez-Iturbe, I. Positive feedbacks promote power-law clustering of Kalahari vegetation. Nature 2007, 449, 209–212. [Google Scholar] [CrossRef]
  34. Scheffer, M. Critical transitions in nature and society; Princeton U. Press: Princeton, 2009. [Google Scholar]
  35. Solé, R.; Bascompte, J.; Valls, J. Nonequilibrium dynamics in lattice ecosystems: Chaotic stability and dissipative structures. Chaos 1992, 2, 387–395. [Google Scholar] [CrossRef]
  36. Solé, R.; Bascompte, J. Self-organization in complex ecosystems; Princeton U. Press: Princeton, USA, 2007. [Google Scholar]
  37. Solé, R. Phase Transitions; Princeton University Press: Princeton, 2011. [Google Scholar]
  38. Solé, R. Bioengineering the biosphere? Ecol. Complex. 2015, 22, 40–49. [Google Scholar] [CrossRef]
  39. Solé, R.V.; Montanez, R.; Duran-Nebreda, S. Synthetic circuit designs for earth terraformation. Biology Direct 2015, 10, 1–10. [Google Scholar] [CrossRef] [PubMed]
  40. Solé, R.V.; Montanez, R.; Duran-Nebreda, S.; Rodriguez-Amor, D.; Vidiella, B.; Sardanyés, J. Population dynamics of synthetic terraformation motifs. Royal Society Open Science 2018, 5, 180121. [Google Scholar] [CrossRef] [PubMed]
  41. Solé, R.; Levin, S. Ecological complexity and the biosphere: The next 30 years. Philosophical Transactions of the Royal Society B 2022, 377, 20210376. [Google Scholar] [CrossRef] [PubMed]
  42. Strogatz, S.H. Nonlinear dynamics and chaos: With applications to physics, biology, chemistry, and engineering; CRC press: 2018.
  43. Van Oppen, M.J.; Oliver, J.K.; Putnam, H.M.; Gates, R.D. Building coral reef resilience through assisted evolution. Proceedings of the National Academy of Sciences 2015, 112, 2307–2313. [Google Scholar] [CrossRef]
  44. van Oppen, M.J.; Blackall, L.L. Coral microbiome dynamics, functions and design in a changing world. Nature Reviews Microbiology 2019, 17, 557–567. [Google Scholar] [CrossRef]
  45. Vidiella, B.; Sardanyes, J.; Solé, R. Exploiting delayed transitions to sustain semiarid ecosystems after catastrophic shifts. Journal of The Royal Society Interface 2018, 15, 20180083. [Google Scholar] [CrossRef]
  46. Vidiella, B.; Sardanyes, J.; Solé, R. Synthetic soil crusts against green-desert transitions: A spatial model. Royal Society open science 2020, 7, 200161. [Google Scholar] [CrossRef]
  47. Vila, J.C.; Jones, M.L.; Patel, M.; Bell, T.; Rosindell, J. Uncovering the rules of microbial community invasions. Nature ecology and evolution 2019, 3, 1162–1171. [Google Scholar] [CrossRef]
Preprints 88250 g001
Figure 1. Targeting endangered ecosystems using synthetic microbiomes. Drylands (a,b) and coral reefs (c,d) are two well-known examples of ecosystems threatened by global warming and other Anthropogenic drivers. They both involve complex microbiomes (c,d) that is key to preserve their resilience and biodiversity and are also the target for potential engineering strategies. One way of modelling the potential impact of such strategy is the use of a resource-consumer network (e) where two sets R and C indicate available resources and those species exploiting them (links indicate such interactions and the radius of the circles would scale as population size). Figure (d) adapted from (Van Oppen and Blackall, 2019).
Figure 1. Targeting endangered ecosystems using synthetic microbiomes. Drylands (a,b) and coral reefs (c,d) are two well-known examples of ecosystems threatened by global warming and other Anthropogenic drivers. They both involve complex microbiomes (c,d) that is key to preserve their resilience and biodiversity and are also the target for potential engineering strategies. One way of modelling the potential impact of such strategy is the use of a resource-consumer network (e) where two sets R and C indicate available resources and those species exploiting them (links indicate such interactions and the radius of the circles would scale as population size). Figure (d) adapted from (Van Oppen and Blackall, 2019).
Preprints 88250 g001
Preprints 88250 g002
Figure 2. The simplest case study of the general RC model would include two resources and two strains, one of which (the engineered one) reduces the loss of R 2 . The populations of the wild type and synthetic strains are indicated by N w and N s , respectively. The synthetic would be obtained by a small engineering of the initial strain, here indicated as an open circle (indicating for example an engineered plasmid).
Figure 2. The simplest case study of the general RC model would include two resources and two strains, one of which (the engineered one) reduces the loss of R 2 . The populations of the wild type and synthetic strains are indicated by N w and N s , respectively. The synthetic would be obtained by a small engineering of the initial strain, here indicated as an open circle (indicating for example an engineered plasmid).
Preprints 88250 g002
Preprints 88250 g003
Figure 3. Population dynamics of engineered ecosystems where a synthetic strain is inoculated at τ 1 = 800 . Thick orange, blue and green represent wild type, synthetic and the other species, respectively. In (a) we have η w t = η s y n which gives coexistence. In contrast, if η s y n = η w t + 0.1 η w t (b), a switch occurs, with the exclusion of the resident wild type by the synthetic. Finally, in (c) the growth rate of the synthetic is a 10 % smaller than the wild type due the extra metabolic load, leading to an extinction of the introduced strain after a transient time.
Figure 3. Population dynamics of engineered ecosystems where a synthetic strain is inoculated at τ 1 = 800 . Thick orange, blue and green represent wild type, synthetic and the other species, respectively. In (a) we have η w t = η s y n which gives coexistence. In contrast, if η s y n = η w t + 0.1 η w t (b), a switch occurs, with the exclusion of the resident wild type by the synthetic. Finally, in (c) the growth rate of the synthetic is a 10 % smaller than the wild type due the extra metabolic load, leading to an extinction of the introduced strain after a transient time.
Preprints 88250 g003
Preprints 88250 g004
Figure 4. Statistical distributions of population changes for different scenarios, as defined by the population change Δ ( N j ) = N j ( τ 1 ) − N j ( τ 2 ) after the intervention (deployment of the synthetic) has been performed. Population expansion or shrink correspond to Δ ( N j ) < 0 and Δ ( N j ) > 0 , respectively). The graph displays the accumulation of occurrences observed throughout 500 iterations. Graphs (a–c) correspond to the symmetric scenario where the synthetic strain replicates the wild type in terms of the resource-consumer interaction matrix. Distribution asymmetries are observed: values of skewness of 4.5, 3.2, 4, 1.6, 1 and 6.3 apply to 4a to 4f respectively. Kurtosis values (42.2, 37.7, 35.7, 52.6, 32.8 and 160) are also measured. Conversely, graphs (d–f) represent the non-symmetric scenario where the R-C interaction matrix of the synthetic strain differs from that of the wild type. These statistical distributions provide valuable insights into the dynamics of population changes and highlight the statistically positive effects of the synthetic intervention on the community.
Figure 4. Statistical distributions of population changes for different scenarios, as defined by the population change Δ ( N j ) = N j ( τ 1 ) − N j ( τ 2 ) after the intervention (deployment of the synthetic) has been performed. Population expansion or shrink correspond to Δ ( N j ) < 0 and Δ ( N j ) > 0 , respectively). The graph displays the accumulation of occurrences observed throughout 500 iterations. Graphs (a–c) correspond to the symmetric scenario where the synthetic strain replicates the wild type in terms of the resource-consumer interaction matrix. Distribution asymmetries are observed: values of skewness of 4.5, 3.2, 4, 1.6, 1 and 6.3 apply to 4a to 4f respectively. Kurtosis values (42.2, 37.7, 35.7, 52.6, 32.8 and 160) are also measured. Conversely, graphs (d–f) represent the non-symmetric scenario where the R-C interaction matrix of the synthetic strain differs from that of the wild type. These statistical distributions provide valuable insights into the dynamics of population changes and highlight the statistically positive effects of the synthetic intervention on the community.
Preprints 88250 g004
Preprints 88250 g005
Figure 5. Statistical distributions of population changes for different scenarios of random invaders. Histograms defined in Figure 4 caption. Graph (a) depicts random invaders with a positive effect over a given resource. Graph b) shows random invaders with no effect on any resource. Distribution asymmetries are observed: values of skewness of -7.4 and -9.6 apply to (a,b), respectively. Kurtosis values (115.1 and 145.2) are also measured.
Figure 5. Statistical distributions of population changes for different scenarios of random invaders. Histograms defined in Figure 4 caption. Graph (a) depicts random invaders with a positive effect over a given resource. Graph b) shows random invaders with no effect on any resource. Distribution asymmetries are observed: values of skewness of -7.4 and -9.6 apply to (a,b), respectively. Kurtosis values (115.1 and 145.2) are also measured.
Preprints 88250 g005
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.
Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.
Prerpints.org logo

Preprints.org is a free preprint server supported by MDPI in Basel, Switzerland.

facebook logotwitter logolinkedin logo
MDPI Initiatives
Important Links
Subscribe

Disclaimer

Terms of Use

Privacy Policy

© 2024 MDPI (Basel, Switzerland) unless otherwise stated