Prerpints.org logo
Preprint
Article

Optimization of Electron and Hole Transport Layer to Model A Lead-Free Inorganic Cs3Bi2I9 Based Perovskite Solar Cell and Investigating the Effects of Different Attributes on Device Performance

Altmetrics

Downloads

402

Views

241

Comments

0

A peer-reviewed article of this preprint also exists.

This version is not peer-reviewed

Submitted:

19 May 2023

Posted:

25 May 2023

You are already at the latest version

Alerts
Abstract
Research on the lead halide-based perovskite solar cells have obtained considerable interest in photovoltaic industry owing to their higher efficiency, easy manufacturing, light-weight and low cost. However, these lead halide-based solar cells are not suitable to manufacture commercially because of the toxicity of lead-based materials. In this context, a lead-free perovskite, cesium-bismuth iodide (Cs3Bi2I9) is considered as a potential alternative to the lead halide-based cell due to their non-toxicity and stability, but this perovskite cannot be matched with random hole transport layer (HTL) and electron transport layer (ETL) materials compared to lead halide-based perovskite because of their crystal structure and band gap. Therefore, in this study, performance comparison of different ideal HTL and ETL materials for Cs3Bi2I9 perovskite layer were studied using SCAPS-1D device simulation on the basis of open circuit voltage, short circuit current, power conversion efficiency (PCE) and fill factor (FF) as well as several novel PSC configuration model were designed that can direct for further experimental research for PSC device commercialization. Results from this investigation reveals that the maximum efficiency of 20.96% is obtained for the configuration ITO/WS2/Cs3Bi2I9­/NiO/Au with optimized parameters such as thickness 400 nm, band gap 2.1eV, absorber layer defect density 1012 cm-3, donor density of ETL 1018 cm-3 and the acceptor density of HTL 1020 cm-3.
Keywords: 
Subject: Engineering  -   Mechanical Engineering

1. Introduction

The consumption of power and energy is increasing with accelerated commercialization and industrialization[1]. The continuous utilization of conventional fuels such as natural gas, oils, hydrocarbon gas liquids, fossil fuels and the severe environmental effect for using these materials raises serious concerns about the research of alternate energy resources [2,3,4]. To replace the non-renewable energy resources and to fulfill the increasing energy demand in an environment friendly way, proper utilization of renewable energy sources is badly needed [5,6]. Solar energy stands out as a viable renewable energy resource among different potential renewable sources such as wind energy, geothermal energy, hydro power, ocean energy, bioenergy and tidal energy. In recent years, solar cell production is expanding significantly today as the cost of solar cells lowers. However, in order to compete with fossil fuels and transform into a substantial energy source, the expenses of solar cells must be minimized. Considerable initiatives have been taken to create novel cell materials, and recently, a new generation of perovskite solar cells (PSCs) has been established that shows satisfactory performances to go for commercialization. The PSC will most likely have a huge impact on the future solar cell industry due to the low cost of raw materials and the simple manufacturing method, and this kind of cell may also be competitive with natural gas [7].
The solar research field have been recently captured by organic-inorganic PSCs due to having exceptional and excellent properties such as high absorptivity, low atomic energy, improved dielectric constant, favorable deposition by solution processing technique, high electron mobility, high hole mobility, suitable with low manufacturing cost and low-temperature deposition than conventional silicon-based solar cells [8,9]. The efficiency and stability of perovskites solar cells show tremendous improvement such as in just 10 years perovskite solar cells developed from unstable 3% efficiency to stable 32% efficiency [10] and this improvement shows the potentiality of perovskite solar cells for which these solar cells have raised as strong competitor in the photovoltaic industry [11,12,13].
Thin-film PSC technology has improved due to the ease fabrication, energy gap adjustability, and the photon conversion efficiency (PCE) above 30% of lead (Pb)-compounded organic inorganic halide PSCs [14]. Although these achievements, the existence of emerging contaminants (Pb) that causes toxicity is the fundamental issues in the applications of lead-based PSCs and this problem is still a significant barrier to commercialization of PSCs [15]. Additionally, the perovskite layer's organic components contribute to the solar cell's instability. Similarly, the presence of organic elements in the perovskite layer causes instability of the solar cell. Therefore, lead based organic halide perovskite solar cells are not suitable and preferable for industrial application and commercialization. To eliminate the toxicity researchers have carried out experiments to develop lead-free perovskite material and to minimize instability utilizing inorganic materials have gathered attractive attention which can replace organic materials [16,17,18]. Ahmad et al. simulated a Cs3Bi2I9 based 2D PSC device where they employed TiO2 as ETL material and Spiro-MeOTAD as HTL material with gold as back contact[19]. Their simulation results revealed that their PSC device could gain an efficiency of 11.54% and their experimental results showed 1.66% efficiency for the similar configuration. Researchers are also working for stabilizing experimented PSC devices against several influencing natural factors such as moisture, temperature and dust. Hamukwaya et al.[20] experimented to investigate the performance after adding KI as additive with Cs3Bi2I9 perovskite layer. This mixing of KI caused the highest efficiency as 2.81% the Cs₃Bi₂I₉ perovskite layer highly stabilizes the resultant PSC device against humidity to the extent that it maintains 98% of the initial PCE after 90 days, which is suitable for solar cell applications.
Homo-valent component such as Ge2+ and Sn2+ can be a potential choice which can eliminate toxicity; however, these components decrease the stability of PSCs when it performs at ambient temperature [21,22,23]. For alternation of such materials different hetero-valent materials are tested in lab-based experiments to investigate their suitability and stability for using in perovskite layers and among those materials Bi3+ and Sb3+ which have stable +3 oxidation phase have gathered much attention[24]. Bi3+ have good optoelectronic properties as Pb2+ due to ionic radius and electronic structure similarities of these materials. Among different Bi halide-based materials Cs2Bi2I9 achieved the greatest interest due to its higher PCE and more stability than other Bi based perovskite materials [25,26]. Summary of different works on the PSC performance analysis are listed in Table 1.
Cs3Bi2I9 is a hybrid organic-inorganic perovskite material that has gained attention in the field of photovoltaics as a potential absorber layer in solar cells. This material has a range of advantages that make it an attractive candidate for this application. One of the significant advantages of Cs3Bi2I9 is its high absorption coefficient. This characteristic enables it to absorb light effectively across a broad range of the solar spectrum, which is essential for the efficient operation of solar cells. The high absorption coefficient of Cs3Bi2I9 is comparable to other well-known perovskite absorbers like MAPbI3 (methylammonium lead iodide). Another advantage of Cs3Bi2I9 is its high stability. Many perovskite materials are known to be unstable under ambient conditions, which can limit their practical applications. However, Cs3Bi2I9 has been shown to be highly stable under various environmental conditions, including humidity, light, and heat. This stability makes it an attractive option for use in real-world applications where stability is crucial. Cs3Bi2I9 also has high carrier mobility, which is a desirable property for efficient charge transport and collection in photovoltaic devices. Furthermore, this material has a direct bandgap, which is crucial for efficient light absorption and conversion into electrical energy in photovoltaic devices[24].
In this study, the simulation has been carried out in two steps, where the first step consists of comparison of suitable ETL and HTL materials with Cs3Bi2I9 absorber layer to find out the best configuration for which higher performance has been observed. In second step, the selected model has been optimized for improving its performance parameters such as Jsc, Voc, PCE and FF. To achieve the optimized system, around 45 models with different ETL and HTL materials have been performed. In this process, a best performance for ITO/WS2/Cs3Bi2I9/NiO/Au has been attained. For further improvement of this configuration, optimization of various adjustable attributes such as thickness and bandgap of absorber layer, defect density of absorber layer and charge carrier density of HTL and ETL materials has been done. After tuning input attributes, 20.96% of PCE has been obtained for this model.

2. Model development and perovskite solar cell structure

2.1. Numerical modeling

In order to construct any form of a practical solar cell, numerical models have become a crucial tool. Perovskite solar cells’ numerical modeling is a crucial technique for evaluating the validity of the proposed physical reasons and predicting the impact of physical modifications on cell performance [38]. Numerical modeling is required because perovskite solar cells are so complicated in their behavior [39].
Numerical simulation software offers useful information to select materials before experiment and commercialization. The One Dimension Solar Cell Capacitance Simulator (SCAPS-1D) program which is created by Burgelman et al. [40] can be used to do the numerical calculations of PSCs [41]. SCAPS-1D software solves the charge carrier continuity Equations such as hole continuity Equation 1 and electron continuity Equation 2, the semiconductor Poisson Equation 3 in one direction, total charge transport Equation 4, electron transport Equation 5, hole transport Equation 6 and optical absorption coefficient Equation 7.
d n p d t = G n − n p − n p 0 τ n + n p μ n d ξ d x + μ n ξ d n p d s + D n d 2 n p d x 2
d n n d t = G p − p n − p n 0 τ p + p n μ p d ξ d x + μ p ξ d n n d s + D p d 2 p n d x 2      
d 2 ∅ ( x ) d x 2 = q ϵ o ϵ r p x − n x + N D − N A + − 0.3 ρ p − − 0.3 ρ n
J = J n + J p        
J n = D n d n d x + μ n n d ϕ d x
J p = D p d p d x + μ p p d ϕ d x    
α λ = A + B h v h v − E g
where, ξ is the electric field, q denotes electrical charge whose typical value is considered as 1.602 × 10 − 19 C, ϵ o is the vacuum absolute permittivity and ϵ r is the semiconductor relative permittivity, ND and NA represent donor doping density and acceptor doping density respectively, p(x) and n(x) are carrier density of hole and electron, -0.3 ρ p is the defect density of hole and -0.3 ρ n is the defect density of electron, Gn and Gp indicates electron generation rate and hole generation rate respectively, Jn and Jp are current density and hole current density of electron, respectively, μ n and μ p are electron and hole mobilities, τ n and τ p represents lifetime of electrons and holes respectively, Dp and Dn represents diffusion coefficient of free hole and electron. v represents optical frequency, A and B depicts arbitrary constant while Eg represents bandgap, h represents plank constant and α λ depicts absorption coefficient. More information about these equations can be learned from somewhere [42,43,44,45,46].

2.2. PSC structure and material charateristics

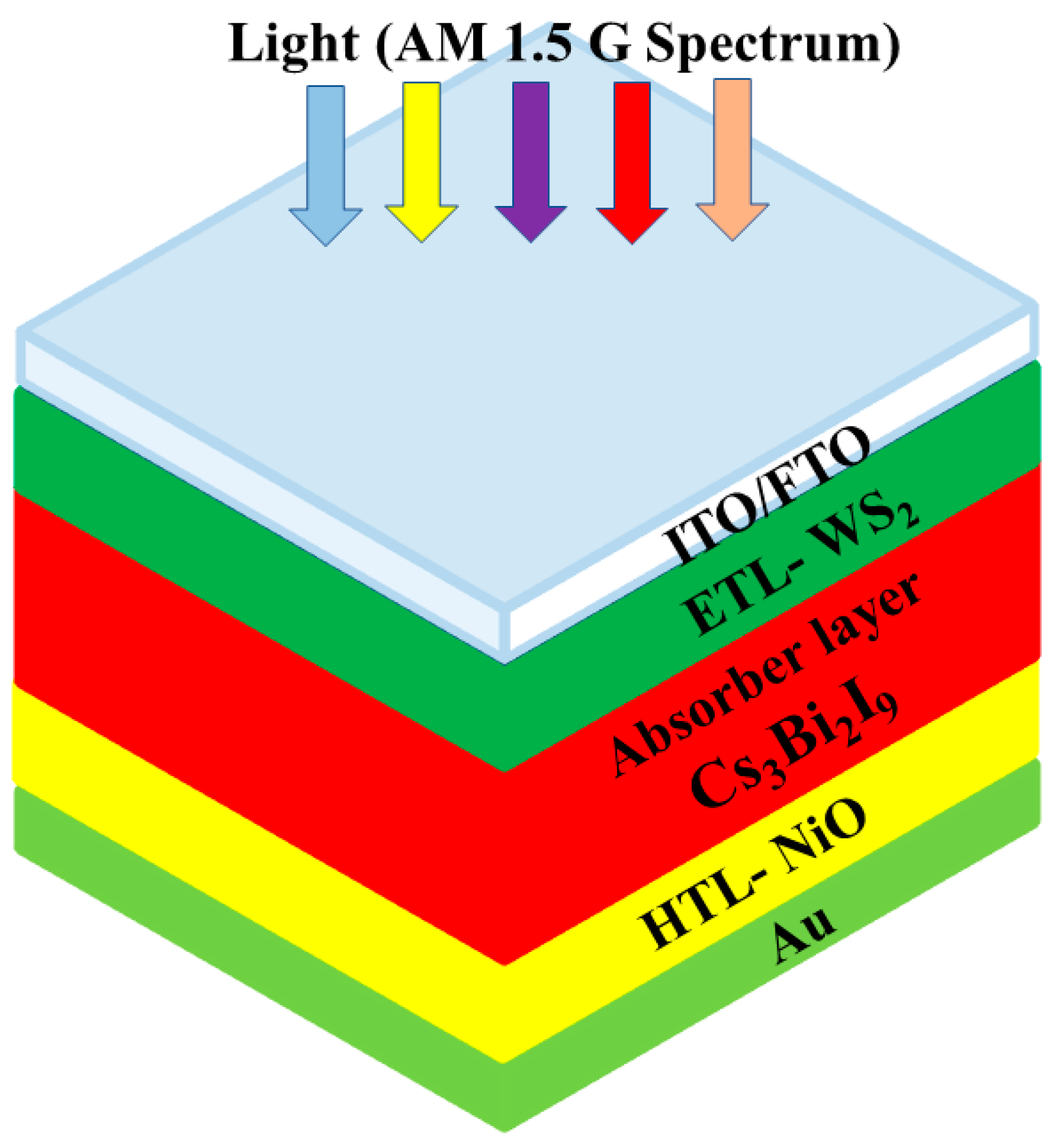
2.2.1. PSC structure

The device structure in this paper is Au/HTL/absorber layer/ETL/ITO/glass, where Au is employed as back contact having work function of 5.1eV and Cs3Bi2I9 is applied as absorber or perovskite layer. The simulation is carried out with different ETLs and HTLs to obtain a novel optimized configuration. The ETLs that are simulated in this study include TiO2, PCBM, WS2, IGZO and C60 whereas CuO, Cu2O, PEDOT:PSS, P3HT, CuSCN, CuSbS2, NiO, Spiro-OMeTAD and CuI are applied as hole transport layer material.
Figure 1 shows a typical model of PSC with different layers such as ITO, ETL, absorber layer and HTL.
The band diagram of our selected configuration is showed in Figure 2, from where it can be seen that the blue curve depicts the conduction band line and red curve shows the valence band line.

2.2.2. Physical input parameters and methodology

The AM1.5 illumination spectrum is used by default in this study. The incident light power (Ps) and temperature are fixed at 1000 W/m2 and 300 K, respectively. In every layer, the thermal velocities of the electrons and holes are fixed at 107 cm/s. The absorption co-efficient ( α ) of ETL and HTL layers are determined in SCAPS-1D through Equation 8 [47], like in many works on PSCs,
α = A a √ ( h v − E g )    
where, Aa is a layer-dependent pre-factor in the simulation. The application of interface defects has schemed the design more realistic and assisted to predict the experimental behavior of the solar cell model.
PSC device investigation has been carried out in two different steps where the first step includes building up a PSC device configuration with suitable HTL and ETL for Cs3Bi2I9 absorber layer. Different input attributes for nine HTL materials have been listed in Table 2 and input parameters for five ETL materials has been listed in Table 3. With these various ETL and HTL materials 45 different configurations have been simulated. After scrutinized comparison, it was found that when WS2 as ETL and NiO as HTL were applied as charge transporting layers then the configuration (ITO/WS2/Cs3Bi2I9/NiO/Au) have showed best results with higher performance parameters. In second stage, the selected model (ITO/WS2/Cs3Bi2I9/NiO/Au) has been optimized by tuning bandgap and thickness of absorber layer, defect density of absorber layer and carrier density of ETL and HTL.

3. Results and discussion

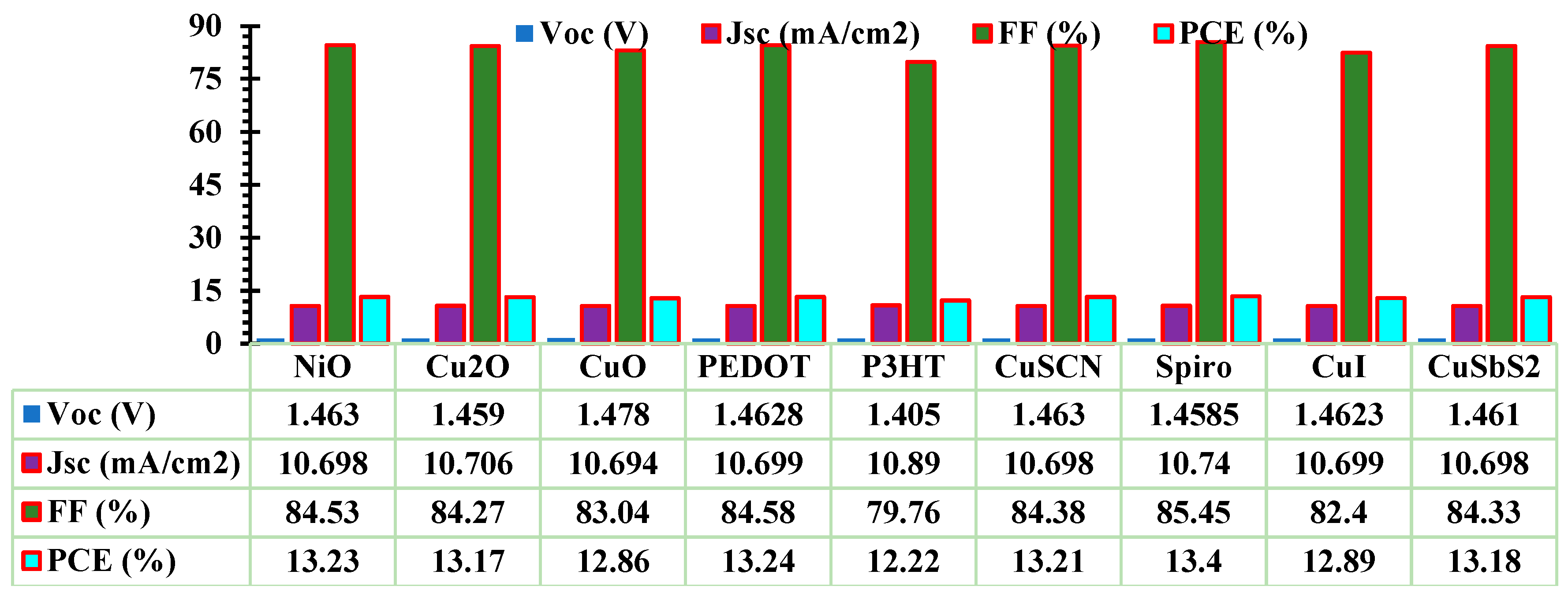
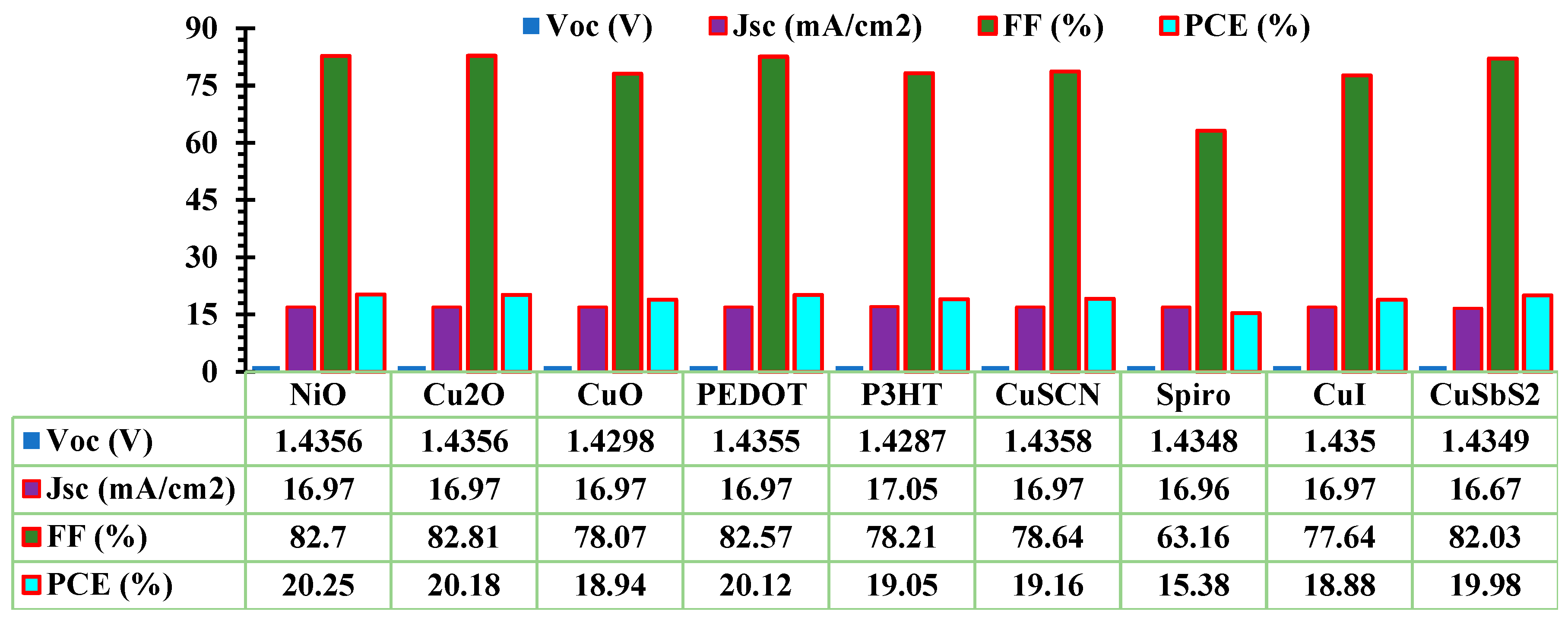
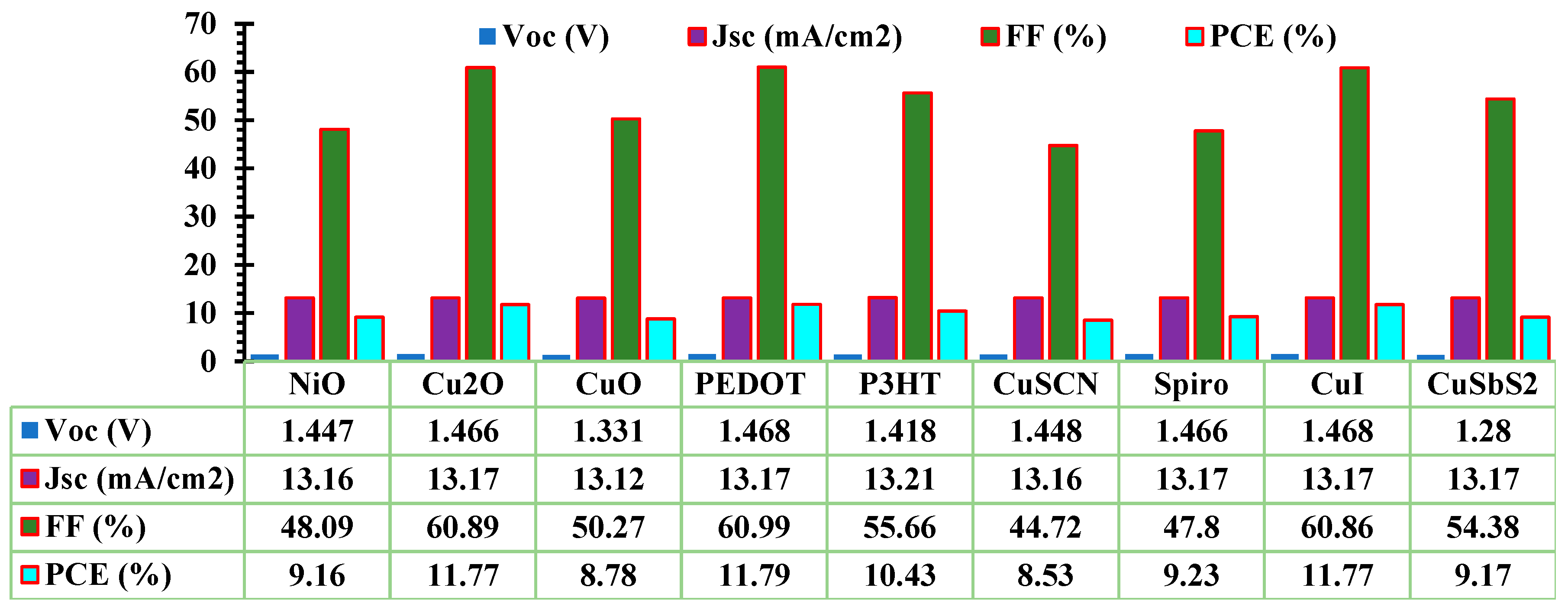
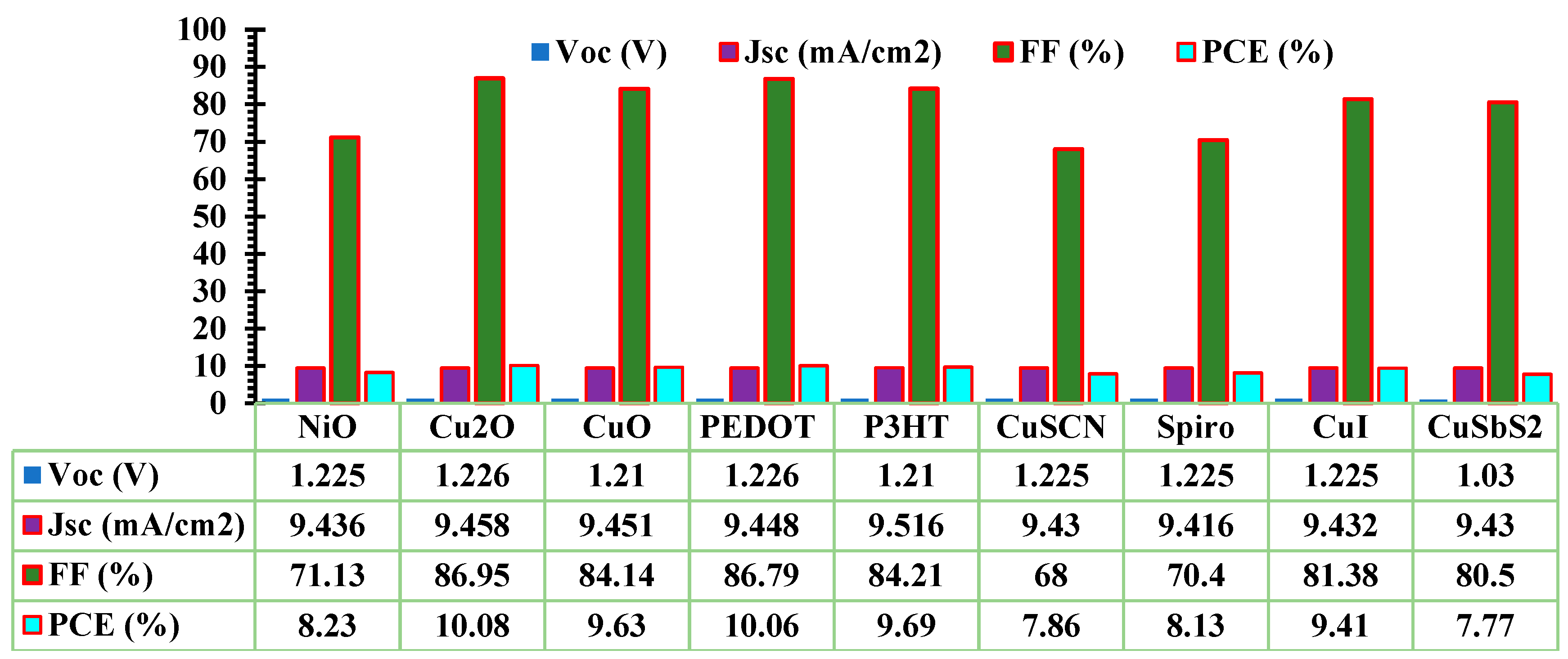
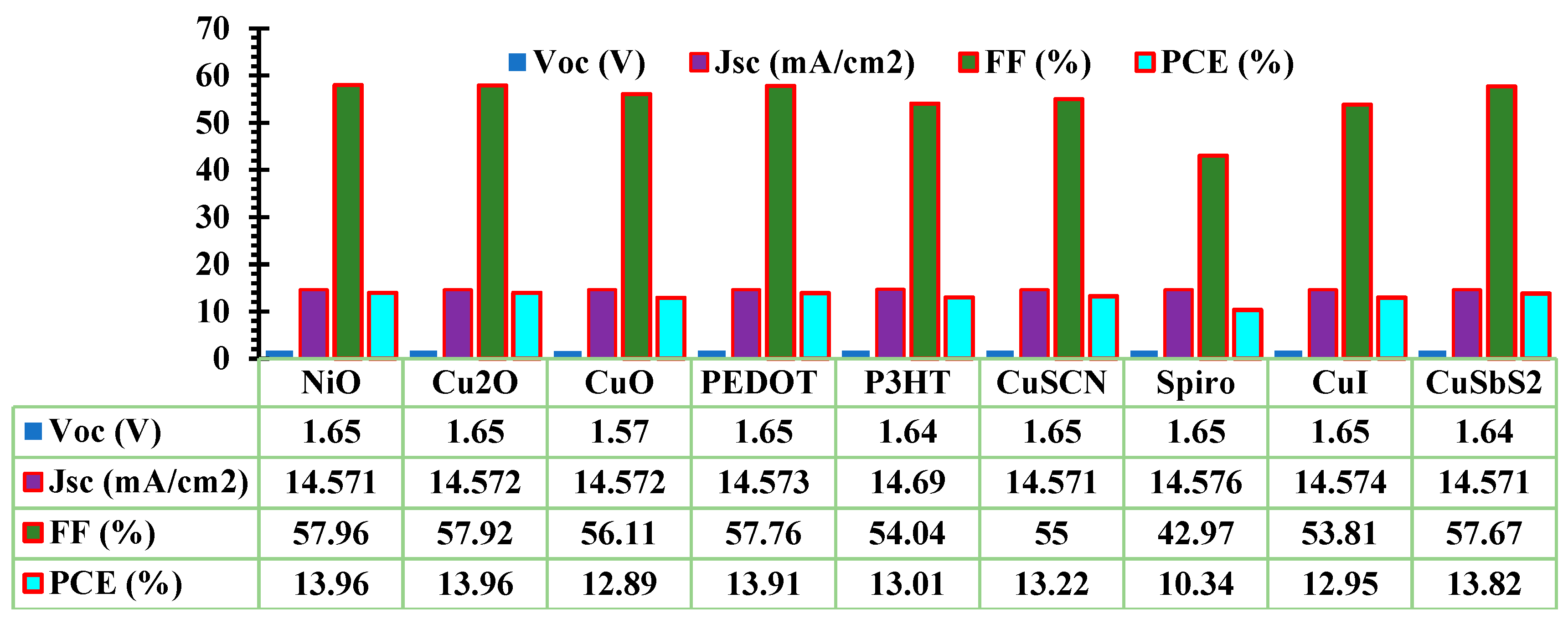
3.1. Optimization of ETL and HTL

In this study, Cs3Bi2I9 was selected as absorber layer due to its non-toxicity and better optoelectronic parameter, however it’s hard enough to match this absorber layer with appropriate ETL and HTL due to band structure of Cs3Bi2I9. To obtain the best performance, simulation of the configuration (ITO/ETL/Cs3Bi2I9/HTL/Au) for five different ETL materials and nine different HTL materials have been carried out.
Figure 3 shows performance parameters of different PSC configurations for different HTLs where PCBM and Cs3Bi2I9 were applied as ETL and absorber layer respectively. In a similar way, Figure 4 shows performance parameters for WS2 ETL, Figure 5 shows comparison for IGZO ETL, Figure 6 reveals performance comparison for C60 ETL as well as comparison for TiO2 ETL can be observed in Figure 7.
After scrutinized comparison, it can be observed from these figures that when NiO and WS2 were applied as HTL and ETL, respectively, the configuration ITO/WS2/Cs3Bi2I9/NiO/Au shows best performance characteristics. The optimized characteristics are given in From Figure 4, Figure 5, Figure 6 and Figure 7, it can be observed that the maximum 20.25% PCE can be achieved when WS2 and NiO were employed as ETL and HTL material respectively with Cs3Bi2I9 perovskite layer. Cu2O also showed extraordinary performance with WS2 ETL and Cs3Bi2I9 absorber layer. However, as the configuration ITO/WS2/Cs3Bi2I9/NiO/Au shows best performance so further optimization was carried out for this model.
Table 4 for which improved performance characteristics were obtained. From Figure 4, Figure 5, Figure 6 and Figure 7, it can be observed that the maximum 20.25% PCE can be achieved when WS2 and NiO were employed as ETL and HTL material respectively with Cs3Bi2I9 perovskite layer. Cu2O also showed extraordinary performance with WS2 ETL and Cs3Bi2I9 absorber layer. However, as the configuration ITO/WS2/Cs3Bi2I9/NiO/Au shows best performance so further optimization was carried out for this model.

3.2. Effect of absorber layer thickness

The light-absorbing layer thickness has a great impact on the performance of PSCs. The layer needs an optimized thickness for the collection of solar radiation basically to collect photons and facilitates the electron and hole pair generation. The photon absorption density drops hence the efficiency when there is a decrease in layer thickness from the optimized value [68]. And with the augmentation of thickness the photon absorption falls down because of the recombination of electron hole pair [69]. In this paper, the thickness of Cs3Bi2I9 was varied from 400 to 5000 nm for getting optimized thickness for the model. There was change in VOC, JSC, FF and PCE with the variation in absorber layer thickness. These changes have been graphically represented on the Figure 8.
Firstly, it has been observed that with the extension of absorber layer thickness, the VOC decreases from 1.4368 to 1.4279 V. The reason behind this is the recombination of charge carrier for their longer travel path. But the JSC has been increased with the increase in absorber layer thickness. This is because of the rise in the spectral response when wavelength is longer. On the contrary the FF get reduced from 84.85% to 72.06% and the reason is the enhancement of series resistance and might be because of the charge carrier recombination along with the resistant losses. The maximum value of PCE was found 20.59% for the thickness of 400 nm which was taken as optimum thickness. For further augmentation of thickness there was drop in PCE. This is because of the charge pathway resistance and enhanced radiative recombination [70].

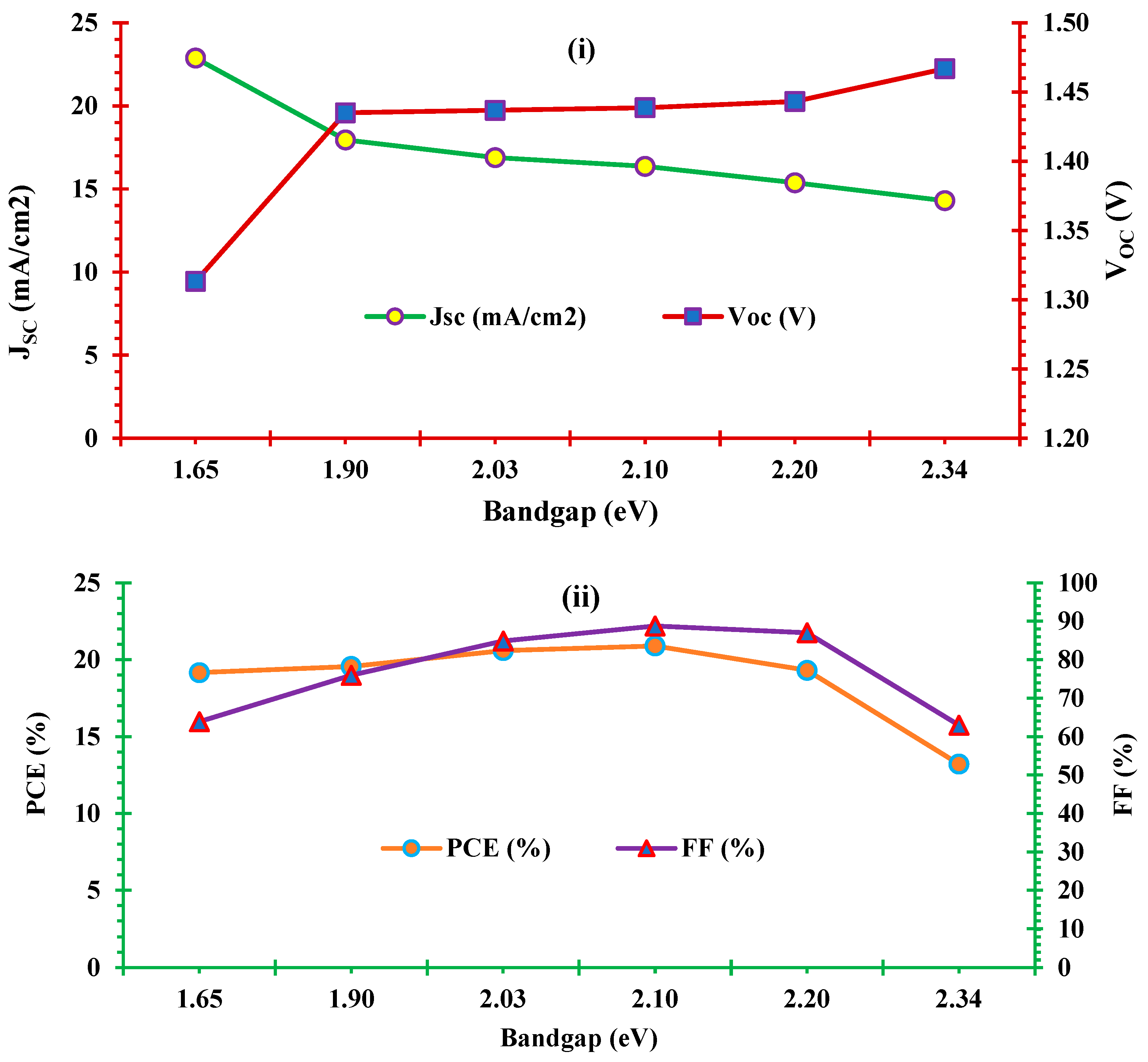
3.3. Effect of absorber layer band gap

The absorber layer band gap is an important parameter for the absorber layer, and it has a major impact on the effectiveness of the PSCs. In this regard, the tunability is the most important property of PSCs. The energy gap of perovskite absorber is tuned from 1.65 eV to 2.34 eV to investigate the performance of the PSC. Figure 9 reported that the maximum value of VOC 1.4669V is obtained at 2.34 eV, JSC of 22.88 mA/cm2 at 1.65 eV, and the maximum PCE and FF of the device were found 20.9% and 88.79%, respectively at 2.1 eV.
The FF and PCE increased from 63.87% to 88.79% and 19.16% to 20.9% with the augmentation of bandgap from 1.65 to 2.1 eV. After there was a decrease in FF and PCE with increase in band gap because of lowering the band gap increases the number of electrons but the problem is the energy of the electrons wasted as heat energy. On the other hand, higher the band gap the generation of electrons drops for some of the photon’s higher energy [71]. The optimum value of bandgap was taken 2.1 eV for the maximum PCE of 20.9%.

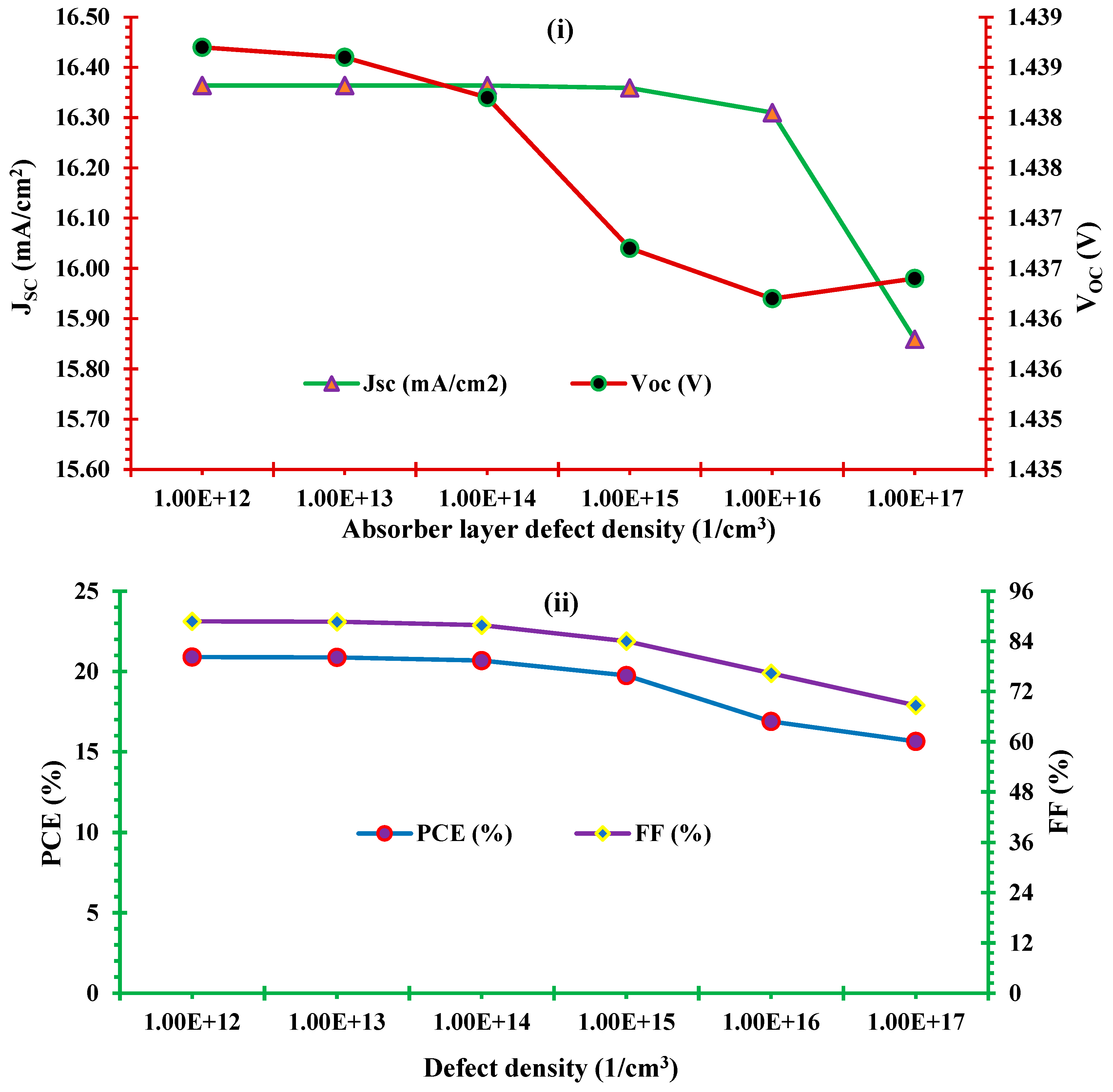
3.4. Effect of absorber layer defect density

In order to attain the stable PV output parameters, the proper amount of defect density is important. The defect density impacts directly on the recombination and generation of electron hole pairs which also has an impact on the efficiency of the PSCs [72]. Defect density depends on the quality of the absorber layer. If the quality is poor, then this causes higher defect density. For this reason, recombination of electron hole pair increases hence reduce the efficiency of the perovskite film.
And this recombination rate depends on the diffusion length, which is affected by the bulk defect density of the PSC. Shockley-Read-Hall (SRH) recombination is the most important type of recombination in PSCs, the calculation of the diffusion length can be done by the trap assisted SRH recombination model [73]. Following two Equations (9 and 10) is used to describe SRH recombination.
R S R H = n p − n i 2 π p + n + 2 n i cosh ⁡ E i − E t k T      
τ = 1 σ × N t × V t h
where, τ represents the life time of charge carriers, σ is the capture cross section of charge carriers, Nt is the defect density of the perovskite absorber layer, Vth is the thermal velocity of charge carriers.
The diffusion length, L = D τ , where D = k T e μ . Here, D refers to the diffusion coefficient and τ refers to the lifetime of minority carriers. In addition to that k denotes as Boltzmann’s constant, e refers to the charge of electron, T refers to the temperature, and µ denotes as mobility of charge carrier.
The defect density has an impact on the value of VOC by the following Equation 11.
V o c = k T q ln ⁡   J s c J o + 1
where, JO and JSC represent the recombination current density and short-circuit current density, respectively.
In order to get the optimum defect density, Nt of the absorber layer on the PSCs performance is analyzed by taking the values from 1012 cm-3 to 1017 cm-3. Figure 10 shows with the increase in defect density all the photovoltaic parameters decrease. The VOC drops from 1.4387 V to 1.4364 V and the Jsc from 16.364 to 15.859 mA/cm2. A high density of defects can lead to a decrease in VOC due to the increase in recombination. In devices with high defect densities, the recombination rate becomes dominant, leading to a decrease in VOC. In addition, the increase in defect density can lead to an increase in the trap-assisted recombination rate, which can also reduce the VOC of the device. The values PCE and FF remains almost similar up to the defect density of 1012 cm-3 to 1014 cm-3 and reduce significantly after 1015 cm-3. Therefore, the optimal defect density is taken as 1012 cm-3. The maximum PCE and FF is found to be 20.9% and 88.79% respectively for the defect density of 10-12 cm-3.

3.5. Effect of carrier density

The doping of ETL and HTL can be carried out using one of the two methods. Minority carriers can be used to accomplish the doping rate., however this method dramatically reduces the photovoltaic characteristics. On the other hand, most carriers with greatly improved PV characteristics can also achieve it. PSC performance will be improved with an intermediate level of doping density.

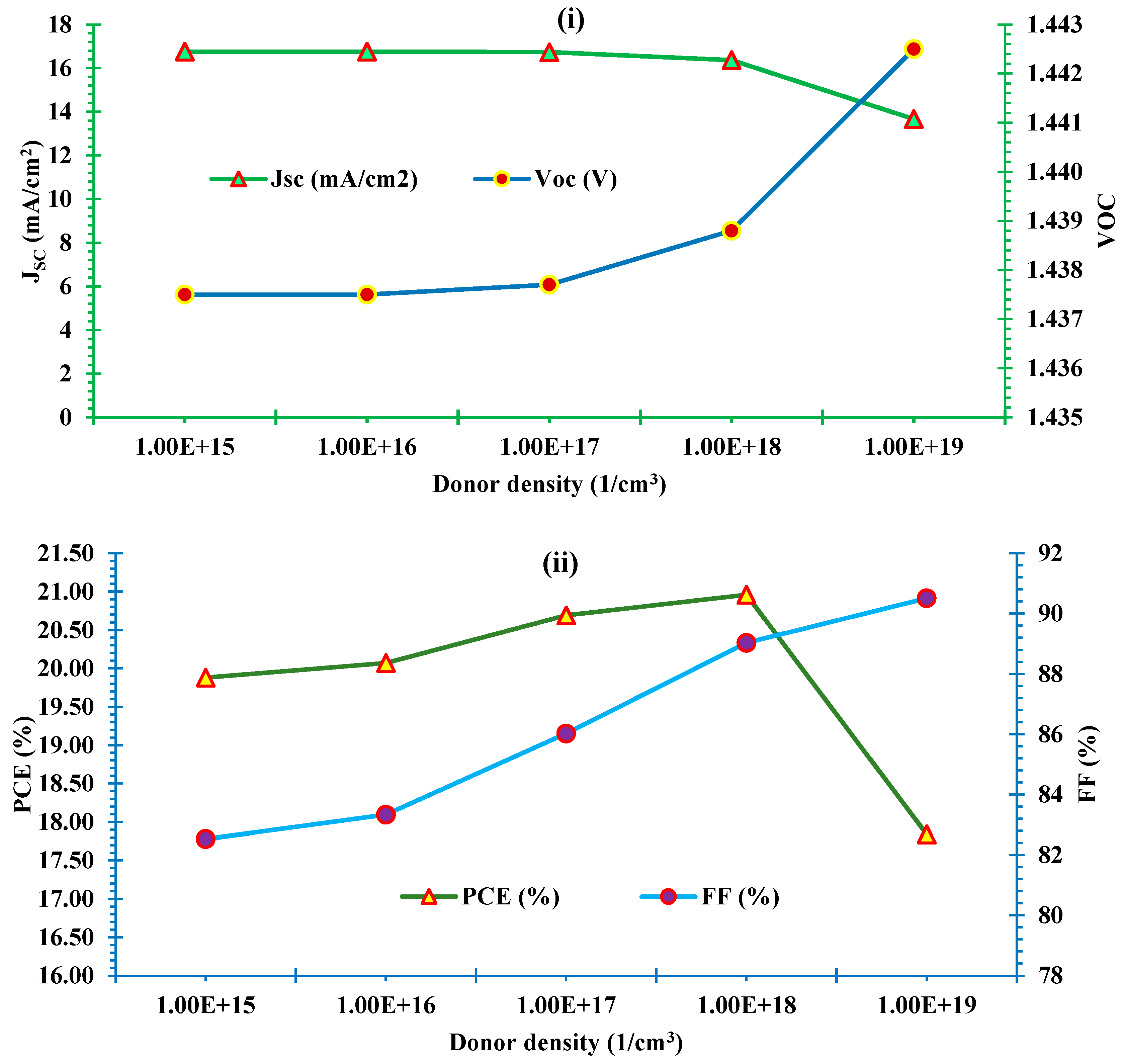
3.5.1. Effect of donor density of ETL

In order to find the best suitable doping concentration of ETL, the donor density for WS2 was enhanced from 1015 cm-3 to 1019 cm-3. The variation of Voc, Jsc, FF and the PCE was shown in Figure 6. The PCE and FF increased from 19.88% to 20.96% and 82.53% to 89.03%, respectively with the increase in donor density from 1015 to 1018 cm-3. The Jsc was almost constant with the variation and there was a sudden drop after 1018 cm-3. Additionally, the Voc enhanced from 1.43V to 1.44V with the rise in doping concentration. The optimal value of donor density was taken as 1018 cm-3 as the maximum PCE 20.96% was found at that value. The higher value of ND makes it easy to extract charge and transportation of charge at the ETL/perovskite interface [74].

3.5.2. Effect of acceptor density of HTL

The variation of acceptor density of HTL(NA) has a major influence on the performance of PSCs. Small amount of variation in acceptor concentration caused variation in the stability of the PSCs. To obtain the optimum value of NA, the NA was varied from 1016 cm-3 to 1020 cm-3. There was a small increase in Voc and Jsc from 1.4385V to 1.4388V and 16.359 mA/cm2 to 16.366 mA/cm2 with the increase in HTL acceptor density.
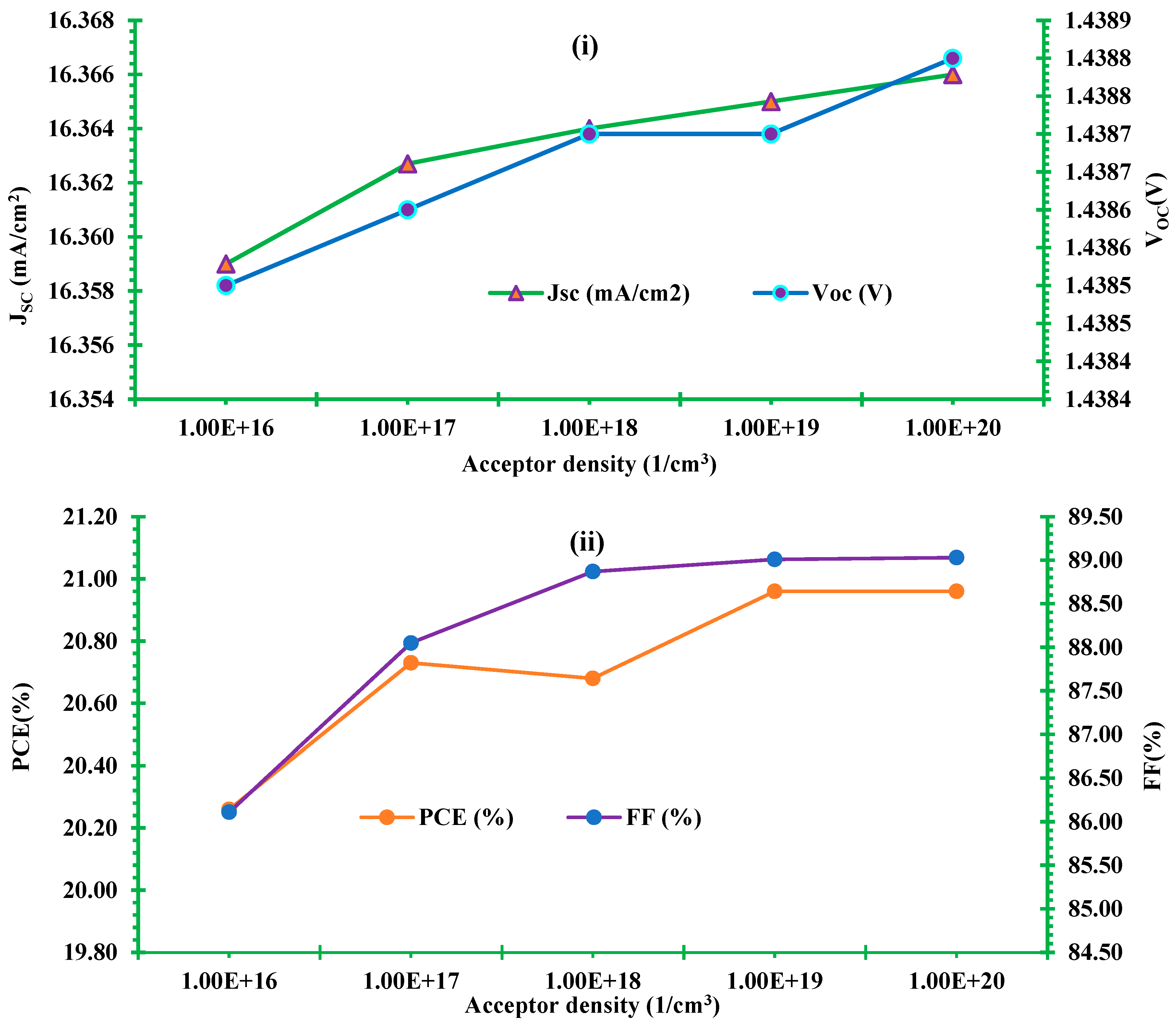
Preprints 74115 g012
Figure 12. Effect of acceptor density of HTL(NiO) on (i) Jsc, Voc, and (ii) FF, PCE.
Figure 12. Effect of acceptor density of HTL(NiO) on (i) Jsc, Voc, and (ii) FF, PCE.
Preprints 74115 g012
In addition to that the PCE and FF was improved from 20.26% to 20.96% and 86.11% to 89.03%, respectively with the augmentation of NA. Therefore, the optimum value of NA was taken 1020 cm-3 as the maximum PCE 20.96% was found at that value of acceptor concentration. The higher the NA, the production of interface electric field among the PSC layer is higher. It causes the increase in electric potential. However, this growth in PCE brings a higher recombination of charge carriers, which causes an increase in dopant concentration in the absorber layer[74,75].

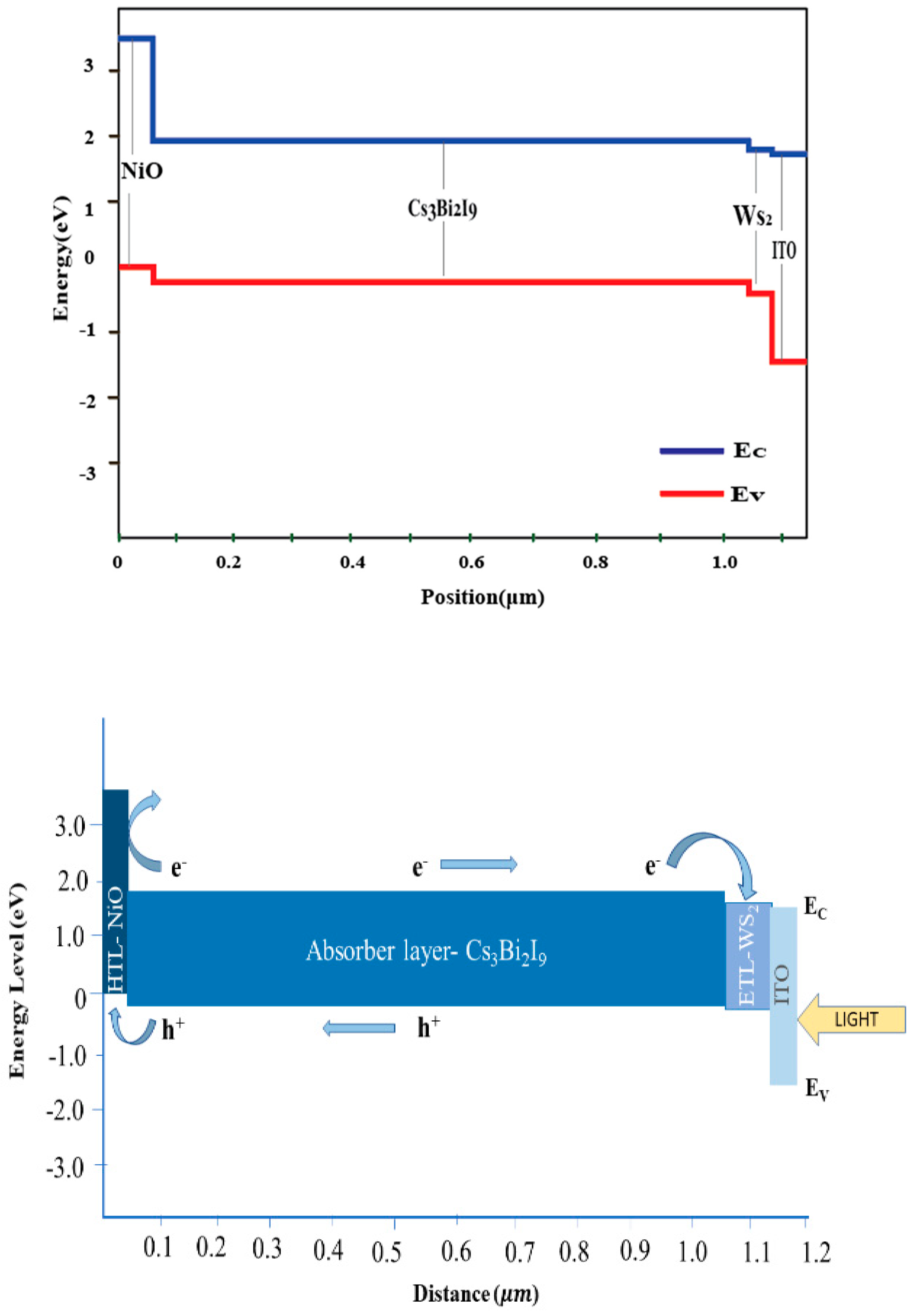
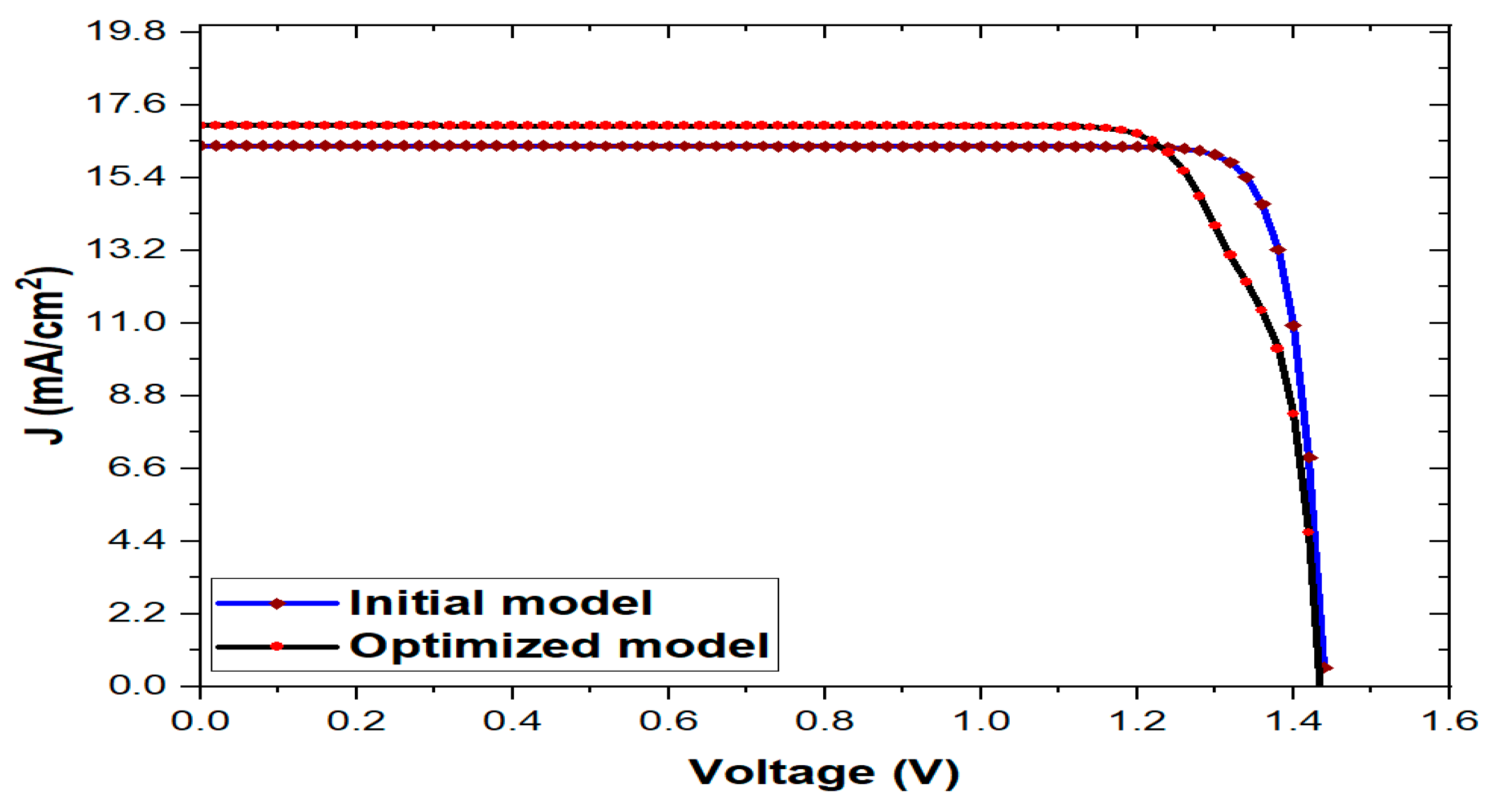
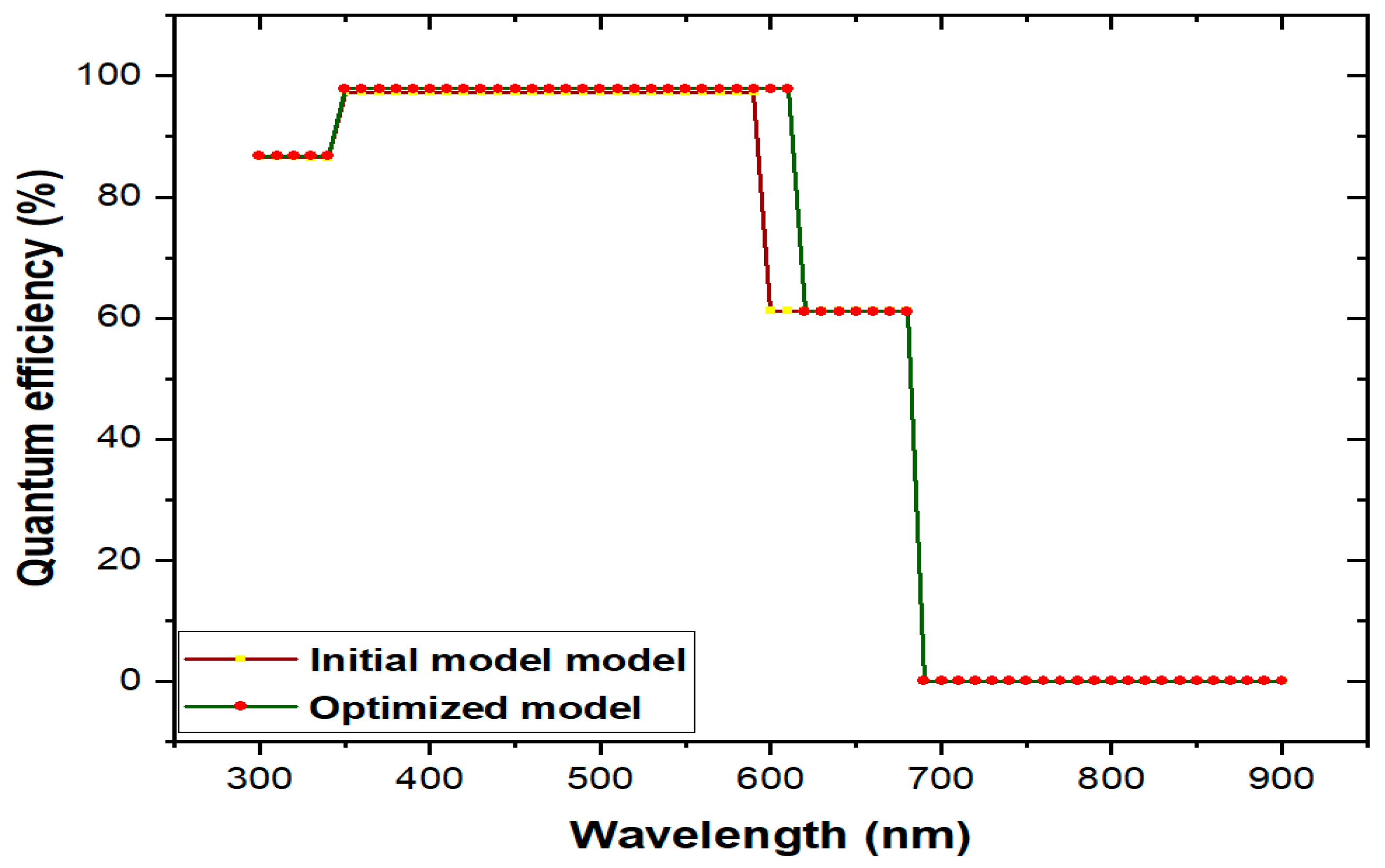
3.6. Comparison of initial and optimized final model

An improvement of current-voltage characteristic can be seen from Figure 13 for the optimized final model than the initial model. From the J-V characteristic curve, performance parameters of a PSC device can be understood. Here, from the J-V curve it can be observed that for the final optimized model an improved I-V curve is obtained than that of initial model.
Figure 14 depicts that the quantum efficiency in optimized final model is higher than the quantum efficiency of initial model. To obtain proper knowledge about quantum efficiency of the initial model and optimized final model, the wavelength was varied from 300 nm to 900 nm. In this wavelength range, the quantum efficiency varied due to tuning of different input attributes such as bandgap and thickness of absorber layer, carrier density and defect density of absorber material.
Quantum efficiency (QE) measures a solar cell's capacity to produce charge carriers from photon energy. From Figure 14, it’s clear that higher quantum efficiency can be obtained by tuning the PSC device in a proper way, thus higher amount of charge carriers can be produced from the absorber layer, that means generation rate would be increased. As a result, better performance can be obtained due greater generation of electron-hole pairs.

3.7. Comparison with literature

Organic spiro-OMeTAD can be fabricated in flexible and simple method of manufacture, therefore, is the material that is most frequently employed in the commercial and industrial sectors [76]. Despite this, the material is unsuitable for PSCs due to poor hole mobility, low conductivity, high manufacturing costs, and instability brought on by moisture, oxidation, and light. Additionally, TiO2 is another popular n-type material which is most commonly used as ETL. Despite having potential for excellent photovoltaic function, photo corrosion resistance, superior thermal stability, and the 3.2eV bandgap presents a difficulty [77]. PSC configurations with these materials and lead-based perovskite shows better characteristics that is clear from table, however due to their toxicity and instability problem further improvement are required through investigating new materials to replace these toxic and instable materials.
In this study, a novel PSC model was designed and simulated that shows better performance characteristics after optimization which can be seen from Table 5. Additionally, the selected perovskite material (Cs3Bi2I9) is considered much stable [85] which is introduced in the previous section. Therefore, the designed model in this present work can be considered for further experiment and commercialization.

4. Conclusions

In this paper, the modeling and performance analysis was done for the Cs3Bi2I9 based PSC using SCAPS-1D. The lead-free Cs3Bi2I9 was used as the absorber layer and the selection of this layer was based on the better stability and non-toxicity of this material. WS2, PCBM, C60, TiO2, IGZO were used as the ETL material and Cu2O, CuSCN, CuSbS2, P3HT, PEDOT:PSS, Spiro-OMeTAD, NiO, CuI, CuO was used as the HTL material. Total of 45 different PSC models were simulated with the combination of these HTL and ETL with the Cs3Bi2I9 based absorber layer. In addition, Au was taken as the back contact material. After the numerical simulation of these models, the combination of WS2-Cs3Bi2I9-NiO was found to give the maximum PCE of 20.25%. This combination is the novel model in which WS2 is used as ETL with Cs3Bi2I9 perovskite layer. In order to enhance the performance parameters (VOC, Jsc, FF, PCE) of the PSC and to achieve the maximum PCE, this model was scrutinized by varying the parameters like absorber layer thickness, band gap, defect density and carrier density of the ETL and HTL. The thickness of absorber layer was found to be 400 nm as optimum as PCE was maximum 20.59% at 400 nm. Thin absorber layer was found to give the good efficiency for the perovskite model. There was a significant change in the performance with the variation of absorber layer band gap. For the band gap of 2.1 eV, the PCE was the highest among others. There was found a significant increase in PCE from 20.59% to 20.9% for this bandgap. Though, the defect density has a major impact on the effectiveness of the PSCs, there was observed no such changes in the maximum efficiency with the variation of defect density. The maximum efficiency of 20.9% was found at the absorber layer dopant density of 1012 cm-3. There was a gradual increase in the performance parameters with the variation in carrier density. The maximum of 20.96 % PCE was obtained with the ETL donor density of 1018 cm-3 which was the best we found in our numerical analysis. Since, higher the ND makes the extraction of the charge easier to the ETL/ perovskite layer. The optimum acceptor density of HTL was found to be 1020 cm-3 and here also the maximum PCE was found to be 20.96%. Finally, after the full optimization the PSC attained a PCE of 20.96% which was initially found to be 20.25%.

Acknowledgement

Authors are thankful to Prof. M. Burgelman and his co-workers, Department of Electronics and Information Systems, University of Gent, Belgium for supporting with the SCAPS-1D simulation software.

References

  1. Fichera, A.; Samanta, S.; Datta Peu, S.; Das, A.; Sanowar Hossain, M.; Abdul Mannan Akanda, M.; et al. A Comprehensive Review on Recent Advancements in Absorption-Based Post Combustion Carbon Capture Technologies to Obtain a Sustainable Energy Sector with Clean Environment. Sustainability 2023, 15, 5827. [Google Scholar] [CrossRef]
  2. Azam, W.; Khan, I.; Ali, S.A. Alternative energy and natural resources in determining environmental sustainability: a look at the role of government final consumption expenditures in France. Environmental Science and Pollution Research 2022, 1, 1–17. [Google Scholar] [CrossRef]
  3. Tofu, D.A.; Wolka, K.; Woldeamanuel, T. The impact of alternative energy technology investment on environment and food security in northern Ethiopia. Scientific Reports 2022, 12, 1–11. [Google Scholar] [CrossRef]
  4. Das, A.; Peu, S.D. A Comprehensive Review on Recent Advancements in Thermochemical Processes for Clean Hydrogen Production to Decarbonize the Energy Sector. Sustainability 2022, 14, 11206. [Google Scholar] [CrossRef]
  5. Das, A.; Peu, S.D.; Hossain, M.d.S.; Akanda, M.A.M.; Salah, M.M.; Akanda, M.M.H.; et al. Metal Oxide Nanosheet: Synthesis Approaches and Applications in Energy Storage Devices (Batteries, Fuel Cells, and Supercapacitors). Nanomaterials 2023, 13, 1066. [Google Scholar] [CrossRef]
  6. Zafeiriou, E.; Sariannidis, N.; Tsiantikoudis, S.; Das, A.; Datta Peu, S.; Abdul Mannan Akanda, M.; et al. Peer-to-Peer Energy Trading Pricing Mechanisms: Towards a Comprehensive Analysis of Energy and Network Service Pricing (NSP) Mechanisms to Get Sustainable Enviro-Economical Energy Sector. Energies 2023, 16, 2198. [Google Scholar] [CrossRef]
  7. Ma, S.; Yuan, G.; Zhang, Y.; Yang, N.; Li, Y.; Chen, Q. Development of encapsulation strategies towards the commercialization of perovskite solar cells. Energy Environ Sci 2022, 15, 13–55. [Google Scholar] [CrossRef]
  8. Kim, Y.H.; Cho, H.; Heo, J.H.; Kim, T.S.; Myoung, N.S.; Lee, C.L.; et al. Multicolored Organic/Inorganic Hybrid Perovskite Light-Emitting Diodes. Advanced Materials 2015, 27, 1248–1254. [Google Scholar] [CrossRef]
  9. Dou, L.; Yang, Y.M.; You, J.; Hong, Z.; Chang, W.H.; Li, G.; et al. Solution-processed hybrid perovskite photodetectors with high detectivity. Nature Communications 2014, 5, 1–6. [Google Scholar] [CrossRef]
  10. Australian manufacturer achieves 32% efficiency for inorganic perovskite solar cell – pv magazine Australia n.d. Available online: https://www.pv-magazine-australia.com/2022/10/18/australian-manufacturer-achieves-32-efficiency-for-inorganic-perovskite-solar-cell/ (accessed on 18 October 2022).
  11. Kojima, A.; Teshima, K.; Shirai, Y.; Miyasaka, T. Organometal halide perovskites as visible-light sensitizers for photovoltaic cells. J Am Chem Soc 2009, 131, 6050–6051. [Google Scholar] [CrossRef]
  12. Ameri, M.; Ghaffarkani, M.; Ghahrizjani, R.T.; Safari, N.; Mohajerani, E. Phenomenological morphology design of hybrid organic-inorganic perovskite solar cell for high efficiency and less hysteresis. Solar Energy Materials and Solar Cells 2020, 205, 110251. [Google Scholar] [CrossRef]
  13. Xiang, T.; Zhang, Y.; Wu, H.; Li, J.; Yang, L.; Wang, K.; et al. Universal defects elimination for high performance thermally evaporated CsPbBr3 perovskite solar cells. Solar Energy Materials and Solar Cells 2020, 206, 110317. [Google Scholar] [CrossRef]
  14. Bi, H.; Han, G.; Guo, M.; Ding, C.; Zou, H.; Shen, Q.; et al. Multistrategy Preparation of Efficient and Stable Environment-Friendly Lead-Based Perovskite Solar Cells. ACS Appl Mater Interfaces 2022, 14, 35513–35521. [Google Scholar] [CrossRef]
  15. Shivesh, K.; Alam, I.; Kushwaha, A.K.; Kumar, M.; Singh, S.V. Investigating the theoretical performance of Cs2TiBr6-based perovskite solar cell with La-doped BaSnO3 and CuSbS2 as the charge transport layers. Int J Energy Res 2022, 46, 6045–6064. [Google Scholar] [CrossRef]
  16. Shi, Z.; Guo, J.; Chen, Y.; Li, Q.; Pan, Y.; Zhang, H.; et al. Lead-Free Organic–Inorganic Hybrid Perovskites for Photovoltaic Applications: Recent Advances and Perspectives. Advanced Materials 2017, 29, 1605005. [Google Scholar] [CrossRef]
  17. Ustinova, M.I.; Babenko, S.D.; Luchkin, S.Y.; Talalaev, F.S.; Anokhin D v Olthof, S.; et al. Experimental evaluation of indium(I) iodide as a lead-free perovskite-inspired material for photovoltaic applications. J Mater Chem C Mater 2022, 10, 3435–3439. [Google Scholar] [CrossRef]
  18. Romani, L.; Speltini, A.; Dibenedetto, C.N.; Listorti, A.; Ambrosio, F.; Mosconi, E.; et al. Experimental Strategy and Mechanistic View to Boost the Photocatalytic Activity of Cs3Bi2Br9 Lead-Free Perovskite Derivative by g-C3N4 Composite Engineering. Adv Funct Mater 2021, 31, 2104428. [Google Scholar] [CrossRef]
  19. Ahmad, K.; Khan, M.Q.; Khan, R.A.; Kim, H. Numerical simulation and fabrication of Pb-free perovskite solar cells (FTO/TiO2/Cs3Bi2I9/spiro-MeOTAD/Au). Opt Mater (Amst) 2022, 128, 112458. [Google Scholar] [CrossRef]
  20. Hamukwaya, S.L.; Hao, H.; Mashingaidze, M.M.; Zhong, T.; Tang, S.; Dong, J.; et al. Potassium Iodide-Modified Lead-Free Cs3Bi2I9 Perovskites for Enhanced High-Efficiency Solar Cells. Nanomaterials 2022, 12, 3751. [Google Scholar] [CrossRef]
  21. Koh, T.M.; Krishnamoorthy, T.; Yantara, N.; Shi, C.; Leong, W.L.; Boix, P.P.; et al. Formamidinium tin-based perovskite with low Eg for photovoltaic applications. J Mater Chem A Mater 2015, 3, 14996–15000. [Google Scholar] [CrossRef]
  22. Noel, N.K.; Stranks, S.D.; Abate, A.; Wehrenfennig, C.; Guarnera, S.; Haghighirad, A.A.; et al. Lead-free organic–inorganic tin halide perovskites for photovoltaic applications. Energy Environ Sci 2014, 7, 3061–3068. [Google Scholar] [CrossRef]
  23. Krishnamoorthy, T.; Ding, H.; Yan, C.; Leong, W.L.; Baikie, T.; Zhang, Z.; et al. Lead-free germanium iodide perovskite materials for photovoltaic applications. J Mater Chem A Mater 2015, 3, 23829–23832. [Google Scholar] [CrossRef]
  24. Das, A.; Peu, S.D.; Akanda, M.A.M.; Salah, M.M.; Hossain, M.S.; Das, B.K. Numerical Simulation and Optimization of Inorganic Lead-Free Cs3Bi2I9-Based Perovskite Photovoltaic Cell: Impact of Various Design Parameters. Energies 2023, 16, 2328. [Google Scholar] [CrossRef]
  25. Lehner, A.J.; Fabini, D.H.; Evans, H.A.; Hébert, C.A.; Smock, S.R.; Hu, J.; et al. Crystal and Electronic Structures of Complex Bismuth Iodides A3Bi2I9 (A = K, Rb, Cs) Related to Perovskite: Aiding the Rational Design of Photovoltaics. Chemistry of Materials 2015, 27, 7137–7148. [Google Scholar] [CrossRef]
  26. Park, B.W.; Philippe, B.; Zhang, X.; Rensmo, H.; Boschloo, G.; Johansson, E.M.J. Bismuth Based Hybrid Perovskites A3Bi2I9 (A: Methylammonium or Cesium) for Solar Cell Application. Advanced Materials 2015, 27, 6806–6813. [Google Scholar] [CrossRef]
  27. Ahmad, K.; Khan, M.Q.; Kim, H. Simulation and fabrication of all-inorganic antimony halide perovskite-like material based Pb-free perovskite solar cells. Opt Mater (Amst) 2022, 128, 112374. [Google Scholar] [CrossRef]
  28. Feng, X.; Guo, Q.; Xiu, J.; Ying, Z.; Ng, K.W.; Huang, L.; et al. Close-loop recycling of perovskite solar cells through dissolution-recrystallization of perovskite by butylamine. Cell Rep Phys Sci 2021, 2, 100341. [Google Scholar] [CrossRef]
  29. Cacovich, S.; Vidon, G.; Degani, M.; Legrand, M.; Gouda, L.; Puel, J.B.; et al. Imaging and quantifying non-radiative losses at 23% efficient inverted perovskite solar cells interfaces. Nature Communications 2022, 13, 1–9. [Google Scholar] [CrossRef]
  30. Zheng, X.; Hou, Y.; Bao, C.; Yin, J.; Yuan, F.; Huang, Z.; et al. Managing grains and interfaces via ligand anchoring enables 22. 3%-efficiency inverted perovskite solar cells. Nature Energy 2020, 5, 131–140. [Google Scholar] [CrossRef]
  31. Chen, M.; Ju, M.G.; Garces, H.F.; Carl, A.D.; Ono, L.K.; Hawash, Z.; et al. Highly stable and efficient all-inorganic lead-free perovskite solar cells with native-oxide passivation. Nature Communications 2019, 10, 1–8. [Google Scholar] [CrossRef]
  32. Tai, Q.; Guo, X.; Tang, G.; You, P.; Ng, T.W.; Shen, D.; et al. Antioxidant Grain Passivation for Air-Stable Tin-Based Perovskite Solar Cells. Angewandte Chemie International Edition 2019, 58, 806–810. [Google Scholar] [CrossRef] [PubMed]
  33. Lee, S.; Kang, D.W. Highly Efficient and Stable Sn-Rich Perovskite Solar Cells by Introducing Bromine. ACS Appl Mater Interfaces 2017, 9, 22432–22439. [Google Scholar] [CrossRef]
  34. Fievez, M.; Singh Rana, P.J.; Koh, T.M.; Manceau, M.; Lew, J.H.; Jamaludin, N.F.; et al. Slot-die coated methylammonium-free perovskite solar cells with 18% efficiency. Solar Energy Materials and Solar Cells 2021;230. [CrossRef]
  35. Wang, J.T.W.; Wang, Z.; Pathak, S.; Zhang, W.; Dequilettes, D.W.; Wisnivesky-Rocca-Rivarola, F.; et al. Efficient perovskite solar cells by metal ion doping. Energy Environ Sci 2016, 9, 2892–2901. [Google Scholar] [CrossRef]
  36. Bansode, U.; Naphade, R.; Game, O.; Agarkar, S.; Ogale, S. Hybrid perovskite films by a new variant of pulsed excimer laser deposition: A roomerature dry process. Journal of Physical Chemistry C 2015, 119, 9177–9185. [Google Scholar] [CrossRef]
  37. Noel, N.K.; Stranks, S.D.; Abate, A.; Wehrenfennig, C.; Guarnera, S.; Haghighirad, A.A.; et al. Lead-free organic–inorganic tin halide perovskites for photovoltaic applications. Energy Environ Sci 2014, 7, 3061–3068. [Google Scholar] [CrossRef]
  38. Doroody, C.; Rahman, K.S.; Kiong, T.S.; Amin, N. Optoelectrical impact of alternative window layer composition in CdTe thin film solar cells performance. Solar Energy 2022, 233, 523–530. [Google Scholar] [CrossRef]
  39. Zuo, C.; Ding, L. Solution-Processed Cu2O and CuO as Hole Transport Materials for Efficient Perovskite Solar Cells. Small 2015, 11, 5528–5532. [Google Scholar] [CrossRef]
  40. Burgelman, M.; Nollet, P.; Degrave, S. Modelling polycrystalline semiconductor solar cells. Thin Solid Films 2000, 361–362, 527–532. [CrossRef]
  41. Burgelman, M.; Nollet, P.; Degrave, S. Modelling polycrystalline semiconductor solar cells. Thin Solid Films 2000, 361–362, 527–532. [CrossRef]
  42. Burgelman, M.; Decock, K.; Khelifi, S.; Abass, A. Advanced electrical simulation of thin film solar cells. Thin Solid Films 2013, 535, 296–301. [Google Scholar] [CrossRef]
  43. Xiao, Z.; Yuan, Y.; Wang, Q.; Shao, Y.; Bai, Y.; Deng, Y.; et al. Thin-film semiconductor perspective of organometal trihalide perovskite materials for high-efficiency solar cells. Materials Science and Engineering: R: Reports 2016, 101, 1–38. [Google Scholar] [CrossRef]
  44. Burgelman, M.; Verschraegen, J.; Degrave, S.; Nollet, P. Modeling thin-film PV devices. Progress in Photovoltaics: Research and Applications 2004, 12, 143–153. [Google Scholar] [CrossRef]
  45. Verschraegen, J.; Burgelman, M. Numerical modeling of intra-band tunneling for heterojunction solar cells in scaps. Thin Solid Films 2007, 515, 6276–6279. [Google Scholar] [CrossRef]
  46. Moiz, S.A.; Alahmadi, A.N.M.; Aljohani, A.J. Design of a Novel Lead-Free Perovskite Solar Cell for 17. 83% Efficiency. IEEE Access 2021, 9, 54254–54263. [Google Scholar] [CrossRef]
  47. Sobayel, K.; Akhtaruzzaman, M.; Rahman, K.S.; Ferdaous, M.T.; Al-Mutairi, Z.A.; Alharbi, H.F.; et al. A comprehensive defect study of tungsten disulfide (WS2) as electron transport layer in perovskite solar cells by numerical simulation. Results Phys 2019, 12, 1097–1103. [Google Scholar] [CrossRef]
  48. Islam, M.T.; Jani, M.R.; Shorowordi, K.M.; Hoque, Z.; Gokcek, A.M.; Vattipally, V.; et al. Numerical simulation studies of Cs3Bi2I9 perovskite solar device with optimal selection of electron and hole transport layers. Optik (Stuttg) 2021, 231, 166417. [Google Scholar] [CrossRef]
  49. Lakhdar, N.; Hima, A. Electron transport material effect on performance of perovskite solar cells based on CH3NH3GeI3. Opt Mater (Amst) 2020, 99, 109517. [Google Scholar] [CrossRef]
  50. Wang, Y.; Xia, Z.; Liu, Y.; Zhou, H. Simulation of perovskite solar cells with inorganic hole transporting materials. 2015 IEEE 42nd Photovoltaic Specialist Conference, PVSC 2015 2015. [CrossRef]
  51. Stamate, M.D. On the dielectric properties of dc magnetron TiO2 thin films. Appl Surf Sci 2003, 218, 318–323. [Google Scholar] [CrossRef]
  52. Niemegeers, A.; Burgelman, M. Numerical modelling of ac-characteristics of CdTe and CIS solar cells. Conference Record of the IEEE Photovoltaic Specialists Conference 1996, 901–904. [Google Scholar] [CrossRef]
  53. Husainat, A.; Ali, W.; Cofie, P.; Attia, J.; Fuller, J. Simulation and Analysis of Methylammonium Lead Iodide (CH3NH3PbI3) Perovskite Solar Cell with Au Contact Using SCAPS 1D Simulator. Http://WwwSciencepublishinggroupCom 2019, 7, 33. [Google Scholar] [CrossRef]
  54. Sobayel, K.; Akhtaruzzaman, M.; Rahman, K.S.; Ferdaous, M.T.; Al-Mutairi, Z.A.; Alharbi, H.F.; et al. A comprehensive defect study of tungsten disulfide (WS2) as electron transport layer in perovskite solar cells by numerical simulation. Results Phys 2019, 12, 1097–1103. [Google Scholar] [CrossRef]
  55. Wojciechowski, K.; Leijtens, T.; Siprova, S.; Schlueter, C.; Hörantner, M.T.; Wang, J.T.W.; et al. C60 as an efficient n-type compact layer in perovskite solar cells. Journal of Physical Chemistry Letters 2015, 6, 2399–2405. [Google Scholar] [CrossRef]
  56. Islam, A.M.; Islam, S.; Sobayel, K.; Emon, E.I.; Jhuma, F.A.; Shahiduzzaman, M.; et al. Performance analysis of tungsten disulfide (WS2) as an alternative buffer layer for CdTe solar cell through numerical modeling. Opt Mater (Amst) 2021, 120, 111296. [Google Scholar] [CrossRef]
  57. Zuo, C.; Ding, L. Solution-Processed Cu2O and CuO as Hole Transport Materials for Efficient Perovskite Solar Cells. Small 2015, 11, 5528–5532. [Google Scholar] [CrossRef]
  58. Raoui, Y.; Ez-Zahraouy, H.; Tahiri, N.; el Bounagui, O.; Ahmad, S.; Kazim, S. Performance analysis of MAPbI3 based perovskite solar cells employing diverse charge selective contacts: Simulation study. Solar Energy 2019, 193, 948–955. [Google Scholar] [CrossRef]
  59. Kumar, M.H.; Dharani, S.; Leong, W.L.; Boix, P.P.; Prabhakar, R.R.; Baikie, T.; et al. Lead-Free Halide Perovskite Solar Cells with High Photocurrents Realized Through Vacancy Modulation. Advanced Materials 2014, 26, 7122–7127. [Google Scholar] [CrossRef] [PubMed]
  60. Chen, D.; Wang, Y.; Lin, Z.; Huang, J.; Chen, X.; Pan, D.; et al. Growth strategy and physical properties of the high mobility p-type cui crystal. Cryst Growth Des 2010, 10, 2057–2060. [Google Scholar] [CrossRef]
  61. Hodes, G. Perovskite-Based Solar Cells. Science (1979) 2013, 342, 317–318. [Google Scholar] [CrossRef]
  62. Liu, D.; Gangishetty, M.K.; Kelly, T.L. Effect of CH3NH3PbI3 thickness on device efficiency in planar heterojunction perovskite solar cells. J Mater Chem A Mater 2014, 2, 19873–19881. [Google Scholar] [CrossRef]
  63. Wu, H.; Wang, L.S. A study of nickel monoxide (NiO), nickel dioxide (ONiO), and Ni(O2) complex by anion photoelectron spectroscopy. J Chem Phys 1998, 107, 16. [Google Scholar] [CrossRef]
  64. Hock, R.; Mayer, T.; Jaegermann, W. P-type doping of spiro-MeOTAD with WO 3 and the spiro-MeOTAD/WO 3 interface investigated by synchrotron-induced photoelectron spectroscopy. Journal of Physical Chemistry C 2012, 116, 18146–18154. [Google Scholar] [CrossRef]
  65. Du, H.-J.; Wang, W.-C.; Zhu, J.-Z.; Du, H.-J.; Wang, W.-C.; Zhu, J.-Z. Device simulation of lead-free CH3NH3SnI3 perovskite solar cells with high efficiency. Chinese Physics B 2016, 25, 108802–108802. [Google Scholar] [CrossRef]
  66. Anwar, F.; Mahbub, R.; Satter, S.S.; Ullah, S.M. Effect of Different HTM Layers and Electrical Parameters on ZnO Nanorod-Based Lead-Free Perovskite Solar Cell for High-Efficiency Performance. International Journal of Photoenergy 2017, 2017. [Google Scholar] [CrossRef]
  67. Ameri, M.; Mohajerani, E.; Ghafarkani, M.; Safari, N.; Alavi, S.A. The investigation of the unseen interrelationship of grain size, ionic defects, device physics and performance of perovskite solar cells. J Phys D Appl Phys 2019, 52, 125501. [Google Scholar] [CrossRef]
  68. Bag, A.; Radhakrishnan, R.; Nekovei, R.; Jeyakumar, R. Effect of absorber layer, hole transport layer thicknesses, and its doping density on the performance of perovskite solar cells by device simulation. Solar Energy 2020, 196, 177–182. [Google Scholar] [CrossRef]
  69. Lin, L.; Jiang, L.; Li, P.; Fan, B.; Qiu, Y. A modeled perovskite solar cell structure with a Cu2O hole-transporting layer enabling over 20% efficiency by low-cost low-temperature processing. Journal of Physics and Chemistry of Solids 2019, 124, 205–211. [Google Scholar] [CrossRef]
  70. Alam, I.; Ashraf, M.A. Effect of different device parameters on tin-based perovskite solar cell coupled with In2S3 electron transport layer and CuSCN and Spiro-OMeTAD alternative hole transport layers for high-efficiency performance. [CrossRef]
  71. Sadanand Dwivedi, D.K. Modeling of photovoltaic solar cell based on CuSbS absorber for the enhancement of performance. IEEE Trans Electron Devices 2021, 68, 1121–1128. [Google Scholar] [CrossRef]
  72. He, Y.; Xu, L.; Yang, C.; Guo, X.; Li, S. Design and Numerical Investigation of a Lead-Free Inorganic Layered Double Perovskite Cs4CuSb2Cl12 Nanocrystal Solar Cell by SCAPS-1D. Nanomaterials 2021, 11, 2321. [Google Scholar] [CrossRef]
  73. Chen, Y.; Shen, H.; Altermatt, P.P. Analysis of recombination losses in screen-printed aluminum-alloyed back surface fields of silicon solar cells by numerical device simulation. Solar Energy Materials and Solar Cells 2014, 120, 356–362. [Google Scholar] [CrossRef]
  74. Mohandes, A.; Moradi, M.; Nadgaran, H. Numerical simulation of inorganic Cs2AgBiBr6 as a lead-free perovskite using device simulation SCAPS-1D. Optical and Quantum Electronics 2021, 53, 1–22. [Google Scholar] [CrossRef]
  75. Salah, M.M.; Abouelatta, M.; Shaker, A.; Hassan, K.M.; Saeed, A. A comprehensive simulation study of hybrid halide perovskite solar cell with copper oxide as HTM. Semicond Sci Technol 2019, 34, 115009. [Google Scholar] [CrossRef]
  76. Alam, I.; Mollick, R.; Ashraf, M.A. Numerical simulation of Cs2AgBiBr6-based perovskite solar cell with ZnO nanorod and P3HT as the charge transport layers. Physica B Condens Matter 2021, 618, 413187. [Google Scholar] [CrossRef]
  77. Ghrib, T.; AL-Saleem, N.K.; AL-Naghmaish, A.; Elshekhipy, A.A.; Brini, S.; Briki, K.; et al. Annealing effect on the microstructural, optical, electrical, and thermal properties of Cu2O/TiO2/Cu2O/TiO2/Si heterojunction prepared by sol-gel technique. Micro and Nanostructures 2022, 164, 107119. [Google Scholar] [CrossRef]
  78. Khattak, Y.H.; Vega, E.; Baig, F.; Soucase, B.M. Performance investigation of experimentally fabricated lead iodide perovskite solar cell via numerical analysis. Mater Res Bull 2022, 151, 111802. [Google Scholar] [CrossRef]
  79. Jeon, Y.J.; Lee, S.; Kang, R.; Kim, J.E.; Yeo, J.S.; Lee, S.H.; et al. Planar heterojunction perovskite solar cells with superior reproducibility. Scientific Reports 2014, 4, 1–7. [Google Scholar] [CrossRef] [PubMed]
  80. Azri, F.; Meftah, A.; Sengouga, N.; Meftah, A. Electron and hole transport layers optimization by numerical simulation of a perovskite solar cell. Solar Energy 2019, 181, 372–378. [Google Scholar] [CrossRef]
  81. Ahn, N.; Son, D.Y.; Jang, I.H.; Kang, S.M.; Choi, M.; Park, N.G. Highly Reproducible Perovskite Solar Cells with Average Efficiency of 18. 3% and Best Efficiency of 19.7% Fabricated via Lewis Base Adduct of Lead(II) Iodide. J Am Chem Soc 2015, 137, 8696–8699. [Google Scholar] [CrossRef] [PubMed]
  82. Christians, J.A.; Fung, R.C.M.; Kamat P, v. An inorganic hole conductor for Organo-lead halide perovskite solar cells. improved hole conductivity with copper iodide. J Am Chem Soc 2014, 136, 758–764. [Google Scholar] [CrossRef] [PubMed]
  83. Zhang, H.; Ren, X.; Chen, X.; Mao, J.; Cheng, J.; Zhao, Y.; et al. Improving the stability and performance of perovskite solar cells via off-the-shelf post-device ligand treatment. Energy Environ Sci 2018, 11, 2253–2262. [Google Scholar] [CrossRef]
  84. Islam, M.T.; Jani, M.R.; Shorowordi, K.M.; Hoque, Z.; Gokcek, A.M.; Vattipally, V.; et al. Numerical simulation studies of Cs3Bi2I9 perovskite solar device with optimal selection of electron and hole transport layers. Optik (Stuttg) 2021, 231, 166417. [Google Scholar] [CrossRef]
  85. Chaudhary, D.K.; Sharma, A.; Kumar, A.; Chauhan, U.; Bhasker, D.r.H.a.r.i.P.; Dhawan, D.r.P.K.; et al. Solvent Engineering of Cs3bi2i9 Perovskite Films for Lead-Free Flexible Semi-Transparent Perovskite Solar Cell Devices with Enhanced Efficiency. SSRN Electronic Journal 2022. [CrossRef]
Preprints 74115 g001
Figure 1. Model of a perovskite-based solar cell with different layers.
Figure 1. Model of a perovskite-based solar cell with different layers.
Preprints 74115 g001
Preprints 74115 g002
Figure 2. Energy band diagram for the selected configuration in this study.
Figure 2. Energy band diagram for the selected configuration in this study.
Preprints 74115 g002
Preprints 74115 g003
Figure 3. Performance parameters for different HTLs with PCBM ETL and Cs3Bi2I9 absorber layer.
Figure 3. Performance parameters for different HTLs with PCBM ETL and Cs3Bi2I9 absorber layer.
Preprints 74115 g003
Preprints 74115 g004
Figure 4. Performance parameters for different HTLs with WS2 ETL and Cs3Bi2I9 absorber layer.
Figure 4. Performance parameters for different HTLs with WS2 ETL and Cs3Bi2I9 absorber layer.
Preprints 74115 g004
Preprints 74115 g005
Figure 5. Performance parameters for different HTLs with IGZO ETL and Cs3Bi2I9 absorber layer.
Figure 5. Performance parameters for different HTLs with IGZO ETL and Cs3Bi2I9 absorber layer.
Preprints 74115 g005
Preprints 74115 g006
Figure 6. Performance parameters for different HTLs with C60 ETL and Cs3Bi2I9 absorber layer.
Figure 6. Performance parameters for different HTLs with C60 ETL and Cs3Bi2I9 absorber layer.
Preprints 74115 g006
Preprints 74115 g007
Figure 7. Performance parameters for different HTLs with TiO2 ETL and Cs3Bi2I9 absorber layer.
Figure 7. Performance parameters for different HTLs with TiO2 ETL and Cs3Bi2I9 absorber layer.
Preprints 74115 g007
Preprints 74115 g008
Figure 8. Effect of absorber layer thickness on PSC device' performance parameters (i). (Jsc, Voc), and (ii) (FF, PCE).
Figure 8. Effect of absorber layer thickness on PSC device' performance parameters (i). (Jsc, Voc), and (ii) (FF, PCE).
Preprints 74115 g008
Preprints 74115 g009
Figure 9. Effect of absorber layer bandgap on (i) Jsc, Voc, and (ii) FF, PCE.
Figure 9. Effect of absorber layer bandgap on (i) Jsc, Voc, and (ii) FF, PCE.
Preprints 74115 g009
Preprints 74115 g010
Figure 10. Effect of absorber layer defect density on (i) Jsc, Voc, and (ii) FF, PCE.
Figure 10. Effect of absorber layer defect density on (i) Jsc, Voc, and (ii) FF, PCE.
Preprints 74115 g010
Preprints 74115 g011
Figure 11. Effect of donor density of ETL (WS2) on (i) Jsc, Voc, and (ii) FF, PCE.
Figure 11. Effect of donor density of ETL (WS2) on (i) Jsc, Voc, and (ii) FF, PCE.
Preprints 74115 g011
Preprints 74115 g013
Figure 13. Comparison of J-V characteristic curve of initial and final optimized model.
Figure 13. Comparison of J-V characteristic curve of initial and final optimized model.
Preprints 74115 g013
Preprints 74115 g014
Figure 14. Comparison of capacitance of initial and final optimized model as a function of wavelength.
Figure 14. Comparison of capacitance of initial and final optimized model as a function of wavelength.
Preprints 74115 g014
Table 1. Literature review on recent experimental perovskite-based solar cells performance.
Table 1. Literature review on recent experimental perovskite-based solar cells performance.
Device structure Year PCE(%) VOC(V) JSC(mA/cm2) FF(%) Ref
Au/spiro-OMeTAD/ FTO/TiO2 2022 12.54 1.32 13.13 72.01 [27]
HTL/back contact /MAPbBr3/SnO2/ FTO 2021 25.40 1.19 25.09 84 [28]
Ag/BCP/PCBM/(Cs0.05(FA5/MAI) 0.95Pb(I0.9Br0.1)3)/PTAA/TTO/Glass 2021 23 1.16 24 82 [29]
Cu/BCP/ITUC60/Cs0.05(FA0.92MA0.08)0.95Pb(I0.92Br0.08)3/ PTAA/ITO 2020 22.30 1.71 24.10 81 [30]
Au/ Spiro-OMeTAD/CsSn0.5Ge0.5I3/PCBM/FTO 2019 7.11 0.63 18.61 60.6 [31]
ITO/NiOx/FASnI3/PCBM/Ag 2018 6.70 0.60 17.53 65 [32]
Ag/PCBM/MASn0.6Pb0.4I3-xBrx/PEDOT:PSS/ITO 2017 12.10 0.78 20.65 75 [33]
Au/Spiro-OMeTAD/Cs0.16FA0.84Pb(I0.88Br0.12)3/SnO2/FTO 2016 18 1.02 22.40 78 [34]
Ag/BCP/PCBM/0.15 mol% Al3+-dopedCH3NH3PbI3/ Poly-TPD/FTO 2016 19.10 1.01 22.40 78 [35]
Au/spiro-OMeTAD /MASnI3/ ZnO/ITO 2015 7.66 0.97 11.10 66 [36]
Au/SpiroOMeTAD + LiTFSI + tBP /MASnI3/ m-TiO2/ TiO2 2014 6.40 0.88 16.80 42 [37]
Table 2. Input attributes for perovskite material, different electron transport layer (ETL) materials and ITO.
Table 2. Input attributes for perovskite material, different electron transport layer (ETL) materials and ITO.
Parameter Cs3Bi2I9
[48]		 PCBM[49,50] TiO2 [51,52,53] WS2 [54] IGZO [49] C60 [55] ITO
[56]
Electron affinity, X (eV) 3.40 3.90 4.26 3.95 4 3.90 4.1
Relative permittivity ( ε r ) 9.68 4 100 13.60 9 4.20 10
Thickness(nm) 1000 30 30 100 30 50 60
Bandgap, Eg (eV) 2.1 2 3.20 1.80 3.50 1.70 3.6
State density of conduction band, NC (1/cm3) 4.98×1019 1 × 10 21 2 × 10 18 107 5 × 10 18 8.0 × 10 19 2.2 × 10 18
State density of valence band, NV (1/cm3) 2.11×1019 2 × 10 20 1.8 × 10 19 107 5 × 10 18 8.0 × 10 19 1.8 × 10 19
AL defect density, Nt (1/cm3) 1014 1 × 10 14 1 × 10 15 1015 1 × 10 15 1 × 10 14 -
Mobility of electron, μ n (cm2/Vs) 107 1 × 10 − 2 2 × 10 4 100 15 8.0 × 10 − 2 107
Mobility of hole, μ p (cm2/Vs) 107 1 × 10 − 2 1 × 10 3 100 0.20 3.5 × 10 − 3 107
AD, NA(1/cm3) 1019 - - - - - -
DD, ND(1/cm3) 1019 1 × 10 20 6 × 10 19 1018 1 × 10 17 2.6 × 10 17 1019
Table 3. Input attributes for different hole transport layer (HTL) materials.
Table 3. Input attributes for different hole transport layer (HTL) materials.
Parameter NiO [50] CuO [57] Cu2O [58] PEDOT [59] P3HT [58] CuSCN [58] CuI [60,61,62,63] Spiro-OMeTAD [64] CuSbS2 [65,66,67]
Relative permittivity ( ε r ) 11.75 18.1 7.1 3 3 10 6.5 3 14.6
Bandgap, Eg(eV) 3.6 31.5 2.17 3.6 1.7 3.4 2.98 2.9 1.58
Electron affinity, X(eV) 2.1 4.07 3.2 1.57 3.5 2.1 2.1 2.2 4.2
Thickness(nm) 50 50 50 50 50 50 50 350 50
AL defect density, Nt (1/cm3) 1 × 10 8 1 × 10 13 1 × 10 13 1 × 10 14 1 × 10 14 1 × 10 8 1 × 10 15 1 × 10 13 1 × 10 18
State density of conduction band, NC (1/cm3) 2.5 × 10 20 2.2 × 10 19 2.5 × 10 20 2.2 × 10 18 2 × 10 18 2.5 × 10 18 2.8 × 10 19 2.5 × 10 18 2 × 10 18
State density of valence band, NV (1/cm3) 2.5 × 10 20 5.5 × 10 20 2.5 × 10 20 1.8 × 10 19 2 × 10 19 1.8 × 10 19 1 × 10 19 1.8 × 10 19 1 × 10 18
Mobility of electron, μ n   (cm2/Vs) 1 × 10 − 3 100 200 100 1.8 × 10 − 3 2 × 10 − 4 1.69 × 10 − 4 2 × 10 − 4 49
Mobility of hole, μ p (cm2/Vs) 1 × 10 − 3 0.1 8600 4 1.8 × 10 − 2 2 × 10 − 4 1.69 × 10 − 4 2 × 10 − 4 49
AD, NA(1/cm3) 1 × 10 19 1 × 10 15 1 × 10 19 2 × 10 19 1 × 10 18 1 × 10 17 1 × 10 18 1 × 10 17 1 × 10 18
DD, ND(1/cm3) - - - - - - - - -
Table 4. Optimized input attributes for the selected configuration in this study.
Table 4. Optimized input attributes for the selected configuration in this study.
Parameters ITO WS2 Cs3Bi2I9 NiO
Electron affinity (eV) 4.1 3.95 3.4 2.1
Bandgap (eV) 3.6 1.8 2.10 3.6
Thickness (nm) 60 100 400 150
Dielectric permittivity (relative) 10 13.6 9.68 11.75
Thermal velocity of hole (cm/s) 107 107 107 107
Mobility of electron (cm2/Vs) 50 100 4.3 10-3
CB effective density of states (cm-3) 2.2 × 1018 2 × 1018 4.98 × 1019 2.5 × 10 20
VB effective density of states (cm-3) 1.8 × 1019 2 × 1018 2.11 × 1019 2.5 × 10 20
Thermal velocity of electron (cm/s) 107 2 × 105 107 107
Mobility of hole (cm2/Vs) 75 100 1.7 10-3
Shallow uniform DD, ND (cm-3) 1019 1018 1019 -
Shallow uniform AD, NA (cm-3) - - 1019 1 × 10 20
Defect density of AL, Nt (cm-3) - 1013 1012 1 × 10 14
Note: The bold attributes depicts the optimized input paramters.
Table 5. Comparison of different established model with the present model in this study.
Table 5. Comparison of different established model with the present model in this study.
Models Methods VOC(V) JSC(mA/cm2) FF(%) PCE(%) Ref
FTO/TiO2/Cs3Sb2I9/spiro-OMeTAD/Au Simulation 1.32 13.13 72.01 12.54 [27]
CZTSe/MAPbI3/Cd1-xZnxS/FTO Simulation 1.12 26.45 88.90 27.13 [78]
PTAA/MAPbI3/TiO2 Experimental 1.11 19.58 76 16.46 [79]
Spiro − OMeTAD/MAPbI3/TiO2 Simulation 1.27 21.87 79.58 22.13 [80]
Spiro − OMeTAD/MAPbI3/TiO2 Experimental 1.09 23.83 76.2 19.71 [81]
CuI /MAPbI3/TiO2 Simulation 1.27 21.89 83.12 23.14 [80]
CuI /MAPbI3/TiO2 Experimental 0.55 17.8 62 6 [82]
NiOx/MAPbI3/PCBM : C60/Zr Experimental 1.08 23.47 79.4 20.13 [83]
FTO/TiO2/Cs3Bi2I9/spiro-MeOTAD/Au Simulation 1.03 21.02 73.4 11.14 [84]
FTO/TiO2/Cs3Bi2I9/NiO Simulation 0.92 22.07 68.21 13.82 [84]
ITO/WS2/Cs3Bi2I9 /NiO/Au Simulation 1.438 16.366 89.03 20.96 [Present work]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.
Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.
Prerpints.org logo

Preprints.org is a free preprint server supported by MDPI in Basel, Switzerland.

facebook logotwitter logolinkedin logo
MDPI Initiatives
Important Links
Subscribe

Disclaimer

Terms of Use

Privacy Policy

© 2024 MDPI (Basel, Switzerland) unless otherwise stated