Prerpints.org logo
Preprint
Article

Design and Operation of a Gripper for a Berthing Task

Altmetrics

Downloads

118

Views

52

Comments

0

A peer-reviewed article of this preprint also exists.

Submitted:

24 May 2023

Posted:

25 May 2023

You are already at the latest version

Alerts
Abstract
The idea of an extension of life for CubeSats is proposed to reduce space debris in a low-earth orbit. In this work, a gripper is designed for geometry-based grasping in berthing tasks. The grasping operation is outlined for square- and rectangle-profiled CubeSats. Equilibrium conditions are used to choose fingertips shape and parameters for grasping the CubeSat body. A design scheme is proposed to provide the required accuracy. A design concept is developed into a lab prototype by using low-cost 3D printing technique, and a mock-up grasping task that is representative of the berthing operation is evaluated with the lab prototype. Center-mass hanging setup for the prototype and grasped body is used to evaluate the impact of grasping, partially replicating the conditions in space by reducing the effect of gravity on the system.
Keywords: 
Subject: Engineering  -   Aerospace Engineering

1. Introduction

The number of satellites on orbit increases every year, but a satellite is designed for a limited time of mission. Non-functioning satellites become uncontrollable space debris, which is a threat to working ones. Therefore, the probability of a chain reaction of collisions increases with every launch of satellites, as described by Kessler more than 40 years ago [1]. Currently, the only way to avoid space debris is to burn satellites in the atmosphere at the end of their mission [2]. For higher attitude orbits, a graveyard orbit is set instead.
Another more sustainable way to decrease the number of debris, however, is to prolong the life of satellites. On low-earth orbits, satellites lose their attitude faster because of the stronger atmosphere influence. So, it is possible to prolong the lifetime of a satellite by moving it to a higher attitude. The process of space systems maintenance is called “on-orbit servicing” (OOS). Maintenance on potentially working satellite with no crucial malfunctioning (for example, out of fuel) is cost-effective [3]. An OOS system includes a base or servicing satellite with a manipulator installed on it, a grasping end-effector at the extremity of the manipulator, and a target satellite to be maintained. A successful example of a working OOS system is the International Space Station (ISS). During more than twenty years of life, several service operations were conducted. Currently, three manipulators are in use on the ISS: SSRMS or Canadarm2 [4], JEMRMS [5], and ERA [6]. Thanks to their considerable size, they can manipulate objects up to 116,000 kg (with the Canadarm2). They are used to inspect the ISS and moving spacecraft modules.
To maintain spacecraft, robotic systems for extravehicular activity (EVA) are being developed and tested. With ETS-VII [7], the Japanese Space Agency tested on-orbit service technologies, such as monitoring the other satellite, docking, refueling, and replacement of parts. The German Space Agency (DLR) in collaboration with the Russian and Canadian Space Agencies (Roscosmos and CSA, respectively) in the TECSAS project [8], and DAPRA Orbital express mission [9]. These projects aimed to prolong the lifetime of existing satellites by refueling them or replacing the components. The deorbiting of a nonfunctioning satellite is shown in a DLR project called DEOS [10]. The OOS satellites from [7-10] were designed with a single manipulator, but multi-arm robotic systems can be used for more complex tasks. These types of systems were proposed in the Advanced Telerobotic Manipulator System (ATLAS) project [10], in kinematic models proposed by Moosavian and Papadopoulos [11] as two-arm systems, and in the TORVEASTRO project [12,13] as a three-link system for EVA in ISS. Repair or change of small modules is still conducted by astronauts. Projects were proposed for humanoid robotic systems in space, such as Justin from DLR [14], Robonaut 2 [15] from NASA, and Fyodor from RSA [16].
CubeSats are a new type of microsatellites [17]. Their small standard size and weight, as well as simplicity when compared with larger satellites, made them widely popular. They are used in many fields, such as telecommunication, meteorology, scientific research. Mostly, CubeSats are based in low-earth orbit, which is also occupied by other types of satellites [18]. In low-earth orbit, atmosphere slows satellites, making them lose attitude and burn in atmosphere. Most CubeSats are designed without a propulsion system for orbit correction, but a service satellite with an active propulsion system can move the CubeSats on higher attitudes and prolong their lifetime.
For the OOS, the target satellite should be reached by the base satellite with far- and close-range rendezvous maneuvers and captured. The process of capturing and fixture the target satellite into the special port is called berthing [19]. Currently, berthing is widely used in ISS for large manned and unmanned satellites, such as Dragon or Progress, and the berthing port for these satellites has dimensions around 1 m [20]. With dimensions 10 cm for 1U CubeSats, these satellites are small enough for existing berthing port designs. Most other projects for OOS [8,10] use peg-in-hole mechanisms to capture the satellites by their nozzle; others use small grippers to hold the satellite by the solar panels or special flanges.
Most CubeSats do not have nozzles, flanges, and ports for berthing. Using the open solar panels risks damaging them during the berthing process.
In this paper, a novel design of a space berthing end effector for grasping CubeSats with standard dimensions from 1U to 12U is proposed based on the geometry characteristics of CubeSats. A specific grasping is analyzed for the berthing task of CubeSats. The characteristic operation is characterized by experimental tests with a proper shaped fingertips and their adjustable grasping configuration.

2. Materials and Methods

2.1. Problems and requirements

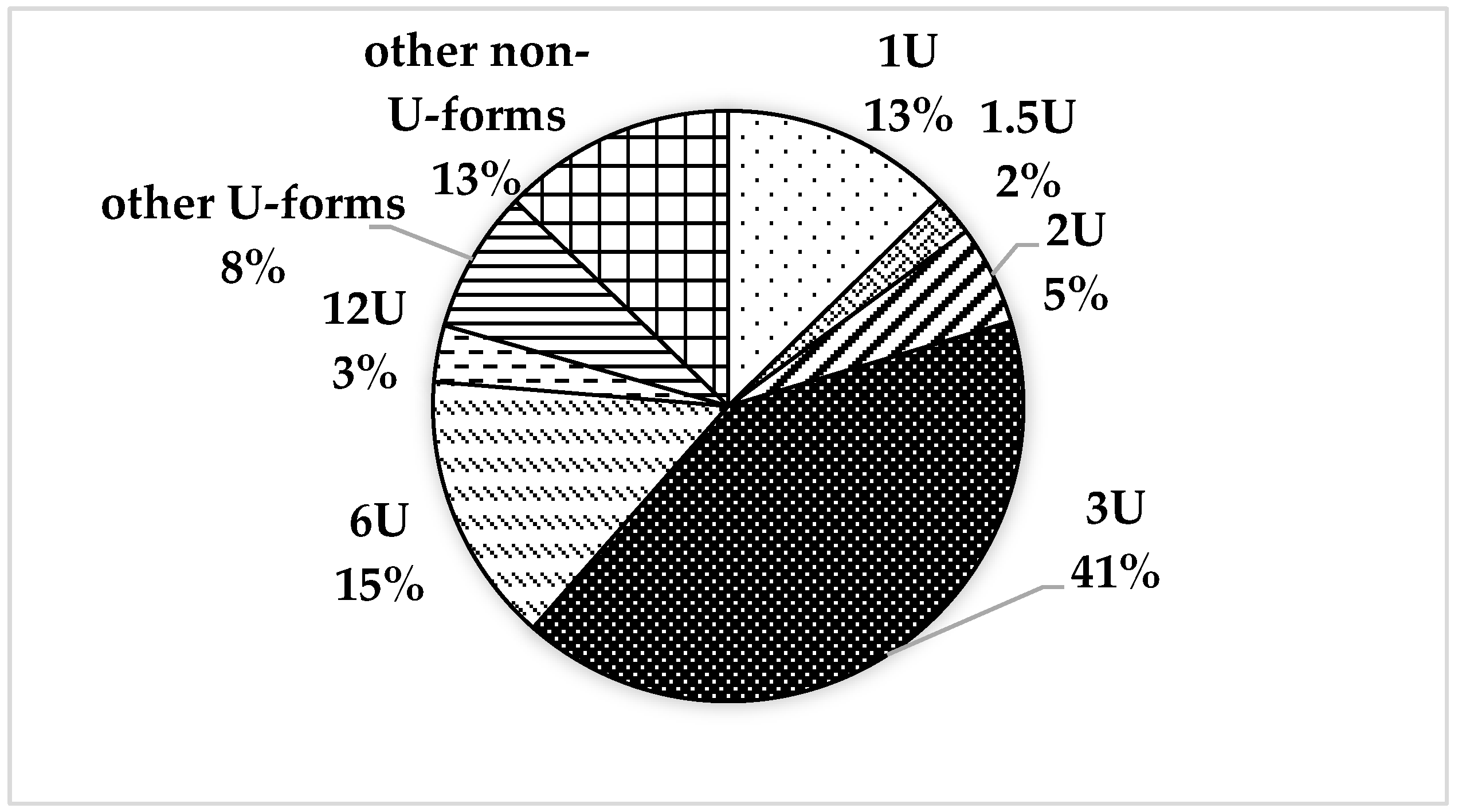
According to the Nanosatellite and CubeSat database [18], 3,163 out of 3,627 nanosatellites are CubeSats of the U form factor, and 41% of these satellites are designed in 3U size.
Preprints 74605 g001
Figure 1. A chart of CubeSat dustribution by types [18].
Figure 1. A chart of CubeSat dustribution by types [18].
Preprints 74605 g001
The problems for a gripper design and operation in berthing tasks can be summarized in the following aspects:
  • geometry-based grasping of CubeSats
  • keeping the CubeSat after grasping
  • minimization of mass, inertial characteristics of the gripper
  • lightweight and low-cost solution for terrestrial testing
In previous works [21,22], geometry-based grasping is planned along CubeSats’ diagonal ribs by using L-shaped fingertips. In general, CubeSats are not designed with docking or berthing ports, but their shape and dimensions are standardized. A gripper design can be based on its geometry so that a standard grasping can be planned for these types of satellites.
After grasping, a CubeSat should be firmly kept by the gripper and not to slip out from its fingertips while being transferred to the berthing port. Grasping force in this case should be large to keep the CubeSat and to avoid its slip, but small enough to not damage it. The berthing operation from [21,22] also considers keeping multiple satellites on the base station and using only one manipulator only. Therefore, berthing ports based on CubeSats’ geometry, are required to be on the base station. Around a half of CubeSats use foldable structures such as solar panels or antennas. Unfolded elements of CubeSat can prevent it to be grasped or entering in the berthing port.
CubeSats’ body dimensions do not exceed 36 centimeters in size and 24 kg in mass [18]. For such small satellites, both the manipulator and the gripper can be designed with suitable mass and dimensions and make the base station for maintaining CubeSats cost-efficient. Manipulators like Canadarm2 [4] with Dextre or ERA [6] with their size, mass, and complexity, are overengineered for this task. Focusing on the berthing can help minimize the mass and inertia characteristic of the gripper. A folding gripper structure is one of the ways to reduce volume in the launcher spacecraft. To reduce development costs, a prototype for preliminary testing of grasping mechanics can be designed using low-cost materials and manufacturing technics, such as 3D-printing.

2.2. Grasping analysis

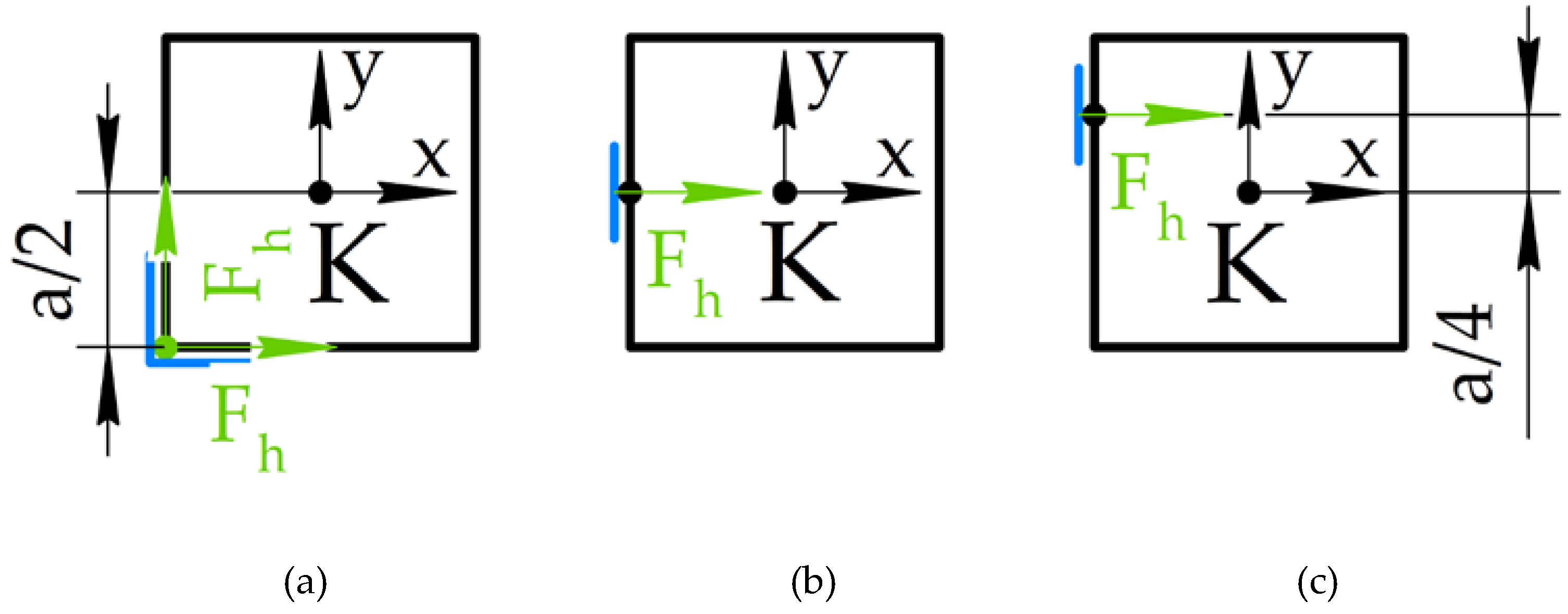
To find a suitable gripper configuration, a typical static planar task is presented in Figure 2 in different ways of contact with the grasped body and the gripper fingertip. A square profile of CubeSat is considered as a grasped body in the presented task. The mass center K with the coordinate system Kxy is placed in the center of the square with the side equal to a. It is assumed that a CubeSat is in contact with fingertips with forces Fh. Three types of contact are presented in this task. The first is a L-shaped fingertip presented in Figure 2a. It contacts with the grasped body in its corner. The holding forces Fh act from the contact point along the sides of the grasped body. The planar fingertip grasping by the middle of the side of the body with the force Fh is presented in Figure 2b. The planar fingertip contact by the edge of the side of the body with the force Fh is shown in Figure 2c.
These types of contact can be used in different combinations of each other applied to the different corners and sides of the grasped body. According to [23], static equilibrium can be ensured with two contact points. The sum of forces and moments acting on the body is equal to zero, which is a representation of the equilibrium condition.
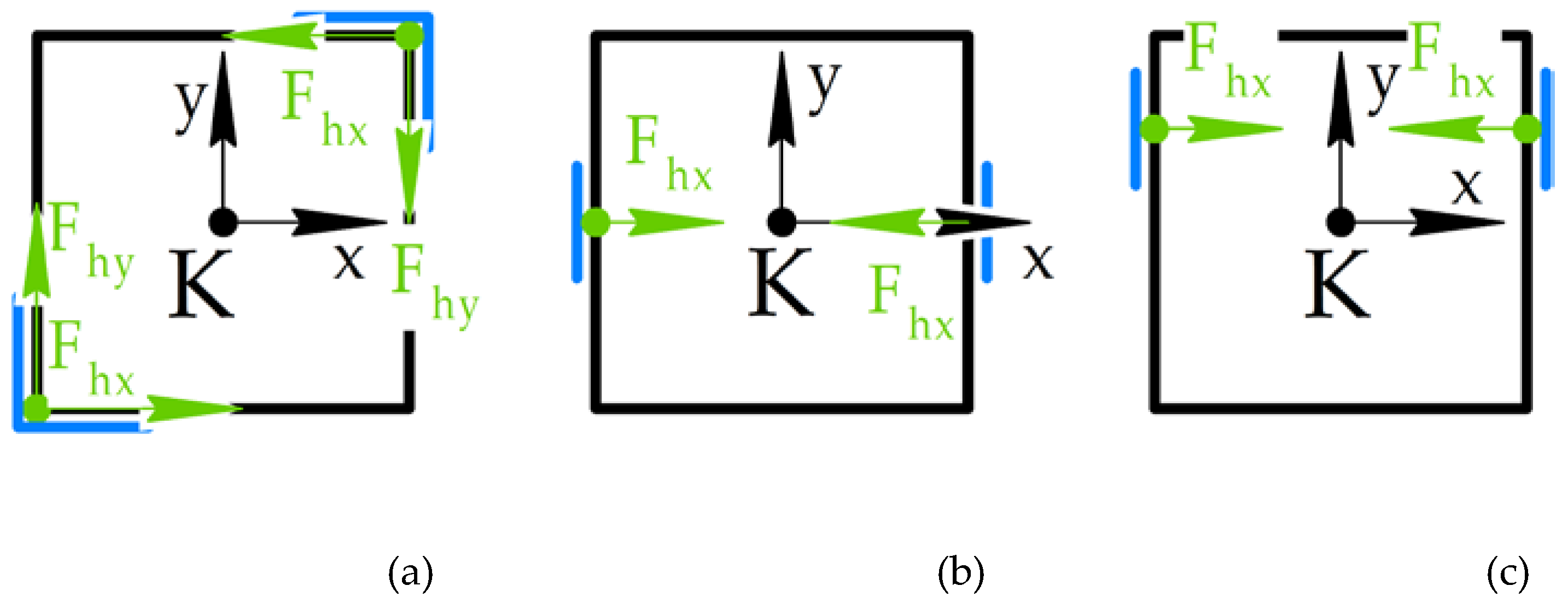
To balance the forces, two similar fingertips should act to the counter sides of the grasped body. For example, two L-shaped fingertips from Figure 2a should act on the counter corners of the grasped body, as shown in Figure 3a. The same condition is applied for the fingertips in Figure 2b and 2c, which is shown in Figure 3b and 3c, respectively.
Other combinations give unbalanced forces or moments to the grasped body. The equilibrium conditions for three ways of contact for fingertips from Figure 3a – 3c, named as FT3a, FT3b, FT3c, respectively, can be expreesed as:
for FT3a:
Σ F x = F h x + − F h x = 0 ;
Σ F y = F h y + − F h y = 0 ;
Σ M K = 2 F h   ∙   a 2 − 2 F h   ∙   a 2 = 0
for FT3b:
Σ F x = F h x + − F h x = 0
Σ F y = 0 ;
Σ M K = 0  
for FT3c:
Σ F x = F h x + − F h x = 0 ;
Σ F y = 0 ;
Σ M K = F h x   ∙   a 4 + − F h x   ∙   a 4 = 0
In Equations 1 – 3, the holding forces Fhx and Fhy keep the grasped body on all its sides. This way is also because the ribs of the body are considered more rigid, and it is possible to apply larger Fh to ensure object keeping. In addition, force keeping in planar type fingertips is limited and not always possible because of sensors or solar panels installed on CubeSat’s surfaces.
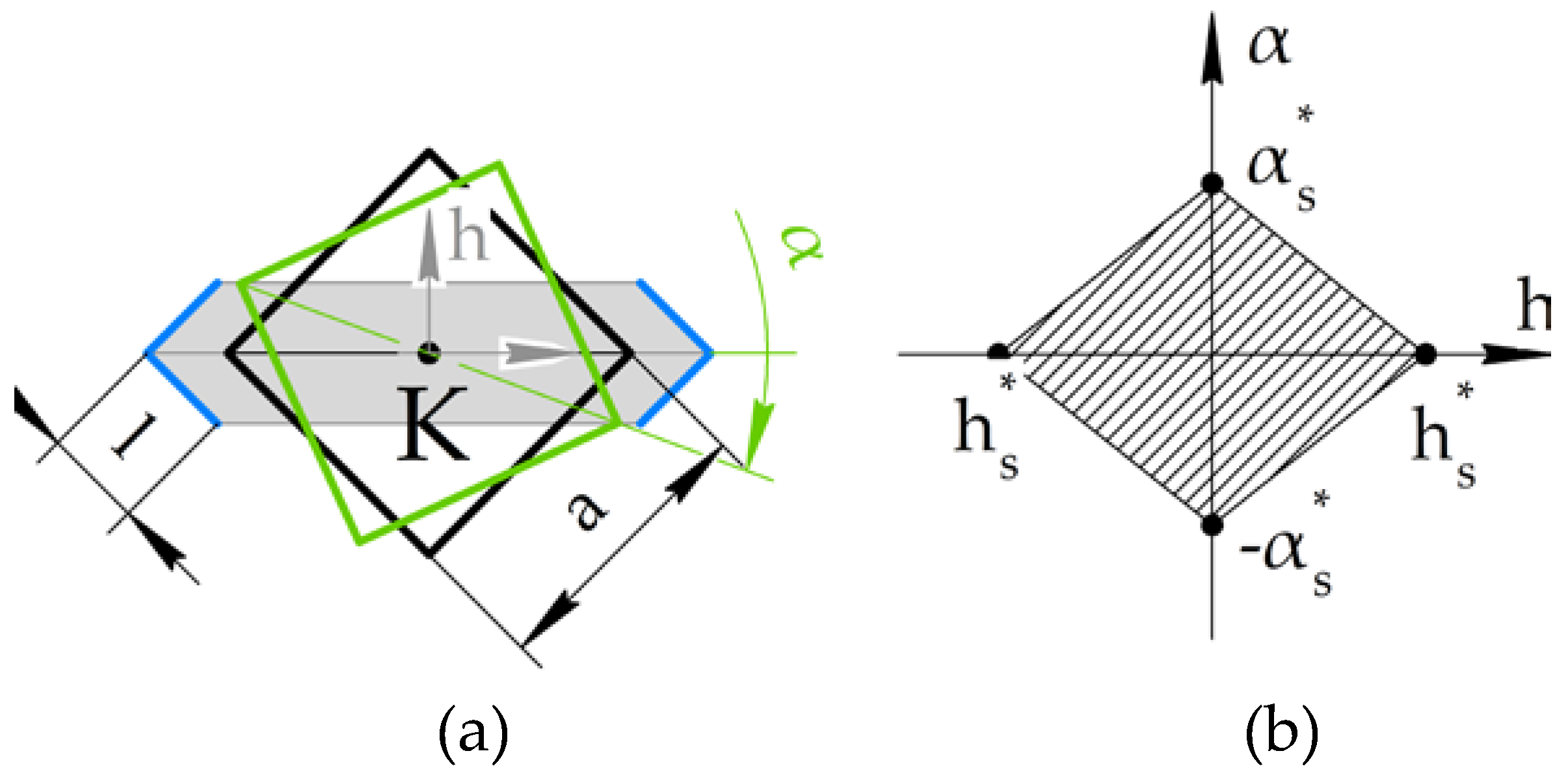
The solution for planar grasping from previous work [24] is based on concept of grasping by diagonals, as shown in Figure 4a. The accuracy limitations of the proposed method are explained below. The grasping zone is limited by the borders of the fingertips. The central line connecting their corners is a bisector of an angle between the fingertips’ sides. For convenience, the coordinate system is set along one of the diagonals of the grasped body. The linear deviation h and the angular α are used to define the grasping area. The profile can be grasped if two of its counter diagonals are placed in the grasping zone. The linear deviation h is measured by the center of the difference between the gripper of the center and the grasped body along the h axis. The angle of deviation α is measured as the angle between two lines, one of which connects the corners of the fingertips, the other is a diagonal of a grasped body. Four points in Figure 4b represent maximum deviations, two of them for linear deviation, and two others are for angular deviation. For square profile of a grasped body with its side equal to a, the diagonal is equal to a 2 . The width of a grasping zone with the fingertip corner side equal to l, is equal to l 2 , where l < a. The linear deviation h corresponds to half of this width in both directions, so the deviations h*s and -h*s are equal l 2 / 2 and − l 2 / 2 , respectively. If to rotate the grasped body around the center in such a way that its counter-diagonals touch borders of the grasping zone, a right triangle can be drawn, where a hypotenuse is equal to a diagonal of the grasped body, and the shortest side of a triangle is equal to the width of the grasping zone. The ratio between the width of the grasping zone and the diagonal of the grasped body is equal to sine of an angular deviation, and, therefore, the maximal angular deviation α can be represented as arcsine of this ratio, as shown in Equation 10.
α s * = sin − 1 ⁡ l 2 a 2 = sin − 1 ⁡ l a
Likewise in Equation 10, − α s * = − sin − 1 ⁡ l a .
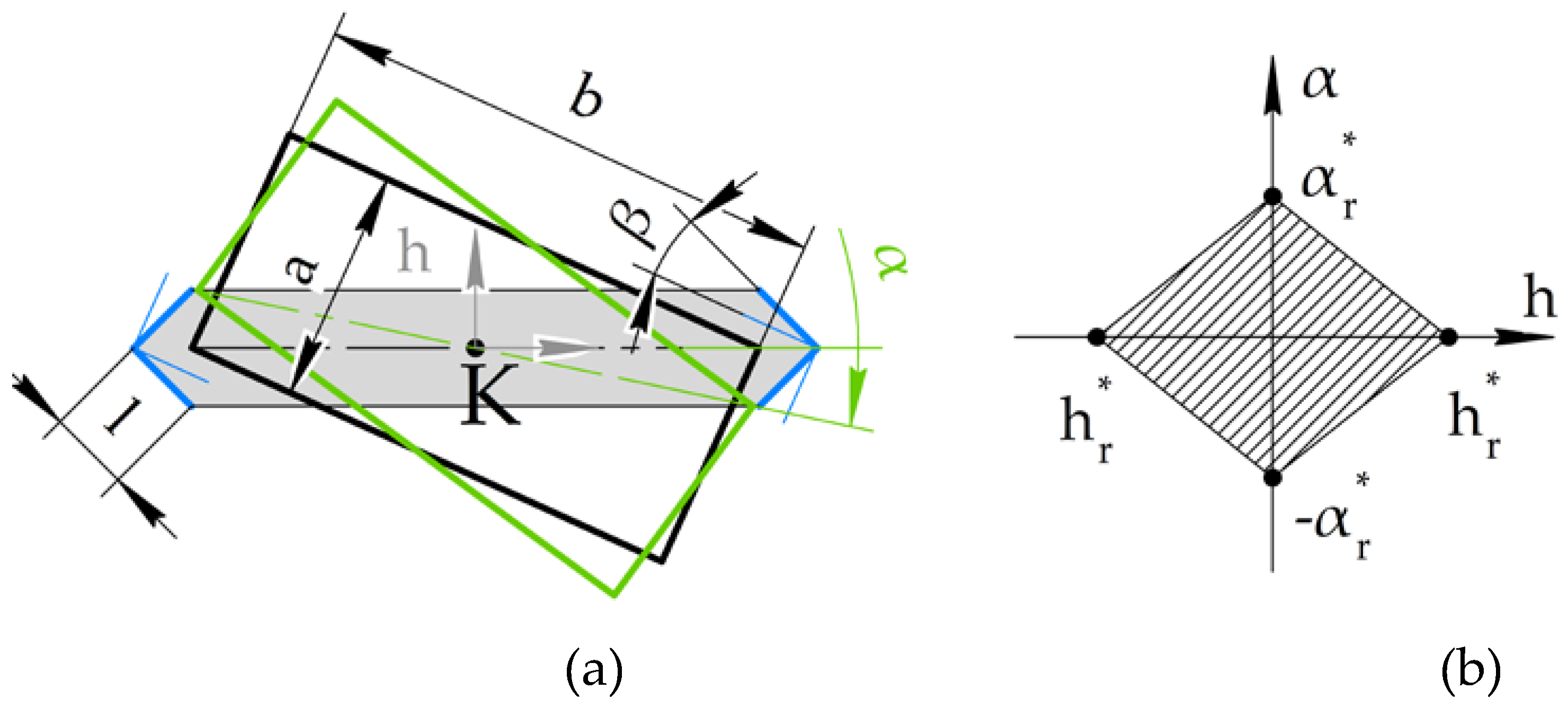
The same way can be used to explain the linear and angular deviations for the rectangular grasped body with sides equal to a and b in Figure 5a. The h-axis is placed perpendicularly to one of the diagonals of the grasped body. The diagonal d for the grasped body can be found by Pythagorean theorem, as a 2 + b 2 . Maximal linear deviation for the rectangular grasped body h*r in Figure 5b remains the same as in the previous task for a square body, or l 2 / 2 . Angular deviation α*r can be presented as a ratio between the grasping zone width and the grasped body diagonal, as
α r * = sin − 1 ⁡ l 2 d = sin − 1 ⁡ l 2 a 2 + b 2
For square grasped body, its diagonals are orthogonal to each other and at 45 degrees to both corresponding sides. Both fingertips are parallel to the sides of the grasped body, and the central line of the grasping zone is coplanar to the diagonal d of the grasped body. But for the rectangular body, the diagonal divides the right angle between its sides into two nonequal angles. To comply with this diagonal, the fingertips should be able to rotate at angle β. As mentioned above, the angle between a central line and each side of a fingertip is equal to 45 degrees. The angle γ between the diagonal of the rectangular grasped body and their sides a and b can be presented as the arctangent function between its sides, or tan − 1 ⁡ a / b . The angle β is a difference between 45 degrees and this function, as
β = 45 − γ = 45 − tan − 1 ⁡ a b
CubeSats 1U-3U and 12U correspond to this task. For grasping rectangular profiled CubeSats 6U, the fingertips should be adaptive and rotate by angle β. Using Equations 10-12, the calculated numerical results for linear h and angular α deviations are listed in Table 1 for the L-shaped fingertips with a side equal to 25 mm.

2.3. Gripper kinematic scheme

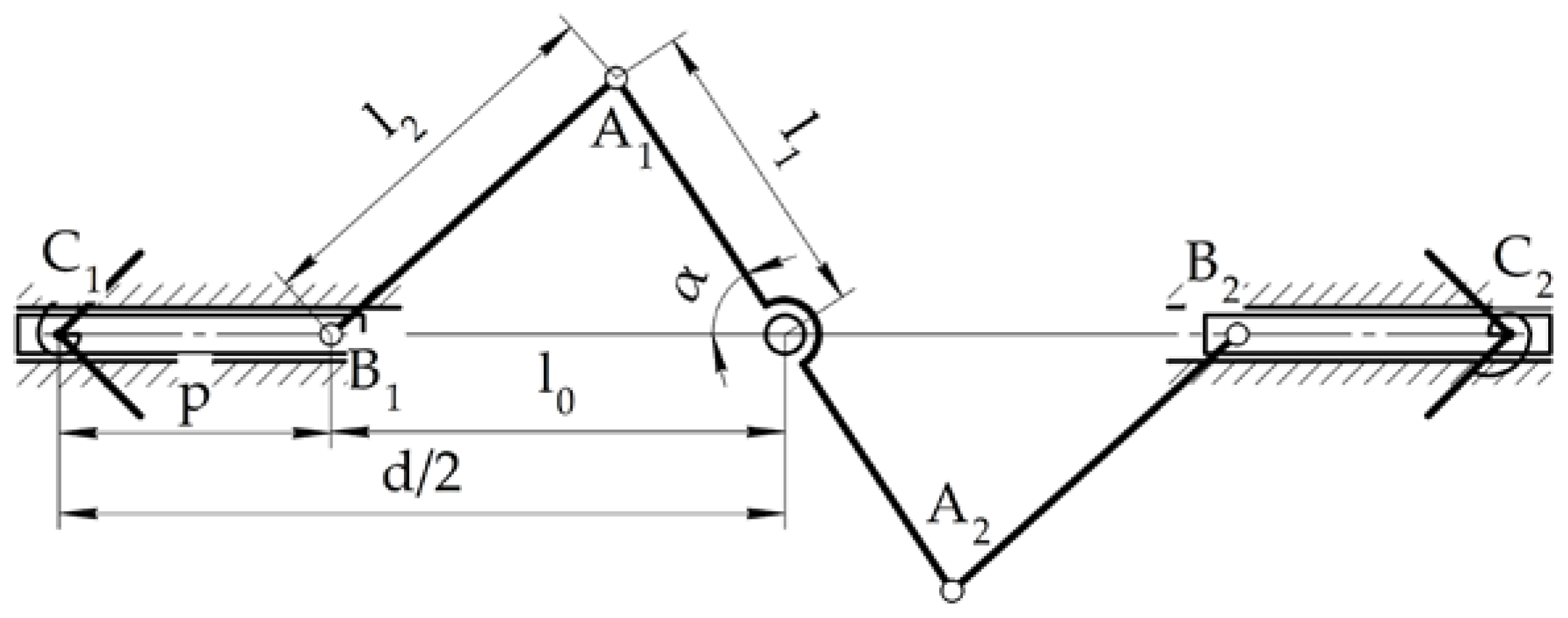
For the grasping task in Figure 4 and Figure 5, a novel gripper design is proposed to grasp different types of CubeSat from 1U to 12U. In previous works [22,24], the conceptual design has been presented as a double slider-crank mechanism, as shown in Figure 6. It has two positions: opened and closed. In the opened position, the distance between fingertips corners dmax is set to be 5% larger than the diagonal of the largest CubeSat 12U for a compact design, or 336.0 mm. For the closed position, the distance dmin is set 1% lower than the diagonal of the smallest CubeSat 1U, or 140.0 mm, to ensure grasping. In Figure 6, the general configuration of a mechanism is presented and distances dmax and dmin are replaced by the distance d/2 from the center of the mechanism to the one of the fingertips. For the gripper design, a distance p equal to 25 mm is set between the fingertip corner C1 or C2 and the crank end B1 and B2, respectively. The distance d/2 in Figure 6 is from the center of the gripper to the corner of the fingertip. In the opened configuration, the distance l0 is the lengths sum of two cranks OA1 and A1B1 for the first finger or OA2 and A2B2 for the second finger. In the closed position, the mechanism becomes the right triangle, where the crank A1B1 with the length l2 is the hypotenuse, and the crank OA1 is one of the cathetes. The distance l0 becomes another cathetus of the right triangle in the closed position. Length l0 is equal to d/2 minus h, and it is known in opened and closed positions of the gripper. Then lengths l1 and l2 of cranks can be found by solving an Equation 13.
l 1 + l 2 + p = d m a x / 2 l 1 2 + d m i n / 2 − p 2 = l 2 2
The length l1 of Equation 5 is equal to 64.4 mm, and the length l2 is equal to 78.6 mm. These lengths are used as crank lengths in the CAD model design.

2.4. Gripper CAD design

The CAD design of a prototype is presented in Figure 7a. A simplified gripper model from [24] has been redesigned for being 3D printed and tested as a lab prototype from Figure 7b, so all the components except ball bearings are designed in PLA. For the input actuation, Dynamixel AX-12A [25] has been chosen. The model of this motor is covered by two parts, which protect the motor from external conditions and are used as basis for other parts. Two rails 180 mm long and 20 mm maximal width are used for translational movement of the fingers. The rails have a trapezoidal profile and a place for ball bearings to keep the fingers. They are inserted into the pockets that are adjusted to the enclosures of the motor. The pockets are designed to fold the gripper rails and keep them unfolded when the gripper is in use. The fingers consist of three parts, such as the car, the fingertip, and the cap with flexible elements. The car is 40 mm long, its profile repeats the profile of the rail with the gap 0.2 mm, and it has sockets for six ball bearings from each side. It has a hole for the crank, and a socket for the fingertip. This socket is designed with the restrictor that limits the free rotation of the fingertip by 21.16 degrees clockwise and counterclockwise. The L-shaped fingertips are designed on a cylindrical platform with diameter of 20 mm. The 25 mm wide and 70 mm long sides of the fingertip are placed 90 degrees related to each other. The central crank is double of the length l1, or 128.8 mm, and the lengths of two other cranks are equal to l2, or 78.6 mm.
For laboratory testing, an adjustable support has been designed. When sensors are installed on fingertips, the center of the mass can slightly move from the initial position. The platform allows to hang and manually center the gripper along two axes in 70×43 mm range.

2.5. Testing design and modes

The lab prototype is made from CAD model from Figure 7. The parts are printed in PLA material with 20% grid infill. The tolerances between the moving parts are 0.2 mm. Flexible elements are taken off to reduce resistance and friction for better adjustment of a fingertip during contact with the grasped body. The final mass of the printed prototype with the installed Arduino board is 215 gram.
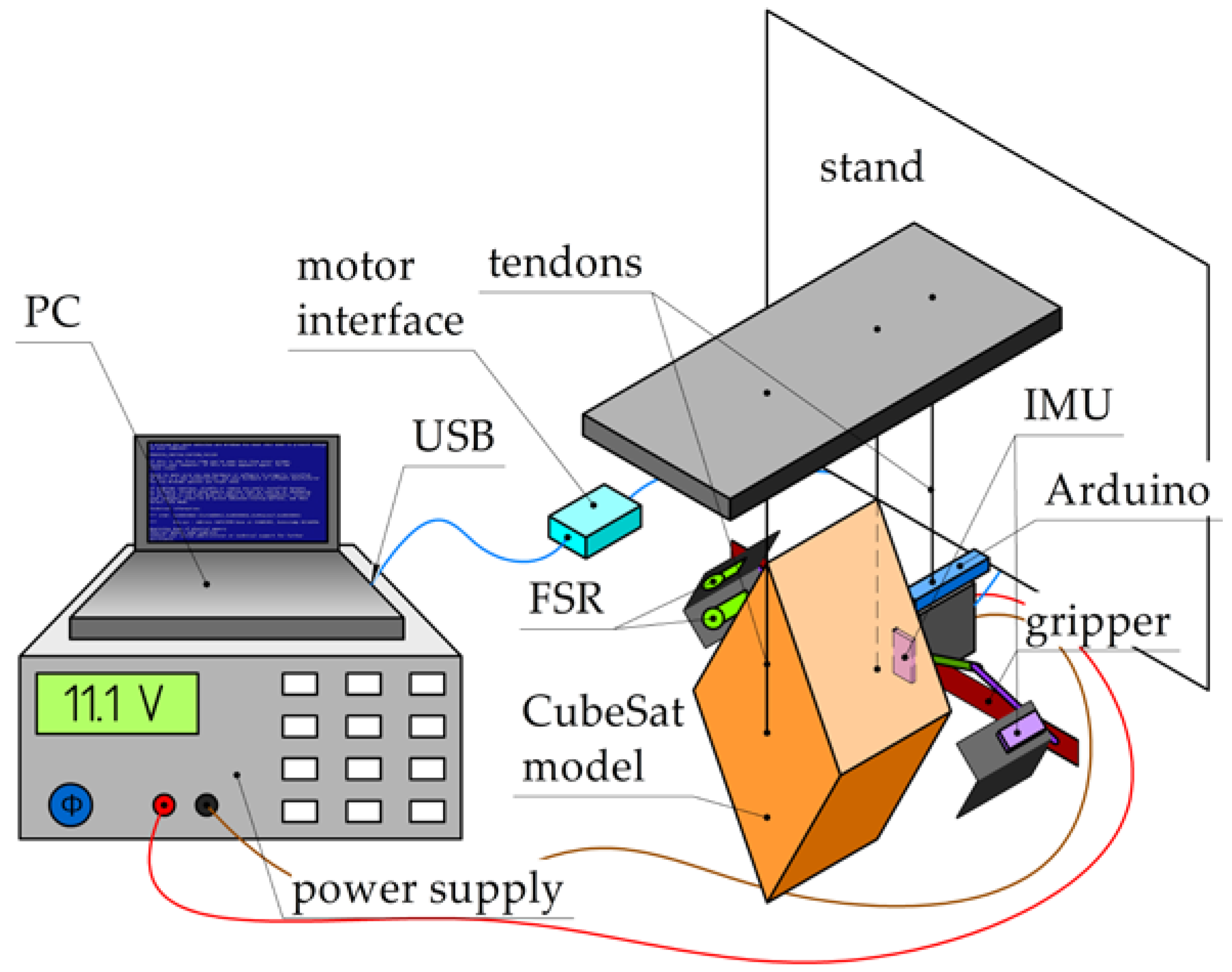
From Figure 8, the grasped body is a cardboard box 210 × 210 × 50 mm, which is close to the dimensions of CubeSat 12U. The larger surface 210 × 210 mm is placed parallel to the gripper mechanism. The distance between the central gripper link and the surface of the gripped body is set 40 mm. The mass of the box is 160 gram.
The Dynamixel AX-12A motor of a gripper is powered by an external 11.1V power supply and controlled by the U2D2 computer interface. The motor is controlled by the software Dynamixel Wizard 2.0. It allows to control the speed, torque, limit rotation angles, and get real-time data, such as current usage and present position. Grasping is performed by movements of the motor, which are manually controlled by the Dynamixel Wizard 2.0 software.
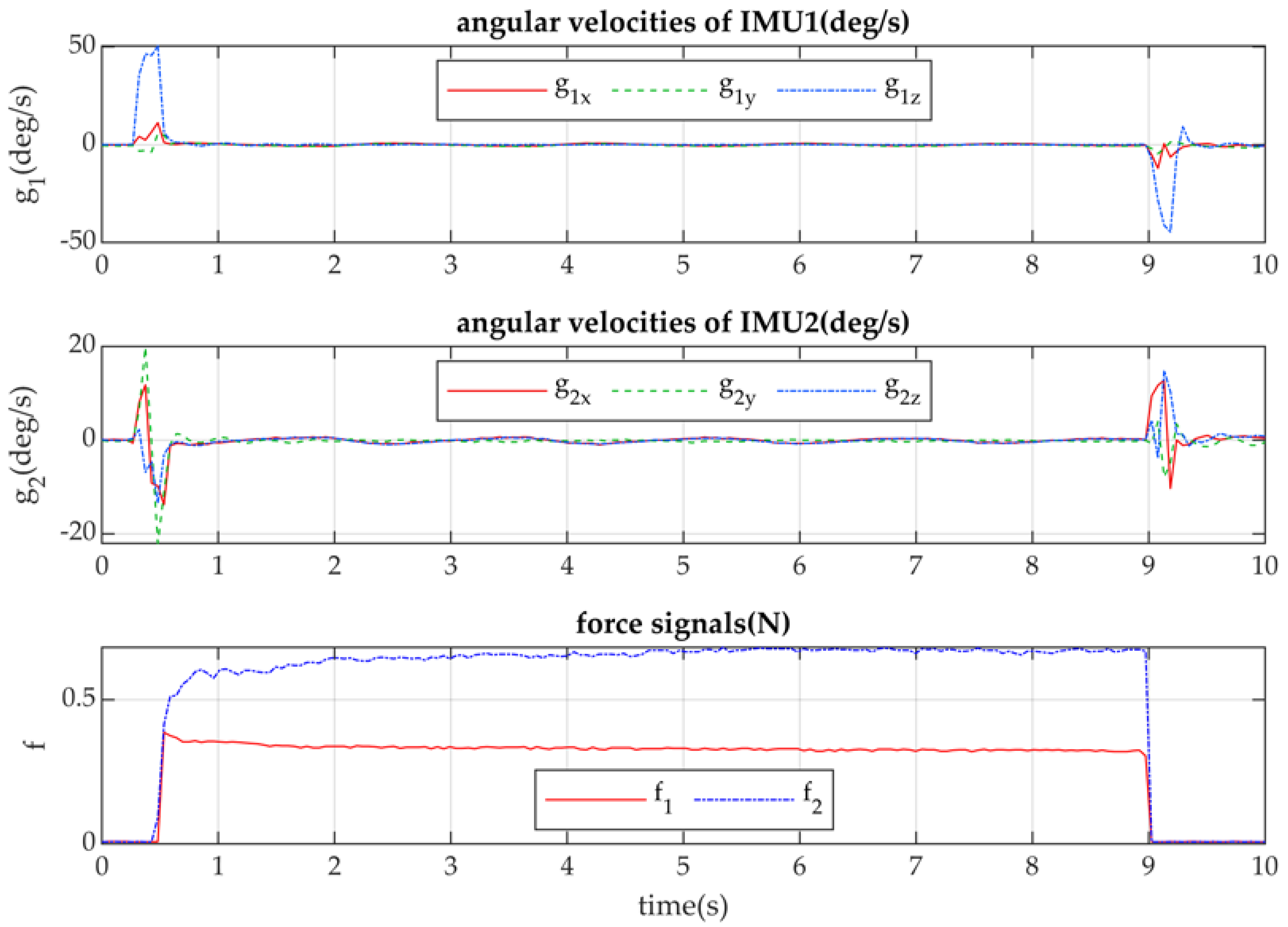
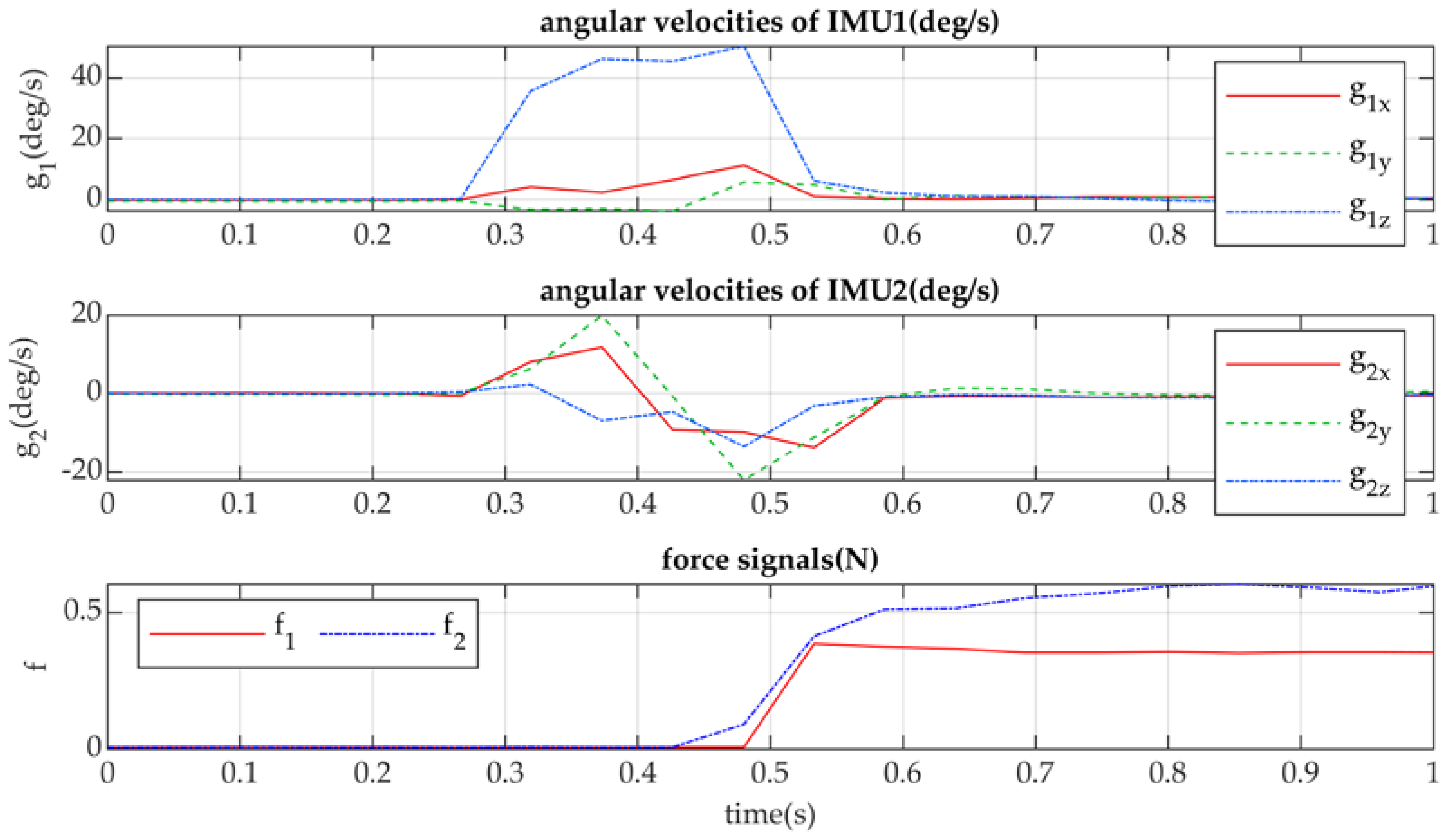
To measure impact during grasping operation, two inertial measurement unit (IMU) sensors BMI160 and two force sensor resistors FSR-400 are installed on the gripper. The first IMU is set in the gripper center on the central crank, and it is used to measure the gyroscope and acceleration data of the gripper center. The second is installed at the fingertip. It shows the data of the fingertip motions. Two force sensors are placed at the fingertip and measure the contact forces when grasping. One force sensor is set between the sides of the fingertip. The ribs of the carton box are with the 1 mm radius, and a small platform is designed to transmit contact forces from this rib to the sensor. Another fingertip is on one side of the fingertip, coordinates of its center are 20 mm from its top and 15 mm from the edge. If the grasping is successful, the surface of the box touches it, and a contact is registered. Another contact platform on the side of the fingertip is used to transmit distributed forces to the small surface of a force sensor.
Force sensor resistors, which are named as FSR in Figure 8, are mostly used to register the existence of a contact, but not for the precise measurements. However, sensors calibration has been conducted using reference weights and Arduino board. The datasheet [26] shows nonlinear resistance or conductance. The sensor was connected to analog pin of Arduino with 10K Ohm resistor, and the data were acquired as a signal from 0 to 1023. The function of the form y = k1 / (x + k2) + k3 , where k1 = -1000, k2 = -1023, and k3 = -0.97 are the empirical coefficients, was applied to the acquired data to convert them into Newtons.
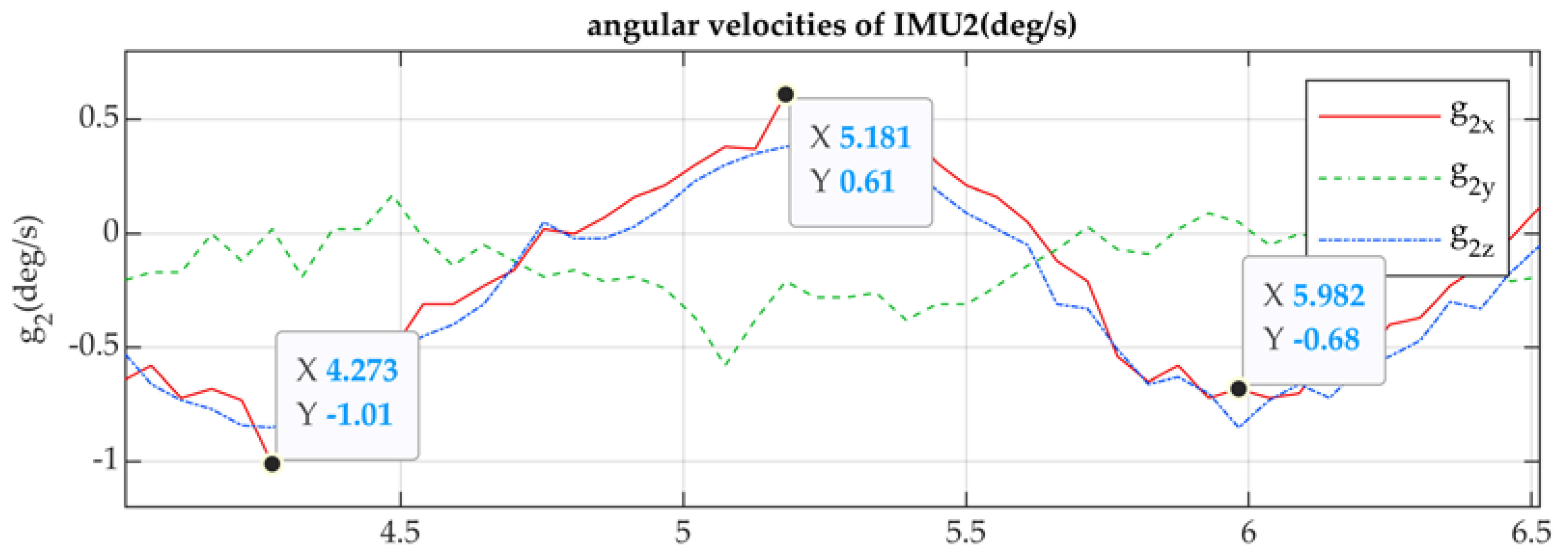
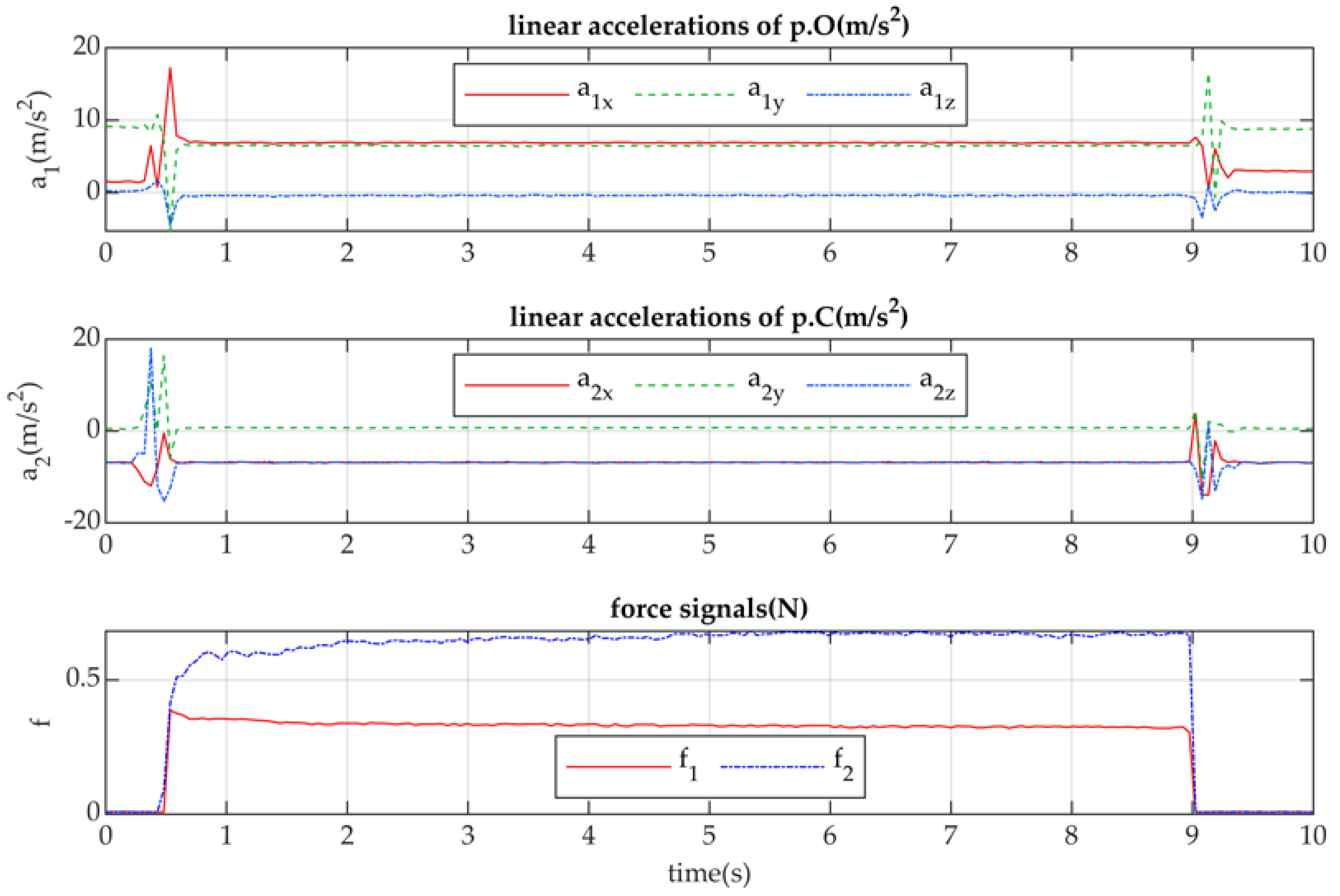
Arduino Nano Every is used to acquire the data from the IMU and force sensors. It is installed on the gripper below the support platform. I2C connection is used to acquire the data from the IMU sensors; three components of angular velocities and three components of linear acceleration are taken from each sensor. Two components of force data are taken from the force sensor resistors. The frequency of acquiring data for 14 components in total is 15 Hz with the 115200 baudrate set on the Arduino board.
The test is planned as a grasping of a box, holding it, and releasing it. The box is fixed in the fingertips during the test. The commands of grasping and releasing are given by user in the Dynamixel Wizard 2.0 software. Grasping time is around 8.5 seconds, as the CubeSat can be held in the berthing operation, and this time is enough to observe the successful operation and behavior of the system, such as gripper oscillations together with the grasped body.
Preprints 74605 g008
Figure 8. A laboratory setup for gripper testing.
Figure 8. A laboratory setup for gripper testing.
Preprints 74605 g008

3. Results

The acquired data from grasping test are shown in Figure 9, Figure 10 and Figure 11. In Figure 9 and Figure 10, IMU1 is the sensor installed on the central link of the gripper. The largest angular velocities of 45 deg/s are along rotation axis Z, and the values of angular velocities decrease when the gripper contacts with the grasped body. The IMU2 installed at the fingertip shows impact when grasping. The velocity components change direction in the moment of a contact.
Acquired data f1 correspond to the force sensor set in the fingertip center. Increasing force data values show no ideal contact with the rib of the grasped body. One of the explanations of this phenomena is the gravitation affecting of the fingertip. It takes more time to adjust the fingertip properly, even if the input motion of the motor is stopped. Instead, the contact with the force sensor f2 on the fingertip surface shows planned behavior with higher values at the beginning and then constant value when the grasped body is held.
The impact of a grasping operation makes the gripper oscillate with a grasped body with the period of 1.7 s and an amplitude 1.6 degrees along X axis, as presented in Figure 11.
Figure 12 can be used not only to evaluate the accelerations of the gripper parts, but also their orientation, because of the gravity force that affects the results.

4. Conclusions

A low-cost lightweight design of a two-finger gripper prototype has been designed for a berthing operation. Double-crank mechanism is used to grasp CubeSat bodies along diagonals from 140 to 330 mm with the maximal size 360 mm of a gripper. The folding scheme allows us to reduce the dimensions of the gripper to keep it in a spacecraft launcher. A CAD design for a prototype is designed ready-to-print. A lab prototype is built for grasp testing. Grasping operation is conducted using the input motion of the motor. Acquired data from IMU and force sensors are used for evaluating and analyze the actual parameters of a grasping operation. The mechanism shows the successful grasping and holding of a body with CubeSat 12U dimensions with the calculated accuracy.
The results in Figure 9, Figure 10, Figure 11 and Figure 12 characterize numerically the prototype, providing a proof-of-concept for the proposed operation. In particular, the acquired angular velocities highlight a smooth motion and limited disturbance after the grasping operation and before release. The force values, despite uncertainties, suggest that the range required for the grasping operation is bound to an upper value lower than 0.7 N, thanks to the angular design of the fingertips that provides a stable grasp by exploiting shape rather than relying on friction/force alone.
As shown in Figure 9, the results from the IMU sensors can be used to monitor and control the residual motion after operation, due to the overall inertia of the system in a low gravity setting. Further information can be extracted from acceleration data, showing the initial impact of the fingertips onto the satellite during the grasping phase and further (more limited) impacts and vibration during the remaining of the grasping phase and release. In future developments, this data can be used for feedback, enabling closed-loop system control, or to improve the design by implementing an embodied damping system (e.g., with soft compliant interfaces).

Author Contributions

Conceptualization, M. Ceccarelli and A. Titov; methodology, A. Titov and M. Russo; formal analysis, A. Titov; investigation, A. Titov, M. Russo and M. Ceccarelli; resources, M. Ceccarelli; data curation, A. Titov and M. Russo; writing—original draft preparation, A. Titov and M. Ceccarelli; writing—review and editing, A. Titov, M. Russo and M. Ceccarelli; visualization, A. Titov; supervision, M. Ceccarelli; project administration, M. Ceccarelli; funding acquisition, M. Ceccarelli. All authors have read and agreed to the published version of the manuscript.

Funding

This research received no external funding.

Data Availability Statement

No other data than in the paper are available.

Conflicts of Interest

The authors declare no conflict of interest.

References

  1. Kessler, D.J.; Cour-Palais, B.G. Collision Frequency of Artificial Satellites: The Creation of a Debris Belt. Journal of Geophysical Research 1978, 83, 2637–2646. [Google Scholar] [CrossRef]
  2. ESA Space Debris Office ESA’s Annual Space Environment Report; ESA ESOC: Darmstadt, Germany, 2022; pp. 1–120.
  3. Liu, Y.; Zhao, Y.; Tan, C.; Liu, H.; Liu, Y. Economic Value Analysis of On-Orbit Servicing for Geosynchronous Communication Satellites. Acta Astronautica 2021, 180, 176–188. [Google Scholar] [CrossRef]
  4. Laryssa, P.; Lindsay, E.; Layi, O.; Marius, O.; Nara, K.; Aris, L.; Ed, T. International Space Station Robotics: A Comparative Study of ERA, JEMRMS and MSS. 7th ESA Workshop on Advanced Space Technologies for Robotics and Automation “ASTRA 2002”, 2002, 1–8.
  5. Kuwao, F.; Otsuka, A.; Hayashi, M.; Aiko, Y.; Wakabayashi, Y.; Sato, N.; Doi, S. Operation Concept of JEMRMS. In Proceedings of the Proceeding of the 7th International Symposium on Artificial Intelligence; Robotics and Automation in Space: i-SAIRAS 2003; May 2003. pp. 19–23.
  6. Boumans, R.; Heemskerk, C. The European Robotic Arm for the International Space Station. Robotics and Autonomous Systems 1998, 23, 17–27. [Google Scholar] [CrossRef]
  7. Oda, M. Summary of NASDA’s ETS-VII Robot Satellite Mission. Journal of Robotics and Mechatronics 2000, 12, 417–424. [Google Scholar] [CrossRef]
  8. Hirzinger, G.; Landzettel, K.; Brunner, B.; Fischer, M.; Preusche, C.; Reintsema, D.; Albu-Schäffer, A.; Schreiber, G.; Steinmetz, B.-M. DLR’s Robotics Technologies for on-Orbit Servicing. Advanced Robotics 2004, 18, 139–174. [Google Scholar] [CrossRef]
  9. Mulder, T. Orbital Express Autonomous Rendezvous and Capture Flight Operations, Part 2 of 2: AR&C Exercise 4,5, and End-Of-Life. In AIAA/AAS Astrodynamics Specialist Conference and Exhibit; American Institute of Aeronautics and Astronautics.
  10. Rupp, T.; Boge, T.; Kiehling, R.; Sellmaier, F. Flight dynamics challenges of the German on-orbit servicing mission DEOS. 21st international symposium on space flight dynamics 2009, 22. [Google Scholar]
  11. Moosavian, S.A.A.; Papadopoulos, E. On the Kinematics of Multiple Manipulator Space Free-Flyers and Their Computation. Journal of Robotic Systems 1998, 15, 207–216. [Google Scholar] [CrossRef]
  12. Samani, F.; Ceccarelli, M. An Experimental Characterization of Torveastro, Cable-Driven Astronaut Robot. Robotics 2021, 10, 1–19. [Google Scholar] [CrossRef]
  13. Cafolla, D.; Araque-Isidro, J.E.; Ceccarelli, M. Design and Testing of Torveastro: An Outer Space Service Robot. Applied Sciences 2023, 13, 1187. [Google Scholar] [CrossRef]
  14. Schmaus, P.; Leidner, D.; Krüger, T.; Schiele, A.; Pleintinger, B.; Bayer, R.; Lii, N.Y. Preliminary Insights From the METERON SUPVIS Justin Space-Robotics Experiment. IEEE Robotics and Automation Letters 2018, 3, 3836–3843. [Google Scholar] [CrossRef]
  15. Diftler, M.A.; Mehling, J.S.; Abdallah, M.E.; Radford, N.A.; Bridgwater, L.B.; Sanders, A.M.; Askew, R.S.; Linn, D.M.; Yamokoski, J.D.; Permenter, F.A.; et al. Robonaut 2 - The First Humanoid Robot in Space. In Proceedings of the 2011 IEEE International Conference on Robotics and Automation; May 2011; pp. 2178–2183. [Google Scholar]
  16. Sofina, D. FEDOR: Meet Russia’s First Robot Astronaut (Who Also Does Splits) Available online:. Available online: https://news.itmo.ru/en/science/cyberphysics/news/8710/ (accessed on 13 March 2023).
  17. Fehse, W. Automated Rendezvous and Docking of Spacecraft; Cambridge University Press: New-York, 2003; ISBN 978-0-521-82492-7. [Google Scholar]
  18. Nanosatellite & CubeSat Database. Available online: https://www.nanosats.eu/database (accessed on 14 February 2023).
  19. ESA Space Debris Office ESA’s Annual Space Environment Report; ESA ESOC: Darmstadt, Germany, 2022; pp. 1–120.
  20. NASA, RSA, ESA, CSA. IDSS International Docking System Standard (IDSS) Interface Definition Document (IDD) Revision E; 2016; pp. 1–142.
  21. Titov, A. , Ceccarelli, M. (2022). Problems and Requirements for Docking Operation in Orbital Stations. In: Niola, V., Gasparetto, A., Quaglia, G., Carbone, G. (eds) Advances in Italian Mechanism Science. IFToMM Italy 2022. Mechanisms and Machine Science, vol 122. Springer, Cham (2022). [CrossRef]
  22. Titov, A.; Ceccarelli, M. Requirements and Problems for Space Berthing System. In Proceedings of the Proceedings of SYROM 2022 & ROBOTICS 2022; Springer International Publishing: Cham, 2023. Vol. 127. pp. 127–135. [Google Scholar]
  23. Ceccarelli, M. Fundamentals of the Mechanics of Grasp. In Fundamentals of Mechanics of Robotic Manipulation; Ceccarelli, M., Ed.; International Series on Microprocessor-Based and Intelligent Systems Engineering; Springer Netherlands: Dordrecht, 2004; pp. 241–304. ISBN 978-1-4020-2110-7. [Google Scholar]
  24. Titov, A.; Ceccarelli, M. Design and Performance Characterization of a Gripper End-Effector for a Space Berthing Manipulator. In Proceedings of the New Advances in Mechanisms, Transmissions and Applications; Springer Nature, 2023; Vol. 124; pp. 15–22. [Google Scholar]
  25. ROBOTIS. E-Manual AX-12+, AX-12A. Available online: https://emanual.robotis.com/docs/en/dxl/ax/ax-12a/ (accessed on 27 April 2023).
  26. FSR® 400 Series Data Sheet. Available online: https://www.digikey.com/htmldatasheets/production/1184367/0/0/1/34-00022.pdf (accessed on 09 May 2023).
Preprints 74605 g002
Figure 2. A grasping task formulation: (a) a corner fingertip example, (b) a middle-side fingertip example, (c) an edge-side fingertip example.
Figure 2. A grasping task formulation: (a) a corner fingertip example, (b) a middle-side fingertip example, (c) an edge-side fingertip example.
Preprints 74605 g002
Preprints 74605 g003
Figure 3. Two-fingertip combinations from Figure 2: (a) two corner fingertips, (b) two middle-side fingertips, (c) two edge-side fingertips.
Figure 3. Two-fingertip combinations from Figure 2: (a) two corner fingertips, (b) two middle-side fingertips, (c) two edge-side fingertips.
Preprints 74605 g003
Preprints 74605 g004
Figure 4. A concept of grasping by diagonals: (a) a planar scheme for grasping a CubeSat 1U with design parameters, (b) grasping zone limits along linear and angular deviation axes.
Figure 4. A concept of grasping by diagonals: (a) a planar scheme for grasping a CubeSat 1U with design parameters, (b) grasping zone limits along linear and angular deviation axes.
Preprints 74605 g004
Preprints 74605 g005
Figure 5. A concept of grasping a rectangle-profiled body by diagonals: (a) a planar scheme for grasping a CubeSat 6U with design parameters, (b) grasping zone limits along linear and angular deviation axes.
Figure 5. A concept of grasping a rectangle-profiled body by diagonals: (a) a planar scheme for grasping a CubeSat 6U with design parameters, (b) grasping zone limits along linear and angular deviation axes.
Preprints 74605 g005
Preprints 74605 g006
Figure 6. A kinematic scheme of the proposed gripper for grasping tasks in Figure 4 and Figure 5.
Figure 6. A kinematic scheme of the proposed gripper for grasping tasks in Figure 4 and Figure 5.
Preprints 74605 g006
Preprints 74605 g007
Figure 7. A design of the proposed gripper from Figure 6: (a) CAD design, (b) a photo of the lab prototype with kinematics drawing and sensor setup.
Figure 7. A design of the proposed gripper from Figure 6: (a) CAD design, (b) a photo of the lab prototype with kinematics drawing and sensor setup.
Preprints 74605 g007
Preprints 74605 g009
Figure 9. Acquired data of angular velocities from IMU corresponding to the force sensors data.
Figure 9. Acquired data of angular velocities from IMU corresponding to the force sensors data.
Preprints 74605 g009
Preprints 74605 g010
Figure 10. Enlarged data of angular velocities and force sensors from Figure 9.
Figure 10. Enlarged data of angular velocities and force sensors from Figure 9.
Preprints 74605 g010
Preprints 74605 g011
Figure 11. Enlarged data of angular velocities of the second IMU from Figure 9.
Figure 11. Enlarged data of angular velocities of the second IMU from Figure 9.
Preprints 74605 g011
Preprints 74605 g012
Figure 11. Acquired data of linear accelerations from IMU corresponding to the force sensors data.
Figure 11. Acquired data of linear accelerations from IMU corresponding to the force sensors data.
Preprints 74605 g012
Table 1. Maximal deviations for grasping CubeSats 1U, 6U, and 12U.
Table 1. Maximal deviations for grasping CubeSats 1U, 6U, and 12U.
l (mm) a (mm) b (mm) d (mm) h (mm) α (deg) β (deg)
1U 25.0 100.0 100.0 141.4 17.678 14.478 –
6U 25.0 100.0 226.3 240.4 17.678 8.216 21.16
12U 25.0 226.3 226.3 320.0 17.678 6.343 –
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.
Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.
Prerpints.org logo

Preprints.org is a free preprint server supported by MDPI in Basel, Switzerland.

facebook logotwitter logolinkedin logo
MDPI Initiatives
Important Links
Subscribe

Disclaimer

Terms of Use

Privacy Policy

© 2024 MDPI (Basel, Switzerland) unless otherwise stated