Prerpints.org logo
Preprint
Article

A Family of Five-Level Pseudo-Totem Pole Dual Boost Converters

Altmetrics

Downloads

111

Views

21

Comments

0

A peer-reviewed article of this preprint also exists.

Submitted:

25 May 2023

Posted:

26 May 2023

You are already at the latest version

Alerts
Abstract
In this paper, based on the pseudo-totem pole (PTP) circuit, a family of five-level PTP dual boost converters (PDBC) is proposed. Dual boost converter has some unique advantages such as no bridge arm shoot-through risk and no switch body diode reverse recovery problem, so that it has a good application prospect. Compared with conventional three-level PTP converters, PDBCs has higher power density, higher efficiency, and low voltage and current stress. The topological derivation process, working principle, modulation and strategy of the topology are analyzed firstly. Further, the number of power devices, the switches voltage and current stress of the proposed topology is analyzed. Finally, a representative five-level PDBC experimental prototype is designed with AC input 220V/50Hz, DC output 400V/1kW, and peak efficiency of 98.27%. The experimental results show that the five-level PDBC proposed in this paper has higher efficiency and verify the correctness of the topology.
Keywords: 
Subject: Engineering  -   Electrical and Electronic Engineering

1. Introduction

With the development of power electronics technology, the neutral point clamped (NPC) multi-level converter has attracted more and more scholars' attention [1,2]. Multi-level NPC converters has the advantages of high efficiency, high power density, low total harmonic distortion (THD), low voltage and current stress [3,4,5]. Therefore, multi-level NPC converters are widely used in medium and high power, medium voltage applications [6,7,8,9], such as electric vehicles (EVs), motor drives, electrical railway traction, and DC-bus microgrids [10,11,12,1310-13].
Compared with IGBT, power MOSFET has some excellent characteristics such as high frequency operation, low switching loss, and low conduction loss. Therefore, power MOSFET is widely used in low-power converters to improve efficiency and reduce the volume. However, due to the poor reverse recovery characteristics of body diode, MOSFET-based have a risk of device failure, which is related to the phase-leg shoot, may cause false triggering of the gate voltage. Therefore, conventional H-bridge converters often used IGBTs [14,15,16,17]. The dual boost/buck converter can avoid the shoot-through problem effectively, and the freewheeling current flows through the independent diode to solve the MOSFET body diode reverse recovery problem [14,15,16,17,18,19,20,21]. However, due to the two inductance structure of the dual boost/buck converter, the volume and weight of the converter will increase. In this regard, in [16,17,22], the multi-level dual boost/buck converter is proposed to reduce the size and weight of this type of topology.
The bridgeless converter has high power factor (PF), low THD, and high efficiency. It usually includes the basic bridgeless converters, the bidirectional-switch bridgeless converters, the totem pole bridgeless converters, and the PTP bridgeless converters [22,23,24]. Among them, the PTP bridgeless converter has a simple structure, few semiconductor devices conducting in the series loop, and a natural dual boost structure. In order to increase the power density and reduce the THD, the PTP bridgeless converter must work at a higher frequency. Moreover, all the active devices in the circuit bear the DC voltage, which cause the high voltage stress [3].
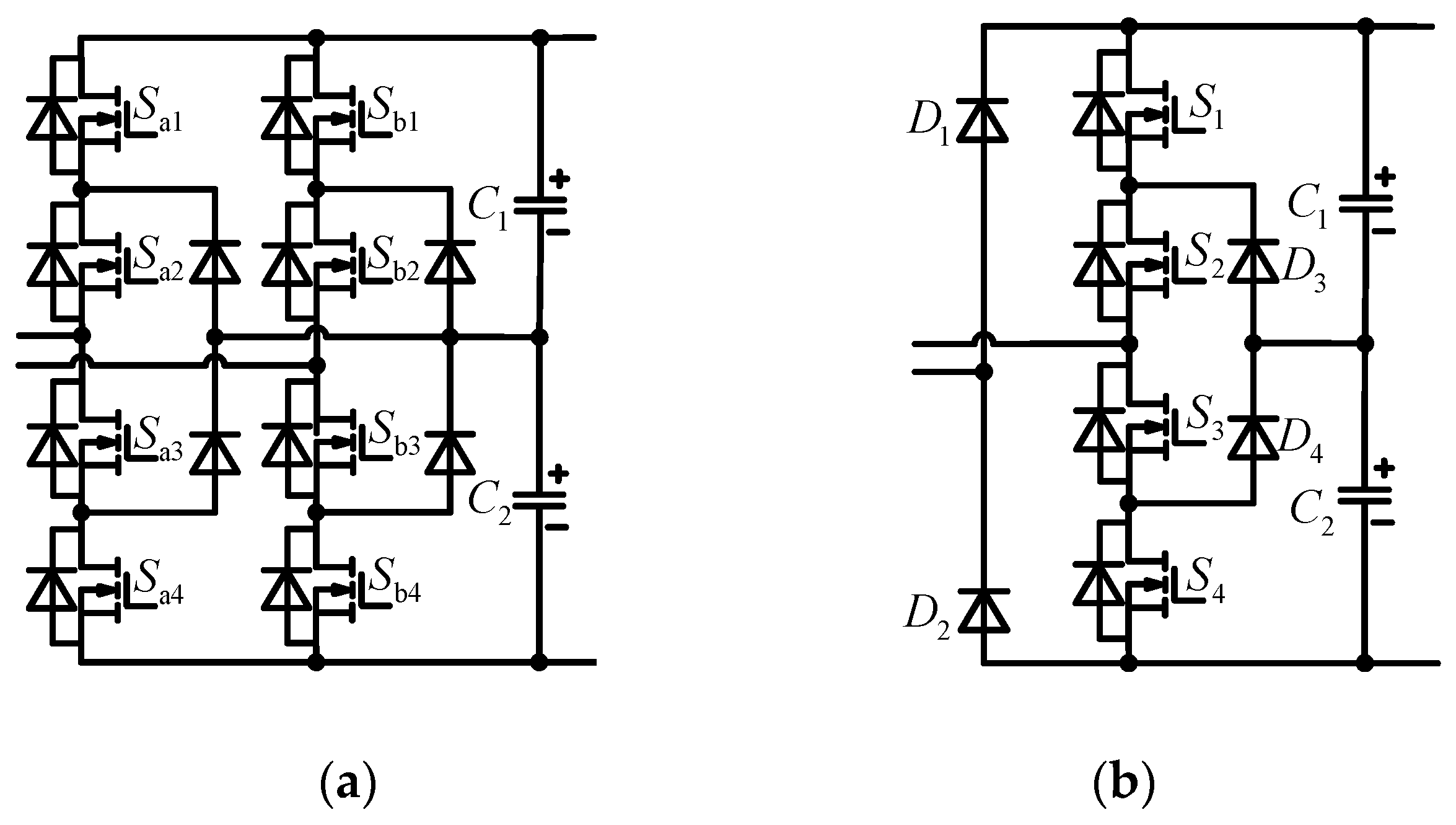
Figure 1 shows two common five-level converter topologies. Figure 1a is conventional five-level converter (CFLC), which is widely used in bidirectional power flow scenario such as vehicle to gird (V2G). However, the number of switch is large, which can be further optimized for reduce the number of switch. Figure 1b is unidirectional five-level converter proposed in [25], which using only one NPC bridge arm in CFLC to reduce the number of switch. However, there is less topology derivation process. In [4], a new five-level converter with high power density is proposed and the current stress is analyzed, however, the number of active devices is large, and the cost is high. In [14,16], the PTP bridgeless structure is adopted to achieve five-level dual buck grid-connected inverter, and summarizes a topology structure method to expand the circuit. However, the utilization of two input inductors is low.
Based on the above analysis, the bridge arm of the topology proposed in [25] is used as the prototype to obtain new five-level bridge arms. By cascading five-level bridge arms with the three-level PTP circuit, a family of five-level PDBCs is proposed. The proposed PDBC optimizes the three-level PTP converter in terms of large volume and large switching loss, and retaining the dual boost structure, which have advantages of high reliability.
The structure of this paper is as follows. Section 2 derives the PDBC in detail and analyzes the working principle. Section 3 designs the control and modulation strategy of PDBC. In section 4, the voltage and current stress are analyzed. Section 5 conducts experimental verification on PDBC. Finally, section 6 concludes the paper.

2. Topological Derivation and Operating Principle

2.1. Topological Derivation

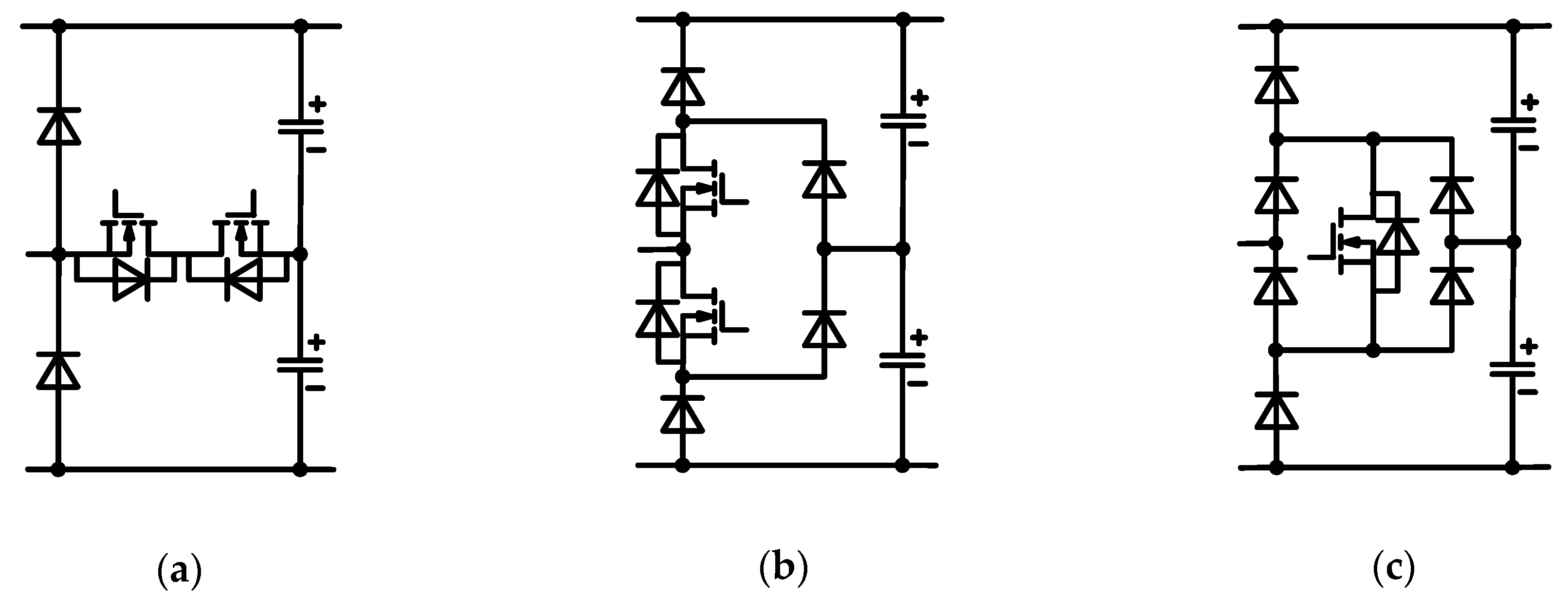
Figure 2 shows the three most commonly used clamping bridge arm structures in five-level converters. A new five-level converter can be obtained by cascading these three clamping bridge arm structures with a three-level circuit.
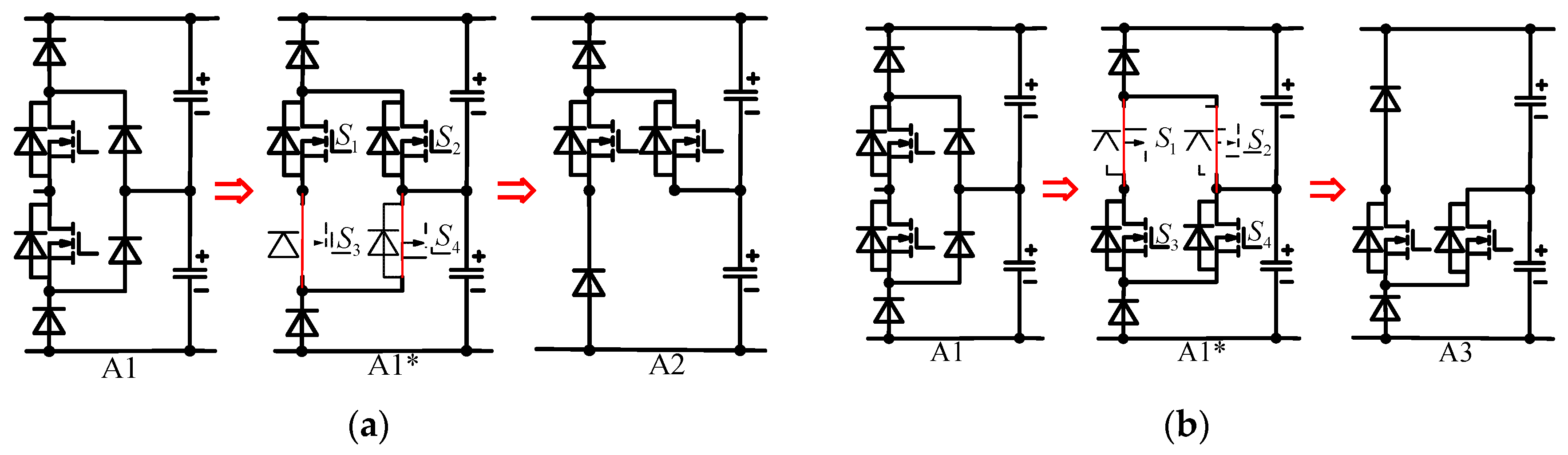
In this paper, the bridge arm shown in Figure 2b is used to generate a new bridge arm, as shown in Figure 3. For ease of description, the bridge arms are numbered below each bridge arms i.e. A1, A2. Firstly, the two diodes on the right side of A4 are replaced with MOSFETs to get A1*. Then removed S2 and S4 of A1*, and reconnected them to get a new bridge arm A2, as shown in Figure 3a. In the same way, remove S1 and S3 of A1*, and then reconnect them to obtain a new bridge arm A3, as shown in Figure 3b.
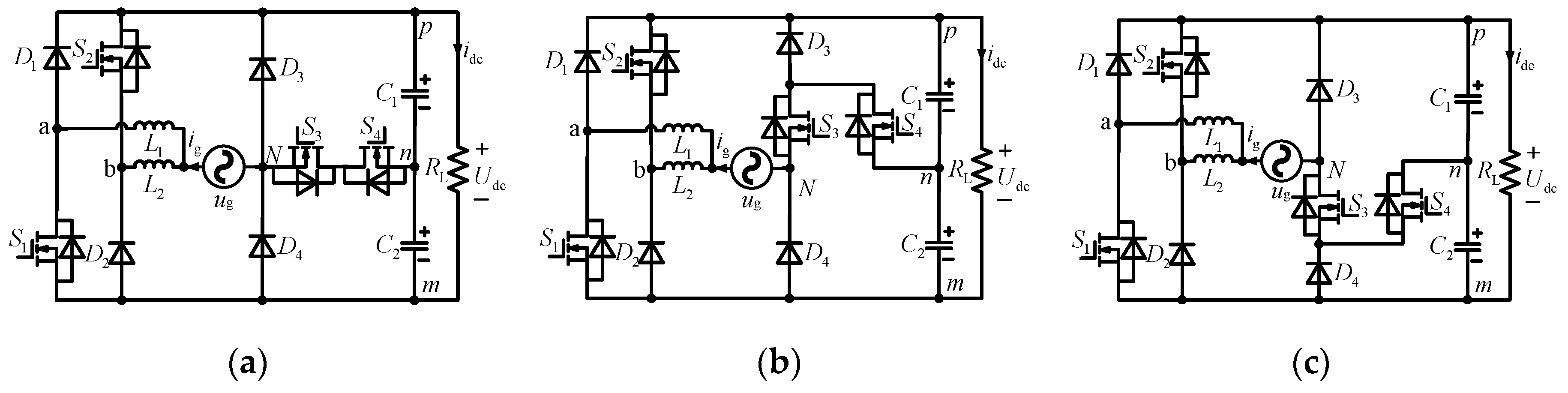
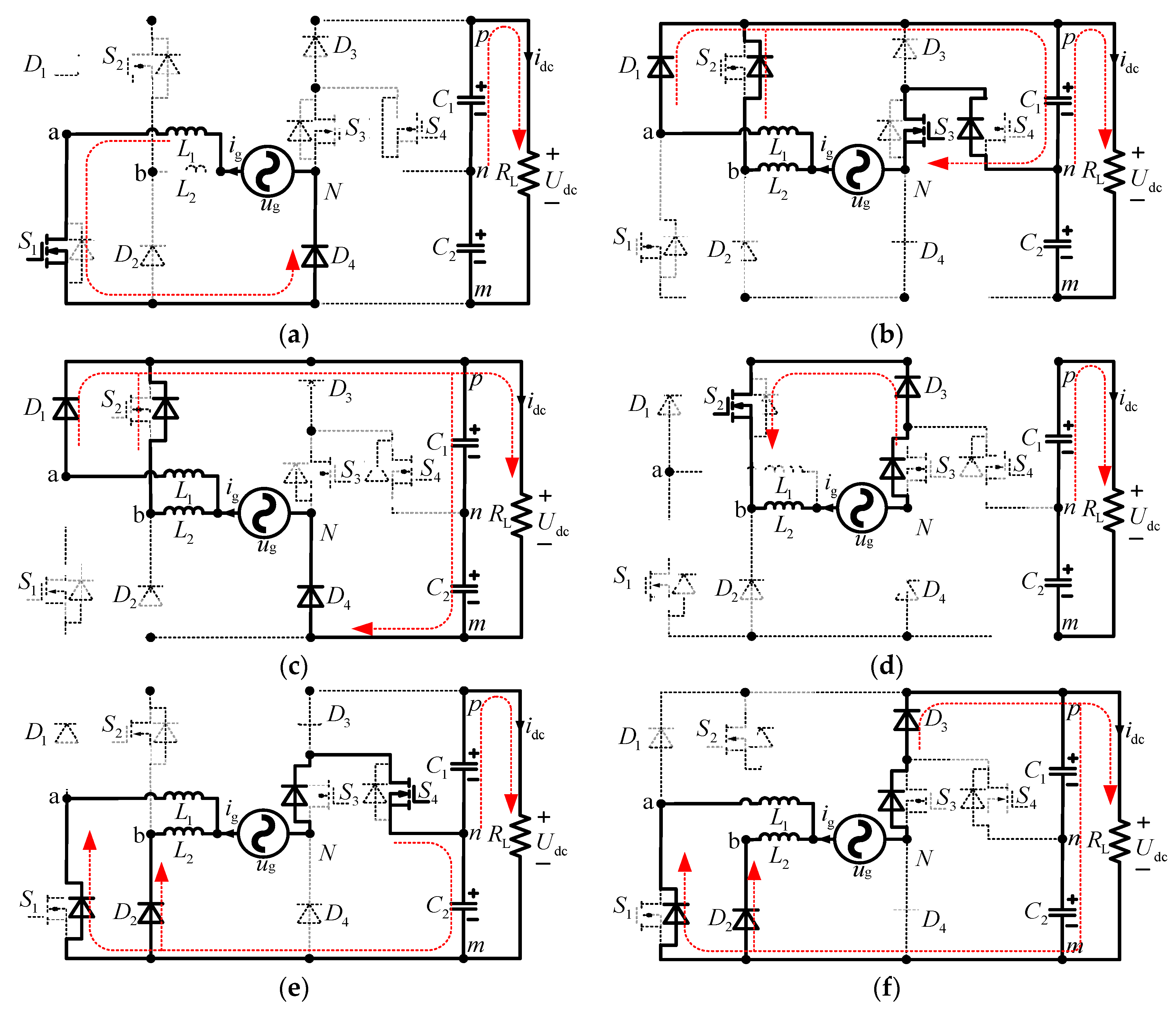
Through the bridge arm transformation in Figure 3, new bridge arms A2 and A3 are derived. Figure 4 shows a family of five-level PTP dual boost converters, which named as PDBC-I, PDBC-II and PDBC-III, respectively. It can be seen in Figure 4, the PTP dual boost converter is cascaded with Figure 2(a), A2, and A3 to generate the PDBCs, respectively.
Compared with the traditional five-level converter, a family of PDBCs proposed in this paper reduces the number of MOSFETs by four, so it can effectively reduce the converter loss. It is worth mentioning that the three power flow converters proposed in this paper can all achieve bidirectional power flow after a slight circuit modification.

2.2. Operating Principle

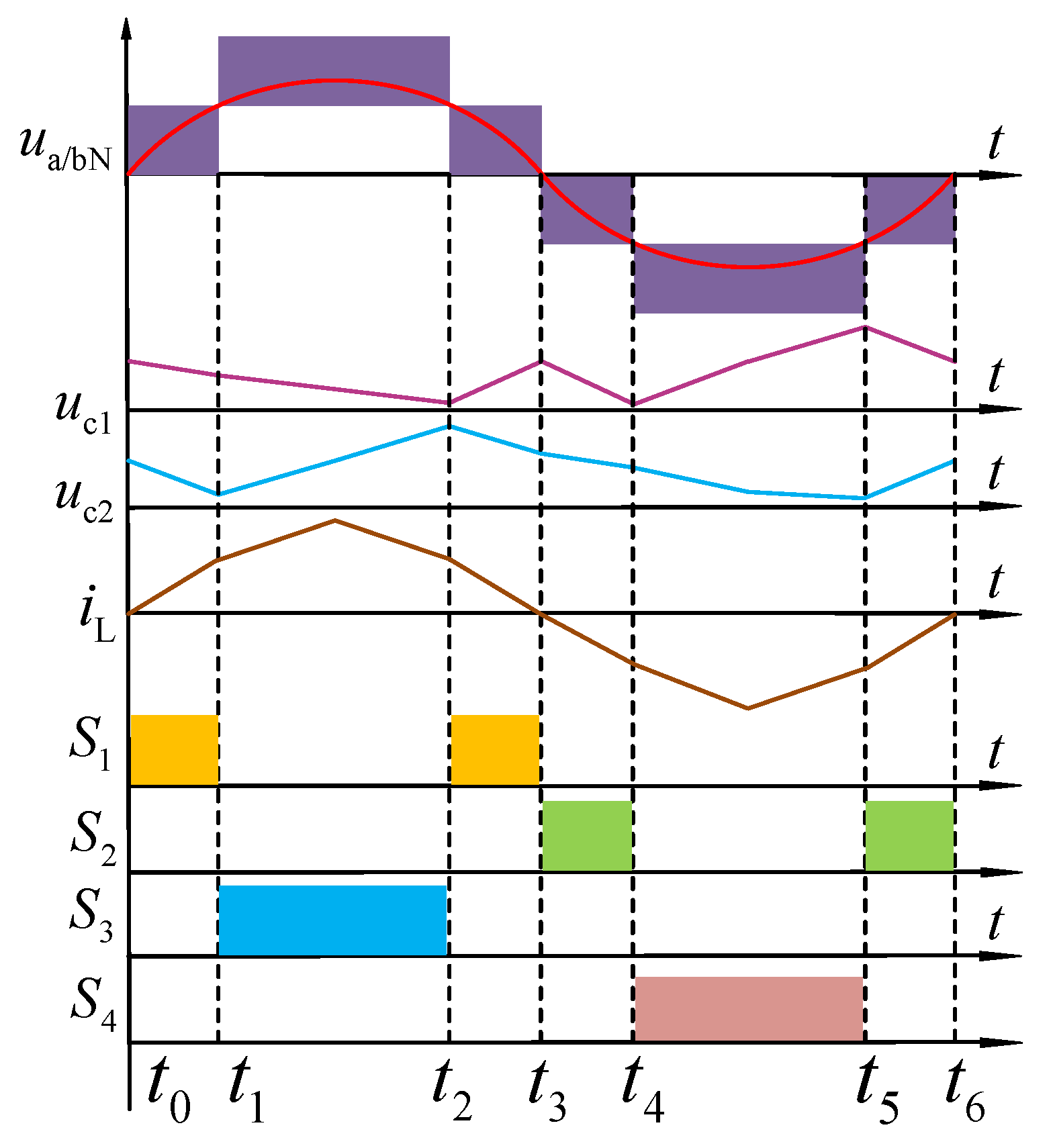
Based on the above analysis, this paper takes the PDBC-II as an example for working mode analysis. Figure 5 shows the key waveforms of one power cycle, which are corresponding to the six working modes in Figure 6. For ease of analysis, it is assumed that the circuit works in continuous conduction mode (CCM), the inductances and capacitors are large enough, the capacitor voltage UC1=UC2=Udc/2, and the DC voltage Udc is remain constant. Figure 6 shows the six working modes of PDBC-II, which are corresponding to 0, ±0.5Udc and ±Udc, respectively. The six working modes are analyzed as follows.
Working mode 1: During [t0, t1] shown in Figure 5, the grid voltage ug>0, uaN=0, ubN=ug. In this mode, the current path is shown in Figure 6a. As shown in Figure 6a, the switch S1 is ON, the diode D4 is ON, and the other active components are OFF. The capacitors C1 and C2 are discharging to the load RL.
Working mode 2: During [t1, t2] shown in Figure 5, the grid voltage ug>0, uaN=ubN=Udc/2. In this mode, the current path is shown in Figure 6b. As shown in Figure 6b, the switch S3 is ON, the body diodes of S2 and S4 are ON, the diode D1 is ON, and the other active components are OFF. The capacitor C1 is charging and C2 is discharging to the load RL.
Working mode 3: During [t2, t3] shown in Figure 5, the grid voltage ug>0, uaN=ubN=Udc. In this mode, the current path is shown in Figure 6c. As shown in Figure 6c, the body diode of S2 is ON, the diodes D1 and D4 are ON, and the other active components are OFF. The capacitors C1 and C2 are charging, and the AC power supplies to the load RL.
Working mode 4: During [t3, t4] shown in Figure 5, the grid voltage ug<0, ubN=ug, ubN=0. In this mode, the current path is shown in Figure 6d. As shown in Figure 6d, the switch S2 is ON, the body diode of S3 is ON, the diode D3 is ON, and the other active components are OFF. The capacitors C1 and C2 are discharging to the load RL.
Working mode 5: During [t4, t5] shown in Figure 5, the grid voltage ug<0, uaN=ubN=−Udc/2. In this mode, the current path is shown in Figure 6e. As shown in Figure 6e, the switch S4 is ON, the body diodes of S1 and S3 are ON, the diode D2 is ON, and the other active components are OFF. The capacitor C2 is charging and C1 is discharging to the load RL.
Working mode 6: During [t5, t6] shown in Figure 5, the grid voltage ug<0, uaN=ubN=−Udc. In this mode, the current path is shown in Figure 6f. As shown in Figure 6f, the body diodes of S1 and S3 are ON, the diodes D2 and D3 are ON, and the other active components are OFF. The capacitors C1 and C2 are charging, and the AC power supplies to the load RL.
Based on the six working mode analysis above, the switching pulse distribution of PDBC-II is summarized, as shown in Table 1. Where "0" and "1" represent switching off and on, "↑" and "↓" represent capacitor charging and discharging, respectively. It can be seen from Table I that the PDBC-II has at most one switch ON in each mode, so the PDBC-II has a lower conduction loss.

3. Control and Modulation Strategy

3.1. Control Strategy

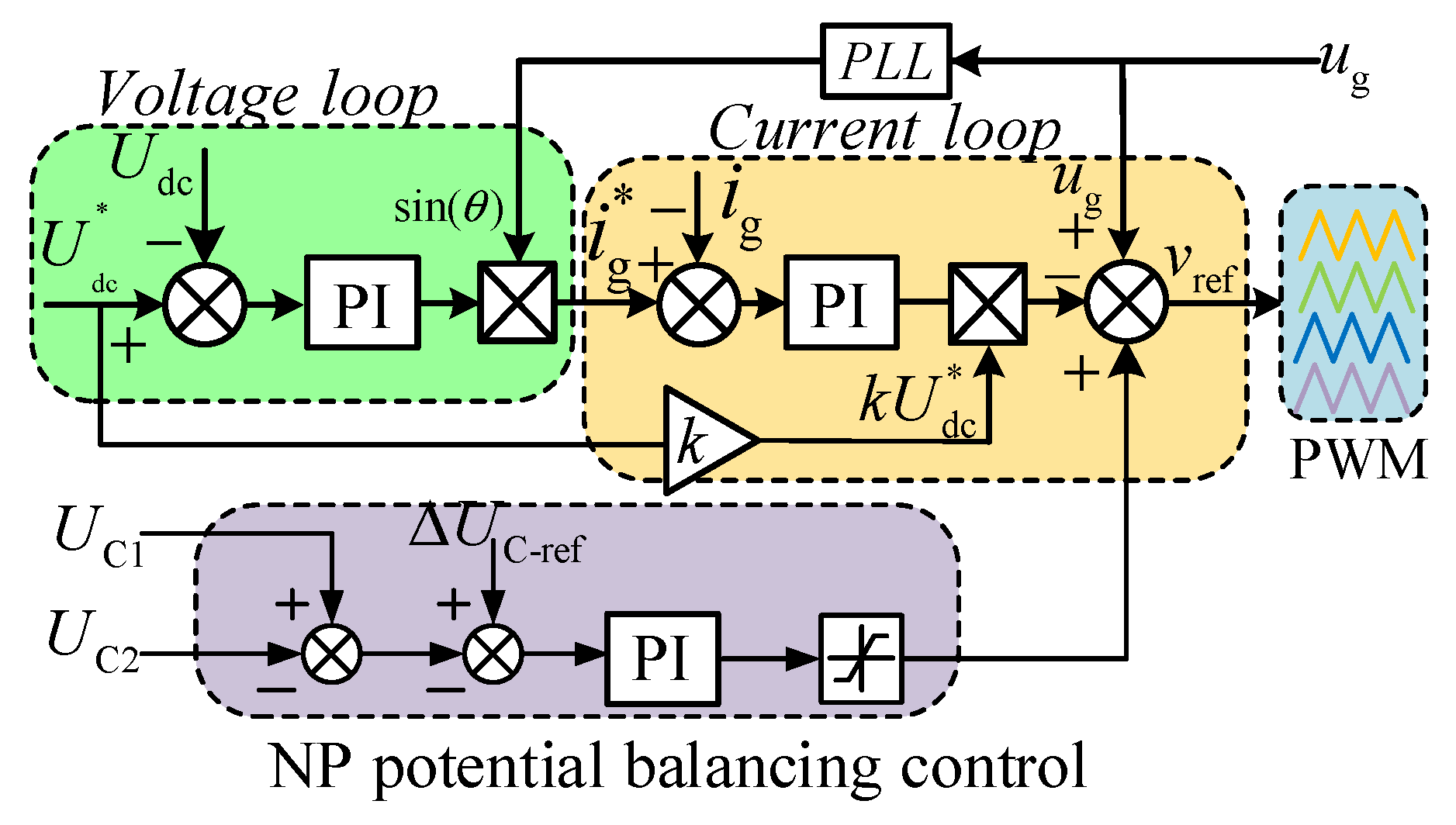
In this paper, a double closed loop control system suit for PDBCs is designed, both the voltage outer loop and the current inner loop adopt PI controller. The control block diagram of the PDBCs is shown in Figure 7. The transfer function of the PI link in Figure 7 can be expressed as (1), where kp and ki are the proportional and integral coefficient, respectively.
G pi = ( k p ⋅ s + k i ) / s
The voltage outer loop is used to keep the output voltage Udc stable, whose output is the reference value of the current inner loop. Firstly, the difference between the DC side voltage Udc and its reference value Udc* is send into the PI controller to obtain an error signal. Then, the error signal is multiply with the phase information of the grid voltage ug. As a result, the input reference signal ig* of the current inner loop is obtained.
The current inner loop is used to ensure that the waveform of ig is sinusoidal and control the power factor close to 1. Firstly, the difference between the AC side current ig and the reference signal ig* (the output of the voltage outer loop) is sent to the PI controller. Then, the output of the PI controller is multiply with kUdc*. Finally, its output is taken the difference with the grid voltage ug to get PWM reference signal vref.
The neutral point (NP) balance of the DC side capacitor is attained by the phase delay control method in this paper. Firstly, the difference between the voltage signals of the capacitors C1 and C2 is compared with the reference value. Then, the result is sent to the PI controller to obtain correction signal, which is added to the modulation wave after limiting the amplitude. Therefore, the NP voltage balance is achieved by adjusting the capacitor charging and discharging time.

3.2. Modulation Strategy

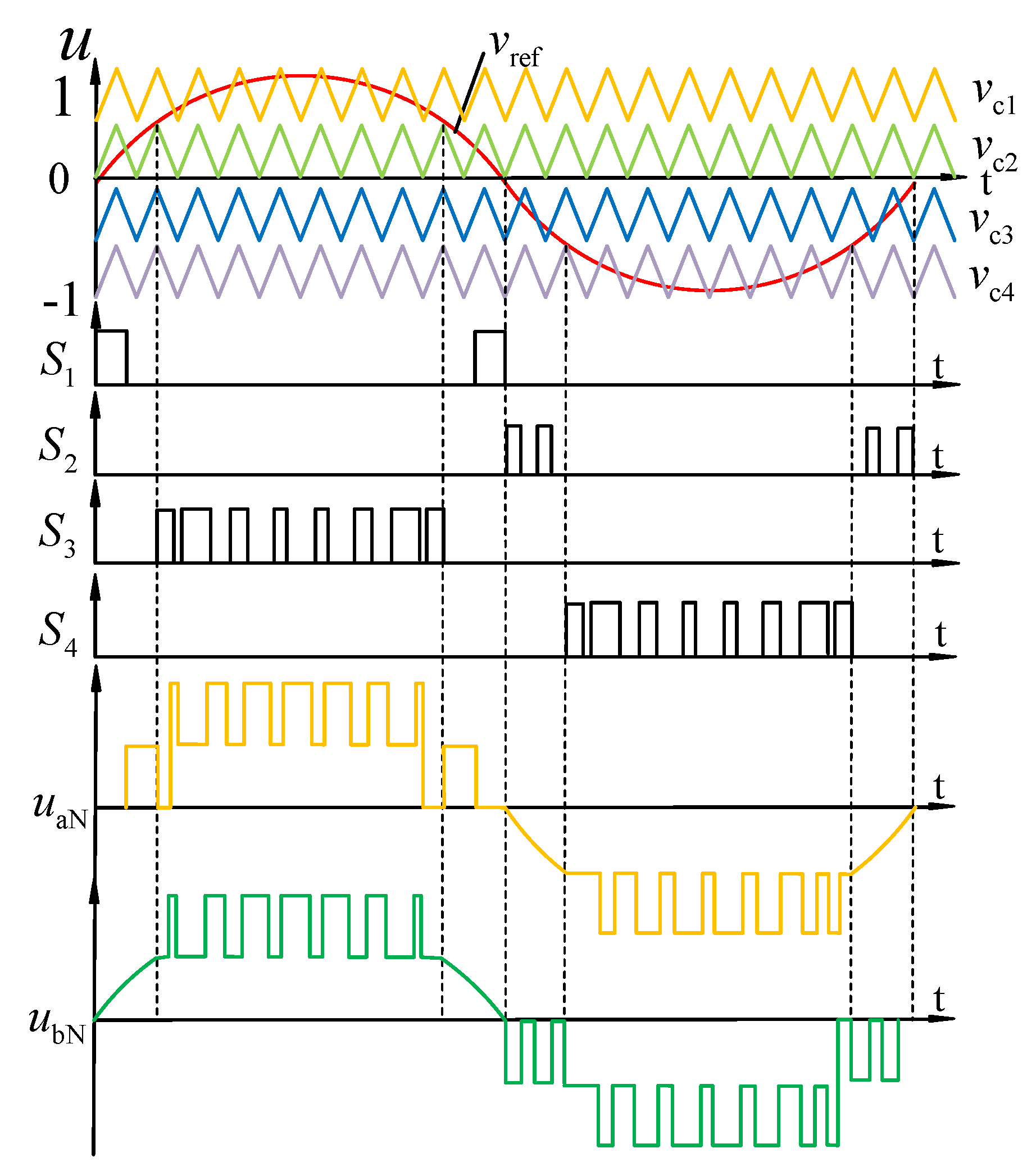
In this paper, the multi-carrier PWM modulation strategy is used to generate switching pulse distribution for proposed PDBCs. The PDBC-II is taken as an example to illustrate the switching pulse distribution and bridge arm voltage uaN, ubN of multi-carrier PWM modulation strategy, as shown in Figure 8, where vc1(t), vc2(t), vc3(t), vc4(t), and vref(t) represent four carrier signals and reference signal, respectively. The reference signal vref(t) is compared with vc1(t), vc2(t), vc3(t), vc4(t) to obtain the switching pulse waveform of the switches S1, S2, S3, and S4.
In the positive half-cycle the PWM modulation strategy, the duty cycle can be derived from (2) to (6). Where Ug,max, Ton, and Toff is the amplitude of AC voltage, the turn on and off time of the switch, respectively. The modulation ratio M and duty ratio D can be defined as follows:
M = U g , max / U dc
D = T on / T on + T off
When 0<vref(t)<0.5, the PDBCs operate alternately in working mode 1 and working mode 2. At this time, the inductance volt-second balance has the following relationship:
u g − 0.5 U dc ⋅ T on = U dc − u g ⋅ T off
The duty cycle D1 is derived from (2) to (4):
D 1 = 1 − 2 M sin w t
Similarly, when 0.5<vref(t)<1, the PDBCs operate alternately in working mode 2 and working mode 3. The duty cycle D2 can be obtained as follows:
D 2 = 2 − 2 M sin w t
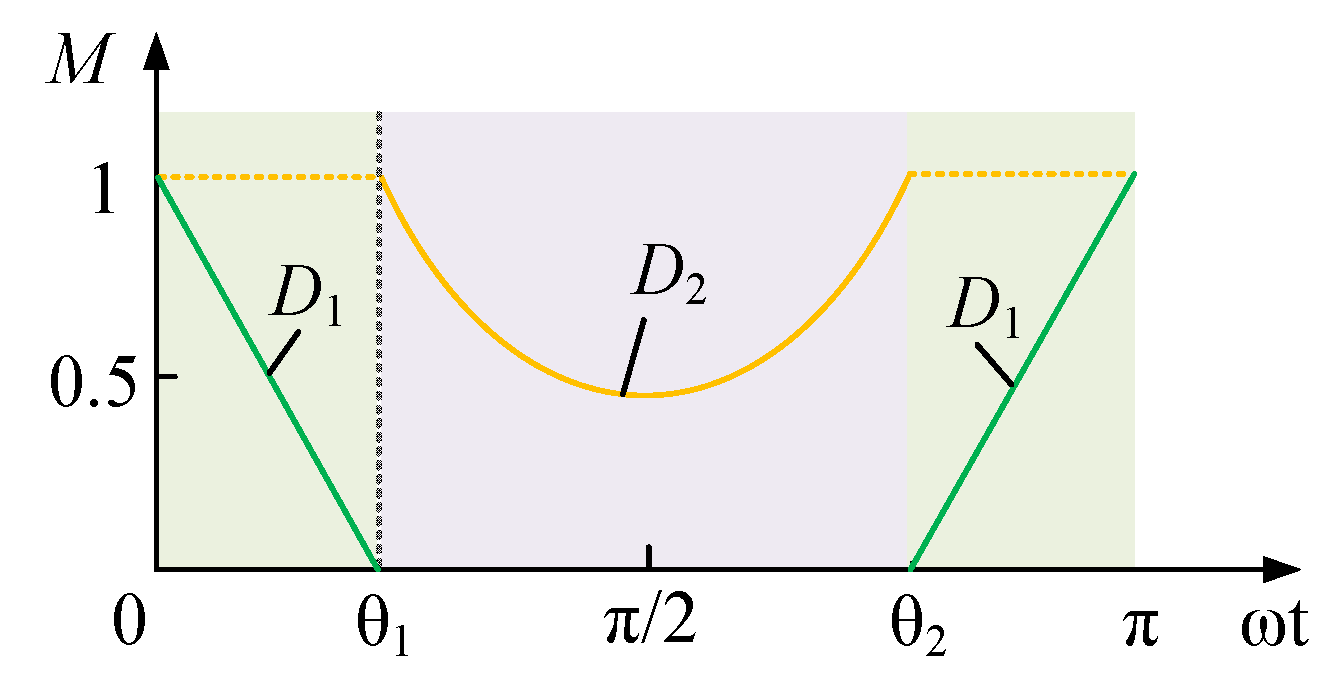
Based on (5) and (6), when PDBCs operates in the positive half-cycle, the duty cycle change curve is shown in Figure 9. Where the green curve represents the duty cycle D1, the yellow curve represents the duty cycle D2, θ1 and θ2 are the two angles of alternation between vc1(t) and vc2(t).
It is assumed that, the amplitude of vref(t) is 1 (after normalization), the θ1 and θ2 can be calculated as follows:
θ 1 = arcsin 0.5 = π 6
D 2 = 2 − 2 M sin w t

4. Performance Analysis

4.1. Voltage Stress Analysis

Based on the working mode analysis of Figure 6, the switches and diodes voltage stress of three PDBCs are summarized, as shown in Table 2. It can be seen from Table 2 that part of the components voltage stress on the three level bridge is reduced by half. In addition, the PDBC-II and PDBC-III have three components voltage stress reduced by half, while PDBC-I only have two components voltage stress reduced by half. Therefore, in terms of cost, PDBC-II and PDBC-III have the lower cost compared with PDBC-I.

4.2. Current Stress Analysis

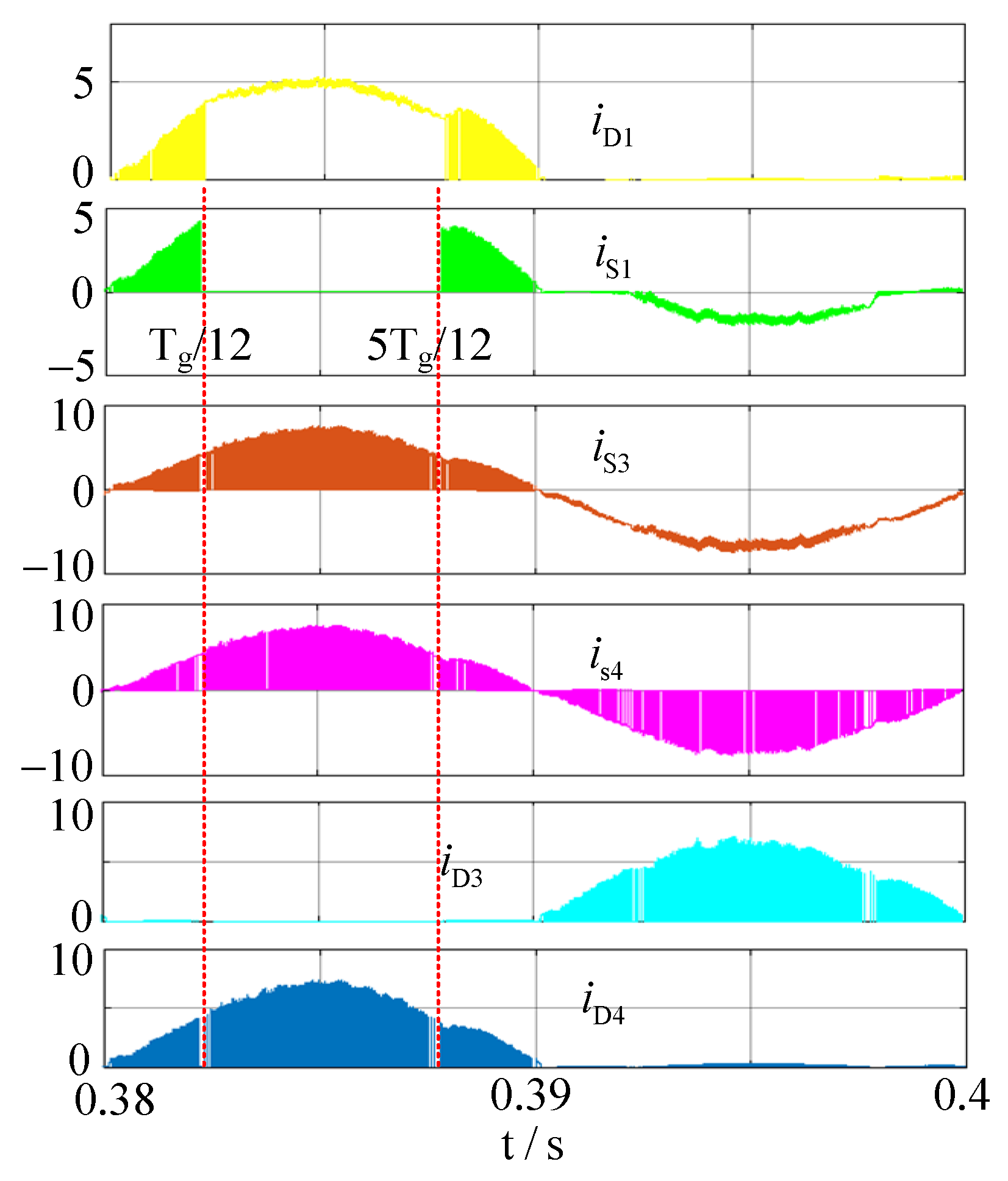
To estimate the conduction loss of the switches and diodes, it is necessary to calculate the average value and the root mean square (RMS) value of the current flowing through the switches and diodes. In this section, PDBC-II is taken as an example to conduct the current stress analysis. Figure 10 shows the current stress simulation waveform of PDBC-II in the Matlab/Simulink environment. It is easy to know from Figure 9, the switching times of two duty cycle D1, D2 in Figure 10 are Tg/12 and 5Tg/12 (Tg is one power frequency cycle), respectively. Based on Figure 10, the theoretical derivation of the average value and RMS value of the current flowing through the semiconductor device can be shown as (9) to (18). For the following calculations, it is assumed that the AC side current is a sine wave, the DC side voltage remains unchanged, and the switching frequency fs is much greater than the grid frequency fg.
The RMS and average value of diode D1, D2 current is calculated by (9):
I D 1 , 2 , rms 2 = 2 T g ∫ 0 T g 12 1 − D 1 ⋅ i g 2 d t + ∫ T g 12 T g 4 i g + 0 . 5 I g , max 2 2 d t I D 1 , 2 , avg = 2 T g ∫ 0 T g 12 1 − D 1 ⋅ i g d t + ∫ T g 12 T g 4 i g + 0 . 5 I g , max 2 d t
Substituting (5) into (9), the RMS and average values of diodes D1, D2 can be obtained:
I D 1 , 2 , rms = 6 I g , max 24 π ⋅ 6 π + 15 3 + 128 − 72 3 M I D 1 , 2 , avg = I g , max 12 π ⋅ π + 3 3 + 2 π − 3 3 M
The RMS and average value of MOSFET S1, S2 current is calculated by (11):
I S 1 , 2 , rms 2 = 2 T g ∫ 0 T g 12 D 1 ⋅ i g 2 d t + ∫ 7 T g 12 3 T g 4 i g + 0.5 I g , max 2 2 d t I S 1 , 2 , a v g = 2 T g ∫ 0 T g 12 D 1 ⋅ i g d t + ∫ 7 T g 12 3 T g 4 i g + I g , max 2 d t
Substituting (5) into (11), the RMS and average values of MOSFET S1, S2 can be obtained:
I S 1 , 2 , rms = 6 I g , max 24 π ⋅ 14 π − 21 3 + 72 3 − 128 M I S 1 , 2 avg = I g , max 12 π ⋅ 12 − π − 3 3 + 3 3 − 2 π M
The RMS and average value of MOSFET S3 current is calculated by (13):
I S 3 , rms 2 = 4 T g ∫ 0 T g 12 D 1 ⋅ i g 2 d t + ∫ T g 12 T g 4 D 2 ⋅ i g 2 d t + ∫ T g 2 3 T g 4 i g 2 d t I S 3 , avg = 2 T g ∫ 0 T g 12 D 1 ⋅ i g d t + ∫ T g 12 T g 4 D 2 ⋅ i g d t + ∫ T g 2 3 T g 4 i g d t
Substituting (5) and (6) into (13), the RMS and average values of MOSFET S3 can be obtained:
I S 3 , rms = I g , max 2 3 π ⋅ 3 3 + 10 π − 32 M I S 3 , avg = I g , max π ⋅ 3 + 2 − π M
The RMS and average value of MOSFET S4 current is calculated by (15):
I S 4 , rms 2 = 4 T g ∫ 0 T g 12 D 1 ⋅ i g 2 d t + ∫ T g 12 T g 4 D 2 ⋅ i g 2 d t I S 4 , avg = 4 T g ∫ 0 T g 12 D 1 ⋅ i g d t + ∫ T g 12 T g 4 D 2 ⋅ i g d t
Substituting (5) and (6) into (15), the RMS and average values of MOSFET S4 can be obtained:
I S 4 , rms = I g , max 2 3 π ⋅ 3 3 + 10 π − 32 M I S 4 , avg = I g , max π ⋅ 3 + 2 − π M
The RMS and average value of diode D3, D4 current is calculated by (17):
I D 3 , 4 , rms 2 = 2 T g ∫ 0 T g 12 1 − D 1 ⋅ i g 2 d t + ∫ T g 12 T g 4 1 − D 2 ⋅ i g 2 d t I D 3 , 4 , avg = 4 T g ∫ 0 T g 12 1 − D 1 ⋅ i g d t + ∫ T g 12 T g 4 1 − D 2 ⋅ i g d t
Substituting (5) and (6) into (17), the RMS and average values of diodes D3, D4 can be obtained:
I D 3 , 4 , rms = I g , max 2 6 π ⋅ 32 M − 3 3 − 4 π I D 3 , 4 , avg = I g , max 2 π ⋅ π M − 3
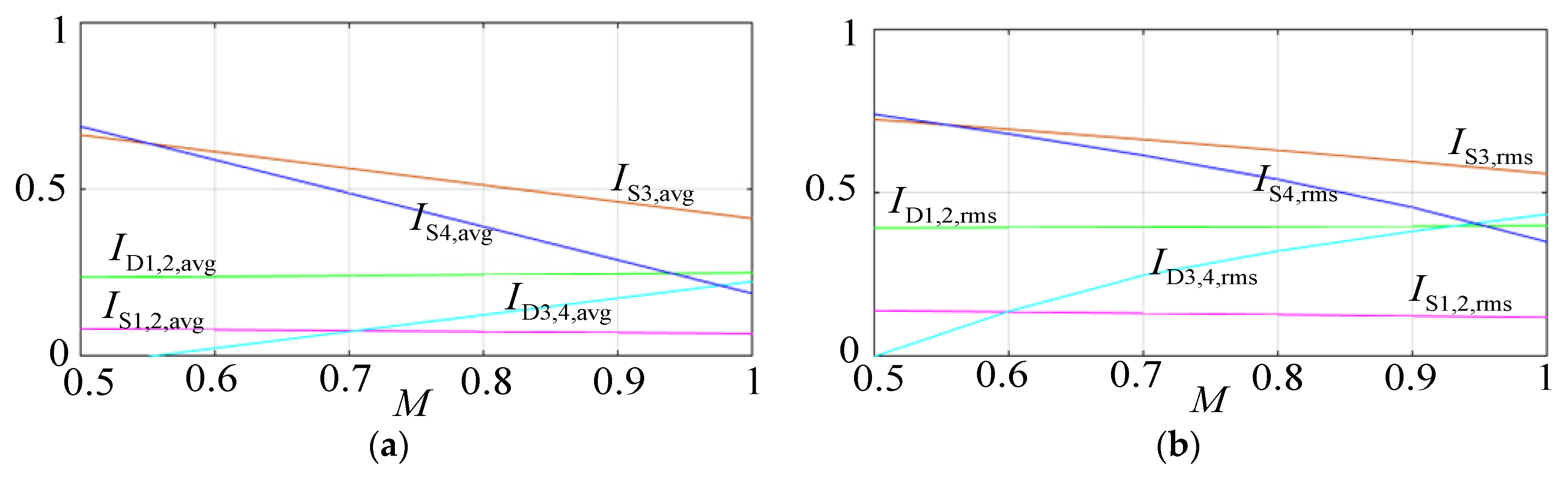
Figure 11 shows the change curve of the average value and RMS value of the switches and diodes with the modulation ratio M after normalization of Ig,max. It can be seen from Figure 11 that the current RMS value and average value of each components have the same trend. Since Ig,max are normalized, the trend shown in Figure 11 is also applicable under different power levels, which is of great significance for studying the working principle of the rectifier.
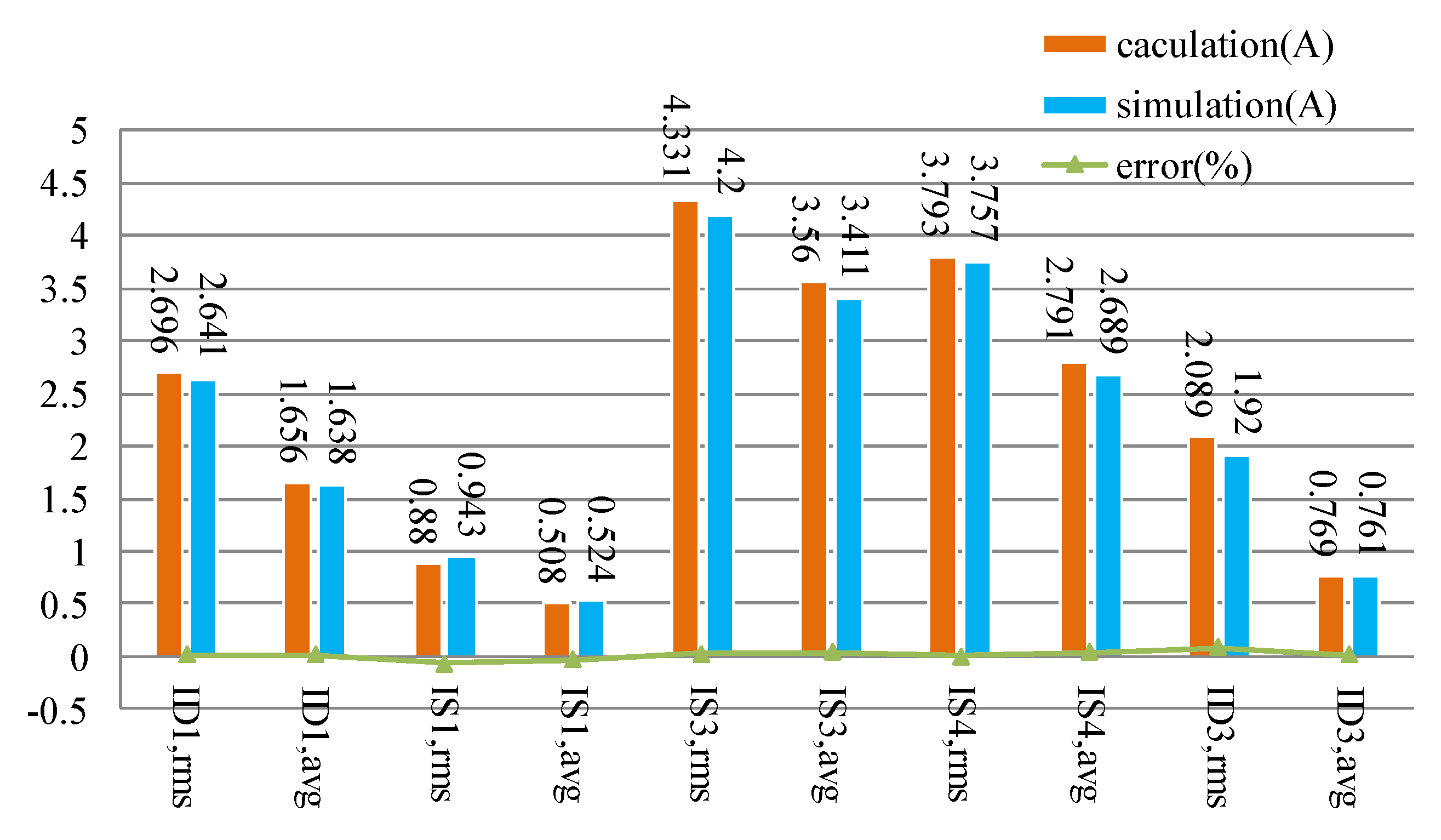
To verify the correctness of the current stress formula deduced in this paper, the current stress value of the switches and diodes is measured in Matlab/Simulink environment under 1kW power rate. Figure 12 shows the comparison between the calculated value and the simulated value of the current stress. It can be seen from Figure 12, the calculated current stress in this paper is consistent with the simulated value, which verifies the correctness of the current stress formula.

4.3. Loss Analysis

Based on the above current stress analysis, this section analyzes the loss and efficiency of the proposed PDBCs. The losses of MOSFET mainly include conduction losses and switching losses. When the MOSFET is on-state, the on-state resistance rds resulting the conduction losses. The conduction losses Pcon can be calculated as (19), where IS,rms is the RMS value of the current flowing through the MOSFET, which can be obtained from the current stress analysis.
P con = I S , rms 2 ⋅ r ds
During the drain current and voltage conversion process of the MOSFET, the switching losses is generated. The switching losses which can be calculated by (20), where Uin, Io, ton, toff, and fs are the RMS value of the input voltage, the output current, the switching process drain current and voltage conversion crossover time, and the switching frequency, respectively.
P sw = 0.5 U in ⋅ I o ⋅ t on + t o f f f s
Similarly, the power losses of the diode in a cycle consists mainly of static losses and dynamic losses. For the static losses, since the fast recovery diode is employed in this paper, there is only the on-state losses are considered. The dynamic losses of the diode can be calculated with (21), where Uf is the forward conduction voltage, ID,avg is the average value of the diode.
P Son = ∫ 0 T g u ⋅ i d t / T g = U f ⋅ I D , avg
Compared with the reverse recovery time tr, the forward recovery time tf is negligible, therefore the turn-on losses can be ignored. The turn-off losses can be calculated with (22), where Urp and Irp are the reverse peak voltage and current, tb is the reverse current fall time.
P Doff = ∫ t 0 t 2 u F t ⋅ i F t d t / T S = 0.5 U rp I rp t b f s
In this paper, the MOSFETs and diodes employ IRFP450 and RHRP3060, respectively. According to the data sheet, the parameters for IRFP450 and RHRP3060 are shown in Table 3. The switching frequency fs=20kHz.
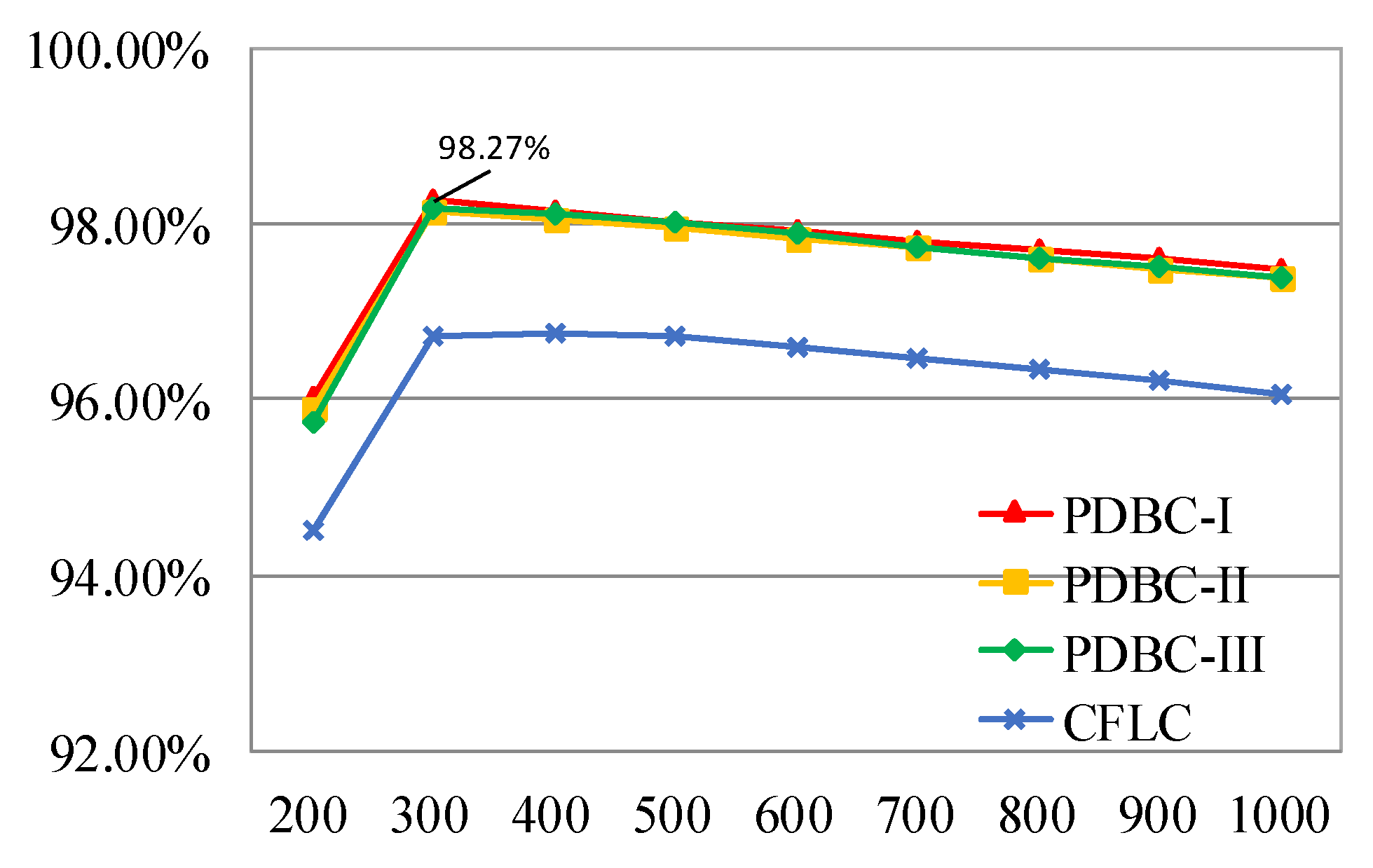
Based on (9) to (22), the losses of the proposed three PDBCs and CFLC at different output power are calculated respectively. According to the results of the losses calculation, the efficiency diagram at different output power rate is generated, as shown in Figure 13. It can be seen from Figure 13, the four circuits reach peak efficiency around 300W. However, when the output power is over 300W, the efficiency declines slowly as the output power increase. The peak efficiency of PDBC-I is 98.27%, which is the highest in the four circuits. In addition, as the output power level increases, the efficiency of the PDBC-I reaches the highest of the four circuits. Therefore, PDBC-I is more suitable at higher power rate.

5. Experimental Verification

In order to verify the feasibility of the PDBC proposed in this paper and the correctness of the theoretical analysis, PDBC-II [shown in Figure 4(b)] is selected for corresponding experimental verification, as shown in Figure 14. The experimental circuit design mainly includes EMI circuit, auxiliary power supply, main power circuit, signal sampling circuit, MOSFET drive circuit, and protection control circuit. The circuit experimental parameters are shown in Table 4, the controller employ DSP28335, the MOSFETs and diodes employ IRFP450 and RHRP3060, respectively.
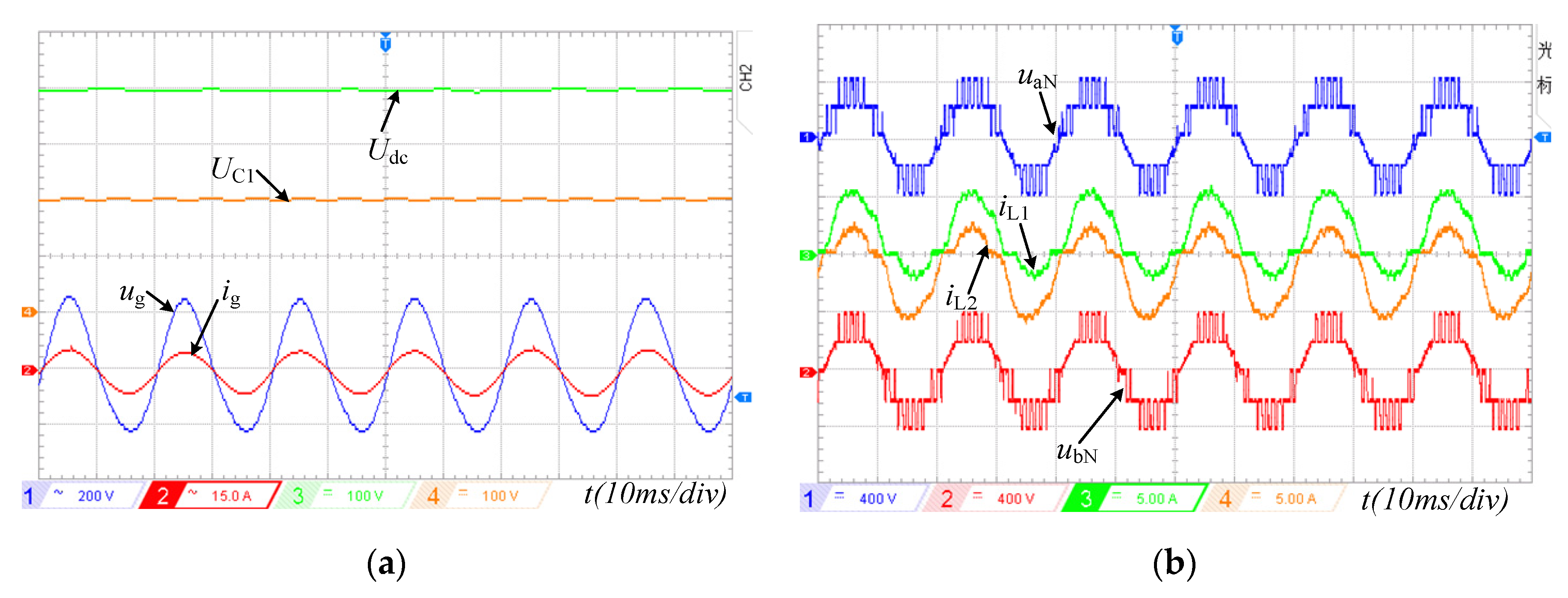
Figure 15 shows the PDBC-II steady-state experimental waveforms of the input and output sides at 1kW rated power. Figure 15a shows the voltage waveforms of the single-phase AC power supply voltage ug, the input side current ig, and the DC side voltage Udc, UC1, UC2. As seen from Figure 15a, the input power supply voltage ug is in phase with the input side current ig, and it is consistent to achieve power factor correction. The DC side voltage Udc is stable at 400V, and the capacitor voltage UC1, UC2 remains dynamically balanced at 200V. Figure 15b shows the bridge arm voltage uaN, ubN waveform and the input inductor current iL1, iL2 waveform. As can be seen from Figure 15b, the waveform of inductor current iL1 phase ahead 180° of inductor current iL2. Similarly, the bridge arm voltage uaN, ubN waveform changes in positive and negative half-cycles alternately, which is consistent with Figure 6 and Table 1.
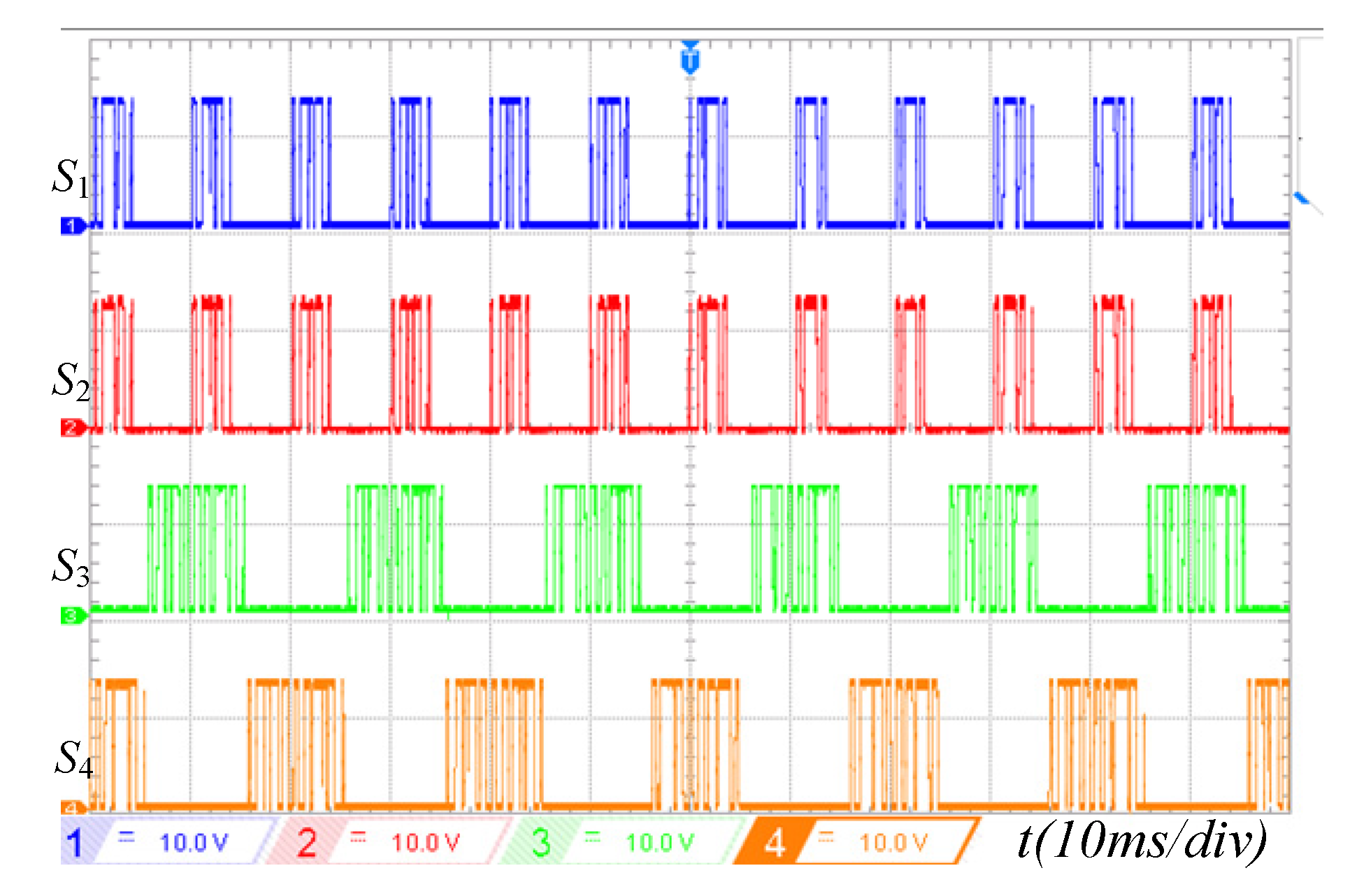
Figure 16 shows the PDBC-II switching pulse distribution experimental waveform. As can be seen from Figure 16, the switches S1-S4 has a short high-frequency switching time. As a result, the switching losses of PDBC-II is relatively low. In addition, the switches S3 and S4 symmetrically action in positive and negative half-cycle, which is consistent with the switching pulse distribution of Table 1.
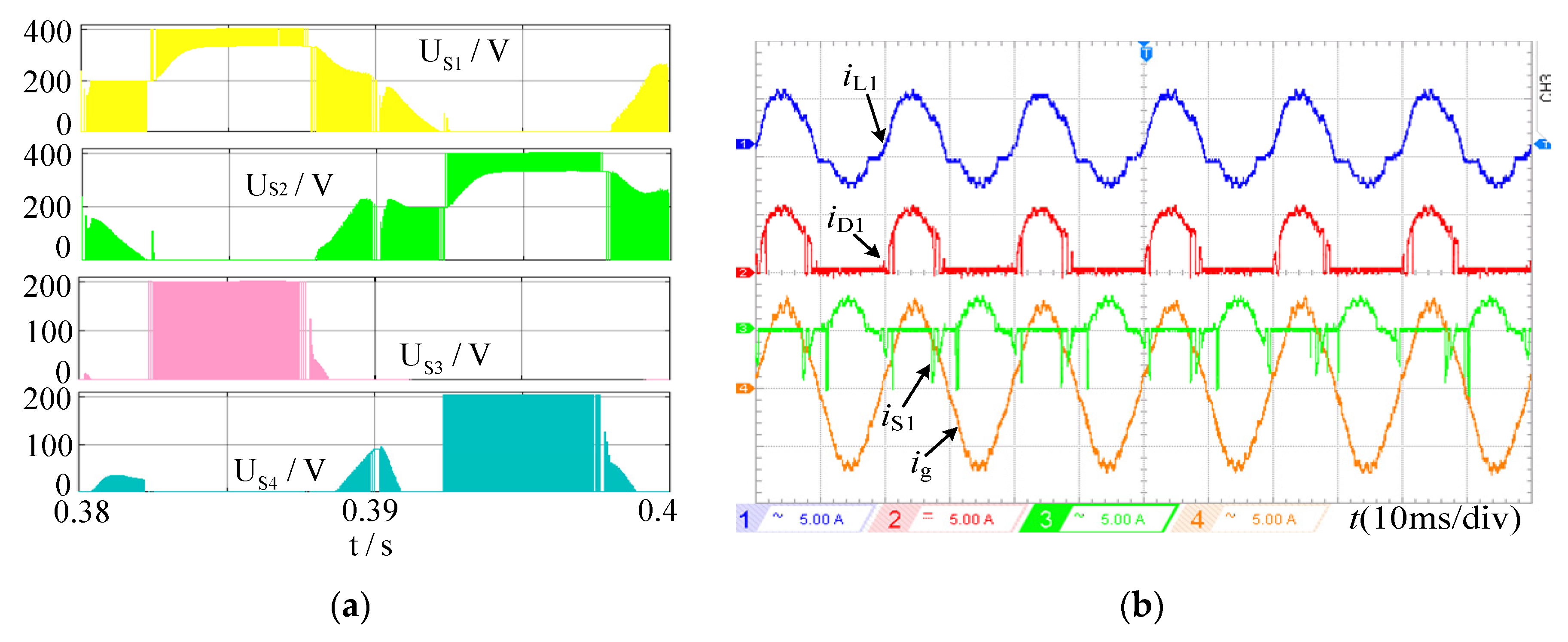
Figure 17 shows the PDBC-II voltage and current stress experimental waveforms of the switches at 1kW rated power. Figure 17a shows the voltage stress waveform of the switches S1-S4. It can be seen from Figure 17a that the maximum voltage stress of the four switches US1=US2≈400V, US3=US4≈200V, i.e. the partial voltage stress is halved, which is consistent with the voltage stress analysis in Table 2. Figure 17b shows the waveform of the inductor current, diode D1 current iD1, the switch S1 current iS1. As can be seen from Figure 17b, the switch current iS1 waveform is enveloped by the inductor L1 current iL1 waveform in the positive half cycle. In addition, the current iD1, iS1 changes at high frequencies during the [0, Tg/12] and [5Tg/12, Tg/2] (where Tg is the grid period), which is the same as the simulation waveforms in Figure 10.
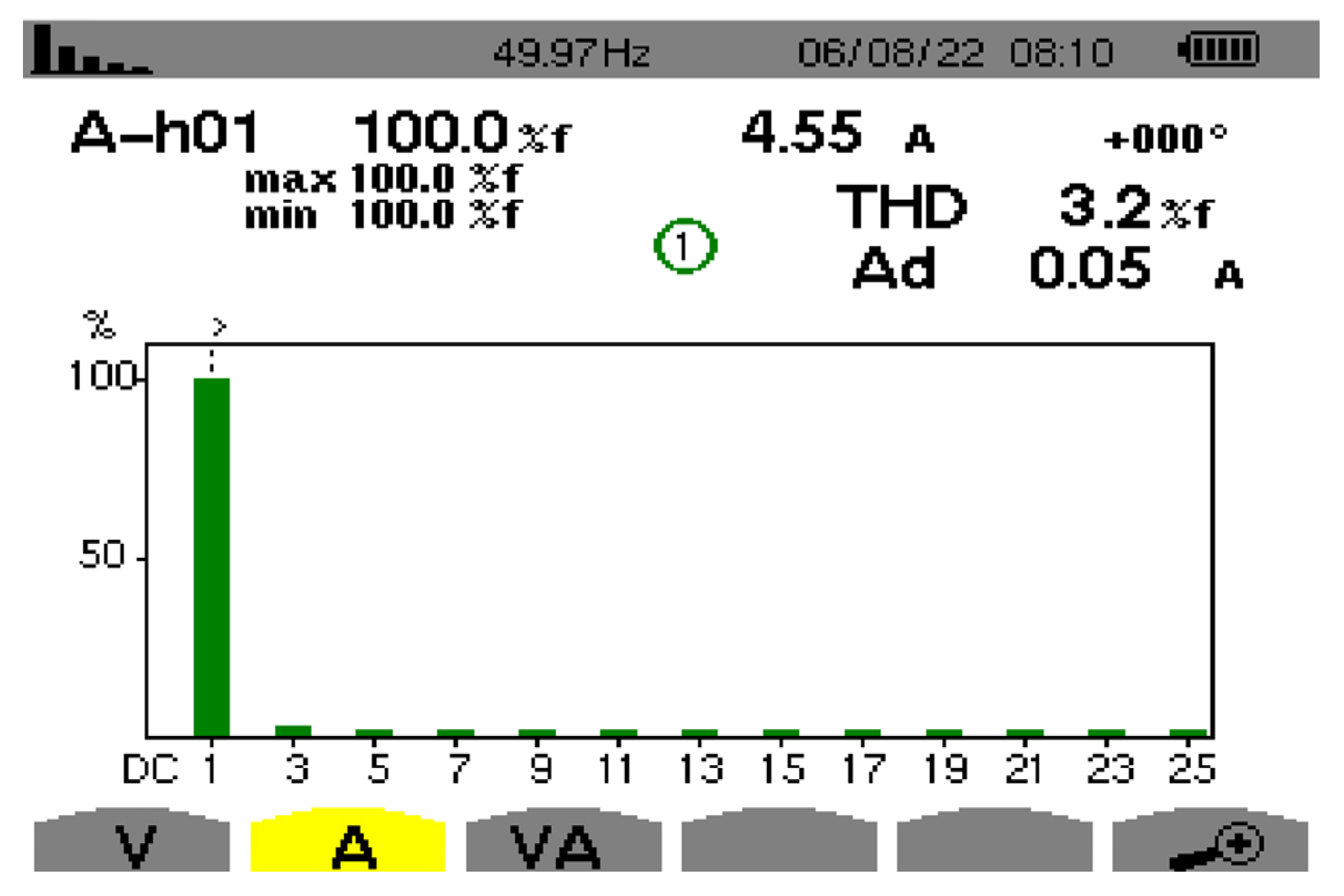
Figure 18 shows the THD test results of PDBC-II at 1kW rated power. As can be seen from Figure 18, at the switching frequency of 20kHz, the THD of PDBC-II is 3.2%, which meets the IEC 6100-3-2 standard.

6. Conclusions

In this paper, combining the three-level PTP circuit and the five-level NPC bridge arm, a family of PDBCs is proposed by transforming the NPC bridge arm. The proposed circuit reduces the volume of the filter inductor to increase the power density of the circuit and improves the working efficiency of the circuit. Through comparative analysis of voltage and current stress, loss, the following conclusions are drawn.
1) The experimental results show that the PDBCs proposed in this paper has a good input and output waveform at low switching frequency. Therefore, the PDBCs can improve overall efficiency by reducing switching losses.
2) The efficiency of the five PDBCs proposed in this paper is higher than CFLC. The PDBC-I has the smallest loss and the highest efficiency, with a peak efficiency of 98.27%, and its overall performance is the best.
3) Compared with the conventional three-level PTP circuit, the five PDBCs proposed in this paper have higher power density, and the voltage stress of some devices is reduced by half. In addition, the PDBC-II and PDBC-III more devices have the voltage stress halved, so their cost is lower.

Conflicts of Interest

The authors declare no conflict of interest.

References

  1. M. T. Shah, S. K. Chauhan and P. N. Tekwani, “Analysis of multiaxis current controller for power system friendly front-end converter employing two-level and three-level topologies,” IEEE Trans. Ind. Electron., vol. 68, no. 1, pp. 586-597, Jan. 2021. [CrossRef]
  2. K. Li, A. Formentini, D. Dewar and P. Zanchetta, “Controller design of an active front-end converter keeping in consideration grid dynamic interaction,” IEEE Trans. Ind. Electron., vol. 69, no. 5, pp. 5195-5206, May 2022. [CrossRef]
  3. M. Gendrin, J. Gauthier and X. Lin-Shi, “A predictive hybrid pulse-width-modulation technique for active-front-end rectifiers,” IEEE Trans. Power Electron., vol. 32, no. 7, pp. 5487-5496, Jul. 2017. [CrossRef]
  4. C. Kang, W. Wang, W. Li, H. Du and L. Diao, “Balance midpoint potential control of three-level boost converter for rail transit application,” IEEE Access, vol. 7, pp. 47737-47746, 2019. [CrossRef]
  5. J. Ebrahimi, H. Karshenas and A. Bakhshai, “A five-level nested diode-clamped converter for medium-voltage applications,” IEEE Trans. Ind. Electron., vol. 69, no. 7, pp. 6471-6483, Jul. 2022. [CrossRef]
  6. Y. Zhang, Y. Bai, H. Yang and B. Zhang, “Low switching frequency model predictive control of three-level inverter-fed IM drives with speed-sensorless and field-weakening operations,” IEEE Trans. Ind. Electron., vol. 66, no. 6, pp. 4262-4272, Jun. 2019. [CrossRef]
  7. G. Zhang, S. Peng, Q. Geng, T. Shi and C. Xia, “Hybrid discontinuous space vector PWM strategy for three-level inverters under two-phase loads condition,” IEEE Trans. Power Electron., vol. 37, no. 2, pp. 1711-1721, Feb. 2022. [CrossRef]
  8. P. Montero-Robina, F. Umbría, F. Salas and F. Gordillo, “Integrated control of five-level diode-clamped rectifiers,” IEEE Trans. Ind. Electron., vol. 66, no. 9, pp. 6628-6636, Sept. 2019. [CrossRef]
  9. F. Sebaaly, H. Vahedi, H. Y. Kanaan and K. Al-Haddad, “Experimental design of fixed switching frequency model predictive control for sensorless five-level packed U-cell inverter,” IEEE Trans. Ind. Electron., vol. 66, no. 5, pp. 3427-3434, May 2019. [CrossRef]
  10. Y. P. Siwakoti, A. Palanisamy, A. Mahajan, S. Liese, T. Long and F. Blaabjerg, “Analysis and design of a novel six-switch five-level active boost neutral point clamped inverter,” IEEE Trans. Ind. Electron., vol. 67, no. 12, pp. 10485-10496, Dec. 2020. [CrossRef]
  11. L. He and C. Cheng, “A flying-capacitor-clamped five-level inverter based on bridge modular switched-capacitor topology,” IEEE Trans. Ind. Electron., vol. 63, no. 12, pp. 7814-7822, Dec. 2016. [CrossRef]
  12. S. P. Gautam, L. Kumar, S. Gupta and N. Agrawal, “A single-phase five-level inverter topology with switch fault-tolerance capabilities,” IEEE Trans. Ind. Electron., vol. 64, no. 3, pp. 2004-2014, Mar. 2017. [CrossRef]
  13. I. M. Alsofyani and K. -B. Lee, “Simple capacitor voltage balancing for three-level NPC inverter using discontinuous PWM method with hysteresis neutral-point error band,” IEEE Trans. Power Electron., vol. 36, no. 11, pp. 12490-12503, Nov. 2021. [CrossRef]
  14. Y. Zhang et al., “A SiC and Si hybrid five-level unidirectional rectifier for medium voltage applications,” IEEE Trans. Ind. Electron., vol. 69, no. 8, pp. 7537-7548, Aug. 2022. [CrossRef]
  15. W. Chen and A. M. Bazzi, “Model-based voltage quality analysis and optimization in post-fault reconFigured N-level NPC inverter,” IEEE Trans. Power Electron., vol. 36, no. 12, pp. 13706-13715, Dec. 2021. [CrossRef]
  16. Z. He et al., “A hybrid DPWM for vienna rectifiers based on the three-level to two-level conversion,” IEEE Trans. Ind. Electron., vol. 69, no. 9, pp. 9429-9439, Sep. 2022. [CrossRef]
  17. S. Wang, J. Ma, B. Liu, N. Jiao, T. Liu and Y. Wang, “Unified SVPWM algorithm and optimization for single-phase three-level NPC converters,” IEEE Trans. Power Electron., vol. 35, no. 7, pp. 7702-7712, Jul. 2020. [CrossRef]
  18. J. Ma, W. Song, S. Wang and X. Feng, “Model predictive direct power control for single phase three-level rectifier at low switching frequency,” IEEE Trans. Power Electron., vol. 33, no. 2, pp. 1050-1062, Feb. 2018. [CrossRef]
  19. J. Kim, S. Lee, W. Cha and B. Kwon, “High-efficiency bridgeless three-level power factor correction rectifier,” IEEE Trans. Ind. Electron., vol. 64, no. 2, pp. 1130-1136, Feb. 2017. [CrossRef]
  20. Z. Liu, Z. Xia, F. Li, G. Wang and C. Li, “A capacitor voltage precharge method for back-to-back five-level active neutral-point-clamped converter,” IEEE Trans. Ind. Electron., vol. 68, no. 10, pp. 9277-9286, Oct. 2021. [CrossRef]
  21. L. Zhang, K. Sun, Y. Xing and J. Zhao, “A family of five-level dual-buck full-bridge inverters for grid-tied applications,” IEEE Trans. Power Electron., vol. 31, no. 10, pp. 7029-7042, Oct. 2016. [CrossRef]
  22. C. Rech and W. A. P. Castiblanco, “Five-level switched-capacitor ANPC inverter with output voltage boosting capability,” IEEE Trans. Ind. Electron. [CrossRef]
  23. V. Monteiro, J. C. Ferreira, A. A. Nogueiras Meléndez and J. L. Afonso, “Model predictive control applied to an improved five-level bidirectional converter,” IEEE Trans. Ind. Electron., vol. 63, no. 9, pp. 5879-5890, Sep. 2016. [CrossRef]
  24. H. Ma, K. Zheng, H. Jiang and H. Yin, “A family of dual-boost bridgeless five-level rectifiers with common-core inductors,” IEEE Trans. Power Electron., vol. 36, no. 11, pp. 12565-12578, Nov. 2021. [CrossRef]
  25. H. Vahedi, A. A. Shojaei, A. Chandra and K. Al-Haddad, “Five-level reduced-switch-count boost PFC rectifier with multicarrier PWM,” IEEE Trans. Ind. Appl., vol. 52, no. 5, pp. 4201-4207, Sep./Oct. 2016. [CrossRef]
Preprints 74713 g001
Figure 1. The common five-level converter topologies. (a) Conventional five-level converter; (b) Converter proposed in [25].
Figure 1. The common five-level converter topologies. (a) Conventional five-level converter; (b) Converter proposed in [25].
Preprints 74713 g001
Preprints 74713 g002
Figure 2. Three most commonly used clamping bridge arm structures. (a) T-type three-level bridge arm structure; (b) Diode Neutral Point Clamping (DNPC) three-level bridge arm structure; (c) Single switch three-level bridge arm structure.
Figure 2. Three most commonly used clamping bridge arm structures. (a) T-type three-level bridge arm structure; (b) Diode Neutral Point Clamping (DNPC) three-level bridge arm structure; (c) Single switch three-level bridge arm structure.
Preprints 74713 g002
Preprints 74713 g003
Figure 3. Topology derivation. (a) Topology derivation of A2; (b) Topology derivation of A3.
Figure 3. Topology derivation. (a) Topology derivation of A2; (b) Topology derivation of A3.
Preprints 74713 g003
Preprints 74713 g004
Figure 4. A family of five-level PTP dual boost converters. (a) PDBC-I; (b) PDBC-II; (c) PDBC-III.
Figure 4. A family of five-level PTP dual boost converters. (a) PDBC-I; (b) PDBC-II; (c) PDBC-III.
Preprints 74713 g004
Preprints 74713 g005
Figure 5. Key waveforms of six working modes in one cycle.
Figure 5. Key waveforms of six working modes in one cycle.
Preprints 74713 g005
Preprints 74713 g006
Figure 6. The six working mode of PDBC-II. (a) Working mode 1; (b) Working mode 2; (c) Working mode 3; (d) Working mode 4; (e) Working mode 5; (f) Working mode 6.
Figure 6. The six working mode of PDBC-II. (a) Working mode 1; (b) Working mode 2; (c) Working mode 3; (d) Working mode 4; (e) Working mode 5; (f) Working mode 6.
Preprints 74713 g006
Preprints 74713 g007
Figure 7. Key waveforms of six working modes in one cycle.
Figure 7. Key waveforms of six working modes in one cycle.
Preprints 74713 g007
Preprints 74713 g008
Figure 8. Diagram of modulation strategy.
Figure 8. Diagram of modulation strategy.
Preprints 74713 g008
Preprints 74713 g009
Figure 9. Change curve of duty cycle in the positive half-cycle.
Figure 9. Change curve of duty cycle in the positive half-cycle.
Preprints 74713 g009
Preprints 74713 g010
Figure 10. The current stress of PDBC-II.
Figure 10. The current stress of PDBC-II.
Preprints 74713 g010
Preprints 74713 g011
Figure 11. Power component average & RMS current stress as functions of the modulation ratio M normalized: Ig,max. (a) Average value; (b) RMS value.
Figure 11. Power component average & RMS current stress as functions of the modulation ratio M normalized: Ig,max. (a) Average value; (b) RMS value.
Preprints 74713 g011
Preprints 74713 g012
Figure 12. Current stress comparison of calculated and simulated value.
Figure 12. Current stress comparison of calculated and simulated value.
Preprints 74713 g012
Preprints 74713 g013
Figure 13. Diagram of efficiency analysis.
Figure 13. Diagram of efficiency analysis.
Preprints 74713 g013
Preprints 74713 g014
Figure 14. Experimental platforms.
Figure 14. Experimental platforms.
Preprints 74713 g014
Preprints 74713 g015
Figure 15. Steady-state experimental waveforms. (a) The voltage waveforms of power supply voltage ug, current ig, and the DC side voltage Udc, UC1, UC2; (b) The bridge arm voltage uaN, ubN and the inductor current iL1, iL2.
Figure 15. Steady-state experimental waveforms. (a) The voltage waveforms of power supply voltage ug, current ig, and the DC side voltage Udc, UC1, UC2; (b) The bridge arm voltage uaN, ubN and the inductor current iL1, iL2.
Preprints 74713 g015
Preprints 74713 g016
Figure 16. Switching pulse distribution experimental waveform.
Figure 16. Switching pulse distribution experimental waveform.
Preprints 74713 g016
Preprints 74713 g017
Figure 17. Voltage and current stress experimental waveforms. (a) The voltage stress waveform of switches S1-S4; (b) The inductor current iL1, diode D1 current iD1, and the switch S1 current iS1.
Figure 17. Voltage and current stress experimental waveforms. (a) The voltage stress waveform of switches S1-S4; (b) The inductor current iL1, diode D1 current iD1, and the switch S1 current iS1.
Preprints 74713 g017
Preprints 74713 g018
Figure 18. THD test results of PDBC-II.
Figure 18. THD test results of PDBC-II.
Preprints 74713 g018
Table 1. Switching pulse distribution of PDBC-II.
Table 1. Switching pulse distribution of PDBC-II.
Mode ig S1 S2 S3 S4 C1 C2 uaN ubN
1 >0 1 0 0 0 ↓ ↓ 0 ug
2 >0 0 0 1 0 ↑ ↓ Udc/2 Udc/2
3 >0 0 0 0 0 ↑ ↑ Udc Udc
4 <0 0 1 0 0 ↓ ↓ ug 0
5 <0 0 0 0 1 ↓ ↑ −Udc/2 −Udc/2
6 <0 0 0 0 0 ↑ ↑ −Udc −Udc
Table 2. Voltage stress of three PDBCs.
Table 2. Voltage stress of three PDBCs.
Components PDBC-I PDBC-II PDBC-III
S1,2 Udc Udc Udc
S3,4 Udc/2 Udc/2 Udc/2
D1,2 Udc Udc Udc
D3 Udc Udc/2 Udc
D4 Udc Udc Udc/2
Table 3. Component parameters.
Table 3. Component parameters.
Components Parameters Values
IRFP450 The on-state resistance rds 0.4Ω
The on-delay time td(on) 17ns
The rise time tr 47ns
The turn-off delay time td(off) 92ns
The fall time tf 44ns
RHRP3060 The conduction voltage Uf 1.7V
The reverse peak voltage Urp 600V
The reverse peak current Irp 250μA
The reverse current fall time tb 18ns
Table 4. Main parameters.
Table 4. Main parameters.
Parameters Label Value
The input filter inductors L1, L2 2mH
The DC-side capacitors C1, C2 1000μF
The input voltage ug RMS 220V
The output voltage Udc 400V
The rated output power Po 1000W
The grid frequency fg 50Hz
The switching frequency fs 20kHz
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.
Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.
Prerpints.org logo

Preprints.org is a free preprint server supported by MDPI in Basel, Switzerland.

facebook logotwitter logolinkedin logo
MDPI Initiatives
Important Links
Subscribe

Disclaimer

Terms of Use

Privacy Policy

© 2024 MDPI (Basel, Switzerland) unless otherwise stated