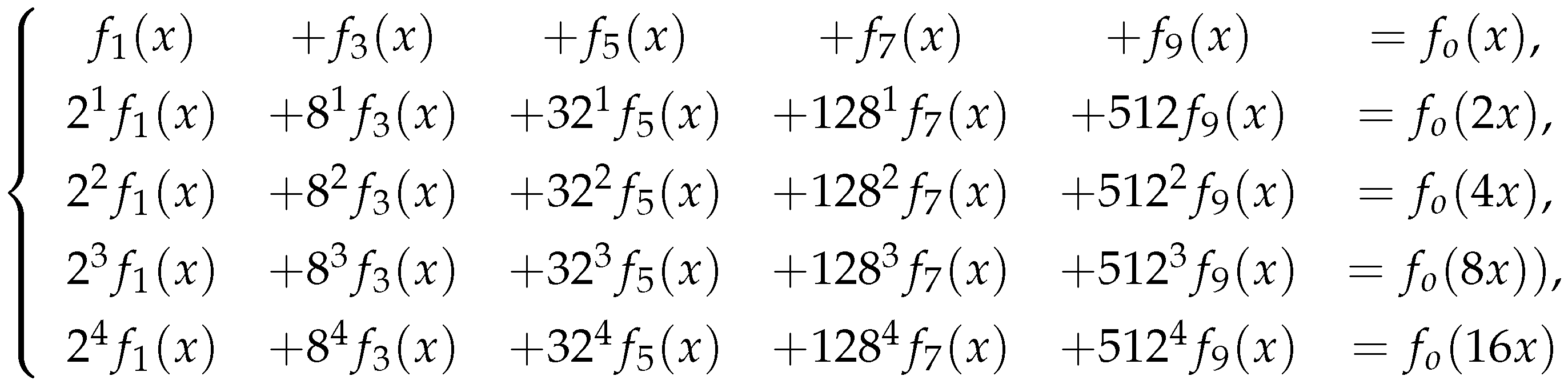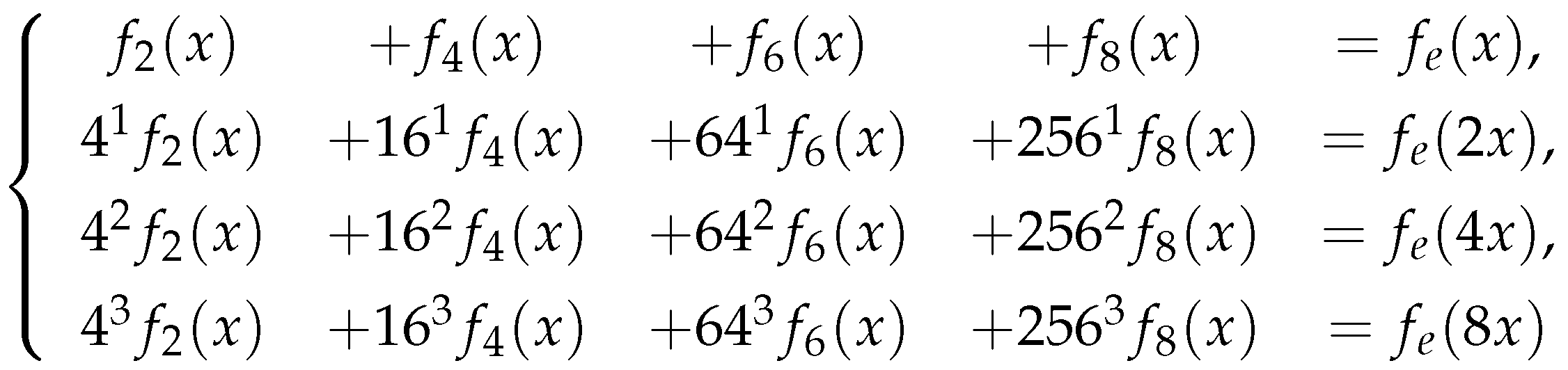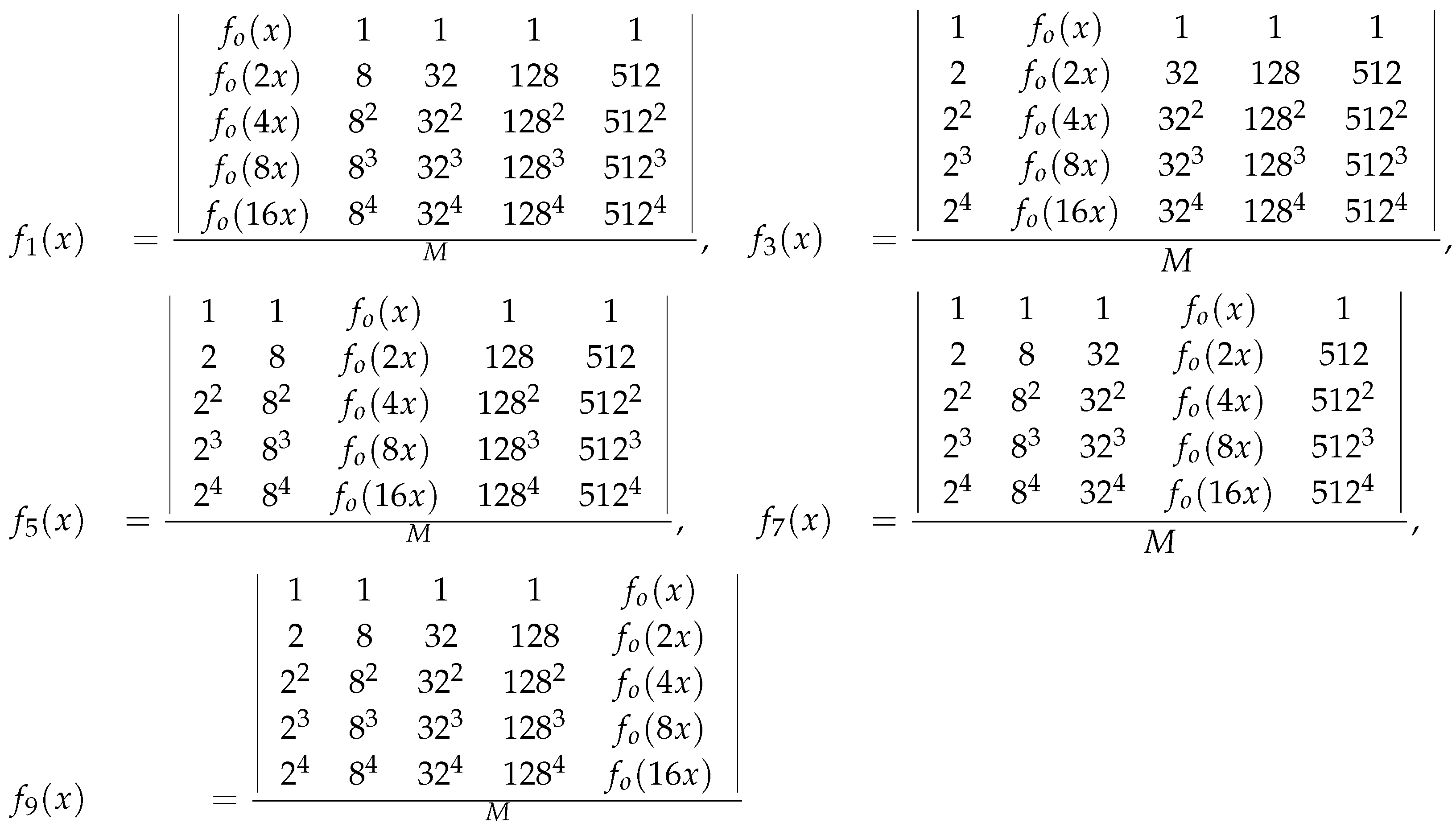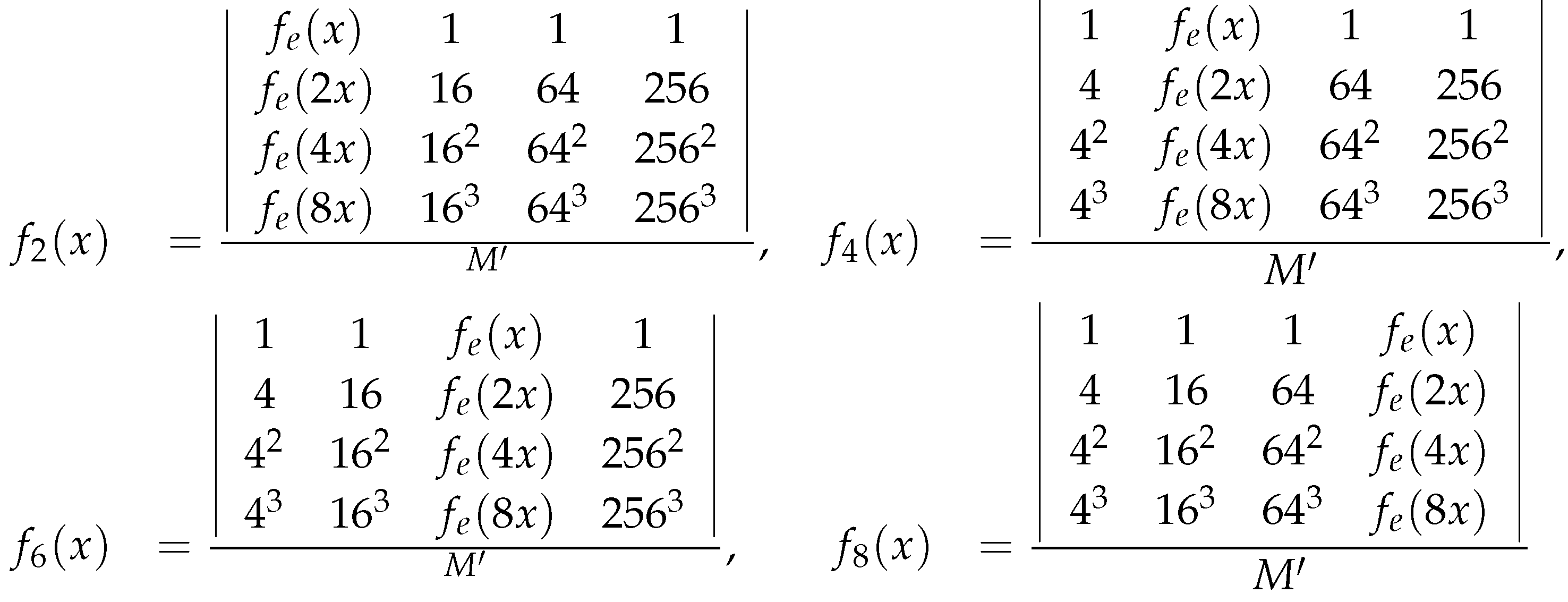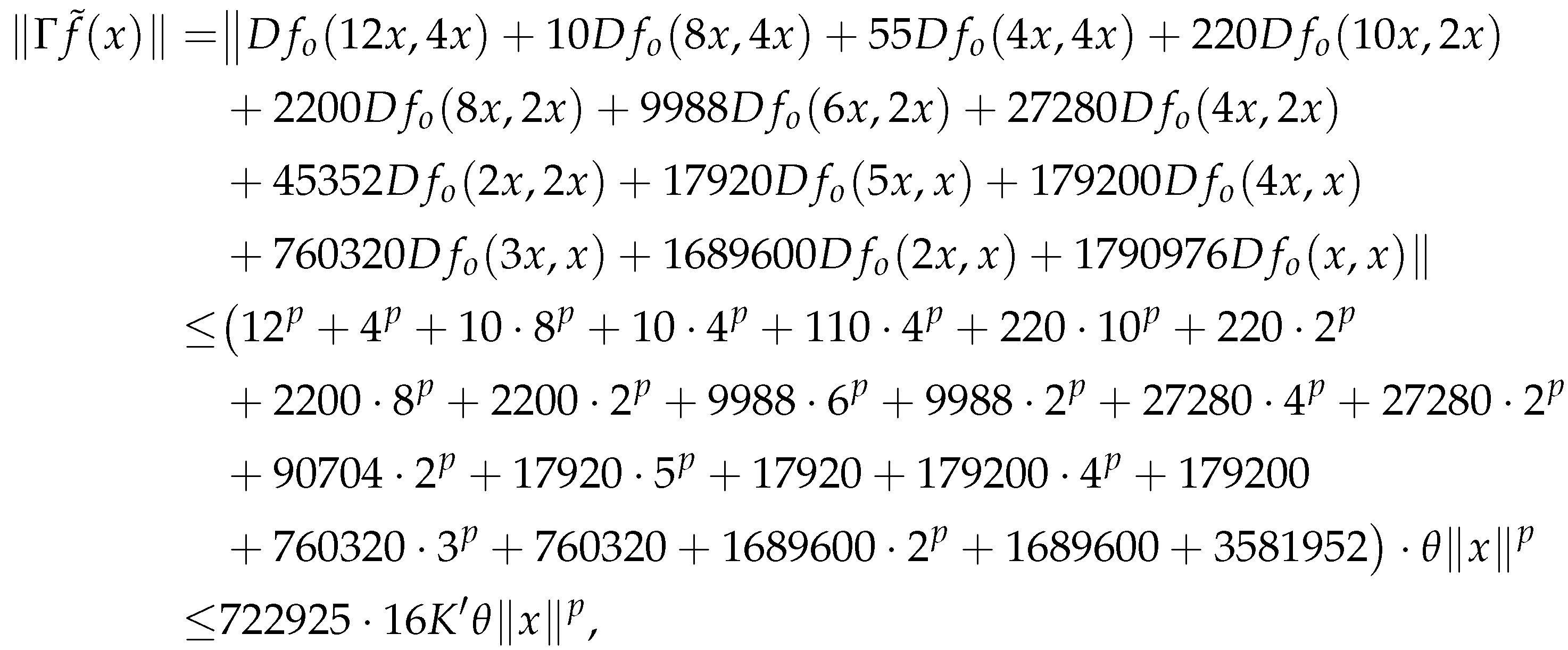4. Stability of the general nonic functional equation
In this section, we will consider the stability of the general nonic functional equation
Theorem 2.
Let be a nonnegative real number. Suppose that is a mapping such that for all
Then, there exists a unique mapping F satisfying and
for all where and
Proof. From the definition of
we get
and
By (4.1) and the definition of
and
we have that
for all
Next, for we will find to make = For each given we will use different approach to find the functions
•
Setting Let
. It follows from Lemma 4 and (4.3) that
for all
Notice that for all
which implies that
for all
and
. By (4.5), the sequence
is Cauchy for all
because of the fact that
Since
Y is complete, the sequence
converges. Hence, we may define a mapping
by
Moreover, letting
and taking the limit
in (4.5), we get the inequality
By the definition of
we easily get
for all
and
for all
Let
It follows from Lemma 4 and (4.3) that
for all
Because of the fact that
for all
we have
for all
and
. Since
, by (4.6), the sequence
is Cauchy for all
. By the completeness of
we know that the sequence
converges. Hence, we can define a mapping
by
However, letting
and passing the limit
in (4.6) we get the inequality
From the definition of , we easily get for all and for all
•
Setting Let
It follows from Lemma 4 and (4.4) that
for all
and
Since
we have from (4.7) that the sequence
is Cauchy for all
. By the completeness of
the sequence
converges. Hence, we can define a mapping
by
Now, letting
and passing the limit
in (4.7), we obtain that
From the definition of , we then have for all and for all
Let
It follows from Lemma 4 and (4.4) that
for all
and
Since
we have by (4.9) that the sequence
is Cauchy for all
Since
Y is complete, the sequence
converges. Then, we can define a mapping
by
In (4.9), puting
and passing the limit
one obtains that
According the definition of , we arrive at for all and for all
•
Setting Let
It follows by Lemma 4 and (4.3) that
for all
and
. Since
we see by (4.10) that the sequence
is Cauchy for all
. From the completeness of
the sequence
converges. So, we may define a mapping
by
Taking
and sending the limit
in (4.10), we find that
for all
Based on the definition of
, we yield that
for all
and
for all
Let
The lemma 4 and (4.3) guarantee that
for all
and
Since
we have from (4.11) that
is a Cauchy sequence for all
. So, because
Y is complete, the sequence
converges. Then, we may define a mapping
by
Let
and take the limit
in (4.11) and then
The definition of gives that for all and for all
•
Setting Let
It follows from Lemma 4 and (4.4) that
for all
and
Considering
and (4.12), the sequence
is Cauchy for all
. Since
Y is complete, the sequence
converges. Thereby, we can define a mapping
by
Now, by letting
and passing the limit
in (4.12), we obtain the inequality
We have from the definition of that for all and for all
Let
Lemma 4 and (4.4) imply that
for all
and
. Since
we have by (4.13) that
is a Cauchy sequence for all
. Since
Y is complete, the sequence
converges. Thus, we can define a mapping
by
Meanwhile, in (4.13), letting
and passing the limit
we then have the inequality
From the definition of , we see that for all and for all
•
Setting Let
It follows from Lemma 4 and (4.3) that
for all
and
We have assume that
So, we have by (4.14) that
is a Cauchy sequence for all
. Since
Y is complete, the sequence
converges. Hence, we can define a mapping
by
Moreover, letting
and passing the limit
in (4.14), we get the inequality
With the help of the definition of , we obtain that for all and for all
Let
In view of Lemma 4 and (4.3), we have that
for all
and
. It follows from
and (4.15) that the sequence
is Cauchy for all
Since
Y is complete, we see that the sequence
converges. So, one can define a mapping
by
Furthermore, setting
and sending the limit
in (4.15), we lead to
By virtue of the definition of , we find that for all and for all
•
Setting Let
Combine Lemma 4 and (4.4) to find that
for all
and
. Then, since
it follows by (4.16) that
is a Cauchy sequence for all
The completeness of
Y ensures that the sequence
converges, so that, we define a mapping
by
But then, let
and take the limit as
in (4.16) to get
According to the definition of , we have shown that for all and for all
Let
It follows from Lemma 4 and (4.4) that
for all
and
Since
we see from (4.17) that the sequence
is Cauchy for all
Thus, by the completeness of
Y, we find that the sequence
converges. Hence, we can define a mapping
by
In addition, put
and then let
in (4.17) to have
From the definition of , we get for all and for all
•
Setting Let
We know by Lemma 4 and (4.3) that
for all
and
Based on the fact that
and (4.18), the sequence
is Cauchy for all
Since
Y is complete, the sequence
converges. So, one can define a mapping
by
Moreover, letting
and passing the limit
in (4.18), we yield that
By the definition of , we have that for all and for all
Let
Note that, by Lemma 4 and (4.3), we have
for all
and
On the basis of the assumption
and (4.19), we see that
is a Cauchy sequence for all
. Since
Y is complete, the sequence
converges for all
Therefore, we can define a mapping
by
In (4.19), set
and then let
to find
By the definition of , it is shown that for all and for all
•
Setting Let
It follows from Lemma 4 and (4.4) that
for all
and
By the assumption
and (4.20), the sequence
is Cauchy for all
Since
Y is complete, the sequence
converges. Hence, we can define a mapping
by
Letting
and passing the limit
in (4.20), we then have the following inequality
From the definition of we are forced to conclude that for all and for all
Let
Observe that, by Lemma 4 and (4.4), we obtain that
for all
and
It follows from the assumption
and (4.21) that
is a Cauchy sequence for all
The completeness of
Y implies that the sequence
converges, so that, we can define a mapping
by
Put
and then take
in (4.21) to get
According to the definition of , we find that for all and for all
•
Setting Let
It follows from Lemma 4 and (4.3) that
for all
and
We then have by the assumption
and (4.22) that
is a Cauchy sequence for all
Since
Y is complete, the sequence
converges. Then, one can define a mapping
by
On the other hand, letting
and passing the limit
in (4.22), we deduce that
We have from the definition of that for all and for all
Let
Using Lemma 4 and (4.3), we have
for all
and
From
and (4.23), it follows that the sequence
is Cauchy for all
By the completeness of
the sequence
converges. Thereby, we can define a mapping
by
In particular, put
and then let
in (4.23) to have
With the aid of the definition of , one obtains that for all and for all
Finally, we set a mapping
F as
Since
for all
we have
Next, we are in the position to prove that the mapping
F satisfies the inequality (4.2). Since
we have
and so we obtain the desired result (4.2).
It remains to prove that
F is unique : Suppose that
be another mapping with
satisfying the relation
and the inequality (4.2). We have by Lemma 5 that for each
the mappings
satisfy
To verify the uniqueness of
we want to prove it only if
This is because other cases of
p can be showed in a similar fashion. Therefore, let us assume that
Then, we see that for
and
for all
and all positive integer
where
Taking the limit in the above relations as
we obtain the equality
which means that
and
for all
Employing the similar way, it is easily shown that for each
the equalities
hold. Note that
This completes the proof of the uniqueness of F for
For other p cases, the uniqueness proof of F can be proved very same to the proof for □