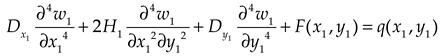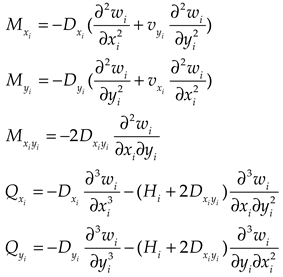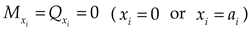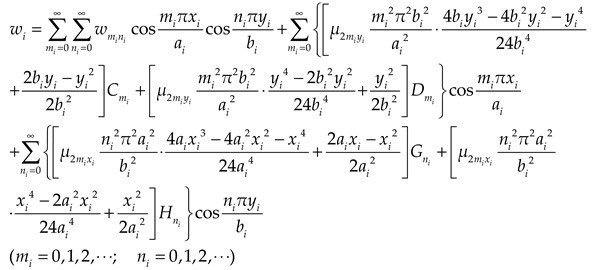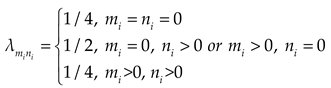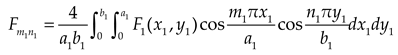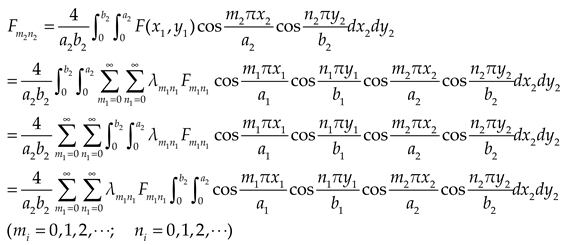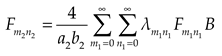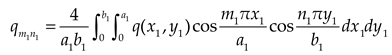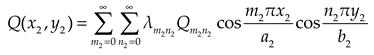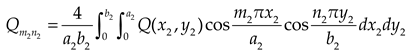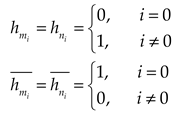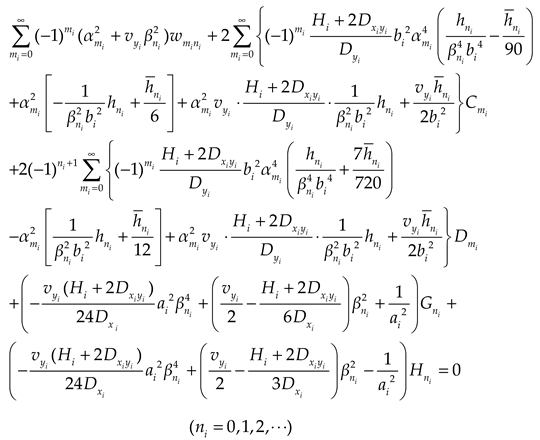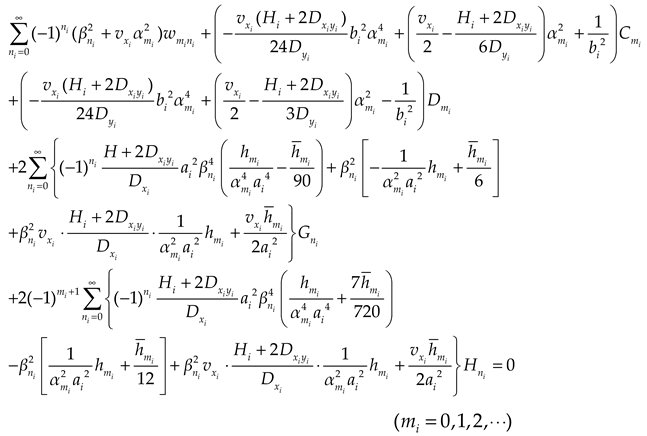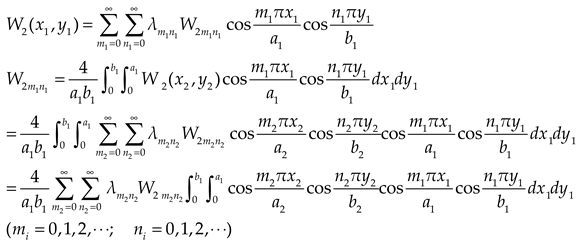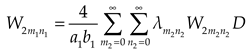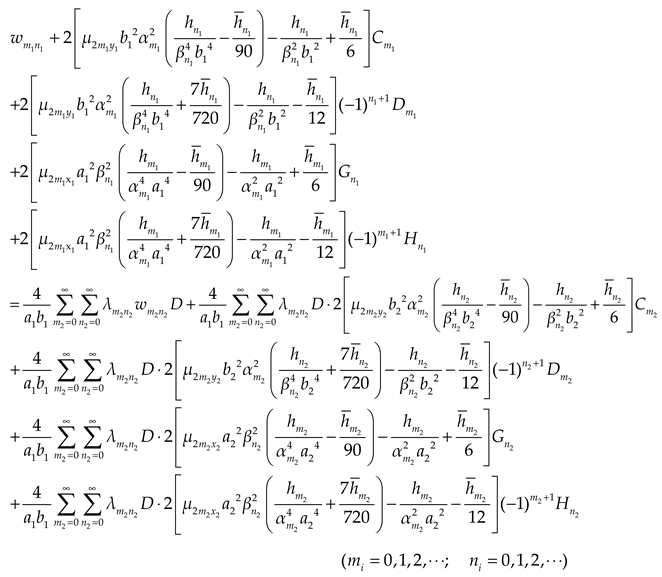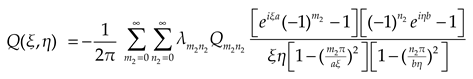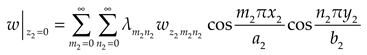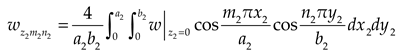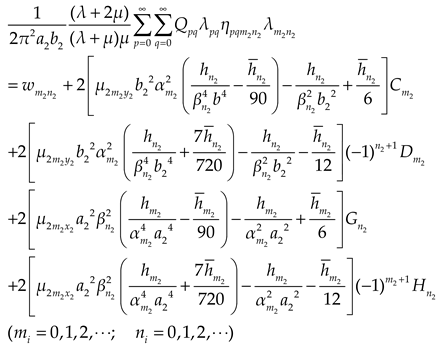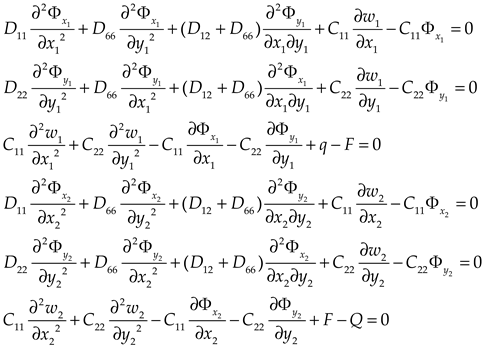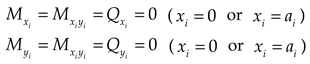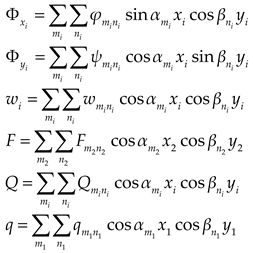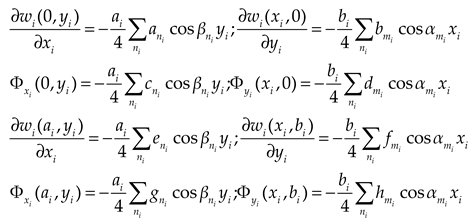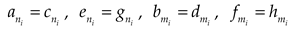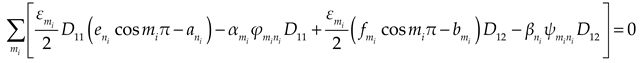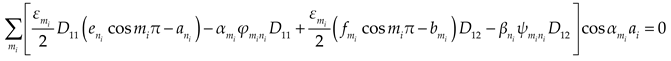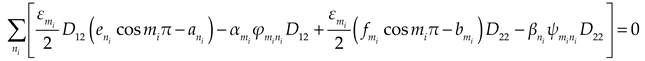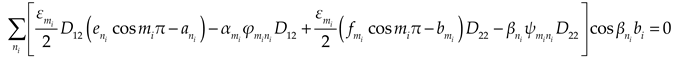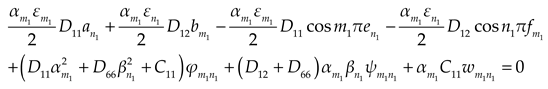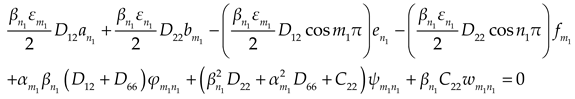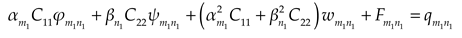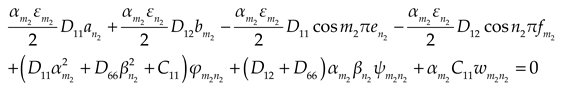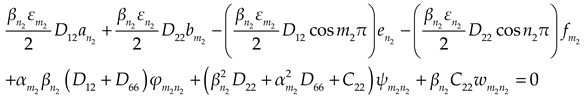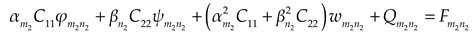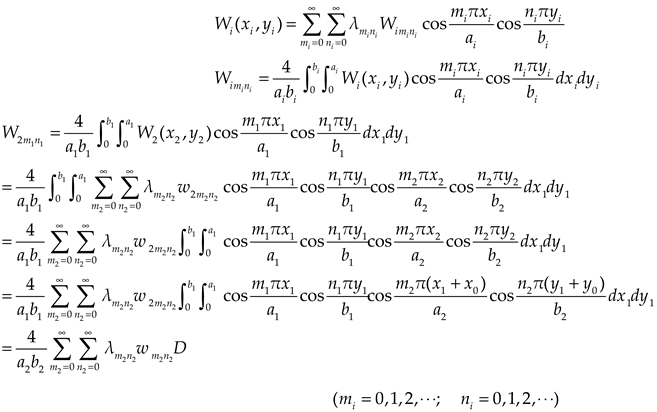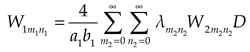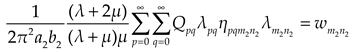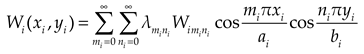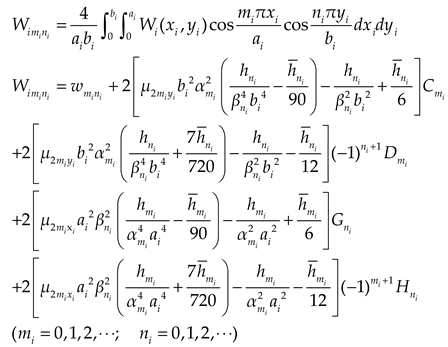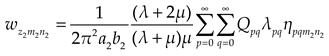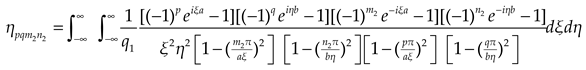Bending Analysis of Stepped Rectangular Plates Resting on Elastic Half-Space Foundation

1. Introduction

The bending problems of plates and stepped rectangular plates resting on the elastic half-space foundation play an important role in practical engineering. These plates could be found in actual engineering, such as foundation plates in civil engineering [1] and piezoelectric laminated plates in electronic engineering [2].

Shao et al. [3] used Fourier differential quadrature method to study the bending problems of irregular thin plate on Winkler foundation, and the accuracy of this method was verified by numerical analysis. Guarracino et al. [4] gave an example of numerical analysis of thin plates buckling which could ensure that the relationship between load and displacement was correct. Kim et al. [5] introduced a novel analytical solution that could be used to solve the flexural responses of annular sector thin plates, the accuracy of which was demonstrated by existing research conclusions and numerical results. Besides the thin plates, moderately thick plates had also been studied by researchers. Tuivey [6] studied the flexural properties of moderately thick laminated plates on Winkler-Pasternak elastic foundations, and the numerical results were demonstrated by computer implementation. Alinaghizadeh et al. [7] investigated the moderately thick plates rested on two-parameter elastic foundation by employing Generalized Differential Quadrature, and the results were in good agreement with the numerical results. Khezri et al. [8] studied the application of a shear-locking-free formulation based on first-order Mindlin theory formulation, and adopted reproducing kernel particle method to demonstrate the accuracy of the presented method.

Winkler foundation [9,10] and two-parameter foundation [11,12] were two commonly used analysis models for the analysis of mechanical properties of plate. Although the Winkler foundation model was simple, the displacement of the foundation was limited to the loaded area which could not effectively reflect the stress diffusion and deformation, meaning that the accuracy of the calculation results was difficult to be guaranteed. The two-parameter foundation model used two independent parameters to reflect the soil properties, and though this model improved the discontinuity of the Winkler foundation model, the two-parameters were very difficult and complex to be determined.

Therefore, some studies have been done to solve the problem of flexural properties of stepped rectangular plates. Cheung et al. [13] and Cho et al. [14] utilized the finite element method to analyze the mechanical performance of the stepped rectangular plate. Xiang et al. [15] and Radosavljević et al. [16] used Levy type solution method to deal with the stepped rectangular plates. Rahai et al. [17] chose energy method based on modified buckling mode shapes to analyze the buckling performance of stepped plates.

These works provided important insight into the characteristics of the rectangular stepped plates, however, the methods they used are mainly numerical method and finite element method. Therefore, analytical method is proposed to study the flexural response of stepped rectangular plate resting on elastic half-space foundation in this paper, which subjected to static load. The stepped rectangular plate is considered to be composed of two plates with different dimensions and properties (upper and lower plates), and taking into account the thickness of the upper and lower plates, the analytical method is divided into three cases: (1) The upper and lower plates are both thin plates; (2) One plate is thin plate, while the other one is moderately thick plate; (3) The upper and lower plates are both moderately thick plates. Fourier series with supplementary terms are used to obtain the analytical solution, and also, the influence of theory of plate, elastic modulus and dimensions of the plate on the bending performance of stepped rectangular plate are analyzed.

2. Governing equations and results

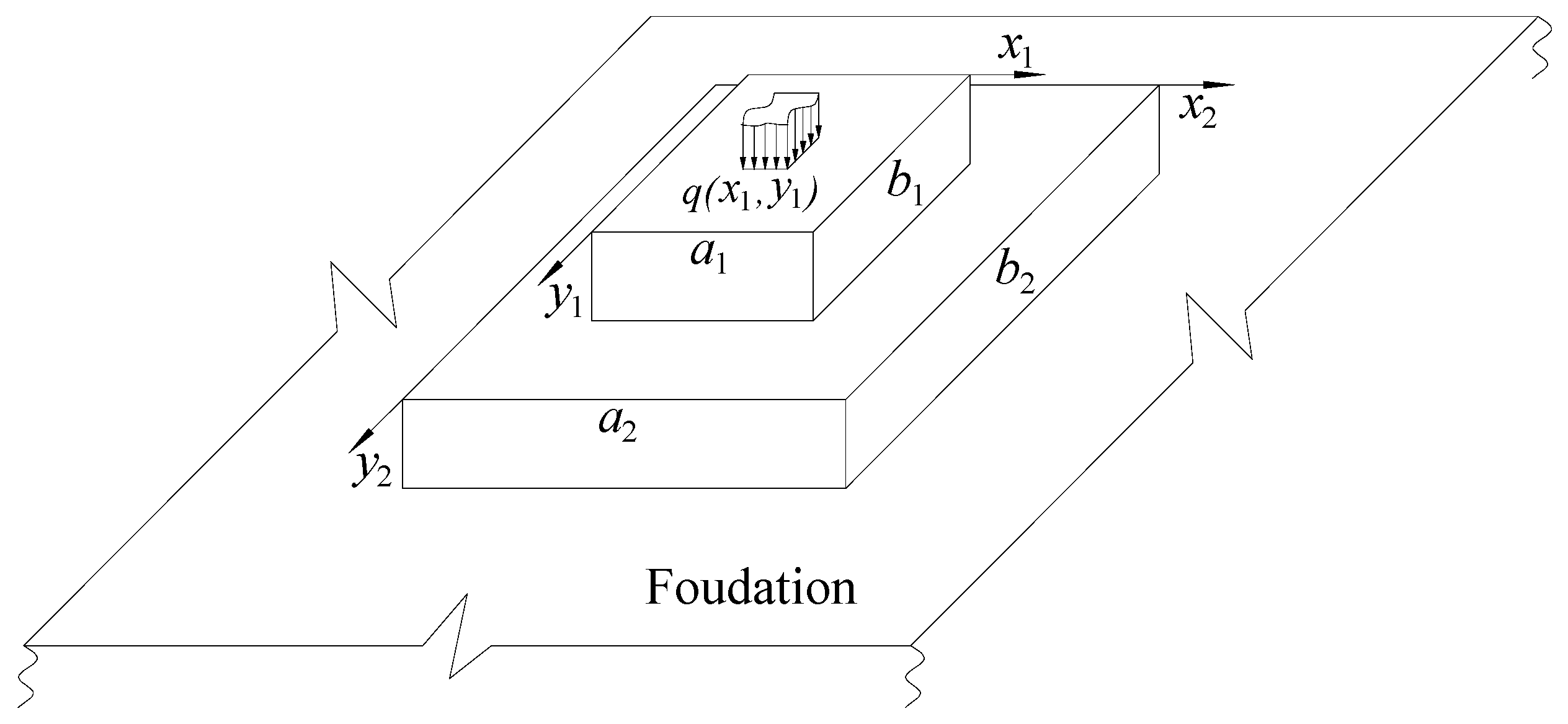
A stepped rectangular plate, whose upper and lower dimensions of plates are a₁×b₁ (length×width) and a₂× b₂ (length×width) respectively, is referred to the Cartesian systems of coordinates x₁y₁ and x₂y₂ associated with the external surfaces of upper and lower plates (Figure 1). The contact surface between the upper and lower plates is assumed to exclude their mutual slipping. Uniformly distributed load $q(x_1,y_1)$ is applied to the external surface of upper plate.

2.1. Both upper and lower parts of the plate are thin plates

2.1.1. Basic equations and boundary conditions

Governing differential equations of the upper and lower plates are given as

(1a)

(1b)

where $D_{x_i}$ and $D_{y_i}$ are bending stiffness, $w_i$ is deflection, $F(x_1,y_1)$ is interaction force between the upper and lower plates, $Q(x_2,y_2)$ is subgrade reaction, $H_i=D_{x_i}{v}_{y_i}+2D_{x_i{y}_i}$ is equivalent stiffness, $v_{x_i}$ and $v_{y_i}$ are Poisson ratio, $D_{x_i{y}_i}$ is torsional stiffness. The upper and lower plates are numbered $i=1$ and $i=2$, respectively.

The internal force of the upper and lower plates could be written in terms of deflection functions:

(2)

in which $M_{x_i}$ is bending moment, $M_{x_i{y}_i}$ is twisting moment, $Q_{x_i}$ is shear force.

Boundary restrictions are given as

(3a)

(3b)

(3c)

2.1.2. Coordination equation and analytical solution

The deflections of the upper and lower plates can be expressed as double cosine series with supplementary terms:

(4)

where ${\mu }_{2m_i{x}_i}=\frac{H_i+2D_{x_i{y}_i}}{D_{x_i}}$, ${\mu }_{2m_i{y}_i}=\frac{H_i+2D_{x_i{y}_i}}{D_{y_i}}$, $w_{m_i{n}_i}$, $C_{m_i}$, $D_{m_i}$, $G_{n_i}$, $H_{n_i}$ are undetermined parameters.

Eq. (4) has four steps’ derivation for rectangular plate with four free edges, which could satisfy the boundary conditions, such as the corner condition and shear force at the boundary. If the plate is made of isotropic material, the Eq. (4) can degenerate into an expression of an isotropic rectangular plate.

Based on Eq. (1), it could be found that $F(x_1,y_1)$ is related to the control differential equations of the upper and lower plates, so $F(x_1,y_1)$ can be expanded into double cosine series represented by $x_1$, $y_1$ and $x_2$, $y_2$.

(5)

where

(6a)

(6b)

(6c)

$x_0$, $y_0$ represent the relationship between $x_1{y}_1$ and $x_2{y}_2$ coordinate systems, and substituting $x_2=x_1+x_0$, $y_2=y_1+y_0$ into the integral part of the Eq. (6c):

Hence, Eq. (6) is rewritten as

$q(x_1,y_1)$ is expanded into double cosine series represented by $x_1$ and $y_1$.

(7)

where

Subgrade reaction can be expressed in terms of double cosine series as

where

Substituting Eqs. (1a), (5) and (7) into Eqs. (3)~(4), and then expanding the polynomial of the supplementary terms in the formulas to cosine series. Comparing the coefficients of the corresponding items on both sides of the Eqs. (3)~(4), we could obtain the expressions as

(8)

(9)

where ${\alpha }_{m_i}=\frac{m_i\pi }{a_i}$, ${\beta }_{m_i}=\frac{n_i\pi }{b_i}$ and

Considering the boundary conditions of bending moment, we could obtain:

(1) When $x_i=0$, $M_{x_i}=0$

(10)

(2) When $x_i=a_i$, $M_{x_i}=0$

(11)

(3) When $y_i=0$, $M_{y_i}=0$

(12)

(4) When $y_i=b_i$, $M_{y_i}=0$

(13)

The deflection of the upper and lower plate could be expressed by formula [18]

where

Expanding the deflections of the lower plate into double cosine series at the contacting position with the upper plate

(14)

Substituting $x_2=x_1+x_0$, $y_2=y_1+y_0$ into Eq. (14), we obtain

Eq. (8) can be rewritten as

Taking into account that the deflections of upper and lower plates at the contact position are the same, the deformation equation of compatibility is expressed as

(15)

The double Fourier transform of the ground reaction force is expressed as

(16)

Expanding $w\left|{}_{z_2=0}\right.$ into double cosine series form

(17)

in which

(18)

In view of the research contents in the literature [19], $w\left|{}_{z_2{m}_2{n}_2}\right.$ could be expressed as

(19)

where

Eq. (4) could be rewritten in double cosine series form, and considering that the plate and surface of the elastic foundation have the same vertical displacement, thus the coefficients of corresponding items are also the same. The deformation equation of compatibility is given as

(20)

According to Eqs. (8)~(13) and (15)~(20), the undetermined coefficients $w_{m_1{n}_1}$, $F_{m_1{n}_1}$, $C_{m_1}$, $D_{m_1}$, $G_{n_1}$, $H_{n_1}$, $w_{m_2{n}_2}$, $Q_{m_2{n}_2}$, $C_{m_2}$, $D_{m_2}$, $G_{n_2}$, $H_{n_2}$ could be solved. Substituting the solved coefficients into Eq. (1) and Eq. (4), the subgrade reaction, deflection and internal force of the plate could be obtained.

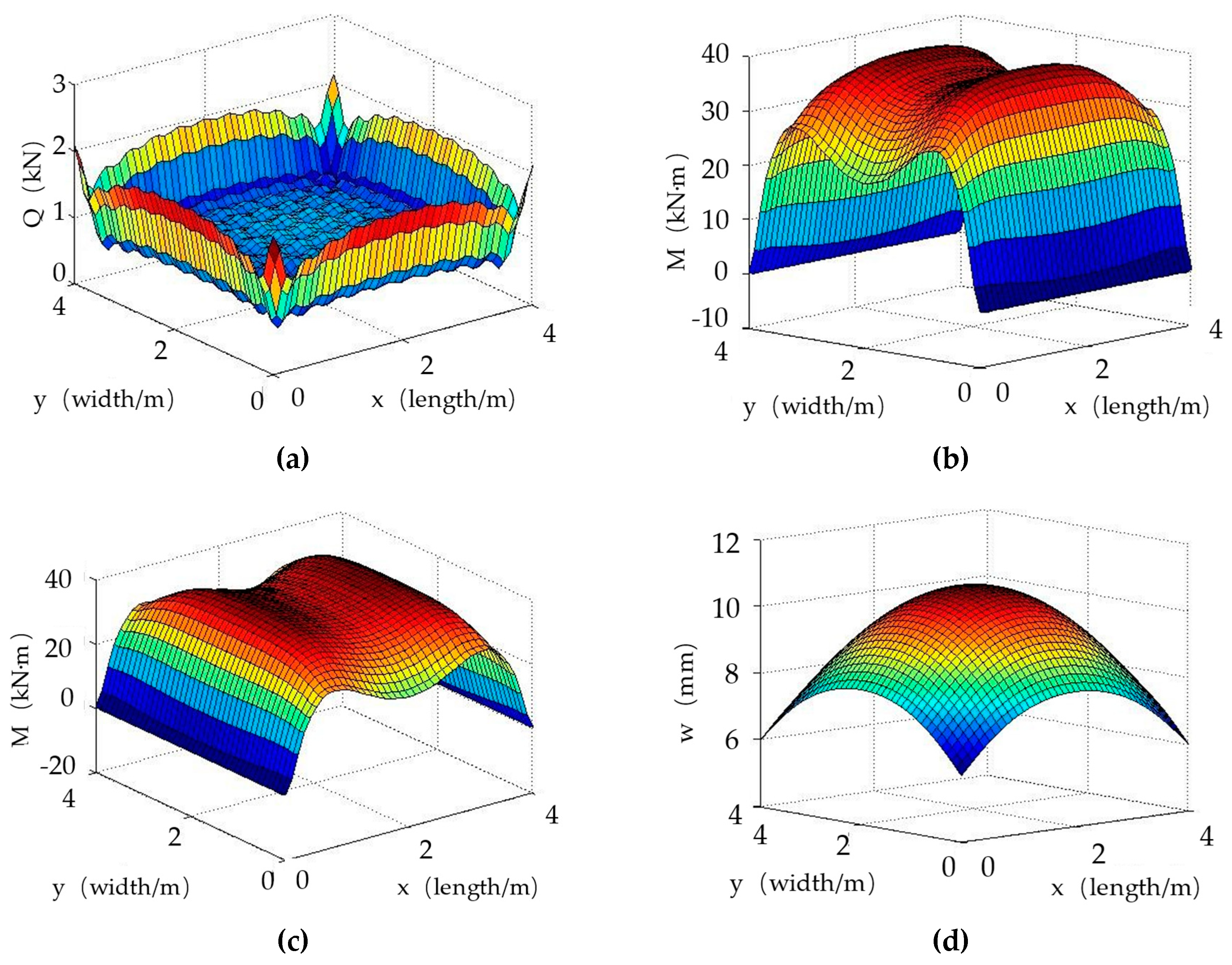
2.1.3. Example

We consider a stepped rectangular plate resting on the surface of an elastic half space foundation. The dimensions of the upper and lower plate are 4.0m×0.2m (side length × thickness) and 4m×0m (side length × thickness) respectively, and the uniform load $q(x_1,y_1)$ on the plate is 0.98MPa. In this case, the stepped rectangular plate degenerates into a rectangular plate. The performance parameters of plate and foundation are given in Table 1.

The subgrade reaction, bending moment and deflection of the plate could be obtained by the solution, as shown in Figure 2.

Table 2 shows that the calculated results are consistent with the results in [19]. This comparison proves the effectiveness of the theory proposed in this paper.

2.2. Both upper and lower parts of the plate are moderately thick plates

2.2.1. Basic equations and boundary conditions

The governing differential equations of moderately thick plate are determined by formulas [20]

(21)

where ${\Phi }_{x_i}$, ${\Phi }_{y_i}$, $w_i$, $F$, $Q$ are unknown coefficient.

Boundary restrictions are given as

2.2.2. Coordination equation and analytical solution

Expanding ${\Phi }_{x_i}$, ${\Phi }_{y_i}$, $w_i$, $F$, $Q$, $q$ into Fourier series

in which ${\Phi }_{m{}_{i}n{}_i}$, ${\psi }_{m_i{n}_i}$, $w_{m_i{n}_i}$, $F_{m_2{n}_2}$, $q_{m_1{n}_1}$ and $Q_{m_i{n}_i}$ are unknown coefficients.

Taking into account the continuous differentiability of the formula on the boundary of the plate, we can write

where $a_{n_i}$, $b_{m_i}$, $c_{n_i}$, $d_{m_i}$, $e_{n_i}$, $f_{m_i}$, $g_{n_i}$ and $h_{m_i}$ are unknown coefficients. According to boundary conditions, we obtain the expressions

(1) Derived from $M_{x_i}=0$ on the edge $x_i=0$, we obtain the expression

(2) Derived from $M_{x_i}=0$ on the edge $x_i=a_i$, we obtain the expression

(3) Derived from $M_{y_i}=0$ on the edge $y_i=0$, we obtain the expression

(4) Derived from $M_{y_i}=0$ on the edge $y_i=b_i$, we obtain the expression

Substituting the unfolded Fourier form of ${\Phi }_{x_i}$, ${\Phi }_{y_i}$ and $w$ into the Eq. (17), the expressions are given as

(22a)

(22b)

(22c)

(22d)

(22e)

(22f)

Considering the same displacement of upper and lower plate at the contacting position, thus the deflection equations of the upper and lower plate could be expanded into double cosine series as

(22)

The deformation coordination equation between the upper and the lower plates is expressed as

The deformation coordination equation between the lower plate and the foundation is given as

(23)

Through the Eqs. (21), (22), (22) and (23), the undetermined coefficients $m_i$, $a_{n_i}$, $b_{m_1}$, $e_{n_1}$, $f_{m_1}$, ${\phi }_{m_i{n}_i}$, ${\psi }_{m_i{n}_i}$, $w_{m_i{n}_i}$, $F_{m_i{n}_i}$, $Q_{m_2{n}_2}$ could be simultaneously solved. Substituting the solved coefficients into related formulas, the subgrade reaction, deflection and internal force of the plate could be obtained.

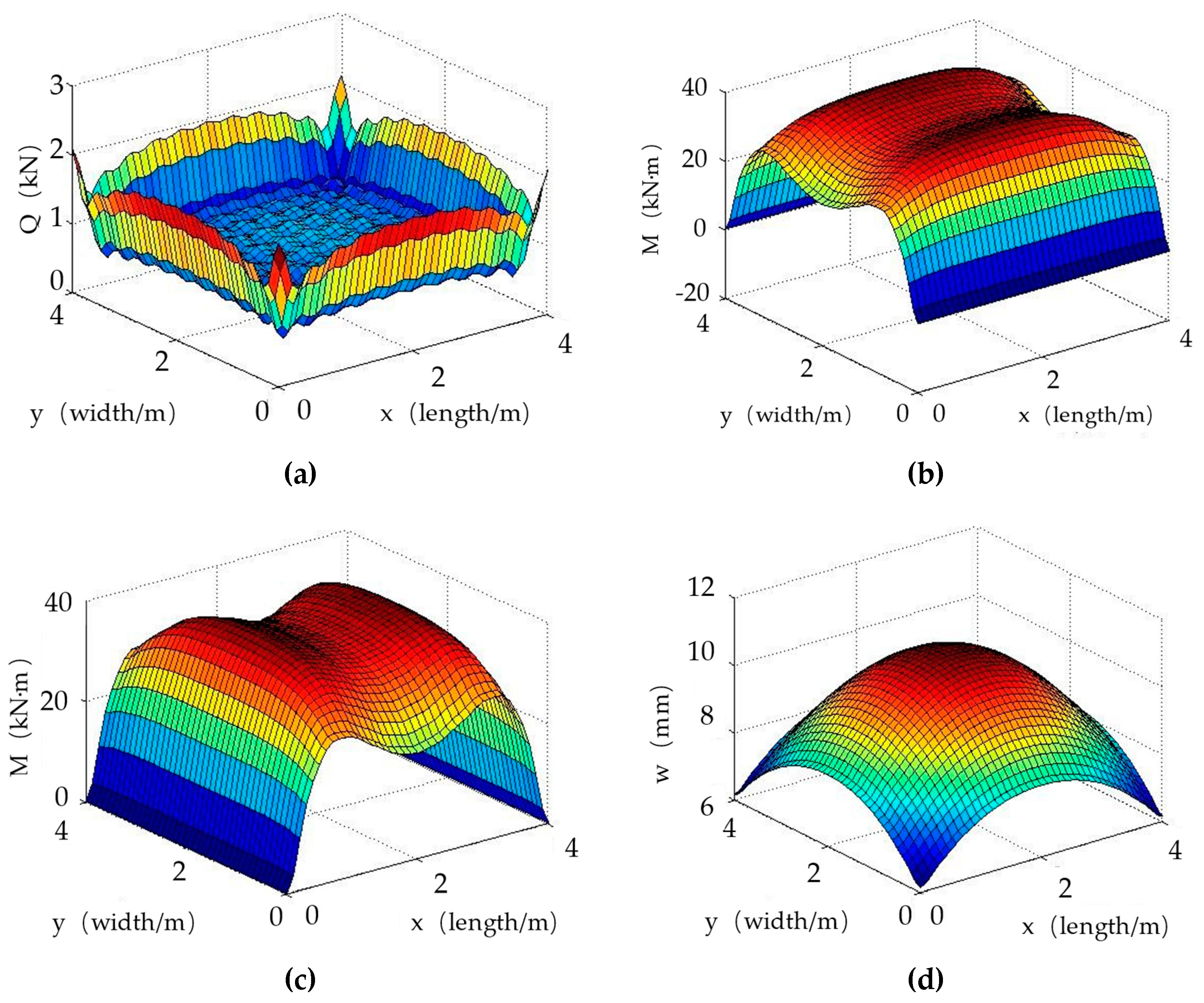
2.2.3. Example

Recalculating the example in 2.1.3 according to the theory mentioned in this section, the results are given in Figure 3.

The calculated results in this paper are consistent with the results in [19], as shown in Table 3. This comparison proves the effectiveness of the theory proposed in this paper.

When the stepped rectangular plate is simultaneously analyzed using moderately thick plate theory and thin plate theory, the same method (as shown in 2.1 and 2.2) could be used to solve the bending moment and deflection formula of the plate.

3. Discussions

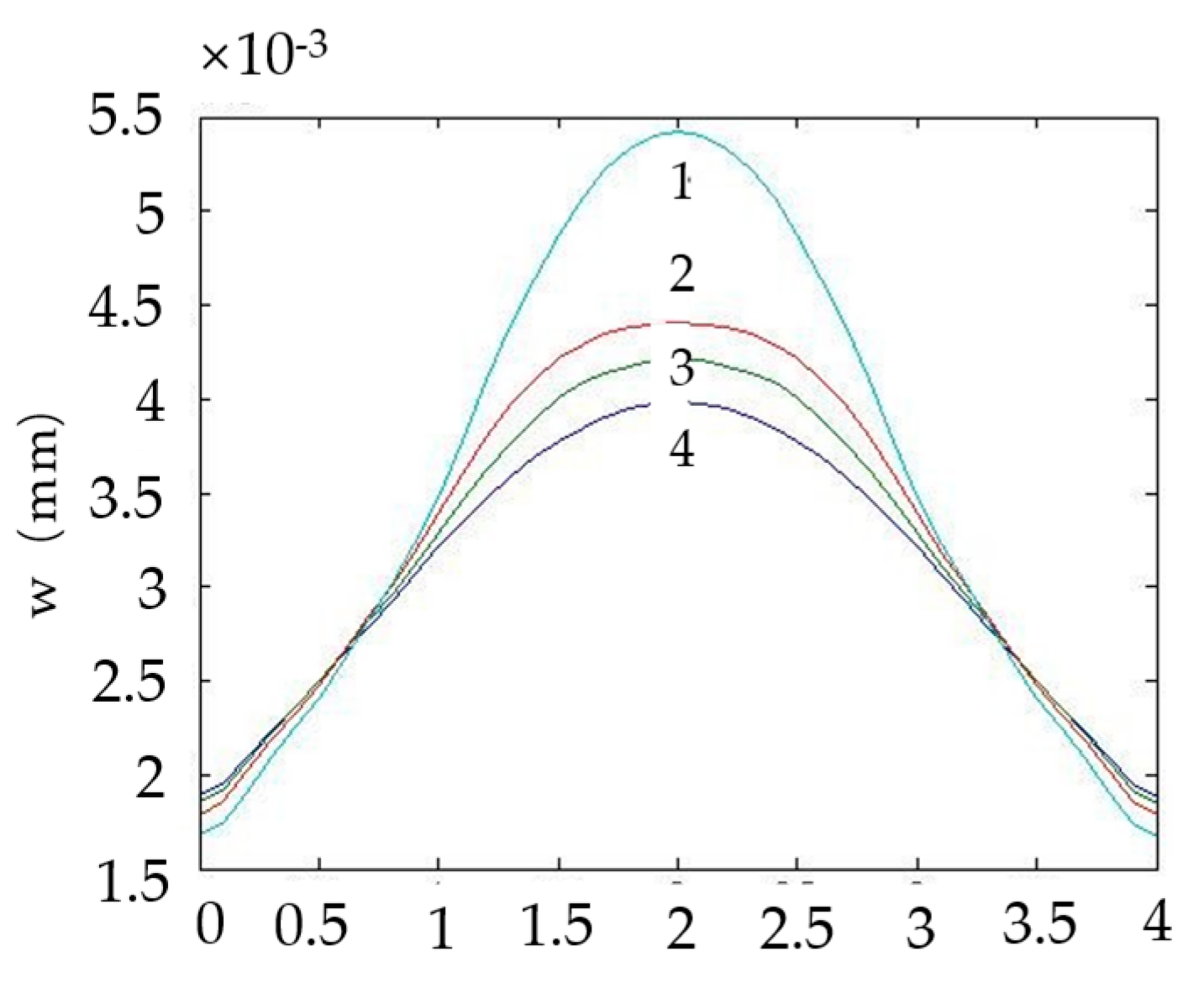
3.1. Effect of elastic modulus on the deflection of plate

The dimensions, Poisson ratios and elastic modulus of the rectangular stepped plate and foundation are given in Table 4. The vertical uniform load value is 0.98MPa. The deflection curve of the center line of the plate is shown in Figure 4, in which the number of the curves 1, 2, 3, and 4 indicate that the elastic modulus of the upper plate are 34300MPa, 343000MPa, 686000MPa, and 1029000MPa, respectively.

Through Figure 4, it could be concluded that with the increase of the elastic modulus of the upper plate, deflection at the center of the plate decreases, while the deflection at the edge of the plate increases.

3.2. Influence of plate theory on calculation results of plate deflection

The dimensions, Poisson ratios and elastic modulus of the rectangular stepped plate and foundation are given in Table 5. The vertical uniform load value is 0.98MPa, the thickness of lower plate is 0.2m, 0.3 m, 0.4m, 0.5m, 0.6m, 0.7m, 0.8m, 0.9m, and 1.0m, respectively. The deflection of the center of the lower plate is given in Table 6, in which $w_1$ and $w_2$ are the deflection values calculated by thin plate theory and moderately thick plate theory, respectively.

Through the calculation results in Table 6, it can be obtained that when the thickness of the plate is small, the calculation results using the thin plate theory and the moderately thick plate theory are basically the same.

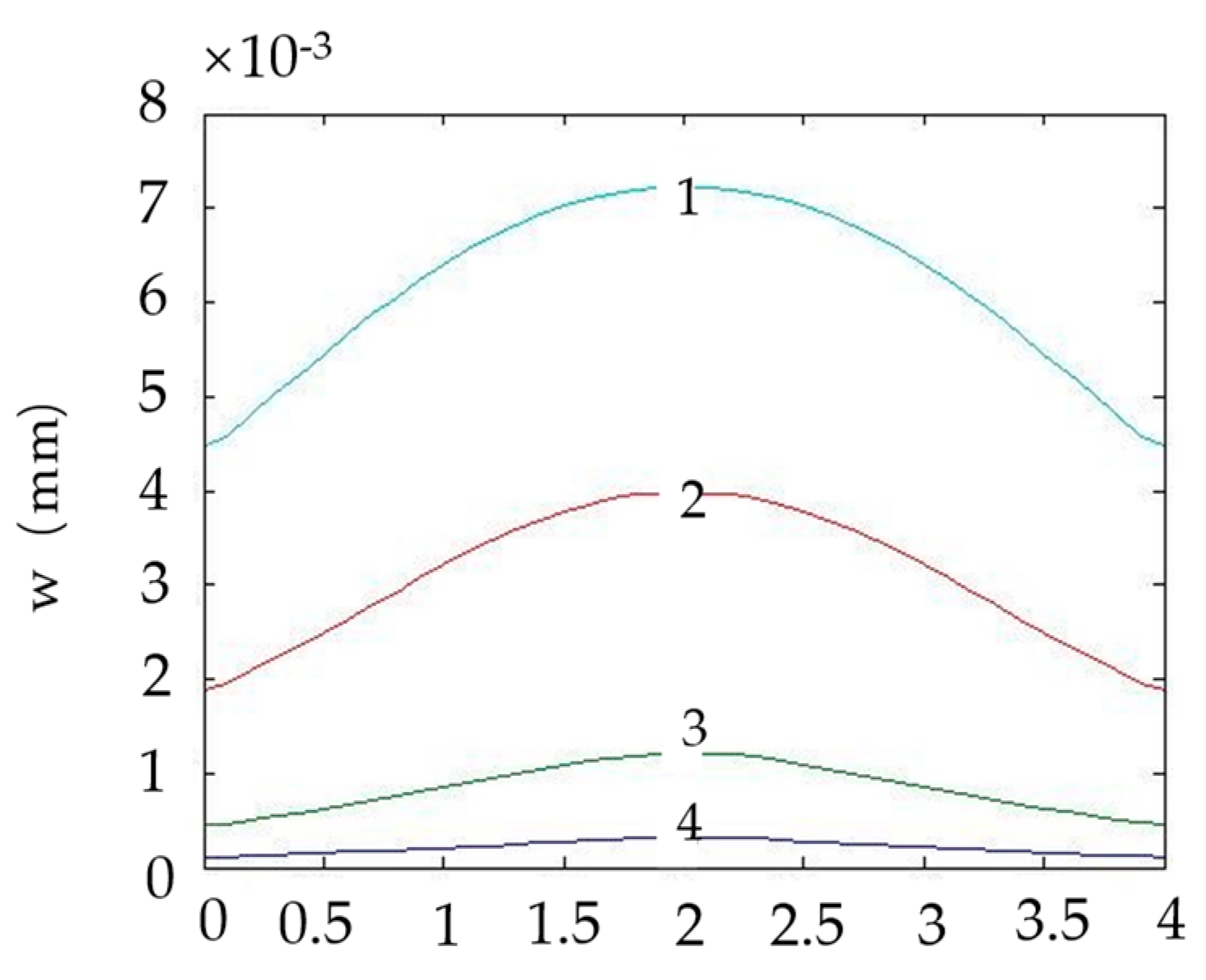
3.3. Influence of side length of upper and lower plates on calculation results of plate deflection

The dimensions of the stepped rectangular plates are given in Table 7. The vertical uniform load value is 0.98MPa. Calculation results can be seen in Figure 5, in which 1, 2, 3, and 4 indicate the side length of the upper plate are 3.0m, 2.0m, 1.0m, and 0.5m, respectively. It could be concluded that the deflection of the center of the plate increases as the size of the upper plate increases.

4. Conclusions

This paper presents a new solving method to obtain the bending moment and deflection of the stepped rectangular plate by using conventional thin plate theory and moderately thick plate theory. Several conclusions can be drawn as following.

(1) Analytical solution of stepped rectangular plate using thin plate theory and moderately thick plate theory is given by formula derivation. Comparing with existing research, it shows that the analysis results are reliable.

(2) The increase of the elastic modulus of the upper plate can effectively reduce the deflection at the center of the plate and slightly increase the deflection at the edge of the plate.

(3) When the thickness of the plate is not large enough, the deflection calculation results using thin plate theory and the moderately thick plate theory are basically the same.

(4) The greater the difference in the side length of the upper and lower plates, the greater the deflection of the stepped rectangular plate. The increase of the deflection at the edge of the plate is not as significant as that at the center of the plate.