Centralization and Sharing of Information to Improve Local Decision-Making in a Home Health Care Center

Home care centers face both an increase in demand and many variations during the execution of routes, compromising the routes initially planned: robust solutions are not effective enough, it is necessary to move on to resilient approaches. We create a close to reality use case supported by interviews of staff at home health care centers, where caregivers are faced with unexpected events that compromise their initial route. We model, analyze and compare three resilient approaches to deal with these disruptions: a baseline approach without any collaboration, a distributed collaborative approach, and a centralized collaborative approach, where we propose a centralization and sharing of information to improve local decision-making. The latter reduces the number of late arrivals by 11% and the total time of late arrival by 21%, and also halves the number of routes exceeding the end of work time (contrary to the distributed collaborative approach, due to the time wasted reaching colleagues). The use of a device, such as a smartphone application, to centralize and share information thus allows better mutual assistance between caregivers. Moreover, we highlight several possible openings like the coupling of simulation and optimization to propose a more resilient approach.

Keywords:

Subject: Public Health and Healthcare - Health Policy and Services

1. Introduction

Thanks to scientific developments and concurrent improvements in healthcare, hygiene, nutrition and social conditions, the life expectancy of humans has consistently increased in the developed world over the last century, and, coupled with a steadily declining birth rate over the course of recent decades, has resulted in an increasingly aging population. In 2020, 20% of the French population was over 60 years old in France, and according to the Institut National de la Statistique et des Etudes Economiques this will rise to 30% by 2070 [1]. In addition, there is a desire to reduce the demand for medical structures (e.g., hospitals), exerting pressure on people to return home as quickly as possible. As a result, the demand for home health care services has increased sharply in recent years, as well as the number of studies on this topic.

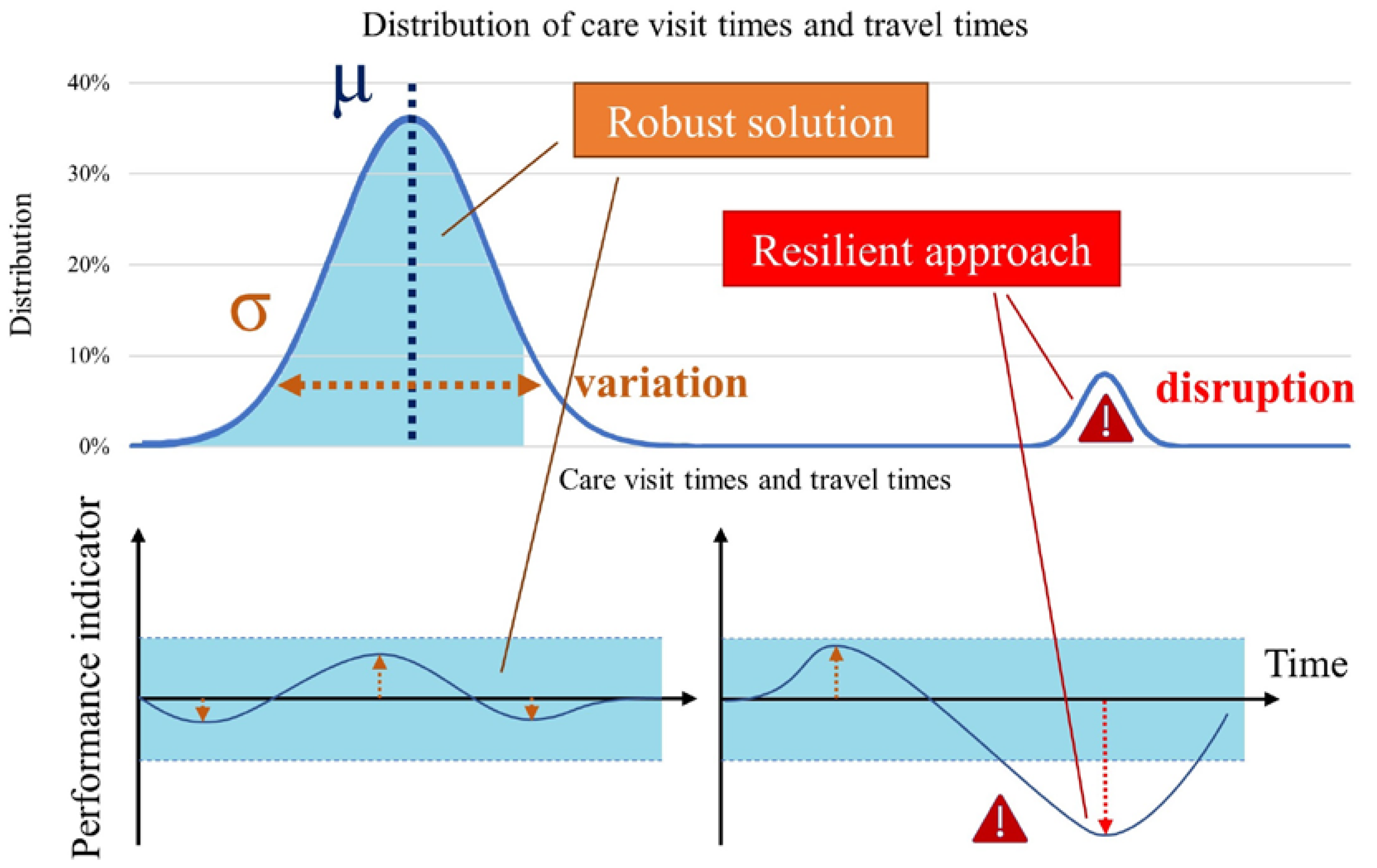
In the scientific literature, the management of home care routes is known as the Home Health Care Routing & Scheduling Problem (HHCRSP) and has been studied for fifty years [2]. The goal is to find the best possible routes according to the characteristics of the problem e.g., strategies to minimize travel times, maximize stakeholders’ satisfaction, taking time windows and difficulty of care visit provision into consideration, etc. Although the variability of HHCRSP systems is increasingly under scrutiny, most studies are carried out in a deterministic environment. For the past five years, an ever-larger number of publications have considered uncertainties (especially for travel times and visit times) and propose robust solutions to absorb these variations. The study of resilient approaches to counter high impact disruptions remains one of the gaps to be filled in the spectrum of HHCRSP publications. In addition, it is difficult to find a clear, realistic and readily available use case in the scientific literature.

The aim of this paper is to analyze and compare the performance of resilient approaches applied to a use case close to reality, open to the scientific community, and inspired by home health care centers in the department of Tarn (France) in an environment subject to both variations and high impact disruptions. Three different approaches are analyzed using discrete event simulation, including an empirical approach modeling what is done today in the home health care centers interviewed, and a new approach based on the centralization and sharing of information between caregivers to improve local decision-making.

2. Literature Review

The HHCRSP is a highly pertinent issue and widely studied in the literature, as evidenced by the numerous states of the art published recently [3,4]. In this section, we present an overview of the existing work to contextualize our contribution.

HHCRSP problems cover a wide range of constraints and objectives. They may include typical features of Vehicle Routing Problems (VRP), such as time windows (hard or soft) [5], and temporal dependencies (precedence, synchronization, or disjunction) [6], but also more specific features related to the field such as continuity of care [7], skills requirements [8], or incompatibilities [9]. The objective is often cost-related, whether it comes to minimizing travel costs or staffing costs [10,11], or is stakeholder-oriented [5].

As a variant of VRP, approaches seeking to address the issues around HHCRSP are manifold. In small instances, exact methods are developed e.g., mathematical programming [12], logic-based Benders decomposition [13], branch and price and cut [14], etc. Larger instances are generally solved with classic metaheuristics or approximation algorithms from the operations research field: population-based algorithms [15], neighborhood searches [16], and decomposition methods, for instance [17].

In practice, caregivers encounter various problems during their route, that can impact the remainder of their working day. Hence, deterministic approaches do not enable us to capture the whole complexity of the HHCRSP, at least not at the operational decision-making level. There are an increasing number of articles currently assessing the HHCRSP in view of various types of uncertainties (e.g., stochastic travel times or visit times, patient cancellations, emergencies, vehicle breakdown, etc.) and propose robust or resilient solutions: visits have an expected duration but can last longer [18] or they are normally distributed [8], and travel times are estimated with a kernel regression, for example [19].

In this paper, we focus on two forms of uncertainties regarding visit and travel times: small variations due to the stochasticity of the data, and more punctual but also more impactful disruptions such as traffic jams. The robustness of a system is defined as the ability “to maintain its function despite internal or external disruption” [20], whereas resilience is “the ability of a system to return to its original state, within an acceptable period of time, after being disturbed” [21]. A robust solution is therefore used to absorb a variation, and a resilient approach is used to counter a disruption, as represented in Figure 1.

These uncertainties can be addressed at different decision-making levels: Nikzad et al propose a two-stage stochastic programming model to tackle both uncertain visit and travel times [22], and Zhan et al propose a mixed-integer linear program and adapt the L-shaped method to solve the HHCRSP with stochastic visit times [23]. Another option to deal with uncertainties is to anticipate different disrupted scenarios and build robust solutions: in the study by Shi et al, each visit and travel time belongs to an uncertainty set based on the theory of budget uncertainty [24]. Since their solutions to the deterministic problem are not robust, they adapt several classic heuristics to build a solution that always remains feasible, despite visit and travel time uncertainties. Cappanera et al also choose a robust method to study uncertain demands from the patients and illustrate the need for a trade-off between a deterministic optimal solution that is particularly susceptible to any small disruption, and an extremely robust solution that is very expensive and often “underused” [25].

Resilient approaches must then be deployed at the operational level to repair the routes in the case of high-impact disruption: Alves et al use a multi-agent system to deal with unexpected events, such as vehicle breakdown, where visits are dynamically reassigned to another vehicle [26]. Marcon et al use a similar two-level architecture with an off-line module that assigns caregivers to patients and an online multi-agent module that takes local decisions to overcome disruptions [27]. In the study by Yuan et al, patients can require new visits during the execution of the routes, so the routes are re-optimized with a tabu-search, with the objective of minimizing deviations from the original plan [28].

In summary, the HHCRSP has been studied for a long time and increasingly in a stochastic environment, where many robust solutions have been proposed in the literature but few resilient approaches have been published. Moreover, it is difficult to find a use case that is clear, realistic and available to the scientific community. For this reason, in this article we propose to examine a realistic use case, the result of numerous interviews, and we analyze and compare three resilient approaches to counter the disruptions of home care routes.

3. Methods

3.1. Use case creation

In order to create a realistic use case to share with the HHCRSP scientific community, staff at seven home health care or service structures were interviewed in the department of Tarn in France during the months of September and October 2022. The aim was to collect information on the working environment: e.g., operating methods, problems encountered, existing and envisaged solutions, tools used, needs, etc. Having identified the challenges of the home care centers, we decided to create a use case inspired by two of these nursing care structures, which has the following characteristics:

There are five caregivers performing five routes;
Routes start at 7 a.m. from the health care center, and end between 12 p.m. and 1 p.m. at the same location;
There are 140 care visits to perform, which are requested by 140 patients (one visit per patient);
When the caregivers have finished their routes, they can help their colleagues if needed or do administrative tasks at the health care center until 1 p.m.;
Travel times are often short (usually less than five minutes) and are triangularly distributed more or less 30% around the average value;
Care visit times are generally five minutes, but can sometimes last 10 minutes; They are both subject to variations (such as travel times, with the same distribution) and to disruptions (whose distribution is detailed in the design of experiments);
Time windows (i.e., time slot during which the caregiver must begin the care visit) last one hour for each visit; and
There is an early and late tolerance of five minutes and if the caregiver arrives more than five minutes early then they must wait before starting the care visit.

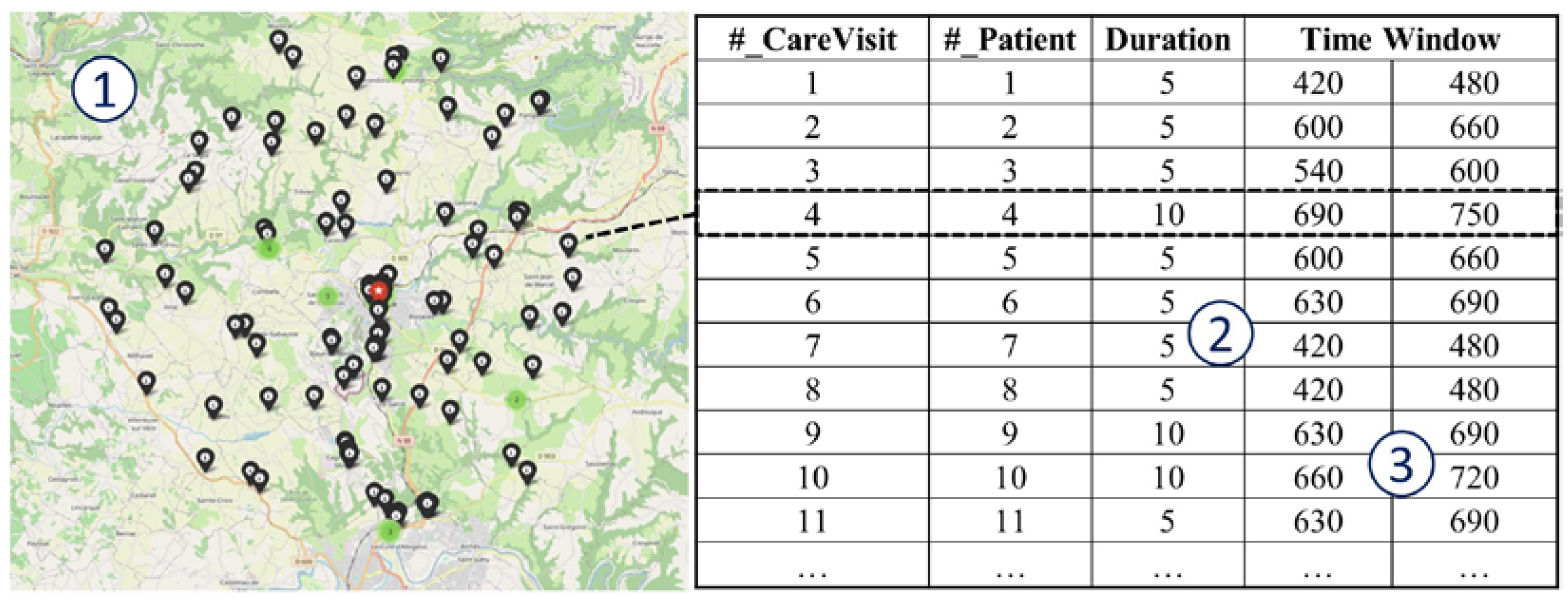
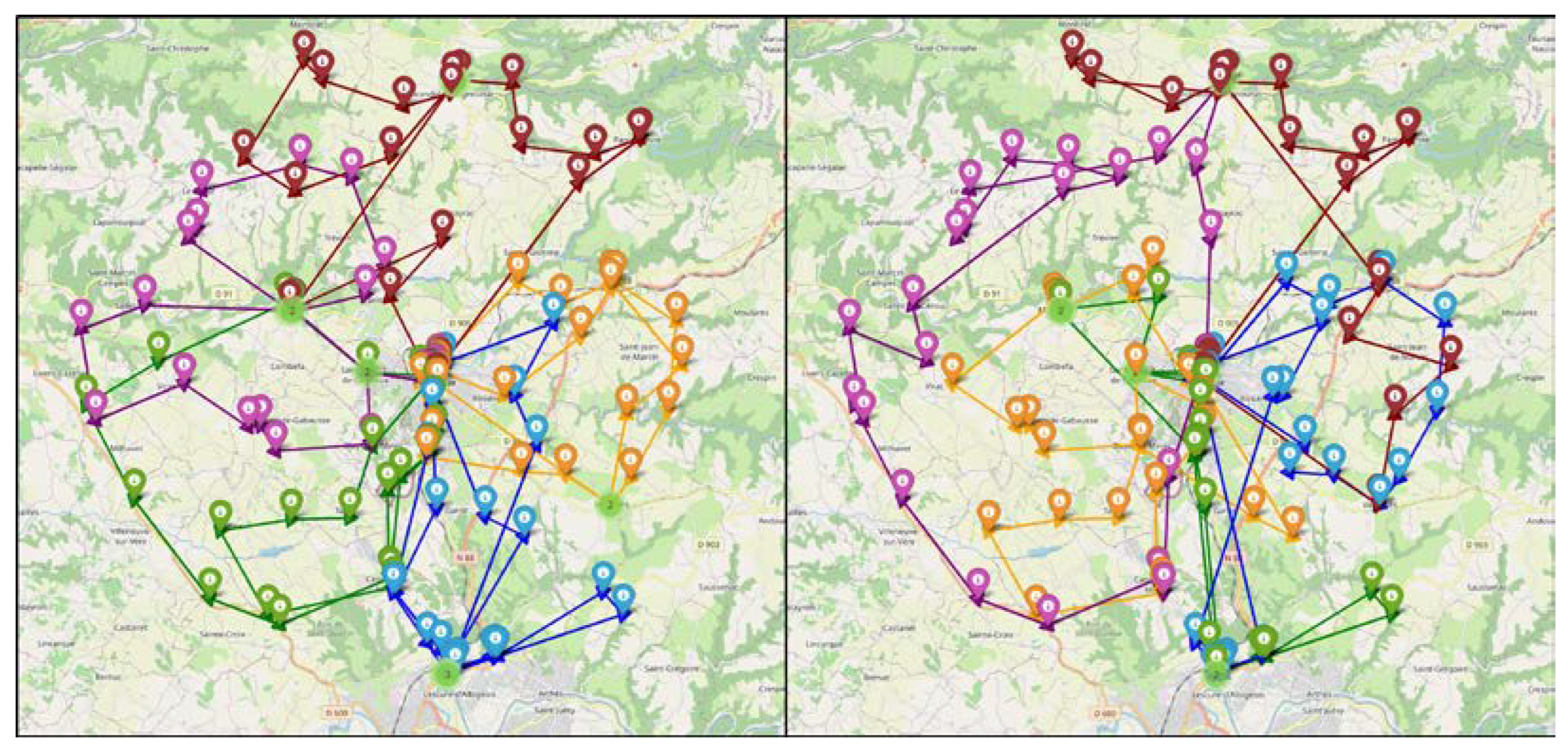
The website https://geodatamine.fr/ was used to generate random and unidentifiable addresses for patients (e.g., businesses, churches, parking spaces, etc.) around the city of Carmaux (France): the map is presented in Figure 2 on the left (1) where the library folium in Python was used to place the patients on a Leaflet map. The health care center was indicated in the city, and the 140 other addresses were randomly distributed to the patients. The website https://openrouteservice.org/ was used, by a query in a Python script, to create a matrix of real travel times between patients.

There are two types of visit: the short visits of 5 minutes which represent 75% of the visits, and the long visits lasting 10 minutes (Figure 2, (2)). Thus, 106 care visits last 5 minutes, distributed randomly among the patients, and the other 34 last 10 minutes.

Finally, the time windows must be determined for each visit (Figure 2, (3)). There are 11 possible time windows between 7 a.m. and 1 p.m. (7 a.m. – 8 a.m.; 7:30 a.m. – 8:30 a.m., 11:30 a.m. – 12:30 p.m., and 12 p.m. – 1 p.m.), evenly distributed among the visits in order to find feasible and realistic solutions.

The map, the coordinates of the addresses and the care visits file are available in the attached archive.

3.2. Home health care

Discrete-event simulation was chosen as the tool-based method as it allows complex environments with several sources of variability to be easily modeled and analyzed [29].

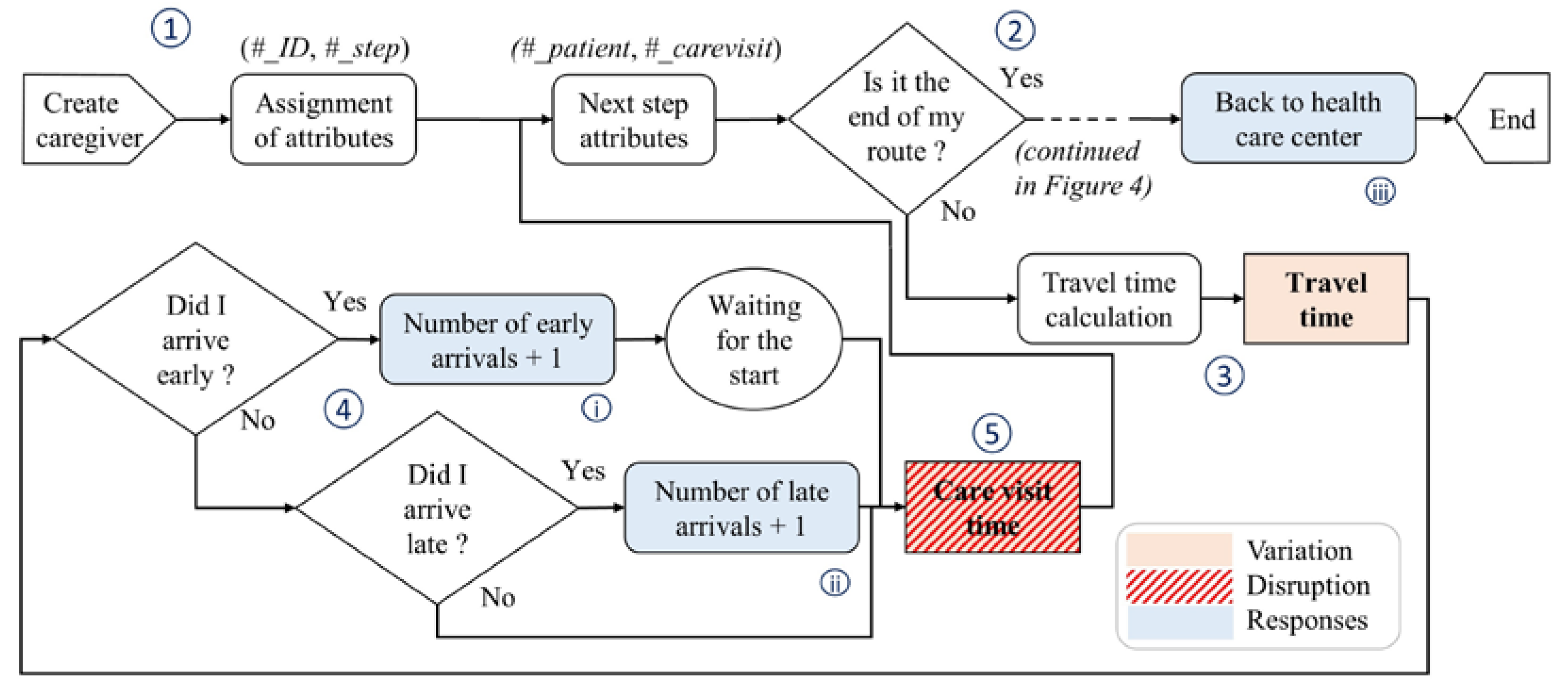
The simulation model, represented in Figure 3, is built as follows: (1) the five caregivers are created and their attributes are assigned to them, then they retrieve the information for their next visit; (2) if they have finished their route, they go back to the center or they help their colleagues (not represented here, more details in the next subsection); if not (3), the travel time to the next patient is calculated; (4) if the caregiver arrives more than 5 minutes early at the patient’s address, the total number of early arrivals is incremented and the caregivers waits. If they arrive more than 5 minutes late, the total number of late arrivals is incremented; and (5) the care visit is carried out before they move on to the next patient.

The performance measures of the model are: (i) the total number of early arrivals and the cumulative early arrival time; (ii) the total number of late arrivals and the cumulative late arrival time; and (iii) the end time of each route (knowing that a caregiver must normally finish before 1 p.m.).

3.3. Design of Experiments

The Design of Experiments (DoE) consists of three dimensions detailed below: the resilient approaches, the different disruptions, and the schedule solutions.

3.3.1. The resilient approaches

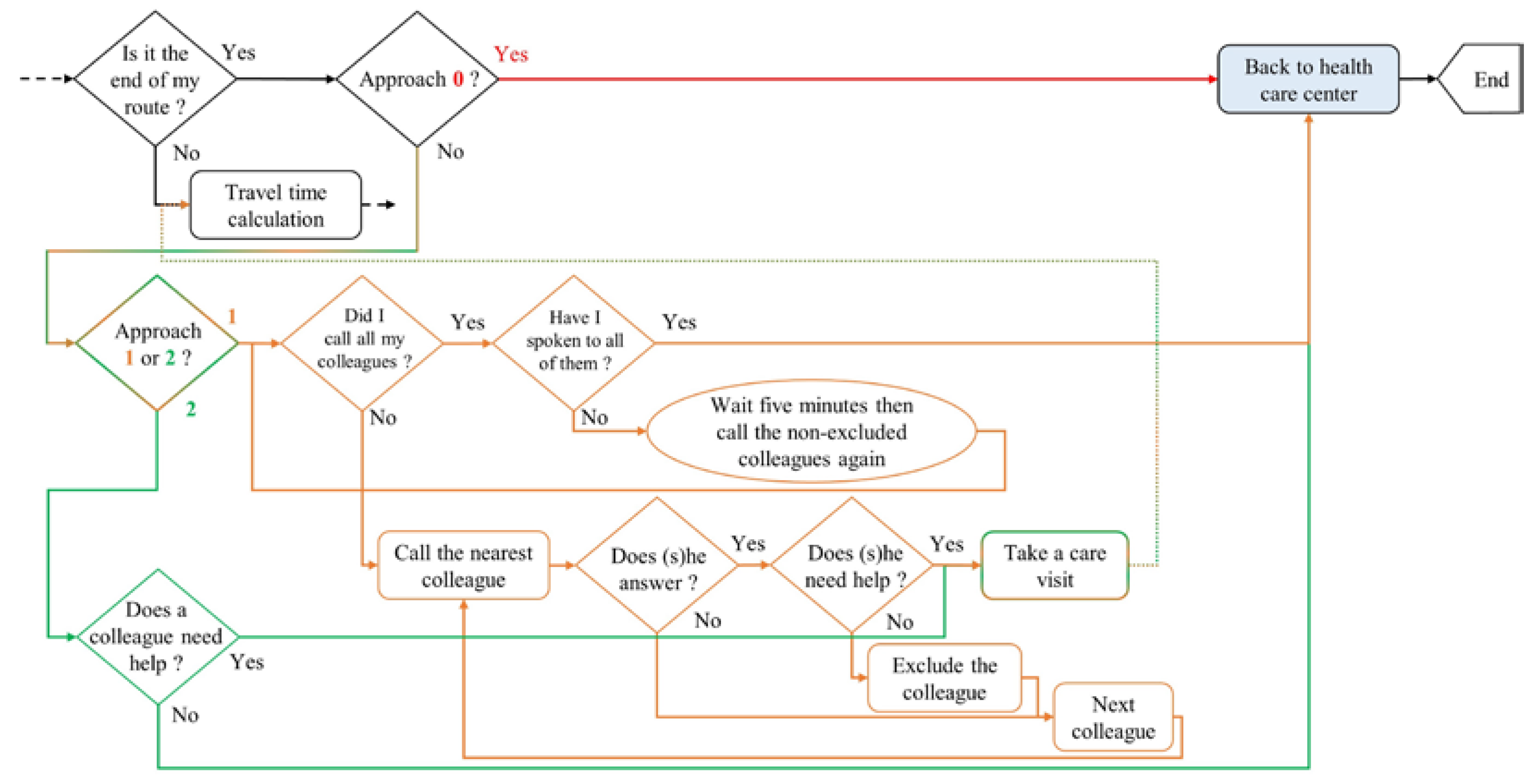
Three different resilient approaches, represented in Figure 4 as a complement to the previous figure, are compared: a baseline approach without any collaboration, a distributed collaborative approach (the one used today by the nursing care structures interviewed), and a centralized collaborative approach.

In the baseline approach (named “approach 0” and represented in red), there is no cooperation between the caregivers: when a caregiver finishes their route, they return to the health care center to carry out administrative tasks.

In the distributed collaborative approach (named “approach 1” and represented in orange), when a caregiver finishes their route, they try to reach their colleagues to help them. The caregiver knows each colleague’s work areas and therefore starts by calling those closest to them: a colleague does not answer the call if they are out on a care visit, unless the latter is disrupted, whereas a colleague who is driving will always respond using a hands-free kit. If the colleague does not answer the call, the caregiver moves on to the next closest individual. Otherwise, they ask them if they need help (i.e., if they are late because they experienced a disruption during their route): if this is the case, they will take a care visit from them, otherwise they will remove this colleague from the list and move on to the next one. If they have called and spoken to all their colleagues, they go back to the health care center to carry out administrative tasks. Otherwise, they wait five minutes and call their colleagues who are still on the list again.

In the centralized collaborative approach (named “approach 2” and represented in green), the information is centralized and easily available to everyone. Using a device (e.g., a smartphone application), a caregiver knows directly if their colleagues need help and where they are. If this is the case, they will take a care visit, otherwise they go back to the health care center to carry out administrative tasks.

Finally, for the two approaches 1 and 2, there are three possible sub-approaches. These sub-approaches are subsequently named X-1, X-2, and X-3 where X = approach 1 or 2. For X-1 approaches, when a colleague needs help, the available caregiver will take the next care visit closest to them. For X-2, they will take the next care visit indicated on the route, regardless of their distance from the patient. And for X-3, they will take the last care visit on the route.

3.3.2. The disruptions

According to the interviews, the disruptions encountered generally last one hour: if a patient dies for example, a doctor, the family, and the funeral directors must be advised and the caregivers have to wait until the patient is taken care of, or if a patient is drunk, the caregiver must wait until the patient is sober again to prevent injury.

To first analyze the impact of the variation, a first scenario without variation or disruption was modeled, as well as a second scenario by adding only the variations (modeled by a triangular distribution at ± 30% around the mean value).

Then, four disruption scenarios were created: a case with a single one-hour disruption, a case with two 30-minute disruptions, a case with two one-hour disruptions, and a case with one two-hour disruption. The disruptions are uniformly distributed among the patients for each replication.

3.3.3. The schedule solution

Two schedule solutions were compared: (1) a handmade schedule as is the case in the health care centers interviewed, and (2) an optimized schedule based on the simplified OptaPlanner-oriented model presented by Zhang et al [30], with the utilization of one embedded "Late Acceptance" metaheuristic for solution generation. The considered constraint is the respect for time windows (to limit the number of late or early arrivals) and the objective function was to minimize travel times (to finish as soon as possible).

For the two solutions, represented in Figure 6, the average occupation rate of the caregivers without disruption is 90% and 87% respectively. The occupation rate includes travel times and care visit times, with the latter representing 55% of the occupation rate on average.

Thus, the DoE is made of 2 x (2 + 7 x 4) = 60 scenarios: two schedule solutions times two scenarios without disruption plus seven resilient approaches times four scenarios with disruptions.

To ensure that we had significant results, we seek the number of replications necessary for each disruption (i.e. each disturbed patient by an unforeseen event), using the confidence interval method from [31]. Initially, 1000 replications for the same disturbed patient are carried out, where the output data was the total time of late arrival, and the percentage deviation of the confidence interval about the mean time of late arrival is calculated using Equation (1):

d = t_{n - 1, α / 2} \frac{S}{\bar{X} \times \sqrt{n}}

(1)

where:

\bar{X} =

average total time of late arrival

S =

standard deviation of the output data from the replications

n =

number of replications

t_{n - 1, α / 2} =

value from Student’s t -distribution with

n - 1

degree of freedom and a significance level of

α / 2

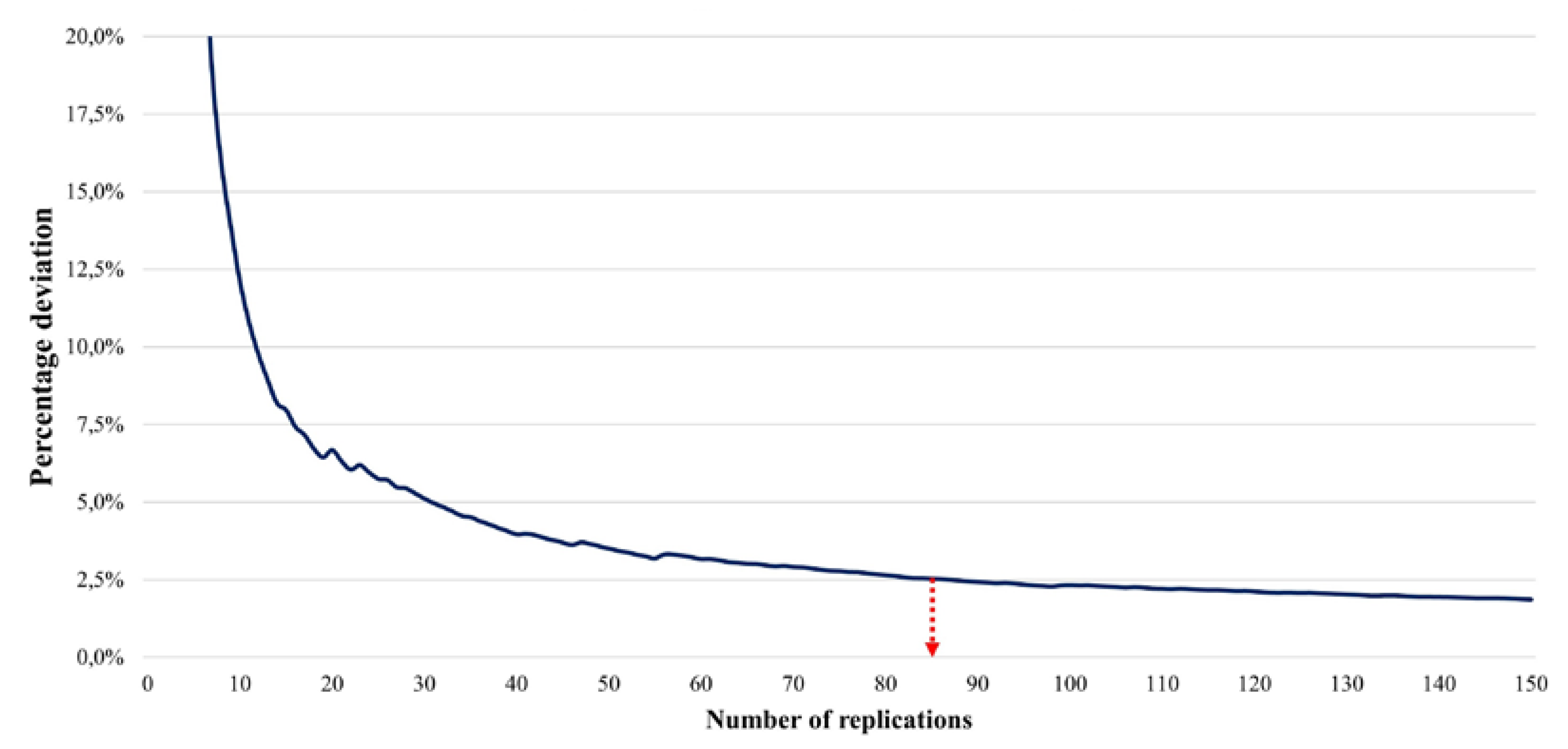
We chose a significance level α of 2.5% (i.e. there is a 97.5% probability that the value of the true mean lies within the confidence interval), and we seek a percentage deviation of maximum 2.5%. The percentage deviation depending on the number of replications for the first 150 replications is presented in Figure 6.

According to the calculation of the percentage deviation, it takes at least 85 replications per scenario. Therefore, in order to obtain significant and homogeneous results, we performed 100 replications for each scenario (i.e. disturbed patient), so a total of 14,000 replications since there are 140 patients.

The model and the simulations were made using Python scripts to facilitate the exchange between the different files and applications.

4. Results

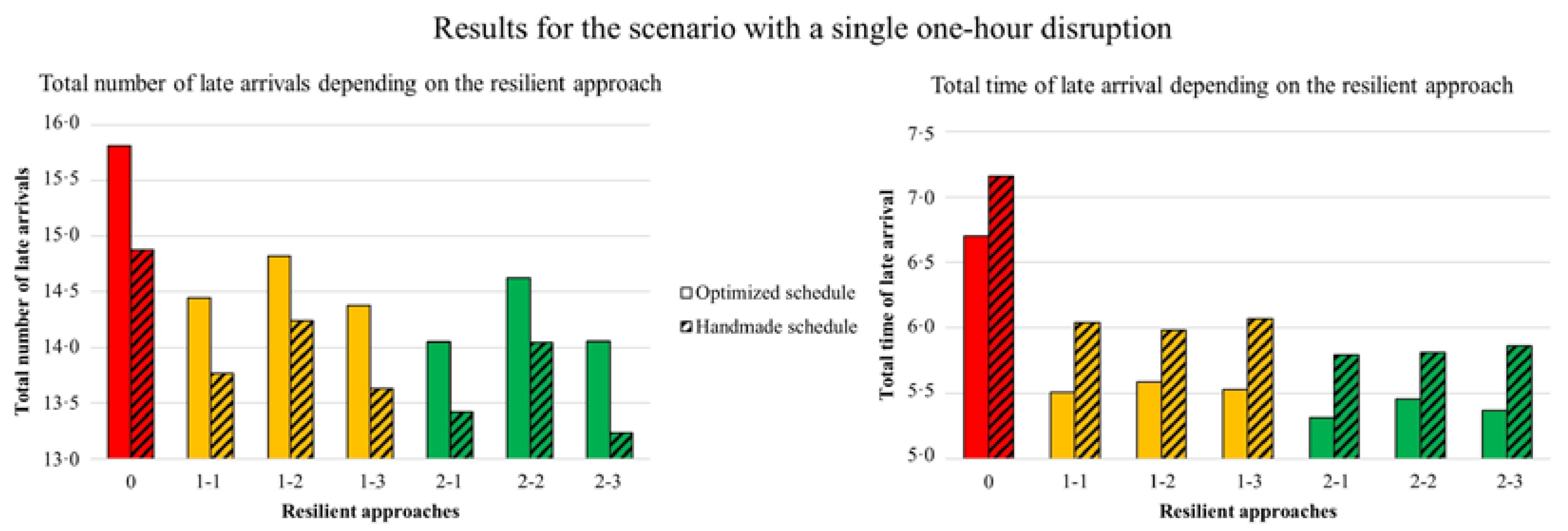
All the results are available in the attached archive. For reasons of space and as it is the most likely outcome, only results on late arrivals for a scenario with a single one-hour disruption are presented in Figure 6. Resilient approaches are on the abscissa, the mean total numbers of late arrivals are on the left, the mean total times of late arrival are on the right, and the results for the handmade schedule are hatched unlike those for the optimized schedule.

The approach 0 in red presents the worst performances: 15.8 late arrivals on average (i.e., 11.3% of care visits are late) with a total of 6.7 hours of late arrival in the optimized schedule, and 14.9 late arrivals and 7.2 hours in the handmade schedule. Overall, the two other approaches (in yellow and green) are better, with the X-1 sub-approaches yielding the best results. With approach 1-1, the number of late arrivals is reduced by 9% in the optimized schedule (7% in the handmade one), with the total time of late arrival reduced by 18% (16% in the case of the handmade). With approach 2-1, the number of late arrivals is reduced by 11% in the optimized schedule (10% in the handmade one), with the total time of late arrival reduced by 21% (19% in the case of the handmade). The 2-1 approach therefore improves performance. The X-2 approaches are the worst performing sub-approaches, while the X-3 perform better than the X-1 as regards the number of late arrivals but not in terms of the total time of late arrival. Finally, there is a slight difference between the two schedule solutions, but the previous remarks are valid for both.

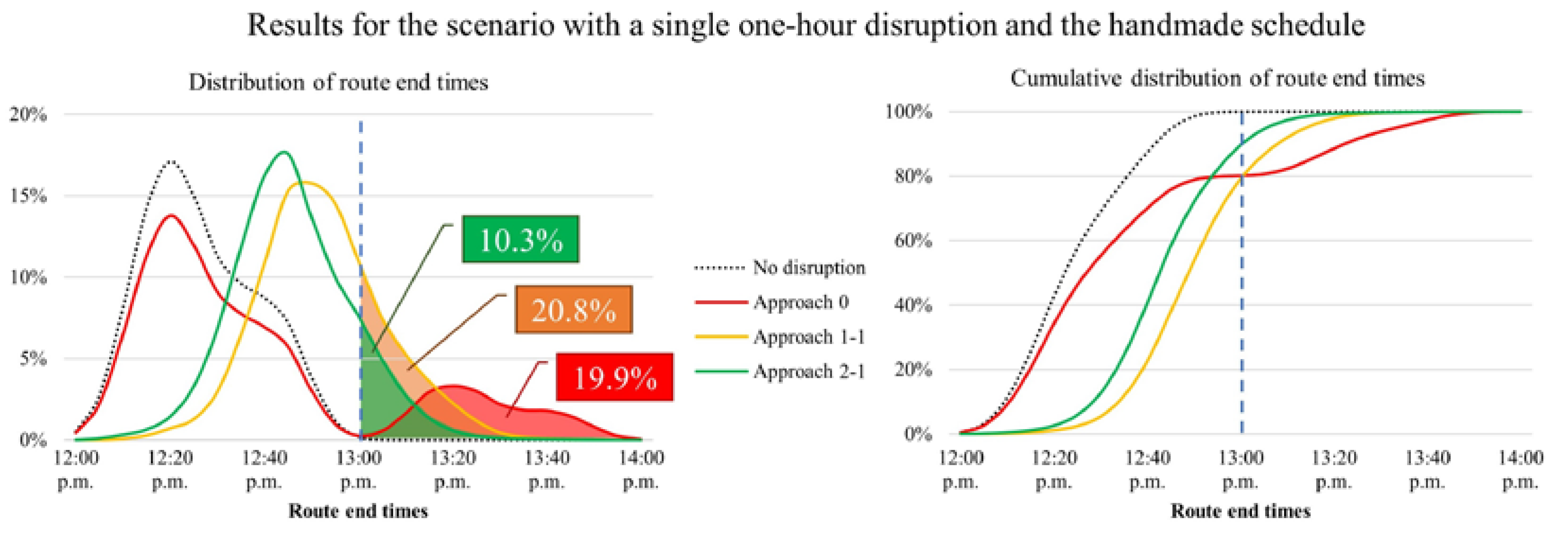
To better understand the effect of the resilient approaches on the route end times, their distribution and cumulative distribution are presented in Figure 8. Since caregivers must finish before 1 p.m., a dashed blue line has been added to the center in each graph.

The dotted black curve represents the distribution when there is no disruption: in this case, all routes end before 1 p.m. with an average of 12:24 p.m. With approach 0 in red, the distribution splits into two parts and 20% of the routes finish after 1 p.m. (this corresponds to the disrupted route out of the five) with an average of 12:36 p.m. With approach 1-1 in yellow, the average rises to 12:50 p.m., with almost 21% of the routes ending after 1 p.m. because of time wasted reaching colleagues. Finally, thanks to approach 2-1 in green, only 10% of the routes go beyond 1 p.m. (i.e. twice less), with the average end time dropping to 12:44 p.m.

Approach 2-1 thus enables a reduction in the number of late arrivals, the total time of late arrival, and the number of routes ending after 1 p.m.

5. Conclusion and openings

In this paper, we first create a use case close to reality which is available to the scientific community working on the HHCRSP. This use case is the result of several interviews with staff at different home health care centers in France. Then, we model three different resilient approaches to counter the high impact disruptions encountered by caregivers on their routes. Hence, we analyze and compare the existing solution with a proposal for centralization and sharing of information to improve local decision-making.

By using discrete event simulation, we show that the centralized collaborative approach enables both a reduction in the number of late arrivals and the total time of late arrival, but above all the number of routes ending before the work end time to be halved (contrary to the distributed collaborative approach). These results hold true regardless of the number and duration of disruptions we tested, as well as the initial schedule solution (handmade or optimized).

As regards managerial insights, we recommend that home health care centers:

Promote the centralization and sharing of information between caregivers to improve mutual aid;
In cases of mutual assistance between two caregivers, the helper must take the care visit closest to them.

To take this line of research further, other resilient approaches are considered, in particular to improve response times to disruptions and thus reduce recovery time (which we do not discuss in this paper). The coupling of optimization and simulation seems to be a powerful and appropriate tool. Moreover, the simulation plays a double role: firstly, to compare resilient approaches with each other, as is the case here, and secondly to find a better initial or intermediate schedule solution. Finally, it is also possible to no longer plan the routes but to monitor them in real time by assigning the care visits on an ongoing basis and taking variations and disruptions in the environment into consideration.

Author Contributions

Literature research, G.D., C.M. and L.Z.; study design, G.D.; data collection, G.D.; data analysis, G.D.; data interpretation, G.D.; writing, G.D., C.M. and L.Z.; supervision, C.B. and F.F.; validation, F.F.

Funding

This research was funded by Plan France Relance and Berger-Levrault.

Data Availability Statement

The case study data and results are currently being added as supplementary material to the article deposit. Upon acceptance of the article, the archive containing all the information will be publicly accessible online.

Conflicts of Interest

The authors declare no conflict of interest.

References

INSEE. D’ici 2070, un tiers des régions perdraient des habitants − Projections de population 2018-2070 | Insee [Internet]. 2021 [cited 2023 Mar 22]. 665. Available online: https://www.insee.fr/fr/statistiques/6658362.
Fernandez, A.; Gregory, G.; Hindle, A.; Lee, A.C. A Model for Community Nursing in a Rural County. J Oper Res Soc. Taylor & Francis 1974, 25, 231–239. [Google Scholar] [CrossRef]
Cissé, M.; Yalcindag, S.; Kergosien, Y.; Şahin, E.; Lenté, C.; Matta, A. OR problems related to Home Health Care: A review of relevant routing and scheduling problems. Oper. Res. Health Care 2017, 13–14, 1–22. [Google Scholar] [CrossRef]
Di Mascolo, M.; Martinez, C.; Espinouse, M.-L. Routing and scheduling in Home Health Care: A literature survey and bibliometric analysis. Comput. Ind. Eng. 2021, 158, 107255. [Google Scholar] [CrossRef]
Trautsamwieser, A.; Hirsch, P. Optimization of daily scheduling for home health care services. J Appl Oper Res. 2011, 3, 124–36. [Google Scholar]
Frifita, S.; Masmoudi, M. VNS methods for home care routing and scheduling problem with temporal dependencies, and multiple structures and specialties. Int. Trans. Oper. Res. 2020, 27, 291–313. [Google Scholar] [CrossRef]
Lahrichi, N.; Lanzarone, E.; Yalçındağ, S. A First Route Second Assign decomposition to enforce continuity of care in home health care. Expert Syst. Appl. 2022, 193, 116442. [Google Scholar] [CrossRef]
Liu, R.; Jiang, Z.; Yuan, B. A branch-and-price algorithm for the home health care scheduling and routing problem with stochastic service times and skill requirements. Int J Prod Res. 2015, 53, 7450–7464. [Google Scholar] [CrossRef]
Chaieb, M.; Jemai, J.; Mellouli, K. A decomposition - construction approach for solving the home health care scheduling problem. Health Care Manag. Sci. 2019, 23, 264–286. [Google Scholar] [CrossRef]
Bard, J.F.; Shao, Y.; Wang, H. Weekly scheduling models for traveling therapists. Socioecon Plann Sci. 2013, 47, 191–204. [Google Scholar] [CrossRef]
Luna, F.; Cervantes, A.; Isasi, P.; Valenzuela-Valdés, J.F. Grid-enabled evolution strategies for large-scale home care crew scheduling. Clust. Comput. 2017, 21, 1261–1273. [Google Scholar] [CrossRef]
Liu, R.; Yuan, B.; Jiang, Z. Mathematical model and exact algorithm for the home care worker scheduling and routing problem with lunch break requirements. Int J Prod Res. 2017, 55, 558–575. [Google Scholar] [CrossRef]
Heching, A.; Hooker, J.N.; Kimura, R. A Logic-Based Benders Approach to Home Healthcare Delivery. Transp. Sci. 2019, 53, 510–522. [Google Scholar] [CrossRef]
Bard, J.F.; Shao, Y.; Qi, X.; Jarrah, A.I. The traveling therapist scheduling problem. IIE Trans. 2014, 46, 683–706. [Google Scholar] [CrossRef]
Akjiratikarl, C.; Yenradee, P.; Drake, P.R. PSO-based algorithm for home care worker scheduling in the UK. Comput. Ind. Eng. 2007, 53, 559–583. [Google Scholar] [CrossRef]
Frifita, S.; Masmoudi, M.; Euchi, J. General variable neighborhood search for home healthcare routing and scheduling problem with time windows and synchronized visits. Electron. Notes Discrete Math. 2017, 58, 63–70. [Google Scholar] [CrossRef]
Fikar, C.; Hirsch, P. A matheuristic for routing real-world home service transport systems facilitating walking. J. Clean. Prod. 2015, 105, 300–310. [Google Scholar] [CrossRef]
Carello, G.; Lanzarone, E. A cardinality-constrained robust model for the assignment problem in Home Care services. Eur. J. Oper. Res. 2014, 236, 748–762. [Google Scholar] [CrossRef]
Yalçındağ, S.; Matta, A.; Şahin, E.; Shanthikumar, J.G. The patient assignment problem in home health care: using a data-driven method to estimate the travel times of care givers. Flex. Serv. Manuf. J. 2016, 28, 304–335. [Google Scholar] [CrossRef]
Kitano, H. Biological robustness. Nat Rev Genet. Nature Publishing Group; 2004;5:826–37.
Christopher M, Peck H. Building the resilient supply chain. MCB UP Ltd/Emerald Group Publishing Limited; 2004 [cited 2023 Mar 6]. Available online: https://dspace.lib.cranfield.ac.uk/handle/1826/2666.
Nikzad, E.; Bashiri, M.; Abbasi, B. A matheuristic algorithm for stochastic home health care planning. Eur. J. Oper. Res. 2021, 288, 753–774. [Google Scholar] [CrossRef]
Zhan, Y.; Wang, Z.; Wan, G. Home service routing and appointment scheduling with stochastic service times. Eur. J. Oper. Res. 2021, 288, 98–110. [Google Scholar] [CrossRef]
Shi, Y.; Boudouh, T.; Grunder, O. A robust optimization for a home health care routing and scheduling problem with consideration of uncertain travel and service times. Transp. Res. Part E: Logist. Transp. Rev. 2019, 128, 52–95. [Google Scholar] [CrossRef]
Cappanera P, Scutellà MG, Nervi F, Galli L. Demand uncertainty in robust Home Care optimization. Omega [Internet]. 2017 [cited 2018 Apr 17]. Available online: http://www.sciencedirect.com/science/article/pii/S0305048316309008.
Alves F, Pereira AI, Barbosa J, Leitão P. Scheduling of Home Health Care Services Based on Multi-agent Systems. In: Bajo J, Corchado JM, Navarro Martínez EM, Osaba Icedo E, Mathieu P, Hoffa-Dąbrowska P, et al., editors. Highlights Pract Appl Agents Multi-Agent Syst Complex PAAMS Collect. Springer International Publishing; 2018. p. 12–23.
Marcon, E.; Chaabane, S.; Sallez, Y.; Bonte, T.; Trentesaux, D. A multi-agent system based on reactive decision rules for solving the caregiver routing problem in home health care. Simul Model Pract Theory 2017, 74, 134–151. [Google Scholar] [CrossRef]
Yuan, B.; Jiang, Z. Disruption Management for the Real-Time Home Caregiver Scheduling and Routing Problem. Sustainability 2017, 9, 2178. [Google Scholar] [CrossRef]
Mourtzis, D. Simulation in the design and operation of manufacturing systems: state of the art and new trends. Int. J. Prod. Res. 2020, 58, 1927–1949. [Google Scholar] [CrossRef]
Zhang, L.; Pingaud, H.; Fontanili, F.; Lamine, E.; Martinez, C.; Bortolaso, C.; Derras, M. Balancing the satisfaction of stakeholders in home health care coordination: a novel OptaPlanner CSP model. Health Syst. Taylor & Francis 2023, 0, 1–21. [Google Scholar] [CrossRef]
Robinson S. Simulation: The Practice of Model Development and Use. Bloomsbury Publishing; 2014.

Figure 1. Difference between variation and disruption and between robust solution and resilient approach.

Figure 2. Map of the surroundings of Carmaux with the patients (in black) and the health care center (in red) on the left, and example of care visits with durations and time windows on the right.

Figure 3. Representation of the main simulation model.

Figure 4. Decision-making algorithm modeling the three resilient approaches.

Figure 5. The five routes of the handmade schedule solution on the left, and the optimized schedule solution on the right.

Figure 6. Percentage deviation of the confidence interval about the mean time of late arrival depending on the number of replications.

Figure 7. Number of late arrivals (on the left) and total time of late arrival (on the right) depending on the resilient approach - scenario with a single one-hour disruption.

Figure 8. Distribution of route end times (on the left) and cumulative distribution (on the right) for the handmade schedule - scenario with a single one-hour disruption.

Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.

© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).

Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.

MDPI Initiatives

Important Links

Choose an area of interest and we will send you notifications of new preprints at your preferred frequency.

Disclaimer