A Source Seeking Method for the Implicit Information Field Based on a Balanced Searching Strategy

Preprint

Article

A Source Seeking Method for the Implicit Information Field Based on a Balanced Searching Strategy

Altmetrics

Downloads

129

Views

Comments

A peer-reviewed article of this preprint also exists.

Kun Liu^*

Yang Bi^*

Qi Zhang,JunFang Li

Kun Liu^*

Yang Bi^*

Qi Zhang,JunFang Li

This version is not peer-reviewed

Submitted:

29 May 2023

Posted:

31 May 2023

You are already at the latest version

Alerts

Abstract

To solve the problem of low efficiency of source seeking in implicit information field, this paper presents an autonomous souring method based on balanced searching strategy is enlighten by biological homing behaviors. At the beginning of the research, the source seeking task come down to a multi-objective convergence issue. By taking the feasibility search behaviors as the individual sample of the evolutionary population drawing on the thought of evolutionary algorithms, then combine motion searching with population evolution, so the carrier can be guide to complete source seeking task by solving the multi-objective problem. Furthermore, the distribution entropy is also considerated d to measure the searching bias in the process of source seeking. Combined with the demand of the source seeking process, a new source seeking method of balanced searching strategy is designed. Ultimately, through theoretical analysis and simulation verification confirm the effectiveness and rationality of the proposed method.

Keywords:

Subject: Computer Science and Mathematics - Artificial Intelligence and Machine Learning

1. Introduction

The implicit information field is a common source of information in nature, such as odor field, geomagnetic field, gravity field, etc. Compared with explicit information, implicit information field is limited by information distribution characteristics and measurement methods, and also limited by certain observation boundedness. It can hardly obtain data from the adjacent space outside boundary and often requires measurement in site to obtain data[1,2]. From the perspective of characteristic distribution, although the implicitit information distribution between adjacent elements has a certain continuity, its gradient direction varies, therefore it is difficult to use the measured data to deduce the data in the unreachable area. This issue cause difficulties to the development and utilization of implicit information field, such as geomagnetic navigation [3,4] and the odor source finding [5]. In the modern industrial environment, there are similar scenes, such as nuclear leakage environment, carrying out the search for nuclear leakage source [6]; In the fingerprint positioning application, the reverse positioning of the faulty fingerprint source is reversed [7].

At present, for the source seeking problem of implicit information fields, the searching method mainly based on searching method by path planning and searching method data driving.

The searching method based on path planning means that the carrier moves along the way which was planned to searching the target source, and the typical methods are traversal searchand Z-shape search, etc [8,9,10]. This method does not distinguish the types of information sources, and with certain universality characteristic by optimization of the path and the expansion of detection capabilities [11,12,13,14]. By optimizing the path and expanding the detection ability, the search efficiency can be improved to a certain extent. However, the shortcoming of this method lies in the exponential relationship between the searching time and the searching space, which is difficult to be accepted in the context of large scene applications.

The data-driven searching method refers to the research of the source seeking method from the perspective of data acquisition and data utilization [15,16,17]. For example, although the formation cooperative searching method improves the measurement ability of the environmental characteristics of implicit information field and then can obtain more data. However, it is prone to information redundancy or conflict, which leads to the failure of source search [18,19]. Probabilistic predictive searching which based on the historical measured data uses the method of statistical probability to predict the position of the target point, and adjusts the predicted results constantly in the subsequent searching, so as to guide the carrier to realize the source searching[20]. However, this method is easy to fall into partial minimum.

At present, with the development of technology and our exploration of the environment, knowledge seeking forms and occasions are more and more diverse. However, not all scenarios can predict its structure and internal correlation, and also many scenarios are presented as the black box solving problems[21,22,23]. In these problems, there are some black box problems with solvable properties. For example, underwater organisms can complete thousand-mile migration by using magnetic field characteristics without any prior database, but it is difficult for humans to achieve navigation tasks without prior geomagnetic database. Dogs can accurately detect odor sources in unfamiliar environments without relying on the misty rain model of odor. Similar posterior detection problems are presented in the scenarios of nuclear radiation source search, pseudo-WIFI source search, and alien exploration.

This paper proposes a source seeking method based on balanced searching strategy from the perspective of autonomous search which is inspired by the biological source seeking behavior [26,27]. From the perspective of biological autonomous search, and due to the lack of reference of the a priori database, the source seeking behavior shows the exploration of the environment and the exploitation of the previous information in the implicit information field. The autonomous searching behavior is carried out by taking the characteristic parameters of the information source at the target as the convergence target.

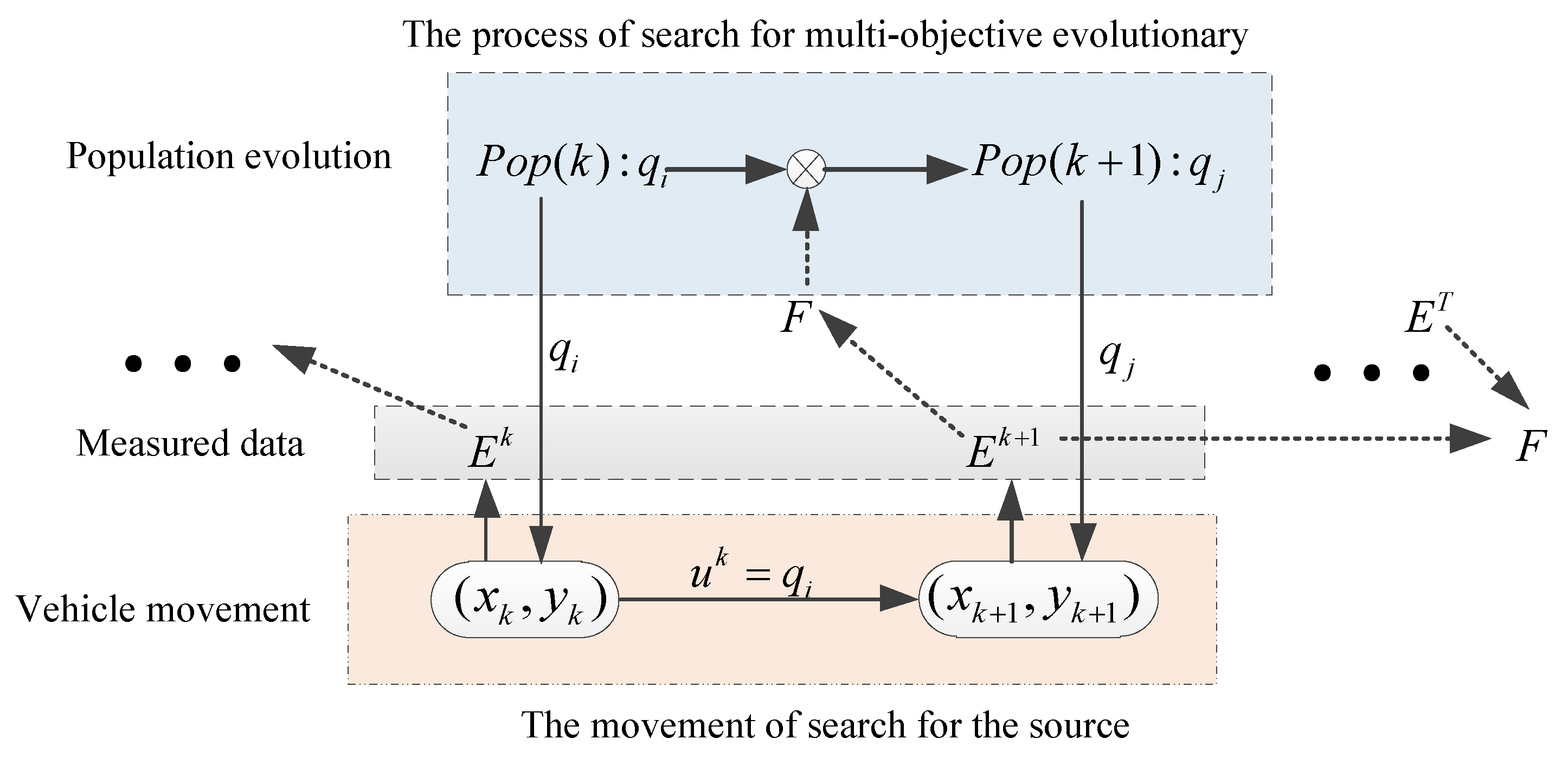
2. Problem description

In general, the implicit information field that can be sourced or used for localization which have many parameters to be described, and can be uniquely characterized by a variety of feature parameters [28], as shown in the following equation:

(1)

where, E stands for the set of an implicit information field features, characterized by n parameters

e_{1}, e_{2}, \dots, e_{n}

; P stands for any position in space (x, y, z), there is a one-to-one mapping relationship between P and E. In the implicit information field, this mapping is ambiguous. As a result, historical information cannot be used to accurately build mapping models.

Here, we note the target information source features as

E^{T}

. Then the problem of source seeking for implicit information field can be described as the process of the carrier uses the measured data combined with autonomous search to achieve the search of the target source. Without loss of generality, the implicit information source finding problem can be reduced to the following: the convergence of various environmental parameters to the target environmental parameters without prior database [29], as shown below:

\min F (E, k) = {(f_{1} (e_{1}, k), f_{2} (e_{2}, k), \dots, f_{n} (e_{n}, k))}^{T}

(2)

where k represents moment information; Objective function F is k-time, and the difference between

E^{K}

the measured environmental characteristics

E^{T}

and the target environmental characteristics.

The termination conditions of the source seeking task are given from the perspectives of parametric convergence and position convergence, respectively, as shown in the following equation.

{\begin{cases} | e_{i}^{k} - e_{i}^{T} | \to 0, i \in n \\ \sqrt{{(x_{k} - x_{T})}^{2} + {(y_{k} - y_{T})}^{2} + {(z_{k} - z_{T})}^{2}} \leq γ \end{cases}

(3)

where, the T represents the target location,

e_{i}^{T}

which is the characteristic parameter of the i-th target environment;

(x_{T}, y_{T}, z_{T})

is the spatial position

P_{T}

γ

is a constant, and represents the source precision. The above equation represents the true spatial position of the k-time, the environmental feature e converges to the respective target value, and the carrier reaches or approaches the target point.

The specific form of function F in Equation (2) cannot be established accurately combing with the content described in Equation (1). It should be emphasized that this paper does not carry out the research on how to establish the specific form of function F and assumes that the function F is unknown.

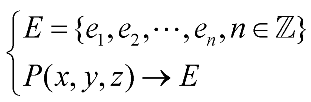
3. A source seeking method based on balanced searching strategy

Obviously, it is too difficult to solve the multi-objective convergence problem described in Equation (2) when the specific form of F is unknown. Therefore, in this section, firstly, the characteristics and existence conditions of the solution of the implicit information field that can be found is given. Then, by introducing the search path into the source seeking problem, the relationship between search behavior and parameter variation is established. Finally, according to the principle of information tendency, a search behavior based on balanced searching strategy is proposed, and a source seeking algorithm is given by combining the idea of evolutionary algorithm.

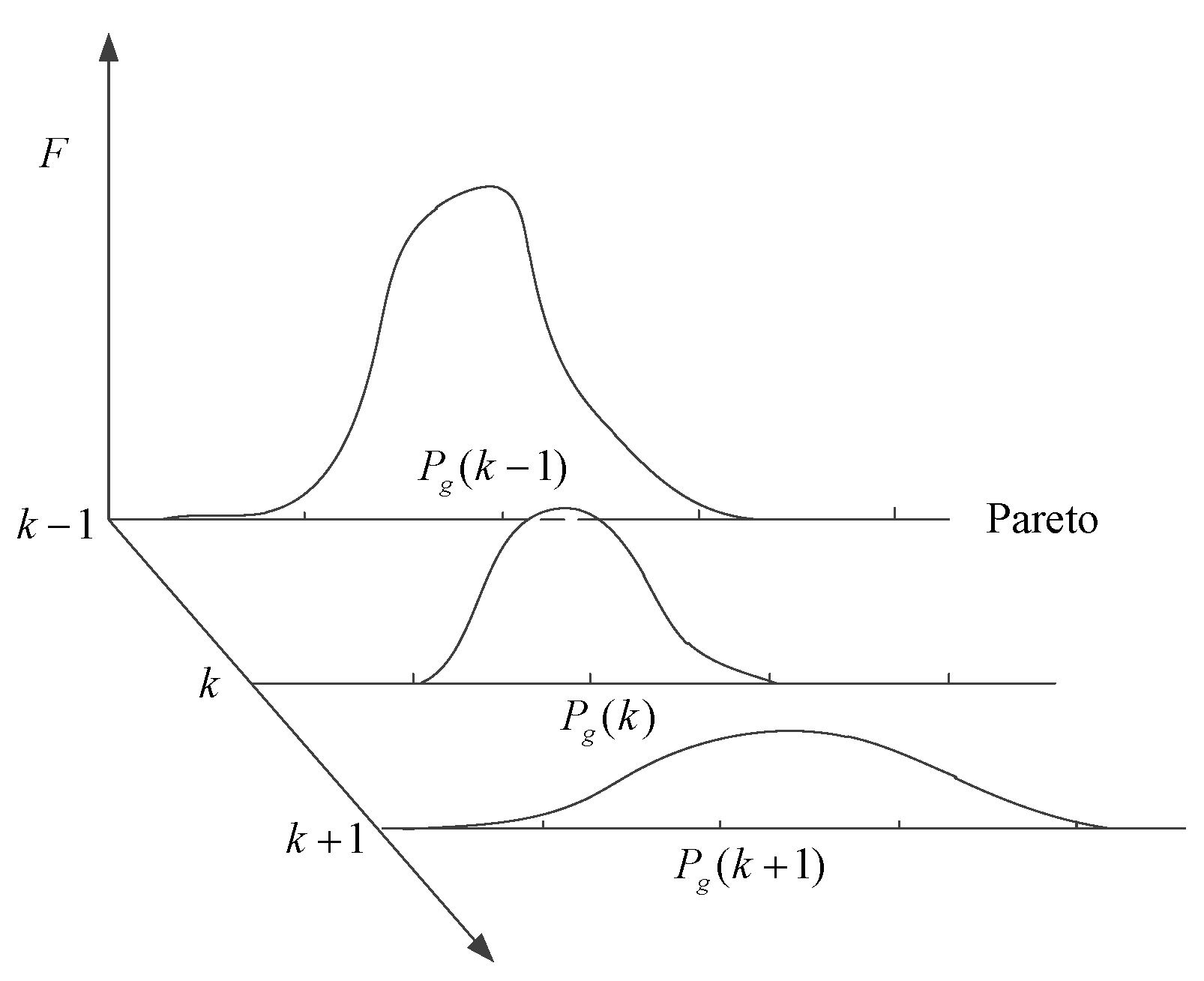
3.1. Characteristic analysis of the source of implicit information field

In nature, there are a variety of implicit information fields can be used as navigation information sources for animals, such as odor field and geomagnetic field, gravity field, other hidden information fields [17,18]. For example, Guiding animals to complete homing, migration and other source seeking tasks, whose source seeking span is often tens or even thousands of kilometers. In this process, it is obvious that the simple brain structure of animals cannot store a complete "map" beforehand. It is believed that in the process of animal source search, implicit information field provides one or even more winding paths to guide animals to the source.

In order to accelerate the analysis of the characteristics of the source solution of the implicit information field, we could assume that the distribution of the environmental feature E in Equation (2) is known, so the source seeking problem can be reduced to a multi-objective convergence one.

Therefore, the distribution characteristics of the implicit information field source seeking problem solution can be analyzed from the perspective of Pareto optimal solution with the help of multi-objective optimization theory.

Consider in a two-dimensional plane, assuming that the carrier is located at the k-moment

P_{k} = (x_{k}, y_{k})

. Within adjacent cells, there will be a closed region G consisting of Pareto solution sets (see Figure 1).

In Figure 1,

\exists x^{*} \in G

within the region G, satisfied

F 〈 x^{*}, t_{i} 〉 < F (x, t_{i})

, that is the region G represents the closed region composed of the Pareto solution set, and arrow "

\to

" represents the direction pointing to Pareto solution set.

The solution of the source seeking problem can be regarded as the process of finding the region G in the search space within a particular time. Generally, when the number of searches is enough that the parameter space can be traversed, then the search behavior could be entering the Pareto solution set region and obtain the source direction at the current moment.

When time changes from k to k+1, region G will also move, and its changing process can be shown in the following Figure 2.

In Figure 2,

P_{g} (k)

shows the optimal solution in the k-time within G-region. It can be seen that the size and position of the optimal solution will change as the moment changes. When

k \in [k_{1}, k_{g}]

changes continuously, there exists an optimal solution

P_{g} (k)

at the current moment at every moment, which is enclosed by the optimal solution cluster enclosed by

P_{S} (k)

(see Figure 3).

In Figure 3, the time-optimal solution cluster at the continuous time is presented as a channel shape. By connecting the optimal solutions at the continuous time in the channel, a curve will be obtained, which is called the solution curve. The solution curve connects the known solution (starting point) and the solution (ending point), and the solution curve can be tracked to solve the multi-objective problem.

The solution curve is the result of the source seeking issue at different times, and tracking the curve can guide the search algorithm to converge to the global optimal solution. In the source finding issue, this curve is the moving trajectory of the carrier in space, connecting the starting point and the end point of navigation, so this curve can also be called the source finding solution curve.

3.2. Source seeking behavior of implicit information field based on motion path

Due to the limitation of measurement for implicit information field characteristics, we cannot get the data of the unreached area or unit. The measurement of environmental characteristics in implicit information field depends on the motion path. For example, olfactory navigation, where you can't predict the intensity of odours in neighbouring locations. Therefore, it is necessary to introduce the motion path into the issue described in Equation 2.

Considering the moving carrier as a particle in a two-dimensional plane, the kinematic equation of the carrier can be described as follows.

{\begin{cases} x_{k + 1} = x_{k} + L \cos (θ) \\ y_{k + 1} = y_{k} + L \sin (θ) \\ u = (L, θ) \end{cases}

(4)

where,

P_{k} = (x_{k}, y_{k})

represents the position of the carrier at time

k

; The motion parameter u consisting of step length

L

and motion direction

θ

. Record the position experienced by the carrier at successive moments, which will constitute a motion trajectory guiding the carrier to reach the target point.

Equation 4 is introduced into the issue of source seeking for implicit information field, then the multi-objective search problem is obtained as shown in Equation 5 below.

{\begin{cases} \min F (E, k) = {(f_{1} (e_{1}, k), f_{2} (e_{2}, k), \dots, f_{n} (e_{n}, k))}^{T} \\ s . t . G (E, k, u) \leq 0 \end{cases}

(5)

where, G is the constraint function of search behaviors, which is composed of environment parameter E, motion parameter u and time information k. After the introduction of constraint function G, the change of objective function F can be caused by the execution of u, and the connection between objective function F and u is indirectly established, which provides the possibility of solving the subsequent source search issue.

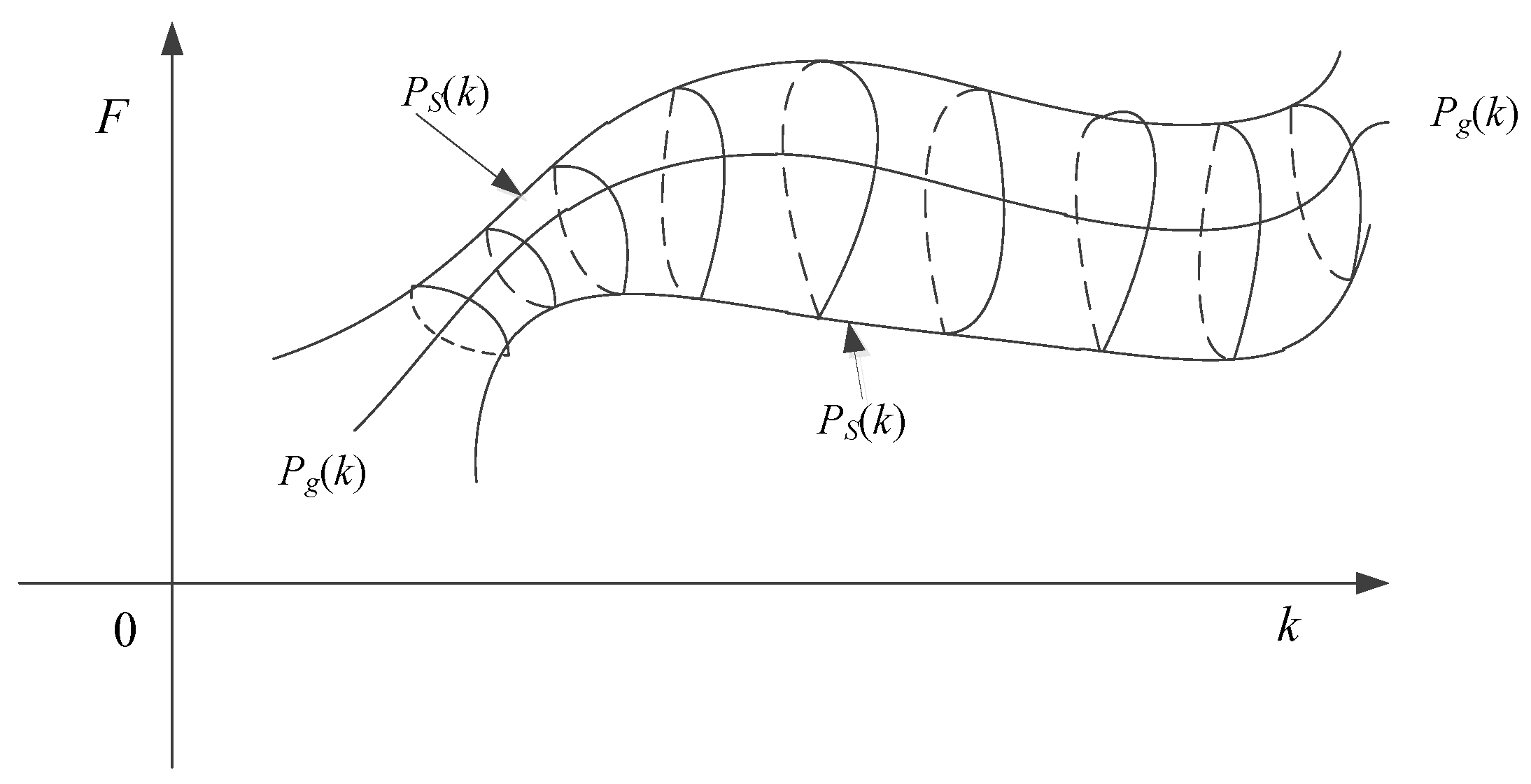
3.3. Balance searching strategy

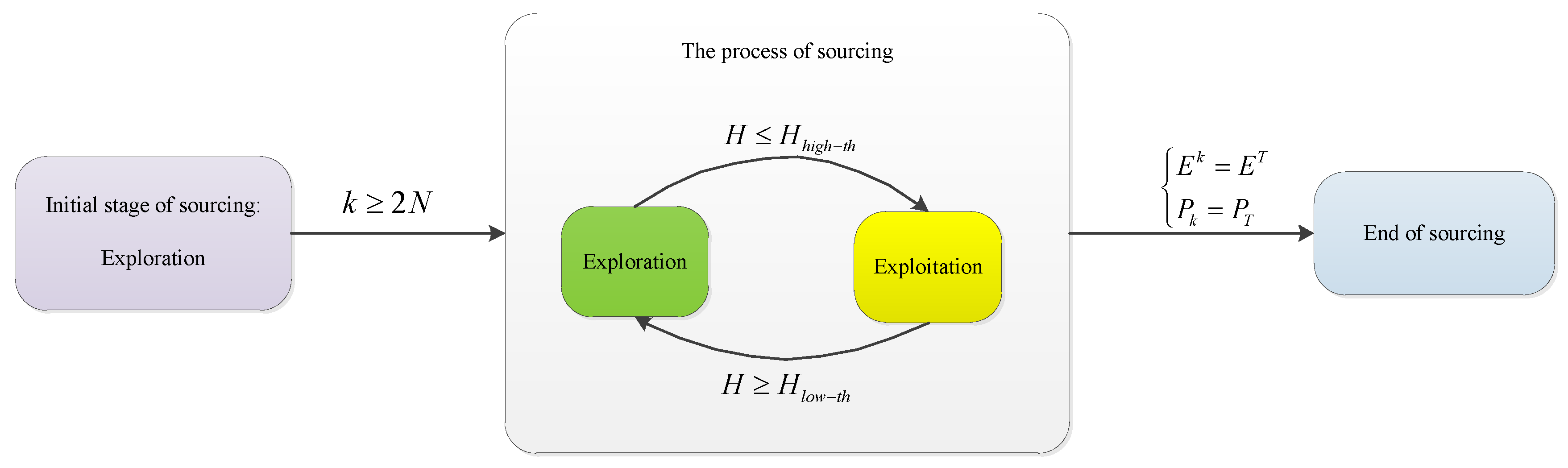
3.3.1. Exploration and exploitation

Exploration and exploitation are two basic strategies in the process of search optimization [26,30]. Among them, exploration refers to the searching strategy aimed at obtaining the information of objective function from the perspective of breadth in the searching process. On the other hand, exploitation refers to the searching strategy based on the function information obtained by exploration, which aims to find the optimal solution at the depth level.

In nature, animals homing in unknown environments through the exploration of unknown environment and the exploitation of historical information. The source seeking process can be described as follows: in the initial stage, animals may explore the environment through their own movement to obtain the distribution information of features to make up for the lack of environmental cognition; then use the accessed information, search for the source path, and respond to the change of the environmental features of distribution, search behaviors to maintain equilibrium between the exploration and exploitation, in order to obtain maximum profits (here, the benefits including the information of the cognition of environmental benefits and the optimization of target point of convergence), thus guide individuals to arrive at the target point.

Inspired by the homing behaviors of animals, we propose a balanced searching strategy, which focuses on the exploration and exploitation of environmental information, and focuses on the dynamic balanced of information returns and optimization returns, then combines different stages of searching to carry out equilibrium searching. In the early stage of searching, the environment information is explored through random roaming, and the trend movement is gradually formed. In the stage of source searching, the searching bias is dynamically adjusted between exploration and exploitation for the purpose of maximizing revenue.

3.3.2. The algorithm of source seeking

(1) Search behaviors design based on evolutionary algorithm

In the following, a source seeking algorithm is proposed based on the balanced searching strategy.

The searching process depends on the movement of the carrier, and its searching behaviors can be characterized by the motion parameter u. Drawing on the idea of evolutionary algorithm, the evolutionary population is constructed by taking the feasible searching behaviors as the sample of evolutionary population. So, the j-th sample individual can be defined as follow:

Q_{j} = θ_{R} = D_{θ} \times R, j = 1, \dots, N_{p o p}

(6)

Where,

R \in [1, \dots, 2 π / D_{θ}]

is a random number;

D_{θ}

is searching space compression ratio;

N_{p o p}

stands for population size; usually, set as

N_{p o p} > (2 π / D_{θ}

The carrier's searching for the target features of environment depends on the movement in space. Multi-target searching and the movement of the source space have the temporal characteristics as shown in the following Figure 4.

Combined with the Figure 4, the source seeking process can be described as follow. At the k-time, select a certain

Q_{i}^{k}

from the evolutionary population Pop(k) with medium probability as the motion parameter of the carrier, and the carrier will obtain the motion displacement of

L^{k}

by executing

Q_{i}^{k}

. The

E^{k}

and

E^{k + 1}

at positions

P_{k}

and

P_{k + 1}

were measured by carrier movement, then substitute it into Equation 5 for multi-objective solution and calculate multi-objective function F. According to the convergence state of the multi-objective function F, the source seeking performance of the executed samples is evaluated, and the breeding or elimination operation is used to increase or decrease the proportion of such samples. Through the mutation operation to improve the population diversity, a new population Pop(k+1) is obtained, and the next round of searching process is re-entered. Through repeated iterations, the multi-objective function converges to the minimum and the source search task is realized.

(2) Search bias measure

The bias of search behaviors can be measured by the diversity of the evolving population. The higher population diversity, the more scattered the sample distribution in the population, resulting in greater randomness of the search behaviors, and the search behaviors is biased towards exploration at this moment; the lower population diversity, the more concentrated the distribution of samples in the population, resulting in less randomness in the search behaviors, which is biased toward development at this time. For measuring the populations diversity, the concept of distributed entropy is introduced here.

Definition 1: Distributed entropy: The sample type is class N and the sample individual can be represented as

C_{1}, \dots, C_{N}

. At some point in the evolution of the group, the proportion of sample individuals in the group is

p_{1}, \dots, p_{N}

respectively, and satisfied

\sum_{i = 1}^{N} p_{i} = 1

,then the distribution entropy is:

H (p_{1}, p_{2}, \dots, p_{N}) = - \sum_{i = 1}^{N} p_{i} \ln p_{i}

(7)

The distribution entropy is nonnegative, symmetric, and additive in the distribution space, and which is a strictly concave function. When all samples are uniformly distributed, H has a unique maximum value; When one type of individual dominates the population, that is

p_{1} \to 1

p_{i} \to 0 (\forall i > 1)

there are:

(8)

Distribution entropy is lowest currently.

The distribution entropy quantifies the population diversity and reflects the searching bias of the population. Exactly, the larger the entropy value is, the stronger the global exploration behaviors of the population will be. The smaller the entropy value is, the stronger the local exploitation ability of the population will be.

(3) The strategy of balance

Combined with the analysis of the source seeking path of implicit information field in Section 3.1, the source seeking path will change with the spatial position. It is not conducive to the tracking of the source path when distribution entropy of the evolutionary population is too large or too small in the source seeking process. Therefore, we combine the structural characteristics of evolutionary algorithms and the distribution characteristics of source paths to give a specific algorithm of balanced searching strategy. We divided the source searching process into three stages (see Figure5).

Figure 5. Schematic diagram of decomposition in source searching stage.

In the first stage, the initial stage of source seeking, the searching behaviors is mainly exploration. When the population sample species at time k is greater than 1 time, it will enter the source seeking stage.

In the second stage, the process of source seeking, the searching behaviors changes dynamically between exploration and exploitation.

When the distribution entropy H is less than or equal to the highest threshold entropy

H_{h i g h - t h}

, the searching process is exploitation-oriented to avoid too much random motion leading to the failure of the search. When the distribution entropy H is greater than or equal to the lowest threshold entropy

H_{l o w - t h}

, the process of source seeking enters the searching process dominated by exploration to avoid the premature population problem caused by low population diversity. Other time, the carrier carries out the search task according to the results of population evolution.

In the third stage, the end of source seeking. When the parameter space reaches and the real space reaches in Equation 3, the source seeking task can be completed.

So far, we give the source seeking method based on balanced searching strategy, and then combine mathematical analysis and experimental simulation to verify the effectiveness and rationality of the algorithm.

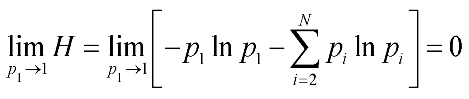
4. Algorithm performance analysis

4.1. Analysis for the convergence of the algorithm

Using the balanced searching method is based on genetic evolution, we can obtain the source path by solving the multi-objective function and guide the carrier to the target source position. The essence of the algorithm is still a multi-objective evolutionary algorithm.

For the optimization issue, the global convergence of the algorithm should meet the following two conditions:

Strictly covered variation distribution, so that any individual

x' \in X

can be generated by individual

x \in X

according to a certain mutation probability.

In evolutionary algorithms, the population sequence

P o p (0), P o p (1), \dots, P o p (k), \dots

is monotone, means that the entire evolutionary process does not degenerate the population due to the loss of the optimal individual.

For condition (1), it is easily guaranteed in evolutionary algorithms that include mutation operations.

Considering that the transfer probability from individual i to individual j is

r_{i j}

, and considering the limiting behaviors in the finite search space

k \to \infty

,there is

\lim_{k \to \infty} r_{i j} (\infty) = 1

. It’s means that the balanced searching strategy with genetic variation as the core can ensure that any individual can be generated by another individual.

Proof.

For condition (2), it can be proved from the perspective of population learning.

During the searching process, the progeny population consists of two parts, one part is the parent population that was not selected

P o p^{'}

, and the other part is the new population that has been learned through trial and error

\tilde{P o p}

The source seeking algorithm selects only one sample of the population to reproduce in any one evolution.

When the population reaches a certain size, the performance

{h^{'}}_{p} (k)

of the old population

P o p'

is equal to the performance

h_{p} (k - 1)

of the parent population

P o p (k - 1)

, so

{h^{'}}_{p} (k) = h_{p} (k - 1)

The

\tilde{P o p}

performance of the progeny population obtained through learning

\tilde{h_{p} (k)}

will be superior to

h_{p} (k - 1)

, so

\tilde{h_{p} (k)} > h_{p} (k - 1)

If sample

q_{i}

is selected and the evaluation result is excellent, the breeding operation will be performed.

The next generation population is composed of the progeny population

\tilde{P o p (k)}

and the parent population

P o p^{'} (k)

. Then the performance of the next generation population is:

h_{p} (k) = h_{p} (k - 1) + \tilde{h_{p} (k)} > h_{p} (k - 1)

(9)

If sample

q_{i}

is selected and the evaluation result is inferior, and the elimination operation will be performed to generate new sample individuals according to the probability. In terms of its results, its performance is no lower than that of its parent population.

Therefore, after performing an evolutionary operation, the performance of the progeny population will be no worse than that of the parent population, and the population sequence for continuous time

P o p (0), P o p (1), \dots, P o p (k), \dots

will be monotonous.

Proof.

4.2. Analysis for the performance of source seeking

As for the source seeking algorithm based on balanced searching strategy, its source searching ability can be clarified from the perspective of obtaining and tracking the solution.

At k-time, the purpose of the source seeking is to find the closed region G composed of Pareto solution set. Because of the carrier searching behaviors is limited, and the mutation operation is used between behaviors, it has the connective reachability.

Therefore, the source seeking issue at k-time can be optimized.

When the closed region G is obtained at k-time, and the optimal solution G contained in this region is wrapped by the Pareto boundary, it will be formed a meandering channel to reach the global optimal solution.

Under the constraint of balanced searching strategy, it can get the solution curve by the search behaviors. And the multiple parameters of environmental will converge to the global optimal solution at the T-time.

Therefore, the source seeking process based on balanced searching strategy can converge to the target point when one or more source paths exist in the source search space.

5. Experiment

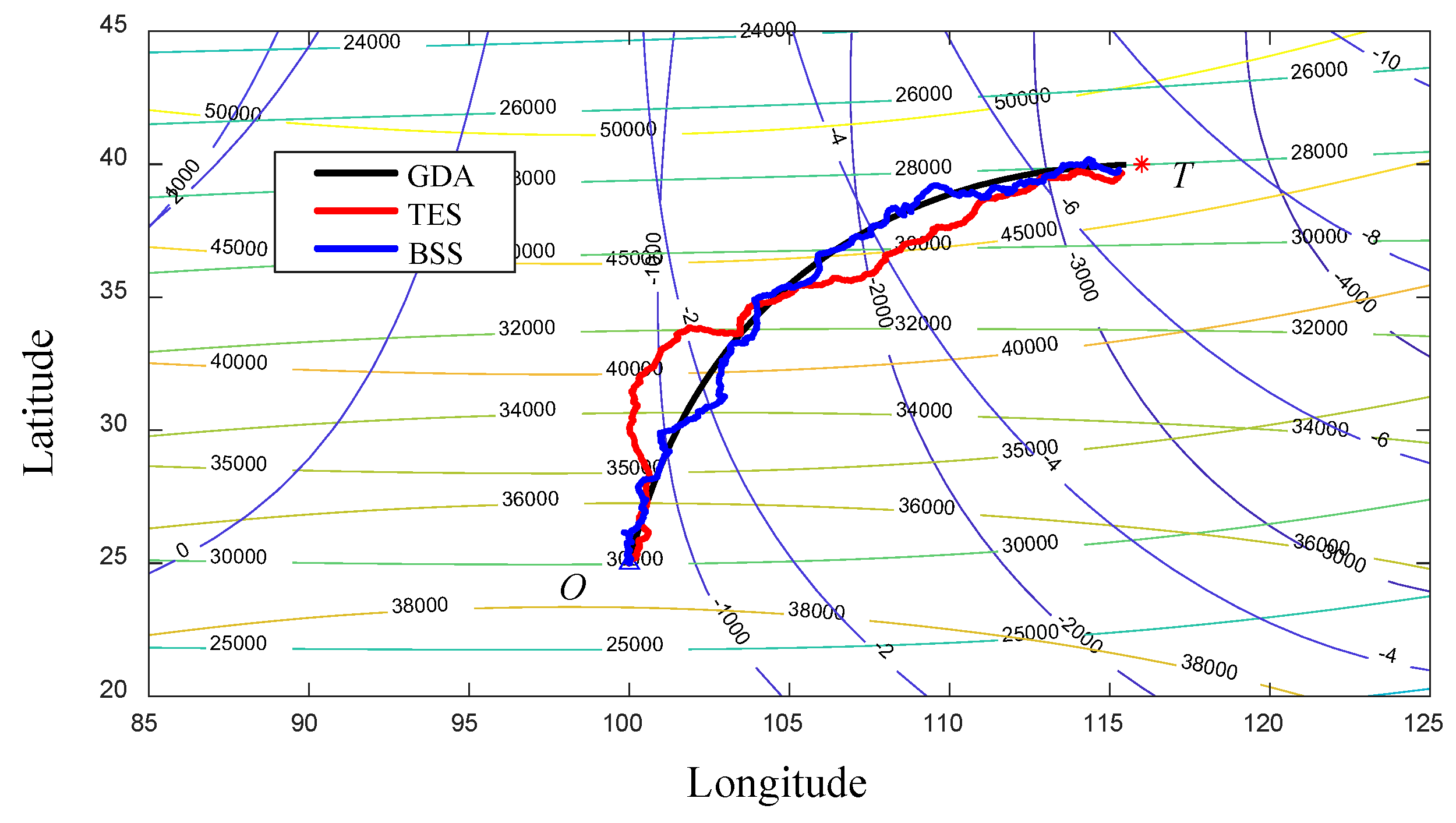
5.1. Simulation background field and source-seeking parameter setting

Geomagnetic field is a natural resource of the earth with abundant characteristic parameters and is a natural navigation information source in nature. It is a typical implicit information field because of the complex nonlinear mapping relationship between parameter distribution and geographical location. In this paper, we take the source seeking behaviors of animals using geomagnetic field, such as migration, homing and migration, as the prototype to verify the source seeking method.

(1) Parameter setting for carrier movement

The global geomagnetic model WMM2020 is employed to construct the source seeking environment in MATLAB. Considering the accuracy of the actual geomagnetic field sensor, set the movement step length L=500m, and each movement step will cause the change of the total field strength of about 1~2nt.

The characteristic parameters of geomagnetic environmental are selected as

B = {B_{x}, B_{y}, B_{z}}

Therefore, we can obtain the form of G function in normalized as follows：

G (B, k) = \sum_{i = 1}^{3} | \frac{B_{i}^{T} - B_{i}^{k}}{B_{i}^{T} - B_{i}^{o}} |

(10)

(2) Parameter setting for BSS algorithm

Set the sampling interval as

D_{θ} = 30^{°}

and population size as

N_{p o p} = 36

, propagation operator P_b=2, mutation operator P_mut=0.02.

Choose the intermediate threshold entropy

H_{t h} = \frac{H_{h i g h - t h} + H_{l o w - t h}}{2}

. And

H \in

[min(H), Max (H)], where min(H)=0, Max (H)=2.3. Here set

H_{t h}

=1.5,

H_{h i g h - t h}

=1.8,

H_{l o w - t h}

=1.2.

5.2. Comparison of different algorithms

Gradient descent algorithm (GDA)：Assuming that the mobile carrier can obtain the magnetic field distribution of adjacent elements, the source finding issue described in Equation 5 is transformed into a dynamic multi-objective optimization issue, and the source finding path can be solved by using the gradient descent method. This result is denoted as the ideal path.

In literature [31,32], a timing evolution searching strategy (TES) is employed as reference algorithm.

Here, we set the target parameter set as (28126nT, -3121.3nT, 54480nT).

The above three algorithms are used in the simulation experiment, and the source seeking path is obtained (see Figure 6).

In the Figure 6, “O” is the initial position of the carrier; “T” is the position of the source target. The black route is the source seeking route obtained by using GDA, which does not exist in the real environment due to the limitation of sensor perception ability, and is only used as an ideal route to test the effectiveness of the algorithm. The red route is the source seeking route obtained by TES; The blue route is the route obtained by using the proposed algorithm BSS. It can be seen that all the three routes can converge to the target point. Compared with the red route, the blue route and the black route are more closely aligned, indicating that the proposed algorithm can better track the solution curve and find the target point.

In the background field, five groups of source searching tasks were randomly set. Further more, three algorithms of GDA and TES, BSS algorithms were used for source seeking. Among them, TES and BSS were used to carry out 1000 times source seeking experiments, then the time of source seeking was calculated in the following Table 1.

As can be seen from the Table 1, the source searching time of TES is about 2.0 times that of GDA, while the source seeking time of BSS is about 1.8 times that of GDA. Obviously, the source seeking effect of BSS is better than that of TES.

5.3. Influence of different parameters on algorithm performance

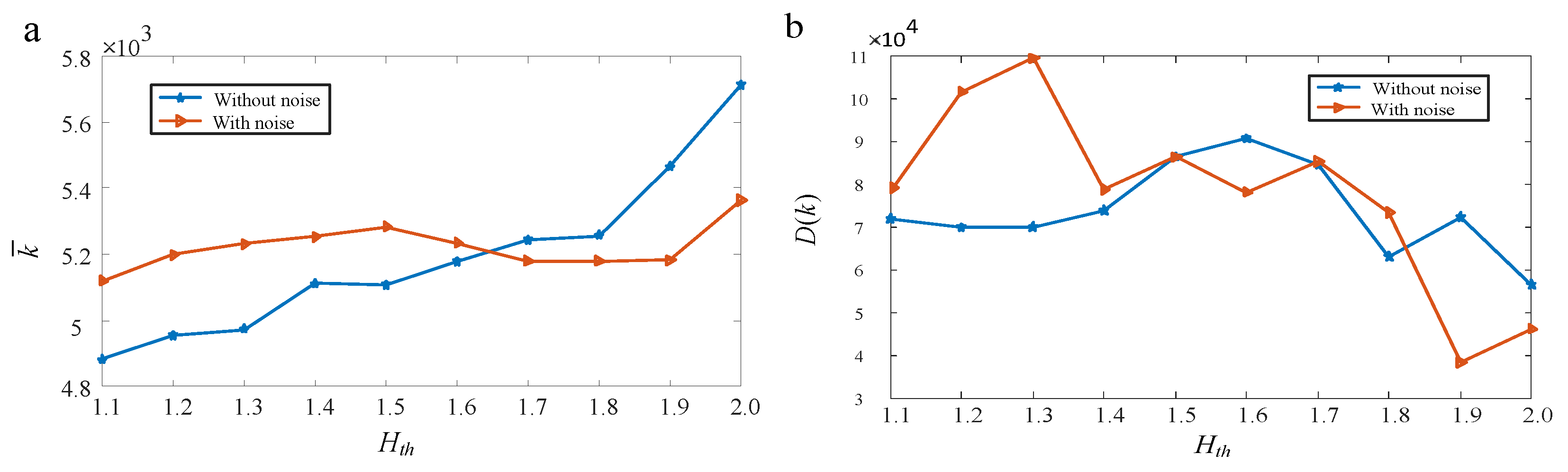
5.3.1. Analysis of the influence of $H_{t h}$

Under the condition that

Δ H

is unchanged, the setting of different behaviors entropy equilibrium points

H_{t h}

and the influence of sensor noise on source seeking performance are analyzed.

In simulation, set

Δ H

=0.4; the equilibrium point is set

H_{t h}

from 1.1 to 2.0, and the threshold entropy is set as follows.

{\begin{cases} H_{l o w - t h} = H_{t h} - Δ H \\ H_{h i g h - t h} = H_{t h} + Δ H \end{cases}

(11)

Other parameters are the same as those in the previous section. Each group of experiments is simulated for 100 times, and we can get the simulation results in Figure 7.

In the Figure 7, the blue line segment represents the data obtained without noise ,and the red line represents the data obtained when there is noise interference. The Figure 7(a) is the average of source seeking time, and figure (b) is the variance of source seeking time.

It can be seen that the change of

H_{t h}

has a significant impact on the performance of the algorithm. When setting

H_{t h}

is small, the algorithm is biased towards exploitation; When the setting is large, the algorithm is biased towards exploration. Overall, when the algorithm is biased towards exploitation, the time consumption is significantly lower than that when the algorithm is biased towards exploration. In combination with variance statistics, it can be seen that the time of source seeking is less and the performance of source seeking effect is better than other in the interval

H_{t h}

∈ [1.3,1.6]. When

H_{t h}

≥1.6, the source seeking effect is better than that in the environment without noise.

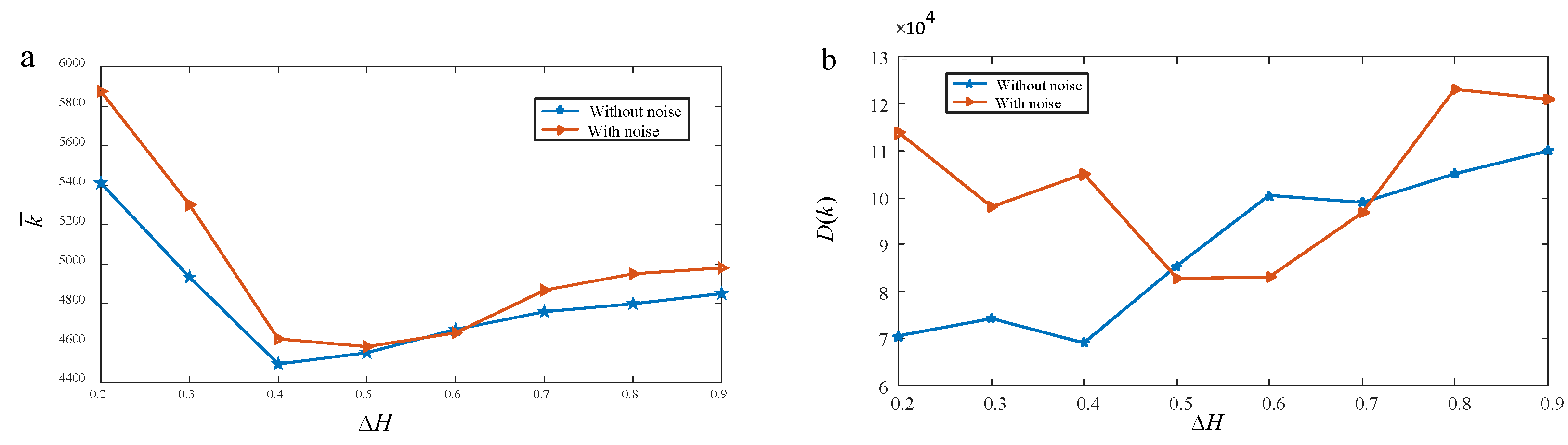
5.3.2. Analysis of the influence of $Δ H$

Set

H_{t h}

=1.4. According to Equation10, the threshold entropy

Δ H

under different conditions can be obtained. Other parameters are the same as those in the previous section. Each group of experiments is simulated 100 times, and the simulation results see the Figure 8.

In the Figure 8, the blue line segment represents the data obtained without noise and the red line represents the data obtained when there is noise interference. Figure 8(a) is the average of source seeking time, and Figure 8(b) is the variance of source seeking time.

It can be seen that the change of

Δ H

has a significant impact on the performance of the algorithm. The more binding the algorithm search bias when the value of

Δ H

is small, and the weaker the constraint on the search bias of the algorithm when the value of

Δ H

is large. Because in the implicit information field, the behaviors of source seeking needs to explore the environment. However, when the constraint is strong, the algorithm is not easy to explore the surrounding. Therefore, the time and variance of source seeking are large. Then, with the continuous increase of

Δ H

, the constraint of threshold entropy on the algorithm bias is weakened, and the source searching process depends on the search bias regulation of the evolutionary algorithm itself, and the time of source seeking tends to be constant. On the whole, the source finding performance is better when

Δ H \in [0.4, 0.7]

6. Conclusions

This paper studies the implicit information field source seeking method from the angle of search behaviors bias. A balanced searching strategy is proposed, which introduces the search path into the solution of the source seeking problem, constructs the evolutionary population with the feasibility search behaviors as the individual, introduces the metric search bias of distribution entropy, and designs a balanced searching strategy combining the evolutionary optimization and source seeking process. Through the performance analysis and simulation experiments, the validity and rationality of the method are verified. The next step is to consider the implicit information field source seeking method with local minima.

Data Availability: The experimental data used to support the findings of this study are available from the corresponding authors upon request.

Author Contributions

Conceptualization and writing—original draft preparation, C.Z.; methodology and software, J.L.; validation and formal analysis W.M.; investigation and writing—review and editing, B.L.; C.Z. analyzed experimental data and results, realized data visualization, and wrote the first draft of the paper. All authors have read and agreed to the published version of the manuscript.

Funding

This work was funded in part by the Aeronautical Science Foundation under Grant No. 2019ZH0T7001, and in part by the Shaanxi Provincial Key Research and Development Plan under Grant No. 2023-YBGY-019.

Data Availability Statement

Not applicable. All data generated or analyzed during this study are included in this article.

Conflicts of Interest

The authors declare that they have no known competing financial interests of personal relationships that could have appeared to influence the work reported in this paper..

Code availability: Not applicable.

Ethical approval: This article does not contain any studies with human participants or animals performed by any of the authors.

Informed consent: Informed consent was obtained from all individual participants included in the study.

References

Zhang, C. , et al. "Source Seeking with Nonholonomic Unicycle Without Position Measurement---Part I: Tuning of Forward Velocity," Systems & Control Letters, vol. 56, no. 3, pp. 245-252, 2007.
Cochran, J. , et al. "Source seeking with a nonholonomic unicycle without position measurements and with tuning of angular velocity — Part II: Applications," Proceedings of the IEEE Conference on Decision and Control (2007), pp. 1951-1956.
Khyade, V. B. , and E. R. Kandel. "Geomagnetic Field and Animal Orientation." International Journal of Social Science and Humanities Research, vol. 6, no. 4, 2018, pp. 27-42.
Putman N, F. “Animal Navigation: Seabirds Home to a Moving Magnetic Target,” Current Biology, vol. 30, no. 14, pp. 802-804, 2020.
Willis, M. A. "Odor-modulated Navigation in Insects and Artificial Systems," Chemical Senses, vol. 30, no. 1, pp. 287-288, 2005.
Anderson, R. B. , et al. "Mobile Robotic Radiation Surveying with Recursive Bayesian Estimation and Attenuation Modelling," E Transactions on Automation Science and Engineering, vol 19, no. 1, pp. 410-424, 2020.
Oconnor, Alan, P. Setlur, and N. Devroye. "Single-sensor RF emitter localization based on multipath exploitation," IEEE Transactions on Aerospace & Electronic Systems, vol. 51, no. 3, pp. 1635-1651, 2015.
Jing, T., Q. Meng, and H. Ishida. "Recent Progress and Trend of Robot Odor Source Localization." IEEJ Transactions on Electrical and Electronic Engineering, vol. 16. no. 7, pp.938-953, 2021.
Golov, Y. , et al. "Navigation in an odorant-landscape: mate finding and mate choice in a nocturnal moth." Entomologia Generalis, vol. 42, no. 2, pp. 323-334, 2021.
Atanasov, N. A., J. L. Ny, and G. J. Pappas. "Distributed Algorithms for Stochastic Source Seeking with Mobile Robot Networks: Technical Report," Journal of Dynamic Systems Measurement & Control, vol. 137, no. 3, DOI：10.1115/1.4027892, 2015.
Wu, W., I. D. Couzin, and F. Zhang. "Bio-inspired Source Seeking with no Explicit Gradient Estimation," IFAC Proceedings Volumes, vol. 45, no. 26, pp. 240-245, 2012.
N. Atanasov, J. Le Ny, N. Michael and G. J. Pappas, "Stochastic source seeking in complex environments," 2012 IEEE International Conference on Robotics and Automation, doi: 10.1109/ ICRA.2012.6225289, pp. 3013-3018, 2012.
M. Q. Liu, B. Li and Y. F. Chen et al., “Location Parameter Estimation of Moving Aerial Target in Space-Air-Ground Integrated Networks-Based IoV,” IEEE Internet of Things Journal.
M. Q. Liu, C. H. Liu and M. Li et al., “Intelligent passive detection of aerial target in space-air-ground integrated networks,” China Communications, vol.19, no.1, pp.52–63, 2022.
Paliotta, C., D. Belleter, and K. Y. Pettersen. "Adaptive Source Seeking with Leader-Follower Formation Control," Ifac Papersonline, vol. 48, no. 16, pp. 285-290, 2015.
Gronemeyer, M., M. Alpen, and J. Horn. "Limited Gradient Criterion for Global Source Seeking with Mobile Robots," IFAC-PapersOnLine, vol. 53, no. 2, pp. 15288-15293, 2020.
Massimo, V., V. Emmanuel, and B. I. Shraiman. "'Infotaxis' as a strategy for searching without gradients," Nature, vol. 445, no. 7126, pp. 406-415, 2007.
Loisy, A. , and C. Eloy. "Searching for a source without gradients: how good is infotaxis and how to beat it," arXiv e-prints, vol. 478, no. 2262, Article Id.20220118, 2022.
M. Q. Liu, Z. L. Liu and W. D. Lu et al., “Distributed Few-Shot Learning for Intelligent Recognition of Communication Jamming,” IEEE Journal of Selected Topics in Signal Processing.
M. Q. Liu, J. K. Wang and N. Zhao et al., "Radio Frequency Fingerprint Collaborative Intelligent Identification Using Incremental Learning, " IEEE Transactions on Network Science and Engineering.
Mingqian Liu, Chunheng Liu, Yunfei Chen, Zhiwen Yan,Nan Zhao, Radio Frequency Fingerprint Collaborative Intelligent Blind Identification for Green Radios, IEEE Transactions on Green Communications and Networking.
Mingqian Liu, Hongyi Zhang, Zilong Liu, Nan Zhao, Attacking Spectrum Sensing With Adversarial Deep Learning in Cognitive Radio-Enabled Internet of Things, IEEE Transactions on Reliability, DOI: 10.1109/TR.2022.3179491, 2022.
Mingqian Liu, Zhenju Zhang, Yunfei Chen, Jianhua Ge, Nan Zhao. Adversarial Attack and Defense on Deep Learning for Air Transportation Communication Jamming, IEEE Transactions on Intelligent Transportation Systems, 2023, DOI: 10.1109/TITS.2023.3262347.
Fuqing Zhao, Lixin Zhang, Jie Cao, Jianxin Tang, "A cooperative water wave optimization algorithm with reinforcement learning for the distributed assembly no-idle flowshop scheduling problem, " Computers & Industrial Engineering,vol. 153. No. 1082, pp. 1-16, 2021.
F. Zhao, S. Di, J. Cao, J. Tang and Jonrinaldi, "A Novel Cooperative Multi-Stage Hyper-Heuristic for Combination Optimization Problems," in Complex System Modeling and Simulation, vol. 1, no. 2, pp. 91-108, 2021.
Crepinsek, Matej, S. H. Liu, and M. Mernik. "Exploration and exploitation in evolutionary algorithms: A survey," ACM Computing Surveys, vol. 45, no. 3.
Nguyen, Ttv, MD Phung, and Q. V. Tran. "Behavior-based Navigation of Mobile Robot in Unknown Environments Using Fuzzy Logic and Multi-Objective Optimization," International Journal of Control and Automation, vol. 10, no. 2, pp. 349-364, 2017.
Anagnostopoulos, G. G., M. Deriaz, and D. Konstantas. "A Multiobjective Optimization Methodology of Tuning Indoor Positioning Systems," 2017 International Conference on Indoor Positioning and Indoor Navigation (IPIN), pp. -8.
Giagkiozis, I. , and P. J. Fleming. "Methods for multi-objective optimization: An analysis," Information Sciences, vol. 293, no. 1, pp. 338-350, 2015.
Salazar, J. Z. , et al. "Balancing exploration, uncertainty and computational demands in many objective reservoir optimization," Advances in Water Resources, vol. 109, no. 1, pp. 196-210, 2017.
Liu M, Liu K, Li H, et al. “A Study of Bio-Inspired Geomagnetic Navigation Using Timing Evolution Searching Strategy.” Journal of Northwestern Ploytechnical University, vol.32, no.6, pp.894–898, 2014.
H. Li, M. Liu and K. Liu, "Bio-inspired geomagnetic navigation method for autonomous underwater vehicle," Journal of Systems Engineering and Electronics, vol. 28, no. 6, pp. 1203-1209,2017.

Figure 1. Schematic diagram of static solution distributed in the two-dimensional plane.

Figure 2. The distribution of solutions at different times.

Figure 3. Schematic diagram of the distribution of solutions at continuous time.

Figure 4. The principle diagram of source seeking.

Figure 6. The route of source seeking.

Figure 7. Influence of

H_{t h}

on source seeking performance. (a) The average source seeking time; (b) The variance of source seeking time.

Figure 7. Influence of

H_{t h}

on source seeking performance. (a) The average source seeking time; (b) The variance of source seeking time.

Figure 8. Influence of

Δ H

on source seeking performance. (a) The average source seeking time; (b) The variance of source seeking time.

Figure 8. Influence of

Δ H

on source seeking performance. (a) The average source seeking time; (b) The variance of source seeking time.

Table 1. Comparison of source finding time of different algorithms.

Algorithm	Source seeking Task
Algorithm	1	2	3	4	5
GDA	2787	2266	2406	2490	2413
TES	5828	4868	5036	5168	5110
BSS	5016	4223	4406	4486	4398

Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.

© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).

Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.

MDPI Initiatives

Important Links

Choose an area of interest and we will send you notifications of new preprints at your preferred frequency.

Disclaimer

A Source Seeking Method for the Implicit Information Field Based on a Balanced Searching Strategy

Abstract

1. Introduction

2. Problem description

3. A source seeking method based on balanced searching strategy

3.1. Characteristic analysis of the source of implicit information field

3.2. Source seeking behavior of implicit information field based on motion path

3.3. Balance searching strategy

3.3.1. Exploration and exploitation

3.3.2. The algorithm of source seeking

4. Algorithm performance analysis

4.1. Analysis for the convergence of the algorithm

4.2. Analysis for the performance of source seeking

5. Experiment

5.1. Simulation background field and source-seeking parameter setting

5.2. Comparison of different algorithms

5.3. Influence of different parameters on algorithm performance

5.3.1. Analysis of the influence of H t h

5.3.2. Analysis of the influence of Δ H

6. Conclusions

Author Contributions

Funding

Data Availability Statement

Conflicts of Interest

References

MDPI Initiatives

Important Links

Subscribe

5.3.1. Analysis of the influence of $H_{t h}$

5.3.2. Analysis of the influence of $Δ H$