Prerpints.org logo
Preprint
Article

An Improved Doppler-Aided Smoothing Code Algorithm for Bds-2/Bds-3 Un-geo Satellites in Consideration of Satellite Code Bias

Altmetrics

Downloads

128

Views

24

Comments

0

A peer-reviewed article of this preprint also exists.

This version is not peer-reviewed

Submitted:

02 June 2023

Posted:

02 June 2023

You are already at the latest version

Alerts
Abstract
The extensive use of carrier-aided smoothing code (CSC) filter has led to reduce the noise level of raw code measurements in GNSS positioning and navigation applications. However, the existing CSC technique is sensitive to the changes of the integer ambiguity and then the smoothing proce-dure needs to be restarted in the presence of cycle-slips. As the Doppler shift is instantaneous ob-servation and immune to cycle-slips, Doppler-aided smoothing code (DSC) algorithm would be more promising in challenged environment. Based on the Hatch-filter, an optimal DSC approach is proposed with the principle of minimum variance. Meanwhile, to inhibit the effect of integral cumulative error of Doppler, a balance factor is adopted to adjust the contributions of raw code and DSC. The noise level of code observable is not only affected by thermal noise, but also limited by systematic bias. Satellite code bias (SCB) has been identified in the raw code observable on each frequency for each BDS-2 satellite. By minimizing the sum of absolute value of residuals, polyno-mial segment fitting algorithm as a function of elevation-angles is applied to establish the SCB cor-rection model based on epoch-differenced Multipath (MP) deviations. Finally, numerical experi-ments demonstrate the validity and efficiency of the refined DSC filter with SCB corrections on each available frequency for BDS-2 un-GEO satellites.
Keywords: 
Subject: Environmental and Earth Sciences  -   Other

1. Introduction

Currently, single-point positioning (SPP) and differential Global Navigation Satellite System (DGNSS) are widely used for navigation and positioning applications at the meter and sub-meter levels [1,2]. Code measurement is preferred over carrier-phase in these cases due to its free of integer ambiguity [3]. However, the presence of random and systematic noise in code observation result in defective solutions, restricting its reliability. To suppress thermal noise, various carrier-aided smoothing methods have been proposed, including the Hatch filter which is essentially a low-pass filter that attenuates high-frequency noise [4], and its improved versions with smoothing-weight factors (SWF) [5,6]. More details of improved CSC methods can be found in the literatures [7,8,9]. Nevertheless, these methods assume that the integer ambiguity is invariant, which is not valid in situations, especially in challenged environment [10,11]. In such cases, the cycle slip is inevitable and then the filtering process need be restarted, leading to undesirable performance in navigation and positioning applications.
Typically, smoothed code measurement is obtained through the weighted mean of the actual code observable and the predicted value which consists of the smoothed code at the previous epoch and delta-range [12,13,14]. Theoretically, delta-range can be computed from the differencing phase observations in successive epochs or from Doppler measurement, which is immune to cycle-slips. Therefore, Doppler-aided smoothing code filter in the range domain may be more advantageous than the CSC method in challenging environments due to its higher accuracy and availability.
Although Doppler measurement has previously been utilized for velocity and acceleration determination [15,16,17,18], few studies have explored its potential in range domain smoothing filters. Bahrami and Ziebart [19] suggested that Doppler could be employed to smooth the code measurement similarly to CSC, however, the accuracy of DSC differs from CSC as it is dependent on both the noise-level of Doppler and the sampling-interval. To address this, Zhou and Li [20] utilized minimum variance principle to develop an optimal DSC filter, while Zhang et al. [21] proposed an optimized kinematic positioning method with DSC and a constant acceleration model, leading to improved positioning accuracy (by nearly 85%) compared to chipset original solutions. Zhou et al. [22] investigated the optimal smoothing window of DSC for low-cost GNSS receivers and the results show that DSC can improve positioning accuracy by up to 29.9% and 26.9%, respectively. Although most of the above Doppler-aided filters are established for GNSS, few DSC algorithms are validated by BeiDou navigation satellite system (BDS) measurements. Considering the different satellite orbits (i.e., Geostationary Earth Orbit (GEO), Inclined Geo-Synchronous Orbit (IGSO) and Medium Earth Orbit (MEO)) and unique development strategy (i.e., BDS-1, BDS-2 and BDS-3) [23,24], it is questionable whether these methods are applicable to BDS.
The CSC or DSC filter can be used to improve the code precision by assuming that the measurement noise can be accurately modeled as a zero-mean Gaussian random variable, which means that the systematic bias should be removed from the raw code observation. Unfortunately, previous studies indicate that a systematic bias is observed in raw BDS code observables which would result in code-phase divergence of more than 1.0 m [25]. After numerous researches, it has been identified that this new type of code bias originates from the spacecraft internal multipath [26,27], so it can be termed satellite code bias (SCB). Due to the mismatch between the antenna element and power-divider network of space satellite, for BDS user-end, the SCB represents to be dependent of elevation-angle and frequency, rather than receiver-type or location. Based on large datasets (almost 24 months), Guo et al. [28] refined the SCB correction model in consideration of the stochastic information and the experiments show that the refined SCB model is more suitable for BDS-2 satellites. Afterwards, Lou et al. [29] presented an assessment of SCB in BDS triple-frequency ambiguity resolutions and the results suggest that the success rate of the wide-lane ambiguity resolution can be evidently improved with corrected code observations.
In view of the cognition that the SCB is orbit-dependent, the above SCB correction models are established as different groups regarding to the orbit types, thus the differences of the bias among various satellites are ignored. To deal with this problem, Zou et al. [30] developed individual correction model for each IGSO and MEO satellite by differencing MP combinations between epochs, and the performances show that, compared to the above orbit-dependent correction models, the proposed correction models can achieve a significant improvement (approximately 20%). To describe more details in the SCB variations, Pan et al. [31] proposed an improved SCB piecewise correction model for each BDS satellite and each frequency as a function of elevation and the elevation node separation is shrunk down to 1° to improve the precision of the model. A few studies have been also conducted to further improve the SCB correction models and similar conclusions have obtained [32]. However, for majority of the above SCB correction models, a simple numerical average method is used to obtain MP estimators, which may be difficult to acquire optimal values of MP variations, so more efficient assessment method needs further research.
Our study briefly reviews the principle and basic model of CSC. Subsequently, the impacts of systematic bias and measurement noise are analyzed with final-value theorem of Laplace transform. Then an improved SCB model is proposed to reduce this systematic bias. A balance factor is introduced, followed by an optimal DSC strategy based on minimum variance principles. Rigorous analysis informs the proposed improved SCB piecewise correction model for each BDS un-GEO satellite and each available frequency. Finally, we analyze the experimental results and draw meaningful conclusions.

2. Methods

In this section, the principle of pure CSC strategy is expressed and then an improved SCB correction model is presented. With the discussion of features and stability of DSC, the refinement of DSC with a balance factor is developed according to the principle of minimum variance.

2.1. Basic model of carrier smoothed code

The code psedorange and carrier phase at epoch k can be modeled as [1]:
P k = ρ k + I k + M k + ε P , k ϕ k = ρ k + λ N k − I k + m k + ε ϕ , k
where the subscript is the epoch index; P and ϕ denote code and carrier phase in meters; ρ is the equivalent distance which includes the geometric distance between the satellite and receiver antenna, tropospheric delay, and receiver and satellite clock errors; λ is the wavelength of carrier phase; N is the integer ambiguity; I is the ionospheric path delay; M and m denote multipath effects in code and phase observables, respectively; ε p and ε ϕ are code and phase measurement errors, respectively.
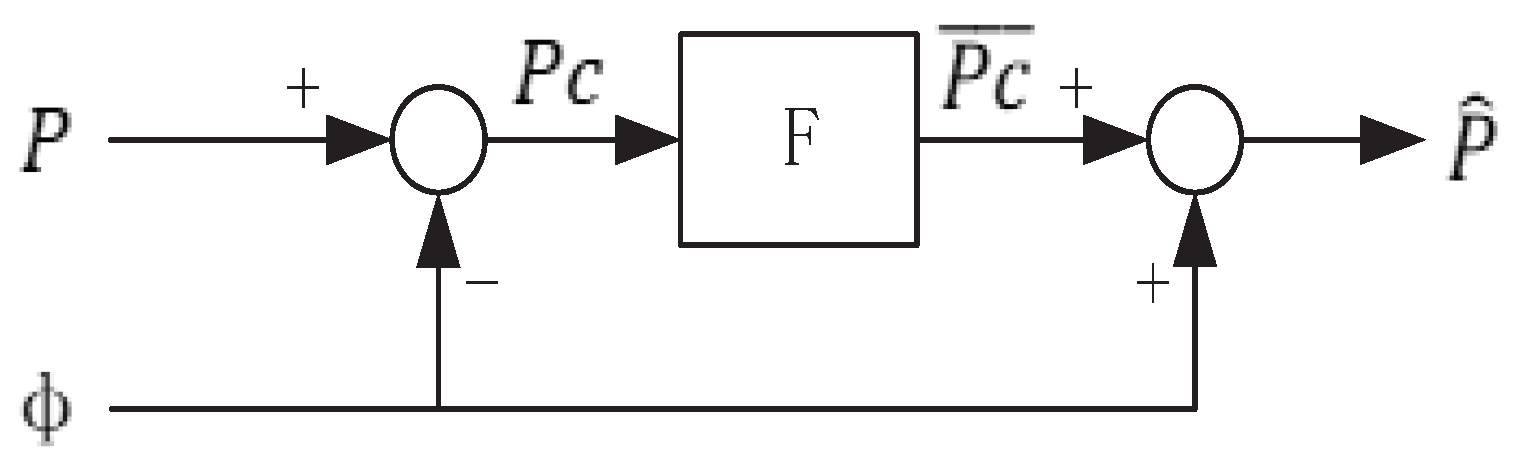
The model of phase is similar to that of code, with the exception that the ionospheric delay changes sign and the phase ambiguity has been added. Since the carrier-phase noise, at the order of 1 mm or below, can be modeled as a zero-mean Gaussian random variable, Hatch firstly proposed a classical filter to improve the code as Figure 1.
In Figure 1, P c and P c ¯ denote the code-minus-carrier (CMC) signal and the filtered signal; P ^ is CSC signal. F is the transfer function in frequency domain:
F s = ( τ s + 1 ) − 1
where τ is the smoothing time of Hatch filter; s is Laplacian Operator.
For single-frequency receiver, the CMC signal can be calculated by
P c = P − ϕ = P − λ φ = 2 I − λ N + ( M − m + ε p − ε ϕ )
After the adoption of low-pass filter, more accurate code can be obtained by
P c ¯ = F ⋅ P c = 2 F ⋅ I − λ N + F ⋅ ( M − m + ε p − ε ϕ )
Then the CSC can be defined as
P ^ = P c ¯ + ϕ = ρ + I + Μ + N I = 2 F − 1 ⋅ I M = F ⋅ M + ( 1 − F ) ⋅ m N = F ⋅ ε P + ( 1 − F ) ⋅ ε ϕ
It is evident that the precision of CSC is determined by the ionospheric delay, multipath effect and measurement errors.

2.2. Error analysis of carrier smoothed code

Assuming that the measurement noises between different epochs is not relevant, the standard error ( σ ) of CSC can be approximately described as
σ ≅ ε P T s / τ
where T s is output period of receiver. Since the smoothing time is normally much greater than output period ( τ ≫ T s ), the precision of CSC is better than raw code.
Inspired by [33], the ionospheric delay in the time domain can be modeled by
I t = I c + I v ⋅ t
where I c and I v denote the constant and rate of ionospheric delay.
Using the Laplace transform, the ionospheric delay in frequency domain can be written as
I s = I c s + I v s 2
where s is complex variable ( s = σ + j ω ,   σ ∈ R , ω ∈ R ).
Then the difference ( d I ) between the original ionospheric delay and the filtered one can be solved by
d I = I − Ι = 2 1 − F I = 2 τ s τ s + 1 I
Using the final-value theorem of Laplace transform, the steady-state error of d I ( d I s s ) can be computed as
d I s s = lim s → 0 ⁡ s ⋅ 2 τ s τ s + 1 I c s + I v s 2 = 2 τ ⋅ I v
If the ionospheric delay is stable, the rate of the delay is approaching zero, leading to non-effect on CSC signal.
Similarly, the multipath effect in the time domain can also be modeled by
M t = M c + M v ⋅ t + 1 2 M a ⋅ t 2
where M c , M v , M a denote the constant, rate and acceleration of multipath.
Then the multipath in the frequency domain can be expressed by using Laplace transform
M s = M c s + M v s 2 + M a s 3
Neglecting multipath in phase observable due to the small magnitude compared with the one of code, the formula for calculating the change of multipath effect ( d M ) after low-pass filtering can be obtained by
d M = M − Μ = 1 − F M = τ s τ s + 1 M
The steady-state error of d M ( d M s s ) can be determined by using the final-value theorem of Laplace transform:
d M s s = lim s → 0 ⁡ s ⋅ τ s τ s + 1 M c s + M v s 2 + M a s 3 = τ ⋅ M v + τ τ s 2 + s M a
Concerning the multipath is time-variant, the steady-state error in CSC includes both constant and linear errors, which are positively correlated with the smoothing time. As such, increasing the smoothing time and active multipath effect leads to a significant increase in steady-state error. Consequently, it is crucial to reduce the multipath effect to optimize CSC performance. The GNSS multipath effect arises from both user-end and satellite-end sources. The former can be controlled or eradicated by choosing an open environment or using a choke ring while the latter (mainly refers to SCB) is challenging to deal with except through empirical correction model.

2.3. Empirical correction of multipath effect in the satellite-end

The multipath combination, a special linear combination of single-frequency code and dual-frequency phase measurements, has been widely used to analyze the SCB [25,26,28] and its formula can be written as
M P i = P i + β i j k − 1 · ϕ j − β i j k · ϕ k = N ~ i j k + B i
with
β i j k = ( λ i 2 + λ j 2 ) / ( λ j 2 − λ k 2 ) N ~ i j k = β i j k − 1 N j − β i j k N k B i = M i + ε i + β i j k − 1 m j + δ j − β i j k m i + δ i
where i , j , k denote the carrier frequencies; β denotes the linear factor; M P is the MP combination ; N ~ refers to the ambiguity of carrier-phase that involves constant satellite- and receiver-dependent hardware delays; B respects to sum of multipath and measurement noise.
Since the MP combination is a geometry-free (GF) combination, the geometric terms in Equation (1) (i.e., geometric distance, receiver and satellite clock offsets, tropospheric delay) can be removed sufficiently. Meanwhile, due to the linear factor (refers to β ), the first-order ionospheric delay can also be eliminated with efficiency. Then the N ~ , determined as a constant over whole tracking arc, can also be subtracted from the MP time series by using difference algorithm. It should be noted that the phase-multipath is ignored because of its small magnitude compared with the code-multipath. Therefore, the MP combination is applicable to analyze the characters of SCB and establish correction model [29,34].
The traditional SCB correction models are usually built based on the assumption that the N ~ in Equation (15) keeps stable during satellite tracking. However, if the tracking arc becoming longer (e.g., 6 hours), this assumption would be difficult to satisfied. To address this problem, an improved SCB approach is proposed in this paper. Firstly, epoch-difference (ED) method is applied to remove the stable terms (here mainly refer to phase-ambiguity and hardware-delays). The ED-SCB modeling on the i th frequency between consecutive epochs can be described as:
∆ S i E l k d a = M P i E l k d a − M P i E l k − 1 d a
where a denotes space satellite; d denotes day of year (doy); E l k is the satellite-elevation at epoch k , and ∆ S refers to the ED-SCB.
In order to correct the SCB efficiently and precisely, the node-separation of elevation should be determined appropriately. If the node is oversized, plenty of details of MP series would be ignored, thereby decreasing the precision of SCB modeling. Therefore, the node-separation of this article is 1° rather than 5° or larger. Besides, the difference between E l k in Equation (17) and the required elevation-angle should not exceed one-tenth of node-separation.
As there would be numerous ∆ S at required E l for all measurement days on the same frequency of same satellite, mean method is used to achieve optimal estimation of ED-SCB as
∆ S ¯ i E l a = ∑ j = 1 n ∆ S i E l j a / n
where n is total number of ED-SCB estimators for satellite a at required elevation E l .
For satellite a on ith frequency, assuming the ED-SCB at medium-elevation ( E m e d ) of epoch ( k 0 ) is θ , the absolute SCB at required elevation-angle E l can be calculated as:
S i ( E l ) a = θ i a + ∑ t = k 0 k − 1 ∆ S ¯ i E l s , E l > E m e d S i ( E l ) a = θ i a ,                                                                     E l = E m e d   S i ( E l ) a = θ i a − ∑ t = k k 0 − 1 ∆ S ¯ i E l s , E l < E m e d
To fix the absolute level of SCB estimators, inspired by [31], a zero-mean restriction has also been introduced in this improved modeling as
∑ l = 1 m S i ( E l ) l a = 0
where l is the total number of SCB estimators for satellites a . Due to the above constraint, the remaining unknown parameter in Equation (20) can be solved and then SCB estimators over tracking arc can be obtained.
The ED method is instrumental in removing the unchanged biases in Equation (15), whilst the noise level of code measurements would be enlarged via error-propagation law. To deal with this problem, polynomial segment fitting algorithm by minimizing the sum of absolute value of residuals is adopted to establish the SCB correction model
S ^ i ( E l ) a = γ 4 ⋅ S i ( E l ) a 4 + γ 3 ⋅ S i ( E l ) a 3 + γ 2 ⋅ S i ( E l ) a 2 + γ 1 ⋅ S i ( E l ) a 1 + γ 0 , E l > E l m e d S ^ i ( E l ) a = θ i a ,                                                                                                                                                                                                                                                           E l = E l m e d   S ^ i ( E l ) a = δ 4 ⋅ S i ( E l ) a 4 + δ 3 ⋅ S i ( E l ) a 3 + δ 2 ⋅ S i ( E l ) a 2 + δ 1 ⋅ S i ( E l ) a 1 + δ 0 , E l < E l m e d
where γ i , δ i , ( i = 0,1 , 2,3 , 4 ) represent the coefficients of the above quartic polynomials. It should be noted that the SCB correction model and SCB estimators are opposite in sign.

2.4. Basic model of Doppler smoothed code

After subtracting the SCB, the performance of CSC would be desirable. Unfortunately, rather small effects (i.e., unexpected high user dynamics, short signal blocking, high noise) may disturb the tracking loop design (PLL) and phase lock can ultimately be lost, easily resulting in the occurrence of cycle slip. Therefore, the efficiency of above CSC filter is mainly restrained by cycle-slip which is unavoidable and unpredictable, especially in urban areas. Once cycle-slip occurs, the smoothing processor need be rebooted, leading a sudden change of position dilution and pollution of positioning accuracy. Hence Doppler observable, immune to cycle-slip, can be alternative to smooth raw code observation.
Similar to CSC, the basic DSC model can be expressed as
P ̄ k = α k P k + ( 1 − α k ) P ̄ k − 1 + d R k
where the subscript is the epoch index; α is the smoothing-weight factor; d R k is the dalte-range of receiver-to-satellite between consecutive epochs; P and P ¯ denote the raw code and smoothed code measurement in meters, respectively.
Assuming the ionospheric delay keeps stable and the multipath is reduced, d R k can be described by Doppler observables as
d R k = ϕ k − ϕ k − 1 = λ ∫ t k − 1 t k D t d t ≈ 1 2 λ T ( D k + D k − 1 )
with T = t k − t k − 1 . Obviously, if the noise level of Doppler measurement is stable, the precision of d R k mainly depends on the sampling-interval ( T ).
With α k = 1 / k , inserting Equation (23) into (22) yields
P ̄ k = 1 k ∑ i = 1 k P i + λ T 4 k − 1 D k + λ T 2 k ∑ i = 1 k − 1 ( n − i ) D i
Assuming that there is no time-correlation existing in Doppler measurements, we can define a function to describe the variance of DSC based on error-propagation law as:
F 1 k = σ P ̄ k 2 = σ p 2 k + λ T 4 2 ( k − 1 ) 2 σ D 2 + λ T 2 k 2 k ( k − 1 ) ( 2 k − 1 ) 6 σ D 2 = σ p 2 k + λ T σ D 2 k 2 16 − k 24 − 1 16 + 1 24 k
where σ P ̄ k 2 is the variance of DSC, and σ p and σ D denote the noise level of code and Doppler observable, respectively.
The variance of DSC is positive relevance with SWF, but unlike CSC, it is not monotonously decrease with increasing SWF, which means that the size of smoothing window (SW) for DSC should be limited (see Figure 1).
To obtain the optimal SW for DSC, setting the derivative of F 1 k regarding k equal to zero yields
d F 1 ( k ) k = − σ p 2 k 2 + λ T 2 σ D 2 k 8 − 1 24 − 1 2 4 k 2 = 0
with β = σ p 2 / ( λ σ D ) 2 , Equation (26) can be further simplified as
k 3 − k 2 3 − ( 24 β + T 2 3 T 2 ) = 0
As Equation (27) is a cubic equation and the coefficient of quadratic term is 0, the discriminant of roots of Shengjin's formulas is
Δ = 9 24 β + T 2 2 4 T 4 + 96 β + 4 T 2 27 T 2 > 0
Therefore, there are three different solutions for k , among which only one solution is real and the others are conjugate complex. Theoretically, k should be positive integer, so the real solution is required and the optimal SW can be obtained by
k ^ = c e i l [ k ]
where c e i l ( * ) is the round-up operator.
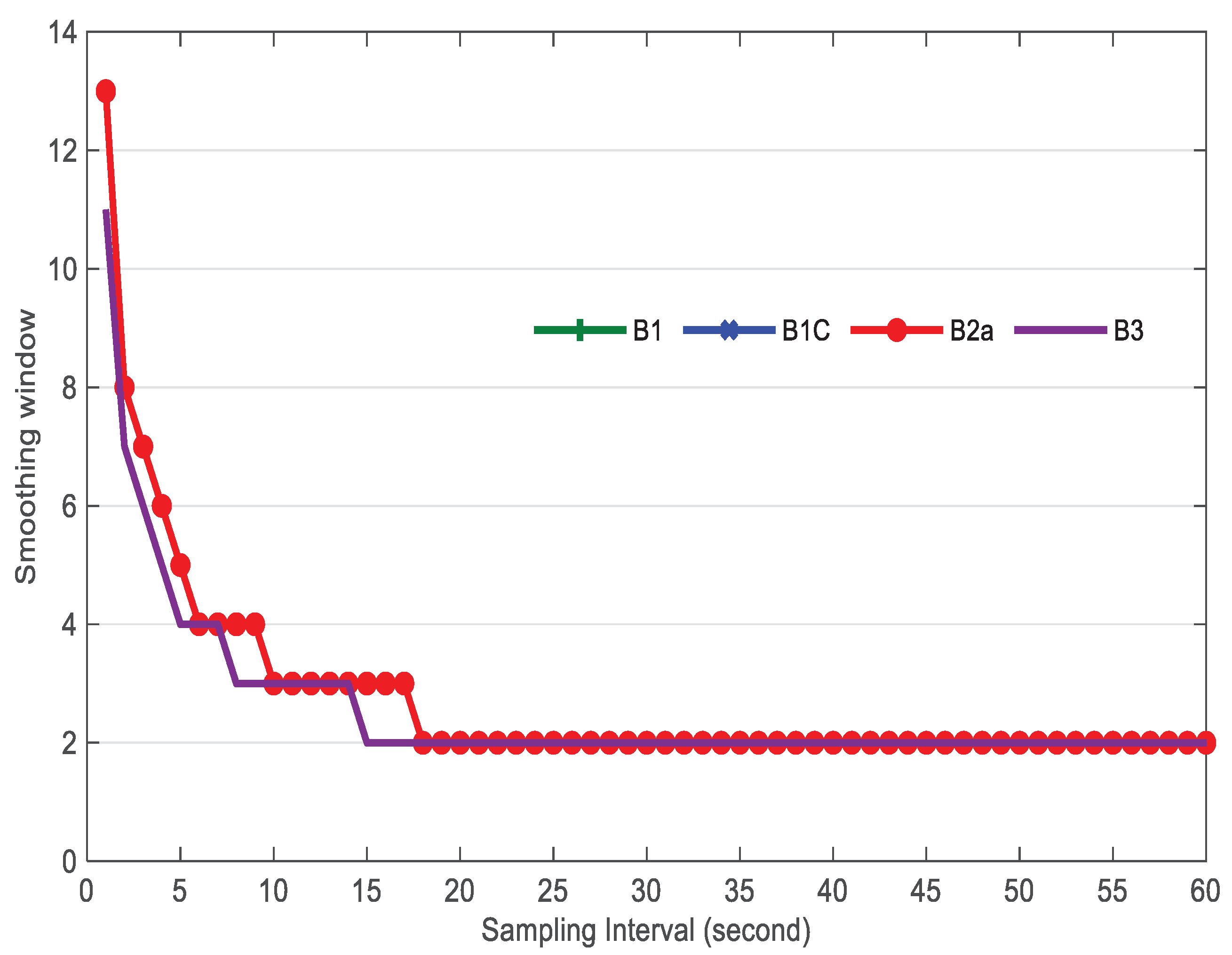
In the case of σ p =0.3 m and σ D =0.1 cycle, the relationship between the sampling-interval and SW can be shown in Figure 2. It is obvious that, based on the principle of minimum variance, the SW decreases dramatically when the sampling-interval increases from 1 s to 10 s for all available signals (i.e., B1, B1C, B2a and B3). When the interval exceeds 10 s, the SW is approaching 1.6. Since the raw BDS measurements would be split into different sampling-intervals to verify the effectiveness of our proposed method, the SW is determined to 2 to make sure that observations of adjacent epochs can be used in the following study.

2.5. Refined model of Doppler smoothed code

Doppler shift can be used to smooth code measurement based on the assumption that the noise level of Doppler is superior to that of raw code. However, when the sampling-interval increases, this assumption may be invalid because of the significant increase of integral cumulative error of Doppler observation [5,20].
To deal with this problem, a balance factor is introduced to refine the DSC and then the refined DSC (RDSC) can be obtained by:
P ^ k = 1 − μ P k + μ P ̄ k = 1 − μ P k + μ k ∑ i = 1 k P i + μ λ T 4 k − 1 D k + μ λ T 2 k ∑ i = 1 k − 1 n − i D i
where μ is the balance factor.
Similarly, another function ( F 2 ) has been derived to describe the variance of RDSC as
F 2 ( k ) = σ P ^ k 2 = 1 − μ 2 σ p 2 + μ 2 k σ p 2 + μ λ T 4 σ D 2 ( k − 1 ) 2 + μ λ T 2 k σ D 2 k ( k − 1 ) ( 2 k − 1 ) 6
where σ P ^ k 2 is the variance of RDSC.
In terms of the d F 2 / d μ = 0 , the minimal σ P ^ k 2 can be obtained at
μ = 48 k β 48 k β + 48 β + ( 3 k 3 − 2 k 2 − 3 k + 2 ) T 2
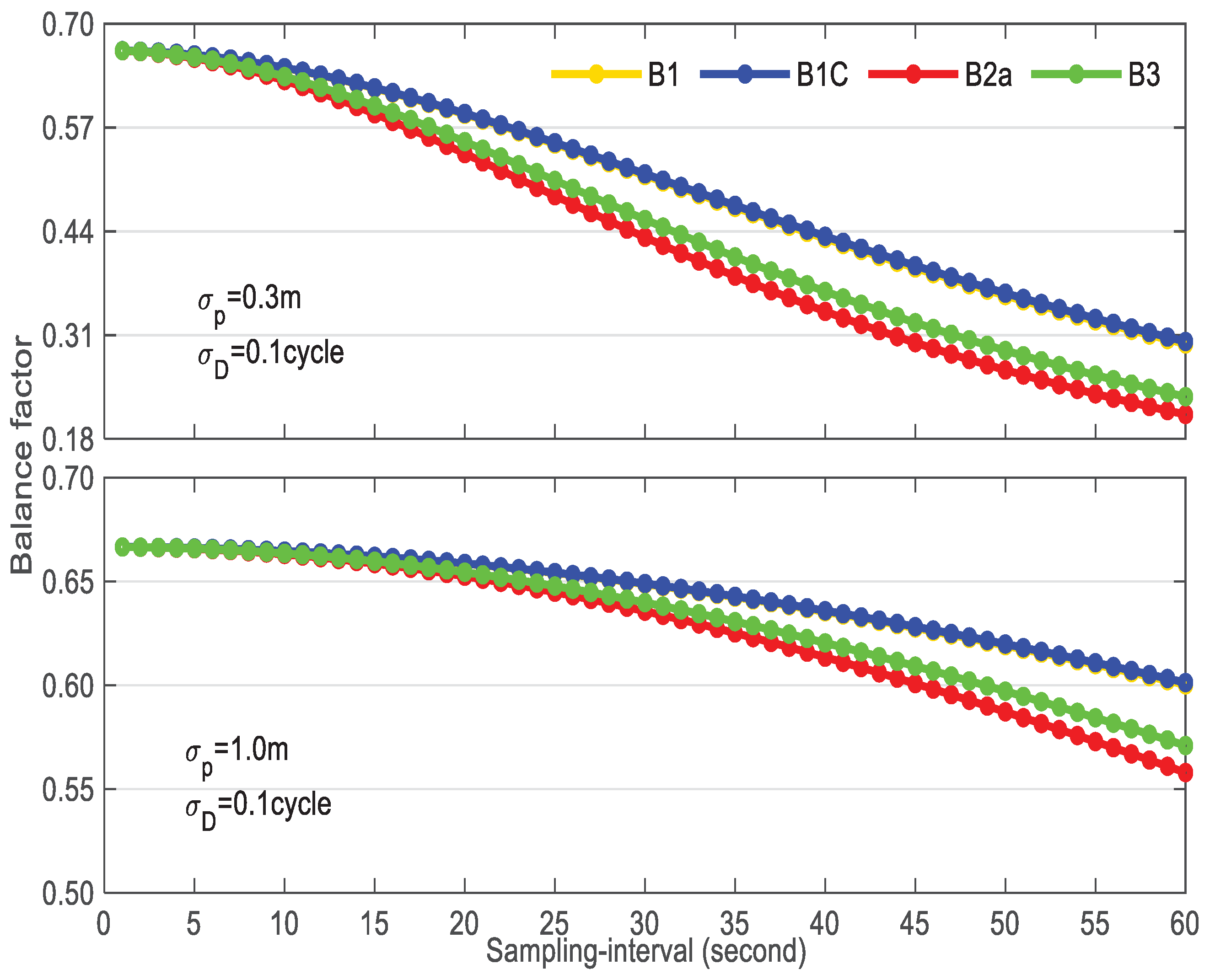
Figure 3 shows the relationships between sampling-interval and balance factor for all tracked signals (B1, B1C, B2a and B3). We should note that the noise level of raw-code measurement ranges from 0.3 m (upper subgraph) to 1.0 m (bottom subgraph) while the Doppler accuracy keeps stable (0.1 cycle). With the principle of minimal variance, the balance factor becomes smaller significantly with increasing sampling-interval, especially when the raw-code accuracy is sub-meter level. Although the downward trend of balance factor has slowed down, it is less than 0.5 ( σ p =0.3 m) for all signals when the sampling-interval is 30 s, which is instrumental in suppressing the integral cumulative error of Doppler and reducing the noise level of DSC.

3. Results

3.1. Datasets

The datasets were observed at the XIA1 station (outline coordinate: 34°22′N, 109°13′E), which is part of the international GNSS Monitoring and Assessment System (iGMAS) and is situated in Xi'an, Shaanxi Province. The GNSS receiver used at XIA1 is the CETC-54-GMR-4016, which can track all available B1/B3 BDS-2 (2I/6I) and B1/B1C/B2a/B3/BDS-3 (2I/1B/5I/6I) signals, except for the B2 signal. The datasets used in this article span from March 7th to March 10th, 2023, and include measurements of code, phase, Doppler, and SNR. The raw data has a sampling interval of 1 second, resulting in a total of 86,400 epochs in theory per day.

3.2. Elevation-dependent SCB correction model for BDS satellites

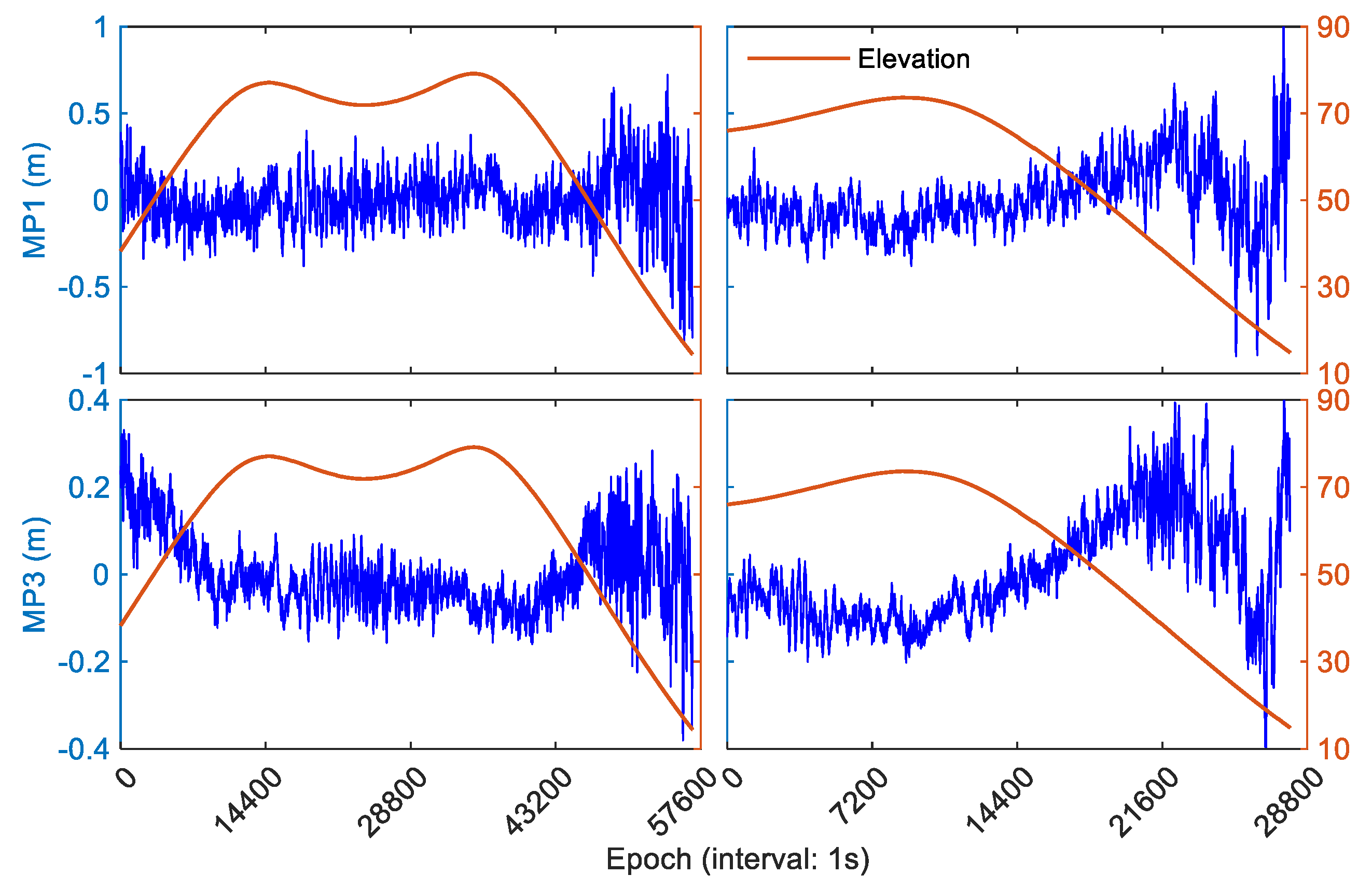
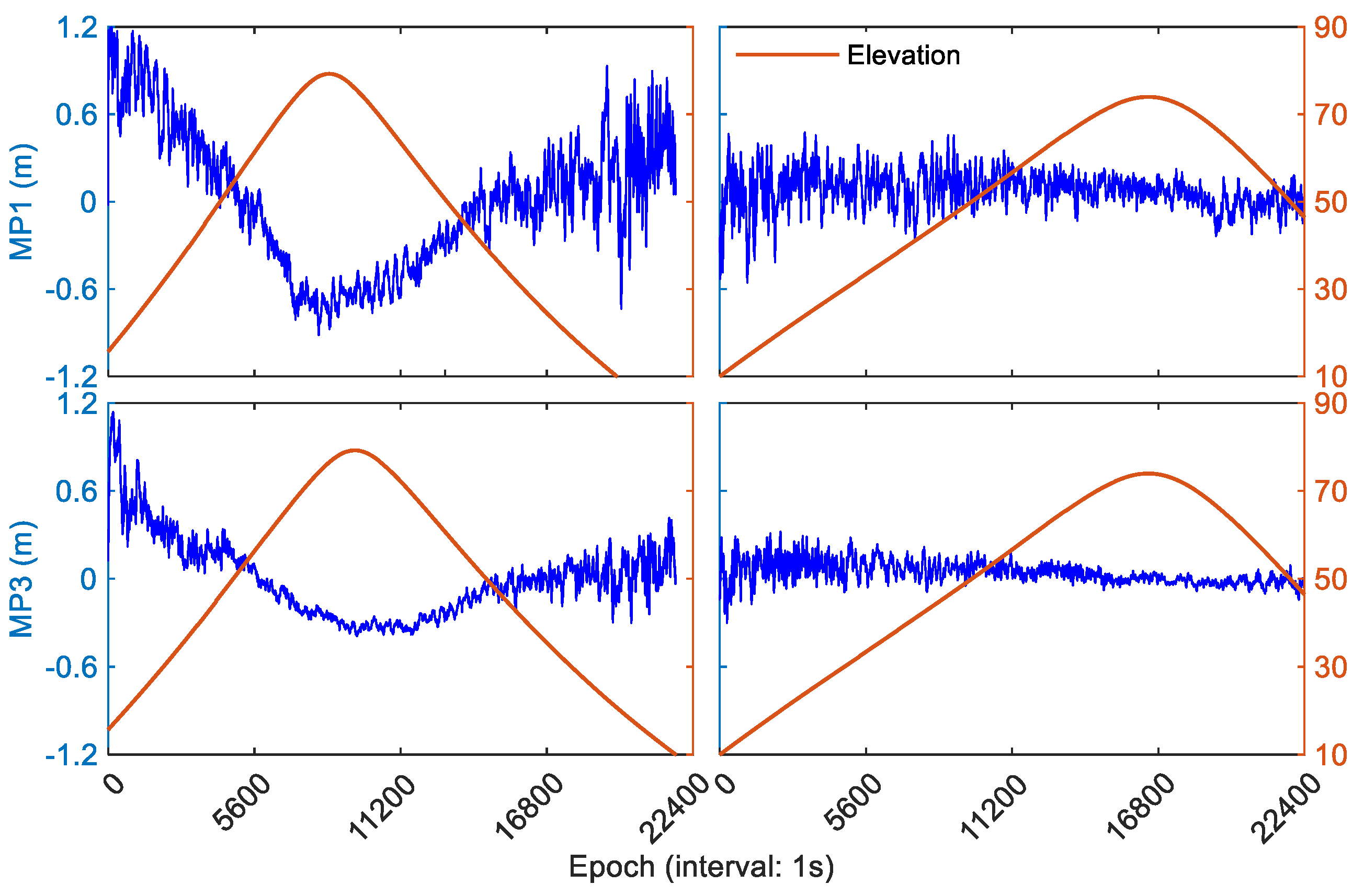
This section focuses on the SCB correction models for BDS un-GEO satellites based on the measurements from XIA1 station. For comparative analysis, the MP deviations and correction models of both IGSO and MEO satellites are provided. Two BDS-2 IGSO satellites (PRN: C07, C16), launched in 2011 and 2018, respectively, were selected to analyze the characters of MP time series due to their long observation durations.
Figure 4 illustrates the MP deviations of C07 and C16 as a function of time using raw code observables. The blue and red solid lines represent the MP series and elevation angles, respectively. To better represent the variations of SCB, the Y-axis scales of MP1 and MP3 are adjusted differently. Unlike random noise distribution, the SCB deviations exhibit apparent systematic bias in all instances, with a magnitude that can reach up to 1.0 m. Due to significant code noise, large fluctuations in MP deviations can be observed during satellites' ascent and descent epochs. The Root-Mean-Square (RMS) error is used to quantify the dispersion of the MP time series which can be calculated as
R M S = ∑ i = 1 n S i 2 n
where S i refers to the MP deviation and n is the total number of the MP series.
The RMS errors of MP deviations for the two selected IGSO satellites on B1 frequency are 0.16 and 0.20 m, respectively. In contrast, the RMS errors for these IGSO satellites on B3 frequency are better than 0.09 and 0.12 m, respectively. Analysis indicates that the SCB magnitude in code observables on both B1 and B3 frequencies for BDS-2 IGSO satellites are sub-meter level, and the code observation on B1 frequency is more sensitive to SCB than B3, resulting in an increase of RMS by approximately 50%.
Similarly, two MEO satellites (PRN: C12 and C24, launched in 2012 and 2018, respectively) were selected due to their longer measurement duration, and their MP time series as a function of time have been displayed in Figure 5. In comparison with IGSO satellites, it is evident that the code observables of BDS-2 MEO satellites are more susceptible to SCB. Negative correlation between this systematic bias and elevation-angle can be discovered in both MP1 and MP3 series, particularly in epochs with high elevation. The RMS errors of MP deviations of C12 are 0.47 and 0.27 m, respectively. Conversely, the RMS errors of C24 on B1 and B3 frequencies are reduced by 49.0% and 51.8% to 0.24 and 0.13 m, respectively. The results indicate that the systematic bias exists in code measurements on both B1 and B3 frequencies of BDS-2 MEO satellites, and the former is more easily affected by SCB than the latter, which happens to coincide with the conclusion of IGSO satellites.

3.3. Reconstruction and analysis of MP deviations with corrected code measurements

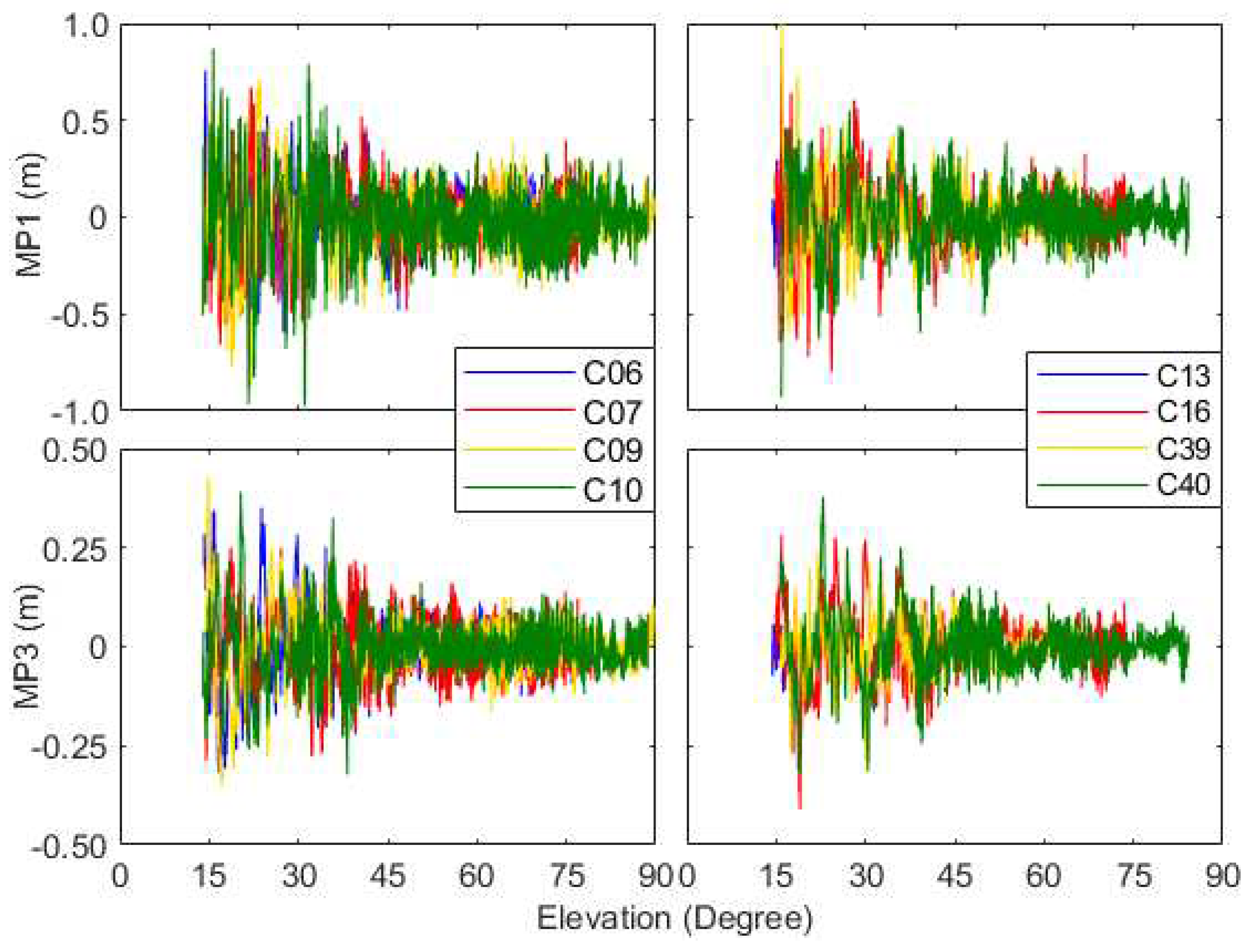
To verify the effectiveness of the previously established SCB correction model, the MP deviations were recalculated as a function of elevation angles on B1 and B3 frequencies for BDS IGSO satellites using corrected code observations (refer to Figure 6). The subfigure on the left displays the MP series of BDS-2 IGSO satellites (PRN: C06, C07, C09 and C10) launched before 2012, while the subfigure on the right shows the MP deviations of BDS-2/BDS-3 IGSO satellites (PRN: C13, C16, C39 and C40) launched after 2016. Due to the code multipath of surroundings and noise, there is a stochastic fluctuation, rather than a systematic bias, existing in the MP time series for all IGSO satellites on each frequency, especially in the conditions of low elevation. The maximum of MP1 deviations at these epochs can reach 1.0 m while the one of MP3 series are no more than 0.5 m. Compared to the results from Figure 3, the MP deviations on B1 and B3 frequencies approach zero with increasing elevation, thereby indicating that the corrections of SCB on raw code observables for BDS IGSO satellites are valid and effective. Moreover, the MP series from BDS-2 to BDS-3 IGSO satellites exhibit similar characteristics, as there are no apparent differences between them after the subtracting the SCB effect.
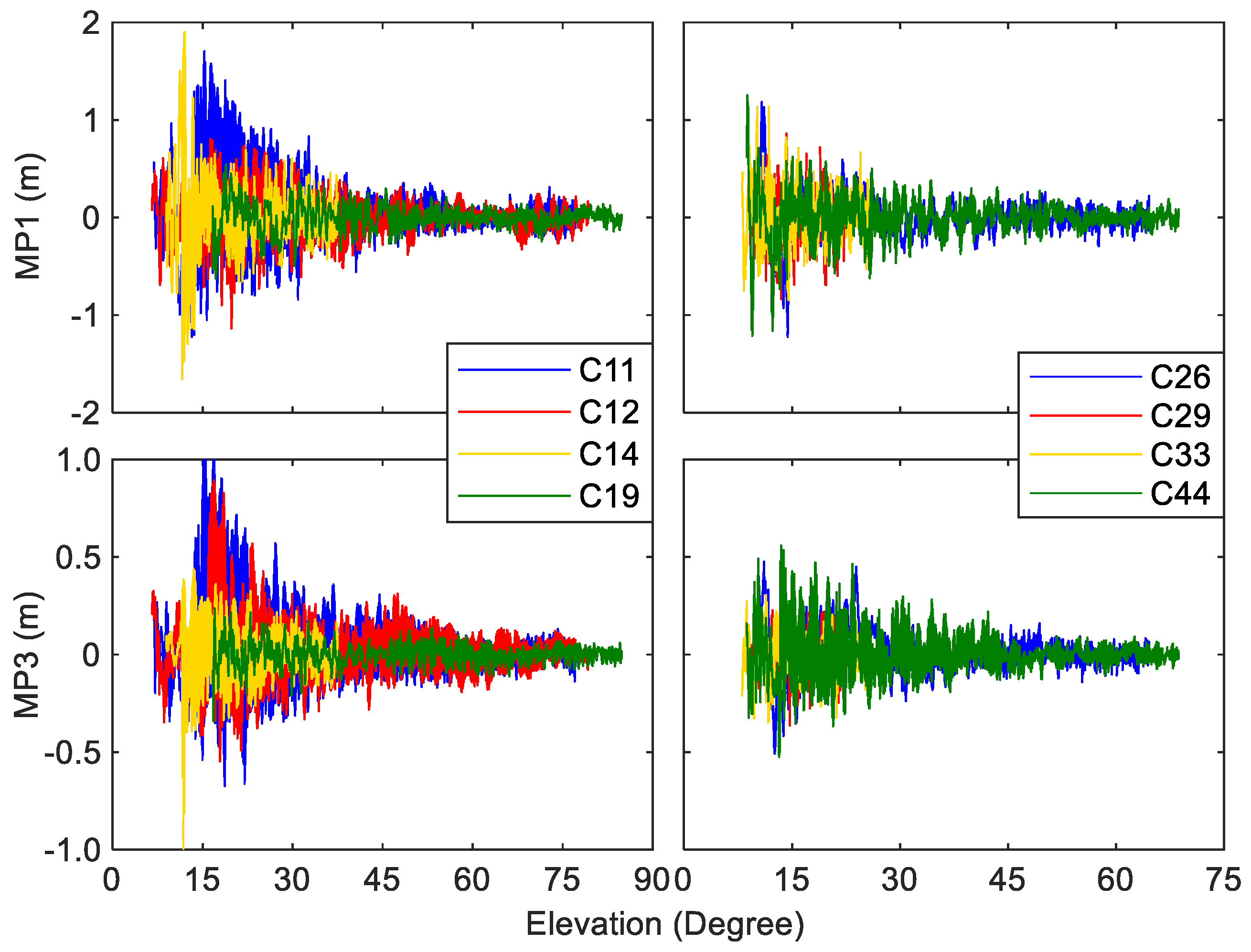
Figure 7 displays the MP deviations of BDS MEO satellites using corrected code measurements. The MP series of three BDS-2 MEO satellites (PRN: C11, C12, and C14, launched in 2012) and five BDS-3 MEO satellites (PRN: C19, C26, C29, C33, and C44, launched after 2017) are presented. The RMS of MP combinations on the B1 frequency is significantly larger than that on the B3 frequency, which may be attributed to the B3 frequency's code rate being five times higher than that of the B1 frequency, despite both using QPSK modulation. Furthermore, even with improved code observables, the maximums of MP1 and MP3 from BDS-2 MEO satellites can reach 2.0 and 1.0 meters, respectively, which is much larger than those from BDS-3 MEO satellites. Although there is no systematic bias observed in both MP1 and MP3 series, MP deviations of MEO satellites show significant fluctuations, particularly for BDS-2 MEO satellites, when compared to the results of IGSO satellites.
To further analyze the availability of the corrected code measurements, we have listed the RMS errors of MP time series for BDS satellites using raw and corrected code observables in Table 1. For BDS-2 IGSO satellites, the RMS errors of MP1 deviations using raw code measurements range from 0.16 to 0.22 m, whereas those of MP3 series using raw code measurements are much better (ranging from 0.09 and 0.18 m). For BDS-2 MEO satellites, the RMS errors of MP1 deviations range from 0.35 m to 0.54 m while the RMS errors of MP3 deviations range from 0.18 m to 0.30 m.
After applying the SCB correction model, for BDS-2 IGSO satellites, the maximum improvement of RMS errors of MP1 and MP3 are 33.3% and 66.7%, respectively. For BDS-2 MEO satellites, with the corrected code measurements, the RMS errors of MP1 can be reduced by 70.4%, 40.0% and 25.7% to 0.21, 0.17 and 0.14 m, respectively, which means that the code observations of BDS-2 MEO satellites are more susceptible to SCB. Compared with MP1, the improvement rates of MP3 only range from 22.2% (PRN: C14) to 32.0% (PRN: C12).
Compared with BDS-2 satellites, a reduction of below 28.6% in the RMS errors of MP deviations on BDS-3 satellites can be noticed, especially for BDS-3 MEO satellites, which reveals that the code observables from BDS-3 satellites are more resistant to the effect of SCB on both B1 and B3 frequencies.

3.4. Statistic and anylisis of code measurements with epoch-difference method

Now that the systematic bias in the raw code observations has been corrected through the application of SCB, our attention turns to reducing the measurement noise present in the data. As the ED method has been widely used to remove the effects of stable biases for GNSS signals, the noise level of ED-code can validate the effectiveness of the proposed smoothed-method and the formula can be expressed as [35]
Δ ε p 1 = Δ P 1 − Δ ϕ 1 − 2 Δ I 1 Δ ε p j = Δ P j − Δ ϕ j − 2 f 1 2 f j 2 Δ I 1
with
Δ I 1 = Δ ϕ 1 − Δ ϕ j f 1 2 / f j 2 − 1
where the subscript denotes the frequency ( j = 2,3 , ⋯ ), Δ P is the ED code measurement and Δ ϕ represents the time-differenced phase observable in meters.
With 24-hours clear GNSS measurements (here mainly refers to free of cycle-slip) from Xia1 station (doy: 066) and the empirical assumptions (i.e., σ p =0.3 m and σ D =0.1 cycle), the RMS errors of raw code, DSC and RDSC on B1 (upper) and B3 (bottom) frequencies are provided in Figure 8. To show the RMS errors clearly, the intervals of Y-axis are different. More specifically, the subfigures illustrate the noise level of code observations from BDS-2 IGSO satellites (PRN: C06-C10, C13 and C16) and MEO satellites (PRN: C11, C12, C14 and C24), respectively.
It is clear that the RMS errors of ED-code measurements become larger with interval-sampling increasing regardless of orbit types, especially when the sampling-interval exceeds 5 seconds. With respect to the noise magnitude of ED raw-code, they are basically at centimeter level, and the maximum of that is 16.5, 51.2, 94.4, 126.7 and 173.8 mm on B1 frequency, respectively when the sampling intervals vary from 1 to 30 s. Whereas the noise level on B3 frequency is better and the maximum of the RMS errors is 11.1, 22.0, 37.4, 52.8 and 86.2 mm, respectively. After the introduction of Doppler observables, the maximum RMS error of ED-DSC on B1 frequency is 15.1, 47.9, 83.5, 110.3 and 158.8 mm, respectively. By contrast, the maximum RMS error of ED-DSC on B3 frequency is smaller than those on B1 frequency, which can be reduced -3.8, -26.8, -48.6 and -63.8 and -95.8 mm with interval ranging from 1 to 30 s, respectively. These statistics reveal that the accuracy of ED-DSC is better than ED raw-code, which can be well-explained by the adoption of Doppler measurements. However, it should be noted that as the interval increase, this improvement become smaller or worse, indicating that the integral cumulative error of Doppler would affect the raw code accuracy with large sampling-interval.
For suppression of the integral cumulative error of Doppler, a balance factor is adopted to refine the DSC and the RMS errors of ED-RDSC have also been represented in Figure 6. Compared with results of DSC, the maximum of RMS errors on B1 frequency are reduced by 4.8%, 1.2%, 1.8%, 8.3% and 21.9% to 14.4, 47.3, 82.0, 101.1 and 124.0 mm, respectively. Meanwhile, the maximum of RMS errors on B3 frequency are reduced by 3.9%, -0.3%, -0.5%, 1.0%, 3.5%, respectively. Obviously, when the sampling interval is below 10 s, the integral cumulative error of Doppler is not large enough to affect the code precision, leading slight differences of RMS errors between DSC and RDSC. However, as the sampling interval gradually increases, the integral cumulative error of Doppler increases rapidly, causing negative impact on accuracy of DSC.
Based on the above findings, we can conclude that Doppler measurement is conducive to improving the accuracy of raw code observation with limited smooth window. Benefiting from the consideration of the balance factor, the integral cumulative error of Doppler is suppressed and RDSC can be widely used in challenged environment. It is noticed that the SCB correction model is not considered in this section. The main reason is that the SCB model is elevation-dependent and established by polynomial segment fitting algorithm (see Equations (21)), which means that the SCB corrections between consecutive epochs are basically identical because of the similar elevation-angles and then the SCB corrections would be removed with ED method.

3.5. Positioning accuracy of SPP with BDS-2 code measurements

In this section, the positioning performance of stand-alone positioning is provided with real measurements from XIA1 station. In consideration of weighted least square method, four schemes have been designed to calculate SPP: (1) raw code; (2) CSC; (3) DSC; (4) RDSC. For fair comparison, the smoothing window of above schemes is set at two, and Klobuchar and Saastamoninen models are applied to weaken the atmospheric delays. It should be noted that one GEO satellite (PRN: C05) is excluded because of its unhealth status and one IGSO satellite (PRN: C06) is also excluded due to its frequent data loss.
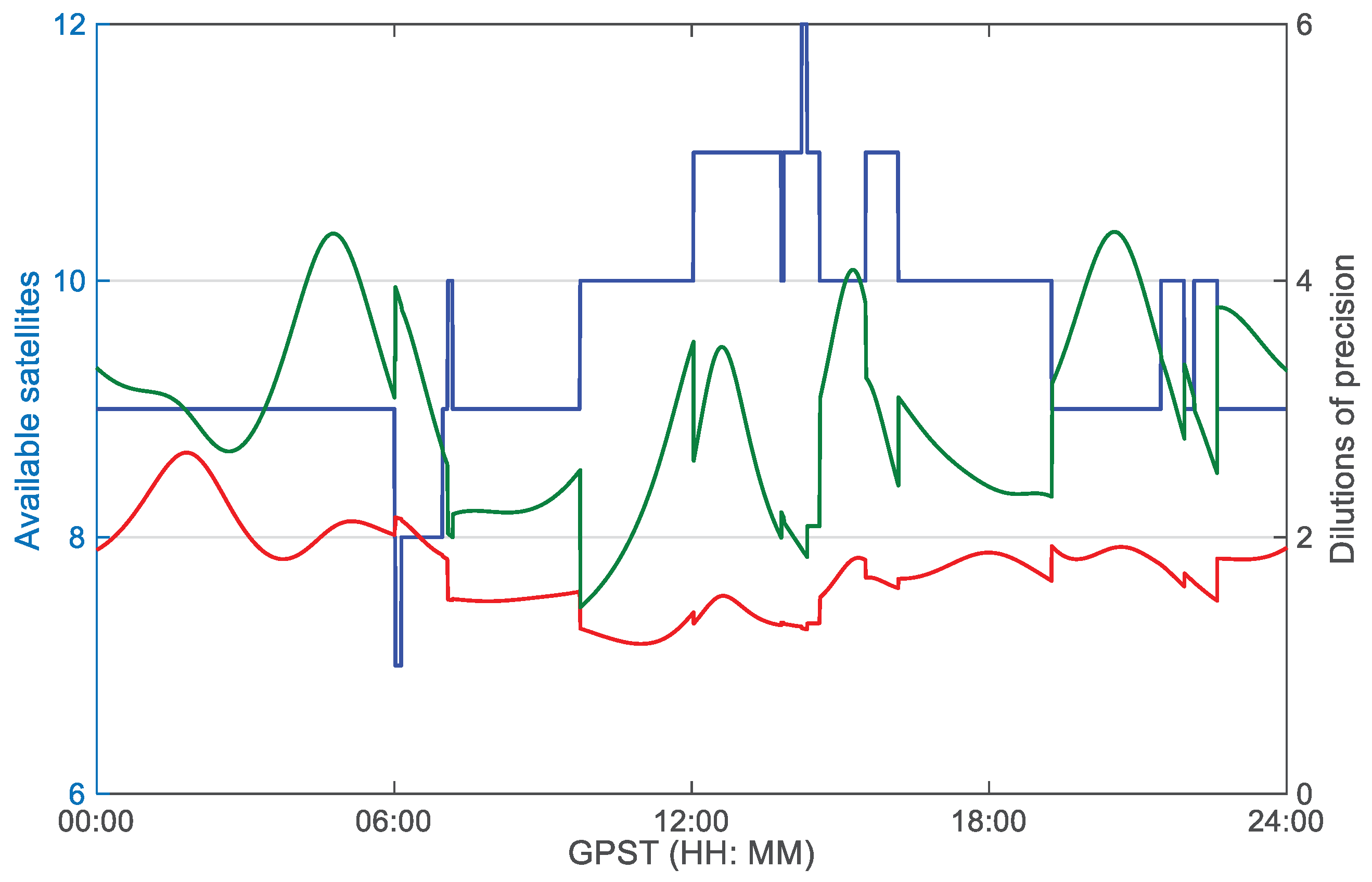
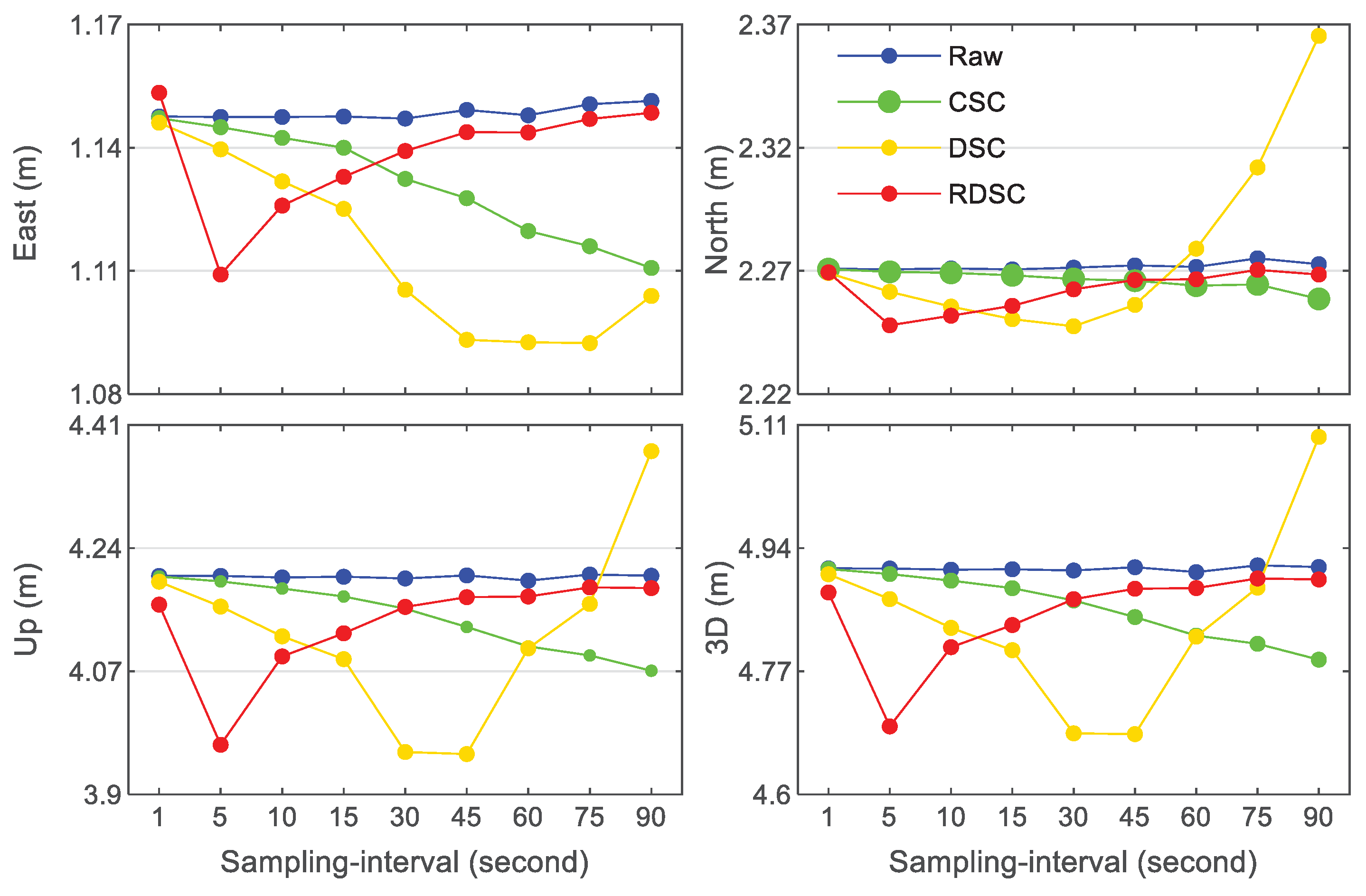
The available satellite numbers (PRN: C01-C04, C07-C14, C16), the horizontal and vertical dilutions of precision (HDOP and VDOP) have been shown in Figure 9. We noticed that the change of the available satellites results in the variation of dilution of precision (DOP). For an illustrative purpose, the final standard point positioning solution with dual-frequency phase observations is used as reference and then the RMS errors for three directions calculated by Equation (35) with changing sampling-intervals for above schemes are presented in Figure 10. The 3D RMS errors can be computed by
R M S ( 3 D ) = R M S ( E ) 2 + R M S ( N ) 2 + R M S ( U ) 2
The scheme (1) with raw code in Figure 9 usually produces worst positioning results and the RMS errors in the east, north and up directions can reach 1.51, 2.28 and 4.20 m, respectively, which remain almost same despite the changing sampling-intervals. On the contrary, during the increase of sampling-intervals, the RMS errors of the scheme (2) with CSC progressively decrease and they are better than 1.11, 2.26 and 4.07 m, respectively, which can be well-explained by the reduction of thermal noise. Similarly, the RMS errors of the scheme (3) with DSC become smaller with increasing sampling-interval, especially in the situations with small intervals. However, as a result of the integral cumulative error of Doppler observable, the RMS errors of DSC significantly increase when the sampling-interval exceeds 45 s, especially in north and up directions. When the interval is 90 s, the 3D RMS error of DSC is 5.09 m, which is raised by 3.7% in comparison with the one of raw code. Due to the introduction of the balance factor, the RMS errors of RDSC are better than those of DSC when the sampling-interval is more than 15 s, indicating that the balance factor can effectively adjust the contribution of raw code and smoothed code measurements.
For comparative analysis, the SPP performance of SCB with and without SCB correction has been listed in Table 2. The RMS errors of RDSC without SCB correction in east, north and up directions are given in Column 2 to 4, while the ones of RDSC with SCB correction (RDSC-SCB) are given in Column 5 to 7. Compared with the positioning statistics of raw code measurements, the improvement rates of RDSC and RDSC-SCB are presented in the last column. Regarding the SPP positioning precision, they are at meter level for RDSC, the mean RMS errors of which are 1.14, 2.26 and 4.17 m, respectively. Owing to the adjustment of balance factor, the differences of RMS errors between raw code and RDSC are getting smaller and the improvement rates are closer to zero with sampling-interval increasing from 1 to 90 s. After the application of SCB correction, the mean RMS errors in east and north directions increased by 3.75% and 1.46% to 1.187 and 2.298 m, respectively, whereas the mean RMS error in up direction is reduced by 10.14% to 3.743 m. The main reason may be that the effect of SCB on up direction is larger than that on horizontal directions in user-end, which coincides with the characters of multipath effect by previous research.

4. Discussion

The noise level of raw code observables from BDS-2 satellites is limited by thermal noise and systematic bias. To address the former, the CSC filter has been widely used in GNSS preprocessing processors with the prediction that carrier measurements lack cycle-slips. As the Doppler measurement is robust and immune to cycle-slip, it can be used to smooth raw code observation that resembles CSC. However, when the sampling-interval increase, the precision of DSC would decrease due to the significant increase of integral cumulative error of Doppler. Therefore, a balance factor is introduced to adjust the contributions of raw code and DSC, which can be helpful to enhance the reliability of SPP, especially in up-direction. When the GNSS is used in the challenged environment, the benefit from Doppler-aided smoothing code for position solution would be more significant.
Since the code measurements of BDS-2 satellite suffer from the systematic bias (SCB) which has proved to be dependent on elevation-angles and carrier-frequency. Therefore, in this paper, with minimizing the sum of absolute value of residuals, polynomial segment fitting algorithm is introduced to established the SCB correction as a function of elevation-angles for each BDS-2 un-GEO satellite and each frequency. After the applying the SCB correction model for each BDS-2 un-GEO satellite, the RMS values of MP time series can be reduced. For BDS-2 IGSO satellites, compared with MP1 deviations using raw code, the improvement rate of RMS errors of MP1 deviations can reach up to 66.7%. For BDS-2 MEO satellites, a reduction of 70.4% in the RMS errors of MP1 can be obtained. In addition, by contrast with MP1, the RMS errors of MP3 are obviously smaller than those of MP1, and most of the improvement rates is no more than 32.0%. These numerical experiments reveal that the code measurements of MEO satellites are more susceptible to SCB than IGSO satellites and the code observables on B3 frequency are more resistant to SCB than B1 frequency.
The positioning accuracies of the raw code are 1.514, 2.275 and 4.202 m, respectively, while the RMS errors of the CSC are better than 1.111, 2.259 and 4.071 m, respectively. Similarly, the RMS errors of the DSC become smaller with increasing sampling-interval in the situations of small intervals. However, when the interval increases from 45 to 90 s, the 3D RMS error of DSC become worst (5.094 m). Due to the introduction of the balance factor, the RMS errors of RDSC are better than those of DSC when the sampling-interval is more than 15 s. After the application of SCB correction, the mean RMS errors in east and north directions increased by 3.75% and 1.46% to 1.187 and 2.298 m, respectively, whereas the mean RMS error in up direction is reduced by 10.14% to 3.743 m. One possible reason is that the SCB correction models are simply established for BDS-2 un-GEO satellites expect for GEO satellites, leading the decrease of the SPP precision.
Due to the orbit characteristic of GEO satellite, few studies pay attention to the SCB correction model for GEO satellite, which will be the focus of our future research. Then, with continuous improvement of SCB model for each BDS satellite, a better performance of stand-alone positioning with code observations would be more promising.

5. Conclusions

As the Doppler measurement is robust and immune to cycle-slip, it can be used to smooth raw code observation that resembles CSC. Compared with raw code and CSC, the noise level and positioning accuracy of DSC can be improved, especially in the situation of high sampling frequency. However, when the sampling-interval increase, the precision of DSC would decrease due to the significant increase of integral cumulative error of Doppler observation. Therefore, a balance factor is introduced to adjust the contributions of raw code and DSC, which can be helpful to enhance the reliability of SPP. When the GNSS receiver is located in the challenged environment, the benefit from Doppler-aided smoothing code for position solution would be more significant.
The smoothed filter, such as the CSC and DSC, can significantly enhance the precision of code measurements by assuming that the measurement noise follows a zero-mean Gaussian distribution. However, this assumption can be violated by the SCB effect present in the code measurements of BDS satellites. As a result, extensive research has been conducted to investigate the SCB variations of un-GEO satellites, and applying the SCB correction model for each un-GEO satellite and frequency has been found to effectively reduce the RMS values of MP time series and improve SPP performance.
Despite these efforts, few studies have focused on developing an SCB correction model for GEO satellites, owing to their unique orbit characteristics. Therefore, our future research will aim to address this gap and develop an effective SCB correction model for GEO satellites. With continuous improvements in the SCB model for each BDS satellite, we can expect a significant enhancement in the performance of stand-alone positioning with code observations.

Author Contributions

Conceptualization, X.G. and Z.M.; methodology, X.G. and L.P.; software, X.G.; validation, X.G. and L.J.; formal analysis, X.G. and Z.M.; investigation, X.G. and L.P.; resources, X.G.; data curation, L.J.; writing—original draft preparation, X.G. and L.P.; writing—review and editing, Z.M. and L.P.; visualization, L.J. and L.P.; supervision, L.P.; project administration, X.G.; funding acquisition, X.G. All authors have read and agreed to the published version of the manuscript.

Funding

This research is funded by the National Natural Science Foundation of China (No. 62276207), the Key Research and Development Project of Shaanxi Construction Engineering Holding Group (No. 20211177-ZKT05) and the Key Research and Development Project of China Energy Engineering Group Co., Ltd. (No. CEEC2022-ZDYF-01). We would like to express our sincere gratitude to the iGMAS and its Multi-GNSS Experiment for providing the real measurements.

Data Availability Statement

Publicly available datasets were analyzed in this study. This data can be found from iGMAS.

Acknowledgments

The contribution of data from iGMAS is appreciated.

Conflicts of Interest

The authors declare no conflict of interest. The funders had no role in the design of the study; in the collection, analyses, or interpretation of data; in the writing of the manuscript, or in the decision to publish the results.

References

  1. Hofmann-Wellenhof, B.; Lichtenegger, H.; Collins, J. Global positioning system: theory and practice, 5th ed.; Springer: New York, USA, 2001; pp. 181–188. [Google Scholar]
  2. Xu, G.; Xu, Y. Parameterization and algorithms of GPS data processing. In GPS theory, algorithms and applications, 3rd ed.; Springer: New York, USA, 2016; pp. 291–300. [Google Scholar]
  3. Won, J.H.; Pany, T. Signal processing. In Springer handbook of global navigation satellite systems, 1st ed.; Teunissen, P.J.G., Montenbruck, O., Eds.; Springer: New York, USA, 2017; pp. 428–434. [Google Scholar]
  4. Hatch, R. The synergism of GPS code and carrier measurements. In Proceedings of the 3rd international geodetic symposium on satellite Doppler positioning, Las Cruces, New Mexico, USA, 8-12 February 1982. [Google Scholar]
  5. Hatch, R. Dynamic differential GPS at the centimeter level. In Proceedings of the 4th international geodetic symposium on satellite positioning, Austin, Texas, USA, 28 April-2 May 1986. [Google Scholar]
  6. Hwang, P.Y.; McGraw, G.A.; Bader, J.R. Enhanced differential GPS carrier-smoothed code processing using dual-frequency measurements. Navigation 1999, 46, 127–138. [Google Scholar] [CrossRef]
  7. Bisnath, S.B.; Langley, R.B. High-precision, kinematic positioning with a single GPS receiver. Navigation 2002, 49, 161–169. [Google Scholar] [CrossRef]
  8. Park, B.; Sohn, K.; Kee, C. Optimal Hatch filter with an adaptive smoothing window width. J Navig 2008, 61, 435–454. [Google Scholar] [CrossRef]
  9. Gunther, C. , Henkel, P. Reduced-noise ionosphere-free carrier smoothed code. IEEE T AERO ELEC SYS 2010, 46(1), 323–334. [Google Scholar] [CrossRef]
  10. Gao, X.; Yang, Z.; Du, Y.; Yang, B. An improved real-time cycle slip correction algorithm based on Doppler-aided signals for BDS triple-frequency measurements. Adv Space Res 2021, 67, 223–233. [Google Scholar] [CrossRef]
  11. Geng, J. , Jiang, E., Li, G., Xin, S., Wei, N. An Improved Hatch Filter Algorithm towards SubMeter Positioning Using only Android Raw GNSS Measurements without External Augmentation Corrections. Remote Sens 2019, 11, 1679. [Google Scholar] [CrossRef]
  12. Cheng, P. Remarks on Doppler-aided smoothing of code ranges. J Geod 1999, 73(1), 23-2. [Google Scholar] [CrossRef]
  13. Kubo, N. Advantage of velocity measurements on instantaneous RTK positioning. GPS Solut 2009, 13(4), 271–280. [Google Scholar] [CrossRef]
  14. Chen, C. , Chang, G., Luo, F., Zhang, S. Dual-frequency carrier smoothed code filtering with dynamical ionospheric delay modeling. Adv Space Res 2019, 63(2), 857–870. [Google Scholar] [CrossRef]
  15. Bruton, A.M.; Glennie, C.L.; Schwarz, K.P. Differentiation for high-precision GPS velocity and. acceleration determination. GPS Solut 1999, 2(4), 7–21. [Google Scholar] [CrossRef]
  16. Lee, H.; Rizos, C.; Jee, G.I. Position domain filtering and range domain filtering for carrier-smoothed-code DGNSS: an analytical comparison. IEE Proc. Radar Sonar Navig 2005, 152(4), 271–276. [Google Scholar] [CrossRef]
  17. Zhang, J.; Zhang, K.; Grenfell, R.; Deakin, R. Short note: on the relativistic Doppler effect for precise velocity determination using GPS. J Geod 2006, 80, 104–110. [Google Scholar] [CrossRef]
  18. Zhang, X.; Guo, B.; Guo, F.; Du, C. Influence of clock jump on the velocity and acceleration estimation with a single GPS receiver based on carrier-phase-derived Doppler. GPS Solut 2013, 17, 549–559. [Google Scholar] [CrossRef]
  19. Bahrami, M.; Ziebart, M. A Kalman filter-based Doppler-smoothing of code pseudoranges in GNSS-challenged environments. In Proceedings of the 24th international technical meeting of the satellite division of the institute of navigation (ION GNSS 2011), Portland, Oregon, USA, 19-23 September 2011. [Google Scholar]
  20. Zhou, Z.; Li, B. Optimal Doppler-aided smoothing strategy for GNSS navigation. GPS Solut 2017, 21, 197–210. [Google Scholar] [CrossRef]
  21. Zhang, K.; Jiao, W.; Wang, L.; Li, Z.; Li, J.; Zhou, K. Smart-RTK: Multi-GNSS kinematic positioning approach on android smart devices with Doppler-smoothed-code filter and constant acceleration model. Adv Space Res 2019, 64, 1662–1674. [Google Scholar] [CrossRef]
  22. Zhou, H.; Li, Z.; Liu, C.; Xu, J.; Li, S.; Zhou, K. Assessment of the performance of carrier-phase and Doppler smoothing code for low-cost GNSS receiver positioning. Results Phys 2020, 19, 103574. [Google Scholar] [CrossRef]
  23. Li, R.; Zheng, S.; Wang, E. et al. Advances in BeiDou Navigation Satellite System (BDS) and satellite navigation augmentation technologies. Satell Navig 2020, 1, 12. [Google Scholar] [CrossRef]
  24. Yang, Y. , Ren, X., Jia, X., Sun, B. Development trends of the national secure PNT system based on BDS. Sci. China Earth Sci. 2023, 66, 929–938. [Google Scholar] [CrossRef]
  25. Hauschild, A.; Montenbruck, O.; Sleewaegen, J.M.; Huisman, L.; Teunissen, P.J.G. Characterization of COMPASS M-1 signals. GPS Solut 2012, 16, 117–126. [Google Scholar] [CrossRef]
  26. Wanninger, L.; Beer, S. BeiDou satellite-induced code pseudorange variations: Diagnosis and therapy. GPS Solut 2015, 19, 639–648. [Google Scholar] [CrossRef]
  27. Lei, W.; Wu, G.; Tao, X.; Bian, L.; Wang, L. BDS satellite-induced code multipath: Mitigation and assessment in new-generation IOV satellites. Adv Space Res 2017, 60, 2672–2679. [Google Scholar] [CrossRef]
  28. Guo, F.; Li, X.; Liu, W. Mitigating BeiDou Satellite-Induced Code Bias: Taking into Account the Stochastic Model of Corrections. Sensors 2016, 16, 909. [Google Scholar] [CrossRef]
  29. Lou, Y.; Gong, X.; Gu, S.; Zheng, F.; Feng, Y. Assessment of code bias variations of BDS triple-frequency signals and their impacts on ambiguity resolution for long baselines. GPS Solut 2017, 21, 177–186. [Google Scholar] [CrossRef]
  30. Zou, X.; Li, Z.; Li, M.; Tang, W.; Deng, C.; Chen, L.; Wang, C.; Shi, C. Modeling BDS pseudorange variations and models assessment. GPS Solut 2017, 21, 1661–1668. [Google Scholar] [CrossRef]
  31. Pan, L.; Guo, F.; Ma, F. An improved bds satellite-induced code bias correction model considering the consistency of multipath combinations. Remote Sens 2018, 10, 1189. [Google Scholar] [CrossRef]
  32. Zhang, X.; Li, X.; Lu, C.; Wu, M.; Pan, L. A comprehensive analysis of satellite-induced code bias for BDS-3 satellites and signals. Adv Space Res 2019, 639, 2822–2835. [Google Scholar] [CrossRef]
  33. McGraw, G.A. Generalized divergence-free carrier smoothing with applications to dual frequency differential GPS. Navigation 2009, 56(2), 115–122. [Google Scholar] [CrossRef]
  34. Shu, B.; Liu, H.; Xu, L.; Gong, X.; Qian, C.; Zhang, M.; Zhang, R. Analysis of satellite-induced factors affecting the accuracy of the BDS satellite differential code bias. GPS Solut 2017, 21, 905–916. [Google Scholar] [CrossRef]
  35. Zhou, R.; Hu, Z.; Zhao, Q.; Li, P.; Wang, W.; He, C.; Cai, C.; Pan, Z. Elevation-dependent pseudorange variation characteristics analysis for the new-generation BeiDou satellite navigation system. GPS Solut 2018, 22, 60. [Google Scholar] [CrossRef]
Preprints 75473 g001
Figure 1. Traditional Hatch filter algorithm diagram.
Figure 1. Traditional Hatch filter algorithm diagram.
Preprints 75473 g001
Preprints 75473 g002
Figure 2. Relationship between sampling-interval and SW ( σ p =0.3 m and σ D =0.1 cycle).
Figure 2. Relationship between sampling-interval and SW ( σ p =0.3 m and σ D =0.1 cycle).
Preprints 75473 g002
Preprints 75473 g003
Figure 3. Relationship between the sampling-interval and balance factor (Upper: σ p =0.3m and σ D =0.1 cycle; Bottom: σ p =1.0 m and σ D =0.1 cycle)
Figure 3. Relationship between the sampling-interval and balance factor (Upper: σ p =0.3m and σ D =0.1 cycle; Bottom: σ p =1.0 m and σ D =0.1 cycle)
Preprints 75473 g003
Preprints 75473 g004
Figure 4. MP time series (blue) and elevation angles (red) of BDS-2 IGSO satellites as a function of time using raw code measurements (Left: C07; Right: C16).
Figure 4. MP time series (blue) and elevation angles (red) of BDS-2 IGSO satellites as a function of time using raw code measurements (Left: C07; Right: C16).
Preprints 75473 g004
Preprints 75473 g005
Figure 5. MP time series and elevation angles of BDS MEO satellites as a function of time using raw code measurements (Left: C12; Right: C24).
Figure 5. MP time series and elevation angles of BDS MEO satellites as a function of time using raw code measurements (Left: C12; Right: C24).
Preprints 75473 g005
Preprints 75473 g006
Figure 6. MP time series of BDS IGSO satellites as a function of elevation angles using improved code measurements corrected by previously established SCB correction model (Upper; MP1; Bottom: MP3).
Figure 6. MP time series of BDS IGSO satellites as a function of elevation angles using improved code measurements corrected by previously established SCB correction model (Upper; MP1; Bottom: MP3).
Preprints 75473 g006
Preprints 75473 g007
Figure 7. MP time series of BDS MEO satellites as a function of elevation angles using improved code measurements corrected by previously established SCB correction model (Upper; MP1; Bottom: MP3).
Figure 7. MP time series of BDS MEO satellites as a function of elevation angles using improved code measurements corrected by previously established SCB correction model (Upper; MP1; Bottom: MP3).
Preprints 75473 g007
Preprints 75473 g008
Figure 8. RMS errors of ED-code measurements for BDS satellites (Left: raw code; Middle: DSC; Right: RDSC).
Figure 8. RMS errors of ED-code measurements for BDS satellites (Left: raw code; Middle: DSC; Right: RDSC).
Preprints 75473 g008
Preprints 75473 g009
Figure 9. Number of available satellites, HDOP and VDOP series using dataset collected at XIA1 station on March 7th, 2023 (sampling-interval: 1s).
Figure 9. Number of available satellites, HDOP and VDOP series using dataset collected at XIA1 station on March 7th, 2023 (sampling-interval: 1s).
Preprints 75473 g009
Preprints 75473 g010
Figure 10. RMS errors of SPP in east, north and up directions with different sampling-intervals using BDS raw code and smoothed code measurements.
Figure 10. RMS errors of SPP in east, north and up directions with different sampling-intervals using BDS raw code and smoothed code measurements.
Preprints 75473 g010
Table 1. RMS errors of MP time series on B1 and B3 frequencies for BDS available satellites with and without SCB corrections.
Table 1. RMS errors of MP time series on B1 and B3 frequencies for BDS available satellites with and without SCB corrections.
BDS-2
PRN		 Orbit Type Launch Date RMS of Raw Code RMS of Corrected Code Improvement
B1 B3 B1 B3 B1 B3
C06 IGSO 2010-08-01 0.21 0.11 0.14 0.07 33.3% 36.4%
C07 IGSO 2010-12-18 0.16 0.09 0.14 0.06 12.5% 33.3%
C09 IGSO 2011-07-27 0.19 0.12 0.17 0.07 10.5% 41.7%
C10 IGSO 2011-12-02 0.22 0.09 0.16 0.06 27.3% 33.3%
C13 IGSO 2016-03-30 0.21 0.18 0.14 0.06 33.3% 66.7%
C16 IGSO 2018-07-10 0.21 0.13 0.15 0.07 28.6% 46.2%
C39 IGSO 2019-06-25 0.21 0.07 0.19 0.05 9.5% 28.6%
C40 IGSO 2019-11-05 0.13 0.06 0.13 0.06 0 0
C11 MEO 2012-04-30 0.54 0.30 0.16 0.21 70.4% 30.0%
C12 MEO 2012-04-30 0.45 0.25 0.27 0.17 40.0% 32.0%
C14 MEO 2012-09-19 0.35 0.18 0.26 0.14 25.7% 22.2%
C19 MEO 2017-11-05 0.19 0.06 0.19 0.05 0 16.7%
C26 MEO 2018-07-29 0.22 0.11 0.16 0.08 27.3% 27.3%
C29 MEO 2018-03-30 0.29 0.12 0.27 0.11 6.9% 8.3%
C33 MEO 2018-09-19 0.30 0.12 0.26 0.09 13.3% 25.0%
C44 MEO 2019-11-23 0.19 0.13 0.19 0.12 0 7.7%
Table 2. RMS statistics of positioning errors in east, north and up directions for BDS-2 satellites using RDSC with and without SCB correction (unit: m).
Table 2. RMS statistics of positioning errors in east, north and up directions for BDS-2 satellites using RDSC with and without SCB correction (unit: m).
Interval
(second)		 RMS of RDSC RMS of RDSC-SCB 3D Improvement rate (%)
East North Up East North Up
1 1.153 2.269 4.162 1.111 2.312 3.693 0.68 / 8.46
15 1.133 2.256 4.122 1.186 2.299 3.716 1.57 / 6.20
30 1.139 2.262 4.159 1.195 2.286 3.752 0.81 / 5.44
45 1.144 2.266 4.172 1.200 2.289 3.773 0.60 / 5.13
60 1.144 2.267 4.173 1.203 2.291 3.772 0.45 / 5.19
75 1.147 2.270 4.186 1.207 2.309 3.781 0.37 / 5.00
90 1.148 2.268 4.185 1.206 2.303 3.815 0.35 / 4.58
* Improvement rate is the ratio of 3D RMS of RDSC or RDSC-SCB to 3D RMS of raw code.
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.
Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.
Prerpints.org logo

Preprints.org is a free preprint server supported by MDPI in Basel, Switzerland.

facebook logotwitter logolinkedin logo
MDPI Initiatives
Important Links
Subscribe

Disclaimer

Terms of Use

Privacy Policy

© 2024 MDPI (Basel, Switzerland) unless otherwise stated