Prerpints.org logo
Preprint
Article

Predicting the Effect of Mutations on Protein Stability and Binding: Assessment of Leading Algorithms Performance and Databases Content with Respect to Types of Mutations

Altmetrics

Downloads

271

Views

184

Comments

0

A peer-reviewed article of this preprint also exists.

supplementary.zip (10.16MB )

Submitted:

01 June 2023

Posted:

02 June 2023

You are already at the latest version

Alerts
Abstract
Development of methods and algorithms to predict the effect of mutations on protein stability, protein-protein, and protein-DNA/RNA binding is necessitated by the needs of protein engineering and for understanding the molecular mechanism of disease-causing variants. The vast majority of the leading methods are either methods with adjustable parameters or machine learning algorithms, both requiring a database of experimentally measured folding and binding free energy changes. These databases are collections of experimental data taken from scientific investigations typically aimed at probing the role of particular residue on the above-mentioned thermodynamics characteristics, i.e., the mutations are not introduced at random and do not necessarily represent mutations originating from single nucleotide variant (SNV). Thus, the reported performance of the leading algorithms assessed on these databases or other limited cases, may not be applicable for predicting the effect of SNVs seen in the human population. Indeed, we demonstrate that the SNVs and non-SNVs are not equally presented in the corresponding databases and the distribution of the free energy changes are not the same. Furthermore, the Pearson correlation coefficients (PCCs) obtained on cases involving SNVs are less impressive than for non-SNVs, indicating that caution should be used in applying them to reveal the effect of human SNVs. All methods are found to underestimate the energy changes by roughly a factor of 2.
Keywords: 
Subject: Biology and Life Sciences  -   Biochemistry and Molecular Biology

1. Introduction

Biological macromolecules, proteins, DNA, and RNAs, perform their function by adopting a particular 3D structure and being involved in a set of interactions. For many proteins, excluding intrinsically disordered proteins (IDPs), the correctly folded 3D structure is needed to prevent them from protease degradation and to form the desired catalytic set of residues, binding interface, and other functionally important structural features [1,2]. The assessment of the stability of such a 3D structure is done via a thermodynamic quantity called folding free energy, i.e., the difference between folded free and unfolded free energies (ΔGfolding). Another important process is the binding of biological macromolecules at which they adopt particular 3D complexes, including the cases of IDPs which upon the binding form a well-defined 3D structure [3,4]. Similarly, as above, the ability of macromolecules to form a macromolecular complex is assessed via binding free energy (ΔGbinding), i.e., the difference between the free energy of bound and unbound states. Thus, because of their importance for the biological function of macromolecules, the ΔGfolding and ΔGbinding were extensively investigated experimentally and many methods for predicting them were developed [5,6,7,8,9,10].
The vast majority of the experimental works were done to assess the impact of a given residue on either ΔGfolding or ΔGbinding, involving the substitution of wild-type residue to alanine (alanine scanning) [11,12,13]. This raises the question about the balance of investigator-initiated mutations versus mutations seen in nature, i.e., in the human population which are single nucleotide variants (SNVs). It should be mentioned that mutations and SNVs are both, types of genetic variations that can occur in the DNA sequence (this article focuses on missense mutations, i.e., mutations that result in a change of the amino acid sequence of the corresponding protein). However, there is a subtle difference between the two terms, since a mutation is a broader term that refers to any change in the DNA sequence that is different from the wild type or the reference sequence, while SNV is a specific type of mutation that involves the substitution of a single nucleotide (A, T, C, or G) at a specific position in the DNA sequence. Thus, SNVs are a type of mutation, but not all mutations are SNVs. In this article, we will provide an assessment of the distribution of SNVs and non-SNVs and the corresponding free energy changes reported in the most popular databases.
Here we briefly outline some of the popular databases of experimentally measured thermodynamic quantities related to protein stability, protein-DNA interaction and protein-protein binding often used by researchers for developing and assessing the performance of new methods for predicting the stability of proteins and their interactions with other protein and/or DNA. ProTherm [14,15] is a database that consists of the experimentally measured ΔGfolding of wild-type protein along with single and multiple mutations. In addition, it also provides information about the experimental conditions such as pH and temperature. ProNIT and ProNAB are databases of experimentally determined protein-nucleic acid ΔGbinding [16,17]. Both these databases contain a variety of parameters including information about the experimental conditions. Similarly, SKEMPI (Structural Kinetics and Energetics of Mutant Protein Interactions) is a database of experimentally measured binding free energy changes [18,19]. It includes data for a wide range of protein-protein complexes, and the mutations are annotated with information about their structural and functional effects.
There are numerous computational methods available for predicting the effect of mutations on protein stability and binding [20,21,22,23]. These methods can be broadly divided into two categories: empirical/machine learning (ML) methods and physics-based methods. Empirical methods are based on a statistical analysis of experimental data and use machine learning algorithms to predict the effect of mutations on ΔGfolding and ΔGbinding. Physics-based methods, on the other hand, use principles of thermodynamics and statistical mechanics to predict the effect of mutations on protein stability. However, these methods can account for the complex physical interactions that determine protein stability but require detailed structural information about the protein and are computationally expensive, which makes them non-applicable for genome-scale investigations. In this article, we only deal with fast methods, the methods using either adjustable parameters or utilizing machine learning.
For predicting the effect of mutation on protein stability several methods have been developed, which can be broadly grouped into structure-based methods and sequence-based methods. The structure-based methods use the protein structure information to derive the features for the wild-type and the mutant protein and then predict the free energy change of the protein due to mutation. The list of the most popular structure-based methods includes FoldX [24], PoPMuSiC [25], mCSM [26], STRUM [27], SDM2 [28], and SAAFEC [29]. The main limitation of these methods is the availability of the 3D structure of the protein of interest. Indeed, only a tiny fraction of known proteins have 3D structures experimentally determined, which limits the applicability of these methods. This prompted the development of methods that utilize sequence information alone, the sequence-based methods. The most popular include I-Mutant 2.0 [30], Evolutionary, Amino acid, and Structural Encodings with Multiple Models [31], Impact of Non-synonymous mutations on Protein Stability [32], BoostDDG [33], and SAAFEC-SEQ [34]. These methods can be applied to genome-scale investigations. Furthermore, it was demonstrated that they outperform some of the structure-based methods despite using sequence information only [34].
The protein-protein binding affinity change of point mutation has also drawn the attention of the research community. Several computational methods have been reported in the literature for the prediction of binding free energy change due to point mutations. These methods can be classified into physics-based and knowledge-based methods. The knowledge-based/empirical methods are generally fast and hence better suited for genome-level screening applications like FoldX [24], SAAMBE [35], SAAMBE-3D [36], BindProfX [37], iSEE [38], BeAtMuSiC [39], mCSM-PPI2 [40], MutaBind2 [41] require the 3D structure of the complex. In addition, there are a couple of sequence-based methods like SAAMBE-SEQ [42] and ProAffiMuSeq [43] which require sequence only to predict the ΔΔGbinding due to the mutation.
Similarly, computational methods for predicting the effect of mutation on protein-nucleic acid ΔGbinding have also been developed. The available methods are fewer than the methods for predicting the change of the folding or binding free energy of protein-protein interactions, and they all require structural information. The list is quite short and includes FoldX [24], mCSM-NA [44], PremPDI [45], SAMPDI [46], and SAMPDI-3D [47]. It is also to be noted down here that except SAMPDI-3D, which is a machine learning-based method, all other methods available for the prediction are either physics-based or empirical. In addition, only SAMPDI-3D [47] allows the prediction of change in protein-DNA binding affinity caused by mutation of DNA bases.
The predictions of the effect of mutations on ΔGfolding and ΔGbinding are essential for protein engineering and understanding the effect of natural variants, i.e., SNVs. We argue that these two tasks may require slightly different approaches and methods. Thus, protein engineering requires methods capable of correctly predicting the effect of any type of mutation on either ΔGfolding and ΔGbinding, with the goal to design more stable proteins or protein-protein and protein-DNA/RNA complexes with better affinity, without any restriction of the type of substitution. In contrast, the methods for predicting ΔGfolding and ΔGbinding of SNVs focus on mutations seen in nature, i.e., in the human population. The goal of this work is to provide an assessment of leading predictors with respect to predicting the change of ΔGfolding and ΔGbinding caused by SNV versus non-SNV. It should be mentioned that our investigation sheds light on another aspect of performance assessment, which is different from previous works focusing on the effect of enrichment of destabilizing mutations in the existing experimental databases [48]. Such enrichment was attributed to the less accurate predictions of stabilizing mutations and prompted the creation of balanced datasets [49,50]. Other studies on the performance of the leading algorithms suggested that the problem is in overfitting and the features used in the models are not sufficiently informative for the task [21], and the quality of experimental data as well [51].

2. Results

Assessment of SNV and non-SNV energy change distribution in experimental databases and types of amino acid changes

Below we provide the change of the folding and binding free energies distribution in the leading databases for the entire dataset, and for SNVs and non-SNVs (Figure 1). It should be mentioned again that the change of the folding free energy vs change of the binding free energy is calculated differently (see eq. (1,2)). Thus, a negative change in the folding free energy indicates destabilization, while a positive change in the binding free energy points to weaker affinity.
The first observation confirms the previously noticed enrichment of destabilizing mutations, i.e., the vast majority of mutations make the corresponding folding or binding weaker. This is an expected observation since proteins fold toward their lowest folded free energy state. Similarly, the protein-protein and protein-DNA binding free energy is optimized (see [52]). This observation holds for the entire databases and for the subsets, the SNVs and non-SNVs (with a slight exception for protein-DNA databases, the S419 and ProNAB-237 databases, for which the SNVs distribution is more symmetrical than of non-SNVs). Such imbalance is illustrated in Table 1, where the number of cases with free energy change (positive or negative) larger than 2 kcal/mol and 1 kcal/mol is provided for each of the databases. Indeed, the ratio of destabilizing vs stabilizing mutations is approximately 8.4 to 16, taking 2 kcal/mol as cut off. The ratio is approximately the same (7.7 to 13.7) when the cut-off was decreased to 1 kcal/mol.
In terms of amino acid changes present in the database, the results are provided in the supplementary material (Figure S1a-o). In the S2648 dataset, most of the mutations have been made from Val (319) to other amino acids followed by Ile (253) and Glu (200) (Figure S1a). In terms of mutations, most mutations have been made to Ala as alanine scanning is one of the most popular methods to study change in folding free energy as a result of mutation. We see 109 Val to Ala mutations and 85 Leu to Ala mutations both of which are SNVs (Figure S1b). In case of non-SNVs, we see more cases of Ile to Val mutations (78) and Ala to Gly mutations (75). Considering the property of amino acids, we see more cases of hydrophobic to hydrophobic mutations followed by large to small mutations. SNV cases are dominated by hydrophobic to hydrophobic and small to small mutations while non-SNVs by large to small and polar to hydrophobic mutations (Figure S1c).
The trend of amino acid change is slightly different in case of SKEMPI-SEQ-2388 (Figure S1d,e,f) and SKEMPI-3D-3775 datasets (Figure S1g,h,i). While we see more cases where Arg (238) is mutated to other amino acid followed by Glu (235) and Lys (217) in SKEMPI-SEQ-2388 dataset, SKEMPI-3D-3775 dataset has more cases of Lys (354) and Arg (352) mutations to other amino acids followed by glutamic acid (320) (Figure S1d,e and Figure S1g,h). Again, most of the amino acids have been mutated to Ala with Glu to Ala mutations (case of SNV) being the prominent ones in both the datasets. With reference to the property of amino acid, most of the mutations have been made from polar to hydrophobic and large to small in both the datasets. Both the dataset is dominated by non-SNV mutations from large to small amino acids (Figure S1f and Figure S1h).
Similar to the S2648 and two SKEMPI datasets, the datasets used for studying the effect of mutation on protein-DNA binding free energy is also dominated by mutations to alanine (Figure S1j,k,l and Figure S1m,n,o). In both the datasets (S419 and ProNAB-237), most of the mutations have been made from Arg to other amino acids (S419: 76 and ProNAB-237: 57), with Arg to Ala being the prominent ones (Figure S2j and S2m). We see more cases of large to small and polar to hydrophobic mutations in S419 and ProNAB-237 dataset (Figure S1l and Figure S1o).

Assessment of leading algorithms performance

In this section, we benchmark the leading free energy change predictors against the datasets listed above. It must be clarified that the benchmarking is done with the sole purpose to reveal the difference of performance between SNVs vs non-SNV cases. It is understood that these algorithms were trained on the above listed databases and thus their absolute performance should not be evaluated on the same datasets.
Table 2 and Table S1 show the Person correlation coefficient (PCC) and Mean squared error (MSE) (defined in eq 3 and eq 4, respectively) of predictions of folding free energy changes (the linear fit graphs of predicted vs experimentally measured folding free energy changes are shown in Figure S2a,b,c,d. Two observations can be made: almost all algorithms perform better on non-SNV cases compared with the whole dataset, and almost all algorithms perform much better on non-SNVs. The largest difference between SNVs and non-SNVs was found for MAESTRO, mCSM, PoPMuSiC and DUET. In contrast, the MSE is worse for non-SNVs compared with SNV cases. The best slope of the fitting lines was obtained in the case of SAAFEC-SEQ; however, there is practically very minor difference in the performance of the SAAFEC-SEQ on the whole dataset, SNV and non-SNV. The largest difference in the slope of the fitting lines was seen in case of MAESTRO, DUET, mCSM and PoPMuSiC when comparing SNV and non-SNV cases. The average slope obtained in the case of the whole dataset was 0.48, SNV was 0.4 while for non-SNV it was 0.54, again demonstrating that the method works better on non-SNVs. It is interesting to mention that the slope of the fitting line for all algorithms is about 0.5, indicating that they underpredict the change of the folding free energy by a factor of 2.
Table 3 summarizes the results for protein-protein binding free energy changes predictors (the linear fit graphs of predicted vs experimentally measured binding free energy changes are shown in Figure S3a,b. Similarly, as above, two observations can be made: all algorithms (except for MutaBind2) perform slightly better on non-SNV cases compared with the whole dataset, and all algorithms perform better on non-SNVs compared with SNVs (except MutaBind2). However, the differences in PCC are not large as they were in the case of folding free energy change predictors. The slope of the fitting lines is nearly identical for SNV and non-SNV in the case of SAAMBE-3D and MutaBind2 (Table 3); however, we see a better slope for non-SNV in the case of mCSM-PPI2 (SNV = 0.60 and non-SNV=0.68). The slope of BeAtMuSiC is very small, reaching 0.13 for SNVs cases, indicating that the predicted binding free energy changes are grossly underestimated. All other methods also underestimate the change of the binding free energy by about a factor of 1.5.
Lastly, Table 4 provides PCC and MSE for protein-DNA binding free energy changes predictors (the linear fit graphs of predicted vs experimentally measured binding free energy changes are shown in Figure S4a,b. The mCSM-NA results indicate that it performs better on SNV cases, while both SAMPDI-3D and PremPDI have almost identical performance on SNV and non-SNV cases on the S419 dataset. The corresponding MSEs for SNVs and non-SNVs are almost identical for SAMPDI-3D and opposite in tendency for the other two algorithms. It should be noted that the slopes of fitting lines in the case of mCSM-NA are very low for both SNVs and non-SNVs underestimating the binding free energy change by a factor of 4. Similarly, the PremPDI predictions on SNVs case are underestimated by a factor of 3. The performance is the opposite in the case of the ProNAB-237 dataset. All the three methods perform better on non-SNVs as compared to SNV. The slopes of the fitting lines are not impressive resulting in an underestimation of a factor of 3 to 4.

3. Discussion

This article aimed at revealing the differences between SNVs and non-SNVs in terms of their distributions in the corresponding databases and the performance of leading algorithms for free energy change predictions. Three types of databases were considered, the folding free energy changes, the protein-protein binding free energy changes, and protein-DNA binding free energy changes. It should be mentioned that the first two are much larger than the third one and therefore the observations made are statistically more meaningful for the first two. The common observation is that SNVs and non-SNVs are almost equally presented in the databases, roughly speaking 50% are SNVs and 50% are non-SNVs. The corresponding free energy changes, ΔGfolding and ΔGbinding, are similar as well, except for protein-DNA databases, where ΔGbinding of SNVs does not have as many destabilizing cases as non-SNVs do. The main difference between SNVs and non-SNVs in the corresponding databases is the types of mutations. For instance, SNV cases in S2648 are dominated by hydrophobic to hydrophobic and small to small mutations while non-SNVs by large to small and polar to hydrophobic mutations whereas SNV cases in both SKEMPI-SEQ-2388 and SKEMPI-3D-3775 is dominated by small-small and polar to hydrophobic mutations while non-SNV mutations from large to small amino acids. We see more cases of polar to hydrophobic and small to small mutation in the case of SNV for S419 and ProNAB-237 dataset and non-SNV by large to small and polar to hydrophobic mutations. These differences between SNVs and non-SNVs should be taken into consideration in selecting features for machine learning algorithms for predicting the effects of SNVs. Alternatively, if the goal is to develop a method that predicts the effects of SNVs only, only SNVs cases should be used for the training set.
In terms of the performance of the leading predictors of the free energy change, ΔGfolding, and ΔGbinding, we would like to reiterate again that our goal is not to compare their absolute performance but rather to see the difference of the performance on SNVs vs non-SNVs cases. Comparison of their performance has been done in numerous papers of the developers [26,28,30,32,34,36,39,40,41,42,44,45,47,53,54,55,56] as well as third-party manuscripts [57]. The common observation is that almost all algorithms as tested on the corresponding datasets perform worse on SNVs as compared with non-SNVs. In some cases, the PCC for SNVs is two times lower than the PCC for non-SNVs. This observation should be considered in asserting the effect of SNVs, both benign and pathogenic, on protein stability and macromolecular interactions. Especially since there is a strong linkage between thermodynamics and pathogenicity [58].

4. Methods

Databases of experimentally measured changes of ΔGfolding and ΔGbinding.

Databases of folding free energy changes (main source ProTherm database)
ProTherm is a database of experimentally measured thermodynamic quantities for wild-type and mutant proteins [14,15]. The database includes information about protein stability in the form of unfolding free energy and thus provides important clues about stability and its association with structure as a result of mutation. This database has been widely utilized as a training dataset for developing in-silico methods for the prediction of change in folding free energy as an effect of the mutation. It is to be noted down here that the majority of the methods are trained on the subset of the ProTherm database named as S2648 dataset.
S2648: The S2648 dataset, originally curated by Dehouck et al. [55] comprises 2648 single-point mutations from 131 proteins. The criteria used for defining the dataset are described in the article by Dehouck et al. [55]. For the current work, we used S2648 for the benchmarking purpose. One of the structures (PDB Id: 2A01) is now marked as obsolete, which corresponds to one entry in the dataset that was removed. The final S2648 dataset used in the current work consists of 2647 single-point mutations from 130 proteins.

Databases of binding free energy changes of protein-protein interactions (main source SKEMPI database)

Using the Structural Kinetic and Energetic database of Mutant Protein Interactions (SKEMPI) [18] as the main source of information, two datasets were created to benchmark the methods for computing the change in ΔGbinding as a result of mutation from the second version of SKEMPI database called SKEMPI-2.0 [19]. First, to benchmark the sequence-based methods, and second, to benchmark the structure-based methods. We named these datasets SKEMPI-SEQ-2388 (sequence information only) and SKEMPI-3D-3775 (SKEMPI entries with the corresponding 3D structures). Both these datasets were built by considering single-point mutations only. The criteria used for curating the two datasets are described below:
SKEMPI-SEQ-2388: SKEMPI-SEQ-2388 dataset is a curated subset of the SKEMPI-2.0 database which has 7085 mutations from 348 protein-protein complexes. The curation starts with purging entries that have missing temperature or missing exact Kd value for wild-type or mutant followed by considering only single point mutations resulting in 4827 mutations over 316 protein complexes. Subsequently, 3000 mutant cases from 210 protein-protein complexes involving only dimers were considered and multimers were filtered out. Then we calculated the average and standard deviation of binding free energy changes for all the mutations with multiple experimental values in the dataset. We removed all duplicated mutations if the corresponding ΔΔGbinding had a standard deviation greater than 1 kcal/mol and collapsed the rest into a single entry if the standard deviation was less than 1 kcal/mol, resulting in 2450 mutations and over 210 complexes. Finally, we filtered out cases where any of the involved protein chains have less than 20 amino acids, resulting in a dataset of 2388 mutations from 200 protein-protein complexes.
SKEMPI-3D-3775: SKEMPI-3D-3775 is also a curated subset of the SKEMPI-2.0 database. The first curation step is identical to that for the SKEMPI-SEQ-2388 dataset, and it resulted in 4827 mutations from 316 proteins. In mutation entries where multiple experimental values are listed, the mean and standard deviation of the ΔΔGbinding for the mutation is computed and if the standard deviation of ΔΔGbinding is greater than 1.0 kcal/mol the mutant data point is eliminated otherwise we consider the average ΔΔGbinding for the mutation and it will be included in the cleaned dataset only once. After this cleaning step, we got 4067 mutations from 316 protein-protein complexes. Afterward, cases having missing residues in the -5 to +5 position of the mutation site were also discarded, as this information is required by some of the methods [36]. Some of the structures have non-standard amino acid analogs, such amino acids were reverted to their respective parent amino acids. Structures containing non-standard residues with RCSB PDB chemical Ids CGU or LLP were purged from the dataset. Finally, our curated dataset consists of 3775 mutations from 300 protein-protein complexes.

Databases of binding free energy changes of protein-DNA interactions

ProNIT [16] and ProNAB [17] are the two databases that contain information about the experimental binding data for protein-nucleic acid complexes. ProNIT release 2.0 [59] contains 4900 from 158 proteins. The database contains information about several thermodynamic quantities like Gibbs free energy change (ΔG), enthalpy change (ΔH), dissociation constant (Kd), association constant (Ka), heat capacity change (ΔCp), and structural information of the protein-nucleic acid complexes and other information like experimental conditions, literature information, etc. The database is currently not active. ProNAB (Harini et al., 2022) is a database of experimentally measured protein-nucleic acid binding affinities of wild-type and mutant proteins. The database is cross-linked with multiple databases like UniProt, GenBank, PDB, PROSITE, ProThermDB, DisProt, and Pubmed. The current version of ProNAB consists of 20219 entries from 1041 proteins which include 14732 cases of Protein-DNA, 5326 cases of Protein-RNA, and 161 cases with Protein-DNA/RNA hybrid binding affinity. We used two datasets for the benchmarking purpose which are described below.
S419: This dataset has been curated by Gen Li et al. [47] and has been used as the training set for SAMPDI-3D [47]. The S419 dataset comprises 419 single-point mutations from 96 proteins. The dataset was created by merging two datasets: a) the S219 dataset: collected from ProNIT and dbAMEPNI, which was used as the training set for the development of PremPDI [45], and b) the S200 dataset: collected from the recently published literature [47].
ProNAB-237: ProNAB-237 is a subset of the ProNAB database [17] used in the current study. ProNAB includes cases of both single-point mutations and multiple mutations. We only considered single-point mutations for the current work. We collected 4806 cases of nucleic acid-protein free binding energies with a single amino acid substitution. The dataset was filtered to exclude cases where the nucleic acid type was either RNA or other. This step resulted in 860 data points. The dataset was further filtered to remove cases where PDB structure is not reported for the protein-DNA complex, resulting in 631 cases from 137 proteins. For cases where multiple measurements were reported for the same mutation, the standard deviation was calculated for the changes in the binding affinity and only those cases were considered where the standard deviation was less than 1.0 kcal·mol−1 for a given mutation. For these cases, the average value of the change in binding free energy was taken into account and was used for benchmarking. The dataset was further pruned to remove mutations for which atomic coordinates were absent in the PDB. In some PDBs the mutation residue listed in the database does not map to the residue in it, such cases were also removed, and finally, we have a dataset of 237 mutations is created. We named this dataset ProNAB-237.

Computational methods for predicting ΔGfolding or ΔGbinding

Methods for predicting folding free energy change caused by mutation.

Altogether eight different methods were used for the benchmarking, wherein three are sequence-based methods while others require 3D structure as the input for making predictions. Below we briefly outline these methods. While there are plenty of methods available for the prediction, the following methods were used because they are popular methods, ease of use and installation.
  • SAAFEC-SEQ [34]: SAAFEC-SEQ is a gradient-boosting decision tree machine learning method that uses physicochemical properties, sequence features, and evolutionary information features to predict changes in folding free energy caused by amino acid mutation. The method utilizes amino acid sequence as the input for making predictions.
  • INPS-MD [32,53]: INPS-MD has been implemented as both sequence (INPS) and structure-based method (INSPS-3D). Both are machine learning methods based on support vector regression (SVR).
  • I-mutant 2.0 [30]: I-mutant 2.0 is a support vector machine (SVM) based method for prediction of folding free energy as an effect of mutation. The method is implemented as both sequence and structure based.
  • mCSM [26]: mCSM is a web-based predictor that uses a graph-based approach to predict the impact of missense mutations on protein stability. The predictive models in mCSM are trained with the atomic distance patterns of different amino acid residues.
  • MAESTRO [54]: MAESTRO is a structure-based method that utilizes a multi-agent machine learning system for predicting the impact of mutation on folding free energy.
  • PoPMuSic [60]: PoPMuSiC is a web server that predicts the thermodynamic stability changes caused by single site mutations in proteins, using a linear combination of statistical potentials whose coefficients depend on the solvent accessibility of the mutated residue.
  • SDM [61] : Site Directed Mutator (SDM) uses statistical potential energy function to calculate the stability score which uses amino-acid substitution frequencies within homologous protein families. The metric is analogous to the free energy difference between wild-type and mutant protein. The method is 3D structure based and is available as a webserver.
  • DUET [56]: DUET is a 3D structure-based method that uses mCSM and SDM for the consensus prediction. The results from these methods are combined and optimized using Support Vector Machines (SVM) to make the final prediction. The method is available as a webserver.

Methods for predicting binding free energy changes of protein-protein interactions caused by mutation.

Overall, the following listed computational methods were considered in this work. We could not include methods that are designed for predicting the effects of single amino acid mutation on binding free energy change for dimeric complexes or whose online servers were slow or busy and stand-alone versions were not available or not trivial to install and configure locally.
  • SAAMBE-SEQ [42]: It is a sequence-based machine-learning technique that can predict how a single mutation will affect the binding energy of protein-protein complexes. In contrast to other methods already in use, SAAMBE-SEQ does not require a 3D protein-protein complex structure as input. Note that it uses features that require the length of interacting partners to be longer than 20 amino acids and thus it is not expected to perform well on protein-peptide binding cases.
  • SAAMBE-3D [36]: SAAMBE-3D is a machine learning-based method that takes a PDB file as its input and can estimate the effect of a single amino acid modification on protein-protein binding. This tool enables the investigation of two types of inquiries: (1) forecasting alterations in binding free energy resulting from a mutation, and (2) predicting whether a mutation causes a disturbance in protein-protein interactions.
  • mCSM-PPI2 [40]: mCSM-PPI2 is a computational technique that uses machine learning to forecast the impact of missense mutations on protein-protein binding affinity. It employs an enhanced graph-based signature strategy to model changes in the network of non-covalent interactions between residues using graph kernels, complex network metrics, evolutionary data, and energetic terms. This approach is available for free at https://biosig.lab.uq.edu.au/mcsm_ppi2/
  • MutaBind2 [41]: MutaBind2 is a tool that assesses the influence of individual-site and multi-site mutations on protein-protein binding affinities in soluble complexes. This method utilizes statistical potentials, molecular mechanics, force fields, and the structure of the protein-protein complex.
  • BeAtMuSiC [39]: BeAtMuSiC is a method based on a set of statistical potentials derived from known protein structures, in addition, it accounts for the effect of the mutation on the strength of the interactions at the interface as well as the overall stability of the complex. This method is available as an online web server free of charge at http://babylone.3bio.ulb.ac.be/beatmusic/index.php

Methods for predicting binding free energy changes of protein-DNA interactions caused by mutation.

Three methods were utilized for benchmarking the binding free energy changes of protein-DNA interactions in the presence of a chemical modification. Both methods rely on a three-dimensional structure for the prediction of binding free energy of protein-DNA interactions.
  • SAMPDI-3D [47]: SAMPDI-3D uses a gradient-boosting decision tree machine learning method to predict the change in the protein-DNA binding free energy brought on by mutations in the binding protein or the bases of the corresponding DNA. It takes the structure of the complex i.e., a PDB file as an input.
  • mCSM-NA [44]: The mCSM-NA method is based on graph-based structural signatures to predict the DDG caused by mutations in proteins bound to DNA/RNA.
  • PREMPDI [45]: PremPDI is a physics-based method that relies on the 3D structure of the protein-nucleic acid complex for making predictions. The method is based on molecular mechanics force fields and fast side-chain optimization algorithms.

SNV vs non-SNV cases

The SNV cases were extracted from the experimental database using the lookup table provided in the supplementary material (Figure S5a,b). The rest of the cases were considered non-SNV. In the S2648 dataset, there are 1493 cases of SNVs and 1154 cases of non-SNVs. In the case of SKEMPI-SEQ-2388 and SKEMPI-3D-3775, there are 1081 & 1692 SNVs and 1307 & 2083 non-SNVs, respectively. Similarly, for S419 and ProNAB-237, there are 164 & 79 cases of SNVs and 255 & 158 cases of non-SNVs. It is to be noted down here that the cases of SNVs and non-SNVs are not equal in all the datasets. Except for S2648, where cases of SNVs are more compared to non-SNVs, all other datasets have more cases of non-SNVs.

Free energy changes

Following previous papers, the change of the folding free energy is calculated as the change of the folding or binding free energy produced by a single amino acid substitution as the difference of the folding and binding free energy of the wild type and the mutant [42,62]. However, the corresponding free energy changes are calculated differently for folding free energy change versus binding free energy changes. Thus, the change of the folding free energy caused by a mutation is calculated with eq. (1), and a positive ΔΔG indicates a mutation that makes the protein stable while a negative value is representative of destabilization.
ΔΔGfolding = ΔGwt – ΔGmutant
In contrast, the change of the binding free energy for both protein-protein and protein-DNA complexes was calculated as
ΔΔGbinding = ΔGmut – ΔGwt
and thus, a positive number indicates that the mutation destabilizes binding, while a negative number is a case when the mutation makes the affinity stronger.

Assessment of Predictions

The accuracy of the predictions was assessed using two measures namely Pearson correlation coefficient (PCC) and mean-square-error (MSE) which are defined below.
P C C = ∑ i = 1 n ( x i − x ¯ ) ( y i − y ¯ ) ∑ i = 1 n   ( x i − x ¯ ) 2 ( y i − y ¯ ) 2  
where x i and y i refer to the true and predicted value of the ith sample.
M S E y , y ^ = 1 n s a m p l e s ∑ i = 0 n s a m p l e s − 1 ( y − y ^ ) 2
where y i is the true value and y ^ i is the predicted value of the ith sample.

5. Conclusions

The paper showed that the distribution of SNV vs non-SNV types of mutations are different in the corresponding databases of experimentally measured quantities. This should be taken into consideration when one applies methods of predicting the effect of missense mutation seen in the human population. Furthermore, the work indicated that the leading algorithms for predicting folding and binding free energy changes caused by mutations perform differently in cases of SNVs and non-SNVs. This is an important observation since there is a strong linkage between the change of the folding and binding free energies and the probability of mutation being pathogenic [58]. Overall PCC is better for non-SNVs, which points out that the methods may not be accurate in ranking SNV cases. In contrast, in terms of MSE, most of methods have larger MSE for non-SNV cases which may indicate that they are more accurate in predicting individual energy changes for non-SNVs. However, this comes with an overall worsen slope of the fitting line, which indicates an underestimation of the energy change.

Supplementary Materials

The supporting information can be downloaded at : Preprints.org.

Author Contributions

PP – created the datasets, carried out calculations; SP – created the datasets, carried out calculations; PR – carried out calculations, NA – carried out calculations, EA – supervised the work, all authors write the paper.

Funding

NIH: R01GM093937.

Institutional Review Board Statement

Not applicable.

Informed Consent Statement

Not applicable.

Data Availability Statement

Data is available at http://compbio/clemson.edu.

Acknowledgments

We thank Clemson University Palmetto supercomputer.

Conflicts of Interest

The authors declare no conflict of interest.

References

  1. Kent, S.; Marshall, G.R.; Wlodawer, A. Determining the 3D Structure of HIV-1 Protease. Science (1979) 2000, 288, 1590. [CrossRef]
  2. Naddaf, M. How Do We Smell? First 3D Structure of Human Odour Receptor Clues. Nature 2023. [CrossRef]
  3. Pacheco-Fiallos, B.; Vorländer, M.K.; Riabov-Bassat, D.; Fin, L.; O’Reilly, F.J.; Ayala, F.I.; Schellhaas, U.; Rappsilber, J.; Plaschka, C. MRNA Recognition and Packaging by the Human-Export Complex. Nature 2023, 616, 828–835. [CrossRef]
  4. Pradhan, B.; Kanno, T.; Umeda Igarashi Miki and Loke, M.S.; Baaske, M.D.; Wong, J.S.K.; Jeppsson, K.; Björkegren, C.; Kim, E. The Smc5/6 Complex Is a DNA Loop-Extruding Motor. Nature 2023, 616, 843–848. [CrossRef]
  5. Bell, D.R.; Cheng, S.Y.; Salazar, H.; Ren, P. Capturing RNA Folding Free Energy with Coarse-Grained Dynamics Simulations. Sci. Rep. 2017, 7, 45812. [CrossRef]
  6. Hazel, A.J.; Walters, E.T.; Rowley Christopher N and Gumbart, J.C. Folding Free Energy Landscapes of -Sheets with Non-polarizable and Polarizable CHARMM Force Fields. J. Chem. Phys. 2018, 149, 72317. [CrossRef]
  7. Krivov, S. V Protein Folding Free Energy Landscape along the Committor - the Optimal Folding Coordinate. J. Chem. Theory Comput. 2018, 14, 3418–3427. [CrossRef]
  8. Nawrocki, G.; Leontyev, I.; Sakipov, S.; Darkhovskiy, M.; Kurnikov, I.; Pereyaslavets Leonid and Kamath, G.; Voronina, E.; Butin, O.; Illarionov, A.; Olevanov, M.; et al. Protein-Ligand Binding Free-Energy Calculations with ARROW─A Purely First-Principles Parameterized Polarizable Field. J. Chem. Theory Comput. 2022, 18, 7751–7763. [CrossRef]
  9. Fu, H.; Chipot, C.; Shao, X.; Cai, W. Achieving Accurate Standard Protein-Protein Binding Free Energy through the Geometrical Route and Ergodic Sampling. J. Chem. Inf. Model. 2023, 63, 2512–2519. [CrossRef]
  10. Molani, F.; Webb, S.; Cho, A.E. Combining QM/MM Calculations with Classical Mining Minima to Predict Protein-Ligand Binding Free Energy. J. Chem. Inf. Model. 2023, 63, 2728–2734. [CrossRef]
  11. Proniewicz, E.; Burnat, G.; Domin, H.; Małuch, I.; Makowska, M.; Prahl, A. Application of Alanine Scanning to Determination of Amino Acids for Peptide Adsorption at the Solid/Solution and Binding to the Receptor: Surface-Enhanced/Infrared Spectroscopy versus Bioactivity Assays. J. Med. Chem. 2021, 64, 8410–8422. [CrossRef]
  12. Tanaka, T.; Asano, T.; Sano, M.; Takei, J.; Hosono, H.; Nanamiya, R.; Tateyama, N.; Kaneko, M.K.; Kato, Y. Epitope Mapping of the Anti-California Sea Lion Podoplanin Antibody PMab-269 Using Alanine-Scanning and ELISA. Monoclon. Antib. Immunodiagn. Immunother. 2021, 40, 196–200. [CrossRef]
  13. Isoda, Y.; Tanaka, T.; Suzuki, H.; Asano, T.; Kitamura, K.; Kudo, Y.; Ejima, R.; Ozawa, K.; Yoshikawa, T.; Kaneko, M.K.; et al. Epitope Mapping of the Novel Anti-Human CCR9 Monoclonal (CMab-11) by 2 Alanine Scanning. Monoclon. Antib. Immunodiagn. Immunother. 2023, 42, 73–76. [CrossRef]
  14. Gromiha, M.M.; An, J.; Kono, H.; Oobatake, M.; Uedaira H and Sarai, A. ProTherm: Thermodynamic Database for Proteins and Mutants. Nucleic Acids Res. 1999, 27, 286–288. [CrossRef]
  15. Nikam, R.; Kulandaisamy, A.; Harini, K.; Sharma Divya and Gromiha, M.M. ProThermDB: Thermodynamic Database for Proteins and Mutants after 15 Years. Nucleic Acids Res. 2021, 49, D420–D424. [CrossRef]
  16. Prabakaran, P.; An, J.; Gromiha, M.M.; Selvaraj, S.; Uedaira, H.; Kono, H.; Sarai, A. Thermodynamic Database for Protein-Nucleic Acid Interactions(ProNIT). Bioinformatics 2001, 17, 1027–1034. [CrossRef]
  17. Harini, K.; Srivastava, A.; Kulandaisamy Arulsamy and Gromiha, M.M. ProNAB: Database for Binding Affinities of Protein-Nucleic Acid and Their Mutants. Nucleic Acids Res. 2022, 50, D1528–D1534. [CrossRef]
  18. Moal, I.H.; Fernández-Recio, J. SKEMPI: A Structural Kinetic and Energetic Database of Mutant Interactions and Its Use in Empirical Models. Bioinformatics 2012, 28, 2600–2607. [CrossRef]
  19. Jankauskaite, J.; Jiménez-Garc\’\ia, B.; Dapkunas, J.; Fernández-Recio, J.; Moal, I.H. SKEMPI 2.0: An Updated Benchmark of Changes in Protein-Protein Energy, Kinetics and Thermodynamics upon Mutation. Bioinformatics 2019, 35, 462–469. [CrossRef]
  20. Gromiha, M.M.; Huang, L.-T. Machine Learning Algorithms for Predicting Protein Folding rates and Stability of Mutant Proteins: Comparison with Statistical. Curr. Protein Pept. Sci. 2011, 12, 490–502. [CrossRef]
  21. Fang, J. A Critical Review of Five Machine Learning-Based Algorithms for predicting Protein Stability Changes upon Mutation. Brief. Bioinform. 2020, 21, 1285–1292. [CrossRef]
  22. Pucci, F.; Schwersensky, M.; Rooman, M. Artificial Intelligence Challenges for Predicting the Impact of mutations on Protein Stability. Curr. Opin. Struct. Biol. 2022, 72, 161–168. [CrossRef]
  23. Sora, V.; Laspiur, A.O.; Degn Kristine and Arnaudi, M.; Utichi, M.; Beltrame, L.; De Menezes, D.; Orlandi, M.; Stoltze, U.K.; Rigina, O.; Sackett, P.W.; et al. RosettaDDGPrediction for High-Throughput Mutational Scans: From to Binding. Protein Sci. 2023, 32, e4527. [CrossRef]
  24. Guerois, R.; Nielsen, J.E.; Serrano, L. Predicting Changes in the Stability of Proteins and Protein: A Study of More than 1000 Mutations. J. Mol. Biol. 2002, 320, 369–387. [CrossRef]
  25. Gilis, D.; Rooman, M. PoPMuSiC, an Algorithm for Predicting Protein Mutant Stability: Application to Prion Proteins. Protein Eng. 2000, 13, 849–856. [CrossRef]
  26. Pires, D.E. V; Ascher, D.B.; Blundell, T.L. MCSM: Predicting the Effects of Mutations in Proteins Using-Based Signatures. Bioinformatics 2014, 30, 335–342. [CrossRef]
  27. Quan, L.; Lv, Q.; Zhang, Y. STRUM: Structure-Based Prediction of Protein Stability changes upon Single-Point Mutation. Bioinformatics 2016, 32, 2936–2946. [CrossRef]
  28. Pandurangan, A.P.; Ochoa-Montaño, B.; Ascher, D.B.; Blundell, T.L. SDM: A Server for Predicting Effects of Mutations on Protein. Nucleic Acids Res. 2017, 45, W229–W235. [CrossRef]
  29. Getov, I.; Petukh, M.; Alexov, E. SAAFEC: Predicting the Effect of Single Point Mutations on Protein Folding Free Energy Using a Knowledge-Modified/PBSA Approach. Int. J. Mol. Sci. 2016, 17, 512. [CrossRef]
  30. Capriotti, E.; Fariselli, P.; Casadio, R. I-Mutant2.0: Predicting Stability Changes upon Mutation from the Protein Sequence or Structure. Nucleic Acids Res. 2005, 33, W306–10. [CrossRef]
  31. Folkman, L.; Stantic, B.; Sattar, A.; Zhou, Y. EASE-MM: Sequence-Based Prediction of Mutation-Induced Changes with Feature-Based Multiple Models. J. Mol. Biol. 2016, 428, 1394–1405. [CrossRef]
  32. Savojardo, C.; Fariselli, P.; Martelli, P.L.; Casadio, R. INPS-MD: A Web Server to Predict Stability of Protein variants from Sequence and Structure. Bioinformatics 2016, 32, 2542–2544. [CrossRef]
  33. Lv, X.; Chen, J.; Lu, Y.; Chen, Z.; Xiao, N.; Yang, Y. Accurately Predicting Mutation-Caused Stability Changes from Protein Sequences Using Extreme Gradient Boosting. J. Chem. Inf. Model. 2020, 60, 2388–2395. [CrossRef]
  34. Li, G.; Panday, S.K.; Alexov, E. SAAFEC-SEQ: A Sequence-Based Method for Predicting the Effect of Single Point Mutations on Protein Thermodynamic Stability. Int. J. Mol. Sci. 2021, 22. [CrossRef]
  35. Petukh, M.; Dai, L.; Alexov, E. SAAMBE: Webserver to Predict the Charge of Binding Free Energy by Amino Acids Mutations. Int. J. Mol. Sci. 2016, 17, 547. [CrossRef]
  36. Pahari, S.; Li, G.; Murthy, A.K.; Liang, S.; Fragoza, R.; Yu, H.; Alexov, E. SAAMBE-3D: Predicting Effect of Mutations on Protein-Protein. Int. J. Mol. Sci. 2020, 21. [CrossRef]
  37. Xiong, P.; Zhang, C.; Zheng, W.; Zhang, Y. BindProfX: Assessing Mutation-Induced Binding Affinity Change by Protein Interface Profiles with Pseudo-Counts. J. Mol. Biol. 2017, 429, 426–434. [CrossRef]
  38. Geng, C.; Vangone, A.; Folkers, G.E.; Xue, L.C.; Bonvin, A.M.J.J. ISEE: Interface Structure, Evolution, and Energy-Based Machine Predictor of Binding Affinity Changes upon Mutations. Proteins 2019, 87, 110–119. [CrossRef]
  39. Dehouck, Y.; Kwasigroch, J.M.; Rooman, M.; Gilis, D. BeAtMuSiC: Prediction of Changes in Protein-Protein Binding on Mutations. Nucleic Acids Res. 2013, 41, W333–9. [CrossRef]
  40. Rodrigues, C.H.M.; Myung, Y.; Pires Douglas E V and Ascher, D.B. MCSM-PPI2: Predicting the Effects of Mutations on protein-Protein Interactions. Nucleic Acids Res. 2019, 47, W338–W344. [CrossRef]
  41. Zhang, N.; Chen, Y.; Lu, H.; Zhao, F.; Alvarez, R.V.; Goncearenco, A.; Panchenko, A.R.; Li, M. MutaBind2: Predicting the Impacts of Single and Multiple on Protein-Protein Interactions. iScience 2020, 23, 100939. [CrossRef]
  42. Li, G.; Pahari, S.; Murthy, A.K.; Liang, S.; Fragoza, R.; Yu, H.; Alexov, E. SAAMBE-SEQ: A Sequence-Based Method for Predicting Mutation on Protein-Protein Binding Affinity. Bioinformatics 2021, 37, 992–999. [CrossRef]
  43. Jemimah, S.; Sekijima, M.; Gromiha, M.M. ProAffiMuSeq: Sequence-Based Method to Predict the Binding Free Change of Protein-Protein Complexes upon Mutation Using Classification. Bioinformatics 2020, 36, 1725–1730. [CrossRef]
  44. Pires, D.E. V; Ascher, D.B. MCSM-NA: Predicting the Effects of Mutations on Protein-Nucleic Interactions. Nucleic Acids Res. 2017, 45, W241–W246. [CrossRef]
  45. Zhang, N.; Chen, Y.; Zhao, F.; Yang, Q.; Simonetti, F.L.; Li, M. PremPDI Estimates and Interprets the Effects of Missense on Protein-DNA Interactions. PLoS Comput. Biol. 2018, 14, e1006615. [CrossRef]
  46. Peng, Y.; Sun, L.; Jia, Z.; Li, L.; Alexov, E. Predicting Protein-DNA Binding Free Energy Change upon Missense Using Modified MM/PBSA Approach: SAMPDI Webserver. Bioinformatics 2018, 34, 779–786. [CrossRef]
  47. Li, G.; Panday, S.K.; Peng, Y.; Alexov, E. SAMPDI-3D: Predicting the Effects of Protein and DNA on Protein-DNA Interactions. Bioinformatics 2021, 37, 3760–3765. [CrossRef]
  48. Benevenuta, S.; Birolo, G.; Sanavia, T.; Capriotti, E.; Fariselli, P. Challenges in Predicting Stabilizing Variations: An Exploration. Front Mol Biosci 2022, 9, 1075570. [CrossRef]
  49. Usmanova, D.R.; Bogatyreva, N.S.; Ariño Bernad, J.; Eremina, A.A.; Gorshkova, A.A.; Kanevskiy, G.M.; Lonishin, L.R.; Meister, A. V; Yakupova, A.G.; Kondrashov, F.A.; et al. Self-Consistency Test Reveals Systematic Bias in Programs for prediction Change of Stability upon Mutation. Bioinformatics 2018, 34, 3653–3658. [CrossRef]
  50. Iqbal, S.; Li, F.; Akutsu, T.; Ascher, D.B.; Webb, G.I.; Song, J. Assessing the Performance of Computational Predictors for estimating Protein Stability Changes upon Missense Mutations. Brief. Bioinform. 2021, 22. [CrossRef]
  51. Fang, J. The Role of Data Imbalance Bias in the Prediction of Protein Change upon Mutation. PLoS One 2023, 18, e0283727. [CrossRef]
  52. Brock, K.; Talley, K.; Coley, K.; Kundrotas, P.; Alexov, E. Optimization of Electrostatic Interactions in Protein-Protein. Biophys. J. 2007, 93, 3340–3352. [CrossRef]
  53. Fariselli, P.; Martelli, P.L.; Savojardo, C.; Casadio, R. INPS: Predicting the Impact of Non-Synonymous Variations on protein Stability from Sequence. Bioinformatics 2015, 31, 2816–2821. [CrossRef]
  54. Laimer, J.; Hofer, H.; Fritz, M.; Wegenkittl, S.; Lackner, P. MAESTRO–Multi Agent Stability Prediction upon Point Mutations. BMC Bioinformatics 2015, 16, 116. [CrossRef]
  55. Dehouck, Y.; Grosfils, A.; Folch, B.; Gilis, D.; Bogaerts, P.; Rooman, M. Fast and Accurate Predictions of Protein Stability Changes upon mutations Using Statistical Potentials and Neural Networks: PoPMuSiC-2.0. Bioinformatics 2009, 25, 2537–2543. [CrossRef]
  56. Pires, D.E. V; Ascher, D.B.; Blundell, T.L. DUET: A Server for Predicting Effects of Mutations on Protein Using an Integrated Computational Approach. Nucleic Acids Res. 2014, 42, W314–9. [CrossRef]
  57. Zhang, X.; Mei, L.; Gao, Y.; Hao, G.; Song, B. Web Tools Support Predicting Protein–Nucleic Acid Complexes Stability with Affinity Changes. WIREs RNA 2023. [CrossRef]
  58. Pandey, P.; Ghimire, S.; Wu, B.; Alexov, E. On the Linkage of Thermodynamics and Pathogenicity. Curr Opin Struct Biol 2023, 80, 102572. [CrossRef]
  59. Kumar, M.D.S. ProTherm and ProNIT: Thermodynamic Databases for Proteins and Protein-Nucleic Acid Interactions. Nucleic Acids Res 2006, 34, D204–D206. [CrossRef]
  60. Dehouck, Y.; Kwasigroch, J.M.; Gilis, D.; Rooman, M. PoPMuSiC 2.1: A Web Server for the Estimation of Protein Changes upon Mutation and Sequence Optimality. BMC Bioinformatics 2011, 12, 1–12. [CrossRef]
  61. Worth, C.L.; Preissner, R.; Blundell, T.L. SDM–a Server for Predicting Effects of Mutations on Protein and Malfunction. Nucleic Acids Res. 2011, 39, W215–22. [CrossRef]
  62. Peng, Y.; Alexov, E. Investigating the Linkage between Disease-Causing Amino Acid and Their Effect on Protein Stability and Binding. Proteins 2016, 84, 232–239. [CrossRef]
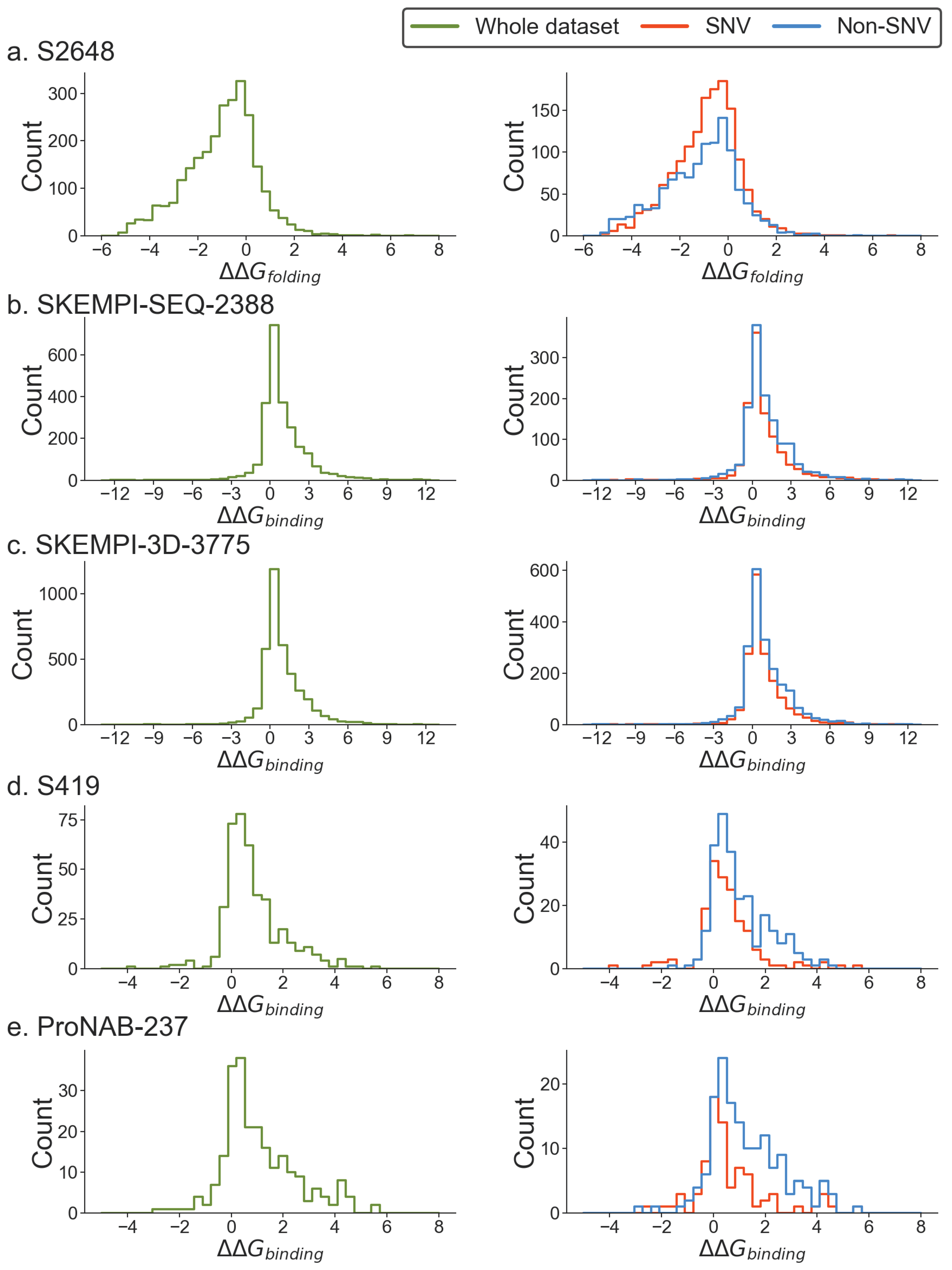
Preprints 75413 g001
Figure 1. Distribution of change in folding and binding free energy for different datasets.
Figure 1. Distribution of change in folding and binding free energy for different datasets.
Preprints 75413 g001
Table 1. Total number of stabilizing and destabilizing mutations in the datasets.
Table 1. Total number of stabilizing and destabilizing mutations in the datasets.
Datasets Cut-off
> 2 kcal/mol > 1 kcal/mol
No. of stabilizing mutations No. of destabilizing mutations No. of stabilizing mutations No. of destabilizing mutations
S2648 42 621 152 1192
SKEMPI-SEQ-2388 56 470 117 903
SKEMPI-3D-3775 67 742 159 1398
S419 4 64 10 137
ProNAB-237 3 53 9 100
Table 2. Performance comparison of methods on S2648 dataset.
Table 2. Performance comparison of methods on S2648 dataset.
Methods S2648
Whole Dataset SNV Non-SNV
PCC MSE Slope PCC MSE Slope PCC MSE Slope
SAAFEC-SEQa 0.91 0.45 0.66 0.90 0.44 0.64 0.92 0.46 0.69
I-mutant 2.0a 0.55 1.68 0.45 0.52 1.50 0.38 0.57 1.92 0.52
I-mutant 2.0 0.60 1.51 0.51 0.56 1.40 0.44 0.63 1.66 0.57
INPSa 0.57 1.56 0.39 0.52 1.50 0.33 0.60 1.65 0.43
INPS-3D 0.64 1.30 0.41 0.59 1.27 0.35 0.68 1.33 0.46
mCSM 0.69 1.15 0.42 0.62 1.19 0.34 0.74 1.11 0.50
MAESTRO 0.66 1.29 0.52 0.58 1.31 0.43 0.72 1.26 0.61
PoPMuSiC 0.62 1.34 0.41 0.55 1.33 0.33 0.67 1.36 0.48
SDM 0.46 2.34 0.43 0.40 2.14 0.36 0.50 2.59 0.50
DUET 0.68 1.17 0.50 0.62 1.19 0.41 0.74 1.14 0.59
a Sequence-based method.
Table 3. Performance comparison of methods on SKEMPI-SEQ-2388 and SKEMPI-3D-3775 datasets.
Table 3. Performance comparison of methods on SKEMPI-SEQ-2388 and SKEMPI-3D-3775 datasets.
Methods SKEMPI-SEQ-2388
Whole Dataset SNV Non-SNV
PCC MSE Slope PCC MSE Slope PCC MSE Slope
SAAMBE-SEQ 0.88 0.82 0.72 0.86 0.86 0.69 0.89 0.78 0.73
SKEMPI-3D-3775
Whole Dataset SNV Non-SNV
PCC MSE Slope PCC MSE Slope PCC MSE Slope
SAAMBE 3D 0.90 0.66 0.64 0.90 0.64 0.63 0.91 0.68 0.65
MutaBind2 0.90 0.62 0.70 0.90 0.58 0.69 0.90 0.64 0.70
mCSM-PPI2 0.91 0.65 0.65 0.88 0.75 0.60 0.93 0.57 0.68
BeAtMuSiC 0.35 2.73 0.18 0.31 2.53 0.13 0.37 2.90 0.21
Table 4. Performance comparison of methods on S419 and ProNAB-237 datasets.
Table 4. Performance comparison of methods on S419 and ProNAB-237 datasets.
Methods S419
Whole Dataset SNV Non-SNV
PCC MSE Slope PCC MSE Slope PCC MSE Slope
SAMPDI-3D 0.83 0.46 0.53 0.84 0.48 0.52 0.81 0.45 0.52
mCSM-NA 0.37 1.56 0.33 0.42 1.45 0.36 0.28 1.63 0.25
PremPDI 0.44 1.53 0.45 0.40 1.31 0.30 0.41 1.67 0.47
ProNAB-237
Whole Dataset SNV Non-SNV
PCC MSE Slope PCC MSE Slope PCC MSE Slope
SAMPDI-3D 0.58 1.39 0.30 0.50 1.59 0.21 0.59 1.29 0.31
mCSM-NA 0.43 2.08 0.35 0.28 3.21 0.28 0.52 1.51 0.38
PremPDI 0.52 1.76 0.42 0.45 2.20 0.38 0.51 1.54 0.37
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.
Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.
Prerpints.org logo

Preprints.org is a free preprint server supported by MDPI in Basel, Switzerland.

facebook logotwitter logolinkedin logo
MDPI Initiatives
Important Links
Subscribe

Disclaimer

Terms of Use

Privacy Policy

© 2024 MDPI (Basel, Switzerland) unless otherwise stated