Privacy-Preserving and Secure Solutions for Online English Education Platforms

1. Introduction

Internet of Things (IoTs) have drawn attentions from both industry and academic fields to its advantages for years, such as efficiency and providing more secure communication environments. Among them, the mobile Internet of Things (MIoT) for online English education has quickly become an important means and main tool for people to learn and communicate in English. This is a new type of English education. This method realizes the English education model with students as the main body and software platform as the carrier [1,2]. Compared with traditional offline classroom education, online English education has the characteristics and advantages of high efficiency [3], students and teachers are not limited by geographical distance [4]. Here, online learning devices (OLDs) able to get access to MIoTs and communicate with other devices and infrastructures like roadside units in some models [5]. Thus, OLDs are allowed to report information and emergencies, which will be used to improve the quality of services [6]. However, if OLDs are allowed to broadcast messages without any verification or limitation, the communication mechanism will become vulnerable and easy to compromise [7,8,9]. For example, if messages sent in MIoTs are not signed with online learning device’s unique identities, then a malicious user can broadcast fraud messages, or sign them with fabricated identities to bypass a weak system. To solve problems in secure communication, some works have been dedicated to design privacy-preserving authentication schemes [10,11,12,13,14]. However, due to the feature of changing topology, it is hard to balance efficiency and security in conventional MIoTs. Then, a brand-new technology came into researchers’ sights.

Software-defined network (SDN) is a new-emerging technology, which represents a network structure differing from traditional networks [15]. In SDN, controlling and forwarding are separated and work in different layers [16]. The control plane represents the centralized point as the brain of the whole architecture [17]. The data plane communicates with control plane via southbound interfaces. It is mainly responsible to query controllers for forwarding tables and forward packets. Using the programmability and scalability, the combination of VANETs and SDN offers new approach to solve inherent problems in VANETs.

Software-defined MIoTs has been proposed for years, and there have been many research efforts demonstrating the advantages of this new combination [18,19,20]. Meanwhile, some schemes are proposed to cope with problems in quality of services (QoS) [21], heterogeneous network accessing [22], factory managing [23], and so many others in different fields by combining with SDN [24]. Inspired by [25], we design a scheme that uses multicast technology to solve the driving direction and secure communication problems in Software-defined MIoTs.

In traditional MIoTs, OLDs mainly rely on broadcasting each other to receive network condition information, which lacks timeliness and overall planning [26,27]. By introducing multicast, the controller is allowed to manage OLDs and balance networks throughputs more efficiently. Besides, some technology used not to be suitable for MIoTs, like Steiner Tree, which is computation intense and scale sensitive [25]. But with SDN introduced, those algorithms can provide new methods for the development of MIoTs [28].

Thus, we propose a new secure communicating and device movement path scheme in this paper. By using multicast [29] and privacy-preserving authentication technologies, we aim to design a secure and efficient model in Software-defined MIoTs. Concretely, the main contributions of this paper are listed below.

1.1. Our Contribution

The main contributions of this work are summarized as follows.

(1)

We propose a novel Software-defined MIoTs-based model providing security communication in underlying data plane. The outstanding computing power of control plane greatly relieves the overhead of upper layer, which offer users higher-quality services.

(2)

We design an authentication system to ensure the authenticity and reliability of messages, so that OLDs are encouraged to spread real information. Otherwise, they will ge punished. Besides, an emergency-dealing scheme is offered to provide in-time services based on multicast, which not only takes current networks situation into consideration, but also the prediction of instantaneously changing.

(3)

A security analysis proves that our proposed scheme is able to achieve the security goals of Software-defined MIoTs. In addition, adopting elliptic curve cryptography avoids heavy overhead brought by bilinear pairing operations, which is demonstrated by the comparison results.

The remainder of this paper is organized as following. We introduce related works in Section 2. in Section 3, we illustrate system models and our design goals. Section 4 introduces the proposed scheme in detail. Security analysis is given in Section 5, and the comparison of computation overhead is in Section 6, respectively. Section 7 gives the conclusions.

2. Related Works

In the security in MIoTs and Software-defined MIoTs research field, Shao $et.al$ [7] proposed a threshold anonymous authentication protocol with gourp signature scheme. In this scheme, the decentralized group model is integrated. It achieved threshold authentication, anonymity, unforgeability, tracability and revocation of MIoTs communication. However, the huge computation cost of bilinear pairing may cause obstacles to implementation. Azees $et.al$ [30] proposed a scheme that enabled roadside units to authenticate vehicles anonymously before providing certain messages to them. It also allowed vehicles to communicate with roadside units anonymously. The scheme reduced costs of certificate and signature verification, and achieved traceability and privacy preserving in vehicular ad hoc networks. However, there was no timestamps attached to messages, which could be used by malicious parities to start replay attacks.

To solve the problems of insecurity of master keys, invalidity of PIDs in [10], Li $et.al$ [31] proposed a certificate-less protocol and demonstrated the security of it. And to cope with inherent problems in MIoTs, Garg $et.al$ [28] proposed secure communication models by introducing SDN architecture. They enabled both mutual authentication among communicating entities, and a intrusion detecting systems to detect potential attacks from the underling networks.

In the multicast in SDN research field, Zhou $et.al$ [25] proposed the cost-efficient Degree-dependent Branch-node Weighted Steiner Tree (DBWST) problem in the SDN architecture. It solved the scalability problem of multicast by introducing Steiner tree to span nodes. The scheme reduced the total cost and the number of branch nodes when generating the multicast tree T. Do $et.al$ [24] proposed an architecture that allowed both multicast and broadcast services in the SDN-based mobile packet core. It took the advantages of programmability and flexibility of SDN, and reduced the signaling cost comparing with traditional network paradigms. However, the system may suffer certain security problems in terms of communication.

Lai $et.al$ [32] proposed an integrated network architecture for secure group communication in SDN-based 5G vehicular ad hoc networks. The scheme was group-oriented vehicular environment, in which vehicles are divined into group based on their geographic positions. This also inspired us to manage vehicles by divining them in transaction-oriented way. Then, Kim $et.al$ [23] proposed a multicast scheme with Gropu Shared Tree (GST) switching in large-scale IIoT networks. To overcome inherent problems, such as transmitting multicast packets under congestions and configuring optimal path dynamically, it adopted SDN-based architecture. They proved that the new architecture outperformed.

3. Models and Design Goals

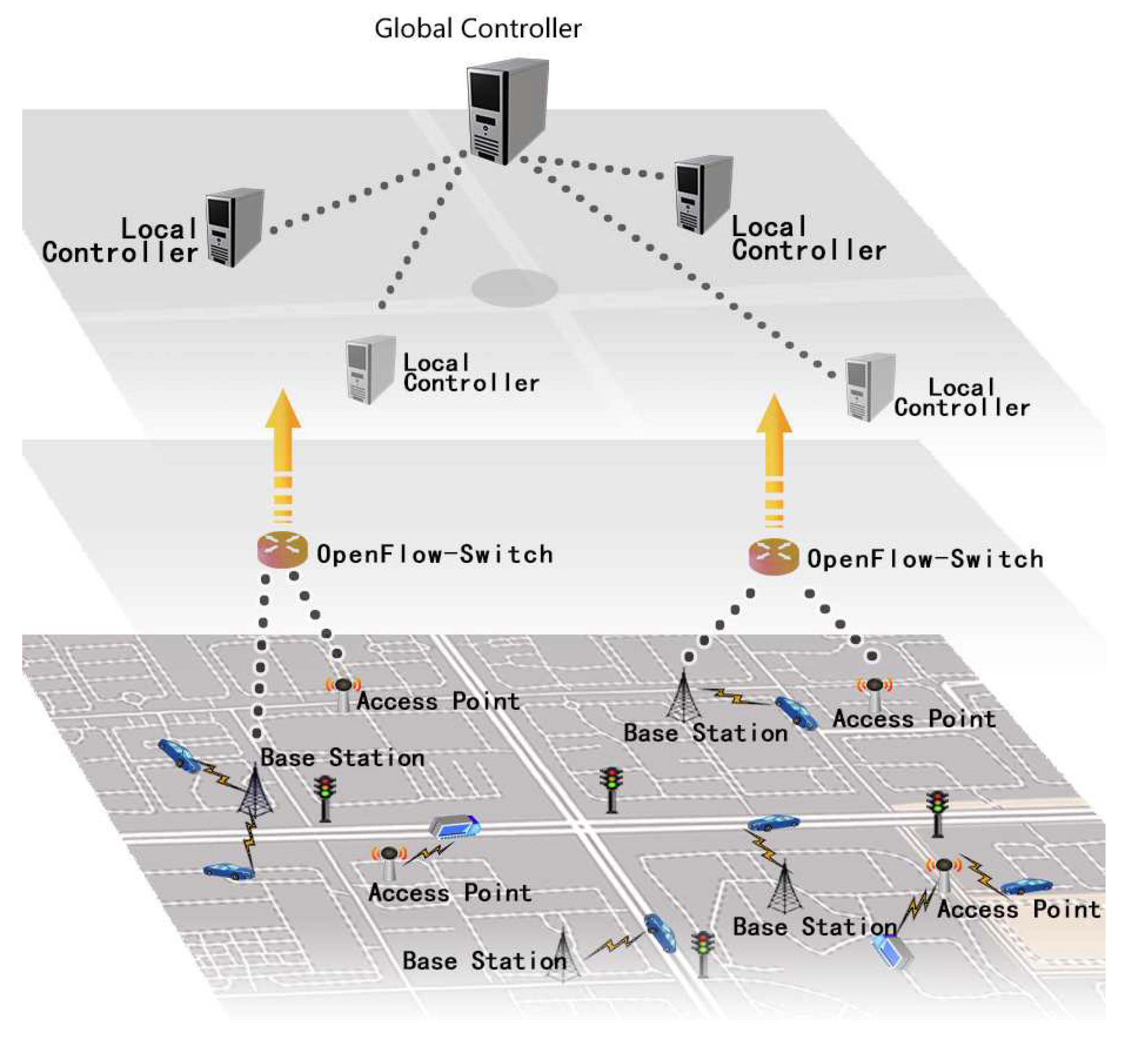
3.1. System Model and Assumptions

According to [11], the layered control plane is thought to be more realistic in practical applications. Based on that, our system is composed of following parties: the Global Controller (GC), many Local Controllers (LCs), many OpenFlow Switches (OF-Switches), Base Stations(BSs), Access Points (APs), and online learning devices (OLDs). GC and LCs are responsible for dealing with collected information, and making optimal decisions. The others make up the data plane, which is mainly to transport packages and collect road information. The system model is shown in Figure 1.

(1)

GC:It’s the main controller of the control plane. In traditional SDN systems, the controller is a logically centralized point that has extremely outstanding storage and computing capabilities. Typically, it directs switches to deliver and forward packages by building routing rules. In our system, the GC is mainly responsible for generating system parameters, computing the movement path of the device, and building route tables for OF-Switches. When there are accidents or emergencies happening, it also selects impacted devices and forms a temporary multicast group. It generates a multicast tree for this group to inform them of conditions in time.

(2)

LCs:They are distributed geographically and manage a specific small area respectively. In our system, LCs exist mainly for balancing the computation and storage burdens of the GC. It can reduce realistic deployment costs as well. LCs set system parameters and communicate with OLDs. They can verify messages in their local areas and compute fine-grained navigation for OLDs. When there are road situations, they also compose of multicast nodes to inform and direct OLDs in their areas.

(3)

OF-Switches:Different from conventional switches, OF-Switches are OpenFlow-enabled data switches that communicate with external controllers over OpenFlow channel. OpenFlow protocol offers separation of programming network devices and underlying hardwares [32]. In our system, OF-Switches perform package lookup and forwarding according to flow tables installed on them.

(4)

OLDs:OLDs offer network access services via wireless communication capabilities, which have limited computing power and storage [33]. Also a tamper-proof equipment is embedded in each OLDs, which is robust and responsible for generating key cryptographical parameters, and performing many encryption and decryption operations [34].

(5)

BSs and APs:OLDs get access to Internet via various ways. Cellular networks like 5G network via BSs, and city WiFi via APs are both supported by our system. For Software-defined MIoTs, to balance heterogeneous networks and allow OLDs in different networks to communicate is much easier compared with conventional networks.

*

The GC is fully trusted and will not be compromised. It has ample computing power and storage space.

*

LCs are trustworthy, but in case it is compromised, we don’t provide them capabilities of trace OLDs’ real identities. LCs have sufficient computing and storage space.

*

The parameters and data stored in OLDs are not available for others.

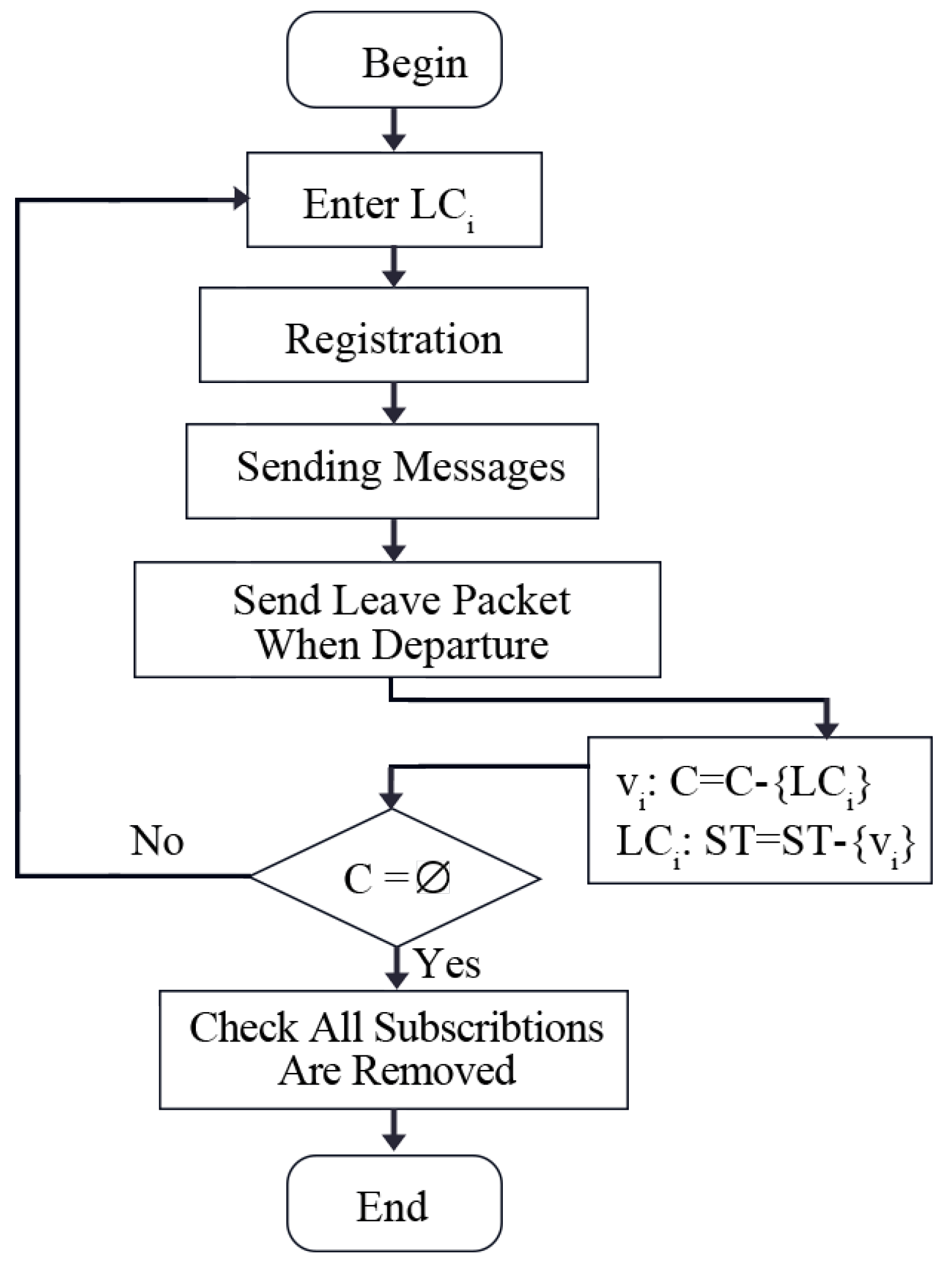
3.2. Multicast Subsystem

When an emergency occurs, impacted OLDs may request new movement paths rather than staying been stuck. Commonly, the conventional systems only replan new paths based on the present road conditions but do not take dynamically instantaneous changing into consideration. We design a multicast mechanism-based emergency system, which uses Stein Tree to compute a multicast tree between those nodes to inform affected OLDs in time.

3.2.1. Steiner Tree

In general, to connect n nodes, the Minimum Spanning Tree (MST) is the most commonly selected algorithm. But in networks, there are lots of factors needed to be taken into consideration, such as bandwidth and transport delay of networks, and so on. Hence, Steiner Tree, an spanning tree algorithm with weights, is more suitable. The generation of Steiner tree is thought to be computation intensive, so there are few applications in conventional multicast schemes. But as for SDN controller, it becomes feasible since the forwarding information is preloaded in network switches. Besides that, the global visibility and programmability can also help to construct a better multicast tree more efficiently [20].

Algorithm 1 Directing Process

Input: input departure, $Dp$; destination,$Ds$ Output: reach $Ds=1$ 1: $OL{D}_i$ request path   2: control plane return path $C={\left\{L{C}_k\right\}}^{*}$,$0<k<n$   3: $L{C}_k:ST=ST+\left\{OL{D}_i\right\}$   4: while$C!=\varnothing$do   5:     $OL{D}_i$ leaves $L{C}_k$   6:     // $OL{D}_i$ does:   7:     $C=C-\left\{L{C}_k\right\}$, $1<k\le n$   8:     // $L{C}_k$ does   9:     $ST=ST-OL{D}_i$, $0\le \left|ST\right|\le n$   10:     if $L{C}_k$ unreachable = true then   11:         $T=DBWST(d,n)$   12:         // d is the number of affected vehicles   13:         // $0<d\le m$   14:         jump tp line 1   15:     end if  16: end while  17: end while

3.2.2. Multicast Tree

In our scheme, we take the Degree-dependent Branch-node Weighted Steiner Tree (DBWST) proposed in [20] to construct our multicast tree. Based on the DBWST, consider an undirected graph $G_v=\{V,L\}$, in which V denotes OLDs and other entities taking part in communication in Software-defined MIoTs, and L is the set of links. For example, the link $l=(v,w)\in L$ denotes the link from $v\in V$ and $w\in V$. Then the cost of link l is $Cst\left(l\right):L\mapsto R^{+}$, where $R^{+}$ is nonnegative. Let s be the source of a multicast, and $U\subset V-\left\{s\right\}$ is the set of destination node, which is our system is the affected OLDs. The number of $\left|R\right|$ will be the size of this group. Let $T=(s,U)$ denotes the multicast tree whose source is s, and spanning all nodes $OL{D}_i\in U$, $1<i<\left|U\right|$. According to the definition of branch node in Steiner Tree, if the degree of node $OL{D}_i$ is no less than three, then $OL{D}_i$ would be one. Let ${\pi }_u$ represents that u is a branch node in T. Based on above description, finally the cost of the tree T can be denoted as:

$$Cst\left(T\right)=\sum _{l\in T}Cst\left(e\right)+\sum _{u\in T}{\pi }_u·Cst\left(u\right)$$

(1)

Based on the DBWST, it’s computationally uncomplicated to find a tree $T=(s,U)$ which makes the $Cst\left(T\right)$ lowest. The constructed multicast tree can not only help to distribute messages more efficiently, but also applied to other fields, such as video conferences and streaming media subscribing.

3.2.3. Application Process

With the multicast tree has been constructed, the process will be described as following. When a OLD starts driving, firstly it will request a path to the controller. Commonly, it tends to store all the forwarding entries in control plane to program routing process. However, given m OLDs and n LCs, the worst condition is that the spatial complexity will reach $O\left(n^m\right)$. Even the lowest will reach $O\left(n^2\right)$. So, we propose to only maintain a subscriber table in each LC. For example, a OLD $OL{D}_i$ gained a path passing through x consecutive LCs. Let C denote the set of x LCs, $\left|C\right|=x$. Then each LC will add $OL{D}_i$ into its subscriber table $ST$. Every time when $OL{D}_i$ leaves an area, it will send leaving packet to control plane. After that, $OL{D}_i$ and LCs will perform $C=C-\left\{L{C}_k\right\}$,$1<k\le n$, and $ST=ST-\left\{OL{D}_i\right\}$, $0\le \left|ST\right|\le m$, respectively. This step is designed to prevent OLDs that have passed through the area would still be rearranged. By only maintaining subscriber tables, the spatial complexity can be decreased to $O\left(m^n\right)$, where $n\ll m$. The process of subscribing is shown as Figure 2.

3.3. Design Goals

Our goal is to design an efficient system to offer OLDs a secure environment to communicate, and services such as avoiding risks. It will satisfy the following desirable properties. $RoutingPlan$: Taking use of the global ability, the control plane will generate the most suitable using plan for OLDs. $EmergencyHandling$: When emergencies occurred, to avoid secondary happening, control system will inform the impacted OLDs promptly by its multicast mechanism. Then it replans new routes for OLDs by balancing all networks situations. $SecureCommunication$: The most important is that all the messages sent by OLDs need to ensured trustworthy and factual. Considering that, the system should have the following security properties.

(1)

Anonymity: OLDs in our system will not communicate with other entities with real identities. Only by virtue of messages sent by OLDs and some public information, malicious users are not able to obtain the sender’s real identity. By this, OLDs are allowed to send messages without exposing sensitive privacy.

(2)

Authentication and Privacy: All interactive parties in our system can authenticate each other to ensure the reliability and legitimacy. Especially, in different areas, messages sent by OLDs should reflect the present LC’s information without exposing them to adversaries, which makes sure the location privacy would not be damaged.

(3)

Traceability: We won’t exclude the possibility of malicious entities’ existences. They aim to interrupt or interfere normal communications, or spread false and deceptive messages to gain conveniences and benefits for themselves. When misbehavior occurs, the controller plane should be able to trace the real identities and punish them by cutting services or submitting their information to related authorities.

(4)

Unlinkability: The proposed scheme would not enable third parties to link scattered messages to the same OLDs. That is to say, no third party could know one specific OLD’s activities by analysing those intercepted messages.

(5)

Resistance to common attacks: The scheme should also be able to resist common attacks that happen in conventional networks. For instance, replay attack, impersonation attack, modification attack, and so on.

4. Proposed Scheme

Here, we propose our secure communication scheme in Software-defined MIoTs. In our scheme, firstly messages should be signed then distributed to ensure non-repudiation. Then, to prevent the privacies of vehicles are exposed, OLDs should communicate via pseudo identities, which conclude a rough location of its current LC area. All above information can only be derived by GC but not other third party. When emergencies occur, GC will extract OLDs’ locations from messages they sent. When malicious messages are found, GC will extract OLDs’ real identities from those messages, and take actions to punish them.

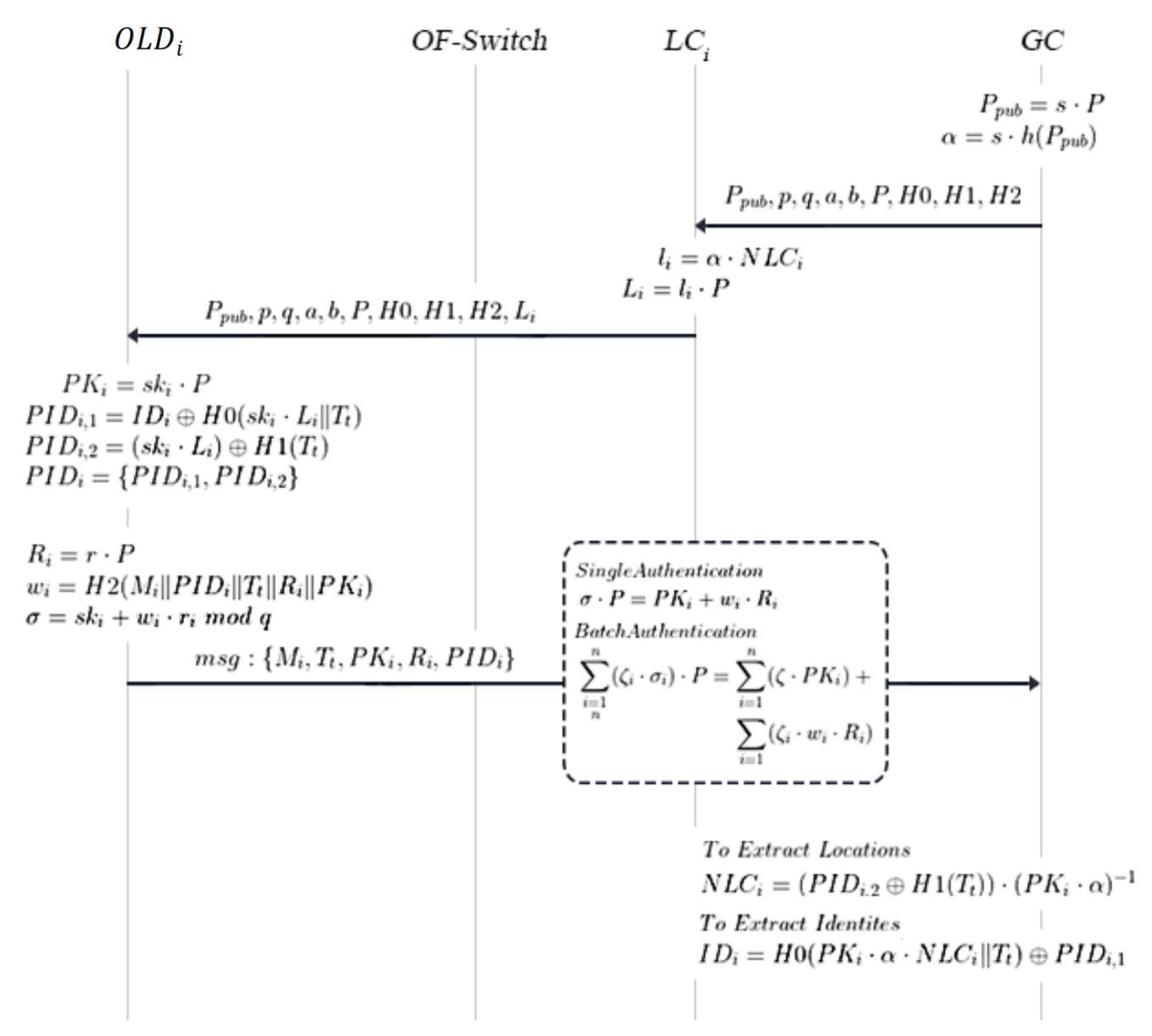
4.1. Control Plane Initialization

Let $F_p$ be the finite field over a large prime p, and p denotes the size of this field. $(a,b)\in F_p$ are the parameters of elliptic curve $E:y^2=x^3+ax+bmodp$. The system generates a group G from E, where P is the generator and q is the prime order of E. Other notations and definitions in our scheme are presented in Table 1.

1)

GC Initialization:The GC randomly selects the master key $s\in Z_q$, and computes $P_{pub}=s·P$ as its public key, and makes $\alpha =s·h\left(P_{pub}\right)$. Then it selects $h:G$$\to Z_q^{*}$, $H0:G\times {\{0,1\}}^{*}\to Z_q^{*}$, $H1$$:{\{0,1\}}^{*}$$\to Z_q^{*}$, $H2:{\{0,1\}}^{*}\times {\{0,1\}}^{*}\times {\{0,1\}}^{*}\times G\times G\to Z_q^{*}$. It sends $\alpha$ to LCs and publishes {$P_{pub},p,q,a,b,P,H0,H1,H2$} as the system parameters. To ensure the security of the whole system, hash function h should be kept secret to GC.

2)

LCs Initialization:After receiving $\alpha$ via secure channel in control plane, $L{C}_i$ computes $l_i=\alpha ·NL{C}_i$ as its secret key, where $NL{C}_i$ is a unique number of each LC and a list of them is only stored in the GC. Since s is unknown to any third party, and each $NL{C}_i$ also stays secret, it’s also difficult to compute $l_i$ based on public parameters. Then it computes $L_i=l_i·P$ as its public key, and adds $L_i$ in to GC’s system parameters. Finally, {$P_{pub},p,q,a,b,P,H0,H1,H2,L_i$} is the local system parameters of this specific area.

4.2. Online Learning Devices Initialization

When a online learning devices $OL{D}_i$ enters into the area of $L{C}_i$ and it requires to publish messages in current environment, it loads parameters and randomly selects $s{k}_i\in Z_q$ as its private key, and calculates $P{K}_i=s{k}_i·P$ as the public key. Then $PI{D}_{i,1}=I{D}_i\oplus H0(s{k}_i·L_i\parallel T_t)$, $PI{D}_{i,2}=(s{k}_i·L_i)\oplus H1\left(T_t\right)$. It uses $PI{D}_i=\{PI{D}_{i,1},PI{D}_{i,2}\}$ as its pseudo name.

4.3. One-time Key Generation and Message Signature

A message $M_i$ could include status, emergency information or other related requests. When $OL{D}_i$ tends to send message $M_i$, it will firstly select a number $r_i$ randomly, and computes $R_i=r·P$. Let $w_i=H2(M_i\parallel PI{D}_i\parallel T_t\parallel R_i\parallel P{K}_i)$, where $T_t$ is the current timestamp. Then it signs $M_i$ with $\sigma =s{k}_i+w_i·r_{i}modq$. Then, $OL{D}_i$ will send encapsulated $msg:\{M_i,T_t,P{K}_i,R_i,PI{D}_i\}$ to nearby communication-related entities.

4.4. Emergency Location Extraction

To ensure the basic location privacy of OLDs, the specific LC where it locates can’t be exposed in $msg$. Otherwise, by connecting and analysing several messages it has sent, it’s feasible for malicious parties to draw a rough activity areas of one OLD. But when emergency happens, control plane needs to roughly located affected OLDs. By fully balancing affected and unaffected areas’ densities of OLDs, the control plane is able to construct a most efficient multicast tree with average lowest sources consumption $Cst\left(T\right)$.

When there are abnormal conditions, OLDs around will broadcast a message $msg$ to report. After receiving those $msg$s, the GC will perform following computing to decide a rough location of LC.

$$\begin{array}{cc}\hfill PI{D}_{i,2}& =(s{k}_i·L_i)\oplus H1\left(T_t\right)\hfill \\ \hfill & =(s{k}_i·\alpha ·NL{C}_i·P)\oplus H1\left(T_t\right)\hfill \\ \hfill & =(P{K}_i·\alpha ·NL{C}_i)\oplus H1\left(T_t\right))\hfill \\ \hfill & \Downarrow \hfill \\ \hfill NL{C}_i& =(PI{D}_{i,2}\oplus H1\left(T_t\right))·{(P{K}_i·\alpha )}^{-1}\hfill \end{array}$$

(2)

By locating the LC, the GC will handle this area’s packets preferentially to deal with emergencies.

4.5. Message Authentication

To verify whether OLDs have sent false messages or packets have been modified, other entities can verify signatures of received messages. To improve the efficiency of verification, the proposed scheme also support to verify messages in batch simultaneously. The single-message verification and batch-message verification are described as below respectively.

(1)

Single Verification

After receiving a message $\{M_i,T_t,P{K}_i,R_i,PI{D}_i\}$, to verify its validation, a receiver will perform following steps by order with the system parameters {$P_{pub},p,q,a,b,P,H0,H1,$$H2,L_i$}.

*

Check if the timestamp $T_t$ is fresh. If not, it abandons the received message. If so, keep performing.

*

The receiver performs $\sigma ·P$ and $P{K}_i+w_i·R_i$ and calculates if they equal. If does not, the receiver chooses to abandon it. If equals, it admit the validation of this message.

Since $P_{pub}=s·P$, $w_i=H2(M_i\parallel PI{D}_i\parallel T_t\parallel R_i\parallel P{K}_i)$, $R_i=r·P$, $P{K}_i=s{k}_i·P$, and $PI{D}_i=\{PI{D}_{i,1},PI{D}_{i,2}\}$, where $PI{D}_{i,1}=I{D}_i\oplus H0(s{k}_i·L_i\parallel T_t)$, $PI{D}_{i,2}=(s{k}_i·L_i)\oplus H1\left(T_t\right)$, and $\sigma =s{k}_i+w_i·r_{i}modq$, following equations can be derived.

$$\begin{array}{cc}\hfill \sigma ·P& =(s{k}_i+w_i·r_i)·P\hfill \\ \hfill & =s{k}_i·P+w_i·r_i·P\hfill \\ \hfill & =P{K}_i+w_i·R_i\hfill \end{array}$$

(3)

(2)

Batch Verification

When a receiver obtains n messages in a short interval, verifying them one by one will consume lots of time and computing power. So our scheme supports batch verification to save sources. Firstly, to ensure the non-repudiation of signatures using batch verification, we choose a vector consisting of small random integers. Let the vector $\zeta =\{{\zeta }_1,{\zeta }_2,{\zeta }_3,...,{\zeta }_n\}$, where ${\zeta }_i\in [1,2^{\xi }]$, and $\zeta$ is a secure parameter. After receiving a message $\{M_1,T_{t,1},P{K}_1,R_1,PI{D}_1\}$, $\{M_2,T_{t,2},P{K}_2,R_2,PI{D}_2\}$, ..., $\{M_n,T_{t,n},P{K}_n,R_n,PI{D}_n\}$, to verify its validation, a receiver will perform following steps by order with the system parameters {$P_{pub},p,q,a,b,P,H0,H1,H2,L_i$}.

*

Check if the timestamp $T_{t,1},T_{t,2},...,T_{t,i},...T_{t,n}(1<i\le n)$ are fresh. If not, it abandons the received message. If so, keep performing.

*

The receiver performs $\left(4\right)$ and calculates if they equal. If does not, the receiver will find the malicious message via the invalid signature search algorithm and chooses to abandon it[cite]. If equals, it admits the validation of this series of messages.

$$\begin{array}{cc}\hfill \sum _{i=1}^n({\zeta }_i·{\sigma }_i)·P& =(\sum _{i=1}^n{\zeta }_i·(s{k}_i+w_i·r_i))·P\hfill \\ \hfill & =\sum _{i=1}^n({\zeta }_i·(s{k}_i·P+w_i·r_i·P))\hfill \\ \hfill & =\sum _{i=1}^n({\zeta }_i·P{K}_i+{\zeta }_i·w_i·R_i)\hfill \\ \hfill & =\sum _{i=1}^n(\zeta ·P{K}_i)+\sum _{i=1}^n({\zeta }_i·w_i·R_i)\hfill \end{array}$$

(4)

By this, the validation of the batch verification of a series of message is proved. The interaction of above parties is shown as Figure 3.

5. Security Proof and Analysis

In this part, we will analyze the security of communications in our proposed scheme. In Section 2 we have demonstrated some our security goals and threats it may meet. Firstly we introduce the definition of the elliptic curve discrete logarithm problem (ECDLP) that the whole analysis based on.

Definition 1(ECDLP): $n\in Z_q$ and $N=nP\in G$, where P is the generator of the group G. Given $N=nP$ it’s infeasible to compute n. Based on the network described before, a game between adversary $\mathcal{A}$ and challenger $\mathcal{C}$ is defined to set up the security model of the proposed scheme.

5.1. Security Proof

The adversary $\mathcal{A}$ is allowed to make following queries in this game.

• Setup-Oracle: $\mathcal{C}$ generates the private key and corresponding system parameters. Then it sends them to $\mathcal{A}$ when $\mathcal{A}$ revokes the query.
• $H0$-Oracle: $\mathcal{C}$ chooses a random point $d\in Z_q$, and insert $\{m,d\}$ into its list $L_{H0}$. Then it returns d to $\mathcal{A}$ when $\mathcal{A}$ revokes the query.
• $H1$-Oracle: $\mathcal{C}$ chooses a random number $d\in Z_q$, and insert $\{m,d\}$ into its list $L_{H1}$. Then it returns d to $\mathcal{A}$ when $\mathcal{A}$ revokes the query.
• $H2$-Oracle: $\mathcal{C}$ chooses a random point $d\in Z_q$, and insert $\{m,d\}$ into $L_{H2}$. Then it returns d to $\mathcal{A}$ when $\mathcal{A}$ revokes the query.
• Sign-Oracle: based on the $M_i$ sent by $\mathcal{A}$, $\mathcal{C}$ computes a $msg:\{M_i,T_t,P{K}_i,R_i,PI{D}_i\}$. Then $\mathcal{C}$ returns $\{M_i,T_t,P{K}_i,R_i,PI{D}_i\}$ to $\mathcal{A}$ when $\mathcal{A}$ revokes the query.

If adversary $\mathcal{A}$ could forge a valid login request message, then we say that $\mathcal{A}$ could violate the proposed secure communication scheme. Let $\Phi \left(\mathcal{A}\right)$ denote the probability that $\mathcal{A}$ violates the scheme.

Definition 2. Our scheme is secure if $\Phi \left(\mathcal{A}\right)$ is negligible for any polynomial adversary $\mathcal{A}$.

By evaluating the security of our scheme in random oracle, we make following theorem.

Theorem 1. The proposed scheme is secure in the random oracle model.

Proof: Suppose that there exists an adversary $\mathcal{A}$ that could forge a $msg:\{M_i,T_t,P{K}_i,R_i,$$PI{D}_i\}$. We construct a challenger $\mathcal{C}$ to perform our signature scheme. By performing following queries revoked by $\mathcal{A}$, challenger $\mathcal{C}$ is able to solve the ECDLP problem with a non-negligible probability by running $\mathcal{A}$ as a subroutine.

Setup Oracle: Firstly a key parameter k is taken as input. Then $\mathcal{C}$ randomly selects a number s as its private key and computes $P_{pub}=s·P$ and $\mathcal{C}$ sends {$P_{pub},p,q,a,b,P,H0,H1,$$H2$} to $\mathcal{A}$.

H0 Oracle: $\mathcal{C}$ keeps a list $L_{H0}:(s{k}_i,L_i,T_t,h_{0,i})$ initialized to empty. When $\mathcal{A}$ invokes this query with $(s{k}_i,L_i,T_t)$, $\mathcal{C}$ checks if $L_{H0}:(s{k}_i,L_i,T_t,h_{0,i})$ already exists in $L_{H0}$. If so, $\mathcal{C}$ returns $h_{0,i}$. Otherwise, it selects a random $h_{0,i}=H0(s{k}_i·L_i\parallel T_t)$, inserts $L_{H0}:(s{k}_i,L_i,T_t,h_{0,i})$ and returns $h_{0,i}$ to $\mathcal{A}$.

H1 Oracle: $\mathcal{C}$ keeps a list $L_{H1}:(T_t,h_{1,i})$ initialized to empty. When $\mathcal{A}$ invokes this query with $\left(T_t\right)$, $\mathcal{C}$ checks if $L_{H1}:(T_t,h_{1,i})$ already exists in $L_{H1}$. If so, $\mathcal{C}$ returns $h_{1,i}$. Otherwise, it selects a random $h_{1,i}=H1\left(T_t\right)$, inserts $L_{H1}:(T_t,h_{1,i})$ and returns $h_{1,i}$ to $\mathcal{A}$.

H2 Oracle: $\mathcal{C}$ keeps a list $L_{H2}:(PI{D}_i,L_i,T_t,R_i.P{K}_i,M_i,h_{2,i})$ initialized to empty. When $\mathcal{A}$ invokes this query with $(PI{D}_i,L_i,T_t,R_i.P{K}_i,M_i)$, $\mathcal{C}$ checks if $L_{H2}:(PI{D}_i,L_i,T_t,R_i.P{K}_i,$$M_i)$ already exists in $L_{H2}$. If so, $\mathcal{C}$ returns $h_{2,i}$. Otherwise, it selects a random $h_{2,i}=H2(PI{D}_i\parallel L_i\parallel$$T_t\parallel R_i\parallel P{K}_i\parallel M_i)$, inserts $L_{H2}:(PI{D}_i,L_i,T_t,R_i.P{K}_i,M_i,h_{2,i})$ and returns $h_{2,i}$ to $\mathcal{A}$.

Sign Oracle: On receiving $\mathcal{A}$’s query with message $M_i$ and pseudo identity $PI{D}_i$, $\mathcal{C}$ checks if $(s{k}_i,L_i,T_t,h_{0,i})$ and $(T_t,h_{1,i})$ already exist in $L_{H0}$ and $L_{H1}$ respectively. $\mathcal{C}$ gains $h_{0,i}$ from $(s{k}_i,L_i,T_t,h_{0,i})$ and $h_{1,i}$ from $(T_t,h_{1,i})$. Otherwise, $\mathcal{C}$ selects three random numbers $\sigma ,w_i,PI{D}_i\in Z_q$, where $PI{D}_i=f1(h_{0,i},h_{1,i})$, $\sigma =f2(w_i,PI{D}_i)$. Then $\mathcal{C}$ sends $\{M_i,T_t,P{K}_i,R_i,PI{D}_i\}$ to $\mathcal{A}$. It’s feasible to verify that $\sigma ·P=P{K}_i+w_i·R_i$ hold.

Based on Forking lemma, suppose that $\mathcal{A}$ has generated two valid signatures, we have $\sigma ·P=P{K}_i+w_i·R_i$ and $\tilde{\sigma }·P=P{K}_i+{\tilde{w}}_i·R_i$. To violate the $\sigma$, $\mathcal{A}$ will perform following steps.

$$\begin{array}{cc}\hfill (\sigma -\tilde{\sigma })·P& =\sigma ·P-\tilde{\sigma }·P\hfill \\ \hfill & =(P{K}_i+w_i·R_i)·P-(P{K}_i+{\tilde{w}}_i·R_i)·P\hfill \\ \hfill & =w_i·Ri·P-{\tilde{w}}_i·Ri·P\hfill \\ \hfill & =(w_i-{\tilde{w}}_i)·r_i·P^2\hfill \end{array}$$

(5)

$\mathcal{C}$ compute $(\sigma -\tilde{\sigma }){((w_i-{\tilde{w}}_i)·P^2)}^{-1}$. As the result shows, $\mathcal{A}$ solves the ECDLP problem in a polynomial time, which contradicts Definition 1. Hence, we come to the conclusion that communications in our scheme are secure against adaptive chosen message attack in the random oracle model.

5.2. Security Analysis

We set several security goals in Section II. Here, we analyse the security properties of the proposed scheme.

(1)

Anonymity: OLDs in our system will not communicate with other entities with pseudo identities $PI{D}_i$, where $PI{D}_i=\{PI{D}_{i,1},PI{D}_{i,2}\},PI{D}_{i,1}=I{D}_i\oplus H0(s{k}_i·L_i\parallel T_t),PI{D}_{i,2}=(s{k}_i·L_i)\oplus H1\left(T_t\right)$. Malicious users are not able to obtain the sender’s privacy only via public parameters and messages it sent. By this, vehicles are allowed to send messages without exposing their real identities.

(2)

Authentication and Privacy: All messages sent by communicating parties should sign these messages before sending. They compute $\sigma =s{k}_i+w_i·r_{i}modq$, where $w_i=H2(M_i\parallel PI{D}_i\parallel T_t\parallel R_i\parallel P{K}_i)$. Then encapsulated messages $msg=\{M_i,T_t,P{K}_i,R_i,PI{D}_i\}$ are broadcasted. Thus, all interactive parties in our system can authenticate each other to ensure the reliability and legitimacy. Besides, an encapsulated message $msg$ include no LC’s $NL{C}_i$ explicitly, which will keep the basic location privacy of OLDs. But when it’s needed, the GC can derive the rough location of $v_i$ by computing $(PI{D}_{i,2}\oplus H1\left(T_t\right))·{(P{K}_i·\alpha )}^{-1}$ from the $msg$.

(3)

Traceability: When malicious messages are detected, the GC will extract vehicles’ real identities by computing $I{D}_i=H0(P{K}_i·\alpha ·NL{C}_i\parallel T_t)\oplus PI{D}_{i,1}$, since $s{k}_i·L_i=s{k}_i·\alpha ·NL{C}_i·P=P{K}_i·\alpha ·NL{C}_i$, and $NL{C}_i=(PI{D}_{i,2}\oplus H1\left(T_t\right))·{(P{K}_i·\alpha )}^{-1}$ can be easily derived via messages.

(4)

Unlinkability: Every time to generate a message $msg:\{M_i,T_t,P{K}_i,R_i,PI{D}_i\}$, a random number $r_i\in Z_q$ will be reselected, and a new $w_i=H2(M_i\parallel PI{D}_i\parallel T_t\parallel R_i\parallel P{K}_i)$ will be recomputed. Due to the randomness of $r_i$ and variability of $w_i$, a malicious party is unable to link messages sent by one OLDs to itself. Therefore, the proposed scheme offers unlinkability in interactive communications.

(5)

Resistance to common attacks: Our scheme can also be able to resist common attacks that happen in conventional networks. Such as,

*

Replay Attack: The encapsulated message contains timestamp $T_t$, which can prevent messages are saved then reforwarded. When receives messages, receivers check the freshness of messages at the very first beginning. If it’s still fresh, receiver will start to verify the validation of these messages. Otherwise, messages will be abandoned.

*

Impersonation Attack: If an adversary tries to impersonate a legal vehicle, it has to generate a signature of the message $msg$ which satisfies $\sigma ·P=P{K}_i+w_i·R_i$. But according to Theorem 1, no adversary can generate such messages in the polynomial time, which proofs that our scheme is able to resist impersonation attack.

*

Modification Attack: A signature $\sigma =s{k}_i+w_i·r_{i}modq$ is a digital signature related to $M_i$ since $w_i=H2(M_i\parallel PI{D}_i\parallel T_t\parallel R_i\parallel P{K}_i)$. If $M_i$ is modified by a malicious party, then $w_i$ will change consequently, which makes $\sigma$ change as well. Hence, the modification can be easily detected if message itself is modified. By that, our scheme is able to resist modification attack.

*

Sybil Attack: To start a sybil attack, the adversary must generate multiple identities to play multiple roles. However, the pseudo identities are computed by a tamper-proof device. An adversary must violate the device first to generate those identities, which is infeasible via current technologies. Therefore, our scheme is able to resist sybil attack.

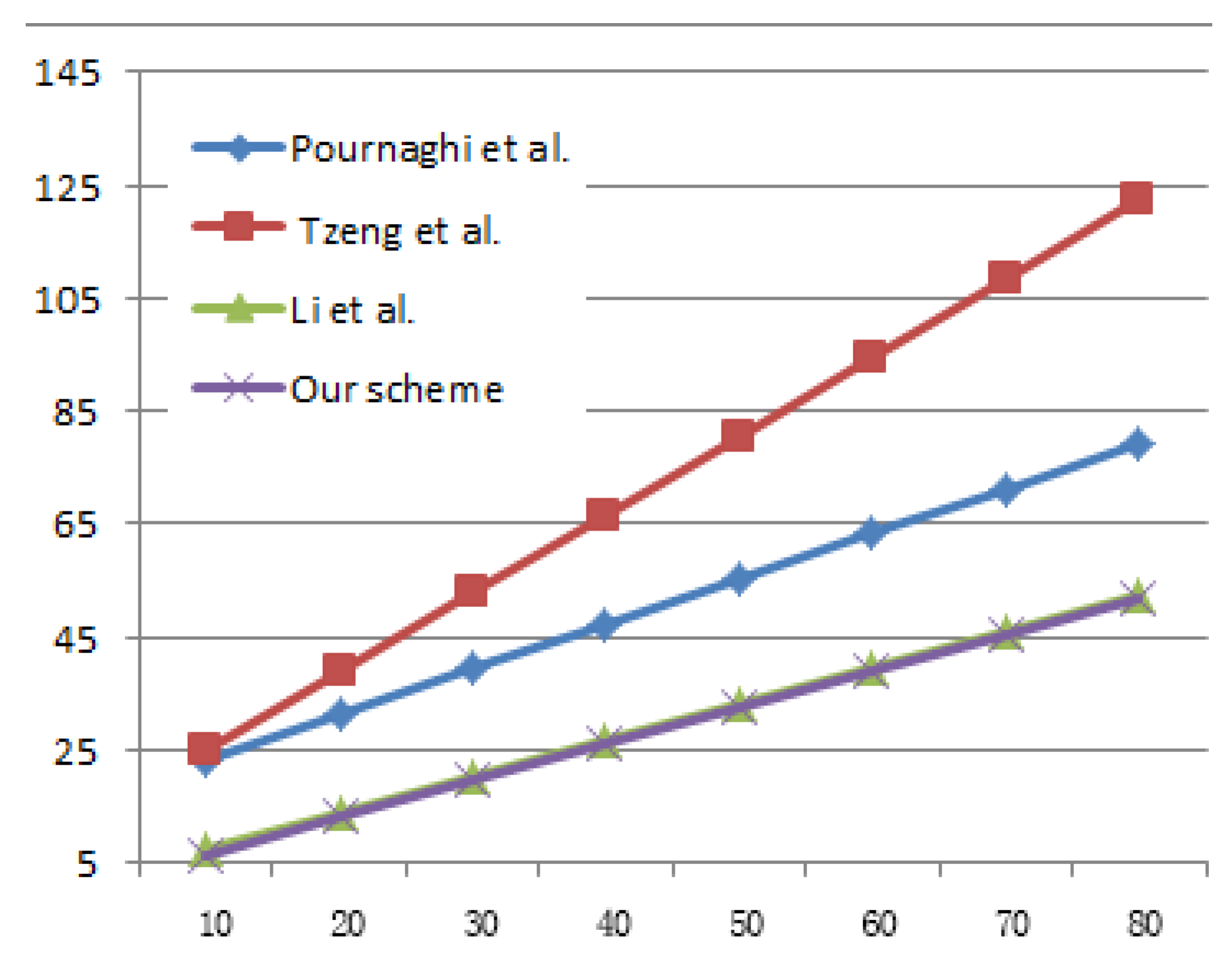
6. Performance Analysis

Here, we analyse the performance of our scheme with comparison of schemes of Pournaghi $etal.$ [35], Li $etal.$ [5] and Tzeng $etal.$ [36]. The processor is Intel Core CPU i7-6700 at 3.40GHz and 8GB RAM, and the operation system is Windows 7. Firstly, we set the bilinear pairing $E:G_1\times G_1\to G_T$ reaching a security level of 80 bits, where $P^{\prime }$ is the generator of $G_1$. And $G_1$ with order $q^{\prime }$ is the super singular elliptic curve $E^{\prime }:y^2=x^3+xmod{p}^{\prime }$, where $p^{\prime }$ is a 512-bit prime number and $q^{\prime }$ is a 160-bit prime number respectively. Then let order q of group G on the super elliptic curve $E:y^2=x^3+ax+bmodp,(a,b\in Z_p^{*})$, where q, p are 160-bit prime numbers. The notations used in this part are presented as below:

-

$T_{bp}$: The time spent on performing a bilinear pairing operation $e(Q^{\prime },R^{\prime }),Q^{\prime },R^{\prime }\in G_1$.

-

$T_{bm}$: The time spent on performing a scale multiplication operation $x^{\prime }·P^{\prime }$ of bilinear paring, , where $x^{\prime }\in Z_{q^{\prime }},P^{\prime }\in G_1$.

-

$T_{ba}$: The time spent on performing a point addition $Q^{\prime }+R^{\prime }$ of the bilinear pairing, where $Q^{\prime },R^{\prime }\in G_1$.

-

$T_{mtp}$: The time spent on performing a MapToPoint hash operation of the bilinear pairing.

-

$T_{em}$: The time spent on performing a scale multiplication operation $x·P$, where $x\in Z_q,P\in G$.

-

$T_{ea}$: The time spent on performing a point addition operation $Q+R$, where $Q,R\in G$.

-

$T_h$: The time required for performing an one-way hash function operation.

The execution time of each operations are shown in Table 2.

6.1. Computation Cost Analysis

In the scheme of Pournaghi $etal.$ [35], to sign a single message, four scale multiplication operations of the bilinear pairing, an addition operation of the bilinear pairing two hash function operations, a MapToPoint functions of the bilinear paiairng, and two hush functions are required, which is $4T_{bm}+T_{ba}+T_{mtp}+2T_h\approx 2.8790ms$. And when the batch verification is implemented, $3(n-1)$ addition operations of bilinear pairing, n scalar multiplication operations of bilinear pairing, three bilinear pairing operations, n MapToPint operations, and n one-way hash functions are performed, which is $3(n-1)T_{ba}+n{T}_{bm}+3T_{bp}+n{T}_{mtp}+n{T}_h\approx 0.7996n+15.2598ms$.

In the scheme of Tzeng $etal.$ [36], to sign a single message, three scale multiplication operations of the bilinear pairing, two hash function operations are required, which is $3T_{bm}+2T_h\approx 2.0840ms$. And when the batch verification is implemented, $(2n+1)$ addition operations of bilinear pairing, $(2n+1)$ scalar multiplication operations of bilinear pairing, two bilinear pairing operations, and n one-way hash functions are performed, which is $(2n+1)T_{ba}+(2n+1)T_{bm}+2T_{bp}+n{T}_h\approx 1.3926n+10.8678ms$.

In the scheme of Li $etal.$ [5], to sign a single message, one scale multiplication and two one-way hash functions are required, which is $1T_{em}+2T_h\approx 0.3238ms$. And when the batch verification is implemented, $(2n+2)$ scale multiplications, n point additions and $\left(2n\right)$ one-way hash functions are performed, which is $(2n+2)T_{em}+n{T}_{ea}+\left(2n\right)T_h\approx 0.648n+0.6436ms$.

In our scheme, to sign a single message, one scale multiplication and two one-way hash functions are required, which is $1T_{em}+T_h\approx 0.3228ms$. And when the batch verification is implemented, $2n$ scale multiplications, n point additions and n one-way hash functions are performed, which is $2n{T}_{em}+n{T}_{ea}+n{T}_h\approx 0.647nms$.

As Figure 4 shows, to sign a message, our scheme costs lower computation power than other three schemes. In Figure 5, we compare the execution time of batch verifications, and the result shows that our scheme achieve better performance.

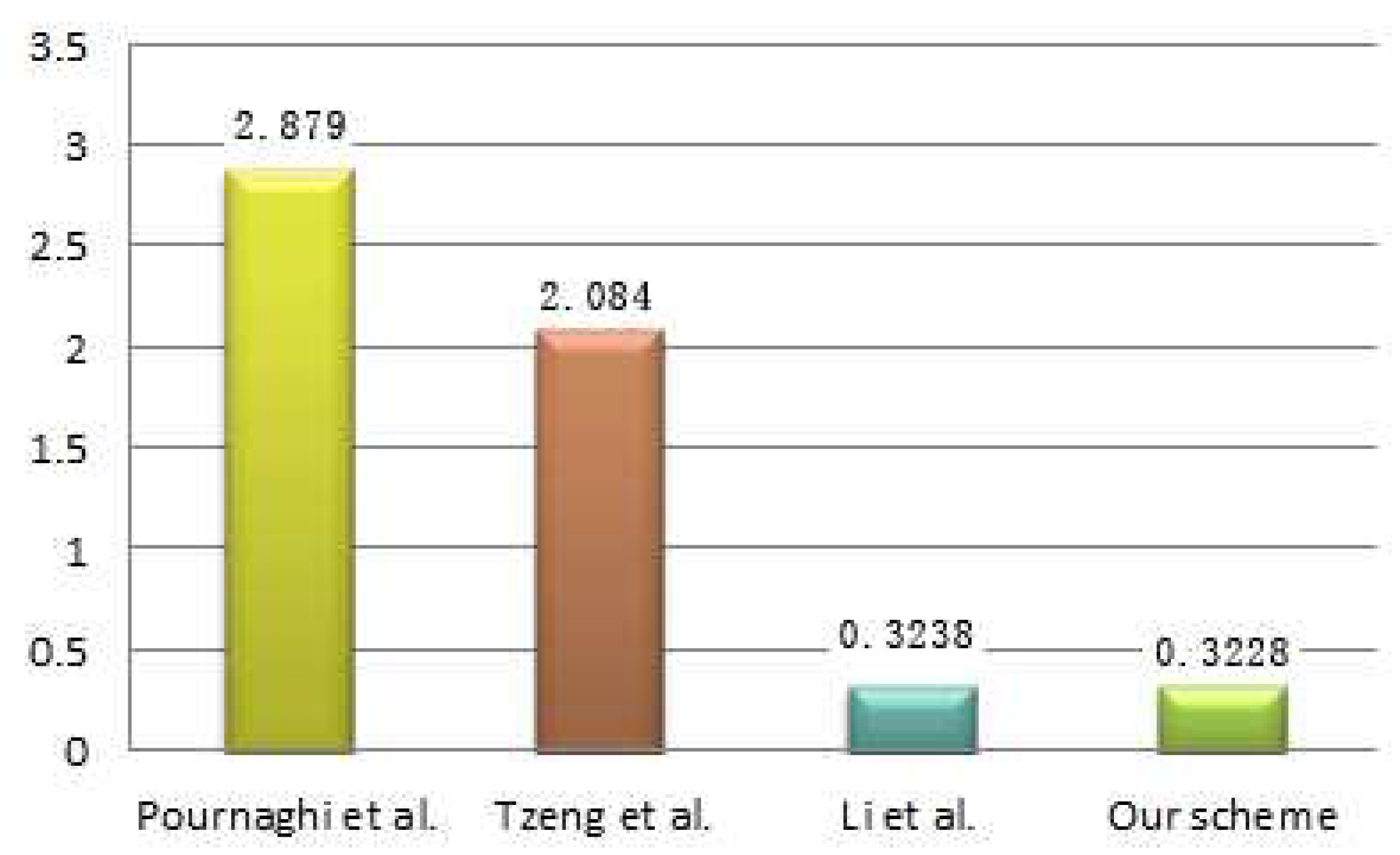
6.2. Communication Cost Analysis

We only analyze our scheme in detail since the analyzing process is the same. In our scheme, the online learning devices will send the anonymous identity and signature $\{M_i,T_t,P{K}_i,R_i,PI{D}_i\}$, in which $PI{D}_i=\{PI{D}_{i,1},PI{D}_{i,2}\}\in G,\sigma \in Z_q$, and $T_t$ is the timestamp. Accordingly, the communication cost is $40\times 4+20+4=184$ bytes. Similarly, the communication cost of Pournaghi $etal.$ [35] is 296 bytes, and 388 bytes in Tzeng $etal.$ [36], and in 144 bytes in Li $etal.$ [5].

The summarized comparison of both computation and communication costs is shown in Table 3.

7. Conclusions

This paper proposes a secure communication scheme based on multicast mechanism in Software-defined MIoTs. First, a multicast tree protocol is designed, which introduces the multicast mechanism to quickly establish the multicast tree after the occurrence of emergencies, so that the affected online learning devices can be informed in time. Then, the signature authentication scheme adapted to our system ensures the security of multi-party communication, so that the system can achieve security requirements of anonymity, privacy preserving, and traceability. Finally, the security proof of the scheme under random oracle indicates that the scheme can meet the requirements of secure communications in Software-defined MIoTs. The performance comparison of the scheme shows that the scheme has better performance in both computing and communication. In the future, we will focus on how to group online learning devices based on the proposed scheme, which helps to manage online learning devices more efficiently in device-intensive areas.