Preprint

Review

A Comparative Analysis of Two-Phase Flow Boiling Heat Transfer Coefficient and Correlations for Hydrocarbons and Ethanol

Altmetrics

Downloads

202

Views

Comments

A peer-reviewed article of this preprint also exists.

This version is not peer-reviewed

Submitted:

02 June 2023

Posted:

05 June 2023

You are already at the latest version

Alerts

Abstract

This study will present a comprehensive review of the two-phase flow boiling heat transfer coefficient of hydrocarbons such propane (R-290), butane (R-600) and iso-butane (R-600a) and ethanol at various experimental conditions. Studying the multiphase flow heat transfer coefficient has a crucial importance for many heat transfer equipment to achieve higher efficiency for more compact design and cost reduction. One reason behind choosing hydrocarbons as refrigerants in this study is because hydrocarbons have zero ozone depletion potential (ODP=0) and insignificant direct global warming potential (GWP = 3). Moreover, thermodynamic and thermophysical characteristics of hydrocarbons qualify them to be a strong candidate for more heat transfer applications. Initially, by constructing a database for the working fluids from various experimental work available in the literature. The current data that this study has collected for the flow boiling of spans wide ranges of parameters, such as: mass flux, heat flux, operating pressure, and saturation temperature, etc. Furthermore, by comparing the experimental multiphase heat transfer coefficient database with the anticipated values of each correlation, the prediction performance of 26 correlations found in the literature was assessed. This study leads to the selection of the best prediction method based on the minimum deviation of predicted results from the experimental database provided by calculated mean absolute error (MAE) from the assessed correlations. The findings of this study can also be useful in the development of more accurate correlation methods for these fluids and improve the prediction of their flow boiling characteristics.

Keywords:

Subject: Engineering - Mechanical Engineering

1. Introduction

In recognition environmental challenges such as ozone depletion and global warming, there is a growing interest among manufacturers, end-users, and scientific researchers regarding the utilization of natural operating fluids in air conditioning, heat pump, and refrigeration systems [1].

However, the use of natural refrigerants has become increasingly complex, involving countless experimental research on heat transfers, pressure drops, and fluid flow patterns. Natural refrigerant research has become extremely active, with the goal of establishing more precise design methodologies and more energy-efficient cycles using natural refrigerants.

Natural refrigerants such as ethanol, hydrocarbons such as propane (R290), butane (R600)/isobutene (R600a), and others have been studied over the last decade as a replacement for CFCs, HCFCs, and HFCs in refrigeration, air conditioning, and heat pump systems [1,2,3].The ozone depletion potentials (ODPs) of these natural refrigerants are zero, and most of them have close-to-zero global warming potentials (GWPs) in comparison to CFCs and HCFCs [1,2,3].

Hydrocarbons had earlier been employed as refrigerants. Because of increased concern for the environment, their use has recently been reassessed. Hydrocarbon (HC) refrigerants are already used in small freezers in some European countries. Propane, isobutane, n-butane, perfluorocyclobutane, cyclopropane, propylene, and other common hydrocarbons are under investigation [4]. In low-temperature applications, R290 is thought to be a suitable alternative for R22 and R502. In household refrigerators, R290 mixtures with R600a or R600 are proposed as R12 substitutions.

For those reasons, hydrocarbons such as Propane (R290) are commonly utilized as a refrigerant in a large cascade refrigeration system in ethylene manufacturing facilities. Germany has recently considered using propane and propane/n-butane mixes as a replacement for CFCs, HCFCs, and HFCs [5]. Furthermore, iso-butane is now used in the majority of new residential refrigerators in Germany. As a result, the usage of hydrocarbons as refrigerants is increasing due to their effectiveness.

The only issue is that hydrocarbon refrigerants are highly flammable. However, most refrigerators use a hermetic compressor, which seals the entire system. Furthermore, because hydrocarbons have a higher specific volume of liquid when compared to traditional refrigerants, the refrigerant charge is reduced.

The utilization of natural refrigerants has become progressively intricate, necessitating numerous experimental studies on heat transfer of these fluids. Along with the goal of developing more precise design techniques and energy-efficient cycles that use natural refrigerants, research in this area has become highly active. Nevertheless, many aspects of the present correlations require enhancement to attain the aimed level of accuracy for the design of refrigerant evaporators, as observed by Thome (1996) [6], from a predictive perspective.

Therefore, the aim of the present study is to present a comprehensive review on two-phase flow boiling heat transfer coefficient of ethanol and hydrocarbons (R290, R600, and R600a) refrigerants. Firstly, the experimental work done in literature was discussed. Then, a description of the available flow boiling heat transfer characteristic of the mentioned fluids and the two-phase heat transfer coefficient prediction correlations was assessed. Since each correlation is derived based on its own data, fluids, geometry, and operating conditions. Therefore, there are no specific prediction methods for ethanol and hydrocarbon. Furthermore, studying the operating fluids and using their data to evaluate the performance of the prediction correlations will be definitely an efficient way that might help in better understanding the complexity of natural refrigerants in the field of boiling two-phase flow. Leading to developing better designs and optimization methods for manufacturing and heat transfer equipment.

2. Experimental Studies on Hydrocarbons and Pure Ethanol

A literature survey on experimental studies in the literature has been conducted to create a database of hydrocarbons (R290, R600, R600a) and pure ethanol for analysis purposes. Table 1 summarizes various experimental work done by researchers studying the flow boiling of hydrocarbons. As well as Table 2 shows the experimental work done for pure ethanol. These studies are listed according to author/year, tube material, inner diameter, also the ranges of the experimental conditions in each experiment such as saturation temperature, heat flux, mass flux, and vapor quality.

2.1. Description of Experimental Work on Hydrocarbons

Cichong et al. [7] have reported that Propane exhibits considerable promise as a refrigerant for next-generation refrigeration systems, barring its flammability. One possible solution to address this issue is the use of low-charge systems. The boiling and evaporation heat transfer of propane increases in proportion to the heat flux, till reaching dry-out. Nevertheless, the correlation between boiling and evaporation heat transfer with mass flux and vapor quality is complex and heavily dependent on the operating conditions. The dry-out inception point is likewise strongly contingent on the flow mechanism.

Col et al. [8] investigated, the thermal performance of propane in enhanced mini-channels with an internal diameter of 0.96mm and a rough internal surface was scrutinized under a range of mass fluxes, from 100 to 600 kg/m²s and evaporation temperature of 31°C. The authors discovered that the flow was characterized by a slug and annular flow region according to Tibirica and Ribatski's [9] classification, within the range of vapor quality from 0.05-0.6 and heat flux from 10-315 kW/m². It was observed that within this region, the heat transfer coefficient increased with the rise in heat flux and had little dependence on other operating conditions. Moreover, the authors observed that the heat transfer coefficients decrease with an increase in vapor quality, Within the vapor quality range of 0.16-0.36, the heat transfer coefficient was found to be unaffected by mass fluxes.

Maqbool et al. [10] conducted experiments to analyze the flow boiling heat transfer of propane in a smooth vertical mini channel with an internal diameter of 1.7mm, mass flux of 100-400 kg/m²s, heat flux of 5 -240 kW/m², and saturation temperature of 23°C. The authors showed that boiling heat transfer coefficient was found to be independent of mass flux. They also concluded that, with the exception of higher vapor qualities, the local boiling heat transfer coefficients were mainly independent of vapor quality but increased with increasing heat fluxes. Moreover, a maximum point was determined where heat transport begins to decrease and proposed that this is the beginning of dry-out.

Wang et al. (2014) [11] performed experiments on propane boiling in a copper tube with an inner diameter of 6 mm under mass fluxes ranging from 62 to 104 kg/m²s, heat fluxes ranging from 11.7 to 87.1 kW/m², and saturated temperatures ranging from -35 °C to -1.9 °C. The authors observed that mass flux had a neglected effect at low vapor quality, but it had a more significant impact at high vapor quality, with a 60% increase in mass flow leading in a 20% increase in heat transfer coefficient. However, the heat flux had a substantial influence, with an almost linear increase in the heat transfer coefficient observed with an increase in heat flux. The saturation temperature had a negligible effect at small heat fluxes, but with increasing heat fluxes, it caused an increase in the heat transfer coefficients. They observed that the vapor quality effects were influenced by boiling number and liquid-to-vapor density ratio (Kandlikar and Steinke [12]), which depended on the flow boiling mechanism.

Jung et al. [13] Investigated the nucleate boiling heat transfer coefficients of some refrigerants, including propane, on a 19 mm outer diameter horizontal smooth tube. Where the saturation temperature of 7 °C and a heat flux of 10-80 kW/m². The results pointed out that propane has a heat transfer coefficient that is just 2.5% greater than R22.

Choi et al. [14] studied the flow boiling heat transfer and pressure drop characteristics of propane in horizontal mini channels with inner diameters of 1.5mm and 3mm, heat fluxes of 5-20 kW/m², mass fluxes of 50-400 kg/m2, saturation temperatures of 10.5 and 0 °C, and vapor quality up to 1.0. They demonstrated that mass flux has no influence on heat transfer coefficient prediction in the low-quality region but can induce a heat transfer decrease in the high-quality region. In contrast to mass flow, heat flux has a considerable influence on heat transfer coefficient in the low-moderate quality region, whereas the influence decreases in the high-quality region. Furthermore, the decrease in inner tube diameter and the rise in saturation temperature cause an increase in the heat transfer coefficient.

Maqbool et al. [15] studied propane heat transfer and pressure behaviors in a vertical circular mini channel with an inner diameter of 1.7mm at saturation temperatures of 23.33 and 43°C, heat fluxes of 5-280 kW/m², and mass fluxes of 100-500 kg/m²s. Their outcomes show that the heat transfer coefficient has a negligible association with vapor quality and mass flux, however, it increases with heat flux and saturation temperature. Lee et al. [16] conducted a study on four refrigerants, namely R290, R600a, R1270, and R22, using a 12.70mm tube and a mass flux ranging from 50-200 kg/m²s. They observed that the evaporative heat transfer coefficient increases with an increase in vapor quality until it sharply decreases after reaching 0.85 due to dry-out. R290 exhibited an average evaporative heat transfer coefficient 67.6% higher than that of R22.

Shin et al. [17] Investigated the flow boiling heat transfer of propane, isobutane, and propane (25, 50, and 75wt%/isobutene mixes) in a horizontal plain tube having an inner diameter of 7.7 mm. They discovered that the local heat transfer coefficients were substantially reliant on heat flux in the poor-quality zone and became independent as vapor quality increased. The propane/i-butane mixture outperformed R22 in terms of heat transfer coefficients. They compared their pure fluid heat transfer data to the Gungor and Winterton (1986) correlation and their mixture heat transfer data to Thome and Shakir's [18] modified Gungor-Winterton [19] correlation for refrigerant mixes. Both correlations outperformed the experimental data.

Wen and Ho (2005) [20] tested propane, butane, and propane/butane (55%/45wt %) in a horizontal plain tube with an inner diameter of 2.46 mm. They observed two-phase pressure decreases and local heat transfer coefficients. At equal heat and mass fluxes, the heat transfer coefficients of propane, butane, and propane/butane mixture were much higher than those of R134a, while the corresponding two-phase frictional pressure drops were lower. To anticipate their data for pure refrigerants, they presented a new heat transfer correlation based on a superposition model. Thome and Shakir [18] modified Gungor-Winterton [19] correlation for mixtures was tested against their mixed data and found to be highly accurate. This conclusion, however, contradicts the already cited Shin et al. [17] study. Because both studies. It is difficult to explain this because both investigations employed the same refrigerant blends with slightly varying component concentrations. Because mixture flow boiling is much more complex than pure refrigerant flow boiling, it is suggested that additional experiments for hydrocarbon mixtures be performed to validate this mixture boiling model and provide a larger database.

Chien et al. [21] investigated the boiling heat transfer coefficient and pressure drop of R410A, R32, and R290 in micro-channels. The experiments were carried out in horizontal stainless-steel tubes with inner diameters of 0.3 and 1.5 mm. The experimental results revealed that the heat transfer coefficients R32 and R290 increased as the heat flux increased. The contribution of nucleate boiling is the most significant. The experimental results were compared to several well-known heat transfer coefficient and pressure drop correlations. The present experimental data were well predicted by a modified heat transfer coefficient correlation for alternative and natural refrigerants. The one proposed by Liu and Winterton [22] makes the best forecast. A modified heat transfer coefficient correlation was also developed using current data. The mean and average deviations were reported to be roughly 16.80% and -0.23%, respectively.

Yunos et al. [23] studied the contributions of various heat transfer mechanisms in two phase flow boiling heat transfer coefficient for R290 (propane) in a narrow channel. The effects of heat flux and mass flux on heat transfer are investigated by comparing experimental data from a 7.6 mm diameter horizontal channel. It was discovered that experimental and optimized R290 findings coincided in the low vapor quality zone, with the heat transfer coefficient increasing with increasing heat flow.

Kanizawa et al. [24] reported on the heat transfer coefficient during flow boiling of the refrigerants R134a, R245fa, and R600a inside small diameter tubes with internal diameters ranging from 0.38 to 2.6 mm. They discovered that in conditions dominated by convective effects, the heat transfer coefficient increases with vapor quality until surface dry out is reached, at which point subsequent rises in vapor quality result in a significant fall in the heat transfer coefficient. In contrast, heat transfer coefficient increases with increasing heat flux and saturation temperature in flow circumstances dominated by nucleate boiling effects.

Wen et al. [25] evaluated the boiling heat transfer and pressure drop of R600a (iso-butane) flowing in a circular pipe with dispersed-copper porous inserts. They found that an increase in mass velocity and heat flux, as well as a loss in quality, raise the heat transfer coefficients of the current test tubes.

2.2. Description of Experimental Work on Ethanol

Ethanol has been characterized as a very promising fluid as a result of its intermediate thermodynamic and transport characteristics. However, due to its high flammability, which may pose a considerable risk to the experimental labor, there is a significant lack of experimental data for ethanol in the new literature. Because of its thermos-physical characteristics, ethanol requires less heat to reach boiling.

Mastrullo et al. [27] investigated anhydrous ethanol (purity grade of 99.8%) experimentally. All of the flow boiling tests were carried out in 6.0 mm stainless horizontal steel tube, with various operating conditions in terms of mass velocities ranging from 85 to 127 kg.m-2 s-1, saturation temperatures ranging from 64.5 to 85.8 °C. Furthermore, the heat flux ranged from 10.0 to 40.3 kW/m². The authors discovered that the local heat transfer efficiency exhibits pure convective behavior, with an increasing trend with vapor quality up to the occurrence of dry-out. Ethanol has been studied and found to be effective in heat pipe applications.

Robertson et al. [28] studied the boiling of ethanol in a 10 mm internal diameter and 3 m long vertical tube. Their experiments utilized a wide range of heat fluxes range (25.5 - 104.6 KW/m²), vapor quality ranging from 0.03 to 0.6, and two mass velocities (145 and 290 Kg. m-2. s-1). Based on precise measurements of ethanol at saturation conditions, the authors demonstrate the interaction between nucleate and convective boiling as a function of vapor quality.

Vasileiadou et al. [29]performed an experimental investigation of boiling multiphase flow heat transfer for ethanol as a pure component and as binary mixture with water (5%v/v) in borosilicate glass using vertical tantalum surface square channel with 5 mm inner hydraulic diameter, wall thickness 0.7 mm, heated length 72 mm, heat flux range 2.8-6.1 kW/m², and mass flux 0.33-1.0 kg.m-2 s-1 and constant, saturation temperature of 40 °C. The authors demonstrate the effect of fluid composition on flow boiling heat transfer by demonstrating that the addition of ethanol into water (5%v/v) might increase the heat transfer coefficient when compared to the pure components. They also realized that the amplitude of wall temperature heating variation is significantly lower in pure liquids, leading to a more stable heat transfer process.

3. Assessment of Previous Correlations

Many researchers offered a number of correlations to predict the heat transfer coefficient of flow boiling. The applicability of these prediction approaches, on the other hand, is often dependent on a specific database and is derived based on their operating conditions such as saturation temperature, pressure, heat flux, and mass flux ranges. The correlations are also dependent on their own experimental geometry, which includes tube orientation (e.g., horizontal, vertical, inclined), tube diameter, etc. In general, these correlations can be classified into two main categories: (A) the superposition model, which combines nucleate boiling and two-phase forced convection mechanisms, and (B) functions of the most significant dimensionless groups.

Review of Flow Boiling Heat Transfer Coefficient Correlations

Chen Correlation [30] is considered to be a leading method for calculating heat transfer coefficients in convective boiling Chen employed a superposition model (Category A) summarized in Table 3, which combines nucleate pool boiling with convective heat transmission. Nevertheless, convection is responsible for the suppression of nucleate boiling. Chen declared that when flow rate increases, the temperature gradient near the wall decreases, reducing the temperature difference between the tube inner wall and bubbles forming outside the wall. Numerous studies of flow boiling heat transfer correlations based on the Chen superposition model have been proposed to date, including the Liu-Winterton [22], Gungor-Winterton [19], and Saitoh et al. [31], Jung et al. [32], Bennett and Chen [33] and Choi et al. [34] Correlations.

Bennett and Chen [30] employed Chen superposition model for over 1,000 data sets for forced convective boiling of pure water, ethylene glycol, and aqueous ethylene glycol mixes. The majority of these measurements were made in the annular flow regime. Their study's aims were to collect forced convective boiling heat transfer data for a liquid with a relatively high Prandtl number and for aqueous mixtures, and to develop a correlation based on these data sets that would be applicable to other pure com-ponents and binary mixtures. The authors expected that their proposed correlation would be valid for boiling of binary mixtures anticipated to be in the annular and annular dispersed flow regimes. It should also be applicable for boiling liquids with Prandtl values between unity and ten under saturated circumstances. Furthermore, because it reduces to the normal Chen correlation for pure liquids with Prandtl values close to unity, it should be applicable for the same range of flow conditions as the Chen equation.

Lazarek and Black [38] introduced a new method for constructing correlation by fitting experimental data which consist of 728 data points and R113 was used a working fluid as a function of the most important dimensionless groups (Category B) as shown in Table 4. The authors used mini and micro-channels with 3.1 mm diameter and range G = 125 - 750 kg/m²s, q = 14 – 380 kW/m² and P = 1.3 - 4.1 bar. The liquid only Reynolds number and the boiling number were utilized by the authors. The influence of mass flux on the proposed correlation was negligible.

In contrast to Chen's superposition concept, Kenning and Cooper [44] suggested that the heat transfer mechanism in narrow tubes could be more like an enhancement of single-phase forced convection heat transfer. The expression of enhanced convective heat transfer was then proposed. To express the effect of two-phase flow, they used the LockhatMartinelli parameter ‘Xtt’. The correlation of Kenning and Cooper [44] takes the form of the product of single-phase forced convection and the function of the Lockhart-Martinelli parameter. However, Kenning and Cooper's experimental correlation data were still based on water as working fluid in a macro-scale tube with range of diameter of 9.6 - 14.1mm, x = 0 - 1, p = 0.16 - 0.6 MPa and G = 123 - 630 kg/m2s

Saitoh et al. [31] developed a correlation for the boiling heat transfer of R-134a in horizontal tubes including the effect of tube diameter were developed here for both the pre- and post-dry out regions. The authors modified Chen correlation model for flow boiling heat transfer was established, which includes the effect of tube diameter. The Weber number was used to describe the effect of tube diameter on flow boiling heat transfer. For a wide range of tube diameters from 0.51 to 10.92 mm, the correlation corresponded reasonably well with experimental results.

Jung et al. [32] studied the mixture effect on a horizontal flow boiling heat trans-fer. More than 2000 local heat transfer coefficients are obtained with the azeotropic R12/R152a mixture and compared against the previously measured data with the non-azeotropic R22/Rll4 mixture. He modified the superposition model suggested by chen using only phase equilibrium data to consider mixture effects to develop his correlation. Firstly, they replaced Forster and Zuber’s [48] nucleate pool boiling correlation shown in Equation (1) by Stephan and Abdelsalam correlation [49] as shown in Equation (2).

h_{n b} = 0.00122 [\frac{K_{L}^{0.79} C_{P_{L}}^{0.45} ∆ T_{e}^{0.24} ∆ P_{s a t}^{0.75}}{σ^{0.5} μ_{L}^{0.29} ∆ h_{v}^{0.24} ρ_{v}^{0.24}}]

(1)

h_{n b} = 207 \frac{K_{L}}{d_{b}} {[\frac{q d_{b}}{K_{L} T_{s}}]}^{0.745} {[\frac{ρ_{v}}{ρ_{L}}]}^{0.581} P_{r_{L}}^{0.533}

(2)

Secondly, they discussed that in a given quality in the partial boiling regime, nu-cleate boiling coefficient is a strong function of heat flux. It is also a function of mass flow rate for a given heat flux. Consequently, it becomes a function of quality, heat flux, and mass flow rate. After Since the derived their own suppression factor ‘S’ which is a strong function of heat flux which is differs from other similar factors such as the other suppression factors by Chen [30] and by Gungor and Winterton [19] fac-tors which are independent of heat flux.

Choi et al. [34] conducted experiments on the convective boiling heat transfer in horizontal mini channels with CO2. The test section is made of stainless-steel tubes with inner diameters of 1.5 and 3.0 mm and range of G= 200 – 600 kg/m2s, x= 0 – 1, Tsat = 0, 10, -5, -10 °C. In their developed correlation, the have used chen superposition model, however they developed their own suppression factor and enhancement factor by including the two-phase frictional multiplier that is based on pressure gradient for liquid only flow according to Chisholm [50]. They discovered that the heat transfer co-efficient at low vapor qualities (up to 0.2) is independent of mass flux and vapor quality but reliant on heat flux, and the boiling regime was designated as nucleate boiling. In the convective boiling regime, the heat transfer coefficient increases with mass flux and vapor quality. At high vapor quality (0.5-1), a drop in heat transfer coefficient happened more rapidly for higher mass fluxes due to the annular regime occurring earlier at a higher mass flow as shown in Equation (3).

ϕ_{f}^{2} = 1 + \frac{C}{X_{t t}} + \frac{1}{X_{t t}^{2}}

(3)

ElFaham and Tang [51] conducted a review study for the flow boiling heat transfer of pure ethanol in various experimental work. A wide range of parameters has been used in their study, Where Tsat = 4.-86.6 °C, G = 0.33 - 290 kg/m2s, q = 2.8 - 104 kW/m2 and x= 0.11 – 0.91. As well as the range of internal diameter is 5-10 mm. Their findings were Liu-Winterton [22] and Chen [30] correlations showed a good prediction among 14 correlations in the study. The authors have used the same approach as Liu-Winterton [22] correlation to derive their proposed correlation. Furthermore, they modified the suppression factor ‘S’ by introducing a suppression factor multiplier (Ms) to control the performance of suppressing the nucleate boiling contribution. They also classified their dataset into 4 regions using boiling number intervals to identify the value of (Ms) in each region [35]. Also, they used Cooper’s correlation as shown in Equation (4) and Dittus-Boelter correlation shown in Equation (5) to calculate the nucleate boiling and single-phase heat transfer coefficient.

h_{n b} = 55 q^{0.67} P_{R}^{0.12} {(- \log_{10} P_{R})}^{- 0.55} M^{- 0.5}

(4)

h_{s p} = 0.023 R {e_{L}}^{0.8} {P_{r_{L}}}^{0.4}

(5)

Warrier et al. (2002) [43] conducted sub-cooled and saturated nucleate boiling experiments in a multi micro-channel section with 5 rectangular channels with a hydraulic diameter of 0.75 mm. FC-84 is the test fluid. Their saturated boiling studies revealed that for a given Boiling number, the boiling heat transfer coefficient falls with increasing vapor quality. They presented an empirical correlation for saturated nucleate boiling and vapor qualities up to 0.55, with the heat transfer coefficient associated with the liquid heat transfer coefficient, boiling number, and vapor quality, with a maximum divergence with experimental data of 28%.

The flow boiling heat transfer characteristics were investigated by Tran [45] for R12 as working fluid. The authors used in their experiments small circular and rectangular tubes with diameters of d_in= 2.46 mm, d_h = 2.4 mm respectively. Moreover, a range of vapor quality (x = 0 - 0.94), Mass Flux (G = 44 – 832 kg/m²s) and Heat flux (q = 7.5 – 129 kW/m²). He emphasized that nucleate boiling contribution predominates in high-wall superheat conditions, while forced convection is the primary heat transfer mechanism in low-wall superheat conditions.

Wattelet et al. [37] The authors conducted their experiment for R-134a, MP-39, and R-12 in horizontal smooth 7.04 mm internal diameter copper tube, with testing parameters with ranges of G = 25-100 kg/m²s, q = 2-10 kW/m², x=0.1 - 0.9, T_sat = -15 – 5 °C. Experimental heat transfer coefficients were reported from their experimental work. In addition, an empirical correlation developed for annular flow data using an asymptotic form was modified to account for the decrease in heat transfer due to the wavy-stratified flow pattern in the low mass flux cases.

Yoon et al. [36] measured heat transfer coefficients and pressure drop during evaporation process of carbon dioxide in a horizontal smooth stainless-steel tube with internal diameter 7.53 mm. Experiments were conducted at Tsat = 4 – 20 °C, q = 12 - 20 kW/m² and G = 200 - 530 kg/m²s. They developed a correlation for carbon dioxide during evaporation was developed by considering the critical quality. They proposed that the correlation can predict the critical quality at which the liquid film breaks down at top of tube. Before the critical quality, the Liu and Winterton correlation is used to predict the heat transfer coefficient. After the critical quality, the Dittus–Boelter equation for vapor flow and the Gungor and Winterton correlation for liquid flow is superposed to predict the heat transfer coefficient of carbon dioxide.

Kew and Cornwell [39] introduced the confinement number in their model to take into consideration for the effect of bubbles limited by the mini-channel wall. They identified three types of flow patterns in mini-scale tubes: isolated bubble regime, restricted bubble regime, and annular-slug flow. In terms of bubble regime, nucleate boiling is the primary heat transfer mechanism, whereas convection is more important in the confined bubble regime and annular-slug flow. However, the authors presented the concept of confinement number for the correlation, but the final version proposed by Kew and Conwell is an improved correlation based on Lazarek and Black [38] correlation that takes vapor quality into account. They found that nucleate boiling in pre and post dry out zones is related to mass flux, boiling number, and vapor quality. It was shown that forced convection is the major mechanism of flow boiling heat transfer in small channels under their experimental conditions. They also considered the impact of equilibrium quality.

Yu et al. [42] used his experimental results to propose a correlation that was the same as Tran.[45] Water, ethylene glycol, and aqueous mixtures of ethylene glycol was the experimental fluids at high temperatures up to 250 °C, pressure (<345 kPa), G= 50 – 200 kg/m²s. The proposed correlation for two-phase heat transfer coefficient based on water flow boiling in a small 2.98 mm diameter horizontal channel which is also developed based on boiling results with refrigerants under similar conditions.

Sun and Mishima [41] used a relatively large database of 2050 data points from 20 published studies to propose a correlation based on the Lazarek and Black [36] correlation which is a function of the most important dimensionless groups as shown in Table 5.

The experimental results of Tran [45] reveal that nucleate boiling is the major process and that the effect of mass flux is insignificant. Furthermore, Tran's formula is totally empirical, with R12 as the working fluid in a circular channel with a hydraulic diameter of 2.46 mm and a tiny rectangular channel with a hydraulic diameter of 2.4 mm.

Agostini and Bontemps [46] have tested flow boiling of R-134a in multiple mini-channels experimentally. The tube is made up of 11 rectangular channels with a hydraulic diameter of 2.01 mm. They discovered a convective to nucleate boiling regime transition for a wall superheat greater than 3 K and heat flux greater than 14 kW. m2, which was consistent with Tran et al. [45] findings. They also observed dry-out at a critical quality of 0.4, without considering heat or mass flux.

Hamdar et al. [40] investigated the boiling heat transfer coefficient and pressure drop of R-152a in a 1-mm square mini-channel under test circumstances of G= 200-600 kg m-2 s-1, q= 10-60 kW/m², P= 600 Kpa, and T_sat = 25.2 °C. The Nusselt number and the dimensionless groups defined by Tran et al. [45] are used to correlate the experimental data matching their results. For the data set, the correlation coefficients are determined using a linear multi-regression technique.

4. Results and Discussion

The present study provides a comprehensive review of the flow boiling heat transfer coefficient of ethanol and hydrocarbons such, propane (R-290), butane (R-600), and iso-butane (R-600a) at various experimental conditions. A database was constructed based on various experimental works available in the literature for the mentioned fluids. This assessment includes a dataset consisting of 900 flow boiling heat transfer coefficient data point for hydrocarbons. On the other hand, 720 data point of flow boiling heat transfer coefficient of ethanol.

4.1. Assessment of Existing Correlations

The performance of 26 correlations identified in the literature, for predicting flow boiling heat transfer coefficient was evaluated by comparing their results with the experimental database of hydrocarbons, ethanol, and Propane (R290). To determine a reliable prediction method, a selection criterion was employed which involved assessing the minimum absolute deviation between the predicted results and the experimental database using Equation (6). Additionally, the mean relative deviation was also computed by Equation (7) to enhance the reliability of the prediction methods.

M A E = \sum_{i = 1}^{N} |\frac{h {(i)}_{p r e d} - h {(i)}_{e x p}}{h {(i)}_{e x p}}|

(6)

M R E = \sum_{i = 1}^{N} \frac{h {(i)}_{p r e d} - h {(i)}_{e x p}}{h {(i)}_{e x p}}

(7)

4.2. Comparison to Hydrocarbons Dataset

The deviations in the predictions made by the 26 correlations have been summarized in Table 5 for hydrocarbons and Table 6 for ethanol. Among the correlations tested for hydrocarbons, the top four that exhibited the lowest mean absolute deviation were Kew and Cornwell [39] (24.6%), Lazarek and Black [38] (25.7%), Liu and Winterton [22] (33.1%), and ElFaham and Tang [35] (36.7%). The mean relative deviations for the same correlations are -12.9%, -18.7%, -3.3%, -6.1% respectively. The performance of the assessed correlations is listed in Table 6:

The Kew and Cornwell [39] correlation exhibits an MRE of -12.89%, signifying that the predictions derived from this correlation tend to consistently underestimate the actual values. Likewise, the Lazarek and Black [38] correlation demonstrates an MRE of -18.72%, indicating a similar pattern of underestimation. On the other hand, the Liu and [22] correlation reveals an MRE of -3.33%, suggesting a relatively small deviation from the actual values and implying a reasonable level of accuracy in its predictions. Furthermore, the ElFaham and Tang [35] correlation showcases an MRE of -6.16%, aligning with the previous correlations by displaying a slight underestimation. The MRE values provided in Table 6 are supported by the graphical comparison depicted in Figure 1, which allows for a visual assessment of the correlation's performance in relation to the actual values.

4.3. Comparison to Ethanol Dataset

In the evaluation of correlations pertaining to ethanol, it was determined that among the various correlations examined, ElFaham and Tang [35]. displayed the most notable precision with a mean absolute deviation of 15.3%. Following ElFaham and Tang correlation, other correlations such as Chen [30] at 25%, Liu and Winterton [22] at 25.1%, and YU [42] at 25.7% exhibited relatively smaller mean absolute deviations. In terms of the mean relative deviations, the aforementioned correlations recorded values of -5.8%, 20%, -14.8%, and -8.2% respectively. The performance of the assessed correlations for ethanol is listed in Table 7.

ElFaham and Tang [35] correlation exhibits a Mean Relative Error (MRE) of -5.83%. This negative MRE indicates a subtle underestimation of the actual values by this correlation. Conversely, the Chen [30] correlation demonstrates an MRE of 20%. The positive MRE suggests that this correlation tends to overestimate the actual values. In the case of the Liu and Winterton [22] correlation, an MRE of -14.81% is observed, reflecting a significant and consistent underestimation of the actual values. Similarly, the YU [42] correlation displays an MRE of -8.17%, which aligns with ElFaham in terms of a slight underestimation of the actual values. The MRE values listed in Table 7 provide insights into the overestimation and underestimation tendencies performed by each correlation. These behaviors can be observed more distinctly through the graphical representation depicted in Figure 2.

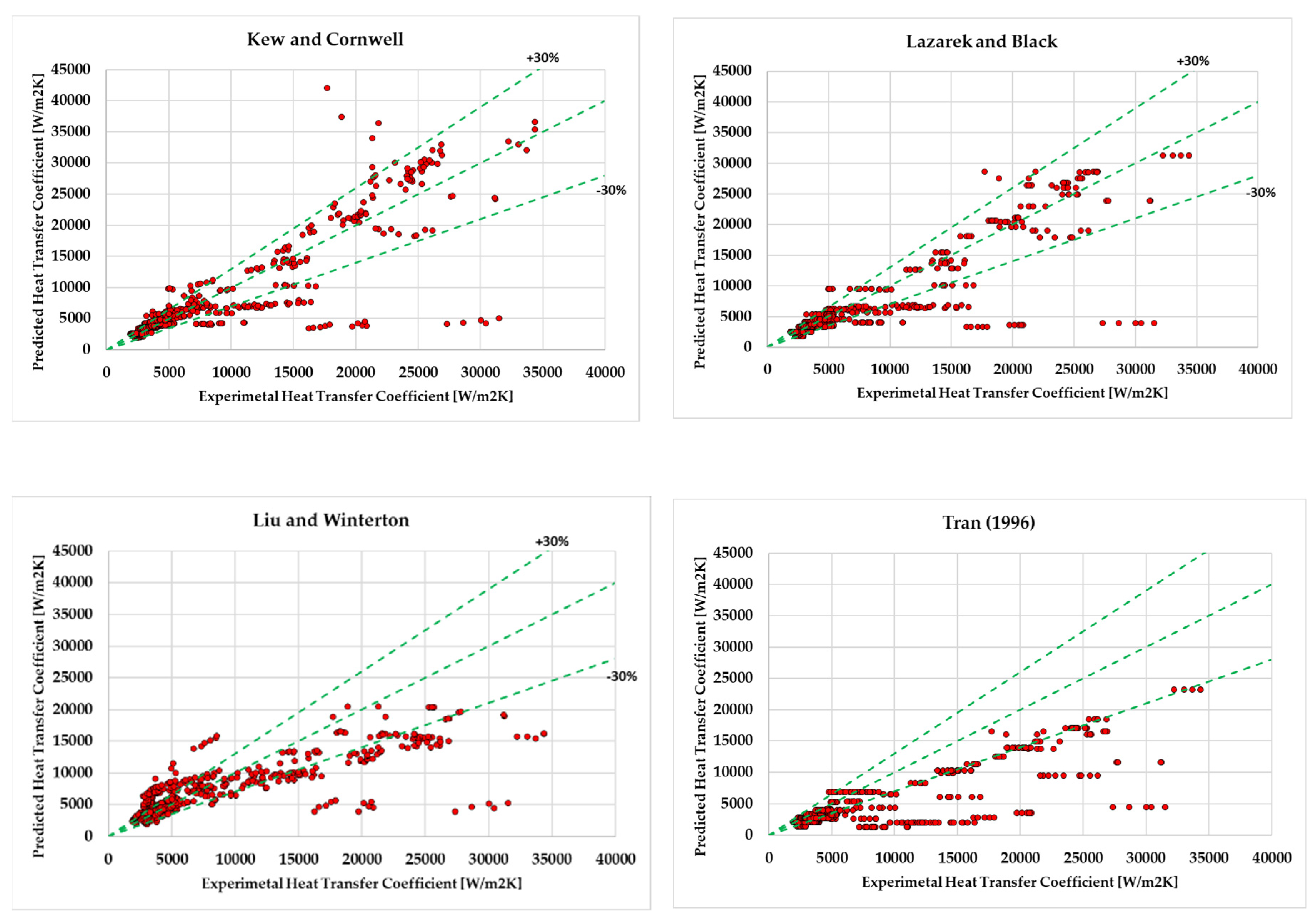
4.4. Comparison to Propane (R290) Dataset

Upon analyzing R290 dataset, it is evident that each correlation demonstrates distinct Mean Absolute Error (MAE) values, representing the average absolute deviation of their predictions from the actual values. The correlation denoted as Kew and Cornwell [39] is associated with an MAE of 17.66. Similarly, the correlation attributed to Lazarek and Black demonstrates an MAE of 18.28%. Moving on to the Liu and Winterton correlation [22], it presents an MAE of 31.17%. Furthermore, the correlation related to Tran (1966) [45] showcases an MAE of 32.4. Lastly, the ElFaham and Tang [35] correlation is characterized by an MAE of 34.96%. Through a careful analysis of the MAE values, a comprehensive understanding can be obtained regarding the accuracy and precision of each correlation's predictions in relation to the actual values which summarized in Table 7.

In the examination of the provided data, it is evident that each correlation demonstrates distinct Mean Relative Error (MRE) values. Kew and Cornwell [39] exhibit an MRE of -1.85%, indicating a slight underestimation of the actual values. Similarly, Lazarek and Black [38] display an MRE of -9.13%, signifying an underestimation that is slightly more pronounced. Conversely, Liu and Winterton’s [22] correlation boasts an MRE of 5.8%, suggesting a tendency to overestimate the actual values. In stark contrast, the Tran [45] correlation reveals a significantly negative MRE of -30.4%, indicative of a consistent and substantial underestimation of the actual values. Lastly, the ElFaham and Tang [35] correlation registers an MRE of 5.48%, aligning with Liu and Winterton in its inclination to overestimate the actual values, albeit to a slightly lesser degree. Through an analysis of the MRE values, valuable insights emerge regarding the deviations and tendencies of each correlation in relation to the actual values, enabling a comprehensive evaluation of their performance and reliability within the given context.

5. Conclusions

A comprehensive review of two-phase flow boiling heat transfer coefficient hydrocarbons and ethanol is presented in this paper. The following results were reached after analyzing and comparing the available heat transfer prediction methods to experimental data.

A database was created based on 11 published papers from 10 independent laboratories for hydrocarbons (R290, R600, and R600a). This evaluation comprises 900 flow boiling heat transfer coefficient data points for hydrocarbons. Moreover, a dataset of 720 experimental data points was collected for the flow boiling heat transfer coefficients of ethanol.
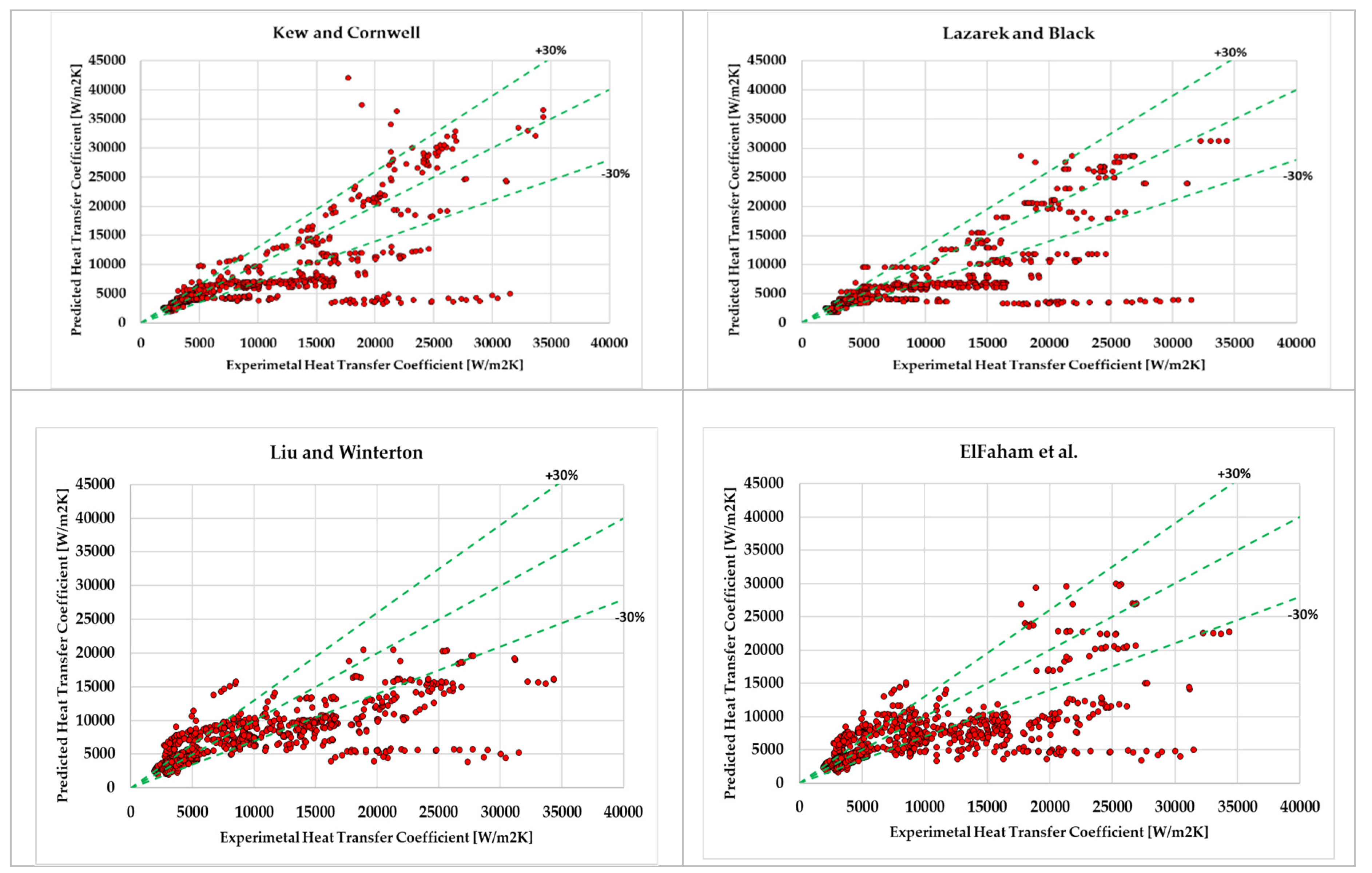
It was found that for hydrocarbons Kew and Cornwell [39] (24.6%), Lazarek and Black [38] (25.7%) correlation has achieved the least mean absolute deviation which is less than 30%. However, Liu and Winterton [22] (33.1%), ElFaham and Tang [35] (36.7%), Tran (38.2%) had the tendency to show relatively low Mean Absolute deviation. On the other hand, Agostini et al. [46], Sun and Mishima [41] , Chaddock and Brunemann [58] , Bennet and Chen [33] were out of prediction and their results were unsatisfactory.
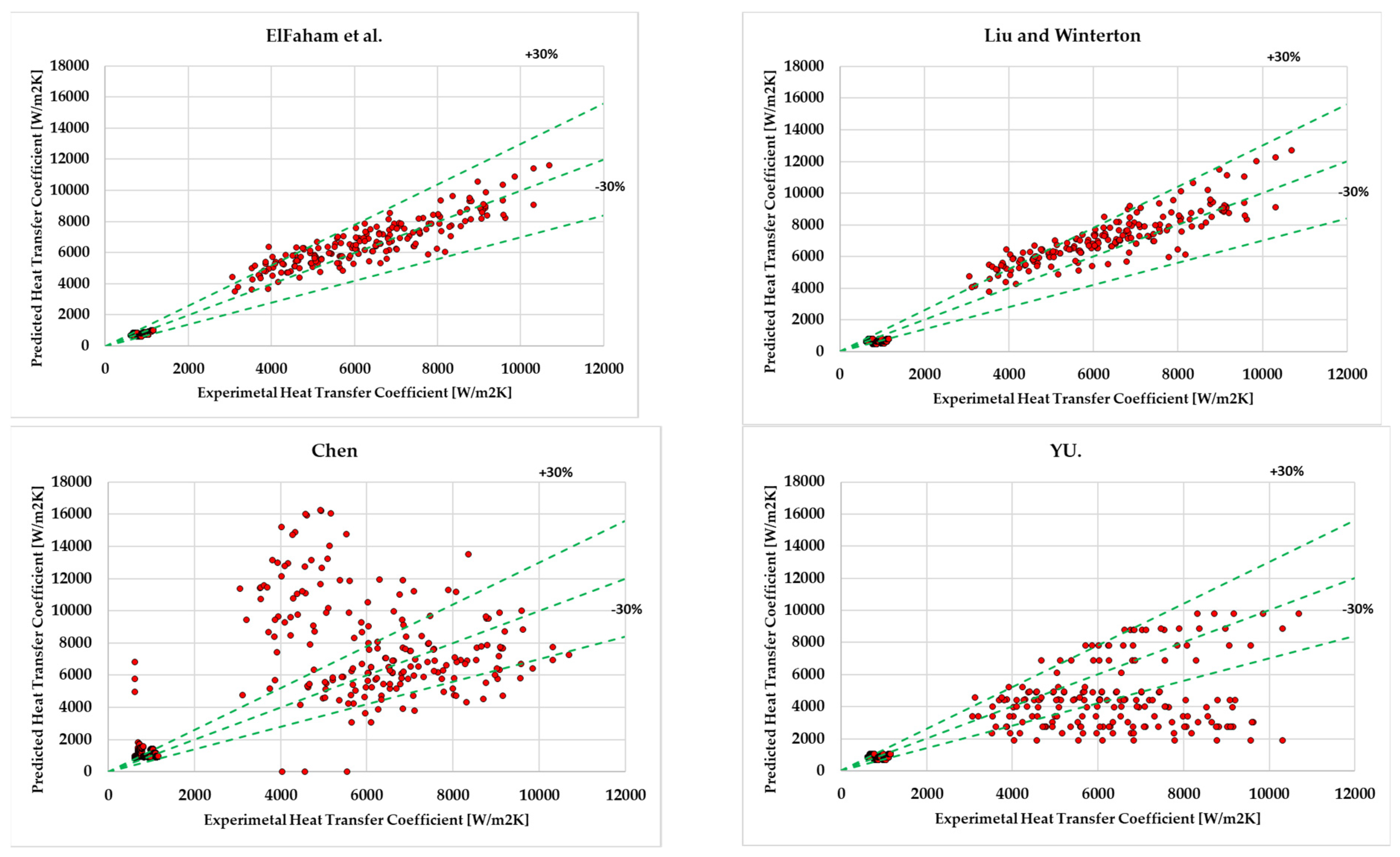
It has been observed that among the assessed correlations for ethanol, ElFaham and Tang [35] achieved the lowest mean absolute deviation (15.3%). Nevertheless, Chen [30] (25%), Liu and Winterton [22] (25.1%), and YU [42] (25.7%) exhibited a range of mean absolute deviation less than 30%, which is considered to be in an outstanding position.
There is an extreme shortage of experimental data on ethanol in the novel of literature. As a result, additional research should be conducted on ethanol, as it is a very promising fluid in many industrial applications. Furthermore, after analyzing the current data set of ethanol, it is recommended to utilize a heat flux range of 7 kW. m-2 to 20 kW. m-2 to fill the gap displayed in Figure 2.
Due to the fact that each correlation developed using its own data, fluids, geometry, and operating conditions. As a result, no specific universal prediction method exists. This study used an assessment of the same correlations for different fluids to benchmark its findings, demonstrating that each fluid has a varied performance for prediction. Therefore, when comparing Table 6, Table 7 and Table 8, each correlation appears in a different place.

References

Lorentzen, G. The use of natural refrigerants: a complete solution to the CFC/HCFC predicament. Int. J. Refrig. 1995, 18, 190–197. [Google Scholar] [CrossRef]
Cavallini, A. Working fluids for mechanical refrigeration—Invited paper presented at the 19th International Congress of Refrig-eration, The Hague, August 1995. International Journal of Refrigeration 1996, 19, 485–496. [Google Scholar] [CrossRef]
Dzigbor, A.; Chimphango, A. Evaluating the potential of using ethanol/water mixture as a refrigerant in adsorption cooling system by using activated carbon - sodium chloride composite adsorbent. Int. J. Refrig. 2019, 97, 132–142. [Google Scholar] [CrossRef]
Thome, J.R.; Cheng, L.; Ribatski, G.; Vales, L.F. Flow boiling of ammonia and hydrocarbons: A state-of-the-art review. Int. J. Refrig. 2008, 31, 603–620. [Google Scholar] [CrossRef]
Granryd, E. , Hydrocarbons as refrigerants—an overview. International journal of refrigeration 2001, 24, 15–24. [Google Scholar] [CrossRef]
Thome, J.R. Boiling of new refrigerants: a state-of-the-art review. Int. J. Refrig. 1996, 19, 435–457. [Google Scholar] [CrossRef]
Liu, C.; et al. , Literature review of condensation and evaporation of R290. 2016.
Del Col, D.; Bortolato, M.; Bortolin, S. Comprehensive experimental investigation of two-phase heat transfer and pressure drop with propane in a minichannel. Int. J. Refrig. 2014, 47, 66–84. [Google Scholar] [CrossRef]
Tibiriçá, C.B.; Ribatski, G. Flow patterns and bubble departure fundamental characteristics during flow boiling in microscale channels. Exp. Therm. Fluid Sci. 2014, 59, 152–165. [Google Scholar] [CrossRef]
Maqbool, M.H. , et al. Saturated flow boiling heat transfer characteristics of propane in a smooth vertical minichannel up to dryout incipience. in 23rd IIR Congress of Refrigeration, Prague, Czech Republic, 21–26 August 2011. [Google Scholar]
Wang, S.; Gong, M.; Chen, G.; Sun, Z.; Wu, J. Two-phase heat transfer and pressure drop of propane during saturated flow boiling inside a horizontal tube. Int. J. Refrig. 2013, 41, 200–209. [Google Scholar] [CrossRef]
Kandlikar, S.G.; Steinke, M.E. Flow Boiling Heat Transfer Coefficient in Minichannels− Correlation and Trends. In Interna-tional Heat Transfer Conference Digital Library.; Begel House Inc., 2022. [Google Scholar]
Jung, D.; Lee, H.; Bae, D.; Oho, S. Nucleate boiling heat transfer coefficients of flammable refrigerants. Int. J. Refrig. 2004, 27, 409–414. [Google Scholar] [CrossRef]
Choi, K.-I.; et al. Pressure drop and heat transfer during two-phase flow vaporization of propane in horizontal smooth minichan-nels. International Journal of Refrigeration 2009, 32, 837–845. [Google Scholar] [CrossRef]
Maqbool, M.H., B. Palm, and R. Khodabandeh, Investigation of two phase heat transfer and pressure drop of propane in a ver-tical circular minichannel. Experimental Thermal and Fluid Science 2013, 46, 120–130. [Google Scholar] [CrossRef]
Lee, H.-S.; Yoon, J.-I.; Kim, J.-D.; Bansal, P. Characteristics of condensing and evaporating heat transfer using hydrocarbon refrigerants. Appl. Therm. Eng. 2006, 26, 1054–1062. [Google Scholar] [CrossRef]
Shin, J.Y.; Kim, M.S.; Ro, S.T. Experimental study on forced convective boiling heat transfer of pure refrigerants and refriger-ant mixtures in a horizontal tube. International Journal of Refrigeration 1997, 20, 267–275. [Google Scholar] [CrossRef]
Thome, J.; Shakir, S. A new correlation for nucleate pool boiling of aqueous mixtures, in Heat Transfer: Pittsburgh 1987, 1987.
Gungor, K.E.; Winterton, R.H.S. A general correlation for flow boiling in tubes and annuli. Int. J. Heat Mass Transf. 1986, 29, 351–358. [Google Scholar] [CrossRef]
Wen, M.-Y.; Ho, C.-Y. Evaporation heat transfer and pressure drop characteristics of R-290 (propane), R-600 (butane), and a mixture of R-290/R-600 in the three-lines serpentine small-tube bank. Appl. Therm. Eng. 2005, 25, 2921–2936. [Google Scholar] [CrossRef]
Chien, N.-B.; et al. , An experimental investigation of convective boiling heat transfer using alternative and natural refrigerants inside horizontal microchannels. 2016.
Liu, Z.; Winterton, R.H.S. A general correlation for saturated and subcooled flow boiling in tubes and annuli, based on a nucleate pool boiling equation. Int. J. Heat Mass Transf. 1991, 34, 2759–2766. [Google Scholar] [CrossRef]
Yunos, Y.M.; Ghazali, N.M.; Pamitran, A.; Novianto, S. Analysis of the Two-Phase Heat Transfer Coefficient of Propane in a Small Channel. Energy Procedia 2017, 105, 4635–4640. [Google Scholar] [CrossRef]
Kanizawa, F.T.; Tibiriçá, C.B.; Ribatski, G. Heat transfer during convective boiling inside microchannels. Int. J. Heat Mass Transf. 2016, 93, 566–583. [Google Scholar] [CrossRef]
Wen, M.-Y.; Jang, K.-J.; Ho, C.-Y. The characteristics of boiling heat transfer and pressure drop of R-600a in a circular tube with porous inserts. Appl. Therm. Eng. 2014, 64, 348–357. [Google Scholar] [CrossRef]
Copetti, J.; Macagnan, M.; Zinani, F. Experimental study on R-600a boiling in 2.6 mm tube. Int. J. Refrig. 2013, 36, 325–334. [Google Scholar] [CrossRef]
Mastrullo, R.; Mauro, A.; Revellin, R.; Viscito, L. Flow boiling heat transfer and pressure drop of pure ethanol (99.8%) in a horizontal stainless steel tube at low reduced pressures. Appl. Therm. Eng. 2018, 145, 251–263. [Google Scholar] [CrossRef]
Steiner, D.; Taborek, J. Flow boiling heat transfer in vertical tubes correlated by an asymptotic model. Heat Transf. Eng. 1992, 13, 43–69. [Google Scholar] [CrossRef]
Vasileiadou, P.; Sefiane, K.; Karayiannis, T.G.; Christy, J.R. Flow boiling of ethanol/water binary mixture in a square mini-channel. Appl. Therm. Eng. 2017, 127, 1617–1626. [Google Scholar] [CrossRef]
Chen, J.C. Correlation for Boiling Heat Transfer to Saturated Fluids in Convective Flow. Ind. Eng. Chem. Process. Des. Dev. 1966, 5, 322–329. [Google Scholar] [CrossRef]
Saitoh, S.; Daiguji, H.; Hihara, E. Correlation for boiling heat transfer of R-134a in horizontal tubes including effect of tube diameter. Int. J. Heat Mass Transf. 2007, 50, 5215–5225. [Google Scholar] [CrossRef]
Jung, D.; McLinden, M.; Radermacher, R.; Didion, D. A study of flow boiling heat transfer with refrigerant mixtures. Int. J. Heat Mass Transf. 1989, 32, 1751–1764. [Google Scholar] [CrossRef]
Bennett, D.L.; Chen, J.C. Forced convective boiling in vertical tubes for saturated pure components and binary mixtures. AIChE J. 1980, 26, 454–461. [Google Scholar] [CrossRef]
Choi, K.-I.; Pamitran, A.; Oh, J.-T. Two-phase flow heat transfer of CO2 vaporization in smooth horizontal minichannels. Int. J. Refrig. 2007, 30, 767–777. [Google Scholar] [CrossRef]
ElFaham, M. , A development of a general heat transfer correlation for boiling two-phase flow of pure ethanol based on experimental datasets and correlations. 2022.
Yoon, S.H.; Cho, E.S.; Hwang, Y.W.; Kim, M.S.; Min, K.; Kim, Y. Characteristics of evaporative heat transfer and pressure drop of carbon dioxide and correlation development. Int. J. Refrig. 2003, 27, 111–119. [Google Scholar] [CrossRef]
Wattelet, J.; et al. , Evaporative characteristics of R-134a, MP-39, and R-12 at low mass fluxes. ASHRAE transactions, 1993.
Lazarek, G.M.; Black, S.H. Evaporative heat transfer, pressure drop and critical heat flux in a small vertical tube with R-113. Int. J. Heat Mass Transf. 1982, 25, 945–960. [Google Scholar] [CrossRef]
Kew, P.A.; Cornwell, K. Correlations for the prediction of boiling heat transfer in small-diameter channels. Appl. Therm. Eng. 1997, 17, 705–715. [Google Scholar] [CrossRef]
Hamdar, M.; Zoughaib, A.; Clodic, D. Flow boiling heat transfer and pressure drop of pure HFC-152a in a horizontal mini-channel. Int. J. Refrig. 2009, 33, 566–577. [Google Scholar] [CrossRef]
Sun, L.; Mishima, K. An evaluation of prediction methods for saturated flow boiling heat transfer in mini-channels. Int. J. Heat Mass Transf. 2009, 52, 5323–5329. [Google Scholar] [CrossRef]
Yu, W.; France, D.; Wambsganss, M.; Hull, J. Two-phase pressure drop, boiling heat transfer, and critical heat flux to water in a small-diameter horizontal tube. Int. J. Multiph. Flow 2002, 28, 927–941. [Google Scholar] [CrossRef]
Warrier, G.R.; Dhir, V.K.; Momoda, L.A. Heat transfer and pressure drop in narrow rectangular channels. Exp. Therm. Fluid Sci. 2002, 26, 53–64. [Google Scholar] [CrossRef]
Kenning, D.; Cooper, M. Saturated flow boiling of water in vertical tubes. Int. J. Heat Mass Transf. 1989, 32, 445–458. [Google Scholar] [CrossRef]
Tran, T.N.; Wambsganss, M.W.; France, D.M. Small circular- and rectangular-channel boiling with two refrigerants. Int. J. Multiph. Flow 1996, 22, 485–498. [Google Scholar] [CrossRef]
Agostini, B.; Bontemps, A. Vertical flow boiling of refrigerant R134a in small channels. Int. J. Heat Fluid Flow 2005, 26, 296–306. [Google Scholar] [CrossRef]
Tran, T. , et al. A correlation for nucleate flow boiling in small channels. In Compact Heat Exchangers for the Process Industries.; Begel House Inc., 1997. [Google Scholar]
Forster, H.K.; Zuber, N. Dynamics of vapor bubbles and boiling heat transfer. AIChE J. 1955, 1, 531–535. [Google Scholar] [CrossRef]
Stephan, K.; Abdelsalam, M. Heat-transfer correlations for natural convection boiling. Int. J. Heat Mass Transf. 1980, 23, 73–87. [Google Scholar] [CrossRef]
Chisholm, D. A theoretical basis for the Lockhart-Martinelli correlation for two-phase flow. Int. J. Heat Mass Transf. 1967, 10, 1767–1778. [Google Scholar] [CrossRef]
ElFaham, M.; Tang, C.C. Review of Datasets and Correlations for Two-Phase Flow Boiling Heat Transfer of Pure Ethanol and Ethanol/Water Binary mixtures. in Heat Transfer Summer Conference. American Society of Mechanical Engineers., 2022. [Google Scholar]
Wojtan, L., T. Ursenbacher, and J.R. Thome, Investigation of flow boiling in horizontal tubes: Part II—Development of a new heat transfer model for stratified-wavy, dryout and mist flow regimes. International journal of heat and mass transfer 2005, 48, 2970–2985. [Google Scholar] [CrossRef]
Pujol, L. and A.H. Stenning, coefficients have been measured in a heat transfer loop consisting of two upward and two downward sections formed by bending a twenty. Cocurrent Gas-Liquid Flow, 1969, 401.
Li, W.; Wu, Z. A general criterion for evaporative heat transfer in micro/mini-channels. Int. J. Heat Mass Transf. 2010, 53, 1967–1976. [Google Scholar] [CrossRef]
Oh, H.-K.; Son, C.-H. Evaporation flow pattern and heat transfer of R-22 and R-134a in small diameter tubes. Heat Mass Transf. 2011, 47, 703–717. [Google Scholar] [CrossRef]
Hu, H.; Ding, G.; Huang, X.-C.; Deng, B.; Gao, Y.-F. Experimental investigation and correlation of two-phase heat transfer of R410a/oil mixture flow boiling in a 5-mm microfin tube. J. Enhanc. Heat Transf. 2011, 18, 209–220. [Google Scholar] [CrossRef]
Lavin, J.G.; Young, E.H. Heat transfer to evaporating refrigerants in two-phase flow. AIChE J. 1965, 11, 1124–1132. [Google Scholar] [CrossRef]
Chaddock, J.B.; Brunemann, H. Forced convection boiling of refrigerants in horizontal tubes: phase 3. 1967: laboratories.

Figure 1. Comparison between experimental and predicted flow boiling heat transfer coefficient for hydrocarbons of the top four correlations in the assessment.

Figure 2. Comparison between experimental and predicted flow boiling heat transfer coefficient for ethanol of the top four correlations in the assessment.

Figure 3. Comparison between experimental and predicted flow boiling heat transfer coefficient for propane of the top four correlations in the assessment.

Table 1. Summary of flow boiling experimental studies on hydrocarbons.

Author/year	Fluids	Tube material/inside diameter (mm)	Saturation temperature/Vapor quality	Heat flux (kW/m2)	Mass flux (kg/m2s)
Shin et al. (1997) [17]	R22, R32, R134a, R290, R600a refrigerant mixtures	Horizontal/Stainless steel tube din= 7.7	Tsat = 12 x = 0.05-0.7	q = 10-30	G = 424-583
Wang et al. (2014) [11]	R290	Horizontal, copper tube din = 6	Tsat = -35 – -1.9 x = 0.14 - 0.75	q = 11.7-87.1	G = 62 -104
Wen et al. (2005) [20]	R290, R600, R290/R600	Horizontal/Copper tube din=2.46	Tsat = 6 x = 0-0.86	q = 5-21	G = 250-500
Chien et al. (2016)	R290, R32, R410a	Horizontal/ Stainless steel tube(microchannel) din= 0.3mm, 1.5	Tsat = 10 x = 0.1 – dry out	q = 10-20	G = 200-500
Yunos et al. (2017) [23]	R290	Horizontal/ single circular stainless-steel tube din= 7.6	Tsat = 6-20 x = 0.01-0.15	q = 5-22	G = 200-650
Kanizwa et al. (2016) [24]	R600a, R134a, R245fa	stainless steel tube din = 0.38-2.6	Tsat= 22 x = 0.01 - 0.69	q = 46-100	G = 240-400
Del Col et al. (2014) [8]	R290	Horizontal, Copper mini-channel din =0.96	Tsat = 31 x =0.05-0.6	q = 10-315	G = 100-600
Wen et al. (2014) [25]	R600a	Horizontal, Circular pipe within dispersed-copper porous inserts. din =0.168-0.506	Tsat = 10 x = 0.076-0.87	q= 12-65	G = 120-1100
Maqbool et al. (2011) [10]	R290	Vertical, stainless steel mini-channel din =1.7	Tsat = 23, 33, 43 x = 0-1	q = 5-280	G = 100-500
Copetti et al. (2013) [26]	R600a, R134a	Horizontal mini channel/ smooth stainless-steel tube din = 2.6	Tsat = 22 x = 0.076 - 0.87	q = 44-95	G = 240-440
Choi et al. (2009) [14]	R290	Horizontal, smooth stainless steel mini channels din = 1.5, 3	Tsat =0,5,10 x = 0-1	q = 5-20	G = 50-400

Table 2. Summary of flow boiling experimental studies on ethanol.

Author/year	Fluids	Tube material/inside diameter (mm)	Saturation temperature/Vapor quality	Heat flux (kW/m²)	Mass flux (kg/m²s)
Mastrullo et al. (2018) [27]	Ethanol	Horizontal stainless-steel tube din = 6.0	T_sat= 64.5-85.8 x = 0.11-0.91	q = 10-40.3	G = 85-127
Robertson et al. (1988) [28]	Ethanol	Vertical copper tube din = 10	T_sat = 88.6 x = 0.03-0.6	q = 25.5-1.4.6	G = 145-290
Vasileiadou et al. (2017) [29]	Ethanol, Deionized water, 5% v/v Ethanol/water	borosilicate glass square channel din = 5	T_sat= 40	q = 2.8-6.1	G = 0.3-1

Table 3. Flow boiling heat transfer coefficient prediction methods (Category A).

Author (Year)	Correlations
Chen (1966) [30]	$h_{t p} = S h_{n b} + F (X_{t t}) h_{s p}$ $F (X_{t t}) = 2.35 {(X_{t t}^{- 1} + 0.213)}^{0.736}$ $h_{s p} = 0.023 (\frac{K_{L}}{d_{i n}}) R {e_{L}}^{0.8} {P_{r_{L}}}^{0.4}$ $h_{n b} = 0.00122 [\frac{K_{L}^{0.79} C_{P_{L}}^{0.45} ∆ T_{e}^{0.24} ∆ P_{s a t}^{0.75}}{σ^{0.5} μ_{L}^{0.29} ∆ h_{v}^{0.24} ρ_{v}^{0.24}}]$ $h_{s p} = 0.023 R {e_{L}}^{0.8} {P_{r_{L}}}^{0.4}$
Bennett and Chen (1980) [33]	$h_{t p} = S h_{n b} + F h_{s p}$ $F = {[1 + (\frac{1}{{X_{t t}}^{0.5}})]}^{1.78} {[\frac{P_{r_{L}} + 1}{2}]}^{0.44}$ $S = 0.9622 - 0.5822 [\tan^{- 1} (\frac{{Re}_{L} F^{1.25}}{61800})]$ $h_{n b}$ is calculated using Equation (1) $h_{s p}$ is calculated using Equation (5)
ElFaham and Tang (2022) [35]	$h_{t P} = {[{(S . h_{n b})}^{2} + {(E . h_{s p})}^{2}]}^{1 / 2}$ $S = [{(1 + 0.055 . E^{0.1} . {R e}_{L}^{0.16})}^{- 1}] \times M_{s}$ $E = {[1 + x . P_{r_{L}} (\frac{ρ_{L}}{ρ_{V}} - 1)]}^{0.35}$ $M_{s} = \{\begin{matrix} 0.7, 1 \times 10^{- 5} \leq B O < 1 \times 10^{- 3} \\ 1.5, 1 \times 10^{- 3} \leq B O < 5 \times 10^{- 3} \\ 1.3, 5 \times 10^{- 3} \leq B O < 1 \times 10^{- 2} \\ 1.1, B O \geq 1 \times 10^{- 2} \end{matrix}$ $h_{n b} = 55 q^{0.67} P_{R}^{0.12} {(- \log_{10} P_{R})}^{- 0.55} M^{- 0.5}$ $h_{s p}$ is calculated using Equation (5)
Jung et al. (1989) [32]	$h_{t p} = S h_{n b} + F h_{s p}$ $d_{b} = 0.51 [\frac{2 σ}{g (ρ_{L} - ρ_{v}}]$ $F = 2.37 {[0.29 + \frac{1}{X_{t t}}]}^{0.85}$ $S = \{\begin{matrix} 4048 X_{t t}^{1.22} {B o}^{1.13}, X_{t t} < 1 \\ 2 - 0.1 X_{t t}^{- 0.28} B o^{- 0.33}, 1 \leq X_{t t} \leq 5 \end{matrix}$ $h_{n b} = 207 \frac{K_{L}}{d_{b}} {[\frac{q d_{b}}{K_{L} T_{s}}]}^{0.745} {[\frac{ρ_{v}}{ρ_{L}}]}^{0.581} P_{r_{L}}^{0.533}$ $h_{s p}$ is calculated using Equation (5)
Saitoh et al. (2007) [31]	$h_{t p} = E h_{s p} + S h_{n b} S = 1 + 0.4 {({Re}_{L} \times 1 0^{- 4})}^{- 1.4}$ $E = {\frac{1 + (\frac{1}{X_{t t}})}{1 + W e_{v}^{- 0.4}}}^{1.05}$ $h_{n b}$ is calculated using Equation (4) $h_{s p}$ is calculated using Equation (5)
Choi et al. (2007) [34]	$h_{t p} = S h_{n b} + F h_{s p}$ $S = 7.2694 {(ϕ_{f}^{2})}^{0.0094} B o^{0.2814}$ $F = 0.05 (ϕ_{f}^{2}) + 0.95$ $ϕ_{f}^{2} = 1 + \frac{C}{X_{t t}} + \frac{1}{X_{t t}^{2}}$ $h_{n b}$ is calculated using Equation (4) $h_{s p}$ is calculated using Equation (5)
Liu-Winterton(1991) [21]	$h_{t P} = {[{(S . h_{n b})}^{2} + {(E . h_{s p})}^{2}]}^{1 / 2}$ $S = {[(1 + 0.055 . E^{0.1} . {R e}_{L}^{0.16})]}^{- 1}$ $E = {[1 + x . P_{r_{L}} (\frac{ρ_{L}}{ρ_{V}} - 1)]}^{0.35}$ $h_{n b}$ is calculated using Equation (4) $h_{s p}$ is calculated using Equation (5)
Yoon et al. (2004) [49]	$h_{t P} = {[{(S . h_{n b})}^{2} + {(F . h_{s p})}^{2}]}^{1 / 2}$ where $x < x_{c r}$ $x_{c r} = 0.0012 {R e}_{L}^{2.79} {(B o \times 10^{3})}^{0.06} B d^{- 4.76}$ $F = {[1 + 9360 x P_{r_{L}} (\frac{ρ_{L}}{ρ_{v} - 1})]}^{0.11}$ $S = \frac{1}{1 + 1.62 \times 10^{- 6} F^{- 0.69} {R e}_{L}^{1.11}}$ $h_{n b}$ is calculated using Equation (4) $h_{s p}$ is calculated using Equation (5)
Wattelet et al. (1994) [46]	$h_{t p} = {[h_{n b}^{2.5} + {(F . R . h_{s p})}^{2.5}]}^{\frac{1}{2.5}}$ $F = 1 + 1.925 X_{t t}^{- 0.83}$ $R = \{\begin{matrix} 1.32 F_{r_{L}}^{0.2}, F_{r_{L}} < 0.25 \\ 1, F_{R_{L}} \geq 0.25 \end{matrix}$ $h_{n b}$ is calculated using Equation (4) $h_{s p}$ is calculated using Equation (5)

Table 4. Flow boiling heat transfer coefficient prediction methods (Category B).

Author (Year)	Correlations
Lazarek and Black (1982) [36]	$h_{t p} = 30 R {e_{L}}^{0.857} {B o}^{0.714} \frac{K_{L}}{d_{i n}}$
Kew and Cornwell (1997) [37]	$h_{t p} = 30 R {e_{L}}^{0.857} {B o}^{0.714} \frac{K_{L}}{d_{i n}} {(1 - x)}^{- 0.143}$
Hamdar et al. (2010) [42]	$h_{t p} = 6942.8 {(B o^{2} W e_{L})}^{0.2415} {(\frac{ρ_{v}}{ρ_{L}})}^{0.22652} (\frac{K_{L}}{d_{i n}})$
Sun and Mishima (2009) [38]	$h_{t p} = 6 R {e_{L}}^{1.05} B o^{0.54} {[W e_{L}^{0.191} {(\frac{ρ_{v}}{ρ_{L}})}^{0.142}]}^{- 1} (\frac{K_{L}}{d_{i n}})$
Yu et al. (2002) [40]	$h_{t p} = 640,000 B o^{0.54} W e_{L}^{0.27} {(\frac{ρ_{L}}{ρ_{v}})}^{- 0.2}$
Warrier et al. (2002) [50]	$h_{t p} = [1 + 6 B o^{\frac{1}{16}} - 5.3 (1 - 855 B o) x^{0.65}] h_{n b}$
Kenning and Cooper (1989) [35]	$h_{t p} = (1 + 1.8 X_{t t}^{- 0.87}) h_{s p}$ $h_{s p}$ is calculated using Equation (5)
Tran et al. (1996) [39]	$h_{t p} = 840,000 B o^{0.6} W e_{L}^{0.3} {(\frac{ρ_{L}}{ρ_{v}})}^{- 0.4}$
Agostini et al. (2005) [41]	$h_{t p} = \{\begin{matrix} 28 q^{\frac{1}{3}} G^{- 0.26} x^{0.1}, x \leq 0.43 \\ 28 q^{\frac{1}{3}} G^{0.64} x^{- 2.058}, x > 0.43 \end{matrix}$
Tran et al. (1997) [51]	$h_{t p} = 770 {(R e_{L} N_{c o n f} B o)}^{0.62} (\frac{ρ_{v}}{ρ_{L}}) (\frac{K_{L}}{d_{i n}})$

Table 5. Summary of the dimensionless equations used in flow boiling correlations.

Dimensionless Number	Equation
Reynolds number for liquid phase	$R e_{L} = \frac{G D}{µ_{L}}$
Boiling number	Bo = $\frac{q}{G {Δ h}_{l g}}$
Bond number	Bd = $\frac{g (ρ_{L} - ρ_{v}) D}{σ}$
Weber number for Liquid phase	$W e_{L} = \frac{G^{2} D}{ρ_{L} σ}$
Froude number for liquid phase	${F r}_{L} = \frac{G^{2}}{g D ρ_{L}^{2}}$
Lockharte-Martinelli parameter	$X_{t t} = {(\frac{1 - x}{x})}^{0.9} {(\frac{ρ_{v}}{ρ_{L}})}^{0.5} {(\frac{µ_{L}}{µ_{v}})}^{0.1}$
Convection number	$C O = {(\frac{1 - x}{x})}^{0.8} {(\frac{ρ_{v}}{ρ_{L}})}^{0.5}$
Confinement number	$N_{c o n f .} = \sqrt{\frac{σ}{g (ρ_{L} - ρ_{v}) D^{2}}}$

Table 6. Prediction performance of the selected correlations for hydrocarbons.

Correlations (Year)	MAE (%)	MRE (%)
Kew and Cornwel [39] (1997)	24.6	-12.89
Lazarek and Black [38] (1982)	25.73	-18.72
Liu and Winterton [22] (1991)	33.02	-3.33
ElFaham and Tang [35] (2022)	36.69	-6.16
Tran [45] (1996)	38.16	-36.22
Yoon [36] (2004)	40.64	14.02
Wojtan et al. [52] (2005)	42.54	-41.39
Hamdar [40] (2010)	47.01	-5.01
Warrier [43] (2002)	51.25	-40.72
Pujol and Stenning [53] (1969)	56.12	10.5
Li and Wu [54] (2010)	57.64	13.22
Saitoh [31] (2007)	60.57	27.7
YU [42] (2002)	65.03	-9.56
Wattelet [37] (1994)	67.98	54.04
Kenning Copper [44] (1989)	68.59	38.71
Oh and Son [55] (2011)	73.27	19.26
Hu et al. [56] (2011)	80.39	15
Gungor and Winterton [19] (1986)	83.51	75.43
Chen [30] (1966)	83.75	75.31
Lavin and Young [57] (1965)	83.8	49.16
Jung [32] (1989)	94.97	61.01
Choi [34] (2007)	104.56	73.16
Bennett and Chen [33] (1980)	104.6	74.28
Chaddock and Brunemann [58] (1967)	104.8	83.69
Sun and Mishima [41] (2009)	116.8	96.85
Kew and Cornwell [39] (1997)	186.97	177.68

Table 7. Prediction performance of the selected correlations for ethanol.

Correlations (Year)	MAE (%)	MRE (%)
ElFaham and Tang [35] (2022)	15.29	-5.83
Chen [30] (1966)	25.02	20
Liu and Winterton [22] (1991)	25.12	-14.81
YU [42] (2002)	25.7	-8.17
Saitoh [31] (2007)	26.78	-10.38
Yoon [36] (2004)	27.37	-20.03
Wattelet [37] (1994)	28.39	-8.35
Sun and Mishima [41] (2009)	29.69	18.58
Wojtan et al. [52] (2005)	40.57	-40.57
Jung [32] (1989)	47.25	-14.42
Gungor and Winterton [19] (1986)	52.28	51.61
Hu et al. [56] (2011)	56.76	56.01
Hamdar [40] (2010)	58.56	-58.57
Bennett and Chen [] (1980)	59.6	59.75
Kenning Copper [44] (1989)	64.66	-51.01
Oh and Son [55] (2011)	66.01	-52.44
Pujol and Stenning [53] (1969)	73.54	-73.34
Lavin and Young [57] (1965)	76.43	-74.91
Chaddock and Brunemann [58] (1967)	77.27	-29.97
Warrier [43] (2002)	79.67	-79.65
Tran [45] (1996)	83.36	-83.35
Kew and Cornwell [39] (1997)	83.91	-83.91
Tran et al. [47] (1997)	84.02	-84.02
Lazarek and black [38] (1982)	85.17	-85.17
Choi [34] (2007)	119.07	118.89
Li and Wu [54] (2010)	574.76	569.49

Table 8. Prediction performance of the selected correlations for Propane(R290).

Correlations (Year)	MAE (%)	MRE (%)
Kew and Cornwell [39] (1997)	17.66	-1.85
Lazarek and black [38] (1982)	18.28	-9.13
Liu and Winterton [22] (1991)	31.17	5.8
Tran [45] (1996)	32.4	-30.4
ElFaham and Tang [35] (2022)	34.96	5.48
Wojtan et al. [52] (2005)	37.78	-35.99
Yoon [36] (2004)	40.94	28.97
Hamdar [40] (2010)	43.11	13.32
Warrier [43] (2002)	48.09	-35.09
Pujol and Stenning [53] (1969)	58.25	26.35
Li and Wu [54] (2010)	63.01	35.31
Saitoh [31] (2007)	67.88	4.8
Wattelet [37] (1994)	75.55	63.57
Kenning Copper [44] (1989)	79.25	39.85
YU [42] (2002)	80.66	66.6
Oh and Son [55] (2011)	87.04	36.72
Chen [30] (1966)	96.18	76.92
Gungor and Winterton [19] (1986)	102.31	99.98
Hu et al. [56] (2011)	102.34	99.97
Lavin and Young [57] (1965)	113.88	94.54
Jung [32] (1989)	123.46	99.67
Tran et al. [47] (1997)	128.08	111.93
Choi [34] (2007)	130.29	123.6
Bennett and Chen [33] (1980)	138.48	127.86
Chaddock and Brunemann (1967)	220.54	218.07
Sun and Mishima [41] (2009)	252.15	250.39

Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.

© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).

Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.