Prerpints.org logo
Preprint
Article

Dynamic Response of a Light-Modulated Magnetometer to Time Dependent Field

Altmetrics

Downloads

126

Views

58

Comments

0

A peer-reviewed article of this preprint also exists.

Submitted:

05 June 2023

Posted:

06 June 2023

You are already at the latest version

Alerts
Abstract
The dynamic response of a Bell-and-Bloom magnetometer to a parallel (to the bias field) time-dependent field is modelled beyond the commonly assumed quasi-static regime. The results unveil features that are related to the parametric nature of the considered system. It is shown that a for low-amplitude time-dependent field different operating conditions are possible and that, beside the commonly reported low-pass-filter behaviour, a band-pass response emerges. Moreover, we numerically show that for larger field amplitude the system, due to its parametric nature, has a kind of ``non-linear'' response.
Keywords: 
Subject: Physical Sciences  -   Applied Physics

1. Introduction

Resonant magneto-optics and the related field of atomic magnetometry have a history started in the late Fifties of the past century with research of Dehmelt [1] and Bell and Bloom [2,3] prosecuting in the Sixties, particularly with the work Cohen-Tannoudji [4,5]. The following decades brought important progresses in the comprehension of optical pumping phenomena [6,7] and prepared the conditions for an important revival at the beginning of the current century, which was inspired by numerous attracting applications and facilitated by several elapsed technological progresses.
Most of the application fields envisaged for atomic magnetometers are identified on the basis of their excellent sensitivity, and, in the case of RF magnetometers, on their response to high-frequency fields. Among these application fields, emerge the detection of bio-magnetism, e.g., in the construction of magneto-encephalographs [8,9], magneto-cardiographs [10,11,12], magneto-miographs [13]. Another promising area is represented by nuclear magnetic resonance in ultra-low (e.g., at microtesla level) or even vanishing fields, where atomic magnetometers find use as non-inductive detectors [14,15,16,17,18] also for imaging experiments [19,20,21,22]. RF magnetometers find other interesting applications in the detection and imaging of eddy currents [23,24], with implications in non-destructive test of materials [25], security [26], and biomedicine [27]. Further perspectives originate from the possibility of producing miniaturized sensors [28,29,30,31] and arranging them in arrays [32].
There exist a variety of atomic magnetometers, nowadays also produced as commercial devices. However, they all share several common features [33]. Generally, the working principle consists in using (near) resonant light to orient atoms in a long lived state (or to induce alignment or higher order momenta); making atoms evolve in the magnetic field under measurement, which thus imprints its features in the subsequent state; and eventually interrogating the atomic sample by means of probe radiation that characterises its optical (absorptive/dispersive) behaviour.
The above mentioned three-step (pumping-evolution-interrogation) procedure [34] can be performed in a sequence or simultaneously, numerous interaction geometries (e.g., relative orientation of field, pump beam and probe beam) can be considered, tailored time-dependent fields can be applied, various approaches (absorption, dispersion, polarimetry) can be used at the interrogation stage etc.: a pletora of configurations can be proposed and this large variety comes with wide ranges of sensitivity, bandwidth, dynamical range, time and space resolution etc.
An interesting implementation consists in pumping atoms synchronously with their precession around a (nearly) static field. In this case the pumping radiation must be modulated (in terms of amplitude, polarisation or wavelength) and the probe radiation detects a time dependent optical behaviour. Such light-modulated setup was firstly proposed by Bell and Bloom [2], who used amplitude-modulated light from a Caesium discharge lamp.
The ideal (optimal) configuration of a Bell-and-Bloom setup considers a static magnetic field B oriented transversely with respect to the pump-radiation wave vector. This causes the resonantly induced macroscopic magnetisation to precess in a plane perpendicular to B . This precession can be profitably analysed by probe radiation propagating in that plane. The Faraday rotation effect offers a favourable detection scheme based on polarimetric measurement: the probe radiation is linearly polarised and the polarisation plane is rotated by an angle that oscillates at the precession frequency. The amplitude of this oscillation is maximised when the pumping radiation is modulated at the Larmor frequency set by the static field, i.e., at an atomic magnetic resonance.
If the pump modulation frequency is fixed, small and slow variations of the static field bring the system in a near-resonant condition, with the typical effects of signal reduction and dephasing, the latter being more effectively and easily detected, thanks to its (nearly) linear dependence on the detuning.
This classical picture of Bell-and-Bloom behaviour applies when the field variation is small compared with the magnetic resonance line-width and slow with respect to the relaxation time of the atomic orientation. Most of literature reporting Bell-and-Bloom magnetometers interprets the detected signals in terms of such quasi-static and near-resonant condition [35], furthermore considering optimal field orientation. In other terms, the field is usually assumed to be (nearly) perpendicular to the pump and probe propagation, (nearly) time-independent, and (nearly) matching the Larmor resonant condition.
This paper aims to provide a more general analysis of the behaviour of a Bell-and-Bloom magnetometer when it operates in the presence of a generic time dependent field that is parallel to the static (bias) one. The availability of a more accurate model is of relevance when the output of a magnetometer is used as an error-signal to implement feedback based field-stabilization systems [36,37,38,39,40], as well as when designing feed-forward ones [41] or when evaluating the effects of strong stray fields. The later is of particular relevance for systems operated in unshielded environment [9,42].
This paper is organised as follows. In Section 2 we describe the mathematical approaches used to solve the Larmor equation under the generic conditions mentioned above. In Section 3 we report the numerical findings of the model, while the main outcomes are discussed in Section 4 and some conclusions are drawn in Section 5.

2. Model

The starting point in modeling of the spin response is the Larmor equation for the magnetization vector M :
M ˙ = − Γ M + γ B ( t ) × M + f ( t ) .
Here Γ represents a relaxation mechanism (assumed isotropic), f ( t ) the action of the forcing term obtained through optical pumping (see [43] for details), γ is the gyromagnetic factor and B ( t ) is the applied magnetic field.
In this paper we are interested in a configuration where the pumping light and the magnetic field are orthogonal. We take the x axis along the pump (so f ( t ) = f ( t ) ( 1 , 0 , 0 ) ) and the y axis along the magnetic field, which, in turn, is composed of a static B 0 and a time-dependent B ‖ ( t ) part. Introducing the frequencies ω 0 = γ B 0 and ω ‖ = γ B ‖ the relevant Larmor equation becomes
M ˙ = − Γ M − i ( ω 0 + ω ‖ ( t ) ) M + f ( t ) ,
where M = M x + i M z , and we are interested in M x = Re ( M ) , which is the quantity related to the Faraday rotation of the probe laser collinear with the pump as, for example, in [43,44].
The solution of (2) can be written as
M ( t ) = e − Γ t − i ω 0 t − i θ ‖ ( t ) M ( 0 ) + e − Γ t − i ω 0 t − i θ ‖ ( t ) ∫ 0 t d t ′ e Γ t ′ + i ω 0 t ′ + i θ ‖ ( t ′ ) f ( t ′ ) ,
where we introduced the Larmor angle associated with the time-dependent field
θ ‖ ( t ) = ∫ 0 t ω ‖ ( s ) d s .
We assume that both the forcing and the time-dependent field are real-valued periodic functions:
f ( t ) = ∑ n = − ∞ + ∞ f n e i n Ω t f − n = f n *
ω ‖ ( t ) = ∑ n = − ∞ + ∞ x n e i n ω t x − n = x n *
and we can put x 0 = 0 (otherwise redefine ω 0 ) obtaining that also θ ‖ is a periodic function which permits to write
e i θ ‖ ( t ) = ∑ n = − ∞ + ∞ G n e i n ω t e − i θ ‖ ( t ) = ∑ n = − ∞ + ∞ G − n * e i n ω t ,
where the G n coefficients are complicated functions of x n / n ω . It is worth noticing that, in case of pure sinusoidal time-dependent field, the G n coefficients are related to the Bessel functions of first kind.
Now the steady-state (SS) solution, valid for t ≫ 1 / Γ , of (3) becomes
M ( t ) = e − i θ ‖ ( t ) ∑ n , m G n f m Γ + i ( ω 0 + n ω + m Ω ) e i ( n ω + m Ω ) t ,
which is still a complicated expression that can be simplified noticing that in the usual experimental condition the pumping frequency is (nearly) resonant with the Larmor frequency set by the static field, that is Ω ≈ ω 0 resulting in
M ( t ) ≈ e − i θ ‖ ( t ) ∑ n f − 1 G n e i n ω t Γ + i ( ω 0 − Ω + n ω ) e − i Ω t = ∑ s ∑ n f − 1 G n G n − s * e i s ω t Γ + i δ + i n ω e − i Ω t ≡ ∑ s Z s e i s ω t e − i Ω t ≡ Z ( t ) e − i Ω t ,
where we introduced the detuning δ = ω 0 − Ω , implicitly defined the Z s coefficients and the Z ( t ) complex function.
We would like to point out that the result (8) has a more general validity: indeed it is valid also when the experimental apparatus track the component at fundamental frequency of the pumping modulation. After this demodulation the quantity monitored is the phase of Z ( t ) , which is still a periodic function
φ ( t ) ≡ arg ( Z ( t ) ) = Im ( log ( Z ( t ) ) ) = ∑ n φ n e i n ω t φ − n = φ n * ,
where, in general, the φ n coefficients can be evaluated only numerically as
φ n = 1 2 π ∫ 0 2 π e − i n θ arg ∑ s Z s e i s θ d θ .
A notable exception is the case of low intensity time-dependent field which is discussed in the following.

2.1. Low-Intensity Limit

When the time-dependent field is small with respect to the static one, which in our formalism means that the x n coefficients are small quantities, the Larmor angle θ ‖ is a small quantity too. It follows that e i θ ‖ ≈ 1 + i θ ‖ and G 0 ≈ 1 − ∑ n ( x n / n ω ) , G n ≈ x n / n ω for n ≠ 0 . Substituting in the first line of (8) one obtains
Z ( t ) = e − i θ ‖ f − 1 G 0 Γ + i δ + ∑ n ≠ 0 G n Γ + i δ + i n ω e i n ω t ≈ e − i θ ‖ f − 1 Γ + i δ 1 − ∑ n x n n ω + ∑ n ≠ 0 x n n ω 1 − i n ω Γ + i δ + i n ω e i n ω t = e − i θ ‖ f − 1 Γ + i δ 1 + ∑ n x n n ω e i n ω t − 1 − i ∑ n x n Γ + i δ + i n ω e i n ω t .
Considering that the second term in parenthesis is i θ ‖ and that log ( 1 + X ) ≈ X for small X, one obtains
φ pert ( t ) = arg f − 1 Γ + i δ − Im i ∑ n x n Γ + i δ + i n ω e i n ω t
and neglecting the first, uninteresting term, the final result is
φ pert ( t ) = − 1 2 ∑ n 1 Γ + i δ + i n ω + 1 Γ − i δ + i n ω x n e i n ω t ,
which is identical to the expression reported in [45] and can be recast as the output of a linear system
φ pert ( t ) = − ∫ 0 t e − Γ ( t − t ′ ) cos ( δ ( t − t ′ ) ) ω ‖ ( t ′ ) d t ′ .

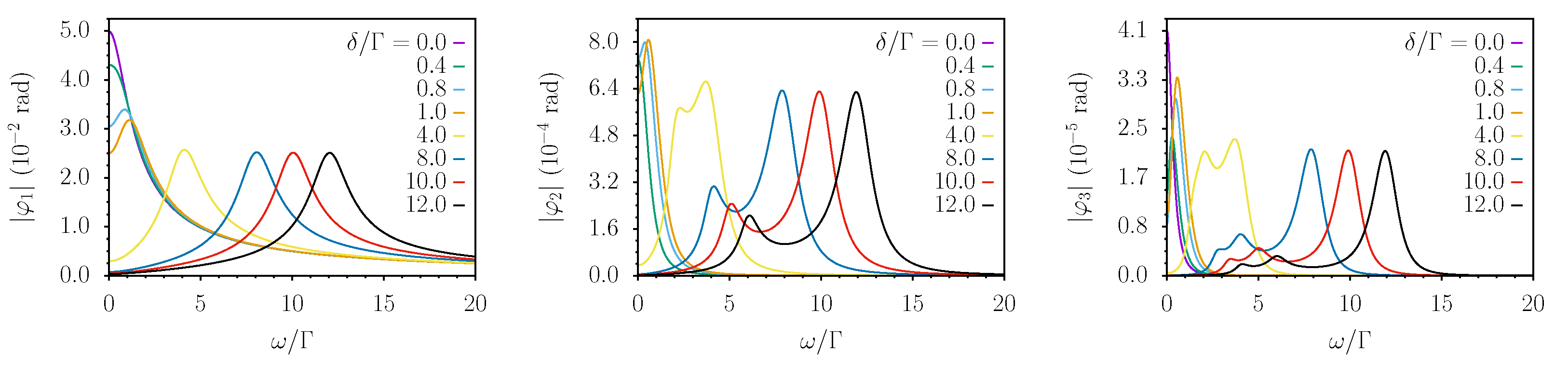
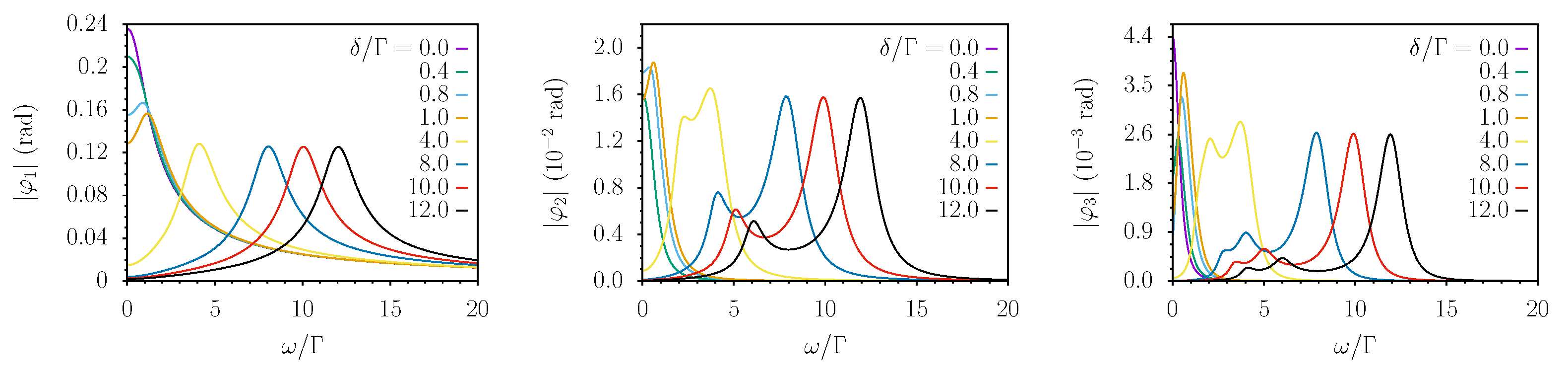
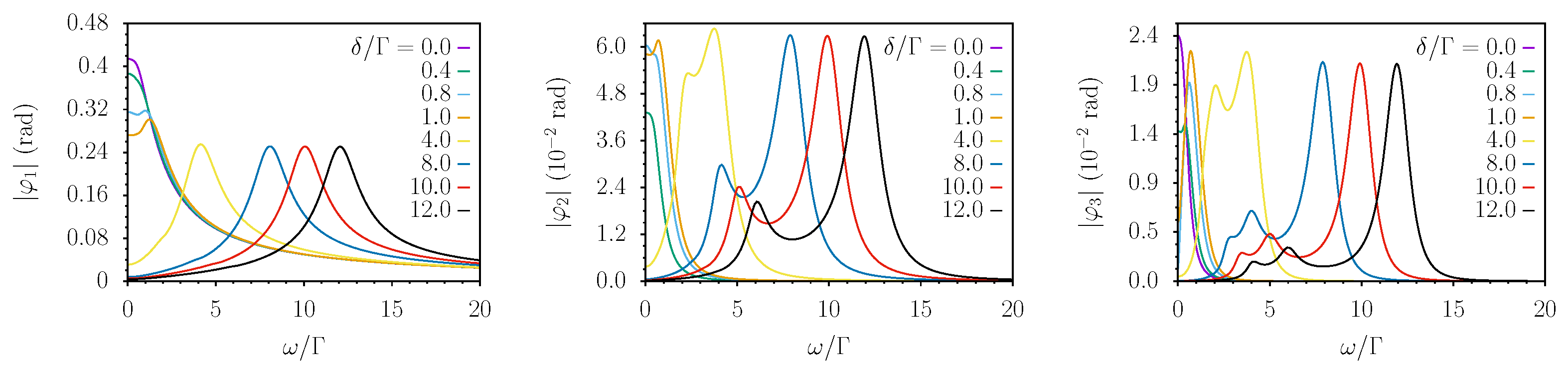
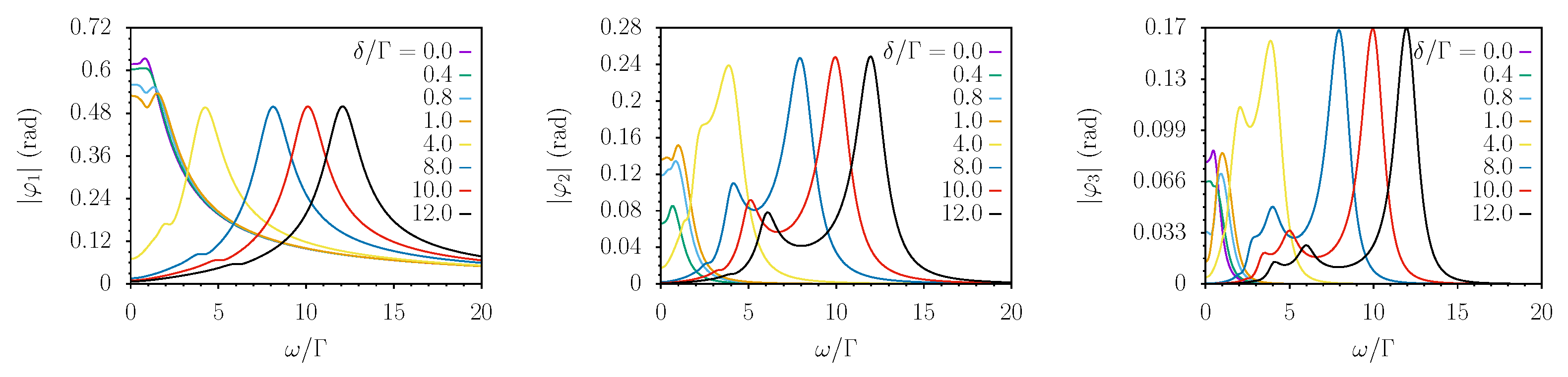
3. Results

The result reported in (8) is quite general and applies to complicated time-dependence of ω ‖ which would require to consider many x n parameters, as well as to the case of a simple sinusoidal oscillation.
It is worth noticing that in the phase time signal (Equation (9)) the coefficient f − 1 gives only a constant contribution which amounts to an experimental offset and can be safely neglected, resulting in an experimental advantage because one does not need to take into account the precise form of the pumping signal. This is not the case if one chooses to monitor the modulus of Z ( t ) where the f − 1 coefficient enters in a multiplicative way.
Because of the complicated dependence of the G n coefficients on the x n , it is difficult to draw conclusions valid for arbitrary values of the parameters. In such sense it is a nice result the analytical low-intensity limit of Equation (12), which allows a discussion in term of linear time-invariant systems. However, in this paper we explore the complementary regime presenting results obtained as explained in the previous section.
To be more concrete we fix the time-dependence as a simple cosine, namely, ω ‖ = Ω ‖ cos ( ω t ) so that G n ≡ J n ( Ω ‖ / ω ) are the Bessel functions of first kind and the coefficients Z s can be written as
Z s = f − 1 ∑ n J n J n − s Γ + i δ + i n ω
and we expect that for not-so-small Ω ‖ also the higher-harmonics coefficients φ n ( n > 1 ) will become important. In fact, the system is a parametric one and it will show a kind of “non-linear” behaviour. In other terms, even for a simple sinusoidal time-dependent field as “input”, higher order harmonics will appear in the monitored phase.
In the following pictures we present numerical results for the first Fourier coefficients of the phase for different values of the amplitude of the time-dependent field.
In the Figure 1, Figure 2, Figure 3 and Figure 4 the modulus of φ n n = 1 , 2 , 3 (from left to right) is reported as a function of ω for fixed values of Ω ‖ / Γ = 0.1 , 0.5 , 1.0 , 2.0 , respectively. Each curve represents a different value of the detuning δ in units of Γ .
As can be seen in Figure 1 where Ω ‖ = 0.1 Γ the perturbative limit of Equation (13) applies. In fact the φ 2 and φ 3 are two and three orders of magnitude smaller than φ 1 respectively. However, as can be seen in the Figure 2, Figure 3 and Figure 4  φ 2 and φ 3 become more and more comparable in magnitude with φ 1 increasing the amplitude Ω ‖ of the time-dependent field.
Let us consider the behaviour of φ 1 for different values of δ / Γ . For small δ / Γ the curve can be interpreted as the response of a low-pass filter, while increasing δ / Γ it becomes resembling a band-pass filter centred in ω ≈ δ . This point of view is reinforced in the low Ω ‖ regime by the result of Equation (13). However, as can be seen in the pictures, this interpretation can be pushed also for higher values of Ω ‖ even if some structure starts appearing close to ω ≈ δ / 2 .
The behaviour of φ 2 is more structured. For δ / Γ = 0 is zero (we observed this for all the even coefficients φ 2 n ), then a “low-pass” profile evolves into a double peaked structure with the highest peak centred around ω ≈ δ and the other around ω ≈ δ / 2 . Increasing Ω ‖ gives rise to a small structure close to ω ≈ δ / 3 .
Similar conclusions can be drawn for φ 3 : here the number of visible peaks is three even for small Ω ‖ . It seems reasonable to assume that this is the general behaviour of the coefficients φ n , i.e., increasing Ω ‖ increase both the number of “relevant” φ n and for each φ n the number of visible peaks centred at ω ≈ δ / k .

4. Discussion

The main scope of this paper is to investigate the dynamic response of a Bell-and-Bloom system to a time dependent field parallel to the bias one. This subject is often presented in terms of an approximation whose validity requires that the time dependent field is small, varies slowly with respect to relaxation time and that the pumping radiation is modulated in resonance with the precession frequency set by the dominant static field. Under these stringent but frequently fulfilled conditions, the systems permits a simplified treatment and behaves as a linear forced-damped oscillator with a low-pass (Butterworth filter) response [8,46].
We have previously analysed the behaviour of such a system , using a perturbative approach in the amplitude of the time dependent field [45], in a more general configuration, as a generic orientation of the field was considered. Before discussing the results presented in Sec.Section 3 it is worth recalling the main outcomes obtained with that approach.

4.1. Perturbative Results

An interesting feature, resulting at the first order perturbative approximation, emerges when the pump radiation is modulated at a frequency detuned from the exact resonance. Under this condition, the simplified low-pass response becomes inadequate and a band-pass behaviour is observed, with an enhanced response to AC components at frequencies close to the pump-frequency detuning δ , as also observed in Ref. [40].
In application, this feature may help tailor the system response to the detection of oscillating terms at frequencies around δ . For instance, a magnetometer with a resonance as narrow as 20Hz maybe used to detect with a good efficiency an AC field oscillating at 200Hz, provided that the pump light is modulated at a frequency 200Hz away from γ B D C .
An interesting behaviour is obtained at an intermediate detuning, δ ≈ Γ / 2 . This condition produces a nearly flat amplitude response up to a cut-off frequency set by Γ / 2 . Such extended flat bandwidth is obtained at expenses of a slight reduction of the signal amplitude, if compared to the δ = 0 case. Concerning the phase of the magnetometric signal, a maximally extended constant-phase (non dispersive) response is instead achieved under the condition δ = Γ .
In this first-order approximation, the precessing spins do not respond to field variations along directions perpendicular to the static field, while such a response appears in the next order. Indeed, the perturbative treatment developed in [45] shows that the second-order approximation predicts terms that double and mix the frequencies at which time-dependent fields are applied. It is worth noting that the frequency mixing among diverse components of the time-dependent field comes with several peculiar features and it does not occurs among all the couples of components, as detailed [45].
Further increase of the time-dependent field makes also the second-order approximation inadequate and the numerical analysis developed in Section 2 becomes necessary. For the sake of simplicity, in this work the time-dependent field is considered at arbitrarily high amplitude, but only along the bias field direction. Moreover the presented results are obtained with a single-frequency term, so that no frequency mixing occur and the non-linearities are pointed out in terms of a harmonic analysis.

4.2. Non-Perturbative Results

The numerical analysis performed at rather weak intensity is perfectly consistent with the first-order perturbative analysis recalled in Section 4.1. In particular the leftmost plot in Figure 1 shows that at resonance ( δ = 0 ) the system has a low-pass response, which evolves into an extended-flat response when δ ≈ Γ and becomes a band-pass one for δ > Γ . At large detunings (band-pass regime) the peak response is half the maximum observed at low frequency and vanishing detunings. A harmonic analysis shows that in the low-field regime ( Ω ‖ ≪ Γ ) the anharmonicity of the response is negligible. A close inspection to the vertical scales in Figure 1 points out that the second- and third-harmonic terms ( φ 2 , φ 3 ) are depressed by two and three order of magnitudes with respect to the fundamental one, respectively.
Figure 2 and Figure 3 show the effects of a moderate increase in the amplitude of the time-dependent field. Under conditions in which Ω ‖ ≈ Γ , the low-pass and band-pass behaviour does not change appreciably, while the anharmonicity becomes progressively more evident, e.g., for Ω ‖ = Γ the third harmonic peaks observed at large detunings are only one order of magnitude weaker than the fundamental one.
The results obtained at small and moderate amplitude of the time dependent field (Figure 1, Figure 2, and Figure 3) show pretty similar features in the spectral response, and the main difference concerns only the anharmonicity level. The response observed for large δ / Γ is characterised by a peak at ω ≈ δ for all the harmonic terms. However, the second harmonic term ( φ 2 ) has also a secondary peak at ω ≈ δ / 2 and an additional peak at ω ≈ δ / 3 emerges for the third harmonic term, φ 3 .
The Figure 4 shows new spectral features in the responses. Strong time-dependent fields cause extra peaks emerge in the plots. In particular, the leftmost plot ( φ 1 ) of Figure 4 shows the appearance of an extra peak at ω ≈ δ / 2 .

5. Conclusion

We studied the effect of a time dependent magnetic on the Bell-and-Bloom magnetometer in the configuration where the time dependent magnetic field is parallel to the bias static one. We generalised the analysis beyond the quasi-static and low amplitude regime usually found in the literature, unveiling interesting features such as confirming the low-pass to band-pass transition also for a large amplitude of the time-dependent field. Moreover, for large amplitude of the time-dependent field, the emergence of “non-linear” behaviour of the system is put in evidence.

Acknowledgments

G.B. is partially supported by the GNFM of Indam.

References

  1. Dehmelt, H.G. Modulation of a Light Beam by Precessing Absorbing Atoms. Phys. Rev. 1957, 105, 1924–1925. [Google Scholar] [CrossRef]
  2. Bell, W.E.; Bloom, A.L. Optical Detection of Magnetic Resonance in Alkali Metal Vapor. Phys. Rev. 1957, 107, 1559–1565. [Google Scholar] [CrossRef]
  3. Bell, W.E.; Bloom, A.L. Optically Driven Spin Precession. Phys. Rev. Lett. 1961, 6, 280–281. [Google Scholar] [CrossRef]
  4. Dupont-Roc, J. Détermination par des méthodes optiques des trois composantes d’un champ magnétique très faible. Rev. Phys. Appl. (Paris) 1970, 5, 853–864. [Google Scholar] [CrossRef]
  5. Dupont-Roc, J.; Haroche, S.; Cohen-Tannoudji, C. Detection of very weak magnetic fields (10-9gauss) by 87Rb zero-field level crossing resonances. Physics Letters A 1969, 28, 638–639. [Google Scholar] [CrossRef]
  6. Happer, W. Optical Pumping. Rev. Mod. Phys. 1972, 44, 169–249. [Google Scholar] [CrossRef]
  7. Happer, W.; Jau, Y.; Walker, T., Optical Pumping of Atoms. In Optically Pumped Atoms; John Wiley & Sons, Ltd, 2010; chapter 5, pp. 49–71. [CrossRef]
  8. Colombo, A.P.; Carter, T.R.; Borna, A.; Jau, Y.Y.; Johnson, C.N.; Dagel, A.L.; Schwindt, P.D.D. Four-channel optically pumped atomic magnetometer for magnetoencephalography. Opt. Express 2016, 24, 15403–15416. [Google Scholar] [CrossRef]
  9. Wu, T.; Peng, X.; Chen, J.; Guo, H., Fiber-Coupled OPM in Purely Coil-Shielded Environment. In Flexible High Performance Magnetic Field Sensors: On-Scalp Magnetoencephalography and Other Applications; Labyt, E.; Sander, T.; Wakai, R., Eds.; Springer International Publishing: Cham, 2022; pp. 161–177. [CrossRef]
  10. Bison, G.; Castagna, N.; Hofer, A.; Knowles, P.; Schenker, J.L.; Kasprzak, M.; Saudan, H.; Weis, A. A room temperature 19-channel magnetic field mapping device for cardiac signals. Applied Physics Letters 2009, 95. [Google Scholar] [CrossRef]
  11. Kamada, K.; Ito, Y.; Kobayashi, T. Human MCG measurements with a high-sensitivity potassium atomic magnetometer. Physiological measurement 2012, 33, 1063. [Google Scholar] [CrossRef]
  12. Kim, Y.J.; Savukov, I.; Newman, S. Magnetocardiography with a 16-channel fiber-coupled single-cell Rb optically pumped magnetometer. Applied Physics Letters 2019, 114. [Google Scholar] [CrossRef]
  13. Broser, P.J.; Knappe, S.; Kajal, D.S.; Noury, N.; Alem, O.; Shah, V.; Braun, C. Optically Pumped Magnetometers for Magneto-Myography to Study the Innervation of the Hand. IEEE Trans Neural Syst Rehabil Eng 2018, 26, 2226–2232. [Google Scholar] [CrossRef]
  14. Savukov, I.M.; Romalis, M.V. NMR Detection with an Atomic Magnetometer. Phys. Rev. Lett. 2005, 94, 123001. [Google Scholar] [CrossRef]
  15. Bevilacqua, G.; Biancalana, V.; Dancheva, Y.; Vigilante, A.; Donati, A.; Rossi, C. Simultaneous Detection of H and D NMR Signals in a micro-Tesla Field. The Journal of Physical Chemistry Letters 2017, 8, 6176–6179. [Google Scholar] [CrossRef]
  16. Tayler, M.C.; Gladden, L.F. Scalar relaxation of NMR transitions at ultralow magnetic field. Journal of Magnetic Resonance 2019, 298, 101–106. [Google Scholar] [CrossRef] [PubMed]
  17. Savukov, I.; Kim, Y.J.; Schultz, G. Detection of ultra-low field NMR signal with a commercial QuSpin single-beam atomic magnetometer. Journal of Magnetic Resonance 2020, 317, 106780. [Google Scholar] [CrossRef]
  18. Eills, J.; Cavallari, E.; Carrera, C.; Budker, D.; Aime, S.; Reineri, F. Real-Time Nuclear Magnetic Resonance Detection of Fumarase Activity Using Parahydrogen-Hyperpolarized [1-(13)C]Fumarate. J Am Chem Soc (ISSN: 0002-7863linking, 0002-7863print) 2019, 80, 20209–20214. [Google Scholar] [CrossRef]
  19. Savukov, I.; Karaulanov, T. Magnetic-resonance imaging of the human brain with an atomic magnetometer. Applied Physics Letters 2013, 103. [Google Scholar] [CrossRef] [PubMed]
  20. Savukov, I.; Karaulanov, T. Anatomical MRI with an atomic magnetometer. Journal of Magnetic Resonance 2013, 231, 39–45. [Google Scholar] [CrossRef] [PubMed]
  21. Bevilacqua, G.; Biancalana, V.; Dancheva, Y.; Vigilante, A. Restoring Narrow Linewidth to a Gradient-Broadened Magnetic Resonance by Inhomogeneous Dressing. Phys. Rev. Applied 2019, 11, 024049. [Google Scholar] [CrossRef]
  22. Bevilacqua, G.; Biancalana, V.; Dancheva, Y.; Vigilante, A. Sub-millimetric ultra-low-field MRI detected in situ by a dressed atomic magnetometer, Appl.Phys.Lett. 2019, 115, 174102. [Google Scholar] [CrossRef]
  23. Deans, C.; Marmugi, L.; Hussain, S.; Renzoni, F. Electromagnetic induction imaging with a radio-frequency atomic magnetometer. Applied Physics Letters 2016, 108. [Google Scholar] [CrossRef]
  24. Bevington, P.; Gartman, R.; Chalupczak, W. Object detection with an alkali-metal spin maser. Journal of Applied Physics 2021, 130. [Google Scholar] [CrossRef]
  25. Bevington, P.; Gartman, R.; Chalupczak, W.; Deans, C.; Marmugi, L.; Renzoni, F. Non-destructive structural imaging of steelwork with atomic magnetometers. Applied Physics Letters 2018, 113. [Google Scholar] [CrossRef]
  26. Darrer, B.J.; Watson, J.C.; Bartlett, P.; Renzoni, F. Magnetic Imaging: a New Tool for UK National Nuclear Security. Scientific Reports 2015, 5. [Google Scholar] [CrossRef] [PubMed]
  27. Marmugi, L.; Renzoni, F. Optical Magnetic Induction Tomography of the Heart. Scientific Reports 2016, 6. [Google Scholar] [CrossRef] [PubMed]
  28. Gerginov, V.; Pomponio, M.; Knappe, S. Scalar Magnetometry Below 100 fT/Hz1/2 in a Microfabricated Cell. IEEE Sensors Journal 2020, 20, 12684–12690. [Google Scholar] [CrossRef] [PubMed]
  29. Scholtes, T.; Woetzel, S.; IJsselsteijn, R.; Schultze, V.; Meyer, H.G. Intrinsic relaxation rates of polarized Cs vapor in miniaturized cells. Applied Physics B 2014, 117, 211–218. [Google Scholar] [CrossRef]
  30. Zhang, Y.; Tian, Y.; Li, S.; Chen, J.; Gu, S. Faraday-Rotation Atomic Magnetometer Using Triple-Chromatic Laser Beam. Phys. Rev. Appl. 2019, 12, 011004. [Google Scholar] [CrossRef]
  31. Li, S.; Zhang, Y.; Tian, Y.; Chen, J.; Gu, S. Faraday-rotation Bell–Bloom atomic magnetometer using an alternating pump–probe beam. Journal of Applied Physics 2021, 130. [Google Scholar] [CrossRef]
  32. Nardelli, N.V.; Perry, A.R.; Krzyzewski, S.P.; Knappe, S.A. A conformal array of microfabricated optically-pumped first-order gradiometers for magnetoencephalography. EPJ Quantum Technology 2014, 7. [Google Scholar] [CrossRef]
  33. Fabricant, A.; Novikova, I.; Bison, G. How to build a magnetometer with thermal atomic vapor: a tutorial. New Journal of Physics 2023, 25, 025001. [Google Scholar] [CrossRef]
  34. Weis, A.; Bison, G.; Pazgalev, A.S. Theory of double resonance magnetometers based on atomic alignment. Phys. Rev. A 2006, 74, 033401. [Google Scholar] [CrossRef]
  35. Zhang, R.; Wu, T.; Chen, J.; Peng, X.; Guo, H. Frequency Response of Optically Pumped Magnetometer with Nonlinear Zeeman Effect. Applied Sciences 2020, 10. [Google Scholar] [CrossRef]
  36. Li, S.; Liu, J.; Jin, M.; Tetteh Akiti, K.; Dai, P.; Xu, Z.; Eric-Theophilus Nwodom, T. A kilohertz bandwidth and sensitive scalar atomic magnetometer using an optical multipass cell. Measurement 2022, 190, 110704. [Google Scholar] [CrossRef]
  37. Bevilacqua, G.; Biancalana, V.; Dancheva, Y.; Vigilante, A. Self-Adaptive Loop for External-Disturbance Reduction in a Differential Measurement Setup. Phys. Rev. Applied 2019, 11, 014029. [Google Scholar] [CrossRef]
  38. Pyragius, T.; Jensen, K. A high performance active noise control system for magnetic fields. Review of Scientific Instruments 2021, 92. [Google Scholar] [CrossRef] [PubMed]
  39. Yan, Y.; Lu, J.; Zhang, S.; Lu, F.; Yin, K.; Wang, K.; Zhou, B.; Liu, G. Three-axis closed-loop optically pumped magnetometer operated in the SERF regime. Opt. Express 2022, 30, 18300–18309. [Google Scholar] [CrossRef] [PubMed]
  40. Ding, Y.; Xiao, W.; Zhao, Y.; Wu, T.; Peng, X.; Guo, H. Dual-Species All-Optical Magnetometer Based on a Cs-K Hybrid Vapor Cell. Phys. Rev. Appl. 2023, 19, 034066. [Google Scholar] [CrossRef]
  41. O’Dwyer, C.; Ingleby, S.J.; Chalmers, I.C.; Griffin, P.F.; Riis, E. A feed-forward measurement scheme for periodic noise suppression in atomic magnetometry. Review of Scientific Instruments 2020, 91. [Google Scholar] [CrossRef]
  42. Cooper, R.J.; Prescott, D.W.; Lee, G.J.; Sauer, K.L. RF atomic magnetometer array with over 40 dB interference suppression using electron spin resonance. Journal of Magnetic Resonance 2018, 296, 36–46. [Google Scholar] [CrossRef]
  43. Bevilacqua, G.; Biancalana, V.; Dancheva, Y. Atomic orientation driven by broadly-frequency-modulated radiation: Theory and experiment. Phys. Rev. A 2016, 94, 012501. [Google Scholar] [CrossRef]
  44. Bevilacqua, G.; Biancalana, V.; Chessa, P.; Dancheva, Y. Multichannel optical atomic magnetometer operating in unshielded environment. Applied Physics B 2016, 122, 103. [Google Scholar] [CrossRef]
  45. Bevilacqua, G.; Biancalana, V.; Dancheva, Y.; Fregosi, A.; Vigilante, A. Spin dynamic response to a time dependent field. Applied Physics B 2021, 127, 128. [Google Scholar] [CrossRef]
  46. Zhang, R.; Pang, B.; Li, W.; Yang, Y.; Chen, J.; Peng, X.; Guo, H. Frequency Response of a Close-Loop Bell-Bloom Magnetometer. 2018 IEEE International Frequency Control Symposium (IFCS), 2018, pp. 1–3. [CrossRef]
Preprints 75762 g001
Figure 1. The modulus of the first Fourier coefficients of the phase for Ω ‖ = 0.1 Γ . From left to right: | φ 1 | , | φ 2 | and | φ 3 | .
Figure 1. The modulus of the first Fourier coefficients of the phase for Ω ‖ = 0.1 Γ . From left to right: | φ 1 | , | φ 2 | and | φ 3 | .
Preprints 75762 g001
Preprints 75762 g002
Figure 2. The modulus of the first Fourier coefficients of the phase for Ω ‖ = 0.5 Γ . From left to right: | φ 1 | , | φ 2 | and | φ 3 | .
Figure 2. The modulus of the first Fourier coefficients of the phase for Ω ‖ = 0.5 Γ . From left to right: | φ 1 | , | φ 2 | and | φ 3 | .
Preprints 75762 g002
Preprints 75762 g003
Figure 3. The modulus of the first Fourier coefficients of the phase for Ω ‖ = 1.0 Γ . From left to right: | φ 1 | , | φ 2 | and | φ 3 | .
Figure 3. The modulus of the first Fourier coefficients of the phase for Ω ‖ = 1.0 Γ . From left to right: | φ 1 | , | φ 2 | and | φ 3 | .
Preprints 75762 g003
Preprints 75762 g004
Figure 4. The modulus of the first Fourier coefficients of the phase for Ω ‖ = 2.0 Γ . From left to right: | φ 1 | , | φ 2 | and | φ 3 | .
Figure 4. The modulus of the first Fourier coefficients of the phase for Ω ‖ = 2.0 Γ . From left to right: | φ 1 | , | φ 2 | and | φ 3 | .
Preprints 75762 g004
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.
Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.
Prerpints.org logo

Preprints.org is a free preprint server supported by MDPI in Basel, Switzerland.

facebook logotwitter logolinkedin logo
MDPI Initiatives
Important Links
Subscribe

Disclaimer

Terms of Use

Privacy Policy

© 2024 MDPI (Basel, Switzerland) unless otherwise stated