1. Background
In a recent publication, an investigation of propagation on an open wire as related to microwave communication systems on power lies was reported [
1,
2]. More specifically, the use of the low loss Sommerfeld-Goubau (SG) mode on the lossy bare wires of power lines has been proposed the foundation for high bandwidth communications [
3,
4,
5]. [
1] was written in order to clarify the relationship between the discrete SG modal current and total current since it is the total current that is relevant to the performance of these systems. There is significant history to this subject beginning with the work of Sommerfeld [
6]. However, it is not repeated here since it is outlined in [
1].
In [
1], a closed form solution for the current induced on an isolated infinitely long lossy conductor by a voltage source in series with it or an electric dipole in close proximity to it was found. This model included contributions from the continuous spectrum of radiation modes as well as the low loss discrete SG mode. While the relative magnitudes of these two components was shown to be sensitive to frequency and wire conductivity, the total current on a lossy conductor is nearly the same as for a perfect conductor over distances comparable to power line communication repeater spacing. Hence, it was shown possible to use a simple expression for the total current from antenna theory to evaluate the performance of these power line communication systems. Further, for observation points not near the source, the current induced by the voltage and dipole sources differs only by a known constant. Dipole sources were considered since voltage sources cannot be inserted into power line conductors. Finally, the advantage of a single conductor communication channel over a wireless channel using high gain antennas was quantified.
However, it was also noted in [
1] that power line conductors are not isolated and, given the fact that SG mode fields decay slowly in the transverse plane, the influence of parallel conductors could be important. Some recent work has appeared on the topic of the SG mode on a pair of wires, but it did not
incorporate the full expression for current which would include the continuous spectrum [
7]. Hence, the impact of a parallel conductor is investigated in this paper. More specifically, a single additional conductor will be assumed parallel to the one that is discussed in [
1]. The two conductor case is considered since its solution can be decomposed into simple common and differential modes leading to additional insight into the solution.
2. Problem Definition and Exact Solution
The problem is illustrated in
Figure 1. Here, two infinitely long parallel lossy (conductivity
σw) conductors each of radius a and spaced a distance d apart are placed in the z direction. A voltage source of amplitude V volts at z = 0 and/or a y oriented elementary electric dipole of length dl at a distance h from the origin along the y axis are used to excite currents on both conductors.
The approach here is to solve for the currents excited by the voltage source and then (later) to use the fixed relation between dipole and voltage sources derived in [
1] to calculate those due to the dipole source.
Mirroring the solution in [
1], an exact expression for the currents can be developed in the following way. Two coupled inhomogeneous Fredholm integral equations of the second kind are set up for the induced currents. These equations are Fourier transformed into the spatial transform domain using the convolution theorem. While details of this process are given in [
1], the primary difference is the inclusion of a term that accounts for the influence of each wire on the other. The resulting transformed equations are solved by expanding the currents in the system eigenvectors (i.e., the common and differential modes) and pre-multiplying by the inverse of the eigenvector matrix. The resulting exact currents (expressed in the Fourier transform domain) induced on the two wires by the voltage source (V) are
for the common (superscript c and/or + sign) and differential (d superscript and/or - sign) modes.
The denominator of (1) can be written as
where
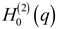
is the Hankel function of second kind, order zero and argument q,

, Im(
ζ) ≤ 0 (in order to satisfy
the radiation condition) where
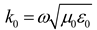
,
γ is the
spatial Fourier transform variable,
ε0 is the permittivity of
free space and
ω is the radian frequency. The other variable in (2) is
δiw
= 4
ωε0ziw where the intrinsic impedance per
unit length of the wire at microwave frequencies is
and
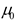
is the permeability
of free space. For (1), the thin wire boundary condition
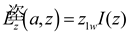
was applied at the
inside surface of each conductor radius. The caret notation, ^, indicates a
phasor quantity while the tilde notation “~” indicates the Fourier transform.
The formal solution to the integral equations for modal currents in the space domain can be written using the inverse Fourier transform as
where
Finally the individual currents in each wire can be written as
and
3. The Spectral Solution
Solving (4) involves deforming the integration along the
real γ axis into the complex γ plane as shown in
Figure 2 and
Figure 3. To accomplish this, it is
first necessary to discuss the singularities of the integrand of (4) in this
plane. Given the multivalued square root function, branch point pairs can be
identified at
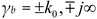
with branch cuts
connecting them defined as shown in
Figure 2.
As a further comment, the “proper” Riemann sheet is defined as Im(
ζ) ≤ 0.
Since the branch cuts in
Figure 2 and
Figure 3
are defined so that Im(
ζ) ≤ 0, the visible (i.e., top) portion of the
complex plane is the proper sheet where Im(
ζ) ≤ 0. In addition to the
branch points and cuts, there is a pole
γp which occurs on
the proper sheet at
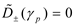
which
is different for the common and differential modes.
First, (4) for the common mode will be evaluated. In this case (i.e.,
Figure 2), the solution will be the branch cut integration plus the residue of a pole
γmSG that corresponds to the SG pole described in [
1] modified by the presence of the second wire.
The result will be quite similar to the case discussed in [
1] except that the details of the branch cut integration and the mSG mode are different. Note also that if the conductivity becomes infinite, the mSG pole will disappear into the branch cut at
k0. One consequence is the more complicated branch cut integration due to the additional term containing the distance d.
The case for the differential mode is somewhat different as illustrated in
Figure 3. Here there is no pole that corresponds to the SG pole in the case for a single wire. This can be illustrated through an examination of the denominator of (4). In the single wire case, there is only a single Hankel function and the SG pole occurs because this function has a logarithmic singularity near
k0. In the case for the two wire differential mode, the second Hankel function cancels this singularity and there is no mSG pole. However, there is another pole that corresponds to the well-known quasi-TEM mode for a pair of parallel wires.
3.1. Calculation of Pole Locations
The zero of (5) (i.e., either the mSG or quasi-TEM pole of the integrand of (4) here given as
γp and known to be near
k0) can be found using Newton’s iterative method. In this case, an initial guess for the zero is selected as γ
p(0) and successive approximations are found as
where
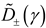
is given as (7) and
its derivative with respect to γ,
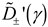
, can be shown to be
[
8]
It has been found that the sequence (8) converges quickly if the initial value γp(0) is selected to be near k0.
A good approximation for the quasi-TEM mode propagation constant (using small argument expansions for the Hankel function in (5) with the minus sign) is
3.2. Evaluation of the Current
Given the singularities of
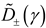
, (4) can now be
evaluated by deforming the original contour around the lower branch cut
entirely on the proper Riemann sheet as illustrated in
Figure 2 and
Figure 3. Given the factor
e−jγz in the integrand of (4), the
integrations along the lower infinite semicircle are zero. Hence the original
integrations reduce to integrations along both sides of the branch cut as
shown. However, because the pole at γ
p is enclosed by the original
and new contours, its residue must be added to each integration.
Equation (4) is integrated around the branch cut using the identities [
8]
where
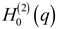
,
J0(
q)
and
Y0(
q)are respectively the Hankel function of the
first kind and Bessel functions of the first and second kind or order zero and
argument
q. After multiplying the numerator and denominator by
ζ2
to avoid an infinity in the denominator at
γ =
k0, the
horizontal portion of the branch cut integral between 0 and
k0 is
where
The vertical portion of the branch cut integral from γ =
-j∞ to γ = 0 can be written (after using the substitutions
γ =
−
ju,
dγ = −
ju) and defining
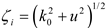
as
where
The subscripts “
h” and “
v” in (14) and (16)
indicate the contribution from the horizontal and vertical portions of the
branch cut integration rfespectively. If
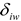
is finite, (14) and
(16) are relatively straightforward to integrate numerically.
As noted earlier in Figures
2 and 3, there is a pole on the proper Riemann sheet in the common mode
case (i.e., the mSG pole) and in the differential mode case (i.e., the
Quasi-TEM pole) located between the original contour and integration contour
used in this work. Hence, the appropriate residue must be added to the branch
cut integral in each case. This residue can be found directly from (5) by
expanding
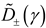
as a
Taylor series around
γp. The result is
where
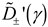
can be found in (9).
The total induced modal currents then are
for the common mode and
for the differential mode.
3.3. The Special Case for Perfectly Conducting Conductors
In the case
δiw = 0 the term 1/ζ
2 in the denominator of (14) and (16)
grows without bound near (due to the fact
that the pole has been absorbed into
k0). However, in the
common mode case, (13) is still integrable since the sum of Neumann functions
in the denominator limit this growth. However, more care must be used to
evaluate the integral. Note that this does not happen in the differential mode
case because the difference in Neumann functions does not grow near k
0..
Given this difficulty, (14) is separated into two parts.
where the first is
and the second (following the method of [
1]) is
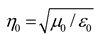
is
the impedance of free space, γ
e is the Euler constant, Δ is small
enough that
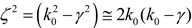
and
small argument approximations can be used for the Bessel functions [8]. In this solution, the substitutions
u =
(
k0 −
γ) and
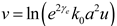
have been used. Note
that (23) accounts for the mSG pole residue which (for
δiw =
0) has been absorbed into
k0. Finally, (16) along
the vertical portion of the branch cut (but with
δiw = 0) can
be evaluated numerically as earlier.
Since the pole at
γp is absorbed into
k0, there is no separate residue term. Given these results, the current induced on a perfect conductor by the voltage source is
3.4. Relationship to Dipole Excitation
It was shown in [1] that
there is a simple relationship between the current excited by a voltage source
and that by a dipole in the immediate proximity of the conductor. To convert
from the voltage source solution to that for a dipole with current
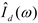
and length
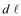
with its center at a
distance from
the outer surface of the conductor, one must multiply the voltage solution by
the factor
Since the dipole is assumed to be very close to the conductor, its influence is limited to that of that conductor in its proximity. Hence, this factor can also be used to convert the two wire case for a voltage source on one conductor only to the dipole solution for the two wire case.
3.5. A Simple Solution
Shen, Wu and King [
9]
have developed a simplified solution for the total current in the single
conductor perfectly conducting case that is valid for

. It is
It was shown in [
1] that
(26) is a very good approximation for the total current (i.e., continuous
spectrum plus the SG mode) induced on a conductor with typical conductivity.
Hence it was used as an simple approximation for the total current on a lossy
wire. It will be shown in the next section that it is reasonable to use (26)
for the common mode current in the two wire case if the wire radius “
a”
is replaced by the geometric mean radius of the two wires
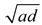
, . That this is
reasonable can be shown by examining (23) and noting that a major contribution
to the common mode current is the same as that for the single wire case in [1}
but with “
a” replaced by
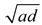
.
It will also be demonstrated shortly that the quasi-TEM mode contribution to the differential mode is the dominant contribution away from the immediate vicinity of the source. Its residue (using small argument expansions for the Hankel functions in (9) is
Hence, a reasonable approximation for the total current on the two wires is
where the plus (minus) sign is for the current on wire one (two).
4. Results
4.1. Pole Locations
The first result (shown inn
Table 1) is a set of propagation constants for the SG (single wire) mode discussed in [
1], and the mSG (two wire common) and quasi-TEM (differential) modes for 1 and 10 GHz. The SG and mSG modes were found using a numerical solution of (5) set to zero without (for the SG mode) and with (for the mSG mode assuming the + sign) the second Hankel function. The quasi-TEM pole location has been determined using (5) set to zero with a minus sign or (10).
It is clear that the mSG mode has slightly less loss than the SG mode. This is due to the fact that the current is spread out over a larger area of wire surface. However, the Quasi-TEM mode has a significantly larger loss factor. Hence, for communication systems, it is important to examine the excitation of each mode in the single and two wire cases.
4.2. Common vs Differential Mode Solutions
In
Figure 4, results are shown for the magnitude of the current distributions at 1 GHz for the common and differential modes. Two methods are used for calculating the differential mode current; the perfect conducting method of (21) and the lossy conductor case in (19). There is little difference between these two methods over typical communication ranges as was the case in [
1]. Hence, perfect conductor theory can be used. Second, both the continuous spectrum and the mSG modal component are important for typical communication distances. There is no important condition (for communications) for which the mSG mode dominates the continuous spectrum (at least for the source studied here). Note however, that for the differential mode, the quasi-TEM mode dominates even at very short distances away from the source.
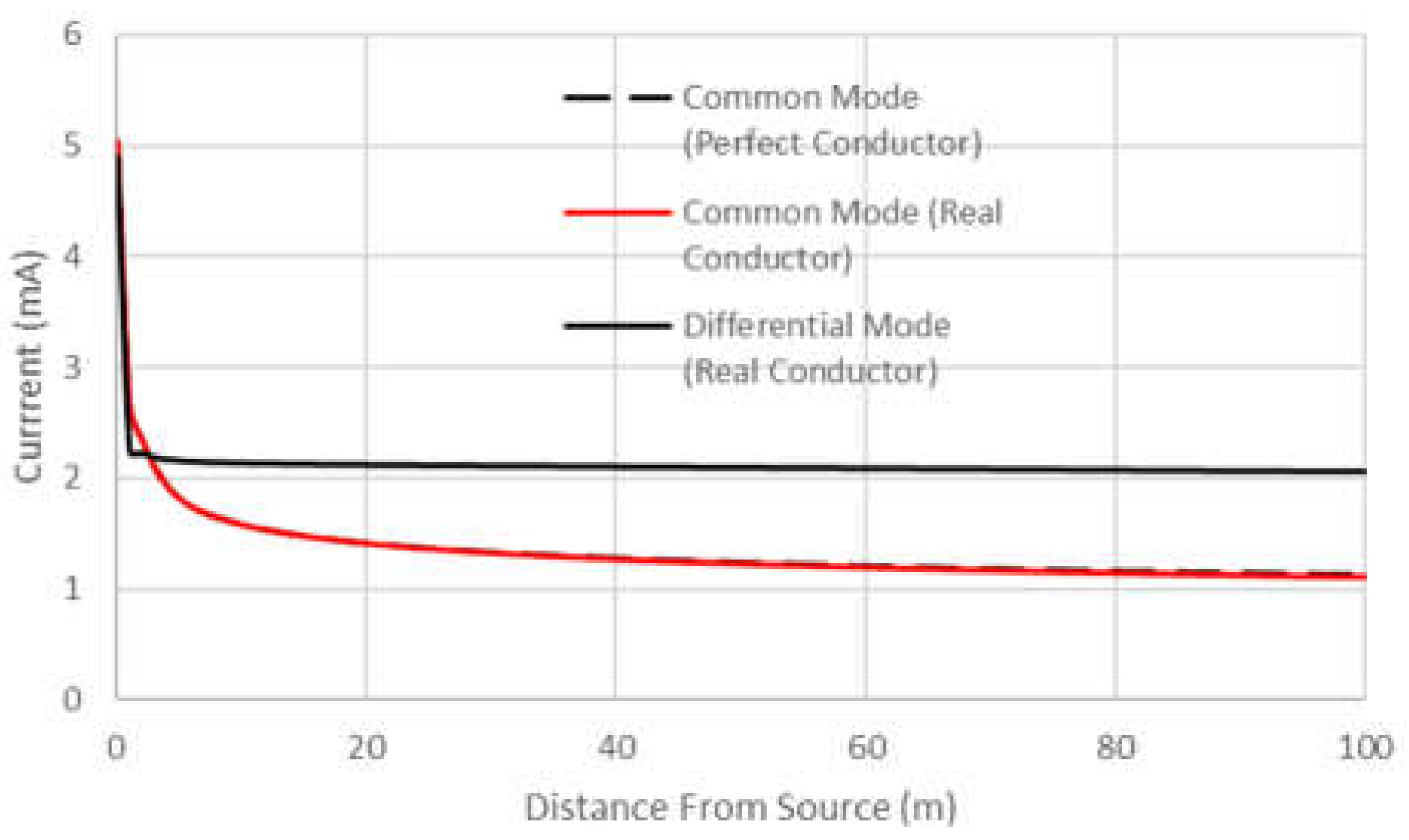
Figure 5 illustrates
that (26) is a reasonable approximation for the total common mode current,
(18), with
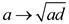
especially
at lower microwave frequencies. When this substitution is made, the branch cut
integration of (13) – (15) can be avoided.
Figure 6 and
Figure 7 are
plots of the individual wire currents excited by a voltage generator at z = 0
on wires 1 and 2 as well as the single wire current from [
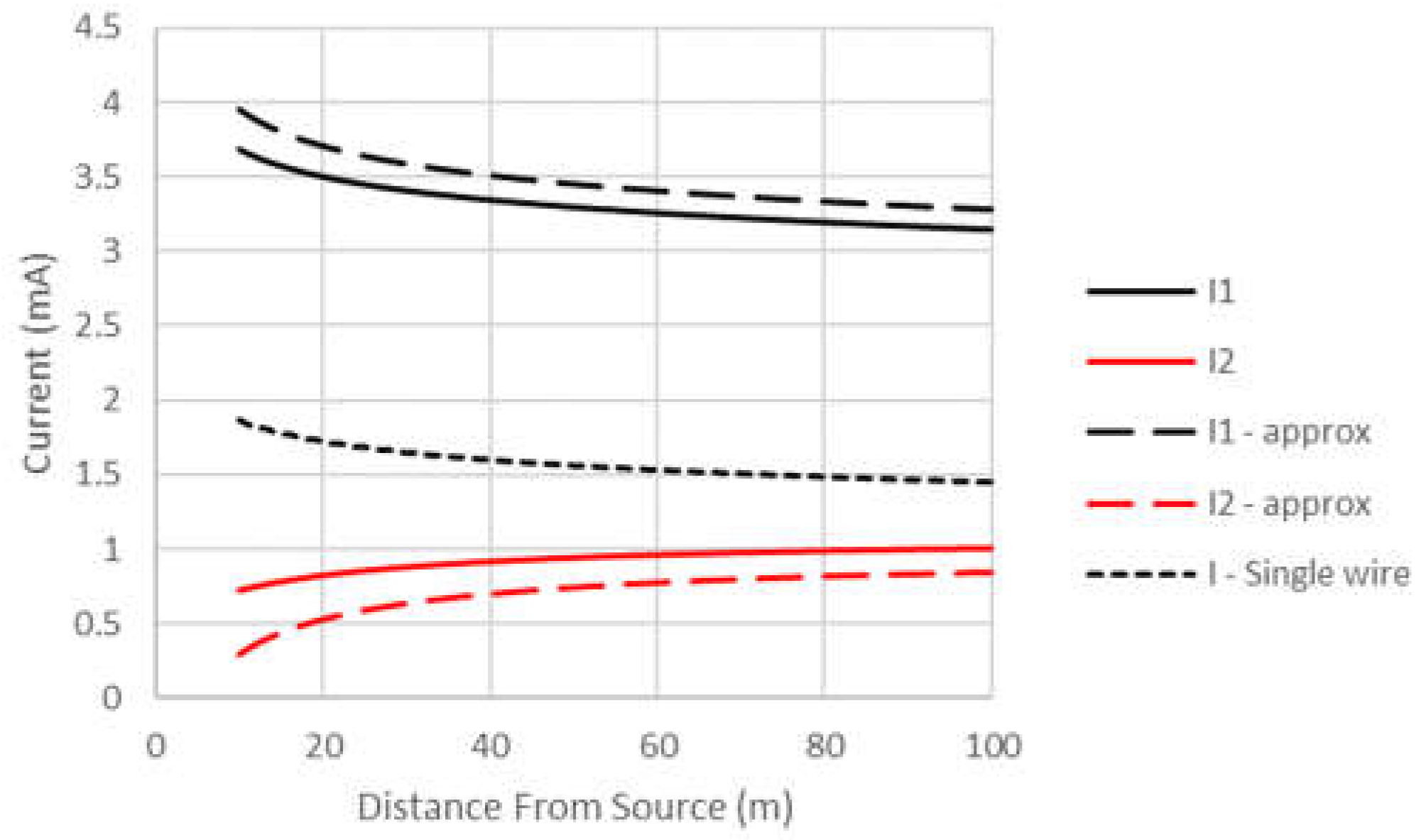
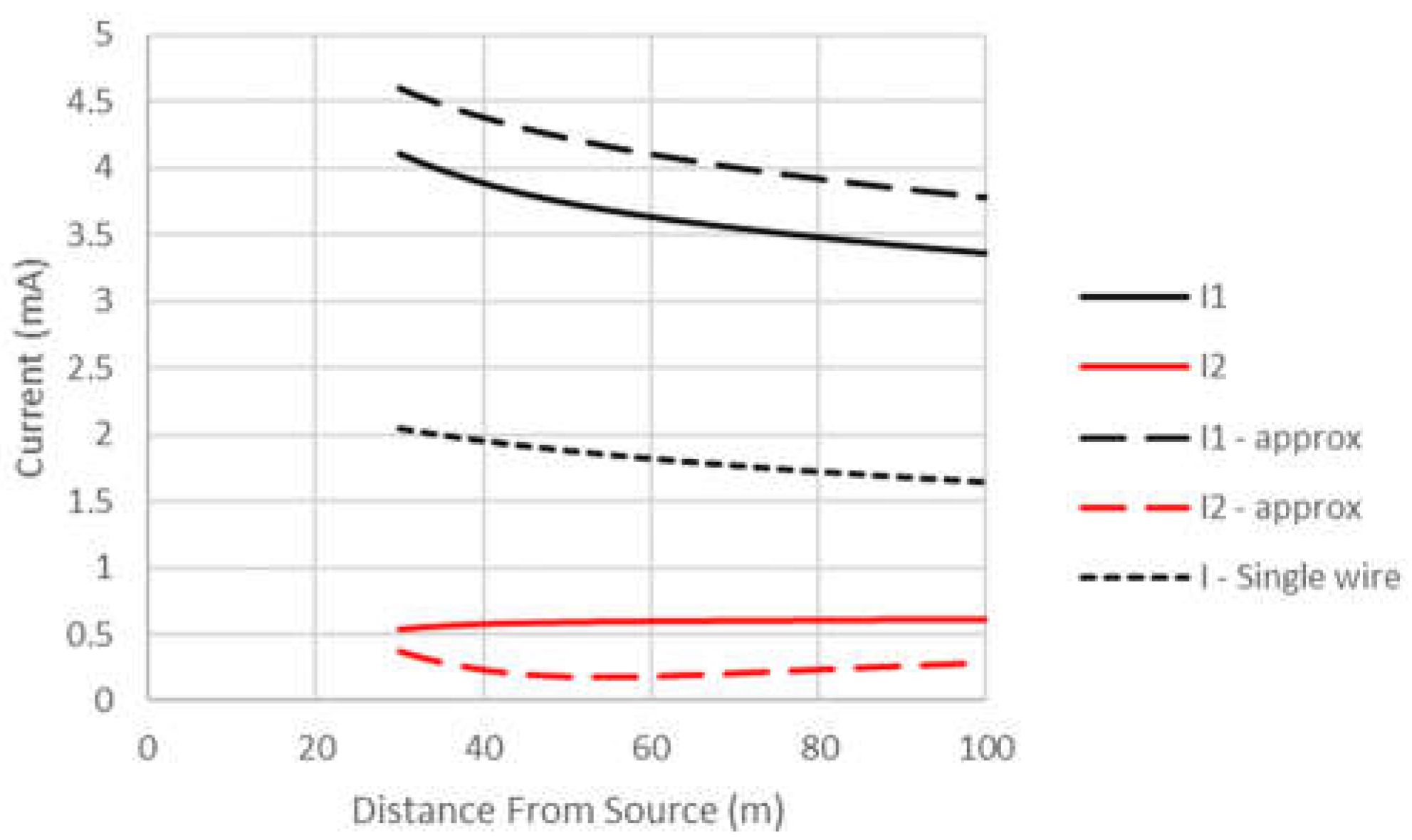
1] for frequencies of 1 and 10 GHz respectively. As
expected, the current on wire 1 exceeds that on wire 2 in the two wire case.
Also of interest is the fact that the current on wire 1 at 100 meters for the
two wire case is significantly higher than that on the single wire. This
indicates that the performance of a microwave power line communication system
can be enhanced by the existence of parallel wires. This conclusion is
consistent with that reported in [
7]. Also,
when approximations of (25) – (27) can be used, very simple expressions for the
currents result. This is more commonly true for
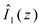
which has smaller
error and is also more important for evaluating communication systems.
5. Conclusions
Closed form solutions for the common and differential mode currents excited on a pair of parallel wires by a voltage source on one wire have been derived. Spectral solutions using a continuous spectrum of currents and the modified Sommerfeld-Goubau (mSG) and quasi-TEM modes in the common and differential mode cases respectively are given.
A simple formula for total current on the driven wire may often be used to approximate the total induced current in the two wire case.
For distances comparable to microwave power line communication system repeater spacing, the second wire can enhance system performance.
Acknowledgments
The author would like to thank Dr. Daiki Tashiro of CRIEPI in Japan for reading and commenting on the manuscript.
References
- R. G. Olsen, “On Single Wire Power Line Microwave Communication Using Low-Loss Modes,” IEEE Transactions on Antennas and Propagation Early Access article Digital Object Identifier: 10.1109/TAP.2021.3088584. [CrossRef]
- R. E. Collin, Field Theory of Guided Waves, 2nd Ed., pp. 718-720, IEEE Press, New York, 1991.
- G. Goubau ; C. Sharp ; S. Attwood, “Investigation of a surface-wave line for long distance transmission,” Transactions of the IRE Professional Group on Antennas and Propagation Vol. PGAP-3 | pp. 263-267, 1952.
- G. Elmore, “Introduction to the Propagating Wave on a Single Conductor,” Corridor Systems, Inc., White Paper, Jul. 2009. [Online].Available: http://www.corridor.biz/FullArticle.pdf.
- AT&T Press Release (Sep. 2016). “AT&T Labs’ Project AirGig Nears First Field Trials for Ultra-Fast Wireless Broadband Over Power Lines”. [Online]. Available: http://about.att.com/newsroom/att_to_test_delivering_multi_gigabit_wireless_internet_speeds_using_power_lines.html.
- Sommerfeld, “Ueber die Fortpflanzung elektrodynamischer Wellen längs eines Drahtes,” Ann. Physik Chem, vol. 303, no. 2, pp. 233–290, 1899. (See J. A. Stratton, “Electromagnetic theory,” McGraw Hill, New York, p. 527,1941).
- D. Molnar, T. Schaich, A. Al-Rawi and M. Payne, “Interaction between Surface Waves on Wire Lines,” The Royal Society, Proceedings A doi.org/10.1098/rspa.2020.0795, November 2021. [CrossRef]
- M. Abramowitz and I. A. Stegun, “Handbook of Mathematical Functions,” National Bureau of Standards, Applied Mathematics Series 55. Washington DC, 1964.
- L. Shen, T. T. Wu and R.W. P King, “A Simple Theory of Dipole Antennas” NASA Scientific Report No. 10, September 1967.
Biography
Robert G. Olsen (S’66–F’92–LF’11) received the B.S.E.E. degree from Rutgers University, New Brunswick, NJ, USA, in 1968, and the M.S. and Ph.D. degrees from the University of Colorado, Boulder, CO, USA, in 1970 and 1974, respectively.Since 1973, he has been with Washington State University, Pullman, WA, USA. Dr. Olsen is Fellow of the IEEE and an Honorary Life Member of the IEEE Electromagnetic Compatibility (EMC) Society. He is Past Associate Editor for the IEEE Transactions on Electromagnetic Compatibility and Radio Science
|
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
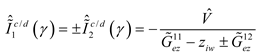
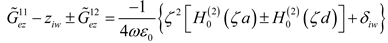
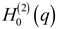 is the Hankel function of second kind, order zero and argument q,
is the Hankel function of second kind, order zero and argument q,  , Im(ζ) ≤ 0 (in order to satisfy
the radiation condition) where
, Im(ζ) ≤ 0 (in order to satisfy
the radiation condition) where 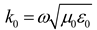 , γ is the
spatial Fourier transform variable, ε0 is the permittivity of
free space and ω is the radian frequency. The other variable in (2) is δiw
= 4ωε0ziw where the intrinsic impedance per
unit length of the wire at microwave frequencies is
, γ is the
spatial Fourier transform variable, ε0 is the permittivity of
free space and ω is the radian frequency. The other variable in (2) is δiw
= 4ωε0ziw where the intrinsic impedance per
unit length of the wire at microwave frequencies is

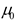 is the permeability
of free space. For (1), the thin wire boundary condition
is the permeability
of free space. For (1), the thin wire boundary condition 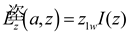 was applied at the
inside surface of each conductor radius. The caret notation, ^, indicates a
phasor quantity while the tilde notation “~” indicates the Fourier transform.
was applied at the
inside surface of each conductor radius. The caret notation, ^, indicates a
phasor quantity while the tilde notation “~” indicates the Fourier transform. 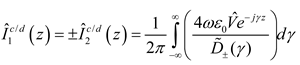
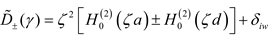
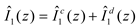
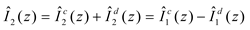
 with branch cuts
connecting them defined as shown in Figure 2.
As a further comment, the “proper” Riemann sheet is defined as Im(ζ) ≤ 0.
Since the branch cuts in Figure 2 and Figure 3
are defined so that Im(ζ) ≤ 0, the visible (i.e., top) portion of the
complex plane is the proper sheet where Im(ζ) ≤ 0. In addition to the
branch points and cuts, there is a pole γp which occurs on
the proper sheet at
with branch cuts
connecting them defined as shown in Figure 2.
As a further comment, the “proper” Riemann sheet is defined as Im(ζ) ≤ 0.
Since the branch cuts in Figure 2 and Figure 3
are defined so that Im(ζ) ≤ 0, the visible (i.e., top) portion of the
complex plane is the proper sheet where Im(ζ) ≤ 0. In addition to the
branch points and cuts, there is a pole γp which occurs on
the proper sheet at 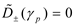 which
is different for the common and differential modes.
which
is different for the common and differential modes. 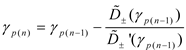
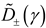 is given as (7) and
its derivative with respect to γ,
is given as (7) and
its derivative with respect to γ, 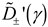 , can be shown to be
[8]
, can be shown to be
[8]
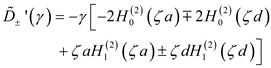
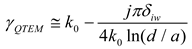
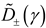 , (4) can now be
evaluated by deforming the original contour around the lower branch cut
entirely on the proper Riemann sheet as illustrated in Figure 2 and Figure 3. Given the factor e−jγz in the integrand of (4), the
integrations along the lower infinite semicircle are zero. Hence the original
integrations reduce to integrations along both sides of the branch cut as
shown. However, because the pole at γp is enclosed by the original
and new contours, its residue must be added to each integration.
, (4) can now be
evaluated by deforming the original contour around the lower branch cut
entirely on the proper Riemann sheet as illustrated in Figure 2 and Figure 3. Given the factor e−jγz in the integrand of (4), the
integrations along the lower infinite semicircle are zero. Hence the original
integrations reduce to integrations along both sides of the branch cut as
shown. However, because the pole at γp is enclosed by the original
and new contours, its residue must be added to each integration. 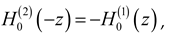
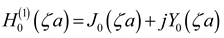
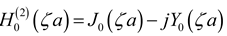
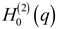 , J0(q)
and Y0(q)are respectively the Hankel function of the
first kind and Bessel functions of the first and second kind or order zero and
argument q. After multiplying the numerator and denominator by ζ2
to avoid an infinity in the denominator at γ = k0, the
horizontal portion of the branch cut integral between 0 and k0 is
, J0(q)
and Y0(q)are respectively the Hankel function of the
first kind and Bessel functions of the first and second kind or order zero and
argument q. After multiplying the numerator and denominator by ζ2
to avoid an infinity in the denominator at γ = k0, the
horizontal portion of the branch cut integral between 0 and k0 is
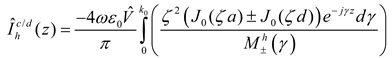
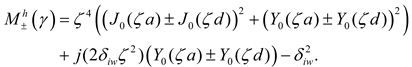
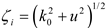 as
as
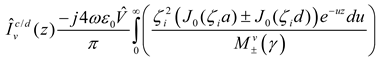
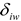 is finite, (14) and
(16) are relatively straightforward to integrate numerically.
is finite, (14) and
(16) are relatively straightforward to integrate numerically. 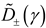 as a
Taylor series around γp. The result is
as a
Taylor series around γp. The result is
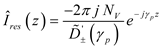
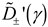 can be found in (9).
can be found in (9).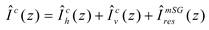


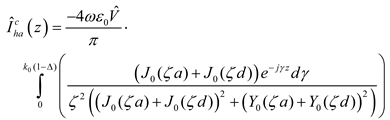
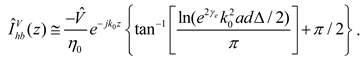
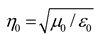 is
the impedance of free space, γe is the Euler constant, Δ is small
enough that
is
the impedance of free space, γe is the Euler constant, Δ is small
enough that 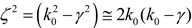 and
small argument approximations can be used for the Bessel functions [8]. In this solution, the substitutions u =
(k0 − γ) and
and
small argument approximations can be used for the Bessel functions [8]. In this solution, the substitutions u =
(k0 − γ) and 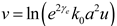 have been used. Note
that (23) accounts for the mSG pole residue which (for δiw =
0) has been absorbed into k0. Finally, (16) along
the vertical portion of the branch cut (but with δiw = 0) can
be evaluated numerically as earlier.
have been used. Note
that (23) accounts for the mSG pole residue which (for δiw =
0) has been absorbed into k0. Finally, (16) along
the vertical portion of the branch cut (but with δiw = 0) can
be evaluated numerically as earlier. 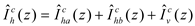
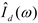 and length
and length 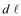 with its center at a
distance from
the outer surface of the conductor, one must multiply the voltage solution by
the factor
with its center at a
distance from
the outer surface of the conductor, one must multiply the voltage solution by
the factor
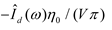
 . It is
. It is
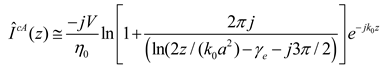
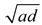 , . That this is
reasonable can be shown by examining (23) and noting that a major contribution
to the common mode current is the same as that for the single wire case in [1}
but with “a” replaced by
, . That this is
reasonable can be shown by examining (23) and noting that a major contribution
to the common mode current is the same as that for the single wire case in [1}
but with “a” replaced by 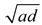 .
. 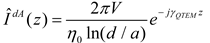
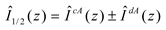
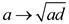 especially
at lower microwave frequencies. When this substitution is made, the branch cut
integration of (13) – (15) can be avoided.
especially
at lower microwave frequencies. When this substitution is made, the branch cut
integration of (13) – (15) can be avoided. 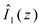 which has smaller
error and is also more important for evaluating communication systems.
which has smaller
error and is also more important for evaluating communication systems.


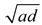 is
substituted for the individual wire radius a. The parameters are given in Table 1.
is
substituted for the individual wire radius a. The parameters are given in Table 1.
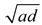 is
substituted for the individual wire radius a. The parameters are given in Table 1.
is
substituted for the individual wire radius a. The parameters are given in Table 1.