Prerpints.org logo
Preprint
Article

Novel Land Cover Change Detection Deep Learning Framework with Very Small Initial Samples Using Heterogeneous Remote Sensing Images

Altmetrics

Downloads

131

Views

54

Comments

0

This version is not peer-reviewed

Submitted:

09 June 2023

Posted:

09 June 2023

You are already at the latest version

Alerts
Abstract
Change detection with heterogeneous remote sensing images (Hete-CD) plays an important role in practical applications, especially when homogenous remote sensing images are unavailable. However, bitemporal heterogeneous remote sensing images (HRSIs) cannot compare directly to measure change magnitude, and many deep learning methods require large amounts of samples to train the module. Moreover, labeling many samples for land cover change detection with HRSIs is time-consuming and labor-intensive. Therefore, acquiring satisfactory performance of Hete-CD remains a challenge for deep learning networks with very small training samples. In this study, we promote a novel deep-learning framework for Hete-CD to obtain satisfactory performance while the initial samples are very small. We initially design a multiscale network with select kernel-attention module to focus on capturing different change targets with various sizes and shapes. Then, a simple yet effective non-parametric sample-enhanced algorithm based on the Pearson correlation coeffi-cient is promoted to explore potential samples around each initial sample. Finally, the proposed network and sample-enhanced algorithm are fused into one iterative framework to improve the change detection performance with very small samples. Experimental results conducted on four pairs of actual HRSIs indicated that the proposed framework can achieve competitive accuracies with very small samples for initialization when compared with some state-of-the-art methods. For example, the improvement is approximately 3.38% and 1.99% when compared with the selected traditional methods and deep learning methods, respectively.
Keywords: 
Subject: Environmental and Earth Sciences  -   Remote Sensing

1. Introduction

Land cover change detection (LCCD) with remote sensing images is defined by comparing the bi-temporal images and extracting the land cover change[1]. LCCD with remote sensing images can obtain large-scale land change on the earth’s surface promptly, and the land cover change information plays a vital role in landslide and earthquake inventory mapping [2,3,4], environmental quality assessment [5,6,7], natural resource monitoring [8,9], urban development decision-making [10,11,12], crop yield estimation [13], and other applications [14]. Therefore, LCCD with remote sensing images is attractive in practical applications [15,16,17,18].
In the previous decades, various LCCD methods have been developed. According to the difference in the bi-temporal images used for LCCD, these methods can be divided into two major groups [19]: change detection with homogeneous remote sensing images (Homo-CD) and change detection with heterogeneous remote sensing images (Hete-CD). Details of each group were reviewed as follows:
Homo_CD indicates that the images used for LCCD are homogeneous data acquired with the same remote sensors, have the same spatial-spectral resolution, and performed with the same reflectance signatures [14]. Therefore, the images can compare directly to measure the change magnitude and obtain land cover change information. Researchers have promoted many methods for Homo_CD. One of the most popular methods is the contextual information-based method [20], such as the sliding window-based approach [21], the mathematical model-based method [22], and the adaptive region-based approach [23,24]. In addition, a deep learning method for Homo_CD has been widely used, such as convolutional neural networks [25,26,27] and fully convolutional Siamese networks [28,29]. To cover more ground targets and utilize deep features, a large number of deep learning networks were constructed with multiscale convolution [30,31] and deep feature fusion [32,33]. Moreover, the change trend detection with multitemporal images is attractive and popular in recent years [15,34,35]. Despite various change detection methods that have been promoted and their excellent performance demonstrating their feasibility and advantages for Homo_CD, two major flaws remain: deep learning neural network training required many samples, and preparing a large number of training samples is labor-intensive and time-consuming.
Moreover, due to the rapid development of remote sensing techniques, homogeneous images may be unavailable in considerable application scenarios. For example, optical satellite image is usually unavailable for detecting land cover change caused by night wildfire or flood, yet the pre-event optical images are easily obtained with satellites. In addition, the image quality of optical satellite images is easily affected by weather [36,37]. Therefore, to solve the limitation of Homo_CD in practical applications, Hete-CD is promoted and has become popular in recent years [38].
Compared with Homo_CD, the images used for Hete-CD are heterogeneous remote sensing images (HRSIs). The HRSIs have an advantage in complementing the insignificance of homogeneous images, such as an optical image reflecting the appearance of ground targets by visible, near-infrared, and short-wave infrared sensors. Thus, the illumination and atmosphere conditions strongly affect the optical image quality. While Synthetic Aperture Radar (SAR) image represents the physical scattering of ground targets, the appearance of a target in SAR image depends on its roughness and wavelength of microwave energy. Therefore, when an optical image is available before a night flood or landslide, SAR image is an alternative after the disaster because it is independent of visual light and weather conditions [39]. Therefore, immediate assessment of the damage of natural disasters using optical and SAR images for some urgent cases is possible. The superiority of Hete-CD increases the corresponding demand in practical engineering.
In recent years, various methods have been promoted for Hete-CD. The most popular approach of Hete-CD focused on exploring the shared features and measuring the similarity between the shared features to bitemporal HRSIs. Wan et al. explored statistical features from multisensor images for LCCD [40]. Lei et al. extracted the adaptive local structure from HRSIs for Hete-CD [41]. Sun et al. improved the adaptive structure feature based on sparse theory for Hete-CD [42]. In addition, image regression [43,44,45], graph representation theory [46,47,48,49,50], and pixel transformation [51] are feasible for exploring the shared feature to achieve change detection tasks with HRSIs. Although considerable traditional methods and their applications have demonstrated the feasibility and advantages of using HRSIs in LCCD, these algorithms are usually complex and their optimal parameter requires trial-and-error experiments.
In addition, deep learning techniques have been widely used to explore deep features from HRSIs and make them comparable for change detection. Zhan et al. promoted a log-based transformation feature learning network for Hete-CD [52]. Wu et al. developed a commonality auto-encoder for learning common features for Hete-CD [53], and Niu presented a conditional adversarial network for Hete-CD [54]. Although some applications indicated that deep learning techniques can learn deep features from HRSIs to be comparable, the deep learning-based Hete-CD methods usually required a large amount of training samples.
Particularly, the challenges of Hete-CD were summarized as follows: 1) bi-temporal HRSIs cannot be compared directly for detecting change; 2) achieving satisfactory performance with very small samples for training is challenging for a number of existing deep learning approaches; 3) labeling training samples for deep learning based methods is necessary, but time-consuming and labor-intensive. We promoted a novel framework to achieve change detection with HRSIs under very small initial sample set to deal with the challenges of Hete-CD. The major contribution of the proposed framework can be briefly summarized as follows:
  • A novel deep-learning framework is designed for Hete-CD. In particular, we demonstrated that the simple framework has some advantages in improving the detection accuracies with very small initial samples. A simple yet competitive performance of the deep learning framework is attractive and preferred for practical engineering.
  • A non-parametric sample-enhanced algorithm is proposed to be embedded into a neural network. In particular, it explores the potential samples around each initial sample in a non-parametric and iterative approach. Although this idea was verified by Hete-CD with HRSIs in this study, it may be useful for other supervised remote sensing image applications, such as land cover classification, scene classification, and Homo-CD.
The remainder of this paper is organized as follows. Section II presents the details of the proposed framework. Section III presents the experiments and the related discussion. The conclusion is given in Section IV.

2. Methods

In this section, we provide a detailed description of the proposed framework for Hete-CD, including an overview and backbone of the proposed neural network, non-parametric sample enhanced algorithm, and accuracy assessment. Each part is detailed in the following section.

Overview

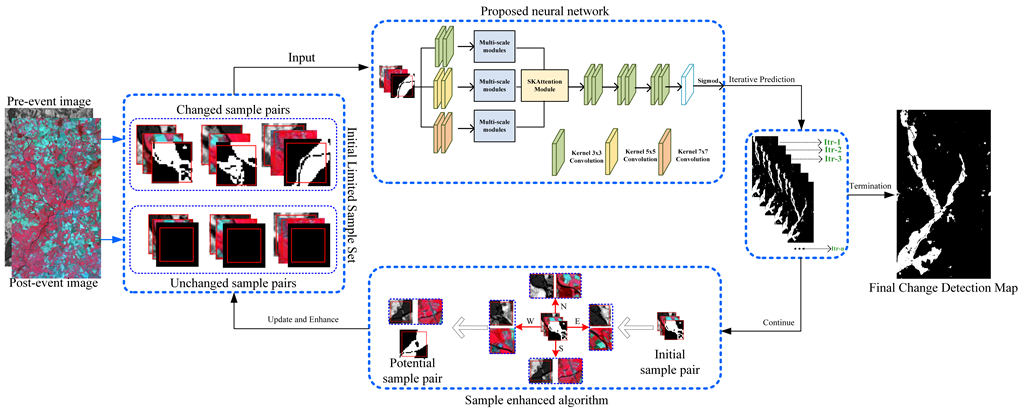
The motivation of this study lies in achieving change detection performance with very small samples for Hete-CD. A novel framework was designed here to achieve the objective. As shown in Figure 1, the proposed framework has three major parts.
The overview of the proposed framework indicates that the proposed framework generated change detection map iteratively, and the final detection map was output until the iteration is terminated. Moreover, the framework was initialized with very small sample, and then the initial training sample set was amplified by a proposed non-parametric sample-enhanced algorithm in each iteration. Details of the termination condition of the proposed framework are presented in the following section.
To clarify this concept, the matched pixels for changed and unchanged classes between three adjacent iterations are defined in (1), as follows:
M k − 1 , k L − M k , k + 1 L ≤ ε ,
M k − 1 , k L = c o u n t ( M k − 1 L ↔ M k L ) W × H ,
M k , k + 1 L = c o u n t ( M k L ↔ M k + 1 L ) W × H ,
where in L ∈ 0,1   , 0 and 1 denote the unchanged and changed class, respectively. M k − 1 , k L and M k , k + 1 L are calculated by (2) and (3), respectively; they indicate the similarity between the detection map from the (k-1)th and k-th and k-th and (k+1)th iterations. In addition, ε is a very small constant, and it is fixed at 0.0001 in our proposed framework. The training sample was adjusted dynamically in the iterative progress. For example, if the change class satisfies the (1), then the corresponding changed sample will not be enhanced in the next iteration, and (1) will be checked again in each iteration. Therefore, (1) implies that the iteration of the proposed framework is terminated until the difference between the matched ratio among the (k-1)th, k-th, and (k+1) detection maps is less than ε for the unchanged and changed classes.
In addition to the overview of the proposed framework, the two major parts are the proposed deep learning neural network and non-parametric sample enhanced algorithm; details are presented as follows.

Proposed deep-learning neural network

Intuitively, different ground targets are performed with different sizes in remote sensing images, and distinguishing a target, such as a lake or a building, requires an appropriate scale from the viewpoint of human vision [55,56]. Therefore, as shown in Figure 1-(a), three aspects are considered in the proposed neural network. First, the bi-temporal images were concatenated into one image and then feed it into three parallel branches. Each branch contained two convolution layers and one multiscale module, and each convolution layer in each branch has a different kernel size. The motivation of this operation lies in learning multiscale features for describing the various targets with different sizes. Second, aiming at guiding the module learning a selective scale for a specific target, a selective kernel (SK) attention module [57] is used here to adaptively adjust its receptive field size based on multiple scales of the input information. Then, six convolutional layers with a 3 × 3 kernel size are used, following the SK-attention to further smoothen the detection noise. Finally, the proposed neural network is activated by the Sigmoid function.
In addition, the proposed neural network was trained with 20 epochs for one iteration in the entire framework and then used to predict one change detection map. When the training samples were enhanced, the proposed neural network was trained again with the new sample set. In the training progress, a widely used loss function named cross-entropy was adopted, and a r g m a x ( · ) was used for prediction.

Nonparametric sample enhanced algorithm

The labeling training sample is well-known to be time-consuming and labor-intensive, and sufficient samples are required for training a deep learning model [58]. Therefore, a non-parametric sample-enhanced algorithm is promoted and embedded in our proposed framework. Details of the sample-enhanced algorithm are presented as follows:
Two image blocks, X i j and Y i j , are symbolized for the pre-event and post-event and defined as a known sample. Their neighboring image blocks around the known sample position (i,j) are selected as the potential training samples, and each potential sample is overlapped a quarter with the known sample. In this study, the correlation between X i j and Y i j   was measured by the Pearson Correlation Coefficient (PCC), as follows:
P X i j , Y i j = E ( x i j − μ x i j ) ( y i j − μ y i j ) δ ( x i j ) δ ( y i j )
where E ( · ) is an expectation, and x i j   and μ x i j represent the pixel within the spatial domain of X i j and the mean of these pixels in terms of gray value, respectively. σ ( · ) is the standard deviation of the pixels within X i j . P X i j , Y i j reflects the linear correlation between the pixels of the samples from the HRSIs. Based on the definition, the label of the samples around the known sample pair X i j   Y i j is distinguished as follows:
P L S i j t 1 , S i j t 2 = L = 1 , i f   P S i j t 1 , S i j t 2 ≤ P 1 ( X i j , Y i j ) L = 0 , i f   P S i j t 1 , S i j t 2 ≥ P 0 ( X i j , Y i j )
where L denotes the sample’s label, and L = 1 and L = 0 denote the changed and unchanged classes, respectively. The defined rules indicated that when the label of the known sample is “changed,” and if the correlation between the pairwise neighboring potential samples ( S i j t 1 and S i j t 2   ) is less than or equal to that of the known sample ( X i j and Y i j   ), then the label of the pairwise neighboring potential sample will be marked as “changed.” On the contrary, when the label of the known sample is “unchanged,” and if P S i j t 1 , S i j t 2 ≥ P 0 ( X i j , Y i j ) , then the label of the pairwise neighboring potential sample will be marked as “unchanged.” Based on this definition, the initial sample set with a very limited size is gradually amplified in the progress of iteration, and the enhanced sample set is re-used for training the proposed neural network to generate a preferred detection performance.
These rules based on PCC is effective for exploring potential samples around each known sample with regard to the following intuitive assumptions: (1) PCC can measure the correlation between two datasets from different modality; (2) around a sample with changed label, the lower correlation between pairwise of heterogonous image blocks indicates the lower possibility of change between them; (3) around a sample with unchanged label, the higher correlation between pairwise of heterogonous image blocks indicates higher possibility of change between them.

2.4. Accuracy assessment

To investigate the performance quantitively, nine widely used evaluation indicators are used in our study; details are summarized in Table I. Here, four variables are defined to clarify the referred indicators: true positive (TP) refers to the number of accurately detected changed pixels, true negative (TN) is the number of accurately detected unchanged pixels, false positive (FP) is the number of inaccurately detected changed pixels, and false negative (FN) is the number of inaccurately detected unchanged pixels.
Table I. Quantitative accuracy evaluation indicators for each experiment.
Table I. Quantitative accuracy evaluation indicators for each experiment.
Evaluation Indicators Formula Definition
False alarm (FA) F A = F P T N + F P FA is the ratio between false changed and unchanged pixels of ground truth.
Missed alarm (MA) M A = F N T P + F N MA is the ratio between false unchanged and changed pixels of ground truth.
Total error (TE) T E = F P + F N T P + T N + F P + F N TE is the ratio between the summary of false changed and false unchanged pixels and the total pixels of the ground map.
Overall accuracy (OA) O A = T P + T N T P + T N + F P + F N OA is the accurately detected pixels between the total pixels of the ground map.
Average accuracy (AA) A A = T P T P + F N + T N T N + F P / 2 AA is the mean of accurately detected changed and accurately unchanged ratios.
Kappa coefficient (Ka) P 0 = T P + T N T P + T N + F P + F N
P e = T P + F P × T P + F N + ( F N + T N ) × ( F P + T N ) ( T P + T N + F P + F N ) 2
K a = P 0 − P e 1 − P e 		Ka reflects the reliability of the detection map by measuring inter-rater reliability for changed and unchanged classes.
Precision (Pr) P r = T P T P + F P Pr is the ratio between the accurately detected changed and total changed pixels in a detention map.
Recall (Re) R e = T P T P + F N Re is the ratio between the accurately detected changed and total changed pixels in the ground truth map.
F1-score (F1) F 1 = 2 × p r e c i s i o n × r e c a l l p r e c i s i o n + r e c a l l F1 is the harmonic mean of precision and recall.

3. Experiments

Two experiments are designed here to verify the superiority and performance of our proposed framework for Hete-CD. The experiments are performed on four pairs of actual HRSIs. Detailed descriptions of the experiments are presented in the following section.

3.1. Dataset Description

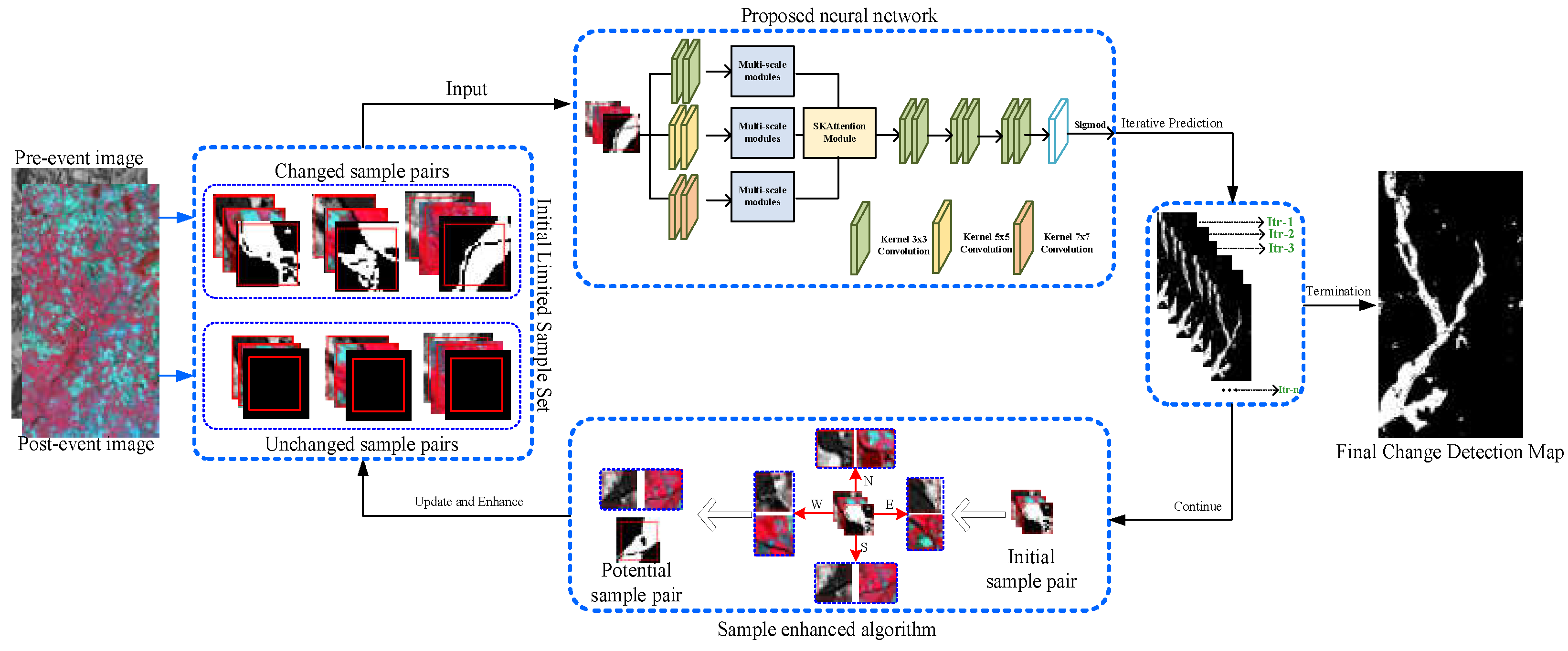
Four pairs of HRSIs are used for the experiments. As shown in Figure 2, these images referred to water body change, building construction, flood, and wildfire change events. Details of each image pair are detailed as follows:
Dataset-1: This dataset refers to different optical images, which are acquired from different sources. The pre-event image was acquired by Landsat-5 in September 1995 and has a size of 300 × 400 × 1 pixels with 30 meters/pixel. The post-event image was acquired in July 1996, and it was clipped from Google Earth; its size is 300 × 400 × 3 pixels with 30 meters per pixel. The type of pairwise HRSIs is easily available. Here, they are used to detect the expansion area of the Sarindia (Italy) Lake.
Dataset-2: This dataset contains one SAR pre-event image, which was acquired with the Radarsat-2 satellite in June 2008, and one optical post-event image, which was extracted from Google Earth in September 2012. The size of the HRSIs is 593 × 921 × 1 pixels and 593 × 921 × 3 pixels with 8 meters per pixel. The change event is the building construction located at Shuguang Village, China.
Dataset-3: This dataset includes SPOT Xs-ERS image and SPOT image for pre-event and post-event, respectively. The pre-event image and post-event image were acquired in October 1999 and October 2000 before and after a flood over Gloucester, U.K. Particularly, the ERS image reflects the roughness of the ground before the flood, and the multispectral SPOT HRV image describes the color of the ground during the flood. The detection task aims at calculating the change areas by comparing the bitemporal heterogonous images.
Dataset-4: This dataset is composed of two images acquired by different sensors (Landsat-5 TM and Landsat-8) over Bastrop County, Texas, USA for a wildfire event on September 4, 2011. The bi-temporal images have the size of 1534 × 808 × 3 pixels and with a 30 meter/pixel resolution. The modality difference of the bi-temporal images lies in the pre-event image, which was acquired by Landsat-5 and composed of 4-3-2 bands, and the post-event image, which was obtained by Landsat-8 and composed of 5-4-3 bands.

3.2. Experimental Setup

In the experiments, nine state-of-the-art change detection methods, including three traditional methods and six deep learning methods, are selected for comparison. Details are presented as follows:
(i) In the first part of the experiments, three relatively new and highly cited related methods, namely, adaptive graph and structure cycle consistency (AGSCC)1[45], the graph-based image regression and MRF segmentation method (GIR-MRF) 2[50], and the sparse constrained adaptive structure consistency based method (SCASC) 3[59], were compared with our proposed framework. In the comparisons, the parameters of the selected methods [45,50,59] are the same as those used in the original studies. For our proposed framework, 12 pairs of unchanged samples (six pairs) and changed samples (six pairs) are randomly selected from the ground reference map for framework initialization.
(ii) The second part of the experiments aims at verifying the advantages and feasibility of the proposed framework while comparing it with some state-of-the-art deep learning methods, including fully convolutional Siamese difference (FC-Siam-diff) [28], crosswalk detection network (CDNet) [56], feature difference convolutional neural network (FDCNN) [26], deeply supervised image fusion network (DSIFN) [60], cross-layer convolutional neural network (CLNet) [27], and multiscale fully convolutional network (MFCN) [30]. The following parameters are set for each network: learning rate=0.0001, batch size=3, and epochs =20. In addition, to guarantee comparative fairness, all the selected deep learning methods used the same training samples randomly clipped and extracted from the ground reference map. Moreover, the quantity of the training samples for the state-of-the-art deep learning methods is close to the number of samples at the end of the iteration of our proposed framework.

3.3. Experimental Results

The experimental results for the four pairs of HRSIs were obtained according to the above parameter setting. Details are as follows:
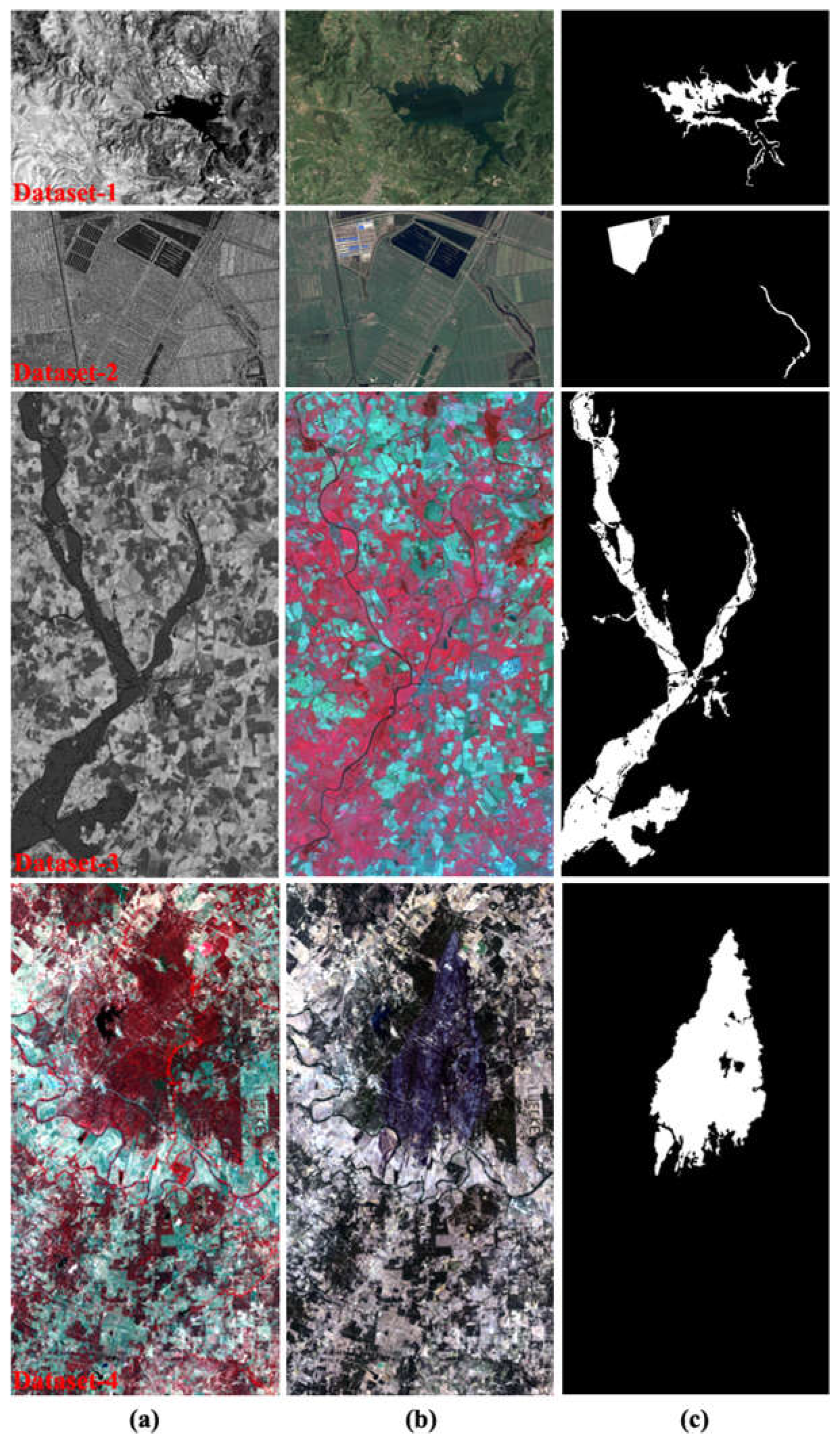
(i) Comparisons with traditional methods: The visual performance of AGSCC [45], GIR-MRF [50], SCASC [59] is presented in Figures 3-(a), -(b), and -(c), respectively. Compared with the results based on our proposed framework, Figure 3-(d) shows that our proposed framework achieved the detection performance with the least false alarm (green) and missed alarm (red) pixels. The corresponding quantitative results in Table 2 further supported the conclusion from the visual observation comparisons. For example, for the four datasets, the proposed framework achieved 99.04%, 98.75%, 96.77%, and 97.92% in terms of OA; these values are the best among the results from AGSCC [45], GIR-MRF [50], SCASC [59], and our proposed framework.
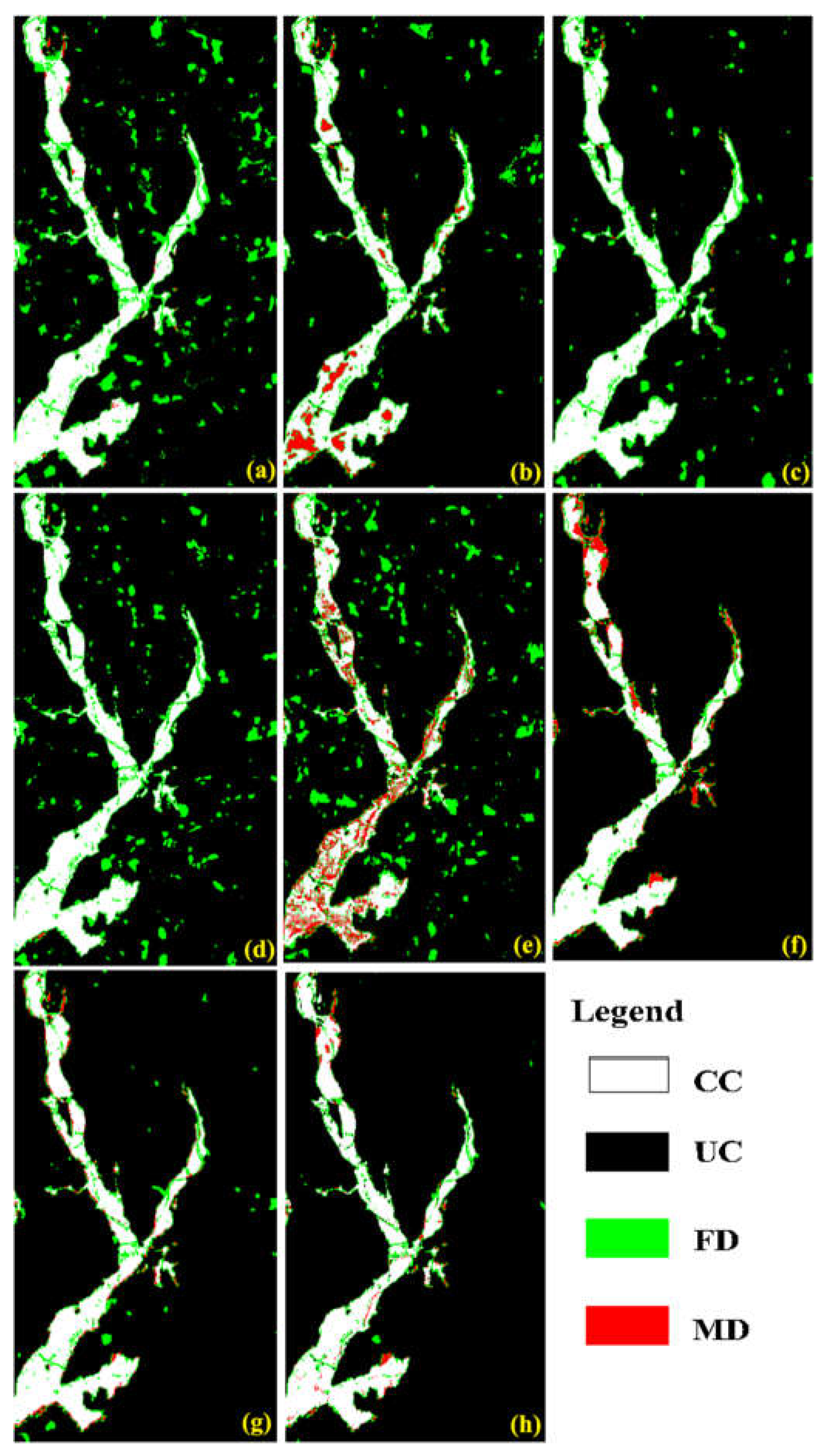
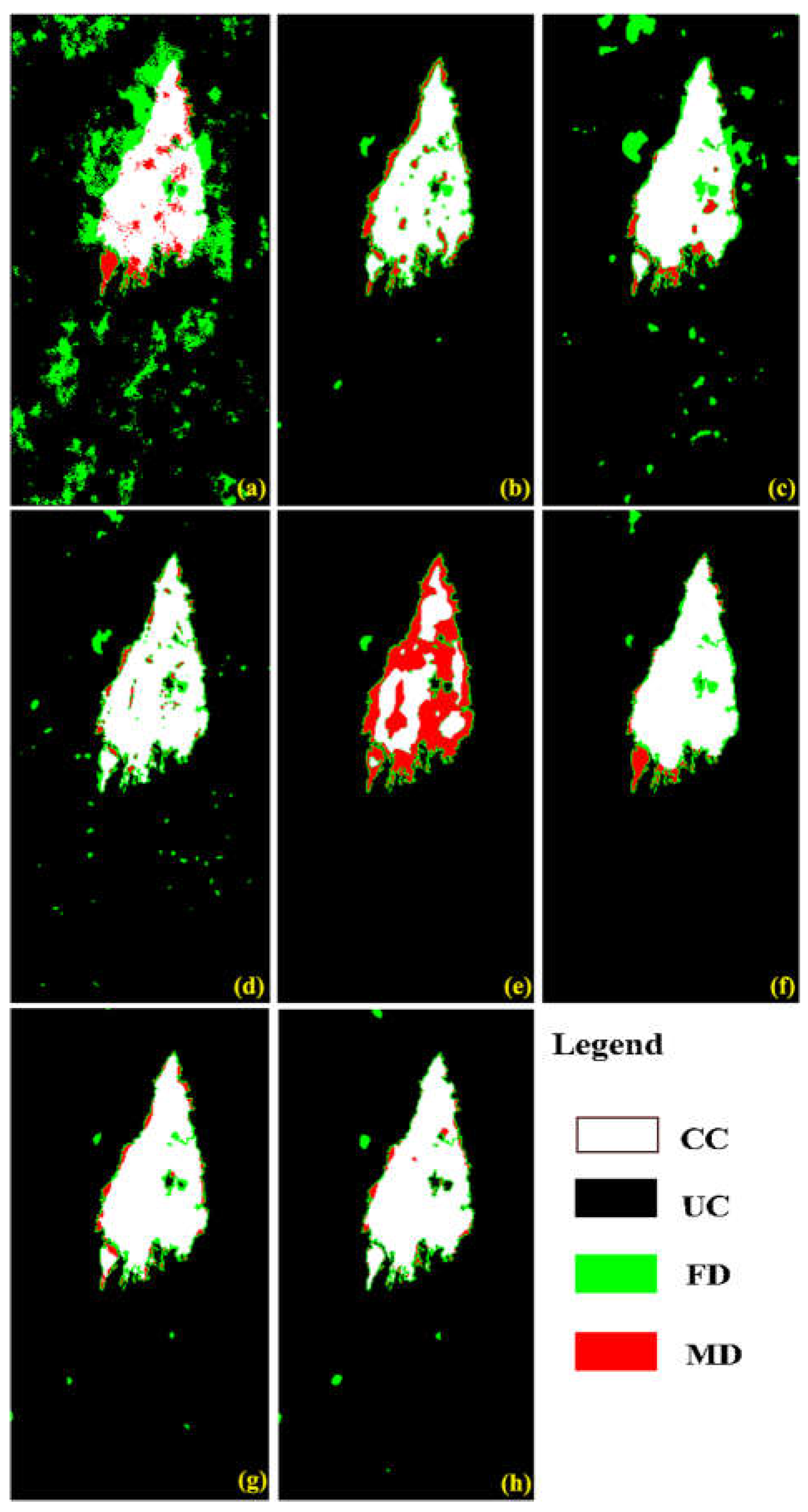
(ii) Comparisons with deep learning methods: We further verify the robustness of the proposed framework by comparing it with some state-of-the-art deep learning methods. The detection maps presented in Figure 4, Figure 5, Figure 6 and Figure 7 are acquired by different deep learning methods for the four datasets. These visual comparisons indicated that the proposed framework achieved better performance with fewer false alarms and missed alarms. Moreover, while removing the sample enhanced algorithm from the entire proposed framework, as denoted by “Proposed-” in Table 3, Table 4, Table 5 and Table 6, the improvement was achieved compared with that of other approaches for the same datasets. Multiscale information extraction and selective kernel attention in the promoted neural network are complementary to learning more accuracy in our proposed framework. The following quantitative comparisons in Table 3, Table 4, Table 5 and Table 6 further supported the visually observed conclusion.

3.4. Discussion and Analysis

To promote the widely use and further understanding of the proposed framework, two aspects of the training samples for the proposed framework are discussed and analyzed, as follows:
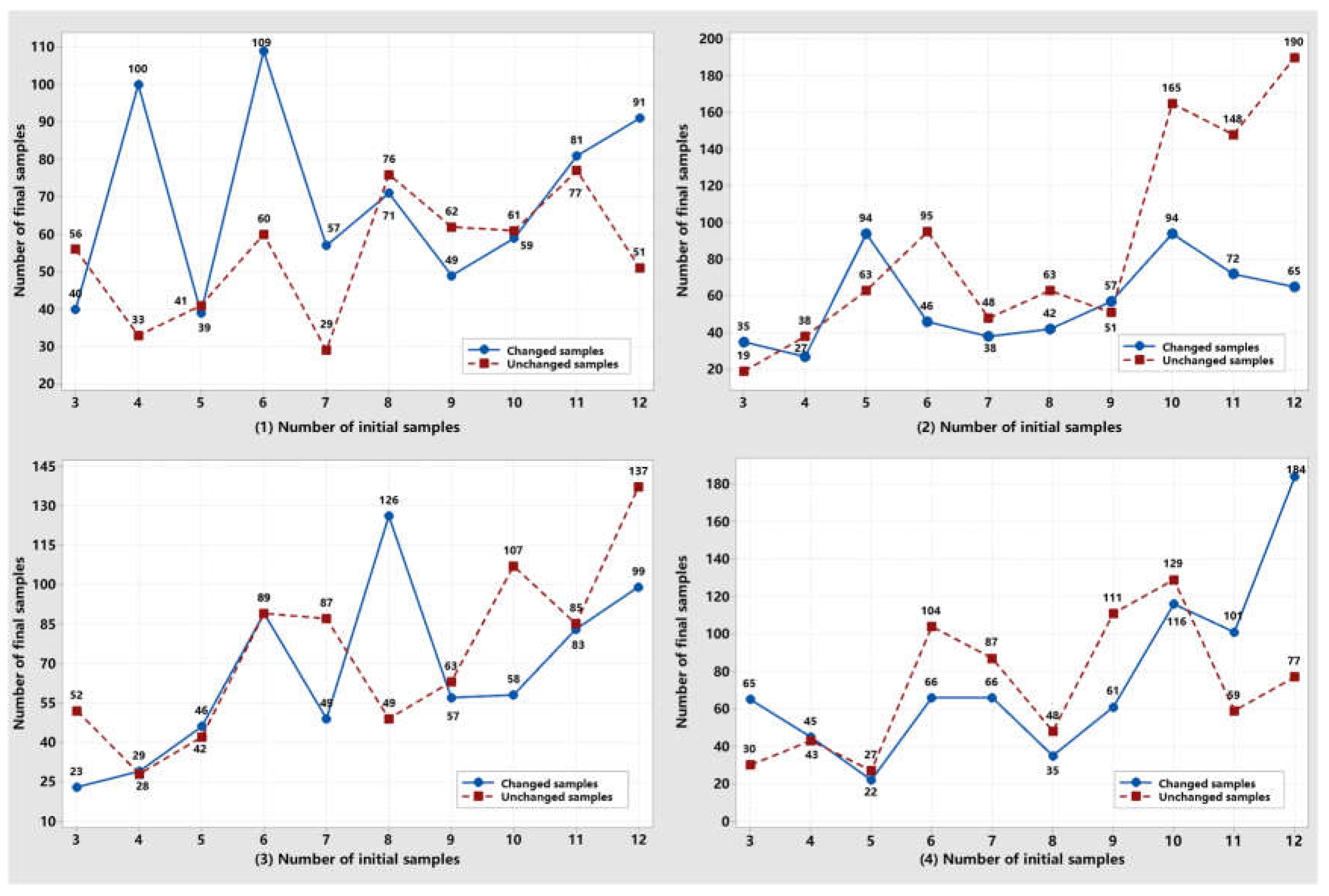
(i) Relationship between the initial and final samples: as stated in Section II, the proposed framework was initialized with very small training samples, which were amplified iteratively at each iteration. Therefore, observing the relationship between the initial samples and the final samples helps in understanding the balancing ability for unchanged and changed classes in our proposed framework. Figure 8 indicated that the quantity of samples for the changed and unchanged classes is equal for initialization. When the iteration of the proposed framework was terminated, the number of samples for the unchanged and changed classes was adjusted automatically to be different because the size of the area was different in an image scene. Detecting them with an unequal sample is beneficial for balancing their detection accuracies. In addition, Figure 8 also demonstrated that the relationship between the initial samples and the final sample is nonlinear. For example, for the unchanged and changed sample of Dataset-1, when the initial samples for the unchanged class increased from three to four pairs, its final samples decreased from 56 pairs to 33 pairs. Moreover, different datasets exhibit the relationship between the initial samples and the final sample for our proposed framework. Therefore, the suitable quantity of samples for the initialization of the proposed framework may require trial-and-error experiments in practical applications.
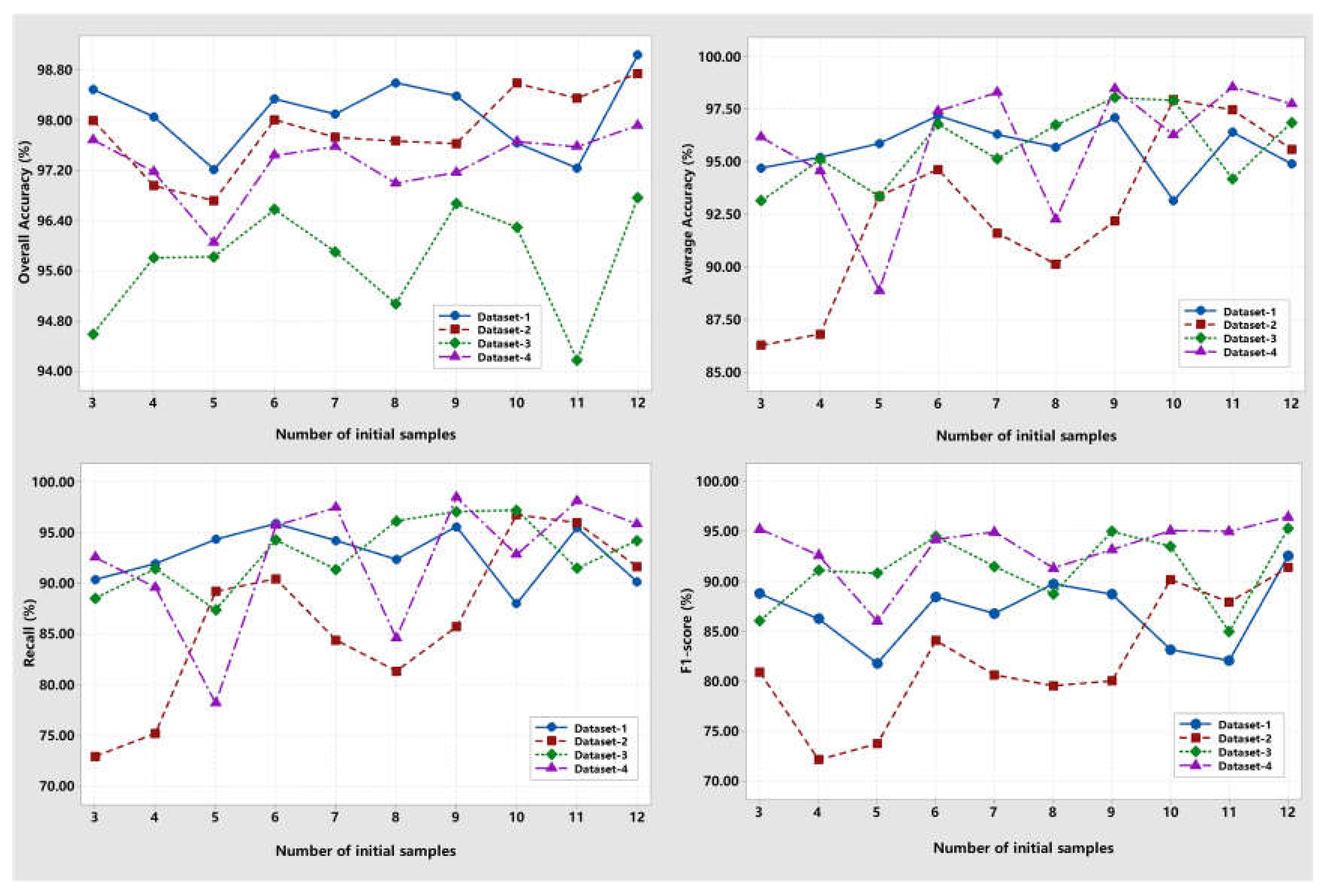
(ii) Relationship between the initial samples and detection accuracies: As shown in Figure 9, the observation indicated that the detection accuracies initially decreased with the increment of the initial samples for some datasets, and then the accuracies increased and posed to be a state with a small variation. For example, the OA for Dataset-2 and -4 decreased when the initial samples increased from three pairs to four pairs, and then it increased and vibrated within [96.72%, 98.75%] and [96.05%, 97.92%], respectively. Some explored samples may be marked with missed labels, which negatively affect the learning performance. However, with the increment of the initial training samples, the sample with missed labels becomes the minority in the total enhanced sample set. Therefore, an uncertainty relationship may cause detection accuracy variation when training our proposed framework with the sample set.

4. Conclusion

In this study, a novel deep learning-based framework is proposed to achieve change detection with heterogeneous remote sensing images when the training samples are very small. To achieve the motivation of acquiring satisfied detection performance with very small initial training samples, the proposed framework fused a novel multiscale neural network and a novel non-parametric sample-enhanced algorithm into iterative progress. The advantages of the proposed framework are summarized as follows:
(i) Advanced detection accuracies are obtained with the proposed framework. The comparative results with four pairs of actual HTRSIs indicated that the proposed framework outperforms three traditional cognate methods (AGSCC [45], GIR-MRF [50], and SCASC [59],) and six state-of-the-art deep learning methods (FC-Siam-diff [28], CDNet [61], FDCNN [26], DSIFN [60], CLNet [27], and MFCN [30]) in terms of visual performance and nine quantitative evaluation metrics.
(ii) Training deep learning neural networks iteratively with a non-parametric sample-enhanced algorithm is effective to improve the detection performance with very limited initial samples. This work is the first to couple a non-parametric sample enhanced algorithm with a deep learning neural network for training the neural network iteratively with the enhanced training samples from each iteration. Experimental results and comparisons demonstrate the feasibility and effectiveness of the recommended sample enhanced algorithm and training strategy for our proposed framework
(iii) A simple, robust, and non-parametric framework is preferred and acceptable for practical engineering applications. In addition to the very small initial training samples for initialization, the proposed framework has no parameters that required hard tuning. This characteristic can be easily applied to practical engineering.
Despite these advantages of the proposed framework, the widespread applications with large areas and other types of change events should be further investigated. In our future study, we will focus on collecting more types of HTRSIs, and multiclass change detection will be considered.

Author Contributions

Dr. YangPeng Zhu was primarily responsible for the original idea and the experimental design. QianYu Li performed the experiments. ZhiYong Lv provided ideas to improve the quality of the paper, Nicoal Falco provides supervision and language revision.

Funding

This work was supported by Shaanxi Provincial Department of Science and Technology Fund Project "Shaanxi Provincial Innovation Capability Support Program" (No. 2021PT-009) for funding the research.

Acknowledgments

The authors wish to thank the editor-in-chief, associate editor and reviewers for their insightful comments and suggestions.

Conflicts of Interest

The authors declare no conflict of interest.

References

  1. Singh, A. Review article digital change detection techniques using remotely-sensed data. International journal of remote sensing 1989, 10, 989–1003. [Google Scholar] [CrossRef]
  2. Anniballe, R.; Noto, F.; Scalia, T.; Bignami, C.; Stramondo, S.; Chini, M.; Pierdicca, N. Earthquake damage mapping: An overall assessment of ground surveys and vhr image change detection after l'aquila 2009 earthquake. Remote sensing of environment 2018, 210, 166–178. [Google Scholar] [CrossRef]
  3. Li, Z.; Shi, W.; Lu, P.; Yan, L.; Wang, Q.; Miao, Z. Landslide mapping from aerial photographs using change detection-based markov random field. Remote Sensing Of Environment 2016, 187, 76–90. [Google Scholar] [CrossRef]
  4. Li, Z.; Shi, W.; Myint, S.W.; Lu, P.; Wang, Q. Semi-automated landslide inventory mapping from bitemporal aerial photographs using change detection and level set method. Remote Sensing Of Environment 2016, 175, 215–230. [Google Scholar] [CrossRef]
  5. Bouziani, M.; Goïta, K.; He, D.-C. Automatic change detection of buildings in urban environment from very high spatial resolution images using existing geodatabase and prior knowledge. ISPRS Journal of Photogrammetry and Remote Sensing 2010, 65, 143–153. [Google Scholar] [CrossRef]
  6. Coppin, P.; Jonckheere, I.; Nackaerts, K.; Muys, B.; Lambin, E. Review articledigital change detection methods in ecosystem monitoring: A review. International journal of remote sensing 2004, 25, 1565–1596. [Google Scholar] [CrossRef]
  7. Leichtle, T.; Geiß, C.; Wurm, M.; Lakes, T.; Taubenböck, H. Unsupervised change detection in vhr remote sensing imagery–an object-based clustering approach in a dynamic urban environment. International Journal of Applied Earth Observation and Geoinformation 2017, 54, 15–27. [Google Scholar] [CrossRef]
  8. Munyati, C. Wetland change detection on the kafue flats, zambia, by classification of a multitemporal remote sensing image dataset. International journal of remote sensing 2000, 21, 1787–1806. [Google Scholar] [CrossRef]
  9. Xian, G.; Homer, C.; Fry, J. Updating the 2001 national land cover database land cover classification to 2006 by using landsat imagery change detection methods. Remote Sensing of Environment 2009, 113, 1133–1147. [Google Scholar] [CrossRef]
  10. Gao, J.; Liu, Y. Determination of land degradation causes in tongyu county, northeast china via land cover change detection. International Journal of Applied Earth Observation and Geoinformation 2010, 12, 9–16. [Google Scholar] [CrossRef]
  11. Taubenböck, H.; Esch, T.; Felbier, A.; Wiesner, M.; Roth, A.; Dech, S. Monitoring urbanization in mega cities from space. Remote sensing of Environment 2012, 117, 162–176. [Google Scholar] [CrossRef]
  12. Zhang, T.; Huang, X. Monitoring of urban impervious surfaces using time series of high-resolution remote sensing images in rapidly urbanized areas: A case study of shenzhen. IEEE Journal of Selected Topics in Applied Earth Observations and Remote Sensing 2018, 11, 2692–2708. [Google Scholar] [CrossRef]
  13. Awad, M.M. An innovative intelligent system based on remote sensing and mathematical models for improving crop yield estimation. Information Processing in Agriculture 2019, 6, 316–325. [Google Scholar] [CrossRef]
  14. Lv, Z.; Liu, T.; Benediktsson, J.A.; Falco, N. Land cover change detection techniques: Very-high-resolution optical images: A review. IEEE Geoscience and Remote Sensing Magazine 2021, 10, 44–63. [Google Scholar] [CrossRef]
  15. Zhu, Z. Change detection using landsat time series: A review of frequencies, preprocessing, algorithms, and applications. ISPRS Journal of Photogrammetry and Remote Sensing 2017, 130, 370–384. [Google Scholar] [CrossRef]
  16. Hachicha, S.; Chaabane, F. On the sar change detection review and optimal decision. International Journal Of Remote Sensing 2014, 35, 1693–1714. [Google Scholar] [CrossRef]
  17. ZhiYong, L.; Liu, T.; Benediktsson, J.A.; Falco, N. Land cover change detection techniques: Very-high-resolution optical images: A review. IEEE Geoscience and Remote Sensing Magazine 2021, 2–21. [Google Scholar]
  18. Wen, D.; Huang, X.; Bovolo, F.; Li, J.; Ke, X.; Zhang, A.; Benediktsson, J.A. Change detection from very-high-spatial-resolution optical remote sensing images: Methods, applications, and future directions. IEEE Geoscience and Remote Sensing Magazine 2021. [Google Scholar] [CrossRef]
  19. Lv, Z.; Huang, H.; Li, X.; Zhao, M.; Benediktsson, J.A.; Sun, W.; Falco, N. Land cover change detection with heterogeneous remote sensing images: Review, progress, and perspective. Proceedings of the IEEE 2022. [Google Scholar] [CrossRef]
  20. Wen, D.; Huang, X.; Bovolo, F.; Li, J.; Ke, X.; Zhang, A.; Benediktsson, J.A. Change detection from very-high-spatial-resolution optical remote sensing images: Methods, applications, and future directions. IEEE Geoscience and Remote Sensing Magazine 2021, 9, 68–101. [Google Scholar] [CrossRef]
  21. Hong, S.; Vatsavai, R.R. Sliding window-based probabilistic change detection for remote-sensed images. Procedia Computer Science 2016, 80, 2348–2352. [Google Scholar] [CrossRef]
  22. Lu, P.; Qin, Y.; Li, Z.; Mondini, A.C.; Casagli, N. Landslide mapping from multi-sensor data through improved change detection-based markov random field. Remote Sensing of Environment 2019, 231, 111235. [Google Scholar] [CrossRef]
  23. Lv, Z.; Liu, T.; Shi, C.; Benediktsson, J.A. Local histogram-based analysis for detecting land cover change using vhr remote sensing images. IEEE Geoscience and Remote Sensing Letters 2020, 18, 1284–1287. [Google Scholar] [CrossRef]
  24. Chen, L.; Liu, C.; Chang, F.; Li, S.; Nie, Z. Adaptive multi-level feature fusion and attention-based network for arbitrary-oriented object detection in remote sensing imagery. Neurocomputing 2021, 451, 67–80. [Google Scholar] [CrossRef]
  25. Mou, L.; Bruzzone, L.; Zhu, X.X. Learning spectral-spatial-temporal features via a recurrent convolutional neural network for change detection in multispectral imagery. IEEE Transactions on Geoscience and Remote Sensing 2018, 57, 924–935. [Google Scholar] [CrossRef]
  26. Zhang, M.; Shi, W. A feature difference convolutional neural network-based change detection method. IEEE Transactions on Geoscience and Remote Sensing 2020, 58, 7232–7246. [Google Scholar] [CrossRef]
  27. Zheng, Z.; Wan, Y.; Zhang, Y.; Xiang, S.; Peng, D.; Zhang, B. Clnet: Cross-layer convolutional neural network for change detection in optical remote sensing imagery. ISPRS Journal of Photogrammetry and Remote Sensing 2021, 175, 247–267. [Google Scholar] [CrossRef]
  28. Daudt, R.C.; Le Saux, B.; Boulch, A. In Fully convolutional siamese networks for change detection, 2018 25th IEEE International Conference on Image Processing (ICIP), 2018; IEEE: pp 4063-4067.
  29. Chen, J.; Yuan, Z.; Peng, J.; Chen, L.; Huang, H.; Zhu, J.; Liu, Y.; Li, H. Dasnet: Dual attentive fully convolutional siamese networks for change detection in high-resolution satellite images. IEEE Journal of Selected Topics in Applied Earth Observations and Remote Sensing 2020, 14, 1194–1206. [Google Scholar] [CrossRef]
  30. Li, X.; He, M.; Li, H.; Shen, H. A combined loss-based multiscale fully convolutional network for high-resolution remote sensing image change detection. IEEE Geoscience and Remote Sensing Letters 2021, 19, 1–5. [Google Scholar] [CrossRef]
  31. Huang, R.; Zhou, M.; Zhao, Q.; Zou, Y. Change detection with absolute difference of multiscale deep features. Neurocomputing 2020, 418, 102–113. [Google Scholar] [CrossRef]
  32. Chen, P.; Li, C.; Zhang, B.; Chen, Z.; Yang, X.; Lu, K.; Zhuang, L. A region-based feature fusion network for vhr image change detection. Remote Sensing 2022, 14, 5577. [Google Scholar] [CrossRef]
  33. Asokan, A.; Anitha, J.; Patrut, B.; Danciulescu, D.; Hemanth, D.J. Deep feature extraction and feature fusion for bi-temporal satellite image classification. Computers, Materials and Continua 2021, 66, 373–388. [Google Scholar] [CrossRef]
  34. Zhang, Z.-D.; Tan, M.-L.; Lan, Z.-C.; Liu, H.-C.; Pei, L.; Yu, W.-X. Cdnet: A real-time and robust crosswalk detection network on jetson nano based on yolov5. Neural Computing and Applications 2022, 1–12. [Google Scholar] [CrossRef]
  35. Yang, B.; Qin, L.; Liu, J.; Liu, X. Utrnet: An unsupervised time-distance-guided convolutional recurrent network for change detection in irregularly collected images. IEEE Transactions on Geoscience and Remote Sensing 2022, 60, 1–16. [Google Scholar] [CrossRef]
  36. Fiorucci, F.; Giordan, D.; Santangelo, M.; Dutto, F.; Rossi, M.; Guzzetti, F. Criteria for the optimal selection of remote sensing optical images to map event landslides. Natural Hazards and Earth System Sciences 2018, 18, 405–417. [Google Scholar] [CrossRef]
  37. Huang, Z.; Zhang, Y.; Li, Q.; Zhang, T.; Sang, N.; Hong, H. Progressive dual-domain filter for enhancing and denoising optical remote-sensing images. IEEE Geoscience and Remote Sensing Letters 2018, 15, 759–763. [Google Scholar] [CrossRef]
  38. You, Y.; Cao, J.; Zhou, W. A survey of change detection methods based on remote sensing images for multi-source and multi-objective scenarios. Remote Sensing 2020, 12, 2460. [Google Scholar] [CrossRef]
  39. Yang, M.; Jiao, L.; Liu, F.; Hou, B.; Yang, S.; Jian, M. Dpfl-nets: Deep pyramid feature learning networks for multiscale change detection. IEEE Transactions on Neural Networks and Learning Systems 2021. [Google Scholar] [CrossRef]
  40. Wan, L.; Zhang, T.; You, H. Multi-sensor remote sensing image change detection based on sorted histograms. International journal of remote sensing 2018, 39, 3753–3775. [Google Scholar] [CrossRef]
  41. Lei, L.; Sun, Y.; Kuang, G. Adaptive local structure consistency-based heterogeneous remote sensing change detection. IEEE Geoscience and Remote Sensing Letters 2020. [Google Scholar] [CrossRef]
  42. Sun, Y.; Lei, L.; Guan, D.; Li, M.; Kuang, G. Sparse-constrained adaptive structure consistency-based unsupervised image regression for heterogeneous remote-sensing change detection. IEEE Transactions on Geoscience and Remote Sensing 2021. [Google Scholar] [CrossRef]
  43. Luppino, L.T.; Bianchi, F.M.; Moser, G.; Anfinsen, S.N. Unsupervised image regression for heterogeneous change detection. arXiv preprint arXiv:1909.05948 2019. arXiv:1909.05948 2019.
  44. Luppino, L.T.; Bianchi, F.M.; Moser, G.; Anfinsen, S.N. In Remote sensing image regression for heterogeneous change detection, 2018 IEEE 28th International Workshop on Machine Learning for Signal Processing (MLSP), 2018; IEEE: pp 1-6.
  45. Sun, Y.; Lei, L.; Guan, D.; Wu, J.; Kuang, G.; Liu, L. Image regression with structure cycle consistency for heterogeneous change detection. IEEE Transactions on Neural Networks and Learning Systems 2022. [Google Scholar] [CrossRef]
  46. Wu, J.; Li, B.; Qin, Y.; Ni, W.; Zhang, H.; Sun, Y. A multiscale graph convolutional network for change detection in homogeneous and heterogeneous remote sensing images. arXiv preprint arXiv:2102.08041 2021. arXiv:2102.08041 2021.
  47. Sun, Y.; Lei, L.; Li, X.; Tan, X.; Kuang, G. Patch similarity graph matrix-based unsupervised remote sensing change detection with homogeneous and heterogeneous sensors. IEEE Transactions on Geoscience and Remote Sensing 2021, 59, 4841–4861. [Google Scholar] [CrossRef]
  48. Sun, Y.; Lei, L.; Li, X.; Tan, X.; Kuang, G. Structure consistency-based graph for unsupervised change detection with homogeneous and heterogeneous remote sensing images. IEEE Transactions on Geoscience and Remote Sensing 2021, 1–21. [Google Scholar] [CrossRef]
  49. Sun, Y.; Lei, L.; Guan, D.; Kuang, G. Iterative robust graph for unsupervised change detection of heterogeneous remote sensing images. IEEE Transactions on Image Processing 2021, 30, 6277–6291. [Google Scholar] [CrossRef] [PubMed]
  50. Sun, Y.; Lei, L.; Tan, X.; Guan, D.; Wu, J.; Kuang, G. Structured graph based image regression for unsupervised multimodal change detection. ISPRS Journal of Photogrammetry and Remote Sensing 2022, 185, 16–31. [Google Scholar] [CrossRef]
  51. Liu, Z.; Li, G.; Mercier, G.; He, Y.; Pan, Q. Change detection in heterogenous remote sensing images via homogeneous pixel transformation. IEEE Transactions on Image Processing 2017, 27, 1822–1834. [Google Scholar] [CrossRef]
  52. Zhan, T.; Gong, M.; Jiang, X.; Li, S. Log-based transformation feature learning for change detection in heterogeneous images. IEEE Geoscience and Remote Sensing Letters 2018, 15, 1352–1356. [Google Scholar] [CrossRef]
  53. Wu, Y.; Li, J.; Yuan, Y.; Qin, A.; Miao, Q.-G.; Gong, M.-G. Commonality autoencoder: Learning common features for change detection from heterogeneous images. IEEE Transactions on Neural Networks and Learning Systems 2021. [Google Scholar] [CrossRef]
  54. Niu, X.; Gong, M.; Zhan, T.; Yang, Y. A conditional adversarial network for change detection in heterogeneous images. IEEE Geoscience and Remote Sensing Letters 2018, 16, 45–49. [Google Scholar] [CrossRef]
  55. Zou, Z.; Shi, Z. Random access memories: A new paradigm for target detection in high resolution aerial remote sensing images. IEEE Transactions on Image Processing 2017, 27, 1100–1111. [Google Scholar] [CrossRef] [PubMed]
  56. Li, Z.; You, Y.; Liu, F. In Multi-scale ships detection in high-resolution remote sensing image via saliency-based region convolutional neural network, IGARSS 2019-2019 IEEE International Geoscience and Remote Sensing Symposium, 2019; IEEE: pp 246-249.
  57. Li, X.; Wang, W.; Hu, X.; Yang, J. In Selective kernel networks, Proceedings of the IEEE/CVF conference on computer vision and pattern recognition, 2019; pp 510-519.
  58. Balki, I.; Amirabadi, A.; Levman, J.; Martel, A.L.; Emersic, Z.; Meden, B.; Garcia-Pedrero, A.; Ramirez, S.C.; Kong, D.; Moody, A.R. Sample-size determination methodologies for machine learning in medical imaging research: A systematic review. Canadian Association of Radiologists Journal 2019, 70, 344–353. [Google Scholar] [CrossRef] [PubMed]
  59. Sun, Y.; Lei, L.; Guan, D.; Li, M.; Kuang, G. Sparse-constrained adaptive structure consistency-based unsupervised image regression for heterogeneous remote-sensing change detection. IEEE Transactions on Geoscience and Remote Sensing 2021, 60, 1–14. [Google Scholar] [CrossRef]
  60. Zhang, C.; Yue, P.; Tapete, D.; Jiang, L.; Shangguan, B.; Huang, L.; Liu, G. A deeply supervised image fusion network for change detection in high resolution bi-temporal remote sensing images. ISPRS Journal of Photogrammetry and Remote Sensing 2020, 166, 183–200. [Google Scholar] [CrossRef]
  61. Zhang, Z.-D.; Tan, M.-L.; Lan, Z.-C.; Liu, H.-C.; Pei, L.; Yu, W.-X. Cdnet: A real-time and robust crosswalk detection network on jetson nano based on yolov5. Neural Computing and Applications 2022, 34, 10719–10730. [Google Scholar] [CrossRef]
1
https://github.com/yulisun/AGSCC
2
https://github.com/yulisun/GIR-MRF
3
https://github.com/yulisun/SCASC
Preprints 76135 g001
Figure 1. Flowchart of the proposed framework for Hete-CD.
Figure 1. Flowchart of the proposed framework for Hete-CD.
Preprints 76135 g001
Preprints 76135 g002
Figure 2. Dataset −1 to −4: (a) Pre-event image, (b) Post-even image, and (c) Ground reference map.
Figure 2. Dataset −1 to −4: (a) Pre-event image, (b) Post-even image, and (c) Ground reference map.
Preprints 76135 g002
Preprints 76135 g003
Figure 3. Comparison of change detection visual performance of some state-of-the-art methods: (a) AGSCC [45], (b) GIR-MRF [50], (c) SCASC [59], (d) Proposed (CC: accurately changed, UC: unchanged, FD: false detection, and MD: missed detection).
Figure 3. Comparison of change detection visual performance of some state-of-the-art methods: (a) AGSCC [45], (b) GIR-MRF [50], (c) SCASC [59], (d) Proposed (CC: accurately changed, UC: unchanged, FD: false detection, and MD: missed detection).
Preprints 76135 g003
Preprints 76135 g004
Figure 4. Detection maps acquired by different deep learning approaches for #1-Dataset: (a) FC-Siam-diff [28], (b) CDNet [61], (c) FDCNN [26], (d) DSIFN [60], (e) CLNet [27], (f) MFCN [30], (g) Proposed-, and (h) Proposed (CC: correctly changed, UC: unchanged, FD: false detection, and MD: missed detection).
Figure 4. Detection maps acquired by different deep learning approaches for #1-Dataset: (a) FC-Siam-diff [28], (b) CDNet [61], (c) FDCNN [26], (d) DSIFN [60], (e) CLNet [27], (f) MFCN [30], (g) Proposed-, and (h) Proposed (CC: correctly changed, UC: unchanged, FD: false detection, and MD: missed detection).
Preprints 76135 g004
Preprints 76135 g005
Figure 5. Detection maps acquired by different deep learning approaches for #2-Dataset: (a) FC-Siam-diff [28], (b) CDNet [61], (c) FDCNN [26], (d) DSIFN [60], (e) CLNet [27], (f) MFCN [30], (g) proposed-, and (h) proposed (CC: correctly changed, UC: unchanged, FD: false detection, and MD: missed detection).
Figure 5. Detection maps acquired by different deep learning approaches for #2-Dataset: (a) FC-Siam-diff [28], (b) CDNet [61], (c) FDCNN [26], (d) DSIFN [60], (e) CLNet [27], (f) MFCN [30], (g) proposed-, and (h) proposed (CC: correctly changed, UC: unchanged, FD: false detection, and MD: missed detection).
Preprints 76135 g005
Preprints 76135 g006
Figure 6. Detection maps acquired by different deep learning approaches for #3-Dataset: (a) FC-Siam-diff [28], (b) CDNet [61], (c) FDCNN [26], (d) DSIFN [60], (e) CLNet [27], (f) MFCN [30], (g) proposed-, and (h) proposed (CC: correctly changed, UC: unchanged, FD: false detection, and MD: missed detection).
Figure 6. Detection maps acquired by different deep learning approaches for #3-Dataset: (a) FC-Siam-diff [28], (b) CDNet [61], (c) FDCNN [26], (d) DSIFN [60], (e) CLNet [27], (f) MFCN [30], (g) proposed-, and (h) proposed (CC: correctly changed, UC: unchanged, FD: false detection, and MD: missed detection).
Preprints 76135 g006
Preprints 76135 g007
Figure 7. Detection maps acquired by different deep learning approaches for #4-Dataset: (a) FC-Siam-diff[28], (b) CDNet [61], (c) FDCNN [26], (d) DSIFN [60], (e) CLNet [27], (f) MFCN [30], (g) proposed-, and (h) proposed (CC: correctly changed, UC: unchanged, FD: false detection, and MD: missed detection).
Figure 7. Detection maps acquired by different deep learning approaches for #4-Dataset: (a) FC-Siam-diff[28], (b) CDNet [61], (c) FDCNN [26], (d) DSIFN [60], (e) CLNet [27], (f) MFCN [30], (g) proposed-, and (h) proposed (CC: correctly changed, UC: unchanged, FD: false detection, and MD: missed detection).
Preprints 76135 g007
Preprints 76135 g008
Figure 8. Relationship between the initial sample and the final sample at the end of the iteration for the proposed framework: (a) Dataset-1, (b) Dataset-2, (c) Dataset-3, and (d) Dataset-4.
Figure 8. Relationship between the initial sample and the final sample at the end of the iteration for the proposed framework: (a) Dataset-1, (b) Dataset-2, (c) Dataset-3, and (d) Dataset-4.
Preprints 76135 g008
Preprints 76135 g009
Figure 9. Relationship between the initial samples and the detection accuracies for the proposed framework.
Figure 9. Relationship between the initial samples and the detection accuracies for the proposed framework.
Preprints 76135 g009
Table 2. Quantitative comparison between three traditional methods and our proposed framework for Hete-CD with four actual datasets.
Table 2. Quantitative comparison between three traditional methods and our proposed framework for Hete-CD with four actual datasets.
Dataset Methods OA Kappa AA FA MA TE Precision Recall F-score
Dataset-1 AGSCC[45] 95.66 0.66 84.08 2.575 29.26 4.341 66.07 70.74 68.33
GIR-MRF[50] 95.43 0.6746 88.34 3.492 19.83 4.573 61.95 80.17 69.89
SCASC[59] 94.38 0.595 83.41 3.951 29.23 5.624 55.94 70.77 62.49
Proposed 99.04 0.9201 94.9 0.33 9.861 0.964 95.04 90.14 92.52
Dataset-2 AGSCC[45] 98.24 0.7732 83.03 0.2824 32.06 1.76 92.14 67.94 78.21
GIR-MRF[50] 98.18 0.81 92.58 1.25 13.60 1.82 77.18 86.40 81.53
SCASC[59] 97.9 0.741 83.84 0.6554 31.67 2.097 83.56 68.33 75.18
Proposed 98.75 0.9097 95.6 0.4129 9.392 0.762 91.13 91.61 91.37
Dataset-3 AGSCC[45] 95.33 0.7904 90.73 3.165 15.37 4.669 78.98 84.63 81.71
GIR-MRF[50] 93.6 0.7386 91.84 5.824 10.5 6.4 68.35 89.5 77.51
SCASC[59] 94.75 0.7704 90.77 3.952 14.5 5.252 75.25 85.5 80.05
proposed 96.77 0.9466 96.87 0.4602 5.805 1.049 96.36 94.2 95.27
Dataset-4 AGSCC[45] 95.81 0.8652 91.38 0.7504 16.5 2.297 92.6 83.5 87.81
GIR-MRF[50] 95.8 0.888 95.16 1.377 8.305 2.037 88.29 91.7 89.96
SCASC[59] 95.27 0.9058 95.09 0.8823 8.931 1.633 91.96 91.07 91.51
Proposed 97.92 0.9607 97.75 0.3272 4.168 0.713 97.11 95.83 96.47
Table 3. Quantitative comparison among different methods for Dataset-1.
Table 3. Quantitative comparison among different methods for Dataset-1.
Methods OA Kappa AA FA MA TE Precision Recall F-score
FC-Siam-diff[28] 97.05 0.7603 87.79 1.53 22.90 2.95 78.12 77.10 77.61
CDNet [61] 97.37 0.7687 85.29 0.78 28.64 2.63 86.61 71.36 78.25
FDCNN [26] 95.36 0.6658 87.42 3.43 21.73 4.64 61.78 78.27 69.05
DSIFN[60] 97.30 0.7807 88.91 1.42 20.76 2.70 79.80 79.24 79.52
CLNet[27] 97.11 0.7553 86.02 1.19 26.76 2.89 81.31 73.24 77.06
MFCN[30] 97.41 0.7921 89.97 1.46 18.59 2.59 79.81 81.41 80.60
Proposed- 97.83 0.808 87.00 0.52 25.48 2.17 91.02 74.52 81.95
Proposed 99.04 0.9201 94.9 0.33 9.861 0.964 95.04 90.14 92.52
Table 4. Quantitative comparison among different methods for Dataset-2.
Table 4. Quantitative comparison among different methods for Dataset-2.
Methods OA Kappa AA FA MA TE Precision Recall F-score
FC-Siam-diff[28] 97.05 0.6378 75.80 0.37 48.03 2.47 86.68 51.97 64.98
CDNet [61] 97.32 0.845 93.16 0.77 12.91 1.26 83.32 87.09 85.16
FDCNN [26] 94.58 0.6308 93.07 3.99 9.87 4.20 51.02 90.13 65.16
DSIFN[60] 97.51 0.7893 83.90 0.11 32.10 1.37 96.23 67.90 79.62
CLNet[27] 97.95 0.8195 87.59 0.33 24.49 1.36 91.29 75.51 82.66
MFCN[30] 97.65 0.7909 91.99 1.28 14.73 1.87 75.48 85.27 80.08
Proposed- 98.12 0.807 84.76 0.06 30.42 1.40 98.10 69.58 81.41
Proposed 98.75 0.9097 95.6 0.4129 9.392 0.762 91.13 91.61 91.37
Table 5. Quantitative comparison among different methods for Dataset-3.
Table 5. Quantitative comparison among different methods for Dataset-3.
Methods OA Kappa AA FA MA TE Precision Recall F-score
FC-Siam-diff[28] 92.25 0.7657 95.85 6.15 2.16 5.57 67.31 97.84 79.76
CDNet [61] 93.62 0.8618 92.28 1.20 14.23 2.51 89.59 85.77 87.64
FDCNN [26] 94.64 0.9081 98.28 2.05 1.39 1.91 86.10 98.61 91.93
DSIFN[60] 93.46 0.8926 98.48 2.63 0.40 2.27 83.11 99.60 90.61
CLNet[27] 89.74 0.6618 84.04 4.10 27.83 6.37 67.76 72.17 69.90
MFCN[30] 95.87 0.8962 92.36 0.31 14.97 1.95 97.26 85.03 90.73
Proposed- 95.88 0.9033 95.45 1.21 7.89 1.93 90.80 92.11 91.45
Proposed 96.77 0.9466 96.87 0.4602 5.805 1.049 96.36 94.2 95.27
Table 6. Quantitative comparison among different methods for Dataset-4.
Table 6. Quantitative comparison among different methods for Dataset-4.
Methods OA Kappa AA FA MA TE Precision Recall F-score
FC-Siam-diff[28] 86.67 0.5282 86.74 11.84 14.68 11.97 45.30 85.32 59.18
CDNet [61] 96.21 0.9126 93.27 0.18 13.29 1.39 98.06 86.71 92.03
FDCNN [26] 94.88 0.8541 95.00 2.25 7.76 2.74 82.28 92.24 86.97
DSIFN[60] 96.82 0.9476 97.24 0.48 5.03 0.91 95.59 94.97 95.28
CLNet[27] 92.38 0.542 70.03 0.11 59.83 6.07 97.57 40.17 56.91
MFCN[30] 97.5 0.9372 96.55 0.56 6.34 1.14 95.09 93.66 94.37
Proposed- 97.75 0.9508 96.87 0.32 5.95 0.88 97.17 94.05 95.58
Proposed 97.92 0.9607 97.75 0.33 4.168 0.713 97.11 95.83 96.47
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.
Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.
Prerpints.org logo

Preprints.org is a free preprint server supported by MDPI in Basel, Switzerland.

facebook logotwitter logolinkedin logo
MDPI Initiatives
Important Links
Subscribe

Disclaimer

Terms of Use

Privacy Policy

© 2024 MDPI (Basel, Switzerland) unless otherwise stated