Ramsey Theory and Transformations of Coordinate Systems

Preprint

Article

Ramsey Theory and Transformations of Coordinate Systems

Altmetrics

Downloads

135

Views

Comments

This version is not peer-reviewed

Submitted:

08 June 2023

Posted:

09 June 2023

You are already at the latest version

Alerts

Abstract

Application of the Ramsey Theory to the set of the points placed in the plane is discussed. Consider a set of N points located in the same plane. The straight lines connecting these points are yikx=αikx+βik i,k=1...N. Listed below values of slopes αik are possible: αik>0; αik=0; αik is not defined; αik<0. Following coloring procedure is introduced: we connect the pairs of points for which αik>0, αik=0 or αik is not defined, with the red links, and the pairs of points for which αik<0 place with green links. The suggested coloring procedure enables building of the complete bi-colored graph for any set containing N points located in the same plane. We apply the Ramsey theorem to the complete graph emerging from the suggested coloring. For the set containing N=6 points at least one monochromatic triangle will necessarily appear in the graph. The values of the slopes αik depend on the chosen coordinate system. The rotation of coordinate axes changes the coloring of the graph; however, at least one monochromatic triangle will be present for N=6. The introduced coloring procedure diminishes the order of the symmetry group of the regular hexagon, irrespectively to the orientation of the coordinate axes. We hypothesized that this will be true for arbitrary regular n-polygon, independently on the orientation of coordinate axes. The inverse bi-color Ramsey graphs arise, when we replace red links appearing in the source graph with red ones, and vice versa. The total number of triangles in the “direct” and “inverse” Ramsey graphs is the same. We considered the particular case of the set of points for which αik>0 or αik<0 is true in the given coordinates. In this particular case, the rotation of the Cartesian coordinate axes to the angle θ=π2 yields the inverse complete graph. Generalization of this coloring for an arbitrary number and arbitrary location of the source points is introduced.

Keywords:

Subject: Computer Science and Mathematics - Discrete Mathematics and Combinatorics

MSC: 05D10; 05C15; 37C83

1. Introduction

The mathematical investigation of combinatorial structures in which a certain degree of order necessarily occurs as the size of the object becomes sufficiently large is labeled in the scientific society as the Ramsey Theory. Ramsey Theory is named after Frank Plumpton Ramsey, who carried out his outstanding research in this area before his untimely death at age 26 in 1930. The theory, introduced by Ramsey, was subsequently developed extensively by Erdős, Gyarfas and Graham [1,2,3,4,5,6,7,8,9]. The typical problem addressed by the Ramsey theory is the party problem, which defines the minimum number of guests

R (m, n)

that must be invited so that at least m of the guests will be familiar, or at least n of them will not know each other [5]. In this case

R (m, n)

is defined a Ramsey number [5]. A typical result in Ramsey theory states that if some mathematical structure is separated into finitely many parts, then one of the parts necessarily must contain a substructure of the predefined type. Consider the following example, it is given that if n is large enough and

℧

is an n-dimensional vector space over the field of integers (mod p), then however

℧

is separated into r sub-spaces, one of the sub-spaces contains an affine subspace of dimension d. When Ramsey theory is re-shaped in the notions of the graph theory, it states that any structure will necessarily contain an interconnected substructure [1,2,3,4,5,6,7,8,9]. The Ramsey theorem, in its graph-theoretic forms, states that one will find monochromatic cliques in any edge color labelling of a sufficiently large complete graph [5,7,8,9]. One more example of the Ramsey-like thinking is exemplified by the van der Waerden’s theorem: colorings of the integers by finitely many colors must have long monochromatic arithmetic progressions [5,7,8,9]. An accessible introduction to the Ramsey theory is found in refs. 6-7. More rigorous approach is presented out in refs. 8-9. Problems in Ramsey theory typically ask a question of the form: "how big must some structure be to guarantee that a particular property holds?" Generalizations of the classical Ramsey Theory are discussed recently in ref. 10; in particular, bipartite Ramsey numbers, k-Ramsey numbers, s-bipartite Ramsey numbers, Ramsey sequences of graphs, and ascending Ramsey indices are considered [10].

We shall adopt the graph-theoretic and Ramsey-theoretic notation and terminology introduced by Roberts [11,12]. Assume that

R (p_{1}, p_{2}, p_{3} \dots p_{t}; ζ)

is the smallest integer N with the property that whenever S is a set of N elements and we divide the r-element subsets of S into t sets,

X_{1}, X_{2} \dots X_{t}

, then for some i, there exists a

p_{i}

-element subset of S all of whose

ζ

-element subsets are in

X_{i}

R (p, q)

R (p, q; 2)

. Eventually if

G_{1}, G_{2} \dots G_{t}

are graphs,

R (G_{1}, G_{2} \dots G_{t})

is the smallest integer N with the property that every coloring of the edges of the complete graph

K_{N}

, in the t colors

(1,2 \dots t)

yields for some i, to a subgraph that is isomorphic to

G_{i}

and is colored all in color i, that is, to a monochromatic graph

G_{i}

[11,12]. We apply the Ramsey theory to the set of points located in the same plane, when coloring is defined by the sign of the slope of straight lines connecting the points and, thus, forming the complete graph. Present work is generalizing the approach introduced in ref. 13, in which the coloring procedure was suggested for the points arranged on a closed contour and connected as a complete graph. The procedure exploited the sign of the slope of the straight line connecting the points placed on the Jordan curve, for coloring. Now we extend the suggested approach for an arbitrary set of points located in the same plane.

2. Results

2.1. Ramsey theory and geometry of closed curves

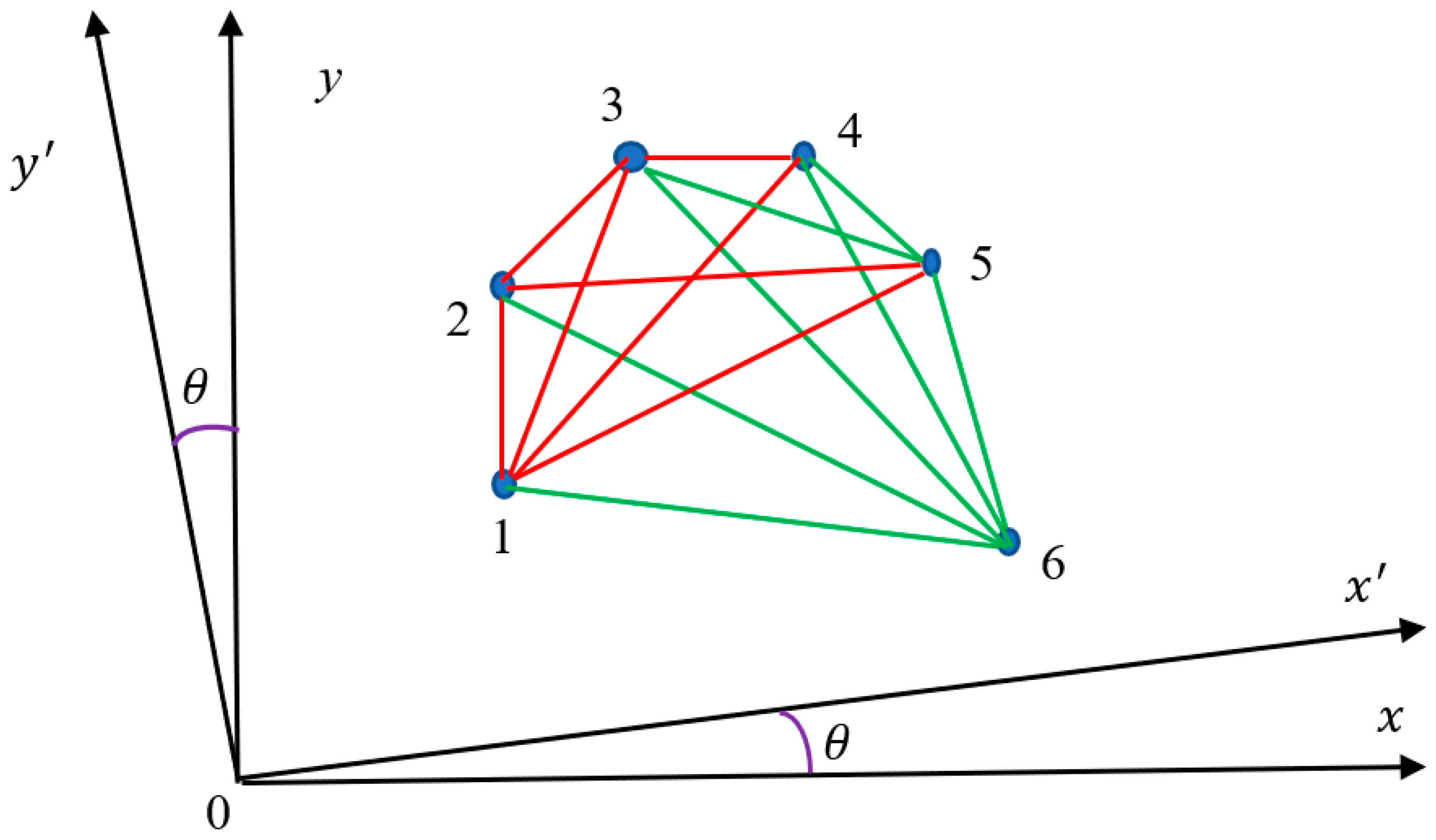
Consider the set of six points placed on the plane

X 0 Y

, as shown in Figure 1. The points are numbered:

(x_{i}, y_{i}); i = 1 \dots 6

depicted in Figure 1 with blue circles.

Now connect the points

i = 1 \dots 6

in pairs. The connection yields a complete graph. Every pare generates straight lines, given in Cartesian coordinate axes by Eq. 1:

y_{i k} (x) = α_{i k} x + β_{i k} (i, k = 1 . . . 6),

(1)

where

y_{i k} (x)

is the equation of the straight line connecting points numbered i and k respectively;

α_{i k}

is the slope of the straight line and

β_{i k}

is its y-intercept. Obviously, Eq. 2 holds:

α_{i k} = t g φ_{i k},

(2)

where

φ_{i k}

is the angle made by the edge connecting the points

(x_{i}, y_{i}); (x_{k}, y_{k})

with the x-axis. Slopes

α_{i k}

depend on the orientation of coordinated axes, namely:

α_{i k} = α_{i k} (θ)

, defined by angle

θ

, as depicted in Figure 1.

Following values of slopes

α_{i k}

are possible:

i.: $α_{i k} > 0$ ; this is true for pairs $(1,3); (2,3); (1,5); (2,5), a s$ shown in Figure 1.
ii.: $α_{i k} = 0$ ; this takes place for the pair $(3.4)$ (see Figure 1).
iii.: $α_{i k}$ is not defined; this occurs for the pair $(1,2)$ (see Figure 1).
iv.: $α_{i k} < 0$ ; this is true for pairs $(3,5); (4,5); (1,6); (3,6); (5,6), a s$ shown in Figure 1.

The aforementioned possibilities exhaust all of the possible mutual locations of the points placed in the plane. Now consider the following coloring procedure: lets us connect the pairs of points for which

α_{i k} > 0

α_{i k} = 0

α_{i k}

is not defined with the red links, and the pairs of points for which

α_{i k} < 0

place with green links, as illustrated with Figure 1. It should be emphasized, that the introduced coloring procedure is non-transitive [14]. The suggested coloring procedure yields the complete bi-color graph, shown in Figure 1. The introduced coloring procedure enables building of the complete bi-colored graph for any set containing six points located in the same plane. It should be emphasized that the values of the slopes

α_{i k}

(and consequently coloring of the graph) depend on the chosen coordinate system

X 0 Y

. Now we can apply the Ramsey theorem to the graph, shown in Figure 1. According to the seminal Ramsey theorem, at least one monochromic triangle should necessarily appear within the aforementioned graph; due to the fact that the Ramsey number is

R (3,3) = 6

. Indeed, the triangle “125” is built of red edges and the triangle “456” contains only green edges (see Figure 1). And this result will be true for any set of six points located in the plane. It should be mentioned that coloring of polygons will depended on the angle

θ

(see Figure 1). This dependence will be addressed below.

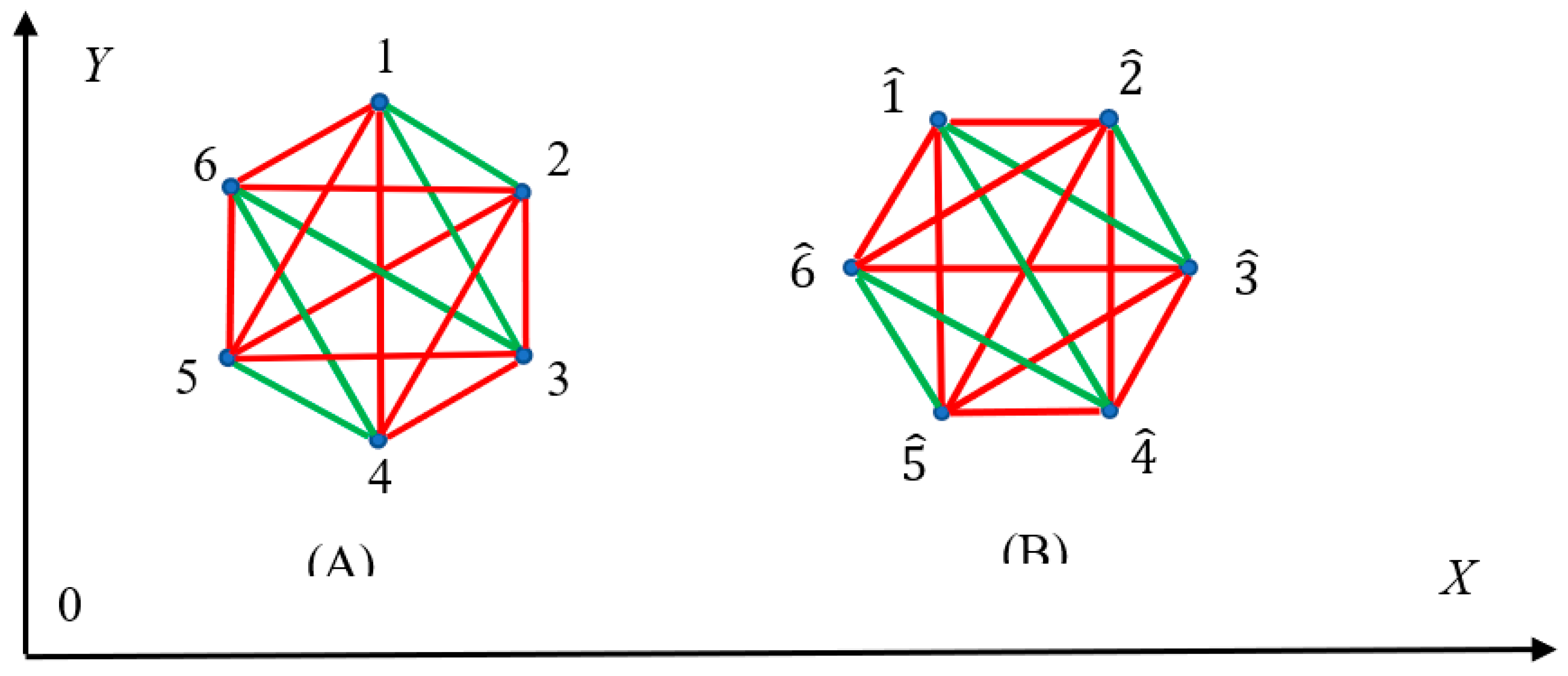
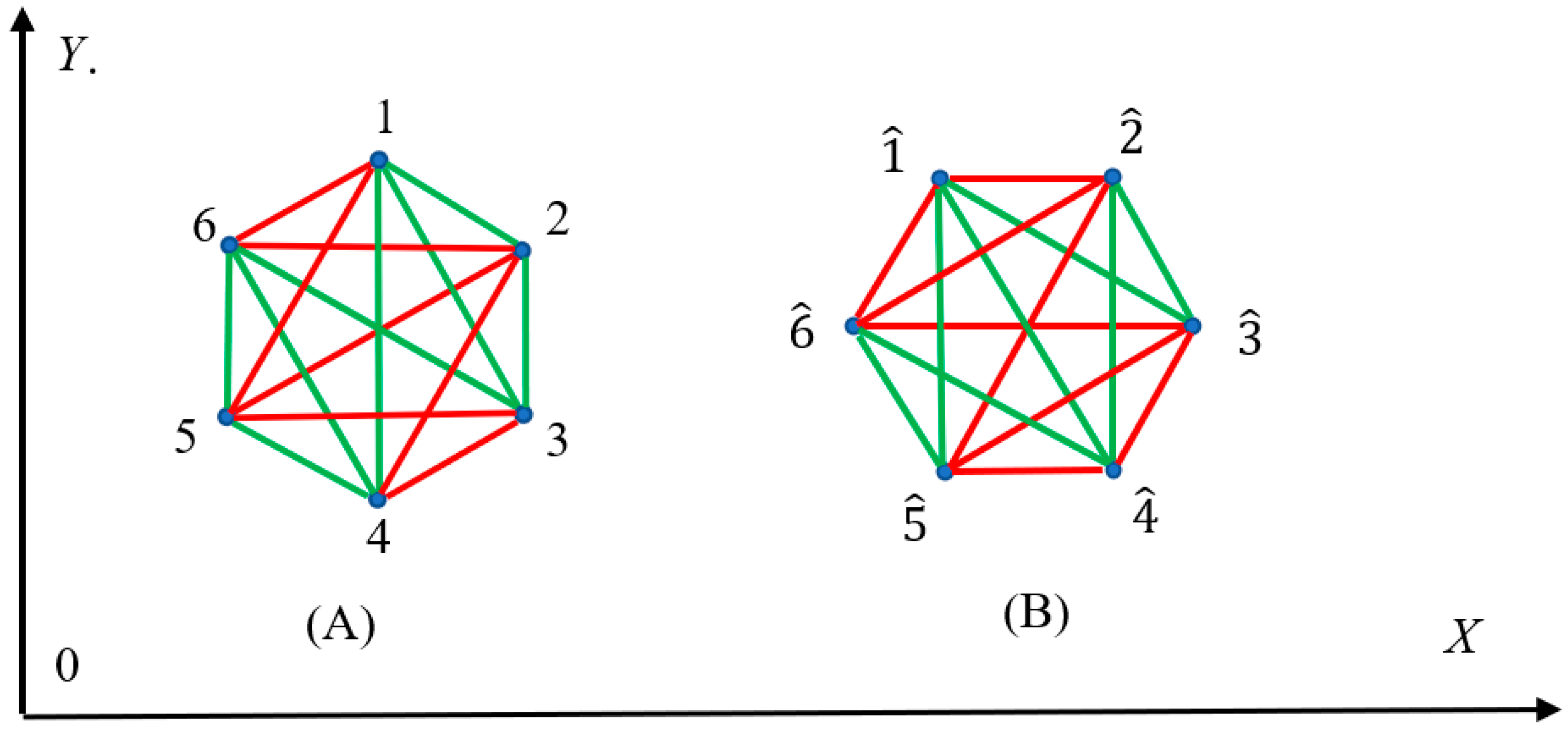
Let us exemplify the suggested procedure with bi-coloring of regular hexagons shown in Figure 2, demonstrating coloring of hexagon (123456) and coloring of the same hexagon rotated counterclockwise to

\frac{π}{3}

and denoted

(\hat{1} \hat{2} \hat{3} \hat{4} \hat{5} \hat{6})

. Monochromatic red triangles (156), (234), (235) and 234 are recognized in inset (A); in turn, monochromatic red triangles

(\hat{1} \hat{2} \hat{5})

(\hat{1} \hat{2} \hat{6})

(\hat{2} \hat{4} \hat{5})

(\hat{3} \hat{4} \hat{5})

appear in inset (B).

It is recognized from Figure 2, that rotation of the pristine hexagon changes its coloring, carried out within the suggested procedure, and this result is quite expectable. Indeed, rotation of the hexagon changes the slopes of its edges. More interesting result is related to the symmetry of the hexagon: the symmetry group of a regular monocromatoc hexagon is a group of order 12, this group is usually labeled as the dihedral group

D_{6}

. The suggested bi-coloring procedure illustrated inset (A) of Figure 2, diminishes the order of the group. The bicolored hexagon is characterized by centrosymmetric point group, which contains an inversion center as one of its symmetry elements; thus the order of the group is reduced to two, containing the inversion and a trivial

2 π

rotation. It is noteworthy that rotation of the colored hexagon depicted in inset (B) of Figure 2 changes the coloring of the hexagon under keeping the symmetry group untouched. Indeed the symmetry of the rotated bi-colored hexagon also characterized by two distinguishable elements, namely: the inversion and trivial

2 π

rotation.

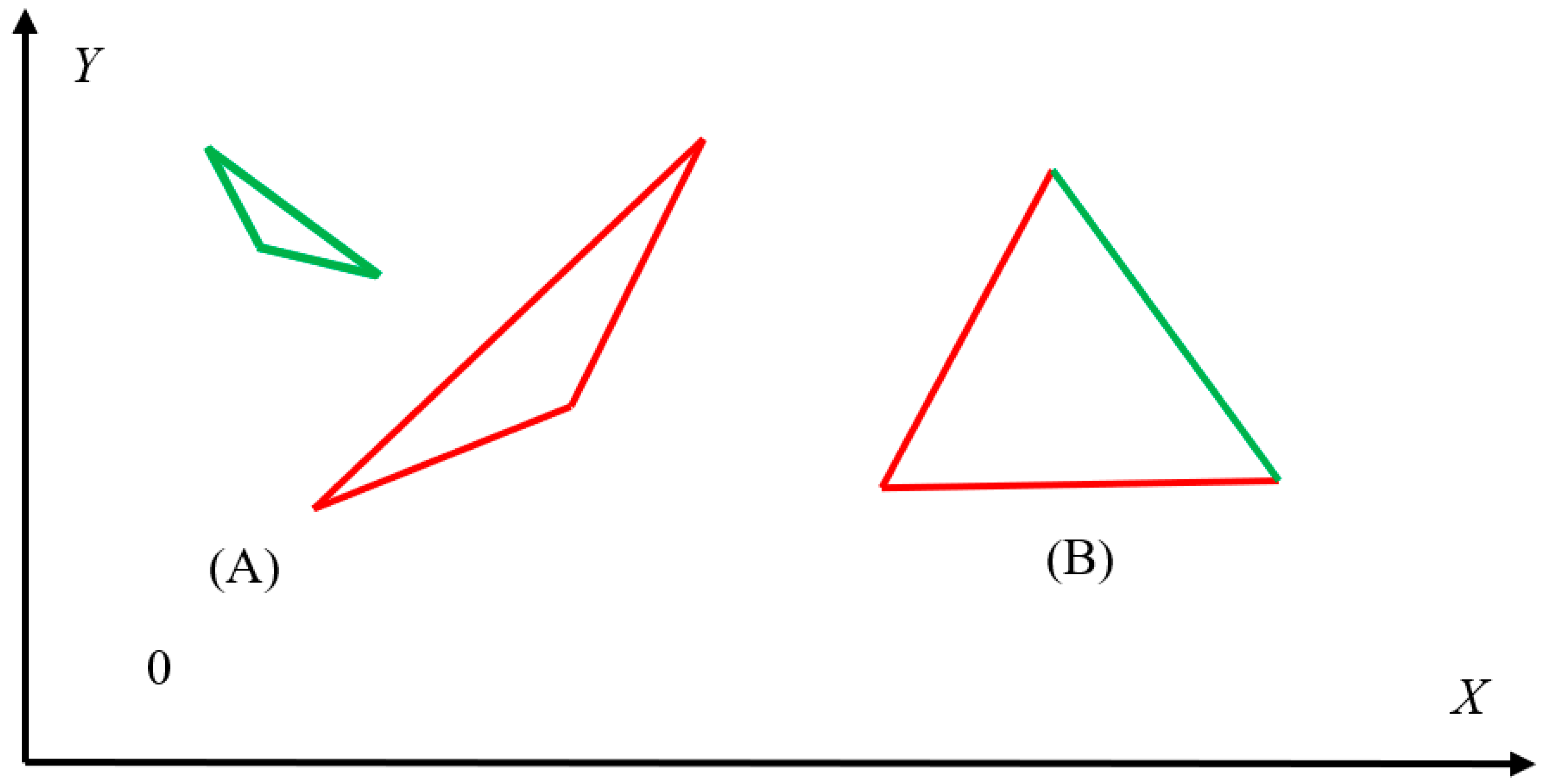
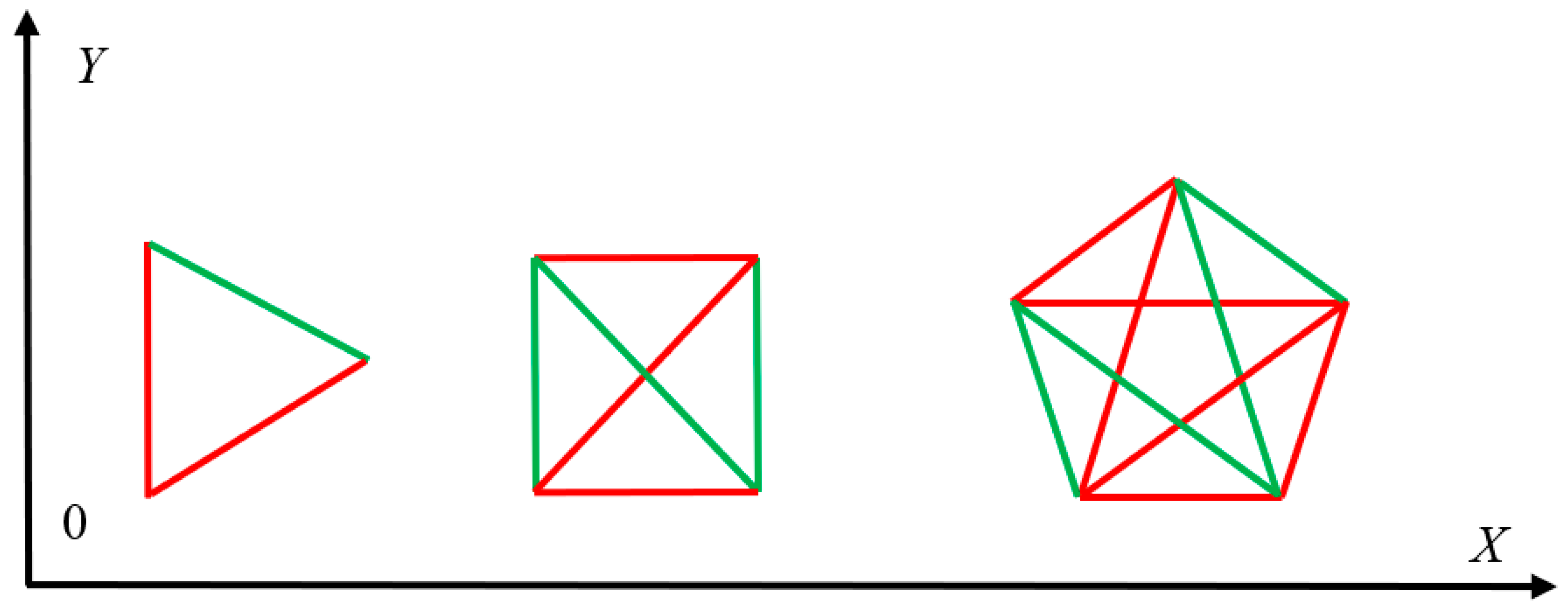
Now we address the minimal complete graphs, arising from triangles, emerging from the suggested coloring procedure and shown in Figure 3.

Obviously monochromatic (red or green) triangles are possible, as shown in inset A of Figure 3, when the aforementioned coloring procedure is adopted. However, equilateral monochromatic triangle is impossible for any value of the rotation angle

θ

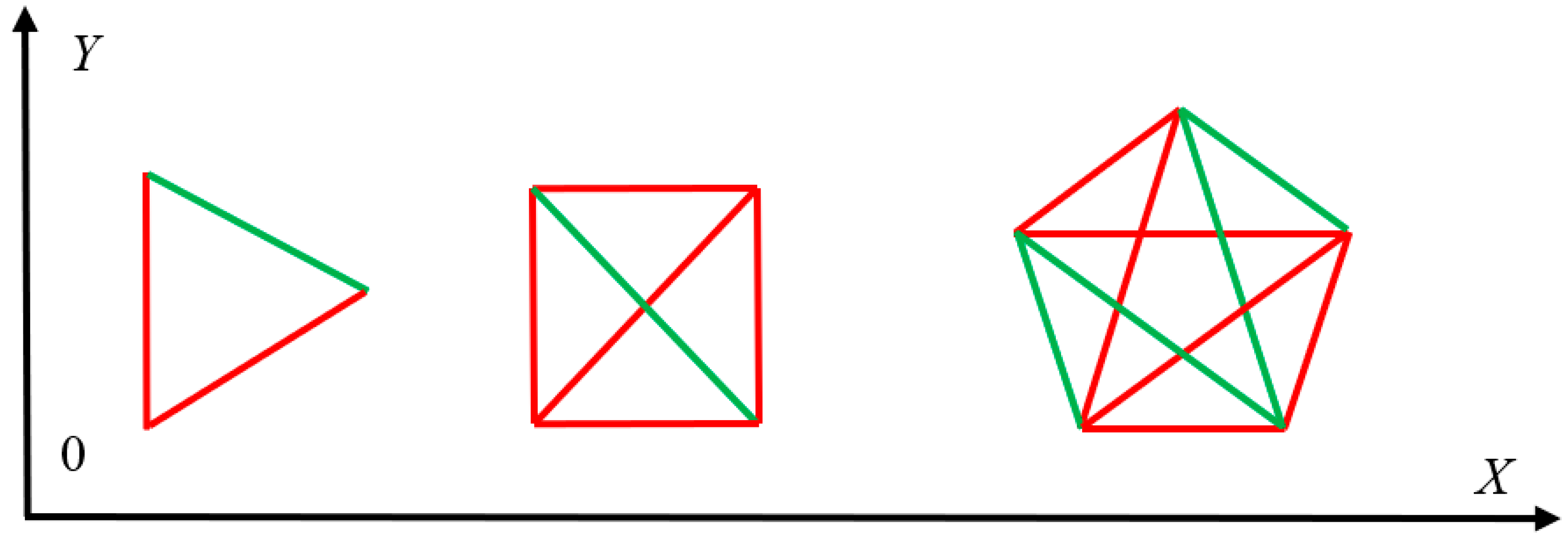
Moreover, monochromatic complete graphs, arising from arbitrary monochromatic regular polygons are impossible as illustrated with Figure 4.

We hypothesize that this result will be true for arbitrary regular n-polygon, independently on the orientation of coordinate axes. This statement should be rigorously proven in our future investigations.

2.2. Ramsey structures and rotations of coordinates

We start from the set of points

(x_{i}, y_{i}), i = 1 \dots 6

located in the plane

X 0 Z

shown in Figure 1. Now we consider rotation of the coordinates about z-axis through an a angle

θ

, as illustrated in Figure 1. The equations of straight lines passing through the vertices of the graph in the new rotated system (primed) now appear as follows:

y_{i k}^{'} (x) = α_{i k}^{'} (θ) x + β_{i k}^{'} (θ),

(3)

α_{i k}^{'} = t g (φ_{i k} - θ)

(4)

The suggestion rotation will change the coloring of the pristine (source) complete graph (we keep the coloring procedure introduced in Section 2.1 untouched). However

R (3,3)

holds; thus, at least one monochromatic triangle will be found in the complete graph, whatever is the rotation angle

θ .

Thus, the following theorem is proven:

Theorem: Consider set of six points

(x_{i}, y_{i})

located on the plane. Connect the lines with straight lines

y_{i k} (x) = α_{i k} x + β_{i k} (i, k = 1 . . . 6) .

Following bi-coloring procedure is introduced: we connect the pairs of points for which

α_{i k} > 0

α_{i k} = 0

α_{i k}

is not defined, with the red links, and the pairs of points for which

α_{i k} < 0

place with green links. The introduced coloring procedure yields the complete bi-color graph including at least one monochromatic triangle, whatever are the Cartesian coordinate axes. Thus, the Ramsey theory supplies a kind of invariant appearing in all of possible Cartesian coordinate axes. The Ramsey generalization of the suggested approach to a set of N arbitrary points belonging to the same plane is straightforward.

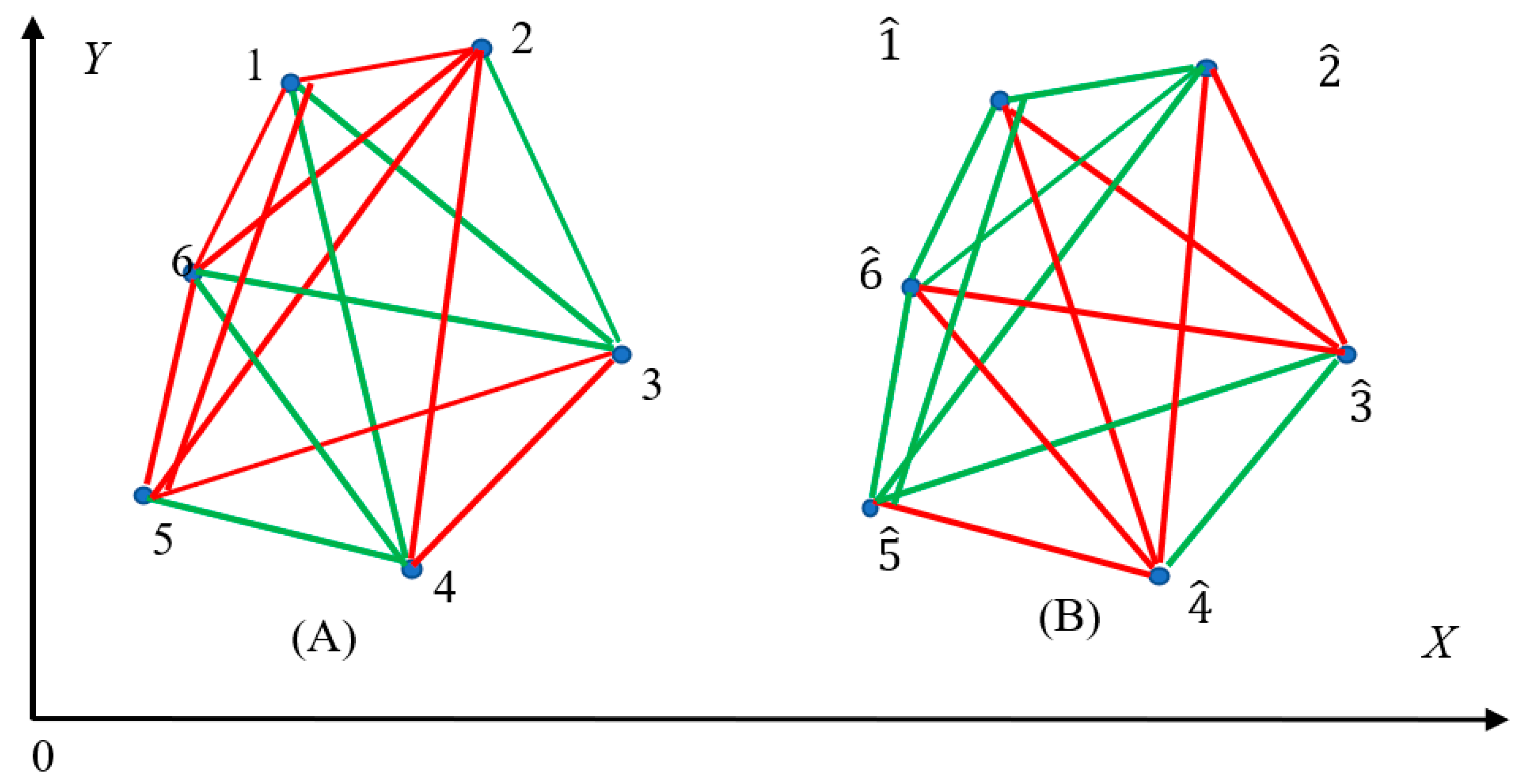
2.3. Direct and inverse Ramsey graphs

Consider set of six arbitrary distinguishable points

(x_{i}, y_{i}); i = 1 \dots 6

located in the plane

X 0 Z,

depicted in Figure 5. Let us connect these points with straight lines and color them, as suggested in Section 2.1. Thus, the source complete graph, shown in inset (A) of Figure 5 is formed. Let us introduce the notion of the inverse bi-color Ramsey graphs, generated by the source graph; namely we replace red links appearing in the source graph with red ones, and vice versa, as shown in inset (B) of Figure 5. The vertices of this complete graph are denoted

(\hat{1}, \dots \hat{6})

in inset (B) of Figure 5. We call such a Ramsey network the “inverse graph”. Obviously, introducing an inverse Ramsey network is possible for any complete source graph. According to the Ramsey theorem both the source and inverse graphs, arising from six vertices, contain at least one monochromatic triangle. Indeed, we recognize red monochromatic triangles

(126)

and

(256)

in inset (A), and, correspondingly green triangles

(\hat{1} \hat{2} \hat{6})

and

(\hat{2} \hat{5} \hat{6})

in inset (b) of Figure 5.

It is noteworthy, that the total number of triangles in the “direct” (source) and “inverse” Ramsey graphs is the same, thus, yielding the conservation law:

ζ = t_{r} + t_{g} = {\hat{t}}_{r} + {\hat{t}}_{g},

(5)

where

t_{r} and t_{g}

are the numbers of red and green triangles in the source graph;

{\hat{t}}_{r} and {\hat{t}}_{g}

are correspondingly the numbers of red and green triangles in the inverse graph. Eq. 5 represents the “conservation law” for the Ramsey complete networks built of six elements. It is noteworthy that direct and inverse graphs form the Abelian (commutative group), when the inversion of the color of the link is taken as an operation.

Generally speaking, rotation of the coordinate axes will change the total number of monochromatic triangles

ζ

in the graph. It should be noted, that Eq. 5 holds for any fixed rotation angle

θ

and arbitrary number of the source points. There exists the particular case of rotation, yielding the inverse graphs, introduced in Section 2.2. This case will be discussed below.

2.4. Rotation of coordinate axes generates inverse complete graphs

Now consider the set of points for which

α_{i k} > 0

α_{i k} < 0

in given coordinates is true, in other words we restrict ourselves with the sets of points for which

φ_{i k} \neq 0; φ_{i k} \neq \frac{π}{2}

takes place. Let us connect the pairs of points for which

α_{i k} > 0

with the red links, and the pairs of points for which

α_{i k} < 0

takes place with the green links. Now consider rotation of coordinate axes to the angle

θ = \frac{π}{2}

. In this particular case, Eq. 6 takes place:

α_{i k}^{'} = - \frac{1}{α_{i k}}

(6)

Hence, the inverse complete graph emerge, and Eqs. 7 occur:

t_{r} = {\hat{t}}_{g}; t_{g} = {\hat{t}}_{r}

(7)

In particular for the complete graph, built of six points, this implies that at least one monochromatic triangle will necessary appear in the “source” and “inverse” complete graphs, colored according to the aforementioned procedure. Again, the generalization of suggested Ramsey approach to complete graphs containing N vertices is straightforward.

Now consider following generalization/symmetrization of the aforementioned coloring procedure. We introduce now the following coloring ,applicable for any set of points belonging to the same plane: lets us connect the pairs of points for which

α_{i k} > 0

or α_{i k} = 0

is not defined with the red links, and the pairs of points for which

α_{i k} < 0

and

α_{i k}

is not defined place with green links, as illustrated for regular polygons with Figure 6.

It is noteworhy that only quandrangle changed its coloring when compared to that depicted in Figure 4. And again no monocromatic regular polygon is recognized. This kind of coloring is of a particular interest due the fact that the rotation of coordinate axes to the angle

θ = \frac{π}{2}

gives rise to the inverse graph for the arbitrary set of points. Let us illustrate the suggested coloring with the complete bi-color graphs, arising from the sets of points forming regular hexagons, shown in Figure 7.

And again, the bicolored hexagons shown in Figure 7 are characterized by centrosymmetric point group, thus the order of the group is two, containing the inversion and a trivial

2 π

rotation. Rotation of the colored hexagon to

\frac{π}{3}

depicted in inset (B) of Figure 7 changes the coloring of the hexagon under keeping the symmetry group untouched. According to the Ramsey Theorem monochromatic triangles inevitably appear in the graphs, depicted in Figure 7.

3. Discussion

Various coloring procedures were introduced for Ramsey graphs [8,9,15]. We introduce the coloring procedure valid for any set of points located in the same plane. The coloring follows the sign of the slope

α_{i k}

of straight lines connecting the points/vertices, numbered correspondingly i and k. For a sake of generalization the certain color is prescribed for the situations when

α_{i k} = 0

α_{i k}

is not defined. Thus, for any set of points located in the same plane the complete graph emerges, and the Ramsey theorem becomes immediately applicable [5,6,7,8,9,10]. When and why the suggested coloring procedure may of interest:

i): The introduced coloring bridges between the Ramsey theory and linear algebra. The reasonable problem to be addressed in future is formulated as follows: what is the interrelation between the properties of the matrix $α_{i k}$ and the number of monochromatic polygons, recognized in the complete graph, built according to the aforementioned procedure?
ii): We introduce the coloring procedure which yields the inverse complete graph arising from an arbitrary set of points belonging to the same plane, when the coordinate axes are rotated to $\frac{π}{2}$ .
iii): Numerous physical processes are described by linear equations such as Ohm’s, Charle’s, Gay-Lussac's law or Hook’s laws. Thus, the $X 0 Y$ plane may be seen, for the example, as maps of thermodynamic states or volt-ampere characteristics. The suggested coloring procedure will supply the predictions related to emerging of cycles in these maps [16,17,18,19,20,21].

4. Conclusions

We introduce the application of the Ramsey theory to the set of the points placed in the plane. We introduce the following coloring procedure: consider a set of arbitrary number N of points located in the same plane. Connect the points in pairs with the straight lines in a given Cartesian coordinates. Thus, the complete graph emerges. The straight lines connecting these points are

y_{i k} (x) = α_{i k} x + β_{i k} (i, k = 1 . . . N) .

Following values of slopes

α_{i k}

are possible:

α_{i k} > 0

;

α_{i k} = 0

;

α_{i k}

is not defined;

α_{i k} < 0 .

The coloring procedure is introduced: we connect the pairs of points for which

α_{i k} > 0

α_{i k} = 0

α_{i k}

is not defined, with the red links, and the pairs of points for which

α_{i k} < 0

place with green links. The introduced coloring procedure yields the complete bi-color graph. The suggested coloring procedure enables building of the complete bi-colored graph for any set containing N points located in the same plane. For the set containing

N = 6

points, at least one monochromatic triangle will necessarily appear in the graph, as it follows from the seminal Ramsey Theorem. The values of the slopes

α_{i k}

depend on the chosen coordinate system. The rotation of coordinate axes changes the coloring of the graph, however at least one monochromatic triangle will be present in the complete graph. Thus, the Ramsey theory supplies a kind of invariant appearing in all of possible Cartesian coordinate axes, irrespectively to their orientation. It is instructive to consider the set of six point forming the regular hexagon. The introduced coloring procedure breaks the symmetry of the hexagon, irrespectively to the orientation of the coordinate axes. The same is true to equilateral triangle, quadrangle and pentagon. We hypothesized that this will be true for any arbitrary regular n-polygon, independently on the orientation of coordinate axes. We introduced the notion of the inverse bi-color Ramsey graphs, generated by the source graph; namely, we replace red links appearing in the source graph with red ones, and vice versa. The total number of triangles in the “direct” (source) and “inverse” Ramsey graphs is the same. We also considered the particular case of the set of points for which

α_{i k} > 0

α_{i k} < 0

in given coordinates is true. In this specific case, the rotation of the Cartesian coordinate axes to the angle

θ = \frac{π}{2}

yields the inverse complete graph for an arbitrary number of the source points. Generalization of the introduced coloring for arbitrary set of points, belonging to the same plane is suggested. Numerous physical processes are described by linear equations. Thus, the coordinate plane may be seen, for the example, as maps of thermodynamic states or volt-ampere characteristics. Hence, the suggested Ramsey approach will supply the predictions related to emerging of cycles in these maps.

Author Contributions

Mark Frenkel – Writing – review & editing, Writing – original draft, Investigation; Formal analysis; Shraga Shoval – Writing – review & editing, Writing – original draft, Supervision; Edward Bormashenko – Writing – review & editing, Writing – original draft; Methodology, Investigation, Formal analysis, Conceptualization.

Funding

This research received no external funding.

Data Availability Statement

The datasets generated during and/or analyzed during the current study are available from the corresponding author on reasonable request.

Acknowledgements

The authors are thankful to Dr. Nir Shvalb for extremely useful discussions.

Conflicts of Interest

The authors declare no conflict of interest.

References

Ramsey, F. P. On a Problem of Formal Logic. In Classic Papers in Combinatorics. Modern Birkhäuser Classics; Gessel, I., Rota, GC. Eds.; Birkhäuser Boston: Boston, USA, 2009; pp. 264–286. [CrossRef]
Gerencsér, L.; Gyárfás, A. On Ramsey-type problems, Ann. Univ. Sci. Budapest. Eötvös Sect. Math 1967, 10, 167-170.
Erdős, P., Gyárfás, A. A variant of the classical Ramsey problem. Combinatorica 1997, 17, 459–467. [CrossRef]
P. Erdős: Solved and unsolved problems in combinatorics and combinatorial number theory,Congressus Numerantium,1981, 32, 49–62.
Katz, M.; Reimann, J. An Introduction to Ramsey Theory: Fast Functions, Infinity, and Metamathematics, Student Mathematical Library; American Mathematical Society: Providence, RI, USA, 2018; Volume 87, pp. 1–34.
Fujita S.; Magnant, C.; Ozeki, K. Rainbow Generalizations of Ramsey Theory: A Survey. Graphs and Combinatorics 2010, 26, 1–30. [CrossRef]
Graham, R. L.; Spencer, J. H. Ramsey Theory. Sci. Am. 1990, 7, 112–117.
Graham, R.; Butler, S. Rudiments of Ramsey Theory (2nd ed.). American Mathematical Society: Providence, Rhode Island, USA, 2015; pp. 7–46.
Graham, R.L.; Rothschild, B. L.; Spencer, J. H. Ramsey theory, 2^nd ed.; Wiley-Interscience Series in Discrete Mathematics and Optimization; John Wiley & Sons, Inc., A Wiley-Interscience Publication: New York, USA, 1990; pp. 10–110.
Chartrand, G.; Zhang P. New directions in Ramsey theory. Discrete Math. Lett. 2021, 6, 84–96. [CrossRef]
Roberts, F. S.; Tesman B. Applied Combinatorics, 2^nd Ed., Chapter 3.3. Graph Coloring and its Applications, pp. 159-161, CRC Press, Boca Raton, Fl. USA.
Roberts, F.S. Applications of Ramsey theory. Discrete Appl. Math. 1984, 9(3), 251–261. [CrossRef]
Shvalb, N.; Frenkel, M.; Shoval, Sh. Bormashenko, Ed. A Note on the Geometry of Closed Loops, Mathematics 2023, 11(8), 1960. [CrossRef]
Choudum, S.A.; Ponnusamy, B. Ramsey numbers for transitive tournaments, Discrete Math. 1999, 206, 119–129.
Lin, S. On Ramsey numbers and $K_{r}$ coloring of graphs, J. Combinatorial Theory, 1972, 12, 82-92. [CrossRef]
Chernov, N.; Markarian, R. Chaotic Billiards, Mathematical Surveys and Monographs, American Mathematical Soc.: N. Y. USA, 2006; v. 127.
Sinai, Ya.G. Dynamical systems with elastic reflections. Ergodic properties of dispersing billiards. Russ. Math. Surv. 1970, 25, 137–189. [CrossRef]
Bunimovich, L.A. On the ergodic properties of nowhere dispersing billiards. Commun. Math. Phys. 1979, 65, 295–312.
Shvalb, N.; Frenkel, M.; Shoval, Sh.; Bormashenko, Ed. Ramsey theory and thermodynamics, Heliyon 2023, 9 (2), e13561. [CrossRef]
Shvalb, N.; Frenkel, M.; Shoval, Sh.; Bormashenko, Ed. Universe as a Graph (Ramsey Approach to Analysis of Physical Systems. World J. Physics; 2023, 1 (1) 1-24. [CrossRef]
Shvalb, N.; Frenkel, M.; Shoval, Sh.; Bormashenko, Ed Dynamic Ramsey Theory of Mechanical Systems Forming a Complete Graph and Vibrations of Cyclic Compounds. Dynamics 2023, 3(2), 272-281. [CrossRef]

Figure 1. Ramsey construction for six points

(x_{i}, y_{i}); i = 1 \dots 6

placed on the plane

X 0 Y

Figure 1. Ramsey construction for six points

(x_{i}, y_{i}); i = 1 \dots 6

placed on the plane

X 0 Y

Figure 2. Bi-coloring of regular hexagons is depicted. Pristine hexagon (123456) is shown in inset (A); inset (B) depicts the same hexagon rotated counterclockwise to

\frac{π}{3}

and denoted

(\hat{1} \hat{2} \hat{3} \hat{4} \hat{5} \hat{6}) .

Figure 2. Bi-coloring of regular hexagons is depicted. Pristine hexagon (123456) is shown in inset (A); inset (B) depicts the same hexagon rotated counterclockwise to

\frac{π}{3}

and denoted

(\hat{1} \hat{2} \hat{3} \hat{4} \hat{5} \hat{6}) .

Figure 3. Coloring of triangles according to the procedure introduced in Section 2.1 is demonstrated. The color of the edge corresponds to the sign of its slope. (A) Monochromatic triangles are shown. (B) Equilateral triangle will be bi-chromatic at any orientation of the triangle relatively to the coordinate axes.

Figure 4. Complete graphs generated by the regular triangle, quadrangle and pentagon are depicted. No monochromatic complete graph is recognized.

Figure 5. Source

(1,2, 3,4, 5.6)

(inset (A)) and inverse

(\hat{1}, \hat{2}, \hat{3}, \hat{4}, \hat{5}, \hat{6})

(inset (B)) complete graphs are depicted. Triangles

(126)

and

(256)

in inset (A), and triangles

(\hat{1} \hat{2} \hat{6})

and

(\hat{2} \hat{5} \hat{6})

are monochromatic.

Figure 5. Source

(1,2, 3,4, 5.6)

(inset (A)) and inverse

(\hat{1}, \hat{2}, \hat{3}, \hat{4}, \hat{5}, \hat{6})

(inset (B)) complete graphs are depicted. Triangles

(126)

and

(256)

in inset (A), and triangles

(\hat{1} \hat{2} \hat{6})

and

(\hat{2} \hat{5} \hat{6})

are monochromatic.

Figure 6. Complete graphs generated by the regular triangle, quadrangle and pentagon are depicted. The pairs of points for which

α_{i k} > 0

or α_{i k} = 0

is not defined are connected with the red links, and the pairs of points for which

α_{i k} < 0

and

α_{i k}

is not defined place are connected with green edges. No monochromatic complete graph is recognized.

Figure 6. Complete graphs generated by the regular triangle, quadrangle and pentagon are depicted. The pairs of points for which

α_{i k} > 0

or α_{i k} = 0

is not defined are connected with the red links, and the pairs of points for which

α_{i k} < 0

and

α_{i k}

is not defined place are connected with green edges. No monochromatic complete graph is recognized.

Figure 7. Bi-coloring of regular hexagons is depicted. Pristine hexagon (123456) is shown in inset (A); inset (B) depicts the same hexagon rotated counterclockwise to

\frac{π}{3}

and denoted

(\hat{1} \hat{2} \hat{3} \hat{4} \hat{5} \hat{6}) .

The pairs of points for which

α_{i k} > 0

or α_{i k} = 0

is not defined are connected with the red edges, and the pairs of points for which

α_{i k} < 0

and

α_{i k}

is not defined place are connected with green edges.

Figure 7. Bi-coloring of regular hexagons is depicted. Pristine hexagon (123456) is shown in inset (A); inset (B) depicts the same hexagon rotated counterclockwise to

\frac{π}{3}

and denoted

(\hat{1} \hat{2} \hat{3} \hat{4} \hat{5} \hat{6}) .

The pairs of points for which

α_{i k} > 0

or α_{i k} = 0

is not defined are connected with the red edges, and the pairs of points for which

α_{i k} < 0

and

α_{i k}

is not defined place are connected with green edges.

Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.

© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).

Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.

MDPI Initiatives

Important Links

Choose an area of interest and we will send you notifications of new preprints at your preferred frequency.

Disclaimer

Ramsey Theory and Transformations of Coordinate Systems

Abstract

1. Introduction

2. Results

2.1. Ramsey theory and geometry of closed curves

2.2. Ramsey structures and rotations of coordinates

2.3. Direct and inverse Ramsey graphs

2.4. Rotation of coordinate axes generates inverse complete graphs

3. Discussion

4. Conclusions

Author Contributions

Funding

Data Availability Statement

Acknowledgements

Conflicts of Interest

References

MDPI Initiatives

Important Links

Subscribe