Prerpints.org logo
Preprint
Article

Characterization of Flow Parameters in Shale Nano-Porous Media Using Pore Network Model: A Field Example from Shale Oil Reservoir in Songliao Basin, China

Altmetrics

Downloads

109

Views

56

Comments

0

A peer-reviewed article of this preprint also exists.

Submitted:

08 June 2023

Posted:

09 June 2023

You are already at the latest version

Alerts
Abstract
The pore-throat radius of shale oil reservoir is extremely small, and it is difficult to accurately obtain the absolute permeability and oil-water two-phase relative permeability of actual oil reservoir through conventional core experiments. However, these parameters are very important for reservoir numerical simulation. In this paper, a method for characterizing flow parameters based on pore network model that considers differential pressure flow and diffusion flow is proposed. Firstly, a digital core was reconstructed using focused ion beam scanning electron microscopy (FIB-SEM) from the Gulong shale reservoir in the Songliao Basin, China, and a pore network model was extracted. Secondly, quasi-static single-phase flow and two-phase flow equations considering diffusion were established in the pore network model. Finally, pore throat parameters, absolute permeability, and oil-water two-phase permeability curves were calculated, respectively. The results show that the pore throat distribution of Gulong shale reservoir is mainly concentrated in the nanometer scale, the mean pore radius is 87 nm, the mean throat radius is 41 nm, and the mean coordination number is 3.97; The calculated permeability considering diffusion is 0.000124mD, which is approximately twice the permeability calculated without considering diffusion; The irreducible water saturation of the Gulong shale reservoir is approximately 0.26, and the residual oil saturation is approximately 0.73. The method proposed in this paper can provide an important approach for characterizing the flow parameters of similar shale oil reservoirs.
Keywords: 
Subject: Engineering  -   Energy and Fuel Technology

1. Introduction

Shale oil reservoirs have a wide distribution of pore throats (ranging from nanoscale to micrometer scale), with complex pore geometries and pore throat structures [1,2]. The micro pore-throat structure is an important factor affecting the macroscopic reservoir properties and fluid flow in shale oil reservoirs [3]. Therefore, quantitative evaluation and characterization of the micro pore throat structure of shale reservoirs [4] (pore geometry, size distribution, connectivity, etc.) is of great significance for understanding the fluid flow patterns of shale reservoirs. The commonly used methods for characterizing the complex pore-throst structure of porous media are digital cores [5,6,7,8,9,10] and pore network models [11,12,13,14,15,16,17]. Direct flow simulation methods based on digital cores (such as lattice Boltzmann method [18,19,20,21], computational fluid dynamics method [22,23] and Monte Carlo simulation [24,25]) take a long time to calculate, require a large amount of memory, and are powerless for large-scale flow simulation and parameter sensitivity analysis. Considering the extremely small pore-throat and strong micro heterogeneity of shale oil reservoirs, which make it difficult to obtain characterization units or have larger sizes, direct flow simulation methods based on digital cores of shale reservoirs will be very challenging. Based on previous studies, it has been shown that pore network simulation is basically consistent with core scale experiments in obtaining macroscopic physical parameters (capillary pressure curves, relative permeability curves, etc.) [26,27,28,29,30,31,32,33,34]. Moreover, pore network simulation computation time is relatively short, which is very advantageous for large-scale flow calculations. Therefore, the pore network model is selected as the method for pore level flow simulation in shale reservoirs in this paper.
Although porous flow parameters such as flow rate-differential pressure curve, permeability, capillary pressure curve and relative permeability curve can be obtained through core experiments [35,36], micro-nano pore throat development of shale rock core and fluid flow in it is very slow, it will be time-consuming and expensive to obtain macro physical parameters such as phase permeability through experiments, and the flow rate is small, resulting in large measurement errors. At present, direct flow simulation methods based on digital cores are time-consuming and occupy a large amount of memory, while pore network simulation can quickly and accurately predict macroscopic physical parameters [37,38,39,40,41,42,43], making it a powerful method for predicting macroscopic physical parameters of shale reservoirs. The pore network model uses regular geometry to replace the characteristics of complex pore throat structure, and uses form factor to characterize the irregularity of pore throat structure. Based on the percolation theory, the pore level flow characteristic of porous media fluid is studied [44,45,46]. In 1957, Broadbent and Hannersley [47] first proposed the concept of percolation and pointed out its prospects in the application of porous flow. Afterwards, many scholars conducted extensive research on the simulation of pore network flow. In the 1970s, Dullien [48] applied the percolation theory to the pore network model and explored the flow rules of fluids in the network model. Lenormand [49] proposed the invasion percolation model and applied it to the simulation of the displacement process simulation of the displaced fluid in porous media. Oak et al. [50] used the pore network model to study the oil-water two-phase and oil gas water three-phase relative permeability curves of water wet Berea sandstone. In recent years, Blunt, Ø ren, and van Dijke et al. [51,52,53,54] have conducted extensive research on the effects of reservoir wettability on pore level flow, three-phase flow, and prediction of capillary pressure and relative permeability curves using pore network models. Capillary pressure is the main driving force determining saturation changes in quasi-static network models. For the capillary pressure at the inlet of each network model, the equilibrium position of the interface between the fluid and the fluid is determined according to the fluid displacement model. Based on the criteria of each displacement mode, displacement and fluid location in the network model occur gradually in order. In addition to being used for theoretical research, many scholars have proposed network models which can be used to predict macroscopic physical property parameters according to research needs. Vogel [55,56] predicted the soil relative permeability using a network model generated by a series of thin slice techniques that can characterize the complex pore structure of soil. In 2002, Blunt et al. [57] pointed out that by combining pore-scale physical phenomena with geometrically equivalent pore-throat cross-section shapes, a representative network model could be used to accurately predict capillary pressure curves and relative permeability curves. In 2005, Piri and Blunt [58] established a pore network flow model that included all the important characteristics of pore scale immiscible fluid flow (such as water film, oil layer, wetting hysteresis and wettability change). The corresponding model was used to calculate oil-water relative permeability, invasion path and capillary pressure curve in different displacement processes. In the water wetting system, the oil-water relative permeability curve predicted by the model was in good agreement with the experimental results. With the deepening of research, the capillary pressure curves and relative permeability curves during different displacement processes under mixed wetting conditions have gradually been successfully predicted. The quasi static pore network model for the three-phase flow of oil, gas, and water has gradually been developed.
In view of the above problems, this paper proposes a characterization method of flow parameters in shale nano-porous media using pore network model. The structure of this article is as follows. In section 2, the FIB-SEM experiment and the calculation method of flow parameters in porous media are introduced. The section of results and discussion is introduced in Section 3. Finally, the conclusion is drawn in section 4.

2. Methodology

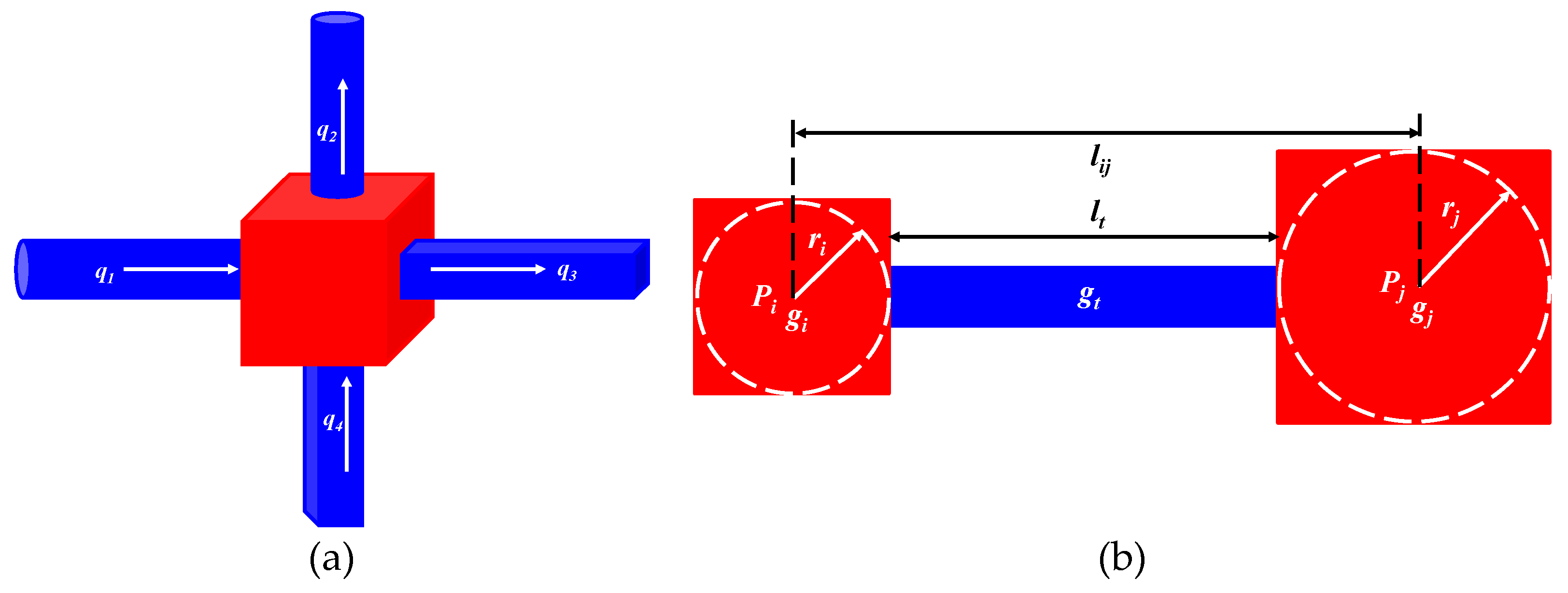
2.1. Establishment of pore network model based on FIB-SEM

The core sample of this experiment is from the Gulong shale oil reservoir in Songliao Basin, China. The experiment used a focused ion beam scanning electron microscope (FIB-SEM) with a resolution of 2nm, Helios 5 CX DualBeam model, to perform high-precision scanning of the shale sample. The electron beam current range is 0.8pA-176nA, and the acceleration voltage range is 200V-30kV. The Ion beam current range is1pA-100nA, and the acceleration voltage range is 500V-30kV.
For the images generated by FIB-SEM, the angle between the ion beam and the electron beam is 52 degrees. Due to the angle between the milled surface and the imaging axis being not 90 degrees, the original image presents geometric artifacts compared to the real profile. Therefore, it is necessary to cut and stretch the image stack to achieve image alignment. In addition, when FIB cutting on the surface of rock samples, the difference in hardness on the surface of the rock sample can cause a difference in cutting speed, resulting in the formation of marks parallel to the cutting direction on the surface of the rock sample. In the FIB-SEM image, it appears as a vertical stripe noise with varying brightness, resembling a curtain, which is called the "curtain effect". Therefore, the preprocessing of FIB-SEM images mainly involves image alignment and denoising filtering. This article uses Avizo software to process FIB-SEM images, providing the FIB Stack Wizard and image filters that can align and preprocess FIB-SEM image stacks. Firstly, the FIB-SEM image stack is aligned and shadow corrected using the FIB stack wizard. Then, the image is denoised and filtered using non-local mean filtering. Then, the striped artifacts caused by the "curtain effect" in the image are eliminated through fast Fourier transform filtering. Finally, the filtered image is edge enhanced through non-sharpening masking to complete image preprocessing. The final FIB-SEM image is shown in Figure 1.
After preprocessing, the signal-to-noise ratio (SNR) of the image can be effectively improved, and then the preprocessed image needs to be segmented, mainly to gain a deeper understanding of the pore structure of the rock and identify the pore phase. Therefore, the Avizo software is used to combine two segmentation methods, interactive threshold segmentation and interactive top hat segmentation, in order to accurately segment the pore structure. Then, the pore network model with true topological relationships is obtained through the pore centered axis method and the maximum sphere method. Figure 2 shows the three-dimensional pore structure of the Gulong shale core after FIB-SEM segmentation and the extracted pore network model.

2.2. Quasi-static single-phase flow equations considering diffusion

The flow rate into and out of a certain pore in the pore network model satisfies the law of mass conservation (Figure 3(a)) [59,60]:
∑ j = 1 N i q i j = 0
Where, Ni is the number of pores connected to pore i; qij is flow into or out of pore i; j is the pore number connected to pore i. The flow from one pore into or out of its adjacent pore qij is satisfied as follows:
q i j = g i j p i − p j L i j
Where, gij is conductivity; pi, pj are pore pressure of pore i, j; Lij is the distance between two adjacent pores. The conductivity gij can be obtained by harmonic average of the conductivity of adjacent pores and the middle throat (Figure 3(b)):
g i j = L i j L i g i + L t g t + L j g j
In addition to pressure difference, diffusion also contributes to flow rate in shale nano-pores. Therefore, based on Knudsen number, the mass transfer modes of Gulong shale oil at different scales are divided. In addition to differential pressure mass transfer, Knudsen diffusion at small pore size, molecular diffusion at large pore size and transition diffusion at medium pore size are respectively established to characterize diffusion coefficients at different scales. Knudsen number Kn is defined as follows:
K n = λ d = k B T 2 π δ 2 p d
where, λ is the mean free path; d is the equivalent pore-throat diameter; kB is the Boltzmann constant, 1.3806488×10-23 J/K; δ is the collision diameter of molecule, m; T is the temperature, K；p is the total pressure, Pa.
Gas diffusion mechanisms in porous media mainly includes Fick diffusion, transition diffusion and Knudsen diffusion. When Kn < 0.1, the flow regime is primarily continuous and slip flow, mainly occurring in large pores. At this time, gas molecules collide with each other and ignore collisions with the pore wall. Diffusion takes the form of Fick diffusion. When Kn > 10, the flow regime is primarily free molecular flow, mainly occurring in small pores. At this time, only a single molecule can pass through the pore, and molecules collide with the pore wall. Diffusion takes the form of Knudsen diffusion. When 0.1 < Kn < 10, the flow regime is primarily transitional flow. At this time, gas molecules and the wall both experience collisions, and diffusion takes the form of transitional diffusion, as shown in Figure 4.
When calculating gas flow velocity caused by diffusion, one of the most important variables is the diffusion coefficient. When Knudsen diffusion is dominant, the diffusion coefficient is the Knudsen diffusion coefficient DK, which can be calculated using the following formula:
D K = d 3 8 R T π M
When Fick diffusion is dominant, the diffusion coefficient is the Fick diffusion coefficient DF, which can be calculated using the following formula:
D F = k B T 3 2 π δ 2 p 8 R T π M
Where, M is molecular molar mass, g/mol; R is the ideal gas constant, 8.314462 J/(mol·K). When transitional flow is dominant, the diffusion coefficient is the transition diffusion coefficient DT, which is a combination of the Fick diffusion coefficient and the Knudsen diffusion coefficient. The calculation formula is as follows:
1 D T = 1 D K + 1 D F
Therefore, after considering diffusion, the flow equation in a single pore-throat is as follows:
Q = Q p + Q d = ( π d 4 128 μ L ρ M + π d 2 4 L D t R T ) Δ p
The pressure at each pore node of the network model can be obtained by combining (1), (2), (3) and the single-phase conductivity coefficients of any shape section. Inlet and outlet nodes were used to calculate the inlet and outlet flow, and Darcy's law was used to calculate the absolute permeability K of the network model:
k abs = Q μ L m A Δ p
Where, Q is the outlet or inlet flow of the network model, m3/s; Lm is length of pore network model, m; A is the cross-sectional area of the network model, m2; △p is the differential pressure at both ends of the network model, Pa.

2.3. Quasi-static two-phase flow equations

The relative permeability of oil and water in the initial displacement process can be calculated at any point in the displacement process. In the two-phase flow process, if there is at least one connected cluster in the network model (the connected cluster in the two-phase flow is defined as: a fluid of a phase in the network model is connected to the inlet and outlet through pores and throats), then the relative permeability of the phase is not zero. On the connected cluster, for each phase of fluid, the flow into and out of a certain pore satisfies the law of conservation of mass [59,60]:
∑ j q p , i j = 0
The flow rate of phase p between pore i and its connected pore j is satisfied as follows:
q p , i j = g p , i j L i j ( P p , i − P p , j )
The conduction coefficient gp,ij between two adjacent pores can be used as the harmonic average of the conduction coefficient between two adjacent pores and the connecting throat:
L i j g p , i j = L i n g p , i n + L i j b g p , i j b + L j n g p , j n
Where, gp,ij is the effective conduction coefficient between pore i and connected pore j; Lij is the distance between pore i and adjacent pore j; Pp,i, Pp,j is the pore i and p phase fluid pressure in j.
In the initial displacement process, oil is the non-wetting phase and water is the wetting phase. At the throat section with corner, the water film is located at the corner, and the oil phase is located at the center of the pore. In the process of two-phase flow, when two phases of oil and water coexist in the same pore or throat, the oil phase conduction coefficient is the bulk phase conduction coefficient, and the water phase conduction coefficient is the sum of all the existing water film conduction coefficients. The expression is:
g o = g o , b ， g w = ∑ k = 1 n g w , c k
By combining the above formulas, the pressure of p-phase fluid at each pore node in the network model can be obtained, and then the effective permeability of p-phase fluid can be obtained by using formula (13):
k p = μ p Q p L T A T Δ p
The calculation formula of relative permeability of p phase is shown in Equation (14):
k r p = k p k abs
In the initial displacement process, water saturation of the pore network model is:
S w = ∑ i = 1 M ∑ j = 1 n A c , j A i V i + ∑ i = 1 N V i ∑ i = 1 M + N V i
Where, Sw is the water saturation of the pore network model; V is volume of pore network model, m3; A is the cross-sectional area of the pore network model, m2.
Table 1. Parameters used in pore network flow simulation.
Table 1. Parameters used in pore network flow simulation.
Simulation parameter Unit Value
Pore number / 8717
Throat number / 18494
Oil density g/cm3 0.7
Water density g/cm3 1
Oil viscosity mPa·s 0.5
Water viscosity mPa·s 1
Oil-water contact angle ° 60
Oil water interfacial tension mN/m 20
Initial temperature ℃ 137
Initial pressure MPa 37.5

3. Results and discussion

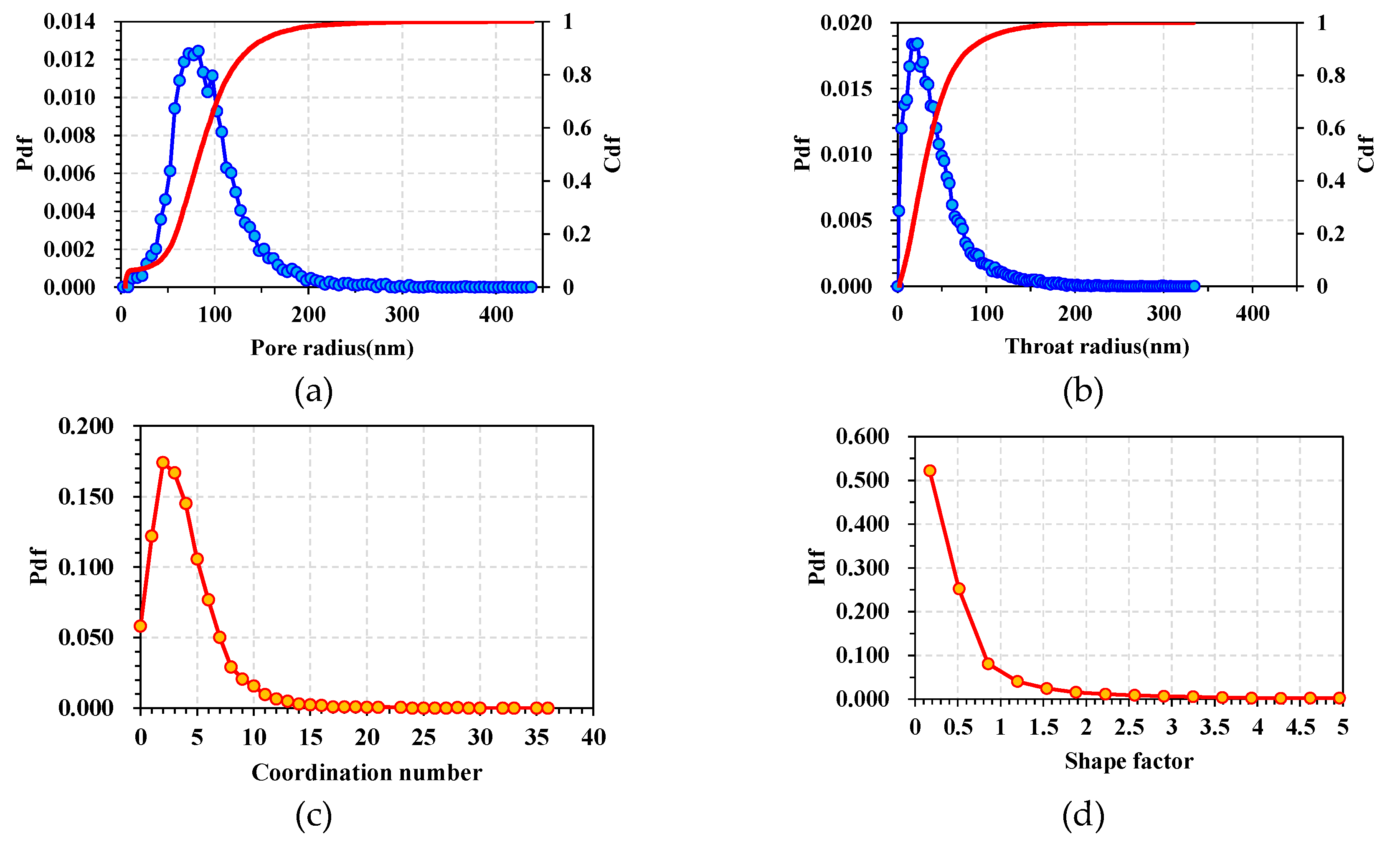
3.1. Pore-throat parameters characterization

The three-dimensional slices of Gulong shale core were obtained by FIB-SEM, and the three-dimensional digital core was constructed. The total porosity is about 9.6%, but the effective connected porosity is only 4.6%. Figure 5(a) and (b) respectively show the radius distribution of pore and throat. The minimum pore radius and throat radius are respectively 2nm and 1nm, the maximum pore radius and throat radius are respectively 438nm and 334nm, the mean pore radius is 87nm, and the mean throat radius is 41nm. Figure 5(c) and (d) respectively show the coordinate number and shape factor of Gulong shale core, and the mean coordination number is 3.97. Generally speaking, pore connectivity of shale is not poor, and the difficulty of development of shale oil reservoir is due to the extremely small pore throat radius.

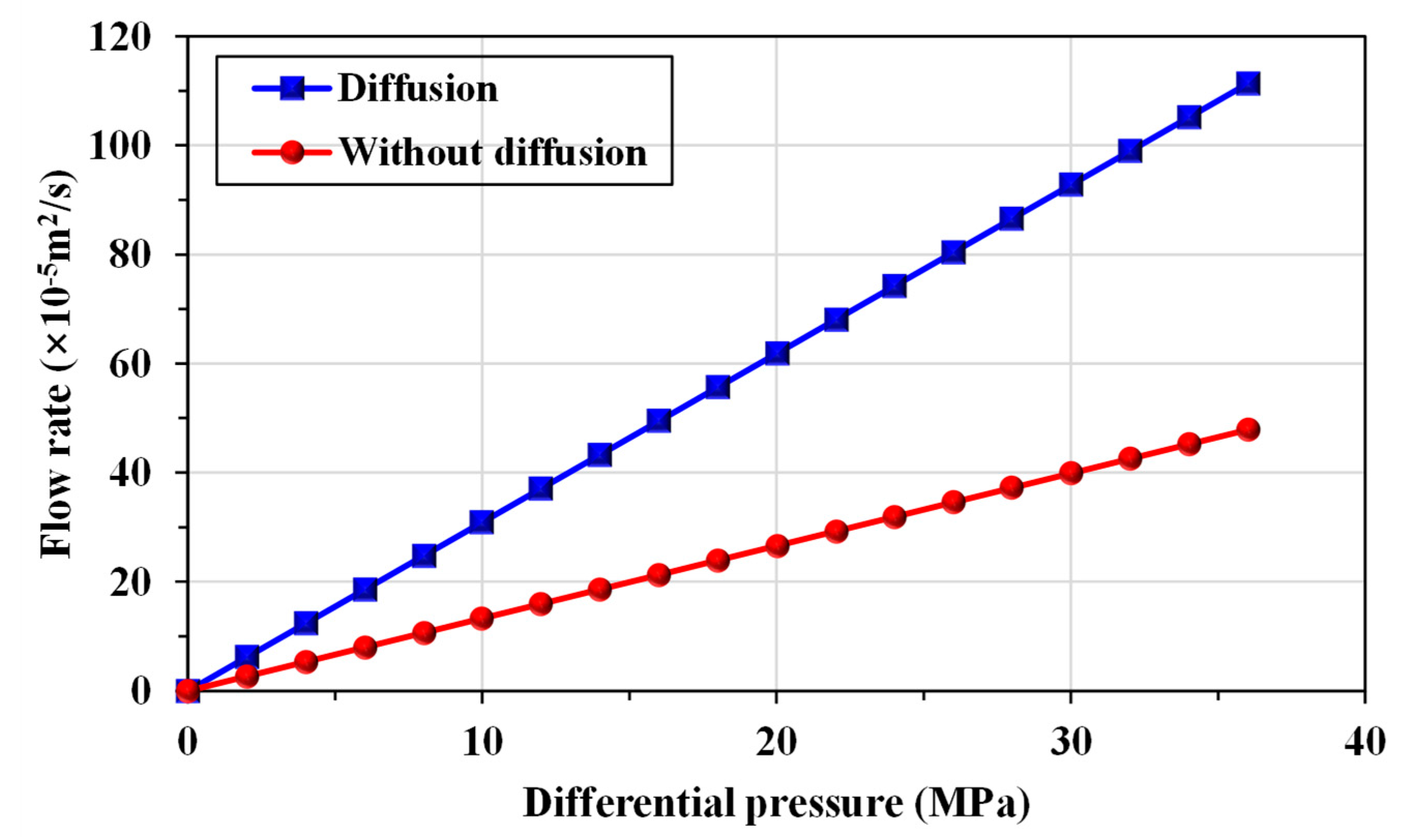
3.2. Apparent permeability characterization

Figure 6 shows the flow rate-differential pressure curve calculated with and without diffusion. The permeability predicted by the combined action of differential pressure displacement and diffusion in micro and nano pores is greater than that under pure differential pressure mass transfer condition, and the permeability calculated with diffusion is 0.000124mD. The permeability calculated without considering diffusion is 0.0000531mD.

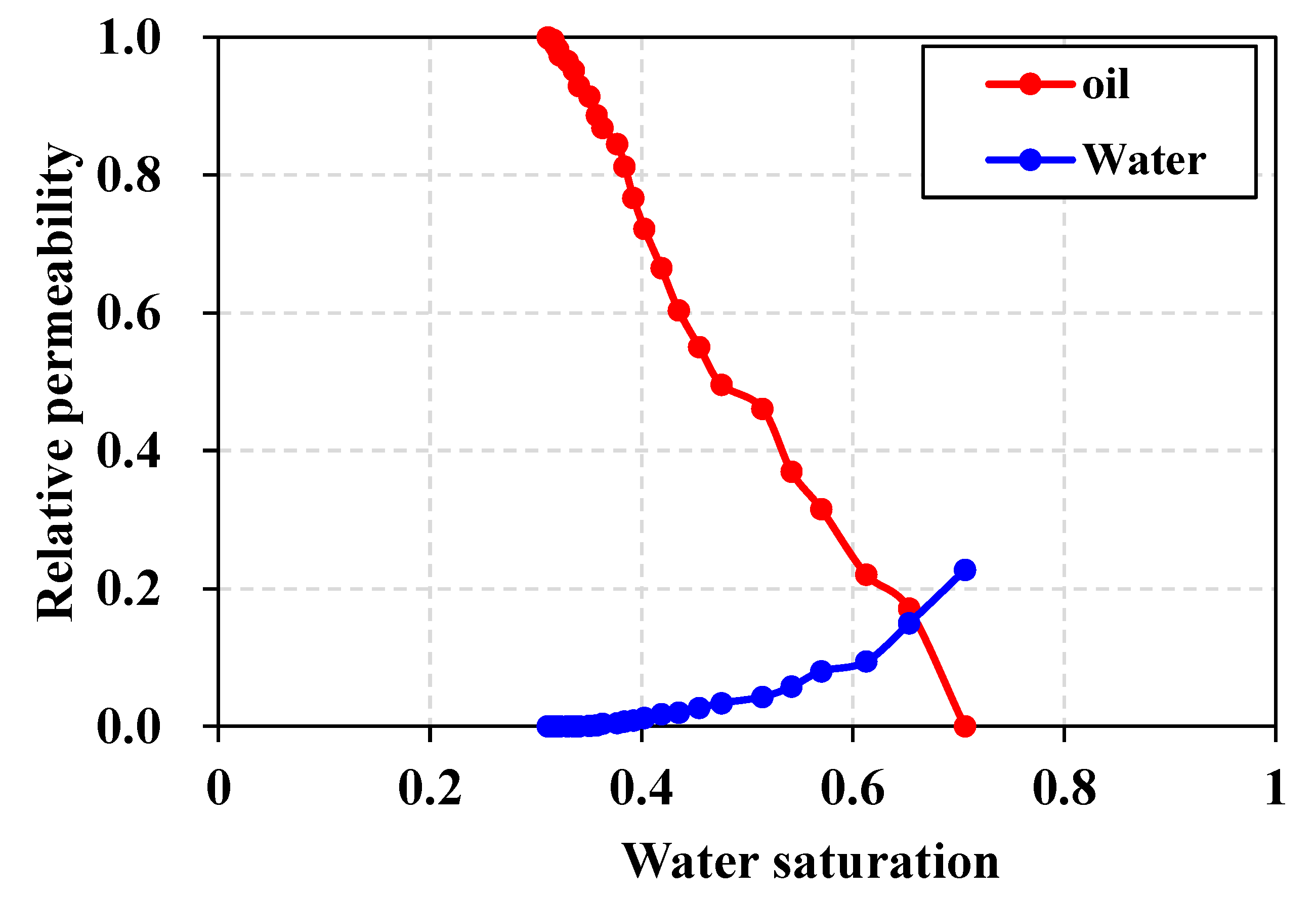
3.3. Relative permeability curves characterization

Figure 7 shows the distribution of oil and water in the pore network model under different water saturation conditions. Injected water preferentially flows along large pore channels, and only with the increase of water saturation can injected water gradually enter small pores.
The relative permeability curve of oil and water in Gulong shale reservoir was calculated through the simulation of oil-water two-phase pore network. The irreducible water saturation of Gulong shale reservoir was calculated to be about 0.26, and the residual oil saturation was about 0.73. The relative permeability curve is shown in Figure 8.

4. Conclusion

In this paper, a characterization method of flow parameters in shale nano porous media using pore network model is proposed to characterize the key flow parameters of the Gulong shale reservoir in the Songliao Basin, China. The conclusions are as follows:
(1) The minimum pore radius and throat radius of Gulong shale are 2nm and 1nm respectively, the maximum pore radius and throat radius are 438nm and 334nm respectively, the mean pore radius is 87nm, the mean throat radius is 41nm, and the mean coordination number is 3.97.
(2) The permeability predicted by considering the combined effects of medium pressure differential displacement and diffusion in micro nano pores is greater than that under pressure differential mass transfer conditions. The calculated permeability considering diffusion is 0.000124mD, while the calculated permeability without diffusion is 0.0000531mD.
(3) The oil-water relative permeability of Gulong shale oil reservoir is calculated through oil-water two-phase pore network simulation. The irreducible water saturation of Gulong shale oil reservoir is about 0.26, and the residual oil saturation is about 0.73.

Author Contributions

Conceptualization, Q.W.; methodology, Z.J.; software, Z.J.; valadation, Q.W.; formal analysis, F.Q.; investigation, D.D; rescources, Q.F.; data curation, Y.L.; writing-original draft preparation, Z.J.; writing—review and editing, P.J.; visualization, Q.W.; supervision, L.C.; project administration, B.L.; funding acquisition, B.L. All authors have read and agreed to the published version of the manuscript.

Funding

This research was funded by CNPC Major Technology Project “Theory and Key Technologies of Exploration and Development of Daqing Gulong Shale Oil”, Topic 2 “Theory and Key Technologies of Beneficial Development of Gulong Shale Oil”, grant number 2021ZZ10-02.

Institutional Review Board Statement

Not applicable.

Informed Consent Statement

Not applicable.

Data Availability Statement

Not applicable.

Conflicts of Interest

The authors declare no conflict of interest.

Nomenclature

A Cross-sectional area of the network model, m2
DK Knudsen diffusion coefficient, m2/s
DF Fick diffusion coefficient, m2/s
DT Transition diffusion coefficient, m2/s
d Equivalent pore-throat diameter, m
gij Conductivity
gp,ij Effective conductivity of p phase
Kn Knudsen number
kB Boltzmann constant, 1.3806488×10-23 J/K
kabs Absolute permeability, mD
kp Effective permeability of p phase, mD
krp Relative permeability of p phase
L Length of pore network model, m
Lij Distance between pore i and adjacent pore j
Ni The number of pores connected to pore i
△p The differential pressure at both ends of the network model, Pa
pi, pj Pore pressure of numbered i, j
Pp,i, Pp,j The pore i and p phase fluid pressure in j
Q The outlet or inlet flow of the network model, m3/s
q Flow into or out of the pore
M Molecular molar mass, g/mol
R Ideal gas constant, 8.314462 J/(mol·K)
Sw Water saturation of the pore network model
V Volume of pore network model, m3
λ Mean free path, m
δ Collision diameter of molecule, m

References

  1. Dou, W.; Liu, L.; Jia, L. Pore structure, fractal characteristics and permeability prediction of tight sandstones: A case study from Yanchang Formation, Ordos Basin, China. Marine and Petroleum Geology 2021, 123, 104737. [Google Scholar] [CrossRef]
  2. Jia, Z.; Cheng, L.; Feng, H. Full composition numerical simulation of CO2 utilization process in shale reservoir using projection-based embedded discrete fracture model (pEDFM) considering nano-confinement effect. Gas Science and Engineering 2023, 111, 204932. [Google Scholar] [CrossRef]
  3. Noiriel, C.; Seigneur, N.; Le Guern, P. Geometry and mineral heterogeneity controls on precipitation in fractures: An X-ray micro-tomography and reactive transport modeling study. Advances in Water Resources 2021, 152, 103916. [Google Scholar] [CrossRef]
  4. Lai, J.; Wang, G.; Wang, Z. A review on pore structure characterization in tight sandstones. Earth-Science Reviews 2018, 177, 436–457. [Google Scholar] [CrossRef]
  5. Hasnan, H.K.; Sheppard, A.; Hassan, M.H. Digital core analysis: Characterizing reservoir quality through thin sandstone layers in heterolithic rocks. Journal of Applied Geophysics 2020, 182, 104178. [Google Scholar] [CrossRef]
  6. Hasnan, H.K.; Sheppard, A.; Hassan, M.H. Digital core analysis: Improved connectivity and permeability characterization of thin sandstone layers in heterolithic rocks. Marine and Petroleum Geology 2020, 120, 104549. [Google Scholar] [CrossRef]
  7. Lv, W.; Chen, S.; Gao, Y. Evaluating seepage radius of tight oil reservoir using digital core modeling approach. Journal of Petroleum Science and Engineering 2019, 178, 609–615. [Google Scholar] [CrossRef]
  8. Ettemeyer, F.; Lechner, P.; Hofmann, T. Digital sand core physics: Predicting physical properties of sand cores by simulations on digital microstructures. International Journal of Solids and Structures 2020, 188–189, 155–168. [Google Scholar] [CrossRef]
  9. Venkatarangan, W. Investigating 3D geometry of porous media from high resolution images. Physics and Chemistry of the Earth, Part A: Solid Earth and Geodesy 1999. [Google Scholar] [CrossRef]
  10. Tan, M.; Su, M.; Liu, W. Digital core construction of fractured carbonate rocks and pore-scale analysis of acoustic properties. Journal of Petroleum Science and Engineering 2021, 196, 107771. [Google Scholar] [CrossRef]
  11. Xiong, Q.; Baychev, T.G.; Jivkov, A.P. Review of pore network modelling of porous media: Experimental characterisations, network constructions and applications to reactive transport. Journal of Contaminant Hydrology 2016, 192, 101–117. [Google Scholar] [CrossRef]
  12. Xu, Z.; Lin, M.; Jiang, W. Rapid multiscale pore network modeling for drainage in tight sandstone. Journal of Petroleum Science and Engineering 2021. [Google Scholar] [CrossRef]
  13. Yi, Z.; Hu, S.; Wu, S. Pore network extraction for shale gas flow in nanoporous media. Marine and Petroleum Geology 2021, 126, 104896. [Google Scholar] [CrossRef]
  14. Meng, Z.; Sun, W.; Liu, Y. Effect of pore networks on the properties of movable fluids in tight sandstones from the perspective of multi-techniques. Journal of Petroleum Science and Engineering 2021, 201, 108449. [Google Scholar] [CrossRef]
  15. El-Zehairy, A.A.; Nezhad, M.M.; Joekar-Niasar, V. Pore-network modelling of non-Darcy flow through heterogeneous porous media. Advances in Water Resources 2019, 131, 103378. [Google Scholar] [CrossRef]
  16. Ahmad, F.; Talbi, M.; Prat, M. Non-local equilibrium continuum modeling of partially saturated drying porous media: Comparison with pore network simulations. Chemical Engineering Science 2020, 228, 115957. [Google Scholar] [CrossRef]
  17. Rodríguez de Castro, A.; Goyeau, B. A pore network modelling approach to investigate the interplay between local and Darcy viscosities during the flow of shear-thinning fluids in porous media. Journal of Colloid and Interface Science 2021, 590, 446–457. [Google Scholar] [CrossRef] [PubMed]
  18. Yin, X.; Zhang, J. An improved bounce-back scheme for complex boundary conditions in lattice Boltzmann method. Journal of Computational Physics 2012, 231, 4295–4303. [Google Scholar] [CrossRef]
  19. Matsuyama, T.; Abe, T.; Yamamoto, H. Lattice Boltzmann method study of Rayleigh instability of a charged droplet. Advanced Powder Technology 2007, 18, 93–104. [Google Scholar] [CrossRef]
  20. Pribec, I.; Hubman, A.; Urbic, T. A discrete reactive collision scheme for the lattice Boltzmann method. Journal of Molecular Liquids 2021, 332, 115871. [Google Scholar] [CrossRef]
  21. Wilde, D.; Krämer, A.; Bedrunka, M. Cubature rules for weakly and fully compressible off-lattice Boltzmann methods. Journal of Computational Science 2021, 51, 101355. [Google Scholar] [CrossRef]
  22. Shams, M.; Raeini, A.Q.; Blunt, M.J. A numerical model of two-phase flow at the micro-scale using the volume-of-fluid method. Journal of Computational Physics 2018, 357, 159–182. [Google Scholar] [CrossRef]
  23. Carrillo, F.J.; Bourg, I.C.; Soulaine, C. Multiphase flow modeling in multiscale porous media: An open-source micro-continuum approach. Journal of Computational Physics: X 2020, 8, 100073. [Google Scholar] [CrossRef]
  24. Sengupta, A.; Adhikari, J. Fluid phase equilibria of triangle-well fluids confined inside slit pores: A transition matrix Monte Carlo simulation study. Journal of Molecular Liquids 2016, 221, 1184–1196. [Google Scholar] [CrossRef]
  25. Karki, S.; Chakraborty, S.N. A Monte Carlo simulation study of hydrogen adsorption in slit-shaped pores. Microporous and Mesoporous Materials 2021, 317, 110970. [Google Scholar] [CrossRef]
  26. Ryazanov, A.V.; Dijke, M.I.; Sorbie, K.S. Two-Phase Pore-Network Modelling: Existence of Oil Layers During Water Invasion. Transport in Porous Media 2009, 80, 79–99. [Google Scholar] [CrossRef]
  27. Høiland, L.K.; Spildo, K.; Skauge, A. Fluid flow properties for different classes of intermediate wettability as studied by network modelling. Transport in Porous Media 2007, 70, 127–146. [Google Scholar] [CrossRef]
  28. Piri, M.; Blunt, M.J. Three-dimensional mixed-wet random pore-scale network modeling of two- and three-phase flow in porous media. I. Model description. Phys Rev E Stat Nonlin Soft Matter Phys 2005, 71 Pt 2, 026301. [Google Scholar] [CrossRef]
  29. Piri, M.; Blunt, M.J. Three-dimensional mixed-wet random pore-scale network modeling of two- and three-phase flow in porous media. II. Results. Phys Rev E Stat Nonlin Soft Matter Phys 2005, 71 Pt 2, 026302. [Google Scholar] [CrossRef] [PubMed]
  30. Valvatne, P.H.; Blunt, M.J. Predictive pore-scale modeling of two-phase flow in mixed wet media. Water Resources Research 2004, 40. [Google Scholar] [CrossRef]
  31. Bakke, S.; Øren, P.E. 3-D Pore-Scale Modelling of Sandstones and Flow Simulations in the Pore Networks. SPE Journal 1997, 2, 136–149. [Google Scholar] [CrossRef]
  32. Bryant, S.; Blunt, M. Prediction of relative permeability in simple porous media. Phys Rev A 1992, 46, 2004–2011. [Google Scholar] [CrossRef] [PubMed]
  33. Ryazanov, A.; Dijke, M.V.; Sorbie, K. Pore-network Prediction of Residual Oil Saturation Based on Oil Layer Drainage in Mixed-wet Systems, SPE Improved Oil Recovery Symposium. 2010. [CrossRef]
  34. Joekar-Niasar, V.; Prodanović, M.; Wildenschild, D. Network model investigation of interfacial area, capillary pressure and saturation relationships in granular porous media. Water Resources Research 2010, 46. [Google Scholar] [CrossRef]
  35. Jones, F.O.; Owens, W.W. A Laboratory Study of Low-Permeability Gas Sands. Journal of Petroleum Technology 1980, 32, 1631–1640. [Google Scholar] [CrossRef]
  36. Tian, X.; Cheng, L.; Cao, R. A new approach to calculate permeability stress sensitivity in tight sandstone oil reservoirs considering micro-pore-throat structure. Journal of Petroleum Science and Engineering 2015, 133, 576–588. [Google Scholar] [CrossRef]
  37. Valvatne, P.H.; Piri, M.; Lopez, X. Predictive Pore-Scale Modeling of Single and Multiphase Flow. Transport in Porous Media 2005, 58, 23–41. [Google Scholar] [CrossRef]
  38. Zheng, D.; Reza, Z. Prediction of pore-scale transport properties in unconventional reservoirs using novel theoretical dendroidal pore-network model. Journal of Petroleum Science and Engineering 2018, 170, 712–720. [Google Scholar] [CrossRef]
  39. Tian, X.; Daigle, H. Permeability prediction from a pore-scale network model constrained by low-pressure nitrogen sorption isotherms. Journal of Petroleum Science and Engineering 2018, 162, 554–566. [Google Scholar] [CrossRef]
  40. Azarafza, A.; King, A.J.; Mead-Hunter, R. Prediction of residual saturation and pressure drop during coalescence filtration using dynamic pore network model. Separation and Purification Technology 2021, 254, 117588. [Google Scholar] [CrossRef]
  41. Merey, Ş. Prediction of transport properties for the Eastern Mediterranean Sea shallow sediments by pore network modelling. Journal of Petroleum Science and Engineering 2019, 176, 403–420. [Google Scholar] [CrossRef]
  42. Dakhelpour-Ghoveifel, J.; Shahverdi, H. Prediction of gas-oil capillary pressure of carbonate rock using pore network modeling. Journal of Petroleum Science and Engineering 2020, 195, 107861. [Google Scholar] [CrossRef]
  43. Xu, Z.; Lin, M.; Jiang, W. Rapid multiscale pore network modeling for drainage in tight sandstone. Journal of Petroleum Science and Engineering 2021, 204, 108682. [Google Scholar] [CrossRef]
  44. Dias, M.M.; Wilkinson, D. Percolation with trapping. Journal of Physics A: Mathematical and General 1986, 19, 3131–3146. [Google Scholar] [CrossRef]
  45. Knackstedt, M.A.; Sahimi, M.; Sheppard, A.P. Invasion percolation with long-range correlations: First-order phase transition and nonuniversal scaling properties. Physical Review E 2000, 61, 4920–4934. [Google Scholar] [CrossRef] [PubMed]
  46. Wilkinson, D.; Willemsen, J.F. Invasion percolation: a new form of percolation theory. Journal of Physics A: Mathematical and General 1983, 16, 3365–3376. [Google Scholar] [CrossRef]
  47. Broadbent, S.R.; Hammersley, J.M. Percolation processes: I. Crystals and mazes. Mathematical Proceedings of the Cambridge Philosophical Society 1957, 53, 629–641. [Google Scholar] [CrossRef]
  48. Dullien, F.A.L. New network permeability model of porous media. Aiche Journal 1975, 21, 299–307. [Google Scholar] [CrossRef]
  49. Lenormand, R.; Zarcone, C.; Sarr, A. Mechanisms of the displacement of one fluid by another in a network of capillary ducts. Journal of Fluid Mechanics 1983, 135. [Google Scholar] [CrossRef]
  50. Oak, M.J.; Baker, L.E.; Thomas, D.C. Three-Phase Relative Permeability of Berea Sandstone. Journal of Petroleum Technology 1990, 42, 1054–1061. [Google Scholar] [CrossRef]
  51. Øren, P.E.; Pinczewski, W.V. Fluid distribution and pore-scale displacement mechanisms in drainage dominated three-phase flow. Transport in Porous Media 1995, 20, 105–133. [Google Scholar] [CrossRef]
  52. Blunt, M.J. Effects of Heterogeneity and Wetting on Relative Permeability Using Pore Level Modeling. SPE Journal 1997, 2, 70–87. [Google Scholar] [CrossRef]
  53. Blunt, M.J. Physically-based network modeling of multiphase flow in intermediate-wet porous media. Journal of Petroleum Science and Engineering 1998, 20, 117–125. [Google Scholar] [CrossRef]
  54. Øren, P.; Bakke, S.; Arntzen, O.J. Extending Predictive Capabilities to Network Models. 1998, 3. 3. [CrossRef]
  55. VOGEL, J. H. Morphological determination of pore connectivity as a function of pore size using serial sections. European Journal of Soil Science 2008, 48, 365–377. [Google Scholar] [CrossRef]
  56. Vogel, H.J. A numerical experiment on pore size, pore connectivity, water retention, permeability, and solute transport using network models. European Journal of Soil Science 2000, 51. [Google Scholar] [CrossRef]
  57. Blunt, M.J.; Jackson, M.D.; Piri, M. Detailed physics, predictive capabilities and macroscopic consequences for pore-network models of multiphase flow. Advances in Water Resources 2002, 25, 1069–1089. [Google Scholar] [CrossRef]
  58. Piri, M.; Blunt, M.J. Three-dimensional mixed-wet random pore-scale network modeling of two- and three-phase flow in porous media. I. Model description. Phys Rev E Stat Nonlin Soft Matter Phys 2005, 71 Pt 2, 026301. [Google Scholar] [CrossRef]
  59. Chen, M.; Cheng, L.; Wang, X. Pore network modelling of fluid flow in tight formations considering boundary layer effect and media deformation. Journal of Petroleum Science & Engineering 2019, 180. [Google Scholar] [CrossRef]
  60. Jia, Z.; Cheng, L.; Zhou, J. Upscaling simulation method of fluid flow for fracturing-shut in-flowback-production process in tight oil reservoirs: Hysteresis effects of capillary pressure and relative permeability. Geoenergy Science and Engineering 2023, 226, 211792. [Google Scholar] [CrossRef]
Preprints 76080 g001
Figure 1. FIB-SEM image results of Gulong shale core.
Figure 1. FIB-SEM image results of Gulong shale core.
Preprints 76080 g001
Preprints 76080 g002
Figure 2. Reconstructed digital core and extracted pore network model. (a) is the pore structure extracted by binarization method; (b) is the pore network model extracted by pore centered axis method and the maximum sphere method.
Figure 2. Reconstructed digital core and extracted pore network model. (a) is the pore structure extracted by binarization method; (b) is the pore network model extracted by pore centered axis method and the maximum sphere method.
Preprints 76080 g002
Preprints 76080 g003
Figure 3. Fluid flowing through pore and conductance between two neighboring pores. (a) is fluid flowing through pore; (b) is the conductance between two neighboring pores [59].
Figure 3. Fluid flowing through pore and conductance between two neighboring pores. (a) is fluid flowing through pore; (b) is the conductance between two neighboring pores [59].
Preprints 76080 g003
Preprints 76080 g004
Figure 4. Various flow regimes and diffusion types depending on Knudsen number.
Figure 4. Various flow regimes and diffusion types depending on Knudsen number.
Preprints 76080 g004
Preprints 76080 g005
Figure 5. Probability density function of pore-throat parameters. (a) is the pore radius distribution; (b) is the throat radius distribution; (c) is the coordination number distribution; (d) is the shape factor distribution.
Figure 5. Probability density function of pore-throat parameters. (a) is the pore radius distribution; (b) is the throat radius distribution; (c) is the coordination number distribution; (d) is the shape factor distribution.
Preprints 76080 g005
Preprints 76080 g006
Figure 6. Flow rate-differential pressure curve. The blue line means that diffusion mass transfer is considered, and the red line means that diffusion mass transfer is not considered.
Figure 6. Flow rate-differential pressure curve. The blue line means that diffusion mass transfer is considered, and the red line means that diffusion mass transfer is not considered.
Preprints 76080 g006
Preprints 76080 g007
Figure 7. Distribution of oil and water in the pore network model under different water satura-tion conditions. (a) is the 30% Sw; (b) is the 40% Sw; (c) is the 50% Sw; (d) is the 60% Sw; (e) is the 70% Sw; (f) is the 80% Sw.
Figure 7. Distribution of oil and water in the pore network model under different water satura-tion conditions. (a) is the 30% Sw; (b) is the 40% Sw; (c) is the 50% Sw; (d) is the 60% Sw; (e) is the 70% Sw; (f) is the 80% Sw.
Preprints 76080 g007
Preprints 76080 g008
Figure 8. Relative permeability curve of Gulong shale oil reservoir calculated by the quasi-static two-phase pore network flow simulation.
Figure 8. Relative permeability curve of Gulong shale oil reservoir calculated by the quasi-static two-phase pore network flow simulation.
Preprints 76080 g008
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.
Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.
Prerpints.org logo

Preprints.org is a free preprint server supported by MDPI in Basel, Switzerland.

facebook logotwitter logolinkedin logo
MDPI Initiatives
Important Links
Subscribe

Disclaimer

Terms of Use

Privacy Policy

© 2024 MDPI (Basel, Switzerland) unless otherwise stated