Analysis of Rigid-Flexible Coupling Characteristics of Pneumatic Modular Soft Joints with Variable Stiffness

Aiming at the problem that soft robots are challenging to take into account both flexibility and bearing capacity, Using the software Pneu-Net driver as the deformation mode, magnetorheological fluid material phase transformation to achieve variable stiffness, A pneumatic modular soft joint structure with dynamically adjustable deformation and stiffness in all directions is proposed. In this paper, mathematical models of deformation and variable stiffness are established. The correspondence between gas pressure and deformation and applied current and joint stiffness is obtained. The finite element analysis method was used to simulate the deformation characteristics and variable stiffness characteristics of modular joints based on the Yeoh model. Finally, the theoretical and simulation results are verified by deformation and variable stiffness tests. It is proved that the modular joint has good rigid-flexible coupling characteristics.

Keywords:

Subject: Engineering - Mechanical Engineering

1. Introduction

A soft robot has good flexibility[1],more degrees of freedom, adapts to active and passive deformation, and is friendly to dynamic, unknown ,and unstructured environments, widely used in military reconnaissance, disaster rescue and scientific exploration, and other vital fields. However, due to the low stiffness of compliant structures and soft materials[2], the bearing capacity of soft robots is generally low. Insufficient carrying capacity[3] has become the most significant obstacle limiting the range of soft robots; It is also a common critical technical problem in this field[4].

In the current research in this area, Various soft robots have been introduced[5]. Most soft robots are inspired by natural creatures; The driving method of the soft robot includes pneumatic[6], Electrically active polymer[7], Shape memory alloy[8], magnetorheological Fluid[9], and cable-driven methods[10]. Due to the PNEU-NET software drive[11], has the advantages of large deformation and high efficiency. It has been widely innovated and applied by researchers. There are several methods for varying stiffness with different techniques, Such as variable stiffness materials[12], Electrically induced unstable stiffness materials[13], and pressure-induced unstable stiffness method[14]. Cheng N G et al.[15] of the University of Hong Kong, China designed and manufactured an elephant trunk-shaped gripper. In the local area, the stiffness can be adjusted by the reversible interference of the particle medium. S.M. Hadi Sadati et al. [16] proposed an idea of scale interference inspired by fish scales. By controlling the Coulomb friction between the rigid hierarchies to control the stiffness of the continuous manipulator, the concept of stiffness control of the soft robot arm is broadened. Ali Shiva et al.[17] took inspiration from the confrontational behavior of the octopus arms and proposed a variable stiffness method that can control the attitude and stiffness of the robot simultaneously by pneumatic and tendon-driven reverse operation. Ying Wei et al.[18] proposed a method to adjust the stiffness of the robot spine based on the spherical joints using vacuum energy. The stiffness can be increased by 13 times, but the positioning control of the mechanism is only analyzed for the controllability of the stiffness. Li et al. [14] designed the gripper based on the concept of passive particle interference. When the pressure changes from 20 KPa to 80 KPa, The stiffness can be increased by more than six times, and the bending process and the stiffness increase are achieved simultaneously. However, the variable stiffness uses particle interference, The bending motion range is still limited, and the fluidity of particles in the particle package will affect the stability of the fixture stiffness. Yanzhi Zhao et al.[19] proposed an extensive range of variable stiffness self-locking soft continuous robots based on interference phenomenon. The textile smooth rope restraint mechanism based the particle interference mechanism uses the low elasticity and high toughness of fiber, the excellent fluidity of spherical particles, and the rigidity of particles themselves. A variable stiffness self-locking soft robot is constructed. The shape of the robot will not change significantly after the stiffness change. Loai A.T. Al A beach et Al. [20] developed a variable stiffness multi-finger dexterous gripper. The gripper uses pneumatic muscles for compliance, and by increasing the pressure on all actuators, It can improve the stiffness of the grip independently without changing the position of the fingers. But the deformation recovery is not ideal. Loai Al Abeach et Al.[21] proposed the design, analysis, and testing of a variable stiffness three-finger soft gripper. It uses pneumatic muscles to drive the finger and changes the stiffness of the finger by particle clamping. As the stiffness of the finger increases due to friction caused by the granular interference, the positioning accuracy of the extended finger (i.e., opening the grip) decreases; that is, the muscle is not pulled back to the original extended length. Yujia Li et al.[22] proposed a flexible robot with variable stiffness based on pre-inflation, particle interference, and origami technology. When the origami structure is compressed, the particles are squeezed by the compression force and the increased pressure of the three air chambers, which increases the overall stiffness of the robot. Tao Wang et al. [23] proposed a new layer interference variable stiffness technology, which uses electrostatic attraction to squeeze the material layer to generate friction, which in turn generates interference. It is characterized by high stiffness variation and space saving. However, the formation of local low pressure areas between the contact surfaces results in a degree of randomness in the stiffness generated under applied voltage. Liu Zhaoyu et al. [24] of Shanghai Jiao Tong University proposed a method combining soft crawling robots with variable stiffness technology to achieve the obstacle avoidance movement of soft crawling robots. When a modular biomimetic soft robot with variable stiffness adjustment passes through obstacles of the same height, There will be no apparent collision with obstacles. Although there are many research results on variable stiffness, the coupling characteristics of deformation and variable stiffness are not studied deeply[25,26]. However, considering the flexibility and bearing capacity of soft robots simultaneously requires good rigid-flexible coupling characteristics [27,28]. From the research literature, there are few reports on this aspect.

Therefore, this study focuses on the innovative new modular soft robot joint with variable stiffness, and conducts research on the coupling characteristics of joint deformation and variable stiffness. The deformation and variable stiffness model of modular soft joints is established and solved to obtain the correspondence between gas pressure and deformation amount and applied current and joint stiffness. The finite element analysis method is used to simulate and analyze the deformation characteristics and variable stiffness characteristics of modular joints based on Yeoh model, and the rigid-flexible coupling characteristics of modular joints are revealed through deformation and variable stiffness tests.

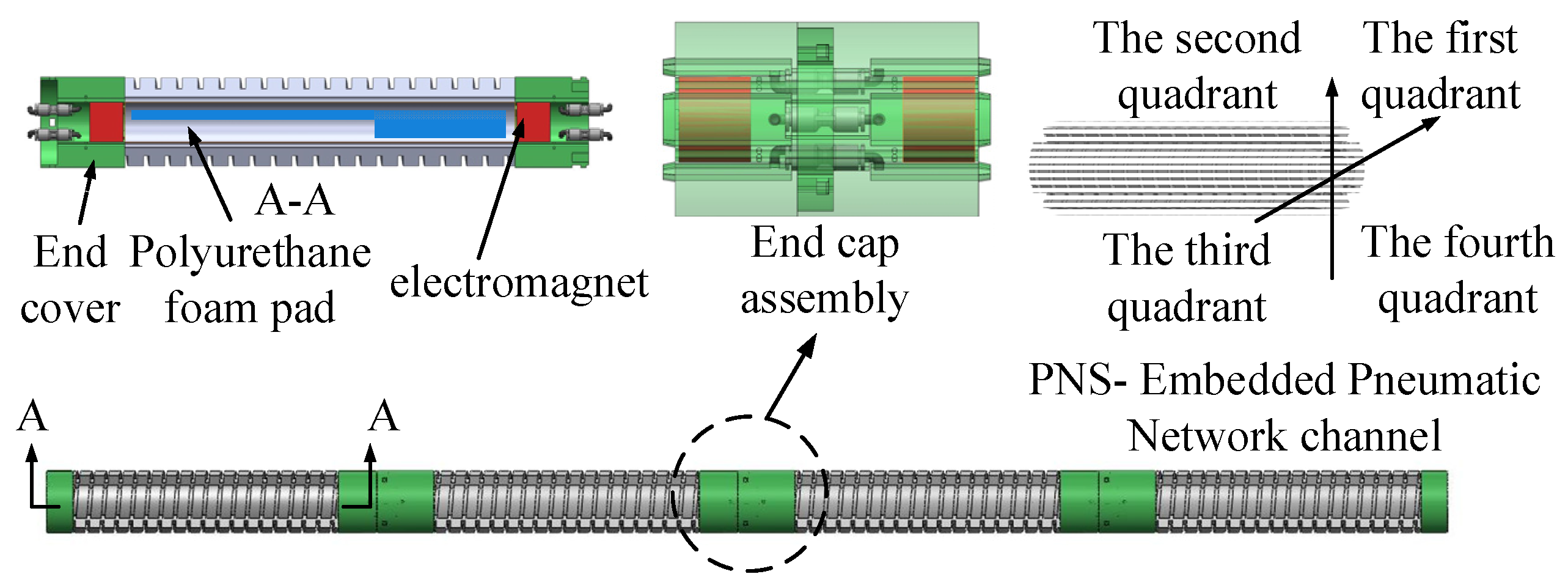
2. Structure Principle

The new modular soft robot joint body material with variable stiffness is made of 50A silicone rubber, and the entire modular joint is composed of four drive modules. As shown in Figure 1, each driver module is divided into three parts: It is composed of a variable stiffness system, a flexible deformation system, and a connecting end cover. As shown in the upper left view and upper right view of Figure 1, the axis of the flexible joint is the first channel for installing polyurethane foam pads, the outer circumference of the flexible joint is provided with a second channel for installing wires, and between the first channel and the second channel there are 4 embedded pneumatic network channels at 90° to each other, distributed in the entire structure of the joint, through the combination of positive and negative pressure gas changes of different pressures of the 4 channels, different degrees of bending in all directions can be realized

The variable stiffness system consists of electromagnets at both ends of the joint and polyurethane foam pads filled with magnetorheological fluid, which are centrally placed at the pivot position of each joint. The electromagnet is powered by the DC power supply, and the current in the electromagnet circuit is adjusted by changing the resistance of the varistor in the electromagnet loop, so that the electromagnet produces different magnetic field strengths, and the viscosity of the magnetorheological fluid is changed by the size of the magnetic field strength[29], so as to realize the dynamic and continuous adjustment of modular joint stiffness.

The flexible deformation system includes a pneumatic flexible pneumatic joint which can bend and deform with the change of air pressure, and a pneumatic system that provides an air source for the joint. Each air chamber of the common is connected at the bottom. Each drive module has four air pipes, and each air pipe is inserted into the pneumatic channel connecting the end cover. When inflating, the air passes through the inflatable tube to each chamber of the soft joint. As the chamber pressure increases, each compartment expands, causing the smooth joints to bend[30]. As shown in Figure 2(b), the air chamber after expansion.

The end caps of the two ends of the flexible joints are 3D printed with PLA material and placed on polyurethane foam pads filled with magnetorheological fluid. Embedded pneumatic network channels in two adjacent loose joints are connected through quick joints and hoses in the end covers.

3. Modeling and Solving

Deformation and variable stiffness are two important indexes to evaluate modular joints. The modular joint is modeled mathematically from these two aspects.

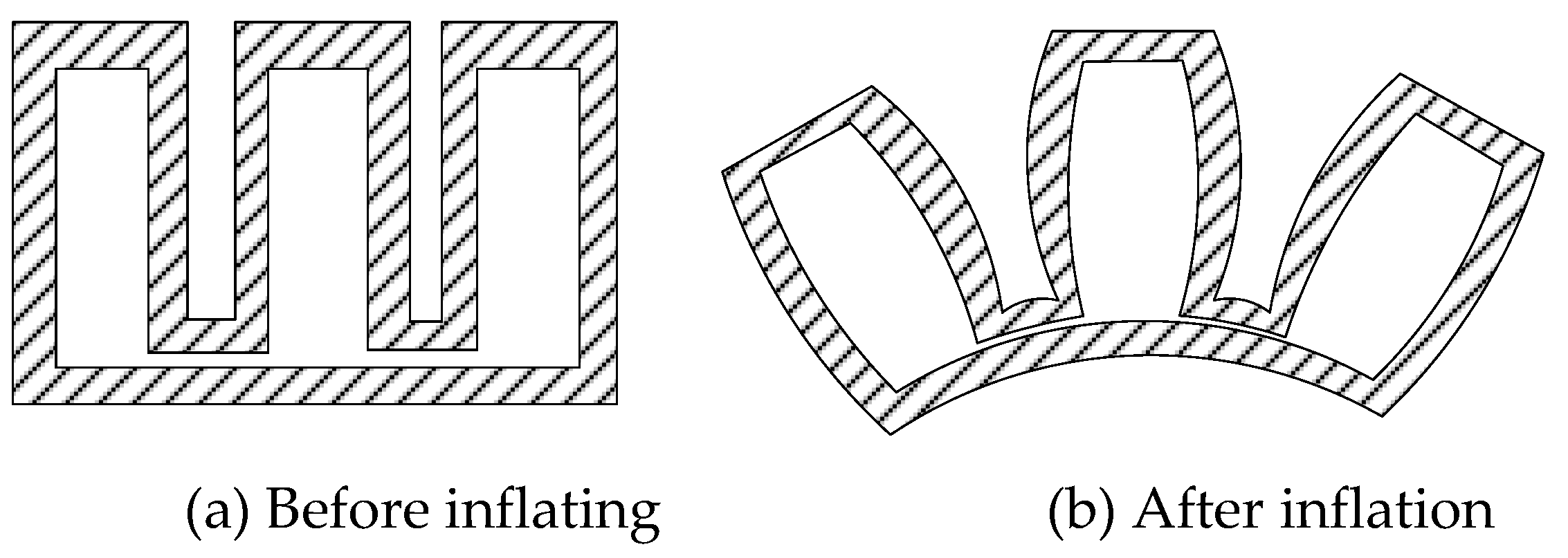
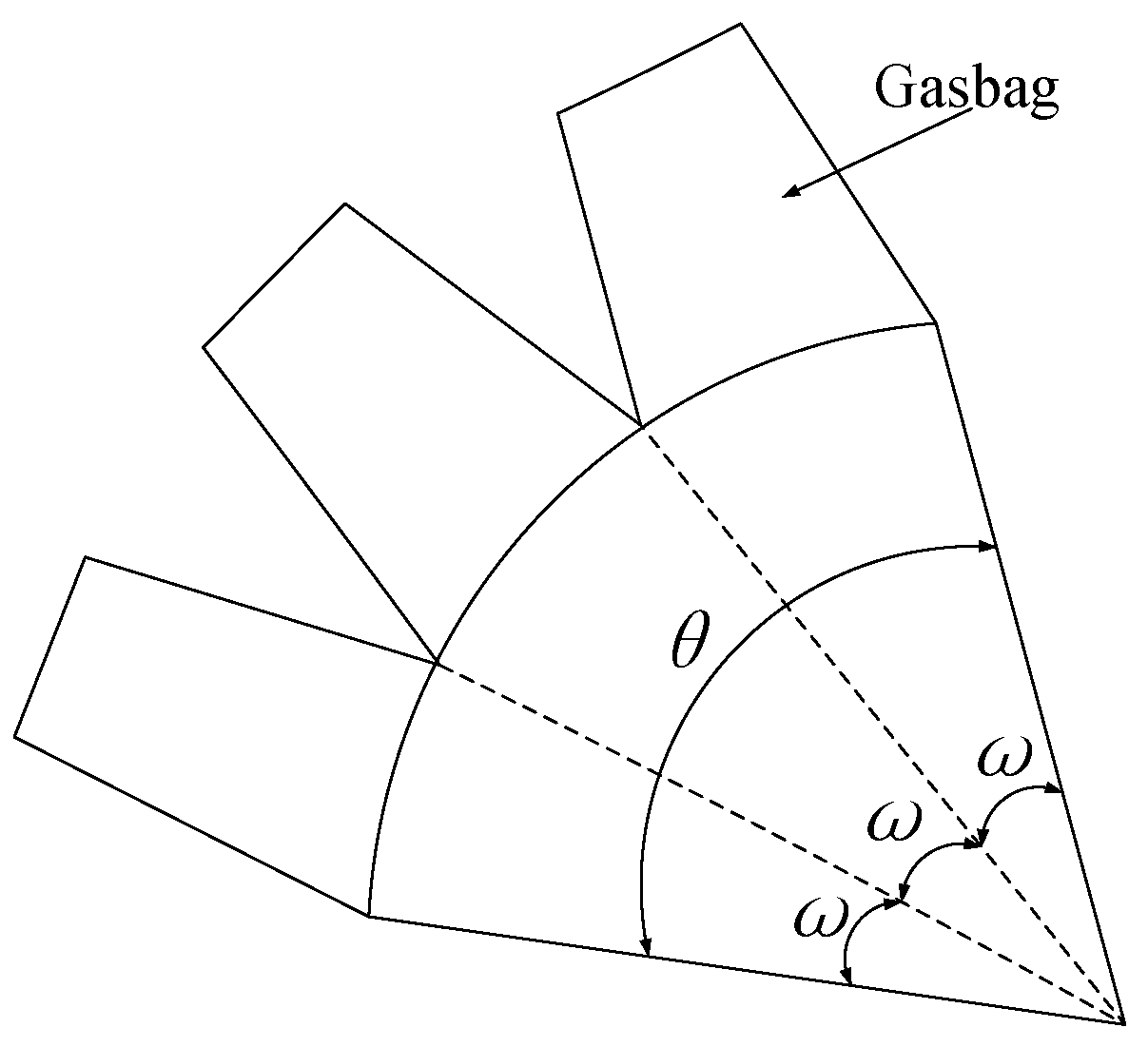
3.1. Deformation Modeling

As shown in Figure 2(a), the cavity in the exhaust state is rectangular, and the elongation of a single embedded pneumatic network channel of the joint after inflation and expansion is less than the elongation away from the axis layer, so that the joint is convex and bent away from the axis layer.

To simplify the model, the following assumptions are proposed :(1) the material used cannot be compressed; (2) The soft joint keeps constant curvature bending during bending. The parameters of the air chamber[31] are shown in Figure 3, and their values are shown in Table 1.

During joint design, each air cavity is designed with a symmetric structure, and the structural parameters are consistent, as shown in Figure 3. Therefore, when ventilating an embedded pneumatic network channel, each air cavity in the medium is subjected to the same pressure and bending Angle.

As shown in Figure 4, the total number of air cavities in this channel is

n

, where the bending Angle of each air cavity is

ω

, then the whole bending Angle is:

θ = n ω

(1)

The relationship between gas pressure and bending angle can be solved by the structural parameters of a single air cavity, assuming that the neutral axis length is unchanged when the modular joint is deformed, and the bending deformation changes uniformly in the length direction, so as to establish an ideal physical model of the joint structure, as shown in Figure 5, the relationship between gas pressure and bending angle can be converted into the relationship between gas pressure and deformation.

Under the condition of ignoring the self-weight of the joint and its external force, it can be seen from the law of conservation of energy that the work done by the pneumatic system to inflate the embedded pneumatic network channel is completely converted into the energy of silica gel deformation, that is, the work done by the gas pressure is equal to the energy of the deformation of the soft joint, which is expressed by its formula as:

P d V_{a} = V_{r} d U

(2)

Among them,

P

is the gas pressure of the pneumatic system to inflate the embedded pneumatic network channel,

V_{a}

is the volume of the air cavity after inflation,

V_{r}

is the volume of silica gel after inflation, and

U

is the strain energy. Since it is assumed that the silica gel is incompressible before and after inflation, its volume remains the same, so it can be obtained:

V_{r} = g (2 d + e) (b + c + a) + g (d + f) (a + b + d) - e (b + c - d) (g - 2 d)

(3)

V

is the total volume after inflation, so

V_{a} = V - V_{r}

, thus:

V_{a} = \frac{g (1 + β) (2 d + e) (b + c + a)}{2} + \frac{g f (a + b + d)}{2}

(4)

Where

β

is the primary elongation in the direction of the air cavity length,

β = \frac{R ω}{R \sin ω} = \frac{ω}{\sin ω}

R

is the curvature radius of joint bending. Taking the derivative of

ω

and combining equations (3) and (4), the relationship between the bending Angle of a single air cavity and the gas pressure can be obtained:

P = \frac{2 {(s i n ω)}^{2} V_{r} \frac{d U}{d ω}}{[(2 d + e) (b + c + a) + f (a + b + d)]} \frac{1}{g (s i n ω - ω c o s ω)}

(5)

Where

a = 4, b = 4.5, c = 14, d = 10, e = 5, f = 7, g = 44, h = 25

, silica gel material is a second-order Yeoh model, So

U = C_{10} (I_{1} - 3) + C_{20} {(I_{2} - 3)}^{2}

, Among them,

I_{1} = I_{2} = β^{2} + \frac{1}{β^{2}} + 1

. When the gas pressure was set to 0KPa, 25KPa, 50KPa, 75KPa, 100KPa, and 125KPa, respectively, the bending Angle results of corresponding joints were solved, as shown in Table 2.

As shown in Figure 5, when the gas with a certain pressure is injected into the joint, the relationship between deformation and bending Angle is as follows:

\{\begin{cases} R_{1} = \frac{L_{0}}{π} \cdot \frac{180 °}{θ} \\ L_{1} = 2 π (R_{1} - R) \cdot \frac{θ}{360 °} \end{cases}

(6)

L_{0} - L_{1} = \frac{π R θ}{180 °}

(7)

Where

R

is the distance of the edge of the joint from the neutral axis,

L_{0}

is the initial length of the joint,

L_{1}

is the length after joint deformation,

θ

is the bending angle of the joint, and

R_{1}

is the bending radius of the joint.

The bending Angle in Table 2 above is transformed into the deformation amount by formula (7), and the deformation amount is used to reflect the deformation effect of the modular joint. The relationship between deformation amount and gas pressure in the theoretical model is shown in Figure 6.

The image of the relationship between gas pressure and joint deformation obtained by kinematically modeling the modular joint conceptual model is shown in Figure 6. When the gas pressure changes from 0 to 100KPa, the deformation increases approximately linearly with the increase of gas pressure, and the gas pressure increases slightly after 100KPa, the deformation has a large increase, and the maximum pressure of the drive module does not exceed 125KPa[32] after strength verification, and the expected deformation effect can be achieved..

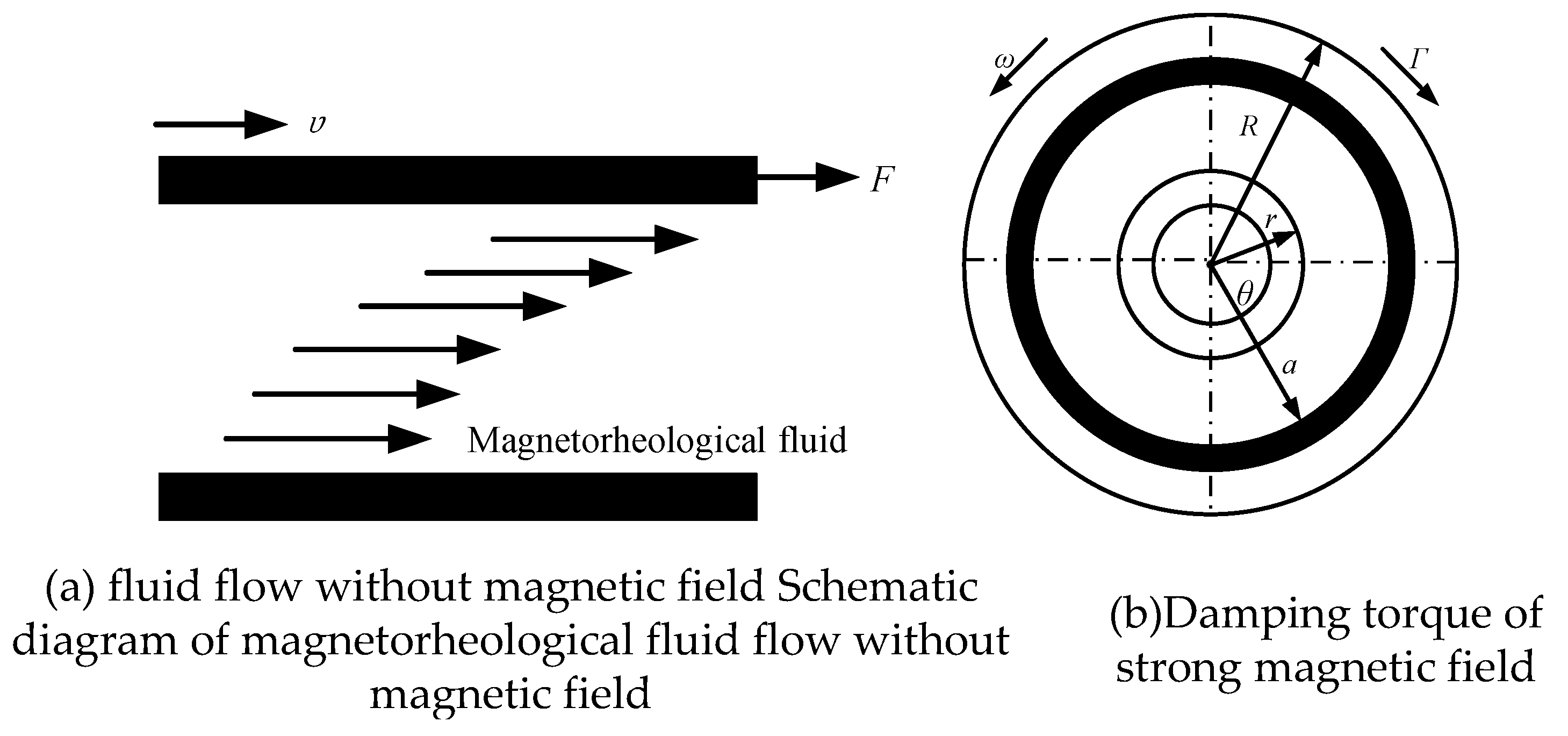
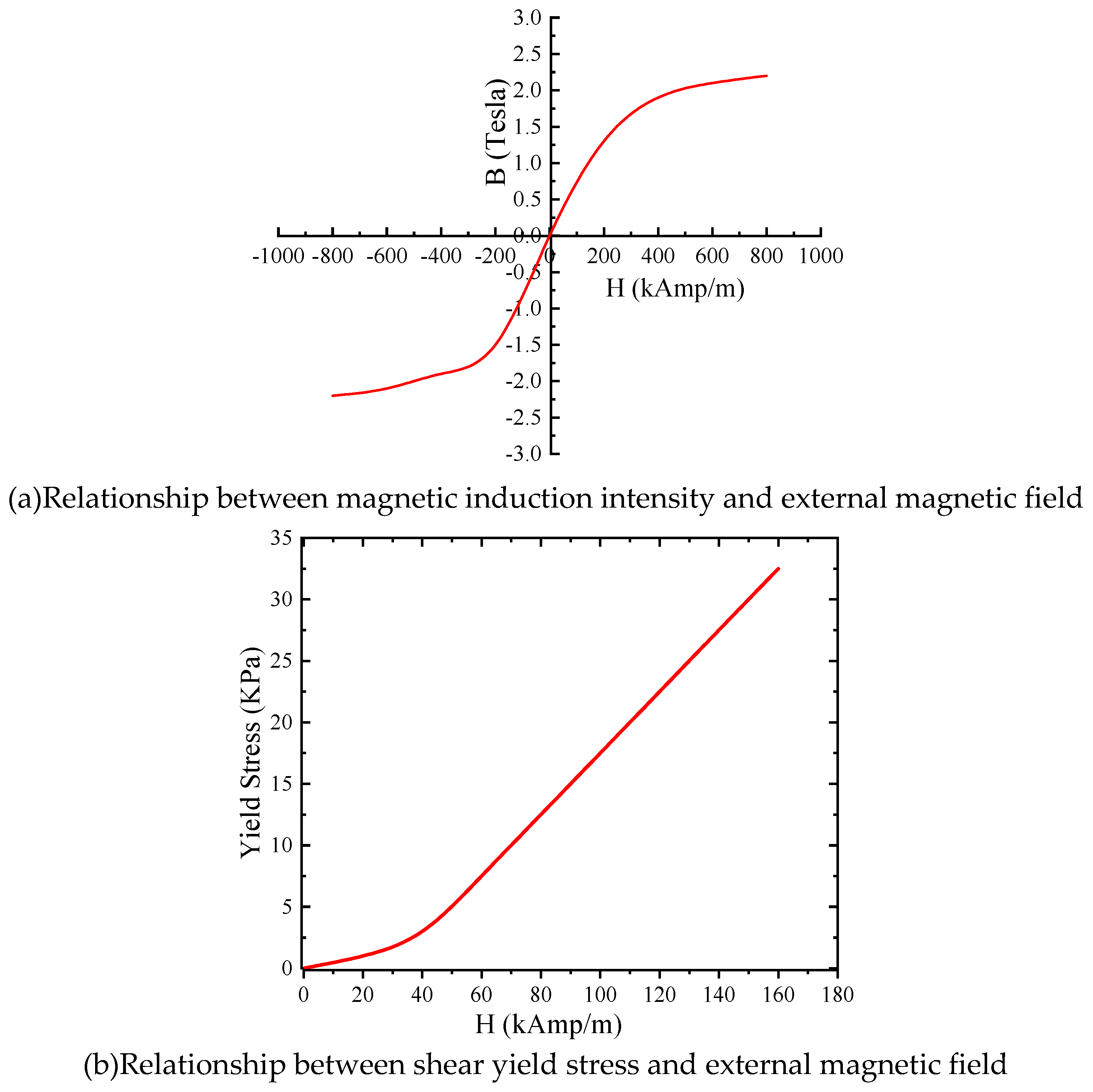
3.2. Variable stiffness modeling

After the soft joint is deformed, a certain stiffness is required to enhance the bearing capacity, and the greater the stiffness, the stronger the bearing capacity. The stiffness of the robot includes a variety of rigidities, such as static stiffness, dynamic stiffness, servo stiffness and mechanical stiffness. Considering that the bending deformation process of soft actuators has little influence on dynamic stiffness, therefore, this paper only analyzes the change of static stiffness[33].

The transformation of force and motion is introduced to establish a variable stiffness model of modular joints. Under the action of external force

f

, the rotational momentum of the joint is

θ

. When the external energy and the rotational speed of the common are small enough, they can be regarded as an approximately linear relationship:

k = \frac{f}{θ}

(8)

Where

k

represents the stiffness of the joint.

For the static stiffness of the drive module, the modular joint can be regarded as a system. When the joint is stationary, the velocity and angular velocity are zero. So angular velocity

\dot{θ}

is equal to zero, Angular acceleration

\ddot{θ}

is equal to zero. Therefore the torque

τ

acting on the joint satisfies:

k_{s} = \frac{τ}{θ}

(9)

Among them,

k_{s}

is the static stiffness of the modular joints.

The operating mode of the variable stiffness model in the drive module is shown in Figure 7(a). When the electromagnet is not energized, magnetorheological fluid is not magnetic, and magnetorheological fluid at this time is a liquid form with low viscosity and almost no damping moment in it. The effect of variable stiffness in flexible joints is virtually zero. When the electromagnet is energized, magnetorheological fluid particles will generate magnetism and connect into a chain structure, and magnetorheological fluid can become a semi-solid state with high viscosity within milliseconds[34]. When the magnetic field encountered by the magnetorheological fluid increases, the magnetorheological fluid will become a solid-like form, and in this change, the shear stress of the magnetorheological fluid will gradually increase, resulting in damping torque. The damping torque diagram of the structure is shown in Figure 7(b).

To solve the flow of the magnetorheological fluid in the driving module, the following assumptions are made [35]:

(1) The magnetorheological fluid cannot be compressed in the flow process and can maintain long-term stability;

(2) The flow effect of magnetorheological fluid in both axial and radial directions of the joint is negligible;

(3) The flow velocity of the magnetorheological fluid in modular joints is only related to the joint radius;

(4) The magnetorheological fluid has the same pressure in the radial direction of the joint.

The distribution of damping torque is concentric circles with a small radius

r

and large radius

R

. When the modular joint moves with angular velocity

ω

, the joint will produce a torque

Γ

in the direction opposite to the angular velocity. Let the annular area of the disk be

d a

and the damping torque produced by the disk be

Γ

Γ = Γ_{H} + Γ_{N} = \frac{2}{3} π τ (H) (R^{3} - r^{3}) + \frac{π η ω}{2 h} (R^{4} - r^{4})

(10)

The

Γ_{H}

is the magneto-induced torque generated by the action of the applied magnetic field on the viscosity of the magnetorheological fluid, and the

Γ_{N}

is the non-magneto-induced torque generated by the density of the magnetorheological fluid after yield.

From the above formula, it can be seen that the stiffness change of the drive module is related to the change of magnetorheological fluid viscosity. When the electromagnet is not energized, the magnetorheological fluid is not magnetic, and the magnetorheological fluid at this time is a liquid form with low viscosity, and the constitutive relationship at any point is:

τ = η \dot{γ}

(11)

Here

τ

is the shear stress generated by the magnetorheological fluid in modular joints,

η

is the viscosity of the magnetorheological fluid in the absence of a magnetic field, and

γ

is the shear strain caused by the magnetorheological fluid viscosity in modular joints.

τ = \{\begin{matrix} sgn (\dot{γ}) τ_{y} (H) + η \dot{γ} τ \geq τ_{γ} \\ 0 τ < τ_{γ} \end{matrix}

(12)

where

τ_{y}

is the shear yield stress generated by the magnetorheological fluid in the modular joint. The magnitude of the magnetic field generated by the electromagnet is positively correlated with the shear yield stress generated by the magnetorheological fluid.

Therefore, the variable stiffness characteristics of magnetorheological fluids can be reflected by electromagnetic field magnetic induction strength analysis. The magnetization curve of magnetorheological fluid is shown in Figure 8.

The stiffness change of the driving module is related to the viscosity change of the magnetorheological fluid. It can be seen from Figure 8 that the magnetic induction intensity

B

increases linearly with the increase of the magnetic field intensity within 400kAmp/m, so the magneto-induced yield stress

τ

and the external magnetic field intensity H have an approximately linear relationship:

τ = α H

(13)

The permeability

μ_{m}

of Fluid is:

μ_{m} = \frac{Β}{H}

(14)

Through equations (10) and (11), we can get:

τ (B) = \frac{α Β}{μ_{m}}

(15)

Magnetic field strength calculation formula:

H = \frac{N I}{L_{e}}

(16)

Substituting equation (13) into equation (10), we can obtain:

τ (I) = \frac{α N I}{L_{e}}

(17)

Equation (17) shows the relationship between magneto-induced shear yield stress, electromagnet parameters, and applied current.

4. Simulation Analysis

The finite element method is used to establish a model, simulate and analyze the aerodynamic loading process of the pneumatic soft robot, and investigate the deformation effect of the flexible joint by introducing different gas pressures into the channel under the same magnetic induction strength. The variable stiffness effect is investigated by the shear modulus of the joint under different magnetic induction strengths.

4.1. Parameter Settings

The viscosity parameter at a certain magnetic induction strength is converted into the shear modulus of the material, replacing the properties of the magnetorheological fluid, so as to determine the influence on the system deformation under different working conditions through simulation.

Disc type electromagnet is selected, and its structural parameters are shown in Table 3.

4.2. Deformation simulation

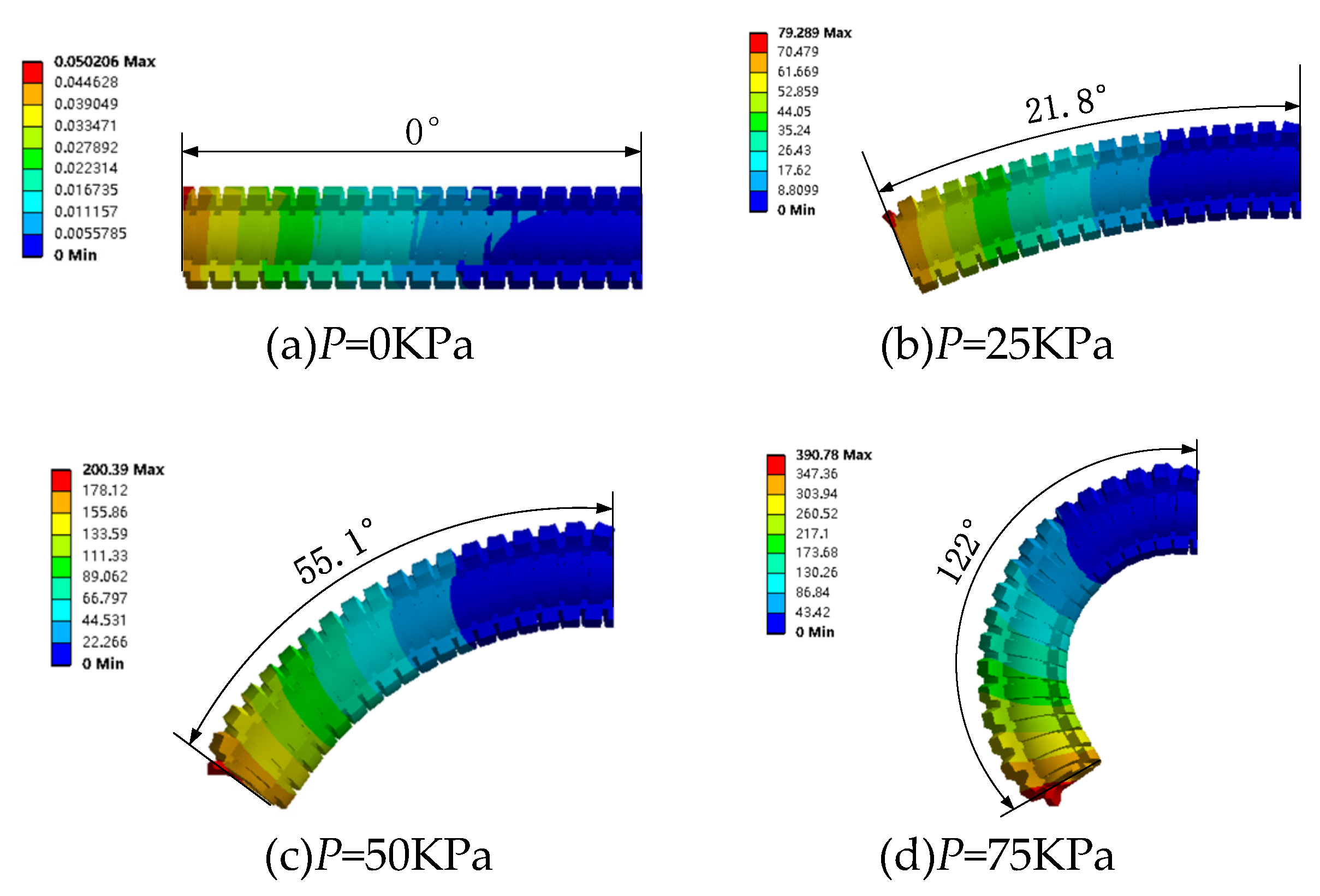
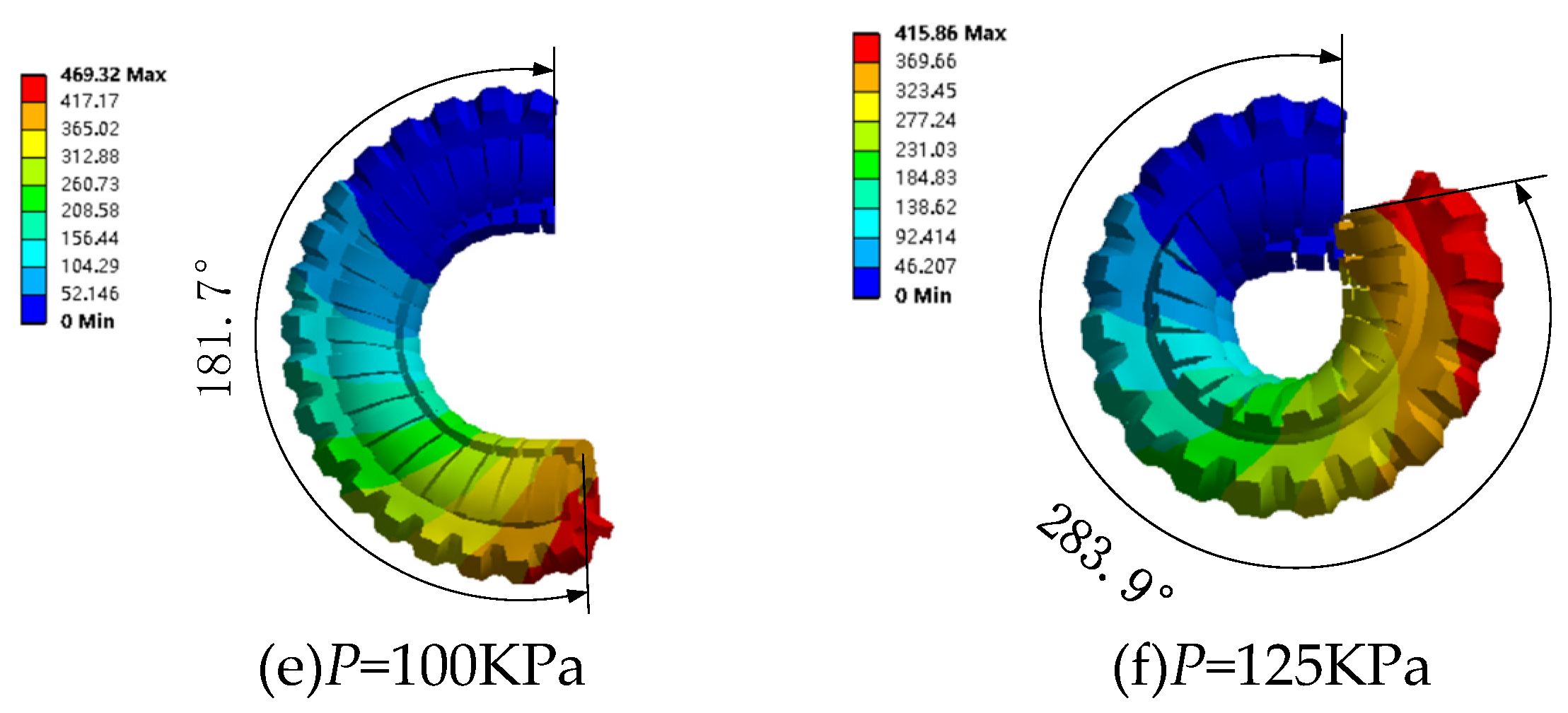
4.2.1. Deformation simulation without magnetic field

The constitutive model is established through the Yeoh model, and its density function is expressed as binomial parameters in the form of:

W = C_{10} (I_{1} - 3) + C_{20} {(I_{1} - 3)}^{2}

(18)

Where

I_{1} = λ_{1} + λ_{2} + λ_{3}

λ_{1}

is the axial stretch ratio,

λ_{2}

is the radial stretch ratio, and

λ_{3}

is the circumferential primary stretch ratio.

C_{10}

and

C_{20}

are the constant coefficients of Yeoh model silica gel materials. Make the material constant coefficients

C_{10} = 0.11

C_{20} = 0.02

The theoretical model of a single soft joint was taken as the object, and the bending deformation Angle was observed by applying 0-125KPa gas pressure to a single channel of the flexible actuator, as shown in Figure 9.

It can be seen from Figure 9 that the bending angle of the soft body joint gradually increases with the increase of gas pressure, the stress concentration appears on the side close to the gas source, and the stress gradually decreases on the side away from the air source, and with the increase of deformation, the stress concentration area begins to expand inward. The relationship curve between gas pressure and joint deformation is shown in Figure 10.

It can be seen from Figure 10 that when the gas pressure changes from 0 to 111KPa, the deformation is roughly linearly related with the increase of gas pressure, and the deformation is significantly deformed with the increase of gas pressure after 111KPa, which is prone to excessive material stress concentration and the risk of material rupture caused by over deformation.

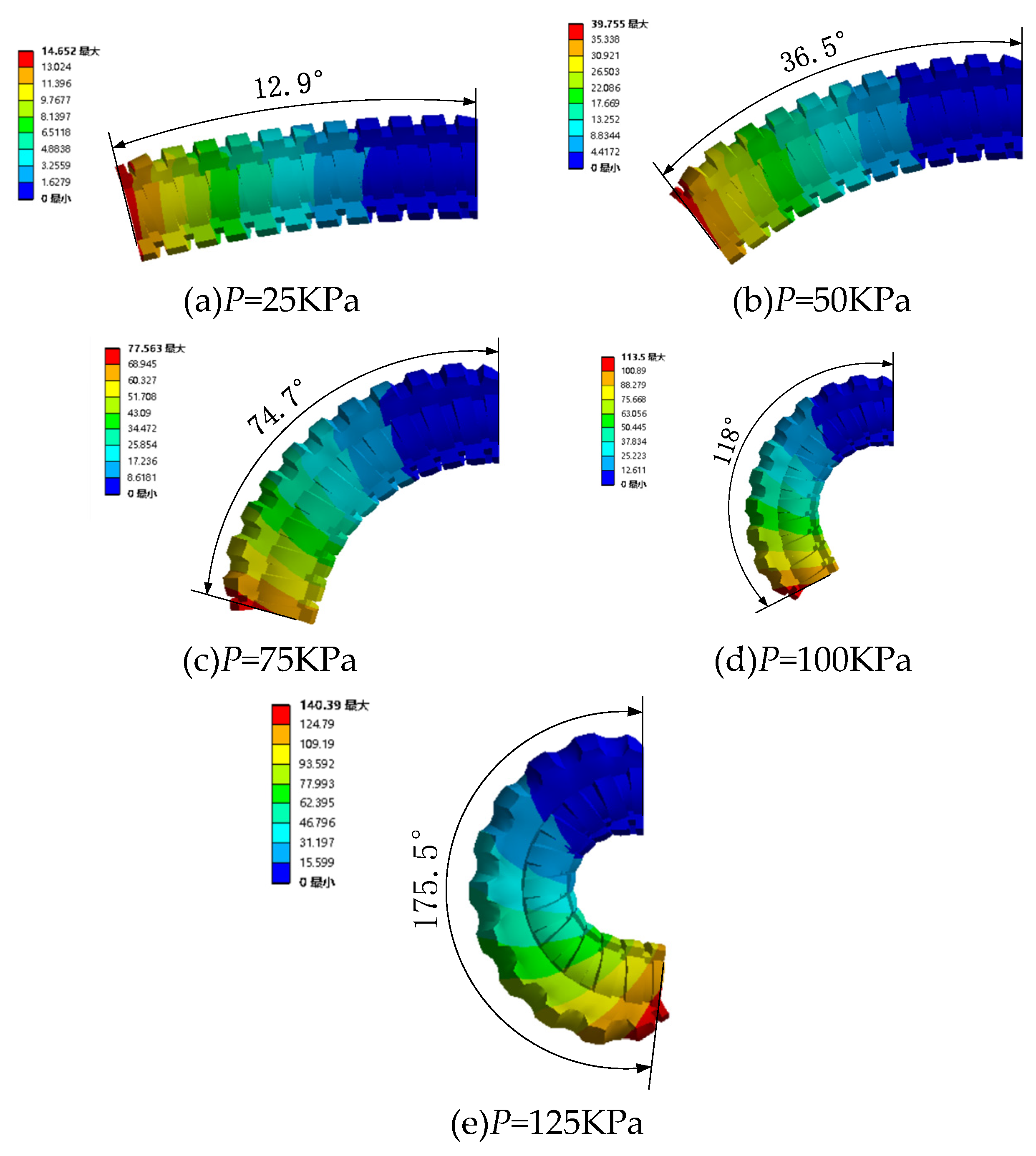
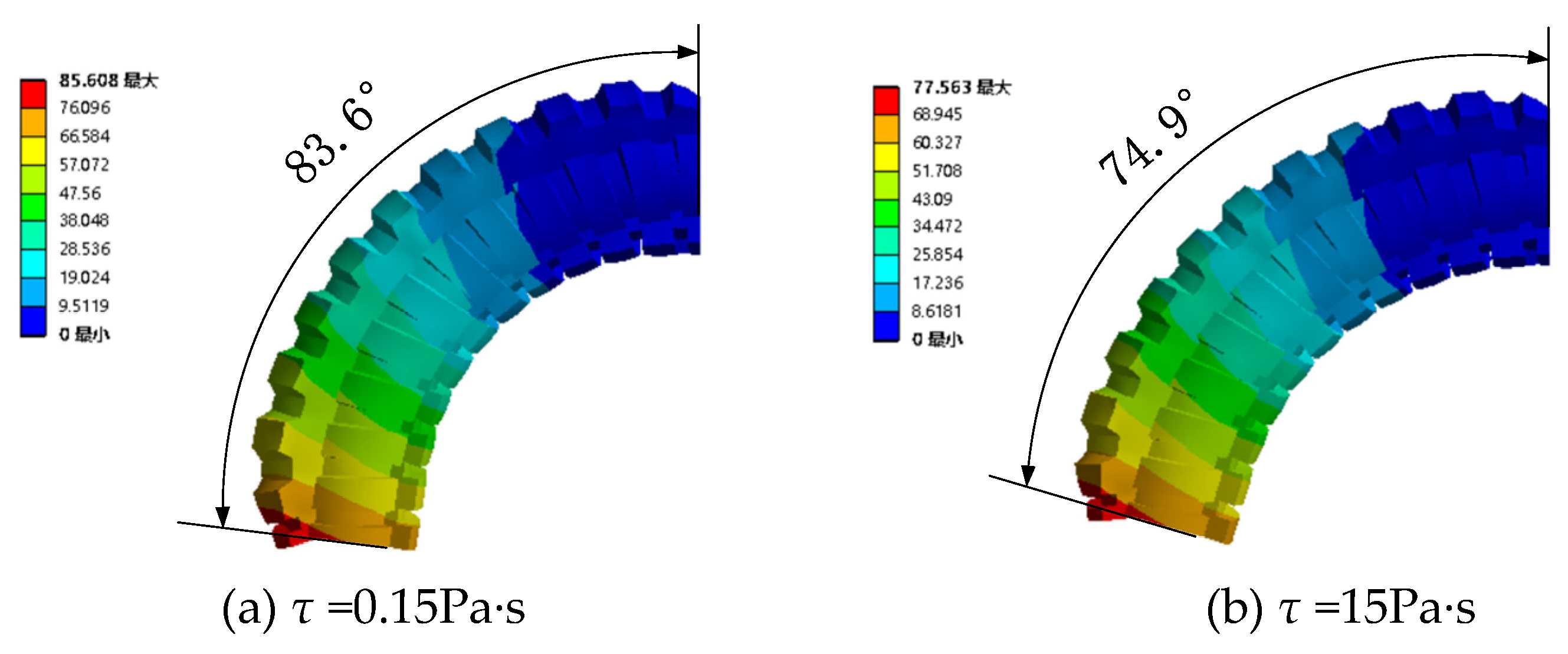
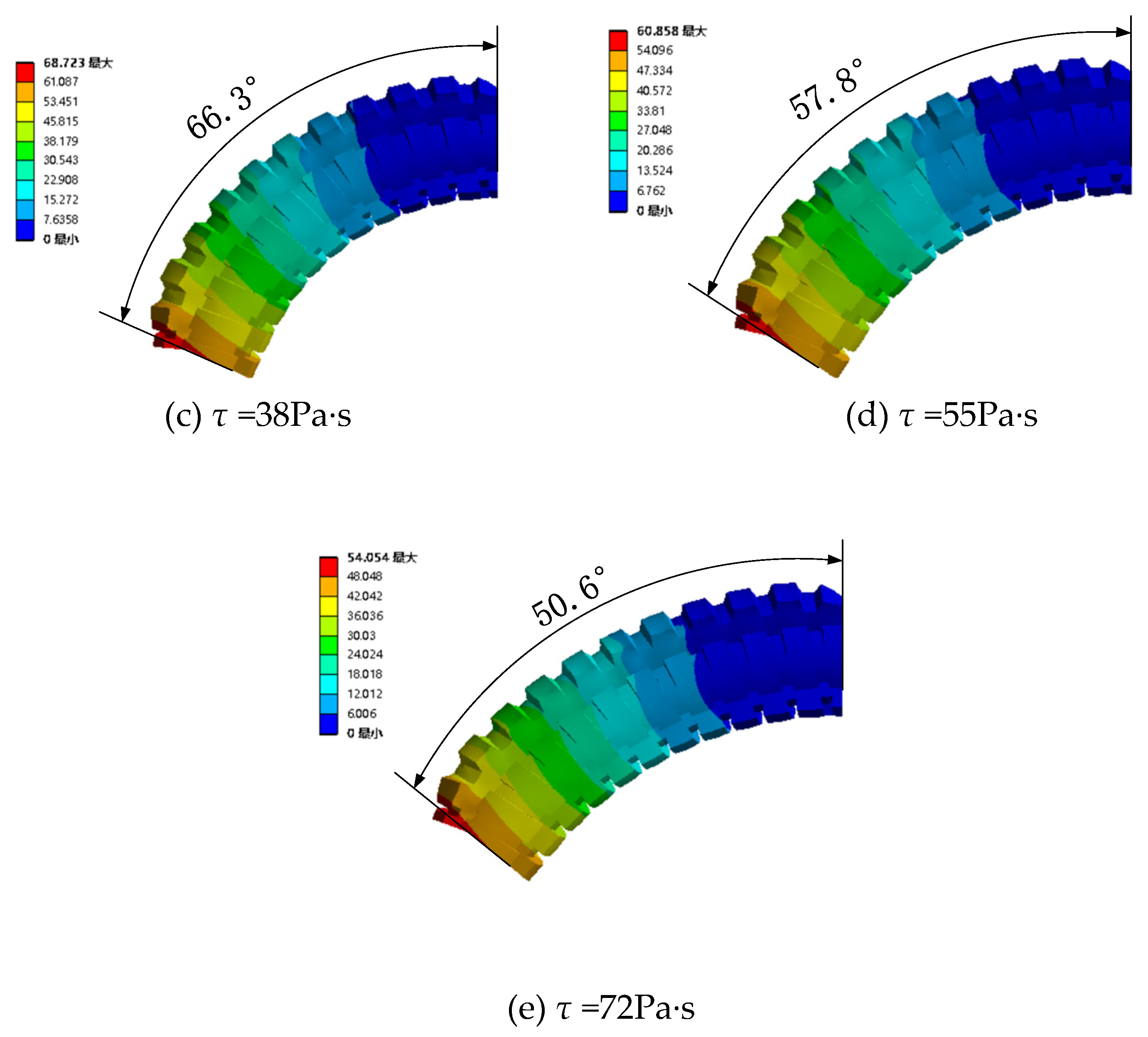
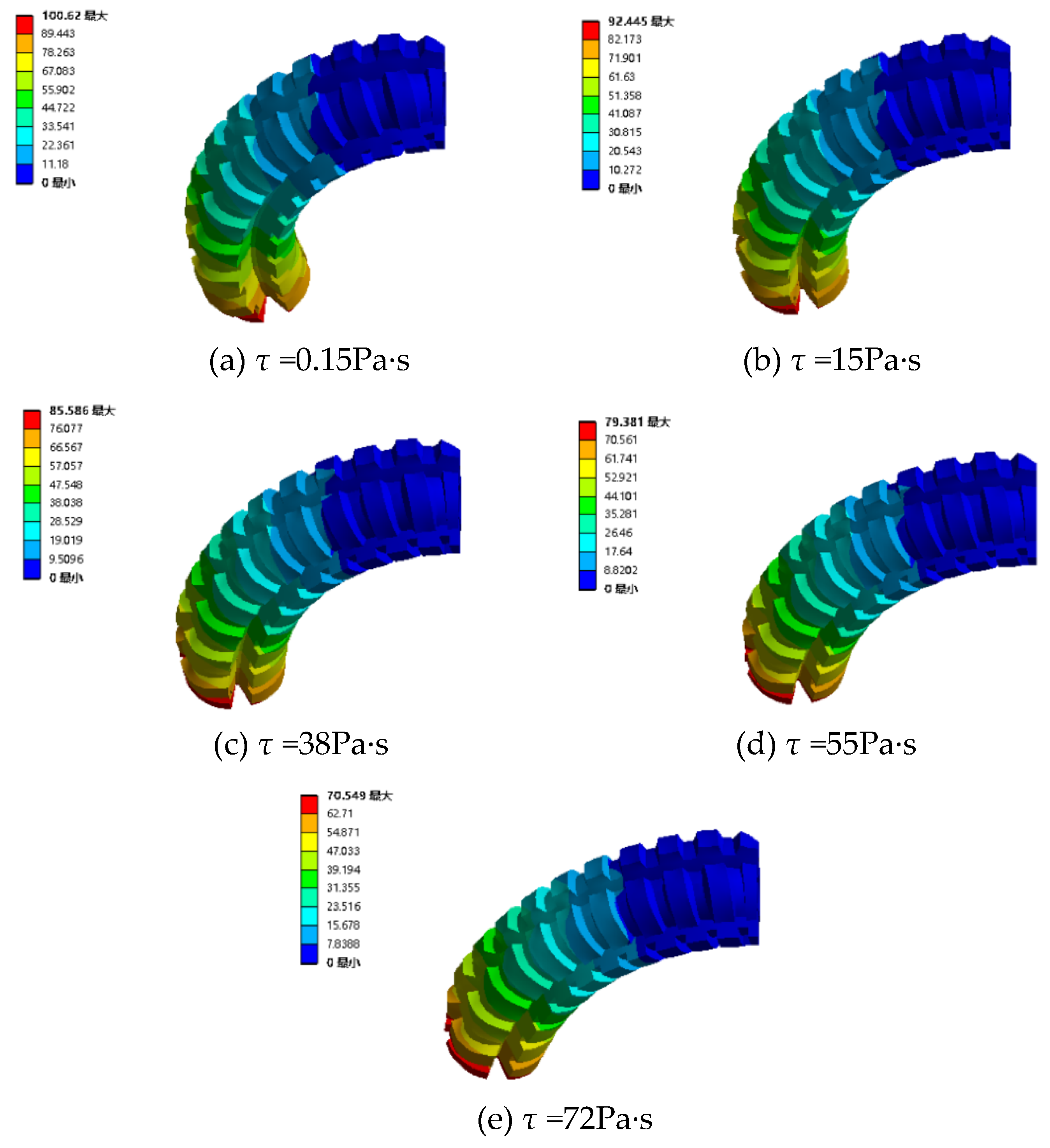
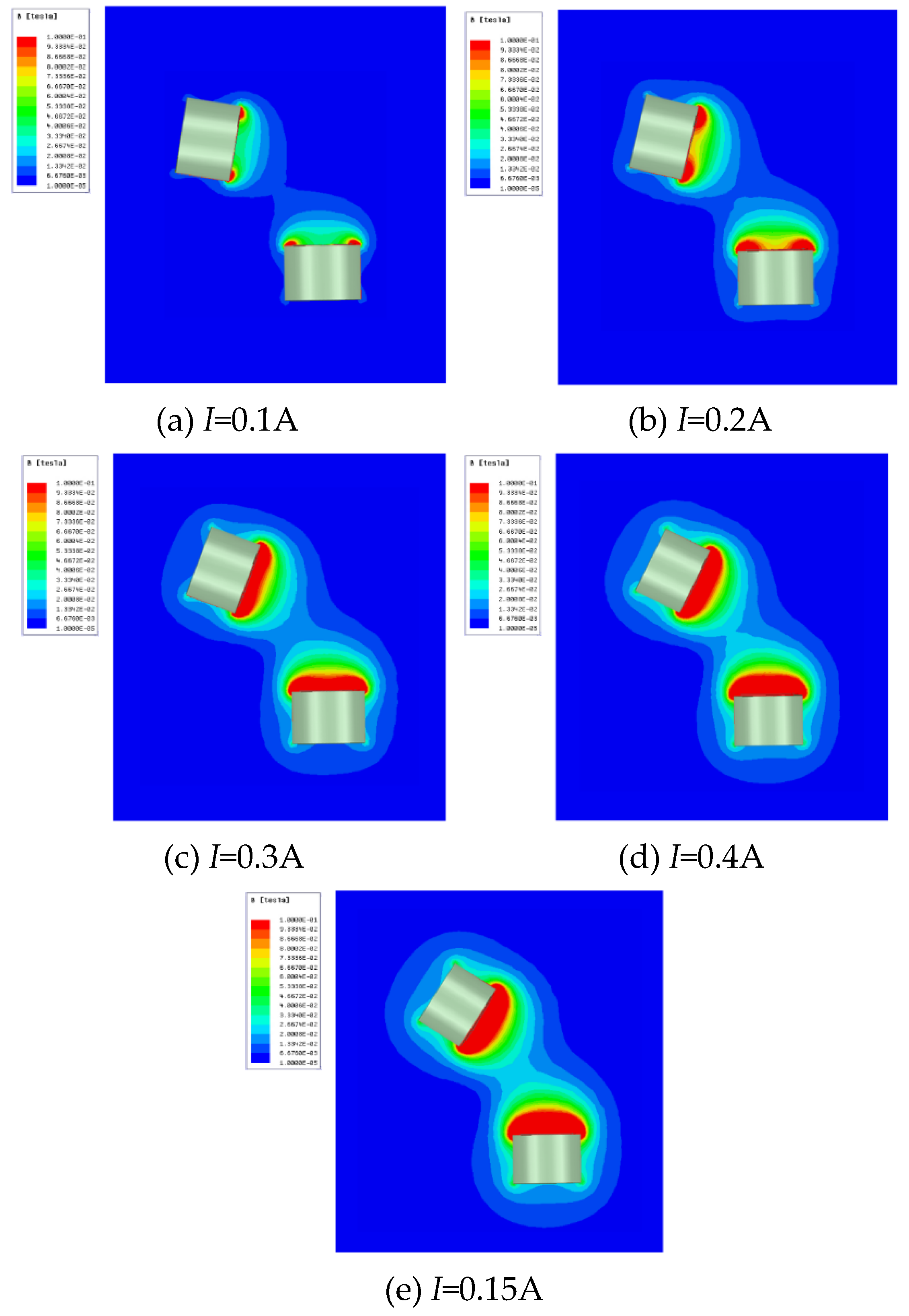
4.2.2. Pressurize single channel with different magnetic fields

Table 4 shows other gradient gas pressures for a single track.

As shown in Figure 11, when the viscosity is 55Pa·s and the gas pressure is 25KPa, 50KPa, 75KPa, 100KPa, and 125KPa, respectively, the deformation amount of soft joint gradually increases with the increase of air pressure.

When a single channel is introduced to a gas pressure of 75KPa, the bending change and stress change are shown in Figure 12, and the viscosity increases gradually as the magnetic field increases. By comparing the bending degree of soft joints with viscosities of 0.15Pa·s, 15Pa·s, 38Pa·s, 55Pa·s, and 72Pa·s, it can be seen that the greater the viscosity, the less obvious the joint deformation, the less obvious the surface stress, and the greater the shear force.

Similarly, since the working conditions of channel 1, channel 2, channel 3, and channel 4 are the same, the analysis results of gas pressure entering other media can be obtained by the same analysis method.

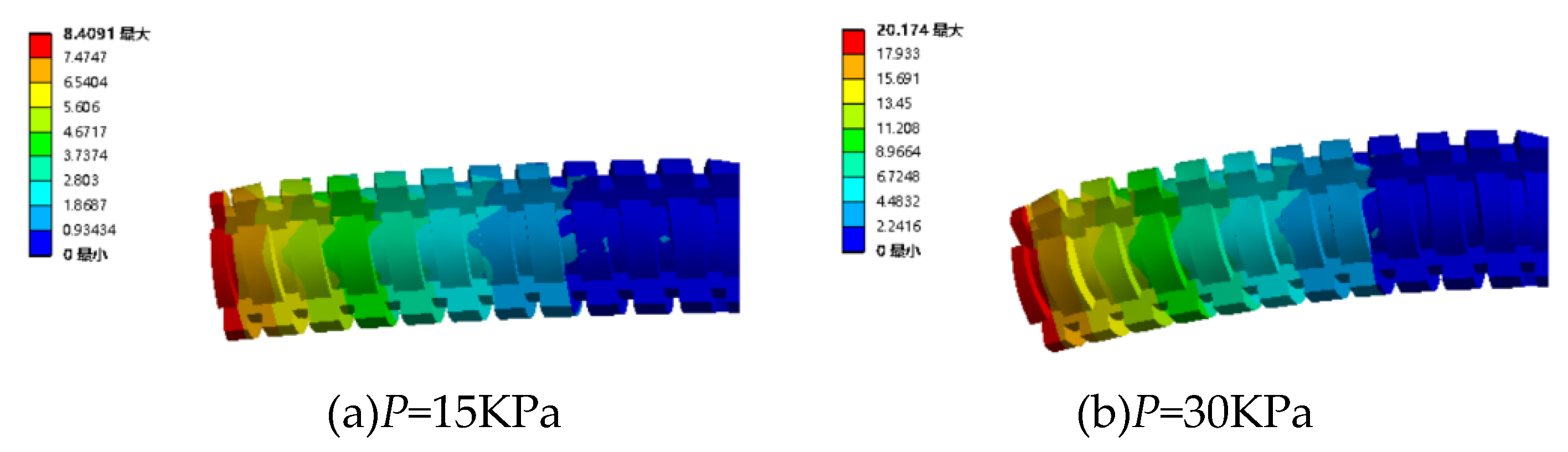
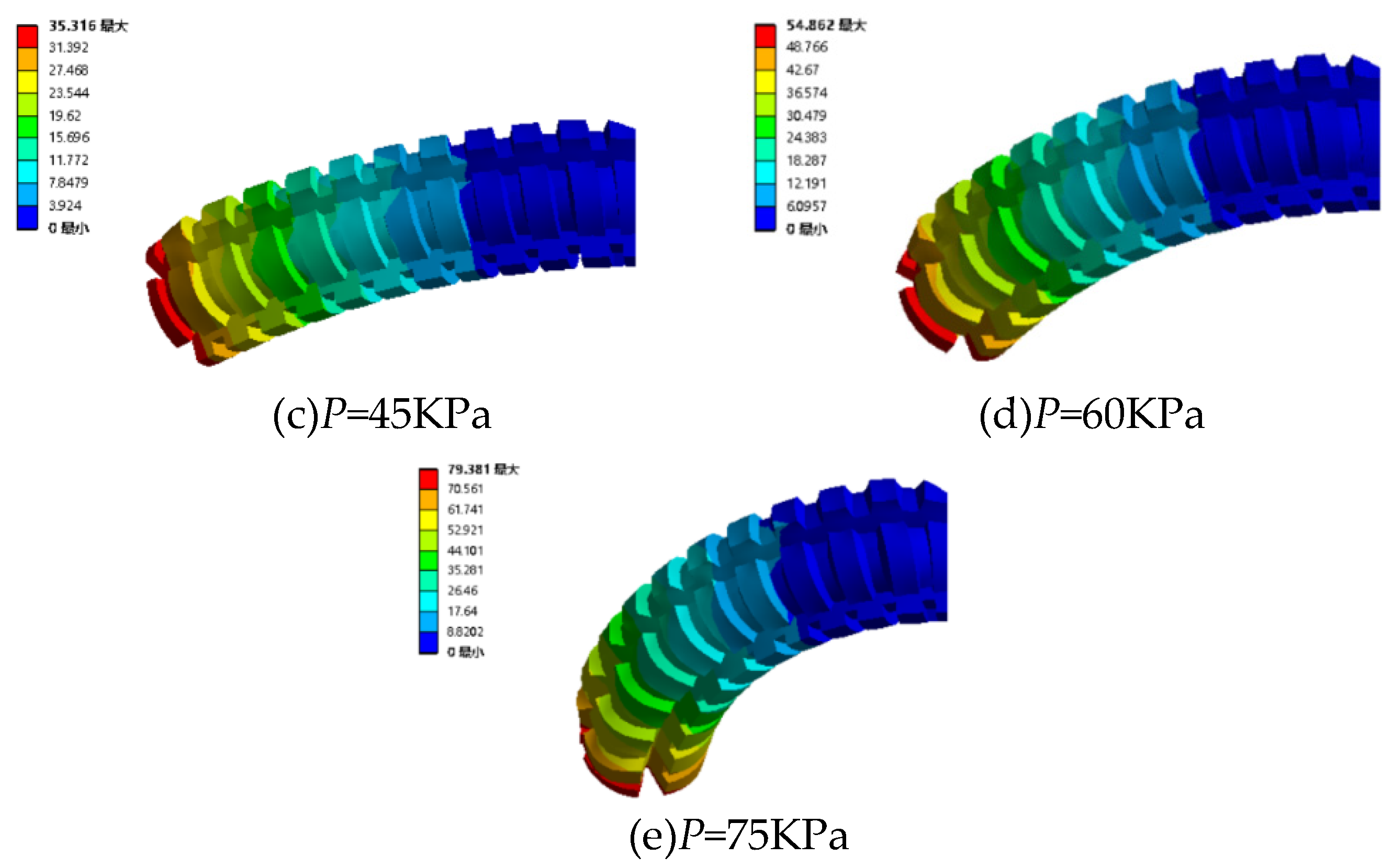
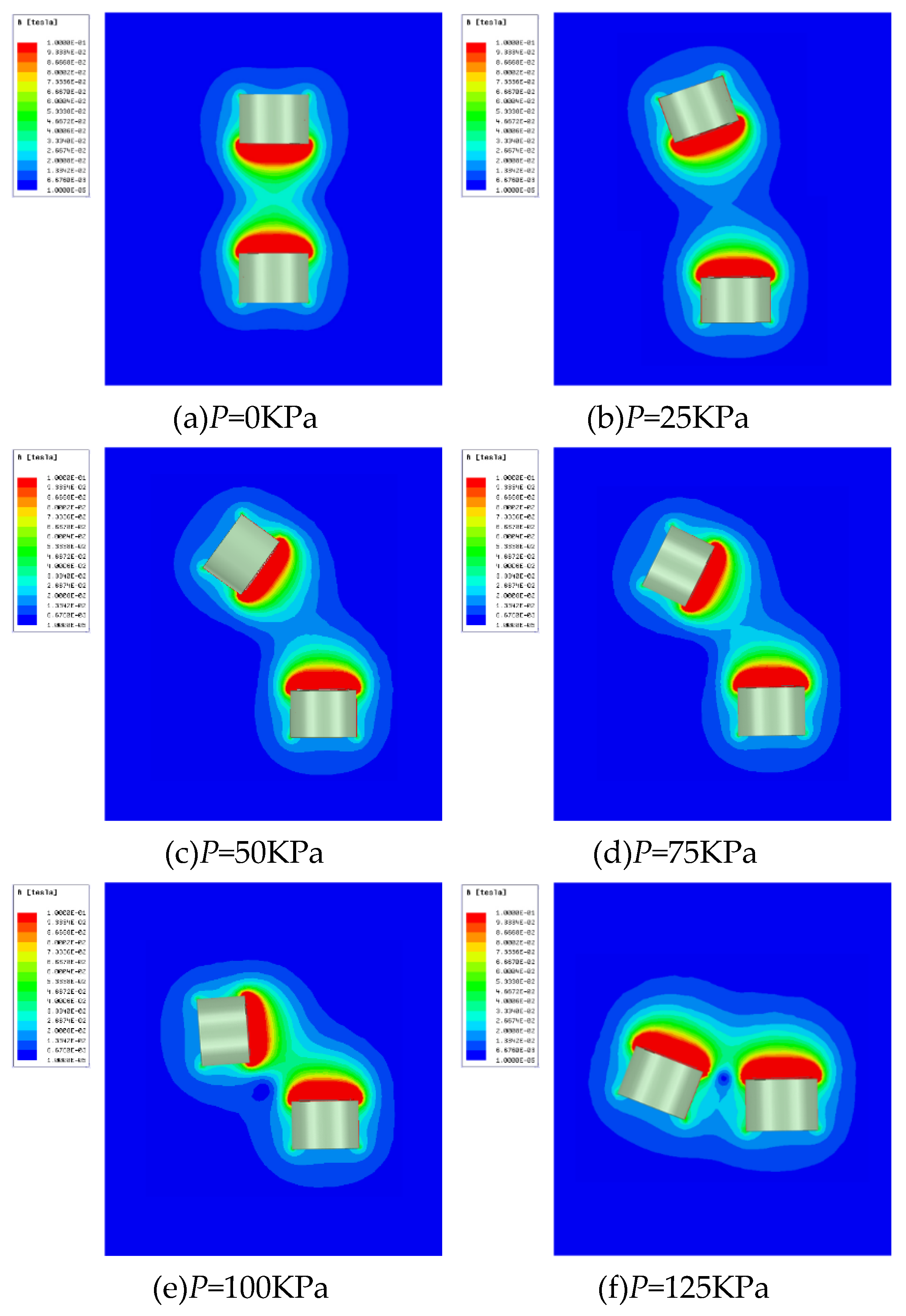
4.2.3. Pressurize the two channels under various magnetic fields

In order to study the effect of variable stiffness on omnidirectional deformation, the adjacent channel 1 and channel 2 are applied 1-5 working conditions at the same time as shown in Table 5. The two adjacent channels with viscosity 55Pa·s simultaneously pass the gas pressure of 15KPa, 30KPa, 45KPa, 60KPa and 75KPa, and the bending angle and stress simulation diagram of the soft joint are shown in Figure 13.

When the gas pressure of 75KPa is introduced into the adjacent two channels, the bending change and stress change are shown in Figure 14, and the viscosity increases gradually as the magnetic field increases. By comparing the bending degree of soft joints with viscosities of 0.15Pa·s, 15Pa·s, 38Pa·s, 55Pa·s, and 72Pa·s, it can be seen that the greater the viscosity, the less obvious the joint deformation, the less obvious the surface stress, and the greater the shear force.

4.3. Variable stiffness simulation

In this section, the variable stiffness model is established for stiffness simulation analysis, and the stiffness analysis method is determined in section 3.2. In the process of measuring the variable stiffness characteristics, the magnetic induction strength of the electromagnetic field is used to reflect the variable stiffness characteristics of the magnetorheological fluid.

When the driving module is fed with 75KPa air pressure, the variable stiffness system is under the applied current of 0.1A, 0.2A, 0.3A, 0.4A, and 0.5A, respectively. As shown in Figure 15, With the increase of the external magnetic field strength, the stiffness of the drive module increases, and the deformation decreases.

Under the magnetic field of 0.4A applied current, when the pressure of the drive module is 0KPa, 25KPa, 50KPa, 75KPa, 100KPa, and 125kP, As shown in Figure 16, with the increase of deformation, the magnetic field at the center of the two electromagnets changes from strong to weak and then to vigorous.

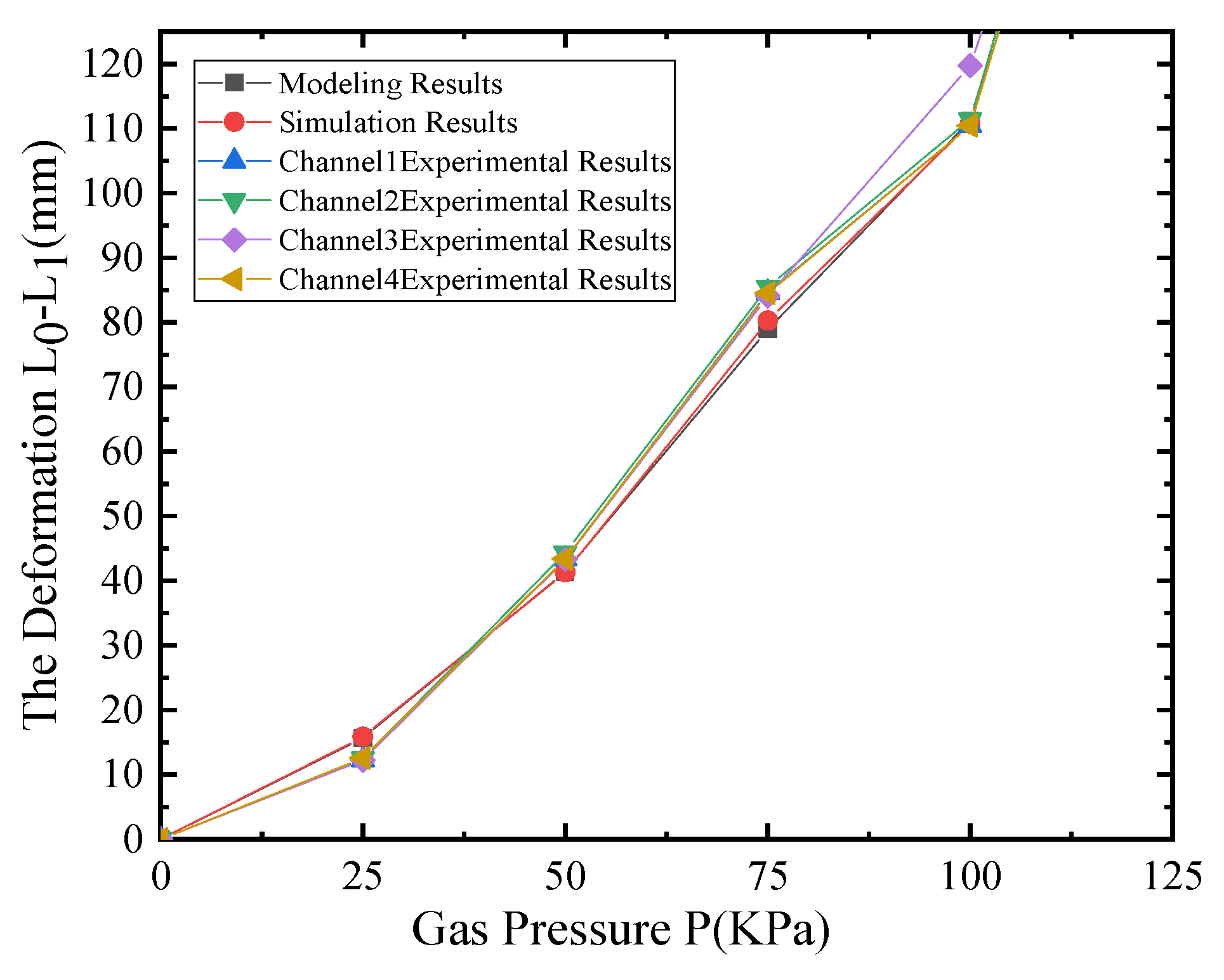
5. Test

5.1. Experimental Design

In order to verify the correctness of the theoretical and simulation results, a test platform for the analysis of rigid and flexible characteristics of modular soft joints was built. As shown in Figure 17, Using the drive module as a simple support beam, the inflatable end and end filled with magnetorheological fluid are constrained by two crab clamps to make the entire structure in a horizontal state, and the bending sensor Flex Sensor 4.5 is attached to the axial direction of the joint to measure the bending angle; By changing the magnetic field strength of the electromagnet, the stiffness is variable.

Several sets of experiments were conducted to verify the deformation and variable stiffness effects of the proposed drive module. Two sets of deformation tests were conducted to test the influence of the combination of positive and negative pressure gas with different pressures on the deformation characteristics of the modular joint. The relationship between gas pressure and joint deformation was tested, and the degree of bending deformation in different directions was measured. Through the variable stiffness experiment, the influence of the variable stiffness characteristic on the bearing capacity of the drive module is tested.

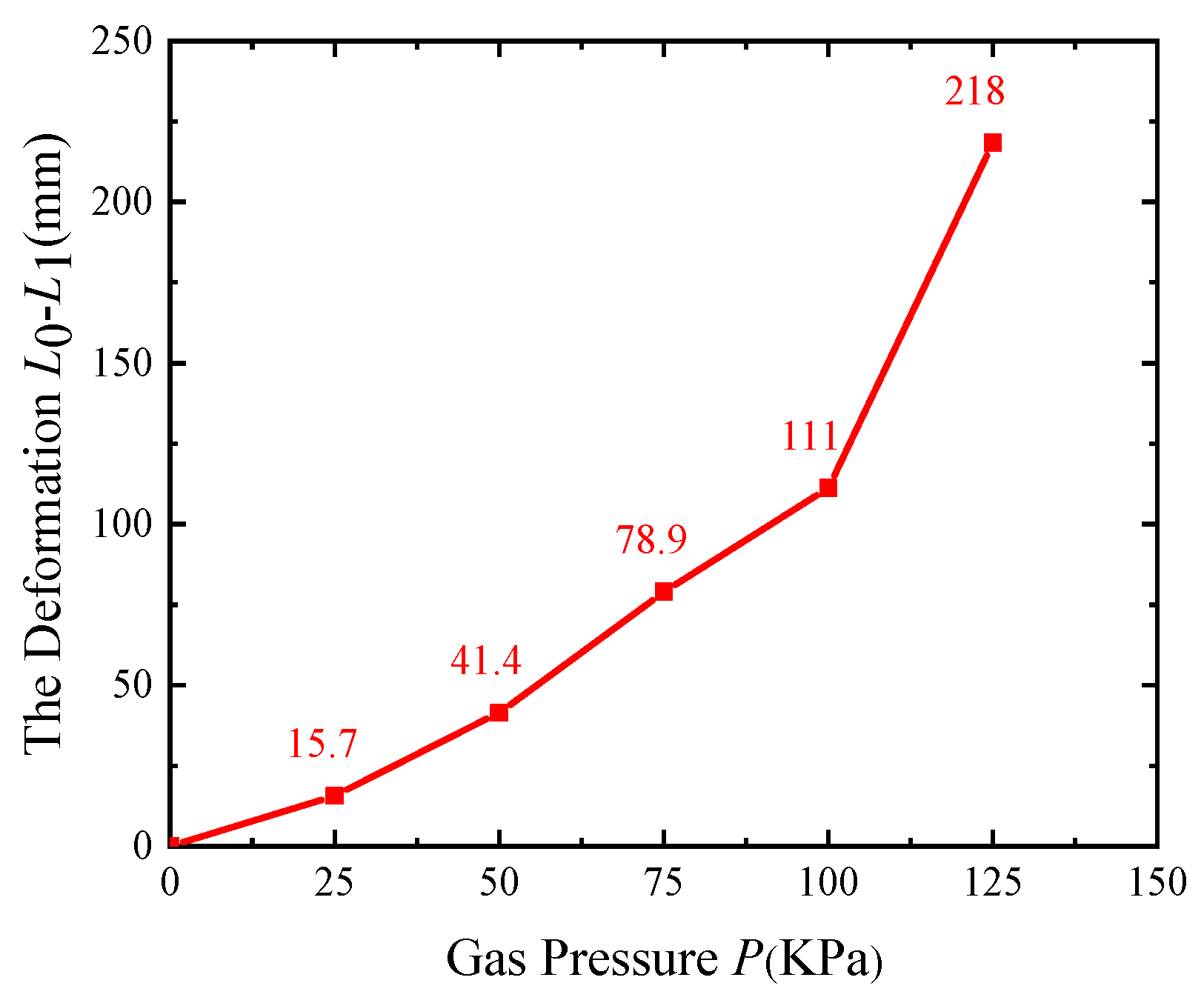
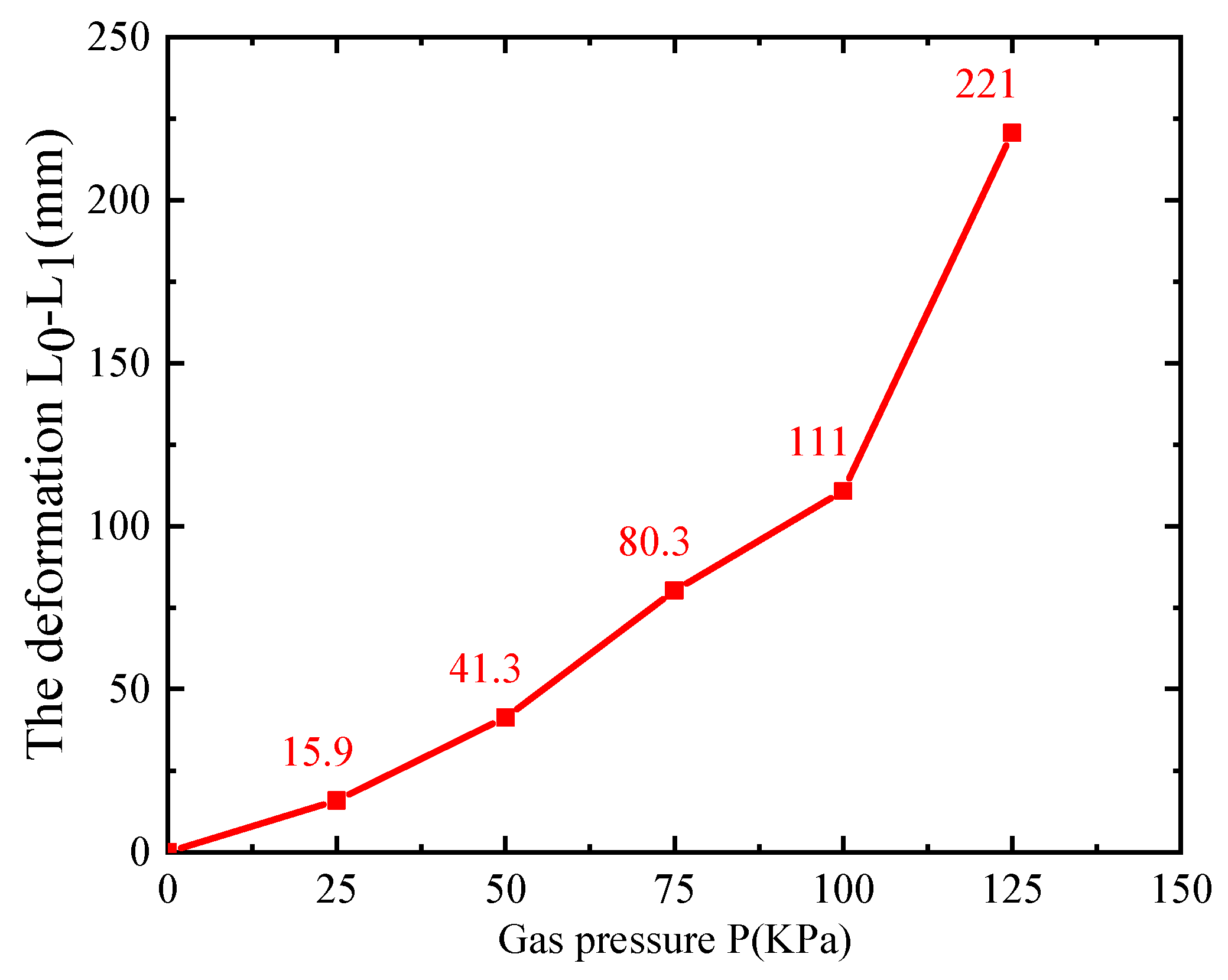
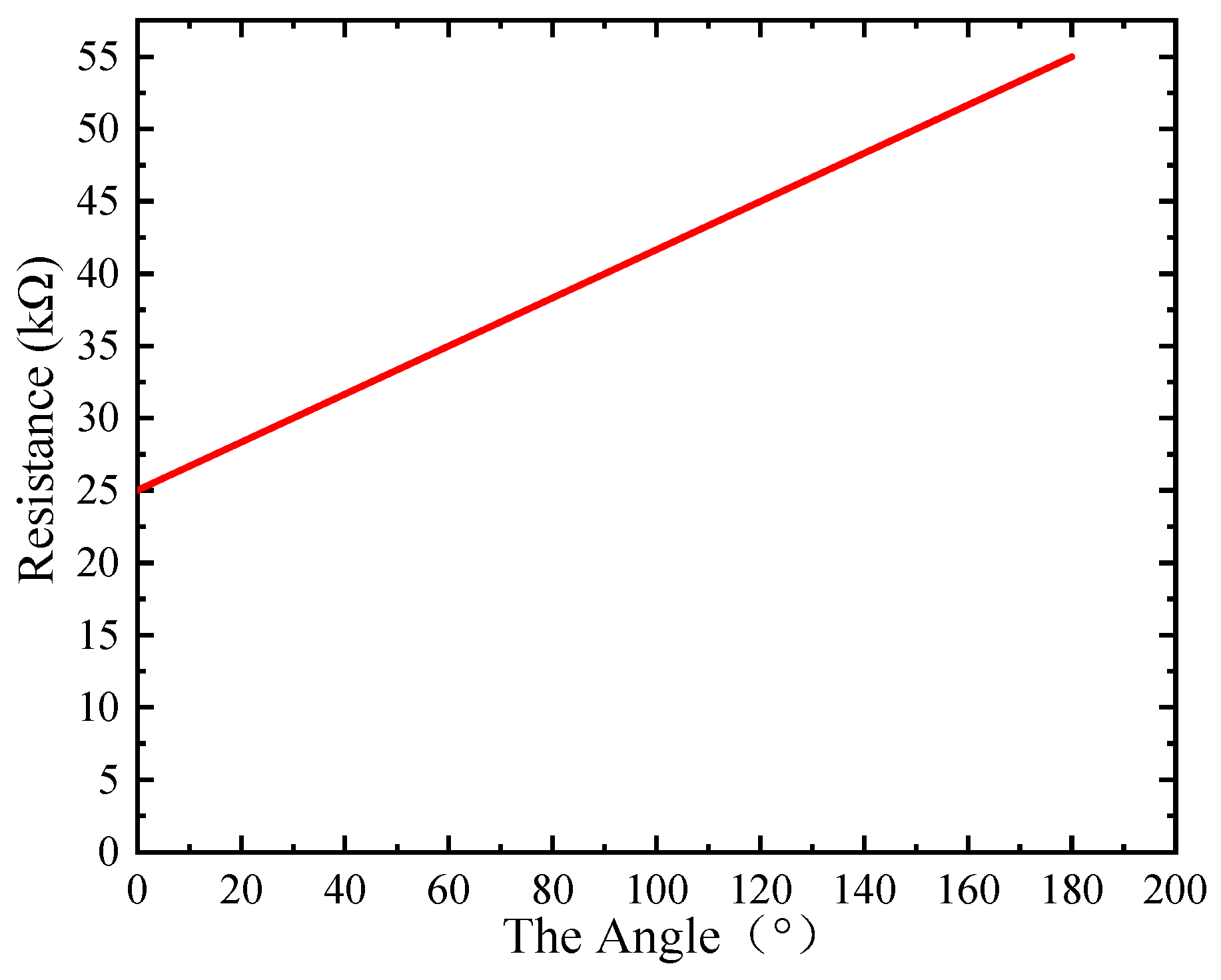
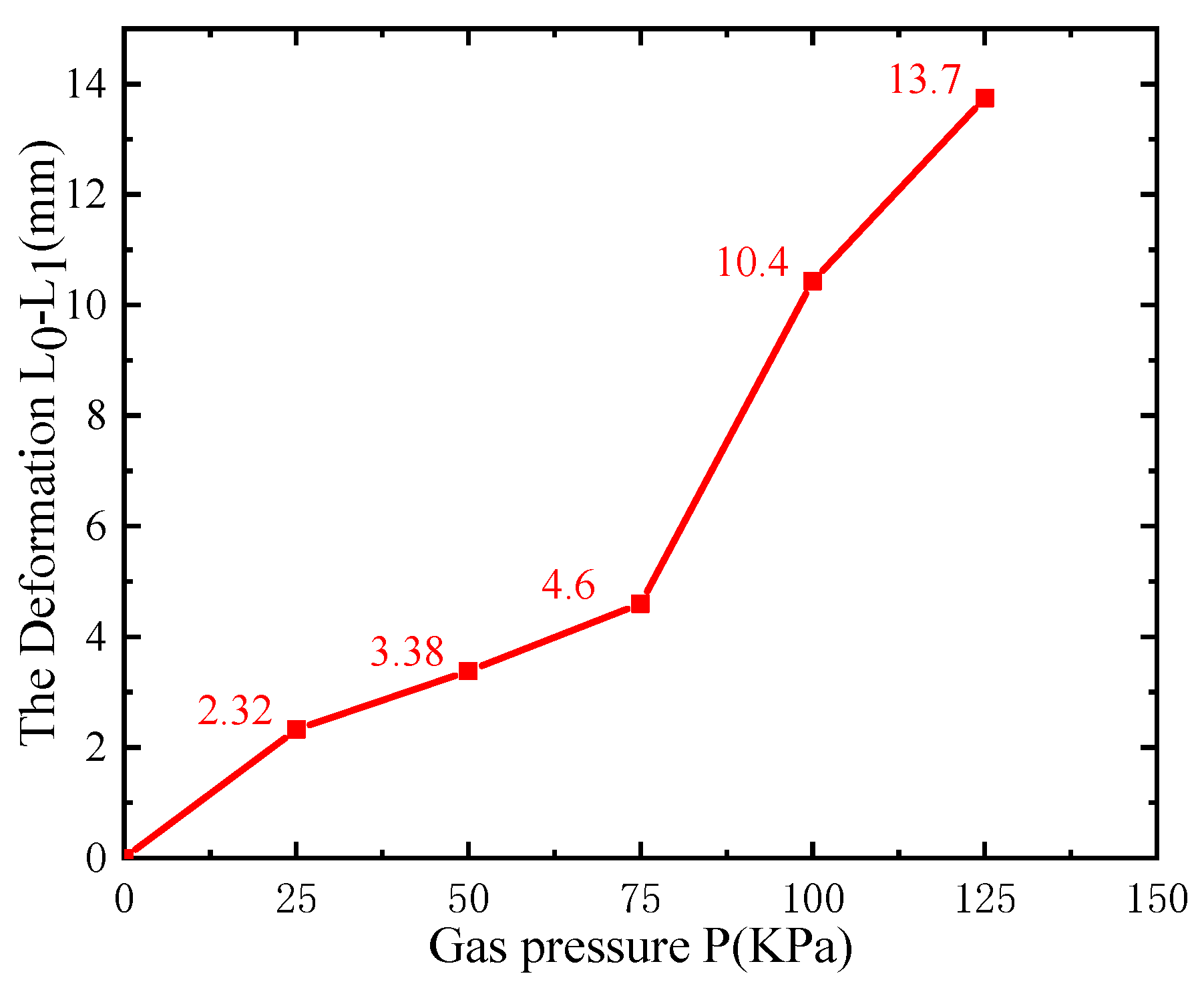
5.1.1. Deformation test

Firstly, the effect of the combination of positive and negative pressure gas changes at different pressures on the deformation characteristics of modular joints is tested. The air pressure of the positive pressure reducing valve is adjusted to 100kPa, and the air pressure of the negative pressure reducing valve is adjusted to -50kPa, and the action of the reversing valve group in the pneumatic system is adjusted in turn, and the actual joint deformation effect is shown in Figure 18, and the deformation is shown in Table 6.

As can be seen from Table 6, 100KPa gas pressure is injected into channels 1, 2, 3, and 4 from state 1 to state 4, the joint deforms to the positive direction of the Y axis, the positive direction of the X axis, the negative direction of the Y axis and the negative direction of the X axis, respectively, with a deformation amount of 10mm. State 5 ~ State 8 is the joint channel combined into 100KPa gas pressure. The soft joint deformation to the first quadrant, the second quadrant, the third quadrant, and the fourth quadrant of the diagonal direction of deformation is 10mm, And according to the size of the gas pressure through the two channels to determine whether the bulging tip is biased to the X axis or Y axis, if the gas pressure through the two channels is the same, the joint will be convex deformation in the direction of the quadrant angular bisector. In states 9 to 12, based on of states 1 to 4, -50KPa gas pressure is applied, and the deformation of soft joints is 13.5mm. The bulging deformation effect is enhanced.

To test the relationship between gas pressure and joint deformation and the degree of bending deformation in different deformation directions; An embedded pneumatic network channel is selected in the experimental flexible joint, and embedded pneumatic network channel 1 is set in this experiment. The pressure-reducing valve controls the pressure gradient of input channel 1, as shown in Figure 19.

Table 7. Resistance values of bending sensors with different gas pressures.

Air pressure (Kpa)	0	25	50	75	100	125
The sensor (KΩ)	25	26.5	27.2	28.1	31.8	34.2

The resistance value fed back by the bending sensor is converted into the bending Angle through the related image of the bending sensor resistance value and bending Angle shown in Figure 20. Then the bending Angle is converted into the deformation amount through equation (7) to obtain the image between the gas pressure and the experimental deformation amount, as shown in Figure 21.

It can be seen from Figure 21, the deformation of the experimental flexible joint gradually increases with the increase of gas pressure, and its change trend is basically the same as the modeling results and simulation results. Using the above method of verifying the relationship between gas pressure and deformation of channel 1, the relationship between gas pressure and deformation of channel 2, channel 3 and channel 4 can be obtained in the same way. The relationship between gas pressure and deformation in theory, simulation and test results is compared, as shown in Figure 22.

It can be seen from the figure that the relationship between gas pressure and deformation of channel 2, channel 3 and channel 4 has the same change trend as the relationship image of channel 1, and the deformation of experimental flexible joints gradually increases with the increase of gas pressure. In the comparison of theory, simulation and test results, the deformation of soft joints gradually increases with the increase of gas pressure, and the change trend is basically consistent, and the test results are consistent with the modeling results and simulation results.

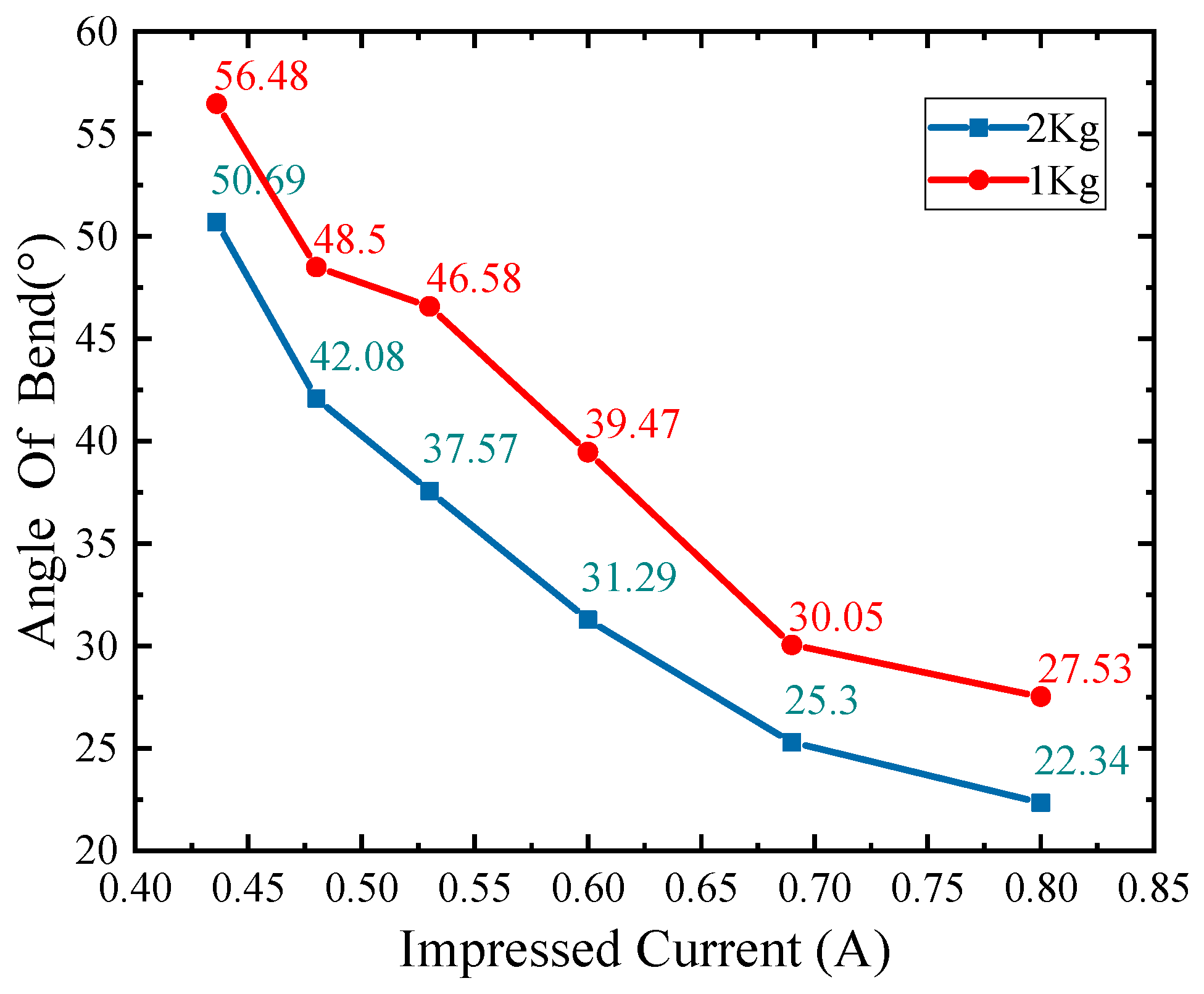
5.1.2. Variable stiffness test

In order to analyze the effect of variable stiffness on the bearing capacity of soft body joints, the test setup equates the variable stiffness structure to a simple support beam structure, hangs a stage at the midpoint of the joint, and places weights to apply a constant force to measure the bending angle of the joint through the bending sensor. The relation between the bending Angle

θ

and the elastic modulus

E

of the flexible joint is:

E = \frac{F L^{2}}{16 θ I}

(18)

Where

F

is the concentrated force, namely the gravity of the weight,

L

is the length of the flexible joint, and

I

is the moment of inertia. According to equation (18), the larger the flexural Angle of the test flexible joint, the smaller the elastic modulus, that is, the smaller the stiffness. According to the above principles, the influence of different applied currents on the stiffness characteristics is analyzed.

Use crab clamps to restrain both ends of the flexible joint to make it in a horizontal position, record its initial position without load through the bending sensor, and then adjust the resistance values of the rheostat to 60

Ω

, 70

Ω

, 80

Ω

, 90

Ω

, 100

Ω

, 110

Ω

respectively, place 1Kg and 2Kg weights on the stage, and after it is stabilized, record the final position of the flexible joint after the load is applied by the bending sensor to obtain the flexible joint bending angle under different loads. Figure 23(a) shows the state before the flexible joint becomes stiff, and Figure 23(b) is the state after the flexible joint becomes stiff.

By converting the rheostat resistance into applied current through the relationship between electromagnet resistance and current, the bending angle of flexible joints with 1Kg load and 2Kg load under different applied currents can be obtained, and the result is shown in Figure 24.

As can be seen from Figure 24 that the bending Angle is approximately linear with the change of applied current. When the load is 1kg, and the applied current is 0.47A to 0.57A, the bending Angle changes gently. With the increased the applied current, the bearing capacity and bending strength of the weak joints are enhanced. With the rise of the applied current, the bending Angle of the flexible joint gradually decreases. That is, the stiffness effect gradually increases, which is consistent with the theoretical results.

6. Conclusion

In this paper, a pneumatic modular joint that can realize the dynamic adjustment of deformation and stiffness in all directions is designed and produced, and its deformation and variable stiffness characteristics are theoretical, simulated, and experimentally analyzed, and the rigid-flexible coupling characteristics of soft joints are revealed. The specific conclusions are as follows:

(1) The deformation and variable stiffness models are established, and the gas pressure and deformation amount, as well as the correspondence between the magnetic field strength and the stiffness of the drive module are obtained.

(2) Through finite element simulation analysis, the change law of pressure and deformation under different stiffness conditions is obtained, and the change law of magnetic field strength and joint stiffness under different deformation conditions is considered.

(3) The theoretical analysis is verified by experiments, and the experiments show that under the simultaneous action of deformation and variable stiffness, the compliance and bearing capacity are taken into account, and the experimental results of the drive module are in good agreement with the calculation and simulation results of the theoretical model.

7. Patents

Author Biography

Siyuan Liu, male, born in 1981, is an associate professor and has a Ph.D. His research focuses on fault diagnosis and condition assessment of intelligent hydraulic systems and components. His email address is liusiyuan@ysu.edu.cn. Yuhang Bian (corresponding author), male, born in 1998, is a master's degree candidate. His research is focused on the analysis of the rigid-flexible coupling characteristics of variable stiffness pneumatic modular soft joints. His email address is 1053858480@qq.com.

Author Contributions

Conceptualization, SiYuan Liu and YuHang Bian ; methodology, SiYuan Liu; software, YiJie Deng; validation, YuHang Bian and JingTao Zhang ; formal analysis, Hongmei Sun ; investigation, SiYuan Liu ; resources, SiYuan Liu ; data curation, YuHang Bian; writing—original draft preparation, YuHang Bian; writing—review and editing, SiYuan Liu; visualization, ZiLong Chen; supervision, SiYuan Liu ; project administration, Wanlu Jiang ; funding acquisition, SiYuan Liu. All authors have read and agreed to the published version of the manuscript.

Funding

This research was supported by the National Natural Science Foundation of China (Nos. 52275069 and 52175065), the Hebei Natural Science Foundation (No. E2022203041) and the Bureau of Science and Technology of Hebei Province, China , grant number (No. E2021203020).

Conflicts of Interest

The authors declare no conflict of interest

References

Xu, F.-Y.; Jiang, F.-Y.; Jiang, Q.-S.; Lu, Y.-X. Soft Actuator Model for a Soft Robot With Variable Stiffness by Coupling Pneumatic Structure and Jamming Mechanism. IEEE Access 2020, 8, 26356-26371. [CrossRef]
Gilday, K.; Hughes, J.; Iida, F. Wrist-driven passive grasping: Interaction-based trajectory adaption with a compliant anthropomorphic hand. Bioinspir Biomim 2021, 16. [CrossRef]
Zhou, P.; Yao, J.; Zhang, S.; Wei, C.; Zhang, H.; Qi, S. A bioinspired fishbone continuum robot with rigid-flexible-soft coupling structure. Bioinspir Biomim 2022, 17. [CrossRef]
Chen, J.; Jin, H.; Iida, F.; Zhao, J. A design concept of parallel elasticity extracted from biological muscles for engineered actuators. Bioinspir Biomim 2016, 11, 056009. [CrossRef]
Wockenfus, W.R.; Brandt, V.; Weisheit, L.; Drossel, W.-G. Design, Modeling and Validation of a Tendon-Driven Soft Continuum Robot for Planar Motion Based on Variable Stiffness Structures. IEEE Robotics and Automation Letters 2022, 7, 3985-3991. [CrossRef]
Wang, Y.; Yang, X.; Chen, Y.; Wainwright, D.K.; Kenaley, C.P.; Gong, Z.; Liu, Z.; Liu, H.; Guan, J.; Wang, T.J.S.R. A biorobotic adhesive disc for underwater hitchhiking inspired by the remora suckerfish. 2017, 2, eaan8072. [CrossRef]
Gu, G.; Zou, J.; Zhao, R.; Zhao, X.; Zhu, X.J.S.R. Soft wall-climbing robots. 2018, 3, eaat2874. [CrossRef]
Seok, S.; Onal, C.D.; Cho, K.-J.; Wood, R.J.; Rus, D.; Kim, S.J.I.A.T.o.m. Meshworm: A peristaltic soft robot with antagonistic nickel titanium coil actuators. 2012, 18, 1485-1497. [CrossRef]
Kashima, S.; Miyasaka, F.; Hirata, K.J.I.T.o.m. Novel soft actuator using magnetorheological elastomer. 2012, 48, 1649-1652. [CrossRef]
Wang, H.; Wang, C.; Chen, W.; Liang, X.; Liu, Y.J.I.A.T.o.M. Three-dimensional dynamics for cable-driven soft manipulator. 2016, 22, 18-28. [CrossRef]
Sun, Y.; Zhang, Q.; Chen, X.; Chen, H.J.M.P.i.E. An Optimum Design Method of Pneu-Net Actuators for Trajectory Matching Utilizing a Bending Model and GA. 2019. [CrossRef]
Zeng, M.; Li, Y.-J.; Ren, T.; Tu, Q.J.P.o.t.I.o.M.E., Part C: Journal of Mechanical Engineering Science. Material stiffness control of compliant tools by using electromagnetic suction. 2019, 233, 4719-4728. [CrossRef]
Yang, Y.; Chen, Y.; Li, Y.; Wang, Z.; Li, Y.J.S.r. Novel variable-stiffness robotic fingers with built-in position feedback. 2017, 4, 338-352. [CrossRef]
Li, Y.; Chen, Y.; Yang, Y.; Wei, Y. Passive Particle Jamming and Its Stiffening of Soft Robotic Grippers. IEEE Transactions on Robotics 2017, 33, 446-455. [CrossRef]
Cheng, N.G.; Lobovsky, M.B.; Keating, S.J.; Setapen, A.M.; Gero, K.I.; Hosoi, A.E.; Iagnemma, K.D. Design and Analysis of a Robust, Low-cost, Highly Articulated manipulator enabled by jamming of granular media. In Proceedings of the 2012 IEEE International Conference on Robotics and Automation, 14-18 May 2012, 2012; pp. 4328-4333. [CrossRef]
Sadati, S.M.H.; Noh, Y.; Elnaz Naghibi, S.; Althoefer, K.; Nanayakkara, T. Stiffness Control of Soft Robotic Manipulator for Minimally Invasive Surgery (MIS) Using Scale Jamming. In Intelligent Robotics and Applications; Lecture Notes in Computer Science; 2015; pp. 141-151. [CrossRef]
Shiva, A.; Stilli, A.; Noh, Y.; Faragasso, A.; Falco, I.D.; Gerboni, G.; Cianchetti, M.; Menciassi, A.; Althoefer, K.; Wurdemann, H.A. Tendon-Based Stiffening for a Pneumatically Actuated Soft Manipulator. IEEE Robotics and Automation Letters 2016, 1, 632-637. [CrossRef]
Wei, Y.; Chen, Y.; Yang, Y.; Li, Y. A soft robotic spine with tunable stiffness based on integrated ball joint and particle jamming. Mechatronics 2016, 33, 84-92. [CrossRef]
Zhao, Y.; Shan, Y.; Guo, K.; Han, L.; Qi, L.; Yu, H. Principle and Performance Analysis of Soft Continuum Robot with Large Range Variable Stiffness Based on Spherical Particles. In Proceedings of the 2019 IEEE 9th Annual International Conference on CYBER Technology in Automation, Control, and Intelligent Systems (CYBER), 29 July-2 Aug. 2019, 2019; pp. 719-724. [CrossRef]
Al Abeach, L.A.T.; Nefti-Meziani, S.; Davis, S. Design of a Variable Stiffness Soft Dexterous Gripper. Soft Robot 2017, 4, 274-284. [CrossRef]
Al Abeach, L.; Nefti-Meziani, S.; Theodoridis, T.; Davis, S. A Variable Stiffness Soft Gripper Using Granular Jamming and Biologically Inspired Pneumatic Muscles. Journal of Bionic Engineering 2018, 15, 236-246. [CrossRef]
Li, Y.; Ren, T.; Chen, Y.; Chen, M.Z. A variable stiffness soft continuum robot based on pre-charged air, particle jamming, and origami. In Proceedings of the 2020 IEEE International Conference on Robotics and Automation (ICRA), 2020; pp. 5869-5875. [CrossRef]
Wang, T.; Zhang, J.; Li, Y.; Hong, J.; Wang, M.Y. Electrostatic Layer Jamming Variable Stiffness for Soft Robotics. IEEE/ASME Transactions on Mechatronics 2019, 24, 424-433. [CrossRef]
Liu, Z.; Wang, Y.; Wang, J.; Fei, Y.; Du, Q. An obstacle-avoiding and stiffness-tunable modular bionic soft robot. Robotica 2022, 40, 2651-2665. [CrossRef]
Luo, Y.; Wright, M.; Xiao, Q.; Yue, H.; Pan, G. Fluid-structure interaction analysis on motion control of a self-propelled flexible plate near a rigid body utilizing PD control. Bioinspir Biomim 2021, 16. [CrossRef]
Wang, C.; Tang, H.; Zhang, X.J.B.; Biomimetics. Fluid-structure interaction of bio-inspired flexible slender structures: A review of selected topics. 2022. [CrossRef]
Moon, D.-H.; Shin, S.-H.; Na, J.-B.; Han, S.-Y. Fluid–Structure Interaction Based on Meshless Local Petrov–Galerkin Method for Worm Soft Robot Analysis. International Journal of Precision Engineering and Manufacturing-Green Technology 2020, 7, 727-742. [CrossRef]
Shan, Y.; Zhao, Y.; Pei, C.; Yu, H.; Liu, P. A novel design of a passive variable stiffness soft robotic gripper. Bioinspir Biomim 2022, 17. [CrossRef]
Sun, W.; Yu, J.; Cai, Y. Influence of magnetic field, magnetic particle percentages, and particle diameters on the stiffness of magnetorheological fluids. Journal of Intelligent Material Systems and Structures 2020, 31, 2312-2325. [CrossRef]
Ilievski, F.; Mazzeo, A.D.; Shepherd, R.F.; Chen, X.; Whitesides, G.M. Soft robotics for chemists. Angew Chem Int Ed Engl 2011, 50, 1890-1895. [CrossRef]
Yap, H.K.; Ng, H.Y.; Yeow, C.-H. High-Force Soft Printable Pneumatics for Soft Robotic Applications. Soft Robotics 2016, 3, 144-158. [CrossRef]
S.Y.Liu; J.T.Zhang; J.Wang; Y.J.Deng; C.T.Xin. Design and simulation analysis of fluid-driven modular soft body bionic elephant trunk joint variable stiffness structure %J Hydraulics and Pneumatics. 2022, 46, 152-158.
Zhang, Y.; Chen, W.; Chen, J.; Cheng, Q.; Zhang, H.; Xiang, C.; Hao, L. Stiffness Analysis of a Pneumatic Soft Manipulator Based on Bending Shape Prediction. IEEE Access 2020, 8, 82227-82241. [CrossRef]
Taniguchi, H.; Miyake, M.; Suzumori, K. Development of new soft actuator using magnetic intelligent fluids for flexible walking robot. In Proceedings of the ICCAS 2010, 27-30 Oct. 2010, 2010; pp. 1797-1801.
Xuan, T.; Li, J.; Li, B.; Fan, W.J.J.o.M.; Materials, M. Effects of the non-uniform magnetic field on the shear stress and the microstructure of magnetorheological fluid. 2021, 535, 168066. [CrossRef]

Figure 1. Modular joint.

Figure 2. Section of air chamber.

Figure 3. Structural parameters.

Figure 4. Flexural Angle of flexible joint.

Figure 5. Ideal physical model of joint structure.

Figure 6. Relationship between deformation and gas pressure in theoretical modeling.

Figure 7. Change under magnetic field of magnetorheological liquid.

Figure 8. Magnetization properties of magnetorheological fluids.

Figure 9. Simulated stress distribution of joints under different gas pressures.

Figure 10. Variation of deformation with gas pressure.

Figure 11. Deformation of a single channel with different gas pressures (τ =15Pa·s).

Figure 12. Deformation simulation of different viscosity (P=75KPa).

Figure 13. Deformation simulation of two adjacent channels with different gas pressures (τ =55Pa·s).

Figure 14. Corresponding deformation of two adjacent channels at different viscosities (P=75KPa).

Figure 15. distribution of magnetic field under different currents at 75KPa.

Figure 16. Magnetic field distribution with different gas pressure at 0.4A current.

Figure 17. Analysis test of rigid-flexible coupling characteristics.

Figure 18. Actual deformation effect of flexible joint.

Figure 19. Flexural degree of flexible joint under different air pressure.

Figure 20. Relationship between resistance value of bending sensor and bending angle.

Figure 21. Relationship between gas pressure and deformation in channel 1.

Figure 22. Relationship between gas pressure and deformation.

Figure 23. Experimental setup before and after variable stiffness.

Figure 24. The relationship between applied current and flexible joint bending angle under different loads.

Table 1. Structural parameters of the air cavity.

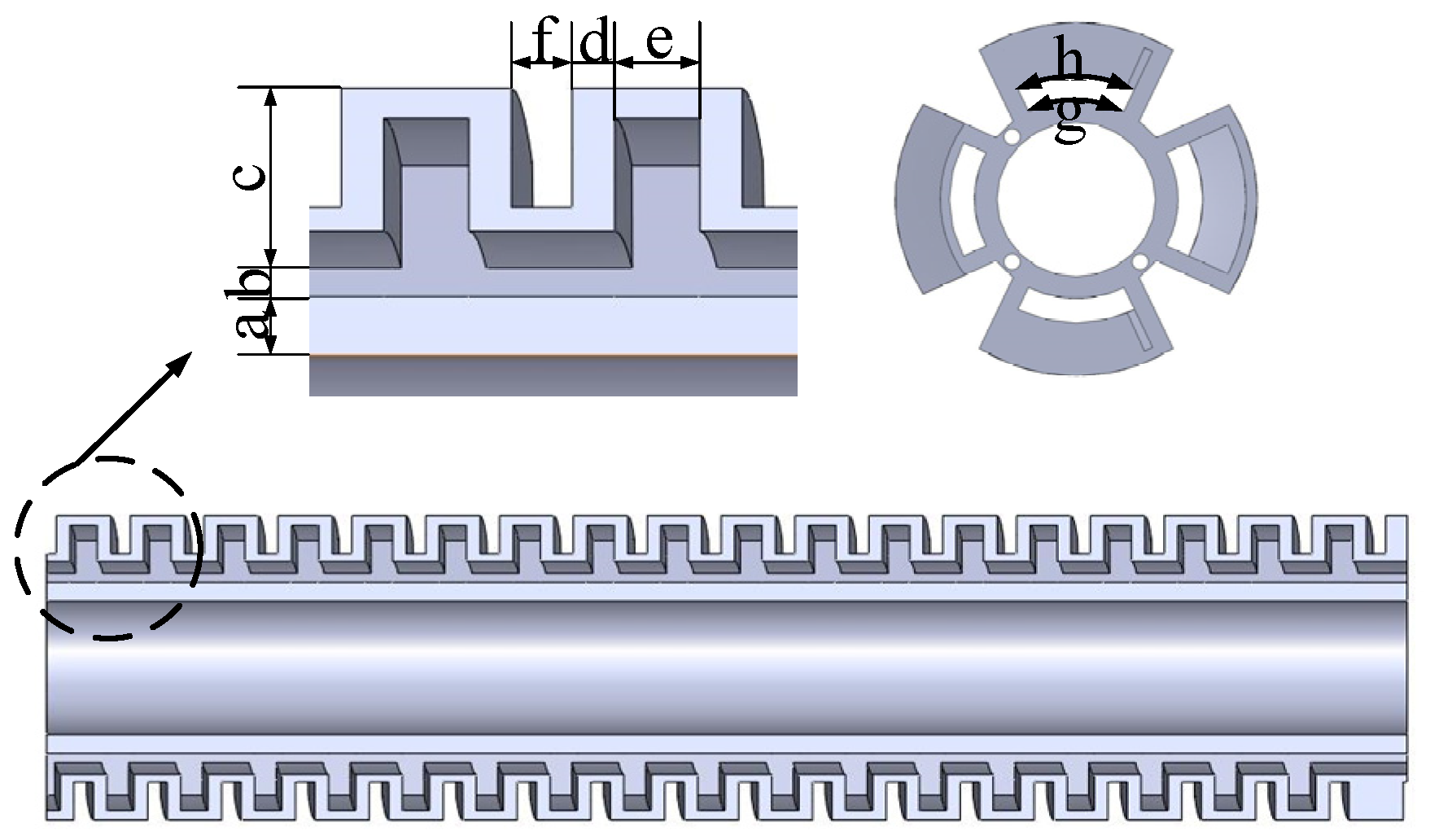
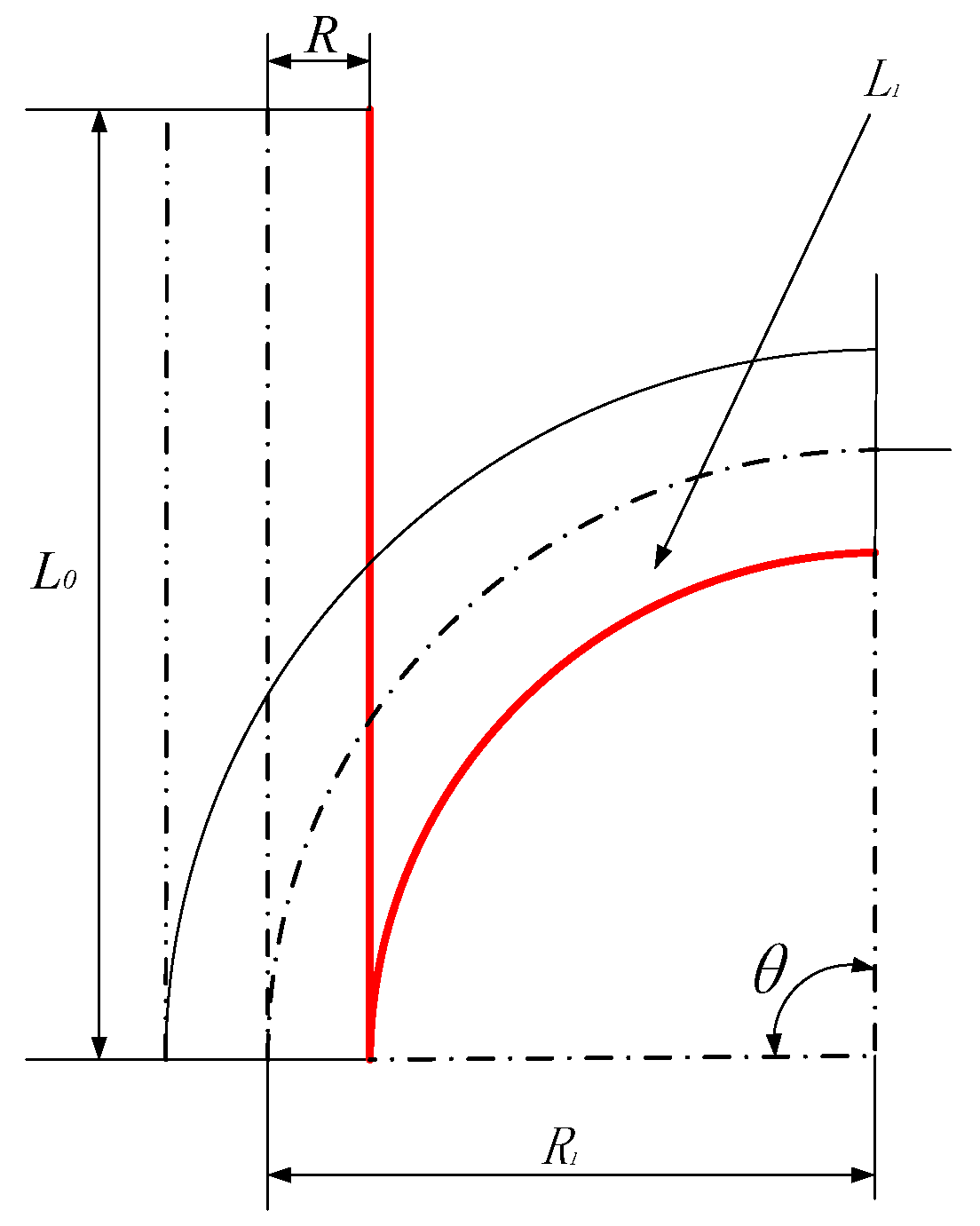
parameter	value
The thickness of a single air chamber constraint layer	$a$
The thickness of the cavity wall in the length direction of a single cavity	$d$
Cavity wall thickness in the height direction	$d$
Cavity wall thickness in the width direction	$d$
The length of the cavity in the direction of the height of a single air cavity	$b + c - d$
Single air cavity length direction empty cavity length	$e$
Width direction cavity length	$g - 2 d$
The spacing between air cavities	$f$
Width of vent between air cavity and air cavity	$h$

Table 2. Bending angles of joints under different pressure.

P(KPa)	0	25	50	75	100	125
θ (°)	0	27.8	51.4	120.3	165.4	335.3

Table 3. Structure parameters of the electromagnet.

Diameter (mm)	high (mm)	Table magnetic intermediate magnetic field strength (T)	nominal voltage (V)	weight (g)
35	30	0.1	24	200

Table 4. Parameter Settings of simulation conditions.

Working condition	Viscosity (Pa·s)	Gas pressure (KPa)	Gas pressure (KPa)	Gas pressure (KPa)	Gas pressure (KPa)	Gas pressure (KPa)
1	0	25	50	75	100	125
2	15	25	50	75	100	125
3	38	25	50	75	100	125
4	55	25	50	75	100	125
5	72	25	50	75	100	125

Table 5. Parameter Settings of simulation conditions.

Working condition	viscosity (Pa·s)	Gas pressure (KPa)	Gas pressure (KPa)	Gas pressure (KPa)	Gas pressure (KPa)	Gas pressure (KPa)
1	0	15	30	45	60	75
2	15	15	30	45	60	75
3	38	15	30	45	60	75
4	55	15	30	45	60	75
5	72	15	30	45	60	75

Table 6. Deformation analysis.

	1	2	3	4	The deformation L0-L1 (mm)
state	1	2	3	4	The deformation L0-L1 (mm)
1	+	0	0	0	10
2	0	+	0	0	10
3	0	0	+	0	10
4	0	0	0	+	10
5	+	+	0	0	10
6	0	+	+	0	10
7	0	0	+	+	10
8	+	0	0	+	10
9	+	0	-	0	13.5
10	0	+	0	-	13.5
11	-	0	+	0	13.5
12	0	-	0	+	13.5

Note: Positive pressure is "+," negative pressure is "-", impassability is "0".

Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.

© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).

Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.

MDPI Initiatives

Important Links

Choose an area of interest and we will send you notifications of new preprints at your preferred frequency.

Disclaimer

Working condition	Viscosity (Pa·s)	Gas pressure (KPa)	Gas pressure (KPa)	Gas pressure (KPa)	Gas pressure (KPa)	Gas pressure (KPa)
1	0	25	50	75	100	125
2	15	25	50	75	100	125
3	38	25	50	75	100	125
4	55	25	50	75	100	125
5	72	25	50	75	100	125

Working condition	viscosity (Pa·s)	Gas pressure (KPa)	Gas pressure (KPa)	Gas pressure (KPa)	Gas pressure (KPa)	Gas pressure (KPa)
1	0	15	30	45	60	75
2	15	15	30	45	60	75
3	38	15	30	45	60	75
4	55	15	30	45	60	75
5	72	15	30	45	60	75

Working condition	Viscosity (Pa·s)	Gas pressure (KPa)	Gas pressure (KPa)	Gas pressure (KPa)	Gas pressure (KPa)	Gas pressure (KPa)
1	0	25	50	75	100	125
2	15	25	50	75	100	125
3	38	25	50	75	100	125
4	55	25	50	75	100	125
5	72	25	50	75	100	125

Working condition	viscosity (Pa·s)	Gas pressure (KPa)	Gas pressure (KPa)	Gas pressure (KPa)	Gas pressure (KPa)	Gas pressure (KPa)
1	0	15	30	45	60	75
2	15	15	30	45	60	75
3	38	15	30	45	60	75
4	55	15	30	45	60	75
5	72	15	30	45	60	75

Analysis of Rigid-Flexible Coupling Characteristics of Pneumatic Modular Soft Joints with Variable Stiffness

Abstract

1. Introduction

2. Structure Principle

3. Modeling and Solving

3.1. Deformation Modeling

3.2. Variable stiffness modeling

4. Simulation Analysis

4.1. Parameter Settings

4.2. Deformation simulation

4.2.1. Deformation simulation without magnetic field

4.2.2. Pressurize single channel with different magnetic fields

4.2.3. Pressurize the two channels under various magnetic fields

4.3. Variable stiffness simulation

5. Test

5.1. Experimental Design

5.1.1. Deformation test

5.1.2. Variable stiffness test

6. Conclusion

7. Patents

Author Biography

Author Contributions

Funding

Conflicts of Interest

References

MDPI Initiatives

Important Links

Subscribe

Working condition	Viscosity (Pa·s)	Gas pressure (KPa)	Gas pressure (KPa)	Gas pressure (KPa)	Gas pressure (KPa)	Gas pressure (KPa)
1	0	25	50	75	100	125
2	15	25	50	75	100	125
3	38	25	50	75	100	125
4	55	25	50	75	100	125
5	72	25	50	75	100	125

Working condition	viscosity (Pa·s)	Gas pressure (KPa)	Gas pressure (KPa)	Gas pressure (KPa)	Gas pressure (KPa)	Gas pressure (KPa)
1	0	15	30	45	60	75
2	15	15	30	45	60	75
3	38	15	30	45	60	75
4	55	15	30	45	60	75
5	72	15	30	45	60	75