Decoding the Profitability of Insurance Products: A Novel Approach to Evaluating Non-Participating and Participating Insurance Policies

This study presents a novel approach to analyzing the present value of total profit for non-participating and participating insurance policies in order to determine the optimal profitability of non-participating and participating insurance policies based on applying the approach used in operations research to the field of finance. As such, a comprehensive insurance product evaluation model was developed using both mathematical models and numerical analysis to evaluate the demand for non-participating and participating life insurance policies in response to changes in interest rates. The findings indicate that non-participating life insurance policies offer greater solvency for insurance companies compared to participating policies. The study also highlights the significance of spontaneous and induced demand in determining the total profit of both types of policies. The study concludes that life insurance companies should focus on generating spontaneous consumer demand, reducing induced demand, and implementing the optimal pricing strategy to achieve maximum profits.

Keywords:

Subject:

Business, Economics and Management - Finance

MSC: 90-10

1. Introduction

In a highly competitive insurance market, insurance companies strive to continuously offer insurance products to their customers while seeking to maximize their profits. (Carriquiry and Osgood [1]; Staikouras [2]). However, this pursuit of success is challenged by the instability of the interest rate environment, leading to difficulties in investment and business operations. These obstacles result in frequent constraints on profits, which limit the scope of operational decisions for insurance companies. As such, in the field of insurance, the modeling of insurance premiums in competitive markets continues to garner significant attention among scholars. According to Cummins [3], insurance is an intangible product, and the actual cost, which refers to the payments made by insurers, is not determined until the policy is in effect. Therefore, insurers determine the estimated life insurance premium of a policy based on the law of large numbers and previous claims experiences. However, if insurers are not proactive, their competition strategy of reducing premiums could lead to financial instability and insolvency in the future (Ai, Bajtelsmit, & Wang [4]; Malinovskii [5]; Cicceri [6]). This highlights the importance of careful and informed decision-making in the pricing of insurance products.

In the field of insurance, the calculation of premiums has garnered much attention from relevant research. According to Kleinow and Willder [7], the premium charged to an individual policyholder cannot surpass established regulations. Meanwhile, the investment strategies employed by insurance companies can impact the price of investment products as indicated in the model proposed by Consiglio et al. [8]. According to Taylor [9], the subjective aspect of insurance underwriting was analyzed within a deterministic discrete-time framework. Through his demand function, an insurer can determine the most appropriate reaction to shifts in the market's premium rates. Furthermore, the aforementioned concerns have been raised in recent studies (Mourdoukoutas et al. [10]; Canh, Wongchoti & Thanh [11]).

In addition, Direr and Ennajar-Sayadi [12] indicate that the increase in life expectancy in developed countries has caused insurers to worry about their solvency due to the increased cost of guaranteed income payments in old age. They thus note an upward trend in the prices of some life insurance products by posing questions about clients' reactions and the future of the life insurance industry. Besides, they also propose examining the price elasticity of demand for life insurance contracts using mathematical models that account for the inventory issue and highlight the significance of boosting an insurer's profitability to address these concerns.

Furthermore, Cohen [13] improved upon the model proposed by Ghare and Schrader [14] by modifying the objective function from cost minimization to profit maximization. Ben-Daya and Roauf [15], drawing inspiration from Liao and Shyu's [16] model, determined the optimal inventory strategy that minimizes the expected total cost for a year, Additionally, Dye [17] extended the findings of Chang and Dye [18] by transforming the demand rate into a decreasing function of the selling price to establish an optimal pricing and ordering strategy. Moreover, some researchers in the field of operations management have begun to investigate the relationship between operations and insurance. For example, Dong and Tomlin [19] and Serpa and Krishnan [20] investigated the relationship between business interruption insurance and operational measures, concluding that, in certain conditions, business interruption insurance, a type of property insurance, can be complementary to operational measures. Martinez et al. [21] created a new approach for combining inventory optimization and insurance optimization.

Nonetheless, we argue that there is a lack of research that comprehensively evaluates the demand for different types of life insurance policies (e.g., non-participating and participating insurance policies) and considers the impact of changes in interest rates after surveying the relevant research. This study may fill this gap by developing a comprehensive insurance product evaluation model, as well as providing valuable insights for life insurance companies to maximize profits. Furthermore, despite the growing literature on operation and property insurance, traditional life insurance-operation linkage research studies are scarce. As a result, the purpose of this study is to present a conceptual framework for linking the value of money with the concept of inventory management model to provide insight into the issue, whereby an insurer can make the optimal solution by focusing on non-participating and participating policies in different circumstances.

This study may contribute to the existing literature in the following aspects. First, it is a pioneering effort from the perspective of a single life insurance company to find the optimal solution for insurance policies using an inventory management model that has not been widely explored in previous insurance research. Second, the study presents a model for evaluating insurance products, demonstrated through numerical examples, that allows a single insurer to refine premium pricing and maximize profits. Finally, the study emphasizes the crucial role of both spontaneous and induced demand in determining the profitability of non-participating and participating life insurance policies and concludes that optimal pricing strategies can significantly enhance the profits of insurance companies.

2. Non-Participating Policies and Participating Policies

A life insurance policy's primary purpose is to provide death benefits. And the insurance benefits are contingent on the insured's survival duration. Furthermore, the premium for whole life insurance policies is calculated using the policy's predetermined interest rate, and the insurer bears all risks.

Our research focuses on the evaluations of non-participating and participating life policies. A non-participating insurance policy, unlike a participating insurance policy, does not pay out dividends based on the insurer's profits; however, these life insurance plans do pay out guaranteed benefits on maturity.

A participating policy is also known as a non-guaranteed cost policy because the dividends are not guaranteed but the premium and cash value are. They are essentially a form of risk sharing in which the insurance company shifts a portion of the risk to policyholders (Cheng & Li [22]; Henckaerts & Antonio [23]). Although it is a dividend policy, whether or not a dividend is distributed is determined by the insurance company's operating performance. If the insurance company's investment performance and business strategy deviations result in losses, the insured may still be unable to receive dividends. However, the dividend policy still has a basic predetermined interest rate, and even if there is no dividend, the policy value may continue to rise if current interest rates fall below such a rate [24].

A non-participating policy is known as a guaranteed-cost policy because every feature of a guaranteed-cost policy is fixed, allowing us to predict future costs. Non-participating policy premiums are typically lower than participating policy premiums due to dividend expense (Picard [25]; Kim et al. [26]), This is because insurers will charge higher premiums than traditional policies on the basis of unpredictable future uncertainties (Bacinello et al. [27]), and thus likely take appropriate measures to distribute dividends to policyholders based on actual performance.

2.1. Assumptions and Notation

In this study, we use the concept of inventory management to develop a new approach to dealing with the aforementioned insurance issue. This entails using mathematical models and conducting numerical analysis to derive a determinate solution for the challenges faced in a highly competitive insurance market. Based on the evaluation model of insurance policies developed in this study, we provide the following symbols and hypotheses to set up the model of traditional life policy, including non-participating and participating policies.

$c_{0}$	Fixed business cost
$c_{1}$	Variable business cost/per piece
$N$	Terms of a valid policy
$M$	Benefit amount due/piece/term
$R$	Claim amount within the policy period in the event of an accident of the beneficiary
$r$	Risk-free rate
$p_{0}$	The occurrence of a covered accident prior to one term (when the proposer purchased the policy)
$p_{j}$	The probability of an insured having a covered accident at the j term,and j=1, 2, …, N-1. (after the proposer purchased the policy)
$p_{N}$	The probability of an insured having no covered accident during the policy
$s$	The premium of a policy/per policy/term, the decision variable
$D (s)$	Policy demand with $D (s) = a - b s,$ where a is spontaneous demand, b is induced demand, and $D (s)$ is a decreasing function with respect to s.

We also set up these assumptions and notations before building our model.

Considering a single insurance product.
The insurers have liability for compensation for the insured’s accident that occurs within the policy period. The claim amount is R. The policy becomes void once the claim is settled.
While the proposer purchases the policy, the probability of accidents equals one, which is

$\sum_{j = 0}^{N} P_{j} = 1$
The demand for the policy is a decreasing function of the premium of the policy.

D(s) satisfies D′(s) < 0

-Following the symbols and hypotheses, we propose the present value function of the total expected profit of the non-participating policy and the participating policy, both of which are described below.

2.2. Non-Participating Policy

The insurance company receives the premium at the start of each period, and the insurance contract is valid until the end of the N period. When the insured has an accident during the contract's validity period and the policy becomes null and void, the insurer must offer the beneficiary a settlement of the claim amount R. If the insured does not have an accident during the contract's validity period and the policy contract expires at the end of the N period, it will be terminated. The following are the relevant revenue and cost functions.

(1): Present value of gross premium income

= [p_{0} s + p_{1} (s + \frac{s}{1 + r}) + \dots + p_{N} \sum_{j = 0}^{N} \frac{s}{{(1 + r)}^{j}}] D (s)

(2): Gross initial business cost

= c_{0} + c_{1} D (s)

(3): Present value of total expected claim amount

= [\sum_{j = 0}^{N} \frac{p_{j} R}{{(1 + r)}^{j}}] D (s)

Based on the above, the present value of the total expected profit (denoted by

{T P}_{1} (s)

) of a life insurance policy is a function of the policy price (s):

{T P}_{1} (s) = \sum_{k = 0}^{N} [p_{k} \sum_{j = 0}^{k} \frac{1}{{(1 + r)}^{j}}] s D (s) - c_{0} - c_{1} D (s) - [\sum_{j = 0}^{N} \frac{p_{j} R}{{(1 + r)}^{j}}] D (s)

(1)

Similarly, we can find the policy premium that maximizes the present value function of the total expected profit of a life insurance policy, which means that the first and second derivatives of the present value function (

{T P}_{1} (s)

) of the total expected profit of the policy respect to the policy price (s) are as follows:

\frac{{d T P}_{1} (s)}{d s} = \sum_{k = 0}^{N} [p_{k} \sum_{j = 0}^{k} \frac{D (s)}{{(1 + r)}^{j}}] + [\sum_{k = 0}^{N} [p_{k} \sum_{j = 0}^{k} \frac{s}{{(1 + r)}^{j}}] - c_{1} - \sum_{j = 0}^{N} \frac{p_{j} R}{{(1 + r)}^{j}}] D' (s)

(2)

And

\frac{{d^{2} T P}_{1} (s)}{d s^{2}} = \sum_{k = 0}^{N} [p_{k} \sum_{j = 0}^{k} \frac{2 D' (s)}{{(1 + r)}^{j}}] + [\sum_{k = 0}^{N} [p_{k} \sum_{j = 0}^{k} \frac{s}{{(1 + r)}^{j}}] - c_{1} - \sum_{j = 0}^{N} \frac{p_{j} R}{{(1 + r)}^{j}}] D^{''} (s) < 0

(3)

As such. we then carry out a second-order differentiation. If the result of the differentiation is negative, it indicates that the solution that meets the requirements is the optimal solution (i.e., the maximum of the present value of the total expected profit of the policy).

2.3. Participating Policy

The policyholder pays the premiums for the insurer at the beginning of each period(n) and claims back the M amount by the end of every two periods. The insurance company needs to settle the claim amount R for the beneficiary while the insured has an accident, then the policy becomes null and void. If the insured has not had an accident within the contract’s period of validity, the policyholder does not need to pay the premium for the insurer upon the expiration of the insurance contract after the N-th policy year, but they can claim back M amount by the end of every two periods until the W-th period. The relevant income and cost functions are described below:

(1): Present value of gross premium income

$= \sum_{k = 0}^{N} p_{k} [\sum_{j = 0}^{k} \frac{s}{{(1 + r)}^{j}}] D (s)$
(2): Gross initial business cost ${= c}_{0} + c_{1} D (s)$
(3): Present Value of the total expected claim amount

$= [\sum_{j = 0}^{N} \frac{p_{j} R}{{(1 + r)}^{j}}] D (s)$
(4): Present Value of the total expected payment due

$= (p_{0} + p_{1}) + (p_{2} + p_{3}) \frac{M}{{(1 + r)}^{2}} + (p_{4} + p_{5}) [\frac{M}{{(1 + r)}^{2}} + \frac{M}{{(1 + r)}^{4}}] + (p_{6} + p_{7}) [\frac{M}{{(1 + r)}^{2}} + \frac{M}{{(1 + r)}^{4}} + \frac{M}{{(1 + r)}^{6}}] + \dots + (p_{N - 2} + p_{N - 1}) \sum_{j = 1}^{N / 2} \frac{M}{{(1 + r)}^{2 j}} + (q_{1} + q_{2}) \sum_{j = 1}^{(\frac{N}{2}) + 1} \frac{M}{{(1 + r)}^{2 j}} + \dots + (q_{W - 1} + q_{W}) \sum_{j = 1}^{(\frac{N + W}{2}) + 1} \frac{M}{{(1 + r)}^{2 j}}$

It is assumed that

p_{N} = \sum_{j = 1}^{W} q_{j}

, and N and W are even numbers.

p_{N}

means the probability that no accident occurs during the payment period;

q_{j}

means the probability that an accident occurs during the non-payment period (where

j = 1, 2, \dots, W

), and W is when the insurance company needs to pay after the N period.

Based on the above, the present value of the total expected total profit (

{T P}_{2} (s)

) of the participating policy is a function of the policy premium.

{T P}_{2} (s) = \{\sum_{k = 0}^{N} p_{k} [\sum_{j = 0}^{k} \frac{s}{{(1 + r)}^{j}}] - c_{1} - \sum_{j = 0}^{N} \frac{p_{j} R}{{(1 + r)}^{j}} - (p_{0} + p_{1}) - (p_{2} + p_{3}) \frac{M}{{(1 + r)}^{2}} - (p_{6} + p_{7}) [\frac{M}{{(1 + r)}^{2}} + \frac{M}{{(1 + r)}^{4}} + \frac{M}{{(1 + r)}^{6}}] - \dots - (p_{N - 2} + p_{N - 1}) \sum_{j = 1}^{N / 2} \frac{M}{{(1 + r)}^{2 j}}

- (q_{1} + q_{2}) \sum_{j = 1}^{(\frac{N}{2}) + 1} \frac{M}{{(1 + r)}^{2 j}} - \dots - (q_{W - 1} + q_{W}) \sum_{j = 1}^{(\frac{N + W}{2}) + 1} \frac{M}{{(1 + r)}^{2 j}}\} D (s) - c_{0}

(4)

Similarly, we can yield the maximum policy premium, which is the present value function of the total expected profit of the participating policy, namely the first and second derivatives of the present value function of the total expected profit of the policy (

{T P}_{2} (s)

) for the policy premium (s) are as follows:

(5)

and

(6)

We can find that the present value function (

{T P}_{2} (s)

) of the total expected profit of the participating policy is the concave function of the policy premium(s) from Eq (6), namely, the solution, which satisfies equation (5) equaling to 0, is the maximum present value of the total expected profit of the policy.

Furthermore, in cases where the outcomes of the second derivative, as presented in Equation (4) and Equation (6), exhibit negative values, it signifies that the optimal solutions satisfy the specified conditions. Nonetheless, determining the exact solutions for both participating and non-participating policies poses a challenge, thereby necessitating the application of numerical analysis techniques, which are elucidated in the ensuing section.

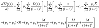
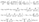
3. Numerical Experiments and Sensitivity Analysis

3.1. Non-Participating Policy

Assuming the given parameter values of an insurance policy are the number of policy contract periods (N) is 6, and the probability of an accident in each period for the policyholder is p₀=0.01, p₁=0.05, p₂=0.1, p₃=0.1, p₄=0.1, p₅=0.1, p₆=0.54. The discount rate is r=0.02, the demand parameters are a=40000 and b=0.06, and the fixed and variable business cost values are c₀=2000 and c₁=200. Given an accident claim amount of R=100,000, the numerical analysis method determines the optimal policy price to be $341,782. Further, the maximum present value of the expected total profit of the policy (

{T P}_{1} (s)

) is estimated to be $34,251,900,000.

In this study, the present value of the maximum policy expected total profit (

{T P}_{1} (s)

), policy price, policy price change percentage, and total profit change percentage are examined with respect to variations in the parameters R, c_0, c₁, r, a, and b in the insurance policy. The parameters R, c0, c1, r, a, and b are modified by +50%, +25%, -25%, and -50%, while keeping the remaining parameter values constant. The results of these calculations are summarized in Table 1.

3.2. Participating Policy

Suppose an insurance policy is defined by the following parameter values: the contract duration (N) is 6 periods, and the payment duration after the policy expiration (W) is 10 periods. The policyholder's accident probability during each period is p₀=0.01, p₁=0.05, p₂=0.1, p₃=0.1, p₄=0.1, p₅=0.1, p₆=0.54, while the accident probability during the non-payment period is q₀=0.05, q₁=0.05, q₂=0.05, q₃=0.05, q₄=0.05, q₅=0.05, q₆=0.05, q₇=0.05, q₈=0.05, q₉=0.05, and q₁₀=0.04. The discount rate r is 0.02, and the demand parameter takes the values a=40000, and b=0.06. The policy entails a fixed business cost of c₀=2000 and a flexible cost of c₁= 200. The accidental claims are R=$10,000, and the payment to be made upon the policy's expiration is M=$500,000. It is found that when the optimal policy price is set at $48,2560, the expected total profit present value (

{T P}_{2} (s)

) is maximized at $10,999,200,000.

To assess the influence of changes in the policy parameters R, M, c₀, c₁, r, a, and b on the present value of the expected total profit (

{T P}_{2} (s)

), policy price, policy price change percentage, and total profit change percentage, we conducted a sensitivity analysis. Each parameter was altered by +50%, +25%, -25%, and -50%, with only one parameter being modified at a time while the other parameter values were held constant. The results of these calculations are presented in Table 2.

3.3. Comparing Non-Participating and Participating Policy Optimal Solutions

Based on the results of the computations described above, Table 3 summarizes the optimal premium and maximum present value of predicted total profit for each policy.

According to Table 3, the non-participating policy generates the greatest profit for an insurance company, followed by the participating policy. Due to the different definitions of these two policies, it is not appropriate to compare the premium of the non-participating policy with that of the participating policy at the same time when determining the optimal premium, so we compare them separately. Most importantly, because dividends are paid, the insurance company charges a higher premium for a participating policy than for a non-participating policy.

In terms of the impact of changing various parameter values on the optimal premium strategy of these two policies, sensitivity analysis provides the following managerial insights. First, there is a positive relationship exists between the claim amount, payment amount due (no payment amounts due for a non-participating policy), and variable business cost with the optimal premium, but there is a negative relationship with the optimal total profit. An increase in the claim amount, payment due, or variable business cost results in an increase in an insurance company's expenses. As a result, the insurance company will raise the premium to reach the break-even point, but higher premiums will reduce consumer willingness to purchase policies, resulting in lower total profits. However, changes in variable business costs have little impact on the premium and total profits.

Second, the changes in fixed business costs have little impact on the optimal premium but have a minor inverse relationship with the optimal total profit. Since it is a fixed cost, the impact is minor compared with that of the variable business cost. Third, when the discount rate increases, the premium will decrease, but the total profit will increase; accordingly, on the contrary, when the discount rate decreases, the premium will increase, and the total profit will decrease accordingly. In other words, the discount rate is inversely related to the optimal premium and positively related to the optimal total profit. The economic implication is that as the discount rate decrease, the premiums for policies with the same insurance amount will be more and more expensive year by year. Moreover, while the discount rate is lower than the return on the stock market, the insurance company will face lapses from customers, consequently a big decrease in the total profits. However, it exists a negative relationship between the discount rate with optimal premium and the optimal total profit in terms of the non-participating policies.

Forth, the demand parameter a is a positive relationship with the premium and total profit. The economic implication is that the demand parameter a is an initiating demand, which implies someone will purchase the policy no matter what the policy premium. Therefore, while the demand is increasing, the premium will increase accordingly. Fifth, the demand parameter b is an inverse relationship with the optimal premium and the optimal total profit. The economic implication is that the demand parameter b is an induced demand, and because policy demand D(s) is a decreasing function, the demand parameter b will be inversely proportional to the demand, and the total profit will decrease accordingly. Besides, when the demand parameter a is fixed, the demand parameter b will also have an inverse relationship with the policy price. Following that, we summarize the effect of each parameter on the premium (s) and the present value of total profit in Table 4.

Furthermore, in Table 4, we argue that the following are worth paying attention to for insurance companies. First, the policy price (s) has a positive relationship with the claim amount R, the policy payment amount M due (non-participating policies not included), the fixed business cost

c_{0}

, the variable business cost

c_{1}

, and the demand parameter a; the policy price (s) has an inverse relationship with the discount rate r and the demand parameter b. Second, the present value of total profit has a positive relationship with the demand parameter a; but the present value of total profit has an inverse relationship with the claim amount R, the policy payment amount M, the fixed business cost

c_{0}

, the variable business cost

c_{1}

, and demand parameter b. Finally, it can be found that the discount rate r has a positive relationship with the present value of total profits of the participating policies, but the discount rate r has an inverse relationship with the present value of total profits of non-participating policies. Accordingly, we summarize the most important parameters that influence both the non-participating and participating policies in Table 5.

From Table 5, the following can be drawn for non-participating policies and participating policies. We showed that the greater the initiating demand a, the greater the marginal impact on the present value of total profits; the smaller the induced demand b is, the greater the marginal impact on the policy premium and the present value of the total profits; regarding policy premium, the non-participating policies are greatly affected by initiating demand a and induced demand b; and in terms of the present value of total profits, the participating policies are greatly affected by initiating demand a and induced demand b.

4. Concluding Remarks

4.1. Conclusions and Discussion

Based on those investors turning to life insurance policies as a means of financial security after experiencing significant losses in volatile stock markets, the study further develops a deterministic model by incorporating the time value of money into the concept of inventory management and provides an optimum solution to find the optimal sales performance and premium strategy. The numerical examples show that the profits created by non-participating life policies are higher than that of participating policies. The sensitivity analysis provides managerial insights, showing that a single insurer can raise profits by considering the balance between initiating demand and induced demand. As such, we derive the following main conclusions in this study.

To begin with, life insurance policies have become increasingly popular among investors looking for more secure and stable investment options due to the volatile nature of stock markets (Delle Foglie & Panetta [28]; Li et al. [29]). As such, insurance companies need to maintain their financial stability while providing adequate coverage to their customers to benefit society and promote economic growth (Cowley & Cummins [30]; Cheng & Yu [31]; Syed et al. [32]) and even under the impact of the COVID-19 pandemic (Richter & Wilson [33]; Valaskova et al. [34]).

Furthermore, the calculation of insurance premiums has been a major focus of research in the insurance industry, as the premium charged to an individual policyholder cannot surpass established regulations (Kleinow & Willder [7]; Huggenberger & Albrecht [35]). Thus, an insurer's investment strategies can impact the price of investment products, and maximizing shareholder value is an important consideration (Consiglio et al. [8]; Zhao et al. [36]). The increase in life expectancy has caused concerns about solvency among life insurance companies due to the increased cost of guaranteed income payments in old age [12].

Moreover, since the optimal pricing strategy for insurance companies can be determined by transforming the demand rate into a decreasing function of the selling price [17], insurance companies can increase their profits by focusing on generating spontaneous consumer demands, reducing induced demands, as well as implementing the optimal pricing strategy. In other words, the study highlights the significance of spontaneous and induced demand in determining the total profit of both types of policies and concludes that life insurance companies should focus on generating spontaneous consumer demand, reducing induced demand, and implementing the optimal pricing strategy to achieve maximum profits.

Overall, the study highlights the importance of insurance companies focusing on preserving solvency and maximizing profits in a highly competitive insurance market. The study provides a valuable framework for insurance companies to evaluate the demand for different types of life insurance policies and determine the optimal pricing strategy to achieve maximum profits.

4.2. Research Implications

We argue that this study has the following essential implication for reference. First, the study highlights the importance of solvency for insurance companies, as non-participating life insurance policies were found to offer greater solvency compared to participating policies. This finding has important implications for insurance companies, as solvency is a crucial aspect of ensuring the long-term viability and stability of the company.

Second, the study also highlights the significance of both spontaneous and induced demand in determining the total profit of both types of policies. This implies that life insurance companies should focus on generating spontaneous consumer demand and reducing induced demand to achieve maximum profits. As such, the study should highlight the significance of spontaneous and induced demand in determining the total profit of life insurance policies. To achieve maximum profits, insurance companies should focus on generating spontaneous consumer demand and reducing induced demand. This requires a comprehensive understanding of consumer behavior, preferences, and demands, as well as an optimal pricing strategy that balances profitability and affordability.

Third, this study develops a deterministic model by explicitly incorporating the time value of money into the concept of inventory management. This helps insurance companies optimize their sales performance and premium strategy, as well as make deliberate considerations between initiating demand and induced demand. The study's numerical examples also show that profits created by non-participating life policies are higher than that of participating policies. This underscores the importance of considering the impact of interest rate fluctuations on insurance products when formulating an investment and operational strategy.

Fourth, the study concludes that life insurance companies should focus on implementing the optimal pricing strategy to achieve maximum profits. This finding has important implications for insurance companies as pricing is a critical aspect of business strategy and can significantly impact the overall financial performance of the company. By focusing on implementing an optimal pricing strategy, insurance companies can ensure long-term profitability and stability.

4.3. Limitations and Future Research

It is important to note that the findings of this study are limited to the specific context in which it was conducted. The insurance market is characterized by significant uncertainty, which can impact the validity of the model's predictions. Additionally, the study only considered the effect of interest rate changes on demand for life insurance policies, but other factors can impact demand for life insurance policies such as changes in tax laws, regulations, and consumer behavior. In addition, we use mathematical models and numerical analysis to derive a deterministic approach in a competitive market based on an annual net premium excluding the loading fee and government price controls because there is no unanimous loading fee and even government price control regulation to follow. This study might be the first attempt to investigate how to implement the optimal pricing strategy to achieve maximum profits for insurance companies by employing the inventory model rarely concerned before. However, developing a comprehensive insurance product evaluation model may not be an easy task because determining how to set the parameters, assumptions, and variables used in this model may not be a unanimous criterion. Nonetheless, this study adds to the existing literature by shedding new light on both mathematical models and numerical analysis to evaluate the demand for non-participating and participating life insurance policies.

Furthermore, this study has identified the premium of a policy as the variable affecting a policy demand function. As a suggestion for future studies, preferences could be incorporated as a demand function. However, a comparative static analysis was performed for the premium while the supply was held constant, which is a limitation of this study. Future studies could incorporate the supply function and provide economic insights into the trade-offs between the two types of policies. Although this study provides valuable insights into the demand for life insurance policies, it has limitations. Therefore, it is necessary to extend the model to a more comprehensive framework as mentioned above. In doing so, we can gain a deeper understanding of spontaneous and induced demand in determining the total profit of both types of policies.

Author Contributions

Conceptualization, methodology, formal analysis, software, C.T Yang; Conceptualization, methodology, writing—original draft, Y. Ni; Formal analysis, validation, writing—original draft, M.H. Yu; Validation, writing—original draft preparation, Y. Chen; Writing—original draft preparation, P. Huang. All authors have read and agreed to the published version of the manuscript.

Funding

The authors received no financial support for the research, authorship, and/or publication of this article.

Conflicts of Interest

The authors declare that there are no conflicts of interest.

References

Carriquiry, M.A.; D. E. Osgood, Index insurance, probabilistic climate forecasts, and production. J. Risk Insur. 2012, 79, 287–300. [CrossRef]
Staikouras, S.K. Business opportunities and market realities in financial conglomerates. Geneva Pap. Risk Insur. Issues Pract. 2006, 31, 124–148. [Google Scholar] [CrossRef]
Cummins, J.D. Risk-based premiums for insurance guaranty funds. J. Finance 1988, 43, 823–839. [Google Scholar]
Ai, J.; V. Bajtelsmit; T. Wang, The combined effect of enterprise risk management and diversification on property and casualty insurer performance. J. Risk Insur. 2018, 85, 513–543. [CrossRef]
Malinovskii, V.K. Business planning for a profit-seeking insurer under deficiency of information. Insur. Math. Econ. 2015, 62, 215–226. [Google Scholar] [CrossRef]
Cicceri, G.; Inserra, G.; Limosani, M. , A machine learning approach to forecast economic recessions—An Italian case study. Mathematics 2020, 8, 241. [Google Scholar] [CrossRef]
Kleinow, T.; Willder, M. , The effect of management discretion on hedging and fair valuation of participating policies with maturity guarantees. Insur. Math. Econ. 2007, 40, 445–458. [Google Scholar] [CrossRef]
Consiglio, A.; D. Saunders; S. A. Zenios, Asset and liability management for insurance products with minimum guarantees: The UK case. J. Bank. Finance 2006, 30, 645–667. [CrossRef]
Taylor, G.C. , Underwriting strategy in a competitive insurance environment. Insur. Math. Econ. 1986, 5, 59–77. [Google Scholar] [CrossRef]
Mourdoukoutas, F.; Boonen, T.J.; Koo, B.; Pantelous, A.A. , Pricing in a competitive stochastic insurance market. Insur. Math. Econ. 2021, 97, 44–56. [Google Scholar] [CrossRef]
Canh, N.P.; U. Wongchoti; S. D. Thanh, 2021. Does economic policy uncertainty matter for insurance development? Evidence from 16 OECD countries. Geneva Pap. Risk Insur. Issues Pract. 2021, 46, 614–648.
Direr, A.; Ennajar-Sayadi, R. How price-elastic is the demand for retirement saving? . Geneva Pap. Risk Insur. Issues Pract. 2019, 2019. 44, 102–122. [Google Scholar] [CrossRef]
Cohen, M.A. , Joint pricing and ordering policy for exponentially decaying inventory with known demand. Nav. Res. Logist. Q. 1977, 24, 257–268. [Google Scholar] [CrossRef]
Ghare, P.M.; G. H. Schrader, A model for an exponentially decaying inventory. J. Ind. Eng. 1963, 14, 238–243.
Ben-Daya, M.A. ; A. Roauf., Inventory models involving lead time as decision variable. J. Oper. Res. Soc.
Liao, C.J.; C. H. Shyu. An analytical determination of lead time with normal demand. Int. J. Oper. Prod. Manage. 1991, 11, 72–78. [CrossRef]
Dye, C.Y. , Joint pricing and ordering policy for a deteriorating inventory with partial backlogging. Omega 2007, 35, 184–189. [Google Scholar] [CrossRef]
Chang, H.J.; C. Y. Dye., An EOQ model for deteriorating items with time varying demand and partial backlogging. J. Oper. Res. Soc. 1999, 50, 1176–1182. [CrossRef]
Dong, L.; B. Tomlin., Managing disruption risk: The interplay between operations and insurance. Manag. Sci. 2012, 58, 1898–1915.
Serpa, J.C.; H. Krishnan. The strategic role of business insurance. Manag. Sci. 2017, 63, 384–404.
Martínez, A.; R. Pascual; S. Maturana. A methodology for integrated critical spare parts and insurance management. Appl. Stoch. Models Bus. Ind. 2016, 32, 90–98. [CrossRef]
Cheng, C.; J. Li., Early default risk and surrender risk: Impacts on participating life insurance policies. Insur. Math. Econ. 2018, 78, 30–43. [Google Scholar] [CrossRef]
Henckaerts, R.; Antonio, K. , The added value of dynamically updating motor insurance prices with telematics collected driving behavior data. Insur. Math. Econ. 2022, 105, 79–95. [Google Scholar] [CrossRef]
Blanchard, O. , Public debt and low interest rates. Am. Econ. Rev. 2019, 109, 1197–1229. [Google Scholar] [CrossRef]
Picard, P. , Participating insurance contracts and the Rothschild-Stiglitz equilibrium puzzle. Geneva Pap. Risk Insur. Issues Pract. 2014, 39, 153–175. [Google Scholar] [CrossRef]
Kim, K.D.; R. J. Funk; P. Yan; B. K. Nallamothu; A. Zaheer, J.M. Hollingsworth, Informal clinical integration in medicare accountable care organizations and mortality following coronary artery bypass graft surgery. Med. Care 2019, 57, 194–201. [CrossRef]
Bacinello, A.R.; P. Millossovich; A. Chen, The impact of longevity and investment risk on a portfolio of life insurance liabilities. Eur. Actuar. J. 2018, 8, 257–290. [CrossRef]
Delle Foglie, A.; Panetta, I.C. , Islamic stock market versus conventional: Are islamic investing a ‘Safe Haven’for investors? A systematic literature review. Pacific-Basin Finance J. 2020, 64, 101435. [Google Scholar] [CrossRef]
Li, Z.; Ao, Z.; Mo, B. , Revisiting the valuable roles of global financial assets for international stock markets: quantile coherence and causality-in-quantiles approaches. Mathematics 2021, 9, 1750. [Google Scholar] [CrossRef]
Cowley, A.; J. D. Cummins, Securitization of life insurance assets and liabilities. J. Risk Insur. 2005, 72, 193–226. [CrossRef]
Cheng, J.; L. Yu. Life and health insurance consumption in China: Demographic and environmental risks. Geneva Pap. Risk Insur. Issues Pract. 2019, 44, 67–101. [CrossRef]
Syed, A.A.; Ahmed, F.; Kamal, M.A.; Trinidad Segovia, J.E. , Assessing the role of digital finance on shadow economy and financial instability: An empirical analysis of selected South Asian countries. Mathematics 2021, 9, 3018. [Google Scholar] [CrossRef]
Richter, A.; T. C. Wilson, Covid-19: implications for insurer risk management and the insurability of pandemic risk. Geneva Pap. Risk Insur. Issues Pract. 2020, 45, 171–199.
Valaskova, K.; Durana, P.; Adamko, P. , Changes in consumers’ purchase patterns as a consequence of the COVID-19 pandemic. Mathematics 2021, 9, 1788. [Google Scholar] [CrossRef]
Huggenberger, M.; P. Albrecht., Risk pooling and solvency regulation: A policyholder's perspective. J. Risk Insur. 2022, 89, 907–950. [CrossRef]
Zhao, H.; Shen, Y.; Zeng, Y.; Zhang, W. , Robust equilibrium excess-of-loss reinsurance and CDS investment strategies for a mean–variance insurer with ambiguity aversion. Insur. Math. Econ. 2019, 88, 159–180. [Google Scholar] [CrossRef]

Table 1. Sensitivity analysis of non-participating policy by various parameters.

		variation（%）
Parameter	variation（%）	The premium of a policy	The total expected profit of policies
R	-50	-1.2332	2.6115
	-25	-0.6166	1.3015
	+25	0.6166	-1.2931
	+50	1.2332	-2.5778
c₀	-50	0.0000	2.91955×10^-6
	-25	0.0000	1.45977×10^-6
	+25	0.0000	-1.45977×10^-6
	+50	0.0000	-2.91955×10^-6
c₁	-50	-0.0027	0.0057
	-25	-0.0013	0.0028
	+25	0.0013	-0.0028
	+50	0.0027	-0.0057
R	-50	0.0515	2.4273
	-25	0.0256	1.1991
	+25	- 0.0252	-1.1709
	+50	- 0.0501	-2.3144
A	-50	-48.7641	-76.2833
	-25	-24.382	-44.7209
	+25	24.382	57.8795
	+50	48.7641	128.917
B	-50	97.5282	105.235
	-25	32.5094	35.0725
	+25	-19.5056	-21.0368
	+50	-32.5094	-35.0556

Table 2. Sensitivity analysis of participating policy by various parameters.

		variation（%）
parameter	variation（%）	The premium of a policy	The total expected profit of policies
R	-50	-0.8734	4.6311
	-25	-0.4367	2.3025
	+25	0.4367	-2.2763
	+50	0.8734	-4.5263
M	-50	-14.5866	91.0835
	-25	-7.2933	41.8874
	+25	7.2933	-34.5786
	+50	14.5866	-61.8483
c₀	-50	0.0000	9.09154×10^-6
	-25	0.0000	4.54577×10^-6
	+25	0.0000	-4.54577×10^-6
	+50	0.0000	-9.09154×10^-6
c₁	-50	-0.0019	0.0100
	-25	-0.0010	0.0050
	+25	0.0010	-0.0050
	+50	0.0019	-0.0100
r	-50	0.9841	-2.6834
	-25	0.4836	-1.2970
	+25	-0.4674	1.2119
	+50	-0.9194	2.3427
a	-50	-34.5380	-99.1027
	-25	-17.2690	-70.0394
	+25	17.2690	111.0150
	+50	34.5380	263.0070
b	-50	69.0760	294.9590
	-25	23.0253	92.8447
	+25	-13.8152	-49.1369
	+50	-23.0253	-76.4200

Table 3. Comparison of each policy's optimal premium and maximum predicted total profit.

Types of policies	Optimum policy premium	Optimal policy sales volume	Maximum present value of expected gross profits
Non-participating policy Participating policy	$34,1782	19494(sheets)	$34,251,900,000
Non-participating policy Participating policy	$48,2560	11046(sheets)	$10,999,200,000

Table 4. The sensitivity direction of each parameter on premium.

Parameter	Premium per policy (s)	Present Value of total profits
R	↑	↓
M	↑	↓
c₀	↑	↓
c₁	↑	↓
r	↓	↑↓
a	↑	↑
b	↓	↓

Notes：↑means positive relationship, ↓means negative relationship, ↑↓ implies a positive relationship with participating policy, inverse relationship with non-participating policy repositions, lemmas, etc. should be numbered sequentially (i.e., Proposition 2 follows Theorem 1). Examples or Remarks use the same formatting, but should be numbered separately, so a document may contain Theorem 1, Remark 1 and Example 1.

Table 5. Parameter variation sensitivity analysis of non-participating and participating.

Parameter	Variation（%）	Non-participating policy		Participating policy
		Variation（%）		Variation（%）
		Policy Price	PV of Expected total profits	Policy Price	PV of Expected total profits
a	-50	-48.7641	-76.2833	-34.5380	-99.1027
	-25	-24.382	-44.7209	-17.2690	-70.0394
	+25	24.382	57.8795	17.2690	111.0150
	+50	48.7641	128.917	34.5380	263.0070
b	-50	97.5282	105.235	69.0760	294.9590
	-25	32.5094	35.0725	23.0253	92.8447
	+25	-19.5056	-21.0368	-13.8152	-49.1369
	+50	-32.5094	-35.0556	-23.0253	-76.4200

Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.

© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).

Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.

Alerts

MDPI Initiatives

Important Links

Choose an area of interest and we will send you notifications of new preprints at your preferred frequency.

Disclaimer