Numerical Solutions of the Nonlinear Dispersive Shallow Water Wave Equations Based on the Space-Time Coupled Generalized Finite Difference Scheme

Preprint

Article

Numerical Solutions of the Nonlinear Dispersive Shallow Water Wave Equations Based on the Space-Time Coupled Generalized Finite Difference Scheme

Altmetrics

Downloads

128

Views

Comments

A peer-reviewed article of this preprint also exists.

This version is not peer-reviewed

Submitted:

12 June 2023

Posted:

12 June 2023

You are already at the latest version

Alerts

Abstract

This paper applied the space-time generalized finite difference scheme for solving the nonlinear dispersive shallow water waves as the modified Camassa−Holm equation, modified Degasperis-Procesi equation, Fornberg-Whitham equation, and its modified form. The proposed meshless numerical scheme was composed of the space-time generalized finite difference method, the two-step Newton-Raphson method, and the time-marching method. The space-time approach can treat the temporal derivative as one of the spatial derivatives. This numerical technique enables all the partial derivatives in the governing equation can be discretized by a spatial discretization method, and the mixed derivative can efficiently deal with using the proposed meshless numerical scheme. The space-time generalized finite difference method is advanced from the Taylor series expansion and the moving-least square method. The numerical discretization process is only related to functional data and weighting coefficients on the central node and its nearby nodes. Thus, the matrix system composed of nonlinear algebraic equations will be a sparse matrix and can be efficiently solved by the two-step Newton-Raphson method. Furthermore, the time-marching method was utilized to proceed with the space-time domain along the time axis. In this paper, several numerical examples were tested to verify the capability of the proposed space-time generalized finite difference scheme.

Keywords:

Subject: Computer Science and Mathematics - Computational Mathematics

1. Introduction

The dispersive shallow water wave is a kind of wave propagation phenomenon that has been widely studied in engineering. It has many applications in physics, engineering, mechanics, and mathematics. In the past few decades [1,2,11,3,4,5,6,7,8,9,10], some partial differential equations (PDEs) have been presented to describe the traveling wave phenomenon, and most of these equations are nonlinear time-dependent PDEs such as the Camassa−Holm equation [2,3], the Degasperis−Procesi equation [3,8,11], the Fornberg−Whitham equation [1,4,5,6,7,9,10,11], and their modified forms. Mathematically, the above-mentioned three equations and their modified forms are transient nonlinear PDE with third (3rd)-order time-space mixed partial derivatives. Therefore, how to obtain the numerical solutions of those PDEs is a significant issue for analyzing the traveling wave phenomenon. In previous studies, there were mainly two types of methods used to obtain solutions for such equations, which included the approximate method and numerical simulation.

To deal with such complicated equations, the exact solution is generally difficult to find, and the numerical ways are important numerical treatments for those equations. By using the numerical methods for temporal and spatial discretization, the classical numerical treatments were inconvenient to adopt due to the high-order mixed partial derivatives. Thus, the approximate methods for presenting the deriving the approximate numerical solutions were widely used by researchers. For example, Wazwaz [3] used the extended tanh method to establish the new solitary wave solutions of the modified Degasperis−Procesi and Camassa−Holm equations. Abidi and Omrani [4] applied the homotopy analysis method (HAM) to acquire the HAM results of the Fornberg−Whitham equation and compared it with Adomian’s decomposition method (ADM). Ahmad et al. [10] utilized the modified variational iteration algorithm (MVIA) to get the approximate numerical solutions of the Fornberg−Whitham equation and its modified form. In addition to the above mentioned, there are other approximate methods such as the method of phase portraits analysis [5], He’s variational iteration method (VIM) [6], and the reproducing kernel Hilbert space method (RKHSM) [7]. Recently, due to the evolution of computer technology and numerical methods, novel numerical schemes have also been applied to solve such equations such as the Godunov method [9], the cubic B-spline quasi-interpolation method [8], and the hybrid radial basis functions method [11].

In the numerical discretization methods for PDEs, they can roughly divide into two families as mesh-based methods and meshless/free methods. The finite difference method (FDM), finite volume method, and finite element method are the famous mesh-based methods that are widely used. Those methods were developed and modified for solving the engineering problem and analyzed some physical phenomena that are difficult to obtain through practical experiments. Although these mesh-based methods are highly applied, mesh generation is still a troublesome issue today. Thus, the idea that using the numerical discretization methods without mesh becomes one of the important research directions. The meshless methods can avoid generating mesh, and make it easy to solve problems in a computational domain with complex shapes. In addition, the numerical discretization only needs to construct interpolation functions on arbitrary distribution nodes for the governing equation. After years of development, meshless methods have the advantages of simple numerical processes, easy programming, flexibility, and even the ability to construct a hybrid numerical scheme customized by researchers. At present, there are several meshless numerical methods, for example, the radial basis functions collocation method (RBFCM) [11], the virtual boundary meshless Galerkin method [12], the moving particle semi-implicit method [13], the radial point interpolation meshless method [14], the singular boundary method [15], the localized scheme based on boundary-type method [16,17,18], the generalized finite difference method (GFDM) [19,20,29,21,22,23,24,25,26,27,28], etc.

The GFDM is a localized domain-type meshless collocation method based on the multivariate Taylor series expansion theory and the moving least-square method. In 1980, the idea that the FDM without mesh was proposed by Liszka and Orkisz [19]. After Benito et al. [20] proposed the explicit numerical process in 2001, numerical applications related to the GFDM have been proposed in the past two decades. By utilizing the GFDM, the approximate expression of the partial derivative terms can be represented by a linear combination of the weight coefficients and function values in a local support domain. This support domain only contains the goal node and its nearby nodes. Once the nodes are distributed in the computational domain, the governing equation can be discretized into a system of algebraic equations. In addition, the resultant matrix system is a sparse matrix due to the localized property of the GFDM. The above characteristics make the GFDM enable to apply for complex problems, such as the theoretical analysis [29], shallow water equation [21,22], porous media flow [23], wave propagation [24], elliptic interface problems [25], theoretical analysis, extended Fisher–Kolmogorov equation [26], stream function formulation [27], and elastic wave [28]. In this research, the space-time GFDM (ST–GFDM) was applied as the foundation of the proposed meshless numerical scheme, and it is an extended meshless method from the GFDM.

The space-time (ST) coupled approach is a numerical technique that treated the temporal derivative as one of a spatial derivative. Before ST coupled approach was used, the original way to solve a time-dependent problem is that apply a numerical scheme that combines the spatial discretization method and temporal discretization method to solve. That caused the accuracy and stability of the numerical scheme to be hard to define. By utilizing the ST coupled approach, an (n)-dimensional time-dependent problem will transfer into an (n+1)-dimensional steady-state problem, then all of the partial derivatives in the governing equation can be discretized by the numerical method which applies for spatial discretization. Thus, the properties of the numerical scheme will much easier to determine. Recently, the ST coupled approach is widely combined with meshless methods such as the ST localized RBFCM [30], ST kernel-based method [31], ST localized method of fundamental solutions [32,33], ST Trefftz Method [34,35], ST backward substitution method [36] and ST-GFDM [37,38,39,40,41,42,43,44,45]. Based on the flexibility of the ST-GFDM, researchers applied this meshless method for engineering problems in the past few years, for example, the heat conduction problems [37,46], Burgers’ equations [38], parabolic PDEs [39], unsteady double-diffusive natural convection [40], thin elastic plate bending problem [41], thermoelasticity problems [42], equal-width equation [43], Zakharov–Kuznetsov-Modified equal-width equation [44], and hyperbolic PDEs [45], etc. The above achievements indicate that the ST-GFDM is one of the meshless method that have potential for engineering applications. In this research, the ST-GFDM is applied to combine with the two-step Newton’s method and time-marching approach for solving the dispersive shallow water wave problem.

After the motivation and the discussions of relevant works of literature are described in the first section. The governing equations of the dispersive shallow water wave are represented in Section 2. In the section of proposed ST-GFDM, the numerical process is described and four numerical examples are simulated to verify the proposed method in section 4. Then, the conclusions are represented in the final section.

2. The Mathematical Models of the Dispersive Shallow Water Waves

The dispersive shallow water wave represents the behavior of the wave propagation, breaking wave, and dynamic system of the fluid. It is an important phenomenon in physics and engineering. In the past few decades, several researchers have proposed the mathematical model of the dispersive shallow water wave problem, and its general form of the governing equation [1,2,3] is described as,

\frac{\partial u}{\partial t} - \frac{\partial^{3} u}{\partial x^{2} \partial t} + (α + β u^{k}) \frac{\partial u}{\partial x} = q \frac{\partial u}{\partial x} \frac{\partial^{2} u}{\partial x^{2}} + u \frac{\partial^{3} u}{\partial x^{3}}, a \leq x \leq b, t \geq 0,

(1)

where u is the wave speed; x and t are the spatial- and temporal- axis; α, β, k, and q are the constants. The initial conditions and boundary conditions are represented as,

{\begin{matrix} u (x, 0) = U_{0} (x) \\ u (a, t) = f_{1} (t) \\ u (b, t) = f_{2} (t) \end{matrix} .

(2)

By applying the constants, a, b, k, and q, three different type of the dispersive shallow water wave equation are defined. The first one is the Fornberg–Whitham equation [1,6,7,9,10] that is given with α=1, β=1, k=1, and q=3 as,

\frac{\partial u}{\partial t} - \frac{\partial^{3} u}{\partial x^{2} \partial t} + (1 + u) \frac{\partial u}{\partial x} = 3 \frac{\partial u}{\partial x} \frac{\partial^{2} u}{\partial x^{2}} + u \frac{\partial^{3} u}{\partial x^{3}}, a \leq x \leq b, t \geq 0,

(3)

and its modified form [4,7,10] is given (α=1, β=1, k=2, and q=3) as,

\frac{\partial u}{\partial t} - \frac{\partial^{3} u}{\partial x^{2} \partial t} + (1 + u^{2}) \frac{\partial u}{\partial x} = 3 \frac{\partial u}{\partial x} \frac{\partial^{2} u}{\partial x^{2}} + u \frac{\partial^{3} u}{\partial x^{3}} .

(4)

The remaining two are similar; they are the Camassa–Holm equation [2,3] and Degasperis–Procesi equation [3,8,11], respectively. By giving with α=0, β=3, k=1, and q=2, the Camassa–Holm equation can be denote as

\frac{\partial u}{\partial t} - \frac{\partial^{3} u}{\partial x^{2} \partial t} + 3 u \frac{\partial u}{\partial x} = 2 \frac{\partial u}{\partial x} \frac{\partial^{2} u}{\partial x^{2}} + u \frac{\partial^{3} u}{\partial x^{3}},

(5)

and the Degasperis–Procesi equation (α=0, β = 4, k = 0, and q=3) is described as

\frac{\partial u}{\partial t} - \frac{\partial^{3} u}{\partial x^{2} \partial t} + 4 u \frac{\partial u}{\partial x} = 3 \frac{\partial u}{\partial x} \frac{\partial^{2} u}{\partial x^{2}} + u \frac{\partial^{3} u}{\partial x^{3}},

(6)

As same to the relationship of the Fornberg–Whitham equation and its modified form, the modified form of the Camassa–Holm equation [3] and Degasperis–Procesi equation [3,8,11] are represented by changing nonlinear term

u \frac{\partial u}{\partial x}

into

u^{2} \frac{\partial u}{\partial x}

. Then, they can be described as follows,

\frac{\partial u}{\partial t} - \frac{\partial^{3} u}{\partial x^{2} \partial t} + 3 u^{2} \frac{\partial u}{\partial x} = 2 \frac{\partial u}{\partial x} \frac{\partial^{2} u}{\partial x^{2}} + u \frac{\partial^{3} u}{\partial x^{3}},

(7)

and

\frac{\partial u}{\partial t} - \frac{\partial^{3} u}{\partial x^{2} \partial t} + 4 u^{2} \frac{\partial u}{\partial x} = 3 \frac{\partial u}{\partial x} \frac{\partial^{2} u}{\partial x^{2}} + u \frac{\partial^{3} u}{\partial x^{3}},

(8)

Eqs. (1) and (3)-(7) are highly nonlinear PDEs and have 3rd-order mixed partial derivatives as

\frac{\partial^{3} u}{\partial x^{2} \partial t}

. Its complexity caused the original explicit or implicit numerical schemes to be difficult to solve, and most of the researchers proposed approximate or exact solutions for dispersive shallow water wave equations. Therefore, the applications of the numerical scheme for such equations are still in the early stages of enlightenment. In this research, the Fornberg–Whitham equation and its modified form, modified Camassa–Holm equation, and modified Degasperis–Procesi equation are solved by the proposed ST-GFDM scheme. The numerical procedures of the proposed ST-GFDM scheme is introduced in the next section.

3. The Proposed Meshless Numerical Scheme

The numerical procedures of the proposed ST-GFDM scheme is described in this section. The proposed numerical scheme applies ST-GFDM for numerical discretization to obtain the nonlinear algebraic equations. Then, the nonlinear algebraic system is solved by the two-step Newton’s method. For saving the computational resource and solving the numerical problems within unpredictable end-time, the simple technique, named time-marching method, is applied.

3.1. Space-Time Generalized Finite Difference Method

In this subsection, the numerical process of ST-GFDM is described. Once the time-dependent problem is determined, the distribution nodes can be set in the corresponding computational domain. For the one-dimensional (1D) time-dependent problem, the ST approach defines a two-dimensional (2D) steady-state problem in an x-t field. Since the ST approach is applied, the distribution nodes are set both in the space- and time-axis, and named ST-domain [38,40,41] as Figure 1(a).

A supporting domain is set up by choosing ns nearest nodes within central i node in Figure 1(b), and

(x_{i}, t_{i}), i = 1, 2, ..., N_{T}

is defined as the coordinate of the ith node. On the other hand,

(x_{i, j}, t_{i, j}), j = 1, 2, ..., n_{s}

, is represented the coordinates of the nodes in the supporting domain. By applying the n-order Taylor expansion and the weighting function, a residual function

B_{n} (u_{i})

can be written as [27,43],

B_{n} (u_{i}) = \sum_{j = 1}^{n_{s}} {[(- u_{i, j} + \sum_{0 \leq o, m \leq n, o + m \leq n}^{} \frac{1}{o! m!} \cdot \frac{\partial^{o + m} u_{i}}{\partial^{o} x \partial^{m} t} \cdot h_{i, j}^{o} \cdot l_{i, j}^{m} + E_{n}) w (h_{i, j}, l_{i, j})]}^{2},

(9)

where

u_{i}

and

u_{i, j}

denotes the unknowns at the ith node and unknowns inside the ith supporting domain, respectively;

E_{n}

is the truncation error of the n-order Taylor expansion; o and m is the natural number;

h_{i, j} = x_{i} - x_{i, j}

;

l_{i, j} = t_{i} - t_{i, j}

; and

w

is the quartic spline function and describes as follows,

w (h_{i, j}, l_{i, j}) = {\begin{cases} 1 - 6 {(\frac{d_{i, j}}{d m_{i}})}^{2} + 8 {(\frac{d_{i, j}}{d m_{i}})}^{3} - 3 {(\frac{d_{i, j}}{d m_{i}})}^{4}, d_{i, j} \leq d m_{i} \\ 0, d_{i, j} > d m_{i} \end{cases},

(10)

where

d_{i, j}

is a distance between the ith node and the each node inside the ith supporting domain, and ; and

d m_{i}

is the maximum distance.

In this study, the 3rd-order ST-GFDM was applied, and Eq. (9) can be written as,

B_{3} (u_{i}) = \sum_{j = 1}^{n_{s}} {[(\begin{array}{l} u_{i} - u_{i, j} + h_{i, j} {\frac{\partial u}{\partial x} |}_{i} + l_{i, j} {\frac{\partial u}{\partial t} |}_{i} + \frac{h_{i, j}^{2}}{2} {\frac{\partial^{2} u}{\partial x^{2}} |}_{i} + h_{i, j} l_{i, j} {\frac{\partial^{2} u}{\partial x \partial t} |}_{i} + \frac{l_{i, j}^{2}}{2} {\frac{\partial^{2} u}{\partial t^{2}} |}_{i} + ... \\ \frac{h_{i, j}^{3}}{6} {\frac{\partial^{3} u}{\partial x^{3}} |}_{i} + {\frac{h_{i, j}^{2} l_{i, j}^{}}{2} \frac{\partial^{3} u}{\partial x^{2} \partial t} |}_{i} + \frac{h_{i, j}^{} l_{i, j}^{2}}{2} {\frac{\partial^{3} u}{\partial x \partial t^{2}} |}_{i} + \frac{l_{i, j}^{3}}{6} {\frac{\partial^{3} u}{\partial t^{3}} |}_{i} \end{array}) w_{i, j}]}^{2},

(11)

and minimalized

B_{3} (u_{i})

respecting to,

D_{u_{i}} = {[{\frac{\partial u}{\partial x} |}_{i}, {\frac{\partial u}{\partial t} |}_{i}, {\frac{\partial^{2} u}{\partial x^{2}} |}_{i}, {\frac{\partial^{2} u}{\partial x \partial t} |}_{i}, {\frac{\partial^{2} u}{\partial t^{2}} |}_{i}, {\frac{\partial^{3} u}{\partial x^{3}} |}_{i}, {\frac{\partial^{3} u}{\partial x^{2} \partial t} |}_{i}, {\frac{\partial^{3} u}{\partial x \partial t^{2}} |}_{i}, {\frac{\partial^{3} u}{\partial t^{3}} |}_{i}]}^{T},

(12)

a linear system

A D_{u_{i}} = b U_{i}

is obtained. In this linear system, the matrix A is denoted as where

P = {[\begin{matrix} h_{i, 1} & l_{i, 1} & \frac{h_{i, 1}^{2}}{2} & h_{i, 1} l_{i, 1} & \frac{l_{i, 1}^{2}}{2} & \frac{h_{i, 1}^{3}}{6} & \frac{h_{i, 1}^{2} l_{i, 1}}{2} & \frac{h_{i, 1} l_{i, 1}^{2}}{2} & \frac{l_{i, 1}^{3}}{6} \\ h_{i, 2} & l_{i, 2} & \frac{h_{i, 2}^{2}}{2} & h_{i, 2} l_{i, 2} & \frac{l_{i, 2}^{2}}{2} & \frac{h_{i, 2}^{3}}{6} & \frac{h_{i, 2}^{2} l_{i, 2}}{2} & \frac{h_{i, 2} l_{i, 2}^{2}}{2} & \frac{l_{i, 2}^{3}}{6} \\ ⋮ & ⋮ & ⋮ & ⋮ & ⋮ & ⋮ & ⋮ & ⋮ & ⋮ \\ h_{i, j} & l_{i, j} & \frac{h_{i, j}^{2}}{2} & h_{i, j} l_{i, j} & \frac{l_{i, j}^{2}}{2} & \frac{h_{i, j}^{3}}{6} & \frac{h_{i, j}^{2} l_{i, j}}{2} & \frac{h_{i, j} l_{i, j}^{2}}{2} & \frac{l_{i, j}^{3}}{6} \\ ⋮ & ⋮ & ⋮ & ⋮ & ⋮ & ⋮ & ⋮ & ⋮ & ⋮ \\ h_{i, n_{s}} & l_{i, n_{s}} & \frac{h_{i, n_{s}}^{2}}{2} & h_{i, n_{s}} l_{i, n_{s}} & \frac{l_{i, n_{s}}^{2}}{2} & \frac{h_{i, n_{s}}^{3}}{6} & \frac{h_{i, n_{s}}^{2} l_{i, n_{s}}}{2} & \frac{h_{i, n_{s}} l_{i, n_{s}}^{2}}{2} & \frac{l_{i, n_{s}}^{3}}{6} \end{matrix}]}_{n_{s} \times 9},

(13)

W = d i a g (w_{i, 1}, w_{i, 2}, \dots, w_{i, n_{s}})

; b is a coefficient matrix whose size is

9 \times (n_{s} + 1)

and is written as

b = [\begin{matrix} P^{Τ} w & P^{Τ} W^{2} \end{matrix}]

;

U_{i} = {[u_{i}, u_{i, 1}, u_{i, 2}, ..., u_{i, n_{s}}]}^{T}

; and the superscript T is a symbol of transpose. By solving this linear system, the approximate expression of

D_{u_{i}}

can be written as,

D_{u_{i}} = A^{- 1} b U_{i} = E_{i} U_{i},

(14)

where

E_{i}

is the matrix of weighting coefficients within sized

9 \times (n_{s} + 1)

. Then, the derivatives are denoted as follows,

{\begin{matrix} {\frac{\partial u}{\partial x} |}_{i} = w x_{i, 0}^{} u_{i} + \sum_{j = 1}^{n_{s}} w x_{i, j}^{} u_{i, j} \\ {\frac{\partial u}{\partial t} |}_{i} = w t_{i, 0}^{} u_{i} + \sum_{j = 1}^{n_{s}} w t_{i, j}^{} u_{i, j} \\ {\frac{\partial^{2} u}{\partial x^{2}} |}_{i} = w x x_{i, 0}^{} u_{i} + \sum_{j = 1}^{n_{s}} w x x_{i, j}^{} u_{i, j} \\ {\frac{\partial^{2} u}{\partial x \partial t} |}_{i} = w x t_{i, 0}^{} u_{i} + \sum_{j = 1}^{n_{s}} w x t_{i, j}^{} u_{i, j} \\ {\frac{\partial^{2} u}{\partial t^{2}} |}_{i} = w t t_{i, 0}^{} u_{i} + \sum_{j = 1}^{n_{s}} w t t_{i, j}^{} u_{i, j} \\ {\frac{\partial^{3} u}{\partial x^{3}} |}_{i} = w x x x_{i, 0}^{} u_{i} + \sum_{j = 1}^{n_{s}} w x x x_{i, j}^{} u_{i, j} \\ {\frac{\partial^{3} u}{\partial x^{2} \partial t} |}_{i} = w x x t_{i, 0}^{} u_{i} + \sum_{j = 1}^{n_{s}} w x x t_{i, j}^{} u_{i, j} \\ {\frac{\partial^{3} u}{\partial x \partial t^{2}} |}_{i} = w x t t_{i, 0}^{} u_{i} + \sum_{j = 1}^{n_{s}} w x t t_{i, j}^{} u_{i, j} \\ {\frac{\partial^{3} u}{\partial t^{3}} |}_{i} = w t t t_{i, 0}^{} u_{i} + \sum_{j = 1}^{n_{s}} w t t t_{i, j}^{} u_{i, j} \end{matrix},

(15)

where

{w x_{i, j}}_{j = 0}^{n_{s}}

{w t_{i, j}}_{j = 0}^{n_{s}}

{w x x_{i, j}}_{j = 0}^{n_{s}}

{w x t_{i, j}}_{j = 0}^{n_{s}}

{w t t_{i, j}}_{j = 0}^{n_{s}}

{w x x x_{i, j}}_{j = 0}^{n_{s}}

{w x x t_{i, j}}_{j = 0}^{n_{s}}

{w x t t_{i, j}}_{j = 0}^{n_{s}}

, and

{w t t t_{i, j}}_{j = 0}^{n_{s}}

are the weighting coefficients, and gained by solving Eq. (14). Eq. (15) is a significant part of the proposed ST-GFDM in that the partial derivatives are approximated by a linear combination of the weight coefficients and function values in a local support domain. Thus, the discretized governing equations and boundary conditions only relate to the central i node and its nearby n_s nodes in the local support domain. In addition, the numerical process of Eqs. (9)-(15) will apply for each node to obtain the weighting coefficients matrix

E_{i}

of each node. Finally, the resultant matrix system, formed by the algebraic equations after discretization, is a sparse matrix.

The following contexts demonstrate the numerical discretization for the governing equation and boundary conditions to form the nonlinear algebraic systems. Since the simulate start, N_b1, N_b2, N_b3 and N_b4 nodes are set up along the

Γ_{1}

Γ_{2}

Γ_{3}

and

Γ_{4}

, respectively. Meanwhile, N_i nodes are distributed inside the computational domain

Ω

. (see Figure 1(a)). The nodes along

Γ_{1}

are satisfied the initial conditions

U_{0} (x)

and the nodes along

Γ_{2}

and

Γ_{3}

are satisfied the boundary conditions

f_{1} (a, t)

and

f_{2} (b, t)

, respectively. Therefore, the algebraic equations along the

Γ_{1}

Γ_{2}

and

Γ_{3}

are described as,

{\begin{cases} F_{i}^{} = u_{i} - U_{0} (x_{i}), i = 1, 2, ..., N_{b 1}, \\ F_{i}^{} = u_{i} - f_{2} (a, t_{i}), i = N_{b 1} + 1, N_{b 1} + 2, ..., N_{b 1} + N_{b 2}, \\ F_{i}^{} = u_{i} - f_{1} (b, t_{i}), i = N_{b 1} + N_{b 2} + 1, N_{b 1} + N_{b 2} + 2, ..., N_{b 1} + N_{b 2} + N_{b 3}, \end{cases}

(16)

The remaining domain,

Γ_{4}

and

Ω

, are both satisfied the governing equation, Eq. (1), and they can be discretized by Eq. (15) as,

\begin{array}{l} F_{i}^{} = {\begin{cases} (w t_{i, 0}^{} u_{i} + \sum_{j = 1}^{n_{s}} w t_{i, j}^{} u_{i, j}) - (w x x t_{i, 0}^{} u_{i} + \sum_{j = 1}^{n_{s}} w x x t_{i, j}^{} u_{i, j}) + ... \\ (a + b u_{i}^{k}) (w x_{i, 0}^{} u_{i} + \sum_{j = 1}^{n_{s}} w x_{i, j}^{} u_{i, j}) - ... \\ q (w x_{i, 0}^{} u_{i} + \sum_{j = 1}^{n_{s}} w x_{i, j}^{} u_{i, j}) (w x x_{i, 0}^{} u_{i} + \sum_{j = 1}^{n_{s}} w x x_{i, j}^{} u_{i, j}) - ... \\ u_{i} (w x x x_{i, 0}^{} u_{i} + \sum_{j = 1}^{n_{s}} w x x x_{i, j}^{} u_{i, j}) \end{cases}}, \\ i = N_{b 1} + N_{b 2} + N_{b 3} + 1, N_{b 1} + N_{b 2} + N_{b 3} + 2, ..., N_{B}, N_{B} + 1, N_{B} + 2, ..., N_{T}, \end{array}

(17)

where

N_{B}

is a number of nodes set up on the whole boundary, and defined as

N_{B} = N_{b 1} + N_{b 2} + N_{b 3} + N_{b 4}

;

N_{T}

is the number of total nodes in the computational domain as

N_{T} = N_{B} + N_{i}

. In Eqs. (16)-(17),

N_{T}

algebraic equations are acquired, and denoted as

F = {[F_{1}^{}, F_{2}^{}, ..., F_{i}^{}]}^{T}, i = 1, 2, ..., N_{T}

. Meanwhile,

N_{T}

unknown values are defined as,

U = {[u_{1}^{}, u_{2}^{}, ..., u_{i}^{}]}^{T}, i = 1, 2, ..., N_{T}

. Then, the two-step Newton’s method is applied to solve this nonlinear algebraic system, and the specific numerical process is described in next subsection.

3.2. Two-Step Newton’s Method

In this research, the famous nonlinear solve, the Newton’s method, was applied for iterating the numerical solution of the proposed ST-GFDM. The Newton’s method is a classic solver for nonlinear systems, and bases on the first (1st) -order Taylor expansion formula. It has characteristics that simple to programming and fast convergence. The iteration formula for the Newton’s method is written as follows

U^{k + 1} = U^{k} - {(J^{- 1})}^{k} F^{k}, k = 1, 2, 3, ...,

(18)

where J is the Jacobian matrix, and the elements are expressed as

J_{i, j} = \partial F_{i} / \partial U_{j}

; k is the number of iteration;

U^{k + 1}

and

U^{k}

are the vectors of unknowns at the (k +1)-th and k-th iteration, respectively. Although the Newton’s method is simple to apply, the inverse matrix of J is a troublesome issue during the simulation. To avoid the computation of the inverse matrix, the two-step iteration of the Newton’s method is given [38,40,43] as ,

J^{k} Δ U^{k} = - F^{k},

(19)

U^{k + 1} = U^{k} + Δ U^{k},

(20)

where

Δ U^{k}

is the numerical increment at kth-step iteration.

The inverse matrix of the Jacobian is prevented by using the two-step process of Eqs. (19)-(20), and the

Δ U^{k}

can be solved as a linear system. Thus, the nonlinear algebraic system, obtained by the ST-GFDM can be solved efficiently. Furthermore, the iterative system will converge once the convergence condition

δ = M a x | Δ U^{k} | \leq 10^{- 9}

is reached, and the numerical solutions of the proposed ST-GFDM are gained.

3.3. Time-Marching Approach

In the previous subsections, the numerical process of the proposed ST-GFDM scheme has actually been introduced, but those processes only work in a single ST-domain,

Ω = [a, b] \times [0, dt]

. To deal with the numerical problems has unpredictable end-time or long temporal scales, the simple technique, the time-marching approach, is composed in the proposed numerical scheme. The schematics of the time-marching approach is demonstrated as Figure 2. In Figure 2(a), a small-scale ST domain,

D 1 = [a, b] \times [0, dt]

is formed when the simulation start, and the distribution of nodes is set up like Figure 1(a). In this ST domain, the initial conditions

U_{0} (x)

is satisfied along

Γ_{1}^{1}

Γ_{2}^{1}

and

Γ_{3}^{1}

are satisfied the boundary conditions

f_{1} (a, t)

and

f_{2} (b, t)

, respectively. The governing equation (Eq. (1)) is satisfied on

Γ_{4}^{1}

and

Ω

. Then, the numerical processes in section 3.1 and 3.3 are applied for obtaining the numerical solutions in D1 domain. Once the numerical procedures within D1 are completed, the D1 will be shifted by distance dt along the t-axis, and the 2nd small-scale ST domain

D 2 = [a, b] \times [dt, 2 dt]

is formed as Figure 2(b).

The numerical processes within the D2 are as same as the D1, but the boundary conditions along

Γ_{1}^{2}

is different. In

Γ_{1}^{2}

, the numerical solutions at

Γ_{4}^{1}

in D1 are treated as the initial conditions for D2. Thus, the numerical solutions in D2 can be solved by the proposed ST-GFDM and the two-step Newton’s method. It shall be noticed that the coordinates between D1 and D2 are the relative locations. Thus, the weighting coefficients of the proposed ST-GFDM in D1 are as same as each ST domain generated by the time-marching approach. After moving the ST domain within n-times, the n-th ST domain,

Dn = [a, b] \times [(n - 1) dt, n * dt]

, is generated (see Figure 2(c)), and the numerical solutions are solved. The simulation will finish when n*dt reaches the specified end-time which is determined by the numerical example. In the next section, four numerical examples are provided to verify the proposed ST-GFDM scheme.

4. Numerical Examples

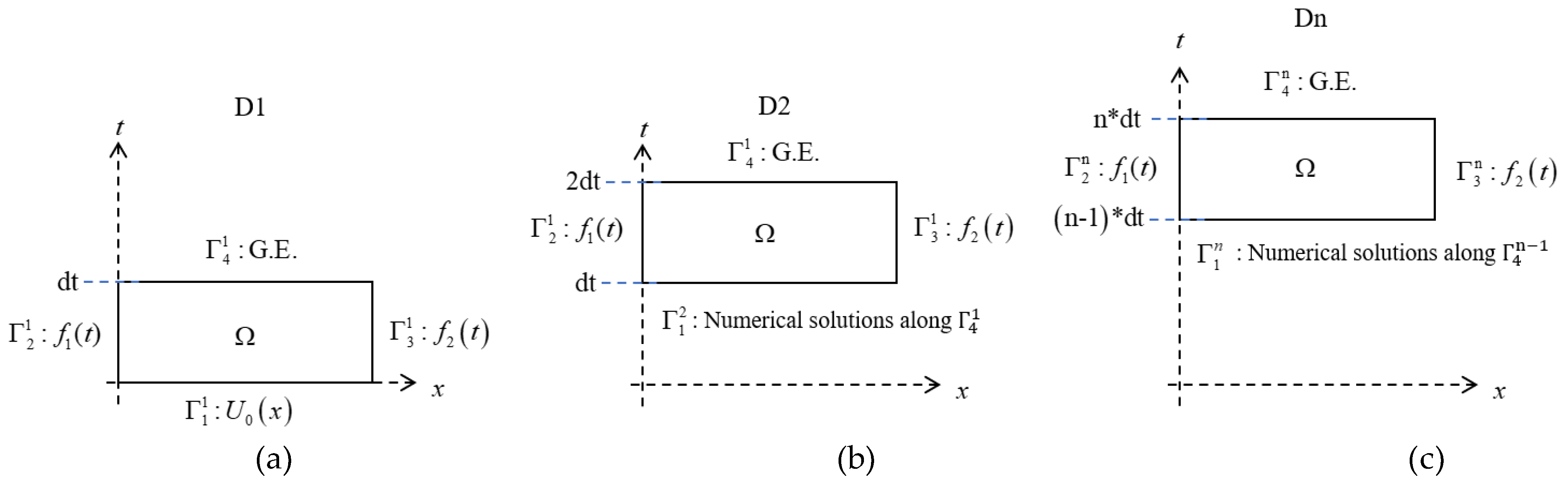
In this section, four numerical examples are tested to verify the proposed ST-GFDM, there are the examples of the Fornberg–Whitham equation and its modified form, modified Camassa–Holm equation, and modified Degasperis–Procesi equation, respectively. The following symbols are defined: T is the end time of the numerical problem, N_D is the number of times that the ST domain has been moved by the time-marching method, and written as

N_{D} = T / dt

. The distribution of nodes for each example is displayed in Figure 1(a). To analyze the accuracy of the proposed ST-GFDM, the numerical errors are defined in this study as follows,

{\begin{cases} L_{\infty, n} = {\max_{1 \leq i \leq N_{T}} | u_{i}^{e x t} - u_{i}^{n u m} | |}^{n}, \\ L_{\infty} = \max \underset{1 \leq n \leq N_{D}}{{L_{\infty, n}},} \end{cases}

(21)

{\begin{cases} {RMSE}_{n} = {\sqrt{\sum_{i = 1}^{N_{T}} | u_{i}^{e x t} - u_{i}^{n u m} | / N_{T}} |}^{n}, \\ RMSE = \max \underset{1 \leq n \leq N_{D}}{{{RMSE}_{n}},} \end{cases}

(22)

where superscript ext is the exact solution; num denotes numerical solutions. In Eq. (21),

L_{\infty, n}^{}

is the maximum absolute errors (MAE) in Dn, and

L_{\infty}^{}

is the maximum MAEs in the entire simulation. Meanwhile, root-mean-squared error (RMSE) in each ST domain is defined as RMSE_n in Eq. (22), and RMSE is the maximum RMSEs in the whole simulation. In addition, the initial guesses are the initial conditions of each numerical problem for iteration in D1, and the numerical solutions in Dn-1 are initial guesses of numerical processes in Dn.

4.1. Example 1

In this subsection, the Fornberg–Whitham equation [1,5] is solved. This mathematic model is presented to describe the behavior of the breaking wave and have the solitary or traveling wave solutions. The exact solution of the 1st numerical example is described as,

u^{e x t} (x, t) = e^{(\frac{x}{2} - \frac{2 t}{3})},

(23)

and the initial condition and boundary conditions are represented as,

U_{0} (x) = e^{\frac{x}{2}}, f_{1} (t) = e^{(\frac{a}{2} - \frac{2 t}{3})}, f_{2} (t) = e^{(\frac{b}{2} - \frac{2 t}{3})} .

(24)

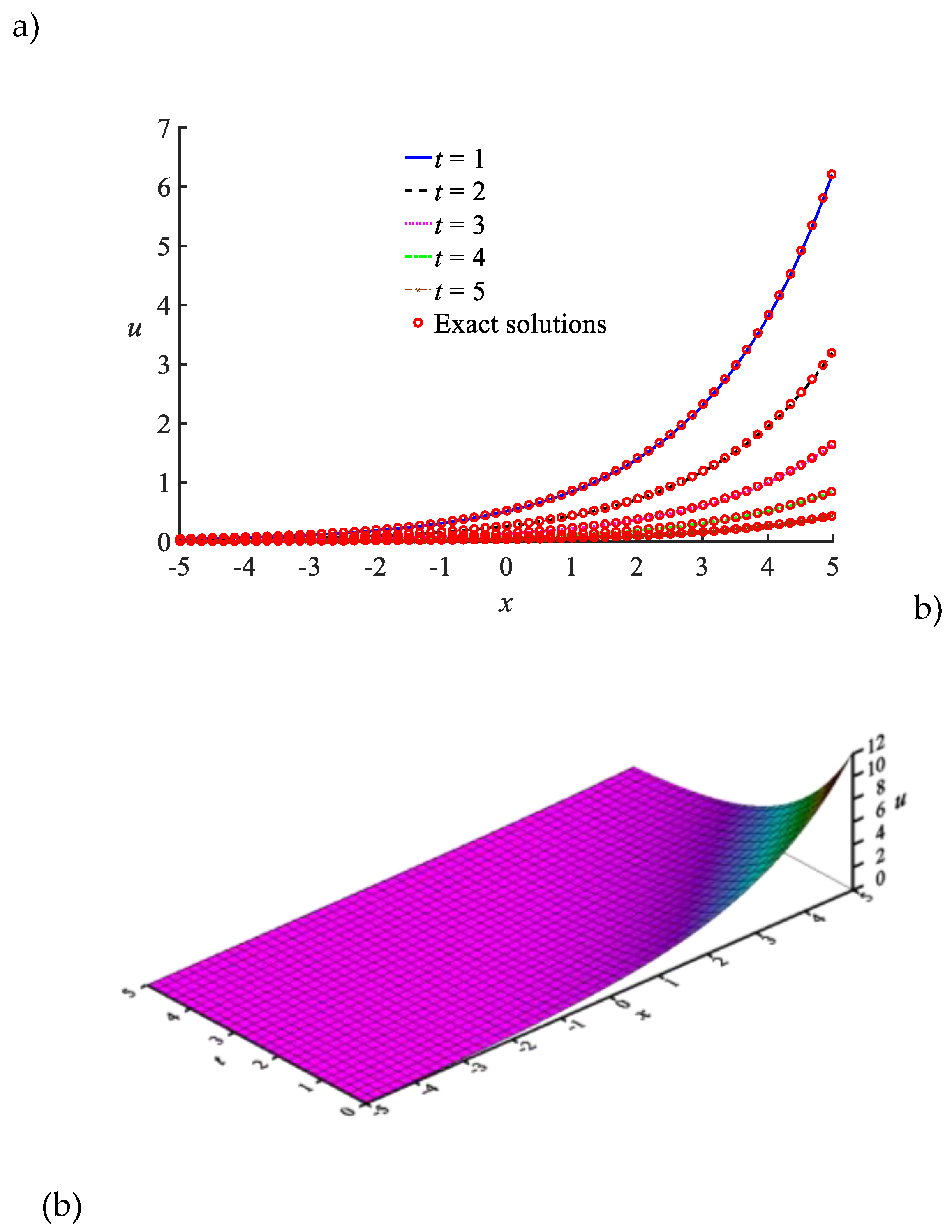
The following parameters are applied in this numerical example: a = -5, b = 5, dt = 0.5, T = 5, and N_D = 10. In Figure 3, the numerical solutions are obtained by applying N_T = 8421 and n_s = 23. The numerical solutions in different time levels are compared with the exact solutions and demonstrated in Figure 3(a). This figure shows that the numerical solutions have a good agreement with the exact solutions. Figure 3(b) is a 3D surface plot of numerical solutions to observe the numerical behavior of the Fornberg–Whitham equation through time.

Table 1, Table 2 and Table 3 are presented to verify the accuracy and parameter sensitivity, MAEs and RMSEs are obtained by utilizing different numbers of N_T and n_s at different time levels. In Table 1, the total number of nodes N_T is tested, and MAEs in different time levels are displayed. These error values indicate that more accurate numerical solutions will be obtained as N_T increases. Meanwhile, MAEs and RMSEs are also presented by using different n_s in Table 2. These errors show that n_s is a parameter with low sensitivity. Furthermore, both tables demonstrate that there is no accumulation of errors during the numerical simulation, and numerically indicate that the ST approach can effectively avoid the accumulation of numerical error that a hybrid numerical scheme may encounter when apply to time-dependent problems.

In order to further validate the capability of the proposed numerical scheme, the numerical solutions locate at specific positions (x,t) are presented in Table 3, and compared with the exact solutions. In this table, the function values are taken to eight decimal places to show the precision accuracy of the proposed ST-GFDM. Besides, the proposed ST-GFDM is compared with the HAM [4], ADM [7], RKHSM [7], and MVIA-I [10], those comparisons are shown in Table 3. In these comparative data, it can be seen that the proposed ST-GFDM performs better than the HAM and ADM. Although the accuracy is weaker than the RKHSM and MVIA-I, the solutions with numerical errors below 10^-6 or even 10^-7 can be obtained, which is already an acceptable numerical result for engineering applications. The above discussions show that the proposed ST-GFDM can accurately and stably solve the Fornberg–Whitham equation. Since the capability of the proposed ST-GFDM has been verified in this numerical example, the following numerical tests are solved by using specific parameters, and the obtained numerical results are compared with other approximation algorithms.

4.2. Example 2

The 2nd example is a numerical test for the modified Fornberg–Whitham equation [5,7,9,10,11], the exact solution is given as follows,

u^{e x t} (x, t) = \frac{3}{4} (\sqrt{15} - 5) {sech}^{2} (c (x - (5 - \sqrt{15}) t)),

(25)

where

c = \frac{1}{20} \sqrt{10 (5 - \sqrt{15})}

. The initial condition and boundary conditions are denoted as,

{\begin{cases} U_{0} (x) = \frac{3}{4} (\sqrt{15} - 5) {sech}^{2} (c x), \\ f_{1} (t) = \frac{3}{4} (\sqrt{15} - 5) {sech}^{2} (c (a - (5 - \sqrt{15}) t)), \\ f_{2} (t) = \frac{3}{4} (\sqrt{15} - 5) {sech}^{2} (c (b - (5 - \sqrt{15}) t)) . \end{cases}

(26)

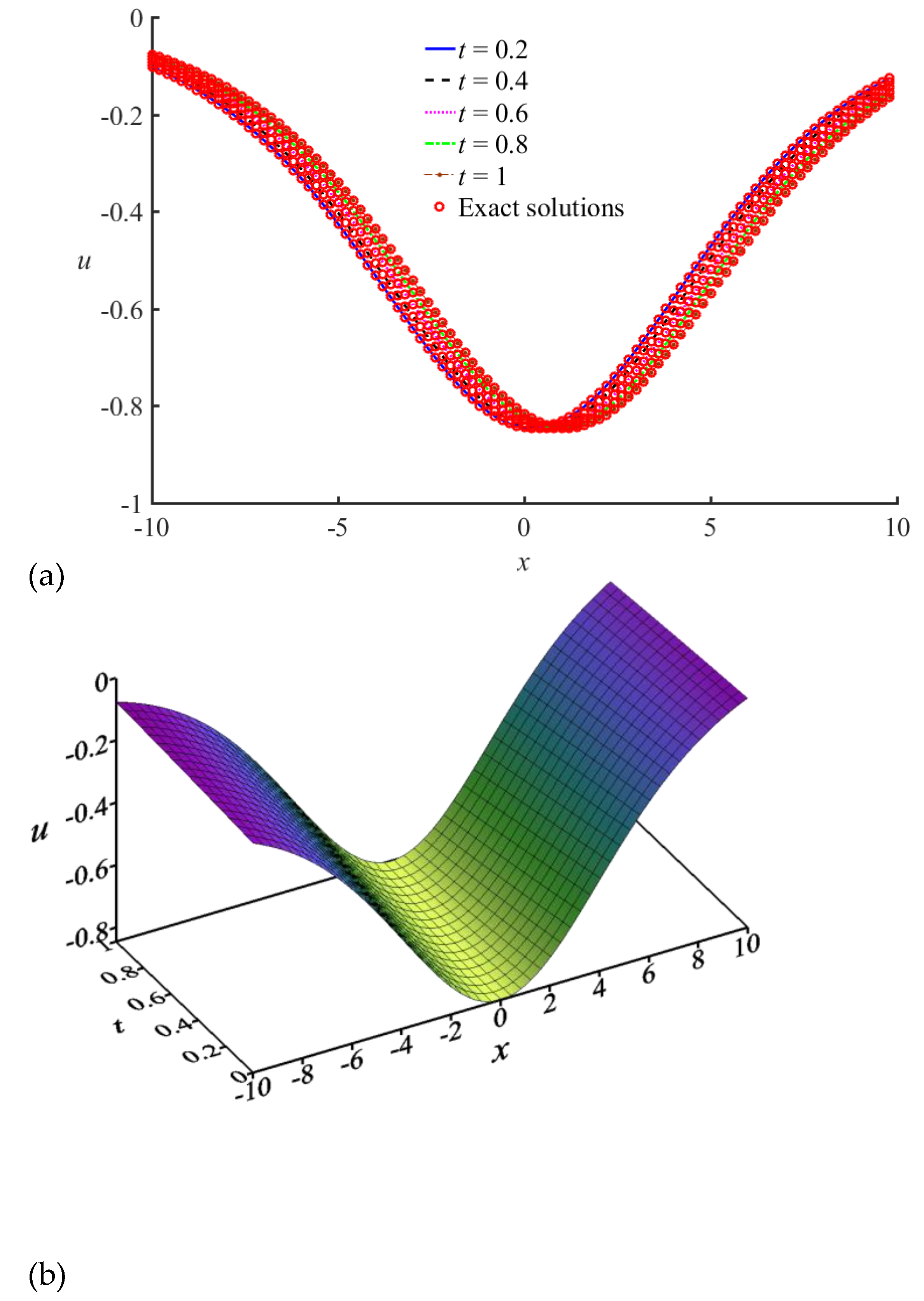
The following parameters are used in this numerical example: a = -10, b = 10, dt = 0.2, T = 1, N_D = 10, N_T = 40421 and n_s = 20. The numerical solutions are displayed in Figure 4. In Figure 4(a), the comparison of the exact solutions and the numerical solutions at specific time levels, t=0.2, 0.4, 0.8, and 1, are shown, and these numerical results have a good agreement with the exact solutions. In addition, the MAEs at specific (x,t) are listed in Table 5 with the errors of the MVIA[10] and VIM [6]. Obviously, the error performance of the proposed numerical scheme is better than the other two approximation algorithms and also verifies that the proposed ST-GFDM is fully capable of handling such complex PDEs.

4.3. Example 3

The 3rd example is the modified Camassa-Holm equations [2,3], the exact solution is given as follows,

u^{e x t} (x, t) = - 2 {sech}^{2} (\frac{x}{2} - t),

(26)

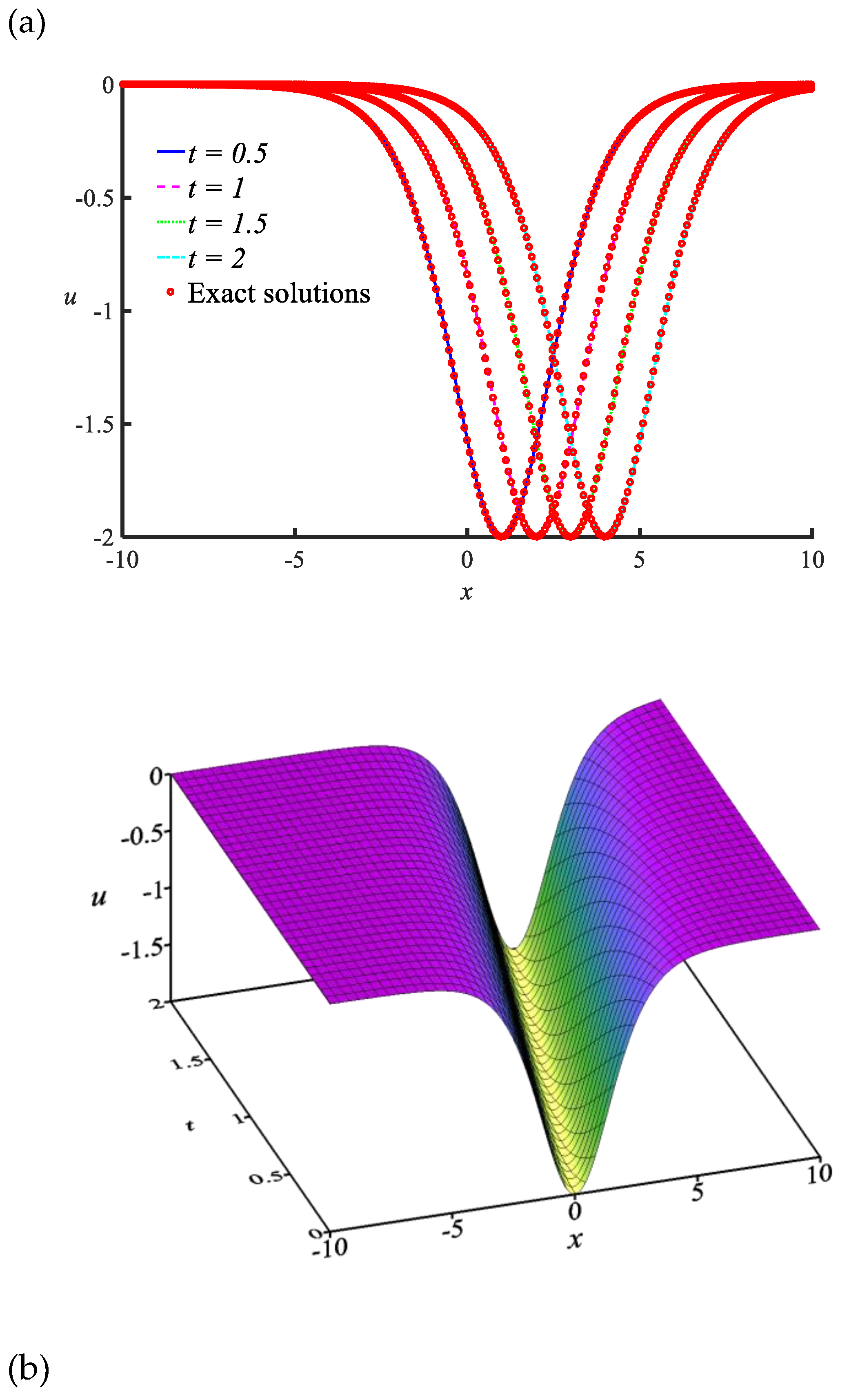
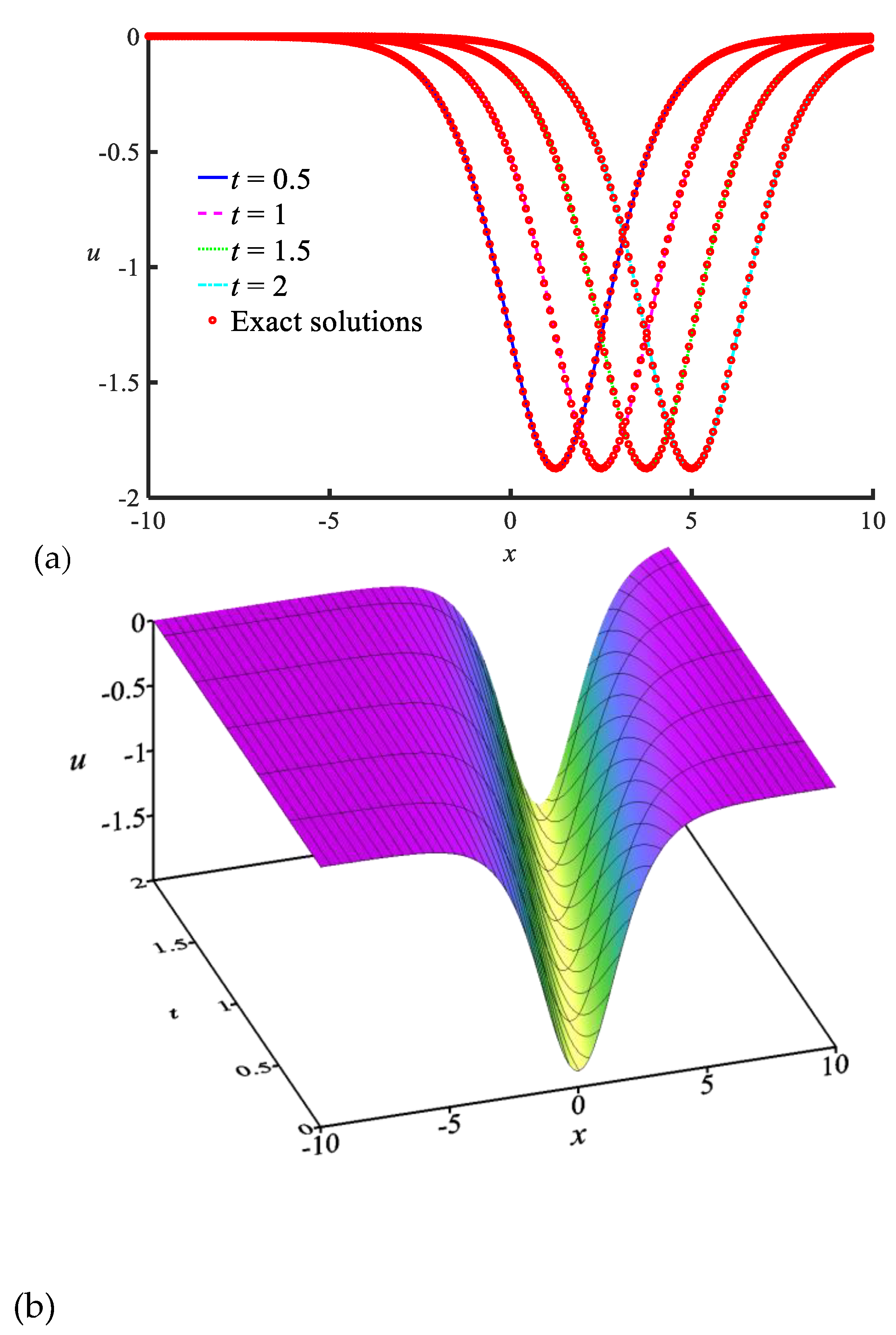
The follows are applied in this numerical example: a = -10, b = 10, dt = 0.5, T = 2, N_D = 4, N_T = 37231 and n_s = 20. The initial condition and boundary conditions are gained by introducing the above parameters into Eq. (26). The numerical solutions are demonstrated in Figure 5. In those plots, the obtained numerical results are compared well with the exact solution in Figure 5(a), and the physical behavior of the wave transmission can be watched in Figure 5(b). Meanwhile, the numerical results located at various locations are presented with the numerical results of the VIM [3] in Table 6. This table shows that the proposed ST-GFDM can successfully solve the Camassa-Holm equation, and can obtain accurate numerical solutions.

4.4. Example 4

The final example is the modified Degasperis−Procesi equation [3,11], the exact solution is given as follows,

u^{e x t} (x, t) = - \frac{15}{8} {sech}^{2} (\frac{x}{2} - \frac{5 t}{4}),

(27)

boundary condition and initial condition can obtain from Eq. (27). The following parameters are used: a = -10, b = 10, dt = 0.5, T = 2, N_D = 4, N_T = 37231 and n_s = 20. The numerical solutions and data are given in Figure 5 and Table 7, respectively. Due to the similarity of the modified Degasperis−Procesi equation and the modified Camassa-Holm equation, the behavior of the numerical solutions is similar as well. In those comparisons, the proposed ST-GFDM can obtain accurate numerical results as shown in the above numerical examples. As has been described above, the proposed ST-GFDM successfully solved the shallow water wave problem, and has the capable to stably simulate the long time scale problems.

5. Conclusions

In this research, the proposed ST-GFDM scheme is adopted for numerical solving the nonlinear shallow water wave equations in which, the modified Camassa−Holm equation, the modified Degasperis-Procesi equation, the Fornberg-Whitham equation, and its modified form. The ST-GFDM is proposed to discretize the governing equations in an ST domain, and the nonlinear algebraic system is solved by the two-step Newton’s method. By applying the ST-GFDM, mesh generation is avoided and makes the numerical processes simpler. On the other hand, the two-step Newton's method has the characteristic of second-order convergence, it correspondingly improves the efficiency for solving the problem that has a heavy computational burden in solving the inverse of a sparse matrix. To deal with long-time-scale numerical problems, the time-marching method is applied for moving the ST domain and saves the computational resource thereby addressing the shortcomings of the ST approach.

Four numerical examples are presented to verify the proposed ST-GFDM scheme. By changing different parameters in the first numerical case, it can be concluded that increasing the total number of nodes can obtain more accurate numerical solutions. Meanwhile, the tests in adjusting n_s in a supporting domain verify that n_s is an insensitive parameter. The numerical solutions have good agreements with exact solutions and the solutions of other approximation methods in four examples. Besides, the accumulation of numerical errors is not significant during the process of time progression, indicating that the proposed ST-GFDM scheme has a strong advantage for solving transient problems. In the future, it can be applied to solve more complex PDEs and engineering problems.

Author Contributions

Conceptualization, P.-W. Li and S.-H. Hu; Methodology, P.-W. Li; Software, S.-H. Hu and M.-Y. Zhang; Validation, S.-H. Hu and M.-Y. Zhang; Writing—original draft preparation, P.-W. Li; Writing—review and editing, P.-W. Li; Funding acquisition, P.-W, Li. All authors have read and agreed to the published version of the manuscript.

Funding

This research was funded by Natural Science Foundation of Shandong Province of China, grant number ZR2021QA012.

Institutional Review Board Statement

Not applicable.

Informed Consent Statement

Not applicable.

Data Availability Statement

Research data are available on request.

Acknowledgments

The authors sincerely Thank that Natural Science Foundation of Shandong Province of China for providing financial support

Conflicts of Interest

The authors declare no conflict of interest.

References

Fornberg, B.; G. B. Whitham A Numerical and Theoretical Study of Certain Nonlinear Wave Phenomena. Philos. Trans. R. Soc. London. Ser. A, Math. Phys. Sci. Phys. Sci. 1978, 289, 373–404. [Google Scholar]
Camassa, R.; Holm, D.D. An Integrable Shallow Water Equation with Peaked Solitons. Phys. Rev. Lett. 1993, 71, 1661–1664. [Google Scholar] [CrossRef]
Wazwaz, A.M. New Solitary Wave Solutions to the Modified Forms of Degasperis-Procesi and Camassa-Holm Equations. Appl. Math. Comput. 2007, 186, 130–141. [Google Scholar] [CrossRef]
Abidi, F.; Omrani, K. The Homotopy Analysis Method for Solving the Fornberg-Whitham Equation and Comparison with Adomian’s Decomposition Method. Comput. Math. with Appl. 2010, 59, 2743–2750. [Google Scholar] [CrossRef]
He, B.; Meng, Q.; Li, S. Explicit Peakon and Solitary Wave Solutions for the Modified Fornberg-Whitham Equation. Appl. Math. Comput. 2010, 217, 1976–1982. [Google Scholar] [CrossRef]
Lu, J. An Analytical Approach to the FornbergWhitham Type Equations by Using the Variational Iteration Method. Comput. Math. with Appl. 2011, 61, 2010–2013. [Google Scholar] [CrossRef]
Boutarfa, B.; Akgül, A.; Inc, M. New Approach for the Fornberg–Whitham Type Equations. J. Comput. Appl. Math. 2017, 312, 13–26. [Google Scholar] [CrossRef]
Zhang, J.H.; Zheng, J.S.; Gao, Q.J. Numerical Solution of the Degasperis–Procesi Equation by the Cubic B-Spline Quasi-Interpolation Method. Appl. Math. Comput. 2018, 324, 218–227. [Google Scholar] [CrossRef]
Hörmann, G.; Okamoto, H. Weak Periodic Solutions and Numerical Case Studies of the Fornberg-Whitham Equation. Discret. Contin. Dyn. Syst. Ser. A 2019, 39, 4455–4469. [Google Scholar] [CrossRef]
Ahmad, H.; Seadawy, A.R.; Ganie, A.H.; Rashid, S.; Khan, T.A.; Abu-Zinadah, H. Approximate Numerical Solutions for the Nonlinear Dispersive Shallow Water Waves as the Fornberg–Whitham Model Equations. Results Phys. 2021, 22, 103907. [Google Scholar] [CrossRef]
Shaheen, S.; Haq, S.; Ghafoor, A. A Meshfree Technique for the Numerical Solutions of Nonlinear Fornberg–Whitham and Degasperis–Procesi Equations with Their Modified Forms. Comput. Appl. Math. 2022, 41, 1–22. [Google Scholar] [CrossRef]
Ling, J.; Wang, H.; Mou, H. An Efficient Boundary-Type Meshless Computational Approach for the Axial Compression on the Part Boundary of the Circular Shaft (Brazilian Test). Appl. Sci. 2022, 12, 11806. [Google Scholar] [CrossRef]
Guo, K.; Li, S.; Zhong, Y.; Chen, R.; Wang, M.; Qiu, S.; Tian, W.; Su, G. Heat Transfer Mechanism Investigation of Bubble Growth on the Superhydrophilic Nano-Structured Surface Using Moving Particle Semi-Implicit Method. Appl. Sci. 2023, 13, 4114. [Google Scholar] [CrossRef]
Belinha, J.; Aires, M. Elastoplastic Analysis of Plates with Radial Point Interpolation Meshless Methods. Appl. Sci. 2022, 12, 12842. [Google Scholar] [CrossRef]
Cheng, S.; Wang, F.; Li, P.-W.; Qu, W. Singular Boundary Method for 2D and 3D Acoustic Design Sensitivity Analysis. Comput. Math. with Appl. 2022, 119, 371–386. [Google Scholar] [CrossRef]
Yue, X.; Wang, F.; Li, P.-W.; Fan, C.-M. Local Non-Singular Knot Method for Large-Scale Computation of Acoustic Problems in Complicated Geometries. Comput. Math. with Appl. 2021, 84, 128–143. [Google Scholar] [CrossRef]
Liu, S.; Li, P.W.; Fan, C.M.; Gu, Y. Localized Method of Fundamental Solutions for Two- and Three-Dimensional Transient Convection-Diffusion-Reaction Equations. Eng. Anal. Bound. Elem. 2021, 124, 237–244. [Google Scholar] [CrossRef]
Fu, Z.; Tang, Z.; Xi, Q.; Liu, Q.; Gu, Y.; Wang, F. Localized Collocation Schemes and Their Applications. Acta Mech. Sin. 2022, 38, 422167. [Google Scholar] [CrossRef]
Liszka, T.; Orkisz, J. The Finite Difference Method at Arbitrary Irregular Grids and Its Application in Applied Mechanics. Comput. Struct. 1980, 11, 83–95. [Google Scholar] [CrossRef]
Benito, J.J.; Ureña, F.; Gavete, L. Influence of Several Factors in the Generalized Finite Difference Method. Appl. Math. Model. 2001, 25, 1039–1053. [Google Scholar] [CrossRef]
Li, P.-W.; Fan, C.M. Generalized Finite Difference Method for Two-Dimensional Shallow Water Equations. Eng. Anal. Bound. Elem. 2017, 80, 58–71. [Google Scholar] [CrossRef]
Li, P.-W.; Fan, C.-M.; Grabski, J.K. A Meshless Generalized Finite Difference Method for Solving Shallow Water Equations with the Flux Limiter Technique. Eng. Anal. Bound. Elem. 2021, 131, 159–173. [Google Scholar] [CrossRef]
Rao, X.; Zhao, H.; Liu, Y. A Novel Meshless Method Based on the Virtual Construction of Node Control Domains for Porous Flow Problems. Eng. Comput. 2023. [Google Scholar] [CrossRef]
Flores, J.; Salete, E.; Benito, J.J.; Vargas, A.M.; Conde, E.R. Generalized Finite Difference Method Applied to Solve Seismic Wave Propagation Problems. Examples of 3D Simulations. Math. Methods Appl. Sci. 2023. [Google Scholar] [CrossRef]
Qin, Q.; Song, L.; Wang, Q. High-Order Meshless Method Based on the Generalized Finite Difference Method for 2D and 3D Elliptic Interface Problems. Appl. Math. Lett. 2023, 137, 108479. [Google Scholar] [CrossRef]
Ju, B.; Qu, W. Three-Dimensional Application of the Meshless Generalized Finite Difference Method for Solving the Extended Fisher–Kolmogorov Equation. Appl. Math. Lett. 2023, 136, 108458. [Google Scholar] [CrossRef]
Li, P.W.; Fan, C.M.; Yu, Y.Z.; Song, L. A Meshless Generalized Finite Difference Scheme for the Stream Function Formulation of the Naiver-Stokes Equations. Eng. Anal. Bound. Elem. 2023, 152, 154–168. [Google Scholar] [CrossRef]
Liu, S.; Zhou, Z.; Zeng, W. Simulation of Elastic Wave Propagation Based on Meshless Generalized Finite Difference Method with Uniform Random Nodes and Damping Boundary Condition. Appl. Sci. 2023, 13, 1312. [Google Scholar] [CrossRef]
Zheng, Z.; Li, X. Theoretical Analysis of the Generalized Finite Difference Method. Comput. Math. with Appl. 2022, 120, 1–14. [Google Scholar] [CrossRef]
Hamaidi, M.; Naji, A.; Charafi, A. Space-Time Localized Radial Basis Function Collocation Method for Solving Parabolic and Hyperbolic Equations. Eng. Anal. Bound. Elem. 2016, 67, 152–163. [Google Scholar] [CrossRef]
Uddin, M.; Ali, H. The Space-Time Kernel-Based Numerical Method for Burgers’ Equations. Mathematics 2018, 6, 2–11. [Google Scholar] [CrossRef]
Wang, F.; Fan, C.-M.; Zhang, C.; Lin, J. A Localized Space-Time Method of Fundamental Solutions for Diffusion and Convection-Diffusion Problems. Adv. Appl. Math. Mech. 2020, 12, 940–958. [Google Scholar] [CrossRef]
Qiu, L.; Lin, J.; Qin, Q.-H.; Chen, W. Localized Space–Time Method of Fundamental Solutions for Three-Dimensional Transient Diffusion Problem. Acta Mech. Sin. 2020, 36, 1051–1057. [Google Scholar] [CrossRef]
Ku, C.-Y.; Liu, C.-Y.; Yeih, W.; Liu, C.-S.; Fan, C.-M. A Novel Space–Time Meshless Method for Solving the Backward Heat Conduction Problem. Int. J. Heat Mass Transf. 2019, 130, 109–122. [Google Scholar] [CrossRef]
Ku, C.-Y.; Hong, L.-D.; Liu, C.-Y.; Xiao, J.-E.; Huang, W.-P. Modeling Transient Flows in Heterogeneous Layered Porous Media Using the Space–Time Trefftz Method. Appl. Sci. 2021, 11, 3421. [Google Scholar] [CrossRef]
Lin, J.; Zhang, Y.; Reutskiy, S.; Feng, W. A Novel Meshless Space-Time Backward Substitution Method and Its Application to Nonhomogeneous Advection-Diffusion Problems. Appl. Math. Comput. 2021, 398, 125964. [Google Scholar] [CrossRef]
Lei, J.; Wang, Q.; Liu, X.; Gu, Y.; Fan, C.-M. A Novel Space-Time Generalized FDM for Transient Heat Conduction Problems. Eng. Anal. Bound. Elem. 2020, 119, 1–12. [Google Scholar] [CrossRef]
Li, P.W. Space–Time Generalized Finite Difference Nonlinear Model for Solving Unsteady Burgers’ Equations. Appl. Math. Lett. 2021, 114, 106896. [Google Scholar] [CrossRef]
Benito, J.J.; García, Á.; Negreanu, M.; Ureña, F.; Vargas, A.M. A Novel Spatio-Temporal Fully Meshless Method for Parabolic PDEs. Mathematics 2022, 10, 1870. [Google Scholar] [CrossRef]
Li, P.W.; Grabski, J.K.; Fan, C.M.; Wang, F. A Space-Time Generalized Finite Difference Method for Solving Unsteady Double-Diffusive Natural Convection in Fluid-Saturated Porous Media. Eng. Anal. Bound. Elem. 2022, 142, 138–152. [Google Scholar] [CrossRef]
Liu, F.; Song, L.; Jiang, M. Space-Time Generalized Finite Difference Method for Solving the Thin Elastic Plate Bending under Dynamic Loading. Eng. Anal. Bound. Elem. 2022, 143, 632–638. [Google Scholar] [CrossRef]
Lei, J.; Wei, X.; Wang, Q.; Gu, Y.; Fan, C.-M. A Novel Space–Time Generalized FDM for Dynamic Coupled Thermoelasticity Problems in Heterogeneous Plates. Arch. Appl. Mech. 2022, 92, 287–307. [Google Scholar] [CrossRef]
Li, P.W. The Space–Time Generalized Finite Difference Scheme for Solving the Nonlinear Equal-Width Equation in the Long-Time Simulation. Appl. Math. Lett. 2022, 132, 108181. [Google Scholar] [CrossRef]
Benito, J.J.; García, A.; Negreanu, M.; Ureña, F.; Vargas, A.M. Two Finite Difference Methods for Solving the Zakharov–Kuznetsov-Modified Equal-Width Equation. Eng. Anal. Bound. Elem. 2023, 153, 213–225. [Google Scholar] [CrossRef]
Flores, J.; García, A.; Negreanu, M.; Salete, E.; Ureña, F.; Vargas, A.M. A Spatio-Temporal Fully Meshless Method for Hyperbolic PDEs. J. Comput. Appl. Math. 2023, 430, 115194. [Google Scholar] [CrossRef]
Qu, W.; He, H. A Spatial–Temporal GFDM with an Additional Condition for Transient Heat Conduction Analysis of FGMs. Appl. Math. Lett. 2020, 110, 106579. [Google Scholar] [CrossRef]

Figure 1. The schematic diagram of (a) nodes and (b) a supporting domain of the GFDM in the x-t domain.

Figure 2. The schematic diagrams of the time-marching approach in the proposed ST-GFDM. (a) 1st domain, (b) 2nd domain, and (c) n-th domain.

Figure 3. (a) The comparisons of the u^ext and u^num at different t and (b) the surface plot of u^num in the entire x-t domain of the example 1.

Figure 4. (a) The comparisons of the u^ext and u^num at different t and (b) the surface plot of u^num in the entire x-t domain of the example 2.

Figure 5. (a) The comparisons of the u^ext and u^num at different t and (b) the surface plot of u^num in the entire x-t domain of the example 3.

Figure 5. (a) The comparisons of the u^ext and u^num at different t and (b) the surface plot of u^num in the entire x-t domain of the example 4.

Table 1. MAEs and RMSEs of the example 1 with n_s = 20 by using different N_T at different t.

	t = 1 (n = 2)		t = 3 (n = 6)		t = 5 (n = 10)
N_T	$L_{\infty, 2}$	RMSE₂	$L_{\infty, 6}$	RMSE₆	$L_{\infty, 10}$	RMSE₁₀
2211	1.725e-04	2.424e-05	2.251e-05	4.081e-06	3.250e-05	5.891e-06
8421	3.267e-05	3.071e-06	6.677e-06	8.855e-07	9.153e-06	1.214e-06
18631	1.313e-05	9.162e-07	3.856e-06	4.747e-07	4.927e-06	5.949e-07

Table 2. MAEs and RMSEs of example 1 with N_T = 8421 by using different ns at different t.

	t = 1 (n = 2)		t = 3 (n = 6)		t = 5 (n = 10)
n_s	$L_{\infty, 2}$	RMSE₂	$L_{\infty, 6}$	RMSE₆	$L_{\infty, 10}$	RMSE₁₀
20	3.267e-05	3.071e-06	6.677e-06	8.855e-07	9.153e-06	1.214e-06
23	5.158e-05	5.737e-06	1.961e-05	2.011e-06	1.301e-05	1.563e-06
26	5.093e-05	5.713e-06	3.067e-05	3.064e-06	1.264e-05	1.566e-06

Table 3. Comparisons of the numerical results of example 1 with exact solution at various locations at different time levels. (N_T=8421 and n_s=23).

		t = 1 (n = 2)		t = 3 (n = 6)		t = 5 (n = 10)
		u^ext	ST-GFDM	u^ext	ST-GFDM	u^ext	ST-GFDM
x	−4	0.06948345	0.06948238	0.01831564	0.01831622	0.00482795	0.00483149
	−2	0.18887560	0.18887409	0.04978707	0.04978139	0.01312373	0.01312198
	0	0.51341712	0.51342701	0.13533528	0.13532764	0.03567399	0.03566356
	2	1.39561243	1.39565330	0.36787944	0.36788606	0.09697197	0.09696040
	4	3.79366789	3.79371117	1.00000000	1.00001868	0.26359714	0.26359633
$L_{\infty, n}$		5.158e-05		1.961e-05		1.301e-05

Table 4. Comparisons of the numerical results of example 1 with exact solution and the other approximation methods at various locations at t = 5. (n = 10, N_T =8421 and n_s =23)

x	u^ext	HAM [4]	ADM [7]	RKHSM [7]	MVIA-I [10]	ST-GFDM	MAEs
−4	0.00482795	0.00487526	0.00317192	0.00482795	0.00482795	0.00482958	1.626e-06
−2	0.01312373	0.01325233	0.00862217	0.01312373	0.01312373	0.01312294	7.893e-07
0	0.03567399	0.03602358	0.02343750	0.03567400	0.03567399	0.03566866	5.337e-06
2	0.09697197	0.09792224	0.06370972	0.09697195	0.09697197	0.09696298	8.992e-06
4	0.26359714	0.26618027	0.17318095	0.26359729	0.26359714	0.26359021	6.925e-06

Table 5. MAEs of example 2 with exact solution and the other numerical methods.

	x = 2.5			x = 5
t	MVIA [10]	VIM [6]	ST-GFDM	MVIA [10]	VIM [6]	ST-GFDM
0.02	3.780e-05	1.180e-04	1.883e-07	9.966e-06	2.124e-05	4.272e-08
0.04	7.240e-05	2.363e-04	1.949e-07	1.778e-05	4.797e-05	4.077e-08
0.06	1.036e-04	3.547e-04	1.996e-07	2.333e-05	8.029e-05	3.867e-08
0.08	1.313e-04	4.731e-04	2.042e-07	2.653e-05	1.183e-04	3.647e-08
0.1	1.552e-04	5.914e-04	2.087e-07	2.727e-05	1.622e-04	3.419e-08

Table 6. Comparisons of the numerical results of example 3 with exact solution and the other numerical methods at various locations at t = 0.05 and t = 0.1.

x	t	u^ext	ST-GFDM	VIM [3]	MAEs
6	0.05	-0.021795977	-0.021798486	-0.019790189	2.508360E-06
8	0.05	-0.002963750	-0.002960395	-0.002682964	3.355673E-06
6	0.1	-0.024074444	-0.024070611	-0.019848303	3.832791E-06
8	0.1	-0.003275195	-0.003265414	-0.002684058	9.781412E-06

Table 7. Comparisons of the numerical results of example 4 with exact solution and the other numerical methods at various locations at t = 0.05 and t = 0.1.

x	t	u^ext	ST-GFDM	VIM [3]	MAEs
6	0.05	-0.020951831	-0.020948113	-0.018566923	3.717910e-06
8	0.05	-0.002851900	-0.002848801	-0.002682964	3.099397e-06
6	0.1	-0.023714184	-0.023719627	-0.018635025	5.443036e-06
8	0.1	-0.003229560	-0.003227788	-0.002516809	1.771923e-06

Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.

© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).

Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.

MDPI Initiatives

Important Links

Choose an area of interest and we will send you notifications of new preprints at your preferred frequency.

Disclaimer

Numerical Solutions of the Nonlinear Dispersive Shallow Water Wave Equations Based on the Space-Time Coupled Generalized Finite Difference Scheme

Abstract

1. Introduction

2. The Mathematical Models of the Dispersive Shallow Water Waves

3. The Proposed Meshless Numerical Scheme

3.1. Space-Time Generalized Finite Difference Method

3.2. Two-Step Newton’s Method

3.3. Time-Marching Approach

4. Numerical Examples

4.1. Example 1

4.2. Example 2

4.3. Example 3

4.4. Example 4

5. Conclusions

Author Contributions

Funding

Institutional Review Board Statement

Informed Consent Statement

Data Availability Statement

Acknowledgments

Conflicts of Interest

References

MDPI Initiatives

Important Links

Subscribe