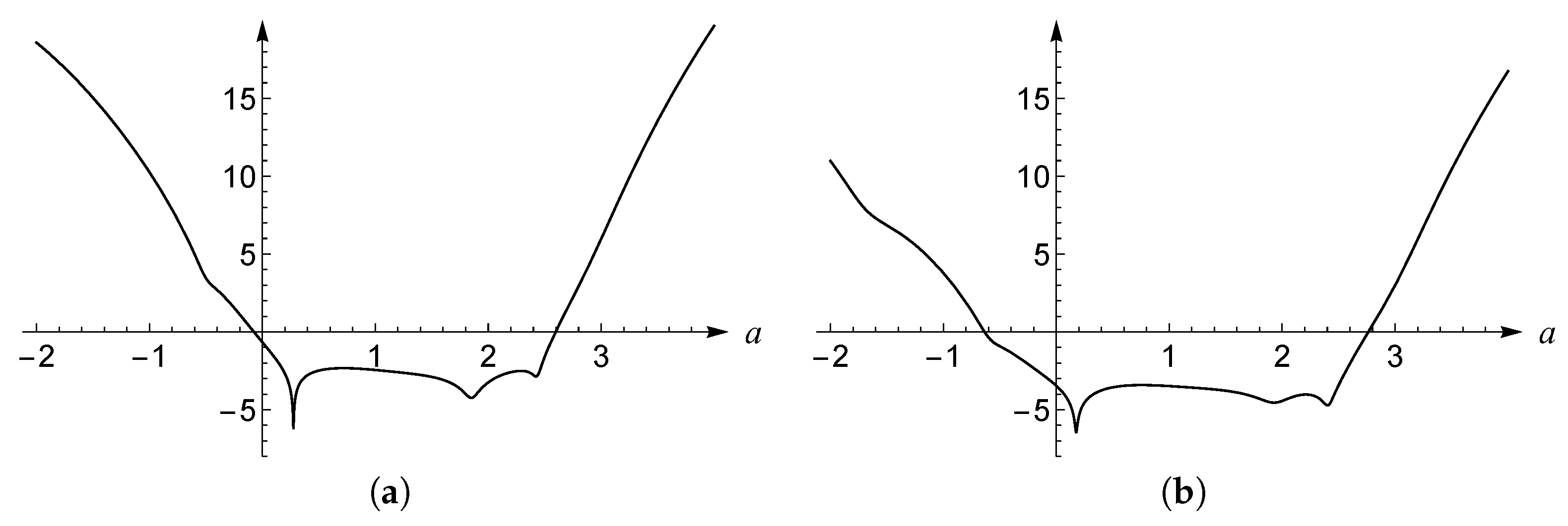Analytical Approximations to Charged Black Hole Solutions in Einstein-Maxwell-Weyl Gravity

1. Introduction

It is widely recognized that the theory of general relativity (GR) does not qualify as a renormalizable quantum field theory within the framework of effective field theory. Therefore, to achieve the ultimate goal of unifying GR with quantum theory, it is imperative to explore alternative theories that go beyond GR. Among these theories, those featuring higher curvature corrections are particularly significant, as they are predicted by the low-energy limit of string theory [1]. In four-dimensional spacetime, the most comprehensive theory that includes second-order derivative terms in the curvature can be expressed as follows[2,3]

$$\mathcal{I}=\int d^{4}x\sqrt{-g}\left(\gamma R-\alpha C_{\mu \nu \rho \sigma }{C}^{\mu \nu \rho \sigma }+\beta R^2\right),$$

(1)

where the parameters $\alpha$, $\beta$, and $\gamma$ are constants, and $C_{\mu \nu \rho \sigma }$ is the Weyl tensor. In addition, black holes are fundamental objects in theories of gravity and serve as powerful tools for studying the intricate global aspects of the theory. Subsequently, Lü et al.[3,4] derived numerical solutions of non-Schwarzschild black holes (NSBH) in the Einstein-Weyl gravity [Eq.(1)] by considering the disappearance of the Ricci scalar for any static spherically symmetric black hole solution ($R=0$). Actually, the no-go theorem also implies that the Ricci scalar R must be zero for a black hole in the case of pure gravity or with a traceless matter stress tensor. In Refs. [3,4], they further investigated some thermodynamic properties of NSBH and discovered several remarkable features: 1) the NSBH can have positive and negative masses; 2) as the coupling constant $\alpha$ approaches its extreme value, the black hole tends towards a massless state while maintaining a nonzero radius. Recently, Held et al.[5] discussed the linear stability of these two branches of black hole solutions. In addition, charged black holes in the Einstein-Weyl gravity coupled with (nonlinear-) Maxwell field were constructed in Refs. [6,7] and our previous works [8,9], where two sets of numerical solutions were obtained: the charged generalization of Schwarzschild solution and charged generalization of non-Schwarzschild solution. The analysis of quasinormal modes of the non-Schwarzschild and charged black holes was performed in the Einstein-Weyl gravity [10,11,12], where the linear relation between quasinormal modes frequencies and the parameter was recovered. Later, the black holes with massive scalar hair were obtained in Ref. [13], where it discussed the effects of the scalar field on the black hole structure. Recently, some novel solutions of black holes were also studied in the Einstein-Weyl gravity [14,15], including the phase diagram of Einstein-Weyl gravity [16].

However, the numerical solutions for non-Schwarzschild black holes have limitations in providing a clear understanding of the dependence of the metric on physical parameters, as they are obtained at fixed parameter values and displayed as curves in figures rather than explicit expressions. This makes it difficult for researchers to use these solutions in their work without recalculating them. Fortunately, there are general methods available for parametrizing black hole space-times, such as the Continued Fractions Method (CFM) [17,18] and the Homotopy Analysis Method (HAM) [19,20]. In this paper, we focus on the HAM. It is considered as a very useful method for obtaining analytical approximate solutions for various nonlinear differential equations, including those arising in different areas of science and engineering. Despite its widespread use in other fields, the HAM has been limited in the fields of general relativity and gravitation. Recently, we constructed analytical approximation solutions of scalarized AdS black holes in Einstein-scalar-Gauss-CBonnet gravity by using of HAM [21]. Moreover, this HAM has been adopted to derive the analytical approximation solutions of non-Schwarzschild black holes in the Einstein-Weyl gravity [22], analytic approximate solutions of hairy black holes in Einstein-CWeyl-scalar gravity [23] as well as for the Regge-Wheeler equations under metric perturbations on the Schwarzschild spacetime [24]. The above works inspire us to continue exploring the application of homotopy analysis in modified gravity theory. In this work, we wish to apply the HAM to obtain analytical approximation solutions of charged black holes in the Einstein-Maxwell-Weyl gravity.

The plan of the paper is as follows. In Section 2 we review the Einstein-Weyl gravity coupled with Maxwell field and present the numerical solutions for charged black hole in the Einstein-Maxwell-Weyl gravity. Section 3 is devoted to deriving the analytical approximation solutions by using the HAM method, where two solutions are accurate in the whole space outside the event horizon. The paper ends with a discussion of the results obtained in Section 4.

2. The Einstein-Maxwell-Weyl gravity

The action of Einstein-Weyl gravity in the presence of Maxwell field is given by [6]

$$\mathcal{I}=\int d^{4}x\sqrt{-g}\left(\gamma R-\alpha C_{\mu \nu \rho \sigma }{C}^{\mu \nu \rho \sigma }+\beta R^2-\kappa F_{\mu \nu }{F}^{\mu \nu }\right),$$

(2)

where the parameters $\gamma$, $\alpha$, $\beta$, and $\kappa$ are coupling constants, $F_{\mu \nu }={\nabla }_{\mu }{A}_{\nu }-{\nabla }_{\nu }{A}_{\mu }$ is the electromagnetic tensor and $C_{\mu \nu \rho \sigma }$ is the Weyl tensor. Since resulting tensors in the equations of motion that comes from the Weyl and Maxwell energy momentum tensors are traceless, a charged black hole solution in this theory should not need of the contribution from $\beta R^2$ term [6]. Taking $\beta =0$ and $\gamma =1$, the corresponding field equations are obtained as

$$\begin{array}{ccc}& & R_{\mu \nu }-\frac{1}{2}{g}_{\mu \nu }R-4\alpha B_{\mu \nu }-2\kappa T_{\mu \nu }=0,\hfill \end{array}$$

(3)

$$\begin{array}{ccc}& & {\nabla }_{\mu }{F}^{\mu \nu }=0,\hfill \end{array}$$

(4)

where the trace-free Bach tensor $B_{\mu \nu }$ and energy-momentum tensor of electromagnetic field $T_{\mu \nu }$ are defined as

$$\begin{array}{c}\hfill B_{\mu \nu }=\left({\nabla }^{\rho }{\nabla }^{\sigma }+\frac{1}{2}{R}^{\rho \sigma }\right)C_{\mu \nu \rho \sigma },\\ \hfill T_{\mu \nu }=F_{\alpha \mu }{F^{\alpha }}_{\nu }-\frac{1}{4}{g}_{\mu \nu }{F}_{\alpha \beta }{F}^{\alpha \beta }.\end{array}$$

(5)

Considering the static and spherical symmetry metric ansatz

$$\begin{array}{c}\hfill d{s}^2=-h\left(r\right)d{t}^2+\frac{1}{f\left(r\right)}d{r}^2+r^2({d\theta }^2+{sin}^2\theta {d\varphi }^2),\end{array}$$

(6)

and substituting the metric ansatz into the field equations (3)(4), we can obtain three independent equations.

$$\begin{array}{ccc}\hfill & & \frac{2h}{r^{2}f}(f+1-r{f}^{\prime })-\frac{h^{\prime 2}}{2h}+\frac{(4f+r{f}^{\prime })h^{\prime }}{2rf}+h^{″}=0,\hfill \\ & & f^{″}-\frac{3h{f}^{\prime 2}}{2f(2h-r{h}^{\prime })}+\frac{2rfh{h}^{\prime }+r^{2}f{h}^{\prime 2}+4h^{2}f(f-1)}{2rfh(2h-r{h}^{\prime })}{f}^{\prime }\hfill \\ & & -\frac{f{h}^{\prime 2}(r{h}^{\prime }-3h)}{2h^2(2h-r{h}^{\prime })}+\frac{4h(f-1)}{r^2(2h-r{h}^{\prime })}+\frac{r^{3}f{h}^{\prime }+(r^{2}f-r^2+\kappa Q_0^2)h}{\alpha r^{2}f(2h-r{h}^{\prime })}=0,\hfill \\ & & A_t^{\prime }+\frac{Q_0}{r^2}\sqrt{\frac{h}{f}}=0,\hfill \end{array}$$

(7)

where the prime (′) denotes differentiation with respect to r, and $Q_0$ denotes electric charge. Now we derive the numerical solutions of charged black holes. Here we suppose that the spacetime has only one horizon to make easier the expansion of $f\left(r\right)$, $h\left(r\right)$ and $A_t\left(r\right)$ around the event horizon $r_0$

$$\begin{array}{ccc}& & h\left(r\right)=h_1\left(r-r_0\right)+h_2{\left(r-r_0\right)}^2+h_3{\left(r-r_0\right)}^3+...,\hfill \\ & & f\left(r\right)=f_1\left(r-r_0\right)+f_2{\left(r-r_0\right)}^2+f_3{\left(r-r_0\right)}^3+...,\hfill \\ & & A_t\left(r\right)=A_{t1}\left(r-r_0\right)+A_{t2}{\left(r-r_0\right)}^2+A_{t3}{\left(r-r_0\right)}^3+...,\hfill \end{array}$$

(8)

$h_i$, $f_i$ and $A_{ti}$ are constant coefficients of the expansions. Note that we set $h_1=f_1$ for the sake of convenience in following calculations. Then, substituting the above equations (8) into the field equations (7), arbitrary coefficients $h_j$, $f_j$ and $A_{ti}$ with $j\ge 2$ can be expressed in terms of $f_1$, for example, $h_2$, $f_2$, $A_{t2}$ and $A_{t1}$ are expressed as

$$\begin{array}{ccc}& & h_2=\frac{1-2f_1{r}_0}{r_0^2}-\frac{r_0^2-f_1{r}_0^3-\kappa Q_0^2}{8\alpha f_1{r}_0^3},\hfill \end{array}$$

(9)

$$\begin{array}{ccc}& & f_2=\frac{1-2f_1{r}_0}{r_0^2}-\frac{3\left(r_0^2-f_1{r}_0^3-\kappa Q_0^2\right)}{8\alpha f_1{r}_0^3},\hfill \end{array}$$

(10)

$$\begin{array}{ccc}& & A_{t1}=-\frac{Q_0}{r_0^2},A_{t2}=\frac{Q_0}{r_0^3}+\frac{Q_0\left(r_0^3{f}_1+\kappa Q_0^2-r_0^2\right)}{8\alpha r_0^5{f}_1^2}.\hfill \end{array}$$

(11)

On the other hand, at the radial infinity $(r\to \infty )$, the metric functions and vector potential can be expanded in power series, this time in terms of $1/r$. Demanding that the metric components reduces to those of the asymptotically flat Minkowski spacetime

$$\begin{array}{ccc}& & h\left(r\right)=1-\frac{2M}{r}+...,f\left(r\right)=1-\frac{2M}{r}+...,\hfill \\ & & A_t\left(r\right)=\Phi -\frac{Q_0}{r}+....\hfill \end{array}$$

(12)

Taking $\alpha =\frac{1}{2}$ and $\kappa =1$, we assume the initial values of the parameters $Q_0$ and $f_1$ at a radius $r_i=r_0+\frac{1}{1000}$ just outside the horizon $r_0$, and then use numerical routines in Mathematica to integrate the equations out to large radius, so that these interpolation functions of metric functions $h\left(r\right)$ and $f\left(r\right)$ and vector potential $A_t\left(r\right)$ satisfy the boundary condition (12). 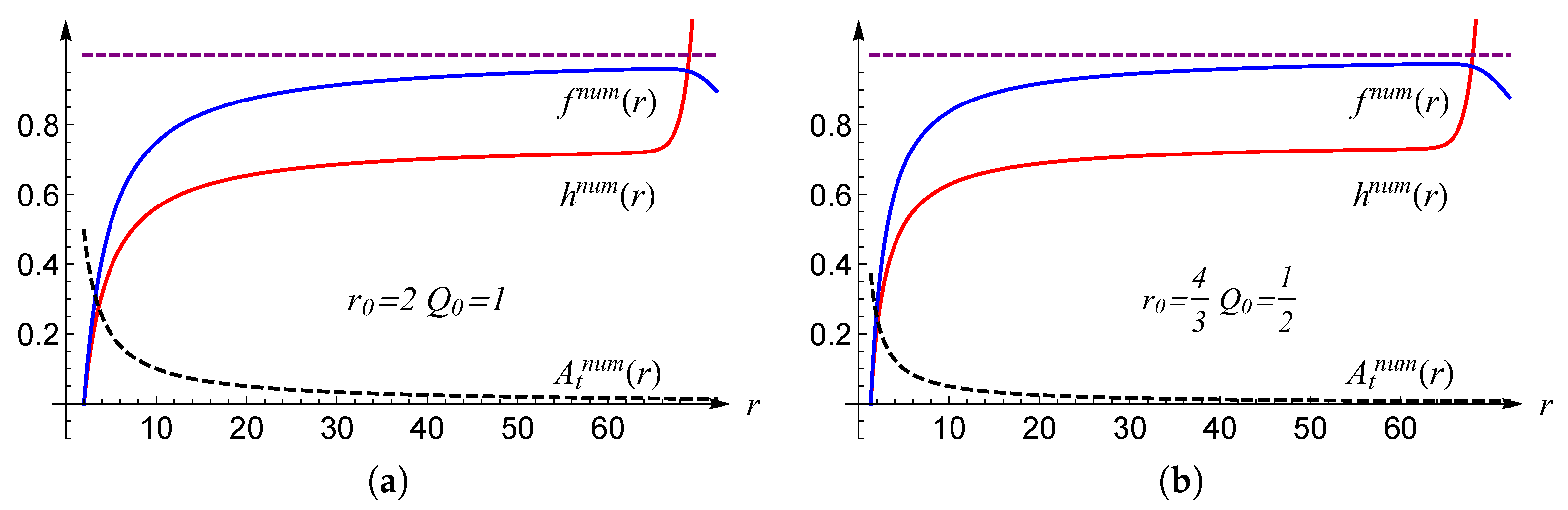The corresponding numerical solutions can be obtained in Figure 1, as shown in Ref.[6].

3. Analytically approximate solutions

In general, it is a difficult task to find exact solutions of nonlinear differential equations. In Refs. [25], the HAM was developed to obtain analytical approximate solutions to nonlinear differential equations. In this section, we will derive the analytical approximate solutions of metric functions and the electric potential function by using the HAM.

Consider n-nonlinear differential equations system, where $y_i\left(t\right)$ is the solution of the nonlinear operator $N_i$ as a function of t

$$\begin{array}{c}\hfill N_i\left[y_i\left(t\right)\right]=0,i=1,2,...,n,\end{array}$$

(13)

with unknown function $y_i\left(t\right)$ and a variable t. Then, the zero-order deformation equation can be written as

$$\begin{array}{c}\hfill (1-q)L[{\varphi }_i(t;q)-y_{i0}\left(t\right)]=q{h}_i{H}_i\left(t\right)N_i\left[{\varphi }_i(t;q)\right].\end{array}$$

(14)

The HAM constructs a topological homotopy for linear auxiliary operator L and nonlinear operator $N_i$. Introducing an embedding parameter $q\in [0,1]$, when q continuously changes from 0 to 1, the solution of the entire equation will also continuously change from the solution $y_{i0}\left(t\right)$ of our selected linear auxiliary operator L to the solution $y_i\left(t\right)$ of the nonlinear equation $N_i$. In order to control the convergence of the solution, an auxiliary function $H_i\left(t\right)$ and a convergence control parameter $h_i$ are also introduced into the homotopy equation (14). By selecting appropriate auxiliary function $H_i\left(t\right)$ and convergence control parameter $h_i$, the solution can converge more rapidly.

To decompose the nonlinear problem into a series of linear subproblems, now make Taylor expansions of ${\varphi }_i(t;q)$ with respect to q around $q=0$

$$\begin{array}{c}\hfill {\varphi }_i(t;q)=y_{i0}\left(t\right)+\sum _{m=1}^{\infty }{y}_{im}\left(t\right)q^m.\end{array}$$

(15)

Where the coefficient $y_{im}\left(t\right)$ of the m-th order of q is

$$\begin{array}{c}\hfill y_{im}\left(t\right)=\frac{1}{m!}\frac{{\partial }^m{\varphi }_i(t;q)}{\partial q^m}.\end{array}$$

(16)

When $q=1$, it is the expansion of the solution of the nonlinear equation (13)

$$\begin{array}{c}\hfill y_i\left(t\right)={\varphi }_i(t;1)=y_{i0}\left(t\right)+\sum _{m=1}^{\infty }{y}_{im}\left(t\right).\end{array}$$

(17)

By solving $y_{im}\left(t\right)$, the expansions of the solutions of the nonlinear equations can be found. To achieve it, the operation for the zero order deformation equation (14) will be as follows: First, substitute the expansion (15) into (14). Second, take the m-th derivative of q on (14) both sides. Third, after calculating the derivatives, set $q=0$. The so-called higher order deformation equation (mth-order deformation equation) is obtained, which is summarized as

$$\begin{array}{c}\hfill L[y_{im}\left(t\right)-{\chi }_m{y}_{im-1}\left(t\right)]=h_i{H}_i\left(t\right)R_{im}\left(y_{im-1}\right).\end{array}$$

(18)

Where the term $R_{im}$ on the right-hand side with respect to the nonlinear operator is

$$\begin{array}{c}\hfill R_{im}\left(y_{im-1}\right)=\frac{1}{(m-1)!}\frac{{\partial }^{m-1}{N}_i\left[{\sum }_{m=0}^{\infty }{y}_{im}\left(t\right)q^m\right]}{\partial q^{m-1}}{\mid }_{q=0},\end{array}$$

(19)

The highest term on the right-hand side of equation (19) can only reach up to the $y_{im-1}$ term. It is found that $y_{im}\left(t\right)$ is related to $y_{im-1}$, and it is possible to find $y_{im}\left(t\right)$ of arbitrary order based on this relation. The value of constant ${\chi }_m$ is

$$\begin{array}{c}\hfill {\chi }_m=\left\{\begin{array}{cc}\hfill 0& :m\le 1,\hfill \\ \hfill 1& :m>1.\hfill \end{array}\right.\end{array}$$

(20)

In the calculation, we take a finite order to ensure that the error is small enough, a finite M-order approximation

$$\begin{array}{c}\hfill y_i^M\left(t\right)=y_{i0}\left(t\right)+\sum _{m=1}^M{y}_{im}\left(t\right),\end{array}$$

(21)

the $y_i^M\left(t\right)$ are the M-th order approximate solution of the original equation (13).

The selection of linear auxiliary operator L, initial guess $y_{i0}\left(t\right)$, auxiliary function $H_i\left(t\right)$, and convergence control parameter $h_i$ has great freedom, making homotopy analysis method highly adaptable to different nonlinear problems. However, precisely because there is a great deal of freedom in selecting these quantities, how to choose these quantities more appropriately still requires a theoretical basis, and related work can be found in [26][27].

Next, we will use the HAM to obtain analytically approximation solutions of charged black holes in the Einstein-Maxwell-Weyl gravity. In order to do it, we choose a coordinate transformation $z=1-\frac{r_0}{r}$ , such that the region of $r\to \infty$ becomes a finite value $z=1$. Then, the field equations under this coordinate transformation become

$$\begin{array}{ccc}& & h^{″}\left(z\right)-\frac{h^{\prime }{\left(z\right)}^2}{2h\left(z\right)}+\frac{f^{\prime }\left(z\right)h^{\prime }\left(z\right)}{2f\left(z\right)}+\frac{2h\left(z\right)\left[-(z-1)f^{\prime }\left(z\right)+f\left(z\right)-1\right]}{{(z-1)}^{2}f\left(z\right)}=0,\hfill \\ & & f\left(z\right)f^{″}\left(z\right)\left[2\alpha {(z-1)}^{5}h{\left(z\right)}^2{h}^{\prime }\left(z\right)+4\alpha {(z-1)}^{4}h{\left(z\right)}^3\right]\hfill \\ & & +f^{\prime }\left(z\right)\{f\left(z\right)\left[\alpha {(z-1)}^{5}h\left(z\right)h^{\prime }{\left(z\right)}^2+2\alpha {(z-1)}^{4}h{\left(z\right)}^2{h}^{\prime }\left(z\right)+12\alpha {(z-1)}^{3}h{\left(z\right)}^3\right]\hfill \\ & & -4\alpha {(z-1)}^{3}h{\left(z\right)}^3\}-3\alpha {(z-1)}^{4}h{\left(z\right)}^3{f}^{\prime }{\left(z\right)}^2+f\left(z\right)\left[-2{r_0}^2(z-1)h{\left(z\right)}^2{h}^{\prime }\left(z\right)\right.\hfill \\ & & \left.+2{r_0}^{2}h{\left(z\right)}^3+8\alpha {(z-1)}^{2}h{\left(z\right)}^3\right]+f{\left(z\right)}^2\left[-\alpha {(z-1)}^5{h}^{\prime }{\left(z\right)}^3-3\alpha {(z-1)}^{4}h\left(z\right)h^{\prime }{\left(z\right)}^2\right.\hfill \end{array}$$

(22)

$$\begin{array}{ccc}& & \left.-8\alpha {(z-1)}^{2}h{\left(z\right)}^3\right]+2\kappa {Q_0}^2{(z-1)}^{2}h{\left(z\right)}^3-2{r_0}^{2}h{\left(z\right)}^3=0,\hfill \end{array}$$

(23)

$$\begin{array}{ccc}& & \frac{Q_0\sqrt{\frac{h\left(z\right)}{f\left(z\right)}}}{r_0}+{A_t}^{\prime }\left(z\right)=0,\hfill \end{array}$$

(24)

where the prime (′) denotes the differentiation of the function with respect to z, and $r_0$ the event horizon of black hole. Notice that Maxwell equation (24) is a linear one, and (22) (23) are second-order derivative equations with respect to $h\left(z\right)$ and $f\left(z\right)$. Therefore, we derive $h\left(z\right)$ and $f\left(z\right)$ by applying the HAM to the two nonlinear equations (22) and (23), after then solve equation (24) for $A_t\left(z\right)$.

In the homotopy equation, the auxiliary function can be coded into the initial guess solution, i.e., the $H_i\left(z\right)$ on the right side of the zero-order deformation Eq. (14) can be moved to the left side [26], so without loss of generality we take the auxiliary function $H_i\left(z\right)=1,i=1,2$. The initial guess is

$$\begin{array}{ccc}& & h_0\left(z\right)=f_0\left(z\right)=z\left(1-a\left(1-z\right)\right),V_{t0}\left(z\right)=1-z.\hfill \end{array}$$

(25)

And corresponding linear auxiliary linear operators (whose construction method is shown in [26][27])

$$\begin{array}{c}\hfill L_i\left[{\varphi }_i(z;q)\right]=\frac{z^2}{2}\frac{{\partial }^2{\varphi }_i(z;q)}{\partial z^2}-z\frac{\partial {\varphi }_i(z;q)}{\partial z^2}+{\varphi }_i(z;q),i=1,2.\end{array}$$

(26)

$$\begin{array}{c}\hfill L_3\left[{\varphi }_3(z;q)\right]=\frac{\partial {\varphi }_3(z;q)}{\partial z}.\end{array}$$

(27)

The following boundary conditions are used in the process of solving the nonlinear equations using the homotopy analysis method,

$$\begin{array}{c}\hfill h\left(0\right)=0=f\left(0\right),h\left(1\right)=1=f\left(1\right),V_t\left(1\right)=0.\end{array}$$

(28)

The chosen of the initial guess solutions (25) is required to satisfy the boundary conditions (28).

The nonlinear equations (13) $N_i$ is provided by Eqs. (22) and (23), and M-order analytical approximate solution (21) is obtained by solving $y_{im}\left(z\right)$ from the higher order deformation equation (18). Here, we do the second-order approximation $M=2$, and the result is related to the parameter a of the initial guessed solution and the convergence control parameters $h_1$,$h_2$ and $h_3$. We fix the convergence control parameters such that $h_1=h_2=h_3=-1$ and obtain the second order approximation to the solution with respect to z and a, which are shown in the Appendix.

In order to select the appropriate parameter a, we substitute Eqs. (A1)(A2) into the left side of the nonlinear equations (22) (23), and obtain

$$\begin{array}{ccc}\hfill & & \Delta e{q}_1=\left|N_1[h(z,a),f(z,a)]\right|,\hfill \end{array}$$

(29)

$$\begin{array}{ccc}\hfill & & \Delta e{q}_2=\left|N_2[h(z,a),f(z,a)]\right|,\hfill \end{array}$$

(30)

$$\begin{array}{ccc}\hfill & & \Delta e{q}_3=\left|N_3[h(z,a),f(z,a),A_t(z,a)]\right|,\hfill \end{array}$$

(31)

which represented as the deviations between the analytical approximate solutions and the exact solutions.

If the above three equations are as close to zero as possible in $z\in [0,1]$, then that means the approximate solutions are as close as possible to the analytical solutions. We can also use the averaged square residual error [20] to represent the total deviation between the approximate solutions and the exact solutions,

$$\begin{array}{ccc}\hfill E\left(a\right)=& & \frac{1}{S+1}\sum _{k=0}^S\{{\left(N_1[h(z_k,a),f(z_k,a)]\right)}^2+{\left(N_2[h(z_k,a),f(z_k,a)]\right)}^2\hfill \\ & & +{\left(N_3[h(z_k,a),f(z_k,a),A_t(z_k,a)]\right)}^2\},\hfill \end{array}$$

(32)

with

$$\begin{array}{c}\hfill z_k=k\Delta z=k\frac{1}{S},k=0,1,2,...,S.\end{array}$$

(33)

We choose $S=40$ and use the averaged square residual error (32) as a function with the undetermined parameter a as a variable to draw images of $ln\left[E\left(a\right)\right]$ to check the relationship between the averaged square residual error and a.

In Figure 2, it shows the relationships between $E\left(a\right)$ and a when $Q_0=2$, $r_0=1$, and $Q_0=\frac{4}{3}$, $r_0=\frac{1}{2}$. The optimal value of $a^{*}$ in the initial guess can be obtained from the averaged square residual error, which makes the solution converge more effectively. $a^{*}$ is at a point such that the averaged square residual error is minimized, and the optimal value of $a^{*}$ is mathematically represented as

$$\begin{array}{c}\hfill a^{*}=min\left\{E\left(a\right)\right\}.\end{array}$$

(34)

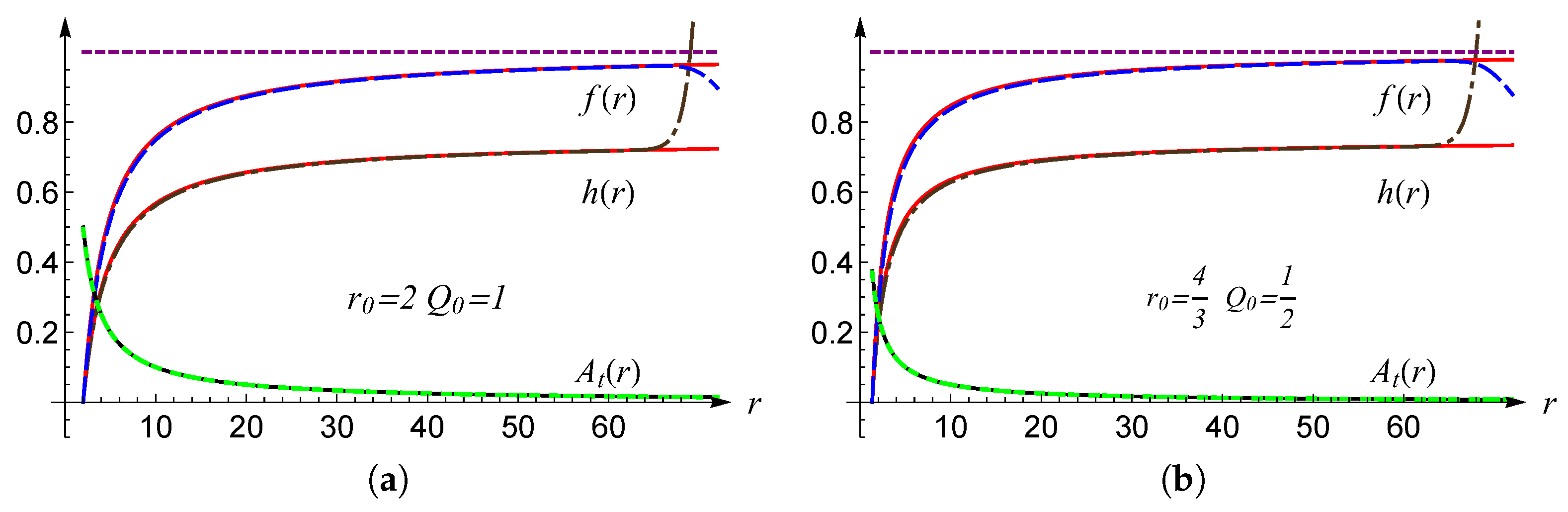
Both curves have a minimum point, which means that at these points, the square residual is the smallest. In the above two figures, these points correspond to $a^{*}=0.27478$ and $a^{*}=0.17611$. Substituting $Q_0$, $r_0$ and the corresponding a into Eqs. (A1), (A2) and (A3)), after reverting back to the radial coordinate r, the analytical approximate solutions of Einstein-Maxwell-Weyl gravity can be obtained for the different configurations of $Q_0$ and $r_0$. The comparison between the analytical approximation solutions obtained by HAM and numerical solutions is plotted in Figure 3.

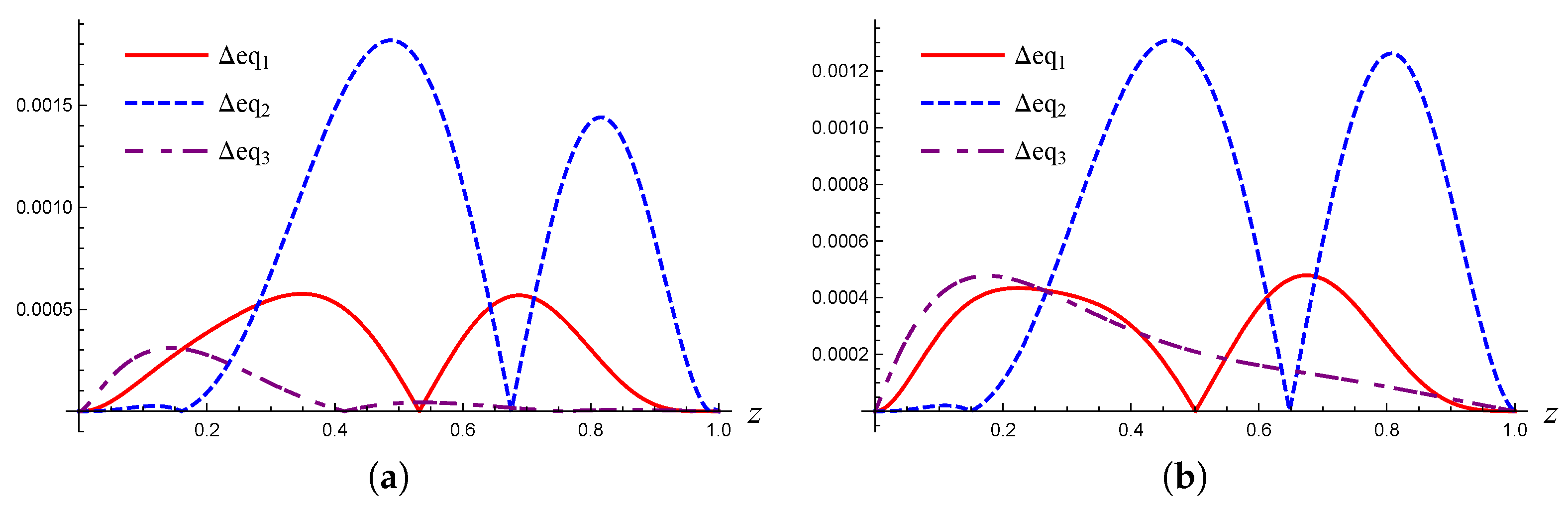
It is interesting to check the accuracy of the analytical approximate solutions. We plot these curves describing the deviations (Eqs.(29) and (30)) of the analytical approximate solutions from the exact solutions, as shown in Figure 4.

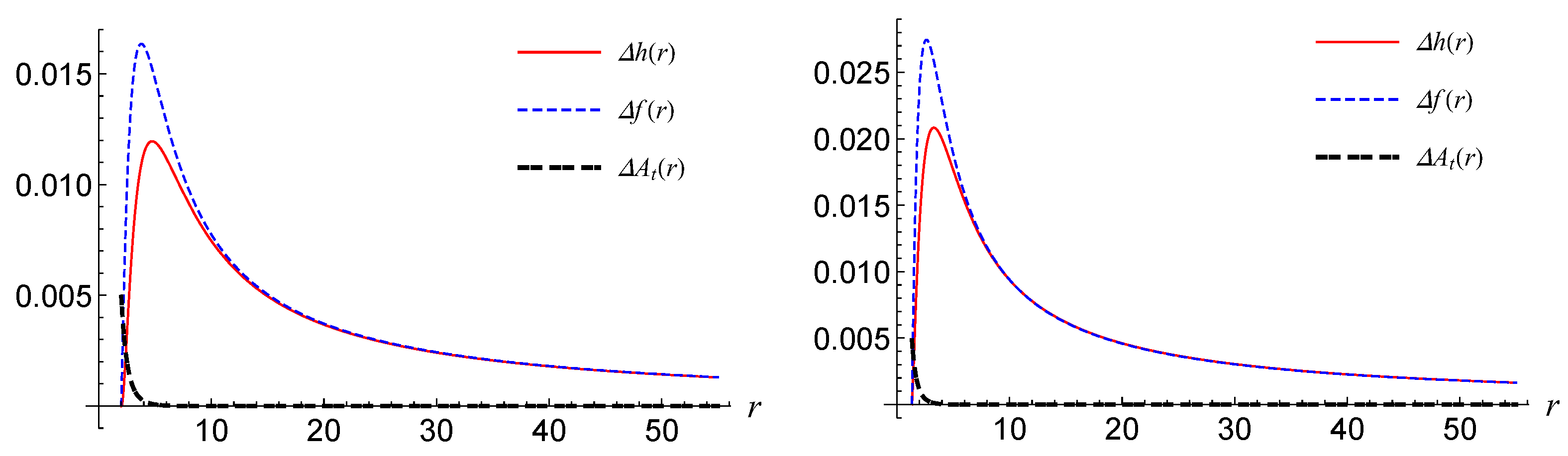
In order to compare with the numerical solutions, we will calculate the absolute errors between the analytical approximate and numerical solutions in Figure 5.

$$\begin{array}{c}\Delta h\left(r\right)=|h^{num}\left(r\right)-h^{ana}\left(r\right)\left]\right|,\Delta f\left(r\right)=|f^{num}\left(r\right)-f^{ana}\left(r\right)\left]\right|,\hfill \\ \Delta A_t\left(r\right)=|A_t^{num}\left(r\right)-A_t^{ana}\left(r\right)\left]\right|.\hfill \end{array}$$

(35)

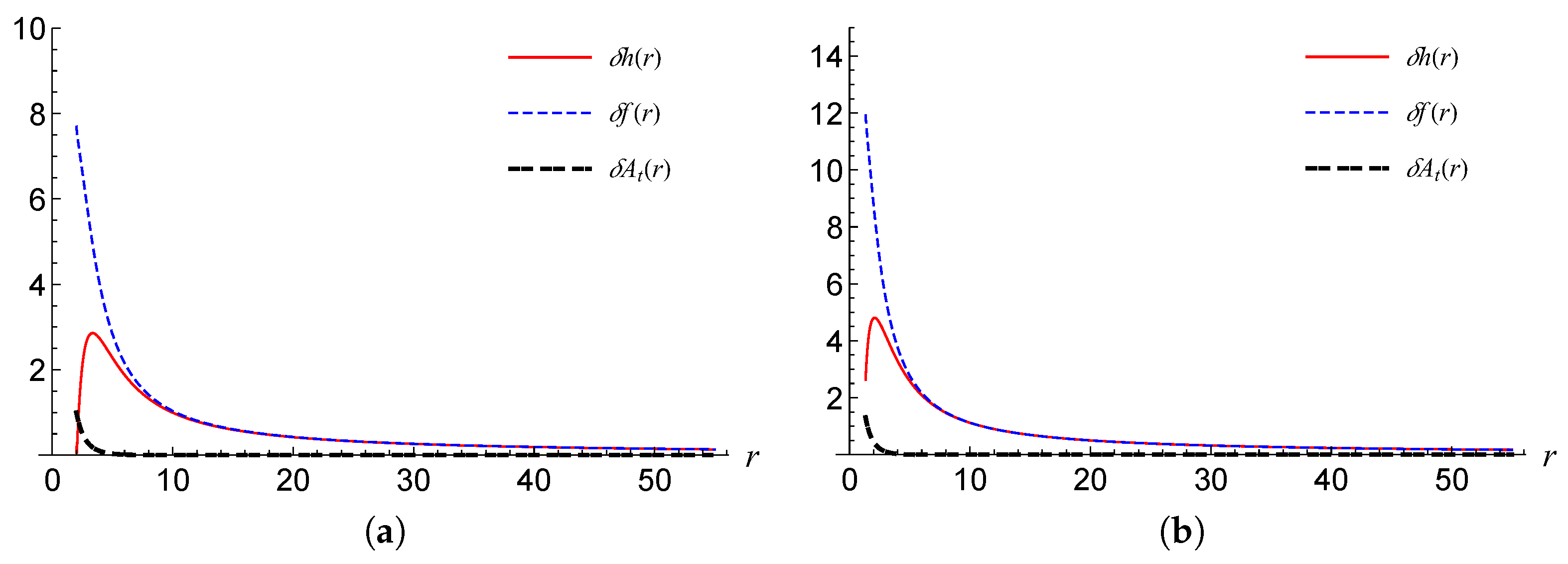
and the relative errors in Figure 6

$$\begin{array}{c}\delta h\left(r\right)=\frac{|h^{num}\left(r\right)-h^{ana}\left(r\right)\left]\right|}{h^{num}\left(r\right)}\times 100\%,\delta f\left(r\right)=\frac{|f^{num}\left(r\right)-f^{ana}\left(r\right)\left]\right|}{f^{num}\left(r\right)}\times 100\%,\hfill \\ A_t\left(r\right)=\frac{|A_t^{num}\left(r\right)-A_t^{ana}\left(r\right)\left]\right|}{A_t^{num}\left(r\right)}\times 100\%.\hfill \end{array}$$

(36)

4. Conclusions and Discussions

In this paper, we discuss the charged black holes in Einstein-Weyl gravity in the presence of Maxwell field. By using Homotopy Analysis Method, we obtain analytical approximation to charged black hole solutions of Einstein-Maxwell-Weyl gravity, which has been also derived numerically by Lin et al.[6]. The region and rate of convergence of the series solution for the HAM does not depend on the choice of the initial guess function, auxiliary linear operator, and an auxiliary function, but it can be effectively controlled by using a convergence control parameter. Since the approximation is significantly accurate in the entire space-time outside the event horizon, it can be used for studying the properties of this particular black hole and the various phenomena. The present work is considered as an important work because we confirm that numerical solutions are consistent with an analytical approximate solution for the charged black holes.