Prerpints.org logo
Preprint
Article

Electron Mean Free Path Effect on Vortex Matter in a Superconducting Pb Island Grown on Si (111)

Altmetrics

Downloads

99

Views

29

Comments

0

A peer-reviewed article of this preprint also exists.

Submitted:

12 June 2023

Posted:

13 June 2023

You are already at the latest version

Alerts
Abstract
In this work we report recent theoretical calculations of a superconducting island in a strong vortex confinement regime. The obtained results reveal the evolution of superconducting condensate as a function of electron mean-free path (l) with the evolution of an applied magnetic field H0. The results of this study provide an insight about the emergent superconducting properties under such conditions, using the Ginzburg-Landau numerical simulations where spatial variation of thickness d on island, omnipresent in these kind of structures grown on Si (111), is taken into account. These results offer a new route to tailor superconducting circuits by using the controlled bombardment, in order to explore the impact on vortex distribution, phase of order parameter, number of vortices, free energy and the first H1 and second critical field H2.
Keywords: 
Subject: Physical Sciences  -   Condensed Matter Physics

0. Introduction

Superconductivity is an electronic state of matter characterized by specific length scales: the coherence length ξ , the length scale of the Cooper-paired electrons, and the London penetration length λ , the length scale of magnetic field penetration into the superconductor [1]. The superconducting state is attained below certain critical values of temperature, magnetic field, vortex structures and applied current, which can change dramatically when the size of a superconductor becomes comparable with the characteristic lengths [9,10,11]. In this state, the resistance to the passage of an electric current exhibited by the material is zero [12]. In past decades several theoretical studies focused on the confinement effects in superconductors of a size lower than one or both of these characteristic scales [2,3,4], but also, focused on the effect of symmetry on condensate confinement comparing mesoscopic disks, squares and triangles [5,6,7,8]. The theoretical macroscopic framework that built upon the definition of a superconducting wavefunction that characterizes the superconducting state, comes from the Ginzburg–Landau theory [2] which is used in this work.
Most experimental focused on measuring the overall response of previous mentioned systems and superconducting islands [13,14,15,16,17,18], or to the local study of the magnetic confinement of vortices considering low magnetizing field H ⋘ H c 2 on large samples d ∼ λ ⋙ ξ [19,20]. The vortex configuration in real space at high fields H ⋙ H c 1 was studied in [16], but low confinement conditions are still considered, d ⋙ ξ . Nowadays, penetration and expulsion of vortices in mesoscopics superconducting samples has been studied in Ref. [21,22,23,24], but the detailed picture of a strongly confined superconducting state d ∼ ξ ⋘ λ e f f is still missing, including the influence of changing electron mean free path l , not only experimentally but also theoretically.
There are two effective techniques for modifying the mean free path of the electron l, such Focused Ion Beam Induced Deposition (FIBID) and Focused Electron Beam Induced Deposition (FEBID), which are two very similar nanopatterning techniques that use of a focused beam of charged particles, either ions or electrons [25,26,27]. In general, irradiation-induced doping or disorder exhibits higher accuracy compared to others such as substitutional chemestry, in which there are greater uncertainties and inhomogeneity in phase distribution in the induced disorder [28,29]. Irradiation of superconductors generally leads to a significant increase in the normal-state resistivity and suppression of T c , as well as an enhancement of the critical current density when efficient pinning centers are created [30].
This has driven nanofabrication techniques because there is a perennial need for both industry and research to exploit such fundamental effects for the development of quantum technologies [31], in which superconducting nanodevices represent a field of research. Such devices include magnetic sensors in the form of superconducting interference superconducting quantum interference devices (SQUIDs) [32], single-photonic detectors [33], quantum bits [34] and quantum switches [35].

1. Materials and Methods

We simulated a superconducting Pb island grown on a silicon substrate (111) as illustrated in Figure 1, but also, the thickness change d and the mean free path l e . The framework for our theoretical studies is the phenomenological Ginzburg-Landau (GL) theory [1]. We used the expressions for GL coeficients α and β in the dirty limit, to include the variation l e the electron mean free path in the sample, i.e.
α ( T ) = − 1.36 ℏ 2 m * ξ 0 l ξ 1 − T T c = α 0 l ξ 0 1 − T T c
β = 0.2 N ( 0 ) ℏ 2 2 m * ξ 0 l e k B T c 2 = β 0 l ξ 0 2
Where l ξ = l e ξ 0 is the ratio of the electron mean free path and BCS coherence length. The dimensionless form of the GL equations can be written as follow:
( − i ∇ − A ) 2 Ψ = 1.367 l ξ 0 − 1 l ξ 0 2 | Ψ | 2 Ψ
Where lengths are scaled to ξ 0 , penetration depth λ 0 is defined as λ 0 2 = m c 2 β 0 / 16 π | a 0 | e 2 , the vector potential A is expressed ϕ 0 / 2 π ξ 0 , and the order parameter is in units of Ψ 0 = − α / β .

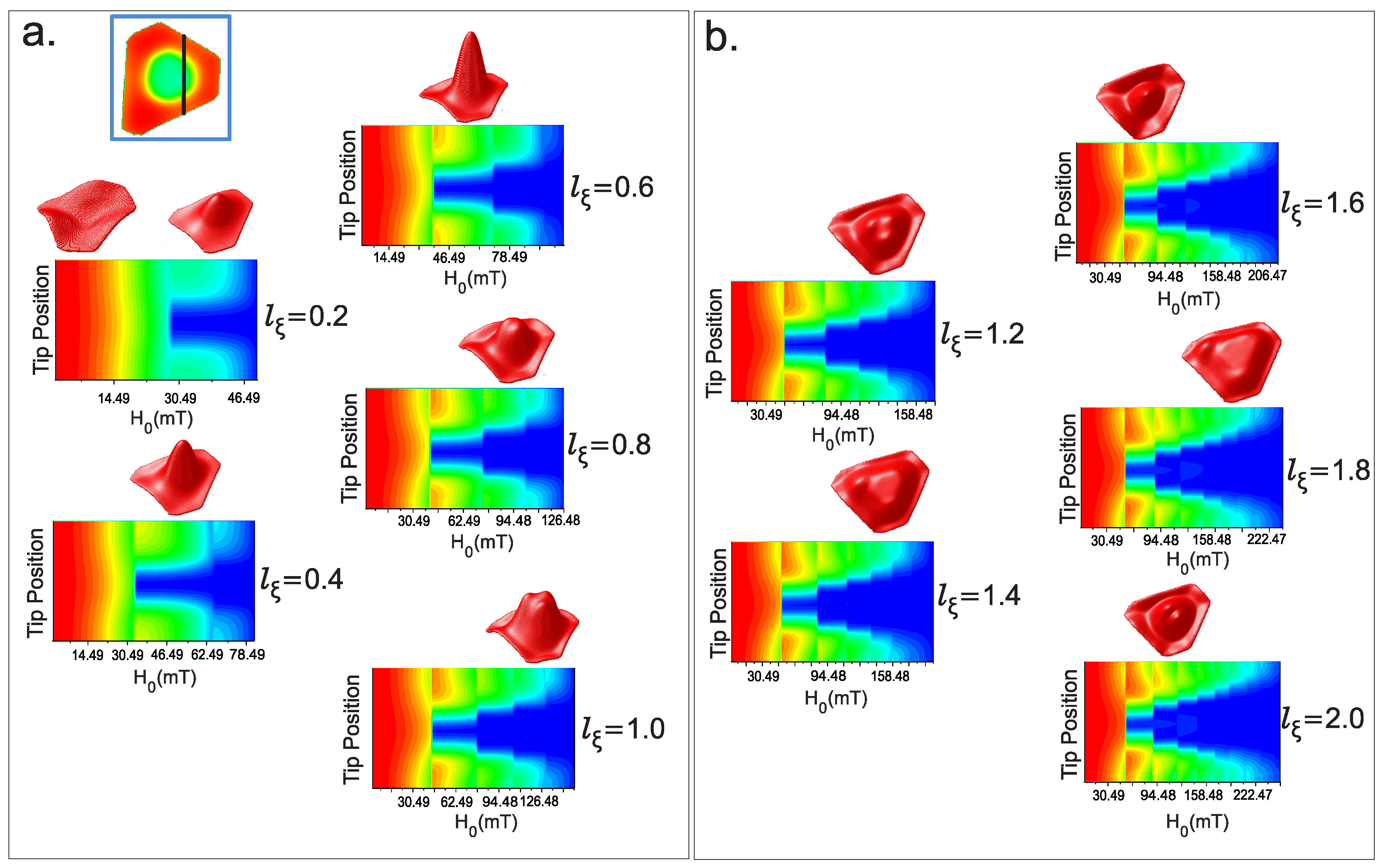
2. Results and discussion

Process started calculating the full free-energy (F) spectrum and the corresponding vortex states as a function of applied magnetic field ( H 0 ) for the island with a central hole and l ξ = 1.0  Figure 2. Initially, the magnetic field was kept perpendicular to the plane bottom of Pb island. The method for finding vortex states is multifold: First step, applied magnetic field is increased and decreased in the considered range with a kept history of the previously found states in the field sweep and the second step, considering each value of magnetic field, the calculation is initialize from the fluctuating normal state (randomized | Ψ | < 0.01 ) and from the from the fully superconducting state ( | Ψ | ≈ 1 ). Following this steps, we construct the energy diagram of all stable vortex states, including those with higher energy. As a result, we found more than one stable vortex distribution, i.e. one with lowest energy (ground state) and several others with higher energy (usually called metastable).
We show lower energies and a higher stabilities represented in the wide ranges of magnetic fields in which the same number of vortices remains (see Figure 2, cases a.,b.,c.,d. and e.). This finding demonstrates the strong confinement imposed on vortices by Meissner currents on the edge of the island (see Figure 1), where the Meissner current is strongest, as we can notice in the snapshots of superconducting current (see Figure 2 (left) inset) and it confines vortices toward the interior of the sample. On the other hand, It can also be noted that stability decreases with the entry of a greater number of vortices when the magnetic field is increasing (see Figure 2, cases f.,h. and g.), due to vortices are basically parallel magnetic moments that destroy the superconductivity with increase of their number. Additionally, other evidence of the strong confinement on the superconducting island can be noticed that vortices repel each other, and this repulsion, in the absence of sample boundaries, leads to the formation of a triangular (Abrikosov) lattice, which is not the case in this research.
Figure 3a–d inset show some states where vortices have reached the center of superconductor island which can be verified by the circular diagram phase of the order parameter on the top of the island simulation. The vortex state is characterized by the total angular momentum L through Ψ = ψ e x p ( i L ϕ ) , but, we can introduce an analog to the total angular momentum which is still a good quantum number. Choosing circular loops at the periphery of the center of the island, we find that the effective angular momentum L = Δ ϕ / 2 π , and each time that in the path the color went from red to blue a vortex is found L = 1 , 2 , 3 , . . . . The superconducting order parameter | Ψ | , nucleated at the sample surface, traps then inside, in the island hole, carrying flux L ϕ 0 where ϕ 0 is the quantum flux . To check this ‘‘flux compression’’ model quantitatively, the self-consistent solution of the full Ginzburg-Landau (GL) equations is necessary Eq.3
The transition between the two quantum states L = 0 (zero vortex) and L = 1 (one vortex) can be used to calculate the field H 1 , corresponding to the penetration of the first flux line into a superconducting island. One option to find the value of H 0 in which this transitions take place is considering every curve of Figure 3a–d where the peaks obtained at a lower value of applied magnetic fields in every curve of Figure 3 (F versus H 0 ), represent the first vortex entrance in the superconducting island, we can notice that it take place at different values of H 0 . Figure 3 also can be used to calculate the field H 0 corresponding to the penetration of one flux line at different electron mean-free path l ξ , and thus the transition between the two quantum states L = 0 and L = 1 , as well as by using l we can tune the number of peaks or transitions.
The characteristics lengths of a superconductor, the coherence length and the penetration depth, take the effective values λ e f f = 0.65 λ 0 ξ 0 / l and ξ e f f = 0.85 l ξ 0 considering l ξ = l 0 / ξ 0 . Thus, the situation in the island is similar to that of a type II superconductor in the diffusive limit, in which correlation length ξ and penetration depth λ in a magnetic field depends on l 0.5 and l − 0.5 respectively. Therefore, the magnetic field in a superconductor is affected due to the increment of λ with the increases of concentration of impurities, but also a strong variation of the number of superconducting electrons, i.e. electrons linked in Cooper pairs with the decrease of ξ . This behaviour is shown in Figure 2 and Figure 3. (inset) where variations of condensate are reached considering a spatial change of the electron mean free path.
In addition, the order parameter | Ψ 0 | 2 is modified through the sample with the modification of l, as we expected, according to the proportionality between the order parameter and penetration depth which is | Ψ 0 | 2 ∼ 1 / λ . It implies changes on strong screening supercurrents (see Figure 2 inset) that may circulate in the island, where strong supercurrent carry on a strong diamagnetic (Meissner) effect as we can notice in Figure 3 where the H 1 (first vortex entry) is reached (see also Table A1 apendix A). It also can be noticed in the modification of l at different zones of sample (see Figure A1 apendix B) which allow to chose not only the location of vortex entrance, but also, the value of H 0 .
Figure 4 (left) shows the proportionality of the green curve corresponding to the values of the second critical magnetic field where the normal state is reached ( H 2 ) versus the mean free path (l), which shows a result not reported before for this type of heterostructures. The fine tune of H 2 shows great applications for the design of electronic devices, through the bombardment of the Pb islands, which can be controlled using high precision with current technologies. Thus, it is clear that H 1 can be tuned, which supposes a variation in the Meissner current and with it the repulsion of the applied magnetic field H 0 and entry of vortices in the superconducting island. We know that flux penetration in type-II superconductors occurs in form of quantized, flux-enclosing, supercurrent vortices. However, a more detailed analysis shows that, this flux penetration must first overcome an energy barrier at the surface which is called Bean-Livinstong barrier (BLB). Corresponding variations of the Gibbs free energy with l, for several values of H 0 , are shown in Figure 3. One can see that H 1 take different values due to, in order to penetrate the superconductor island, vortex must first overcome BLB.
In order to identify the observed quantum phenomenon, we explored the evolution and stability of the superconductivity in the islands with the magnetic field (Figure 2, Figure 3 and Figure 4). At zero magnetic field, Figure 2 snapshot (a.) shows a spatially homogeneous superconducting condensate to exist in the entire nanoisland, evidencing the Meissner ( L = 0 ) state. As the field increases further, the snapshots in Figure 2 and Figure 3 reveal novel intriguing vortex configurations, evolving till the normal state is achieved in each the superconducting island, but in order to get a deeper insight into the field evolution of the condensate confined we need to focus on their phases.
In Figure 5 we present a color-coded diagram of (ZBC) vs magnetic field taken over a line crossing the island (depicted as a black line in the blue frame). This diagram shows a series of abrupt steplike transitions which are identified in a separating the states with different vorticity L, where color from red (superconducting state) to blue (normal state) corresponds to the local strength of superconducting condensate. Precisely, until H 0 ≈ 27.5 m T the island remain in the Meissner state ( L = 0 ) for l = 0.2 , in agreement with the color map in Figure 5. Also, we can notice that only one vortex penetrate due to only one steplike transition take place for l = 0.2 until reach the total normal state at H 0 ≈ 46.49 m T (all region became blue). In order to get a deeper insight into these phases, we focused on the field evolution of the condensate confined in the superconducting island with l = 1.2 . At H 0 ≈ 46.49 m T T the first vortex appears in the sample; it is clearly identified by its normal state core (blue region). This single vortex state lasts until H 0 ≈ 78.49 m T . The L = 2 phase occurs at H 0 ≈ 78.49 m T < H 0 < H 0 ≈ 110.49 m T , followed by the L = 3 state, that also can be noticed in the CPD in the red snapshot located up of the H 0 ≈ 110.49 m T < H 0 < H 0 ≈ 134.49 m T .
Remarkably, in L = 2 for l = 0.8 looks like a single round object located at the island center, instead of two individual vortices. The straightforward conclusion is that here one (two) individual vortex cores are merged to form a single giant vortex.

3. Conclusions

In conclusion, strong vortex confinement effects were studied in Pb island grown on Si (111), taking into account several changes of electron mean-free path, considering that experimentally to ion bombardment can be done over a superconducting sample, by using the expressions for Ginzburg-Landau (GL) coefficients α and β in the dirty limit. In these type II superconducting island an unexpected behaviour of vortex configuration was studied, but also, their critical parameters which allow to control this heteroestructure in order to be applied in electronic devices.

Author Contributions

Derived G-L equations for dirty limit and performed the simulations, J.D. González and J.E. González; prepared the figures, F. Durán and C. Salas; software, J.D. González; formal analysis,J.D. González and J.E. González; writing original draft preparation, J. Gómez and J.D. González.

Acknowledgments

This work was partially financed by the Universidad del Magdalena (Fonciencias) and Dirección de Investigación (Colombia) y Transferencia (DIT) Universidad Pontificia Bolivariana (Colombia).

Conflicts of Interest

The authors declare no conflict of interest. The founding sponsors had no role in the design of the study; in the collection, analyses, or interpretation of data; in the writing of the manuscript, and in the decision to publish the results.

Appendix A

Appendix A.1

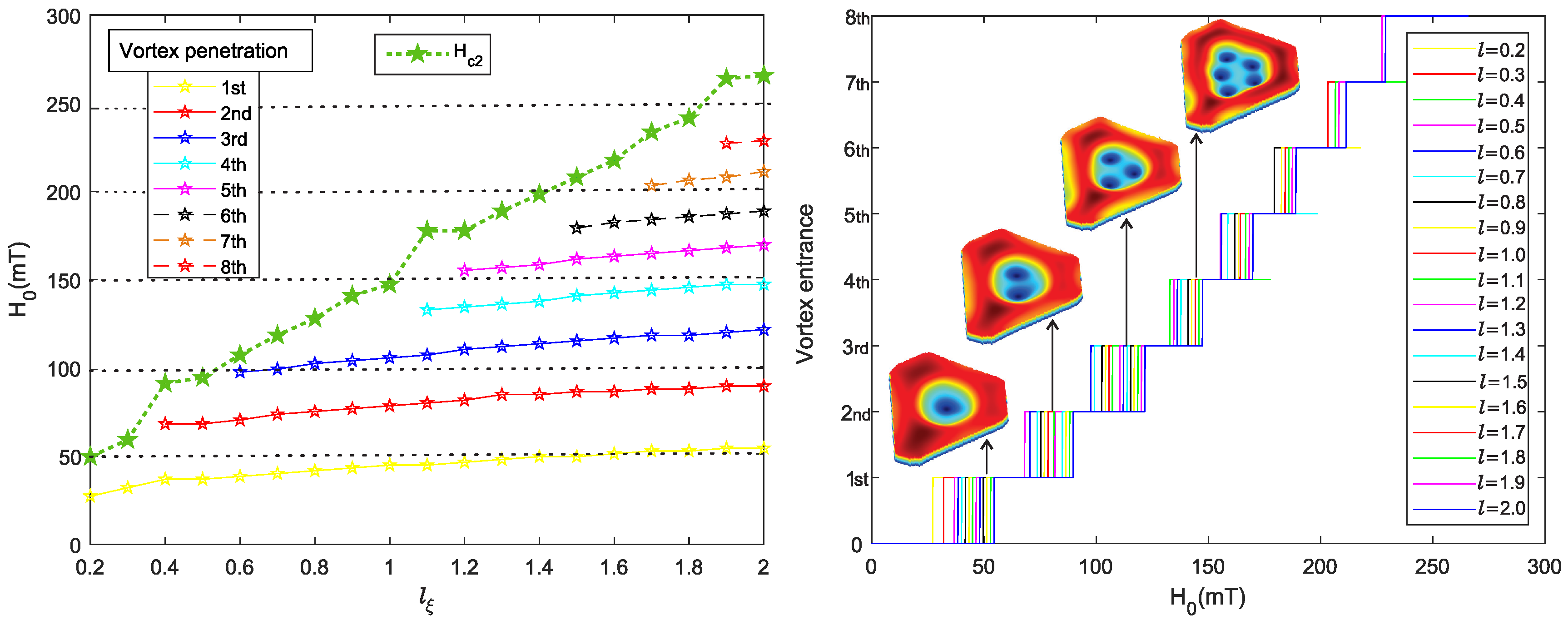
Table A1. Stability range of vortex states for each value of the mean free path studied. Second critical field is included in the last column.
Table A1. Stability range of vortex states for each value of the mean free path studied. Second critical field is included in the last column.
l/ n m 1 s t / m T 2 n d / m T 3 r d / m T 4 t h / m T 5 t h / m T 6 t h / m T 7 t h / m T 8 t h / m T H 2 / m T
0.2 27.29 49.69
0.3 32.09 59.29
0.4 36.89 68,89 91.28
0.5 36.89 68,29 94.48
0.6 38,49 70,49 97.68 107.28
0.7 40,09 73,69 99.28 118.48
0.8 41,69 75,29 102.48 128.08
0.9 43,29 76,89 104.08 140.88
1.0 44,89 78,49 105.68 147.28
1.1 44,89 80,09 107.28 132.88 177.67
1.2 46,49 81,68 110.48 134.48 155.28 177.67
1.3 48,09 84,88 112.08 136.08 156.88 188.87
1.4 49,69 84,88 113.68 137.68 158.48 198.47
1.5 49,69 86,48 115.28 140.88 161.68 179.27 208.07
1.6 51,29 86,48 116.88 142.48 163.28 182.47 217.67
1.7 52,89 88,08 118.48 144.08 164.87 184.07 203.27 233.67
1.8 52,89 88,08 118.48 145.68 166.47 185.67 206.47 241.67
1.9 54,49 89,68 120.08 147.28 168.07 187.27 208.07 227.27 264.06
2.0 54,49 89,68 121.68 147.27 169.67 188.87 211.27 228.80 265.66
* Tables may have a footer.

Appendix B

Figure A1 shows the modification of the mean free path in selected zones of Pb island, which is totally possible using nanopattering Ion technique [25,26,27].
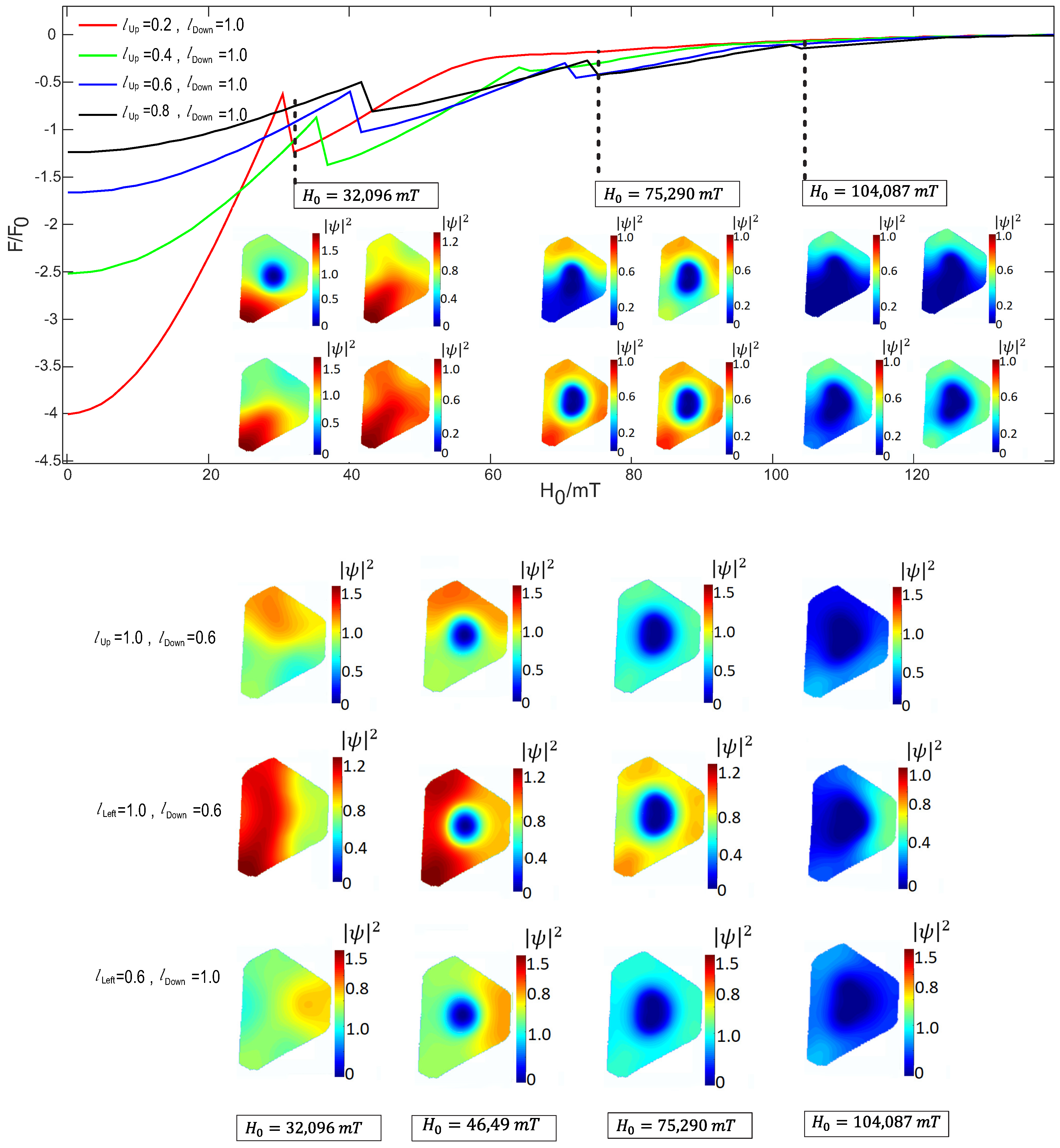
Preprints 76373 g0a1
Figure A1. The figure shows the free energy as a function of the applied magnetic field. l u p and l d o w n show the values of mean free path at the top and bottom respectively, while l l e f t shows l r i g t h for the left and right zones. Inside the figure we can see the clear modification of the vortex input under the influence of the mean free path, which implies a greater control of the superconducting condensate and the vortex configuration.
Figure A1. The figure shows the free energy as a function of the applied magnetic field. l u p and l d o w n show the values of mean free path at the top and bottom respectively, while l l e f t shows l r i g t h for the left and right zones. Inside the figure we can see the clear modification of the vortex input under the influence of the mean free path, which implies a greater control of the superconducting condensate and the vortex configuration.
Preprints 76373 g0a1

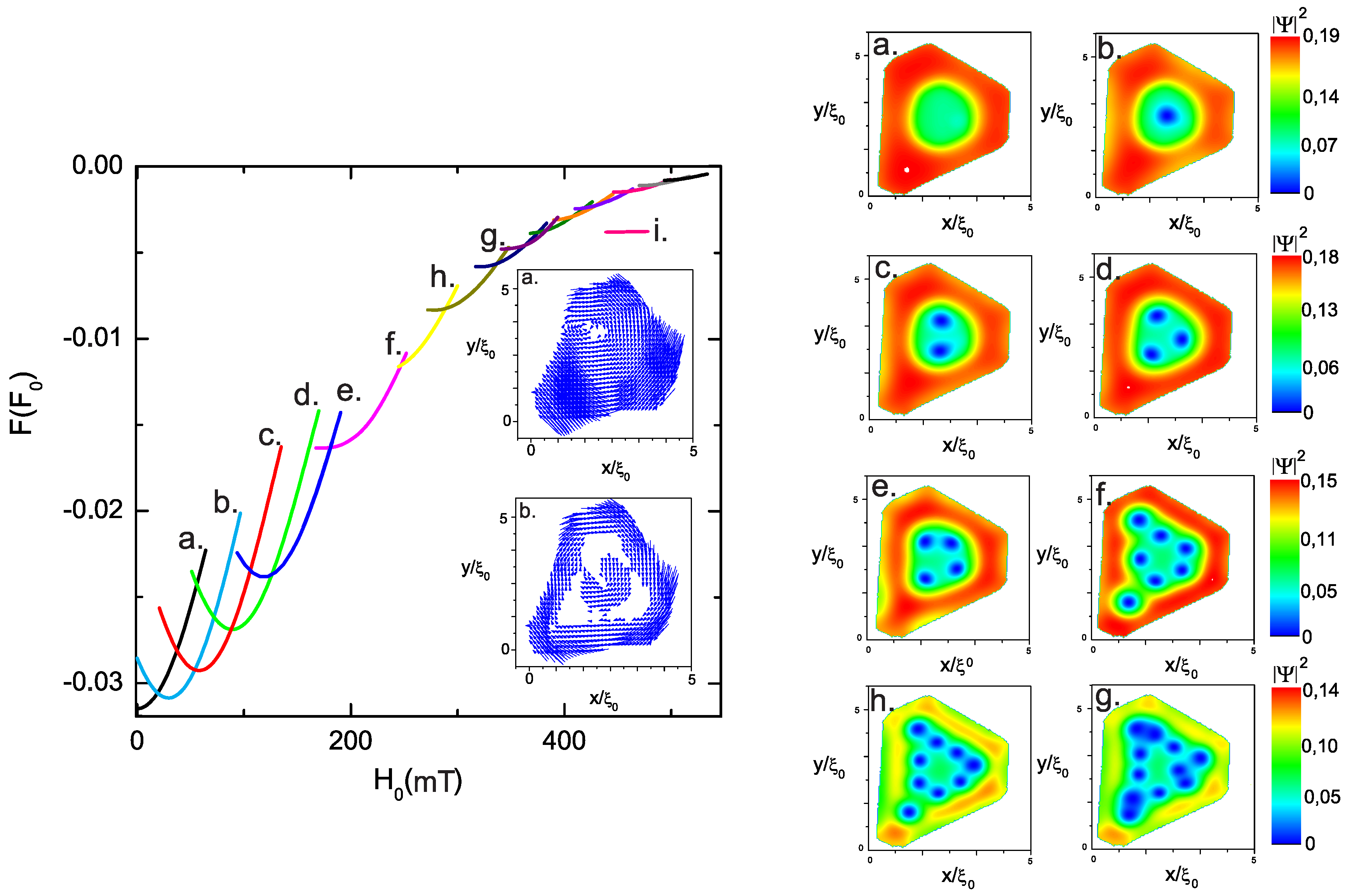
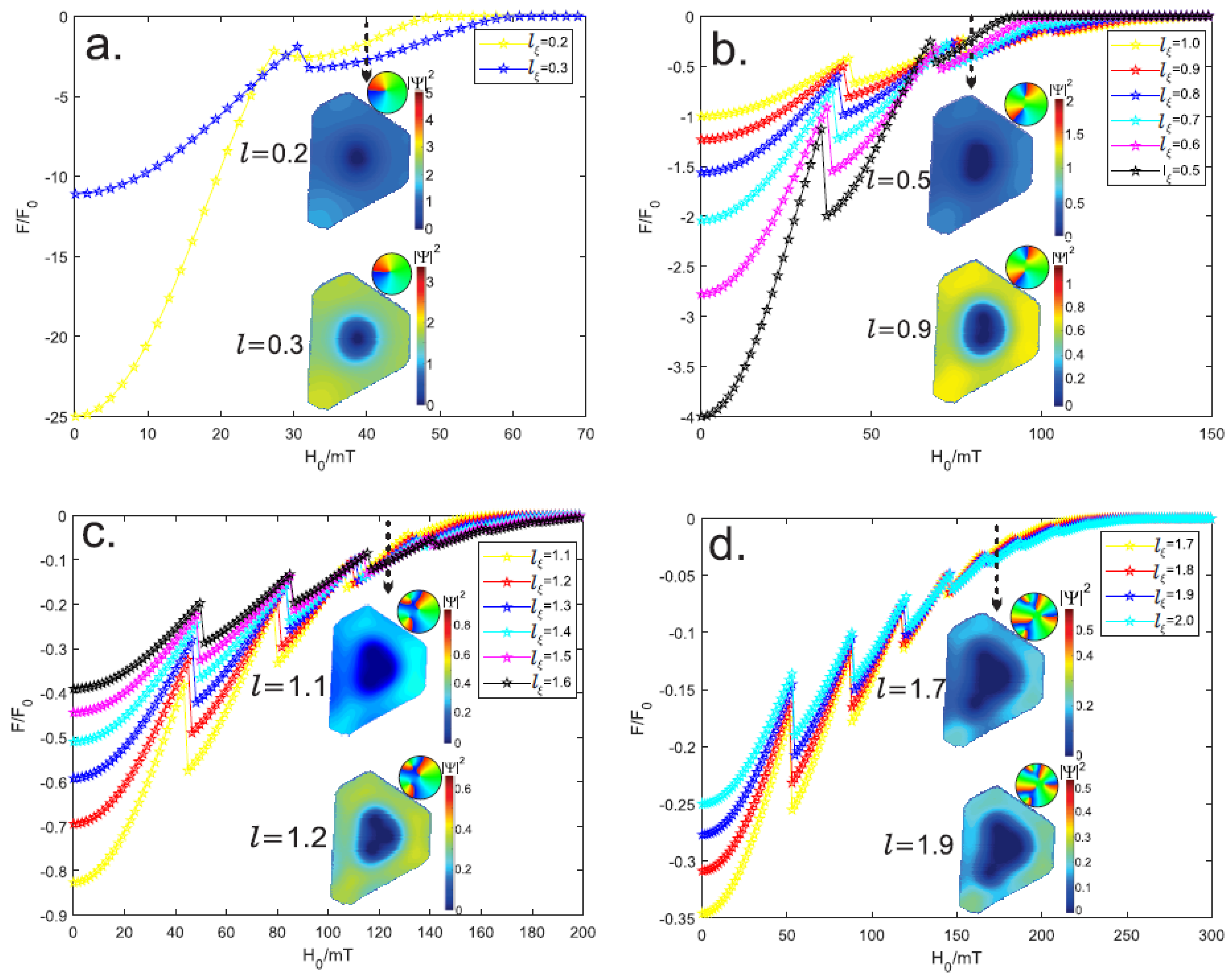
References

  1. Tinkham, M. Introduction to Superconductivity, 2nd ed.; Dover Publications, Inc.: New York, USA, 2004. [Google Scholar]
  2. Moshchalkov, V. V.; Qiu, X. G.; Bruyndoncx, V. Paramagnetic Meissner effect from the self-consistent solution of the Ginzburg-Landau equations. Phys. Rev. B 1997, 55, 173. [Google Scholar] [CrossRef]
  3. Schweigert, V. A.; Peeters, F. M.; Singha Deo, P. Vortex Phase Diagram for Mesoscopic Superconducting Disks. Phys. Rev. Lett. 1998, 81, 2783. [Google Scholar] [CrossRef]
  4. Mel’nikov, A.S.; Ryzhov, D. A.; Silaev, M.A. Electronic structure and heat transport of multivortex configurations in mesoscopic superconductors. Phys. Rev. B. 2008, 78, 064513. [Google Scholar] [CrossRef]
  5. Geim, A. K.; Grigorieva, I. V.; Dubonos, S. V.; Lok, J. G. S.; Maan, J. C.; Filippov, A. E.; Peeters, F. M. Phase transitions in individual sub-micrometre superconductors. Nature 1997, 390, 259. [Google Scholar] [CrossRef]
  6. V. A. Schweigert and F. M. Peeters. Flux Penetration and Expulsion in Thin Superconducting Disks. Phys. Rev. Lett. 1999, 83, 2409. [Google Scholar] [CrossRef]
  7. Gonzáleza, J.D.; Joya, M.R.; Barba-Ortega, J. Flux Vortex state in thermally-induced pinning patterns in superconducting film. Phys. Lett. A. 2018, 382, 3103–3108. [Google Scholar] [CrossRef]
  8. Gonzáleza, J.D.; Gaona, O.J.; Barba-Ortega, J. Flux Vortex state in thermally-induced pinning patterns in superconducting film. J. Low Temp. Phys. 2020, 198, 123–134. [Google Scholar]
  9. Milošević, M.; Peeters, F. M. Vortex manipulation in a superconducting matrix with view on applications. Appl. Phys. Lett. 2010, 96, 192501. [Google Scholar] [CrossRef]
  10. Berdiyorov, G. R.; Baelus, B. J.; Milošević, M. V.; Peeters, F. M. Stability and transition between vortex configurations in square mesoscopic samples with antidots. Phys. Rev. B 2003, 68, 174521. [Google Scholar] [CrossRef]
  11. Berdiyorov, G. R.; Baelus, B. J.; Milošević, M. V.; Peeters, F. M. The superconducting state in square mesoscopic samples with two and four antidots. Physica C:Superconductivity 2004, 404, 1–4. [Google Scholar] [CrossRef]
  12. Jelić, Ž. L.; Milošević, M. V.; Silhanek, A. V. Velocimetry of superconducting vortices based on stroboscopic resonances. Sci Rep 2016, 6, 35687. [Google Scholar] [CrossRef]
  13. Little, W. A.; Parks, R.D. Observation of Quantum Periodicity in the Transition Temperature of a Superconducting Cylinder. Phys. Rev. Lett. 1962, 9, 9. [Google Scholar] [CrossRef]
  14. Boato, G.; Gallinaro, G.; Rizzuto, C. Direct evidence for quantized flux threads in type - II superconductors. Solid State Communications 1962, 3, 173–176. [Google Scholar] [CrossRef]
  15. Moshchalkov, V.V.; Gielen, L.; Strunk, C.; Jonckheere, R.; Qiu, X.; Van Haesendonck, C.; Bruynseraede, Y. Effect of sample topology on the critical fields of mesoscopic superconductors. nature 1995, 373, 319–322. [Google Scholar] [CrossRef]
  16. Nishio, T. et al. Scanning Hall probe microscopy of vortex patterns in a superconducting microsquare. Phys. Rev. B. 2008, 77, 012502. [Google Scholar] [CrossRef]
  17. Kanda, A.; Baelus, B.J.; Peeters, F. M.; Kadowaki, K.; Ootuka, Y. Experimental Evidence for Giant Vortex States in a Mesoscopic Superconducting Disk. Phys. Rev. Lett. 2004, 93, 257002. [Google Scholar] [CrossRef]
  18. Nishio, T. et al.; et al. Superconductivity of nanometer-size Pb islands studied by low-temperature scanning tunneling microscopy. Appl. Phys. Lett. 2006, 88, 113115. [Google Scholar] [CrossRef]
  19. Okayasu, S. et al. Vortex imaging in microscopic superconductors with a scanning SQUID microscope. IEEE Transactions on Applied Superconductivity 2005, 15, 696–698. [Google Scholar] [CrossRef]
  20. Karapetrov, G.; Fedor, J.; Iavarone, M.; Rosenmann, D.; Kwok, W. K. Vortex imaging in microscopic superconductors with a scanning SQUID microscope. Phys. Rev. Lett. 2005, 95, 167002. [Google Scholar] [CrossRef] [PubMed]
  21. Cren, T.; Fokin, D.; Debontridder, F.; Dubost, V.; Roditchev, D. Ultimate Vortex Confinement Studied by Scanning Tunneling Spectroscopy. Phys. Rev. Lett. 2009, 102, 127005. [Google Scholar] [CrossRef] [PubMed]
  22. Nishio, T. et al. D. Superconducting Pb Island Nanostructures Studied by Scanning Tunneling Microscopy and Spectroscopy. Phys. Rev. Lett. 2008, 101, 167001. [Google Scholar] [CrossRef]
  23. Roditchev, D.; Brun, C.; Sierrer-Garcia, L.; Cuevas, J.; Liola, V.; Milošević, M.; Debontridder, F.; Stolyarov, V.; Cren, T. Direct observation of Josephson vortex cores. Nature 2015, 11, 332–337. [Google Scholar] [CrossRef]
  24. Miller, J.H., Jr.; Villagrán, M.Y.S. Time-Correlated Vortex Tunneling in Layered Superconductors. Condens. Matter 2017, 2, 21. [Google Scholar] [CrossRef]
  25. Orús, P.; Córdoba, R.; De Teresa, J.M. Nanofabrication: Nanolithography techniques and their applications, 1st ed.; IOP Publishing: United Kindom, 2020. [Google Scholar]
  26. Utlaut, M. Focused ion beams for nano-machining and imaging, 1st ed.; Woodhead Publishing: USA, 2014. [Google Scholar]
  27. Orús, P.; Sigloch, F.; Sangiao, S.; De Teresa, J.M. Superconducting Materials and Devices Grown by Focused Ion and Electron Beam Induced Deposition. Nanomaterials 2022, 12, 1367. [Google Scholar] [CrossRef]
  28. Geahel, M.; Jouanny, I.; Gorse-Pomonti, D.; Poirier-Quinot, M.; Briatico, J.; Van der Beek, C.J. Edge Contamination, Bulk Disorder, Flux Front Roughening, and Multiscaling in Type II Superconducting Thin Films. Condens. Matter 2017, 2, 27. [Google Scholar] [CrossRef]
  29. Maccari, I.; Benfatto, L.; Castellani, C. Uniformly Frustrated XY Model: Strengthening of the Vortex Lattice by Intrinsic Disorder. Condens. Matter 2021, 6, 42. [Google Scholar] [CrossRef]
  30. Chong, S. V. et al. Surface superconductivity on SrFe2As2 single crystals induced by ion implantation. EPL 2011, 94, 37009. [Google Scholar] [CrossRef]
  31. Koren, G. Magnetoresistance, Gating and Proximity Effects in Ultrathin NbN-Bi2Se3 Bilayers. Condens. Matter 2017, 2, 14. [Google Scholar] [CrossRef]
  32. Fagaly, R. L. Superconducting quantum interference device instruments and applications. Review of Scientific Instruments 2006, 77, 101101. [Google Scholar] [CrossRef]
  33. Natarajan, C.M.; Tanner, M.G.; Hadfield, R.H. Superconducting nanowire single-photon detectors: physics and applications. Superconductor science and technology 2012, 25, 063001. [Google Scholar] [CrossRef]
  34. Vion, D.; Aassime, A.; Cottet, A.; Joyez, P.; Pothier, H.; Urbina, C.; Esteve, D.; Devoret, M. H. Manipulating the Quantum State of an Electrical Circuit. Science 2002, 296, 886–889. [Google Scholar] [CrossRef] [PubMed]
  35. Chiorescu, I.; Nakamura, Y.; Harmans, C.M.; Mooij, J. Coherent Quantum Dynamics of a Superconducting Flux Qubit. Science 2003, 299, 1869–1871. [Google Scholar] [CrossRef] [PubMed]
  36. Bean, C.P.; Livingston, J.D. Surface Barrier in Type-II Superconductors. Phys. Rev. Lett. 1964, 12, 14. [Google Scholar] [CrossRef]
Preprints 76373 g001
Figure 1. (Color online) (Left) Computational simulation: Pb superconducting island using data extracted from the experiment, which gives greater precision to the results obtained. (Rigth) Experimental results: Scanning tunneling microscopy (STM) images of Pb islands on Si(111) surface taken on a large scale (a) and on a local scale (b) showing locations C and E correspond, respectively, to the island center and edge [21]. The effective diameter of the studied Pb island was estimated as D e f f ≈ 3.6 n m and its thickness in the border as d ≈ 8.4 n m whereas inside the island hole d i n t ≈ 2.52 n m , corresponding to 2–3 single atomic layers of Pb in (111) direction.
Figure 1. (Color online) (Left) Computational simulation: Pb superconducting island using data extracted from the experiment, which gives greater precision to the results obtained. (Rigth) Experimental results: Scanning tunneling microscopy (STM) images of Pb islands on Si(111) surface taken on a large scale (a) and on a local scale (b) showing locations C and E correspond, respectively, to the island center and edge [21]. The effective diameter of the studied Pb island was estimated as D e f f ≈ 3.6 n m and its thickness in the border as d ≈ 8.4 n m whereas inside the island hole d i n t ≈ 2.52 n m , corresponding to 2–3 single atomic layers of Pb in (111) direction.
Preprints 76373 g001
Preprints 76373 g002
Figure 2. (Color online) (left) Free-energy curves and corresponding vortex states in a Pb island with one central hole, in a magnetic field perpendicular to the sample. The insets show the superconducting current for selected cases. (Right) Contour plots of the Cooper-pair density for selected different vortex states, the color bar of the islands snapshot evolves from red to blue, reflecting the reduction of the condensate strength.
Figure 2. (Color online) (left) Free-energy curves and corresponding vortex states in a Pb island with one central hole, in a magnetic field perpendicular to the sample. The insets show the superconducting current for selected cases. (Right) Contour plots of the Cooper-pair density for selected different vortex states, the color bar of the islands snapshot evolves from red to blue, reflecting the reduction of the condensate strength.
Preprints 76373 g002
Preprints 76373 g003
Figure 3. (Color online) Free-energy curves for island with different values of l as a function of applied magnetic field perpendicular to the sample. Insets show the Intersection of the sections of curves representing the state without vortices and the first vortex entry, representing the first critical field H 1 .
Figure 3. (Color online) Free-energy curves for island with different values of l as a function of applied magnetic field perpendicular to the sample. Insets show the Intersection of the sections of curves representing the state without vortices and the first vortex entry, representing the first critical field H 1 .
Preprints 76373 g003
Preprints 76373 g004
Figure 4. (Color online) (Left) Values of the applied magnetic field H 0 versus electron mean free path l, the green curve shows the values of the second critical magnetic field H 2 reached for each value of l selected, evidencing the direct proportionality between both magnitudes. While the yellow curve shows the values of H 0 for which the Bean-Livistong barrier (BLB) [36] is exceeded H 1 (first critical field) or first entry of vortices, whose inclination from l = 0.2 to l = 2.0 of the BLB because in the first case the sample is in the dirty limit ( l ≪ ξ ), while in the second case it is in the clean limit ( l ≫ ξ ). (Right) Entry of vortices in the sample as a function of H 0 , inset some configurations of vortices that show that up to approximate values of H 0 = 150 m T the vortices penetrate one by one. Each line in this graph has a correspondence in Figure 3, where each jump in the Gibbs free energy curve evidences the entry of vortices.
Figure 4. (Color online) (Left) Values of the applied magnetic field H 0 versus electron mean free path l, the green curve shows the values of the second critical magnetic field H 2 reached for each value of l selected, evidencing the direct proportionality between both magnitudes. While the yellow curve shows the values of H 0 for which the Bean-Livistong barrier (BLB) [36] is exceeded H 1 (first critical field) or first entry of vortices, whose inclination from l = 0.2 to l = 2.0 of the BLB because in the first case the sample is in the dirty limit ( l ≪ ξ ), while in the second case it is in the clean limit ( l ≫ ξ ). (Right) Entry of vortices in the sample as a function of H 0 , inset some configurations of vortices that show that up to approximate values of H 0 = 150 m T the vortices penetrate one by one. Each line in this graph has a correspondence in Figure 3, where each jump in the Gibbs free energy curve evidences the entry of vortices.
Preprints 76373 g004
Preprints 76373 g005
Figure 5. (Color online) (a,b) Phase diagrams of the value of Cooper-pair density (CPD) under the tip as a function of magnetic field, obtained as the tip is moved along the line that runs through the island, and taken during sweep up and down of the magnetic field. The corresponding spatial distribution of CDP (red shapshot) for selected steplike transitions where every peak correspond to vortex position in the island. Black line on figure inside blue frame indicates the trajectory over which the tip was moved in order to simulate the scanning tunneling microscope (STM) to obtain the zerobias conductance (ZBC) phase diagram.
Figure 5. (Color online) (a,b) Phase diagrams of the value of Cooper-pair density (CPD) under the tip as a function of magnetic field, obtained as the tip is moved along the line that runs through the island, and taken during sweep up and down of the magnetic field. The corresponding spatial distribution of CDP (red shapshot) for selected steplike transitions where every peak correspond to vortex position in the island. Black line on figure inside blue frame indicates the trajectory over which the tip was moved in order to simulate the scanning tunneling microscope (STM) to obtain the zerobias conductance (ZBC) phase diagram.
Preprints 76373 g005
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.
Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.
Prerpints.org logo

Preprints.org is a free preprint server supported by MDPI in Basel, Switzerland.

facebook logotwitter logolinkedin logo
MDPI Initiatives
Important Links
Subscribe

Disclaimer

Terms of Use

Privacy Policy

© 2024 MDPI (Basel, Switzerland) unless otherwise stated