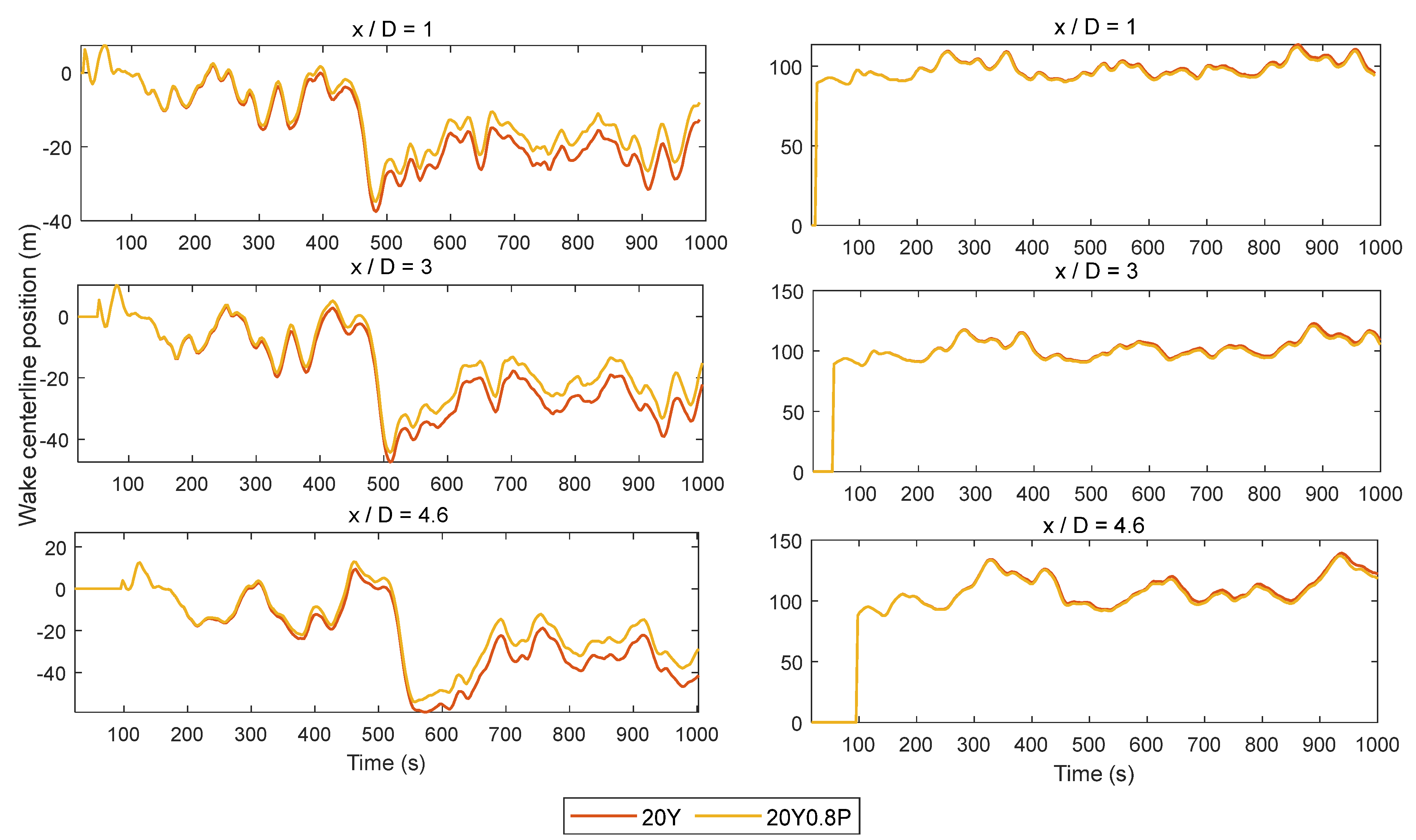Prerpints.org logo
Preprint
Article

Study on Mitigation of Wake Interference by Combined Control of Yaw Misalignment and Pitch

Altmetrics

Downloads

128

Views

24

Comments

0

A peer-reviewed article of this preprint also exists.

Submitted:

13 June 2023

Posted:

13 June 2023

You are already at the latest version

Alerts
Abstract
Yaw misalignment can make a wake steer, which is an effective method to increase the power of wind farms, but it also increases the fatigue load of the turbines. In this paper, the method of combining yaw misalignment and pitch control (CYMP) is proposed to investigate the potential to mitigate wake interference, the wind velocity distribution and turbulence distribution in the wake, as well as the power and load changes of the wind turbine are studied, focusing on power in-crement and fatigue damage reduction. Although some studies have found that the method of CYMP are beneficial to increase power generation and reduce fatigue loads, there are no papers that have made a detailed analysis of the effects of wake turbulence, wind speed distribution, power, especially fatigue damage under this control. Simulation tool FAST.Farm is used to model and analyze wind farms, obtain the variation details of wake and provide simulation data for calculating power and fatigue load. The pitch control brings bias to the CYMP optimization results was neglected, the case studies show that the method of CYMP can reduce the fatigue load by 10.29% and increase the total power by 1.7% compared with only wake steering. The Model Predictive Control collaborative method based on CYMP is proposed, which can increase power by more than 2% and reduce thrust by more than 4% under 10m/s turbulent wind.
Keywords: 
Subject: Engineering  -   Marine Engineering

1. Introduction

Offshore wind power has grown rapidly in the past few years, it is estimated that the total installed capacity of global offshore wind power will reach 200GW by 2030 [1,2]. The proportion of offshore wind power is growing fast, which is of great significance to achieving the goal of carbon neutrality. Compared with the onshore wind farm, the turbulence intensity of offshore wind farm is low, and the wake is not easy to dissipate, therefore, the wake interference is serious. The maximum annual power generation loss caused by wake is 54% [3], and the wake also reduces the reliability of turbines [4].
Nowadays, there are three methods to mitigate wake interference in the wind farm, which are mic-sitting, layout optimization of the wind farm, and wind farm control. The first two methods were constrained by wind farm space [5], electrical cost [6], maintenance cost [7], and sea terrain [8]. Wind farm control uses the freedom degree of a single wind turbine to achieve the wind farm wake interference goal, which is easier to achieve compared with the first two methods [9].
Wake steering is a method to mitigate wind farm wake, which has attracted great attention. The yaw misalignment of the upwind turbine makes the wake steer [10,11], and the downwind turbine is away from the wake center and the power increases. Wake steering is considered to be an effective method to increase power output [11,12]. Adaramola and Krogstad [13] studied the wake steering in a wind tunnel test, and they found that when the upwind turbine yawed by 30°, the total power output could be increased by 12%. Campagnolo et al. [14] changed the wind tunnel test conditions, and it was found that when the upstream turbine yaw misalignment was set to 20°, the maximum power gain was 7.0%. Howland et al. [15] conducted a series of field tests and found that an appropriate yaw misalignment control could increase the wind farm power output by about 10%. However, the fatigue load of the turbine always increases under wake steering. The turbine increases its fatigue load due to yaw offset [16]. Lin and Port'e-Agel [17] used the method of multi-objective parameter optimization to determine the maximum power output and the minimum fatigue load in the wind tunnel test. The wake steering also increases the fatigue load of the downwind turbine. Churchfield et al. [18] also found that although the wake steering made the downwind power increase, the fluctuation of blade root flap-wise moment was significantly increased, and the root mean square of bending moment of the turbine blade affected by partial wake was increased by at least 15% in CFD simulation analysis.
Pitch control [19,20,21] has also attracted much attention in the study of relieving wake effect [22,23]. Corten and Schaak [24] tested 24 turbines (3 × 8) with 25 cm rotor diameter in the wind tunnel, and they found that the pitch control of the front row turbines made the total power output increase by 4.6%, meanwhile, the increase of the power was the most pronounced in the second-row turbines. However, pitch control did not always improve the power generation of wind farms. Bartl and Sætran [25] set the constant average wind speeds and varied the turbulence intensity in the wind tunnel test, the rotor diameter of the two turbines was 90 cm, and the pitch control did not improve the total power. Campagnolo et al. [26] also applied wind tunnel experiments to investigate the pitch control, and they found that only when the first two turbines were considered, the pitch control could increase total power, but when the third turbine was considered, the total power output did not increase. Kim et al. [27] validated that the atmospheric turbulence and Reynolds number affected the pitch control, i.e., when the atmospheric turbulence intensity was low, the wake expansion rate was slow [4], also, when the Reynolds number was low, the rate of wake expansion was slow [28], so the momentum recovery was low. Annoni et al. [29] found that when the downwind turbines were affected by full wake, the upwind turbines were pitched, and the kinetic power along the wake boundary was significantly increased, but with the wake expansion, the swept area of the downwind turbine was away from the boundary, which had little influence on the power increase of the downstream turbines. Combining the experiments and analysis above, Ha et al. concluded that the pitch control effect was greatly affected by the environment [30].
Reducing the axial inducement factor can reduce the thrust of the rotor to the wind, which plays an important role in reducing the turbulence and wake deficit of the wake [31,32]. Pitch is one of the methods to change the axial induce factor. Although the pitch control does not significantly improve the wind farm power, it helps to reduce the wake turbulence intensity.
Bossanyi [32] has proposed a combining yaw and induction control method to optimize wind farm power and reduce fatigue load. This method takes advantage of changes in wind direction and speed in the wind field to maximize power output and reduce fatigue load by adjusting the yaw angle and blade pitch angle of the wind turbine. The fundamental theory of the method is that the yaw misalignment control makes the downwind turbine away from the wake center or close to the wake boundary, and the pitch-control reduces the axial induction factor of the upstream turbine and increases the recovery of kinetic energy along the wake boundary. This paper examines a joint yaw and pitch control method, but its primary focus is on analyzing the impact of wind speed and turbulence distribution changes on the wake of a wind turbine under various control methods. Specifically, this study examines how these changes affect the downwind turbine's power output and load fluctuations, while also analyzing the resulting power and fatigue damage under different control modes. Fatigue damage is a key factor in predicting the expected life of wind turbines, as it is the result of repeated loading and unloading of turbine components under different wind and operating conditions. This damage leads to small cracks and material degradation that can build up over time, eventually leading to structural failure. The hope is that the fatigue damage analysis under different control will help researchers reduce the costs associated with maintenance and operation over the life cycle of turbines.
The paper is arranged as follows. Section 2 introduces the simulation tool FAST.Farm and simulation setup, section 3 gives the case analysis and discussion points, and section 4 summarizes the whole paper.

2. Methodology

2.1. Overview of FAST.Farm

FAST.Farm is a simulation tool developed by the National Renewable Energy Laboratory (NREL), which is an extension of the OpenFast. The wake calculation is conducted by modifying and extending the dynamic wake meandering (DWM) model. FAST.Farm is used to describe wake development and evolution, explain the wake interference effect, and describe the fatigue load and power of the turbine under wake interference.
The thin shear layer approximation of Reynolds averaged Navier-Stokes equation under quasi-steady-state conditions is used to simulate wake deficit, and the turbulent closure captured with eddy viscosity formula [33] is also applied.

2.2. Wind Turbine Model

The NREL's 5 MW baseline turbines model is used, the parameters of wind turbines are listed in Table 1.
The control of pitch and yaw misalignment change the momentum deficit of air passing through the wind turbine, which is related to the thrust of the wind turbine rotor. Thrust is the basis of fatigue load, and the azimuthally averaged thrust-force coefficient is normal to the rotor disk.

2.3. Wake Model2.3. CYMP and Presentation of Results

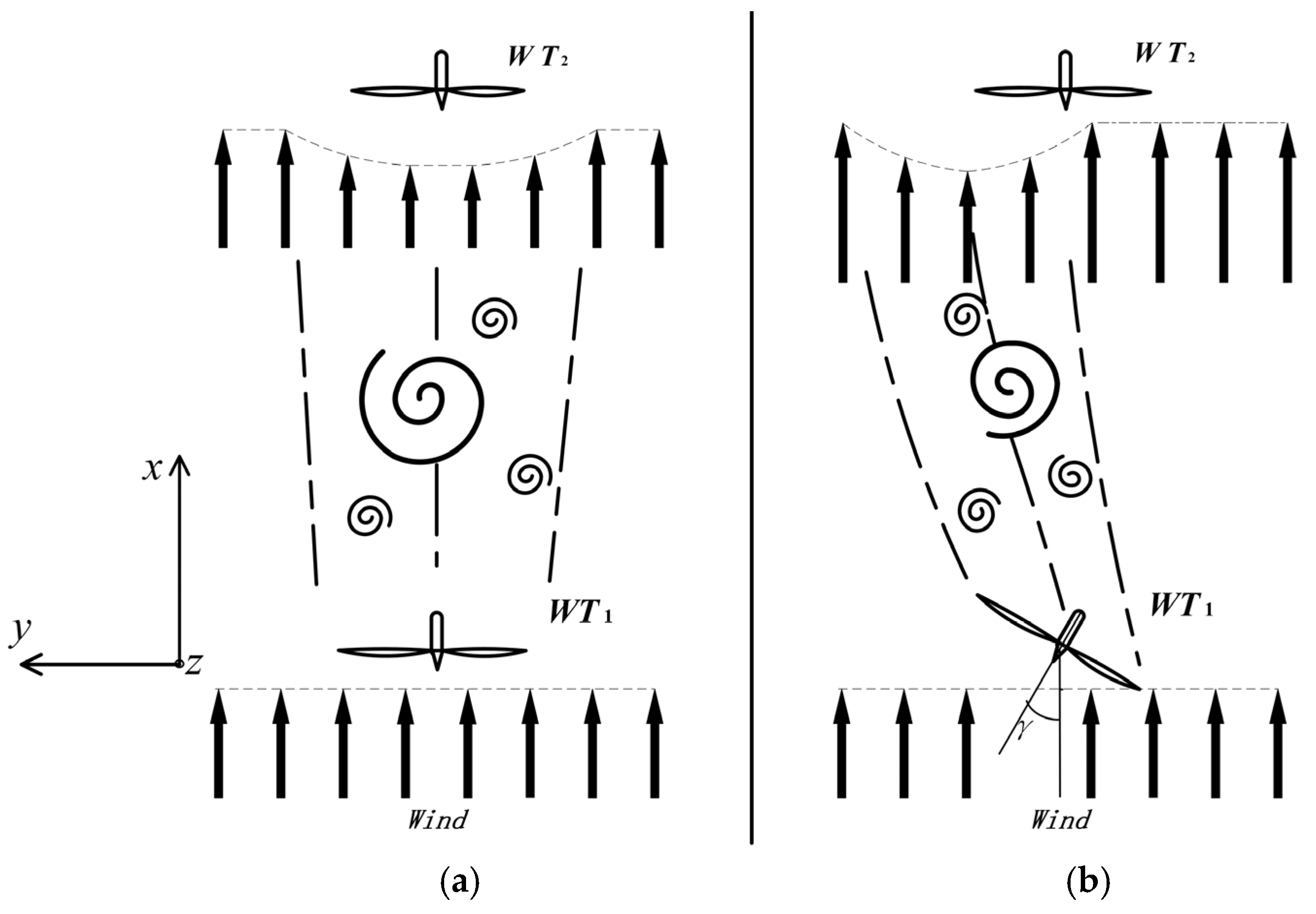
The flow field of the downwind turbine has changed when compared with the free flow field. This change is due to the wake generated by the upwind turbine, and the turbulence intensity increases as the average wind speed decreases. The wake interference diagram is shown in Figure 1, where the parameter γ is the angle between the rotor axis and wind direction, it is called the yaw misalignment angle, and the parameter β is the pitch angle.
In Figure 1 (a), in the case of the wind speed below the rated speed, the turbine WT1 is in free flow and has no control over the wake, γ and β are 0°, and the power of WT1 reaches the optimum. At this time, the wind speed of the wake is very low, the turbulence intensity is high, and WT2 is seriously affected by the wake, resulting in the decrease of WT2 power and the increase of fatigue load [2]. The CYMP method is a combination of yaw misalignment and pitch control. Yaw misalignment makes the wake steer, and the downwind turbine far away from the wake center. The upwind turbine reduces the thrust to the wind through pitch, while reducing the thrust to the wind of the upstream turbine will reduce the turbulence in the wake [29].
In Figure 1 (b), the CYMP method is applied to make velocity recover (dashed arrow) and wake centerline offset, where both γ and β are not 0°. WT1 applies the CYMP method, which makes C P reduced, as shown in Eq. (11),
C P β i , λ i , γ i = C P β i , λ i   η c o s ⁡ ( γ i ) 2
where C P is deduced from the experiment of Medici [34], and it is a function of β , λ   a n d   γ , λ is the tip speed ratio. η is the loss factor. C P β i , λ i is obtained from C P -curve without yaw. The power of WT1 P i reduces, as Eq. (12) [35].
P i = 1 2 ρ A i C P β i , λ i , γ i v i 3   ( i = 1 ,   2 ,   3 … )
where i is the wind turbines number, ρ is the air density, A i is the turbine rotor swept domain, v is the efficient wind speed.
Repeated fatigue load accumulation will cause fatigue damage to turbine materials, for example, cracks appear, consequently reducing the service life of the turbine. According to Eq. (13)
D = ∑ i n i N
where ni is the number of fatigue load cycles, and N is the number of cycles causing fatigue load failure. In this paper, damage equivalent fatigue load (DEL) is applied to fatigue loads in different simulations.
D E L = ∑ i n i m N 1 m
where m is Wöhler exponents, the value of m varies with different materials. In the fatigue load analysis of Section 3, the Blade out-of-plane moment at the blade root is selected as the object, and m is defined as 10.

2.4. Simulation Setup

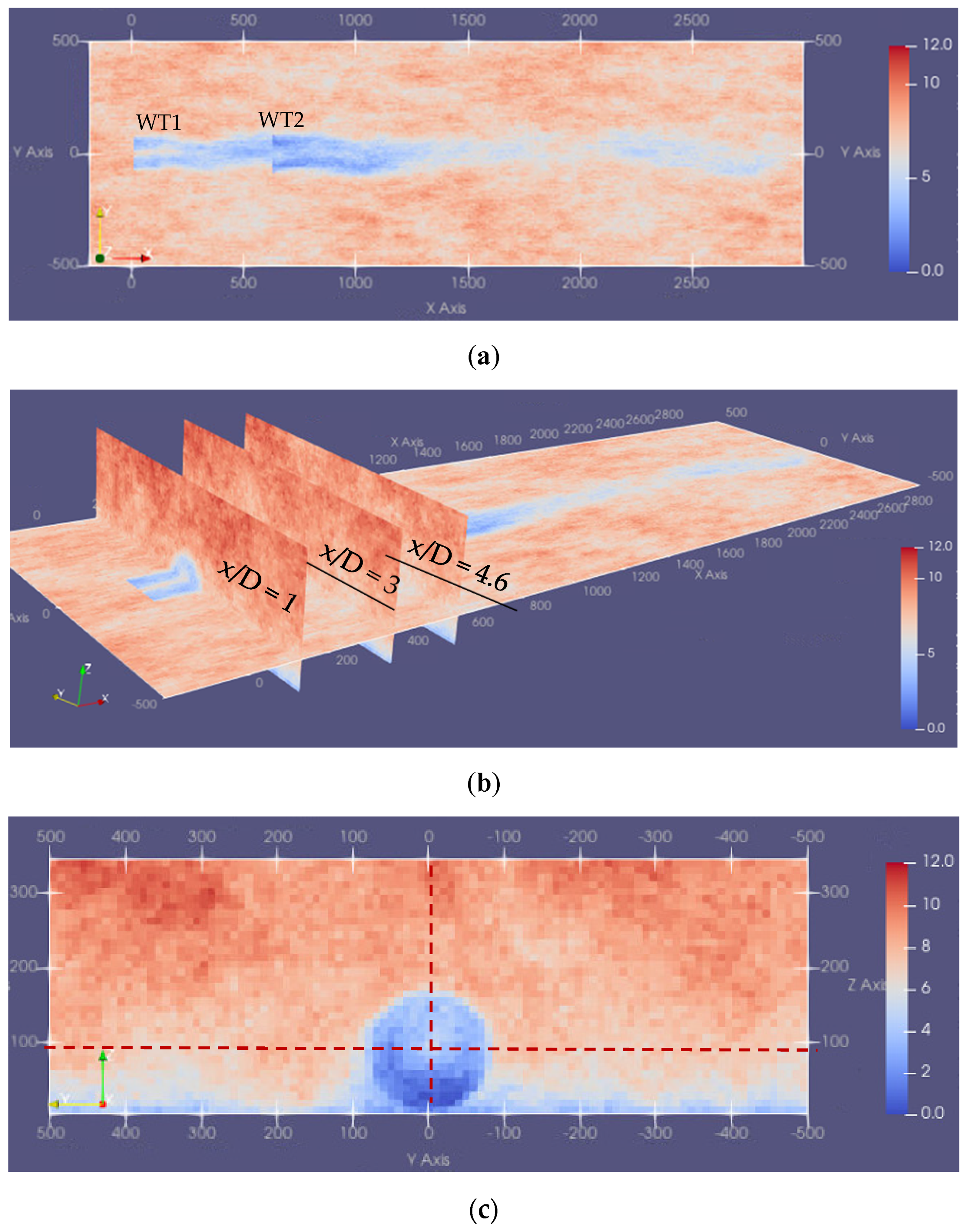
The visualization image of the flow field of two turbines (WT1 and WT2) is shown in Figure 2, which provides the intuitive flow field characteristics. Figure 2 (a) shows that the layout is 5 diameters (D) apart from the inter row, and the wind direction is along the X-axis. WT1 is the upwind turbine, followed by WT2 in the downwind. As shown in Figure 2 (a) and (c), the size of the wind farm is set to 3130 m × 1010 m × 350 m. The low-resolution domain in Figure 2 (a) is mainly responsible for wake wandering and merging, and it encompasses the entire wind farm. The spacing of spatial nodes is 10 m in FAST.Farm, the number of spatial nodes is 313 × 101× 35, the temporal resolution is 3 s; the high-resolution domain is responsible for the wake formation and inflow, located around the turbines, the spacing of spatial nodes is 10 m, the number of spatial nodes is 18 × 17 × 17, the temporal resolution is 0.1 s. In Figure 2 (b), wake evolution can be seen in the XY plane as well as the wake cross-section, three wake cross-sections at x/D=1, x/D=3, and x/D=4.6 are researched.
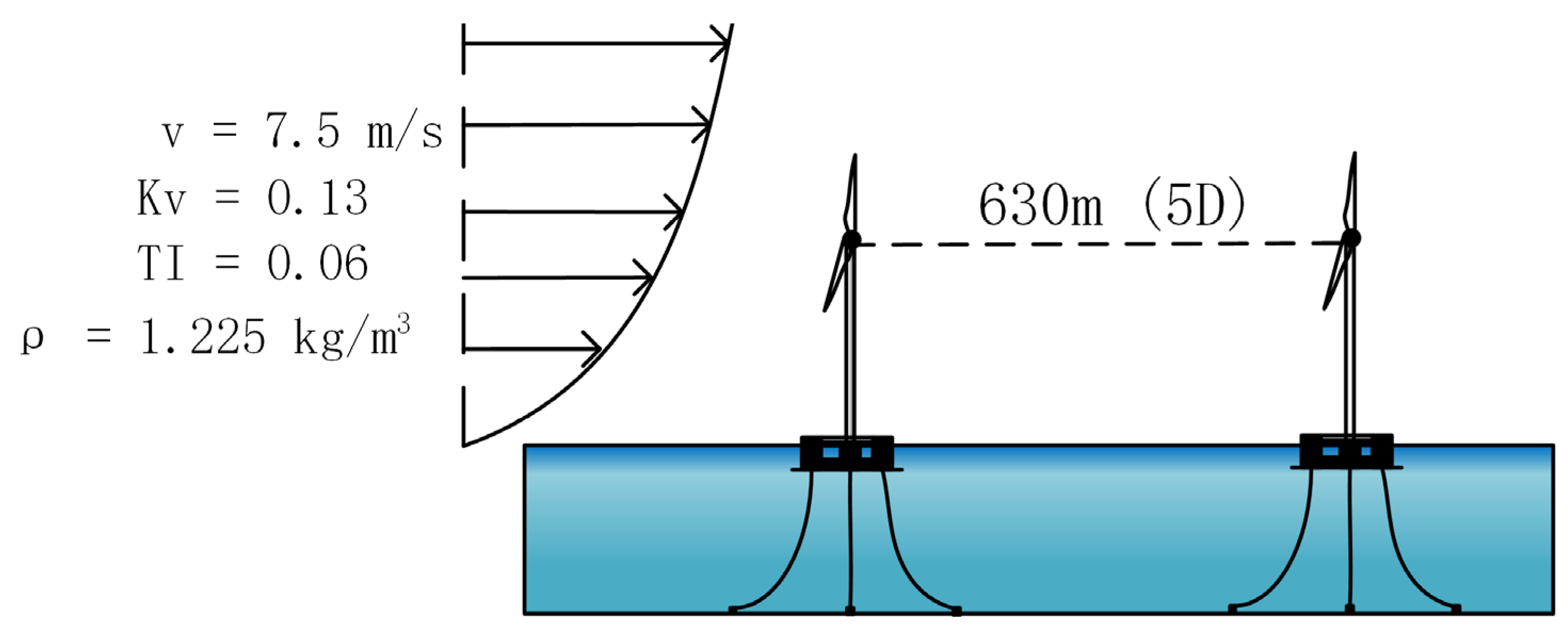
The average wind speed (v) of 7.5 m/s is researched in simulation. The wind characteristics of this region are: a) obvious wake interference; b) when the wind speed is lower than rated, the pitch control is easy to achieve. The characteristics of turbine operation in those regions are: a) the rotor speed increases and the pitch angle is 0°; b) the rotor speed control follows the optimal Cp tracking. Turbulence intensity (TI) of 6 % , a wind shear(kv) of 0.13, ari density ( ρ ) of 1.225 kg/ m 3   are typical offshore wind characteristics, The distance of the two wind turbine in the wind direction is 5D.
Turbsim is a tool for generating wind by NREL [39]. It is most applicable to the simulation of small wind farms, and it has lower computational complexity than CFD simulation tools. The turbulent wind is generated by Turbsim, the specific settings are as follows:
a. The turbulence degree is 6%, the average wind speed is 7.5 m/s, and the turbulence model-Kaimal model;
b. Wind shear adopts power exponent 0.13.
The simulation time under each control mode is 1000 s. To make the downwind wake fully develop, the analysed data between 200 s and 1000 s is chosen .

3. Result Analysis

In this section, the three aspects are studied and analysed, which are the wake visualization, the impact of the CYMP on the wake, and the impact of the wake on the downwind turbine under the control of CYMP.

3.1. Flow Visualizations

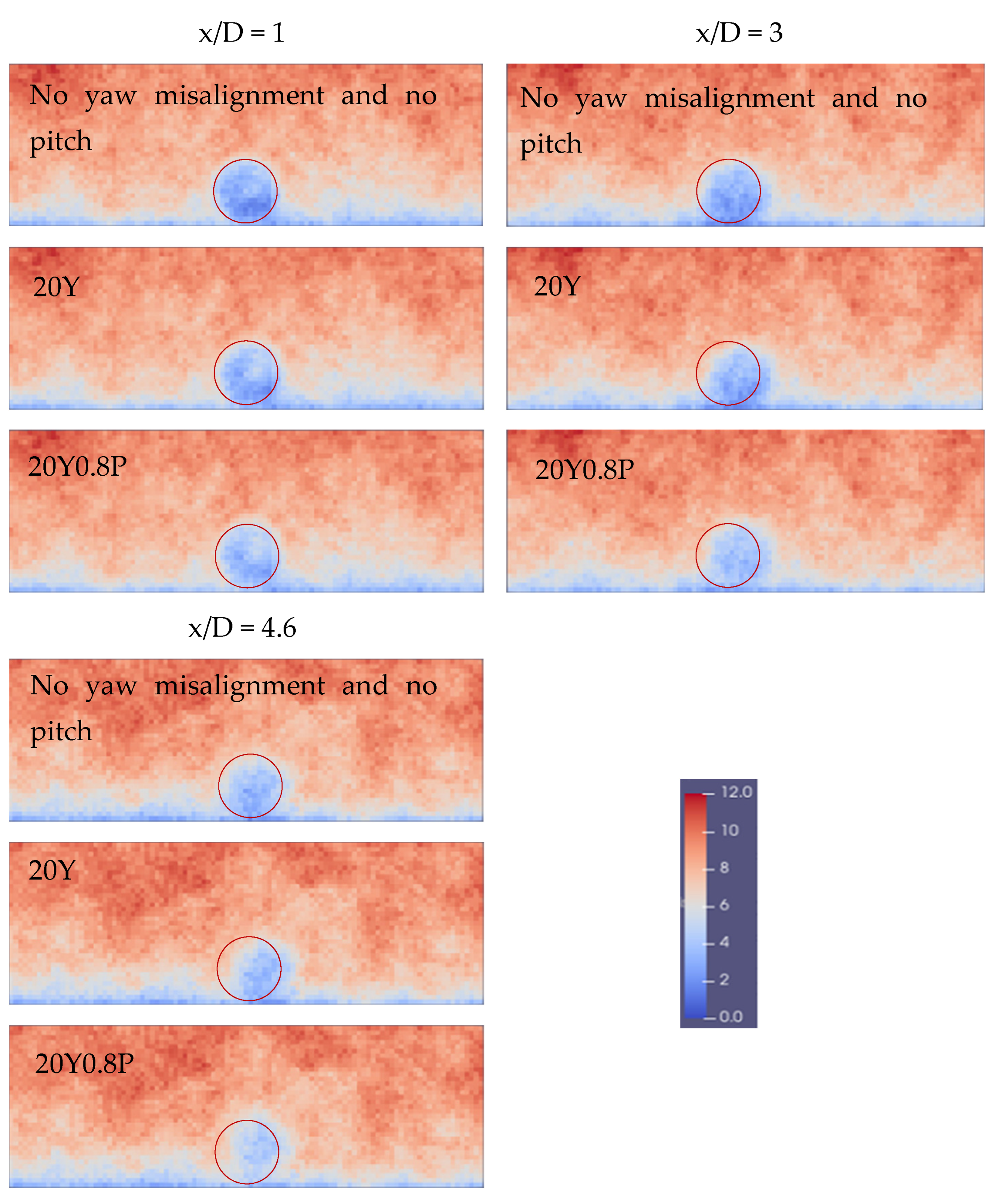
The visualization of the wake plane can vividly show the changes in the wake. Just take the results of three different cases as examples, which are no yaw misalignment and no pitch, 20° pitch (20Y), and 20° yaw misalignment and 0.8° pitch (20Y0.8P) the yaw angle of 20° and the pitch angle of 0.8°, there is no particular reason. In each case, three YZ-wake planes (the plane positions are as shown in Figure 2 (b)) are captured at 477s as in Figure 2. The wake states in. As shown in Figure 3, 20Y and 20Y0.8P make the wake center offset to the right, and the farther the distance downwind of WT1, the greater offset to the right of the wake center. This result is consistent with the characteristics of yaw misalignment control [36]. Wind shear results in a lower wind speed within the lower half of the swept area, and it is one of the important factors that cause the increase of the fatigue load [37]. Compared with the control result of 20Y, 20Y0.8P makes the wind speed at the wake boundary recover faster, which is manifested in the reduction of wake radius in Figure 3.
The XY plane in Figure 1 (a) shows the meandering and offset of the wake. Figure 1 (b) shows the YZ plane in different downwind distances (x/D=1, x/D=3, x/D=4.6), and the variation of wind speed at different downstream distances can be observed. Figure 1 (c) shows the YZ plane at WT1, and its wake characteristics are that the wind shear causes the wind speed on the lower side to be lower than that on the upper side.

3.2. Effect on the Wake

This part is the quantification of the wake characteristics in Section 3.1, and the axial velocity deficits, wake turbulence and wake center-line offset are analysed.
In Figure 5, the characteristics of the wake center-line offset can be found that the yaw misalignment makes the wake center-line offset in the y-axis direction, whereas it is not obvious in the z-axis direction. The distance of the wake center-line offset under the 20Y0.8P control is less than the 20Y control, and this may be caused by the difference in the wake speed. Wake deficits and turbulence also have such characteristics, so they are analysed only in the y-axis direction.
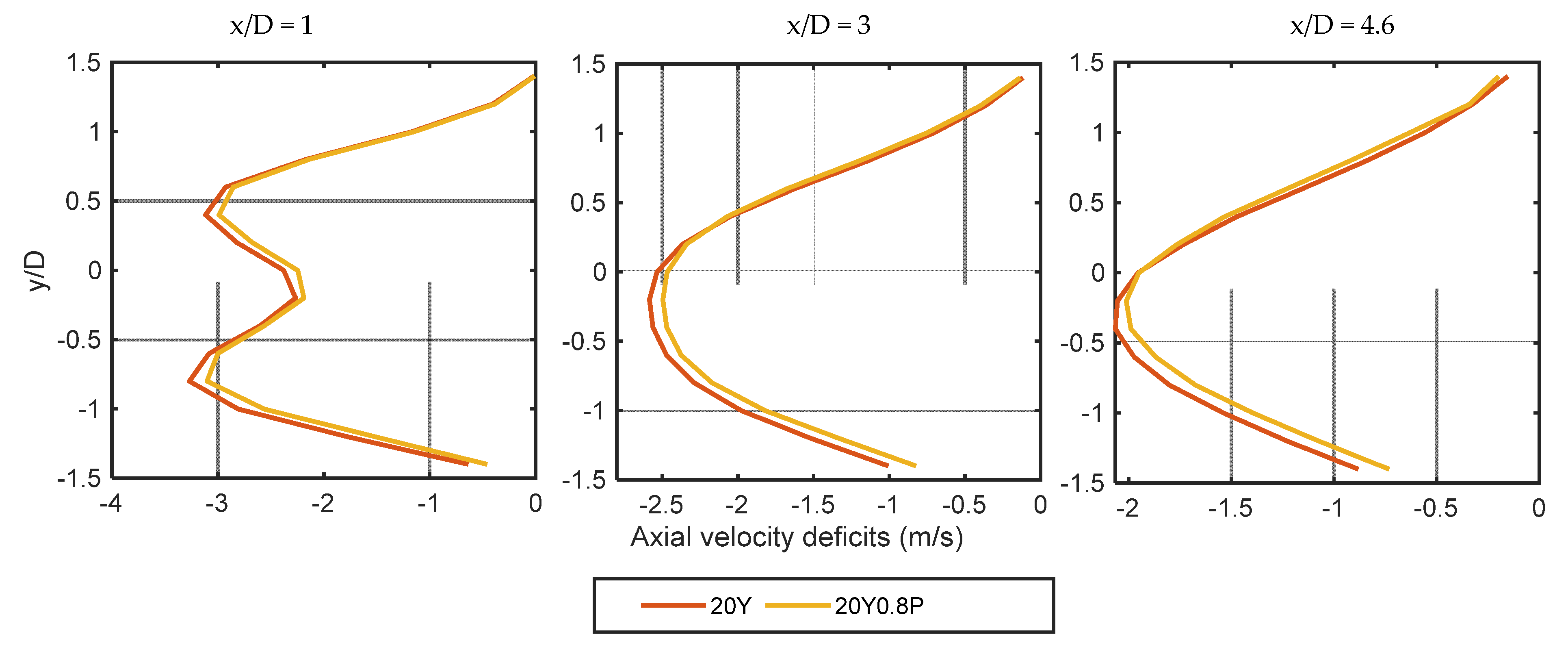
The recovery of the wake is generally considered from two aspects, which are wake deficit and wake turbulence. As shown in Figure 6, the controls of 20Y and 20Y0.8P make the wake deficit center offset to the right (y<0) by 0.2 times the rotor radius(R) because of the upwind turbine yaw misalignment. The ability to capture energy at 0.6-0.8 0.6-0.8R from the hub center is the greatest, and the wake deficit is the most at 0.6-0.8R as shown at x/D=1. With the evolution of wake downwind, compared with at x/D=1, the wind speed of x/D=3 at 0.6-0.8 r recovers rapidly. At x/D=4.6, the wind deficit at the wake center is the most, and the closer to the boundary, the lower the wind deficit.
There is little difference in the wake deficit on the left side of the hub center between the controls of 20Y and 20Y0.8P, and on the right side of the wake plane (y<0), the wake deficit of the 20Y control is less than that of the 20Y0.8P control. At x/D=4.6 and the 0.6-0.8R position, the 20Y0.8P control makes wind speed 0.18 m/s higher than that of the 20Y control. This can be explained that under the 20Y0.8P control, the wind speed of the downwind wake recovers quickly, which helps improve the power of the downwind turbines. This conclusion is consistent with the visualization results in Figure 4
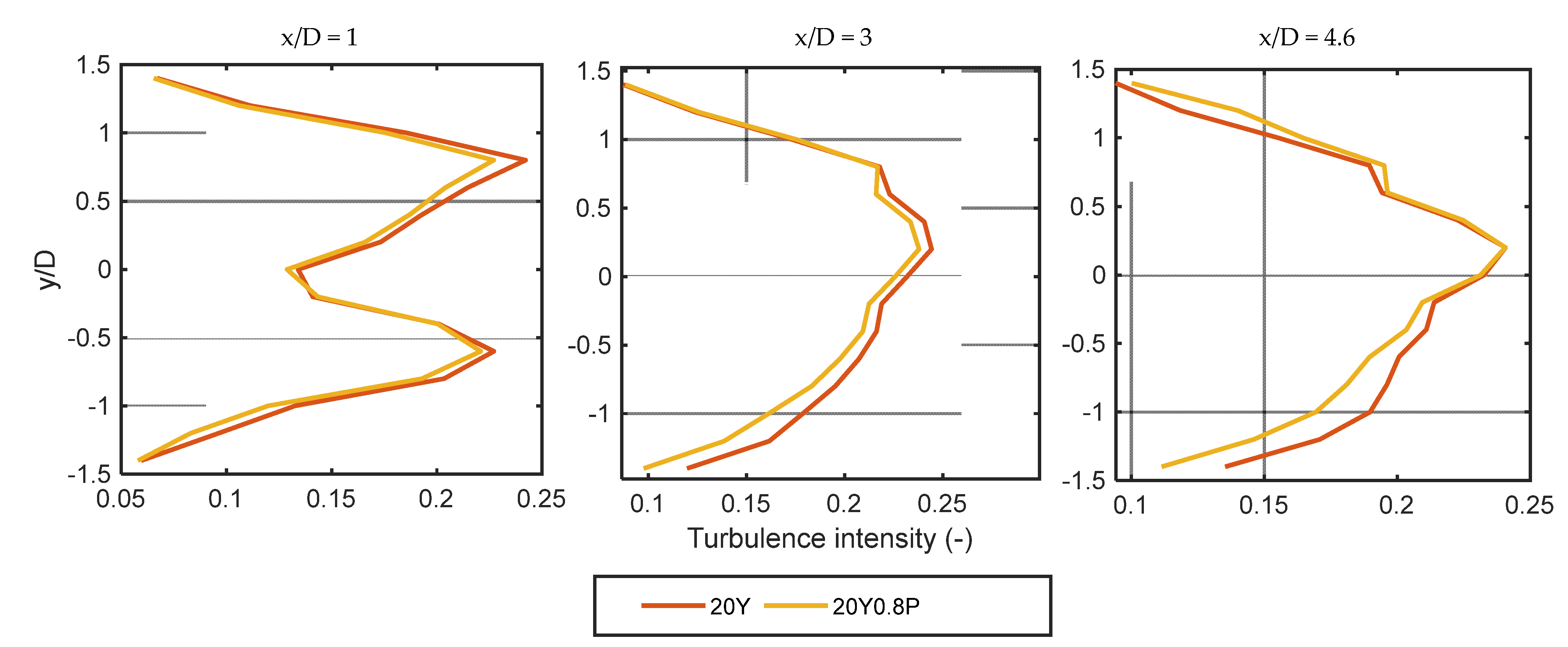
Turbulence is an important factor to affect the fatigue load. As shown in Figure 7, at x/D=1, the 20Y0.8P control makes the turbulence of 0.6-0.8 R lower than that of the 20Y control. This is caused by the reduction of the thrust of the upwind turbine, and the difference in other regions of the y-axis is not obvious. At x/D=3, the turbulence intensity on the left side (y>0) of the wake plane is higher than that on the right side, but the opposite is true at x/D=4.6. In the right side of the wake plane at x/D=4.6, 20Y0.8P makes the turbulence reduced by 1.25% at the 0.6-0.8 times rotor radius position, and this is also one of the factors to reduce the fatigue load of downwind turbines.
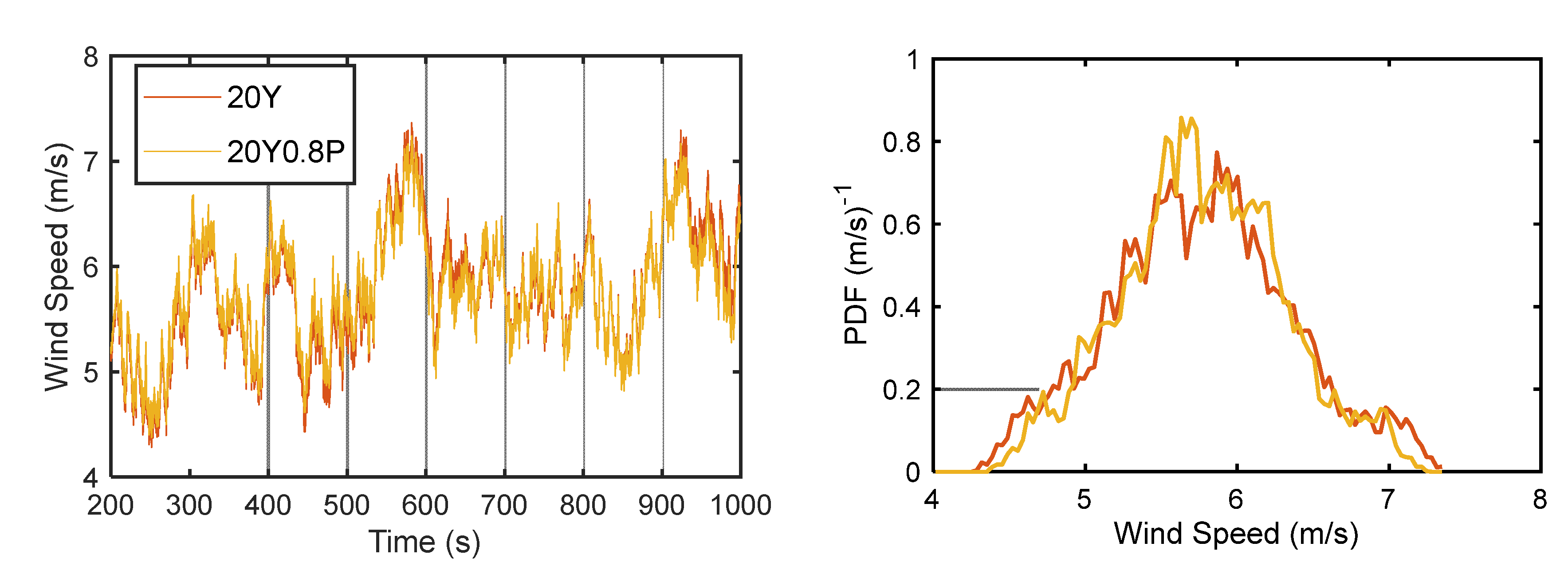
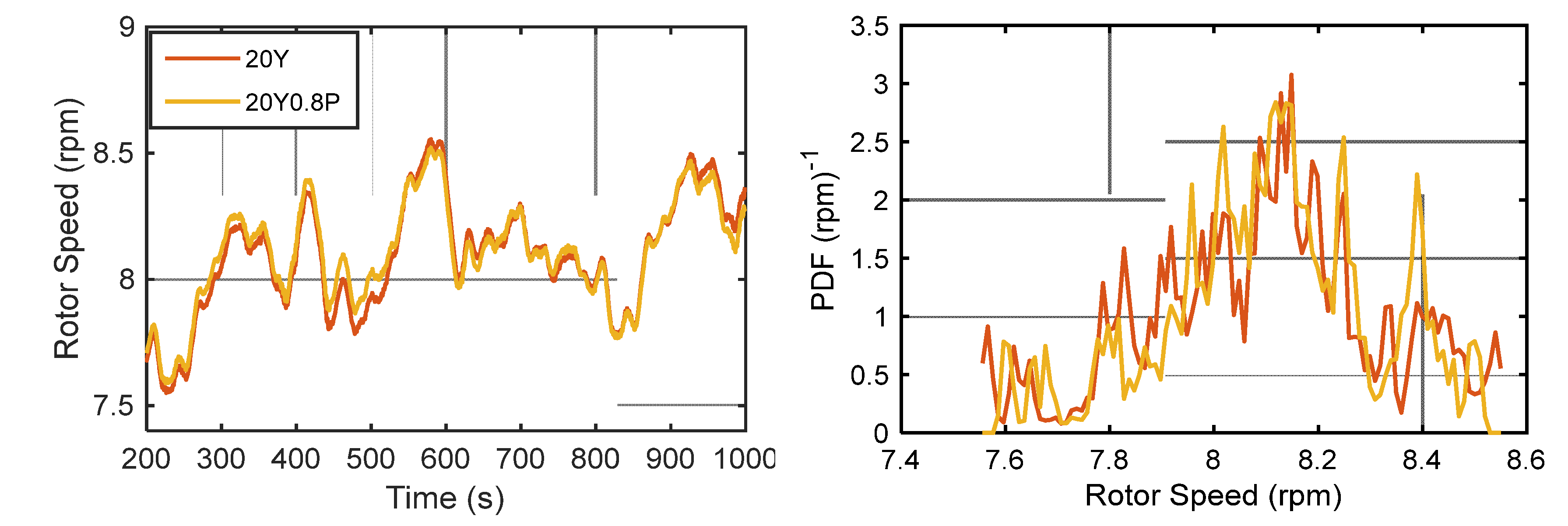
The wind speed at the hub center and rotor speed of WT2 are shown in Figure 8 and Figure 9, respectively. As shown in Figure 8, under the control of 20Y0.8P, although the wind speed of WT2 has not been significantly improved, the Probability Density Functions (PDF) of the wind speed of WT2 greatly changed. This is important for the rotor speed increase of WT2. For the average wind speed greater than 5.5 m/s, the PDF under 20Y0.8P control is higher than that of 20Y. The rotor speed of WT2 shows consistency with the wind speed distribution. As shown in Figure 8, when the rotor speed is greater than 8 rpm, the PDF of 20Y0.8P is greater than 20Y. When the rotor speed is around 8.4 rpm, the PDF value under 20Y0.8P control is twice that of 20Y.

3.3. Turbine Performance Impact

To study the impact of CYMP on turbine performance clearly, more cases are studied, which are listed in Table 2. The yaw misalignment angle varies from 0° to 40° (positive for clockwise yaw) with a gradient of 5°, the pitch angle changes from 0° to 1.0° with a gradient of 0.2°. The fatigue load and total power of CYMP are shown in Figure 10 and Figure 11, respectively. To observe the effect of CYMP on turbine performance, the wake steering is used as a comparison. The results are normalized by the value of no yaw offset and no pitch. 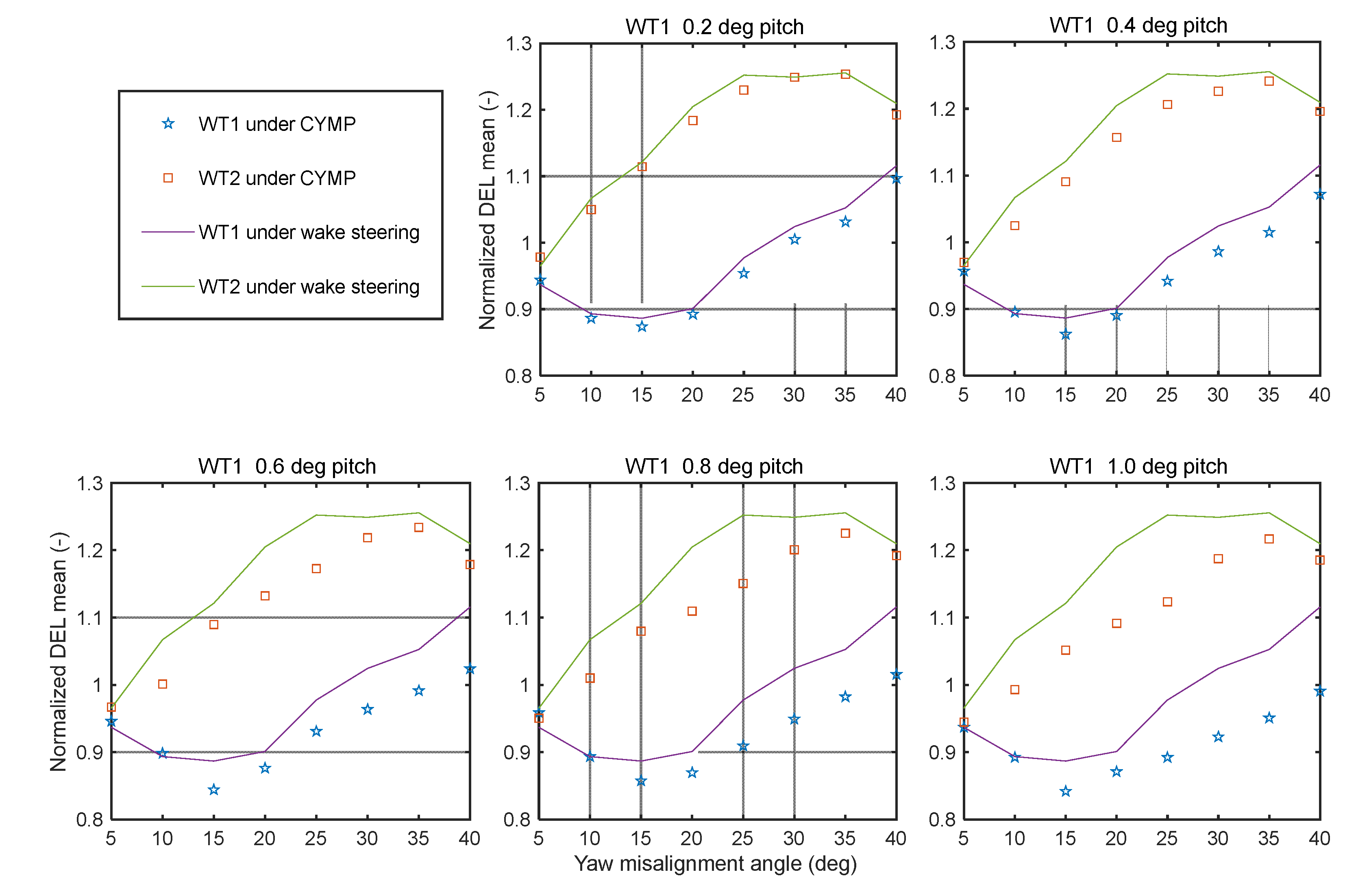As shown in Figure 10, the turbine blade root out-of-plane moment is used to calculate DEL as fatigue load, normalized by the WT1 DEL value of no yaw misalignment and pitch. When the method of only wake steering is chosen, some clockwise yaw misalignment of WT1 makes the fatigue load of WT1 decrease, which is consistent with Kragh’s research [37]. The fatigue load of WT2 increases because of the partial overlaps. The fatigue damage of WT1 and WT2 under the CYMP method is both lower than that of wake steering only. When the WT1 pitch angle is 1.0°, the fatigue damage of the two turbines decreases the most. When the yaw misalignment angle is 30°, the fatigue damage of WT1 is decreased by 9.94%. When the yaw misalignment angle is 25°, the fatigue damage of WT2 is decreased by 10.29%. Therefore, the high fatigue damage of WT2 caused by yaw misalignment can be effectively reduced under the CYMP method.
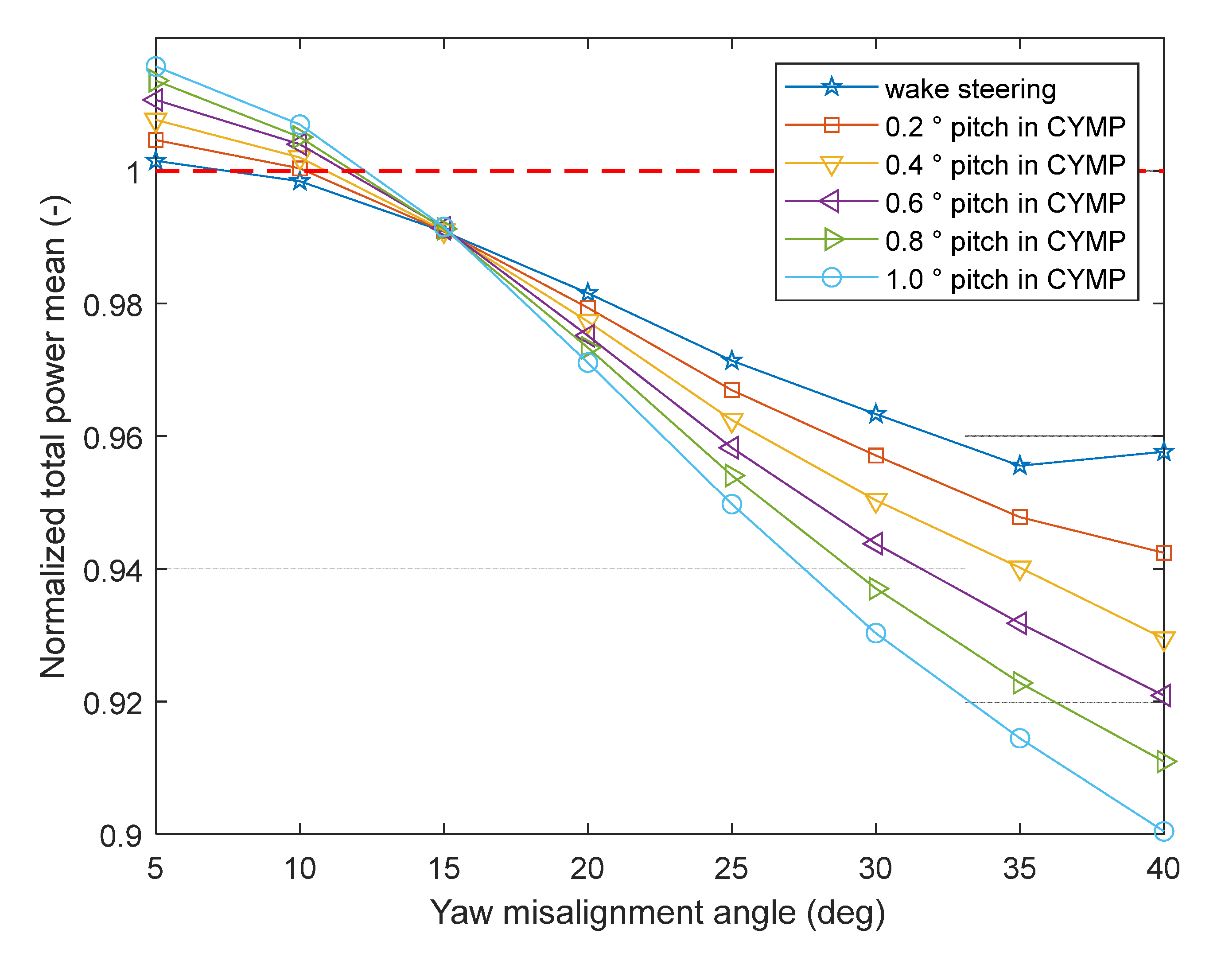
Figure 11 shows the total power under the CYMP method, which used wake steering as a comparison. 5° yaw misalignment and the 1.0° pitch of WT1 make total power maximal improved by 1.7%. When WT1 yaw misalignment is greater than 15°, the CYMP method reduces the total power. It can be seen that when WT1 takes the CYMP control, the captured power of WT1 reduces, while the power boosted by WT2 downwind is less than this value, as a result, the total power reduces. This value may be improved when adding downwind turbines, and more research will be undertaken in the future.

4. Cooperative Control of Wind Farm Based on Model Predictive Control of CYMP

For offshore wind farms, a multi-Model Predictive controller collaborative control strategy (CoMPC) is proposed, and joint pitch and yaw control actions can increase power generation and reduce wind turbine loads.

4.1. Method Design

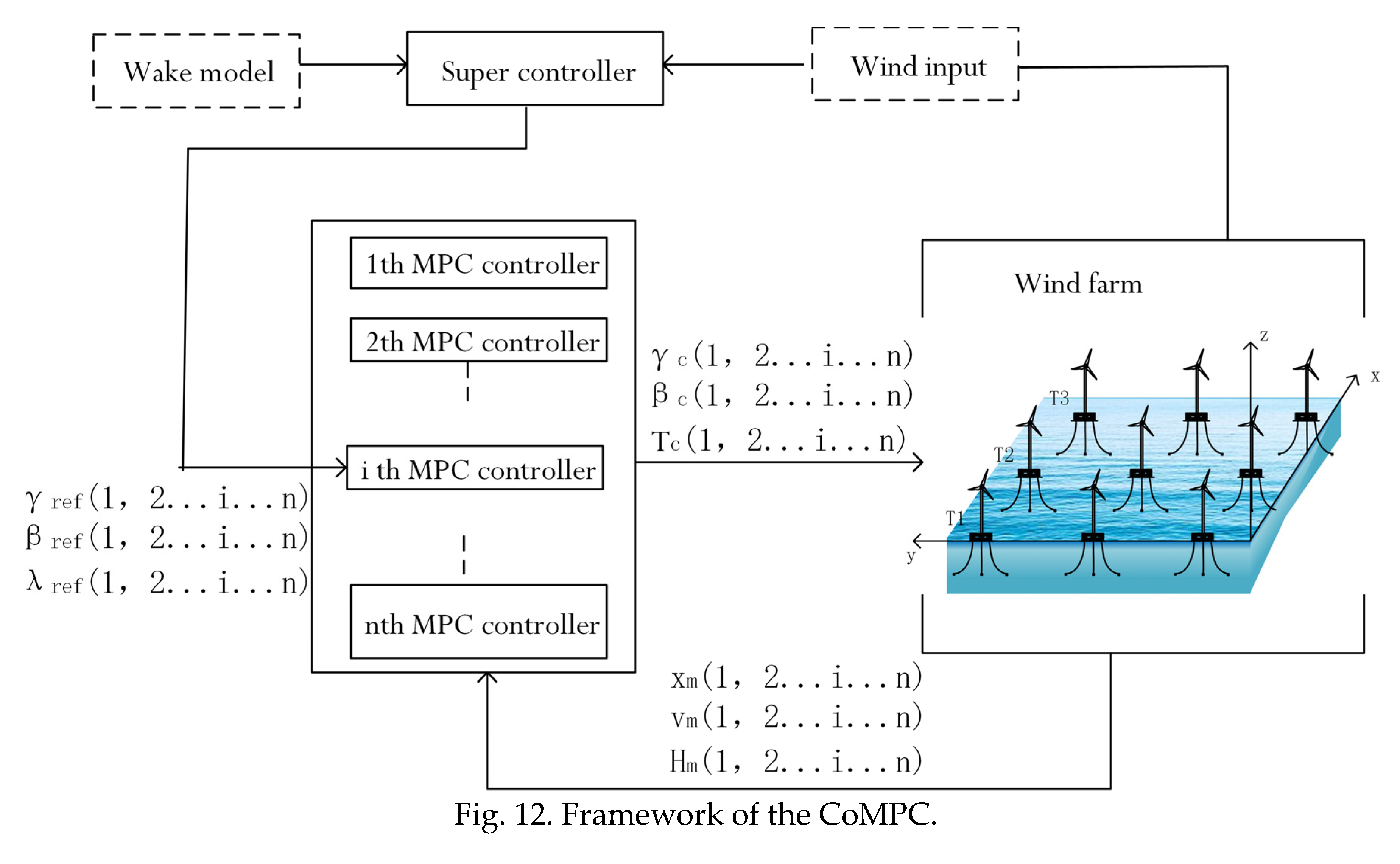
Model Predictive control MPC is a commonly used control method for wind turbines. According to the control needs of offshore semi-submersible floating wind farms, this paper proposes CoMPC. The framework of CoMPC is shown in Figure 12. The super-controller is for wind farms, the optimization algorithm “Fmincon” to calculate the optimal references including yaw angle, pitch angle and rotor speed of each wind turbine corresponding to the optimal target, and considers the free flow wind speed, wind direction and wind turbine arrangement. Then the super-controller transmits the optimal operating value of the wind turbine to each MPC controller. The MPC controller tracks the reference value and controls the wind turbine action. At the same time, the operating data and wind of the wind farm is fed back to the super-controller continuously and each MPC controller for real-time adjustment of optimal value selection and tracking of control actions, realizing dynamic active wake control of CYMP.

4.1.1. Super-Controller Design

The goal of the super controller is to maximize the power ∑ i ∈ n P i of the entire wind farm while ensuring that the load is reduced. For the convenience of calculation, the load is specified as the thrust ∑ i ∈ n F i of the wind turbine. According to the total power and thrust of all generators in the wind farm, it is expressed as follows:
∑ i ∈ n P i = ŋ ρ π R 2 v f 3 2 ∑ i ∈ n C P i [ 1 − δ v i ( C T j ) j ∈ W i ] 3
∑ i ∈ n F i = ρ π R 2 v f 2 2 ∑ i ∈ n C T i [ 1 − δ v i ( C T j ) j ∈ W i ] 2
where ρ is air density, π R 2 is the plane area of the rotor, v f is the wind farm free-flow wind speed, δ v i ( C T j ) j ∈ W i indicates that the wind deficit of the i t h wind turbine affected by other wind turbines W i in the wind farm. The wind speed deficit caused by wake, which is obtained by the classic wake model Jensen model [38] [39], the wake deflection caused by yaw is calculated by the Jiménez model [40]. These two models are not the focus of this article and will not be introduced in the article, please refer to the paper for details if needed, C T j indicates the thrust coefficient of the i t h wind turbine, C P i , C t i are affected by the pitch angle β and rotor speed ω at the same time, so the super-controller also needs to consider the control of ω, C P i , C t i are obtained from the look-up table. The objective function of the super-controller is set as:
m a x ⁡ ( f γ , β , ω ) = m a x ⁡ ( ∑ i ∈ n ( a P i − b F i ) )
where, a and b are the weights for power and thrust respectively. The goal of the super controller is to find γ r e f , β r e f , ω r e f when f γ , β , ω is maximized, and take them as the best operating point of each wind turbine.
For a wind farm with n wind turbines, when the function f ( γ , β , ω ) is maximum, there are 3 n optimization parameters. When n is large, the number of large parameters will increase the computational burden. Due to changing wind conditions, too long calculation times makes the optimal reference invalidate. In response to this problem, this paper proposes to partition the wind farm, with wind turbines in the upwind direction as the dominant factor, and the wind turbines that are seriously disturbed by the wake of this wind turbine are divided into the same area. 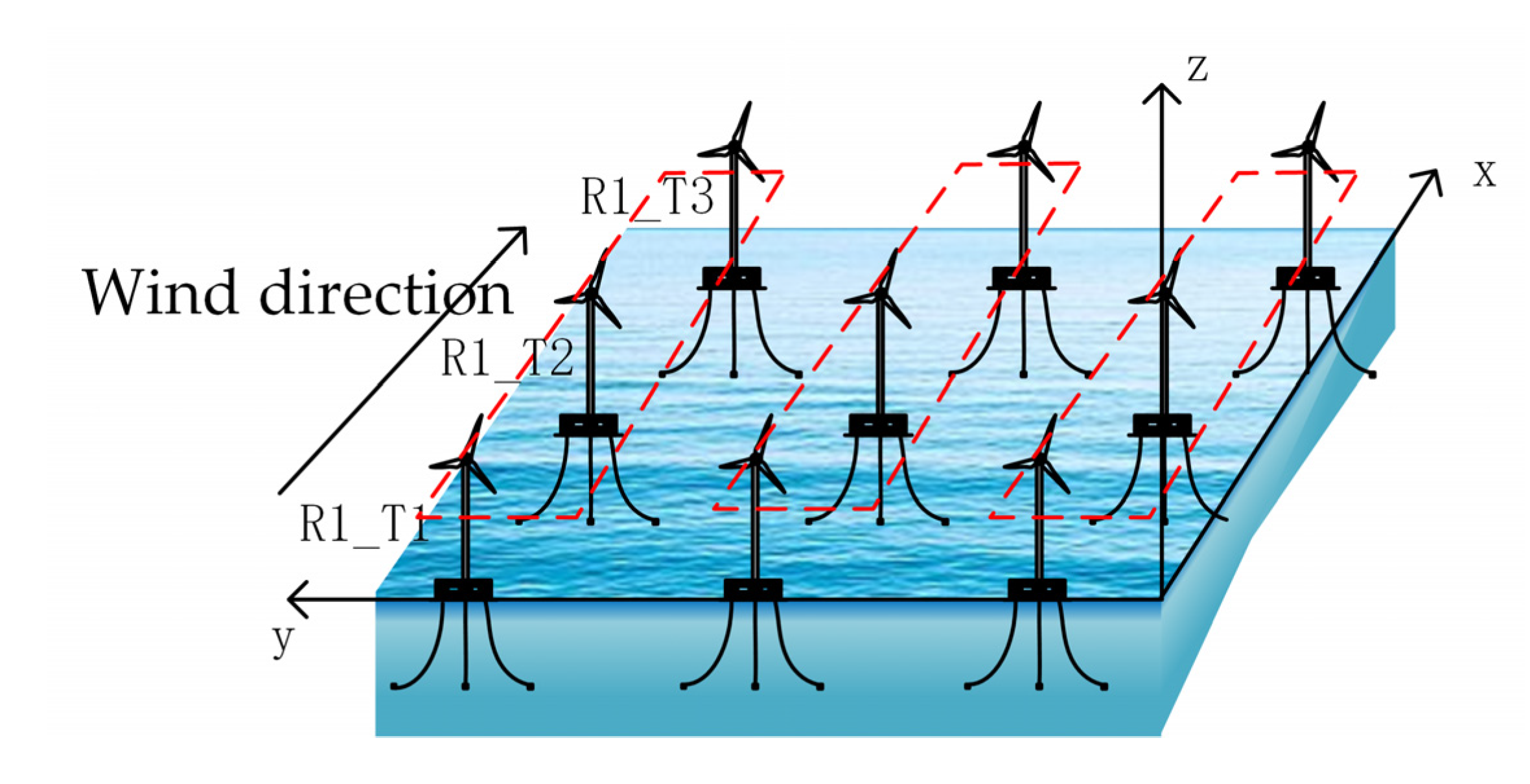The schematic diagram is shown in Figure 13.
Firstly, obtain the wind direction wd, coordinates of all wind turbines ( x ( i ) , y ( i ) ) ;
Secondly, rotate the coordinates of all wind turbines according to the wind direction w d according to the Equation (18), and obtain the new coordinates of the wind turbines ( x _ w d ( i ) , y _ w d ( i ) ) ,
x w d ( i ) y w d ( i ) = c o s ⁡ ( w d ) − s i n ⁡ ( w d ) s i n ⁡ ( w d ) c o s ⁡ ( w d ) x ( i ) y ( i )
Thirdly, select the wind turbine with the smallest x coordinate value and name it R 1 _ T 1 , R 1 represents the first area, R 1 _ T 1 represents the first wind turbine in the first region; Look for the wind turbine with less x w d , y w d is the y coordinate of the wind turbine. If x w d − x w d R 1 _ T 1 ≤ 4 R 2 + y w d − y w d R 1 _ T 1 R is satisfied, it is determined that the wind turbine is affected by the wake interference of R 1 _ T 1 , where, x w d R 1 _ T 1 , y w d R 1 _ T 1 is the x coordinate of R 1 _ T 1 , R = 63 m . If yes, name the wind turbine R 1 _ T 2 , and if no, name it R 2 _ T 1 . In the same way, find the wind turbines with lower x _ w d order again to determine whether they are interfered by R 1 _ T 1 and R 1 _ T 2 (or R 2 _ T 1 ) , and name them according to the naming rules, until all the wind turbines are named and the partition is completed, area R1, R2… Rk (k≤n) can be got.
Fourth, the wind turbine in the same area is considered as an optimization target, and the Equation (17) is used to find the optimal.
This method is based on the assumption that each area does not interfere with each other.

4.1.2. Control Model of Semi-Submersible Floating Wind Turbine

For semi-submersible floating wind turbine, a control-oriented four-input and two-output four-order incremental state space expression is established as follows:
x ˙ = A x + B u y ˙ = C x + D u
State variable x = ω r , ω g , β , γ , T T , which are rotor speed, generator speed, pitch angle, yaw angle, generator torque; control input u = β c , γ c , T c , v , H T , which are respectively the controlled pitch angle, the controlled yaw angle, the controlled generator torque, the wind speed of each wind turbine, and the wave height of each wind turbine; y = P T , P is generator power.
A , B , C , D in formula (19) are obtained by linearizing the NREL, semi-submersible floating wind turbine nonlinear model:
ω ˙ r = 1 J r [ K T ω ω r − B d ( ω r − ω g N g ) + K T β β + K T γ γ + K T v v + K T H H
ω ˙ g = 1 J g [ − T + K g B d ( ω r − ω g N g ) ]
β ˙ = ( β c − β ) / τ β
γ ˙ = ( γ c − γ ) / τ γ
T ˙ = T c − T / τ g
P = ŋ ω g T
where the rotor torque of inertia J r = 5.34 · 10 6 k g . m 2 , the generator torque of inertia J g = 534 k g . m 2 , the gearbox growth ratio N g = 97 , the drive shaft damping coefficient B d = 6.215 · 10 6 k g · m 2 / r a d · s , K T ω ,   K T β , K T γ , K T v , K T H , K g , ε t ， K M ， K B is the identification parameter, τ β is the inertia time constant of variable pitch, τ γ is the yaw inertia time constant, τ g is the generator torque inertia time constant, and the power generation efficiency ŋ = 0.944 .

4.1.3. MPC Controller for Wind Turbine

After discretizing Equation (19), Equation (26) is obtained.
x k + 1 = A k x k + B k u k
where A k and B k are obtained by discretization of the state. References to state variables are as follows:
x r e f = m a x ( ω r , m i n , m i n ( ω r , r e f , ω r , n o m ) ) m a x ( ω g , m i n , m i n ( ω g , r e f , ω g , n o m ) ) β r e f γ r e f m i n ⁡ ( T m a x , P n o m ŋ ω g , 0 )
where the minimum of rotor speed ω r , m i n = 0.723 r a d / s , the nominal rotor speed ω r , n o m = 1.267 r a d / s , the minimum of generator speed ω g , m i n = ω r , m i n N g , the nominal generator speed ω g , n o m = ω r , n o m N g , the maximum of generator torque T m a x = 47403 N m , the nominal generator power P n o m = 5 M W , ω g , 0 is the generator speed measurement during state equilibrium, which means x ˙ = 0 .
The goal of MPC in this paper is to minimize the deviation between the predicted state and the reference value, and to avoid frequent action of the controller and reduce the mechanical load of the unit. Therefore, the value function of the optimization problem can be described as:
J = m i n ∑ k = k 0 k 0 + N P − 1 x ~ T k Q c x ~ k + u c ^ T k R c u c ^ k + x T k 0 + N P P c x k 0 + N P
where, x ~ = x ( k ) − x r e f , u c ^ = u c ( k ) − u c m , u c 0 is the measurement of control inputs during state equilibrium. Q c and R c are weight. With dynamic state space equation constraints:
x ~ k + 1 = A k x ~ k + B c k u c ^ k
where control input u c ^ = [ γ ^ c , β ^ c , T ^ c ] T , the constraints of u c ^ are as follows：
if ω g < ω g , n o m ,
u ^ m i n = m a x ( − γ 0 , − γ r a t e ) m a x ( − β 0 , − β r a t e ) m a x ( − T 0 , − T r a t e ) , u ^ m a x = m a x ( − γ 0 , − γ r a t e ) m a x ( − β 0 , − β r a t e ) m i n ( T m a x − T 0 , P n o m ŋ ω g , 0 − T 0 , T r a t e )
if ω g ≥ ω g , n o m ,
u ^ m i n = m a x ( − γ 0 , γ r a t e ) m a x ( − β 0 , β r a t e ) m i n ( T m a x − T 0 , P n o m ŋ ω g , 0 − T 0 , T r a t e ) u ^ m a x m i n ( γ m a x − γ m , γ r a t e ) m i n ( β m a x − β m , β r a t e ) m i n ( T m a x − T 0 , P n o m ŋ ω g , 0 − T 0 , T r a t e )
where γ 0 is the yaw angle measurement of control inputs during state equilibrium, yaw rate γ r a t e = 0.3 ° / s , maximum yaw angle γ m a x = 45 ° ; β 0 is the pitch angle measurement of control inputs during state equilibrium，pitch rate β r a t e = 8 ° / s , maximum pitch angle β m a x = 90 ° ; T 0 is the yaw angle measurement of control inputs during state equilibrium, generator torque rate T r a t e = 15000 N m / s , maximum generator torque T m a x = 40000 N m .

4.2. Result

Taking the wind farm layout in Figure 13 as an example, when the wind direction is as shown in the figure, the wind farm is divided into 3 zones, assuming that each zone does not affect each other. The optimization performance of CoMPC for wind farm is proved by the optimization effect of region 1. The X-axial spacing of each wind turbine in region 1 is 5D, and the Y-axis direction has no spacing (In addition to the displacement changes caused by the movement of the wind tuebine).
According to the wind condition characteristics of an offshore wind farm, the simulated v is 10m/s, TI is 6%, kv is 0.13, and the wave height (WH) are 1.2 and 3m, respectively, with Gaussian white noise. Wind speed changes and WH changes are shown in Figure 14.
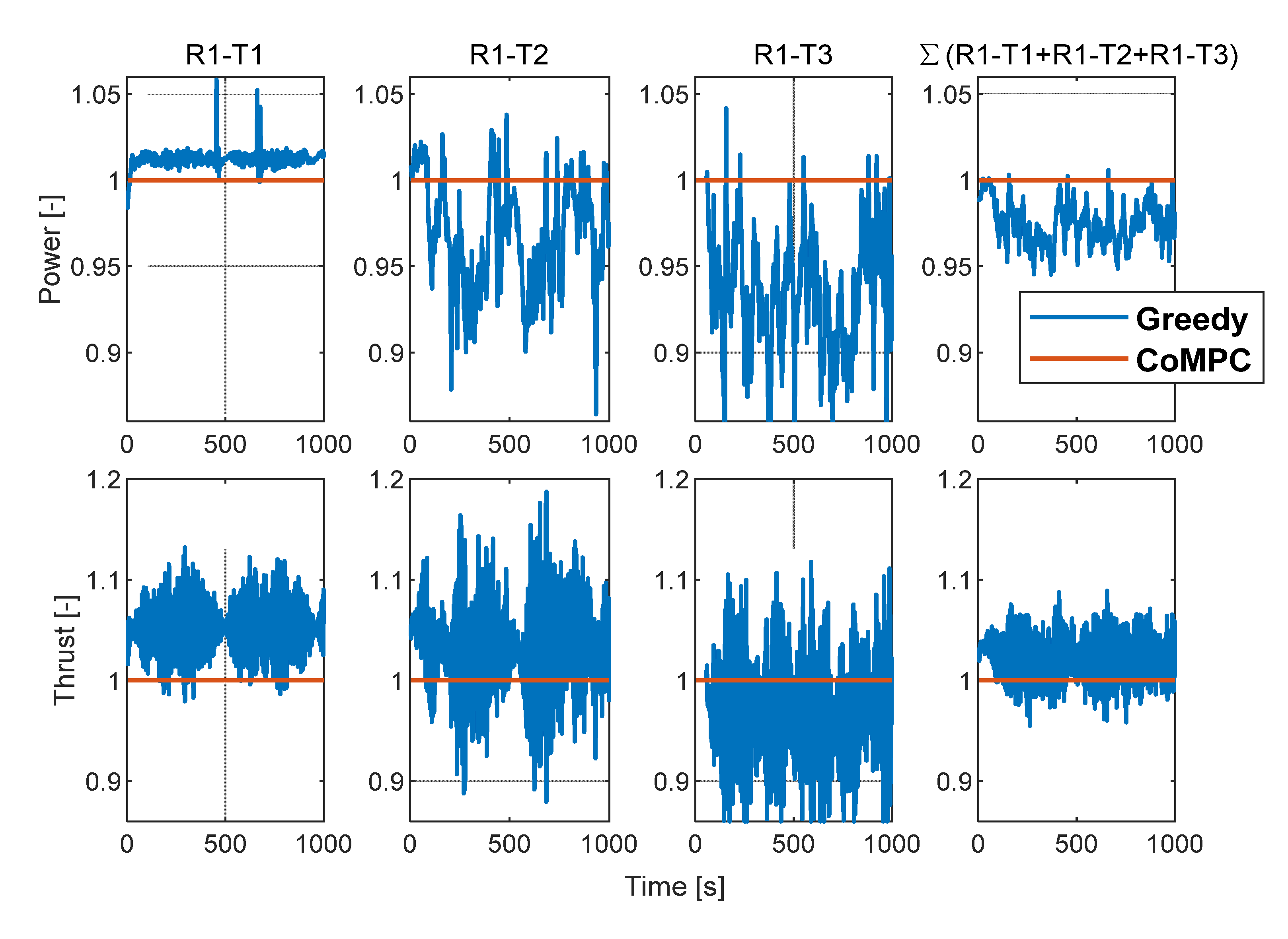
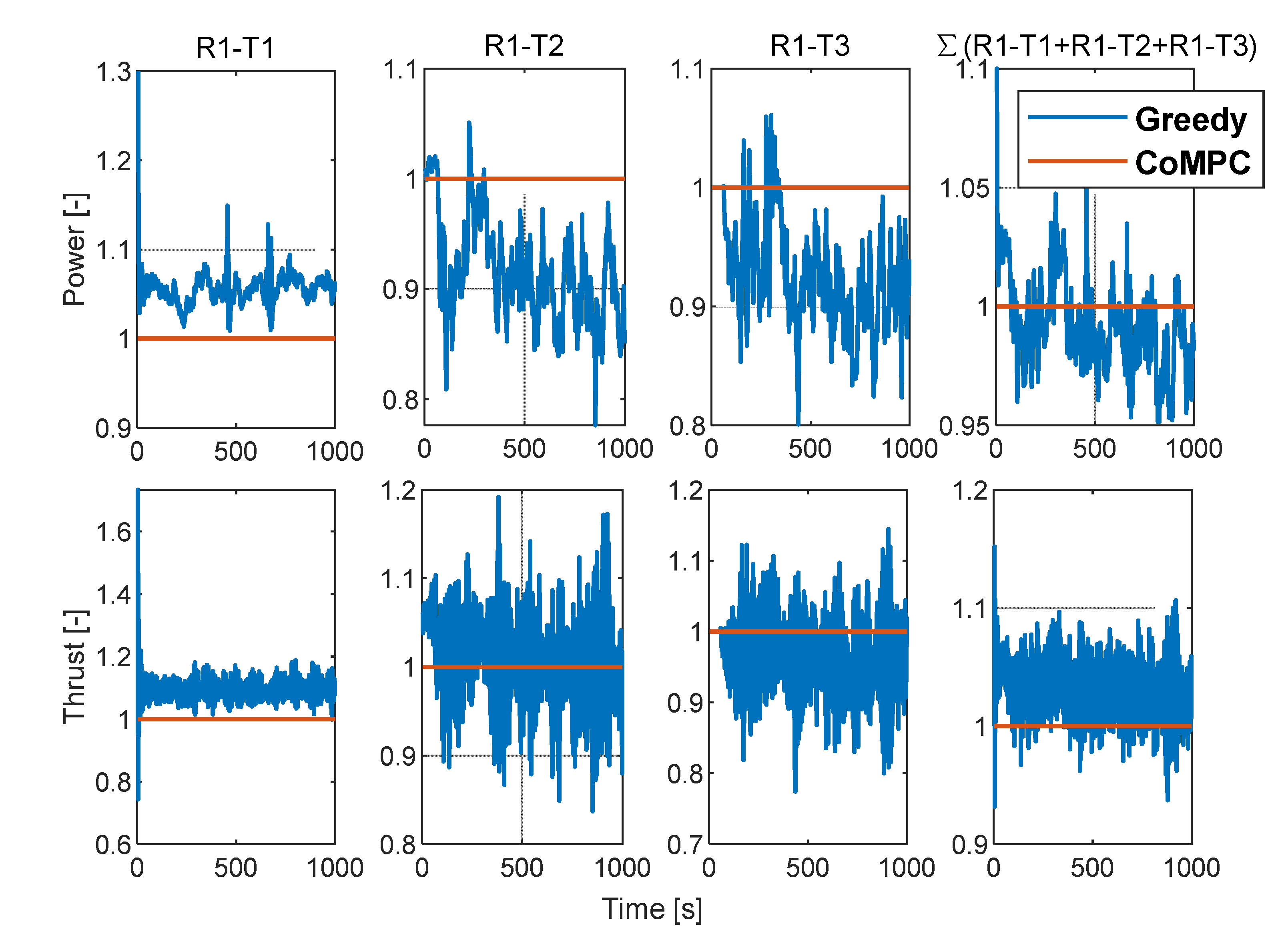
The Greedy algorithm means that there is no collaboration between wind turbines and each wind turbine is in the optimal power generation operation state. The following results are compared with the Greedy algorithm. As shown in Figure 15 and 16, the total power controlled by CoMPC is higher than that controlled by Greedy, while the total thrust is also lower. According to statistical calculations, when the WH is 1.2m, the average power is increased by about 2.5%, and the average load is reduced by about 4%. At a WH of 3m, the average power increase is about 2.1% and the average load decrease is about 4.5%.
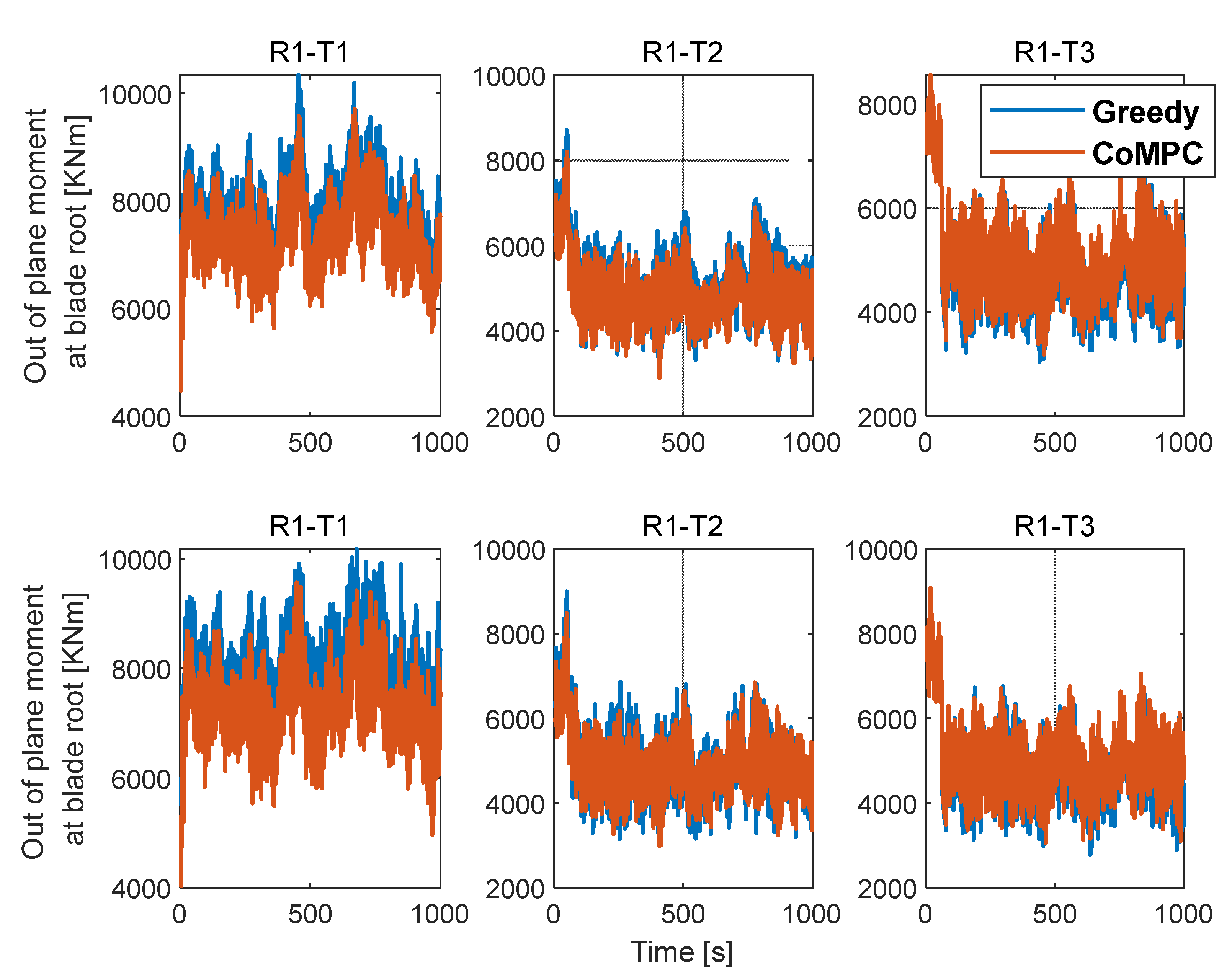
As shown in Figure 17, under CoMPC control, the out-of-plane moment at blade root of R1-T1 and R1-T2 wind turbine decreases compared with greedy control, while under CoMPC control, the power capture of R1-T3 wind turbine increases, and the corresponding out-of-plane moment at blade root increases slightly, but very little.
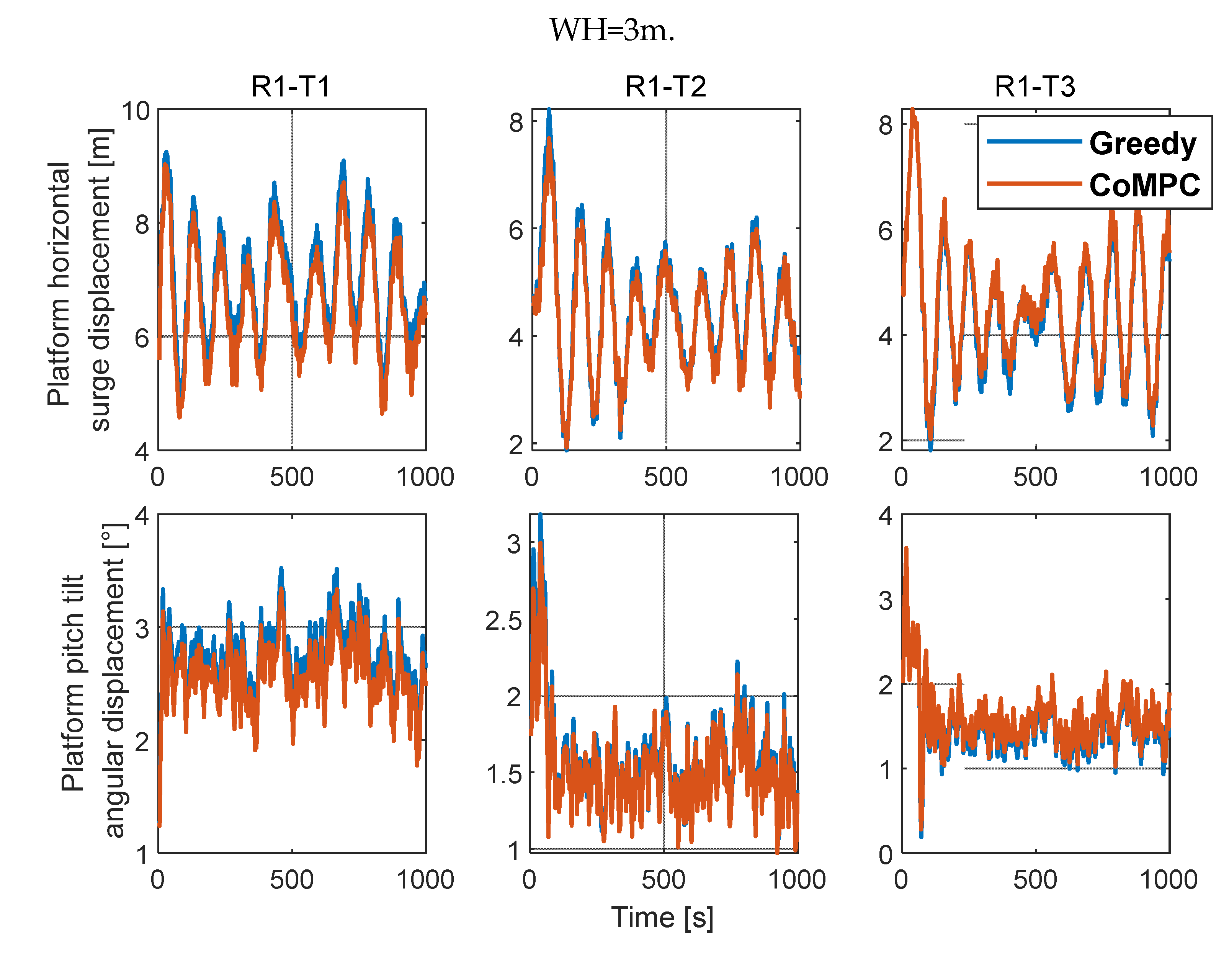
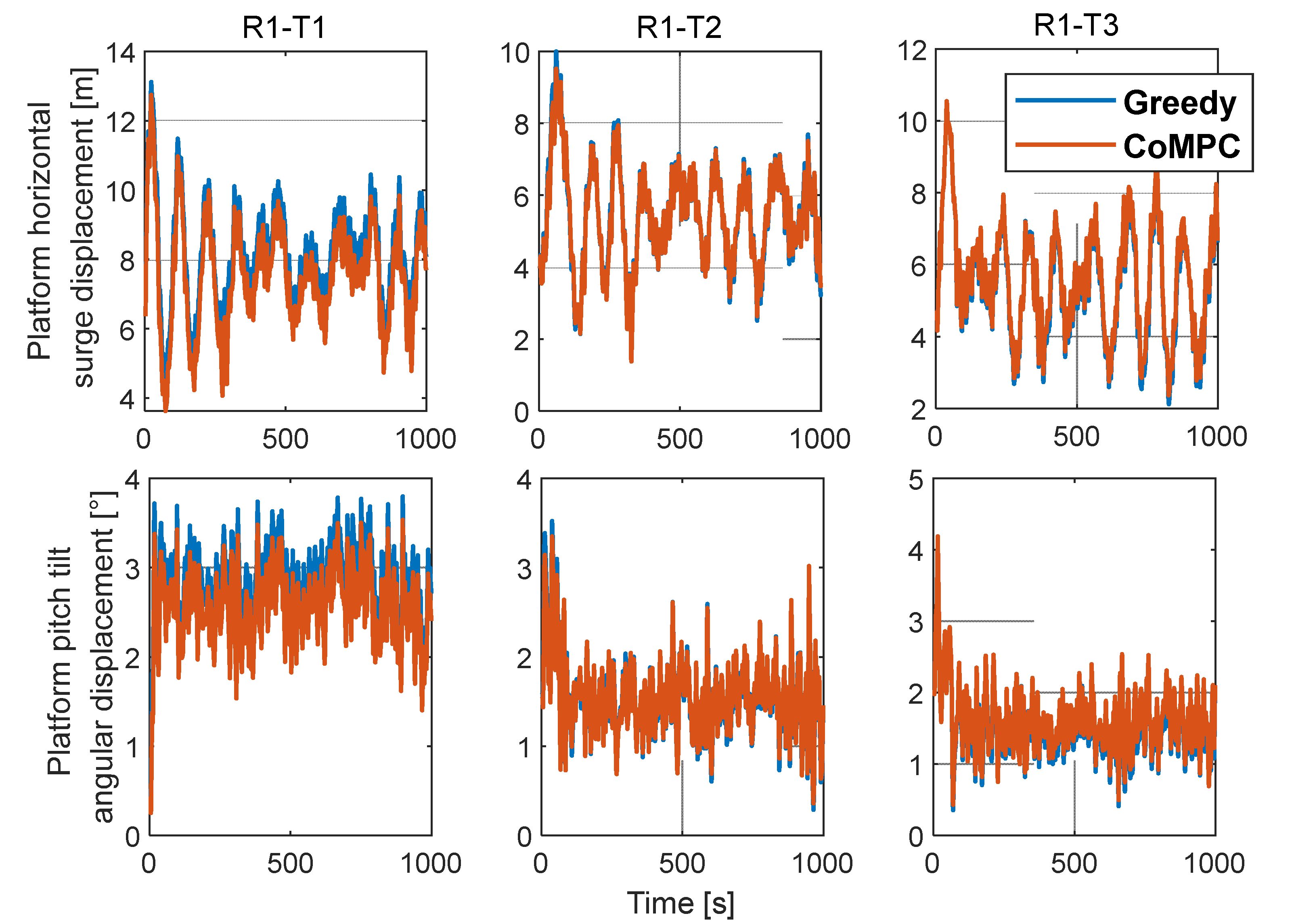
The movement of the semi-submersible floating wind turbine platform is one of the important criteria to evaluate the operation of the wind turbine. As shown in Figure 18 and 19, under the control of CoMPC, the surge displacement and pitch tilt angular displacement of R1-T1 wind turbine are large and significantly reduced, while the R1-T3 wind turbine still increases slightly due to the increase in power capture, but the motion range is still small.
As shown in Figure 14-18, it is difficult to see a significant difference in the CoMPC optimization effect of two groups of different wave heights, so it is temporarily believed that wave heights have no influence on this method.

5. Conclusion

In this paper, a method to mitigate wake interference is studied. The upwind wind turbine with CYMP is used to optimize the fatigue load caused by wake steering and increase the total power. The paper starts from the influence of CYMP control on the distribution characteristics of the flow field, and analyzes the control principle of CYMP, which has not been paid attention to in previous papers, and the feasibility of CYMP method to reduce wake disturbance is proved by simulation. Several cases study show that the CYMP method can reduce the fatigue load by 10.29% and increase the total power by 1.7% compared with only wake steering. FAST.Farm does not consider the influence of the atmospheric boundary layer, resulting in inaccurate control of the pitch angle, which will lead to deviations in the optimization results, so this study cannot be repeated to demonstrate the performance of CYMP, and further verification in modeling is needed.
Proper combination of yaw and pitch angles is critical to reduce fatigue loads and increase overall power, which is a complex and critical part of CYMP. In this paper, the CoMPC based on CYMP is proposed, and the concept of super-controller is used to calculate the optimal control action under the corresponding wind condition under the steady-state wake model, and it is used as a reference for MPC, so as to realize the purpose of the whole wind farm collaborative control. To solve the problem of large number of wind turbines in a wind farm, a novel wake zoning method is proposed, which greatly reduces the dimensionality of the optimization target. Although the steady-state Jensen model and Jimenez's deflection model are used in the calculation, the super controller constantly adjusts the optimal value according to the periodic feedback to adapt to the dynamic change of the wake. At 10m/s turbulent wind, the average power is increased by more than 2%, and the average load is reduced by more than 4%. This result shows that this method is promising.

Author Contributions

Conceptualization, L.Z., Y.X.; Methodology, L.Z.; Formal analysis, L.Z.; writing—original draft preparation, L.Z.; Writing-review and editing, F.G., B.Z., Y.X.; Visualization, J.W., L.X; Data curation, Y.X.; Funding acquisition, Y.X. All authors have read and agreed to the published version of the manuscript.

Funding

This work was supported by the Offshore Wind Power Intelligent Measurement and Control Research Centre and Laboratory Construction at the Ocean University of China grant number 861901013159, and Shandong Provincial Natural Science Foundation, grant number ZR2021ZD23.

Institutional Review Board Statement

Not applicable.

Informed Consent Statement

Not applicable.

Acknowledgments

The author is very grateful to China Electric Power Research Institute for its support in parameters of the wind farm.

Conflicts of Interest

The authors declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper.

References

  1. Council, G.W.E. Global Wind Report 2021. Available online: https://gwec. net/wp-content/uploads/2021/03. GWEC-Global-Wind-Report-2021. pdf 2020.
  2. Council, G.W.E. Global Wind Report 2022. Available online: https://gwec.net/global-wind-report-2022/. GWEC-Global-Wind-Report-2022. pdf 2021.
  3. Nilsson, K.; Ivanell, S.; Hansen, K.S.; Mikkelsen, R.; Sørensen, J.N.; Breton, S.; Henningson, D. Large-eddy simulations of the Lillgrund wind farm. Wind. Energy 2014, 18, 449–467. [Google Scholar] [CrossRef]
  4. Lissaman, P.B.S. Energy Effectiveness of Arbitrary Arrays of Wind Turbines. J. Energy 1979, 3, 323–328. [Google Scholar] [CrossRef]
  5. Manwell; F. , J.; McGowan, J.G., Ed.; Rogers, A.L. Wind energy explained: theory, design and application. John Wiley & Sons 2010. [Google Scholar]
  6. Estate, C. Offshore wind cost reduction pathways study. Crown Estate 2012.
  7. Ren, Z.; Verma, A.S.; Li, Y.; Teuwen, J.J.; Jiang, Z. Offshore wind turbine operations and maintenance: A state-of-the-art review. Renew. Sustain. Energy Rev. 2021, 144, 110886. [Google Scholar] [CrossRef]
  8. Ju Feng, W.Z.S. Design optimization of offshore wind farms with multiple types of wind turbines. Applied Energy 2017, 205, 1283–1297. [Google Scholar] [CrossRef]
  9. Andersson, L.E.; Anaya-Lara, O.; Tande, J.O.; Merz, K.O.; Imsland, L. Wind farm control - Part I: A review on control system concepts and structures. IET Renew. Power Gener. 2021, 15, 2085–2108. [Google Scholar] [CrossRef]
  10. Speakman, G.A.; Abkar, M.; Martínez-Tossas, L.A.; Bastankhah, M. Wake steering of multi-rotor wind turbines: a new wind farm control strategy. arXiv e-prints, 2020; arXiv:2006.11874. [Google Scholar]
  11. Dou, B.; Guala, M.; Lei, L.; Zeng, P. Experimental investigation of the performance and wake effect of a small-scale wind turbine in a wind tunnel. Energy 2018, 166, 819–833. [Google Scholar] [CrossRef]
  12. Archer, C.L.; Vasel-Be-Hagh, A. Wake steering via yaw control in multi-turbine wind farms: Recommendations based on large-eddy simulation. Sustain. Energy Technol. Assessments 2019, 33, 34–43. [Google Scholar] [CrossRef]
  13. Adaramola, M.S.; Krogstad, P. Experimental investigation of wake effects on wind turbine performance. Renew. Energy 2011, 36, 2078–2086. [Google Scholar] [CrossRef]
  14. Campagnolo, F.; Petrović, V.; Schreiber, J.; Nanos, E.M.; Croce, A.; Bottasso, C.L. Wind tunnel testing of a closed-loop wake deflection controller for wind farm power maximization. In Proceedings of the Journal of Physics: Conference Series; 2016; p. 032006. [Google Scholar]
  15. Howland, M.F.; Lele, S.K.; Dabiri, J.O. Wind farm power optimization through wake steering. Proceedings of the National Academy of Sciences 2019, 116, 14495–14500. [Google Scholar] [CrossRef]
  16. Schreiber, J.; Salbert, B.; Bottasso, C. Study of wind farm control potential based on SCADA data. In Proceedings of the Journal of Physics: Conference Series; 2018; p. 032012. [Google Scholar]
  17. Lin, M.; Porté-Agel, F. Power Maximization and Fatigue-Load Mitigation in a Wind-turbine Array by Active Yaw Control: an LES Study. J. Physics: Conf. Ser. 2020; 1618. [Google Scholar] [CrossRef]
  18. Churchfield, M.J.; Fleming, P.; Bulder, B.; White, S.M. Wind turbine wake-redirection control at the Fishermen's Atlantic City windfarm. In Proceedings of the Offshore Technology Conference; 2015. [Google Scholar]
  19. Dilip, D.; Porté-Agel, F. Wind Turbine Wake Mitigation through Blade Pitch Offset. Energies 2017, 10, 757. [Google Scholar] [CrossRef]
  20. Lee, J.; Son, E.; Hwang, B.; Lee, S. Blade pitch angle control for aerodynamic performance optimization of a wind farm. Renew. Energy 2013, 54, 124–130. [Google Scholar] [CrossRef]
  21. Behnood, A.; Gharavi, H.; Vahidi, B.; Riahy, G. Optimal output power of not properly designed wind farms, considering wake effects. International Journal of Electrical Power & Energy Systems 2014, 63, 44–50. [Google Scholar]
  22. Navarrete, E.C.; Perea, M.T.; Correa, J.J.; Serrano, R.C.; Ríos-Moreno, G. Expert Control Systems Implemented in a Pitch Control of Wind Turbine: A Review. IEEE Access 2019, 7, 13241–13259. [Google Scholar] [CrossRef]
  23. Tian, J.; Zhou, D.; Su, C.; Blaabjerg, F.; Chen, Z. Optimal Control to Increase Energy Production of Wind Farm Considering Wake Effect and Lifetime Estimation. Appl. Sci. 2017, 7, 65. [Google Scholar] [CrossRef]
  24. Corten, G.; Schaak, P. Heat and Flux. Increase of Wind Farm Production by Reduction of the Axial Induction. 2003.
  25. Bartl, J.; Sætran, L. Experimental testing of axial induction based control strategies for wake control and wind farm optimization. J. Physics: Conf. Ser. 2016, 753, 032035. [Google Scholar] [CrossRef]
  26. Campagnolo, F.; Petrović, V.; Bottasso, C.L.; Croce, A. Wind tunnel testing of wake control strategies. In Proceedings of the 2016 American Control Conference (ACC); 2016; pp. 513–518. [Google Scholar]
  27. Kim, H.; Kim, K.; Paek, I. Model Based Open-Loop Wind Farm Control Using Active Power for Power Increase and Load Reduction. Appl. Sci. 2017, 7, 1068. [Google Scholar] [CrossRef]
  28. McTavish, S.; Feszty, D.; Nitzsche, F. Evaluating Reynolds number effects in small-scale wind turbine experiments. J. Wind. Eng. Ind. Aerodyn. 2013, 120, 81–90. [Google Scholar] [CrossRef]
  29. Annoni, J.; Gebraad, P.M.; Scholbrock, A.K.; Fleming, P.A.; Wingerden, J.W.v. Analysis of axial-induction-based wind plant control using an engineering and a high-order wind plant model. Wind Energy 2016, 19, 1135–1150. [Google Scholar] [CrossRef]
  30. Ha, K.; Truong, H.V.A.; Dang, T.D.; Ahn, K.K. Recent control technologies for floating offshore wind energy system: A review. International Journal of Precision Engineering and Manufacturing-Green Technology 2021, 8, 281–301. [Google Scholar] [CrossRef]
  31. Ishihara, T.; Qian, G.-W. A new Gaussian-based analytical wake model for wind turbines considering ambient turbulence intensities and thrust coefficient effects. J. Wind. Eng. Ind. Aerodyn. 2018, 177, 275–292. [Google Scholar] [CrossRef]
  32. Smith, S.D. Thrust-anemometer measurements of wind turbulence, Reynolds stress, and drag coefficient over the sea. Journal of Geophysical Research 1970, 75, 6758–6770. [Google Scholar] [CrossRef]
  33. Ainslie, J.F. Calculating the flowfield in the wake of wind turbines. Journal of wind engineering and Industrial Aerodynamics 1988, 27, 213–224. [Google Scholar] [CrossRef]
  34. Medici, D. Experimental studies of wind turbine wakes: power optimisation and meandering. KTH, 2005.
  35. Bianchi, F.D.; De Battista, H.; Mantz, R.J. Wind turbine control systems: principles, modelling and gain scheduling design; Springer: 2007; Volume 19.
  36. Gebraad, P.M.O.; Teeuwisse, F.W.; van Wingerden, J.W.; Fleming, P.A.; Ruben, S.D.; Marden, J.R.; Pao, L.Y. Wind plant power optimization through yaw control using a parametric model for wake effects-a CFD simulation study. Wind. Energy 2014, 19, 95–114. [Google Scholar] [CrossRef]
  37. Kragh, K.A.; Hansen, M.H. Load alleviation of wind turbines by yaw misalignment. Wind. Energy 2013, 17, 971–982. [Google Scholar] [CrossRef]
  38. Jensen, N.O. A note on wind generator interaction. 1983.
  39. Katic, I.; Højstrup, J.; Jensen, N.O. A simple model for cluster efficiency. In Proceedings of the European wind energy association conference and exhibition; 1986; pp. 407–410. [Google Scholar]
  40. Jiménez. ; Crespo, A.; Migoya, E. Application of a LES technique to characterize the wake deflection of a wind turbine in yaw. Wind. Energy 2009, 13, 559–572. [Google Scholar] [CrossRef]
Preprints 76486 g001
Figure 1. Wake interference diagram: (a) Free stream state; (b) CYMP operation of the upwind wind turbine.
Figure 1. Wake interference diagram: (a) Free stream state; (b) CYMP operation of the upwind wind turbine.
Preprints 76486 g001
Preprints 76486 g002
Figure 2. Visualization of wind farm flow field in a different position: (a) Visualization of wind farm flow field in XY plane at hub center height; (b) Visualization of wind farm with three wake sections. Along the X direction, the disks are at x/D=1, x/D=3, x/D=4.6; (c) YZ plane at WT1. The dotted line in the figure calibrates the height of the hub center.
Figure 2. Visualization of wind farm flow field in a different position: (a) Visualization of wind farm flow field in XY plane at hub center height; (b) Visualization of wind farm with three wake sections. Along the X direction, the disks are at x/D=1, x/D=3, x/D=4.6; (c) YZ plane at WT1. The dotted line in the figure calibrates the height of the hub center.
Preprints 76486 g002
Preprints 76486 g003
Figure 3. Explicit boundary conditions schematic.
Figure 3. Explicit boundary conditions schematic.
Preprints 76486 g003
Preprints 76486 g004
Figure 4. Instantaneous flow velocity visualization on YZ planes downstream from WT1. Red circles indicate a rotor located directly downwind of the turbine. The color bar indicates the wind velocity corresponding to the different colors in the figures. 20Y means control at yaw error angle of 20°; 20Y0.8P means combination control of 20° yaw error and 0.8 degree pitch.
Figure 4. Instantaneous flow velocity visualization on YZ planes downstream from WT1. Red circles indicate a rotor located directly downwind of the turbine. The color bar indicates the wind velocity corresponding to the different colors in the figures. 20Y means control at yaw error angle of 20°; 20Y0.8P means combination control of 20° yaw error and 0.8 degree pitch.
Preprints 76486 g004
Preprints 76486 g005
Figure 5. Wake centerline offset on y- axis (left) and z- axis (right). 20Y means control at yaw error angle of 20°; 20Y0.8P means combination control of 20° yaw error and 0.8 degree pitch.
Figure 5. Wake centerline offset on y- axis (left) and z- axis (right). 20Y means control at yaw error angle of 20°; 20Y0.8P means combination control of 20° yaw error and 0.8 degree pitch.
Preprints 76486 g005
Preprints 76486 g006
Figure 6. Spanwise profiles of the velocity deficit at the hub height for the incoming flow. 20Y means control at yaw error angle of 20°; 20Y0.8P means combination control of 20° yaw error and 0.8 degree pitch.
Figure 6. Spanwise profiles of the velocity deficit at the hub height for the incoming flow. 20Y means control at yaw error angle of 20°; 20Y0.8P means combination control of 20° yaw error and 0.8 degree pitch.
Preprints 76486 g006
Preprints 76486 g007
Figure 7. Spanwise profiles of the turbulence intensity for the inflow wind. 20Y means control at yaw error angle of 20°; 20Y0.8P means combination control of 20° yaw error and 0.8 degree pitch.
Figure 7. Spanwise profiles of the turbulence intensity for the inflow wind. 20Y means control at yaw error angle of 20°; 20Y0.8P means combination control of 20° yaw error and 0.8 degree pitch.
Preprints 76486 g007
Preprints 76486 g008
Figure 8. Wind speed variation (left) and PDF (right) in the hub center of WT2. PDF is an abbreviation for Probability Density Function, which is used to represent the probability distribution of wind speed. 20Y means control at yaw error angle of 20°; 20Y0.8P means combination control of 20° yaw error and 0.8 degree pitch.
Figure 8. Wind speed variation (left) and PDF (right) in the hub center of WT2. PDF is an abbreviation for Probability Density Function, which is used to represent the probability distribution of wind speed. 20Y means control at yaw error angle of 20°; 20Y0.8P means combination control of 20° yaw error and 0.8 degree pitch.
Preprints 76486 g008
Preprints 76486 g009
Figure 9. Rotor speed variation (left) and PDF (right) of WT2. PDF is an abbreviation for Probability Density Function, which is used to represent the probability distribution of wind speed. 20Y means control at yaw error angle of 20°; 20Y0.8P means combination control of 20° yaw error and 0.8 degree pitch.
Figure 9. Rotor speed variation (left) and PDF (right) of WT2. PDF is an abbreviation for Probability Density Function, which is used to represent the probability distribution of wind speed. 20Y means control at yaw error angle of 20°; 20Y0.8P means combination control of 20° yaw error and 0.8 degree pitch.
Preprints 76486 g009
Preprints 76486 g010
Figure 10. Effect on fatigue load of turbines with the CYMP control method in wake interference conditions.
Figure 10. Effect on fatigue load of turbines with the CYMP control method in wake interference conditions.
Preprints 76486 g010
Preprints 76486 g011
Figure 11. The total power using the CYMP method, normalized by the total power with no yaw and no pitch. It is worth noting that the dynamic wake model in FAST Farm does not capture the effect of the atmospheric boundary layer, however, the pitch angle settings need to be considered in the specific atmospheric condition [3,29], so the results are biased in this paper. Although the pitch angle setting deviates from the actual optimization effect, it is enough to prove that this method has the potential to optimize the wake effect.
Figure 11. The total power using the CYMP method, normalized by the total power with no yaw and no pitch. It is worth noting that the dynamic wake model in FAST Farm does not capture the effect of the atmospheric boundary layer, however, the pitch angle settings need to be considered in the specific atmospheric condition [3,29], so the results are biased in this paper. Although the pitch angle setting deviates from the actual optimization effect, it is enough to prove that this method has the potential to optimize the wake effect.
Preprints 76486 g011
Preprints 76486 g012
Figure 12. Framework of the CoMPC.
Figure 12. Framework of the CoMPC.
Preprints 76486 g012
Preprints 76486 g013
Figure 13. Partition diagram of wind farm wake. Each red rectangle represents one wake disturbance area.
Figure 13. Partition diagram of wind farm wake. Each red rectangle represents one wake disturbance area.
Preprints 76486 g013
Preprints 76486 g014
Figure 14. Simulation conditions, the left picture is wind speed, the right picture is wave height.
Figure 14. Simulation conditions, the left picture is wind speed, the right picture is wave height.
Preprints 76486 g014
Preprints 76486 g015
Figure 15. WH= 1.2m, power (top row) and thrust (bottom row).
Figure 15. WH= 1.2m, power (top row) and thrust (bottom row).
Preprints 76486 g015
Preprints 76486 g016
Figure 16. WH= 3m, power (top row) and thrust (bottom row).
Figure 16. WH= 3m, power (top row) and thrust (bottom row).
Preprints 76486 g016
Preprints 76486 g017
Figure 17. Out-of-plane moment at blade root. In top row, WH=1.2m, In bottom row, WH=3m.
Figure 17. Out-of-plane moment at blade root. In top row, WH=1.2m, In bottom row, WH=3m.
Preprints 76486 g017
Preprints 76486 g018
Figure 18. WH= 1.2m, platform movement. The top row shows platform horizontal surge displacement, the bottom row shows pitch tilt angular displacement.
Figure 18. WH= 1.2m, platform movement. The top row shows platform horizontal surge displacement, the bottom row shows pitch tilt angular displacement.
Preprints 76486 g018
Preprints 76486 g019
Figure 19. WH= 3m, platform movement. The top row shows platform horizontal surge displacement, the bottom row shows pitch tilt angular displacement.
Figure 19. WH= 3m, platform movement. The top row shows platform horizontal surge displacement, the bottom row shows pitch tilt angular displacement.
Preprints 76486 g019
Table 1. Turbine parameters.
Table 1. Turbine parameters.
Parameter Value
Rated power (MW) 5
Blades number (-) 3
Cut-in, cut-out, rated wind speed (m/s) 3, 25, 11.4
Cut-in, rated rotor speed (rpm) 6.9, 12.1
Hub height (m) 90
Rotor diameter (m) 126
Table 2. Simulation cases.
Table 2. Simulation cases.
Method name Yaw misalignment [°] Pitch angle [°]
entry 1 5/10/15/20/
25/30/35/40		 0
entry 2 5 0.2/0.4/0.6/0.8/1.0
10
15
20
25
30
35
40
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.
Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.
Prerpints.org logo

Preprints.org is a free preprint server supported by MDPI in Basel, Switzerland.

facebook logotwitter logolinkedin logo
MDPI Initiatives
Important Links
Subscribe

Disclaimer

Terms of Use

Privacy Policy

© 2024 MDPI (Basel, Switzerland) unless otherwise stated