Preprint
Article
Influence of Torque on Platform Deformity of the Tri-channel Implant: Two and Three-Dimensional Analysis Using Micro Computed Tomography
Altmetrics
Downloads
116
Views
28
Comments
0
A peer-reviewed article of this preprint also exists.
Submitted:
13 June 2023
Posted:
14 June 2023
You are already at the latest version
Alerts
Abstract
Background and Objectives: Mechanical and biological complications can lead to system fracture or screw loss on dental implants. Narrow and regular platforms have been used without a consensus about the effect of distance the abutment from the prosthetic platform margin. The aim of this study is to evaluate different insertion torques in the deformation of tri-channel platform connections through two- and three-dimensional measurements with micro-CT. Materials and Methods: 164 implants were divided into groups (platform diameter and type): 3.5, 3.75, and 4.3 mm NP (Narrow Platform), and 4.3 mm RP (Regular Platform). Each implant-platform group was then divided into four subgroups (n = 10) with different torques: T45 (45 Ncm), T80 (80 Ncm), T120 (120 Ncm) and T150 (150 Ncm). The implant-abutment-screw assemblies were scanned and the images obtained were analyzed. Results: A significant difference was observed for the linear and volume measures between the different platforms (p <0.01) and the different implant insertion torques (p <0.01). Qualitative analysis suggested higher deformation resistance for the 3.75 NP compared to the 3.5 NP, and RP was more resistant compared to the NP. Conclusions: The 0.25-mm increment in the implant platform did not increase the resistance to the applied insertion torques; the 4.3-mm implant was significantly stronger compared to the 3.5-mm implant and the proposed micro-CT analysis was considered valid for both 2D and 3D analyses of micro gaps, qualitatively and quantitatively.
Keywords:Â
Subject: Medicine and Pharmacology -  Dentistry and Oral Surgery
1. Introduction
Osseointegrated implants have a high scientific consensus in dentistry and great success rates are achieved with their use in oral rehabilitation [1,2] due to the synergistic combination of numerous biomechanical factors [3,4].
To overcome the disadvantages of external (loosening of the screw) and internal (low mechanical strength) hexagon connections, the tri-channel connection has emerged, allowing for better force distribution, reduced micro-movement, and increased resistance to high insertion torques [5], advantages especially important for immediate loading cases [2,6].
In implantology, primary implant stability is decisive for a successful osseointegration process. In cases of immediate loading, there is a direct relationship between osseointegration and implant insertion torque [5], which is an excellent clinical parameter for the evaluation of primary stability [7,8]. Also, there is the platform switching concept [9,10], based on the change of the implant/abutment connection, as well as the action of extrinsic-intrinsic factors to the central region of the implant, thus promoting bone maintenance [11,12].
However, clinical investigations underlined how mechanical complications (such as instability of the implant-abutment assembly, the abutment screw loosening or fracture and implant structural problems) generate detrimental forces between connecting structures and bone tissue that can lead to system fracture or loss, or biological problems due to bacterial infiltration in micro gaps of the interface [13].
The modification of the bone tissue related to mechanical influence has also been focused in literature by several years [1,2,14]. The continuous bone resorption presents clinical disadvantages for both dental implant and prostheses, which is why these parameters must be analyzed before planning dental rehabilitation in order to achieve clinical success [14,15].
Nowadays, digital technology represents a virtual access to human tissues and structures (like bone, teeth, gums and face) in a single 3D model [12]. Hence, studies have been focused on three-dimensional methods and digital dentistry (CAD/CAM) to consider the risk factors related to some of the dental implants characteristics because they influence the tension and the bone resorption and remodeling [11,14]. That is why is fundamental to analyze and understand the stress involving the complex system around bone, dental implants and prosthodontics components before planning any surgeries in rehabilitation [15].
In oral rehabilitation, some methods are being develop with new digital technologies and are important parameter for prognosis, that improves its predictability, such as the finite element methods (FEM), which creates a virtual model of biomedical device and allows the stress distribution on important area [13,14]. According to Cicciù [15], FEM analysis has been used to evaluate some dental planning procedures in 3D, as in maxillofacial and implant surgeries; to investigate dental loading conditions and also to evaluate the impact of implant diameter in stress around dental tissues; to support the dental field understanding stress distribution and geometry evaluation [14,15]. Besides FEM, the Von Mises analysis is been applied in 3D technology to help identifying areas where high and low strength around the bone and implant system are located [15].
Another digital technology in dentistry is micro computed tomography (micro-CT) analysis, that has been proposed for detection and evaluation of deformations and micro gaps between implant and abutment, as it allows the acquisition of three-dimensional images with sample preservation [16,17]. Moreover, Scarano et al. [16] demonstrated the use of micro-CT to analyze margin discrepancies and the interface between dental implant and prosthetic components.
Thus, the objective of the present study was to evaluate different insertion torques in the deformation of tri-channel narrow platform (NP) connections and regular platform (RP) connections through two- and three-dimensional (2D and 3D) measurements with micro-CT. The hypothesis tested was that micro-CT analysis is valid for 2D and 3D micro gap evaluations. The null hypothesis was that the deformation of different implant platforms and diameters is not affected by the insertion torque applied.
2. Materials and Methods
For the present study, 164 13-mm-long implants with tri-channel connections (Dérig Bioneck, Barueri, SP, Brazil) were divided into groups according to the platform diameter and type: 3.5, 3.75, and 4.3 mm NPs, and 4.3 mm RP (Figure 1).
For analysis of insertion torque resistance, each implant-platform group was randomly divided into four subgroups (n = 10): Group T45 (45 Ncm torque), Group T80 (80 Ncm torque), Group T120 (120 Ncm torque), and Group T150 (150 Ncm torque).
Insertion torques were applied with 22 RinGrip insertion wrench (TRI, Dérig Bioneck, Dérig) in a torsion machine (Biopdi, Brazil). One wrench per group was used for the T45 and T80 groups and one wrench per implant was used for the T120 and T150 groups, to prevent driver deformation due to higher torques. Samples were coupled to stainless steel cylinders (26 × 20 mm) with lateral screws, keeping the implant platform at the upper level of the cylinder (Figure 2).
Abutments and their respective screws were installed in the implants with a torque of 32 Ncm using a RinGrip hex wrench, according to the manufacturer's recommendations. A new implant-platform sample was used as control for each group.
2.1. Micro-CT deformation analysis
The implant-abutment-screw assemblies were scanned on the SkyScan Model 1176 microtopography scanner (Bruker micro-CT, Kontich, Belgium) operated at 90 kV, 278 mA (0.1 mm Cu filter). A 180-degree rotation scanning was performed around the vertical axis with a rotation step of 0.5 at an isotropic resolution of 8.6 μm. The images were reconstructed using the NRecon v.1.6.9.18 (Bruker-micro-CT) software providing axial cross-sections of inner structures. The images obtained before and after applying the different torques were superimposed using DataViewer v.1.5.0 software (Bruker micro-CT). Then, 2D and 3D evaluations of the tri-channel deformation were performed using the CTAn v.1.17.7.2+ (Bruker micro-CT) software.
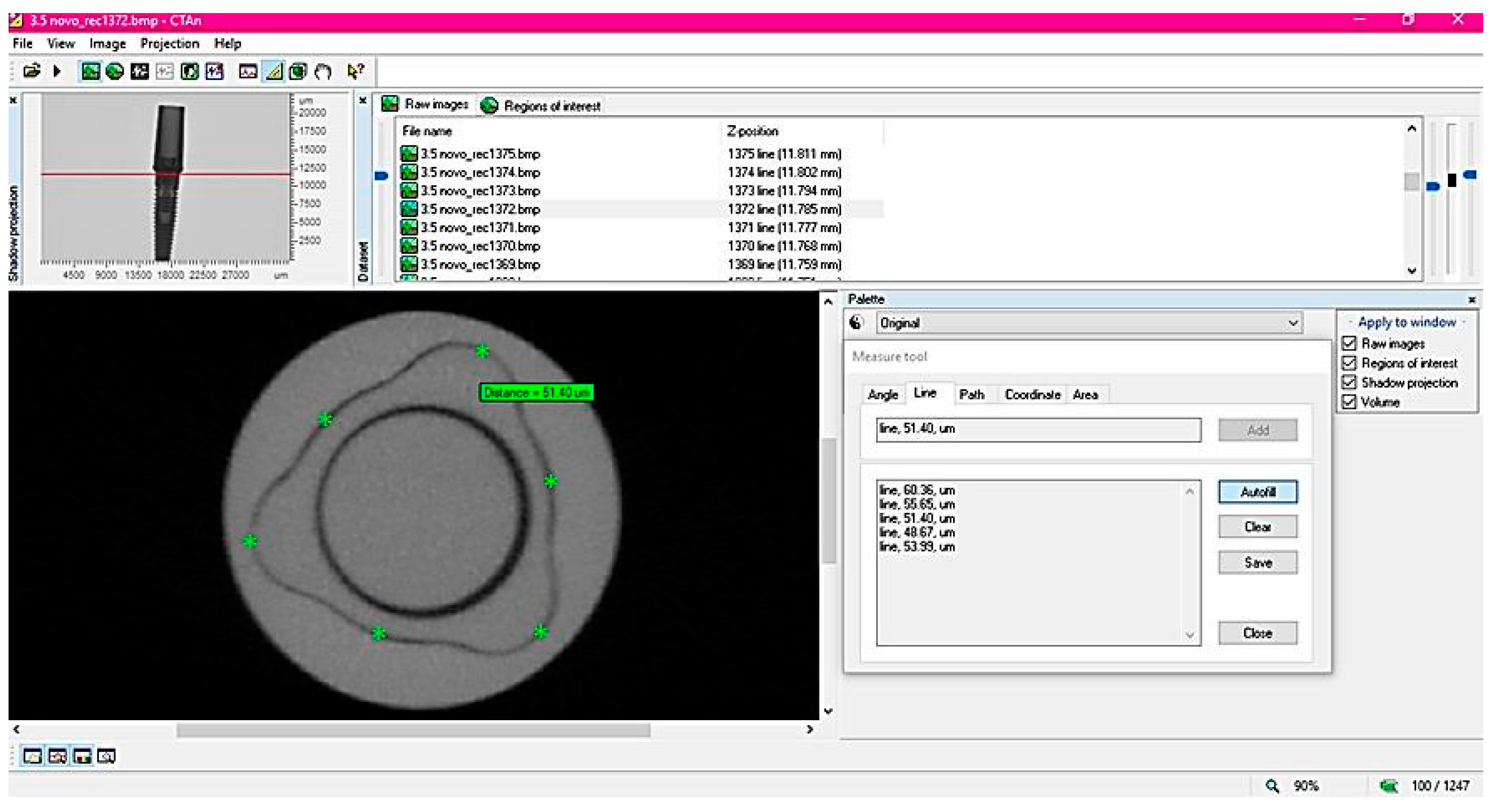
For the 2D evaluation, 10 equidistant sections were used in sagittal and coronal directions. Micro gaps were measured with the Measure tool of the software in six platform regions, three in the tri-channel lobes and three in the implant-abutment edges (Figure 3).
Sixty measurements were obtained per sample (n = 10), totaling 640 measurements per torque group.
For the 3D evaluation, the volume of interest (VOI, mm³) was obtained from the sharpest image of the tri-channel connection, which was in the central section of the sample. From the central section, 425 sections to the cervical direction and 425 sections to the apical direction were used as limits, totaling 850 sections per sample. The percent difference of the initial and final deformations were measured and values (µm) for each group and torque were compared with those of the new implant-abutment-screw assemblies according to the formula [5]:
2.2. Statistical analysis
Comparisons between insertion torques, platform types, and differences in volume were performed by two-way analysis of variance (Two-way ANOVA) using the SAS software version 9.4. The fit of the models was verified by residual analysis. For the 2D measure, comparisons between insertion torques, platform types, and their interactions were performed through orthogonal contrasts, using the linear effect model with random effects. This model considers the repeated measurements of each specimen as a random effect, and the group and force were considered fixed effects. The fit of the model was verified by residual analysis.
3. Results
A significant difference was observed for the linear and volume measures between the different platforms (p <0.0001) and the different implant insertion torques (p<0.0001). The interaction between platform and insertion torque was significant (p<0.0001), indicating that the tested platforms have different behavior depending on the different insertion torques, as can be observed in Table 1, Table 2, Table 3 and Table 4.
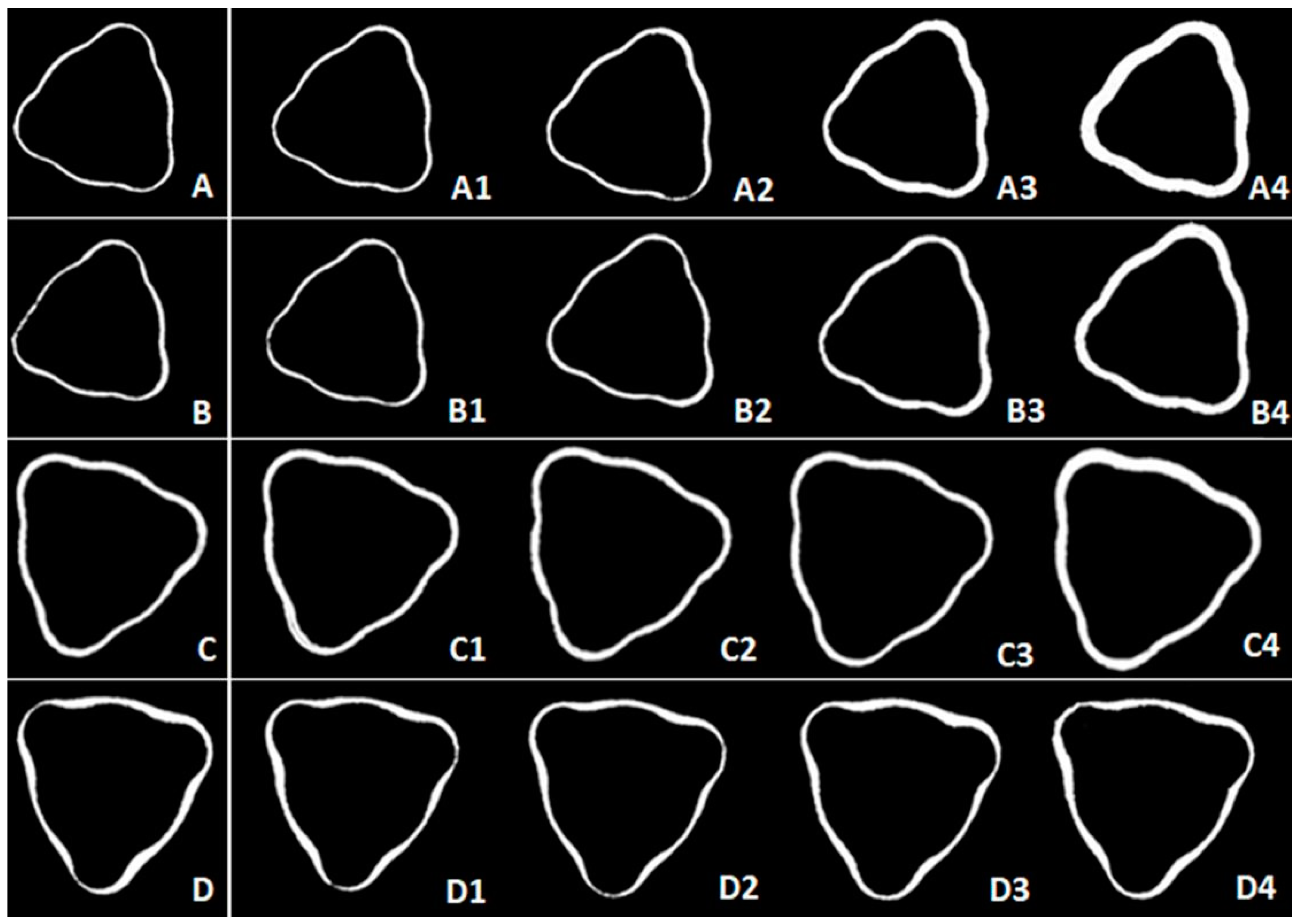
Images of the micro gap formed between the tri-channel platform and the prosthetic abutment were generated. Comparisons between the control and the experimental samples (45, 80, 120 and 150 Ncm) are shown in Figure 4.
A change in micro gap volume was found between the tri-channel platform and prosthetic abutment, especially for smaller diameter groups (3.5 NP and 3.75 NP) at higher torques (80, 120, and 150 Ncm), with few variations among the larger diameters. The 150 Ncm insertion torque caused a significant volumetric deformation in all groups. The qualitative analysis suggested higher deformation resistance for the 3.75 NP compared to the 3.5 NP, due to the 0.25 mm increase in the body of the former. In addition, the RP was more resistant compared to the NP, with the 4.3 RP group showing no evident change in the gap in relation to the control group.
4. Discussion
In the present study, tri-channel dental implants with different diameters and platforms were evaluated for insertion torque resistance with micro-CT analyzes to verify possible deformations. Based on results, the test hypothesis was accepted and that the null hypothesis was partially rejected.
Studies have been conducted to establish the possible correlation between implant insertion torque and primary stability [8,18]. Li et al. [18] emphasize that high insertion torques (>50 Ncm) might be beneficial for securing the implant, especially in bones of lower density. However, the authors affirm that the ideal amount of force is unclear and, as observed in the present study, significant deformations can occur in narrow platforms (3.5 NP, 3.75 NP and 4.3 NP).
The use of micro-CT for 2D and 3D investigations of platform deformations and the adaptation of components was considered because most of the previous research regarding implant failures is directed to biological aspects, giving secondary importance to reports on mechanical causes of failure [12,19,20]. Also, digital dentistry technology improves the predictability of the treatment, providing a high-resolution CT radiology examination [16,21,22].
Significant differences in deformation were found for different platforms and insertion torques, (in both 2D and 3D analyses). In addition to the associated patient discomfort, the discrepancy between the prosthetic component and the implant causing a micro gap at the implant-prosthetic abutment interface can lead to the penetration of microorganisms and contamination of the peri-implant tissue over time [19,23]. Still, the contact between an implant and a new prosthetic component is subject to micro gaps, with values between 40 and 100 µm (depending on their characteristics) [21,24], in accordance with micrographs shown in Figure 4 - A, B, C and D. However, to date, there are few reports that associate failures at the implant platform level (deformation) with the adaptation of the prosthetic abutment after insertion with high torques [24,25,26].
Based on the micro-CT results showing micro gaps generation after the implant insertion using different torques, we can state that mechanical complications may occur prior to the clinical use of the dental implant [27,28]. As observed, during the insertion of the implant in the crestal bone, platform deformations might occur leading to discrepancies of the prosthetic components (especially for narrow platform implants). This may be the cause of many of the failures reported that are only associated to microbial infiltration or bone resorption [21,22].
The results found in the present study corroborate previous studies, indicating that the adaptation of the prosthetic component and the implant insertion wrench might deform depending on the applied torque [27]. Such deformations can result in biomechanical complications over time, compromising a proper functioning and stability of implant prostheses [18,24,25].
The differences found between 3.5 NP and 3.75 NP groups indicated that the 0.25 mm reinforcement of the 3.5-mm implant was not sufficient to prevent damage to the tri-channel connector. However, the volume alteration analysis shows a smaller micro gap with the 3.75 NP using higher torques (over 100 Ncm) compared to 3.5 NP. The results suggest that the reinforcement of the 3.75 NP could be more useful if placed in the region where the installation wrench is connected (near the cervical third), in the resistant area of the implant [24] and not in the implant body [18]. According to Maeda et al. [24], the area and thickness of the external and internal walls of the implant directly influence the resistance of the implant-installation wrench combo to the applied insertion torque and, as shown in this study, additional reinforcement should be placed nearest to the connecting area (at platform level) for the best resistance possible. Likewise, with the 4.3-mm implants, significant differences were found for deformations in the NP platform compared to PR with torques above 45 Ncm.
To eliminate or minimize micro gaps that can lead to peri-implant problems, implant manufacturers have been designing more stable connections, with more accurate adaptation between prosthetic components and implant platform, and keeping micro gaps in the internal region of the connection [22,26,27]. This type of connection has been considered of superior stability [22,28]. However, according to results of the present study, the reduced platform was more susceptible to deformations and had lower resistance to insertion torques greater than 80 Ncm compared to the regular platform. Similar findings were found by Kwon et al. [21], and Bambini et al. [22], where the application of 60 Ncm torques and higher also caused deformations in the platform, compromising the adaptation of the prosthetic abutment.
Cervino et al. [19] demonstrated that, according to the Federal Drug Administration FDA (in 2016), digital technology using computational modeling represents a safety and effectiveness method to predict clinical situations and, in this study, the micro-CT analysis was fundamental to quantify and qualify micro gaps, highlighting the need to clinically investigate the effect of these prosthetic mismatches [11] and the greater susceptibility of microbial infiltration. Deformations that occurred on the implants platform were not visible to the naked eye, thus impossible to be detected by the dentist. New investigations must be carried out in order to improve and modify the physical-mechanical properties of the implants used, especially those with smaller dimensions in diameter and platform, because the clinical success depends on several factors, and it is suggested the development of new equipment that can standardize methodologies of application of high torques, as well as clinical evidence to evaluate parameters biomechanics of implants subjected to high insertion torques. Also, digital dentistry analysis has demonstrated predictability of the patient’s planning and treatment [12,14,15]. Based on these results, thermomechanical and microbiological simulation analyzes are recommended to assess the clinical implication of these deformations and their impact on mechanical and biological failures of implants, which usually have been attributed to generic causes, and reported as limitation in studies [15,19,27,28].
5. Conclusions
Based on the results of the present study, the 0.25-mm increment in the implant platform did not increase the resistance to the applied insertion torques; the 4.3-mm implant was significantly stronger compared to the 3.5-mm implant. In addition, the proposed micro-CT analysis was considered valid for both 2D and 3D analyses of micro gaps, qualitatively and quantitatively, of the new implant-abutment assemblies, which showed deformations and increased micro gaps after insertion torque application in all tested groups.
Author Contributions
Conceptualization, R.F.R. and R.C.S.R.; methodology, R.F.R., R.C.S.R., A.C.L.F., I.C.M.M. and G.B.L..; software, R.F.R.; validation, A.C.L.F., I.C.M.M. and G.B.L..; formal analysis, R.F.R., R.C.S.R., A.C.L.F., I.C.M.M. and G.B.L.; investigation, R.C.deM. and A.A.S.; resources, R.F.R.; data curation, R.C.deM. and A.C.L.F.; writing—original draft preparation, R.C.deM. and A.A.S.; writing—review and editing, A.C.L.F., I.C.M.M., R.C.S.R. and R.F.R.; visualization, A.C.L.F., I.C.M.M., R.C.S.R. and R.F.R.; supervision, A.C.L.F., R.C.S.R. and R.F.R.; project administration, R.F.R.; funding acquisition, R.F.R. All authors have read and agreed to the published version of the manuscript.
Funding
This work was supported by the State of Sao Paulo Research Foundation (FAPESP - São Paulo, SP, Brazil), DDS Scholarship (#2015/13199-5). A.A.S. and R.C.deM. received a PhD scholarship from Agency for the High-Standard Promotion of Graduate Courses—CAPES, which also support the Oral Rehabilitation Graduate Program—code 001.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
The data that support the findings of this study are available from the corresponding author upon reasonable request.
Acknowledgments
The authors gratefully acknowledge to Dérig Implants (Barueri, SP, Brazil) for providing the implants and components for the study; to Dr. AbÃlio Ricciardi Coppedê (Dérig Implants - Barueri, SP, Brazil) for technical support; and Dr. Yara Teresinha Corrêa Silva Sousa (Department of Dentistry, Ribeirão Preto University, SP, Brazil) for allowing the use of micro computed tomography equipment.
Conflicts of Interest
The authors declare no conflict of interest in relation to this study.
References
- Griggs, J.A. Dental Implants. Dent. Clin. North Am. 2017, 61, 857–871. [Google Scholar] [CrossRef]
- Gaviria, L.; Salcido, J.P.; Guda, T.; Ong, J.L. Current Trends in Dental Implants. J. Korean Assoc. Oral Maxillofac. Surg. 2014, 40, 50. [Google Scholar] [CrossRef] [PubMed]
- Chrcanovic, B.R.; Albrektsson, T.; Wennerberg, A. Reasons for Failures of Oral Implants. J. Oral Rehabil. 2014, 41, 443–476. [Google Scholar] [CrossRef] [PubMed]
- Ryu, H.S.; Namgung, C.; Lee, J.H.; Lim, Y.J. The Influence of Thread Geometry on Implant Osseointegration under Immediate Loading: A Literature Review. J. Adv. Prosthodont. 2014, 6, 547–554. [Google Scholar] [CrossRef] [PubMed]
- Coppedê, A.R.; Faria, A.C.L.; Mattos, M. da G.C. de; Rodrigues, R.C.S.; Shibli, J.A.; Ribeiro, R.F. Mechanical Comparison of Experimental Conical-Head Abutment Screws with Conventional Flat-Head Abutment Screws for External-Hex and Internal Tri-Channel Implant Connections: An In Vitro Evaluation of Loosening Torque. Int. J. Oral Maxillofac. Implants 2013, 28, e321–e329. [Google Scholar] [CrossRef]
- Nary Filho, H.; Calvo Guirado, J.L.; Matsumoto, M.A.; Bresaola, M.D.; Aur, R. Biomechanical Evaluation of Resistance to Insertion Torque of Different Implant Systems and Insertion Driver Types. Implant Dent. 2015, 24, 211–216. [Google Scholar] [CrossRef]
- Santiago, J.F.; De Souza Batista, V.E.; Verri, F.R.; Honório, H.M.; De Mello, C.C.; Almeida, D.A.D.; Pellizzer, E.P. Platform-Switching Implants and Bone Preservation: A Systematic Review and Meta-Analysis. Int. J. Oral Maxillofac. Surg. 2016, 45, 332–345. [Google Scholar] [CrossRef]
- Chrcanovic, B.R.; Albrektsson, T.; Wennerberg, A. Platform Switch and Dental Implants: A Meta-Analysis. J. Dent. 2015, 43, 629–646. [Google Scholar] [CrossRef]
- Salamanca, E.; Lin, J.C.Y.; Tsai, C.Y.; Hsu, Y.S.; Huang, H.M.; Teng, N.C.; Wang, P.D.; Feng, S.W.; Chen, M.S.; Chang, W.J. Dental Implant Surrounding Marginal Bone Level Evaluation: Platform Switching versus Platform Matching - One-Year Retrospective Study. Biomed Res. Int. 2017, 2017, 1–9. [Google Scholar] [CrossRef]
- Cicciù, M.; Cervino, G.; Milone, D.; Risitano, G. FEM Investigation of the Stress Distribution over Mandibular Bone Due to Screwed Overdenture Positioned on Dental Implants. Materials (Basel). 2018, 11. [Google Scholar] [CrossRef]
- Lavorgna, L.; Cervino, G.; Fiorillo, L.; Leo, G. Di; Troiano, G.; Ortensi, M.; Galantucci, L.; Cicci, M. Reliability of a Virtual Prosthodontic Project Realized through a 2D and 3D Photographic Acquisition: An Experimental Study on the Accuracy of Di Ff Erent Digital Systems. 1–15.
- Cicciù, M. Bioengineering Methods of Analysis and Medical Devices: A Current Trends and State of the Art. Materials (Basel). 2020, 13, 14–18. [Google Scholar] [CrossRef]
- Abdelhamed, M.I.; Galley, J.D.; Bailey, M.T.; Johnston, W.M.; Holloway, J.; Mcglumphy, E.; Leblebicioglu, B. A Comparison of Zirconia and Titanium Abutments for Microleakage. Clin. Implant Dent. Relat. Res. 2015, 17, e643–e651. [Google Scholar] [CrossRef] [PubMed]
- Cicciù, M.; Bramanti, E.; Cecchetti, F.; Scappaticci, L.; Guglielmino, E.; Risitano, G. FEM and Von Mises Analyses of Different Dental Implant Shapes for Masticatory Loading Distribution. ORAL Implantol. 2014, 7, 1–10. [Google Scholar] [CrossRef]
- Cicciù, M.; Cervino, G.; Milone, D.; Risitano, G. FEM Analysis of Dental Implant-Abutment Interface Overdenture Components and Parametric Evaluation of Equator® and Locator® Prosthodontics Attachments. Materials (Basel). 2019, 12. [Google Scholar] [CrossRef]
- Scarano, A.; Mortellaro, C.; Mavriqi, L.; Pecci, R.; Valbonetti, L. Evaluation of Microgap with Three-Dimensional x-Ray Microtomography: Internal Hexagon versus Cone Morse. J. Craniofac. Surg. 2016, 27, 682–684. [Google Scholar] [CrossRef]
- Greenstein, G.; Cavallaro, J. Implant Insertion Torque: Its Role in Achieving Primary Stability of Restorable Dental Implants. Compend. Contin. Educ. Dent. 2017, 38, 88–95; quiz 96. [Google Scholar] [PubMed]
- Li, H.; Liang, Y.; Zheng, Q. Meta-Analysis of Correlations Between Marginal Bone Resorption and High Insertion Torque of Dental Implants. Int. J. Oral Maxillofac. Implants 2015, 30, 767–772. [Google Scholar] [CrossRef] [PubMed]
- Cervino, G.; Fiorillo, L.; Arzukanyan, A.V.; Spagnuolo, G.; Campagna, P.; Cicciù, M. Application of Bioengineering Devices for Stress Evaluation in Dentistry: The Last 10 Years FEM Parametric Analysis of Outcomes and Current Trends. Minerva Stomatol. 2020, 69, 55–62. [Google Scholar] [CrossRef]
- Farronato, D.; Pieroni, S.; Mangano, F.G.; Briguglio, F.; Re, D. Effects of Different Abutment Material and Surgical Insertion Torque on the Marginal Adaptation of an Internal Conical Interface: An in Vitro Study. J. Prosthodont. Res. 2014, 58, 230–236. [Google Scholar] [CrossRef]
- Kwon, J.H.; Han, C.H.; Kim, S.J.; Chang, J.S. The Change of Rotational Freedom Following Different Insertion Torques in Three Implant Systems with Implant Driver. J. Adv. Prosthodont. 2009, 1, 37–40. [Google Scholar] [CrossRef]
- Bambini, F.; Memè, L.; Pellecchia, M.; Sabatucci, A.; Selvaggio, R. Comparative Analysis of Deformation of Two Implant/Abutment Connection Systems during Implant Insertion. An in Vitro Study. Minerva Stomatol. 2005, 54, 129–138. [Google Scholar] [PubMed]
- Sotto-Maior, B.S.; Rocha, E.P.; de Almeida, E.O.; Freitas-Júnior, A.C.; Anchieta, R.B.; Del Bel Cury, A.A. Influence of High Insertion Torque on Implant Placement - an Anisotropic Bone Stress Analysis. Braz. Dent. J. 2010, 21, 508–514. [Google Scholar] [CrossRef] [PubMed]
- Maeda, Y.; Satoh, T.; Sogo, M. In Vitro Differences of Stress Concentrations for Internal and External Hex Implant-Abutment Connections: A Short Communication. J. Oral Rehabil. 2006, 33, 75–78. [Google Scholar] [CrossRef] [PubMed]
- Sasada, Y.; Cochran, D. Implant-Abutment Connections: A Review of Biologic Consequences and Peri-Implantitis Implications. Int. J. Oral Maxillofac. Implants 2017, 32, 1296–1307. [Google Scholar] [CrossRef]
- D’Ercole, S.; Scarano, A.; Perrotti, V.; Mulatinho, J.; Piattelli, A.; Iezzi, G.; Tripodi, D. Implants With Internal Hexagon and Conical Implant-Abutment Connections: An In Vitro Study of the Bacterial Contamination. J. Oral Implantol. 2014, 40, 31–36. [Google Scholar] [CrossRef]
- Alqutaibi, A.Y.; Aboalrejal, A.N. Microgap and Micromotion at the Implant Abutment Interface Cause Marginal Bone Loss Around Dental Implant but More Evidence Is Needed. J. Evid. Based. Dent. Pract. 2018, 18, 171–172. [Google Scholar] [CrossRef]
- Gehrke, S.A. lexandr.; Shibli, J.A. wa.; Aramburú Junior, J.S. ard.; de Val, J.E.M. at. S.; Calvo-Girardo, J.L.; Dedavid, B.A. nin. Effects of Different Torque Levels on the Implant-Abutment Interface in a Conical Internal Connection. Braz. Oral Res. 2016, 30, 1–7. [Google Scholar] [CrossRef]
Figure 1.
Platform and diameter sizes for implants used in the study. Black line: platform size; Yellow line: diameter; Red line: bevel showing the difference between platform and diameter sizes). A: 3.5 narrow platform (NP) implant; B: 3.75 NP implant; C: 4.3 NP implant; D: 4.3 regular platform (RP) implant.
Figure 1.
Platform and diameter sizes for implants used in the study. Black line: platform size; Yellow line: diameter; Red line: bevel showing the difference between platform and diameter sizes). A: 3.5 narrow platform (NP) implant; B: 3.75 NP implant; C: 4.3 NP implant; D: 4.3 regular platform (RP) implant.
Figure 2.
Metal cylinder-implant assembly and wrench coupled to the torque machine for the application of the teste insertion torques, according to the study methodology.
Figure 2.
Metal cylinder-implant assembly and wrench coupled to the torque machine for the application of the teste insertion torques, according to the study methodology.
Figure 3.
Representation of linear (two-dimensional) analysis in CT analysis. The reconstructed image (upper left corner) was fixed in the region of interest (ROI) and 10 sections were selected in that region for six measurements (asterisks) on the tri-channel platform.
Figure 3.
Representation of linear (two-dimensional) analysis in CT analysis. The reconstructed image (upper left corner) was fixed in the region of interest (ROI) and 10 sections were selected in that region for six measurements (asterisks) on the tri-channel platform.
Figure 4.
Microtopography images with the drawing of the tri-channel deformation (white area). A, B, C, and D: 3.5 NP, 3.75 NP, 4.3 NP and 4.3 RP new implant groups (control), respectively. A1, B1, C1, and D1: images after 45-Ncm torque. A2, B2, C2, and D2: images after 80 Ncm torque. A3, B3, C3, and D3: images after 120 Ncm torque. A4, B4, C4, and D4: images after 150 Ncm torque.
Figure 4.
Microtopography images with the drawing of the tri-channel deformation (white area). A, B, C, and D: 3.5 NP, 3.75 NP, 4.3 NP and 4.3 RP new implant groups (control), respectively. A1, B1, C1, and D1: images after 45-Ncm torque. A2, B2, C2, and D2: images after 80 Ncm torque. A3, B3, C3, and D3: images after 120 Ncm torque. A4, B4, C4, and D4: images after 150 Ncm torque.
Table 1.
Comparisons of the volume (three-dimensional analysis) among insertion torques and interactions with platform types.
Table 1.
Comparisons of the volume (three-dimensional analysis) among insertion torques and interactions with platform types.
| Comparisons | Estimated difference between means | P-value | Confidence interval | ||
|---|---|---|---|---|---|
| Lower | Upper | ||||
| 45 Ncm | 3.5 NP x 3.75 NP | 4.67 | <.001 | 3.12 | 6.22 |
| 3.5 NP x 4.3 NP | -0.10 | <.001 | 12.05 | 15.16 | |
| 3.5 NP x 4.3 RP | 2.67 | <.001 | 12.91 | 16.02 | |
| 3.75 NP x 4.3 NP | 13.30 | <.001 | 7.42 | 10.46 | |
| 3.75 NP x 4.3 RP | 13.61 | <.001 | 8.28 | 11.31 | |
| 4.3 NP x 4.3 RP | 19.52 | 0.270 | -0.66 | 2.37 | |
| 80 Ncm | 3.5 NP x 3.75 NP | 32.12 | 0.897 | -1.62 | 1.42 |
| 3.5 NP x 4.3 NP | 46.58 | <.001 | 18.00 | 21.03 | |
| 3.5 NP x 4.3 RP | 14.46 | <.001 | 21.00 | 24.03 | |
| 3.75 NP x 4.3 NP | 22.51 | <.001 | 18.10 | 21.13 | |
| 3.75 NP x 4.3 RP | 37.67 | <.001 | 21.10 | 24.13 | |
| 4.3 NP x 4.3 RP | 57.49 | 0.000 | 1.48 | 4.51 | |
| 120 Ncm | 3.5 NP x 3.75 NP | 8.94 | 0.001 | 1.15 | 4.18 |
| 3.5 NP x 4.3 NP | 19.62 | <.001 | 30.61 | 33.64 | |
| 3.5 NP x 4.3 RP | 29.45 | <.001 | 36.16 | 39.19 | |
| 3.75 NP x 4.3 NP | 33.29 | <.001 | 27.94 | 30.97 | |
| 3.75 NP x 4.3 RP | 9.80 | <.001 | 33.49 | 36.52 | |
| 4.3 NP x 4.3 RP | 22.61 | <.001 | 4.04 | 7.07 | |
| 150 Ncm | 3.5 NP x 3.75 NP | 35.01 | <.001 | 11.78 | 14.81 |
| 3.5 NP x 4.3 NP | 44.19 | <.001 | 45.07 | 48.10 | |
| 3.5 NP x 4.3 RP | 0.86 | <.001 | 55.98 | 59.01 | |
| 3.75 NP x 4.3 NP | 2.30 | <.001 | 31.77 | 34.80 | |
| 3.75 NP x 4.3 RP | 5.55 | <.001 | 42.69 | 45.71 | |
| 4.3 NP x 4.3 RP | 10.91 | <.001 | 9.39 | 12.42 | |
Table 2.
Comparisons of the volume (three-dimensional analysis) among platforms and interactions with insertion torques.
Table 2.
Comparisons of the volume (three-dimensional analysis) among platforms and interactions with insertion torques.
| Comparisons | Estimated difference between means | P-value | Confidence interval | ||
|---|---|---|---|---|---|
| Lower | Upper | ||||
| 3.5 NP | 45 N x 80 N | -8.53 | <.001 | -10.09 | -6.97 |
| 45 N x 120 N | -24.72 | <.001 | -26.28 | -23.17 | |
| 45 N x 150 N | -45.77 | <.001 | -47.32 | -44.21 | |
| 80 N x 120 N | -16.19 | <.001 | -17.71 | -14.68 | |
| 80 N x 150 N | -37.24 | <.001 | -38.75 | -35.72 | |
| 120 N x 150 N | -21.04 | <.001 | -22.56 | -19.53 | |
| 3.75 NP | 45 N x 80 N | -13.30 | <.001 | -14.81 | -11.781 |
| 45 N x 120 N | -26.72 | <.001 | -28.24 | -25.21 | |
| 45 N x 150 N | -37.14 | <.001 | -38.65 | -35.62 | |
| 80 N x 120 N | -13.43 | <.001 | -14.94 | -11.91 | |
| 80 N x 150 N | -23.84 | <.001 | -25.35 | -22.32 | |
| 120 N x 150 N | -10.41 | <.001 | -11.93 | -8.90 | |
| 4.3 NP | 45 N x 80 N | -2.62 | 0.001 | -4.14 | -1.10 |
| 45 N x 120 N | -6.21 | <.001 | -7.72 | -4.69 | |
| 45 N x 150 N | -12.79 | <.001 | -14.31 | -11.27 | |
| 80 N x 120 N | -3.59 | <.001 | -5.10 | -2.07 | |
| 80 N x 150 N | -10.17 | <.001 | -11.69 | -8.65 | |
| 120 N x 150 N | -6.58 | <.001 | -8.10 | -5.06 | |
| 4.3 RP | 45 N x 80 N | -0.48 | 0.53 | -2.00 | 1.03 |
| 45 N x 120 N | -1.51 | 0.05 | -3.03 | 0.00 | |
| 45 N x 150 N | -2.74 | 0.00 | -4.26 | -1.22 | |
| 80 N x 120 N | -1.03 | 0.18 | -2.55 | 0.49 | |
| 80 N x 150 N | -2.26 | 0.00 | -3.77 | -0.74 | |
| 120 N x 150 N | -1.23 | 0.11 | -2.74 | 0.29 | |
Table 3.
Comparisons of the linear measure (two-dimensional analysis) among insertion torques and interactions with platform types.
Table 3.
Comparisons of the linear measure (two-dimensional analysis) among insertion torques and interactions with platform types.
| Comparisons | Estimated difference between means | P-value | Confidence interval | ||
|---|---|---|---|---|---|
| Lower | Upper | ||||
| 45 N | 3.5 NP x 3.75 NP | -5.76 | <.001 | -7.98 | -3.55 |
| 3.5 NP x 4.3 NP | 3.55 | 0.002 | 1.33 | 5.77 | |
| 3.5 NP x 4.3 RP | -8.13 | <.001 | -10.34 | -5.91 | |
| 3.75 NP x 4.3 NP | 9.31 | <.001 | 7.10 | 11.53 | |
| 3.75 NP x 4.3 RP | -2.36 | 0.036 | -4.57 | -0.15 | |
| 4.3 NP x 4.3 RP | -11.68 | <.001 | -13.89 | -9.46 | |
| 80 N | 3.5 NP x 3.75 NP | -5.77 | <.001 | -7.98 | -3.55 |
| 3.5 NP x 4.3 NP | 4.43 | <.001 | 2.22 | 6.64 | |
| 3.5 NP x 4.3 RP | -6.859 | <.001 | -9.07 | -4.64 | |
| 3.75 NP x 4.3 NP | 10.20 | <.001 | 7.98 | 12.41 | |
| 3.75 NP x 4.3 RP | -1.09 | 0.333 | -3.30 | 1.12 | |
| 4.3 NP x 4.3 RP | -11.29 | <.001 | -13.89 | -9.08 | |
| 120 N | 3.5 NP x 3.75 NP | -5.94 | <.001 | -8.16 | -3.73 |
| 3.5 NP x 4.3 NP | 4.46 | <.001 | 2.24 | 6.67 | |
| 3.5 NP x 4.3 RP | -1.35 | 0.233 | -3.56 | 0.87 | |
| 3.75 NP x 4.3 NP | 10.40 | <.001 | 8.19 | 12.61 | |
| 3.75 NP x 4.3 RP | 4.59 | <.001 | 2.38 | 6.81 | |
| 4.3 NP x 4.3 RP | -5.80 | <.001 | -8.02 | -3.59 | |
| 150 N | 3.5 NP x 3.75 NP | -2.87 | 0.011 | -5.08 | -0.66 |
| 3.5 NP x 4.3 NP | 8.25 | <.001 | 6.04 | 10.47 | |
| 3.5 NP x 4.3 RP | 4.05 | 0.003 | 1.84 | 6.26 | |
| 3.75 NP x 4.3 NP | 11.12 | <.001 | 8.91 | 13.34 | |
| 3.75 NP x 4.3 RP | 6.92 | <.001 | 4.71 | 9.18 | |
| 4.3 NP x 4.3 RP | -4.20 | 0.002 | -6.42 | -1.99 | |
Table 4.
Comparisons of the linear measure (two-dimensional analysis) among insertion torques and interactions with platform types.
Table 4.
Comparisons of the linear measure (two-dimensional analysis) among insertion torques and interactions with platform types.
| Comparisons | Estimated difference between means | P-value | Confidence interval | ||
|---|---|---|---|---|---|
| Lower | Upper | ||||
| 3.5 NP | 45 N x 80 N | -1.31 | 0.242 | -3.49 | 0.88 |
| 45 N x 120 N | -6.91 | <.001 | -9.09 | -4.72 | |
| 45 N x 150 N | -12.49 | <.001 | -14.67 | -10.30 | |
| 80 N x 120 N | -5.60 | <.001 | -14.67 | -10.30 | |
| 80 N x 150 N | -11.18 | <.001 | -13.36 | -8.99 | |
| 120 N x 150 N | -5.58 | <.001 | -7.76 | -3.39 | |
| 3.75 NP | 45 N x 80 N | -1.31 | 0.240 | -3.49 | 0.87 |
| 45 N x 120 N | -7.08 | <.001 | -9.27 | -4.90 | |
| 45 N x 150 N | -9.59 | <.001 | -11.78 | -7.41 | |
| 80 N x 120 N | -5.77 | <.001 | -7.96 | -3.59 | |
| 80 N x 150 N | -8.28 | <.001 | -10.47 | -6.10 | |
| 120 N x 150 N | -2.50 | 0.025 | -4.69 | -0.32 | |
| 4.3 NP | 45 N x 80 N | -0.42 | 0.703 | -2.61 | 1.76 |
| 45 N x 120 N | -6.00 | <.001 | -8.18 | -3.81 | |
| 45 N x 150 N | -7.78 | <.001 | -9.97 | -5.60 | |
| 80 N x 120 N | -5.57 | <.001 | -7.76 | -3.39 | |
| 80 N x 150 N | -7.36 | <.001 | -9.54 | -5.17 | |
| 120 N x 150 N | -1.78 | 0.110 | -3.97 | 0.40 | |
| 4.3 RP | 45 N x 80 N | -0.04 | 0.972 | -2.22 | 2.15 |
| 45 N x 120 N | -0.13 | 0.909 | -2.31 | 2.06 | |
| 45 N x 150 N | -0.31 | 0.782 | -2.49 | 1.88 | |
| 80 N x 120 N | -0.09 | 0.937 | -2.27 | 2.10 | |
| 80 N x 150 N | -0.27 | 0.809 | -2.45 | 1.91 | |
| 120 N x 150 N | -0.18 | 0.871 | -2.37 | 2.00 | |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.
MDPI Initiatives
Important Links
© 2024 MDPI (Basel, Switzerland) unless otherwise stated