A Calibration Study With CFD Methodology for Self-propulsion Simulations at Ship Scale

Preprint

Article

A Calibration Study With CFD Methodology for Self-propulsion Simulations at Ship Scale

Altmetrics

Downloads

112

Views

Comments

A peer-reviewed article of this preprint also exists.

Vladimir Krasilnikov^*,

Vegard Slettahjell Skjefstad^*,

Kourosh Koushan

,Hans Jørgen Rambech

Vladimir Krasilnikov^*,

Vegard Slettahjell Skjefstad^*,

Kourosh Koushan

,Hans Jørgen Rambech

This version is not peer-reviewed

Submitted:

14 June 2023

Posted:

15 June 2023

You are already at the latest version

Alerts

Abstract

This paper summaries the main findings from the full-scale CFD analyses conducted at SINTEF Ocean on the case of MV REGAL, which is one of the benchmark vessels studied in the ongoing joint industry project JoRes. The numerical approach is described in detail, and comparative results are presented regarding the propeller open water characteristics, ship towing resistance, and ship self-propulsion performance. The focus of numerical investigations is on the assessment of the existing simulation best practices applied to a ship scale case in a blind simulation exercise, and performance of thereof with different turbulence modelling methods. The results are compared directly with full-scale performance predictions based on model tests conducted at SINTEF Ocean and sea trails data obtained in the JoRes project.

Keywords:

Subject: Engineering - Marine Engineering

1. Introduction

Model testing has been and still is the dominant method to predict propulsion performance of ships. However, the methods of Computational Fluid Dynamics (CFD) are more and more frequently used for the same purpose, and they are also becoming an integral part of ship design process. The greatest advantage of CFD is the possibility to perform predictions directly at full scale and thereby reduce uncertainties related to the influence of Reynolds number (known as scale effect). Numerical simulations are performed in a strictly controlled environment, and are therefore characterized by high repeatability. They can be conducted in a time- and cost-effective manner, especially when the best practices are established, and automated templates are developed. Considering the increasing importance of numerical simulations in both the research and industrial settings, from as early as 2011, ITTC are developing and continuously updating the recommended procedures and guidelines for CFD analysis of ship performance [1] with specific sections addressing resistance and flow, propulsion, manoeuvrability, as well as uncertainty analysis and quality assurance. The recent IMO Resolutions MEPC.350(78) and MEPC.351(78) consider numerical calculations as an acceptable way to derive ship’s performance in the EEXI regulatory framework [2]. To this end, the International Association of Classification Societies (IACS) have proposed the dedicated guidelines regarding the definition of the reference speed used to forecast from CFD simulations the impact of an energy efficiency technology applied on a ship [3]. The said guidelines include, among other things, the three optional approaches to perform calibration of a CFD method used for speed/power prediction: 1-Calibrated CFD with sea trials or model tests of parent hull; 2-Calibrated CFD with model test of similar ship; 3-Calibrated CFD with sea trials of a set of comparable ships. It is generally assumed that the calibration factor, which is defined as the ratio between the shaft delivered power found from sea trails (or model test prognosis) and the same quantity found from a CFD calculation, should lie between 0.95 and 1.05 to be accepted by a verifier without further technical justification. At the same time, it is understood that successful calibration alone does not necessarily mean that the CFD method in question solves correctly the governing equations of the problem, and that it accurately represents physical phenomena significant to the problem solution. The classical example is given by the RANS method which normally shows sufficient accuracy in prediction of ship resistance and propulsion characteristics, but reveals limitation in the analysis of propeller cavitation in the wake behind ship hull and associated pressure pulses on the hull and radiated noise [4]. To answer the latter questions, verification and validation procedures need to be employed on a systematic basis, following formal procedures for the analysis of errors and uncertainties [5].

In public domain, the experimental material on ship propulsion available for verification, validation and calibration exercises has largely been limited to the results of models tests with such benchmark ship cases as KCS, KVLCC1, KVLCC2, JBC, DTMB5415 and DTC, see for example the proceedings of the CFD Workshops in Ship Hydrodynamics held in Gothenburg (2010) [6] and Tokyo (2015) [7]. More recently, new benchmark datasets have emerged dealing with contemporary designs of next generation ships such as for example SOBC-1 by SINTEF Ocean [8]. A “blind” comparison of CFD predictions with sea trials data in full-scale has been addressed in the 2016 Workshop on Ship Scale Hydrodynamic Computer Simulation for the case of the general cargo vessel MV REGAL [9]. Presently, the same ship is also used in the ongoing project JoRes [10] where SINTEF Ocean contribute with both the model tests and CFD simulations. The findings from the referred works highlight that numerical results often appear sensitive to how the CFD model is constructed, especially computation grid, near-wall treatment, surface roughness model, boundary conditions and turbulence modelling approach. Representative examples of the scatter found in practical full-scale predictions are documented in [9]. To improve predictive capabilities of CFD methods and increase confidence in numerical prognoses, calibration and validation of CFD methods against model tests and sea-trials data need to be continued. Such an effort is also seen as an important step in the direction of better understanding of the physics behind the effect of Reynolds number and elaboration of scaling procedures employed by testing facilities.

In the present study, the open benchmark dataset of the vessel MV REGAL shown in Figure 1 is chosen by the authors to assess the accuracy of their current CFD simulation practices and study the influence of different turbulence modelling approaches for ship resistance, propeller open water, and ship self-propulsion calculations.

The range of turbulence modelling approaches includes conventional Reynolds-averaged Navier-Stokes (RANS) method and Scale-Resolving Simulation (SRS) techniques such as Detached Eddy Simulation (DES) and Large Eddy Simulation (LES). The LES results are only provided for the case of propeller in open water. All simulations are performed in full-scale conditions. The results of resistance and open water calculations are compared with the predictions using SINTEF Ocean’s scaling procedure based on the results of model tests. The results of self-propulsion simulations are compared with both the performance predictions and full-scale trials in terms of propeller RPM and shaft delivered power at ship self-propulsion points for several speeds. In addition, cavitation patterns on propeller blades are visually compared with full-scale observations on cavitation for selected conditions. Due to the restrictions regarding the data distribution which currently apply in the JoRes Consortium, most of the comparisons are presented in the form of relative differences and as plots without scale. Finally, it has to be noted that all CFD results have been produced in spring of 2021 by running “blind” simulations and following SINTEF Ocean’s modelling best practices, before either sea trials data or model test results have become available. This places the present study in the category of CFD calibration exercise, whereas the employed simulations templates have been subject to earlier verification and validation studies using both the open access data and SINTEF Ocean internal datasets.

2. Research Methodology

For the numerical simulations conducted in the present study the commercial CFD software STAR-CCM+ (version 15.06.007-R8) was employed. Trimmed hexahedral mesher with prism layers on the wall boundaries was used in all the main types of simulations (towing resistance, propeller in open water and ship self-propulsion calculations) as well as additional simulations with flat plate which were used to assess the influence of surface roughness height. All simulations, except for the flat plate calculations, were carried out in a time-dependent manner, using the implicit unsteady segregated flow solver. Simulations involving rotating propeller (open water, and self-propulsion) were performed using the Sliding Mesh technique to fully account for the interaction between the rotating and stationary components in the setup. Water and air properties applied in the simulations were derived from values recorded during the sea-trials of MV REGAL. Simulations were performed for full-scale conditions corresponding to sea trials, as specified in the case description for the JoRes CFD Workshop regarding the MV REGAL vessel [11]. Three ship speeds (9, 10.5 and 12 knots) were subject to investigation in the resistance and self-propulsion scenarios, while in the open water case, the advance coefficient (J) values of 0.2, 0.3, 0.4, 0.5 and 0.6 were used. The case specific details of numerical setups are addressed below for each individual simulation scenario.

Separately, as a part of the JoRes project SINTEF Ocean have conducted a model test campaign with the MV REGAL vessel, comprising towing resistance, open water and propulsion tests in calm water, at the scale of 1:23.111. The results of model tests were used in full-scale performance prediction for the sea trial conditions, following the standard procedure applied at SINTEF Ocean to single-screw ships [12]. The results of performance prediction were compared against the sea-trials data post-processed according to the ISO15016 standard [13] and CFD calculations in full-scale in terms of propeller RPM and propeller shaft power, P_D. Additional comparisons were made between the CFD calculations and model test results extrapolated to full-scale conditions in terms of towing resistance of the ship, its dynamic position, and propeller characteristics in open water.

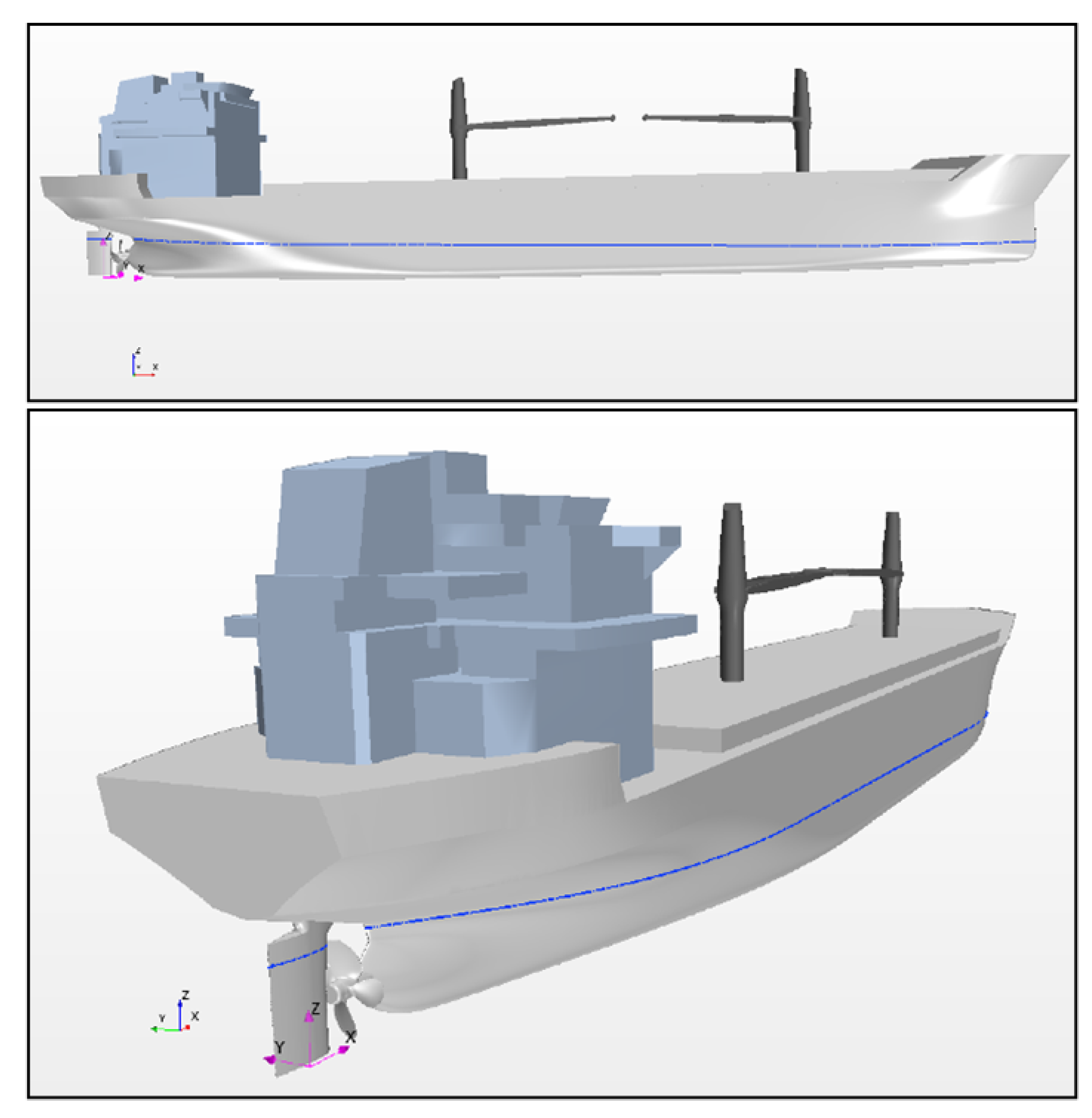
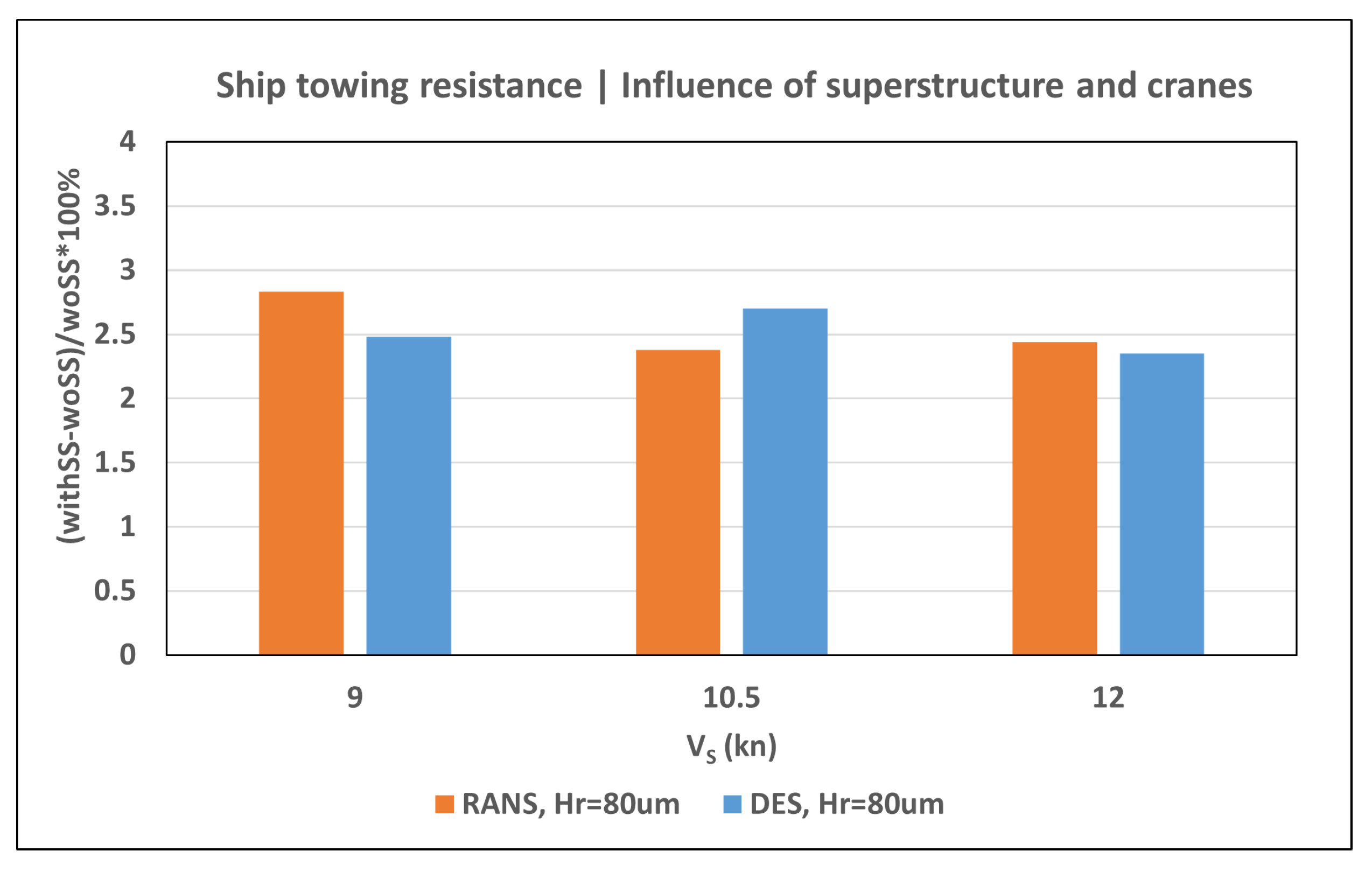
MV REGAL is a single-screw general cargo vessel having the length between perpendiculars LPP = 138 m, breadth B = 23 m, and gross tonnage 11542 t. It is equipped with a 4-bladed fixed pitch propeller having the diameter D = 5.2 m, pitch ratio P(0.7)/D = 0.6781, and blade area ratio Ae/Ao = 0.57. The ship features a semi-balanced rudder with fixed horn. The main particulars of the MV REGAL vessel, its propeller and rudder arrangements can be found in [9,11]. It needs to be remarked that the geometries provided for the JoRes CFD Workshop are different from those used in the earlier Lloyd’s Register Workshop organized in 2016 on the same ship case. While the 2016 Workshop used the STL models of ship hull, propeller and rudder derived from the 3D laser scan data, the present JoRes geometries were provided as clean solids which were prepared using both the reconstructed 3D laser scan data and original documentation and drawings. Further, such constructive features as bilge keels and protective anodes installed on the ship hull and rudder were removed from the CFD model, and no respective corrections were applied in the performance prediction based on model tests. The ship does not have tunnel thrusters. The approximate geometry models of the superstructure, deck hatches and coamings, and the two cranes on the deck were included in the resistance and self-propulsion CFD simulations to account for aerodynamic resistance of the ship in a more accurate manner. The initial hydrostatic position of the ship was set according to the draft measurements before the JoRes sea trials, resulting in the draught values at the fore and aft marks of 2.97 m and 5.865 m, respectively, which corresponds to ballast condition. The presence of hull sagging, hogging and list are disregarded in the draught measurements. The general view of MV REGAL self-propulsion simulation setup is shown in Figure 2.

2.1. Open water propeller simulations

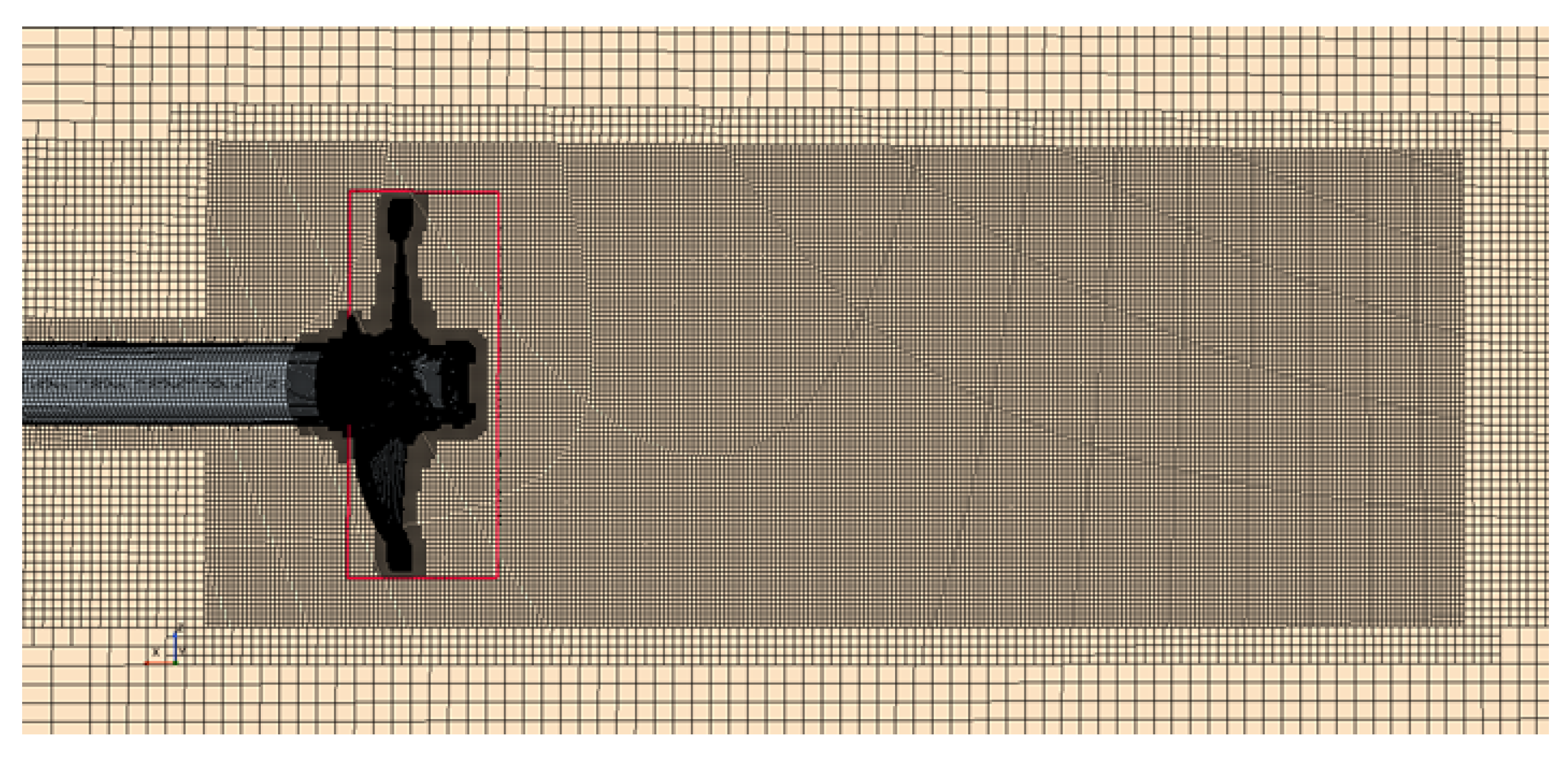
The open water simulations were performed in full scale using the same propeller setup as in self-propulsion conditions. It means that, unlike conventional open water model test setup, the propeller is driven not from downstream but from upstream, thus operating in pushing mode as behind ship hull in the propulsion setup, and also having the same hub cap. This setup is illustrated in Figure 3, which also gives appreciation of overall mesh refinement pattern around the propeller.

The cylindrical rotating propeller region used in Sliding Mesh calculation has the dimensions 0.125D (upstream), 0.288D (downstream) and 0.5385D (radius), as measured from propeller plane, where D is the propeller diameter. Such dimensions are smaller than normally applied in the SINTEF Ocean standard open water CFD setup, since in the self-propulsion case studied in this work, the propeller region had to be fit in a quite tight space between the ship hull and rudder, as it can be seen in Figure 2. The rationale was then to use the same region dimensions in open water calculations to avoid the influence of region size when deriving propulsion factors. The respective dimensions of the main fluid region (also cylindrical in this case) were 5D (inlet), 15D (outlet), and 5D (radius), as measured from propeller center. Additional simulations were performed to assess the influence of the downstream extension of the sliding mesh region on propeller open water characteristics and quality of resolution of propeller slipstream.

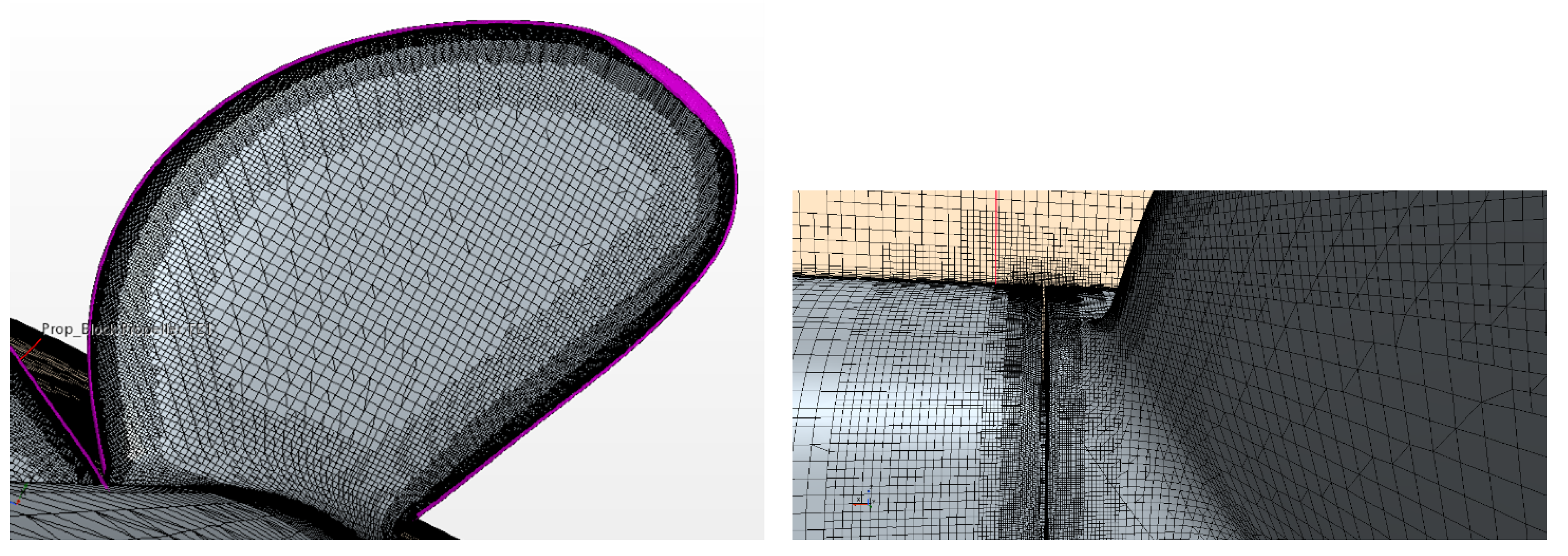
The cell size in the propeller region and the first (finest) volumetric control around the propeller and slipstream (seen in Figure 3) was set to 1.3 % of the base size which was equal to propeller diameter, D. The said volumetric control extends to the distance of 3D downstream. On the propeller blades, the maximum target cell size equals to 0.65 % of base, and it is reduced to the minimum size of 0.0203125 % of base at the blade edges and tip. The edge and tip refinements are achieved using the surface patches extracted from the initial CAD geometry of propeller, as shown in Figure 4. In absence of such patches, similar refinement can be achieved by means of volumetric controls in the shape of a tube following the leading edge feature curve, which is usually easy to extract from blade surface wireframe. The propeller model included a gap between the rotating propeller hub and stationary shaft, which had the size of 17 mm, exactly as in the self-propulsion setup. The inclusion of hub gap in the numerical model allows to compute forces acting on the propeller more accurately by avoiding the uncertainty related to the integration of pressure on the side of propeller hub facing the shaft. The total number of cells in the open water setup was 22.1 million cells, of which 18.6 million cells were accommodated in the propeller region.

Figure 5 illustrates the arrangement of prism layers on propeller blades. The prism layer mesh consists of 10 layers. The height of the first near-wall cell is chosen to target the average Wall Y+ around 60 in the middle part of the blade, thus implying the use of wall functions, for the reasons of computational efficiency and inclusion of surface roughness. The total thickness of prism layers is 0.235 % of propeller diameter. The present settings result in the layer stretch factor about 1.35 and Wall Y+ distribution shown in Figure 6. With a coarse near-wall mesh, one cannot achieve a uniform distribution of Y+ over the whole blade, but as it can be seen, the applied settings provide a favorable Y+ range between 30 and 100, avoiding buffer zone everywhere except the gap and hub vortex separation area. The same Y+ range on propeller is also met at other advance coefficients and in self-propulsion calculations.

In the open water scenario, several turbulence modelling approaches were subject to investigation. These included: (i) the traditional unsteady RANS method using the k-

ω

SST model with linear constitutive relation [14]; (ii) the Improved Delayed Detached Eddy Simulation (IDDES) method [15] where the subgrid length-scale includes a dependence on the wall distance and therefore allows the RANS part of the solution to be used in the thin near-wall region where the wall distance is smaller than the boundary layer thickness. The DES formulation with the k-

ω

SST turbulence model in the RANS zones was used [16]; (iii) Large Eddy Simulation (LES) method with the Smagorinsky Subgrid Scale model [17] and Modified Van Driest damping function [18]; (iv) Scale-Resolving Hybrid (SRH) turbulence model [19] which is a continuous hybrid RANS-LES technique that switches continuously (unlike the DES method) from the RANS model to LES model when the mesh resolution is fine and the time step is small. Similar to the DES solution, the SRH method was applied with the k-

ω

SST model in the RANS part of the solution. Open water calculations were conducted with both the smooth and rough propeller surfaces. The influence of surface roughness was accounted for by using roughness-modified wall functions which move the log layer of the inner part of the boundary layer closer to the wall. Mathematically, it is achieved by means of a roughness function [20] that modifies the log law offset coefficient depending on the equivalent sand-grain roughness height, viscosity and velocity scale. The influence of roughness was investigated only with the RANS and DES method, assuming the two values of roughness height; 8.68 µm resulting from the JoRes propeller surface roughness measurements, and 30.0 µm which is a standard value of sand-grain roughness used at SINTEF Ocean in CFD calculation on older ship propellers in-service that have been subject to cleaning and polishing before trials.

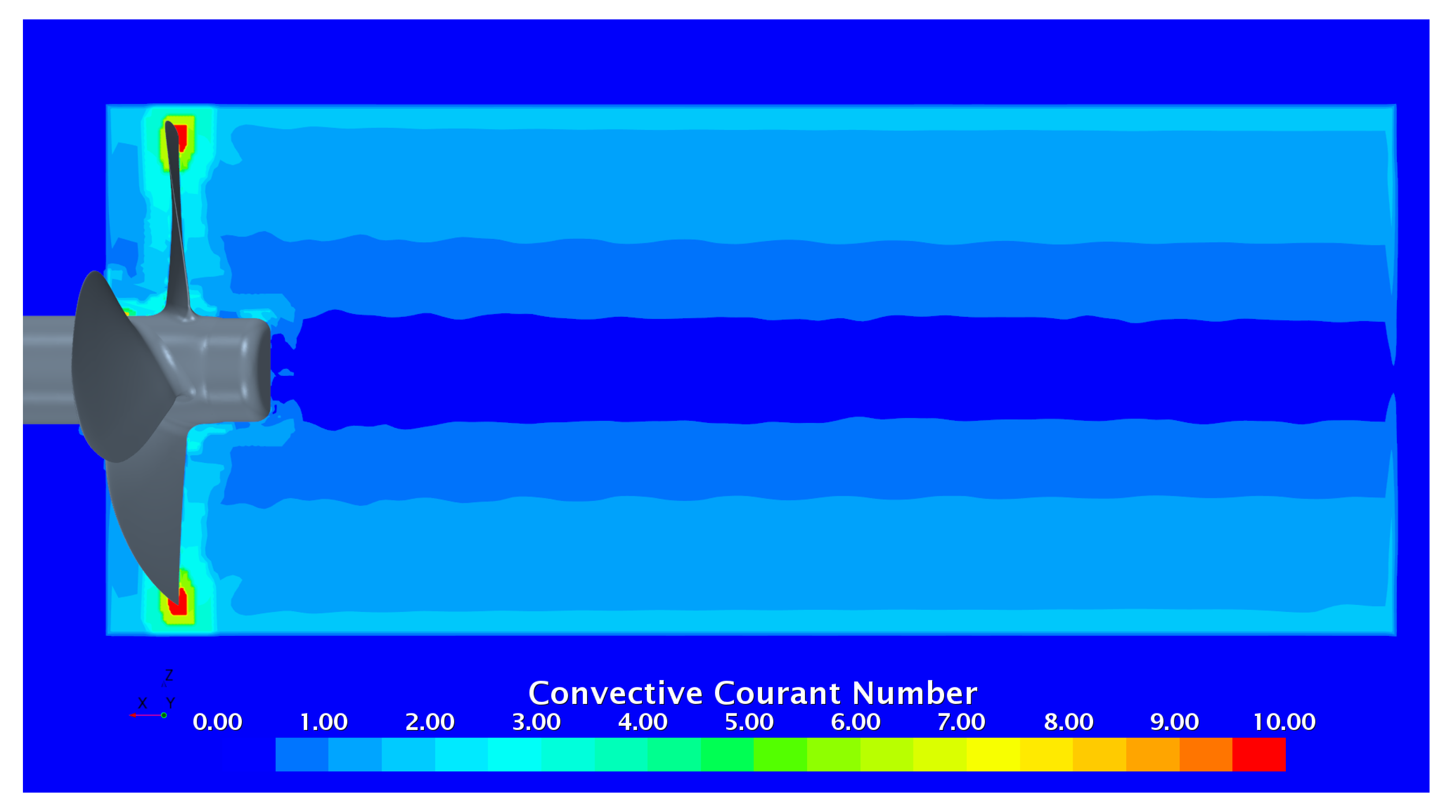
The time-accurate solution is achieved by rotating the sliding mesh region (propeller region) about the shaft axis for a certain angular step. The time step corresponding to 2 deg of propeller rotation was applied in both the open water and self-propulsion calculation, which in authors’ experience is sufficient in most practical cases. However, an additional test with the step of 1 deg was made to assess the sensitivity of the LES and SRH models to time step. Representative levels of Courant number obtained with the time step of 2 deg are shown in Figure 7. Reduction of time step to 1 deg lowers the Courant number by the factor of 2.

The open water simulations were performed using the multi-phase flow formulation with the Volume of Fluid (VOF) model, like in self-propulsion calculations, but with the reference pressure set to atmospheric conditions to prevent occurrence of cavitation.

2.2. Hull resistance simulations

The resistance simulations were performed in full scale for the geometry model consisting of the ship’s hull, rudder, and propeller hub. The calculation matrix included both the cases with and without superstructure and cranes to evaluate the influence of the said on-deck features on the resistance of the ship and its dynamic position. The initial hydrostatic position for the resistance simulations was the same as in the self-propulsion case, and it corresponded to the draught marks provided by JoRes as specified above. The dimensions of the rectangular computation domain were assigned according to the existing practices to minimize the influence of the outer boundaries on the quality of numerical solution: 4LPP in X (inlet and outlet) / Y (side boundaries) directions from the ship’s aft perpendicular/center plane, 2LPP in Z direction to the bottom boundary, and 1LPP in Z direction to the top boundary, from base. As an additional measure to mitigate wave reflections, VOF Damping method described in [21] was employed with the damping zone extending to the distance of 2LPP from the inlet, outlet and side boundaries. The resistance simulations were performed using the full hull model.

The Trimmer hexahedral mesh used in the resistance case was built to provide the refinement in the vicinity of free surface equal to 0.1 % of LPP in Z direction. In the bow and stern regions, this is also the size of isotropic cells around the hull. In the mid-ship area, the cells are anisotropic, their aspect ratio varying from 2 to 4. Conventional Kelvin’s wake refinement controls were used to capture the wave systems generated by the ship. Figure 8 and Figure 9 give illustrations of the mesh around ship hull with superstructure and cranes, and in the area of free surface.

Additional mesh refinement controls are placed around the location of propeller and rudder to provide the refinement level sufficient to capture the salient features of separated hull wake. In this area, the refinement pattern is isotropic, and the cell size equals to 1.35 % of propeller diameter – the same size as applied in the propeller slipstream in open water and self-propulsion calculations.

The prism layer mesh on the hull is constructed of 16 layers, where the height of the first near-wall cell is chosen to target average Wall Y+ about 130 on the hull and 50 on the rudder. The total boundary layer thickness is chosen from the considerations of stretch factor (varies between 1.30 and 1.35) and reasonably smooth transition to the core mesh, which is particularly relevant in the stern area. 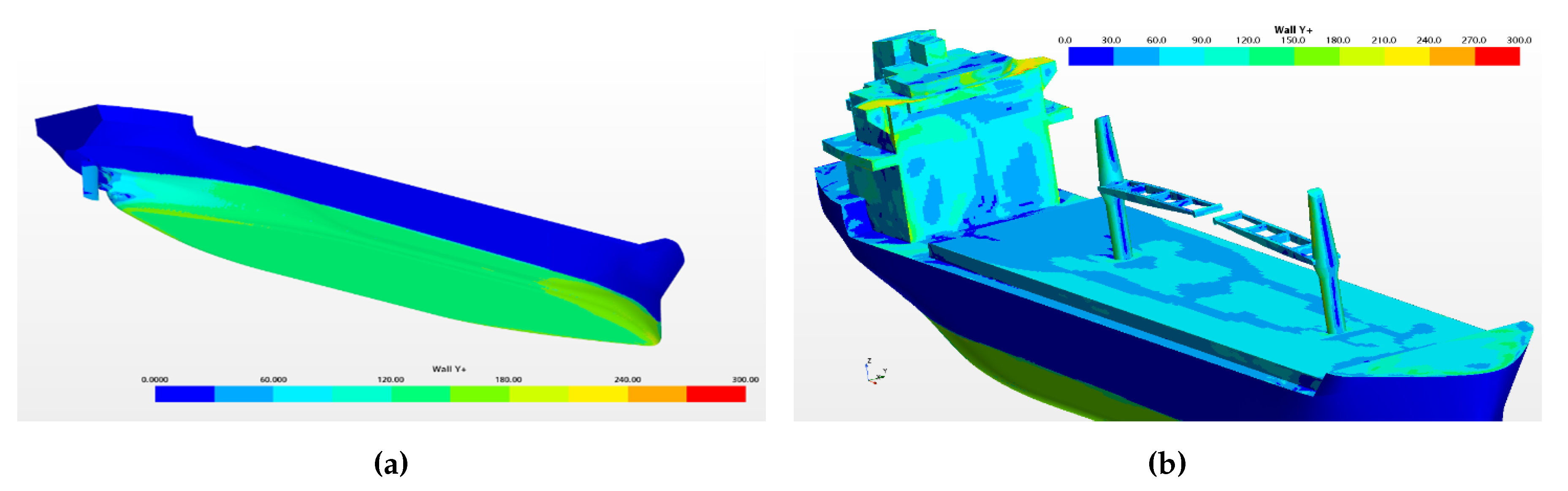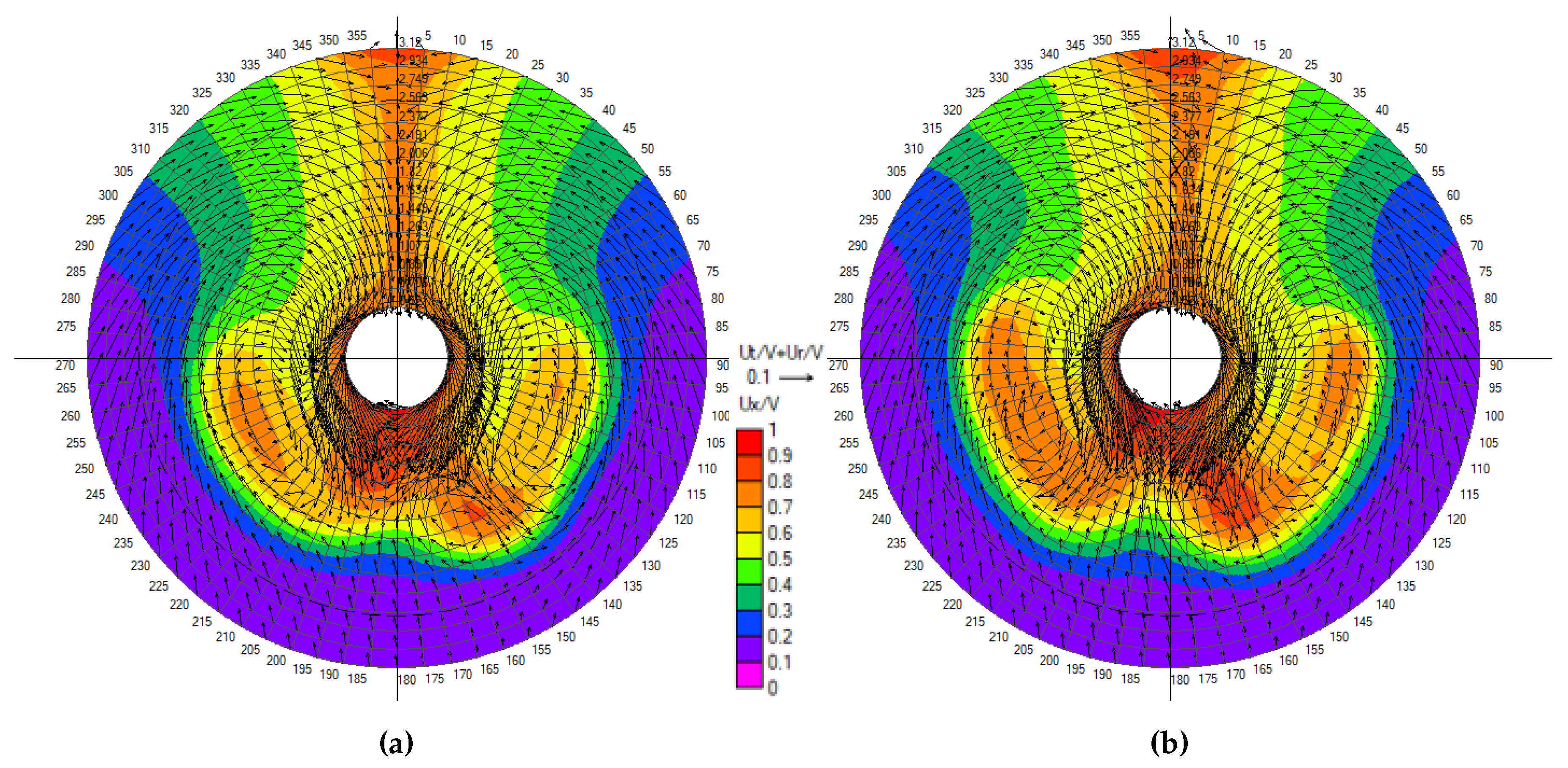A typical distribution of Wall Y+ on the ship is presented in Figure 10a. Like in the case of propeller, it is impossible to provide a uniform distribution of Y+, but its values are kept above the buffer region (i.e., above 30) everywhere expect the flow separation zones.

The number of prism layers on the deck, superstructure and cranes is reduced to 6. Since these parts are subject to intensive separation of the air flow with multiple stall areas, the Y+ varies significantly. However, the range of Y+ between 30 and 240 is well preserved, as shown in Figure 10b. The total number of cells in the present resistance setup was 15.8 million, a higher cell count than commonly used in routine resistance calculations, which is mainly due to the inclusion of the on-deck features and finer resolution of propulsor area.

The numerical solution for the free surface is obtained using the VOF method with Flat VOF Wave model and the blended High-Resolution Interface Capturing (HRIC) scheme [22]. The Courant number limits in the blended HRIC scheme are set to high values (Co_l = 200 and Co_u = 250) to ensure that the HRIC is used irrespective of the time step. These settings mitigate solution dependency on chosen time step, which is essential when processing the results of resistance and self-propulsion calculations to, for example, derive thrust deduction factor. 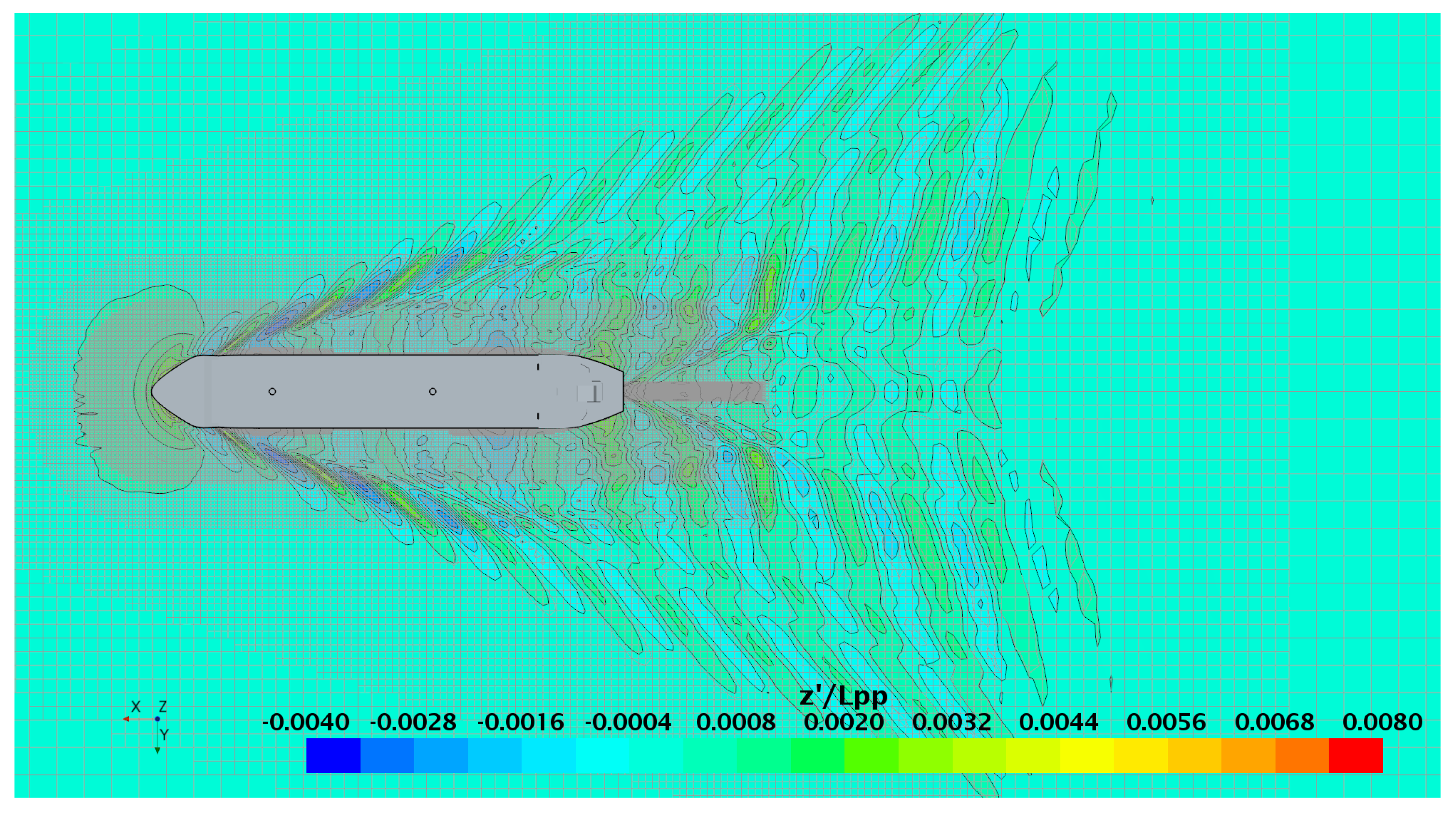A representative distribution of Courant number around the ship observed in the present resistance simulations is shown in Figure 11.

The Courant number is below 2.0 for the greatest part of the domain, and it is elevated to 7.0 - 8.0 in the areas of generation of ship’s bow and stern wave systems, and to 9.0 - 10.0 in the area where the stern wave interacts with rudder. These higher values of Courant number are the natural result of high induced velocities and finer mesh size in the mentioned areas. In propulsion simulations, due to the small time step (

Δ

t ∼ 2 deg), the Courant number is well below 1.0 everywhere. Special tests were carried out to verify that the mentioned differences in Courant number have little, if any, impact on the computed ship resistance. The Dynamic Fluid-Body Interaction (DFBI) model with two degrees of freedom in heave and pitch was used to solve the hydrodynamic position of the ship. The DFBI solver was applied to the whole domain. The Equilibrium body motion option was chosen to accelerate convergence towards the sought steady-state solution. On a caution side it needs to be noted that, depending on the case, the equilibrium solution may lead to large variations in body’s position at the intermediate time steps and introduce disturbances which exist in the numerical solution for a long time. This effect is particularly noticeable in the DFBI solutions conducted without mesh morphing.

The studies regarding the turbulence model were primarily focused on two solutions: the RANS method with the k-

ω

SST model, and the IDDES method with the k-

ω

SST model in the RANS domain. Preliminary studies on the case without superstructure also included the LES method which was found to provide good prognosis of total resistance of the smooth hull, but larger discrepancies with the RANS and DES solutions in terms of pressure and viscous resistance components. Besides, the LES model is not applicable with rough surfaces, which limits its use in the present case where the influence of hull roughness is essential. The results obtained with the SRH model reveal dependency on time step, since as the time step decreases, a larger part of the solution is treated by LES, and eventually when the time step is small (as in the self-propulsion case) the SRH solution is found equivalent to that of LES.

Assigning appropriate value of sand-grain roughness on ship hull required separate investigations. Surface roughness of 3.244 mm was initially provided in the JoRes case description from measurements on the hull using an underwater roughness scanner. One can hypothesize that such a high value is caused by two main factors: vessel age and quality of underwater hull cleaning. Further, the available photos of the hull surface revealed numerous patches, pits and bumps. These imperfections may be regarded as a macro-scale roughness that measures in mm rather than µm. At a later stage, JoRes provided another estimation of hull roughness using an alternative approach and resulting in the value of 440 µm. Converting the measured value of technical averaged hull roughness (AHR) to the equivalent sand-grain roughness height used in the wall functions is not straightforward. Therefore, the value of this parameter was derived from additional calculations with a flat plate model.

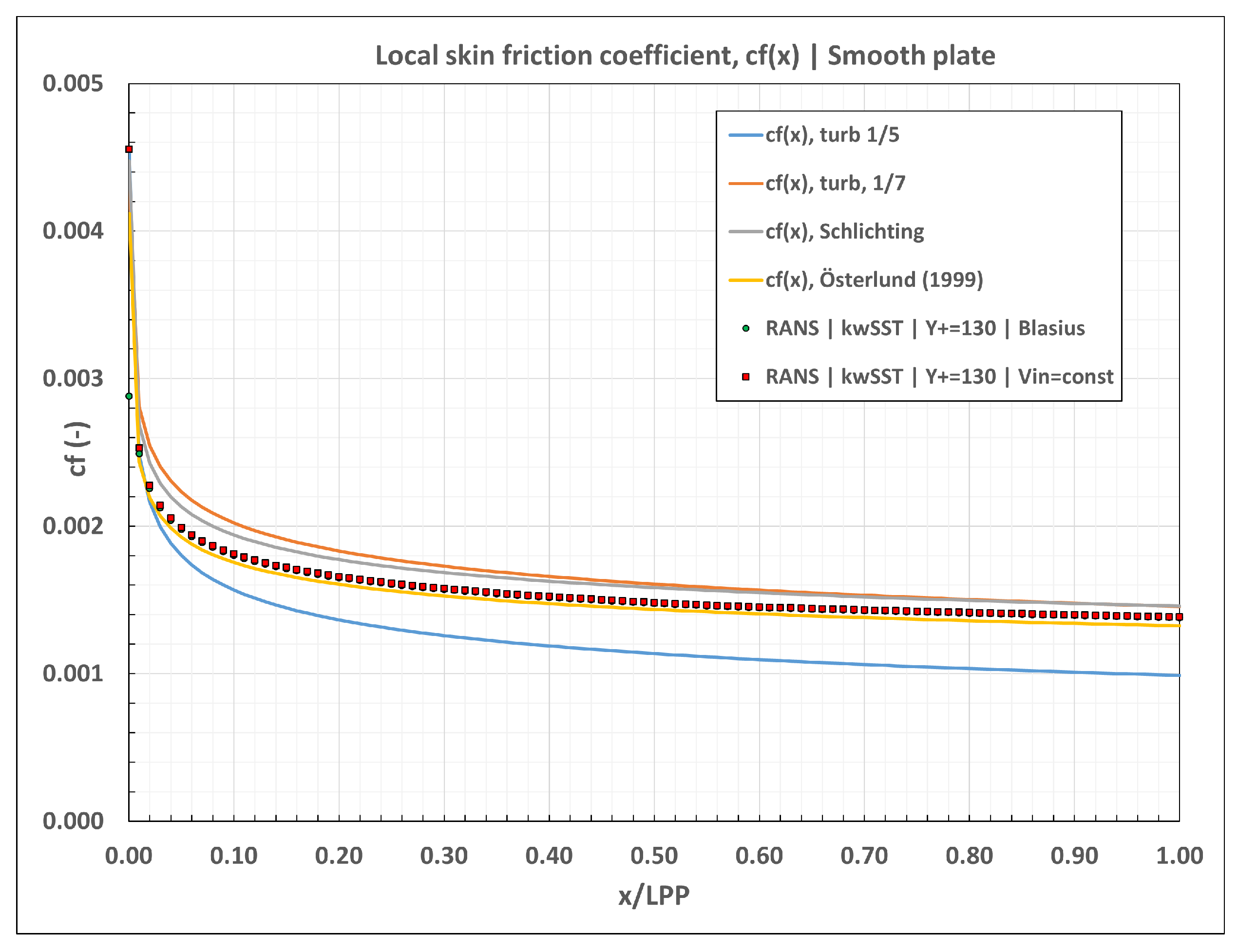
In these calculations, the computational domain consisted of a rectangular box of the length equal to ship LPP. The bottom surface of the domain was set as the no-slip wall boundary (flat plate). The upstream boundary was set as the velocity inlet, the downstream and top boundaries were set as pressure outlet, while on both side boundaries the symmetry boundary condition was imposed. The computation mesh was constructed in such a way that it replicated the prism layer mesh settings used in the ship resistance calculations and provided the same target Wall Y+. At the inlet, the Blasius velocity profile representing theoretical solution for the streamwise and normal velocities in the laminar boundary layer over the smooth plate was used. This was done in the attempt to mitigate a slight acceleration in the boundary layer that may occur locally when using a constant velocity profile. The Blasius profile applied at the inlet was calculated at the distance of x/L = 0.005 from the plate leading edge. The calculations were performed with the smooth surface and equivalent roughness height (r_g) equal to 50, 100, 150 and 200 µm. 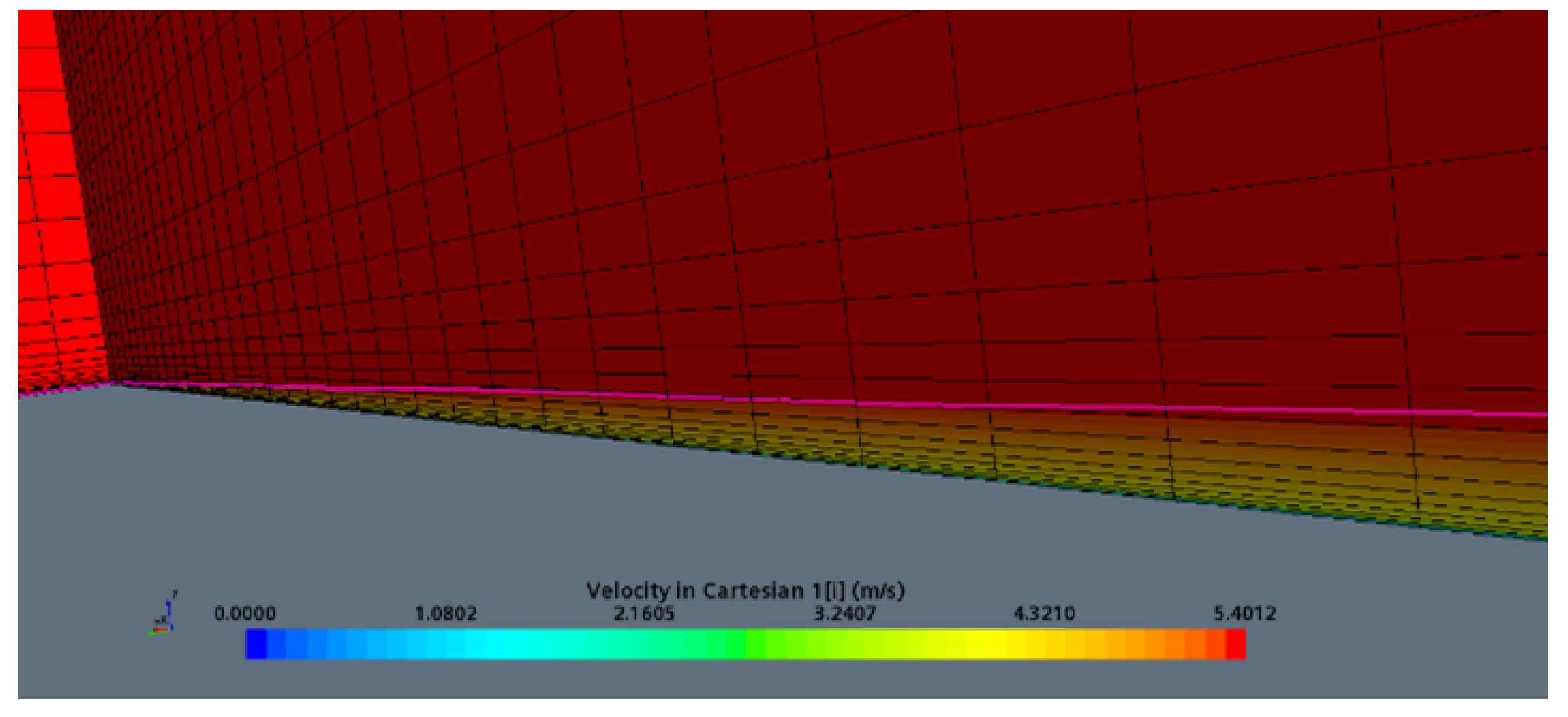Figure 12 shows the computation mesh and field of streamwise (axial) velocity in the near-wall region of the smooth flat plate.

In Table 1 the computed values of the integral friction coefficient (C_F) are compared with the ITTC friction lines used in the ship performance prediction procedures and experimental correlations by Österlund [23]. The calculation results for the smooth plate are about 2 % below the ITTC57 friction line, and 1 % above the experimental results by Österlund. The computed streamwise distributions of the local friction coefficient (cf) are presented in Figure 13 where they are compared with different theoretical solutions and experimental correlations, showing a good agreement with Österlund’s data. Minor difference between the CFD solutions using the constant velocity profile and Blasius profile at the inlet are noticed in the very vicinity of the plate leading edge.

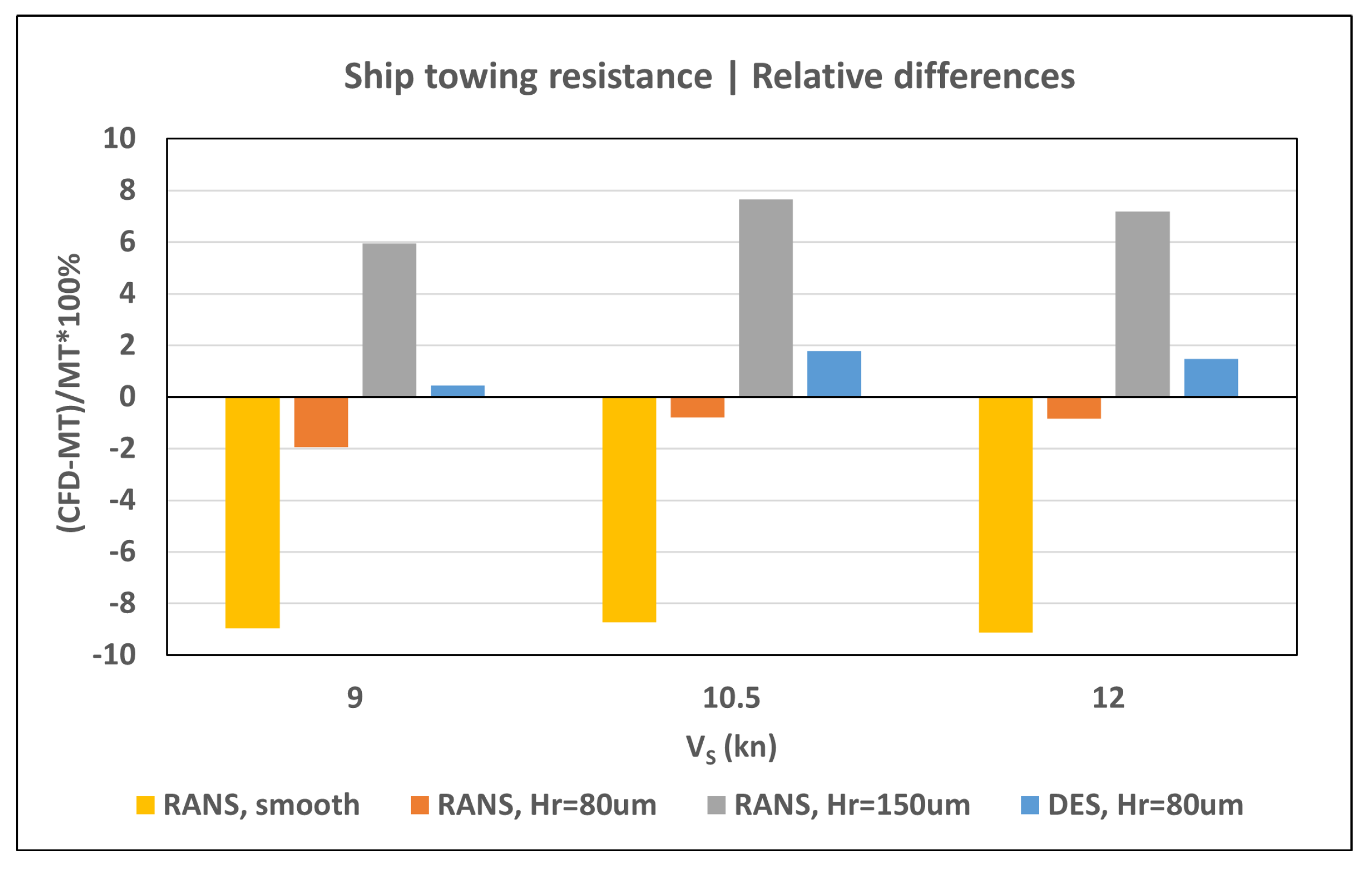
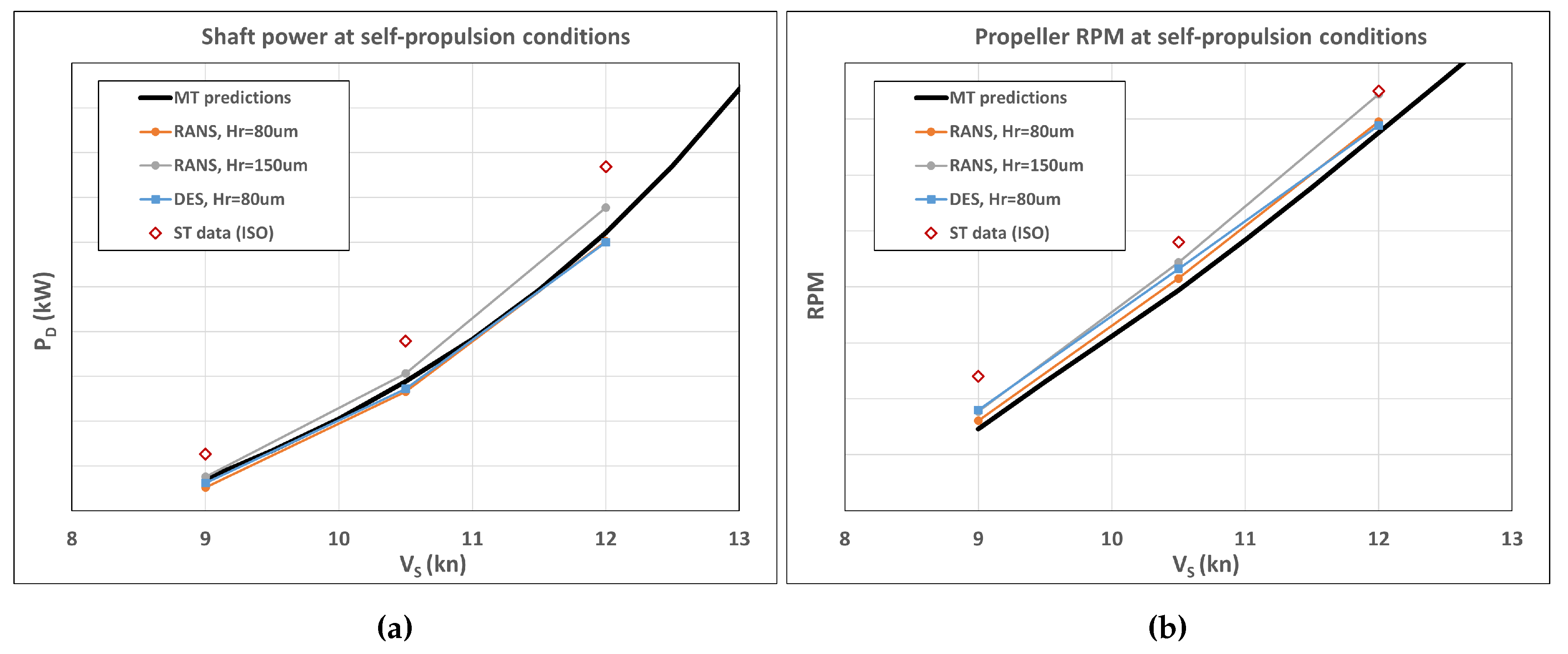
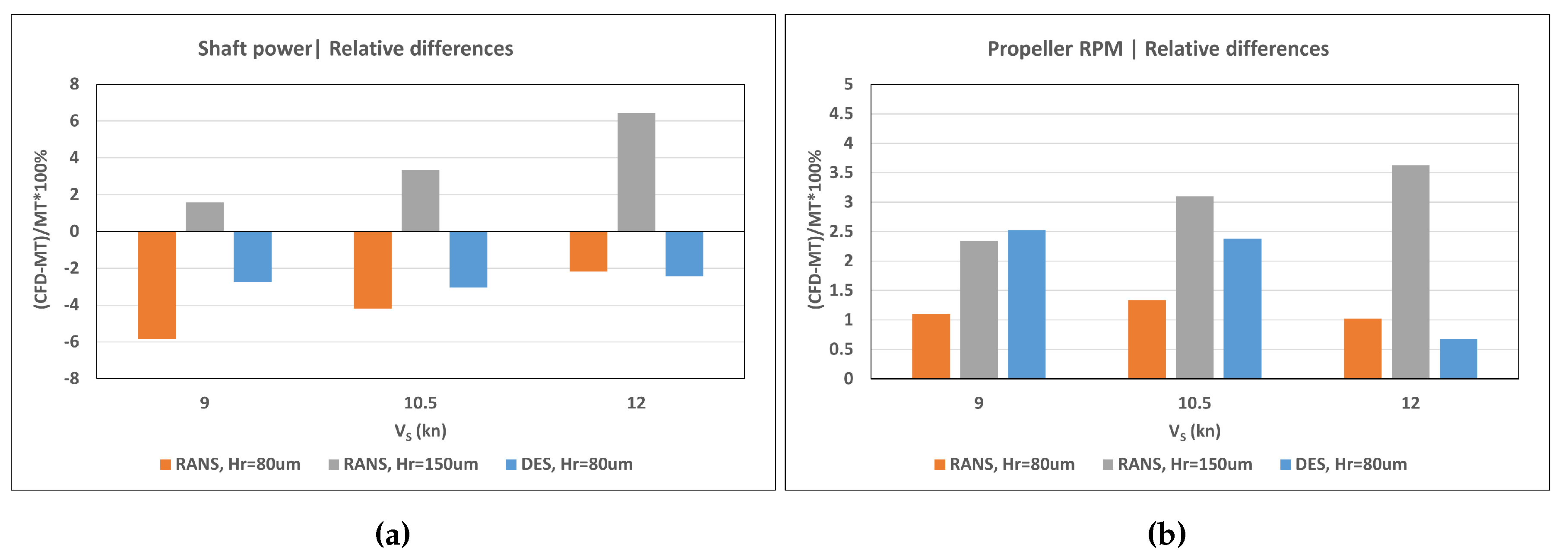
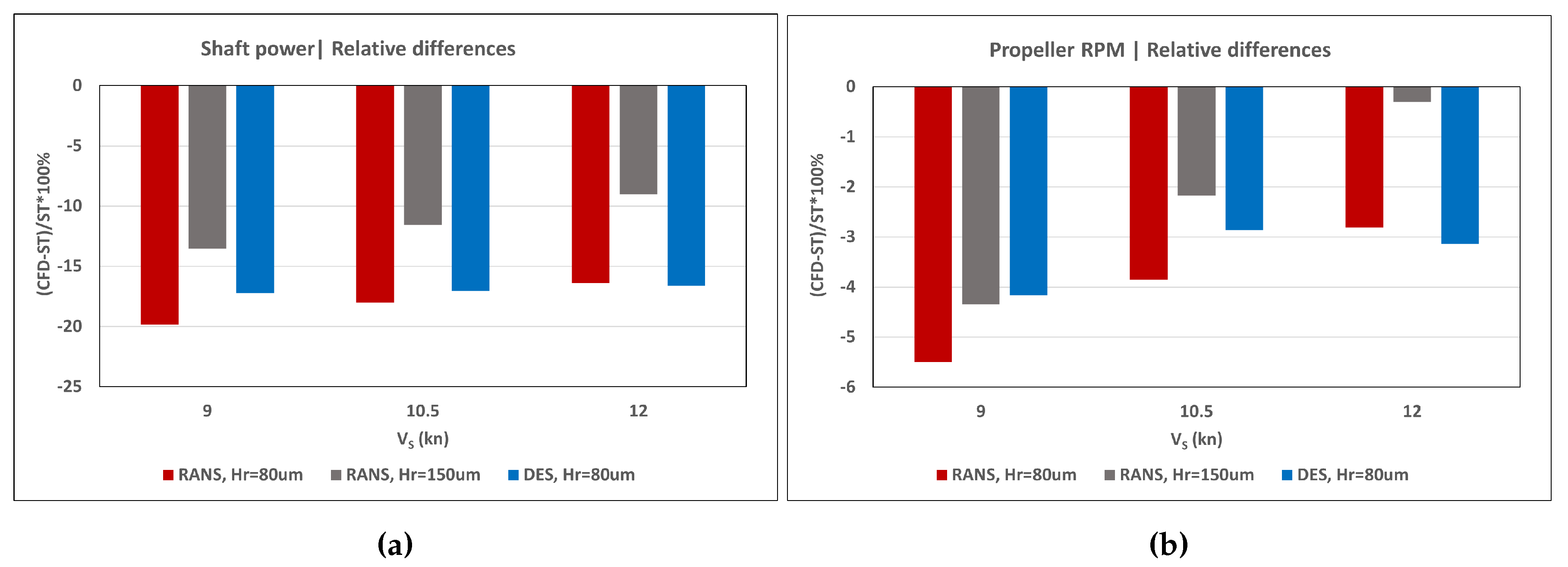
Regarding the case of plate with roughness, the ITTC57 friction line results for C_F corrected with the ITTC78 roughness correction are found to be between the CFD results for the flat plate with sand-grain roughness heights of 50 µm and 100 µm, see Table 1. Based on these findings, the height of sand roughness equal 80 µm was chosen to be applied in the main resistance and self-propulsion simulations for comparison with the predictions based on model tests data. To assess the influence of higher roughness, and with the high roughness values measured on MV REGAL in mind, additional simulations were performed with r_g = 150 µm. The same values of roughness height were applied on ship hull and rudder surfaces.

2.3. Self-propulsion simulations

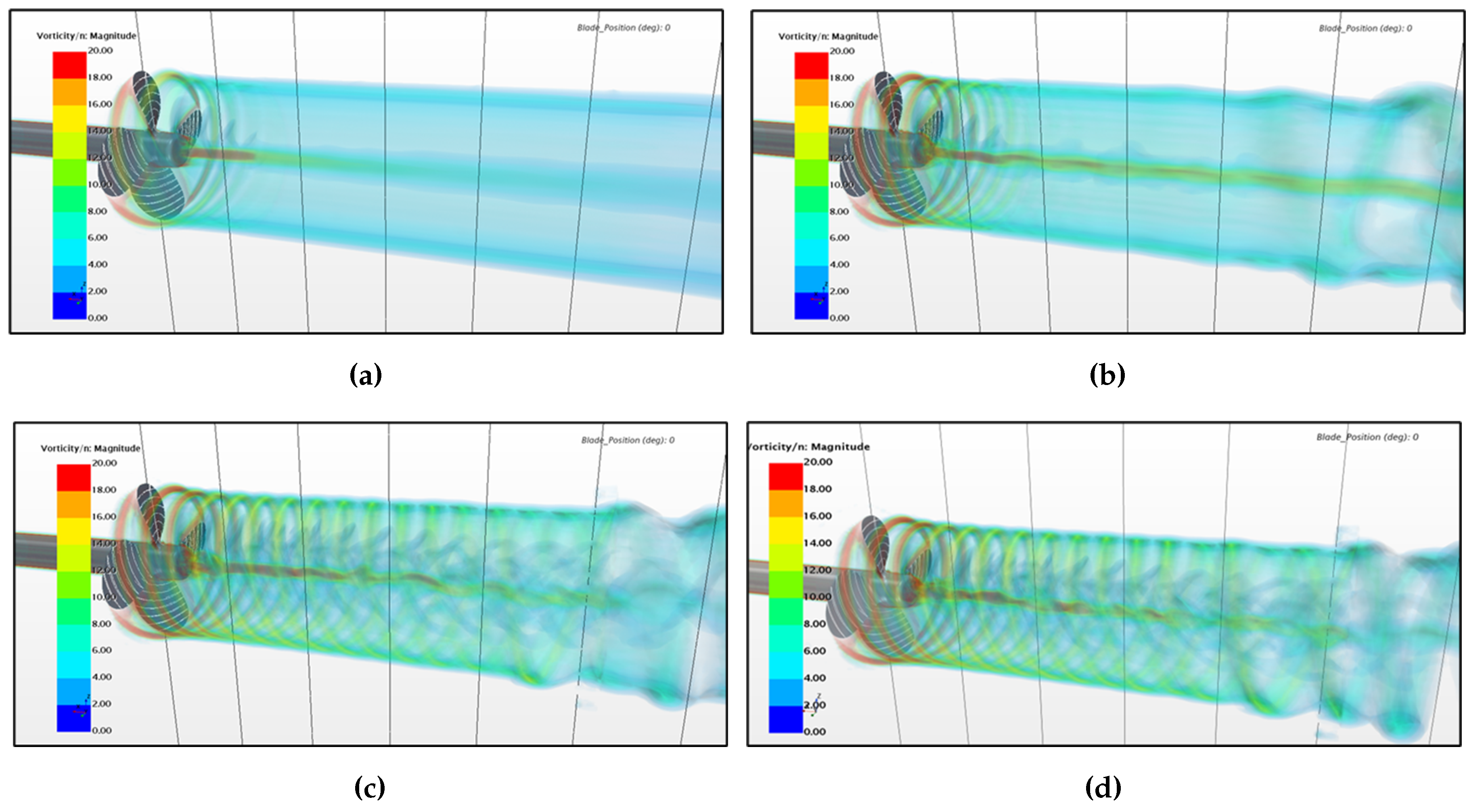
As far as the topology of computation domain and mesh regions, and mesh settings on the ship and propeller are concerned, the self-propulsion simulation setup is, to a large degree, a combination of the setups used in the resistance and open water simulations. Figure 14 gives an illustration of the mesh in the aftship area, where the sliding mesh propeller region is fit in the space between the ship hull and rudder. As in the open water case, this region accommodates the entire propeller hub and cap. The total number of cells in the self-propulsion setup is 32.8 million of which 13.3 million are in the main fluid region, and 19.5 million are in the propeller region.

The self-propulsion calculation is performed in several steps. At the first step, the propeller region is fixed, and the solution is performed using the Moving Reference Frame (MRF) method until convergence is attained for the free surface flow. At the second step, the sliding mesh region is set in motion with the initial value of propeller RPM, which is thereafter adjusted to find the vessel self-propulsion point where the following force balance equation 1 is satisfied:

| R_{S P} + Δ R - T_{P X} | \leq ε,

(1)

where

R_{S P}

is the ship resistance with operating propeller,

Δ R

is the correction accounting for addition resistance components that are not modelled in the simulation (set to 0 in the present case),

T P X

is the X-component of propeller thrust, and

ε

is the solution tolerance (set to 0.5 % of propeller thrust).

Finally, at the third step, the phase transfer solver with the cavitation model by Scherr-Sauer [24] is activated, and the saturation pressure is gradually ramped through the first propeller revolution to its value specified in water properties to address possible occurrence of cavitation. At the stage of cavitation calculation, it is assumed that thrust-resistance balance is not violated, and therefore propeller RPM is fixed to its value found at the second step.

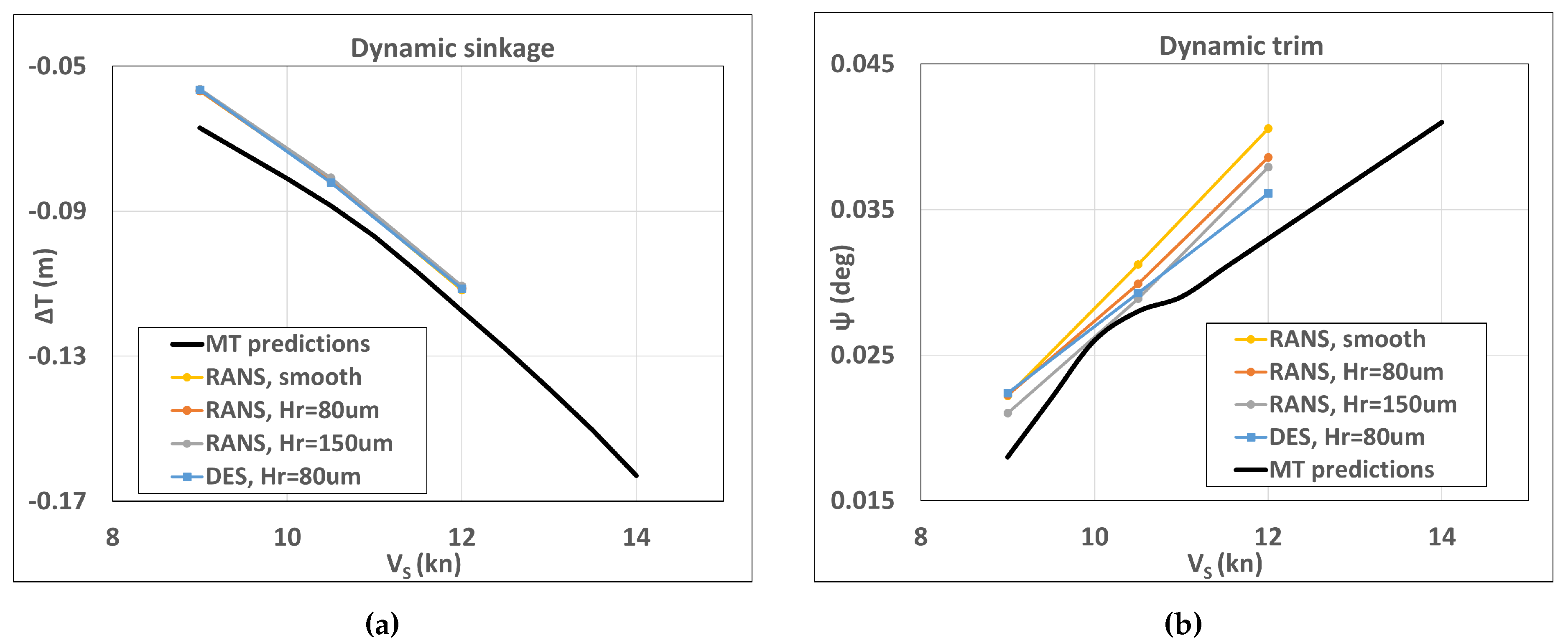
In the present study, the ship was fixed in the self-propulsion analysis at the values of dynamic sinkage and trim found from the DFBI resistance calculation. The RANS and DES turbulence modelling approaches were investigated where the equivalent sand grain roughness height of 80 µm was applied on the ship hull and rudder, and it was assumed equal to 30 µm on the propeller. An additional run with the RANS method using the roughness height of 150 µm on the hull and rudder was conducted after the fashion of resistance analyses.

3. Results and Comparisons

In this section the results of resistance, open water, and self-propulsion simulations are presented and compared with the experimental data. In all the scenarios, comparisons are made in full scale, using the results of model tests at SINTEF Ocean extrapolated to full-scale conditions. For the self-propulsion cases, comparisons are complemented by the results of sea-trials conducted in the JoRes project. Respecting the current restrictions regarding the data distribution in the JoRes Consortium, the comparisons are presented in the form of relative differences and as plots without scale.

3.1. Results of open water calculations

Figure 15 present comparisons between the values of propeller thrust coefficient, propeller torque coefficient and open water efficiency computed using different turbulence modelling approaches and experimental data. The numerical results presented in these figures correspond to smooth propeller surface. The three aspects need to be specifically mentioned concerning the experimental results. Firstly, in accordance with SINTEF Ocean’s performance prediction procedures, propeller open water characteristics obtained in model tests are not scaled. Secondly, the model test characteristics consider the propeller blades only where the hub thrust and torque is excluded. Thirdly, as described in Section 2.1, while the geometry of propeller blades and hub were exactly the same in the simulations and model tests, different shaft arrangements and hub caps were used. It is mainly the third aspect that explains the differences of 4 - 5 % in propeller thrust and torque in the range of advance coefficient (J) from 0.2 to 0.5. The presence of dynamometer shaft downstream of the propeller results in increase of propeller loading by affecting the contraction of propeller slipstream. At the highest J = 0.6, which is already beyond the point of maximum efficiency, the influence of Reynolds number becomes more prominent, which explains larger difference in propeller torque, and hence efficiency. The different turbulence models used in CFD calculations show a good agreement in terms of predicted propeller characteristics. Only slightly larger differences are noticed for the LES and SRH solutions, particularly at the highest J = 0.6.

The influence of surface roughness on propeller performance in open water is illustrated in Figure 16. Only the RANS and DES simulations included the roughness model. Both the numerical solutions predict close magnitudes of roughness effect, whose manifestation is mainly seen in the increase of propeller torque and, consequently, decrease of propeller efficiency. The mentioned influences become larger at higher J values where the relative contribution of the frictional component is greater. It is the increase of surface friction that is mainly behind the observed roughness effect, as one can see from the plots of skin friction distribution on propeller blade shown in Figure 17. Surface roughness also leads to the reduction of blade section lift, but it is counteracted by local changes in the flow pattern near the trailing edge where roughness delays flow separation. This explains a minor increase of propeller thrust shown by the calculations including roughness at J = 0.2 to 0.4. Further studies are needed to understand whether this result is entirely physical, or it is partly caused by the modified wall functions in use.

Scale-Resolving turbulence methods provide a better basis for detailed resolution of vortical structures generated by the propeller, even when using a fairly modest mesh as in the present study. This is illustrated by Figure 18 showing the field of vorticity magnitude in propeller slipstream. The DES method is found to improve the resolution of the tip vortex in the near-field, and the hub vortex in the large part of the domain. The LES and SRH methods offer superior resolution of tip vortices compared to both the RANS and DES methods in the whole domain. It is important to emphasize that with the present solution settings, the accuracy of prediction of the integral propeller characteristics is comparable for all methods. Another aspect revealed by the present study is related to the influence of sliding mesh interfaces. It was found that the presence of sliding interface downstream of propeller facilitates premature diffusion of the tip vortex, and it also introduces changes in the dynamic behaviour of the hub vortex. This aspect may be of lesser importance for the calculation of ship propulsion performance, but it is certainly relevant to the prediction of cavitation and noise characteristics, and unsteady loads on the rudder. The vorticity fields presented in Figure 18 were obtained with the long propeller region, extending 2.5D downstream of propeller. However, it is impossible to use such a region in self-propulsion simulation with the sliding mesh method. The influence of Sliding Mesh region extension on the integral characteristics of propeller is negligible.

3.2. Results of resistance calculations

For the reasons mentioned in Section 2.2, the ship towing resistance simulations were performed only with the RANS and DES method, both including the cases of smooth hull and hull with equivalent sand-grain roughness of 80 µm. An additional calculation with the RANS method was performed using a higher value of roughness height 150 µm. In Figure 19, the total resistance of ship hull, superstructure and cranes predicted by these simulations is compared to the predictions based on model tests data. Figure 20 shows the same comparison as relative differences, in percent, for selected ship speeds.

The calculations done with the smooth surfaces of hull and rudder underpredict the resistance for about 9 %. A good agreement (within 1 - 2 % depending on speed) is obtained with both the RANS and DES methods when using the sand-grain roughness height 80 µm as recommended from the flat plate studies described in Section 2.2. The DES method predicts higher values of resistance which is due to a larger pressure component of hull resistance. This is explained by the DES capturing more accurately the flow separation at the aftship. The frictional component of hull resistance and rudder resistance predicted by DES are slightly lower compared to the RANS predictions.

Figure 21 shows the results for the aerodynamic resistance of superstructure and cranes. These values were obtained by conducting separate calculations without and with the mentioned on-deck features. According to both the RANS and DES methods, the superstructure and cranes add about 2.5 % to the total resistance of the ship. They have a relatively small effect on the dynamic position of the vessel, reducing both the sinkage and positive trim (by bow up). The computed values of sinkage and trim are compared with experimental predictions in Figure 22.

While the predictions of ship resistance and dynamic position by the RANS and DES methods are generally close, the influence of turbulence modelling method is more pronounced in the picture of nominal wake on propeller plane, see Figure 23.

As expected, the DES solution results in a heavier wake field (nominal wake fraction 0.518 compared to 0.495 predicted by RANS) with better resolved separation areas on the portside, starboard and below the stern tube. The wake pictures shown in Figure 23 were obtained by time averaging of the wake field data recorded over last 50 s of simulation time. It is however the time varying wake field where the differences are most prominent. While the wake field in the RANS method hardly shows any changes with time, the wake field resulting from the DES simulation is highly unsteady. The mentioned separation zones downstream of the shaft tube contain the assemblies of eddies of different size and intensity. These eddies participate in constant interaction, so that the shape and extent of the separation zones changes in time. As an illustration, Figure 24 presents instantaneous snapshots of the wake field from the DES simulation taken with a time interval of 5 s.

3.3. Results of self-propulsion calculations

The RPM and shaft delivered power of propeller found from self-propulsion calculations according to the RANS and DES methods are compared with the model test predictions and sea trials data provided by JoRes project in Figure 25. The relative differences for these values against model test predictions and sea trials data are shown in Figure 26 and Figure 27, respectively. Similar to the resistance case, both the RANS and DES solutions were computed with equivalent sand-grain roughness on ship hull and rudder surfaces equal to 80 µm. An additional calculation with the RANS method was performed using a higher value of roughness height 150 µm. The propeller surface roughness value of 30 µm was adopted in these analyses. The presented values are obtained by time averaging over the last 5 propeller revolutions. The total number of propeller revolutions varied in each case, and it depended on how fast the self-propulsion condition was attained. The accuracy of satisfaction of self-propulsion condition given by the equation 1 was within 0.2 % in all cases.

It can be concluded that both the RANS and DES methods provide comparable prognoses of ship’s propulsion performance when using the hull roughness of 80 µm, which is close to the predictions derived from model tests data. The DES results are somewhat closer to model tests predictions in terms of shaft power with relative differences about 2.5 % at all ship speeds. The respective differences in terms of propeller RPM are also within 2.5 %.

The RANS results are closer to model tests data in terms of RPM (about 1 %), but they reveal larger deviations in shaft power (2 - 6 % depending on speed). Both the CFD calculations and model tests prognosis underpredict shaft power and RPM compared to the sea trials data post-processed according to the ISO15016 standard. For the CFD results, the said underpredictions amount 3 - 4 % in terms of RPM and 17 % in terms of shaft power, when using the DES method and hull surface roughness of 80 µm. The RANS calculations done with the increased value of hull surface roughness of 150 µm reduce these differences to about 2 % and 12 %, respectively. High values of hull surface roughness and numerous surface imperfections documented on MV REGAL in the JoRes project indicate that hull surface conditions may indeed be one of the factors explaining the deviations between the predictions and sea trials. However, in authors’ opinion, an even more likely reason is related to the presence of bilge keels on the ship hull and sacrificial anodes on both the hull and rudder, which were not considered in the CFD simulations and model tests predictions. According to authors’ experience, a combined contribution of these constructive features can easily amount to 11 - 13 % of increased hull resistance in propulsion conditions. The said increase may be even higher in the case of bilge keel misalignment. Combined with the surface conditions of a 25-year-old ship hull, these influences may result to the increased power demand of 15 %. Therefore, the differences between the performance predictions and sea trials data found in the present case are not at all surprising, and even quite expected. Comparing these findings with the results of simulations conducted on MV REGAL during the 2016 Workshop [9], it is worth noting that a much closer agreement with sea trials data in terms of shaft delivered power (within 1.5 %) was obtained by the authors while applying very similar settings in the CFD model. The 2016 exercises dealt with a different loading condition of the ship corresponding to the draught values of 4.899 m and 5.597 m at the fore and aft marks, instead of 2.97 m and 5.865 m, respectively, applied in the present case. Further, as already mentioned earlier in Section 2, the 2016 simulations used the geometries of ship hull, propeller and rudder derived from the 3D laser scan data (with some of the surface imperfection and constructive features naturally present), whereas the present simulations used clean CAD geometries reconstructed from the drawings. This latter aspect may be critical for direct comparisons with sea trials data.

For the speed of 10.5 knots, the RANS self-propulsion simulation done with hull roughness of 150 µm was extended with the cavitation simulation using a phase change model. Fifteen additional propeller revolutions were performed at the same propeller RPM as found from self-propulsion analysis. The cavitation images were compared with borescope photography done during the sea trials. This comparison is presented in Figure 28 for the selected positions of the blade on the starboard and portside of the ship.

The experimental images reveal considerable presence of bubbles swept by the flow from the ship bow, under the hull and onto the propeller. Further, the propeller loading at the observation conditions was higher than achieved in the CFD simulation. The difference in propeller loading and use of the RANS method presumably explain smaller extent of tip vortex cavitation shown by the simulations, while an overall cavitation pattern is captured realistically. A better resolution of the tip vortex flow would be achieved with the DES method, but the DES simulations were not performed for the case of increased hull roughness at the time of preparation of the present manuscript.

4. Conclusions

Full-scale CFD calculations have been conducted on the benchmark ship case of MV REGAL used in the joint industry project JoRes, to calibrate the existing modelling practices, after the fashion of a "blind" simulation exercise. When the experimental predictions based on model tests and sea-trials data have become available, detailed comparisons have been made regarding the propeller characteristics in open water, ship towing resistance and ship self-propulsion performance. Along with traditionally used unsteady RANS method, Scale-Resolving Simulations such as DES, LES and SRH turbulence modeling approaches have also been included in the study.

The analysis of comparative results demonstrates that the applied CFD modelling best practices are mature and capable of predicting the performance characteristics in question with an accuracy sufficient for practical applications. The CFD predictions in full scale according to the RANS, and particularly DES method, are found to be in a good agreement with the prognosis based on model tests that follows the current performance prediction procedure at SINTEF Ocean. In this case, the differences between CFD using the DES method and experimental predictions of shaft delivered power and propeller RPM are within 2.5 %, thus being well within the accepted range of CFD/EFD calibration factor, according to [3].

Both the CFD calculations and model test prognosis underpredict the levels of shaft delivered power and propeller RPM when compared to the sea trials data obtained on the same vessel in the JoRes project. Several factors are thought to contribute to the mentioned differences, including the additional resistance of bilge keels and sacrificial anodes which were not included in the numerical model, as well as the surface conditions of ship hull for which high values of surface roughness and numerous macro-scale imperfections are documented. The use of accurately scanned hull, propeller and rudder geometries is deemed highly important for an adequate direct comparison between full-scale CFD predictions and sea-trials data on old ships in service. The influence of surface roughness of hull and propeller, particularly the accuracy of roughness measurements, conversion of measured values to equivalent sand-grain roughness height used in CFD, and roughness distribution pattern on the hull require closer investigation, concerning with both their impacts on hull resistance and wake field.

The DES method is found to provide a good compromise between the fidelity of resolution of flow details in the hull wake and propeller slipstream, on the one hand, and accuracy of prediction of propeller and hull forces, on the other hand. This method also supports surface roughness wall functions, and it generally shows little dependence on the simulation time step, both features being essential for the prediction of ship performance in full scale.

Author Contributions

Conceptualization, V.K. and K.K.; Formal analysis, V.K. and V.S.S.; Funding acquisition, V.K. and K.K.; Investigation, V.K., V.S.S., K.K. and H.J.R.; Methodology, V.K. and V.S.S.; Project administration, V.K. and K.K.; Supervision, V.K.; Visualization, V.K and V.S.S.; Writing—original draft, V.K.; Writing—review & editing, V.K., V.S.S. and K.K.

Funding

The model test campaign of MV REGAL was funded by the JoRes project (https://jores.net/).

Acknowledgments

The authors acknowledge the use of experimental data acquired in the project JoRes. The authors would like to express their gratitude to Dr. Dmitriy Ponkratov of Royal Institution of Naval Architects, the manager of JoRes, for insightful discussions during the JoRes workshops and for his review of the present manuscript.

Conflicts of Interest

The authors declare no conflict of interest.

Abbreviations

The following abbreviations are used in this manuscript:

CFD	Computational Fluid Dynamics
RANS	Reynolds-Averaged Navier-Stokes
SRS	Scale-Resolving Simulation
DES	Detached Eddy Simulation
LES	Large Eddy Simulation
IDDES	Improved Delayed Detached Eddy Simulation
SRH	Scale-Resolving Hybrid
VOF	Volume of Fluid
HRIC	High-Resolution Interface Capturing
DFBI	Dynamic Fluid-Body Interaction
AHR	Averaged Hull Roughness
MT	Model Test
ST	Sea Trial
EFD	Experimental Fluid Dynamics

References

ITTC Recommended Procedures and Guidelines. Section 7.5-03 CFD. Effective Date 2021, Revision 09, 2021.
IMO RESOLUTION MEPC.350(78). Guidelines on the method of calculation of the attained energy efficiency existing ship index (EEXI), June 10, 2022. 10 June.
IACS Guidelines on Numerical Calculations for the purpose of deriving the Vref in the framework of the EEXI Regulation. No.173, November 10, 2022. 10 November.
Krasilnikov, V.I., Savio, L., Koushan, K., Felli, M., Abdel-Maksoud, M., Kimmerl, J., Reichstein, N., Fageraas, A. and Sun, J. Towards Reliable Prediction of Propeller Noise: Challenges and Findings of the Project ProNoVi. Proceedings of the 7th International Symposium on Marine Propulsors SMP’22, Wuxi, China, October 17-21, 2022. 17 October.
Ferziger, J.H. and Perić, M. Computational Methods for Fluid Dynamics, Springer-Verlag, 3rd ed., 2002.
Larsson, L. Larsson, L., Stern, F. and Visonneau, M. (Editors). Proceedings of the Workshop on Numerical Ship Hydrodynamics – Gothenburg 2010, Chalmers University of Technology, Gothenburg, Sweden. Available online: http://www.gothenburg2010.org/.
Hino, T., Stern, F., Larsson, L., Visonneau, M., Hirata, N. and Kim, J. Numerical Ship Hydrodynamics: An Assessment of the Tokyo 2015 Workshop, Springer Nature, 2020.
Lindstad, E. and Krasilnikov, V.I. Is it feasible to reduce fuel consumption of dry bulkers with 50% by combining WASP, Gate Rudder and a slender design? Presentations of the BlueWeek 2023, Natural Propulsion Seminar, Palma de Mallorca, Spain, April 17-21, 2023. 17 April.
Ponkratov, D. Proceedings of the 2016 Workshop on Ship Scale Hydrodynamic Computer Simulation, Lloyd’s Register Report Ref. 8428, February 10, 2017. 10 February.
JoRes - Joint Research Project: Development of an industry recognized benchmark for Ship Energy Efficiency Solutions. Available online: https://jores.net/.
Ponkratov, D. Description of cases. REGAL. JoRes: Development of Industry Recognized Benchmark for Ship Energy Efficiency Solutions, April 2021. 20 April.
Rambech, H.J. Calm Water Model Tests of MV REGAL. SINTEF Ocean Report OC2021 F-077, September 2021. 20 September.
ISO 15016:2015. Ships and marine technology — Guidelines for the assessment of speed and power performance by analysis of speed trial data. ISO/TC 8/SC 6 Navigation and ship operations, April, 2015.
Menter, F.R. Two-equation eddy-viscosity turbulence modeling for engineering applications, AIAA Journal, 32(8), 1994, pp. 1598-1605. [CrossRef]
Shur, M.L., Spalart, P.R., Strelets, M.Kh., and Travin, A.K. A hybrid RANS-LES approach with delayed-DES and wall-modelled LES capabilities, International Journal of Heat and Fluid Flow, 29(6), 2008, pp. 1638-1649. [CrossRef]
Menter, F. R. and Kuntz, M. Adaptation of Eddy Viscosity Turbulence Models to Unsteady Separated Flows Behind Vehicles, in The Aerodynamics of Heavy Vehicles: Trucks, Buses and Trains, Springer, 2002, Asilomar, CA.
Smagorinsky, J. General Circulation Experiments with the Primitive Equations: Part I, The Basic Experiment, Monthly Weather Review, 91, 1963, pp. 99-164. [CrossRef]
Balaras, E., Benocci, C., and Piomelli, U. Two-Layer Approximate Boundary Conditions for Large-Eddy Simulations, AIAA Journal 34(6), 1996, pp. 1111-1119. [CrossRef]
Duffal, V., de Laage de Meux, B., and Manceau, R. Development and validation of a hybrid RANS-LES approach based on temporal filtering, Proceedings of the 8th Joint Fluids Engineering Conference, 2019, San Francisco, USA.
Jayatilleke, C.L. The influence of Prandtl number and surface roughness on the resistance of the laminar sub-layer to momentum and heat transfer, Progress in Heat and Mass Transfer, 1, 1969, pp. 193-330.
Choi, J and Sung, B.Y. Numerical simulations using momentum source wave-maker applied to RANS equation model, Coastal Engineering, 56 (10), 2009, pp. 1043 - 1060. [CrossRef]
Muzaferija, S. and Peric, M. Computation of free surface flows using interface-tracking and interface-capturing methods, Chap. 2 in O. Mahrenholtz and M. Markiewicz (eds.), Nonlinear Water Wave Interaction, Computational Mechanics Publications, WIT Press, 1999, Southampton.
Österlund, J.M. Experimental Studies of Zero Pressure Gradient Boundary Layer Flow. Department of Mechanics, Royal Institution of Technology, Stockholm, Sweden, December 1999. 19 December.
Sauer, J. Instationaer kavitierende Stroemungen - Ein neues Modell, basierend auf Front Capturing VOF und Blasendynamik, Dissertation, Universitaet Kalrsruhe, 2000. (in German).

Figure 1. General cargo vessel MV REGAL used as the case study in the present work.

Figure 2. Geometry assembly of the MV REGAL used in self-propulsion simulations. Blue line shows the free surface level at the initial hydrostatic position.

Figure 3. Open water simulation setup. Mesh refinement pattern around propeller. Rotating propeller region is show by the red contour.

Figure 4. Mesh refinement on propeller blade and in the hub gap region.

Figure 5. Prism layer mesh around propeller blade. The areas of blade tip and leading edge of the section 0.7R.

Figure 6. Distribution of Wall Y+ on the suction side of propeller. Open water calculation, J = 0.4 (DES).

Figure 7. Typical levels of Courant number in propeller slipstream obtained with the present spatial and temporal discretization settings. Open water calculation, J = 0.4 (LES, time step ∼ 2 deg).

Figure 8. Overall mesh refinement around the ship with superstructre, cranes and free surface.

Figure 9. Mesh refinement in horizontal plane on free surface.

Figure 10. Distribution of Wall Y+ on the underwater part of the hull a, and on the deck, superstructure and cranes b. Resistance calculation, Vs = 10.5 knots (DES).

Figure 11. Distribution of Courant number in flow around the ship. Resistance calculation, Vs = 10.5 knots (DES).

Figure 12. Computation mesh and field of streamwise velocity in the near-wall region of the smooth flat plate. Vs = 10.5 knots = 5.4012 m/s. The magenta line shows the computed 99 % boundary layer thickness.

Figure 13. Comparison of streamwise distributions of local friction coefficient of the flat plate. Vs = 10.5 knots = 5.4012 m/s.

Figure 14. Mesh in the aftship area used in self-propulsion calculation.

Figure 15. Comparison between computed and measured propeller thrust a, torque b and efficiency c in open water conditions.

Figure 16. Influence of surface roughness on propeller thrust a, torque b and efficiency c in open water conditions.

Figure 17. Distribution of skin friction over the smooth blades a and blade with 30 µm roughness b. J = 0.4 (DES).

Figure 18. Field of vorticity magnitude in propeller slipstream computed by different turbulence modelling approaches. J = 0.4. RANS a, DES b, LES c, SRH d.

Figure 19. Full-scale ship resistance curve computed by CFD simulations and predicted from model tests (MT).

Figure 20. Relative differences between the computed full-scale ship resistance and model tests predictions.

Figure 21. Additional resistance due to superstructure and cranes predicted by CFD simulations.

Figure 22. Computed and measured dynamic sinkage a and trim b of the ship

Figure 23. Time-average nominal wake field on propeller plane predicted by the RANS a and DES b methods. Vs = 12 knots, Smooth hull.

Figure 24. Instantaneous snapshots of the nominal wake field from the DES simulation taken with the time interval of 5 s. Vs = 12 knots, Smooth hull.

Figure 25. Comparison of propeller shaft delivered power a and RPM b at self-propulsion point in full scale.

Figure 26. Relative differences between the computed propeller shaft delivered power a and RPM b at self-propulsion point and model tests prediction.

Figure 27. Relative differences between the computed propeller shaft delivered power a and RPM b at self-propulsion point and sea trials data.

Figure 28. Comparison between the numerical simulation and full-scale observations on propeller cavitation. Vs = 10.5 knots (RANS, hull roughness 150 µm).

Table 1. Computed values of the integral friction coefficients (C_F) of the flat plate compared with the ITTC friction lines.

	C_F · 10³
Velocity [knots]	9.0	10.5	12.0
ITTC57 (smooth)	1.6164	1.5851	1.5587
ITTC57 + ITTC78 (rough)	1.6854	1.6795	1.6742
Österlund (exp., smooth)	1.5666	1.5368	1.5116
RANS (smooth)	1.5847	1.5542	1.5287
RANS (r_g = 50 $μ$ m)	1.6314	1.6200	1.6128
RANS (r_g = 100 $μ$ m)	1.7644	1.7659	1.7690
RANS (r_g = 150 $μ$ m)	1.8798	1.8863	1.8922
RANS (r_g = 200 $μ$ m)	1.9746	1.9790	1.9681

Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.

© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).

Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.

MDPI Initiatives

Important Links

Choose an area of interest and we will send you notifications of new preprints at your preferred frequency.

Disclaimer

A Calibration Study With CFD Methodology for Self-propulsion Simulations at Ship Scale

Abstract

1. Introduction

2. Research Methodology

2.1. Open water propeller simulations

2.2. Hull resistance simulations

2.3. Self-propulsion simulations

3. Results and Comparisons

3.1. Results of open water calculations

3.2. Results of resistance calculations

3.3. Results of self-propulsion calculations

4. Conclusions

Author Contributions

Funding

Acknowledgments

Conflicts of Interest

Abbreviations

References

MDPI Initiatives

Important Links

Subscribe