Ultra-large cold-water pipes (CWP) may present structural instability phenomenon under complex and variable operating conditions, and the current theoretical analysis rarely takes into account the influence of multiple key parameters at the same time, resulting in some errors between the prediction results and the actual deformation behavior of the pipe. Considering this issue, this paper establishes a computational analysis model of the mechanical performance of the CWP based on the Euler-Bernoulli beam theory, considering the effect of waves, the clump weight at the bottom, internal flow and sea current, and gives a time-dependent solution of the mechanical response of the pipe with the action of multiple key parameters using the differential quadrature method (DQM). Additionally, the correctness and validity of the theoretical model are well verified by comparing the numerical solution with the theoretical results. Finally, to study the effects of operating conditions on the mechanical response of the pipe, the effects of waves, the clump weight, internal flow and sea current on the lateral deflection and maximum bending moment of the pipeline are discussed based on numerical simulation and orthogonal experimental method. The results show that changing the wave strength and internal flow velocity has little effect on the lateral deflection of the CWP, and the clump weight at the bottom can effectively suppress the lateral deflection of the pipeline, but increasing the current velocity can significantly increase the lateral deflection of the pipeline, which can lead to the instability of the pipe. Nevertheless, the effects of waves, the clump weight, internal flow and sea current on the maximum bending moment of the pipeline are basically the same, all of them increase sharply at first, and then decrease gradually until they level off, and the differences in the effects are mainly reflected in the different locations of the pipe sections. This paper suggests the design guidance of CWP in aspect of dynamic response depending on the operating condition.

Keywords:

Subject: Engineering - Marine Engineering

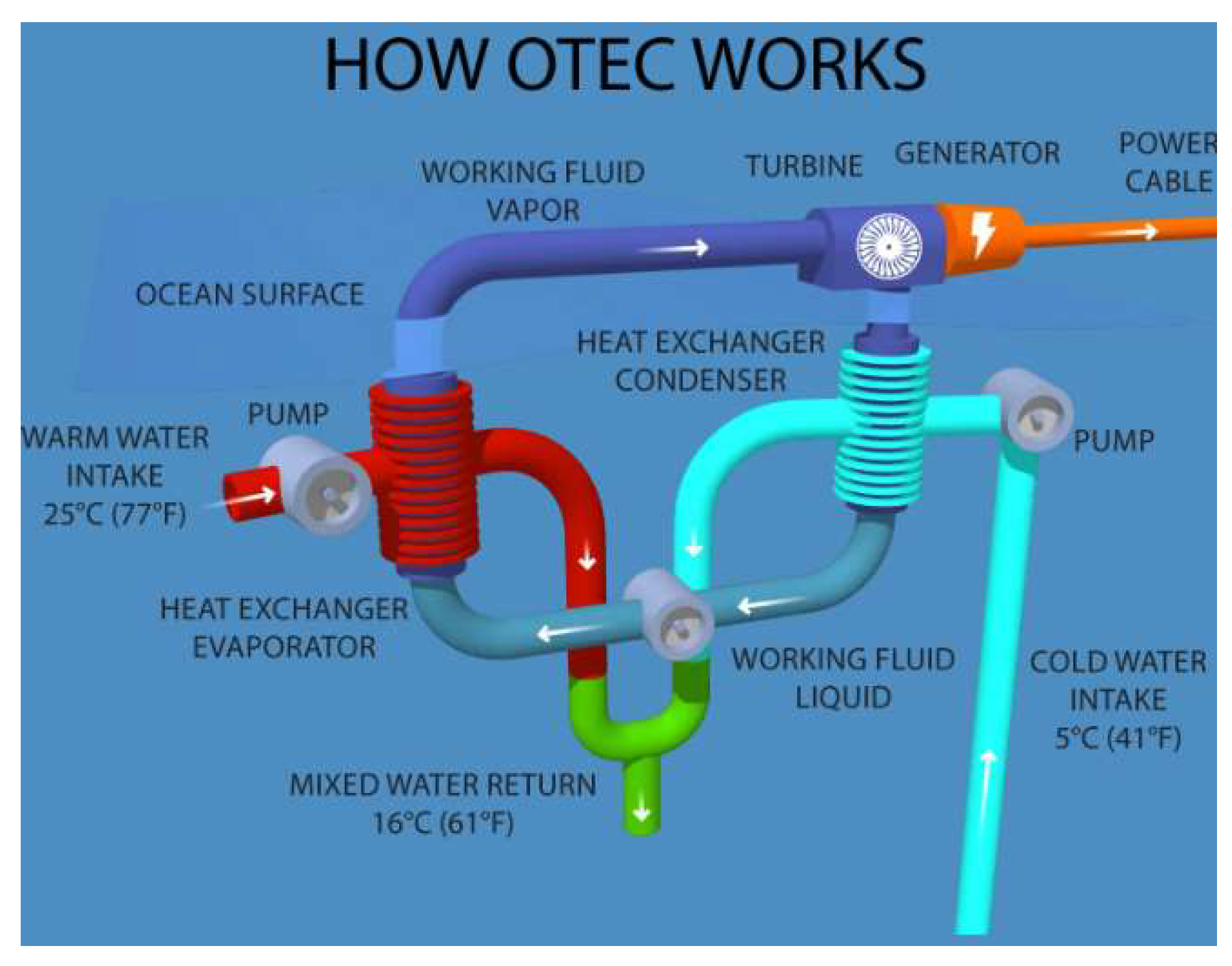
1. Introduction

With petroleum resources production is peaking and demand increasing, humanity will face a steadily diminishing supply of fossil fuels. It seems sensible to consider ocean energy resources as some of the replacement “fuels” for the future energy technologies. Ocean thermal resource as one of the three major ocean energy is always available while all other ocean energy resources are intermittent. Ocean Thermal Energy Conversion (OTEC) is a process that can produce electricity by utilizing the temperature difference between deep cold water and surface warm water, as shown in Figure 1 [1]. The cold-water pipe (CWP) is a novel and most challenging component of floating structures for OTEC, which is used to transport deep cold water to floating platforms [2]. For commercial-scale, the CWP is are large as 12m in diameter and up to 1000m in length [3]. Ultra-large cold-water pipe will be subjected to wind, waves, currents, collisions and platform movements in the complex marine environment. These internal and external factors can directly affect the dynamic response of CWP and the safety of in-situ operation. To ensure the safe and smooth operation of CWP, it is necessary to analyze the dynamic response of the pipe in the marine environment in order to obtain reliable prediction results.

Since the concept of chilled water pipe was first proposed to be applied in OTEC systems, the study of the dynamic performance of chilled water pipes has been a key research object in OTEC installations. As a typical marine riser, the design of cold-water pipe can be divided into three main issues [4]: strength analysis, which includes limit analysis and crush analysis; cold-water pipe-platform coupling analysis; and cold-water pipe vibration analysis, which includes internal flow excitation and vortex excitation vibration. When Kuiper et al [5] investigated the stability of suspended flow transfer pipes, they found errors between theoretical predictions and experiments, which were caused by the incorrect description of the negative pressure of the pipe Halkyard et al [6] summarized the research work on cold-water pipes in the past three decades (2014) and found that the research work mainly focused on the analysis of the dynamic performance of cold-water pipes under the action of waves, currents and platform motion, and little consideration was given to the effect of instream flow. Adiputra [2] focused on the effects of pipe material, top connection, and bottom support system on the dynamic performance of cold-water pipe. Additionally, the self-induced vibration of the cold-water pipe was analyzed and solved numerically. The results showed that the critical flow velocity predicted in the time domain was on average 20% higher compared to the frequency domain, and the clump weight at the bottom under the lighter material had a more significant effect on the critical flow velocity compared to the relatively high-density material [3]. Shan [7] established an OTEC hull cold-water pipe coupling analysis and benchmarked the cold-water pipe through a coupling analysis software program. Halkyard and Associates [8] determined the dynamic strain imparted to the cold-water pipe due to waves and currents through simulations using the offshore dynamic analysis program HARP; this was verified by Makai Offshore using OrcaFlex software, which showed that the maximum pipe strain was within 25% of the HARP prediction. Xiang [9] based on a study of the cold-water pipe vibration problem The dynamic response of the cold-water pipe to extreme conditions was investigated, and vortex-induced vibration response and other design issues of the cold-water pipe were discussed.

As typical conveying fluid riser, a lot of research work has been done by domestic and foreign scholars for the vibration problem of the pipe. Aitken [10] first experimentally illustrated the equilibrium between tension and centrifugal forces induced by motion in 1876, which was the earliest work to study the dynamics of pipes conveying fluids. In 1939, Bourrieres [11] studied the oscillatory instability of cantilevered pipes conveying fluids theoretically and experimentally, deriving the equations of motion of the pipes. Feodos'ev and Housner[12] found that the internal flow velocity significantly affects the pipe's buckling. Poussins[13,14] demonstrated theoretically and experimentally that cantilevered pipes undergo oscillatory instability (chattering) at sufficiently high flow velocities. Benjamin [15] found that vertical cantilevered systems subjected to gravity are susceptible to buckling instability. Paidoussis et al. [16] used the micro-element method to establish the equations of motion of a suction pipe in still water. Based on the finite unit method, Guo [17] and Li [18] studied the static and dynamic characteristics of a riser containing internal flow. Based on the above-related studies, it can be seen that a large number of scholars have done a lot of research work on the dynamic pipeline response problem, while the current research on the dynamic response of the pipe has not considered the problem of the fluid inside the pipe. Meanwhile, the external flow field (sea current, waves) has not been explored in depth during the study of the fluid transfer pipe. Therefore, studying the dynamic response under the collective excitation of internal flow, sea current, and waves must be studied in depth.

Using analytical methods to predict the dynamic response behavior of cold-water pipe can provide a clearer insight into the nature of the problem. At the same time, the analytical method can accurately and quickly extract the influence of critical parameters on the structural dynamic behavior of chilled water pipes efficiently and rapidly, thus guiding the design of cold-water pipes. When using the analytical method to study the dynamic response of the pipe, it is usually desirable to consider the mechanical properties of the pipe comprehensively in the calculation. However, the difficulty of the calculation is always proportional to the comprehensiveness of the mechanical properties of the pipe. Therefore, in most cases, the analysis is focused on a single mechanical property of the pipe or a single boundary condition. The commonly used analytical methods in dealing with the relevant dynamic pipe response problems are the Galerkin method[19,20,21,22], Finite Element Method (FEM)[23,24], Finite Difference Method (FDM)[25,26,27,28], Transfer (Matrix Method)[29,30]. However, the above methods have the disadvantages of computational limitations and complexity.

This paper uses a semi-analytical method that can accurately and quickly solve high-order nonlinear partial differential equations. Liang[31] et al. studied the effect of pipe end boundary conditions and geometric parameters on pipe displacements using the differential product (DQM) method. The results showed that the displacement increases with the increase of pipe degrees of freedom increases with the increase of length-diameter ratio, and decreases with the increase of thickness-diameter ratio. An and Su[32,33] used the generalized integral transformation (GITT) method to derive a semi-analytical solution for the vibration of a flow transport pipe due to two-phase flow under solid-supported-solid-supported boundary conditions and analyzed the effect of gas volume fraction and volume flow rate in two-phase flow on the dynamic behaviour of the pipe. Li[34] et al. used the GITT method to analyze the effect of different internal and external flow velocities and different soil stiffness on the dynamic response of a free-hanging span pipe. Li[35] applied the GITT method to study the effect of damping ratio on the dynamic behaviour of a pipe under simply-supported-simply-supported boundary conditions and verified it by comparing it with existing experimental results to obtain dimensionless structural parameters that can control the standardized stability envelope of the pipe. Ni and Qian[36] studied the bifurcation and chaotic motion of fluid transport bends under nonlinear constraints based on the DQM method. The discrete form of the system's equations of motion was established and solved numerically.

In this paper, based on the Euler-Bernoulli beam theory and Morrison equation theory, we establish the lateral motion control equation of large diameter cold-water pipe based on the Euler-Bernoulli beam theory and Morrison equation theory, and consider the effect of internal flow, current and wave excitation comprehensively, and use DQM method to obtain its semi-analytical solution. By comparing with the finite element simulation results of Orcaflex, the correctness of the semi-analytical solution is verified, and the effects of the wave, current velocity, internal flow velocity and the clump weight on the dynamic response characteristics of the large diameter cold-water pipe are analyzed by combining with the orthogonal experimental method. The main parameter variables in the paper are shown in Table 1.

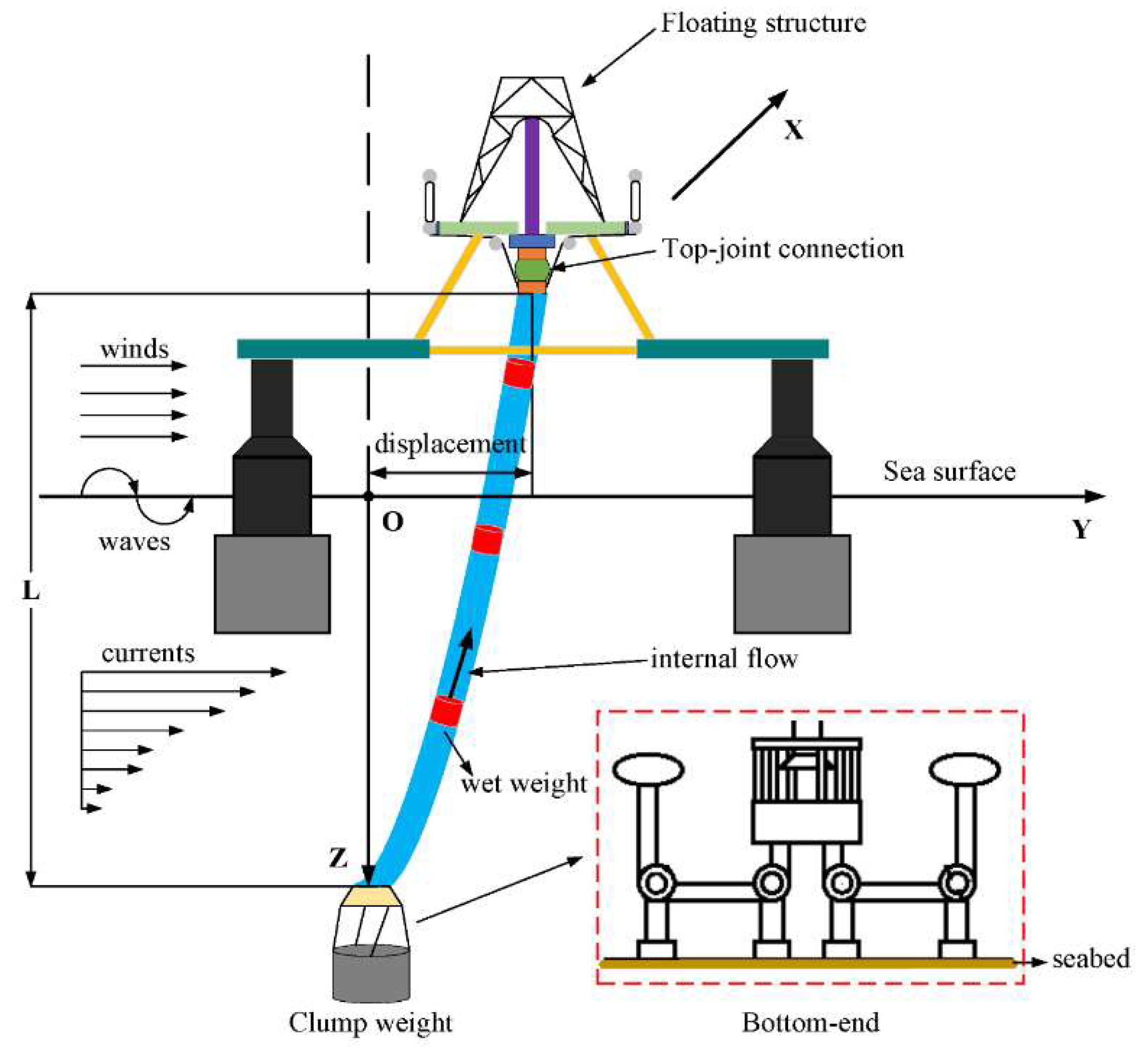
2. Analytical Simulation

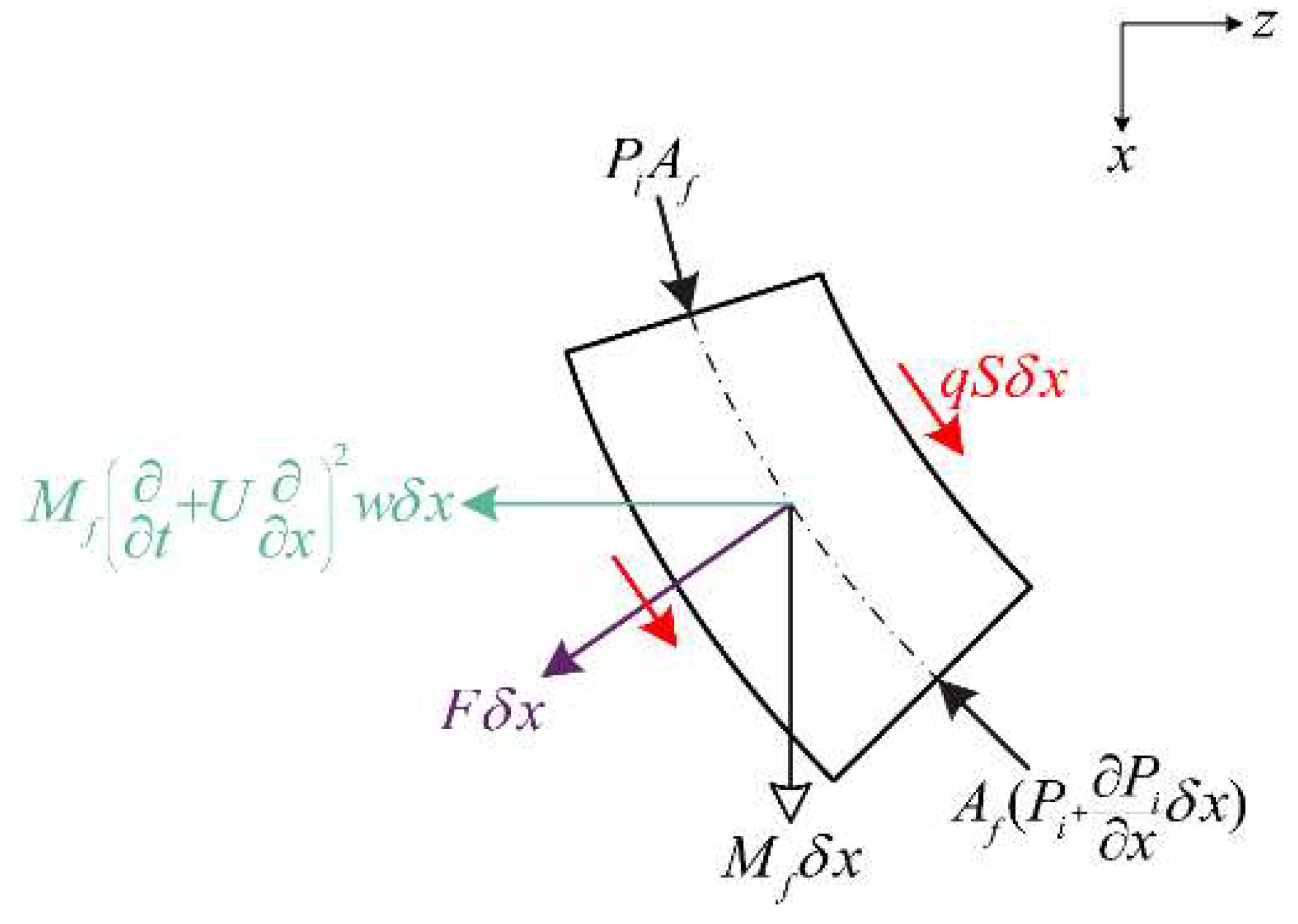
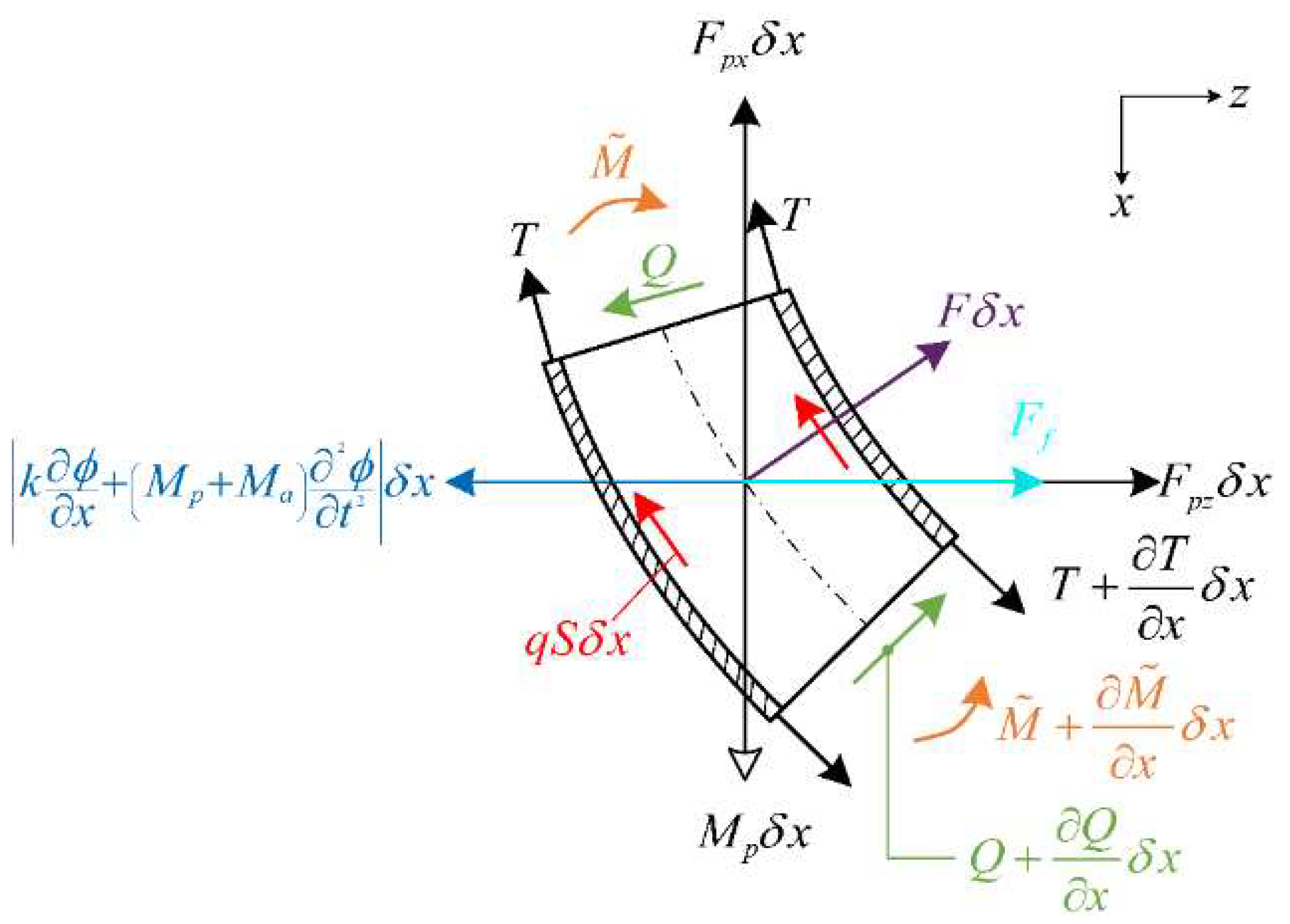
2.1. Governing General Equation

The analytical model of the cold-water pipe shown in Figure 2 is established and simplified as an Euler-Bernoulli beam. The cold-water pipe is a vertical cantilevered pipe, which is restrained at the upper end by articulation and at the lower end by a counterweight block and carries deep cold water upward from a water depth of 1200 m. The top of the cold-water pipe is subjected to the top tension applied by lifting and sinking compensator-tensioner. Before analysing the cold-water pipe, reasonable assumptions[37] are required.

(1) Assume that the cold-water pipe is composed of homogeneous, isotropic, viscoelastic material, ignoring the effect of the connecting joint between the pipes.

(2) Meet the Euler-Bernoulli theory model, ignoring the effect of axial shear.

(3) The incompressible fluid inside and outside the pipe.

The calculation of hydrodynamic loads is generally performed using Morrison equation, the rounding theory, and the Froude-Krylov assumption. Since the structures in this paper are slender marine structures, Morrison equation is used for the calculation. The basic idea of Morrison equation will divide the forces of waves and currents on the pipe into drag and inertia forces[38]. The use of Morrison equation for hydrodynamic load calculations requires reasonable assumptions.

(4) The ratio of the diameter of the member to the wavelength is not greater than 0.2, i.e.

D / L \leq 0.2

(5) The member is rigid, has a smooth surface, and is perpendicular to the seafloor.

According to the analysis of the engineering condition of the temperature difference energy cold-water pipe, the load acting on the pipe system includes two categories of environmental and operational load. Environmental loads include: waves, currents and sea wind loads; operational loads include: the gravity and buoyancy of the pipe itself, hydrodynamic loads, the gravity of counterweight blocks and internal fluid loads, etc.

As shown in Figure 2, the length of the cold-water pipe for L uniform pipe, the internal perimeter S, the internal cross-sectional area of the pipe

A_{f}

, the external cross-sectional area of the pipe

A_{o}

, the mass of the fluid inhaled per unit length

M_{f}

, the mass of the pipe per unit length

M_{p}

, the bending stiffness of the pipe EI, the intra-pipe flow rate of the fluid in the pipe

U

, the uniform cross-section of the pipe. The pipe is in an equilibrium position along the

x

-axis when no vibration occurs, and the effect of gravity is not negligible. The flow velocity may be affected by minor external disturbances, so generally

d U / d t \neq 0

. Considering that the pipe is a slender structure, its lateral motion is small, and its wavelength is long relative to its diameter; therefore, the curvilinear coordinates s and

x

coordinates along the centerline of the pipe can be used interchangeably according to the previous discussion. Consider both the fluid and the pipe microelements, as shown in Figure 3 and Figure 4.

As shown in Figure 3, the fluid micro-element is subjected to axial pressure (

P = P (x, t)

), and the internal hydrostatic pressure (

P_{i}

) and external hydrostatic pressure (

P_{o}

) on the cold-water pipe, respectively, the tangential fluid force tangential to the fluid micro-element (

q S δ x

), the average fluid force perpendicular to the fluid element (

F δ x

) (the reaction force of the pipe on the fluid), the axial, lateral, centrifugal, and kurtosis inertia forces of the fluid itself, and gravity (

M_{f} δ x

). According to Newton's second law of motion and Euler-Bernoulli beam theory, the pipe is a slight deformation, neglecting the second-order term of acceleration of the pipe in the

x

direction, as well as transverse shear deformation and rotational inertia, the fluid unit Axial direction force equilibrium equation is as follows.

- A_{f} \frac{\partial P_{i}}{\partial x} + q S + M_{f} g + F \frac{\partial ϕ}{\partial x} + M_{f} \frac{\partial U}{\partial t} = 0

(1)

The force balance equation in the z-axis direction of the fluid unit is as follows.

F + M_{f} {(\frac{\partial}{\partial t} + U \frac{\partial}{\partial x})}^{2} ϕ + A_{f} \frac{\partial}{\partial x} (P_{i} \frac{\partial y}{\partial x}) - q S \frac{\partial ϕ}{\partial x} - M_{f} \frac{\partial U}{\partial t} \frac{\partial ϕ}{\partial x} = 0

(2)

The pipe micro-element is subjected to axial tension perpendicular to the pipe cross-section (

T

), transverse shear force in the pipe (

Q

), bending moment (

\tilde{M}

), normal (

F δ x

) and tangential (

q S δ x

) forces of the fluid on the pipe, gravity (

M_{p} δ x

) , hydrostatic pressure of the fluid around the pipe in any direction , external fluid forces on the pipe (

F_{f}

), forces generated by the additional mass of the pipe and surrounding fluid (

(M_{p} + M_{a}) \frac{\partial^{2} ϕ}{\partial x^{2}} δ x

), and forces generated by friction-related damping (

k \frac{\partial ϕ}{\partial x} δ x

), according to Newton's second law and Euler Bernoulli beam theory, the pipe is a slight deformation, ignoring the second-order acceleration term in the direction of the pipe, as well as transverse shear deformation and rotational inertia, for the pipe unit in the

x

axial and

z

axial directions respectively, the force balance equations and moment balance equations, as shown in Figure 4.

The equation for the balance of forces in the

x

axial direction is as follows.

\frac{\partial T}{\partial x} - q S + M_{p} g - F_{p x} - F \frac{\partial ϕ}{\partial x} = 0

(3)

The equation for the balance of forces in the

z

axial direction is as follows.

\frac{\partial Q}{\partial x} + F - (M_{f} + M_{a}) \frac{\partial^{2} ϕ}{\partial t^{2}} - k \frac{\partial ϕ}{\partial t} + \frac{\partial}{\partial x} (T \frac{\partial y}{\partial x}) - q S \frac{\partial ϕ}{\partial x} + F_{p z} + F_{f} = 0

(4)

The moment balance equation for the micro-element column is as follows.

Q = - \frac{\partial \tilde{M}}{\partial x}

(5)

The pipe is a viscoelastic material subject to Kelvin-Voigt type internal dissipation and follows the following stress-strain relationship.

σ = E ε + E^{*} \frac{\partial ε}{\partial x} = (E + a E \frac{\partial}{\partial x}) ε

(6)

Where E is the modulus of elasticity of the pipe material,

E^{*}

is the dissipation coefficient of the pipe material, and

a

is the viscoelastic coefficient of the pipe. From Equation (6), the bending moment

\tilde{M}

can be expressed as follows.

\tilde{M} = (E + E^{*} \frac{\partial}{\partial x}) I \frac{\partial^{2} ϕ}{\partial x^{2}}

(7)

Substituting (7) into (5) yields.

Q = - (E + E^{*} \frac{\partial}{\partial x}) I \frac{\partial^{3} ϕ}{\partial x^{3}}

(8)

Considering the fluid as incompressible and neglecting the temperature effect of the fluid, there is a simple linear relationship between the pressure in hydrostatic water and[39,40].

P_{o} (x) = P_{o L} \frac{x}{L}

(9)

It can therefore be concluded that.

F_{p x} = 0 ， F_{p z} = \frac{\partial}{\partial x} (P_{o} A_{o} \frac{\partial ϕ}{\partial x})

(10)

Taking Equations (9) into (10) gives.

F_{p z} = \frac{A_{o} P_{o L}}{L} \frac{\partial ϕ}{\partial x} + \frac{A_{o} P_{o L} x}{L} \frac{\partial^{2} ϕ}{\partial x^{2}}

(11)

By adding up Equations (1) and (3) and substituting into (10), we obtain

\frac{\partial}{\partial x} (T - P_{i} A_{f}) + (M_{f} + M_{p}) g + M_{f} \frac{\partial U}{\partial t} = 0

(12)

The additional axial force generated by the pressure on the fluid at the lowermost end of the pipe is

P_{0 L} (1 - 2 ν δ)

. The axial force

δ

at the end of the pipe is equal to 1 when the pipe is restrained and 0 when it is free. Secondly, the axial force at the pipe is generated by the gravity of the counterweight minus its buoyancy, i.e.

\bar{T} = \bar{M} - F_{b}

(13)

Integrating (12) from to gives.

{(T - P_{i} A_{f})}_{x} = \bar{T} - P_{o L} A_{f} (1 - 2 ν δ) + [(M_{f} + M_{p}) g + M_{f} \frac{\partial U}{\partial t}] (L - x)

(14)

Subtracting from Equations (2) and (4) gives

\begin{array}{l} - \frac{\partial Q}{\partial x} + M_{f} {(\frac{\partial}{\partial x} + U \frac{\partial}{\partial x})}^{2} w + \frac{\partial}{\partial x} ((T - A_{f} P_{i}) \frac{\partial ϕ}{\partial x}) + (M_{f} + M_{a}) \frac{\partial^{2} ϕ}{\partial t^{2}} \\ + k \frac{\partial ϕ}{\partial t} - M_{f} \frac{\partial U}{\partial t} \frac{\partial ϕ}{\partial x} - F_{p z} - F_{f} = 0 \end{array}

(15)

Taking (8), (10), (11) and (14) into the above equation yields.

\begin{array}{l} (E + E^{*} \frac{\partial}{\partial x}) I \frac{\partial^{4} ϕ}{\partial x^{4}} + {M_{f} U^{2} - \bar{T} + P_{o L} A_{f} (1 - 2 ν δ) \\ - [(M_{f} + M_{p}) g + M_{f} \frac{\partial U}{\partial t}] (L - x) - \frac{A_{o} P_{o L} x}{L}} \frac{\partial^{2} ϕ}{\partial x^{2}} \\ + [(M_{f} + M_{p}) g - \frac{A_{o} P_{o L}}{L}] \frac{\partial ϕ}{\partial x} + 2 M_{f} U \frac{\partial^{2} ϕ}{\partial t \partial x} \\ + (M_{f} + M_{p} + M_{a}) \frac{\partial^{2} ϕ}{\partial t^{2}} + k \frac{\partial ϕ}{\partial t} - F_{f} = 0 \end{array}

(16)

According to the Morison[38] equation, the total drag force acting on the vertical column structure per unit length can be obtained as.

F_{D} = \frac{1}{2} C_{D} ρ_{w} D_{O} V | V |

(17)

Where

F_{D}

is the horizontal drag force,

C_{D}

is the drag force coefficient. When the Reynolds number

R_{e} < 3 \times 10^{5}

C_{D} = 1.2

ρ_{w}

is the seawater density,

D_{O}

is the riser outer diameter,

V

is the current flow velocity.

The inertial force acting on a vertical cylindrical structure per unit length can be expressed as.

F_{I} = ρ_{w} \frac{π D^{2}}{4} \frac{\partial V}{\partial t} + C_{a} ρ_{w} \frac{π D^{2}}{4} \frac{\partial V}{\partial t} = C_{m} ρ_{w} \frac{π D^{2}}{4} \frac{\partial V}{\partial t}

(18)

Where

C_{a}

is the additional mass coefficient,

C_{a} = 1.2

C_{m}

is the inertia force coefficient (

C_{m} = C_{a} + 1

Then the hydrodynamic load acting on the vertical cylindrical structure per unit length can be obtained as.

F_{f} = F_{D} + F_{I} = \frac{1}{2} C_{D} ρ_{w} D_{O} V | V | + C_{m} ρ_{w} \frac{π D^{2}}{4} \frac{\partial V}{\partial t}

(19)

In summary, combining Equations (16) and (19) yields the differential equations of motion for the pipeline under internal flow, sea current and wave excitation as.

\begin{array}{l} (E + E^{*} \frac{\partial}{\partial x}) I \frac{\partial^{4} ϕ}{\partial x^{4}} + {M_{f} U^{2} - \bar{T} + P_{o L} A_{f} (1 - 2 ν δ) \\ - [(M_{f} + M_{p}) g + M_{f} \frac{\partial U}{\partial t}] (L - x) - \frac{A_{o} P_{o L} x}{L}} \frac{\partial^{2} ϕ}{\partial x^{2}} \\ + [(M_{f} + M_{p}) g - \frac{A_{o} P_{o L}}{L}] \frac{\partial ϕ}{\partial x} + 2 M_{f} U \frac{\partial^{2} ϕ}{\partial t \partial x} \\ + (M_{f} + M_{p} + M_{a}) \frac{\partial^{2} ϕ}{\partial t^{2}} + k \frac{\partial ϕ}{\partial t} - \frac{1}{2} C_{D} ρ_{w} D_{o} V | V | - C_{m} ρ_{w} \frac{π D_{o}^{2}}{4} \frac{\partial V}{\partial t} = 0 \end{array}

(20)

2.2. Boundary Condition and General Solutions

Assuming that the pipe boundary conditions are simply supported at both ends, the expressions are.

\begin{array}{l} E I ϕ^{‴} (0) = - K_{1} ϕ (0), E I ϕ^{″} (0) = K_{T 1} ϕ^{'} (0) \\ E I ϕ^{‴} (L) = K_{2} ϕ (L), E I ϕ^{″} (L) = - K_{T 2} ϕ^{'} (L) \end{array}

(21)

Where

K_{1}, K_{2}

is the top and bottom linear spring stiffness, respectively, and

K_{T 1}, K_{T 2}

is the top and bottom torsional spring stiffness, respectively. In this paper, the boundary conditions of the water pipe: the top is supported, i.e., the top displacement and bending moment are 0; the bottom is a constraint with a concentrated mass (

\bar{M}

), i.e., the bottom bending moment is equal to 0. The mathematical formula can express the boundary conditions.

\begin{array}{l} ϕ (0) = ϕ^{″} (0) = 0, ϕ^{″} (L) = 0 \\ E I ϕ^{‴} (L) = \bar{M} ω^{2} ϕ (L) \end{array}

(22)

Where

K_{1} \to \infty

K_{T 1} = 0

K_{2} = \bar{M} ω^{2}

K_{T 2} = 0

, and

a^{4} = \frac{ω^{2} \bar{M}}{E I}

The differential equation of motion of the cold-water pipe is simplified by introducing dimensionless coefficients, which are as follows.

\begin{array}{l} ξ = \frac{x}{L}, η = \frac{ϕ}{L}, τ = \sqrt{\frac{E I}{M}} \frac{t}{L^{2}}, u = \sqrt{\frac{M_{f}}{E I}} U L, β = \frac{M_{f}}{M_{p}}, \\ γ = \frac{(M_{p} + M_{f}) L^{3}}{E I} g, ς = \frac{P_{o L} A_{o} L^{2}}{E I}, Γ = \frac{(\bar{M} - F_{b}) L^{2}}{E I}, \\ Π = \frac{P_{o L} A_{f} L^{2}}{E I}, α = \sqrt{\frac{I}{E M_{p}}} \frac{E^{*}}{L^{2}}, d = \frac{D_{o}}{L}, \\ v = \sqrt{\frac{M_{p}}{E I}} V L, w = \sqrt{\frac{M_{p}}{E I}} w_{s} L^{2}, ρ = \frac{L^{2}}{M_{p}} ρ_{w}, \\ k_{1} = \frac{L^{3}}{E I} K_{1}, k_{2} = \frac{L^{3}}{E I} K_{2}, k_{T 1} = \frac{L}{E I} K_{T 1}, k_{T 2} = \frac{L}{E I} K_{T 2} \end{array}

(23)

The primary consideration in this study is that the internal fluid is a constant flow, i.e., for the stability problem of self-excited vibration, so Equation (20) is simplified to

\begin{array}{l} α {\dot{η}}^{''''} + η^{''''} + {u^{2} + Γ + Π (1 - 2 ν δ) - γ (I - ξ) - ς ξ} η^{″} + (γ - ς) {\dot{η}}^{'} \\ + 2 \sqrt{β} u {\dot{η}}^{'} + \ddot{η} + r w ρ d^{2} \dot{η} - \frac{1}{2} C_{D} ρ d v^{2} - \frac{1}{4} π C_{m} ρ d^{2} \dot{v} = 0 \end{array}

(24)

The boundary conditions are simplified as.

\begin{array}{l} η^{‴} (0) = - k_{1} η (0), η^{'} (0) = k_{T 1} η^{'} (0) \\ η^{‴} (1) = k_{2} η (1), η^{'} (1) = - k_{T 2} η^{'} (1) \end{array}

(25)

The Differential quadrature method is a standard numerical solution for solving ordinary and partial differential equations. The basic idea is to approximate the derivative of a particular point in the computational region concerning the spatial variables by a weighted sum of the function values of all points in the computational region. It is assumed that the solution of Equation (24) is obtained in the form of as follows.

η (ξ, τ) = ϕ (ξ) \exp (Ω τ)

(26)

Substituting equation (26) into Equations (24) and (25) yields.

\begin{array}{l} (1 + α Ω) {ϕ^{'}}^{'}^{'}^{'} + {u^{2} + Γ + Π (1 - 2 ν δ) - γ (Ι - ξ) - ς ξ} {ϕ^{'}}^{'} \\ + (γ - ς + 2 \sqrt{β} u Ω) ϕ^{'} + (r w ρ d^{2} Ω + Ω^{2}) ϕ = 0 \end{array}

(27)

The boundary condition of the pipe.

\begin{array}{l} ϕ^{‴} (0) = - k_{1} ϕ (0), ϕ^{'} (0) = k_{T 1} ϕ^{'} (0) \\ ϕ^{‴} (1) = k_{T 2} ϕ (1), ϕ^{'} (1) = - k_{T 2} ϕ^{'} (1) \end{array}

(28)

Then the DQM discrete format of the control equation for the lateral vibration motion of the cold-water pipe under the action of the internal and external flow is as follows.

\begin{array}{l} \sum_{j = 1}^{N} {A_{i j}^{(4)} + [u^{2} + Γ + Π (1 - 2 ν δ) - γ (Ι - ξ_{i}) - ς ξ_{i}] A_{i j}^{(2)} + (γ - ς) A_{i j}^{(1)}} ϕ_{j} \\ + Ω \sum_{j = 1}^{N} [(α A_{i j}^{(4)} + 2 \sqrt{β} u A_{i j}^{(1)}) + r w ρ d^{2}] {\dot{ϕ}}_{j} + Ω^{2} ϕ_{i} = 0 \end{array}

(29)

The DQM discrete format of the boundary conditions is as follows.

\begin{array}{l} \sum_{j = 1}^{N} A_{1, j}^{(3)} + k_{1} ϕ_{1} = 0, \sum_{j = 1}^{N} A_{2, j}^{(2)} ϕ_{j} - k_{T 1} \sum_{j = 1}^{N} A_{2, j}^{(1)} ϕ_{j} = 0, \\ \sum_{j = 1}^{N} A_{N - 1, j}^{(3)} ϕ_{j} - k_{2} ϕ_{N - 1} = 0, \sum_{j = 1}^{N} A_{N, j}^{(2)} ϕ_{j} + k_{T 2} \sum_{j = 1}^{N} A_{N, j}^{(1)} ϕ_{j} = 0. \end{array}

(30)

Use the subscript b to denote the boundary and d to denote the non-boundary, i.e.

ϕ_{b} = {ϕ_{1}, ϕ_{2}, ϕ_{N - 1}, ϕ_{N}}^{T}, ϕ_{d} = {ϕ_{3}, ϕ_{4}, ϕ_{N - 4}, ϕ_{N - 3}}^{T}

(31)

Substituting Equation (31) into Equations (29) and (30), respectively, the following matrix form is obtained.

Ω^{2} I ϕ_{d} + Ω (G_{d b} ϕ_{b} + G_{d d} ϕ_{d}) + (K_{d b} ϕ_{b} + G_{d d} ϕ_{d}) = 0

(32)

K_{b b} ϕ_{b} + K_{b d} ϕ_{d} = 0

(33)

Solving Equation (33) by matrix operations and substituting the result into Equation (32) yields

G = - G_{d b} K_{b b}^{- 1} K_{b d} + G_{d d}

(34)

K = - K_{d b} K_{b b}^{- 1} K_{b d} + K_{d d}

(35)

Equation (33) has a non-zero solution of sufficient necessary conditions for the determinant of the matrix

Ω^{2} I + Ω G + K

to be zero so that the eigenvalues of the transverse vibration equation of the pipe can be solved, combined with Mathematica software to write the program, and finite element software Ocraflex simulation, using the cold-water pipe parameters and fluid parameters as shown in Table 2, to analyze the characteristics of the dynamic response of the pipe.

2.3. Convergence and Accuracy

To verify the effectiveness of the DQM method, the software Ocraflex was used to calculate the transverse vibration amplitude of the cold-water pipe at water depths of 100m, 300m, 500, 700m and 900m, and the results were compared with those solved by the DQM method, which are shown in Table 3 and as shown in Figure 5.

As seen from Table 3, the results of the finite element of transverse vibration amplitude at different locations of the pipe are very close to the theoretical solution, proving the method's effectiveness and correctness. As seen in Figure 5, the vibration response at the top of the pipe is the largest, and with the increase of water depth, the vibration response of the cold-water pipe keeps decreasing.

3. Results and Discussion

In the actual design process of the cold-water pipe project, three factors, waves, the clump weight, and internal flow velocity, respectively, significantly impact the lateral displacement and maximum bending moment of the cold-water pipe. This section will detail the impact of the appeal parameters on the mechanical properties of the chilled water pipe. The parameters shown in Table 2 and Table 4 are still used in the analysis process.

3.1. Parameter Sensitivity Analysis

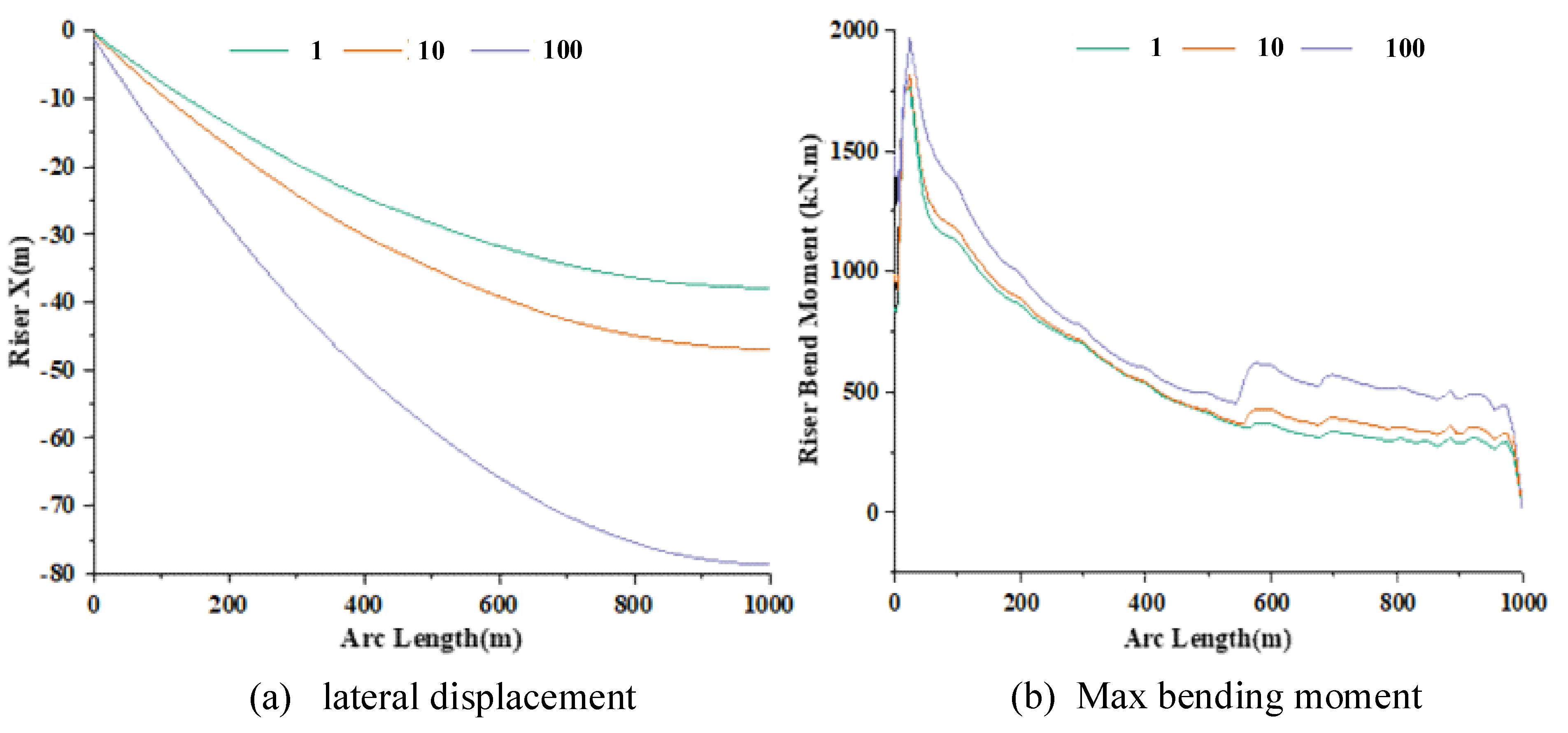
3.1.1. Effects of Waves

The impact of waves on the cold-water pipe can be divided into two main aspects: one is the hydrodynamic load acting directly on the pipe; the other is the dynamic boundary conditions at the top of the pipe changed by acting on the floating body platform, while the movement of the floating body platform will also cause a more significant impact on the offset and vibration response of the pipe. In order to investigate the effect of waves on the lateral deflection and maximum bending moment of the pipe, three sets of wave parameters are selected for comparison and analysis in this subsection: 1-year, 10-year and 100-year encounters.

Figure 6(a) shows the variation of lateral deflection with wave intensity at different pipeline locations. It can be seen that the hydrodynamic load generated by the waves on the pipe gradually accumulates with the water depth. Thus the lateral deflection of the pipe gradually increases, and its maximum can reach about 40m. The lateral displacement of the pipe is almost constant under the three wave intensities, mainly because the pipe is a large-scale structure and the wave parameters are not significantly different. The maximum bending moment development curve of the pipe considering only the wave strength is given in Figure 6(b). It can be found that the wave strength has a more significant influence on the bending moment of the cold seawater pipe; when the wave strength is the same, with the increase of water depth, the bending moment of the pipe shows a trend of first increasing and then decreasing. The maximum bending moment appears in the upper part of the pipe, especially at the top, where the abrupt change of the maximum bending moment occurs. The larger the wave strength is, the more abrupt change slightly decreases.

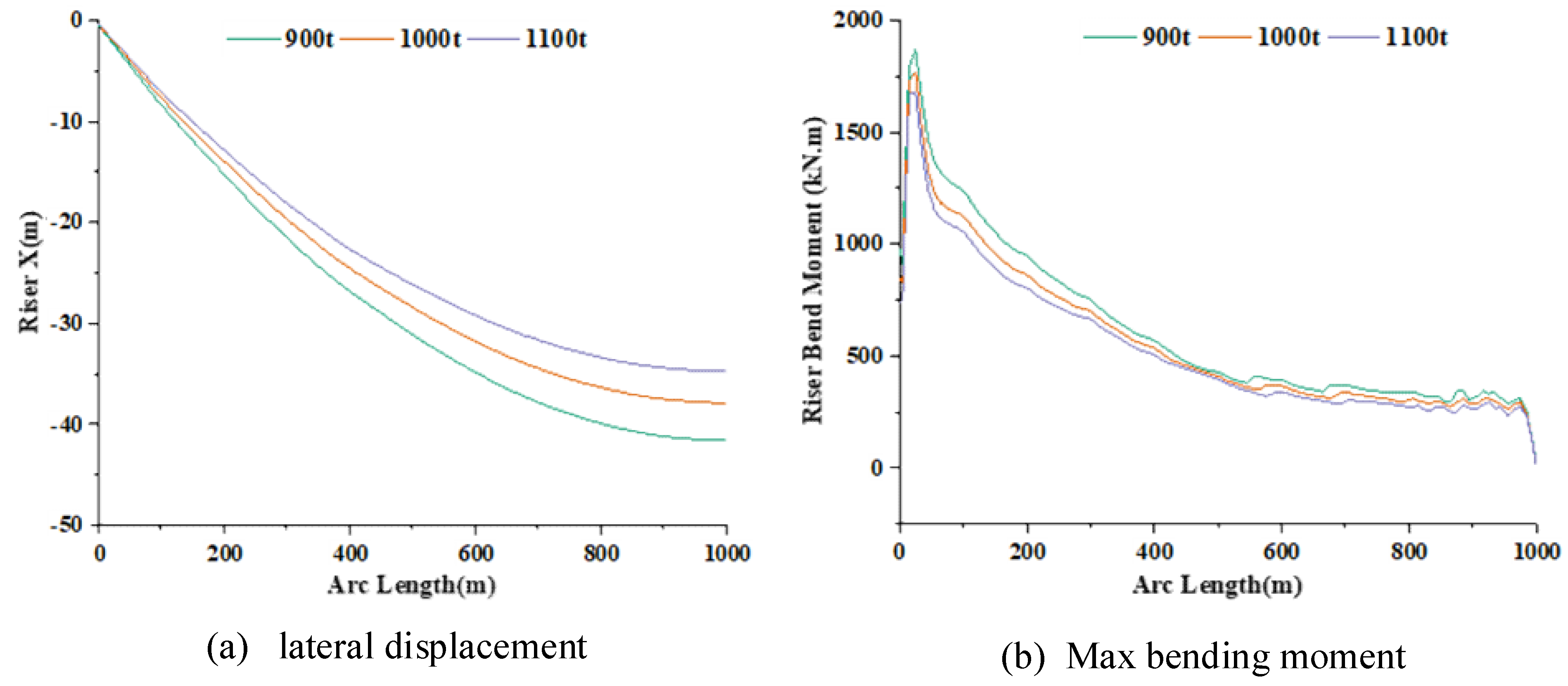
3.1.2. Effects of the Clump Weight

This section focuses on the effect of the bottom counterweight block on the dynamic response of the cold seawater pipe. The counterweight weights of 900t, 1000t and 1100t are selected for comparative analysis, and other parameters are still selected from Table 4. Figure 7 shows the curves of the development of the pipe's lateral deflection and maximum bending moment with water depth under different counterweight weights.

Figure 7(a) gives a graph of the development of the lateral offset of the pipe with the water depth at the different weights of the bottom counterweight. It can be found that with the increase of water depth, the lateral offset of the pipe gradually increases, and the growth of the lateral offset of the pipe tends to level off at 900-1000m. With the increase in the weight of the bottom counterweight, the pipeline's lateral offset gradually decreases, indicating that the bottom counterweight can effectively reduce the lateral offset of the pipeline. According to Figure 7(b), when the weight of the counterweight is 900t, the maximum bending moment of the pipe increases sharply with the increase of water depth and then decreases gradually and levels off at 500-1000m. When increasing the bottom counterweight's weight, the pipeline's maximum bending moment can be effectively reduced in the water depth range of 100-200m.

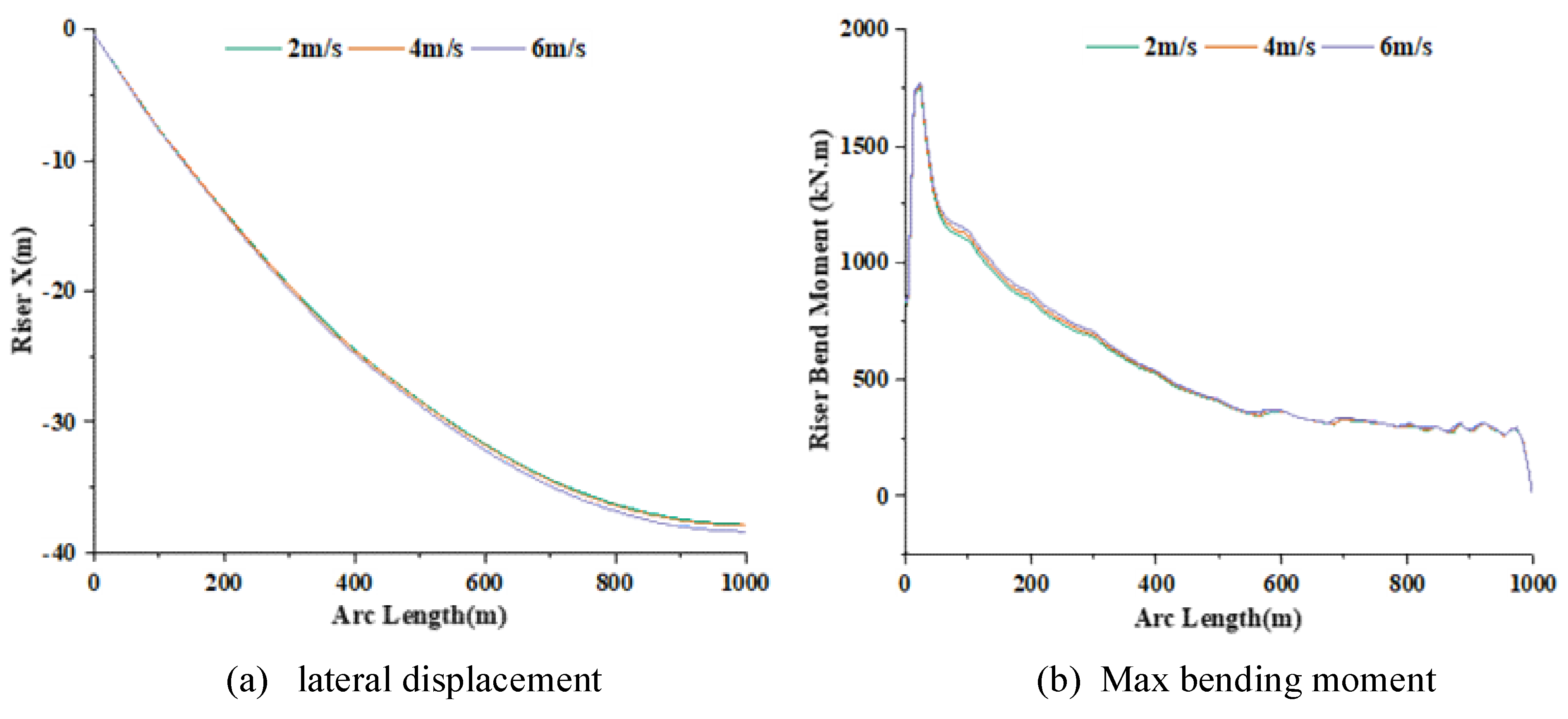
3.1.3. Effects of Internal Flow Velocity

This section studies the effect of the internal flow velocity on the lateral deflection and maximum bending moment of the pipe. Three groups of internal flow velocities, 2m/s, 4m/s and 6m/s, are selected respectively for comparison and analysis, while other parameters are still selected from Table 4. Figure 8 shows the curves of the development of lateral deflection and maximum bending moment of the pipe with water depth under different internal flow velocities.

Figure 8(a) shows the development curve of lateral deflection of the pipe under the effect of internal flow only. It can be seen that the effect of the internal flow velocity on the lateral offset of the cold seawater pipe is negligible. With the increase of the water depth, the lateral offset increases, and the maximum offset of the cold seawater pipe under the three internal flow velocities are about 40m, in line with the requirements of the actual project, the lateral offset of 40m is not more than 5% of the water depth of 1200m. Figure 8(b) is the development curve of the maximum bending moment of the pipe with the water depth under different internal flow velocities, the maximum bending moment of the cold seawater pipe is not significantly affected by the change of the internal flow velocity, and there is a sharp increase in the water depth of 30m. The overall trend is that the maximum bending moment decreases gradually with the increase of water depth.

3.1.4. Effects of Current Velocity

In order to investigate the effect of sea current on the lateral deflection and maximum bending moment of the pipeline, three sets of sea current flow parameters of 1-year 1-interval, 10-year 1-interval and 100-year 1-interval are selected for simulation in this section. Figure 9 shows the graphs of lateral deflection and maximum bending moment development of the pipeline under different sea current flow rates.

From Figure 9(a), it can be seen that the current velocity has a significant influence on the lateral offset of the cold-water pipe; with the increase of the current velocity, the lateral offset of the pipe increases; when the occasional 100-year one encounter sea current is encountered, the lateral offset reaches 80m, which exceeds 5% of the seawater depth of 1200m and is not in line with the engineering reality, so special attention needs to be paid to the influence of the change of the current sea velocity on the lateral offset of the pipe. It can be seen from Figure 9(b) that the effect of sea current velocity changes on the maximum bending moment of the cold-water pipe is mainly manifested in two aspects, one is the difference of the peak near the top of the cold seawater pipe, and the other is that the maximum bending moment of the pipe increases with the increase of current velocity, but its change trend is the same. The change in current velocity significantly impacts the maximum bending moment of the pipe.

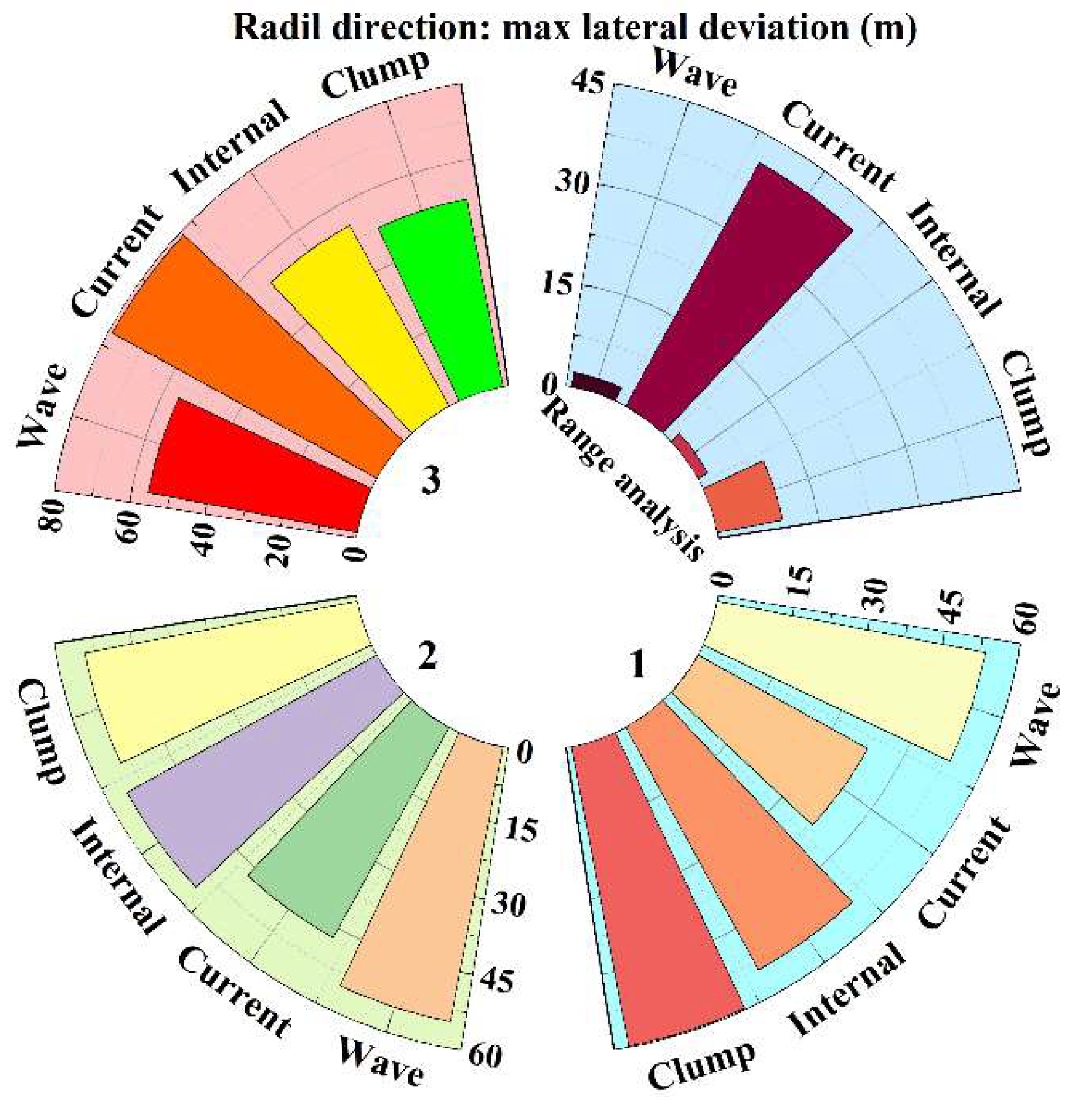
3.2. Orthogonal Analysis of Key Parameters

The analysis in the previous section shows that the four factors of the wave, the clump weight, internal flow velocity and current influence the mechanical properties of the pipe. In order to further analyze the degree of influence of the three influencing factors on the cold-water pipe, this subsection, through the orthogonal test design, is for a comprehensive analysis of the degree of influence of cold-water pipe.

3.2.1. Analysis of Orthogonal Experiments

This multi-factor and multi-level analysis method of the number of simulation experiments into a power increase, the use of this comprehensive experimental approach requires a large number of simulation experiments, the workload is quite large, resulting in tedious work. In this paper, the orthogonal experiment method is used, which is a feasible method to improve the efficiency of seeking the optimal level of combination and is widely used.

Through the analysis of the three factors in the previous section to get the wave, the clump weight, internal flow velocity and sea current on the dynamic characteristics of the cold-water pipe more significant, therefore, the four factors to analyze the degree of influence on the dynamic response of the cold-water pipe. The orthogonal test matrix table with four factors and three levels was designed as shown in Table 5.

In analysing the impact of different factors on the cold-water pipe, at the same time, consider each factor set several parameters. The orthogonal 3⁴ orthogonal test form was used to carry out the orthogonal test design, and the protocol was developed concerning the orthogonal form, as shown in Table 6.

3.2.2. Simulation Date Analysis

In this subsection, the dynamic response analysis of the cold-water pipe was carried out using the finite element software Ocraflex simulation method, and nine numerical calculations were performed. The relevant data obtained are shown in Table 7.

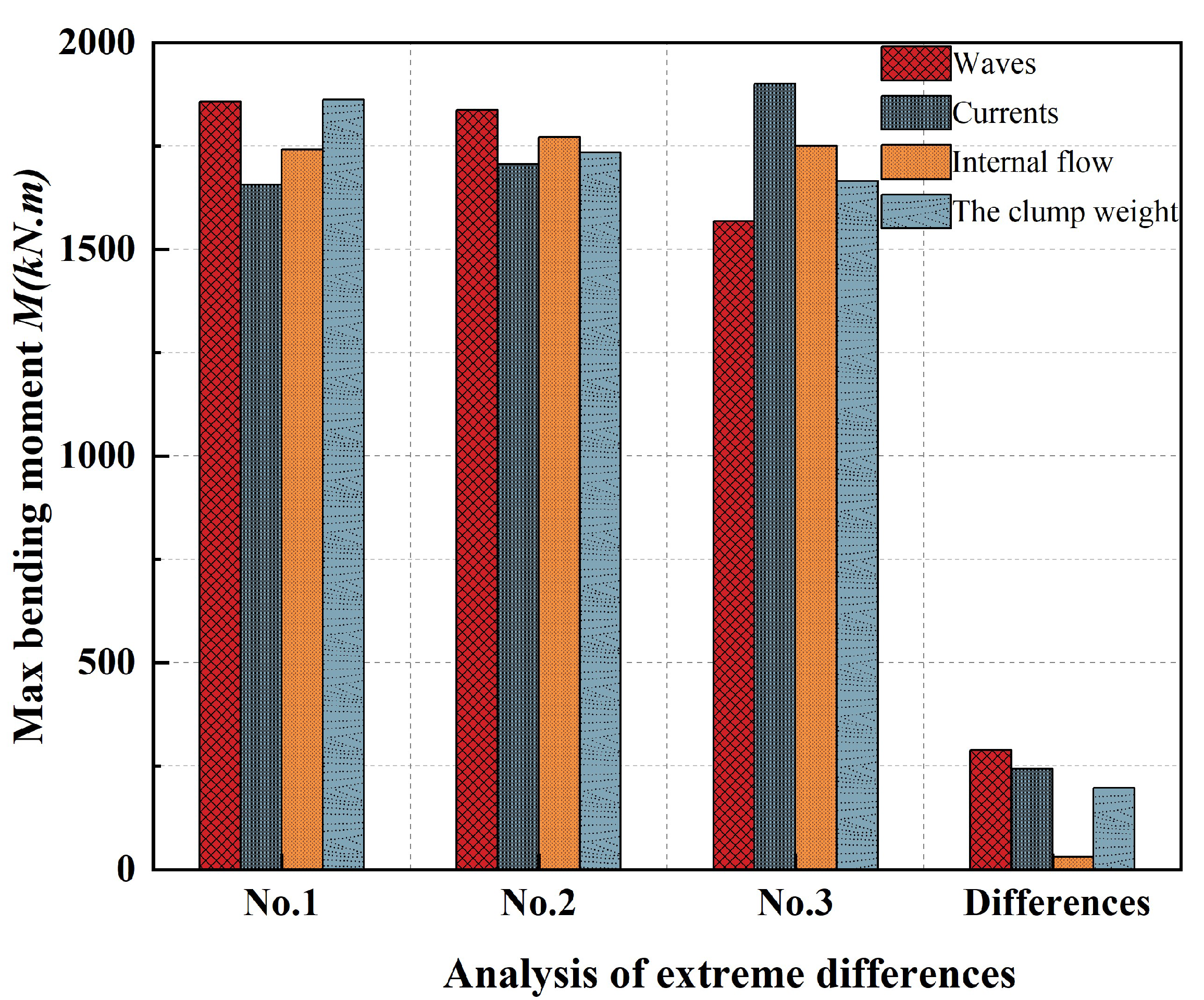
3.2.3. Extremum Difference Analysis

In this subsection, four factors affecting the power response of the pipe and their three different levels are analyzed in an orthogonal simulation. In order to see the sensitivity of the different levels of different factors to the influence of the pipe dynamic response, the sensitivity is analyzed by the polar difference method. The basic principle of the polar difference method is divided into two steps: (1) calculate the average value of the same level under the conditions of different factors; (2) calculate the fluctuation range of the average value of the same factor under the conditions of different levels, the value of the fluctuation range is the resulting polar difference.

(1) The results of the maximum lateral displacement of the cold-water pipe obtained from the orthogonal experiment are post-processed to obtain the polar difference based on the maximum lateral displacement and plotted as shown in Figure 10. It can be seen that: the order of importance affecting the lateral displacement of the cold-water pipe are: current, the clump weight, wave and internal flow; when the lateral offset of the cold-water pipe reaches the maximum, the parameters are: wave is 6.5m, current velocity is 1.42m/s, the internal flow velocity is 5m/s, and the clump weight is 900t.

(2) The results of the maximum bending moment of the cold-water pipe obtained from the orthogonal experiment were post-processed to obtain the extreme difference based on the maximum bending moment and plotted as shown in Figure 11. It can be seen that: the order of importance of the maximum bending moment affecting the cold-water pipe are: wave, sea current, the clump weight, and internal flow velocity; when the bending stress of the cold-water pipe reaches the maximum, the parameters are: wave is 4.8m, sea current is 1.42m/s, the internal flow velocity is 5m/s, the clump weight is 900t.

Through the above extreme difference analysis of the lateral offset and maximum bending moment of the cold-water pipe, it is concluded that: the influence of wave order in the first place twice, which fully indicates that the change of wave has the most significant impact on the maximum bending moment of the cold-water pipe, which is the most critical factor affecting the dynamic response characteristics of the cold-water pipe; the change of the current velocity has the most apparent impact on the lateral offset of the cold-water pipe; in summary, it can be seen that the wave, the current velocity and the clump weight at the bottom have a significant impact on the dynamic response of the cold-water pipe, therefore, in the design and manufacture of the cold-water pipe and the installation and operation process need to pay attention to these three parameters.

4. Conclusions

In this paper, the mechanical properties of ultra-large cold-water pipe for Ocean Thermal Energy Conversion is addressed. The lateral motion control equations of the pipe are derived based on the structural dynamics and semi-analytical solution methods, and the effect of the parameters of waves, the clump weight, internal flow and sea current are analyzed using finite element software, and the specific conclusion are as follows.

(ⅰ). Based on the Euler-Bernoulli beam theory and differential quadrature method, the mechanical model of transverse vibration control of ultra-large cold-water pipe is established by comprehensively considering the effects of wave, sea current, internal flow and the clump weight, and the semi-analytical solution of the mechanical response of the pipe is derived, and the correctness of the theoretical model is verified by comparing with the numerical simulation results.

(ⅱ). The wave strength, the clump weight, internal flow velocity and sea current velocity can gradually increase the lateral deflection of the cold-water pipe, but different wave strength and internal flow velocity have little effect on the lateral deflection of the pipe. Increasing the clump weight at the bottom can effectively suppress the lateral deflection of the pipe, and the suppression effect is better near the location of the bottom counterweight; the larger the sea current velocity is, the larger the lateral deflection of the pipe is, which is likely to cause the cold-water pipe strength failure problem.

(ⅲ). Wave strength, the clump weight, internal flow velocity and sea current velocity have a greater effect on the maximum bending moment of the pipe, and their effects are first sharply increased, and then gradually decreased until leveling off. However, the effect of the parameters is different in the location of the pipe section, at 100-200m, the greater the wave strength, the smaller the maximum bending moment, and at 600m, the maximum bending moment changes begin to level off. At 50m-150m, the clump weight at the bottom and the velocity of the current are larger, the maximum bending moment decreases gradually, and at 600m, the maximum bending moment begins to level off.

(ⅳ). Based on the orthogonal analysis of key parameters, the change of wave has the greatest influence on the maximum bending moment of cold seawater pipe, the change of sea current velocity has the most obvious influence on the lateral deflection of cold seawater pipe, and the clump weight at the bottom can effectively suppress the lateral deflection and maximum bending moment of pipe.

Acknowledgments

The authors gratefully acknowledge the financial support provided by and the Found of Southern Marine Science and Engineering Guangdong Laboratory (Zhanjiang) (Grant No. ZJW-2019-05), and the National Natural Science Foundation of China (Grant No. 52201347).

References

Makai ocean engineering. ocean thermal energy conversion [EB / OL]. Available online: https:∥www. makai. com/ ocean-thermal-energy conversion.
Herrera, J.; Sierra, S.; Ibeas, A. Ocean Thermal Energy Conversion and Other Uses of Deep Sea Water: A Review. J. Mar. Sci. Eng. 2021, 9, 356. [Google Scholar] [CrossRef]
Adiputra, R.; Utsunomiya, T. Stability based approach to design cold-water pipe (CWP) for ocean thermal energy conversion (OTEC). Appl. Ocean Res. 2019, 92, 101921. [Google Scholar] [CrossRef]
Adiputra, R.; Utsunomiya, T. Linear vs non-linear analysis on self-induced vibration of OTEC cold water pipe due to internal flow. Appl. Ocean Res. 2021, 110, 102610. [Google Scholar] [CrossRef]
Xiang, S.; Cao, P.; Erwin, R.; Kibbee, S. OTEC Cold Water Pipe Global Dynamic Design for Ship-Shaped Vessels. Ocean. Renew. Energy 2013. [Google Scholar] [CrossRef]
Kuiper, G.; Metrikine, A. Dynamic stability of a submerged, free-hanging riser conveying fluid. J. Sound Vib. 2005, 280, 1051–1065. [Google Scholar] [CrossRef]
Halkyard, J.; Sheikh, R.; Marinho, T.; Shi, S.; Ascari, M. Current Developments in the Validation of Numerical Methods for Predicting the Responses of an Ocean Thermal Energy Conversion (OTEC) System Cold Water Pipe. Volume 7: Ocean Space Utilization; Professor Emeritus J. Randolph Paulling Honoring Symposium on Ocean Technology 2014. [CrossRef]
Shi, S.; Halkyard, J.; Kurup, N.; Jiang, L. Coupled Analysis Approach in OTEC System Design. Volume 4: Offshore Geotechnics; Ronald W. Yeung Honoring Symposium on Offshore and Ship Hydrodynamics. 2012. [Google Scholar]
Lockheed Martin. 2011. NAVFAC Ocean Thermal Energy Conversion (OTEC) Project. Port Hueneme, CA: Naval Facilities Engineering Command. Port Hueneme, CA.
Xiang, S.; Cao, P.; Erwin, R.; Kibbee, S. OTEC Cold Water Pipe Global Dynamic Design for Ship-Shaped Vessels. Ocean. Renew. Energy 2013, 8. [Google Scholar] [CrossRef]
Aitken, J. XIV. An account of some experiments on rigidity produced by centrifugal force. London, Edinburgh, Dublin Philos. Mag. J. Sci. 1878, 5, 81–105. [Google Scholar] [CrossRef]
Bourriéres, F. (1939). Sur un phénomène d'oscillation auto-entretenue en mécanique des fluides réels.
Housner, G.W. Bending Vibrations of a Pipe Line Containing Flowing Fluid. J. Appl. Mech. 1952, 19, 205–208. [Google Scholar] [CrossRef]
R. W. GREGORY and M. P. PAIDOUSSIS 1966a Proceedings of the Royal Society (London) A, 293, 512-527. Unstable oscillation of tubular cantilevers conveying fluid. I. Theory.
R. W. GREGORY and M. P. PAIDOUSSIS 1966b Proceedings of the Royal Society (London) A, 293, 528-542. Unstable oscillation of tubular cantilevers conveying fluid. II. Experiments.
T. BROOKE BENJAMIN 1961a Proceedings of the Royal Socicty (London) A, 261,457-486. Dynamics of a system of articulated pipes conveying fluid. I. Theory.
Wu, M.C.; Lou, J.Y.K. Effects of rigidity and internal flow on marine riser dynamics. Appl. Ocean. Res. 1991, 13, 235–244. [Google Scholar]
Guo, H.Y.; Wang, S.Q.; Wu, J.N.; et al. Dynamic Characteristics of Marine Risers Conveying Fluid[J]. China Ocean Engineering. 2000, 14, 153–160. [Google Scholar]
Li, X.M.; Guo, H.Y.; Meng, F.S. Effect of internal flow on the dynamic behavior of top tensioned riser[J]. Journal of Ship Mechanics 2010, 14, 1021–1030. [Google Scholar]
Jung, D.; Chung, J. In-plane and out-of-plane motions of an extensible semi-circular pipe conveying fluid[J]. Journal of Sound and Vibration 2008, 311, 408–420. [Google Scholar] [CrossRef]
Ghayesh, M.H.; Païdoussis, M.P.; Modarres-Sadeghi, Y. Three-dimensional dynamics of a fluid-conveying cantilevered pipe fitted with an additional spring support and an end-mass[J]. Journal of Sound and Vibration 2011, 330, 2869–2899. [Google Scholar] [CrossRef]
Uczko, J.; Czerwiński, A. Parametric vibrations of flexible hoses excited by a pulsating fluid flow, Part I: modelling, solution method and simulation[J]. Journal of Fluids and Structures, 2015; 55, 155–173. [Google Scholar] [CrossRef]
Uczko, J.; Czerwiński, A. Nonlinear three-dimensional dynamics of flexible pipes conveying fluids[J]. Journal of Fluids and Structures, 2017; 55, 235–260. [Google Scholar] [CrossRef]
Misra, A.; Païdoussis, M.; Van, K. On the dynamics of curved pipes transporting fluid. Part I: Inextensible theory. J. Fluids Struct. 1988, 2, 221–244. [Google Scholar] [CrossRef]
Misra, A.; Païdoussis, M.; Van, K. On the dynamics of curved pipes transporting fluid Part II: Extensible theory. J. Fluids Struct. 1988, 2, 245–261. [Google Scholar] [CrossRef]
Patel, M.H.; Seyed, F.B. Review of flexible riser modelling and analysis techniques[J]. Engineering Structures 1995, 17, 293–304. [Google Scholar] [CrossRef]
Zare, K.; Datta, T.K. Vibrations of lazy "S" risers due to vortex shedding under lock-in[C]. Offshore Technology Conference, Texas, USA, 1988; pp. 451–458. [Google Scholar]
Jain, A.K. Review of flexible risers and articulated storage systems[J]. Ocean Engineering 1994, 21, 733–750. [Google Scholar] [CrossRef]
Chatjigeorgiou, I.K. A finite differences formulation for the linear and nonlinear dynamics of 2D catenary risers[J]. Ocean Engineering 2008, 35, 616–636. [Google Scholar] [CrossRef]
Huang, Y.; Zeng, G.; Wei, F. A new matrix method for solving vibration and stability of curved pipes conveying fluid[J]. Journal of Sound and Vibration 2002, 251, 215–225. [Google Scholar] [CrossRef]
Shen, H.J.; Wen, J.H.; Yu, D.L.; et al. The vibration properties of a periodic composite pipe in 3D space[J]. Journal of Sound and Vibration 2009, 328, 57–70. [Google Scholar] [CrossRef]
Liang, X.; Zha, X.; Jiang, X.; Wang, L.; Leng, J.; Cao, Z. Semi-analytical solution for dynamic behavior of a fluid-conveying pipe with different boundary conditions. Ocean Eng. 2018, 163, 183–190. [Google Scholar] [CrossRef]
An, C.; Su, J. Dynamic Behavior of Pipes Conveying Gas–Liquid Two-Phase Flow. Nuclear Engineering and Design 2015, 292, 204–212. [Google Scholar] [CrossRef]
An, C.; Su, J. Vibration behavior of marine risers conveying gas-liquid two-phase flow. In Proceedings of the 34th International Conference on Ocean, Offshore and Arctic Engineering, American Society of Mechanical Engineers, Newfoundland, Canada; 2015. [Google Scholar]
Li, T.; An, C.; Liang, W.; Duan, M.; Estefen, S.F. Semi-analytical solution for soil-constrained vibration of subsea free-spanning pipelines. Ships Offshore Struct. 2018, 13, 666–676. [Google Scholar] [CrossRef]
Li, F.; An, C.; Duan, M.; Su, J. Combined damping model for dynamics and stability of a pipe conveying two-phase flow. Ocean Eng. 2019, 195, 106683. [Google Scholar] [CrossRef]
Qiao, N.; Lin, W.; Qin, Q. Bifurcations and chaotic motions of a curved pipe conveying fluid with nonlinear constraints. Comput. Struct. 2006, 84, 708–717. [Google Scholar] [CrossRef]
Paidoussis, M.P. Fluid-Structure interactions: Slender structures and axial flow; Academic Press: London, 1998; Volume l. [Google Scholar]
Chibueze, N.O.; Ossia, C.V.; Okoli, J.U. On the Fatigue of Steel Catenary Risers. Strojniški Vestnik-Journal of Mechanical Engineering, 2016; 62, 751–756. [Google Scholar] [CrossRef]
Paidoussis, M.P.; Luu, T.P. Dynamics of a Pipe Aspirating Fluid Such as Might be Used in Ocean Mining. J. Energy Resour. Technol. 1985, 107, 250–255. [Google Scholar] [CrossRef]
Paidoussis, M.P. Dynamics of Tubular Cantilevers Conveying Fluid. J. Mech. Eng. Sci. 1970, 12, 85–103. [Google Scholar] [CrossRef]

Figure 1. Ocean Thermal Energy Conversion operating principle.

Figure 2. Schematic diagram of load of CWP system.

Figure 3. Force analysis diagram of fluid elements.

Figure 4. Pipe element force analysis diagram.

Figure 5. Lateral vibration amplitudes at different water depths (Ocraflex).

Figure 6. The lateral displacement and max bending moment of the pipe with respect to different wave intensities.

Figure 7. The transverse displacement and max bending moment of the pipe with respect to different clump weight at the bottom.

Figure 8. The transverse displacement and bending moment of the pipe with respect to the internal flow velocity.

Figure 9. The transverse displacement and max bending moment of the pipe with respect to the external flow velocity.

Figure 10. Range analysis of max lateral deviation range of CWP.

Figure 11. Range analysis max bending stress of CWP.

Table 1. The main parameters of the CWP.

Nomenclature	Description
EI	Bending stiffness (N/m²)
L	Pipe length (m)
M_p	Mass of the internal flow per unit length (kg/m)
M_f	Mass of the pipe per unit length (kg/m)
T	Axial equivalent tension (N)
U	Velocity of the internal flow (m/s)
$ϕ (x, t)$	Transverse displacement of the pipe (m)
A_f	Internal cross-sectional areas (m²)
A₀	External cross-sectional areas (m²)
$ρ_{w}$	Density of the seawater (kg/m³)
C_a	Added mass coefficient
$P_{i}$	Internal pressure of the pipe
$P_{0}$	External pressure of the pipe
C_d	Adapted drag coefficient

Table 2. Physical properties of CWP.

Property	Value
Bending stiffness (Gpa)	30
Inner diameter (m) Outer diameter (m)	1.5 1.6
Density of the seawater (kg/m³) The density of the pipe (kg/m³)	1025 1760
Pipe length (m)	1000
Axial equivalent tension	0
External flow velocity (m/s)	1.09
Velocity of the internal flow (m/s)	5.0
Top fluid pressure (Pa)	$1.0 \times 10^{5}$
Poisson's ratio	0.3
Adapted drag coefficient Additional mass coefficient	1.0 1.0

Table 3. Transverse vibration amplitude at different point of the pipe.

Pipe Section Location	Numerical Simulation Method (m)	DQM METHOD (m)
0.1	0.8536	0.8934
0.3	0.4952	0.4879
0.5	0.3016	0.2991
0.7	0.1954	0.2047
0.9	0.1187	0.1152

Table 4. Environmental parameters of current and wave.

Periodicity (year)		1	10	100
Wave	Significant wave height (m)	4.8	5.8	6.5
	Max wave height (m)	8.3	10.0	11.3
	Period (s)	7.8	9.0	9.8

Table 5. CWP orthogonal test matrix table.

Horizontal	Factors
Horizontal	Wave (m)	Current (m/s)	Internal Flow Velocity (m/s)	The Clump Weight (t)
1	4.8	0.99	2	900
2	5.8	1.09	4	1000
3	6.5	1.42	6	1100

Table 6. Orthogonal test table of CWP.

Number	Wave (m)	Current (m/s)	Internal Flow Velocity (m/s)	The Clump Weight (t)
1	4.8	0.99	2	900
2	4.8	1.09	4	1000
3	4.8	1.42	6	1100
4	5.8	0.99	4	1100
5	5.8	1.09	6	900
6	5.8	1.42	2	1000
7	6.5	0.99	6	1000
8	6.5	1.09	2	1100
9	6.5	1.42	4	900

Table 7. Simulation data of nine groups CWP tests.

Numbers	Max Lateral Displacement (m)	Max Bending Moment (kN.m)
1	41.46	1854.8
2	46.8	1806.88
3	72.33	1910.79
4	34.73	1668.64
5	51.57	1892.18
6	78.35	1950.59
7	37.96	1446.81
8	42.88	1417.94
9	86.16	1840.65

Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.

© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).

Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.

MDPI Initiatives

Important Links

Choose an area of interest and we will send you notifications of new preprints at your preferred frequency.

Disclaimer

Investigation on Dynamic Behavior of Ultra-Large Cold-water Pipe for Ocean Thermal Energy Conversion

Abstract

1. Introduction

2. Analytical Simulation

2.1. Governing General Equation

2.2. Boundary Condition and General Solutions

2.3. Convergence and Accuracy

3. Results and Discussion

3.1. Parameter Sensitivity Analysis

3.1.1. Effects of Waves

3.1.2. Effects of the Clump Weight

3.1.3. Effects of Internal Flow Velocity

3.1.4. Effects of Current Velocity

3.2. Orthogonal Analysis of Key Parameters

3.2.1. Analysis of Orthogonal Experiments

3.2.2. Simulation Date Analysis

3.2.3. Extremum Difference Analysis

4. Conclusions

Acknowledgments

References

MDPI Initiatives

Important Links

Subscribe