Prerpints.org logo
Preprint
Review

Progressive Collapse Resistance of Steel Frame Buildings and the Role of Beam-Column Connections

Altmetrics

Downloads

225

Views

100

Comments

0

A peer-reviewed article of this preprint also exists.

This version is not peer-reviewed

Submitted:

16 June 2023

Posted:

19 June 2023

You are already at the latest version

Alerts
Abstract
The behaviour of steel frame buildings under progressive collapse conditions depends on a combination of several parameters including the interplay between different collapse resistance mechanisms mobilized in different structural components. Previous studies have shown that the extent to which these mechanisms may contribute to progressive collapse resistance depends on the ability of the beam-column connections to undergo large inelastic deformations prior to reaching their deformation capacity limits. For this reason, and due to the important role of their flexural strength and tying capacity in the development of essential collapse resistance mechanisms, the response of beam-column connections is one of the most important features of progressive collapse performance. Based on the knowledge gained through previous studies on the mechanics of the problem, the role of the connections is critically reviewed by examining the results of several experimental studies conducted during the past decade. The factors that may adversely affect progressive collapse resistance – such as failure modes of certain connection types – are evaluated, and novel approaches of limiting these factors which are currently under development are reviewed. The assessment of these parameters leads to useful conclusions of practical significance, while highlighting the aspects of the problem that need further study and understanding.
Keywords: 
Subject: Engineering  -   Civil Engineering

1. Introduction

The traditional methods available in current design codes for assessing resistance of building structures to progressive collapse have mainly been derived from the work conducted in the UK following the Ronan Point collapse [1]. In their simplest form, these methods are mainly prescriptive since they only impose certain conditions on the basis that their inclusion will simply ensure a potentially better performance. One such approach is the provision of a suitable level of tying resistance in structural components, with the aim of increasing the degrees of continuity, ductility, and load transfer capacity. Various forms of the tying force method are addressed in current design codes such as the Eurocodes [2] and the US guidelines to structural robustness [3,4]. However, these approaches do not account for all the key features of the problem, and therefore they cannot provide a reliable indication of progressive collapse resistance [5,6,7,8,9]. For this reason, a replacement of the traditional form of the tying force method is currently in process [10,11].
Since general interest in the more scientific treatment of the problem has heightened significantly during the past two decades, especially after the 9/11 events, the need for a sound understanding of the mechanics of progressive collapse has become more important [12]. The research activity has focused on changing the design basis from prescriptive requirements to performance-based methods that rely on understanding, modelling, and quantitative assessment. Therefore, particular attention was given to the study of the problem through the “alternate load path” approach, which allows the quantitative assessment of structural resistance to progressive collapse based on the analysis of the actual mechanics of structural behaviour [13,14,15,16,17].
The alternate load path method is usually applied by considering a threat-independent loss of a load-bearing element – e.g., a column member – and by examining the consequences of this action to the remaining structure [18]. It may incorporate essential features of the ensuing structural behaviour such as dynamic effects (provided the load-bearing member is removed instantaneously to simulate the scenarios of blast or impact), loading redistribution, large deformations, material nonlinearity, and second-order geometry effects. The gravity loading that was initially carried by the missing element may effectively be redistributed to the remaining structure through the activation of different collapse resistance mechanisms. Progressive collapse may therefore be arrested once the structure attains a new state of stable equilibrium; otherwise, the increased loading and deformation demands may cause separation at key locations, which may lead to collapse propagation. Most likely, separations may occur at the connections between structural components, and thus the response of the connections represents a key feature of the progressive collapse behaviour [19].
The role of the connections in the progressive collapse resistance of steel frame buildings is the subject of this paper. First, the different collapse resistance mechanisms mobilized in steel frame structures under the action of notional column removal are described based on findings from previous studies. Attention is then focused on the double-span beam mechanism, which represents the lowest level of structural idealization in a progressive collapse analysis, but it is considered particularly suitable for studying the behaviour of beam-column connections. Having identified the main characteristics of the connection behaviour in progressive collapse, the results of various experimental studies are evaluated with respect to these characteristics and several conclusions of substantial practical significance are derived.

2. Collapse resistance mechanisms mobilized by a column removal

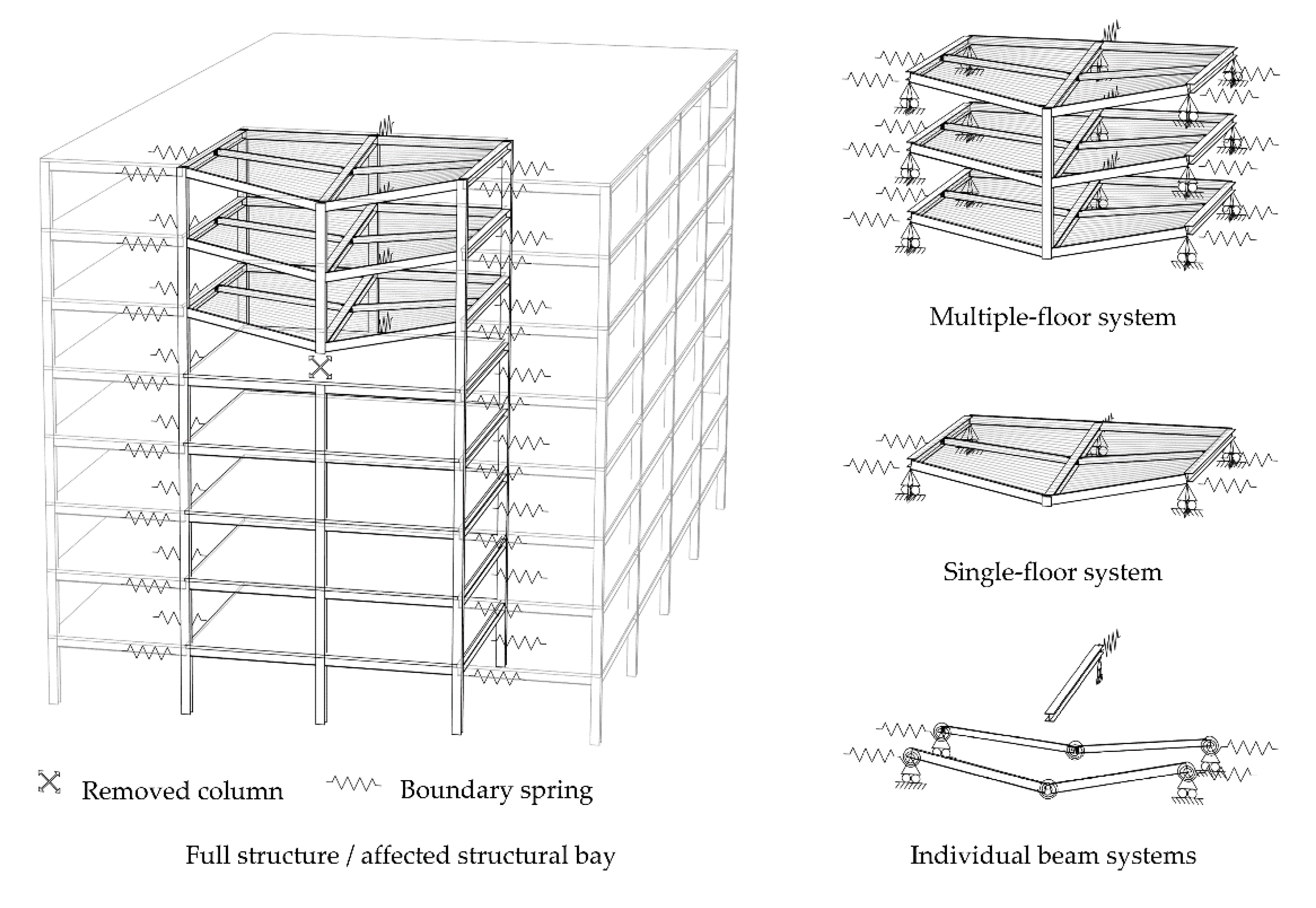
The column removal approach involves assessment of the response of a frame structure to notional removal of a single column. Although a column loss scenario may affect the overall behaviour of the structure, simplified structural idealizations can be considered in the analysis [20] as shown in Figure 1. Provided the interaction with the surrounding structure is simulated by appropriate boundary conditions, consideration may be given only to the affected bay instead of the full structure. If the stability of the remaining columns is not a critical parameter for structural resistance, a reduced model comprising only the floors above the level of the initial damage may be considered. Provided these floors are identical in terms of structure and loading, the model may be further restricted to a single floor system. By ignoring the contribution of the slab, the model is simplified to a grillage structure in which each beam system may be analyzed individually.
Unless the removed column is located at the corner of the structure [21], the latter simplification leads to the concept of a double-span beam mechanism created by two adjacent beams after removal of the intermediate column, which represents a common approach for examining the progressive collapse behaviour of beams and beam-column connections, as further discussed in the next section. In the presence of axial restraint, the progressive collapse resistance of a double-span beam system can be enhanced by the mobilization of different load resistance mechanisms, such as compressive arching action and/or tensile catenary action. Although these mechanisms may have a substantial contribution to overall structural performance, the resistance of the entire structure is usually affected by several additional factors, such as the collapse resistance mechanisms mobilized in the slabs when subject to large deflections, the presence of infill walls and/or diagonal bracing in the affected structural bays, the number of floors above the missing column, and the load-carrying capacity of the remaining columns.
Floor slabs may contribute to structural resistance to progressive collapse through membrane action. In the presence of lateral restraint compressive membrane action may increase the punching shear capacity at small deflections, but it usually has only little effect on collapse resistance [22]. On the other hand, tensile membrane action may considerably enhance the resistance to progressive collapse at large deflections [23,24,25]. Performance can be supported by the presence of lateral restraint and/or by compressive ring action which enables self-equilibration [26,27,28]. However, some studies have shown that, although tensile membrane action can make a significant contribution to the resistance against progressive collapse, it cannot form the principal collapse resisting mechanism in the absence of other load redistribution paths [23,29]. Therefore, a comparable contribution from the framework of the supporting beams and their end connections through effective activation of flexural, arching and/or tensile catenary actions is required [7,17,30,31,32,33,34].
Recent studies have examined the progressive collapse behaviour of steel frame structures in the presence of masonry infill walls in the structural bays above the removed column. A numerical study reported in [35] revealed that infill walls may considerably contribute to collapse resistance, but they may also increase the stiffness of the structure and thus lead to different failure modes. In a different numerical study [36] it was shown that the presence of openings on the walls may affect performance, while the extent to which infill walls may enhance the structural resistance depends on the structural properties of the beam-column connections. The experimental study conducted by Qian et al. [37] focused exclusively on the possible effects of infill walls on the progressive collapse resistance against a corner column removal. It was found that the progressive collapse resistance of corner areas of steel frame structures – which are usually prone to progressive collapse due to the absence of sufficient load redistribution paths – is extremely enhanced by the development of effective compressive struts in the walls which contribute to the transfer of gravity loading from the exposed area to the surrounding structure.
The presence of steel bracing members in the structural bays above the missing column may also influence progressive collapse resistance as demonstrated by recent experimental and numerical studies. This, however, depends on the type of the bracing system since X-bracing, for instance, may ensure an increased resistance while V-bracing may have a detrimental effect on performance [38]. Concentric diagonal bracing can affect performance in very different ways depending on whether the bracing members are subject to tension or compression following column loss [39]. These conflicting conclusions indicate that the response of bracing systems should not be considered as a reliable collapse resistance mechanism, but instead special attention should be paid to their possible negative influence. The only exception is probably the cases of corner areas, which are extremely prone to progressive collapse due to the absence of effective alternate load paths, the response of which can benefit from any type of bracing systems [40].
So far, research studies have mainly focused on the behaviour of specific structural components such as beams, connections, and slabs. One main reason is because these components have a major contribution to the overall structural resistance to progressive collapse. Another reason is because the problem, whether approached by experimental, numerical, or analytical methods, is considerably simplified when focusing on a reduced model of structural idealization. Few experimental studies have considered the behaviour of two-storey [41,42] or three-storey [43,44] plane frames following simulated column loss. These studies were mainly aimed at identifying possible differences between the contribution of different storeys to the total resistance. However, what is probably more important in a multi-storey frame structure is the stability of the surrounding columns. While it is necessary to make sure that beams and slabs can safely transfer their loads to the remaining columns, the latter should also be able to carry these loads. Very few studies have focused exclusively on this problem [45,46,47,48,49,50], but their findings indicate that bucking of the remaining columns is a possible mode of failure in a column removal scenario, which may lead to extensive collapse propagation.

3. The double-span beam mechanism

3.1. Mechanics of structural behaviour

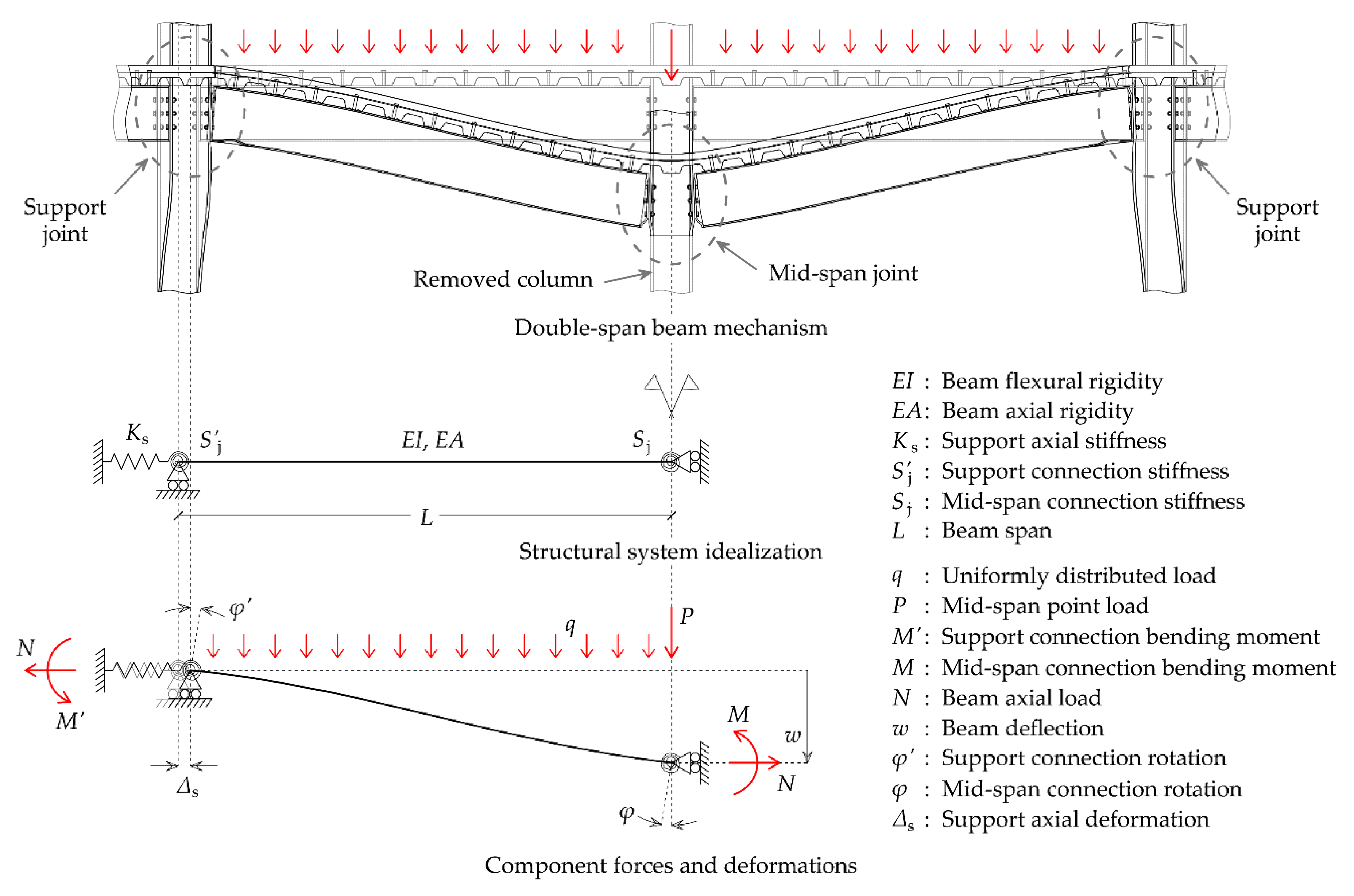
As noted previously, the present study focuses on the role of beam-column connections in the progressive collapse response of steel frame buildings. The double-span mechanism created by two adjacent beams following removal of the intermediate column, as illustrated in Figure 2 [51], represents a simple approach for examining the progressive collapse behaviour of beams and beam-column connections. The axial restraint provided by the surrounding structure should be taken into account by considering appropriate boundary conditions. Assuming a symmetric structure, the response can be analyzed based on the structural idealization shown in Figure 2, where the various structural parameters that influence performance are identified. A suitable representation of the connection behaviour is required, that explicitly accounts for the connection moment-rotation response in the presence of axial force [52,53,54,55].
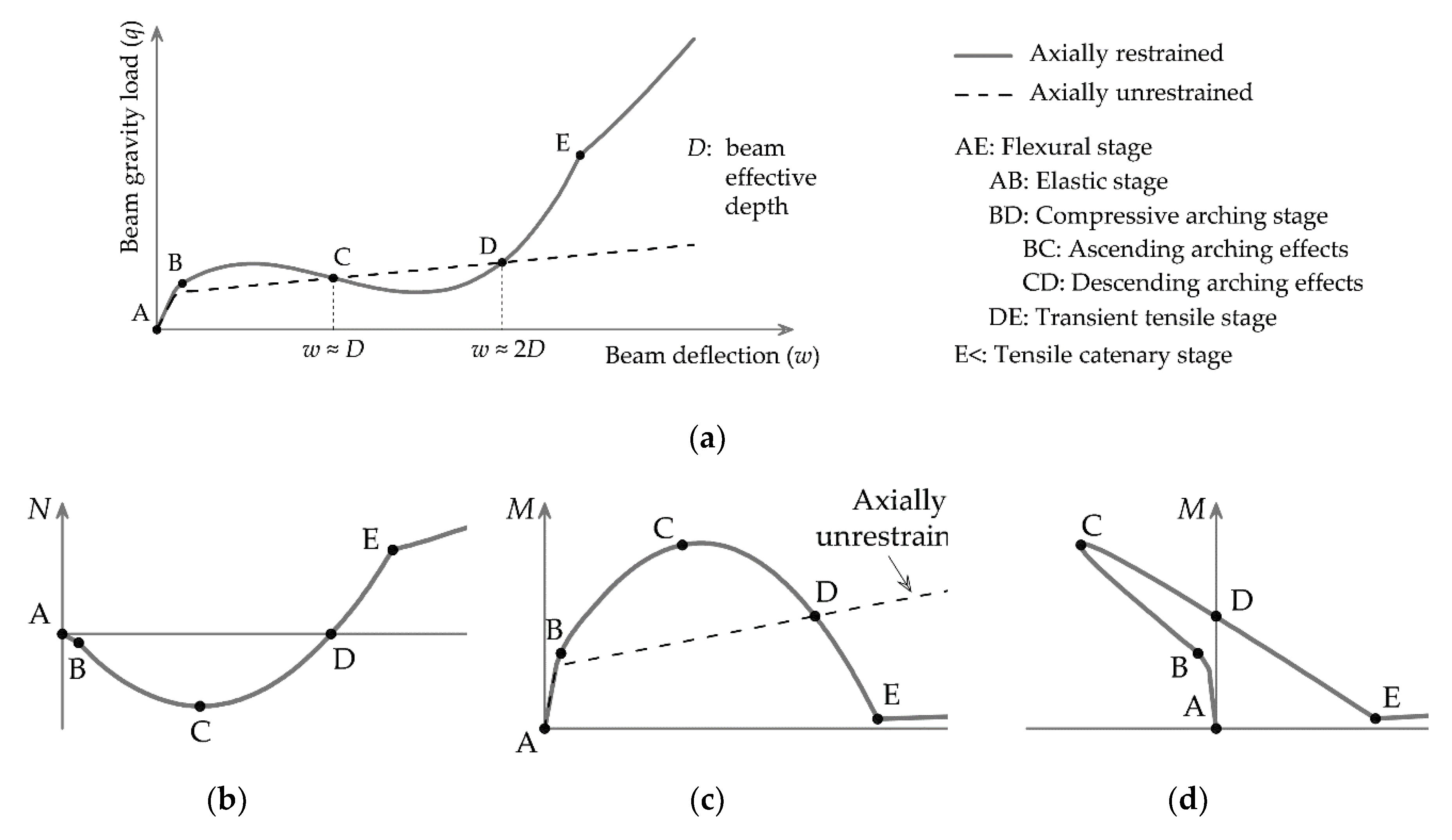
The typical nonlinear static behaviour of a double-span beam mechanism is described in Figure 3 [56]. In practice, it is not always possible to reach every stage of the response, since the deformation capacity can be exhausted at any point along the load-deflection curve [7,19,32,55,56,57]. The comparison with the response of an equivalent axially unrestrained system demonstrates the significant effects of axial restraint. The axial force generated in axially restrained beams may mobilize compressive arching and tensile catenary actions at small and large deflections respectively. In both cases, the load-carrying capacity may considerably increase. As shown in Figure 3, the maximum compressive arching capacity is reached at a beam deflection less than the beam depth (D), while tensile catenary action is mobilized when the beam deflection becomes greater than twice the beam depth (2D).
The above conclusions only concern the case of an elastic compressive arching behaviour, which means that all structural components subject to axial compression (e.g., beam compression flanges) exhibit a linear elastic behaviour [58]. When the resistance of any of the components participating in the development of compressive arching action is exhausted, the system response changes as described in the examples of Figure 4. Previous studies [58,59] have shown that compressive arching action may still occur provided the beam-column connections are classified as partial-strength; that is, the connection tension zone resistance is less than the connection compression zone resistance. In this case, the beam deflection corresponding to the maximum compressive arching capacity decreases, while tensile catenary action is activated earlier, at a deflection value between the beam depth (D) and twice the beam depth (2D). The response of a system with full-strength connections – which practically corresponds to the case when the connection tension zone resistance is not less than the connection compression zone resistance – is only governed by flexural action at small deflections, followed by tensile catenary action at large deflections in the presence of axial restraint. In this case, tensile catenary action is activated when the beam deflection equals the beam depth (D). On the other hand, beam systems with nominally pinned connections may resist gravity loading only through tensile catenary action. This is essentially equivalent to the absence of connection compression resistance, which means that the connections are not able to resist bending moments [58].
The previous studies also demonstrated how the different collapse resistance mechanisms are affected by various structural parameters [58,59]:
  • The flexural action effects increase as the beam span decreases, and/or the bending moment capacities of the beam-column connections increase.
  • The compressive arching action effects increase as the beam span-to-depth ratio decreases, and/or the compression zone resistances of the connections increase, and/or the axial and flexural stiffness of the beam increase.
  • The tensile catenary action effects increase as the beam span decreases, and/or the tensile resistance of the connections increase, and/or the post-limit tensile stiffness of the connections increase.

3.2. Common configurations of test specimens

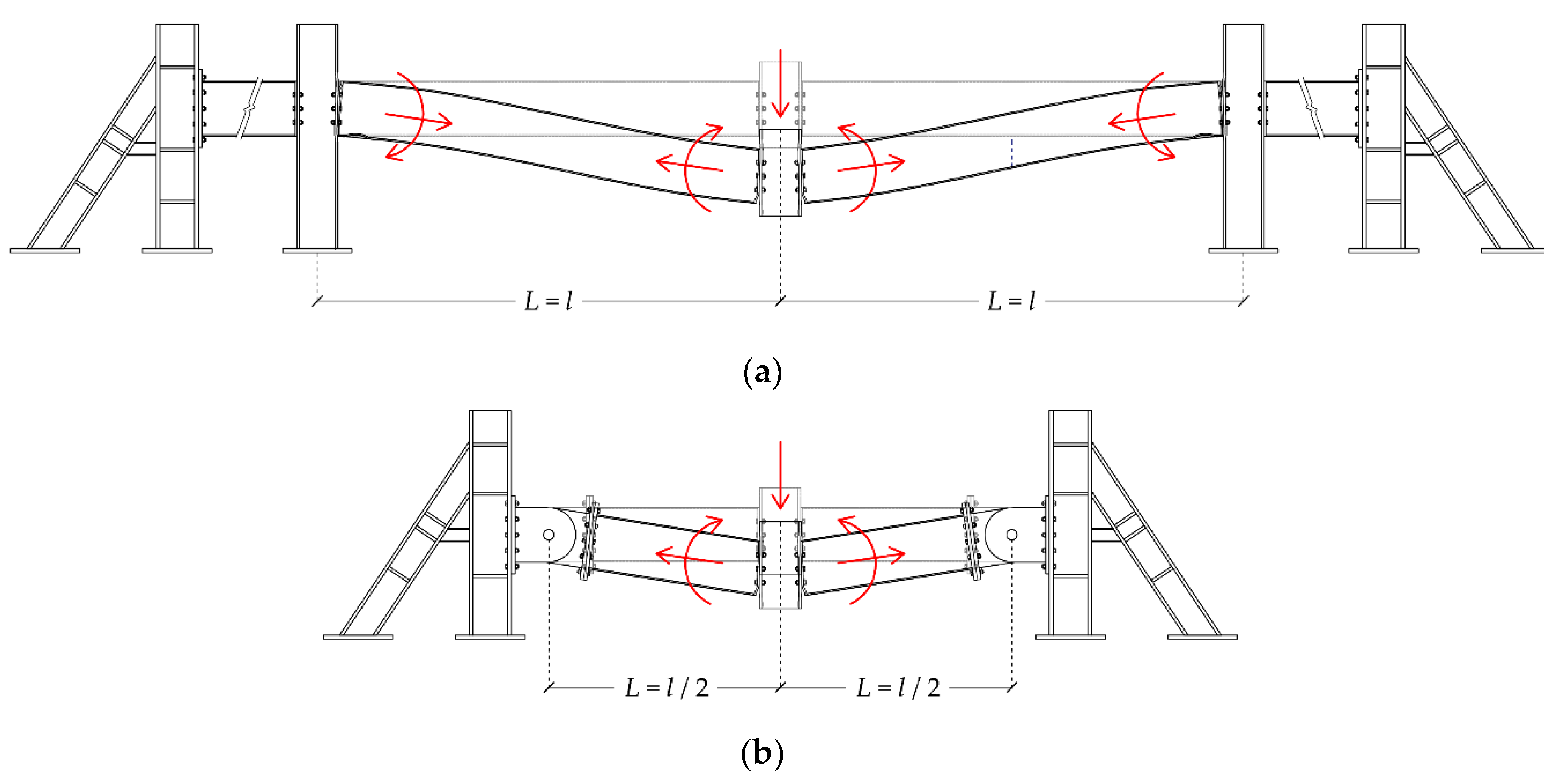
In relevant experimental studies, one of the two main test configurations shown in Figure 5 is usually adopted. In both cases, the test is conducted under static loading, by applying an incremental point load at the mid-span under displacement control until failure. The first configuration shown in Figure 5a represents a complete double-span beam system created after column loss, which comprises the midspan region and two support regions, including details of the corresponding beam-column connections. The second configuration shown in Figure 5b represents a simplification of the double-span mechanism. On the presumption that the point of inflection is located at the mid-span of each beam section, only a half of the section is considered, and the supports are modelled as hinged. This configuration is probably more appropriate for studying the behaviour of the midspan joint rather than the response of the complete double-span beam system.
Previous experimental studies that employed the simplified setup approach have provided essential information about the behaviour of different connection types and connection arrangements, especially in relation to their potential contribution to the load-carrying capacity and the deformation capacity of the structure. Nevertheless, the focus of these studies was the prediction of the load-deflection response, that is the relationship between the applied loading and the mid-span deflection. However, the results obtained from a simple setup configuration should be carefully evaluated, because they may lead to inaccurate conclusions about the significance of each collapse resisting mechanism [59]. In particular, according to the information given in section 3.1:
  • The span length influences differently each collapse resistance mechanism.
  • The exclusion of the support connections results in a decrease in the flexural action effects.
  • The use of hinged supports results in a decrease in the effective depth (D) used for the prediction of the span-do-depth ratio, which influences the compressive arching action effects.
  • The replacement of the support connections by axially stiff pinned supports increases the axial stiffness of the system and, therefore, enhances the tensile catenary action effects.
Therefore, the load-deflection curves obtained using the simplified configuration of Figure 5b may underestimate the potential effects of flexural and compressive arching actions, while overestimating the effects of tensile catenary action.

4. Summary and review of experimental studies

During the past decade several experimental studies have examined the behaviour of axially restrained steel and composite beam systems under simulated column loss. These studies are reviewed in this section and their results are evaluated based on the information about the mechanics of structural behaviour given in the previous section.

4.1. Summary of experimental studies

A list of several experimental studies that examined the behaviour of steel and composite double-span beam structures is given in Table 1. These studies are described in terms of the structure type (bare steel or steel-concrete composite beams), the test setup configuration (detailed or simplified, as defined in the previous section), the beam span length (L), the beam depth (D), and the type of steelwork connections employed. Their main results, as defined in terms of the main parameters that govern the different collapse resistance mechanisms described in the previous section, are collected in Table 2. Besides the span-to-depth ratio (L/D) which has a direct influence on the compressive arching action, two other ratios are defined:
  • The ratio between the ultimate load-carrying capacity at a level of deflection greater than the beam depth (Pu) and the maximum value of load-carrying capacity up to a deflection level equal to the beam depth (Pw≤D).
  • The ratio between the ultimate deflection (wu) and the beam depth (D).
A value of the former ratio (Pu/Pw≤D) greater than 1.0 indicates that the progressive collapse resistance has been enhanced by tensile catenary action, since catenary action effects may develop beyond w=D, unless tensile catenary action is the only collapse resistance mechanism (i.e., in the absence of flexural action and/or compressive arching action). A value of the latter ratio (wu/D) less than 1.0 indicates that the structure has exhibited limited deformation capacity (thus, it has failed during the flexural/arching stage), while a value greater than 2.0 indicates that the structure has exhibited high deformation capacity (thus, it has failed after the development of substantial tensile catenary action forces).
In accordance with the values of these ratios, and based on further information obtained from each study, the collapse resistance mechanisms (i.e., flexural action, compressive arching action, and tensile catenary action) that have been activated in each specimen are also specified in Table 2. The last column of the table defines the failure mode, that is the mode of failure of the most critical connection component that essentially triggered overall failure of the specimen. 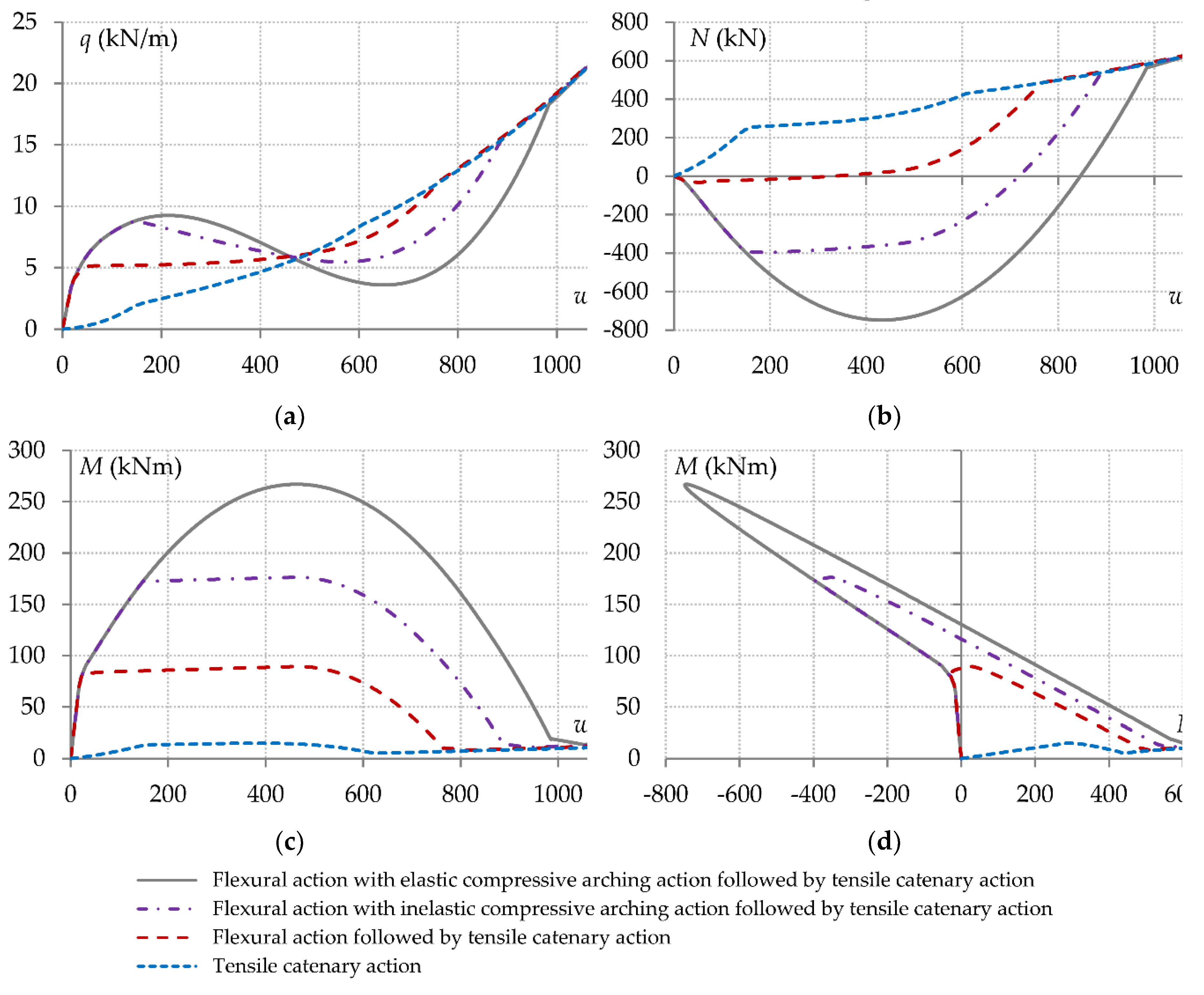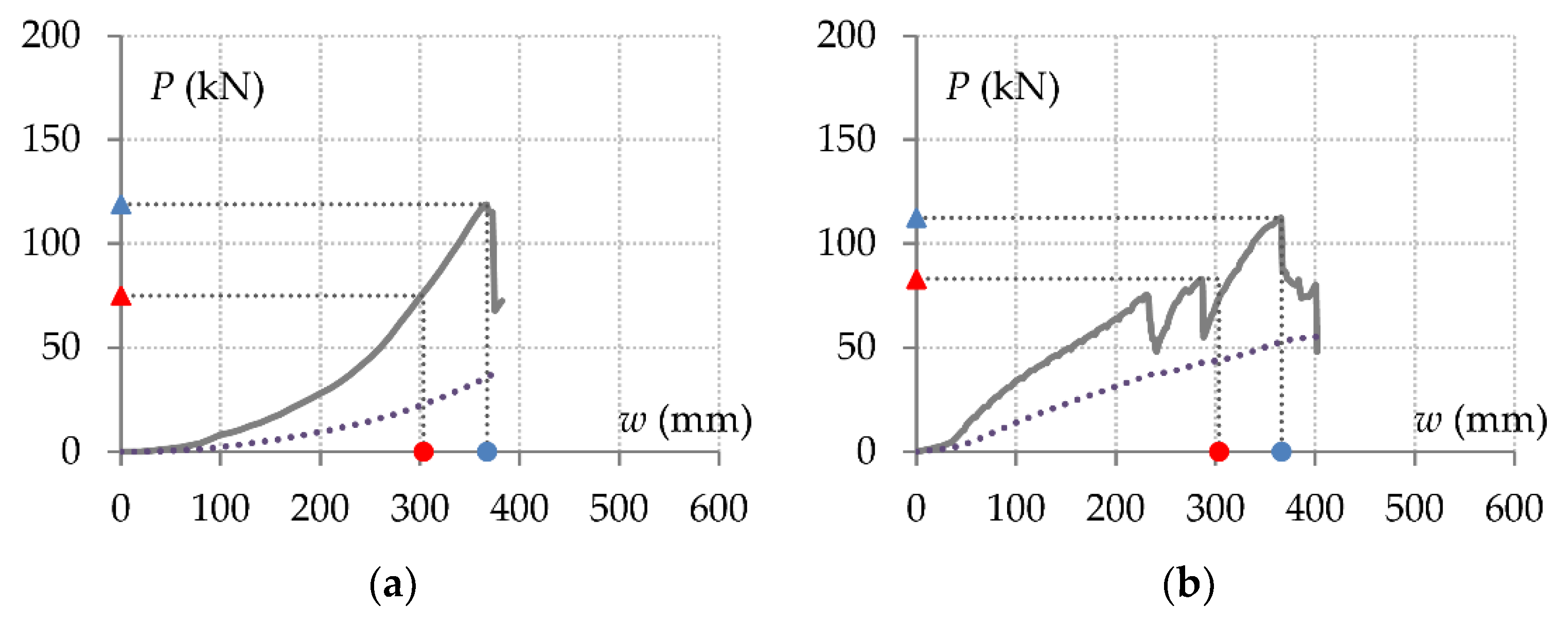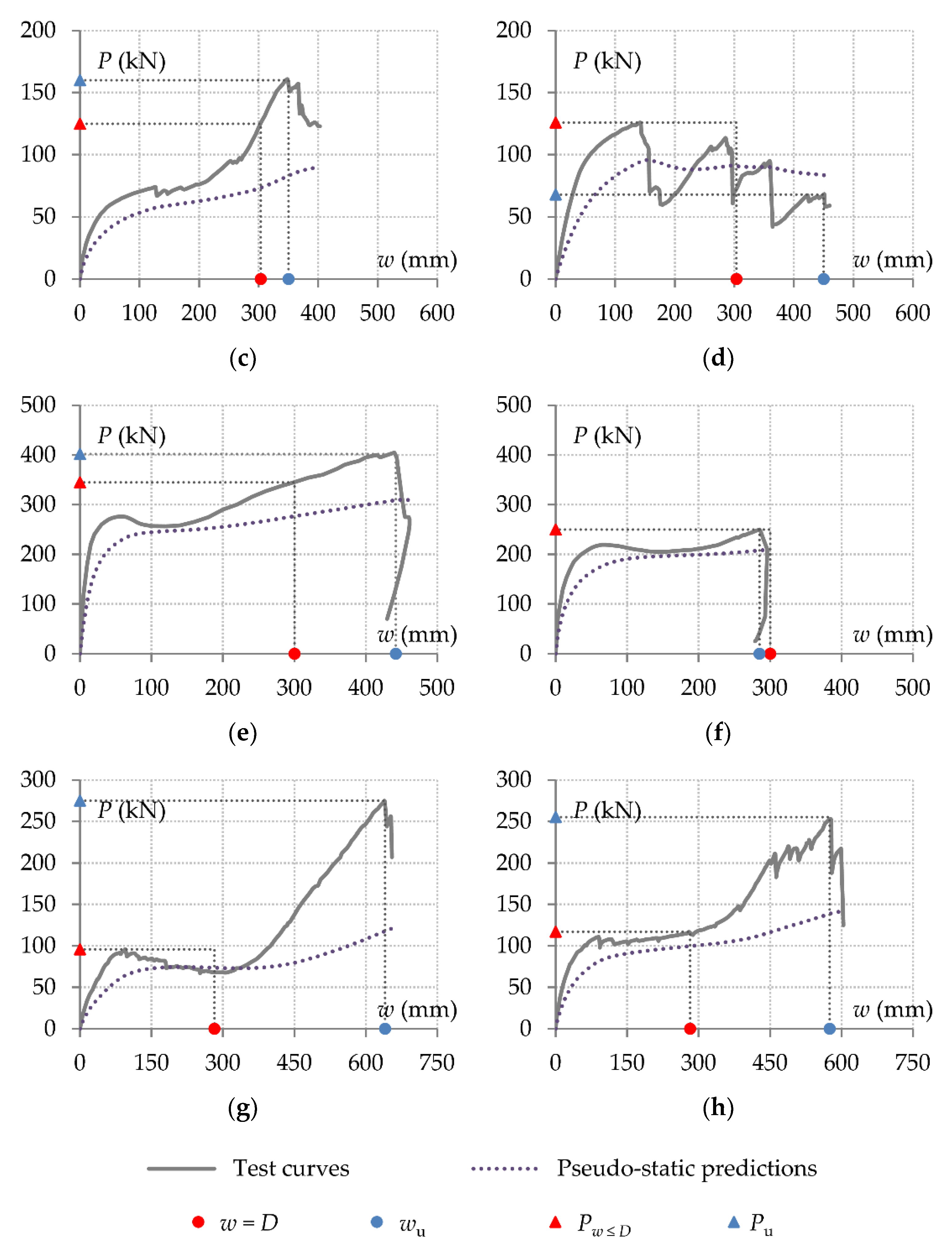The load-deflection curves of selected specimens from those listed in Table 1 and Table 2 are shown in Figure 6, on which the various key parameters described above are identified.

4.2. Pseudo-static response representation

All the tests listed in Table 1 and Table 2 were conducted under static loading, by applying an incremental vertical force at the mid-span under displacement control. Therefore, the nonlinear static load-deflection responses of the specimens were obtained. However, since events in progressive collapse usually take place in a short timescale, it is quite important to identify how the behaviour changes when the load is applied instantaneously which corresponds to a sudden column removal scenario (e.g., caused by blast or impact). Since the dynamic analysis of the problem is particularly demanding, especially in experimental applications, alternative solutions have been proposed. Izzuddin et al. [20] derived a simplified method to predict the dynamic response based on static analysis principles. It has been shown that the maximum dynamic displacement under the action of a given value of gravity loading is developed when the work done by the load becomes equal to the energy absorbed by the structure. Therefore, from a static load-deflection curve, it is possible to derive a step-by-step representation of the dynamic load-deflection curve by calculating the maximum dynamic displacement at each step. Since the dynamic load-deflection curve is based on static analysis principles, it is defined as “pseudo-static”.
By examining the different pseudo-static predictions derived from the experimental load-deflection curves shown in Figure 6, some important conclusions are drawn:
  • The poor behaviour of a double-span system with nominally pinned connections which is solely governed by tensile catenary action is further degraded when considering dynamic effects, as shown in Figure 6a,b.
  • The increase in the load-carrying capacity due to tensile catenary action that develops after the flexural/arching stage becomes much less significant when the static response is converted to pseudo-static, as shown in Figure 6c,g,h.
  • When the load-carrying capacity is gradually decreased due to successive failure of various connection components, without leading to total collapse of the double-span system, the rate of decrease in the pseudo-static capacity is smaller, as shown in Figure 6d.
  • A system that demonstrates stiff initial response and substantial flexural action tends to exhibit enhanced pseudo-static resistance, as shown in Figure 6e,f.
  • The effects of compressive arching action are less pronounced in a pseudo-static load-deflection curve, as shown in Figure 6g.
These conclusions are very useful to better assess the true significance of the various collapse resistance mechanisms in the progressive collapse response of steel frame structures following sudden column removal.

4.3. Review of experimental results

One of the earliest experimental studies was performed at the University of Liège as part of the collaborative research project on structural robustness described in [60]. The study adopted the concept of column removal to examine the progressive collapse resistance of a composite frame building designed according to the provisions of the Eurocode. A substructure was isolated from the frame and tested against simulated column removal, by adopting the detailed test setup configuration described previously. The structure comprised HEA160 steel columns and IPE140 steel beams acting compositely with a 500 × 120 mm solid concrete slab. Flush endplate connections with two bolt rows and endplate thickness equal to 8 mm were employed. In addition, 3Ø8 rebars were arranged on either side of the columns. The response was first governed by flexural action without evident compressive arching effects, but the structure was able to undergo large inelastic deformations and exhibited substantial tensile catenary action prior to failure due to rebar rupture at a beam deflection of approximately 2.4 times the beam depth.
The simplified test specimen was first adopted by Yang and Tan [61], in a study that examined the progressive collapse behaviour of bare steel beams with various steelwork connection types. Beam systems with simple shear connections such as double web cleat and fin plate were only able to sustain gravity loading through tensile catenary action (Figure 6a,b). The behaviour of beams with more substantial arrangements (e.g., top and seat angle, top/seat and web angle) was somewhat enhanced by flexural action, but their resistance was limited by premature fracture of the seat angles at the mid-span joints. The effects of flexural action were better illustrated by the behaviour of beam systems with flush and extended endplate connections. The former was able to demonstrate significant tensile catenary action (Figure 6c) prior to tensile fracture of the bolts, while the latter did not benefit from tensile catenary action due to premature fracture of the welds, which caused the successive failure of other connection components and thus led to a progressive reduction in load-carrying capacity (Figure 6d).
By employing the detailed setup configuration, Lew et al. [62] tested two bare steel double-span beam specimens with welded unreinforced flange-bolted web (WUF-B) and reduced beam section (RBS) connections respectively. The response of the former was initially described by the effects of compressive arching action, which however had a minor influence on overall performance. The resistances of both specimens were greatly enhanced by the development tensile catenary action at large deflections. The resistance of the WUF-B connection was first reduced by shear failure of the beam web bolts prior to complete failure of the specimen due to fracture of the beam flange. The RBS specimen failed at a comparatively later stage due to fracture of the beam flange at the reduced area of the section.
The progressive collapse behaviour of a double-span composite beam with two different steelwork connections was examined by Guo et al. [63,64]. In both cases, the total depth of the composite section was 300 mm, comprising the steel section with a height of 200 mm and the slab with a height of 100 mm. The slab had a width of 800 mm and closely spaced longitudinal reinforcement bars Ø12. Welded [63] and flush endplate [64] beam-column connections were employed in the two specimens respectively. The first specimen exhibited limited compressive arching action but substantial tensile catenary action (Figure 6e) since failure occurred at a deflection of approximately 1.5 times the beam depth due to fracture of the welds. The compressive arching effects were rather more pronounced in the response of the second specimen, but the tensile catenary action effects were limited (Figure 6f) by premature tensile fracture of the bolts at the mid-span joint. The premature failure of the mid-span connections was mainly due to the presence of the concrete slab in the compression zone. Since the mid-span connections are subject to sagging bending moments, the centre of rotation is in the concrete slab and therefore further away from the lower bolt-rows. For this reason, these bolt-rows undergo increased deformations for lower connection rotation values.
In a different study, Li et al. [65] employed the simplified test setup configuration to explore the behaviour of welded unreinforced flange-bolted web (WUF-B) connections between I-beams and square hollow sections under simulated column removal. Two different connection geometries were considered, having the same number of bolts arranged in one and two rows respectively. Both specimens exhibited similar responses, which were mainly governed by flexural action, but their resistances were limited by fracture of the beam bottom flange at the midspan region. An extension of this study was presented elsewhere [66], where another alternative WUF-B arrangement and an equivalent welded connection were examined. Similar experimental results in terms of overall performance and load resistance mechanisms as those reported in [62] were obtained. The fracture of the beam bottom flange in the region of the mid-span joint was the initial failure mechanism for both connection types.
Yang et al. [67] compared the role of different steelwork connections in the progressive collapse response of composite frames. Detailed test setup configurations were employed, in which the composite beams had a total depth of 282 mm, comprising UB203×133×30 steel sections and a composite slab with or without longitudinal reinforcement bars. The steelwork connections were either double web cleat or flush endplate. Although these connections are classified differently in terms of stiffness and strength, the responses of both specimens in the presence of longitudinal reinforcement were similar since they were both enhanced by compressive arching and, especially, by tensile catenary effects (Figure 6g,h). This demonstrates the significant contribution of the slab reinforcement to the tensile catenary behaviour. The failure modes were the same as those observed in [61], that is web angle fracture and bolt tensile fracture respectively.
The objective of the study conducted by Dinu et al. [68] was to investigate the contribution of different types of semi-rigid and rigid connections to the progressive collapse response of steel frame structures. Based on a detailed representation of the double-span beam mechanism, four specimens with different connections – i.e., welded cover plate flange-bolted web, haunch endplate, reduced beam section, and extended endplate – were tested. Apart from the latter, the other three specimens were able to sustain large deformations, allowing for the development of tensile catenary action prior to failure. Flange cover plate fracture, bolt tensile failure, beam flange fracture, and premature bolt tensile fracture were the observed failure modes for the four specimens, respectively.
Another study performed by Zhong et al. [69] employed the detailed test setup configuration to study the performance of different types of bare steel connections. One of the connection types was welded unreinforced flange-bolted web (WUF-B), which demonstrated similar behaviour to that described by previous studies [62,65]. Apart from the WUF-B connection, the study also examined the behaviour of beam systems with double angle cleat and TSWA (top/seat and web angles) connections. Due to their substantial deformation capacity, both connections enabled the development of tensile catenary action prior to failure. The failure modes of these connections were similar to those observed in relevant previous studies [61].
Based on the simplified test setup configuration, the behaviour of bare steel systems was further studied by Li et al. [70]. The test specimen comprised two I-beam sections connected with a square hollow column through WUF-B connection arrangements. Similar to relevant previous studies, the load-carrying capacity was mainly limited by premature fracture of the beam bottom flanges in the region of the mid-span joint, which occurred at a relatively small beam deflection. Although this reduced considerably the load-carrying capacity, the specimen was able to undergo quite large inelastic deformations to attain the tensile catenary stage, but the catenary action forces were not sufficient for the structure to recover its initial load-carrying capacity.
Xu et al. [71] and Gao et al. [72] studied the progressive collapse resistance of steel frame systems comprising I-beam sections and concrete filled steel tubular (CFST) columns, based on the simplified test setup configuration and by considering different alternative solutions for the beam-column connections. Instead of the conventional blind bolts that are commonly used in these frame systems, long bolts passing through the column section were adopted. The former study examined the behaviour of flush endplate, extended endplate and stiffened angle connections, while the latter study focused on different arrangements of stiffened angle connections. The failure of all specimens was triggered by either thread stripping or pull-out of the most heavily loaded bolts. The responses of the specimens with flush endplate and the extended endplate connections were enhanced by tensile catenary action effects, while the specimens with stiffened angle connections failed at comparatively earlier stages and thus prior to significant activation of tensile forces in the beams.
Another experimental program was conducted by Alrubaidi et al. [73] to study the behaviour of bare steel frames with different connection types based on the detailed test setup configuration. Three connection types were considered, that is fin plate, WUF-B, and extended endplate. Similar to previous studies, the response of the specimen with fin plate connections was mainly described by tensile catenary action. Although the connections exhibited an increased deformation capacity, allowing for the beam deflection to reach a value of approximately 1.8 times the beam depth, the tying resistance of the connections was not sufficiently high to ensure significant load-carrying capacity, especially compared to the other two specimens. Owing to the increased flexural strength of the WUF-B and extended endplate connections, the ultimate resistance of those specimens was 3-4 times greater than the load-carrying capacity of the specimen with fin plate connections. However, the capacity of the WUF-B specimen was limited by premature fracture of the beam bottom flange prior to the activation of tensile catenary action. Although the behaviour of the third specimen was enhanced by tensile catenary action at large deflections, this occurred after thread stripping of some bolts and thus it had a minor practical significance.
Meng et al. [74] examined the effects of web openings on the progressive collapse resistance of composite frames. Two specimens with detailed setup configurations that included welded unreinforced flange-bolted web (WUF-B) connections were tested. The steel beam cross-section was the same in both specimens. The total beam depth was 205 mm, including a concrete slab with a height of 55 mm. While in the first specimen the beam webs were solid, in the second specimen the beam webs had circular openings at closely spaced intervals throughout the span. The experimental results showed that the web openings had a beneficial influence on progressive collapse resistance. Both specimens failed due to fracture of the beam tension flange in the mid-span joint region. Meanwhile, however, the mid-span connections of the second specimen had already undergone greater deformations as compared to the first specimen, due to the presence of the web openings in the vicinity of the mid-span region. For this reason, the response of the specimen with web openings was enhanced to a significantly greater extent by the effects of tensile catenary action.
The significance of web openings in the vicinity of the beam-column connections was further investigated by the experimental studies conducted by Qiao et al. [75] and Lin et al. [76]. In these studies, there were no web openings along the entire length of the beam, but only one opening next to each connection. For this reason, the connection type was defined as reduced web section (RWS). The studies employed simplified test setup configurations and they were restricted to bare steel specimens. The beam-column connections were welded. Qiao et al. [75] compared the cases of a solid beam section, a reduced flange section (RBS), and a section with both reduced flange and reduced web (RBS-RWS). Lin et al. [76] compared a solid beam section with two reduced web sections, RWS1 and RWS2. In the RWS2 specimen, the web opening had a smaller diameter, and it was located at a greater distance from the edge of the beam. Failure occurred due to fracture of either the welds or the beam flange. It was found, however, that performance can be improved by a reduction in either the beam flange or the beam web. The latter can become more effective depending on the dimensions and the location of the web opening.
The experimental study conducted by Kukla and Kozlowzki [77] confirmed the significance of the beam span-to-depth ratio on the progressive collapse resistance of steel frame structures. The study employed the simplified test setup configuration, but the span-to-depth ratio on either side of the removed column was only 3.2. Six specimens with flush endplate and extended endplate connections and various endplate thicknesses were examined. Table 2 only presents the results for the two connection types with endplate thickness equal to 20 mm. Regardless of the connection type and the endplate thickness, the responses of all specimens were very similar. They were mainly governed by flexural action without evident compressive arching effects, but the specimens failed prior to the development of tensile catenary forces due to premature fracture of the bolts. That is, because the beam-column connections were subject to large rotations at relatively small beam deflections.

5. Novel approaches to improve performance

The experimental studies described in the previous section revealed several factors that may adversely affect the resistance of steel and composite frame structures to progressive collapse. These factors mainly concern the limited deformation capacity of certain types of connections due to premature failure of specific components, such as fracture of welds, shear or tensile failure of bolts, fracture of angle cleats, fracture of beam flanges (especially in reduced beam sections), etc. Based on these findings, recent research studies have focused on possible methods of limiting these effects, and thus enhancing overall structural performance.
Reduced beam sections (RBS) offer important advantages in terms of increased rotation capacity and increased energy absorption capacity under seismic actions. Under the action of column removal, however, structural resistance heavily depends on the ability of the reduced section to carry the combined forces that develop. Therefore, the failure of frame systems comprising reduced beam sections is usually triggered by fracture of the beam tension flanges [62,68,75]. In order to overcome this limitation, Meng et al. [78] proposed a novel strengthening approach, which involves the addition of V-shaped reinforcing plates on the inner faces of the beam flanges, bridging over the reduced areas. The aim is for these plates to act as backup components and prevent the rapid failure propagation in the case of a flange fracture. This strengthening technique has only been studied through numerical modelling, but quite promising results have been obtained. In particular, it was found that the load-carrying capacity and ultimate deflection can increase up to 180.9% and 85.8% respectively.
According to previous experimental studies, the progressive collapse resistance of steel or composite beams with fully welded beam-column connections is usually limited by premature weld fracture or brittle cracking at the beam root [63,66,75,76]. The study presented in [79] aimed to resolve this problem by proposing a different design solution for welded connections. The objective is both to limit the concentration of stresses at the critical area of the welds and to enable the formation of plastic zones outside this area. The solution involves the addition of suitably configured energy dissipation cover plates on the outer surfaces of the beam flanges, which would indirectly connect the beam flanges with the column. The mechanical behaviour of the cover plates was studied in isolation through tensile tests. However, the progressive collapse behaviour of the proposed connection configuration was only studied through numerical modelling. The study has shown that energy dissipation cover plates may increase the progressive collapse resistance and deformation capacity by 78%-120% and 140%-182% respectively.
Previous experimental studies have also shown that extended endplate connections may suffer premature failure when exposed to the effects of column removal, due to weld fracture [61], or tensile fracture of bolts [68,77], or bolt thread stripping [71,73]. Avoiding these failure modes could increase the connection deformation capacity and thus enhance structural resistance to progressive collapse. Towards this goal, Meng et al. [80] proposed a strengthening technique for extended endplate connections, which involved the addition of bending stiffened plates between the outer surfaces of the beam flanges and the connected column. The objective is for these bending plates to replace the loss of welds or bolts in extreme loading conditions. A numerical study was conducted to examine the prospect of this solution, and it has been found that the resistance of a double-span beam sub-structure to progressive collapse can increase up to 248%, while the deformation capacity may increase up to 151%.
The progressive collapse resistance of top-and-seat angle with double web-angle (TSWA) connections is usually controlled by the ability of the top/seat angles to respond to the increased loading demands while undergoing very large deformations. Previous experimental studies have shown that failure is usually governed by fracture of these angles [61,69]. The study presented in [81] focused on the idea of replacing the traditional right web angles with bending angles, as well as adding bending angles to the inner surfaces of the beam flanges. On the presumption that bending angles will have a greater deformation capacity, the overall deformation capacity of the connection would increase. The study presented in [81] is only restricted to tensile tests of T-stub models comprising bending angles. The results indicate that the proposed solution offers greater strength and deformation capacity, and it may therefore become effective in enhancing the progressive collapse behaviour of steel frame structures with TSWA connections.
Since shear connections such as fin plate and double cleat are normally designed as nominally pinned and they are only required to resist shear forces, their bending moment capacity under normal loading conditions is of minor significance. This is the reason why tensile catenary action is the only mechanism that can be mobilized in a double-span beam system with shear connections under the action of gravity loading, according to the conclusions of relevant experimental studies [61,69,73]. With the aim of improving the performance of these structures, Alrubaidi et al. [82] investigated possible strengthening techniques. The objective was to achieve a level of performance equivalent to that of corresponding structures with moment connections. The results of a previous experimental study conducted by the same research group [73] were used as a guide to determine strengthening requirements. Two strengthening approaches were proposed, including welded double side plates and pretensioned high-strength hot-rolled steel rods within the connection region, respectively. The study, which involved both experimental testing and numerical analyses, has shown that the two strengthening schemes may effectively enhance performance of shear beam-column connections, leading to substantial increases in progressive collapse resistance. A possible disadvantage of these approaches, however, is that they seem to be rather complex and potentially costly solutions.
In order to increase the tying resistance and rotation capacity of nominally pinned connections, Ghorbanzadeh et al. [83] and Bregoli et al. [84] proposed and investigated a different strengthening approach. This involves reinforcement of the joint region by duplex stainless steel pins passing through the beam web, which aim at carrying tensile catenary action forces at large deformations through bending, without affecting the shear resistance of the connections under normal loading conditions. Experimental results have shown that this technique may enhance to a considerable extent the tying resistance and rotation capacity of fin plate connections. This may lead to a substantial increase in the load-carrying capacity of a double-span beam mechanism, which may become more than 8 times higher than the capacity of an equivalent un-strengthened arrangement. Despite the significant improvement, however, tensile catenary action remains the dominant collapse resistance mechanism.
According to several experimental studies, failure of flush and extended endplate connections exposed to progressive collapse conditions is usually triggered by tensile fracture of bolts [61,64,67,68,77]. This represents an undesirable brittle mode of failure which usually results in significant reduction in the connection strength and overloading of other connection components, thus rapidly leading to a complete failure of the connection. A relatively simple solution to this problem was proposed by Shaheen et al. [85]. This involves the addition a steel sleeve between the steel endplate and the washer, with the primary purpose of enhancing the deformation capacity of the bolt. The sleeve must be properly designed by specifying the appropriate length, thickness, and wall curvature to ensure the best possible performance. Numerical studies have exploited this approach to evaluate its effects on the progressive collapse performance of flush endplate [86] and extended endplate [87] connections. The results indicate that significant increases in the connection rotation capacity can be achieved, on the order of approximately 50-150%. However, there is still a lack of experimental validation.
As described in the previous section, recent studies have shown that the deformation capacity of beam-column connections under the action of column removal can be considerably enhanced by the presence of openings on the webs of the connected beams in the vicinity of the connection regions [74,75,76]. This essentially represents another effective approach of increasing the progressive collapse resistance of steel frame structures, since the higher deformation capacity allows for the development of tensile catenary forces at large deflections prior to reaching the ultimate deformation limit. Experimental results are already available for both the cases of circular [75,76] and rectangular [88] openings, with the findings and conclusions from all studies being quite promising. However, while the shape and dimensions of the web opening as well as its distance from the beam edge may influence structural response in certain ways [76], they may also be controlled and limited by other factors such as the beam shear capacity and seismic performance, which should probably be examined in future studies.

6. Conclusions

Considerable progress has been made in recent years to develop an understanding of the role of beam-column connections in the overall behaviour of steel frame buildings in progressive collapse. A common approach for assessing structural performance, which is based on the alternate load path concept, considers the consequences of a threat-independent column loss on the surrounding structure. Beams and beam-column connections, slabs, infill walls, and bracing members may act as alternate load paths to enable redistribution of loading to the neighboring intact columns, which should be able to respond to these increased loading demands. The overall structural behaviour is governed by different collapse resistance mechanisms mobilized in these structural components. In this process, the role of the beam-column connections is extremely important, because they should be able to transfer a varying combination of bending, axial and shear forces from the supported beams to the supporting columns whilst undergoing very large inelastic deformations.
The axially restrained double-span beam mechanism is the most common approach of examining the response of beam-column connections to column loss. A double-span beam system may resist gravity loading through flexural, compressive arching, and tensile catenary actions. The flexural action depends on the flexural strength of the connections and the beam span, and it mainly describes the flexural resistance of the structure. The compressive arching action depends on the beam span-to-depth ratio and the resistance of the constitutive components to axial compression, and it may affect performance at small deflections. The tensile catenary action depends on the beam span and the strength and post-yielding tensile stiffness of the constitutive components, and it can improve the load-carrying capacity at large deflections. The presence of a concrete slab acting compositely with steel beams also influences performance, because it may affect the bending moment capacities and the rotation capacities of the beam-column connections.
At the experimental research level, the double-span beam mechanism has been used in two main alternative ways. Its detailed representation involves the complete sub-structure comprising a missing column between two adjacent beams which are supported by two other columns on their other ends, while the simplified representation considers only half of the beam spans and hinged supports on either end simulating the points of inflection. Although the simplified representation cannot describe accurately the actual behaviour of a double-span beam system, it can provide essential information about the performance of beam-column connections under the conditions imposed by a column removal. Most experimental studies involved static application of a point load at the mid-span directly above the missing column under displacement control. The overall response of each tested specimen was therefore described by a static load-deflection curve.
Another important feature of the problem is that events in progressive collapse usually take place in a very short timescale and, therefore, dynamic effects should also be taken into account. In this case, the performance of a double-span beam structure can be described more appropriately by instantaneous column removal or by a sudden application of the gravity loading. Alternatively, the results of a static analysis can be utilized for the prediction of the dynamic response by converting the static load-deflection curve into a pseudo-static load-deflection curve based on an energy-balance approach proposed in the literature. In a pseudo-static response representation, however, the effects of compressive arching and tensile catenary actions on collapse resistance become considerably less significant, while the rate of decrease in load-carrying capacity due to premature failure of constitutive components decreases.
In this paper, the results of 44 test specimens from 18 different experimental studies were collected and evaluated with respect to the information provided above. Only 7 out of 44 specimens comprised composite beams of steel and concrete, while the remaining 37 specimens comprised bare steel beam sections. In addition, 19 specimens employed the detailed test setup configuration, whereas the simplified configuration was adopted in the remaining 25 specimens. The average span-to-depth ratio of the 44 specimens was 8.6, where only one of them had a span-depth ratio greater than 15 and three specimens had a ratio value of less than 6.5. For the detailed specimens, the average span-to-depth ratio was 10.6, while for the simplified specimens the corresponding value was only 7.1. The high span-depth ratios of the detailed specimens justify the limited contribution of compressive arching action, while the smaller value for the simplified specimens has a minor significance since the simplified configuration does not favor the development of compressive arching action.
Except for the four specimens that involved nominally pinned beam-column connections (i.e., double web cleat or fin plate) the responses of the remaining 40 specimens that employed moment connections were governed by flexural action. The results indicate that in the absence of flexural action the progressive collapse resistance of a double-span beam system is rather low, since tensile catenary action alone cannot ensure a substantial load-carrying capacity, regardless of the deformation capacity of the connections. The beneficial effects of flexural action, however, are of essential practical importance only when the structure has an increased deformation capacity. From the 40 specimens that exhibited flexural action response, 8 specimens with different connection types failed at a beam deflection value less than the beam depth. This means that these structural systems failed prior to the development of tensile catenary action. Among these specimens, however, only one of them employed the detailed setup configuration, but this specimen had a comparatively low span-to-depth ratio.
The remaining 32 specimens with moment connections that exhibited flexural action were able to undergo large deflections on the order of the beam depth or greater. Nine of them, in particular, were able to undergo even larger deflections on the order of twice the beam depth or greater. The load-carrying capacity of only 6 of these specimens decreased within the deflection range between the beam depth and twice the beam depth, due to partial failure of the connections (i.e., failure of some connection components that did not lead directly to a total failure of the connection). The load-carrying capacity of the remaining 26 specimens was increased by the effects of tensile catenary action. The average ultimate deflection of these 32 specimens was 1.56 times the beam depth. The load-carrying capacity of the 26 specimens increased by 50% in average due to tensile catenary action.
Although the general impression is that certain connection types (e.g., flush endplate, welded, RBS, etc.) may perform better as compared to others (e.g., extended endplate, WUF-B, TSWA, etc.), this is not always the case. What is more important is that the interplay between the key connection properties, regardless of the connection type, ensures the best possible behaviour. By taking into account other important factors that influence overall performance, such as dynamic effects and the contribution of other collapse resistance mechanisms mobilized in different structural components, it is concluded that the most important properties of the connection response are the initial stiffness, the flexural strength and the deformation capacity. As the initial flexural stiffness and the flexural strength of the connections increase, the pseudo-static capacity of the double-span beam system increase. As the deformation capacity of the connections increase, the pseudo-static capacity may increase provided the response is governed by tensile catenary action or it may barely decrease when fracture of some connection components has already occurred. In either case, the deformation capacity of the connections will enable the structure to undergo large deflections which may enable mobilization of additional collapse resistance mechanisms such as membrane tensile action in the slabs.
Therefore, rigid or semi-rigid moment connections with a proven capability of sustaining large deformations are likely to make a positive contribution to the progressive collapse resistance of steel frame buildings. While any required level of flexural stiffness and strength can potentially be achieved by common assemblies of steelwork connections employed in design practice, the required levels of ductility that will ensure beam deflections in the event of column loss on the order of approximately twice the beam depth are not always guaranteed. This is the reason why current studies mainly focus on deriving novel approaches of enhancing the deformation capacity of common connection types by employing additional components that aim at minimising the consequences of premature failure of certain connection components (e.g., bolts, welds, angles, etc.). The prospects of the solutions proposed in these studies are quite promising, but most of these solutions have not been validated through experimental testing yet.
Besides the connection ductility issue, another aspect of the problem that requires further study and understanding is the interplay between the different collapse resistance mechanisms. The main resistance mechanisms mobilized individually in a double-span beam system or in a reinforced concrete slab have been studied extensively and they are now well understood. Different mechanisms mobilized in the presence of masonry infill walls or steel bracing systems have also been studied. However, the simultaneous activation of these mechanisms and the interplay between the various parameters that may have different effects on some of these mechanisms may considerably change the problem. Similarly, little attention has been paid so far to the behaviour of the surrounding columns which are expected to carry an increased level of gravity loading transferred from the beam-column connections through varying combinations of shear, axial and bending forces. This is a particularly important aspect of the problem, since the failure of surrounding columns will trigger a different mode of progressive collapse as compared to the failure of beam-column connections.

Author Contributions

Conceptualization, methodology, investigation, resources, writing—original draft preparation, writing—review and editing, P.S. and J.B. All authors have read and agreed to the published version of the manuscript.

Funding

This research received no external funding.

Data Availability Statement

No new data was created in this study.

Conflicts of Interest

The authors declare no conflict of interest.

References

  1. MHCLG (Ministry of Housing, Communities and Local Government). The Building Regulations 2010, Structure: Approved Document A: A3 Disproportionate Collapse. London, UK; 2013.
  2. EN 1991-1-7, Eurocode 1: Actions on Structures – Part 1-7: General Actions – Accidental Actions, Brussels; 2006.
  3. GSA (General Services Administration), Alternate Path Analysis and Design Guidelines for Progressive Collapse Resistance, Washington, D.C., USA; 2016.
  4. DoD (Department of Defense), Unified Facilities Criteria - Design of Buildings to Resist Progressive Collapse, Washington, D.C., USA; 2016.
  5. Liu, R.; Davison, B.; Tyas, A. A Study of Progressive Collapse in Multi-Storey Steel Frames. ASCE Structures Congress: New York, 2005, 1-9. [CrossRef]
  6. Byfield, M.; Paramasivam, S. Catenary action in steel-framed buildings. ICE Proceedings, Structure Buildings. 2007, 160, 247–257. [CrossRef]
  7. Vlassis, A.; Izzuddin, B.; Elghazouli, A.; Nethercot, D. Progressive collapse of multi-storey buildings due to sudden column loss—Part II: Application. Eng. Struct. 2008, 30, 1424–1438. [Google Scholar] [CrossRef]
  8. Nethercot, D.A.; Stylianidis, P.; Izzuddin, B.A.; Elghazouli, A.Y. Resisting progressive collapse by the use of tying resistance. In: Uy B., editor. Steel and Composite Structures. Research Publishing; 2010, 94-109.
  9. Nethercot, D.A.; Stylianidis, P. Utilising catenary action as a method for resisting progressive collapse. In: Hieng Ho Lau, editor. Advances in Steel and Aluminium Structures. Research Publishing. 2011; 22-28. [CrossRef]
  10. Izzuddin, B.A. Rational Robustness Design of Multistory Building Structures. J. Struct. Eng. 2022, 148, 04021279. [Google Scholar] [CrossRef]
  11. Izzuddin, B.A.; Sio, J. Rational horizontal tying force method for practical robustness design of building structures. Eng. Struct. 2021, 252, 113676. [Google Scholar] [CrossRef]
  12. Nethercot, D.A.; Izzuddin, B.A.; Elghazouli, A.Y.; Vlassis, A.G. Aligning progressive collapse with conventional structural design. In: Liew J.Y.R and Choo, Y.S., eds. Advances in Steel Structures, Research Publishing; 2007, 1-21.
  13. Marjanishvili, S.; Agnew, E.; Ph. D.; M.Asce Comparison of Various Procedures for Progressive Collapse Analysis. J. Perform. Constr. Facil. 2006, 20, 365–374. [Google Scholar] [CrossRef]
  14. Kim, J.; Kim, T. Assessment of progressive collapse-resisting capacity of steel moment frames. J. Constr. Steel Res. 2008, 65, 169–179. [Google Scholar] [CrossRef]
  15. Fu, F. Progressive collapse analysis of high-rise building with 3-D finite element modeling method. J. Constr. Steel Res. 2009, 65, 1269–1278. [Google Scholar] [CrossRef]
  16. Khandelwal, K.; El-Tawil, S. Pushdown resistance as a measure of robustness in progressive collapse analysis. Eng. Struct. 2011, 33, 2653–2661. [Google Scholar] [CrossRef]
  17. Jahromi, H.Z.; Vlassis, A.; Izzuddin, B. Modelling approaches for robustness assessment of multi-storey steel-composite buildings. Eng. Struct. 2013, 51, 278–294. [Google Scholar] [CrossRef]
  18. Gudmundsson, G.V.; Izzuddin, B.A. The ‘sudden column loss’ idealisation for disproportionate collapse assessment. Structural Engineer. 2010, 88(6), 22–26. [Google Scholar]
  19. Stylianidis, P.M.; Nethercot, D.A.; Izzuddin, B.A.; Elghazouli, A.Y. Progressive collapse: Failure criteria used in engineering analysis. In: Proceedings of the 2009 Structures Congress. ASCE; 2009, 1811-1820. [CrossRef]
  20. Izzuddin, B.A.; Vlassis, A.G.; Elghazouli, A.Y.; Nethercot, D.A. Progressive collapse of multi-storey buildings due to sudden column loss — Part I: Simplified assessment framework. Eng. Struct. 2008, 30, 1308–1318. [Google Scholar] [CrossRef]
  21. Fu, Q.; Tan, K.-H. Numerical study on steel-concrete composite floor systems under corner column removal scenario. Structures 2019, 21, 33–44. [Google Scholar] [CrossRef]
  22. Keyvani, L.; Sasani, M.; Mirzaei, Y. Compressive membrane action in progressive collapse resistance of RC flat plates. Eng. Struct. 2014, 59, 554–564. [Google Scholar] [CrossRef]
  23. Alashker, Y.; El-Tawil, S.; Sadek, F.; Ph. D.; M.Asce Progressive Collapse Resistance of Steel-Concrete Composite Floors. J. Struct. Eng. 2010, 136, 1187–1196. [Google Scholar] [CrossRef]
  24. Li, H.; El-Tawil, S. Three-Dimensional Effects and Collapse Resistance Mechanisms in Steel Frame Buildings. J. Struct. Eng. 2014, 140, A4014017. [Google Scholar] [CrossRef]
  25. Kim, S.; Lee, C.-H.; Lee, K. Effects of floor slab on progressive collapse resistance of steel moment frames. J. Constr. Steel Res. 2015, 110, 182–190. [Google Scholar] [CrossRef]
  26. Pham, A.T.; Lim, N.S.; Tan, K.H. Investigations of tensile membrane action in beam-slab systems under progressive collapse subject to different loading configurations and boundary conditions. Eng. Struct. 2017, 150, 520–536. [Google Scholar] [CrossRef]
  27. Zandonini, R.; Baldassino, N.; Freddi, F.; Roverso, G. Steel-concrete frames under the column loss scenario: An experimental study. J. Constr. Steel Res. 2019, 162, 105527. [Google Scholar] [CrossRef]
  28. Zhang, J.-Z.; Li, G.-Q.; Jiang, J. Collapse of steel-concrete composite frame under edge-column loss—Experiment and its analysis. Eng. Struct. 2020, 209, 109951. [Google Scholar] [CrossRef]
  29. Sadek, F.; El-Tawil, S.; Lew, H.S. Effects of Robustness of composite floor systems with shear connections: modelling, simulation and evaluation. Journal of Structural Engineering. 2008, 134(11), 1717–1725. [Google Scholar]
  30. Nethercot, D.; Stylianidis, P.; Izzuddin, B.; Elghazouli, A. Enhancing the robustness of steel and composite buildings. Advanced Steel Construction. 2011, 7(1), 64-85. [CrossRef]
  31. Dinu, F.; Marginean, I.; Dubina, D.; Petran, I. Experimental testing and numerical analysis of 3D steel frame system under column loss. Eng. Struct. 2016, 113, 59–70. [Google Scholar] [CrossRef]
  32. Stylianidis, P.; Nethercot, D.; Izzuddin, B.; Elghazouli, A. Robustness assessment of frame structures using simplified beam and grillage models. Eng. Struct. 2016, 115, 78–95. [Google Scholar] [CrossRef]
  33. Jeyarajan, S.; Liew, J.R. Robustness analysis of 3D Composite buildings with semi-rigid joints and floor slab. Structures 2016, 6, 20–29. [Google Scholar] [CrossRef]
  34. Li, H.; Cai, X.; Zhang, L.; Zhang, B.; Wang, W. Progressive collapse of steel moment-resisting frame subjected to loss of interior column: Experimental tests. Eng. Struct. 2017, 150, 203–220. [Google Scholar] [CrossRef]
  35. Shan, S.; Li, S.; Wang, S. Effect of infill walls on mechanisms of steel frames against progressive collapse. J. Constr. Steel Res. 2019, 162, 105720. [Google Scholar] [CrossRef]
  36. Alrubaidi, M.; Alhammadi, S. Effectiveness of masonry infill walls on steel frames with different beam-column connections under progressive collapse. Structures 2022, 38, 202–224. [Google Scholar] [CrossRef]
  37. Qian, K.; Lan, X.; Deng, X.-F.; Li, Z. Effects of Infilled Walls with and without Openings on Progressive Collapse Resistance of Steel Frames under Corner Column Loss Condition. J. Struct. Eng. 2023, 149, 04023098. [Google Scholar] [CrossRef]
  38. Qian, K.; Lan, X.; Li, Z.; Fu, F. Effects of Steel Braces on Robustness of Steel Frames against Progressive Collapse. J. Struct. Eng. 2021, 147, 04021180. [Google Scholar] [CrossRef]
  39. Tan, Z.; Zhong, W.-H.; Meng, B.; Zheng, Y.-H.; Duan, S.-C.; Qu, Z.-Y. Numerical evaluation on collapse-resistant performance of steel-braced concentric frames. J. Constr. Steel Res. 2022, 193, 107268. [Google Scholar] [CrossRef]
  40. Lan, X.; Li, Z.; Fu, F.; Qian, K. Robustness of steel braced frame to resist disproportionate collapse caused by corner column removal. J. Build. Eng. 2023, 69, 106226. [Google Scholar] [CrossRef]
  41. Wang, F.; Yang, J.; Pan, Z. Progressive collapse behaviour of steel framed substructures with various beam-column connections. Eng. Fail. Anal. 2020, 109, 104399. [Google Scholar] [CrossRef]
  42. Qian, K.; Lan, X.; Li, Z.; Li, Y.; Fu, F. Progressive collapse resistance of two-storey seismic configured steel sub-frames using welded connections. J. Constr. Steel Res. 2020, 170, 106117. [Google Scholar] [CrossRef]
  43. Zhong, W-H.; Tan, Z.; Tian, L-M.; Meng, B.; Zheng, Y-H.; Daun, S-C. Collapse-resistant performance of a single-story frame assembly and multi-story sub-frame under an internal column-removal scenario. Steel and Composite Structures. Steel and Composite Structures. 2021, 41(5), 663–679.
  44. Tan, Z.; Zhong, W.-H.; Meng, B.; Zheng, Y.-H.; Duan, S.-C. Effect of various boundary constraints on the collapse behavior of multi-story composite frames. J. Build. Eng. 2022, 52, 104412. [Google Scholar] [CrossRef]
  45. Gerasimidis, S.; Deodatis, G.; Kontoroupi, T.; Ettouney, M. Loss-of-stability induced progressive collapse modes in 3D steel moment frames. Struct. Infrastruct. Eng. 2014, 11, 334–344. [Google Scholar] [CrossRef]
  46. Gerasimidis, S.; Deodatis, G.; Yan, Y.; Ettouney, M. Global Instability Induced Failure of Tall Steel Moment Frame Buildings. J. Perform. Constr. Facil. 2017, 31, 04016082. [Google Scholar] [CrossRef]
  47. Pantidis, P.; Gerasimidis, S. New Euler-Type Progressive Collapse Curves for Steel Moment-Resisting Frames: Analytical Method. J. Struct. Eng. 2017, 143, 04016082. [Google Scholar] [CrossRef]
  48. Li, L.-L.; Li, G.-Q.; Jiang, B.; Lu, Y. Analysis of robustness of steel frames against progressive collapse. J. Constr. Steel Res. 2018, 143, 264–278. [Google Scholar] [CrossRef]
  49. Zhang, W-Z.; Li, G-Q.; Zhang, J-Z. Progressive collapse mechanism of steel framed-structures subjected to a middle-column loss. Advanced Steel Construction. 2021, 17(2), 199-209.
  50. Naghavi, F.; Tavakoli, J.R. Probabilistic prediction of failure in columns of a steel structure under progressive collapse using response surface and artificial neural network methods. Iranian Journal of Science and Technology, Transactions of Civil Engineering. 2022, 46, 801–817. [Google Scholar]
  51. Stylianidis, P.; Nethercot, D.; Izzuddin, B.; Elghazouli, A. Modelling of beam response for progressive collapse analysis. Structures 2015, 3, 137–152. [Google Scholar] [CrossRef]
  52. Del Savio, A.; Nethercot, D.; Vellasco, P.; Andrade, S.; Martha, L. Generalised component-based model for beam-to-column connections including axial versus moment interaction. J. Constr. Steel Res. 2009, 65, 1876–1895. [Google Scholar] [CrossRef]
  53. Stylianidis, P.; Nethercot, D. Representation of connection behaviour for progressive collapse response. Int. J. Struct. Eng. 2010, 1, 340–360. [Google Scholar] [CrossRef]
  54. Stylianidis, P.; Nethercot, D. Modelling of connection behaviour for progressive collapse analysis. J. Constr. Steel Res. 2015, 113, 169–184. [Google Scholar] [CrossRef]
  55. Cassiano, D.; D'Aniello, M.; Rebelo, C. Parametric finite element analyses on flush end-plate joints under column removal. J. Constr. Steel Res. 2017, 137, 77–92. [Google Scholar] [CrossRef]
  56. Stylianidis, P.M.; Nethercot, D.A. Simplified Methods for Progressive Collapse Assessment of Frame Structures. J. Struct. Eng. 2021, 147, 04021183. [Google Scholar] [CrossRef]
  57. Gomes, V.R.; Tenchini, A.; Lima, L.; Vellasco, P. Robustness assessment of semi-rigid steel multi-storey frames. Structures 2020, 25, 849–860. [Google Scholar] [CrossRef]
  58. Stylianidis, P.; Nethercot, D.; Izzuddin, B.; Elghazouli, A. Study of the mechanics of progressive collapse with simplified beam models. Eng. Struct. 2016, 117, 287–304. [Google Scholar] [CrossRef]
  59. Stylianidis, P.; Nethercot, D. Considerations for Robustness in the Design of Steel and Composite Frame Structures. Struct. Eng. Int. 2017, 27, 263–280. [Google Scholar] [CrossRef]
  60. Demonceau, J.-F.; Jaspart, J.-P. Experimental test simulating a column loss in a composite frame. Advanced Steel Construction. 2010, 891–913. [CrossRef]
  61. Yang, B.; Tan, K.H. Experimental tests of different types of bolted steel beam–column joints under a central-column-removal scenario. Eng. Struct. 2013, 54, 112–130. [Google Scholar] [CrossRef]
  62. Lew, H.S.; Main, J.A.; Robert, S.D.; Sadek, F.; Chiarito, V.P.; Ph. D.; F.Asce; A.M.Asce; M.Asce; P.E. Performance of Steel Moment Connections under a Column Removal Scenario. I: Experiments. J. Struct. Eng. 2013, 139, 98–107. [Google Scholar] [CrossRef]
  63. Guo, L.; Gao, S.; Fu, F.; Wang, Y. Experimental study and numerical analysis of progressive collapse resistance of composite frames. J. Constr. Steel Res. 2013, 89, 236–251. [Google Scholar] [CrossRef]
  64. Guo, L.; Gao, S.; Fu, F. Structural performance of semi-rigid composite frame under column loss. Eng. Struct. 2015, 95, 112–126. [Google Scholar] [CrossRef]
  65. Li, L.; Wang, W.; Chen, Y.; Lu, Y. Effect of beam web bolt arrangement on catenary behaviour of moment connections. J. Constr. Steel Res. 2015, 104, 22–36. [Google Scholar] [CrossRef]
  66. Wang, W.; Fang, C.; Qin, X.; Chen, Y.; Li, L. Performance of practical beam-to-SHS column connections against progressive collapse. Eng. Struct. 2016, 106, 332–347. [Google Scholar] [CrossRef]
  67. Yang, B.; Tan, K.H.; Xiong, G.; Nie, S.D. Experimental study about composite frames under an internal column-removal scenario. J. Constr. Steel Res. 2016, 121, 341–351. [Google Scholar] [CrossRef]
  68. Dinu, F.; Marginean, I.; Dubina, D. Experimental testing and numerical modelling of steel moment-frame connections under column loss. Eng. Struct. 2017, 151, 861–878. [Google Scholar] [CrossRef]
  69. Zhong, W.; Meng, B.; Hao, J. Performance of different stiffness connections against progressive collapse. J. Constr. Steel Res. 2017, 135, 162–175. [Google Scholar] [CrossRef]
  70. Li, L.; Wang, W.; Teh, L.H.; Chen, Y. Effects of span-to-depth ratios on moment connection damage evolution under catenary action. J. Constr. Steel Res. 2017, 139, 18–29. [Google Scholar] [CrossRef]
  71. Xu, M.; Gao, S.; Zhang, S.; Li, H. Experimental study on bolted CFST-column joints with different configurations in accommodating column-loss. J. Constr. Steel Res. 2018, 151, 122–131. [Google Scholar] [CrossRef]
  72. Gao, S.; Xu, M.; Fu, F.; Guo, L. Performance of bolted steel-beam to CFST-column joints using stiffened angles in column-removal scenario. J. Constr. Steel Res. 2019, 159, 459–475. [Google Scholar] [CrossRef]
  73. Alrubaidi, M.; Elsanadedy, H.; Abbas, H.; Almusallam, T.; Al-Salloum, Y. Investigation of different steel intermediate moment frame connections under column-loss scenario. Thin-Walled Struct. 2020, 154, 106875. [Google Scholar] [CrossRef]
  74. Meng, B.; Zhong, W.; Hao, J.; Tan, Z.; Wang, L. Anti-progressive collapse performance analysis of composite frame with openings on beam web. J. Constr. Steel Res. 2020, 173, 106251. [Google Scholar] [CrossRef]
  75. Qiao, H.; Chen, Y.; Wang, J.; Chen, C. Experimental study on beam-to-column connections with reduced beam section against progressive collapse. J. Constr. Steel Res. 2020, 175, 106358. [Google Scholar] [CrossRef]
  76. Lin, S.; Qiao, H.; Wang, J.; Shi, J.; Chen, Y. Anti-collapse performance of steel frames with RWS connections under a column removal scenario. Eng. Struct. 2020, 227, 111495. [Google Scholar] [CrossRef]
  77. Kukla, D.; Kozlowski, A. Parametric study of steel flush and extended end-plate joints under column loss scenario. Eng. Struct. 2021, 237, 112204. [Google Scholar] [CrossRef]
  78. Meng, B.; Zhong, W.; Hao, J.; Song, X. Improving anti-collapse performance of steel frame with RBS connection. J. Constr. Steel Res. 2020, 170, 106119. [Google Scholar] [CrossRef]
  79. Meng, B.; Li, L.; Zhong, W.; Tan, Z.; Du, Q. Improving anti-progressive collapse capacity of welded connection based on energy dissipation cover-plates. J. Constr. Steel Res. 2021, 188, 107051. [Google Scholar] [CrossRef]
  80. Meng, B.; Li, F.; Zhong, W.; Zheng, Y.; Du, Q. Strengthening strategies against the progressive collapse of steel frames with extended end-plate connections. Eng. Struct. 2023, 274, 115154. [Google Scholar] [CrossRef]
  81. Meng, B.; Qiangqiang, D.; Zhong, W.; Tan, Z.; You, K. Tensile resistance and deformation of novel bending T-stub connections against progressive collapse. J. Constr. Steel Res. 2023, 201, 107733. [Google Scholar] [CrossRef]
  82. Alrubaidi, M.; Abbas, H.; Elsanadedy, H.; Almusallam, T.; Iqbal, R.; Al-Salloum, Y. Experimental and FE study on strengthened steel beam-column joints for progressive collapse robustness under column-loss event. Eng. Struct. 2022, 258, 114103. [Google Scholar] [CrossRef]
  83. Ghorbanzadeh, B.; Bregoli, G.; Vasdravellis, G.; Karavasilis, T.L. Pilot experimental and numerical studies on a novel retrofit scheme for steel joints against progressive collapse. Eng. Struct. 2019, 200, 109667. [Google Scholar] [CrossRef]
  84. Bregoli, G.; Vasdravellis, G.; Karavasilis, T.L.; Cotsovos, D.M. Static and dynamic tests on steel joints equipped with novel structural details for progressive collapse mitigation. Eng. Struct. 2021, 232, 111829. [Google Scholar] [CrossRef]
  85. Shaheen, M.A.; Foster, A.S.J.; Cunningham, L.S. A novel device to improve robustness of end plate beam-column connections. Structures 2020, 28, 2415–2423. [Google Scholar] [CrossRef]
  86. Shaheen, M.A.; Galal, M.A.; Cunningham, L.S.; Foster, A.S.J. New Technique to Improve the Ductility of Steel Beam to Column Bolted Connections: A Numerical Investigation. CivilEng 2021, 2, 929–942. [Google Scholar] [CrossRef]
  87. Shaheen, M.A.; Atar, M.; Cunningham, L.S. Enhancing progressive collapse resistance of steel structures using a new bolt sleeve device. J. Constr. Steel Res. 2023, 203, 107843. [Google Scholar] [CrossRef]
  88. Lin, S.; Xue, X.; Qiao, H.; Chen, Y. Prediction model for catenary action of welded RWS connections using PVM link element. J. Constr. Steel Res. 2022, 191, 107207. [Google Scholar] [CrossRef]
Preprints 76867 g001
Figure 1. Levels of structural idealization for progressive collapse assessment.
Figure 1. Levels of structural idealization for progressive collapse assessment.
Preprints 76867 g001
Preprints 76867 g002
Figure 2. Representation of the double-span beam mechanism [51].
Figure 2. Representation of the double-span beam mechanism [51].
Preprints 76867 g002
Preprints 76867 g003
Figure 3. Structural response following column removal involving elastic compressive arching action: (a) Beam load-deflection; (b) Beam axial force; (c) Connection bending moment; (d) Connection moment-axial force interaction.
Figure 3. Structural response following column removal involving elastic compressive arching action: (a) Beam load-deflection; (b) Beam axial force; (c) Connection bending moment; (d) Connection moment-axial force interaction.
Preprints 76867 g003
Preprints 76867 g004
Figure 4. Comparison between responses governed by different collapse resistance mechanisms: (a) Load-deflection curves; (b) Beam axial forces vs. beam deflections; (c) Connection bending moments vs. beam deflections; (d) Connection bending moments vs. beam axial forces.
Figure 4. Comparison between responses governed by different collapse resistance mechanisms: (a) Load-deflection curves; (b) Beam axial forces vs. beam deflections; (c) Connection bending moments vs. beam deflections; (d) Connection bending moments vs. beam axial forces.
Preprints 76867 g004
Preprints 76867 g005
Figure 5. Common configurations of test specimens (where l is the span of the beam): (a) Detailed; (b) Simplified.
Figure 5. Common configurations of test specimens (where l is the span of the beam): (a) Detailed; (b) Simplified.
Preprints 76867 g005
Preprints 76867 g006aPreprints 76867 g006b
Figure 6. Experimental load-deflection curves and pseudo-static predictions: (a) Bare steel specimen 2a [61]; (b) bare steel specimen 2c [61]; (c) Bare steel specimen 2e [61]; (d) Bare steel specimen 2f [61]; (e) Composite specimen 4 [63]; (e) Composite specimen 5 [64]; (g) Composite specimen 8a [67]; (h) Composite specimen 8b [67].
Figure 6. Experimental load-deflection curves and pseudo-static predictions: (a) Bare steel specimen 2a [61]; (b) bare steel specimen 2c [61]; (c) Bare steel specimen 2e [61]; (d) Bare steel specimen 2f [61]; (e) Composite specimen 4 [63]; (e) Composite specimen 5 [64]; (g) Composite specimen 8a [67]; (h) Composite specimen 8b [67].
Preprints 76867 g006aPreprints 76867 g006b
Table 1. Summary of test specimens employed in experimental studies.
Table 1. Summary of test specimens employed in experimental studies.
Specimen No. Reference Structure
type		 Test setup
configuration		 Beam span (mm) * Beam depth (mm) ** Steelwork
connection type ***
1 Demonceau and Jaspart., 2010 [60] Composite Detailed 4000 260 Flush endplate
2a Yang and Tan, 2013 [61] Bare steel Simplified 2434 303.4 Web cleat
2b Yang and Tan, 2013 [61] Bare steel Simplified 2434 303.4 Top-seat angles
2c Yang and Tan, 2013 [61] Bare steel Simplified 2434 303.4 TSWA
2d Yang and Tan, 2013 [61] Bare steel Simplified 2434 303.4 Fin plate
2e Yang and Tan, 2013 [61] Bare steel Simplified 2434 303.4 Flush endplate
2f Yang and Tan, 2013 [61] Bare steel Simplified 2434 303.4 Extended endplate
3a Lew et al., 2013 [62] Bare steel Detailed 6096 539.5 WUF-B
3b Lew et al., 2013 [62] Bare steel Detailed 6096 615.95 RBS
4 Guo et al., 2013 [63] Composite Detailed 2000 300 Welded
5 Guo et al., 2015 [64] Composite Detailed 2000 300 Flush endplate
6a Li et al., 2015 [65] Bare steel Simplified 2250 300 WUF-B (1)
6b Li et al., 2015 [65] Bare steel Simplified 2250 300 WUF-B (2)
7a Wang et al., 2016 [66] Bare steel Simplified 2250 300 Welded
7b Wang et al., 2016 [66] Bare steel Simplified 2250 300 WUF-B
8a Yang et al., 2016 [67] Composite Detailed 3000 282 Web cleat
8b Yang et al., 2016 [67] Composite Detailed 3000 282 Flush endplate
9a Dinu et al., 2017 [68] Bare steel Detailed 3000 220 WCF-B
9b Dinu et al., 2017 [68] Bare steel Detailed 3000 220 Haunch endplate
9c Dinu et al., 2017 [68] Bare steel Detailed 3000 220 RBS
9d Dinu et al., 2017 [68] Bare steel Detailed 3000 220 Extended endplate
10a Zhong et al., 2017 [69] Bare steel Detailed 1500 150 WUF-B
10b Zhong et al., 2017 [69] Bare steel Detailed 1500 150 TSWA
10c Zhong et al., 2017 [69] Bare steel Detailed 1500 150 Web cleat
11 Li et al., 2017 [70] Bare steel Simplified 1200 300 WUF-B
12a Xu et al., 2018 [71] Bare steel Simplified 1800 244 Flush endplate
12b Xu et al., 2018 [71] Bare steel Simplified 1800 244 Extended endplate
12c Xu et al., 2018 [71] Bare steel Simplified 1800 244 Stiffened angle
13a Gao et al., 2019 [72] Bare steel Simplified 1800 244 Stiffened angle (1)
13b Gao et al., 2019 [72] Bare steel Simplified 1800 244 Stiffened angle (2)
13c Gao et al., 2019 [72] Bare steel Simplified 1800 244 Stiffened angle (3)
14a Alrubaidi et al., 2020 [73] Bare steel Detailed 2000 194 Fin plate
14b Alrubaidi et al., 2020 [73] Bare steel Detailed 2000 194 WUF-B
14c Alrubaidi et al., 2020 [73] Bare steel Detailed 2000 194 Extended endplate
15a Meng et al., 2020 [74] Composite Detailed 1500 205 WUF-B
15b Meng et al., 2020 [74] Composite Detailed 1500 205 WUF-B/RWS
16a Qiao et al., 2020 [75] Bare steel Simplified 1520 200 Welded
16b Qiao et al., 2020 [75] Bare steel Simplified 1520 200 RBS
16c Qiao et al., 2020 [75] Bare steel Simplified 1520 200 RBS-RWS
17a Lin et al., 2021 [76] Bare steel Simplified 1510 200 Welded
17b Lin et al., 2021 [76] Bare steel Simplified 1510 200 RWS (1)
17c Lin et al., 2021 [76] Bare steel Simplified 1510 200 RWS (2)
18a Kukla and Kozlowski, 2021 [77] Bare steel Simplified 945 300 Flush endplate
18b Kukla and Kozlowski, 2021 [77] Bare steel Simplified 945 300 Extended endplate
* The beam span is defined for each test setup configuration as shown in Figure 5. ** The beam depth includes the height of the slab in the presence of composite action. *** TSWA: top/seat and web angle; WUF-B: welded unreinforced flange-bolted web; WCF-B: welded cover plate flange-bolted web; RBS: reduced beam section; RWS: reduced web section.
Table 2. Summary of results obtained from experimental studies.
Table 2. Summary of results obtained from experimental studies.
4 Reference L/D* Pu/Pw≤D** wu/D *** Mechanisms **** Failure mode
FA CAA TCA
1 Demonceau and Jaspart., 2010 [60] 15.38 1.92 2.38 ✓ ✓ Rebar rupture
2a Yang and Tan, 2013 [61] 8.02 1.60 1.22 ✓ Web angle fracture
2b Yang and Tan, 2013 [61] 8.02 1.00 2.01 ✓ ✓ Flange angle fracture
2c Yang and Tan, 2013 [61] 8.02 1.36 1.21 ✓ ✓ Flange angle fracture
2d Yang and Tan, 2013 [61] 8.02 - 0.86 ✓ Bolt shear failure
2e Yang and Tan, 2013 [61] 8.02 1.28 1.15 ✓ ✓ Bolt tensile fracture
2f Yang and Tan, 2013 [61] 8.02 0.54 1.48 ✓ ✓ Weld fracture
3a Lew et al., 2013 [62] 11.30 0.62 1.33 ✓ ✓ ✓ Bolt shear failure
3b Lew et al., 2013 [62] 9.90 1.17 1.40 ✓ ✓ Beam flange fracture
4 Guo et al., 2013 [63] 6.67 1.16 1.47 ✓ ✓ Weld fracture
5 Guo et al., 2015 [64] 6.67 - 0.95 ✓ ✓ Bolt tensile fracture
6a Li et al., 2015 [65] 7.50 1.09 1.13 ✓ Beam flange fracture
6b Li et al., 2015 [65] 7.50 1.00 1.30 ✓ Beam flange fracture
7a Wang et al., 2016 [66] 7.50 - 0.67 ✓ Beam flange fracture
7b Wang et al., 2016 [66] 7.50 0.93 1.33 ✓ Beam flange fracture
8a Yang et al., 2016 [67] 10.64 2.89 2.27 ✓ ✓ ✓ Web angle fracture
8b Yang et al., 2016 [67] 10.64 2.32 2.04 ✓ ✓ ✓ Bolt tensile fracture
9a Dinu et al., 2017 [68] 13.64 2.31 2.36 ✓ ✓ Flange plate fracture
9b Dinu et al., 2017 [68] 13.64 1.85 2.00 ✓ ✓ Bolt tensile fracture
9c Dinu et al., 2017 [68] 13.64 2.00 2.18 ✓ ✓ Beam flange fracture
9d Dinu et al., 2017 [68] 13.64 0.36 1.66 ✓ Bolt tensile fracture
10a Zhong et al., 2017 [69] 10.00 1.09 1.13 ✓ Beam flange fracture
10b Zhong et al., 2017 [69] 10.00 2.65 2.37 ✓ ✓ Flange angle fracture
10c Zhong et al., 2017 [69] 10.00 5.69 2.83 ✓ Web angle fracture
11 Li et al., 2017 [70] 4.00 0.82 1.03 ✓ Beam flange fracture
12a Xu et al., 2018 [71] 7.38 2.00 1.27 ✓ ✓ Bolt thread stripping
12b Xu et al., 2018 [71] 7.38 1.02 1.27 ✓ ✓ Bolt thread stripping
12c Xu et al., 2018 [71] 7.38 1.11 1.17 ✓ ✓ Bolt pull-out
13a Gao et al., 2019 [72] 7.38 - 0.74 ✓ ✓ Bolt pull-out
13b Gao et al., 2019 [72] 7.38 1.11 1.19 ✓ ✓ Bolt pull-out
13c Gao et al., 2019 [72] 7.38 - 0.94 ✓ ✓ Bolt pull-out
14a Alrubaidi et al., 2020 [73] 10.31 2.52 1.80 ✓ Fin plate fracture
14b Alrubaidi et al., 2020 [73] 10.31 1.05 1.16 ✓ Beam root fracture
14c Alrubaidi et al., 2020 [73] 10.31 0.71 2.35 ✓ ✓ Bolt thread stripping
15a Meng et al., 2020 [74] 7.32 1.16 1.34 ✓ ✓ Beam flange fracture
15b Meng et al., 2020 [74] 7.32 1.67 1.78 ✓ ✓ Beam flange fracture
16a Qiao et al., 2020 [75] 7.60 - 0.90 ✓ ✓ Weld fracture
16b Qiao et al., 2020 [75] 7.60 1.23 1.15 ✓ ✓ Beam flange fracture
16c Qiao et al., 2020 [75] 7.60 1.26 1.18 ✓ ✓ Beam flange fracture
17a Lin et al., 2021 [76] 7.55 - 0.93 ✓ ✓ Weld fracture
17b Lin et al., 2021 [76] 7.55 1.00 1.55 ✓ ✓ Beam flange fracture
17c Lin et al., 2021 [76] 7.55 1.20 1.13 ✓ ✓ Weld fracture
18a Kukla and Kozlowski, 2021 [77] 3.15 - 0.33 ✓ Bolt tensile fracture
18b Kukla and Kozlowski, 2021 [77] 3.15 - 0.42 ✓ Bolt tensile fracture
* Beam span-to-span ratio based on the span and depth values given in Table 1. ** Ratio between the ultimate load-carrying capacity and the maximum value of load-carrying capacity up to a deflection level equal to the beam depth. *** Ratio between the ultimate deflection and the beam depth. **** FA: flexural action; CAA: compressive arching action; TCA: tensile catenary action.
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.
Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.
Prerpints.org logo

Preprints.org is a free preprint server supported by MDPI in Basel, Switzerland.

facebook logotwitter logolinkedin logo
MDPI Initiatives
Important Links
Subscribe

Disclaimer

Terms of Use

Privacy Policy

© 2024 MDPI (Basel, Switzerland) unless otherwise stated