Proposition of FSR Photon Suppression Employing a Two Positron Decay Dark Matter Model To Explain Positron Anomaly in Cosmic Rays

Preprint

Communication

Proposition of FSR Photon Suppression Employing a Two Positron Decay Dark Matter Model To Explain Positron Anomaly in Cosmic Rays

Altmetrics

Downloads

115

Views

Comments

A peer-reviewed article of this preprint also exists.

Ramin Barak^*,

Ramin Barak^*,

This version is not peer-reviewed

Submitted:

18 June 2023

Posted:

19 June 2023

You are already at the latest version

Alerts

Abstract

The origin of an anomalous excess of high-energy (about 100 GeV and higher) positrons in cosmic rays is one of the rare problems in this field which is proposed to be solved with dark matter (DM). Attempts to solve this problem are faced with the issue of having to satisfy the data on cosmic positrons and cosmic gamma-radiation, which inevitably accompanies positron production such as FSR (final state radiation), simultaneously. We have been trying to come up with a solution by means of two approaches: making assumptions (*) about the spatial distribution of the dark matter, and (**) about the physics of its interactions. This work is some small final step of a big investigation regarding the search for gamma suppression by employing the second approach and a model with a doubly charged particle decaying into two positrons (X++→e+e+) is suggested as the most prospective one from those considered before.

Keywords:

Subject: Physical Sciences - Particle and Field Physics

1. Introduction

Physical nature of dark matter (DM) is the subject of long-term investigations. Different sophisticated research methods have been elaborated. Among them there are indirect ones concerning possible explanation of cosmic ray (CR) anomalies. Cosmic positrons manifest anomalous growth in the energy spectrum in the range of 10–500 GeV, as observed by PAMELA [1], AMS-2 [2] and Fermi [3], and possibly at higher energies, as pointed out by, e.g., DAMPE [4] (positron anomaly (PA)). Basically two following explanations are suggested: the ones related to pulsars [5,6] and the ones related to the annihilation or decay of DM particles (see, e.g., [7,8,9,11]). There have also been attempts, based on supernova explosions [12,13], changes of CR propagation model [14,15,16] and some others. However, all of these at least suffer from the problem of fine-tuning of model parameter magnitudes.

Here we are trying to reduce the fine-tuning problem in the framework of DM explanation of PA. This explanation faces the issue of disagreement with data on cosmic gamma radiation, first of all, the so-called Isotropic Gamma-Ray Background (IGRB) obtained by Fermi-LAT [9], illustration is provided in Figure 1. The authors are aware that Figure 1 does not contain the latest data from the AMS experiment [10]. However, the choice for this particular figure was made nonetheless in order to portray the issue which only intensifies in case of an increase of energy range as in new AMS data. Any positrons (electrons)

e^{+} e^{-}

produced by annihilation or decay of DM particles induce prompt photons (mainly, final state radiation (FSR)) and photons due to interaction of

e^{+} e^{-}

with medium photons (mainly, due to inverse Compton (IC) scattering on starlight). As one can see from Figure 1, the main problem arises due to, basically, FSR photons, and occurs at high energies.

2. Approaches to the Positron Anomaly Solution with Dark Matter

It is possible to propose two approaches for solving the problem of disagreement with gamma-ray data in DM explanation of PA. First one is due to spacial distribution of DM components, including DM clumps and other structures like dark disk. Second approach is related to the physical properties of DM particles which govern decay/annihilation process.

Our group proposed the so-called "dark disk model" [22,23,24,25,26] in the framework of first approach in order to explain positron anomaly in AMS-02 data. The idea is the following. The contradiction is caused by a finite travelling length of high energy positrons because of energy losses they suffer and the existence of a magnetic field around the Galactic Disk, which does not allow positrons born outside of it to reach the Earth. However, gammas are unaffected by these and therefore contribute to the total gamma-ray flux. This enables one to artificially decrease the amount of gamma flux while keeping the amount of positrons unchanged by "cutting off" an area of space outside the magnetic disk. In fact, there can be one minor "active" component of DM which gives a positron signal and a major passive one which forms a halo of the Galaxy. It was shown in [8] that the implementation of this particular model greatly reduces the contradiction with IGRB data.

In the framework of the second approach, different attempts were undertaken to find a physical model of DM (Lagrangian) to provide suppression of gamma-ray output. However, the focus here lies on doubly charged DM particles.

Earlier, DM models based on technicolor [17,18], where doubly charged techniparticles in composition of dark atoms decay into two positronse (

X^{+ +} \to e^{+} e^{+}

), were considered. Details on technicolour DM model can b found in Appendix A.

Also, different DM models with doubly charged particles, based on various standard model extensions [19,20,21], were discussed and elaborated to solve contradiction of the results of underground experiment DAMA with the results of other similar experiments. As to positron anomaly, model with the decay

X^{+ +} \to e^{+} e^{+}

has a simple advantage as compared to the more traditional one

X^{0} \to e^{+} e^{-}

, since there are twice as many positrons per one FSR photon.

In this short letter we follow the second approach related to the physical properties of DM which account for decay with positron production. More specifically, our aim was to point out that the DM model with a double charged unstable particle has one more advantage in the context of positron anomaly solution. This additional advantage is associated with two identical particles in the final state [8]. Such a system (

e^{+} e^{+}

) does not have classical dipole radiation since it has zero electric dipole moment. The so-called ”single photon theorem” (or ”radiation zeros”) [28] claims partial suppression of identically charged particles radiation, thus restoring a correspondence between classical and quantum descriptions to some extent. Here we demonstrate a possible role of this suppression in relation to the physics of dark matter in explaining the cosmic positron anomaly.

3. Models Used

Following theoretical simplification of the model in [8], two models of decaying dark matter particle were considered.

A model with a decay of a scalar DM particle into two positrons

$X \to e^{+} + e^{+}$

(1)

according to Lagrangian

$L_{i n t} = X {\bar{Ψ}}^{C} (a + b γ_{5}) Ψ + h . c .$

(2)

with an accompanying decay of DM particle into two positrons and FSR photon

$X \to e^{+} + e^{+} + γ;$

(3)
and more conventional model, to be compared with, with decay of scalar DM particle into an electron and a positron

$X \to e^{+} + e^{-}$

(4)

according to Lagrangian

$L_{i n t} = X \bar{Ψ} (a + b γ_{5}) Ψ + h . c .$

(5)

respectively accompanied by decay

$X \to e^{+} + e^{-} + γ .$

(6)

Ψ

represents the positron/electron wave function, index C stands for charge conjugation,

a = b = 1

was used in this work during calculations, and

γ_{5}

is the Dirac matrix.

Photon (FSR) suppression is of interest to us, since it is necessary to eliminate the contradiction with the excess of IGRB during the decay of DM particles. This implies that the ratio of the width of the three-body to two-body decay should be minimal [29]:

\frac{Γ (X \to e^{+} e^{\pm} γ)}{Γ (X \to e^{+} e^{\pm})} \equiv B r (X \to e^{+} e^{\pm} γ) = m i n .

(7)

Here we denoted this ratio as

B r

, which is (since

Γ (X \to e^{+} e^{\pm} γ) ≪ Γ (X \to e^{+} e^{\pm})

) close to the branching ratio.

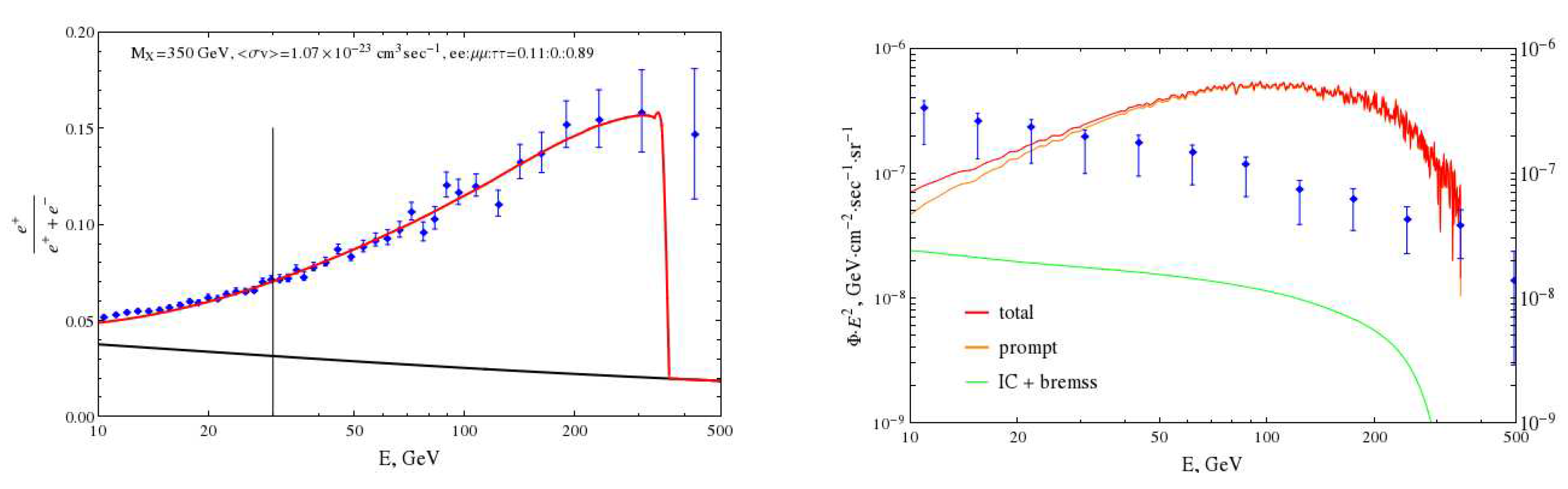
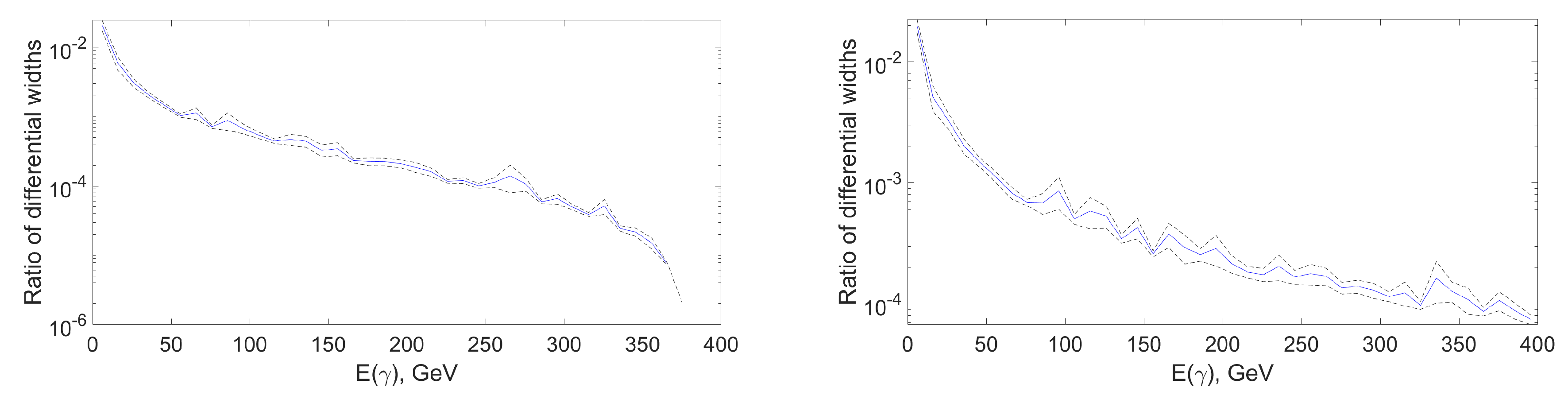
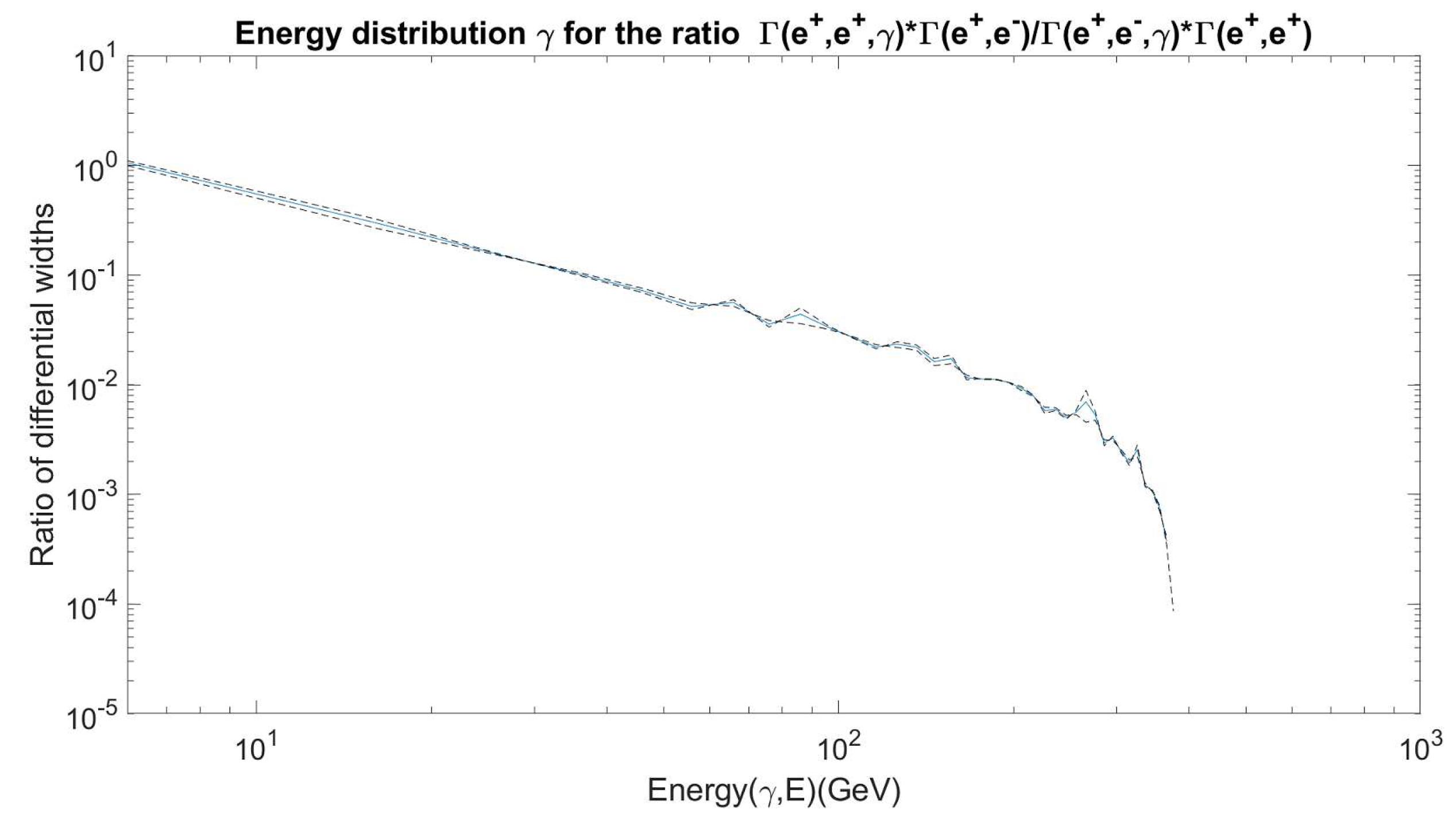
4. Results

Processes (1),(3),(4),(6) were simulated by making use of the CompHEP [30]–[32] and MadGraph [33] MC-generators. Numerical results were obtained for the mass of X being equal to 1000 GeV. For the presentation of the results the relation (7) is used in differential form for photon energy spectra in both model cases (

e^{+} e^{-}

and

e^{+} e^{+}

\frac{d B r_{e^{+} e^{\pm} γ} (E)}{d E} \equiv \frac{1}{Γ_{e^{-} e^{\pm}}} \frac{d Γ_{e^{-} e^{\pm} γ} (E)}{d E},

(8)

where

Γ_{i}

and

B r_{i}

are the widths of the respective processes and their ratio (according to (7)), and E is the FSR photon energy.

The results for these two types of processes are shown in Figure 2. As one can note,

X \to e^{+} e^{-} γ

mode has a more smooth drop in photon energy, especially at the upper kinematic limit. This can finally be observed in Figure 3, where the ratio of these two spectra

R (E) = \frac{d B r_{e^{+} e^{+} γ} (E) / d E}{d B r_{e^{+} e^{-} γ} (E) / d E}

(9)

is shown. This is the main result which shows essential suppression of FSR photons in the model with decay

X^{+ +} \to e^{+} e^{+} γ

as compared to

X^{0} \to e^{+} e^{-} γ

with the growth of photon energy, as was necessary for the resolution of contradiction between DM explanation of PA and data on IGRB.

This behaviour of spectra ratio has a qualitative explanation. The highest FSR photon energy corresponds to the situation when two charged leptons move with the maximum possible energy in the direction opposite to that of the photon (lepton and photon momenta are related as follows:

{\vec{p}}_{e 1} = {\vec{p}}_{e 2} = - {\vec{p}}_{γ} / 2

). However, two positrons cannot be born with identical momenta because of Pauli exclusion principle.

5. Conclusion

In this work, an overview of prerequisites for solving the problem of DM explanation of positron anomaly in CR was conveyed. Such an explanation faces discrepancy with data on cosmic gamma-rays. The result of this note is a suggestion of the model which provides suppression of FSR photons in comparison with the traditional case. The model suggested is based on a decaying double charged DM particle

X^{+ +} \to e^{+} e^{+}

. This displays suppression of the FSR photon yield for two reasons: firstly, we have half as many positrons per photon as compared to the more conventional case

X^{0} \to e^{+} e^{-}

; secondly, which is the main result of this note, is the effect of suppression of FSR photons due to an identity of final charged fermions. The latter leads to an additional essential suppression of FSR. This suppression takes place in the classical case since two same charged particles do not have an electric dipole momentum and therefore radiation. In the quantum case, the so-called single photon theorem tells a similar thing in an implicit way. We have shown here an effect in a specific model example that is yet to be applied to concrete astrophysical and cosmological problems. We do not show here how this suppression helps in explaining the PA problem further. This requires a separate comprehensive study. In any case, such an effect will facilitate its solution, and this is what we pay attention to.

Acknowledgments

The work was performed with the financial support provided by the Russian Ministry of Science and Higher Education, project “Fundamental and applied research of cosmic rays”, No. FSWU-2023-0068. The authors would also like to thank R.Budaev, A.Kamaletdinov, A.Kirillov, M.Khlopov, M.Laletin, S.Rubin, M.Solovyov for their contribution to the work in this investigative direction or/and useful discussions.

Appendix A

In the minimal model of walking technicolor there are two technical quarks U and D, which are being transformed by a single representation of the technicolor group

S U (2)

, and two technileptons

ν

’ and

ζ

. Electric charges can be chosen in the following way: +1 and 0 for U and D, -1 and -2 for

ν

’ and

ζ

. 9 Goldstone bosons are produced in the model. In these models one can implement the possibility of DM in the form of doubly charged particles. Two different cases can be considered. In the first case an excess of

\bar{U}

\bar{U}

with a charge of -2 and a smaller excess of

ζ

with a charge of +2. In this case the main component of the DM will consist of bound states of helium and

\bar{U}

\bar{U}

H e

\bar{U}

\bar{U}

. The are the so-called SIMPs (Strongly Interacting Massive Particles). A small component will consist in the form of bound states

ζ

\bar{U}

\bar{U}

, which are the so-called WIMPs (Weakly Interacting Massive Particles). In the second case, on the other hand, an excess of

ζ

and a smaller excess of

U U

are assumed. In this case, the main component of the DM will consist of the states

H e

ζ

(SIMP) and a small component will consist of the states

U U

ζ

(WIMP).

In both cases, it is assumed that

U U

is the lightest technibaryon, and

ζ

is the lightest technilepton. The assumption of the smallness of the WIMP component is due to the results of underground experiments on the direct search for DM. The constraint obtained from the underground experiments requires that the relative fraction of the WIMP component has to be at the level of

\sim 10^{- 6}

[17]. This value of the WIMP fraction and the corresponding values of initial excesses between particles and antiparticles can be obtained on the base of the mechanism of sphaleron transitions in the early Universe and can be associated with an excess of baryons and leptons [17]. It is important to note that

U U

state has both charge +2 and spin 0 which is important for our final goal.

References

Adriani, Oscar, et al. An anomalous positron abundance in cosmic rays with energies 1.5–100 GeV. Nature 458.7238 2009: 607-609. [CrossRef]
Aguilar, M., et al. First result from the Alpha Magnetic Spectrometer on the International Space Station: precision measurement of the positron fraction in primary cosmic rays of 0.5–350 GeV. Physical Review Letters 110.14 2013: 141102. [CrossRef]
Ackermann, Markus, et al. Measurement of separate cosmic-ray electron and positron spectra with the Fermi Large Area Telescope. Physical Review Letters 108.1 2012: 011103. [CrossRef]
G. Ambrosi, et al., DAMPE collaboration, Direct detection of a break in the teraelectronvolt cosmic-ray spectrum of electrons and positrons, Nature 552 2017 63–66. [CrossRef]
D. Hooper, I. Cholis, T. Linden, K. Fang, Hawc observations strongly favor pulsar interpretations of the cosmic-ray positron excess, Phys. Rev. D 96 2017 103013. [CrossRef]
S. Profumo, J. Reynoso-Cordova, N. Kaaz, M. Silverman, Lessons from HAWC pulsar wind nebulae observations: the diffusion constant is not a constant; pulsars remain the likeliest sources of the anomalous positron fraction; cosmic rays are trapped for long periods of time in pockets of inefficient diffusion, Phys. Rev. D 97 2018 123008,. [CrossRef]
Belotsky, Konstantin M. and Kamaletdinov, Airat Kh. and Shlepkina, Ekaterina S. and Solovyov, Maxim L., Cosmic Gamma Ray Constraints on the Indirect Effects of Dark Matter Particles 2020, 3, 336–-344. [CrossRef]
Belotsky, K. M. and Esipova, E. A. and Kamaletdinov, A. Kh. and Shlepkina, E. S. and Solovyov, M. L., Indirect effects of dark matter International Journal of Modern Physics D 2019, 28, 1941011. [CrossRef]
Belotsky, Konstantin and Budaev, Ruslan and Kirillov, Alexander and Laletin, Maxim, Fermi-LAT kills dark matter interpretations of AMS-02 data. Or not? Journal of Cosmology and Astroparticle Physics 2017, 2017, 021–-021. [CrossRef]
Aguilar, M. ; Ali Cavasonza, L. ; Ambrosi, G. ; Arruda, L. ; Attig, N. ; Barao, F. ; Barrin, L. ; Bartoloni, A. ; Başeğmez-du Pree, S. ; Bates, J. ; Battiston, R. ; Behlmann, M. ; Beischer, B. ; Berdugo, J. ; Bertucci, B. ; Bindi, V. ; de Boer, W. ; Bollweg, K. ; Borgia, B. ; Boschini, M. J. ; Bourquin, M. ; Bueno, E. F. ; Burger, J. ; Burger, W. J. ; Burmeister, S. ; Cai, X. D. ; Capell, M. ; Casaus, J. ; Castellini, G. ; Cervelli, F. ; Chang, Y. H. ; Chen, G. M. ; Chen, H. S. ; Chen, Y. ; Cheng, L. ; Chou, H. Y. ; Chouridou, S. ; Choutko, V. ; Chung, C. H. ; Clark, C. ; Coignet, G. ; Consolandi, C. ; Contin, A. ; Corti, C. search by orcid ; Cui, Z. ; Dadzie, K. ; Dai, Y. M. ; Delgado, C. ; Della Torre, S. ; Demirköz, M. B. ; Derome, L. ; Di Falco, S. ; Di Felice, V. ; Díaz, C. ; Dimiccoli, F. ; von Doetinchem, P. ; Dong, F. ; Donnini, F. ; Duranti, M. ; Egorov, A. ; Eline, A. ; Feng, J. ; Fiandrini, E. ; Fisher, P. ; Formato, V. ; Freeman, C. ; Galaktionov, Y. ; Gámez, C. ; García-López, R. J. ; Gargiulo, C. ; Gast, H. ; Gebauer, I. ; Gervasi, M. ; Giovacchini, F. ; Gómez-Coral, D. M. ; Gong, J. ; Goy, C. ; Grabski, V. ; Grandi, D. ; Graziani, M. ; Guo, K. H. ; Haino, S. ; Han, K. C. ; Hashmani, R. K. search by orcid ; He, Z. H. ; Heber, B. ; Hsieh, T. H. ; Hu, J. Y. ; Huang, Z. C. ; Hungerford, W. ; Incagli, M. ; Jang, W. Y. ; Jia, Yi ; Jinchi, H. ; Kanishev, K. ; Khiali, B. ; Kim, G. N. ; Kirn, Th. ; Konyushikhin, M. ; Kounina, O. ; Kounine, A. ; Koutsenko, V. ; Kuhlman, A. ; Kulemzin, A. ; La Vacca, G. search by orcid ; Laudi, E. ; Laurenti, G. ; Lazzizzera, I. ; Lebedev, A. ; Lee, H. T. ; Lee, S. C. ; Leluc, C. ; Li, J. Q. ; Li, M. ; Li, Q. ; Li, S. ; Li, T. X. ; Li, Z. H. ; Light, C. ; Lin, C. H. ; Lippert, T. ; Liu, Z. ; Lu, S. Q. ; Lu, Y. S. ; Luebelsmeyer, K. ; Luo, J. Z. ; Lyu, S. S. ; Machate, F. ; Mañá, C. ; Marín, J. ; Marquardt, J. ; Martin, T. ; Martínez, G. ; Masi, N. ; Maurin, D. ; Menchaca-Rocha, A. ; Meng, Q. ; Mo, D. C. ; Molero, M. ; Mott, P. ; Mussolin, L. ; Ni, J. Q. ; Nikonov, N. ; Nozzoli, F. ; Oliva, A. ; Orcinha, M. ; Palermo, M. ; Palmonari, F. ; Paniccia, M. ; Pashnin, A. ; Pauluzzi, M. ; Pensotti, S. ; Phan, H. D. ; Plyaskin, V. ; Pohl, M. ; Porter, S. ; Qi, X. M. ; Qin, X. ; Qu, Z. Y. ; Quadrani, L. ; Rancoita, P. G. ; Rapin, D. ; Reina Conde, A. ; Rosier-Lees, S. ; Rozhkov, A. ; Rozza, D. ; Sagdeev, R. ; Schael, S. ; Schmidt, S. M. ; Schulz von Dratzig, A. ; Schwering, G. ; Seo, E. S. ; Shan, B. S. ; Shi, J. Y. ; Siedenburg, T. ; Solano, C. ; Song, J. W. ; Sonnabend, R. ; Sun, Q. ; Sun, Z. T. ; Tacconi, M. ; Tang, X. W. ; Tang, Z. C. ; Tian, J. ; Ting, Samuel C. C. ; Ting, S. M. ; Tomassetti, N. ; Torsti, J. ; Tüysüz, C. ; Urban, T. ; Usoskin, I. ; Vagelli, V. ; Vainio, R. ; Valente, E. ; Valtonen, E. ; Vázquez Acosta, M. ; Vecchi, M. ; Velasco, M. ; Vialle, J. P. ; Wang, L. Q. ; Wang, N. H. ; Wang, Q. L. ; Wang, S. ; Wang, X. ; Wang, Z. X. ; Wei, J. search by orcid ; Weng, Z. L. ; Wu, H. ; Xiong, R. Q. ; Xu, W. ; Yan, Q. search by orcid ; Yang, Y. ; Yi, H. ; Yu, Y. J. ; Yu, Z. Q. ; Zannoni, M. ; Zhang, C. ; Zhang, F. ; Zhang, F. Z. ; Zhang, J. H. ; Zhang, Z. ; Zhao, F. ; Zheng, Z. M. ; Zhuang, H. L. ; Zhukov, V. ; Zichichi, A. ; Zimmermann, N. ; Zuccon, P. ; AMS Collaboration, The Alpha Magnetic Spectrometer (AMS) on the international space station: Part II - Results from the first seven years Physics Reports 2021, 894, p. 1-116. [CrossRef]
Belotsky, Konstantin and Kamaletdinov, Airat and Laletin, Maxim and Solovyov, Maxim, The DAMPE excess and gamma-ray constraints Physics of the Dark Universe 2019, 26, 100333. [CrossRef]
K. Fang, X.-J. Bi, P.-F. Yin, Explanation of the knee-like feature in the dampe cosmic e− + e+ energy spectrum, Astrophys. J. 854 2018 57,. [CrossRef]
M. Kachelrieß, A. Neronov, D.V. Semikoz, Cosmic ray signatures of a 2–3myr old local supernova, Phys. Rev. D 97 2018 063011,. [CrossRef]
Blum K., Katz B., Waxman E. AMS-02 Results Support the Secondary Origin of Cosmic Ray Positrons. Physical Review Letters 111.21 2013 (2013): 211101. [CrossRef]
Tomassetti N. Cosmic-ray protons, nuclei, electrons, and antiparticles under a two-halo scenario of diffusive propagation. Physical Review D 92.8 2015 (2015): 081301. [CrossRef]
Kappl R., Reinert A. Secondary Cosmic Positrons in an Inhomogeneous Diffusion Model. Physics of the Dark Universe 16 2017 (2017): 71–80. [CrossRef]
Belotsky, Konstantin, et al. Decaying Dark Atom constituents and cosmic positron excess. Advances in High Energy Physics 2014 (2014): 1-10. [CrossRef]
Belotsky, K. and Khlopov, M. and Kouvaris, C. and Laletin, M., High-energy positrons and gamma radiation from decaying constituents of a two-component dark atom model International Journal of Modern Physics D 2015, 24, 1545004. [CrossRef]
Khlopov, Maxim Yu. Physics of dark matter in the light of dark atoms. Modern Physics Letters A 26.38 2011: 2823-2839. [CrossRef]
Khlopov, Maxim Yu, and Chris Kouvaris. Composite dark matter from a model with composite Higgs boson. Physical Review D 78.6 2008: 065040. [CrossRef]
Khlopov, M. Yu, C. A. Stephan, and D. Fargion. Dark matter with invisible light from heavy double charged leptons of almost-commutative geometry?. Classical and Quantum Gravity 23.24 2006 7305. [CrossRef]
K. M. Belotsky, R. I. Budaev, A. A. Kirillov and M. L. Solovyov, Gamma-rays from possible disk component of dark matter J. Phys. Conf. Ser. 798 2017: 012084. [CrossRef]
V. V. Alekseev, K. M. Belotsky, Y. V. Bogomolov, R. I. Budaev, O. A. Dunaeva, A. A. Kirillov et al., High-energy cosmic antiparticle excess vs. isotropic gamma-ray background problem in decaying dark matter universe Journal of Physics: Conference Series 675 2016: 012023. [CrossRef]
V. V. Alekseev, K. M. Belotsky, Y. V. Bogomolov, R. I. Budaev, O. A. Dunaeva, A. A. Kirillov et al., On a possible solution to gamma-ray overabundance arising in dark matter explanation of cosmic antiparticle excess Journal of Physics: Conference Series 675 2016: 012026. [CrossRef]
V. V. Alekseev, K. M. Belotsky, Y. V. Bogomolov, R. I. Budaev, O. A. Dunaeva, A. A. Kirillov et al., Analysis of a possible explanation of the positron anomaly in terms of dark matter Physics of Atomic Nuclei 80 2017: 713–717. [CrossRef]
K. M. Belotsky, A. A. Kirillov and M. L. Solovyov, Development of dark disk model of positron anomaly origin Int. J. Mod. Phys. D27 2018: 1841010. [CrossRef]
M.L. Solovyov, M.A. Rakhimova, K.M. Belotsky, The “Dark disk” model in the light of DAMPE experiment Proceedings of the 23rd Bled Workshop "What Comes Beyond Standard Models?" 21.2 2020: 156–161. [CrossRef]
Brown, Robert W. Understanding something about nothing: radiation zeros. AIP Conference Proceedings Vol. 350. No. 1. American Institute of Physics, 1995. [CrossRef]
Shlepkina, E., POSSIBLE EFFECTS IN COSMIC GAMMA RADIATION DUE TO THE DECAY OR ANNIHILATION OF DARK MATTER PARTICLES. Master’s Thesis, National Research Nuclear University MEPhI (Moscow Engineering Physics Institute), Moscow, 2020.
E. Boos, V. Bunichev, M. Dubinin, L. Dudko, V. Ilyin, A. Kryukov, V. Edneral, V. Savrin, A. Semenov, A. Sherstnev (the CompHEP collaboration), CompHEP 4.4 - Automatic Computations from Lagrangians to Events 2004. [CrossRef]
A.Pukhov, E.Boos, M.Dubinin, V.Edneral, V.Ilyin, D.Kovalenko, A.Kryukov, V.Savrin, S.Shichanin, A.Semenov, CompHEP - a package for evaluation of Feynman diagrams and integration over multi-particle phase space. User’s manual for version 33 2004, 534, 250–259. [CrossRef]
http://comphep.sinp.msu.ru.
J. Alwall, R. Frederix, S. Frixione, V. Hirschi, F. Maltoni, O. Mattelaer, H.-S. Shao, T. Stelzer, P. Torrielli, M. Zaro, The automated computation of tree-level and next-to-leading order differential cross sections, and their matching to parton shower simulations Journal of High Energy Physics 2014, 2014. [CrossRef]

Figure 1. A comparison of the data of CR experiments and the predicted results of the model for decaying DM: (left) cosmic positron fraction, red line indicates the theoretical prediction, black line is the expected background and datapoints are from AMS-02; (right) IGRB, red line corresponds to the total expected contribution of photons of the same DM model as in the left plot, and the datapoints are of the Fermi/LAT. Figures were taken from [9].

Figure 2. Energy distribution of photons

\frac{d B r_{e^{+} e^{\pm} γ} (E)}{d E}

from DM particle decay through

e^{+} e^{+}

mode (left) and

e^{+} e^{-}

one (right). Dotted lines show errors.

Figure 2. Energy distribution of photons

\frac{d B r_{e^{+} e^{\pm} γ} (E)}{d E}

from DM particle decay through

e^{+} e^{+}

mode (left) and

e^{+} e^{-}

one (right). Dotted lines show errors.

Figure 3. The ratio

R (E)

of photon energy spectra from the two processes

X \to e^{+} e^{+} γ

and

X \to e^{+} e^{-} γ

Figure 3. The ratio

R (E)

of photon energy spectra from the two processes

X \to e^{+} e^{+} γ

and

X \to e^{+} e^{-} γ

Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.

© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).

Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.

MDPI Initiatives

Important Links

Choose an area of interest and we will send you notifications of new preprints at your preferred frequency.

Disclaimer

Proposition of FSR Photon Suppression Employing a Two Positron Decay Dark Matter Model To Explain Positron Anomaly in Cosmic Rays

Abstract

1. Introduction

2. Approaches to the Positron Anomaly Solution with Dark Matter

3. Models Used

4. Results

5. Conclusion

Acknowledgments

Appendix A

References

MDPI Initiatives

Important Links

Subscribe