Optimality Comparison of Object Safe Trajectory in a Multi-Object Passing Situation for Different Quantities of Acceptable Game and Non-Game Control Strategies

Preprint

Technical Note

Optimality Comparison of Object Safe Trajectory in a Multi-Object Passing Situation for Different Quantities of Acceptable Game and Non-Game Control Strategies

Altmetrics

Downloads

Views

Comments

Józef Lisowski^*

This version is not peer-reviewed

Submitted:

18 June 2023

Posted:

19 June 2023

You are already at the latest version

Alerts

Abstract

This paper presents an analysis of the sensitivity of controlling an autonomous surface object among a group of encountered objects to the inaccuracy of state control process data. For this purpose, a safe and optimal model of the control process was defined. An algorithm for determining the optimal and safe trajectory of an object, based on the multi-object game model, was developed; for comparative analysis, an algorithm for calculating only the optimal trajectory, not taking into account the maneuverability of other objects, was additionally developed. First, simulation-based studies of the algorithms enabled a comparative analysis of a number of different acceptable strategies for optimally shifting the trajectory of maneuvering objects from a single initial direction. Thereafter, the main goal of this paper was implemented: an analysis of the sensitivity characteristics of safe control, assessed with the risk of collision, both on the inaccuracy of navigation data and on the number of possible control strategies. Finally, final conclusions and a plan for further research on the subject of the paper were formulated.

Keywords:

Subject: Engineering - Control and Systems Engineering

1. Introduction

Currently, in marine technology, autonomous navigation of such marine objects as ships, offshore units, and unmanned vehicles is gaining increasing importance from the perspective of maritime traffic safety.

1.1. State of Knowledge

One of the oldest reviews of the state of development of autonomous surface vehicles is the work of Zhao et al. [1], which describes ASCs (autonomous surface crafts), also called ASVs (autonomous surface vehicles), as autonomous marine vehicle without direct human service.

The research, production, and service development of USVs (unmanned surface vehicles) in shipping were described by Barrera et al. [2], showing a multidisciplinary approach to this field.

Choi et al. [3] presented a test stand for the validation of basic navigation technologies for autonomous marine robots for the purpose of tracking waypoints and avoiding obstacles. Two methods of underwater location were used, in the forms of acoustic navigation, based on the Kalman filter, and navigation based on geophysics, using a particle filter.

Much work has been devoted, in recent years, to the use of autonomous surface vehicles for the detection, recognition, and tracking of various objects. Thus, Chen et al. [4] presented a solution in the form of an autonomous USV that could acquire and process mission data, as well as use a deep convolutional neural network in order to identify approaching vehicles and transmit their information to the ground station controlling the sea area.

The design of a surface vehicle, which was capable of detecting objects at the bottom of a larger reservoir, navigating in the direction of the object, and picking the object up using the attached grapple, was presented by Sneha [5]. Control is first performed with a PID controller for proof of concept, and then with an LQR controller and observer for optimal control.

Omrani et al. [6] presented the use of an aircraft ASV for monitoring marine facilities and ports by implementing a stereovision system for detecting and tracking both static and dynamic obstacles.

Zhang et al. [7] proposed a method of accurate target detection with long-strip targets on the water, based on a convolutional neural network, for detecting and tracking targets in the processes of sea exploration and protection. The closed control system with a PID controller ensures its optimal approximation to the longitudinal target.

In addition, Lee and Lin [8], using an extensive neural network, designed a process for identifying and controlling an unmanned surface vehicle.

Currently, there is a growing interest in technology regarding the intelligent navigation of autonomous ships in planning the optimal voyage route and preventing collisions. For this purpose, Hongguang and Yong [9] proposed the use of the artificial potential field method for the synthesis of anti-collision trajectories.

Zhou et al. [10] and Due et al. [11] reviewed research on the route planning of USVs based on the multimodality constraint, which can be divided into the following stages: route planning, trajectory planning, and traffic planning.

Martins et al. [12] designed a docking system for a surface ASV cooperating with an underwater AUV in a river environment.

Park et al. [13] described object recognition based on images from several cameras in order to detect obstacles on autonomous ships and then to track the movements of recognized ships.

Moreover, Li et al. [14] designed a USV and a UAV path-following system in the presence of structural uncertainties and external disturbances, consisting of three-dimensional mapping guidance and an adaptive fuzzy control algorithm.

Wang et al. [15] introduced Roboat’s autonomy system for urban waterways, based on the extended Kalman filter, calculation of optimal trajectories to avoid static and dynamic obstacles, and predictive steering to accurately track the trajectory from the planner in rough water.

Hongguang and Yong [16] presented a deterministic method of real-time route planning for autonomous ships or unmanned surface vehicles (USVs), taking into account the function of the repulsive potential field and the corresponding virtual forces, constrained by COLREG rules for own-ship actions.

Recently, USVs that ensure traffic safety by taking the COLREG rules into account, thus preventing collisions with other vessels, have been actively developed. Thus, Kim et al. [17] proposed an algorithm that predicts dangerous situations based on the distance to the nearest DCPA approach point and the time to the nearest TCPA approach point.

However, Zhong et al. [18] proposed an ontological model of ship behavior based on the COLREGs using knowledge graph techniques, aiming to help the machine interpret the rules of COLREGs; in this model, the ship is perceived as a spatiotemporal object and its behavior is described as changing the elements of the object on spatiotemporal scales using resource description framework, function, and method mappings for set expressions.

Moreover, Hu et al. [19] reviewed recent advances in COLREG rules-compliant ASV navigation from a traditional approach to a learning-based approach in implementing the three steps of safe navigation, namely from collision detection, to decision making, and then to rerouting.

Furthermore, the topic of ensuring the safety of a USV moving among a group of other USVs has been raised.

Sun et al. [20] proposed a method of cooperation for many USVs in the process of chasing intelligent escapees, in which the collision avoidance method is based on the artificial field potential for ships between USVs and the strategy for dynamic obstacle–ship collision avoidance is based on the COLREG rules.

1.2. Paper Thesis and Objectives

An analysis of the literature review shows that, so far, the problem of the dependence of the game control motion security level of an autonomous surface object acting among a group of other encountered objects on both the inaccuracy of navigation information and on the range of acceptable control strategies has not been addressed.

Therefore, the aim of this article is to show that, by analyzing the sensitivity of the collision risk, it is possible to assess the range of acceptable values for both the inaccuracy of individual components of navigation information and the number of acceptable control strategies.

The scientific goal is to analyze the game and optimal control sensitivity to changes in the state and control process of autonomous surface object movement among a group of other encountered objects. The index of the game control is the collision risk value, and the index of the optimal control is the final deviation of the trajectory from its predetermined direction.

The aim of this research is to conduct an experimental comparative analysis of game control against non-game control with a number of different acceptable strategies for controlling objects.

1.3. Paper Content Plan

This paper is organized as follows. First, the autonomous control process of a surface object is described, in the forms of state equations, constraints, and control objective functions. The next section describes our new safe trajectory algorithms: first, the game control algorithm, and then, for comparison, the non-game control algorithm. The subsequent section presents a computer simulation using the developed algorithms on the example of a real navigational situation at sea. The test results, as a comparison of trajectory optimalty and safe control sensitivity characteristics, are illustrated. The conlusion section summarizes the results of the research and presents the scope of future work on the subject of this paper.

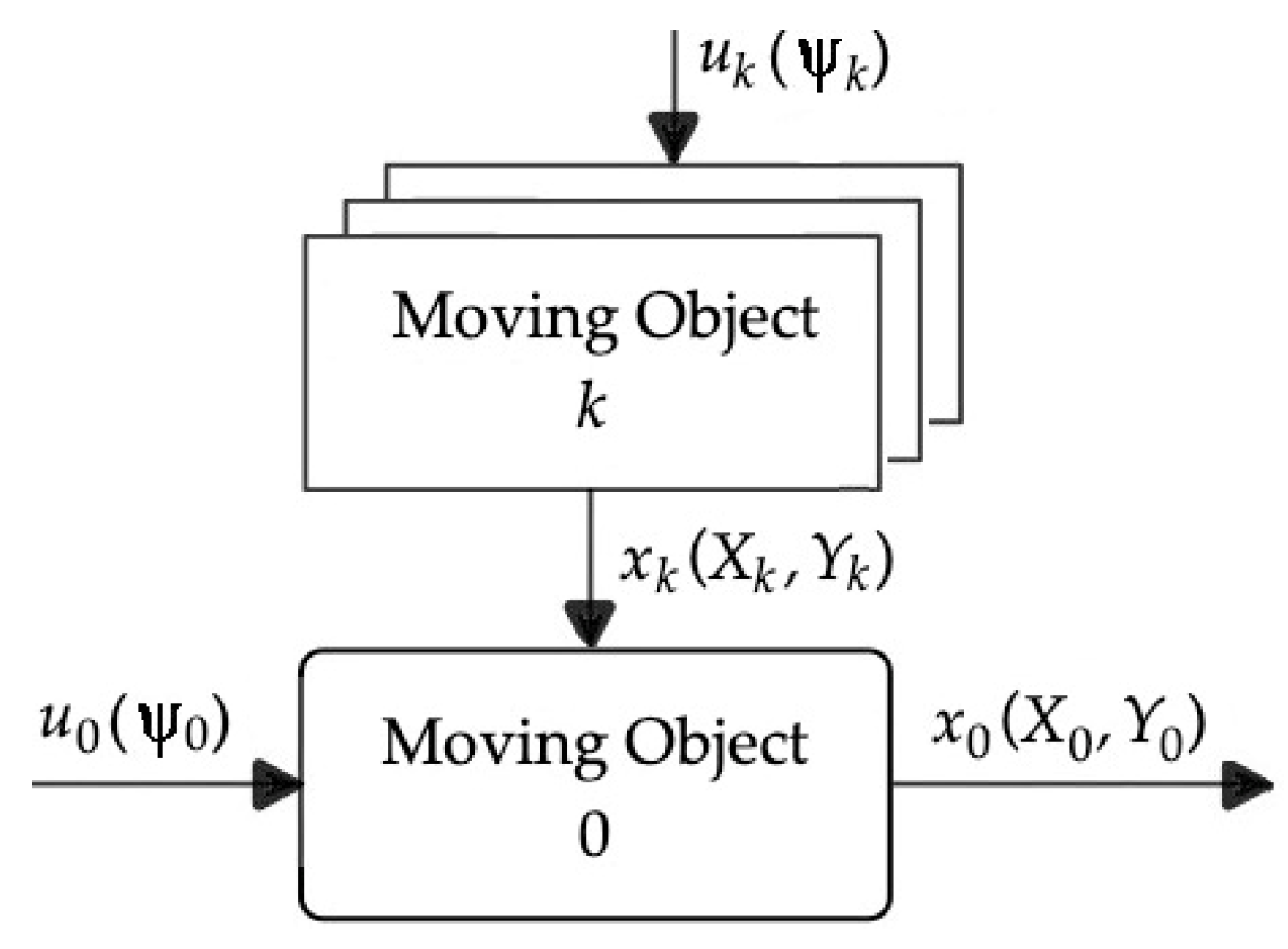
2. Autonomous Surface Object Control Process

The control process for a group of autonomous surface objects, where our autonomous surface object 0, which controls collision avoidance by using the change in course ψ₀ as control u₀, is positioned at (X₀, Y₀), and a group of other autonomous surface objects k, which controls their course ψ_k via control u_k, are positioned at (X_k, Y_k), is presented in Figure 1.

The control of individual objects affect their relative movement and the distance at which they will pass each other, which becomes the basis for whether the model involves a cooperative game or a non-cooperative game. When following COLREGs, we are dealing with a cooperative game.

However, difficult environmental conditions, disturbances in the measurements of data-controlled autonomous objects, and various subjective factors make up a non-cooperative game.

The control process of our autonomous surface object 0 among the group of k autonomous surface objects, shown in Figure 2, consists of the state equations of this process:

\dot{x} (t) = f (x, u, t)

(1)

where x(D_k, N_k, X_k, Y_k) are state variables; u(ψ_k) is the control variable; k = 1, 2, ..., K—represents the number of autonomous objects; D_k and N_k are, respectively, the distance from and bearing to the k autonomous surface object; X_k, Y_k are the position coordinates of k autonomous surface objects; and ψ_k is the course of autonomous surface object k.

State and control constraints in general notation have the following form:

g (x, u, t) \geq 0

(2)

while, here, they result from the need to keep a safe distance between objects

D_{m i n}^{k} \geq D_{s}

D_{m i n}^{k} (V_{0}, V_{k}, ψ_{0}, ψ_{k}, X_{k}, Y_{k}) - D_{s} \geq 0

(3)

where

D_{\min}^{k}

is the shortest passing distance of our autonomous surface object and k autonomous surface object; D_s is a safe distance for passing objects, depending on the state of visibility at sea; and ψ₀ is the course of our autonomous surface object.

The control objective function as an index of optimal control quality in general form:

Q = Q (x, u, t) \to m i n

(4)

takes the form of r_k collision risk in the process of safe object control:

Q_{0}^{k} = r_{0}^{k} (D_{m i n}^{k}, D_{s}, T_{m i n}^{k}, T_{s}, D_{k}) \to m i n

(5)

where

T_{m i n}^{k}

is the shortest passing time of our autonomous surface object and autonomous surface object k, and T_s is a safe passing time, depending on the state of visibility at sea.

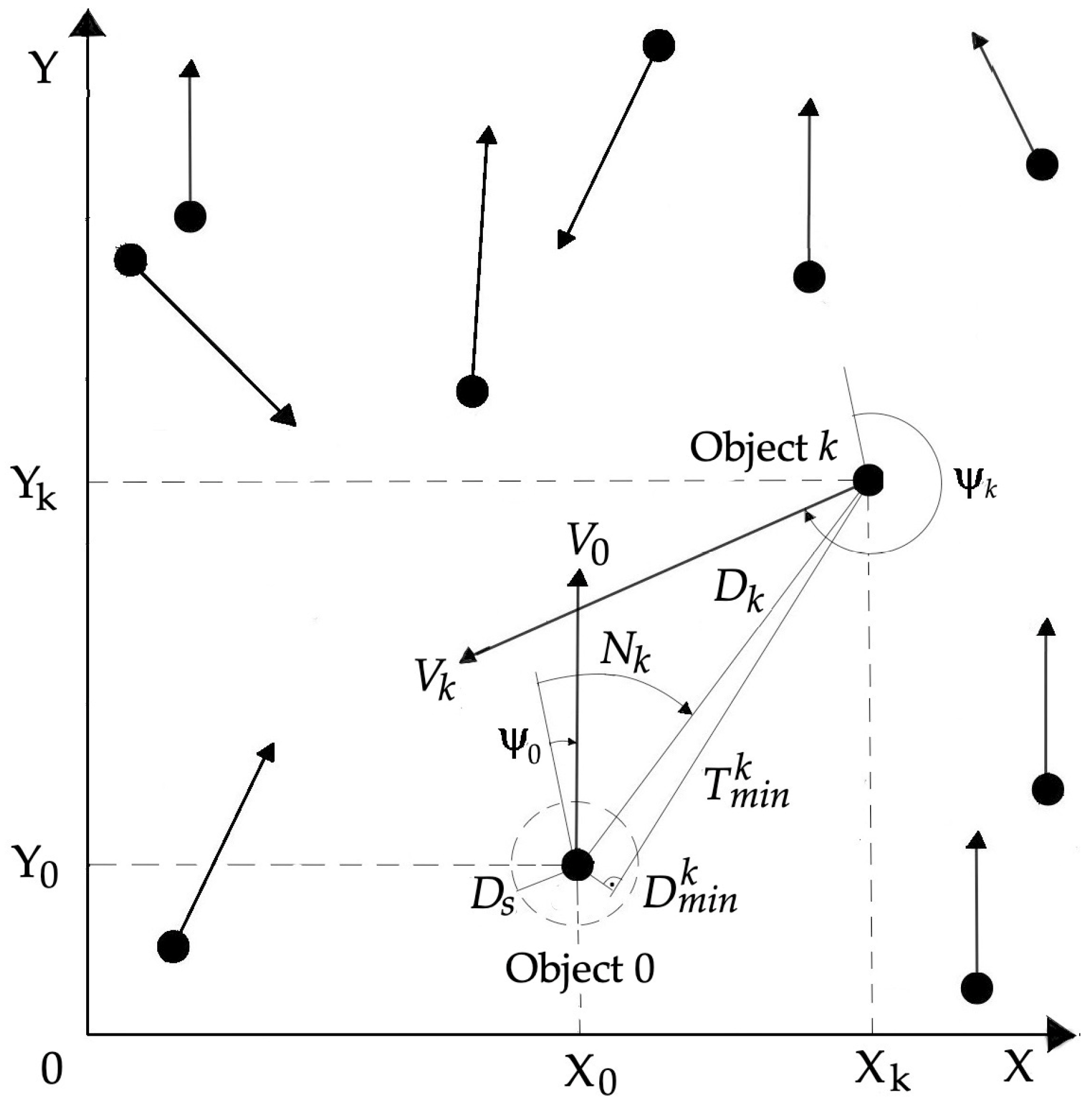
3. Algorithms for Determining a Safe Trajectory

3.1. Game Control Algorithm

Our autonomous surface object has control

u_{0} (Δ ψ_{0}^{i})

, where i = 1, 2, ..., I is the number of times it is allowed to change courses in order to carry out an anti-collision maneuver at a distance of no less than D_s (see Figure 3). Similarly, at each k, another autonomous surface object uses control

u_{k} (Δ ψ_{k}^{j})

, where j = 1, 2, …, J is the number of times it is allowed to change courses in order to carry out an anti-collision maneuver.

A collision risk matrix

R [r_{k} (Δ ψ_{0,}^{i} Δ ψ_{k}^{j})]

is created, where the risk of collision r_k is the relative measure of safety when autonomous objects pass each other. The current situation CS is described by values

C S (D_{m i n}^{k}, T_{m i n}^{k}, D_{k})

. A safe situation SS is defined by quantities SS(D_s, T_s). The author of this paper defines the collision risk r_k as the mean squared reference measure of the assessment of the current situation CS and the proximity of objects to the assessment of the expected safe situation SS:

r_{k} = {[c_{d} {(\frac{D_{m i n}^{k}}{D_{s}})}^{2} + c_{t} {(\frac{T_{m i n}^{k}}{T_{s}})}^{2} + c {(\frac{D_{k}}{D_{s}})}^{2}]}^{- \frac{1}{2}}

(6)

where c_d, c_t, and c represent weighting factors depending on environmental conditions, with values from 0 to 1; for example, in situations with concentrated object movement, c_d = c_t = 0.4 and c = 0.5 and in situations with greater distances between objects, c_d = c_t = 0.5 and c = 0.1 [21] .

The safe and optimal game trajectory for our autonomous surface object 0 in a group of other autonomous surface objects k can be computed via dual linear programming:

Q_{0, k}^{G} = \min_{i} \max_{j} r_{k}

(7)

It is assumed that, for various unknown reasons, a k autonomous object’s course leads to a collision using strategy j, maximizing the risk of collision. Thereafter, its own autonomous surface object, in response, determines its area of acceptable strategies and, from there, selects the strategy i, minimizing the risk of collision, and implements the anti-collision maneuver.

The operation of the game control algorithm G, developed by the author of the article for determining the safe trajectory of an autonomous surface object among a group of autonomous surface objects as a multi-stage decision-making process, was tested using MATLAB/Simulink version R2023a software (Algorithm 1).

Algorithm 1: Game control of autonomous surface object.

The original, innovative algorithm G segment forms a collision risk matrix based on current information about the navigation situation from the ARPA anti-collision system and then applies dual linear programming in order to find optimal strategies in each subsequent step of the game flow. In this way, a multi-step game control algorithm is synthesized. Therefore, Algorithm G computes the elements of the collision risk matrix, where the number of rows equals the number of strategies available to our autonomous surface object, and the number of columns equals the total number of strategies available to all other autonomous surface objects.

3.2. Non-Game Control Algorithm

Assuming that other autonomous objects move without changing course over time, the game control task is reduced to the non-game control task:

Q_{0, k}^{N G} = \min_{i} r_{k}

(8)

The NG algorithm is used in this paper only for the comparative analysis of game control with classic optimal control. The operation of the non-game control algorithm for determining a safe trajectory in a group of autonomous surface objects as a multi-stage decision-making process was tested using MATLAB/Simulink version R2023a software (Algorithm 2).

Algorithm 2: Non-game control of autonomous surface object.

4. Computer Simulation

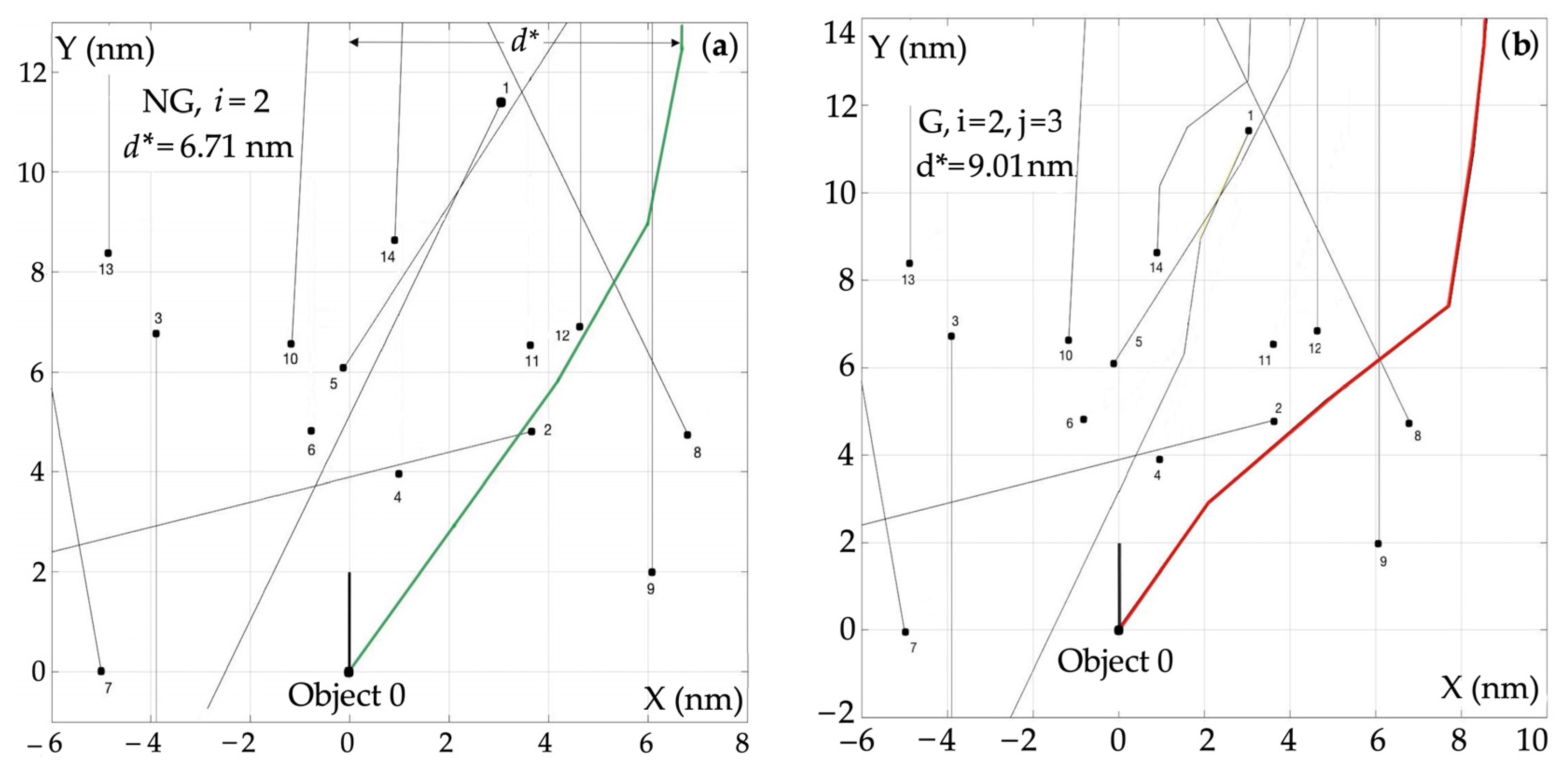
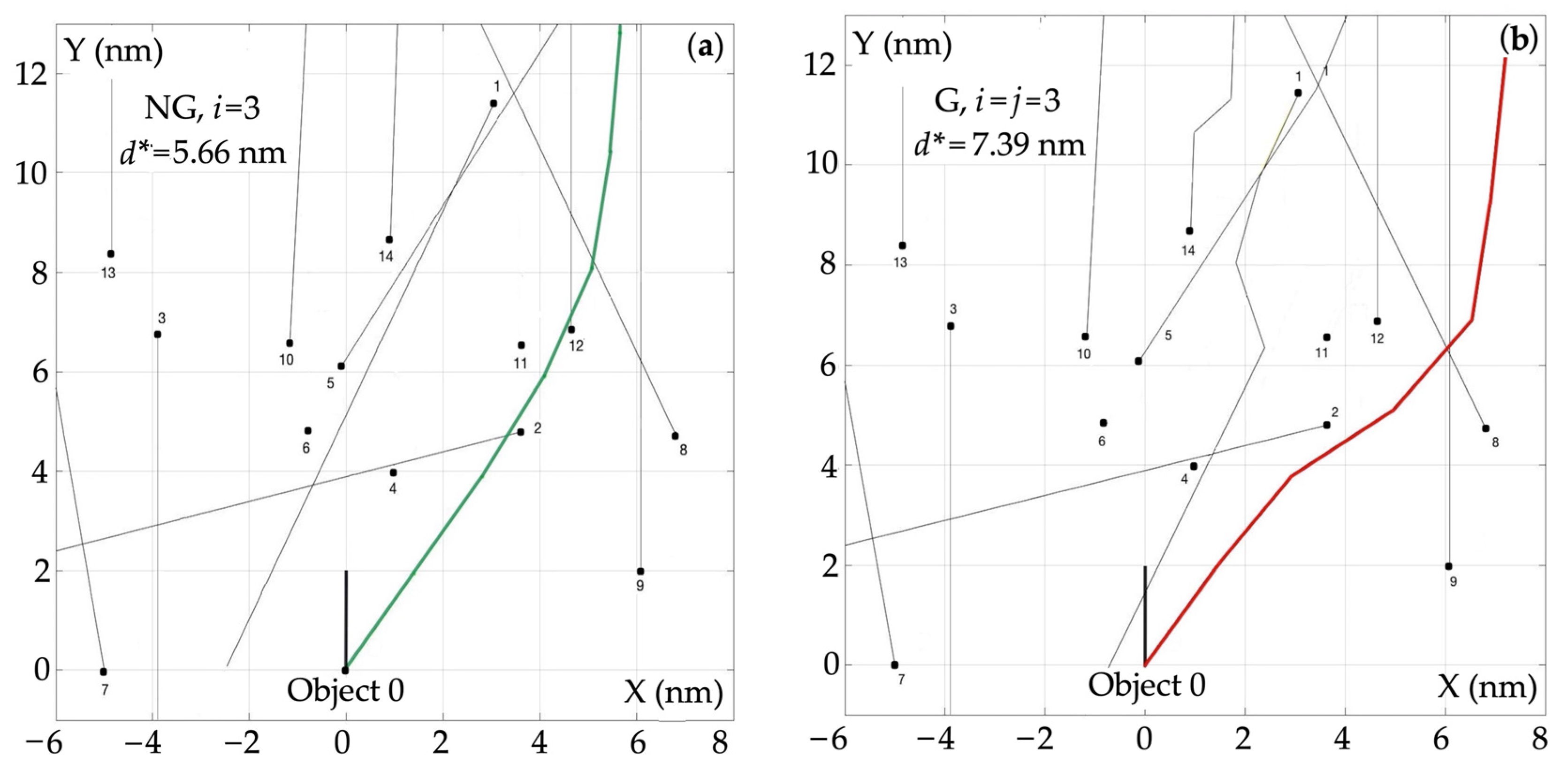
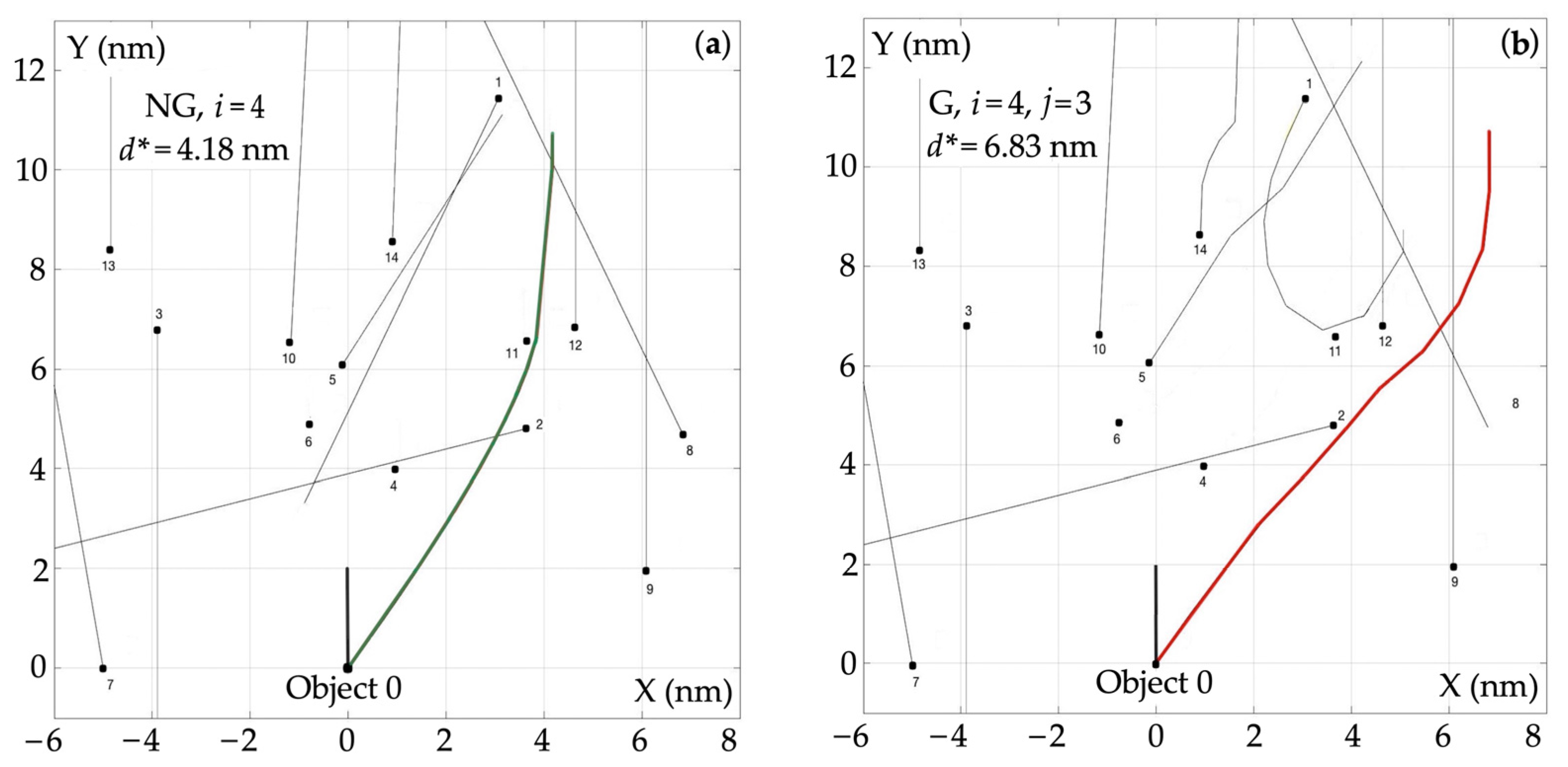
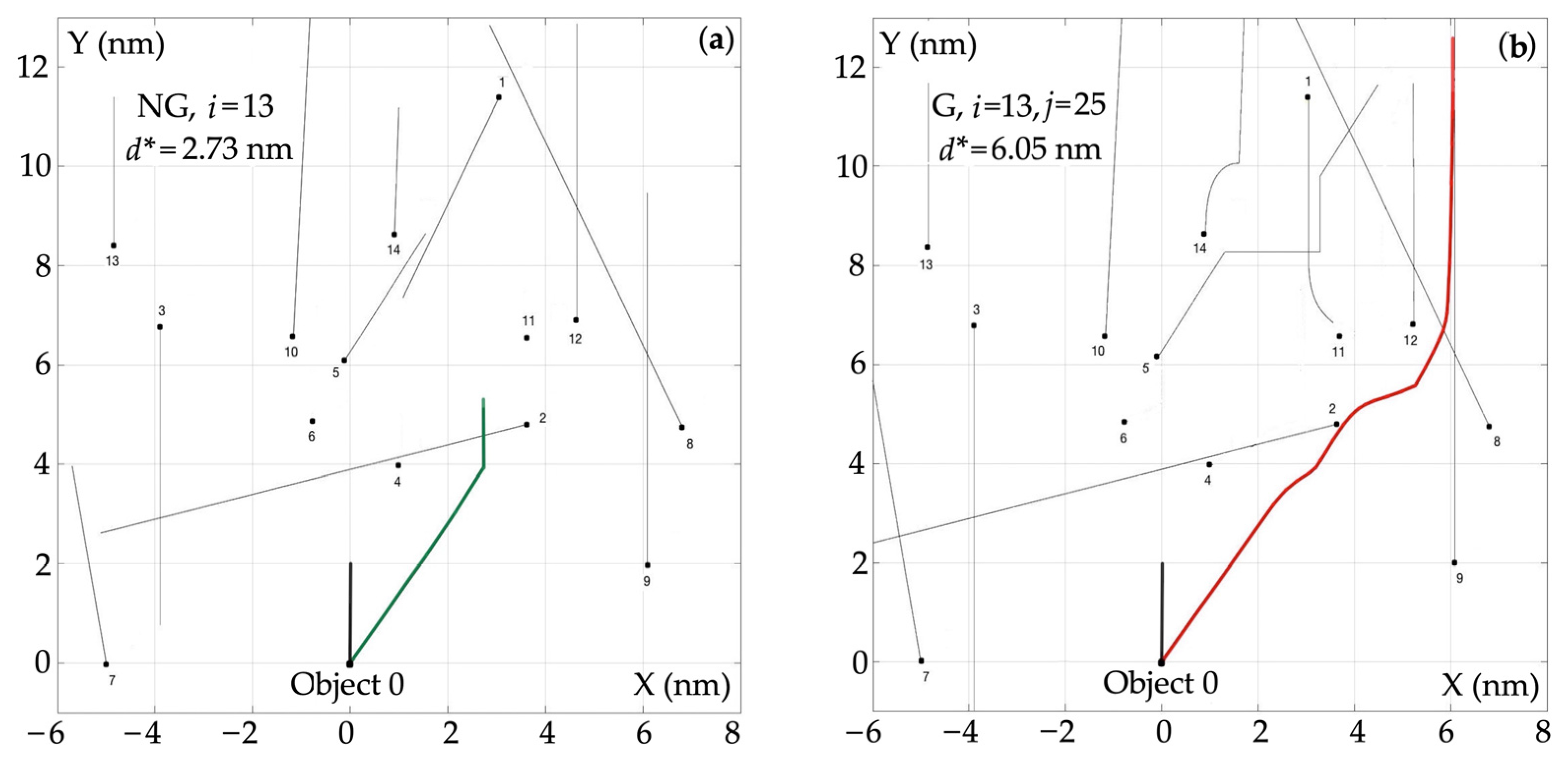
4.1. Comparison of Trajectories for Optimality

The G and NG algorithms for calculating the safe path of our autonomous surface vehicle through a group of k = 14 autonomous surface targets were subjected to simulation tests on the example described in Table 1 and shown in Figure 4, Figure 5, Figure 6, Figure 7 and Figure 8.

We assume that autonomous surface objects are equipped with regulators programmed in a microcontroller or programmable logic controller (PLC), and their motion control takes predetermined discrete values, which are called control strategies.

For the simulation tests, five sets of object maneuvering strategies were adopted, which are presented in Table 2.

Figure 7a and Figure 8a for non-game NG algorithm are the same for comparison with the game G algorithm results for different quantities control strategies shown in Figure 7b and Figure 8b.

Comparing the results from experimental studies of the safe path algorithms for our autonomous surface object through a group of other autonomous surface targets, we can conclude the following:

The greater number of admissible strategies available for the objects, i.e., the greater the angular resolution of the course change, the smaller the deviation d* of the safe trajectory: for the non-game algorithm NG, about three times and for the game algorithm G, about two times;
With a small number of acceptable strategies, the deviation of the safe path is 30–60% greater for the G algorithm than for the NG algorithm;
With a greater number of acceptable strategies, the safe path deviation becomes 200 ÷ 300% greater for the G algorithm than for the NG algorithm.

The above differences result from the specificity of the G algorithm, which takes unforeseen maneuvers of other autonomous surface objects into account.

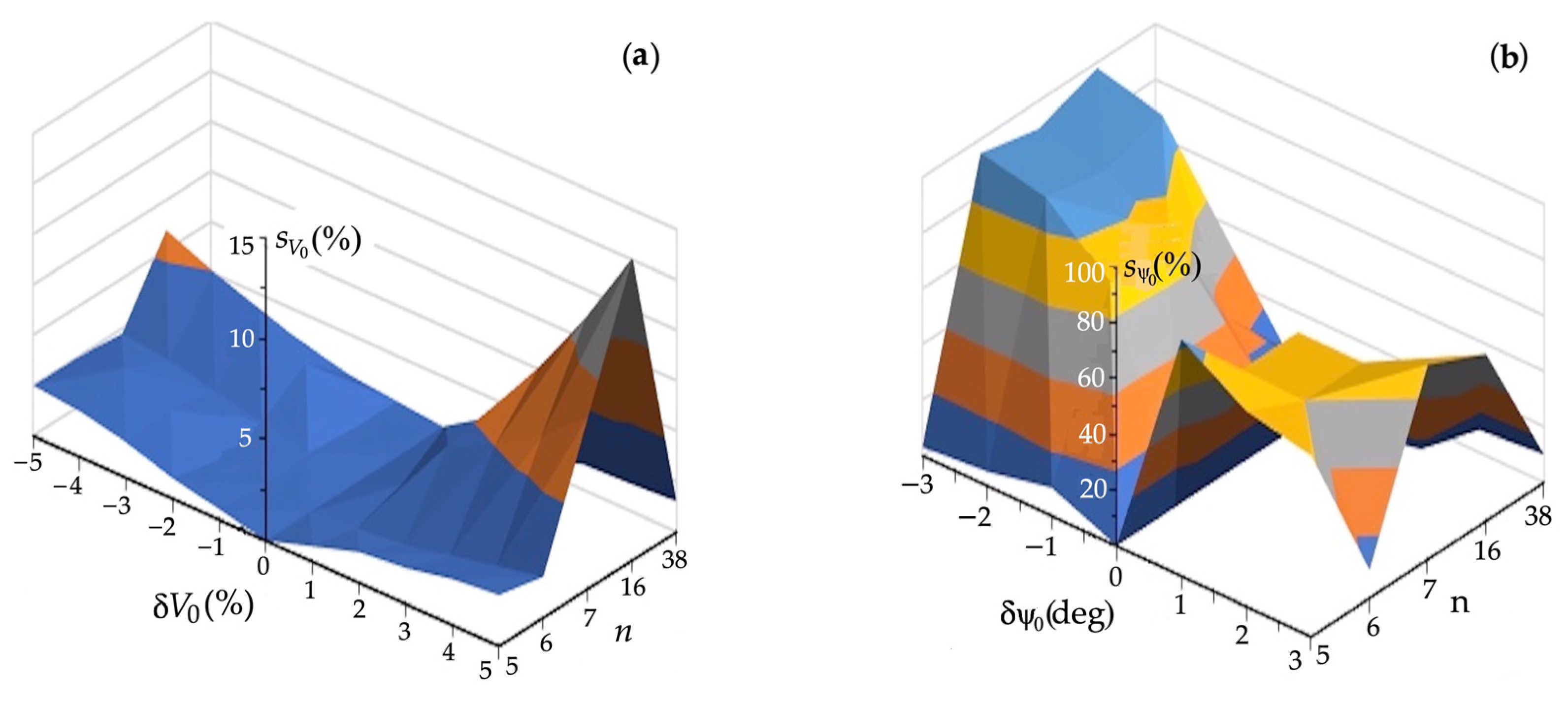
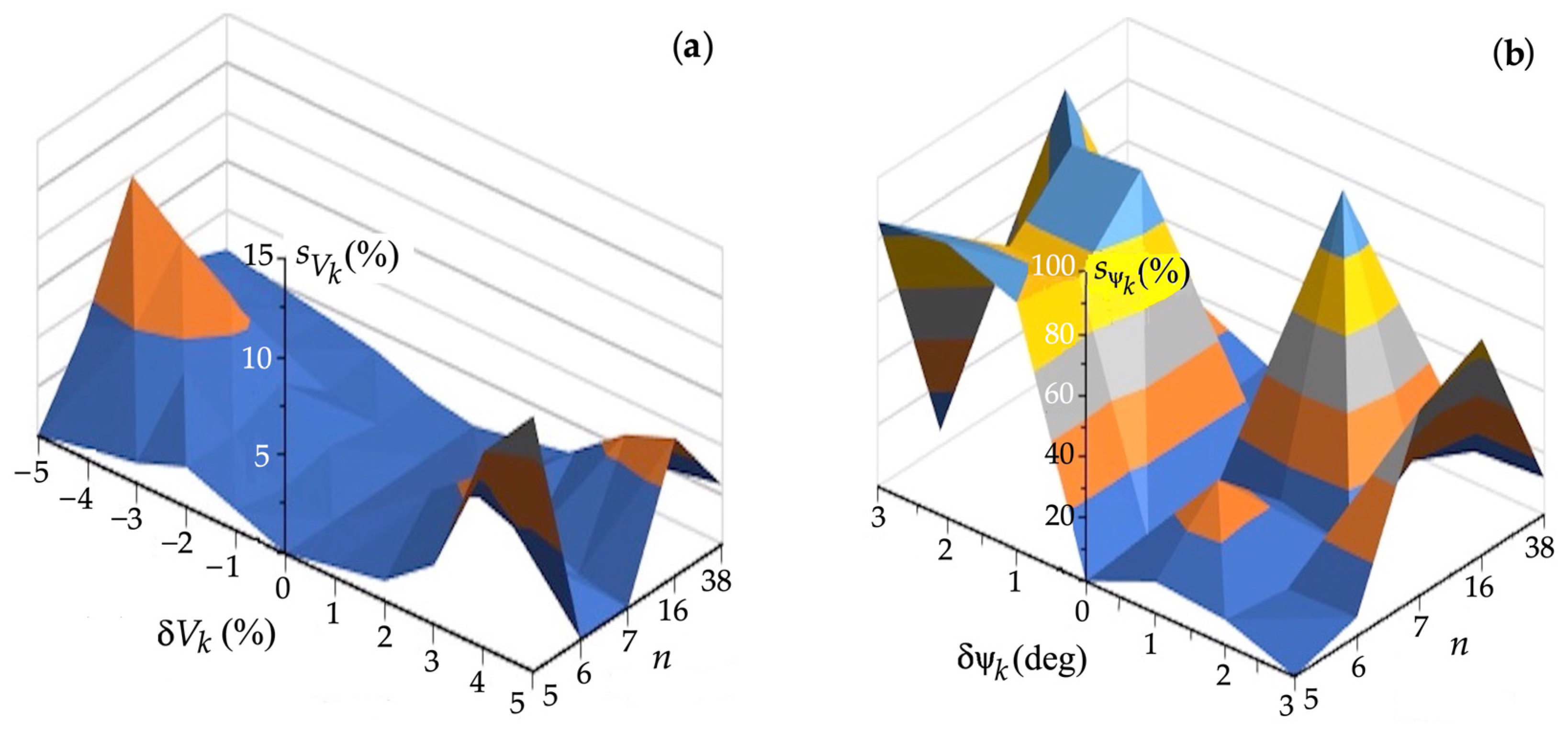
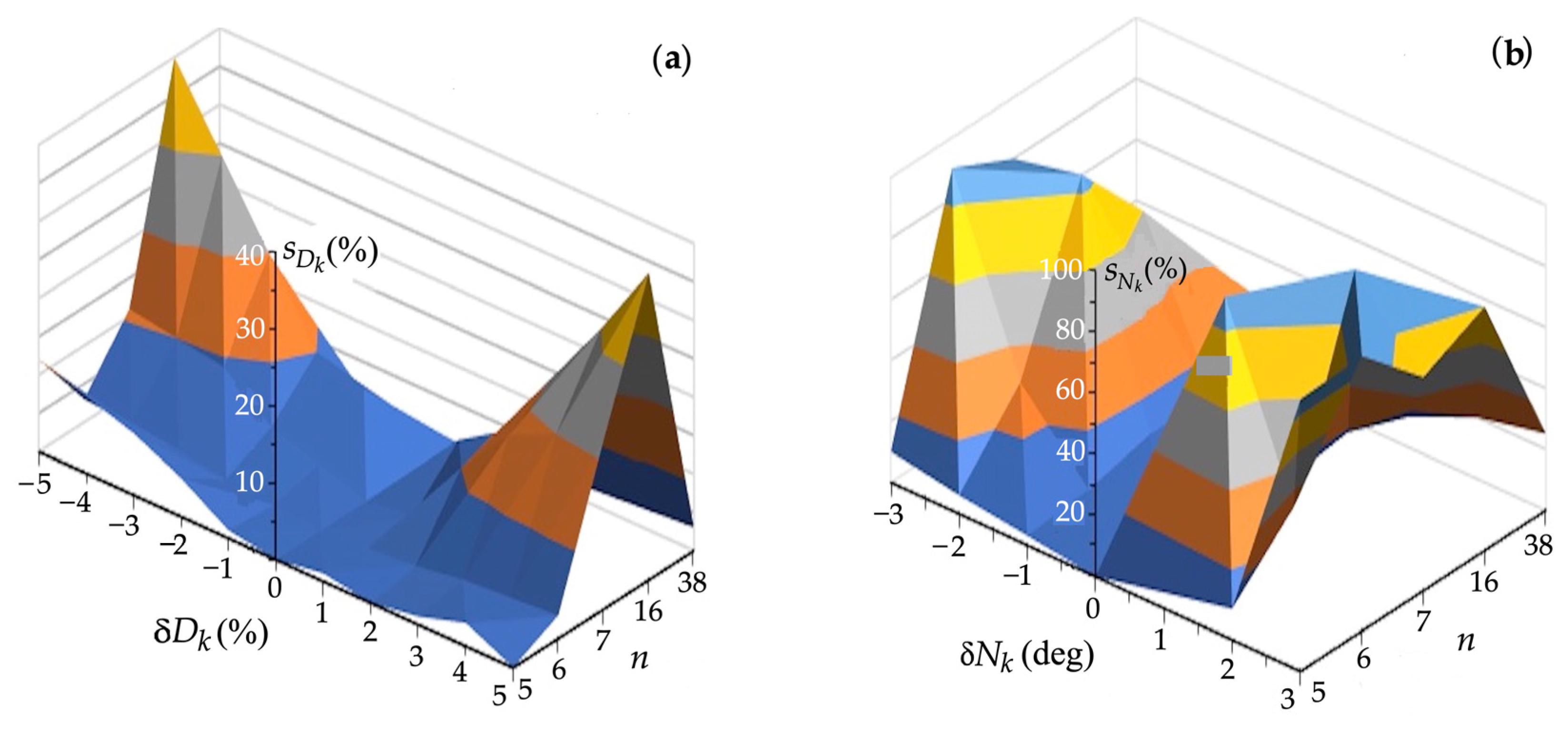
4.2. Safe Control Sensitivity

Sensitivity analysis concerns an assessment of the quality of optimal and safe system control of autonomous surface objects. The sensitivity functions s_x of the optimal and safe control u of the game process described by state variables x can be presented as partial derivatives of the quality control index Q [22,23]:

s_{x} = \frac{\partial Q [x (u)]}{\partial x}

(9)

where Q is an index of the optimal control quality described by Formula (4).

The sensitivity of safe control is treated as the sensitivity s_x of the collision risk r_k to deviations of the measured values x_e of the individual components of the process state from their actual values x, as follows:

s_{x} = \frac{\partial Q_{0}^{k}}{\partial x} = \frac{\partial r_{k}}{\partial x} = \frac{r_{k} (x_{e}) - r_{k} (x)}{r_{k} (x)} = {s_{V 0}, s_{ψ 0}, s_{V k}, s_{ψ k}, s_{D k}, s_{N k}, s_{D s}, s_{t s}}

(10)

where x(V₀, ψ₀, V_k, ψ_k, D_k, N_k, D_s, t_s, n) is a set of real values about the process state; t_s is the step time calculation trajectory; n = i + j is the number of admissible strategies for autonomous surface objects; and x_e(V₀ ± δV₀, ψ₀ ± δψ₀V_k ± δV_k, ψ_k± δψ_k, D_k ± δD_k, N_k ± δN_k, D_s ± δD_s, t_s ± δt_s, n ± δn) is a set of real values about the process state with measurement errors or possibility control.

Figure 9, Figure 10, Figure 11 and Figure 12 show the sensitivity characteristics of the collision risk to changes in the eight components involved in the motion of objects and to a different number of acceptable strategies for autonomous surface objects.

The sensitivity of the control process depends on the inaccuracy of information from the ARPA anti-collision radar about the current situation and on changes in its parameters.

The inaccuracy of the sensors are as follows:

Log speed δV₀, δV_k: ±0.5 kn;
Gyrocompass course δψ₀, δψ_k: ±0.5°;
Radar distance δD_k: ±0.05 nm, bearing δN_k: ±0.25°;
COLREG safe distance δD_s: +100%/−40%; subjective error of the navigator in assessing the situation.

The algebraic sum of all errors affecting the image of the navigational situation cannot exceed ±5% for absolute values and ±3° for angular parameters.

The course of the s_V and s_V_k characteristics shows that, in order to reduce the sensitivity of the safe control by half, the velocity of the objects should be measured with an acceptable error of no more than δV₀ = δV_k = 0.2 kn.

On the other hand, the course of the s_ψ and s_ψk characteristics shows that, in order to reduce the sensitivity of the safe control by half, the course of the objects should be measured with an acceptable error of no more than δψ₀ = δψ_k = 0.2 deg.

The course of the s_D and s_Dk characteristics shows that, in order to reduce the sensitivity of the safe control by half, the distances of the objects should be measured with an acceptable error of no more than δD_k = 0.02 nm.

On the other hand, the course of the s_N and s_Nk characteristics shows that, in order to reduce the sensitivity of the safe control by half, the bearings of the objects should be measured with an acceptable error of no more than δN_k = 0.1 deg.

The analysis of the sensitivity characteristics for the collision risk of the autonomous surface object’s control allows us to draw the following conclusions:

Sensitivity is the greatest source of measurement errors for angular variables of the process state in the form of course and bearing;
Sensitivity increases with increasing traffic safety requirements, defined by safe distance D_s between objects;
Sensitivity decreases with increasing step time t_s value;
Underestimating own speed V₀ is better than overestimating because the risk of collision increases as the speed of the moving object increases;
Sensitivity decreases with an increase in the number of acceptable strategies, n, of autonomous surface objects k, which is a positive feature of robust control systems on the impact of any external influences, and results from the possibility of more accurate control with a larger number n of acceptable control strategies.

5. Conclusions

Based on the analysis of the algorithms for the safe control of a group of autonomous surface objects, and the results of their computer simulation studies, the following final conclusions were formulated:

The multi-stage matrix game model enables the synthesis of a computer program for calculating the safe path of an autonomous surface object through a group of other autonomous surface objects that can perform unforeseen maneuvers;
The safe path of an autonomous surface feature and its deviation from its initial trajectory depends on the number of allowed strategies for this autonomous surface feature and other autonomous surface features; the greater the angular resolution of the course change, the smaller the deviation of the safe path from the initial direction of motion;
Based on the sensitivity characteristics of the collision risk, the required accuracy of measurement can be determined for individual state variables—the speed and course of objects, as can the distance and bearing to objects.

This article has not yet solved many of the problems associated with the design, testing, and application of new game control systems for autonomous surface objects. Future research should consider the following:

Development of a process model that takes the non-linear dynamic properties of objects into account;
Appropriate semantic interpretation of COLREG requirements;
More accurate representation of the optimal control process using selected methods of artificial intelligence.

Funding

This research was funded by a research project of the Electrical Engineering Faculty, Gdynia Maritime University, Poland, No. WE/2023/PZ/02: “Control algorithms synthesis of autonomous objects”.

Institutional Review Board Statement

Not applicable.

Informed Consent Statement

Not applicable.

Data Availability Statement

This study did not report any data.

Conflicts of Interest

The author declares no conflict of interest. The funders had no role in the design of the study; in the collection, analyses, or interpretation of data; in the writing of the manuscript; or in the decision to publish the results.

References

Zhao, J.; Yan, W.; Jin, X. Brief review of autonomous surface crafts. ICIC Express Lett. 2011, 5, 4381–4386. [Google Scholar]
Barrera, C.; Padron, I.; Luis, F.S.; Llinas, O. Trends and challenges in unmanned surface vehicles (USV): From survey to shipping. TransNav Int. J. Mar. Navig. Saf. Sea Transp. 2021, 15, 135–142. [Google Scholar] [CrossRef]
Choi, J.; Park, J.; Jung, J.; Lee, Y.; Choi, H.T. Development of an Autonomous Surface Vehicle and Performance Evaluation of Autonomous Navigation Technologies. Int. J. Control Autom. Syst. 2020, 18, 535–545. [Google Scholar] [CrossRef]
Chen, Y.; Chen, X.; Zhu, J.; Lin, F.; Chen, B.M. Development of an Autonomous Unmanned Surface Vehicle with Object Detection Using Deep Learning. In Proceedings of the IECON 2018—44th Annual Conference of the IEEE Industrial Electronics Society, Washington, DC, USA, 26 December 2018; pp. 5636–5641. [Google Scholar] [CrossRef]
Sneha, T. The Design and Control of an Economical Autonomous Surface Vehicle for Object Detection; Princeton University: Princeton, NJ, USA, 2020. [Google Scholar]
Omrani, E.; Mousazadeh, H.; Omid, M.; Masouleh, M.T.; Jafarbiglu, H.; Salmani-Zakaria, Y.; Makhsoos, A.; Monhaseri, F.; Kiapei, A. Dynamic and static object detection and tracking in an autonomous surface vehicle. Ships Offshore Struct. 2020, 15, 711–721. [Google Scholar] [CrossRef]
Zhang, M.; Zhao, D.; Sheng, C.; Liu, Z.; Cai, W. Long-Strip Target Detection and Tracking with Autonomous Surface Vehicle. J. Mar. Sci. Eng. 2023, 11, 106. [Google Scholar] [CrossRef]
Lee, M.F.R.; Lin, C.Y. Object Tracking for an Autonomous Unmanned Surface Vehicle. Machines 2022, 10, 378. [Google Scholar] [CrossRef]
Hongguang, L.; Yong, Y. Fast Path Planning for Autonomous Ships in Restricted Waters. Appl. Sci. 2018, 12, 2592. [Google Scholar] [CrossRef]
Zhou, C.; Gu, S.; Wen, Y.; Du, Z.; Xiao, C.; Huang, L.; Zhu, M. The review unmanned surface vehicle path planning: Based on multi-modality constraint. Ocean. Eng. 2020, 200, 107043. [Google Scholar] [CrossRef]
Du, Z.; Negenborn, R.R.; Reppa, V. Review of floating object manipulation by autonomous multi-vessel systems. Annu. Rev. Control. 2022, 1, 1. [Google Scholar] [CrossRef]
Martins, A.; Almeida, J.M.; Ferreira, H.; Silva, H.; Dias, N.; Dias, A.; Almeida, C.; Silva, E.P. Autonomous Surface Vehicle Docking Manoeuvre with Visual Information. In Proceedings of the IEEE International Conference on Robotics and Automation, Roma, Italy, 10–14 April 2007. [Google Scholar] [CrossRef]
Park, H.; Ham, S.H.; Kim, T.; An, D. Object Recognition and Tracking in Moving Videos for Maritime Autonomous Surface Ships. J. Mar. Sci. Eng. 2022, 10, 841. [Google Scholar] [CrossRef]
Li, J.; Zhang, G.; Shan, Q.; Zhang, W. A Novel Cooperative Design for USV-UAV Systems: 3D Mapping Guidance and Adaptive Fuzzy Control. IEEE Trans. Control. Netw. Syst. 2022, 11, 1–11. [Google Scholar] [CrossRef]
Wang, W.; Gheneti, B.; Mateos, L.A.; Duarte, F.; Ratti, C.; Rus, D. Roboat: An Autonomous Surface Vehicle for Urban Waterways. In Proceedings of the IEEE/RSJ International Conference on Intelligent Robots and Systems (IROS), Macau, China, 3–8 November 2019; pp. 6340–6347. [Google Scholar] [CrossRef]
Hongguang, L.; Yong, Y. COLREGS-Constrained Real-time Path Planning for Autonomous Ships Using Modified Artificial Potential Fields. J. Navig. 2018, 72, 588–608. [Google Scholar] [CrossRef]
Kim, H.G.; Yun, S.J.; Choi, G.H.; Ryu, J.K.; Suh, J.H. Collision Avoidance Algorithm Based on COLREGs for Unmanned Surface Vehicle. J. Mar. Sci. Eng. 2021, 9, 863. [Google Scholar] [CrossRef]
Zhong, S.; Wen, Y.; Huang, Y.; Cheng, X.; Huang, L. Ontological Ship Behavior Modeling Based COLREGs for Knowledge Reasoning. J. Mar. Sci. Eng. 2022, 10, 203. [Google Scholar] [CrossRef]
Hu, L.; Hu, H.; Naeem, W.; Wang, Z. A review on COLREGs-compliant navigation of autonomous surface vehicles: From traditional to learning-based approaches. J. Autom. Intell. 2022, 1, 100003. [Google Scholar] [CrossRef]
Sun, Z.; Sun, H.; Li, P.; Zou, J. Self-organizing cooperative pursuit strategy for multi-USV with dynamic obstacle ships. J. Mar. Sci. Eng. 2022, 10, 562. [Google Scholar] [CrossRef]
Lisowski, J. Multi-criteria Optimization of Multi-step Matrix Game in Collision Avoidance of Ships. TransNav—Int. J. Mar. Navig. Saf. Sea Transp. 2019, 13, 125–131. [Google Scholar] [CrossRef]
Eslami, M. Theory of Sensitivity in Dynamic Systems; Springer-Verlag: Berlin, Germany, 1994; ISBN 978-3-662-01632-9. [Google Scholar]
Rosenwasser, E.; Yusupov, R. Sensitivity of Automatic Control Systems; CRC Press: Boca Raton, FL, USA, 2000; ISBN 978-0-849-3229293-8. [Google Scholar]

Figure 1. Graphical model of a group game involving autonomous surface objects.

Figure 2. Variables describing the movement of a group of autonomous surface objects: V₀ and ψ₀ are, respectively, the speed and the course of our autonomous surface object; V_k and ψ_k are, respectively, the speed and the course of another autonomous surface object k; D_k and N_k are, respectively, the distance from and the bearing to the k autonomous surface object;

D_{m i n}^{k}

and

T_{m i n}^{k}

stand, respectively, for the minimum distance from and the time of passing autonomous surface objects; D_s is the safe passing distance of autonomous surface objects; and (X, Y) are the position coordinates of autonomous surface objects.

D_{m i n}^{k}

and

T_{m i n}^{k}

Figure 3. Sets of the number of acceptable strategies i for our autonomous surface object 0 and the number of acceptable strategies j for another autonomous surface object k.

Figure 4. Safe trajectory of our autonomous surface object, using set A of object maneuvering strategies: (a) non-game control; (b) game control.

Figure 5. Safe trajectory of our autonomous surface object, using set B of object maneuvering strategies: (a) non-game control; (b) game control.

Figure 6. Safe trajectory of our autonomous surface object, using set C of object maneuvering strategies: (a) non-game control; (b) game control.

Figure 7. Safe trajectory of our autonomous surface object, using set D of object maneuvering strategies: (a) non-game control; (b) game control.

Figure 8. Safe trajectory of our autonomous surface object, using set E of object maneuvering strategies: (a) non-game control; (b) game control.

Figure 9. The dependence of the collision risk sensitivity of s_V₀ and s_ψ0 on the inaccuracy of the measurement of the (a) speed δV₀ and (b) course δψ₀ of our autonomous surface object 0, and the number of acceptable strategies, n, for autonomous surface objects.

Figure 10. The dependence of the collision risk sensitivity of s_Vk and s_ψk on the inaccuracy of the measurement of the (a) speed δV_k and (b) course δψ_k of another autonomous surface object k, and the number of acceptable strategies, n, for autonomous surface objects.

Figure 11. The dependence of the collision risk sensitivity of s_Dk and s_Nk on the inaccuracy of the measurement of the (a) distance δD_k and (b) bearing δN_k of another autonomous surface object k, and the number of acceptable strategies, n, for autonomous surface objects.

Figure 12. The dependence of the collision risk sensitivity of s_Ds and s_ts on the inaccuracy of the measurement of the (a) safe distance δD_s and (b) step time δt_s of calculations, and the number of acceptable strategies, n, for autonomous surface objects.

Table 1. Parameters describing the movement of a group of autonomous surface objects.

Autonomous Surface Object k	Speed V_k (kn)	Course ψ_k (deg)	Distance D_k (nm)	Bearing N_k (deg)
0	12	0	0	0
1	9	206	11.8	15
2	18	256	6.0	37
3	12	180	7.8	330
4	0	0	4.1	14
5	6	33	6.1	359
6	0	0	4.9	270
7	8	359	5.0	85
8	18	334	8.3	55
9	15	0	6.4	72
10	13	3	6.7	350
11	0	0	7.5	29
12	12	0	8.3	34
13	6	0	9.7	330
14	5	2	8.7	6

Table 2. The sets of strategies controlling the movement of the autonomous surface vehicles adopted for simulation tests.

Strategies Sets	Our Autonomous Surface Object 0	Other Autonomous Surface Objects k
A	i = 2 $u_{0} = Δ ψ_{0}^{i} = 0, 60^{o}$	j = 3 $u_{k} = Δ ψ_{k}^{j} = - 30^{o}, 0, 30^{o}$
B	i = 3 $u_{0} = Δ ψ_{0}^{i} = 0, 30^{o}, 60^{o}$	j = 3 $u_{k} = Δ ψ_{k}^{j} = - 30^{o}, 0, 30^{o}$
C	i = 4 $u_{0} = Δ ψ_{0}^{i} = 0, 20^{o}, 40^{o}, 60^{o}$	j = 3 $u_{k} = Δ ψ_{k}^{j} = - 30^{o}, 0, 30^{o}$
D	i = 13 $u_{0} = Δ ψ_{0}^{i} = 0 \div 60^{o} for each 5^{o}$	j = 3 $u_{k} = Δ ψ_{k}^{j} = - 30^{o}, 0, 30^{o}$
E	i = 13 $u_{0} = Δ ψ_{0}^{i} = 0 \div 60^{o} for each 5^{o}$	j = 25 $u_{k} = Δ ψ_{k}^{j} = - 60 \div 60^{o} for each 5^{o}$

Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.

© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).

Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.

MDPI Initiatives

Important Links

Choose an area of interest and we will send you notifications of new preprints at your preferred frequency.

Disclaimer

Optimality Comparison of Object Safe Trajectory in a Multi-Object Passing Situation for Different Quantities of Acceptable Game and Non-Game Control Strategies

Abstract

1. Introduction

1.1. State of Knowledge

1.2. Paper Thesis and Objectives

1.3. Paper Content Plan

2. Autonomous Surface Object Control Process

3. Algorithms for Determining a Safe Trajectory

3.1. Game Control Algorithm

3.2. Non-Game Control Algorithm

4. Computer Simulation

4.1. Comparison of Trajectories for Optimality

4.2. Safe Control Sensitivity

5. Conclusions

Funding

Institutional Review Board Statement

Informed Consent Statement

Data Availability Statement

Conflicts of Interest

References

MDPI Initiatives

Important Links

Subscribe