Prerpints.org logo
Preprint
Article

Commuted PD Controller for Nonlinear Systems: Glucose-Insulin Regulatory Case

Altmetrics

Downloads

106

Views

26

Comments

0

A peer-reviewed article of this preprint also exists.

Submitted:

19 June 2023

Posted:

19 June 2023

You are already at the latest version

Alerts
Abstract
As an option to deal with the insulin-dependent disease, a recent commuted PD control strategy is designed and carefully analyzed for different clinic diabetic patients. This controller approach is mainly conceived to stabilize the glucose blood concentration in a diabetic patient around its basal value, hence avoiding extreme situations such as hypoglycemia and hyperglycemia. This control strategy receives two inputs carefully tuned to actuate when the measured variable is out of a prescribed healthy zone. Therefore, one of these variables is invoked to decrease the glucose concentration to insulin injection, and the other is employed to increase the glucose absorption, both by using a proper PD controller. According to our numerical experiments, our controller approach performs well, even when there is an external disturbance in the controlled system.
Keywords: 
Subject: Engineering  -   Other

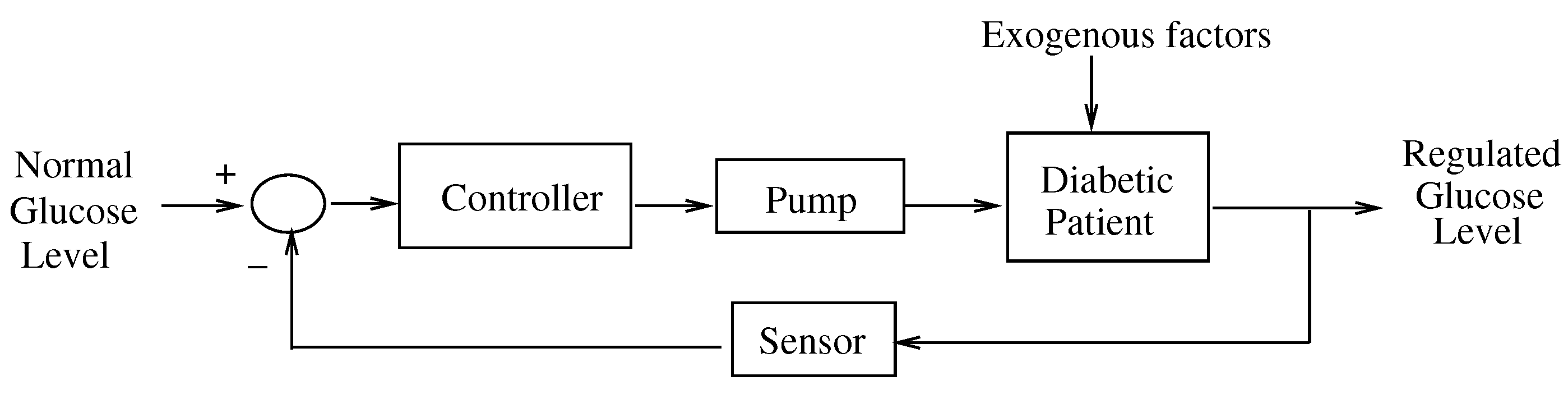
1. Introduction

Diabetes (Diabetes mellitus) is a chronic disease that affects millions of persons worldwide (see, for instance, [1,2,3], and [4]). This disease is characterized by inadequate control of the blood glucose concentration in the body, leading to complications such as limb loss, blindness, ischemic heart disease, and end-stage renal disease [3]. Besides, for diabetic patients with insulin-dependent diabetes, the glucose/insulin regulatory system can be viewed as a feedback-control example where the blood glucose levels are frequently measured to control it (see, for instance, [2,5,6,8] and [9]). Additionally, and according to the Diabetes Control and Complications Trial (DCCT), the blood glucose concentration should be within the range of 50-120 mg/dL [4]. In [10], the range from 60 mg/dL to 110 mg/dL is considered as the normal blood glucose concentration level in humans. Therefore, by correctly applying insulin, this glucose level can be correctly (healthy) manipulated. As reference values, above 120mg/dL the state of the patient is known as hyperglycemia, and below of 50mg/dL, the state is known as hypoglycemia. Both states are harmful to the diabetic patient [4]. Exogenous factors that can affect glucose include food intake, rate of digestion, exercise, and reproductive state, among others ([2,4]). Hence, for control performance evaluation, it is also important that the designed controller be robust in front of any real kind of internal or external perturbations.
Figure 1 shows the block diagram of a closed-loop controlled system of diabetic patients using insulin pumps ([4,6]). In this scheme, the glucose sensor can be embedded under the skin, and the insulin pump can be implanted in the abdomen. So, the control objective consists to keep regulating the glucose level in the body. In this scenario, the patient is said to be under metabolic control. The pump injects insulin through a catheter. The system shown in Figure 1 can be referred to as artificial pancreas due to this closed-loop system replaces, in some way, the pancreas activity in controlling the glucose level of the body of a healthy person [2].
In literature, several approaches have been used to design artificial pancreas. For instance, a robust controller using higher-order sliding mode control is studied in [6]. Using optimal H ∞ control theory, an insulin injection control is analyzed in [5]. And employing a parametric programming approach for the control design is considered in [4]. On the other hand, in [11], control algorithms using standard linear control techniques, like the proportional-derivative controller, are studied, as in [12,13,14]. In this paper, the feedback measurement signal is assumed available at discrete-time moments which results in an interesting and useful technological fact for an artificial pancreas design. In contrast, we claim that no significant benefit is obtained in using a nonlinear model-based control design strategy. For instance, in [15], an impulsive model predictive control is presented, but the mathematical model has to be linear, and in [16], miss undertaken internal dynamics. On the other hand, PID controllers in the artificial pancreas has been studied in [17], but only for hyperglycemic condition, and in [18] a PID robust control is presented for the hypoglycemic situation, but both conditions are not studied simultaneously, as in the present work. However, the nonlinear techniques can offer new ways of control implementation that can face some nonlinearities ignored in by the linear controller tools. Some of these nonlinear control design strategies involve sliding mode control [6,7], delay control [19], optimal control [20], switched LPV control [21], sub-optimal control [22], model predictive control [23], fuzzy control [24], reinforcement learning [25], etc. Therefore, the use of these control design tools allows us to innovate new developments for artificial pancreas approaches. Our proposal aims to act upon the control part of an insulin-dependent diabetic system to develop an effective and simple solution to avoid non-desired clinical problems.
The main objective of the present work is to design a robust control for an artificial pancreas to minimize the effect of extreme situation as hyperglycemia or hypoglycemia. Additionally, we evaluate our artificial pancreas performance under different scenarios. Our control strategy uses a novel switched strategy: when a peak value on glucose blood concentration is detected, then the controller tries to minimize its level by injecting insulin to the system; and when the glucose blood concentration is minor than healthy level, then glucose ingestion is administrated by the controller. The objective is to maintain a healthy level of glucose. The control strategy is based on a Proportional-Derivative (PD) theory, where the input signal is the detected peak value of the glucose blood concentration. The PD controller format is considered due to its simple and easy realization [12], as pointed out by [13,20]. We avoid using the PID controller because its integral action may be useless [14]. This is also evidenced, in our numerical experiments, when we noticed that strong hypoglycemia occurs during a long period of time when the integral part is considered. But in order to complete the study of the proposed switched strategy, a reset integral part is considered, defining a commuted Proportional Integral Derivative (PID) controller. This approach is based on Clegg integrator [26], where a reset signal is introduced to face the overshoots produced by the integral part of the controller as suggested in [27] and [28].
The rest of the paper is organized as follows. First, the nonlinear mathematical model and the proposed controller are presented in Section 2. Then, Section 3 shows the performance of the combined PD controller in different scenarios: with decaying disturbance; with external additive perturbation; and in the presence of dynamical plant changes. Also, in this section, a resetting-PID is evaluated to see the undesired chattering effect due to the integral part of the control architecture. Finally, Section 4 discusses the obtained results.

2. Materials and Methods

2.1. Dynamical Model of the Glucose-Insulin Regulatory System

The main objective of this paper is to design a robust PD controller for an artificial pancreas able to stabilize the glucemia blood level around its basal value and prevent hypoglycemia from appearing when the administrated insulin is not well assimilated by the patient. In the recent literature, there are some glucose-insulin regulatory mathematical models [29]. In this paper, we consider the minimal model called the Bergman minimal model. See, for instance, [4,5,6,11] and references therein. This is due to its simplicity. This model is as described follows:
x ˙ 1 ( t ) = − p 1 ( x 1 ( t ) − G b ) − x 1 ( t ) · x 2 ( t ) + D ( t ) ,
x ˙ 2 ( t ) = − p 2 x 2 ( t ) + p 3 ( x 3 ( t ) − I b ) ,
x ˙ 3 ( t ) = − n ( x 3 ( t ) − I b ) + γ [ x 1 ( t ) − σ ] + t + u ( t ) ,
where x 1 ( t ) , x 2 ( t ) and x 3 ( t ) are the blood plasma glucose concentration (mg/dL), the insulin’s effect on the net glucose disappearance (1/min) and the insulin concentration in plasma ( μ U/ml), respectively. [ x 1 − σ ] + means that when x 1 ( t ) is greater that σ , then the value is taken to be [ x 1 − σ ] , otherwise, its value is zero. G b and I b are the basal value levels of pre-injection level of glucose (mg/dL) and the pre-injection level of insulin ( μ U/ml), respectively. These values can be also called the subject’s baseline glycemia ( G b ) and the subject’s baseline insulinemia ( I b ) [19]. Remark that σ is greater than G b . D ( t ) represents the exogenous factors, and u ( t ) defines the insulin injection rate being the control input. Parameters p 1 , p 2 , p 3 , n and γ are the system parameters. These are described, for instance, in [6,19]. Additionally, x 1 ( 0 ) , x 2 ( 0 ) , and x 3 ( 0 ) are the corresponding initial conditions. Finally, x 1 ( t ) is the available output system for the control algorithm.
According to [6], D ( t ) is supposed to be reduced to zero or to some constant value in finite-time, and it represents the rate at which glucose is absorbed by the regulatory system. One possible mathematical representation of D ( t ) is as follows [4,6,7,20]:
D ( t ) = A e − B t , B > 0 .
Therefore, mathematical model (1)-() will be taken as a reference pancreas system.

2.2. Modified Mathematical Model

Because the dynamic of glucose concentration is reduced when hypoglycemia occurs, and to increase its concentration, the control action has to administrate glucose to the pancreas system. In consequence, equation (1) is modified to include this control manipulation:
x ˙ 1 ( t ) = − p 1 ( x 1 ( t ) − G b ) − x 1 ( t ) · x 2 ( t ) + D ( t ) + u g ( t ) ,
x ˙ 2 ( t ) = − p 2 x 2 ( t ) + p 3 ( x 3 ( t ) − I b ) ,
x ˙ 3 ( t ) = − n ( x 3 ( t ) − I b ) + γ [ x 1 ( t ) − σ ] + t + u ( t ) .
From here, the term u g ( t ) corresponds to the controller part that is activated under hypoglycemia. This modified mathematical model defined by equations (5)-() allows us to direct influence on the glucose level of the pancreas system.

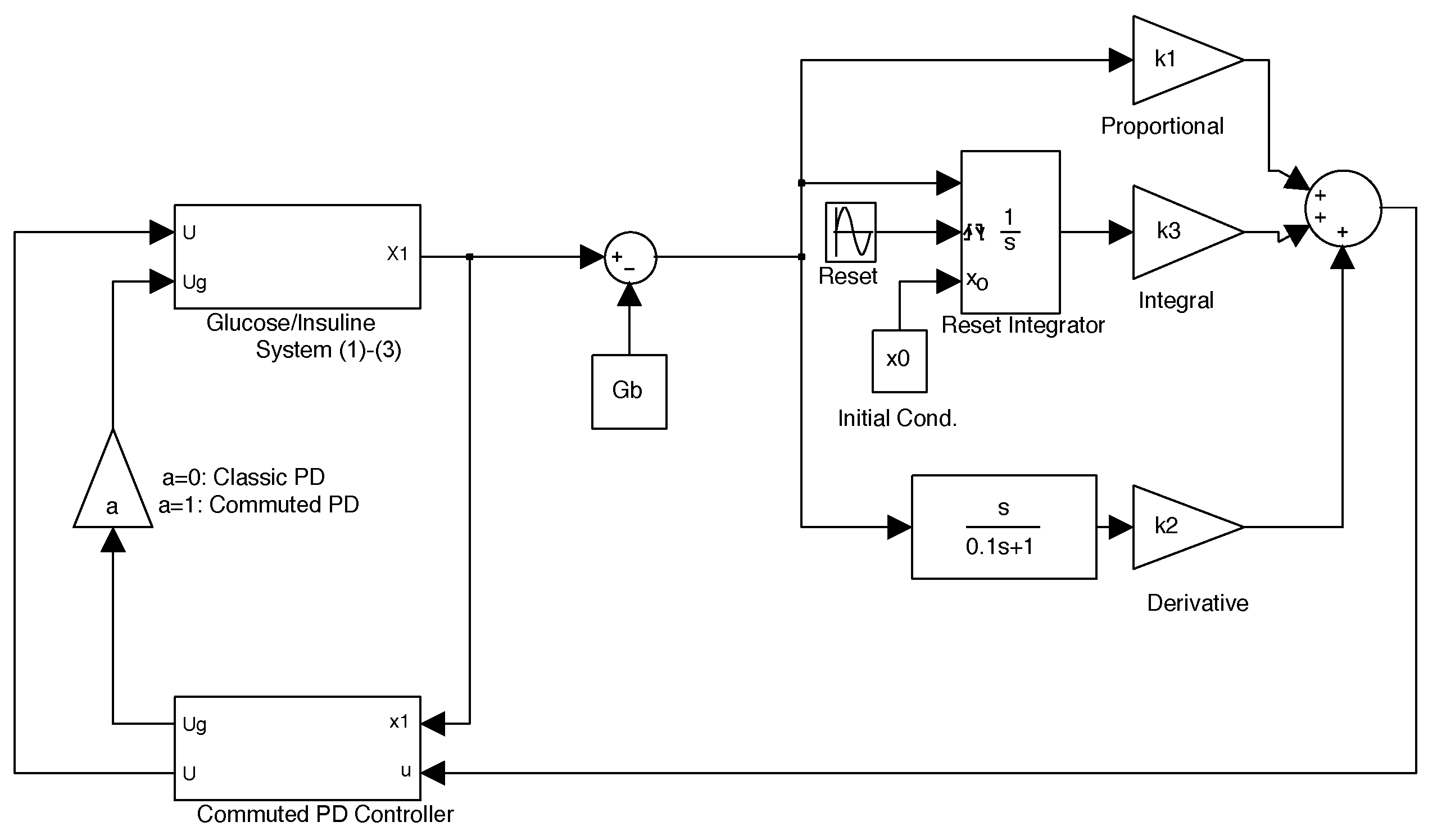
2.3. Commuted PD Control

The control objective is to stabilize the glucose blood concentration around the nominal value G b . First, we deal with the following PD control law:
u P D ( t ) = k 1 x 1 ( t ) − G b + k 2 x ˙ 1 ( t ) ,
where control parameters k 1 and k 2 must be tuned off-line. Once we have determined their nominal values, we have to implement the combined strategy to face hypo- and hyperglycemia states. The purpose is to reduce the time that the patient suffers from these unhealthy states. In this section, we do not consider the integrator term of the classical PID controller. As mentioned in [14], the integral action can be neglected in front of the proportional and derivative ones. But to obtain a more complete study, we deal with PID version in Section 3.4. Also, from simulation experiments, we notice that strong hypoglycemia occurs during a long time period of PID control action.
To mitigate the strong effect of insulin, we propose to administrate a slight dose of glucose. The control action must be present in glucose dynamic (5) and in insulin dynamic () too. To identify when the patient is in a critical situation, we test if the glucose blood concentration x 1 ( t ) is in a healthy range 60-110 mg/dL. In fact, from the literature, this range can be larger, as 50-120 mg/dL [4]. The idea of the switched strategy is as follows:
  • Hyperglycemia: to decrease the glucose blood concentration, an insulin injection is needed, in terms of the PD controller. In system equation (), the control u ( t ) is:
    u ( t ) = u P D ( t ) x 1 ( t ) > x 1 H 0 otherwise .
    This administration has to be always positive. The control designer has to decide when this control is activated, in terms of critical glucose blood concentration value x 1 H .
  • Hypoglycemia: to increment the glucose blood concentration, ingestion is necessary. In system equation (5), the control u g ( t ) is:
    u g ( t ) = − u P D ( t ) x 1 ( t ) < x 1 h 0 otherwise .
    Due to the dynamic of glucose blood concentration (5), the control law tries to increment the velocity of glucose blood absorption. The control designer has to decide when this control is activated, in terms of critical glucose blood concentration value x 1 h .
We will call this control strategy the commuted PD controller. This is because we combine insulin and glucose administration following a switched decision rule. The design parameters x 1 H and x 1 h can be off-line determined to ensure the activation when hypoglycemia occurs (we do not have x 3 ( t ) measurements to obtain an adjusted running of this value). In our case, we set x 1 H = 110 and x 1 h = 60 , to meet the given healthy range.
We now discuss why a combined strategy is desirable. First, a PD controller was considered, but simulations show that the insulin infusion rate is greater than its basal value leading to hypoglycemia during a long period of time of control activation. To improve the controller performance, and if possible to not fall into hypoglycemia, one option is to tune the controller’s parameters. Additionally, we decide to restrict the action of insulin administration only when hyperglycemia is really happening. In this case, with control laws { u = u P D , u g = 0 } , the controlled artificial pancreas will try to minimize the error between the measured glucose blood concentration x 1 ( t ) and the basal concentration G b . Then, when the glucose blood concentration of the patient is in a healthy range, no control action is required { u = 0 , u g = 0 } . To complete this strategy, we consider a control action when hypoglycemia occurs: { u = 0 , u g = − u P D } . This action can be seen as an ingestion or administration of glucose. The minus sign in u g is necessary due to the dynamics of (1).

2.4. Robustness and Stability

Our control objective consists of stabilizing the glucose level around the basal value in finite-time. To study the stability, we consider two switching surfaces: s 1 = { x 1 = x 1 h } and s 2 = { x 1 = x 1 H } . So, the glucose level can be into three possible regions:
S 1 = ( 0 , x 1 h ) , S 0 = ( x 1 h , x 1 H ) , S 2 = ( x 1 H , + ∞ ) ,
verifying that x 1 ( t ) ∈ R = S ¯ 1 ∪ S ¯ 0 ∪ S ¯ 2 . Considering x ( t ) = ( x 1 ( t ) , x 2 ( t ) , x 3 ( t ) ) T , the closed-loop system has the following general representation:
x ˙ ( t ) = f ( t , x ( t ) ) ,
with f ( t , x ( t ) ) as a piecewise continuous function in each S j (11). To simplify the presentation, we omit the dependence on t of x ( t ) . Function f ( t , x ) is then defined as:
f ( t , x ) = f 1 ( t , x ) , x 1 ∈ S 1 f 0 ( t , x ) , x 1 ∈ S 0 f 2 ( t , x ) , x 1 ∈ S 2 ,
where
f 1 ( t , x ) = 1 1 − k 2 − ( p 1 + k 1 ) ( x 1 − G b ) − x 1 x 2 + D ( t ) − p 2 x 2 + p 3 ( x 3 − I b ) − n ( x 3 − I b ) ,
f 0 ( t , x ) = − p 1 ( x 1 − G b ) − x 1 x 2 + D ( t ) − p 2 x 2 + p 3 ( x 3 − I b ) − n ( x 3 − I b ) + γ ( x 1 − σ ) + t ,
f 2 ( t , x ) = − p 1 ( x 1 − G b ) − x 1 x 2 + D ( t ) − p 2 x 2 + p 3 ( x 3 − I b ) − n ( x 3 − I b ) + γ ( x 1 − σ ) + t + ( k 1 − p 1 k 2 ) ( x 1 − G b ) − k 2 x 1 x 2 + k 2 D ( t ) .
According to Filippov’s theory (see [31,32] and [33] to an overview on this subject), a vector solution x ( t ) of (12) is said to exist if it is absolutely continuous on [ 0 , ∞ ) , and for almost all t ∈ [ 0 , ∞ ) , x ˙ belongs to C [ f j , f 0 ] with j = 1 , 2 , the convex closure over all sets of measure zero. Moreover, system (12) is quadratically stable if there exist Lyapunov functions V j ( x ) , j = 1 , 2 , verifying two conditions [32]:
(i)
x ∈ R 3 − { s j } : V j ˙ ( x ) < 0 ,
(ii)
x ∈ { s j } : sup α ∈ [ 0 , 1 ] ∂ V i ∂ x α f 0 ( t , x ) + ( 1 − α ) f j ( t , x ) < 0 .
To ensure stability, the control design parameters k 1 and k 2 have to verify (i) and (ii), obtaining a rule on how to choose these values. Appendix A presents stability’s proof details.
The control algorithm to establish a healthy behavior in our pancreatic system can be summarized as follows:
Step 1: Determine parameters x 1 H > 0 and x 1 h > 0 , necessary to active controllers u g ( t ) or u ( t ) .
Step 2: Set the control parameters k 1 > 0 and k 2 > 0 of control u P D ( t ) (8), satisfying the stability conditions.
Step 3: Measure x 1 ( t ) every sample time; and define u ( t ) in () and u g ( t ) in (5) as:
x 1 ( t ) ∈ [ x 1 h , x 1 H ] ⇒ u ( t ) = 0 u g ( t ) = 0 x 1 ( t ) < x 1 h ⇒ u ( t ) = 0 u g ( t ) = − u P D ( t ) x 1 ( t ) > x 1 H ⇒ u ( t ) = u P D ( t ) u g ( t ) = 0

3. Results

Simulation experiments of our controlled pancreatic model are carried out here, and for different patients shown in Table 1 [6] (the value * in Patient 3 denotes a modified value to obtain a notable hyperglycemia case). The total simulation time is over 800 minutes, and the sample time is set to 2s. The control parameter values are stated as k 1 = 0.09 and k 2 = 0.04 [12]. Note that these values verify the stability conditions, as shown in Appendix A. In [30], algorithms to tune PD control parameters are presented. Our purpose is to test the switched strategy, not to find the best PD control parameters.
To test the effectiveness of our switched control strategy, different scenarios are considered: commuted controller (9)-(10) is compared to the uncontrolled situation, and to system (1)-() with the classic PD controller u ( t ) = u c ( t ) defined in [12] and [14]:
x ˙ 1 ( t ) = − p 1 ( x 1 ( t ) − G b ) − x 1 ( t ) · x 2 ( t ) + D ( t ) ,
x ˙ 2 ( t ) = − p 2 x 2 ( t ) + p 3 ( x 3 ( t ) − I b ) ,
x ˙ 3 ( t ) = − n ( x 3 ( t ) − I b ) + γ [ x 1 ( t ) − σ ] + t + u c ( t ) ,
where the control is defined by:
u c ( t ) = k 1 ( x 1 ( t ) − G b ) + k 2 x ˙ 1 ( t ) .
Also, decaying and additive disturbance are considered, all to each patient in Table 1 [6]. Figure 2, Figure 3, Figure 4, Figure 5, Figure 6, Figure 7, Figure 8 and Figure 9 present different scenarios that reinforce our proposal (each one in a different subsection):
  • Decaying exponential disturbance D ( t ) (4): open-loop and closed-loop with commuted PD controller (Figure 2, Figure 3 and Figure 4).
  • Additive disturbance (Figure 5 and Figure 6).
  • Change on the dynamic equation (5), proving the efficiency of our control algorithm against slight modification on glucose assimilation (Figure 7).
  • Finally, a reset-PID controller is implemented, showing that despite the rise time being reduced, the control law presents chattering, a non-desired effect for a pancreatic system (Figure 8 and Figure 9).
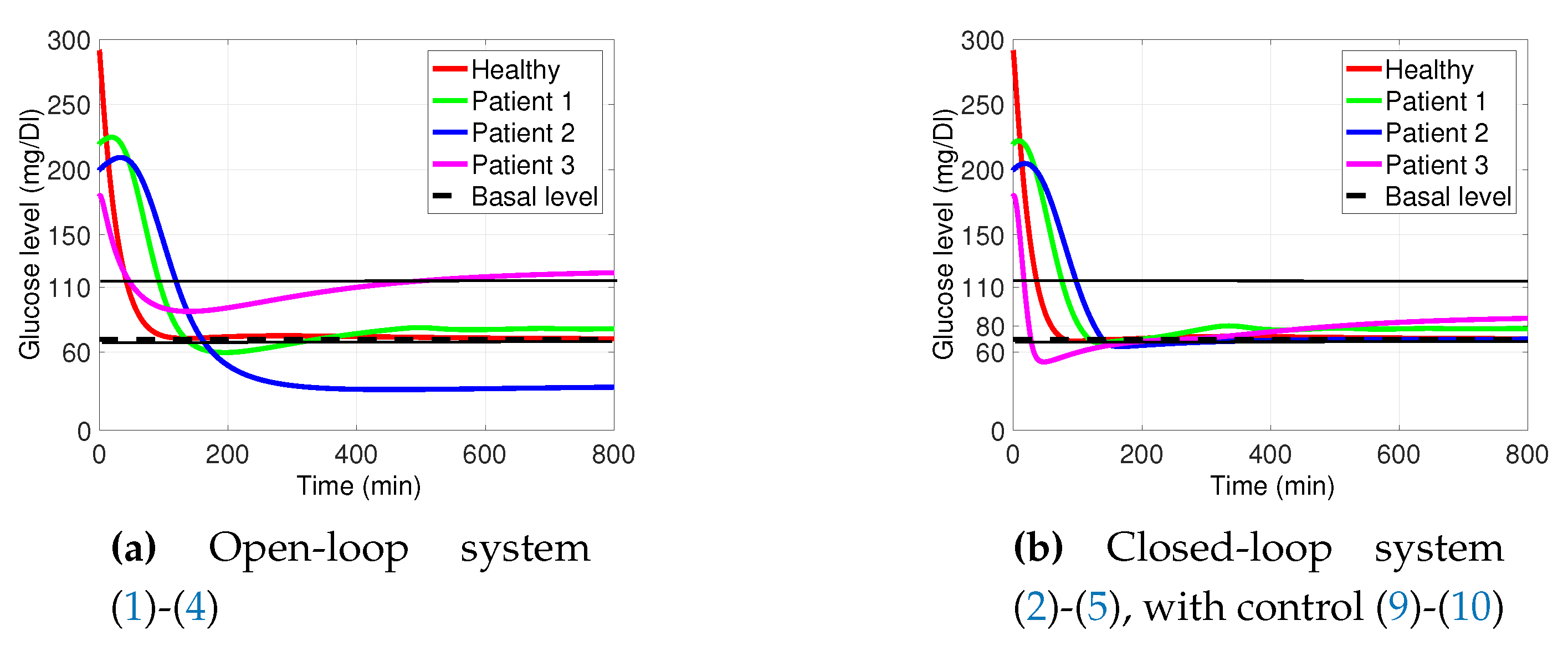
Preprints 77012 g002
Figure 2. From (a), we notice that Patient 2 presents strong hypoglycemia (reaching 30 mg/dl), and Patient 3 hyperglycemia (reaching 120 mg/dl). From closed-loop system (b), only Patient 3 presents hypoglycemia for one hour approximately, reaching the lowest glucose level 52mg/dl (considered healthy in [4]).
Figure 2. From (a), we notice that Patient 2 presents strong hypoglycemia (reaching 30 mg/dl), and Patient 3 hyperglycemia (reaching 120 mg/dl). From closed-loop system (b), only Patient 3 presents hypoglycemia for one hour approximately, reaching the lowest glucose level 52mg/dl (considered healthy in [4]).
Preprints 77012 g002
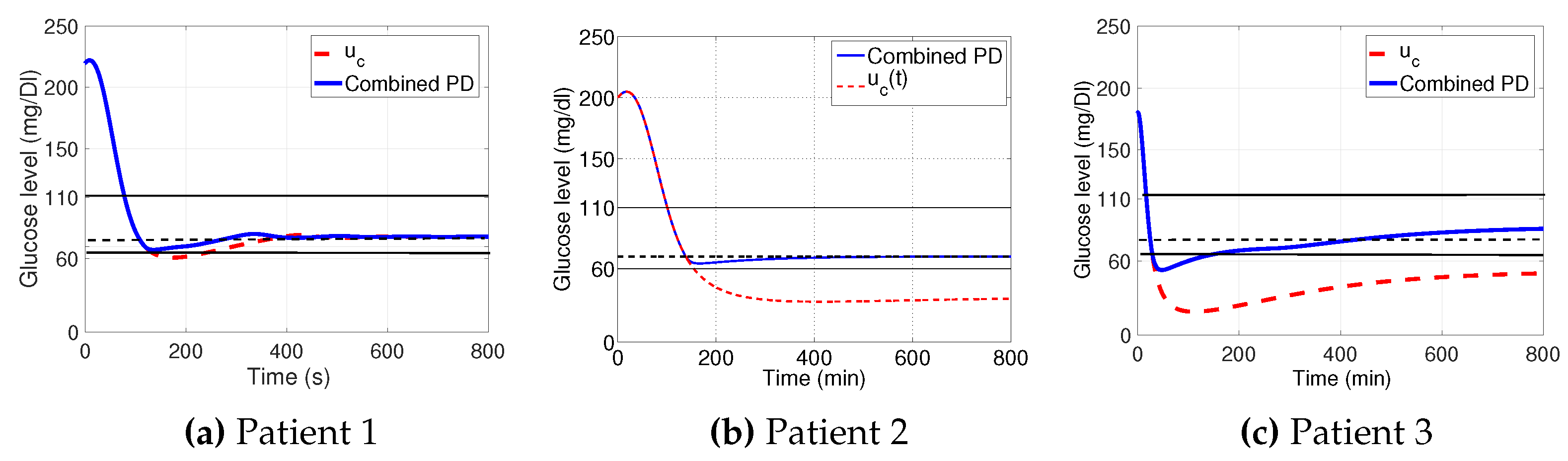
Preprints 77012 g003
Figure 3. Closed-loop simulations. Classic model (16)-() with u c ( t ) (19) from [12], is compared to proposed system ()-(5) with commuted PD controller (9)-(10). It shows how under the commuted PD controller (9)-(10) the glucose blood concentration is stabilized at G b .
Figure 3. Closed-loop simulations. Classic model (16)-() with u c ( t ) (19) from [12], is compared to proposed system ()-(5) with commuted PD controller (9)-(10). It shows how under the commuted PD controller (9)-(10) the glucose blood concentration is stabilized at G b .
Preprints 77012 g003
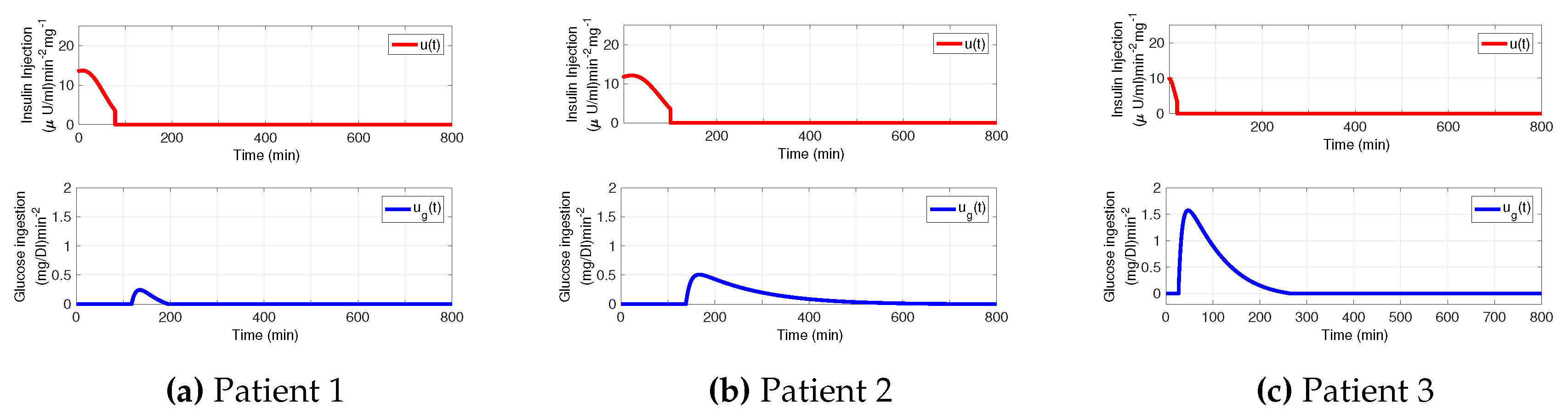
Preprints 77012 g004
Figure 4. Control input u ( t ) (9) and u g ( t ) (10), with D ( t ) defined in (4), for each Patient under study. To prevent hypoglycemia, after a few minutes of the end of its injection, glucose ingestion is needed.
Figure 4. Control input u ( t ) (9) and u g ( t ) (10), with D ( t ) defined in (4), for each Patient under study. To prevent hypoglycemia, after a few minutes of the end of its injection, glucose ingestion is needed.
Preprints 77012 g004
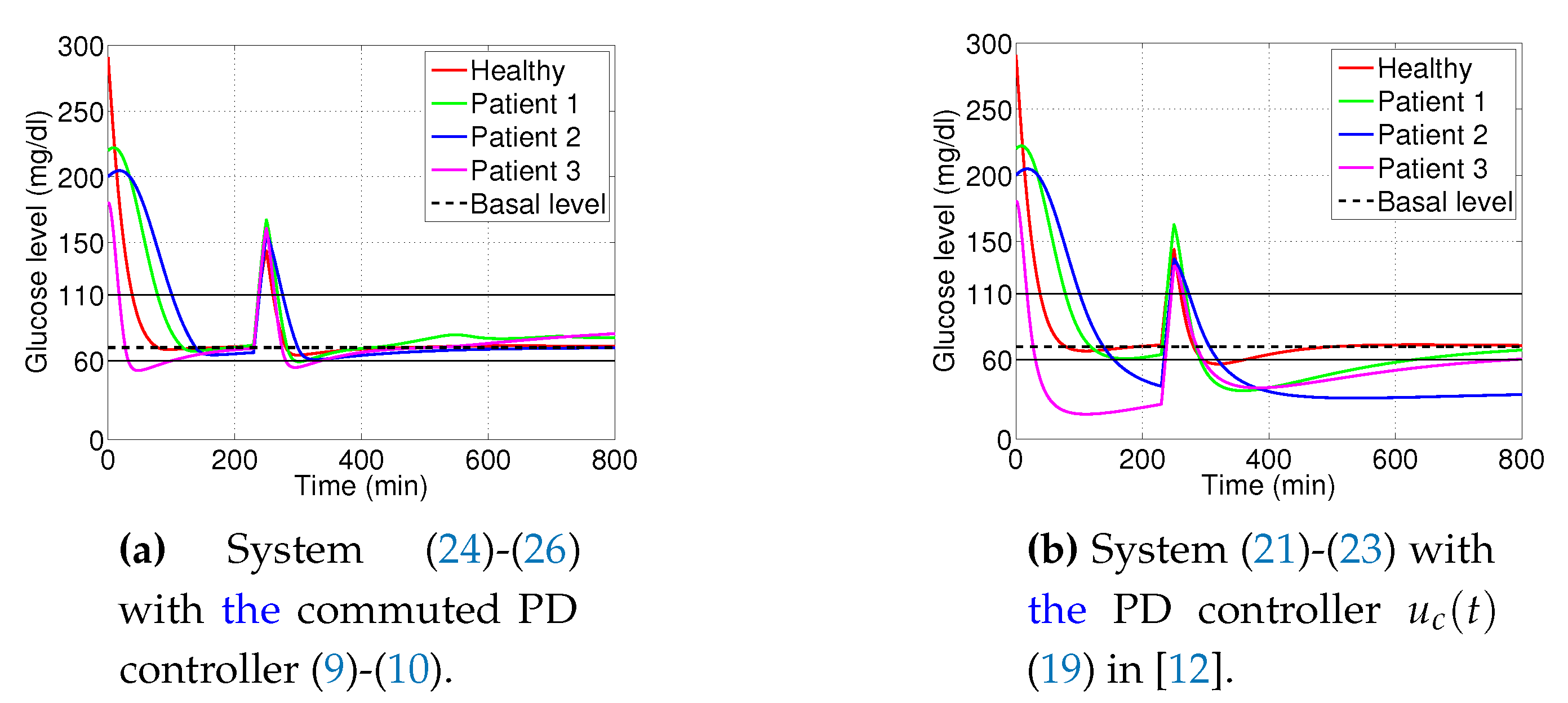
Preprints 77012 g005
Figure 5. Simulations of closed-loop system with external perturbation (20). The proposed control strategy performs better than PD control u c ( t ) [12], noticing that glucose ingestion is needed to prevent hypoglycemia episodes.
Figure 5. Simulations of closed-loop system with external perturbation (20). The proposed control strategy performs better than PD control u c ( t ) [12], noticing that glucose ingestion is needed to prevent hypoglycemia episodes.
Preprints 77012 g005
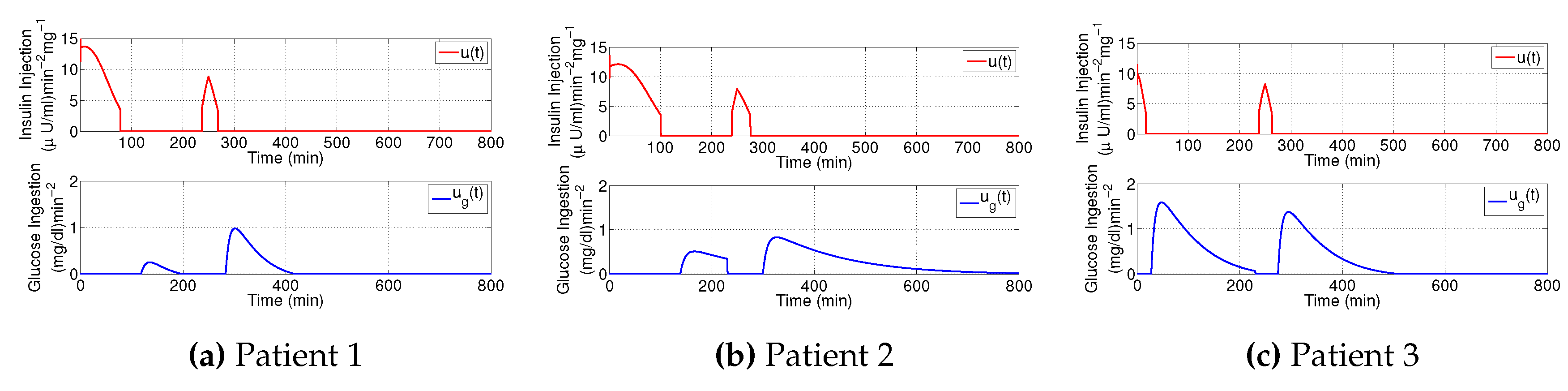
Preprints 77012 g006
Figure 6. Commuted PD controller (9)-(10), under external perturbation (20). Notice that the glucose ingestion suggested is small compared with the glucose blood concentration.
Figure 6. Commuted PD controller (9)-(10), under external perturbation (20). Notice that the glucose ingestion suggested is small compared with the glucose blood concentration.
Preprints 77012 g006
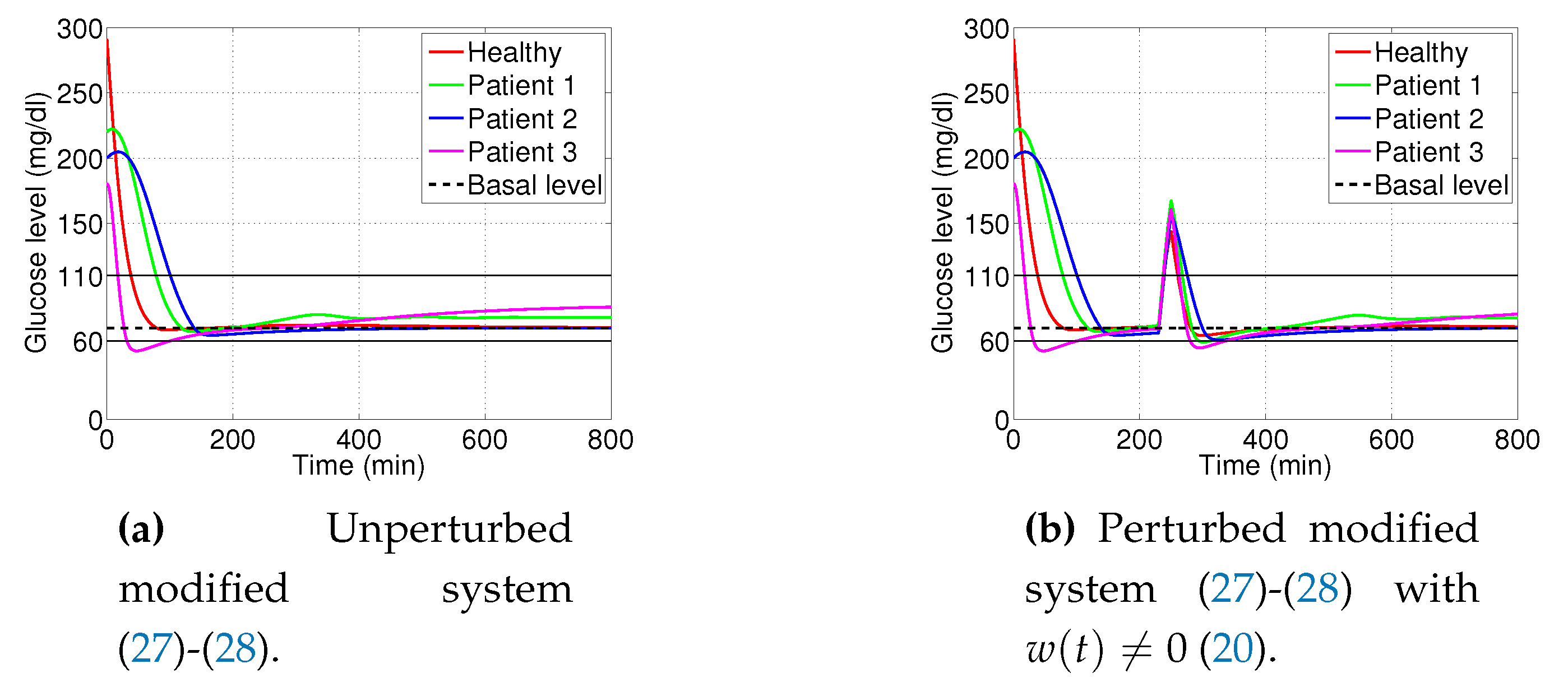
Preprints 77012 g007
Figure 7. Simulations of closed-loop system with commuted PD controller (9)-(10) when dynamical changes on the glucose assimilation are considered (27)-(). Two comparative situations: (a) with w ( t ) = 0 and (b) under external perturbation (20). The behavior is similar to commuted model (5), as Figure 2 and Figure 5 show.
Figure 7. Simulations of closed-loop system with commuted PD controller (9)-(10) when dynamical changes on the glucose assimilation are considered (27)-(). Two comparative situations: (a) with w ( t ) = 0 and (b) under external perturbation (20). The behavior is similar to commuted model (5), as Figure 2 and Figure 5 show.
Preprints 77012 g007
Preprints 77012 g008
Figure 8. Matlab Simulink diagram block model used to study the behavior of the proposed control strategy to our pancreatic plant, considering reset integrator (29). When k 3 = 0 , we obtain the commuted PD controller (9)-(10). As a resetting signal, we use a sinusoidal function r ( t ) = sin ( t ) , and zero initial condition.
Figure 8. Matlab Simulink diagram block model used to study the behavior of the proposed control strategy to our pancreatic plant, considering reset integrator (29). When k 3 = 0 , we obtain the commuted PD controller (9)-(10). As a resetting signal, we use a sinusoidal function r ( t ) = sin ( t ) , and zero initial condition.
Preprints 77012 g008
Preprints 77012 g009
Figure 9. Simulations of closed-loop system with external perturbation (20), using PID with reset integrator (29). The rise time is reduced in 10 minutes approximately compared to Figure 5, but the control laws present chattering.
Figure 9. Simulations of closed-loop system with external perturbation (20), using PID with reset integrator (29). The rise time is reduced in 10 minutes approximately compared to Figure 5, but the control laws present chattering.
Preprints 77012 g009
Each figure of glucose blood concentration displays the healthy range 60-110 [10] to measure the duration of hypo- and hyperglycemia episodes. For each patient, we compute the glucose and insulin blood concentration x 1 ( t ) and x 3 ( t ) respectively, and the control action u ( t ) and u g ( t ) (verifying in this case that they are both positive). The simulation results of patients are obtained using the data in Table 1, with D ( t ) = 0.5 e − 0.005 t [7]. Note that in [6], D ( t ) = 0 is used. We decided to use a different value of it to be more realistic taking the exogenous factor into account. Also, the pump dynamics have been ignored (for a justification, see [6]).

3.1. Decaying Exponential Disturbance Simulations

Figure 2 pictures the open-loop system response (1)-(4) with u ( t ) = 0 . Figure 2 presents the signal output of the closed-loop system ()-(5) with the commuted PD control (9)-(10) showing the effectiveness of the proposed commuted PD controller. Also, a comparison is presented in Figure 3, where the behavior of classic PD control [12] does not perform better than the proposed control strategy. Furthermore, the commuted PD controller stabilizes the glucose blood concentration at the basal value G b in the three cases. As Figure 3 shows, no hypoglycemia is attained when commuted PD control (9)-(10) is chosen. That is not the case when u g ( t ) (10) is not considered, as u c ( t ) behavior shows. In Figure 3, considering commuted controller, in just a few minutes, hypoglycemia occurs. Then, the glucose blood concentration is normalized, but the basal glucose concentration is not reached.
Analysing Figure 4, we see how commuted PD controller works. We comment on the Patient 1 case. During the first minutes after meal ingestion, when D ( t ) is biggest, the system needs insulin injection to reduce the glucose concentration (graphic of u ( t ) in Figure 4). To normalize its level, glucose ingestion is needed an hour after (graphic of u g ( t ) in Figure 4). This is a common situation difficult to deal with. This due to the insulin administration could be too strong for a pancreatic system. To mitigate this effect, we suggest ingesting some controlled quantity of glucose. This is done by u g ( t ) (10) action. The same can be seen for Patients 2 and 3 given in Figure 4 and Figure 4, respectively.

3.2. External Noise Perturbation

We consider now an intake meal after 230 minutes after the controller is activated. It corresponds to the case of additive perturbation on (1) or (5), and defined as:
w ( t ) = 5 H ( t − 230 ) − H ( t − 250 ) + A e − B ( t − 230 ) H ( t − 230 ) ,
where the function H ( t − a ) is the well-known Heaviside expression:
H ( t − a ) = 0 t < a 1 t ≥ a .
Due to the additional glucose ingestion, an additional rate of glucose absorption has to be considered (exponential function in (20)). Hence, the classic mathematical model of the pancreatic system is given by [12]:
x ˙ 1 ( t ) = − p 1 ( x 1 ( t ) − G b ) − x 1 ( t ) · x 2 ( t ) + D ( t ) + w ( t ) ,
x ˙ 2 ( t ) = − p 2 x 2 ( t ) + p 3 ( x 3 ( t ) − I b ) ,
x ˙ 3 ( t ) = − n ( x 3 ( t ) − I b ) + γ [ x 1 ( t ) − σ ] + t + u c ( t ) .
Which modified to our controlled system, results:
x ˙ 1 ( t ) = − p 1 ( x 1 ( t ) − G b ) − x 1 ( t ) · x 2 ( t ) + D ( t ) + u g ( t ) + w ( t ) ,
x ˙ 2 ( t ) = − p 2 x 2 ( t ) + p 3 ( x 3 ( t ) − I b ) ,
x ˙ 3 ( t ) = − n ( x 3 ( t ) − I b ) + γ [ x 1 ( t ) − σ ] + t + u ( t ) ,
with u ( t ) defined in (9) and u g ( t ) in (10).
Figure 5Figure 6 present the simulations of Patients 1, 2, and 3 under the commuted PD controller action. In these cases, the commuted PD controller has a good performance, because no hypoglycemia range is attained. Hyperglycemia is attained only during ingestion, as expected.

3.3. Changes on Glucose Assimilation

Consider a more general case to system in (5), where the dynamic of x 1 ( t ) is modified using an auxiliary variable x a ( t ) with an stable dynamic (27)-():
x ˙ 1 ( t ) = − p 1 ( x 1 ( t ) − G b ) − x 1 ( t ) · x 2 ( t ) + D ( t ) + x a ( t ) ,
x ˙ a ( t ) = − α x a ( t ) − u g ( t ) .
We set α = 2 . Figure 7 presents the simulations, where it can be noticed that its behavior is similar to (5). So, we can conclude that our control algorithm is robust against to changes in patient dynamics for glucose assimilation.

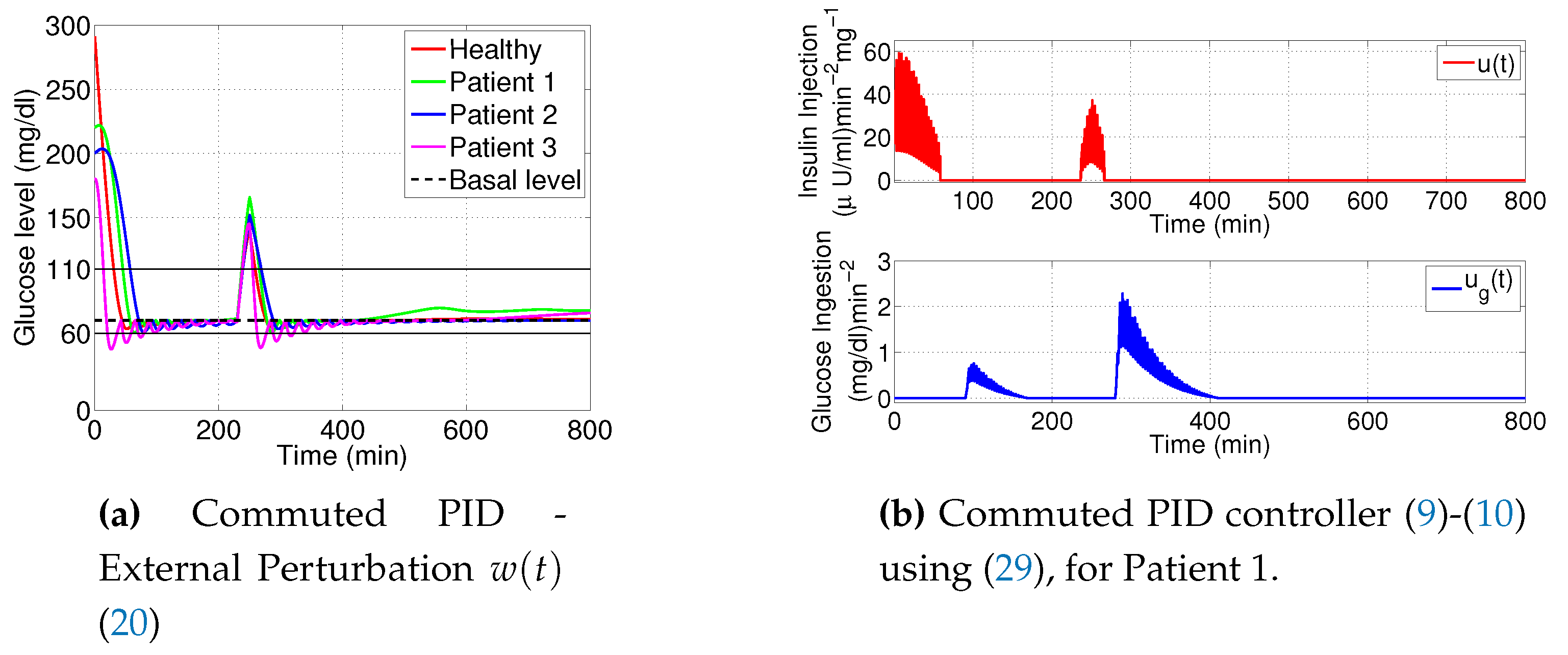
3.4. PID Using Reset Integrator

As was mentioned in the introduction, we noticed from simulations that strong hypoglycemia occurs during a long period of time when the integral part in the PD controller is considered. In order to complete the study of the proposed switched strategy, we consider now a reset integral part. Hence, defining a commuted PID controller as:
u P I D ( t ) = k 1 x 1 ( t ) − G b + k 2 x ˙ 1 ( t ) + k 3 ∫ 0 t x 1 ( τ ) − G b d τ .
The limitations of the linear integrator can be faced using a reset integrator, also named as Clegg integrator [26]. This integrator resets its output to zero whenever its input and output have different signs [27,28]. Due to this resetting condition, the transient response of the controller can be arranged. Figure 8 captures the Matlab Simulink model used to compute the numerical simulation experiments. Based on Clegg integrator [26], we define a reset integrator block by taking into account that we need to integrate the error and to vanishing it. Then, from Figure 8, we set:
  • Clegg integrator Input. The error between glucose blood concentration x 1 ( t ) and the nominal value G b .
  • Clegg integrator Initial condition. After each reset to the Clegg integrator, an initial condition is needed to integrate at each resetting action. We use the zero initial condition setting.
  • Clegg integrator Resetting actions. The block can reset its state to the specified initial condition based on an external signal. We choose to reset the integrator when the sinus function changes its sign.
  • Clegg integrator gain. The parameter k 3 = 0.1 was found by the trial and error method.
Figure 9 shows the behavior of the commuted PID controller (29), where the rise time is reduced to 10 minutes approximately. But the controller presents chattering in all cases (we picture Patient 1 in Figure 9 as an example), and the insulin injection is increased.

4. Discussion of Results

This paper proposes a new strategy to control the glucose blood concentration in a pancreatic system, and with the control objective to reduce the error between this concentration with respect to the basal one. As it is well-known, the main idea is to administrate insulin to prevent hyperglycemia. But this insulin dose could be too strong, falling into the hypoglycemia region. To mitigate this effect, we suggest ingesting some controlled quantity of glucose. The method used to define the controllers is the Proportional-Derivative one, which is able to stabilize the glucose concentration around its basal value. The key feature is to avoid an unhealthy glucose concentration range, combining insulin injection with glucose administration. Then, two control actions are defined: one to modify the insulin dynamic (and prevent hyperglycemia), and the other one to to improve the perform the glucose dynamic (and prevent hypoglycemia).
The simulations test the closed-loop performance on four different human behaviors. Moreover, external perturbations are considered, as meal ingestion. The results are comparable or improved with respect to other works. The purpose of this work is to study the behavior of this novel strategy, and opens the possibility of testing this switched strategy on another type of controller.
Finally, two complementary studies are presented. One is based on modifying the glucose absorption dynamic, to test the robustness of the commuted PD controller. The other study was to include an integral part to our controller approach, defining a PID with a resetting integrator action, showing that despite the rise-time of closed-loop dynamics is reduced, chattering on the controller appears inevitably.

Appendix A

In this appendix, we check the stability conditions established in Section 2.4 without external disturbances, that is, considering D ( t ) = 0 . We apply Filippov’s theory [31]-[33], where a vector solution x ( t ) in (12) is said to exist if it is absolutely continuous on [ 0 , ∞ ) , and for almost all t ∈ [ 0 , ∞ ) , if x ˙ belongs to the convex closure over all sets of measure zero. Moreover, system (12) is quadratically stable if there exist Lyapunov functions V j ( x ) , j = 1 , 2 , verifying two conditions [32]:
(i)
x ∈ R 3 − { s j } : V j ˙ ( x ) < 0 ,
(ii)
x ∈ { s j } : sup α ∈ [ 0 , 1 ] ∂ V i ∂ x α f 0 ( t , x ) + ( 1 − α ) f j ( t , x ) < 0 .
First, we linearize nonlinear system (12) around the equilibrium point ( G b , 0 , I b ) :
f ¯ 1 = − p 1 − k 1 1 − k 2 − G b 0 0 − p 2 p 3 0 0 − n
f ¯ 0 = − p 1 − G b 0 0 − p 2 p 3 0 0 − n
f ¯ 2 = − p 1 − G b 0 0 − p 2 p 3 k 1 − p 1 k 2 − k 2 G b − n
The existence of Lyapunov function of Condition (i) from Filippov’s theory is ensured by the negativeness of the eigenvalues of the matrices (30)-(32) from the linearilized model. Hence, from the triangular expression of (31) the negativeness is obvious. The eigenvalues of (30) have negative real part if − p 1 − k 1 1 − k 2 < 0 , where p 1 > 0 . So, that’s define a condition on PD-control parameters:
− p 1 − k 1 1 − k 2 < 0 ⇒ p 1 + k 1 1 − k 2 > 0 ⇒ k 2 < 1 .
Under assumption k 2 < 1 , the stability of (32) is verified, and the existence of Lyapunov function V j ( x ) is guaranteed if k 1 < n · p 2 G b · p 3 . From the experimental data on Table 1, we obtain k 1 < 0.301 . Condition (ii) ensures the stability where x 1 takes its critical value.

References

  1. M. Nwokolo, R. Hovorka, The Artificial Pancreas and Type 1 Diabetes, The Journal of Clinical Endocrinology and Metabolism (2023). [CrossRef]
  2. E. R. Carson, T. Deutsch, A Spectrum of approaches for controlling diabetes, IEEE Control System Magazine, 12(12) (1992) 25-31. [CrossRef]
  3. C. Cobelli, C. D. Man, G. Sparacino, L. Magni, G. De Nicolao, B. P. Kovatchev, Diabetes: Models, Signals, and Control, IEEE Rev. in Biomedical Eng., 2 (2009) 54-96. [CrossRef]
  4. P. Dua, F. J. Doyle-III, E. N. Pistikopoulos, Model-based glucose control for Type-1 diabetes via parametric programming, IEEE Trans. on Biomedical Eng., 53(8)(2006) 1478-1491. [CrossRef]
  5. F. Chee, A V. Savkin, T. L. Fernando, S. Nahavandi, Optimal H∞ insulin injection control for blood glucose regulation in diabetic patients, IEEE Trans. on Biomedical Eng., 52(10)(2005) 1625-1631. [CrossRef]
  6. P. Kaveh, Y. B. Shtessel, Blood glucose regulation using higher-order sliding mode control, Int. J. of Robust and Nonlinear Control, 18 (2008) 557-569. [CrossRef]
  7. P. Kaveh, Y. B. Shtessel, Blood Glucose Regulation in Diabetics Using Sliding Mode Control Techniques, Proc. of the 38th Southeastern Symposium on System Theory Tennessee Technological University Cookeville, TN, USA, (2006), 5-7. [CrossRef]
  8. B. S. Leon, A. Y. Alanis, E. N. Sanchez, F. Ornelas-Tellez, E. Ruiz-Velazquez, Inverse optimal neural control of blood glucose level for type 1 diabetes mellitus patients, J. of the Franklin Institute, 349 (2012) 1851-1870. [CrossRef]
  9. Anas El Fathi; Mohamed Raef Smaoui; Veronique Gingras; Benoit Boulet; Ahmad Haidar, The Artificial Pancreas and Meal Control: An Overview of Postprandial Glucose Regulation in Type 1 Diabetes, IEEE Control Systems, 38(1) ( 2018), 67 - 85. [CrossRef]
  10. A. Makroglou, J. Li, Y. Kuang, Mathematical models and software tools for the glucose-insulin regulatory system and diabetes: an overview, Applied Numerical Mathematics, 56 (2006) 559-573. [CrossRef]
  11. N. Hernjak, F. J. Doyle-III, Glucose control design using nonlinearity assessment techniques, AIChE Journal, 51(2) (2005) 544-554. [CrossRef]
  12. C. Li, R. Hu, Simulation study on blood glucose control in diabetics, Int. Conf. on Bioinformatics and Biomedical Engineering, (2007). [CrossRef]
  13. S. Amuthameena, A novel strategy for blood glucose control in human body using PID-Fuzzy logic controller, Journal of Chemical and Pharmaceutical Sciences, 8 (2016) 88-92.
  14. G. Marchetti, M. Barolo, L. Jovanovic, H. Zisser, D.E. Seborg, An improved PID switching control strategy for Type 1 Diabetes, IEEE Trans. on Biomedical Engineering, 55(3) (2008) 857-865. [CrossRef]
  15. J. D. Hoyos, F. Bolanos, M. Vallejo, and P. S. Rivadeneira, ”Population-based incremental learning algorithm for identification of blood glucose dynamics model for type-1 diabetic patients, in Proceedings of the International Conference on Artificial Intelligence,(2018), 29-35.
  16. Maria, F. Villa Tamayo, Michelle A. Caicedo Alvarez, and Pablo S. Rivadeneira, Handling Parameter Variations during the Treatment of Type 1 Diabetes Mellitus: In Silico Results, Mathematical Problems in Engineering, vol. 2019, Article ID 2640405, (2019), 1- 21. [CrossRef]
  17. Ndakara, A.I., Essabbar, M., Saikouk, H. Blood Glucose-Insulin Dynamics in Type-1 Diabetic Patients for the Mitigation of Hyperglycemic Conditions: A PID Controller with a Step Response. In: Motahhir, S., Bossoufi, B. (eds) Digital Technologies and Applications. ICDTA 2023. Lecture Notes in Networks and Systems, vol 668 (2023). Springer, Cham. [CrossRef]
  18. S. Syafiie, F. AlHarbi, A. Ali Alshehri, B. Hasanain, PID and LQG controllers for diabetes system with internal delay: a comparison study, Biomed. Phys. Eng. Express 9 (2023), 035031. [CrossRef]
  19. A. De Gaetano, O. Arino, Mathematical modelling of the intravenous glucose tolerance test, J. of Mathematical Biology, 40 (2000), 136-168. [CrossRef]
  20. M. E. Fisher, A semiclosed-loop algorithm for the control of blood glucose levels in diabetics, IEEE Trans. on Biomedical Eng., 38 (1) (1991), 57-61. [CrossRef]
  21. Patricio, H. Colmegna; Ricardo S. Sanchez-Pena; Ravi Gondhalekar; Eyal Dassau; Frank J. Doyle, Switched LPV Glucose Control in Type 1 Diabetes, IEEE Transactions on Biomedical Engineering 63(6) (2016), 1192 - 1200. [CrossRef]
  22. Y. Batmani, Blood glucose concentration control for type 1 diabetic patients: a non-linear suboptimal approach, IET Systems Biology, 11(4) (2017), 119 - 125. [CrossRef]
  23. M. Messori, G.P. Incremona, C. Cobelli, L. Magni, Individualised model predictive control for the artificial pancreas: In silico evaluation of closed-loop glucose control, IEEE Control Systems, 38(1) (2018), 86 - 104. [CrossRef]
  24. N. Ankit Sharma, H.P. Singh, Computer-controlled diabetes disease diagnosis technique based on fuzzy inference structure for insulin-dependent patients. Appl Intell 53 (2023), 1945?1958. [CrossRef]
  25. H.Emerson, M. Guy, R. McConville, Offline reinforcement learning for safer blood glucose control in people with type 1 diabetes, Journal of Biomedical Informatics (2023), 104376. [CrossRef]
  26. J.C. Clegg, A nonlinear integrator for servomechanism, Trans. A.I.E.E., 77(II) (1958) 41-42. [CrossRef]
  27. D. Nesic, L. D. Nesic, L. Zaccarian, A.R. Teel, Stability properties of reset systems, 16th Triennial World Congress, IFAC 2005, 67-72. [CrossRef]
  28. A. Banos, A. A. Banos, A. Barreiro, Reset control systems, (2011) Springer Sciences and Business Media. [CrossRef]
  29. P. Palumbo, S. Ditlevsen, A. Bertuzzi, A. De Gaetano, Mathematical modeling of glucose-insulin system: A review, Mathematical Bioscience, 244(2) (2013), 69-81. [CrossRef]
  30. K.H. Ang, G. K.H. Ang, G. Chong, Y. Li, PID control system analysis, design, and technology, IEEE Trans. on Control Systems Technology, 13(4), (2005) 559-576. [CrossRef]
  31. Filippov, AF. Differential Equations with Discontinuous Right-hand Sides. Kluwer Academic: Boston, 1988. [CrossRef]
  32. H. Frankowska, Filippov’s and Filippov-Wazewski’s theorems on closed domains, Journal of Differential Equations, 161 (2000) 449-478. [CrossRef]
  33. L. Dieci, L. L. Dieci, L. Lopez, Sliding motion in Filippov differential systems: Theoretical results and a computational approach, SIAM Journal on Numerical Analysis, 47(3) (2009), 2023-2051.
  34. F. León-Vargas, F. Garelli, H. De Battista, J. Vehí, Postprandial response improvement via safety layer in closed-loop blood glucose controllers, Biomedical Signal Processing and Control, 16 (2015), 80-87, 2015. [CrossRef]
  35. P. Rossetti, C. Quirós, V. Moscardó, A. Comas, M. Giménez, F. J. Ampudia-Blasco, F. León, E. Montaser, I. Conget, J. Bondia, J. Vehí, Closed-Loop Control of Postprandial Glycemia Using an Insulin-on-Board Limitation Through Continuous Action on Glucose Target, Diabetes Technology and Therapeutics, 19(6) (2017). [CrossRef]
  36. D. Boiroux, A. K. Duun-Henriksen, S. Schmidt, K. Norgaard, N. Kjolstad Poulsen, H. Madsen, J. Bagterp Jorgensen, Adaptive control in an artificial pancreas for people with type 1 diabetes, Control Engineering Practice 58 (2017) 332-342. [CrossRef]
Preprints 77012 g001
Figure 1. Block diagram of the closed-loop controlled system of insulin-dependent diabetic patients.
Figure 1. Block diagram of the closed-loop controlled system of insulin-dependent diabetic patients.
Preprints 77012 g001
Table 1. Parameter values [6]. The value * in Patient 3 denotes a modified value to obtain a notable hyperglycemia case.
Table 1. Parameter values [6]. The value * in Patient 3 denotes a modified value to obtain a notable hyperglycemia case.
Healthy Patient 1 Patient 2 Patient 3
p 1 0.0317 0 0 0
p 2 0.0123 0.02 0.0072 0.0142
p 3 4.92 × 10 − 6 5.3 × 10 − 6 2.16 × 10 − 6 9.94 × 10 − 5
γ 0.0039 0.005 0.0038 0.0 *
n 0.2659 0.3 0.2465 0.2814
σ 79.0353 78 77.5783 82.9370
G b 70 70 70 70
I b 7 7 7 7
x 1 ( 0 ) 291.2 220 200 180
x 2 ( 0 ) 0 0 0 0
x 3 ( 0 ) 364.8 50 55 60
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.
Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.
Prerpints.org logo

Preprints.org is a free preprint server supported by MDPI in Basel, Switzerland.

facebook logotwitter logolinkedin logo
MDPI Initiatives
Important Links
Subscribe

Disclaimer

Terms of Use

Privacy Policy

© 2024 MDPI (Basel, Switzerland) unless otherwise stated