In response to the structural optimization problem of PCB stator coreless disc motors, the orthogonal response surface method was used to optimize the motor structure, determine the basic parameters of the motor preliminarily, and conduct orthogonal experiments on the motor parameters based on the optimization design objectives, The optimization factors were the quantity of magnetic pole of the motor rotor, the ratio of main/auxiliary pole size, the thicknessof the permanent magnet, and the air gap length.The motor torque，the amplitude of magnetic density of the air gap and waveform distortion rateare used as optimization objectives. The motor parameters that make the motor torque reach the maximum, the air gap magnetic density maximum, and the waveform distortion rate minimum. Due to the use of PCB plates instead of motor stator cores in PCB coreless disc motors,The service life of the PCB board during motor operation will be reduced with the temperature rise generated by the stator winding To solve this problem, the response surface analysis of the motor is carried out to reduce the temperature rise of the stator windings during the operation of the motor. PCB board and stator winding are the main factors affecting the temperature rise of the motor.Taking the thickness of the PCB board, the hole diameter on the board, and the uneven width of the stator winding as optimization factors, the motor parameters with the lowest temperature rise of the motor winding are obtained. Simulation analysis is conducted using Ansys/Maxwell software, and the results prove the feasibility of optimization.

Keywords:

Subject: Engineering - Electrical and Electronic Engineering

1. Introduction

High efficiency, high reliability and high power density are the advantages of permanent magnet motors, and has always been the research focus of scholars at home and abroad, especially in the application of motors[1,2,3]. However, for some thin installation scenarios such as electric motors, aerospace vehicles, electric vehicle wheels, and satellite reaction flywheel systems, it is required that the motor must be as thin as possible. This article is based on PCB winding stator coreless disc permanent magnet motor. which is also known as an axial flux motor. This is because the magnetic field of the motor is axial and the motor structure is compact, making the motor thinner and smaller, meeting the requirements of thin installation occasions[4,5,6].

For stator coreless disc motors with PCB windings, they have attracted much attention due to its short axial size and high power density, strong overload capacity, and no cogging torque[7,8]. For stator coreless disc motors, the optimization of the motor is mainly aimed at improving the efficiency of the motor. However, due to the mutual correlation and constraints between the various performance of the motor, an improvement in one performance may lead to a decrease in other performance of the motor[9,10]. With the development of computer technology, scholars at home and abroad have put forward a series of multi-objective optimization design methods for motor: A high-speed BPMSM was designed in reference[11], a multi physical field model was established, and the optimal motor design scheme was obtained based on the decomposed multi-objective evolutionary algorithm; In literature[12], Taguchi method was used to optimize the initial parameters of permanent magnet motor, and orthogonal test was used to improve the output torque characteristics of the motor; Reference[13] used multi-objective genetic algorithm to optimize the saliency rate variable permanent magnet motor, the output torque of the motor is increased, the speed range is extended, and the risk of irreversible demagnetization is reduced; Reference[14] applied particle swarm optimization algorithm to multi-objective optimization design of magnetic steel parameters in permanent magnet synchronous motors, which can reduce the distortion rate of air gap magnetic density waveform.

At present, there are few researches on the multi-objective optimization design of PCB stator disc permanent magnet motor. This paper proposes a orthogonal response surface method to optimize the multi-objective parameters of stator coreless disk type motor. On the basis of determining the optimization variables and optimization goals of the motor, the orthogonalization method is used to analyze the optimization target values under different levels of optimization variables, and preliminarily determine the basic parameters of the motor, Afterwards, the response surface method is used to analyze the parameter changes of the motor under the influence of multiple optimization variables, and finally determine the motor parameters that achieve the optimal multiple parameters. By comparing the motor conditions before and after optimization, the optimization goal is determined.

2. Structure and working principle of the PCB stator coreless disc motor

2.1. Integrated motor system

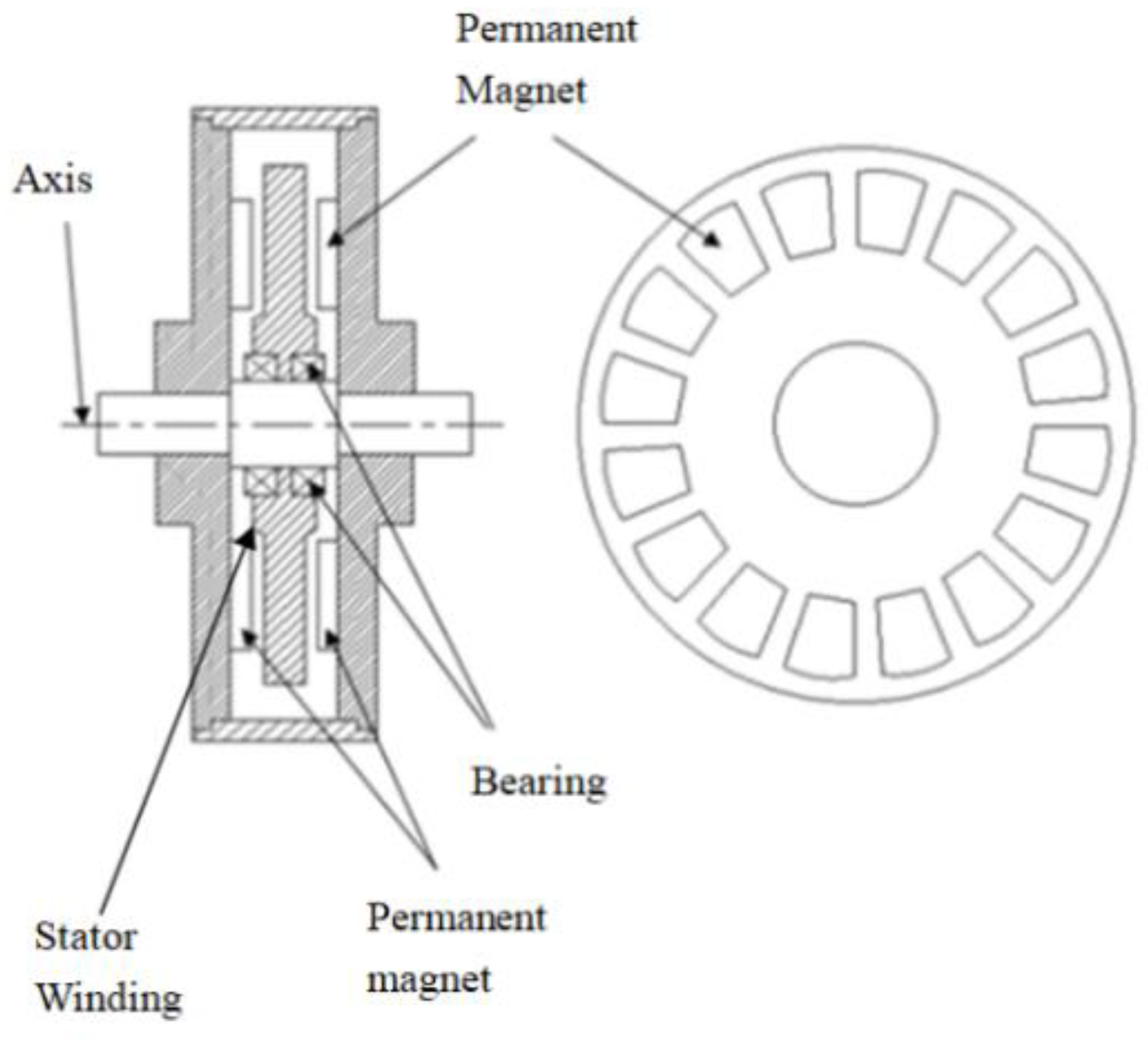
PCB winding and wound winding are the two main structures of stator winding of plateless stator motor. Considering practical application issues, PCB winding stator coreless disk motor as the choice. The motor structure diagram is shown in Figure 1.

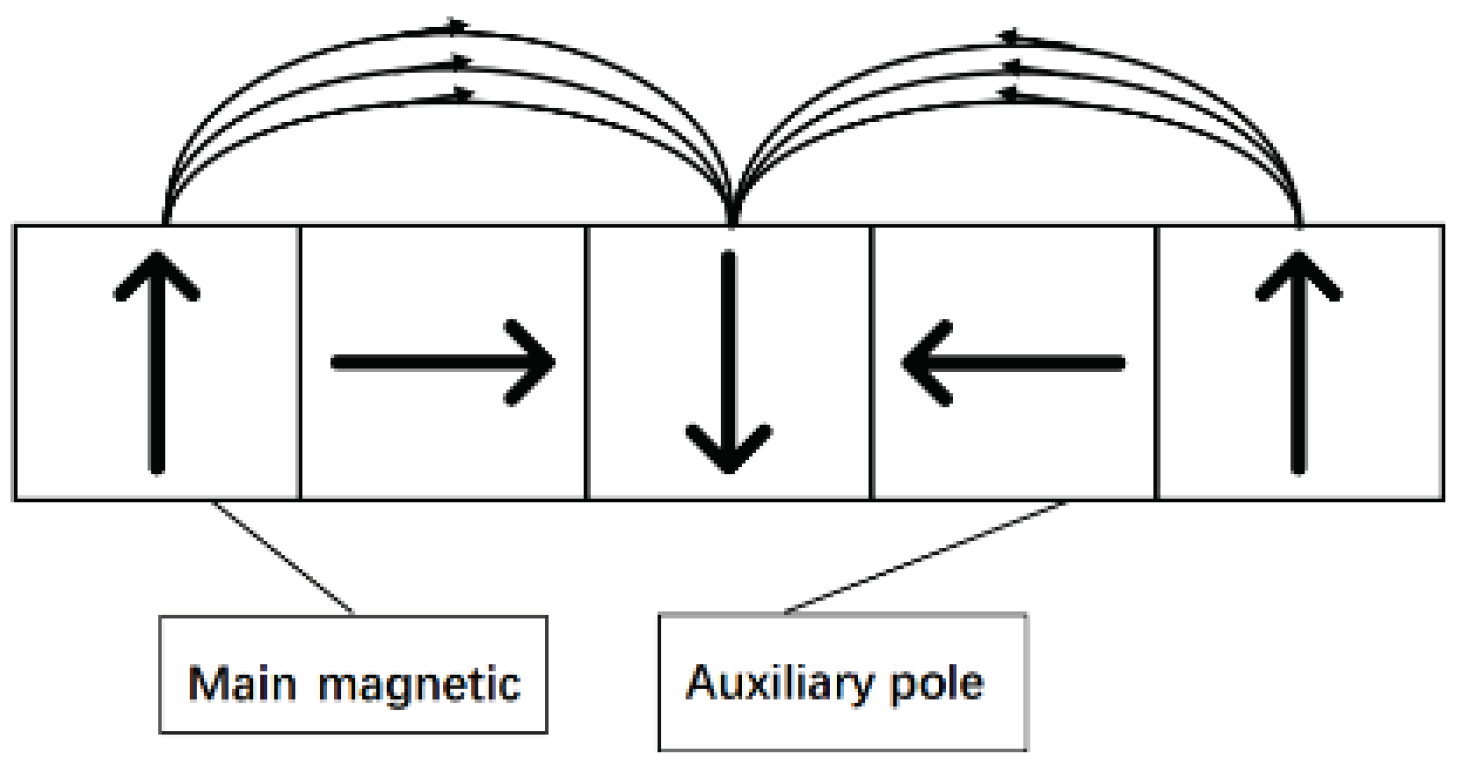
The motor is a single-stator double external rotor structure, and the stator winding is embedded on the printed circuit board, which is located in the center of the motor. The rotor is arranged symmetrically around the stator. The permanent magnet is pasted on the back iron in the form of Halbach array. The arrangement of permanent magnets is shown in Figure 2.

The permanent magnet consists of a main pole in the N-S direction and an auxiliary pole in the horizontal direction. By arranging the main magnetic pole and the auxiliary magnetic pole according to a certain law, the air gap magnetic density of the motor can be increased, and the torque density of the motor can also be increased, reducing the motor volume. The double-sided permanent magnet structure also has the effect of overcoming unilateral magnetic pull and reducing magnetic leakage in the motor [15,16].Table 1 shows the basic parameters of the finite element model.

2.2. Calculation of main parameters of the motor

Formula 1 is the motor torque equation.Formula 2 is the magnetic density of the air gap.

T_{d} = \frac{m}{\sqrt{2}} p N k_{w 1} ϕ_{m} I

(1)

ϕ_{m} = \frac{π}{8 p} α_{i} B_{δ} (D_{o u t}^{2} - D_{i n}^{2})

(2)

Among them,

D_{i n}

D_{o u t}

is the inner and outer diameter of permanent magnet;

ϕ_{m}

represents magnetic flux;

p

represents the polar logarithm;

α_{i}

represents the polar arc coefficient;

B_{δ}

represents the maximum magnetic density of the air gap.

The distortion rate of air gap magnetic density waveform can be calculated

T H D = \frac{\sqrt{A_{2}^{2} + A_{3}^{2} + \dots + A_{n}^{2}}}{A_{1}}

(3)

Among them,

A_{1}

A_{2}

A_{3}

and

A_{n}

represent the fundamental waves of the waveforms obtained from Fourier decomposition separately, second harmonic, third harmonic and nth harmonic.

PCB winding constitutes the stator winding of the disk permanent magnet motor. During operation, the current in the stator PCB winding produces the winding copper loss. The formula of winding current I and power P generated by winding is

P = \sqrt{2} π f B_{m} I \sum_{n = 1}^{N_{m a x}} S_{n} - P_{c u}

(4)

In the formula,

P_{c u}

represents the copper loss of the winding. According to the formula between the two, the output power of the motor decreases with the increase of the PCB stator winding, and the winding current I and the power P generated by the winding increase with the decrease of the PCB stator winding.

The formula for finding the internal resistance of PCB stator winding is

r_{0} = ρ \frac{\sum_{n = 1}^{N_{m a x}} L_{n}}{S_{l}}

(5)

In the formula:

ρ

is the resistivity of the copper wire;

L_{n}

is the length of the nth turn of the coil.

From this, the copper loss of the winding can be obtained as

P_{c u} = I^{2} r_{0}

(6)

With the passage of time, the stator winding in the magnetic field will change, eddy currents will be formed in the winding conductor, resulting in eddy current loss. The eddy current loss is related to the magnetic induction intensity of the magnetic field, the quality and width of the conductor, the changing frequency of the magnetic field and many other factors. The expression [17] is

P_{v} = \frac{π^{2}}{3 ρ} \frac{1}{ρ_{L}} f^{2} ω_{L}^{2} m_{c} (B_{m t 1}^{2} + B_{m a 1}^{2}) η_{d}^{2}

(7)

In the formula:

ρ_{L}

is the density of the guide bar;

ω_{L}

is the line width;

m_{c}

is the mass of the winding without considering the end;

B_{m t 1}

and

B_{m a 1}

are the fundamental magnetic density peaks in the tangential and axial directions, respectively;

η_{d}

is the distortion coefficient of the magnetic density waveform.

Convective heat dissipation between stator and rotor α is

α = 14 (1 + 0.5 \sqrt{ω}) \sqrt[3]{T_{0} / 25}

(8)

In the formula,

ω

is the angular velocity,

T_{0}

is the ambient temperature.

3. Optimization of Motor Parameters Based on Orthogonal Experiments

The main size design of the motor has a direct impact on the performance of the motor. The ultimate goal of motor optimization is to select the motor size that maximizes the performance of the motor. The initial optimization goals are motor power and torque, according to the electromagnetic power equation and torque equation of the motor, it can be determined that these two optimization objectives are affected by the air gap magnetic density and pole number. Because the motor uses Halbach's permanent magnet arrangement, the magnetic density of the air gap generated by the motor is affected by the size of the main pole, the size of the auxiliary pole, the thickness of the permanent magnet and the length of the air gap. Considering these aspects and ensuring the stability of the motor, the final optimization objectives of the motor are determined, including the number of rotor poles

p

, the ratio of the size of the main magnetic pole to the auxiliary magnetic pole

R_{n d}

, the thickness of the permanent magnet

T_{m}

and the length of the air gap

δ

, the torque of the motor

T_{d}

, the air gap flux density

B_{δ}

and the waveform distortion rate of the air gap flux density

T H D

. Table 2 shows the initial design values of the optimization factors

Table 3 shows the average values of each factor at each level, which are obtained through the orthogonal table. The four initial design factors are represented from top to bottom by A, B, C, and D.

By comprehensively considering the relationship between each optimization objective, we strive to achieve the optimal effect of the optimization objective. According to the simulation result data in Table 4, the pole number is finally determined to be 8 when the motor torque is not the maximum. Although the motor torque is not the maximum at this time, the performance of the other two is better when the torque difference is not significant.For the design of permanent magnets, for the design of permanent magnet, the optimal motor effect can be achieved when there is a ratio of 2 between the size of the main magnetic pole and the size of the auxiliary magnetic pole and the thickness of the permanent magnet is 3mm. At this time, the motor torque is maximized, while At the the magnetic density of the air gap is also the largest, and the waveform distortion of the magnetic density of the air gap is the smallest; The performance of the motor is not significantly different when the air gap length is 0.8mm and 1mm. Taking into account the relationship between the three performances, the final determination of the motor air gap length is 1mm. After that, simulation analysis was conducted on the motor with a rotor pole number of 8, a ratio between the size of the main magnetic pole and the size of the auxiliary magnetic pole of the permanent magnet is 2, a thickness of 3mm, and an air gap length of 1mm. The simulation results showed a torque of 157mN · m, and the magnetic gap density is 0.73, The distortion rate of the air gap magnetic density waveform is 21.9%, and the performance of the motor has been improved compared to before optimization.

4. Response Surface Experimental Design

4.1. esponse Surface Algorithm

The most commonly used response surface analysis methods mainly include CCD and BBD. Both models can analyze experimental data results through fitting regression equations. Among them, the experimental running cost of CCD design is higher than that of BBD design[18,19,20]. Therefore, BBD design is selected for fitting analysis of the experimental results, and the optimal solution of the response surface can be obtained. The fitting process is as follows:

The general second-order response surface model can be represented as

y = β_{0} + \sum_{i = 1}^{k} β_{i} x_{i} + \sum_{i = 1}^{k} β_{i i} x_{i}^{2} + \sum_{i < j} β_{i j} x_{i} x_{j} + ε

(9)

Among them,

β_{0}

is a constant term,

β_{i}

is a first-order coefficient,

β_{i i}

is a second-order coefficient,

β_{i j}

is a second-order interaction term coefficient, and

ε

is an error constant.

Using the least squares method to achieve data fitting, the result is

f^{*} = β_{0}^{*} + N^{T} b + N^{T} B N

(10)

Among them,

N = [N_{1}, N_{2}, N_{3}]; b = [β_{1}^{*}, β_{2}^{*}, β_{3}^{*}]

Performing first-order differentiation can determine the optimal solution as

N_{0} = - \frac{1}{2} B^{- 1} b

(11)

The experimental points selected for BBD design have specificity and can evaluate the nonlinear impact of optimization factors on the target within the range of independent variable changes.

4.2. Selection of optimization objectives and factors and experimental results

After completing the orthogonal experimental optimization for motor torque and air gap magnetic density, at this time, the service life of the PCB board has become the biggest problem to be solved. The PCB board is used to replace the stator core of the motor, and the stator winding, the main structure of the motor, is embedded on the PCB board. At this time, the motor is in a coreless form, so there will be no core loss in the stator during the motor operation, However, the stator winding will generate copper loss and eddy current loss during operation, which not only reduces the operating efficiency of the motor, but also transfers heat in the form of heat, causing the temperature of the motor PCB board to be too high and the PCB board is affected and the motor service life is reduced. Due to the fact that these issues are mainly related to the stator design of the motor, the heat dissipation capacity of the stator winding can be enhanced to a certain extent by increasing the thickness of the motor's PCB board, drilling holes on the PCB board, and designing the stator winding with unequal widths. Increasing the thickness of the PCB board will increase the equivalent air gap of the motor, the motor torque will be reduced accordingly. The objective function satisfies mutual constraints. Therefore, the final optimization targets are stator windings temperature rise, motor efficiency and motor torque. The BBD experimental design and simulation results are shown in Table 4

The response surface model of the optimization target can be obtained through response surface analysis of the experimental results in Table 4, and according to the response surface analysis results, the P-values of the Linear model for eddy current loss and average temperature are both less than 0.05, with the P-values of the eddy current loss analysis being less than 0.0001 and the P-values of the Quadratic model for torque being also less than 0.05. Therefore, it can be considered that the model is generally effective.

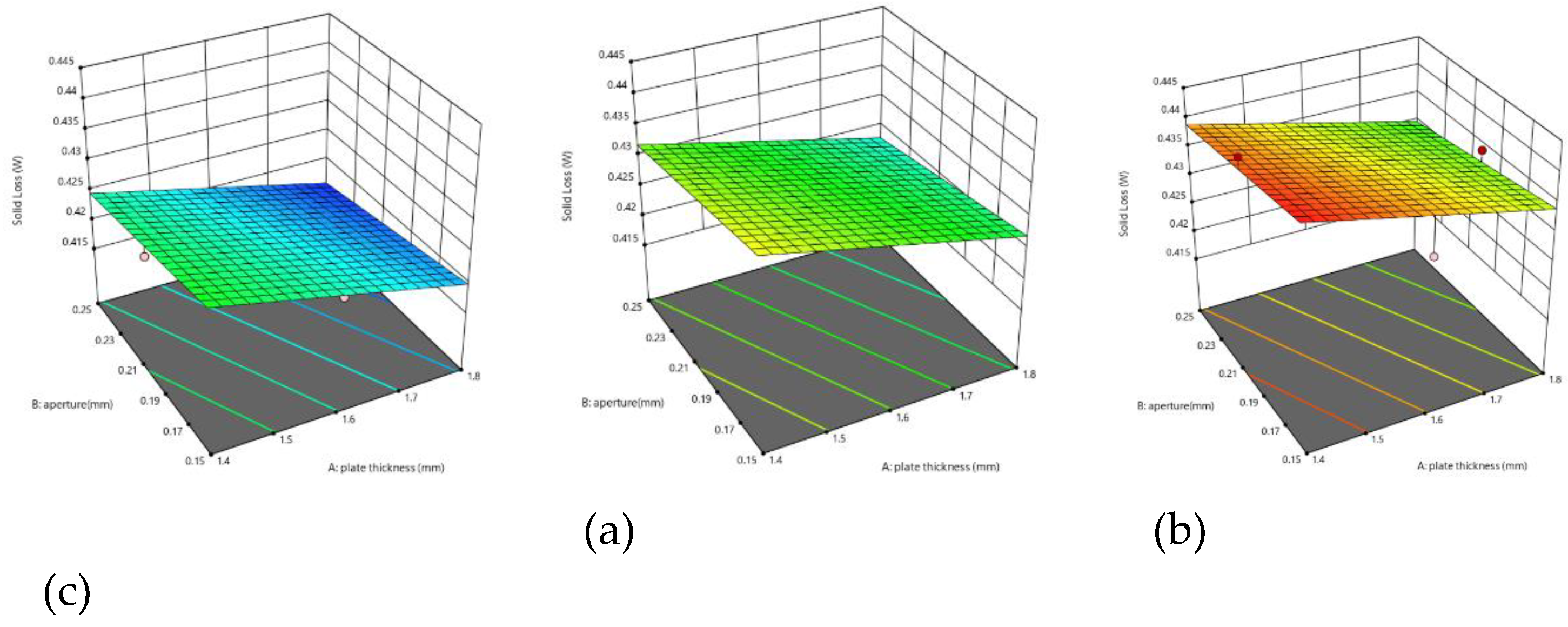
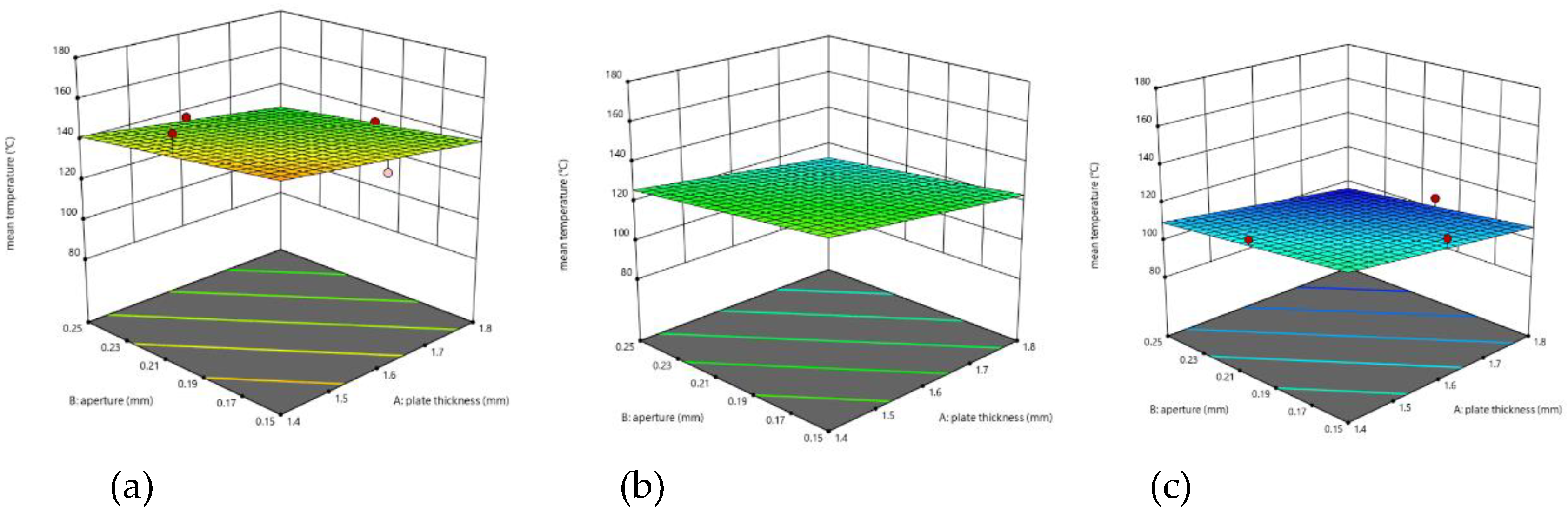
According to the BBD experimental analysis, the response surface maps corresponding to eddy current loss and average temperature can be obtained, as shown in Figure 3 and Figure 4.

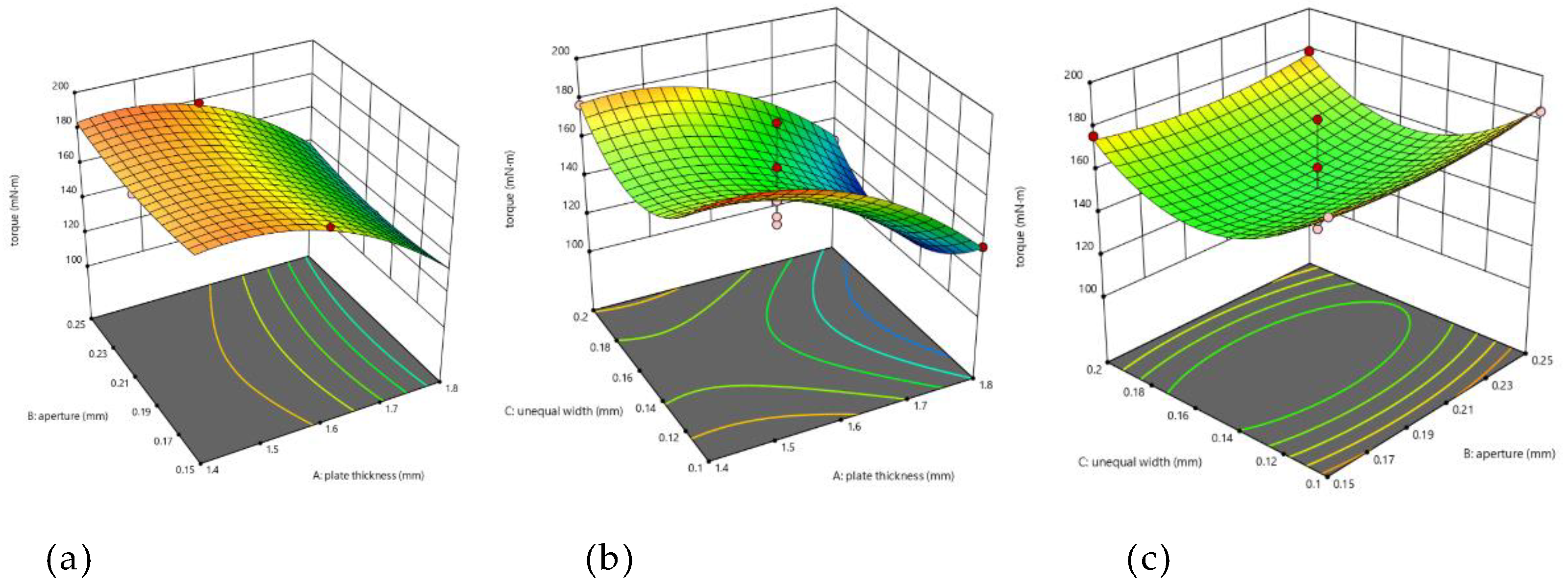
The abscissa of Figure 4 shows the thickness of the PCB board on the stator and the aperture size of the holes on the board. Among them, (a), (b), and (c) are the eddy current losses and average temperature values corresponding to the stator winding at different widths of 0.1mm, 0.15mm, and 0.2mm. From Figure 3 and Figure 4, it can be seen that as the thickness of the motor stator PCB board increases and the aperture size of the holes on the board increases, the eddy current loss is reduced in the running process, and the average temperature generated by the winding is reduced; However, as the unequal width design width between the stator windings increases, the value of eddy current loss is increased, but the average temperature value generated in the winding is reduced. It is necessary to calculate the stator winding unequal width design value, so that the motor eddy current loss is small and the winding average temperature is low.

The regression equation for torque can be obtained from the experimental results as follows

T = 8888.82 + 5000 A + 24.5 B + 128 C + A B + 16 A C - 1160.25 A^{2} - 101.09 B^{2} - 2610.57 C^{2}

(12)

As shown in Figure 5, the response surface analysis diagram obtained by fitting and calculating the torque through the regression equation

In Figure 5, (a), (b), and (c) are the motor torque values under the influence of aperture and plate thickness, unequal width and plate thickness, and aperture and unequal width, respectively. Figure (a) shows that as the thickness of the motor stator PCB board and the hole diameter on the board increase, the motor torque decreases. In Figures (b) and (c), as the abscissa value increases, the motor torque first decreases and then increases.

According to the response surface analysis results, the PCB data of the motor stator can be determined when the motor generates the minimum eddy current loss, the average temperature on the winding is the lowest, and the motor torque reaches the maximum. The plate thickness is 1.62mm, the opening aperture on the stator is 0.25mm, and the non-width width is 0.1mm.

5. Comparative analysis before and after optimization

Comparative analysis can be carried out, and finite element method can be used to compare the motor before and after optimization, so as to determine the effect after optimization, and a comparison diagram of magnetic density, torque, temperature change during winding operation and eddy current loss of the motor before and after optimization is obtained, as shown in Figure 6.

From the comparative analysis of the motor performance before and after optimization in Figure 6, it can be seen that the optimized target motor torque, winding temperature, eddy current loss and axial air gap magnetic density are optimized. After optimization, the amplitude of the air gap magnetic flux density of the motor is 0.73T, the torque is 182mN · m, the average temperature is 134 ℃, and the eddy current loss is 0.42W, achieving the goal of multi-parameter optimization and verifying the feasibility of the optimization.

6. Prototype experiment

The stator coreless disk motor prototype based on PCB winding is manufactured according to the above motor design parameters, as shown in Figure 7, where (a) is the motor rotor, (b) is the PCB stator, and (c) is the overall model diagram of the prototype, and the experimental platform shown in Figure 8 was built for experiments.

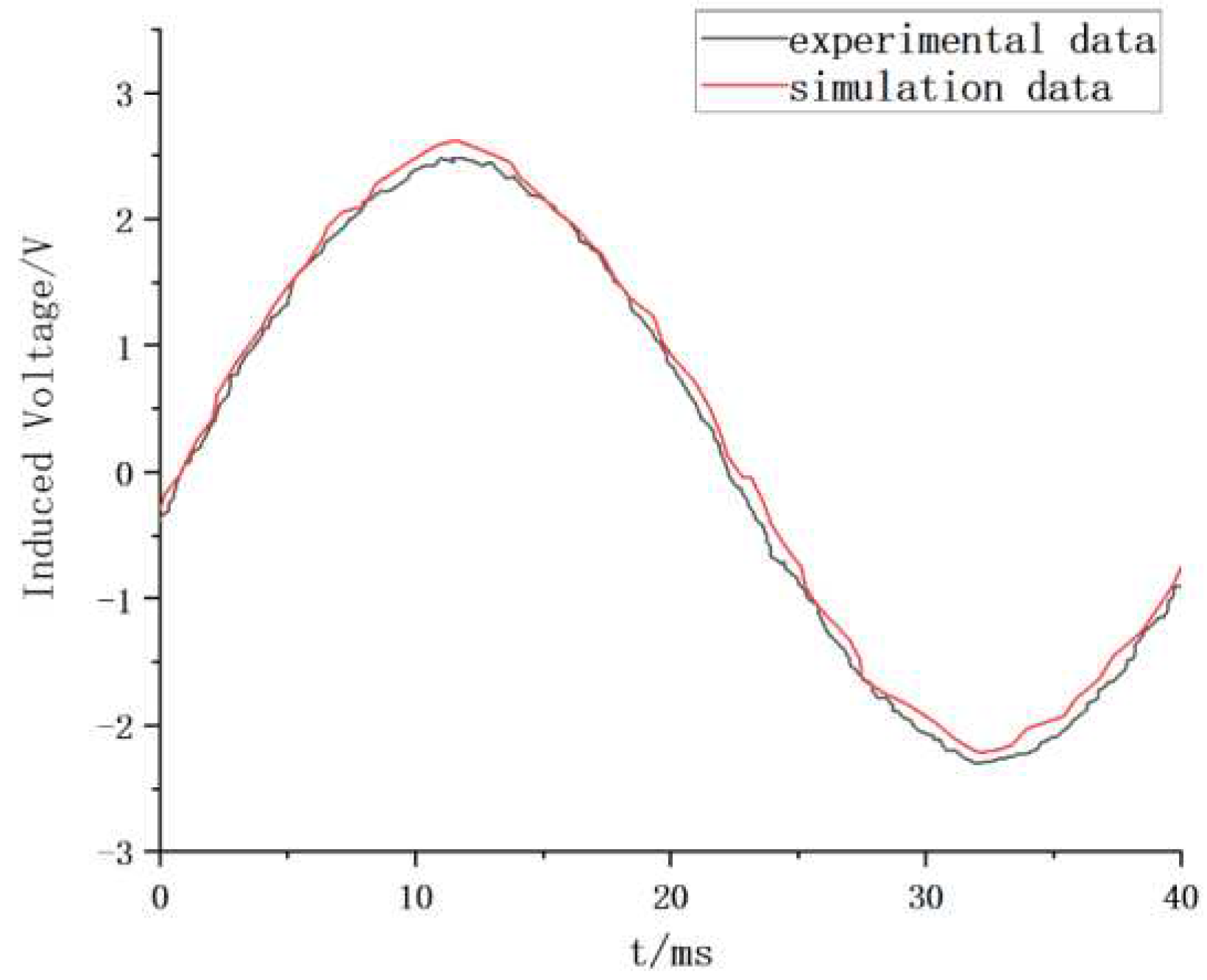
In the experimental platform, a permanent magnet synchronous motor is used as the prime mover to drag the PCB statorless disk motor, and a coupling is used to connect the two. As shown in Figure 9, the no-load back potential of PCB stator coreless disk motor is measured and compared with the simulation results.

The simulation results of no-load back potential in the figure are consistent with the actual measurement results. It can be concluded that the optimal design of the motor is reasonable in this paper.

7. Summary

This article proposes a multi-parameter optimization design algorithm based on orthogonal response surface for the multi parameter optimization problem of PCB stator coreless disc motors. By using orthogonal method, the distortion rate of air gap magnetic density waveform is reduced, and the torque and magnetic density amplitude of air gap are increased, It is determined that the number of rotor poles of the motor is 8, the ratio of the size of the auxiliary magnetic pole of the permanent magnet to the size of the main magnetic pole is 2, the thickness of the permanent magnet is 3mm, and the length of the air gap is 1mm . After that, in order to extend the use time of the PCB board, it began to reduce the winding temperature rise generated when the motor was running, BBD experiments were conducted on the motor stator to obtain optimized motor parameters. The thickness of the motor PCB board was determined to be 1.62mm, the aperture on the board was 0.25mm, and the uneven width of the stator winding was 0.1mm. At this time, the temperature rise of the motor can be minimized.The air gap flux density of the motor permanent magnet after optimization is 0.73T, The distortion rate of the air gap magnetic density waveform is 21.9%, the torque is 182mN · m, the average temperature is 134 ℃, and the eddy current loss is 0.42W. This verifies the effectiveness of multi-objective optimization design and provides a new idea for multi-parameter optimization of PCB stator coreless disc motors in the future.

References

Sultan, H.M. Design and Modeling of a Robust Sensorless Control System for a Linear Permanent Magnet Synchronous Motor. Electronics 2021, 10. [Google Scholar] [CrossRef]
Qiu Ruilin, Hua Qingsong, Zhang Hongxin, et al. Optimization design of permanent magnet synchronous motor rotor based on Taguchi method. Journal of Qingdao University (Engineering Technology Edition) 2020, 35, 57–61. [CrossRef]
Wang Xiaoyuan, Huang Xudong, Li Tianyuan. Optimization design of PCB stator disc permanent magnet motor winding under high-frequency power supply conditions. Journal of China Electrical Engineering 2021, 41, 1937–1946.
Lu Y, Li J, Qu R, et al. Electromagnetic Force and Vibration Analysis of Permanent-Magnet-Assisted Synchronous Reluctance Machines. IEEE Transactions on Industry Applications 2018, 1-1. [CrossRef]
Zhang, W.; Xu, Y.; Zhou, G. Research on a Novel Transverse Flux Permanent Magnet Motor With Hybrid Stator Core and Disk-Type Rotor for Industrial Robot Applications. IEEE Transactions on Industrial Electronics 2021, 68-11. [Google Scholar] [CrossRef]
Zhang C, Chen Z, Mei Q, et al. Application of Particle Swarm Optimization Combined With Response Surface Methodology to Transverse Flux Permanent Magnet Motor Optimization. IEEE Transactions on Magnetics 2017, 53, 1–7. [Google Scholar] [CrossRef]
Abdelrahem M, Hackl C, Kennel R. Robust Predictive Control Scheme for Permanent-Magnet Synchronous Generators Based Modern Wind Turbines. Electronics 2021, 10, 1596. [Google Scholar] [CrossRef]
Tang Renyuan. Theory and Design of Modern Permanent Magnet Motors. Mechanical Industry Press, 2016.
Ma Y , Ching T W , Fu W N , et al. Multi-Objective Optimization of a Direct-Drive Dual-Structure Permanent Magnet Machine. IEEE Transactions on Magnetics 2019. [CrossRef]
Silva A M, Antunes C H, Mendes A, et al. On Phase Shifting and Diversified Coil-Pitch for Enhanced Multiobjective Winding Design Optimization. IEEE Transactions on Energy Conversion 2020, 99, 1–1. [Google Scholar] [CrossRef]
Farhan A, Johnson M, Hanson K, et al. Design of an ultra-high speed bearingless motor for significant rated power[C]//Proceedings of the IEEE Energy Conversion Congress and Exposition. Detroit, USA:IEEE,2020.
Liu Fugui, Wang Pengfei, Lei Yu. Structural Optimization of Permanent Magnet Vernier Motors Based on Taguchi Method. Experimental Technology and Management 2020, 37, 96–100. [Google Scholar]
Zhou X, Zhu X, Wu W, et al. Multi-objective optimization design of variable-saliency-ratio PM motor considering driving cycles. IEEE Transactions on Industrial Electronics 2020, 68, 6516–6526. [Google Scholar] [CrossRef]
Du Xiaobin, Deng Jianhua. Optimization of Air Gap Magnetic Density Waveform of Permanent Magnet Synchronous Motor Based on GPR-PSO Model. Explosion proof Motor 2017, 52, 20. [Google Scholar]
Cao Yongjuan, Huang Yunkai, Jin Long, et al. Design and analysis of axial magnetic field coreless permanent magnet motors with magnetic pole combination. Chinese Journal of Electrical Engineering 2014, 34, 903–909. [Google Scholar]
Gao, F.Y. , Qi, X.D., Li, X.F., Tao, C.X., and Gao, P. Analytical calculation and optimization analysis of electromagnetic performance of unequal-width unequal-thickness Halbach partially segmented permanent magnet synchronous motor. Journal of Electrotechnology 2022, 37, 1398–1414. [Google Scholar] [CrossRef]
Wang Xiaolei. Design and Analysis of a New Type of Coreless Armature Disc Motor; China Shipbuilding Research Institute: Beijing, China, 2012. [Google Scholar]
Du Xiaobin, Huang Kaisheng, Tan Gengrui, Huang Xin. Multi-objective optimization of permanent magnet motor torque based on response surface method. Micro Special Motor 2019, 47, 20–23. [Google Scholar] [CrossRef]
Yang X, Ren Zhouyang, Guo Bing, Ding Yan. Probabilistic optimal energy flow calculation method for electricity-gas interconnection system based on stochastic response surface. New Technology of Electrical Energy 2021, 40, 1–9. [Google Scholar]
Liu G, Wang Y, Chen Q, et al. Multi-Objective Deterministic and Robust Optimization Design of a new Spoke-Type Permanent Magnet Machine for the Improvement of Torque Performance. IEEE Transactions on Industrial Electronics 2020, 99, 1–1. [Google Scholar] [CrossRef]

Figure 1. Schematic diagram of motor structure.

Figure 2. Permanent magnet arrangement

Figure 3. Eddy Current Loss Response Surface Model

Figure 4. Average Temperature Response Surface Model

Figure 5. Torque Response Surface Model

Figure 6. Comparison of motor performance before and after optimization.

Figure 7. Prototype structure diagram

Figure 8. Prototype experiment platform.

Figure 9. no-load counter potential waveform simulation results compared with the measured value

Table 1. Basic parameters of motor finite element model

Parameter	Numerical value
Rated power/w	500
Rated speed/r/min	750
Outer diameter of stator/mm	100
Stator bore/mm	70
Number of PCB coils per layer	3
Coil conductor thickness/mm	0.105
Width of coil conductor/mm	0.70
Insulation distance between conductors/mm	0.20
Number of coil conductor layers	12
PCB Number of sections	1

Table 2. Initial Design Factors.

Initial design factor	Horizontal	Numerical value
Number of rotor poles $p$	1	2
	2	4
	3	6
	4	8
Main/auxiliary magnetic pole size ratio $R_{n d}$	1	0.5
	2	1
	3	2
	4	3
Permanent magnet thickness $T_{m}$ /mm	1	3
	2	4
	3	5
	4	6
Air gap length $δ$ /mm	1	0.5
	2	0.8
	3	1
	4	1.2

Table 3. Average values of various factors at various performance levels

Divisor	Horizontal	$T_{d} / m N \cdot m$	$B_{δ} / T$	$T H D / %$
A	1	93.3	0.43	38.0
	2	42.8	0.56	42.4
	3	74.4	0.60	35.6
	4	81.7	0.66	28.2
B	1	48.1	0.56	54.5
	2	77.9	0.58	42.2
	3	111.7	0.57	25.3
	4	54.3	0.54	22.1
C	1	100.0	0.53	26.5
	2	65.2	0.53	39.2
	3	92.1	0.60	39.9
	4	34.8	0.61	38.6
D	1	58.4	0.61	60.3
	2	80.7	0.55	39.5
	3	90.0	0.52	36.8
	4	63.0	0.58	38.3

Table 4. BBD Experimental Design and Simulation Results

Order number	Plate thickness (mm)	Aperture (mm)	Unequal width (mm)	A	B	C	Eddy current loss (W)	Average temperature (℃)	Torq-ue (mN·m)
1	1.4	0.15	0.15	-1	-1	0	0.436	127.1	161
2	1.8	0.15	0.15	1	-1	0	0.428	130.0	112
3	1.4	0.25	0.15	-1	1	0	0.432	129.7	164
4	1.8	0.25	0.15	1	1	0	0.423	107.4	117
5	1.4	0.20	0.10	-1	0	-1	0.425	158.4	192
6	1.8	0.20	0.10	1	0	-1	0.415	134.4	136
7	1.4	0.20	0.20	-1	0	1	0.443	118.6	177
8	1.8	0.20	0.20	1	0	1	0.434	106.3	129
9	1.6	0.15	0.10	0	-1	-1	0.424	140.4	181
10	1.6	0.25	0.10	0	1	-1	0.418	136.8	184
11	1.6	0.15	0.20	0	-1	1	0.432	119.2	176
12	1.6	0.25	0.20	0	1	1	0.430	97.2	179
13	1.4	0.15	0.10	-1	-1	-1	0.429	162.7	182
14	1.6	0.20	0.15	0	0	0	0.434	130.9	160
15	1.8	0.25	0.20	1	1	1	0.433	102.4	131

Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.

© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).

Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.