Prerpints.org logo
Preprint
Article

Downscaling Land Surface Temperature Using SAR Images: A Machine Learning Framework

Altmetrics

Downloads

233

Views

200

Comments

0

Submitted:

19 June 2023

Posted:

20 June 2023

You are already at the latest version

Alerts
Abstract
Land Surface Temperature (LST) is significant for climatological and environmental studies. LST products from satellites, however, suffer from the tradeoff between spatial and temporal resolution. Spatial downscaling has emerged as a well explored field aiming to overcome limitations arising from this tradeoff. Previous research on regression based LST downscaling models focused on utilizing predictors derived from optical imagery. Weather-dependency of optical imagery data, however, can influence downscaling models by the weather conditions. To cope this issue, in this study, we involve predictors derived from the weather-independent Sentinel-1 Synthetic Aperture Radar (SAR) imagery to downscale Landsat-8 LST data. In this context, we propose to use machine learning techniques, namely Random Forest (RF) and Convolutional Neural Networks (CNN). To demonstrate the applicability and performance of the proposed method, extensive experimental analyses were conducted over Zuid-Holland in the Netherlands. From the experiments, we found that the results obtained with radar predictors were comparable to those achieved using optical predictors. This confirms that the proposed method indeed paves a new way for mapping land surface temperature using SAR images.
Keywords: 
Subject: Environmental and Earth Sciences  -   Remote Sensing

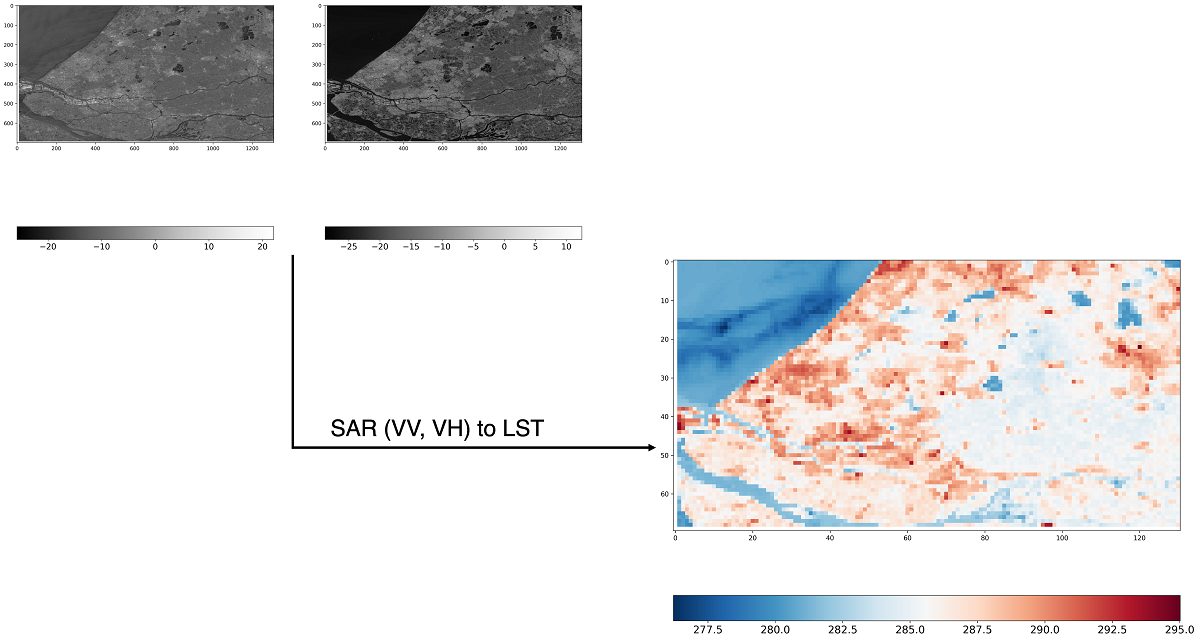
1. Introduction

Land Surface Temperature (LST) is crucial for modeling the Earth's energy balance. LST provides valuable insights for studying urban heat islands [1], soil moisture[2,3], droughts[4], and vegetation[5]. Such applications require detailed LST information at various spatial and temporal scales. Ground weather stations are commonly used to gather detailed LST information, but their sparse distribution limits their effectiveness in mapping LST over large areas [6].
Remote sensing techniques, as an alternative method to estimate LST, allows users to indirectly deduce surface temperature of large areas from space. However, remote sensing techniques employed for retrieving LST information can be challenged by the conflict or the trade-off between spatial and temporal resolution. Indeed, the space-based high spatial resolution LST products generally corresponds to low temporal information and vice versa. Irrespective of the selected LST product, the user would have to deal with uncertainties either related to the spatial or temporal domain. Coarse spatial resolutions LST products (e.g., 1000m) confuse temperatures of different land covers and avoid detailed assessment. Spatial Downscaling (SD) methods can assist in solving this conflict. Spatial downscaling can be defined as the process of translating spatial information from coarse to fine spatial resolution. High spatio-temporal LST products is particularly necessary for urban studies; as the built-up areas have high heterogeneity in terms of land surface information [6]. Furthermore, the availability of high spatio-temporal resolution LST data makes it possible to observe and monitor the temporal change of temperature over distinct land covers such as fields, roads, buildings.
Spatial downscaling methods can be divided into: physical models [7], spatio-temporal fusion models [8,9], and regression-based models [10,11,12]. Out of these, regression-based modelling is the most commonly adopted downscaling method due to its ease of practical implementation as compared to other methods [11]. Regression based methods aim to model the relationship between input predictors (e.g., spectral indices, terrain factors, land use land cover information) and the target variable (LST). The generated model consequently can be used to estimate fine scale LST data when fine scale predictors are used as input.
Several studies investigated LST downscaling problem using regression models. These studies utilized and developed models such as: DisTrad [13], TsHARP [10], NL-DisTrad [14], Geographically Weighted Regression (GWR) [15], Co-Kriging [16], Random Forest (RF) [11,12], and Support Vector Machines (SVM) [12]. Generally, irrespective of the applied methods, predictors such as surface reflectance and spectral indices were commonly derived from optical data. Such predictors apparently rely on clear weather conditions that can hinder the construction and usage of downscaling models due to the lack of cloud-free images. Additionally, these predictors are ineffective during nighttime due to the limitations of optical imagery. In this study, to overcome the above-mentioned limitations, Synthetic Aperture Radar (SAR) data is used for deriving the predictors to downscale LST image. Due to the active imaging mode and the employed microwave electromagnetic waves, radar signals penetrate through clouds, making SAR system capable to acquire information from Earth’s surface during both daytime and night-time and independent of weather condition [17]. The sensitivity of radar backscattering to surface parameters such as surface roughness, soil moisture, surface dielectric constant and vegetation indices has long been established in several studies [18,19,20,21,22,23]. The anticipated relationship between these surface parameters obtained via radar and temperature inspires exploration of the use of SAR images to downscale LST products. In this paper, we investigate the main question: can SAR images be used as a predictor to downscale the available coarse resolution Thermal Infrared (TIR)-based LST products? We conduct several experimental analyses to answer this question. Random Forest (RF) regression and a Convolutional Neural Network (CNN) are considered to perform the downscaling problem.
The rest of the paper is organized as follows: Section 2 introduces the materials and the methods, while the experimental results are given in Section 3. Discussion of the achieved results is presented in Section 4. Finally, Section 5 is dedicated to conclusions.

2. Materials and Methods

2.1. Sudy area

Figure 1 shows the considered study area, the province of Zuid-Holland in the Netherlands. In 2020, Zuid-Holland had a minimum temperature of approximately 281 K, a maximum temperature of 289 K, and a mean temperature of 285 K based on global surface temperature data (https://climateknowledgeportal.worldbank.org/). These statistics provide a broad overview of the temperature regime in the study case. Surface temperature dynamics vary across regions due to factors like topography, land cover, and urbanization. In Zuid-Holland, the landscape consists of grassland, built-up areas, croplands, trees, bare/sparse vegetation, and herbaceous wetland, which can contribute to regional variations in surface temperatures. This study introduces the first use of SAR image for detailed LST mapping and assesses its performance across various types of land covers.

2.2. Datasets

The employed datasets include Landsat 8 collection Tier 1 LST (100 m), Copernicus Sentinel-1 SAR (10 m) and Sentinel-2 Multi Spectral Instrument (MSI) optical data (10 m), and ESA WorldCover v100 land cover information (10 m). To construct the radar-based downscaling models, the Landsat-8 LST data was utilized as the target or reference variable, while the Sentinel-1 SAR Ground Range Detected (GRD) data served as the basis for deriving the predictor variables. The models were trained using both data sets that were aggregated to a spatial resolution of 1000 m. The constructed models were subsequently used to produce a fine resolution radar derived LST map using high-resolution SAR images. Moreover, for subsequent experiments, ESA WorldCover data was also incorporated into the radar-based downscaling models as a predictor variable. The performance of the radar-based downscaling models was evaluated and compared with downscaling models constructed based upon the optical data sets. To this aim, Sentinel-2 MSI data was used as predictor.
All the aforementioned datasets were collected and processed in the Google Earth Engine environment and using Python application programming interface. The considered pre-processing steps included crucial procedures such as clipping, resampling, and reprojection of the datasets to ensure proper coregistration between datasets. To establish a reliable mapping, the reference and predictor data with the closest acquisition dates were utilized in the development of the downscaling models. A concise summary of the datasets utilized in this study can be found in Table 1.

2.3. Downscaling Models

2.3.1. Random Forest

RF [24], has been extensively employed in various studies focusing on the LST downscaling problem [11,12,25,26]. The RF downscaling model can be expressed as a mapping function f   approximated by training the model between the predictors P c (coarse resolution predictors) and the target T c . After training the model and building the mapping function using the coarse resolution data, the predictors at fine resolution are utilized as inputs to the function f to correspondingly estimate the fine scale target value.
The regression models employed for downscaling often fail to capture all the variation present in the target variable. To cope with this, a residual correction procedure, introduced in [13], is incorporated into our proposed downscaling framework as:
Δ T = T f c − T c
where T c is coarse resolution target variable, and T f c is the reaggregated T f from fine resolution to coarse resolution. Finally, the residual corrected downscaled target value T f ′ can be expressed as:
T f ′ = T f + Δ T
where T f   represents the output of the model when high-resolution predictor is fed as an input.
The selection of RF regression for this study is motivated by the successes achieved in previous studies [11,12,25,26]. The advantages highlighted include its non-linear and non-parametric nature, the reduced risk of overfitting, ability to handle high-dimensional datasets, the incorporation of both continuous and categorical variables, efficient computation time, etc.
For the radar-based RF downscaling model, the aggregated versions of Sentinel-1 GRD and Landsat-8 LST at 1000 m spatial resolution were respectively used as predictor and target variables. In this study, we employed the median-based aggregation. The Sentinel-1 GRD data consists of intensity images of two polarization channels (VV and VH), which were both utilized as predictors. Typically, SAR images compared to LST data contains significant backscattering intensity variations over local regions. The pixel values in both VV and VH intensity images do not exhibit the same smooth variations as commonly seen in the bands of optical imageries. Excessive spatial filtering can alleviate this intensity variation. However, this can easily lead to information loss, preventing the model from capturing all the variation in the target variable. To mitigate this limitation, we incorporated the neighboring values of all the pixels in the VV and VH channels as additional features/predictors. The results from both experiments, i.e., with and without the inclusion of neighboring values, are reported in the experimental section. Figure 2a shows visual explanation of this feature inclusion concept.
LST is a complex phenomenon that cannot be adequately modeled using a single source of data. Consequently, in many downscaling studies, researchers strive to integrate multiple sources of information that are correlated with LST to achieve more accurate estimations. In line with this concept, this research also incorporates land cover information as additional predictors for the radar-based downscaling models. However, instead of following the conventional approach of aggregating the land cover image to a coarser resolution and training a model, we calculate the proportion of land cover classes within a coarse pixel and utilized them as additional features. As shown in Figure 2b a 1000 m pixel in the aggregated Landsat-8 LST image (Tc) corresponds to a patch of 100×100 pixels in ESA WorldCover v100 (10 m) (Po) image. Within this patch, the proportion of each land cover class is calculated, which serves as a feature value for that specific pixel. This process is repeated with a patch size of (10, 10) to facilitate the estimation of LST at 100 m resolution.
To validate and compare the performance of the proposed radar-based LST downscaling framework, an optical-based random forest downscaling model was implemented. In particular, six optical bands including blue, green, red, Near Infrared (NIR), Short Wavelength InfraRed (SWIR1, and SWIR2) from the Sentinel-2 MSI data were used as predictors.

2.3.2. Convolutional Neural Networks

In addition to the Random Forest model, we employed Convolutional Neural Networks (CNNs) to downscale LST. CNNs belong to a class of deep learning models that have been significantly experimented and investigated in the fields of computer vision and image processing [27,28]. The convolutional layers of a CNN capture local patterns and features from the input, while subsequent layers, such as fully connected layers, facilitate the regression process by making predictions based on these learned features. In contrast to RF, CNNs excel in extracting spatial information from input data. CNNs possess an inherent ability to learn and exploit the spatial relationships present in the data, rendering them particularly valuable for downscaling tasks. The integration of deep learning, in general, into the domain of LST downscaling has been relatively limited. A previous study by [29] utilized neural networks and proposed a deep learning-based downscaling architecture called GTNNWAR. However, this architecture does not incorporate CNNs for regression-based downscaling. To the best of our knowledge, the incorporation of a regression-based CNN architecture for LST downscaling has not yet been investigated.
In this research, we propose a regression-based CNN architecture for downscaling LST. The architecture aims to establish a mapping between a coarse resolution target image and fine resolution predictor images (See Figure 3). To achieve this, the predictor images derived from radar, land cover, and optical imageries are initially aggregated from their original 10 m resolution to 100 m resolution. Subsequently, (10, 10) patches, covering the corresponding 1000 m target pixel are generated, and considered as inputs for the model. Once the model is trained, the (10, 10) patches are generated again from the original 10 m predictor images and fed into the trained model to generate the corresponding 100 m target LST image. Thus, the model receives inputs with a dimension of 10×10×k, where k represents the number of predictors. For each input patch, the output of the model is a singular value representing the downscaled temperature. Consistent with the RF experiments, the experiments from CNN based downscaling model utilized VV, VH and land cover images collected from Sentinel-1 GRD and ESA WorldCover v100 datasets as predictors. Moreover, for further comparison and evaluation, the optical image with six bands collected from Sentinel-2 MSI dataset was also used as a predictor for the developed CNN model.

2.4. Evaluation framework

The evaluation framework in this research paper employs three metrics: Root Mean Square Error (RMSE), Correlation Coefficient (r), and Coefficient of Determination (R²). In the context of downscaling LST, these metrics can be expressed as
R M S E = ∑ i = 1 n T f ′ − T v 2 n ,           r = ∑ i = 1 n T v − T v ¯   T f ′ − T f ′ ¯ ∑ i = 1 n T v − T v ¯ 2 ∑ i = 1 n T f ′ − T f ′ ¯ 2 ,       R 2 = 1 − ∑ T v − T f ′ 2 ∑ T v − T v ¯ 2
where T f ′ is the final residual corrected downscaled LST (100 m), T f ′ ¯ is the mean of   T f ′ , T v is the validation or reference Landsat-8 LST (100 m), T v ¯ is the mean of T v , and n is the number of pixels.

3. Experimental Results

3.1. Case 1: Results from RF-based Downscaling Models

In this section, three primary experiments were conducted for the radar-based random forest downscaling model. The first experiment involved downscaling the aggregated Landsat-8 LST from 1000 m spatial resolution to 100 m spatial resolution using the VV and VH intensity channels as predictors. The second experiment considers inclusion of 5x5 neighboring values of VV and VH channels as predictors. Thus, the feature dimensionality in the first experiment is 2, while in the second experiment it is increased to 25×2=50. Finally, for the third experiment, proportion of different land covers were incorporated as features increasing the dimensionality to 58 (50 + 8 land cover classes). These experiments were repeated for three specific dates: 25th March 2020, 10th April 2020, and 28th May 2020. The quantitative evaluation metrics obtained by comparing the downscaled LST (100 m) against the Landsat-8 LST (100 m) are presented in Table 2. For qualitative comparison, Figure 4 displays the obtained results from the proposed radar-based downscaling models for 25th March 2020. Figure 5 also shows the results of the RF model with optical data acquired on 25th March 2020. For more analysis, Table 3 shows the quantitative evaluation of the results over the different land cover areas.

3.2. Case 2: Results from CNN-based Downscaling Models

Two primary experiments were undertaken for the CNN-based downscaling model. The first experiment involved utilizing (10, 10) patches extracted from VV, VH, and land cover images as input, while the second experiment employed the six bands of the Sentinel-2 MSI optical image as input. The evaluation metrics obtained for these experiments, comparing the downscaled LST products (100 m) with the corresponding Landsat-8 LST (100 m), are presented in Table 4. Additionally, Figure 6 showcases the CNN-based downscaled LST products (100 m) derived from these experiments, juxtaposed with the validation Landsat-8 LST products (100 m). Table 5 also displays the RMSE values of all the CNN-based downscaling experiments for each land cover in the study area. Furthermore, Table 6 presents the evaluation metrics of the optical-based RF and CNN downscaling experiment conducted specifically for the date of 25th March 2020.

4. Discussion

The primary objective of this research was to evaluate the efficacy of radar-derived predictors in downscaling Land Surface Temperature (LST). The quantitative evaluation metrics presented in Table 2 demonstrate the effectiveness of using the VV and VH bands of Sentinel-1 GRD data as predictors for LST downscaling. 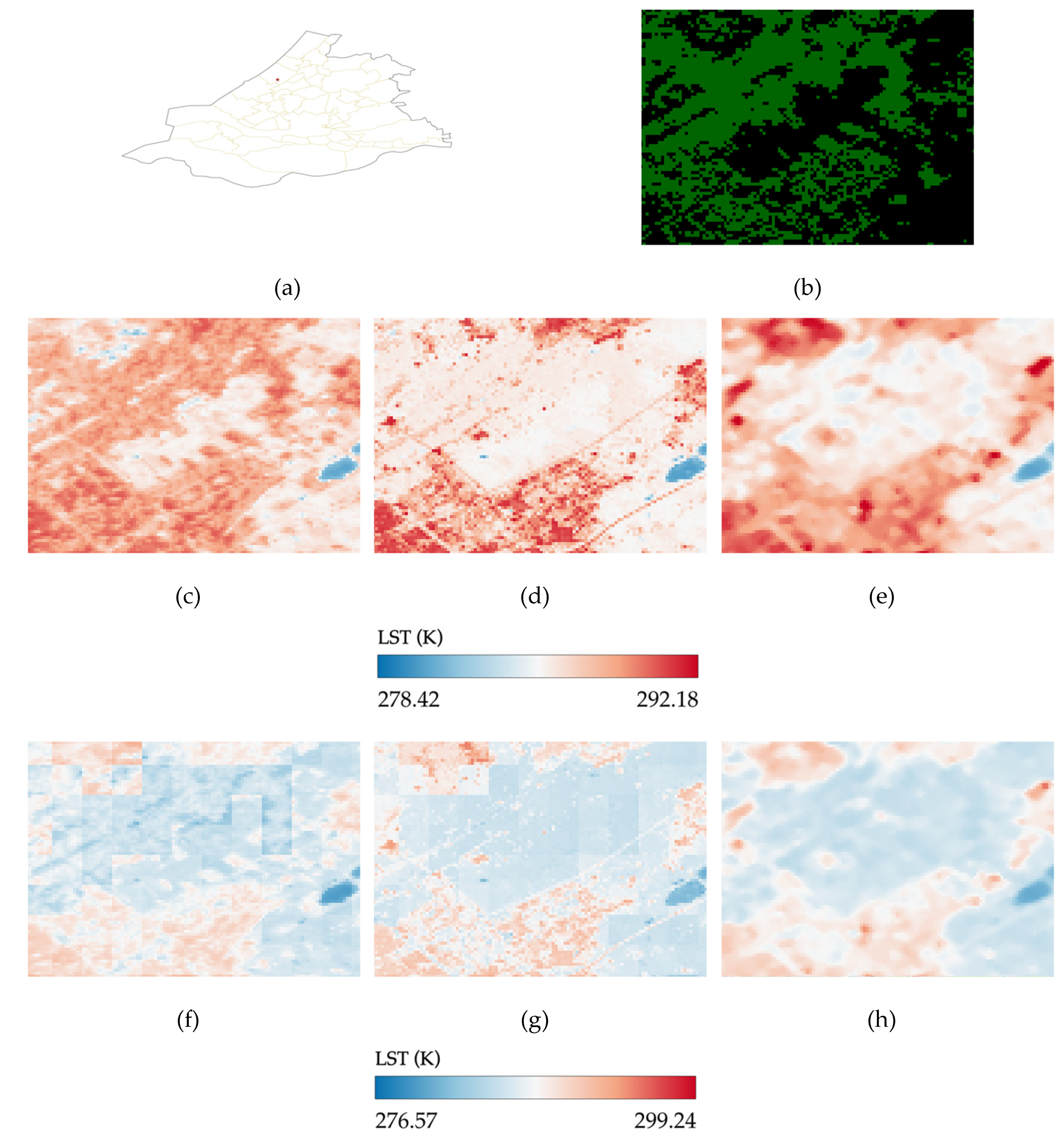The downscaled LST maps generated using the radar-based random forest downscaling models exhibit favorable agreement with the validation data, as depicted in Figure 4. Moreover, the incorporation of feature engineering techniques, such as including neighboring values and land cover proportion, enhances the quantitative performance of the radar-based random forest downscaling models and yields improved qualitative results. To better illustrate the effect of feature inclusion in SAR-based downscaling framework, results from two different small regions over Zuid-Holland province, namely Lansingerland (the red star in Figure 7a) and Wassenaar (the red star in Figure 8a), were reported. In particular, Figure 7 shows the effect of including neighborhood values in the downscaling method with and without residual correction. As can be seen, the LST image generated with the inclusion of neighboring values (Figure 7c and Figure 7e) exhibits smoother and more gradual variations compared to the version without such inclusion (Figure 7b and Figure 7d). Further, the inclusion of neighboring values also mitigates numerous false high LST estimates that may arise from elevated values of the backscattering coefficient. High backscatter values do not necessarily correspond to high LST values, as the raw radar backscatter is influenced by various variables beyond LST alone. Forested areas, for instance are wrongly mapped to high LST values due to high backscatter values. Furthermore, as can be seen in Figure 8, the incorporation of land cover features resolves the issue related to the forested areas. Additionally, the inclusion of land cover features assists in better boundary delineation between different land cover categories, addressing a limitation observed in the downscaled results obtained solely using predictors derived from Sentinel-1 GRD data (VV and VH). In general, comparison of radar-based downscaling LST with original Landsat LST image confirms the applicability of the proposed framework.
Table 7 provides both non-residual corrected and residual corrected RMSE values for all the radar-based random forest downscaling experiments. Although the quantitative performance gains achieved through the inclusion of these features in the models are not substantial, qualitatively, these engineered features effectively address several challenges.
The residual correction process, as described by (1) and (2), effectively addresses certain challenges mentioned above. However, it is important to acknowledge that the application of this process can introduce boxy patterns in regions where the model's predictive capability is limited. This occurs because the residuals are obtained at a coarser scale, and the corresponding fine-scale pixels are adjusted using this constant residual value. The significance of this issue varies depending on the practical use of these downscaled products. Consequently, it is generally preferable to enhance predictive power through the incorporation of additional features rather than relying heavily on the residual correction method.
For further evaluation, the radar-based random forest downscaling is compared with optical-based random forest downscaling model (Table 2 and Table 3, Figure 4 and Figure 5). In terms of quantitative metrics, the optical-based random forest downscaling model exhibits slightly superior performance compared to the radar-based counterpart. Several factors may contribute to the optical dataset outperforming the radar dataset. Firstly, as discussed earlier, radar images typically display more pixel value variations over local regions, whereas optical bands exhibit smoother variations in pixel values. Although efforts were made to address this issue by incorporating neighboring values of radar bands as features, datasets with inherent smooth patterns generally yield better results compared to those without such patterns. Additionally, the boundary delineation observed in the pixel values of optical images between different features in the study area, such as urban and green areas, aligns with the spatial patterns of observed differences in LST values. However, the same cannot be observed for radar images. To mitigate this issue, information from the land cover image was integrated into the model, which successfully addressed the problem. However, integration of land cover information with optical data may result in even better optical-based downscaling models as emphasized in other studies [11,12]. Another characteristic that may contribute to the slightly better performance of the optical dataset is the difference in sensor characteristics between radar and optical data, particularly the disparity in viewing geometry. Sentinel-1 SAR satellites collect images using a side-looking geometry, whereas both Landsat-8 LST and Sentinel-2 optical data are acquired using a nadir-looking geometry, which may introduce some spatial pattern mismatches.
From examining Table 2 and Table 3, the downscaling models for the dates of 10th April 2020 and 28th May 2020 exhibit poorer RMSE values as compared to the model for 25th March 2020. This discrepancy could be attributed to the greater temporal difference between the acquisition of LST and radar images for the dates of 10th April 2020 and 28th May 2020 (1 day) compared to that of 25th March 2020 (same day).
In addition to the conventional random forest downscaling model, this study also introduced a CNN-based regression architecture for LST downscaling. The primary objective was to establish an end-to-end mapping between coarse-scale target values and fine-scale predictor values. As indicated in Table 6, the CNN-based architecture exhibits slightly better quantitative performance compared to the random forest model when utilizing the same optical input. However, the difference in performance is not substantial. From a qualitative standpoint, the CNN-based downscaling model preserves the structural characteristics of features within the study area, in contrast to the RF-based model. Consequently, there are minimal drastic variations observed in the CNN-based downscaled LST values across local regions (Figure 6e and Figure 6h). When using VV, VH, and land cover as predictors without residual correction, the evaluation metrics for the CNN-based downscaling model are inferior to those of the RF-based downscaling model (Table 8). For optical data, the evaluation metrics for RF and CNN models stays the same before residual correction. This discrepancy can be attributed, in part, to the fact that the feature inputs for the radar-based downscaling model, i.e., the neighbors and the land cover proportion do not correlate with the features learned by the convolution layers. Consequently, it may be erroneous to directly compare these models. However, this discrepancy could also be attributed to the fact that incorporation of any images that exhibit noisy spatial patterns like radar would always result in bad estimates due to the nature of the developed architecture. Specifically, the proposed CNN architecture attempts to map the intrinsic fine structure of the coarse resolution pixel with the value of corresponding coarse resolution pixel. Consequently, inputs lacking a smoothly varying pattern can pose challenges for the proposed CNN downscaling architecture in identifying appropriate features. If this hypothesis holds true, it highlights a limitation in the developed architecture and suggests the need for modifications. Potential modifications could involve integrating a fully connected network that functions as a traditional downscaling regression algorithm, where the inputs consist of the coarse-resolution predictors and target images. However, definitive conclusions cannot be drawn without conducting further experimentation.

5. Conclusion

This study introduced a new way to estimate land surface temperature using synthetic aperture radar data. Two different machine learning techniques, i.e., Random Forest and Convolutional Neural network, were experimented to downscale the coarse resolution LST image from 1000 m to 100 m. The information from Sentinel-1 SAR images served as predictors and was fed into the models to obtain high-resolution LST images. The achieved results were evaluated against the original LST information form Landsat-8 images at 100 m spatial resolution. Additionally, the performance of the proposed radar-based downscaling method was compared with the optical-based downscaling method. Remarkably, despite the inherent limitations of radar data such as geometric distortion, the performance of the downscaling models built with radar predictors was comparable to those constructed with optical predictors. A notable advantage of radar data over optical data is however its weather independence, enabling the downscaling models to be similarly unaffected by weather conditions. Additionally, inclusion of additional information from fully polarimetric SAR image, including second order covariance matrix, can also help to improve the performance of the proposed radar based downscaling method. Finally, one of the main challenges in generating high-resolution LST data from coarse-scale predictors is the temporal aspect. While radar images have shown promising results for spatial downscaling, they are not suitable for accurate temporal estimation. Temporal variations in LST values may not align with changes in predictors derived from Sentinel-1 GRD intensity images. To address this issue, incorporating phase information from Sentinel-1 Single Look Complex (SLC) product can help capture the temporal disparities in LST values over time. This presents an avenue for future research to explore and overcome this limitation.

Author Contributions

Conceptualization, methodology, validation, and implementation, N.P.; conceptualization, review, and editing, H.A., F.O, A.S, and M.M. All authors have read and agreed to the published version of the manuscript.

Funding

This research received no external funding.

Data Availability Statement

All the data used in this study are publicly available data.

Conflicts of Interest

The authors declare no conflict of interest.

References

  1. Zakšek, K.; Oštir, K. Downscaling Land Surface Temperature for Urban Heat Island Diurnal Cycle Analysis. Remote Sens. Environ. 2012, 117, 114–124. [Google Scholar] [CrossRef]
  2. Bai, L.; Long, D.; Yan, L. Estimation of Surface Soil Moisture With Downscaled Land Surface Temperatures Using a Data Fusion Approach for Heterogeneous Agricultural Land. Water Resour. Res. 2019, 1105–1128. [Google Scholar] [CrossRef]
  3. Zhang, F.; Zhang, L.W.; Shi, J.J.; Huang, J.F. Soil Moisture Monitoring Based on Land Surface Temperature-Vegetation Index Space Derived from MODIS Data. Pedosphere 2014, 24, 450–460. [Google Scholar] [CrossRef]
  4. Wan, Z.; Wang, P.; Li, X. Using MODIS Land Surface Temperature and Normalized Difference Vegetation Index Products for Monitoring Drought in the Southern Great Plains, USA. Int. J. Remote Sens. 2004, 25, 61–72. [Google Scholar] [CrossRef]
  5. Julien, Y.; Sobrino, J.A. The Yearly Land Cover Dynamics (YLCD) Method: An Analysis of Global Vegetation from NDVI and LST Parameters. Remote Sens. Environ. 2009, 113, 329–334. [Google Scholar] [CrossRef]
  6. Li, Z.L.; Tang, B.H.; Wu, H.; Ren, H.; Yan, G.; Wan, Z.; Trigo, I.F.; Sobrino, J.A. Satellite-Derived Land Surface Temperature: Current Status and Perspectives. Remote Sens. Environ. 2013, 131, 14–37. [Google Scholar] [CrossRef]
  7. Hu, Y.; Tang, R.; Jiang, X.; Li, Z.L.; Jiang, Y.; Liu, M.; Gao, C.; Zhou, X. A Physical Method for Downscaling Land Surface Temperatures Using Surface Energy Balance Theory. Remote Sens. Environ. 2023, 286, 113421. [Google Scholar] [CrossRef]
  8. Weng, Q.; Fu, P.; Gao, F. Generating Daily Land Surface Temperature at Landsat Resolution by Fusing Landsat and MODIS Data. Remote Sens. Environ. 2014, 145, 55–67. [Google Scholar] [CrossRef]
  9. Zhu, X.; Chen, J.; Gao, F.; Chen, X.; Masek, J.G. An Enhanced Spatial and Temporal Adaptive Reflectance Fusion Model for Complex Heterogeneous Regions. Remote Sens. Environ. 2010, 114, 2610–2623. [Google Scholar] [CrossRef]
  10. Agam, N.; Kustas, W.P.; Anderson, M.C.; Li, F.; Neale, C.M.U. A Vegetation Index Based Technique for Spatial Sharpening of Thermal Imagery. Remote Sens. Environ. 2007, 107, 545–558. [Google Scholar] [CrossRef]
  11. Hutengs, C.; Vohland, M. Downscaling Land Surface Temperatures at Regional Scales with Random Forest Regression. Remote Sens. Environ. 2016, 178, 127–141. [Google Scholar] [CrossRef]
  12. Li, W.; Ni, L.; Li, Z.L.; Duan, S.B.; Wu, H. Evaluation of Machine Learning Algorithms in Spatial Downscaling of Modis Land Surface Temperature. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2019, 12, 2299–2307. [Google Scholar] [CrossRef]
  13. Kustas, W.P.; Norman, J.M.; Anderson, M.C.; French, A.N. Estimating Subpixel Surface Temperatures and Energy Fluxes from the Vegetation Index-Radiometric Temperature Relationship. Remote Sens. Environ. 2003, 85, 429–440. [Google Scholar] [CrossRef]
  14. Bindhu, V.M.; Narasimhan, B.; Sudheer, K.P. Development and Verification of a Non-Linear Disaggregation Method (NL-DisTrad) to Downscale MODIS Land Surface Temperature to the Spatial Scale of Landsat Thermal Data to Estimate Evapotranspiration. Remote Sens. Environ. 2013, 135, 118–129. [Google Scholar] [CrossRef]
  15. Luo, X.; Chen, Y.; Wang, Z.; Li, H.; Peng, Y. Spatial Downscaling of MODIS Land Surface Temperature Based on a Geographically and Temporally Weighted Autoregressive Model. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2021, 14, 7637–7653. [Google Scholar] [CrossRef]
  16. Mahour, M.; Tolpekin, V.; Stein, A.; Sharifi, A. A Comparison of Two Downscaling Procedures to Increase the Spatial Resolution of Mapping Actual Evapotranspiration. ISPRS J. Photogramm. Remote Sens. 2017, 126, 56–67. [Google Scholar] [CrossRef]
  17. Li, J.; Wang, S.; Gunn, G.; Joosse, P.; Russell, H.A.J. A Model for Downscaling SMOS Soil Moisture Using Sentinel-1 SAR Data. Int. J. Appl. Earth Obs. Geoinf. 2018, 72, 109–121. [Google Scholar] [CrossRef]
  18. Benallegue, M.; Taconet, O.; Vidal-Madjar, D.; Normand, M. The Use of Radar Backscattering Signals for Measuring Soil Moisture and Surface Roughness. Remote Sens. Environ. 1995, 53, 61–68. [Google Scholar] [CrossRef]
  19. Hoeben, R.; Troch, P.A.; Su, Z.; Mancini, M.; Chen, K.S. Sensitivity of Radar Backscattering to Soil Surface Parameters: A Comparison between Theoretical Analysis and Experimental Evidence. Int. Geosci. Remote Sens. Symp. 1997, 3, 1368–1370. [Google Scholar] [CrossRef]
  20. Ulaby, F.T. Radar Measurement of Soil Moisture Content. IEEE Trans. Antennas Propag. 1974, 22, 257–265. [Google Scholar] [CrossRef]
  21. Yunjin, Kim; van Zyl, J. Yunjin Kim; van Zyl, J. Comparison of Forest Parameter Estimation Techniques Using SAR Data. In Proceedings of the IGARSS 2001. Scanning the Present and Resolving the Future. Proceedings. IEEE 2001 International Geoscience and Remote Sensing Symposium (Cat. No.01CH37217); IEEE, 2001; Vol. 3, pp. 1395–1397.
  22. Oh, Y.; Sarabandi, K.; Ulaby, F.T. An Empirical Model and an Inversion Technique for Radar Scattering from Bare Soil Surfaces. IEEE Trans. Geosci. Remote Sens. 1992, 30, 370–381. [Google Scholar] [CrossRef]
  23. Fung, A.K.; Li, Z.; Chen, K.S. Backscattering from a Randomly Rough Dielectric Surface. IEEE Trans. Geosci. Remote Sens. 1992, 30, 356–369. [Google Scholar] [CrossRef]
  24. Breiman, L. Random Forests. Mach. Learn. 2001, 45, 5–32. [Google Scholar] [CrossRef]
  25. Njuki, S.M.; Mannaerts, C.M.; Su, Z. An Improved Approach for Downscaling Coarse-Resolution Thermal Data by Minimizing the Spatial Averaging Biases in Random Forest. Remote Sens. 2020, 12, 1–23. [Google Scholar] [CrossRef]
  26. Li, X.; Zhang, G.; Zhu, S.; Xu, Y. Step-By-Step Downscaling of Land Surface Temperature Considering Urban Spatial Morphological Parameters. Remote Sens. 2022, 14. [Google Scholar] [CrossRef]
  27. Krizhevsky, A.; Sutskever, I.; Hinton, G.E. ImageNet Classification with Deep Convolutional Neural Networks. In Proceedings of the Advances in Neural Information Processing Systems; Pereira, F., Burges, C.J., Bottou, L., Weinberger, K.Q., Eds.; Curran Associates, Inc., 2012; Vol. 25. [Google Scholar]
  28. Lecun, Y.; Bengio, Y.; Hinton, G. Deep Learning. Nature 2015, 521, 436–444. [Google Scholar] [CrossRef] [PubMed]
  29. Wu, J.; Xia, L.; On Chan, T.; Awange, J.; Zhong, B. Downscaling Land Surface Temperature: A Framework Based on Geographically and Temporally Neural Network Weighted Autoregressive Model with Spatio-Temporal Fused Scaling Factors. ISPRS J. Photogramm. Remote Sens. 2022, 187, 259–272. [Google Scholar] [CrossRef]
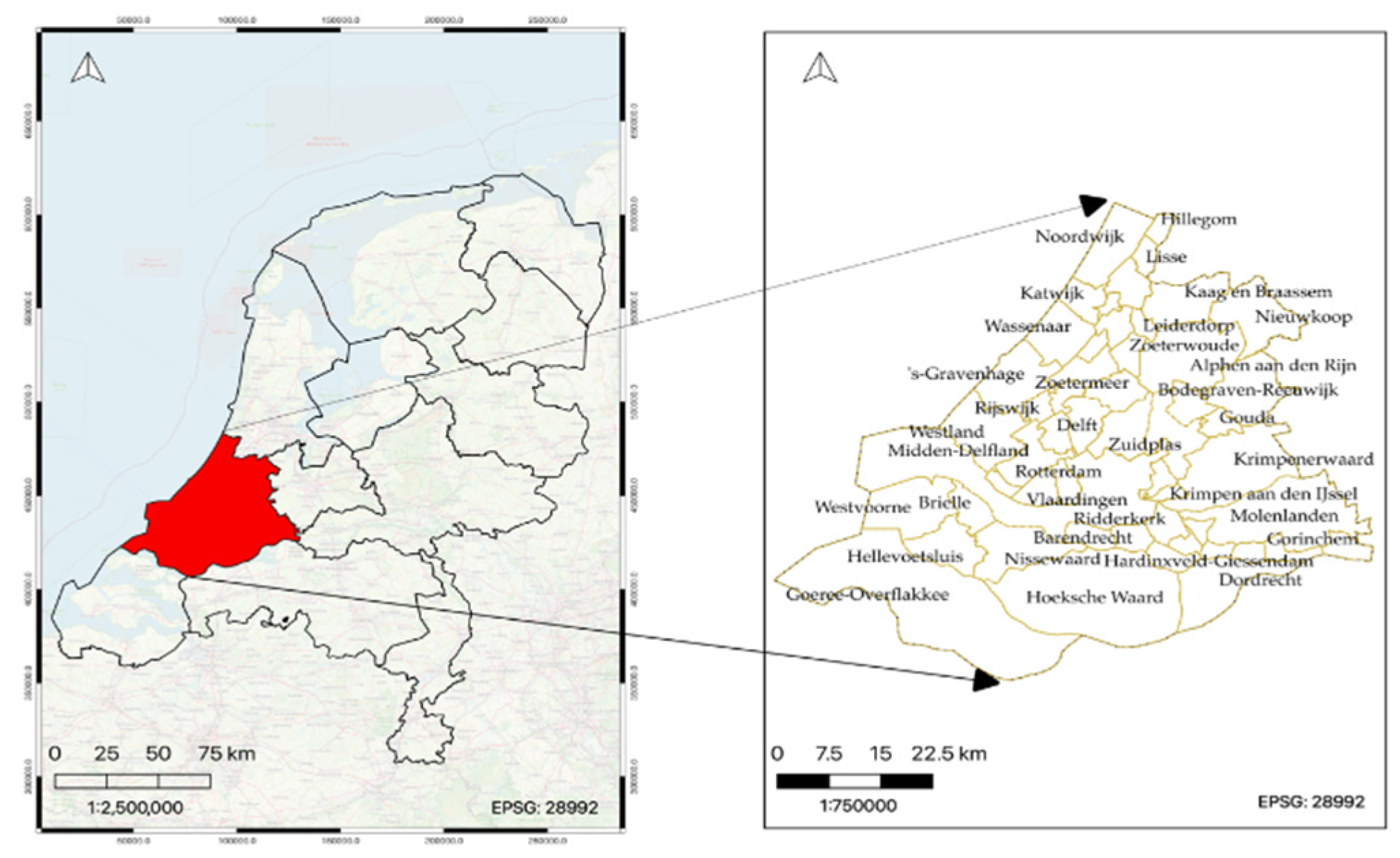
Preprints 77058 g001
Figure 1. Map showing the study area: Zuid-Holland province (left) and various municipalities in Zuid-Holland province (right).
Figure 1. Map showing the study area: Zuid-Holland province (left) and various municipalities in Zuid-Holland province (right).
Preprints 77058 g001
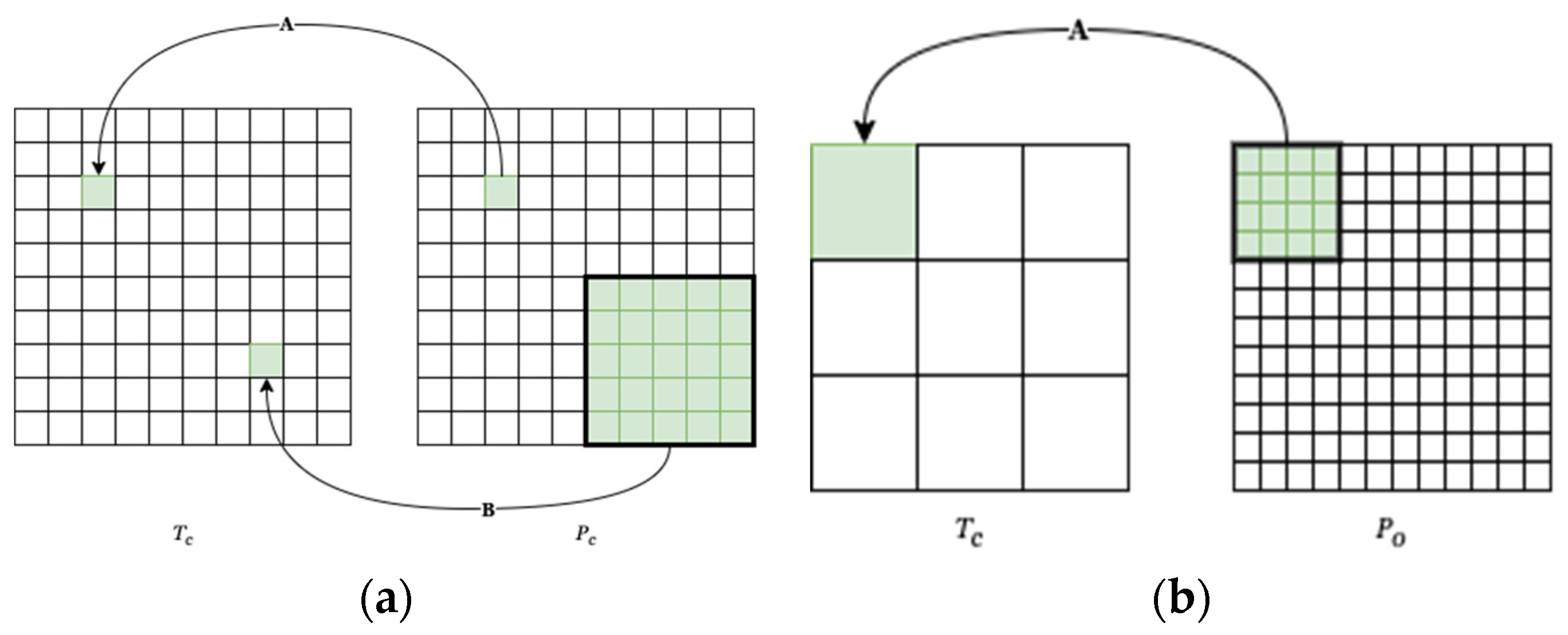
Preprints 77058 g002
Figure 2. (a) Representation of neighboring values integration procedure: connection 'A' represents traditional pixel to pixel mapping, whereas connection 'B' represents neighbourhood to pixel mapping between the predictor image Pc and the target image Tc. (b) Representation land cover proportion integration procedure: Po refers to the predictor land cover image at original 10 m resolution, whereas Tc refer to target values at 1000 m respectively.
Figure 2. (a) Representation of neighboring values integration procedure: connection 'A' represents traditional pixel to pixel mapping, whereas connection 'B' represents neighbourhood to pixel mapping between the predictor image Pc and the target image Tc. (b) Representation land cover proportion integration procedure: Po refers to the predictor land cover image at original 10 m resolution, whereas Tc refer to target values at 1000 m respectively.
Preprints 77058 g002
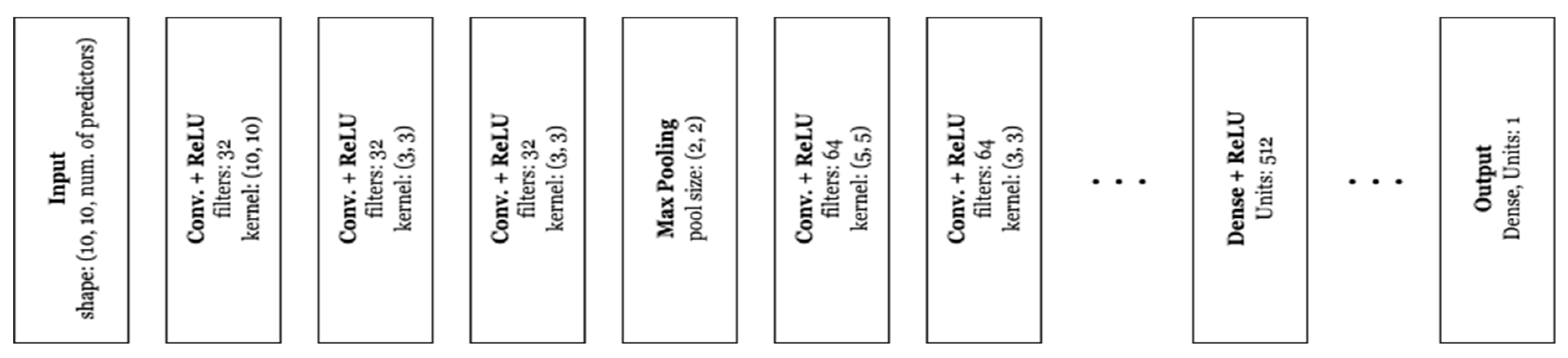
Preprints 77058 g003
Figure 3. Developed model architecture for CNN-based downscaling experiments.
Figure 3. Developed model architecture for CNN-based downscaling experiments.
Preprints 77058 g003
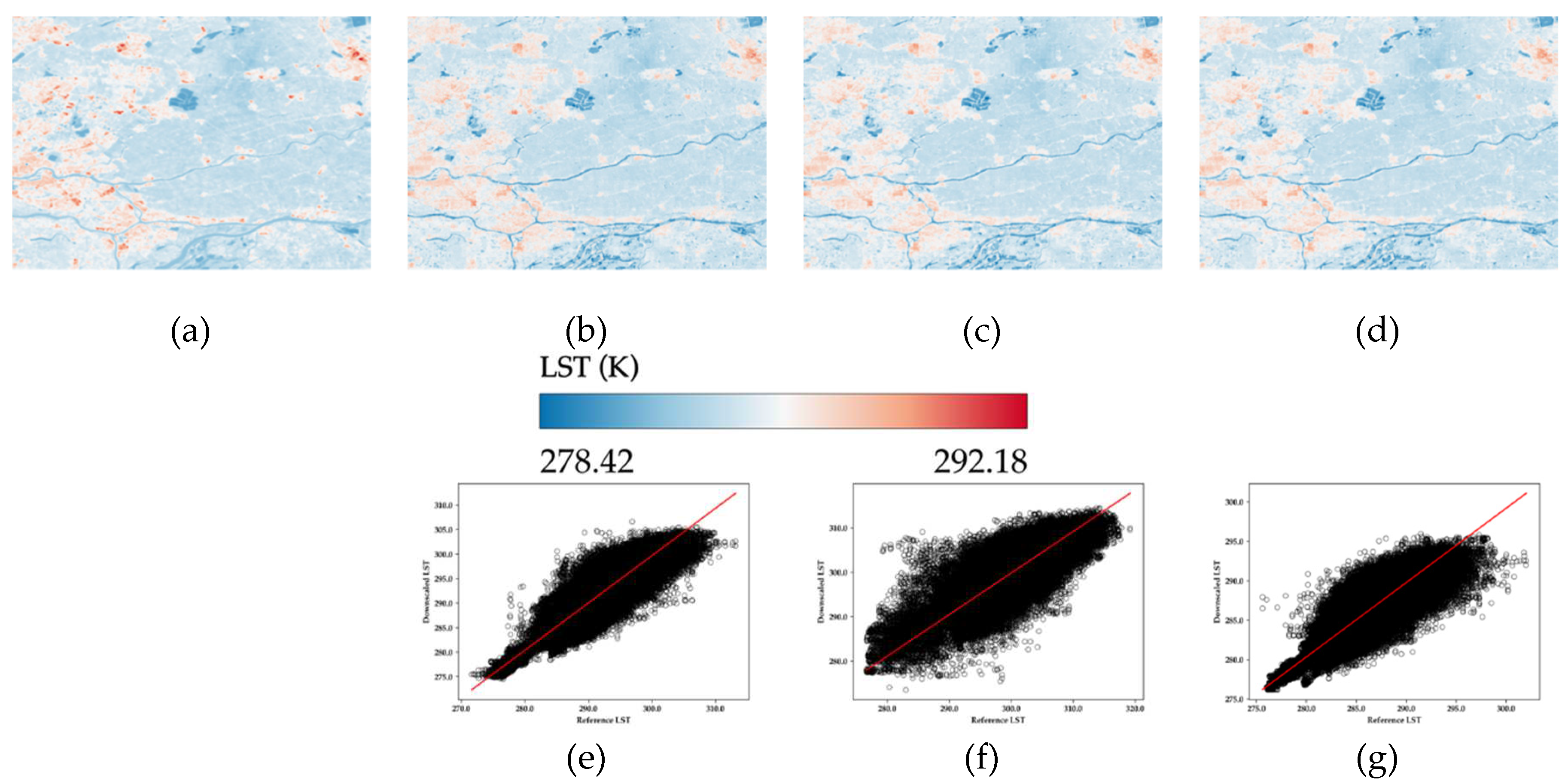
Preprints 77058 g004
Figure 4. Results of the radar-based RF downscaling experiment (SAR image acquisition date: 25th March 2020. (a) the original Landsat-8 validation LST (100 m), (b) downscaled LST (100 m) without neighbours, (c) downscaled LST (100 m) with 5x5 neighbours, (d) downscaled LST (100 m) with 5x5 neighbours and land cover. Second row represents the scatter plot between the validation Landsat-8 LST and downscaled LST (e) without neighbours, (f) with 5x5 neighbours, (g) with 5x5 neighbors and land cover.
Figure 4. Results of the radar-based RF downscaling experiment (SAR image acquisition date: 25th March 2020. (a) the original Landsat-8 validation LST (100 m), (b) downscaled LST (100 m) without neighbours, (c) downscaled LST (100 m) with 5x5 neighbours, (d) downscaled LST (100 m) with 5x5 neighbours and land cover. Second row represents the scatter plot between the validation Landsat-8 LST and downscaled LST (e) without neighbours, (f) with 5x5 neighbours, (g) with 5x5 neighbors and land cover.
Preprints 77058 g004
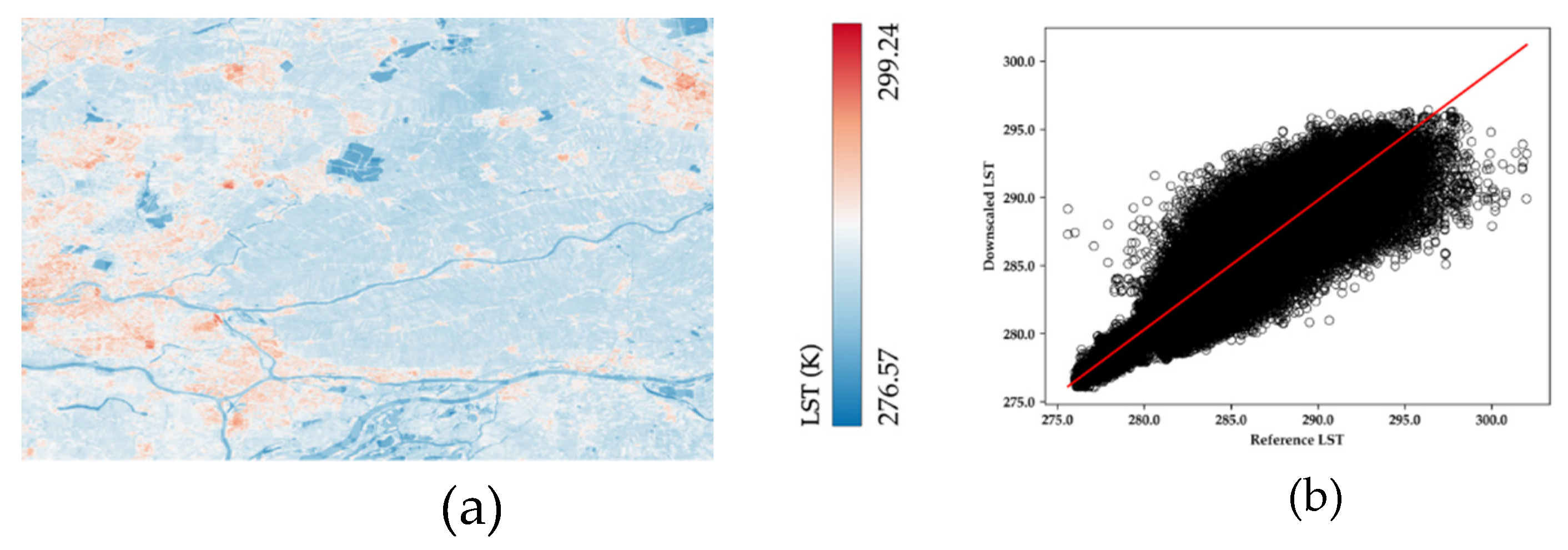
Preprints 77058 g005
Figure 5. Results of the optical based RF downscaling experiments (optical image acquisition date: 26th March 2020). (a) downscaled LST (100 m) using six spectral channels, (b) scatter plot of downscaled image versus the validation Landsat-8 LST image (100 m).
Figure 5. Results of the optical based RF downscaling experiments (optical image acquisition date: 26th March 2020). (a) downscaled LST (100 m) using six spectral channels, (b) scatter plot of downscaled image versus the validation Landsat-8 LST image (100 m).
Preprints 77058 g005
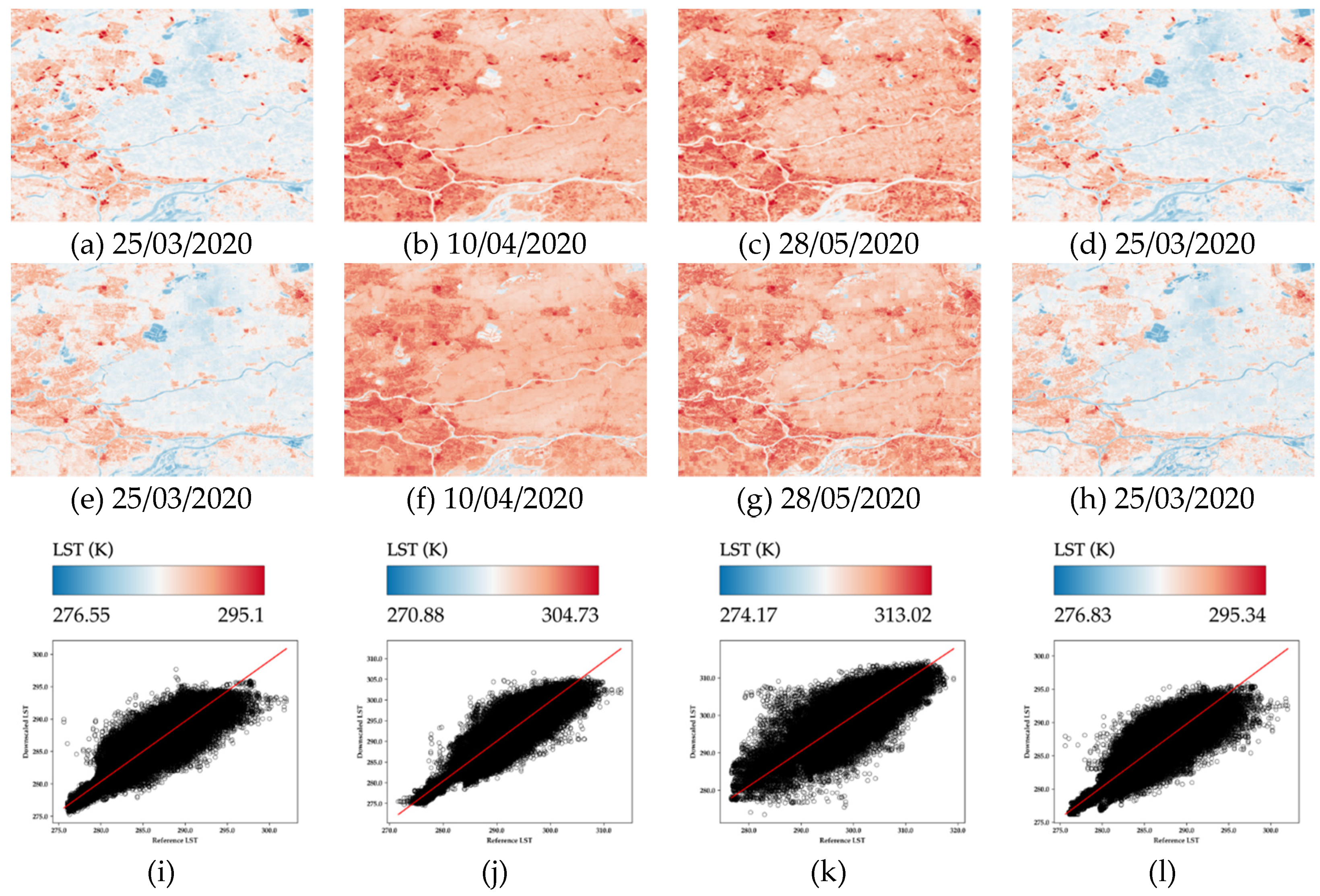
Preprints 77058 g006
Figure 6. Results from the CNN-based downscaling experiments. First row displays Landsat-8 validation LST (100 m) for different dates. Second row shows generated downscaled LST for different dates using CNN. The input predictors in (e, f, & g) are VV, VH, and land cover, while in (h) is optical data. The third row displays the scatterplot with regression line between the downscaled (second row) and validation LST (first row) at 100 m.
Figure 6. Results from the CNN-based downscaling experiments. First row displays Landsat-8 validation LST (100 m) for different dates. Second row shows generated downscaled LST for different dates using CNN. The input predictors in (e, f, & g) are VV, VH, and land cover, while in (h) is optical data. The third row displays the scatterplot with regression line between the downscaled (second row) and validation LST (first row) at 100 m.
Preprints 77058 g006
Preprints 77058 g007
Figure 7. Effect of neighborhood feature inclusion in downscaled LST’s. (a) area of interest: Lansingerland. (b and d) represents downscaled LST’s without inclusion of neighbors and (c and e) with inclusion of 5x5 neighbors. Here, (b and c) are achieved downscaled LST’s before residual correction and (d and e) after residual correction.
Figure 7. Effect of neighborhood feature inclusion in downscaled LST’s. (a) area of interest: Lansingerland. (b and d) represents downscaled LST’s without inclusion of neighbors and (c and e) with inclusion of 5x5 neighbors. Here, (b and c) are achieved downscaled LST’s before residual correction and (d and e) after residual correction.
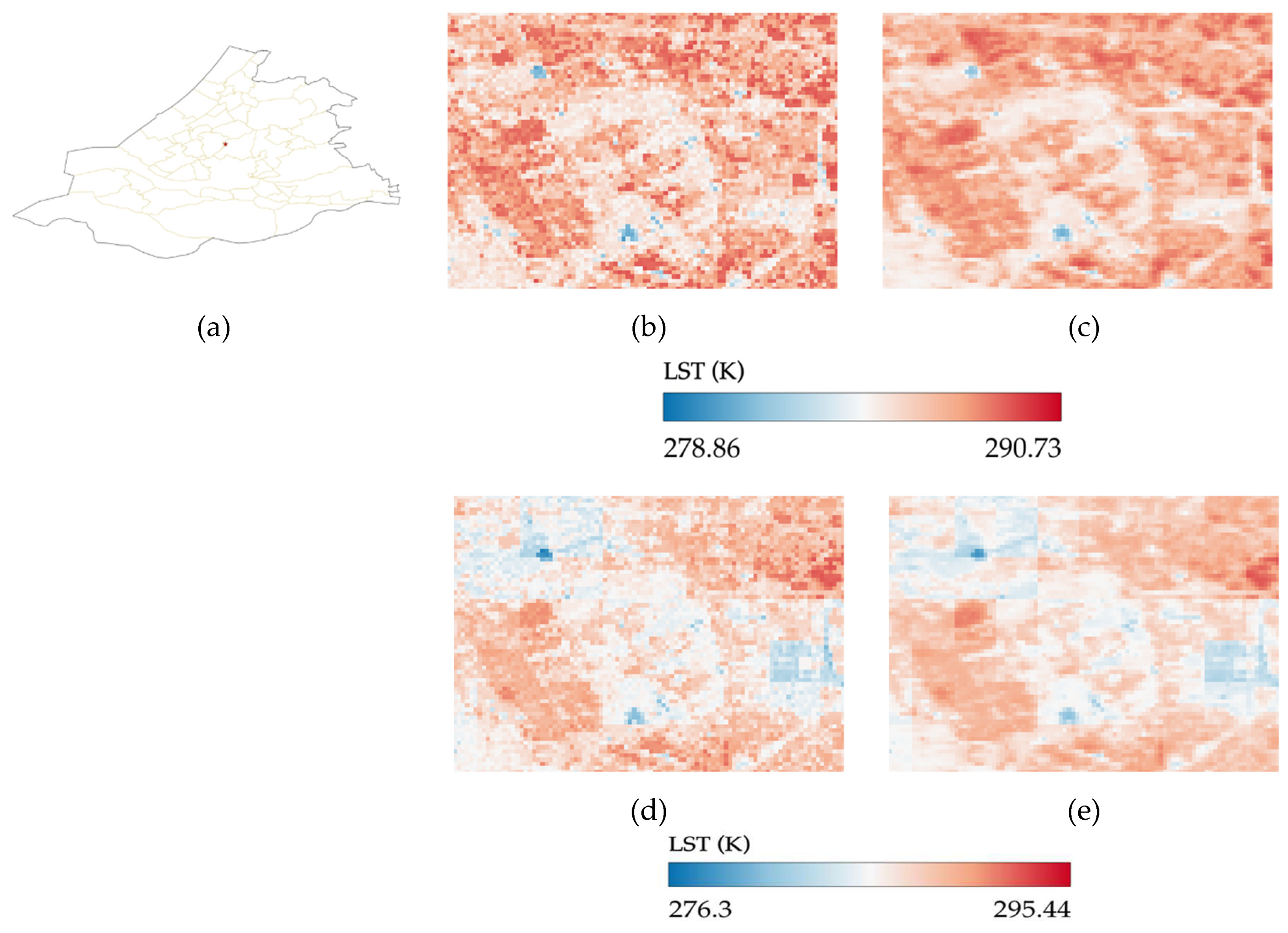
Preprints 77058 g007
Preprints 77058 g008
Figure 8. Effect of land cover feature inclusion in downscaled LST’s. (a) area of interest: Wassenar, (b) represents the mask image of the tree cover class with green color, (c and f) represents the achieved downscaled LST’s with inclusion of 5x5 neighbors, and (d and g) with inclusion of 5x5 neighbors and land cover. (e and h) show the corresponding Landsat-8 validation LST. Here, (c and d) are achieved downscaled LST’s before residual correction and (f and g) after residual correction.
Figure 8. Effect of land cover feature inclusion in downscaled LST’s. (a) area of interest: Wassenar, (b) represents the mask image of the tree cover class with green color, (c and f) represents the achieved downscaled LST’s with inclusion of 5x5 neighbors, and (d and g) with inclusion of 5x5 neighbors and land cover. (e and h) show the corresponding Landsat-8 validation LST. Here, (c and d) are achieved downscaled LST’s before residual correction and (f and g) after residual correction.
Preprints 77058 g008
Table 1. Overview of the datasets used for this study.
Table 1. Overview of the datasets used for this study.
Dataset [spatial resolution], [Google Earth Engine Tag] Acquisition Date [Time] Use case
Landsat-8 LST [60 m],
[“LANDSAT/LC08/C02/T1_L2”]		 25-03-2020 [10:33], 10-04-2020 [10:33],
28-05-2020 [10:33]		 Target variable (Aggregated 1000 m LST),
Validation data (Original 100 m LST)
Sentinel-1 SAR [10 m],
[“COPERNICUS/S1_GRD”]		 25-03-2020 [17:25], 11-04-2020 [17:33],
29-05-2020 [17:33]		 Predictor variable
ESA WorldCover v100 [10 m],
[“ESA/WorldCover/v100”]		 One image for the entire year of 2020 Predictor variable
Sentinel-2 MSI [10 m],
[“COPERNICUS/S2_SR_HARMONIZED”]		 26-03-2020 [10:46] Predictor variable
Table 2. Evaluation metrics for the radar- and optical-based downscaling experiments.
Table 2. Evaluation metrics for the radar- and optical-based downscaling experiments.
Radar Optic
25/03/2020 10/04/2020 28/05/2020 25/03/2020
Without neighbors With 5x5 neighbors 5x5 neighbors and land cover Without neighbors With 5x5 neighbors 5x5 neighbors & land cover Without neighbors With 5x5 neighbors 5x5 neighbors & land cover With six bands
RMSE 1.44 1.25 1.21 2.10 1.93 1.70 2.76 2.61 2.55 1.12
Correlation Coefficient (r) 0.89 0.92 0.93 0.94 0.95 0.96 0.89 0.91 0.91 0.93
Coefficient of determination (R2) 0.80 0.84 0.86 0.88 0.90 0.92 0.80 0.82 0.83 0.87
Table 3. RMSE of all the downscaling experiments by each land cover class in the study area.
Table 3. RMSE of all the downscaling experiments by each land cover class in the study area.
Radar predictors Optical predictors
25/03/2020 10/04/2020 28/05/2020 25/032020
Without neighbors With 5x5 neighbors 5x5 neighbors & land cover Without neighbors With 5x5 neighbors 5x5 neighbors & land cover Without neighbors With 5x5 neighbors 5x5 neighbors & land cover With 6 optical bands
Tree Cover 1.73 1.51 1.20 2.30 2.19 1.67 3.19 3.14 3.31 1.22
Shrubland 3.11 3.03 2.29 4.41 4.48 2.48 6.52 6.60 3.24 2.10
Grassland 1.14 1.00 0.96 1.67 1.56 1.41 2.35 2.19 2.07 0.95
Cropland 1.61 1.42 1.05 2.55 2.18 1.70 3.34 3.32 3.41 0.96
Built-Up 1.83 1.62 1.98 2.25 2.22 2.29 2.81 2.76 3.21 1.68
Bare/sparse vegetation 2.81 2.58 2.10 3.22 3.14 2.81 4.85 4.47 4.30 1.81
Permanent water bodies 1.37 1.09 1.03 2.31 2.01 1.73 2.77 2.45 1.79 0.92
Herbaceous wetland 1.93 1.65 1.37 2.88 2.68 1.91 3.39 3.07 2.36 1.68
Table 4. Evaluation metrics of the CNN-based downscaling experiments.
Table 4. Evaluation metrics of the CNN-based downscaling experiments.
with VV, VH, and land cover with six optical bands
25/03/2020 10/04/2020 28/05/2020 25/03/2020
RMSE 1.04 1.44 2.23 1.09
Correlation Coefficient (r) 0.94 0.97 0.93 0.94
Coefficient of Determination (R2) 0.89 0.94 0.87 0.88
Table 5. RMSE of the CNN-based downscaling experiments for each land cover.
Table 5. RMSE of the CNN-based downscaling experiments for each land cover.
with VV, VH, and land cover with six optical bands
25/03/2020 10/04/2020 28/05/2020 25/03/2020
Tree Cover 1.09 1.50 3.12 1.18
Shrubland 2.18 2.60 3.45 2.36
Grassland 0.87 1.18 1.97 0.92
Cropland 0.99 1.53 2.18 1.04
Built-Up 1.55 1.83 2.52 1.58
Bare/sparse vegetation 2.16 2.60 3.71 2.04
Permanent water bodies 0.85 1.42 1.86 0.89
Herbaceous wetland 1.50 3.21 3.66 1.57
Table 6. Evaluation metrics of the optical based RF and CNN downscaling models.
Table 6. Evaluation metrics of the optical based RF and CNN downscaling models.
with six optical bands
RF CNN
RMSE 1.12 1.09
Correlation Coefficient (r) 0.93 0.94
Coefficient of Determination (R2) 0.87 0.88
Table 7. RMSE before and after residual correction of radar-based RF downscaling experiments.
Table 7. RMSE before and after residual correction of radar-based RF downscaling experiments.
Without neighbors With 5x5 neighbors With 5x5 neighbors and land cover
Without   Δ T With   Δ T Without   Δ T With   Δ T Without   Δ T With   Δ T
25/03/2020 1.80 1.44 1.63 1.25 1.41 1.21
10/04/2020 2.73 2.10 2.56 1.93 2.20 1.70
28/05/2020 3.51 2.76 3.38 2.61 3.19 2.55
Table 8. RMSE values for RF and CNN downscaling models before and after residual correction.
Table 8. RMSE values for RF and CNN downscaling models before and after residual correction.
RF CNN
Without   Δ T With   Δ T Without   Δ T With   Δ T
Predictors derived from VV, VH and land cover 1.41 1.21 2.09 1.04
Predictors derived from six bands of optical imagery 1.39 1.12 1.39 1.09
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.
Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.
Prerpints.org logo

Preprints.org is a free preprint server supported by MDPI in Basel, Switzerland.

facebook logotwitter logolinkedin logo
MDPI Initiatives
Important Links
Subscribe

Disclaimer

Terms of Use

Privacy Policy

© 2024 MDPI (Basel, Switzerland) unless otherwise stated