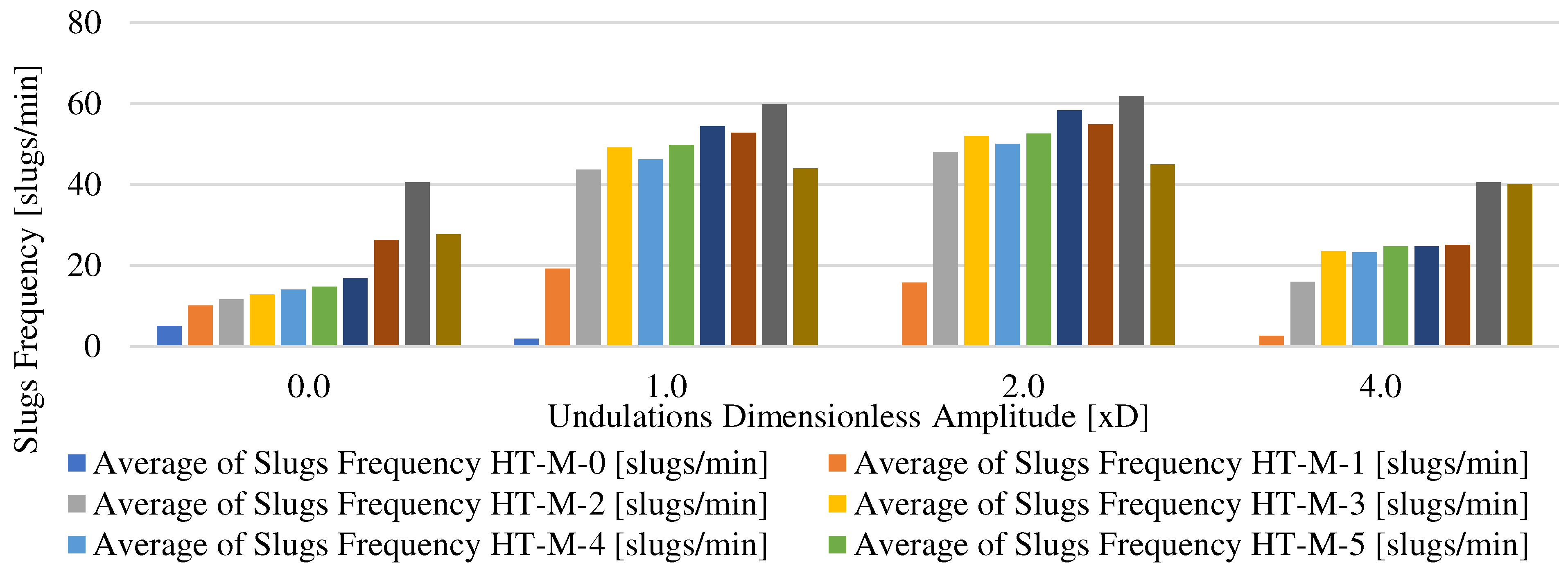Experimental and Numerical Investigations on the Effect of Unconventional Oil Wells Lateral’s Undulating Amplitude on Transient Multiphase Flow Behavior

The increasing popularity of unconventional wells has sparked a heightened interest in evaluating and predicting their production performance. With the use of extended reach well structures, these wells are able to generate and access larger reservoir volumes. Hence, it is crucial to understand how the well's lateral trajectory affects its transient production performance. The assessment of lateral trajectory undulating amplitude effect on the flow behavior is performed in the current study based on the experimental results obtained at the University of North Dakota, Undulated Two-Phase (UTP) Flow Loop, injecting air and water mixture through a variable undulating amplitude section followed by a vertical section. The experiments showed that the undulating amplitude increase induced lower translational velocity, frequency, and length, with a consistent slug acceleration through the system profile from the inlet to the vertical section and a decreasing frequency when the slugs travel through the vertical section. Measured data shows that an increase of the horizontal pressure losses and variability is expected with a higher undulation amplitude, translating the fact that larger instabilities are observed for higher amplitudes. The numerical simulation predicted lower translational velocity and frequency, higher slug’s lengths, and similar vertical pressure losses when compared to the experimental results.

Keywords:

Subject: Engineering - Energy and Fuel Technology

1. Introduction

Horizontal well technology plays a crucial role in the extraction of unconventional resources. The implementation of multistage hydraulic fracturing along the lateral section of these wells enhances the production of tight oil and gas-rich formations, such as the Middle Bakken and Three Forks in the Bakken Basin. As demonstrated by the research conducted by [1], the optimal production of these formations can be achieved through the utilization of horizontal wells with a measured-to-vertical depth ratio of 2 or higher. The Bakken wells are extended-reach wells. Horizontal liquid-producing wells present a flow stability challenge that seems inherent to their structure, as stated by [2]. The severe slugging creates high-pressure oscillations downhole along the lateral section, which do affect the integrity of the hydraulic fracture as demonstrated by [3], and can trigger proppant displacement and fracture closure due to excessive drawdown as demonstrated by [4].

Based on the literature review, it is evident that flow instabilities play a crucial role in the evaluation of horizontal oil well production performance. As such, any factors that influence flow instabilities and oscillations are of significant interest for further understanding. The transient flow behavior is dependent on the fluid properties, flow conditions, and system structure. This study focuses specifically on the effect of well trajectory characteristics on the transient behavior of horizontal wells. [5,6,7] experimentally and numerically studied the effect of trajectory on the flow behavior of horizontal wells. Although focusing on gas wells liquid loading, the mechanisms are similar to the oil wells cases, which showed that the effect of the lateral section on the flow regime is not seen at high velocities. However, the effect of the well trajectory is more pronounced as the velocity decreases. This translates into the fact that as the well moves into more gravity-dominated flow conditions, the effect of its structure becomes more dominant.

The existing literature has explored the impact of well lateral section trajectory on performance, but mostly focusing on single undulation effects, but not the multiple undulations effect on flow performances as per [8]. The fundamental experimental and modeling study shows that for constant flow conditions, liquid film fallback and accumulations are observed for toe-down cases at the low gas flow rate, while, a stratified flow regime with no liquid accumulations in the lateral section is observed for the toe-up configuration. However, for very low gas flowrate, severe slugging is observed with high pressure and rates fluctuations. In the case of one undulation configuration, the study shows that for a moderate gas flow rate, a stratified wavy flow regime is observed, while the low gas flowrate generates slugs at the lowest undulation point, and slug flow is observed for the upward pipe section with large liquid accumulations in the lateral section. Convex (hump) undulations generate higher instabilities when compared to concave (sump) undulations. The study focused on one undulation without considering the effect of the undulation amplitude and multiple undulations. A more practical simulation study presented in [9] showed that the well geometry with 5 undulations, where one hump, sump, toe-up, and toe-down have different impacts on the production performance, especially in low production rates. The optimal configuration for high productivity cases is a toe-up, as opposed to the low productivity formations which perform better with toe-down trajectories, reducing the severity of fluctuations.

No literature focuses on the effect of the amplitude of the undulations. As a higher undulating amplitude creates longer path for the same distance due to higher sinuosity, a higher vertical depth variation along the lateral. It is of importance to understand the effect of the amplitude of the undulation on the transient flow behavior by transient behavior or the steadiness, in case of slugging cyclicity, three phases (oil, gas, and water) flow rates, slugs translational velocity, frequency and length, lateral pressure loss and vertical pressure loss, and the time variability of lateral section pressure and top vertical section. The mentioned parameters constitute the set of key performance indicators (KPIs’) that are used to analyze the experimental test data.

2. Materials and Methods

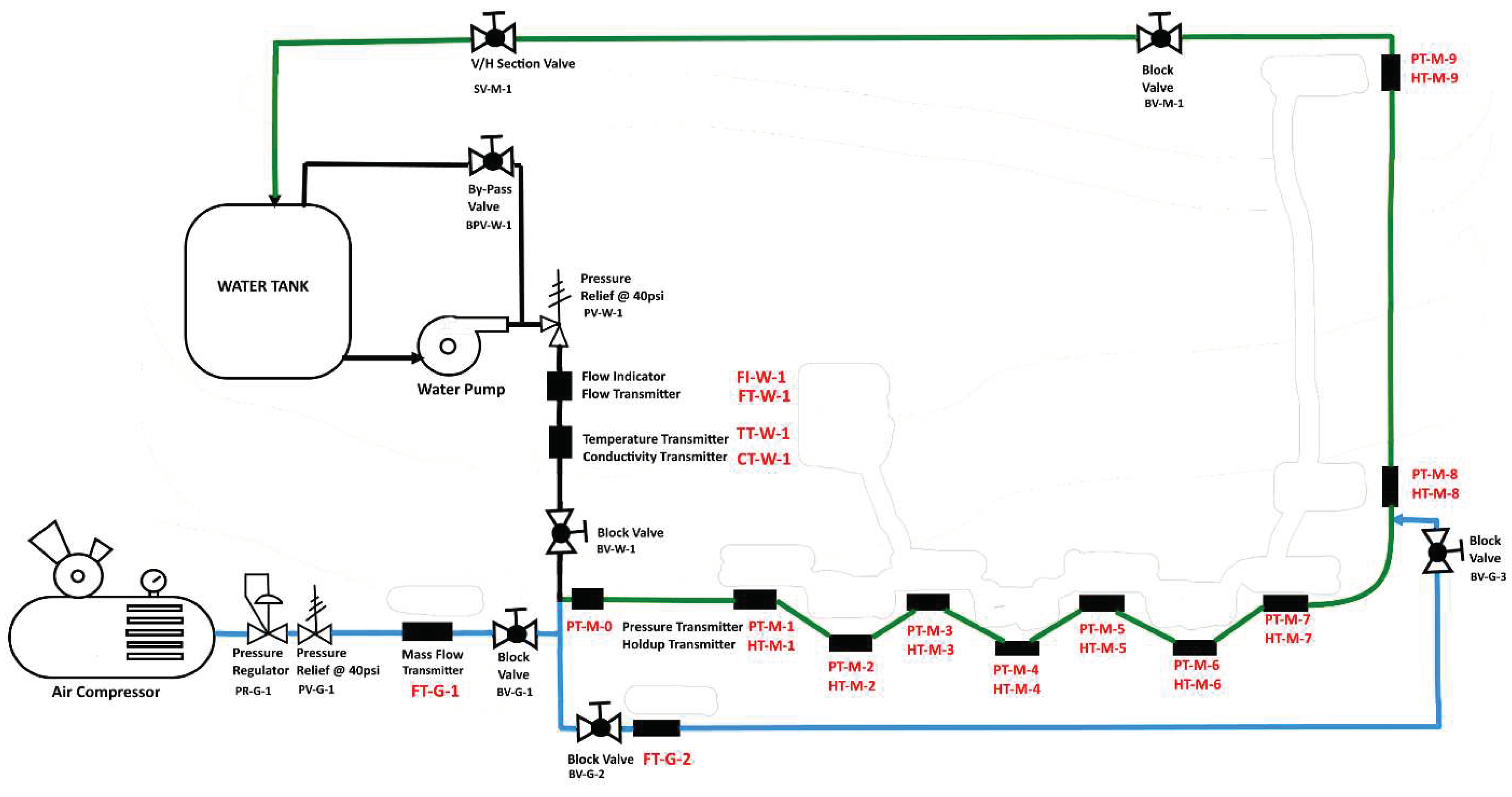
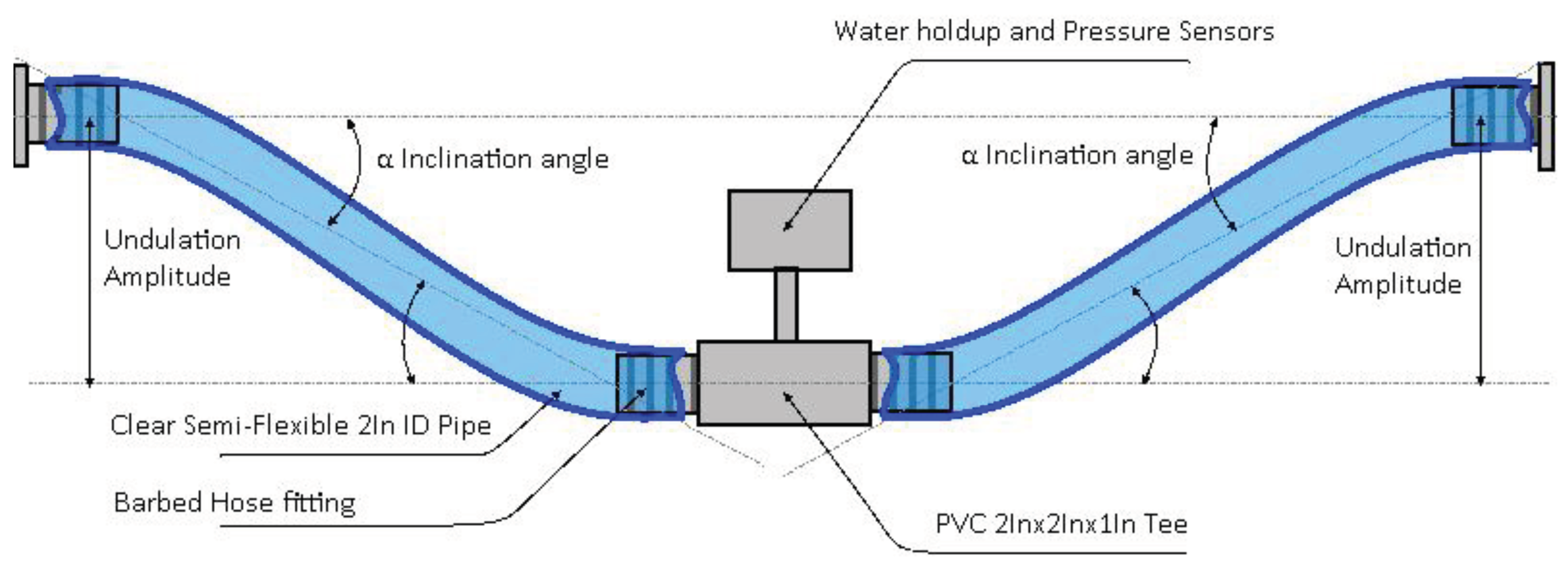
The experimental system consists of the undulated two-phase (UTP) flow loop built for the purpose of this study at the University of North Dakota Petroleum Engineering Department. It is equipped with undulations made of a semi-flexible clear 2” -ID pipe with the possibility to adjust the amplitude of each undulation. As illustrated in Figure 1 the facility is equipped with a water tank that serves as a two phases separator, and from which the liquid is pumped to the desired test inlet pressure by the centrifugal pump. The liquid is metered through a turbine followed by an ultrasonic flowmeters before passing through a control valve and a block valve joining then the mixing tee. The air is compressed by the reciprocating compressor and accumulated in the compressor tank to provide a stable air flowrate and avoid affecting the test flow regimes. The air passes through the filters set, pressure regulator, mass flowmeter and check valve, control valve, and block valve before joining the mixing tee. At the mixing tee, a pressure transmitter captures the test section inlet pressure value then the undulated sections follow with a pressure and water holdup measurement at each inflection point. A maximum of three undulations configuration is achievable. Each piece of equipment, fitting, and instrument is tagged with a physical label and electronically through the DAQ National Instruments® data acquisition system as shown in Figure 1 in red for instruments and fittings (valves). Worth to be mentioned that the flow loop is equipped with a gas lift feature which has not been used for the present study.

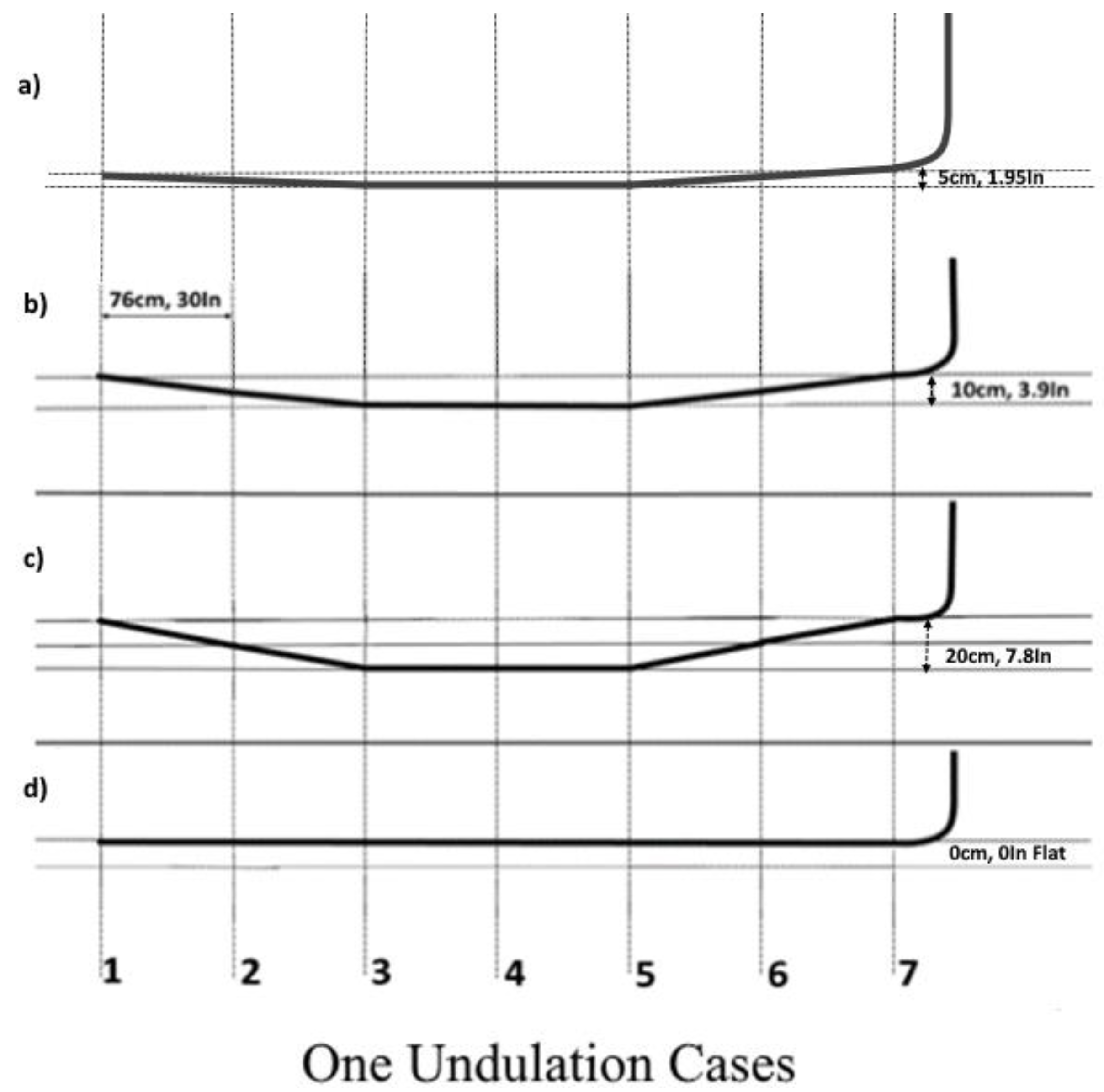
The undulation amplitude is the distance from the horizontal hypothetical line starting at the test section inlet height to the horizontal line formed by the lower inflection points, as shown in Figure 1 for the overall test section structure and Figure 2 for one undulation characteristics. Inclination angle, and undulation amplitude, the variation of the amplitude are obtained by adjusting the height (vertical position) of the water holdup probe and pressure sensor tee. The vertical position could be adjusted in such a way that it produced undulating amplitudes of 0, 5, 10, and 20 cm, representing 0, 1, 2, and 4 times the diameter in terms of dimensionless undulation amplitude.

The operation of the experimental facility is carried out utilizing the equipment specifications detailed in Table 1.

Figure 3 presents a visual representation of the flow loop facility from lateral perspective.

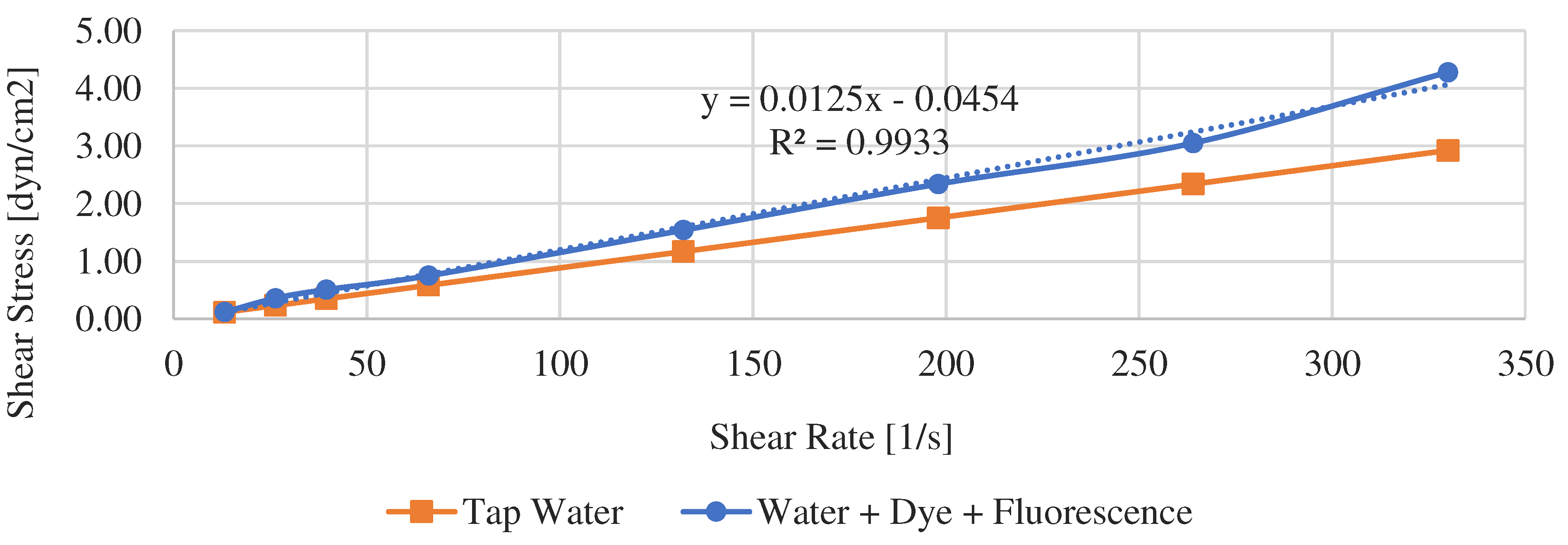
The liquid mixture is made of water, blue dye (unknown composition, and a fluorescent substance based on strontium aluminate. Both products are Non toxic and NSF-compliant. However, the dye and fluorescent product do influence the water viscosity, which leads to higher friction, as shown in Figure 4.

Methodology

To capture the effect of the undulating amplitude on the transient flow behavior as explained in the introduction, the amplitude of the undulations is varied while the flow rates, pressures and water holdups are measured for 10 minutes with a 10-ms data sampling rate. As shown in Table 2, the undulating amplitudes realized for the study are 0, 5, 10, and 20 cm representing 0, 1, 2, and 4 dimensionless amplitudes, which is defined as the ratio of the absolute amplitude value to the undulated pipe diameter value, here 2 In. the inclination angle varies from 3.77⁰ to a maximum of 15.26⁰ as in Table 2. A total of eight configuration cases were investigated. For each case, a set of 10 flow conditions were realized.

The pressure, air and water flowrates and water holdups are acquired in real-time, then were analyzed using Cross-correlation MATLAB® script to capture the lag and calculate the translational velocity as defined by [11]. Then the film and slug regions were identified so that the slug lengths, translational velocity, and frequencies are estimated using MATLAB® scripts.

With regards to the pressure losses, the vertical pressure difference between the PT-M-8 and PT-M-9 is calculated for each time point. Then the average of a time series is calculated and the time-averaged value is reported for each configuration. The horizontal pressure difference is calculated between Pt-M-1 and PT-M-7, representing the lateral section inlet and outlet (elbow), respectively. Then the time average value is calculated with a simple arithmetic average. Finally, to estimate (quantify) the flow instability, the time variability of the pressure is calculated using the standard deviation of the measured pressure time series.

Table 2. Experimental cases, undulating amplitude, and number configuration.

Case	Code	Number of Undulations	Position	Amplitude [cm]	Angle [⁰]
1	1U20A	1	-20	20	15.26
2	1U10A	1	-10	10	7.56
3	1U5A	1	-5	5	3.77
4	0U0A	0	0	0	0.00

In terms of flow conditions, 10 conditions were experimented, called A, B, C, D, E, F, G, H, I, and J for convenience. The flow conditions are performed for each undulation configuration case, as shown in Table 3. Spanning liquid, and air superficial velocities of moderate to low values, similar to the superficial velocities range that can be encountered in horizontal wells laterals, with a liquid superficial velocity ranging from 0.26 to 2.86 ft/s, and air velocity range from 0.80 to 25.21 ft/s were recorded.

The experimental facility is also modeled in the transient multiphase flow simulator OLGA®, for comparison and validation purposes. The same system flow conditions, and geometry (amplitude and number of undulations) were pricesely replicated in the simulaton, as shown in Figure 5.

3. Experimental Results

The experimental results consist of the variations of the time averaged slug characteristics, i.e., slug length, frequency and translational velocity, and the time averaged pressure losses changes, i.e., horizontal and lateral pressure loss and variability of pressure at the elbow as measured at PT-M-7 location shown in Figure 1.

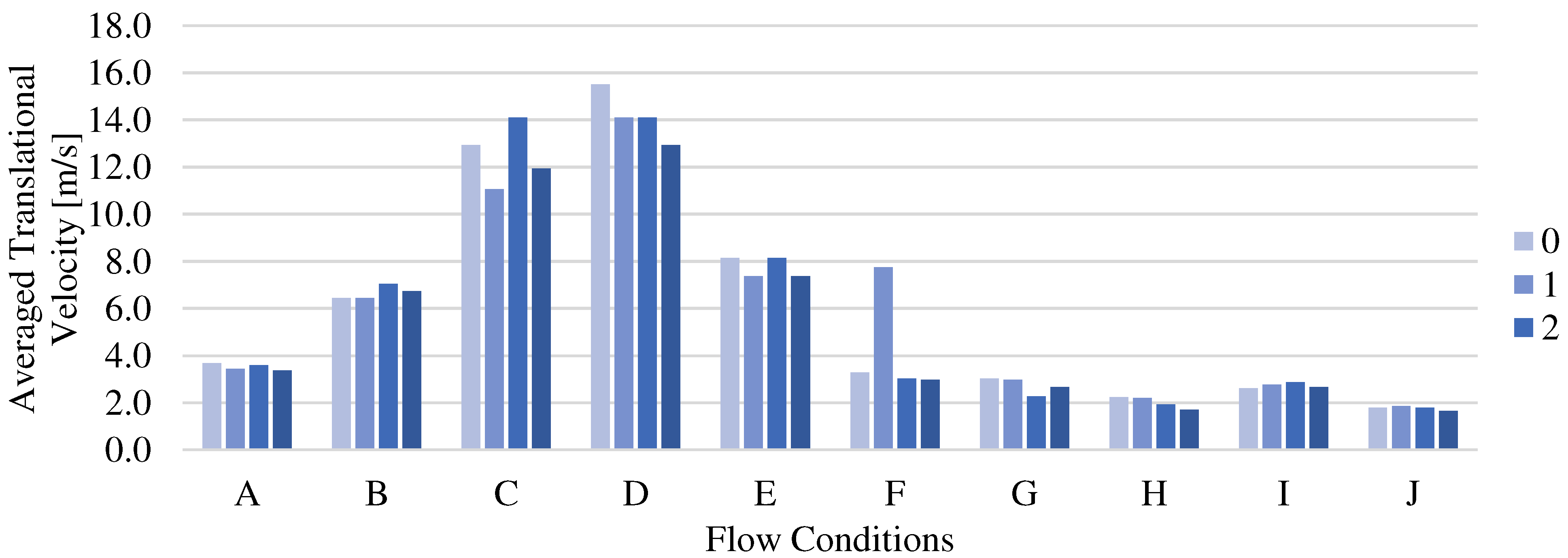
The slug characteristics are highly dependent on the flow conditions as shown in Figure 6. However, two behaviors can be distinguished. One behavior is for flow conditions with relatively high kinetic energy due to the higher superficial air and water velocities representing by cases of A, B, C, D, and E cases as previously shown in Table 3. For these cases, higher slugs translational velocities are observed, with a declining trend (Except for flow Condition B) with respect to undulating amplitude. The second behavior to be mentioned is for lower kinetic energy cases represented by cases of F, G, H, I, and J, where the translational velocity remains lower than 3.5 m/s and stable with respect to undulating amplitude. It is also important to notice that the slugs move at velocities higher than both phases’ superficial velocities.

In terms of slug frequency, the overall trend is downward, meaning that for higher undulation amplitude, lower slug frequency is observed as reported in Figure 7. It is worth noting that 50% of the cases shows that a dimensionless amplitude of 1 generates the maximum slug frequency.

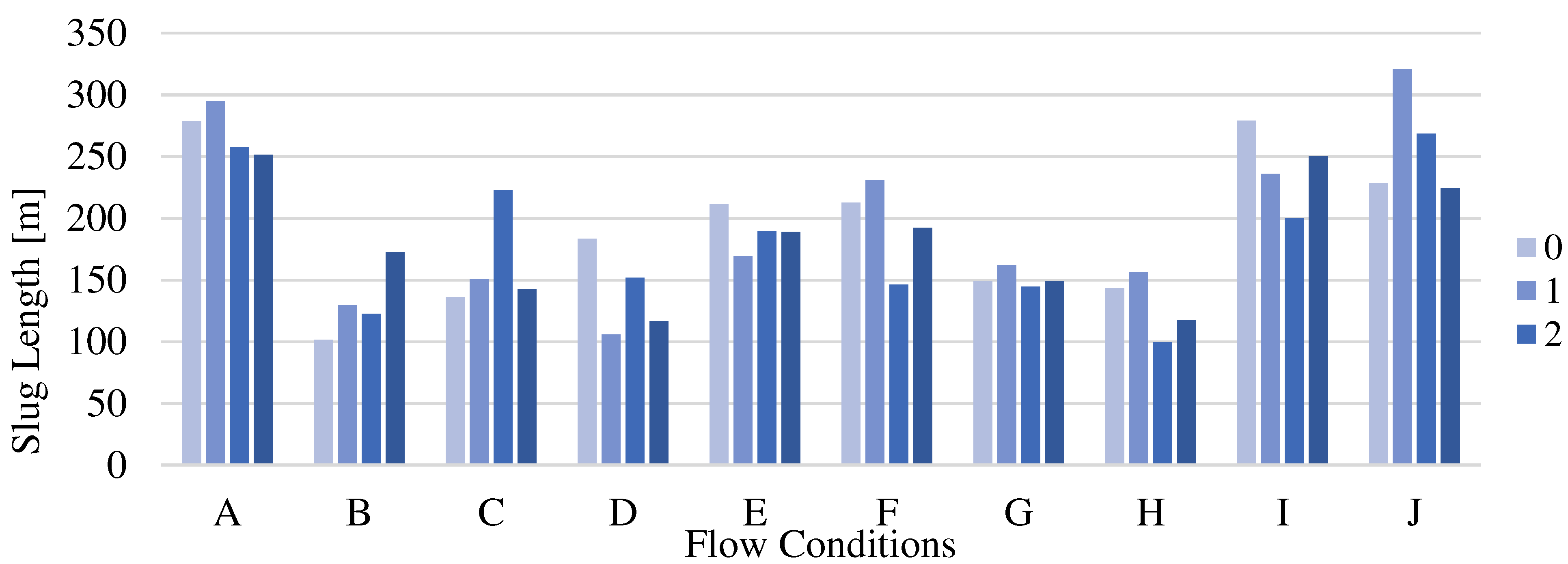
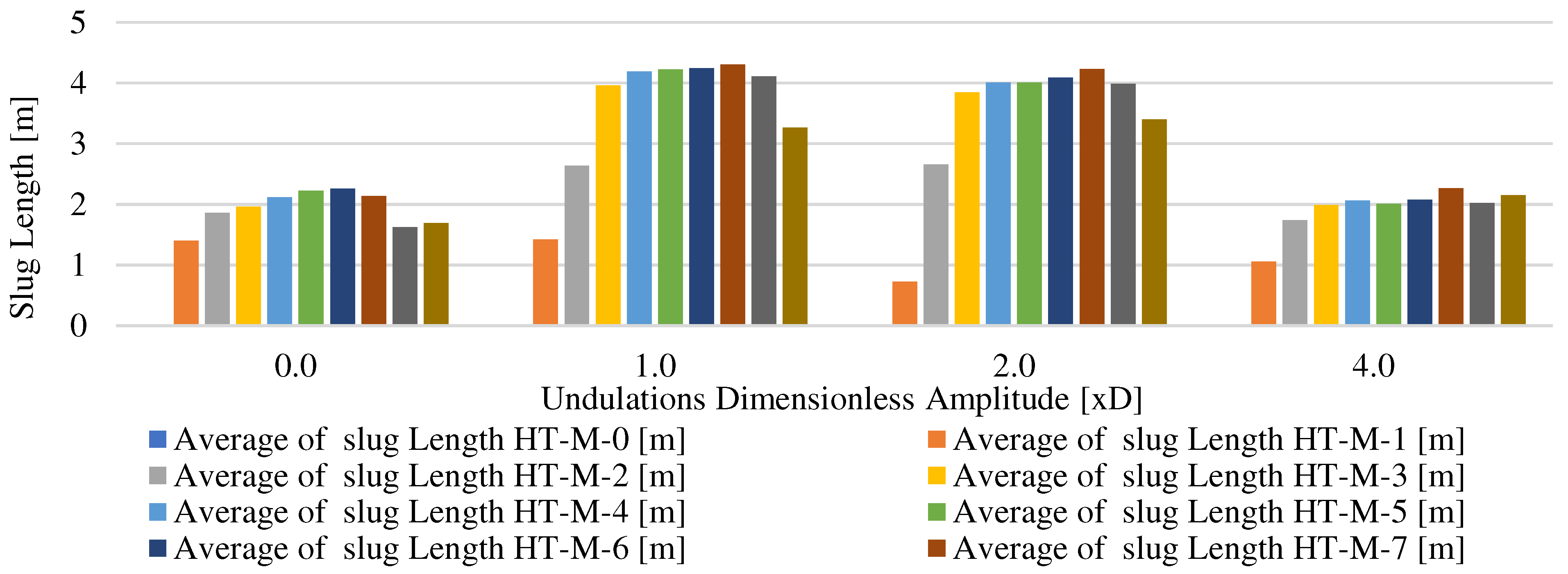
Slug length shows a bell-shaped result with regards to the undulating amplitude with an overall highest length in intermediate dimensionless undulation amplitude and lowest values at highest amplitude for the investigated flow conditions as shown in Figure 8. No dependency on kinetic energy (Cases A, B, C, D, E versus Cases F, G, H, I, J) can be inferred from the reported results as no clear trend can be identified.

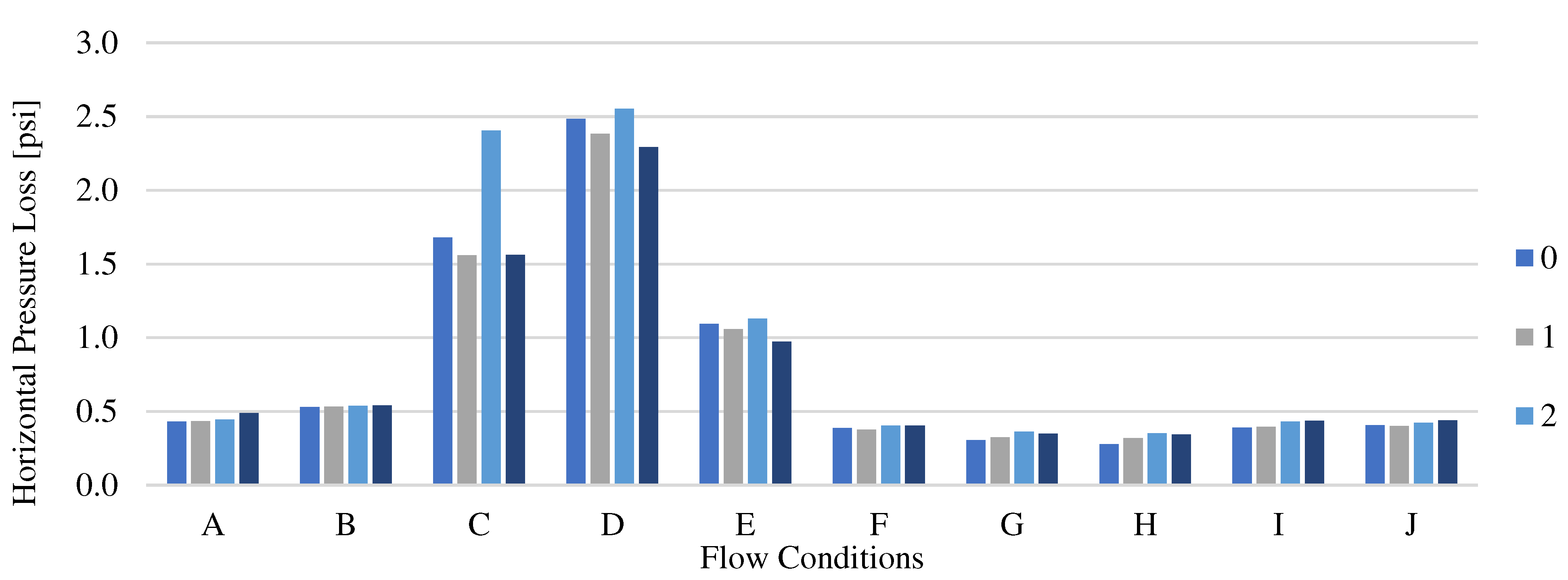
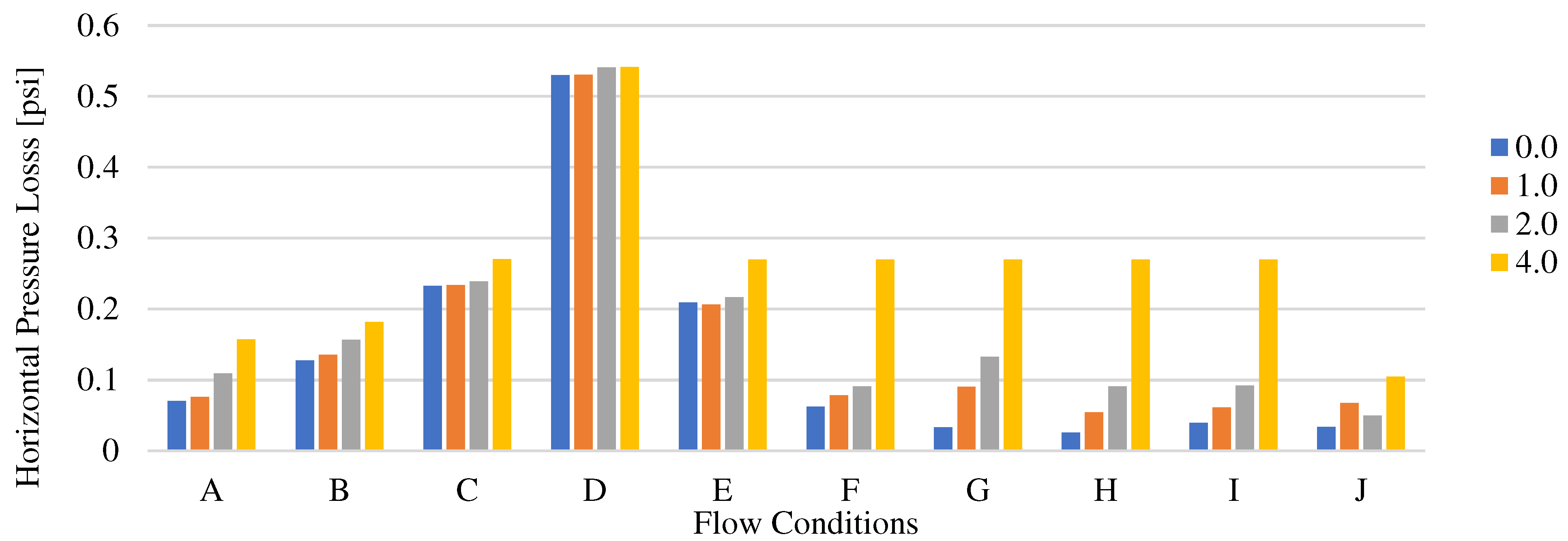
Regarding horizontal pressure loss, although a slight increase with respect to the amplitude is consistently observed (except for flow conditions C and D), the value of lateral pressure loss is relatively constant and weakly depend on the amplitude of the lateral undulations. As expected, dependency on the flow conditions is observed. For higher kinetic energy cases, a higher horizontal pressure loss is captured when compared to lower kinetic energy cases as shown in Figure 9.

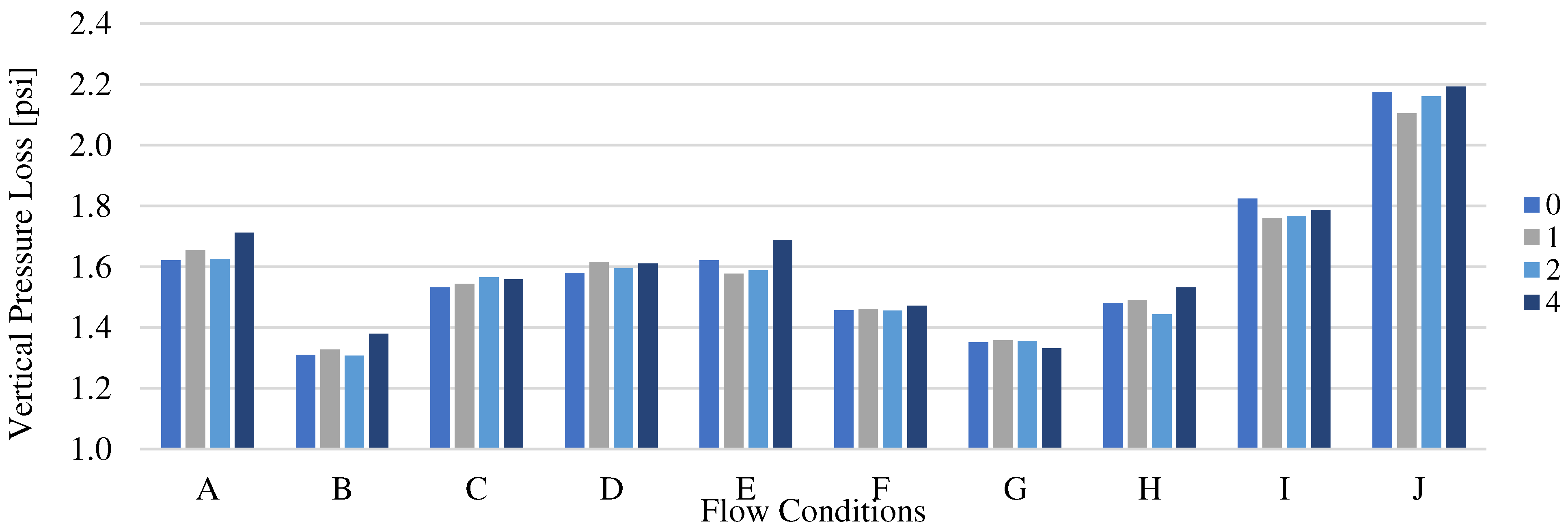
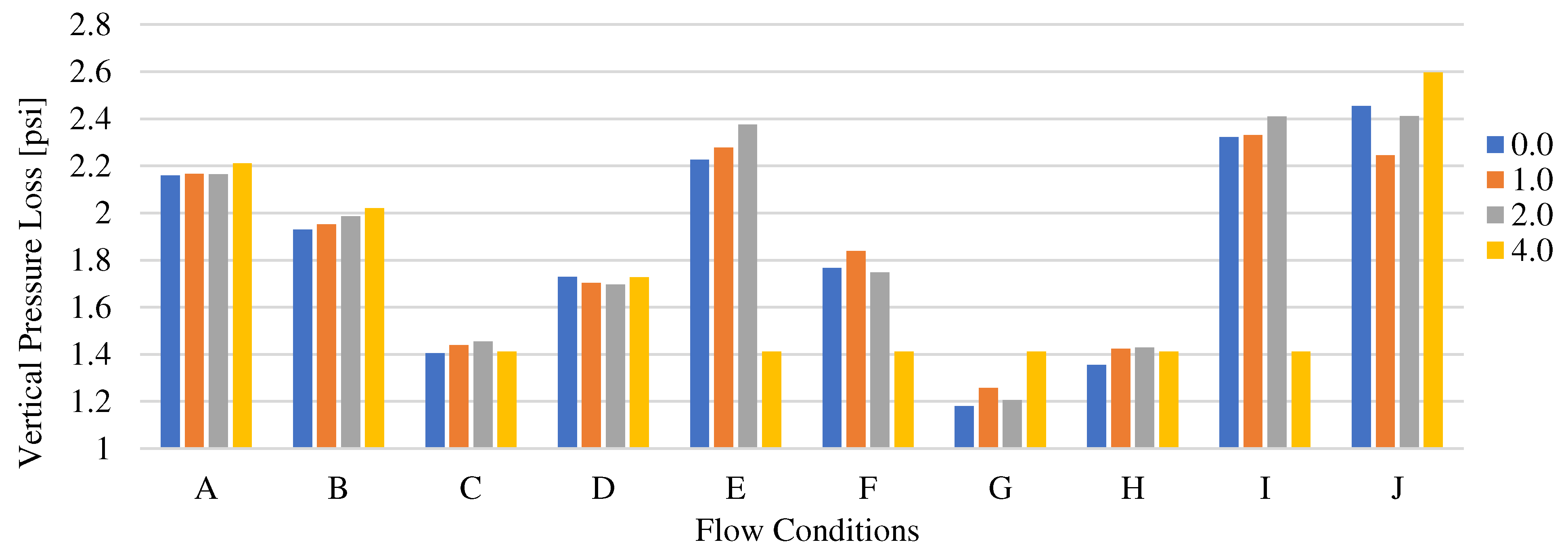
Vertical pressure loss shows small but consistent variation with respect to the undulating amplitude (except for Case G), and is 60% higher for cases of very low kinetic energy when compared to cases of moderate to high kinetic energy. This is due to the increased slug severity which induced larger fluid vertical column head variations in the vertical section. as shown in Figure 10.

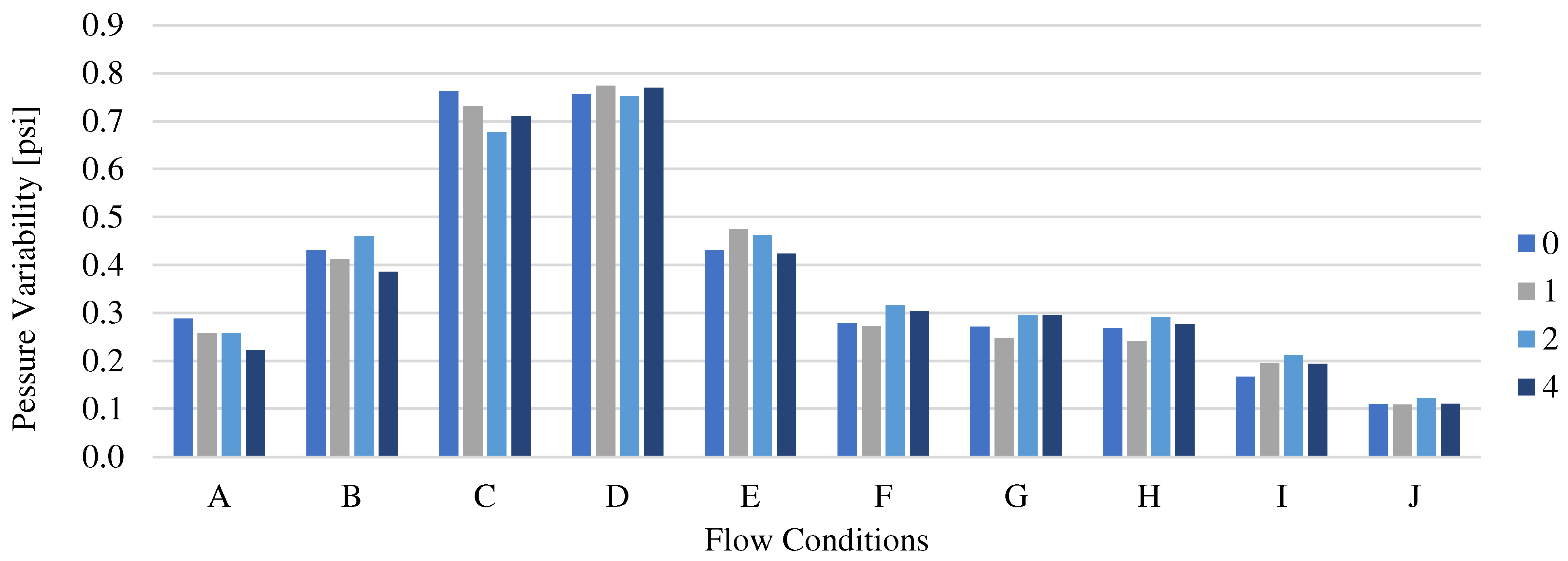
In terms of variability of the pressure at PT-M-7, we observe higher variability for higher kinetic energy cases, with a decreasing variability with respect to dimensionless undulating amplitude and lower variability for lower kinetic energy cases with higher variability versus dimensionless amplitude. In other words the flow is slightly more stable with higher amplitude for high energy cases, and slightly unstable for lower energy cases. Applying this observation to oil production wells, it is reasonable to state that for lower velocities the undulating amplitude increases the instability of the flow. Hence a contribution to a more severe slugging.

Figure 11. Lateral pressure variability versus undulating amplitude for flow conditions from A to J.

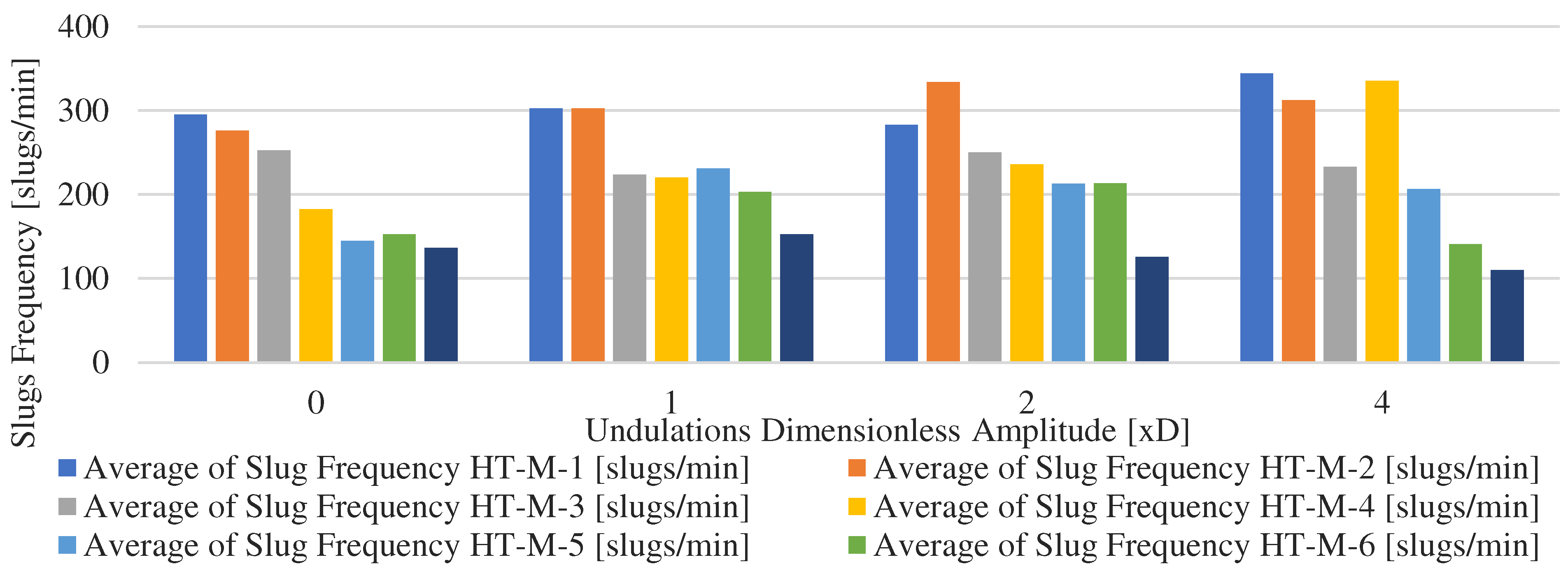
In terms of lateral section profile results, it is observed on the slug frequency profile shown in Figure 12, that the frequency is lower as the slugs move towards the vertical section from HT-M-1 to HT-M-7, meaning that slugs are merging to reach a critical frequency which is transmitted to the vertical section of the flow loop. No undulating amplitude effect is observed apart from a weak downward trend with respect to the last (HT-M-7) probe calculated frequency.

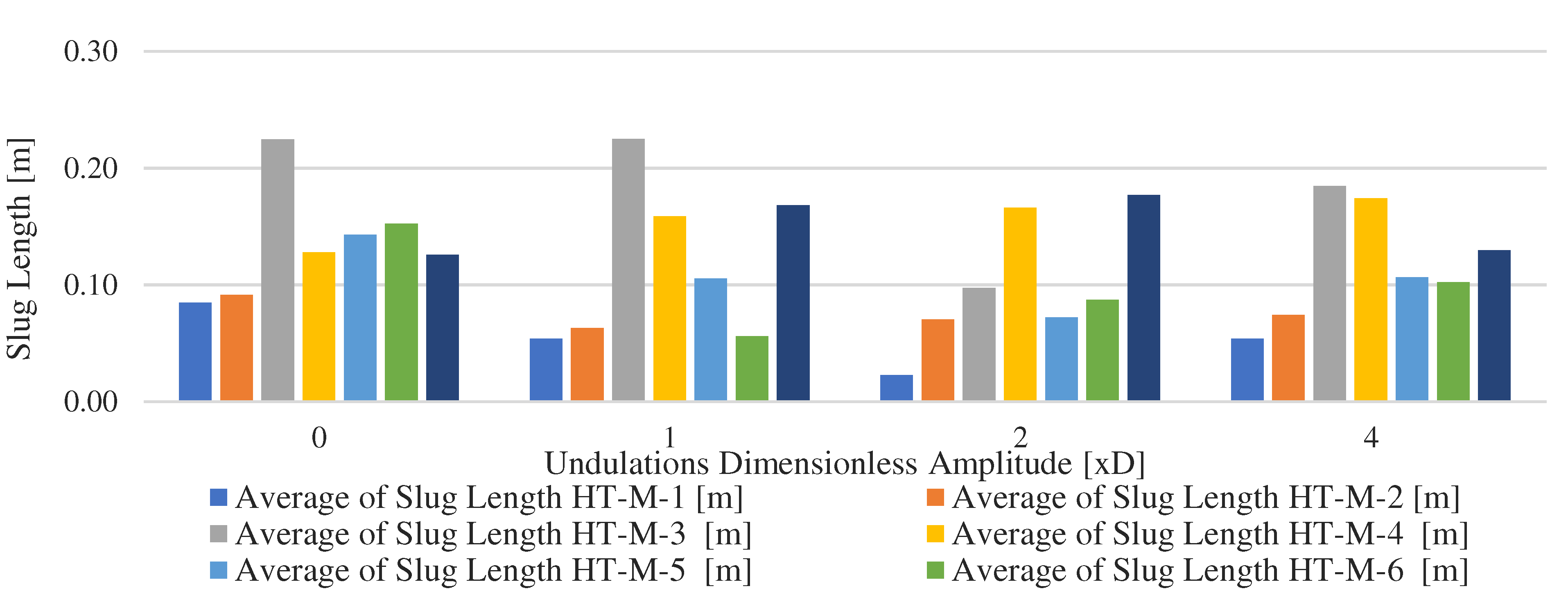
The slug length as detected by the water holdup probes along the lateral section shows a bell-shaped trend with higher slug length at the closest probe to the vertical section when compared to the first (inlet) of the lateral section. No strong dependency on the dimensionless undulating amplitude is observed as illustrated by Figure 13.

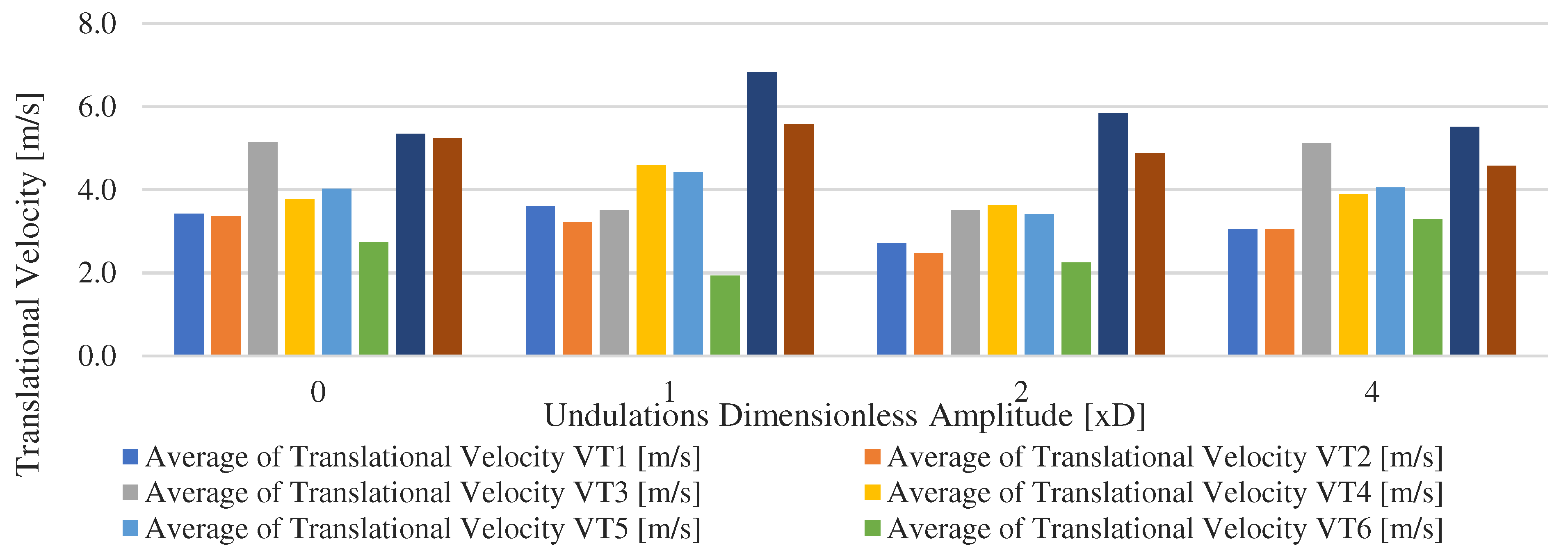
The general trend is a slugs velocity increase towards the center of the undulation, then a decrease at the end of the lateral section due to slugs length increase and frequency reduction as seen in the previous results. The vertical section slug velocity is consistently higher than the lateral section, due to the higher pressure drop lifting the slugs towards the surface as shown in Figure 14. Apart from the case with 0 dimensionless undulation amplitude, the translational velocity of the vertical section (HT-M-7 and HT-M-8) decreases.

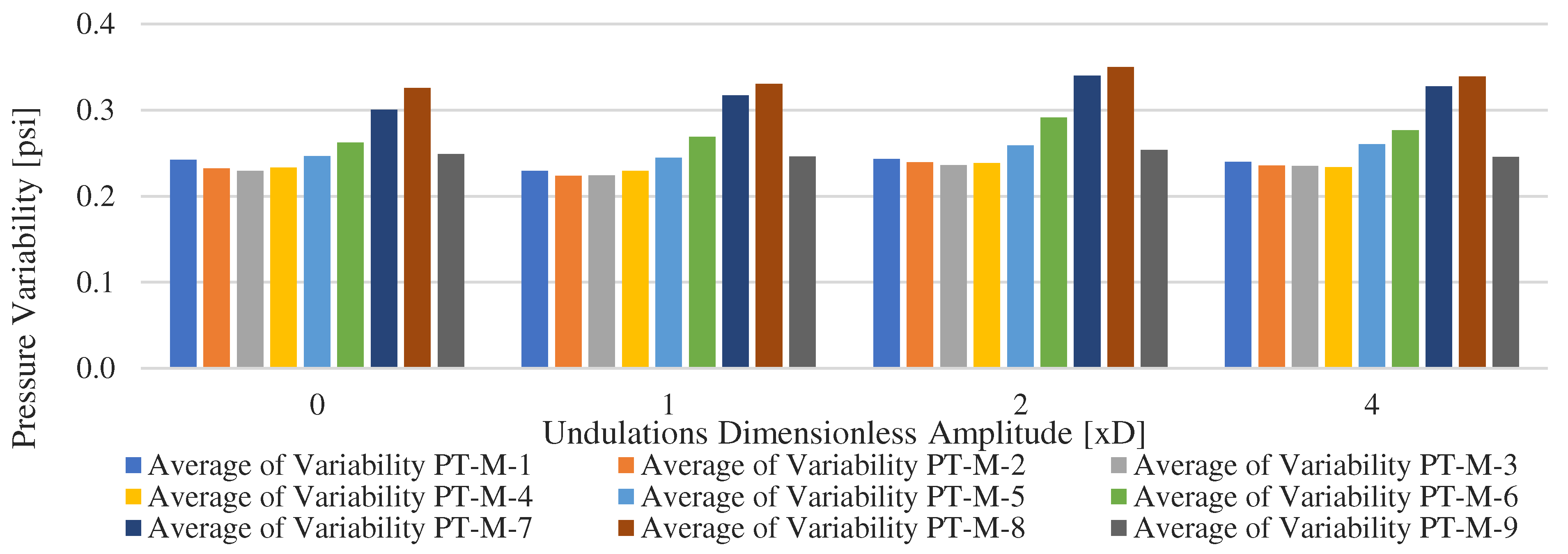
In terms of variability the pressure variability increases in the lateral section towards the vertical section, with the highest-pressure variability recorded at the bottom of the vertical section PT-M-8, a lower variability is recorded at the top of the vertical section. An interesting behavior which indicates that the small variations observed at wellhead level, translates large pressure variation downhole which propagates and is attenuated through the lateral section towards the toe of the well can be seen in Figure 15.

4. Numerical Simulation Results

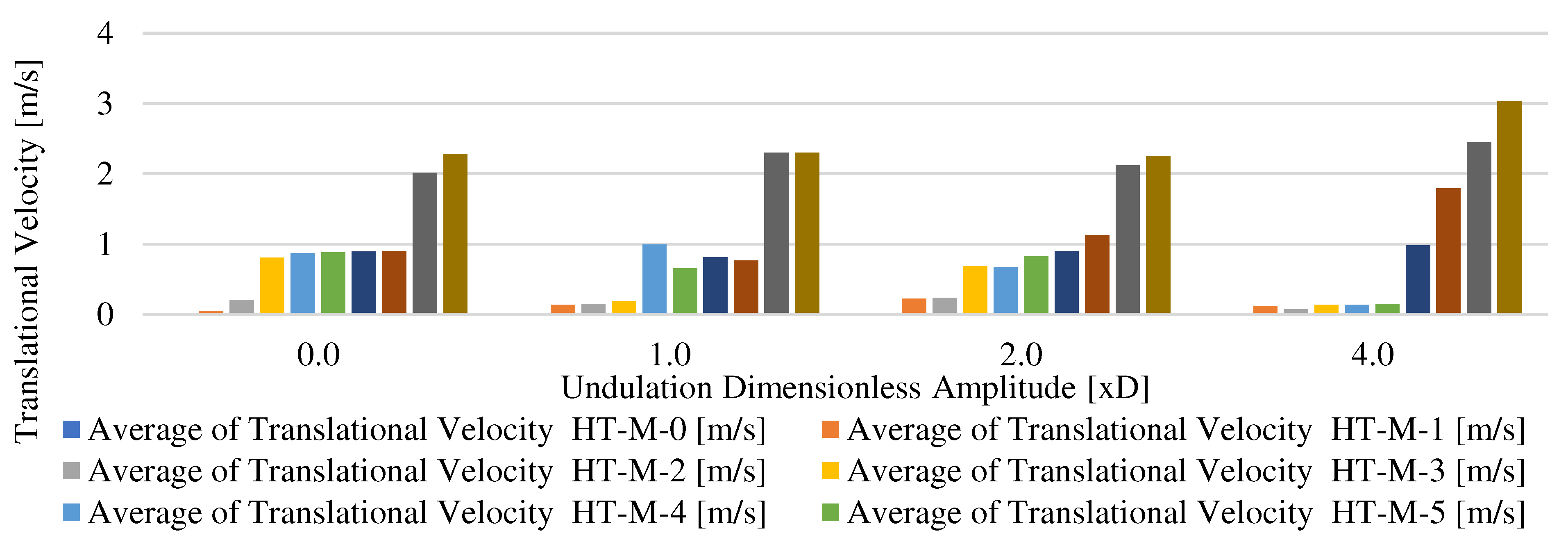
The same system and flow conditions are modeled in the commercial transient multiphase flow simulator OLGA® with slug tracking feature. Although the order of magnitude and the results differs and do not match, the trends agree. The translational velocity gradually increases along the lateral section with highest values in the vertical section due to the higher-pressure gradient in the vertical section, as shown in Figure 16.

The slug frequency increases along the lateral section as shown in Figure 17, indicating a slug dissipation as opposite to the experimental results. This difference can be explained by the lack of liquid fallback effect in the simulation results, as with higher fall back from the vertical to the horizontal section, the accumulated liquid in the outlet of the lateral section creates less liquid holdup variations in the measured experimental results due to slugs merging, as opposite, the simulation results with lower to none liquid fallback, the slugs evolving along the lateral section continue accelerating and moving towards the vertical section. Then through the vertical section, the frequency decreases translating a slug merging in the vertical. No trend with regards to the undulation’s amplitude can be inferred.

In terms of slug length, it increases along the lateral section then a decrease through the vertical section is observed. No clear dependency on undulating amplitude is obtained can be seen in Figure 18. this contradicts the experimental results.

The simulation difference from the experimental results is due to several factors. Firstly, the modeling of such systems of laterals followed by vertical section in multiphase flow presents numerical stability challenges and requires a fine tuning of the slug tracking models. In addition, there is a maximum 12% measurement uncertainty of the water holdup probes. The simulation predicted higher slug length at lower frequencies and lower translational velocities, translating a more severe slugging behavior, with order of magnitude larger and slower slugs.

In terms of pressure losses, Figure 19 shows the lateral pressure losses obtained using the numerical simulation model. For all flow condition cases the lateral pressure loss increase with the increase of the dimensionless undulating amplitude.

The trend for vertical pressure loss with respect to undulating amplitude is less pronounced than the horizontal one as shown in Figure 20. However it still shows that for 50% of the cases, an increase of the vertical pressure loss is observed with regards to undulating amplitude, with no difference between high and low kinetic energy cases.

5. Conclusions

Based on the observed experimental results, the below conclusions are stated:

Undulation amplitude increase induces lower slug translational velocities.
Overall, the slug frequency decreases with the increase of undulation amplitude, except for few outlier cases.
The slug length may decrease or remain constant as the undulation amplitude increases, depending on the flow conditions.
A part for the translational velocity which is higher for high kinetic energy cases, the higher and lower kinetic energy cases show similar trends.
It can be inferred from the pressure loss results that both horizontal and vertical pressure losses increase for higher amplitude situations.
The variability of pressure at the given location decreases with the increase in undulation amplitude for high kinetic energy cases, however, it increases for low energy cases.
Slug merging is observed along the lateral section with a gradually decreasing slug frequency.
Numerical simulation predicted lower translational velocity, higher slug lengths and lower frequency when compared to the experimental results.
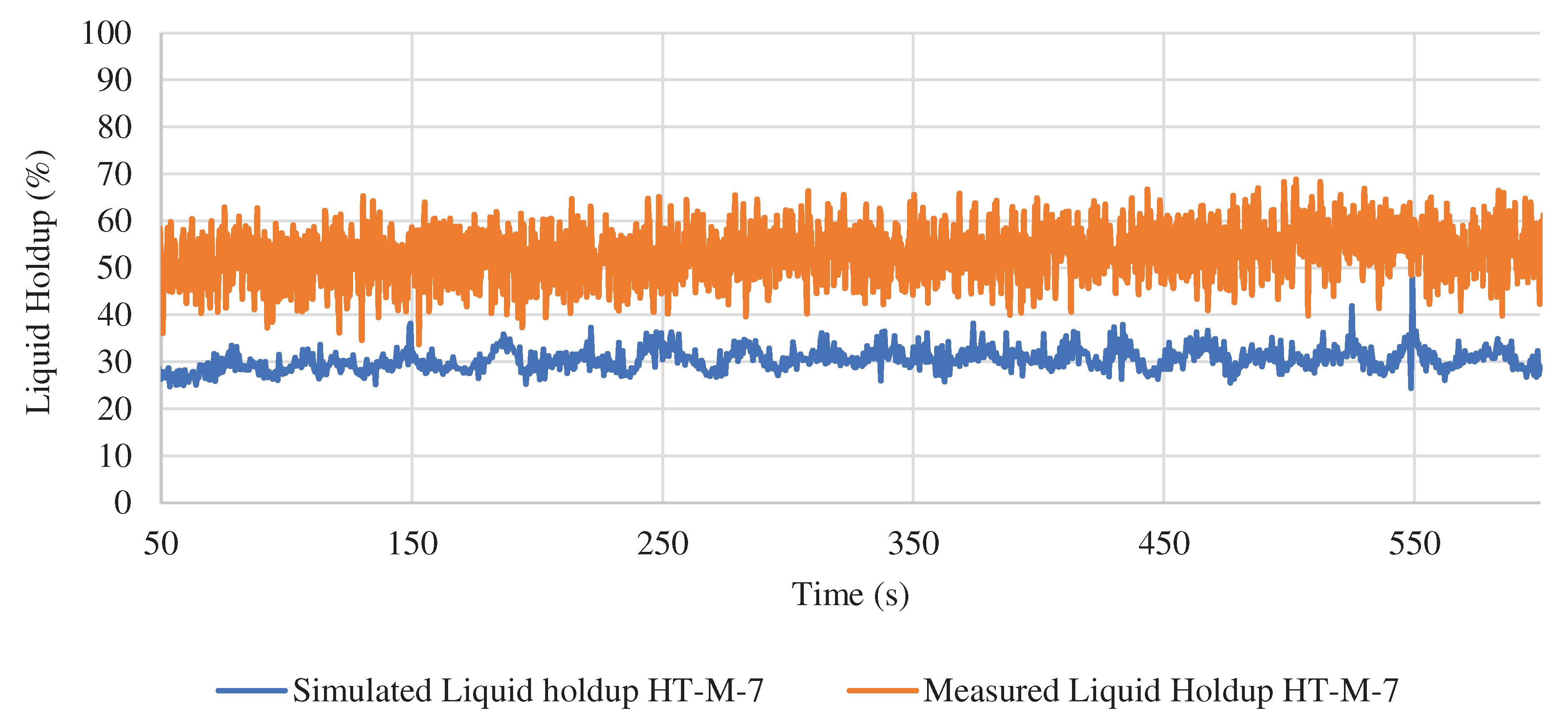
The observed lateral pressure loss is 4-5 folds the numerically obtained pressure losses. This is expected to be due to a lack of liquid fallback effect modeling. The lateral section shows higher liquid hold up versus time in the measured data as shown in the Appendix A.
The observed vertical pressure losses agree in magnitude and trend with the numerical simulation results.

The authors recommend investigating the effect of undulating frequency (Undulations number) on the slug characteristics, pressure loss, and flow stability/variability.

Supplementary Materials

The following are available online at https://data.mendeley.com/datasets/vd2hj27ywy/draft?a=aaec4643-1270-4c5f-95d1-74f581bc170e.

Author Contributions

Khetib.Y.; Conceptualization, Methodology, Investigation, Writing-Original Draft, Data Curation, formal Analysis, Software. Ling.K.; Validation, Supervision, Writing – Review & Editing, Tang.C.; Writing - Review & Editing, Aoun.A E.; Investigation. Samson.F A.; Investigation. Ouadi.H.; Writing - Review & Editing.

Funding

This research was funded by North Dakota Industrial Commission, grant number 43500-2730.

Data Availability Statement

Generated data are available through: KHETIB, Youcef; Ling, Kegang; Feilen, Harry (2023), “University of North Dakota UTP Flow loop Undulations Experiment Data”, Mendeley Data, V3, doi: 10.17632/vd2hj27ywy.3

Acknowledgments

The authors recognize the support of the North Dakota Industrial Commission. Slb for making its OLGA® software available. Harry Feilen and Vamegh Rasouli for their technical and administrative support respectively.

Conflicts of Interest

The authors declare no conflict of interest.

Appendix A

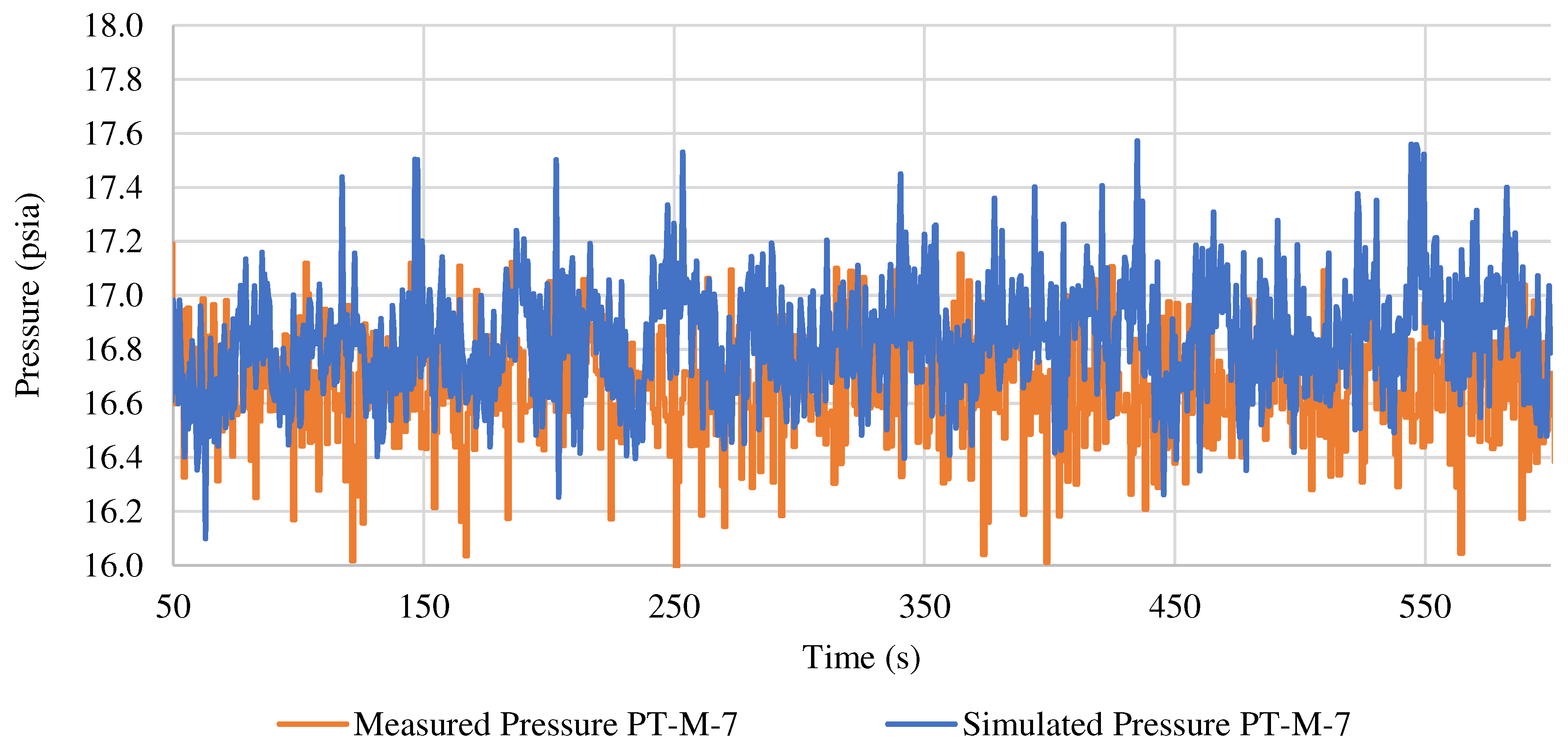
The below Figure A1 and Figure A2 show the history match results of pressure and water holdup parameters for the sensor position M-7, located at the base of the vertical section.

Figure A1. Measured and simulated Pressure at PT-M-7 Probe location.

Figure A2. Measured and simulated Water Holdup at HT-M-7 Probe location.

References

Khetib, Y.; Ling, K.; Allam, L.; Aoun, A.E. Statistical and numerical investigation of the effect of wellbore trajectories in williston basin horizontal wells and their effects on production performance. Petroleum & Petrochemical Engineering Journal 2022. [Google Scholar]
Norris, H.L.; Lee, H. The Use of a Transient Multiphase Simulator to Predict and Suppress Flow Instabilities in a Horizontal Shale Oil Well. SPE. October 2012; 1009–1019. [Google Scholar] [CrossRef]
Khetib, Y.; et al. Modelling Slugging Induced Flow Instabilities and Its Effect on Hydraulic Fractures Integrity in Long Horizontal Wells. In Proceedings of the 56th US Rock Mechanics/Geomechanics Symposium, Santa Fe: ARMA. New Mexico, USA, 26–29 June 2022. [Google Scholar]
Lu, H.; Anifowosh, O.; Xu, L. Understanding the Impact of Production Slugging Behavior on Near-Wellbore Hydraulic Fracture and Formation Integrity. In Proceedings—SPE International Symposium on Formation Damage Control; OnePetro, February 2018; pp. 7–9. [Google Scholar] [CrossRef]
Brito, R.M. Effect of Horizontal Well Trajectory on Two-Phase Gas-Liquid Flow Behavior. 2015. Available online: https://www.proquest.com/openview/02f234dbb748e2e1b02cd2593d596632/1.pdf?pq-origsite=gscholar&cbl=18750 (accessed on 8 January 2023).
Brito, R.; Pereyra, E.; Sarica, C. Existence of Severe Slugging in Toe-Up Horizontal Gas Wells. In Society of Petroleum Engineers—SPE North America Artificial Lift Conference and Exhibition 2016; October 2016; pp. 25–27. [Google Scholar] [CrossRef]
Brito, R.; Pereyra, E.; Sarica, C. Well trajectory effect on slug flow development. J Pet Sci Eng 2016, 167, 366–374. Available online: http://onepetro.org/BHRNACMT/proceedings-pdf/BHR16/All-BHR16/BHR-2016-053/1330257/bhr-2016-053.pdf (accessed on 24 June 2021). [CrossRef]
Brito, R.M. Effect of horizontal well trajectory on two-phase gas-liquid flow behavior. PH.D Dissertation, University of Tulsa, Tulsa, 2015. Available online: https://www.proquest.com/docview/1761846432/A53F663E44D042C4PQ/1?accountid=28267 (accessed on 4 November 2022).
Tran, N.L.; Orazov, B.; Karami, H. Impacts of Well Geometry and Gas Lift on Flow Dynamic and Production of Unconventional Horizontal Wells. [CrossRef]
Khetib, Y.; Ling, K.; Aoun, A.E. Experimental and Numerical Analysis of Toe-up Trajectory Effect on Gas Lifted Unconventional Wells Performances. 2023. [CrossRef]
Gokcal, B. An experimental and theoretical investigation of slug flow for high oil viscosity in horizontal pipes. 2008. [Google Scholar]

Figure 1. Schematic of the University of North Dakota UTP flow loop facility.

Figure 2. One undulation amplitude and inclination angle illustration of the experimental system.

Figure 3. Photo of the flow loop facility and assigned computer and DAQ station, from [10].

Figure 4. Municipal water and test liquid rheogram data.

Figure 5. One undulations cases with 0cm, 5cm, 10cm and, 20cm amplitude shown as case d, a, b, and c figures.

Figure 6. One undulation case slug translational velocity versus the undulating amplitude for flow conditions from A to J.

Figure 7. One undulation case slug frequency versus undulating amplitude for flow conditions from A to J.

Figure 8. One undulation case slug length versus undulating amplitude for flow conditions from A to J.

Figure 9. One Undulation Case Averaged Horizontal Pressure Loss versus the undulation’s amplitude for flow conditions from A to J.

Figure 10. One undulation case vertical pressure loss versus undulating amplitude for flow conditions from A to J.

Figure 12. Slug frequency for each water holdup probe of the lateral section versus dimensionless undulating amplitude.

Figure 13. Slug length for each water holdup probe of the lateral section versus undulations dimensionless amplitude.

Figure 14. Slug translational velocity for each water holdup probe of the lateral section versus dimensionless undulating amplitude.

Figure 15. Pressure variability profile versus undulations dimensionless amplitude.

Figure 16. Simulation translational velocity profile versus undulating amplitude.

Figure 17. Simulation slug frequency profile versus undulations dimensionless amplitude.

Figure 18. Simulation slug length profile along the lateral and vertical section versus undulations dimensionless amplitude.

Figure 19. Simulation Lateral time-averaged pressure loss versus flow conditions, for different undulations dimensionless amplitude.

Figure 20. Simulation Lateral time-averaged pressure loss versus flow conditions, for different undulations dimensionless amplitude.

Table 1. Flow loop facility characteristics.

Equipment name	Tag	Model name	Specifications
Air Compressor	CMP-G-1	Ingersoll Rand Model 7100	15hp, Max Pressure 175 psig, 50 CFM
Water Pump	PMP-W-1	Gorman-Rupp Model 3790-95	7.5hp, max pressure 75 psig, max flowrate 157 gpm.
Liquid Tank	TNK-W-1	Schutz	275 gallons
High-Speed Camera	CAM-N-1	Z-CAM E2	60 fps, max resolution
Pressure Regulator	PR-G-1	Ingersoll Rand	Range [0 to 160 psig]
Heat exchanger	EX-G-1	Ingersoll Rand	Flowrate 64 cfm max temperature 140 F, max pressure 203 psig

Table 3. Experiment flow conditions corresponding to the mass and volumetric flow rates and superficial velocities for water mixture and air.

Parameter	Flow Conditions
Parameter	A	B	C	D	E	F	G	H	I	J	Unit
Water Flow Rate	10.0	10.0	20.0	28.00	20	5	2.5	2.5	10	10	GPM
Water Superficial Velocity	1.0	1.02	2.04	2.86	2.04	0.51	0.26	0.26	1.02	1.02	ft/s
Mass Flow Rate	0.6	0.63	1.26	1.77	1.26	0.32	0.16	0.16	0.63	0.63	Kg/s
Air Flow Rate	5.0	10.0	20.0	33.0	10.0	5.0	5.0	2.8	2.8	1.1	SCFM
Air Superficial Velocity	3.82	7.64	15.28	25.21	7.63	3.83	3.83	2.15	2.15	0.80	ft/s
Mass Flow Rate	0.003	0.006	0.012	0.020	0.006	0.003	0.003	0.0017	0.002	0.0006	Kg/s

Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.

© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).

Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.

MDPI Initiatives

Important Links

Choose an area of interest and we will send you notifications of new preprints at your preferred frequency.

Disclaimer