Prerpints.org logo
Preprint
Article

Model and Simulation of Benefit Distribution of Collaborative Cooperation in the Supply Chain of General Contracting Projects

Altmetrics

Downloads

87

Views

30

Comments

0

A peer-reviewed article of this preprint also exists.

This version is not peer-reviewed

Submitted:

23 June 2023

Posted:

26 June 2023

You are already at the latest version

Alerts
Abstract
To solve the benefit allocation problem between the subjects of the supply chain of general contracting projects. The Cobb-Douglas function is applied to establish the benefit distribution model when the two cooperate in the supply chain system, analyze the optimal benefit situation of one-time cooperation between the two parties under two modes of egoistic decision and collectivistic decision as well as the benefit distribution problem of multiple cooperation, and conduct numerical simulation to calculate the functional relationship between each decision variable and the contribution degree of the general contractor under different effort cost coefficients. The results show that：In the case of one-time cooperation between general contractors and subcontractors, regardless of the decision mode, the degree of effort of both parties is positively related to their own contributions and negatively related to each other's contributions; the overall benefit of the supply chain system is positively proportional to the degree of contribution of the general contractor and inversely proportional to the share of benefit distribution of the subcontractor; in multiple cooperation, the equilibrium result of both parties achieving Pareto optimality at each stage is that both parties choose to cooperate.
Keywords: 
Subject: Engineering  -   Architecture, Building and Construction

1. Introduction

With the development of economic integration and engineering construction market, as well as more transparent and competitive engineering projects, owners are increasingly inclined to adopt the general contracting model for engineering projects in order to obtain more comprehensive services [1]. In 2019, the Ministry of Housing and Urban-Rural Development and the National Development and Reform Commission formulated the Measures for the Management of General Contracting for Housing Construction and Municipal Infrastructure Projects, which emphasizes that "general contracting activities shall follow the principles of legality, fairness, honesty and trustworthiness, reasonably share risks, ensure project quality and safety, save energy, protect ecological environment, and shall not harm the public interests of society and the legitimate rights and interests of others." Due to the need of engineering construction project management and the implementation of national policies, as well as the fact that our construction enterprises currently have no way to form an enterprise with general contracting capability in a short period of time, the consortium of construction general contracting projects has become a trend, and each enterprise can achieve the purpose of reducing costs, sharing risks and improving the efficiency of cooperation by establishing a good cooperative relationship and through resource sharing. The supply chain of general contracting projects is a network structure formed by the general contractor as the core and members of enterprises such as subcontractors and material suppliers in order to meet the construction needs of the owners.
There are many participating subjects in the supply chain of general contracting projects, and interests are the bond and driving force for the development of the relationship among members, which makes the issue of benefit allocation a very critical and complex one, requiring consideration of various factors. Generally speaking, the distribution of interests of general contractors and subcontractors and other subjects should be distributed according to their own contribution degree, but in reality, it is also necessary to consider the competitive environment and market supply and demand. When the interests of each party cannot be fairly and reasonably distributed, it will affect the enthusiasm of cooperation among members or directly lead to the failure of cooperation, so that each subject cannot achieve a win-win situation. In order to achieve the management goal of maximizing the interests of the supply chain itself and sustainable development, it is necessary to design a good mechanism for the distribution of interests among the participating subjects, balance the interests obtained by each participating party, ensure that each subject can obtain reasonable benefits, and solve the contradiction of interests of all parties, which is an urgent problem for general contracting projects, and it is important for fully mobilizing the enthusiasm of general contractors and subcontractors to participate in the construction, and then achieve the mutual. It is of great significance to fully mobilize the enthusiasm of general contractors and subcontractors to participate in the construction, and then maximize the interests of both parties. Therefore, this paper focuses on the benefit distribution between general contractors and subcontractors in the supply chain of general contracting projects, and discusses the cooperation mechanism in one-time cooperation and multiple cooperation.

2. Research overview

Domestic and international research on the issue of benefit distribution mainly includes the following aspects.

2.1. Research on the distribution of engineering benefits

Bai Zhenyu [2] studied the optimal decision of benefit distribution between general contractors and procurement service providers under two situations of cooperation and dispersion on the basis of revenue sharing theory and Stackelberg’s game idea; Guan Baihai [3] used the basic principles of contract theory and game theory idea to The mechanism of benefit distribution between different units as general contractors was analyzed; Sun GS et al [4] studied the benefit distribution problem of PPP projects by constructing a game model and used a case study to investigate the effects of different situations on the outcome of government and social equilibrium strategies. Ren Kai et al [5] studied the use of shapley model to solve the problem of uneven profit distribution between general contractors and subcontractors in EPC projects in railways; Lv Ping et al [6] studied and pointed out that the improved shapley model was more reasonable for the benefit distribution of the general contractor’s engineering construction supply chain on the basis of cooperative alliance; Shi Qianqian et al [7] used the Cobb-Douglas function to analyze the benefit distribution problem of one-time cooperation between major engineering contractors and suppliers; Feng Jingchun et al [8] discussed the benefit distribution of BIM-based collaborative construction projects under the EPC model, and proposed a two-level benefit distribution mechanism based on the dual management system under the EPC model at the macro level, and a three-stage benefit distribution mechanism based on the application characteristics of BIM in the whole project life cycle at the micro level.

2.2. Research on the benefit distribution of supply chain cooperation

Wang Li et al [9] used the idea of Stackelberg game to establish a quantitative model of benefit distribution mechanism of supply chain members’ cooperation; Zhong Changbao et al [10] proposed a new two-stage distribution method of supply chain benefits, the orthogonal projection entropy method, based on the importance of the supply chain benefit distribution mechanism and some existing problems; Han Ting and Li Dengfeng [11] used shapley value method to regulate the benefit allocation game problem among enterprise members with intuitionistic fuzzy alliance; Zou Yong [12] used the maximum entropy method to allocate the profits obtained from the VMI & TPL model in the upstream segment of the supply chain; Mahjoub S and Hennet J C [13] used cooperative game analysis to solve strategic problems such as maximum profit generation and sharing among supply chain companies; Chen C L et al. [14] proposed a two-stage fuzzy decision-making method to maximize the profit of each participating company for a typical multi-echelon supply chain network; Xi Yiheng and Cheng Yangyuan [15] studied the benefit distribution mechanism of supply chain partnership in depth, introduced the benefit distribution principle of supply chain partnership, and constructed a model of benefit distribution ratio of supply chain partnership; Kumoi Y and Matsubayashi N [16] analyzed the supply chain benefit distribution problem on the basis of cooperative game theory, and clearly proposed that the profits of the alliance must be allocated more to retailers and higher-cost members in the revenue distribution.

2.3. Research in benefit distribution models

In a large number of cooperative game studies, it can be further divided into two types of ex ante allocation and ex post allocation, where the specific forms of ex ante allocation generally include revenue sharing contracts [17], quantity flexibility contracts [18] and repurchase contracts [19,20], etc.; expost profit allocation is carried out by Shapley value method [5,6,11,21,22,23,24,25], minimum core method [25], bargaining model [26], the Nash bargaining model [27], and the maximum entropy method [12], among other models. Raza S A [17] proposed solutions for control decisions by analyzing the demand profiles of a quantitative model of joint pricing, inventory (order quantity) and investment used for supply chain social responsibility decisions under three games of decentralized, centralized and revenue sharing contracts; Heydari J et al [18] applied quantity elasticity contract to study the stochastic demand situation of a two-level supply chain consisting of one product and two members (manufacturer and retailer); Luo Chunlin [19] analyzed that when a supply chain can be coordinated through a buy-back contract, the coordination benefits of the supply chain can be arbitrarily distributed between suppliers and retailers; Xiao Qun and Ma Shihua [20] demonstrated that repurchase contracts can be used to eliminate the risk aversion effect and the double marginal effect in the cooperation of the second-level supply chain; Tan Zhongfu et al [23] applied the shapley value method to solve the problem of benefit distribution in the cooperation between the generation side and the supply side; Wang L et al. [24] combined individual characteristic weight coefficients with the shapley values of each hydropower plant and proposed the coefficient of variation-shapley value method for the compensation benefits of multi-owner step hydropower plants; Li Lin and Liu Shaohe [25] combined the minimum core method and the shapley value method to find a practical method for the benefit distribution of cooperative cooperation; In order to solve the benefit allocation problem among members of the consortium of whole-process engineering consulting projects, Sun Linlin et al [28] constructed a benefit allocation model of whole-process engineering consulting projects with modified Shapley value by means of AHP and fuzzy comprehensive evaluation method, and verified the feasibility and effectiveness of the model; Wang Xiaosheng et al [26] proposed a dynamic game benefit allocation scheme based on the bargaining model for the benefit allocation of shared contract water conservation management; Liu Zecheng et al. [29] constructed a benefit distribution model for full-process consulting consortia based on the asymmetric Nash negotiation model, which corrects the shortcomings of the asymmetric Nash negotiation model in terms of benefit distribution averaging.
From the above analysis of the existing literature, the study of the supply chain of general contracting projects has received much attention from scholars, but there is less research on the distribution of benefits among members within general contracting projects, and the utilisation distribution models used are relatively fixed, mostly the shapley value method, and most of them are limited to the one-time cooperation between subjects within the supply chain system, and less involved in the problem of multiple cooperation. However, in real life, general contractors and subcontractors will choose to cooperate multiple times on the basis of satisfactory one-off cooperation, which makes it more important to deal with the distribution of benefits when they cooperate together. Therefore, in the context of the general contracting market, taking general contractors and subcontractors in the supply chain of general contracting projects as the research object, it is of practical guidance to consider the distribution of benefits between the two parties in the supply chain system in one-time cooperation and multiple cooperation, which is of practical significance to the distribution of benefits among the subjects within general contracting projects in China.

3. Basic assumptions and modeling

In general contracting construction, a general contract is signed between the owner and the general contractor, leaving the construction work solely in the hands of the general contractor. Due to the asymmetry of information between the owner and the general contractor, the general contractor may take advantage of this to generate opportunism and lose project output. In order to achieve win-win situation, the owner will often adopt an incentive mechanism to reduce the opportunistic behaviour of the general contractor by signing a fixed lump sum price plus bonus contract with the general contractor, while the general contractor will likewise establish an incentive bonus with its subcontractors in order to obtain the incentive bonus itself The general contractor, in order to obtain incentive bonuses for itself, will likewise ensure the quality and progress of the project by establishing an incentive mechanism with its subcontractors and allocating bonuses according to a certain percentage, thus achieving a win-win outcome.
The basic assumptions in the text are as follows.
(1) The general contractor engineering supply chain is a consortium consisting of two parts: the general contractor and the subcontractors.
(2) The quality of products provided by the upstream supply chain of subcontractors is qualified, i.e. there will not be any problems with the quality of works due to material aspects.
(3) In the past two years, with the normalization of the new crown epidemic, the general contractor and subcontractors are subject to uncertainties such as epidemics and natural disasters in engineering construction, and the field of engineering construction has encountered challenges. Let the risk factor ε obey the standard normal distribution, i.e. ε ∼ N ( 0 , σ 2 ) .
(4) The Cobb-Douglas function is used to express the bonus function F ( e 1 , e 2 ) given by the owner to the general contractor, i.e. F ( e 1 , e 2 ) = e 1 α e 2 1 − α + ε . The expected bonus for the general contractor and the subcontractor is E ( F ) = e 1 α e 2 1 − α , where e i ( i = 1 , 2 ) represents the level of effort of both, α represents the general contractor’s level of contribution, and (1-α) represents the level of contribution of the subcontractor.
(5) The owner and the main contractor enter into a contract in the form of a fixed lump sum price plus bonus, i.e. W = p 1 + F ; the contract between the main contractor and the subcontractor, which is also a fixed lump sum price plus bonus incentive, has P = p 2 + ( 1 − β ) F , where W is the total price of the benefits received by the main contractor at the end of the project, P is the total price of the benefits received by the subcontractor at the end of the project, p i ( i = 1 , 2 ) is the fixed total price of the project contracted by the general contractor and subcontractors, β(0 < β < 1) is the bonus allocation coefficient of the general contractor, and 1 - β is the bonus allocation coefficient of the subcontractors.
(6) The effort cost function paid by the general contractor in the construction of the project is C 1 = 1 2 k 1 e 1 2 , and the effort cost function paid by the subcontractor in the construction process is C 2 = 1 2 k 2 e 2 2 , where k1 represents the effort cost coefficient of the general contractor and k2 represents the effort cost coefficient of the subcontractor.
(7) Assume that the general contractor is risk-neutral in the cooperation process, while the subcontractor is risk-averse, i.e. the general contractor, as the general manager, is neither risky nor conservative in its decision, but the subcontractor, as a member of the project, will choose the riskier one when the expected benefits are the same, as it may bring him greater benefits. (b) For a subcontractor, its cost of risk is c 2 = 1 2 f 2 ( 1 − β ) 2 σ 2 , where f 2 represents the degree of risk preference of the subcontractor and has 0 ≤ f2 ≤ 1. When f2 = 0 represents that the subcontractor is in a risk-neutral state, and when f2 → 1 represents the increasing risk preference possessed by the subcontractor.
(8) The final benefit to the general contractor is:
X = p 1 − p 2 + β E ( F ) − C 1 = p 1 − p 2 + β e 1 α e 2 1 − α − 1 2 k 1 e 1 2
The ultimate benefits to subcontractors are:
Y = p 2 + ( 1 − β ) E ( F ) − C 2 − c 2 = p 2 + ( 1 − β ) e 1 α e 2 1 − α − 1 2 k 2 e 2 2 − 1 2 f 2 ( 1 − β ) 2 σ 2
The ultimate benefits of a general contractor’s engineering supply chain system are:
Z = X + Y = p 1 + e 1 α e 2 1 − α − 1 2 k 1 e 1 2 − 1 2 k 2 e 2 2 − 1 2 f 2 ( 1 − β ) 2 σ 2

4. Model solving and analysis

From Equations (1) and (2), we can see that the interests of the general contractor are related to the subcontractors, and the interests of the subcontractors are also related to each other, which shows that in the general contracting supply chain, in order to maximize their own interests, both parties have to consider the interests of the other party. If both parties do not consider the interests of the other party but only their own interests, then egoistic decision-making will occur; if both parties consider the maximisation of the overall interests, i.e. the maximisation of the interests of the EPC supply chain system, then collectivist decision-making will occur. (Since both p 1 and p 2 are fixed values and not directly related to the conclusion, both p1 and p2 are assumed to be zero in the subsequent calculation)

4.1. Egoistic decision making model (Model I)

Under egoistic decision-making, in the whole supply chain system of general contracting projects, for two subjects, general contractor and subcontractor, it is a Stackelberg game between them. The general contractor is the leader, who first determines its own level of effort and the share of allocated benefits, aiming at maximizing its own benefits, while the subcontractor, as a follower, can determine its own level of effort only after the general contractor has made a decision. The subcontractor, as a follower, determines its own level of effort only after the general contractor has made its decision.
Taking the derivative of X with respect to e1 and making it equal to zero gives: ∂ X ∂ e 1 = α β e 1 α − 1 e 2 1 − α − k 1 e 1 = 0 , which gives: e 1 = α β k 1 e 2 1 − α 1 2 − α .
After determining the choice of the general contractor, the subcontractor chooses its own level of effort in conjunction with the aim of maximising its own interest. Taking the derivative of Y with respect to e2 and making the derivative equal to zero gives: ∂ Y ∂ e 2 = ( 1 − α ) ( 1 − β ) e 1 α e 2 − α − k 2 e 2 = 0 , which gives: e 2 = ( 1 − α ) ( 1 − β ) k 2 e 1 α 1 1 + α .
Substituting the resulting e 2 into X yields:
X = β ( 1 − α ) ( 1 − β ) k 2 1 − α 1 + α e 1 2 α 1 + α − 1 2 k 1 e 1 2
Finding the derivatives of Equation (4) with respect to e 1 and β respectively and making the two derivatives equal to zero as well as relating the system of equations yields:
( 1 − β ) ( 1 − α ) k 2 1 − α 1 + α e 1 α − 1 1 + α − β ( 1 − α ) 1 + α 1 − α k 2 1 − α 1 + α e 1 α − 1 1 + α ( 1 − β ) − 2 α 1 + α = 0 2 α β 1 + α ( 1 − β ) ( 1 − α ) k 2 1 − α 1 + α e 1 α − 1 1 + α − k 1 e 1 = 0
The final solution gives:
The optimal decision allocation share of the general contractor is: β Ⅰ * = 1 + α 2 .
The optimal level of effort for the general contractor and subcontractor respectively is:
e 1 Ⅰ * = ( α k 1 ) 1 + α 2 ( 1 − α ) 2 2 k 2 1 − α 2 e 2 Ⅰ * = ( α k 1 ) α 2 ( 1 − α ) 2 2 k 2 2 − α 2
The optimal returns for the main contractor, subcontractors and the supply chain system of the main contracting works are respectively
X Ⅰ * = p 1 − p 2 + 1 2 ( α k 1 ) α ( 1 − α ) 2 2 k 2 1 − α Y Ⅰ * = p 2 + 1 − α 2 4 ( α k 1 ) α ( 1 − α ) 2 2 k 2 1 − α − 1 2 f 2 ( 1 − β ) 2 σ 2 Z Ⅰ * = X + Y = p 1 + 3 − α 2 4 ( α k 1 ) α ( 1 − α ) 2 2 k 2 1 − α − 1 2 f 2 ( 1 − β ) 2 σ 2
The optimal decision allocation share result for the general contractor shows that the magnitude of this value is positively related to the degree of contribution of the general contractor, and it can be concluded that the allocation share of the general contractor is greater than 1/2 because the degree of contribution of the general contractor α and the degree of contribution of the subcontractor 1-α are both greater than 0. It can be concluded that 0 < α < 1, and thus the allocation share of the general contractor is greater than 1/2. The subcontractor’s The optimal return result indicates that the larger the subcontractor’s share of benefit distribution, the smaller the return it receives, and conversely, the smaller its share of benefit distribution, the larger the return it receives. The relationship between the optimal return of the general contracting supply chain system as a whole and the share of benefits allocated to subcontractors is consistent with the variation between subcontractors and their share of benefits, because as subcontractors have risk appetite, the supply chain system as a whole also has risk appetite.

4.2. Collectivist decision-making model (Model II)

In collectivist decision-making, the two parties collaborate in terms of maximising the overall benefits of the supply chain system for turnkey projects, thereby determining the level of effort of both parties.
Under collectivist decision-making, the two cooperating parties seek to maximise the benefits of the supply chain system, i.e.:
maxZ ⁡ = max ⁡ p 1 + e 1 α e 2 1 − α − 1 2 k 1 e 1 2 − 1 2 k 2 e 2 2 − 1 2 f 2 ( 1 − β ) 2 σ 2
Finding the derivative of the above equation with respect to e 1 , e 2 and making the derivative equal to zero as well as the system of joint cubic equations leads to
α e 1 α − 1 e 2 1 − α − k 1 e 1 = 0 ( 1 − α ) e 1 α e 2 − α − k 2 e 2 = 0
From this it can be found that
The optimal level of effort for the main contractor and the subcontractor are respectively.
e 1 Ⅱ * = ( α k 1 ) 1 + α 2 1 − α k 2 1 − α 2 e 2 Ⅱ * = ( α k 1 ) α 2 1 − α k 2 2 − α 2
The optimal return of the overall supply chain system for a turnkey project is
Z Ⅱ * = X + Y = p 1 + 1 2 ( α k 1 ) α 1 − α k 2 1 − α − 1 2 f 2 ( 1 − β ) 2 σ 2
Summarizing the above two decision models we can get Table 1.

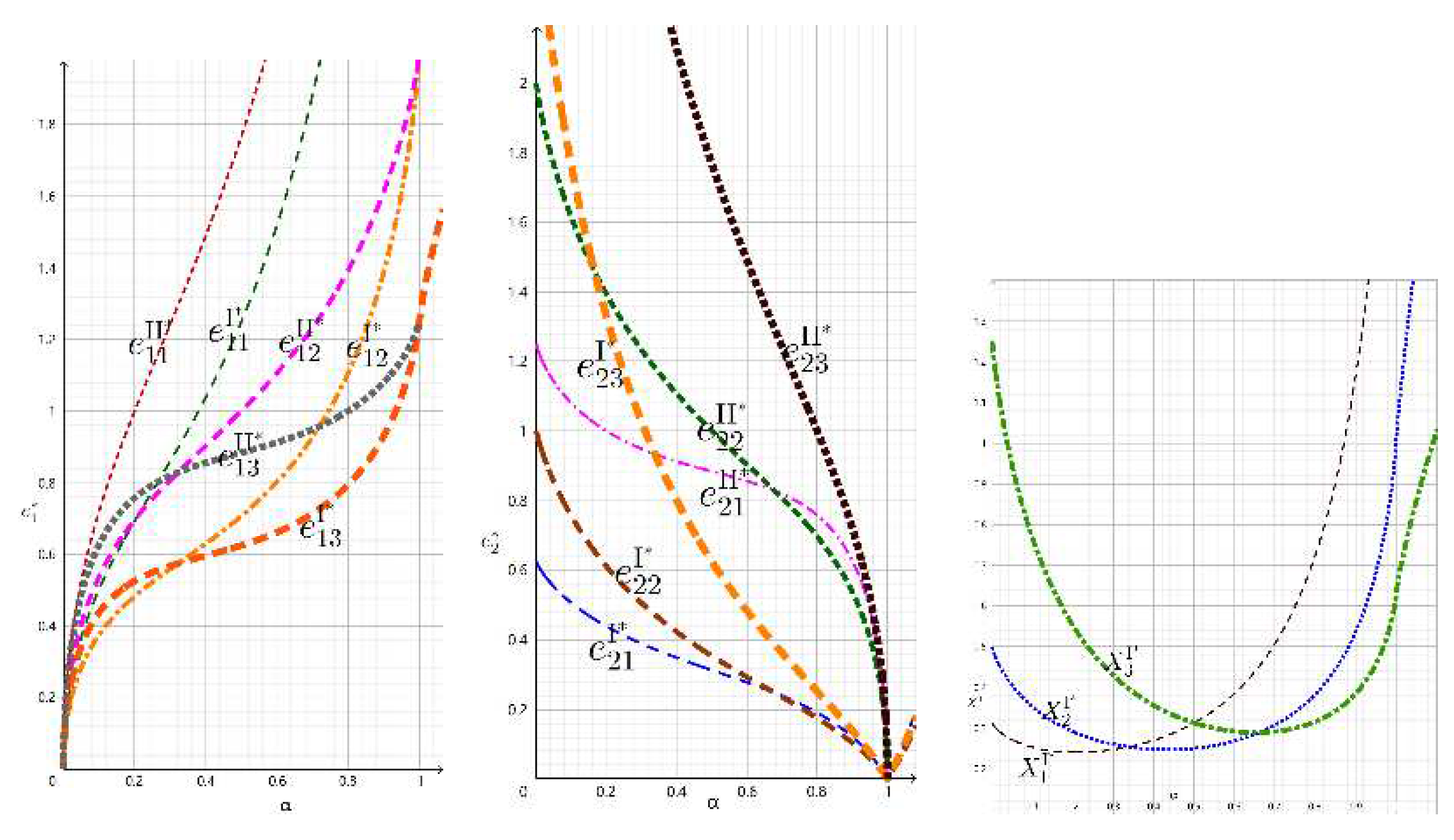
4.3. Numerical analysis

In order to further analyze the relationship between each decision variable and the degree of contribution α and the share of benefit distribution β, Geogebra is applied for numerical simulation calculation. Assuming the basic parameters σ 2 =100 and f 2 =1/2, and since p 1 and p 2 are fixed values that do not affect the analysis results, three simulations are made in the simulation process assuming that p 1 and p 2 are both 0: Simulation 1: set k 1 = 0.2, k 2 = 0.8; Simulation 2: set k 1 = 0.5, k 2 = 0.5; Simulation 3: set k 1 = 0.8, k 2 = 0.2. 2 = 0.2. The following images of the degree of contribution α and the share of benefit distribution β in relation to each of the other variables can be obtained, as shown in Figure 1 and Figure 2.
Figure 1 shows that: (1) the effort level of the main contractor e 1 , increases with the increase of its contribution level, α, and the increase of e 1 decreases and then increases with the increase of α, and the increase of e 1 decreases with the increase of k 1 , and the effort level in the collectivist decision is greater than that in the egoist decision. (2) The level of effort of subcontractors decreases as the level of effort of the general contractor increases, and the magnitude of the decrease decreases and then increases as k 2 decreases, and the level of effort is also higher in the collectivist decision than in the egoist decision. (3) Until the contribution level α reaches a certain value α 0 X , the optimal benefit X obtained by the general contractor increases as its effort cost coefficient k 1 becomes larger, and decreases as k 1 becomes larger after α 0 X . Moreover, under the egoistic decision, the tendency of X to decrease gradually increases as k 1 increases, and the tendency to increase gradually after reaching α 0 X slows down, probably because This is probably because as k 1 becomes larger, the general contractor will pay more and more costs, and when the benefits are certain, the benefits reaped will decrease accordingly. The highest profit of the general contractor is obtained when α < 0.5, k 1 > k 2 and α > 0.5, k 1 < k 2 .
It can be seen from Figure 2 that (1) the optimal benefit Y obtained by the subcontractor is in a decreasing state in the egoistic decision model and becomes progressively greater as k 2 decreases. The highest returns to subcontractors are obtained when α < 0.5, k 1 > k 2 and α > 0.5, k 1 < k 2 . The image of the optimal return Y obtained by the subcontractor about the share of the general contractor’s benefit distribution β conforms to a normal distribution, and the optimal return of the subcontractor is proportional to the general contractor’s benefit distribution in the range of 0 < β < 1. (2) The optimal return of the general contractor’s supply chain system as a whole decreases and then increases as α increases, and the return under collectivist decision-making is higher than that under egoistic decision-making. As k 1 increases, the decreasing trend of Z gradually increases before reaching α 0 Z , and the increasing trend becomes slower after reaching α 0 Z , which is consistent with the change of the general contractor’s optimal benefit, further highlighting the The influence of the general contractor’s effort cost coefficient on the overall return of the supply chain of general contracting works can also be understood: under the collectivist decision-making model, the overall return of the supply chain system is highest when α < 0.5, k 1 > k 2 and α > 0.5, k 1 < k 2 . The optimal return of the supply chain system as a whole is positively related to the share of benefits allocated to the general contractor, which means that as the share of benefits allocated to the general contractor β increases, the overall benefits of the supply chain system of general contracting projects also gradually increase.

5. Distribution of benefits from multiple collaborations

Collaboration between teams reduces the cost for the main contractor to find other subcontractors, and reduces the benefit-gaming process at the beginning of each collaboration between the two parties. Cooperation between the main contractor and subcontractors is based on both parties being satisfied with the last benefit distribution result, i.e. if one party questions the benefit distribution result, the next cooperation will not be established, and only when both parties receive the contracted bonus percentage and are satisfied with the benefit distribution result, will the opportunity for further cooperation arise, and as the number of cooperation increases, the subcontractors gradually tend from risk-averse to risk-neutral, i.e. f 2 →0. (Assuming that subcontractors are risk-neutral in the following analysis)
The cooperation between the subjects of the supply chain system of general contracting works is often based on the repeated game between the two parties many times. At the beginning of the cooperation, the two parties will reach some kind of agreement, promising that both parties will give priority to the overall interests of the supply chain system, and the level of effort exerted by both parties will be e 1 Ⅱ * and e 2 Ⅱ * respectively, and when one party defaults, the level of effort of both parties will change to the sub-optimal e 1 Ⅰ * and e 2 Ⅰ * .
If in a certain cooperation the general contractor does not pay the level of effort e 1 Ⅱ * and the subcontractor still proceeds according to the agreement, i.e. if the general contractor defaults in this cooperation, his level of effort is e 1 Ⅰ * and the subcontractor pays the level of effort e 2 Ⅱ * , but after the end of this cooperation the subcontractor will discover the default of the general contractor, then in this cooperation the general Contractor’s gain from default.
W 1 = ( β ′ λ u e 1 Ⅰ * α e 2 Ⅱ * 1 − α − β ′ λ u e 1 Ⅱ * α e 2 Ⅱ * 1 − α ) + 1 2 k 1 ( e 1 Ⅱ * 2 − e 1 Ⅰ * 2 )
After this default, the subcontractor will not comply with the agreement in its subsequent actions, so the loss of the main contractor in each subsequent period is
S 1 = ( β ′ λ u e 1 Ⅱ * α e 2 Ⅱ * 1 − α − β ′ λ u e 1 Ⅰ * α e 2 Ⅰ * 1 − α ) + 1 2 k 1 ( e 1 Ⅰ * 2 − e 1 Ⅱ * 2 )
If the discount rate for the general contractor is γ 1 , the present value of the cost of default is
∑ n = 1 ∞ 1 1 + γ 1 n S 1 = 1 γ 1 [ ( β ′ λ u e 1 Ⅱ * α e 2 Ⅱ * 1 − α − β ′ λ u e 1 Ⅰ * α e 2 Ⅰ * 1 − α ) + 1 2 k 1 ( e 1 Ⅰ * 2 − e 1 Ⅱ * 2 ) ]
The case of no default by the general contractor is Equation (8) ≤ Equation (10), and the critical value of the general contractor discount rate when taking the critical condition is
γ 1 = ( β ′ λ u e 1 Ⅱ * α e 2 Ⅱ * 1 − α − β ′ λ u e 1 Ⅰ * α e 2 Ⅰ * 1 − α ) + 1 2 k 1 ( e 1 Ⅰ * 2 − e 1 Ⅱ * 2 ) ( β ′ λ u e 1 Ⅰ * α e 2 Ⅱ * 1 − α − β ′ λ u e 1 Ⅱ * α e 2 Ⅱ * 1 − α ) + 1 2 k 1 ( e 1 Ⅱ * 2 − e 1 Ⅰ * 2 )
Similarly, if a subcontractor defaults in a particular collaboration, its gain from default is
W 2 = ( 1 − β ′ ) ( λ u e 1 Ⅱ * α e 2 Ⅰ * 1 − α − λ u e 1 Ⅱ * α e 2 Ⅱ * 1 − α ) + 1 2 k 2 ( e 2 Ⅱ * 2 − e 2 Ⅰ * 2 )
The cost of default for a subcontractor is
∑ n = 1 ∞ 1 1 + γ 2 n S 2 = 1 γ 2 1 − β ′ λ u e 1 Ⅱ * α e 2 Ⅱ * 1 − α − λ u e 1 Ⅰ * α e 2 Ⅰ * 1 − α + 1 2 k 2 e 2 Ⅰ * 2 − e 2 Ⅱ * 2
The case where the subcontractor does not default is Equation (12) ≤ Equation (13), and the critical value of the subcontractor discount rate when taking the critical condition is
γ 2 = ( 1 − β ′ ) ( λ u e 1 Ⅱ * α e 2 Ⅱ * 1 − α − λ u e 1 Ⅰ * α e 2 Ⅰ * 1 − α ) + 1 2 k 2 ( e 2 Ⅰ * 2 − e 2 Ⅱ * 2 ) ( 1 − β ′ ) ( λ u e 1 Ⅱ * α e 2 Ⅰ * 1 − α − λ u e 1 Ⅱ * α e 2 Ⅱ * 1 − α ) + 1 2 k 2 ( e 2 Ⅱ * 2 − e 2 Ⅰ * 2 )
From the above analysis, the condition that the general contractor and subcontractor will still choose to cooperate at stage n+1 is that Equation (8) ≤ Equation (10) and Equation (12) ≤ Equation (13) hold, and the equilibrium result of achieving Pareto optimality at each stage is that both parties choose to cooperate, thus the equilibrium result of repeated games between the main bodies of the general contracting engineering supply chain system is that both parties choose to cooperate.

6. Discussion

First, all benefits are inversely proportional to the effort cost factor. In a general contracting supply chain, the optimal benefits for the general contractor, subcontractors, and the supply chain system as a whole are inversely proportional to the respective effort cost coefficients of the general contractor and subcontractors, i.e., the larger the cost coefficients of both, the smaller their benefits. This is because when general contractors and subcontractors do not play a role in the supply chain system, they have to pay more costs to achieve the same level of effort, which will cause both of them to obtain less benefits, making the supply chain system generate less benefits, as Ma DQ and Hu JS [30] found that the optimal benefits are inversely proportional to their own cost coefficients. This indicates that in the engineering supply chain, attention should be paid to the efforts of the general contractor and subcontractors themselves, and the level of effort of both should be monitored.
Secondly, the benefits of the supply chain system are proportional to the contribution of the general contractor and inversely proportional to the share of subcontractor benefits. No matter in the egoistic decision or collectivist decision, the optimal gain of the total supply chain system gain of general contracting project increases with the increase of the general contractor’s contribution degree α and decreases with the increase of the share of subcontractor’s benefit distribution, that is, the greater the general contractor’s contribution degree or the smaller the share of subcontractor’s benefit distribution, the more the overall gain of the supply chain system gain, which is because the general contractor either wants to This is because the general contractor has to contribute whether it wants to get the maximum benefit for itself or make the maximum benefit for the supply chain as a whole, and the greater its contribution, the more the total benefit of the supply chain system will be, which is in line with the objective situation. From this, it can be understood that the general contractor can be motivated to improve its own efforts by appropriately increasing its benefit distribution ratio, thus making the cooperation between the general contractor and subcontractors more efficient.
Finally, cooperation leads to optimal benefits for the supply chain system. The cooperation selection mode of general contractor and subcontractor is not related to the degree of contribution, and the general contractor prefers the egoistic decision mode, while the subcontractor prefers the centralist decision mode, although both decisions can make the supply chain system gain, but the overall supply chain system should prefer the centralist decision mode in order to get the optimal gain, as Wang ZS et al. [31]: government departments and social capital sectors can gain more benefits after adopting the cooperative model. The same is true for the general contractor and subcontractor, both of them can only cooperate to obtain the maximum benefit, and the optimal outcome of both sides of the game many times is cooperation, which is consistent with the reality.

7. Conclusions

In the supply chain system of general contracting projects, the benefit allocation problem between general contractors and subcontractors is related to the synergistic cooperation between them, and the effective and reasonable allocation of benefits between them can promote further cooperation between them. By using the Cobb-Douglas function to establish the benefit distribution model between general contractors and subcontractors in engineering projects and solving and simulating, we get that all benefits are inversely proportional to the effort cost coefficient; in any case, the effort level of general contractors and subcontractors is positively related to their own contribution degree and negatively related to each other’s contribution degree; and the benefits of general contracting supply chain system are positively proportional to the contribution degree of general contractors and subcontractors. The benefit distribution between the general contractor and subcontractor is inversely proportional to the share of subcontractor’s benefit; analyzing the benefit distribution between the general contractor and subcontractor when they cooperate many times, we can understand that the condition that both parties will still choose to cooperate at stage n+1 is that the benefit of default is not greater than the respective cost of default, and the equilibrium result of achieving Pareto optimality at each stage is that both parties choose to cooperate.
The paper only considers the benefit distribution of synergistic cooperation between general contractors and subcontractors in the supply chain of general contracting projects when they are risk-neutral and risk-averse, and fails to consider the benefit distribution between them when they are both risk-averse and risk-averse, and further discussion and analysis of the benefit distribution of synergistic cooperation between general contractors and other subcontractors and material suppliers are needed in future research.

Author Contributions

Wang Dan and Gao Wenwen participated equally in the conception of the idea, development of the methodology, analysis and interpretation of data, drafting of the article, and critical reviews. All authors have read and agreed to the published version of the manuscript.

Funding

This research was funded by Liaoning Provincial Education Department University Research Fund (LJKMR20220708).

Data Availability Statement

Not applicable.

Conflicts of Interest

Authors declare no conflict of interest.

References

  1. Liu, E. Introduction to international engineering management; Tianjin University Press: Tianjin, China, 2005. [Google Scholar]
  2. Bai, Z. Profit allocation model of general contracting engineering construction considering investment efforts. Journal of Engineering Management 2016, 30, 120–124. [Google Scholar]
  3. Guan, B. Research on profit distribution between general contractors and subcontractors of engineering projects. Journal of railway engineering 2010, 2703, 123–127. [Google Scholar]
  4. Sun, G.; Zhang, W.; Dong, J.; Wan, S.; Feng, J. Behavioral Decision-Making of Key Stakeholders in Public-Private Partnerships: A Hybrid Method and Benefit Distribution Study. CMES-Computer Modeling in Engineering & Sciences 2023, 136, 2895–2934. [Google Scholar] [CrossRef]
  5. Ren, K.; Liu, Y.M.; Zhang, L.Y. Research on profit distribution of total subcontracting in railway EPC projects. Journal of Engineering Management 2020, 34, 131–136. [Google Scholar]
  6. Lv, P.; Zhang, Y.; Mu, F.F. A study on the distribution of supply chain benefits between general contractors and subcontractors based on the improved Shapley value method. Operations Research and Management 2012, 2106, 211–216. [Google Scholar]
  7. Shi, Q.; Zhu, J.; Sheng, Z. Research on benefit distribution of collaborative cooperation in major engineering supply chain. China Management Science 2017, 2505, 42–51. [Google Scholar]
  8. Feng, J.; Wang, T.; Wang, L. Multi-level and multi-stage benefit distribution mechanism of collaborative construction projects based on building information model—design procurement construction model scenario. Science and Technology Management Research 2021, 41, 194–203. [Google Scholar]
  9. Wang, L.; Peng, L.; Meng, Q.L. Construction of profit game and distribution mechanism for three-level supply chain cooperation. Operations Research and Management 2010, 19, 59–65. [Google Scholar]
  10. Zhong, C.; Wei, X.; Nie, M.; et al. A two-stage method for distributing supply chain benefits considering risk—orthogonal projection entropy method. China Management Science 2010, 1802, 68–74. [Google Scholar]
  11. Han, T.; Li, D. Shapley value method for benefit distribution of cooperative enterprises with intuitionistic fuzzy coalition. Systems Science and Mathematics 2016, 3605, 719–727. [Google Scholar]
  12. Zou, Y. Benefit allocation mechanism of VMI&TPL model based on maximum entropy value method. Journal of Systems Science 2018, 26, 100–104. [Google Scholar]
  13. Mahjoub, S.; Hennet, J.C. A Cooperative Game Based Approach for Resource Pooling and Profit Sharing in Supply Chains. IFAC Proceedings Volumes 2012, 45, 554–559. [Google Scholar] [CrossRef]
  14. Chen, C.L.; Wang, B.W.; Lee, W.C.; et al. The optimal profit distribution problem for a supply chain network. Computer Aided Chemical Engineering 2003, 15, 422–427. [Google Scholar] [CrossRef]
  15. Xi, Y.; Cheng, Y. Research on benefit distribution mechanism based on supply chain partnership. Statistics and Decision Making 2019, 35, 59–63. [Google Scholar]
  16. Kumoi, Y.; Matsubayashi, N. Vertical integration with endogenous contract leadership: Stability and fair profit allocation. European Journal of Operational Research 2014, 238, 221–232. [Google Scholar] [CrossRef]
  17. Raza, S.A. Supply chain coordination under a revenue-sharing contract with corporate social responsibility and partial demand information. International Journal of Production Economics 2018, 205, 1–14. [Google Scholar] [CrossRef]
  18. Heydari, J.; Govindan, K.; Nasab, H.; et al. Coordination by quantity flexibility contract in a two-echelon supply chain system: effect of outsourcing decisions. 2020.
  19. Luo, C. Supply chain coordination by risk-averse retailers based on repurchase contracts. Economic Mathematics 2010, 27, 7. [Google Scholar]
  20. Xiao, Q.; Ma, S. Supply chain coordination mechanism considering information prediction cost under CVaR criterion. Systems Engineering Theory and Practice 2014, 34, 7. [Google Scholar]
  21. Wang, Y.X.; Zhao, Z.L.; Balezentis, T. Benefit distribution in shared private charging pile projects based on modified Shapley value. Energy 2023, 263. [Google Scholar] [CrossRef]
  22. Wang, C.; Zhou, Z.; Yu, X.; et al. Research on Profit Allocation of Agricultural Products Co-Delivery Based on Modified Interval Shapley Value. Sustainability 2023, 15, 3303. [Google Scholar] [CrossRef]
  23. Tan, Z.F.; Yu, C.; Li, L.; et al. Optimization model for joint energy saving and SO2 emission reduction benefit distribution between power generation side and power supply side. Systems Engineering Theory and Practice 2011, 31, 9. [Google Scholar]
  24. Wang, L.; Li, Y.; Wang, Y.; et al. Compensation benefits allocation and stability evaluation of cascade hydropower stations based on Variation Coefficient—Shapley Value Method. Journal of Hydrology 2021, 126277. [Google Scholar] [CrossRef]
  25. Li, L.; Liu, S.; Fan, F. A dynamic benefit allocation method for collaborative innovation projects. Statistics and Decision Making 2017, 13, 59–62. [Google Scholar]
  26. Wang, X.S.; Hu, H.; Liu, X.X.; et al. Benefit allocation of shared contractual water conservation management based on bargaining model. Systems Engineering Theory and Practice 2020, 40, 9. [Google Scholar]
  27. Zhang, S.; Li, X.; Wu, Z. A pilot study on the allocation of strategic alliances. Application of system engineering theory and methods 2002, 11, 5. [Google Scholar]
  28. Sun, L.; Zhao, Y.; Liu, L. Research on benefit allocation of whole process engineering consulting based on modified SHAPLEY value. Journal of Engineering Management 2022, 36, 41–45. [Google Scholar]
  29. Liu, Z.; Chu, J.-Y.; Ma, D.-X.; et al. Research on benefit distribution of whole process engineering consulting consortium based on asymmetric Nash negotiation model. Journal of North China University of Technology (Natural Science Edition) 2022, 44, 46–51+67. [Google Scholar]
  30. Ma, D.Q.; Hu, J.S. A dynamic synergistic strategy for quality improvement inputs and marketing efforts considering the delay phenomenon. Operations Research and Management 2021, 30, 181–190. [Google Scholar]
  31. Wang, Z.; Zhou, Y.; Jin, X.; Zhao, N.; Sun, J. Risk allocation and benefit distribution of PPP projects for construction waste recycling: a case study of China. Engineering, Construction and Architectural Management, ahead-of-print. 2022. [Google Scholar] [CrossRef]
Preprints 77468 g001
Figure 1. Comparison of e1, e2, X, and α.
Figure 1. Comparison of e1, e2, X, and α.
Preprints 77468 g001
Preprints 77468 g002
Figure 2. Comparison of the positive lateral relationship between Y, Z and α and β.
Figure 2. Comparison of the positive lateral relationship between Y, Z and α and β.
Preprints 77468 g002
Table 1. Results for each decision variable in the two decision models.
Table 1. Results for each decision variable in the two decision models.
Decision Variables Egoistic decision making Collectivist decision-making
β * 1 + α 2
e 1 * ( α k 1 ) 1 + α 2 ( 1 − α ) 2 2 k 2 1 − α 2 ( α k 1 ) 1 + α 2 1 − α k 2 1 − α 2
e 2 * ( α k 1 ) α 2 ( 1 − α ) 2 2 k 2 2 − α 2 ( α k 1 ) α 2 1 − α k 2 2 − α 2
X * p 1 − p 2 + 1 2 ( α k 1 ) α ( 1 − α ) 2 2 k 2 1 − α
Y * p 2 + 1 − α 2 4 ( α k 1 ) α ( 1 − α ) 2 2 k 2 1 − α − 1 2 f 2 ( 1 − β ) 2 σ 2
Z * p 1 + 3 − α 2 4 ( α k 1 ) α ( 1 − α ) 2 2 k 2 1 − α − 1 2 f 2 ( 1 − β ) 2 σ 2 p 1 + 1 2 ( α k 1 ) α 1 − α k 2 1 − α − 1 2 f 2 ( 1 − β ) 2 σ 2
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.
Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.
Prerpints.org logo

Preprints.org is a free preprint server supported by MDPI in Basel, Switzerland.

facebook logotwitter logolinkedin logo
MDPI Initiatives
Important Links
Subscribe

Disclaimer

Terms of Use

Privacy Policy

© 2024 MDPI (Basel, Switzerland) unless otherwise stated