Prerpints.org logo
Preprint
Article

Modeling of the Peptide Release During Proteolysis of B-Lactoglobulin by Trypsin

Altmetrics

Downloads

95

Views

29

Comments

0

A peer-reviewed article of this preprint also exists.

This version is not peer-reviewed

Submitted:

26 June 2023

Posted:

27 June 2023

You are already at the latest version

Alerts
Abstract
Prospects for predicting the fragmentation of polypeptide chains during their enzymatic hydrolysis using proteolysis models are considered. The opening of the protein substrate during proteolysis and the exposure of its internal peptide bonds for a successful enzymatic attack, the so-called demasking process, were taken into account. The two-step model of proteolysis was used, including the parameters of peptide bond demasking and hydrolysis rate constants for various peptide bonds. Herein, we presented an algorithm for calculating the concentrations of peptide fragments depending on the hydrolysis time or the degree of hydrolysis. The intermediate peptide fragments with two or one internal specific bonds were considered. The fragmentation of β-lactoglobulin (b-LG) with trypsin was predicted, and the calculated concentration curves for peptide fragments were compared with the experimental dependences of concentrations on the degree of hydrolysis. Numerical parameters characterizing the kinetic curves were proposed for the intermediate and final peptide fragments, and they were used to compare the calculated and experimental dependences. The predicted distribution of peptide fragments corresponded to the experimental data on the peptide release during proteolysis of b-LG by trypsin.
Keywords: 
Subject: Biology and Life Sciences  -   Biophysics

1. Introduction

Enzymatic hydrolysis of proteins (proteolysis) gives a mixture of various peptide fragments, the composition of which continuously changes during hydrolysis. The final products of proteolysis, which no longer include enzyme-specific peptide bonds, as well as rather long intermediate peptides, can be biologically active. The intermediate biopeptides can be obtained if the time interval in which the reaction should be stopped to avoid further degradation is known. An aid in the production of bioactive peptides by proteolysis can be the prediction of peptide release using the quantitative models of proteolysis and computer simulations.
It is clear that in order to predict the peptide release during proteolysis, it is necessary to know the quantitative contributions to the specificity of various amino acid residues at different positions closest to the cleaved bond within the conception of primary and secondary specificity [1,2]. In addition to knowing the specificity parameters, one should know whether the conformation of the peptide chain is convenient for the successful enzymatic attack of a given peptide bond, i.e. whether this bond is demasked or not [3]. Various simplifications in calculation algorithm are inevitable when modeling such a complex phenomenon as proteolysis, including decrease in the number of intermediate fragments, approximately definition of the parameters that cannot be determined experimentally, etc. Here, we propose a new algorithm for predicting the release of peptides during proteolysis of β-LG by trypsin with consideration of demasking process.
The first quantitative data on the secondary specificity has been obtained for pepsin, considering up to 10 amino acid residues on both sides of the broken bond [4]. These data were used for the prediction of the peptide release in β-LG with demasked peptide bonds [5]. Efforts are currently ongoing to analyze the secondary specificity of pepsin and model the peptide release kinetics [6,7]. For trypsin, mostly primary substrate specificity was taken into consideration for the proteolysis modelling [1,8], although preferred and undesirable amino acid residues at various positions have also been established and taken into account [9]. Among the modeling the peptide release, we note also studies of proteolysis with proteases from Bacillus licheniformis [10] and Lactococcus lactis [11]. In all these works, it was assumed that any site of the polypeptide chain is freely accessible to the enzyme or some constant factor was introduced for the estimation of limited accessibility of the peptide bonds. There were no attempts to evaluate changes in the accessibility of peptide bonds during proteolysis that means that demasking process was not considered in these studies.
In the protein substrates, trypsin cleaves predominantly peptide bonds at the carboxyl side of lysine and arginine (Arg-X and Lys-X bonds) unless they are followed by proline [12,13,14]. In the addition, the rate of hydrolysis of these bonds depends also on other neighboring amino acid residues [9]. Hydrolysis of some peptide bonds during proteolysis is accompanied by structural changes in the protein, which in turn predetermine the hydrolysis of other bonds. Therefore, the opening of the protein substrate during proteolysis and the corresponding exposure of its internal peptide bonds for successful enzymatic attack, the so-called demasking effect is very important component of proteolysis controlling its overall kinetics [15,16]. In contrast to the hydrolysis of low molecular weight substrates with one hydrolysable bond, proteolysis cleaves a set of peptide bonds of different secondary specificities and different demasking states, the latter being able to change during the process [15,16]. Proteolysis starts from the destruction of the initial structure of the globular protein or protein aggregates (micelles), which increases the accessibility of the remaining peptide bonds for the enzyme. This process provides demasking of peptide bonds, leading to an increase in the rate of hydrolysis when the initially masked bonds become demasked [3]. The opposite process was noted during proteolysis of β-CN by trypsin, when increased aggregation and a local increase in masking was observed in some time after the start of proteolysis [16]. The formation of additionally masked peptide bonds from proteolysis intermediates, as a result of their aggregation or conformational rearrangements, is referred to as the secondary masking. Recently, competition between peptide bond demasking and secondary masking has been shown to explain restriction in substrate structure opening and limitation in peptide bond hydrolysis [17] with a decrease in enzyme concentration.
The hydrolysis of peptide bonds was studied using the two-step proteolysis model that takes into account the demasking process [3,16]. The rate of demasking was determined from the shift in tryptophan fluorescence, which changes as the protein globule degrades or protein micelles are destroyed [15,16]. A complication of the two-step proteolysis model was carried out for the proteolysis of β-LG with trypsin, considering two different stages of demasking, corresponding to the degradation of the protein globule and the destruction of the remaining hydrophobic core [18].
There are two possibilities for describing proteolysis: one can analyze the concentrations of peptide fragments, or one can analyze the probabilities of bond cleavage versus the time of proteolysis. The first method provides more information about proteolysis, although it is more laborious and some of this information may be redundant because it is not known how to interpret it. The probabilities of bond cleavage contain much less information. Having the concentrations of all fragments, one can calculate the bond breaking probabilities, but the reverse is not possible. It was shown that even with the loss of some fragments, it is possible to reliably determine the cleavage probabilities for almost all specific bonds using HPLC-MC data [19]. It was also demonstrated that the changes in the probabilities of bond cleavage reflect the processes of the demasking of these bonds [20].
Herein, we show how proteolysis can be described in terms of fragment concentrations with consideration of demasking of peptide bonds. The concentrations of peptides (final and intermediate products of proteolysis) were calculated and presented as functions of degree of hydrolysis. These data were compared with the experimental data [21,22,23,24,25] on the release of peptides during hydrolysis of β-lactoglobulin by trypsin. Our goal was to present in detail the procedure for choosing the calculation parameters, including the demasking and hydrolysis rate constants. The equations for calculating the concentration of peptide fragments were also presented and the parameters of the concentration curves were considered, which made it possible to compare the simulation results with the experiment.

2. Results

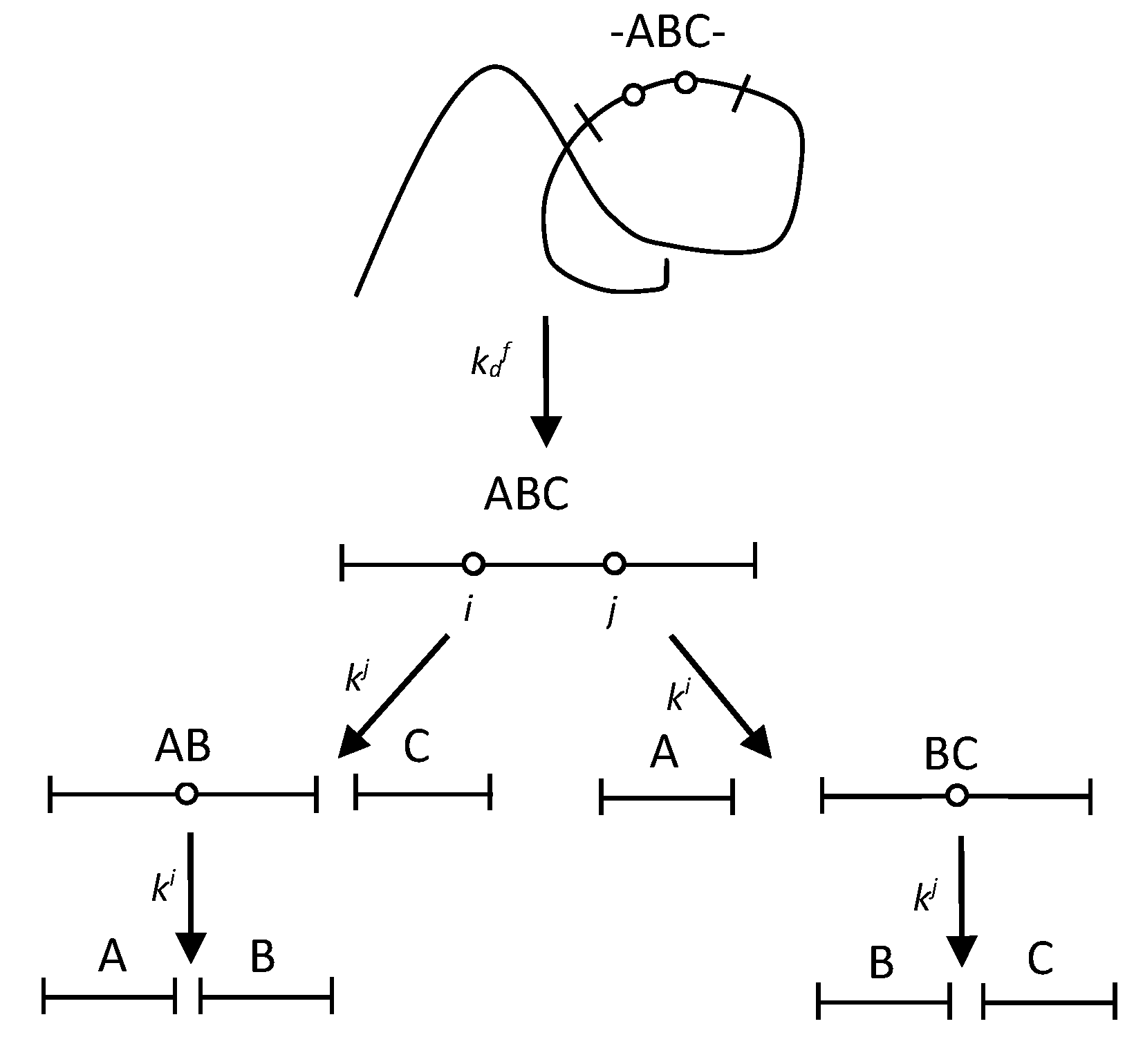
2.1. The polypeptide chain fragmentation with one demasking step

Proteolysis of a protein substrate is described by indicating the path of splitting long fragments of the polypeptide chain into shorter ones. The concentrations of these fragments depending on the hydrolysis time are obtained by solving a system of differential equations describing the fragmentation kinetics, taking into account the material balance equations. In the case when all peptide fragments and all peptide bonds are freely available for the action of the enzyme, which means that there is no masking, the solution of the kinetic task is trivial [26]. If some of the fragments are masked and the peptide bonds in them are inaccessible to the enzyme, then the analysis becomes complex. It is proposed to simplify this task.
It is assumed that the region of the polypeptide chain, located between the most rapidly hydrolyzed peptide bonds, opens up for enzymatic attack as a result of demasking. The rate of hydrolysis of the intrinsic peptide bonds in this region is controlled by demasking, i.e. the rate constants of their hydrolysis are equal or smaller than the rate constant of demasking k d f . Figure 1 shows a diagram of such a process using the example of the formation of the trimer ABC containing two demasked enzyme-specific peptide bonds. The size of the demasked region is limited here to three blocks of amino acid residues, although the kinetics for a longer region can be calculated in a similar way. According to simplification, the hydrolysis of i and j bonds is impossible in the initial polypeptide chain, but it is possible only in ABC trimer and AB and BC dimers. Hydrolysis of the demasked peptide bonds A-B and B-C occurs with the hydrolysis rate constants ki and kj, resulting in fragments AB, BC, A, B, and C.
In this scheme, the demasking process gives both the release of ABC molecule and the opening of AB and BC peptide bonds. The time dependences of the concentrations for all fragments are given in the Methods (Equations (1-6)). The initial concentration of the fragments at any position of the polypeptide chain is taken as a unit, for example, for the fragments containing A, [A]+[AB]+[ABC]+[-ABC-]=1 is valid. Therefore, all concentrations of peptide fragments given here are relative.

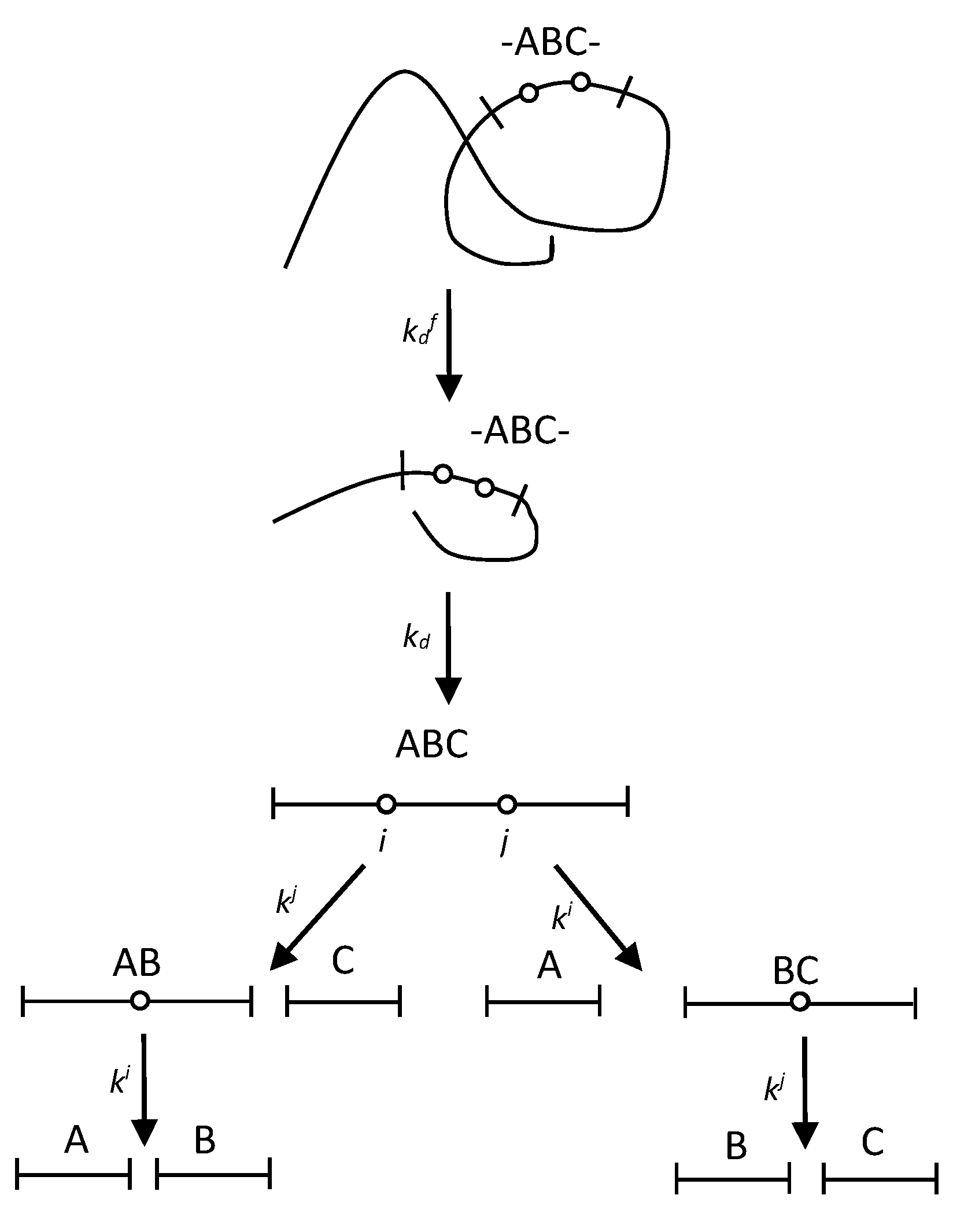
2.2. The polypeptide chain fragmentation with two demasking steps

It has been shown that some sites are demasked in two stages because after the first stage of demasking with the demasking rate constant k d f they are still in a core resistant to hydrolysis [18]. The second demasking step with the rate constant kd yields the demasked trimer ABC containing two demasked enzyme-specific peptide bonds:
In this scheme (Figure 2), the two-stage demasking process gives both the release of ABC molecule and the opening of ith and jth peptide bonds. The hydrolysis of ABC trimer proceeds in the same way as in the previous scheme (Figure 1). The time dependences for the concentrations of all fragments are given in the Methods (Equation (7)).

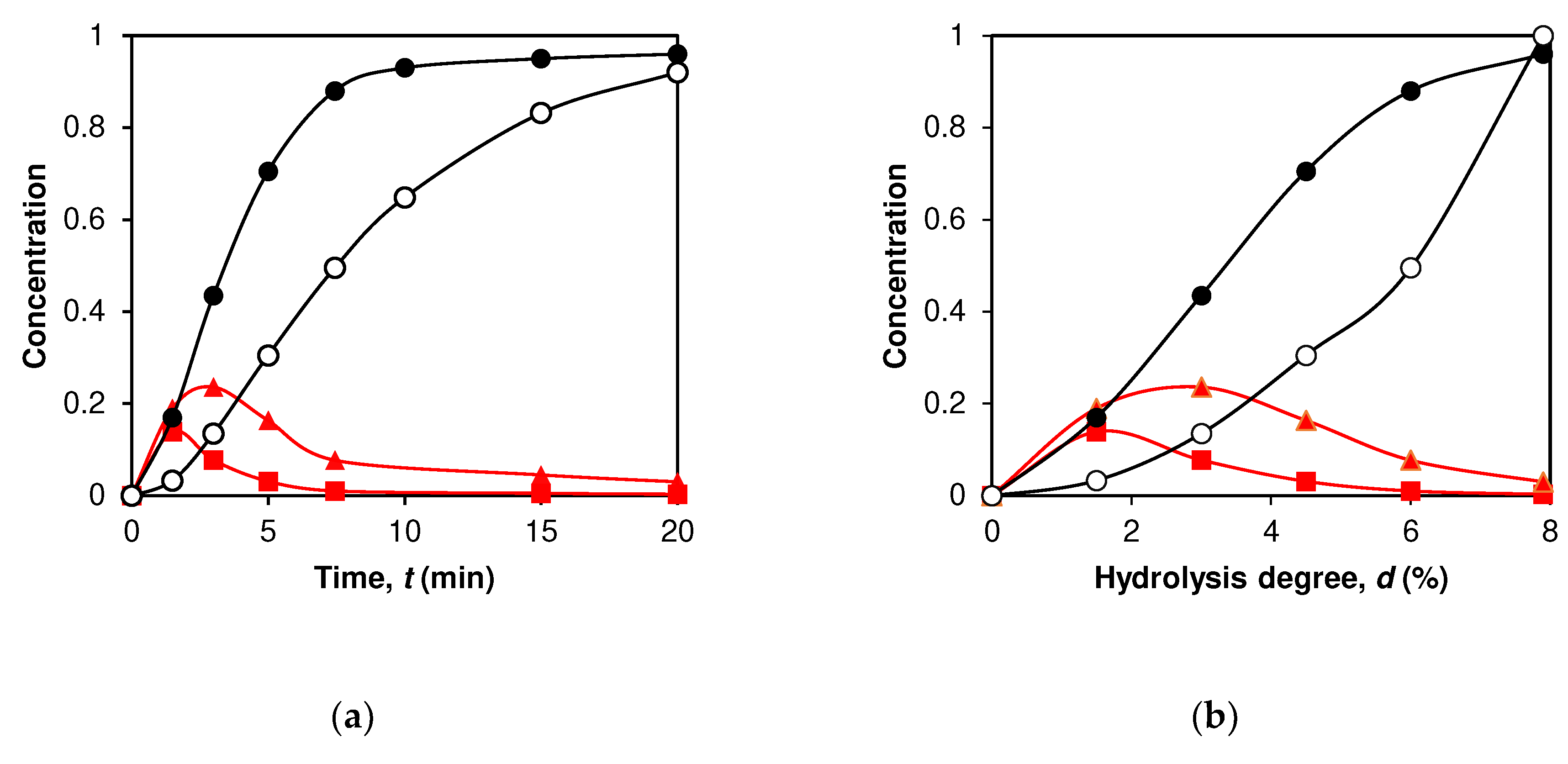
2.3. Application of peptide release schemes to β-LG proteolysis by trypsin.

For the application of the model schemes (Figure 1 and Figure 2) to real proteolysis, we collected here two kinetic parameters published for the proteolysis of β-LG by trypsin (Table 1). These parameters are the enzyme selectivity [9] and phase lag time [18]. Additionally, the hydrolysis rate constant kj, for the peptide bonds j were calculated by Equation (10) (Table 1).
The values of lag phase were used to assign peptide bonds to the type of demasking [18]. The peptide bonds 8, 14, 40, 75, 138, 141, and 148 were assigned to the one-stage demasking, while the peptide bonds 83, 91, 124, and 135 were assigned to the two-stage demasking [18].
Based on the values of selectivity and kj, the peptide bonds 8, 69/70, 75, 141 and 138 were assigned to the group of the most rapidly hydrolysable bonds. The peptide bonds 20 and 60 were assigned to the group of the most slowly hydrolyzed bonds, and therefore, in our calculation, it was assumed that they were not hydrolyzed at all. Thus, taking into account all these estimates, the trimeric fragments of the β-LG polypeptide chain are 9-14, 15-40, and 41-69/70 (one-stage demasking); 76-83, 84-91, and 92-100/101 (two-stage demasking); 101/102-124, 125-135, and 136-138 (two-stage demasking).

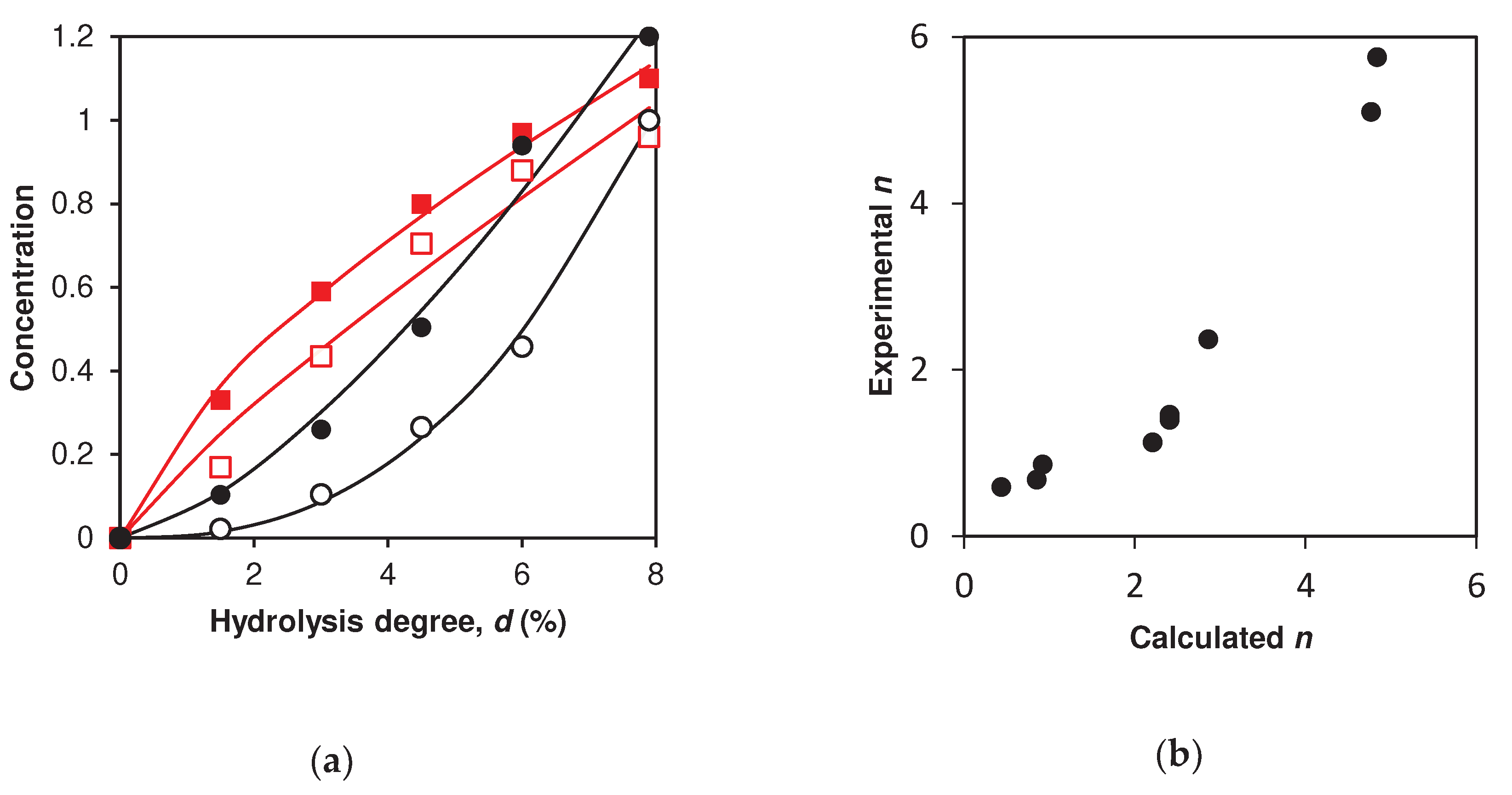
2.4. Simulation of peptide release for β-LG proteolysis by trypsin

An example of the dependences of peptide concentrations on hydrolysis time is given here for the intermediate fragments f(9-70) and f(9-40), as well as for the final products f(76-91) and f(101/102-124) (Figure 3a). The intermediate peptide products (ABC, AB and BC) are first formed and then reduced due to hydrolysis of the internal enzyme-specific peptide bonds (Figure 3a). The final products (A, B and C) accumulate because they do not contain enzyme-specific peptide bonds. When the demasking step is a kinetically significant part of proteolysis, the concentrations of the proteolysis products may increase not immediately with the onset of proteolysis, but with a lag phase [18]. This is also observed for the curves in Figure 3, especially for the peptide f(101/102-124).
The data on the release of peptides during proteolysis are presented here on the degree of hydrolysis. This way of presentation is more convenient for determining the mechanisms by which various bonds are demasked and hydrolyzed. The transformation from time to degree of hydrolysis practically does not change the concentration dependences for intermediate products, but it does change the dependences for the final peptides. For them, the curves for fast-release peptides are still convex curves, while the curves for slow-release peptides become concave (peptide f(101/102-124)) in Figure 3b. For the intermediate products, we did not use any approximate functions, but compared the curves on the basis of the average degrees of hydrolysis (dr). The degree of hydrolysis (dr) at which the main part of a peptide is released was calculated for each of the intermediate products using Equation (8) (Table 2). The calculation methodology is described in detail in the Section 4.3. The curvature of these curves is calculated using Equation (9), which is a power function and allows us to determine the exponent n (Table 3). Thus, we compared the kinetic curves for various final products by simply comparing the parameter n for them.
Figure 4 and Figure 5 show an example of the experimental and simulated dependences of the peptide concentrations as functions of d. The parameters dr for the intermediate peptides and n for the final peptides are shown in Table 2 and 3, respectively. In order to compare the simulation results with the experiment, the parameters dr and n were calculated from the experimental data [9] at the published values of hydrolysis degree 0, 1.5, 3, 4.5, 6 and 7.9%. For the same values of the degree of hydrolysis, the concentrations of peptide fragments were obtained using Equations (1-6) and Equation (7).
The experimental and simulated concentration dependences of the intermediate trimer peptides ABC and dimeric peptides (AB or BC) differ from each other (Table 2, Figure 4 a,b). For all 9 peptide fragments, trimeric peptides are released earlier than dimeric ones, and dr for the trimeric peptide fragments is less than for dimeric ones. The difference in dr for peptides released with the participation of one-stage and two-stage demasking are also different (Figure 4 a,b). This difference in release for peptides ABC (Figure 4a) is higher than that for peptides AB (Figure 4b). To determine the difference between the predicted dr and those determined from the experimental curves, we used seven peptides for which there were experimental data (Table 2). The average difference between the experimental and predicted values of dr was 0.6%, while the range of their variation was from 1.5 to 6.1%.
For the final peptides, the curve was considered convex at n < 1, while at n > 1, the curve was considered concave. The values of n for the calculated and experimental curves were compared with each other (Figure 5b). For the final peptides, it was found that for one group of peptides, the dependencies were upward convex or linear, while for the other, the dependencies were definitely concave (Figure 5a). When peptide bonds were hydrolyzed by the two-stage demasking mechanism, the release of final peptides gives concave curves.
For all three peptides released by the one-step demasking mechanism, lower values of n were obtained compared to the other peptides released by the two-step demasking. This is observed for both experimental and simulated n, although no assumptions about the presence of demasking were made when processing the experimental curves. The coefficient of proportionality between the calculated and experimental values of n was 1.25±0.42 with the expected coefficient of 1 (Figure 5b). Thus, the agreement between simulation and experiment was good.
For the proteolysis of β-LG by trypsin, the release of the peptides was determined experimentally depending on the degree of hydrolysis [27]. In this publication, among the last released intermediate peptides were f(41-60), f(76-83) and f(125-138), as well as peptides f(61-70 + 149-162) and f(41-70 + 142-162) bonded with disulfide bond Cys66-Cys160 [27]. Implementation of the demasking at the second stage may be associated with the destruction of the peptide complex connected by disulfide bridge and degradation of the α-helical region of the polypeptide chain. This is consistent with the fact that amino acid residues 76-138 in β-LG were noted as trypsin-resistant core [28].
Approximately the same cleavage sites were identified by us in β-LG as peptide bonds cleaved by trypsin after two-stage demasking. The indexes of such bonds were 20, 60, 83, 91, 124, and 135 [18] without taking into account the hydrolysis of –Lys-Lys- sequence (cleavage sites 69, 70 and 100, 101). The peptide bonds were classified as hydrolysable by the mechanism of two-stage demasking, if their hydrolysis occurs with the significant time lags [18]. Thus, lag phase estimation on kinetic curves and peptide release sequence can be used to link cleavage sites to demasking mechanisms.
The experimental confirmation of the predicted regularities requires accurate measurements of the concentrations of the released peptides. Among the quantitative studies on this topic, we note experiments in which peptide fractions [29,30] or individual peptides [19,27] were presented as the functions of the degree of hydrolysis. In these works, the changes in proteolysis conditions were due to different concentrations of the enzyme and/or substrate [19,27,29,30], but the presentation of concentration dependences on the degree of hydrolysis made it possible to bring the dependences to the same scale. The hydrolysis of casein by chymotrypsin at various E/S ratios when the substrate concentration changed was interpreted in the framework of two-step proteolysis model [29]. Hydrolysis of casein by chymotrypsin at various E/S ratios with varying substrate concentrations was interpreted in terms of a two-step proteolysis model [29]. It was taken into account that a change in the degree of hydrolysis may be the result of hydrolysis of other peptide bonds, leading to a change in the course of concentration dependences for the studied peptides. A similar effect is observed in the present study, leading to the transformation of the concentration dependences shown in Figure 3a into the dependences of Figure 3b.

3. Discussion

The proposed method for predicting the release of peptides is new, based on the modeling of proteolysis, taking into account the gradual demasking of peptide bonds during the process of proteolysis. This approach was developed by us for the quantitative description of the proteolysis of various proteins by various proteases and was based on the kinetic data on the total hydrolysis of peptide bonds and tryptophan fluorescence [3,15,16,17,18,31]. The importance of taking into account demasking processes in the study of proteolysis was also shown using other analytical and physicochemical methods [20,32,33,34,35].
In the present work, it is shown that, knowing the rate constants of demasking and the rate constants of peptide bond hydrolysis, one can calculate the concentrations of peptide fragments. This is illustrated here by the example of the release of trimeric fragments, which are demasked by the mechanism of one-stage or two-stage demasking. The size of these fragments can be increased and four-dimensional and longer fragments can be considered with the corresponding equations, similar to Equations (1-7). An additional simplification in the calculations was that the hydrolysis of a small number of very slowly hydrolyzed bonds was not taken into account, and they were considered non-hydrolysable (ki=0). When processing experimental data, the concentrations of fragments formed by the hydrolysis of such bonds were small and they were added to the concentrations of the parent peptides. Thus, the concentrations of dimeric peptides with the internal bonds i=20 and 60 were restored. The size of peptide fragments can be increased and all specific bonds, including slowly hydrolyzed ones, can be taken into account, which will increase the accuracy of the prediction of peptide release. However, the equations will be much more complicated.
The concentrations of peptide fragments were calculated using the example of β-LG proteolysis with trypsin as a practically important and experimentally well-studied case. For this case of proteolysis, the demasking parameters were determined using fluorescence spectroscopy [15,18]. The resulting peptides were identified and their concentrations were determined at several values of the proteolysis time, which makes it possible to build concentration dependences for the intermediate and final products of proteolysis [9,27].
We made an assumption that the concentration of the active enzyme is constant throughout the proteolysis, which allowed us to obtain the analytical solutions for the kinetic schemes (Figure 1 and Figure 2). If the effective Michaelis constant is expressed as a function of the degree of hydrolysis, then we can introduce a new time variable, as we showed earlier [31], and thus obtain solution in the analytical form as functions of this variable. A decrease in the concentration of the active enzyme is associated with both the equilibrium inhibition of the enzyme by proteolysis products and the relatively slow irreversible inactivation of the enzyme during proteolysis [36]. The slow inactivation of the enzyme during proteolysis was shown by the example of proteolysis of casein by chymotrypsin [36], and it explained the slowdown of proteolysis in the exponential model of proteolysis [37]. In the general case, one can use numerical integration and obtain solutions of the system of differential equations by specifying a specific form of the dependence of the concentration of the active enzyme on the time of proteolysis.
The description of proteolysis using bond cleavage probabilities is based on a significant simplification, namely on the assumption that the rate constants of hydrolysis of any bond are the same in the various demasked peptides in which this bond is located. During the hydrolysis of the polypeptide chain by the most enzymes, this assumption is justified, since the binding sites of the active sites of these enzymes do not exceed the length of the hydrolyzed fragments. An exception is the hydrolysis of peptides in which specific bonds are located in the neighborhood. For the proteolysis of β-LG by trypsin, the influence of the hydrolysis of the neighboring specific bonds on each other can be first for the cleavage sites 69, 70 and 100, 101 with amino acid sequence –Lys-Lys-. In this case, it is better to use the description of proteolysis in terms of fragment concentrations calculated, for example, by the computer program [5], in which the influence of the ends is taken into account by the corresponding term, which reduces the rate constant of the hydrolysis of bonds in short peptides. An alternative is to simplify the consideration of the –Lys-Lys- site as a single peptide bond Lys-X, as we did in the present study.
Identification and quantitative determination of peptides in hydrolysates is effectively carried out by HPLC-MS methods [9,10,19]. The probability of hydrolysis of a peptide bond is determined by summing the concentrations of all peptides formed as a result of breaking this peptide bond. This technique was used to determine the enzyme selectivity for specific peptide bonds [10,19]. The proteolysis of whey proteins by the Bacillus licheniformis protease was analyzed by the hydrolysis of individual bonds [19] and it was shown that more than half of the kinetic curves have a characteristic shape, indicating the presence of the demasking effect [20]. The proteolysis of whey proteins by the Bacillus licheniformis protease was studied by analyzing the hydrolysis of individual bonds [19], and it was shown that more than a half of kinetic curves have a characteristic shape, indicating the presence of an demasking effect [20]. The fitting such curves with Equation (10) makes it possible to determine the hydrolysis rate constants kj. But these constants are only suitable for the hydrolysis 0f peptide bonds with one-step demasking. Equation (11) in ref. [18] should be used to determine the hydrolysis rate constants for the two-stage demasking. However, the application of this equation requires a more detailed measurement of the kinetic curves than was done in the works [9,10,19,20]. When selecting the values of kj for two-stage demasking, we could not directly use the obtained values of kj (Table 1), but they indicated which of the bonds is hydrolyzed faster and which slower.
To simulate the formation of peptide fragments when considering the complete system of differential equations describing the complete kinetics, it is necessary to know all the hydrolysis constants of specific bonds. For example, for porcine pepsin, an algorithm was proposed for calculating the rate constants of hydrolysis by summing the increments determined for all amino acid residues [4]. Thus, for any amino acid sequences and any cleavable bond positions, the hydrolysis constants should be calculated. This is a very time-consuming task and, therefore, it is necessary to make simplifications.
Our results on the proteolysis of β-LG by trypsin show that determination of the demasking mechanism is of great importance. This includes determining by what mechanism each peptide bond is demasked before its hydrolysis and determining the corresponding demasking rate constants. Apparently, the precise determination of the demasking mechanism may be even more important than the exact determination of the rate constants of hydrolysis for peptide bonds. This looks favorable, since the determination of the demasking parameters by spectral methods is simpler than the kinetic determination of the hydrolysis rate constants. The use of other enzyme-substrate pairs is necessary in further experiments to more fully elucidate the role of peptide bond demasking in predicting the kinetics of peptide release.
The difference between prediction and experiment in modeling the yield of peptides can be due to several reasons. Firstly, this is the imperfection of the model itself and additional simplifications made by us for the convenience of calculations. Secondly, this is insufficiently accurate knowledge of the values of the kinetic parameters included in the model. Third, the experimental data on peptide concentrations themselves contain errors. However, we have obtained a satisfactory agreement between experimental data and simulation results. It should be noted that the methods for comparing the calculated and experimental data on the release of peptides as a result of proteolysis have not been finally determined. In this work, for intermediate peptides, it is proposed to compare the average degrees of hydrolysis of peptide release. For the final peptides, the convexity of the concentration dependences on the degree of hydrolysis is compared. Further research should show if these methods are useful for modeling peptide release or if others are needed.

4. Materials and Methods

4.1. Quantitative modelling of proteolysis with one-stage demasking

To calculate the relative concentrations C(t) of the peptide fragments (Figure 1) at various ptoteolysis times t [min], the following equations must be used:
[ A B C ] = k d f k i + k j − k d f [ e − k d f t − e − ( k i + k j ) t ]
[ A B ] = k d f k j ( k i + k j − k d f ) ( k i − k d f ) e − k d f t + k d f k i + k j − k d f e − ( k i + k j ) t − k d f k i − k d f e − k i t
[ B C ] = k d f k i ( k i + k j − k d f ) ( k j − k d f ) e − k d f t + k d f k i + k j − k d f e − ( k i + k j ) t − k d f k j − k d f e − k j t
[ A ] = 1 − k i k i − k d f e − k d f t + k d f k i − k d f e − k i t
[ B ] = 1 − [ 1 + k d f k i + k j − k d f ( 1 + k i k j − k d f + k j k i − k d f ) ] e − k d f t − k 1 k i + k j − k d f e − ( k i + k j ) t + k d f k j − k d f e − k j t + k d f k i − k d f e − k i t
[ C ] = 1 − k j k j − k d f e − k d f t + k d f k j − k d f e − k j t
In the calculations k d f was 0.46 min-1 [18] and the hydrolysis rate constants were taken from Table 1 for the one-stage type of demasking.

4.2. Quantitative modelling of proteolysis with two-stage demasking

To calculate the relative concentrations of peptide fragments (Figure 2), it is necessary to use the following equation:
C ( t ) = C 0 + C 1 e − k d f t + C 2 e − ( k i + k j ) t + C 3 e − k d t + C 4 e − k i t + C 5 e − k j t
where the constant coefficients C0, C1, C2, C3 are collected in Table 4, while the constant coefficients C4 and C5 are in Table 5. k d f was 0.46 min-1 [18], while kd was accepted to be 0.15 min-1 to keep the ratio k d f / kd around 3 [18]. The hydrolysis rate constants were taken from Table 1 for the two-stage type of demasking.

4.3. Estimation of the parameters for concentration dependences

For the intermediate peptide fragments, the average hydrolysis degree of the peptide release dr was calculated using the following equation:
d r = ∑ i = 1 6 d i × C ( d i ) / ∑ i = 1 6 C ( d i ) ,
where C(di) are the concentrations of peptide fragments determined at six hydrolysis degrees di (0, 1.5, 3, 4.5, 6 and 7.9%). We used the same values of the degrees of hydrolysis that were used in the work [9] with which we compared the simulation results. Concentrations taken from Table S-4 [9] were divided by 50 to obtain the relative concentrations of peptide fragments.
For the final peptides, the parameter n was calculated using the following equation:
C ( d i ) = a ( d i / 7.9 ) n ,
where a is a constant factor and n is the exponent of the power function.
The concentration of the products of the hydrolysis of jth peptide bond is described by the equation (Equation (10) in ref. [18]):
N j ( t ) = N 0 [ 1 − k j e − k d f t ( k j − k d f ) + k d f e − k j t ( k j − k d f ) ] ,
where Nj is the concentration of all products derived from the hydrolysis of jth bond [18]. Equation (10) was used for the determination of the hydrolysis constant kj at a fixed value of k d f = 0.46 min-1 from the experimental kinetic data [9].

Author Contributions

Not applicable.

Funding

This research was supported by Russian Foundation for Basic Research (grant 20-53-46006) and Ministry of Science and Higher Education of the Russian Federation (Contract/agreement No. 075-03-2023-642).

Institutional Review Board Statement

Not applicable.

Informed Consent Statement

Not applicable.

Data Availability Statement

The data presented in this study are available on request from the corresponding author.

Conflicts of Interest

The authors declare that they have no conflict of interest.

References

  1. Niemann, C. Alpha-chymotrypsin and the nature of enzyme catalysis. Science 1964, 143(3612), 1287–1296. [Google Scholar] [CrossRef] [PubMed]
  2. Vorob’ev, M.M.; Dalgalarrondo, M.; Chobert, J.-M.; Haertle, T. Kinetics of β-casein hydrolysis by wild-type and engineered trypsin. Biopolymers 2000, 54, 355–364. [Google Scholar] [CrossRef] [PubMed]
  3. Vorob’ev, M.M. Kinetics of peptide bond demasking in enzymatic hydrolysis of casein substrates. J. Mol. Catal. B 2009, 58, 146–152. [Google Scholar] [CrossRef]
  4. Antonov, V.K. New Data on Pepsin Mechanism and Specificity. In: Tang, J. (eds) Acid Proteases: Structure, Function, and Biology. Advances in Experimental Medicine and Biology, vol 95. Springer: New York, NY, 1977. [CrossRef]
  5. Vorob’ev, M.M.; Goncharova, I.A. Computer simulation of proteolysis. Peptic hydrolysis of partially demasked β-Lactoglobulin. Nahrung-Food 1998, 42, 61–67. [Google Scholar] [CrossRef]
  6. Suwareh, O.; Causeur, D.; Jardin, J.; Briard-Bion, V.; Le Feunteun, S.; Pezennec, S.; Nau, F. Statistical modeling of in vitro pepsin specificity. Food Chem. 2021, 362, 130098. [Google Scholar] [CrossRef]
  7. Tonda, A.; Grosvenor, A.; Clerens, S.; Le Feunteun, S. In silico modeling of protein hydrolysis by endoproteases: a case study on pepsin digestion of bovine lactoferrin. Food Funct. 2017, 8, 4404–4413. [Google Scholar] [CrossRef]
  8. Trusek-Holownia, A.; Noworyta, A. A model of kinetics of the enzymatic hydrolysis of biopolymers – a concept for determination of hydrolysate composition. Chem. Eng. Process.: Process Intensif. 2015, 89, 54–61. [Google Scholar] [CrossRef]
  9. Deng, Y.; van der Veer, F.; Sforza, S.; Gruppen, H.; Wierenga, P.A. Towards predicting protein hydrolysis by bovine trypsin. Process Biochem. 2018, 65, 81–92. [Google Scholar] [CrossRef]
  10. Butré, C.I. Introducing enzyme selectivity as a quantitative parameter to describe the effects of substrate concentration on protein hydrolysis. Thesis, Wageningen University, 2014, ISBN: 978-94-6257-023-8.
  11. Muñoz-Tamayo, R.; De Groot, J.; Wierenga, P.A.; Gruppen, H.; Zwietering, M.H.; Sijtsma, L. Modeling peptide formation during the hydrolysis of β-casein by Lactococcus lactis. Process Biochem. 2012, 47, 83–93. [Google Scholar] [CrossRef]
  12. Polgár, L. The catalytic triad of serine peptidases. Cell. Mol. Life Sci. 2005, 62, 2161–2172. [Google Scholar] [CrossRef]
  13. Olsen, J.V.; Ong, S.-E.; Mann, M. Trypsin cleaves exclusively C-terminal to arginine and lysine residues. Mol. Cell. Proteomics. 2004, 3, 608–614. [Google Scholar] [CrossRef] [PubMed]
  14. Stryer, L. Biochemistry, 3rd ed.; W.H. Freeman and Company: NY, USA, 1988; ISBN 0-7167-1843-x. [Google Scholar]
  15. Vorob’ev, M.M.; Vogel, V.; Güler, G.; Mäntele, W. Monitoring of demasking of peptide bonds during proteolysis by analysis of the apparent spectral shift of intrinsic protein fluorescence. Food Biophys. 2011, 6, 519–526. [Google Scholar] [CrossRef]
  16. Vorob’ev, M.M. Proteolysis of β-lactoglobulin by trypsin: Simulation by two-step model and experimental verification by intrinsic tryptophan fluorescence. Symmetry 2019, 11, 153. [Google Scholar] [CrossRef]
  17. Vorob’ev, M.M. Modeling of proteolysis of β-lactoglobulin and β-casein by trypsin with consideration of secondary masking of intermediate polypeptides. Int. J. Mol. Sci. 2022, 23, 8089. [Google Scholar] [CrossRef]
  18. Vorob’ev, M.M. Tryptophan fluorescence and time-lag hydrolysis of peptide bonds during degradation of β-lactoglobulin by trypsin. Catalysts 2020, 10, 1368. [Google Scholar] [CrossRef]
  19. Butre, C.I.; Sforza, S.; Gruppen, H.; Wierenga, P.A. Introducing enzyme selectivity: a quantitative parameter to describe enzymatic protein hydrolysis. Anal. Bioanal. Chem. 2014, 406, 5827–5841. [Google Scholar] [CrossRef]
  20. Vorob’ev, M.M.; Butré, C.I.; Sforza, S.; Wierenga, P.A.; Gruppen, H. Demasking kinetics of peptide bond cleavage for whey protein isolate hydrolysed by Bacillus licheniformis protease. J. Mol. Catal, B. 2016, 133, 426–431. [Google Scholar] [CrossRef]
  21. Caessens, P.; Visser, S.; Gruppen, H.; Voragen, A. β-Lactoglobulin hydrolysis. 1. Peptide composition and functional properties of hydrolysates obtained by the action of plasmin, trypsin, and Staphylococcus aureus V8 protease. J. Agric. Food Chem. 1999, 47, 2973–2979. [Google Scholar] [CrossRef] [PubMed]
  22. Cheison, S.; Schmitt, M.; Leeb, E.; Letzel, T.; Kulozik, U. Influence of temperature and degree of hydrolysis on the peptide composition of trypsin hydrolysates of β-lactoglobulin: Analysis by LC-ESI-TOF/MS. Food Chem. 2010, 121, 457–467. [Google Scholar] [CrossRef]
  23. Fernandez, A.; Riera, F. β-Lactoglobulin tryptic digestion: A model approach for peptide release. Biochem. Eng. J. 2013, 70, 88–96. [Google Scholar] [CrossRef]
  24. Mao, Y.; Krischke, M.; Kulozik, U. β-lactoglobulin hydrolysis by immobilized trypsin in ethanol/aqueous solvents. Process Biochem. 2019, 82, 84–93. [Google Scholar] [CrossRef]
  25. Cheison, S.; Lai, M.; Leeb, E.; Kulozik, U. Hydrolysis of β-lactoglobulin by trypsin under acidic pH and analysis of the hydrolysates with MALDI–TOF–MS/MS. Food Chem. 2011, 125, 1241–1248. [Google Scholar] [CrossRef]
  26. Emsley, A.M.; Heywood, R.J. Computer modeling of the degradation of linear polymers. Polym. Degrad. Stab. 1995, 49, 145–149. [Google Scholar] [CrossRef]
  27. Leeb, E.; Stefan, T.; Letzel, T.; Hinrichs, J.; Kulozik, U. Tryptic hydrolysis of β-lactoglobulin: A generic approach to describe the hydrolysis kinetic and release of peptides. Int. Dairy J. 2020, 105, 104666. [Google Scholar] [CrossRef]
  28. Cheison, S.C.; Leeb, E.; Letzel, T.; Kulozik, U. Influence of buffer type and concentration on the peptide composition of trypsin hydrolysates of β-lactoglobulin. Food Chem. 2011, 125, 121–127. [Google Scholar] [CrossRef]
  29. Vorob’ev, M.M.; Paskonova, E.A. , Vitt, S.V.; Belikov, V.M. Kinetic description of proteolysis. Part 2. Substrate regulation of peptide bond demasking and hydrolysis. Liquid chromatography of hydrolyzates. Nahrung-Food, 1986, 30, 995–1001. [Google Scholar] [CrossRef]
  30. Chabanon, G.; Chevalot, I.; Framboisier, X.; Chenu, S.; Marc, I. Hydrolysis of rapeseed protein isolates: Kinetics, characterization and functional properties of hydrolysates. Process Biochem. 2007, 42, 1419–1428. [Google Scholar] [CrossRef]
  31. Vorob’ev, M.M. Quantification of two-step proteolysis model with consecutive demasking and hydrolysis of peptide bonds using casein hydrolysis by chymotrypsin. Biochem. Eng. J. 2013, 74, 60–68. [Google Scholar] [CrossRef]
  32. Rivera-Burgos, D.; Regnier, F.E. Disparities between immobilized enzyme and solution based digestion of transferrin with trypsin. J. Sep. Sci. 2013, 36, 454–460. [Google Scholar] [CrossRef]
  33. Melikishvili, S.; Dizon, M. , Hianik, T. Application of high-resolution ultrasonic spectroscopy for real-time monitoring of trypsin activity in β-casein solution. Food Chem. 2021, 337, 127759. [Google Scholar] [CrossRef]
  34. Buckin, V.; Altas, M.C. Ultrasonic monitoring of biocatalysis in solutions and complex dispersions. Catalysts 2017, 7, 336. [Google Scholar] [CrossRef]
  35. Vreeke, G.J.C.; Vincken, J.-P.; Wierenga, P.A. The path of proteolysis by bovine chymotrypsin Food Res. Int. 2023, 165, 112485. [Google Scholar] [CrossRef]
  36. Vorob’ev, M.M.; Vitt, S.V.; Belikov, V.M. Kinetic description of proteolysis. Part 3. Total kinetics of peptide bonds hydrolysis in peptide mixtures. Nahrung-Food 1987, 31, 331–340. [Google Scholar] [CrossRef] [PubMed]
  37. Marquez, M.C.; Fernandez, V. Enzymic hydrolysis of vegetable proteins: mechanism and kinetics. Process Biochem. 1993, 28, 481–490. [Google Scholar] [CrossRef]
Preprints 77728 g001
Figure 1. A scheme of peptide release in proteolysis with one-stage demasking.
Figure 1. A scheme of peptide release in proteolysis with one-stage demasking.
Preprints 77728 g001
Preprints 77728 g002
Figure 2. A scheme of peptide release in proteolysis with two-stage demasking.
Figure 2. A scheme of peptide release in proteolysis with two-stage demasking.
Preprints 77728 g002
Preprints 77728 g003
Figure 3. Simulation of peptide release during proteolysis: (a) Calculated dependences of peptide concentrations on hydrolysis time for the intermediate peptides f(9-70) ■ and f(9-40) □, and for the final products of proteolysis f(76-91) ● and f(101/102-124) ○ . (b) Calculated dependences of peptide concentrations on the degree of hydrolysis for the same peptide fragments.
Figure 3. Simulation of peptide release during proteolysis: (a) Calculated dependences of peptide concentrations on hydrolysis time for the intermediate peptides f(9-70) ■ and f(9-40) □, and for the final products of proteolysis f(76-91) ● and f(101/102-124) ○ . (b) Calculated dependences of peptide concentrations on the degree of hydrolysis for the same peptide fragments.
Preprints 77728 g003
Preprints 77728 g004
Figure 4. Simulation of peptide release during proteolysis: (a) Peptide fragment ABC f(9-79/70) (one-stage demasking) calculated (■) and experimental (●) curves. Peptide fragment ABC f(76-100/101) (one-stage demasking), calculated (□) and experimental (○) curves. (b) Peptide fragment AB f(9-40) (two-stage demasking) calculated (■) and experimental (●) curves. Peptide fragment AB f(76-91) (two-stage demasking), calculated (□) and experimental (○) curves.
Figure 4. Simulation of peptide release during proteolysis: (a) Peptide fragment ABC f(9-79/70) (one-stage demasking) calculated (■) and experimental (●) curves. Peptide fragment ABC f(76-100/101) (one-stage demasking), calculated (□) and experimental (○) curves. (b) Peptide fragment AB f(9-40) (two-stage demasking) calculated (■) and experimental (●) curves. Peptide fragment AB f(76-91) (two-stage demasking), calculated (□) and experimental (○) curves.
Preprints 77728 g004
Preprints 77728 g005
Figure 5. Processing of concentration curves for final products: (a) Concentration dependences for f(9-14) (calculated □, experimental ■) and f(76-83) (calculated ○, experimental ●). Solid lines correspond to Equation (9). (b) Correlation between experimental and calculated parameters n for 9 final products (Table 3).
Figure 5. Processing of concentration curves for final products: (a) Concentration dependences for f(9-14) (calculated □, experimental ■) and f(76-83) (calculated ○, experimental ●). Solid lines correspond to Equation (9). (b) Correlation between experimental and calculated parameters n for 9 final products (Table 3).
Preprints 77728 g005
Table 1. Kinetic parameters for tryptic hydrolysis of β-LG.
Table 1. Kinetic parameters for tryptic hydrolysis of β-LG.
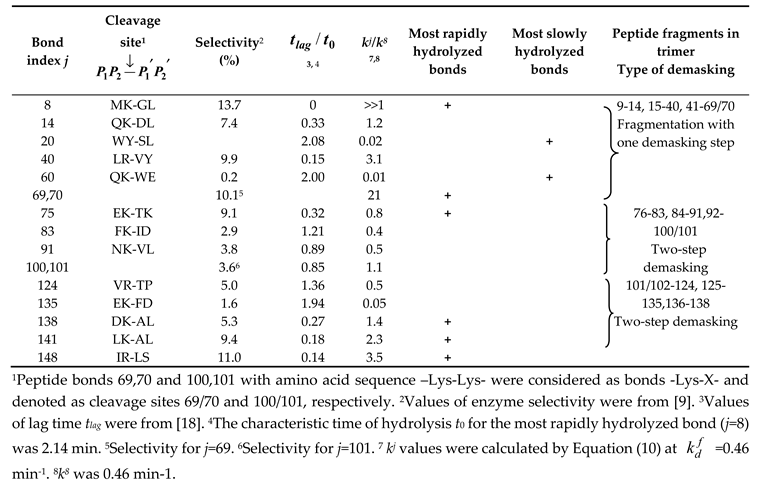
Preprints 77728 i001
Table 2. Simulation of the release of intermediate peptides.
Table 2. Simulation of the release of intermediate peptides.
Peptide Type of demasking Hydrolysis rate constants (min-1) Calculated values of dr (%) Experimental estimation of dr (%)
f(9-69/70) ABC One-stage1 k14=0.53 k40=1.41 2.6 1.53
f(9-40) AB One-stage1 3.5 3.6
f(15-69/70) BC One-stage1 2.8 -4
f(76-100/101) ABC Two-stage k83=1 k91=1 3.9 3.4
f(76-91) AB Two-stage2 4.3 4.4
f(84-100/101) BC Two-stage2 4.3 4,7
f(101/102-138) ABC Two-stage2 k124=2 k138=0.2 3.8 3,4
f(101/102-135)AB Two-stage2 4,1 -4
f(125-138) BC Two-stage2 4.7 6.1
1 k d f was 0.46 min-1 [18]. 2kd was 0.15 min-1 ( k d f / kd=3 [18]). 3Only one concentration at d=1.5% for this fragment was given [9]. 4These peptide fragments were not found [9].
Table 3. Simulation of the release of final peptides.
Table 3. Simulation of the release of final peptides.
Peptide Type of demasking Hydrolysis rate constants (min-1) Calculated values of n3 Experimental estimation of n3
f(9-14) A One-stage1 k14=0.53 k40=1.41 0.85 0.68
f(15-40) B
f(41-69/70) C		 One-stage1
One-stage1 		0.92
0.44		 0.86
0.59
f(76-83) A Two-stage2 k83=1 k91=1 2.41 1.46
f(84-91) B Two-stage2 2.86 2.37
f(92-100/101) C Two-stage2 2.41 1.40
f(101/102-124) A Two-stage2 k124=2 k135=0.2 2.21 1.13
f(125-135) B Two-stage2 4.84 5.76
f(136-138) C Two-stage2 4.77 5.10
1 k d f was 0.46 min-1 [18]. 2 kd was 0.15 min-1( k d f / kd=3 [18]). 3 The exponents of the power function n were determined using Equation (9).
Table 4. Coefficients C0, C1, C2, and C3 for the terms of Equation 7.
Table 4. Coefficients C0, C1, C2, and C3 for the terms of Equation 7.
Peptide fragment Constant term C0 Coefficient   C 1   at   e − k d f t Coefficient   C 2   at   e − ( k i + k j ) t Coefficient   at   C 3   e − k d t
A 1 − k i k d ( k d − k d f ) ( k i − k d f ) 0 k d f k i ( k d − k d f ) ( k i − k d f )
B 1 − k d k i k j ( k i + k j − 2 k d f ) ( k d − k d f ) ( k i + k j − k d f ) ( k j − k d f ) ( k i − k d f ) k d f k d ( k i + k j − k d f ) ( k i + k j − k d ) k d f k i k j ( k i + k j − 2 k d ) ( k d − k d f ) ( k i + k j − k d ) ( k j − k d ) ( k i − k d )
C 1 − k j k d ( k d − k d f ) ( k j − k d f ) 0 k d f k j ( k d − k d f ) ( k j − k d f )
AB 0 k d f k d k j ( k d − k d f ) ( k i + k j − k d f ) ( k i − k d f ) k d f k d ( k i + k j − k d f ) ( k i + k j − k d ) k d f k d k j ( k d − k d f ) ( k i + k j − k d ) ( k i − k d )
BC 0 k d f k d k i ( k d − k d f ) ( k i + k j − k d f ) ( k j − k d f ) k d f k d ( k i + k j − k d f ) ( k i + k j − k d ) k d f k d k i ( k d − k d f ) ( k i + k j − k d ) ( k j − k d )
ABC 0 k d f k d ( k d − k d f ) ( k i + k j − k d f ) k d f k d ( k i + k j − k d f ) ( k i + k j − k d ) − k d f k d ( k d − k d f ) ( k i + k j − k d )
Table 5. Coefficients C4 and C5 for the terms of Equation 7.
Table 5. Coefficients C4 and C5 for the terms of Equation 7.
Peptide fragment Coefficient   C 4   at   e − k i t Coefficient   C 5   at   e − k j t
A − k d f k d [ ( k i + k j ) ( k i + k j − k d f − k d ) + k d f k d ] ( k i − k d f ) ( k i − k d ) ( k i + k j − k d f ) ( k i + k j − k d ) 0
B 0 0
C 0 − k d f k d [ ( k i + k j ) ( k i + k j − k d f − k d ) + k d f k d ] ( k j − k d f ) ( k j − k d ) ( k i + k j − k d f ) ( k i + k j − k d )
AB − k d f k d [ ( k i + k j ) ( k i + k j − k d f − k d ) + k d f k d ] ( k i − k d f ) ( k i − k d ) ( k i + k j − k d f ) ( k i + k j − k d ) 0
BC 0 − k d f k d [ ( k i + k j ) ( k i + k j − k d f − k d ) + k d f k d ] ( k j − k d f ) ( k j − k d ) ( k i + k j − k d f ) ( k i + k j − k d )
ABC − k d f k d [ ( k i + k j ) ( k i + k j − k d f − k d ) + k d f k d ] ( k i − k d f ) ( k i − k d ) ( k i + k j − k d f ) ( k i + k j − k d ) − k d f k d [ ( k i + k j ) ( k i + k j − k d f − k d ) + k d f k d ] ( k j − k d f ) ( k j − k d ) ( k i + k j − k d f ) ( k i + k j − k d )
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.
Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.
Prerpints.org logo

Preprints.org is a free preprint server supported by MDPI in Basel, Switzerland.

facebook logotwitter logolinkedin logo
MDPI Initiatives
Important Links
Subscribe

Disclaimer

Terms of Use

Privacy Policy

© 2024 MDPI (Basel, Switzerland) unless otherwise stated