Prerpints.org logo
Preprint
Article

Characterizing the Spatio-Temporal Variations of Urban Growth with Multifractal Spectrums

Altmetrics

Downloads

81

Views

14

Comments

0

Meng Fu  *

This version is not peer-reviewed

Submitted:

27 June 2023

Posted:

28 June 2023

You are already at the latest version

Alerts
Abstract
Urban morphology exhibits fractal characteristics, which can be described by multifractal scaling. Multifractal parameters under positive moment orders primarily capture information about cen-tral areas with relatively stable growth, while those under negative moment orders mainly reflect information about marginal areas with more active growth. However, effectively utilizing mul-tifractal spectrums to uncover the spatio-temporal variations of urban growth remains a challenge. To addresses this issue, this paper proposes a multifractal measurement by combining theoretical principles and empirical analysis. To capture the difference between growth stability in central areas and growth activity in marginal areas, an index based on generalized correlation dimension Dq is defined. This index takes the growth rate of Dq at extreme negative moment order as the numerator, and that at extreme positive moment order as the denominator. During the stable stage of urban growth, the index demonstrates a consistent pattern over time. While during the active stage, the index may exhibit abnormal fluctuations or even jumps. This indicates that the index can reveal spatio-temporal information about urban evolution that cannot be directly observed through multifractal spectrums alone. By integrating this index with multifractal spectrums, we can more comprehensively characterize the evolutionary characteristics of urban spatial structure.
Keywords: 
Subject: Environmental and Earth Sciences  -   Geography

1. Introduction

Multifractal method has become a crucial tool in urban geography research, as urban systems are complex systems that exhibit scaling symmetry. Traditional mathematical methods fail to capture this characteristic, which necessitates the use of scaling analysis tools like fractal geometry [1,2,3]. Urban fractal research can be broadly classified into two categories: monofractal analysis and multifractal analysis. Monofractal analysis assumes that there is only one scaling process in fractals, and the growth probability of each part is equal, leading to the use of a single fractal dimension for measurement. Multifractal analysis, on the other hand, takes into account the multiple scaling processes in fractals, where the growth probabilities of different parts differ. Therefore, a set of multifractal parameters, known as the multifractal spectrum, is used to describe them. Since real fractals often have more than one scaling process, a single fractal dimension is insufficient to characterize them. A set of comparable parameters is required, which is provided by the multifractal spectrum [4].
The spatio-temporal evolution of urban morphology is a critical focus area within geography, but existing multifractal research is not extensive enough. Urban multifractal research can be classified into three spaces: real space, order space and phase space [4]. Real space corresponds to the spatial subdivision of urban land [5], transportation [6,7,8], population [9,10,11,12], and other elements [13]; Order space refers to the hierarchical subdivision of urban system [14,15]; And phase space corresponds to the dynamic processes. However, compared to other fields such as finance, biology, meteorology and hydrology, multifractal research of phase space in urban geography is relatively lacking, which may be attributed to the lack of higher resolution time series data. On the other hand, in real space, while the spatial meaning of multifractal spectrums is clear, the temporal evolution of these spectrums still requires further investigation. At the spatial level, the spectrums under positive moment orders correspond to central or high-density areas in a city, which are stable areas for urban development and are similar across different cities; The spectrums under negative moment orders, on the other hand, correspond to marginal or low-density areas in a city, which are the most dynamic areas for urban growth and exhibit significant differences between cities [16,17]. At the temporal level, the multifractal parameters in the mathematical world are continuous and stable. Nevertheless, the evolution of cities in the real world, as reflected in multifractal parameters, may exhibit local fluctuations. While many studies focus on seeking macroscopic patterns of urban evolution through spectrum comparison [7,18,19,20,21,22,23] or trend fitting [24], few studies delve into characterizing spatio-temporal variations of urban evolution at a micro level. Hence, by combining the distinct growth characteristics of multifractal parameters under positive and negative moment orders, we can expect to explore more detailed aspects of the spatio-temporal evolution process of urban morphology. This approach will deepen our understanding of the urban evolution process, providing insights into the intricate dynamics shaping cities.
The current multifractal research that characterizes the spatio-temporal variations in the evolution of urban morphology at a micro level is scarce. Therefore, this paper aims to address this gap by introducing a new measurement, which captures the distinct growth characteristics of multifractal spectrums under positive and negative moment orders. The measurement is then used to analyze and characterize the detailed variations in the spatio-temporal evolution process of urban form. The effectiveness of the analysis is verified through case studies. The following is divided into four sections. Section 2 introduces the multifractal model and case studies used in this paper, which are the Pearl River Delta (PRD) and the Yangtze River Delta (YRD), the two largest Chinese urban agglomerations. In Section 3, the conventional multifractal spectrum analysis is combined with the newly proposed measurement to depict the macro laws and micro variations in the spatio-temporal evolution of urban morphology within the study areas. The findings are then compared with regional policies and spatial patterns to validate the effectiveness of the analysis. In Section 4, the achievements, novelties, and limitations of the research methods used in this paper are discussed. Finally, the main conclusions based on the research results and problem discussions are drawn.

2. Materials and Methods

2.1. Multifractal measures

Before delving into the case analysis, let’s first introduce the multifractal measures used in this paper. Multifractals have two sets of parameters: global and local. Global parameters include generalized correlation dimension Dq and mass exponent τq, while local parameters include singularity exponent α and local fractal dimension f(α). The calculation formula of generalized correlation dimension Dq is [25,26]:
D q = { 1 q − 1 lim ε → 0 ln ∑ i = 1 N ( ε ) p i q ln ( ε ) , q ≠ 1 lim ε → 0 ∑ i = 1 N ( ε ) p i ln p i ln ( ε ) , q = 1
When measuring fractal dimension using box-counting method, N(ε) in Equation (1) represents the number of non-empty boxes under box scale ε, while pi represents the probability measure, that is, the ratio of measure Mi in the ith box to total measure M. The moment order q functions like telescopes and microscopes, and is used to highlight either the central areas (if q > 1 and q→+∞) or the marginal areas (if q < 1 and q→-∞), thereby obtaining the corresponding global dimension Dq [5]. Plotting Dq for different moment orders q on the same graph results in the spectrum of generalized correlation dimension. The value of Dq monotonically decreases with q, and the height difference between the upper and lower spectrum is
∆D = D-∞ - D+∞,
representing the spatial heterogeneity and multifractality of the study area [27], with higher values indicating stronger spatial heterogeneity. Another important global parameter is mass exponent τq, which is related to generalized correlation dimension through the equation
τq = (q - 1)Dq.
Since the two are somewhat equivalent, the analysis of global parameters mainly focuses on generalized correlation dimension. On the other hand, singularity exponent α of local parameters is defined based on the probability measure pi as well [28]:
p i ∝ ε α
which means boxes with different probability measures have varying singularity exponents. Lower singularity exponent α implies denser corresponding box, while higher value implies less density. The singularity exponent spectrum is generated by plotting different moment orders q and their corresponding α(q) on the same graph, and its variation trend is generally consistent with the Dq spectrum. Another important local parameter is the local dimension f(α), which represents the local fractal dimension of a subset of boxes with a given singularity exponent α. By plotting α and its corresponding local fractal dimension f(α) on the same graph, we can generate the singularity spectrum. This curve is unimodal and provides important insights into the spatial characteristics of the research area. The singularity spectrum’s maximum value point α0, and its corresponding maximum value f(α0), are all related to the capacity dimension D0. D0 reflects the degree of spatial filling in the research area. A larger D0 indicates a higher level of spatial filling and a more complex spatial structure. The width of singularity spectrum, Δα = α-∞ - α+∞, represents the differences between high- and low-density areas and the spatial heterogeneity of the study area. The height difference between left and right side of the spectrum, Δf = f(α+∞) - f(α-∞), reflects the fractal growth pattern of the study area. If Δf > 0, high-density areas dominate and fractal growth mainly extends outward. On the contrary, if Δf < 0, low-density areas dominate and fractal growth is mainly centered [29]. Although global and local parameters are essentially equivalent and can be transformed into each other through Legendre transformations which are [30]:
τ ( q ) = q α − f ( α ) d τ ( q ) d q = α + q d α ( q ) d q − d f ( α ) d α d α ( q ) d q = α
They offer different perspectives for understanding the fractal characteristics of the study area.
There are two approaches to estimate multifractal parameters. The first is a global-to-local approach, where global parameters are estimated using Equations (1) and (3), followed by estimation of local parameters using Legendre transformation, i.e., Equation (5). However, this method often incurs high errors due to the need for discretization in Legendre transformation of real data. The second approach is a local-to-global approach, where local parameters are calculated first, and then global parameters are inferred using Legendre transformation, i.e., Equation (5). This process does not require discretization and is therefore more accurate than the former approach. The widely used method for estimating local parameters is the normalized μ method [31]. The calculation steps are as follows. Firstly, define the normalized probability μ based on the probability measure pi:
μ i = p i q ∑ i = 1 N ( ε ) p i q
then we can then estimate the singularity exponent α and its local fractal dimension f(α) using
α ( q ) = lim ε → 0 ∑ i = 1 N ( ε ) μ i ln p i ln ε
f ( q ) = lim ε → 0 ∑ i = 1 N ( ε ) μ i ln μ i ln ε
The process of parameter estimation involves different measurement and estimation methods. The probability measure pi, as shown in Equations (1), (7) and (8), is typically obtained using box-counting method. This method is widely used for calculating multifractal parameters, with functional box method being the most convenient form of this method [32,33]. To begin, the minimum area box of the study area is selected as the first level box. Subsequently, each box is divided into four and then sixteen, with the side length of box during each division corresponding to a specific scale ε. On the other hand, the limit condition in Equations (1), (7) and (8) is hard to meet, hence the parameter is usually approximated by the slope of the scatter plot. A variety of parameter estimation methods exist, including Ordinary Least Squares Method (OLS), Maximum Likelihood Method (MLM), etc. [16]. In this paper, we have chosen to use OLS and fix the intercept at 0 during regression [34].

2.2. Temporal evolution of multifractal measures

The multifractal method provides a way to examine different density areas within a city, and the temporal evolution of multifractal parameters can reflect the growth characteristics of the city at multiple levels. Multifractal spectrums under positive moment orders correspond to central areas that are stable areas of urban development. They usually grow steadily over time [7,18], reflecting the stable filling of central areas. On the other hand, multifractal spectrums under negative moment orders correspond to marginal areas that are the most active areas of urban development. They usually change sharply over time, reflecting the dynamic expansion of marginal areas. The distinct evolution of multifractal parameters under positive and negative moment orders leads to significant fluctuations in ΔD over time, as described in Equation (2), reflecting rich spatio-temporal information. As D+∞ usually increases steadily over time, we can categorize the relative changes in D+∞ and D-∞ into three scenarios (Table 1). These scenarios can be summarized by introducing a new measurement, that is named as Dimension Growth Rate Ratio (DGR) in this paper:
D G R = Δ ( D − ∞ ) t Δ ( D + ∞ ) t
whose numerator and denominator represent the changes of D-∞ and D+∞ from time t-1 to time t, respectively.
  • If D+∞ rises faster than D-∞, then ΔD decreases and 0 < DGR < 1. This type of change indicates that the growth of built-up areas is primarily due to filling in central areas, leading to a decrease in spatial heterogeneity. This direction of urban evolution is commonly observed in empirical research.
  • If D-∞ rises faster than D+∞, then ΔD rises and DGR > 1. This type of change indicates that the growth of built-up areas is dominated by filling in marginal areas, leading to an increase in spatial heterogeneity. This marks the beginning of expansion of marginal areas, where the fractal dimension has rapidly increased.
  • If D-∞ decreases, then ΔD decreases and DGR < 0. This type of change indicates that the original low-density areas are rapidly filled into medium- to high-density areas, resulting in fewer new low-density areas, reduced dimensions and spatial heterogeneity. This marks the transformation of original marginal areas into new sub-central areas.
It is evident that DGR can effectively detect the spatio-temporal evolution of urban mophorlogy. If DGR is greater than 1 or less than 0, it indicates that urban growth is primarily driven by expansion in marginal areas. Conversely, if DGR is between 0 and 1, it suggests that urban growth is predominantly focused on filling in central areas. The absolute value of DGR is directly proportional to the grwoth rate of D-∞, reflecting the intensity of the expansion process. A larger |DGR| signifies a faster change in D-∞ and a more significant expansion of marginal areas. To identify outliers in DGR, statistical methods based on the mean and standard deviation can be employed. Specifically, if a value exceeds one-standard-deviation bands, there is a 68% confidence level for determining it as an outlier. Similarly, if a value surpasses two-standard-deviation bands, a 95% confidence level is used to identify it as an outlier. The numerical detection method (0 and 1) and the standard deviation detection method complement each other and provide valuable insights into the variation details of the spatio-temporal evolution of urban morphology. However, it is important to note that the former leans more towards the theoretical interpretation of DGR, where different values of DGR reflect distinct characteristics of urban morphology evolution. On the other hand, the standard deviation detection method leans more towards statistically testing DGR. When the index does not exhibit a clear trend or shows a weak trend, outliers can be intuitively identified using the mean and standard deviation, corresponding to significant expansion in marginal areas. In summary, this paper utilizes various multifractal measurements, including multifractal spectrums and DGR, to comprehensively analyze the spatio-temporal evolution of urban morphology. These measurements are summarized in Table 2.

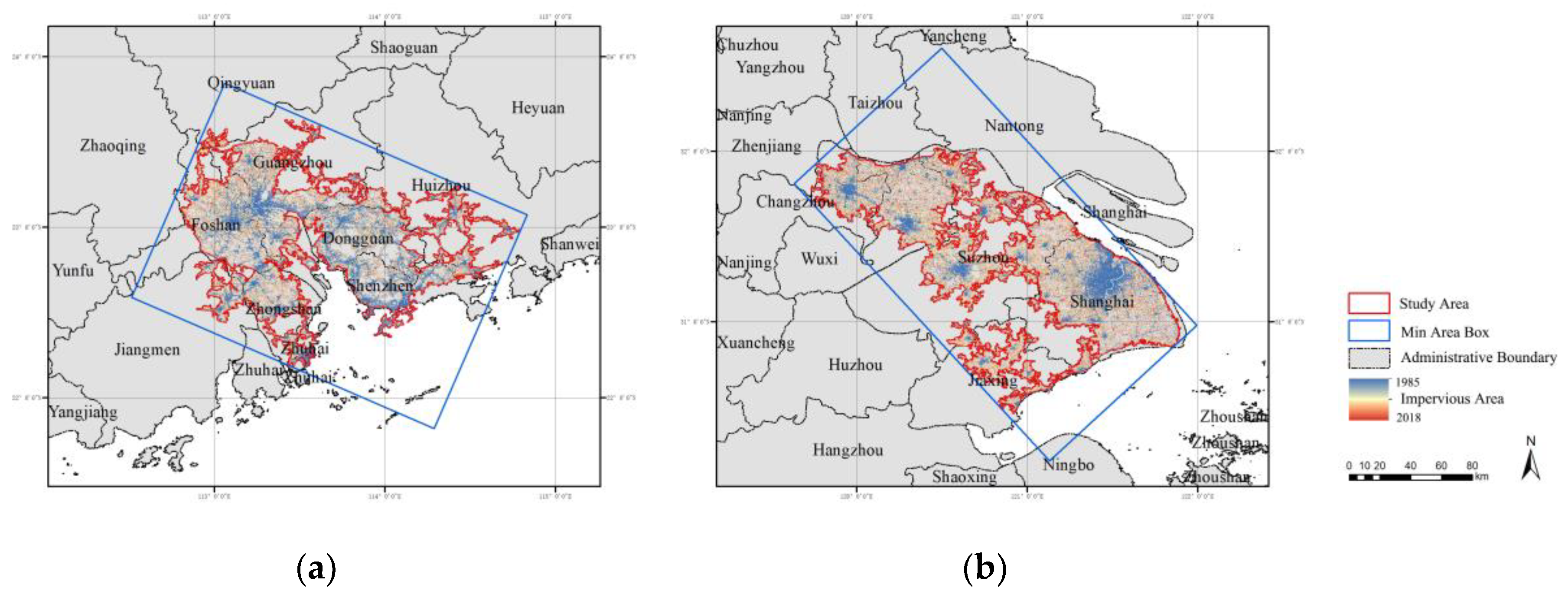
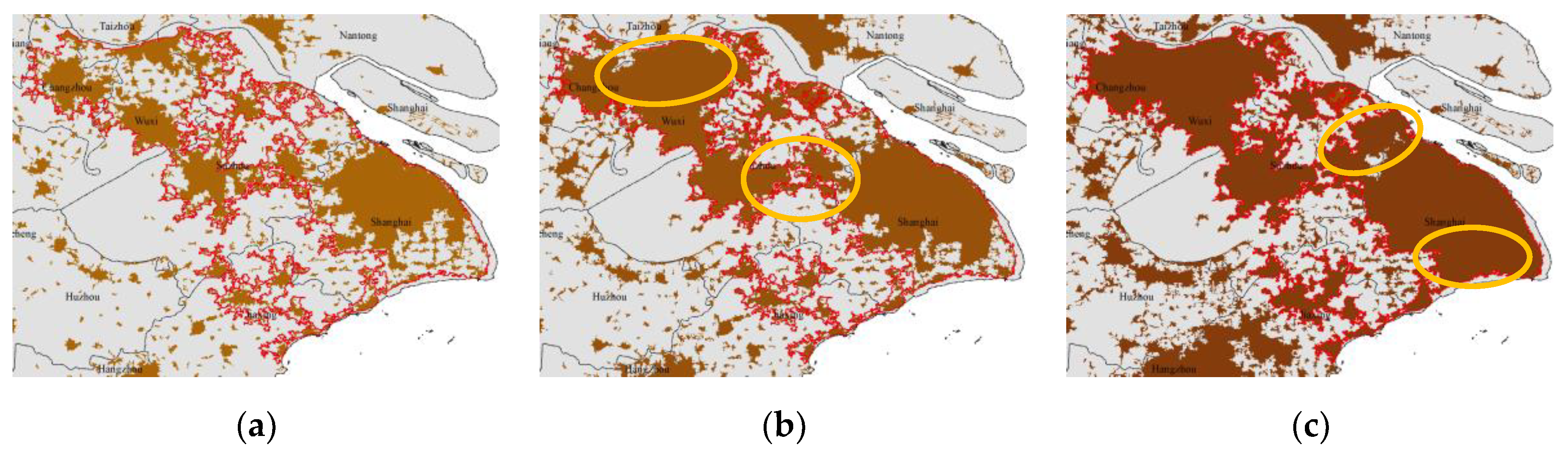
2.3. Study area and data processing

Based on multifractal spectrums and the newly defined DGR, the spatio-temporal evolution and variation details of urban morphology are studied below. The data used for analysis includes annual artificial impervious area from 1985 to 2018 [35] and urban boundaries every 5 years from 1990 to 2018 [36]. In order to conduct the analysis, the impervious area is cropped using the urban boundaries from 2018, then multifractal spectrums and related multifractal measurements are calculated every year based on the minimum area box of the study area. The two largest Chinese urban agglomerations, PRD and YRD, are selected as the research objects in empirical analysis, which are both comparable in terms of area size and both experienced rapid development from 1985 to 2018 (Figure 1 and Table 3). PRD encompasses 10 prefecture cities with central cities being Guangzhou and Shenzhen. On the other hand, YRD includes Shanghai as its central city and six other prefecture cities. The historical background and development characteristics of the two regions make them suitable cases for studying the spatio-temporal evolution and variation details of urban morphology. The raw data is processed using ArcGIS 10.3 and ENVI 5.3, and the multifractal parameters are calculated using Python 3.8 for moment orders q ranging from -20 to 20.

3. Results

Multifractal spectrums and related multifractal measurements of PRD and YRD are calculated from 1985 to 2018, respectively, and the results are shown in Figure 2 and Figure 3 and Table S1. It was found that the multifractal spectrums of PRD in 1985 were significantly lower as shown in Figure 2a,c, and this abnormal year has been excluded from subsequent analysis.
Based on the temporal evolution of multifractal spectrums (Figure 2), we can derive the macroscopic laws in the spatio-temporal evolution of urban morphology in the study areas (Table 4). The following is a summary of these observed patterns:
1.
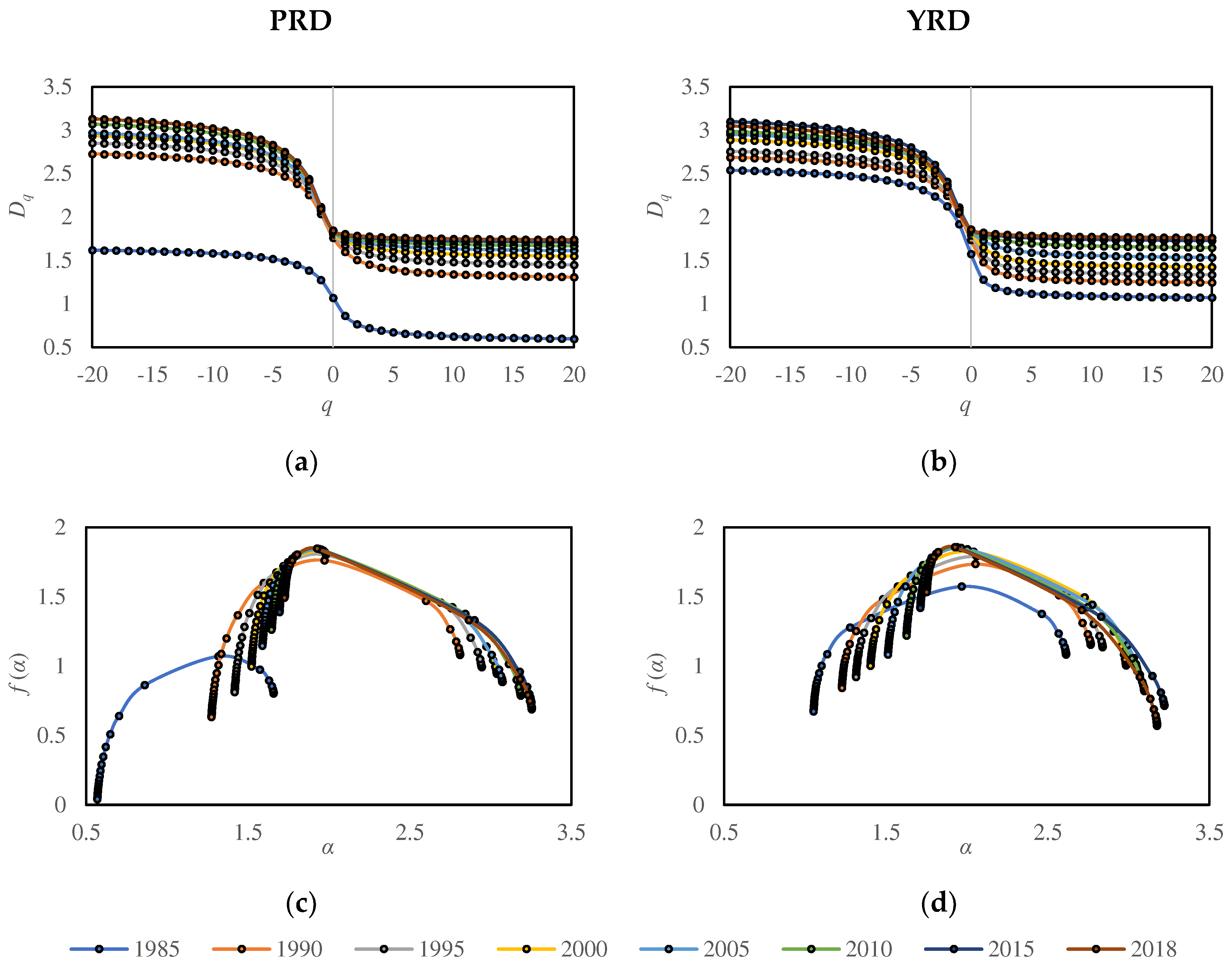
Generalized correlation dimension Dq, as shown in Figure 2a,b:
  • The spectrums continue to rise, indicating ongoing filling of PRD and YRD.
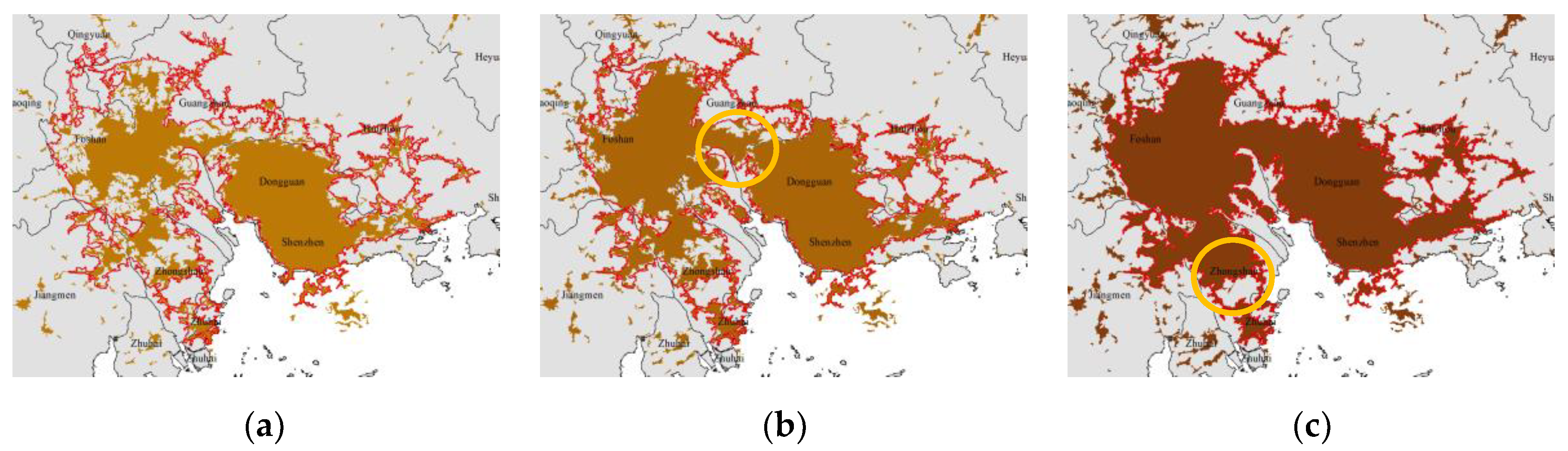
  • The right side of the spectrum (q→+∞) converges rapidly, with an even faster convergence over time. While the left side of the spectrum (q→-∞) does not exhibit a clear convergence trend. This suggests that the central areas have reached a state of saturation in terms of development and filling, and there is still potential for expansion in marginal areas.
2.
Singular spectrum f(α), as shown in Figure 2c,d:
  • The maximum value, f(α0) = D0, keeps increasing, signifying an increasing degree of spatial filling.
  • The left side of the spectrum (q→+∞) shows a rapid rise, while the right side (q→-∞) experiences a gradual decline. This implies that the central areas are rapidly being filled, the marginal areas are expanding and transforming into new sub-centers, resulting in a relatively reduced dimension.
  • In the early stages of the study, the heights of the right side of the spectrums for PRD and YRD are similar, but the left side of YRD is higher. By the end of the research period, the heights of the left side of the spectrums for both regions become similar, but the right side of YRD is lower. This indicates that the central areas in YRD developed earlier compared to PRD, with a higher degree of spatial filling and more advanced development. Moreover, the expansion of marginal areas in YRD has been faster, leading to a lower dimension and more new sub-centers formed during the research period. Although the central areas in PRD started their development later, they progressed rapidly and approached the filling degree observed in YRD by the end of the research period.
  • The height difference between the left and right side of the spectrum, Δf, changed from negative to positive in PRD and YRD in 2000 and 2001, respectively. This shift indicates that the fractal growth pattern of the study areas shifted from concentration to deconcentration during those corresponding years.
By analyzing the temporal evolution of DGR (Figure 3), we can uncover the microscopic variations in the spatio-temporal development of urban morphology in the study areas (Table 4). The generalized correlation dimension Dq exhibits a steady increase under positive moment orders, eventually reaching a stabilized state in the later stages. Furthermore, there is no significant difference observed between PRD and YRD. Under negative moment orders, Dq generally increases, but with notable fluctuations. Particularly significant fluctuations are observed in 2009 in PRD and in 1997 in YRD (Figure 3a,b). The distinct evolution of Dq under positive and negative moment orders leads to significant fluctuations in ΔD (Figure 3c,d). Overall, ΔD decreases, indicating a decreasing trend in spatial heterogeneity within the study areas. However, ΔD for PRD fluctuated significantly in 2009 and 2016, while those for YRD experienced significant fluctuations in 1997, 2015 and 2016, reflecting fluctuations in spatial heterogeneity during the respective years. The aforementioned spatio-temporal variations in urban morphology evolution can be further highlighted by examining the temporal evolution of DGR, providing a more intuitive explanation (Figure 3e,f). In most cases, DGR remains stable between 0 and 1, indicating a consistent filling of central areas. However, there are certain years where DGR shows abnormal fluctuations, surpassing 0 or 1, and even exhibiting sudden jumps. These abnormal fluctuations indicate active expansion in marginal areas. The abnormal fluctuations in DGR can occur at a single point in time or over a period of time. The former marks an important node in the expansion of marginal areas, such as 1994 and 1997 in YRD. The latter marks a period of rapid expansion of marginal areas, namely, the expansion of marginal areas (DGR > 1) → the original marginal areas becoming new sub-central areas (DGR < 0) → the expansion of new marginal areas (DGR > 1) … This type of expansion is particularly evident during 2005 to 2010 and 2013 to 2017 in PRD, as well as 2013 to 2016 in YRD. To detect outliers in DGR, statistical criteria can be established using standard-deviation bands. Applying one standard deviation, we can determine "abnormal" years in PRD as 2009, 2010, 2013, 2014, 2016 and 2017, and in YRD as 1994, 1997, 2013, 2015 and 2016 at a 68% confidence level. Moreover, based on two standard deviations, "abnormal" years in PRD are 2009 and 2016, and in YRD are 1997, 2015 and 2016 at a 95% confidence level. This standard deviation detection method allows for the identification of outliers in DGR.
The abnormal fluctuations in the DGR curve over time indicate active expansion of marginal areas in the study areas. The standard deviation detection reveals that YRD has started rapid growth in its marginal areas since 1994, whereas PRD encountered a similar situation only in 2009. This suggests that the urban development in YRD generally preceded that of PRD, which is consistent with the results from multifractal spectrums. Despite PRD being known as a window for China's reform and opening up policies, YRD holds a longstanding position as an established economic region within China. The active expansion of marginal areas may be attributed to regional or national policies. In 2008, the Outline of the Plan for the Reform and Development of the Pearl River Delta (2008-2020) was approved, aiming to promote regional economic integration and deepen cooperation in the Pan-PRD area. The provincial government aims to achieve A good start in one year, a great development in four years, and a great leap in nine years, so 2009, 2013 and 2017 are key years for the expansion of PRD. In the case of YRD, the establishment of the Seminar on the Work of the Yangtze River Delta Political Consultative Conference in 1994 and the Inter-City Conference on Yangtze River Delta Economic Coordination in 1997 laid the foundation for political and economic cooperation in the region. And the establishment of the China (Shanghai) Pilot Free Trade Zone in 2013 provided further impetus for the integration of YRD. The integrated development of these regions also relies on the support of national policies. In 2016, the 13th Five-Year Plan, adopted during the Fourth Session of the 12th National People's Congress, aimed to optimize and enhance the urban agglomerations in the eastern region, including the Beijing-Tianjin-Hebei, YRD, and PRD. It also emphasized the coordinated development of the upper, middle, and lower reaches of the Yangtze River and regional cooperation in the Pan-PRD, supporting and facilitating further expansions of YRD and PRD. Therefore, the DGR of YRD and PRD both fluctuated significantly in 2016, corresponding to a significant expansion of marginal areas. As a result of the expansion in marginal areas, multiple cities have seen the interconnection of their urban boundaries. In PRD, the marginal areas of southern Guangzhou and western Dongguan expanded significantly from 2005 to 2010, leading to an interconnection of the urban boundaries of Guangzhou, Foshan, Dongguan and Shenzhen, forming an integrated spatial pattern (Figure 4a,b). From 2010 to 2018, Zhongshan and Zhuhai also expanded and connected with the urban boundaries of these cities, further consolidating the integrated spatial pattern (Figure 4b,c). In YRD, the marginal areas of eastern Changzhou, northern Wuxi, Suzhou and Shanghai significantly expanded from 2010 to 2015, leading to an interconnection of urban boundaries of these cities for the first time. As a result, the integrated spatial pattern was initially formed (Figure 5a,b). From 2015 to 2018, the marginal areas of Shanghai continued to expand, further strengthening the integration pattern (Figure 5b,c). In summary, DGR can effectively reflect the spatio-temporal variation of urban evolution. A DGR greater than 1 or less than 0 corresponds to active expansion of marginal areas. Abnormal fluctuations in DGR help capture the variation details in the spatio-temporal evolution of urban growth.

4. Discussion

Multifractal method is a valuable approach for analyzing the spatio-temporal evolution of urban morphology. However, there is still a need to explore the specific details of urban evolution. Therefore, this paper proposes a multifractal measurement called Dimension Growth Rate Ratio (DGR) to characterize the spatio-temporal variation of urban evolution, and it is validated using PRD and YRD as examples. Based on the above calculations and analysis, the research results can be summarized as follows. Firstly, the generalized correlation dimension (Dq) shows a steady increase under positive moment orders and significant fluctuations under negative moment orders. The differences between the two reflect rich spatio-temporal information. Dq under positive moment orders are similar among different cities, demonstrating a consistent increase over time and stabilization in later stages, indicating the stable filling of central areas. On the other hand, Dq under negative moment orders generally increase over time, but with notable fluctuations, reflecting the active expansion of marginal areas. Based on this, the spatio-temporal evolution pattern of urban morphology can be classified into three scenarios: 1) D+∞ rises faster than D-∞, indicating urban growth dominated by filling in central areas, corresponding to the common direction of urban evolution. 2) D-∞ rises faster than D+∞, indicating urban growth dominated by filling in marginal areas, corresponding to the beginning of marginal area expansion. 3) D+∞ increases while D-∞ decreases, suggesting rapid filling of original low-density areas, resulting in fewer new low-density areas and a smaller fractal dimension. This corresponds to the transformation of the original marginal areas into new sub-central areas. Secondly, the spatio-temporal variation of urban evolution can be quantitatively detected using DGR. DGR represents the ratio of the growth rate between D-∞ and D+∞, can comprehensively reflects the evolution of both central and marginal areas. Normally, 0 < DGR < 1 indicates stable growth in central areas. Abnormal fluctuations in DGR reflect the expansion of marginal areas. DGR > 1 corresponds to the beginning of expansion in marginal areas, while DGR < 0 corresponds to the transformation of original marginal areas into new sub-central areas. In some cases, DGR may even exhibit abrupt jumps. Larger |DGR| indicate more significant expansion, and can be tested using standard-deviation bands. Thirdly, abnormal fluctuations in DGR can occur at a single time point or over a certain period of time. A single time point with abnormal fluctuation signifies a crucial node for marginal area expansion, while fluctuations over a period of time mark periods of rapid expansion.
By combining the conventional multifractal spectrums with the proposed DGR measurement, important conclusions can be drawn regarding the spatio-temporal evolution patterns in PRD and YRD. Overall, from 1985 to 2018, both PRD and YRD experienced an increase in the degree of spatial filling and complexity. The central areas reached a saturation point, while there is still potential for expansion in marginal areas. Compared to PRD, the urban growth in YRD occurred earlier and was more developed. YRD exhibited a higher level of filling in its central areas and witnessed faster expansion in the marginal areas. Nevertheless, PRD demonstrated rapid development, and by 2018, the degree of filling in its central areas approached that of YRD. Moreover, in PRD, the pattern of fractal growth shifted from concentration to deconcentration in 2000. Marginal areas expanded rapidly from 2005 to 2010 and from 2013 to 2017, with notable growth observed in 2009 and 2016, leading to the formation and strengthening of regional integration patterns. In YRD, significant expansion nodes occurred in 1994 and 1997, with policies laying political and economic foundation for regional integration. The pattern of fractal growth shifted from concentration to deconcentration in 2001. The period from 2013 to 2016 has witnessed another rapid expansion in marginal areas, indicating the formation and strengthening of regional integration patterns, with notable growth observed in 2015 and 2016. The key nodes and periods in the evolution of urban form may be attributed to regional or national policies and are reflected in spatial patterns.
The spatio-temporal evolution of urban systems is a crucial aspect of urban planning, and multifractal methodology offers an effective tool for studying this evolution. However, due to limited time series data, most studies have focused on comparing changes in multifractal spectrums to understand the general laws of urban development [7,18,19,20,21,22,23], or fitted the time series of Dq using logistic functions to reveal the spatial replacement dynamics of urban development. Based on logistic functions, it is possible to determine the type of urban evolution, predict the time of maximum speed, and divide urban development stages macroscopically [24]. However, these studies have primarily remained at a macro-level analysis of urban evolution, with few exploring the micro-variations within the evolution process. Compared with previous research, this article introduces an innovative approach by employing a newly defined measurement called DGR to detect the detailed spatio-temporal variations in urban evolution. The different values of DGR correspond to the expansion of central or marginal areas, and abnormal fluctuations in these values indicate active expansion in marginal areas. The calculation of DGR is clear, concise, and useful for high temporal resolution data. It could serve as a supplement to previous macro analysis and provide more insights into the spatio-temporal evolution patterns of urban morphology.
This paper has several shortcomings that need to be addressed. Firstly, the algorithm is limited to OLS with a fixed intercept of 0, which might be not comprehensive enough. The parameter estimation of mathematical models depends on algorithms, while the selection of algorithms is subjective. The commonly used algorithms for estimating regression parameters include OLS and MLM. Empirical study shows that when the observed data follows power law, the results of the two algorithms are consistent; when the observation data does not obey power law, OLS gives an approximate value, while MLM gives outlier. Therefore, MLM can be used to detect power laws [16]. Furthermore, OLS for parameter estimation also has two possible scenarios: fixed intercept and unfixed intercept. Previous research indicates that the results from these two methods are consistent when the fractal structure of cities is well-developed. However, if the fractal structure of cities is not sufficiently developed, multifractal measurement depends on the selection of methods [34]. Therefore, integrating multiple algorithms and methods, including both OLS and MLM, fixed and unfixed intercept, can aid in understanding the evolution of urban fractal structure. Unfortunately, due to limited space, this paper only chose to utilize OLS with a fixed intercept for parameter estimation. Future comparative analysis measuring DGR under different algorithms and methods may improve our understanding of urban evolution. Secondly, the research only covers a limited number of cities, the universality of the measurement DGR needs further verification, and the mechanism behind the spatio-temporal variation in urban evolution still needs further exploration.

5. Conclusions

The classic theme in geography focuses on regional differentiation, and geographers are interested in understanding both spatial differences and their underlying similarities. Multifractal methodology offers a way to unify regional differentiation and spatial similarities within a single descriptive framework. When the moment order is greater than 0, the multifractal spectrum provides more information about central areas with high density and growth probability, as well as intra-area stability and inter-area similarity. On the other hand, when the moment order is less than 0, the multifractal spectrum captures more information about marginal areas with low density and growth probability, along with intra-area instability and inter-area differences. Based on these ideas, this article introduces an index using extreme values of generalized correlation dimension, named as DGR, to describe the spatio-temporal evolution characteristics of cities. This index combines two extremes and can effectively capture the detailed features of urban spatio-temporal evolution. Through calculations, analysis, and discussion of problems, the following main conclusions can be drawn. Firstly, the curve of the growth rate of the generalized correlation dimension under extreme positive and negative moment orders (DGR) over time reflects the variation characteristics of urban growth. Urban growth is more active in marginal areas and can be characterized by multifractal parameters under negative moment orders. Conversely, growth in urban central areas is relatively stable and can be characterized by multifractal parameters under positive moment orders. The ratio of the growth rate of the generalized correlation dimension between these two extreme cases reflects the growth rate of marginal areas relative to central areas. Unevenness in the DGR curve over time typically indicates a period of active growth in urban marginal areas. Secondly, the DGR curve serves as a complementary tool of multifractal analysis for urban morphology. In other words, combining the DGR curve with multifractal spectrums allows for a more comprehensive understanding of urban growth. The generalized correlation dimension and related multifractal measurements can effectively reflect the spatio-temporal evolution patterns of urban morphology. The stable filling in central areas represents a normal situation, while expansion in marginal areas indicates an "abnormal" situation, which corresponds to sudden increases or decreases in parameters. The DGR curve captures these abnormal growth patterns and changes. By using various multifractal parameter curves, urban growth characteristics can be comprehensively analyzed from multiple perspectives and levels.

Supplementary Materials

The following supporting information can be downloaded at the website of this paper posted on Preprints.org. Table S1: Multifractal spectrums and related measurements in PRD and YRD from 1985 to 2018; Algorithm S1: The main code to calculate multifractal parameters in Python.

Funding

This research was funded by the National Natural Science Foundation of China (Grant No. 42171192). The support is gratefully acknowledged.

Data Availability Statement

The data presented in this study are available in Supplementary Materials.

Conflicts of Interest

The authors declare no conflict of interest.

References

  1. Mandelbrot, B.B. The fractal geometry of nature; WH freeman: New York, 1982. [Google Scholar]
  2. Batty, M.; Longley, P.A. Fractal cities: a geometry of form and function; Academic press: London, 1994. [Google Scholar]
  3. Batty, M. Cities and Complexity: Understanding Cities with Cellular Automata, Agent- Based Models, and Fractals; The MIT Press: London, 2005. [Google Scholar]
  4. Chen, Y. The solutions to the uncertainty problem of urban fractal dimension calculation. Entropy 2019, 21, 453. [Google Scholar] [CrossRef] [PubMed]
  5. Chen, Y.; Wang, J. Multifractal characterization of urban form and growth: the case of Beijing. Environment and Planning B: Planning and Design 2013, 40, 884–904. [Google Scholar] [CrossRef]
  6. Ariza-Villaverde, A.B.; Jiménez-Hornero, F.J.; de Ravé, E.G. Multifractal analysis of axial maps applied to the study of urban morphology. Computers, Environment and Urban Systems 2013, 38, 1–10. [Google Scholar] [CrossRef]
  7. Murcio, R.; Masucci, A.P.; Arcaute, E.; Batty, M. Multifractal to monofractal evolution of the London street network. Physical Review E 2015, 92, 62130. [Google Scholar] [CrossRef] [PubMed]
  8. Pavón-Domínguez, P.; Rincón-Casado, A.; Ruiz, P.; Camacho-Magriñán, P. Multifractal approach for comparing road transport network geometry: The case of Spain. Physica A: Statistical Mechanics and its Applications 2018, 510, 678–690. [Google Scholar] [CrossRef]
  9. Appleby, S. Multifractal characterization of the distribution pattern of the human population. Geographical Analysis 1996, 28, 147–160. [Google Scholar] [CrossRef]
  10. Cavailhès, J.; Frankhauser, P.; Peeters, D.; Thomas, I. Residential equilibrium in a multifractal metropolitan area. The Annals of regional science 2010, 45, 681–704. [Google Scholar] [CrossRef]
  11. Sémécurbe, F.; Tannier, C.; Roux, S.G. Spatial Distribution of Human Population in France: Exploring the Modifiable Areal Unit Problem Using Multifractal Analysis. Geographical Analysis 2016, 48, 292–313. [Google Scholar] [CrossRef]
  12. Ito, M.I.; Ohnishi, T. Evaluation of the Heterogeneous Spatial Distribution of Population and Stores/Facilities by Multifractal Analysis. Frontiers in Physics 2020, 8, 291. [Google Scholar] [CrossRef]
  13. Hu, S.; Cheng, Q.; Wang, L.; Xie, S. Multifractal characterization of urban residential land price in space and time. Applied Geography 2012, 34, 161–170. [Google Scholar] [CrossRef]
  14. Haag, G. The rank-size distribution of settlements as a dynamic multifractal phenomenon. Chaos, Solitons & Fractals 1994, 4, 519–534. [Google Scholar] [CrossRef]
  15. Chen, Y.; Zhou, Y. Multi-fractal measures of city-size distributions based on the three-parameter Zipf model. Chaos, Solitons & Fractals 2004, 22, 793–805. [Google Scholar] [CrossRef]
  16. Long, Y.; Chen, Y. Multifractal scaling analyses of urban street network structure: The cases of twelve megacities in China. PloS one 2021, 16, e0246925. [Google Scholar] [CrossRef] [PubMed]
  17. Sato, Y.; Munakata, F. Morphological characteristics of self-assembled aggregate textures using multifractal analysis: Interpretation of Multifractal τ (q) Using Simulations. Physica A: Statistical Mechanics and its Applications 2022, 603, 127771. [Google Scholar] [CrossRef]
  18. Man, W.; Nie, Q.; Li, Z.; Li, H.; Wu, X. Using fractals and multifractals to characterize the spatio-temporal pattern of impervious surfaces in a coastal city: Xiamen, China. Physica A: Statistical Mechanics and its Applications 2019, 520, 44–53. [Google Scholar] [CrossRef]
  19. Song, S.; Zeng, L.; Wang, Y.; Li, G.; Deng, X. The response of river network structure to urbanization: A multifractal perspective. Journal of cleaner production 2019, 221, 377–388. [Google Scholar] [CrossRef]
  20. Xiang, J.; Xu, Y.; Yuan, J.; Wang, Q.; Wang, J.; Deng, X. Multifractal Analysis of River Networks in an Urban Catchment on the Taihu Plain, China. Water 2019, 11, 2283. [Google Scholar] [CrossRef]
  21. Nie, Q.; Shi, K.; Gong, Y.; Ran, F.; Li, Z.; Chen, R.; Hua, L. Spatial–temporal variability of land surface temperature spatial pattern: Multifractal detrended fluctuation analysis. IEEE Journal of Selected Topics in Applied Earth Observations and Remote Sensing 2020, 13, 2010–2018. [Google Scholar] [CrossRef]
  22. Wang, J.; Qin, Z.; Shi, Y.; Yao, J. Multifractal Analysis of River Networks under the Background of Urbanization in the Yellow River Basin, China. Water 2021, 13, 2347. [Google Scholar] [CrossRef]
  23. Kimothi, S.; Thapliyal, A.; Gehlot, A.; Aledaily, A.N.; Bilandi, N.; Singh, R. .Akram, S.V. Spatio-temporal fluctuations analysis of land surface temperature (LST) using Remote Sensing data (LANDSAT TM5/8) and multifractal technique to characterize the urban heat Islands (UHIs). Sustainable Energy Technologies and Assessments 2023, 55, 102956. [Google Scholar] [CrossRef]
  24. Chen, Y.; Huang, L. Modeling growth curve of fractal dimension of urban form of Beijing. Physica A: Statistical Mechanics and its Applications 2019, 523, 1038–1056. [Google Scholar] [CrossRef]
  25. Grassberger, P. Generalized dimensions of strange attractors. Physics Letters A 1983, 97, 227–230. [Google Scholar] [CrossRef]
  26. Hentschel, H.G.E.; Procaccia, I. The infinite number of generalized dimensions of fractals and strange attractors. Physica D: Nonlinear Phenomena 1983, 8, 435–444. [Google Scholar] [CrossRef]
  27. Stošić, D.; Stošić, D.; Stošić, T.; Stanley, H.E. Multifractal properties of price change and volume change of stock market indices. Physica A: Statistical Mechanics and its Applications 2015, 428, 46–51. [Google Scholar] [CrossRef]
  28. Halsey, T.C.; Jensen, M.H.; Kadanoff, L.P.; Procaccia, I.; Shraiman, B.I. Fractal measures and their singularities: The characterization of strange sets. Physical review A 1986, 33, 1141–1151. [Google Scholar] [CrossRef] [PubMed]
  29. Chen, Y. Multifractals of central place systems: Models, dimension spectrums, and empirical analysis. Physica A: Statistical Mechanics and its Applications 2014, 402, 266–282. [Google Scholar] [CrossRef]
  30. Frisch, U.; Parisi, G. On the singularity structure of fully developed turbulence. In Turbulence and Predictability in Geophysical Fluid Dynamics and Climate Dynamics; Ghil, M., Benzi, R., Parisi, G., Eds.; North-Holland: New York, 1985; pp. 84–88. [Google Scholar]
  31. Chhabra, A.B.; Meneveau, C.; Jensen, R.V.; Sreenivasan, K.R. Direct determination of the f(α) singularity spectrum and its application to fully developed turbulence. Physical Review A 1989, 40, 5284. [Google Scholar] [CrossRef]
  32. Lovejoy, S.D.A.A.; Schertzer, D.; Tsonis, A.A. Functional box-counting and multiple elliptical dimensions in rain. Science 1987, 235, 1036–1038. [Google Scholar] [CrossRef]
  33. Chen, T. Studies on Fractal Systems of Cities and Towns in the Central Plains of China. Master Dissertation, Department of Geography, Northeast Normal University, Changchun, 1995. [In Chinese]. [Google Scholar]
  34. Huang, L.S.; Chen, Y.G. A comparison between two OLS-based approaches to estimating urban multifractal parameters. Fractals 2018, 26, 1850019. [Google Scholar] [CrossRef]
  35. Gong, P.; Li, X.; Wang, J.; Bai, Y.; Chen, B.; Hu, T. .Zhou, Y. Annual maps of global artificial impervious area (GAIA) between 1985 and 2018. Remote Sensing of Environment 2020, 236, 111510. [Google Scholar] [CrossRef]
  36. Li, X.; Gong, P.; Zhou, Y.; Wang, J.; Bai, Y.; Chen, B. .Zhu, Z. Mapping global urban boundaries from the global artificial impervious area (GAIA) data. Environmental Research Letters 2020, 15, 094044. [Google Scholar] [CrossRef]
Preprints 77839 g001
Figure 1. Study area of the research objects. (a) the Pearl River Delta (PRD); (b) the Yangtze River Delta (YRD). The two are the largest urban agglomerations in China.
Figure 1. Study area of the research objects. (a) the Pearl River Delta (PRD); (b) the Yangtze River Delta (YRD). The two are the largest urban agglomerations in China.
Preprints 77839 g001
Preprints 77839 g002
Figure 2. Multifractal spectrums every five years from 1985 to 2018 in PRD and YRD. (a) generalized correlation dimension spectrum Dq in PRD; (b) generalized correlation dimension spectrum Dq in YRD; (c) singularity spectrum f(α) in PRD; (d) singularity spectrum f(α) in YRD.
Figure 2. Multifractal spectrums every five years from 1985 to 2018 in PRD and YRD. (a) generalized correlation dimension spectrum Dq in PRD; (b) generalized correlation dimension spectrum Dq in YRD; (c) singularity spectrum f(α) in PRD; (d) singularity spectrum f(α) in YRD.
Preprints 77839 g002
Preprints 77839 g003aPreprints 77839 g003b
Figure 3. Temporal evolution of related multifractal measurements from 1985 to 2018 in PRD and YRD. (a) generalized correlation dimension Dq in PRD; (b) generalized correlation dimension Dq in YRD; (c) height difference ∆D in PRD; (d) height difference ∆D in YRD; (e) newly defined measurement DGR in PRD; (f) newly defined measurement DGR in YRD. In subfigures (e) and (f), the light gray and medium gray bands represent the two-standard-deviation and one-standard-deviation bands, respectively. If a data point falls outside the bands, there is a 95% (light gray) or 68% (medium grey) confidence level for considering it as an outlier. The dark gray boundaries are set at 0 and 1. When a data point goes beyond these boundaries, it indicates that urban growth is mainly driven by expansion in marginal areas. On the contrary, it suggests that urban growth is dominated by filling in central areas.
Figure 3. Temporal evolution of related multifractal measurements from 1985 to 2018 in PRD and YRD. (a) generalized correlation dimension Dq in PRD; (b) generalized correlation dimension Dq in YRD; (c) height difference ∆D in PRD; (d) height difference ∆D in YRD; (e) newly defined measurement DGR in PRD; (f) newly defined measurement DGR in YRD. In subfigures (e) and (f), the light gray and medium gray bands represent the two-standard-deviation and one-standard-deviation bands, respectively. If a data point falls outside the bands, there is a 95% (light gray) or 68% (medium grey) confidence level for considering it as an outlier. The dark gray boundaries are set at 0 and 1. When a data point goes beyond these boundaries, it indicates that urban growth is mainly driven by expansion in marginal areas. On the contrary, it suggests that urban growth is dominated by filling in central areas.
Preprints 77839 g003aPreprints 77839 g003b
Preprints 77839 g004
Figure 4. Temporal evolution of urban boundaries in PRD from 2005 to 2018. (a) urban boundaries in 2005; (b) urban boundaries in 2010; (c) urban boundaries in 2018.
Figure 4. Temporal evolution of urban boundaries in PRD from 2005 to 2018. (a) urban boundaries in 2005; (b) urban boundaries in 2010; (c) urban boundaries in 2018.
Preprints 77839 g004
Preprints 77839 g005
Figure 5. Temporal evolution of urban boundaries in YRD from 2010 to 2018. (a) urban boundaries in 2010; (b) urban boundaries in 2015; (c) urban boundaries in 2018.
Figure 5. Temporal evolution of urban boundaries in YRD from 2010 to 2018. (a) urban boundaries in 2010; (b) urban boundaries in 2015; (c) urban boundaries in 2018.
Preprints 77839 g005
Table 1. The classification of temporal evolution of generalized correlation dimension and related multifractal measurements.
Table 1. The classification of temporal evolution of generalized correlation dimension and related multifractal measurements.
Change of Dq Change of related measurements Spatio-temporal information
∆(D+∞)t > ∆(D-∞)t > 0 ΔD decreases
0 < DGR < 1		 Dominated by filling in central areas, spatial heterogeneity decreased: common direction of urban evolution.
∆(D-∞)t > ∆(D+∞)t > 0 ΔD rises
DGR > 1		 Dominated by filling in marginal areas, spatial heterogeneity increased: the beginning of expansion of marginal areas.
∆(D+∞)t > 0 > ∆(D-∞)t ΔD decreases
DGR < 0		 The original low-density areas filled rapidly, new low-density areas reduced and fractal dimension decreased, spatial heterogeneity decreased: the transformation of original marginal areas into new sub-central areas.
Table 2. Main multifractal measurements used in this paper.
Table 2. Main multifractal measurements used in this paper.
Measurement Meaning in spectrum Spatio-temporal information
ΔD = D-∞ –D +∞
Δα = α-∞ – α+∞ 		Height difference between the upper and lower Dq, α(q) spectrum. Differences between high- and low-density areas: the higher, the stronger spatial heterogeneity.
F(α0) = D0 Maximum value of f(α). Degree of spatial filling: the larger, the higher level of spatial filling and the more complex spatial structure.
Δf = f(α+∞) – f(α-∞) Height difference between left and right side of f(α): >0, higher on the left; <0, higher on the right. Fractal growth pattern: >0, high-density areas dominate and fractal growth mainly extends outward; <0, low-density areas dominate and fractal growth is mainly centered.
DGR = ∆(D-∞)t / ∆(D+∞) Ratio of growth rate of Dq at extreme positive and negative moment orders. Variation details in the spatio-temporal evolution of urban morphology: if the curve exhibits steadiness over time, central areas grow steadily; if the curve exhibits abnormal fluctuations, marginal areas expand actively.
Table 3. Research objects: the Pearl River Delta (PRD) and the Yangtze River Delta (YRD).
Table 3. Research objects: the Pearl River Delta (PRD) and the Yangtze River Delta (YRD).
Research objects the Pearl River Delta (PRD) the Yangtze River Delta (YRD)
Cities included 10 prefecture cities: Guangzhou, Shenzhen, Foshan, Dongguan, Zhongshan, Zhuhai, Huizhou, Qingyuan, Jiangmen, Zhaoqing. 1 municipality: Shanghai; 6 prefecture cities: Suzhou, Wuxi, Jiaxing, Changzhou, Nantong, Zhenjiang.
Area/ km2 10711.8 10480.2
Historical background and development characteristics The central cities, Guangzhou in PRD and Shanghai in YRD, have long histories. But the entire region only started to develop rapidly since the reform and opening up. The period between 1985 to 2018 was notable for its significant and speedy progress.
Table 4. Multifractal analysis results of the spatio-temporal evolution of urban morphology in PRD and YRD from 1985 to 2018.
Table 4. Multifractal analysis results of the spatio-temporal evolution of urban morphology in PRD and YRD from 1985 to 2018.
Temporal evolution of multifractal spectrums and related measurements Spatio-temporal information in the evolution of urban morphology
Macroscopic laws Dq rises, f(α0) = D0 increases. Increasing degree of spatial filling.
When q→+∞, Dq converges rapidly, with an even faster convergence over time. While when q→-∞, Dq does not exhibit a clear convergence trend. Central areas have reached saturation in terms of development and filling, and there is still potential for expansion in marginal areas.
When q→+∞, f(α) shows a rapid rise, while when q→-∞, f(α) experiences a gradual decline. Central areas were rapidly being filled, marginal areas were expanding and transforming into new sub-centers, resulting in a relatively reduced dimension.
In the early stages of the study, f(α-∞) for PRD and YRD are similar, but f(α+∞) for YRD is larger. By the end of the research period, f(α+∞) for both regions become similar, but f(α-∞) for YRD is smaller. The central areas in YRD developed earlier compared to PRD, with a higher degree of spatial filling and more advanced development. The expansion of marginal areas in YRD has been faster, leading to more new sub-centers formed during the research period. Although the central areas in PRD started their development later, they progressed rapidly and approached the filling degree observed in YRD by the end of the research period.
ΔD and Δα decrease overall. A decreasing trend in spatial heterogeneity.
Δf changed from negative to positive in 2000 in PRD, and in 2001 in YRD. Fractal growth pattern shifted from concentration to deconcentration in 2000 in PRD, and in 2001 in YRD.
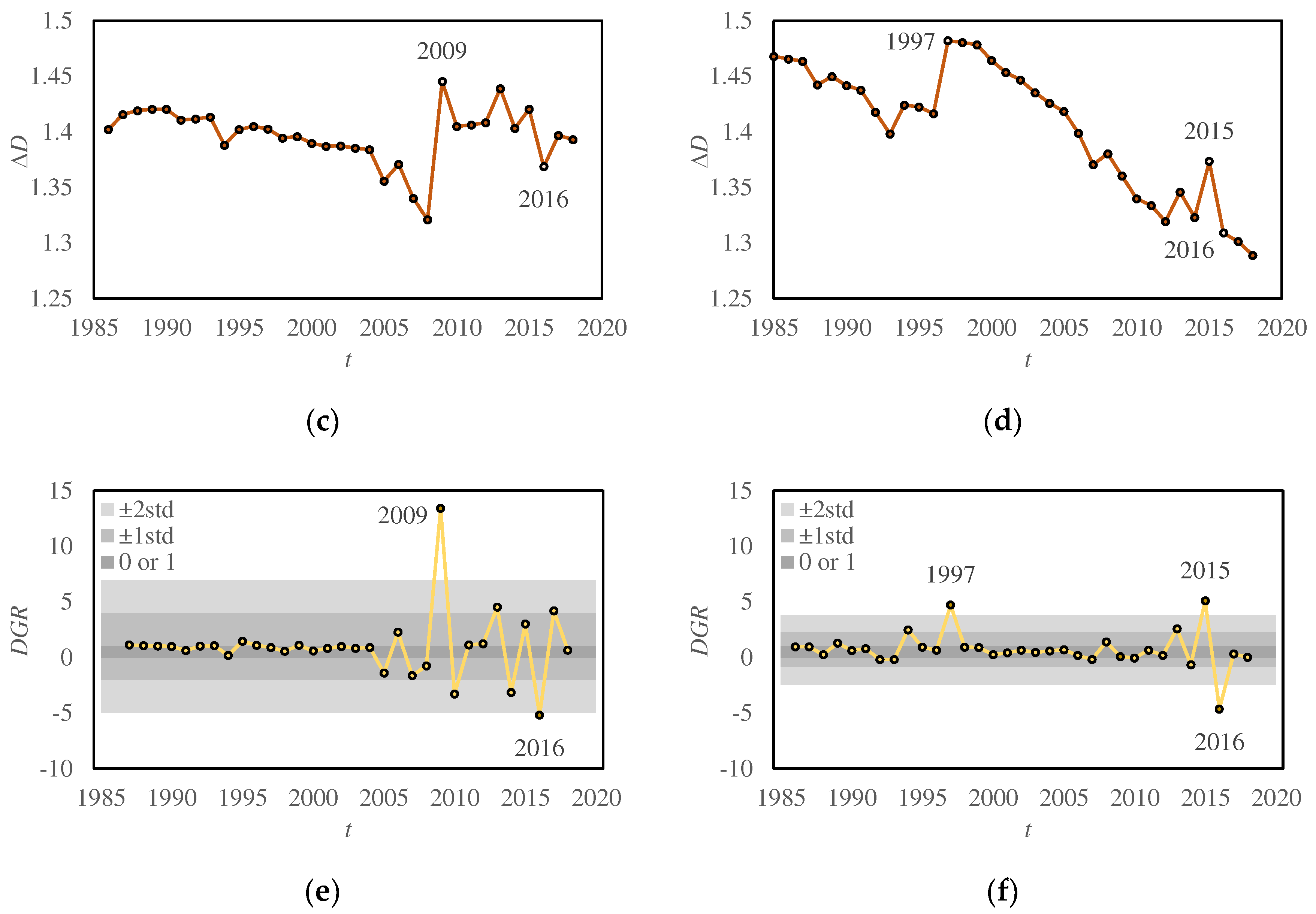
Microscopic variations Dq>0 increase steadily over time, stabilize in the later stages, and exhibit similarities between PRD and YRD. Dq<0 generally increases, but fluctuates sometimes. Central areas were steadily filled and tended to saturation, marginal areas expanded actively.
DGR surpassing 0 or 1: 2005-2010, 2013-2017 in PRD; 1994, 1997, 2013-2016 in YRD. Marginal areas expanded actively in the corresponding years, leading to the interconnection of urban boundaries among multiple cities.
DGR exceeds one-standard-deviation bands, the value is an outlier with a 68% confidence level: 2009, 2010, 2013, 2014, 2016, 2017 in PRD; 1994, 1997, 2013, 2015, 2016 in YRD. The marginal areas witnessed substantial expansion during those specific years, which might be attributed to regional or national policies. YRD has started rapid growth in its marginal areas since 1994, whereas PRD encountered a similar situation only in 2009. The urban development in YRD generally preceded that of PRD. Despite PRD being known as a window for China's reform and opening up policies, YRD holds a longstanding position as an established economic region within China.
DGR exceeds two-standard-deviation bands, the value is an outlier with a 95% confidence level: 2009 and 2016 in PRD; 1997, 2015, 2016 in YRD.
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.
Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.
Prerpints.org logo

Preprints.org is a free preprint server supported by MDPI in Basel, Switzerland.

facebook logotwitter logolinkedin logo
MDPI Initiatives
Important Links
Subscribe

Disclaimer

Terms of Use

Privacy Policy

© 2024 MDPI (Basel, Switzerland) unless otherwise stated