Prerpints.org logo
Preprint
Article

Multiplicity Analysis of a Thermistor Problem

Altmetrics

Downloads

93

Views

39

Comments

0

A peer-reviewed article of this preprint also exists.

This version is not peer-reviewed

Submitted:

28 June 2023

Posted:

28 June 2023

You are already at the latest version

Alerts
Abstract
In the present study a numerical bifurcation analysis of a thermistor problem is carried out, considering a realistic heat dissipation mechanism due to conduction, nonlinear temperature dependent natural convection and radiation. The electric conductivity is modeled as a strongly nonlinear and smooth function of the temperature between two limiting values, based on measurements. The problem formulated in this way admits multiple steady state solutions that do not depend on the external circuit. The analysis reveals that the conduction-convection parameter and the type of the boundary conditions have a profound effect on the solution structure and the temperature profiles. Depending on the boundary conditions the complex multiplicity pattern appears either as a series of nested cusp points or as enclosed branches emanating from pitchfork bifurcation points.
Keywords: 
Subject: Engineering  -   Mechanical Engineering

Introduction

Thermistors are thermally sensitive resistors and have either a negative (NTC) or positive (PTC) resistance/temperature coefficient; we will discuss only the later. Its characteristic feature is the strongly dependent electric conductivity. PTCs are manufactured from silicon, barium, lead and strontium titanates with the addition of yttrium, manganese, tantalium and silica [1,2,3]. PTC thermistors are widely used as current limiting devices, that is as nondestructible (resettable) fuses for electric circuit protection, sensing excessive currents. They can also be encountered as a micro self-heating thermostat for microelectronic, biomedical and chemical applications. Common geometrical configurations are the washer, the disk and the rod type [1,2,3]. Although PTCs and in general electroceramics are in principle loaded electrically a significant number of mechanical failures is being recorded annually. This may be explained on the basis of the Joule self-heating effect which causes temperature differences, thermal strains and excessive thermo-mechanical stresses that may cause failure of the device. As the current technological trends point towards greater device miniaturization while operating at higher power densities there is an increasing demand for thorough analysis and understanding of the underlying coupled electrothermal phenomena in electroceramic devices, Dewitte et al. [4], Supancic [5].
The thermistor as a coupled thermo-electric problem has attracted significant attention. An early result (1900) due to Diesselhorst [6] for the steady state problem shows that the temperature may be expressed as a function of the electric potential provided that certain types of boundary conditions are imposed. Cimmati [7] extended the result of Diesselhorst to obtain existence and uniqueness conditions for the steady state problem. Further results on existence and uniqueness we obtained by Cimatti [8], Cimatti and Prodi [9], Xie and Allegretto [10] and Antontsev and Chipot [11]. Bahadir [12,13] and Çatal [14] employed finite element numerical techniques to solve the thermistor problem assuming a step electric conductivity function. Kutluay et al. [15] obtained a heat balance integral solution of the same problem considering a modified electric conductivity function. Ammi and Torres [16] solved numerically a nonlocal parabolic equation in time and space domains resulting form the thermistor problem. Golosnoy and Sykulski [17] compared various computational techniques for coupled nonlinear thermo-electric problems. The thermistor problem was used as a test case with an electric conductivity being a nonlinear function of the temperature and the electric field intensity. Karpov [18] demonstrated the bistability conditions, the switching autowave properties and the emergence of dissipative structures of essentially a thermistor problem. Apart from the temperature depended electric conductivity, convective heat dissipation with a constant heat transfer coefficient through the device lateral surface was assumed. It is worth noticing that the thermistor problem is closely associated with the flash sintering of ceramics [19], as for instance yttria stabilized zirconia, magnesia doped alumina and strontium titanate among others [20]. The essence of the process is that when an operating parameter such as the furnance temperature exceeds the corresponding limit point, established by the applied voltage that separates the stable from the unstable steady states the Joule heating greatly exceeds the heat dissipation mechanism due to radiation and the temperature blows up. The process controller is then switching from voltage control to current control to maintain the temperature within the specified limits [21,22].
From the literature review above it appears that the thermistor problem has been studied with various assumptions and/or restrictions related primarily with the form of the electric conductivity, the heat dissipation mechanism and in certain cases with the influence of the external electric circuit. The later is also associated with the existence of multiple steady state solutions, up to three, as determined from the number of the intersection points between the current-voltage characteristic curves of the external (linear) circuit and the thermistor, Fowler et al. [23], Howison et al. [24], Zhou and Westbrook [25], Cimatti [26]. In the present study a numerical bifurcation analysis of a thermistor problem is carried out, considering a realistic heat dissipation mechanism due to conduction, nonlinear temperature dependent natural convection and radiation. The electric conductivity is modeled as a strongly nonlinear and smooth function of the temperature between two limiting values, based on measurements. The problem formulated in this way admits multiple steady state solutions that do not depend on the external circuit. The analysis reveals that the conduction-convection parameter and the type of the boundary conditions have a profound effect on the solution structure and the temperature profiles. Depending on the boundary conditions the complex multiplicity pattern appears either as a series of nested cusp points or as enclosed branches emanating from pitchfork bifurcation points.

1. Analysis

1.2. Energy Balance

Consider a horizontal cylindrical segment of a conductor of uniform material density γ with constant thermal conductivity k. The segment has diameter D and length L as it is schematically shown in Figure 1. Heat is being dissipated by conduction through the core of the device and by natural convection and radiation through the lateral surface area, in an ambient environment of constant temperature T ∞ . An energy balance along the longitudinal direction X yields the following differential equation for the device temperature T:
γ C ∂ T ∂ t = ∂ ∂ X ( k ∂ T ∂ X ) − P A [ h c ( T − T ∞ ) + ε σ ( T 4 − T ∞ 4 ) ] + E J
In the equation above, C is the specific heat capacity, A is the cross sectional area, P is the perimeter, h c is the convective heat transfer coefficient, ε is the surface emissivity, σ is the Stefan-Boltzmann constant, E is the electric field intensity and J is the current density through the device.

1.3. Electric Resistivity

A characteristic feature of a ceramic PTC device is the strongly non-linear dependence of its resistivity with respect to temperature. Driven by a transition of the ferroelectric PTC material the resistance increases several orders of magnitude in a relatively small temperature interval, for instance between 100°C and 200°C. The same smooth curve with continuous derivatives, with respect to temperature for the subsequent numerical bifurcation analysis has been adopted from Karpov [18], which represents a barium titanate (BaTiO3) based device:
ρ ^ ( T ) = ρ ^ l + 1 ( ρ ^ h − ρ ^ l ) − 1 + exp [ − 0.12 ( T − 95 ) ]
where ρ ^ l = 2 Ωm and ρ ^ h = 10 4 Ωm are the asymptotic resistivity values corresponding to the low and high operating temperatures respectively. The temperature of 95°C signifies the onset of the transition from the low to the high resistivity value as the contribution of the exponential term in Equation (2) becomes significant. The form of Equation (2) is supported by a significant volume of measurements as for instance reported by Brzozowski and Castro [27], Wang et al. [28], Wang et al. [29], Luo et al. [30], Takeda et al. [31], Rowlands and Vaidhyanathan [32].

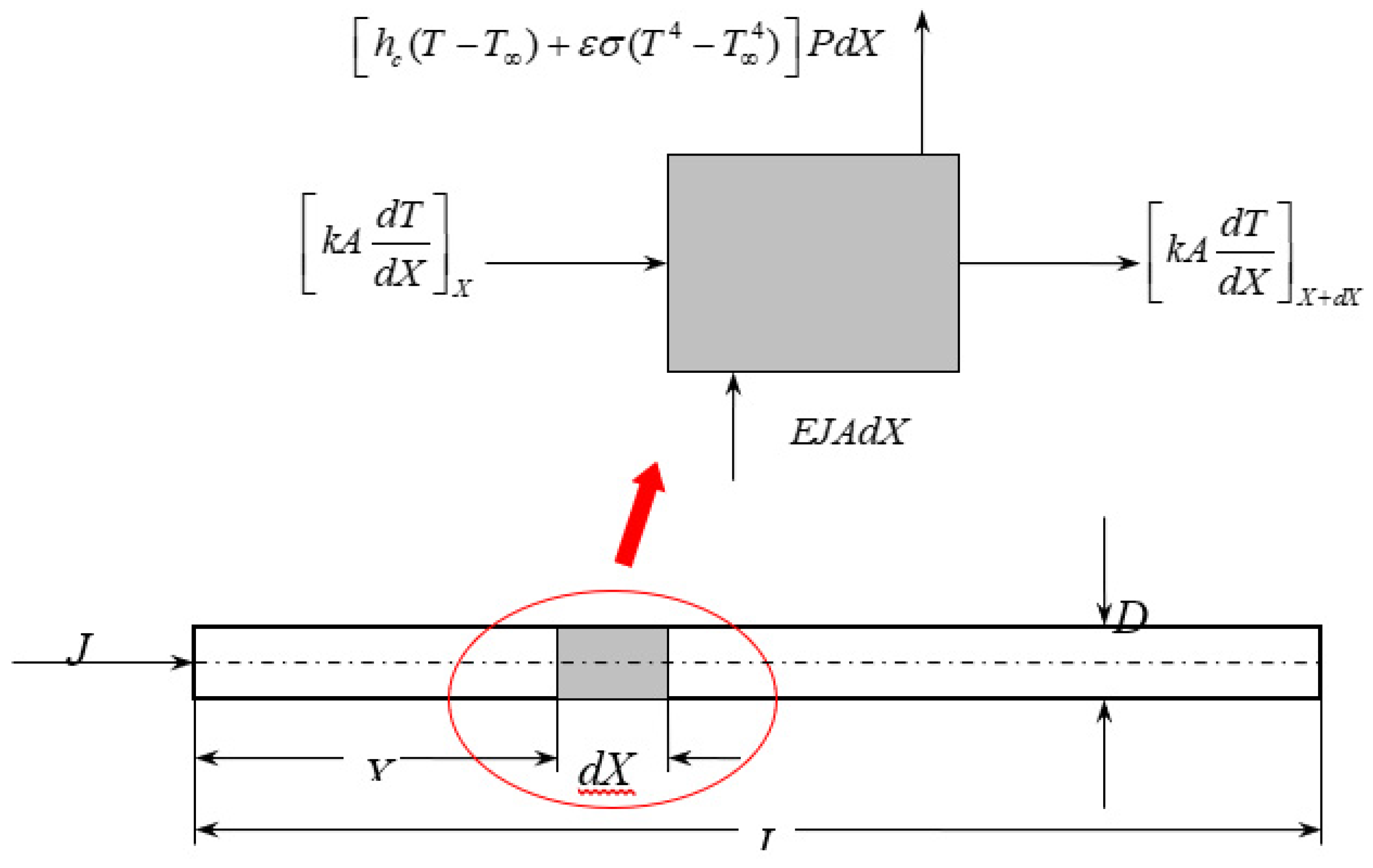
1.4. Heat Transfer Model

The heat generated in the device due to the current flow (Joule heating, Metaxas [33], Lupi [34], Lupi et al. [35]) is dissipated to the surrounding environment through natural convection and radiation exchange. For the circumferential average Nusselt number Nu, the correlation of Churchill and Chu [36] is employed:
Nu = 0.36 + 0.518 Ra 1 / 4 f ( Pr ) ,   f ( Pr ) = [ 1 + ( 0.559 Pr ) 9 / 16 ] 4 / 9
where f ( Pr ) is a weak function of the Prandtl number Pr. Equation (3) covers a very wide range of Rayleigh numbers namely in the range from 10-6 to 109, while it maintains a simple and compact mathematical form. Equation (3) is applied locally in the evaluation of the convective heat transfer coefficient along the device axis, in a similar manner as it was utilized by Faghri and Sparrow [37]. Consequently the local Rayleigh number Ra is evaluated from the local temperature difference as:
Ra = g β D 3 [ T ( X ) − T ∞ ] / α ν
where g is the acceleration due to gravity, β is the thermal expansivity, D is the device diameter, α is the thermal diffusivity and ν is the kinematic viscosity.

1.5. Boundary Conditions. Problems P1 and P2.

As it will be described in the next paragraphs the boundary conditions have a profound effect on the bifurcation structure in general and on the temperature distribution in particular. Thus for problem P1 the edges of the device are considered adiabatic:
∂ T ∂ X | X = 0 = ∂ T ∂ X | X = L = 0
whereas for problem P2 the imposed boundary conditions are:
T | X = L = T e ,   ∂ T ∂ X | X = L / 2 = 0

1.6. The Electrothermal Model in Dimensionless Form

Considering a constant (dc) current flowing through the device, the electric field intensity is related to the current density through Ohm’s law, E = ρ ^ ( T ) J , Metaxas [33], Lupi [34], Lupi et al. [35]. Introducing dimensionless variables
x = X / L ,   τ = α t / L 2 ,   Θ = T / T ∞ ,   ρ = ρ ^ / ρ ^ ref
the temperature distribution along the device takes the form:
∂ Θ ∂ τ = ∂ 2 Θ ∂ x 2 − u 2 [ Nu ( Θ − 1 ) + C h ( Θ 4 − 1 ) − j 2 ρ ]
In the above equation, the conduction- convection parameter (CCP) is defined as:
u 2 = h ref L 2 k ( A / P )
where the reference heat transfer coefficient h ref is defined through the Nusselt number:
Nu = h c k ∞ / D = h c h ref
In terms of the dimensionless variables defined above the local Rayleigh number becomes:
Ra = Ra ∞ ( Θ − 1 ) ,   Ra ∞ = g β D 3 T ∞ α ν
The current density parameter is related to the current density as below
j 2 = J 2 ( A / P ) T ∞ ( ρ ^ h ) ref
and C h is the ratio of the radiative heat transfer coefficient to the reference heat transfer coefficient
C h = ε σ T ∞ 3 h ref = h r h ref
Under steady state conditions the partial differential equation Equation (8) reduces to a two point boundary value problem for the device temperature Θ ( x )
Θ ″ − u 2 [ Nu ( Θ − 1 ) + C h ( Θ 4 − 1 ) − j 2 ρ ] = 0         0 < x < 1
with boundary conditions
Θ ′ ( x = 0 ) = Θ ′ ( x = 1 ) = 0
for problem P1 and
Θ ( x = 1 ) = Θ e ,   Θ ′ ( x = 0.5 ) = 0
for problem P2.

1.7. Stability

The stability of a certain steady state Θ s ( x ) to small perturbations ϑ ( x ) i.e.
Θ ( x , τ ) = Θ s ( x ) + ϑ ( x ) e λ τ
is determined by the eigenvalues λ of the corresponding Sturm-Liouville problem, after substituting Equation (15) into the original partial differential equation, Equation (8),
ϑ ″ − [ u 2 Δ Q Θ + λ ] ϑ = 0 ,   0 < x < 1
where
Δ Q Θ = ∂ ∂ Θ [ Nu ( Θ − 1 ) + C h ( Θ 4 − 1 ) − j 2 ρ ( Θ ) ] Θ = Θ s
The corresponding boundary conditions for problem P1 are ϑ ′ ( 0 ) = ϑ ′ ( 1 ) = 0 and for problem P2 are ϑ ′ ( 0.5 ) = ϑ ( 1 ) = 0 . During branch tracing, for every steady state that has been calculated from Equation (12), the associated eigenvalue problem, Equation (16), is subsequently numerically solved and a sufficient number of eigenvalues is determined. Stable solutions are characterized by negative eigenvalues whereas positive ones correspond to unstable temperature distributions.

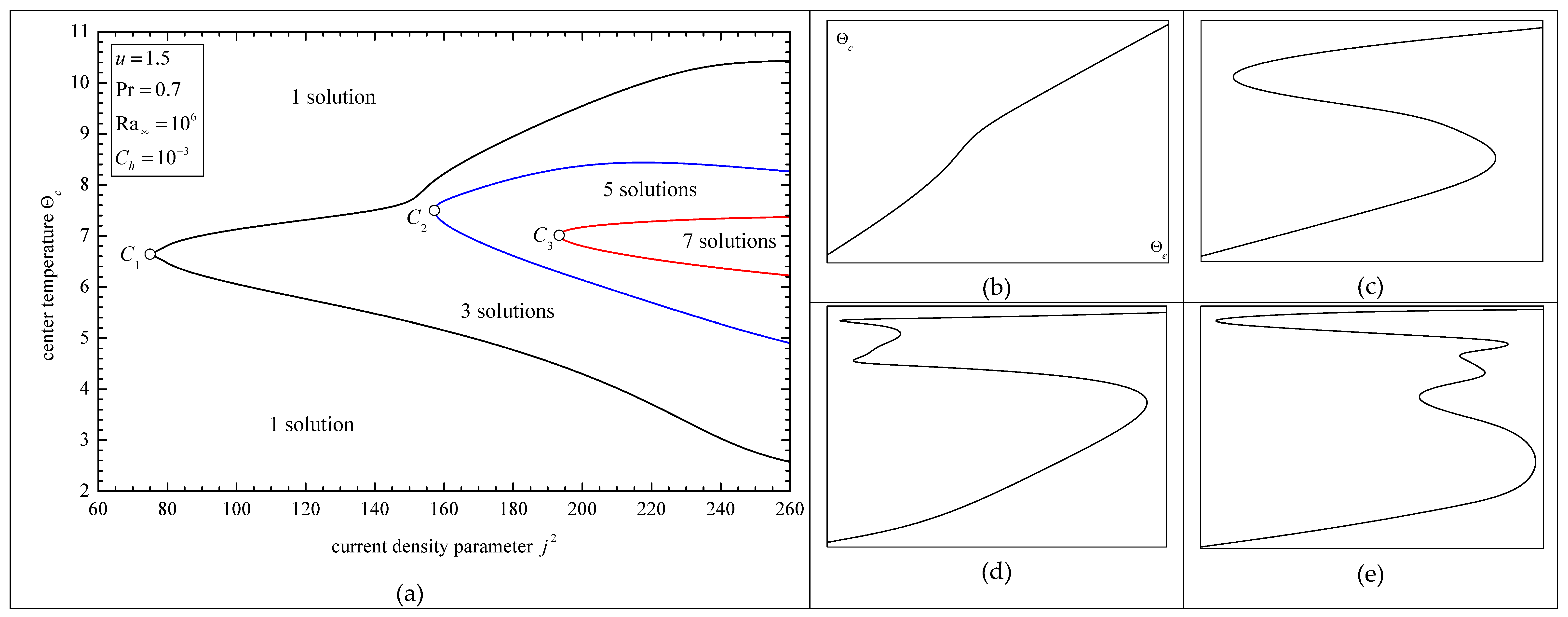
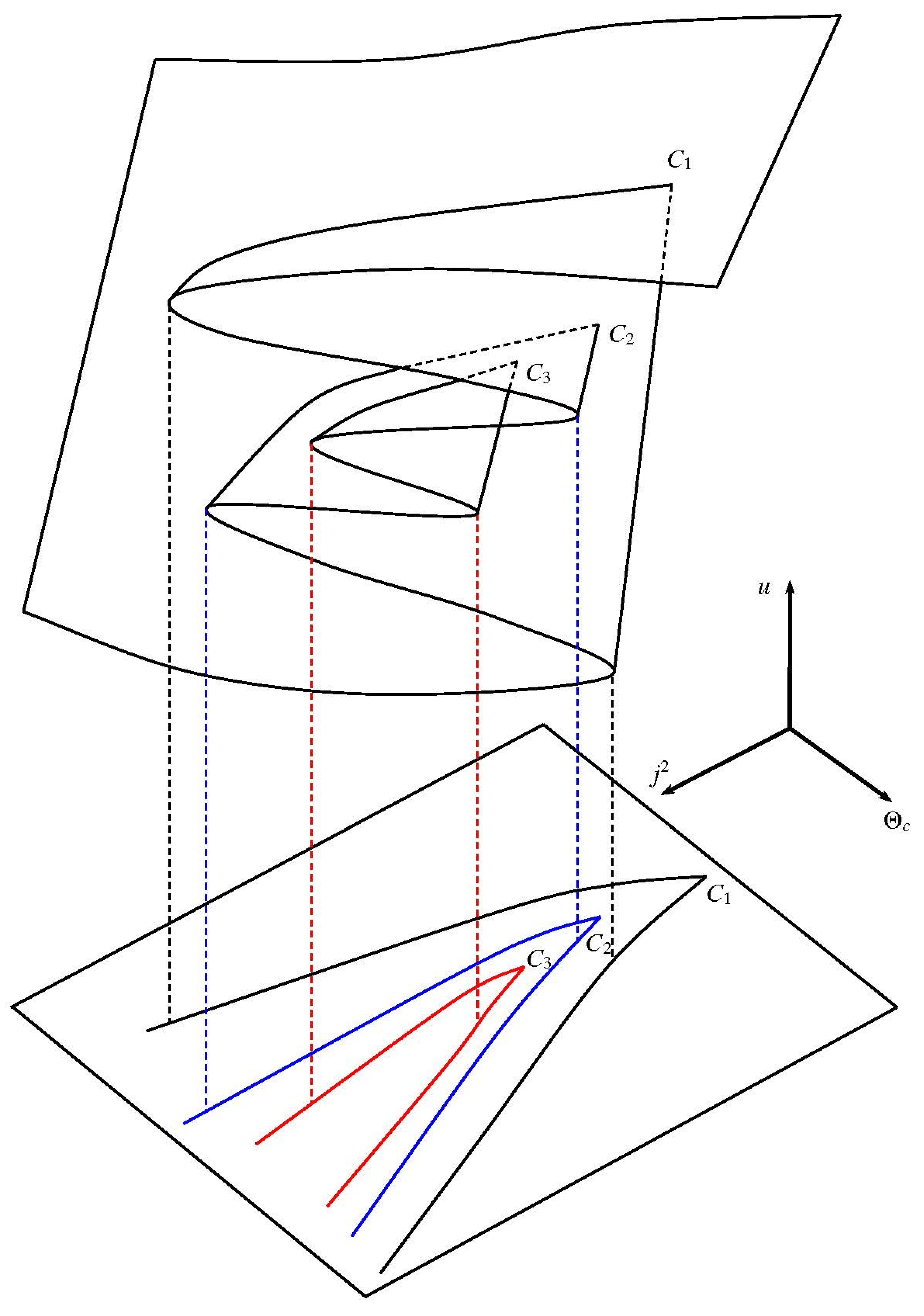
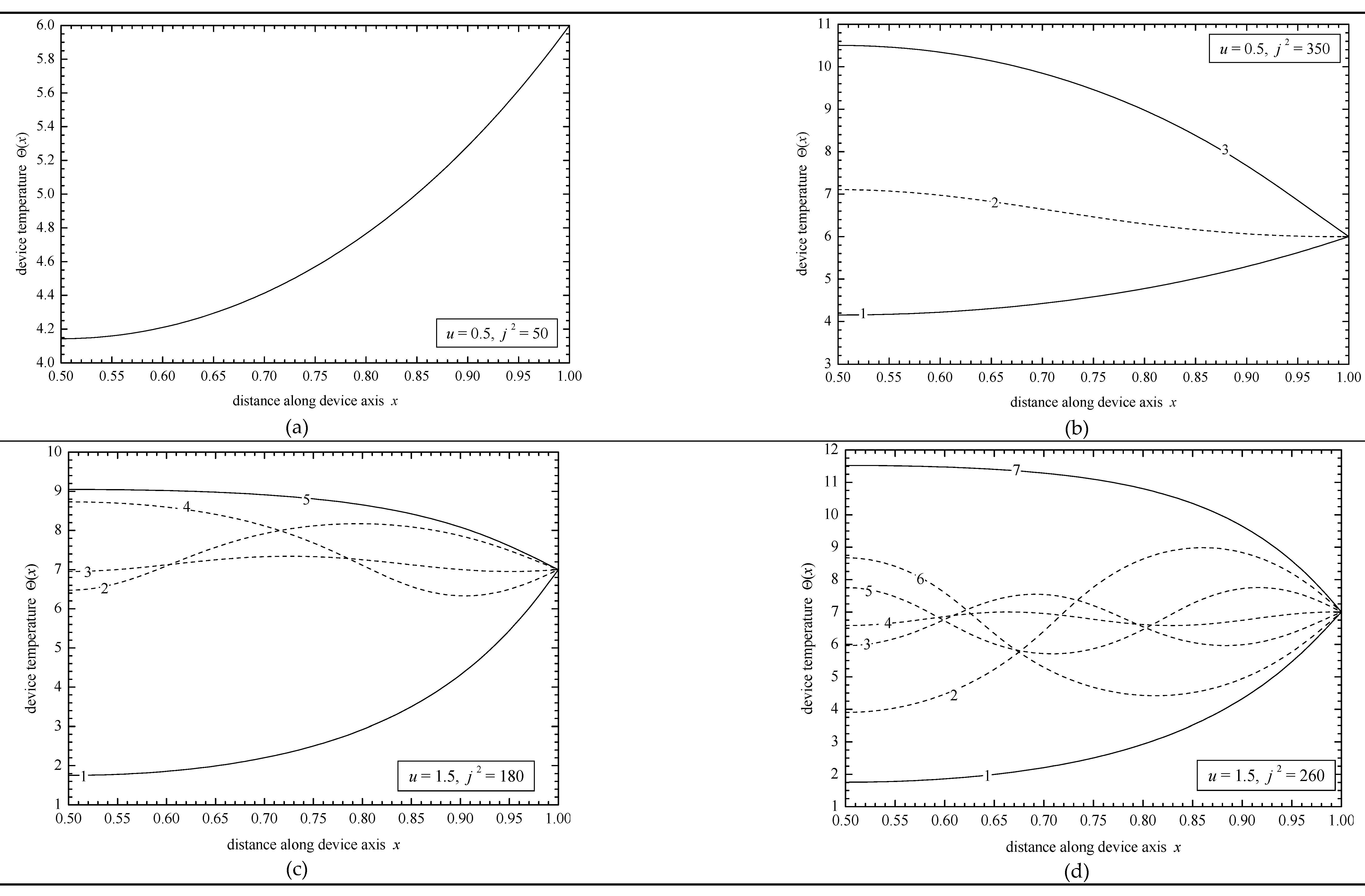
2. Results and Discussion

The second order, two-point boundary value problem described by Equation (12) is transformed into a system of first order equations through the transformation Θ 1 = Θ , Θ 2 = Θ ′ and solved numerically. In order to ensure an accurate and reliable numerical solution, two different methods have been employed resulting in identical results under the strict tolerances imposed. The first one utilizes a multi-shooting Runge-Kutta formula pair of order 8(7), Hairer et al. [38] and the second one a spline collocation method described by Ascher et al. [39]. Continuation along the various branches has been carried out along the lines suggested by Seydel [40]. For the computation of the singular points an extended problem is being formed from the partial derivatives of Equation (12) with respect to the parameters, according to Witmer et al. [41].
Before we analyze the complete numerical solution, it is instructive to discuss first the uniform solutions of Equation (12), which reduces to an algebraic one for a constant temperature profile:
Nu ( Θ − 1 ) + C h ( Θ 4 − 1 ) − j 2 ρ ( Θ ) = 0
A geometrical (graphical) solution is depicted in Figure 2 where the heat generation and the heat dissipation curves are being plotted for a variety of current parameters j 2 and reference Rayleigh numbers Ra ∞ (Figure 2a). In Figure 2b the effect of radiation through C h on the heat rejection rate is demonstrated. Depending on the combination of j 2 , Ra ∞ and C h up to three solutions of Equation (17) may be obtained from the number of the intersection points.

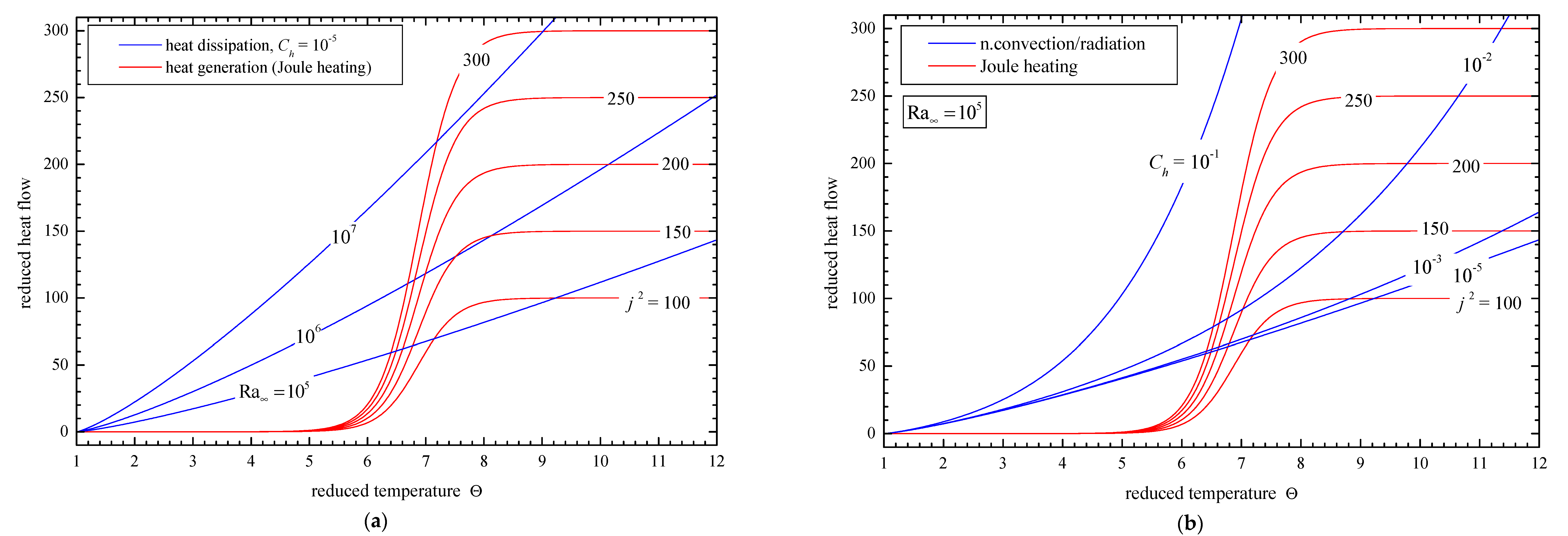
2.1. Problem P1

Interestingly, when the conduction term and the associated conduction-convection parameter u is taken into consideration, a far more complicated solution structure and multiplicity pattern emerges as it is shown in Figure 3, where the edge temperature Θ e = Θ ( 0 ) is plotted against j 2 . For lower values of the conduction-convection parameter ( u = 1 ) the three uniform solutions of Equation (17) are being recovered (Figure 3a). As u increases the number of solutions increases as well. Five for u = 2 in Figure 3b, seven for u = 3 in Figure 3c and eleven for u = 5 in Figure 3d. The corresponding temperature profiles are shown in Figure 4 (a to d). In every case the solution structure is consisting of the three uniform solutions, one stable “cold”, one stable “hot” and one unstable at an intermediate temperature. Additional unstable solutions emerge in the form of standing waves as u gradually increases. It is worth pointing out that the solution obtained by imposing boundary conditions Equation (13) have two salient features. The first one is that as long as the nonuniform solutions are unstable only the uniform ones are physically encountered, the “cold” one being far more preferable from the operating point of view since it results in reduced thermal stresses and thermal loading (reduced fracture probability) of the device. The second one stems from the first and the associated stability analysis, namely the temperature profiles may be obtained from the solution of the simpler algebraic Equation (17) instead of solving the complete boundary value problem, Equation (12). In other words effective control of the boundary conditions (and the edge temperature, say through the application of an insulating layer) appears to have a profound effect on the operating and performance characteristics of the device.

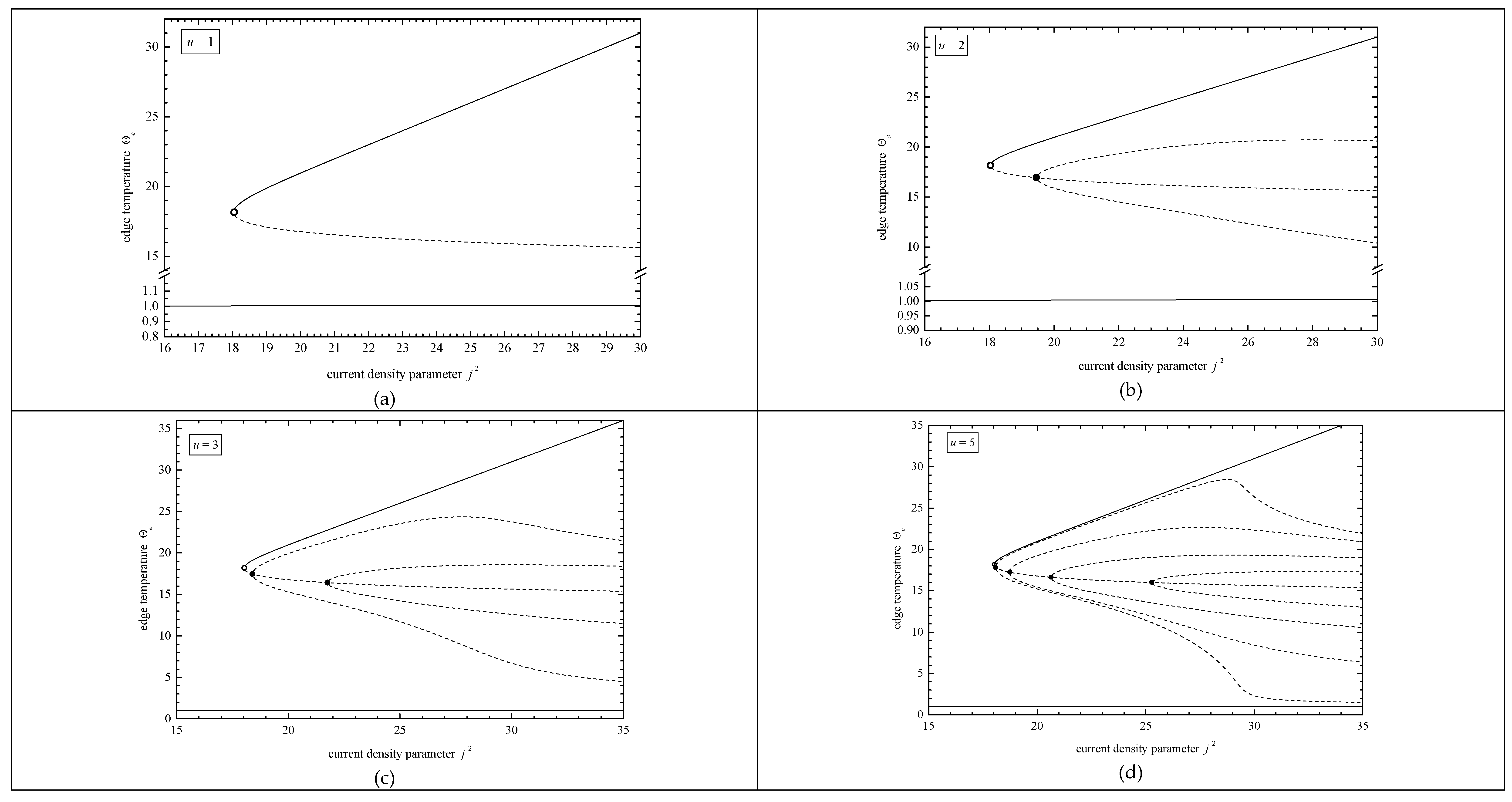
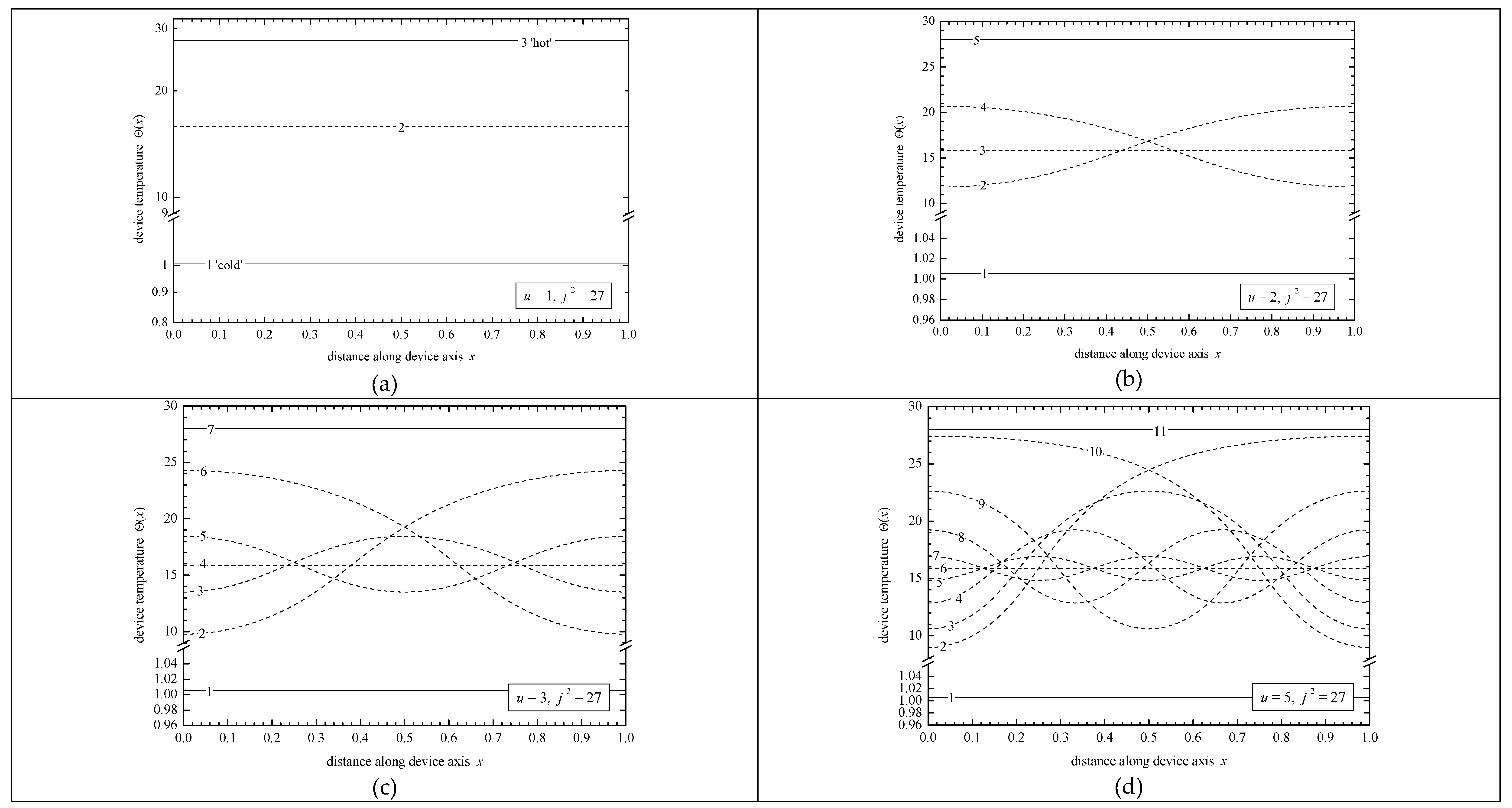
2.2. Problem P2

For the case where the edge temperature is fixed, the bifurcation analysis reveals a rich and interesting pattern, shown in Figure 5. Selecting the center temperature Θ c = Θ ( 0.5 ) as the bifurcation parameter, the projection of the limit points on the ( Θ c , j 2 ) plane forms a pattern of nested cusp points ( C 1 C 2 C 3 ... ) in Figure 5a, where the regions with unique, three, five, seven (and so on) solutions are designated. For a better understanding of the complexity of the solution structure and the clarity of the exposition a geometrical perspective of the nested cusps is depicted in Figure 6. Again the CCP has a profound effect on the solution structure since the number of the steady states calculated depend on its magnitude. Indeed starting from u = 0.5 and a unique solution in Figure 5b, three solutions emerge for u = 1 in Figure 5c, five for u = 1.5 in Figure 5d and seven in Figure 5e for u = 2 . The temperature profiles for problem P2 are symmetrical with respect to the center of the device. For the unique solution calculated in Figure 7a the center is maintained at a lower temperature, while it increases towards the edge ( Θ c < Θ e ) . When the CCP increases and three solutions are present as in Figure 7b, for the same edge temperature Θ e two stable solutions exist one “cold” ( Θ c < Θ e ) and one “hot” ( Θ c > Θ e ) . In contrast to the “cold” solution described earlier, the peak temperature for the “hot” one now appears around the center and gradually decreases to Θ e . As CCP further increases more solutions emerge, five in Figure 7c for u = 1.5 and seven in Figure 7d when u = 2 . Yet the stable ones remain the “cold” and “hot” set described earlier whereas the ones appearing as standing waves are unstable. In other words the bistability is retained as the CCP increases and several solutions emerge. Furthermore, as u increases a temperature plateau around the center is being formed and the temperature gradient along the device although it cannot be entirely eliminated as it was the case in problem P1, it is definitely reduced. It is worth pointing out that a multiplicity structure consisting of nested cusps is not a unique feature of this particular electrothermal problem. Aris [42] was the first to publish imbedded cusps in the study of first order reaction in spherical pellet. The same solution structure emerged in the analysis of another chemical reacting system, namely an isothermal Langmuir-Hinshelwood reaction in a cylindrical or spherical pellet, Witmer et al. [43]. Another example of similar multiplicity behavior is encountered when the three boiling modes (nucleate, transition and film) are being excited by a uniform heat generating source along a non-isothermal extended surface immersed in a boiling liquid, Krikkis [44].

3. Conclusions

An electrothermal model for a barium titanate based thermistor has been set up, featuring a nonlinear temperature dependent natural convection combined with radiation heat rejection mechanism through the device lateral surface. A smooth and strongly temperature dependent electric conductivity function based on experimental data has been adopted. As a result the problem formulated in this way admits multiple steady state solutions which do not depend on the external circuit.
Important findings are the profound effect of the conduction-convection parameter and of the boundary conditions on the multiplicity structure. Regardless of the type of the boundary conditions imposed, the number of the multiple steady states depends on the magnitude of the conduction-convection parameter, as for instance up to eleven solutions have been calculated when the edges of the device are insulated (problem P1) and up to seven when the edge temperature is being fixed (problem P2). The stability analysis reveals that for problem P1 only the uniform solutions are stable, namely one “cold” and one “hot”. Therefore, control and effective reduction of the heat transmitted through the edges results in a reduced thermal loading of the device both in the steady state operation and during transients since the temperature gradient across the device is vanishing.

Nomenclature

A cross sectional area [m2]
C specific heat capacity [J/(kgK)]
D device diameter [m]
E electric field intensity [V/m]
f function of Prandtl number in Equation (3) [-]
g acceleration due to gravity [-]
h c convective heat transfer coefficient [W/(m2K)]
h r ( ε σ T ∞ 3 ) radiative heat transfer coefficient [W/(m2K)]
j current density parameter [-]
J current density [A/m2]
k thermal conductivity [W/(mK)]
L device length [m]
Nu Nusselt number, Equation (3) [-]
P perimetry [m]
Pr Prandtl number, Equation (3) [-]
Ra Rayleigh number, Equation (4) [-]
t time [sec]
T temperature [K]
u conduction-convection parameter [-]
x ( X / L ) dimensionless distance [-]
X longitudinal distance along device [m]
  • Greek Symbols
α thermal diffusivity [m2/s]
β thermal expansivity [K-1]
γ material density [kg/m3]
ε emissivity [-]
Θ ( T / T ∞ ) dimensionless temperature [-]
λ eigenvalue [-]
ν kinematic viscosity [m2/s]
ρ ( ρ ^ / ρ ^ ref ) reduced electric resistivity [-]
ρ ^ electric resistivity [Ω m]
σ Stefan-Boltzmann constant [Wm-2K-4]
τ dimensionless time [-]
  • Subscripts
b position at x = 1
c position at x = 0.5
e position at x = 0
ref reference value
s steady state
∞ ambient environment
  • Superscripts
( ′ ) derivative with respect to x
  • Abbreviations
CCP Conduction-Convection Parameter
NTC Negative Temperature Coefficient
PTC Positive Temperature Coefficient

References

  1. T. G. Glaggett, R. W. Worrall, B. G. Lipták and P. M. B. Silva Girão, Thermistors, in: B. G. Lipták (Editor), Instrument Engineers’ Handbook, Process Measurement and Analysis, Vol 1, CRC Press, 4th ed., 2003, pp. 66-672.
  2. J. Fraden, Handbook of Modern Sensors. Physics, Designs and Applications, (2004), 3rd ed., AIP Press, New York, pp. 477-481.
  3. M. Sapoff, Thermistor Thermometers, in: J. G. Webster (Editor), The Measurement, Instrumentation and Sensors Handbook, CRC Press/IEEE Press, 1999.
  4. C. Dewitte, R. Elst and F. Delannay (1994) “On the mechanism of delamination fracture of BaTiO3-based PTC thermistors”, J. Eur. Ceram. Soc. 14, pp. 481-492.
  5. P. Supancic (2000) “Mechanical stability of BaTiO3-based PTC thermistors components: experimental investigation and theoretical modeling”, J. Eur. Ceram. Soc. 20(12), pp. 2009-2024.
  6. H. Diesselhorst (1900) “Uber das Probleme das Electrisch Erwärmter Leiter”, Ann. Phys. 1, pp. 312-325.
  7. G. Cimatti (1989) “Remark on existence and uniqueness for the thermistor problem under mixed boundary conditions”, Quart. Appl. Math. 47, pp. 117-121.
  8. G. Cimatti (1988) “A bound for temperature in thermistor problem”, IMA J. Appl. Math. 40, pp. 15-22.
  9. G. Cimatti and G. Prodi (1988) “Existence results for a nonlinear elliptic system modeling a temperature dependent electrical resistor”, Ann Mat. Pure Appl. 152, pp. 227-236.
  10. H. Xie and W. Allegretto (1991) “Cα(Ω) solutions of a class of nonlinear degenerate elliptic systems arising in the thermistor problem”, SIAM J. Math. Anal. 22, pp. 1491-1499.
  11. S. N. Antontsev and M. Chipot (1994) “The Thermistor Problem: Existence, smoothness, uniqueness, blowup”, SIAM J. Math. Anal. 25, pp. 1128-1156.
  12. A.R. Bahadir (2002) “Steady state solution of the PTC thermistor using a quadratic spline finite element method”, Mathematical Methods in Engineering 8(2), pp. 101-109.
  13. R. Bahadir (2004) “Application of cubic B-spine finite element technique to the thermistor problem”, Applied Mathematics and Computation 149, pp. 379-387.
  14. S. Çatal (2004) “Numerical solution of the thermistor problem”, Applied Mathematics and Computation 152, pp. 743-757.
  15. S. Kutluay, A. S. S. Kutluay, A. S. Wood and A. Esen (2006) “A heat balance integral solution of the thermistor with a modified electrical conductivity”, Applied Mathematical Modelling 30, pp. 386-394.
  16. M. R. S. Ammi and D. F. M. Torres (2008) “Numerical analysis of a nonlocal parabolic problem resulting from thermistor problem”, Mathematics and Computers in Simulation 77, pp. 291-300.
  17. O. Golosnoy and J. K. Sykulski (2009) “Numerical modeling of non-linear coupled thermo-electric problems. A comparative study”, International Journal for Computation and Mathematics in Electrical and Electronic Engineering 28(3), pp. 639-655.
  18. E. G. Karpov (2012) “Bistability, autowaves and dissipative structures in semiconductor fibers with anomalous resistivity properties”, Philosophical Magazine 92(10), pp. 1300-1316.
  19. J. Hewitt, A. A. Lacey and R. I. Todd (2015) “A mathematical model for flash sintering”, Math. Model. Nat. Phenom. 10(6), pp. 77-89. [CrossRef]
  20. R. Raj (2012) “Joule heating during flash-sintering”, Journal of the European Ceramic Society 32, pp. 2293-2301.
  21. R. I. Todd, E. Zapata-Solvas, R. S. Bonilla, T. Sneddon and P. R. Wilshaw (2015) “Electrical characteristics of flash sintering: thermal runaway of Joule heating”, Journal of the European Ceramic Society 35, pp. 1865-1877.
  22. G. Pereira da Silva, H. A. Al-Qureshi, F. Keil, R. Janssen (2016) “A dynamic bifurcation criterion for thermal runaway during the flash sintering of ceramics”, Journal of the European Ceramic Society 36, pp. 1261-1267.
  23. A.C. Fowler, I. Frigaard and S. D. Howison (1992) “Temperature surges in current-limiting circuit devices”, SIAM J. Appl. Math. 52, pp. 998-1011.
  24. S. D. Howison, J. F. Rodrigues and M. Shilor (1993) “Stationary solutions to the thermistor problem”, Journal of Mathematical Analysis and. Applications, 174, pp. 573-588.
  25. S. Zhou and D. R. Westbrook (1997) “Numerical solutions of the thermistor equations”, Journal of Computational and Applied Mathematics 79, pp. 101-118.
  26. G. Cimatti (2011) “Remark on the number of solutions in the thermistor problem”, Le Mathematische, Vol. LXVI, pp. 49-60.
  27. E. Brzozowski and M. S. Castro (2000) “Conduction mechanism of barium titanate ceramics”, Ceramics International, 26, pp. 265-269.
  28. X. Wang, H. L. W. Chan and C. L. Choy (2003) “Semiconducting barium titanate ceramics prepared by using yttrium hexaboride as sintering aid”, Materials Science and Engineering B, 100(3), pp. 286-291.
  29. X. Wang, H. L. W. Chan G. K. H. Pang and C. L. Choy (2004) “Positive temperature coefficient of resistivity effect in niobium doped barium titanate ceramics obtained at low sintering temperature”, J. Eur. Ceram. Soc. 24(6), pp. 1227-1231.
  30. Y. Luo, X. Lin X. Li and G. Lin (2006) “PTCR effect in BaBiO3-doped BaTiO3 ceramics”, Solid State Ionics, 177, pp. 1543-1546.
  31. H. Takeda, H. Harinaka, T. Shiosaki, M. A. Zubair, C. Leach, R. Freer, T. Hoshina, T. Tsurumi (2010) “Fabrication and positive temperature coefficient of resistivity properties of semiconducting ceramics based on the BaTiO3-(Bi1/2K1/2TiO3 system”, J. Eur. Ceram. Soc, 30, pp. 555-559.
  32. W. Rowlands and B. Vaidhyanathan (2019) “Additive manufacturing of barium titanate based ceramic heaters with positive temperature coefficient (PTCR)”, J. Eur. Ceram. Soc, 39, pp. 3475-3483.
  33. A.C. Metaxas (1996), Foundations of Electroheat. A Unified Approach, John Wiley & Sons, New York.
  34. S. Lupi (2017), Foundamentals of Electroheat. Electrical Technologies for Process Heating, Springer, Switzeland.
  35. S. Lupi, M. Forzan. A. Aliferov (2015), Induction and Direct Resistance Heating. Theory and Numerical Modeling, Springer, Switzerland.
  36. S. W. Churchill and H. H. S. Chu (1975) “Correlating equations for laminar and turbulent free convection from a horizontal cylinder”, Int. J. Heat Mass Transfer 18, pp. 1049-1053.
  37. M. Faghri and E. M. Sparrow (1986) “Forced convection in a horizontal pipe subjected to nonlinear external natural convection and to external radiation”, Int. J. Heat Mass Transfer 23, pp. 861-872.
  38. E. Hairer, S. P. Nørsett and G. Wanner, Solving Ordinary Differential Equations I. Nonstiff Problems, (1987) Springer-Verlag, New York.
  39. U. M. Ascher, R. M. M. Mattheij and R. D. Russel Numerical Solution of Boundary Value Problems for Ordinary Differential Equations, (1995) 2nd ed., SIAM, Philadelphia.
  40. R. Seydel, Practical Bifurcation and Stability Analysis, (2009), 3rd ed., Springer-Verlag, New York.
  41. G. Witmer, V. Balakotaih and D. Luss, (1986) “Finding singular points of two-point boundary value problems”, Journal of Computational Physics 65, pp. 244–250.
  42. R. Aris, (1979) “Chemical reactors and some bifurcation phenomena” In Bifurcation Theory and Applications in Scientific Disciplines, Annals New York Acad. of Sci., vol 316, pp. 314-331.
  43. G. Witmer, V. Balakotaih and D. Luss, (1986) “Multiplicity features of distributed systems – I. Langmuir-Hinshelwood reaction in a porous catalyst”, Chemical Engineering Science 41, pp. 179–186.
  44. R. Krikkis, (2015) “On the multiple solutions of boiling fins with heat generation”, Int. J. Heat Mass Transfer, vol. 80, pp. 236-242.
Preprints 77959 g001
Figure 1. Conductor geometry and energy balance.
Figure 1. Conductor geometry and energy balance.
Preprints 77959 g001
Preprints 77959 g002
Figure 2. Uniform solutions and energy balance on the device. (a) heat dissipation by primarily natural convection and (b) by combined natural convection and radiation.
Figure 2. Uniform solutions and energy balance on the device. (a) heat dissipation by primarily natural convection and (b) by combined natural convection and radiation.
Preprints 77959 g002
Preprints 77959 g003
Figure 3. Multiplicity pattern for Problem P1. (a) three (3) uniform solutions, u = 1 . (b) five (5) solutions, u = 2 , (c) seven (7) solutions, u = 3 , (d) eleven (11) solutions, u = 5 . Solid line: stable, dashed line: unstable.
Figure 3. Multiplicity pattern for Problem P1. (a) three (3) uniform solutions, u = 1 . (b) five (5) solutions, u = 2 , (c) seven (7) solutions, u = 3 , (d) eleven (11) solutions, u = 5 . Solid line: stable, dashed line: unstable.
Preprints 77959 g003
Preprints 77959 g004
Figure 4. Solution structure for Problem P1, corresponding to multiplicity pattern in Figure 3. (a) three (3) uniform solutions, u = 1 . (b) five (5) solutions, u = 2 , (c) seven (7) solutions, u = 3 , (d) eleven (11) solutions, u = 5 . Solid line: stable, dashed line: unstable.
Figure 4. Solution structure for Problem P1, corresponding to multiplicity pattern in Figure 3. (a) three (3) uniform solutions, u = 1 . (b) five (5) solutions, u = 2 , (c) seven (7) solutions, u = 3 , (d) eleven (11) solutions, u = 5 . Solid line: stable, dashed line: unstable.
Preprints 77959 g004
Preprints 77959 g005
Figure 5. Problem P2. (a) projection of the singular points on the ( j 2 , Θ c ) plane. (b) one solution, u = 0.5 , (c) three solutions, u = 1 . 0 , (d) five solutions, u = 1 . 5 and (e) seven solutions, u = 2 . 0 .
Figure 5. Problem P2. (a) projection of the singular points on the ( j 2 , Θ c ) plane. (b) one solution, u = 0.5 , (c) three solutions, u = 1 . 0 , (d) five solutions, u = 1 . 5 and (e) seven solutions, u = 2 . 0 .
Preprints 77959 g005
Preprints 77959 g006
Figure 6. Geometrical perspective of nested cusps.
Figure 6. Geometrical perspective of nested cusps.
Preprints 77959 g006
Preprints 77959 g007
Figure 7. Solution structure for Problem P2, corresponding to multiplicity pattern in Figure 3. (a) three (3) uniform solutions, u = 1 . (b) five (5) solutions, u = 2 , (c) seven (7) solutions, u = 3 , (d) eleven (11) solutions, u = 5 . Solid line: stable, dashed line: unstable.
Figure 7. Solution structure for Problem P2, corresponding to multiplicity pattern in Figure 3. (a) three (3) uniform solutions, u = 1 . (b) five (5) solutions, u = 2 , (c) seven (7) solutions, u = 3 , (d) eleven (11) solutions, u = 5 . Solid line: stable, dashed line: unstable.
Preprints 77959 g007
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.
Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.
Prerpints.org logo

Preprints.org is a free preprint server supported by MDPI in Basel, Switzerland.

facebook logotwitter logolinkedin logo
MDPI Initiatives
Important Links
Subscribe

Disclaimer

Terms of Use

Privacy Policy

© 2024 MDPI (Basel, Switzerland) unless otherwise stated