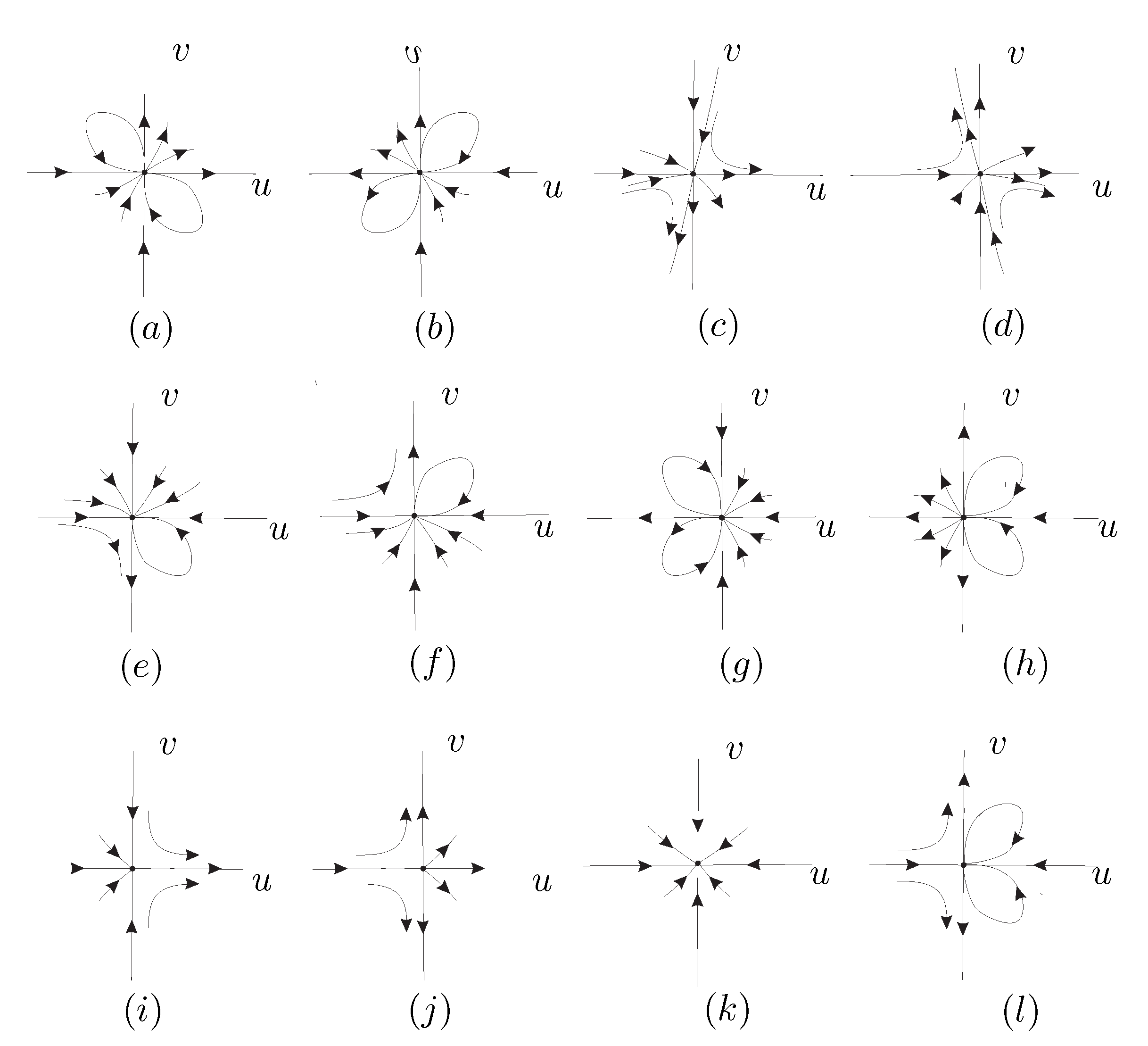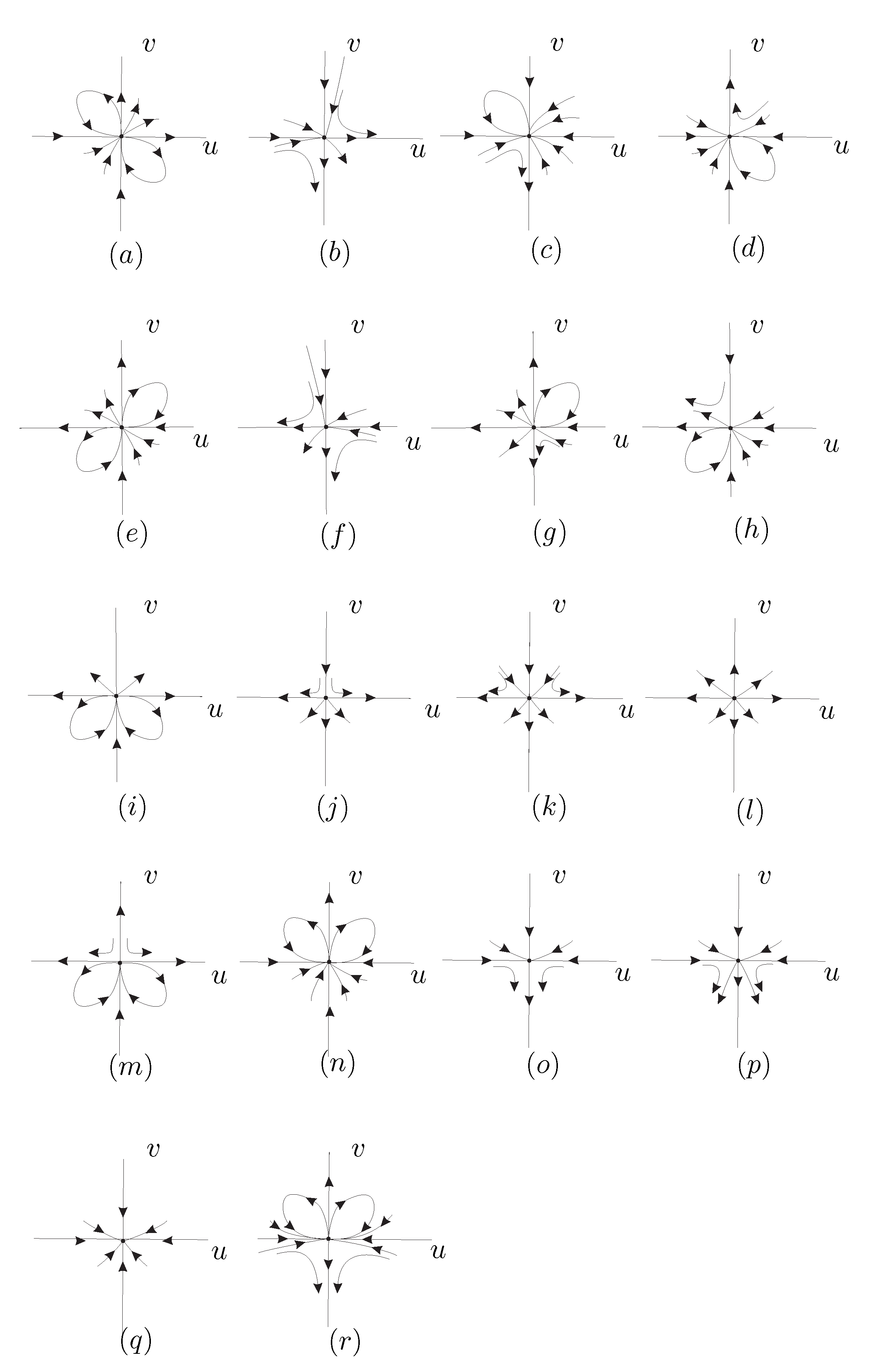4.3. the Infinite Singular Point at the Origin of the Chart
Studying the infinite singular points in the local chart we also have studied the infinite singular points in the local chart . So only remains to see if the origins of the local charts and are infinite singular points or not.
System (
3) in the local chart
writes
so the origin of
always is an infinite singular point. The eigenvalues of the Jacobian matrix of the system at the origin are
with multiplicity two. Therefore the origin is a hyperbolic node, stable if
, and unstable if
.
If
then the Jacobian matrix of the system at the origin is the zero matrix and we need to make blow-ups in order to study the local phase portrait at the origin of
. Before doing a vertical blow-up we need to be sure that
is not a characteristic direction. If
is a characteristic direction then
u is a factor of the polynomial
, where
and
are the terms of lowest degree of
and
. In our case
. So
is characteristic direction and consequently before doing a vertical blow-up, we must do a twist in order that
do not be a characteristic direction. This is done with the change of variables
where
,
. Doing this change of variables the differential system (
8) writes
The characteristic directions of this system are given by the polynomial
, so
is not a characteristic direction and we can do a vertical blow-up. This vertical blow-up is given by the change of variables
where
Then system (
9) becomes
Now doing a rescaling of the time with the factor
we obtain the system
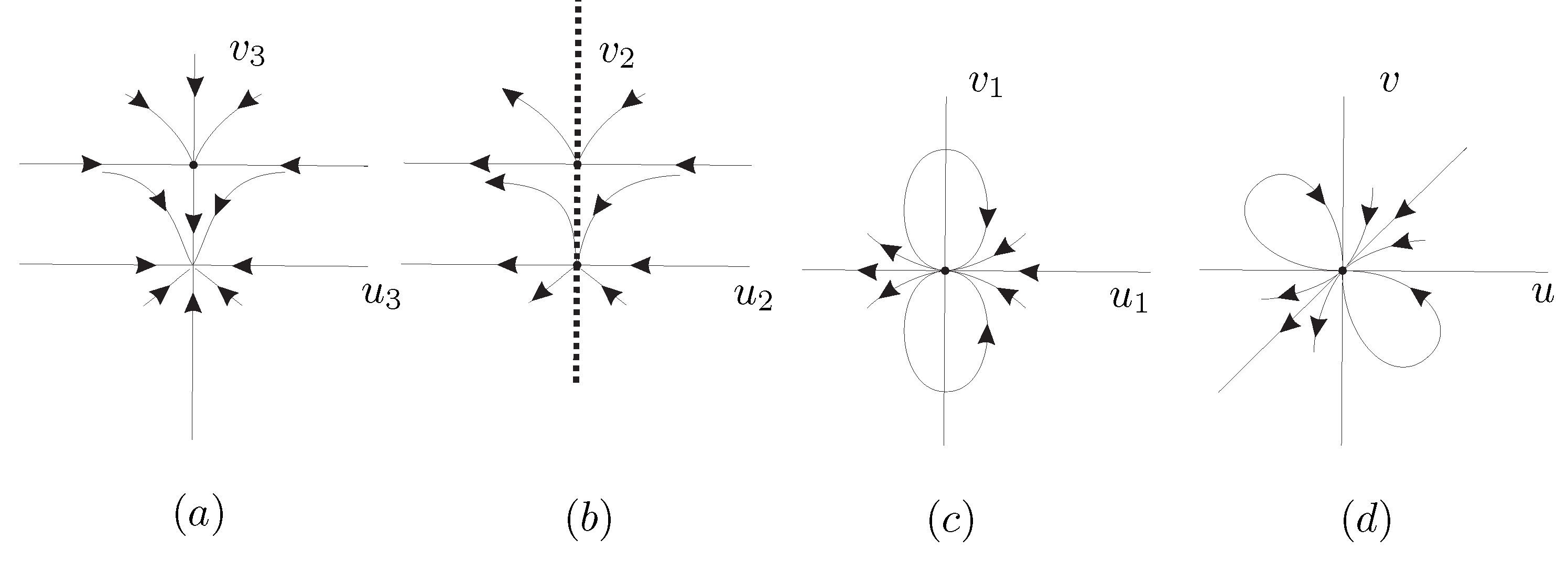
The singular points of system (
11) on
are
which is double and
. The eigenvalues of the Jacobian matrix at
are 0 and
. So the
is a semi-hyperbolic singular point, applying to it Theorem 2.19 of [
7] it is a saddle-node. The eigenvalues of the Jacobian matrix at
are 1 and
. So this singular point is hyperbolic, a saddle if
, an unstable node if
, see
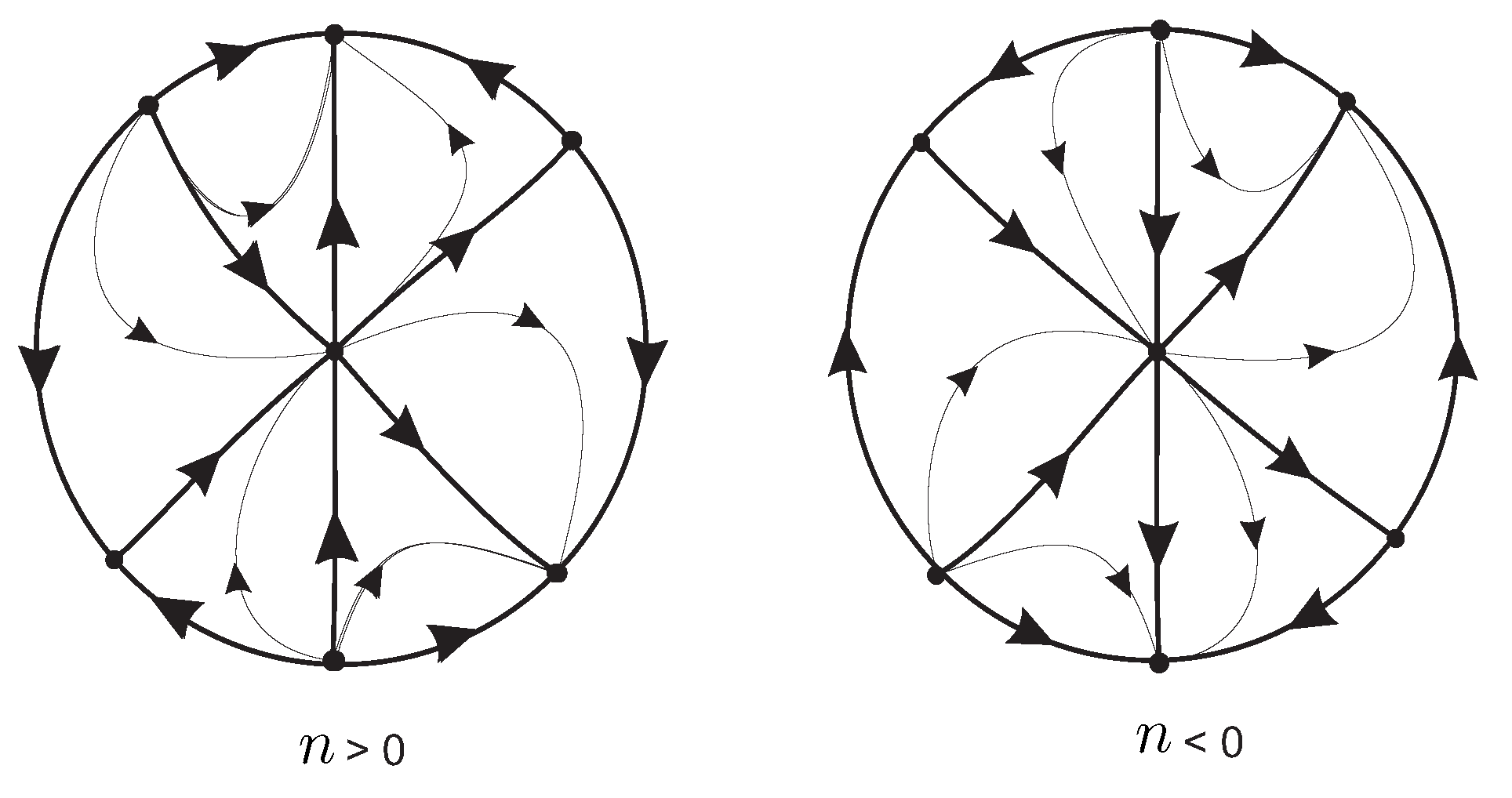
Figure 8(a) when
,
and
.
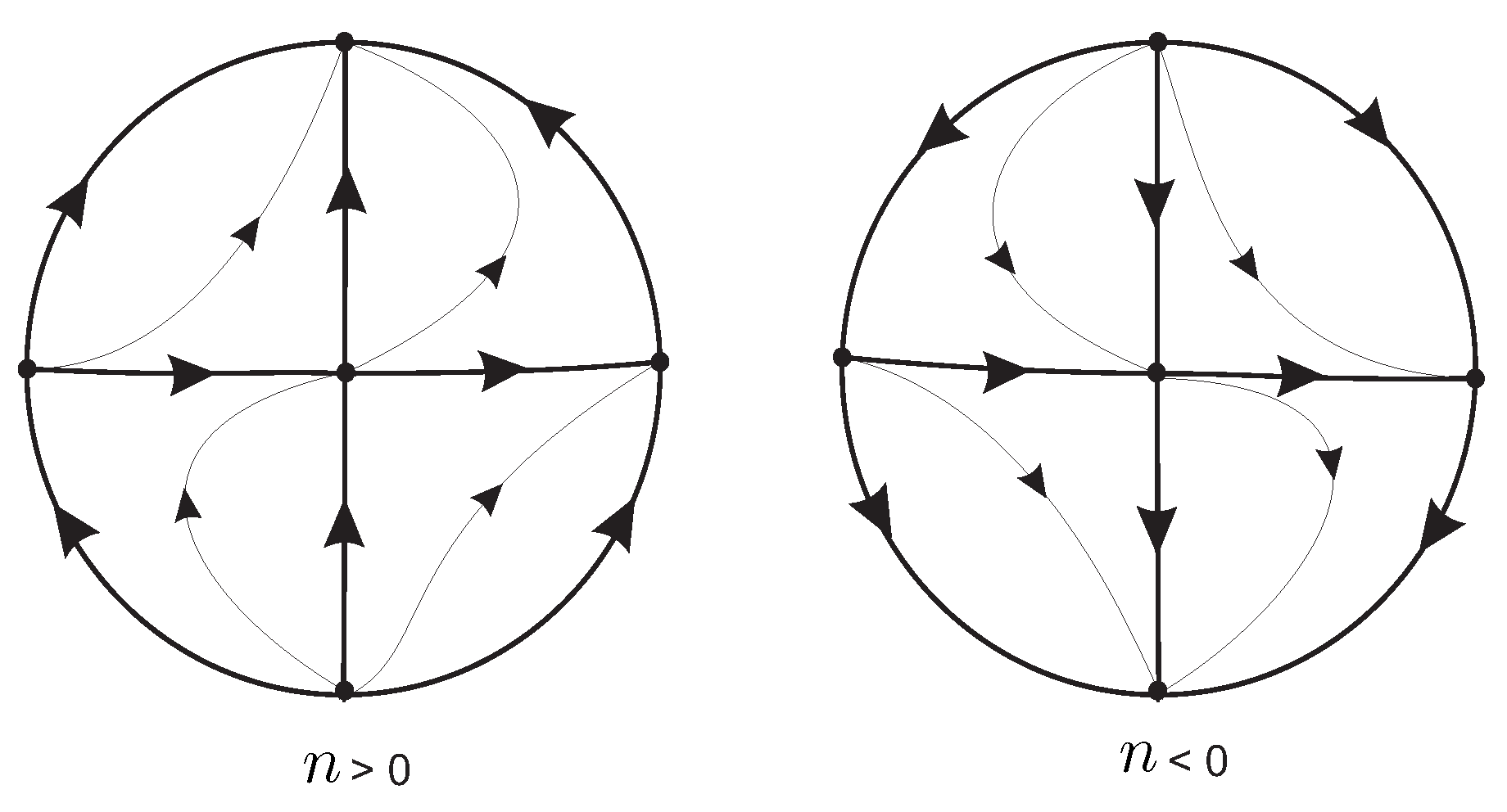
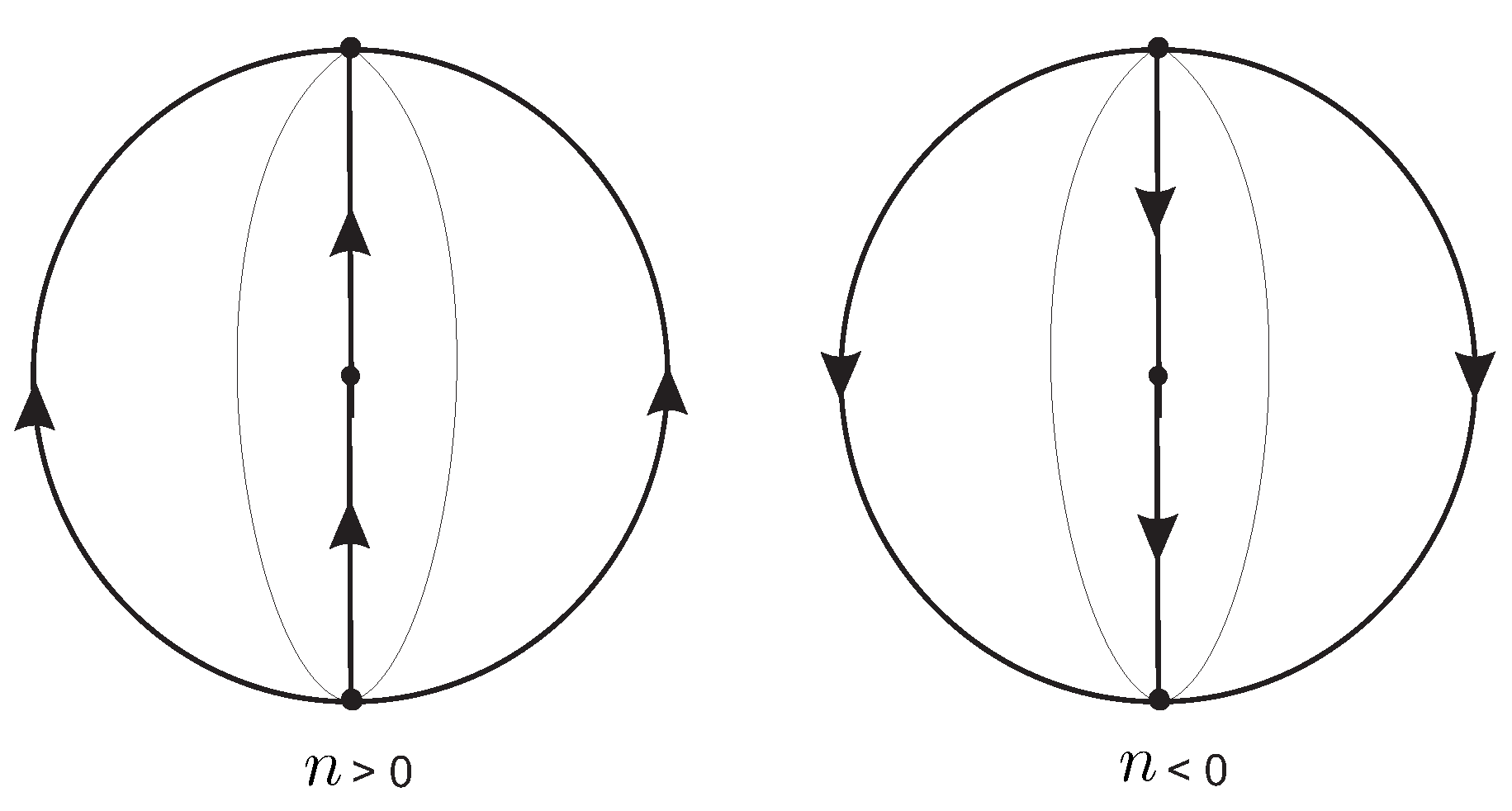
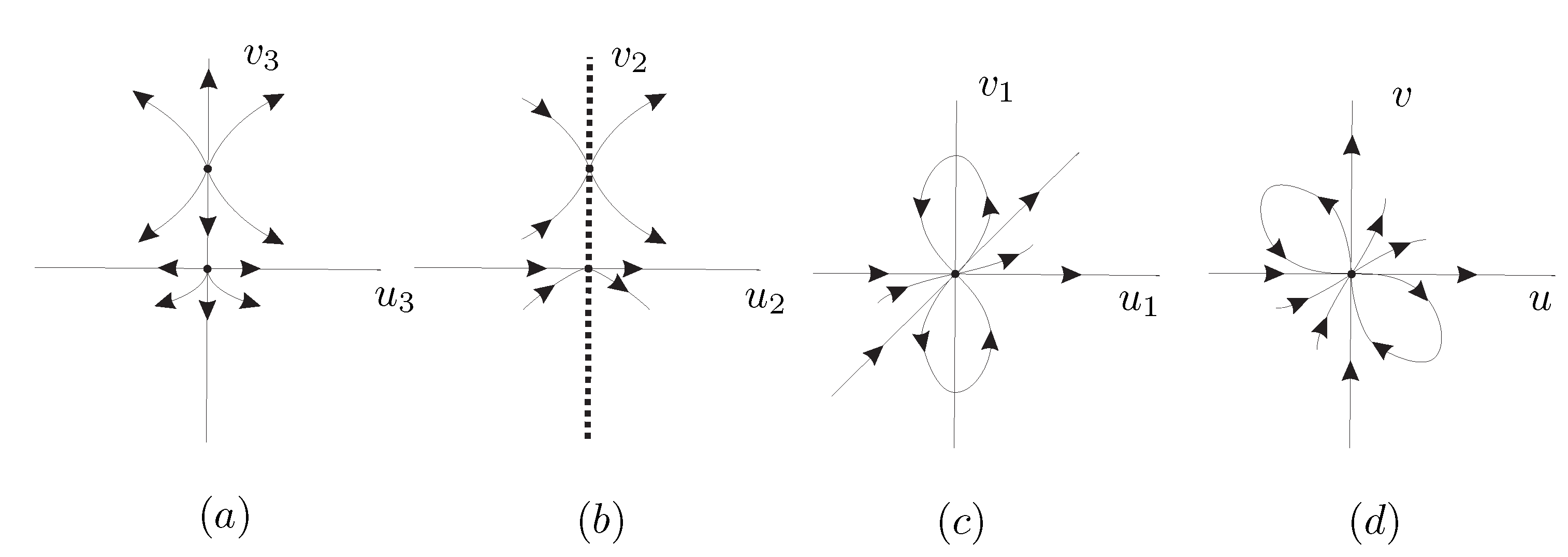
From
Figure 8(a) we obtain that the local phase portrait at the axis
of system (
10) is given in
Figure 8(b). Now going back through the vertical blow up and taking into account the value of
we obtain the local phase portrait at the origin of system (
8) in
Figure 8(c). Finally unding the twist we get the local phase portrait at the origin of the local chart
which is shown in
Figure 8(d) and
Figure 9(a).
Working in a similar way to the case
,
and
, i.e. doing the convenient blow ups and using Theorems 2.15 and 2.19 of [
7] we obtain all the local phase portraits at the origin of the local chart
in
Figure 9 for the following cases:
,
,
, and
in
Figure 9(c);
,
and
, in
Figure 9(d);
,
,
and
in
Figure 9(g);
,
,
and
in
Figure 9(h);
,
,
and
in
Figure 9(i);
,
,
and
in
Figure 9(j);
,
,
and
in
Figure 9(k);
,
,
,
and
in
Figure 9(l);
,
,
,
and
in
Figure 9(m);
,
,
,
and in
Figure 9(n);
,
,
and
in
Figure 9(o);
,
,
and
in
Figure 9(p);
,
,
,
and
in
Figure 9(q);
,
,
and
in
Figure 9(r).
4.4. The Global Phase Portaits
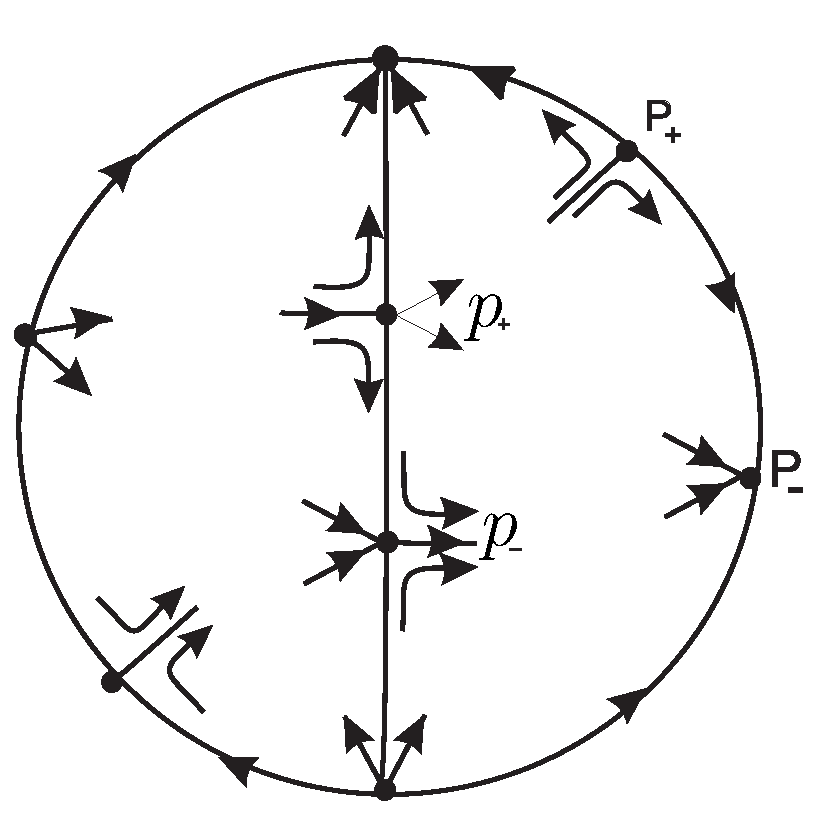
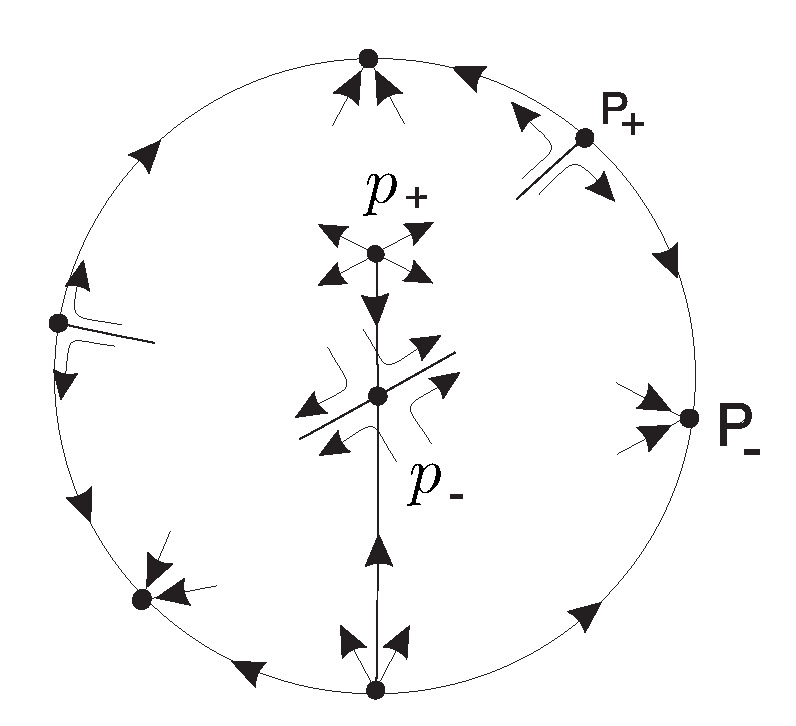
The preceding results for the finite and infinite singular points, allow to obtain the global phase portraits quite easily, taking into account that the straight line is invariant.
First we consider the case satisfying the following conditions:
,
and
. We have seen that
denotes a stable hyperbolic node at the origin of the chart
,
indicates the existence of two real finite singular points (
a hyperbolic unstable node and
a hyperbolic saddle), and
imply two infinite singular points in the chart
(
and
which are nilpotent saddle-nodes). The local phase portraits at all these singular points are shown in
Figure 10.
With the help of Mathematica we have proved that in order that the conditions
,
and
hold, the parameters of the differential system (
3) must satisfy one of the conditions:
- (i)
, , and ;
- (ii)
, , , and ;
- (iii)
, , , and ;
- (iv)
, , and ;
- (v)
, , , and ;
- (vi)
, , , and ;
- (vii)
, , and ;
- (viii)
, , , and ;
- (ix)
, , , and ;
- (x)
, , and ;
- (xi)
, , , and ;
- (xii)
, , , and ;
- (xiii)
, , and ;
- (xiv)
, , , and ;
- (xv)
, , , and .
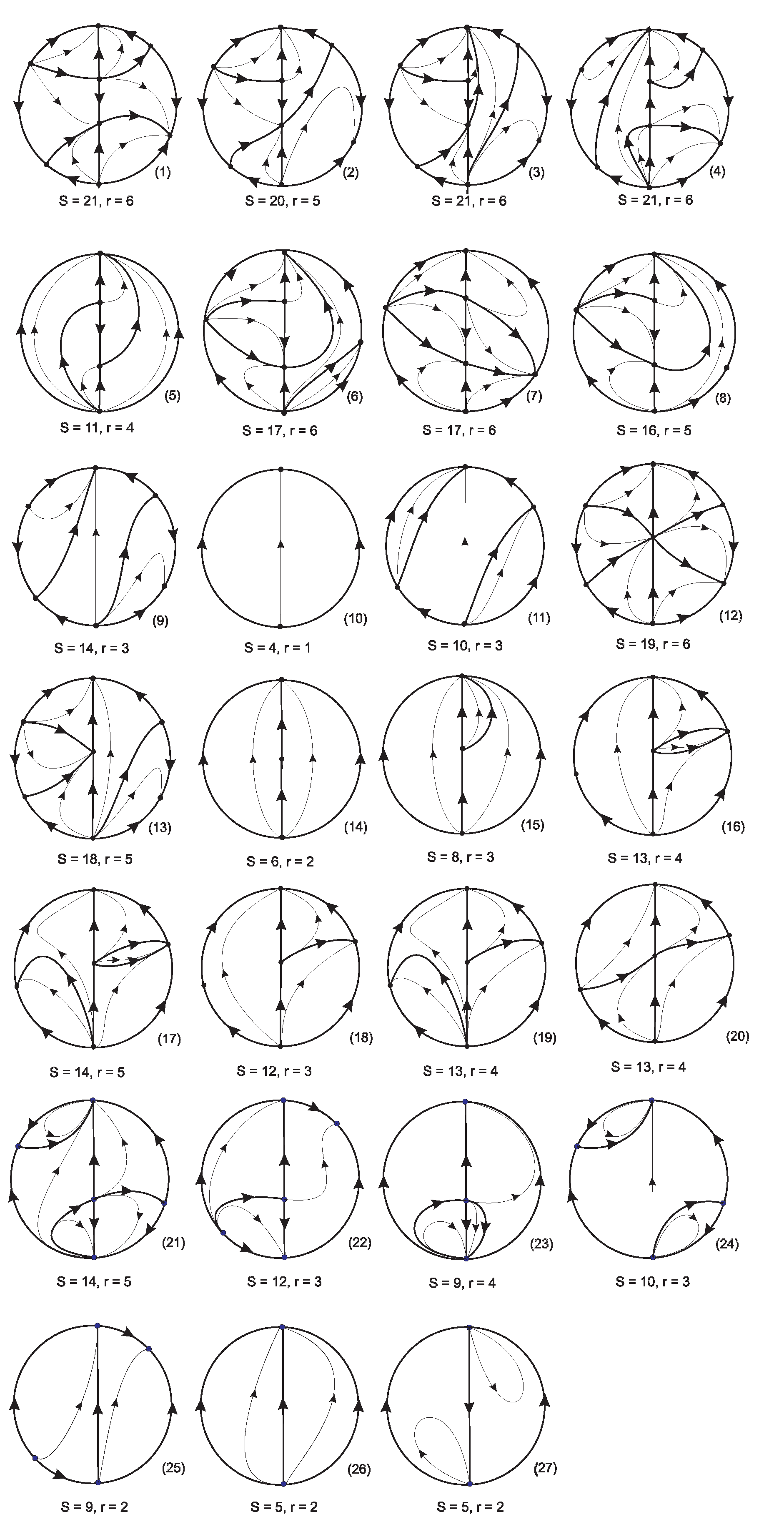
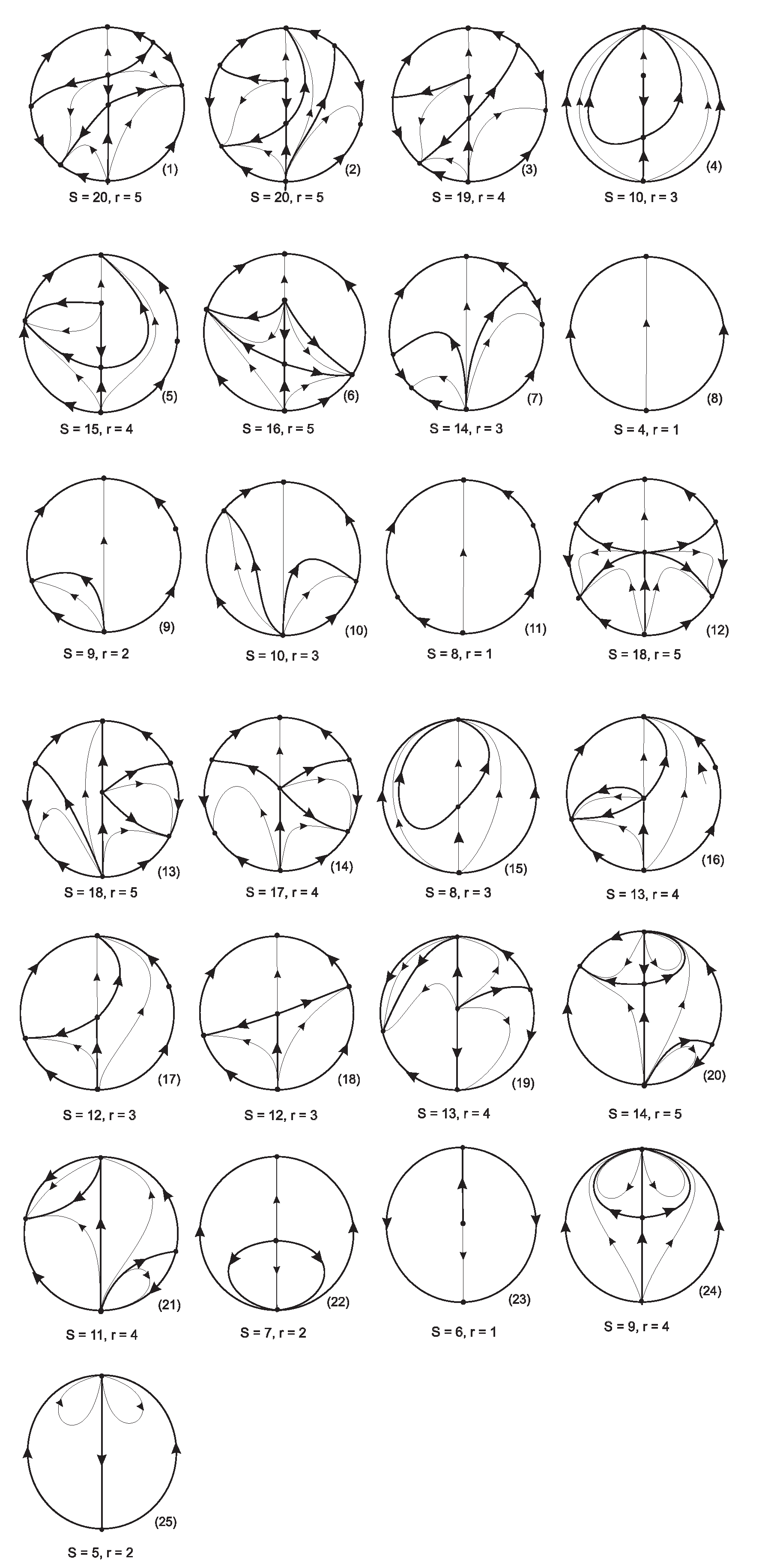
We have proved that in the cases (i), (ii), (iv), (vii) and from (ix) to (xv) we get the phase portrait (1) of
Figure 11; in the cases (iii), (vi) and (viii) we obtain the phase portrait (2) of
Figure 11; and finally in the case (v) we get the phase portrait symetric to the phase portrait (2) with respect to the straigt line
. For instance: the phase portrait (1) of
Figure 11 is obtained when the parameters of system (
3) are
,
,
,
and
; the phase portrait (2) of
Figure 11 is obtained when the parameters are
,
,
,
and
.The phase portrait (3) of
Figure 11 exists by continuity going from the phase portrait (1) to the phase portrait (2).
We recall that the
separatrices of a polynomial differential system in the Poincaré disc are all the orbits at infinity, the finite singularities and the two orbits at the boundary of an hyperbolic sector. Also the limit cycles are separatrices but the quadratic system VIII has no limit cycles. If in a phase portrait of the Poincaré disc we remove all the separatrices the open components which remain are called the
the canonical regions of the phase portrait. For more details on the separatrices and canonical regions see [
10,
11].
The tools for studying the phase portraits of system (
3) for the case
,
and
are used in the following cases, leading to the next results:
,
, and
in
Figure 11(4);
,
,
and
in
Figure 11(5);
, , and in this case the phase portrait is symmetric with respect to the straight line of the phase portrait of the previous case;
,
,
and
in
Figure 11(6);
,
, and
in
Figure 11(7);
,
, and
in
Figure 11(8);
,
,
and
in
Figure 11(9);
, , and this case is a symetric phase portrait with respect to the straight line of the previous phase phase portrait;
,
,
and
in
Figure 11(10) and
Figure 11(11);
,
, and
in
Figure 11(15);
,
and
in
Figure 11(16) and
Figure 11(17);
,
,
and
in
Figure 11(18);
The cases with are the symetric with respect to the straight line to all the preceding cases;
,
and
in
Figure 11(21);
, and this case has a symmetric phase portrait with respect to to the previous case;
The phase portraits of the cases and are symmetric with respect to the straight line of the phase portraits of the cases and
,
and
in
Figure 11(22);
, and this case has a symetric phase portrait with respect to the axis;
,
and
in
Figure 11(23);
,
and
in
Figure 11(24);
, and the phase portrait of this case is symetric with respect to the straight line of the previous phase portrait;
,
,
and
in the
Figure 11(25);
, , and the phase portrait of this case is symetric with respect to the straight line of the previous phase portrait;
,
,
and
this case has the same phase portrait of
Figure 11(8);
,
,
and
this case has the symetric phase portrait with respect to the straight line
to the phase portrait of
Figure 11(8).
Of course from the Table 2 the phase portraits with different number of separatrices and canonical regions are topologically distinct. Now we shall see that the phase portraits with the same number of separatrices and canonical regions of the Table 2 also are topologically different.
The phase portraits 4 and 10 of Figure 12 are topologically different because the phase portrait 4 has two finite singular points and the phase portrait 10 has no finite singular points.
Table 2.
Here p.p. denotes phase portrait in the Poincaré disc, s denotes the number of separaratrices of the phase portrait, and r denotes the number of canonical regions of the phase portrait.
Table 2.
Here p.p. denotes phase portrait in the Poincaré disc, s denotes the number of separaratrices of the phase portrait, and r denotes the number of canonical regions of the phase portrait.
| s |
4 |
5 |
6 |
7 |
8 |
8 |
9 |
9 |
10 |
11 |
| r |
1 |
2 |
1 |
2 |
1 |
3 |
2 |
4 |
3 |
4 |
| p.p. |
8 |
25 |
23 |
22 |
11 |
15 |
9 |
24 |
4,10 |
21 |
| s |
12 |
13 |
14 |
14 |
15 |
16 |
17 |
18 |
19 |
20 |
| r |
3 |
4 |
3 |
5 |
4 |
5 |
4 |
5 |
4 |
5 |
| p.p. |
17,18 |
16,19 |
7 |
20 |
5 |
6 |
14 |
12,13 |
3 |
1,2 |
The phase portraits 17 and 18 (respectively 16 and 19) of Figure 12 are topologically different because the phase portrait 17 (respectively 16) has two orbits going to the origin of the chart , and such orbits do not exist in the phase portrait 18 (respectively 19).
The phase portrait 14 of Figure 12 has three pairs of infinite singular points while the phase portrats 16 and 19 only have only two pairs of infinite singumlar, so the phase portrait 14 is different from the phase portraits 16 and 19.
We note that the phase portrait 13 of Figure 12 has three pairs of infinite singular points, while the phase portrait 20 has only two pairs, so these two phases portraits are topologically disctinct.