Prerpints.org logo
Preprint
Article

Biomechanical Investigation of Red Cell Sedimentation Using Blood Shear Stress and Blood Flow Image in a Capillary Chip

Altmetrics

Downloads

156

Views

105

Comments

0

A peer-reviewed article of this preprint also exists.

This version is not peer-reviewed

Submitted:

03 July 2023

Posted:

05 July 2023

You are already at the latest version

Alerts
Abstract
Blood image intensity has been used to detect erythrocyte sedimentation rate (ESR). However, it does not give an information on biophysical properties of blood sample under continuous ESR. In this study, three physical properties, including, τ0, ESRτ, and AII, are suggested to quantify mechanical variations of blood under continuous ESR. To demonstrate the proposed method, blood sample is loaded into a driving syringe. The blood flow rate is set in a periodic on–off pattern. Blood sample is then supplied into a capillary chip, and microscopic blood images are captured at specific intervals. Blood shear stress is quantified from the interface of blood stream in the coflowing channel. Both τ0 and ESRτ are then obtained by analyzing the blood shear stress. Simultaneously, the AII is evaluated by analyzing the image intensity of blood flow. According to the experimental results, the τ0 exhibits consistent trends with respect to hematocrit as well as diluent. The ESRτ and AII showed a reciprocal relationship each other. Three suggested properties represented substantial differences for suspended blood samples (i.e., hardened red blood cells, different concentration of dextran solution and fibrinogen). In conclusion, the present method can detect variations of blood sample under continuous ESR effectively.
Keywords: 
Subject: Engineering  -   Bioengineering

1. Introduction

Because red blood cells (RBCs) are more numerous than other cells (such as white blood cells and platelets), the rheological properties of RBCs play a significant role in determining the blood flow. Owing to their distinctive advantages (i.e., high surface area/volume and flexible membranes), RBCs are easily deformed under external shear stress [1]. High deformability helps RBCs pass through micron-sized capillaries to transport gases and waste into peripheral tissues [2]. In microcirculation, RBCs are exposed to high shear stress as well as oxidative stress [3]. To resist these stresses and provide sufficient functionality, biochemical and structural alterations of RBCs occur sensitively depending on stress conditions [4]. The mechanical properties of RBCs are then substantially altered. Therefore, significant alterations in the mechanical properties of RBCs can be used as biomarkers for diagnosing such pathological disorders as hypertension [5], diabetes [6,7,8], malaria [9], and cardiovascular diseases [10,11,12]) or detecting storage-induced lesions [13,14,15,16,17,18,19] as well as senescence [4].
Several researchers have reported a substantial correlation between coronary heart disease and the mechanical properties of blood [20,21,22]. Probing the mechanical properties of blood is crucial for diagnosing and monitoring diseases [2,23]. Currently, microfluidic techniques, which have several merits such as a high sensitivity, small volume, short measurement period, and disposability), have been employed extensively to measure the mechanical properties of blood (i.e., viscosity [24,25,26,27], deformability [24,28,29,30,31], hematocrit [32,33], erythrocyte sedimentation rate (ESR) [34,35], and aggregation [36,37,38,39]).
Blood viscosity is often determined by injecting blood into a specific microfluidic device [40]. The blood viscosity obtained at a low shear rate is determined substantially by RBC aggregation. RBC deformation or alignment contributes to decreasing blood viscosity at higher shear rates. In a microfluidic environment, it is extremely difficult to obtain a consistent viscosity at low shear rates (or flow rates) because a syringe pump does not supply consistent blood flow at extremely low flow rates [41]. Instead of blood viscosity, RBC aggregation has been obtained by analyzing blood flow at extremely low flow rates or stasis [35,42,43]. After blood is injected into a microfluidic channel, the blood flows or stops with external sources (i.e., a solenoid valve [44], pinch valve [35], vibration motor [45], and pump). Unlike RBC aggregation, the ESR is obtained without external flow controllers. When blood (approximately 1 mL) is loaded into a vertical capillary tube, gravity forces the RBCs to fall to the bottom of the tube. When the ESR in the tube is obtained, RBC aggregation causes an increase in cell-to-cell interactions and large voids in the network, resulting in faster sedimentation. The ESR is then interpreted as a comparable measure of RBC aggregation [34]. The interface movement after 1 hour is called as the sedimentation velocity (mm/h). The sedimentation velocity is routinely used as an ESR index to detect chronic diseases and immune disorders [3,46]. However, the conventional ESR test does not provide information on variations in RBC distributions resulting from RBC sedimentation. Instead of a vertical capillary tube, a driving syringe is employed to supply blood to the microfluidic device. As RBC sedimentation occurs in the syringe, the hematocrit increases in the bottom regions of the syringe. When supplying blood to a microfluidic channel from the bottom region, variations in the RBCs in the tube can be monitored by analyzing the image intensity of the blood flow. Alterations in image intensity are interpreted as an increase in the hematocrit resulting from RBC sedimentation [47,48,49,50]. However, image intensity does not provide mechanical information about the blood. More recently, our group suggests the shear stress for monitoring the effect of the hematocrit on blood flow because it is influenced by the hematocrit [51]. A new ESR index (ESRτ) has been suggested using the blood shear stress under continuous blood flow. This index provides consistent results compared with the conventional sedimentation velocity. However, the image intensity of the blood flow remains unchanged under continuous blood flow. It is impossible to compare the two indices obtained using blood shear stress and image intensity. To compare the two indices quantitatively, it is necessary to stop and run the blood flow because RBC aggregation occurs at stasis or extremely low shear rates.
In this study, by supplying or stopping blood flow into a microfluidic device with a syringe pump, the blood shear stress and image intensity were obtained at the turn-on and turn-off periods, respectively. Two indices for quantifying the ESR in the driving syringe were obtained by analyzing the blood shear stress and blood image intensity at specific intervals. The contributions of the blood delivery period, air cavity secured into the syringe, and hematocrit to the performance were quantified by measuring the variations in the two indices. To compare the indices quantitatively, several types of suspended blood were prepared by adding normal RBCs to the diluent (i.e., dextran solution and fibrinogen) and by adding thermally hardened RBCs to dextran solution.
Compared with the conventional ESR method (i.e., sedimentation velocity), the proposed method can monitor RBC distributions resulting from the ESR in a driving syringe by analyzing the blood flow in microfluidic channels. The variation in the ESR in the driving syringe is then monitored by temporal variations of blood shear stress and blood image intensity. The shear stress measured during the initial period can be used to detect differences in the blood (i.e., hematocrit, or diluent). The three physical properties (i.e., τ0, ESRτ, and AII) exhibited substantial differences for suspended blood samples. Namely, in an experiment of less than 10 min, three suggested properties can detect variations of blood sample under continuous ESR effectively.

2. Materials and Methods

2.1. Microfluidic Device Fabrication and Experimental Setup Preparation

As shown in Figure 1A, a microfluidic platform was prepared to quantify the continuous ESR occurring in the driving syringe. It consisted of a microfluidic device, two syringe pumps, and an image acquisition system. The microfluidic device was composed of two inlets (a, b), a reference fluid channel (RC, width = 1 mm), a blood channel (BC, width = 1 mm), a coflowing channel (width [w] = 1 mm), and one outlet. To stop the blood flow shortly and avoid the invasion of the reference fluid into the blood channel, a relatively small-sized microfluidic channel (width = 100 µm) was positioned between the blood channel and the coflowing channel. The channel depth [h] was set to 50 μm.
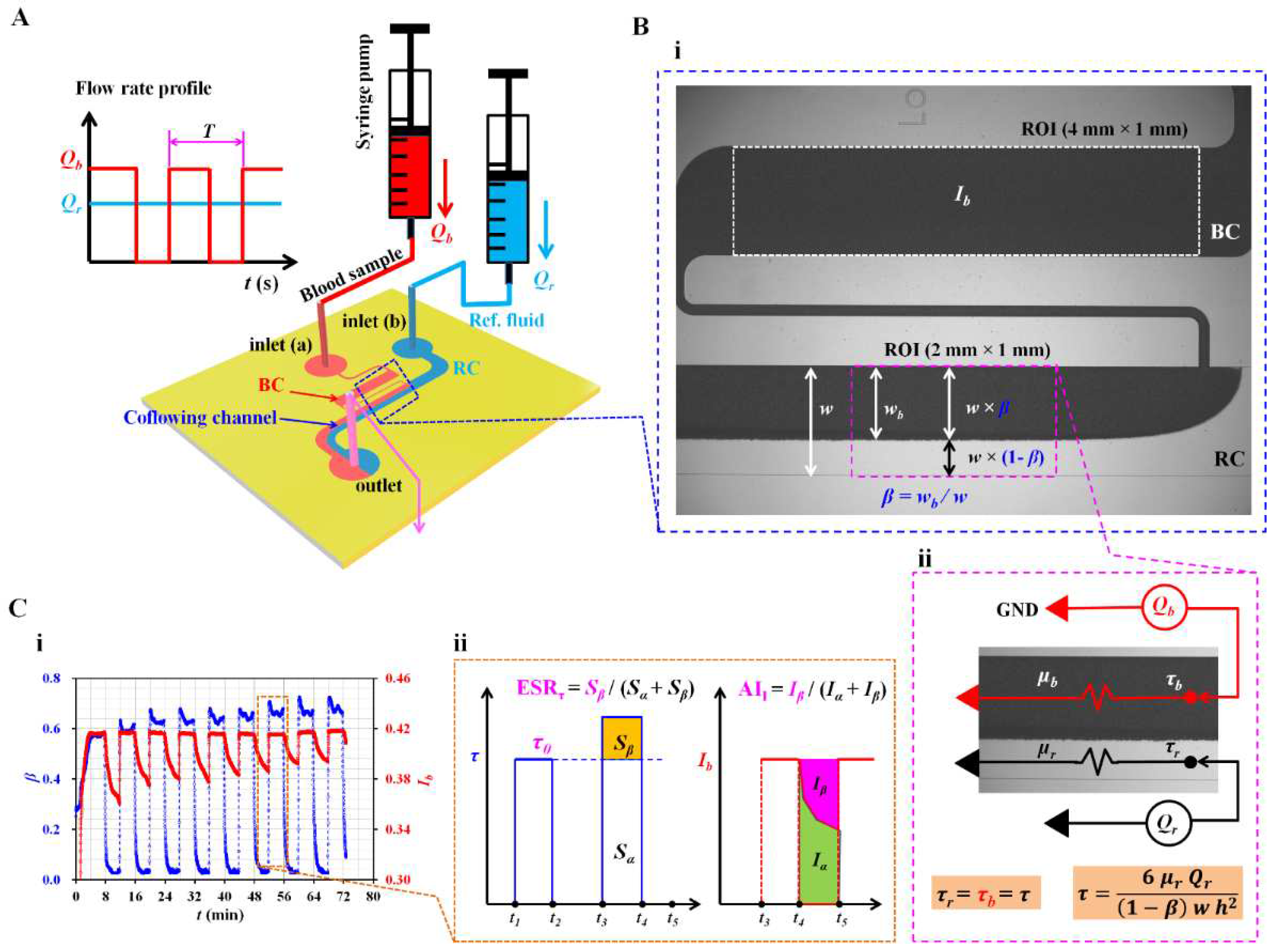
Preprints 78399 g001
Figure 1. Proposed method for quantification of red blood cell sedimentation using blood shear stress and blood flow image in a capillary chip. (A) Schematics of experimental setup, including, a microfluidic device, and two syringe pumps. The microfluidic device consisted of two inlets (a, b), reference channel (RC), blood channel (BC), coflowing channel, and one outlet. As shown in left side panel, using two syringe pumps, flow rate of reference fluid set to constant value of Qr. Flow rate of blood (Qb) set to square wave profile (i.e., amplitude, period [T]). (B) Quantification of image intensity and shear stress of microscopic blood flow. (i) Selection of two regions-of-interest (ROIS) for estimating image intensity (Ib) in the blood channel and interface (β) in coflowing channel. (ii) Estimation of blood shear stress (τ) using discrete fluidic circuit model. (C) Quantification of ESR index and aggregation index. (i) Temporal variations of β and Ib under on-off blood flow (ii) Definition of ESR index (ESRτ) and aggregation index (AII) in terms of blood shear stress and blood flow image intensity, respectively.
Figure 1. Proposed method for quantification of red blood cell sedimentation using blood shear stress and blood flow image in a capillary chip. (A) Schematics of experimental setup, including, a microfluidic device, and two syringe pumps. The microfluidic device consisted of two inlets (a, b), reference channel (RC), blood channel (BC), coflowing channel, and one outlet. As shown in left side panel, using two syringe pumps, flow rate of reference fluid set to constant value of Qr. Flow rate of blood (Qb) set to square wave profile (i.e., amplitude, period [T]). (B) Quantification of image intensity and shear stress of microscopic blood flow. (i) Selection of two regions-of-interest (ROIS) for estimating image intensity (Ib) in the blood channel and interface (β) in coflowing channel. (ii) Estimation of blood shear stress (τ) using discrete fluidic circuit model. (C) Quantification of ESR index and aggregation index. (i) Temporal variations of β and Ib under on-off blood flow (ii) Definition of ESR index (ESRτ) and aggregation index (AII) in terms of blood shear stress and blood flow image intensity, respectively.
Preprints 78399 g001
A polydimethylsiloxane (Sylgard 184, Dow Corning, Midland, MI, USA) microfluidic device was fabricated using a conventional micro-electromechanical system technique and soft lithography [52].
The microfluidic device was positioned on an inverted microscope (IX81, Olympus, Tokyo, Japan) with a 4× objective lens (numerical aperture = 0.1). Two Tygon Tubing (inside diameter = 250 µm, outside diameter = 750 µm, length = 400 mm, Cole-Parmer, Vernon Hills, IL, USA) was fitted into each inlet. The other Tygon Tubing (inside diameter = 250 µm, outside diameter = 750 µm, length = 200 mm) was fitted to the outlet. To repel air in the microfluidic channels and avoid nonspecific binding of plasma proteins to the inner surfaces, the microfluidic channels were filled with bovine serum albumin (2 mg/mL). This condition was maintained for 10 min. Next, 1× phosphate-buffered saline (PBS) was loaded into the microfluidic channels. Two disposable syringes (approximately 1 mL) were filled with blood and a reference fluid (glycerin solution [30%]), respectively.
As shown in the right panel of Figure 1A, the syringes were installed using two syringe pumps (NeMESYS, Cetoni GmbH, Germany) that were installed vertically against the gravitational direction. As shown in the left panel of Figure 1A, reference fluid was supplied at a constant flow rate (Qr = 0.5, or 1 mL/h). However, the flow rate of the blood sample (Qb) was set to a square-wave profile (amplitude = 0.5 mL/h, period: T).
A high-speed camera (FASTCAM MINI, Photron, Tokyo, Japan) was used to capture microscopic images of the blood flow in the blood channel and the interface in the coflowing channel. The camera speed was set to 2000 fps, and microscopic images were then recorded at intervals of 1 s. Experiments were conducted at a constant room temperature of 25 °C.

2.2. Quantification of Blood Flow Inside the Capillary Chip

To quantify the ESR occurring in the driving blood syringe, the image intensities in the blood channel and the interface in the coflowing channel were quantified by analyzing the microscopic blood flow images recorded by the high-speed camera.
First, as shown in Figure 1B(i), to obtain the image intensity of the blood flow, a specific region of interest (ROI) of 4 mm × 1 mm was selected within the blood channel. The image intensity of the blood flow was obtained by conducting digital image processing using MATLAB 2019 (MathWorks, Natick, MA, USA). The average image intensity (Ib) was calculated by averaging the image intensities distributed within the ROI.
Second, to obtain the interface (or blood-filled width) in the coflowing channel, a specific ROI (2 mm × 1 mm) was selected at the downstream position where the interface remained distinctively straight. Based on the intensity threshold algorithm (Otsu’s method) [53], a grayscale image was converted into a binary image. The blood-filled width (wb) was obtained by averaging the interfaces distributed within the ROI. The interface was calculated as β = wb / w. Based on the interface (β), the width of each stream was obtained as w × β for the blood stream and w × (1 − β) for the reference fluid stream.

2.3. Simple Mathematical Model for Estimating Shear Stress of Blood Flow in the Coflowing Channel

As shown in Figure 1B(ii), a discrete fluidic circuit model was constructed to estimate the blood shear stress in the coflowing channel. The flow rate of each fluid is represented as Qr for the reference fluid and Qb for the blood. Both fluid streams in the coflowing channel were modeled as two fluidic resistances connected in parallel. A symbol (◄) indicates zero value of pressure (i.e., P = 0), designated as GND (ground condition). As both fluid streams flowed in the straight coflowing channel, they had the same pressure condition (i.e., the pressure of the reference fluid stream equals the pressure of the blood stream). According to previous studies [25,54,55], the approximation error between the mathematical model and the real physical model contributed substantially to the worsening of accuracy, especially when an interface was relocated near both walls. To compensate for the approximation error, a correction factor (Cp), which can be obtained by conducting experiments or numerical simulations, was proposed. For a rectangular channel with a low aspect ratio (i.e., h / w = 50 / 1000), the shear stress formulas for the reference fluid stream and blood stream were derived as
τ r = 6   μ r   Q r 1 − β w   h 2
and,
τ b = 6   μ b   Q b C p   β   w   h 2
Here, the subscripts r and b represent the reference fluid stream and blood stream, respectively. In addition, µr and µb are the viscosity of the reference fluid and viscosity of the blood sample, respectively. The viscosity of the reference fluid (glycerin [30%]) was set to µr = 3 cP [56]. Based on the force balance condition (i.e., the pressure-drop-induced force equals the shear-stress-induced force) for each stream in the coflowing channel, it can be concluded that both fluid streams had the same shear stress (i.e., τr = τb = τ). Thus, it was possible to obtain the shear stress of the blood stream in terms of Equation (1) or Equation (2). If the flow rate and blood viscosity were not specified, the blood shear stress could not be obtained using Equation (2). However, the flow rate and viscosity of the reference fluid stream remained unchanged throughout the experiments. Based on Equation (1), the blood shear stress could be estimated easily when an interface was available.

2.4. Blood Sample Preparation

This study was conducted in accordance with the Declaration of Helsinki and approved by the ethics committee of Chosun University under reference code (2-1041055-AB-N-01-2021-80). To prepare suspended blood (i.e., normal RBCs in diluent), concentrated RBCs and fresh frozen plasma (FFP) were purchased from the Gwangju–Chonnam Blood Bank (Gwangju, South Korea). They were stored in a refrigerator prior to the experiments. According to the specific washing procedures [52], normal packed RBCs were collected by discarding the buffy coat. In addition, the FFP was defrosted at room temperature. Autologous plasma was obtained by passing FFP into syringe filtration. Several types of suspended blood were prepared by adding normal RBCs to a specific diluent (i.e., 1× PBS, autologous plasma, dextran solution, and fibrinogen) or hardened RBCs to specific concentrations of dextran solution. To quantify the contribution of the hematocrit to the ESR in the driving syringe, suspended blood was prepared by adding normal RBCs to a specific dextran solution (10 mg/mL). To increase RBC aggregation in normal RBCs, normal RBCs were added to five different dextran solutions (Cdex = 10, 20, 40, 60, and 80 mg/mL) prepared by dissolving dextran powder (Leuconostoc spp., MW = 450–650 kDa; Sigma-Aldrich, St. Louis, MO, USA) in 1× PBS. To quantify the contribution of fibrinogen to the ESR, suspended blood was prepared by adding normal RBCs into three different fibrinogen solutions (Cfib = 4, 8, and 12 mg/mL), which were dissolved by adding human plasma fibrinogen (F3879-250 mg, Sigma Aldrich Co., St. Louis, USA) into autologous plasma. To evaluate the effect of the hardened RBCs on the ESR, two different degrees of fixed RBCs were obtained by exposing normal RBCs to either 50 °C for 30 min or 50 °C for 60 min inside a convective oven.

3. Results and Discussion

3.1. Definition of ESR Index and Aggregation Index in Terms of Blood Shear Stress and Blood Image Intensity

To investigate the contributions of the ESR to the two parameters (β, Ib) over time, suspended blood was prepared by adding normal RBCs to a specific dextran solution (10 mg/mL). As shown in Figure 1A, the flow rate of the reference fluid was set to 0.5 mL/h. Simultaneously, the flow rate of blood was set to a square-wave profile (i.e., amplitude = 0.5 mL/h, T = 8 min). Figure 1C(i) shows temporal variations of β and Ib. When the syringe pump for suspended blood was turned on, β tended to increase gradually over time. When the blood syringe pump was turned off, the RBC aggregation caused Ib to decrease significantly over time. The variation range of Ib decreased continuously with an increase in the period. Based on these results, Ib can be used to estimate RBC aggregation or the ESR, especially under periodic on–off blood flow. According to a previous study, the ESR in the driving syringe causes a change in the image intensity of the blood flow in a microfluidic channel under periodic on–off blood flow [50]. In addition, it contributes to increasing blood shear stress (τ), even under a constant blood flow [51] — that is, Ib and τ can be employed to quantify variations in the ESR occurring in the driving syringe. According to Equation (1), blood shear stress can be calculated when β is specified. In Figure 1C(ii), variations in τ and Ib are redrawn simply with respect to specific time. First, the initial shear stress (τ0) (i.e., the reference value) is defined as the maximum shear stress during the first period of blood flow (from t = t1 to t = t2). In the next period of blood flow (from t = t3 to t4), the ESR in the syringe contributes to an increase in the hematocrit (or viscosity) of the blood flow. Thus, blood shear stress increases significantly when compared with τ0 as the reference value. Based on an experimental investigation, to calculate the variation range of blood shear stress for a single period, two parameters (Sα and Sβ) were suggested and calculated previously [51]:
S α = ∫ t 3 t 4 τ 0 d t
and,
S β = ∫ t 3 t 4 τ − τ 0 d t
ESRτ is then defined as ESRτ = Sβ / (Sα + Sβ). If there is little variation in the ESR, the blood shear stress remains unchanged for each period. ESRτ is then estimated as zero because Sβ = 0. As shown in Figure 1C(i), the blood shear stress tends to increase over time — that is, the ESR in the driving syringe caused to increase Sβ.
As a comparable parameter to the ESR, the image intensity of blood flow was used to estimate the trends of RBC aggregation in blood. In the absence of blood flow (from t = t4 to t = t5), the RBC aggregation contributed to decreasing Ib over time. Based on previous studies [37,45], two parameters (Iα and Iβ) were obtained by analyzing the temporal variations of Ib. AII was defined as AII = Iβ / (Iα + Iβ). As shown in Figure 1C(i), the Ib obtained in the absence of blood flow decreased with an increase in the period. Specifically, AII tended to decrease with an increase in the period. The ESR can be monitored in terms of AII. Subsequently, two indices (ESRτ and AII) were calculated in terms of blood shear stress (i.e., the blood flow condition) and image intensity of blood flow (i.e., the blood flow at stasis), respectively. Initial shear stress and both indices were used to quantify the continuous ESR in the driving syringe.

3.2. Contribution of Dynamic Blood Flow to ESR Quantification

In previous studies [35,45], RBC aggregation was obtained by analyzing blood flow after stopping it completely. Under the square-wave profile of blood flow, the blood flow did not stop immediately because of the time delay of the fluidic system (i.e., the time constant) [57]. The time constant was determined by the fluidic resistance and system compliance (i.e., time constant = fluidic resistance × system compliance). Here, two vital factors (the on–off period [T] and air cavity secured in the driving syringe [Vair]) were adjusted to investigate the contributions of the time constant to the ESRτ and AII.
First, to evaluate the contributions of the period of the on–off blood flow to both indices, the period was adjusted from T = 0 (continuous blood flow) to T = 8 min. The amplitude of the square-wave profile of the blood flow was set to 0.5 mL/h. The flow rate of the reference fluid was set to 0.5 mL/h. To stimulate test blood with a high degree of aggregation, normal RBCs (Hct = 50%) were added to a specific concentration of dextran solution (10 mg/mL) rather than autologous plasma. Figure 2A shows temporal variations of τ and Ib with respect to period (T) ((i) T = 0, (ii) T = 4 min, (iii) T = 6 min, and (iv) T = 8 min). At a continuous blood flow (T = 0), the ESR during driving caused an increase in blood shear stress over time. However, the image intensity did not differ substantially over time. In other words, for quantifying the ESR under continuous blood flow, the blood shear stress was much better than the blood image intensity [51,58]. Shin et al. reported the critical shear stress required for RBC aggregation under transient blood flow [59]. However, under periodic on–off blood flow, the shear stress increased gradually with an increase in period.
Preprints 78399 g002
Figure 2. Contributions of on-off period of blood flow (T) to ESR index (ESRτ) and aggregation index (AII). (A) Temporal variations of blood shear stress (τ) and image intensity (Ib) with respect to period (T) ((i) T = 0, (ii) T = 4 min, (iii) T = 6 min, and (iv) T = 8 min). (B) Contribution of period (T) to ESRτ and AII. (i) Temporal variations of ESRτ with respect to T = 4, 6, and 8 min. (ii) Temporal variations of AII with respect to T.
Figure 2. Contributions of on-off period of blood flow (T) to ESR index (ESRτ) and aggregation index (AII). (A) Temporal variations of blood shear stress (τ) and image intensity (Ib) with respect to period (T) ((i) T = 0, (ii) T = 4 min, (iii) T = 6 min, and (iv) T = 8 min). (B) Contribution of period (T) to ESRτ and AII. (i) Temporal variations of ESRτ with respect to T = 4, 6, and 8 min. (ii) Temporal variations of AII with respect to T.
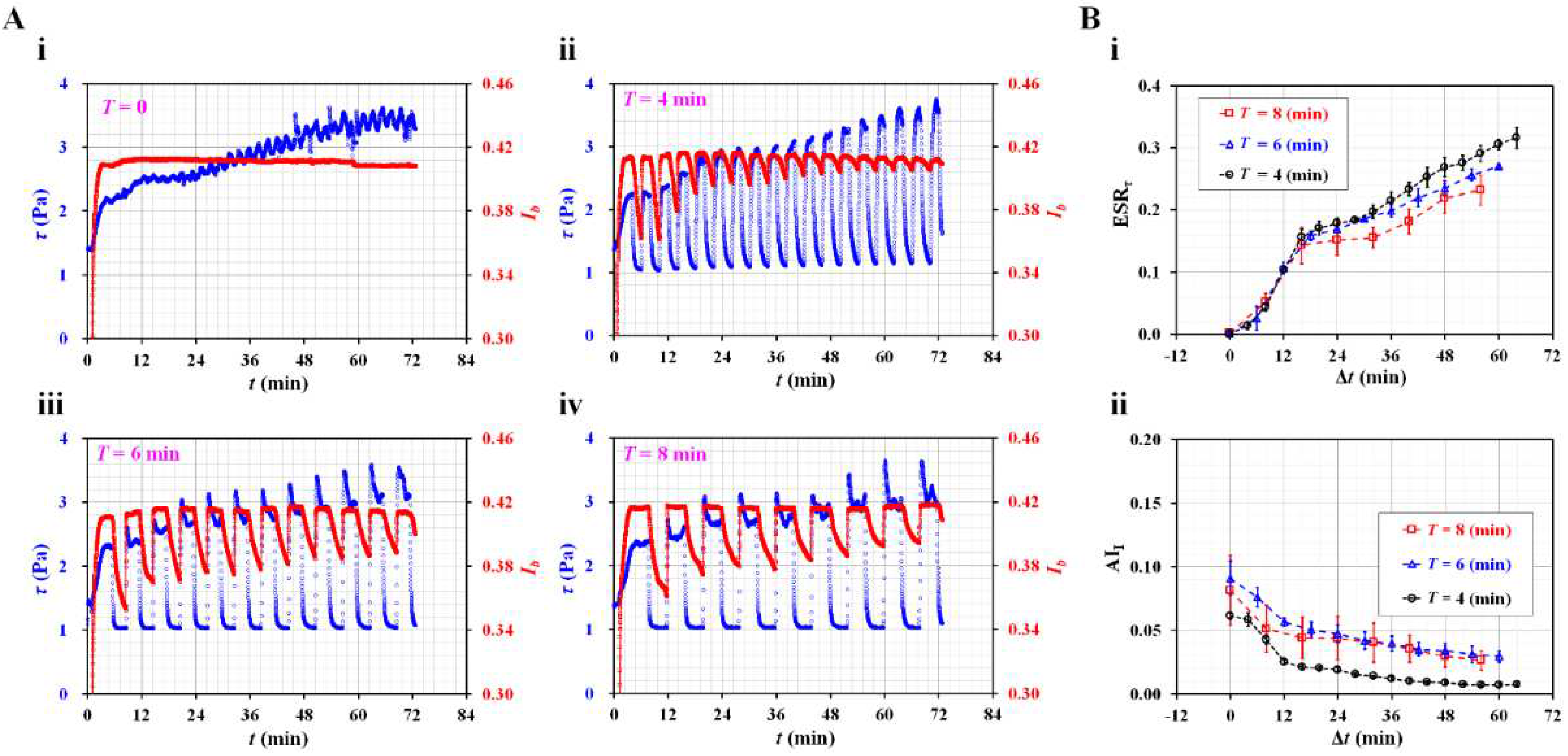
Preprints 78399 g002
As blood was supplied from the bottom region of the driving syringe, the hematocrit of the blood flow tended to increase over time in the microfluidic channel [50]. As expected, RBC aggregation contributed to a significant decrease in the image intensity in the absence of blood flow. The Ib value changed distinctively depending on the period; however, it decreased substantially over time. Based on the temporal variations of τ and Ib, two indices, i.e., ESRτ and AII, were obtained for every period. For continuous blood flow (T = 0), ESRτ = 0.274–0.309 and AII = 0. As shown in Figure 2B(i), temporal variations of ESRτ were obtained with respect to T = 4, 6, and 8 min. The ESRτ was represented as mean ± standard deviation (n = 3). Below Δt = 15 min, the ESRτ increased significantly over time. This period did not have a substantial influence on the ESRτ. After Δt = 24 min, a shorter period (T = 4 min) led to a higher value of the ESRτ compared with a longer period (T = 8 min). Previously, Yeom et al. reported that oscillational motion of the air cavity caused the ESR to increase in the syringe tube [60]. Shin et al. also showed that the critical shear stress tended to increase gradually during four consecutive periods (i.e., T = 5 s) [44]. Based on the previous results, it was inferred that a shorter period contributed to the acceleration of the ESR in the driving syringe. Figure 2B(ii) shows the temporal variations in AII with respect to T. The AII is represented as mean ± standard deviation (n = 3). With an increase in the period, the AII tended to decrease gradually because of the ESR in the driving syringe. As shown in Figure 2A, the Ib decreased significantly over a longer period (T = 6 or 8 min). A longer period led to a higher value of AII than a shorter period. After Δt = 24 min, the AII did not exhibit a substantial difference between T = 6 min and T = 8 min. In a previous study, a long period with no blood flow had a positive influence on RBC aggregation over consecutive periods of 6 min [61] — that is, a longer period led to an increase in AII compared with a shorter period. In the experimental investigations, a shorter period (T = 4 min) resulted in a high sensitivity of ESRτ. To obtain the ESR in the driving syringe, the period of the square-wave profile was set to T = 4 min during all following experiments.
Second, the compliance effect of the fluidic system caused the time delay to increase or the pulsatile flow to be regulated. Even though the syringe pump was turned off, the blood flow did not stop immediately because of the compliance effect. In the microfluidic system, several components (i.e., a PDMS microfluidic device, flexible tubing, and an air cavity in the syringe) induced compliance effects. Because the RBC aggregation was influenced significantly by dynamic blood flow, it was necessary to quantify the contribution of the compliance effect to the ESR. For convenience, the air cavity secured in the syringe was adjusted to vary the magnitude of the compliance effect. As shown in Figure 3A(i), the air cavity was set to Vair = 0, 0.1, and 0.2 mL by moving a piston in blood syringe. Vair = 0 indicated that there was no air cavity in the blood syringe. The test blood (Hct = 50%) was prepared by adding normal RBCs to a specific dextran solution (10 mg/mL). The flow rate of the reference fluid was set to 0.5 mL/h. Blood was supplied in an on–off fashion (i.e., amplitude = 0.5 mL/h and T = 4 min).
Preprints 78399 g003
Figure 3. Contribution of air cavity set inside the blood syringe (Vair) to ESRτ and AII in a periodic on-off fashion. (A) Temporal variations of blood shear stress and image intensity with respect to air cavity. (i) Snapshots for showing air cavity secured inside the driving syringe (Vair) (Vair = 0, 0.1, and 0.2 mL). Temporal variations of τ and Ib were obtained with respect to Vair ((ii) Vair = 0, (iii) Vair = 0.1 mL, and (iv) Vair = 0.1 mL). (B) Contribution of air cavity to ESRτ and AII. (i) Temporal variations of ESRτ with respect to Vair. (ii) Temporal variations of AII with respect to Vair.
Figure 3. Contribution of air cavity set inside the blood syringe (Vair) to ESRτ and AII in a periodic on-off fashion. (A) Temporal variations of blood shear stress and image intensity with respect to air cavity. (i) Snapshots for showing air cavity secured inside the driving syringe (Vair) (Vair = 0, 0.1, and 0.2 mL). Temporal variations of τ and Ib were obtained with respect to Vair ((ii) Vair = 0, (iii) Vair = 0.1 mL, and (iv) Vair = 0.1 mL). (B) Contribution of air cavity to ESRτ and AII. (i) Temporal variations of ESRτ with respect to Vair. (ii) Temporal variations of AII with respect to Vair.
Preprints 78399 g003
As shown in Figure 3A(ii–iv), temporal variations of τ and Ib were obtained with respect to Vair. With respect to Vair = 0.1 and 0.2 mL, blood shear stress increased over time. As the air cavity contributed to a reduction in the alternating components of the blood flow [41,57,62], the fluctuation range of the shear stress decreased significantly at a high air cavity volume. At higher volumes of the air cavity, the blood flow did not stop immediately. Because the air cavity hindered RBC aggregation, the Ib value remained constant over time. Based on temporal variations of τ and Ib, two indices (i.e., ESRτ and AII) were obtained over time.Figure 3B(i) shows the temporal variations in ESRτ with respect to Vair. The condition without an air cavity (Vair = 0) had higher value of ESRτ when compared with Vair = 0.1 or 0.2 mL. Figure 3B(ii) shows the temporal variations of AII with respect to Vair. The AII had a high value when there was no air cavity. When the air cavity was set to 0.1 or 0.2 mL, AII decreased significantly. The experimental results revealed that no air cavity provided a high sensitivity of ESRτ as well as AII. Therefore, to monitor the ESR in the blood syringe with high sensitivity, it was necessary to confirm that any air cavity inside the blood syringe was small.

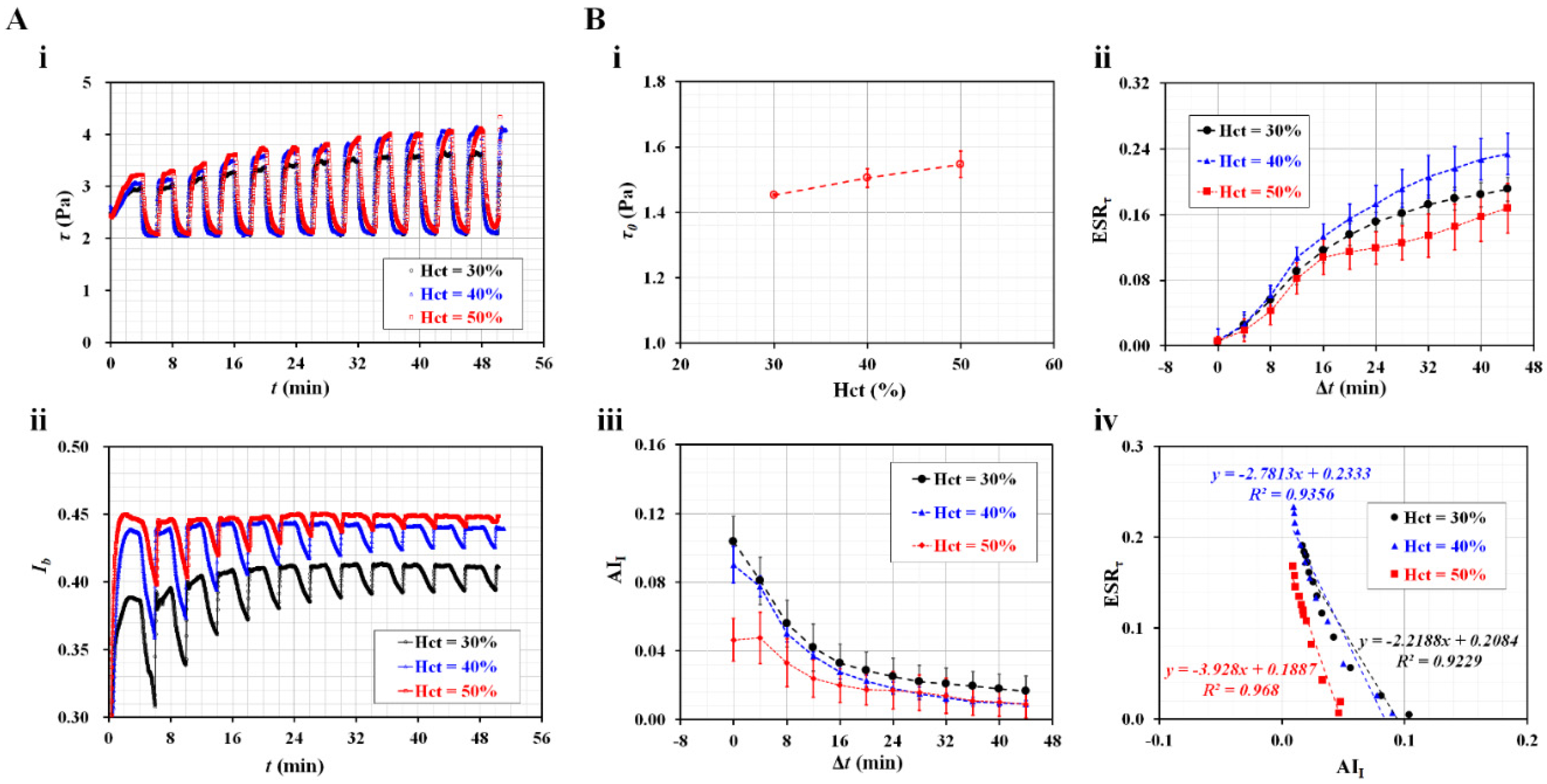
3.3. Contribution of Hematocrit to ESR in Driving Syringe

Previous researchers reported that hematocrit has a strong influence RBC aggregation [37,39,45,50,54,60,63]. In addition, RBC stiffness contributes to changes in RBC aggregation [38,44,47,52]. Based on the previous studies, the hematocrit (i.e., RBC volume in relation to total blood volume) was set from 30 to 50%. In addition, to change the stiffness of the RBC, normal RBCs were hardened thermally. To accelerate RBC aggregation, a dextran solution (10 mg/mL) was selected as the diluent. The test blood was prepared by adding normal or hardened RBCs to a specific dextran solution. The ESR in the syringe caused variations in the hematocrit of the blood flow, which contributed to the shifting of the interface toward the channel wall. When the interface was relocated near the channel wall, the modeling accuracy of Equation (1) deteriorated [55]. Thus, the flow rate of the reference fluid was adjusted from 0.5 to 1 mL/h (i.e., Qr = 1 mL/h). Test blood was supplied at the square-wave profile (amplitude = 0.5 mL/h, period = 4 min).
First, the contributions of the hematocrit to the ESR were obtained by changing the Hct ranging from 30 to 50%. Figure 4A(i) shows temporal variations of τ with respect to Hct. As expected, the hematocrit caused an increase in blood shear stress. The τ increased significantly over time. Figure 4A(ii) shows the temporal variations of Ib with respect to Hct. Under blood flow, the hematocrit caused Ib to increase. A significant difference was observed between Hct = 30% and Hct = 50%. Previous researchers reported that RBC aggregation or ESR tended to decrease with increasing hematocrit [50,63,64]. Because the fluctuation range of Ib (i.e., Iβ, as shown in Figure 1C(ii)) was proportional to the magnitude of RBC aggregation, it tended to decrease substantially with respect to Hct. In addition, the variation range of Ib decreased gradually over time. As shown in Figure 1C(ii), τ0 was obtained as the maximum shear stress during the first period. For convenience, the elapsed time was reset to zero (i.e., Δt = 0). As shown in Figure 4B, the variation of the ESR was summarized in terms of three physical properties, i.e., τ0, ESRτ, and AII. Three representative properties of blood samples are expressed as mean ± standard deviation (n = 4). Figure 4B(i) shows variations of τ0 with respect to Hct. According to Equation (2), the shear stress is proportional to blood viscosity. Because Hct was strongly related to blood viscosity [24,65,66], it was reasonable that the Hct contributed to a substantial increase in τ0.
Preprints 78399 g004
Figure 4. Contribution of hematocrit to ESR index as well as aggregation index. (A) Temporal variations of blood shear stress and image intensity with respect to hematocrit. (i) Temporal variations of τ with respect to Hct = 30%, 40%, and 50%. (ii) Temporal variations of Ib with respect to Hct. (B) Contribution of hematocrit to initial shear stress (τ0), ESRτ, and AII. (i) Variations of τ0 with respect to Hct. (ii) Temporal variations of ESRτ with respect to Hct. (iii) Temporal variations of AII with respect to Hct. (iv) Linear relationship between ESRτ and AII with respect to Hct.
Figure 4. Contribution of hematocrit to ESR index as well as aggregation index. (A) Temporal variations of blood shear stress and image intensity with respect to hematocrit. (i) Temporal variations of τ with respect to Hct = 30%, 40%, and 50%. (ii) Temporal variations of Ib with respect to Hct. (B) Contribution of hematocrit to initial shear stress (τ0), ESRτ, and AII. (i) Variations of τ0 with respect to Hct. (ii) Temporal variations of ESRτ with respect to Hct. (iii) Temporal variations of AII with respect to Hct. (iv) Linear relationship between ESRτ and AII with respect to Hct.
Preprints 78399 g004
Figure 4B(ii) shows temporal variations of ESRτ with respect to Hct. Interestingly, within 16 min, the ESRτ did not differ substantially with respect to Hct. Based on the results, the ESRτ obtained within a short duration (less than 16 min) did not depend on the Hct in the range from 30 to 50%. However, after 20 min, the ESRτ tended to decrease with respect to the Hct. According to a previous study [51], the ESRτ decreased at a higher Hct under a continuous blood flow. The ESRτ did not exhibit a substantial difference between Hct = 30% and Hct = 40%, but it did show a substantial difference between Hct = 30% and Hct = 50%. Thus, it was inferred that the ESRτ tended to decrease at a higher Hct without respect to the blood flow pattern (i.e., continuous or square-wave blood flow). Figure 4B(iii) shows the temporal variations of AII with respect to Hct. The AII did not exhibit a substantial difference between Hct = 30% and Hct = 40%. A high Hct (50%) caused a decrease in AII when compared with a low Hct (30 or 40%). After 16 min, the Hct did not contribute to variations in AII. The trends of AII were quite similar to those of ESRτ with respect to the Hct. To find out the relationship between the two indices, the ESRτ and AII (i.e., Figure 4B(ii,iii)) were replotted on the Y-axis and X-axis, respectively. A linear regression analysis was performed using Microsoft Excel Ver. 2019 (Microsoft, Redmond, Washington, USA). According to the results, the slope of each Hct was obtained as (a) ΔESRτ /ΔAII = −2.2188 (Hct = 30%), (b) ΔESRτ /ΔAII = −2.7813 (Hct = 40%), and (c) ΔESRτ /ΔAII = −3.928 (Hct = 50%). Both indices had a reciprocal relationship (i.e., negative slope). The slope tended to increase with respect to Hct. Because the regression coefficients had higher values of R2 = 0.923–0.968, it was confirmed that the indices had a strong linear relationship.
Second, two indices were employed to quantify the ESR of the hardened RBCs in the blood syringe. According to previous studies [44,50,67,68], normal RBCs were thermally hardened at high temperatures of either 50 °C for 30 min or 50 °C for 60 min. Hardened blood samples (Hct = 50%) were prepared by adding the hardened RBCs to a specific dextran solution (10 mg/mL). To quantify the contribution of the hardened RBCs to the ESR in the blood syringe, τ and Ib were obtained over time. As shown in Figure 5A(i), temporal variations of τ were obtained with respect to normal and hardened blood, i.e., 50 °C × 30 min and 50 °C × 60 min. When compared with normal RBCs, thermally shocked RBCs caused the variation range of τ to decrease substantially over time. For hardened RBCs, i.e., 50 °C × 60 min, τ remained constant over time. The longer the exposure time to thermal shock, the smaller the variation range of the shear stress. Highly hardened RBCs did not contribute to a change in τ over time.
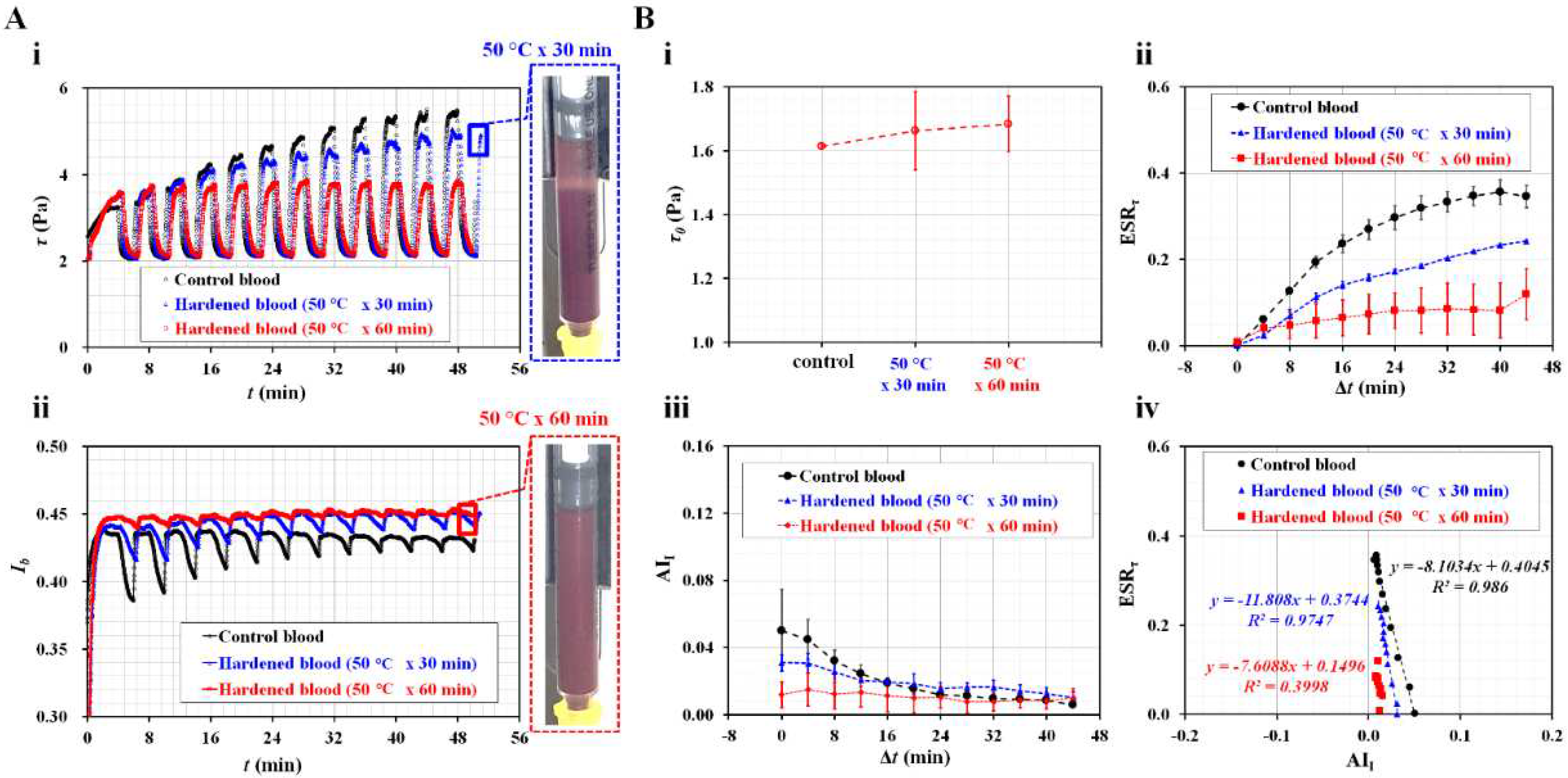
Preprints 78399 g005
Figure 5. Detection of thermally hardened RBCs in terms of three suggested properties. (A) Temporal variations of shear stress and image intensity with respect to control blood and two hardened bloods. As shown in right side panel, two snapshots of blood syringe filled with heat-treated RBCs (i.e., 50 °C × 30 min, and 50 °C × 60 min) were captured at the end of experiment. (i) Temporal variations of τ with respect to control blood and two hardened bloods. (ii) Temporal variations of Ib with respect to blood samples. (B) Quantification of thermally hardened RBCs in terms of τ0, ESRτ, and AII. (i) Variations of τ0 with respect to heat treatment condition. (ii) Temporal variations of ESRτ with respect to heat treatment condition. (iii) Temporal variations of AII with respect to heat treatment condition. (iv) Linear relationship between ESRτ and AII for three blood samples.
Figure 5. Detection of thermally hardened RBCs in terms of three suggested properties. (A) Temporal variations of shear stress and image intensity with respect to control blood and two hardened bloods. As shown in right side panel, two snapshots of blood syringe filled with heat-treated RBCs (i.e., 50 °C × 30 min, and 50 °C × 60 min) were captured at the end of experiment. (i) Temporal variations of τ with respect to control blood and two hardened bloods. (ii) Temporal variations of Ib with respect to blood samples. (B) Quantification of thermally hardened RBCs in terms of τ0, ESRτ, and AII. (i) Variations of τ0 with respect to heat treatment condition. (ii) Temporal variations of ESRτ with respect to heat treatment condition. (iii) Temporal variations of AII with respect to heat treatment condition. (iv) Linear relationship between ESRτ and AII for three blood samples.
Preprints 78399 g005
Figure 5A(ii) shows the temporal variations of Ib with respect to the control blood and hardened blood. The variation range of Ib tended to decrease with longer heat treatment exposure times — that is, hardened RBCs at 50 °C × 60 min had a smaller Ib range compared with normal RBCs. The right panel shows two snapshots of the blood syringe filled with hardened RBCs with respect to the heat treatment conditions (50 °C × 30 min and 50 °C × 60 min) captured at the end of the experiment. Slightly hardened RBCs (50 °C × 30 min) exhibited a clear interface in the blood syringe. However, there was no clear interface between the diluent and RBCs in the blood syringe for highly hardened RBCs (50 °C × 60 min). According to the results, when normal RBCs were exposed to heat treatment (50 °C × 60 min), the blood shear stress and image intensity did not exhibit substantial differences over time. Furthermore, the ESR was not detected in the blood syringe. As shown in Figure 5B, to quantify the thermally hardened RBCs, three properties (τ0, ESRτ, and AII) were summarized as mean ± standard deviation (n = 2 or 3). Figure 5B(i) shows variations of τ0 with respect to the heat treatment condition. Although τ0 tended to increase gradually with respect to the heat treatment exposure time, there was no statistical difference between 30 min and 60 min. Figure 5B(ii) shows temporal variations of ESRτ with respect to the heat treatment condition. Compared with normal RBCs, the ESRτ tended to decrease substantially with respect to the heat treatment exposure time. The longer exposure time (60 min) had the smallest ESRτ variation. Figure 5B(iii) shows the AII temporal variations with respect to the heat treatment conditions. The AII tended to decrease over time. After 16 min, the AII did not change over time. Before Δt = 16 min, the AII exhibited a promising difference with respect to the heat treatment conditions. Highly hardened RBCs (50 °C × 60 min) did not exhibit a substantial difference in AII over time. As shown in Figure 5B(iv), an X–Y plot (X-axis: AII, Y-axis: ESRτ) was constructed to validate the correlation between the two indices. Because the highly hardened RBCs (50 °C × 60 min) did not show a substantial variation of ESRτ and AII, the indices did not have a linear relationship (i.e., R2 = 0.4). However, with respect to the control blood and slightly hardened blood (50 °C × 30 min), the coefficients of linear regression were estimated to have high values of R2 = 0.974–0.986. Thus, the two indices had a strong linear relationship. The experimental investigations indicated that the two indices could be used to detect differences between normal and hardened RBCs with sufficient consistency.

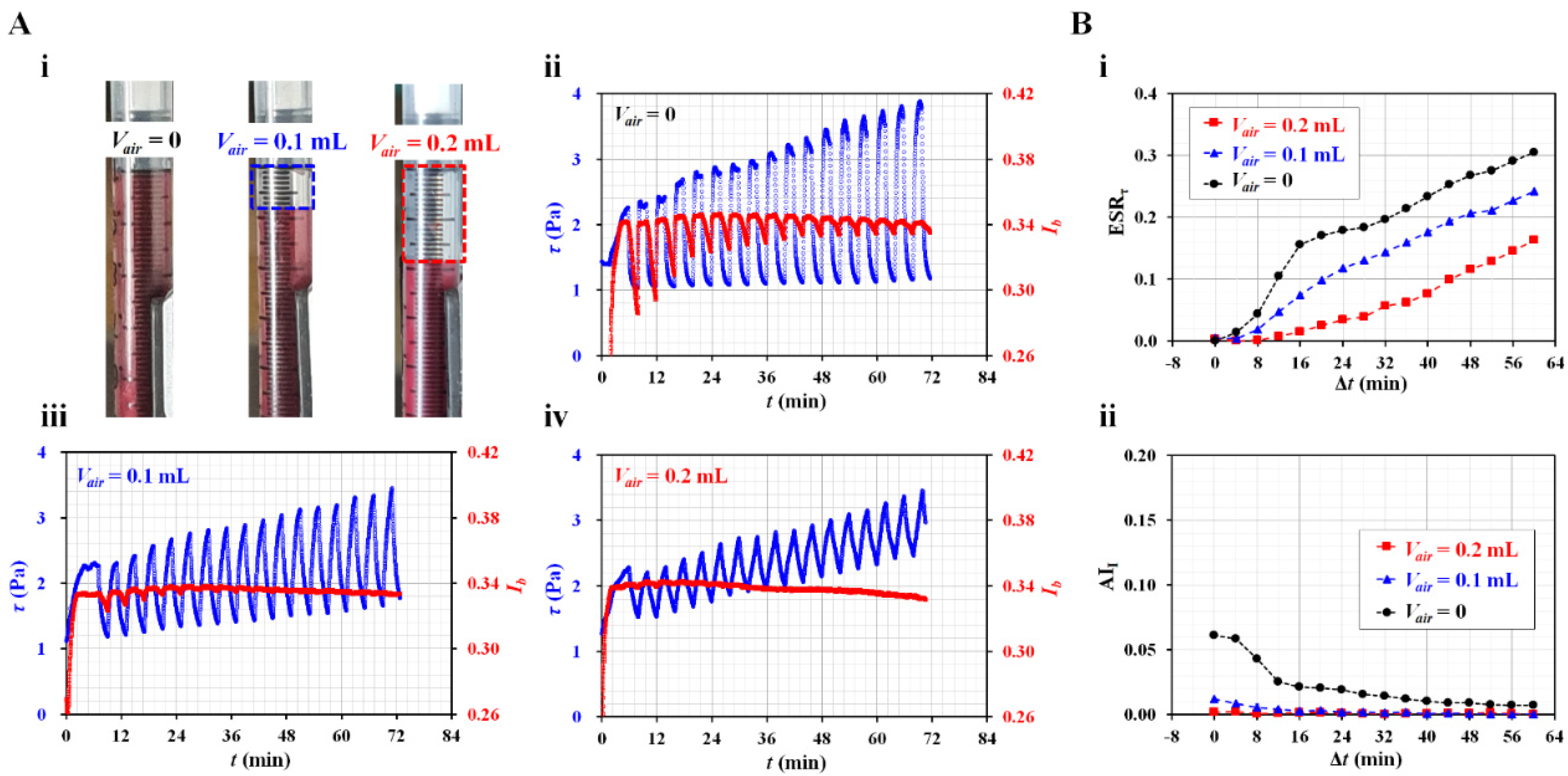
3.4. Contributions of Diluent to ESR in the Driving Syringe

According to previous studies, diluents (dextran solution [45,51,52,63,69,70,71,72,73] and fibrinogen [34,74]) contribute to increasing RBC aggregation or ESR [75]. To quantify the effect of the diluent on the ESR, test blood was prepared by adding normal RBCs to two types of diluent (dextran solution and fibrinogen). The present method was used to measure variations of the two indices for the test blood.
First, the proposed method was used to detect variations of two indices for test blood, which was prepared by adding normal RBCs into dextran solution (Cdex = 0, 10, 20, 40, 60, and 80 mg/mL). Here, Cdex = 0 represents 1× PBS. Figure 6A(i) shows variations of τ0 with respect to Cdex. The τ0 tended to increase significantly with respect to Cdex. Previously, by supplying suspended blood to a microfluidic device under constant blood flow, the shear stress and blood viscosity were obtained with respect to dextran solutions ranging from 5 to 80 mg/mL [51]. In a previous study, it was found that blood viscosity and shear stress tended to increase substantially at higher concentrations of dextran solution, especially under a constant blood flow. However, in the present study, the test blood was supplied to the microfluidic channel in a square-wave profile, as shown in Figure 1A. Because the test blood was prepared with the same normal RBCs, the difference in diluent (i.e., different concentrations of dextran solution) led to an increase in τ0. Based on Equation (2), it was confirmed that the τ0 increased because of the higher concentration of the dextran solution. Compared with a previous study, the τ0 tended to increase substantially, regardless of the blood flow pattern (constant or square wave). The τ0 could be then used to detect the change in the diluent of test blood. Figure 6A(ii) shows the temporal variations of ESRτ with respect to Cdex. Below Cdex = 40 mg/mL, the ESRτ tended to increase substantially with respect to Cdex, which gradually increases during this period. However, above Cdex = 40 mg/mL, the ESRτ tended to decrease with respect to Cdex. Interestingly, for dextran solutions with Cdex = 60 or 80 mg/mL, the ESRτ tended to increase for up to 24 min. After 32 min, the ESRτ tended to decrease over time. According to a previous study conducted under a constant blood flow [51], ESRτ did not exhibit a substantial difference between 15 and 40 mg/mL. In addition, it significantly decreased between 60 and 80 mg/mL. However, according to the present study, which was conducted at a square-wave blood flow, ESRτ tended to increase significantly between 10 and 40 mg/mL. Thus, it was inferred that the difference in blood flow pattern (constant or square-wave profile) can lead to different ESRτ trends. Figure 6A(iii) shows temporal variations of AII with respect to Cdex. The AII tended to increase up to Cdex = 40 mg/mL. It tended to decrease above Cdex = 40 mg/mL and tended to decrease significantly over time. The results confirmed that the two indices have promise for detecting test blood with different concentrations of dextran.
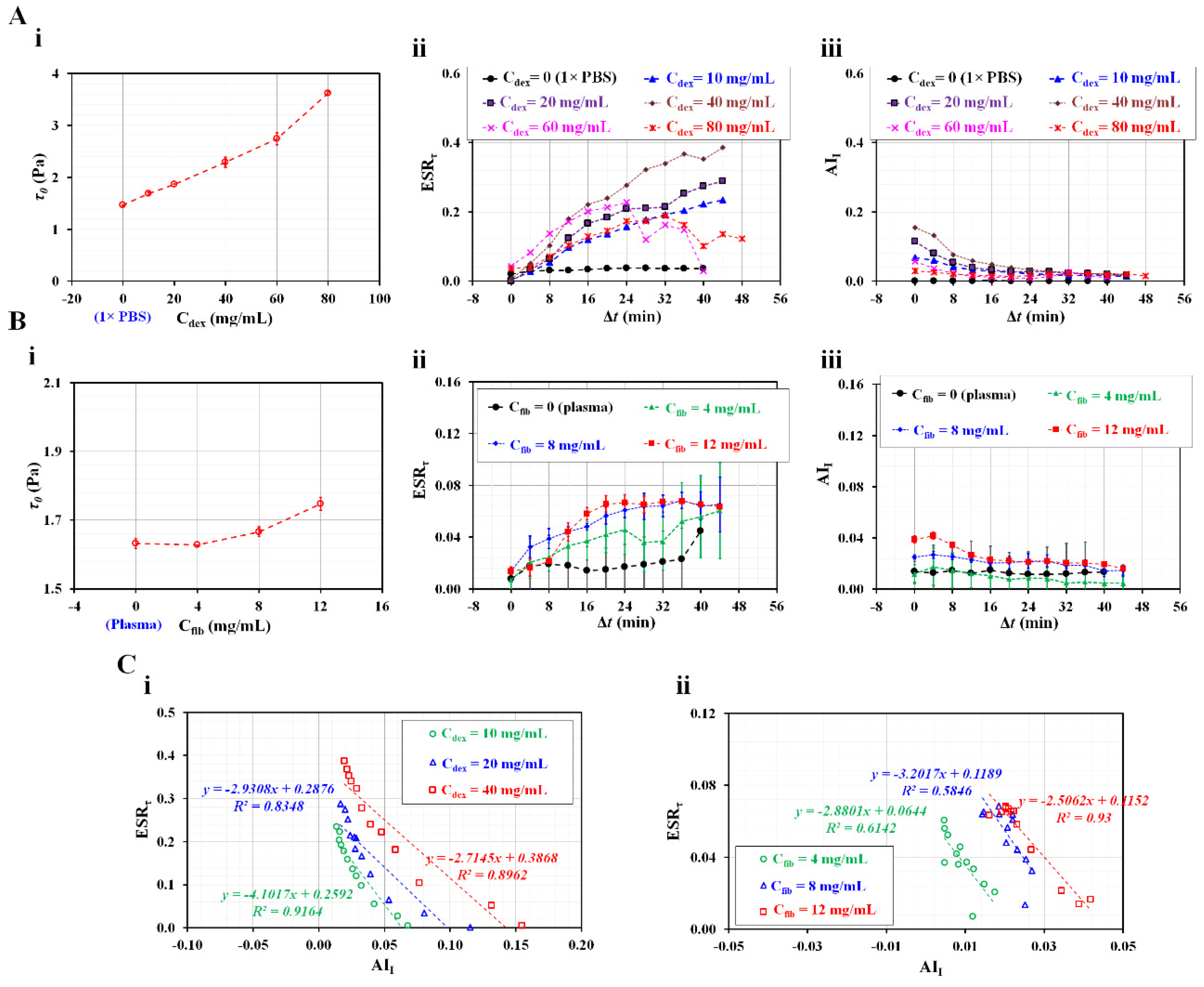
Preprints 78399 g006
Figure 6. Detection of different diluent (i.e., dextran solution, fibrinogen) in terms of τ0, ESRτ, and AII. (A) Detection of difference in dextran concentration in terms of three properties. (i) Variations of τ0 with respect to Cdex = 0, 10, 20, 40, 60, and 80 mg/mL. (ii) Temporal variations of ESRτ with respect to Cdex. (iii)Temporal variations of AII with respect to Cdex. (B) Detection of difference in fibrinogen concentration in terms of three properties. (i)Variations of τ0 with respect to Cfib = 0, 4, 8, and 12 mg/mL. (ii) Temporal variations of ESRτ with respect to Cfib. (iii) variations of AII with respect to Cfib. (C) Correlation between ESR index and aggregation index for test bloods diluted by dextran or fibrinogen. (i) Linear relationship between ESRτ and AII with respect to concentration of dextran. (ii) Linear relationship between ESRτ and AII with respect to concentration of fibrinogen.
Figure 6. Detection of different diluent (i.e., dextran solution, fibrinogen) in terms of τ0, ESRτ, and AII. (A) Detection of difference in dextran concentration in terms of three properties. (i) Variations of τ0 with respect to Cdex = 0, 10, 20, 40, 60, and 80 mg/mL. (ii) Temporal variations of ESRτ with respect to Cdex. (iii)Temporal variations of AII with respect to Cdex. (B) Detection of difference in fibrinogen concentration in terms of three properties. (i)Variations of τ0 with respect to Cfib = 0, 4, 8, and 12 mg/mL. (ii) Temporal variations of ESRτ with respect to Cfib. (iii) variations of AII with respect to Cfib. (C) Correlation between ESR index and aggregation index for test bloods diluted by dextran or fibrinogen. (i) Linear relationship between ESRτ and AII with respect to concentration of dextran. (ii) Linear relationship between ESRτ and AII with respect to concentration of fibrinogen.
Preprints 78399 g006
Second, the present method was employed to detect differences in two indices for test blood, which was prepared by adding normal RBCs into fibrinogen. For healthy control blood, fibrinogen levels ranging from 2 to 4 mg/mL were considered to be the normal range [69]. According to an optical tweezer study, disaggregating force increased significantly above Cfib = 4 mg/mL (i.e., the abnormal range). Furthermore, the AII increased substantially in the abnormal range [76]. Based on previous studies, the fibrinogen was set to more than 4 mg/mL (i.e., Cfib = 0, 4, 8, and 12 mg/mL). Here, Cfib = 0 means autologous plasma. Figure 6B(i) shows variations of τ0 with respect to Cfib. The τ0 remained unchanged below Cfib = 4 mg/mL (i.e., τ0 = 1.628–1.632 Pa). Above Cfib = 4 mg/mL, the τ0 of each fibrinogen increased as τ0 = 1.666 ± 0.014 Pa (Cfib = 8 mg/mL) and τ0 = 1.747 ± 0.019 Pa (Cfib = 12 mg/mL). The τ0 increased substantially in the abnormal range (more than 4 mg/mL) compared with the normal range (less than 4 mg/mL). Compared with the previous optical tweezer study [69], the τ0 had a similar trend with respect to fibrinogen. Figure 6B(ii) shows temporal variations of ESRτ with respect to Cfib. When compared with autologous plasma (Cfib = 0), fibrinogen contributed to an increase in ESRτ. The ESRτ tended to increase at higher concentration of fibrinogen (i.e., Cfib = 4–8 mg/mL). The ESRτ tended to increase over time. For higher concentrations of fibrinogen (i.e., Cfib = 8 or 12 mg/mL), when Δt was less than 12 min, the ESRτ of Cfib = 12 mg/mL was smaller than that of Cfib = 8 mg/mL. After 16 min, there was no substantial difference between Cfib = 8 and Cfib = 12 mg/mL. Figure 6B(iii) shows variations of AII with respect to Cfib. At Δt = 0, the AII tended to increase with respect to Cfib. However, after Δt = 16 min, the AII did not show a substantial difference with respect to Cfib — that is, fibrinogen did not contribute substantially to the change in AII. Compared with ESRτ (Figure 6B(ii)), the variation range of AII was much smaller. Therefore, it was inferred that measuring the variation in ESR in terms of AII is difficult.
Finally, it was necessary to validate the linear relationship between the two indices. As shown in Figure 6C, ESRτ and AII were constructed using an X–Y plot. Figure 6C(i) shows a linear relationship between ESRτ and AII with respect to three types of dextran solution (Cdex = 10, 20, and 40 mg/mL). The slope varied from −4.101 to −2.715. The coefficient of linear regression was estimated to have a high value of R2 = 0.835–0.916. Figure 6C(ii) shows a linear relationship between ESRτ and AII with respect to three types of fibrinogen (Cfib = 4, 8, and 12 mg/mL). The slope varied from −3.202 to −2.506. With respect to Cfib = 4 or 8 mg/mL, the coefficient of linear regression obtained had a lower value of R2 = 0.584–0.614 because AII did not show distinctive trends over time. However, the higher concentration of fibrinogen (Cfib = 12 mg/mL) had a higher value of R2 = 0.93. The linear regression analysis revealed that both indices had a strong correlation (i.e., ESRτ ~ AII), especially under periodic on–off blood flow.

4. Conclusions

Three physical properties of blood samples (initial shear stress [τ0], ESR index [ESRτ], and aggregation index [AII]) were used to quantify biophysical variations of blood samples during the continuous ESR. Blood was supplied from a blood driving syringe to a microfluidic channel in a periodic on–off manner. Both τ0 and ESRτ were obtained by analyzing the temporal variations of the blood shear stress. Furthermore, AII was calculated by analyzing the image intensity of the blood flow. According to the experimental results related to several factors (on–off period, air cavity secured in the blood syringe, and hematocrit), a shorter period of T = 4 min and no air cavity were fixed to obtain high sensitivity of the two indices (ESRτ and AII). The τ0 was linearly proportional to the hematocrit. The contribution of hematocrit (30–50%) to ESRτ was negligible during the short duration of the experiment (less than 16 min). In conclusion, the three biophysical properties exhibited substantial differences in several types of suspended blood (i.e., thermally hardened RBCs, dextran, and fibrinogen). In the future, this method will be used to detect blood collected from patients with cardiovascular diseases. Furthermore, it is necessary to improve the present method for testing different types of blood in clinical settings.

Acknowledgments

This work was supported by a research fund from the Chosun University (2023).

Conflicts of Interest

The author has no conflict to disclose.

References

  1. Noguchi, H.; Gompper, G. Shape transitions of fluid vesicles and red blood cells in capillary flows. Proc. Natl. Acad. Sci. U. S. A. 2005, 102, 14159–14164. [Google Scholar] [CrossRef] [PubMed]
  2. Tomaiuolo, G. Biomechanical properties of red blood cells in health and disease towards microfluidics. Biomicrofluidics 2014, 8, 051501. [Google Scholar] [CrossRef] [PubMed]
  3. Barshtein, G. Biochemical and biophysical properties of red blood cells in disease. Biomolecules 2022, 12, 923. [Google Scholar] [CrossRef] [PubMed]
  4. Lutz, H.U.; Bogdanova, A. Mechanisms tagging senescent red blood cells for clearance in healthy humans. Front. Physiol. 2013, 4, 387. [Google Scholar] [CrossRef] [PubMed]
  5. Spencer, C.; Lip, G. Haemorheological factors in hypertension. J. Hum. Hypertens. 2000, 14, 291–293. [Google Scholar] [CrossRef]
  6. Lee, H.; Na, W.; Lee, S.B.; Ahn, C.W.; Moon, J.S.; Won, K.C.; Shin, S. Potential Diagnostic Hemorheological Indexes for Chronic Kidney Disease in Patients With Type 2 Diabetes. Front. Physiol. 2019, 10, 1062. [Google Scholar] [CrossRef]
  7. Agrawal, R.; Smart, T.; Nobre-Cardoso, J.; Richards, C.; Bhatnagar, R.; Tufail, A.; Shima, D.; Jones, P.H.; Pavesio, C. Assessment of red blood cell deformability in type 2 diabetes mellitus and diabetic retinopathy by dual optical tweezers stretching technique. Sci. Rep. 2016, 6, 15873. [Google Scholar] [CrossRef]
  8. Cho, Y.I.; Mooney, M.P.; Cho, D.J. Hemorheological disorders in diabetes mellitus. J. Diabetest Sci. Technol. 2008, 2. [Google Scholar] [CrossRef]
  9. Guo, Q.; Duffy, S.P.; Matthews, K.; Deng, X.; Santoso, A.T.; Islamzada, E.; Ma, d.H. Deformability based sorting of red blood cells improves diagnostic sensitivity for malaria caused by Plasmodium falciparum. Lab Chip 2016, 16, 645–654. [Google Scholar] [CrossRef]
  10. Olumuyiwa-Akeredolu, O.-o.O.; Soma, P.; Antoinette V., Buys; Debusho, L.K.; Pretorius, E. Characterizing pathology in erythrocytes using morphological and biophysical membrane properties: Relation to impaired hemorheology and cardiovascular function in rheumatoid arthritis. Biochim. Biophys. Acta-Biomembr 2017, 1859, 2381–2391. [Google Scholar] [CrossRef]
  11. Upadhyay, R.K. Emerging risk biomarkers in cardiovascular diseases and disorders. J. Liqids 2015, 2015, 971453. [Google Scholar] [CrossRef] [PubMed]
  12. Lowe, G.; Rumley, A.; Norrie, J.; Ford, I.; Shepherd, J.; Cobbe, S.; Macfarlane, P.; Packard, C. Blood rheology, cardiovascular risk factors, and cardiovascular disease: the west of scotland coronary prevention study. Thromb. Haemost. 2000, 84, 553–558. [Google Scholar] [PubMed]
  13. Islamzada, E.; Matthews, K.; Lamoureux, E.; Duffy, S.P.; Scott, M.D.; Ma, H. Blood unit segments accurately represent the biophysical properties of red blood cells in blood bags but not hemolysis. Transfusion 2022, 62, 448–456. [Google Scholar] [CrossRef]
  14. Jeon, H.-J.; Qureshi, M.M.; Lee, S.Y.; Chung, E. Optofluidic laser speckle image decorrelation analysis for the assessment of red blood cell storage. PLoS One 2019, 14, e0224036. [Google Scholar] [CrossRef] [PubMed]
  15. Xu, Z.; Zheng, Y.; Wang, X.; Shehata, N.; Wang, C.; Sun, Y. Stiffness increase of red blood cells during storage. Microsystems & Nanoengineering 2018, 4, 17103. [Google Scholar]
  16. Park, H.; Lee, S.; Ji, M.; Kim, K.; Son, Y.; Jang, S.; Park, Y. Measuring cell surface area and deformability of individual human red blood cells over blood storage using quantitative phase imaging. Sci. Rep. 2016, 6, 34257. [Google Scholar] [CrossRef]
  17. Huang, S.; Hou, H.W.; Kanias, T.; Sertorio, J.; Chen, H.; Sinchar, D.; Gladwin, M.; Han, J. Towards microfluidic-based depletion of stiff and fragile human red cells that accumulate during blood storage. Lab Chip 2015, 15, 448–458. [Google Scholar] [CrossRef]
  18. Daly, A.; Raval, J.S.; Waters, J.H.; Yazer, M.H.; Kameneva, M.V. Effect of blood bank storage on the rheological properties of male and female donor red blood cells. Clin. Hemorheolo. Microcir. 2014, 56, 337–345. [Google Scholar] [CrossRef]
  19. Cluitmans, J.C.A.; Chokkalingam, V.; Janssen, A.M.; Brock, R. ; S.Huck, W.T.; GielJ.C.G.M.Bosman. Alterations in red blood cell deformability during storage: a microfluidic approach. Biomed Res. Int. 2014, 2014, 764268. [Google Scholar]
  20. Yayan, J. Erythrocyte sedimentation rate as a marker for coronary heart disease. Vasc. Health Risk Manag. 2012, 8, 219–223. [Google Scholar] [CrossRef]
  21. Cho, Y.-I.; Cho, D.J. Hemorheology and Microvascular Disorders. Korean Cir. J. 2011, 41, 287–295. [Google Scholar] [CrossRef]
  22. Danesh, J.; Collins, R.; Peto, R.; Lowe, G.D.O. Haematocrit, viscosity, erythrocyte sedimentation rate: meta-analyses of prospective studies of coronary heart disease. Eur. Heart J. 2000, 21, 515–520. [Google Scholar] [CrossRef] [PubMed]
  23. Trejo-Soto, C.; Lázaro, G.R.; Pagonabarraga, I.; Hernández-Machado, A. Microfluidics approach to the mechanical properties of red blood cell membrane and their effect on blood rheology. Membranes 2022, 12, 217. [Google Scholar] [CrossRef] [PubMed]
  24. Kim, B.J.; Lee, Y.S.; Zhbanov, A.; Yang, S. A physiometer for simultaneous measurement of whole blood viscosity and its determinants: hematocrit and red blood cell deformability. Analyst 2019, 144, 3144–3157. [Google Scholar] [CrossRef] [PubMed]
  25. Hintermüller, M.A.; Offenzeller, C.; Jakoby, B. A microfluidic viscometer with capacitive readout using screen-printed electrodes. IEEE Sensors J. 2021, 21, 2565–2021. [Google Scholar] [CrossRef]
  26. Kang, H.; Jang, I.; Song, S.; Bae, S.-C. Development of a paper-based viscometer for blood plasma using colorimetric analysis. Anal. Chem. 2019, 91, 4868–4875. [Google Scholar] [CrossRef] [PubMed]
  27. Solomon, D.E.; Abdel-Raziq, A.; Vanapalli, S.A. A stress-controlled microfluidic shear viscometer based on smartphone imaging. Rheol. Acta 2016, 55, 727–738. [Google Scholar] [CrossRef]
  28. Link, A.; Franke, T. Acoustic erythrocytometer for mechanically probing cell viscoelasticity. Lab Chip 2020, 20, 1991–1998. [Google Scholar] [CrossRef]
  29. Stathoulopoulos, A.; Passos, A.; Balabani, S. Flows of healthy and hardened RBC suspensions through a micropillar array. Med. Eng. Phys. 2022, 107, 103874. [Google Scholar] [CrossRef]
  30. Piety, N.Z.; Stutz, J. Piety, N.Z.; Stutz, J.; NidaYilmaz; Xia, H.; TatsuroYoshida; Shevkoplyas, S.S. Microfuidic capillary networks are more sensitive than ektacytometry to the decline of red blood cell deformability induced by storage. Sci. Rep. 2021, 11, 604. [Google Scholar] [CrossRef]
  31. Urbanska, M.; Muñoz, H.E.; Bagnall, J.S.; Otto, O.; Manalis, S.R.; Carlo, D.D.; Guck, J. A comparison of microfluidic methods for high-throughput cell deformability measurements. Nat. Methods 2020, 17, 587–593. [Google Scholar] [CrossRef]
  32. Hyakutake, T.; Abe, H.; Miyoshi, Y.; Yasui, M.; Suzuki, R.; Tsurumaki, S.; Tsutsumi, Y. In vitro study on the partitioning of red blood cells using a microchannel network. Microvasc. Res. 2022, 140, 104281. [Google Scholar] [CrossRef] [PubMed]
  33. Zhbanov, A.; Yang, S. Electrochemical impedance spectroscopy of blood for sensitive detection of blood hematocrit, sedimentation and dielectric properties. Anal. Methods 2017, 9, 3302–3313. [Google Scholar] [CrossRef]
  34. Dasanna, A.K.; Darras, A.; John, T.; Gompper, G.; Kaestner, L.; Wagner, C.; Fedosov, D.A. Erythrocyte sedimentation: Effect of aggregation energy on gel structure during collapse. Phys. Rev. E 2022, 105, 024610. [Google Scholar] [CrossRef] [PubMed]
  35. Isiksacan, Z.; Erel, O.; Elbuken, C. A portable microfluidic system for rapid measurement of the erythrocyte sedimentation rate. Lab Chip 2016, 16, 4682–4690. [Google Scholar] [CrossRef]
  36. Pasias, D.; Passos, A.; Constantinides, G.; Balabani, S.; Kaliviotis, E. Surface tension driven flow of blood in a rectangular microfluidic channel: Effect of erythrocyte aggregation. Phys. Fluids 2020, 32, 071903. [Google Scholar] [CrossRef]
  37. Baskurt, O.K.; Uyuklu, M.; Meiselman, H.J. Time Course of Electrical Impedance During Red Blood Cell Aggregation in a Glass Tube: Comparison With Light Transmittance. IEEE Trans. Biomed. Eng. 2010, 57, 969–978. [Google Scholar] [CrossRef]
  38. Antonova, N.; Riha, P.; Ivanov, I. Time dependent variation of human blood conductivity as a method for an estimation of RBC aggregation. Clin. Hemorheolo. Microcir. 2008, 39, 69–78. [Google Scholar] [CrossRef]
  39. Zhbanov, A.; Yang, S. Effects of aggregation on blood sedimentation and conductivity. PLoS One 2015, 10, e0129337. [Google Scholar] [CrossRef]
  40. Kang, Y.J.; Lee, S.-J. In vitro and ex vivo measurement of the biophysical properties of blood using microfluidic platforms and animal models. Analyst 2018, 143, 2723–2749. [Google Scholar] [CrossRef]
  41. Kang, Y.J.; Yang, S. Fluidic low pass filter for hydrodynamic flow stabilization in microfluidic environments. Lab Chip 2012, 12, 1881–1889. [Google Scholar] [CrossRef]
  42. Lim, H.-J.; Lee, Y.-J.; Nam, J.-H.; Chung, S.; Shin, S. Temperature-dependent threshold shear stress of red blood cell aggregation. J. Biomech. 2010, 43, 546–550. [Google Scholar] [CrossRef] [PubMed]
  43. Shin, S.; Hou, J.X.; Suh, J.-S. Measurement of cell aggregation characteristics by analysis of laser-backscattering in a microfluidic rheometry. Korea-Aust. Rheol. J. 2007, 19, 61–66. [Google Scholar]
  44. Nam, J.-H.; Xue, S.; Lim, H.; Shin, S. Study of erythrocyte aggregation at pulsatile flow conditions with backscattering analysis. Clin. Hemorheol. Microcirc. 2012, 50, 257–266. [Google Scholar] [CrossRef]
  45. Namgung, B.; Lee, T.; Tan, J.K.S.; Poh, D.K.H.; Park, S.; Chng, K.Z.; Agrawal, R.; Park, S.-Y.; Leo, H.L.; Kim, S. Vibration motor-integrated low-cost, miniaturized system for rapid quantification of red blood cell aggregation. Lab Chip 2020, 20, 3930–3937. [Google Scholar] [CrossRef] [PubMed]
  46. Lapić, I.; Padoan, A.; Bozzato, D.; Plebani, M. Erythrocyte sedimentation rate and C-reactive protein in acute inflammation. Am. J. Clin. Pathol. 2020, 153, 14–29. [Google Scholar] [CrossRef] [PubMed]
  47. Kang, Y.J. Microfluidic-based measurement of RBC aggregation and the ESR using a driving syringe system. Anal. Methods 2018, 10, 1805–1816. [Google Scholar] [CrossRef]
  48. Kang, Y.J. Contributions of red blood cell sedimentation in a driving syringe to blood flow in capillary channels. Micromachines 2022, 13, 909. [Google Scholar] [CrossRef]
  49. Kang, Y.J. Sequential quantification of blood and diluent using red cell sedimentation-based separation and pressure-induced work in a microfluidic channel. Anal. Methods 2022, 14, 1194–1207. [Google Scholar] [CrossRef]
  50. Kang, Y.J. Microfluidic-based measurement method of red blood cell aggregation under hematocrit variations. Sensors 2017, 17, 2037. [Google Scholar] [CrossRef]
  51. Kang, Y.J. Red Blood Cell Sedimentation Index Using Shear Stress of Blood Flow in Microfluidic Channel. Biosensors 2022, 12, 547. [Google Scholar] [CrossRef]
  52. Kim, G.; Jeong, S.; Kang, Y.J. Ultrasound standing wave-based cell-to-liquid separation for measuring viscosity and aggregation of blood sample. Sensors 2020, 20, 2284. [Google Scholar] [CrossRef] [PubMed]
  53. Otsu, N. A threshold selection method from gray-level histograms. IEEE Trans. Syst. Man. Cybern. 1979, 9, 62–66. [Google Scholar] [CrossRef]
  54. Kang, Y.J. Continuous and simultaneous measurement of the biophysical properties of blood in a microfluidic environment. Analyst 2016, 141, 6583–6597. [Google Scholar] [CrossRef] [PubMed]
  55. Kang, Y.J. Quantitative monitoring of dynamic blood flows using coflowing laminar streams in a sensorless approach. App. Sci.-Basel 2021, 11, 7260. [Google Scholar] [CrossRef]
  56. Cheng, N.-S. Formula for the viscosity of a glycerol−water mixture. Ind. Eng. Chem. Res. 2008, 47, 3285–3288. [Google Scholar] [CrossRef]
  57. Kang, Y.J. Experimental investigation of air compliance effect on measurement of mechanical properties of blood sample flowing in microfluidic channels. Micromachines 2020, 11, 460. [Google Scholar] [CrossRef]
  58. Lim, H.-J.; Nam, J.-H.; Lee, B.-K.; Suh, J.-S.; Shin, S. Alteration of red blood cell aggregation during blood storage. Korea-Aust. Rheol. J. 2011, 23, 67–70. [Google Scholar] [CrossRef]
  59. Shin, S.; Nam, J.-H.; Hou, J.-X.; Suh, J.-S. A transient microfluidic approach to the investigation of erythrocyte aggregation: The threshold shear-stress for erythrocyte disaggregation. Clin. Hemorheol. Microcirc. 2009, 42, 117–125. [Google Scholar] [CrossRef]
  60. Hong, H.; Song, J.M.; Yeom, E. Micro-vibrational erythrocyte sedimentation rate (ESR) for sensitive measurement of erythrocyte aggregation. J. Vis. 2021, 24, 749–760. [Google Scholar] [CrossRef]
  61. Kang, Y.J. A disposable blood-on-a-chip for simultaneous measurement of multiple biophysical properties. Micromachines 2018, 9, 475. [Google Scholar] [CrossRef]
  62. Zhou, Y.; Liu, J.; Yan, J.; Zhu, T.; Guo, S.; Li, S.; Li, T. Standing air bubble-based micro-hydraulic capacitors for flow stabilization in syringe pump-driven systems. Micromachines 2020, 11, 396. [Google Scholar] [CrossRef] [PubMed]
  63. Yeom, E.; Lee, S.-J. Microfluidic-based speckle analysis for sensitive measurement of erythrocyte aggregation: A comparison of four methods for detection of elevated erythrocyte aggregation in diabetic rat blood. Biomicrofluidics 2015, 9, 024110. [Google Scholar] [CrossRef] [PubMed]
  64. Kang, Y.J.; Ha, Y.-R.; Lee, S.-J. Microfluidic-based measurement of erythrocyte sedimentation rate for biophysical assessment of blood in an in vivo malaria-infected mouse. Biomicrofluidics 2014, 8, 044114. [Google Scholar] [CrossRef] [PubMed]
  65. Kang, Y.J. Microfluidic-based effective monitoring of bloods by measuring RBC aggregation and blood viscosity under stepwise varying shear rates. Korea-Aust. Rheol. J. 2020, 32, 15–27. [Google Scholar] [CrossRef]
  66. Tomaiuolo, G.; Carciati, A.; Caserta, S.; Guido, S. Blood linear viscoelasticity by small amplitude oscillatory flow. Rheol. Acta 2016, 55, 485–495. [Google Scholar] [CrossRef]
  67. Kang, Y.J.; Lee, S.-J. Blood viscoelasticity measurement using steady and transient flow controls of blood in a microfluidic analogue of Wheastone-bridge channel. Biomicrofluidics 2013, 7, 054122. [Google Scholar] [CrossRef]
  68. lerche, D.; Baumler, H. Moderate heat treatment of only red blood cells (RBC) slows down the rate of RBC-RBC aggregation in plasma. Biorheology 1984, 21, 393–403. [Google Scholar] [CrossRef]
  69. Lee, K.; Kinnunen, M.; Khokhlova, M.D.; Lyubin, E.V.; Priezzhev, A.V.; Meglinski, I.; Fedyanin, A.A. Optical tweezers study of red blood cell aggregation and disaggregation in plasma and protein solutions. J. Biomed. Opt. 2016, 21, 035001. [Google Scholar] [CrossRef]
  70. Ermolinskiy, P.; Lugovtsov, A.; Yaya, F.; Lee, K.; Kaestner, L. ; ChristianWagner; Priezzhev, A. Effect of red blood cell aging in vivo on their aggregation properties in vitro: measurements with laser tweezers. App. Sci.-Basel 2020, 10, 7581. [Google Scholar]
  71. Reinhart, W.H.; Piety, N.Z.; Shevkoplyas, S.S. Influence of red blood cell aggregation on perfusion of an artificial microvascular network. Microcirculation 2017, 24, e12317. [Google Scholar] [CrossRef]
  72. Sherwood, J.M.; Dusting, J.; Kaliviotis, E.; Balabani, S. The effect of red blood cell aggregation on velocity and cell-depleted layer characteristics of blood in a bifurcating microchannel. Biomicrofluidics 2012, 6, 024119. [Google Scholar] [CrossRef]
  73. Neu, B.; Wenby, R.; Meiselman, H.J. Effects of dextran molecular weight on red blood cell aggregation. Biophys. J. 2008, 95, 3059–3065. [Google Scholar] [CrossRef] [PubMed]
  74. Xue, S.; Lee, B.-K.; Shin, S. Disaggregating shear stress: The roles of cell deformability and fibrinogen concentration. Clin. Hemorheol. Microcirc. 2013, 55, 231–240. [Google Scholar] [CrossRef] [PubMed]
  75. Baskur, O.K.; Meiselman, H.J. Erythrocyte aggregation: Basic aspects and clinical importance. Clin. Hemorheol. Microcirc. 2013, 53, 23–37. [Google Scholar] [CrossRef] [PubMed]
  76. Lominadze, D.; Schuschke, D.A.; Joshua, I.G.; Dean, W.L. Increased ability of erythrocytes to aggregate in spontaneously hypertensive rats. Clin. Exp. Hypertens. 2002, 24. [Google Scholar] [CrossRef] [PubMed]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.
Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.
Prerpints.org logo

Preprints.org is a free preprint server supported by MDPI in Basel, Switzerland.

facebook logotwitter logolinkedin logo
MDPI Initiatives
Important Links
Subscribe

Disclaimer

Terms of Use

Privacy Policy

© 2024 MDPI (Basel, Switzerland) unless otherwise stated