Submitted:
05 July 2023
Posted:
06 July 2023
You are already at the latest version
Abstract
Keywords:
1. Introduction
2. PV Modeling and Problem Formulation
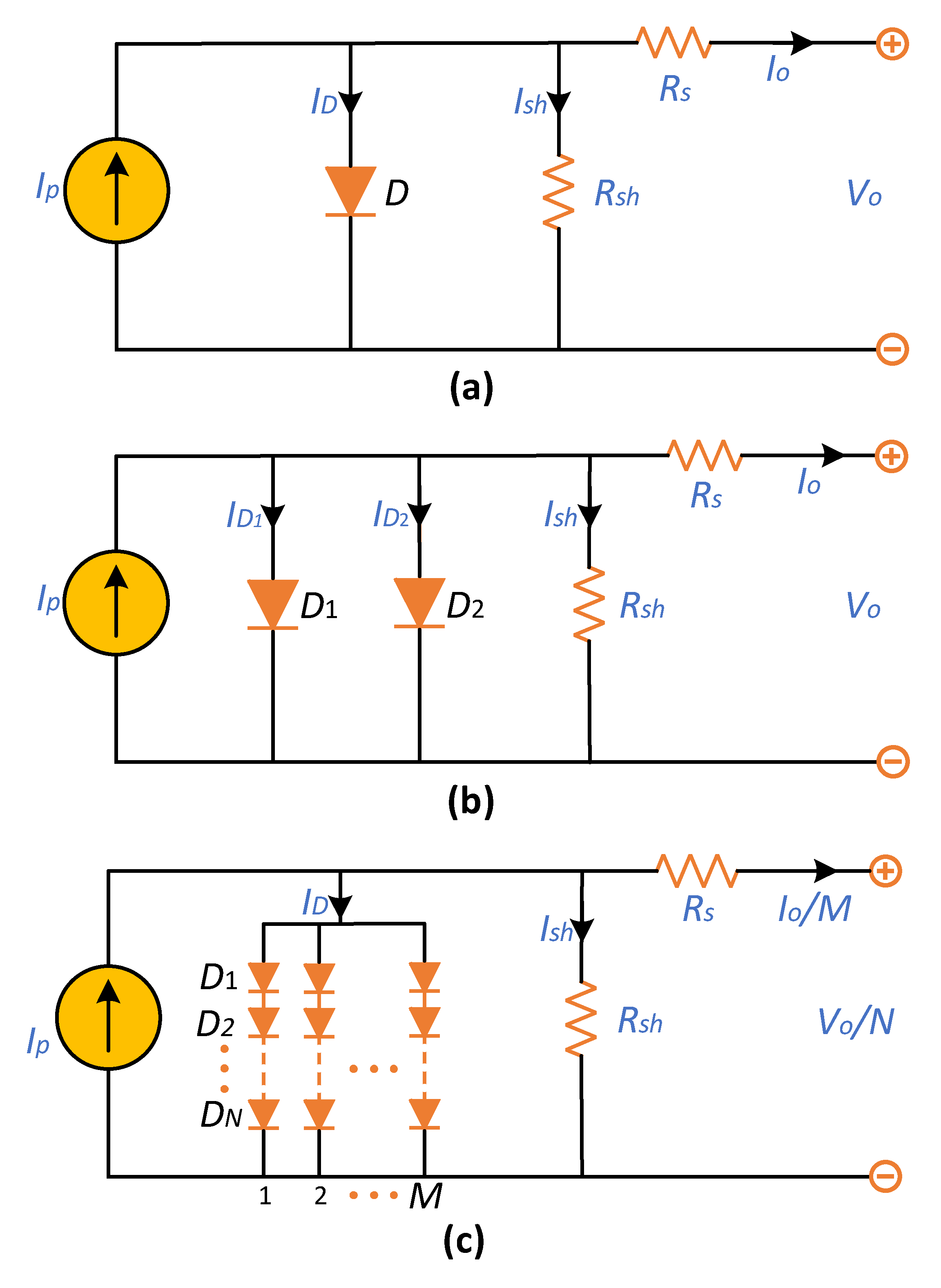
2.1. The Model of a Solar Cell
2.1.1. SDM
2.1.2. DDM
2.2. PVMM
2.3. Problem Formulation
3. Proposed Optimization Algorithm
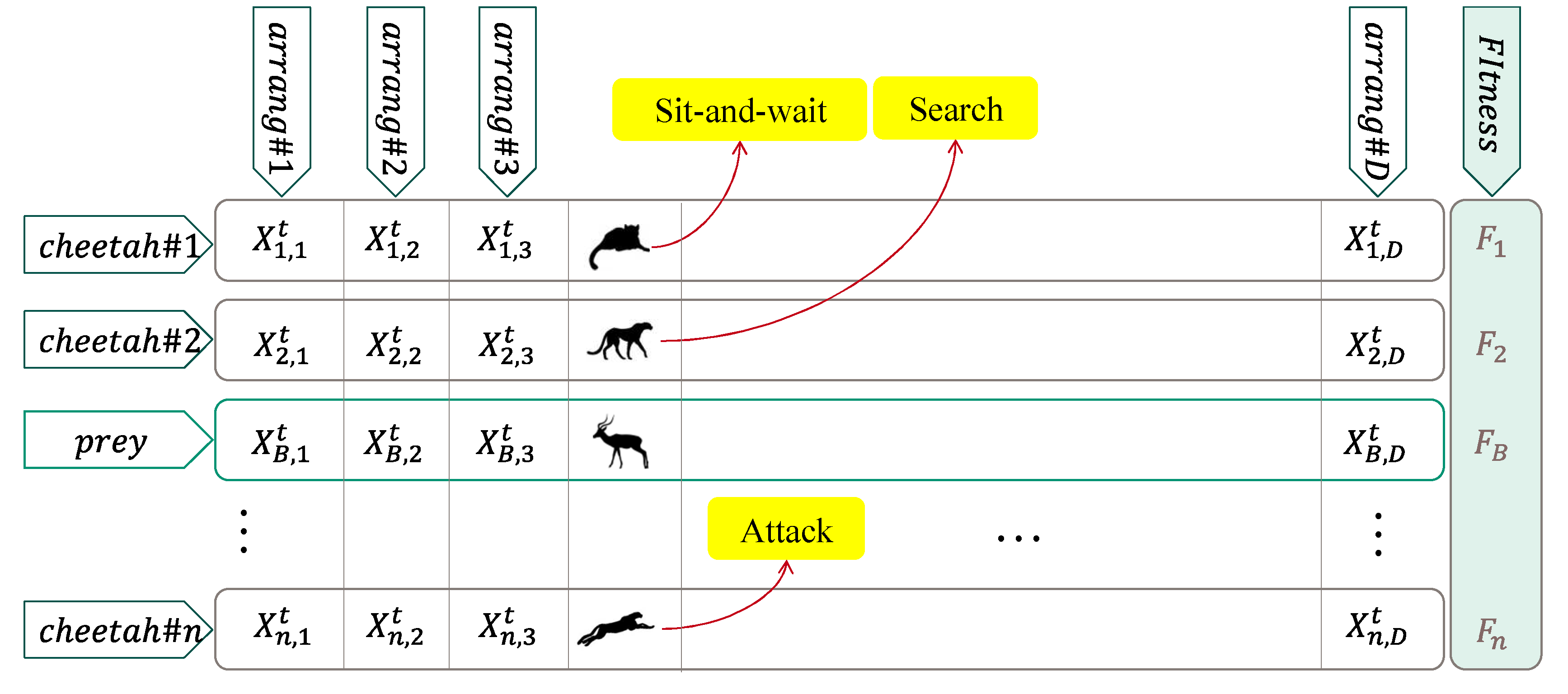
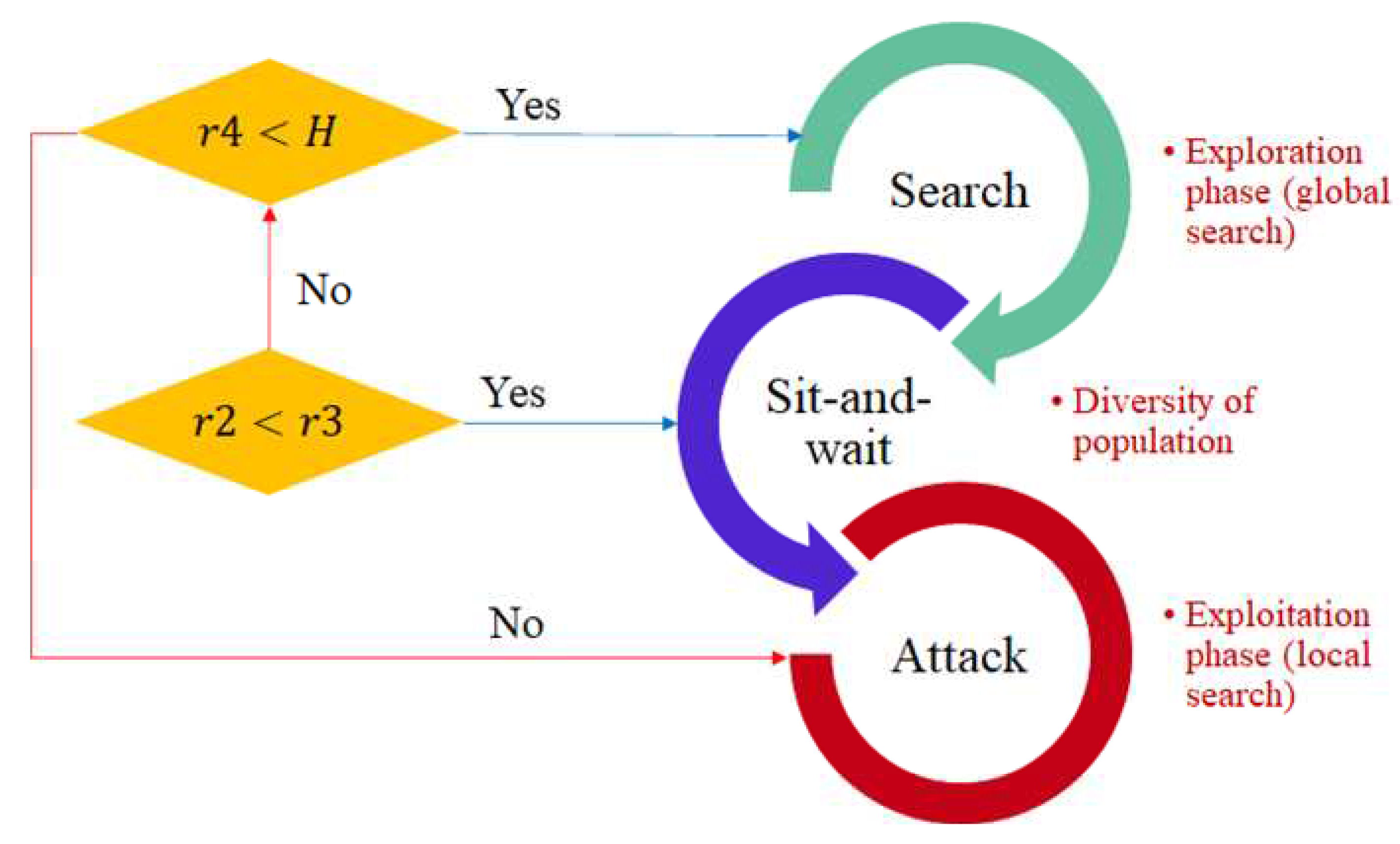
3.1. Overview of CO Algorithm
3.1.1. Searching Strategy
3.1.2. Sitting-and-Waiting Strategy
3.1.3. Attacking Strategy
3.1.4. Strategy Selection Mechanism
| Algorithm 1: The CO Algorithm |
 |
3.2. Improved Cheetah Optimizer (ICO) Algorithm
3.2.1. Searching Strategy
3.2.2. Attacking Strategy
| Algorithm 1: The ICO Algorithm |
 |
4. Experimental Results
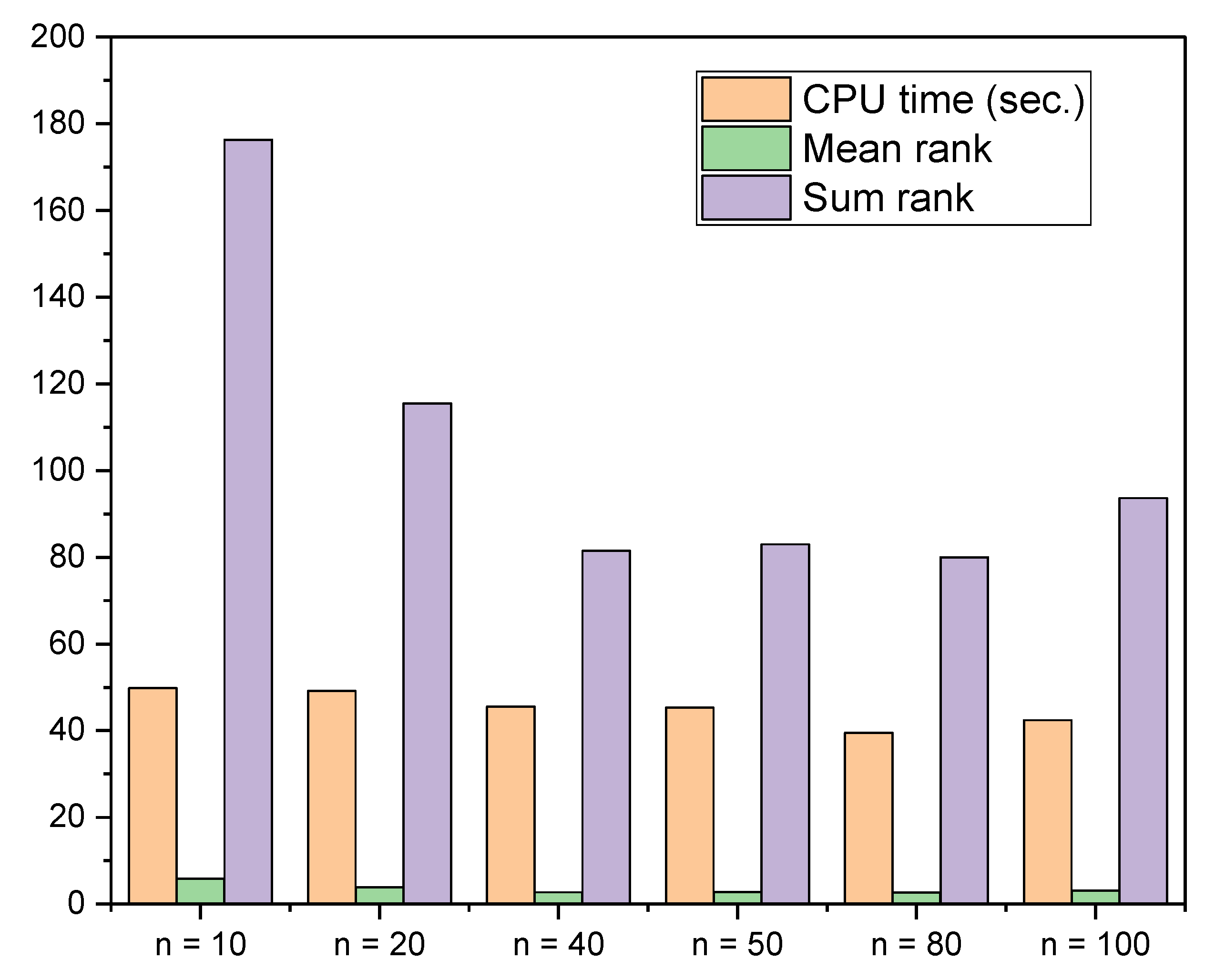
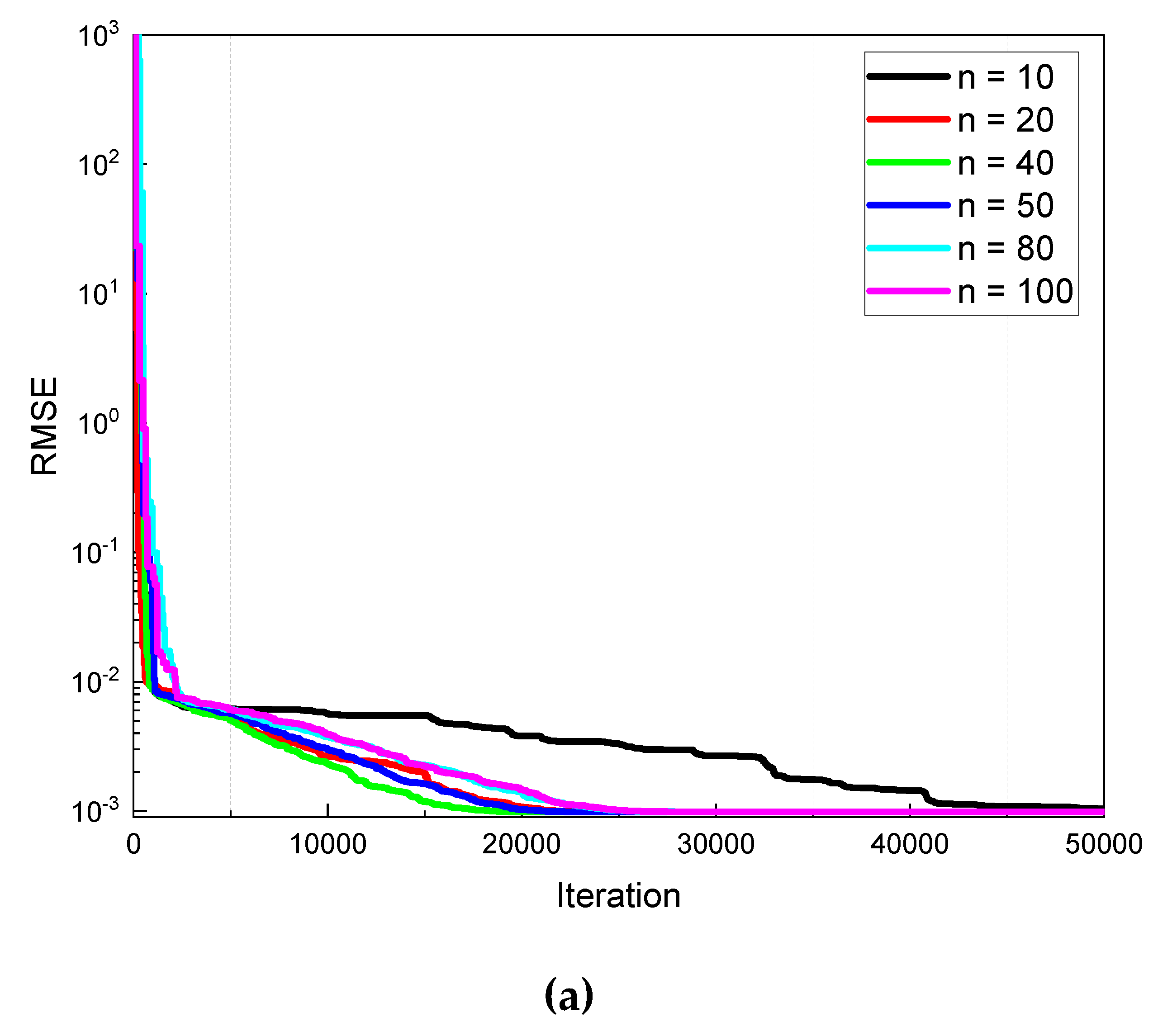
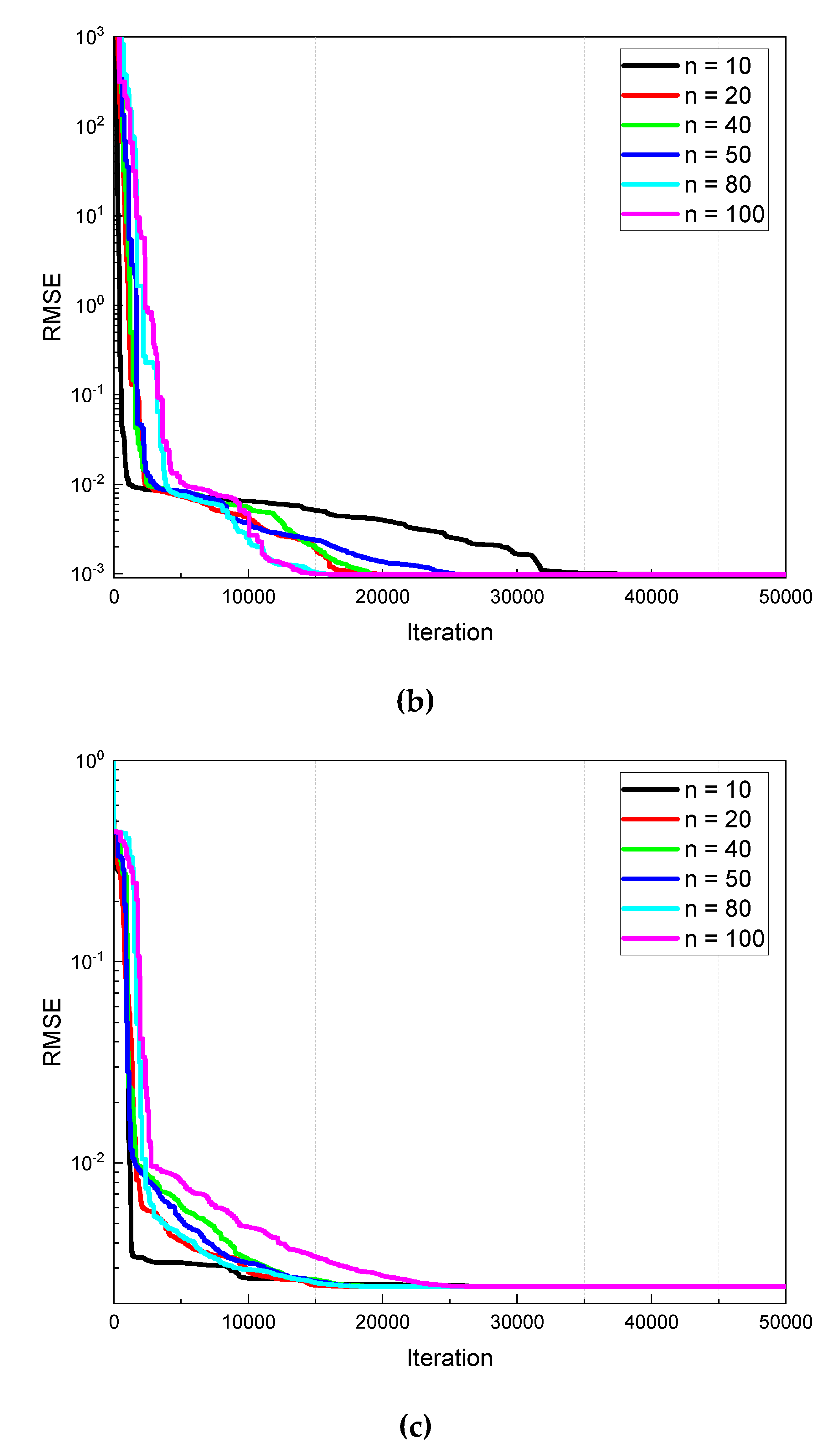
4.1. Population Size Analysis
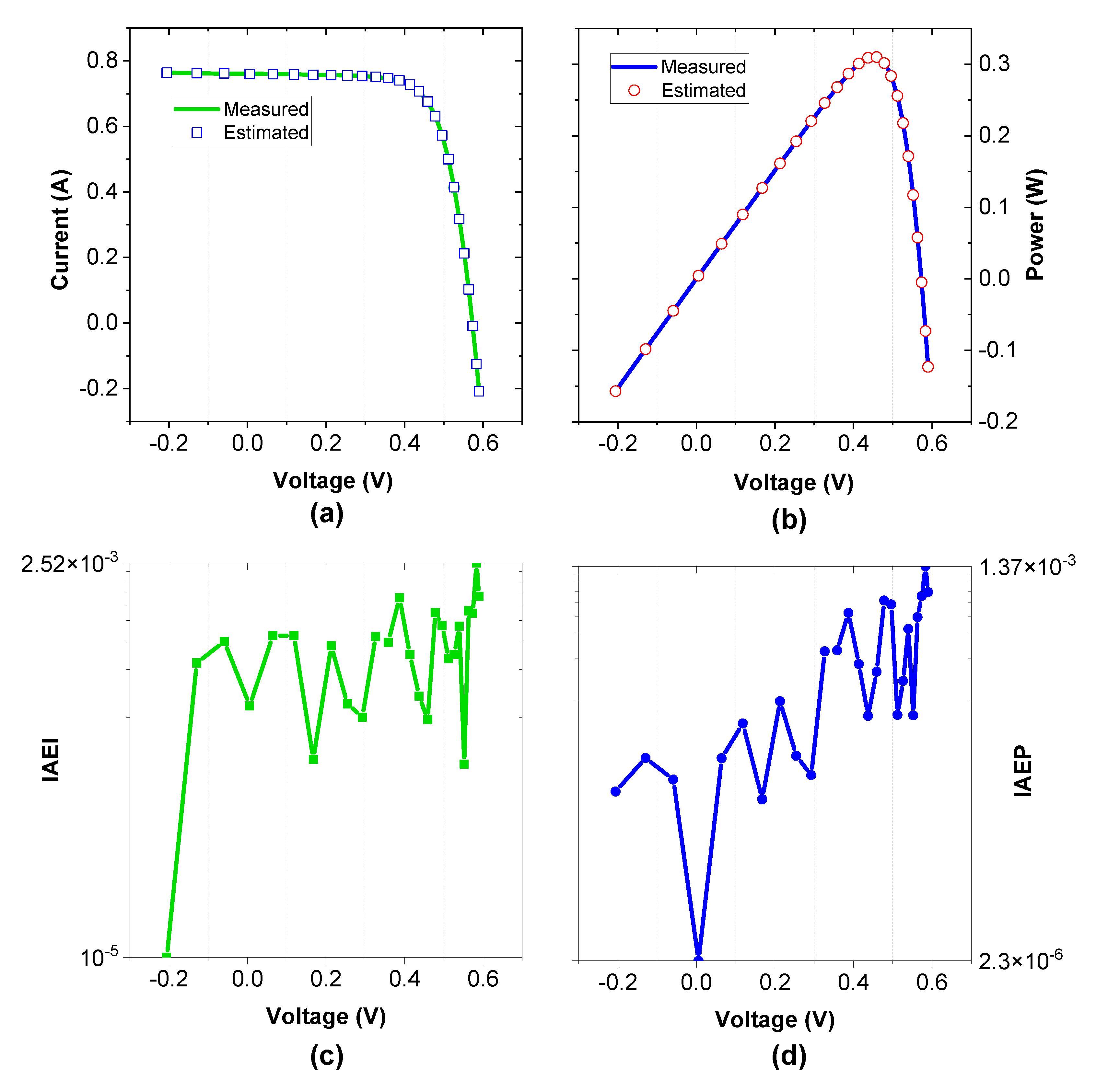
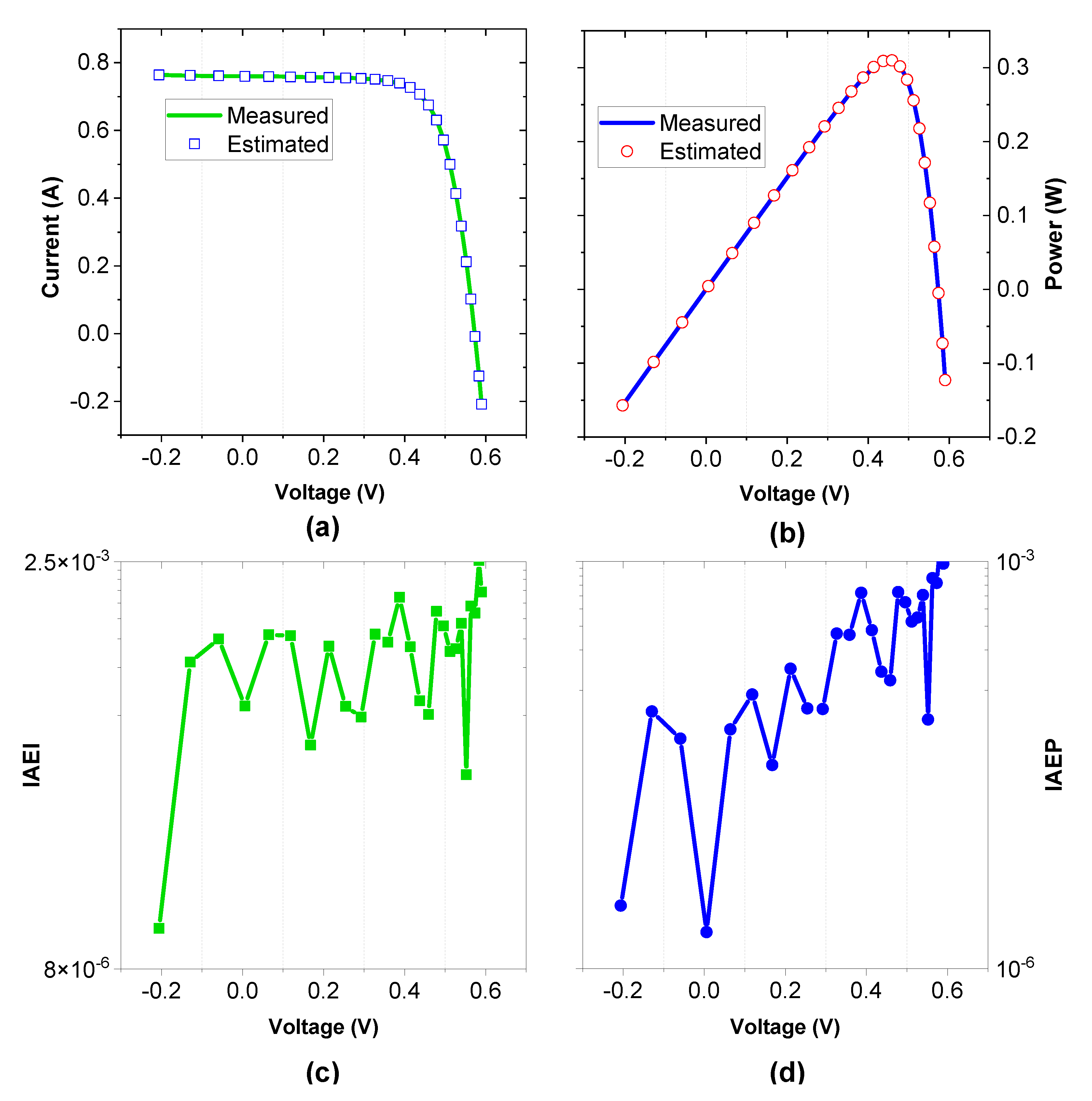
4.2. Results of Parameter Extraction Based on SDM
4.3. Results of Parameter Extraction Based on DDM
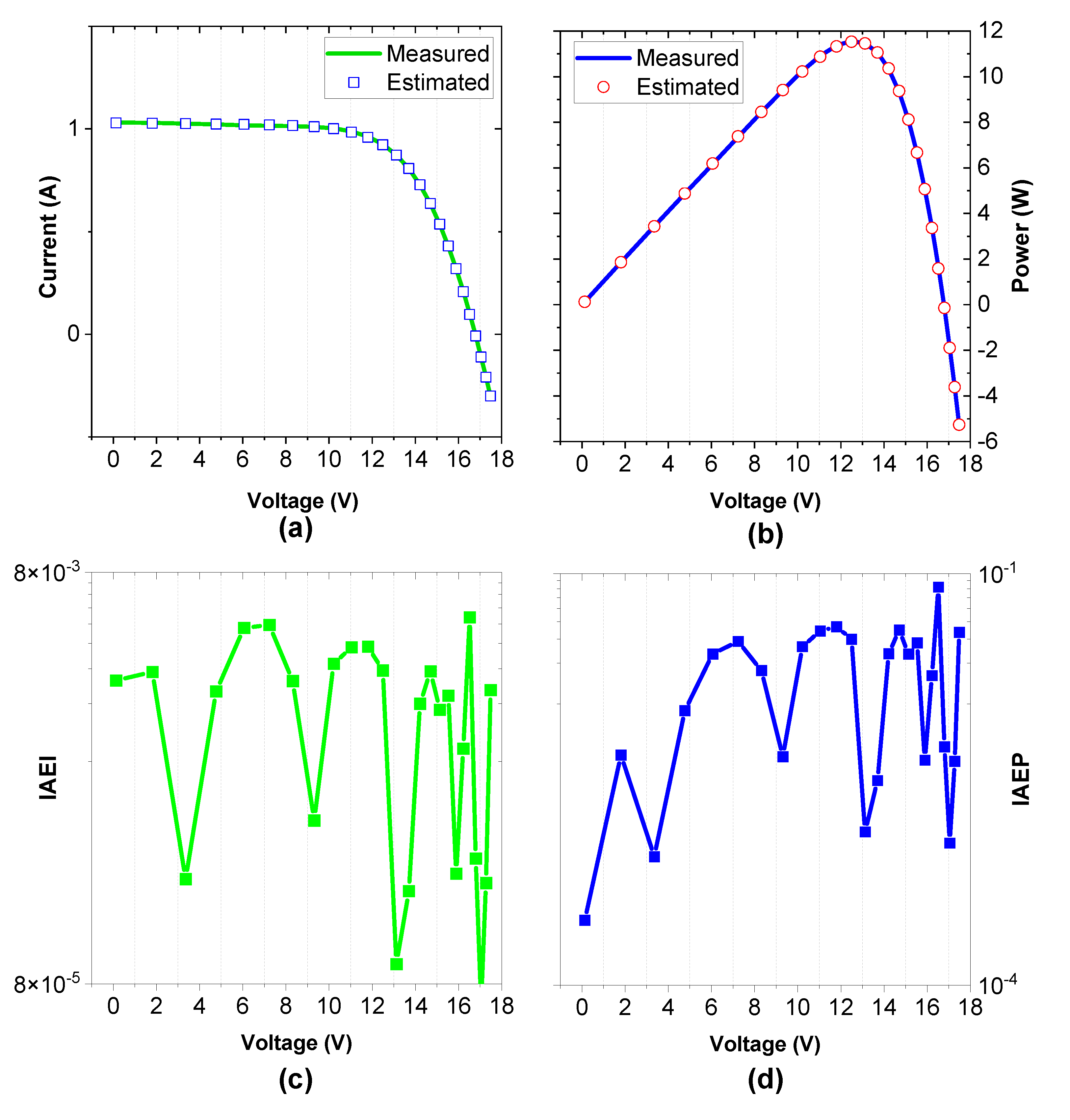
4.4. PVMM-Based Photo Watt-PWP 201
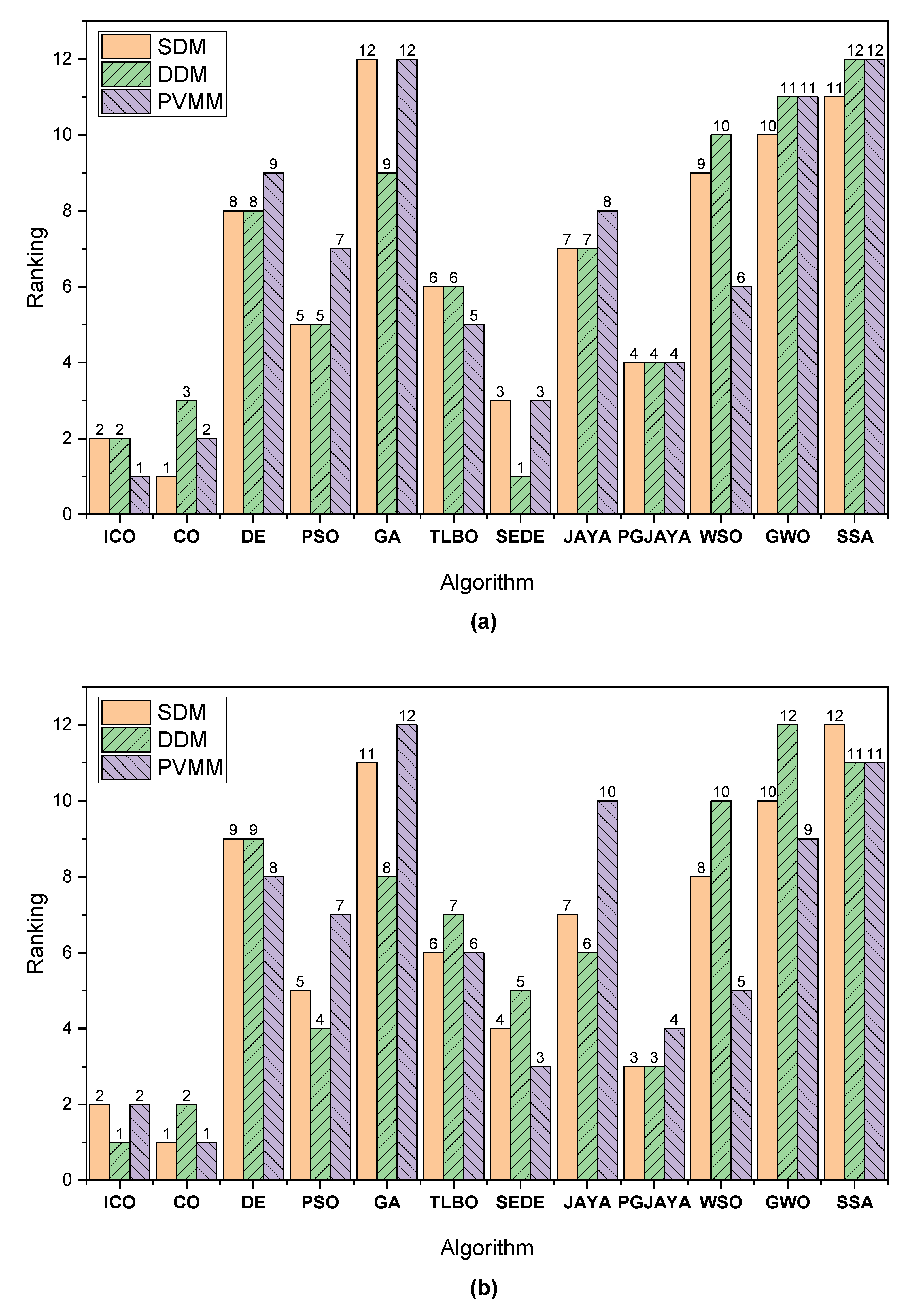
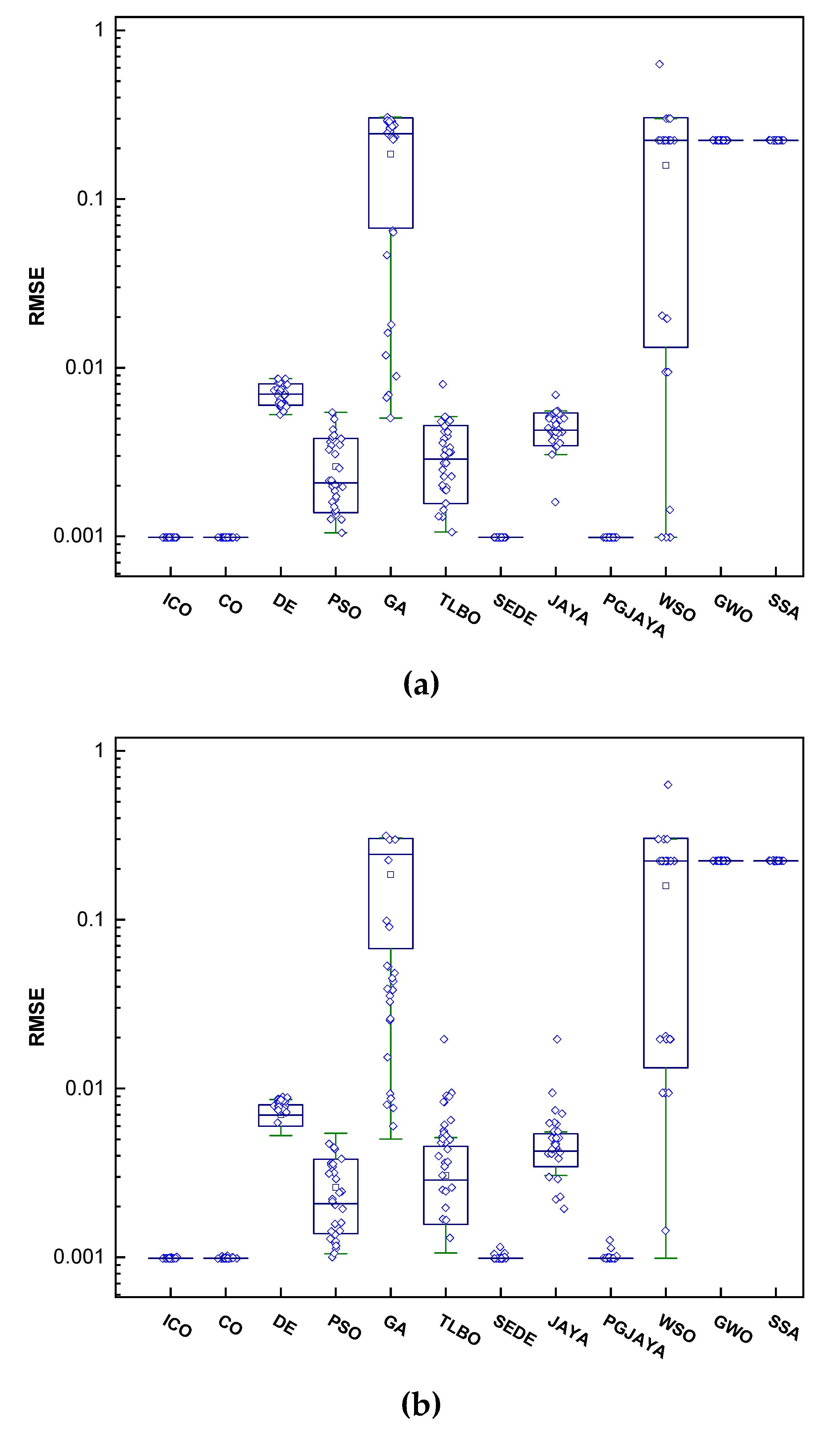
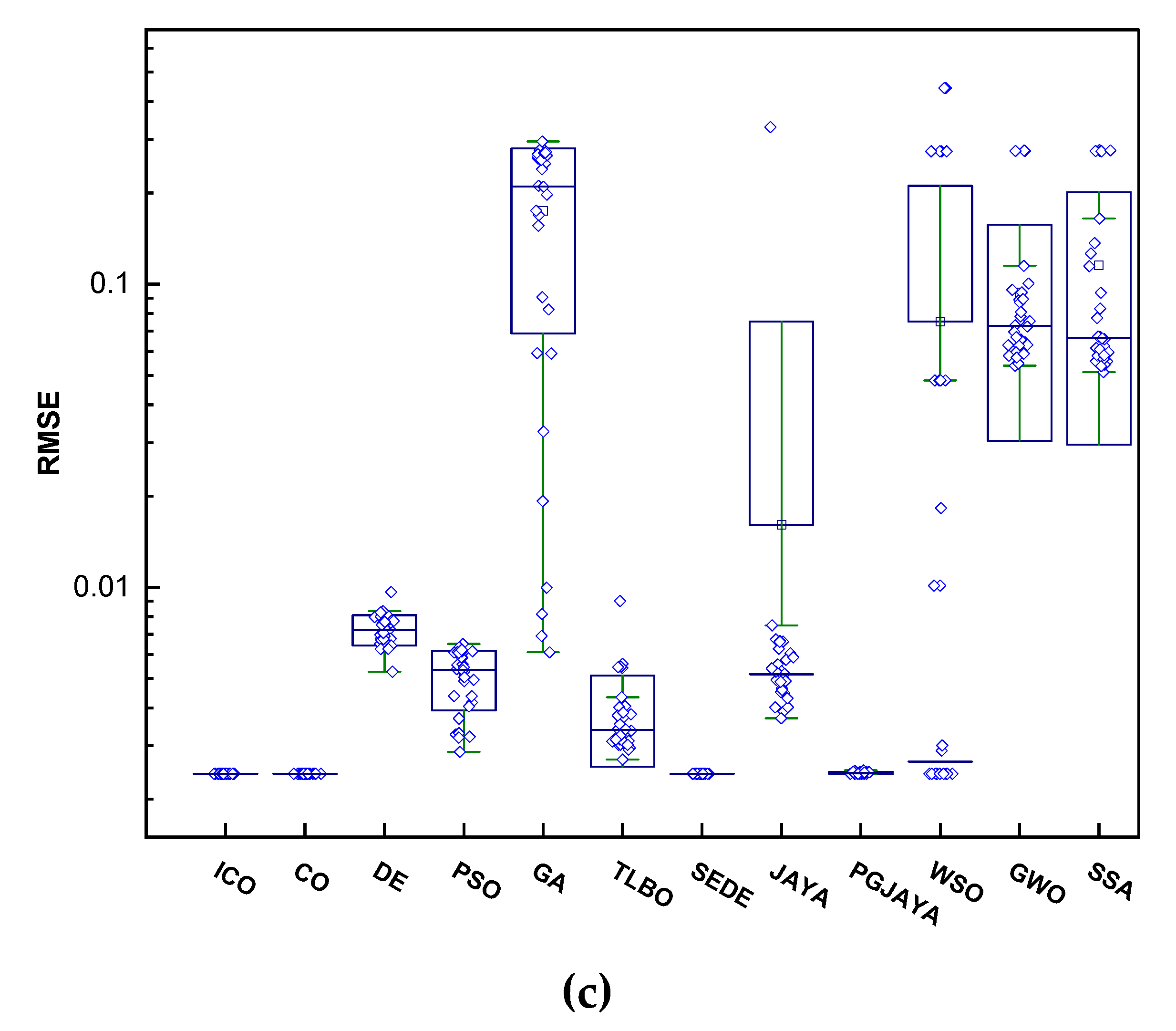
4.5. Comparison of Statistical Results
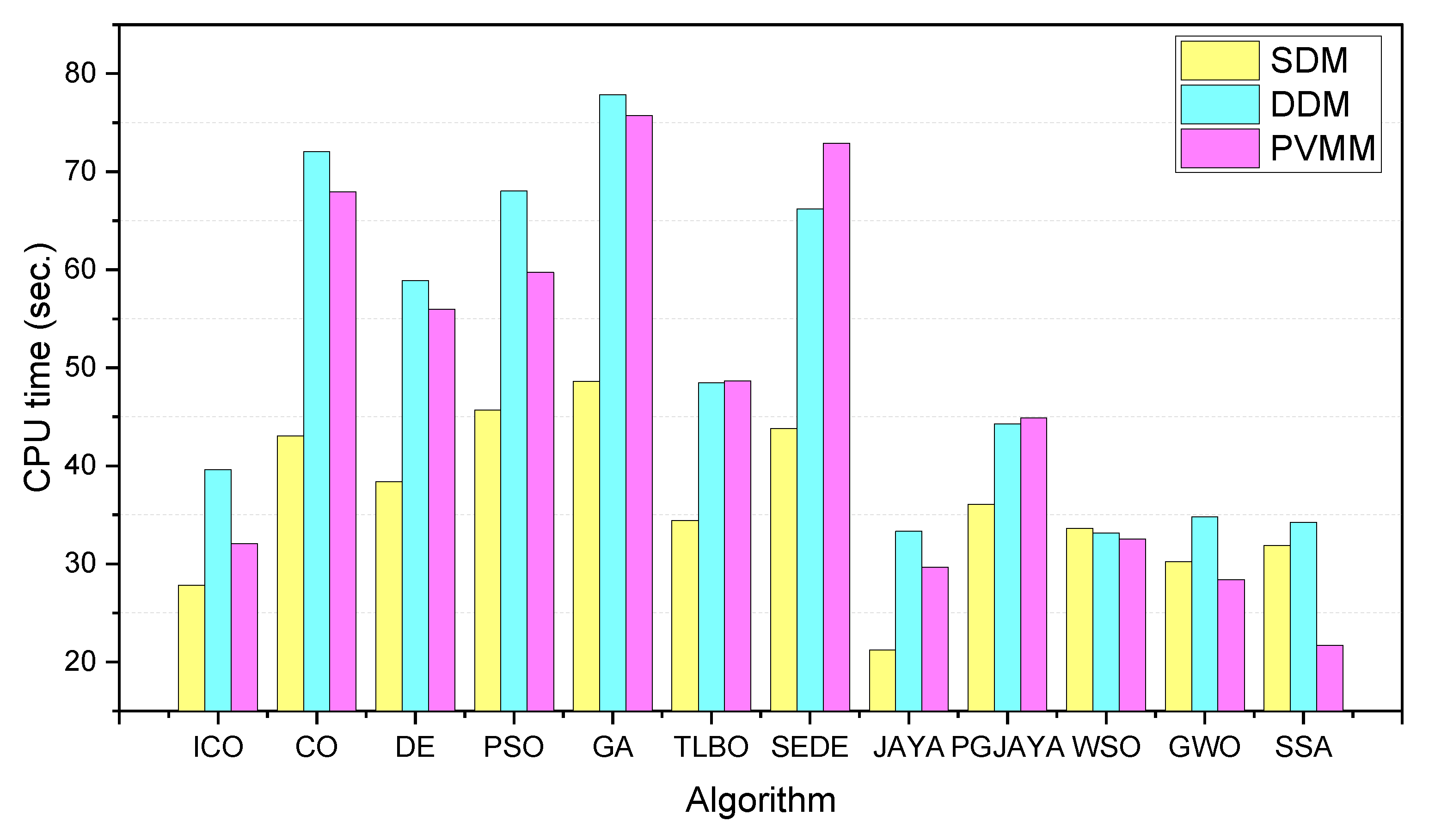
4.6. Computational Time
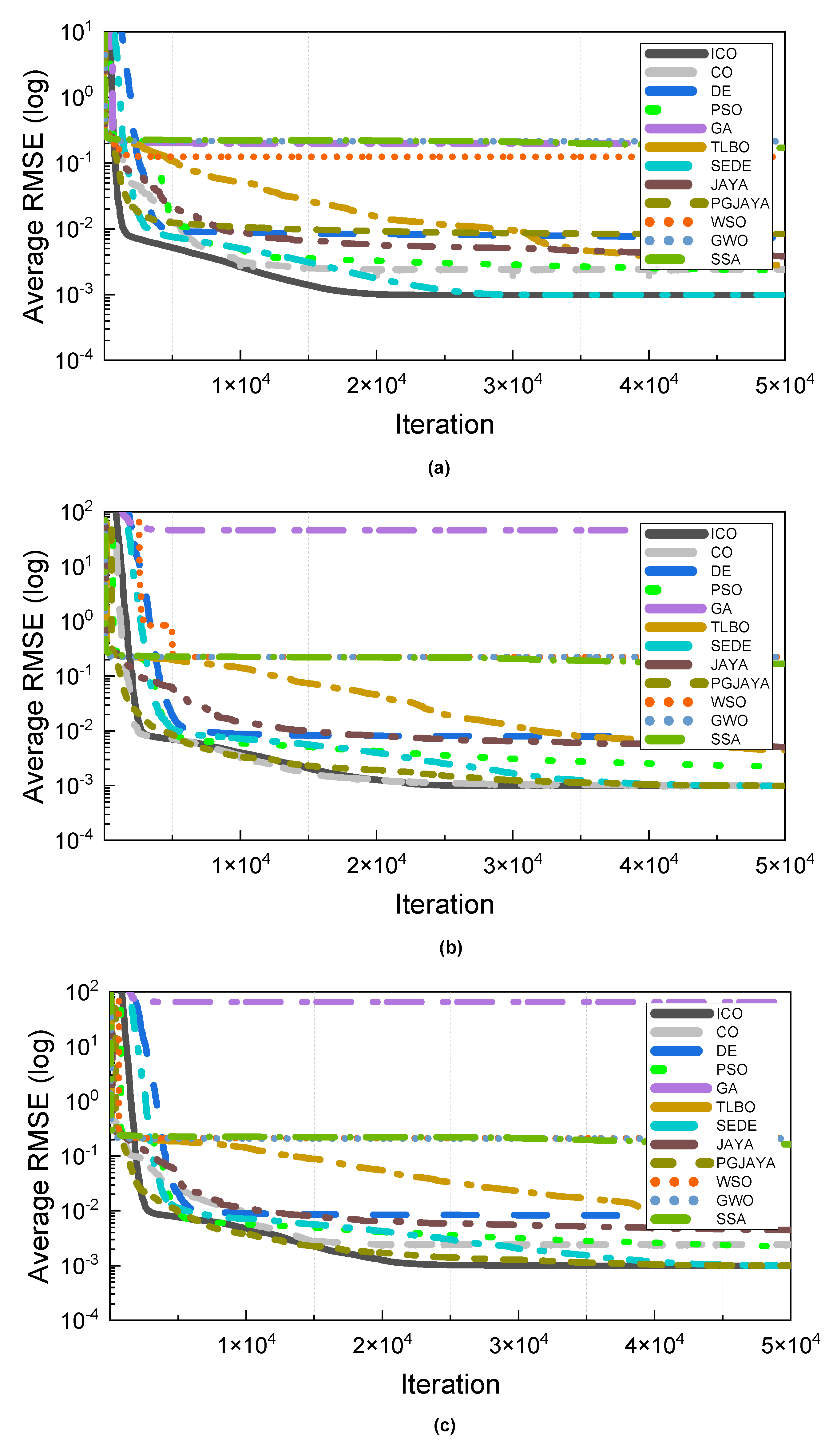
4.7. Convergence Characteristics
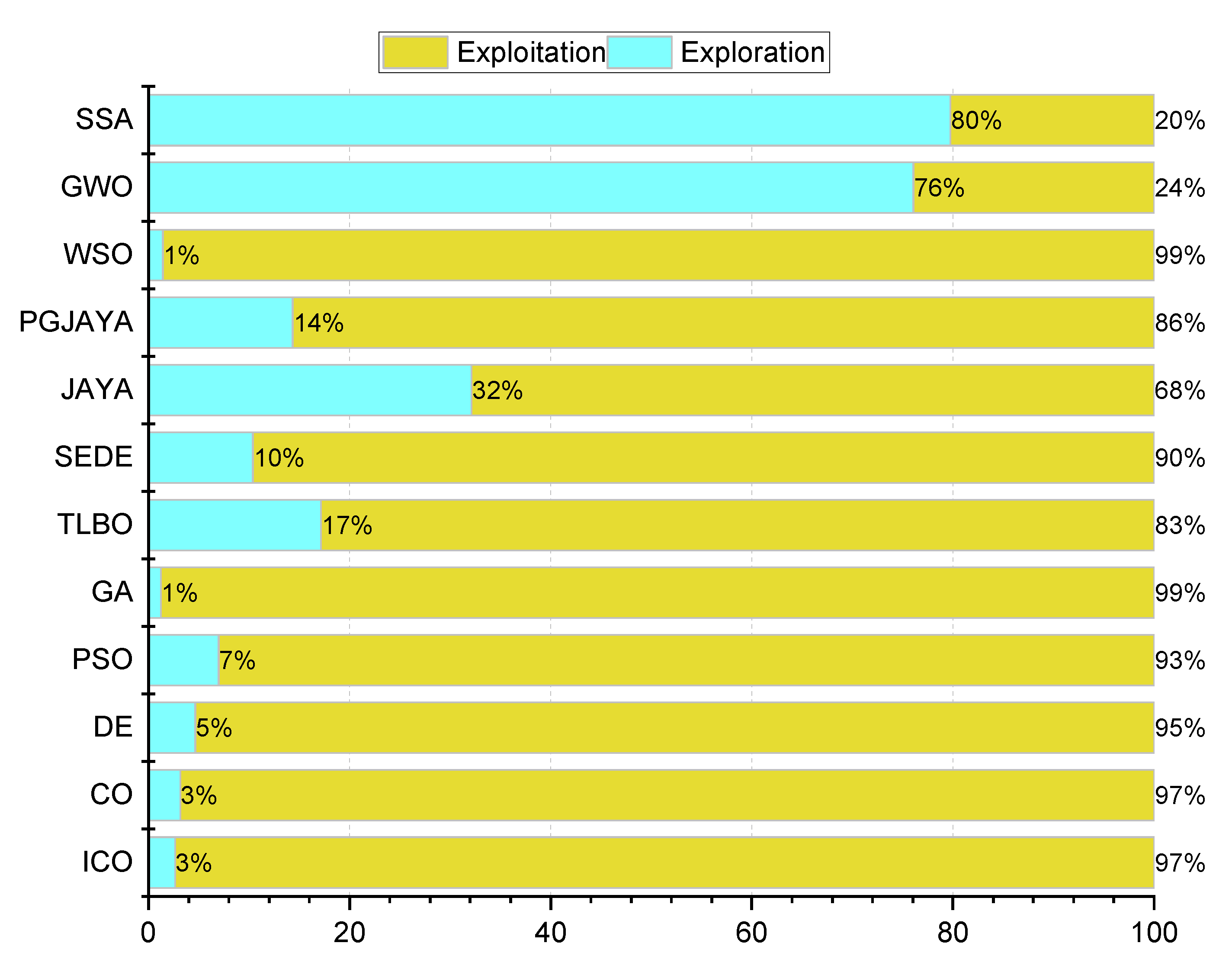
4.8. Exploration and Exploitation Analysis
5. Conclusion
Acknowledgments
References
- Sheng, R.; Du, J.; Liu, S.; Wang, C.; Wang, Z.; Liu, X. Solar Photovoltaic Investment Changes across China Regions Using a Spatial Shift-Share Analysis. Energies 2021, 14, 6418. [Google Scholar] [CrossRef]
- Chen, H.; Jiao, S.; Heidari, A.A.; Wang, M.; Chen, X.; Zhao, X. An opposition-based sine cosine approach with local search for parameter estimation of photovoltaic models. Energy Convers. Manag. 2019, 195, 927–942. [Google Scholar] [CrossRef]
- Jiang, L.L.; Maskell, D.L.; Patra, J.C. Parameter Estimation of Solar Cells and Modules Using an Improved Adaptive Differential Evolution Algorithm. Appl. Energy 2013, 112, 185–193. [Google Scholar] [CrossRef]
- Rasheduzzaman, M.; Fajri, P.; Kimball, J.; Deken, B. Modeling, Analysis, and Control Design of a Single-Stage Boost Inverter. Energies 2021, 14, 4098. [Google Scholar] [CrossRef]
- Yu, K.; Chen, X.; Wang, X.; Wang, Z. Parameters identification of photovoltaic models using self-adaptive teaching-learning-based optimization. Energy Convers. Manag. 2017, 145, 233–246. [Google Scholar] [CrossRef]
- Yu, K.; Qu, B.; Yue, C.; Ge, S.; Chen, X.; Liang, J. A performance-guided JAYA algorithm for parameters identification of photovoltaic cell and module. Appl. Energy 2019, 237, 241–257. [Google Scholar] [CrossRef]
- Mehta, H.K.; Warke, H.; Kukadiya, K.; Panchal, A.K. Accurate Expressions for Single-Diode-Model Solar Cell Parameterization. IEEE J. Photovolt. 2019, 9, 803–810. [Google Scholar] [CrossRef]
- Hejri, M.; Mokhtari, H.; Azizian, M.R.; Ghandhari, M.; Soder, L. On the Parameter Extraction of a Five-Parameter Double-Diode Model of Photovoltaic Cells and Modules. IEEE J. Photovoltaics 2014, 4, 915–923. [Google Scholar] [CrossRef]
- Chin, V.J.; Salam, Z. A New Three-point-based Approach for the Parameter Extraction of Photovoltaic Cells. Appl. Energy 2019, 237, 519–533. [Google Scholar] [CrossRef]
- Ishaque, K.; Salam, Z. An improved modeling method to determine the model parameters of photovoltaic (PV) modules using differential evolution (DE). Sol. Energy 2011, 85, 2349–2359. [Google Scholar] [CrossRef]
- Dali, A.; Bouharchouche, A.; Diaf, S. Parameter Identification of Photovoltaic Cell/Module Using Genetic Algorithm (GA) and Particle Swarm Optimization (PSO). In Proceedings of the 2015 3rd International Conference on Control, Engineering & Information Technology (CEIT); IEEE, 2015; pp. 1–6. [CrossRef]
- Khanna, V.; Das, B.; Bisht, D.; Vandana; Singh, P. A three diode model for industrial solar cells and estimation of solar cell parameters using PSO algorithm. Renew. Energy 2015, 78, 105–113. [Google Scholar] [CrossRef]
- Ayyarao, T.L.V.; Kumar, P.P. Parameter estimation of solar PV models with a new proposed war strategy optimization algorithm. Int. J. Energy Res. 2022, 46, 7215–7238. [Google Scholar] [CrossRef]
- Liang, J.; Qiao, K.; Yu, K.; Ge, S.; Qu, B.; Xu, R.; Li, K. Parameters estimation of solar photovoltaic models via a self-adaptive ensemble-based differential evolution. Sol. Energy 2020, 207, 336–346. [Google Scholar] [CrossRef]
- Abbassi, R.; Abbassi, A.; Heidari, A.A.; Mirjalili, S. An efficient salp swarm-inspired algorithm for parameters identification of photovoltaic cell models. Energy Convers. Manag. 2019, 179, 362–372. [Google Scholar] [CrossRef]
- Yu, K.; Liang, J.; Qu, B.; Chen, X.; Wang, H. Parameters identification of photovoltaic models using an improved JAYA optimization algorithm. Energy Convers. Manag. 2017, 150, 742–753. [Google Scholar] [CrossRef]
- Premkumar, M.; Babu, T.S.; Umashankar, S.; Sowmya, R. A new metaphor-less algorithms for the photovoltaic cell parameter estimation. Optik 2020, 208, 164559. [Google Scholar] [CrossRef]
- Jamadi, M.; Merrikh-Bayat, F.; Bigdeli, M. Very accurate parameter estimation of single- and double-diode solar cell models using a modified artificial bee colony algorithm. Int. J. Energy Environ. Eng. 2016, 7, 13–25. [Google Scholar] [CrossRef]
- Sheng, H.; Li, C.; Wang, H.; Yan, Z.; Xiong, Y.; Cao, Z.; Kuang, Q. Parameters Extraction of Photovoltaic Models Using an Improved Moth-Flame Optimization. Energies 2019, 12, 3527. [Google Scholar] [CrossRef]
- Hasanien, H.M. Shuffled Frog Leaping Algorithm for Photovoltaic Model Identification. IEEE Trans. Sustain. Energy 2015, 6, 509–515. [Google Scholar] [CrossRef]
- Liao, Z.; Chen, Z.; Li, S. Parameters Extraction of Photovoltaic Models Using Triple-Phase Teaching-Learning-Based Optimization. IEEE Access 2020, 8, 69937–69952. [Google Scholar] [CrossRef]
- Oliva, D.; Abd El Aziz, M.; Hassanien, A.E. Parameter estimation of photovoltaic cells using an improved chaotic whale optimization algorithm. Appl. Energy 2017, 200, 141–154. [Google Scholar] [CrossRef]
- Montoya, O.D.; Gil-González, W.; Grisales-Noreña, L.F. Sine-Cosine Algorithm for Parameters’ Estimation in Solar Cells Using Datasheet Information. In Proceedings of the Journal of Physics: Conference Series; IOP Publishing, 2020; Vol. 1671, p. 12008.
- Long, W.; Cai, S.; Jiao, J.; Xu, M.; Wu, T. A new hybrid algorithm based on grey wolf optimizer and cuckoo search for parameter extraction of solar photovoltaic models. Energy Convers. Manag. 2020, 203, 112243. [Google Scholar] [CrossRef]
- Diab, A.A.Z.; Sultan, H.M.; Do, T.D.; Kamel, O.M.; Mossa, M.A. Coyote Optimization Algorithm for Parameters Estimation of Various Models of Solar Cells and PV Modules. IEEE Access 2020, 8, 111102–111140. [Google Scholar] [CrossRef]
- Soliman, M.A.; Hasanien, H.M.; Alkuhayli, A. Marine Predators Algorithm for Parameters Identification of Triple-Diode Photovoltaic Models. IEEE Access 2020, 8, 155832–155842. [Google Scholar] [CrossRef]
- Kumari, P.A.; Geethanjali, P. Adaptive Genetic Algorithm Based Multi-Objective Optimization for Photovoltaic Cell Design Parameter Extraction. Energy Procedia 2017, 117, 432–441. [Google Scholar] [CrossRef]
- Abdel-Basset, M.; Mohamed, R.; Mirjalili, S.; Chakrabortty, R.K.; Ryan, M.J. Solar photovoltaic parameter estimation using an improved equilibrium optimizer. Sol. Energy 2020, 209, 694–708. [Google Scholar] [CrossRef]
- Kumar, C.; Premkumar, M.; Raj, T.D. A new stochastic slime mould optimization algorithm for the estimation of solar photovoltaic cell parameters. Optik 2020, 223, 165277. [Google Scholar] [CrossRef]
- Jiao, S.; Chong, G.; Huang, C.; Hu, H.; Wang, M.; Heidari, A.A.; Chen, H.; Zhao, X. Orthogonally adapted Harris hawks optimization for parameter estimation of photovoltaic models. Energy 2020, 203, 117804. [Google Scholar] [CrossRef]
- Wolpert, D.H.; Macready, W.G. No free lunch theorems for optimization. IEEE Trans. Evol. Comput. 1997, 1, 67–82. [Google Scholar] [CrossRef]
- Akbari, M.A.; Zare, M.; Azizipanah-Abarghooee, R.; Mirjalili, S.; Deriche, M. The cheetah optimizer: a nature-inspired metaheuristic algorithm for large-scale optimization problems. Sci. Rep. 2022, 12, 1–20. [Google Scholar] [CrossRef]
- Storn, R.; Price, K. Differential evolution—A simple and efficient heuristic for global optimization over continuous spaces. J. Glob. Optim. 1997, 11, 341–359. [Google Scholar] [CrossRef]
- Kennedy, J.; Eberhart, R. Particle Swarm Optimization. In Proceedings of the Proceedings of ICNN’95-international conference on neural networks; IEEE, 1995; Vol. 4, pp. 1942–1948.
- Mitchell, M. An Introduction to Genetic Algorithms; MIT press, 1998.
- Rao, R.; Savsani, V.; Vakharia, D. Teaching–Learning-Based Optimization: An optimization method for continuous non-linear large scale problems. Inf. Sci. 2012, 183, 1–15. [Google Scholar] [CrossRef]
- Rao, R.V. Jaya: A simple and new optimization algorithm for solving constrained and unconstrained optimization problems. Int. J. Ind. Eng. Comput. 2016, 7, 19–34. [Google Scholar] [CrossRef]
- Mirjalili, S.; Gandomi, A.H.; Mirjalili, S.Z.; Saremi, S.; Faris, H.; Mirjalili, S.M. Salp Swarm Algorithm: A Bio-Inspired Optimizer for Engineering Design Problems. Adv. Eng. Softw. 2017, 114, 163–191. [Google Scholar] [CrossRef]
- Mirjalili, S.; Mirjalili, S.M.; Lewis, A. Grey Wolf Optimizer. Adv. Eng. Softw. 2014, 69, 46–61. [Google Scholar] [CrossRef]
- AlRashidi, M.; AlHajri, M.; El-Naggar, K.; Al-Othman, A. A new estimation approach for determining the I–V characteristics of solar cells. Sol. Energy 2011, 85, 1543–1550. [Google Scholar] [CrossRef]
- Easwarakhanthan, T.; Bottin, J.; Bouhouch, I.; Boutrit, C. Nonlinear Minimization Algorithm for Determining the Solar Cell Parameters with Microcomputers. Int. J. Sol. Energy 1986, 4, 1–12. [Google Scholar] [CrossRef]
- Hussain, K.; Salleh, M.N.M.; Cheng, S.; Shi, Y. On the exploration and exploitation in popular swarm-based metaheuristic algorithms. Neural Comput. Appl. 2018, 31, 7665–7683. [Google Scholar] [CrossRef]

| Algorithm | PV Type | PV model | Disadvantage | Advantage |
|---|---|---|---|---|
| PGJAYA [6] | RTC France Si cell and PhotoWatt-PWP201 | SDM, DDM, PVMM | Insufficient reliability | Acceptable accuracy |
| DE [10] | SM55 Module | SDM | The parameters need to be adjusted Insufficient capability for exploitation |
Accurate performance under a variety of operating conditions Possessing good exploration capabilities |
| PSO [12] | Not specified | SDM, DDM | Stuck in local minima Convergence at the beginning |
High level of accuracy in the solution Ease of implementation Robustness |
| SEDE [14] | RTC France Si cell and PhotoWatt-PWP201 | SDM, DDM, PVMM | High computation time | High accuracy and robustness |
| WSO [13] | RTC France silicon solar cell, Photo watt-PWP 201, and STM6-40/36 PV modules | SDM, DDM, PVMM | Insufficient robustness | New optimization algorithm for parameter extraction of PV cells and modules, low CPU time |
| SSA [15] | TITAN-12-50 | DDM | Caught within local minimums Convergence occurs early in the process |
Low computational time |
| IJAYA [16] | RTC France Si cell | SDM, DDM | Caught by local minima Inaccurate solution |
A simpler and more efficient algorithm Convergence and robustness are high |
| Rao [17] | RTC France Si cell and PhotoWatt-PWP201 | SDM, DDM | Stuck in local minima Commercial modules haven't been tested |
Ease of implementation The ability to explore well |
| MABC [18] | RTC France Si cell | SDM, DDM | Excessive computation time Parameters need to be adjusted frequently Achieving convergence early |
High accuracy and robustness Insensitive to noise |
| IMFO [19] | Q6-1380 solar cell and CS6P-240P module | SDM, DDM | It takes a long time to compute Commercial modules have not been tested |
Convergence speed is high It is simpler |
| SFLA [20] | KC200GT and MSX-60 | SDM | Not accurateA lot of control parameters | Fast convergence |
| TPTLBO [21] | RTC France Si cell | SDM, DDM | High computational costs Uncertainty about the solution |
Ease of implementation Fewer control parameters Fast convergence |
| ICWO [22] | KC200GT | SDM, DDM | Inability to explore Caught within local minimums Convergence occurs early in the process |
Easily implemented A lower cost of computationCapacity for fair exploitation |
| SCA [23] | KC200GT | SDM | KC200GT module only tested A local minimum trap |
Easy to implement and simple to use A fair degree of accuracy |
| GWO-CS [24] | KC200GT | SDM | The convergence speed is very slow |
A robust design Reduced possibility of local optima trapping The accuracy of the solution is high |
| COA [25] | RTC France Si cell, PhotoWatt-PWP201, KC200GT, ST40, and SM55 | SDM, DDM | Insufficient ability to exploit Convergence at an early stage |
The quality of the solution is high High convergence speed |
| MPA [26] | KC200GT and MSX-60 | DDM | Convergence at an early stage Stuck in local minima |
A high degree of accuracy in the solution Excel exploratory skills |
| AGA [27] | RTC France Si cell | SDM | Caught in the trap of local minima A lack of local search capability |
A reasonable degree of accuracy Identify promising search areas to find solutions |
| IEO [28] | RTC France Si cell, PhotoWatt-PWP201, ST40, and SM55 | SDM, DDM | Long computation times | High level of accuracy A good ability to explore and exploit |
| SMA [29] | RTC France Si cell and PhotoWatt-PWP201 | SDM, DDM | It takes a long time to compute | A high degree of accuracy A good ability to explore and exploit |
| OAHHO [30] | RTC France Si cell, PhotoWatt-PWP201, PVM 752 GaAs, ST40, and SM55 | SDM, DDM | Not specified | Rapid convergence rates Avoiding local optimum situations High-quality solutions |
| Model | |||||||||||||||
| Min | Max | Min | Max | Min | Max | Min | Max | Min | Max | ||||||
| SDM | 0 | 1 | 0 | 1 | 1 | 2 | 0 | 0.5 | 0 | 100 | |||||
| DDM | 0 | 1 | 0 | 1 | 1 | 2 | 0 | 0.5 | 0 | 100 | |||||
| PV module | 0 | 2 | 0 | 50 | 1 | 50 | 0 | 2 | 0 | 2000 | |||||
| Model | n | Min | Mean | Max | SD | CPU time (sec.) | Mean rank in the Freidman test | Sum rank in the Freidman test |
|---|---|---|---|---|---|---|---|---|
| SD | 10 | 9.860219E-04 | 1.006557E-03 | 1.268819E-03 | 5.47E-05 | 48.59 | 6.0 | 180 |
| 20 | 9.860219E-04 | 9.860219E-04 | 9.860219E-04 | 8.17E-17 | 48.02 | 3.6 | 106.5 | |
| 40 | 9.860219E-04 | 9.860219E-04 | 9.860219E-04 | 6.30E-17 | 37.42 | 2.6 | 76.5 | |
| 50 | 9.860219E-04 | 9.860219E-04 | 9.860219E-04 | 3.24E-17 | 40.23 | 2.5 | 74.5 | |
| 80 | 9.860219E-04 | 9.860219E-04 | 9.860219E-04 | 4.85E-17 | 41.11 | 2.9 | 87 | |
| 100 | 9.860219E-04 | 9.860219E-04 | 9.860219E-04 | 4.66E-17 | 50.89 | 3.5 | 105.5 | |
| DD | 10 | 9.849747E-04 | 1.046876E-03 | 1.199696E-03 | 5.90E-05 | 52.52 | 5.6 | 169 |
| 20 | 9.832470E-04 | 9.909079E-04 | 1.016172E-03 | 8.43E-06 | 55.21 | 3.9 | 116 | |
| 40 | 9.824888E-04 | 9.869534E-04 | 1.002805E-03 | 4.35E-06 | 53.12 | 2.9 | 87 | |
| 50 | 9.825601E-04 | 9.861925E-04 | 9.948859E-04 | 2.43E-06 | 50.93 | 3.0 | 90 | |
| 80 | 9.824849E-04 | 9.860955E-04 | 9.895027E-04 | 1.43E-06 | 38.32 | 2.6 | 78 | |
| 100 | 9.836909E-04 | 9.878873E-04 | 1.014303E-03 | 6.14E-06 | 36.53 | 3.0 | 90 | |
| PVM | 10 | 2.425075E-03 | 2.435752E-03 | 2.498069E-03 | 1.99E-05 | 48.36 | 6.0 | 180 |
| 20 | 2.425075E-03 | 2.425075E-03 | 2.425075E-03 | 2.14E-16 | 44.27 | 4.1 | 124 | |
| 40 | 2.425075E-03 | 2.425075E-03 | 2.425075E-03 | 1.24E-16 | 46.07 | 2.7 | 81 | |
| 50 | 2.425075E-03 | 2.425075E-03 | 2.425075E-03 | 3.65E-17 | 44.76 | 2.8 | 84.5 | |
| 80 | 2.425075E-03 | 2.425075E-03 | 2.425075E-03 | 2.65E-17 | 39.16 | 2.5 | 75 | |
| 100 | 2.425075E-03 | 2.425075E-03 | 2.425075E-03 | 3.17E-17 | 39.84 | 2.9 | 85.5 |
| n | Algorithm | RMSE | |||||
| 40 | ICO | 0.761 | 3.23E-07 | 53.719 | 0.0364 | 1.4812 | 9.860218778914E-04 |
| CO | 0.761 | 3.23E-07 | 53.719 | 0.0364 | 1.4812 | 9.860218778914E-04 | |
| DE | 0.763 | 3.18E-06 | 100.000 | 0.0243 | 1.7547 | 5.274028415510E-03 | |
| PSO | 0.761 | 2.67E-07 | 48.768 | 0.0371 | 1.4623 | 1.049908843005E-03 | |
| GA | 0.764 | 2.63E-06 | 70.532 | 0.0257 | 1.7285 | 5.028715197625E-03 | |
| TLBO | 0.761 | 3.77E-07 | 63.546 | 0.0358 | 1.4967 | 1.061394487359E-03 | |
| SEDE | 0.761 | 3.23E-07 | 53.719 | 0.0364 | 1.4812 | 9.860218778915E-04 | |
| JAYA | 0.761 | 6.08E-07 | 70.138 | 0.0337 | 1.5478 | 1.596303286167E-03 | |
| PGJAYA | 0.761 | 3.23E-07 | 53.713 | 0.0364 | 1.4812 | 9.860219332331E-04 | |
| WSO | 0.761 | 3.23E-07 | 53.719 | 0.0364 | 1.4812 | 9.860218778915E-04 | |
| GWO | 0.838 | 0.00E+00 | 1.139 | 0.0000 | 2.0000 | 2.228699161204E-01 | |
| SSA | 0.835 | 0.00E+00 | 1.162 | 0.0000 | 1.0000 | 2.228762271791E-01 | |
| 80 | ICO | 0.761 | 3.23E-07 | 53.719 | 0.0364 | 1.4812 | 9.860218778914E-04 |
| CO | 0.761 | 3.23E-07 | 53.719 | 0.0364 | 1.4812 | 9.860218778914E-04 | |
| DE | 0.763 | 1.54E-06 | 99.600 | 0.0296 | 1.6569 | 3.541687987531E-03 | |
| PSO | 0.761 | 3.54E-07 | 56.556 | 0.0360 | 1.4903 | 1.001530647734E-03 | |
| GA | 0.759 | 1.29E-07 | 46.427 | 0.0399 | 1.3938 | 2.248309383635E-03 | |
| TLBO | 0.761 | 3.40E-07 | 55.608 | 0.0362 | 1.4865 | 9.917684200620E-04 | |
| SEDE | 0.761 | 3.36E-07 | 54.054 | 0.0362 | 1.4852 | 9.902825250634E-04 | |
| JAYA | 0.762 | 9.73E-07 | 88.523 | 0.0312 | 1.6013 | 2.589835639165E-03 | |
| PGJAYA | 0.761 | 3.23E-07 | 53.722 | 0.0364 | 1.4812 | 9.860220454267E-04 | |
| WSO | 0.761 | 3.23E-07 | 53.719 | 0.0364 | 1.4812 | 9.860218778915E-04 | |
| GWO | 0.769 | 4.43E-06 | 24.455 | 0.0200 | 1.8059 | 9.281563258264E-03 | |
| SSA | 1.000 | 8.72E-07 | 1.098 | 0.0007 | 1.6512 | 1.525312427660E-01 |
| n | Algorithm | RMSE | |||||||
| 40 | ICO | 0.760781 | 7.46E-07 | 2.26E-07 | 0.036740 | 55.456 | 2.000 | 1.4511 | 9.82486099138E-04 |
| CO | 0.760781 | 7.50E-07 | 2.26E-07 | 0.036741 | 55.486 | 2.000 | 1.4510 | 9.82484882272E-04 | |
| DE | 0.764966 | 2.55E-06 | 2.40E-06 | 0.022457 | 100.000 | 1.752 | 1.9806 | 6.28139269321E-03 | |
| PSO | 0.760733 | 1.71E-07 | 1.46E-06 | 0.036757 | 61.054 | 1.429 | 2.0000 | 1.00247341473E-03 | |
| GA | 0.763271 | 0.00E+00 | 4.23E-06 | 0.022775 | 97.844 | 1.670 | 1.7963 | 5.99279194424E-03 | |
| TLBO | 0.760090 | 9.73E-08 | 2.76E-06 | 0.036975 | 100.000 | 1.387 | 1.9994 | 1.30300020067E-03 | |
| SEDE | 0.760769 | 2.14E-07 | 8.07E-07 | 0.036790 | 55.795 | 1.447 | 1.9869 | 9.82753663536E-04 | |
| JAYA | 0.759873 | 5.29E-07 | 4.02E-11 | 0.034438 | 70.729 | 1.532 | 1.8894 | 1.93867560984E-03 | |
| PGJAYA | 0.760782 | 2.45E-07 | 2.90E-07 | 0.036477 | 54.289 | 1.999 | 1.4720 | 9.84193519571E-04 | |
| WSO | 0.759500 | 4.52E-07 | 0.00E+00 | 0.035285 | 100.000 | 1.516 | 2.0000 | 1.43847589737E-03 | |
| GWO | 1.000000 | 0.00E+00 | 1.16E-05 | 0.000000 | 2.179 | 1.000 | 2.0000 | 1.54903625180E-01 | |
| SSA | 0.834308 | 0.00E+00 | 0.00E+00 | 0.000000 | 1.152 | 1.000 | 1.0000 | 2.22868413284E-01 | |
| 80 | ICO | 0.760780 | 6.63E-07 | 2.36E-07 | 0.036695 | 55.257 | 2.000 | 1.4547 | 9.82538943274E-04 |
| CO | 0.760781 | 2.22E-07 | 7.72E-07 | 0.036757 | 55.539 | 1.450 | 1.9969 | 9.82528425982E-04 | |
| DE | 0.763865 | 5.19E-08 | 9.13E-06 | 0.023974 | 99.963 | 1.407 | 1.9937 | 6.73013079580E-03 | |
| PSO | 0.760797 | 6.03E-07 | 2.03E-07 | 0.036852 | 54.797 | 1.900 | 1.4430 | 9.84648707354E-04 | |
| GA | 0.760727 | 0.00E+00 | 9.74E-07 | 0.031507 | 100.000 | 1.681 | 1.6015 | 2.39573932360E-03 | |
| TLBO | 0.760754 | 3.22E-07 | 5.04E-17 | 0.036453 | 55.423 | 1.481 | 1.0230 | 9.95677091382E-04 | |
| SEDE | 0.760178 | 8.63E-07 | 2.07E-07 | 0.034961 | 82.980 | 1.806 | 1.4577 | 1.47037750973E-03 | |
| JAYA | 0.761997 | 1.39E-06 | 0.00E+00 | 0.028824 | 100.000 | 1.644 | 2.0000 | 3.57709882707E-03 | |
| PGJAYA | 0.760851 | 5.18E-07 | 2.30E-07 | 0.036667 | 54.633 | 1.917 | 1.4533 | 9.84200147988E-04 | |
| WSO | 0.760776 | 0.00E+00 | 3.23E-07 | 0.036377 | 53.719 | 2.000 | 1.4812 | 9.86021877892E-04 | |
| GWO | 0.999003 | 0.00E+00 | 5.29E-06 | 0.000514 | 1.373 | 2.000 | 1.8772 | 1.38743574369E-01 | |
| SSA | 0.836762 | 1.17E-09 | 0.00E+00 | 0.000071 | 1.149 | 1.121 | 1.4507 | 1.57126305055E-01 |
| n | Algorithm | RMSE | |||||
| 40 | ICO | 1.03051 | 3.48E-06 | 27.277 | 0.0334 | 1.3512 | 2.425074868095030E-03 |
| CO | 1.03051 | 3.48E-06 | 27.277 | 0.0334 | 1.3512 | 2.425074868094980E-03 | |
| DE | 1.02991 | 1.49E-05 | 1065.617 | 0.0284 | 1.5261 | 5.266650305240960E-03 | |
| PSO | 1.02677 | 5.98E-06 | 88.261 | 0.0318 | 1.4111 | 2.864391667859010E-03 | |
| GA | 1.02370 | 1.52E-05 | 1944.805 | 0.0278 | 1.5294 | 6.099240455880790E-03 | |
| TLBO | 1.02611 | 4.78E-06 | 75.270 | 0.0325 | 1.3855 | 2.700403640152360E-03 | |
| SEDE | 1.03051 | 3.48E-06 | 27.277 | 0.0334 | 1.3512 | 2.425074868095090E-03 | |
| JAYA | 1.02742 | 8.89E-06 | 911.208 | 0.0305 | 1.4586 | 3.697656950234140E-03 | |
| PGJAYA | 1.03052 | 3.48E-06 | 27.250 | 0.0334 | 1.3511 | 2.425077305006140E-03 | |
| WSO | 1.03051 | 3.48E-06 | 27.277 | 0.0334 | 1.3512 | 2.425074868095050E-03 | |
| GWO | 1.04843 | 5.00E-05 | 3.016 | 0.0000 | 1.7509 | 5.383466416567090E-02 | |
| SSA | 1.15116 | 5.00E-05 | 2.191 | 0.0129 | 1.7224 | 5.130174319081860E-02 | |
| 80 | ICO | 1.03051 | 3.48E-06 | 27.277 | 0.0334 | 1.3512 | 2.425074868095010E-03 |
| CO | 1.03051 | 3.48E-06 | 27.277 | 0.0334 | 1.3512 | 2.425074868094990E-03 | |
| DE | 1.02868 | 2.27E-05 | 1968.622 | 0.0264 | 1.5866 | 6.921126739647050E-03 | |
| PSO | 1.02664 | 6.66E-06 | 115.721 | 0.0314 | 1.4238 | 3.029451135597340E-03 | |
| GA | 1.03138 | 2.87E-05 | 2000.000 | 0.0252 | 1.6215 | 7.712963596737400E-03 | |
| TLBO | 1.02522 | 5.63E-06 | 881.405 | 0.0321 | 1.4034 | 3.244452302450550E-03 | |
| SEDE | 1.03013 | 3.56E-06 | 28.820 | 0.0333 | 1.3536 | 2.427164258722220E-03 | |
| JAYA | 1.02758 | 1.51E-05 | 1713.306 | 0.0277 | 1.5278 | 5.590302366807740E-03 | |
| PGJAYA | 1.02922 | 4.29E-06 | 33.745 | 0.0327 | 1.3739 | 2.518017787843970E-03 | |
| WSO | 1.03051 | 3.48E-06 | 27.277 | 0.0334 | 1.3512 | 2.425074868095060E-03 | |
| GWO | 1.07157 | 5.00E-05 | 5.528 | 0.0187 | 1.7213 | 2.019064583084870E-02 | |
| SSA | 1.06056 | 4.31E-05 | 12.652 | 0.0238 | 1.6888 | 1.554532543514840E-02 |
| n | Algorithm | Min | Mean | Max | SD | Mean rank | Sum rank | Significance |
|---|---|---|---|---|---|---|---|---|
| 40 | ICO | 9.86021877891E-04 | 9.86021877892E-04 | 9.86021877892E-04 | 3.091E-17 | 1.633 | 49 | |
| CO | 9.86021877891E-04 | 9.86021877892E-04 | 9.86021877893E-04 | 2.299E-16 | 1.600 | 48 | ||
| DE | 5.27402841551E-03 | 7.00472269280E-03 | 8.61400240318E-03 | 1.008E-03 | 8.200 | 246 | ||
| PSO | 1.04990884301E-03 | 2.59824261345E-03 | 5.43861383375E-03 | 1.215E-03 | 5.700 | 171 | ||
| GA | 5.02871519763E-03 | 1.85106717646E-01 | 3.05981702986E-01 | 1.178E-01 | 10.933 | 328 | ||
| TLBO | 1.06139448736E-03 | 3.05558085709E-03 | 7.98832352445E-03 | 1.489E-03 | 5.867 | 176 | ||
| SEDE | 9.86021877891E-04 | 9.86021877892E-04 | 9.86021877892E-04 | 4.368E-17 | 2.867 | 86 | ||
| JAYA | 1.59630328617E-03 | 4.42292722271E-03 | 6.90548939964E-03 | 9.777E-04 | 6.933 | 208 | ||
| PGJAYA | 9.86021933233E-04 | 9.86276195755E-04 | 9.89060476576E-04 | 6.385E-07 | 4.133 | 124 | ||
| WSO | 9.86021877892E-04 | 1.58438200609E-01 | 6.30741696212E-01 | 1.452E-01 | 8.733 | 262 | ||
| GWO | 2.22869916120E-01 | 2.23053219785E-01 | 2.23414777753E-01 | 1.541E-04 | 10.600 | 318 | ||
| SSA | 2.22876227179E-01 | 2.23093108473E-01 | 2.23798438512E-01 | 1.976E-04 | 10.800 | 324 | ||
| 80 | ICO | 9.86021877891E-04 | 9.86021877892E-04 | 9.86021877892E-04 | 5.21E-17 | 1.933 | 58 | |
| CO | 9.86021877891E-04 | 9.86021877891E-04 | 9.86021877892E-04 | 1.02E-16 | 1.267 | 38 | ||
| DE | 3.54168798753E-03 | 7.44468352091E-03 | 8.66642059402E-03 | 8.63E-04 | 8.233 | 247 | ||
| PSO | 1.00153064773E-03 | 2.60127712828E-03 | 4.82228315158E-03 | 1.30E-03 | 5.633 | 169 | ||
| GA | 2.24830938364E-03 | 1.73964495048E-01 | 2.97093810571E-01 | 9.96E-02 | 10.767 | 323 | ||
| TLBO | 9.91768420062E-04 | 5.34155103461E-03 | 1.97944235719E-02 | 4.83E-03 | 6.600 | 198 | ||
| SEDE | 9.90282525063E-04 | 1.01400153629E-03 | 1.09363977975E-03 | 2.20E-05 | 4.033 | 121 | ||
| JAYA | 2.58983563916E-03 | 5.68192621557E-03 | 9.00499477318E-03 | 1.14E-03 | 7.067 | 212 | ||
| PGJAYA | 9.86022045427E-04 | 1.01574698584E-03 | 1.18949290801E-03 | 4.93E-05 | 3.767 | 113 | ||
| WSO | 9.86021877892E-04 | 3.86485383212E-02 | 2.99953326338E-01 | 8.23E-02 | 7.233 | 217 | ||
| GWO | 9.28156325826E-03 | 2.08662190383E-01 | 2.22887009586E-01 | 5.41E-02 | 10.650 | 319.5 | ||
| SSA | 1.52531242766E-01 | 1.76192424924E-01 | 2.22861399093E-01 | 2.22E-02 | 10.817 | 324.5 |
| n | Algorithm | Min | Mean | Max | SD | Mean rank | Sum rank | Sign. |
|---|---|---|---|---|---|---|---|---|
| 40 | ICO | 9.82486099138221E-04 | 9.87266271841069E-04 | 1.00565345910251E-03 | 5.0E-06 | 2.400 | 72 | |
| CO | 9.82484882272263E-04 | 9.90014277022917E-04 | 1.02092378170200E-03 | 9.2E-06 | 2.667 | 80 | ||
| DE | 6.28139269320691E-03 | 8.08813241671442E-03 | 8.93742409284825E-03 | 5.8E-04 | 7.867 | 236 | ||
| PSO | 1.00247341473318E-03 | 2.42462675866429E-03 | 4.70972999662043E-03 | 1.2E-03 | 5.233 | 157 | ||
| GA | 5.99279194423828E-03 | 9.40346251766308E-02 | 3.14531449266952E-01 | 9.2E-02 | 9.533 | 286 | ||
| TLBO | 1.30300020066498E-03 | 5.31395638216597E-03 | 1.95451852804007E-02 | 3.5E-03 | 6.533 | 196 | ||
| SEDE | 9.82753663536365E-04 | 9.96916197397831E-04 | 1.15176160603947E-03 | 3.4E-05 | 2.133 | 64 | ||
| JAYA | 1.93867560984064E-03 | 5.30491570084624E-03 | 1.95452348011886E-02 | 3.1E-03 | 6.567 | 197 | ||
| PGJAYA | 9.84193519571165E-04 | 1.00336927015568E-03 | 1.26370280495224E-03 | 5.6E-05 | 2.867 | 86 | ||
| WSO | 1.43847589736749E-03 | 1.86584575264940E-01 | 6.30741696211904E-01 | 1.5E-01 | 9.967 | 299 | ||
| GWO | 1.54903625179668E-01 | 2.21100841293962E-01 | 2.24562995128955E-01 | 1.3E-02 | 11.067 | 332 | ||
| SSA | 2.22868413284217E-01 | 2.23443763002107E-01 | 2.24750772827690E-01 | 5.3E-04 | 11.167 | 335 | ||
| 80 | ICO | 9.8253894327E-04 | 9.8641995737E-04 | 9.9981923040E-04 | 3.134E-06 | 1.633 | 49 | |
| CO | 9.8252842598E-04 | 9.9825780367E-04 | 1.0827441957E-03 | 2.432E-05 | 1.900 | 57 | ||
| DE | 6.7301307958E-03 | 8.0618449324E-03 | 8.8108931833E-03 | 6.169E-04 | 7.933 | 238 | ||
| PSO | 9.8464870735E-04 | 2.3813391278E-03 | 5.5055357165E-03 | 1.184E-03 | 4.533 | 136 | ||
| GA | 2.3957393236E-03 | 2.2114853037E-02 | 1.1924927342E-01 | 3.269E-02 | 7.800 | 234 | ||
| TLBO | 9.9567709138E-04 | 1.8966303725E-02 | 6.2679374194E-02 | 1.887E-02 | 7.700 | 231 | ||
| SEDE | 1.4703775097E-03 | 2.6141249460E-03 | 4.0397037616E-03 | 8.191E-04 | 4.833 | 145 | ||
| JAYA | 3.5770988271E-03 | 6.7480847825E-03 | 9.7931015684E-03 | 1.726E-03 | 7.067 | 212 | ||
| PGJAYA | 9.8420014799E-04 | 1.0315913230E-03 | 1.3731176270E-03 | 7.747E-05 | 2.700 | 81 | ||
| WSO | 9.8602187789E-04 | 1.1327669684E-01 | 2.9995332634E-01 | 1.185E-01 | 9.700 | 291 | ||
| GWO | 1.3874357437E-01 | 1.6797247572E-01 | 2.2219565068E-01 | 1.317E-02 | 11.167 | 335 | ||
| SSA | 1.5712630505E-01 | 1.6563118085E-01 | 1.7878158052E-01 | 5.962E-03 | 11.033 | 331 |
| n | Algorithm | Min | Mean | Max | SD | Mean rank | Sum rank | Sign. |
|---|---|---|---|---|---|---|---|---|
| 40 | ICO | 2.4250748680950E-03 | 2.4250748680950E-03 | 2.4250748680950E-03 | 4.998E-17 | 1.917 | 57.5 | |
| CO | 2.4250748680950E-03 | 2.4250748680950E-03 | 2.4250748680950E-03 | 1.105E-16 | 1.983 | 59.5 | ||
| DE | 5.2666503052410E-03 | 7.2566226992670E-03 | 9.6379708296680E-03 | 8.375E-04 | 8.433 | 253 | ||
| PSO | 2.8643916678590E-03 | 5.0462723254080E-03 | 6.5034717549490E-03 | 1.123E-03 | 6.800 | 204 | ||
| GA | 6.0992404558810E-03 | 1.7462237365350E-01 | 2.9547389242870E-01 | 1.059E-01 | 11.000 | 330 | ||
| TLBO | 2.7004036401520E-03 | 3.8363781147850E-03 | 9.0053151975850E-03 | 1.277E-03 | 5.933 | 178 | ||
| SEDE | 2.4250748680950E-03 | 2.4250748680950E-03 | 2.4250748680950E-03 | 2.319E-17 | 2.833 | 85 | ||
| JAYA | 3.6976569502340E-03 | 1.6079498126920E-02 | 3.2966678818700E-01 | 5.923E-02 | 7.333 | 220 | ||
| PGJAYA | 2.4250773050060E-03 | 2.4419751596470E-03 | 2.4895343685670E-03 | 1.780E-05 | 4.467 | 134 | ||
| WSO | 2.4250748680950E-03 | 7.5247794485460E-02 | 4.4356045864950E-01 | 1.357E-01 | 6.100 | 183 | ||
| GWO | 5.3834664165670E-02 | 9.3745614784530E-02 | 2.7590077173170E-01 | 6.334E-02 | 10.633 | 319 | ||
| SSA | 5.1301743190820E-02 | 1.1525567589300E-01 | 2.7696629442010E-01 | 8.570E-02 | 10.567 | 317 | ||
| 80 | ICO | 2.4250748680950E-03 | 2.4250748680951E-03 | 2.4250748680952E-03 | 3.193E-17 | 2.083 | 62.5 | |
| CO | 2.4250748680950E-03 | 2.4250748680950E-03 | 2.4250748680952E-03 | 4.371E-17 | 1.300 | 39 | ||
| DE | 6.9211267396471E-03 | 8.2205499846706E-03 | 9.1644830901135E-03 | 5.053E-04 | 7.733 | 232 | ||
| PSO | 3.0294511355973E-03 | 5.6849600297253E-03 | 7.4169012983030E-03 | 1.083E-03 | 6.267 | 188 | ||
| GA | 7.7129635967374E-03 | 1.8430319719111E-01 | 4.0758844972356E-01 | 1.287E-01 | 10.533 | 316 | ||
| TLBO | 3.2444523024506E-03 | 5.3311216098958E-03 | 9.2734827389708E-03 | 1.343E-03 | 6.033 | 181 | ||
| SEDE | 2.4271642587222E-03 | 2.4987409190963E-03 | 2.6543169613205E-03 | 5.638E-05 | 3.533 | 106 | ||
| JAYA | 5.5903023668077E-03 | 6.1914139863795E-02 | 1.2797477931005E-01 | 3.926E-02 | 9.800 | 294 | ||
| PGJAYA | 2.5180177878440E-03 | 2.8115756633088E-03 | 3.0907794548476E-03 | 1.572E-04 | 4.533 | 136 | ||
| WSO | 2.4250748680951E-03 | 9.1707088610467E-02 | 4.4400407477152E-01 | 1.376E-01 | 5.983 | 179.5 | ||
| GWO | 2.0190645830849E-02 | 8.4207804663943E-02 | 2.7422933458200E-01 | 9.724E-02 | 9.767 | 293 | ||
| SSA | 1.5545325435148E-02 | 1.4408325701658E-01 | 2.7424833297126E-01 | 1.240E-01 | 10.433 | 313 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).





