Prerpints.org logo

Submitted:

04 July 2023

Posted:

05 July 2023

You are already at the latest version

A peer-reviewed article of this preprint also exists.

Abstract
Porous ferroelectric lead zirconate-titanate (PZT) films are a promising material for various electronics applications. This study focuses on understanding how structure-directing agent (polyvinylpyrrolidone) can change structure and electrical properties of porous PZT films prepared by chemical solution deposition. The films with various porosity up to ~ 40 vol.% and pore connectivity changing from 3-0 to 3-3 were prepared and studied by capacitance-voltage, dielectric hysteresis, transient current, photocurrent, and local current techniques. We have found that the linear decrease in the material volume in a porous film is not the only factor governing film properties. The key role in changing electrical properties plays the creation of new internal grain boundaries. This research expands the understanding of physical phenomena in porous ferroelectric films and may enable the development of new materials and devices.
Keywords: 
Subject: 
Chemistry and Materials Science  -   Surfaces, Coatings and Films

1. Introduction

Manufacturers of ferroelectric ceramics generally aim to increase the ceramic density in order to obtain better electrical performance. Pores and voids after high temperature sintering are considered as defects. However, some applications need introducing an artificial porosity to meet some special materials properties. Firstly, porous ferroelectric ceramics are used in hydrophones, where porosity provides better figure of merit (FOM) and acoustic coupling to water [1]. Another application is IR detectors, where a better FOM results from a decrease in permittivity and volume specific heat [2]. The same reason for choosing porous ceramics (better FOMs due to lower permittivity) is a rapidly developing field of energy harvesting based on piezo- and pyroelectric effects and improved dynamic mechanical and electrical performance under shock compression in power supply devices. [3,4]. Variety of processing techniques to obtain porous ceramics with different internal structure were proposed, including polymer sphere burning, polymer sponge method, freeze casting, 3D printing, etc. [4,5].
Thin films of ferroelectric ceramics are less studied and exploited than bulk ones. The driving force to introduce porosity in ferroelectric thin films was increasing the film thickness. A film thickness of lead zirconate titanate (PZT) deposited by chemical solution deposition (CSD) is limited by ~30-50 nm due to cracking caused by film shrinkage related to loss of solvent and organics, as well as crystallization. Repeated cycles of deposition and heat treatment are employed to produce thick films [6]. For example, the coating and baking processes need to be repeated 20 to 30 times to achieve the ~2 µm film thickness required in MEMS devices, resulting in low throughput and high scrap rates in mass production.
H. Kozuka et al propose to increase ceramic film thickness by incorporating polyvinylpyrrolidone (PVP) in precursor solutions as a stress-relaxing agent [7,8,9]. An idea to use N, N-dialkyl- or N-alkylcarboxamide precursors in combination with sol-gel hydrolysis and condensation of silicon alkoxide belongs to T. Saegusa and Y. Chujo [10,11]. They have shown that when a silicon-oxide network is formed in the presence of an organic polymer, which is a strong acceptor of hydrogen to form hydrogen bonds, the organic polymer is to be drawn into the three-dimensional network of silica. This inorganic-organic gel can be transformed into a porous material by destruction of organic species during a heat treatment. H. Kozuka et all have extended this approach to ferroelectric PZT and BaTiO3 films preparation: they speculate that in a PVP-modified system, the strong intermolecular interaction between the carbonyl groups (C=O) of PVP and the hydroxyl radicals (OH) of the metal-oxide network can play a critical role in retarding the condensation reaction and promoting the stress release [7,9,12].
The introduction of porosity changes the microstructure and electrical properties of ferroelectric films. The main influence that is important for applications is a reduction in the permittivity in a wide frequency range up to THz, [13,14,15,16], which makes it possible, for example, to increase the pyroelectric performance [17,18]. Polarization decreases with increasing porosity [19,20,21], however, there are no systematic data on the dependences of the polarization and coercive field on porosity for thin films, as it has been done for bulk ceramics [22]. Yu. Podgorny et al. reported a larger dead layer thickness at the porous PZT-metal interface and a higher leakage current in contrast to the dense PZT film [23,24]. Higher leakages may be caused by different reasons, including chemical defects [25], grain boundary charge carrier transport [26], carbon residuals [27], and may strongly affect device performance and leakage mechanisms, and should therefore be studied.
Thus, despite the fact that porous ferroelectric films have been studied for more than 20 years, there is no clear understanding of their application areas due to the lack of systematic studies and models describing the dependence of electrical properties on porosity. Whether this is only the way to obtain ceramics films with higher thickness but inferior to dense films properties or porosity may be useful in itself to meet some specific electrical properties? To give insight on electrical properties of porous films we have performed a detailed study of PZT films prepared by CSD method with a wide range of PVP content from 1 to 20 wt.% to obtain films with various porosity and internal structure varied from isolated pores to highly interconnected ones. The film structure was studied by SEM, XRD and AFM methods. Characterization of electrical properties include polarization hysteresis loops and their asymmetry, dielectric constant, polarization dependences of the transient current and short-circuited photocurrents, and local current distribution. As a result of this study, we show that introducing porosity in ferroelectric ceramic films provides tuning their electrical properties and can be used in device manufacturing.

2. Materials and Methods

A film-forming solution was prepared using zirconium and titanium isopropoxides, and dry lead acetate obtained directly from PbO according to the method described in [28,29]. The Zr/Ti ratio was chosen to be 48/52, a 14 mol.% excess of Pb relative to the stoichiometric composition was added to the film-forming solution to compensate for the PbO loss at the high-temperature treatment. Polyvinylpyrrolidone (C6H9ON)n with a molecular weight of 360,000 was used as a porogen. Different amounts from 1 to 20 wt.% of PVP were added to the PZT stock solution as is shown in Table 1. The films were spin coated onto 6” silicon wafer with the following structure: Si -SiO2 (300 nm)-TiO2 (10 nm)-Pt (160 nm) produced by Inostek, Korea. Spin-on deposition was performed using a spin coater (WS-650-8NPP, Laurell, USA) at a rotation speed of 2500 rpm for 15 s. The films were grown by repeated cycles of solution deposition and drying. Each deposited layer was dried at 200oC (soft bake) and 400°С (hard bake) for 10 min to remove organic residuals. After the final layer was deposited, the samples were annealed at T = 650°С for 15 min to perform crystallization.
Film thickness d and refractive index np were estimated by spectroscopic ellipsometry (Sentech SE-850, Germany). The ellipsometry data were fitted using the Bruggemann and the Tauc-Lorentz optical models. The optical (volume) porosity p of the film was estimated from the Lorentz-Lorentz relationship using the refractive indexes of dense and porous films. Some samples could not be measured by ellipsometry because of excessive light scattering.
Ferroelectric polarization was recorded using AixACCT TF 2000 (AixACCT, Germany). Capacitor-voltage dependences were obtained with an LCR meter (4284A, Agilent, USA). A mercury probe (model 802-150, MDC, MDC Corp, USA) with an area of 0.53 mm2 was used for metal contact connection. Semitransparent Pt 10 nm-thick top electrodes with an area of 10-3 cm2 were formed by DC magnetron sputtering to study the film properties in the geometry of the applied field perpendicular to the plane of the film, that is, between the top and bottom electrodes. These includes the asymmetry of hysteresis loops, as well as the polarization dependences of the transient current and short circuited photocurrent which were measured using a Keithley 6487 Picoammeter/Voltage Source (Keithley Instruments, USA). To excite charge carriers under visible light illumination we used a Cree XLamp 7090 LED with a wavelength of 457 nm and a pump power on the film surface of 25 mW/cm2. The crystalline structure was studied using a DRON-3 (Burevesnik, Russia) diffractometer (scanning mode Θ-2Θ, Cu Kα1 radiation). Microstructure was studied by the scanning electron microscope (SEM) FEI NovaNanoSEM 230 (FEI, USA). Grain size distribution and film’s porosity were estimated with the ImageScope software. The surface topography and local current distribution in the PZT films were studied using conductive atomic force microscopy (c-AFM) with a Ntegra Aura (NT-MDT Co., Russia) scanning probe laboratory.

3. Results

3.1. General Characterization of the Films Thickness and Microstructure

As the film thickness affects their electrical properties, two groups of samples were prepared: the first has a thickness of about 400 nm (“thin” films), while the second has a thickness in the range of 600–700 nm (“thick” films). Detailed information including PVP content, number of applied layers, refractive index, volume porosity calculated from the refractive index, film thickness and thickness per one layer deposition are collected in Table 1.
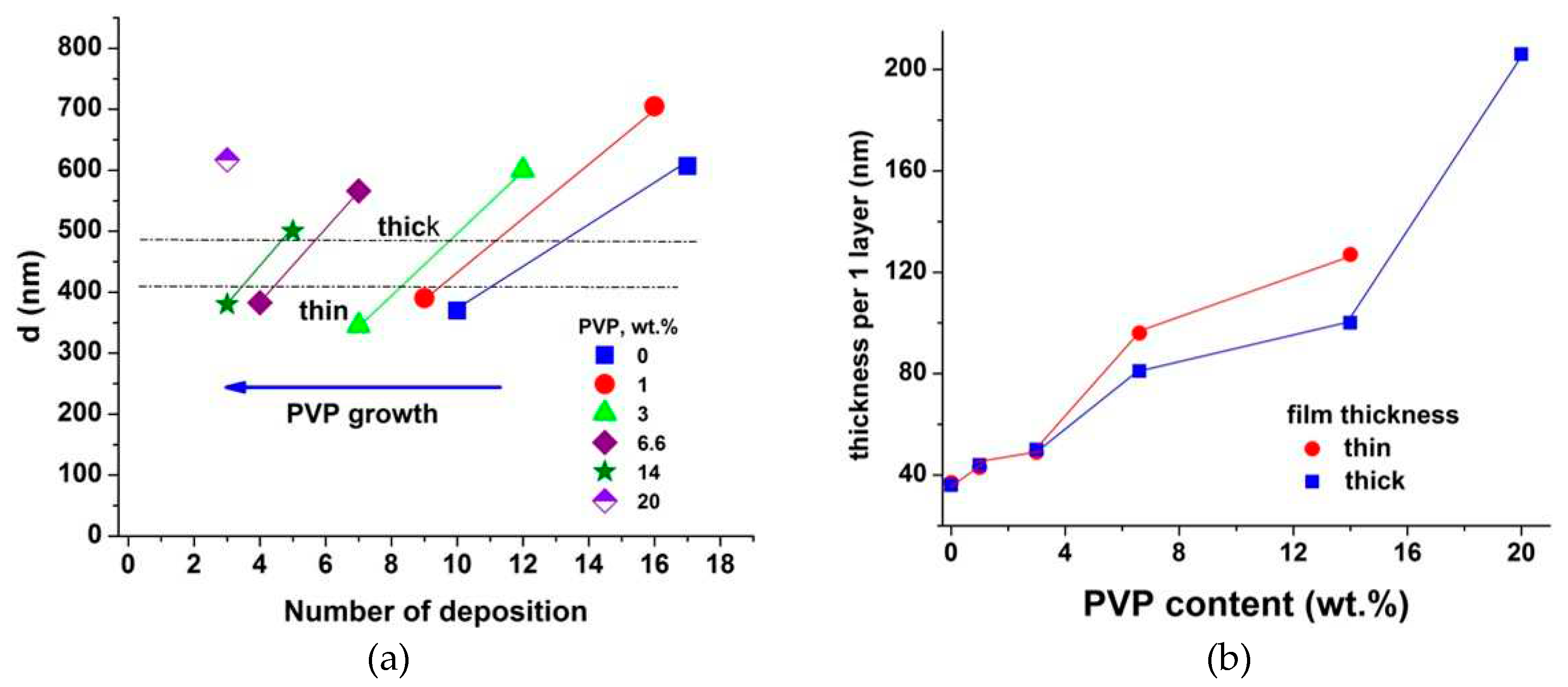
Figure 1 shows how the film thickness depends on the number of applied layers at different PVP content (a), and the thickness of one applied layer on the PVP content (b). The film thickness increases with the PVP content, as a result a thicker film can be obtained via a less number of deposition steps, as it is illustrated in Figure 1a.
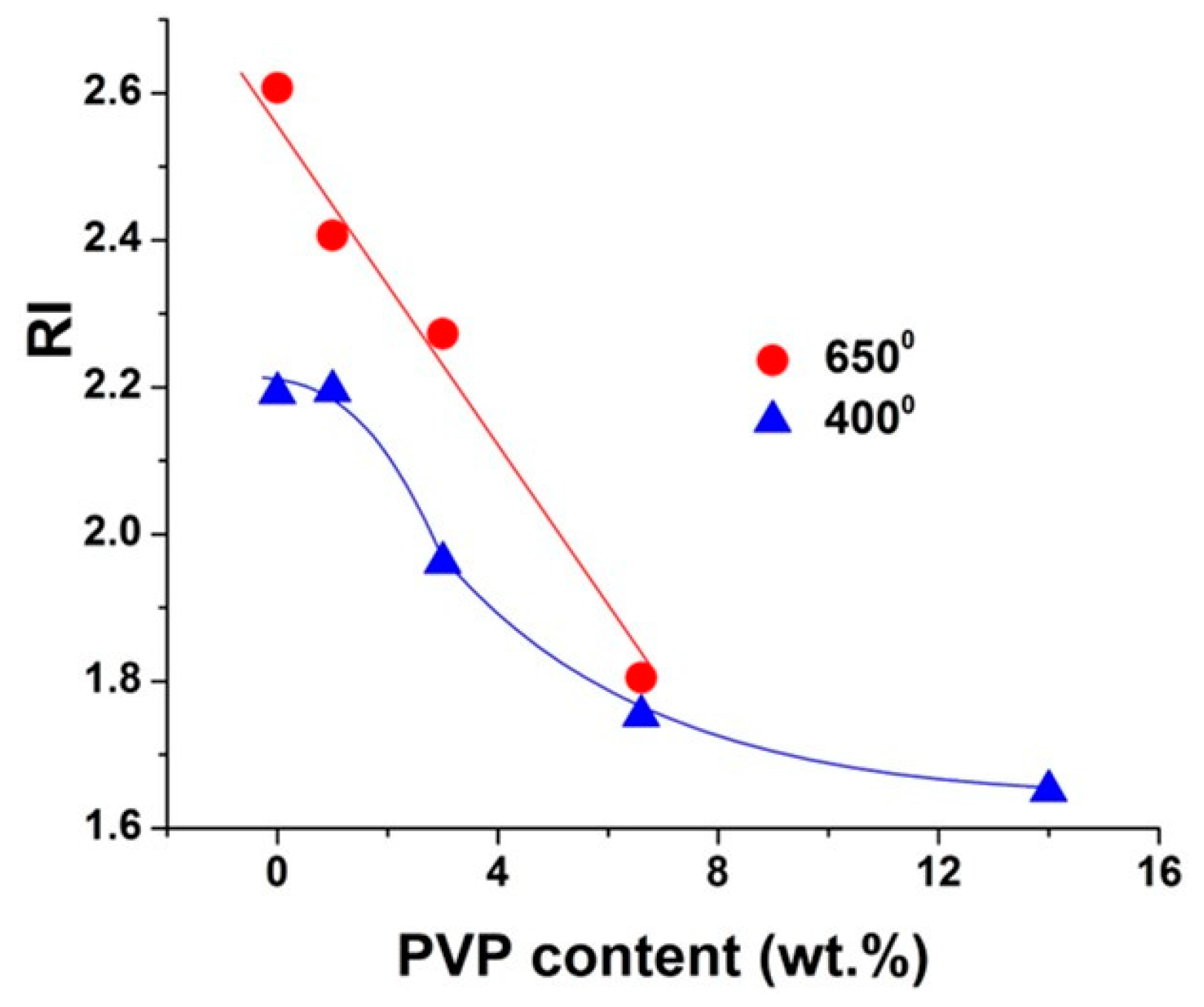
Figure 2 shows the dependences of the refractive index on PVP content. Two types of measurements were carried out in the samples: the data found before crystallization of the structure correspond to annealing at 4000C, and the data obtained after crystallization refer to annealing at 6500C. Refractive index decreases with the PVP content due to increasing porosity. The volume porosity calculated by the Lorentz-Lorentz relationship is
Preprints 78576 g002
Figure 2. Refractive index vs PVP content, measured before (4000C) and after (6500C) crystallization.
Figure 2. Refractive index vs PVP content, measured before (4000C) and after (6500C) crystallization.
Preprints 78576 g002
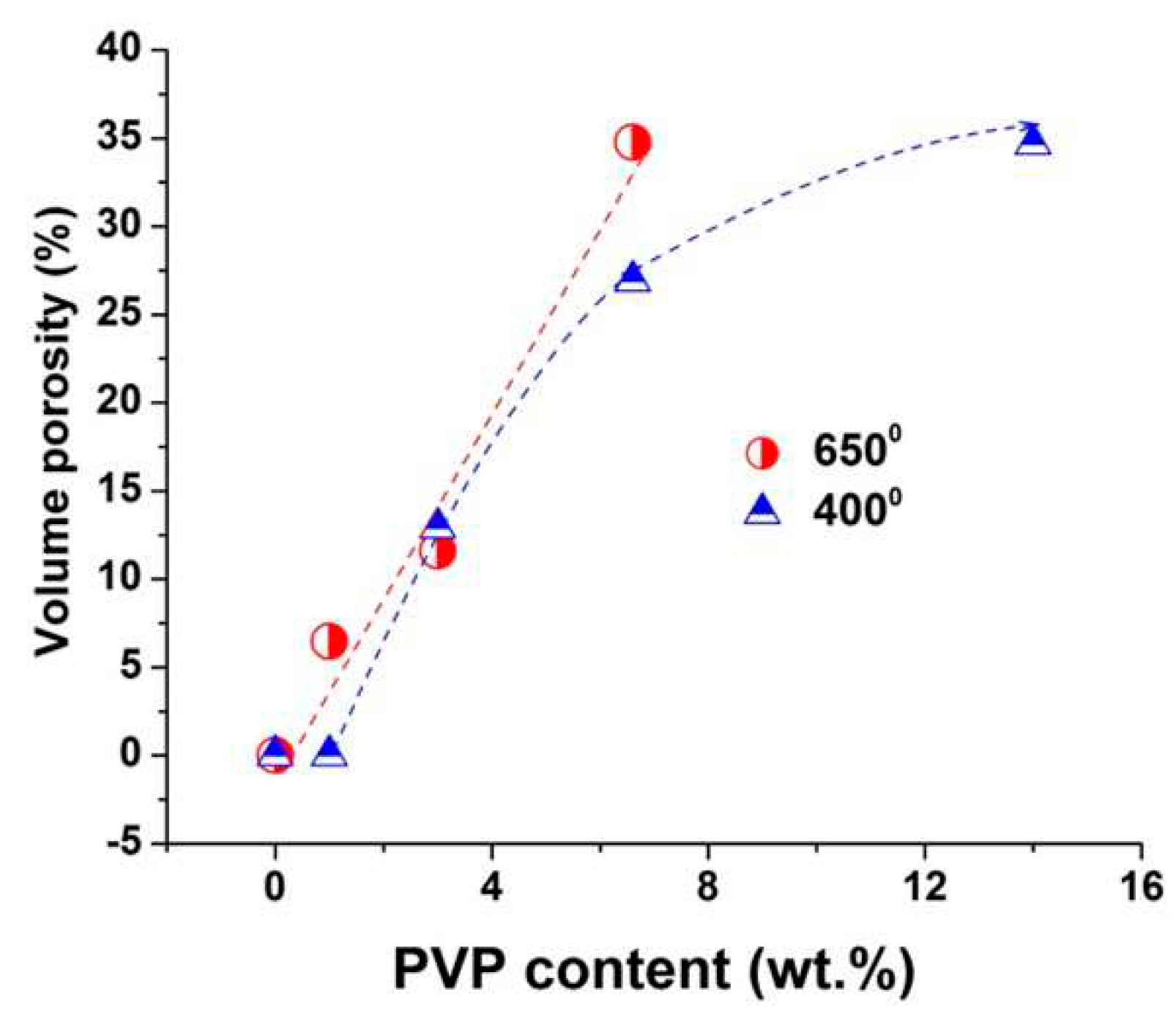
Preprints 78576 g003
Figure 3. Volume porosity vs PVP content shown in Figure 3. The volume porosity increases almost linearly up to 6.6 wt.% PVP content. Higher PVP content complicates ellipsometry measurementins due to the light scattering, however data obtained after annealing at 4000C before crystallization started shows further increase in porosity for a film with 14 wt.% PVP content.
Figure 3. Volume porosity vs PVP content shown in Figure 3. The volume porosity increases almost linearly up to 6.6 wt.% PVP content. Higher PVP content complicates ellipsometry measurementins due to the light scattering, however data obtained after annealing at 4000C before crystallization started shows further increase in porosity for a film with 14 wt.% PVP content.
Preprints 78576 g003
Figure 4 shows the cross sectional (top) and in-plane (bottom) SEM images of dense PZT film (a) and ones with varied PVP content (b)–(f). The initial dense PZT film exhibits a pronounced columnar grain structure which is typical for PZT grown on (111) Pt [28,29]. The addition of 1 to 3 wt.% PVP induces isolated pores included into perovskite grains as it is seen in Figure 4b,c, and can be refers to a 3-0 connectivity [30]. Detailed description of films microstructure can be found in Ref. [31]. A further increase in the PVP content leads to a strong transformation of the film structure. With an excess of 6.6 wt.% PVP content, the films lose their columnar grain structure and become polycrystalline, consisting of fairly fine grains about 50 nm in size. It is characterized by irregular and highly interconnected pores, as it can be seen in Figure 4 d-f. This percolated structure can be attributed to a 3-3 connectivity [30].
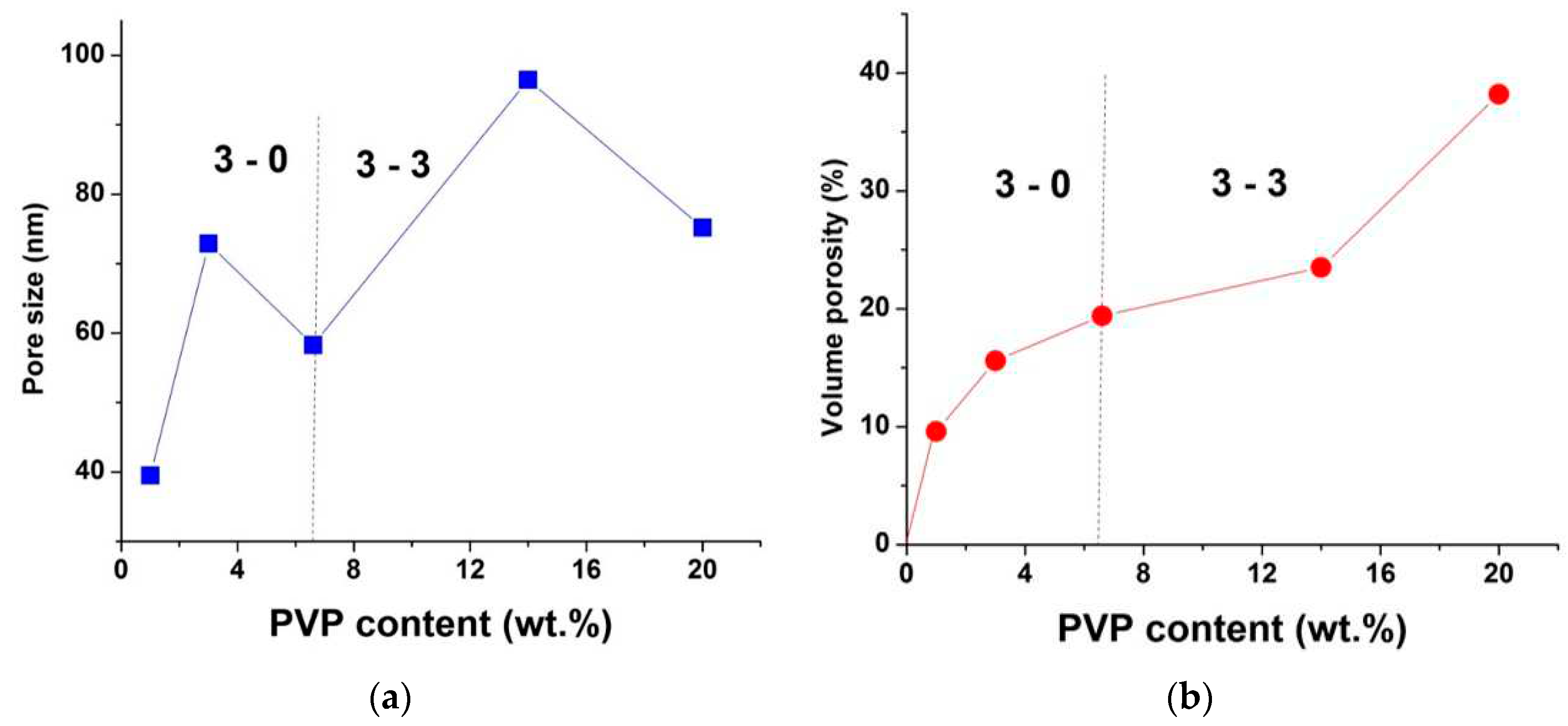
Statistical processing of plane-view SEM images shows an increase in the average pore size and volume porosity with increasing PVP content, see Figure 5. A decrease in the mean pore size at 6.6 wt.% may be caused by reaching percolation threshold and appearance of narrow interconnecting mouths (ink-bottle pores) and internal voids [32].

3.2. X-ray Diffraction Study

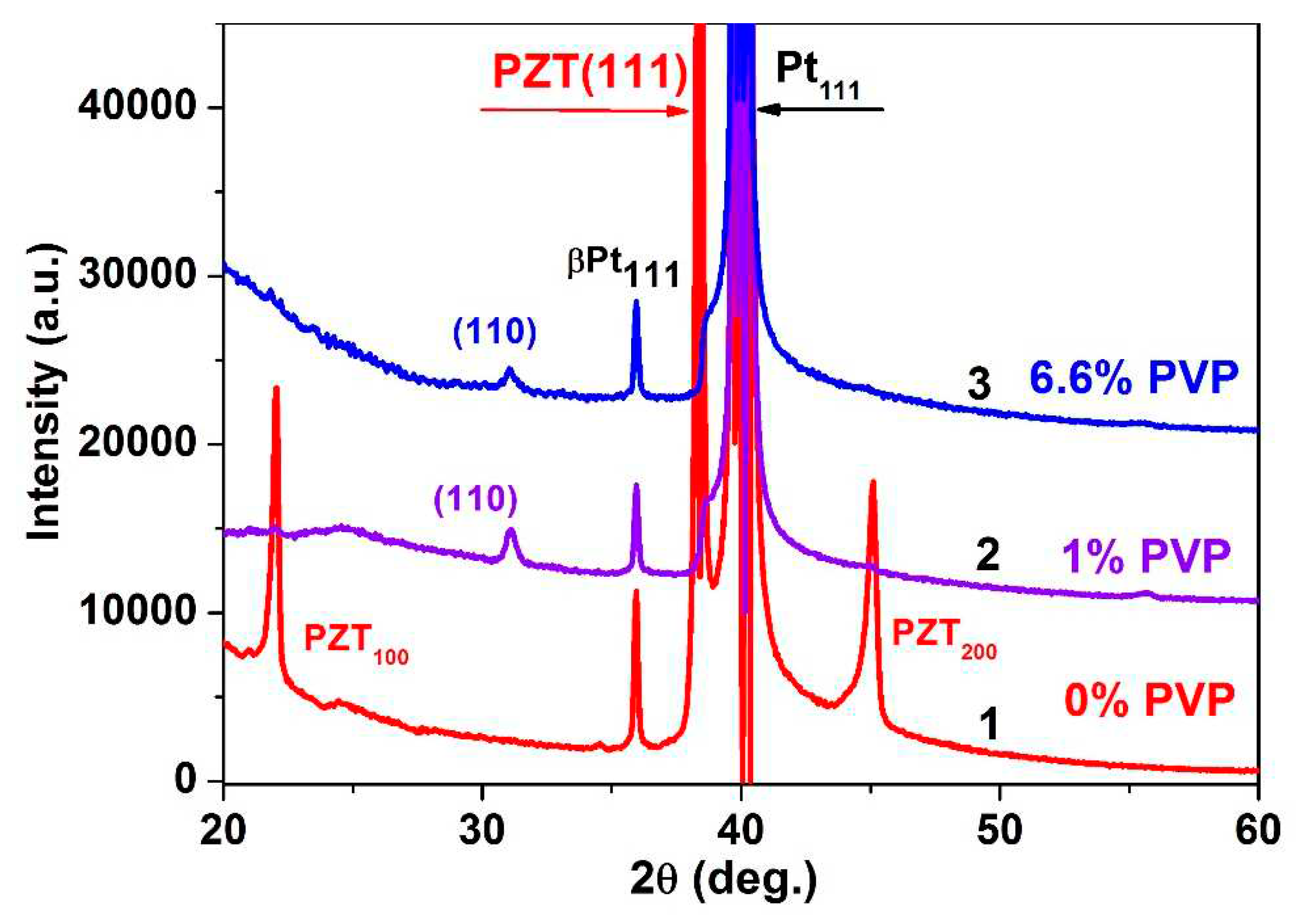
The X-ray diffraction (XRD) data confirms the crystal structure transformation. Figure 6 presents XRD patterns measured in the dense PZT film (curve 1) and those prepared with the PVP content of 1 wt.% (curve 2) and 6.6 wt.% (curve 3). It is seen that the dense film shows a predominant (111) Pe texture along the volume diagonal and a weaker (100) direction, which is typical for columnar grain films grown on (111) Pt. In porous PZT films, the strong columnar grain texture is destroyed and changes to the predominant Pe (110) and weaker (211), the peak intensity decreasing with increasing porosity.
The ratios of the reflection intensities found from the diffraction peaks are listed in Table 2.
The lattice parameters calculated from the XRD-measured interplane distances under the assumption of a pseudo-cubic lattice are shown in Table 3 (JCPDS International Centre for Diffraction Data). In a dense film, the found lattice constants are less than the value for an unstressed PZT powder, which indicates the presence of compressive stresses in the dense PZT film. However, in porous films with increasing porosity the pseudocubic lattice parameter increases and for (110) reflection the stress is removed already at 3 wt.% PVP, while for (211) reflection the stress decreases, but still remains at 14 wt.% PVP. In general, the measured lattice constant increases with the PVP content, which evidences for the stress relaxation. This is the reason for the better resistance of porous films to cracking.

3.3. Dielectric Constant, Polarization, Coercive Field

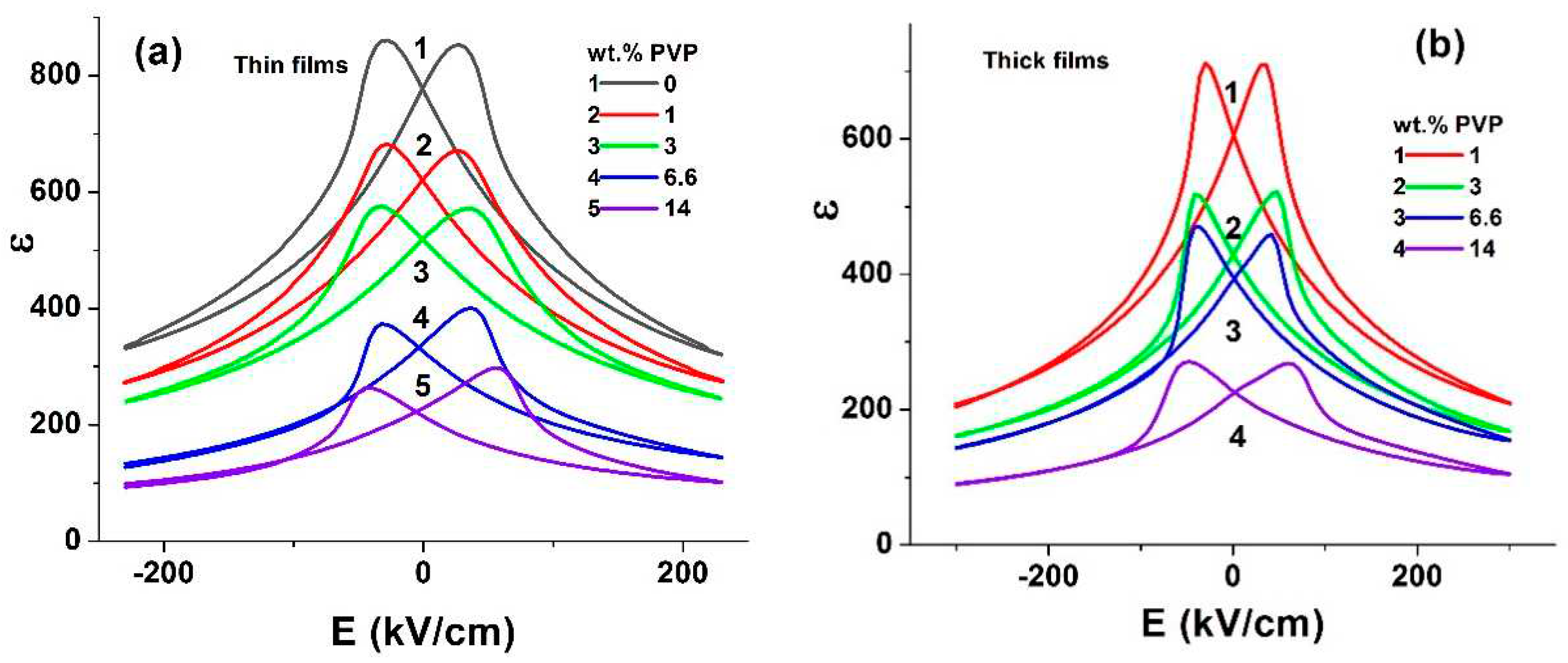
Figure 7 presents the dielectric constant vs the electric field, found from the capacitance-voltage (CV) curves measured in porous PZT films. These dependences are typical for PZT films and demonstrate a decrease in the permittivity with increasing the PVP content, while maintaining the characteristic shape.
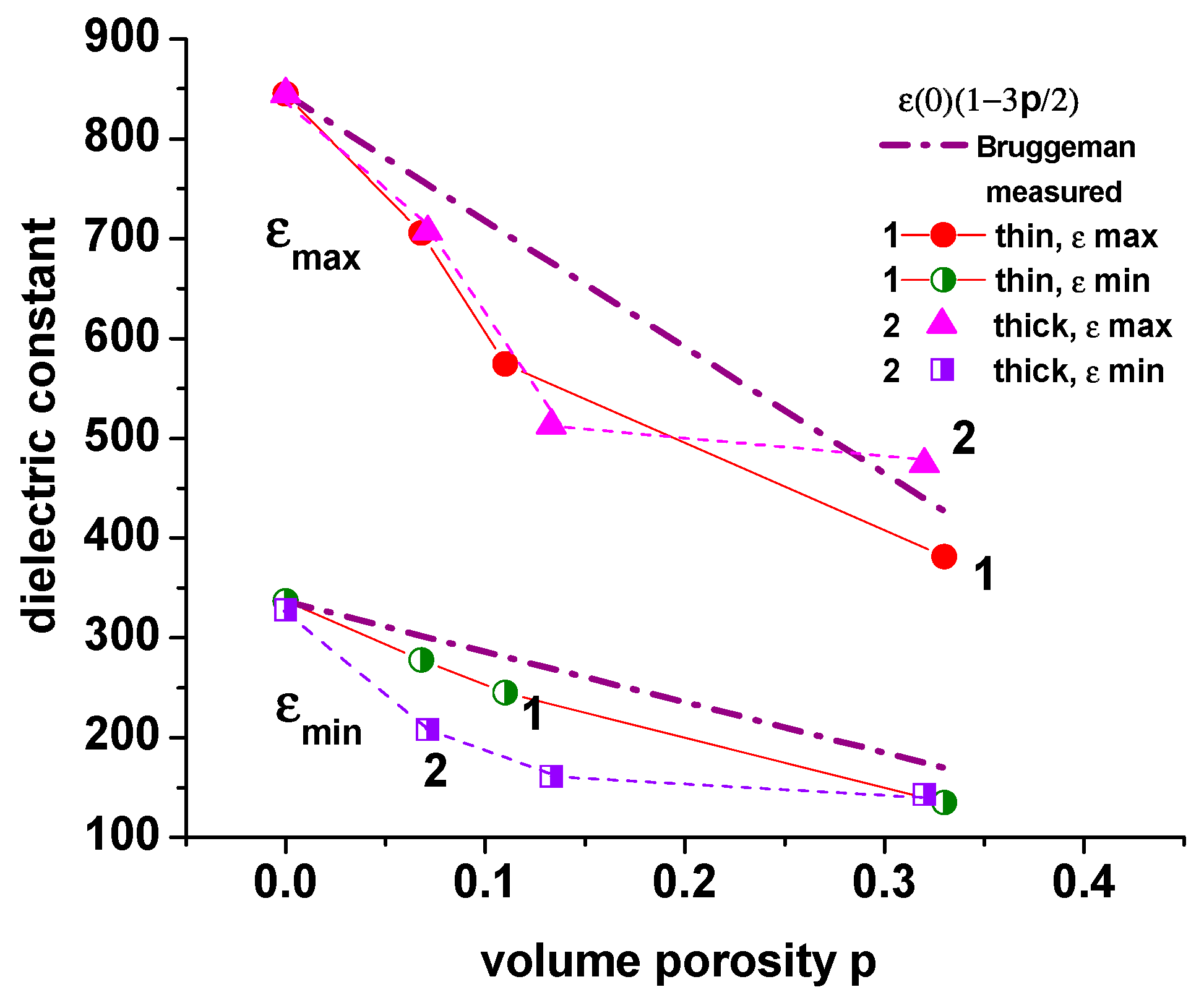
The maximum and minimum values of the permittivity found from the CV curves depending on the volume porosity (estimated from optical measurements) are plotted in Figure 8. The Brüggemann's approximation for binary composites is usually used to estimate an effective permittivity taking into account a volume porosity ε(p) = ε(0)ˑ(1-3p/2), where ε(p) is the permittivity of porous film, ε(0) is the permittivity of dense film, p is the porosity [33]. The approximation is seen to give larger values compared to the measured ones (Figure 8), indicating the existence of additional reasons for the reduction in the dielectric constant (loss of texture, change in perovskite grain size).
The operation of most electronic devices using ferroelectric film is based on the existence of the spontaneous polarization and its switching by an electric field. Therefore, the retention of the polarization magnitude and the symmetry of the hysteresis loop are important factors in determining the performance and reliability of the device. To study the asymmetry of the hysteresis loops, the Sawyer-Tower method was used, supplemented by a depolarization procedure, in which a decaying sinusoidal voltage was applied to the bottom electrode of the Pt/PZT/Pt structure connected in series with a 220-nF reference capacitor. Polarization was recorded by the amount of the charge on the reference capacitor [34]. This method makes it possible to transfer the film to the initial depolarized state and, thereby, to establish a reference point on the charge axis, relative to which to reveal a possible asymmetry of polarization switching under the action of an applied bias.
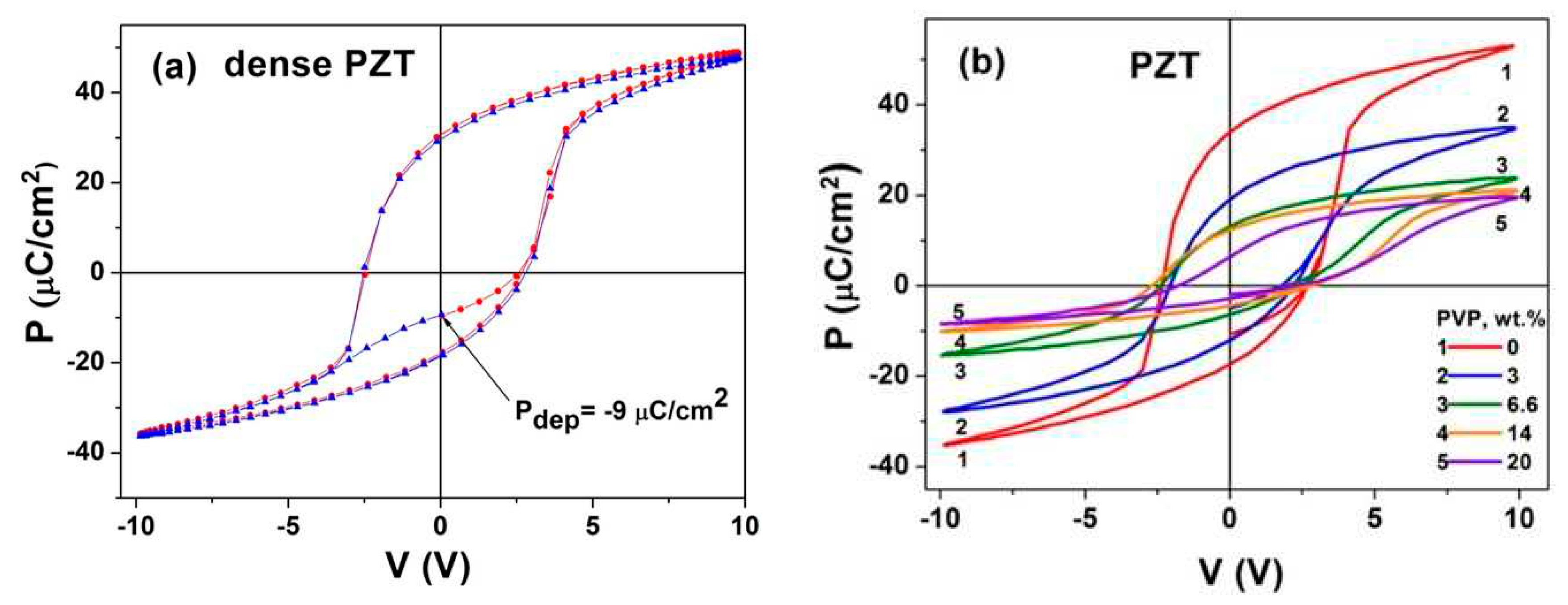
The hysteresis loops measured from the depolarized state by applying three half-periods of sinusoidal voltage with an amplitude of ±10 V and a frequency of 64 Hz are shown in Figure 9a for the dense PZT film. It is seen that the measured hysteresis loops turned out to be strongly asymmetric: the noticeable excess of the positive remanent polarization over the negative one suggests that the PZT film has an unswitchable positive polarization, which manifests itself in the depolarized state as the value Pdep = ̶ 9 µC/cm2. This is due to the presence of stresses in the film [34].
Hysteresis loops measured from the depolarized state in porous PZT films are given in Figure 9b. It is also seen that the porosity growth leads to a decrease in the polarization magnitude and hysteresis area as well as to tilting the loops and a reduction in their rectangularity beginning with 20 wt.% PVP. Similar results were reported for PZT ceramics in [22]. Increasing porosity leads as well to loss of saturation (bird beak region) due to leakage increase [35].
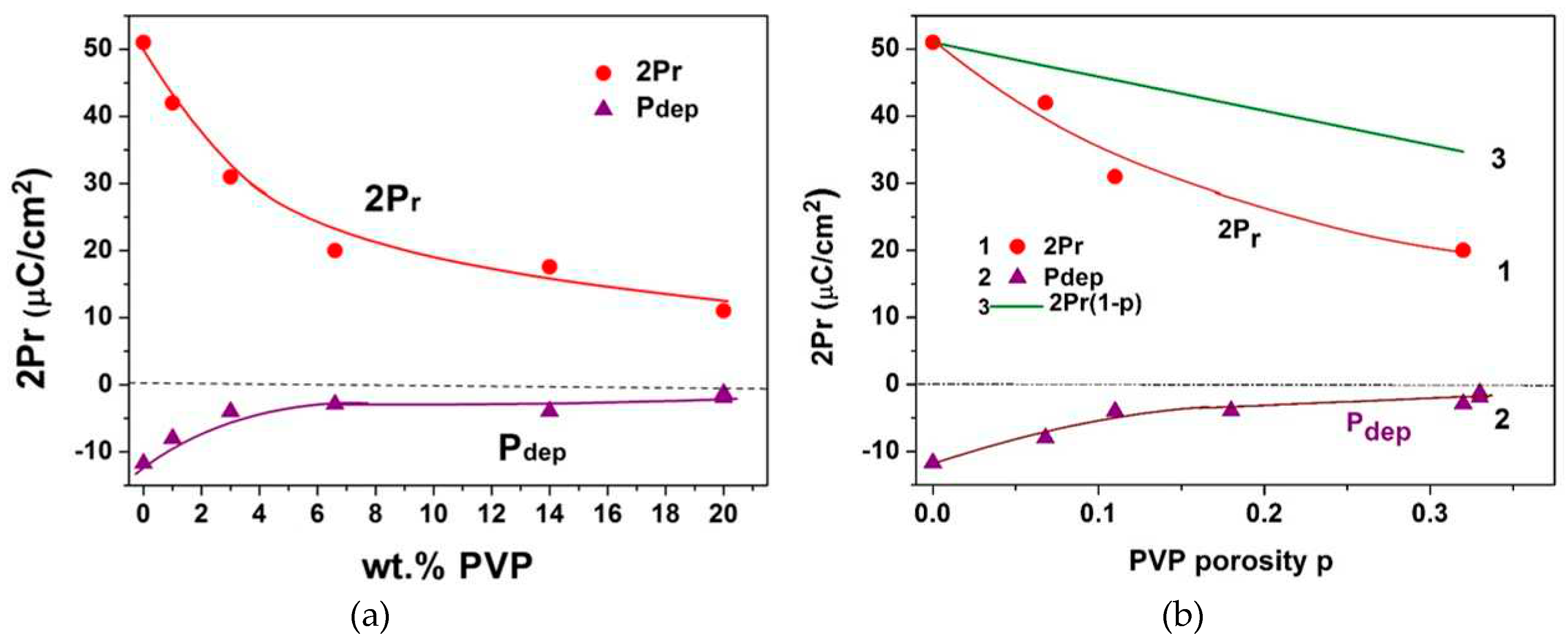
Figure 10 shows the switchable polarization 2Pr and polarization in the depolarized state Pdep as functions of the PVP content in weight percent (a) and volume porosity (b).
W. Wersing et al. [33] within the Marukate’s effective medium approximation [36] have found an approximation that adequately describes the polarization in porous ceramics: P = P0 (1-p), where P0 is the polarization of dense ceramics. Y. Zhang et al [22] studying polarization-electric field behavior of ferroelectric materials introduce a depolarization factor (dP): P = dP‧P0 (1-p). They have obtained dP in the range of 0.5-0.8 depending on pore configuration and alignment.
It can be seen, that the switchable polarization in PZT films decreases with porosity faster than the linear reduction in Wersing’s approximation, shown by curve 3 in Figure 10b. The depolarization factor was estimated to be within the range of 0.9 - 0.59. This correlates with the results obtained for ceramics [22,37] and indicates the presence of an additional depolarization factor associated not only with a decrease in the volume of the ferroelectric material. At the same time, the value of Pdep associated with the unswitchable polarization also decreases with increasing PVP, which indicates stress relaxation in the porous film.
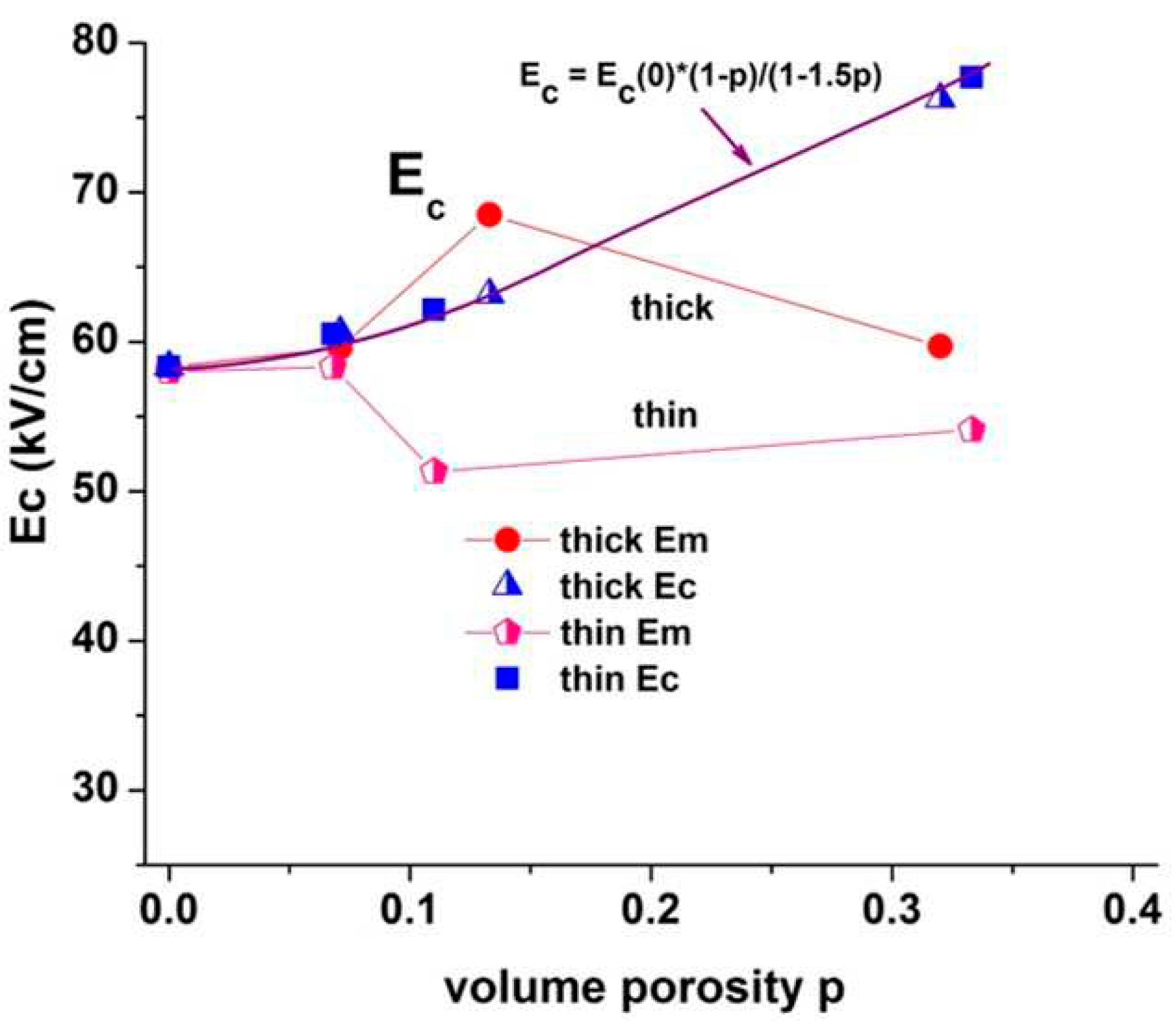
The value of the coercive field EC extracted from the hysteresis loops both in thin and thick films as a function of the volume porosity p is shown in Figure 11. According to W. Wersing et al [33], in bulk porous PZT ceramic coercive field EC have to increase monotonically as EC = EC(0)ˑ(1-p)/(1 - 3p/2), where EC(0) is the coercive field of the dense ceramics, as it is shown in Figure 11. Interestingly, the measured films do not show a sufficient increase in the coercive field.

3.4. Polarization Dependences of the Transient Current

To elucidate the behavior of the polarization vector with growing porosity, we study the polarization dependences of the transient current in porous PZT films. Previously, we experimentally showed that the appearance of pronounced current peaks in the current-voltage (IV) curves of epitaxial or well-textured polycrystalline PZT films with non-conductive grain-boundaries can occur when the directions of the polarization vector and external bias coincide [26,38]. To explain the nature of these peaks, we formulated a model of non-stationary charge carrier transport in an n-type PZT film, where electrons generated by oxygen vacancies are captured by Ti+3 levels [39,40] and move between them under the action of an electric field [41,42]. The model and the performed numerical simulation showed that a necessary condition for a current peak to appear is the presence of an electron accumulated space charge layer (SCL) near that electrode, where a significant positive uncompensated polarization charge has formed. Therefore, the observation of the current peak means that at least the polarization vector retains its magnitude and direction throughout the film thickness up to the electrodes. Note that a pronounced current peak in the IV curves of well-textured PZT film with conductive grain-boundaries can appear if an external bias is applied against the polarization [26]. [26]. [26]. vector [26].
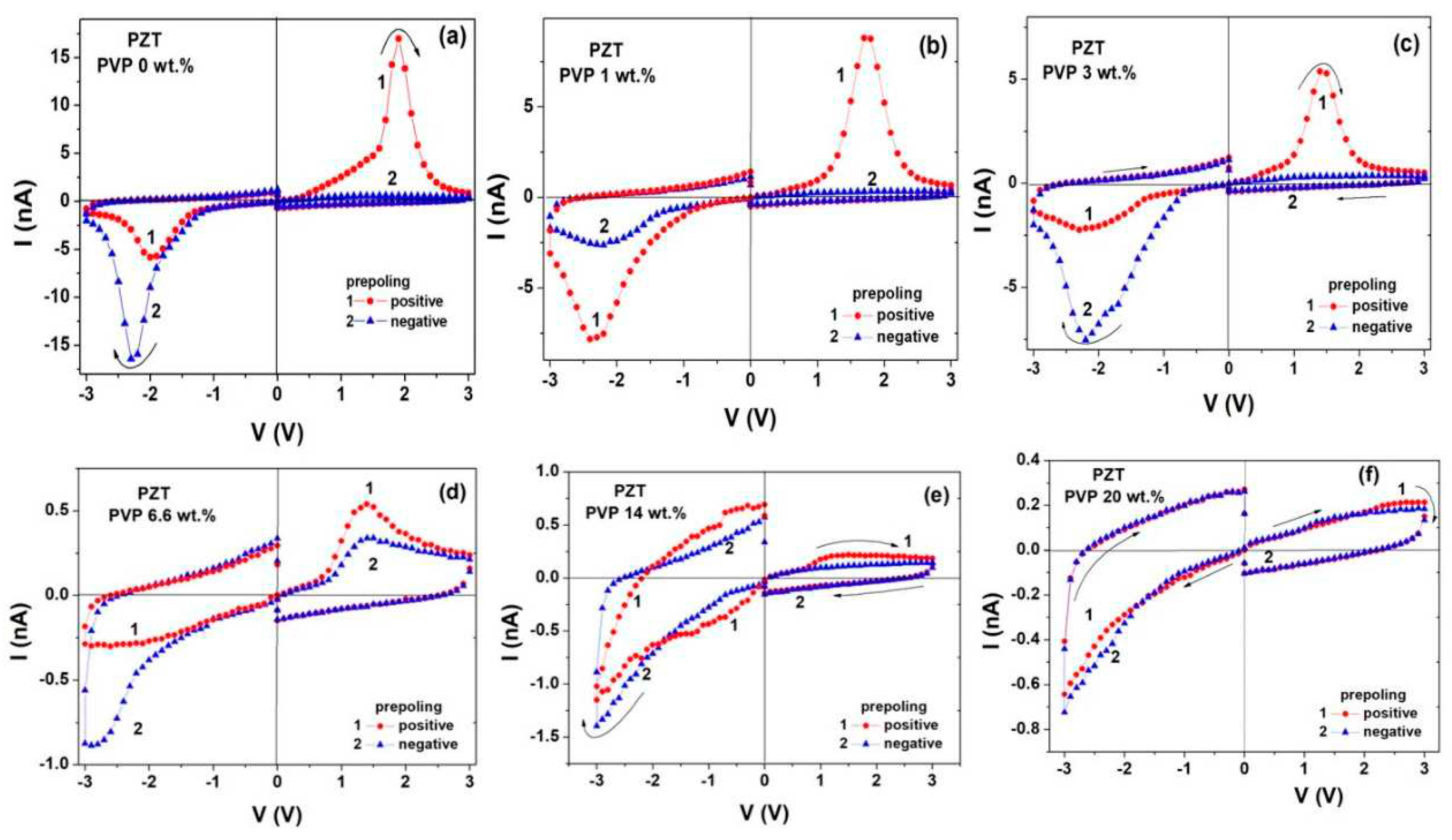
During the experiments, the bias is applied in a sequence of steps, each with an amplitude of 0.1 V and a duration of 0.2 s, and the current is recorded at the end of the step. The voltage changes from 0 to 3 V and then back to 0. In the measurement circuit, the domain-switching time is ~2 ms, therefore, by the time the current is recorded, the current caused by the domain switching has already passed through the external circuit. As a result, the recorded current is transient, i.e. associated with the movement of mobile charge carriers and variations of the electric field in time.
For both bias directions, the measurements were carried out at different preliminary polarizations. Before each measurement, the film was depolarized, and then polarized in a certain direction by applying a bias pulse of V = ±6 V for 2 s. Figure 12 shows the current-voltage curves measured in PZT films with different PVP content at positive (curves 1) and negative (curves 2) preliminary polarizations. In the dense PZT film, curves 1 and 2 exhibit pronounced current peaks (±16 nA) when the directions of the bias and the polarization vector coincide, Figure 12a. Similar current peaks but with lower current values are observed in PZT films with 1–3 wt.% PVP content and pore connectivity 3–0, Figure 12b,c. Whereas with exceeding 6 wt.% PVP, both pronounced peaks and their dependence on the polarization direction actually disappeared, Figure 12d–f. More details are provided in Table 4.
Indeed, above 6 wt.% PVP content, there are no more peaks at negative bias, possibly, because the value of the negative remanent polarization -Pr is too small to induce an accumulated SCL at the bottom electrode. At a positive bias, an intermediate situation takes place: there are no peaks in 42% of all structures, and a weak current peak appears either at P > 0 in 35% or at P < 0 in 23% of the structures, the latter corresponding to a conductive grain boundary [26]. At 14 wt.% PVP at V > 0, there are no peaks in 70% of all structures, only a weak plateau appears either at P > 0 in 15%, or at P < 0 in 15% of structures. At 20 wt.% PVP at V > 0, half of the structures have no peak, the other half show a weak plateau at P > 0.

3.5. Polarization Dependences of the Short-Circuited Photocurrent

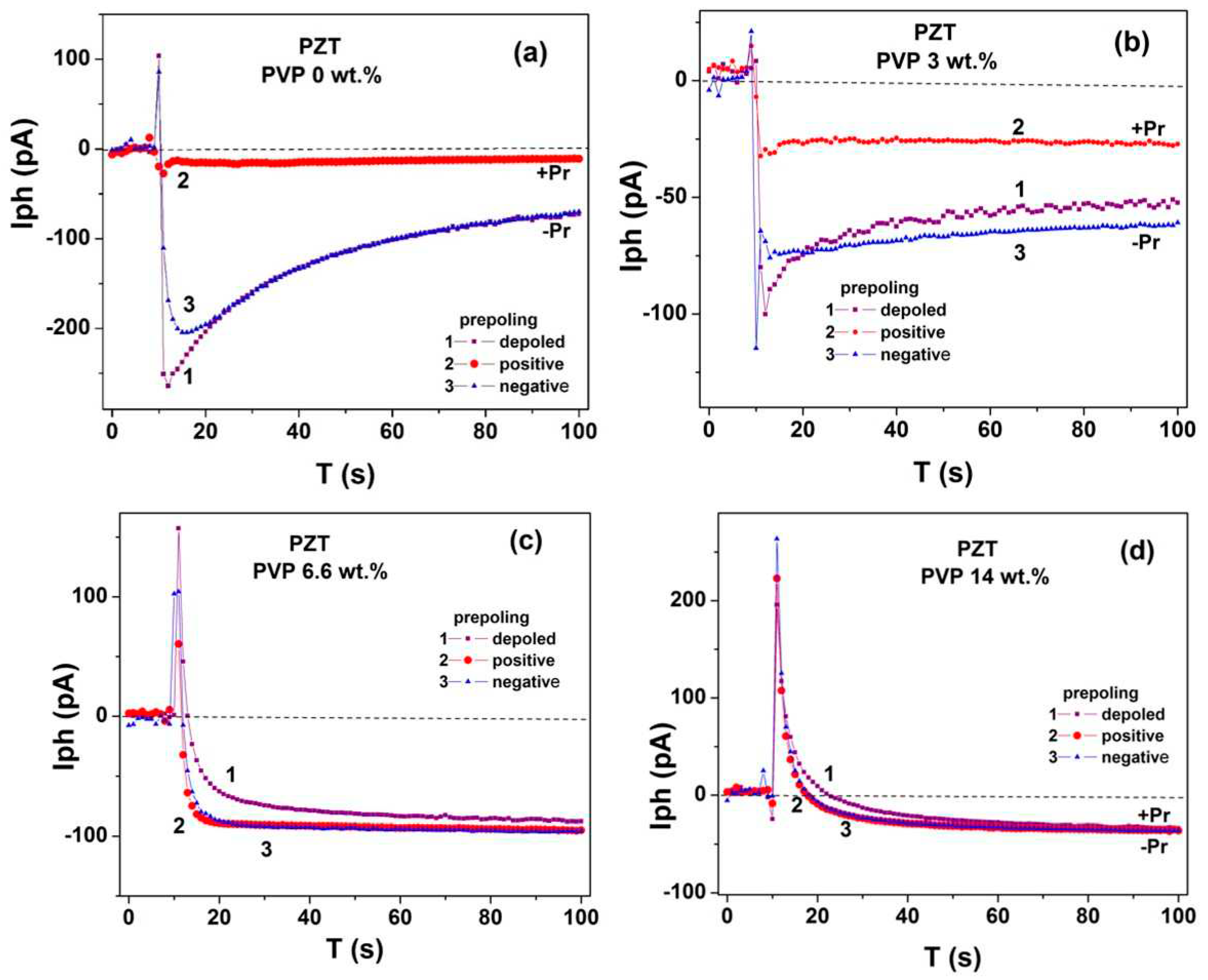
Measuring a photocurrent under short-circuit conditions is a well-known method to study internal electric fields in a film. The time-dependent photocurrent of the short-circuited capacitor M/PZT/M was measured at various pre-polarizations. First, the film was depolarized and then polarized in the dark by a bias pulse of ± 6 V for 2 s. After the bias was switched off, the external circuit was shorted. When the transient dark current decreased to zero, the film was illuminated by visible light with a wavelength of 457 nm (2.7 eV), and a photocurrent flowing in the external circuit was recorded at 1 s interval.
Figure 13 presents the photocurrents measured in the dense (a) and porous (b–d) PZT films at various pre-polarizations. Initially, there is a burst of the photocurrent, which then relaxes to some stationary value. In depolarized state of the dense film, a negative stationary photocurrent flowing downward from the top electrode to the bottom one is observed, indicating the existence of a downward built-in averaged electric field in the film, curve 1 in Figure 13a. The effect of positive polarization significantly, by 59 pA, reduces the magnitude of the negative stationary photocurrent, curve 2, while the negative polarization has almost no effect on the photocurrent magnitude, curve 3. Nevertheless, the large difference in the photocurrent values measured at the positive and negative directions of the polarization indicates a noticeable effect of the polarization vector on the photocurrent in a dense film.
It is seen in Figure 13b that at 3 wt.% PVP the photovoltaic current retains all the characteristic features of the dense film photocurrent: a negative initial burst and relaxation to a stationary negative value and the same polarization effect, but with a weaker influence on the current magnitude. Indeed, the positive pre-polarization reduced the stationary photocurrent of the depoled state only by 25 pA, curve 2, and the difference between the photocurrents measured at positive and negative pre-polarization was 34 pA, curve 3 in Figure 13b. When exceeding 6 wt.% PVP content, an initial positive burst of the photocurrent occurs, followed by its relaxation to a negative stationary value, which has lost its dependence on the polarization, Figure 13 c,d. Moreover, as it is seen in Figure 13d, the value of the stationary negative photocurrent decreases with increasing porosity, which indicates a weakening of the averaged built-in electric field in the film.

3.6. Local Current Study by c-AFM

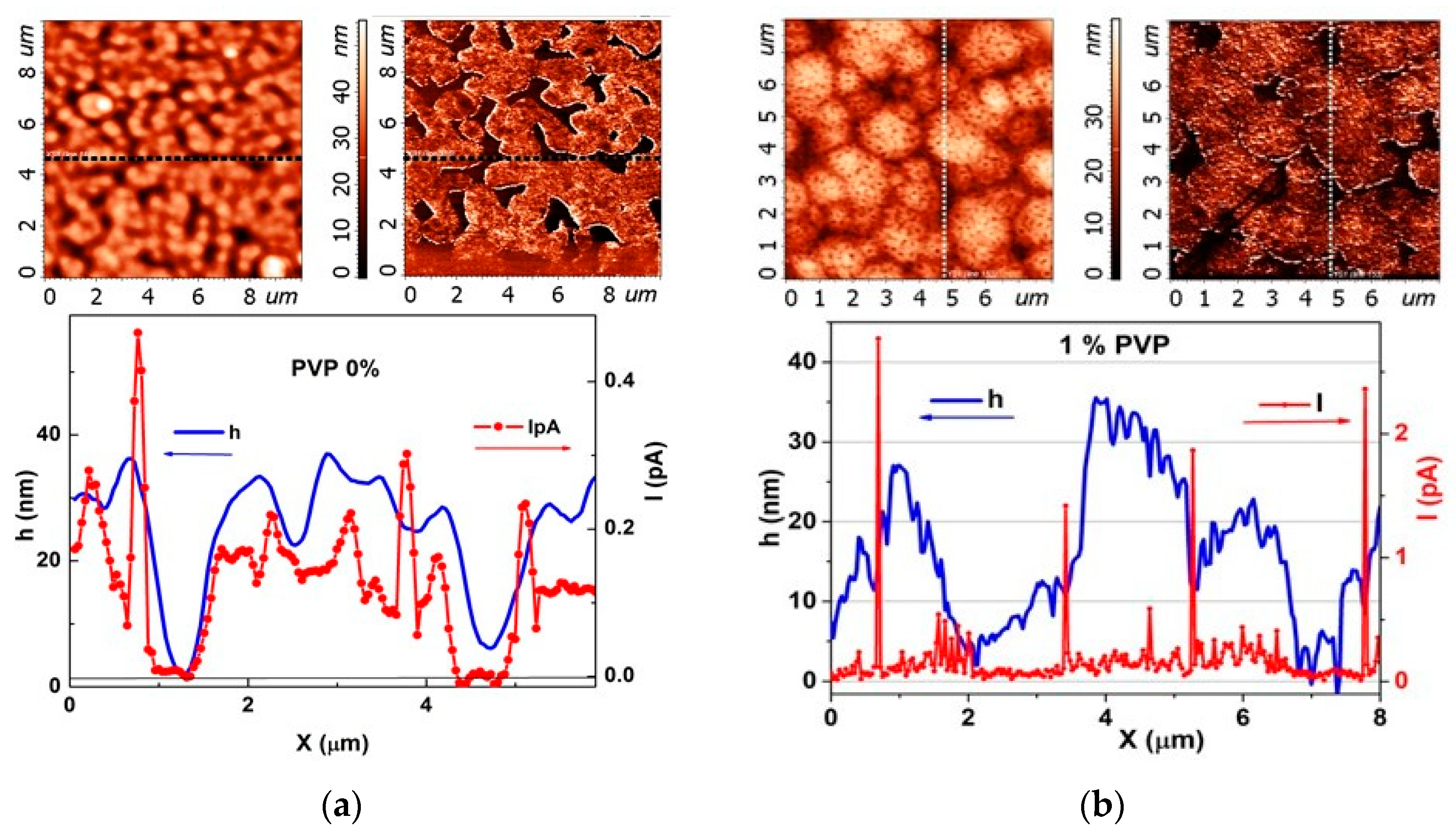
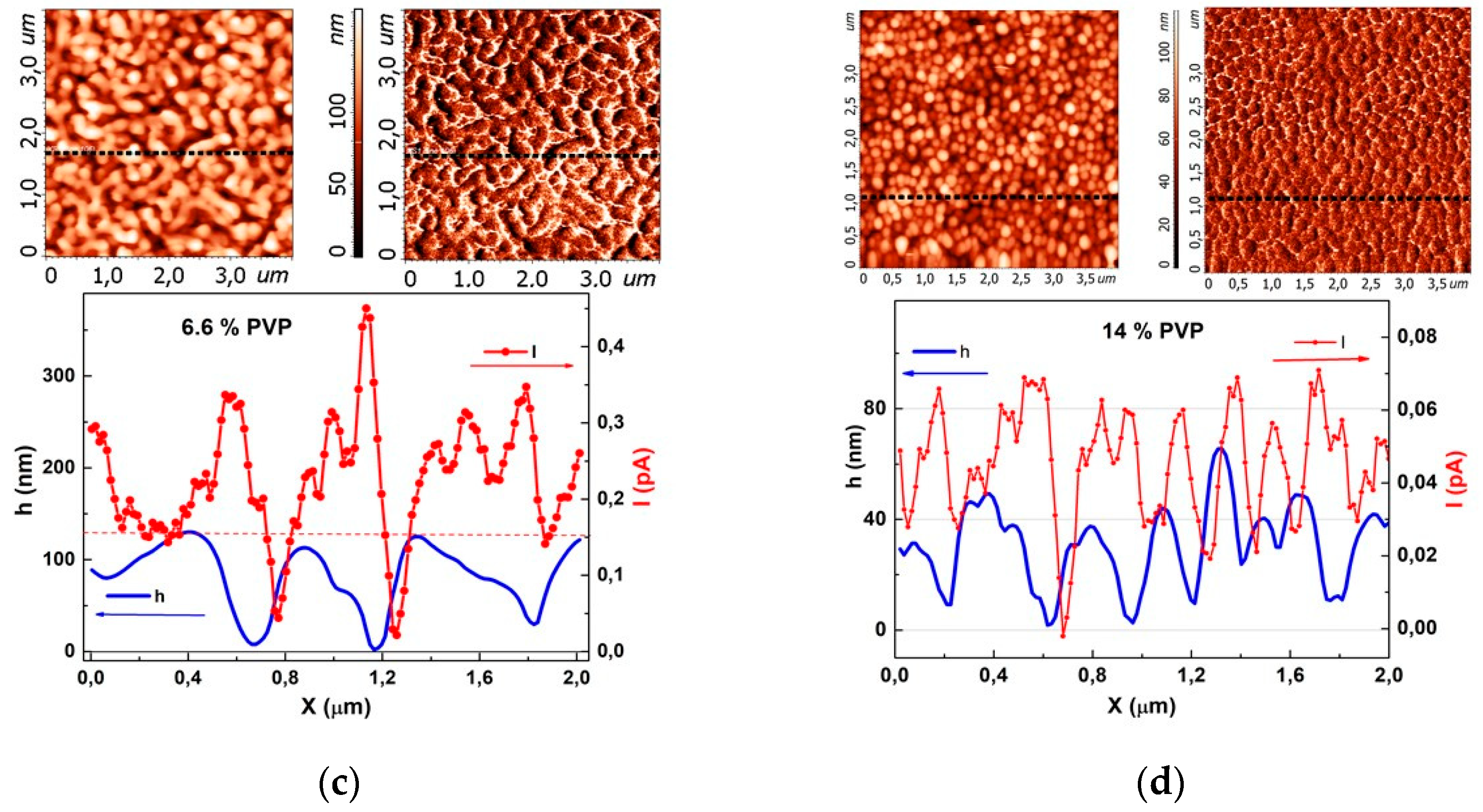
The local current distributions were studied by the c-AFM method, which makes it possible to measure simultaneously the surface topography and local current map of the film. Rigid (stiffness coefficient ~5--20 N/m) conductive probes with a wear-resistant diamond-coated cantilever were used for imaging, which retained their conductive properties even when a voltage of ±10 V was applied. The interaction force between the c-AFM probe and the surface under study is F ≈ 300–500 nN. The probe tip radius is ~100 nm, and the radius of the contact area is ~15 nm. An external bias of ~6 -7 V was applied to the bottom electrode, while the top electrode was grounded.
Figure 14 shows the results of the c-AFM study in PZT films with various PVP content. For each PZT film, the 2D images of the topography and local current maps obtained by scanning the PZT film are shown, as well as the topographic signal and local current flowing along the profile selected in the images. Figure 14a shows that in the dense film the white areas of increased conductivity in the local current map are correlated with the light areas in the 2D image of the topography, which correspond to grain heights. The grain width is within the range of 0.15-0.4 μm, the minima in the topographic signal correspond to the grain boundaries. It can be seen that the change in the local current actually repeats the profile of the topography, and there are separate current peaks inside the grains. In addition, zero current positions correlate with the grain boundaries, thereby confirming that the grain boundaries are non-conductive. One can say that in the dense film local currents flow inside the grains, forming a dense columnar structure.
In films with 1 wt.% PVP, individual peaks of the intergrain current are observed, which significantly exceed the very low current flowing inside the grains, see Figure 14b. With exceeding 6 wt.% PVP, the distribution of the local current changes radically, Figure 14c--d. It can be seen that variations in the local current no longer repeat the profile of the grain relief, but, on the contrary, the current sharply increases in the region of grain boundaries and pore boundaries.

4. Discussion

4.1. Structure - Polarization

The film thickness at a single spin-on deposition increases by almost fivefold with the addition of 20 wt.% PVP, see Figure 1b. The main reason is the increase in the viscosity of the film-forming solution. According to Meyerhofer’s approximation for spin-on deposition a film thickness d ~ ν1/3, where ν is the viscosity of solution [43]. No cracking was observed in all samples studied in this research. The addition of a stress-relaxing agent, polyvinylpyrrolidone (PVP), to the PZT precursor solution leads to an increase in the film thickness and prevents film cracking [7,8,12]. Kozuka et al observed that the tensile stress in the BST films is greatly reduced with increasing PVP content.
According to the study of the silicate sol-gel process with PVP by Saegusa and Chujo, PVP forms hydrogen bonds with oxoalkoxides, slowing down the polycondensation reaction [10,11]. Kozuka et al suggest an interaction between PVP and PZT precursors via carbonyl groups (C=O) and the hydroxyl bonds (OH) [7]. However, the synthesis of a film-forming solution in our case does not assume any water addition for hydrolysis (see Section 2). Lead acetate is also free of water according to its direct preparation from PbO [44]. We assume that intermolecular interaction between PVP and PZT oxoalkoxide occurs via donor-acceptor mechanism.
The film thickness is increased without any saturation region up to 20 wt.% PVP content (Figure 1b). In contrast, the addition of surfactant Brij, used as a porogen for preparation of silica and PZT porous films, demonstrates saturation region at the film thickness - porogen content dependences, as there are no sufficient terminal hydroxyls to provide interaction between Brij and metal-oxide network [31,45]. This fact limits the porosity of films prepared by EISA with Brij surfactant [31]. In contrast, the PVP-based process can provide higher porosity for PZT films. The porosity value obtained from ellipsometry data increases with the PVP content in the range 1-6.6 wt.% reaching about 32 % (Figure 3). A further growth of PVP content leads to an increase in the porosity. Indeed, the refractive index of PZT film before crystallization shows further decrease (Figure 2), while the calculated value of porosity increases (Figure 3). A rough estimation from in-plane SEM images analysis supports the porosity increase in the range of PVP content from 1 to 20 wt.% up to the value about 40%, see Figure 5b.
The films demonstrate a rather high average pore size of 40-100 nm (Figure 5a). This value coincides with the data obtained by transmission electron microscopy in [31]. It should be noted that the EISA process with the Brij precursor provides a smaller pore size and a uniform pore distribution [31].
SEM study showed a columnar grain structure of a dense PZT film, isolated disk-shaped pore inclusions inside the PZT grains at 1 to 3 wt. % PVP (3-0 connectivity), and percolated porous structure when exceeding 6.6 wt. % PVP. In the latter case, the porous structure becomes continuous and is attributed to a 3-3 connectivity. The X-ray diffraction data confirms the crystal structure transformation: the strong columnar grain Pe (111) texture in the dense film is destroyed and changes to the predominant Pe (110) and weaker (211) in porous films. The lattice constants in the dense film are less than in PZT powder, indicating the presence of compressive stress. While in porous films, the lattice constant increases with the PVP content, which evidences for the stress relaxation. This explains the better cracking resistance of porous films.
The CV curves of all samples demonstrate nonlinear butterfly-like behavior typical for ferroelectrics, see Figure 7 [46]. All films demonstrate as well polarization hysteresis (Figure 9). Introducing porosity decreases electrical nonlinearity but the ferroelectric behavior persists even in the case of high film porosity. Both the maximum permittivity value representing the contribution of the domain walls movement near the coercive field, and the minimum permittivity value related to low contribution of domain walls due to their electric field clamping, show a decrease with increasing porosity (Figure 8). However, the Brüggemann's approximation for binary composites gives larger values of the effective permittivity compared to the experimental data (Figure 8). Dielectric hysteresis loops also showed faster decrease in the remanent polarization, than predicted by the Wersing's approximation [33], see Figure 10. This indicates that, in addition to the decrease in the volume of the ferroelectric material, which is taken into account in these models, there are other factors that affect the electrical properties. Among them are the texture destruction, an emergence of additional interfaces and defects that cause depolarization fields and domain walls clamping. On the other hand, the relaxation of mechanical stresses in porous films leads to a decrease in the nonswitchable polarization Pdep [34], see Figure 10. We can suggest that this is a reason of the weak dependence of the coercive field on porosity (Figure 11) in contrast to the monotonic growth with porosity predicted in [33].

4.2. Рolarization Dependences of the Transient Current

The depolarized Pt/PZT/Pt structure contains two Schottky barriers with depleted SCLs created by the positive charge of oxygen vacancies and a quasi-neutral region between them, where the positive charge of oxygen vacancies is compensated by the negative charge of electrons captured by Ti+3 atoms. As was shown in [41], at the contact of a polarized film where a negative polarization charge arises, the thickness of the depleted SCL increases, while at the opposite contact it decreases, and if the polarization exceeds a certain level, then the depleted SCL at this contact is replaced by the accumulated layer. When an external bias is applied in the direction of the polarization, the electric field begins to pull electrons from the accumulated SCL and transfer them to the depleted SCL at the opposite contact, compensating for the charge of vacancies and thereby reducing the resistance of this layer and the entire film. This causes an increase in the current and the formation of a current peak. When the accumulated layer has exhausted all the electrons, further electrons taken from the already depleted layer increase the thickness of this SCL and, hence, the film resistance, which leads to a decrease in the current and completes the formation of the current peak. Thus, there are several factors, necessary to appear the current peak: (1) the presence of an accumulated SCL and (2) coincidence of the directions of the applied bias and the polarization vector.
In the dense PZT film, all necessary conditions are present, therefore we can see the highest current peaks in both bias directions. At 1 - 3 wt.% PVP, there are pronounced current peaks, but with a lower current value. The latter can be explained by a decrease in an electron density of the accumulated layer due to the polarization reduction with increasing porosity. The current peak is formed by electrons of the accumulated layer and their hopping over Ti levels inside the grains. When pores are introduced into the PZT matrix, a new current component appears which is associated with carrier hopping through deep levels along the grain boundaries and pore boundaries. It is unlikely that this current contributes to the formation of the current peak, since the dependence of this current on the polarization direction is not visible.
At 6.6 wt.% PVP content and more the film structure suffers strong distortion. This leads to appearance of numerous depolarizing fields associated with charged pore boundaries and significant variations in both the direction and magnitude of the electric field throughout the film, which, in turn, leads to a general decrease in the polarization magnitude, the emergence of poled areas with different poling directions, and even the presence of unpoled areas [47]. As a result, the averaged built-in electric field responsible for the transfer of carriers between the contacts is weakened, while conductive grain boundaries appear. The disappearance of the current peaks can be explained by the simultaneous influence of a decrease in the polarization, a weakening of electron transfer across titanium levels, and competitive conductivity along the grain boundaries.

4.3. Рolarization Dependences of the Photocurrent

We assume that when illuminated by visible light with a photon energy less than the band gap PZT, an electron in the valence band absorbs an energy quantum and is excited to the Ti level located by 1 eV below the bottom of the conduction band, while a free hole appears in the valence band. The electrons excited from the Ti level to the conduction band fall back to the Ti level or move in the electric field to the contact for a time much shorter than 1 s, therefore they do not contribute to the measured photocurrent. The initial burst of the photocurrent is defined by the direction of the built-in electric field in the film. In a dense PZT film, the built-in field is most likely to be the downwards electric field of the bottom Schottky barrier. Therefore, the initial burst of the photocurrent is negative. Further relaxation of the photocurrent to its stationary value reflects the establishment of an equilibrium between the processes of photoexcitation, recombination, and charge carrier transport. As a result, in the depolarized state, the stationary negative photocurrent density was 7ˑ10-7 A/cm2 at an illumination intensity of 0.025 W/cm2. This magnitude agrees well with the photovoltaic current value of 4.7ˑ10-7 A/cm2 for a 210-nm-thick PLZT film at an illumination intensity of 0.05 W/cm2 reported in [48].
An effect of the preliminary polarization on the photocurrent can be explained by the bulk photovoltaic effect, in which a photocurrent is induced in the polarization direction. In the case of +Pr = 24 µC/cm2, it seems that the action of the bulk photovoltaic effect almost completely compensates for the action of the built-in electric field associated with Schottky barriers and polarization charges. As a result, the negative photocurrent decreases to -11 pA. In the case of –Pr = -9 µC/cm2, the contribution to the negative photocurrent can occur due to the bulk photovoltaic effect, while the positive photocurrent can appear due to the depolarizing field or a field enhancement of the top Schottky barrier. As results for -Pr, the induced photocurrent is too small to change significantly the negative stationary photocurrent of the depolarized state
The film with 3 wt.% PVP retains all the features of the dense film photocurrent: a negative burst followed by a relaxation to a stationary negative value and the same dependence on the polarization, but with a weaker influence on the current magnitude, since the polarization value has already decreased due to porosity. However, with exceeding 6 wt.% PVP, the initial burst of the photocurrent changes its direction from the negative to the positive one. The film is illuminated from the side of the top electrode, where a higher density of excited carriers can occur due to a non-uniform light absorption across the film thickness as well as light scattering associated with the presence of pores. Therefore, at the first illumination moment, most of the excited carriers are exposed to the action of the positive electric field of the top Schottky barrier and exhibit a positive current burst, followed by a relaxation to a stationary negative photocurrent. Moreover, the magnitude of the stationary photocurrent decreases with increasing porosity, indicating a weakening of the averaged built-in electric field in the film and practically independent of the polarization direction.
Analyzing the photovoltaic current measurements, one can conclude the following. Charged pore boundaries in the films with 3-3 connectivity leads to the appearance of numerous depolarizing fields and not only to a decrease in the magnitude of the polarization, but also to the loss of a single direction of the polarization vector throughout the film.

4.4. Local Current Study

A dense PZT film with a columnar grain structure contains grains and grain-boundaries. The c-AFM study showed that in the dense PZT film the local current flows between the bottom and top electrodes through the PZT grains, while the grain boundaries are non-conductive. Scheme 1a is a sketch illustrating the current flowing in the dense PZT film.
The introduction of pores into a PZT film creates a new type of interface—pore boundaries. Inside the film, there are grains, grain boundaries, pores inside the grains. A pore may appear between the grains, but it remains a part of the grain boundary. Furthermore, since a polarization charge can exist at the grain boundaries, the pore boundaries also can be charged. The resulting pore boundaries are new pathways for the flow of the electric current. Electrons move either inside the PZT grain, or along pore boundaries, or grain boundaries. At low PVP content below 6.6 wt.% (3-0 connectivity), individual intergrain current peaks are observed, which significantly exceed the very small current flowing inside the grains, see Scheme 1b. At higher PVP content (3-3 connectivity) the grain size decreases, but the number of current pathways along the pore boundaries increases, so that the currents flowing along the pore boundaries exceed those flowing inside the grains, as it is seen in Figure 14c,d and Scheme 1c. As a result, the conductivity and leakage current in the porous films increase compared to the dense film.

5. Conclusions

Thе research focuses on understanding structural and electrical properties of porous ferroelectric PZT films prepared by CSD technique. The film porosity is engineered using various amounts of PVP as a structure-directing agent. SEM and X-ray diffraction show that PVP addition significantly changes the (111) textured columnar perovskite grains structure of the dense film. At low PVP content (below 6 wt. %) the films retain columnar grain structure with inclusions of pores (3-0 connectivity). Under these conditions, the polarization magnitude and permittivity decrease, the direction of the polarization vector is retained throughout the film thickness up to the electrodes. In the film, there is an averaged built-in electric field directed from the top electrode to the bottom one, and the dependence of the photovoltaic current on the polarization direction is observed. The local current flows mainly inside the grains while individual high intergrain current peaks are found.
Higher PVP content, exceeding 6.6 wt.%, leads to a stronger transformation of the structure. The films lose their columnar grain structure and become a fine-grained and spongy-granular, while the porous structure becomes continuous with a 3-3 connectivity. Structure transformation is accompanied by the mechanical stresses relaxation of the initially compressed film, including the disappearance of the hysteresis loop asymmetry with porosity increase. This explains the better resistance of porous films to cracking.
It is shown that the switchable polarization decreases with increasing volume porosity faster than the linear reduction predicted by the Wersing's approximation. This indicates the presence of an additional depolarization factor associated not only with a decrease in the volume of the ferroelectric material. The introduction of low permittivity pores into a ferroelectric matrix with high dielectric constant leads to the appearance of a new type of interfaces between an air pore and a grain, which is the pore boundary. Furthermore, the pore boundary can also be charged. This leads to the appearance of numerous depolarizing fields and significant variations in both the direction and magnitude of the electric field throughout the film. The latter, in turn, leads to a general decrease in the polarization magnitude, and the direction of the polarization vector is not preserved throughout the film thickness.
The pore boundaries are new pathways for the flow of the electric current, the number of which increases with increasing porosity above 6.6 wt.%, so that the currents flowing along the pore boundaries exceeds those flowing inside the grains. As a result, the leakage current in the porous films increases compared to the dense film.
We suggest that understanding of structural peculiarities and physical processes in porous PZT films opens way for their applications in electronics, including MEMS, pyroelectric infrared detectors, sensors, etc.

Author Contributions

Conceptualization, K.V.; Methodology, K.V., L.D., D.S., N.Z., and E.G.; Validation, L.D., D.S., and K.V.; Formal Analysis, N.Z.. and G.O..; Investigation, L.D., D.S., G.O., N.Z., and E.G.; Resources, K.V., L.D., and A.S.; Data Curation, L.D., D.S., and K.V.; Writing – Original Draft Preparation, L.D., and K.V.; Writing – Review & Editing, L.D., A.S., and K.V.; Visualization, L.D.; Supervision, A.S. and K.V.; Project Administration, L.D., and K.V.; Funding Acquisition, A.S. All authors have read and agreed to the published version of the manuscript.

Funding

This work was supported by the Ministry of Science and Higher Education of the Russian Federation [project № FSFZ -2023-0005 – in part of development and characterization of ferroelectric heterostructures], and Russian Scientific Foundation [grant № 23-79-30016 in part of the program conceptualization and selection of the material for this research].

Data Availability Statement

Data are contained within the article. The raw data presented in this study are available on request from the authors.

Acknowledgments

The authors are grateful to D.A. Abdullaev and N.M. Kotova for assistance and helpful discussion.

Conflicts of Interest

The authors declare no conflict of interest. The funders had no role in the design of the study; in the collection, analyses, or interpretation of data; in the writing of the manuscript; or in the decision to publish the results.

Sample Availability

Not applicable for this work.

References

  1. Li, J.F.; Takagi, K.; Ono, M.; Pan, W.; Watanabe, R.; Almajid, A.; Taya, M. Fabrication and evaluation of porous piezoelectric ceramics and porosity-graded piezoelectric actuators. Journal of the American Ceramic Society 2003, 86, 1094–1098. [Google Scholar] [CrossRef]
  2. Shaw, C.P.; Whatmore, R.W.; Alcock, J.R. Porous, functionally gradient pyroelectric materials. Journal of the American Ceramic Society 2007, 90, 137–142. [Google Scholar] [CrossRef]
  3. Nie, H.; Yu, Y.; Liu, Y.; He, H.; Wang, G.; Dong, X. Enhanced shock performance by disperse porous structure: A case study in PZT95/5 ferroelectric ceramics. Journal of the American Ceramic Society 2017, 100, 5693–5699. [Google Scholar] [CrossRef]
  4. Roscow, J.; Zhang, Y.; Taylor, J.; Bowen, C. R. Porous ferroelectrics for energy harvesting applications. European Physical Journal: Special Topics 2015, 224, 2949–2966. [Google Scholar] [CrossRef]
  5. Mercadelli, E.; Galassi, C. How to make porous piezoelectrics? Review on processing strategies. IEEE Transactions on Ultrasonics, Ferroelectrics, and Frequency Control 2020, 68, 217–228. [Google Scholar] [CrossRef]
  6. Corkovic, S.; Whatmore, R.W.; Zhang, Q. Sol-gel fabrication of PZT thick films for MEMS. Integrated Ferroelectrics 2007, 88, 93–102. [Google Scholar] [CrossRef]
  7. Kozuka, H.; Kajimura, M.; Hirano, T.; Katayama, K. Crack-free, thick ceramic coating films via non-repetitive dip-coating using polyvinylpyrrolidone as stress-relaxing agent. Journal of Sol-Gel Science and Technology 2000, 19, 205–209. [Google Scholar] [CrossRef]
  8. Kozuka, H.; Kajimura, M. Achievement of crack-free BaTiO3 films over 1 μm in thickness via non-repetitive dip-coating. Chemistry Letters 1999, 10, 1029–1030. [Google Scholar] [CrossRef]
  9. Kozuka, H.; Takenaka, S. Single-Step Deposition of Gel-Derived Lead Zirconate Titanate Films: Critical Thickness and Gel Film to Ceramic Film Conversion. Journal of the American Ceramic Society 2002, 85, 2696–2702. [Google Scholar] [CrossRef]
  10. Saegusa, T.; Chujo, Y. Macromolecular engineering on the basis of the polymerization of 2-oxazolines. Makromolekulare Chemie. Macromolecular Symposia 1991, 51, 1–10. [Google Scholar] [CrossRef]
  11. Saegusa, T.; Chujo, Y. An Organic/Inorganic Hybrid Polymer. Journal of Macromolecular Science: Part A - Chemistry 1990, 27, 1603–1612. [Google Scholar] [CrossRef]
  12. Kozuka, H.; Kajimura, M. Single-Step Dip Coating of Crack-Free BaTiO3 Films &gt; 1 μm Thick: Effect of Poly(vinylpyrrolidone) on Critical Thickness. Journal of the American Ceramic Society 2000, 83, 1056–1062. [Google Scholar] [CrossRef]
  13. Komandin, G.A.; Porodinkov, O.E.; Spektor, I.E.; Volkov, A.A.; Vorotilov, K.A.; Seregin, D.S.; Sigov, A.S. Terahertz-infrared electrodynamics of lead zirconate-titanate films on a platinum sublayer. Physics of the Solid State 2015, 57, 1155–1159. [Google Scholar] [CrossRef]
  14. Komandin, G.A.; Porodinkov, O.E.; Spektor, I.E.; Volkov, A.A.; Vorotilov, K.A.; Seregin, D.S.; Sigov, A.S. The Mechanisms of Absorption of Terahertz and Infrared Radiation in PZT Films. Physics of the Solid State 2018, 60, 1226–1234. [Google Scholar] [CrossRef]
  15. Ohya, Y.; Yahata, Y.; Ban, T. Dielectric and piezoelectric properties of dense and porous PZT films prepared by sol-gel method. Journal of Sol-Gel Science and Technology 2007, 42, 397–405. [Google Scholar] [CrossRef]
  16. Stancu, V.; Boerasu, I.; Lisca, M.; Pintilie, L.; Popescu, M.; Sava, F. Structural and microstructural properties of porous PZT films. Journal of Optoelectronics and Advanced Materials 2006, 8, 1492–1497. [Google Scholar]
  17. Suyal, G.; Setter, N. Enhanced performance of pyroelectric microsensors through the introduction of nanoporosity. Journal of the European Ceramic Society 2004, 24, 247–251. [Google Scholar] [CrossRef]
  18. Zhang, Q.; Corcovic, S.; Shaw, C.P.; Huang, Z.; Whatmore, R.W. Effect of porosity on the ferroelectric properties of Sol-Gel prepared Lead Zirconate Titanate thin films. Thin Solid Films 2005, 488, 258–264. [Google Scholar] [CrossRef]
  19. Seregin, D.S.; Vorotilov, K.A.; Sigov, A.S.; Zubkova, E.N.; Abdullaev, D.A.; Kotova, N.M.; Vishnevskiy, A.S. Formation and properties of porous films of lead zirconate titanate. Physics of the Solid State 2015, 57, 499–502. [Google Scholar] [CrossRef]
  20. Seregin, D.; Vorotilov, K.; Sigov, A.; Kotova, N. Porous PZT films prepared by PVP assisted sol-gel process. Ferroelectrics 2015, 484, 43–48. [Google Scholar] [CrossRef]
  21. Stancu, V.; Lisca, M.; Boerasu, I.; Pintilie, L.; Kosec, M. Effects of porosity on ferroelectric properties of Pb(Zr0.2Ti0.8)O3 films. Thin Solid Films 2007, 515, 6557–6561. [Google Scholar] [CrossRef]
  22. Zhang, Y.; Roscow, J.; Lewis, R.; Khanbareh, H.; Topolov, V.Y.; Xie, M.; Bowen, C.R. Understanding the effect of porosity on the polarisation-field response of ferroelectric materials. Acta Materialia 2018, 154, 100–112. [Google Scholar] [CrossRef]
  23. Podgorny, Y.; Vorotilov, K.; Lavrov, P.; Sigov, A. Leakage currents in porous PZT films. Ferroelectrics 2016, 503, 77–84. [Google Scholar] [CrossRef]
  24. Podgornyi, Y.V.; Vorotilov, K.A.; Sigov, A.S. Determination of the Steady State Leakage Current in Structures with Ferroelectric Ceramic Films. Physics of the Solid State 2018, 60, 433–436. [Google Scholar] [CrossRef]
  25. Izyumskaya, N.; Alivov, Y.I.; Cho, S.J.; Morkoç, H.; Lee, H.; Kang, Y.S. Processing, structure, properties, and applications of PZT thin films. In Critical Reviews in Solid State and Materials Sciences 2007, 32, 111–202. [Google Scholar] [CrossRef]
  26. Delimova, L.A.; Guschina, E.V.; Seregin, D.S.; Vorotilov, K.A.; Sigov, A.S. Unexpected behavior of transient current in thin PZT films caused by grain-boundary conduction. J. Appl. Phys. 2017, 121, 224104. [Google Scholar] [CrossRef]
  27. Krishtab, M.; Afanas’Ev, V.; Stesmans, A.; De Gendt, S. Leakage current induced by surfactant residues in self-assembly based ultralow-k dielectric materials. Appl. Phys. Lett. 2017, 111, 032908. [Google Scholar] [CrossRef]
  28. Sigov, A.S.; Vorotilov, K.A.; Zhigalina, O.M. Effect of Lead Content on Microstructure of Sol-Gel PZT Structures. Ferroelectrics 2012, 433, 146–157. [Google Scholar] [CrossRef]
  29. Vorotilov, K.; Sigov, A.; Seregin, D.; Podgorny, Yu.; Zhigalina, O.; Khmelenin, D. Crystallization behavior of PZT in multilayer heterostructures. Phase Trans. 2013, 86, 1152–1165. [Google Scholar] [CrossRef]
  30. Newnham, R.E.; Skinner, D.P.; Cross, L.E. Connectivity and Piezoelectric-Pyroelectric Composites. Mater Res Bull 1978, 13, 525–536. [Google Scholar] [CrossRef]
  31. Atanova, A. V.; Zhigalina, O.M.; Khmelenin, D.N.; Orlov, G.A.; Seregin, D.S.; Sigov, A.S.; Vorotilov, K.A. Microstructure Analysis of Porous Lead Zirconate–Titanate Films. Journal of the American Ceramic Society 2022, 105, 639–652. [Google Scholar] [CrossRef]
  32. Vishnevskiy, A.S.; Naumov, S.; Seregin, D.S.; Wu, Y.-H.; Chuang, W.-T.; Rasadujjaman, M.; Zhang, J.; Leu, J.; Vorotilov, K.A.; Baklanov, M.R. Effects of Methyl Terminal and Carbon Bridging Groups Ratio on Critical Properties of Porous Organosilicate-Glass Films. Materials 2020, 13, 4484. [Google Scholar] [CrossRef] [PubMed]
  33. Wersin, W.; Lubits, K.; Mohaupt, J. Dielectric, Elastic and Piezoelectric Properties of porous PZT ceramics. Ferroelwectrics 1986, 68, 77–97. [Google Scholar] [CrossRef]
  34. Delimova, L.A.; Zaitseva, N.V.; Ratnikov, V.V.; Yuferev, V.S.; Seregin, D.S.; Vorotilov, K.A.; Sigov, A.S. Comparison of Characteristics of Thin PZT Films on Si-on-Sapphire and Si Substrates. Physics of the Solid State 2021, 63, 1224–1231. [Google Scholar] [CrossRef]
  35. Podgorny, Y.； Sigov, A.; Vorotilov, K. Once again on the hysteresis loop: Leakage current consideration. Ferroelectrics 2021, 573, 1–8. [Google Scholar] [CrossRef]
  36. Marutake, M. A Calculation of Physical Constants of Ceramic Barium Titanate. Journal of the Physical Society of Japan 1956, 11, 807–814. [Google Scholar] [CrossRef]
  37. Nagata, K. Effects of porosity and grain size on hysteresis loops of piezoelectric ceramics (Pb-La)(Zr-Ti)O3. Electr. Eng. Jpn. 1980, 11, 1–8. [Google Scholar] [CrossRef]
  38. Delimova, L.A.; Gushchina, E.V.; Yuferev, V.S.; Grekhov, I.V. Investigation of the polarization dependence of the transient current in polycrystalline and epitaxial Pb(Zr,Ti)O3 thin films. Physics of the Solid State 2014, 56, 2451–2460. [Google Scholar] [CrossRef]
  39. Robertson, J.; Warren, W.L.; Tuttle, B.A.; Dimos, D.; Smith, D.M. Shallow Pb3+ hole traps in lead zirconate titanate ferroelectrics. Appl. Phys. Lett. 1993, 63, 1519–1521. [Google Scholar] [CrossRef]
  40. Warren, W.L.; Robertson, J.; Dimos, D.B.; Tuttle, B.A.; Smyth, D.M. Transient hole traps in PZT. Ferroelectrics 1994, 153, 303–308. [Google Scholar] [CrossRef]
  41. Delimova, L.A.; Yuferev, V.S. Transient carrier transport and rearrangement of Schottky barrier layers under theaction of a bias applied to the M/PZT/M structure. J. Appl. Phys. 2018, 124, 184102. [Google Scholar] [CrossRef]
  42. Delimova, L.A.; Yuferev, V.S. Transient carrier transport and rearrangement of space charge layers under the bias applied to ferroelectric M/PZT/M structures. J. Phys. Conf. Ser. 2019, 1400, 055003. [Google Scholar] [CrossRef]
  43. Meyerhofer, D. Characteristics of resist films produced by spinning. J. Appl. Phys. 1978, 49, 3993–3997. [Google Scholar] [CrossRef]
  44. Kotova, N. M.; Vorotilov, K. A.; Seregin, D. S.; Sigov, A. S. Role of precursors in the formation of lead zirconate titanate thin films. Inorganic Materials 2014, 50, 612–616. [Google Scholar] [CrossRef]
  45. Nenashev, R. N.; Kotova, N. M.; Vishnevskii, A. S.; Vorotilov, K. A. Effect of the Brij 30 porogen on the properties of sol–gel derived thin polymethylsilsesquioxane films. Inorganic Materials 2016, 52, 968–972. [Google Scholar] [CrossRef]
  46. Vorotilov, K.A.; Yanovskaya, M.I.; Dorokhova, O.A. Effect of annealing conditions on alkoxy-derived PZT thin films. Microstructural and CV study. Integrated Ferroelectrics 1993, 3, 33–49. [Google Scholar] [CrossRef]
  47. Lewis, R.W.C.; Dent, A.C.E.; Stevens, R.; Bowen, C.R. Microstrutural modelling of the polarization and properties of porous ferroelectrics. Smart Mater. Struct. 2011, 20, 085002. [Google Scholar] [CrossRef]
  48. Batra, V.; Kotru, S. A simulation model for understanding the charge transport and recombination behavior in PLZT based ferroelectric photovoltaic devices. Ferroelectrics 2018, 532, 121–137. [Google Scholar] [CrossRef]
Preprints 78576 g001
Figure 1. A film thickness vs number of applied layer (a) and a thickness of one applied layer on PVP content (b).
Figure 1. A film thickness vs number of applied layer (a) and a thickness of one applied layer on PVP content (b).
Preprints 78576 g001
Preprints 78576 g004
Figure 4. Cross-sectional (top) and in-plane (bottom) SEM images of PZT films prepared with different PVP content, wt.%: 0 - (a); 1 – (b); 3 – (c); 6.6 – (d); 14 – (e); 20 – (f).
Figure 4. Cross-sectional (top) and in-plane (bottom) SEM images of PZT films prepared with different PVP content, wt.%: 0 - (a); 1 – (b); 3 – (c); 6.6 – (d); 14 – (e); 20 – (f).
Preprints 78576 g004
Preprints 78576 g005
Figure 5. In-plane SEM results: pore size on the left (a), porosity on the right (b) depending on the PVP content. Data obtained by statistical processing of in-plane SEM pictures in ImageScope software.
Figure 5. In-plane SEM results: pore size on the left (a), porosity on the right (b) depending on the PVP content. Data obtained by statistical processing of in-plane SEM pictures in ImageScope software.
Preprints 78576 g005
Preprints 78576 g006
Figure 6. X-ray diffraction patterns of PZT films prepared with different wt.% PVP: (1) – 0; (2) - 1; (3) - 6.6.
Figure 6. X-ray diffraction patterns of PZT films prepared with different wt.% PVP: (1) – 0; (2) - 1; (3) - 6.6.
Preprints 78576 g006
Preprints 78576 g007
Figure 7. The dielectric constant vs the electric field in thin (a) and thick (b) PZT film.
Figure 7. The dielectric constant vs the electric field in thin (a) and thick (b) PZT film.
Preprints 78576 g007
Preprints 78576 g008
Figure 8. The dielectric constant εmax and εmin as a function of volume porosity measured in curves: (1) thin films, and (2) thick films; dashed lines correspond to the calculated Brüggemann's approximation for pores with a 3-3 connectivity.
Figure 8. The dielectric constant εmax and εmin as a function of volume porosity measured in curves: (1) thin films, and (2) thick films; dashed lines correspond to the calculated Brüggemann's approximation for pores with a 3-3 connectivity.
Preprints 78576 g008
Preprints 78576 g009
Figure 9. The polarization vs sample voltage in the dense (a), and porous PZT films (b).
Figure 9. The polarization vs sample voltage in the dense (a), and porous PZT films (b).
Preprints 78576 g009
Preprints 78576 g010
Figure 10. The polarizations 2Pr and Pdep vs PVP content in weight percentage (a) and volume porosity (b).
Figure 10. The polarizations 2Pr and Pdep vs PVP content in weight percentage (a) and volume porosity (b).
Preprints 78576 g010
Preprints 78576 g011
Figure 11. The dependences of the coercive field vs volume porosity in the measured PZT films.
Figure 11. The dependences of the coercive field vs volume porosity in the measured PZT films.
Preprints 78576 g011
Preprints 78576 g012
Figure 12. Current-voltage curves measure at different pre-polarization in PZT films with various PVP content, wt.%: (a) – 0; (b) – 1; (c) – 3: (d) – 6.6; (e) – 14; (f) – 20.
Figure 12. Current-voltage curves measure at different pre-polarization in PZT films with various PVP content, wt.%: (a) – 0; (b) – 1; (c) – 3: (d) – 6.6; (e) – 14; (f) – 20.
Preprints 78576 g012
Preprints 78576 g013
Figure 13. Dependences of the photocurrent on the illumination time at different pre-polarization in PZT film with PVP content, wt.%: (a) – 0; (b) – 3; (c) – 6.6; (d) - 14.
Figure 13. Dependences of the photocurrent on the illumination time at different pre-polarization in PZT film with PVP content, wt.%: (a) – 0; (b) – 3; (c) – 6.6; (d) - 14.
Preprints 78576 g013
Preprints 78576 g014aPreprints 78576 g014b
Figure 14. The results of the c-AFM study in PZT films with various PVP content, wt.%: (a) - 0; (b) - 1; (c) - 6.6; (d) - 14. For each PZT film, the 2D images (upper left) of the topography and (upper right) maps of local currents obtained by scanning the PZT film are shown; Below are the profiles of the topographic signal h (left scale, solid line) and local current I (right scale, circles) flowing along the profile shown above by the dotted line.
Figure 14. The results of the c-AFM study in PZT films with various PVP content, wt.%: (a) - 0; (b) - 1; (c) - 6.6; (d) - 14. For each PZT film, the 2D images (upper left) of the topography and (upper right) maps of local currents obtained by scanning the PZT film are shown; Below are the profiles of the topographic signal h (left scale, solid line) and local current I (right scale, circles) flowing along the profile shown above by the dotted line.
Preprints 78576 g014aPreprints 78576 g014b
Preprints 78576 sch001
Scheme 1. Sketch, illustrating the current flowing across the dense (a) and porous PZT films with pore interconnectivity (3-0) – (b) and (3-3) – (c). The red arrows indicate the currents flowing through the grains (thin) and along the boundaries of grains and pores (thick). White color indicates air pores.
Scheme 1. Sketch, illustrating the current flowing across the dense (a) and porous PZT films with pore interconnectivity (3-0) – (b) and (3-3) – (c). The red arrows indicate the currents flowing through the grains (thin) and along the boundaries of grains and pores (thick). White color indicates air pores.
Preprints 78576 sch001
Table 1. General characteristics of porous thin and thick (bold font) PZT films.
Table 1. General characteristics of porous thin and thick (bold font) PZT films.
PVP wt.% Volume porosity,% Number of layers Thickness d, nm Refractive index Thickness per layer
0 0 10 370 2.54 37
0 0 17 607 2.61 36
1 6.8 9 390 2.40 43
1 7.1 16 705 2.39 44
3 11.0 7 345 2.29 49
3 13.3 12 600 2.23 50
6.6 33.3 4 383 1.83 96
6.6 32.0 7 566 1.85 81
14 * 3 380 * 127
14 * 5 500 * 100
20 * 3 617 * 206
*Ellipsometric measurements were not meaningful because of light scattering.
Table 2. The percentage ratios of the reflection intensities found from the diffraction peaks in porous PZT films.
Table 2. The percentage ratios of the reflection intensities found from the diffraction peaks in porous PZT films.
PVP wt.% XRD texture
0 (111)100% (100) 28% (200)22%
1 (110)100% (211)14%
3 (110)100% (211)7%
6.6 (110)100% (211)16%
14 (110)100% (211)5%
20 (110)100%
Table 3. The lattice parameters in porous PZT films.
Table 3. The lattice parameters in porous PZT films.
XRD reflexes 100 110 111 200 211
PZT powder reflex, % 20% 100% 20% 22% 26%
Lattice constant, Å 4.068 4.068 4.068 4.068 4.068
PVP, wt.% Lattice constant in PZT, Å
0 4.029 4.061 4.019
1 4.061 4.047
3 4.072 4.027
6.6 4.072 4.055
14 4.072 4.062
20 4.073
Table 4. Characteristics of the I-V curves in polarized PZT films with different PVP content.
Table 4. Characteristics of the I-V curves in polarized PZT films with different PVP content.
PVP, wt.% I-V peak is observed when:
0 P//V, nonconductive grain boundaries (GB) columnar grain structure
1 P//V, 100% nonconductive GB columnar grain structure
porous 3-0 connectivity
3
6.6 V < 0 there are no peaks, 100% porous 3-3 connectivity
causes a destruction of the
columnar grain structure;

numerous depolarizing fields induced by polarization charges at pore boundaries lead to a decrease in the polarization and vanishing the current peaks;
V > 0 there are no peaks, 42%
35% weak peaks at P>0, nonconductive GB
23% weak peaks at P<0, conductive GB
14 V < 0 there are no peaks, 100%
V > 0 there are no peaks, 70%
15% weak plateau at P > 0
15% weak plateau at P < 0
20 V < 0 there are no peaks, 100%
V > 0 there are no peaks, 50%
50% weak plateau at P > 0
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.
Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.
Alerts
Prerpints.org logo

Preprints.org is a free preprint server supported by MDPI in Basel, Switzerland.

facebook logotwitter logolinkedin logo
MDPI Initiatives
Important Links
Subscribe

Disclaimer

Terms of Use

Privacy Policy

© 2025 MDPI (Basel, Switzerland) unless otherwise stated