Material Point Simulation Method for Concrete Medium Fracture and Fragmentation under Blast Loading

The nature of the fracture and fragmentation process of concrete medium under blast loading is the transformation process of the medium from continuum to discontinuity, coupled with the significant rate correlation of concrete medium, its mechanical behavior presents a high degree of complexity. Problems such as grid distortion and even negative volume are often encountered in the finite element method and others when solving this problem, while the material point method can effectively avoid these problems. In addition, the widely used HJC concrete constitutive model does not take into account the segmented characteristics of the calculation function for dynamic increasing factor. Therefore, in this paper, firstly, the calculation function for dynamic increasing factor in the HJC concrete model is modified by SHPB experiment, and the improved HJC concrete model is proposed; secondly, the material point method simulation program is developed, and the improved HJC concrete model is embedded into the simulation program; finally, the simulation program is verified by numerical examples, and the results show that the developed simulation program can better simulate the fracture and fragmentation process of concrete medium under blast loading, especially the pulverization characteristics of the medium in the near zone of the load.

Keywords:

Subject: Engineering - Civil Engineering

1. Introduction

The mechanical performance characteristics of concrete medium are: when external forces reach a certain limit, the concrete medium will undergo abrupt failure without prior warning; it has significant strength asymmetry, with compressive strength far greater than tensile strength; the failure is random and is a typical disordered medium, with an extremely small ultimate strain value during failure; it exhibits significant rate sensitivity under blast loading. In addition, the process of concrete medium failure under blast loading exhibits significant progressive (dynamic evolution process of failure), grading (scale of fragments), and zoning (mechanical response differences at different distances from the load source) characteristics: the medium in the near zone undergoes violent deformation and shows characteristics of crushing failure; the medium in the middle zone undergoes elastic-plastic deformation, and the degree of fragmentation is relatively larger compared to the medium in the near zone; the medium in the far zone undergoes elastic vibration. Therefore, the mechanical behavior of concrete medium under blast loading is highly complex.

Numerical simulation studies of concrete medium under blast loading mainly include finite element method, discontinuous deformation analysis method, and discrete element method. S.M., Martin, Jian, Jeong, et al. used finite element software to simulate the mechanical behavior of the concrete medium under blast loading and compared with the experimental results [1,2,3,4]. In order to solve discontinuous mechanical problems and break the limitations of the finite element method, the extended finite element method has been developed in recent years. Baietto et al. analyzed the two-dimensional and three-dimensional contact-type crack expansion, based on contact fatigue tests and empirical formulas for friction-type cracks [5,6]. However, the finite element method based on continuum mechanics often encounter grid distortion or even negative volume problems when solving the problem, resulting in abnormal termination of calculations.

The discontinuous deformation analysis (DDA) is a numerical model proposed by Shi Genhua for analyzing the motion and deformation of block systems [7]. DDA is capable of solving problems such as large displacements, large deformations, and discontinuous movements such as slipping, cracking, and rotating which are difficult to solve using traditional finite element methods. In recent years, scholars have started using this method to simulate the failure process of reinforced concrete structures and have achieved good results [8,9]. However, this method is currently limited to simulating two-dimensional problems and is still a certain distance away from simulating three-dimensional problems.

The discrete element method was first proposed by Professor Cundall P.A. in 1971 in the United States, suitable for solving large displacement and nonlinear problems [10]. Zhang et al used a two-dimensional discrete element model to study the failure process of concrete, it was verified that the concrete material failure simulation based on the discrete element method can truly simulate the entire process of crack generation, expansion and failure [11]. Sebastien et al used a three-dimensional discrete element model to study the dynamic behavior of concrete, and verified the rate effect of concrete through dynamic tensile tests [12]. Qin et al used the discrete element method to establish a two-dimensional concrete model, they further simulated the Brazilian splitting test of concrete and obtained a significant rate effect on the tensile strength of concrete [13,14,15]. Wu et al studied the crack propagation modes and the relationship between kinetic energy and strain energy under different strain rates [16,17]. However, the discrete element method simulates through iterative calculations, which requires a huge amount of computational resources; additionally, this method only uses cohesion to reflect the strength characteristics of the research object when simulating the damage of concrete medium, which is quite different from the actual situation.

The material point method (MPM) is developed from the Particle-in-Cell method, and combines the advantages of Lagrange and Euler methods, the material point moves in a background grid and the motion equation is solved on the background grid, avoiding the problem of grid distortion, it is particularly suitable for solving problems that involve large deformations or even material failure [18,19]. Therefore, this paper developed an MPM calculation program using C++ language based on the existing theoretical foundation of the material point method, and improved the widely used HJC concrete constitutive model. Finally, it was used to simulate the process of concrete medium fracture and fragmentation under blast loading.

2. Fundamental theory of the material point method

The material point method discretizes the continuum into a series of material points, each material point represents a material region and carries all the material information of that region, such as mass, velocity, stress, and strain, the collection of all material points represents the entire material area. Therefore, the density of the continuum can be approximated as.

ρ (x_{i}) = \sum_{p = 1}^{n_{p}} m_{p} δ (x_{i} - x_{i p})

(1)

In the equation,

n_{p}

represents the total number of material points,

m_{p}

is the mass of the material point,

δ

is the Dirac Delta function, and

x_{i p}

represents the coordinates of the material point.

Similar to the finite element method of Lagrange, the solution format of the material point method is also based on the weak form. The solution format of the material point method is as follows:

\int_{Ω} ρ {\ddot{u}}_{i} δ u_{i} d V + \int_{Ω} ρ σ_{i j}^{s} δ u_{i, j} d V - \int_{Ω} ρ b_{i} δ u_{i} d V - \int_{Γ_{t}} ρ {\bar{t}}_{i}^{s} δ u_{i} d A = 0

(2)

In the equation,

ρ

is the density,

{\ddot{u}}_{i}

is the acceleration,

b_{i}

is the force acting on unit mass of the object,

Ω

is the solving area,

Γ_{t}

is the given surface force boundary,

σ_{i j}^{s} = σ_{i j} / ρ

is the comparing stress,

{\bar{t}}_{i}^{s} = {\bar{t}}_{i} / ρ

is the comparing boundary surface force.

Substituting Equation (1) into Equation (2), we obtain:

\sum_{p = 1}^{n_{p}} m_{p} {\ddot{u}}_{i p} δ u_{i p} + \sum_{p = 1}^{n_{p}} m_{p} σ_{i j p}^{s} δ u_{i p, j} - \sum_{p = 1}^{n_{p}} m_{p} b_{i p} δ u_{i p} - \sum_{p = 1}^{n_{p}} m_{p} {\bar{t}}_{i p}^{s} h^{- 1} δ u_{i p} = 0

(3)

In the equation,

u_{i p} = u_{i} (x_{p})

δ u_{i p, j} = δ u_{i, j} (x_{p})

σ_{i j p}^{s} = σ_{i j}^{s} (x_{p})

b_{i p} = b_{i} (x_{p})

{\bar{t}}_{i p}^{s} = {\bar{t}}_{i}^{s} (x_{p})

h

is used to introduced a hypothetical boundary layer thickness in order to convert the final term of the left-hand side boundary integral in Equation (2) into a volume integral. As shown in Equation (3), the material point method converts the integrals in Equation (2) into the product of the value of the integrand at each material point and the volume represented by the material point, which is a form of point integration.

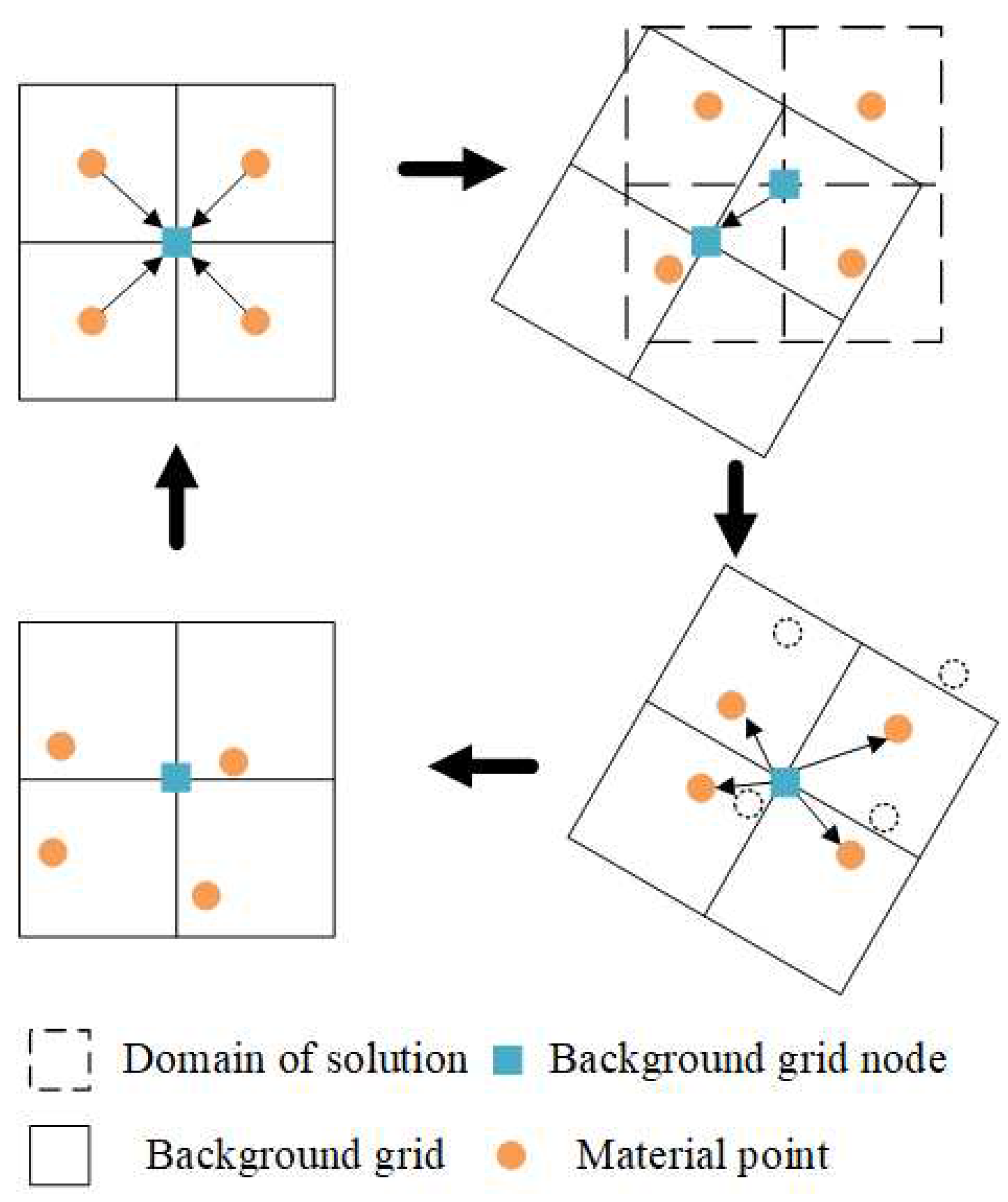
The material point method arranges a background grid in the material domain and uses the principle of virtual work to approximate the momentum equation. The displacement field is constructed using finite element shape functions on the regular grid and spatial derivatives are solved to establish the motion equation of the background grid nodes. At each time step, the material points move together with the background grid, and there is no need to handle the convection term. At the end of each time step, all motion information is recorded on the material points, and a new regular background grid is used in the next step. The solution process of the material point method in a single step is shown in Figure 1, and the calculation algorithm is shown in Figure 2.

3. An improved HJC concrete model considering the segmentation of DIF function

3.1. HJC concrete model

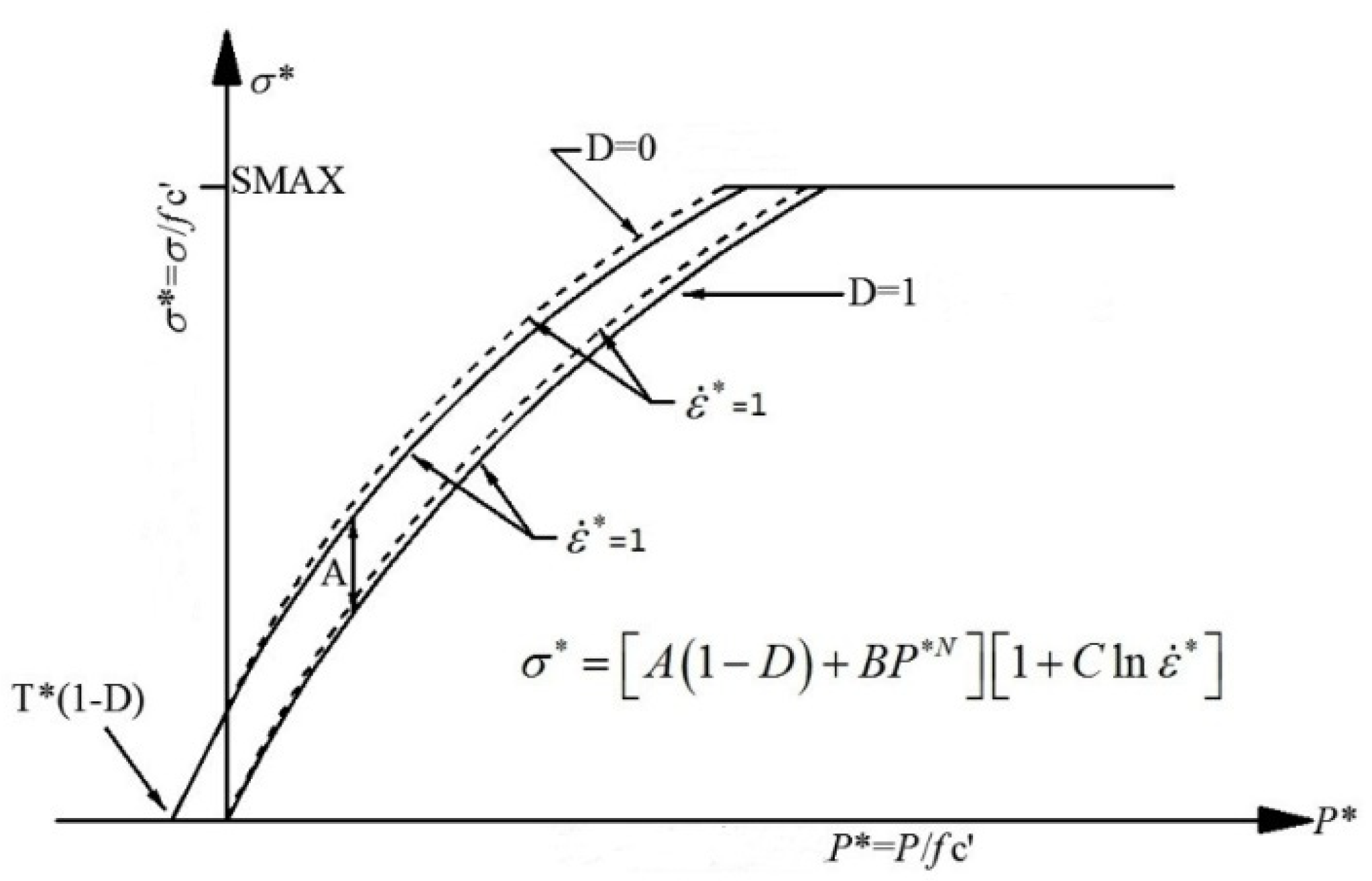
The HJC concrete model was proposed by Holmquist, Johnson, Cook et al [20]. This model proposes corresponding state equations and yield functions for concrete under high confinement pressure and large deformation at high strain, which can effectively simulate the mechanical behavior of concrete materials under high-speed impact, while reasonably considering the damage and failure of concrete during this process. The equation of the yield surface is shown in Figure 3.

The yield stress of the HJC concrete model is

σ_{y}^{*} = \{\begin{matrix} [A (1 - D) + B p^{* n}] D I F & p^{*} \geq 0 \\ [A (1 - D + p^{*} / T^{*})] D I F & p^{*} < 0 \end{matrix}

(4)

In the equation,

D I F = 1 + C \ln {\dot{ε}}^{*}

is the dynamic increasing factor,

σ_{y}^{*} = σ_{y} / f_{c}^{'}

is the normalized yield stress,

σ_{y}

is the yield stress,

f_{c}^{'}

is the unconfined compressive strength,

D

is the damage factor (

0 \leq D \leq 1

p^{*} = p / f_{c}^{'}

is the normalized pressure (

p

is the actual pressure),

{\dot{ε}}^{*} = \dot{ε} / {\dot{ε}}_{0}

is the dimensionless equivalent strain rate (

{\dot{ε}}_{0} = 1 s^{- 1}

is the reference strain rate),

A

is the normalized cohesive material strength,

B

is the normalized pressure hardening coefficient,

n

is the pressure hardening index,

C

is the strain rate coefficient.

The HJC model comprehensively considers the hydrostatic pressure effect and strain rate effect of concrete materials, as well as damage evolution caused by plastic strain and plastic volumetric strain. However, the HJC model itself still has certain shortcomings: (1) The model cannot well describe the failure mode dominated by tensile failure; (2) The influence of the third deviatoric stress invariant on the strength surface has not been considered; (3) The strain hardening behavior of concrete materials has not been taken into account.

In response to these deficiencies, researchers have made some improvements to the HJC model to improve its calculation accuracy under different loading conditions. Polanco-Loria et al. modified the HJC model by considering the hydrostatic pressure effect, the third deviatoric stress invariant, and the tensile-compression-shear composite damage, and used the improved HJC model to calculate uniaxial compression, biaxial compression, strain softening, and projectile penetration effects on concrete targets, and compared the results with other experimental results as well as the original HJC model calculation results [21]. M.J.Islam et al. mainly modified the strain rate effect part of the HJC model based on the experimental results of the dynamic increasing factor (DIF) of concrete material strength growth. At the same time, they considered the temperature effect in the HJC model and used the improved HJC model to calculate an example of projectile penetration into a concrete target, and compared it with the original HJC model [22]. Zhang Fengguo et al. in China corrected the deficiency of the tension damage model in the HJC model and verified the improved model through a 2-D program [23].

3.2. The improved method of HJC concrete model

In addition to the above shortcomings, a large number of research results have shown that the HJC model can well reflect the influence of low strain rates on the dynamic strength of concrete, but cannot accurately describe the significant enhancement effect of concrete dynamic strength under high strain rate conditions. That is, the dynamic strength calculated by the DIF function in the HJC model under high strain rate conditions deviates greatly from experimental results.

Therefore, based on the Hopkinson bar, this paper carried out dynamic uniaxial compression and dynamic split tension experiments on concrete to obtain the dynamic compressive and tensile strength of concrete under high strain rates, and improved the DIF function in the HJC model in combination with experimental data, making it have segmentation. That is, there is a critical strain rate. When the strain rate is lower than the critical strain rate, the strain rate effect on the strength of concrete is not obvious, but when the strain rate is higher than the critical strain rate, the degree to which the strength of concrete increases with the strain rate is significantly improved.

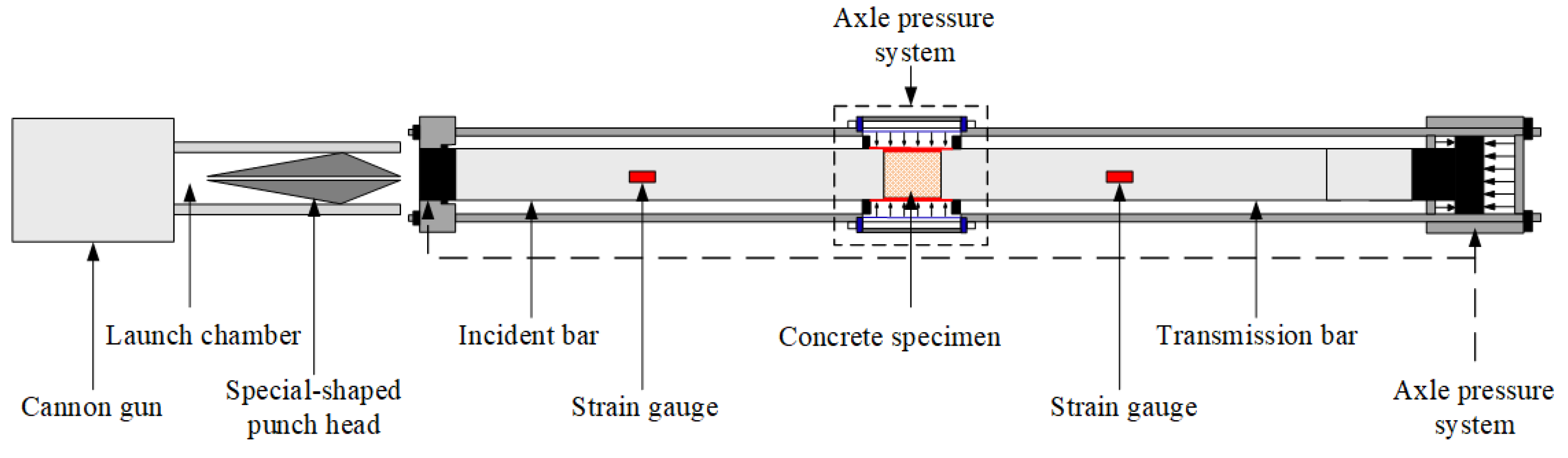
The Split-Hopkinson Pressure Bar (SHPB) experiment is the primary method of studying the mechanical properties of materials at high strain rates (10²~10⁴s-1). A modern conventional SHPB consists of a gas gun (cannon or launching device), a bullet, an incident bar, a transmission bar, an energy absorption device and a data acquisition system (as shown in Figure 4).

Several circular concrete specimens with a size of Φ50×25mm (as shown in Figure 5) were prepared for dynamic compression and dynamic Brazilian splitting tests using a 400mm cylindrical punch. Throughout the experiment, it is required that the cross-sectional area of the specimen is always smaller than or equal to that of the rod. In addition, the incident rod must be long enough (more than twice the length of the bullet) to avoid overlapping of incident and reflected waves, and the material must remain within the elastic range during the experiment. To improve the accuracy of the test, it is also required that the contact surface between the rod and the specimen must remain flat and parallel to each other throughout the experiment.

The concrete specimen is loaded between the incident and transmission bars. The bullet is propelled by high-pressure gas and is fired from the launching device at a certain velocity, striking the incident bar and generating a pressure pulse in the incident bar, known as the incident wave (measured by the resistance strain gauge attached to the incident bar). The pressure pulse propagates forward in the incident bar, and when it reaches the interface between the incident bar and the specimen, the entire specimen is compressed due to the inertial effect of the specimen and the transmission bar. Meanwhile, due to the wave impedance difference between the bar and specimen, the incident wave is partially reflected as a reflected wave back to the incident bar, and the other part passes through the specimen as a transmission wave and enters the transmission bar. The reflected wave is also measured by the resistance strain gauge attached to the incident bar, and the transmission wave is measured by the resistance strain gauge attached to the transmission bar. By processing the measured incident wave, reflected wave, and transmission wave, the deformation and failure of the material can be obtained, and the dynamic performance data of the material can be obtained.

To comprehensively consider the effect of strain rate on the dynamic compressive strength and dynamic tensile strength, compression dynamic increasing factor and tensile dynamic increasing factor are separately defined. The compression dynamic increasing factor (

D I F_{c}

) is defined as

D I F_{c} = f_{c d} / f_{c}^{'}

(5)

The tensile dynamic increasing factor (

D I F_{t}

) is defined as

D I F_{t} = f_{t d} / f_{t}^{'}

(6)

In the equation,

f_{c d}

is the dynamic uniaxial compressive strength,

f_{c}^{'}

is the quasi-static uniaxial compressive strength,

f_{t d}

is the dynamic uniaxial tensile strength, and

f_{t}^{'}

is the quasi-static uniaxial tensile strength.

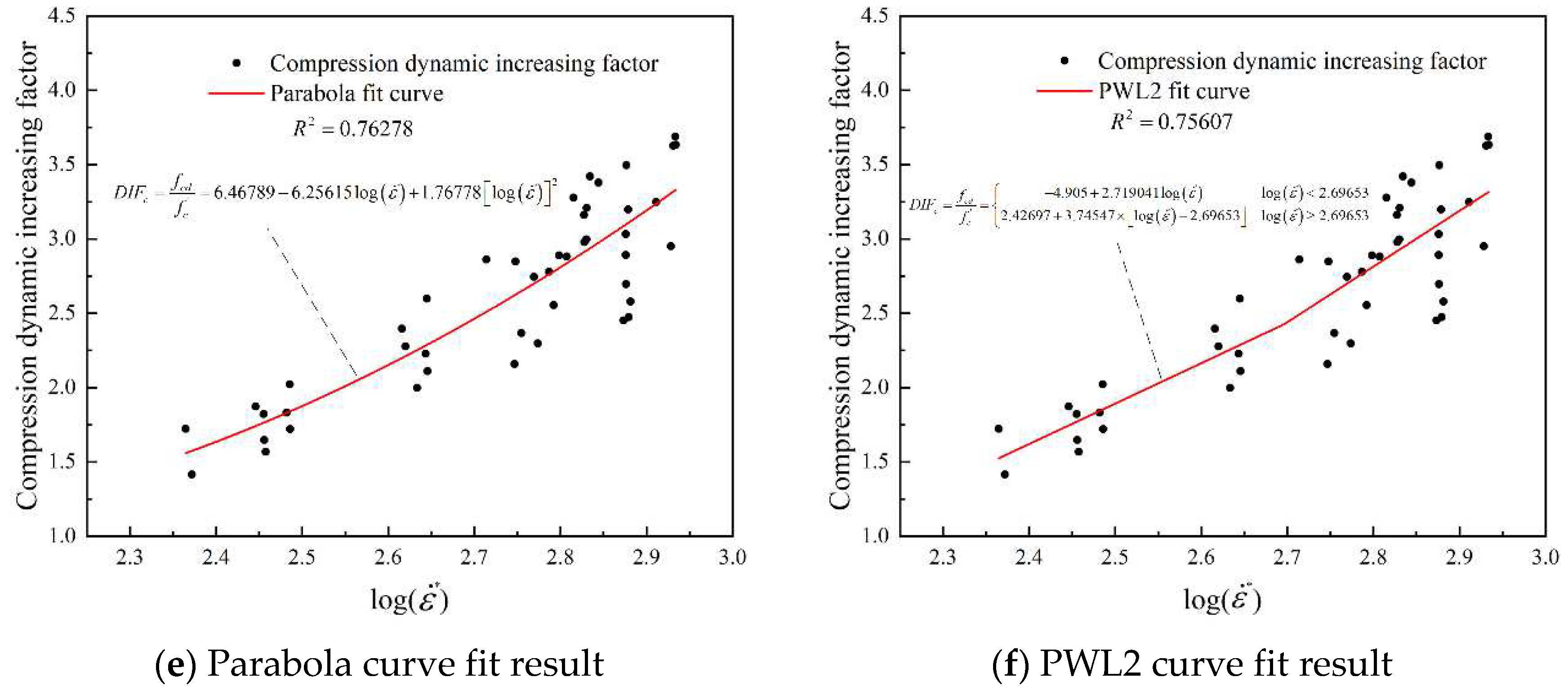
3.2.1. Calculation expression of the $D I F_{c}$

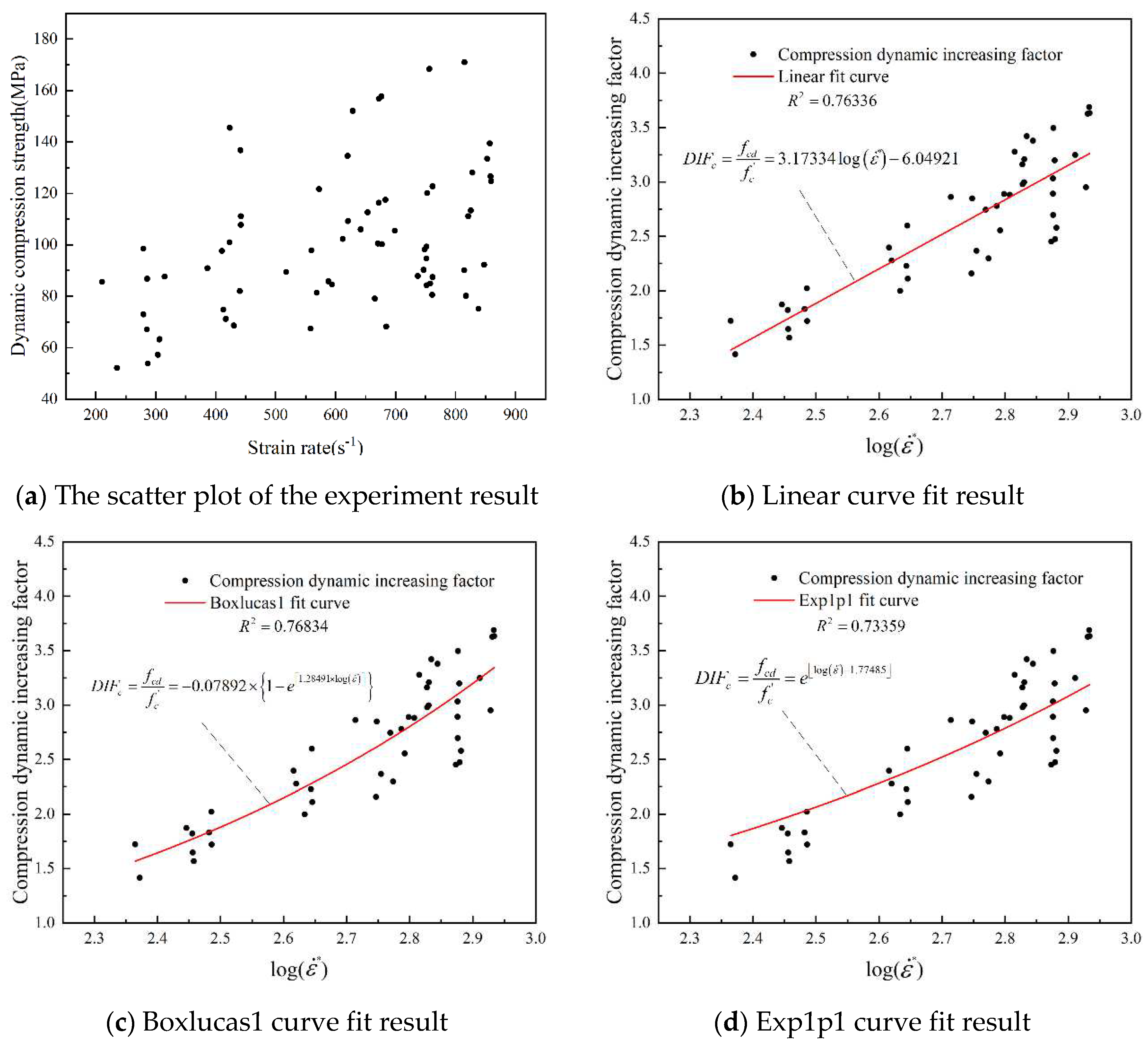
According to the results of the SHPB dynamic uniaxial compression experiment, multiple function forms are used to fit the experiment results, and the fitting goodness of each function curve is compared and analyzed. The scatter plot of the experiment results is shown in Figure 6a, it can be seen that high strain rates have a significant strengthening effect on the dynamic compressive strength of concrete, while the DIF function in the original HJC model does not reflect this characteristic. The fitting results of various curves of the compression dynamic increasing factor of concrete are shown in Figure 6b–f. Before fitting the data, it is necessary to remove some "bad points" with large data dispersion.

By analyzing and comparing the goodness of fit of each curve, it can be found that compared to other curves, the Boxlucas1 curve has a higher goodness of fit. Therefore, the compression dynamic increasing factor is calculated using the Boxlucas1 curve. Thus, the formula for calculating the compression dynamic increasing factor of concrete considering strain rate segmentation characteristics is:

D I F_{c} = \{\begin{matrix} D I F & \dot{ε} \leq 10^{2} s^{- 1} \\ - 0.07892 \times \{1 - e^{[1.28491 \times \log ({\dot{ε}}^{*})]}\} & \dot{ε} > 10^{2} s^{- 1} \end{matrix}

(7)

In the equation,

D I F = 1 + C \ln {\dot{ε}}^{*}

is the formula for calculating the dynamic increasing factor in the HJC model,

\dot{ε}

is the strain rate,

{\dot{ε}}^{*} = \dot{ε} / {\dot{ε}}_{0}

is the dimensionless equivalent strain rate (

{\dot{ε}}_{0} = 1 s^{- 1}

is reference strain rate).

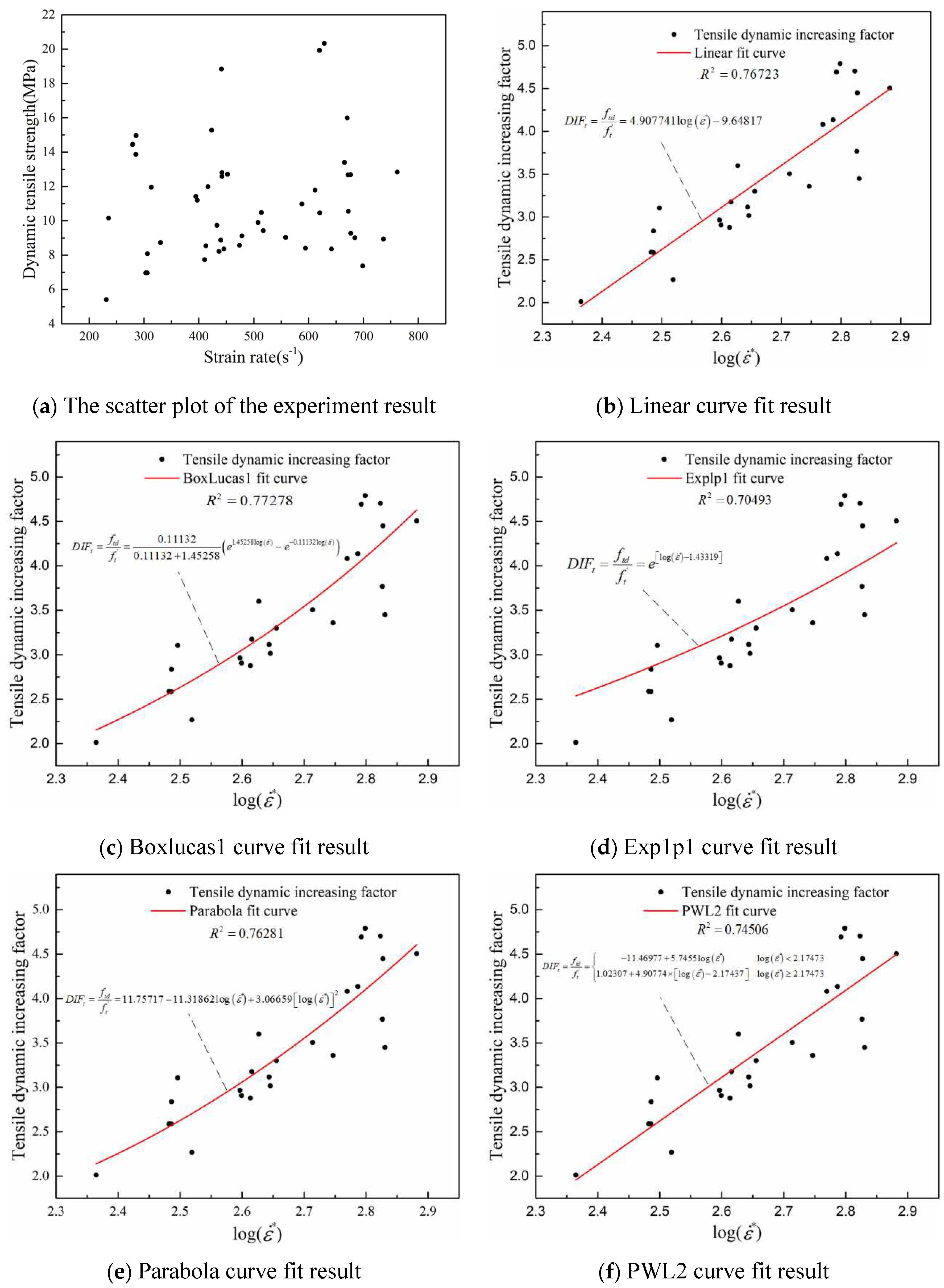
3.2.2. Calculation expression of the $D I F_{t}$

According to the results of the SHPB dynamic split tension experiment, multiple function forms are used to fit the experiment results, and the goodness of fit of the curves of each function is compared and analyzed. The scatter plot of the experiment results is shown in Figure 7a, it can be seen that high strain rates also have a significant strengthening effect on the dynamic tensile strength of concrete, and the dynamic tensile strength of concrete shows higher sensitivity to strain rates. However, the DIF function in the original HJC model does not reflect this characteristic. The fitting results of the various curves of the tensile dynamic increasing factor of concrete are shown in Figure 7b–f. Before fitting the data, it is necessary to remove some "bad points" with large data dispersion.

By analyzing and comparing the goodness of fit of each curve, it can be found that compared to other curves, the Boxlucas1 curve has a higher goodness of fit. Therefore, the tensile dynamic increasing factor is calculated using the Boxlucas1 curve. Therefore, the formula for calculating the tensile dynamic increasing factor of concrete considering the strain rate segmentation characteristics is:

D I F_{t} = \{\begin{matrix} D I F & \dot{ε} \leq 10^{2} s^{- 1} \\ \frac{0.11132}{0.11132 + 1.45258} (e^{1.45258 \log ({\dot{ε}}^{*})} - e^{- 0.11132 \log ({\dot{ε}}^{*})}) & \dot{ε} > 10^{2} s^{- 1} \end{matrix}

(8)

In the equation,

D I F = 1 + C \ln {\dot{ε}}^{*}

is the formula for calculating the dynamic increasing factor in the HJC model,

\dot{ε}

is the strain rate,

{\dot{ε}}^{*} = \dot{ε} / {\dot{ε}}_{0}

is the dimensionless equivalent strain rate (

{\dot{ε}}_{0} = 1 s^{- 1}

is reference strain rate).

Therefore, the yield stress of the improved HJC concrete model is

σ_{y}^{*} = \{\begin{matrix} [A (1 - D) + B p^{* n}] D I F_{c} & p^{*} \geq 0 \\ [A (1 - D + p^{*} / T^{*})] D I F_{t} & p^{*} < 0 \end{matrix}

(9)

In the equation,

T^{*}

is the normalized maximum static tensile stress, and the other symbols are explained in the previous text.

4. Numerical example

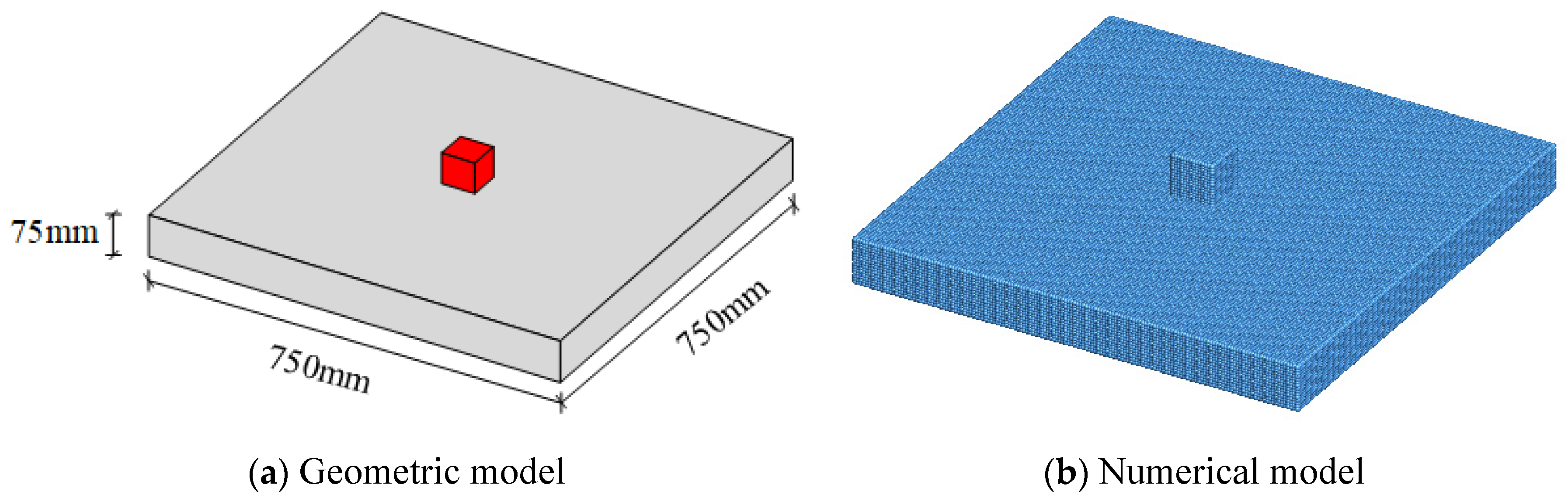
Embed the improved HJC concrete constitutive model into the developed material point calculation program and use it to simulate the fracture and fragmentation process of a concrete slab under blast loading. This calculation example is a contact explosion experiment of a plain concrete slab done by Alok et al [24]. The dimension of the concrete slab is 750mm×750mm×75mm, The concrete slab was reinforced with 12-mm-diameter rebar mesh spaced at 100 mmc/c each way at the top and bottom with 30-mm cover. The concrete slab was supported on a 900-mm-high steel frame without edge fixity. Experimental test were performed to investigate both failure modes by subjecting the concrete slab to contact explosion effects of 500-g TNT. The experiment result is shown as Figure 8.

Before solving the problem using the material point method, first establish the numerical model of the simulation object. The material points are used to discretize the charge and concrete slab, and a background grid is generated. The spacing between material points of the charge is set to 0.005m, resulting in a total of 2184 material points. The spacing between material points of the concrete slab is also set to 0.005m, producing a total of 339684 material points. The range of the background grid is set to X: 0.0m~0.75m, Y: 0.0m~0.75m, Z: -0.8m~0.3m, with a spacing of 0.01m. Boundary conditions are applied to the concrete slab using the background grid, with the length and width being fixed and the thickness being free. The explosive calculation model in contact with the concrete slab is shown in Figure 9.

The plain concrete slab uses the improved HJC concrete model, and the charge uses the high-energy explosive model and JWL state equation. The model parameter values are shown in Table 1, Table 2, Table 3, Table 4 and Table 5.

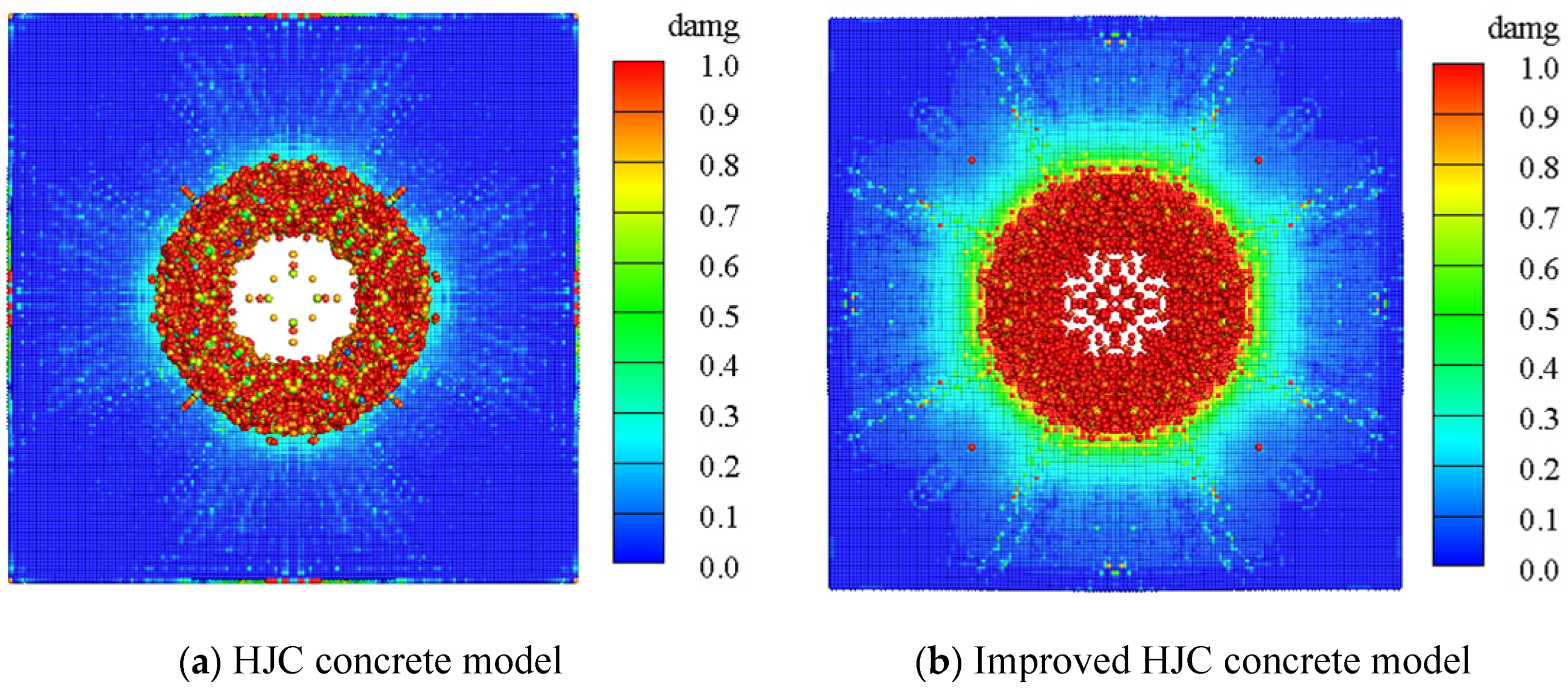
The final damage distribution of the concrete slab under explosive contact is shown in Figure 11 and Figure 12, calculated using the original HJC concrete model and the improved HJC concrete model. From the figures, it can be seen that the improved HJC concrete model can better reflect the influence of high strain rate on the dynamic strength of concrete material, particularly the significant enhancement of dynamic tensile strength under high strain rate.

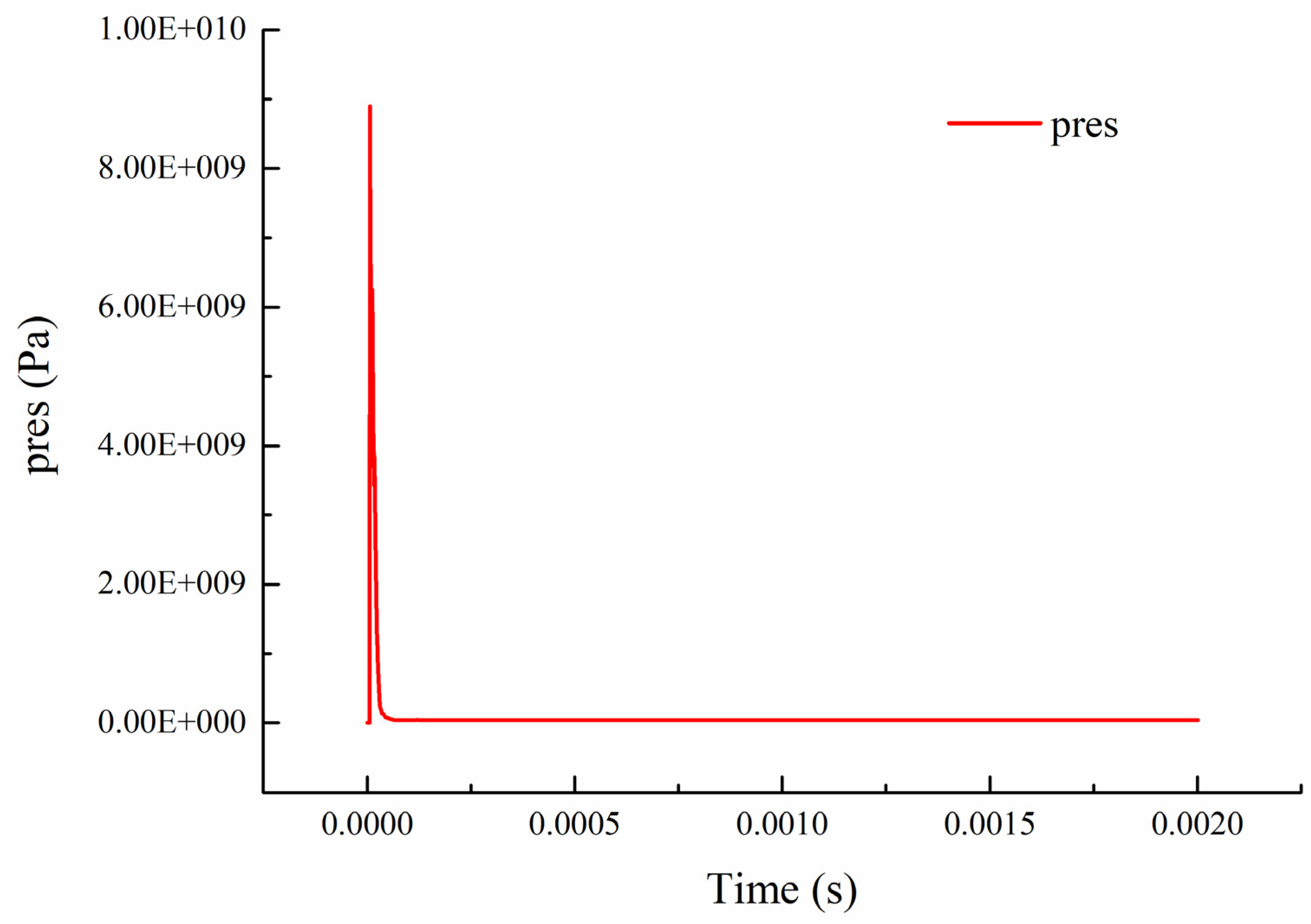
The failure mode of the concrete slab under explosive contact is mainly local crushing, cutting damage, and bottom collapse and peeling damage. After the charge is detonated, the high-pressure shock wave generated will directly act on the blast surface of the concrete slab, the pressure amplitude reached 9GPa and then rapidly attenuated, as shown in Figure 10, and this pressure is often higher than the compressive strength of the concrete, causing a crushed area to appear on the slab facing the explosion, that is, the appearance of a blast pit, as shown in Figure 11; after the shock wave pressure propagates to the inside of the concrete slab, it will spread to the bottom in the form of a compression wave, and the tensile wave formed by reflection on the bottom surface will cause a collapse and peeling area on the bottom surface, while a penetrating hole will be formed at the center of the slab, as shown in Figure 12.

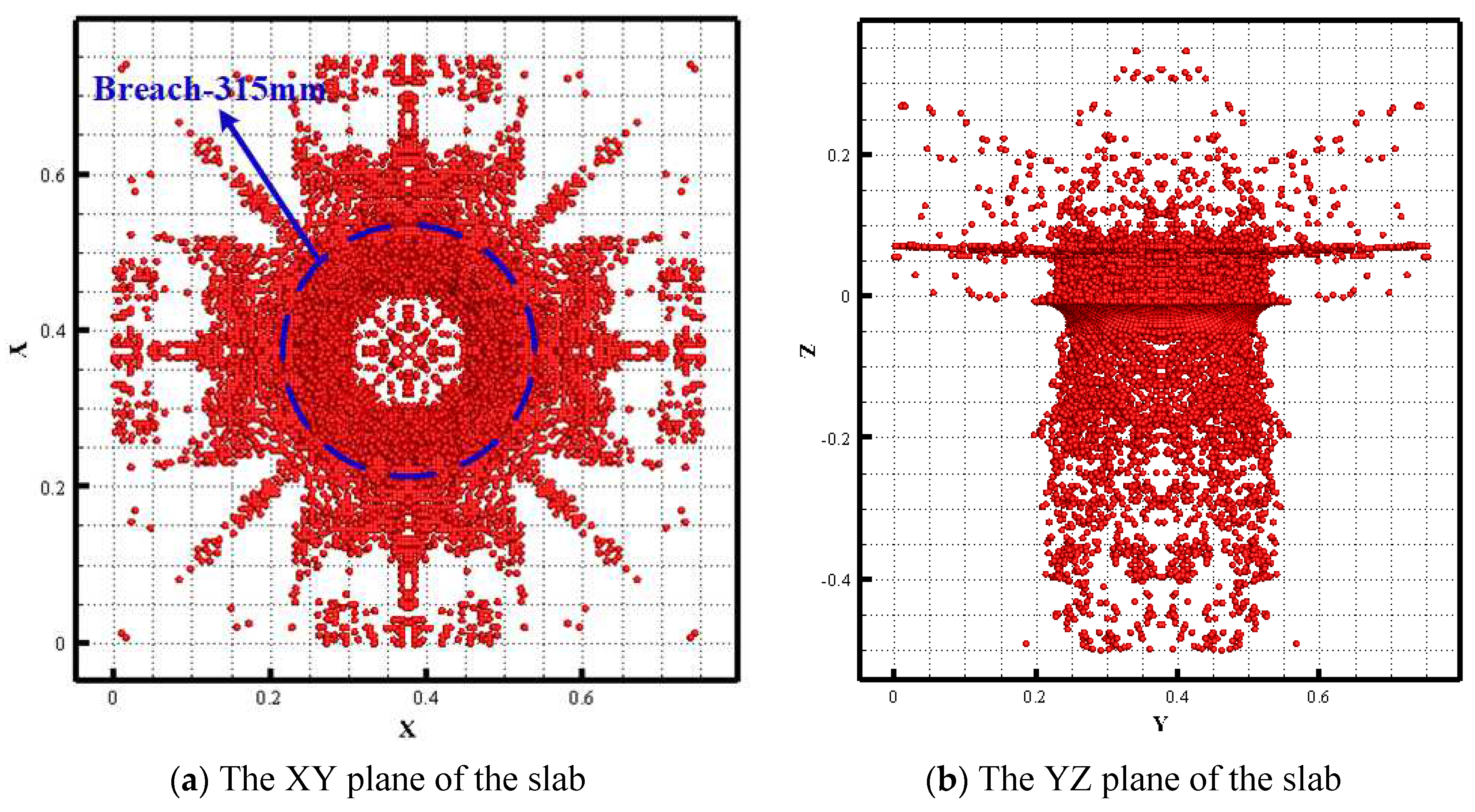
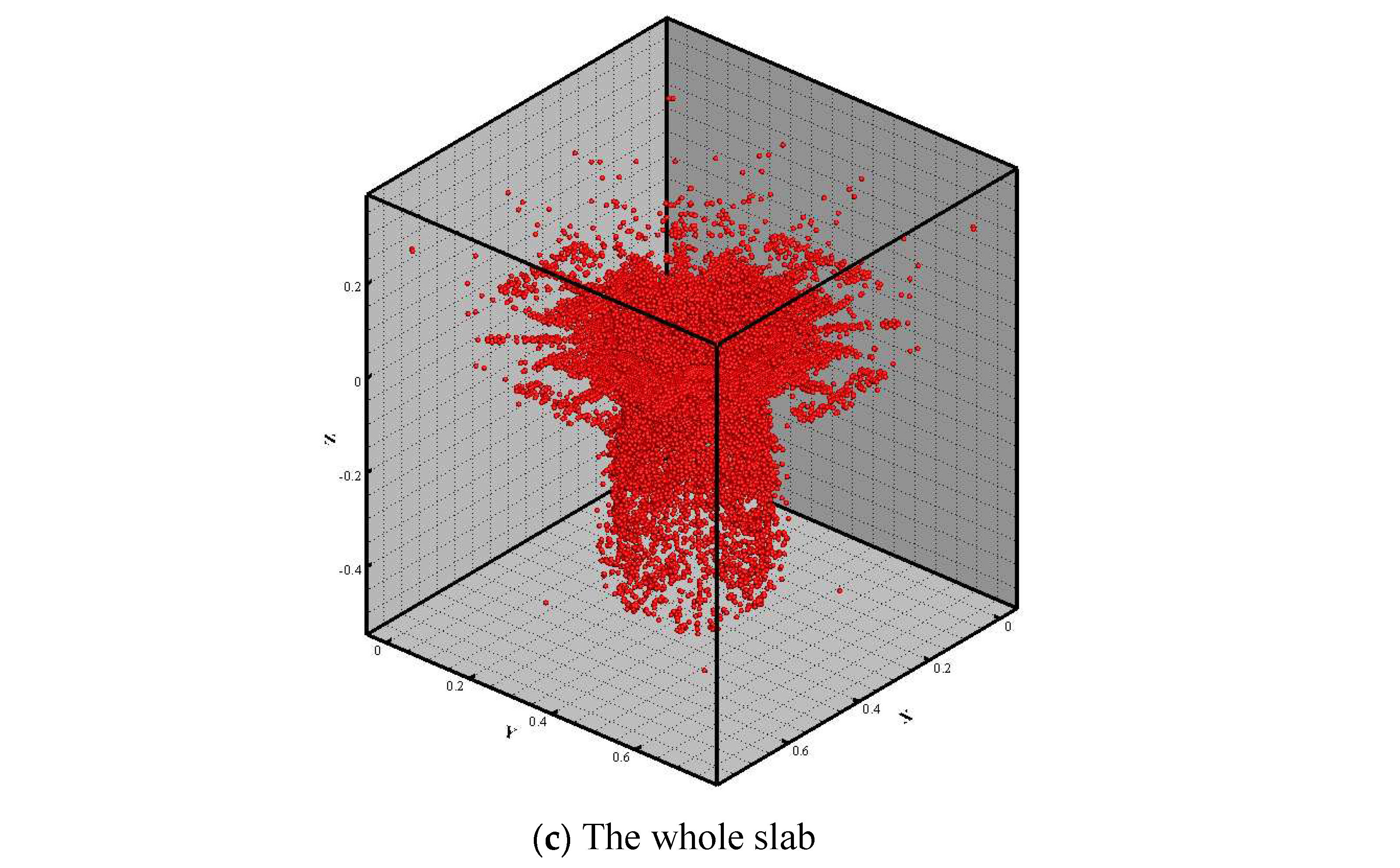
When the damage value of a certain material point inside the slab exceeds 1.0, it is considered that the material point has failed. Therefore, the area with a damage value of 1.0 is extracted, as shown in Figure 13. From the figure, it can be seen that after the detonation of the charge, the first damage caused is the crushing damage of the slab facing the explosion, followed by the formation of a through-hole at the center of the slab, and finally the tensile damage on the back of the slab facing away from the explosion, with the damage area on the back of the slab being significantly larger than that on the front. The diameter of the damage area on the front of the slab calculated by the material point method is 315mm, with an error rate of 10% compared to the experimental results, indicating that the improved HJC concrete constitutive model and material point method can accurately simulate the process of concrete medium under blast loading.

The process of the change in system energy over time is shown in Figure 14. When the charge detonates, it produces a huge amount of energy instantaneously. The concrete slab experiences compression and tensile failure. As the explosive burns fully, the internal energy of the explosive gradually transforms into the system's kinetic energy. However, the total energy of the system remains conserved before and after the explosive detonation, which also indirectly reflects the accuracy of the material point method calculation program and the improved HJC concrete constitutive model.

5. Conclusion

The main conclusions of this paper are as follows:

(1): Based on the SHPB experiment, the dynamic compression and tension strength of concrete under medium and high strain rates were obtained. The DIF function in the HJC concrete model was modified according to the experimental data, making it piecewise, On this basis, an improved HJC concrete model was proposed, and the calculation expressions of the compression dynamic increasing factor and tensile dynamic increasing factor of concrete were given separately;
(2): On the existing theoretical basis of the material point method, a calculation program for the material point method was developed using C++ language, and the improved HJC concrete model was embedded into the material point calculation program, thus breaking through the limitations of methods such as finite element method based on continuous medium mechanics in simulating concrete medium fracture and fragmentation under blast loading;
(3): The developed calculation program was verified through numerical examples, and the results showed that the improved HJC concrete model can better characterize the rate sensitivity of material strength, especially the rate sensitivity of the strength of concrete materials under high strain rate conditions. While the material point method can accurately simulate the fracture and fragmentation process of concrete medium under blast loading, particularly the pulverization characteristics of medium in the near zone of the load.

Data Availability Statement

Some or all data, models, or code that support the findings of this study are available from the corresponding author upon reasonable request.

Acknowledgments

This work was supported by the National Natural Science Foundation of China (n0. 51874118) and the Postgraduate Research& Practice Innovation Program of Jiangsu Province KYCX20_0443.

Conflicts of Interest

The authors declare no potential conflicts of interest with respect to the research, authorship, and/or publication of this article.

References

Anas, S.; Alam, M.; Umair, M. Experimental and numerical investigations on performance of reinforced concrete slabs under explosive-induced air-blast loading: A state-of-the-art review. Structures. 2021, 31, 428–461. [Google Scholar] [CrossRef]
Kristoffersen, M.; Hauge, K.O.; Minoretti, A.; Børvik, T. Experimental and numerical studies of tubular concrete structures subjected to blast loading. Eng. Struct. 2021, 233, 111543. [Google Scholar] [CrossRef]
Tao, J.; Yang, X.G.; Li, H.T.; Zhou, J.W.; Qi, S.C.; Lu, G.D. Numerical investigation of blast-induced rock fragmentation. Comput. Geotech. 2020, 128, 103846. [Google Scholar] [CrossRef]
Jeong, H.; Jeon, B.; Choi, S.; Jeon, S. Fracturing Behavior around a Blasthole in a Brittle Material under Blasting Loading. Int. J. Impact Eng. 2020, 140, 103562. [Google Scholar] [CrossRef]
Bagault, C.; Nélias, D.; Baietto, M.C. Contact Analyses for Anisotropic Half Space: Effect of the Anisotropy on the Pressure Distribution and Contact Area. J. Tribol. 2012, 134, 031401. [Google Scholar] [CrossRef]
Trollé, B.; Baietto, M.C.; Gravouil, A.; Mai, S. H.; Nguyen-Tajan, T. M. L. XFEM Crack Propagation under Rolling Contact Fatigue. Procedia Eng. 2013, 66, 775–782. [Google Scholar] [CrossRef]
Shi, G.H. Block System Modeling by Discontinuous Deformation Analysis. Computational Mechanics Publications. 1993. [Google Scholar]
Pearce, C.; Thavalingam, A.; Liao, Z.; Bićanić, N. Computational aspects of the discontinuous deformation analysis framework for modelling concrete fracture. Eng. Fract. Mech. 2000, 65, 283–298. [Google Scholar] [CrossRef]
Zhao, G.; Zhang, W.X.; Li, Y.C. DDA numerical simulation of directional blasting parameters and effect in demolition of reinforced concrete chimney. Eng. Blasting. 2006, 12, 19–21. [Google Scholar]
Cundall, P.A. A computer model for simulating progressive large-scale movements in blocky rock system. Proc. Symp. Int. Soc. Rock Mech. 1971, 2, 129–136. [Google Scholar]
Zhang, Z.J.; Liu, J.; Hu, W.; Yun, B.; Zhao, C.B. Two-dimensional simulation of concrete material fracturing by discrete element method. J. Hydroelectr. Eng. 2010, 29, 22–27. [Google Scholar]
Hentz, S.; Donzé, F. V.; Daudeville, L. Discrete Element Modelling of Concrete Submitted to Dynamic Loading at High Strain Rates. Comput. Struct. 2004, 82, 2509–2524. [Google Scholar] [CrossRef]
Qin, C.; Zhang, C. Numerical Study of Dynamic Behavior of Concrete by Meso-Scale Particle Element Modeling. Int. J. Impact Eng. 2011, 38, 1011–1021. [Google Scholar] [CrossRef]
Haeri, H.; Sarfarazi, V. Numerical Simulation of Tensile Failure of Concrete Using Particle Flow Code (PFC). Comp. Concrete. 2016, 18, 39–51. [Google Scholar] [CrossRef]
Wu, M.; Chen, Z.; Zhang, C. Determining the Impact Behavior of Concrete Beams through Experimental Testing and Meso-Scale Simulation: I. Drop-Weight Tests. Eng. Fract. Mech. 2015, 135, 94–112. [Google Scholar] [CrossRef]
Wu, M.; Zhang, C.; Chen, Z. Determining the Impact Behavior of Concrete Beams through Experimental Testing and Meso-Scale Simulation: II. Particle Element Simulation and Comparison. Eng. Fract. Mech. 2015, 135, 113–125. [Google Scholar] [CrossRef]
Wu, M.; Zhang, C.; Chen, Z. Drop-Weight Tests of Concrete Beams Prestressed with Unbonded Tendons and Meso-Scale Simulation. Int. J. Impact Eng. 2016, 93, 166–183. [Google Scholar] [CrossRef]
Sulsky, D.; Zhou, S.J.; Schreyer, H. L. Application of a Particle-in-Cell Method to Solid Mechanics. Comput. Phys. Commun. 1995, 87, 236–252. [Google Scholar] [CrossRef]
Sulsky, D.; Schreyer, H. L. Axisymmetric Form of the Material Point Method with Applications to Upsetting and Taylor Impact Problems. Comput. Methods Appl. Mech. Eng. 1996, 139, 409–429. [Google Scholar] [CrossRef]
Holmquist, T.J.; Johnson, G.R. A computational constitutive model for glass subjected to large strains, high strain rates and high pressures. J. Appl. Mech. 2011, 78, 051003. [Google Scholar] [CrossRef]
Polanco-Loria, M.; Hopperstad, O. S.; Børvik, T.; Berstad, T. Numerical Predictions of Ballistic Limits for Concrete Slabs Using a Modified Version of the HJC Concrete Model. Int. J. Impact Eng. 2008, 35, 290–303. [Google Scholar] [CrossRef]
Islam, M.J.; Swaddiwudhipong, S.; Liu, Z.S. Penetration of concrete targets using a modified Holmquist–Johnson–Cook material model. Int. J. Comput. Methods 2012, 9, 1250056. [Google Scholar] [CrossRef]
Zhang, F.G.; Li, E.Z. A computational model for concrete subjected to large strains, high strain rates, and high pressures. Explos. Shock Waves 2002, 22, 198–202. [Google Scholar]
Dua, A.; Braimah, A. Assessment of Reinforced Concrete Slab Response to Contact Explosion Effects. J. Perform. Constr. Facil. 2020, 34, 04020061. [Google Scholar] [CrossRef]

Figure 1. Solution process of the MPM in a single step.

Figure 2. MPM calculation algorithm.

Figure 3. Equation of the yield surface [20].

Figure 4. Conventional Hopkinson bar experiment system.

Figure 5. Concrete specimen.

Figure 6. Fitting results of the compression dynamic increasing factor.

Figure 7. Fitting results of the tensile dynamic increasing factor.

Figure 8. Response of the concrete slab to contact explosion effect [24].

Figure 9. Calculation model for contact explosion of concrete slab.

Figure 10. Pressure time curve of charge detonation point.

Figure 11. Damage area on the front of the slab.

Figure 12. Damage area on the back of the slab.

Figure 13. Area with a damage value of 1.0.

Figure 14. System energy time curve.

Table 1. Parameters of high-energy explosives model.

$ρ (k g / m^{3})$	$D (m / s)$
1630	6930.0

Table 2. Parameters of JWL equation of state.

$A (P a)$	$B (P a)$	$R_{1}$	$R_{2}$	$w$	$E_{0} (J / m^{3})$
3.712e11	3.23e9	4.15	0.95	0.30	7.0e9

Table 3. Parameters of improved HJC state equation.

$P_{c r u s h} (M P a)$	$μ_{c r u s h}$	$P_{l o c k} (M P a)$	$μ_{p l o c k}$	$K_{1} (M P a)$	$K_{2} (M P a)$	$K_{3} (M P a)$
16	0.001	800	0.127	16e3	0.0	0.0

Table 4. Parameters of improved HJC strength model.

$G (M P a)$	$A$	$B$	$C$	$N$	$f_{c} (M P a)$	$T (M P a)$	$S_{\max}^{f}$
14.86e3	0.79	1.6	0.007	0.61	48.0	4.0	7.0

Table 5. Parameters of improved HJC damage model.

$ε_{\min}^{f}$	$D_{1}$	$D_{2}$
48.0	4.0	7.0

Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.

© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).

Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.

MDPI Initiatives

Important Links

Choose an area of interest and we will send you notifications of new preprints at your preferred frequency.

Disclaimer

Material Point Simulation Method for Concrete Medium Fracture and Fragmentation under Blast Loading

Abstract

1. Introduction

2. Fundamental theory of the material point method

3. An improved HJC concrete model considering the segmentation of DIF function

3.1. HJC concrete model

3.2. The improved method of HJC concrete model

3.2.1. Calculation expression of the D I F c

3.2.2. Calculation expression of the D I F t

4. Numerical example

5. Conclusion

Data Availability Statement

Acknowledgments

Conflicts of Interest

References

MDPI Initiatives

Important Links

Subscribe

3.2.1. Calculation expression of the $D I F_{c}$

3.2.2. Calculation expression of the $D I F_{t}$