Prerpints.org logo
Preprint
Article

Characterisation of the Contact between Cross-Country Skis and Snow: On the Multi-Scale Interaction between Ski Geometry and Ski-Base~Texture

Altmetrics

Downloads

202

Views

276

Comments

0

A peer-reviewed article of this preprint also exists.

Submitted:

04 July 2023

Posted:

05 July 2023

You are already at the latest version

Alerts
Abstract
At the highest level of endurance sports, the differences in finishing times are small, so equipment is constantly being constantly improved to enhance the athletes' performance. For instance, one dominant resistive force in connection with cross-country skiing is the friction between the skis and snow and since the 1930s, research designed to understand and reduce this friction has been ongoing. The mechanisms involved in ski-snow friction include compaction, micro-ploughing, adhesion, viscosity, and water-bridging. Of these, adhesive and viscous friction have been most studied, while much less is presently known about compaction, micro-ploughing, and water-bridging. At the macro-scale, the ski-camber profile plays a key role in determining whether, with respect to friction, a particular cross-country ski is suitable for use under a given set of conditions. Through its influence on where ski-snow contact occurs, this ski-camber profile has a profound impact on adhesive and viscous friction, micro-ploughing, the formation of water bridges, and the rate of compaction. Different contact zones with different apparent areas of contact and pressure have been found to be most suitable for different conditions. In addition, the micro-scale texture of the ski base is also an important determinant of ski-snow friction. Topographical measurements of this texture can be achieved with white-light interferometer and recent characterisation has focused on the mechanical properties of contact. In numerous tribological studies the interactions between features at different scales are modelled. In most tribological systems, features on several scales influence friction and ski-snow contact is certainly no exception. Accordingly, the current investigation was designed to evaluate the multi-scale properties of different combinations of two skis with two different base textures. The real area of contact and the average interfacial separation and total average reciprocal interfacial separation between the ski and snow were taken into consideration. We found that different macro- and micro-scale properties of the ski favour different mechanisms of friction. Both the profile of the ski camber and texture of the base play decisive roles in determining viscous friction. At the same time, the texture of the ski base exerts a greater impact on the average real contact pressure, real contact area and minimal average interfacial separation between the ski and snow than does the ski-camber profile.
Keywords: 
Subject: Engineering  -   Mechanical Engineering

Nomenclature

A Nominal micro-scale area m 2
A r , n Real contact area m 2
E ′ Effective Young’s modulus Pa
E s n o w Young’s modulus of the virtual snow Pa
E b a s e Young’s modulus of the ski-base material Pa
F Equivalent load N
h * Micro-scale topography height function m
h n Micro-scale clearance/interfacial separation m
h ¯ n Average interfacial separation m
1 / h ¯ n Average reciprocal interfacial separation m
H Apparent macro-scale clearance between the ski-base and the virtual snow m
H * ANN prediction of measured ski-camber height profile m
n Porosity −
p n Micro-scale pressure distribution Pa
P Apparent (macro-scale) contact pressure Pa
P n Nominal load Pa
( x , y ) Micro-scale coordinates m
X Macro-scale coordinates m
ν Poisson’s ratio −
ω Micro-scale computational domain m 2
ω g Part of ω where there is a gap m 2
ω c Part of ω where there is solid–solid contact m 2
| ω * | Area of ω * m 2

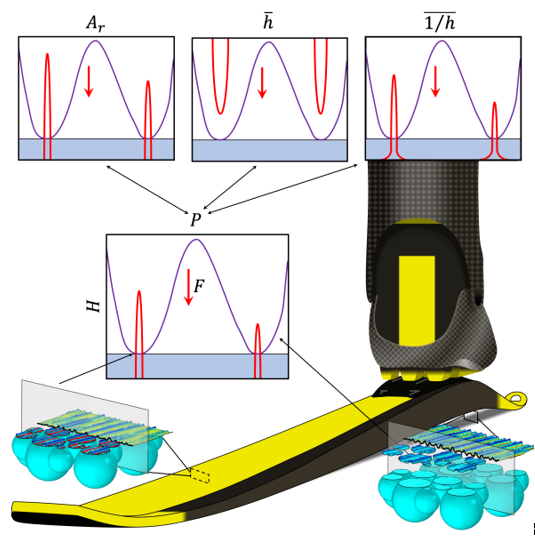
1. Introduction

At the top level of endurance sports, the race times are long but the difference between the finishing times can be small. Therefore, in most endurance sports, the equipment is constantly improved, e.g., minimised in weight to increase the athletes’ performance. Reduced equipment weight helps the athlete overcome gravitational forces, which is one of the resistive forces present in many sports. In some sports, other resistive forces are present, e.g., in cross-country skiing where friction is one of the dominant resistive forces [1]. In cross-country skiing, friction has even been correlated with the winning time [2]. Friction in contacts involving snow has interested researchers for quite some time, already in 1939, Bowden [3] published a paper on this topic. In the years thereafter, several papers discussing this topic were published, e.g., [4,5], and even in recent years researchers are still trying to fully understand the physics and phenomenons [6] associated with the snow contact.
In the literature, several friction mechanisms occurring in the ski-snow contact are considered. For example, compaction, micro-ploughing, adhesion, viscous and water-bridging, which are mentioned in Almqvist et al. [1]. The ones considered most commonly are the adhesive and viscous contributions to friction, see e.g., [7,8,9,10,11,12,13]. Lever et al. [14] showed that abrasive friction in the form of micro-ploughing was dominating, in the absence of meltwater at sub-zero temperatures. Friction, originating from compaction, micro-ploughing and water bridges, in the ski-snow contact, is, however, yet not well-enough understood.
When trying to estimate friction in cross-country skiing, it is crucial to consider the entire ski. The ski-camber profile is often used to determine how well-suited a ski is for a particular condition. Breitschadel et al. [15] did, for instance, conclude that skis that were determined by the Norwegian Ski Team to work at a given condition had similar ski-camber profiles. In another paper, Breitschadel et al. [16], also investigated how different attributes of the ski-camber profiles changed when subjected to temperatures at which skiing often occurs compared to room temperature, at which the ski-camber profile usually is characterised. They observed an increase in stiffness and shorter contact zones as the temperature decreased. Recently, Kalliorinne et al. [17] showed how the skiers’ pose during tucking influenced the length of the rear- and front contact zones, as well as the load partitioning between them.
Although a lot of information can be extracted from a ski-camber profile, e.g., the apparent length (thus area) of the rear- and front contact zones and the topology of the kick-wax zone at a given loading condition. It does, however, not provide information on how the nominal load, i.e., the meso-scale pressure defined in [18], is distributed over the contact zones. Neither does it tell us what the contact will look like at the micro-scale, in terms of real contact area and the corresponding real contact pressure distribution.
Measuring the pressure between the ski and a rigid counter-surface, at a given magnification, gives some information about the contact interface. Accordingly, both Bäckström et al. [19] and Schindelwig et al. [20] developed techniques for measuring the contact pressure between a ski and a counter body that can be considered rigid in comparison to snow. The advantage of this method is that the apparent area and contact pressure distribution can be estimated, the drawback being that it will not be the same as for the ski-snow contact. The counter body can, however, be replaced, Mössner et al. [21] recently developed a system for measuring the “penetration depth of the cross-country ski in an elastomer pad”, used to simulate a ski in contact with snow. They then obtained the contact pressure using Euler–Bernoulli beam theory, as previously described in [22]. Another way of obtaining the contact pressure is to use a Boundary Element Model (BEM) to simulate the contact between a ski-camber profile and a virtual snow counter surface, as in Kalliorinne et al. [18]. This method enables a variety of counter-surface material properties, as well as, non-flat counter surfaces.
Both ski-camber profile and contact pressure measurements consider the ski in a stationary setting, but while skiing, it will be loaded dynamically and vibrate at the ends. Already in the 80s Lehtovaara et al. [23] found that vibrations could decrease the friction between a polymer sample and ice. As a successor of this work, Koptyug et al. [24,25,26] continued and it was concluded that a beam model of the entire ski is necessary to fully understand the ski vibrations in the interaction between ski and snow. Another related work is the one by Nam et al. [27], who developed a numerical model for jumping ski vibration, he concluded that the relation between friction and mode/amplitude is more complex than what was reported in Lehtovaara et al. [23], since full-sized skis behave differently than a small-sized polymer sample.
It is no question that the structural mechanics of the ski is a key determinant when it comes to ski-snow friction, but perhaps equally important is the snow counter-surface. Gold [28] studied the compression strength of snow while considering the density, temperature and snow crystal size and presented a relation between these parameters and the hardness of the snow. It was also noted that the compression strength could differ by several orders of magnitudes for the same parameter values. Bader [29] did a thorough work on the properties of snow, in which 14 properties that characterise snow were listed. It was stated that at least 5 of these, i.e., density, hardness, grain size, grain shape and temperature, which were viewed as the most important for characterising the snow should always be used. Lintzén and Edeskär studied uni-axial compression of snow and observed that there are both an elastic and a plastic region in the stress–strain curve. They also found that there exists a critical compression rate at which the snow becomes brittle, and in connection to this, that old machine-made snow is more brittle than new machine-made snow. However, as discussed in [30,31], it should be taken into consideration that the behaviour due to the small deformations that occur in a ski track may be different from the behaviour of the bulk of snow during compression.
Apart from the macro-scale properties of the ski, the micro-scale properties have also been studied to a large extent. Moldestad et al. [32] developed a methodology for measuring ski-base textures in 3D, which nowadays is a standard procedure used for the characterisation of the topography of the ski-base surfaces. Jordan et al. [33], found that fractal analysis was a better tool than the standard roughness parameters and FFT techniques for differentiating ski-base textures. Ski-base textures are most commonly fabricated through a stone grinding procedure, see e.g., Breitschädel et al. [34,35], where different techniques for changing/obtaining new ski-base textures, such as manual texturing with an embossment tool, and texturing the ski base with a milling machine, were discussed.
Giesbrecht et al. [36], tested ski-base materials, surface roughness and texture orientation by means of miniature skis, they found that there was an optimal roughness in the range of R a = 0 . 5 − 1 . 0 , and they also observed that the texture orientation had less of an impact on the surfaces with lower R a -values. Rohm et al. [37] performed friction tests with two different surface textures with completely different bearing ratios. They found that the surface with the higher core roughness value, i.e., “the bearing surface”, exhibited lower friction at lower temperatures ( − 19   ∘ C ) and that the other surface, i.e., “the non-bearing surface”, exhibited lower friction at higher temperatures ( − 2 . 6   ∘ C ). Recently, Scherge et al. [38] studied five different ski-base textures and found that the sliding times increased with increasing contact area. Along with the contact area being highlighted as one of the important parameters in ski-snow friction, different methods for evaluating the contact area have been presented, e.g., [39,40]. The latter of the two, which was developed within the same group as the present work, employs a BEM-based method for evaluating the contact mechanical response for different ski-base textures in contact with virtual snow.
There are a large number of length scales to be considered in most tribological applications, and specific numerical models have been, and are still being, developed for each one of the length scales, see [41]. When a model considers two or more scales, it is denoted as multi-scale, and when using a multi-scale model the interaction between different scales can be studied. In many tribological applications, there are several topographical scales present, and these have been readily assessed and may be found in the literature. Tribology research does, in general, show that the multi-scale interaction between different topographical scales has a considerable influence on friction [42]. The ski-snow contact is no exception, with at least three clearly distinguishable geometrical scales present at the same time.
The interaction between the ski’s macro-scale mechanics and geometry and its micro-scale, encompassing the ski-base texture, and how the interplay between them is connected to the frictional performance, has, however, not yet been thoroughly studied. Accordingly, the objective of the present work is to combine the methods developed for Macro-[18] and Micro-Scale [40] ski-snow contact simulations to present metrics that describe the multi-scale contact.
By employing the novel multi-scale method presented herein, we study the ski–snow contact of four combinations of two pairs of skis (with significantly different ski-camber profiles) and two different ski-base textures. The results are presented in terms of four functional parameters, namely the real area of contact, the corresponding average real contact pressure, the minimum average interfacial separation, and the total average reciprocal interfacial separation. The analysis shows that different macro- and micro-scale properties of the ski are related to different friction mechanisms and that both the ski-camber profile and the texture of the ski-base play decisive roles in determining the viscous contribution to friction.

2. Theory

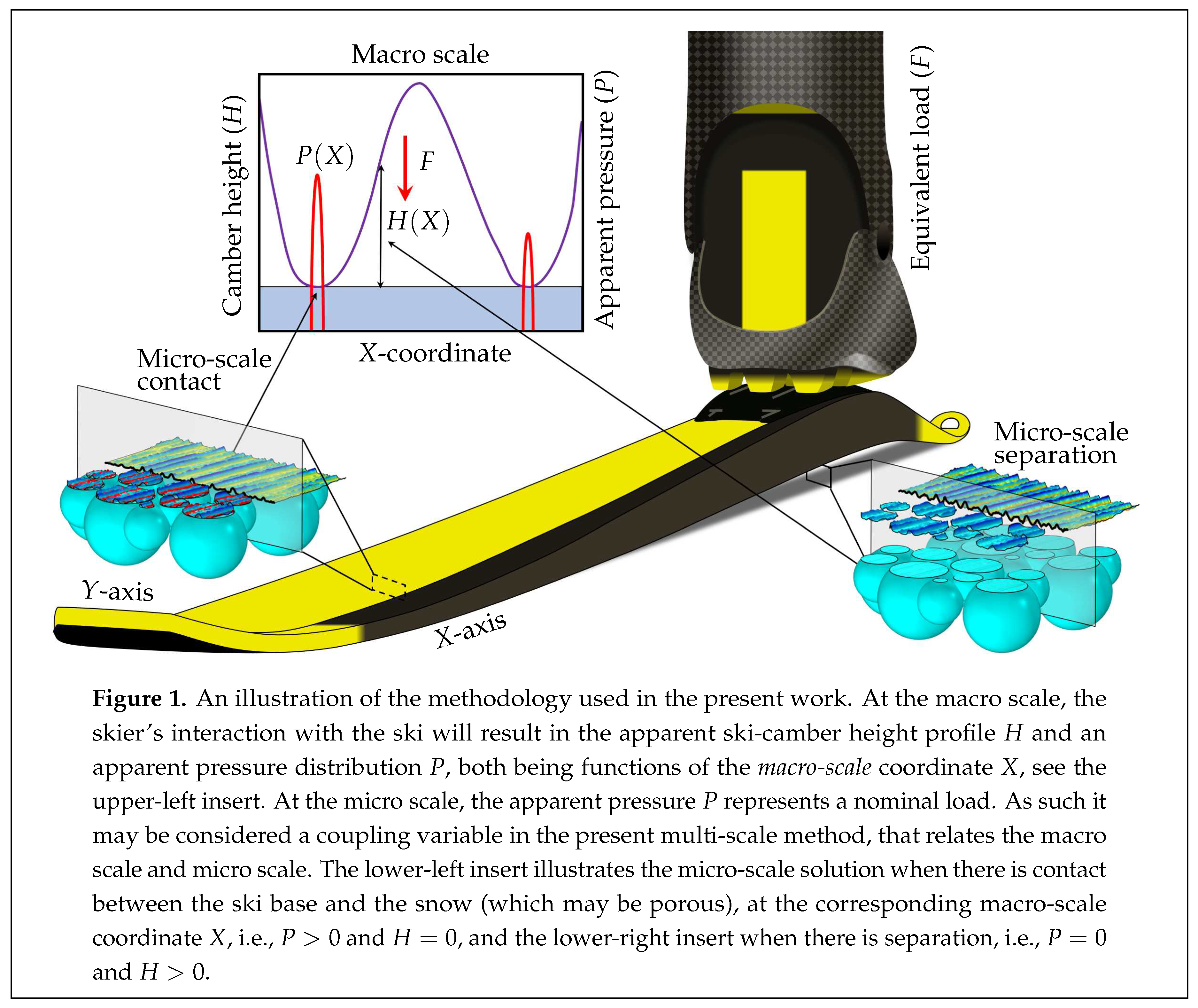
In this section, we will present a novel multi-scale approach that combines the methods developed for Macro-[18] and Micro-Scale [40] ski-snow contact simulations. Figure 1 is an effort to graphically illustrate the present method, in which the geometry of the selected ski is measured using a ski-camber profile measurement device, according to the principles presented in [18]. This macro-scale ski-camber profile data, which can be viewed in the upper-left insert, together with the corresponding apparent pressure distribution, is used to train an ANN with a carefully designed architecture (also described in [18]). The lower-left insert of Figure 1 presents a micro-scale perspective of a situation when the ski-base texture is in contact with virtual snow, under the apparent pressure acting over the rear contact zone. Similarly, the lower-right insert shows the same ski-base texture at a location where it is separated from the virtual snow.
Given an equivalent load (position and magnitude), corresponding to the plantar pressure exerted by the athlete during, e.g., tucking downhill corresponding half body weight at 16 c m behind the balance point [17], the ANN can be employed to predict the geometry of the ski-camber profile as a function of the coordinate along the ski. Hence, the predicted ski-camber profile may be used as input in the BEM-based model presented [18], to simulate the macro-scale contact between the ski-camber profile and virtual snow.
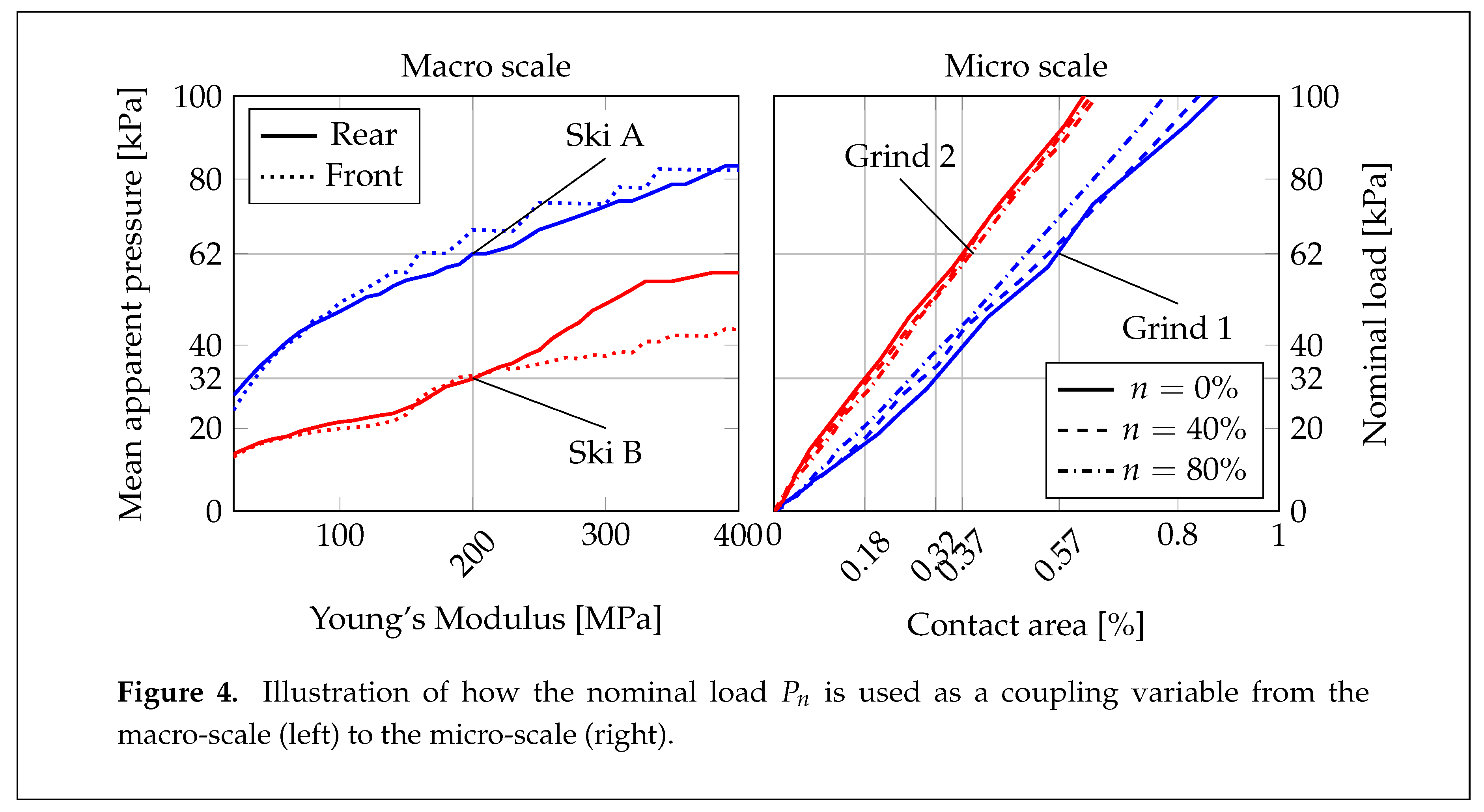
The main output from a numerical simulation, based on this macro-scale method, is the contact mechanical response in terms of the apparent contact area and pressure between the ski and the virtual snow. In the present multi-scale method, the apparent pressure represents a coupling variable between the macro- and the micro scale, at which it defines the nominal load (in Pa ) that the ski-base texture should be pressed against the virtual snow with.
Preprints 78530 i001
More precisely, for a given loading condition a prediction of the ski-camber profile H * as a function of the macro-scale X-coordinate ( H * = H * ( X ) ), along the entire ski, which consitutes the macro-scale computational domain Ω , can be obtained by the ANN. In turn, the ski-camber profile H * (which represents the undeformed geometry of the rigid half space), the loading condition, and the effective Youngs modulus E ′ of the virtual snow and the ski base (which describes the effective material properties of the deformable half space), defined as
2 E ′ = 1 − ν 2 E s n o w + 1 − ν 2 E b a s e
are input to the macro-scale BEM-model [18], which can be used to determine the apparent pressure P as a function of the X-coordinate ( P = P ( X ) ), as well as the apparent clearance H ( X ) between the ski and deformed counter body, made of virtual snow, for which the classical complementarity P · H = 0 holds.
The inputs to the micro-scale BEM-model [40] can be specified in terms of a nominal load F / A ( Pa ), where F is the load and A is the nominal area, an effective Youngs modulus E ′ (defined as in (1)), and a surface topography with height function h * . Furthermore, when the snow porosity is introduced as the ratio between the pore surface area and nominal area, i.e., 0 ≤ n ≤ 1 , the nominal load at the micro scale P n , and the apparent pressure at the macro scale (P) are related by
P n ( X ) = P ( X ) · ( 1 − n ) .
The output of the micro-scale BEM-model can, therefore, be expressed as the clearance h n and the corresponding pressure p n , for which p n · h n = 0 holds. Note that the subscript n denotes both the dependence of X-coordinate and the porosity n.
With P n , E ′ , and the ski-base texture, h * = h * ( x , y ) , where ( x , y ) ∈ ω are the micro-scale coordinates, as input to the micro-scale BEM-model, the real contact area, interfacial separation and the corresponding contact pressure can be determined as functions of ( x , y ) , for each X-coordinate along the ski and snow porosity n. This means that the real contact area may be considered a function of the X-coordinate, parameterised using n in the same way as the nominal load P n ( X ) , i.e.,
A r , n ( X ) : = A r ( P n ( X ) ) = A r ( P ( X ) · ( 1 − n ) ) .
We may now also define the average interfacial separation as a function of X as
h ¯ n ( X ) = 1 | ω | ∫ Ω h n ( x , y ) + H ( X ) d x d y = 1 | ω | ∫ Ω h n ( x , y ) d x d y + H ( X ) ,
where the nominal area | ω | = A is the area of ω . The average reciprocal interfacial separation may now be described in the same way, i.e.,
1 / h ¯ n ( X ) = 1 − n | ω g | ∫ ω g d x d y h n ( x , y ) + H ( X ) .
where ω g = ω ∖ ω c is the part of the domain at the micro-scale where there is a gap (and possibly solid–liquid contact) between the surfaces and ω c is the part of the domain where there is solid–solid contact.
The multi-scale metrics considered in the present work are functional parameters deduced from the definitions of the real area of contact and the average interfacial separation and average reciprocal interfacial separation presented above. These functional parameters are, the total contact area, the corresponding average real contact pressure, the minimum average interfacial separation, and total average reciprocal interfacial separation. That is, these can simply be calculated by integrating (3), (2), (4) and (5), over the entire length of the ski ( Ω ).

3. Method

To show how the present multi-scale method can be used to analyse the contact mechanical response, we present a study in which two different ski-base textures are applied to two pairs of skis with significantly different ski-camber profiles, leading to four combinations in total.
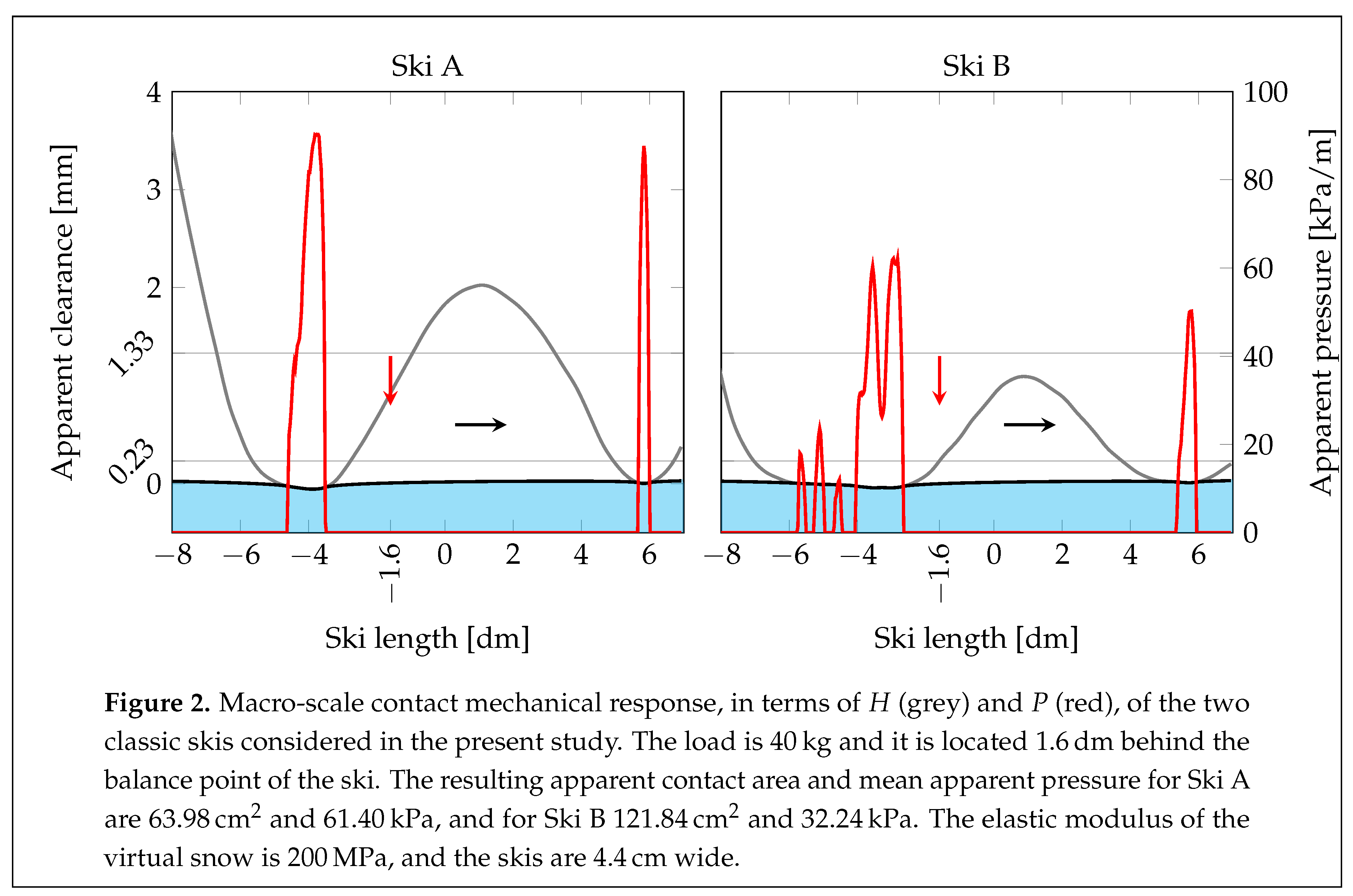
The macro-scale contact mechanics response of two pairs of classic skis, named “Ski A” and “Ski B”, considered in the present work was simulated under 40 k g of load placed 1 . 6   d m behind the balance point. The reason for choosing this loading condition is that it was found in [17] to be the equivalent load corresponding to the neutral G7 position for a skier with 80 k g body weight. The results, in terms of H and P, are depicted in Figure 2. It is clear that the two pairs render completely different contact mechanical responses under the same load. That is, Ski A exhibits higher mean apparent pressure of 61 . 40   k Pa over a smaller apparent contact area 63 . 98   c m 2 than Ski B with the lower mean apparent pressure 32 . 24   k Pa over a larger apparent contact area 121 . 84   c m 2 . The elastic modulus of the virtual snow is specified as E s n o w = 200 M Pa .
Preprints 78530 i002
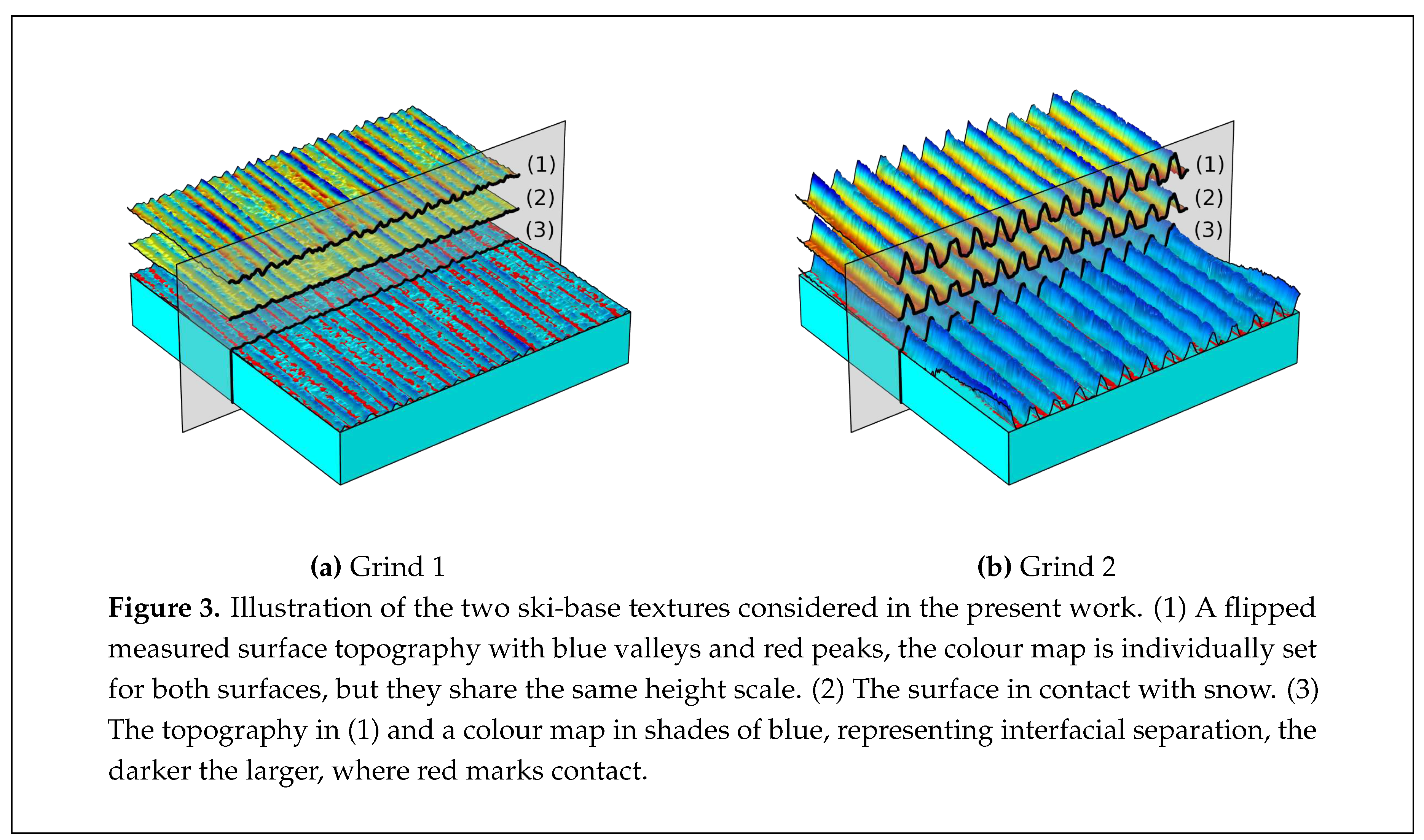
Two different ski-base textures, herein named Grind 1 and Grind 2, are considered and their micro-scale topography can be seen in Figure 3. These have previously been used in the work by Kalliorinne et al. [40], where they were named “Linear 1” and `Linear 3”. Both these topographies were produced on the skis by running a single pass through a stone grinding machine, where the dressing speed of the diamond was varied to obtain linear textures with varying pitches. Table 1 presents a group of common surface roughness parameters for these two surfaces.
Depicted in Figure 4 (left) are the mean apparent pressures for the rear and front friction interface in contact with a range of differently stiff virtual-snow with elastic modulus ranging from 20-400 M Pa . It is clear that the ski-camber profile of Ski A yields higher mean apparent pressure over the whole range of counter-surface stiffness. Figure 4 (right) shows the relation between the micro-scale contact area A r , n and the nominal pressure P n for the two ski-base textures, the relation is shown for 3 different porosities of the snow. Grind 1 develops contact area faster when subjected to load than Grind 2, e.g., 54% more contact area at 62 k Pa apparent pressure. It is also clear that Grind 1 exhibits a higher variability with the porosity and that Grind 2 yields a lower real area of contact.
Preprints 78530 i003Preprints 78530 i004

4. Results and Discussion

In this section, the multi-scale results obtained by combining macro and micro-scale contact mechanics are presented. Depicted in Figure 5 are the distributions of the real area of contact for the 4 combinations of skis and ski-base textures along the apparent contact of the ski. As already shown in Figure 4, Grind 1 clearly yields a larger contact area than Grind 2. The micro-scale contact areas’ almost linear dependency on the load shown in Figure 4 is also visible here, as the distributions closely follow the shape of the apparent pressure distributions.
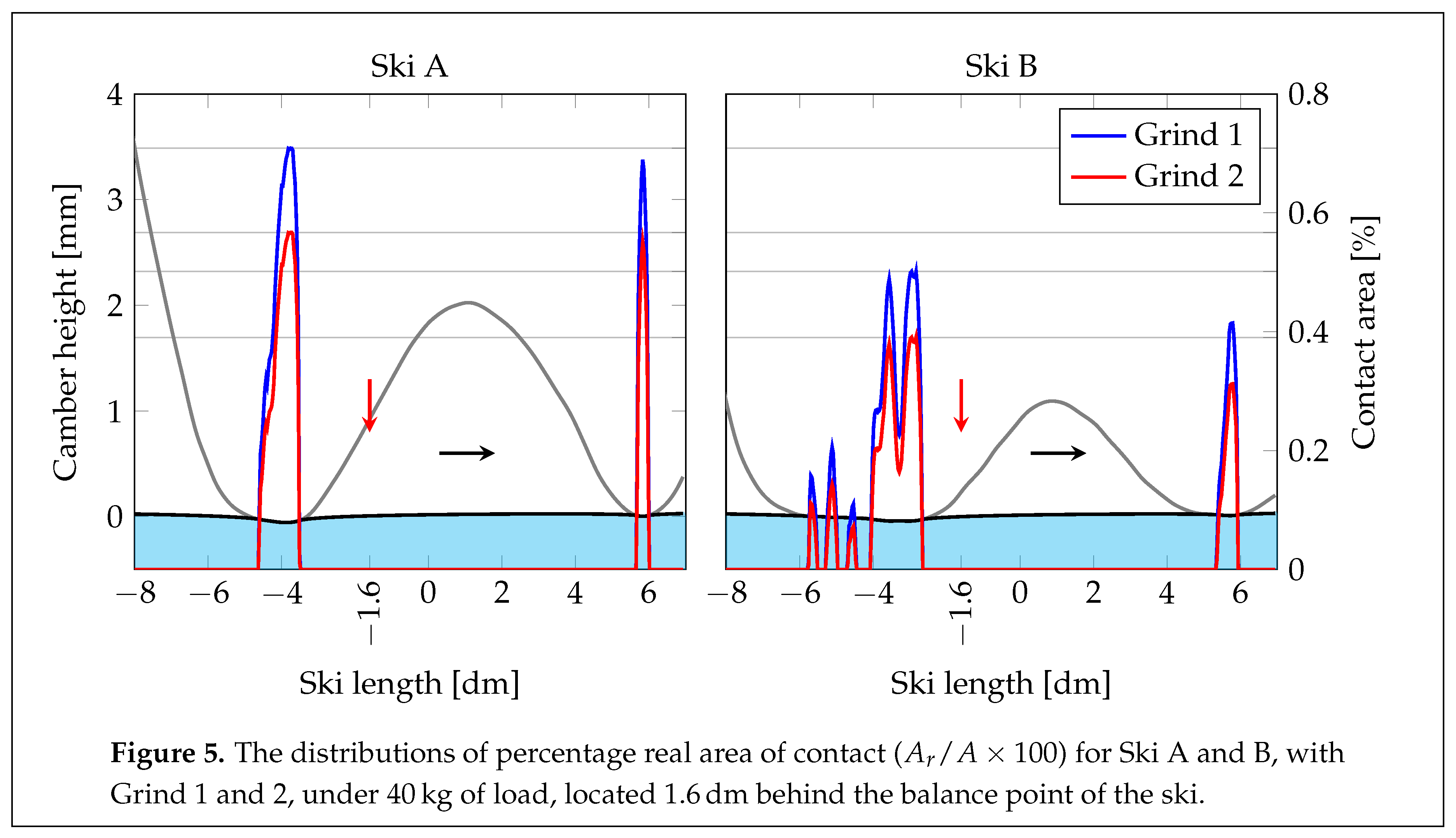
Preprints 78530 i005
By integrating the distributions of the real area of contact along the ski (3), the total contact area of contact A t o t that the ski makes with the snow can be obtained. This is actually the real area of contact A r , n ( X ) integrated over the entire length of the ski Ω ), i.e., A t o t = ∫ Ω A r , n ( X ) d X . The results are presented in Table 2, and they show the total area of contact is in principle solely determined by the grind, with a rather large difference between Grind 1 and 2 for both Ski A and B, i.e., ≈ 28% and ≈ 34%, respectively. However, when comparing the variability in A t o t with the different ski-base textures the differences for Ski A and Ski B are only ≈ 4 % and ≈ 0 . 4 %, respectively. Most of the available adhesive friction models take the total real area of contact as its main input, and in all of them, a lower contact area renders less friction. Hence, the present results suggest that the ski-base texture might be the denominator of the adhesive friction contribution in the ski–snow contact.
Likewise, as shown in Table 3, the average nominal load (the nominal load integrated over the entire length of the ski Ω ) ∫ Ω P n ( X ) d X , which corresponds to the total real area of contact, depends on the ski-base texture to a larger degree than the ski-camber profile. The average nominal load can be viewed as a measurement of the abrasive part of the friction, acting as a counterpart to the contact area. At a certain limit, the snow will yield and abrasion/micro-ploughing will result in higher friction. In turn, this limits the minimisation of the real area of contact and does, therefore, create an optimum. This was highlighted by Lever et al. [14] as one of the dominant factors of snow friction and perhaps connected to the second phase of snow contact described by Theile et al. [30]. Higher apparent pressure may cause abrasive friction on the macro scale, i.e. compaction of the snow, but it does not affect the micro-ploughing component as much as the ski-base texture.
Figure 6 depicts the distributions of the average interfacial separation for the different combinations of skis and ski-base textures. The figure also indicate its minimum value for Grind 1 and 2 applied to both Ski A and B, and it is clear that the ski-camber profile has a very small contribution, but that the ski-base texture highly influences the resulting minimum average interfacial separation. This was also shown in Kalliorinne et al. [40], where only a minute variation of the average interfacial separation with load was found as soon as the load increased above 10 k Pa . The ski-camber profile does, however, determine the number of local minimum interfacial separation points.
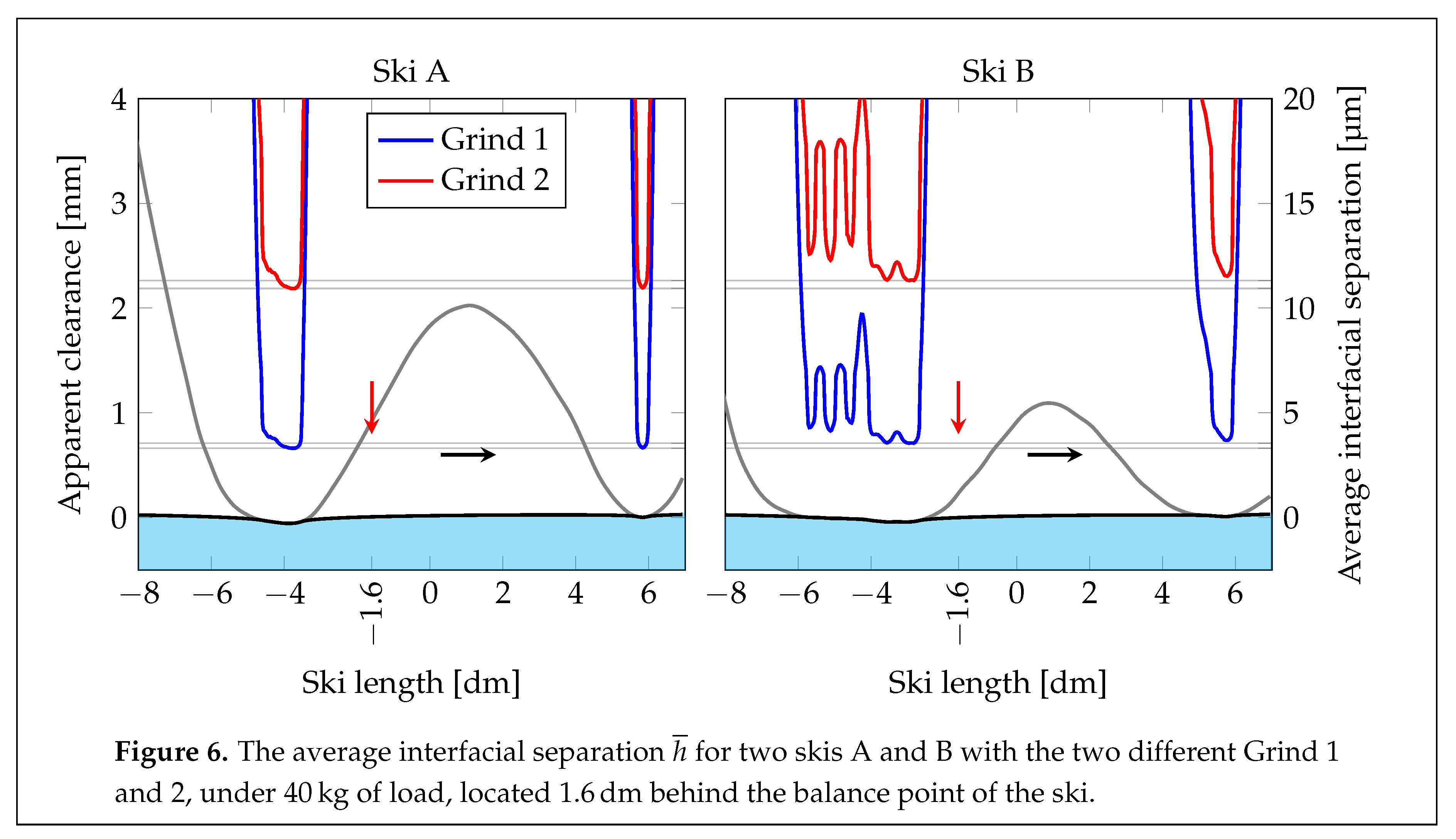
Preprints 78530 i006
Table 4 shows the minimum interfacial separation along the ski for the 4 combinations of skis and ski-base textures. The differences between Ski A and B with the same ski-base texture are 6 . 84 % and 3 . 31 %, respectively. The differences between Grind 1 and 2, on the same pair of skis are, however, 319% and 331%, for Ski A and B, respectively. In a situation where the counter-surface is smooth and non-porous, a too small average interfacial separation could result in a restriction of water transportation, and the consequence could be going from a boundary lubricated regime to a hydrodynamically lubricated contact, which does not necessarily favour the glide. The present analysis suggest that the ski-base texture has a larger impact than ski-camber profile with respect to water transport. The number of local minima and/or the total area of low interfacial separation are probably also very important, as it might increase the likelihood that a restriction will occur.
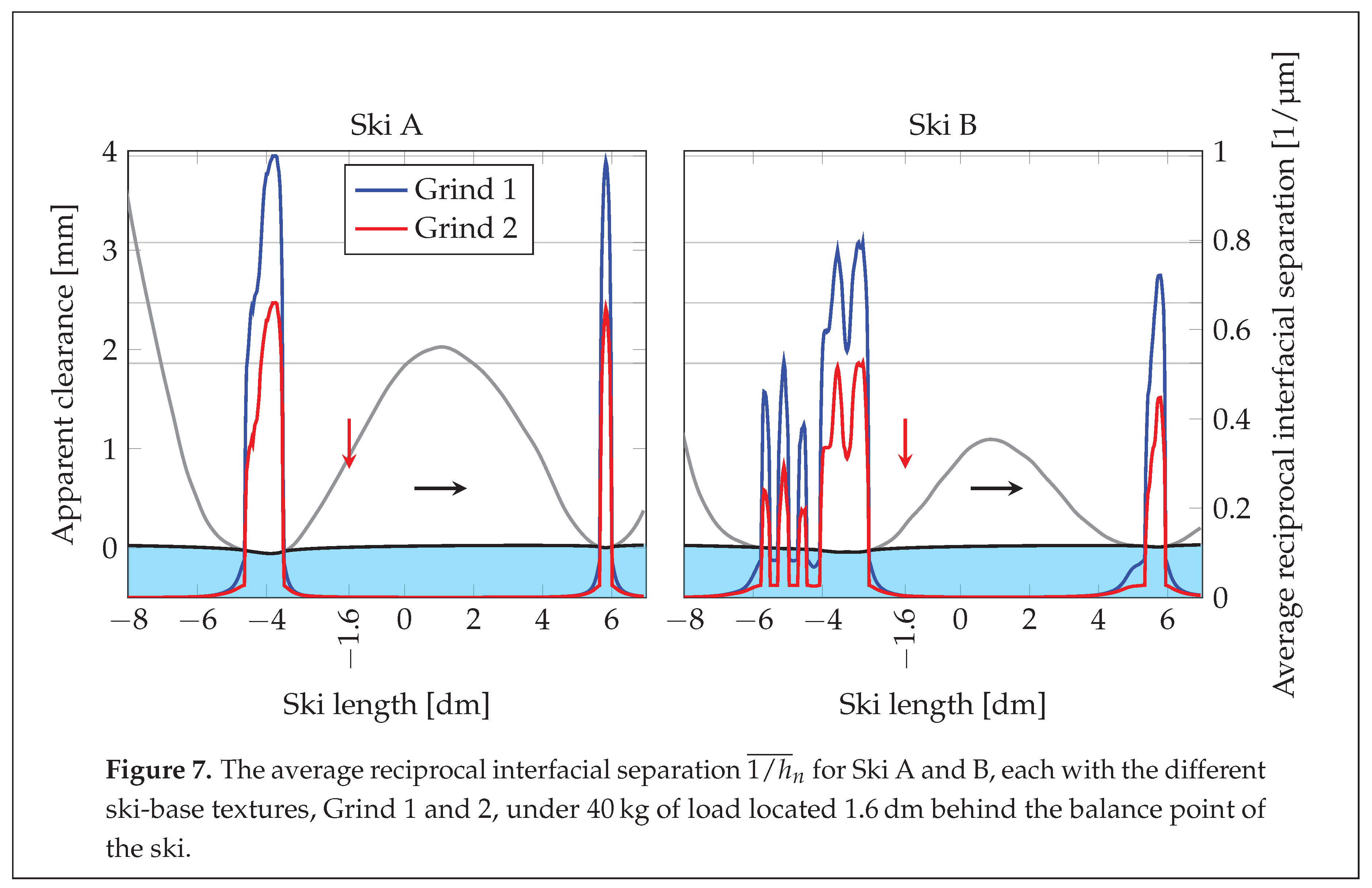
Preprints 78530 i007
Depicted in Figure 7 is the average reciprocal interfacial separation for the different combinations of skis and ski-base textures. One of the things worth noting here is that all maximum values are different in each case. It should also be noted that the average reciprocal interfacial separation takes values outside the regions where there is contact (where the surfaces are separated), and in these regions, it is clear that Grind 1 yields a larger values than Grind 2.
Table 5 shows the average reciprocal interfacial separation, integrated along the entire length of the ski. Contrary to the previous results we can see that all 4 combinations of skis and ski-base textures render considerably different values. More precisely, there is a decrease when changing from Grind 1 to Grind 2 for Ski A and B, which is 40 . 9 % and 23 . 4 %, respectively, and there is an increase when changing from Ski A to Ski B for Grind 1 and 2 which is 31 . 3 % and 23 . 8 %, respectively. The reciprocal interfacial separation is linked to the viscous friction induced by shearing the water film, hence, the results may be interpreted as that the ski-camber and the ski-base texture both play an important role in reducing the viscous friction.

5. Conclusions

To conclude the present paper, two methods for determining the multi-scale contact mechanical response of the ski–snow contact were combined. One considers the macro-scale response of the entire ski and the other one the micro-scale response of the ski-base structure. The analysis based on the functional parameters considered in this work it is suggested that the ski-base texture has a larger impact on the ski-snow friction than the ski-camber profile has itself. The ski-camber profile had the largest impact on the integrated average reciprocal interfacical separation, but impact of the ski-base texture was larger on all four of the function parameters considered.
Related to ski–snow friction, these are the specific findings of the present work:
  • Abrasive friction: The ski-base texture is the deciding factor for average real contact pressure.
  • Adhesive friction: The ski-base texture is the deciding factor for the real contact area.
  • Viscous friction: The ski and the grind are both deciding factor for viscous friction.
  • Friction regime: The ski-base texture is the deciding factor for the minimum average interfacial separation, but the ski-camber profile could decrease risk of transitioning between the regimes by minimising the apparent contact area.
It should be noted, that according to the general consensus, the ski is the most important aspect of ski–snow friction, and thereby there are probably other aspects of the ski–snow contact that has to be considered for a full understanding of the friction in this particular system.

Acknowledgments

The authors would like to acknowledge the support from SOK (Swedish Olympic Committee). The authors would like to acknowledge the support from VR (The Swedish Reseach Council): DNR 2019-04293.

References

  1. Almqvist, A.; Pellegrini, B.; Lintzén, N.; Emami, N.; Holmberg, H.C.; Larsson, R. A Scientific Perspective on Reducing Ski-Snow Friction to Improve Performance in Olympic Cross-Country Skiing, the Biathlon and Nordic Combined. Frontiers in Sports and Active Living 2022, 4, 844883. [Google Scholar] [CrossRef]
  2. Street, G.M.; Gregory, R.W. Relationship between Glide Speed and Olympic Cross-Country Ski Performance. Journal of Applied Biomechanics 1994, 10, 393–399, ZSCC: 0000022. [Google Scholar] [CrossRef]
  3. Bowden, F. The mechanism of sliding on ice and snow. Proceedings of the Royal Society of London. Series A. Mathematical and Physical Sciences 1939, 172, 280–298. [Google Scholar] [CrossRef]
  4. Eriksson, R. Friction of runners on snow and ice. Meddelanden från Föreningen Skogsarbetens och Kungl. Domänstyrelsens Arbetsstudieavdelning 1949. Document Type: Journal Article Bibliographic Level: Analytic Source Note: P.1-63 In Swedish with English summary. Fören. Skogsarbet. Kgl. Domänstyrelsens Arbetsstud. Medd. No.34-35, 1949. 12 refs. CRREL Acc. No: 06007558 GeoRef ID: 7151 crossref: https://www.coldregions.org/vufind/Record/7151.
  5. Bowden, F.P. Some Recent Experiments in Friction: Friction on Snow and Ice and the Development of some Fast-Running Skis. Nature 1955, 176, 946–947. [Google Scholar] [CrossRef]
  6. Lever, J.H.; Asenath-Smith, E.; Taylor, S.; Lines, A.P. Assessing the Mechanisms Thought to Govern Ice and Snow Friction and Their Interplay With Substrate Brittle Behavior. Frontiers in Mechanical Engineering 2021, 7, 690425. [Google Scholar] [CrossRef]
  7. Glenne, B. Sliding Friction and Boundary Lubrication of Snow. Journal of Tribology 1987, 109, 614–617. [Google Scholar] [CrossRef]
  8. Lehtovaara, A. Kinetic friction between ski and snow; Finnish Academy of Technology, 1989.
  9. Bejan, A. The Fundamentals of Sliding Contact Melting and Friction. Journal of Heat Transfer 1989, 111, 13–20, [https://asmedigitalcollection.asme.org/heattransfer/article-pdf/111/1/13/5910218/13_1.pdf]. [CrossRef]
  10. Bejan, A. Contact Melting Heat Transfer and Lubrication. In Advances in Heat Transfer; Elsevier, 1994; Vol. 24, pp. 1–38. [CrossRef]
  11. Makkonen, L. Application of a new friction theory to ice and snow. Annals of Glaciology 1994, 19, 155–157. [Google Scholar] [CrossRef]
  12. Bäurle, L.; Kaempfer, T.; Szabó, D.; Spencer, N. Sliding friction of polyethylene on snow and ice: Contact area and modeling. Cold Regions Science and Technology 2007, 47, 276–289. [Google Scholar] [CrossRef]
  13. Matveev, K.I. An analytical model for flat-ski friction in steady horizontal gliding. Sports Engineering 2017, 20, 293–298. [Google Scholar] [CrossRef]
  14. Lever, J.H.; Taylor, S.; Hoch, G.R.; Daghlian, C. Evidence that abrasion can govern snow kinetic friction. Journal of Glaciology 2019, 65, 68–84. [Google Scholar] [CrossRef]
  15. Breitschädel, F. Variation of Nordic Classic Ski Characteristics from Norwegian national team athletes. Procedia Engineering 2012, 34, 391–396. [Google Scholar] [CrossRef]
  16. Breitschädel, F. Effects of temperature change on cross-country ski characteristics. Procedia Engineering 2010, p. 6.
  17. Kalliorinne, K.; Hindér, G.; Sandberg, J.; Larsson, R.; Holmberg, H.C.; Almqvist, A. The impact of cross-country skiers’ tucking position on ski-camber profile, apparent contact area and load partitioning. Proceedings of the Institution of Mechanical Engineers, Part P: Journal of Sports Engineering and Technology 2023, 0, 0. [CrossRef]
  18. Kalliorinne, K.; Sandberg, J.; Hindér, G.; Larsson, R.; Holmberg, H.C.; Almqvist, A. Characterisation of the Contact between Cross-Country Skis and Snow: A Macro-Scale Investigation of the Apparent Contact. Lubricants 2022, 10, 279. [Google Scholar] [CrossRef]
  19. Bäckström, M.; Dahlen, L.; Tinnsten, M. Essential Ski Characteristics for Cross-Country Skis Performance (P251). In The Engineering of Sport 7; Springer Paris: Paris, 2008; pp. 543–549. [CrossRef]
  20. Schindelwig, K.; Hasler, M.; Van Putten, J.; Rohm, S.; Nachbauer, W. Temperature Below a Gliding Cross Country Ski. Procedia Engineering 2014, 72, 380–385. [Google Scholar] [CrossRef]
  21. Mössner, M.; Schindelwig, K.; Heinrich, D.; Hasler, M.; Nachbauer, W. Effect of load, ski and snow properties on apparent contact area and pressure distribution in straight gliding. Cold Regions Science and Technology 2023, 208, 103799. [Google Scholar] [CrossRef]
  22. Renshaw, A.; Mote, C. A model for the turning snow ski. Skiing Trauma and Safety: Eighth International Symposium; Mote, C.D.J.; Johnson, R.J., Eds.; ASTM International: Philadelphia, US-PA, 1991; pp. 217–238. [CrossRef]
  23. Lehtovaara, A. Influence of vibration on the kinetic friction between plastics and ice. Wear 1987, 115, 131–138. [Google Scholar] [CrossRef]
  24. Koptyug, A.; Bäckström, M.; Tinnsten, M.; Carlsson, P. Cross-country ski vibrations and possible mechanisms of their influence on the free gliding. Procedia Engineering 2012, 34, 473–478, ZSCC: 0000017. [Google Scholar] [CrossRef]
  25. Koptyug, A.; Bäckström, M.; Tinnsten, M. Studies into the Mechanisms of the Cross-country Ski Vibrations and Possible Models of the Phenomenon. Procedia Engineering 2013, 60, 40–45, ZSCC: 0000003. [Google Scholar] [CrossRef]
  26. Koptyug, A.; Bäckström, M.; Tinnsten, M. Gliding-induced Ski Vibrations: Approaching Proper Modeling. Procedia Engineering 2014, 72, 539–544, ZSCC: 0000004. [Google Scholar] [CrossRef]
  27. Nam, Y.; Gim, J.; Jeong, T.; Rhee, B.; Kim, D.N. A Numerical Study for the Effect of Ski Vibration on Friction. Multiscale Science and Engineering 2019, 1, 256–264, ZSCC: 0000001. [Google Scholar] [CrossRef]
  28. Gold, L.W. The Strength of Snow in Compression. Journal of Glaciology 1956, 2, 719–725. [Google Scholar] [CrossRef]
  29. Bader, H. The Physics and Mechanics of Snow as a Material. Cold regions science and engineering. 1962, p. 96.
  30. Theile, T.; Szabo, D.; Luthi, A.; Rhyner, H.; Schneebeli, M. Mechanics of the Ski–Snow Contact. Tribology Letters 2009, 36, 223–231. [Google Scholar] [CrossRef]
  31. Rohm, S.; Unterberger, S.; Hasler, M.; Gufler, M.; van Putten, J.; Lackner, R.; Nachbauer, W. Wear of ski waxes: Effect of temperature, molecule chain length and position on the ski base. Wear 2017, 384-385, 43–49. [Google Scholar] [CrossRef]
  32. Moldestad, D.A.; Løset, S. The Ski Base Structure Analyser (SSA). Modeling, Identification and Control: A Norwegian Research Bulletin 2003, 24, 15–26. [Google Scholar] [CrossRef]
  33. Jordan, S.; Brown, C. Comparing texture characterization parameters on their ability to differentiate ground polyethylene ski bases. Wear 2006, 261, 398–409. [Google Scholar] [CrossRef]
  34. Breitschädel, F. Cross country ski base tuning with structure imprint tools. Procedia Engineering 2010, p. 5.
  35. Breitschädel, F. A new approach for the grinding of Nordic skis. Procedia Engineering 2015, 112, 385–390. [Google Scholar] [CrossRef]
  36. Giesbrecht, J.L.; Smith, P.; Tervoort, T.A. Polymers on snow: Toward skiing faster. Journal of Polymer Science Part B: Polymer Physics 2010, 48, 1543–1551. [Google Scholar] [CrossRef]
  37. Rohm, S.; Kno, C.; Hasler, M.; Kaserer, L.; van Putten, J.; Unterberger, S.H.; Lackner, R. Effect of Different Bearing Ratios on the Friction between Ultrahigh Molecular Weight Polyethylene Ski Bases and Snow. ACS Appl. Mater. Interfaces 2016, p. 6.
  38. Scherge, M.; Stoll, M.; Moseler, M. On the influence of microtopography on the sliding performance of cross country skis. Frontiers in Mechanical Engineering 2021, 7, 659995. [Google Scholar] [CrossRef]
  39. Mössner, M.; Hasler, M.; Nachbauer, W. Calculation of the contact area between snow grains and ski base. Tribology International 2021, 163, 107183. [Google Scholar] [CrossRef]
  40. Kalliorinne, K.; Persson, B.N.J.; Sandberg, J.; Hindér, G.; Larsson, R.; Holmberg, H.C.; Almqvist, A. Characterisation of the Contact between Cross-Country Skis and Snow: A Micro-Scale Study Considering the Ski-Base Texture. Lubricants 2023, 11, 225. [Google Scholar] [CrossRef]
  41. Vakis, A.; Yastrebov, V.; Scheibert, J.; Nicola, L.; Dini, D.; Minfray, C.; Almqvist, A.; Paggi, M.; Lee, S.; Limbert, G.; Molinari, J.; Anciaux, G.; Aghababaei, R.; Echeverri Restrepo, S.; Papangelo, A.; Cammarata, A.; Nicolini, P.; Putignano, C.; Carbone, G.; Stupkiewicz, S.; Lengiewicz, J.; Costagliola, G.; Bosia, F.; Guarino, R.; Pugno, N.; Müser, M.; Ciavarella, M. Modeling and simulation in tribology across scales: An overview. Tribology International 2018, 125, 169–199. [Google Scholar] [CrossRef]
  42. Grützmacher, P.G.; Profito, F.J.; Rosenkranz, A. Multi-Scale Surface Texturing in Tribology—Current Knowledge and Future Perspectives. Lubricants 2019, 7, 95. [Google Scholar] [CrossRef]
Table 1. Surface roughness parameters for the ski-base textures shown in Figure 3.
Table 1. Surface roughness parameters for the ski-base textures shown in Figure 3.
Textures S a  (μm) S q  (μm) S s k (-) S k u (-) S d q (μm/mm) S p k  (μm) S k  (μm) S v k  (μm)
Grind 1 1.77 2.16 -0.16 2.58 65.79 1.44 6.01 1.92
Grind 2 8.77 9.62 -0.43 1.63 185.77 2.16 11.65 20.02
Table 2. The total real area of contact for the 4 combinations of skis and grinds.
Table 2. The total real area of contact for the 4 combinations of skis and grinds.
A t o t Grind 1 Grind 2
Ski A 31.52  mm2 24.62  mm2
Ski B 32.89  mm2 24.52  mm2
Table 3. The average nominal load for the 4 combinations of skis and grinds.
Table 3. The average nominal load for the 4 combinations of skis and grinds.
F / A t o t Grind 1 Grind 2
Ski A 12.46   M Pa 15.95   M Pa
Ski B 11.94   M Pa 16.02   M Pa
Table 4. The minimum average interfacial separation along the ski for the 4 combinations of skis and grinds.
Table 4. The minimum average interfacial separation along the ski for the 4 combinations of skis and grinds.
min ( h ¯ n ) Grind 1 Grind 2
Ski A 3.31  μm 10.94  μm
Ski B 3.55  μm 11.32  μm
Table 5. The integrated average reciprocal interfacial separation for the 4 combinations of skis and grinds.
Table 5. The integrated average reciprocal interfacial separation for the 4 combinations of skis and grinds.
∫ Ω 1 / h ¯ n ( X ) d X Grind 1 Grind 2
Ski A 5.472   k m 3.439   k m
Ski B 7.967   k m 4.512   k m
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.
Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.
Prerpints.org logo

Preprints.org is a free preprint server supported by MDPI in Basel, Switzerland.

facebook logotwitter logolinkedin logo
MDPI Initiatives
Important Links
Subscribe

Disclaimer

Terms of Use

Privacy Policy

© 2024 MDPI (Basel, Switzerland) unless otherwise stated