Regional Frequency Analysis of Extreme Wind in Pakistan Using Robust Estimation Methods

The quantile estimation of extreme wind speed is needed in various environmental fields such as climatology, design of structures, renewable energy sources and agricultural operations. These calculations are crucial for the coding of wind speed. In this study, the required wind speed series of 16 stations in Khyber Pakhtunkhwa, Pakistan, was obtained from the NASA official website and measured in meters per second (m/s) at a 10-meter distance. A Regional Frequency Analysis of 16 AMWS stations was performed using L-moments. The quantile estimates of extreme wind speed are needed for various areas of interest using Regional Frequency Analysis (RFA) and extreme value theory. These calculations are crucial for the coding of wind speed. The data was taken from the NASA official website at a 10-meter distance and measured in meter per second (m/s). A Regional Frequency Analysis of AMWS using L-moments is performed utilizing wind speed data from sixteen sites (16) in Pakistan's Khyber Pakhtunkhwa province. There are no sites that are found to be discordant. The wards method is used to construct a homogenous region and make two homogenous regions from 16 sites. The heterogeneity test justifies that both clusters are homogeneous. The most appropriate probability distribution from the Generalized Normal (GNO), Generalized Logistic (GLO), Pearson Type-3 (P3), Generalized Pareto (GPA), and Generalized Extreme Value (GEV) distributions are chosen to calculate regional quantiles. According to the L-moments diagram and Z statistics, GEV for Cluster- Ι and GLO for Cluster- ΙΙ are the best suggestions from the others. Both clusters’ robustness is measured utilizing Relative Bias (RB) and Relative Root Mean Square Error (RRMSE). Overall, GEV distribution is fit for cluster-Ι, and the GLO distribution is fit for cluster-ΙΙ. Utilizing the site mean and median as index parameters, we can also find at-site quantiles from regional quantiles. The study’s quantile estimates can be employed in codified structural designs with policy consequences.

Keywords:

Subject: Environmental and Earth Sciences - Atmospheric Science and Meteorology

1. Introduction

Wind speed is also known as wind flow speed. It is a basic atmospheric volume produced by air flowing from high to low pressure due to temperature variations. Due to the earth’s rotation, the direction of the wind is usually parallel to the isobar. Anemometers are usually used to measure wind speed. Wind speed affects weather forecasts, aviation, and maritime operations; wind energy is a source of energy that is fast growing in popularity worldwide. It is clean and brings many benefits to human beings. There are many different wind sources, and they change throughout time in different regions (Ma, 1997). Many countries support the use of renewable energy sources; one of the most prominent cleaner energy sources is wind energy (Sarrias et al., 2010). Environmental challenges have arisen due to the rising cost of fossil fuels and other factors. It is important to appreciate the potential of unconventional energy generations. The most parts of our country, the wind speed is slow. There are many places where wind power can be generated. Coastal regions are prospective locations for wind turbine development and some hilly regions (Ahmed and Ahmad, 2004). Fossil fuel power generation technologies, which have been used for centuries, are becoming problematic as the world’s energy consumption and pollution levels rise, many countries are considering shifting away from fossil fuels and toward non-fossil fuels as their economies grow to help mitigate climate change, which is mostly caused by excessive carbon emissions around the world (Fawad et al., 2019). Wind, solar, and geothermal energy are examples of fuel sources for energy generation. Renewable energy is defined as energy that is regularly regenerated for human benefit while posing no significant environmental risk.

Wind energy, often known as wind power, is a clean, low-cost, and renewable resource. The process of using wind power to transform the kinetic energy of the wind into mechanical or electrical energy via a wind turbine is known as “wind energy generation.” Wind energy generation does not release pollutants and is often referred to as “Green Power Technology” because it does not threaten the global environment.

Compared with fossil fuels, wind energy has no negative influence on the environment or ecosystems (Dai et al., 2015). That is why more than 100 countries use wind energy (Huang and McElroy, 2015). Many countries are currently heavily investing in wind energy. As a result, the worldwide market for wind energy is rapidly rising (Darbandi et al., 2012). According to the Pakistan meteorological department (PMD), the alternative energy development board (AEDB), and the national renewable energy laboratory in Pakistan, the overall installed capacity in Pakistan is expected to be around 346 GW (Aized et al., 2019). According to estimates, wind energy is suitable for roughly 9.06 percent of Pakistan’s geographical zone (Hulio et al., 2019).

The most important part of wind energy is wind speed. Policymakers can use wind speed data to choose whether or not to construct and build a wind farm in a certain region. Before a wind conversion system can be implemented, the potential wind energy of a certain region must be determined. Wind speed varies randomly; hence proper modelling of wind speed is required for future wind energy design. Then probabilistic modeling of wind speed data is required. To anticipate the energy output of a wind conversion system for a specific site,

Two procedures are utilized to evaluate extreme events. At-site frequency analysis and regional frequency analysis are two types of frequency analysis. The primary drawbacks of at-site frequency include sampling variability, which is especially problematic for quantile estimates overhead for a long period (Hosking and Wallis, 1993). The RFA of AMWS data examined at sixteen sites in Khyber Pakhtunkhwa, Pakistan, was also explored in this research.

The objective of this study consists of: 1) ensuring that all study sites fulfil assumptions of stationarity, independence, and homogeneity; 2) Data screening for regional frequency analysis. 3) Identifying homogeneous regions for a set number of sites. 4) Determine the best probability distribution for the identified homogeneous regions. 5) Determine the quantiles for different return periods by estimating the parameters of the various best-fit regional distributions identified in this study. 6) To give some solutions to mitigate the losses due to these extreme events for policy implications and to address the advantages of wind energy.

The remainder of this work is structured as follows. Section 2 will go through the materials and techniques utilized in this paper in detail; Section 3 will go over the study area; Section 4 will go over the results and discussion, and Section 5 will finalize the paper.

In Pakistan’s Khyber Pakhtunkhwa region, the first RFA of AMWS utilizing linear moments is planned. NASA provided the AMWS data for these sites, which is measured in m/sec.

2. Methodology

The analysis of the AMWS is discussed in this section. The AMWS was fitted with a variety of distributions, and goodness of fit tests was employed to evaluate the results.

2.1. The Initial Examination of the Annual Maximum Wind Speed (AMWS) Series

Before the regional frequency analysis, we check the basic assumptions, which are stationarity, independence and homogeneity. These are also mutual assumptions for the RFA of maximum events, such as maximum floods, rainfall, and droughts. For stationarity, Spearman’s order rank correlation test, for independence, the Wald-Wolfowitz test, and for homogeneous Man-Whitney U (MWU) test is used in this study.

2.1.1. Spearman’s Order Rank Correlation Test for Checking the Trend

The spearman’s order rank correlation test is based on a rank, which is a non-parametric test and is used for checking the monotonic pattern of increasing or decreasing trend in the data. In statistical methods, we call it a monotonic trend. “Spearman’s order correlation coefficient” refers to the well-known non-parametric statistical dependence measure named after British psychologist Charles Spearman (1863-1945). It indicates if the trend is positive, negative, or non-existent. The null and alternative hypothesis of the spearman’s order rank correlation test is

H_o:

there is no trend in the series

H₁:

there is trend in the series

The significance threshold is 0.05, and the test statistics are

ρ = 1 - \frac{6 - \sum {d_{i}}^{2}}{n (n^{2} - 1)}

(1)

While

ρ =

Spearman’s rank correlation coefficient,

d_{i}

= difference between the two ranks of each observation,

n =

Number of observations

2.1.2. The Wald-Wolfowitz (WW) Test for Checking Independence

According to the Independence, at the site, observed data of wind speed cannot affect the occurrence or non-occurrence of any other observed wind speed at that site. The assumptions of independence are checked frequently for hydrological data, which includes yearly means, totals, maxima, or minima, monthly, seasonal, and other time interval data, such as non-annual maximum data samples and partial duration series. The nonparametric WW test, first introduced by (Wald and Wolfowitz, 1943), is widely used to test the independence of observations in a recorded series. It’s also utilized to see whether there are any trends in the data. Let

X_{1}

X_{2}

X_{3}

……………

X_{n}

represent the experimental values of the variable under investigation. The Rao and Hamed recommended R statistics are

R = \sum_{i = 1}^{n - 1} x_{i} x_{i + 1} + x_{1} x_{n}

(2)

The

R

statistic follows a normal distribution with the mean and variance shown below.

Ṝ = \frac{({S_{1}}^{2} - S_{2})}{n - 1}

(3)

V a r (R) = \frac{({S_{1}}^{2} - S_{2})}{n - 1} - Ṝ^{2} + \frac{({S_{1}}^{4} - 4 {S_{1}}^{2} S_{2} + 4 S_{1} S_{3} + {S_{2}}^{2} - 2 S_{4})}{(n - 1) - (n - 2)}

(4)

Where the term

S_{r} = n ḿ_{r}

and

ḿ_{r}

is the

r^{t h}

moment with respect to the origin of the sample. The test statistics of the WW test is given as

u = \frac{R - Ṝ}{\sqrt{v a r (R)}}

(5)

Where

u

is used to test the data set for independence at 5 % level of significance.

2.1.3. Mann-Whitney U (MWU) test for Homogeneity

The Mann-Whitney U (MWU) test is a non-parametric test devised by (Mann and Whitney, 1947) to test the null hypothesis that the two samples come from the same population or not. When the data does not follow the normality assumption, the MWU test is the alternative to the t-test. The MWU test, often known as the U test, is frequently used in frequency analysis of extreme occurrences to test the homogeneity assumption. Let’s say we have two independent samples of sizes

n_{1}

and

n_{2}

, and the total sample size

N

, which is

N = n_{1} + n_{2}

almost similar length yielding

n_{1} \leq n_{2}

. All of the samples are ranked from best to worst. The MWU test is based on the lowest value of “U,” which is the minimum of the V and W variables defined in.

V = R_{1} - \{\frac{n_{1} (n_{1} + 1)}{2}\}

(6)

W = n_{1} n_{2} - V

(7)

U = \min (V, W)

(8)

Where

n_{1}

and

n_{2}

are both sample,

R_{1}

is the sum ranking order of the first sub sample

n_{1}

in the combined series N,

R_{1} = \sum_{i = 1}^{n} R_{i}

where

R_{i}

is the rank of the first sample

n_{1}

in the combined series N. where

V

denotes the number of times an element from the first sample

n_{1}

is ranked after an element from the second sample

n_{2}

. Similarly, W denotes the case in which the second sample

n_{2}

is ranked after the first sample

n_{1}

. When

N \geq 20

and

n_{1}

n_{2} \geq 3

under the same null hypothesis, the

U

test statistic can be regarded normally distributed. The

U

statistic is written as follows.

U = \frac{U - Ū}{\sqrt{V a r (U)}}

(9)

Ū = \frac{n_{1} n_{2}}{2}

(10)

V a r (U) = [\frac{n_{1} n_{2} (n_{1} {+ n}_{2} + 1}{12}]

(11)

The formula for the variance of U should be modified as follows in the presence of tied ranks.

V a r (U) = (\frac{n_{1} n_{2}}{12}) [(N + 1) - \sum_{i = 1}^{k} \frac{{J_{i}}^{3} - J_{i}}{N (N - 1)}]

(12)

Where

J_{i}

is the number of observations that share rank

i

and

k

is the number of ranks that are tied.

2.2. Linear Moments

In this work, the method of L-moments was utilized to estimate the parameters of PDs, which has been employed in the frequency analysis of severe wind speeds (Fawad et al., 2018; Goel et al., 2004; Modarres, 2008; Yu et al., 2016). The L-moments are more reliable than the method of moments and the maximum likelihood approach because they are less sensitive to outliers and are suited for smaller sample sizes (Alam et al., 2016; Hosking, 1990).

(Hosking, 1990) defines a L-moment as the expectation of a linear arrangement of order statistics. They may be used to explain any random variable with a mean. Let

Χ_{1}, Χ_{2}, \dots, Χ_{r}

represent a random sample of magnitude r with cumulative distributions functions F(X) and quantile functions X (F). Let

Χ_{1 : r} \leq Χ_{2 : r} \leq \dots \leq Χ_{r : r}

be the random sample order statistics. (Hosking, 1990) explained the r^th population L-moment for the random variable X as follows:

λ_{r} = \frac{1}{r} \sum_{k = 0}^{r - 1} {(- 1)}^{k} (\binom{r - 1}{k}) Ε (X_{r - k : r}) r = 1, 2 \dots

(13)

When it comes to L-moments,

λ_{r}

is a linear function of the predicted order of statistics according to L-moments. The following have provided the first four L-moments

λ_{1} = Ε (Χ_{1 : 1})

(14)

λ_{2} = \frac{1}{2} Ε (Χ_{2 : 2} - Χ_{1 : 2})

(15)

λ_{3} = \frac{1}{3} Ε (Χ_{3 : 3} - 2 Χ_{2 : 3} + Χ_{1 : 3})

(16)

λ_{4} = \frac{1}{4} Ε (Χ_{4 : 4} - 3 Χ_{3 : 4} + 3 Χ_{2 : 4} + Χ_{1 : 4})

(17)

The ratio of L-moments will be determined as follows

τ = \frac{λ_{2}}{λ_{1}}

(18)

τ_{3} = \frac{λ_{3}}{λ_{2}}

(19)

τ_{4} = \frac{λ_{4}}{λ_{2}}

(20)

λ_{1}

Is the measure of locations,

τ

is the measure of L-coefficient of variations (L-cv),

τ_{3}

and

τ_{4}

are L- skewness and L-Kurtosis, respectively in the preceding equation.

2.3. Application of the L-Moments Based on Regional Frequency Analysis

(Hosking and Wallis, 1997) proposed the following four steps for regional frequency analysis of extreme occurrence based on L- moment’s theory. These steps are as follows.

Screening of the data
Recognition of Homogeneous Regions
Selections of the best fit distribution
Quantile estimation

2.3.1. Screening of the Data

Before beginning with statistical analysis, data screening ensures that the data is clean and ready. The data must be checked to ensure that it is available, trustworthy, and suitable for testing the causality theory. On the LM basis (Hosking and Wallis, 1997) depicted a discordance amount

D_{i}

to differentiate those locations that are completely discordant with the group as a whole

D_{i} = \frac{1}{3} {(u_{i} - \bar{u})}^{T} S^{- 1} (u_{i} - \bar{u})

(20)

S = \frac{1}{N - 1} \sum_{i = 1}^{N} (u_{i} - \bar{u}) {(u_{i} - \bar{u})}^{T}

(21)

Sum of Squares and Cross Products Matrix Where

u_{i}

= [

t^{(i)}

t_{3}^{(i)}

t_{4}^{(i)}

] vector consisting sample LMR

\bar{u}

N^{- 1} \sum_{i = 1}^{N} u_{i}

,N = Total enumerate of sites Hosking plied a touchstone for discordancy statistic, site’s collection and relevant

D_{i}

brink point.

2.3.2. Recognition of Homogeneous Regions

The development of homogeneous regions is the most important phase in RFA. A region is said to be homogenous if all of its sites share some common characteristics. There is a substantial quantity of literature on various grouping strategies, such as geographical convenience, subjective partitioning, objective partitioning, and cluster analysis. According to (Hosking and Wallis, 1997), administrative zones or focal physical groupings include adjacent sites in a region for geographical convenience. Many site characteristics, including sewerage zone, mean annual rainfall, wind speed, latitude, longitude, drainage area, and time of occurrence of the most significant flood in the year, can be used to characterize regions subjectively. Using Ward’s methods for hierarchical clustering in this study, all sixteen sites were classified as two homogeneous clusters. Their homogeneity was confirmed using the regional heterogeneity measure, ensuring that both clusters are two homogeneous clusters. Cluster analysis is a multivariate approach to data analysis used to form groups having the least variability, similar characteristics and features. Each site is assigned a data vector, which is then dispersed or combined into a set of uniform vectors formation of regions can have practiced. At-site characteristics are commonly used in cluster analysis to structure homogenous regions, but site statistics can also strengthen the process. Characteristics of the site can be latitude and longitude, annual average rainfall, level of elevation and drainage area can be added to construct cluster (Ouarda et al., 2008).

2.3.2.1. Cluster Analysis

Cluster analysis is a multivariate technique used to form groups having the least variability, matching characteristics, and matching features. By allocating a data vector to each site and adding these sites into groups of uniform vectors, regions can be practiced. Site characteristics are commonly used in cluster analysis to structure homogenous regions, but additionally, site statistics can strengthen the process. The characteristics of a site can be latitude and longitude, the annual average maximum wind, level of elevation, and drainage area can be added to the constructed cluster.

2.3.2.2. Hierarchical Clustering

Hierarchical clustering is a well-known and simple clustering technique. One of them is agglomerative hierarchical clustering.Agglomerative Hierarchical Clustering Technique In this method, each data point is treated as a separate cluster at first. Similar clusters merge with other clusters in each repetition until one cluster or K clusters are produced.

2.3.2.3. Ward’s Method

Ward’s approach is based on hierarchical clustering (Ward, 1963). Because entering a group causes one to become a square hierarchal clustering is based on the standardized Euclidean distance (d), which is provided in equations

d^{2} (p, q) = (x_{p} - x_{q}) D^{- 1} (x_{p} - x_{q})^{T}

(22)

Where

x_{p}

and

x_{q}

are the physiographic coordinates of places

p

and

q

respectively and

D^{- 1}

is a diagonal matrix each coordinate is expressed as a sum of squares because the variables are presented in different units. To avoid proportional effects, this coordinate is inversely weighted by the sample variance. In terms of variables, the cluster’s sum of squares inside the cluster (GSS is defined as the sum of the distances between all objects in the cluster and their center of gravity (Ouarda et al., 2008). An equation can be used to express it as.

G S S_{r} = \sum_{i = 1}^{n_{r}} d^{2} (x_{r i} - \bar{x_{r}})

(23)

where

n_{r}

and

\bar{x_{r}}

are the cluster r size and centroid, respectively.

2.3.2.4. Heterogeneity Test

Hosking and Wallis discuss the homogeneity test (1997). By using

H

test, we approach the homogeneity of the sites in the region, whether the region is homogenous or heterogeneous.

H = \frac{(v - μ_{v})}{δ_{v}}

(24)

“Where v is standard deviation of sample lcv”

V = {\{\frac{\sum_{i = 1}^{n} n_{i} {(t^{i} - t^{R})}^{2}}{\sum_{i = 1}^{n} n_{i}}\}}^{\frac{1}{2}}

(25)

t^{R}

lcv of regional average

t^{R} = \frac{\sum_{i = 1}^{N} n_{i} t^{(i)}}{\sum_{i = 1}^{N} n_{i}}

(26)

μ_{V}, σ_{V}

Represents the mean and variance of population

V

. According to the criteria, if

H

< 1, the region is homogeneous,

H

is in among 1 and 2. It can be considered homogeneous but not perfectly homogeneous.

H

≥ 2, then the region will be considered as perfectly heterogeneous. The use of Kappa distribution for simulations is common because of its tremendous qualities, generated by emerging two gamma distributions, having four parameters (

α, ξ, k, h

) indicating scale, location, shape and redundant shape parameter, x values lower and upper as

[ξ + \frac{α}{k} (1 - \frac{1}{h^{k}}), ξ + \frac{α}{k}

]. Kappa distribution is generalizing GEV distribution when h=0, of GPA, if h=1, of EXP if

h = 1

k = 0

, of Uniform distribution (UD) at

h = 1

k = 1

and GLO when

h = - 1

. Its density, distribution and quantile functions are given below.

f (x) = \frac{{\{1 - k (x - \frac{ξ}{α})\}}^{(\frac{1}{k} - 1)}}{α} {\{F (x)\}}^{1 - h}

(27)

F (x) = {[1 - h \{1 - k {(x - \frac{ξ}{α})}^{(\frac{1}{k} - 1)}\}]}^{\frac{1}{h}}

(28)

x (F) = ξ + \frac{α}{k} \{1 - (\frac{1 - F^{h}}{h})\}

(29)

2.3.3. Selections of the Best Fit Distribution

The next stage is to select the right distribution after passing the homogeneity test. After making homogeneous regions, the following step is the description of the appropriate statistical model by choosing a suitable regional frequency distribution.

(Peel et al., 2001) suggested an L-Moment (LM) ratio diagram to select suitable probability distribution in regional frequency analysis of homogeneous regions. (Vogel and Fennessey, 1993) determined that in the use of extreme events in hydrology, LM ratio diagrams are always employed instead of product-moment ratio diagrams. (Hosking, 1990) found that LM ratio diagrams can distinguish between candidate distributions and explain regional data.

Low flow occurrences within the regions be analyzed based on the fitted regional distribution using goodness-of-fit criterion in terms of L-moments using L-moments ratio diagrams and Z-Statistics (Hosking and Wallis, 1997). The average moments of the regional data are compared to the moments of the distribution in this criterion. The main goal is to choose the optimal distribution for the observed data among the above-mentioned simulated candidate distributions. The best fit of the simulated distribution depends on how well L-skewness and L-kurtosis support regional average L-Skewness and L-kurtosis.

The procedure for selection of distribution accordingly is as follows.

Z^{D i s t} = \frac{τ_{4}^{D i s t} - τ_{4}^{R} + B_{4}}{σ_{4}}

(30)

Where

B_{4} = \frac{\sum_{m = 1}^{N s i m} (t_{4}^{(m)} - t_{4}^{R})}{N}

(31)

σ_{4} = {[\frac{{\sum_{m = 1}^{N s i m} (t_{4}^{(m)} - t_{4}^{R}) - N_{s i m} B_{4}^{2}}}{{(N}_{s i m} - 1)}]}^{\frac{1}{2}}

(32)

$t_{4}^{D i s t} = L - C k o f f i t t e d d i s t r i b u t i o n$
$B_{4} = R e g i o n a l B i a s$
$σ_{4} = R e g i o n a l S t a n d a r d D e v i a t i o n$
$N_{s i m} = Q u a n t i t y o f S i m u l a t e d R e g i o n a l D a t a b y K a p p a D i s t r i b u t i o n$

The fit is considered to be good if

|Z^{D i s t}|

have the small value or sufficiently close to zero. In the statistical technique of hypothesis testing if

|Z^{D i s t}| \leq 1.64

, then at 90% confidence level, the candidate distribution is considered the best-fitted probability distribution. If more than one candidate probability distribution meets the above criteria, the distribution with the lowest

|Z^{D i s t}|

value is chosen as the best-suited probability distribution.

2.3.4. Quantile Estimation

The final phase of RFA is to estimate the parameters of the chosen frequency distribution and assess its robustness in giving valid quantile estimates for all sites in the homogenous region. (Hosking and Wallis, 1997) suggested that the regional L-moment algorithm is more convenient despite the non-fulfillment of some fundamental assumptions of the index flood procedure. For various non-exceedance probabilities, regional quantiles estimations are calculated using a simulation process. Furthermore, by scaling

Q (.)

with an estimate of the scaling factor of

μ_{i}

corresponding to non-exceedance probability

F

, the quantile estimates of each site might be obtained as follows:

{\hat{Q}}_{i} (Ϝ) = l_{1}^{(i)} \hat{q} (Ϝ)

(33)

where

{\hat{Q}}_{i} (Ϝ)

is the estimation of the at-sit quantile,

l_{1}^{(i)}

is the individual sites mean and

\hat{q} (Ϝ)

is refers to the regional quantile function. Other scaling factors that can be used include median, mean, etc. We used the Monte Carlo simulation technique given by (Meshgi and Khalili, 2009) to test the robustness of the specified regional frequency distribution in this work, with 10,000 simulations. We calculated the errors between simulated quantiles and calculated regional quantiles estimations using this technique. These differences are then used to calculate relative bias (RB) and relative root mean square error (RRMSE) for various non exceedance probabilities, which are then used to examine the robustness of best fit distributions. Below is the mathematical form of RB and RRMSE.

R B = \frac{1}{M} \sum_{m = 1}^{M} \{\frac{{\hat{Q}}_{i}^{[m]} - Q_{i} (F)}{Q_{i} (F)}\}

(34)

R R M S E = \sqrt{\frac{1}{M} {\sum_{m = 1}^{M} \{\frac{{\hat{Q}}_{i}^{[m]} - Q_{i} (F)}{Q_{i} (F)}\}}^{2}}

(35)

Here

M

is the sample size,

{\hat{Q}}_{i}^{[m]} (F)

and

Q_{i} (F)

is the simulated and computed regional quantiles, respectively, in the above equation.

On the basis of standard error of at-site quantile estimations under best-fit distribution, (Hosking and Wallis, 1997) proposed the following equation to check robustness.

v a r \{{\hat{Q}}_{i} (Ϝ)\} \approx {x (F; θ_{°})}^{2} v a r ({\hat{μ}}_{i}) + {\hat{μ}}_{i}^{2} v a r {x (F; \hat{θ})\}

(36)

This can be further written like this

v a r \{{\hat{Q}}_{i} (Ϝ)\} \approx {q_{i} (F)}^{2} \frac{{σ i}^{2}}{n} + {\bar{x}}_{i}^{2} {R e g i o n a l R M S E - (R e g i o n a l B i a s)^{2}\}

(37)

In additions we can use sample variance of median and sample median instead of sample mean of variance and sample mean. In that case the relationship will become

v a r \{{\hat{Q}}_{i} (Ϝ)\} \approx {q_{i} (F)}^{2} \frac{{π σ i}^{2}}{2 n} + {\bar{x}}_{i}^{2} {R e g i o n a l R M S E - (R e g i o n a l B i a s)^{2}\}

(38)

Where the

x -

represent the sample median and

\frac{{π σ i}^{2}}{2 n}

is the sample variance of median.

3. Study Area and Data

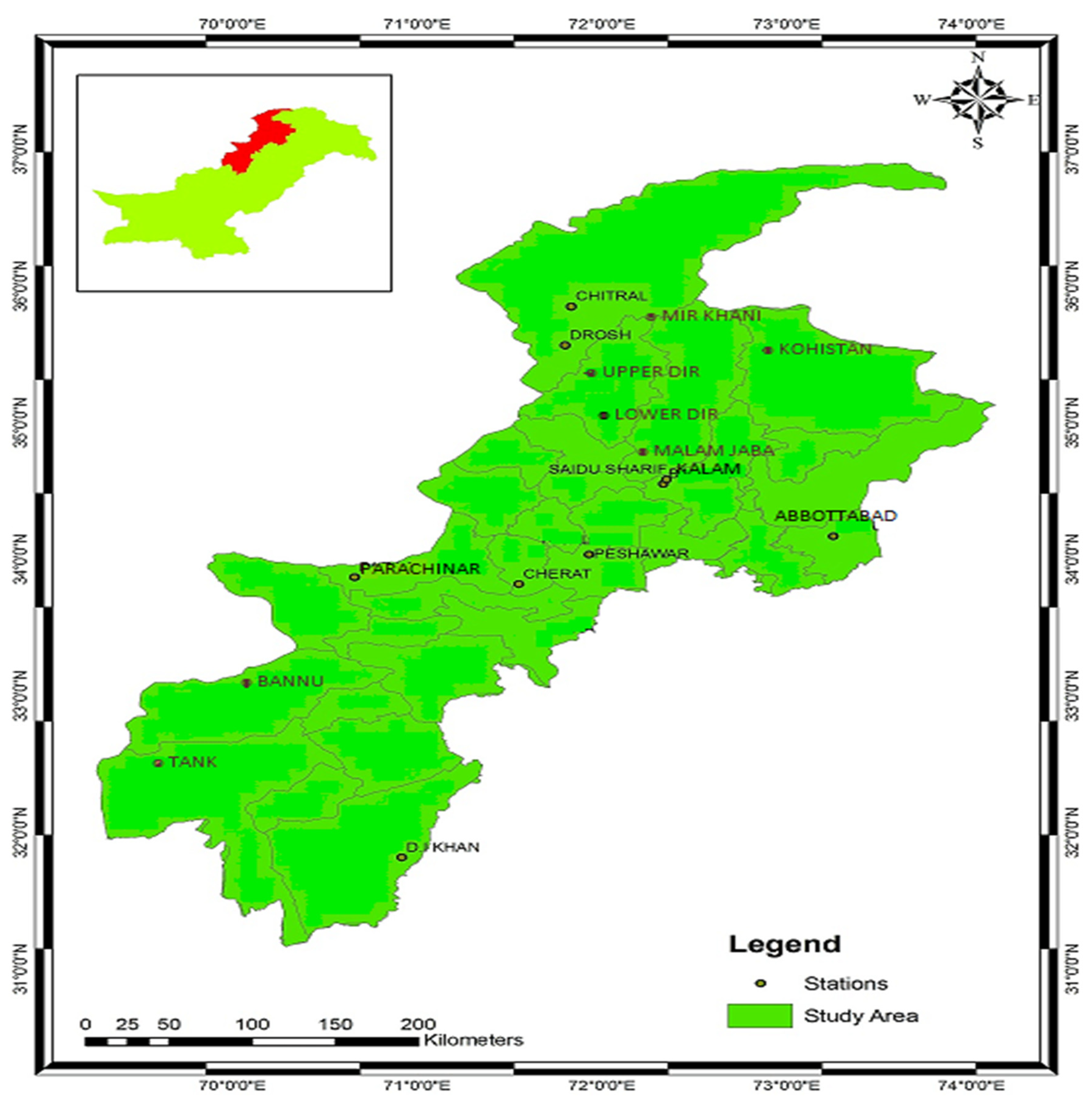
Khyber Pakhtunkhwa (30⁰-35N & 67⁰-72⁰E) is one of Pakistan’s five provinces, It is located on the Iranian plateau and Eurasian land plate with an area of 74,521 km², It is separated into two zones geographically, from the Hindu Kush to the northern section of Peshawar and from Peshawar to the southern half of the Derjat basin, KPK climate shifted from severely cold (in places like Chitral) to highly hot (in places like Dera Ismail Khan) (Lubna and Sapna, 2019). On availability of required data sets, only sixteen (16) palaces of KPK (Cherat, Chitral, D.I. Khan, Tang, UpperDir, Drosh, Kakul(Abbottabad), Parachinar, SaiduSharif, Kalam, Malam Jabba, MirKhani, Peshawar, LowerDir, Kohistan) were selected for this study. All site names and characteristics are shown in Table 1 and Figure 1.

4. Results and Discussion

4.1. Basic Assumption

Prior to performing the RFA of AMWS, we investigated three main assumptions of RFA: independence, homogeneity, and stationarity. The term “independence” refers to the notion that no single observation in a data series affects subsequent observations. In practice, the degree of dependency between successive portions of a series varies with the interval between them and is commonly small between yearly maximum values, but the degree of dependence between consecutive daily values is typically substantial. The term “homogeneity” means that all observations within a data series originate from the same population. When the variety in severe events such as floods, snowmelt, rainfall, wind speed, and drought is large, it becomes hard to identify non-homogeneity. Stationarity implies that the AMWS series is invariant in time, excluding random variations. Trends, leaps, and cycles describe non-stationarity. While trends may be attributed to periodic changes in climatic circumstances, cycles can be linked to long-term climate oscillations. Jumps occur most often in flood series caused by a sudden change in the river system, such as the structure of a dam.

The required assumptions should fulfill by the data of annual maximum wind speed. Therefore time series graphs and various non-parametric tests are applied to justify these assumptions.

The Wald-Wolfowitz Test is used to verify AMWS’ assumption of independence. The results are given in detail in Table 1. The Wald-Wolfowitz test statistic values are usually small, and the p-value is greater than the (0.05) for each site. According to this test, we conclude that AMWS data of the different sites is independent.

We used the Man-Whitney U (MWU) test to check the assumption of homogeneity in the data of AMWS. The results verified that the probability “P” value is greater than the critical value of 0.05 such that It means that we accept the null hypothesis (the sample comes from a homogenous population) of the MWU test and we conclude that the data of AMWS is homogeneous. The details of the results are given in Table 1.

We used the Spearman order rank correlation test to check the stationarity of AMWS. The Spearman’s rank order correlation test statistic values for each site are small, and the p-value is larger than the level of significance, i.e. (p > 0.05). Therefore, we conclude that based on the results given in Table 1, the data of each site of AMWS fulfills the assumption of stationarity.

4.1.2. Time Series Plots

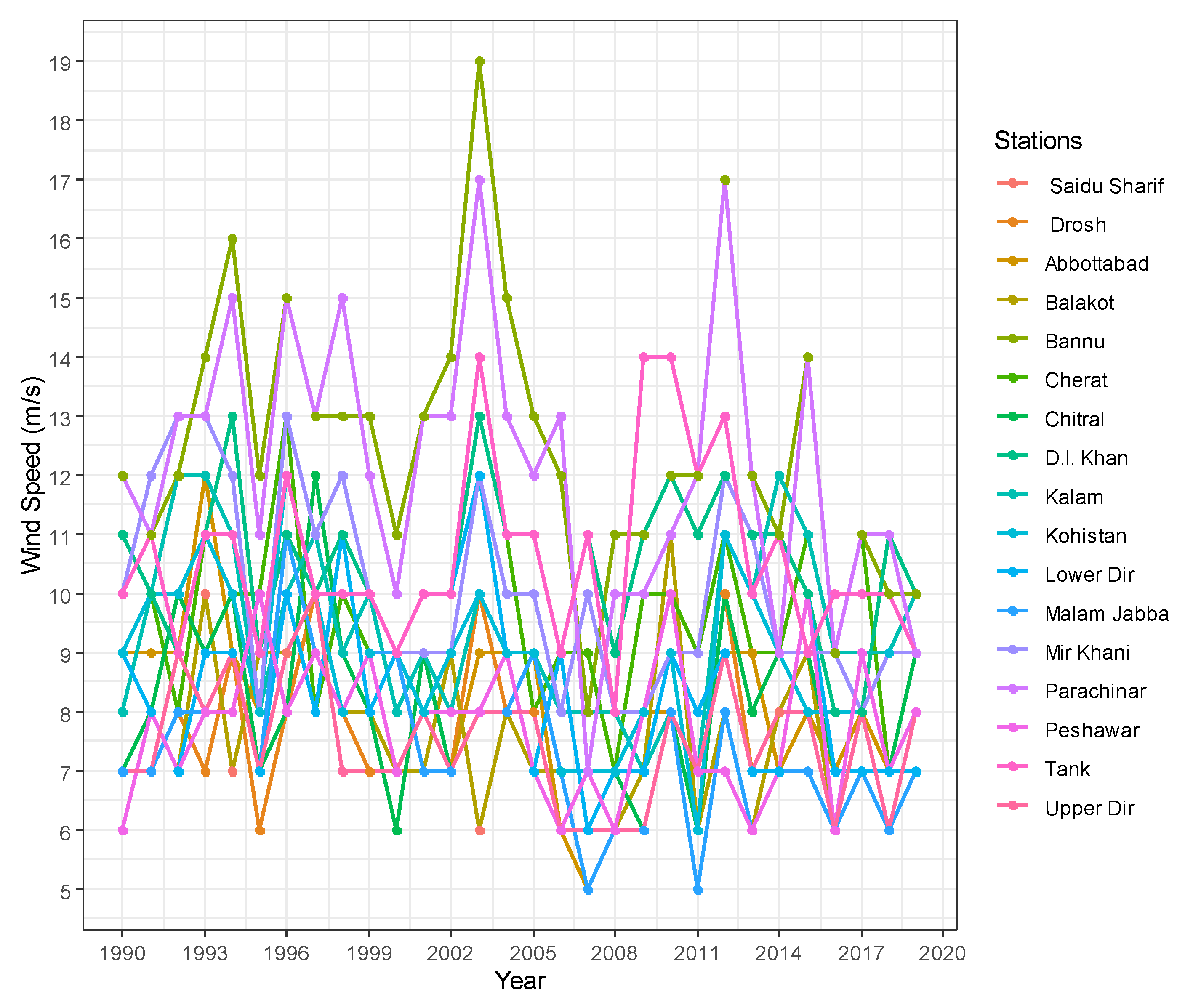
As time goes by, stationarity is one of the basic assumptions when dealing with hydrological data. The graphs of ordered data on variables give us a good understanding of stationarity. The time series plots in Figures 4.1 and 4.2 show that the data series of Cherat and D.I. Khan Sites have a uniform increasing/declining trend, indicating randomness in the observation of all sites and that the time series data is stationary.

Figure 2. Time series plot of all stations.

4.2. Screening of the Data Using Discordancy Measure

The data screening to detect certain discordant sites is the initial stage in regional frequency analysis. We analyzed two clusters, the first of which has 12 sites and the second of which have four, and we calculated the discordancy measure for each site. For each site, the discordancy statistics are computed. As shown in Table 2 and Table 3, for all sites, the computed values are less than the critical value of 3.

In Table 2 and Table 3,

n

denotes the record length, which is set at 30 across all sites.

l_{1}

Stands for the sample mean,

t

for the sample L-CV,

t_{3}

for the sample L-skewness, and

t_{4}

for the sample L-kurtosis. The mean of the data in Table 2 of cluster-Ι ranges from 7.390667 to 10.03833, whereas sample L-CV ranges from 0.079843 to 0.102031. The data skewnes coefficient ranges from 0.006789 to 0.179212.

Similarly, the average value of the data in Cluster-ΙΙ in Table 3 varies from 10.50267 to 12.48133, while the sample L-CV is 0.066783 to 0.107685. The skewness coefficient for data varies between 0.017385 and 0.177261. In both Clusters, all sites are favorably skewed.

4.3. Cluster Analysis

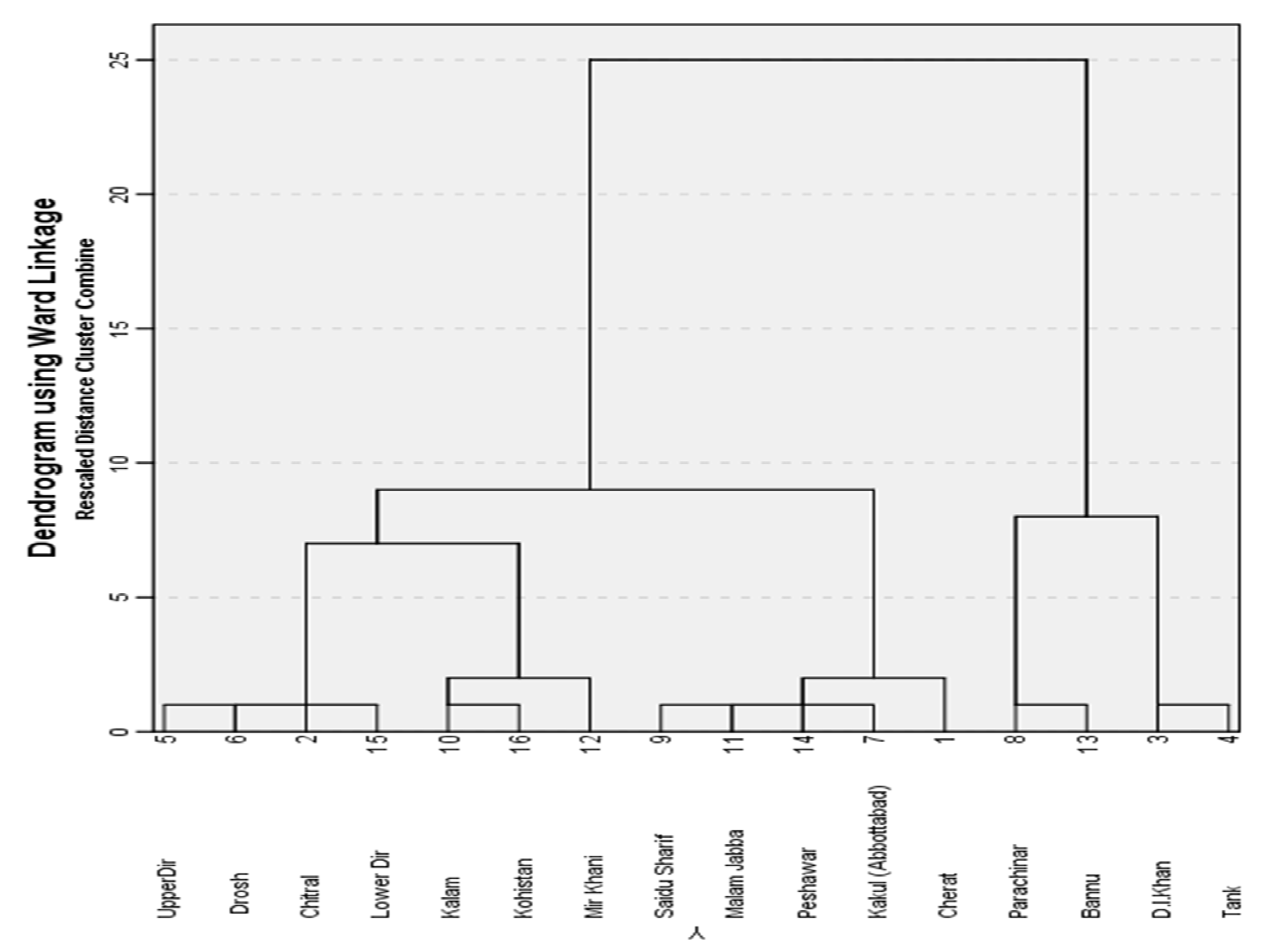
Cluster analysis is used to split data into several groups such that places belonging to the same cluster have related climatic/geographical features. The Ward algorithm is utilized in this work to create Clusters based on the basin average slope and drainage area; because this technique may produce homogenous Clusters of the same size (Ward et al. 1963).

We applied the wards method for further clarification and justification about the number of homogenous regions. This method investigated that there are more than two homogenous regions in this study.

4.3.1. Regions and Heterogeneity Measure

The next stage in RFA is to examine the heterogeneity value of the underwork areas after obtaining the discordancy value. It’s basically a heterogeneity assessment employing L-CV, L-Skewness, and L-kurtosis for

H_{1}

H_{2}

and

H_{3}

. In practice

H_{1}

, is regarded as a good indicator of observed with L-CV. Similarly, if the L-skewness and L-Kurtosis are naturally larger, the

H_{2}

and

H_{3}

measurements have less discriminating value.

The cluster analysis findings are shown in Table 4. Table 4 shows that both Clusters Ι and ΙΙ are “acceptably homogenous.”

(Hosking and Wallis, 1997) give three different aspects of heterogeneity values. If

H

<1, the region is completely homogeneous.If 1≤

H

≤2, the region can be homogeneous. If, on the other hand,

H \geq 2

, the region is completely heterogeneous. In the Table 4 the values of

H

of both clusters indicate that no value is greater than 2, which meet the criteria of homogeneous region.

4.4. Selections of Best Fit Distribution

The third stage of RFA is fitting of the distribution and selection of the best fitting distributions. (Hosking and Wallis, 1997) used standards to determine the first three perimeter distributions, such as Generalize Pareto (GPA), Generalized Logistic (GLO), Generalize Extreme Value (GEV), Generalize Normal (GNO), and Generalize Pearson type 3 ( P3). When starting this process, we will keep two goals in mind. The first is the nomination of the best distribution. The ordinal is the estimate of the quantile for each region in several time periods. Hosking provides two methods to achieve the best distribution. Mainly Z-fit, others are ratio graphs

The selections of the fit distribution for each cluster are based on the L-moment ratio diagram, and Z statistical test. Z- Fit applies through the critical value if

|Z^{D i s t}| \leq 1.64

at level of Significance 5%. It might be possible that more than one distribution strike to the said limits, than the distribution approaching to zero will be best considered as best fit.

Table 5 summarizes the appropriate Z statistics and best distributions of both homogeneous clusters. For cluster-Ι the values of GEV and P3 are the smallest among other values. The values of GEV and P3 are less than the critical values of 1.64 and the selected distribution is required to be closer to zero. Therefore, according to this criterion, it can be said that the distribution of GEV and P3 is acceptable if the statistic is less than 1.64. Similarly, for cluster-ΙΙ the values of GLO and GNO are the smallest among other values. The values of GLO and GNO are less than the critical values of 1.64 and the selected distribution is required to be closer to zero. Therefore, according to this criterion, it can be said that the distribution of GLO and GNO is acceptable if the number is less than 1.64.

4.4.1. L-Moments Ratio Diagram

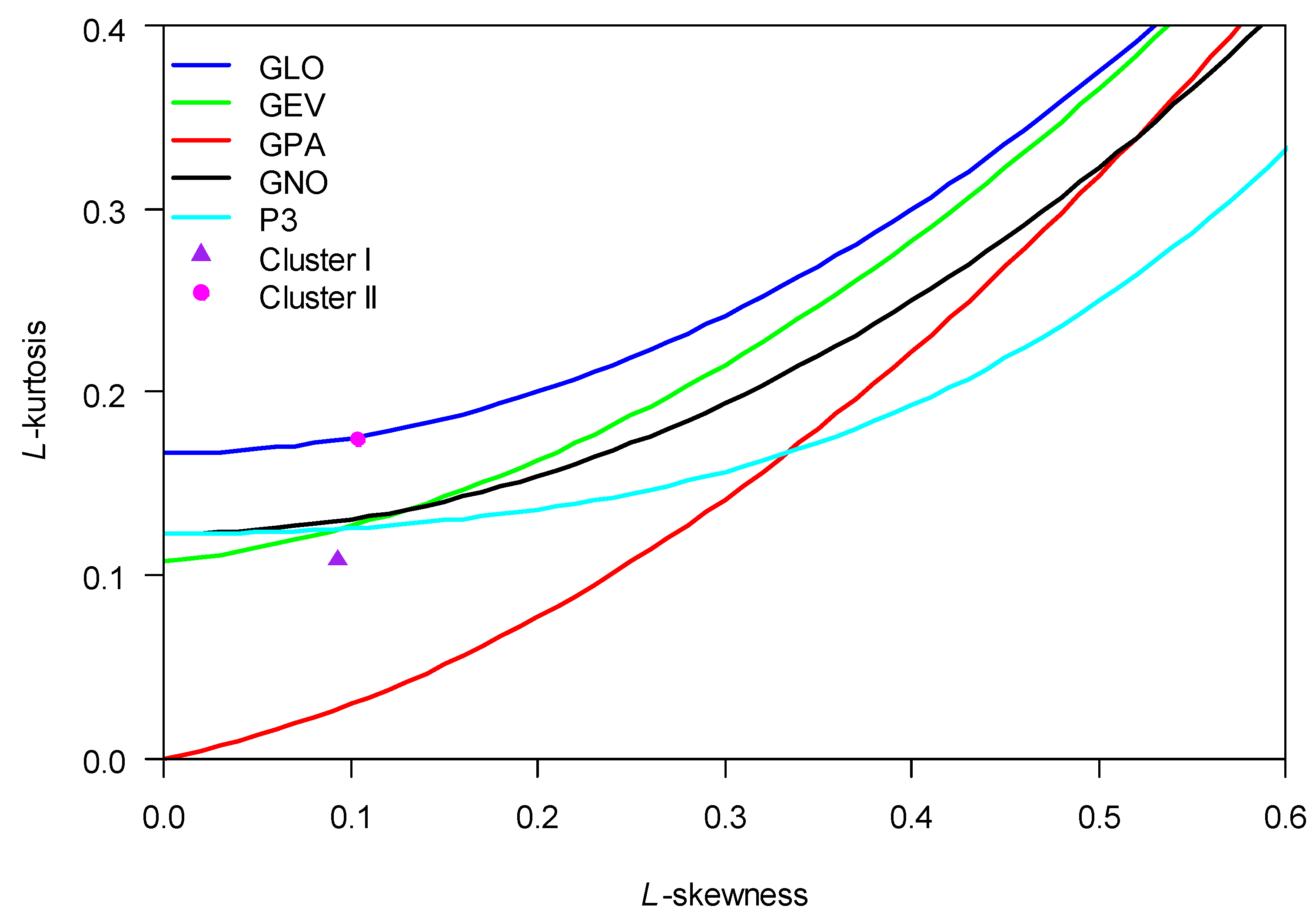
L-moment ratio diagrams (scatter plots) display L-moments of various distributions that are commonly used and are useful for providing guidelines for selecting an appropriate distribution for the study area based on average values of L-Skewness and L-Kurtosis. Although it is a subjective method, it is a very popular tool for selecting candidate distributions at the outset. Another advantage of the L-moments Ratio Diagram is the ability to display moment ratios from multiple distributions on the same graph paper.

L-moments ratio diagram/plot for two Clusters is shown in Figure 3a and Figure 4b. For Cluster-I regional average L-Skewness and L-Kurtosis average lies closest to the GEV distribution similarly for Cluster-II regional average L-Skewness and L-Kurtosis average lies closest to GLO. In the Both diagram points (L, N, G, E, U) stand for Logistic distribution, Normal distribution, Gumbel distribution, Exponential Distribution, and Uniform Distribution, respectively.

4.4.2. Constructions of Growth Curves and Accuracy Measures for Best Fit Distributions

To evaluate which of these two distributions was the most accurate we performed a Monte Carlo simulation provided by (Meshgi and Khalili, 2009). For design flood estimate relative bias (RB) and relative root mean square error (RRMSE) were used to examine the robustness of the RFA distributions.

For the Cluster-Ι Table 7 shows the RB and RRMSE simulation results for GEV and P3 distributions for various return times up to 1,000 years. Table 7 shows that the RB values for GEV are lower than the P3 distribution at all periods of return except years 2. As a result of the RB measures, GEV is the best robust distributions. Also the value of RRMSE outperforms the P3 distributions during return period of 5 and 10 years. However, the RRMSE of the GEV distribution is higher than that of the P3 distribution for return periods 2, 20, 50, 100, 500, and 1,000. Overall, Table 7 shows that the GEV distribution outperforms than the P3 distribution however RRMSE shows that P3 has little advantage over GEV over longer return periods.

Similarly Table 6 shows the RB and RRMSE simulation results for GLO plus GNO distributions for various return times up to 1,000 years for Cluster-ΙΙ. Table 6 shows that the RB values for the GLO distribution are lower than the GNO distribution for all return periods except 2 and 1000 years. As a result of the RB measures, GLO is most robust distribution. Also the RRMSE value of the GLO distribution outperforms than the GNO distribution during return periods of 2, 5, 10, 20, 50, and 100 years. However, at return times of 500 and 1,000 the GLO a distribution has a higher RRMSE than the GNO distributions. General Table 7 shows that the GLO distribution outperforms than the GNO distribution however RRMSE shows that GNO has a little advantage above GLO for longer return period. So the GLO distributions is a robust distributions for cluster-ΙΙ

4.5. Regional Quantiles Estimations for Different Return Periods

After selecting the best fit distributions, the next stage in regional frequency analysis is to find the quantile estimates for each return period. The return period “T” can be defined as the likelihood of repeated interval estimates, such as floods, droughts, stream flow, rainfall or earthquakes. The return time period T can be called

\frac{1}{P}

with its exceedance probability P. The probability of occurrence or exceedance is the chance of an event occurring within a specific time period, that is,

P = \frac{1}{T}

probability of occurrence. For example, in the case of 20 years (

\frac{1}{20} = 0.05

) can be defined as the chance of exceeding, where

(1 - \frac{1}{20} = 0.95

) is the probability of non-exceedance.

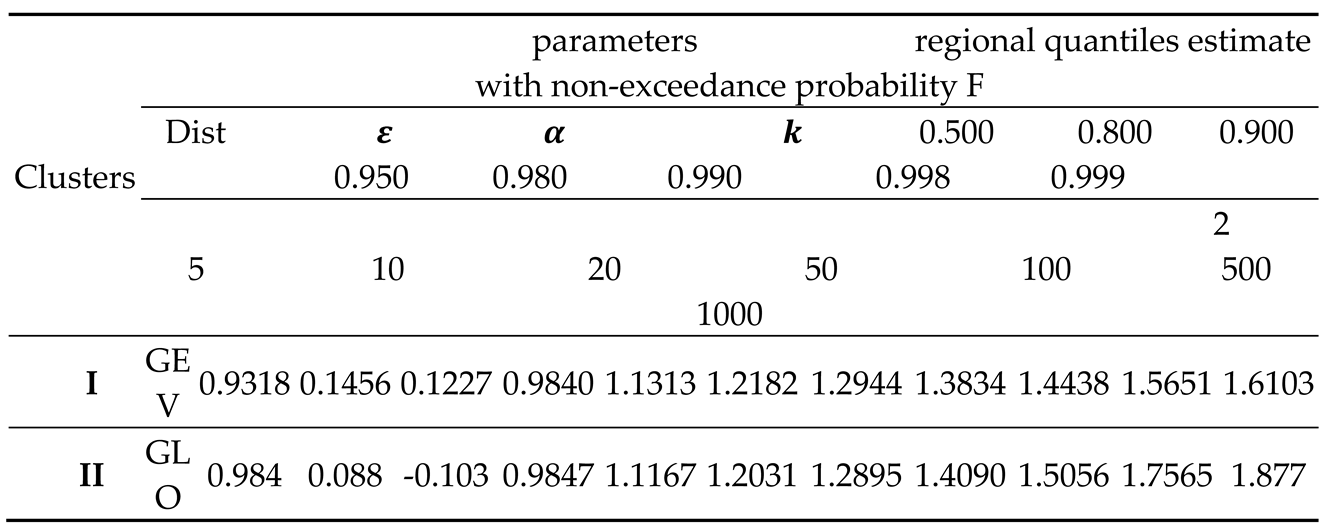
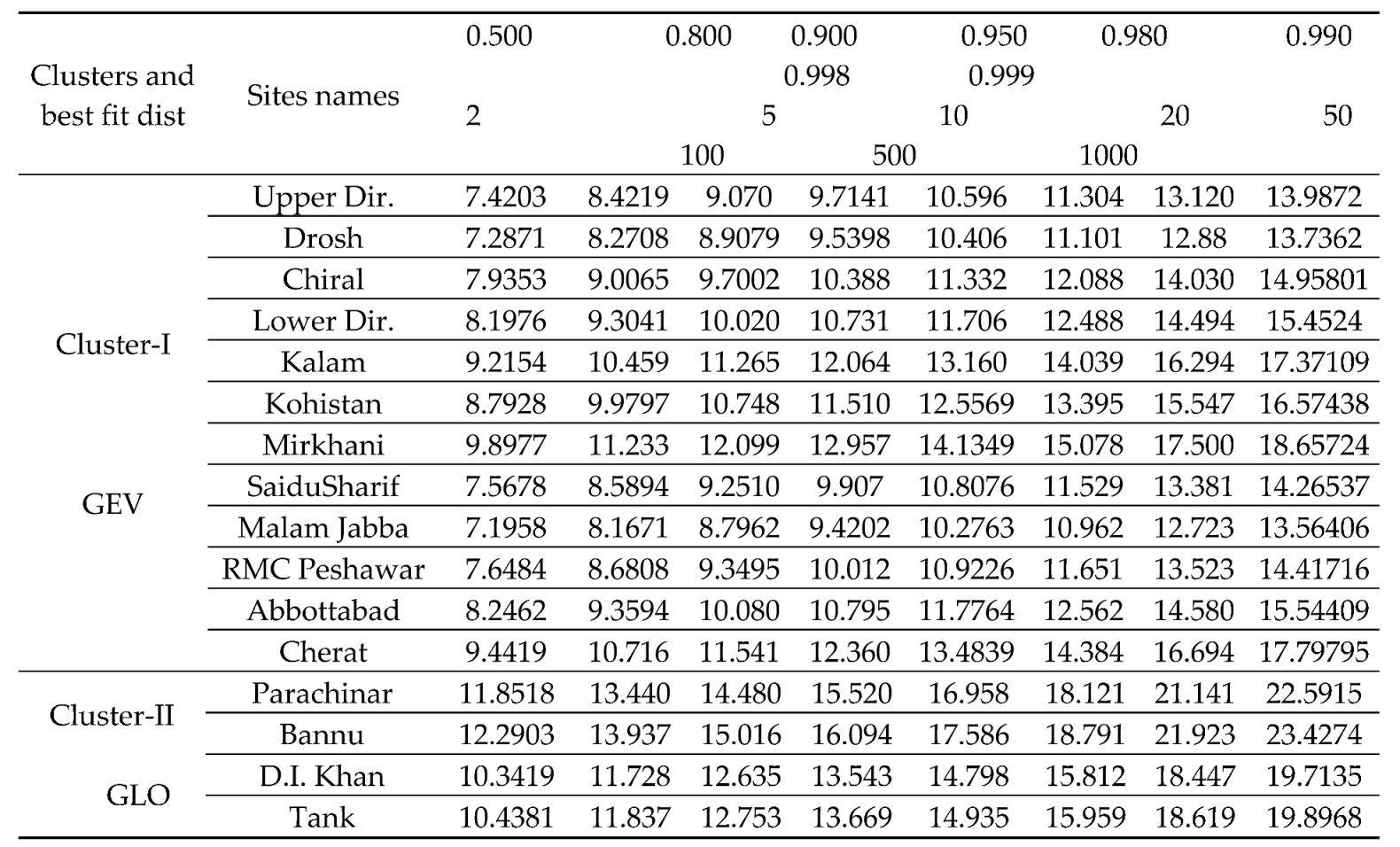
After selecting the most suitable regional distribution, we estimate the regional quantiles and parameters of the two clusters. Table 7 shows the best-fit distribution of both Clusters and regional quantiles.

Table 7. Regional quantile estimation for best fit Distributions of both clusters.

4.5.1. At-sites Quantiles Estimations by using Mean as Index Parameter

For fitted regional frequency distributions, the regional At-sit quantile may be calculated by multiply the regional quantile by the sample mean a single site. By definition, the regional At-site quantile estimation by mean is

{\hat{Q}}_{i} (Ϝ) = l_{1}^{(i)} \hat{q} (Ϝ)

(33)

Where

{\hat{Q}}_{i} (Ϝ)

is the regional at-sit quantiles estimations,

l_{1}^{(i)}

is the individual sites mean and

\hat{q} (Ϝ)

is the functions quantile of the fitted, RFD.

The results of regional at-sits quantiles estimate by using the sample mean for Cluster-Ι and cluster- ΙΙ the following Table 8 show the results. We find at-site quantile estimate for that cluster which is best fit distribution. For Cluster-Ι the best fit distributions is GEV and we can interpret as a 1000 years return period computed in Table 8. We may calculate quantile estimate for each

i^{t h}

site in the Cluster-Ι for a particular return period. We consider the site Upper Dir which has on the average annual maximum wind speed is 7.525667.we obtained by multiplying the regional quantile estimate to the mean of the relevant site. As the

{\hat{q}}_{G E V} (0.980)

=1.3834, interpretable as 7.525667* 1.3834=10.596 is the amount of extreme wind once in coming 50 years (for given return period) with non-exceedance probability 0.980. All other sites and for cluster-II can be interpreted in the similar way.

4.5.2. The Standard Errors of the Estimated At-Site Quantile

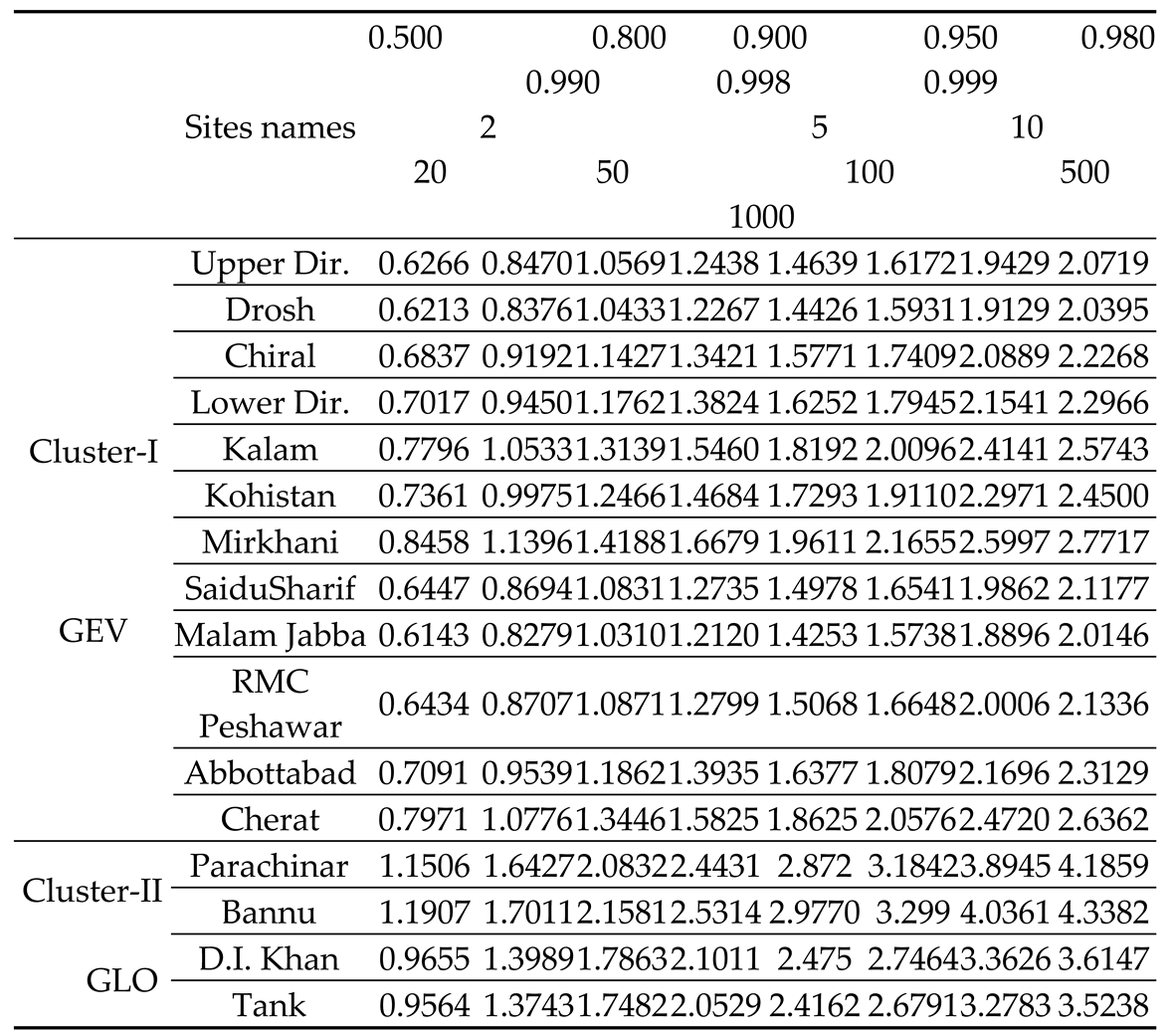
For the (Hosking and Wallis, 1997) simulation process (algorithm), accuracy estimation is usually done by “Abs. Bias”, “Bias” and “RMSE” for regional assessment. However, we can use the extra results to get the standard mistake of the calculated amount of each site in the region.

For all sites, we used Equation (36) to compute the standard errors of these at site quantile estimations. The at-site quantile estimates for both clusters are calculated use the sample mean as index parameter, and the best-fit regional frequency distribution is GEV for cluster-I and GLO is for cluster-II, Table 9 show the results of both cluster.

5. Summary and Conclusions

This study investigated the RFA of AMWS at 16 stations in Khyber Pakhtunkhwa, Pakistan. The initial screening of the AMWS is checked through the time series plot, spearman test, Mann-Whitney U test, and Wald and Wolfowitz test. The finding indicates that all 16 stations of AMWS passed the initial screening and were used further for RFA of AMWS. In the first step of RFA of AMWS, the discordancy measure was used, and the findings revealed that none of the sites was discordant, suggesting that all 16 stations should be included in RFA. All sixteen stations were identified as two homogeneous clusters using Ward’s hierarchical clustering techniques. According to the Z Statistics criterion and the L-moment ratio diagram, the GEV and GLO distributions were the best fit among all other PDFs for clusters I and II, respectively.

The Monte Carlo method was used to test the accuracy and efficacy of the estimated quantiles for Clusters I and II by running ten thousand simulations. Measures including Root Mean Square Error (RMSE), Relative Bias, Relative Absolute Bias, Lower Error bound, and Upper Error bound were established and introduced in Table 8 and Table 9 to examine the quantile estimates and growth curves of both clusters during the Monte Carlo simulation technique.

The robustness of both clusters was assessed using the RB and RRMSE measures. When RB and RRMSE measures are employed to compare GEV and P3 distributions in cluster-Ι, the results demonstrate that GEV distribution has smaller RB and RRMSE measures generally, while P3 performs better to some extend at longer return periods. In cluster-ΙΙ, RB and RRMSE measures are employed to analyses GLO and GNO distributions, and the results demonstrate that GLO distribution has lower RB and RRMSE measures generally, while GNO perform better to some extent at longer return periods. The GEV distribution for Cluster-Ι and the GLO distribution for Cluster- ΙΙ are the most acceptable choices for regional AMWS analysis in this study, according to the Z-test and LM ratio diagram.

By multiplying the regional quantiles by the sample mean and median as index parameters, we were able to derive the at-site quantiles (index flood procedure). The standards errors of these at site quantiles were likewise discovered under both index parameters. Frequency analysis at the site can be performed to compare these results to quantiles and standard errors. For Cluster-I, the sites including Upper Dir, Lower Dir, Kalam, Kohistan, and Peshawar have lesser standard errors for all return periods when using mean as index parameters. On the other hand, Mirkhani and Kakul (Abbottabad) with median as index parameters had considerably lesser standard errors for all return periods than the same sites with mean as index parameters. Furthermore, Drosh, Chitral, SaiduSharif, Malam Jabba, and Cherat with median as index parameters had considerably reduced standard errors for all return periods except 2 and 5 years when compared to data from the same sites with mean as the index parameters. Similarly, the D.I. Khan and Tank sites in cluster-ΙΙ had lower standard errors for all return periods when using mean as the index parameters, as compared to the same sites’ findings when using median as the index parameters. When comparing the findings of the same sites using median as the index parameters, the Parachinar site has a lower mean except for 50, 100, 500, and 1000 years. In contrast, when using the bannu median as index parameters, the standard errors for all return periods except 2 and 5 years are significantly lower than when using the mean as index parameters.

The predicted AMWS quantiles from these distributions might be used for policy implications in codifying the wind load for various codified structural designs to avoid losses due to high wind speeds.

Acknowledgments

This research has been funded by Deputy for Research & Innovation, Ministry of Education through Initiative of Institutional Funding at University of Ha’il - Saudi Arabia through project number IFP-22 055.

References

Ahmad, I., Fawad, M., Akbar, M., Abbas, A., & Zafar, H. (2016). Regional Frequency Analysis of Annual Peak Flows in Pakistan Using Linear Combination of Order Statistics. Polish Journal of Environmental Studies, 25(6). [CrossRef]
Ahmed, M. A., & Ahmad, F. (2004). Estimation of Wind Power Potential for Pasni, Coast of Baluchistan, Pakistan. Journal of Research (Science), 455-460.
Aized, T., Sohail Rehman, S. M., Kamran, S., Kazim, A. H., & Ubaid ur Rehman, S. (2019). Design and analysis of wind pump for wind conditions in Pakistan. Advances in Mechanical Engineering, 11(9), 1687814019880405. [CrossRef]
Alam, J., Muzzammil, M., & Khan, M. K. (2016). Regional flood frequency analysis: comparison of L-moment and conventional approaches for an Indian catchment. ISH Journal of Hydraulic Engineering, 22(3), 247-253. [CrossRef]
Carta, J. A., Ramirez, P., & Velazquez, S. (2009). A review of wind speed probability distributions used in wind energy analysis: Case studies in the Canary Islands. Renewable and sustainable energy reviews, 13(5), 933-955. [CrossRef]
Clausen, B., & Pearson, C. P. (1995). Regional frequency analysis of annual maximum streamflow drought. Journal of Hydrology, 173(1-4), 111-130. [CrossRef]
Cunnane, C. (1988). Methods and merits of regional flood frequency analysis. Journal of Hydrology, 100(1-3), 269-290. [CrossRef]
Dai, K., Bergot, A., Liang, C., Xiang, W. N., & Huang, Z. (2015). Environmental issues associated with wind energy–A review. Renewable Energy, 75, 911-921. [CrossRef]
Darbandi, S., Aalami, M. T., & Asadi, H. (2012). Comparison of four distributions for frequency analysis of wind speed. Environment and Natural Resources Research, 2(1), 96. [CrossRef]
Fawad, M., Ahmad, I., Nadeem, F. A., Yan, T., & Abbas, A. (2018). Estimation of wind speed using regional frequency analysis based on linear-moments. International Journal of Climatology, 38(12), 4431-4444. [CrossRef]
Fawad, M., Yan, T., Chen, L., Huang, K., & Singh, V. P. (2019). Multiparameter probability distributions for at-site frequency analysis of annual maximum wind speed with L-moments for parameter estimation. Energy, 181, 724-737. [CrossRef]
Goel, N. K., Burn, D. H., Pandey, M. D., & An, Y. (2004). Wind quantile estimation using a pooled frequency analysis approach. Journal of wind engineering and industrial aerodynamics, 92(6), 509-528. [CrossRef]
Hong, H. P., & Ye, W. (2014). Estimating extreme wind speed based on regional frequency analysis. Structural Safety, 47, 67-77. [CrossRef]
Hosking, J. R. (1990). L-moments: Analysis and estimation of distributions using linear combinations of order statistics. Journal of the Royal Statistical Society: Series B (Methodological), 52(1), 105-124. [CrossRef]
Hosking, J. R. M., & Wallis, J. R. (1993). Some statistics useful in regional frequency analysis. Water resources research, 29(2), 271-281. [CrossRef]
Hosking, J.R. and Wallis, J.R. (1997) Regional Frequency Analysis: An Approach based on L-moments. Cambridge: Cambridge University Press.
Huang, J., & McElroy, M. B. (2015). A 32-year perspective on the origin of wind energy in a warming climate. Renewable Energy, 77, 482-492. [CrossRef]
Hulio, Z. H., Jiang, W., & Rehman, S. (2019). Techno-Economic assessment of wind power potential of Hawke’s Bay using Weibull parameter: A review. Energy Strategy Reviews, 26, 100375. [CrossRef]
Kidson, R., & Richards, K. S. (2005). Flood frequency analysis: assumptions and alternatives. Progress in Physical Geography, 29(3), 392-410. [CrossRef]
Ma, X.(1997). Adaptive extremum control and wind turbine control (Doctoral dissertation, Technical University of Denmark).
Mann, H. B., & Whitney, D. R. (1947). On a test of whether one of two random variables is stochastically larger than the other. The annals of mathematical statistics, 50-60. [CrossRef]
Meshgi, A., & Khalili, D. (2009). Comprehensive evaluation of regional flood frequency analysis by L-and LH-moments. I. A re-visit to regional homogeneity. Stochastic Environmental Research and Risk Assessment, 23(1), 119-135. [CrossRef]
Mirza, I. A., Khan, N. A., & Memon, N. (2010). Development of benchmark wind speed for Gharo and Jhimpir, Pakistan. Renewable Energy, 35(3), 576-582. [CrossRef]
Modarres, R. (2008). Regional maximum wind speed frequency analysis for the arid and semi-arid regions of Iran. Journal of Arid Environments, 72(7), 1329-1342. [CrossRef]
Murtagh, F., & Legendre, P. (2011). Ward’s hierarchical clustering method: clustering criterion and agglomerative algorithm. arXiv preprint arXiv:1111.6285. [CrossRef]
Ouarda, T. B., Bâ, K. M., Diaz-Delgado, C., Cârsteanu, A., Chokmani, K., Gingras, H., ... & Bobée, B. (2008). Intercomparison of regional flood frequency estimation methods at ungauged sites for a Mexican case study. Journal of Hydrology, 348(1-2), 40-58. [CrossRef]
Ouarda, T. B., Charron, C., Shin, J. Y., Marpu, P. R., Al-Mandoos, A. H., Al-Tamimi, M. H., ... & Al Hosary, T. N. (2015). Probability distributions of wind speed in the UAE. Energy conversion and management, 93, 414-434. [CrossRef]
Peel, M. C., Wang, Q. J., Vogel, R. M., & McMAHON, T. A. (2001). The utility of L-moment ratio diagrams for selecting a regional probability distribution. Hydrological Sciences Journal, 46(1), 147-155. [CrossRef]
RAFİQ, L. (2019). EXPLORING WIND ENERGY POTENTIAL IN KPK-PAKISTAN BY USING MULTI CRITERIA APPROACH. Anadolu Üniversitesi Bilim Ve Teknoloji Dergisi A-Uygulamalı Bilimler ve Mühendislik, 20(2), 171-178. [CrossRef]
Rao, A. R., & Hamed, K. H. (2019). Flood frequency analysis. CRC press.
Sarrias, R., Fernández, L. M., García, C. A., & Jurado, F. (2010). Energy storage systems for wind power application. European Association for the Development of Renewable Energies. [CrossRef]
Vogel, R. M., & Fennessey, N. M. (1993). L moment diagrams should replace product moment diagrams. Water resources research, 29(6), 1745-1752. [CrossRef]
Wald, A., & Wolfowitz, J. (1943). An exact test for randomness in the non-parametric case based on serial correlation. The Annals of Mathematical Statistics, 14(4), 378-388. [CrossRef]
Ward Jr, J. H. (1963). Hierarchical grouping to optimize an objective function. Journal of the American statistical association, 58(301), 236-244.
Yu, I., Kim, J., & Jeong, S. (2016). Development of probability wind speed map based on frequency analysis. Spatial Information Research, 24(5), 577-587. [CrossRef]

Figure 1. Geographical locations of the 16 stations of KPK, Pakistan.

Figure 3. Dendrogram using Wards Methods.

Figure 4. L-Moments Ratio Diagram for both regions.

Table 1. The results of basic assumptions for 16 sites.

Name of the sites	Spearman test		Wald & Wolfowitz test		Mann Whitney U test
Name of the sites	Test statistic	P-value	Test statistic	P-value	Test statistic	P-value
Abbottabad	0.569	0.285	-1.135	0.128	-0.975	0.165
Bannu	-0.806	0.210	-0.857	0.196	-0.767	0.221
Cherat	-0.861	0.195	0.353	0.362	-1.597	0.055
Chitral	-0.717	0.237	0.791	0.214	-1.389	0.082
D.I. Khan	0.274	0.392	0.837	0.201	-0.353	0.362
Drosh	-0.837	0.201	0.814	0.208	-1.638	0.051
Kalam	-0.277	0.391	0.081	0.468	-0.306	0.380
Kohistan	-1.017	0.154	0.940	0.174	-1.016	0.155
Lower Dir	-1.305	0.096	0.376	0.353	-1.472	0.070
Malam Jabba	0.598	0.275	1.558	0.060	-0.353	0.363
Mir Khani	0.720	0.236	0.968	0.166	-0.726	0.234
Parachinar	-0.372	0.355	0.097	0.461	-0.228	0.410
Peshawar	0.059	0.477	-1.029	0.152	-0.643	0.260
Saidu Sharif	-0.658	0.255	-0.409	0.341	-1.390	0.341
Tank	-0.492	0.311	0.405	0.343	-0.311	0.378
Upper Dir	-0.416	0.339	0.402	0.344	-1.141	0.127

Table 2. Summary Statistics Based on L-moments for Cluster-Ι various Wind Sites.

Stations	Latitude (North)	Longitude (East)	Elevation (meter)	l1	t	t3	t4	Di
Abbottabad	34.11	73.15	1418.53	8.363	0.099	0.053	0.167	1.22
Bannu	33	70.06	1337.87	12.481	0.101	0.177	0.241	2.11
Cherat	33.49	71.33	632.28	9.576	0.083	0.161	0.171	1.24
Chitral	35.51	71.50	3392.71	8.048	0.102	0.106	0.082	0.75
D.I. Khan	31.49	70.56	294.41	10.503	0.068	0.017	0.119	2.28
Drosh	35.34	70.47	3174.26	7.390	0.093	0.130	0.128	0.14
Kalam	35.5	72.59	3782.04	9.346	0.090	0.028	0.030	1.04
Kohistan	35.06	73	2969.68	8.918	0.080	0.007	0.121	1.08
Lower Dir	34.5	70.49	2061.64	8.314	0.096	0.148	0.116	0.41
Malam Jabba	34.45	72.44	706.05	7.298	0.093	0.082	0.127	0.08
Mir Khani	35.30	74.42	3462.82	10.038	0.095	0.179	0.067	1.91
Parachinar	33.52	70.05	1727.58	12.036	0.108	0.071	0.143	1.66
Peshawar	34.02	71.56	713.79	7.757	0.083	0.099	0.094	0.23
Saidu Sharif	34.44	72.21	706.05	7.675	0.094	0.083	0.068	0.48
Tank	31.55	70.52	256.26	10.600	0.085	0.148	0.191	1.04
Upper Dir	35.12	70.51	3061.05	7.526	0.087	0.044	0.119	0.32

Table 3. Summary Statistics Based on L-moments for Cluster-ΙΙ various Wind Sites.

Name	n	l₁	t	t₃	t₄	D_i
Bannu	30	12.481	0.101	0.177	0.241	2.11
Tank	30	10.600	0.085	0.148	0.191	1.04

Table 4. Homogeneity measures of both Clusters.

Cluster	Number of sites	$H_{1}$	$H_{2}$	$H_{3}$	Homogeneity
Cluster-Ι	12	-1.76	-1.26	-1.77	Homogeneous
Cluster -ΙΙ	04	0.90	-0.36	-0.69	Homogeneous

Table 5. Goodness of Fit test for Homogeneous Clusters.

Clusters	Distributions	GLO	GEV	GNO	P3	GPA
Cluster-Ι	\| $Z^{D i s t}$ \|	3.69 ^a	$1.01 *$	1.26	$1.02 * *$	4.36 ^a
Cluster-ΙΙ	\| $Z^{D i s t}$ \|	$0.02 *$	1.22	$1.14 * *$	1.27	3.74 ^a

* show the best distribution; ** show the second best distribution; ^a indicates that the calculated values are more than the critical value of 1.64.

Table 6. Accuracy Measure for best fit Distributions for Cluster-Ι and Cluster-II.

Distributions		Measures	Q2	Q5	Q10	Q20	Q50	Q100	Q500	Q1000
Cluster-Ι	GEV	RB	0.0003	0.0001	-0.0001	-0.0002	-0.0000	0.0002	0.001	0.0025
	GEV	RRMSE	0.0062	0.0117	0.0186	0.0261	0.0363	0.0446	0.0642	0.0738
	PE3	RB	-0.0000	0.0004	0.0008	0.0011	0.0015	0.0018	0.0026	0.0029
	PE3	RRMSE	0.0057	0.0129	0.0192	0.0249	0.0319	0.0368	0.0475	0.0519
Cluster-ΙΙ	GLO	RB	0.0008	0.00002	-0.0002	-0.0002	0.0003	0.0013	0.0058	0.0089
	GLO	RRMSE	0.008	0.0172	0.0283	0.0393	0.0547	0.0674	0.1012	0.117
	GNO	RB	0.0003	0.0001	0.0004	0.00097	0.002	0.003	0.0059	0.0073
	GNO	RRMSE	0.009	0.0214	0.0343	0.0461	0.0607	0.0714	0.0956	0.1058

Table 8. At site Quantiles Estimate for the best fit Distributions using mean as Index Parameter of Cluster-Ι and cluster-II.

Table 9. Standard Errors of At-site Quantile Estimate using median as an index parameter for both Clusters.

Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.

© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).

Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.

MDPI Initiatives

Important Links

Choose an area of interest and we will send you notifications of new preprints at your preferred frequency.

Disclaimer

Regional Frequency Analysis of Extreme Wind in Pakistan Using Robust Estimation Methods

Abstract

1. Introduction

2. Methodology

2.1. The Initial Examination of the Annual Maximum Wind Speed (AMWS) Series

2.1.1. Spearman’s Order Rank Correlation Test for Checking the Trend

2.1.2. The Wald-Wolfowitz (WW) Test for Checking Independence

2.1.3. Mann-Whitney U (MWU) test for Homogeneity

2.2. Linear Moments

2.3. Application of the L-Moments Based on Regional Frequency Analysis

2.3.1. Screening of the Data

2.3.2. Recognition of Homogeneous Regions

2.3.2.1. Cluster Analysis

2.3.2.2. Hierarchical Clustering

2.3.2.3. Ward’s Method

2.3.2.4. Heterogeneity Test

2.3.3. Selections of the Best Fit Distribution

2.3.4. Quantile Estimation

3. Study Area and Data

4. Results and Discussion

4.1. Basic Assumption

4.1.2. Time Series Plots

4.2. Screening of the Data Using Discordancy Measure

4.3. Cluster Analysis

4.3.1. Regions and Heterogeneity Measure

4.4. Selections of Best Fit Distribution

4.4.1. L-Moments Ratio Diagram

4.4.2. Constructions of Growth Curves and Accuracy Measures for Best Fit Distributions

4.5. Regional Quantiles Estimations for Different Return Periods

4.5.1. At-sites Quantiles Estimations by using Mean as Index Parameter

4.5.2. The Standard Errors of the Estimated At-Site Quantile

5. Summary and Conclusions

Acknowledgments

References

MDPI Initiatives

Important Links

Subscribe