New Analytical Expresions of Concentrations in Packed Bed Immobilized-Cell Electrochemical Photobioreactor

Preprint

Article

New Analytical Expresions of Concentrations in Packed Bed Immobilized-Cell Electrochemical Photobioreactor

Altmetrics

Downloads

144

Views

Comments

A peer-reviewed article of this preprint also exists.

Ponraj Jeyabarathi,

Marwan Abukhaled^*,

Murugesan Kannan,Lakshmanan Rajendran,

Michael Edward Gerard Lyons^*

Ponraj Jeyabarathi,

Marwan Abukhaled^*,

Murugesan Kannan,Lakshmanan Rajendran,

Michael Edward Gerard Lyons^*

This version is not peer-reviewed

Submitted:

05 July 2023

Posted:

07 July 2023

You are already at the latest version

Alerts

Abstract

In this paper, Akbari-Ganji's and Taylor series methods are applied to find analytical solutions to nonlinear differential equations that arise in an immobilized-cell photobioreactor. Approximate analytical expressions for substrate and product concentrations and both liquid and gas phases for various parameter values are derived using both methods. Efficiency, accuracy, and convergence of the two methods relative to highly accurate numerical methods are investigated to establish reliable profiles of these two methods for solving general nonlinear equations that model various physical phenomena. Numerical simulations are presented to validate the theoretical investigations.

Keywords:

Subject: Chemistry and Materials Science - Electrochemistry

1. Introduction

Nonlinear systems of equations usually present real-world physical applications. Over the past three decades, the search for efficient and reliable analytical asymptotic methods to solve these systems has intensified [1]. Of the methods have received a great attention are the perturbation method (PM) [4], homotopy perturbation method (HPM) [5,6,7,8,9,10,11], variational iteration method (VIM) [12,13,14,15,16], homotopy analysis method (HAM)[17,18,19,20], differential transform method (DTM) [21,22], Adomian decomposition method (ADM) [23,24], and Green’s function iterative method [25,26].

Two-phase flow and mass transport coupled with biochemical reactions co-occur in an operating photobioreactor. Therefore, a better understanding of the complicated transport mechanism will promote the application of electrochemical photobioreactors[28,29].This communication directs our attention to the analytical and numerical method of solving nonlinear equations in immobilized-cell photobioreactor [2,3]. A comparison study between Akbari-Ganji's method (AGM) [27,28,29] and the renowned Taylors series method (see [30,31] and the references therein are presented. We aim to derive approximate analytical expressions of the concentrations of substrate and product and both liquid and gas phases for various parameter values by using these two methods. This paper will present a profile of reliability, efficiency, and convergence of both approaches.

2. Mathematical Formulation of the Problems

An immobilized-cell photo bioreactor packed with transparent gel-granules containing immobilized PSB developed and modeled by Shirejini et al. [3] is illustrated in Figure 1(a).Figure 1(b) shows a schematic diagram of mass transfer in a single gel graule, such that the mass transfer of all reactants and products is dominated by diffusion. Using Fick’s law, the mass transport equations for substrate and the hydrogen inside the gel granules are given by[32]:

Figure 1. Schematic of the entrapped-cell photobioreactor.

D_{granule}^{S} [\frac{1}{r^{2}} \frac{d}{d r} (r^{2} \frac{d C_{granule}^{S}}{d r})] = ϕ_{granule}^{S}

(1)

D_{granule}^{H_{2}} [\frac{1}{r^{2}} \frac{d}{d r} (r^{2} \frac{d C_{granule}^{H_{2}}}{d r})] = ϕ_{granule}^{H_{2}}

(2)

ϕ_{granule}^{S} = \frac{μ X_{cell}}{Y_{X / S}^{*}} + m X_{cell}, ϕ_{granule}^{H_{2}} = \frac{α^{*} μ X_{cell}}{Y_{X / S}^{*}} + β X_{cell}, μ_{\max} = \frac{C_{granule}^{S}}{K_{S} + C_{granule}^{S}}

(3)

where

D_{granule}^{S}

and

D_{granule}^{H_{2}}

are the significant diffusion coefficients of glucose and hydrogen in the gelgranule,

C_{granule}^{S}

and

C_{granule}^{H_{2}}

are the local concentrations of glucose and hydrogen inside the gel granule,

ϕ_{granule}^{S}

is the consumption rate of glucose,

ϕ_{granule}^{H_{2}}

is the generation rate of hydrogen. The parameter

α^{*}

represents the growth associated kinetic constant for hydrogenproduction,

β

is the non-growth associated kinetic constant,

X_{cell}

is the initial cell density,

Y_{X / S}^{*}

is the cell yield, and

K_{S}

is a Monod constant. Furthermore,

μ_{\max}

denotes the maximum specific growth rate, and

μ

is the growth rate. The boundary conditions for the above system of Equations(1) and (2) are given by

{\frac{d C_{granule}^{S}}{d r}|}_{r = 0} = {\frac{d C_{granule}^{H_{2}}}{d r}|}_{r = 0} = 0

(4)

{C_{granule}^{S}|}_{r = R} = C_{l}^{S}, {C_{granule}^{H_{2}}|}_{r = R} = C_{g}^{H_{2}}

(5)

where

C_{l}^{S}

and

C_{g}^{H_{2}}

are bulk solutions, and

R

is the radius of catalyst. The source terms

φ^{s}, φ^{H_{2}}

and

φ^{C O_{2}}

are defined by:

φ^{s} = α D_{g r a n u l e}^{s} {(\frac{d C_{g r a n u l e}^{s}}{d r})}_{r = R}, φ^{H_{2}} = α D_{g r a n u l e}^{H_{2}} {(\frac{d C_{g r a n u l e}^{H_{2}}}{d r})}_{r = R}, φ^{C O_{2}} = \frac{M^{C O_{2}}}{2 M^{H_{2}}} φ^{H_{2}}

(6)

where

α

is the specific area of the gel granule. The source terms of the liquid phase and gas phase are expressed by:

m_{l}^{•} = - φ^{s}, m_{g}^{•} = φ^{H_{2}} + φ^{C O_{2}}

(7)

By introducing the dimensionless parameters

Φ_{1} = \frac{X_{cell} μ_{m a x} R^{2}}{Y_{\frac{X}{S}}^{*} D_{granule}^{S} K_{S}}, Φ_{2} = \frac{X_{cell} μ_{m a x} R^{2} C_{l}^{S}}{Y_{\frac{X}{S}}^{*} D_{granule}^{S} K_{S} C_{g}^{H_{2}}}, γ_{1} = \frac{X_{cell} m R^{2}}{D_{granule}^{S} K_{S}}, γ_{2} = \frac{X_{cell} m R^{2}}{D_{granule}^{S} C_{l}^{S}}, γ_{3} = \frac{X_{cell} m R^{2} C_{l}^{S}}{D_{granule}^{S} K_{S} C_{g}^{H_{2}}}, γ_{4} = \frac{X_{cell} m R^{2}}{D_{granule}^{H_{2}} C_{g}^{H_{2}}}

ζ = \frac{r}{R}, u = \frac{C_{g r a n u l e}^{s}}{C_{g}^{s}}, v = \frac{C_{g r a n u l e}^{H_{2}}}{C_{g}^{H_{2}}}, α_{1} = \frac{C_{l}^{S}}{K_{S}}

(8)

Equations (1) and (2),take the dimensionless forms:

\frac{1}{ζ^{2}} \frac{d}{d ζ} (ζ^{2} \frac{d u (ζ)}{d ζ}) = \frac{(φ_{1} + γ_{1}) u (ζ) + γ_{2}}{(1 + α_{1} u (ζ))}

(9)

\frac{1}{ζ^{2}} \frac{d}{d ζ} (ζ^{2} \frac{d v (ζ)}{d ζ}) = \frac{(φ_{2} + γ_{3}) u (ζ) + γ_{4}}{(1 + α_{1} u (ζ))}

(10)

with the dimensionless boundary conditions:

\frac{d u (ζ)}{d ζ} = \frac{d v (ζ)}{d ζ} = 0 at ζ = 0

(11)

u (ζ) = v (ζ) = 1 at ζ = 1

(12)

The normalized steady-state source terms of liquid and gas phases is given by

ψ_{l} = \frac{m_{l}^{•} R}{α D_{g r a n u l e}^{s} C_{l}^{s}} = - {(\frac{d u}{d ζ})}_{ζ = 1}

(13)

ψ_{g} = \frac{m_{g}^{•} R}{α D_{g r a n u l e}^{H_{2}} C_{g}^{H_{2}}} = (\frac{2 + ω}{2}) {(\frac{d v}{d ζ})}_{ζ = 1} where ω = \frac{M^{C O_{2}}}{M^{H_{2}}}

(14)

3. Analytical expression of the concentrations using Akbari-Ganji’s method

In this section, we use AGM to derive explicit expressions for the concentrations of glucose and hydrogen. The AGM is a semi-analytical approach that has shown efficacy in solving nonlinear equations [33,34,35]. The AGM procedure begins by assuming a solution function with unknown constant coefficients, which are determined by solving a system of algebraic equations that is constructed from the differential equations and the initial conditions.

3.1. Concentration of Glucose (substrate)

Let

u (ζ) = a_{0} + a_{1} ζ + a_{2} ζ^{2}

(15)

be a trial solution of Equation (9), where

a_{0}, a_{1}, a_{2}

are constants. The boundary conditions (11) and (12) imply

1 = a_{0} + a_{1} + a_{2}, a_{1} = 0 .

(16)

Now define the function

F

F (ζ) : \frac{1}{ζ^{2}} \frac{d}{d ζ} (ζ^{2} \frac{d u (ζ)}{d ζ}) - \frac{(φ_{1} + γ_{1}) u (ζ) + γ_{2}}{(1 + α_{1} u (ζ))} = 0

(17)

then

F (ζ = 1) : 2 a_{1} + 6 a_{2} - \frac{(φ_{1} + γ_{1}) (a_{0} + a_{1} + a_{2}) + γ_{2}}{(1 + α_{1} (a_{0} + a_{1} + a_{2}))} = 0

(18)

Using Equation (16) in Equation (18), gives

a_{2} = \frac{φ_{1} + γ_{1} + γ_{2}}{6 (1 + α_{1})}, a_{0} = 1 - \frac{φ_{1} + γ_{1} + γ_{2}}{6 (1 + α_{1})}

(19)

By substituting Equations (16) and (18) into Equation (15), the analytical expression for the substrate is

u (ζ) = 1 + \frac{φ_{1} + γ_{1} + γ_{2}}{6 (1 + α_{1})} (ζ^{2} - 1)

(20)

3.2. Concentration of Hydrogen (product)

Assume the following solution to Equation (10):

v (ζ) = b_{0} + b_{1} ζ + b_{2} ζ^{2}

(21)

From boundary conditions (11) and (12), we obtain:

1 = b_{0} + b_{1} + b_{2}, and b_{1} = 0 .

(22)

Define the G function by

G (ζ) : \frac{1}{ζ^{2}} \frac{d}{d ζ} (ζ^{2} \frac{d v (ζ)}{d ζ}) - \frac{(φ_{2} + γ_{3}) u (ζ) + γ_{4}}{(1 + α_{1} u (ζ))} = 0,

(23)

then

G (ζ = 1) : 2 b_{1} + 6 b_{2} - \frac{(φ_{2} + γ_{3}) (a_{0} + a_{1} + a_{2}) + γ_{4}}{(1 + α_{1} (a_{0} + a_{1} + a_{2}))} = 0

(24)

Substituting Equation (22) into Equation (24) leads to

b_{2} = \frac{φ_{2} + γ_{3} + γ_{4}}{6 (1 + α_{1})}, b_{0} = 1 - \frac{φ_{2} + γ_{3} + γ_{4}}{6 (1 + α_{1})},

(25)

and substituting Equations (22) and (25) into Equation (16), the analytical expression for the product is

v (ζ) = 1 + \frac{φ_{2} + γ_{3} + γ_{4}}{6 (1 + α_{1})} (ζ^{2} - 1)

(26)

3.3. Normalized steady-state source terms of liquid and gas phases

The analytical expressions of normalized steady-state source terms of liquid and gas phases aregiven by:

ψ_{l} = - \frac{(φ_{1} + γ_{1} + γ_{2})}{3 (1 + α_{1})}

(27)

ψ_{g} = \frac{(2 + ω)}{2} (\frac{(φ_{2} + γ_{3} + γ_{4})}{3 (1 + α_{1})})

(28)

Remark 1. The analytical expressions given by Equations (20) and (26) for the concentrations of glucose and hydrogen, respectively, are identical to the expressions obtained by the Adomian decomposition method (ADM) [2] and the homotopy perturbation method [3].

4. Analytical expression of the concentrations using Taylor series method

The three-century-old Taylor series method (TSM) has been recently revived and exploited to accurately and efficiently solve many nonlinear differential equations representing nonlinear models in various sciences and engineering applications Equations [36,37]. In this section, we employ TSM to find the substrate and product concentrations.

4.1. Concentration of Glucose (substrate)

First, we assume that

u (0) = m

(29)

where

m

is an unknown constant to be determined. Steady state nonlinear reaction–diffusion equations can be written in the form:

(ζ u^{''} (ζ) + 2 u^{'} (ζ)) (1 + α_{1} u (ζ)) = (φ_{1} + γ_{1}) ζ u (ζ) + γ_{2} ζ

(30)

Taking the first three derivatives of Equation (30) with respect to

' ζ'

gives

(ζ u^{'''} (ζ) + 3 u^{''} (ζ)) (1 + α_{1} u (ζ)) + (ζ u^{''} (ζ) + 2 u^{'} (ζ)) α_{1} u' (ζ) = (φ_{1} + γ_{1}) (u (ζ) + ζ u^{'} (ζ)) + γ_{2}

(31)

(ζ u^{''''} (ζ) + 4 u^{'''} (ζ)) (1 + α_{1} u (ζ)) + 2 (ζ u^{'''} (ζ) + 3 u^{''} (ζ)) α_{1} u^{'} (ζ) + (ζ u^{''} (ζ) + 2 u^{'} (ζ)) α_{1} u^{''} (ζ) = (φ_{1} + γ_{1}) (2 u^{'} (ζ) + ζ u^{''} (ζ))

(32)

(ζ u^{' V} (ζ) + 5 u^{''''} (ζ)) (1 + α_{1} u (ζ)) + 3 (ζ u^{''''} (ζ) + 4 u^{'''} (ζ)) α_{1} u^{'} (ζ) + 3 (ζ u^{'''} (ζ) + 3 u^{''} (ζ)) α_{1} u^{''} (ζ) + (ζ u^{''} (ζ) + 2 u^{'} (ζ)) α_{1} u^{'''} (ζ) = (φ_{1} + γ_{1}) (3 u^{''} (ζ) + ζ u^{'''} (ζ))

(33)

For

ζ = 0

, Equations (31)–(33) give the following identities:

u^{''} (0) = \frac{m (φ_{1} + γ_{1}) + γ_{2}}{3 (1 + α_{1} m)} u^{'''} (0) = 0, u^{''''} (0) = \frac{(m (φ_{1} + γ_{1}) + γ_{2}) (φ_{1} + γ_{1} - α_{1} γ_{2})}{5 (α_{1} m + 1)^{3}}, u^{v} (0) = 0 u^{v i} (0) = \frac{(m (φ_{1} + γ_{1}) + γ_{2}) (φ_{1} + γ_{1} - α_{1} γ_{2}) ((φ_{1} + γ_{1}) (3 - 10 α_{1} m) - 13 α_{1} γ_{2})}{7 (α_{1} m + 1)^{5}} .

(34)

The substrate concentration,using the Taylor’s series, is expressed by the expansion

u (ζ) = u (0) + u^{'} (0) \frac{ζ}{1!} + u^{''} (0) \frac{ζ^{2}}{2!} + u^{'''} (0) \frac{3 ζ}{3!} + . . . = m + u_{1} \frac{ζ^{2}}{2!} + u_{2} \frac{ζ^{4}}{4!} + u_{3} \frac{ζ^{6}}{6!}

(35)

where

u_{1} = \frac{m (φ_{1} + γ_{1}) + γ_{2}}{3 (α_{1} m + 1)}, u_{2} = \frac{(m (φ_{1} + γ_{1}) + γ_{2}) (φ_{1} + γ_{1} - α_{1} γ_{2})}{5 (α_{1} m + 1)^{3}}, u_{3} = \frac{(m (φ_{1} + γ_{1}) + γ_{2}) (φ_{1} + γ_{1} - α_{1} γ_{2}) ((φ_{1} + γ_{1}) (3 - 10 α_{1} m) - 13 α_{1} γ_{2})}{7 (α_{1} m + 1)^{5}}

(36)

Using the boundary conditions

ζ = 1, u (ζ) = 1

in Equation (35) implies that

m + u_{1} \frac{1}{2!} + u_{2} \frac{1}{4!} + u_{3} \frac{1}{6!} = 1

(37)

from which the unknown constant m can be obtained. For the fixed values of the parameters:

φ_{1} = 5, γ_{1} = 0.1, γ_{2} = 0.1

and

α_{1} = 5

, the numerical value of m is found to be

m = 0.85803

and from Equation (36), we obtain

u_{1} = 0.141015, u_{2} = 0.001159

and

u_{3} = - 0.000207

, and thus from Equation (35), we obtain the analytical expression of the substrate expressed by

u (ζ) . = 0.85803 + 0.141015 \frac{ζ^{2}}{2!} + 0.001159 \frac{ζ^{4}}{4!} - 0.000207 \frac{ζ^{6}}{6!}

(38)

4.2. Concentration of Hydrogen (product)

Similar to the approach in Section 4.1, we begin by assuming that

v (0) = l,

(39)

where l is an unknown constant to be determined and by direct differentiation of

v (ζ)

, we obtain,

v^{''} (0) = \frac{m (φ_{2} + γ_{3}) + γ_{4}}{3 (1 + α_{1} m)}, v^{'''} (0) = 0, v^{''''} (0) = \frac{(m (φ_{1} + γ_{1}) + γ_{2}) (φ_{2} + γ_{3} - α_{1} γ_{4})}{5 (1 + α_{1} m)^{3}}, v^{v} (0) = 0, v^{v i} (0) = \frac{(m (φ_{` 1} + γ_{1}) + γ_{2}) (φ_{2} + γ_{3} - α_{1} γ_{4}) ((φ_{1} + γ_{1}) (1 - α_{1} m) - 2 α_{1} γ_{2})}{7 (1 + α_{1} m)^{5}} .

(40)

Now, the product concentration is readily obtained using Taylor’s series

v (ζ) = v (0) + v^{'} (0) \frac{ζ}{1!} + v^{''} (0) \frac{ζ^{2}}{2!} + v^{'''} (0) \frac{ζ^{3}}{3!} + \dots

(41)

Using the boundary condition,

v (1) = 1,

in Equation (41) gives the numerical value of l. For the fixed values of the parameters

φ_{1} = 1, γ_{1} = 1, γ_{2} = 1, φ_{2} = 5, γ_{3} = 0.1, γ_{4} = 0.1, α_{1} = 5

, and

m = 0.915769

, we obtain

l = 0.8563317

. The analytical expression for the product concentration takes on the form

v (ζ) = 0.8563317 + 0.1425122 \frac{ζ^{2}}{2!} + 0.0011589 \frac{ζ^{4}}{4!} - 0.0000581 \frac{ζ^{6}}{6!}

(42)

4.3. Normalized steady-state source terms of liquid and gas phases

The analytical expression of the normalized steady-state source terms of liquid phases,

ψ_{l}

, is obtained from the equation,

- ψ_{l} = u_{1} + u_{2} \frac{1}{6} + u_{3} \frac{1}{120}

(43)

Using, the values

u_{1} = 0.141015, u_{2} = 0.001159

and

u_{3} = - 0.000207

, we obtain

- ψ_{l} = 0.141207

. The analytical expression of normalized steady-state terms of gas phases,

ψ_{g}

, is given by

ψ_{g} = \frac{2 + ω}{2} [v_{1} + v_{2} \frac{1}{6} + v_{3} \frac{1}{120}]

(44)

where

ψ_{g} = 0.214057

when

ω = 1 .

5. Numerical simulations and Discussion

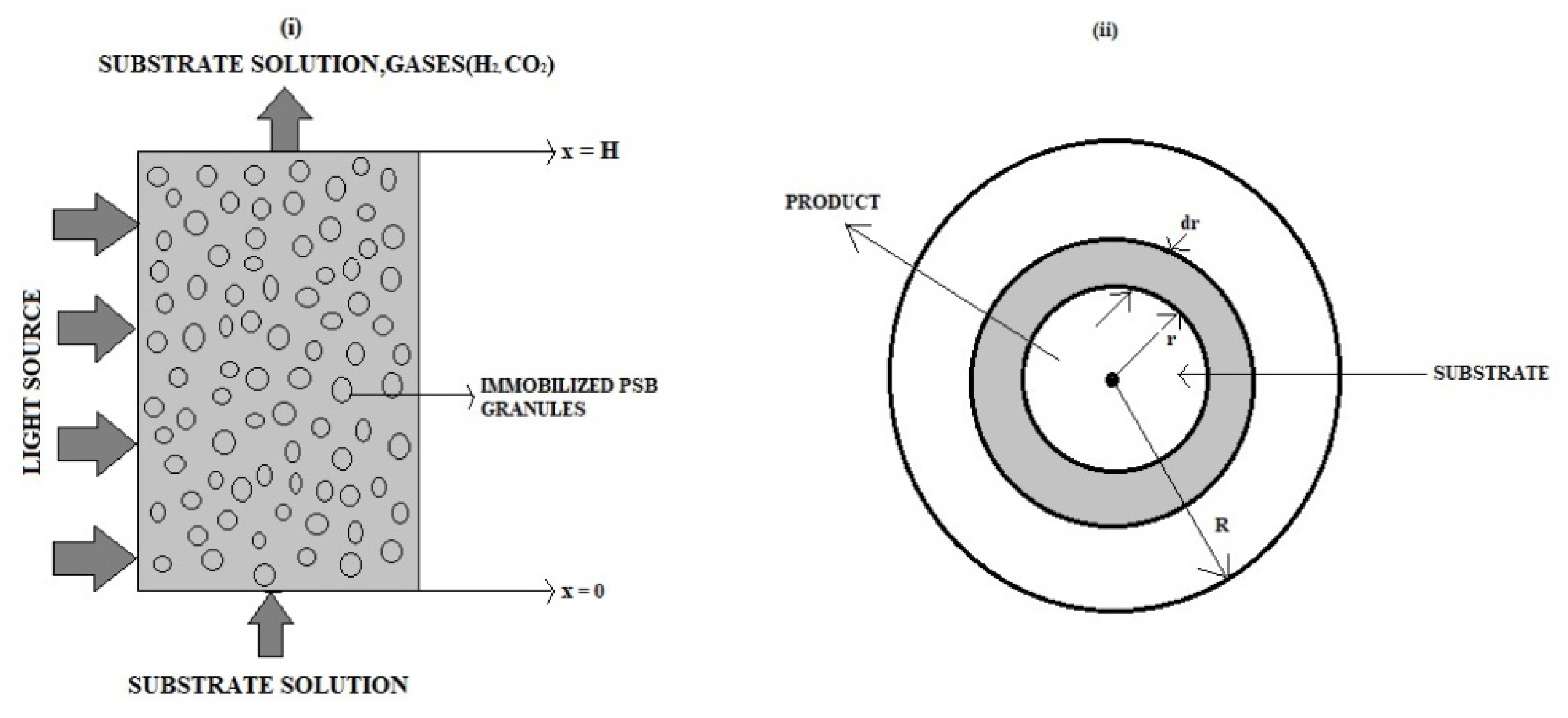
Nonlinear equations in the immobilized-cell photobioreactor are analytically solved. The approximate analytical expressions of concentrations of glucose and hydrogen inside the gel and granule in addition to approximate analytical expressions of steady-state source terms of liquid and gas phases are derived using Taylor series (TSM) and Akbari-Ganji (AGM) methods.

The reaction-diffusion equations representing the packed bed photobioreactor with immobilized-cell were solved using the Adomian decomposition method (ADM) [2] and the homotopy perturbation method (HPM) [3]. Interstingly, the semi-analytical expressions of the concentrations of substrate and product obtained by the ADM, HPM, and AGM were identical (Equations (20) and (26)) for all values of parameters.

To examine the accuracy of the two proposed analytical approaches, we compared their results with numerical results obtained from the reliable MATLAB pdepe function (Appendix A) and with analytical results of other methods available in the literature. The approximate analytical and numerical concentrations of substrate and product for various parameters are summarized in Table 1, Table 2, Table 3, Table 4, Table 5 and Table 6. Even though both methods gave satisfactory results, TSM is notably more accurate. The maximum relative error average is 0.6% for the TSM and 5% for the AGM. Comparisons of normalized steady-state source terms of both liquid and gas phases for various values of parameters

φ_{1}, φ_{2}

and

α_{1}

are given in Table 7 and Table 8.

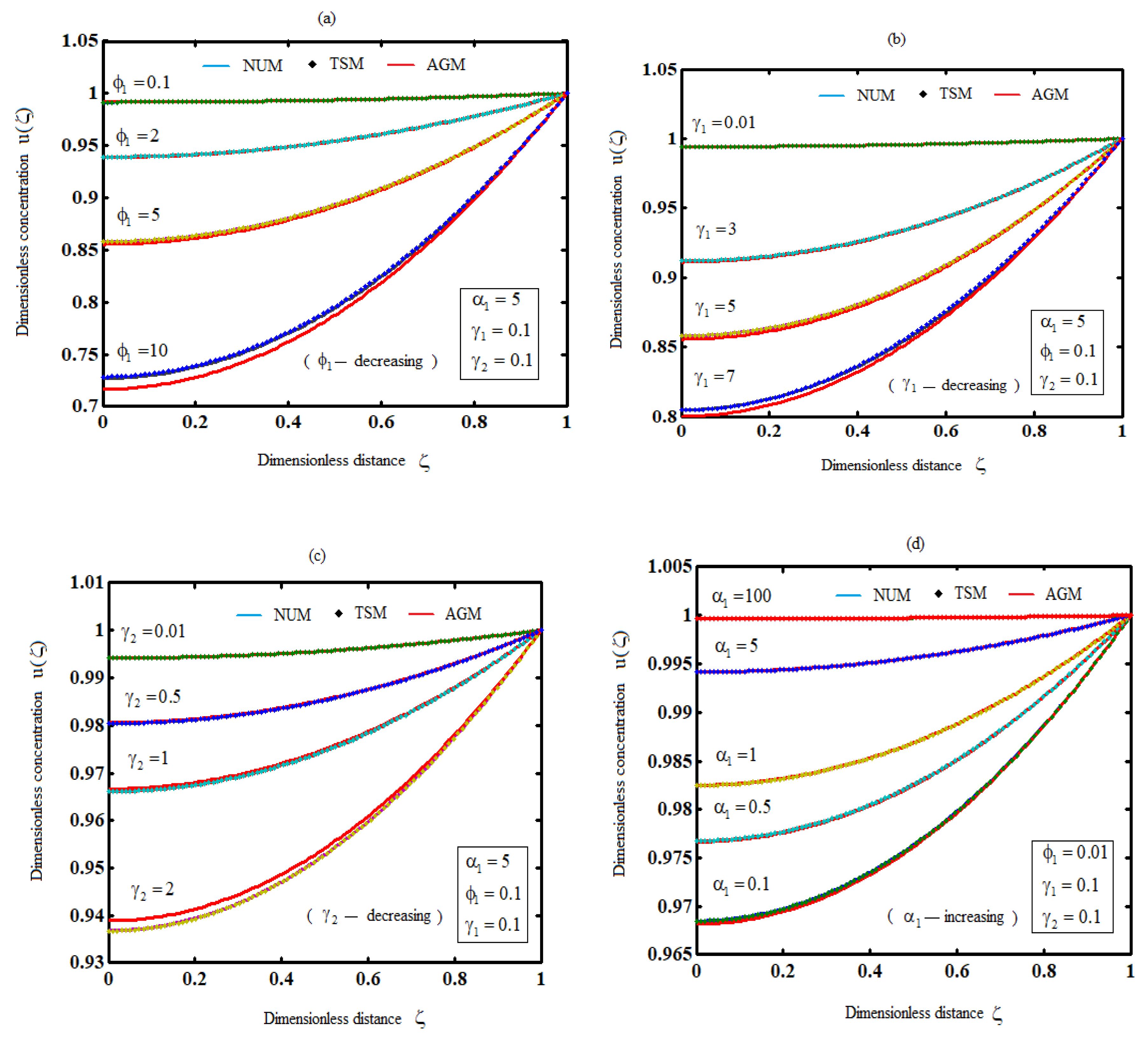
Figures 2(a)-2(c) illustrate the behavior of the biodegradation of substrate for different values of the parameters. It is noticed that as any of the parameters

ϕ_{1}, γ_{1}, or γ_{2}

decreases, the substrate concentration increases. In contrast, Figure 2(d) confirms a direct relationship between the parameter

α_{1}

and the substrate concentration.

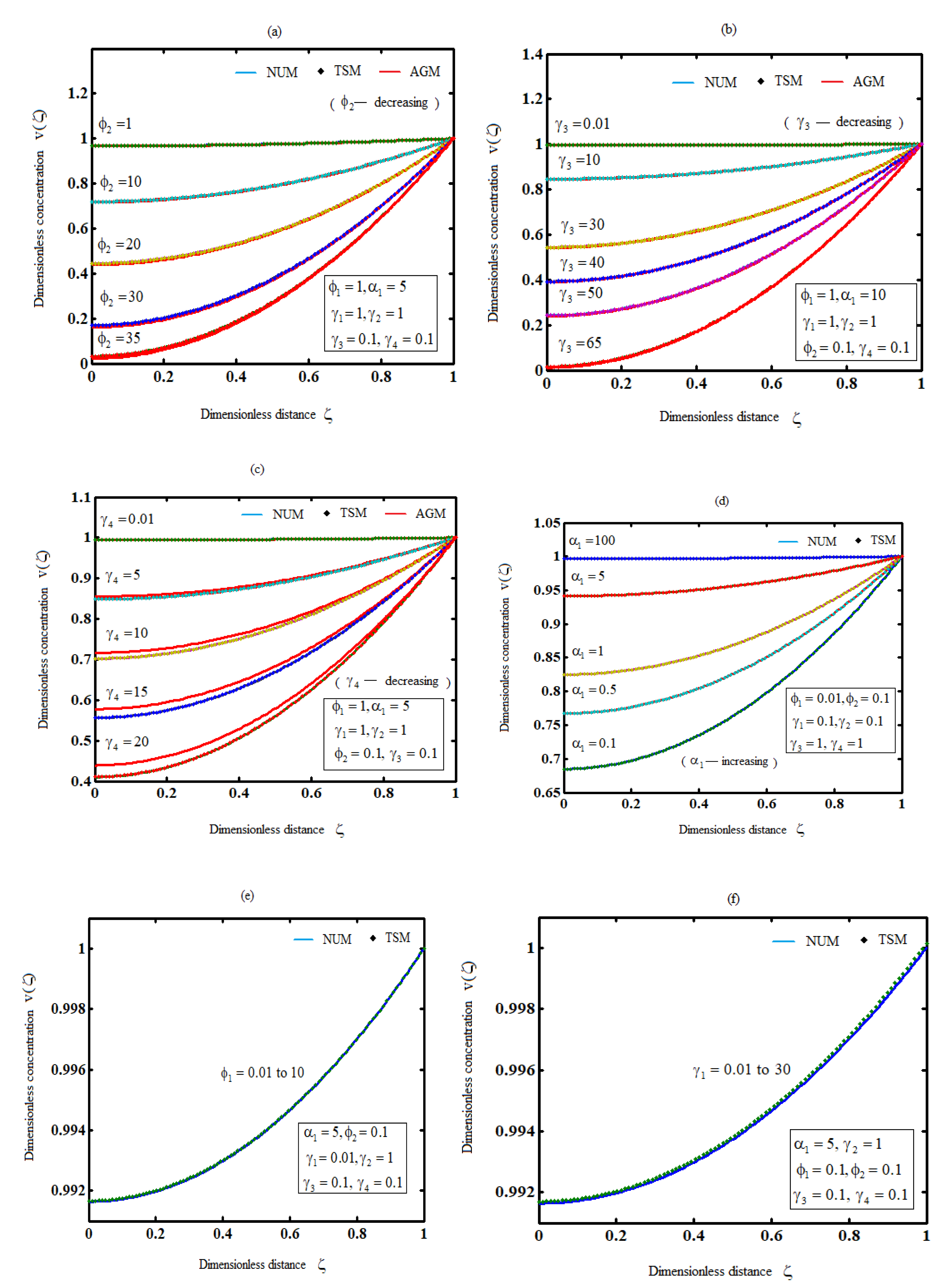
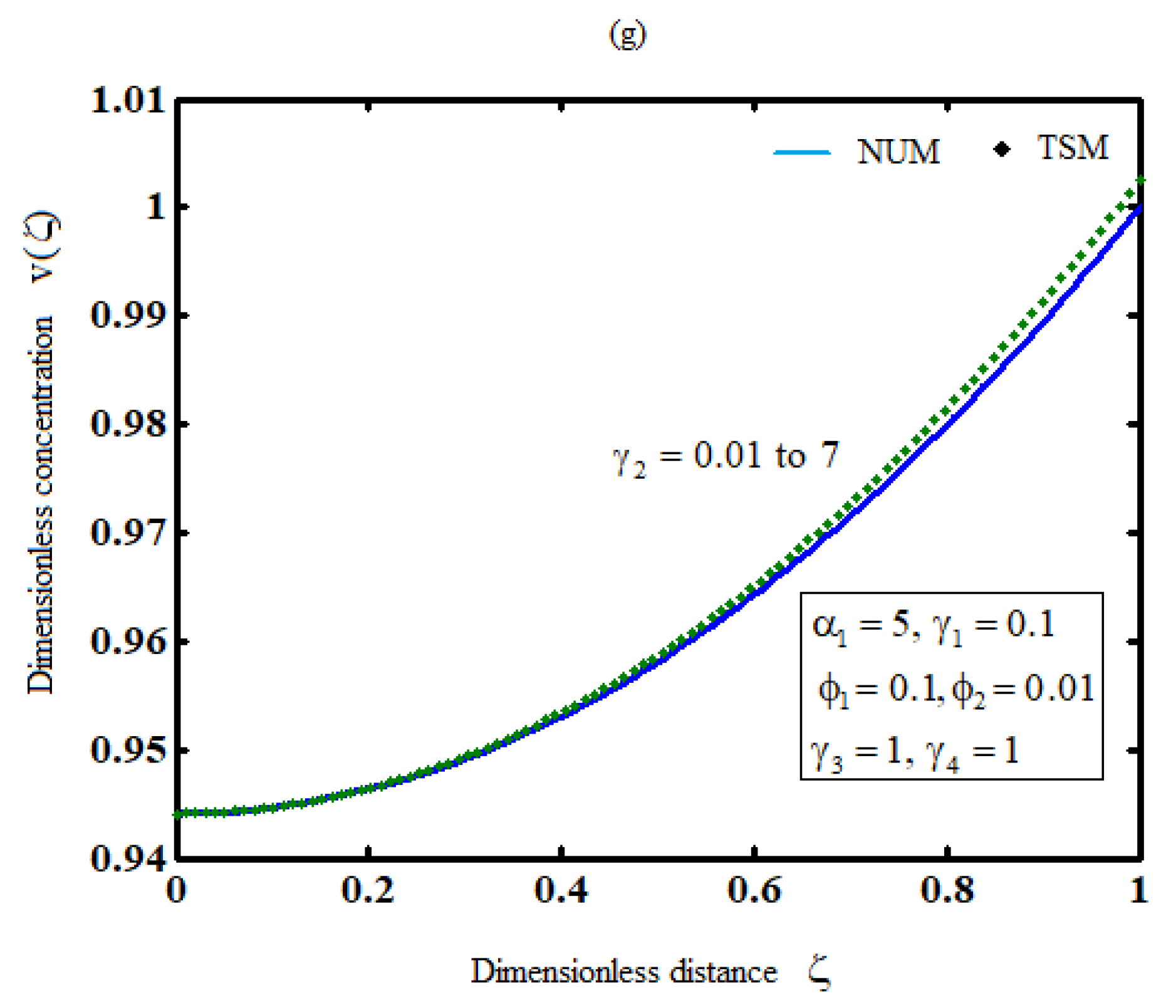
The effects of all parameters on the hydrogen production profiles are shown in Figures 3(a)-3(g),where it is noticed that the concentration of hydrogen increases the parameters

ϕ_{2}, γ_{3}, or γ_{4}

decreases or the parameter

α_{i}

increases. However, the concentration of hydrogen is independent of any of the parameters

ϕ_{1}, γ_{1}, and γ_{2}

Figure 2. Plot of substrate concentration for various values of parameters (Equations (20) and (35)).

Figure 3. Plot of product concentration,

v (ζ)

, for various values of the parameters

ϕ_{1}, ϕ_{2}, γ_{1}, γ_{2}, γ_{3}, γ_{4},

and

α

(Equations (26) and (41)).

Figure 3. Plot of product concentration,

v (ζ)

, for various values of the parameters

ϕ_{1}, ϕ_{2}, γ_{1}, γ_{2}, γ_{3}, γ_{4},

and

α

(Equations (26) and (41)).

Table 1. Comparison beteween numerical and analytical results for dimensionless concentration of substrate

u (ζ)

for various values of parameter

φ_{1}

when

γ_{1} = γ_{2} = 0.1

and

α_{1} = 5

Table 1. Comparison beteween numerical and analytical results for dimensionless concentration of substrate

u (ζ)

for various values of parameter

φ_{1}

when

γ_{1} = γ_{2} = 0.1

and

α_{1} = 5

$ζ$	$φ_{1} = 10$ $and m = 0.728557$					$φ_{1} = 15$ $and m = 0.610154$
$ζ$	Num.Equation (9)	AGMEq.(20)	TSMEq.(35)	Error % ofAGMEq.(20)	Error % of TSMEquation (35)	NumEquation (9)	AGMEq.(20)	TSMEq.(35)	Error % ofAGMEq.(20)	Error % of TSMEquation (35)
0	0.73	0.72	0.73	1.37	0.00	0.60	0.58	0.61	3.33	1.67
0.2	0.74	0.73	0.74	1.35	0.00	0.62	0.59	0.63	4.84	1.61
0.4	0.77	0.76	0.77	1.30	0.00	0.67	0.65	0.67	2.98	0.00
0.6	0.83	0.82	0.83	1.20	0.00	0.75	0.73	0.75	2.67	0.00
0.8	0.90	0.90	0.90	0.00	0.00	0.86	0.85	0.86	1.16	0.00
1	1.00	1.00	1.00	0.00	0.00	1.00	1.00	1.00	0.00	0.00
	Average error %			0.87	0.00	Average error %			2.50	0.55

Table 2. Comparison beteween numerical and analytical results for dimensionless concentration of substrate

u (ζ)

for various values of parameter

γ_{1}

when

φ_{1} = γ_{2} = 0.1

and

α_{1} = 5

Table 2. Comparison beteween numerical and analytical results for dimensionless concentration of substrate

u (ζ)

for various values of parameter

γ_{1}

when

φ_{1} = γ_{2} = 0.1

and

α_{1} = 5

$ζ$	$γ_{1} = 7$ $and m = 0.805191$					$γ_{1} = 15$ $and m = 0.610124$
$ζ$	Num.Equation (9)	AGMEq.(20)	TSMEq.(35)	Error % ofAGMEq.(20)	Error % of TSMEquation (35)	NumEquation (9)	AGMEq.(20)	TSMEq.(35)	Error % ofAGMEq.(20)	Error % of TSMEquation (35)
0	0.80	0.80	0.80	0.00	0.00	0.60	0.58	0.61	3.33	1.67
0.2	0.81	0.81	0.81	0.00	0.00	0.62	0.59	0.63	4.84	1.61
0.4	0.84	0.83	0.84	1.20	0.00	0.67	0.65	0.67	2.98	0.00
0.6	0.88	0.87	0.88	1.14	0.00	0.75	0.73	0.75	2.67	0.00
0.8	0.93	0.93	0.93	0.00	0.00	0.86	0.85	0.86	1.16	0.00
1	1.00	1.00	1.00	0.00	0.00	1.00	1.00	1.00	0.00	0.00
	Average error %			0.39	0.00	Average error %			2.50	0.55

Table 3. Comparison beteween numerical and analytical results for dimensionless concentration of substrate

u (ζ)

for various values of parameter

γ_{2}

when

γ_{1} = φ_{1} = 0.1

and

α_{1} = 5

Table 3. Comparison beteween numerical and analytical results for dimensionless concentration of substrate

u (ζ)

for various values of parameter

γ_{2}

when

γ_{1} = φ_{1} = 0.1

and

α_{1} = 5

$ζ$	$γ_{2} = 5$ $and m = 0.839877$					$γ_{2} = 7$ $and m = 0.762254$
$ζ$	Num.Equation (9)	AGMEquation (20)	TSMEq.(35)	Error % ofAGMEq.(20)	Error % of TSMEquation (35)	NumEquation (9)	AGMEq.(20)	TSMEq.(35)	Error % ofAGMEq.(20)	Error % of TSMEquation (35)
0	0.84	0.86	0.84	2.38	0.00	0.77	0.80	0.76	3.90	1.30
0.2	0.85	0.86	0.85	1.18	0.00	0.78	0.81	0.77	3.85	1.28
0.4	0.87	0.88	0.87	1.15	0.00	0.81	0.83	0.80	2.47	1.23
0.6	0.90	0.91	0.90	1.11	0.00	0.86	0.87	0.85	1.16	1.16
0.8	0.95	0.95	0.94	0.00	1.05	0.92	0.93	0.92	1.09	0.00
1	1.00	1.00	1.00	0.00	0.00	1.00	1.00	1.00	0.00	0.00
	Average error %			0.97	0.17	Average error %			2.09	0.83

Table 4. Comparison beteween numerical and analytical results for dimensionless concentration of product

v (ζ)

for various values of parameter

φ_{2}

when

γ_{1} = 1, γ_{2} = 1, γ_{3} = 0.1, γ_{4} = 1, α_{1} = 5

and

m = 0.915769

Table 4. Comparison beteween numerical and analytical results for dimensionless concentration of product

v (ζ)

for various values of parameter

φ_{2}

when

γ_{1} = 1, γ_{2} = 1, γ_{3} = 0.1, γ_{4} = 1, α_{1} = 5

and

m = 0.915769

$ζ$	$φ_{2} = 20$ $and l = 0.4444703$					$φ_{2} = 35$ $and l = 0.0320751$
$ζ$	Num.Eq.(10)	AGMEq.(26)	TSMEq.(41)	Error% ofAGMEq.(26)	Error% ofTSMEquation (41)	NumEq.(10)	AGMEq.(26)	TSMEq.(41)	Error% ofAGMEq.(26)	Error% ofTSMEquation (41)
0	0.44	0.44	0.44	0.00	0.00	0.03	0.02	0.03	33.33	0.00
0.2	0.47	0.46	0.47	2.13	0.00	0.07	0.06	0.07	14.29	0.00
0.4	0.53	0.53	0.53	0.00	0.00	0.19	0.18	0.19	5.26	0.00
0.6	0.65	0.64	0.65	1.54	0.00	0.39	0.38	0.39	2.56	0.00
0.8	0.81	0.80	0.81	1.23	0.00	0.66	0.66	0.66	0.00	0.00
1	1.00	1.00	1.00	0.00	0.00	1.00	1.00	1.00	0.00	0.00
	Average error %			0.82	0.00	Average error %			9.24	0.00

Table 5. Comparison beteween numerical and analytical results for dimensionless concentration of product

v (ζ)

for various values of parameter

γ_{3}

when

γ_{1} = 1, γ_{2} = 1, φ_{1} = 0.1, γ_{4} = 1, α_{1} = 10

and

m = 0.954173

Table 5. Comparison beteween numerical and analytical results for dimensionless concentration of product

v (ζ)

for various values of parameter

γ_{3}

when

γ_{1} = 1, γ_{2} = 1, φ_{1} = 0.1, γ_{4} = 1, α_{1} = 10

and

m = 0.954173

$ζ$	$γ_{3} = 40$ $and l = 0.39268025$
$ζ$	Num.Eq.(10)	AGMEq.(26)	TSMEq.(41)	Error % ofAGMEq.(26)	Error % of TSMEquation (41)	NumEq.(10)	AGMEq.(26)	TSMEq.(41)	Error % ofAGMEq.(26)	Error % of TSMEquation (41)
0	0.39	0.39	0.39	0.00	0.00	0.01	0.01	0.01	0.00	0.00
0.2	0.42	0.42	0.42	0.00	0.00	0.05	0.05	0.05	0.00	0.00
0.4	0.49	0.49	0.49	0.00	0.00	0.18	0.17	0.18	5.55	0.00
0.6	0.62	0.61	0.62	1.61	0.00	0.38	0.37	0.38	2.63	0.00
0.8	0.79	0.79	0.79	0.00	0.00	0.66	0.66	0.66	0.00	0.00
1	1.00	1.00	1.00	0.00	0.00	1.00	1.00	1.00	0.00	0.00
	Average error %			0.27	0.00	Average error %			1.36	0.00

Table 6. Comparison beteween numerical and analytical results for dimensionless concentration of product

v (ζ)

for various values of parameter

γ_{4}

when

γ_{1} = 1, γ_{2} = 1, γ_{3} = 0.1, φ_{1} = 1, α_{1} = 5

and

m = 0.915769

Table 6. Comparison beteween numerical and analytical results for dimensionless concentration of product

v (ζ)

for various values of parameter

γ_{4}

when

γ_{1} = 1, γ_{2} = 1, γ_{3} = 0.1, φ_{1} = 1, α_{1} = 5

and

m = 0.915769

$ζ$	$γ_{4} = 10$ $and l = 0.70248543$					$γ_{4} = 20$ $and l = 0.41040946$
$ζ$	Num.Eq.(10)	AGMEq.(26)	TSMEq.(41)	Error % ofAGMEq.(26)	Error % of TSMEquation (41)	NumEq.(10)	AGMEq.(26)	TSMEq.(41)	Error % ofAGMEq.(26)	Error % of TSMEquation (41)
0	0.70	0.72	0.70	2.86	0.00	0.41	0.44	0.41	7.32	0.00
0.2	0.71	0.73	0.71	2.82	0.00	0.43	0.46	0.43	6.98	0.00
0.4	0.75	0.76	0.75	1.33	0.00	0.51	0.53	0.51	3.92	0.00
0.6	0.81	0.82	0.81	1.23	0.00	0.63	0.64	0.63	1.59	0.00
0.8	0.90	0.90	0.90	0.00	0.00	0.80	0.80	0.80	0.00	0.00
1	1.00	1.00	1.00	0.00	0.00	1.00	1.00	1.00	0.00	0.00
	Average error %			1.37	0.00	Average error %			3.30	0.00

Table 7. Comparison between numerical and analytical normalized steady-state source terms of liquid phase

- ψ_{l}

for various values of parameter

φ_{1}

and

α_{1}

when

γ_{1} = γ_{2} = 0.1

Table 7. Comparison between numerical and analytical normalized steady-state source terms of liquid phase

- ψ_{l}

for various values of parameter

φ_{1}

and

α_{1}

when

γ_{1} = γ_{2} = 0.1

$φ_{1}$	$α_{1} = 0.1$					$α_{1} = 0.5$
$φ_{1}$	Num.Eq.(13)	AGMEq.(27)	TSMEq.(43)	Error% ofAGMEq.(27)	Error% ofTSMEquation (43)	Num.Eq.(13)	AGMEquation (27)	TSMEq.(43)	Error% ofAGMEq.(27)	Error%ofTSMEquation (43)
0	0.06	0.06	0.06	0.00	0.00	0.04	0.04	0.04	0.00	0.00
0.1	0.09	0.09	0.09	0.00	0.00	0.07	0.07	0.07	0.00	0.00
0.5	0.20	0.21	0.21	5.00	5.00	0.15	0.15	0.15	0.00	0.00
1	0.34	0.37	0.34	8.82	0.00	0.26	0.27	0.26	3.85	0.00
5	1.25	1.56	1.33	24.8	6.40	1.00	1.15	1.01	15.00	1.00
10	2.08	3.09	2.42	48.56	16.35	1.74	2.27	1.90	30.46	9.19
50	5.64	15.2	5.23	169.7	7.27	4.81	11.15	5.22	131.8	8.52
100	7.75	30.4	5.66	291.7	26.97	7.31	22.27	5.66	204.6	22.57
	Average error %			68.68	7.75	Average error %			48.22	5.16

Table 8. Comparison between numerical and analytical normalized steady-state source terms of gas phase

ψ_{g}

for various values of parameter

φ_{2}

and

α_{1}

when

γ_{1} = γ_{2} = 1, γ_{3} = γ_{4} = 0.1, φ_{1} = 1

and

ω = 1

Table 8. Comparison between numerical and analytical normalized steady-state source terms of gas phase

ψ_{g}

for various values of parameter

φ_{2}

and

α_{1}

when

γ_{1} = γ_{2} = 1, γ_{3} = γ_{4} = 0.1, φ_{1} = 1

and

ω = 1

$φ_{2}$	$α_{1} = 0.1$
$φ_{2}$	Num.Eq.(14)	AGMEq.(28)	TSMEq.(44)	Error % ofAGMEq.(28)	Error % of TSMEquation (44)	Num.Eq.(14)	AGMEquation (28)	TSMEquation (44)	Error % ofAGMEq.(28)	Error % of TSMEquation (44)
0	0.08	0.09	0.09	12.50	12.50	0.06	0.07	0.06	16.67	0.00
0.1	0.12	0.14	0.12	16.67	0.00	0.10	0.10	0.10	0.00	0.00
0.5	0.27	0.32	0.28	18.52	3.70	0.22	0.23	0.22	4.54	0.00
1	0.47	0.54	0.47	14.87	0.00	0.37	0.40	0.37	8.11	0.00
5	2.02	2.36	2.03	16.83	0.49	1.58	1.73	1.60	9.49	1.27
10	3.96	4.64	3.98	17.17	0.50	3.10	3.40	3.14	9.68	1.29
50	19.5	22.8	19.55	17.21	0.41	15.26	16.73	15.42	9.63	1.05
100	38.9	45.5	39.02	17.19	0.41	30.46	33.40	30.78	9.65	1.05
	Average error %			16.37	2.25	Average error %			8.47	0.58

7. Conclusions

The objective of this research is multi-folded. First, we successfully employed two widely used analytical methods (AGM and TSM) to solve two reaction-diffusion equations representing the packed bed photobioreactor with immobilized-cell, and derive simple semi-analytical expressions of the substrate and product concentrations and analytical expressions of steady-state source terms of liquid and gas phases. Second, we studied the effect of the reaction-diffusion parameters on the concentrations of substrate and product. Third, we added to the literature some useful information about the exploitation of some of the widely used methods, in particular the AGM and TSM. As both methods appear to be effective and reliable in solving nonlinear systems, it is noticed that the AGM is more or less a modification of the Adomian decomposition method and is likely to involve some tedious algebraic computations. The TSM, on the other hand, involves less algebraic computations, gives more accurate results, and guarantees convergence if the conditions of Taylor’s theorem are met.

Author Contributions

Conceptualization, M.A. and L.R.; methodology, M.E.G.L..; software, P.J; validation, M.A., and P.J.; formal analysis, L.R.; investigation, M.E.G.L.; resources, P.J.; data curation, P.J.; writing—original draft preparation, M.A.; writing—review and editing, P.J.; visualization, L.R; supervision, M.E.G.L.; and L.R.; project administration, M.E.G.L.; All authors have read and agreed to the published version of the manuscript.

Funding

The authors have not received any funds.

Institutional Review Board Statement

Not applicable.

Informed Consent Statement

Not applicable.

Conflicts of Interest

The author declare no conflict of interest.

List of Symbols

Symbols	Description	Units
$C$	Local substrate concentration	kg/m³
$R$	Radius of the gel granule	m
$D$	Diffusion coefficient	m²/s
$K$	Absolute permeability	m²
$M$	Molecular weight	kg mol^-1
$H$	Photobioreactor height	m
$m$	Maintenance coefficient	h^-1
$\dot{m}$	Source item in mass conservation equation	$kg m^{- 1} s^{- 1}$
$φ$	Source item in species conservation equation	$kg m^{- 1} s^{- 1}$
$α$	Specific area	m²/kg
$α^{*}$	Growth associated kinetic constant for hydrogen production	None
$β$	Non- growthassociated kinetic constant	h^-1
$μ$	Specific growth rate	h^-1
$μ_{m a x}$	Maximum specific growth rate	h^-1
$u (ζ)$	Dimensionless substrate concentration	None
$v (ζ)$	Dimensionless product concentration	None
$α_{1}$	Dimensionless parameter	None
$γ_{1}, γ_{2}, γ_{3}, γ_{4}$	Dimensionless parameter	None
$φ_{1}, φ_{2}$	Dimensionless parameter	None
$ψ_{l}, ψ_{g}$	Dimensionless parameter	None
$ω$	Dimensionless parameter	None
$ζ$	Dimensionless distance	None
Superscripts
S	Substrate
H₂	Hydrogen
CO₂	Carbon dioxide
Subscripts
g	Gas phase
l	Liquid phase

Appendix A

function pdex4

m = 2;

x = linspace(0,1);

t=linspace(0,10);

sol = pdepe(m,@pdex4pde,@pdex4ic,@pdex4bc,x,t);

u1 = sol(:,:,1);

u2 = sol(:,:,2);

%------------------------------------------------------------------

figure

plot(x,u1(end,:))

title('u1(x,t)')

xlabel('Distance x')

ylabel('u1(x,1)')

%------------------------------------------------------------------

figure

plot(x,u2(end,:))

title('u2(x,t)')

xlabel('Distance x')

ylabel('u2(x,2)')

% -----------------------------------------------------------------

function [c,f,s] = pdex4pde(x,t,u,DuDx)

c = [1; 1];

f = [1; 1] .* DuDx;

a1=10; p1=30;p2=0.1; r1=0.1; r2=0.1;r3=0.1;r4=0.1; %

F1=-(((p1+r1)*u(1)+r2)/(1+a1*u(1)));

F2= -(((p2+r3)*u(1)+r4)/(1+a1*u(1)));

s=[F1; F2];

% -----------------------------------------------------------------

function u0 = pdex4ic(x)

u0 = [0; 0];

% -----------------------------------------------------------------

function [pl,ql,pr,qr]=pdex4bc(xl,ul,xr,ur,t)

pl = [ul(1)-0; ul(2)-0];

ql = [1; 1];

pr = [ur(1)- 1; ur(2)-1];

qr = [0; 0];

References

Rajendran, L; Swaminathan, R; Chitra Devi, M. A Closer Look of Nonlinear Reaction-Diffusion Equations, nova publishers,2020.
Praveen, T; Rajendran , L. Theoretical analysis through mathematical modeling of two-phase flow transport in an immobilized-cell photobioreactor, Chemical Physics Letters, 2015, 625, 193-201. [CrossRef]
ZeibiShirejini, S; Fattahi, M. Mathematical modeling and analytical solution oftwo-phase flow transport in an immobilized-cellphotobioreactor using the homotopy perturbationmethod (HPM), Int. J Hydrogen Energy, 2016, 1-13. [CrossRef]
Ganji, D; Hosseini, M.; Shayegh, J. Some nonlinear heat transfer equations solved by three approximate methodsInt. Commun. Heat Mass Transf, 2007, 34, 1003-1016. [CrossRef]
He JH., Homotopy perturbation technique, Comput Methods Appl Mech Eng, 1999, 178(3–4) 257-262. [CrossRef]
Manimegalai, B; Lyons, MEG; Rajendran, L. Transient chronoamperometric current at rotating disc electrode for second-order ECE reactions. J. Electroanal. Chem. 2021, 902: 115775. [CrossRef]
Umadevi, R; Venugopal, K; Jeyabarathi, P; Rajendran, L; Abukhaled, M. Analytical study of nonlinear roll motion of ships: A Homotopy perturbation approach. Palestine Journal of Mathematics. 2022; 11:316-325.
Swaminathana, R; Venugopal, K; Rasi, M; Abukhaled, M. Rajendran, L. Analytical expressions for the concentration and current in the reduction of hydrogen peroxide at a metal-dispersed conducting polymer film,Quim. Nova, 2020, 43, 1, 58-65. [CrossRef]
Joy Salomi, R; Vinolyn Sylvia, S; Abukhaled, M; Lyons, MEG; Rajendran, L; Theoretical Analysis of Transient Responses of Amperometric Biosensor Based on the Phenol–Polyphenol Oxidase Model, Int. J. Electrochem. Sci., 2022, 17, Article Number: 22047. [CrossRef]
Swaminathan, R; Narayanan, KL; Mohan, V; Saranya, K; Rajendran, L; Reaction/Diffusion Equation with Michaelis-Menten Kinetics in Microdisk Biosensor: Homotopy Perturbation Method Approach,Int. J. Electrochem. Sci., 2019, 14, 3777 – 3791. [CrossRef]
Chitra Devi, M; Pirabaharan, P; Rajendran, L.; Abukhaled, M; Amperometric biosensors in an uncompetitive inhibition process: a complete theoretical and numerical analysis. React. Kinet. Mech. Catal. 2021, 133, 655-668. [CrossRef]
He, JH. Variational iteration method for autonomous ordinary differential systems, Appl. Math. Compute, 2000, 114(2-3),115-123. [CrossRef]
Ghafoori, S; Motevalli, M; Nejad, MG; Shakeri, F; Ganji, DD; Jalaal, M. Efficiency of differential transformation method for nonlinear oscillation: Comparison with HPM and VIM, Curr Appl Phys, 2011, 11(4), 965-971. [CrossRef]
Rahamathunissa, G; Rajendran, L; Application of He’s variational iteration method in nonlinear boundary value problems in enzyme–substrate reaction diffusion processes: part 1. The steady-state amperometric, 2008, J. Math. Chem., 44 (3), 849-861. [CrossRef]
Abukhaled, M. Variational iteration method for nonlinear singular two-point boundary value problems arising in human physiology, J. Math, 2013, Article ID 720134. [CrossRef]
Eswari, A; Rajendran, L. Application of variational iteration method and electron transfer mediator/catalyst composites in modified electrodes, Nat. sci, 2010, 2 (6), 612-625. [CrossRef]
Liao, SJ. The proposed homotopy analysis technique for the solution of nonlinear problems, Ph.D. Thesis, Shanghai Jiao Tong University, 1992.
Liao, SJ. Beyond Perturbation: Introduction to Homotopy Analysis Method, Chapman & Hall/CRC, 2003.
Liao, SJ. Notes on the homotopy analysis method: some definitions and theorems, Commun. Nonlinear Sci. Numer. Simul. 2009, 14, 14,983–997. [Google Scholar] [CrossRef]
Liao, S. On the homotopy analysis method for nonlinear problems. Appl. Math. Comput. 2004, 147(2), 499–513. [Google Scholar] [CrossRef]
Arikoglu, A.; Ozkol, I. Solution of difference equations by using differential transform method, Appl. Math. Comput, 2006, 174(2), 1216-1228. [CrossRef]
Soltanalizadeh, B. Differential transformation method for solving one-space-dimensional telegraph equation, Comput. Appl. Math, 2011, 30(3). [CrossRef]
Jeyabarathi, P.; Kannan,M.; Rajendran, L.Approximate analytical solutions of biofilm reactor problem in applied biotechnology. Theor. Found. Chem. Eng.2021, 55(5), 851-861. [CrossRef]
Jeyabarathi,P.; Rajendran,L.; Abukhaled,M.; Kannan,M.; Semi-analytical expressions for the concentrations and effectiveness factor for the three general catalyst shapes. React. Kinet. Mech. Catal.2022, 1-16. [CrossRef]
Abukhaled, M; Khuri, SA. Efficient numerical treatment of a conductive-radiative fin with temperature-dependent thermal conductivity and surface emissivity, Int J. Comput. Methods Eng. Sci. Mech, 2020, 21 (4) 159–168. [CrossRef]
Abukhaled, M. Green’s function iterative method for Solving a class of boundary value problems arising in heat transfer, Appl. Math. Inf. Sci., 2017,11 (1) 229–234. [CrossRef]
Sheikholeslami, M; Ganji, DD. Applications of Semi-Analytical Methods for Nanofluid Flow and Heat Transfer. Oxford: Elsevier, 2018.
Jeyabarathi,P.; Rajendran,L.; Lyons,MEG. Reaction-diffusion in a packed-bed reactors: Enzymatic isomerization with Michaelis-Menten KineticsJ. Electroanal. Chem. 2022, 910, 116184. [CrossRef]
Jeyabarathi, P.; Rajendran, L.; Lyons M. E., G.; Abukhaled, M. Theoretical Analysis of Mass Transfer Behavior in Fixed-Bed Electrochemical Reactors: Akbari-Ganji’s Method. Electrochem 2022, 3, 699–712. [Google Scholar] [CrossRef]
He, CH; Shen, Y; Ji, FY; He, JH. Taylor series solution for Fractal Bratu-Type equation arising in electrospinning process, Fractals, 2020, 28, 1-8. [CrossRef]
Lilly Clarance Mary, M.; Chitra Devi, M.; Meena, A; Rajendran, L.; Abukhaled, M. A reliable Taylor series solution to the nonlinear reaction-diffusion model representing the steady-state behaviour of a cationic glucose-sensitive membrane, J. Math. Comput. Sci. 2021, 11, 8354–8381. [CrossRef]
Liao, Q; Liu, DM; Ye, DD; Zhu, X; Lee, DJ. Mathematical modeling of two-phase flow and transport in an immobilized-cell photobioreactor, Int. J. Hydrogen Energy, 2011,36, 13936-13948. [CrossRef]
Akbari, MR; Ganji, DD; Nimafar, M; Ahmadi, AR. Significant progress in solution of nonlinear equations at displacement of structure and heat transfer extended surface by new AGM approach. Front. Mech. Eng, 2014, 9(4), 390–401. [CrossRef]
Akbari, M. Nonlinear Dynamic in Engineering by Akbari-Ganji’s Method, Xlibris Corporation, 2015.
Ganji, DD; Talarposhti, RA. Numerical and Analytical Solutions for Solving Nonlinear Equations in Heat Transfer, Hershey, PA: Technology and Engineering, IGI Global, 2017.
AlRasheed, NN. Adaptation of Taylor’s Formula for Solving System of Differential Equations, Nonlinear Differ. Equ. App,, 2016, 4(2), 95 – 107. [CrossRef]
El-Ajou,A; Abu Arqub, O; Al-Smadi, M. A general form of the generalized Taylor’s formula with some applications, Appl. Math. Comput., 2015, 256, 851-859. [CrossRef]

Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.

© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).

Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.

MDPI Initiatives

Important Links

Choose an area of interest and we will send you notifications of new preprints at your preferred frequency.

Disclaimer

New Analytical Expresions of Concentrations in Packed Bed Immobilized-Cell Electrochemical Photobioreactor

Abstract

1. Introduction

2. Mathematical Formulation of the Problems

3. Analytical expression of the concentrations using Akbari-Ganji’s method

3.1. Concentration of Glucose (substrate)

3.2. Concentration of Hydrogen (product)

3.3. Normalized steady-state source terms of liquid and gas phases

4. Analytical expression of the concentrations using Taylor series method

4.1. Concentration of Glucose (substrate)

4.2. Concentration of Hydrogen (product)

4.3. Normalized steady-state source terms of liquid and gas phases

5. Numerical simulations and Discussion

7. Conclusions

Author Contributions

Funding

Institutional Review Board Statement

Informed Consent Statement

Conflicts of Interest

List of Symbols

Appendix A

References

MDPI Initiatives

Important Links

Subscribe