Prerpints.org logo
Preprint
Article

An Intelligent Physiological Control Method Using Sliding Mode Neural Network for Left Ventricular Assist Device

Altmetrics

Downloads

122

Views

96

Comments

0

A peer-reviewed article of this preprint also exists.

This version is not peer-reviewed

Submitted:

05 July 2023

Posted:

06 July 2023

You are already at the latest version

Alerts
Abstract
The technology of left ventricular assist devices (LVADs) requires developing and implementing an intelligent control systems to optimize pump speed to achieve a physiological metabolic demands for heart failure (HF) patients. This work aimed to present an advanced control algorithm to drive an LVAD under different physiological conditions. Pole placement method in conjunction with of sliding mode control approach (PP-SMC) was utilized to design and construct the proposed control method. In this design, the method was adopted to use neural networks to eliminate system uncertainties of disturbances. An elastance function was also developed and used as an input signal to mimic the physiological perfusion of HF patients. Two scenarios ranging from rest to exercise were introduced to evaluate the proposed technique. In this technique, a lumped parameter model of cardiovascular system (CVS) was used for this evaluation. The results demonstrated that the designed controller was robustly tracking the input signal in the presence of the system parameter variations of CVS. In both scenarios, the proposed method shows that the controller automatically drive the LVAD with a minimum flow of 1.7 L/min to prevent suction and 5.7 L/min to prevent over-perfusion.
Keywords: 
Subject: Engineering  -   Bioengineering

1. Introduction

Heart failure (HF) is a disease that occurs when cardiac muscle exhibits an insufficient capacity to adequately circulate blood [1,2]. A left ventricular assist device (LVAD) has emerged as a valuable solution to help patients suffering from this issue. Different studies have shown that left ventricular assist devices positively affect patient outcomes, including increased survival rates, symptom relief, and overall quality of life for individuals with advanced HF [3–5].
LVADs can exert a significant influence on the physiology of the cardiovascular system (CVS) [6,7]. As a result, one of the primary goals of enhancing the state of LVAD technology entails formulating a control approach that can adaptively regulate pump speed to accommodate differences in metabolic requirements [8,9]. Therefore, physiological control management of this type of device entails monitoring and adjusting device parameters to enhance its efficiency for a given patient. The main goal of LVAD treatment is to provide adequate assistance to the heart and maintain proper blood circulation throughout the body. Therefore, it is necessary to carefully observe the flow rate of the LVAD and determine the volume of blood circulated by the LVAD per unit of time. The LVAD flow rate is tailored to the patient's requirements and can be adjusted up or down to maintain optimal blood pressure and cardiac output. The aspiration inhibition system of LVADs is an essential physiological control parameter. Excessive suction from an LVAD can damage the heart muscle and cause the device to malfunction. To mitigate the incidence of aspiration, LVAD devices are equipped with suction prevention mechanisms that supervise intracardiac pressure levels and regulate device flow rate accordingly to avoid undue suction [10,11].
LVADs show limited preload sensitivity, indicating their inability to detect or perceive the amount of blood they receive [9]. Thus, it is critical to implement a pump control approach to maintain a safe operating range, where pump flow corresponds to right heart output [12]. Inadequate action may lead to ventricular collapse caused by excessive pumping or decreased preload, reversed pump flow (regurgitation), and pulmonary edema due to insufficient pumping and consequent decrease in applied differential pressure [13,14]. Adverse circumstances can cause harm to the patient; Therefore, it is essential to identify and prevent them in individuals receiving implants promptly. Moreover, the ability to approximate direct values of pump flow and differential pressure is crucial to pump control approaches. For example, ensuring a minimum average pump flow rate or achieving maximum differential pressure restriction requires careful evaluation of these parameters [15].
Various control techniques have been proposed for LVAD devices, including conventional PID controllers [16,17], optimized controllers [18–20], sliding mode controllers [21,22], H-infinity controller based on the estimator model [23], fuzzy logic controllers [24–26], deadbeat controllers [27,28], and predictive model controllers [29–31]. However, these methods may not be effective in dealing with the uncertainty and disturbances common in LVAD systems [32]. Recently, a model-free adaptive control technique has been used to regulate the speed of the LVAD pump in response to changes in the patient's CVS [33]. The methodology in this study, designed an algorithm that calculates a coefficient of control over time and then uses existing data on the manipulated and control variables. The performance of this controller was evaluated and verified using computer simulations. The results indicate that LVAD can effectively adapt to changes in blood demand, whether constant or fluctuating. An alternative study presented a supervised adaptive fuzzy control approach featuring pulse-ratio modulation [34]. This study aimed to ensure adequate blood circulation perfusion and reduce the phenomena of aspiration. The results of this study indicate that implementing a supervised adaptive fuzzy controller can effectively prevent the system from experiencing suction hooking compared to conventional approaches. However, most adaptive control techniques suffer from the system convergence phenomenon of chatter, which causes stability convergence to slow down.
Among the above techniques, an extremum-seeking control is technique that attempts to determine the optimal value of the performance index by processing the control input of the LVAD. A study conducted by Sadatieh et al. [35] proposed a nonlinear controller that uses extremum-seeking theory to regulate cardiac performance. The primary objective of the control unit was to improve the pump flow rate while at the same time minimizing the incidence of suction phenomena. In-silico model was used to evaluate the proposed controller, and the results indicate that it can effectively maintain an appropriate cardiac response. Moreover, it is observed that the mean arterial pressure remains within the required range, thus preventing aspiration. The optimization control unit then modulates the LVAD pump speed by analyzing the system's response to the perturbation signal to optimize cardiac output and reduce energy consumption. A valuable feature of the control-seeking maximalist is its ability to adapt to changes in the system or the surrounding environment without needing a mathematical representation of the system [36]. This property makes them highly compatible with left ventricular assist devices, which may be subject to fluctuations in a patient's cardiovascular system or medical condition. Despite its potential benefits, monitoring search for extremes may be subject to measurement noise and other perturbations. In addition, achieving optimal performance may require fine-tuning the perturbation signal and control parameters. Implementing extreme case-control as a control strategy for the LVAD requires detailed design and rigorous testing to ensure its safety and efficacy in clinical settings [37].
This paper proposes a novel control strategy that combine a sliding mode control, pole placement method, and neural network to achieve automatic regulation of an LVAD. The proposed method is implemented to design a control algorithm that minimizes tracking errors between desired and actual heart flow rates while ensuring that system states remain within the safe range [38]. In this work, the neural network approach is utilized to drive the system states toward the sliding surface, allowing the SMC technique to achieve quick convergence and robustness against any uncertainties or disturbances. To our knowledge, this is the first study in which the PP-SMC in combination with neural network method employed to control an LVAD.

2. Materials and Methods

2.1. Hemodynamic Characteristics of CVS Model

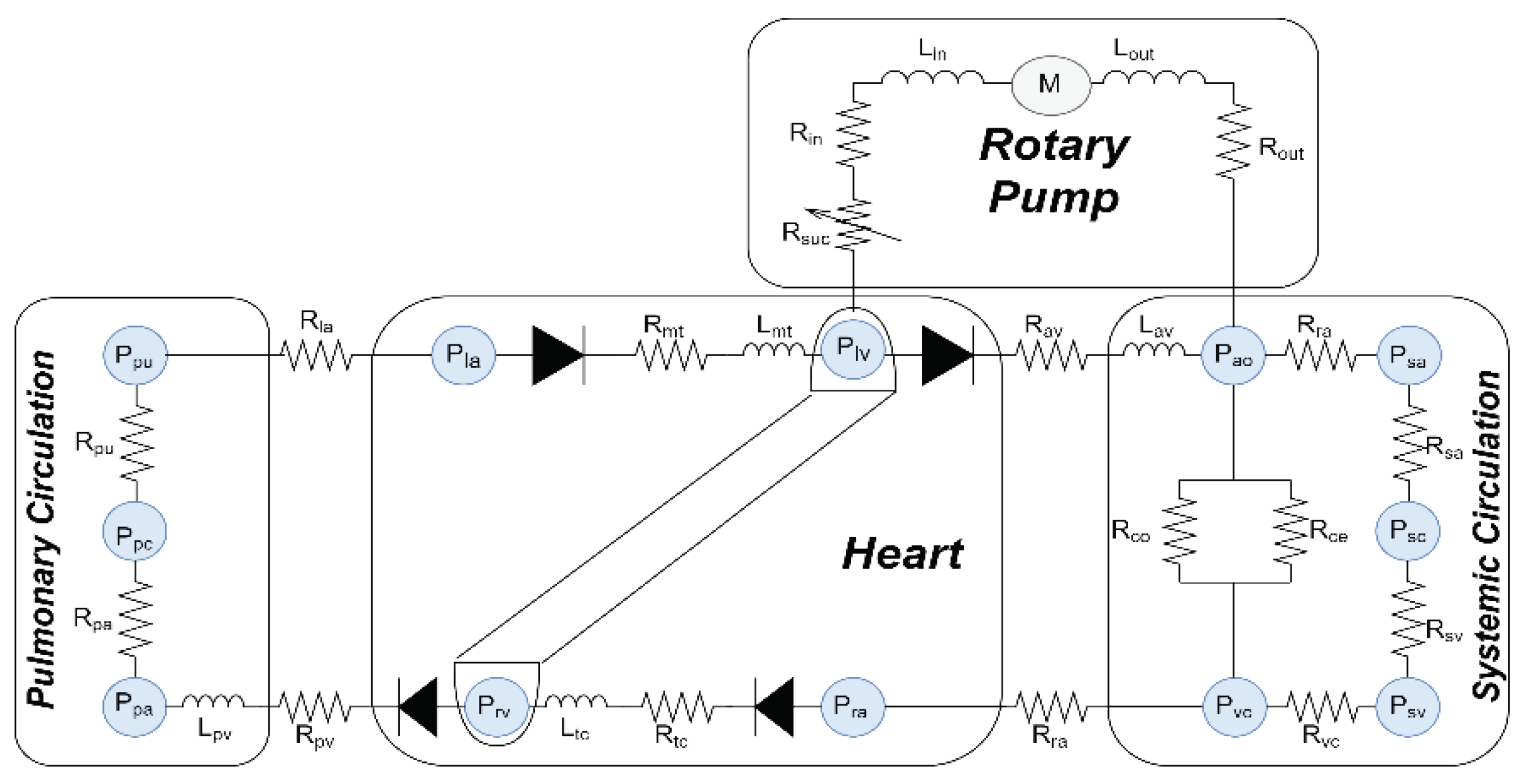
To examine the work of the proposed control system method and how it works with physiological interactions, a software model of the lumped parameters model was used [39]. In this model, the CVS is combined with the LVAD model, as shown in Figure 1. The hydraulic properties of the CVS system, which contains the right and left side of the heart, regular circulatory system, and circulation pulmonary are described as:

2.1.1. Blood Flow across the Valves

The hemodynamic movement of blood through the cardiac valves (tricuspid, pulmonary, aortic, and mitral valve) is expressed as:
Q n = { p n − p n + 1 R n p n ≥ p n + 1 0 p n < p n + 1
where, p n is the upstream pressure, p n + 1 is the downstream pressure, R n is representing the resistance of each valve, and n represents the four cardiac valves.

2.1.2. Function Blood Vessel in Chambers

The function of blood vessels in chambers for aorta, pulmonary veins, vena cava, and pulmonary peripheral vessel of the CVS are depicted as:
P n = v n − v u n , n c n
where v n is the volume in vessel, v u n , i is the unstressed volume of the vessel, c n is the compliance, and n represents of vessels in chambers.

2.2. Blood Flow between Chambers

The circulation of blood between different chambers can be described as follows:
Q n = p n − p n + 1 R n
The term Rn denotes the resistance of the respective chamber.
In this model, the steady flow resistance ( R i n and R o u t ) and serial inductance ( L i n and L o u t ) are utilized for each inflow and outflow cannula to reduce stress and resistance of flow rate changes. The resistance ( R s u c ) has been incorporated prior to the intake cannula to emulate suction events.

2.3. LVAD Estimator Model

Our research team has developed and validated a dynamical model for estimating an average pump flow ( Q p ) of an LVAD [32]. In this developments, two auto-regressive (ARX) models with exogenous input were utilized for system modelling and configuration. Pulse-width modulation ( P W M ) signal was used as input signal for the first ARX model to estimate the pulsatility index of pump rotational speed ( P I ω ). Secondly, P I ω was utilized as the input for the subsequent ARX model to estimate Q p . A recursive of least square approach were used to estimate the system parameters. Accordingly, the obtained dynamic estimator model can be expressed as follows:
χ ( n + 1 ) = A χ ( n ) + δ A χ ( n ) + B u ( n ) + ξ ( n ) Q p ( n ) = C χ ( n )
where " χ ∈ R n " represents the states of the system, “ δ A ” is the system parameter variation, " u = P W M " represents the control input, " ξ " is the system disturbance, " Q p " refers to the system output, and " A , B , and C " represent matrices of appropriate dimensions.

2.4. Control Design

To design a physiological controller that maintains the optimal functioning of the blood pump, we need to keep the left atrial pressure within the appropriate physiological range to prevent aspiration or pulmonary congestion. Therefore, to achieve this design, we assume the aortic valve is fully closed. For this reason we utilize the elastance function ( E t ) to determine the cardiac output. In this work, we propose that in each cardiac cycle E t was linearly and exponentially varied during end-systolic and end-diastole respectively. As a result, if the blood flow exceeds the physiological requirement, it is imperative to adjust the estimated value of Q p . In order to ensure that pump flow remains at a consistent level, it was deemed necessary to increase Q r in the event that it falls below the body's physiological requirements. 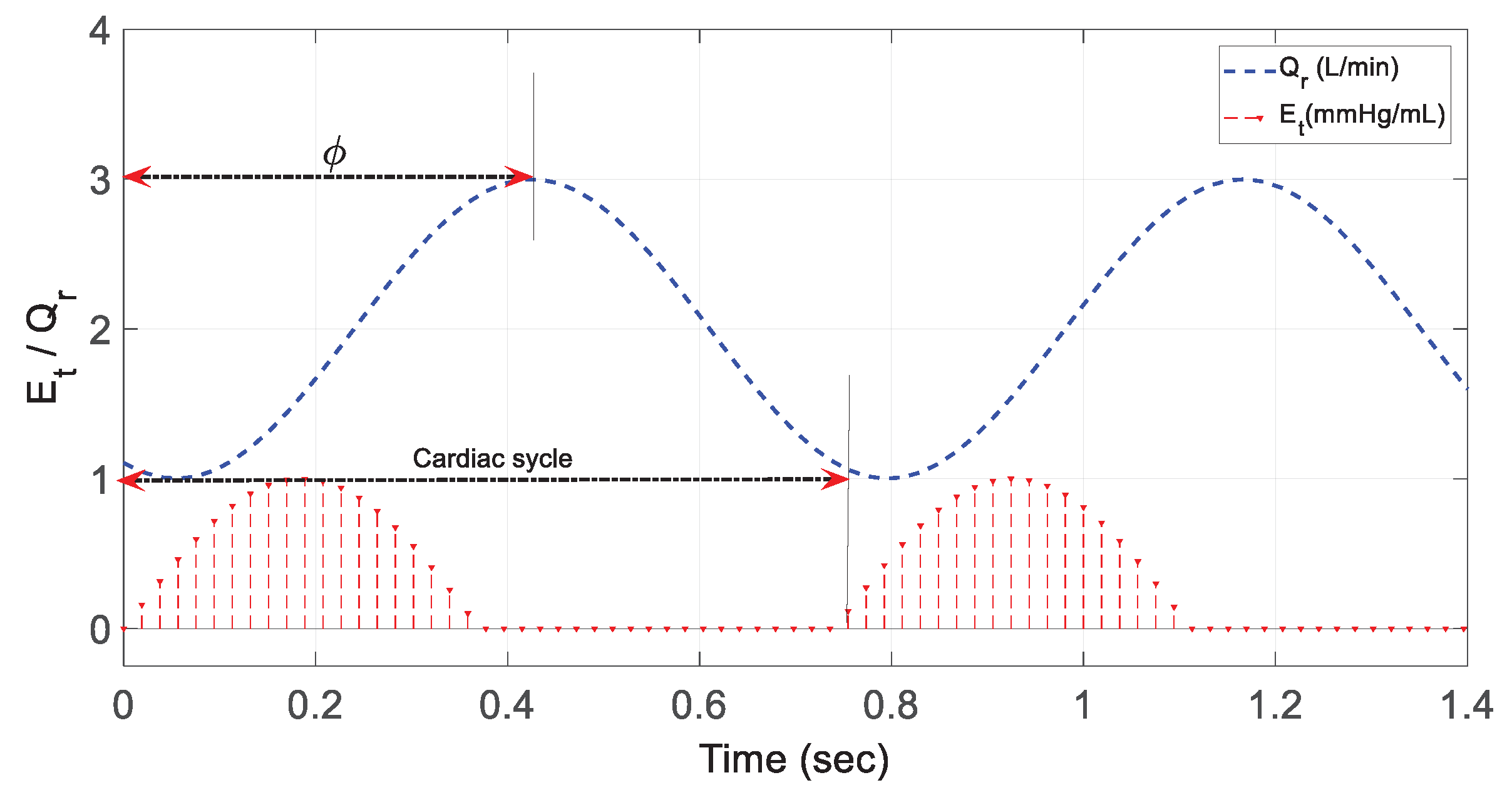Figure 2. depicts the phase shift that exists between the sinusoidal Q r and E t . The value of Q r was deemed to be zero during the phase shift, notwithstanding the observation of the peak value of Q p during end-systole when E t was at its maximum value.
This mechanism was achieved through the utilization of the following sinusoidal function as:
Preprints 78679 g002
Figure 2. Phase shift for Q r in comparison with E t .
Figure 2. Phase shift for Q r in comparison with E t .
Preprints 78679 g002
Q r = a + β sin ( 2 π t T + φ )
In this equation, a and β are fixed values, T represents the cardiac cycle, and φ denotes the phase shift.
To implement the control algorithm, we suggest to use the pole placement SMC (PP-SMC) approach. In this approach we invoke neural network to eliminate the error resulting due the system parameter variation and disturbance. As a result, in this particular methodology the control system matrix is represented by ( A − B K ). The gain matrix K is derived by assigning n-desired eigenvalues in the pole placement, where K ∈ R n .
In this method, we propose to use the following sliding surface which given by:
σ ( n ) = γ e ( n ) = γ ( χ d − χ ( n ) )
the constant vector γ has been formulated to guarantee the asymptotic stability for σ ( n ) = 0 and χ d is the desired states.
From Equation (6) we can write:
σ ( n + 1 ) = γ e ( n + 1 ) = γ ( χ d ( n + 1 ) − χ ( n + 1 ) )
In order to achieve the requirements of the strong reachability, we propose to use the updated Gao formula as:
σ ( n + 1 ) = ( 1 − Δ T ) σ ( n ) − τ T s i g n ( σ ( n ) )
where, T is the sampling period, and the both terms Δ ≥ 0 , τ > 0 satisfies that 0 < ( 1 − Δ T ) < 1 .
Equalization of Equations (5), (7), and (8) can gives:
σ ( n + 1 ) = γ ( χ d ( n + 1 ) − ( ( A − B K ) χ ( n ) + δ A χ ( n ) + B u ( n ) + ξ ( n ) ) ) = ( 1 − Δ T ) σ ( n ) − τ T s i g n ( σ ( n ) )
Upon solving the Equation (9), yields the control command signal ( u ( n ) ) as:
u ( n ) = − ( γ B ) − 1 ( γ ( A − B K ) χ ( n ) + γ δ A χ ( n ) + γ ξ ( n ) − γ χ d ( n + 1 ) + ( Δ T − 1 ) γ σ ( n ) + τ T s i g n ( σ ( n ) ) )
The control command signal ( u ( n ) ) in Equation (10) can be constructed as equivalent ( u e ( n ) ) and corrective ( u c ( n ) ) parts:
u ( n ) = u e ( n ) + u c ( n )
For the equivalent part we can write:
u e ( n ) = − ( γ B ) − 1 ( γ ( ( A − B K ) χ ( n ) + δ A χ ( n ) + ξ ( n ) − χ d ( n + 1 ) ) )
For the corrective part we can write:
u c ( n ) = − ( γ B ) − 1 ( Δ T − 1 ) γ σ ( n ) + τ T s i g n ( σ ( n ) )
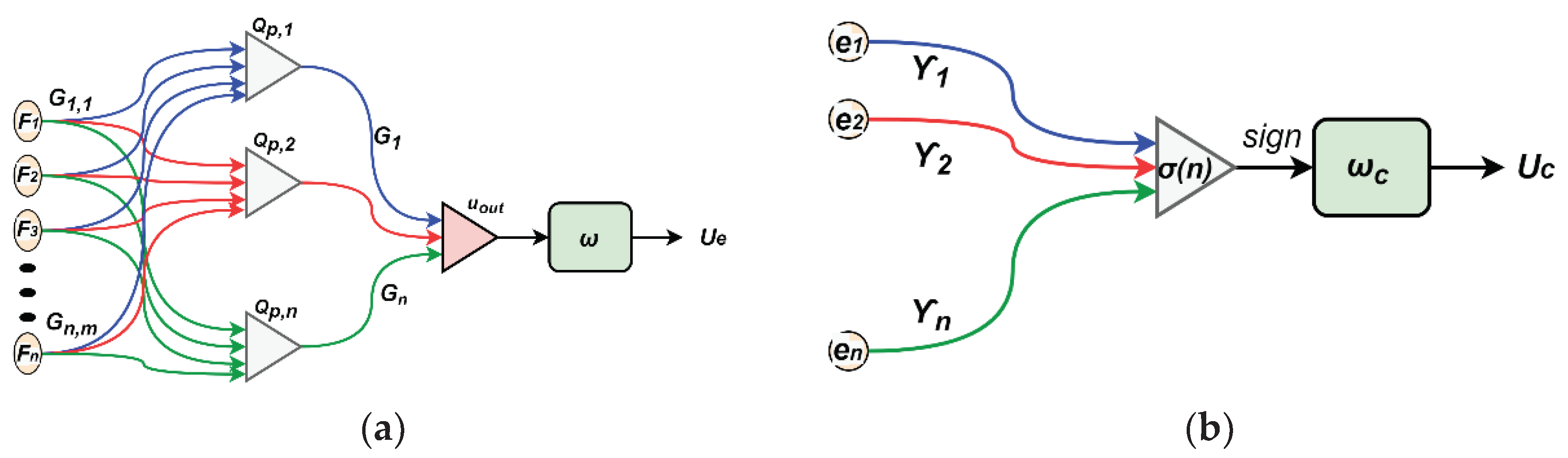
To adjust the values varying of the system parameters and disturbances, we propose to use neural networks for estimating both equivalent and corrective and the control lows as shown in Figure 3.
To maintain the system states on the proposed sliding surface ( σ ( n ) = 0 ) we need to estimate the equivalent control law as:
u ⌢ e ( n ) = ω . s i g n ( σ ( n ) ) ( ∑ i = 1 m G i . s i g n ( σ ( n ) ) ( ∑ j = 1 n G ¯ j , i . F i ) )
In order to restore the plants' state to the sliding surface when they are no longer in contact with said surface, we need to train the estimated corrective control law as:
u ⌢ c ( n ) = ω c . s i g n ( σ ( n ) ) ( ∑ j = 1 n γ j e j ( n ) )
To achieve a robust estimation for u ⌢ e ( n ) and u ⌢ c ( n ) , the training methods employ the following cost functions based on iterative steepest descent algorithm to reduce the mean square errors between the desired and actual values as:
Ε = ( u e ( n ) − u ⌢ e ( n ) ) 2 2
Τ = ( σ ( n ) ) 2 2
Based on Equation (16), the weight updating law to reduce Ε can be written as:
δ G i = − β ∂ Ε / ∂ G i = ( β . σ ( n ) . ω . Q p − β . σ ( n ) . ω . s i g n ( σ ( n ) ) u 2 n e t Q p ) 2
δ G ⌢ j , i = − β ∂ Ε ∂ G ⌢ j , i = ( β . σ ( n ) . ω . G i − β . σ ( n ) . ω . s i g n ( σ ( n ) ) u 2 n e t G i ) ( 1 − s i g n ( σ ( n ) ) Q 2 p ) F i 4
where, β > 0
Based on Equation (17), the weight updating law to reduce Τ can be written as:
δ γ j = − α ∂ Τ ∂ γ j = − α . σ ( n ) . e j ( n )
where, α > 0
For K in Equation (10), can be calculated based on the updated vector γ as:
K = λ ( γ T B ) − 1
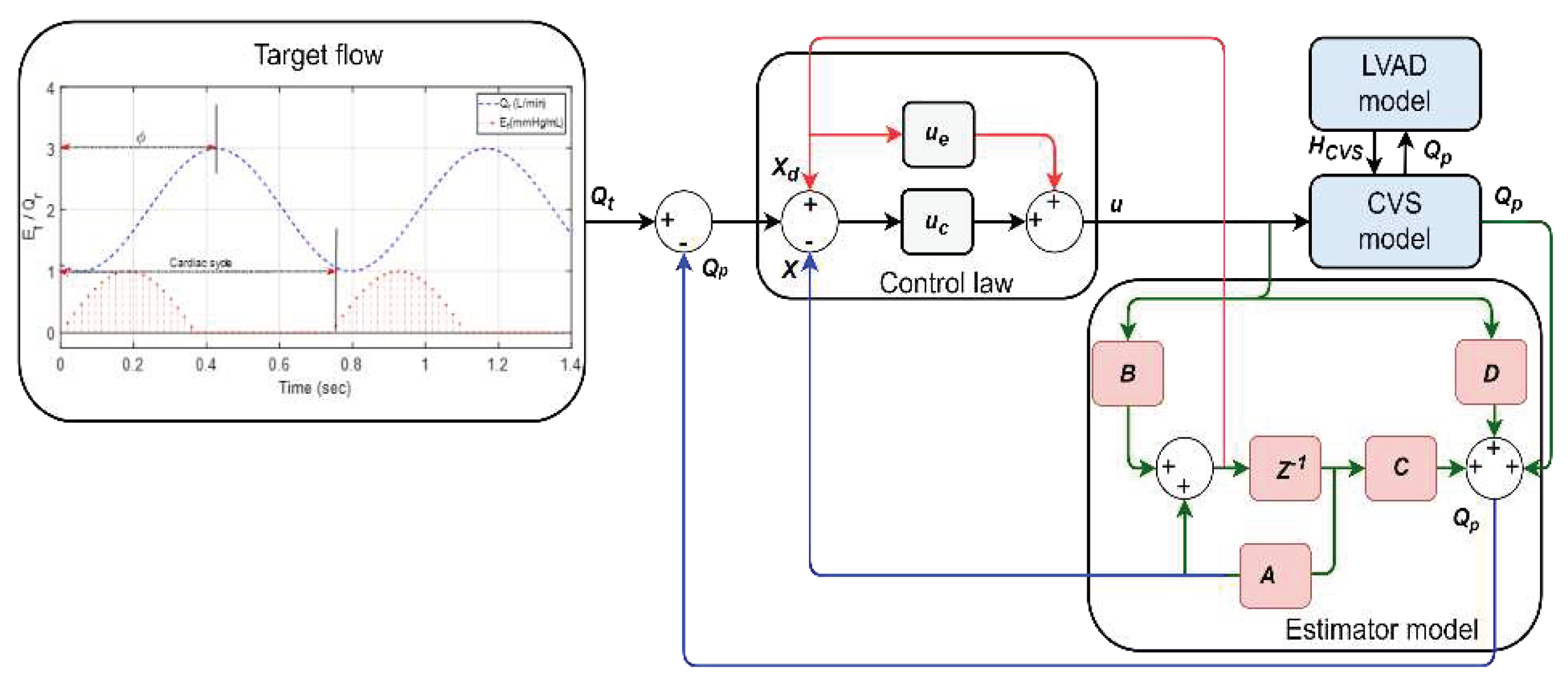
where, λ > 0 . Figure 4 depicts the block diagram of the proposed system.

2.5. Software Simulation Environments Protocols

This study was implemented using MATLAB-Simulink and it involved carefully adjusting the model's parameters. The work was carried out to generate two different physiological simulations (rest and exercise) for HF patients. Table 1 provides information on the modifications made to the model's parameters to represent the HF condition accurately. These modifications were made to the contractility of the left/ right ventricle, systemic peripheral resistance, and total blood volume.
To simulate the rest scenario, the CVS model parameters were varied at t = 25s in one cardiac cycle. This includes decreases in the total blood volume with 500mL, an increase in the left/ right ventricle contractility by 15%, and keeping systemic peripheral resistance with the same values. This scenario was conducted to ensure the controller was robust enough to provide sufficient perfusion support to the HF patient.
Subsequently, the simulation was conducted to simulate the transition of system parameters from rest to one physical exertion to ensure that the control algorithm robustly automated the LVAD to provide a minimum flow to the patient. In the scenario, the CVS model parameters were varied at t = 25s in one cardiac cycle. They prolonged for an additional 35s in order to give the CVS system enough time to attain a steady state condition. During this scenario, the total blood volume was increased by 500mL, the left/ right ventricle contractility decreased by 20%, and systemic peripheral resistance increased by 15%.
In Equation (10), the parameters for the control law are given as “ γ = [ 1.2 − 0.95 ] and“ τ T = 0.24 ”.

3. Results

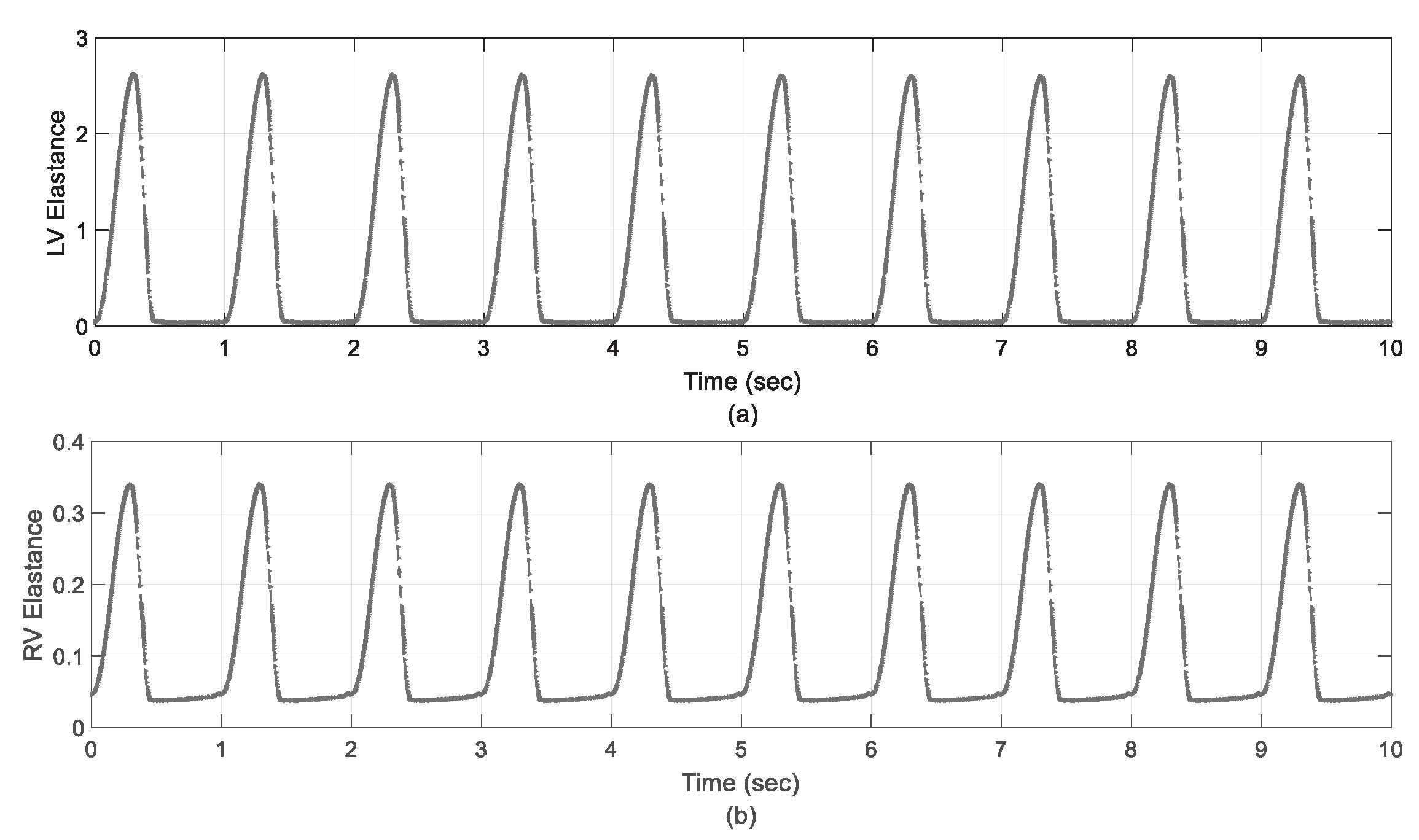
Figure 5 shows the left/right elastance function curves during system simulation, which was designed as the system input signal for CVS. In both scenarios, the results indicate that the controller was able to modulate flexibility to achieve the suggested input signal (stream) given in Section (5). This confirms that the controlled act obtained physiological perfusion to prevent excessive pulmonary aspiration or regurgitation.

3.1. Results in Rest Scenario

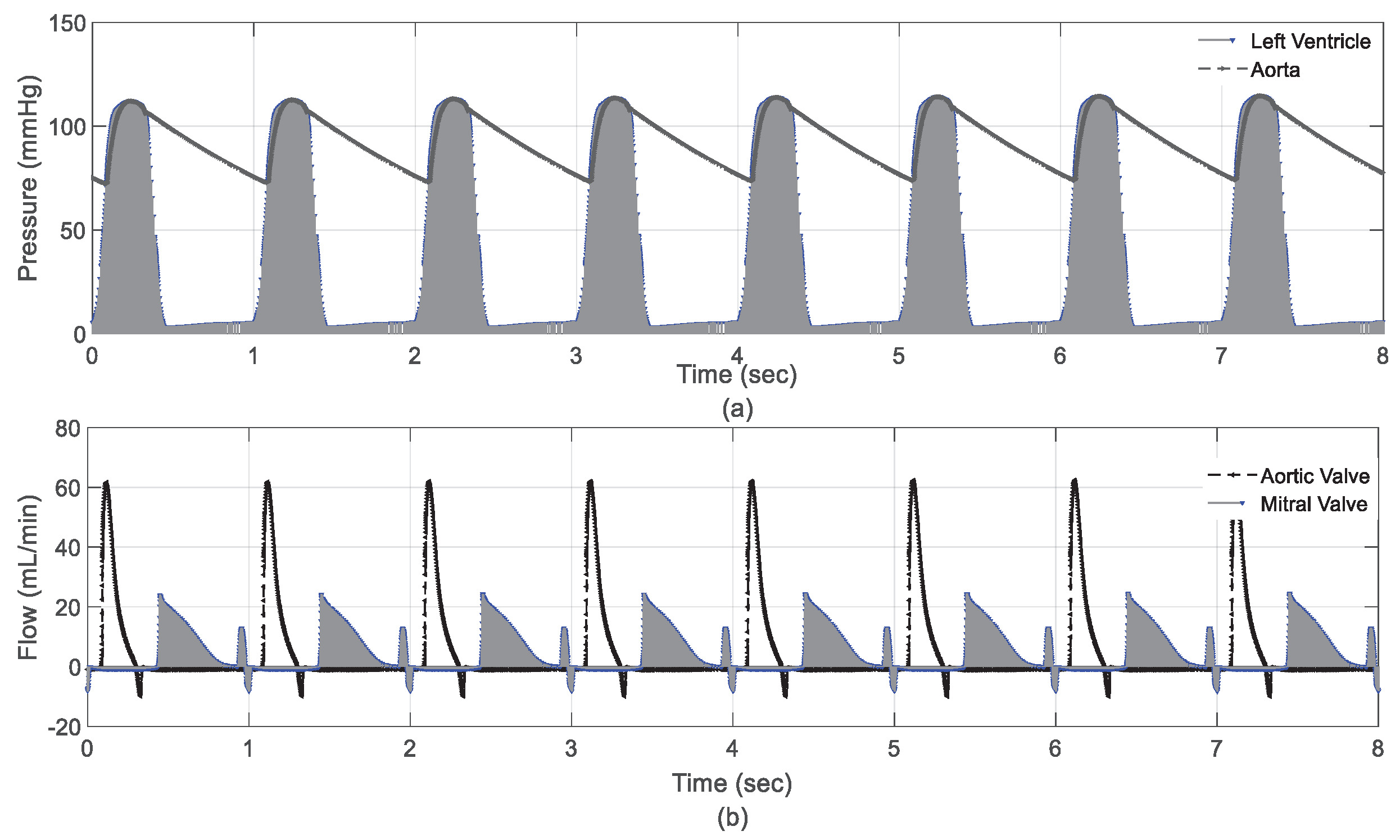
Figure 6 presents the hemodynamic variables of CVS during the rest scenario. The results showed that left ventricular and aortic valve pressure decreased within a safe operating range, as shown in Figure 6a. This means the control unit effectively maintained systemic flow at a safe level of 4.5 L/min during this process. As a result, the flow crossing the aortic and mitral valve remained within clinical limits with a maximum recording of 60 ml and 22 ml, respectively, as shown in Figure 6b.

3.2. Results in Exercise Scenario

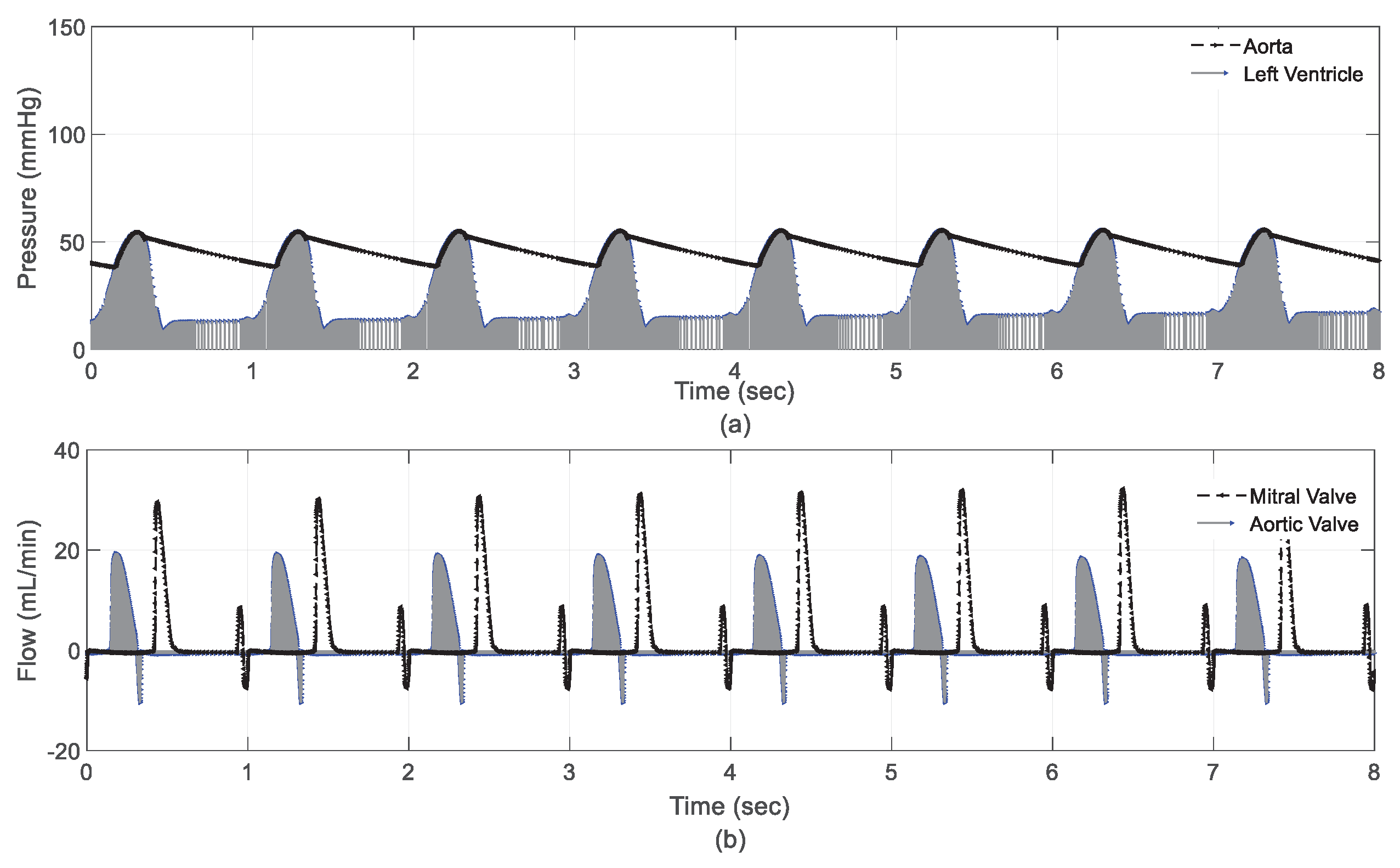
The results of the hemodynamic variables during the exercise scenario are depicted in Figure 7. The results showed a significant decrease in pressure on the left ventricle and aorta, as shown in Figure 7a. Left ventricular diastolic and systolic pressures decreased to 41 mmHg and 20 mmHg, respectively. Despite these significant reductions, the control unit increased the volume of the regular flow by 1.7 l/min to secure the dynamic flow. The results also show that the flow crossing the aortic and mitral valves remained within clinical conditions, as shown in Figure 7b. Table 2 presents hemodynamic variables for CVS in a healthy individual and HF patient.

4. Discussion

One of the primary goals needed to improve LVAD technology involves developing a control strategy that automatically adjusts pump speed to meet changes in metabolic demand. In the normal functioning of the heart, the pumping process is subject to the Frank-Starling mechanism [8,9]. This mechanism ensures that left ventricular stroke volume is adjusted to compensate for left ventricular end-diastolic pressure-volume changes. or the preload associated with it so that all blood exits the left ventricle regardless of the volume of blood it receives. In order to obtain results that simulate this theory, in this work the pump flow was chosen as a significant parameter for the design of the control system. The elastance function was chosen as a basic input signal that was designed to obtain a rate of change in the flow that synchronizes the work of HF patients. The results demonstrated that this function was able to simulate the proposed flow to balance the physiological status of HF patients as shown in Figure 5. However, other studies chose the pump differential pressure as an essential control parameter to obtain significant results to simulate HF status [10,16].
Eliminating disturbances and parameter variation during controller operation is the significant challenge often found in the operation of this type of pump. Therefore, many control systems are designed to minimize or eliminate these issues [11]. In this regard, this work utilized neural network method to eliminate any presence of disturbance or parameter variation. The design method introduced the numerical analysis based on PP-SMC while subjecting to a variety of various physiological situations. According to the findings, the performance of PP-SMC is superior to other control methods [16,17,18,19,20,21,22,23,24,25,26,27,28,29,30,31]. For instance, The findings presented in Figure 5, Figure 6 and Figure 7 and Table 2 demonstrate that the neural PP-SMC can increase tracking performance because it can alter its parameters in an adaptive manner based on the input/output data of the CVS. Interpatient and interpatient differences automatically adjust the settings of CVS, and CVS can respond to any unpredicted changes in hemodynamics thanks to the adaptive structure of the controller. Our results also demonstrate that employing our strategy will eventually decrease error tracking between the desired and measured outputs. Because of the reduced elastance on control tracking performance, the estimated pump flow output will follow the target output flow in the range of 1.5 to 7 L/min faster and with fewer amplitude oscillations, resulting in fewer ventricular suctions and pulmonary congestion occurrences. It is evident from the findings that in the two patient situations (growing vascular resistance, rest to exercise, reducing postural change), lowering postural change was more likely to occur in the patient with the increased vascular resistance. Compared to the other controllers' performance, the PP-SMC controller's control tracking performance can be improved further by optimizing the process of determining the controller's parameters.
In terms of limitation, the baroreflex was not modeled in this particular study, which may have affected both performance and hemodynamics. However, the design method of PP-SMC can appropriately compensate for its effects since any changes caused by the baroreflex can be perceived as a nonlinearity similar to a distinct patient state or scenario which, allows it to work properly. In addition, the Frank-Starling technique for achieving a balance between systemic and pulmonary flows has yet to be incorporated into the methodology that has been developed. Physiological control systems similar to Frank-Starling controllers, which configure the flow rate to be a preload function, have been created and demonstrated to be among the most effective of these systems. However, determining the Frank-Starling process for each patient can be challenging due to their various illnesses..

5. Conclusions

This work presents the design and development of an intelligent control method for driving LVAD under different physiological conditions. The proposed method uses PP-SMC in combination with a neural network to achieve physiological performance in the presence of variability and perturbations in system parameters. For the neural network, we have developed an equivalent and corrective law to eliminate any discrepancies and disturbances that may occur in any conditions. The cost function is proposed in each law of control to achieve robust estimation. Two scenarios (rest and exercise) were proposed to evaluate the control method using a CVS aggregated parameter model. In both scenarios, the parameters of the CVS model varied in terms of left/right ventricular systole, systemic peripheral resistance, and total blood volume to obtain the physiological conditions of the HF patients. The results show that the proposed method can alter CVS parameters to prevent aspiration or over-perfusion.

Funding Statement

The author received no specific funding for this study.

Acknowledgments

The authors extend their appreciation to the Deanship of Scientific Research - Majmaah University, for supporting this research work under project number R-2023-000.

Conflicts of Interest

The authors declare no conflict of interest.

References

  1. F. Edelmann, C. Knosalla, K. Mörike, C. Muth, P. Prien et al., “Chronic Heart Failure,”. Dtsch Arztebl Int, vol. 115, pp. 124-130, 2018. https://doi.org/10.3238/arztebl.2018.0124. [CrossRef]
  2. E. J. Benjamin, M. J. Blaha, S. E. Chiuve, M. Cushman, S. R. Das et al., "Heart Disease and Stroke Statistics’2017 Update: A Report from the American Heart Association,”. Circulation, vol. 135, no. 10, 2017. https://doi.org/10.1161/CIR.0000000000000485. [CrossRef]
  3. Montalto, A. Loforte, F. Musumeci, T. Krabatsch, and M. Slaughter, Mechanical circulatory support in end-stage heart failure. Switzerland: Springer International Publishing. 2017. https://doi.org/10.1007/978-3-319-43383-7. [CrossRef]
  4. K. G. Soucy, G. A. Giridharan, Y. Choi, M. A. Sobieski, G. Monreal et al. “Rotary pump speed modulation for generating pulsatile flow and phasic left ventricular volume unloading in a bovine model of chronic ischemic heart failure,”. J Hear Lung Transplant, vol. 34, no. 1, pp. 122–131, 2015. https://doi.org/10.1016/j.healun.2014.09.017. [CrossRef]
  5. M. R. Mehra, N. Uriel, Y. Naka, J. C. Cleveland, M. Yuzefpolskaya et al. “A fully magnetically levitated left ventricular assist device - Final report,”. N Engl J Med, vol. 380, pp. 1618–1627, 2019. https://doi.org/10.1056/NEJMoa1900486. [CrossRef]
  6. Levine and A. Gass, “Third-Generation LVADs: Has Anything Changed?,” Cardiol Rev, vol. 27, no. 6, pp. 293–301, 2019. https://doi.org/10.1097/CRD.0000000000000268. [CrossRef]
  7. H. Hoshi, T. Shinshi and S. Takatani, “Third-generation blood pumps with mechanical noncontact magnetic bearings,” Artif Organs, vol. 30, no. 5, pp. 324–38, 2006. https://doi.org/10.1111/j.1525-1594.2006.00222.x. [CrossRef]
  8. M. C. Stevens, A. Stephens, A. H. H. AlOmari and F. Moscato, Physiological control. Elsevier Inc.; 2018. https://doi.org/10.1016/B978-0-12-810491-0.00020-5. [CrossRef]
  9. R. F. Salamonsen, E. Lim, N. Gaddum, A. H. H. Alomari, S. D. Gregory et al. “Theoretical Foundations of a Starling-Like Controller for Rotary Blood Pumps,” Artif Organs, 2012;vol. 36, no. 9, pp. 787–796, 2012. https://doi.org/10.1111/j.1525-1594.2012.01457.x. [CrossRef]
  10. H. H. Alomari, A. V. Savkin, M. Stevens, D. G. Mason, D. L. Timms et al “Developments in control systems for rotary left ventricular assist devices for heart failure patients: A review,”. Physiol Meas, vol. 34, 2013. https://doi.org/10.1088/0967-3334/34/1/R1. [CrossRef]
  11. S. Bozkurt “Physiologic outcome of varying speed rotary blood pump support algorithms: a review study,” Australas Phys Eng Sci Med , vol. 39, pp.13–28, 2016. https://doi.org/10.1007/s13246-015-0405-y. [CrossRef]
  12. M. A. Bakouri, R. F. Salamonsen, A. V. Savkin, A. H. H. Alomari, E. Lim et al, “A Sliding Mode-Based Starling-Like Controller for Implantable Rotary Blood Pumps,”. Artif Organs;vol. 38, no. 7, pp. 587–593, 2014. https://doi.org/10.1111/aor.12223. [CrossRef]
  13. J. Cysyk, R. Newswanger, E. Popjes, W. Pae, C. S. Jhun, et al, “Cannula tip with integrated volume sensor for rotary blood pump control: Early-stage development,” ASAIO J 2019; vol. 65, no. 4, pp. 318–323. https://doi.org/10.1097/MAT.0000000000000818. [CrossRef]
  14. J. T. Horobin, M. J. Simmonds, D. Nandakumar, S. D. Gregory, G. Tansley et al., “Speed Modulation of the HeartWare HVAD to Assess In Vitro Hemocompatibility of Pulsatile and Continuous Flow Regimes in a Rotary Blood Pump,” Artif Organs, vol. 42, no. 9, pp. 879–890, 2018. https://doi.org/10.1111/aor.13142. [CrossRef]
  15. M. Meki, Y. Wang, P. Sethu, M. Ghazal, A. El-Baz et al., “A Sensorless Rotational Speed-Based Control System for Continuous Flow Left Ventricular Assist Devices,”. IEEE Trans Biomed Eng, vol. 67, no. 4, pp. 1050–1060, 2020. https://doi.org/10.1109/TBME.2019.2928826. [CrossRef]
  16. Y. Wang, S. C. Koenig, Z. Wu, M. S. Slaughter and G. A. Giridharan “Sensor-based physiologic control strategy for biventricular support with rotary blood pumps,” ASAIO J, vol. 64, no. 3, pp.338–350, 2018. https://doi.org/10.1097/MAT.0000000000000671. [CrossRef]
  17. F. Stephens, M. C. Stevens, S. D. Gregory, M. Kleinheyer and R. F. Salamonsen “In Vitro Evaluation of an Immediate Response Starling-Like Controller for Dual Rotary Blood Pumps,” Artif Organs, vol. 41, no. 10, pp. 911–922, 2017. https://doi.org/10.1111/aor.12962. [CrossRef]
  18. K. W. Gwak, M. Ricci, S. Snyder, B. E. Paden, J. R. Boston et al., “In vitro evaluation of multiobjective hemodynamic control of a heart-assist pump,” ASAIO J 2005; vol. 51, no. 4, pp.329–335. https://doi.org/10.1097/01.mat.0000169122.64794.28. [CrossRef]
  19. M. Ketelhut, F. Schrödel, S. Stemmler, J. Roseveare, M. Hein et al., “Iterative Learning Control of a Left Ventricular Assist Device,” IFAC-PapersOnLine, vol. 50, no. 1, pp. 6684–6690, 2017. https://doi.org/10.1016/j.ifacol.2017.08.1161. [CrossRef]
  20. Y. Wu, P. E. Allaire, G. Tao, M. Adams, Y. Liu et al., “A bridge from short-term to long-term left ventricular assist device - Experimental verification of a physiological controller,” Artif Organs, vol. 28, no. 4, pp. 927–932, 2004. https://doi.org/10.1111/j.1525-1594.2004.07381.x. [CrossRef]
  21. M. Bakouri “Evaluation of an advanced model reference sliding mode control method for cardiac assist device using a numerical model,” IET Syst Biol, vol. 12, no. 2, pp. 68–72, 2018. https://doi.org/10.1049/iet-syb.2017.0052. [CrossRef]
  22. Y. Chang and B. Gao “A global sliding mode controller design for an intra-aorta pump,”. ASAIO J, vol. 56, no. 6, pp. 510–516, 2010. https://doi.org/10.1097/MAT.0b013e3181ede369. [CrossRef]
  23. M. Bakouri, A. Alassaf, K. Alshareef, S. Abdelsalam, H. F. Ismail et al., “An Optimal H-Infinity Controller for Left Ventricular Assist Devices Based on a Starling-like Controller: A Simulation Study,”. Mathematics, vol. 10, no. 5, pp.731, 2022. https://doi.org/10.3390/math10050731. [CrossRef]
  24. F. Huang, X. Ruan and X. Fu. “Pulse-pressure-enhancing controller for better physiologic perfusion of rotary blood pumps based on speed modulation,” ASAIO J, vol. 60, no. 3, pp. 269–279, 2014. https://doi.org/10.1097/MAT.0000000000000059. [CrossRef]
  25. M. Bakouri, A. Alassaf, K. Alshareef, A. Smida, I. AlMohimeed et al., “A Feasible Method to Control Left Ventricular Assist Devices for Heart Failure Patients: A Numerical Study,” Mathematics, vol. 10, no. 13, pp. 2251, 2022. https://doi.org/10.3390/math10132251. [CrossRef]
  26. M. Bakouri, A. Alassaf, K. Alshareef, I. AlMohimeed, A. Alqahtani et al., “In Silico Evaluation of a Physiological Controller for a Rotary Blood Pump Based on a Sensorless Estimator,” Appl. Sci. 2022, vol. 12, no. 22, pp. 11537, 2022. https://doi.org/10.3390/app122211537. [CrossRef]
  27. E. Lim, A. H. H. Alomari, A. V. Savkin, S. Dokos, J. F. Fraser et al., “A method for control of an implantable rotary blood pump for heart failure patients using non-invasive measurements,” Artif Organs, vol. 35, no. 8, pp. E174–80, 2011. https://doi.org/10.1111/j.1525-1594.2011.01268.x. [CrossRef]
  28. H. H. Alomari, A. V. Savkin, P. J. Ayre, E. Lim, D. G. Mason et al., “Non-invasive estimation and control of inlet pressure in an implantable rotary blood pump for heart failure patients,” Physiol Meas, vol. 32, pp. 1035–1060, 2011. https://doi.org/10.1088/0967-3334/32/8/004. [CrossRef]
  29. V. C. A. Koh, J. P. Pauls, E. L. Wu, M. C. Stevens, Y. K. Ho et al., “A centralized multiobjective model predictive control for a biventricular assist device: An in vitro evaluation,” Biomed Signal Process Control, vol. 59, pp. 137–148, 2020. https://doi.org/10.1016/j.bspc.2020.101914. [CrossRef]
  30. V. C. A. Koh, Y. K. Ho, M. C. Stevens, R. F. Salamonsen, N. H. Lovell et al., “Synergy of first principles modelling with predictive control for a biventricular assist device: In silico evaluation study,” in Proc EMBS, pp. 1291–1294, 2017. https://doi.org/10.1109/EMBC.2017.8037068. [CrossRef]
  31. C. Ng, R. F. Salamonsen, S. D. Gregory, M. C. Stevens , Y. Wu et al. “Application of multiobjective neural predictive control to biventricular assistance using dual rotary blood pumps,” Biomed Signal Process Control, vol. 39, pp. 81-93, 2018. https://doi.org/10.1016/j.bspc.2017.07.028. [CrossRef]
  32. M. A. Bakouri, A. V. Savkin and A. H. Alomari AH, “Non-linear modelling and control of left ventricular assist device,” Electron Letter, vol. 51, no. 8 , pp. 613–615, 2015. https://doi.org/10.1049/el.2014.4330. [CrossRef]
  33. J. Son and Y. Du, “Model-Free Adaptive Control of the Failing Heart Managed by Mechanical Supporting Devices,” IFAC-PapersOnLine, vol. 55, no. 7, pp.750-755, 2022.
  34. M. Azizkhani and Y. Chen “Supervised Adaptive Fuzzy Control of LVAD with Pulsatility Ratio Modulation,” in Proc. IEEE 18th CASE, pp. 2429-2434, 2022. https://doi.org/10.1109/CASE49997.2022.9926444. [CrossRef]
  35. S. Sadatieh, M. Dehghani, M. Mohammadi and R. Boostani, “Extremum-seeking control of left ventricular assist device to maximize the cardiac output and prevent suction,” Chaos, Solitons & Fractals, vol. 148, pp.111013, 2021. https://doi.org/10.1016/j.chaos.2021.111013. [CrossRef]
  36. K. W. Gwak, “Application of extremum seeking control to turbodynamic blood pumps,” ASAIO, vol. 53, no. 4, pp. 403–409, 2007. https://doi.org/10.1097/MAT.0b013e31806ada0a. [CrossRef]
  37. Arndt, P. Nüsser and B. Lampe, “Fully autonomous preload-sensitive control of implantable rotary blood pumps,” Artif Organs, vol. 34, no. 9, 2010. https://doi.org/10.1111/j.1525-1594.2010.01092.x. [CrossRef]
  38. M. A. Bakouri, A. V. Savkin and A. H. H. Alomari, “A method for physiological control of a cardiac assist device,” in Proc. 10th ASCC, Sabah, Malaysia, pp. 1-5, 2015. https://doi.org/10.1109/ASCC.2015.7244808. [CrossRef]
  39. E. Lim, S. Dokos, R. Salamonsen, F. Rosenfeldt, P. Ayre et al., “Numerical Optimization Studies of Cardiovascu-lar-Rotary Blood Pump Interaction,” Artificial Organs, vol. 36, no. 5, pp. E110-E124, 2012. https://doi.org/10.1111/j.1525-1594.2012.01449.x. [CrossRef]
Preprints 78679 g001
Figure 1. The CVS combined with the LVAD rotary pump.
Figure 1. The CVS combined with the LVAD rotary pump.
Preprints 78679 g001
Preprints 78679 g003
Figure 3. Neural networks for estimating control lows; a: Equivalent control; b: Corrective Control.
Figure 3. Neural networks for estimating control lows; a: Equivalent control; b: Corrective Control.
Preprints 78679 g003
Preprints 78679 g004
Figure 4. Proposed of control method.
Figure 4. Proposed of control method.
Preprints 78679 g004
Preprints 78679 g005
Figure 5. Left/ right elastance of CVS.
Figure 5. Left/ right elastance of CVS.
Preprints 78679 g005
Preprints 78679 g006
Figure 6. Hemodynamic variables. (a): Pressure vs Time; (b): Flow vs Time.
Figure 6. Hemodynamic variables. (a): Pressure vs Time; (b): Flow vs Time.
Preprints 78679 g006
Preprints 78679 g007
Figure 7. Hemodynamic variables. (a): Pressure vs Time; (b): Flow vs Time.
Figure 7. Hemodynamic variables. (a): Pressure vs Time; (b): Flow vs Time.
Preprints 78679 g007
Table 1. CVS model parameters.
Table 1. CVS model parameters.
Parameter HF Healthy
Systemic peripheral resistance
(mm Hg*s/mL)		 1.1200 0.7501
Left ventricle contractility
(mm Hg/mL)		 0.7111 3.4900
Right ventricle contractility
(mm Hg/mL)		 0.5299 1.7510
Total blood volume
(mL)		 5798 5298
Table 2. CVS variables from the simulation results.
Table 2. CVS variables from the simulation results.
Parameters Healthy HF + LVAD
Exercise Rest
Aortic pressure (mmHg) 120 77 105
Left ventricle pressure (mmHg) 120 81 97
Output flow ( Q p ) (L/min) 5.5 2 2.4
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.
Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.
Prerpints.org logo

Preprints.org is a free preprint server supported by MDPI in Basel, Switzerland.

facebook logotwitter logolinkedin logo
MDPI Initiatives
Important Links
Subscribe

Disclaimer

Terms of Use

Privacy Policy

© 2024 MDPI (Basel, Switzerland) unless otherwise stated